METODE PEMISAH VARIABEL: PERSAMAAN LAPLACE
|
|
|
- Vera Sumadi
- 7 tahun lalu
- Tontonan:
Transkripsi
1 METODE PEMISAH VARIABEL: PERSAMAAN LAPLACE M. Jamhuri April 1, 2013
2 Salah satu metode untuk menyelesaikan persamaan Laplace adalah dengan metode pemisahan variabel. Misalkan diberikan persamaan laplace 2D pada domain terbatas pada 0 < x < a, 0 < y < b, dengan kondisi batas u xx + u yy = 0 (1) u(0, y) = 0, u x (a,y) = 0 (2) u y (x,0)+u(x,0) = 0, u(x,b) = g (x). (3) Misalkan u(x, y) = X (x) Y (y), kemudian substitusikan pada (1), diperoleh X Y + XY = 0 X Y = XY X = Y X Y Ruas kiri dari persamaan (4) hanya bergantung pada x saja, segkan ruas kanan hanya bergantung pada y saja. Persamaan tersebut hanya mungkin dipenuhi jika keduanya merupakan konstanta. Misalkan konstanta itu λ, maka (4) X X = Y Y = λ (5)
3 Persamaan (5) dapat dituliskan secara terpisah sebagai X +λx = 0 (6) Y λy = 0 (7) Tuliskan kondisi batas (2) (3) kita tuliskan kedalam bentuk variabel terpisah, yaitu u(0, y) = X (0) Y (y) = 0 u x (a,y) = X (a)y (y) = 0 (8) u y (x,0)+u(x,0) = X (x)y (0)+X (x)y (0) = 0 (9) u(x,b) = X (x)y (b) = g (x) (10) Jika kita mislkanλ = β 2, maka persamaan (6) menjadi X +β 2 X = 0 ( d 2 ) dx +β2 X = 0 ( )( ) d d dx + iβ dx iβ X = 0 (11)
4 Misalkan Selesaikan (13) terlebih dahulu, yaitu ( ) d dx iβ X = A (12) ( ) d dx + iβ A = 0 (13) da dx + iβa = 0 da = iβa dx da = iβdx ˆ A ˆ 1 A da = iβdx Jika (14) kita substitusikan pada (12), diperoleh log A = iβx + c 1 A = c 1 e iβx (14) dx dx iβx = c 1e iβx (15)
5 Untuk menyelesaikan (15), kita gunakan faktor integrasi I = e ( iβ)dx = e iβx (16) Kalikan kedua ruas dari persamaan (15) dengan faktor integrasi (16), yaitu iβx dx e dx iβe iβx X d ( ) e iβx X dx = c 1 e 2iβx Integralkan kedua sisi dari persamaan (17), yaitu ˆ ( ) d e iβx X = c 1ˆ e 2iβx dx [ e iβx X = c 1 1 ] 2iβ e 2iβx + c 2 ( e iβx X = c ) 1 e 2iβx + c 1 c 2 2iβ X = ( c 1 2iβ = c 1 e 2iβx (17) ) e iβx +(c 1 c 2 ) e iβx (18) Misalkan c 1 2iβ = k 1, c 1 c 2 = k 2, maka persamaan (18) menjadi X = k 1 e iβx + k 2 e iβx (19)
6 Jika (19) kita tuliskan dalam bentuk sinusoidal, maka X = k 1 [cos(βx) i sin(βx)]+k 2 [cos(βx)+ i sin(βx)] = [k 1 + k 2 ] cos(βx)+[ ik 1 + ik 2 ]sin(βx) X (x) = A cos(βx)+ B sin(βx) (20) Gunakan kondisi batas (8), maka sehingga (20) menjadi karena λ = β 2, maka X (a) = 0 B cos(βa) = 0 X (0) = 0 Acos 0+B sin0 = 0 A = 0 X (x) = B sin(βx) (21) βa = arccos 0 (2n + 1)π βa =, {n = 0, 1,2,...} 2 ( ) 2n + 1 β = π (22) 2a ( ) 2n λ n = π 2 (23) 2a
7 λ n disebut nilai eigen, segkan fungsi eigennya adalah ( ) (2n + 1)πx X n (x) = sin 2a Selanjutnya kita selesaikan Y (y) dari persamaan (7), yaitu Misalkan Solusi dari (27) adalah (24) d 2 dy 2 Y λy = 0 ( d 2 ) dy 2 β2 Y = 0 ( )( ) d d dy +β dy β Y = 0 (25) ( ) d dy β Y = A (26) ( ) d dy +β A = 0 (27) da dy da A = βa = βdy
8 ˆ 1 A da Substitusikan (28) pada (26), yaitu ( ) d dy β Y ˆ = βdy log A = βy + c 1 A = c 1 e βy (28) = A Faktor integrasi untuk ODE (29) diatas adalah dy dy βy = c 1e βy (29) I = e βdy = e βy (30) Kalikan ruas kiri ruas kanan dari (29) dengan (30), diperoleh βy dy e dy βe βy Y d ( ) e βy Y dy ˆ d ( ) e βy Y = c 1 e 2βy = c 1 e 2βy = c 1ˆ e 2βy dy [ e βy Y = c 1 1 ] 2β e 2βy + c 2
9 Next... e βy Y = Y = ( Jika kita misalkan konstan-konstan persamaan (31) diatas menjadi Karena sehingga (32) sama dengan sinhx = ex e x ( c 1 2β ( c 1 2β c 1 2β ) e 2βy + c 1 c 2 ) e βy +(c 1 c 2 ) e βy (31) ) = k 1 (c 1 c 2 ) = k 2, maka Y = k 1 e βy + k 2 e βy (32) 2 cosh x = ex + e x 2 (33) Y n (y) = Acosh(β ny)+ B sinh(β ny) (34) Berikutnya gunakan kondisi batas (9) pada (34), yaitu karena maka Y (0)+Y (0) = 0 Y (y) = β na sinh(β ny)+β nb cosh(β ny) Y (0) = β nb Y (0) = A β nb + A = 0 (35)
10 atau Jika A kita substitusikan pada (34), diperoleh A = β nb (36) Y n = B [ β n cosh(β ny)+sinh(β ny)] (37) Selanjutnya solusi u dapat diperoleh dengan mensubstitusikan kembali (24) (37) pada pemisalan u(x,y) = X (x)y (y), yaitu atau u n (x,y) = B sin(β nx)(β n cosh(β ny) sinh(β ny)) u(x,y) = B n sin(β nx)(β n cosh(β ny) sinh(β ny)) (38) n=0 Notasi B n adalah gabungan dari konstanta pada Y konstanta yang ada pada saat pembentukan kombinasi linier. konstanta B n akan kita tentukan dengan menggunakan kondisi batas (10) yaitu pada saat y = b, g (x) = B n sin(β nx)(β n cosh(β nb) sinh(β nb)) (39) n=0 yang berlaku untuk 0 < x < a.
11 Selanjutnya dengan menggunakan deret Fourier kita peroleh ˆ B n = [β n cosh(β nb) sinh(β nb)] 1 2 a g (x)sin(β nx)dx a 0
12 Contoh 1 Diberikan persamaan Laplace u xx + u yy = 0 pada domain D = {(x,y) : 0 < x < 10, 0 < y < π} dengan kondisi batas u(0,y) = 0 u x (10, y) = 0 u y (x,0)+u(x,0) = 0, u(x,π) = (x 10) sinπx (40) Dengan menggunkan metode pemisahan variabel seperti yang dijelaskan sebelumnya, maka diperoleh solusi u(x,y) = B n sin(β nx)(β n cosh(β ny) sinh(β ny)) (41) n=0 jika kondisi batas (40) disubstitusikan pada (41) diperoleh (x 10) sin(πx) = B n sin(β nx)[β n cosh(β nπ) sinh(β nπ)] n=0 dengan β n = ( ) 2n+1 2a π, dengan menggunakan deret Fourier diperoleh B n = [β n cosh(β nπ) sinh(β nπ)] 1 1 ˆ 10 (x 10)sin(πx)sin(β nx)dx (42) 5 0
13 Contoh 2 Diketahui pada domain h 1 < y < η(x,t), pada domain h 2 < y < h 1, dengan kondisi batas φ xx +φ yy = 0 (43) φ xx + φ yy = 0 (44) φ y = α φ y, pada y = h 1 φ y = 0, pada y = h 2 Misalkan φ(x,y,t) = S (x,t)f (y). jika diketahui S (x,t) = ig η(x,t) (45) ω maka φ(x,y,t) = ig η(x,t)f (y) (46) ω Jika (46) kita substitusikan pada (43), diperoleh 2 η(x,t) x 2 F (y)+η(x,t) d2 F (y) = 0 (47) dy2
14 Solusi untuk φ Persamaan (47) dapat kita tuliskan sebagai ηxx η = Fyy F = λ (48) Persamaan (48) dapat dituliskan sebagai dua persamaan terpisah η xx +λη = 0 (49) F yy λf = 0 (50) Misalkan λ = β 2, maka dapat diperoleh solusi dari persamaan (50), yaitu Jika digunakan F (0) = 1, maka F (y) = Ae βy + Be βy (51) F (0) = A+B = 1 A = 1 B F (y) = (1 B) e βy + Be βy F (y) = (1 B)βe βy Bβe βy untuk F (0) = ω2 g,diperoleh (1 B)β βb = ω2 g (52)
15 Next... (1 2B)β = ω2 g β = ω 2 (1 2B) g versi yang lain: Misalkan konstan A B kita tuliskan dalam bentuk konstan yang lain, yaitu A = C 1 + C 2 2 dengan C 1 C 2, maka F (y) = Ae βy + Be βy ( ) C1 + C 2. = e βy +. = 2 [ C1 2 eβy + C 1 2 e βy. = C 1 ( e βy + e βy 2 maka B = C 1 C 2 2 ( ) C1 C 2 e βy 2 ] [ C2 + 2 eβy C ] 2 2 e βy ( e )+C βy e βy ) 2 2 F (y) = C 1 cosh(βy)+c 2 sinh(βy) (53) DIketahui kondisi batas F (0) = 1, F (0) = ω2 g maka F (0) = 1 C 1 = 1
16 maka F (y) = cosh(βy)+ C 2 sinh(βy) (54) F (y) = β sinh(βy)+c 2 β cosh(βy) maka C 2 β = ω2 g C 2 = ω2 gβ Jika C 2 kita substitusikan pada (54), maka F (y) = cosh(βy)+ ω2 gβ sinh(βy) fungsi potensial φ(x,y,t) = ig [ ] ω η(x,t) cosh(βy)+ ω2 gβ sinh(βy) (55)
17 Dari syarat batas φ y = 0 pada y = h 2, maka φ y (x,y,t) = ig [ ] ω η(x,t) β sinh(βy)+ ω2 g cosh(βy) ] ig [β ω η(x,t) sinh( βh 2 )+ ω2 g cosh( βh 2) = 0 β sinh(βh 2 )+ ω2 g cosh(βh 2) = 0 ω 2 g cosh(βh 2) = β sinh(βh 2 ) ω 2 = gβ sinh(βh 2) cosh(βh 2 ) atau ω 2 = gβ tanh(βh 2 ) (56)
18 Next... Perhatikan, S xx +λs = 0 (57) Jika S (x,t) = ig ω η(x,t), η(x,t) = ae i(kx ωt) maka Maka 2 x 2 S (x,t) = ig ω ηxx = g ka( ik) e i(kx ωt) ω S xx = igk2 η(x,t) (58) ω Jika kita gunakan (58) (45) pada (57), maka igk2 ω η(x,t)+ ig ω β2 η(x,t) = 0 k 2 η +β 2 η = 0 β 2 η = k 2 η sehingga β = k, persamaan (56) dapat kita tulis sebagai atau ω 2 = gk tanh(kh 2 ) ω = gk tanh(kh 2 ) (59)
19 Solusi untuk φ Misalkan dimana S (x,t) sama dengan (45), maka φ(x,y,t) = S (x,t) G (y) dengan fungsi tak diketahui G memenuhi dengan kondisi φ(x,y,t) = ig η(x,t) G (y) (60) ω G k 2 G = 0 (61) G (0) = 1, G (0) = ω2 g Sama dengan solusi dari (50), maka solusi untuk (61) kondisi (62) adalah G (y) = cosh(ky)+ ω2 gk sinh(ky) (62) Now φ(x,y,t) = ig [ ] ω η(x,t) cosh(βy)+ ω2 gβ sinh(βy) φ(x,y,t) = ig [ ] ω η(x,t) Acosh(ky)+ ω2 gk B sinh(ky) (63) (64)
20 φ y = α φ y pada y = h 1 (65) y φ(x,y,t) = ig ] [k ω η(x,t) sinh(ky)+ ω2 g cosh(ky) y φ(x, h 1,t) = ig ω η(x,t) [ k sinh(kh 1 )+ ω2 g cosh(kh 1) ] (66) y φ(x, h 2,t) = 0 y φ(x, h 2, t) = ig ] [Ak ω η(x,t) sinh( kh 2 )+ ω2 g B cosh( kh 2) = 0 Ak sinh(kh 2 )+ ω2 g B cosh(kh 2) = 0 ω 2 g B cosh(kh 2) = Ak sinh(kh 2 ) B = Akg ω 2 tanh(kh 2)
21 y φ(x,y,t) = ig ] [Ak ω η(x,t) sinh(ky)+ ω2 g B cosh(ky) = ig [ ω η Ak sinh(ky)+ ω2 kg g ω 2 Atanh(kh 2)cosh(ky) = ig ω η[ak sinh(ky)+ak tanh(kh 2)cosh(ky)] = igak ω η[sinh(ky)+tanh(kh 2) cosh(ky)] y φ(x, h 1,t) = igak ω η[sinh( kh 1)+tanh(kh 2 )cosh( kh 1 )] = igak ω η[ sinh(kh 1)+tanh(kh 2 )cosh(kh 1 )] (67) Selanjutnya kita gunakan (67) (66) pada (65), yaitu k sinh(kh 1 )+ ω2 g cosh(kh 1) = αak [ sinh(kh 1 )+tanh(kh 2 ) cosh(kh 1 )] ] αka = A = k sinh(kh 1 )+ ω2 g cosh(kh 1) sinh(kh 1 )+tanh(kh 2 )cosh(kh 1 ) k sinh(kh 1 )+ ω2 g cosh(kh 1) αk [ sinh(kh 1 )+tanh(kh 2 )cosh(kh 1 )] (68)
22 sinh(kh 1)cosh(kh 2 ) + sinh(kh 2)cosh(kh 1 ) cosh(kh 2 ) cosh(kh 2 ) sinh([h 2 h 1 ]k) cosh(kh 2 ) sehingga, A = ] [ k sinh(kh 1 )+ ω2 g cosh(kh cosh(kh 2 ) 1) αk sinh([h 2 h 1 ] k) = k sinh(kh 1) cosh(kh 2 )+ ω 2 g cosh(kh 1)cosh(kh 2 ) αk sinh([h 2 h 1 ]k) cosh([h 2 h 1 ]k) = cosh(h 2 k) cosh(h 1 k) sinh(h 2 k) sinh(h 1 k) cosh(h 2 k) cosh(h 1 k) = cosh([h 2 h 1 ]k)+sinh(h 2 k) sinh(h 1 k) sinh([h 2 h 1 ]k) = sinh(h 2 k) cosh(h 1 k) sinh(h 1 k) cosh(h 2 k) sinh(h 1 k) cosh(h 2 k) = sinh(h 2 k) cosh(h 1 k) sinh([h 2 h 1 ]k)
23 A = k sinh(kh 1)cosh(kh 2 )+ ω 2 g [cosh([h 2 h 1 ]k)+sinh(kh 1 )sinh(kh 2 )] αk sinh([h 2 h 1 ] k) k sinh(kh 1 )cosh(kh 2 )+ ω2 g sinh(kh 1)sinh(kh 2 ) k [sinh(h 2 k) cosh(h 1 k) sinh([h 2 h 1 ] k)]+ ω2 g sinh(kh 1) sinh(kh 2 ) ) ( k cosh(h 1 k)+ ω2 g sinh(kh 1) sinh(kh 2 )+k sinh([h 2 h 1 ] k)
24 t φ(x, h 1, t) = α φ(x, h 1,t)+ωf φ(x, h 1, t) t φ(x,0,t) = gη(x,t) t φ(x,y,t) = ig [ ] ω η(x,t) cosh(βy)+ ω2 gβ sinh(βy) φ(x,y,t) = ig ω η(x,t) [ A cosh(ky)+ ω2 gk [ Akg ω 2 tanh(kh 2) = ig ω η(x,t)[a cosh(ky)+a tanh(kh 2)sinh(ky)] ] ] sinh(ky) t φ(x,y,t) = ig ] ηt (x,t) [cosh(βy)+ ω2 ω gβ sinh(βy) φ(x,y,t) = ig t ω ηt (x,t)[a cosh(ky)+a tanh(kh 2)sinh(ky)]
Soal Ujian 2 Persamaan Differensial Parsial
 Soal Uian 2 Persamaan Differensial Parsial M. Jamhuri April 15, 2013 1 Buktikan bahwa ux,t) = πˆ 1 x e θ2 dθ merupakan solusi persamaan difusi u t = u xx untuk setiap x R,t > 0. Untuk x 0 tunukkan bahwa
Soal Uian 2 Persamaan Differensial Parsial M. Jamhuri April 15, 2013 1 Buktikan bahwa ux,t) = πˆ 1 x e θ2 dθ merupakan solusi persamaan difusi u t = u xx untuk setiap x R,t > 0. Untuk x 0 tunukkan bahwa
Persamaan Diferensial Parsial CNH3C3
 Persamaan Diferensial Parsial CNH3C3 Week 4: Separasi Variabel untuk Persamaan Panas Orde Satu Tim Ilmu Komputasi Coordinator contact: Dr. Putu Harry Gunawan phgunawan@telkomuniversity.ac.id 1 Persamaan
Persamaan Diferensial Parsial CNH3C3 Week 4: Separasi Variabel untuk Persamaan Panas Orde Satu Tim Ilmu Komputasi Coordinator contact: Dr. Putu Harry Gunawan phgunawan@telkomuniversity.ac.id 1 Persamaan
Persamaan Difusi. Penurunan, Solusi Analitik, Solusi Numerik (Beda Hingga, RBF) M. Jamhuri. April 7, UIN Malang. M. Jamhuri Persamaan Difusi
 Persamaan Difusi Penurunan, Solusi Analitik, Solusi Numerik (Beda Hingga, RBF) M Jamhuri UIN Malang April 7, 2013 Penurunan Persamaan Difusi Misalkan u(x, t) menyatakan konsentrasi dari zat pada posisi
Persamaan Difusi Penurunan, Solusi Analitik, Solusi Numerik (Beda Hingga, RBF) M Jamhuri UIN Malang April 7, 2013 Penurunan Persamaan Difusi Misalkan u(x, t) menyatakan konsentrasi dari zat pada posisi
Bab 4 DINDING SINUSOIDAL SEBAGAI REFLEKTOR GELOMBANG
 Bab 4 DINDING SINUSOIDAL SEBAGAI REFLEKTOR GELOMBANG Pada bab sebelumnya telah dibahas mengenai dasar laut sinusoidal sebagai reflektor gelombang. Persamaan yang digunakan untuk memodelkan masalah dasar
Bab 4 DINDING SINUSOIDAL SEBAGAI REFLEKTOR GELOMBANG Pada bab sebelumnya telah dibahas mengenai dasar laut sinusoidal sebagai reflektor gelombang. Persamaan yang digunakan untuk memodelkan masalah dasar
BAB III KONDUKSI ALIRAN STEDI - DIMENSI BANYAK
 BAB III KONDUKSI ALIRAN SEDI - DIMENSI BANYAK Untuk aliran stedi tanpa pembangkitan panas, persamaan Laplacenya adalah: + y 0 (6-) Aliran kalor pada arah dan y bisa dihitung dengan persamaan Fourier: q
BAB III KONDUKSI ALIRAN SEDI - DIMENSI BANYAK Untuk aliran stedi tanpa pembangkitan panas, persamaan Laplacenya adalah: + y 0 (6-) Aliran kalor pada arah dan y bisa dihitung dengan persamaan Fourier: q
NOISE TERMS PADA SOLUSI DERET DEKOMPOSISI ADOMIAN DALAM MENYELESAIKAN PERSAMAAN DIFERENSIAL PARSIAL ABSTRACT
 NOISE TERMS PADA SOLUSI DERET DEKOMPOSISI ADOMIAN DALAM MENYELESAIKAN PERSAMAAN DIFERENSIAL PARSIAL Heni Kusnani 1, Leli Deswita, Zulkarnain 1 Mahasiswa Program Studi S1 Matematika Dosen Jurusan Matematika
NOISE TERMS PADA SOLUSI DERET DEKOMPOSISI ADOMIAN DALAM MENYELESAIKAN PERSAMAAN DIFERENSIAL PARSIAL Heni Kusnani 1, Leli Deswita, Zulkarnain 1 Mahasiswa Program Studi S1 Matematika Dosen Jurusan Matematika
Persamaan Diferensial Parsial CNH3C3
 Persamaan Diferensial Parsial CNH3C3 Tim Ilmu Komputasi Week 6: Separasi Variabel untuk Persamaan Gelombang Orde dua dan Koesien Fourier Coordinator contact: Dr. Putu Harry Gunawan phgunawan@telkomuniversity.ac.id
Persamaan Diferensial Parsial CNH3C3 Tim Ilmu Komputasi Week 6: Separasi Variabel untuk Persamaan Gelombang Orde dua dan Koesien Fourier Coordinator contact: Dr. Putu Harry Gunawan phgunawan@telkomuniversity.ac.id
PENGARUH JUMLAH SUKU FOURIER PADA PENDEKATAN POLAR UNTUK SISTEM GEOMETRI KARTESIAN
 PENGARUH JUMLAH SUKU FOURIER PADA PENDEKATAN POLAR UNTUK SISTEM GEOMETRI KARTESIAN IRMA ISLAMIYAH 1105 100 056 FISIKA FMIPA INSTITUT TEKNOLOGI SEPULUH NOPEMBER SURABAYA 2010 PENDAHULUAN LATAR BELAKANG
PENGARUH JUMLAH SUKU FOURIER PADA PENDEKATAN POLAR UNTUK SISTEM GEOMETRI KARTESIAN IRMA ISLAMIYAH 1105 100 056 FISIKA FMIPA INSTITUT TEKNOLOGI SEPULUH NOPEMBER SURABAYA 2010 PENDAHULUAN LATAR BELAKANG
Evolusi Gelombang Harmonik melalui Serangkaian Pemecah Gelombang berupa Balok Berpori
 Evolusi Gelombang Harmonik melalui Serangkaian Pemecah Gelombang berupa Balok Berpori Mohammad Jamhuri, M.Si dan Evawati Alisah, M.Pd Jurusan Matematika UIN Maulana Malik Ibrahim November 14, 2015 Mohammad
Evolusi Gelombang Harmonik melalui Serangkaian Pemecah Gelombang berupa Balok Berpori Mohammad Jamhuri, M.Si dan Evawati Alisah, M.Pd Jurusan Matematika UIN Maulana Malik Ibrahim November 14, 2015 Mohammad
BAB 2 PERSAMAAN DIFFERENSIAL BIASA
 BAB 2 BIASA 2.1. KONSEP DASAR Persamaan Diferensial (PD) Biasa adalah persamaan yang mengandung satu atau beberapa penurunan y (varibel terikat) terhadap x (variabel bebas) yang tidak spesifik dan ditentukan
BAB 2 BIASA 2.1. KONSEP DASAR Persamaan Diferensial (PD) Biasa adalah persamaan yang mengandung satu atau beberapa penurunan y (varibel terikat) terhadap x (variabel bebas) yang tidak spesifik dan ditentukan
Ringkasan Kalkulus 2, Untuk dipakai di ITB 1. Integral Lipat Dua Atas Daerah Persegipanjang
 ingkasan Kalkulus 2, Untuk dipakai di ITB 1 Integral Lipat Dua Atas Daerah Persegipanjang Perhatikan fungsi z = f(x, y) pada = {(x, y) : a x b, c y d} Bentuk partisi P atas daerah berupa n buah persegipanjang
ingkasan Kalkulus 2, Untuk dipakai di ITB 1 Integral Lipat Dua Atas Daerah Persegipanjang Perhatikan fungsi z = f(x, y) pada = {(x, y) : a x b, c y d} Bentuk partisi P atas daerah berupa n buah persegipanjang
Pertemuan 1 dan 2 KONSEP DASAR PERSAMAAN DIFERENSIAL
 Pertemuan 1 dan 2 KONSEP DASAR PERSAMAAN DIFERENSIAL A. PENGERTIAN PERSAMAAN DIFERENSIAL Dalam pelajaran kalkulus, kita telah berkenalan dan mengkaji berbagai macam metode untuk mendiferensialkan suatu
Pertemuan 1 dan 2 KONSEP DASAR PERSAMAAN DIFERENSIAL A. PENGERTIAN PERSAMAAN DIFERENSIAL Dalam pelajaran kalkulus, kita telah berkenalan dan mengkaji berbagai macam metode untuk mendiferensialkan suatu
PROPOSAL TUGAS AKHIR PENGARUH JUMLAH SUKU FOURIER PADA PENDEKATAN POLAR UNTUK SISTEM GEOMETRI KARTESIAN OLEH : IRMA ISLAMIYAH
 PROPOSAL TUGAS AKHIR PENGARUH JUMLAH SUKU FOURIER PADA PENDEKATAN POLAR UNTUK SISTEM GEOMETRI KARTESIAN OLEH : IRMA ISLAMIYAH 1105 100 056 JURUSAN FISIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT
PROPOSAL TUGAS AKHIR PENGARUH JUMLAH SUKU FOURIER PADA PENDEKATAN POLAR UNTUK SISTEM GEOMETRI KARTESIAN OLEH : IRMA ISLAMIYAH 1105 100 056 JURUSAN FISIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT
perpindahan, kita peroleh persamaan differensial berikut :
 1.1 Pengertian Persamaan Differensial Banyak sekali masalah terapan (dalam ilmu teknik, ilmu fisika, biologi, kimia, sosial, dan lain-lain), yang telah dirumuskan dengan model matematika dalam bentuk persamaan
1.1 Pengertian Persamaan Differensial Banyak sekali masalah terapan (dalam ilmu teknik, ilmu fisika, biologi, kimia, sosial, dan lain-lain), yang telah dirumuskan dengan model matematika dalam bentuk persamaan
KONSEP DASAR PERSAMAAN DIFERENSIAL
 KONSEP DASAR PERSAMAAN DIFERENSIAL A. PENGERTIAN PERSAMAAN DIFERENSIAL Dalam pelajaran kalkulus, kita telah berkenalan dan mengkaji berbagai macam metode untuk mendiferensialkan suatu fungsi (dasar). Sebagai
KONSEP DASAR PERSAMAAN DIFERENSIAL A. PENGERTIAN PERSAMAAN DIFERENSIAL Dalam pelajaran kalkulus, kita telah berkenalan dan mengkaji berbagai macam metode untuk mendiferensialkan suatu fungsi (dasar). Sebagai
BAB III HASIL DAN PEMBAHASAN. analitik dengan metode variabel terpisah. Selanjutnya penyelesaian analitik dari
 BAB III HASIL DAN PEMBAHASAN Pada bab ini akan dibahas penurunan model persamaan panas dimensi satu. Setelah itu akan ditentukan penyelesaian persamaan panas dimensi satu secara analitik dengan metode
BAB III HASIL DAN PEMBAHASAN Pada bab ini akan dibahas penurunan model persamaan panas dimensi satu. Setelah itu akan ditentukan penyelesaian persamaan panas dimensi satu secara analitik dengan metode
BAB I PERSAMAAN DIFERENSIAL LINIER ORDE I
 BAB I PERSAMAAN DIFERENSIAL LINIER ORDE I. Pengertian PD, Orde (tingkat), & Derajat (Pangkat) Persamaan diferensial adalah suatu persamaan yang memuat derivatifderivatif (turunan) sekurang-kurangnya derivatif
BAB I PERSAMAAN DIFERENSIAL LINIER ORDE I. Pengertian PD, Orde (tingkat), & Derajat (Pangkat) Persamaan diferensial adalah suatu persamaan yang memuat derivatifderivatif (turunan) sekurang-kurangnya derivatif
MODUL MATEMATIKA II. Oleh: Dr. Eng. LILYA SUSANTI
 MODUL MATEMATIKA II Oleh: Dr. Eng. LILYA SUSANTI DEPARTEMEN RISET TEKNOLOGI DAN PENDIDIKAN TINGGI UNIVERSITAS BRAWIJAYA FAKULTAS TEKNIK JURUSAN TEKNIK SIPIL KATA PENGANTAR Puji sukur kehadirat Allah SWT
MODUL MATEMATIKA II Oleh: Dr. Eng. LILYA SUSANTI DEPARTEMEN RISET TEKNOLOGI DAN PENDIDIKAN TINGGI UNIVERSITAS BRAWIJAYA FAKULTAS TEKNIK JURUSAN TEKNIK SIPIL KATA PENGANTAR Puji sukur kehadirat Allah SWT
Persamaan Differensial Biasa
 Bab 7 cakul fi5080 by khbasar; sem1 2010-2011 Persamaan Differensial Biasa Dalam banyak persoalan fisika, suatu topik sering dinyatakan dalam bentuk perubahan (laju perubahan). Telah disinggung sebelumnya
Bab 7 cakul fi5080 by khbasar; sem1 2010-2011 Persamaan Differensial Biasa Dalam banyak persoalan fisika, suatu topik sering dinyatakan dalam bentuk perubahan (laju perubahan). Telah disinggung sebelumnya
Persamaan diferensial adalah suatu persamaan yang memuat satu atau lebih turunan fungsi yang tidak diketahui.
 1 Persamaan diferensial adalah suatu persamaan yang memuat satu atau lebih turunan fungsi yang tidak diketahui. Jika persamaan diferensial memiliki satu peubah tak bebas maka disebut Persamaan Diferensial
1 Persamaan diferensial adalah suatu persamaan yang memuat satu atau lebih turunan fungsi yang tidak diketahui. Jika persamaan diferensial memiliki satu peubah tak bebas maka disebut Persamaan Diferensial
PERSAMAAN DIFERENSIAL I PERSAMAAN DIFERENSIAL BIASA
 PERSAMAAN DIFERENSIAL I PERSAMAAN DIFERENSIAL BIASA Persamaan Diferensial Biasa 1. PDB Tingkat Satu (PDB) 1.1. Persamaan diferensial 1.2. Metode pemisahan peubah dan PD koefisien fungsi homogen 1.3. Persamaan
PERSAMAAN DIFERENSIAL I PERSAMAAN DIFERENSIAL BIASA Persamaan Diferensial Biasa 1. PDB Tingkat Satu (PDB) 1.1. Persamaan diferensial 1.2. Metode pemisahan peubah dan PD koefisien fungsi homogen 1.3. Persamaan
Bab 2 LANDASAN TEORI. 2.1 Penurunan Persamaan Air Dangkal
 Bab 2 LANDASAN TEORI 2.1 Penurunan Persamaan Air Dangkal Persamaan air dangkal atau Shallow Water Equation (SWE) berlaku untuk fluida homogen yang memiliki massa jenis konstan, inviscid (tidak kental),
Bab 2 LANDASAN TEORI 2.1 Penurunan Persamaan Air Dangkal Persamaan air dangkal atau Shallow Water Equation (SWE) berlaku untuk fluida homogen yang memiliki massa jenis konstan, inviscid (tidak kental),
DASAR SINUSOIDAL SEBAGAI REFLEKTOR GELOMBANG
 h Bab 3 DASAR SINUSOIDAL SEBAGAI REFLEKTOR GELOMBANG 3.1 Persamaan Gelombang untuk Dasar Sinusoidal Dasar laut berbentuk sinusoidal adalah salah satu bentuk dasar laut tak rata yang berupa fungsi sinus
h Bab 3 DASAR SINUSOIDAL SEBAGAI REFLEKTOR GELOMBANG 3.1 Persamaan Gelombang untuk Dasar Sinusoidal Dasar laut berbentuk sinusoidal adalah salah satu bentuk dasar laut tak rata yang berupa fungsi sinus
Fourier Analysis & Its Applications in PDEs - Part I
 Fourier Analysis & Its Applications in PDEs Hendra Gunawan http://personal.fmipa.itb.ac.id/hgunawan/ Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA WIDE 2010 5-6 August
Fourier Analysis & Its Applications in PDEs Hendra Gunawan http://personal.fmipa.itb.ac.id/hgunawan/ Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA WIDE 2010 5-6 August
PERSAMAAN DIFERENSIAL LINIER NON HOMOGEN
 LINIER NON HOMOGEN Contoh PD linier non homogen orde 2. Bentuk umum persamaan PD Linier Non Homogen Orde 2, adalah sebagai berikut : y + f(x) y + g(x) y = r(x) ( 2-35) Solusi umum y(x) akan didapatkan
LINIER NON HOMOGEN Contoh PD linier non homogen orde 2. Bentuk umum persamaan PD Linier Non Homogen Orde 2, adalah sebagai berikut : y + f(x) y + g(x) y = r(x) ( 2-35) Solusi umum y(x) akan didapatkan
LAMPIRAN I. Alfabet Yunani
 LAMPIRAN I Alfabet Yunani Alha Α Nu Ν Beta Β Xi Ξ Gamma Γ Omicron Ο Delta Δ Pi Π Esilon Ε Rho Ρ Zeta Ζ Sigma Σ Eta Η Tau Τ Theta Θ Usilon Υ Iota Ι hi Φ, Kaa Κ Chi Χ Lambda Λ Psi Ψ Mu Μ Omega Ω LAMPIRAN
LAMPIRAN I Alfabet Yunani Alha Α Nu Ν Beta Β Xi Ξ Gamma Γ Omicron Ο Delta Δ Pi Π Esilon Ε Rho Ρ Zeta Ζ Sigma Σ Eta Η Tau Τ Theta Θ Usilon Υ Iota Ι hi Φ, Kaa Κ Chi Χ Lambda Λ Psi Ψ Mu Μ Omega Ω LAMPIRAN
Solusi Numerik Persamaan Transport dengan RBF
 Solusi Numerik Persamaan Transport dengan RBF Unpublished M. Jamhuri UIN Malang March 30, 013 Hampiran RBF RBF singkatan dari radial basis function φ(r), adalah sebuah fungsi kontinu dengan satu peubah
Solusi Numerik Persamaan Transport dengan RBF Unpublished M. Jamhuri UIN Malang March 30, 013 Hampiran RBF RBF singkatan dari radial basis function φ(r), adalah sebuah fungsi kontinu dengan satu peubah
Persamaan Diferensial Parsial CNH3C3
 Persamaan Diferensial Parsial CNH3C3 Week 5: Separasi Variabel untuk Persamaan Panas Orde Satu - Tim Ilmu Komputasi Coordinator contact: Dr. Putu Harry Gunawan phgunawan@telkomuniversity.ac.id 1 Review
Persamaan Diferensial Parsial CNH3C3 Week 5: Separasi Variabel untuk Persamaan Panas Orde Satu - Tim Ilmu Komputasi Coordinator contact: Dr. Putu Harry Gunawan phgunawan@telkomuniversity.ac.id 1 Review
PERSAMAAN DIFFERENSIAL LINIER
 PERSAMAAN DIFFERENSIAL LINIER Persamaan Differensial Linier Pengertian : Suatu persamaan differensial orde satu dikatakan linier jika persamaan tersebut dapat dituliskan sbb: y + p x y = r(x) (1) linier
PERSAMAAN DIFFERENSIAL LINIER Persamaan Differensial Linier Pengertian : Suatu persamaan differensial orde satu dikatakan linier jika persamaan tersebut dapat dituliskan sbb: y + p x y = r(x) (1) linier
Persamaan Diferensial Biasa
 Persamaan Diferensial Biasa Pendahuluan, Persamaan Diferensial Orde-1 Toni Bakhtiar Departemen Matematika IPB September 2012 Toni Bakhtiar (m@thipb) PDB September 2012 1 / 37 Pendahuluan Konsep Dasar Beberapa
Persamaan Diferensial Biasa Pendahuluan, Persamaan Diferensial Orde-1 Toni Bakhtiar Departemen Matematika IPB September 2012 Toni Bakhtiar (m@thipb) PDB September 2012 1 / 37 Pendahuluan Konsep Dasar Beberapa
PDP linear orde 2 Agus Yodi Gunawan
 PDP linear orde 2 Agus Yodi Gunawan Pada bagian ini akan dipelajari tiga jenis persamaan diferensial parsial (PDP) linear orde dua yang biasa dijumpai pada masalah-masalah dunia nyata, yaitu persamaan
PDP linear orde 2 Agus Yodi Gunawan Pada bagian ini akan dipelajari tiga jenis persamaan diferensial parsial (PDP) linear orde dua yang biasa dijumpai pada masalah-masalah dunia nyata, yaitu persamaan
BAB II KAJIAN TEORI. dalam penulisan bab III. Materi yang diuraikan berisi tentang definisi, teorema,
 BAB II KAJIAN TEORI Pada bab ini akan dibahas tentang beberapa hal yang menjadi landasan dalam penulisan bab III. Materi yang diuraikan berisi tentang definisi, teorema, dan beberapa kajian matematika,
BAB II KAJIAN TEORI Pada bab ini akan dibahas tentang beberapa hal yang menjadi landasan dalam penulisan bab III. Materi yang diuraikan berisi tentang definisi, teorema, dan beberapa kajian matematika,
UJI KONVERGENSI. Januari Tim Dosen Kalkulus 2 TPB ITK
 UJI KONVERGENSI Januari 208 Tim Dosen Kalkulus 2 TPB ITK Uji Integral Teorema 3 Jika + k= u k adalah deret dengan suku-suku tak negatif, dan jika ada suatu konstanta M sedemikian hingga s n = u + u 2 +
UJI KONVERGENSI Januari 208 Tim Dosen Kalkulus 2 TPB ITK Uji Integral Teorema 3 Jika + k= u k adalah deret dengan suku-suku tak negatif, dan jika ada suatu konstanta M sedemikian hingga s n = u + u 2 +
TEORI GELOMBANG AMPLITUDO KECIL DAN PERAMALAN GELOMBANG
 Bahan Ajar TEORI GELOMBANG AMPLITUDO KECIL DAN PERAMALAN GELOMBANG Ahmad Zakaria,Ph.D. JURUSAN TEKNIK SIPIL FAKULTAS TEKNIK UNIVERSITAS LAMPUNG Januari 2009 Kata Pengantar Bahan Ajar ini dibuat dengan
Bahan Ajar TEORI GELOMBANG AMPLITUDO KECIL DAN PERAMALAN GELOMBANG Ahmad Zakaria,Ph.D. JURUSAN TEKNIK SIPIL FAKULTAS TEKNIK UNIVERSITAS LAMPUNG Januari 2009 Kata Pengantar Bahan Ajar ini dibuat dengan
Bab 3 Fungsi Elementer
 Bab 3 Fungsi Elementer Bab 3 ini direncanakan akan disampaikan dalam 3 kali pertemuan, dengan perincian sebagai berikut: (1) Pertemuan I: Fungsi Eksponensial dan sifat-sifatnya, Fungsi Trigonometri. ()
Bab 3 Fungsi Elementer Bab 3 ini direncanakan akan disampaikan dalam 3 kali pertemuan, dengan perincian sebagai berikut: (1) Pertemuan I: Fungsi Eksponensial dan sifat-sifatnya, Fungsi Trigonometri. ()
BAB 3 PERAMBATAN GELOMBANG MONOKROMATIK
 BAB 3 PERAMBATAN GELOMBANG MONOKROMATIK Dalam bab ini, kita akan mengamati perambatan gelombang pada fluida ideal dengan dasar rata. Perhatikan gambar di bawah ini. Gambar 3.1 Aliran Fluida pada Dasar
BAB 3 PERAMBATAN GELOMBANG MONOKROMATIK Dalam bab ini, kita akan mengamati perambatan gelombang pada fluida ideal dengan dasar rata. Perhatikan gambar di bawah ini. Gambar 3.1 Aliran Fluida pada Dasar
12. Teorema Inversi Fourier dan Transformasi Fourier di L 2 (R)
 1. Teorema Inversi Fourier dan Transformasi Fourier di L (R) 1.1 Teorema Inversi Fourier Dari hasil hitung-hitungan kasar di awal bagian ke-10, kita ingin membuktikan bahwa, dalam kondisi tertentu, kita
1. Teorema Inversi Fourier dan Transformasi Fourier di L (R) 1.1 Teorema Inversi Fourier Dari hasil hitung-hitungan kasar di awal bagian ke-10, kita ingin membuktikan bahwa, dalam kondisi tertentu, kita
KONSEP METODE ITERASI VARIASIONAL ABSTRACT
 KONSEP METODE ITERASI VARIASIONAL Yuliani 1, Leli Deswita 2, Agusni 2 1 Mahasiswa Program Studi S1 Matematika 2 Dosen Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Riau Kampus
KONSEP METODE ITERASI VARIASIONAL Yuliani 1, Leli Deswita 2, Agusni 2 1 Mahasiswa Program Studi S1 Matematika 2 Dosen Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Riau Kampus
Program Interaktif berbasis Web untuk menghitung Panjang Gelombang dan Pasang Surut
 seri komputasi pantai Dasar Teori dan Aplikasi Program Interaktif berbasis Web untuk menghitung Panjang Gelombang dan Pasang Surut (Edisi Pertama) Ahmad Zakaria Penerbit Magister Teknik Sipil Universitas
seri komputasi pantai Dasar Teori dan Aplikasi Program Interaktif berbasis Web untuk menghitung Panjang Gelombang dan Pasang Surut (Edisi Pertama) Ahmad Zakaria Penerbit Magister Teknik Sipil Universitas
Pengantar Metode Perturbasi Bab 4. Ekspansi Asimtotik pada Persamaan Diferensial Biasa
 Pengantar Metode Perturbasi Bab 4. Ekspansi Asimtotik pada Persamaan Diferensial Biasa Mahdhivan Syafwan Jurusan Matematika FMIPA Universitas Andalas PAM 454 KAPITA SELEKTA MATEMATIKA TERAPAN II Semester
Pengantar Metode Perturbasi Bab 4. Ekspansi Asimtotik pada Persamaan Diferensial Biasa Mahdhivan Syafwan Jurusan Matematika FMIPA Universitas Andalas PAM 454 KAPITA SELEKTA MATEMATIKA TERAPAN II Semester
Suku Banyak Chebyshev
 Bab 3 Suku Banyak Chebyshev Suku banyak Chebyshev, yang diberi nama oleh Pafnuty Chebyshev, merupakan suatu deret dari suku banyak ortogonal yang dapat dituliskan secara rekursif. Suku banyak ini dibedakan
Bab 3 Suku Banyak Chebyshev Suku banyak Chebyshev, yang diberi nama oleh Pafnuty Chebyshev, merupakan suatu deret dari suku banyak ortogonal yang dapat dituliskan secara rekursif. Suku banyak ini dibedakan
KB 2. Nilai Energi Celah. Model ini menjelaskan tingkah laku elektron dalam sebuah energi potensial yang
 KB. Nilai Energi Celah 1. Model Kronig-Penney Model ini menjelaskan tingkah laku elektron dalam sebuah energi potensial yang periodik, dengan menganggap energi potensial periodik itu merupakan deretan
KB. Nilai Energi Celah 1. Model Kronig-Penney Model ini menjelaskan tingkah laku elektron dalam sebuah energi potensial yang periodik, dengan menganggap energi potensial periodik itu merupakan deretan
Persamaan Poisson. Fisika Komputasi. Irwan Ary Dharmawan
 (Pendahuluan) 1D untuk syarat batas Robin 2D dengan syarat batas Dirichlet Fisika Komputasi Jurusan Fisika Universitas Padjadjaran http://phys.unpad.ac.id/jurusan/staff/dharmawan email : dharmawan@phys.unpad.ac.id
(Pendahuluan) 1D untuk syarat batas Robin 2D dengan syarat batas Dirichlet Fisika Komputasi Jurusan Fisika Universitas Padjadjaran http://phys.unpad.ac.id/jurusan/staff/dharmawan email : dharmawan@phys.unpad.ac.id
BAB 2 TINJAUAN PUSTAKA
 BAB TINJAUAN PUSTAKA. Definisi Gelombang dan klasifikasinya. Gelombang adalah suatu gangguan menjalar dalam suatu medium ataupun tanpa medium. Dalam klasifikasinya gelombang terbagi menjadi yaitu :. Gelombang
BAB TINJAUAN PUSTAKA. Definisi Gelombang dan klasifikasinya. Gelombang adalah suatu gangguan menjalar dalam suatu medium ataupun tanpa medium. Dalam klasifikasinya gelombang terbagi menjadi yaitu :. Gelombang
Bab III Respon Sinusoidal
 Bab III Respon Sinusoidal Sinyal sinusiodal digunakan sebagai input ui terhadap kinera sistem, misal untuk mengetahui respon frekuensi, distorsi harmonik dan distorsi intermodulasi... Bentuk Amplituda-fasa
Bab III Respon Sinusoidal Sinyal sinusiodal digunakan sebagai input ui terhadap kinera sistem, misal untuk mengetahui respon frekuensi, distorsi harmonik dan distorsi intermodulasi... Bentuk Amplituda-fasa
DERET FOURIER. n = bilangan asli (1,2,3,4,5,.) L = pertemuan titik. Bilangan-bilangan untuk,,,, disebut koefisien fourier dari f(x) dalam (-L,L)
 DERET FOURIER Bila f adalah fungsi periodic yang berperioda p, maka f adalah fungsi periodic. Berperiode n, dimana n adalah bilangan asli positif (+). Untuk setiap bilangan asli positif fungsi yang didefinisikan
DERET FOURIER Bila f adalah fungsi periodic yang berperioda p, maka f adalah fungsi periodic. Berperiode n, dimana n adalah bilangan asli positif (+). Untuk setiap bilangan asli positif fungsi yang didefinisikan
Program Interaktif berbasis Web untuk menghitung Panjang Gelombang dan Pasang Surut
 seri komputasi pantai Dasar Teori dan Aplikasi Program Interaktif berbasis Web untuk menghitung Panjang Gelombang dan Pasang Surut (Edisi Pertama) Ahmad Zakaria Magister Teknik Sipil Universitas Lampung
seri komputasi pantai Dasar Teori dan Aplikasi Program Interaktif berbasis Web untuk menghitung Panjang Gelombang dan Pasang Surut (Edisi Pertama) Ahmad Zakaria Magister Teknik Sipil Universitas Lampung
Department of Mathematics FMIPAUNS
 Lecture 2: Metode Operator A. Metode Operator untuk Sistem Linear dengan Koefisien Konstan Pada bagian ini akan dibicarakan cara menentukan penyelesaian sistem persamaan diferensial linear dengan menggunakan
Lecture 2: Metode Operator A. Metode Operator untuk Sistem Linear dengan Koefisien Konstan Pada bagian ini akan dibicarakan cara menentukan penyelesaian sistem persamaan diferensial linear dengan menggunakan
Dr. Ir. Bib Paruhum Silalahi, M.Kom
 Metode Descent Oleh : Andaikan fungsi tujuan kita adalah minf(x);x R n. Secara umum f(x) dapat berupa fungsi nonlinear. Metode-metode descent adalah metode iteratif untuk memperoleh solusi pendekatan dari
Metode Descent Oleh : Andaikan fungsi tujuan kita adalah minf(x);x R n. Secara umum f(x) dapat berupa fungsi nonlinear. Metode-metode descent adalah metode iteratif untuk memperoleh solusi pendekatan dari
Reflektor Gelombang 1 balok
 Bab 3 Reflektor Gelombang 1 balok Setelah diperoleh persamaan yang menggambarkan gerak gelombang air setiap saat yaitu SWE, maka pada bab ini akan dielaskan mengenai pengaruh 1 balok terendam sebagai reflektor
Bab 3 Reflektor Gelombang 1 balok Setelah diperoleh persamaan yang menggambarkan gerak gelombang air setiap saat yaitu SWE, maka pada bab ini akan dielaskan mengenai pengaruh 1 balok terendam sebagai reflektor
Aplikasi Persamaan Bessel Orde Nol Pada Persamaan Panas Dua dimensi
 JURNAL FOURIER Oktober 2013, Vol. 2, No. 2, 113-123 ISSN 2252-763X Aplikasi Persamaan Bessel Orde Nol Pada Persamaan Panas Dua dimensi Annisa Eki Mulyati dan Sugiyanto Program Studi Matematika Fakultas
JURNAL FOURIER Oktober 2013, Vol. 2, No. 2, 113-123 ISSN 2252-763X Aplikasi Persamaan Bessel Orde Nol Pada Persamaan Panas Dua dimensi Annisa Eki Mulyati dan Sugiyanto Program Studi Matematika Fakultas
4. Dibawah ini persamaan diferensial ordo dua berderajat satu adalah
 Pilihlah jawaban yang benar dengan cara mencakra huruf didepan jawaban yang saudara anggap benar pada lembar jawaban 1. Dibawah ini bentuk persamaan diferensial biasa linier homogen adalah a. y + xy =
Pilihlah jawaban yang benar dengan cara mencakra huruf didepan jawaban yang saudara anggap benar pada lembar jawaban 1. Dibawah ini bentuk persamaan diferensial biasa linier homogen adalah a. y + xy =
FUNGSI EVANS, SIFAT-SIFAT DAN APLIKASINYA PADA PELACAKAN NILAI EIGEN DARI MASALAH STURM-LIOUVILLE
 Jurnal Matematika UNAND Vol. 4 No. Hal. 23 3 ISSN : 233 29 c Jurusan Matematika FMIPA UNAND FUNGSI EVANS, SIFAT-SIFAT DAN APLIKASINYA PADA PELACAKAN NILAI EIGEN DARI MASALAH STURM-LIOUVILLE HILDA FAHLENA,
Jurnal Matematika UNAND Vol. 4 No. Hal. 23 3 ISSN : 233 29 c Jurusan Matematika FMIPA UNAND FUNGSI EVANS, SIFAT-SIFAT DAN APLIKASINYA PADA PELACAKAN NILAI EIGEN DARI MASALAH STURM-LIOUVILLE HILDA FAHLENA,
BAB II TINJAUAN PUSTAKA
 BAB II TINJAUAN PUSTAKA 2.1 Transformasi Laplace Salah satu cara untuk menganalisis gejala peralihan (transien) adalah menggunakan transformasi Laplace, yaitu pengubahan suatu fungsi waktu f(t) menjadi
BAB II TINJAUAN PUSTAKA 2.1 Transformasi Laplace Salah satu cara untuk menganalisis gejala peralihan (transien) adalah menggunakan transformasi Laplace, yaitu pengubahan suatu fungsi waktu f(t) menjadi
MA1201 KALKULUS 2A (Kelas 10) Bab 8: Bentuk Tak Tentu d
 MA1201 KALKULUS 2A (Kelas 10) Bab 8: dan Do maths and you see the world ? Pengantar Bentuk tak tentu? Bentuk apa? Bentuk tak tentu yang dimaksud adalah bentuk limit dengan nilai seolah-olah : 0 0 ; ; 0
MA1201 KALKULUS 2A (Kelas 10) Bab 8: dan Do maths and you see the world ? Pengantar Bentuk tak tentu? Bentuk apa? Bentuk tak tentu yang dimaksud adalah bentuk limit dengan nilai seolah-olah : 0 0 ; ; 0
Kalkulus Multivariabel I
 Maksimum, Minimum, dan Statistika FMIPA Universitas Islam Indonesia Titik Kritis Misalkan p = (x, y) adalah sebuah titik peubah dan p 0 = (x 0, y 0 ) adalah sebuah titik tetap pada bidang berdimensi dua
Maksimum, Minimum, dan Statistika FMIPA Universitas Islam Indonesia Titik Kritis Misalkan p = (x, y) adalah sebuah titik peubah dan p 0 = (x 0, y 0 ) adalah sebuah titik tetap pada bidang berdimensi dua
Fourier Analysis & Its Applications in PDEs - Part II
 Fourier Analysis & Its Applications in PDEs Hendra Gunawan http://personal.fmipa.itb.ac.id/hgunawan/ Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA WIDE 2010 5-6 August
Fourier Analysis & Its Applications in PDEs Hendra Gunawan http://personal.fmipa.itb.ac.id/hgunawan/ Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA WIDE 2010 5-6 August
PENYELESAIAN PERSAMAAN DIFFERENSIAL ORDE 1 - I
 PENYELESAIAN PERSAMAAN DIFFERENSIAL ORDE 1 - I 1. Pendahuluan Pengertian Persamaan Diferensial Metoda Penyelesaian -contoh Aplikasi 1 1.1. Pengertian Persamaan Differensial Secara Garis Besar Persamaan
PENYELESAIAN PERSAMAAN DIFFERENSIAL ORDE 1 - I 1. Pendahuluan Pengertian Persamaan Diferensial Metoda Penyelesaian -contoh Aplikasi 1 1.1. Pengertian Persamaan Differensial Secara Garis Besar Persamaan
Barisan dan Deret Agus Yodi Gunawan
 Barisan dan Deret Agus Yodi Gunawan Barisan. Definisi. Barisan tak hingga adalah suatu fungsi dengan daerah asalnya himpunan bilangan bulat positif dan daerah kawannya himpunan bilangan real. Notasi untuk
Barisan dan Deret Agus Yodi Gunawan Barisan. Definisi. Barisan tak hingga adalah suatu fungsi dengan daerah asalnya himpunan bilangan bulat positif dan daerah kawannya himpunan bilangan real. Notasi untuk
Catatan Kuliah FI1101 Fisika Dasar IA Pekan #8: Osilasi
 Catatan Kuliah FI111 Fisika Dasar IA Pekan #8: Osilasi Agus Suroso update: 4 November 17 Osilasi atau getaran adalah gerak bolak-balik suatu benda melalui titik kesetimbangan. Gerak bolak-balik tersebut
Catatan Kuliah FI111 Fisika Dasar IA Pekan #8: Osilasi Agus Suroso update: 4 November 17 Osilasi atau getaran adalah gerak bolak-balik suatu benda melalui titik kesetimbangan. Gerak bolak-balik tersebut
7. RESIDU DAN PENGGUNAAN. Contoh 1 Carilah titik singular dan tentukan jenisnya dari fungsi berikut a. f(z) = 1/z
 MATEMATIKA 6 TEKNIK Residu dan Penggunaan 6 7. RESIDU DAN PENGGUNAAN 7.. RESIDU DAN KUTUB disebut titik singular dari f() bila f() gagal analitik di tetapi analitik pada suatu titik dari setiap lingkungan
MATEMATIKA 6 TEKNIK Residu dan Penggunaan 6 7. RESIDU DAN PENGGUNAAN 7.. RESIDU DAN KUTUB disebut titik singular dari f() bila f() gagal analitik di tetapi analitik pada suatu titik dari setiap lingkungan
BAB II PENGANTAR SOLUSI PERSOALAN FISIKA MENURUT PENDEKATAN ANALITIK DAN NUMERIK
 BAB II PENGANTAR SOLUSI PERSOALAN FISIKA MENURUT PENDEKATAN ANALITIK DAN NUMERIK Tujuan Instruksional Setelah mempelajari bab ini pembaca diharapkan dapat: 1. Menjelaskan cara penyelesaian soal dengan
BAB II PENGANTAR SOLUSI PERSOALAN FISIKA MENURUT PENDEKATAN ANALITIK DAN NUMERIK Tujuan Instruksional Setelah mempelajari bab ini pembaca diharapkan dapat: 1. Menjelaskan cara penyelesaian soal dengan
BAB II KAJIAN TEORI. pada penulisan bab III. Materi yang diuraikan berisi tentang definisi, teorema, dan
 BAB II KAJIAN TEORI Pada bab ini akan dibahas beberapa hal yang digunakan sebagai landasan pada penulisan bab III. Materi yang diuraikan berisi tentang definisi, teorema, dan beberapa kajian matematika,
BAB II KAJIAN TEORI Pada bab ini akan dibahas beberapa hal yang digunakan sebagai landasan pada penulisan bab III. Materi yang diuraikan berisi tentang definisi, teorema, dan beberapa kajian matematika,
13. Aplikasi Transformasi Fourier
 13. plikasi ransformasi Fourier Misal adalah operator linear pada fungsi yang terdefinisi pada R dengan sifat: jika [f(x] = g(x, maka [f(x + s] = g(x + s untuk setiap s R. Maka, fungsi f(x = e ax (a C
13. plikasi ransformasi Fourier Misal adalah operator linear pada fungsi yang terdefinisi pada R dengan sifat: jika [f(x] = g(x, maka [f(x + s] = g(x + s untuk setiap s R. Maka, fungsi f(x = e ax (a C
Kalkulus 2. Teknik Pengintegralan ke - 1. Tim Pengajar Kalkulus ITK. Institut Teknologi Kalimantan. Januari 2018
 Kalkulus 2 Teknik Pengintegralan ke - 1 Tim Pengajar Kalkulus ITK Institut Teknologi Kalimantan Januari 2018 Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari 2018 1 / 36 Daftar
Kalkulus 2 Teknik Pengintegralan ke - 1 Tim Pengajar Kalkulus ITK Institut Teknologi Kalimantan Januari 2018 Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari 2018 1 / 36 Daftar
Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Riau Kampus Binawidya Pekanbaru (28293), Indonesia.
 METODE SIMPSON-LIKE TERKOREKSI Ilis Suryani, M. Imran, Asmara Karma Mahasiswa Program Studi S Matematika Laboratorium Matematika Terapan, Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam
METODE SIMPSON-LIKE TERKOREKSI Ilis Suryani, M. Imran, Asmara Karma Mahasiswa Program Studi S Matematika Laboratorium Matematika Terapan, Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam
Bab 2 TEORI DASAR. 2.1 Linearisasi Persamaan Air Dangkal
 Bab 2 TEORI DASAR 2.1 Linearisasi Persamaan Air Dangkal Persamaan air dangkal merupakan persamaan untuk gelombang permukaan air yang dipengaruhi oleh kedalaman air tersebut. Kedalaman air dapat dikatakan
Bab 2 TEORI DASAR 2.1 Linearisasi Persamaan Air Dangkal Persamaan air dangkal merupakan persamaan untuk gelombang permukaan air yang dipengaruhi oleh kedalaman air tersebut. Kedalaman air dapat dikatakan
Geometri pada Bidang, Vektor
 Jurusan Matematika FMIPA Unsyiah September 9, 2011 Sebuah kurva bidang (plane curve) ditentukan oleh pasangan persamaan parametrik x = f(t), y = g(t), t dalam I dengan f dan g kontinu pada selang I. I
Jurusan Matematika FMIPA Unsyiah September 9, 2011 Sebuah kurva bidang (plane curve) ditentukan oleh pasangan persamaan parametrik x = f(t), y = g(t), t dalam I dengan f dan g kontinu pada selang I. I
Bab 2. Landasan Teori. 2.1 Persamaan Air Dangkal (SWE)
 Bab 2 Landasan Teori Dalam bab ini akan dibahas mengenai Persamaan Air Dangkal dan dasar-dasar teori mengenai metode beda hingga untuk menghampiri solusi dari persamaan diferensial parsial. 2.1 Persamaan
Bab 2 Landasan Teori Dalam bab ini akan dibahas mengenai Persamaan Air Dangkal dan dasar-dasar teori mengenai metode beda hingga untuk menghampiri solusi dari persamaan diferensial parsial. 2.1 Persamaan
Bab V Prosedur Numerik
 Bab V Prosedur Numerik Pada bab ini, metode numerik digunakan untuk menghitung medan kecepatan, yakni dengan menghitung batas dan domain integral. Tensor tegangan tak Newton melalui persamaan Maxwell Linear
Bab V Prosedur Numerik Pada bab ini, metode numerik digunakan untuk menghitung medan kecepatan, yakni dengan menghitung batas dan domain integral. Tensor tegangan tak Newton melalui persamaan Maxwell Linear
11. Konvolusi. Misalkan f dan g fungsi yang terdefinisi pada R. Konvolusi dari f dan g adalah fungsi f g yang didefinisikan sebagai.
 11. Konvolusi Operasi konvolusi yang akan kita bahas di sini sebetulnya pernah kita jumpai pada pembahasan deret Fourier (ketika membuktikan kekonvergenan jumlah parsialnya). Operasi konvolusi merupakan
11. Konvolusi Operasi konvolusi yang akan kita bahas di sini sebetulnya pernah kita jumpai pada pembahasan deret Fourier (ketika membuktikan kekonvergenan jumlah parsialnya). Operasi konvolusi merupakan
FISIKA. Sesi GELOMBANG BERJALAN DAN STASIONER A. GELOMBANG BERJALAN
 FISIKA KELAS XII IPA - KURIKULUM KTSP 0 Sesi GELOMBANG BERJALAN DAN STASIONER A. GELOMBANG BERJALAN Gelombang adalah getaran yang merambat. Adapun gelombang berjalan merupakan suatu gelombang di mana setiap
FISIKA KELAS XII IPA - KURIKULUM KTSP 0 Sesi GELOMBANG BERJALAN DAN STASIONER A. GELOMBANG BERJALAN Gelombang adalah getaran yang merambat. Adapun gelombang berjalan merupakan suatu gelombang di mana setiap
PENYELESAIAN PERSAMAAN DIFFERENSIAL ORDE 2 - II
 PENYELESAIAN PERSAMAAN DIFFERENSIAL ORDE - II.Persamaan Homogen dengan Koefisien Konstan Suatu persamaan linier homogen y + ay + by = 0 (1) mempunyai koefisien a dan b adalah konstan. Persamaan ini mempunyai
PENYELESAIAN PERSAMAAN DIFFERENSIAL ORDE - II.Persamaan Homogen dengan Koefisien Konstan Suatu persamaan linier homogen y + ay + by = 0 (1) mempunyai koefisien a dan b adalah konstan. Persamaan ini mempunyai
BAB II KAJIAN TEORI. representasi pemodelan matematika disebut sebagai model matematika. Interpretasi Solusi. Bandingkan Data
 A. Model Matematika BAB II KAJIAN TEORI Pemodelan matematika adalah proses representasi dan penjelasan dari permasalahan dunia real yang dinyatakan dalam pernyataan matematika (Widowati dan Sutimin, 2007:
A. Model Matematika BAB II KAJIAN TEORI Pemodelan matematika adalah proses representasi dan penjelasan dari permasalahan dunia real yang dinyatakan dalam pernyataan matematika (Widowati dan Sutimin, 2007:
KALKULUS MULTIVARIABEL II
 Pada Bidang Bentuk Vektor dari KALKULUS MULTIVARIABEL II (Minggu ke-9) Andradi Jurusan Matematika FMIPA UGM Yogyakarta, Indonesia Pada Bidang Bentuk Vektor dari 1 Definisi Daerah Sederhana x 2 Pada Bidang
Pada Bidang Bentuk Vektor dari KALKULUS MULTIVARIABEL II (Minggu ke-9) Andradi Jurusan Matematika FMIPA UGM Yogyakarta, Indonesia Pada Bidang Bentuk Vektor dari 1 Definisi Daerah Sederhana x 2 Pada Bidang
SISTEM HUKUM KEKEKALAN LINEAR
 Bab 3 SISTEM HUKUM KEKEKALAN LINEAR 3.1 Sistem Linear Hiperbolik Sistem linear dalam pengertian Tugas Akhir ini adalah suatu sistem hukum kekekalan dengan bentuk umum, t u + d A α (t) xα u = 0 (3.1.1)
Bab 3 SISTEM HUKUM KEKEKALAN LINEAR 3.1 Sistem Linear Hiperbolik Sistem linear dalam pengertian Tugas Akhir ini adalah suatu sistem hukum kekekalan dengan bentuk umum, t u + d A α (t) xα u = 0 (3.1.1)
Listrik Statik. Agus Suroso
 Listrik Statik Agus Suroso Muatan Listrik Ada dua macam: positif dan negatif. Sejenis tolak menolak, beda jenis tarik menarik. Muatan fundamental e =, 60 0 9 Coulomb. Atau, C = 6,5 0 8 e. Atom = proton
Listrik Statik Agus Suroso Muatan Listrik Ada dua macam: positif dan negatif. Sejenis tolak menolak, beda jenis tarik menarik. Muatan fundamental e =, 60 0 9 Coulomb. Atau, C = 6,5 0 8 e. Atom = proton
Matematika I: Turunan. Dadang Amir Hamzah. Dadang Amir Hamzah Matematika I Semester I / 61
 Matematika I: Turunan Dadang Amir Hamzah 2015 Dadang Amir Hamzah Matematika I Semester I 2015 1 / 61 Outline 1 Garis Singgung Dadang Amir Hamzah Matematika I Semester I 2015 2 / 61 Outline 1 Garis Singgung
Matematika I: Turunan Dadang Amir Hamzah 2015 Dadang Amir Hamzah Matematika I Semester I 2015 1 / 61 Outline 1 Garis Singgung Dadang Amir Hamzah Matematika I Semester I 2015 2 / 61 Outline 1 Garis Singgung
PENYELESAIAN PERSAMAAN DIFFERENSIAL ORDE 1 - II
 PENYELESAIAN PERSAMAAN DIFFERENSIAL ORDE 1 - II c. Metoda Persamaan Differensial Pasti (Exact) Pada kalkulus bahwa jika suatu fungsi u(x,y) mempunyai turunan parsial yang sifatnya kontinyu, turunan pasti
PENYELESAIAN PERSAMAAN DIFFERENSIAL ORDE 1 - II c. Metoda Persamaan Differensial Pasti (Exact) Pada kalkulus bahwa jika suatu fungsi u(x,y) mempunyai turunan parsial yang sifatnya kontinyu, turunan pasti
PENGANTAR MATEMATIKA TEKNIK 1. By : Suthami A
 PENGANTAR MATEMATIKA TEKNIK 1 By : Suthami A MATEMATIKA TEKNIK 1??? MATEMATIKA TEKNIK 1??? MATEMATIKA TEKNIK Matematika sebagai ilmu dasar yang digunakan sebagai alat pemecahan masalah di bidang keteknikan
PENGANTAR MATEMATIKA TEKNIK 1 By : Suthami A MATEMATIKA TEKNIK 1??? MATEMATIKA TEKNIK 1??? MATEMATIKA TEKNIK Matematika sebagai ilmu dasar yang digunakan sebagai alat pemecahan masalah di bidang keteknikan
MA1201 MATEMATIKA 2A Hendra Gunawan
 MA101 MATEMATIKA A Hendra Gunawan Semester II, 016/017 1 Maret 017 Bab Sebelumnya 9.1 Barisan Tak Terhingga 9. Deret Tak Terhingga 9.3 Deret Positif: Uji Integral 9.4 Deret Positif: Uji Lainnya 9.5 Deret
MA101 MATEMATIKA A Hendra Gunawan Semester II, 016/017 1 Maret 017 Bab Sebelumnya 9.1 Barisan Tak Terhingga 9. Deret Tak Terhingga 9.3 Deret Positif: Uji Integral 9.4 Deret Positif: Uji Lainnya 9.5 Deret
Gambar 1. Bentuk sebuah tali yang direnggangkan (a) pada t = 0 (b) pada x=vt.
 1. Pengertian Gelombang Berjalan Gelombang berjalan adalah gelombang yang amplitudonya tetap. Pada sebuah tali yang panjang diregangkan di dalam arah x di mana sebuah gelombang transversal sedang berjalan.
1. Pengertian Gelombang Berjalan Gelombang berjalan adalah gelombang yang amplitudonya tetap. Pada sebuah tali yang panjang diregangkan di dalam arah x di mana sebuah gelombang transversal sedang berjalan.
log2 PEMBAHASAN SOAL TRY OUT = = 2 1 = 27 8 = 19 Jawaban : C = = = 2( 15 10) Jawaban : B . 4. log3 1 2 (1) .
 TRY OUT AKBAR UN SMA 08 PEMBAHASAN SOAL TRY OUT. 9 6 4 8 7 Jawaban : C 4 4 = = = 7 8 4 = 9. 5 + = 0 5 = 0 5 = 5 0 = ( 5 0). log5 5 log8 log6 4 log log4 = log5 5 4 log log log6 log4 =. log5 5. 4. log log
TRY OUT AKBAR UN SMA 08 PEMBAHASAN SOAL TRY OUT. 9 6 4 8 7 Jawaban : C 4 4 = = = 7 8 4 = 9. 5 + = 0 5 = 0 5 = 5 0 = ( 5 0). log5 5 log8 log6 4 log log4 = log5 5 4 log log log6 log4 =. log5 5. 4. log log
matematika PEMINATAN Kelas X PERSAMAAN DAN PERTIDAKSAMAAN EKSPONEN K13 A. PERSAMAAN EKSPONEN BERBASIS KONSTANTA
 K1 Kelas X matematika PEMINATAN PERSAMAAN DAN PERTIDAKSAMAAN EKSPONEN TUJUAN PEMBELAJARAN Setelah mempelajari materi ini, kamu diharapkan memiliki kemampuan berikut. 1. Memahami bentuk-bentuk persamaan
K1 Kelas X matematika PEMINATAN PERSAMAAN DAN PERTIDAKSAMAAN EKSPONEN TUJUAN PEMBELAJARAN Setelah mempelajari materi ini, kamu diharapkan memiliki kemampuan berikut. 1. Memahami bentuk-bentuk persamaan
GETARAN DAN GELOMBANG
 1/19 Kuliah Fisika Dasar Teknik Sipil 2007 GETARAN DAN GELOMBANG Mirza Satriawan Physics Dept. Gadjah Mada University Bulaksumur, Yogyakarta email: mirza@ugm.ac.id GETARAN Getaran adalah salah satu bentuk
1/19 Kuliah Fisika Dasar Teknik Sipil 2007 GETARAN DAN GELOMBANG Mirza Satriawan Physics Dept. Gadjah Mada University Bulaksumur, Yogyakarta email: mirza@ugm.ac.id GETARAN Getaran adalah salah satu bentuk
PENYELESAIAN PERSAMAAN PANAS DENGAN ANALITIK DAN METODE VOLUME HINGGA HALAMAN JUDUL TUGAS AKHIR SKRIPSI
 PENYELESAIAN PERSAMAAN PANAS DENGAN ANALITIK DAN METODE VOLUME HINGGA HALAMAN JUDUL TUGAS AKHIR SKRIPSI Diajukan kepada Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Yogyakarta untuk
PENYELESAIAN PERSAMAAN PANAS DENGAN ANALITIK DAN METODE VOLUME HINGGA HALAMAN JUDUL TUGAS AKHIR SKRIPSI Diajukan kepada Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Yogyakarta untuk
Fungsi Elementer (Bagian Kedua)
 Fungsi Elementer (Bagian Kedua) Supama Jurusan Matematika, FMIPA UGM Yogyakarta 55281, INDONESIA Email:maspomo@yahoo.com, supama@ugm.ac.id (Pertemuan Minggu IX) Outline 1 Fungsi Hiperbolik 2 sin(iz) =
Fungsi Elementer (Bagian Kedua) Supama Jurusan Matematika, FMIPA UGM Yogyakarta 55281, INDONESIA Email:maspomo@yahoo.com, supama@ugm.ac.id (Pertemuan Minggu IX) Outline 1 Fungsi Hiperbolik 2 sin(iz) =
8. Deret Fourier yang Diperumum dan Hampiran Terbaik di L 2 (a, b)
 8. Deret Fourier yang Diperumum dan Hampiran Terbaik di L (a, b) 8.1 Deret Fourier yang Diperumum Jika {ϕ n } 1 adalah basis ortonormal untuk L (a, b) dan f L (a, b), maka f, ϕ n disebut koefisien Fourier
8. Deret Fourier yang Diperumum dan Hampiran Terbaik di L (a, b) 8.1 Deret Fourier yang Diperumum Jika {ϕ n } 1 adalah basis ortonormal untuk L (a, b) dan f L (a, b), maka f, ϕ n disebut koefisien Fourier
BINOVATIF LISTRIK DAN MAGNET. Hani Nurbiantoro Santosa, PhD.
 BINOVATIF LISTRIK DAN MAGNET Hani Nurbiantoro Santosa, PhD hanisantosa@gmail.com 2 BAB 2 MEDAN LISTRIK DAN HUKUM GAUSS Pendahuluan, Distribusi Muatan Kontinu, Mencari Medan Listrik Menggunakan Integral,
BINOVATIF LISTRIK DAN MAGNET Hani Nurbiantoro Santosa, PhD hanisantosa@gmail.com 2 BAB 2 MEDAN LISTRIK DAN HUKUM GAUSS Pendahuluan, Distribusi Muatan Kontinu, Mencari Medan Listrik Menggunakan Integral,
PEMBAHASAN. (29) Dalam (Grosen 1992), kondisi kinematik (19) dan kondisi dinamik (20) dapat dinyatakan dalam sistem Hamiltonian berikut : = (30)
 5 η = η di z = η (9) z x x z x x Dalam (Grosen 99) kondisi kinematik (9) kondisi dinamik () dapat dinyatakan dalam sistem Hamiltonian : δ H t = () δη δ H ηt = δ Dengan mengenalkan variabel baru u = x maka
5 η = η di z = η (9) z x x z x x Dalam (Grosen 99) kondisi kinematik (9) kondisi dinamik () dapat dinyatakan dalam sistem Hamiltonian : δ H t = () δη δ H ηt = δ Dengan mengenalkan variabel baru u = x maka
FUNGSI. Berdasarkan hubungan antara variabel bebas dan terikat, fungsi dibedakan dua: fungsi eksplisit dan fungsi implisit.
 FUNGSI Fungsi merupakan hubungan antara dua variabel atau lebih. Variabel dibedakan :. Variabel bebas yaitu variabel yang besarannya dpt ditentukan sembarang, mis:,, 6, 0 dll.. Variabel terikat yaitu variabel
FUNGSI Fungsi merupakan hubungan antara dua variabel atau lebih. Variabel dibedakan :. Variabel bebas yaitu variabel yang besarannya dpt ditentukan sembarang, mis:,, 6, 0 dll.. Variabel terikat yaitu variabel
Bab II Konsep Dasar Metode Elemen Batas
 Bab II Konsep Dasar Metode Elemen Batas II.1 II.1.1 Kalkulus Dasar Teorema Gradien Misal menyatakan domain pada ruang dimensi dua dan menyatakan batas i x + j 2 2 x 2 + 2 2 elanjutnya, penentuan integral
Bab II Konsep Dasar Metode Elemen Batas II.1 II.1.1 Kalkulus Dasar Teorema Gradien Misal menyatakan domain pada ruang dimensi dua dan menyatakan batas i x + j 2 2 x 2 + 2 2 elanjutnya, penentuan integral
PERSAMAAN DIFRENSIAL BIASA
 PERSAMAAN DIFRENSIAL BIASA (Buku pegangan mata kuliah Persamaan Difrensial) Oleh Drs. D a f i k, M.Sc. NIP. 132 052 409 Program Pendikan Matematika FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN UNIVERSITAS JEMBER
PERSAMAAN DIFRENSIAL BIASA (Buku pegangan mata kuliah Persamaan Difrensial) Oleh Drs. D a f i k, M.Sc. NIP. 132 052 409 Program Pendikan Matematika FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN UNIVERSITAS JEMBER
Jawaban. atau 1 xkt. h c = = = atau. 4,965k
 Jawaban Diketahui F( λ) π 5 λ hc ex( hc / λk ) a Untuk menemukan nilai maksimum F( λ ), diambil derivatif F( λ ) ke λ kemudian nilanya sama dengan 0 Misalnya Sehingga hc x λk atau xk λ hc Dengan Maka 5
Jawaban Diketahui F( λ) π 5 λ hc ex( hc / λk ) a Untuk menemukan nilai maksimum F( λ ), diambil derivatif F( λ ) ke λ kemudian nilanya sama dengan 0 Misalnya Sehingga hc x λk atau xk λ hc Dengan Maka 5
(T.8) SEBARAN ATIMTOTIK FUNGSI INTENSITAS PROSES POISSON PERIODIK DENGAN TREN FUNGSI PANGKAT
 (T.8) SEBARAN ATIMTOTIK FUNGSI INTENSITAS PROSES POISSON PERIODIK DENGAN TREN FUNGSI PANGKAT Ro fah Nur Rachmawati Universitas Bina Nusantara Jl. K.H. Syahdan No. 9 Palmerah Jakarta Barat 11480 rrachmawati@binus.edu
(T.8) SEBARAN ATIMTOTIK FUNGSI INTENSITAS PROSES POISSON PERIODIK DENGAN TREN FUNGSI PANGKAT Ro fah Nur Rachmawati Universitas Bina Nusantara Jl. K.H. Syahdan No. 9 Palmerah Jakarta Barat 11480 rrachmawati@binus.edu
MATERI 2 MATEMATIKA TEKNIK 1 PERSAMAAN DIFERENSIAL ORDE SATU
 MATERI 2 MATEMATIKA TEKNIK 1 PERSAMAAN DIFERENSIAL ORDE SATU 1 Persamaan diferensial orde satu Persamaan diferensial menyatakan hubungan dinamik antara variabel bebas dan variabel tak bebas, maksudnya
MATERI 2 MATEMATIKA TEKNIK 1 PERSAMAAN DIFERENSIAL ORDE SATU 1 Persamaan diferensial orde satu Persamaan diferensial menyatakan hubungan dinamik antara variabel bebas dan variabel tak bebas, maksudnya
7. Transformasi Fourier
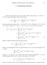 Pengantar Analisis Fourier dan eori Aproksimasi 33 7. ransformasi Fourier Pada bab sebelumnya kita telah melihat bahwa setiap fungsi f L 1 ([0, 1] L ([0, 1] dapat dinyatakan sebagai deret Fourier f(x =
Pengantar Analisis Fourier dan eori Aproksimasi 33 7. ransformasi Fourier Pada bab sebelumnya kita telah melihat bahwa setiap fungsi f L 1 ([0, 1] L ([0, 1] dapat dinyatakan sebagai deret Fourier f(x =
BAB II KAJIAN TEORI. syarat batas, deret fourier, metode separasi variabel, deret taylor dan metode beda
 BAB II KAJIAN TEORI Pada bab ini akan dibahas tentang beberapa teori dasar yang digunakan sebagai landasan pembahasan pada bab III. Beberapa teori dasar yang dibahas, diantaranya teori umum tentang persamaan
BAB II KAJIAN TEORI Pada bab ini akan dibahas tentang beberapa teori dasar yang digunakan sebagai landasan pembahasan pada bab III. Beberapa teori dasar yang dibahas, diantaranya teori umum tentang persamaan
Husna Arifah,M.Sc : Persamaan Bessel: Fungsi-fungsi Besel jenis Pertama
 Bentuk umum PD Bessel : x 2 y"+xy' +(x 2 υ 2 )y =...() Kita asumsikan bahwa parameter υ dalam () adalah bilangan riil dan tak negatif. Penyelesaian PD mempunyai bentuk : y(x) = x r m = a m x m = a m xm
Bentuk umum PD Bessel : x 2 y"+xy' +(x 2 υ 2 )y =...() Kita asumsikan bahwa parameter υ dalam () adalah bilangan riil dan tak negatif. Penyelesaian PD mempunyai bentuk : y(x) = x r m = a m x m = a m xm
Kalkulus Variasi. Masalah Kalkulus Variasi, Fungsional Objektif, Variasi, Syarat Perlu Optimalitas. Toni Bakhtiar. Departemen Matematika IPB
 Kalkulus Variasi Masalah Kalkulus Variasi, Fungsional Objektif, Variasi, Syarat Perlu Optimalitas Toni Bakhtiar Departemen Matematika IPB Februari 2014 tbakhtiar@ipb.ac.id (IPB) MAT332 Kontrol Optimum
Kalkulus Variasi Masalah Kalkulus Variasi, Fungsional Objektif, Variasi, Syarat Perlu Optimalitas Toni Bakhtiar Departemen Matematika IPB Februari 2014 tbakhtiar@ipb.ac.id (IPB) MAT332 Kontrol Optimum
