Fourier Analysis & Its Applications in PDEs - Part I
|
|
|
- Farida Makmur
- 6 tahun lalu
- Tontonan:
Transkripsi
1 Fourier Analysis & Its Applications in PDEs Hendra Gunawan Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA WIDE August 2010
2 Outline 1,, and 2 Persamaan Panas Persamaan Gelombang Persamaan Laplace Domain Tak Terbatas
3 Referensi J. Douandikoetxea, Fourier Analysis G.B. Folland, Fourier Analysis and Its Applications H. Gunawan, Analisis Fourier dan Wavelet M.A. Pinsky, Introduction to Fourier Analysis and Wavelets E.M. Stein, Singular Integrals and Differentiability Properties of Functions E.M. Stein & R. Shakarchi, Fourier Analysis R. Strichartz, The Way of Analysis... dan masih banyak lagi.
4 Deret trigonometri yang kita kenal sekarang sebagai deret Fourier pada mulanya digagas oleh D. Bernoulli pada tahun 1750-an dalam rangka mempelajari persamaan gelombang persamaan diferensial parsial untuk dawai bergetar (vibrating string): dengan syarat batas dan syarat awal u tt = c 2 u xx u(0, t) = u(l, t) = 0 t 0 u(x, 0) = f(x) dan u t (x, 0) = 0 x [0, L]. Di sini c konstanta, L panjang dawai, f keadaan awal dawai, dan u = u(x, t) simpangan vertikal dawai di titik x pada saat t.
5 Bernoulli menemukan bahwa untuk f(x) = sin kπx L, fungsi u(x, t) = sin kπx ckπt cos L L merupakan solusi untuk setiap bilangan bulat positif k. Karena persamaan diferensial tadi merupakan persamaan diferensial parsial linear, maka kombinasi linear dari solusi-solusi di atas juga merupakan solusi. Dalam hal ini, Bernoulli menyimpulkan bahwa u(x, t) = k=1 a k sin kπx L ckπt cos L memenuhi persamaan, dengan syarat awal f(x) = a k sin kπx L. k=1 Bernoulli juga menyatakan bahwa ia telah mendapatkan semua solusi tanpa penjelasan tentang koefisien a k.
6 Temuan Bernoulli ini tak lama kemudian disanggah oleh L. Euler. Bagi Euler, tidak masuk akal sebarang fungsi f yang terdefinisi pada interval [0, L] dengan f(0) = f(l) = 0 dapat dinyatakan sebagai deret tak hingga sinus f(x) = k=1 a k sin kπx L, karena menurutnya deret sinus memiliki sifat khusus, yakni merupakan fungsi ganjil dan periodik dengan periode 2L. Jadi, lanjutnya, kesamaan di atas mustahil dipenuhi oleh, misalnya, f(x) = x(l x) yang bukan fungsi ganjil ataupun periodik.
7 Euler, dan juga D Alembert, pada saat itu telah menemukan solusi dalam bentuk yang berbeda, yaitu sin kπx L u(x, t) = 1 2 ckπt cos L = 1 2 [ f(x + ct) + f(x ct) ] dengan f menyatakan perluasan dari f pada R sedemikian sehingga f ganjil dan periodik dengan periode 2L. Mengingat [sin kπl (x + ct) + sin kπl ] (x ct), solusi Bernoulli dianggap sebagai kasus khusus dari solusi yang ia temukan.
8 Bernoulli tak dapat menanggapi sanggahan Euler dengan baik. Ia hanya menjelaskan bahwa persamaan f(x) = k=1 a k sin kπx L merupakan suatu sistem persamaan linear dengan tak hingga peubah. Kelemahan utama argumennya adalah bahwa ia tak dapat memberikan rumus untuk koefisien a k yang memenuhi persamaan di atas. Rumus itu akhirnya ditemukan oleh Euler beberapa tahun sesudahnya, namun Euler tidak mempelajari lebih lanjut temuannya karena ia terlanjur menolak gagasan Bernoulli sebelumnya.
9 Setengah abad kemudian, tepatnya pada 1807, J. Fourier berhasil mengembangkan apa yang kita kenal sekarang sebagai deret Fourier. Ketika itu ia tertarik dengan persamaan panas atau persamaan difusi: u t = c 2 u xx dengan u = u(x, t) menyatakan suhu kawat yang panjangnya L di titik x pada saat t, dengan syarat batas dan syarat awal u(0, t) = u(l, t) = 0 t 0 u(x, 0) = f(x) x [0, L].
10 Dengan menuliskan f sebagai deret f(x) = Fourier menemukan solusi u(x, t) = k=1 k=1 a k sin kπx L, a k e (c2 k 2 π 2 t)/l 2 sin kπx L. Namun, tak seperti Bernoulli, Fourier memberikan rumus untuk koefisien a k dalam f, yaitu [Ref: Strichartz, 2000] a k = 2 L L 0 f(x) sin kπx L dx.
11 dari sebuah fungsi periodik f merupakan deret trigonometri (persisnya deret sinus dan cosinus) untuk f. Untuk kemudahan kita akan lebih banyak bekerja dengan fungsi eksponensial kompleks e iθ daripada fungsi trigonometri cos θ dan sin θ. Ingat bahwa fungsi-fungsi ini terkait oleh rumus e iθ = cos θ + i sin θ cos θ = 1 2 (eiθ + e iθ ) dan sin θ = 1 2i (eiθ e iθ ). Kelebihan fungsi cosinus dan sinus adalah bahwa mereka bernilai real dan mempunyai sifat simetri, sementara kelebihan fungsi eksponensial adalah rumus turunan (e iθ ) = ie iθ dan rumus jumlah e i(θ+φ) = e iθ e iφ yang relatif lebih sederhana.
12 Misalkan f(θ) adalah sebuah fungsi bernilai kompleks yang terdefinisi pada R sedemikian sehingga f(θ + 2π) = f(θ) θ R, yakni f periodik dengan periode 2π. Asumsikan pula bahwa f terintegralkan Riemann pada sebarang interval terbatas (ini dipenuhi bila, misalnya, f terbatas dan kontinu kecuali di sejumlah terhingga titik pada sebarang interval terbatas). Kita ingin mengetahui kapankah f dapat diuraikan sebagai deret f(θ) = 1 2 a 0 + (a n cos nθ + b n sin nθ). n=1 Di sini 1 2 a 0 merupakan koefisien fungsi konstan cos 0θ = 1 (faktor 1 2 sengaja diikutsertakan untuk kemudahan yang akan kita lihat nanti). Tidak ada b 0 karena sin 0θ = 0.
13 Menggunakan fungsi ekponensial, persamaan tadi menjadi dengan f(θ) = n= c n e inθ c 0 = 1 2 a 0; c n = 1 2 (a n ib n ) dan c n = 1 2 (a n + ib n ), n N atau a 0 = 2c 0 ; a n = c n + c n dan b n = i(c n c n ), n N. Untuk menjawab pertanyaan di atas, kita mencoba terlebih dahulu mencari syarat perlunya. Jika kita mempunyai persamaan di atas, dapatkah kita menyatakan koefisien c n dalam f?
14 Dengan mengalikan kedua ruas dengan e ikθ (k Z), kemudian integralkan dari π sampai π, kita peroleh (dengan menganggap bahwa integral deret sama dengan deret integral) π π Tetapi, untuk n k π π f(θ)e ikθ dθ = e i(n k)θ dθ = sementara untuk n = k π π n= e i(n k)θ dθ = π c n e i(n k)θ dθ. π 1 π i(n k) ei(n k)θ = 0, π π π dθ = 2π.
15 Jadi satu-satunya suku yang bertahan dalam deret tadi adalah suku ke-k, sehingga kita dapatkan π π Ganti k menjadi n, maka c n = 1 2π Dari sini kita peroleh a n = c n + c n = 1 π b n = i(c n c n ) = 1 π f(θ)e ikθ dθ = 2πc k. π π a 0 = 2c 0 = 1 π π π π π f(θ)e inθ dθ, n Z. π π f(θ)dθ f(θ) cos nθ dθ, n = 1, 2, 3,... f(θ) sin nθ dθ, n = 1, 2, 3,....
16 Definisi. Misalkan f periodik dengan periode 2π dan terintegralkan pada [ π, π]. Bilangan c n, atau a n dan b n, sebagaimana dirumuskan di atas, disebut sebagai koefisien Fourier dari f, sementara deret n= c n e inθ atau 1 2 a 0 + (a n cos nθ + b n sin nθ) n=1 disebut sebagai deret Fourier dari f.
17 Catat bahwa yang telah kita dapatkan saat ini baru syarat perlunya saja, belum syarat cukup. Yakni, jika kita mempunyai sebuah fungsi f yang periodik dengan periode 2π dan terintegralkan pada [ π, π], maka kita dapat menghitung koefisien-koefisien Fourier dan deret Fourier dari fungsi tersebut. Namun pertanyaan apakah f sama dengan deret Fouriernya, atau apakah deret Fourier dari f konvergen (titik demi titik) ke f, sama sekali belum terjawab. Sebelum kita menjawab pertanyaan penting tadi, kita tinjau terlebih dahulu dua buah contoh berikut.
18 Contoh 1. Misalkan f periodik dengan periode 2π dan f(θ) = θ, π θ π. Maka, dengan mengingat bahwa f merupakan fungsi genap, kita peroleh a 0 = π, a n = 2 ( 1) n 1 π dan b n 2 n = 0 untuk setiap n N. Namun ( 1) n 1 = 0 bila n genap, dan ( 1) n 1 = 2 bila n ganjil. Dengan demikian deret Fourier dari f adalah π 2 4 π n=1,3,5,... 1 cos nθ. n2
19 Contoh 2. Misalkan g periodik dengan periode 2π dan g(θ) = θ, π < θ π. Maka c 0 = 0 dan c n = ( 1)n+1 in untuk setiap n 0. Jadi deret Fourier dari g adalah ( 1) n+1 n 0 in e inθ atau, mengingat ( 1) n = ( 1) n dan einθ in + e inθ in = 2 n sin nθ, ( 1) n+1 2 sin nθ. n n=1
20 Mari kita lihat apakah deret Fourier dari masing-masing fungsi tersebut konvergen titik demi titik ke fungsi semula, dengan mengamati kecenderungan beberapa jumlah parsial pertamanya. Gambar 1. f(θ) = θ, π θ π. Gambar diberikan di papan tulis.
21 Gambar 2. g(θ) = θ, π < θ π. Perhatikan bahwa pada Gambar 2 ada fenomena menarik di sekitar x = π dan x = π.
22 Ketaksamaan berikut diperlukan kelak dalam pembahasan kekonvergenan deret Fourier. Ketaksamaan Bessel. Jika f periodik dengan periode 2π dan terintegralkan Riemann pada [ π, π], maka koefisien Fourier c n yang ditentukan oleh rumus di atas memenuhi ketaksamaan n= c n 2 1 π f(θ) 2 dθ. 2π π Bukti. Untuk setiap N N, kita mempunyai 0 π π f(θ) N n= N c n e inθ 2 π dθ = f(θ) 2 dθ 2π π N n= N Ambil limitnya untuk N, kita peroleh ketaksamaan yang diinginkan. c n 2.
23 Catatan. Mengingat a 0 2 = 4 c 0 2 dan a n 2 + b n 2 = 2( c n 2 + c n 2 ) untuk n 1, kita peroleh 1 4 a ( a n 2 + b n 2 ) = n=1 n= c n 2 1 π f(θ) 2 dθ. 2π π Akibat (Lemma Riemann-Lebesgue). Koefisien Fourier c n menuju 0 bila n. Koefisien Fourier a n dan b n menuju 0 bila n. Bukti. a n 2, b n 2, dan c n 2 merupakan suku ke-n deret yang konvergen, dan karenanya mereka menuju 0 dan demikian pula halnya dengan a n, b n, dan c n.
24 Soal Latihan 1 Verifikasi perhitungan koefisien a n dan b n pada Contoh 1 dan perhitungan koefisien c n pada Contoh 2. 2 Verifikasi hubungan antara a n, b n, dan c n. 3 Tentukan deret Fourier dari fungsi periodik f dengan periode 2π, dengan f(θ) = 1 jika 0 < θ < π, f(θ) = 1 jika π < θ < 0, dan f(0) = f(π) = 0. 4 Buktikan bahwa untuk setiap N N berlaku π N π n= N c n e inθ dθ = 1 π f(θ)dθ. 2π π
25 Sekarang kita akan membahas kekonvergenan deret Fourier, khususnya kekonvergenan titik demi titik. Barisan fungsi (f n ) dikatakan konvergen titik demi titik ke fungsi f pada himpunan A apabila (f n (x)) konvergen ke f(x) untuk tiap x A. Melalui Contoh 2 yang dibahas pada bab sebelumnya kita mengetahui bahwa secara umum deret Fourier dari suatu fungsi tidak selalu konvergen titik demi titik ke fungsi semula, khususnya di titik di mana fungsi tersebut diskontinu. Namun, kita akan melihat bila fungsi tersebut memenuhi sejumlah hipotesis tertentu, maka deret Fouriernya akan konvergen titik demi titik.
26 Untuk menjawab pertanyaan apakah deret 1 2 a 0 + (a n cos nθ + b n sin nθ) atau n=1 n= c n e inθ, dengan koefisien a n, b n, dan c n sebagaimana diberikan sebelumnya, konvergen ke f(θ), kita tinjau jumlah parsialnya, yakni N S f N (θ) := n= N c n e inθ = 1 2 a 0 + N (a n cos nθ + b n sin nθ). n=1 (Ketika kita bekerja dengan bentuk eksponensial, kita sepakat bahwa kita senantiasa menyatukan suku e inθ dan e inθ. Itu sebabnya kita harus menyelidiki jumlah parsial simetris di atas.)
27 Substitusikan rumus untuk c n ke dalam jumlah parsial tadi, S f N (θ) = 1 2π N n= N π π f(ψ)e in(ψ θ) dψ = 1 2π N n= N π Selanjutnya, dengan substitusi peubah φ = ψ θ dan mengingat bahwa f periodik dengan periode 2π, kita peroleh S f N (θ) = 1 2π N n= N Karena N n= N dengan D N (φ) := 1 2π π+θ π+θ f(θ+φ)e inφ dφ = 1 2π N n= N π π π f(ψ)e in(ψ θ) dψ f(θ+φ)e inφ dφ. π π = π N π n= N..., kita dapat menuliskan π S f N (θ) = f(θ + φ)d N (φ)dφ, N n= N π e inφ.
28 Fungsi D N (φ) dikenal sebagai kernel Dirichlet. Dengan mengenalinya sebagai deret geometri, dengan suku pertama e inφ dan rasio e iφ, kita dapat menyederhanakannya sebagai D N (φ) = 1 2π e i(n+1)φ e inφ e iφ. 1 Selanjutnya, dengan mengalikan pembilang dan penyebut dengan e iφ/2, kita peroleh D N (φ) = 1 e i(n+1/2)φ e i(n+1/2)φ 2π e iφ/2 e iφ/2 = 1 2π sin(n + 1/2)φ. sin φ/2 Grafik D N (φ) untuk N = 25 kurang lebih berbentuk sebagai berikut (di papan tulis).
29 Intuisi mendorong kita untuk menyimpulkan bahwa S f N (θ) f(θ). Dalam hal ini titik puncak D N (φ) yang terjadi di φ = 0 memetik nilai f(θ) pada S f N (θ); sementara osilasi cepat yang terjadi pada D N (φ) untuk φ jauh dari 0 menihilkan bagian lainnya karena adanya pencoretan antara nilai positif dan negatif. Untuk membuktikan kekonvergenan titik demi titik deret Fourier, kita memerlukan lemma berikut mengenai kernel Dirichet dan sejumlah peristilahan. Lemma. Untuk setiap N N berlaku 0 π D N (φ)dφ = π 0 D N (φ)dφ = 1 2.
30 Misalkan < a < b <. Kita katakan bahwa f kontinu bagian demi bagian pada [a, b] apabila f kontinu pada [a, b] kecuali di sejumlah terhingga titik, dan di titik-titik tersebut limit kiri dan limit kanan f ada. Lalu, kita katakan bahwa f mulus bagian demi bagian pada [a, b] apabila f kontinu bagian demi bagian pada [a, b], f ada dan kontintu pada (a, b) kecuali di sejumlah terhingga titik, dan di titik-titik tersebut turunan kiri dan turunan kanan f ada. Sebagai ilustrasi, fungsi yang kontinu bagian demi bagian dan fungsi yang mulus bagian demi bagian digambarkan di papan tulis. Selanjutnya, f dikatakan kontinu (mulus) bagian demi bagian pada R apabila ia kontinu (mulus) bagian demi bagian pada sebarang selang terbatas [a, b].
31 Teorema. Jika f periodik dengan periode 2π dan mulus bagian demi bagian, maka lim N Sf N (θ) = 1 [f(θ ) + f(θ+)], 2 dengan f(θ ) := lim f(θ + h) dan f(θ+) := lim f(θ + h). h 0 h 0 + Bukti. Menurut lemma sebelumnya, f(θ ) = f(θ ) π dan 1 2 f(θ+) = f(θ+) D N (φ)dφ. Karena itu,... 0 π D N (φ)dφ
32 Karena itu, S f N (θ) [f(θ ) + f(θ+)] = [f(θ + φ) f(θ )]D N (φ)dφ + + π π Selanjutnya, kita dapat menuliskan S f N (θ) 1 1 [f(θ ) + f(θ+)] = 2 2π 0 [f(θ + φ) f(θ+)]d N (φ)dφ. π π g(φ)[e i(n+1)φ e inφ ]dφ, dengan g(φ) := f(θ+φ) f(θ ) untuk π < φ < 0 dan e iφ 1 g(φ) := f(θ+φ) f(θ+) untuk 0 < φ < π. e iφ 1
33 Di sini g merupakan fungsi yang mulus seperti halnya f pada [ π, π], kecuali di φ = 0, di mana lim g(φ) = if (θ+) dan φ 0 + lim g(φ) = if (θ ). Jadi g kontinu bagian demi bagian pada φ 0 [ π, π], sehingga koefisien Fouriernya, yakni c g n := 1 2π π π g(φ)e inφ dφ menuju 0 bila n ±. Dengan demikian bentuk di atas, yang merupakan selisih c g (N+1) cg N, akan menuju 0 bila N.
34 Soal Latihan 1 Misalkan f dan g periodik dengan periode 2π, mulus bagian demi bagian, dan f(θ) = 1 2 [f(θ ) + f(θ+)] untuk setiap θ. Buktikan jika f dan g mempunyai koefisien Fourier yang sama, maka f = g. 2 Dengan meninjau nilai deret Fourier dan fungsi g (yang dibahas pada Contoh 2) di θ = 0, buktikan bahwa k=1 1 (2k 1) 2 = π2 8 3 Dengan menggunakan deret Fourier dari fungsi tertentu, buktikan bahwa 1 n 2 = π2 6. n=1
35 Kita telah mempelajari bagaimana menguraikan fungsi periodik dengan periode 2π yang terdefinisi pada R sebagai deret Fourier. Deret trigonometri tersebut sebetulnya dapat pula dipakai sebagai representasi fungsi yang terdefinisi pada interval sebarang yang panjangnya 2π. Misalkan f terdefinisi pada [ π, π], dengan asumsi f( π) = f(π). (Asumsi ini dapat dipenuhi dengan cara mendefinisikan ulang, bila perlu, nilai f di salah satu titik ujungnya.) Selanjutnya misalkan f terbatas dan terintegralkan pada [ π, π]. Kita perluas f pada R sedemikian sehingga f periodik dengan periode 2π, melalui f(θ + 2nπ) = f(θ), θ ( π, π], n Z. Sebagai contoh, fungsi periodik f yang dibahas pada Contoh 1 dapat dipandang sebagai perluasan periodik fungsi f(θ) = θ dari interval ( π, π] ke seluruh R.
36 Jika f mulus bagian demi bagian pada ( π, π], maka kita dapat menguraikannya sebagai deret Fourier. Dengan membatasi kembali peubah θ pada [ π, π], kita peroleh deret Fourier dari fungsi semula. Sekarang misalkan f terdefinisi hanya pada [0, π]. Kita dapat memperluas f pada R sedemikian sehingga ia merupakan fungsi periodik dengan periode 2π, dan kemudian kita peroleh deret Fouriernya. Untuk memperluas f pada R, pertama kita perluas f pada [ π, π]. Ada dua cara yang baku untuk hal ini, yakni dengan membuatnya menjadi fungsi genap atau ganjil.
37 Perluasan genap f genap pada [ π, π] dapat diperoleh melalui f genap ( θ) = f(θ), θ [0, π]; sementara perluasan ganjil f ganjil dapat diperoleh melalui f ganjil ( θ) = f(θ), θ (0, π], f ganjil (0) = 0; Untuk ilustrasi, perhatikan gambar di papan tulis. Keuntungan menggunakan f genap dan f ganjil adalah bahwa koefisien Fouriernya kelak sangat sederhana. Untuk f genap, koefisien sinusnya akan sama dengan nol (karena sin nθ merupakan fungsi ganjil). Untuk f ganjil, koefisien cosinusnya akan sama dengan nol (karena cos nθ merupakan fungsi genap). Jadi, deret Fourier dari f genap hanya melibatkan fungsi cosinus, sementara deret Fourier dari f ganjil hanya melibatkan fungsi sinus.
38 Dengan simetri, perhitungan koefisien lainnya juga menjadi lebih mudah: π π f genap (θ) cos nθ dθ = 2 f(θ) cos nθ dθ, π 0 π π f ganjil (θ) sin nθ dθ = 2 f(θ) sin nθ dθ. π 0 Perhatikan bahwa pada akhirnya fungsi f yang terdefinisi pada [0, π] muncul kembali dalam perhitungan koefisien Fourier di atas.
39 Definisi. Misalkan f terintegralkan pada [0, π]. Deret 1 2 a 0 + n a n cos nθ, n=1 dengan a n = 2 π π 0 f(θ) cos nθ dθ disebut deret cosinus Fourier dari f; sementara deret n b n sin nθ, n=1 dengan b n = 2 π π 0 f(θ) sin nθ dθ, disebut deret sinus Fourier dari f.
40 Teorema. Misalkan f mulus bagian demi bagian pada [0, π]. Maka, deret cosinus Fourier dan deret sinus Fourier dari f konvergen ke 1 2 [f(θ ) + f(θ+)] di setiap θ (0, π). Khususnya, mereka konvergen ke f(θ) jika f kontinu di θ (0, π). Deret cosinus Fourier dari f konvergen ke f(0+) di θ = 0 dan ke f(π ) di θ = π; deret sinus Fourier dari f konvergen ke 0 di kedua titik tersebut.
41 Sekarang misalkan f adalah fungsi periodik dengan periode 2L. Dengan substitusi peubah x = Lθ π, kita peroleh fungsi baru ( Lθ ) g(θ) := f = f(x). π Perhatikan bahwa g merupakan fungsi periodik dengan periode 2π, dan karenanya dapat diuraikan sebagai deret Fourier dengan g(θ) = n= c n e inθ, c n = 1 π g(θ)e inθ dθ, 2π π asalkan g mulus bagian demi bagian.
42 Subtitusikan kembali θ = πx L ke dalam rumus di atas, kita dapatkan deret Fourier dari fungsi f semula: f(x) = n= c n e inπx/l, c n = 1 L f(x)e inπx/l dx. 2L L Dinyatakan dalam cosinus dan sinus, deret ini menjadi a n = 1 L f(x) = 1 2 a 0 + L [a n cos(nπx/l) + b n sin(nπx/l)], n=1 L f(x) cos(nπx/l)dx, b n = 1 L L L f(x) sin(nπx/l)dx.
43 Dengan cara yang serupa seperti sebelumnya kita dapat memperoleh deret cosinus Fourier ATAU deret sinus Fourier dari fungsi f yang mulus bagian demi bagian pada [0, L], yakni f(x) = 1 2 a 0 + a n cos(nπx/l), n=1 dengan ATAU dengan a n = 2 L L 0 f(x) cos(nπx/l)dx, f(x) = b n sin(nπx/l), b n = 2 L L 0 n=1 f(x) sin(nπx/l)dx.
44 Contoh. Deret cosinus Fourier dari fungsi f(x) = x, x [0, 1], adalah π 2 cos(2n 1)πx; (2n 1) 2 n=1 sementara deret sinus-nya adalah 2 π ( 1) n+1 sin nπx. n n=1
45 Soal Latihan 1 Bagaimana anda dapat memperoleh deret Fourier dari sebuah fungsi yang terdefinisi pada sebarang interval [a, b]? Jelaskan secara detil.
46 Teori L 2 untuk Keluarga fungsi {e inθ } membentuk basis ortogonal di ruang L 2 [ π, π], yaitu ruang fungsi f : [ π, π] C yang memenuhi f 2 2 := π π f(θ) 2 dθ <. Ruang L 2 [ π, π] merupakan ruang Hilbert, dengan hasil kali dalam f, g = π π f(θ)ḡ(θ) dθ. Karena itu, setiap f L 2 [ π, π] dapat dinyatakan sebagai f = n Z f, e n e n (konvergen dalam norm). Lebih jauh, kita mempunyai Kesamaan Parseval: f 2 = n Z f, e n 2.
47 Jika f L 1 ([ T 2, T 2 ]), maka kita mempunyai ( 1 f(x) = T n= T/2 T/2 ) f(y)e 2πiny/T dy e 2πinx/T. Bentuk ini mengingatkan kita akan jumlah Riemann atas suatu partisi dengan lebar 1 T, yakni n= ( T/2 T/2 ) f(y)e 2πiξny dy e 2πiξnx ξ n, dengan ξ n = n T dan ξ n = 1 T. Berdasarkan hal ini, dengan mengambil T, kita boleh menduga bahwa untuk f yang cukup bagus akan berlaku f(x) = ( ) f(y)e 2πiξy dy e 2πiξx dξ. (1)
48 Definisi. Misalkan f L 1 (R), yakni f 1 = R f(x) dx <. dari f, f, didefinisikan oleh f(ξ) = f(x)e 2πiξx dx, ξ R. R Seperti halnya dalam pembahasan deret Fourier, pertanyaan kita adalah bagaimana kita dapat memperoleh f kembali dari f. Kesamaan (1) menyarankan kita untuk mendefinisikan invers transformasi Fourier dari g, yang dituliskan sebagai ǧ, sebagai ǧ(x) = g(ξ)e 2πixξ dξ, x R. R
49 Teorema inversi Fourier kelak menyatakan bahwa ( f)ˇ(x) = f(x), h.d.m. asalkan f dan f terintegralkan. Sebelum sampai ke sana, kita mempunyai teorema berikut. Teorema. Jika f L 1 (R), maka f kontinu pada R. Teorema. Jika f L 1 (R), maka f terbatas pada R. Teorema (Riemann-Lebesgue). Jika f L 1 (R), maka f(ξ) = 0 h.d.m. lim ξ Akibat. memetakan L 1 (R) ke C 0 (R). Catatan. C 0 (R) adalah ruang fungsi kontinu dan terbatas pada R dengan limit nol di ±.
50 Contoh 1. Jika f(x) = e πx2, maka f(ξ) = e πξ2. Contoh 2. χ [0,1) (ξ) = e πiξ sin πξ πξ.
51 Definisi. Untuk f, g L 1 (R), kita definisikan konvolusi f g: f g(x) = f(y)g(x y)dy, x R. R Konvolusi bersifat seperti perkalian pada L 1 (R), yakni (i) komutatif: f g = g f; (ii) distributif (karena kelinearan integral): f (g + h) = f g + f h (f + g) h = f h + g h λ(f g) = (λf) g = f (λg) (iii) asosiatif (karena teorema Fubini): (f g) h = f (g h).
52 Jadi L 1 (R) merupakan suatu aljabar komutatif terhadap konvolusi. Lebih jauh, teorema di bawah ini mengatakan bahwa L 1 (R) merupakan aljabar Banach terhadap konvolusi. Teorema. Jika f, g L 1 (R), maka f g L 1 (R) dan f g 1 f 1 g 1. Selanjutnya kita mempunyai teorema berikut, yang merupakan kunci penting dalam aplikasi kelak. Teorema. Jika f, g L 1 (R), maka (f g) = fĝ.
53 Berdasarkan teorema sebelumnya kita mengetahui bahwa L 1 (R) tidak mempunyai identitas terhadap konvolusi: Jika ada e L 1 (R) sedemikian sehingga e f = f f L 1 (R), maka haruslah ê f = f h.d.m. f L 1 (R). Namun ini mengakibatkan ê(ξ) = 1 h.d.m., bertentangan dengan Teorema Riemann-Lebesgue. Walaupun demikian, kita mempunyai identitas hampiran, seperti yang dinyatakan dalam teorema berikut. Teorema. Misalkan φ 0 dan R φ(x) dx = 1. Untuk setiap ɛ > 0, definisikan φ ɛ (x) = 1 ɛ φ( ) x ɛ. Maka, untuk setiap f L 1 (R), kita mempunyai φ ɛ f f 1 0, ɛ 0.
54 Teorema Inversi Fourier. Misalkan f L 1 (R) sedemikian sehingga f L 1 (R). Maka, f(x) = f(ξ)e 2πiξx dξ, h.d.m. yakni, f = ( f)ˇh.d.m. R Akibat. Jika f, g L 1 (R) dan f = ĝ h.d.m., maka f = g h.d.m. Catatan. Akibat di atas mengatakan bahwa transformasi Fourier merupakan pemetaan yang bersifat 1-1 atau injektif h.d.m.
55 Jika deret Fourier memenuhi kesamaan Parseval, maka transformasi Fourier memenuhi kesamaan Plancherel, yakni Teorema (Kesamaan Plancherel). Jika f L 1 (R) L 2 (R), maka f L 2 (R) dan f 2 = f 2. Lebih umum daripada itu, kita mempunyai: Teorema (Kesamaan Plancherel). Jika f, g L 1 (R) L 2 (R), maka f, g = f, ĝ.
56 Soal Latihan 1 Tunjukkan bahwa χ [0,1) (ξ) = e πiξ sin πξ 2 Hitung χ [ T 2, T ](ξ) (T > 0). 2 3 sin πx Diketahui f(x) =. Tentukan f(ξ). πx πξ. 4 Tunjukkan jika f(x) = e πx2, maka f(ξ) = e πξ2. (Petunjuk. Integralkan fungsi kompleks f(z) = e πz2 sepanjang lintasan tertutup γ = [ R, R] + [R, R + iξ] + [R + iξ, R + iξ] + [ R + iξ, R], dan ambil R. Ingat e πx2 dx = 1.) 5 Buktikan jika f, g L 1 f(x)g(x) (R), maka R dx = R f(x)ĝ(x) dx. 6 Buktikan bahwa untuk setiap f dan g L 1 ([0, 1]) berlaku 1 f g = g f; 2 (f g) h = f (g h). 7 Misalkan χ = χ [0,1). Tentukan = χ χ.
57 di L 2 (R) Ruang L 2 (R), yang dilengkapi dengan hasilkali dalam f, g = R f(x)g(x) dx, merupakan ruang Hilbert. Karena L2 (R) bukan himpunan bagian dari L 1 (R), definisi transformasi Fourier tidak langsung berlaku di L 2 (R). Namun demikian, dengan menggunakan fakta bahwa L 1 (R) L 2 (R) padat di L 2 (R), transformasi Fourier dari fungsi f L 2 (R) dapat didefinisikan sebagai limit dari suatu barisan f n (dalam norma di L 2 (R)), dengan f n L 1 (R) L 2 (R) dan f n f (n ) dalam norma di L 2 (R). Semua ini dapat dilakukan sebagaimana dijamin oleh teorema berikut:
58 Teorema. Misalkan f L 2 (R). Untuk n N, definisikan f n = χ [ n,n] f, yakni f n (x) = { f(x), jika x n, 0, jika x > n. Maka, f n L 1 (R) L 2 (R) dan f n L 2 (R), untuk setiap n N. Lebih jauh, f n f (n ) dalam norma di L 2 (R) dan ( f n ) konvergen (dalam norma di L 2 (R)) ke suatu fungsi di L 2 (R).
59 Persamaan Panas Persamaan Gelombang Persamaan Laplace Domain Tak Terbatas Materi ini disadur dari buku G.B. Folland, Fourier Analysis and Its Applications. Persamaan Panas yang terkait dengan perambatan (difusi) panas pada sebuah dawai atau kawat yang panjangnya L adalah u t = ku xx, yang mungkin disertai dengan syarat batas dan syarat awal u(0, t) = u(l, t) = 0 t 0 u(x, 0) = f(x) x [0, L].
60 Persamaan Panas Persamaan Gelombang Persamaan Laplace Domain Tak Terbatas Dengan Metode Pemisahan Peubah, kita misalkan u(x, t) = X(x)T (t). Maka, persamaan tadi menjadi: Dari sini, kita dapatkan XT = kx T, X(0) = X(L) = 0. T kt = X X = A dengan A konstanta yang tidak bergantung pada x ataupun t. Jadi, kita mempunyai dua persamaan: T = AkT dan X = AX.
61 Persamaan Panas Persamaan Gelombang Persamaan Laplace Domain Tak Terbatas Dari persamaan pertama kita peroleh T (t) = C 0 e Akt, sementara dari persamaan kedua kita dapatkan X(x) = C 1 cos λx + C 2 sin λx, λ = A. Substitusikan syarat batas, kita peroleh C 1 = 0 dan (C 2 = 0 atau sin λl = 0). Tentunya kita tidak sedang mencari solusi trivial 0, ) karena itu λl = nπ, n = 1, 2, 3,..., sehingga A = ( nπ 2. L Dengan demikian kita peroleh solusi persamaan panas u n (x, t) = sin nπx n 2 π 2 kt L e L 2, n = 1, 2, 3,....
62 Persamaan Panas Persamaan Gelombang Persamaan Laplace Domain Tak Terbatas Kombinasi linear dari u n juga solusi, dan dengan mengambil limitnya kita simpulkan bahwa u(x, t) = a n u n (x, t) n=1 juga merupakan solusi persamaan panas. Selanjutnya, syarat awal u(x, 0) = f(x) memberikan n=1 a n sin nπx L = f(x), yang tak lain merupakan deret sinus Fourier dari f. Dari sini kita peroleh solusi khusus, dengan a n = 2 L L 0 f(x) sin nπx L dx.
63 Soal Latihan Persamaan Panas Persamaan Gelombang Persamaan Laplace Domain Tak Terbatas Tentukan solusi dari persamaan panas u t = ku xx dengan syarat batas u x (0, t) = u x (L, t) = 0 dan syarat awal u(x, 0) = f(x).
64 Persamaan Panas Persamaan Gelombang Persamaan Laplace Domain Tak Terbatas Persamaan Gelombang untuk dawai bergetar yang panjangnya L adalah u tt = c 2 u xx yang mungkin disertai dengan syarat batas dan syarat awal u(0, t) = u(l, t) = 0 u(x, 0) = f(x) dan u t (x, 0) = g(x).
65 Persamaan Panas Persamaan Gelombang Persamaan Laplace Domain Tak Terbatas Dengan Metode Pemisahan Peubah, yakni dengan pemisalan u(x, t) = X(x)T (t), diperoleh dua persamaan X = λ 2 X dan T = λ 2 c 2 T dengan X(0) = X(L) = 0. Dari kedua persamaan tersebut dan syarat batasnya, kita dapatkan X(x) = C 2 sin nπx L T (t) = C 3 cos nπct L + C 4 sin nπct L.
66 Persamaan Panas Persamaan Gelombang Persamaan Laplace Domain Tak Terbatas Dengan argumen yang serupa seperti untuk Persamaan Panas, kita dapatkan solusi untuk Persamaan Gelombang: u(x, t) = n=1 sin nπx ( a n cos nπct L L + b n sin nπct ). L Solusi khusus dapat diperoleh dengan menghitung koefisien a n dan b n dari kedua syarat awal yang diberikan.
67 Soal Latihan Persamaan Panas Persamaan Gelombang Persamaan Laplace Domain Tak Terbatas Tentukan koefisien a n dan b n bila diketahui f(x) = x(l x) dan g(x) = 0.
68 Persamaan Panas Persamaan Gelombang Persamaan Laplace Domain Tak Terbatas Persamaan Laplace pada persegi [0, 1] [0, 1] adalah u xx + u yy = 0, yang mungkin disertai dengan syarat batas u(0, y) = u(1, y) = 0 u(x, 0) = 0, u(x, 1) = f(x). Dengan pemisahan peubah, u(x, y) = X(x)Y (y), kita peroleh dua persamaan X = λ 2 X dan Y = λ 2 Y. Dari kedua persamaan tersebut, kita dapatkan X = C 1 cos λx + C 2 sin λx dan Y = C 3 e λy + C 4 e λy.
69 Persamaan Panas Persamaan Gelombang Persamaan Laplace Domain Tak Terbatas Substitusikan syarat batas, kita peroleh X(x) = C 2 sin nπx, n = 1, 2, 3,... Y (y) = C 3 sinh nπy, n = 1, 2, 3,... Dengan demikian, solusinya berbentuk u(x, y) = a n sin nπx sinh nπy. n=1 Masih ada satu syarat batas yang belum digunakan, yaitu u(x, 1) = f(x). Dari syarat batas ini kita peroleh a n.
70 Soal Latihan Persamaan Panas Persamaan Gelombang Persamaan Laplace Domain Tak Terbatas Tentukan koefisien a n bila diketahui f(x) = x(1 x).
71 Persamaan Panas Persamaan Gelombang Persamaan Laplace Domain Tak Terbatas Menggunakan transformasi Fourier, kita dapat menyelesaikan persamaan panas, persamaan gelombang, dan persamaan Laplace pada domain tak terbatas, dengan syarat awal tertentu. Sebagai contoh, tinjau persamaan panas pada kawat tak terhingga u t = ku xx, < x <, dengan syarat awal u(x, 0) = f(x). Tidak ada syarat batas karena domain x tak terbatas; namun untuk kemudahan kita asumsikan u(x, t) dan f(x) menuju 0 untuk x ±. Hitung transformasi Fourier dari kedua ruas terhadap x, sehingga kita peroleh û t (ξ, t) = k(2πξ)2 û(ξ, t), û(ξ, 0) = f(ξ).
72 Persamaan Panas Persamaan Gelombang Persamaan Laplace Domain Tak Terbatas Untuk tiap ξ, ini merupakan persamaan diferensial biasa dalam t dengan sebuah syarat awal. Solusinya adalah û(ξ, t) = f(ξ)e k(2πξ)2t. Untuk mendapatkan u(x, t), kita tinggal menghitung inversnya. Ada dua cara untuk itu. Cara pertama, kita gunakan Teorema Inversi Fourier: u(x, t) = f(ξ)e k(2πξ)2t e 2πiξx dξ. R Cara kedua, kita cukup menentukan invers dari e k(2πξ)2t, yaitu H t (x) = 1 4πkt e x2 /4kt.
73 Persamaan Panas Persamaan Gelombang Persamaan Laplace Domain Tak Terbatas Dalam hal ini solusinya dalah u(x, t) = f H t (x) = 1 4πkt R f(y)e (x y)2 /4kt dy. Catatan. H t (x) = 1 kt φ ( x kt ) dengan φ(x) = 1 4π e x2 /4. Soal Latihan 1. Tunjukkan bahwa H t (x) memenuhi Persamaaan Panas; dan dengan pertukaran turunan dan integral, u(x, t) = f H t (x) juga memenuhi Persamaan Panas. Lebih jauh, tunjukkan jika f L 1 (R), maka u(, t) f 1 0 bila t Dengan transformasi Fourier, selesaikan Persamaan Laplace u xx + u yy = 0 (x R, y > 0) dengan syarat awal u(x, 0) = f(x).
7. Transformasi Fourier
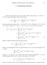 Pengantar Analisis Fourier dan eori Aproksimasi 33 7. ransformasi Fourier Pada bab sebelumnya kita telah melihat bahwa setiap fungsi f L 1 ([0, 1] L ([0, 1] dapat dinyatakan sebagai deret Fourier f(x =
Pengantar Analisis Fourier dan eori Aproksimasi 33 7. ransformasi Fourier Pada bab sebelumnya kita telah melihat bahwa setiap fungsi f L 1 ([0, 1] L ([0, 1] dapat dinyatakan sebagai deret Fourier f(x =
3. Kekonvergenan Deret Fourier
 3. Kekonvergenan Deret Fourier Sekarang kita akan membahas kekonvergenan deret Fourier, khususnya kekonvergenan titik demi titik. Melalui Contoh 2 yang dibahas pada bab sebelumnya kita mengetahui bahwa
3. Kekonvergenan Deret Fourier Sekarang kita akan membahas kekonvergenan deret Fourier, khususnya kekonvergenan titik demi titik. Melalui Contoh 2 yang dibahas pada bab sebelumnya kita mengetahui bahwa
Analisis Fourier dan Wavelet
 0 Hendra Gunawan Analisis Fourier dan Wavelet Hendra Gunawan KK Analisis & Geometri FMIPA-ITB Bandung, 2017 Analisis Fourier dan Wavelet 1 Daftar Isi Kata Pengantar 5 0 Pendahuluan 7 0.1 Notasi dan istilah,
0 Hendra Gunawan Analisis Fourier dan Wavelet Hendra Gunawan KK Analisis & Geometri FMIPA-ITB Bandung, 2017 Analisis Fourier dan Wavelet 1 Daftar Isi Kata Pengantar 5 0 Pendahuluan 7 0.1 Notasi dan istilah,
Hendra Gunawan. KK Analisis & Geometri FMIPA-ITB. Bandung, Maret 2001 [Edisi Revisi II: Mei 2014]
![Hendra Gunawan. KK Analisis & Geometri FMIPA-ITB. Bandung, Maret 2001 [Edisi Revisi II: Mei 2014] Hendra Gunawan. KK Analisis & Geometri FMIPA-ITB. Bandung, Maret 2001 [Edisi Revisi II: Mei 2014]](/thumbs/72/67819562.jpg) Analisis Fourier dan Wavelet 1 Catatan Kuliah Analisis Fourier dan Wavelet Oleh Hendra Gunawan KK Analisis & Geometri FMIPA-ITB Bandung, Maret 2001 [Edisi Revisi II: Mei 2014] 1 2 Hendra Gunawan Daftar
Analisis Fourier dan Wavelet 1 Catatan Kuliah Analisis Fourier dan Wavelet Oleh Hendra Gunawan KK Analisis & Geometri FMIPA-ITB Bandung, Maret 2001 [Edisi Revisi II: Mei 2014] 1 2 Hendra Gunawan Daftar
4. Deret Fourier pada Interval Sebarang dan Aplikasi
 4. Deret Fourier pada Interval Sebarang dan Aplikasi Kita telah mempelajari bagaimana menguraikan fungsi periodik dengan periode 2 yang terdefinisi pada R sebagai deret Fourier. Deret trigonometri tersebut
4. Deret Fourier pada Interval Sebarang dan Aplikasi Kita telah mempelajari bagaimana menguraikan fungsi periodik dengan periode 2 yang terdefinisi pada R sebagai deret Fourier. Deret trigonometri tersebut
4. Deret Fourier pada Interval Sebarang dan Aplikasi
 8 Hendra Gunawan 4. Deret Fourier pada Interval Sebarang dan Aplikasi Kita telah mempelajari bagaimana menguraikan fungsi periodik dengan periode 2 yang terdefinisi pada R sebagai deret Fourier. Deret
8 Hendra Gunawan 4. Deret Fourier pada Interval Sebarang dan Aplikasi Kita telah mempelajari bagaimana menguraikan fungsi periodik dengan periode 2 yang terdefinisi pada R sebagai deret Fourier. Deret
Fourier Analysis & Its Applications in PDEs - Part II
 Fourier Analysis & Its Applications in PDEs Hendra Gunawan http://personal.fmipa.itb.ac.id/hgunawan/ Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA WIDE 2010 5-6 August
Fourier Analysis & Its Applications in PDEs Hendra Gunawan http://personal.fmipa.itb.ac.id/hgunawan/ Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA WIDE 2010 5-6 August
12. Teorema Inversi Fourier dan Transformasi Fourier di L 2 (R)
 1. Teorema Inversi Fourier dan Transformasi Fourier di L (R) 1.1 Teorema Inversi Fourier Dari hasil hitung-hitungan kasar di awal bagian ke-10, kita ingin membuktikan bahwa, dalam kondisi tertentu, kita
1. Teorema Inversi Fourier dan Transformasi Fourier di L (R) 1.1 Teorema Inversi Fourier Dari hasil hitung-hitungan kasar di awal bagian ke-10, kita ingin membuktikan bahwa, dalam kondisi tertentu, kita
10. Transformasi Fourier
 10. Transformasi Fourier Dalam beberapa bab ke depan, kita akan membahas transformasi Fourier, sifatsifatnya, dan aplikasinya. Seperti halnya pada pembahasan deret Fourier, pendekatan yang diambil dalam
10. Transformasi Fourier Dalam beberapa bab ke depan, kita akan membahas transformasi Fourier, sifatsifatnya, dan aplikasinya. Seperti halnya pada pembahasan deret Fourier, pendekatan yang diambil dalam
13. Aplikasi Transformasi Fourier
 13. plikasi ransformasi Fourier Misal adalah operator linear pada fungsi yang terdefinisi pada R dengan sifat: jika [f(x] = g(x, maka [f(x + s] = g(x + s untuk setiap s R. Maka, fungsi f(x = e ax (a C
13. plikasi ransformasi Fourier Misal adalah operator linear pada fungsi yang terdefinisi pada R dengan sifat: jika [f(x] = g(x, maka [f(x + s] = g(x + s untuk setiap s R. Maka, fungsi f(x = e ax (a C
0. Pendahuluan. 0.1 Notasi dan istilah, bilangan kompleks
 0. Pendahuluan Analisis Fourier mempelajari berbagai teknik menganalisis sebuah fungsi dengan menguraikannya sebagai deret atau integral fungsi tertentu (yang sifat-sifatnya telah kita kenal dengan baik,
0. Pendahuluan Analisis Fourier mempelajari berbagai teknik menganalisis sebuah fungsi dengan menguraikannya sebagai deret atau integral fungsi tertentu (yang sifat-sifatnya telah kita kenal dengan baik,
5.1 Fungsi periodik, fungsi genap, fungsi ganjil
 Bab 5 DERET FOURIER Pada Bab sebelumnya kita telah membahas deret Taylor. Syarat fungsi agar dapat diekspansi ke dalam deret Taylor adalah fungsi tersebut harus terdiferensial pada setiap tingkat. Untuk
Bab 5 DERET FOURIER Pada Bab sebelumnya kita telah membahas deret Taylor. Syarat fungsi agar dapat diekspansi ke dalam deret Taylor adalah fungsi tersebut harus terdiferensial pada setiap tingkat. Untuk
11. Konvolusi. Misalkan f dan g fungsi yang terdefinisi pada R. Konvolusi dari f dan g adalah fungsi f g yang didefinisikan sebagai.
 11. Konvolusi Operasi konvolusi yang akan kita bahas di sini sebetulnya pernah kita jumpai pada pembahasan deret Fourier (ketika membuktikan kekonvergenan jumlah parsialnya). Operasi konvolusi merupakan
11. Konvolusi Operasi konvolusi yang akan kita bahas di sini sebetulnya pernah kita jumpai pada pembahasan deret Fourier (ketika membuktikan kekonvergenan jumlah parsialnya). Operasi konvolusi merupakan
BAB II KAJIAN TEORI. pada penulisan bab III. Materi yang diuraikan berisi tentang definisi, teorema, dan
 BAB II KAJIAN TEORI Pada bab ini akan dibahas beberapa hal yang digunakan sebagai landasan pada penulisan bab III. Materi yang diuraikan berisi tentang definisi, teorema, dan beberapa kajian matematika,
BAB II KAJIAN TEORI Pada bab ini akan dibahas beberapa hal yang digunakan sebagai landasan pada penulisan bab III. Materi yang diuraikan berisi tentang definisi, teorema, dan beberapa kajian matematika,
BAB IV DERET FOURIER
 BAB IV DERET FOURIER 4.1 Fungsi Periodik Fungsi f(x) dikatakan periodik dengan perioda P, jika untuk semua harga x berlaku: f (x + P) = f (x) ; P adalah konstanta positif. Harga terkecil dari P > 0 disebut
BAB IV DERET FOURIER 4.1 Fungsi Periodik Fungsi f(x) dikatakan periodik dengan perioda P, jika untuk semua harga x berlaku: f (x + P) = f (x) ; P adalah konstanta positif. Harga terkecil dari P > 0 disebut
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
BAB II KAJIAN TEORI. dalam penulisan bab III. Materi yang diuraikan berisi tentang definisi, teorema,
 BAB II KAJIAN TEORI Pada bab ini akan dibahas tentang beberapa hal yang menjadi landasan dalam penulisan bab III. Materi yang diuraikan berisi tentang definisi, teorema, dan beberapa kajian matematika,
BAB II KAJIAN TEORI Pada bab ini akan dibahas tentang beberapa hal yang menjadi landasan dalam penulisan bab III. Materi yang diuraikan berisi tentang definisi, teorema, dan beberapa kajian matematika,
17. Transformasi Wavelet Kontinu dan Frame
 17. Transformasi Wavelet Kontinu dan Frame Pada 16 kita mempelajari basis ortonormal {e 2πimx g(x n)} dengan g = χ [,1). Transformasi f f(x)g(x n)e 2πimx dx, m, n Z, dikenal sebagai transformasi Fourier
17. Transformasi Wavelet Kontinu dan Frame Pada 16 kita mempelajari basis ortonormal {e 2πimx g(x n)} dengan g = χ [,1). Transformasi f f(x)g(x n)e 2πimx dx, m, n Z, dikenal sebagai transformasi Fourier
DASAR-DASAR TEORI RUANG HILBERT
 DASAR-DASAR TEORI RUANG HILBERT Herry P. Suryawan 1 Geometri Ruang Hilbert Definisi 1.1 Ruang vektor kompleks V disebut ruang hasilkali dalam jika ada fungsi (.,.) : V V C sehingga untuk setiap x, y, z
DASAR-DASAR TEORI RUANG HILBERT Herry P. Suryawan 1 Geometri Ruang Hilbert Definisi 1.1 Ruang vektor kompleks V disebut ruang hasilkali dalam jika ada fungsi (.,.) : V V C sehingga untuk setiap x, y, z
BAGIAN KEDUA. Fungsi, Limit dan Kekontinuan, Turunan
 BAGIAN KEDUA Fungsi, Limit dan Kekontinuan, Turunan 51 52 Hendra Gunawan Pengantar Analisis Real 53 6. FUNGSI 6.1 Fungsi dan Grafiknya Konsep fungsi telah dipelajari oleh Gottfried Wilhelm von Leibniz
BAGIAN KEDUA Fungsi, Limit dan Kekontinuan, Turunan 51 52 Hendra Gunawan Pengantar Analisis Real 53 6. FUNGSI 6.1 Fungsi dan Grafiknya Konsep fungsi telah dipelajari oleh Gottfried Wilhelm von Leibniz
PDP linear orde 2 Agus Yodi Gunawan
 PDP linear orde 2 Agus Yodi Gunawan Pada bagian ini akan dipelajari tiga jenis persamaan diferensial parsial (PDP) linear orde dua yang biasa dijumpai pada masalah-masalah dunia nyata, yaitu persamaan
PDP linear orde 2 Agus Yodi Gunawan Pada bagian ini akan dipelajari tiga jenis persamaan diferensial parsial (PDP) linear orde dua yang biasa dijumpai pada masalah-masalah dunia nyata, yaitu persamaan
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
DERET FOURIER DAN APLIKASINYA DALAM FISIKA
 Matakuliah: Fisika Matematika DERET FOURIER DAN APLIKASINYA DALAM FISIKA Di S U S U N Oleh : Kelompok VI DEWI RATNA PERTIWI SITEPU (8176175004) RIFKA ANNISA GIRSANG (8176175014) PENDIDIKAN FISIKA REGULER
Matakuliah: Fisika Matematika DERET FOURIER DAN APLIKASINYA DALAM FISIKA Di S U S U N Oleh : Kelompok VI DEWI RATNA PERTIWI SITEPU (8176175004) RIFKA ANNISA GIRSANG (8176175014) PENDIDIKAN FISIKA REGULER
Catatan Kuliah MA1123 Kalkulus Elementer I
 Catatan Kuliah MA1123 Kalkulus Elementer I Oleh Hendra Gunawan, Ph.D. Departemen Matematika ITB Sasaran Belajar Setelah mempelajari materi Kalkulus Elementer I, mahasiswa diharapkan memiliki (terutama):
Catatan Kuliah MA1123 Kalkulus Elementer I Oleh Hendra Gunawan, Ph.D. Departemen Matematika ITB Sasaran Belajar Setelah mempelajari materi Kalkulus Elementer I, mahasiswa diharapkan memiliki (terutama):
SYARAT DIRICHLET. 1, 1 < t < 0
 SYARAT DIRICHET Misalkan f t adalah fungsi yang licin bagian demi bagian, berperioda, maka deret fourier konvergen. Ke nilai f t untuk setiap titik di mana fungsi f kontinu.. Ke nilai f t + + f t bagi
SYARAT DIRICHET Misalkan f t adalah fungsi yang licin bagian demi bagian, berperioda, maka deret fourier konvergen. Ke nilai f t untuk setiap titik di mana fungsi f kontinu.. Ke nilai f t + + f t bagi
Bab 3 Fungsi Elementer
 Bab 3 Fungsi Elementer Bab 3 ini direncanakan akan disampaikan dalam 3 kali pertemuan, dengan perincian sebagai berikut: (1) Pertemuan I: Fungsi Eksponensial dan sifat-sifatnya, Fungsi Trigonometri. ()
Bab 3 Fungsi Elementer Bab 3 ini direncanakan akan disampaikan dalam 3 kali pertemuan, dengan perincian sebagai berikut: (1) Pertemuan I: Fungsi Eksponensial dan sifat-sifatnya, Fungsi Trigonometri. ()
KALKULUS BAB II FUNGSI, LIMIT, DAN KEKONTINUAN. DEPARTEMEN TEKNIK KIMIA Universitas Indonesia
 KALKULUS BAB II FUNGSI, LIMIT, DAN KEKONTINUAN DEPARTEMEN TEKNIK KIMIA Universitas Indonesia BAB II. FUNGSI, LIMIT, DAN KEKONTINUAN Fungsi dan Operasi pada Fungsi Beberapa Fungsi Khusus Limit dan Limit
KALKULUS BAB II FUNGSI, LIMIT, DAN KEKONTINUAN DEPARTEMEN TEKNIK KIMIA Universitas Indonesia BAB II. FUNGSI, LIMIT, DAN KEKONTINUAN Fungsi dan Operasi pada Fungsi Beberapa Fungsi Khusus Limit dan Limit
Bab 2 Fungsi Analitik
 Bab 2 Fungsi Analitik Bab 2 ini direncanakan akan disampaikan dalam 4 kali pertemuan, dengan perincian sebagai berikut: () Pertemuan I: Fungsi Kompleks dan Pemetaan. (2) Pertemuan II: Limit Fungsi, Kekontiuan,
Bab 2 Fungsi Analitik Bab 2 ini direncanakan akan disampaikan dalam 4 kali pertemuan, dengan perincian sebagai berikut: () Pertemuan I: Fungsi Kompleks dan Pemetaan. (2) Pertemuan II: Limit Fungsi, Kekontiuan,
Suku Banyak Chebyshev
 Bab 3 Suku Banyak Chebyshev Suku banyak Chebyshev, yang diberi nama oleh Pafnuty Chebyshev, merupakan suatu deret dari suku banyak ortogonal yang dapat dituliskan secara rekursif. Suku banyak ini dibedakan
Bab 3 Suku Banyak Chebyshev Suku banyak Chebyshev, yang diberi nama oleh Pafnuty Chebyshev, merupakan suatu deret dari suku banyak ortogonal yang dapat dituliskan secara rekursif. Suku banyak ini dibedakan
BAB II KAJIAN TEORI. syarat batas, deret fourier, metode separasi variabel, deret taylor dan metode beda
 BAB II KAJIAN TEORI Pada bab ini akan dibahas tentang beberapa teori dasar yang digunakan sebagai landasan pembahasan pada bab III. Beberapa teori dasar yang dibahas, diantaranya teori umum tentang persamaan
BAB II KAJIAN TEORI Pada bab ini akan dibahas tentang beberapa teori dasar yang digunakan sebagai landasan pembahasan pada bab III. Beberapa teori dasar yang dibahas, diantaranya teori umum tentang persamaan
11. FUNGSI MONOTON (DAN FUNGSI KONVEKS)
 11. FUNGSI MONOTON (DAN FUNGSI KONVEKS) 11.1 Definisi dan Limit Fungsi Monoton Misalkan f terdefinisi pada suatu himpunan H. Kita katakan bahwa f naik pada H apabila untuk setiap x, y H dengan x < y berlaku
11. FUNGSI MONOTON (DAN FUNGSI KONVEKS) 11.1 Definisi dan Limit Fungsi Monoton Misalkan f terdefinisi pada suatu himpunan H. Kita katakan bahwa f naik pada H apabila untuk setiap x, y H dengan x < y berlaku
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
UJI KONVERGENSI. Januari Tim Dosen Kalkulus 2 TPB ITK
 UJI KONVERGENSI Januari 208 Tim Dosen Kalkulus 2 TPB ITK Uji Integral Teorema 3 Jika + k= u k adalah deret dengan suku-suku tak negatif, dan jika ada suatu konstanta M sedemikian hingga s n = u + u 2 +
UJI KONVERGENSI Januari 208 Tim Dosen Kalkulus 2 TPB ITK Uji Integral Teorema 3 Jika + k= u k adalah deret dengan suku-suku tak negatif, dan jika ada suatu konstanta M sedemikian hingga s n = u + u 2 +
MA1201 KALKULUS 2A Do maths and you see the world
 Catatan Kuliah MA20 KALKULUS 2A Do maths and you see the world disusun oleh Khreshna I.A. Syuhada, MSc. PhD. Kelompok Keilmuan STATISTIKA - FMIPA Institut Teknologi Bandung 203 Catatan kuliah ini ditulis
Catatan Kuliah MA20 KALKULUS 2A Do maths and you see the world disusun oleh Khreshna I.A. Syuhada, MSc. PhD. Kelompok Keilmuan STATISTIKA - FMIPA Institut Teknologi Bandung 203 Catatan kuliah ini ditulis
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
Daftar Isi 5. DERET ANALISIS REAL. (Semester I Tahun ) Hendra Gunawan. Dosen FMIPA - ITB September 26, 2011
 (Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. September 26, 2011 Diberikan sejumlah terhingga bilangan a 1,..., a N, kita dapat menghitung jumlah a 1 + + a N. Namun,
(Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. September 26, 2011 Diberikan sejumlah terhingga bilangan a 1,..., a N, kita dapat menghitung jumlah a 1 + + a N. Namun,
8. Deret Fourier yang Diperumum dan Hampiran Terbaik di L 2 (a, b)
 8. Deret Fourier yang Diperumum dan Hampiran Terbaik di L (a, b) 8.1 Deret Fourier yang Diperumum Jika {ϕ n } 1 adalah basis ortonormal untuk L (a, b) dan f L (a, b), maka f, ϕ n disebut koefisien Fourier
8. Deret Fourier yang Diperumum dan Hampiran Terbaik di L (a, b) 8.1 Deret Fourier yang Diperumum Jika {ϕ n } 1 adalah basis ortonormal untuk L (a, b) dan f L (a, b), maka f, ϕ n disebut koefisien Fourier
Definisi 4.1 Fungsi f dikatakan kontinu di titik a (continuous at a) jika dan hanya jika ketiga syarat berikut dipenuhi: (1) f(a) ada,
 Lecture 4. Limit B A. Continuity Definisi 4.1 Fungsi f dikatakan kontinu di titik a (continuous at a) jika dan hanya jika ketiga syarat berikut dipenuhi: (1) f(a) ada, (2) lim f(x) ada, (3) lim f(x) =
Lecture 4. Limit B A. Continuity Definisi 4.1 Fungsi f dikatakan kontinu di titik a (continuous at a) jika dan hanya jika ketiga syarat berikut dipenuhi: (1) f(a) ada, (2) lim f(x) ada, (3) lim f(x) =
16. BARISAN FUNGSI. 16.1 Barisan Fungsi dan Kekonvergenan Titik Demi Titik
 16. BARISAN FUNGSI 16.1 Barisan Fungsi dan Kekonvergenan Titik Demi Titik Bila pada bab-bab sebelumnya kita membahas fungsi sebagai sebuah objek individual, maka pada bab ini dan selanjutnya kita akan
16. BARISAN FUNGSI 16.1 Barisan Fungsi dan Kekonvergenan Titik Demi Titik Bila pada bab-bab sebelumnya kita membahas fungsi sebagai sebuah objek individual, maka pada bab ini dan selanjutnya kita akan
FUNGSI dan LIMIT. 1.1 Fungsi dan Grafiknya
 FUNGSI dan LIMIT 1.1 Fungsi dan Grafiknya Fungsi : suatu aturan yang menghubungkan setiap elemen suatu himpunan pertama (daerah asal) tepat kepada satu elemen himpunan kedua (daerah hasil) fungsi Daerah
FUNGSI dan LIMIT 1.1 Fungsi dan Grafiknya Fungsi : suatu aturan yang menghubungkan setiap elemen suatu himpunan pertama (daerah asal) tepat kepada satu elemen himpunan kedua (daerah hasil) fungsi Daerah
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
3 LIMIT DAN KEKONTINUAN
 Menurut Bartle dan Sherbet (1994), Analisis matematika secara umum dipahami sebagai tubuh matematika yang dibangun oleh berbagai konsep limit. Pada bab sebelumnya kita telah mempelajari limit barisan,
Menurut Bartle dan Sherbet (1994), Analisis matematika secara umum dipahami sebagai tubuh matematika yang dibangun oleh berbagai konsep limit. Pada bab sebelumnya kita telah mempelajari limit barisan,
SATUAN ACARA PERKULIAHAN MATA KULIAH KALKULUS LANJUT A (S1 / TEKNIK INFORMATIKA ) KODE / SKS KD
 SATUAN ACARA PERKULIAHAN MATA KULIAH KALKULUS LANJUT A (S1 / TEKNIK INFORMATIKA ) KODE / SKS KD-045315 Mingg u Ke Pokok Bahasan dan TIU Sub-pokok Bahasan dan Sasaran Belajar Cara Pengajaran Media Tugas
SATUAN ACARA PERKULIAHAN MATA KULIAH KALKULUS LANJUT A (S1 / TEKNIK INFORMATIKA ) KODE / SKS KD-045315 Mingg u Ke Pokok Bahasan dan TIU Sub-pokok Bahasan dan Sasaran Belajar Cara Pengajaran Media Tugas
Keterbatasan Operator Riesz di Ruang Morrey
 J. Math. and Its Appl. ISSN: 829-605X Vol. 3, No., May 2006, 27 40 Keterbatasan Operator Riesz di Ruang Morrey Gani Gunawan, Hendra Gunawan Departemen Matematika FMIPA ITB Abstrak Dengan menggunakan transformasi
J. Math. and Its Appl. ISSN: 829-605X Vol. 3, No., May 2006, 27 40 Keterbatasan Operator Riesz di Ruang Morrey Gani Gunawan, Hendra Gunawan Departemen Matematika FMIPA ITB Abstrak Dengan menggunakan transformasi
Aplikasi Deret Fourier (FS) Deret Fourier Aplikasi Deret Fourier
 Aplikasi Deret Fourier (FS) 1. Deret Fourier Menurut Fourier setiap fungsi periodik dapat dinyatakan sebagai jumlah fungsi sinus dan cosinus yang tak berhingga jumlahnya dan dihubungkan secara harmonis.
Aplikasi Deret Fourier (FS) 1. Deret Fourier Menurut Fourier setiap fungsi periodik dapat dinyatakan sebagai jumlah fungsi sinus dan cosinus yang tak berhingga jumlahnya dan dihubungkan secara harmonis.
FT UNIVERSITAS SURABAYA VARIABEL KOMPLEKS SUGATA PIKATAN. Bab V Aplikasi
 Bab V Aplikasi Selain aplikasi yang sudah diperkenalkan di bab I, teori variabel kompleks masih memiliki banyak ragam aplikasi lainnya. Beberapa di antaranya akan dibahas di dalam bab ini. Perhitungan
Bab V Aplikasi Selain aplikasi yang sudah diperkenalkan di bab I, teori variabel kompleks masih memiliki banyak ragam aplikasi lainnya. Beberapa di antaranya akan dibahas di dalam bab ini. Perhitungan
MA1201 KALKULUS 2A (Kelas 10) Bab 8: Bentuk Tak Tentu d
 MA1201 KALKULUS 2A (Kelas 10) Bab 8: dan Do maths and you see the world ? Pengantar Bentuk tak tentu? Bentuk apa? Bentuk tak tentu yang dimaksud adalah bentuk limit dengan nilai seolah-olah : 0 0 ; ; 0
MA1201 KALKULUS 2A (Kelas 10) Bab 8: dan Do maths and you see the world ? Pengantar Bentuk tak tentu? Bentuk apa? Bentuk tak tentu yang dimaksud adalah bentuk limit dengan nilai seolah-olah : 0 0 ; ; 0
Barisan dan Deret Agus Yodi Gunawan
 Barisan dan Deret Agus Yodi Gunawan Barisan. Definisi. Barisan tak hingga adalah suatu fungsi dengan daerah asalnya himpunan bilangan bulat positif dan daerah kawannya himpunan bilangan real. Notasi untuk
Barisan dan Deret Agus Yodi Gunawan Barisan. Definisi. Barisan tak hingga adalah suatu fungsi dengan daerah asalnya himpunan bilangan bulat positif dan daerah kawannya himpunan bilangan real. Notasi untuk
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
digunakan untuk menyelesaikan integral seperti 3
 Bab Teknik Pengintegralan BAB TEKNIK PENGINTEGRALAN Rumus-rumus dasar integral tak tertentu yang diberikan pada bab hanya dapat digunakan untuk mengevaluasi integral dari fungsi sederhana dan tidak dapat
Bab Teknik Pengintegralan BAB TEKNIK PENGINTEGRALAN Rumus-rumus dasar integral tak tertentu yang diberikan pada bab hanya dapat digunakan untuk mengevaluasi integral dari fungsi sederhana dan tidak dapat
Deret Fourier. (Pertemuan XI) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya. Fungsi Genap dan Fungsi Ganjil
 TKS 4007 Matematika III Deret Fourier (Pertemuan XI) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya Fungsi Genap dan Fungsi Ganjil Perhitungan koefisien-koefisien Fourier sering kali
TKS 4007 Matematika III Deret Fourier (Pertemuan XI) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya Fungsi Genap dan Fungsi Ganjil Perhitungan koefisien-koefisien Fourier sering kali
3 LIMIT DAN KEKONTINUAN
 Menurut Bartle dan Sherbet (994), Analisis matematika secara umum dipahami sebagai tubuh matematika yang dibangun oleh berbagai konsep limit. Pada bab sebelumnya kita telah mempelajari limit barisan, kekonvergenan
Menurut Bartle dan Sherbet (994), Analisis matematika secara umum dipahami sebagai tubuh matematika yang dibangun oleh berbagai konsep limit. Pada bab sebelumnya kita telah mempelajari limit barisan, kekonvergenan
BAB I PENDAHULUAN. Integral Lebesgue merupakan suatu perluasan dari integral Riemann.
 BAB I PENDAHULUAN 1.1 Latar Belakang Masalah Integral Lebesgue merupakan suatu perluasan dari integral Riemann. Sebagaimana telah diketahui, pengkonstruksian integral Riemann dilakukan dengan cara pemartisian
BAB I PENDAHULUAN 1.1 Latar Belakang Masalah Integral Lebesgue merupakan suatu perluasan dari integral Riemann. Sebagaimana telah diketahui, pengkonstruksian integral Riemann dilakukan dengan cara pemartisian
BAB III KONDUKSI ALIRAN STEDI - DIMENSI BANYAK
 BAB III KONDUKSI ALIRAN SEDI - DIMENSI BANYAK Untuk aliran stedi tanpa pembangkitan panas, persamaan Laplacenya adalah: + y 0 (6-) Aliran kalor pada arah dan y bisa dihitung dengan persamaan Fourier: q
BAB III KONDUKSI ALIRAN SEDI - DIMENSI BANYAK Untuk aliran stedi tanpa pembangkitan panas, persamaan Laplacenya adalah: + y 0 (6-) Aliran kalor pada arah dan y bisa dihitung dengan persamaan Fourier: q
Bil Riil. Bil Irasional. Bil Bulat - Bil Bulat 0 Bil Bulat + maka bentuk umum bilangan kompleks adalah
 ANALISIS KOMPLEKS Pendahuluan Bil Kompleks Bil Riil Bil Imaginer (khayal) Bil Rasional Bil Irasional Bil Pecahan Bil Bulat Sistem Bilangan Kompleks Bil Bulat - Bil Bulat 0 Bil Bulat + Untuk maka bentuk
ANALISIS KOMPLEKS Pendahuluan Bil Kompleks Bil Riil Bil Imaginer (khayal) Bil Rasional Bil Irasional Bil Pecahan Bil Bulat Sistem Bilangan Kompleks Bil Bulat - Bil Bulat 0 Bil Bulat + Untuk maka bentuk
Kalkulus 2. Teknik Pengintegralan ke - 1. Tim Pengajar Kalkulus ITK. Institut Teknologi Kalimantan. Januari 2018
 Kalkulus 2 Teknik Pengintegralan ke - 1 Tim Pengajar Kalkulus ITK Institut Teknologi Kalimantan Januari 2018 Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari 2018 1 / 36 Daftar
Kalkulus 2 Teknik Pengintegralan ke - 1 Tim Pengajar Kalkulus ITK Institut Teknologi Kalimantan Januari 2018 Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari 2018 1 / 36 Daftar
BAB III HASIL DAN PEMBAHASAN. analitik dengan metode variabel terpisah. Selanjutnya penyelesaian analitik dari
 BAB III HASIL DAN PEMBAHASAN Pada bab ini akan dibahas penurunan model persamaan panas dimensi satu. Setelah itu akan ditentukan penyelesaian persamaan panas dimensi satu secara analitik dengan metode
BAB III HASIL DAN PEMBAHASAN Pada bab ini akan dibahas penurunan model persamaan panas dimensi satu. Setelah itu akan ditentukan penyelesaian persamaan panas dimensi satu secara analitik dengan metode
3 LIMIT DAN KEKONTINUAN
 Menurut Bartle dan Sherbet (1994), Analisis matematika secara umum dipahami sebagai tubuh matematika yang dibangun dari berbagai konsep limit. Pada bab sebelumnya kita telah mempelajari limit barisan,
Menurut Bartle dan Sherbet (1994), Analisis matematika secara umum dipahami sebagai tubuh matematika yang dibangun dari berbagai konsep limit. Pada bab sebelumnya kita telah mempelajari limit barisan,
Modul KALKULUS MULTIVARIABEL II
 Modul KALKULUS MULTIVARIABEL II Oleh Ayundyah Kesumawati, S.Si., M.Si. (Program Studi Statistika) FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS ISLAM INDONESIA 26 Daftar Isi Daftar Isi iv Daftar
Modul KALKULUS MULTIVARIABEL II Oleh Ayundyah Kesumawati, S.Si., M.Si. (Program Studi Statistika) FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS ISLAM INDONESIA 26 Daftar Isi Daftar Isi iv Daftar
BAB III PEMBAHASAN. dengan menggunakan penyelesaian analitik dan penyelesaian numerikdengan. motode beda hingga. Berikut ini penjelasan lebih lanjut.
 BAB III PEMBAHASAN Pada bab ini akan dibahas tentang penurunan model persamaan gelombang satu dimensi. Setelah itu akan ditentukan persamaan gelombang satu dimensi dengan menggunakan penyelesaian analitik
BAB III PEMBAHASAN Pada bab ini akan dibahas tentang penurunan model persamaan gelombang satu dimensi. Setelah itu akan ditentukan persamaan gelombang satu dimensi dengan menggunakan penyelesaian analitik
Analisis Riil II: Diferensiasi
 Definisi Turunan Definisi dan Teorema Aturan Rantai Fungsi Invers Definisi (Turunan) Misalkan I R sebuah interval, f : I R, dan c I. Bilangan riil L dikatakan turunan dari f di c jika diberikan sebarang
Definisi Turunan Definisi dan Teorema Aturan Rantai Fungsi Invers Definisi (Turunan) Misalkan I R sebuah interval, f : I R, dan c I. Bilangan riil L dikatakan turunan dari f di c jika diberikan sebarang
Bagian 2 Matriks dan Determinan
 Bagian Matriks dan Determinan Materi mengenai fungsi, limit, dan kontinuitas akan kita pelajari dalam Bagian Fungsi dan Limit. Pada bagian Fungsi akan mempelajari tentang jenis-jenis fungsi dalam matematika
Bagian Matriks dan Determinan Materi mengenai fungsi, limit, dan kontinuitas akan kita pelajari dalam Bagian Fungsi dan Limit. Pada bagian Fungsi akan mempelajari tentang jenis-jenis fungsi dalam matematika
Persamaan Diferensial Parsial CNH3C3
 Persamaan Diferensial Parsial CNH3C3 Tim Ilmu Komputasi Week 6: Separasi Variabel untuk Persamaan Gelombang Orde dua dan Koesien Fourier Coordinator contact: Dr. Putu Harry Gunawan phgunawan@telkomuniversity.ac.id
Persamaan Diferensial Parsial CNH3C3 Tim Ilmu Komputasi Week 6: Separasi Variabel untuk Persamaan Gelombang Orde dua dan Koesien Fourier Coordinator contact: Dr. Putu Harry Gunawan phgunawan@telkomuniversity.ac.id
TUJUAN INSTRUKSIONAL KHUSUS
 PREVIEW KALKULUS TUJUAN INSTRUKSIONAL KHUSUS Mahasiswa mampu: menyebutkan konsep-konsep utama dalam kalkulus dan contoh masalah-masalah yang memotivasi konsep tersebut; menjelaskan menyebutkan konsep-konsep
PREVIEW KALKULUS TUJUAN INSTRUKSIONAL KHUSUS Mahasiswa mampu: menyebutkan konsep-konsep utama dalam kalkulus dan contoh masalah-masalah yang memotivasi konsep tersebut; menjelaskan menyebutkan konsep-konsep
MATERI 4 MATEMATIKA TEKNIK 1 DERET FOURIER
 MATERI 4 MATEMATIKA TEKNIK 1 DERET FOURIER 1 Deret Fourier 2 Tujuan : 1. Dapat merepresentasikan seluruh fungsi periodik dalam bentuk deret Fourier. 2. Dapat memetakan Cosinus Fourier, Sinus Fourier, Fourier
MATERI 4 MATEMATIKA TEKNIK 1 DERET FOURIER 1 Deret Fourier 2 Tujuan : 1. Dapat merepresentasikan seluruh fungsi periodik dalam bentuk deret Fourier. 2. Dapat memetakan Cosinus Fourier, Sinus Fourier, Fourier
PENGARUH JUMLAH SUKU FOURIER PADA PENDEKATAN POLAR UNTUK SISTEM GEOMETRI KARTESIAN
 PENGARUH JUMLAH SUKU FOURIER PADA PENDEKATAN POLAR UNTUK SISTEM GEOMETRI KARTESIAN IRMA ISLAMIYAH 1105 100 056 FISIKA FMIPA INSTITUT TEKNOLOGI SEPULUH NOPEMBER SURABAYA 2010 PENDAHULUAN LATAR BELAKANG
PENGARUH JUMLAH SUKU FOURIER PADA PENDEKATAN POLAR UNTUK SISTEM GEOMETRI KARTESIAN IRMA ISLAMIYAH 1105 100 056 FISIKA FMIPA INSTITUT TEKNOLOGI SEPULUH NOPEMBER SURABAYA 2010 PENDAHULUAN LATAR BELAKANG
BAB III OPERATOR LINEAR TERBATAS PADA RUANG HILBERT. Operator merupakan salah satu materi yang akan dibahas dalam fungsi
 BAB III OPERATOR LINEAR TERBATAS PADA RUANG HILBERT 3.1 Operator linear Operator merupakan salah satu materi yang akan dibahas dalam fungsi real yaitu suatu fungsi dari ruang vektor ke ruang vektor. Ruang
BAB III OPERATOR LINEAR TERBATAS PADA RUANG HILBERT 3.1 Operator linear Operator merupakan salah satu materi yang akan dibahas dalam fungsi real yaitu suatu fungsi dari ruang vektor ke ruang vektor. Ruang
BAB II PENGANTAR SOLUSI PERSOALAN FISIKA MENURUT PENDEKATAN ANALITIK DAN NUMERIK
 BAB II PENGANTAR SOLUSI PERSOALAN FISIKA MENURUT PENDEKATAN ANALITIK DAN NUMERIK Tujuan Instruksional Setelah mempelajari bab ini pembaca diharapkan dapat: 1. Menjelaskan cara penyelesaian soal dengan
BAB II PENGANTAR SOLUSI PERSOALAN FISIKA MENURUT PENDEKATAN ANALITIK DAN NUMERIK Tujuan Instruksional Setelah mempelajari bab ini pembaca diharapkan dapat: 1. Menjelaskan cara penyelesaian soal dengan
9. Teori Aproksimasi
 44 Hendra Gunawan 9 Teori Aproksimasi Mulai bab ini tema kita adalah aproksimasi fungsi dan interpolasi Diberikan sebuah fungsi f, baik secara utuh ataupun hanya beberapilai di titik-titik tertentu saja,
44 Hendra Gunawan 9 Teori Aproksimasi Mulai bab ini tema kita adalah aproksimasi fungsi dan interpolasi Diberikan sebuah fungsi f, baik secara utuh ataupun hanya beberapilai di titik-titik tertentu saja,
Memahami definisi barisan tak hingga dan deret tak hingga, dan juga dapat menentukan
 4 BARISAN TAK HINGGA DAN DERET TAK HINGGA JUMLAH PERTEMUAN : 5 PERTEMUAN TUJUAN INSTRUKSIONAL KHUSUS : Memahami definisi barisan tak hingga dan deret tak hingga, dan juga dapat menentukan kekonvergenan
4 BARISAN TAK HINGGA DAN DERET TAK HINGGA JUMLAH PERTEMUAN : 5 PERTEMUAN TUJUAN INSTRUKSIONAL KHUSUS : Memahami definisi barisan tak hingga dan deret tak hingga, dan juga dapat menentukan kekonvergenan
16. Analisis Multi Resolusi
 16. Analisis Multi esolusi Esensi dari basis ortonormal yang dibangun oleh sebuah wavelet adalah sifat multi resolusi-nya, sehingga kita dapat menganalisis suatu signal pada berbagai frekuensi di suatu
16. Analisis Multi esolusi Esensi dari basis ortonormal yang dibangun oleh sebuah wavelet adalah sifat multi resolusi-nya, sehingga kita dapat menganalisis suatu signal pada berbagai frekuensi di suatu
DASAR-DASAR ANALISIS MATEMATIKA
 (Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. December 1, 2007 Diberikan sebuah fungsi yang terdefinisi pada interval (a, b) kecuali mungkin di
(Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. December 1, 2007 Diberikan sebuah fungsi yang terdefinisi pada interval (a, b) kecuali mungkin di
BAB III INTEGRAL LEBESGUE. Pada bab sebelumnya telah disebutkan bahwa ruang dibangun oleh
 BAB III INTEGRAL LEBESGUE Pada bab sebelumnya telah disebutkan bahwa ruang dibangun oleh fungsi-fungsi terukur dan memenuhi sifat yang berkaitan dengan integral Lebesgue. Kajian mengenai keterukuran suatu
BAB III INTEGRAL LEBESGUE Pada bab sebelumnya telah disebutkan bahwa ruang dibangun oleh fungsi-fungsi terukur dan memenuhi sifat yang berkaitan dengan integral Lebesgue. Kajian mengenai keterukuran suatu
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
Persamaan Difusi. Penurunan, Solusi Analitik, Solusi Numerik (Beda Hingga, RBF) M. Jamhuri. April 7, UIN Malang. M. Jamhuri Persamaan Difusi
 Persamaan Difusi Penurunan, Solusi Analitik, Solusi Numerik (Beda Hingga, RBF) M Jamhuri UIN Malang April 7, 2013 Penurunan Persamaan Difusi Misalkan u(x, t) menyatakan konsentrasi dari zat pada posisi
Persamaan Difusi Penurunan, Solusi Analitik, Solusi Numerik (Beda Hingga, RBF) M Jamhuri UIN Malang April 7, 2013 Penurunan Persamaan Difusi Misalkan u(x, t) menyatakan konsentrasi dari zat pada posisi
Persamaan Diferensial Parsial CNH3C3
 Persamaan Diferensial Parsial CNH3C3 Week 5: Separasi Variabel untuk Persamaan Panas Orde Satu - Tim Ilmu Komputasi Coordinator contact: Dr. Putu Harry Gunawan phgunawan@telkomuniversity.ac.id 1 Review
Persamaan Diferensial Parsial CNH3C3 Week 5: Separasi Variabel untuk Persamaan Panas Orde Satu - Tim Ilmu Komputasi Coordinator contact: Dr. Putu Harry Gunawan phgunawan@telkomuniversity.ac.id 1 Review
BAB III ANALISIS SPEKTRAL PADA RUNTUN WAKTU MODEL ARIMA. Analisis spektral adalah metode yang menggambarkan kecendrungan osilasi
 BAB III ANALISIS SPEKTRAL PADA RUNTUN WAKTU MODEL ARIMA Analisis spektral adalah metode yang menggambarkan kecendrungan osilasi atau getaran dari sebuah data pada frekuensi tertentu. Analisis spektral
BAB III ANALISIS SPEKTRAL PADA RUNTUN WAKTU MODEL ARIMA Analisis spektral adalah metode yang menggambarkan kecendrungan osilasi atau getaran dari sebuah data pada frekuensi tertentu. Analisis spektral
Hendra Gunawan. 4 September 2013
 MA1101 MATEMATIKA 1A Hendra Gunawan Semester I, 2013/2014 4 September 2013 Latihan (Kuliah yang Lalu) 1. Tentukan daerah asal dan daerah nilai fungsi 2 f(x) = 1 x. sudah dijawab 2. Gambar grafik fungsi
MA1101 MATEMATIKA 1A Hendra Gunawan Semester I, 2013/2014 4 September 2013 Latihan (Kuliah yang Lalu) 1. Tentukan daerah asal dan daerah nilai fungsi 2 f(x) = 1 x. sudah dijawab 2. Gambar grafik fungsi
DASAR-DASAR ANALISIS MATEMATIKA
 (Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. December 11, 2007 Misalkan f terdefinisi pada suatu himpunan H. Kita katakan bahwa f naik pada H apabila
(Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. December 11, 2007 Misalkan f terdefinisi pada suatu himpunan H. Kita katakan bahwa f naik pada H apabila
BAB III FUNGSI TERUKUR LEBESGUE. Setelah dibahas mengenai ukuran Lebesgue dan beberapa sifatnya pada
 BAB III FUNGSI TERUKUR LEBESGUE Setelah dibahas mengenai ukuran Lebesgue dan beberapa sifatnya pada Bab II, selanjutnya pada bab ini akan dipelajari gagasan mengenai fungsi terukur Lebesgue. Gagasan mengenai
BAB III FUNGSI TERUKUR LEBESGUE Setelah dibahas mengenai ukuran Lebesgue dan beberapa sifatnya pada Bab II, selanjutnya pada bab ini akan dipelajari gagasan mengenai fungsi terukur Lebesgue. Gagasan mengenai
BAGIAN PERTAMA. Bilangan Real, Barisan, Deret
 BAGIAN PERTAMA Bilangan Real, Barisan, Deret 2 Hendra Gunawan Pengantar Analisis Real 3 0. BILANGAN REAL 0. Bilangan Real sebagai Bentuk Desimal Dalam buku ini pembaca diasumsikan telah mengenal dengan
BAGIAN PERTAMA Bilangan Real, Barisan, Deret 2 Hendra Gunawan Pengantar Analisis Real 3 0. BILANGAN REAL 0. Bilangan Real sebagai Bentuk Desimal Dalam buku ini pembaca diasumsikan telah mengenal dengan
DASAR-DASAR ANALISIS MATEMATIKA
 (Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. November 19, 2007 Secara geometris, f kontinu di suatu titik berarti bahwa grafiknya tidak terputus
(Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. November 19, 2007 Secara geometris, f kontinu di suatu titik berarti bahwa grafiknya tidak terputus
LIMIT FUNGSI. A. Menentukan Limit Fungsi Aljabar A.1. Limit x a Contoh A.1: Contoh A.2 : 2 4)
 LIMIT FUNGSI A. Menentukan Limit Fungsi Aljabar A.. Limit a Contoh A.:. ( ) 3 Contoh A. : 4 ( )( ) ( ) 4 Latihan. Hitunglah nilai it fungsi-fungsi berikut ini. a. (3 ) b. ( 4) c. ( 4) d. 0 . Hitunglah
LIMIT FUNGSI A. Menentukan Limit Fungsi Aljabar A.. Limit a Contoh A.:. ( ) 3 Contoh A. : 4 ( )( ) ( ) 4 Latihan. Hitunglah nilai it fungsi-fungsi berikut ini. a. (3 ) b. ( 4) c. ( 4) d. 0 . Hitunglah
Ringkasan Materi Kuliah Bab II FUNGSI
 Ringkasan Materi Kuliah Bab II FUNGSI. FUNGSI REAL, FUNGSI ALJABAR, DAN FUNGSI TRIGONOMETRI. TOPIK-TOPIK YANG BERKAITAN DENGAN FUNGSI.3 FUNGSI KOMPOSISI DAN FUNGSI INVERS. FUNGSI REAL, FUNGSI ALJABAR,
Ringkasan Materi Kuliah Bab II FUNGSI. FUNGSI REAL, FUNGSI ALJABAR, DAN FUNGSI TRIGONOMETRI. TOPIK-TOPIK YANG BERKAITAN DENGAN FUNGSI.3 FUNGSI KOMPOSISI DAN FUNGSI INVERS. FUNGSI REAL, FUNGSI ALJABAR,
BAB 4 KEKONSISTENAN PENDUGA DARI FUNGSI SEBARAN DAN FUNGSI KEPEKATAN WAKTU TUNGGU DARI PROSES POISSON PERIODIK DENGAN TREN FUNGSI PANGKAT
 29 BAB 4 KEKONSISTENAN PENDUGA DARI FUNGSI SEBARAN DAN FUNGSI KEPEKATAN WAKTU TUNGGU DARI PROSES POISSON PERIODIK DENGAN TREN FUNGSI PANGKAT 4.1 Perumusan Penduga Misalkan adalah proses Poisson nonhomogen
29 BAB 4 KEKONSISTENAN PENDUGA DARI FUNGSI SEBARAN DAN FUNGSI KEPEKATAN WAKTU TUNGGU DARI PROSES POISSON PERIODIK DENGAN TREN FUNGSI PANGKAT 4.1 Perumusan Penduga Misalkan adalah proses Poisson nonhomogen
MODUL RESPONSI MAM 4222 KALKULUS IV
 MODUL RESPONSI MAM 4222 KALKULUS IV Mata Kuliah Wajib 2 sks untuk mahasiswa Program Studi Matematika Oleh Dr. WURYANSARI MUHARINI KUSUMAWINAHYU, M.Si. PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS
MODUL RESPONSI MAM 4222 KALKULUS IV Mata Kuliah Wajib 2 sks untuk mahasiswa Program Studi Matematika Oleh Dr. WURYANSARI MUHARINI KUSUMAWINAHYU, M.Si. PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS
I. PENDAHULUAN. dan kotoran manusia atau kotoran binatang. Semua polutan tersebut masuk. ke dalam sungai dan langsung tercampur dengan air sungai.
 I. PENDAHULUAN 1.1 Latar Belakang dan Masalah Dalam kehidupan, polusi yang ada di sungai disebabkan oleh limbah dari pabrikpabrik dan kotoran manusia atau kotoran binatang. Semua polutan tersebut masuk
I. PENDAHULUAN 1.1 Latar Belakang dan Masalah Dalam kehidupan, polusi yang ada di sungai disebabkan oleh limbah dari pabrikpabrik dan kotoran manusia atau kotoran binatang. Semua polutan tersebut masuk
BAB 3 REVIEW SIFAT-SIFAT STATISTIK PENDUGA KOMPONEN PERIODIK
 BAB 3 REVIEW SIFAT-SIFAT STATISTIK PENDUGA KOMPONEN PERIODIK 3. Perumusan Penduga Misalkan N adalah proses Poisson non-homogen pada interval 0, dengan fungsi intensitas yang tidak diketahui. Fungsi intensitas
BAB 3 REVIEW SIFAT-SIFAT STATISTIK PENDUGA KOMPONEN PERIODIK 3. Perumusan Penduga Misalkan N adalah proses Poisson non-homogen pada interval 0, dengan fungsi intensitas yang tidak diketahui. Fungsi intensitas
Catatan Kuliah KALKULUS II BAB V. INTEGRAL
 BAB V. INTEGRAL Anti-turunan dan Integral TakTentu Persamaan Diferensial Sederhana Notasi Sigma dan Luas Daerah di Bawah Kurva Integral Tentu Teorema Dasar Kalkulus Sifat-sifat Integral Tentu Lebih Lanjut
BAB V. INTEGRAL Anti-turunan dan Integral TakTentu Persamaan Diferensial Sederhana Notasi Sigma dan Luas Daerah di Bawah Kurva Integral Tentu Teorema Dasar Kalkulus Sifat-sifat Integral Tentu Lebih Lanjut
Hendra Gunawan. 26 Februari 2014
 MA1201 MATEMATIKA 2A Hendra Gunawan Semester II, 2013/2014 26 Februari 2014 9.6 Deret Pangkat Kuliah yang Lalu Menentukan selang kekonvergenan deret pangkat 9.7 Operasi pada Deret Pangkat Mlkk Melakukan
MA1201 MATEMATIKA 2A Hendra Gunawan Semester II, 2013/2014 26 Februari 2014 9.6 Deret Pangkat Kuliah yang Lalu Menentukan selang kekonvergenan deret pangkat 9.7 Operasi pada Deret Pangkat Mlkk Melakukan
BAB IV SEBARAN ASIMTOTIK PENDUGA TURUNAN PERTAMA DAN KEDUA DARI KOMPONEN PERIODIK FUNGSI INTENSITAS PROSES POISSON PERIODIK DENGAN TREN LINEAR
 3 BAB IV SEBARAN ASIMTOTIK PENDUGA TURUNAN PERTAMA DAN KEDUA DARI KOMPONEN PERIODIK FUNGSI INTENSITAS PROSES POISSON PERIODIK DENGAN TREN LINEAR 4.. Sebaran asimtotik dari,, Teorema 4. ( Normalitas Asimtotik
3 BAB IV SEBARAN ASIMTOTIK PENDUGA TURUNAN PERTAMA DAN KEDUA DARI KOMPONEN PERIODIK FUNGSI INTENSITAS PROSES POISSON PERIODIK DENGAN TREN LINEAR 4.. Sebaran asimtotik dari,, Teorema 4. ( Normalitas Asimtotik
Reflektor Gelombang 1 balok
 Bab 3 Reflektor Gelombang 1 balok Setelah diperoleh persamaan yang menggambarkan gerak gelombang air setiap saat yaitu SWE, maka pada bab ini akan dielaskan mengenai pengaruh 1 balok terendam sebagai reflektor
Bab 3 Reflektor Gelombang 1 balok Setelah diperoleh persamaan yang menggambarkan gerak gelombang air setiap saat yaitu SWE, maka pada bab ini akan dielaskan mengenai pengaruh 1 balok terendam sebagai reflektor
1 Sistem Bilangan Real
 Learning Outcome Rencana Pembelajaran Setelah mengikuti proses pembelajaran ini, diharapkan mahasiswa dapat ) Menentukan solusi pertidaksamaan aljabar ) Menyelesaikan pertidaksamaan dengan nilai mutlak
Learning Outcome Rencana Pembelajaran Setelah mengikuti proses pembelajaran ini, diharapkan mahasiswa dapat ) Menentukan solusi pertidaksamaan aljabar ) Menyelesaikan pertidaksamaan dengan nilai mutlak
PENGANTAR ANALISIS REAL
 Seri Analisis dan Geometri No. 1 (2009), -15 158 (173 hlm.) PENGANTAR ANALISIS REAL Oleh Hendra Gunawan Edisi Pertama Bandung, Januari 2009 2000 Dewey Classification: 515-xx. Kata Kunci: Analisis matematika,
Seri Analisis dan Geometri No. 1 (2009), -15 158 (173 hlm.) PENGANTAR ANALISIS REAL Oleh Hendra Gunawan Edisi Pertama Bandung, Januari 2009 2000 Dewey Classification: 515-xx. Kata Kunci: Analisis matematika,
BAB I LIMIT-LIMIT Limit-limit Fungsi
 .. Limit-it Fungsi BAB I LIMIT-LIMIT... Definisi. Misalkan A R. Suatu titik c R adalah titik cluster dari A jika setiap lingkungan-δ dari c, V δ (c) = (c-δ,c+δ), memuat paling sedikit satu titik dari A
.. Limit-it Fungsi BAB I LIMIT-LIMIT... Definisi. Misalkan A R. Suatu titik c R adalah titik cluster dari A jika setiap lingkungan-δ dari c, V δ (c) = (c-δ,c+δ), memuat paling sedikit satu titik dari A
BAB III PEMBAHASAN. Bab III terbagi menjadi tiga sub-bab, yaitu sub-bab A, sub-bab B, dan subbab
 BAB III PEMBAHASAN Bab III terbagi menjadi tiga sub-bab, yaitu sub-bab A, sub-bab B, dan subbab C. Sub-bab A menjelaskan mengenai konsep dasar C[a, b] sebagai ruang vektor beserta contohnya. Sub-bab B
BAB III PEMBAHASAN Bab III terbagi menjadi tiga sub-bab, yaitu sub-bab A, sub-bab B, dan subbab C. Sub-bab A menjelaskan mengenai konsep dasar C[a, b] sebagai ruang vektor beserta contohnya. Sub-bab B
ANALISIS AKIBAT INTEGRAL CAUCHY Ricky Antonius, Helmi, Yudhi INTISARI
 Buletin Ilmiah Mat. Stat. dan Terapannya (Bimaster) Volume 07, No. 1 (2018), hal 41-46. ANALISIS AKIBAT INTEGRAL CAUCHY Ricky Antonius, Helmi, Yudhi INTISARI Analisis kompleks salah satu cabang matematika
Buletin Ilmiah Mat. Stat. dan Terapannya (Bimaster) Volume 07, No. 1 (2018), hal 41-46. ANALISIS AKIBAT INTEGRAL CAUCHY Ricky Antonius, Helmi, Yudhi INTISARI Analisis kompleks salah satu cabang matematika
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
PENGANTAR MATEMATIKA TEKNIK 1. By : Suthami A
 PENGANTAR MATEMATIKA TEKNIK 1 By : Suthami A MATEMATIKA TEKNIK 1??? MATEMATIKA TEKNIK 1??? MATEMATIKA TEKNIK Matematika sebagai ilmu dasar yang digunakan sebagai alat pemecahan masalah di bidang keteknikan
PENGANTAR MATEMATIKA TEKNIK 1 By : Suthami A MATEMATIKA TEKNIK 1??? MATEMATIKA TEKNIK 1??? MATEMATIKA TEKNIK Matematika sebagai ilmu dasar yang digunakan sebagai alat pemecahan masalah di bidang keteknikan
INTISARI KALKULUS 2. Penyusun: Drs. Warsoma Djohan M.Si. Open Source. Not For Commercial Use
 INTISARI KALKULUS 2 Penyusun: Drs. Warsoma Djohan M.Si. Program Studi Matematika - FMIPA Institut Teknologi Bandung Januari 200 Pengantar Kalkulus & 2 merupakan matakuliah wajib tingkat pertama bagi semua
INTISARI KALKULUS 2 Penyusun: Drs. Warsoma Djohan M.Si. Program Studi Matematika - FMIPA Institut Teknologi Bandung Januari 200 Pengantar Kalkulus & 2 merupakan matakuliah wajib tingkat pertama bagi semua
