Kalkulus 2. Teknik Pengintegralan ke - 1. Tim Pengajar Kalkulus ITK. Institut Teknologi Kalimantan. Januari 2018
|
|
|
- Yuliana Indradjaja
- 6 tahun lalu
- Tontonan:
Transkripsi
1 Kalkulus 2 Teknik Pengintegralan ke - 1 Tim Pengajar Kalkulus ITK Institut Teknologi Kalimantan Januari 2018 Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
2 Daftar Isi 1 Teknik Pengintegralan Aturan Dasar Pengintegralan Integrasi Substitusi Integrasi Parsial Latihan Soal Integrasi Parsial Beberapa Integral Trigonometri Jenis 1 ( sin n x dx dan cos n x dx) Jenis 2 ( sin m x cos n x dx) Jenis 3 ( sin mx cos nx dx, sin mx sin nx dx, dan cos mx cos nx dx) Jenis 4 ( tan n x dx dan cot n x dx) Jenis 5 ( tan m x sec n x dx dan cot m x csc n x dx) Latihan Soal Integral Trigonometri Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
3 Kemampuan yang diinginkan pada Bab Ini adalah mahasiswa memiliki kejelian melihat bentuk soal. sehingga faktor latihan sangat penting untuk memperoleh hasil yang diinginkan. Jadi BANYAK BERLATIH dengan soal-soal, maka anda InsyaAllah akan menuai kesuksesan. Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
4 Aturan Dasar Pengintegralan Fungsi - fungsi yang telah kita ketahui bersama adalah fungsi - fungsi Elementer, yaitu fungsi konstanta, fungsi pangkat, fungsi logaritma dan eksponen, trigonometri, dan fungsi invers, serta fungsi yang kita peroleh dari hasil penambahan, pengurangan, perkalian, pembagian, dan komposisi fungsi - fungsi tersebut. jadi f (x) = ex + e x 2 = cosh x adalah fungsi elementer. Integrasi (anti diferensiasi) adalah persoalan yang berbeda dengan diferensiasi/turunan. Integrasi melibatkan sedikit teknik dan lebih banyak akal. dan perlu diingat hasilnya tidak selalu berupa fungsi elementer. misalnya anti turunan dari e x2 bukan fungsi elementer. Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
5 Aturan Dasar Pengintegralan Dua Teknik dasar untuk integrasi adalah substitusi dan integrasi parsial. metode substitusi telah kita kenal pada bab sebelumnya. tetapi yang perlu diingat teknik ini juga banyak digunakan pada bab selanjutnya. Bentuk Baku. Penggunaan secara efektif metode substitusi bergantung ketersediaan daftar integral - integral yang sudah dikenal. Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
6 Beberapa bentuk Integral Baku Konstanta dan pangkat k du = ku + C u r+1 u r du = r + 1 +C ln u +C r = 1 r = 1 Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
7 Beberapa bentuk Integral Baku Konstanta dan pangkat k du = ku + C u r+1 u r du = r + 1 +C ln u +C r = 1 r = 1 Eksponensial e x dx = e x + C a x dx = ax ln a + C, a = 1, a > 0 Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
8 Beberapa bentuk Integral Baku Konstanta dan pangkat k du = ku + C u r+1 u r du = r + 1 +C ln u +C r = 1 r = 1 Eksponensial e x dx = e x + C a x dx = ax ln a + C, a = 1, a > 0 Fungsi Trigonometri cos u du = sin u + C sec 2 u du = tan u + C sin u du = cos u + C csc 2 u du = cot u + C Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
9 Review Integral Substitusi Teknik pengintegralan ini sudah kita kenal dalam bab sebelumnya. berikut teorema yang mendasari teknik integral substitusi, Teorema (Substitusi dalam integral tak tentu) Misalkan g adalah fungsi yang terdiferensiasikan dan misalkan F adalah anti turunan f. Maka, jika u = g(x), f (g(x))g (x) dx = f (u) du = F(u) + C = F(g(x)) + C Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
10 Contoh Integral Substitusi Contoh Carilah x cos x 2 dx. Di dalam pikiran kita, substitusikan u = x 2 sehingga du = 2xdx. Sehingga diperoleh x cos x 2 dx = 1 cos x 2 (2x dx) = 1 cos x 2 dx 2 = sin x2 + C Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
11 Contoh Integral Substitusi Contoh Hitunglah t t 2 4 dt. Misalkan u = t 2 4, sehingga du = 2t dt, sehingga diperoleh t t 2 4dt = 1 (t 2 4 ) 1 2 2t dt = 1 u 1 2 du 2 2 = u C = 3 u u + C = 1 ( t 2 4 ) t C Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
12 Integrasi Parsial Jika integrasi menggunakan substitusi gagal, kita mungkin saja menggunakan substitusi ganda (double substitusion), yang lebih dikenal sebagai integrasi Parsial. Metode ini didasarkan pada integrasi dari rumus untuk turunan dari hasil kali dua fungsi. Misalkan u = u(x) dan v = v(x), maka D x [u(x)v(x)] = u (x)v(x) + u(x)v (x) atau u(x)v (x) = D x [u(x)v(x)] u (x)v(x) dengan mengintegrasi kedua ruas persamaan diperoleh u(x)v (x) dx = u(x)v(x) u (x)v(x) dx dengan dv = v (x) dx dan du = u (x) dx. Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
13 Bentuk rumus Integrasi Definisi Misalkan u = u(x) dan v = v(x), maka rumus integrasi parsial adalah u dv = uv v du yang perlu diperhatikan adalah pemilihan yang tepat untuk u dan dv, kecakapan dan ketepatan dapat diasah melalui banyak berlatih mengerjakan soal latihan. Catatan : Ketentuan bahwa biasanya u adalah fungsi yang mudah jika diturunkan dan dapat habis diturunkan terhadap x, dv adalah bagian yang mudah diintegralkan. Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
14 Integrasi Parsial Contoh Carilah x cos x dx. Kita dapat menuliskan x cos x dx = u dv. Salah satu kemungkinan ialah dengan memisalkan u = x dan dv = cos x dx. Kemungkinan sudah tepat, (ingat dengan ketentuan pada halaman sebelumnya). Karena u = x maka du/dx = 1 diperoleh du = dx dan untuk dv = cos x dx jika diintegralkan kedua ruas diperoleh dv = v = cos x dx = sin x. Ringkasannya sebagai berikut, u = x du = dx Rumus integrasi parsial memberikan }{{} x cos }{{ x dx } = }{{} x sin }{{} x u dv u v dv = cos x dx v = sin x sin x }{{} v }{{} dx = x sin x + cos x + C du Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
15 Integrasi Parsial Contoh Carilah ln x dx. Kita buat substitusi sebagai berikut. (ingat dengan ketentuan pada halaman sebelumnya) maka u = ln ( x ) 1 du = dx x dv = dx v = x ln x dx = x ln x = x ln x x 1 x dx dx = x ln x x + C Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
16 Integrasi Parsial Contoh Carilah x 2 sin x dx. Misalkan maka u = x 2 du = 2x dx dv = sin x dx v = cos x x 2 sin x dx = x 2 cos x + 2 x cos x dx Setelah ini lakukan lagi integrasi parsial pada bagian yang masih harus diintegralkan. karena telah diperoleh pada contoh sebelumnya, maka x 2 sin x dx = x 2 cos x + 2(x sin x + cos x + C) = x 2 cos x + 2x sin x + 2 cos x + K Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
17 Integrasi Parsial Perhatikan contoh soal berikut, hal ini menarik karena hasil integrasi seperti terus berulang. Contoh Carilah e x sin x dx. Gunakan u = e x dan dv = sin x dx. Maka du = e x dx dan v = cos x. Jadi, e x sin x dx = e x cos x + e x cos x dx } {{ } i) Perhatikan bagian i) harus diselesaikan dengan cara yang sama dengan memisalkan u = e x dan dv = cos x dx. Maka du = e x dx dan v = sin x. Maka e x cos x dx = e x sin x e x sin x dx } {{ } i) Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
18 Integrasi Parsial Jika kita substitusikan lagi bagian i) maka kita peroleh e x sin x dx = e x cos x + e x sin x e x sin x dx dengan memindahkan suku terakhir ke ruas kiri dan menggabungkan suku - sukunya, maka diperoleh 2 e x sin x dx = e x cos x + e x sin x + C e x sin x dx = 1 2 ex sin x 1 2 ex cos x + K perhatikan bahwa integral yang hendak kita cari muncul seperti berulang di ruas kanan. Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
19 Latihan Soal Gunakan Integrasi Parsial untuk menghitung Integral - integral di bawah ini. 1 xe 3x dx. Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
20 Latihan Soal Gunakan Integrasi Parsial untuk menghitung Integral - integral di bawah ini. 1 xe 3x dx. 2 x sin 2x dx. Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
21 Latihan Soal Gunakan Integrasi Parsial untuk menghitung Integral - integral di bawah ini. 1 xe 3x dx. 2 x sin 2x dx. 3 ln 3x dx. Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
22 Latihan Soal Gunakan Integrasi Parsial untuk menghitung Integral - integral di bawah ini. 1 xe 3x dx. 2 x sin 2x dx. 3 ln 3x dx. 4 t 3 2t + 7 dt. Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
23 Latihan Soal Gunakan Integrasi Parsial untuk menghitung Integral - integral di bawah ini. 1 xe 3x dx. 2 x sin 2x dx. 3 ln 3x dx. 4 t 3 2t + 7 dt. 5 π/2 π/6 x csc 2 x dx. Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
24 Beberapa Integral Trigonometri Ketika kita menggabungkan metode substitusi dengan penggunaan identitas trigonometri, kita dapat mengintegrasikan banyak bentuk trigonometri. Ada lima bentuk jenis integral yang sering muncul. 1 sin n x dx dan cos n x dx Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
25 Beberapa Integral Trigonometri Ketika kita menggabungkan metode substitusi dengan penggunaan identitas trigonometri, kita dapat mengintegrasikan banyak bentuk trigonometri. Ada lima bentuk jenis integral yang sering muncul. 1 sin n x dx dan cos n x dx 2 sin m x cos n x dx. Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
26 Beberapa Integral Trigonometri Ketika kita menggabungkan metode substitusi dengan penggunaan identitas trigonometri, kita dapat mengintegrasikan banyak bentuk trigonometri. Ada lima bentuk jenis integral yang sering muncul. 1 sin n x dx dan cos n x dx 2 sin m x cos n x dx. 3 sin mx cos nx dx, sin mx sin nx dx, dan cos mx cos nx dx Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
27 Beberapa Integral Trigonometri Ketika kita menggabungkan metode substitusi dengan penggunaan identitas trigonometri, kita dapat mengintegrasikan banyak bentuk trigonometri. Ada lima bentuk jenis integral yang sering muncul. 1 sin n x dx dan cos n x dx 2 sin m x cos n x dx. 3 sin mx cos nx dx, sin mx sin nx dx, dan cos mx cos nx dx 4 tan n x dx dan cot n x dx Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
28 Beberapa Integral Trigonometri Ketika kita menggabungkan metode substitusi dengan penggunaan identitas trigonometri, kita dapat mengintegrasikan banyak bentuk trigonometri. Ada lima bentuk jenis integral yang sering muncul. 1 sin n x dx dan cos n x dx 2 sin m x cos n x dx. 3 sin mx cos nx dx, sin mx sin nx dx, dan cos mx cos nx dx 4 tan n x dx dan cot n x dx 5 tan m x sec n x dx dan cot m x csc n x dx Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
29 Beberapa Identitas Trigonometri Beberapa identitas yang perlu diingat dan berguna, antara lain : Identitas Pythagoras sin 2 x + cos 2 x = 1 sec 2 x tan 2 x = 1 csc 2 x cot 2 x = 1 Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
30 Beberapa Identitas Trigonometri Beberapa identitas yang perlu diingat dan berguna, antara lain : Identitas Pythagoras sin 2 x + cos 2 x = 1 sec 2 x tan 2 x = 1 csc 2 x cot 2 x = 1 Identitas Setengah Sudut sin 2 x = cos 2 x = 1 cos 2x cos 2x 2 Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
31 Jenis 1 Pada bentuk sin n x dx dan cos n x dx, pertama perhatikanlah untuk n adalah bilangan bulat positif ganjil. setelah mengeluarkan salah satu faktor sin x atau cos x dan selanjutnya gunakan identitas. Contoh (n Ganjil) Carilah sin 5 x dx. sin 5 x dx = (1 sin 4 x sin x dx = cos 2 x ) 2 sin x dx ( ) = 1 2 cos 2 x + cos 4 x sin x dx ( ) = 1 2 cos 2 x + cos 4 x ( sin x dx) = cos x cos3 x 1 5 cos5 x + C Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
32 Untuk n genap gunakan identitas setengah sudut Contoh (n Genap) Carilah sin 2 x dx dan cos 4 x dx 1 cos 2x 1 sin 2 cos 2x x dx = dx = dx = 1 dx 1 cos 2x(2 dx) 2 4 = 1 2 x 1 sin 2x + C 4 Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
33 ( ) 1 + cos 2x 2 cos 4 x dx = dx = 1 (1 + 2 cos 2x + cos 2 2x ) dx 2 4 = 1 dx + 1 cos 2x(2 dx) + 1 (1 + cos 4x) dx = 3 dx + 1 cos 2x(2 dx) + 1 cos 4x(4 dx) = 3 8 x sin 2x + sin 4x + C 4 32 Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
34 Jenis 2 Perhatikan bentuk sin m x cos n x dx.jika salah satu dari m atau n adalah bilangan bulat positif ganjil sedangkan yg lainnya sembarang, kita faktorkan sin x atau cos x dan gunakan identitas. Contoh (m atau n ganjil) Carilah sin 3 x cos 2 x dx. sin 3 x cos 2 x dx = (sin 2 x) ( cos 2 x ) (sin x) dx = (1 cos 2 x) ( cos 2 x ) (sin x) dx ( ) = cos 2 x cos 4 x ( sin x dx) = 1 3 cos3 x cos5 x + C Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
35 Jika m dan n keduanya adalah bilangan bulat positif genap, maka gunakanlah identitas setengah sudut. Contoh (m dan n genap) Carilah sin 2 x cos 4 x dx. ( ) ( ) 1 cos 2x 1 + cos 2x 2 sin 2 x cos 4 x dx = dx 2 2 = 1 8 (1 + cos 2x cos 2 2x cos 3 2x ) dx Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
36 = 1 [ 1 + cos 2x 1 ] 8 2 (1 + cos 4x) (1 sin2 2x) cos 2x = 1 [ cos 4x + sin2 2x cos 2x] dx = 1 [ x 1 8 sin 4x + 1 ] 6 sin3 2x + C dx Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
37 Jenis 3 Integral jenis sin mx cos nx dx, sin mx sin nx dx, dan cos mx cos nx dx muncul dalam banyak aplikasi fisika dan engineering (Baca Hal 14, Bab 7 Teknik Pengintegralan, Purcell edisi 9, jilid 2). Untuk menangani integral - integral ini, kita gunakan identitas hasil kali. 1 sin mx cos nx = 1 [sin(m + n)x + sin(m n)x]. 2 Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
38 Jenis 3 Integral jenis sin mx cos nx dx, sin mx sin nx dx, dan cos mx cos nx dx muncul dalam banyak aplikasi fisika dan engineering (Baca Hal 14, Bab 7 Teknik Pengintegralan, Purcell edisi 9, jilid 2). Untuk menangani integral - integral ini, kita gunakan identitas hasil kali. 1 sin mx cos nx = 1 [sin(m + n)x + sin(m n)x]. 2 2 sin mx sin nx = 1 [cos(m + n)x cos(m n)x]. 2 Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
39 Jenis 3 Integral jenis sin mx cos nx dx, sin mx sin nx dx, dan cos mx cos nx dx muncul dalam banyak aplikasi fisika dan engineering (Baca Hal 14, Bab 7 Teknik Pengintegralan, Purcell edisi 9, jilid 2). Untuk menangani integral - integral ini, kita gunakan identitas hasil kali. 1 sin mx cos nx = 1 [sin(m + n)x + sin(m n)x]. 2 2 sin mx sin nx = 1 [cos(m + n)x cos(m n)x]. 2 3 cos mx cos nx = 1 [cos(m + n)x + cos(m n)x] 2 Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
40 Bentuk pertama Contoh Carilah sin 2x cos 3x dx. sin 2x cos 3x dx = 1 [sin(5)x + sin( 1)x] dx 2 = 1 sin 5x (5 dx) 1 sin x dx 10 2 = 1 10 cos 5x cos x + C Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
41 Bentuk Kedua Contoh Carilah sin 3u sin u du. sin 3u sin u du = 1 2 = 1 8 [cos(4)u cos(2)u] du cos 4u (4 du) + 1 cos 2u (2 du) 4 = 1 8 sin 4u + 1 sin 2u + C 4 Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
42 Bentuk Ketiga Contoh Carilah cos t cos( 2t) dt. cos t cos( 2t)dt = 1 2 = 1 2 [cos( 1)t + cos(3)t] dt cos t dt + 1 cos 3t (3 dt) 6 = 1 2 sin t + 1 sin 3t + C 6 Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
43 Jenis 4 Pada Bentuk tan n x dx dan cot n x dx ini, sesungguhnya serupa dengan jenis 1. Namun alat yang diperlukan adalah identitas sec 2 x 1 = tan 2 x dan csc 2 x 1 = cot 2 x. Contoh Carilah cot 4 x dx. cot 4 x dx = cot 2 x ( csc 2 x 1 ) dx = cot 2 x csc 2 x dx cot 2 x dx = (csc cot 2 x ( csc 2 x dx) 2 x 1 ) dx = 1 3 cot3 x + cot x + x + C Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
44 Jenis 4 Untuk bentuk tan n x dx, cobalah cari tan 2 x dx dan tan 5 x dx Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
45 Jenis 5 Pada jenis terakhir ini yaitu tan m x sec n x dx dan cot m x csc n x dx serupa dengan bentuk pada jenis 2. sekali lagi ingatlah dengan identitas sec 2 x tan 2 x = 1 dan csc 2 x cot 2 x = 1. Contoh (m sembarang bilangan, n genap) Carilah tan 3/2 x sec 4 x dx. ( (1 tan 3/2 x sec 4 x dx = tan x) 3/2 + tan 2 x ) sec 2 x dx ( ) = tan 3/2 x sec 2 x dx+ ( ) + tan 1/2 x sec 2 x dx = 2 tan 1/2 x tan3/2 x + C Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
46 Contoh (m ganjil, n Sebarang Bilangan) Carilah tan 3 x sec 1/2 x dx. (tan tan 3 x sec 1/2 x dx = 2 x ) ( sec x) 3/2 (sec x tan x) dx (sec = 2 x 1 ) ( sec x) 3/2 (sec x tan x dx) = sec 1/2 x (sec x tan x dx) + sec 3/2 x (sec x tan x dx) = 2 3 sec3/2 x + 2 sec 1/2 x + C Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
47 Latihan Soal Integral Trigonometri Agar lebih mengenal dan memahami bentuk integral Trigonometri, cobalah beberapa soal di bawah ini Lakukanlah Integrasi pada pada soal - soal di bawah ini. 1 cos 3 θ dθ Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
48 Latihan Soal Integral Trigonometri Agar lebih mengenal dan memahami bentuk integral Trigonometri, cobalah beberapa soal di bawah ini Lakukanlah Integrasi pada pada soal - soal di bawah ini. 1 cos 3 θ dθ 2 sin 4 6x dx. Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
49 Latihan Soal Integral Trigonometri Agar lebih mengenal dan memahami bentuk integral Trigonometri, cobalah beberapa soal di bawah ini Lakukanlah Integrasi pada pada soal - soal di bawah ini. 1 cos 3 θ dθ 2 sin 4 6x dx. 3 π/2 0 cos 5 θ dθ. Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
50 Latihan Soal Integral Trigonometri Agar lebih mengenal dan memahami bentuk integral Trigonometri, cobalah beberapa soal di bawah ini Lakukanlah Integrasi pada pada soal - soal di bawah ini. 1 cos 3 θ dθ 2 sin 4 6x dx. 3 4 π/2 0 cos 5 θ dθ. sin 2 3x cos 3 3x dx. Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
51 Latihan Soal Integral Trigonometri Agar lebih mengenal dan memahami bentuk integral Trigonometri, cobalah beberapa soal di bawah ini Lakukanlah Integrasi pada pada soal - soal di bawah ini. 1 cos 3 θ dθ 2 sin 4 6x dx π/2 0 cos 5 θ dθ. sin 2 3x cos 3 3x dx. cos y cos 4y dy. im Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
52 Latihan Soal Integral Trigonometri Kerjakanlah sebagai latihan dan tugas nomor - nomor ganjil dari no. 17 s.d 29 pada buku Purcell edisi 9, jilid 2 Bab 7 Teknik Pengintegralan, hal 17) Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
53 Daftar Pustaka Varberg, Purcell, Rigdon, Calkulus Ninth Edition, Pearson Education, im Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
54 Daftar Pustaka Varberg, Purcell, Rigdon, Calkulus Ninth Edition, Pearson Education, Azka, M, 2 3 statistic, 2017 im Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari / 36
Kalkulus 2. Teknik Pengintegralan ke - 2. Tim Pengajar Kalkulus ITK. Institut Teknologi Kalimantan. Januari 2018
 Kalkulus 2 Teknik Pengintegralan ke - 2 Tim Pengajar Kalkulus ITK Institut Teknologi Kalimantan Januari 2018 Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari 2018 1 / 24 Daftar
Kalkulus 2 Teknik Pengintegralan ke - 2 Tim Pengajar Kalkulus ITK Institut Teknologi Kalimantan Januari 2018 Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari 2018 1 / 24 Daftar
Kalkulus 2. Teknik Pengintegralan ke - 3. Tim Pengajar Kalkulus ITK. Institut Teknologi Kalimantan. Januari 2018
 Kalkulus 2 Teknik Pengintegralan ke - 3 Tim Pengajar Kalkulus ITK Institut Teknologi Kalimantan Januari 2018 Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari 2018 1 / 27 Daftar
Kalkulus 2 Teknik Pengintegralan ke - 3 Tim Pengajar Kalkulus ITK Institut Teknologi Kalimantan Januari 2018 Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari 2018 1 / 27 Daftar
Teknik Pengintegralan
 Jurusan Matematika 13 Nopember 2012 Review Rumus-rumus Integral yang Dikenal Pada beberapa subbab sebelumnya telah dijelaskan beberapa integral dari fungsi-fungsi tertentu. Berikut ini diberikan sebuah
Jurusan Matematika 13 Nopember 2012 Review Rumus-rumus Integral yang Dikenal Pada beberapa subbab sebelumnya telah dijelaskan beberapa integral dari fungsi-fungsi tertentu. Berikut ini diberikan sebuah
MA1201 KALKULUS 2A (Kelas 10) Bab 7: Teknik Pengintegral
 MA1201 KALKULUS 2A (Kelas 10) Bab 7: Teknik Pengintegralan Do maths and you see the world Integral atau Anti-turunan? Integral atau pengintegral adalah salah satu konsep (penting) dalam matematika disamping
MA1201 KALKULUS 2A (Kelas 10) Bab 7: Teknik Pengintegralan Do maths and you see the world Integral atau Anti-turunan? Integral atau pengintegral adalah salah satu konsep (penting) dalam matematika disamping
Aturan dasar pengintegralan Integral fungsi rasional Integral parsial Integral trigonometri Substitusi yang merasionalkan Strategi pengintegralan
 Aturan dasar pengintegralan Integral fungsi rasional Integral parsial Integral trigonometri Substitusi yang merasionalkan Strategi pengintegralan Kemampuan yang diinginkan: kejelian melihat bentuk soal
Aturan dasar pengintegralan Integral fungsi rasional Integral parsial Integral trigonometri Substitusi yang merasionalkan Strategi pengintegralan Kemampuan yang diinginkan: kejelian melihat bentuk soal
TEKNIK PENGINTEGRALAN
 TEKNIK PENGINTEGRALAN Departemen Matematika FMIPA IPB Bogor, 202 (Departemen Matematika FMIPA IPB) Kalkulus I Bogor, 202 / 2 Topik Bahasan Pendahuluan 2 Manipulasi Integran 3 Integral Parsial 4 Dekomposisi
TEKNIK PENGINTEGRALAN Departemen Matematika FMIPA IPB Bogor, 202 (Departemen Matematika FMIPA IPB) Kalkulus I Bogor, 202 / 2 Topik Bahasan Pendahuluan 2 Manipulasi Integran 3 Integral Parsial 4 Dekomposisi
MA1201 KALKULUS 2A (Kelas 10) Bab 7: Teknik Pengintegral
 MA1201 KALKULUS 2A (Kelas 10) Bab 7: Teknik Pengintegralan Do maths and you see the world Integral atau Anti-turunan? Integral atau pengintegral adalah salah satu konsep (penting) dalam matematika disamping
MA1201 KALKULUS 2A (Kelas 10) Bab 7: Teknik Pengintegralan Do maths and you see the world Integral atau Anti-turunan? Integral atau pengintegral adalah salah satu konsep (penting) dalam matematika disamping
digunakan untuk menyelesaikan integral seperti 3
 Bab Teknik Pengintegralan BAB TEKNIK PENGINTEGRALAN Rumus-rumus dasar integral tak tertentu yang diberikan pada bab hanya dapat digunakan untuk mengevaluasi integral dari fungsi sederhana dan tidak dapat
Bab Teknik Pengintegralan BAB TEKNIK PENGINTEGRALAN Rumus-rumus dasar integral tak tertentu yang diberikan pada bab hanya dapat digunakan untuk mengevaluasi integral dari fungsi sederhana dan tidak dapat
INTISARI KALKULUS 2. Penyusun: Drs. Warsoma Djohan M.Si. Open Source. Not For Commercial Use
 INTISARI KALKULUS 2 Penyusun: Drs. Warsoma Djohan M.Si. Program Studi Matematika - FMIPA Institut Teknologi Bandung Januari 200 Pengantar Kalkulus & 2 merupakan matakuliah wajib tingkat pertama bagi semua
INTISARI KALKULUS 2 Penyusun: Drs. Warsoma Djohan M.Si. Program Studi Matematika - FMIPA Institut Teknologi Bandung Januari 200 Pengantar Kalkulus & 2 merupakan matakuliah wajib tingkat pertama bagi semua
Fungsi F disebut anti turunan (integral tak tentu) dari fungsi f pada himpunan D jika. F (x) = f(x) dx dan f (x) dinamakan integran.
 4 INTEGRAL Definisi 4. Fungsi F disebut anti turunan (integral tak tentu) dari fungsi f pada himpunan D jika untuk setiap D. F () f() Fungsi integral tak tentu f dinotasikan dengan f ( ) d dan f () dinamakan
4 INTEGRAL Definisi 4. Fungsi F disebut anti turunan (integral tak tentu) dari fungsi f pada himpunan D jika untuk setiap D. F () f() Fungsi integral tak tentu f dinotasikan dengan f ( ) d dan f () dinamakan
INTISARI KALKULUS 2. Penyusun: Drs. Warsoma Djohan M.Si. Open Source. Not For Commercial Use
 INTISARI KALKULUS Penyusun: Drs. Warsoma Djohan M.Si. Program Studi Matematika - FMIPA Institut Teknologi Bandung Januari 010 Pengantar Kalkulus 1 & merupakan matakuliah wajib tingkat pertama bagi semua
INTISARI KALKULUS Penyusun: Drs. Warsoma Djohan M.Si. Program Studi Matematika - FMIPA Institut Teknologi Bandung Januari 010 Pengantar Kalkulus 1 & merupakan matakuliah wajib tingkat pertama bagi semua
Fungsi F disebut anti turunan (integral tak tentu) dari fungsi f pada himpunan D jika. F (x) = f(x) dx dan f (x) dinamakan integran.
 4 INTEGRAL Definisi 4.0. Fungsi F disebut anti turunan (integral tak tentu) dari fungsi f pada himpunan D jika untuk setiap D. F () f() Fungsi integral tak tentu f dinotasikan dengan f ( ) d dan f () dinamakan
4 INTEGRAL Definisi 4.0. Fungsi F disebut anti turunan (integral tak tentu) dari fungsi f pada himpunan D jika untuk setiap D. F () f() Fungsi integral tak tentu f dinotasikan dengan f ( ) d dan f () dinamakan
HUBUNGAN ANTARA DIFFERENSIAL DAN INTEGRAL
 HUBUNGAN ANTARA DIFFERENSIAL DAN INTEGRAL Dra.Sri Rejeki Dwi Putranti, M.Kes. Fakultas Teknik - Universitaas Yos Soedarso Surabaya Email : riccayusticia@gmail.com Abstrak Hubungan antara Differensial dan
HUBUNGAN ANTARA DIFFERENSIAL DAN INTEGRAL Dra.Sri Rejeki Dwi Putranti, M.Kes. Fakultas Teknik - Universitaas Yos Soedarso Surabaya Email : riccayusticia@gmail.com Abstrak Hubungan antara Differensial dan
TEKNIK-TEKNIK PENGINTEGRALAN
 TEKNIK-TEKNIK PENGINTEGRALAN 1. Teknik Subtitusi Teorema : Misal g fungsi yang terdiferensialkan dan F suatu anti turunan dari f, jika u = g() maka f(g())g () d = f(u) du = F(u) + c = F(g()) + c sin. 1.
TEKNIK-TEKNIK PENGINTEGRALAN 1. Teknik Subtitusi Teorema : Misal g fungsi yang terdiferensialkan dan F suatu anti turunan dari f, jika u = g() maka f(g())g () d = f(u) du = F(u) + c = F(g()) + c sin. 1.
FUNGSI-FUNGSI INVERS
 FUNGSI-FUNGSI INVERS Logaritma, Eksponen, Trigonometri Invers Departemen Matematika FMIPA IPB Bogor, 202 (Departemen Matematika FMIPA IPB) Kalkulus I Bogor, 202 / 49 Topik Bahasan Fungsi Satu ke Satu 2
FUNGSI-FUNGSI INVERS Logaritma, Eksponen, Trigonometri Invers Departemen Matematika FMIPA IPB Bogor, 202 (Departemen Matematika FMIPA IPB) Kalkulus I Bogor, 202 / 49 Topik Bahasan Fungsi Satu ke Satu 2
KALKULUS INTEGRAL 2013
 KALKULUS INTEGRAL 0 PENDAHULUAN A. DESKRIPSI MATA KULIAH Isi pokok mata kuliah ini memuat pemahaman tentang: () Anti turunan: pengertian anti turunan, teorema-teorema, dan teknik anti turunan, () Integral
KALKULUS INTEGRAL 0 PENDAHULUAN A. DESKRIPSI MATA KULIAH Isi pokok mata kuliah ini memuat pemahaman tentang: () Anti turunan: pengertian anti turunan, teorema-teorema, dan teknik anti turunan, () Integral
Fakultas Teknik UNY Jurusan Pendidikan Teknik Otomotif INTEGRASI FUNGSI. 0 a b X A. b A = f (X) dx a. Penyusun : Martubi, M.Pd., M.T.
 Kode Modul MAT. TKF 20-03 Fakultas Teknik UNY Jurusan Pendidikan Teknik Otomotif INTEGRASI FUNGSI Y Y = f (X) 0 a b X A b A = f (X) dx a Penyusun : Martubi, M.Pd., M.T. Sistem Perencanaan Penyusunan Program
Kode Modul MAT. TKF 20-03 Fakultas Teknik UNY Jurusan Pendidikan Teknik Otomotif INTEGRASI FUNGSI Y Y = f (X) 0 a b X A b A = f (X) dx a Penyusun : Martubi, M.Pd., M.T. Sistem Perencanaan Penyusunan Program
Matematika I: Turunan. Dadang Amir Hamzah. Dadang Amir Hamzah Matematika I Semester I / 61
 Matematika I: Turunan Dadang Amir Hamzah 2015 Dadang Amir Hamzah Matematika I Semester I 2015 1 / 61 Outline 1 Garis Singgung Dadang Amir Hamzah Matematika I Semester I 2015 2 / 61 Outline 1 Garis Singgung
Matematika I: Turunan Dadang Amir Hamzah 2015 Dadang Amir Hamzah Matematika I Semester I 2015 1 / 61 Outline 1 Garis Singgung Dadang Amir Hamzah Matematika I Semester I 2015 2 / 61 Outline 1 Garis Singgung
TURUNAN. Bogor, Departemen Matematika FMIPA-IPB. (Departemen Matematika FMIPA-IPB) Kalkulus: Turunan Bogor, / 50
 TURUNAN Departemen Matematika FMIPA-IPB Bogor, 2012 (Departemen Matematika FMIPA-IPB) Kalkulus: Turunan Bogor, 2012 1 / 50 Topik Bahasan 1 Pendahuluan 2 Turunan Fungsi 3 Tafsiran Lain Turunan 4 Kaitan
TURUNAN Departemen Matematika FMIPA-IPB Bogor, 2012 (Departemen Matematika FMIPA-IPB) Kalkulus: Turunan Bogor, 2012 1 / 50 Topik Bahasan 1 Pendahuluan 2 Turunan Fungsi 3 Tafsiran Lain Turunan 4 Kaitan
BAB: TEKNIK PENGINTEGRALAN Topik: Metode Substitusi
 BAB: TEKNIK PENGINTEGRALAN Topik: Metode Substitusi Kompetensi yang diukur adalah kemampuan mahasiswa menghitung integral fungsi dengan metode substitusi.. UAS Kalkulus Semester Pendek no. b (kriteria:
BAB: TEKNIK PENGINTEGRALAN Topik: Metode Substitusi Kompetensi yang diukur adalah kemampuan mahasiswa menghitung integral fungsi dengan metode substitusi.. UAS Kalkulus Semester Pendek no. b (kriteria:
Kalkulus Diferensial week 09. W. Rofianto, ST, MSi
 Kalkulus Diferensial week 09 W. Rofianto, ST, MSi Tingkat Perubahan Rata-rata Jakarta Km 0 jam Bandung Km 140 Kecepatan rata-rata s t 140Km jam 70Km / jam Konsep Diferensiasi Bentuk y/ disebut difference
Kalkulus Diferensial week 09 W. Rofianto, ST, MSi Tingkat Perubahan Rata-rata Jakarta Km 0 jam Bandung Km 140 Kecepatan rata-rata s t 140Km jam 70Km / jam Konsep Diferensiasi Bentuk y/ disebut difference
TEKNIK PENGINTEGRALAN
 TEKNIK PENGINTEGRALAN KALKULUS S- Teknik Industri Outline Integral Parsial Integral Fungsi Trigonometri Substitusi Trigonometri Integral Fungsi Rasional . Integral Parsial Formula Integral Parsial : u
TEKNIK PENGINTEGRALAN KALKULUS S- Teknik Industri Outline Integral Parsial Integral Fungsi Trigonometri Substitusi Trigonometri Integral Fungsi Rasional . Integral Parsial Formula Integral Parsial : u
Bab 16. LIMIT dan TURUNAN. Motivasi. Limit Fungsi. Fungsi Turunan. Matematika SMK, Bab 16: Limit dan Turunan 1/35
 Bab 16 Grafik LIMIT dan TURUNAN Matematika SMK, Bab 16: Limit dan 1/35 Grafik Pada dasarnya, konsep limit dikembangkan untuk mengerjakan perhitungan matematis yang melibatkan: nilai sangat kecil; Matematika
Bab 16 Grafik LIMIT dan TURUNAN Matematika SMK, Bab 16: Limit dan 1/35 Grafik Pada dasarnya, konsep limit dikembangkan untuk mengerjakan perhitungan matematis yang melibatkan: nilai sangat kecil; Matematika
RUMUS INTEGRAL RUMUS INTEGRAL
 TEKNIK PENGINTEGRALAN TEKNIK PENGINTEGRALAN Berdasarkan Teorema Dasar Kalkulus, maka kita akan mendapatkan integral tak tentu dari fungsi-fungsi yang sudah kita ketahui Beberapa yang telah kita ketahui
TEKNIK PENGINTEGRALAN TEKNIK PENGINTEGRALAN Berdasarkan Teorema Dasar Kalkulus, maka kita akan mendapatkan integral tak tentu dari fungsi-fungsi yang sudah kita ketahui Beberapa yang telah kita ketahui
MA1201 KALKULUS 2A Do maths and you see the world
 Catatan Kuliah MA20 KALKULUS 2A Do maths and you see the world disusun oleh Khreshna I.A. Syuhada, MSc. PhD. Kelompok Keilmuan STATISTIKA - FMIPA Institut Teknologi Bandung 203 Catatan kuliah ini ditulis
Catatan Kuliah MA20 KALKULUS 2A Do maths and you see the world disusun oleh Khreshna I.A. Syuhada, MSc. PhD. Kelompok Keilmuan STATISTIKA - FMIPA Institut Teknologi Bandung 203 Catatan kuliah ini ditulis
PENYELESAIAN PERSAMAAN DIFFERENSIAL ORDE 1 - I
 PENYELESAIAN PERSAMAAN DIFFERENSIAL ORDE 1 - I 1. Pendahuluan Pengertian Persamaan Diferensial Metoda Penyelesaian -contoh Aplikasi 1 1.1. Pengertian Persamaan Differensial Secara Garis Besar Persamaan
PENYELESAIAN PERSAMAAN DIFFERENSIAL ORDE 1 - I 1. Pendahuluan Pengertian Persamaan Diferensial Metoda Penyelesaian -contoh Aplikasi 1 1.1. Pengertian Persamaan Differensial Secara Garis Besar Persamaan
INTEGRAL TAK TENTU 1
 INTEGRAL TAK TENTU 1 Rumus umum integral b a f (x) dx F(x) =lambang integral f(x) = integran (fungsi yg diintegralkan) a dan b = batas pengintegralan a = batas bawah b = batas atas dx = faktor pengintegral
INTEGRAL TAK TENTU 1 Rumus umum integral b a f (x) dx F(x) =lambang integral f(x) = integran (fungsi yg diintegralkan) a dan b = batas pengintegralan a = batas bawah b = batas atas dx = faktor pengintegral
INTEGRAL (ANTI DIFERENSIAL) Tito Adi Dewanto S.TP
 A. Soal dan Pembahasan. ( x ) dx... Jawaban : INTEGRAL (ANTI DIFERENSIAL) Tito Adi Dewanto S.TP ( x) dx x dx x C x C x x C. ( x 9) dx... x Jawaban : ( x 9) dx. (x x 9) dx x 9x C x x x. (x )(x + ) dx =.
A. Soal dan Pembahasan. ( x ) dx... Jawaban : INTEGRAL (ANTI DIFERENSIAL) Tito Adi Dewanto S.TP ( x) dx x dx x C x C x x C. ( x 9) dx... x Jawaban : ( x 9) dx. (x x 9) dx x 9x C x x x. (x )(x + ) dx =.
16. INTEGRAL. A. Integral Tak Tentu 1. dx = x + c 2. a dx = a dx = ax + c. 3. x n dx = + c. cos ax + c. 4. sin ax dx = 1 a. 5.
 6. INTEGRAL A. Integral Tak Tentu. dx = x + c. a dx = a dx = ax + c. x n dx = n+ x n+ + c. sin ax dx = a cos ax + c 5. cos ax dx = a sin ax + c 6. sec ax dx = a tan ax + c 7. [ f(x) ± g(x) ] dx = f(x)
6. INTEGRAL A. Integral Tak Tentu. dx = x + c. a dx = a dx = ax + c. x n dx = n+ x n+ + c. sin ax dx = a cos ax + c 5. cos ax dx = a sin ax + c 6. sec ax dx = a tan ax + c 7. [ f(x) ± g(x) ] dx = f(x)
INTEGRAL PARSIAL DENGAN TEKNIK TURIN. Mintarjo SMK Negeri 2 Gedangsari Gunungkidul
 INTEGRAL PARSIAL DENGAN TEKNIK TURIN Mintarjo SMK Negeri Gedangsari Gunungkidul email : tarjamint@gmailcom Abstrak Matematika merupakan ilmu pengetahuan yang memiliki sifat universal Salah satu cabang
INTEGRAL PARSIAL DENGAN TEKNIK TURIN Mintarjo SMK Negeri Gedangsari Gunungkidul email : tarjamint@gmailcom Abstrak Matematika merupakan ilmu pengetahuan yang memiliki sifat universal Salah satu cabang
FUNGSI dan LIMIT. 1.1 Fungsi dan Grafiknya
 FUNGSI dan LIMIT 1.1 Fungsi dan Grafiknya Fungsi : suatu aturan yang menghubungkan setiap elemen suatu himpunan pertama (daerah asal) tepat kepada satu elemen himpunan kedua (daerah hasil) fungsi Daerah
FUNGSI dan LIMIT 1.1 Fungsi dan Grafiknya Fungsi : suatu aturan yang menghubungkan setiap elemen suatu himpunan pertama (daerah asal) tepat kepada satu elemen himpunan kedua (daerah hasil) fungsi Daerah
Catatan Kuliah MA1123 Kalkulus Elementer I
 Catatan Kuliah MA1123 Kalkulus Elementer I Oleh Hendra Gunawan, Ph.D. Departemen Matematika ITB Sasaran Belajar Setelah mempelajari materi Kalkulus Elementer I, mahasiswa diharapkan memiliki (terutama):
Catatan Kuliah MA1123 Kalkulus Elementer I Oleh Hendra Gunawan, Ph.D. Departemen Matematika ITB Sasaran Belajar Setelah mempelajari materi Kalkulus Elementer I, mahasiswa diharapkan memiliki (terutama):
Matematika I: Turunan. Dadang Amir Hamzah. Dadang Amir Hamzah Matematika I Semester I / 75
 Matematika I: Turunan Dadang Amir Hamzah 2015 Dadang Amir Hamzah Matematika I Semester I 2015 1 / 75 Outline 1 Garis Singgung Dadang Amir Hamzah Matematika I Semester I 2015 2 / 75 Outline 1 Garis Singgung
Matematika I: Turunan Dadang Amir Hamzah 2015 Dadang Amir Hamzah Matematika I Semester I 2015 1 / 75 Outline 1 Garis Singgung Dadang Amir Hamzah Matematika I Semester I 2015 2 / 75 Outline 1 Garis Singgung
Teknik pengintegralan: Integral parsial (Integral by part)
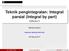 Teknik pengintegralan: Integral parsial (Integral by part) Kalkulus 2 Nanang Susyanto Departemen Matematika FMIPA UGM 06 Februari 2017 NS (FMIPA UGM) Teknik pengintegralan 06/02/2017 1 / 14 Mari mengingat
Teknik pengintegralan: Integral parsial (Integral by part) Kalkulus 2 Nanang Susyanto Departemen Matematika FMIPA UGM 06 Februari 2017 NS (FMIPA UGM) Teknik pengintegralan 06/02/2017 1 / 14 Mari mengingat
KED INTEGRAL JUMLAH PERTEMUAN : 2 PERTEMUAN TUJUAN INSTRUKSIONAL KHUSUS: Materi : 7.1 Anti Turunan. 7.2 Sifat-sifat Integral Tak Tentu KALKULUS I
 7 INTEGRAL JUMLAH PERTEMUAN : 2 PERTEMUAN TUJUAN INSTRUKSIONAL KHUSUS: Memahami konsep dasar integral, teorema-teorema, sifat-sifat, notasi jumlah, fungsi transenden dan teknik-teknik pengintegralan. Materi
7 INTEGRAL JUMLAH PERTEMUAN : 2 PERTEMUAN TUJUAN INSTRUKSIONAL KHUSUS: Memahami konsep dasar integral, teorema-teorema, sifat-sifat, notasi jumlah, fungsi transenden dan teknik-teknik pengintegralan. Materi
MODUL 1. Teori Bilangan MATERI PENYEGARAN KALKULUS
 MODUL 1 Teori Bilangan Bilangan merupakan sebuah alat bantu untuk menghitung, sehingga pengetahuan tentang bilangan, mutlak diperlukan. Pada modul pertama ini akan dibahas mengenai bilangan (terutama bilangan
MODUL 1 Teori Bilangan Bilangan merupakan sebuah alat bantu untuk menghitung, sehingga pengetahuan tentang bilangan, mutlak diperlukan. Pada modul pertama ini akan dibahas mengenai bilangan (terutama bilangan
Hendra Gunawan. 4 September 2013
 MA1101 MATEMATIKA 1A Hendra Gunawan Semester I, 2013/2014 4 September 2013 Latihan (Kuliah yang Lalu) 1. Tentukan daerah asal dan daerah nilai fungsi 2 f(x) = 1 x. sudah dijawab 2. Gambar grafik fungsi
MA1101 MATEMATIKA 1A Hendra Gunawan Semester I, 2013/2014 4 September 2013 Latihan (Kuliah yang Lalu) 1. Tentukan daerah asal dan daerah nilai fungsi 2 f(x) = 1 x. sudah dijawab 2. Gambar grafik fungsi
= + atau = - 2. TURUNAN 2.1 Definisi Turunan fungsi f adalah fungsi yang nilainya di setiap bilangan sebarang c di dalam D f diberikan oleh
 JURUSAN PENDIDIKAN MATEMATIKA FPMIPA-UPI BANDUNG HAND OUT TURUNAN DAN DIFERENSIASI OLEH: FIRDAUS-UPI 0716 1. GARIS SINGGUNG 1.1 Definisi Misalkan fungsi f kontinu di c. Garis singgung ( tangent line )
JURUSAN PENDIDIKAN MATEMATIKA FPMIPA-UPI BANDUNG HAND OUT TURUNAN DAN DIFERENSIASI OLEH: FIRDAUS-UPI 0716 1. GARIS SINGGUNG 1.1 Definisi Misalkan fungsi f kontinu di c. Garis singgung ( tangent line )
FUNGSI LOGARITMA ASLI
 FUNGSI LOGARITMA ASLI............ Definisi Fungsi logaritma asli, dinyatakan oleh ln, didefinisikan sebagai ln (Daerah asalnya adalah., 0 Turunan Logaritma Asli ln, 0 Lebih umumnya, Jika 0 dan f terdifferensialkan,
FUNGSI LOGARITMA ASLI............ Definisi Fungsi logaritma asli, dinyatakan oleh ln, didefinisikan sebagai ln (Daerah asalnya adalah., 0 Turunan Logaritma Asli ln, 0 Lebih umumnya, Jika 0 dan f terdifferensialkan,
DERIVATIVE (continued)
 DERIVATIVE (continued) (TURUNAN) Kus Prihantoso Krisnawan November 25 rd, 2011 Yogyakarta Aturan Turunan Trigonometri Aturan Turunan Trigonometri d (sin x) = cos x d (cos x) = sin x Aturan Turunan Trigonometri
DERIVATIVE (continued) (TURUNAN) Kus Prihantoso Krisnawan November 25 rd, 2011 Yogyakarta Aturan Turunan Trigonometri Aturan Turunan Trigonometri d (sin x) = cos x d (cos x) = sin x Aturan Turunan Trigonometri
= F (x)= f(x)untuk semua x dalam I. Misalnya F(x) =
 Nama : Deami Astenia Purtisari Nim : 125100300111014 Kelas : L / TIP A. Integral Integral merupakan konsep yang bermanfaat, kegunaan integral terdapat dalam berbagai bidang. Misalnya dibidang ekonomi,
Nama : Deami Astenia Purtisari Nim : 125100300111014 Kelas : L / TIP A. Integral Integral merupakan konsep yang bermanfaat, kegunaan integral terdapat dalam berbagai bidang. Misalnya dibidang ekonomi,
4.1 Konsep Turunan. lim Turunan di satu titik. Pendahuluan ( dua masalah dalam satu tema ) a. Garis Singgung Kemiringan tali busur PQ adalah :
 4. TURUNAN 4. Konsep Turunan 4.. Turunan di satu titik Pendahuluan dua masalah dalam satu tema a. Garis Singgung Kemiringan tali busur PQ adalah : m PQ c c Q -c Jika c, maka tali busur PQ akan berubah
4. TURUNAN 4. Konsep Turunan 4.. Turunan di satu titik Pendahuluan dua masalah dalam satu tema a. Garis Singgung Kemiringan tali busur PQ adalah : m PQ c c Q -c Jika c, maka tali busur PQ akan berubah
bila limitnya ada. Dengan penggantian x = c+ h, jika x c h 0 dan x c h turunan fungsi f di c dapat dituliskan dalam bentuk: x c
 Misalkan fungsi f terdefinisi pada selang terbuka I yang memuat c. Turunan pertama dari fungsi f di titik c ditulis f '( c ) didefinisikan sebagai: ( ) ( ) f x f '( c) = lim f c x c x c bila limitnya ada.
Misalkan fungsi f terdefinisi pada selang terbuka I yang memuat c. Turunan pertama dari fungsi f di titik c ditulis f '( c ) didefinisikan sebagai: ( ) ( ) f x f '( c) = lim f c x c x c bila limitnya ada.
MACLAURIN S SERIES. Ghifari Eka
 MACLAURIN S SERIES Ghifari Eka Taylor Series Sebelum membahas mengenai Maclaurin s series alangkah lebih baiknya apabila kita mengetahui terlebih dahulu mengenai Taylor series. Misalkan terdapat fungsi
MACLAURIN S SERIES Ghifari Eka Taylor Series Sebelum membahas mengenai Maclaurin s series alangkah lebih baiknya apabila kita mengetahui terlebih dahulu mengenai Taylor series. Misalkan terdapat fungsi
matematika TURUNAN TRIGONOMETRI K e l a s A. Rumus Turunan Sinus dan Kosinus Kurikulum 2006/2013 Tujuan Pembelajaran
 Kurikulum 006/03 matematika K e l a s XI TURUNAN TRIGONOMETRI Tujuan Pembelajaran Setelah mempelajari materi ini, kamu diharapkan memiliki kemampuan berikut.. Dapat menentukan rumus turunan trigonometri
Kurikulum 006/03 matematika K e l a s XI TURUNAN TRIGONOMETRI Tujuan Pembelajaran Setelah mempelajari materi ini, kamu diharapkan memiliki kemampuan berikut.. Dapat menentukan rumus turunan trigonometri
Gambar 1. Gradien garis singgung grafik f
 D. URAIAN MATERI 1. Definisi dan Rumus-rumus Turunan Fungsi a. Definisi Turunan Sala satu masala yang mendasari munculnya kajian tentang turunan adala gradien garis singgung. Peratikan Gambar 1. f(c +
D. URAIAN MATERI 1. Definisi dan Rumus-rumus Turunan Fungsi a. Definisi Turunan Sala satu masala yang mendasari munculnya kajian tentang turunan adala gradien garis singgung. Peratikan Gambar 1. f(c +
FUNGSI TRIGONOMETRI, FUNGSI EKSPONEN, FUNGSI LOGARITMA
 FUNGSI TRIGONOMETRI, FUNGSI EKSPONEN, FUNGSI LOGARITMA Makalah Ini Disusun Guna Memenuhi Tugas Mata Kuliah Kalkulus Dosen Pengampu : Muhammad Istiqlal, M.Pd. Disusun Oleh:. Mukhammad Rif an Alwi (070600).
FUNGSI TRIGONOMETRI, FUNGSI EKSPONEN, FUNGSI LOGARITMA Makalah Ini Disusun Guna Memenuhi Tugas Mata Kuliah Kalkulus Dosen Pengampu : Muhammad Istiqlal, M.Pd. Disusun Oleh:. Mukhammad Rif an Alwi (070600).
INTEGRAL TAK TENTU (subtitusi parsial) Agustina Pradjaningsih, M.Si. Jurusan Matematika FMIPA UNEJ
 INTEGRAL TAK TENTU subtitusi parsial Agustina Pradjaningsih, M.Si. Jurusan Matematika FMIPA UNEJ agustina.mipa@unej.ac.id DEFINISI Untuk ungsi yang terdeinisi pada selang terbuka I, dpt ditentukan ungsi
INTEGRAL TAK TENTU subtitusi parsial Agustina Pradjaningsih, M.Si. Jurusan Matematika FMIPA UNEJ agustina.mipa@unej.ac.id DEFINISI Untuk ungsi yang terdeinisi pada selang terbuka I, dpt ditentukan ungsi
FT UNIVERSITAS SURABAYA VARIABEL KOMPLEKS SUGATA PIKATAN. Bab V Aplikasi
 Bab V Aplikasi Selain aplikasi yang sudah diperkenalkan di bab I, teori variabel kompleks masih memiliki banyak ragam aplikasi lainnya. Beberapa di antaranya akan dibahas di dalam bab ini. Perhitungan
Bab V Aplikasi Selain aplikasi yang sudah diperkenalkan di bab I, teori variabel kompleks masih memiliki banyak ragam aplikasi lainnya. Beberapa di antaranya akan dibahas di dalam bab ini. Perhitungan
integral = 2 . Setiap fungsi ini memiliki turunan ( ) = adalah ( ) = 6 2.
 integral 13.1 PENGERTIAN INTEGRAL Untuk itu, coba tentukan turunan fungsi berikut. Perhatikan bahwa fungsi ini memiliki bentuk umum 6 2. Jadi, turunan fungsi = 2 =2 3. Setiap fungsi ini memiliki turunan
integral 13.1 PENGERTIAN INTEGRAL Untuk itu, coba tentukan turunan fungsi berikut. Perhatikan bahwa fungsi ini memiliki bentuk umum 6 2. Jadi, turunan fungsi = 2 =2 3. Setiap fungsi ini memiliki turunan
I N T E G R A L (Anti Turunan)
 I N T E G R A L (Anti Turunan) I. Integral Tak Tentu A. Rumus Integral Bentuk Baku. Derifatif d/ X n = nx n- xn = Integral x n+ n. d/ cos x = - sin x sin x = - cos x. d/ sin x = cos x cos x = sin x 4.
I N T E G R A L (Anti Turunan) I. Integral Tak Tentu A. Rumus Integral Bentuk Baku. Derifatif d/ X n = nx n- xn = Integral x n+ n. d/ cos x = - sin x sin x = - cos x. d/ sin x = cos x cos x = sin x 4.
FUNGSI LOGARITMA ASLI
 D.. = D.. = D.. = = 0 D.. = D.. = D.. = 3 FUNGSI LOGARITMA ASLI Definisi Fungsi logaritma asli, dinyatakan oleh ln, didefinisikan sebagai ln = (Daerah asalnya adalah R). t dt, > 0 Turunan Logaritma Asli
D.. = D.. = D.. = = 0 D.. = D.. = D.. = 3 FUNGSI LOGARITMA ASLI Definisi Fungsi logaritma asli, dinyatakan oleh ln, didefinisikan sebagai ln = (Daerah asalnya adalah R). t dt, > 0 Turunan Logaritma Asli
MA1201 KALKULUS 2A (Kelas 10) Bab 8: Bentuk Tak Tentu d
 MA1201 KALKULUS 2A (Kelas 10) Bab 8: dan Do maths and you see the world ? Pengantar Bentuk tak tentu? Bentuk apa? Bentuk tak tentu yang dimaksud adalah bentuk limit dengan nilai seolah-olah : 0 0 ; ; 0
MA1201 KALKULUS 2A (Kelas 10) Bab 8: dan Do maths and you see the world ? Pengantar Bentuk tak tentu? Bentuk apa? Bentuk tak tentu yang dimaksud adalah bentuk limit dengan nilai seolah-olah : 0 0 ; ; 0
BAB VIII. TEKNIK INTEGRASI. Andaikan anda menghadapi suatu integral tak tentu. Jika ini bentuk baku
 9 BAB VIII. TEKNIK INTEGRASI 8.. Integral dengan Substitusi Andaikan anda menghadapi suatu integral tak tentu. Jika ini bentuk baku maka cukup tuliskan jawabannya. Jika tidak, cari tahu substitusi yang
9 BAB VIII. TEKNIK INTEGRASI 8.. Integral dengan Substitusi Andaikan anda menghadapi suatu integral tak tentu. Jika ini bentuk baku maka cukup tuliskan jawabannya. Jika tidak, cari tahu substitusi yang
UJI KONVERGENSI. Januari Tim Dosen Kalkulus 2 TPB ITK
 UJI KONVERGENSI Januari 208 Tim Dosen Kalkulus 2 TPB ITK Uji Integral Teorema 3 Jika + k= u k adalah deret dengan suku-suku tak negatif, dan jika ada suatu konstanta M sedemikian hingga s n = u + u 2 +
UJI KONVERGENSI Januari 208 Tim Dosen Kalkulus 2 TPB ITK Uji Integral Teorema 3 Jika + k= u k adalah deret dengan suku-suku tak negatif, dan jika ada suatu konstanta M sedemikian hingga s n = u + u 2 +
Indikator : Menentukan penarikan kesimpulan dari beberapa premis. Modus Ponens Modus Tollens Silogisme
 Indikator : Menentukan penarikan kesimpulan dari beberapa premis Modus Ponens Modus Tollens Silogisme p q p q p q p ~q q r q ~p p r Bentuk ekuivalen : p q ~q ~p p q ~p q Soal 1 : Diketahui premis : Premis
Indikator : Menentukan penarikan kesimpulan dari beberapa premis Modus Ponens Modus Tollens Silogisme p q p q p q p ~q q r q ~p p r Bentuk ekuivalen : p q ~q ~p p q ~p q Soal 1 : Diketahui premis : Premis
MATEMATIKA INDUSTRI 1 RESUME INTEGRAL DAN APLIKASI
 MATEMATIKA INDUSTRI 1 RESUME INTEGRAL DAN APLIKASI Nama : Syifa Robbani NIM : 125100301111002 Dosen Kelas : Nimas Mayang Sabrina S., STP, MP, MSc : L Nimas Nimas Mayang Sabrina S., STP, MP, MSc Mayang
MATEMATIKA INDUSTRI 1 RESUME INTEGRAL DAN APLIKASI Nama : Syifa Robbani NIM : 125100301111002 Dosen Kelas : Nimas Mayang Sabrina S., STP, MP, MSc : L Nimas Nimas Mayang Sabrina S., STP, MP, MSc Mayang
Catatan Kuliah KALKULUS II BAB V. INTEGRAL
 BAB V. INTEGRAL Anti-turunan dan Integral TakTentu Persamaan Diferensial Sederhana Notasi Sigma dan Luas Daerah di Bawah Kurva Integral Tentu Teorema Dasar Kalkulus Sifat-sifat Integral Tentu Lebih Lanjut
BAB V. INTEGRAL Anti-turunan dan Integral TakTentu Persamaan Diferensial Sederhana Notasi Sigma dan Luas Daerah di Bawah Kurva Integral Tentu Teorema Dasar Kalkulus Sifat-sifat Integral Tentu Lebih Lanjut
APLIKASI INTEGRAL 1. LUAS DAERAH BIDANG
 Bahan ajar Kalkulus Integral 9 APLIKASI INTEGRAL. LUAS DAERAH BIDANG Misalkan f() kontinu pada a b, dan daerah tersebut dibagi menjadi n sub interval h, h,, h n yang panjangnya,,, n (anggap n ), ambil
Bahan ajar Kalkulus Integral 9 APLIKASI INTEGRAL. LUAS DAERAH BIDANG Misalkan f() kontinu pada a b, dan daerah tersebut dibagi menjadi n sub interval h, h,, h n yang panjangnya,,, n (anggap n ), ambil
Bab 3 Fungsi Elementer
 Bab 3 Fungsi Elementer Bab 3 ini direncanakan akan disampaikan dalam 3 kali pertemuan, dengan perincian sebagai berikut: (1) Pertemuan I: Fungsi Eksponensial dan sifat-sifatnya, Fungsi Trigonometri. ()
Bab 3 Fungsi Elementer Bab 3 ini direncanakan akan disampaikan dalam 3 kali pertemuan, dengan perincian sebagai berikut: (1) Pertemuan I: Fungsi Eksponensial dan sifat-sifatnya, Fungsi Trigonometri. ()
Turunan Fungsi. h asalkan limit ini ada.
 Turunan Fungsi q Definisi Turunan Fungsi Misalkan fungsi f terdefinisi pada selang terbuka I yang memuat a. Turunan pertama fungsi f di =a ditulis f (a) didefinisikan dengan f ( a h) f ( a) f '( a) lim
Turunan Fungsi q Definisi Turunan Fungsi Misalkan fungsi f terdefinisi pada selang terbuka I yang memuat a. Turunan pertama fungsi f di =a ditulis f (a) didefinisikan dengan f ( a h) f ( a) f '( a) lim
4. Deret Fourier pada Interval Sebarang dan Aplikasi
 4. Deret Fourier pada Interval Sebarang dan Aplikasi Kita telah mempelajari bagaimana menguraikan fungsi periodik dengan periode 2 yang terdefinisi pada R sebagai deret Fourier. Deret trigonometri tersebut
4. Deret Fourier pada Interval Sebarang dan Aplikasi Kita telah mempelajari bagaimana menguraikan fungsi periodik dengan periode 2 yang terdefinisi pada R sebagai deret Fourier. Deret trigonometri tersebut
Matematika Dasar FUNGSI DAN GRAFIK
 FUNGSI DAN GRAFIK Suatu pengaitan dari himpunan A ke himpunan B disebut fungsi bila mengaitkan setiap anggota dari himpunan A dengan tepat satu anggota dari himpunan B. Notasi : f : A B f() y Himpunan
FUNGSI DAN GRAFIK Suatu pengaitan dari himpunan A ke himpunan B disebut fungsi bila mengaitkan setiap anggota dari himpunan A dengan tepat satu anggota dari himpunan B. Notasi : f : A B f() y Himpunan
Fungsi Gamma dan Fungsi Beta. Ayundyah. Ayundyah Kesumawati. Prodi Statistika FMIPA-UII. March 31, 2015
 Fungsi Kesumawati Prodi Statistika FMIPA-UII March 31, 215 Gamma Fungsi Fungsi Gamma didefinisikan sebagai integral tak wajar berikut: Γ(α) := e x x α 1 dx (1) Integral ini konvergen bila α >. Dengan menerapkan
Fungsi Kesumawati Prodi Statistika FMIPA-UII March 31, 215 Gamma Fungsi Fungsi Gamma didefinisikan sebagai integral tak wajar berikut: Γ(α) := e x x α 1 dx (1) Integral ini konvergen bila α >. Dengan menerapkan
Pengintegralan Fungsi Rasional
 Pengintegralan Fungsi Rasional Ahmad Kamsyakawuni, M.Kom Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Jember 25 Maret 2014 Pengintegralan Fungsi Rasional 1 Pengintegralan Fungsi Rasional 2
Pengintegralan Fungsi Rasional Ahmad Kamsyakawuni, M.Kom Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Jember 25 Maret 2014 Pengintegralan Fungsi Rasional 1 Pengintegralan Fungsi Rasional 2
KONSEP DASAR PERSAMAAN DIFERENSIAL
 KONSEP DASAR PERSAMAAN DIFERENSIAL A. PENGERTIAN PERSAMAAN DIFERENSIAL Dalam pelajaran kalkulus, kita telah berkenalan dan mengkaji berbagai macam metode untuk mendiferensialkan suatu fungsi (dasar). Sebagai
KONSEP DASAR PERSAMAAN DIFERENSIAL A. PENGERTIAN PERSAMAAN DIFERENSIAL Dalam pelajaran kalkulus, kita telah berkenalan dan mengkaji berbagai macam metode untuk mendiferensialkan suatu fungsi (dasar). Sebagai
BAB II KAJIAN TEORI. dalam penulisan bab III. Materi yang diuraikan berisi tentang definisi, teorema,
 BAB II KAJIAN TEORI Pada bab ini akan dibahas tentang beberapa hal yang menjadi landasan dalam penulisan bab III. Materi yang diuraikan berisi tentang definisi, teorema, dan beberapa kajian matematika,
BAB II KAJIAN TEORI Pada bab ini akan dibahas tentang beberapa hal yang menjadi landasan dalam penulisan bab III. Materi yang diuraikan berisi tentang definisi, teorema, dan beberapa kajian matematika,
LUAS DAERAH DI BAWAH KURVA SUATU FUNGSI
 LUAS DAERAH DI BAWAH KURVA SUATU FUNGSI Afrizal, S.Pd, M.PMat Matematika MAN Kampar Juli 2010 Afrizal, S.Pd, M.PMat (Matematika) Luas Daerah Dibawah Kurva Juli 2010 1 / 29 Outline Outline 1 Limit dan Turunan
LUAS DAERAH DI BAWAH KURVA SUATU FUNGSI Afrizal, S.Pd, M.PMat Matematika MAN Kampar Juli 2010 Afrizal, S.Pd, M.PMat (Matematika) Luas Daerah Dibawah Kurva Juli 2010 1 / 29 Outline Outline 1 Limit dan Turunan
Kalkulus II. Institut Teknologi Kalimantan
 Tim Dosen Kalkulus II Tahun Persiapan Bersama Institut Kalkulus Teknologi II Kalimantan January 31, () 2018 1 / 71 Kalkulus II Tim Dosen Kalkulus II Tahun Persiapan Bersama Institut Teknologi Kalimantan
Tim Dosen Kalkulus II Tahun Persiapan Bersama Institut Kalkulus Teknologi II Kalimantan January 31, () 2018 1 / 71 Kalkulus II Tim Dosen Kalkulus II Tahun Persiapan Bersama Institut Teknologi Kalimantan
BAB II PENGANTAR SOLUSI PERSOALAN FISIKA MENURUT PENDEKATAN ANALITIK DAN NUMERIK
 BAB II PENGANTAR SOLUSI PERSOALAN FISIKA MENURUT PENDEKATAN ANALITIK DAN NUMERIK Tujuan Instruksional Setelah mempelajari bab ini pembaca diharapkan dapat: 1. Menjelaskan cara penyelesaian soal dengan
BAB II PENGANTAR SOLUSI PERSOALAN FISIKA MENURUT PENDEKATAN ANALITIK DAN NUMERIK Tujuan Instruksional Setelah mempelajari bab ini pembaca diharapkan dapat: 1. Menjelaskan cara penyelesaian soal dengan
Nughthoh Arfawi Kurdhi, M.Sc Department of Mathematics FMIPA UNS
 Lecture 5. Integral A. Masalah Luas (The Area Problem) Sebelumnya kita pernah mempelajari rumus-rumus luas dari beberapa bentuk geometri. Misalnya, luas daerah persegi panjang adalah panjang kali lebar,
Lecture 5. Integral A. Masalah Luas (The Area Problem) Sebelumnya kita pernah mempelajari rumus-rumus luas dari beberapa bentuk geometri. Misalnya, luas daerah persegi panjang adalah panjang kali lebar,
BAB II MACAM-MACAM FUNGSI
 BAB II MACAM-MACAM FUNGSI (Pertemuan ke 3) PENDAHULUAN Diskripsi singkat Pada bab ini dibahas tentang macam-macam fungsi, yaitu fungsi aljabar, fungsi trigonometri, fungsi logaritma, fungsi eksponensial,
BAB II MACAM-MACAM FUNGSI (Pertemuan ke 3) PENDAHULUAN Diskripsi singkat Pada bab ini dibahas tentang macam-macam fungsi, yaitu fungsi aljabar, fungsi trigonometri, fungsi logaritma, fungsi eksponensial,
MAKALAH MATEMATIKA DASAR TURUNAN (DIFERENSIAL)
 MAKALAH MATEMATIKA DASAR TURUNAN (DIFERENSIAL) KATA PENGANTAR Puji dan Syukur kami panjatkan ke Hadirat Tuhan Yang Maha Esa, karena berkat limpahan Rahmat dan Karunia-nya sehingga kami dapat menyusun makalah
MAKALAH MATEMATIKA DASAR TURUNAN (DIFERENSIAL) KATA PENGANTAR Puji dan Syukur kami panjatkan ke Hadirat Tuhan Yang Maha Esa, karena berkat limpahan Rahmat dan Karunia-nya sehingga kami dapat menyusun makalah
KALKULUS BAB II FUNGSI, LIMIT, DAN KEKONTINUAN. DEPARTEMEN TEKNIK KIMIA Universitas Indonesia
 KALKULUS BAB II FUNGSI, LIMIT, DAN KEKONTINUAN DEPARTEMEN TEKNIK KIMIA Universitas Indonesia BAB II. FUNGSI, LIMIT, DAN KEKONTINUAN Fungsi dan Operasi pada Fungsi Beberapa Fungsi Khusus Limit dan Limit
KALKULUS BAB II FUNGSI, LIMIT, DAN KEKONTINUAN DEPARTEMEN TEKNIK KIMIA Universitas Indonesia BAB II. FUNGSI, LIMIT, DAN KEKONTINUAN Fungsi dan Operasi pada Fungsi Beberapa Fungsi Khusus Limit dan Limit
A B A B. ( a ) ( b )
 BAB. FUNGSI A. Relasi dan Fungsi Misalkan A dan B dua himpunan tak kosong. Relasi T dari himpunan A ke B adalah himpunan bagian dari A B. Jadi relasi A ke B merupakan himpunan (,y), dengan pada himpunan
BAB. FUNGSI A. Relasi dan Fungsi Misalkan A dan B dua himpunan tak kosong. Relasi T dari himpunan A ke B adalah himpunan bagian dari A B. Jadi relasi A ke B merupakan himpunan (,y), dengan pada himpunan
Matematika
 Diferensial/ Diferensial/ dan Aplikasinya D3 Analis Kimia FMIPA Universitas Islam Indonesia Diferensial/ Diferensial/turunan adalah metode atau prosedur untuk menghitung laju perubahan. Definisi Diferensial/
Diferensial/ Diferensial/ dan Aplikasinya D3 Analis Kimia FMIPA Universitas Islam Indonesia Diferensial/ Diferensial/turunan adalah metode atau prosedur untuk menghitung laju perubahan. Definisi Diferensial/
Universitas Indonusa Esa Unggul Fakultas Ilmu Komputer Teknik Informatika. Persamaan Diferensial Orde II
 Universitas Indonusa Esa Unggul Fakultas Ilmu Komputer Teknik Informatika Persamaan Diferensial Orde II PDB Orde II Bentuk umum : y + p(x)y + g(x)y = r(x) p(x), g(x) disebut koefisien jika r(x) = 0, maka
Universitas Indonusa Esa Unggul Fakultas Ilmu Komputer Teknik Informatika Persamaan Diferensial Orde II PDB Orde II Bentuk umum : y + p(x)y + g(x)y = r(x) p(x), g(x) disebut koefisien jika r(x) = 0, maka
BAB VI INTEGRAL TAK TENTU DAN PENGGUNAANNYA
 BAB VI INTEGRAL TAK TENTU DAN PENGGUNAANNYA Jika dari suatu fungsi kita dapat memperoleh turunannya, bagaimana mengembalikan turunan suatu fungsi ke fungsi semula? Operasi semacam ini disebut operasi balikan
BAB VI INTEGRAL TAK TENTU DAN PENGGUNAANNYA Jika dari suatu fungsi kita dapat memperoleh turunannya, bagaimana mengembalikan turunan suatu fungsi ke fungsi semula? Operasi semacam ini disebut operasi balikan
: Pramitha Surya Noerdyah NIM : A. Integral. ʃ f(x) dx =F(x) + c
 Nama : Pramitha Surya Noerdyah NIM : 125100300111022 Kelas/Jur : L/TIP A. Integral Integral dilambangkan oleh ʃ yang merupakan lambang untuk menyatakan kembali F(X )dari F -1 (X). Hitung integral adalah
Nama : Pramitha Surya Noerdyah NIM : 125100300111022 Kelas/Jur : L/TIP A. Integral Integral dilambangkan oleh ʃ yang merupakan lambang untuk menyatakan kembali F(X )dari F -1 (X). Hitung integral adalah
Ringkasan Kalkulus 2, Untuk dipakai di ITB 1
 Ringkasan Kalkulus 2, Untuk dipakai di ITB Deret Tak Hingga Pada bagian ini akan dibicarakan penjumlahan berbentuk a +a 2 + +a n + dengan a n R Sebelumnya akan dibahas terlebih dahulu pengertian barisan
Ringkasan Kalkulus 2, Untuk dipakai di ITB Deret Tak Hingga Pada bagian ini akan dibicarakan penjumlahan berbentuk a +a 2 + +a n + dengan a n R Sebelumnya akan dibahas terlebih dahulu pengertian barisan
INTEGRASI Matematika Industri I
 INTEGRASI TIP FTP UB Pokok Bahasan Pendahuluan Fungsi dari suatu fungsi linear Integral berbentuk Integrasi hasilkali Integrasi per bagian Integrasi dengan pecahan parsial Integrasi fungsi-fungsi trigonometris
INTEGRASI TIP FTP UB Pokok Bahasan Pendahuluan Fungsi dari suatu fungsi linear Integral berbentuk Integrasi hasilkali Integrasi per bagian Integrasi dengan pecahan parsial Integrasi fungsi-fungsi trigonometris
F U N G S I A R U M H A N D I N I P R I M A N D A R I
 F U N G S I A R U M H A N D I N I P R I M A N D A R I DEFINISI Fungsi adalah suatu aturan yang memetakan setiap anggota himpunan A pada tepat satu anggota himpunan B. Dimana: Himpunan A disebut domain
F U N G S I A R U M H A N D I N I P R I M A N D A R I DEFINISI Fungsi adalah suatu aturan yang memetakan setiap anggota himpunan A pada tepat satu anggota himpunan B. Dimana: Himpunan A disebut domain
FUNGSI TRIGONOMETRI, FUNGSI EKSPONENSIAL, dan FUNGSI LOGARITMA
 FUNGSI TRIGONOMETRI, FUNGSI EKSPONENSIAL, dan FUNGSI LOGARITMA Makalah ini disusun untuk memenuhi tugas Mata Kuliah Kalkulus 1 Dosen Pengampu : Muhammad Istiqlal, M.Pd Disusun Oleh : 1. Sufi Anisa (23070160086)
FUNGSI TRIGONOMETRI, FUNGSI EKSPONENSIAL, dan FUNGSI LOGARITMA Makalah ini disusun untuk memenuhi tugas Mata Kuliah Kalkulus 1 Dosen Pengampu : Muhammad Istiqlal, M.Pd Disusun Oleh : 1. Sufi Anisa (23070160086)
BAB VII. FUNGSI TRANSEDEN. Perhatikan adanya kesenjangan tentang turunan berikut.
 64 BAB VII. FUNGSI TRANSEDEN 7.. Fungsi Logaritma Asli Perhatikan adanya kesenjangan tentang turunan berikut. D ( 3 /3) D ( /) D () 0 D (???) - D (- - ) - D (- - /3) -3 Definisi: Fungsi logaritma asli
64 BAB VII. FUNGSI TRANSEDEN 7.. Fungsi Logaritma Asli Perhatikan adanya kesenjangan tentang turunan berikut. D ( 3 /3) D ( /) D () 0 D (???) - D (- - ) - D (- - /3) -3 Definisi: Fungsi logaritma asli
LIMIT FUNGSI. A. Menentukan Limit Fungsi Aljabar A.1. Limit x a Contoh A.1: Contoh A.2 : 2 4)
 LIMIT FUNGSI A. Menentukan Limit Fungsi Aljabar A.. Limit a Contoh A.:. ( ) 3 Contoh A. : 4 ( )( ) ( ) 4 Latihan. Hitunglah nilai it fungsi-fungsi berikut ini. a. (3 ) b. ( 4) c. ( 4) d. 0 . Hitunglah
LIMIT FUNGSI A. Menentukan Limit Fungsi Aljabar A.. Limit a Contoh A.:. ( ) 3 Contoh A. : 4 ( )( ) ( ) 4 Latihan. Hitunglah nilai it fungsi-fungsi berikut ini. a. (3 ) b. ( 4) c. ( 4) d. 0 . Hitunglah
Pecahan Parsial (Partial Fractions)
 oki neswan (fmipa-itb) Pecahan Parsial (Partial Fractions) Diberikan fungsi rasional f (x) p(x) q(x) f (x) r(x) : Jika deg p deg q; maka r (x) ^p (x) q(x) ; dengan deg r < deg q: p (x) q (x) r (x) ^p (x)
oki neswan (fmipa-itb) Pecahan Parsial (Partial Fractions) Diberikan fungsi rasional f (x) p(x) q(x) f (x) r(x) : Jika deg p deg q; maka r (x) ^p (x) q(x) ; dengan deg r < deg q: p (x) q (x) r (x) ^p (x)
matematika PEMINATAN Kelas X PERSAMAAN DAN PERTIDAKSAMAAN EKSPONEN K13 A. PERSAMAAN EKSPONEN BERBASIS KONSTANTA
 K1 Kelas X matematika PEMINATAN PERSAMAAN DAN PERTIDAKSAMAAN EKSPONEN TUJUAN PEMBELAJARAN Setelah mempelajari materi ini, kamu diharapkan memiliki kemampuan berikut. 1. Memahami bentuk-bentuk persamaan
K1 Kelas X matematika PEMINATAN PERSAMAAN DAN PERTIDAKSAMAAN EKSPONEN TUJUAN PEMBELAJARAN Setelah mempelajari materi ini, kamu diharapkan memiliki kemampuan berikut. 1. Memahami bentuk-bentuk persamaan
perpindahan, kita peroleh persamaan differensial berikut :
 1.1 Pengertian Persamaan Differensial Banyak sekali masalah terapan (dalam ilmu teknik, ilmu fisika, biologi, kimia, sosial, dan lain-lain), yang telah dirumuskan dengan model matematika dalam bentuk persamaan
1.1 Pengertian Persamaan Differensial Banyak sekali masalah terapan (dalam ilmu teknik, ilmu fisika, biologi, kimia, sosial, dan lain-lain), yang telah dirumuskan dengan model matematika dalam bentuk persamaan
Matematika
 Diferensial/ Diferensial/ dan Aplikasinya D3 Analis Kimia FMIPA Universitas Islam Indonesia Diferensial/ Diferensial/turunan adalah metode atau prosedur untuk menghitung laju perubahan. Definisi Diferensial/
Diferensial/ Diferensial/ dan Aplikasinya D3 Analis Kimia FMIPA Universitas Islam Indonesia Diferensial/ Diferensial/turunan adalah metode atau prosedur untuk menghitung laju perubahan. Definisi Diferensial/
Definisi 4.1 Fungsi f dikatakan kontinu di titik a (continuous at a) jika dan hanya jika ketiga syarat berikut dipenuhi: (1) f(a) ada,
 Lecture 4. Limit B A. Continuity Definisi 4.1 Fungsi f dikatakan kontinu di titik a (continuous at a) jika dan hanya jika ketiga syarat berikut dipenuhi: (1) f(a) ada, (2) lim f(x) ada, (3) lim f(x) =
Lecture 4. Limit B A. Continuity Definisi 4.1 Fungsi f dikatakan kontinu di titik a (continuous at a) jika dan hanya jika ketiga syarat berikut dipenuhi: (1) f(a) ada, (2) lim f(x) ada, (3) lim f(x) =
BAB 4 SEBARAN ASIMTOTIK PENDUGA KOMPONEN PERIODIK
 BAB 4 SEBARAN ASIMTOTIK PENDUGA KOMPONEN PERIODIK 4. Sebaran Asimtotik,, Teorema 4. (Sebaran Normal Asimtotik,, ) Misalkan fungsi intensitas seperti (3.2) dan terintegralkan lokal. Jika kernel K adalah
BAB 4 SEBARAN ASIMTOTIK PENDUGA KOMPONEN PERIODIK 4. Sebaran Asimtotik,, Teorema 4. (Sebaran Normal Asimtotik,, ) Misalkan fungsi intensitas seperti (3.2) dan terintegralkan lokal. Jika kernel K adalah
KALKULUS 1 HADI SUTRISNO. Pendidikan Matematika STKIP PGRI Bangkalan. Hadi Sutrisno/P.Matematika/STKIP PGRI Bangkalan
 KALKULUS 1 HADI SUTRISNO 1 Pendidikan Matematika STKIP PGRI Bangkalan BAB I PENDAHULUAN A. Sistem Bilangan Real Untuk mempelajari kalkulus kita terlebih dahulu perlu memahami bahasan tentang sistem bilangan
KALKULUS 1 HADI SUTRISNO 1 Pendidikan Matematika STKIP PGRI Bangkalan BAB I PENDAHULUAN A. Sistem Bilangan Real Untuk mempelajari kalkulus kita terlebih dahulu perlu memahami bahasan tentang sistem bilangan
PEMBAHASAN KISI-KISI SOAL UAS KALKULUS PEUBAH BANYAK (TA 2015/2016)
 PEMBAHAAN KII-KII OAL UA KALKULU PEUBAH BANYAK (TA 5/6) Arini oesatyo Putri DEEMBER 3, 5 UNIVERITA ILAM NEGERI UNAN GUNUNG DJATI BANDUNG Pembahasan oal Kisi-Kisi UA Kalkulus Peubah Banyak Tahun Ajaran
PEMBAHAAN KII-KII OAL UA KALKULU PEUBAH BANYAK (TA 5/6) Arini oesatyo Putri DEEMBER 3, 5 UNIVERITA ILAM NEGERI UNAN GUNUNG DJATI BANDUNG Pembahasan oal Kisi-Kisi UA Kalkulus Peubah Banyak Tahun Ajaran
Matematika SMA (Program Studi IPA)
 Smart Solution UJIAN NASIONAL TAHUN PELAJARAN 0/0 Disusun Sesuai Indikator Kisi-Kisi UN 0 Matematika SMA (Program Studi IPA) Disusun oleh : Hario Pamungkas 4.. Menyelesaikan persamaan trigonometri. Nilai
Smart Solution UJIAN NASIONAL TAHUN PELAJARAN 0/0 Disusun Sesuai Indikator Kisi-Kisi UN 0 Matematika SMA (Program Studi IPA) Disusun oleh : Hario Pamungkas 4.. Menyelesaikan persamaan trigonometri. Nilai
Ringkasan Materi Kuliah Bab II FUNGSI
 Ringkasan Materi Kuliah Bab II FUNGSI. FUNGSI REAL, FUNGSI ALJABAR, DAN FUNGSI TRIGONOMETRI. TOPIK-TOPIK YANG BERKAITAN DENGAN FUNGSI.3 FUNGSI KOMPOSISI DAN FUNGSI INVERS. FUNGSI REAL, FUNGSI ALJABAR,
Ringkasan Materi Kuliah Bab II FUNGSI. FUNGSI REAL, FUNGSI ALJABAR, DAN FUNGSI TRIGONOMETRI. TOPIK-TOPIK YANG BERKAITAN DENGAN FUNGSI.3 FUNGSI KOMPOSISI DAN FUNGSI INVERS. FUNGSI REAL, FUNGSI ALJABAR,
BAB II LANDASAN TEORI
 BAB I PENDAHULUAN 1.1 Latar Belakang Matematika sebagai salah satu ilmu dasar, semakin dirasakan interaksinya dengan bidangbidang ilmu lainnya, seperti ekonomi dan teknologi. Peran matematika dalam interaksi
BAB I PENDAHULUAN 1.1 Latar Belakang Matematika sebagai salah satu ilmu dasar, semakin dirasakan interaksinya dengan bidangbidang ilmu lainnya, seperti ekonomi dan teknologi. Peran matematika dalam interaksi
Persamaan diferensial adalah suatu persamaan yang memuat satu atau lebih turunan fungsi yang tidak diketahui.
 1 Persamaan diferensial adalah suatu persamaan yang memuat satu atau lebih turunan fungsi yang tidak diketahui. Jika persamaan diferensial memiliki satu peubah tak bebas maka disebut Persamaan Diferensial
1 Persamaan diferensial adalah suatu persamaan yang memuat satu atau lebih turunan fungsi yang tidak diketahui. Jika persamaan diferensial memiliki satu peubah tak bebas maka disebut Persamaan Diferensial
4. Deret Fourier pada Interval Sebarang dan Aplikasi
 8 Hendra Gunawan 4. Deret Fourier pada Interval Sebarang dan Aplikasi Kita telah mempelajari bagaimana menguraikan fungsi periodik dengan periode 2 yang terdefinisi pada R sebagai deret Fourier. Deret
8 Hendra Gunawan 4. Deret Fourier pada Interval Sebarang dan Aplikasi Kita telah mempelajari bagaimana menguraikan fungsi periodik dengan periode 2 yang terdefinisi pada R sebagai deret Fourier. Deret
Program Perkuliahan Dasar Umum Sekolah Tinggi Teknologi Telkom Persamaan Diferensial Orde II
 Program Perkuliahan Dasar Umum Sekolah Tinggi Teknologi Telkom Persamaan Diferensial Orde II [MA4] PDB Orde II Bentuk umum : y + p(x)y + g(x)y = r(x) p(x), g(x) disebut koefisien jika r(x) = 0, maka Persamaan
Program Perkuliahan Dasar Umum Sekolah Tinggi Teknologi Telkom Persamaan Diferensial Orde II [MA4] PDB Orde II Bentuk umum : y + p(x)y + g(x)y = r(x) p(x), g(x) disebut koefisien jika r(x) = 0, maka Persamaan
SATUAN ACARA PERKULIAHAN JURUSAN TEKNIK INFORMATIKA ITP
 SATUAN ACARA PERKULIAHAN JURUSAN TEKNIK INFORMATIKA ITP Mata kuliah : Kalkulus II Kode Mata Kuliah : TIS2213 SKS : 3 Waktu Pertemuan : 16 kali Pertemuan Deskripsi : Mata kuliah Kalkulus II mempelajari
SATUAN ACARA PERKULIAHAN JURUSAN TEKNIK INFORMATIKA ITP Mata kuliah : Kalkulus II Kode Mata Kuliah : TIS2213 SKS : 3 Waktu Pertemuan : 16 kali Pertemuan Deskripsi : Mata kuliah Kalkulus II mempelajari
