16. Analisis Multi Resolusi
|
|
|
- Johan Sanjaya
- 6 tahun lalu
- Tontonan:
Transkripsi
1 16. Analisis Multi esolusi Esensi dari basis ortonormal yang dibangun oleh sebuah wavelet adalah sifat multi resolusi-nya, sehingga kita dapat menganalisis suatu signal pada berbagai frekuensi di suatu lokasi tertentu. Di bawah ini kita akan membahas apa yang dimaksud dengan analisis multi resolusi dan, pada pasal berikutnya, bagaimana kita dapat mengkontruksi sebuah wavelet dari suatu analisis multi resolusi Analisis Multi esolusi Keluarga subruang tertutup {V j : j Z} dari L 2 () yang memenuhi (a) V j V j+1 untuk setiap j Z; (b) f V j f(2 ) V j+1 untuk setiap j Z; (c) V j = {0}; j Z (d) V j = L 2 (); j Z (e) terdapat ϕ V 0 sedemikian sehingga {ϕ( k) : k Z} merupakan basis ortonormal untuk V 0, disebut analisis multi resolusi (AM) pada L 2 (). Fungsi ϕ pada (e) disebut fungsi skala dalam AM tersebut. Contoh 1. Misalkan V j = {f L 2 () : f konstan pada [2 j k, 2 j (k+1)), k Z}, j Z. Maka, {V j : j Z} memenuhi sifat (a) s/d (d) di atas. Sekarang misalkan ϕ = χ [0,1]. Maka, {ϕ( k) : k Z} membentuk basis ortonormal untuk V 0. Oleh karena itu, {V j : j Z} merupakan suatu AM pada L 2 (). 77
2 Untuk ilustrasi, fungsi f V 0 berbentuk seperti misalnya Teorema. Misalkan {V j : j Z} suatu AM pada L 2 (). Maka, (i) Untuk setiap j Z, f V 0 f(2 j ) V j ; (ii) Untuk setiap k Z, f V 0 f( k) V 0 ; (iii) Untuk setiap j, k Z, f V j f( 2 j k) V j ; (iv) Untuk setiap j, k Z, f V 0 f(2 j k) V j. Bukti. (i) Gunakan sifat (b) dan induksi. (ii) Misalkan f V 0 dan k Z. Maka, berdasarkan sifat (e), f(x) = m Z f, ϕ( m) ϕ(x m), dan karenanya f(x k) = m Z f, ϕ( m) ϕ(x k m). Namun, f, ϕ( m) = f( k), ϕ( k m). Akibatnya, f(x k) = m Z f( k), ϕ( k m) ϕ(x k m) V 0 karena {ϕ( m) : m Z} = {ϕ( k m) : m Z} basis ortonormal untuk V 0. (iii) Gunakan (i) dan (ii). (iv) Gunakan (i) dan (iii). Akibat. Misalkan {V j : j Z} suatu AM pada L 2 () dan ϕ V 0 fungsi skala dalam AM tersebut. Definisikan ϕ j,k (x) = 2 j/2 ϕ(2 j x k), j, k Z. 78
3 Maka, untuk setiap j Z, {ϕ j,k : k Z} merupakan basis ortonormal untuk V j. Bukti. Misalkan j Z. Maka, {ϕ j,k : k Z} merupakan himpunan ortonormal, karena ϕ j,k, ϕ j,m = 2 j ϕ(2 j x k)ϕ(2 j x m)dx = ϕ(x k)ϕ(x m)dx = δ k,m. Selanjutnya, misalkan f V j. Maka, f(2 j ) V 0, dan karenanya f(2 j x) = k Z f(2 j ), ϕ( k) ϕ(x k). Substitusi x = 2 j x memberikan f(x ) = k Z f, ϕ j,k ϕ j,k (x ). Ini membuktikan bahwa {ϕ j,k : k Z} lengkap. Dengan demikian {ϕ j,k : k Z} merupakan basis ortonormal untuk V j Konstruksi Wavelet Misalkan {V j : j Z} suatu AM pada L 2 (). Misalkan W 0 komplemen ortogonal dari V 0 relatif terhadap V 1, yakni V 1 = V 0 W 0. Kemudian, untuk setiap j Z, definisikan W j = {f(2 j ) : f W 0 }. Maka, V j+1 = V j W j, j Z. Karena V j {0} untuk j, kita peroleh j V j+1 = W n, j Z; n= 79
4 dan karena V j L 2 () untuk j, kita peroleh L 2 () = n= Untuk memperoleh wavelet, kita harus mencari ψ W 0 sedemikian sehingga {ψ( k) : k Z} merupakan basis ortonormal untuk W 0. Selanjutnya dapat diperiksa bahwa untuk setiap j Z, {2 j/2 ψ(2 j k) : k Z} membentuk basis ortonormal untuk W j. Dengan demikian, {ψ j,k wavelet yang diinginkan. W n. : j, k Z} merupakan basis ortonormal untuk L 2 () atau ψ adalah Contoh 2. Melanjutkan Contoh 1, wavelet ψ yang kita cari adalah 1, jika 0 x < 1 2 ; ψ(x) = 1, jika 1 2 x < 1; 0, jika x < 0 atau x 1. Periksa bahwa ϕ ψ dan {ψ( k) : k Z} merupakan basis ortonormal untuk W 0. Basis yang dibangun oleh ψ tak lain adalah basis Haar yang dibahas pada Bab Wavelet Bertumpuan Kompak dan Kemulusannya Wavelet Haar merupakan sebuah contoh wavelet yang mempunyai tumpuan kompak, yakni [0, 1]. Pada pasal ini kita akan melihat bahwa wavelet bertumpuan kompak tak mungkin merupakan fungsi C ; semulus-mulusnya ia hanya dapat merupakan fungsi di C n untuk suatu n yang terhingga. Teorema. Misalkan ψ kontinu pada dan memenuhi ψ(x) C (1 + x ) 1+ϵ untuk suatu ϵ > 0. Jika {ψ j,k : j, k Z} ortonormal di L 2 (), maka ψ(x) dx = 0. Bukti. Misalkan a = 2 j k, suatu bilangan diadik, sedemikian sehingga ψ(a) 0. [Karena ψ 2 = 1 dan ψ kontinu, bilangan a demikian dijamin ada.] Berdasarkan hipotesis, kita mempunyai ψ(x)ψ(2 j x k)dx = 0, (j, k) (0, 0). 80
5 Dengan mengambil k = 2 j j k dengan j > maks{j, 0}, kesamaan di atas menjadi ψ(x)ψ(2 j (x a))dx = 0. Sekarang misalkan y = 2 j (x a). Maka ψ(a + 2 j y)ψ(y)dy = 0. Berdasarkan Teorema Kekonvergenan Terdominasi Lebesgue, integral di ruas kiri menuju ψ(a) ψ(y)dy bila j, sehingga kita peroleh ψ(y)dy = 0 karena ψ(a) 0. Catatan. Teorema di atas dapat diperluas dengan menghapuskan asumsi bahwa ψ kontinu, namun buktinya lebih rumit. Lihat Hernandez & Weiss, Proposisi 3.6. Teorema. Misalkan r suatu bilangan bulat tak negatif dan ψ sebuah fungsi di C r () sedemikian sehingga ψ(x) C (1 + x ) r+1+ϵ untuk suatu ϵ > 0, dan ψ (m) terbatas pada untuk m = 0, 1,..., r. Jika {ψ j,k : j, k Z} ortonormal di L 2 (), maka x m ψ(x) dx = 0, yakni, momen ke-m dari ψ bernilai 0, untuk m = 0, 1,..., r. Bukti. Lihat Hernandez & Weiss. Akibat. Misalkan ψ L 2 () sebuah fungsi Schwartz sedemikian sehingga {ψ j,k : j, k Z} merupakan himpunan ortonormal di L 2 (). Maka semua momen dari ψ bernilai 0 atau, setara dengan itu, dm ψ dξ m (0) = 0 untuk setiap m = 0, 1, 2,.... Bukti. Jelas, karena setiap fungsi Schwartz merupakan fungsi C dan memenuhi ketaksamaan pada teorema di atas untuk setiap bilangan bulat tak negatif r, dan dm ψ dξ m (0) = ( 2πi) m xm ψ(x) dx untuk setiap m = 0, 1, 2,
6 Akibat. Misalkan ψ L 2 () sebuah fungsi bertumpuan kompak sedemikian sehingga C. Maka {ψ j,k : j, k Z} tidak mungkin merupakan himpunan ortonormal di L 2 (). Bukti. Jika {ψ j,k : j, k Z} merupakan himpunan ortonormal di L 2 (), maka menurut teorema di atas semua momen dari ψ bernilai 0. Karena itu untuk semua polinom p(x), kita mempunyai p(x)ψ(x) dx = 0. Karena ψ bertumpuan kompak, diberikan ϵ > 0 kita dapat menemukan suatu polinom p(x) sedemikian sehingga sup x K ψ(x) p(x) < ϵ, dengan K menyatakan tumpuan ψ (berdasarkan Teorema Aproksimasi Weierstrass). Akibatnya ψ 2 = ψ(x)ψ(x) dx = [ψ(x) p(x)]ψ(x) dx K ϵ ψ(x) dx = ϵ ψ 1. K Mengingat ψ 1 < dan ϵ > 0 sebarang, kita haruslah mempunyai ψ 2 2 = 0, yang bertentangan dengan keortonormalan {ψ j,k : j, k Z} Teorema Sampling Teorema di bawah ini merupakan bentuk lain dari Teorema Sampling Shannon yang dibahas pada Teorema. Misalkan V j = {f L 2 () : f konstan pada [2 j k, 2 j (k + 1)), k Z}, j Z dan ϕ = χ [0,1). Maka, untuk setiap f V j, berlaku f(x) = f(2 j k)ϕ(2 j x k). k Z Bukti. Kita tahu bahwa {V j } merupakan suatu AM pada L 2 () dan ϕ fungsi skala, yakni {ϕ( k) : k Z} membentuk basis ortonormal untuk V 0. Selanjutnya, keluarga fungsi ϕ j,k (x) = 2 j/2 ϕ(2 j x k), j, k Z membentuk basis ortonormal untuk V j. Karena itu, untuk setiap f V j, berlaku f = k Z f, ϕ j,k ϕ j,k, 82
7 dengan f, ϕ j,k = 2 j/2 = 2 j/2 2 = 2 j/2 2 f(x)ϕ(2 j x k)dx j (k+1) 2 j k j (k+1) 2 j k f(x)dx f(2 j k)dx = 2 j/2 f(2 j k), sesuai dengan yang dinyatakan. Teorema. Misalkan {ψ j,k : j, k Z} basis ortonormal yang diperoleh dari wavelet ψ. Maka, f = (f ψ j,0 )(2 j k)ψ j,k j Z k Z dalam norma L 2 (). (Di sini, g(x) = g( x).) Bukti. Tuliskan Namun, Jadi, seperti yang diinginkan. f = j Z f, ψ j,k = = = = f = j Z f, ψ j,k ψ j,k. k Z f(x)ψ j,k (x) dx f(x)2 j/2 ψ(2 j x k) dx f(x)ψ j,0 (x 2 j k) dx f(x) ψ j,0 (2 j k x) dx = f ψ j,0 (2 j k). (f ψ j,0 )(2 j k)ψ j,k, k Z 16.5 Soal Latihan 1. Misalkan {V j } suatu AM pada L 2 (). Buktikan bahwa V j+1 = V j W j, j Z. 83
8 2. Buktikan jika {ψ( k) : k Z} merupakan basis ortonormal untuk W 0, maka untuk setiap j Z, {2 j/2 ψ(2 j k) : k Z} merupakan basis ortonormal untuk W j. 3. Tunjukkan jika ψ merupakan fungsi C yang bertumpuan kompak pada, maka ψ memenuhi ketaksamaan ψ(x) untuk r = 0, 1, 2,... dan ϵ > 0 sembarang. C (1 + x ) r+1+ϵ 84
11. Konvolusi. Misalkan f dan g fungsi yang terdefinisi pada R. Konvolusi dari f dan g adalah fungsi f g yang didefinisikan sebagai.
 11. Konvolusi Operasi konvolusi yang akan kita bahas di sini sebetulnya pernah kita jumpai pada pembahasan deret Fourier (ketika membuktikan kekonvergenan jumlah parsialnya). Operasi konvolusi merupakan
11. Konvolusi Operasi konvolusi yang akan kita bahas di sini sebetulnya pernah kita jumpai pada pembahasan deret Fourier (ketika membuktikan kekonvergenan jumlah parsialnya). Operasi konvolusi merupakan
12. Teorema Inversi Fourier dan Transformasi Fourier di L 2 (R)
 1. Teorema Inversi Fourier dan Transformasi Fourier di L (R) 1.1 Teorema Inversi Fourier Dari hasil hitung-hitungan kasar di awal bagian ke-10, kita ingin membuktikan bahwa, dalam kondisi tertentu, kita
1. Teorema Inversi Fourier dan Transformasi Fourier di L (R) 1.1 Teorema Inversi Fourier Dari hasil hitung-hitungan kasar di awal bagian ke-10, kita ingin membuktikan bahwa, dalam kondisi tertentu, kita
DASAR-DASAR ANALISIS MATEMATIKA
 (Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. November 19, 2007 Secara geometris, f kontinu di suatu titik berarti bahwa grafiknya tidak terputus
(Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. November 19, 2007 Secara geometris, f kontinu di suatu titik berarti bahwa grafiknya tidak terputus
9. Teori Aproksimasi
 44 Hendra Gunawan 9 Teori Aproksimasi Mulai bab ini tema kita adalah aproksimasi fungsi dan interpolasi Diberikan sebuah fungsi f, baik secara utuh ataupun hanya beberapilai di titik-titik tertentu saja,
44 Hendra Gunawan 9 Teori Aproksimasi Mulai bab ini tema kita adalah aproksimasi fungsi dan interpolasi Diberikan sebuah fungsi f, baik secara utuh ataupun hanya beberapilai di titik-titik tertentu saja,
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
DASAR-DASAR ANALISIS MATEMATIKA
 (Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. December 1, 2007 Diberikan sebuah fungsi yang terdefinisi pada interval (a, b) kecuali mungkin di
(Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. December 1, 2007 Diberikan sebuah fungsi yang terdefinisi pada interval (a, b) kecuali mungkin di
11. FUNGSI MONOTON (DAN FUNGSI KONVEKS)
 11. FUNGSI MONOTON (DAN FUNGSI KONVEKS) 11.1 Definisi dan Limit Fungsi Monoton Misalkan f terdefinisi pada suatu himpunan H. Kita katakan bahwa f naik pada H apabila untuk setiap x, y H dengan x < y berlaku
11. FUNGSI MONOTON (DAN FUNGSI KONVEKS) 11.1 Definisi dan Limit Fungsi Monoton Misalkan f terdefinisi pada suatu himpunan H. Kita katakan bahwa f naik pada H apabila untuk setiap x, y H dengan x < y berlaku
BAGIAN KEDUA. Fungsi, Limit dan Kekontinuan, Turunan
 BAGIAN KEDUA Fungsi, Limit dan Kekontinuan, Turunan 51 52 Hendra Gunawan Pengantar Analisis Real 53 6. FUNGSI 6.1 Fungsi dan Grafiknya Konsep fungsi telah dipelajari oleh Gottfried Wilhelm von Leibniz
BAGIAN KEDUA Fungsi, Limit dan Kekontinuan, Turunan 51 52 Hendra Gunawan Pengantar Analisis Real 53 6. FUNGSI 6.1 Fungsi dan Grafiknya Konsep fungsi telah dipelajari oleh Gottfried Wilhelm von Leibniz
17. Transformasi Wavelet Kontinu dan Frame
 17. Transformasi Wavelet Kontinu dan Frame Pada 16 kita mempelajari basis ortonormal {e 2πimx g(x n)} dengan g = χ [,1). Transformasi f f(x)g(x n)e 2πimx dx, m, n Z, dikenal sebagai transformasi Fourier
17. Transformasi Wavelet Kontinu dan Frame Pada 16 kita mempelajari basis ortonormal {e 2πimx g(x n)} dengan g = χ [,1). Transformasi f f(x)g(x n)e 2πimx dx, m, n Z, dikenal sebagai transformasi Fourier
7. Transformasi Fourier
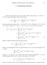 Pengantar Analisis Fourier dan eori Aproksimasi 33 7. ransformasi Fourier Pada bab sebelumnya kita telah melihat bahwa setiap fungsi f L 1 ([0, 1] L ([0, 1] dapat dinyatakan sebagai deret Fourier f(x =
Pengantar Analisis Fourier dan eori Aproksimasi 33 7. ransformasi Fourier Pada bab sebelumnya kita telah melihat bahwa setiap fungsi f L 1 ([0, 1] L ([0, 1] dapat dinyatakan sebagai deret Fourier f(x =
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
DASAR-DASAR TEORI RUANG HILBERT
 DASAR-DASAR TEORI RUANG HILBERT Herry P. Suryawan 1 Geometri Ruang Hilbert Definisi 1.1 Ruang vektor kompleks V disebut ruang hasilkali dalam jika ada fungsi (.,.) : V V C sehingga untuk setiap x, y, z
DASAR-DASAR TEORI RUANG HILBERT Herry P. Suryawan 1 Geometri Ruang Hilbert Definisi 1.1 Ruang vektor kompleks V disebut ruang hasilkali dalam jika ada fungsi (.,.) : V V C sehingga untuk setiap x, y, z
DASAR-DASAR ANALISIS MATEMATIKA
 (Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. December 11, 2007 Misalkan f terdefinisi pada suatu himpunan H. Kita katakan bahwa f naik pada H apabila
(Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. December 11, 2007 Misalkan f terdefinisi pada suatu himpunan H. Kita katakan bahwa f naik pada H apabila
8. Deret Fourier yang Diperumum dan Hampiran Terbaik di L 2 (a, b)
 8. Deret Fourier yang Diperumum dan Hampiran Terbaik di L (a, b) 8.1 Deret Fourier yang Diperumum Jika {ϕ n } 1 adalah basis ortonormal untuk L (a, b) dan f L (a, b), maka f, ϕ n disebut koefisien Fourier
8. Deret Fourier yang Diperumum dan Hampiran Terbaik di L (a, b) 8.1 Deret Fourier yang Diperumum Jika {ϕ n } 1 adalah basis ortonormal untuk L (a, b) dan f L (a, b), maka f, ϕ n disebut koefisien Fourier
10. Transformasi Fourier
 10. Transformasi Fourier Dalam beberapa bab ke depan, kita akan membahas transformasi Fourier, sifatsifatnya, dan aplikasinya. Seperti halnya pada pembahasan deret Fourier, pendekatan yang diambil dalam
10. Transformasi Fourier Dalam beberapa bab ke depan, kita akan membahas transformasi Fourier, sifatsifatnya, dan aplikasinya. Seperti halnya pada pembahasan deret Fourier, pendekatan yang diambil dalam
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016. Hendra Gunawan
 MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 3. Topologi Garis Bilangan Real 3.1 Teori Limit Limit, supremum, dan infimum Titik limit 3.2 Himpunan Buka dan Himpunan Tutup 3.3
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 3. Topologi Garis Bilangan Real 3.1 Teori Limit Limit, supremum, dan infimum Titik limit 3.2 Himpunan Buka dan Himpunan Tutup 3.3
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
13. Aplikasi Transformasi Fourier
 13. plikasi ransformasi Fourier Misal adalah operator linear pada fungsi yang terdefinisi pada R dengan sifat: jika [f(x] = g(x, maka [f(x + s] = g(x + s untuk setiap s R. Maka, fungsi f(x = e ax (a C
13. plikasi ransformasi Fourier Misal adalah operator linear pada fungsi yang terdefinisi pada R dengan sifat: jika [f(x] = g(x, maka [f(x + s] = g(x + s untuk setiap s R. Maka, fungsi f(x = e ax (a C
BAB 4 KEKONSISTENAN PENDUGA DARI FUNGSI SEBARAN DAN FUNGSI KEPEKATAN WAKTU TUNGGU DARI PROSES POISSON PERIODIK DENGAN TREN FUNGSI PANGKAT
 29 BAB 4 KEKONSISTENAN PENDUGA DARI FUNGSI SEBARAN DAN FUNGSI KEPEKATAN WAKTU TUNGGU DARI PROSES POISSON PERIODIK DENGAN TREN FUNGSI PANGKAT 4.1 Perumusan Penduga Misalkan adalah proses Poisson nonhomogen
29 BAB 4 KEKONSISTENAN PENDUGA DARI FUNGSI SEBARAN DAN FUNGSI KEPEKATAN WAKTU TUNGGU DARI PROSES POISSON PERIODIK DENGAN TREN FUNGSI PANGKAT 4.1 Perumusan Penduga Misalkan adalah proses Poisson nonhomogen
BAB V KEKONVERGENAN BARISAN PADA DAN KETERKAITAN DENGAN. Pada subbab 4.1 telah dibahas beberapa sifat dasar yang berlaku pada koleksi
 BAB V KEKONVERGENAN BARISAN PADA DAN KETERKAITAN DENGAN Pada subbab 4.1 telah dibahas beberapa sifat dasar yang berlaku pada koleksi semua fungsi yang terintegralkan Lebesgue, 1. Sebagaimana telah dirumuskan
BAB V KEKONVERGENAN BARISAN PADA DAN KETERKAITAN DENGAN Pada subbab 4.1 telah dibahas beberapa sifat dasar yang berlaku pada koleksi semua fungsi yang terintegralkan Lebesgue, 1. Sebagaimana telah dirumuskan
0. Pendahuluan. 0.1 Notasi dan istilah, bilangan kompleks
 0. Pendahuluan Analisis Fourier mempelajari berbagai teknik menganalisis sebuah fungsi dengan menguraikannya sebagai deret atau integral fungsi tertentu (yang sifat-sifatnya telah kita kenal dengan baik,
0. Pendahuluan Analisis Fourier mempelajari berbagai teknik menganalisis sebuah fungsi dengan menguraikannya sebagai deret atau integral fungsi tertentu (yang sifat-sifatnya telah kita kenal dengan baik,
4. Deret Fourier pada Interval Sebarang dan Aplikasi
 4. Deret Fourier pada Interval Sebarang dan Aplikasi Kita telah mempelajari bagaimana menguraikan fungsi periodik dengan periode 2 yang terdefinisi pada R sebagai deret Fourier. Deret trigonometri tersebut
4. Deret Fourier pada Interval Sebarang dan Aplikasi Kita telah mempelajari bagaimana menguraikan fungsi periodik dengan periode 2 yang terdefinisi pada R sebagai deret Fourier. Deret trigonometri tersebut
Fourier Analysis & Its Applications in PDEs - Part II
 Fourier Analysis & Its Applications in PDEs Hendra Gunawan http://personal.fmipa.itb.ac.id/hgunawan/ Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA WIDE 2010 5-6 August
Fourier Analysis & Its Applications in PDEs Hendra Gunawan http://personal.fmipa.itb.ac.id/hgunawan/ Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA WIDE 2010 5-6 August
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
III. HASIL DAN PEMBAHASAN
 III. HASIL DAN PEMBAHASAN 3.1 Perumusan Masalah Misalkan adalah proses Poisson nonhomogen pada interval dengan fungsi intensitas yang tidak diketahui. Fungsi intensitas diasumsikan terintegralkan lokal
III. HASIL DAN PEMBAHASAN 3.1 Perumusan Masalah Misalkan adalah proses Poisson nonhomogen pada interval dengan fungsi intensitas yang tidak diketahui. Fungsi intensitas diasumsikan terintegralkan lokal
BAB 3 REVIEW SIFAT-SIFAT STATISTIK PENDUGA KOMPONEN PERIODIK
 BAB 3 REVIEW SIFAT-SIFAT STATISTIK PENDUGA KOMPONEN PERIODIK 3. Perumusan Penduga Misalkan N adalah proses Poisson non-homogen pada interval 0, dengan fungsi intensitas yang tidak diketahui. Fungsi intensitas
BAB 3 REVIEW SIFAT-SIFAT STATISTIK PENDUGA KOMPONEN PERIODIK 3. Perumusan Penduga Misalkan N adalah proses Poisson non-homogen pada interval 0, dengan fungsi intensitas yang tidak diketahui. Fungsi intensitas
BAB III FUNGSI TERUKUR LEBESGUE. Setelah dibahas mengenai ukuran Lebesgue dan beberapa sifatnya pada
 BAB III FUNGSI TERUKUR LEBESGUE Setelah dibahas mengenai ukuran Lebesgue dan beberapa sifatnya pada Bab II, selanjutnya pada bab ini akan dipelajari gagasan mengenai fungsi terukur Lebesgue. Gagasan mengenai
BAB III FUNGSI TERUKUR LEBESGUE Setelah dibahas mengenai ukuran Lebesgue dan beberapa sifatnya pada Bab II, selanjutnya pada bab ini akan dipelajari gagasan mengenai fungsi terukur Lebesgue. Gagasan mengenai
DASAR-DASAR ANALISIS MATEMATIKA
 (Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. December 26, 2007 Misalkan f kontinu pada interval [a, b]. Apakah masuk akal untuk membahas luas daerah
(Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. December 26, 2007 Misalkan f kontinu pada interval [a, b]. Apakah masuk akal untuk membahas luas daerah
Memahami definisi barisan tak hingga dan deret tak hingga, dan juga dapat menentukan
 4 BARISAN TAK HINGGA DAN DERET TAK HINGGA JUMLAH PERTEMUAN : 5 PERTEMUAN TUJUAN INSTRUKSIONAL KHUSUS : Memahami definisi barisan tak hingga dan deret tak hingga, dan juga dapat menentukan kekonvergenan
4 BARISAN TAK HINGGA DAN DERET TAK HINGGA JUMLAH PERTEMUAN : 5 PERTEMUAN TUJUAN INSTRUKSIONAL KHUSUS : Memahami definisi barisan tak hingga dan deret tak hingga, dan juga dapat menentukan kekonvergenan
BAB III INTEGRAL LEBESGUE. Pada bab sebelumnya telah disebutkan bahwa ruang dibangun oleh
 BAB III INTEGRAL LEBESGUE Pada bab sebelumnya telah disebutkan bahwa ruang dibangun oleh fungsi-fungsi terukur dan memenuhi sifat yang berkaitan dengan integral Lebesgue. Kajian mengenai keterukuran suatu
BAB III INTEGRAL LEBESGUE Pada bab sebelumnya telah disebutkan bahwa ruang dibangun oleh fungsi-fungsi terukur dan memenuhi sifat yang berkaitan dengan integral Lebesgue. Kajian mengenai keterukuran suatu
KALKULUS BAB II FUNGSI, LIMIT, DAN KEKONTINUAN. DEPARTEMEN TEKNIK KIMIA Universitas Indonesia
 KALKULUS BAB II FUNGSI, LIMIT, DAN KEKONTINUAN DEPARTEMEN TEKNIK KIMIA Universitas Indonesia BAB II. FUNGSI, LIMIT, DAN KEKONTINUAN Fungsi dan Operasi pada Fungsi Beberapa Fungsi Khusus Limit dan Limit
KALKULUS BAB II FUNGSI, LIMIT, DAN KEKONTINUAN DEPARTEMEN TEKNIK KIMIA Universitas Indonesia BAB II. FUNGSI, LIMIT, DAN KEKONTINUAN Fungsi dan Operasi pada Fungsi Beberapa Fungsi Khusus Limit dan Limit
ANALISIS REAL. (Semester I Tahun ) Hendra Gunawan. October 10, Dosen FMIPA - ITB
 (Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. October 10, 2011 Pemahaman yang baik tentang fungsi kontinu merupakan hal yang penting dalam analisis. Dalam optimisasi,
(Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. October 10, 2011 Pemahaman yang baik tentang fungsi kontinu merupakan hal yang penting dalam analisis. Dalam optimisasi,
Catatan Kuliah MA1123 Kalkulus Elementer I
 Catatan Kuliah MA1123 Kalkulus Elementer I Oleh Hendra Gunawan, Ph.D. Departemen Matematika ITB Sasaran Belajar Setelah mempelajari materi Kalkulus Elementer I, mahasiswa diharapkan memiliki (terutama):
Catatan Kuliah MA1123 Kalkulus Elementer I Oleh Hendra Gunawan, Ph.D. Departemen Matematika ITB Sasaran Belajar Setelah mempelajari materi Kalkulus Elementer I, mahasiswa diharapkan memiliki (terutama):
Analisis Riil II: Diferensiasi
 Definisi Turunan Definisi dan Teorema Aturan Rantai Fungsi Invers Definisi (Turunan) Misalkan I R sebuah interval, f : I R, dan c I. Bilangan riil L dikatakan turunan dari f di c jika diberikan sebarang
Definisi Turunan Definisi dan Teorema Aturan Rantai Fungsi Invers Definisi (Turunan) Misalkan I R sebuah interval, f : I R, dan c I. Bilangan riil L dikatakan turunan dari f di c jika diberikan sebarang
BAB III FUNGSI YOUNG DAN KOMPLEMEN YOUNG
 BAB III FUNGSI YOUNG DAN KOMPLEMEN YOUNG Pada bab ini, dibahas tentang definisi fungsi Young dengan domain real diperluas dan komplemennya. Sebelumnya, dalam studi deret Fourier, W. H. Young telah menganalisis
BAB III FUNGSI YOUNG DAN KOMPLEMEN YOUNG Pada bab ini, dibahas tentang definisi fungsi Young dengan domain real diperluas dan komplemennya. Sebelumnya, dalam studi deret Fourier, W. H. Young telah menganalisis
BAB 3 REVIEW PENDUGAAN FUNGSI INTENSITAS LOKAL DAN GLOBAL DARI PROSES POISSON PERIODIK DENGAN TREN FUNGSI PANGKAT
 9 BAB 3 REVIEW PENDUGAAN FUNGSI INTENSITAS LOKAL DAN GLOBAL DARI PROSES POISSON PERIODIK DENGAN TREN FUNGSI PANGKAT Misalkan adalah proses Poisson nonhomogen pada interval dengan fungsi intensitas yang
9 BAB 3 REVIEW PENDUGAAN FUNGSI INTENSITAS LOKAL DAN GLOBAL DARI PROSES POISSON PERIODIK DENGAN TREN FUNGSI PANGKAT Misalkan adalah proses Poisson nonhomogen pada interval dengan fungsi intensitas yang
4. Deret Fourier pada Interval Sebarang dan Aplikasi
 8 Hendra Gunawan 4. Deret Fourier pada Interval Sebarang dan Aplikasi Kita telah mempelajari bagaimana menguraikan fungsi periodik dengan periode 2 yang terdefinisi pada R sebagai deret Fourier. Deret
8 Hendra Gunawan 4. Deret Fourier pada Interval Sebarang dan Aplikasi Kita telah mempelajari bagaimana menguraikan fungsi periodik dengan periode 2 yang terdefinisi pada R sebagai deret Fourier. Deret
BAB I PENDAHULUAN. Integral Lebesgue merupakan suatu perluasan dari integral Riemann.
 BAB I PENDAHULUAN 1.1 Latar Belakang Masalah Integral Lebesgue merupakan suatu perluasan dari integral Riemann. Sebagaimana telah diketahui, pengkonstruksian integral Riemann dilakukan dengan cara pemartisian
BAB I PENDAHULUAN 1.1 Latar Belakang Masalah Integral Lebesgue merupakan suatu perluasan dari integral Riemann. Sebagaimana telah diketahui, pengkonstruksian integral Riemann dilakukan dengan cara pemartisian
16. BARISAN FUNGSI. 16.1 Barisan Fungsi dan Kekonvergenan Titik Demi Titik
 16. BARISAN FUNGSI 16.1 Barisan Fungsi dan Kekonvergenan Titik Demi Titik Bila pada bab-bab sebelumnya kita membahas fungsi sebagai sebuah objek individual, maka pada bab ini dan selanjutnya kita akan
16. BARISAN FUNGSI 16.1 Barisan Fungsi dan Kekonvergenan Titik Demi Titik Bila pada bab-bab sebelumnya kita membahas fungsi sebagai sebuah objek individual, maka pada bab ini dan selanjutnya kita akan
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016. Hendra Gunawan
 MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 4.2 Sifat-Sifat Fungsi Kontinu Diberikan f dan g, keduanya terdefinisi pada himpunan A, kita definisikan f + g, f g, fg, f/g secara
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 4.2 Sifat-Sifat Fungsi Kontinu Diberikan f dan g, keduanya terdefinisi pada himpunan A, kita definisikan f + g, f g, fg, f/g secara
ANALISIS REAL. (Semester I Tahun ) Hendra Gunawan. October 3, Dosen FMIPA - ITB
 (Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. October 3, 2011 6.3 Limit Sepihak, Limit di Tak Hingga, dan Limit Tak Hingga Bila sebelumnya kita mempelajari limit barisan,
(Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. October 3, 2011 6.3 Limit Sepihak, Limit di Tak Hingga, dan Limit Tak Hingga Bila sebelumnya kita mempelajari limit barisan,
BAB IV REDUKSI BIAS PADA PENDUGAAN
 BAB IV REDUKSI BIAS PADA PENDUGAAN 4.1. Asimtotik Orde-2 Berdasarkan hasil simulasi pada Helmers dan Mangku (2007) kasus kernel seragam, aproksimasi asimtotik orde pertama pada ragam dan bias, gagal memprediksikan
BAB IV REDUKSI BIAS PADA PENDUGAAN 4.1. Asimtotik Orde-2 Berdasarkan hasil simulasi pada Helmers dan Mangku (2007) kasus kernel seragam, aproksimasi asimtotik orde pertama pada ragam dan bias, gagal memprediksikan
3 LIMIT DAN KEKONTINUAN
 Menurut Bartle dan Sherbet (1994), Analisis matematika secara umum dipahami sebagai tubuh matematika yang dibangun oleh berbagai konsep limit. Pada bab sebelumnya kita telah mempelajari limit barisan,
Menurut Bartle dan Sherbet (1994), Analisis matematika secara umum dipahami sebagai tubuh matematika yang dibangun oleh berbagai konsep limit. Pada bab sebelumnya kita telah mempelajari limit barisan,
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231. Pengantar Analisis Real. Hendra Gunawan, Ph.D. Semester II, Tahun
 MA3231 Pengantar Analisis Real Semester II, Tahun 2016-2017 Hendra Gunawan, Ph.D. Bab 7 Limit dan Kekontinuan 2 Isaac Newton (1643-1727) Isaac Newton adalah seorang fisikawan & matematikawan Inggris yang
MA3231 Pengantar Analisis Real Semester II, Tahun 2016-2017 Hendra Gunawan, Ph.D. Bab 7 Limit dan Kekontinuan 2 Isaac Newton (1643-1727) Isaac Newton adalah seorang fisikawan & matematikawan Inggris yang
Hendra Gunawan. 11 Oktober 2013
 MA1101 MATEMATIKA 1A Hendra Gunawan Semester I, 2013/2014 11 Oktober 2013 Latihan (Kuliah yang Lalu) Dengan memperhatikan: daerah asal dan daerahhasilnya, titik titik potong dengan sumbu koordinat, asimtot
MA1101 MATEMATIKA 1A Hendra Gunawan Semester I, 2013/2014 11 Oktober 2013 Latihan (Kuliah yang Lalu) Dengan memperhatikan: daerah asal dan daerahhasilnya, titik titik potong dengan sumbu koordinat, asimtot
TUJUAN INSTRUKSIONAL KHUSUS
 PREVIEW KALKULUS TUJUAN INSTRUKSIONAL KHUSUS Mahasiswa mampu: menyebutkan konsep-konsep utama dalam kalkulus dan contoh masalah-masalah yang memotivasi konsep tersebut; menjelaskan menyebutkan konsep-konsep
PREVIEW KALKULUS TUJUAN INSTRUKSIONAL KHUSUS Mahasiswa mampu: menyebutkan konsep-konsep utama dalam kalkulus dan contoh masalah-masalah yang memotivasi konsep tersebut; menjelaskan menyebutkan konsep-konsep
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016. Hendra Gunawan
 MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 3.2 Himpunan Buka dan Himpunan Tutup Titik limit dari suatu himpunan tidak harus merupakan anggota himpunan tersebut. Pada interval
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 3.2 Himpunan Buka dan Himpunan Tutup Titik limit dari suatu himpunan tidak harus merupakan anggota himpunan tersebut. Pada interval
BAB 2 RUANG HILBERT. 2.1 Definisi Ruang Hilbert
 BAB 2 RUANG HILBERT Pokok pembicaraan kita dalam tugas akhir ini berpangkal pada teori ruang Hilbert. Untuk itu di bab ini akan diberikan definisi ruang Hilbert dan ciri-cirinya, separabilitas ruang Hilbert,
BAB 2 RUANG HILBERT Pokok pembicaraan kita dalam tugas akhir ini berpangkal pada teori ruang Hilbert. Untuk itu di bab ini akan diberikan definisi ruang Hilbert dan ciri-cirinya, separabilitas ruang Hilbert,
ANALISIS REAL. (Semester I Tahun ) Hendra Gunawan. August 18, Dosen FMIPA - ITB
 (Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. August 18, 2011 Kita telah mencatat sebelumnya bahwa supremum dan infimum suatu himpunan tidak harus merupakan anggota himpunan
(Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. August 18, 2011 Kita telah mencatat sebelumnya bahwa supremum dan infimum suatu himpunan tidak harus merupakan anggota himpunan
Hendra Gunawan. KK Analisis & Geometri FMIPA-ITB. Bandung, Maret 2001 [Edisi Revisi II: Mei 2014]
![Hendra Gunawan. KK Analisis & Geometri FMIPA-ITB. Bandung, Maret 2001 [Edisi Revisi II: Mei 2014] Hendra Gunawan. KK Analisis & Geometri FMIPA-ITB. Bandung, Maret 2001 [Edisi Revisi II: Mei 2014]](/thumbs/72/67819562.jpg) Analisis Fourier dan Wavelet 1 Catatan Kuliah Analisis Fourier dan Wavelet Oleh Hendra Gunawan KK Analisis & Geometri FMIPA-ITB Bandung, Maret 2001 [Edisi Revisi II: Mei 2014] 1 2 Hendra Gunawan Daftar
Analisis Fourier dan Wavelet 1 Catatan Kuliah Analisis Fourier dan Wavelet Oleh Hendra Gunawan KK Analisis & Geometri FMIPA-ITB Bandung, Maret 2001 [Edisi Revisi II: Mei 2014] 1 2 Hendra Gunawan Daftar
UNIVERSITAS PENDIDIKAN INDONESIA
 Ruang Norm Sumanang Muhtar Gozali UNIVERSITAS PENDIDIKAN INDONESIA Definisi. Misalkan suatu ruang vektor atas. Norm pada didefinisikan sebagai fungsi. : yang memenuhi N1. 0 N2. 0 0 N3.,, N4.,, Kita dapat
Ruang Norm Sumanang Muhtar Gozali UNIVERSITAS PENDIDIKAN INDONESIA Definisi. Misalkan suatu ruang vektor atas. Norm pada didefinisikan sebagai fungsi. : yang memenuhi N1. 0 N2. 0 0 N3.,, N4.,, Kita dapat
Analisis Fourier dan Wavelet
 0 Hendra Gunawan Analisis Fourier dan Wavelet Hendra Gunawan KK Analisis & Geometri FMIPA-ITB Bandung, 2017 Analisis Fourier dan Wavelet 1 Daftar Isi Kata Pengantar 5 0 Pendahuluan 7 0.1 Notasi dan istilah,
0 Hendra Gunawan Analisis Fourier dan Wavelet Hendra Gunawan KK Analisis & Geometri FMIPA-ITB Bandung, 2017 Analisis Fourier dan Wavelet 1 Daftar Isi Kata Pengantar 5 0 Pendahuluan 7 0.1 Notasi dan istilah,
ANALISIS NUMERIK LANJUT. Hendra Gunawan, Ph.D. 2006/2007
 ANALISIS NUMERIK LANJUT Hendra Gunawan, Ph.D. 2006/2007 BAB I. RUANG LINEAR Pelajari definisi dan contoh: ruang linear (hal. 1-3); subruang (hal. 3); kombinasi linear (hal. 4); bebas/bergantung linear
ANALISIS NUMERIK LANJUT Hendra Gunawan, Ph.D. 2006/2007 BAB I. RUANG LINEAR Pelajari definisi dan contoh: ruang linear (hal. 1-3); subruang (hal. 3); kombinasi linear (hal. 4); bebas/bergantung linear
TRANSFORMASI WAVELET DISKRIT PADA SINTETIK PEMBANGKIT SINYAL ELEKTROKARDIOGRAM
 Saintia Matematika ISSN: 2337-9197 Vol. 02, No. 01 (2014), pp. 95 104. TRANSFORMASI WAVELET DISKRIT PADA SINTETIK PEMBANGKIT SINYAL ELEKTROKARDIOGRAM Yedidia Panca, Tulus, Esther Nababan Abstrak. Transformasi
Saintia Matematika ISSN: 2337-9197 Vol. 02, No. 01 (2014), pp. 95 104. TRANSFORMASI WAVELET DISKRIT PADA SINTETIK PEMBANGKIT SINYAL ELEKTROKARDIOGRAM Yedidia Panca, Tulus, Esther Nababan Abstrak. Transformasi
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016. Hendra Gunawan
 MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 5. Kalkulus Diferensial 5.1 Konsep Turunan Beberapa Definisi yang Setara Kekontinuan dan Keterdiferensialan secara Kontinu 5.2 Sifat-Sifat
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 5. Kalkulus Diferensial 5.1 Konsep Turunan Beberapa Definisi yang Setara Kekontinuan dan Keterdiferensialan secara Kontinu 5.2 Sifat-Sifat
BAB IV SEBARAN ASIMTOTIK PENDUGA TURUNAN PERTAMA DAN KEDUA DARI KOMPONEN PERIODIK FUNGSI INTENSITAS PROSES POISSON PERIODIK DENGAN TREN LINEAR
 3 BAB IV SEBARAN ASIMTOTIK PENDUGA TURUNAN PERTAMA DAN KEDUA DARI KOMPONEN PERIODIK FUNGSI INTENSITAS PROSES POISSON PERIODIK DENGAN TREN LINEAR 4.. Sebaran asimtotik dari,, Teorema 4. ( Normalitas Asimtotik
3 BAB IV SEBARAN ASIMTOTIK PENDUGA TURUNAN PERTAMA DAN KEDUA DARI KOMPONEN PERIODIK FUNGSI INTENSITAS PROSES POISSON PERIODIK DENGAN TREN LINEAR 4.. Sebaran asimtotik dari,, Teorema 4. ( Normalitas Asimtotik
Contoh-contoh soal induksi matematika
 Contoh-contoh soal induksi matematika Buktikan bahwa 2 n > n + 20 untuk setiap bilangan bulat n 5. (i) Basis induksi : Untuk n = 5, kita peroleh 2 5 > 5 + 20 adalah suatu pernyataan yang benar. (ii) Langkah
Contoh-contoh soal induksi matematika Buktikan bahwa 2 n > n + 20 untuk setiap bilangan bulat n 5. (i) Basis induksi : Untuk n = 5, kita peroleh 2 5 > 5 + 20 adalah suatu pernyataan yang benar. (ii) Langkah
Analisis Fungsional. Oleh: Dr. Rizky Rosjanuardi, M.Si Jurusan Pendidikan Matematika UNIVERSITAS PENDIDIKAN INDONESIA
 Analisis Fungsional Oleh: Dr. Rizky Rosjanuardi, M.Si Jurusan Pendidikan Matematika UNIVERSITAS PENDIDIKAN INDONESIA Lingkup Materi Ruang Metrik dan Ruang Topologi Kelengkapan Ruang Banach Ruang Hilbert
Analisis Fungsional Oleh: Dr. Rizky Rosjanuardi, M.Si Jurusan Pendidikan Matematika UNIVERSITAS PENDIDIKAN INDONESIA Lingkup Materi Ruang Metrik dan Ruang Topologi Kelengkapan Ruang Banach Ruang Hilbert
asimtot.wordpress.com BAB I PENDAHULUAN
 BAB I PENDAHULUAN. Latar Belakang Kalkulus Differensial dan Integral sangat luas penggunaannya dalam berbagai bidang seperti penentuan maksimum dan minimum. Suatu fungsi yang sering digunakan mahasiswa
BAB I PENDAHULUAN. Latar Belakang Kalkulus Differensial dan Integral sangat luas penggunaannya dalam berbagai bidang seperti penentuan maksimum dan minimum. Suatu fungsi yang sering digunakan mahasiswa
10. TEOREMA NILAI RATA-RATA
 10. TEOREMA NILAI RATA-RATA 10.1 Maksimum dan Minimum Lokal Misalkan f terdefinisi pada suatu interval terbuka (a, b) dan c (a, b). Kita katakan bahwa f mencapai nilai maksimum lokal di c apabila f(x)
10. TEOREMA NILAI RATA-RATA 10.1 Maksimum dan Minimum Lokal Misalkan f terdefinisi pada suatu interval terbuka (a, b) dan c (a, b). Kita katakan bahwa f mencapai nilai maksimum lokal di c apabila f(x)
KALKULUS MULTIVARIABEL II
 Pada Bidang Bentuk Vektor dari KALKULUS MULTIVARIABEL II (Minggu ke-9) Andradi Jurusan Matematika FMIPA UGM Yogyakarta, Indonesia Pada Bidang Bentuk Vektor dari 1 Definisi Daerah Sederhana x 2 Pada Bidang
Pada Bidang Bentuk Vektor dari KALKULUS MULTIVARIABEL II (Minggu ke-9) Andradi Jurusan Matematika FMIPA UGM Yogyakarta, Indonesia Pada Bidang Bentuk Vektor dari 1 Definisi Daerah Sederhana x 2 Pada Bidang
Tugas Statistika Matematika TEORI PELUANG
 Lusi Agustin 131810101004 Ria Ammelia Wahyu 131810101008 Atiqoh Hani R 131810101044 Tugas Statistika Matematika TEORI PELUANG Percobaan acak menjadi percobaan yang hasilnya tidak dapat diprediksi dengan
Lusi Agustin 131810101004 Ria Ammelia Wahyu 131810101008 Atiqoh Hani R 131810101044 Tugas Statistika Matematika TEORI PELUANG Percobaan acak menjadi percobaan yang hasilnya tidak dapat diprediksi dengan
dari ruang vektor berdimensi hingga V (dimana I adalah suatu himpunan indeks) disebut basis bagi V jika V = span(ψ) dan vektorvektor
 BAB 3 FRAME Sinyal kontinu dapat kita diskritisasi dengan menggunakan ekspansi vektor. Sifat yang paling esensial untuk melakukan hal tersebut adalah adanya operator yang menjamin bahwa ekspansi vektor
BAB 3 FRAME Sinyal kontinu dapat kita diskritisasi dengan menggunakan ekspansi vektor. Sifat yang paling esensial untuk melakukan hal tersebut adalah adanya operator yang menjamin bahwa ekspansi vektor
DEFINISI TIPE RIEMANN UNTUK INTEGRAL LEBESGUE 1. Drajad Maknawi 2 dan Muslich 3 Jurusan Matematika FMIPA UNS. Abstrak
 DEFINISI TIPE RIEMANN UNTUK INTEGRAL LEBESGUE 1 An-2 1. PENDAHULUAN Drajad Maknawi 2 dan Muslich 3 Jurusan Matematika FMIPA UNS Abstrak Tujuan dari tulisan ini adalah membahas tentang integral Lebesgue
DEFINISI TIPE RIEMANN UNTUK INTEGRAL LEBESGUE 1 An-2 1. PENDAHULUAN Drajad Maknawi 2 dan Muslich 3 Jurusan Matematika FMIPA UNS Abstrak Tujuan dari tulisan ini adalah membahas tentang integral Lebesgue
DERET TAK HINGGA. Contoh deret tak hingga :,,, atau. Barisan jumlah parsial, dengan. Definisi Deret tak hingga,
 DERET TAK HINGGA Contoh deret tak hingga :,,, atau. Barisan jumlah parsial, dengan Definisi Deret tak hingga,, konvergen dan mempunyai jumlah S, apabila barisan jumlah jumlah parsial konvergen menuju S.
DERET TAK HINGGA Contoh deret tak hingga :,,, atau. Barisan jumlah parsial, dengan Definisi Deret tak hingga,, konvergen dan mempunyai jumlah S, apabila barisan jumlah jumlah parsial konvergen menuju S.
MA2111 PENGANTAR MATEMATIKA Semester I, Tahun 2015/2016. Hendra Gunawan
 MA2111 PENGANTAR MATEMATIKA Semester I, Tahun 2015/2016 Hendra Gunawan 5 KUANTOR II: METODE MEMILIH (c) Hendra Gunawan (2015) 2 Masih Berurusan dengan Kuantor Sekarang kita akan membahas metode memilih,
MA2111 PENGANTAR MATEMATIKA Semester I, Tahun 2015/2016 Hendra Gunawan 5 KUANTOR II: METODE MEMILIH (c) Hendra Gunawan (2015) 2 Masih Berurusan dengan Kuantor Sekarang kita akan membahas metode memilih,
Lampiran 1. Beberapa Definisi dan Lema Teknis
 Lampiran 1. Beberapa Definisi dan Lema Teknis Ruang Contoh, Kejadian dan Peluang Suatu percobaan yang dapat diulang dalam kondisi yang sama, yang hasilnya tidak dapat diprediksi dengan tepat tetapi kita
Lampiran 1. Beberapa Definisi dan Lema Teknis Ruang Contoh, Kejadian dan Peluang Suatu percobaan yang dapat diulang dalam kondisi yang sama, yang hasilnya tidak dapat diprediksi dengan tepat tetapi kita
Integral Tak Tentu. Modul 1 PENDAHULUAN
 Modul 1 Integral Tak Tentu M PENDAHULUAN Drs. Hidayat Sardi, M.Si odul ini akan membahas operasi balikan dari penurunan (pendiferensialan) yang disebut anti turunan (antipendiferensialan). Dengan mengikuti
Modul 1 Integral Tak Tentu M PENDAHULUAN Drs. Hidayat Sardi, M.Si odul ini akan membahas operasi balikan dari penurunan (pendiferensialan) yang disebut anti turunan (antipendiferensialan). Dengan mengikuti
ANALISIS REAL. (Semester I Tahun ) Hendra Gunawan. September 12, Dosen FMIPA - ITB
 (Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. September 12, 2011 Teorema 11 pada Bab 3 memberi kita cara untuk menyelidiki kekonvergenan sebuah barisan tanpa harus mengetahui
(Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. September 12, 2011 Teorema 11 pada Bab 3 memberi kita cara untuk menyelidiki kekonvergenan sebuah barisan tanpa harus mengetahui
MINGGU KE-7 INTEGRAL LEBESQUE
 MINGGU KE-7 INTEGRAL LEBESQUE INTEGRAL LEBESQUE (Ω, A, µ): measure space Fungsi Ψ : Ω R disebut sederhana bila jelajahnya berhingga. Misalkan A A. Maka I A : Ω {0, 1} yang didefinisikan sebagai I A (X
MINGGU KE-7 INTEGRAL LEBESQUE INTEGRAL LEBESQUE (Ω, A, µ): measure space Fungsi Ψ : Ω R disebut sederhana bila jelajahnya berhingga. Misalkan A A. Maka I A : Ω {0, 1} yang didefinisikan sebagai I A (X
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016. Hendra Gunawan
 MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 3.3 Himpunan Kompak Himpunan tak terhingga lebih sulit ditangani daripada himpunan terhingga. Namun ada himpunan tak terhingga yang
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 3.3 Himpunan Kompak Himpunan tak terhingga lebih sulit ditangani daripada himpunan terhingga. Namun ada himpunan tak terhingga yang
Gambar 1. Gradien garis singgung grafik f
 D. URAIAN MATERI 1. Definisi dan Rumus-rumus Turunan Fungsi a. Definisi Turunan Sala satu masala yang mendasari munculnya kajian tentang turunan adala gradien garis singgung. Peratikan Gambar 1. f(c +
D. URAIAN MATERI 1. Definisi dan Rumus-rumus Turunan Fungsi a. Definisi Turunan Sala satu masala yang mendasari munculnya kajian tentang turunan adala gradien garis singgung. Peratikan Gambar 1. f(c +
Catatan Kuliah KALKULUS II BAB V. INTEGRAL
 BAB V. INTEGRAL Anti-turunan dan Integral TakTentu Persamaan Diferensial Sederhana Notasi Sigma dan Luas Daerah di Bawah Kurva Integral Tentu Teorema Dasar Kalkulus Sifat-sifat Integral Tentu Lebih Lanjut
BAB V. INTEGRAL Anti-turunan dan Integral TakTentu Persamaan Diferensial Sederhana Notasi Sigma dan Luas Daerah di Bawah Kurva Integral Tentu Teorema Dasar Kalkulus Sifat-sifat Integral Tentu Lebih Lanjut
3 LIMIT DAN KEKONTINUAN
 Menurut Bartle dan Sherbet (1994), Analisis matematika secara umum dipahami sebagai tubuh matematika yang dibangun oleh berbagai konsep limit. Pada bab sebelumnya kita telah mempelajari limit barisan,
Menurut Bartle dan Sherbet (1994), Analisis matematika secara umum dipahami sebagai tubuh matematika yang dibangun oleh berbagai konsep limit. Pada bab sebelumnya kita telah mempelajari limit barisan,
Ringkasan Kalkulus 2, Untuk dipakai di ITB 1
 Ringkasan Kalkulus 2, Untuk dipakai di ITB Deret Tak Hingga Pada bagian ini akan dibicarakan penjumlahan berbentuk a +a 2 + +a n + dengan a n R Sebelumnya akan dibahas terlebih dahulu pengertian barisan
Ringkasan Kalkulus 2, Untuk dipakai di ITB Deret Tak Hingga Pada bagian ini akan dibicarakan penjumlahan berbentuk a +a 2 + +a n + dengan a n R Sebelumnya akan dibahas terlebih dahulu pengertian barisan
Ayundyah Kesumawati. April 29, Prodi Statistika FMIPA-UII. Deret Tak Terhingga. Ayundyah. Barisan Tak Hingga. Deret Tak Terhingga
 Kesumawati Prodi Statistika FMIPA-UII April 29, 2015 Akar Barisan a 1, a 2, a 3, a 4,... adalah susunan bilangan-bilangan real yang teratur, satu untuk setiap bilangan bulat positif. adalah fungsi yang
Kesumawati Prodi Statistika FMIPA-UII April 29, 2015 Akar Barisan a 1, a 2, a 3, a 4,... adalah susunan bilangan-bilangan real yang teratur, satu untuk setiap bilangan bulat positif. adalah fungsi yang
INTEGRASI NUMERIK DENGAN METODE KUADRATUR GAUSS-LEGENDRE MENGGUNAKAN PENDEKATAN INTERPOLASI HERMITE DAN POLINOMIAL LEGENDRE
 Jurnal Matematika UNAND Vol. 5 No. 1 Hal. 148 153 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND INTEGRASI NUMERIK DENGAN METODE KUADRATUR GAUSS-LEGENDRE MENGGUNAKAN PENDEKATAN INTERPOLASI HERMITE DAN
Jurnal Matematika UNAND Vol. 5 No. 1 Hal. 148 153 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND INTEGRASI NUMERIK DENGAN METODE KUADRATUR GAUSS-LEGENDRE MENGGUNAKAN PENDEKATAN INTERPOLASI HERMITE DAN
MA1201 KALKULUS 2A (Kelas 10) Bab 8: Bentuk Tak Tentu d
 MA1201 KALKULUS 2A (Kelas 10) Bab 8: dan Do maths and you see the world ? Pengantar Bentuk tak tentu? Bentuk apa? Bentuk tak tentu yang dimaksud adalah bentuk limit dengan nilai seolah-olah : 0 0 ; ; 0
MA1201 KALKULUS 2A (Kelas 10) Bab 8: dan Do maths and you see the world ? Pengantar Bentuk tak tentu? Bentuk apa? Bentuk tak tentu yang dimaksud adalah bentuk limit dengan nilai seolah-olah : 0 0 ; ; 0
MA3231. Pengantar Analisis Real. Hendra Gunawan, Ph.D. Semester II, Tahun
 MA3231 Pengantar Analisis Real Semester II, Tahun 2016-2017 Hendra Gunawan, Ph.D. Bab 1 Sifat Kelengkapan Bilangan Real 2 1.1 Paradoks Zeno ACHILLES TORTOISE 0 1 1½ Sumber: skeptic.com 1 1 1... 1 2 4 8?
MA3231 Pengantar Analisis Real Semester II, Tahun 2016-2017 Hendra Gunawan, Ph.D. Bab 1 Sifat Kelengkapan Bilangan Real 2 1.1 Paradoks Zeno ACHILLES TORTOISE 0 1 1½ Sumber: skeptic.com 1 1 1... 1 2 4 8?
BAB III PEMBAHASAN. Bab III terbagi menjadi tiga sub-bab, yaitu sub-bab A, sub-bab B, dan subbab
 BAB III PEMBAHASAN Bab III terbagi menjadi tiga sub-bab, yaitu sub-bab A, sub-bab B, dan subbab C. Sub-bab A menjelaskan mengenai konsep dasar C[a, b] sebagai ruang vektor beserta contohnya. Sub-bab B
BAB III PEMBAHASAN Bab III terbagi menjadi tiga sub-bab, yaitu sub-bab A, sub-bab B, dan subbab C. Sub-bab A menjelaskan mengenai konsep dasar C[a, b] sebagai ruang vektor beserta contohnya. Sub-bab B
3. Kekonvergenan Deret Fourier
 3. Kekonvergenan Deret Fourier Sekarang kita akan membahas kekonvergenan deret Fourier, khususnya kekonvergenan titik demi titik. Melalui Contoh 2 yang dibahas pada bab sebelumnya kita mengetahui bahwa
3. Kekonvergenan Deret Fourier Sekarang kita akan membahas kekonvergenan deret Fourier, khususnya kekonvergenan titik demi titik. Melalui Contoh 2 yang dibahas pada bab sebelumnya kita mengetahui bahwa
tidak terdefinisi ketika x = 1, tetapi dapat kita peroleh
 Lecture 4. Limit A A. Definition of Limit Definisi 4.1 (a). Jika f adalah suatu fungsi, maka kita mengatakan bahwa jika nilai f(x) mendekati L saat x dipilih mendekati a. Dengan kata lain, bilangan L merupakan
Lecture 4. Limit A A. Definition of Limit Definisi 4.1 (a). Jika f adalah suatu fungsi, maka kita mengatakan bahwa jika nilai f(x) mendekati L saat x dipilih mendekati a. Dengan kata lain, bilangan L merupakan
3 LIMIT DAN KEKONTINUAN
 Menurut Bartle dan Sherbet (994), Analisis matematika secara umum dipahami sebagai tubuh matematika yang dibangun oleh berbagai konsep limit. Pada bab sebelumnya kita telah mempelajari limit barisan, kekonvergenan
Menurut Bartle dan Sherbet (994), Analisis matematika secara umum dipahami sebagai tubuh matematika yang dibangun oleh berbagai konsep limit. Pada bab sebelumnya kita telah mempelajari limit barisan, kekonvergenan
OPERATOR PADA RUANG BARISAN TERBATAS
 OPERATOR PADA RUANG BARISAN TERBATAS Muslim Ansori *,Tiryono 2, Suharsono S 2,Dorrah Azis 2 Jurusan Matematika FMIPA Universitas Lampung,2 Jln. Soemantri Brodjonegoro No Bandar Lampung email: ansomath@yahoo.com
OPERATOR PADA RUANG BARISAN TERBATAS Muslim Ansori *,Tiryono 2, Suharsono S 2,Dorrah Azis 2 Jurusan Matematika FMIPA Universitas Lampung,2 Jln. Soemantri Brodjonegoro No Bandar Lampung email: ansomath@yahoo.com
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
Fourier Analysis & Its Applications in PDEs - Part I
 Fourier Analysis & Its Applications in PDEs Hendra Gunawan http://personal.fmipa.itb.ac.id/hgunawan/ Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA WIDE 2010 5-6 August
Fourier Analysis & Its Applications in PDEs Hendra Gunawan http://personal.fmipa.itb.ac.id/hgunawan/ Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA WIDE 2010 5-6 August
SIFAT P-KONVEKS PADA RUANG FUNGSI MUSIELAK-ORLICZ TYPE BOCHNER. Yulia Romadiastri
 Jurnal Matematika Murni dan Terapan εpsilon Vol. 07, No.01, 013, Hal. 1 1 SIFAT P-KONVEKS PADA RUANG FUNGSI MUSIELAK-ORLICZ TYPE BOCHNER Yulia Romadiastri Program Studi Tadris Matematika Fakultas Tarbiyah
Jurnal Matematika Murni dan Terapan εpsilon Vol. 07, No.01, 013, Hal. 1 1 SIFAT P-KONVEKS PADA RUANG FUNGSI MUSIELAK-ORLICZ TYPE BOCHNER Yulia Romadiastri Program Studi Tadris Matematika Fakultas Tarbiyah
BAB III FUNGSI UJI DAN DISTRIBUSI
 BAB III FUNGSI UJI DAN DISTRIBUSI Bab ini membahas tentang fungsi uji dan distribusi di mana ruang yang memuat keduanya secara berturut-turut dinamakan ruang fungsi uji dan ruang distribusi. Ruang fungsi
BAB III FUNGSI UJI DAN DISTRIBUSI Bab ini membahas tentang fungsi uji dan distribusi di mana ruang yang memuat keduanya secara berturut-turut dinamakan ruang fungsi uji dan ruang distribusi. Ruang fungsi
Daftar Isi 3. BARISAN ANALISIS REAL. (Semester I Tahun ) Hendra Gunawan. Dosen FMIPA - ITB
 (Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. August 29, 2011 Dalam kisah Zeno tentang perlombaan lari antara Achilles dan seekor kura-kura, ketika Achilles mencapai
(Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. August 29, 2011 Dalam kisah Zeno tentang perlombaan lari antara Achilles dan seekor kura-kura, ketika Achilles mencapai
BAB I DERIVATIF (TURUNAN)
 BAB I DERIVATIF (TURUNAN) Pada bab ini akan dipaparkan pengertian derivatif suatu fungsi, beberapa sifat aljabar derivatif, aturan rantai, dan derifativ fungsi invers. A. Pengertian Derivatif Pengertian
BAB I DERIVATIF (TURUNAN) Pada bab ini akan dipaparkan pengertian derivatif suatu fungsi, beberapa sifat aljabar derivatif, aturan rantai, dan derifativ fungsi invers. A. Pengertian Derivatif Pengertian
FUNGSI KONTINU. sedemikian sehingga jika x adalah titik dari A (c), maka f (x) berada pada Vg (f (c)). (Lihat Gambar 5.1.1).
 FUNGSI KONTINU 51 FUNGSI KONTINU 511 Definisi A R, f: A R, dan c A Kita mengatakan bahwa f kontinu di c jika, diberi persekitaran Vg (f (c)) dari f (c) terdapat persekitaran (c) dari c sedemikian sehingga
FUNGSI KONTINU 51 FUNGSI KONTINU 511 Definisi A R, f: A R, dan c A Kita mengatakan bahwa f kontinu di c jika, diberi persekitaran Vg (f (c)) dari f (c) terdapat persekitaran (c) dari c sedemikian sehingga
BAB V DUALITAS RUANG ORLICZ
 BAB V DUALITAS RUANG ORLICZ Karena ketaksamaan Holder yang telah dipelajari pada bab sebelumnya, Untuk sembarang h L θ, kita dapat mendefinisikan suatu fungsional linear kontinu l h yang memetakan L θ
BAB V DUALITAS RUANG ORLICZ Karena ketaksamaan Holder yang telah dipelajari pada bab sebelumnya, Untuk sembarang h L θ, kita dapat mendefinisikan suatu fungsional linear kontinu l h yang memetakan L θ
Keterbatasan Lokal Suatu Operator Superposisi Pada Ruang Barisan Real. Lina Nurhayati, Universitas Sanggabuana
 Keterbatasan Lokal Suatu Operator Superposisi Pada Ruang Barisan Real Lina urhayati, Universitas Sanggabuana nurhayati_lina@yahoo.co.id Abstrak Misalkan P suatu operator superposisi terbatas dan T adalah
Keterbatasan Lokal Suatu Operator Superposisi Pada Ruang Barisan Real Lina urhayati, Universitas Sanggabuana nurhayati_lina@yahoo.co.id Abstrak Misalkan P suatu operator superposisi terbatas dan T adalah
BAB I Sekilas tentang Teori-teori sebagai Dasar Program Linear
 BAB I Sekilas tentang Teori-teori sebagai Dasar Program Linear. Himpunan konveks Sebuah himpunan X dalam R n disebut himpunan konveks apabila memenuhi sifat berikut: jika diberikan sebarang dua titik x
BAB I Sekilas tentang Teori-teori sebagai Dasar Program Linear. Himpunan konveks Sebuah himpunan X dalam R n disebut himpunan konveks apabila memenuhi sifat berikut: jika diberikan sebarang dua titik x
Fungsi dan Limit Fungsi 23. Contoh 5. lim. Buktikan, jika c > 0, maka
 Contoh 5 Buktikan jika c > 0 maka c c Analisis Pendahuluan Akan dicari bilangan δ > 0 sedemikian sehingga apabila c < ε untuk setiap ε > 0. 0 < c < δ berlaku Perhatikan: c ( c)( c) c c c c c c c Dapat
Contoh 5 Buktikan jika c > 0 maka c c Analisis Pendahuluan Akan dicari bilangan δ > 0 sedemikian sehingga apabila c < ε untuk setiap ε > 0. 0 < c < δ berlaku Perhatikan: c ( c)( c) c c c c c c c Dapat
PENGANTAR ANALISIS REAL
 Seri Analisis dan Geometri No. 1 (2009), -15 158 (173 hlm.) PENGANTAR ANALISIS REAL Oleh Hendra Gunawan Edisi Pertama Bandung, Januari 2009 2000 Dewey Classification: 515-xx. Kata Kunci: Analisis matematika,
Seri Analisis dan Geometri No. 1 (2009), -15 158 (173 hlm.) PENGANTAR ANALISIS REAL Oleh Hendra Gunawan Edisi Pertama Bandung, Januari 2009 2000 Dewey Classification: 515-xx. Kata Kunci: Analisis matematika,
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016. Hendra Gunawan
 MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 4. Fungsi Kontinu 4.1 Konsep Kekontinuan Fungsi kontinu Limit fungsi dan limit barisan Prapeta himpunan buka 4.2 Sifat-Sifat Fungsi
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 4. Fungsi Kontinu 4.1 Konsep Kekontinuan Fungsi kontinu Limit fungsi dan limit barisan Prapeta himpunan buka 4.2 Sifat-Sifat Fungsi
