Keterbatasan Operator Riesz di Ruang Morrey
|
|
|
- Agus Sudjarwadi
- 6 tahun lalu
- Tontonan:
Transkripsi
1 J. Math. and Its Appl. ISSN: X Vol. 3, No., May 2006, Keterbatasan Operator Riesz di Ruang Morrey Gani Gunawan, Hendra Gunawan Departemen Matematika FMIPA ITB Abstrak Dengan menggunakan transformasi Fourier, didefinisikan operator ( ) α 2, 0 < α < n, yang dikenal sebagai operator Riesz atau operator integral fraksional I α, yaitu I α : ( ) α 2, 0 < α < n. Dalam makalah ini akan diperlihatkan bahwa aksi dari operator tersebut bersifat terbatas dari ruang L p (R n ) ke ruang L q (R n ) jika dan hanya jika dengan α p q n dengan < p < q <. Selanjutnya diperlihatkan juga bahwa operator tersebut terbatas di ruang perumumannya, khususnya di ruang Morrey. Kata Kunci: Operator Riesz, ruang Lebesgue, ruang Morrey. Pendahuluan Diasumsikan f S, dengan S adalah himpunan fungsi yang terdiferensialkan tak hingga kali di R n. Transformasi Fourier dari fungsi f dinotasikan dengan f, dan didefinisikan oleh f (ξ) : f(x)e 2πiξx dx, ξ R n R n Jur. Mat. UNISBA, Mhs S2 Jur. Mat. ITB 27
2 28 Keterbatasan Operator Riesz di Ruang Morrey Jika f menotasikan Laplacian dari f yang didefinisikan oleh f : n j 2 f x 2, maka untuk suatu ξ R n, berlaku ( f) (ξ) 4π 2 ξ 2 f (ξ), lihat ([5], halaman 308). Oleh karena itu melalui persamaan ini didefinisikan untuk 0 < α < n, (( ) α 2 f) (ξ) (2π ξ ) α f (ξ), untuk setiap ξ R n. Karena ( ) α 2 f (( ) α 2 f) ((2π ξ ) α f ) dimana ( ) α 2 f) adalah invers transformasi Fourier dari (( ) α 2 f), maka untuk suatu x R n, ( (2π ξ ) α f ) Γ( n α (x) 2 ) f(y) 2 α π n 2 Γ( α 2 ) dy R x y n α n Uraian dari invers transformasi tersebut dapat dilihat pada ([5], halaman 367) atau ([7], halaman 23). Menurut Stein (lihat [2], halaman 7), dituliskan bahwa Jadi dengan I α f : ( ) α 2 f, 0 < α < n I α f(x) : f(y) dy () Γ(α) R x y n α n Γ(α) π n 2 2 α Γ( α 2 ) Γ( (n α) 2 ) I α pada Persamaan selanjutnya dinamakan sebagai operator Riesz atau operator integral fraksional. Dalam makalah ini akan dilihat bagaimana aksi dari operator tersebut jika dikenakan di ruang L p L p (R n ) dan ruang perumumannya, khususnya di ruang Morrey. Adapun notasi L p L p (R n ), p < disebut juga ruang Lebesgue, yaitu himpunan kelas-kelas ekuivalen fungsi sedemikian sehingga f L p (R n ) <, atau dapat ditulis L p (R n ) : {f : f L p (R n ) < } dengan f L p (R n ) f p adalah norm dari f dan didefinisikan oleh f p : ( R n f(x) p dx) /p, untuk setiap x R n. Sedangkan norm dari f untuk p didefinisikan oleh f : ess sup{ f(x) : x R n } dengan ess sup{ f(x) : x R n } merupakan batas atas terkecil esensial dari f. Diawali dari suatu proposisi mengenai operator I α di ruang L p (R n ), dapat diperlihatkan bahwa melalui operator dilasi yang dikenakan pada opertor I α diperoleh suatu syarat perlu dari keterbatasan operator I α di ruang L p (R n ). Kemudian dengan menggunakan fakta keterbatasan fungsi maksimal atau ketaksamaan Hardy-Littlewood di ruang L p (R n ) dapat ditunjukan juga bahwa operator I α merupakan operator yang terbatas dari L p (R n ) ke L q (R n ) asalkan p q α n dengan < p < q <. Selanjutnya dengan menggunakan ketaksamaan Fefferman-Stein,
3 Gani Gunawan, Hendra Gunawan 29 dapat ditunjukan bahwa operator maksimal juga terbatas di ruang perumumannya, khususnya di ruang Morrey. Berdasar pada fakta ini, akhirnya diperoleh hasil bahwa operator I α juga terbatas di ruang perumumannya, yakni terbatas di ruang Morrey. 2. Keterbatasan Operator I α di Ruang Lebesgue Pertama-tama akan kita lihat aksi dari operator I α ini di ruang L p (R n ) yang mempunyai sifat bahwa operator tersebut terbatas dari L p (R n ) ke L q (R n ) hanya jika p q α n. Untuk melihat sifat ini kita pandang suatu operator dilasi τ δ yang didefinisikan untuk δ > 0 oleh τ δ f(x) : f(δx). Maka dapat dinyatakan suatu lemma berikut, Lemma 2. (a) (b) τ δ f p δ n/p f p τ δ I α f δ α I α τ δ f Bukti: (a). τ δ f p ( ) /p ( ) /p (τ δ f(x)) p dx (f(δx)) p dx R n R ( ) n /p ( (f(x )) p δ n dx δ n/p (f(x ) p dx R n R n ) /p δ n/p f p
4 30 Keterbatasan Operator Riesz di Ruang Morrey (b). [ ] τ δ I α f(x) τ δ x y n+α f(y)dy Γ(α) R n x Γ(α) R δ y n+α f(y)dy n x δy n+α δ n α f(y)dy Γ(α) R n Rn x y n+α δ n δ α f( y Γ(α) δ )dy δ α Rn x y n+α f( y Γ(α) δ )dy δ α x y n+α τ Γ(α) δ f(y )dy R n δ α I α τ δ f(x) Akibat dari Lemma 2. tersebut diperoleh syarat perlu keterbatasan fungsi maksimal di ruang L p (R n ) yang dinyatakan dalam proposisi berikut. Proposisi 2.2 Jika ketaksamaan I α f q A f p, 0 < α < n (2) dipenuhi untuk setiap f dan untuk suatu konstanta A, maka p q α n. Bukti: Akibat dari Lemma 2. bagian (a), dapat ditulis τ δ I α f q δ n/q I α f q bahwa sehingga diperoleh I α f q δ n q τδ I α f q Menurut Lemma 2. bagian (b), τ δ I α f(x) δ α I α τ δ f(x), maka diperoleh I α f q δ n q τδ I α f q δ n q δ α I α τ δ f q δ n q α I α τ δ f q Karena Ketaksamaan 2 dipenuhi, maka diperoleh untuk suatu konstanta A (dalam hal ini A dapat diasumsikan sebagai konstanta terkecil yang memenuhi 2) I α f q Aδ n q α τ δ f q (3) Menurut Lemma 2. bagian (a), τ δ f q δ n q f q. Jadi Ketaksamaan 3 dapat ditulis I α f q Aδ n p n q α f q (4)
5 Gani Gunawan, Hendra Gunawan 3 Ini mungkin hanya jika n p n q α 0. Diamati lebih lanjut, syarat cukup untuk proposisi tersebut juga dapat dipenuhi. Namun untuk kasus p, (maka q n n α ) dan q 8, (maka p n α ) gagal untuk dapat dipenuhi, lihat ([2], halaman 9). Oleh karena itu, setelah melalui pengamatan ini dapat diformulasikan teorema positifnya, yang disebut teorema Hardy-Littlewood-Sobolev. Persisnya kita mempunyai suatu teorema berikut. Teorema 2.3 (Hardy-Littlewood-Sobolev) Jika p q α n dan < p < q < dengan 0 < α < n, maka f α n L q (R n ) A p,q f L q (R n ) Sebelum membuktikan Teorema 2.3 tersebut, pertama-tama perhatikan beberapa definisi, sifat dan fakta yang ada sebagai konsep yang mendasarinya. Sebelumnya, didefinisikan fungsi maksimal Hardy-Littlewood, Mf(x) : f(y) dy, x R n µ(b(x, R)) sup 0<R< B(x,R) dengan f L loc (Rn ), yaitu fungsi terintegralkan secara lokal di R n, dan µ(b(x, R)) adalah ukuran Lebesgue B(x, R) di R n. Dalam hal ini B(R) B(x, R) adalah bola buka di R n yang berpusat di titik x R n dengan radius R > 0, yaitu B(x, R) : {y R n : x y < R}, untuk setiap x R n dan R > 0. Selanjutnya teorema Hardy-Littlewood berikut, yang menyatakan bahwa operator maksimal M tersebut terbatas di ruang L p (R n ), lihat [8]. Teorema 2.4 (Hardy-Littlewood) Jika < p < dan f L p, maka Mf L p dan Mf p C p,n f p. Definisi 2.5 Fungsi f di R n disebut fungsi radial jika nilai f(x) hanya bergantung pada x untuk x R n. Lemma 2.6 Misalkan ψ fungsi non negatif di R n. Jika ψ fungsi radial yang turun, maka sup{ f ψ t (x) : t > 0} Mf(x) ψ dy R n dengan Mf merupakan fungsi maksimal dan ψ t t n ψ( x t )
6 32 Keterbatasan Operator Riesz di Ruang Morrey Bukti: Lihat ([3], halaman 57) Lemma 2.7 Jika f fungsi radial, maka f(x) dx ω n f(r)r n dr, R n 0 x R n dengan ω n 2πn/2 Γ( n 2 ) Lihat ([5], halaman 407). Lemma 2.8 Misalkan φ(y) y k χ B(R) (y), y R n dan y 0. Maka untuk setiap R > 0 dan 0 < k < n, (i). (ii). φ adalah fungsi turun secara radial φ terintegralkan Bukti: (i). (ii). Ambil y, y 2 dengan 0 < y < y 2 R, maka y k > y 2 k. Karena χ B(R) (y) untuk setiap y B(R), sehingga diperoleh χ B(R) (y ) χ B(R) (y 2 ). Jadi φ(y ) y k χ B(R) (y ) y 2 k χ B(R) (y 2 ) φ(y 2 ). Ini berarti φ(y) adalah fungsi turun secara radial untuk setiap y R n. R n φ(y) dy y k χ B(R) (y) dy y k dy R n y <R R r k r n dr dθ θ S n 0 θ S n θ Sn R n k ( n k r n k n k ) rr r0 dθ Rn k n k dθ θ S n Rn k n k ω n Rn k 2π n/2 n k Γ( n 2 ) < dθ
7 Gani Gunawan, Hendra Gunawan 33 Lemma 2.9 Misalkan ψ(y) y k χ CB(R) (y) dengan y R n, y 0 dan R > 0. Jika 0 < k < n dan n kp < 0, maka ψ L p Bukti ψ(y) p dy R n y k χ CB(R) (y) p dy R n y kp χ CB(R) (y)dy R n y kp dy y R θ s n θ s n ( R ) r kp r n dr dθ ( n kp rn kp ) r rr dθ, n kp < 0 Jadi ψ L p. θ sn Rn kp kp dθ Rn kp n kp n ω n Rn kp 2π n/2 kp n Γ(n/2) < Selanjutnya kita lihat pembuktian Teorema 2.3 sebagai berikut, Untuk R > 0 dapat dituliskan bahwa (f α n )(x) f(x y) y α n dy R n f(x y) y α n dy + f(x y) y α n dy (5) y <R y R Perhatikan suku pertama Persamaan 5, dapat ditulis menjadi f(x y) y α n dy ( f α n χ B(R) (y) ) (x) y <R dengan, jika y B(R) χ B(R) (y) 0, jika y / B(R) Dan menurut Definisi 2.5, jika dimisalkan φ(y) y α n χ B(R) (y) maka φ merupakan fungsi radial. Berdasarkan Lemma 2.8 diperoleh bahwa φ adalah fungsi
8 34 Keterbatasan Operator Riesz di Ruang Morrey turun yang terintegralkan. Akibatnya menurut Lemma 2.6, jika φ t t n φ(x/t), maka f φ(x) f φ (x) sup{ f φ t (x) : t > 0} Mf(x) φ(y)dy R n C R α Mf(x), (φ terintegralkan) (6) untuk suatu bilangan real C. Suku kedua dari Persamaan 5 dapat dituliskan menjadi f(x y) y α n dy ( f α n χ CB(R) (y) ) (x) f(x y) y α n χ CB(R) (y)dy y R dengan Oleh karena itu dapat ditulis f(x y) y α n dy y R, jika y C B(R) χ CB(R) (y) 0, jika y / C B(R) f(x y) y α n χ CB(R) (y)dy f(x y) y α n χ CB(R) (y) dy Misalkan u y, maka dapat ditulis f(x y) y α n χ CB(R) (y) dy f(u + x) u α n χ CB(R) (u) du. Jadi menurut ketaksamaan Holder diperoleh f(x y) y α n dy f(u + x) u α n χ CB(R) (u) du y R f +x u α n χ CB(R) (u) f +x p u α n χ CB(R) (u) p f p y α n χ CB(R) (y) p f p ψ p (7) dengan ψ α n χ CB(R). Perhatikan Lemma 2.9 jika k n α, maka kp n ( n q n ( ) p p + n)p n n > 0. q
9 Gani Gunawan, Hendra Gunawan 35 Akibatnya diperoleh n kp < 0. Sehingga menurut Lemma 2.9, dapat dikatakan bahwa ψ L p. Oleh karenanya dapat dipandang untuk suatu bilangan real C 2 ψ p C 2 R n/q (8) Dengan demikian Ketaksamaan 7 menjadi f(x y) y α n dy C 2R n/q f p (9) y R untuk suatu bilangan real C 2. Dari Persamaan 5, 6 dan 9 diperoleh (f α n )(x) C R α Mf(x) + C 2 f p R n/q A[R α Mf(x) + f p R n/q ] dimana A max{c, C 2 }. Selanjutnya pilih R sehingga R α Mf(x) f p R n/q atau R n/p Mf(x) f p. Jadi jika dipilih R n/p Mf(x) f p, maka (f α n )(x) A[Mf(x)] p/q f p/q p Sehingga diperoleh f α n q ( (f α n )(x) q dx) /q [ (A[Mf(x)] p/q f p/q p ) q dx] /q A f p/q p [ (Mf(x)) p ] /q A f p/q p Mf p/q p A f p/q p f p/q p C f p untuk suatu konstanta C yang tergantung pada p, q. Dengan demikian dapat disimpulkan bahwa f α n L q (R n ) A p,q f L q (R n ) 3. Keterbatasan Operator I di Ruang Morrey Ruang Morrey L p,λ (R n ) pertama kali diperkenalkan oleh C.B. Morrey pada tahun 938 dalam suatu jurnal matematika dengan judul on the solutions of quasi linear elliptic partial differential equations. Selanjutnya ruang Morrey banyak ditemukan
10 36 Keterbatasan Operator Riesz di Ruang Morrey pada saat mempelajari perilaku operator Schrodinger dan teori potensial. Tujuan utama kita dalam pembahasan pada bagian ini, akan menunjukan bahwa operator I α juga terbatas di ruang Morrey L p,λ (R n ) ke L q,λ (R n ) asalkan p q α n λ dan 0 λ < n αp. Adapun ruang Morrey itu sendiri didefinisikan sebagai himpunan semua fungsi f yang terintegralkan secara lokal pada R n, yaitu seperti yang dinyatakan dalam definisi berikut, Definisi 3. Untuk p < dan 0 λ n, ruang Morrey L p,λ (R n ) didefinisikan oleh L p,λ (R n ) : {f L p loc (Rn ) : f L p,λ (R n ) < + } dengan f L p,λ(r n ) : ( ) /p sup BB(x,R) R λ f(x) p dx B Dalam hal ini notasi B B(x, R) merupakan bola buka berdimensi n dengan pusat x R n dan berjari-jari R > 0, yaitu B(x, R) : {y R n : x y < R}. Untuk setiap bola B B(x, R) berdimensi n ini dipunyai suatu fakta bahwa B CR n (0) dimana n adalah suatu bilangan dimensi yang tetap dan C adalah konstanta yang tidak bergantung pada x dan R, dengan B menyatakan ukuran Lebesgue dari B, lihat ([5], halaman 3). Dari fakta 0 tersebut dapat dinyatakan suatu lemma berikut. Lemma 3.2 Untuk setiap α > 0, maka berlaku B(x,R) x y dy CR α untuk n α suatu konstanta real C. Bukti: Jika n α, maka jelas bahwa menurut fakta (*), B(x,R) CR α. Sekarang jika n < α, maka x y n α dy B(x,R) C j0 2 j R x y <2 j R j0 j0 x y n α dy B dy x y n α (2 j R) n α B(x, 2 j R) (2 (j+)(n α) R n α C(2 j R) n 2 αj R α CR α j0
11 Gani Gunawan, Hendra Gunawan 37 Selanjutnya sebelum diperlihatkan suatu fakta yang menyatakan bahwa operator I α juga terbatas di ruang Morrey, yakni dari L p,λ (R n ), ke L q,λ (R n ), terlebih dahulu disajikan suatu ketaksamaan Fefferman-Stein yang buktinya dapat dilihat di ([3], halaman 53). Teorema 3.3 (Fefferman-Stein) Misalkan ω adalah fungsi tak negatif dan f adalah fungsi terintegralkan secara lokal di R n. Maka terdapat C p > 0 sedemikian sehingga Mf(x) p ω(x) dx C p R n f(x) p Mω(x) dx R n Dengan menggunakan ketaksamaan Fefferman-Stein ini diperoleh suatu fakta bahwa operator maksimal juga terbatas di ruang Morrey. Seperti dinyatakan dalam teorema berikut, Teorema 3.4 (Chiarenza-Frasca) Misal < p < dan 0 λ < n. Maka Mf L p,λ C f L p,λ, untuk suatu konstanta C yang tidak bergantung pada f. Bukti: Menurut ketaksamaan yang dinyatakan dalam Teorema 3.3, maka Mf(x) p χ(x) dx C R n f(x) p (Mχ(x)) dx R n () untuk suatu fungsi f dan χ yang tak negatif. Ambil f L p,λ, dan χ adalah fungsi karakteristik pada bola B R B(x 0, R). Maka menurut Ketaksamaan di atas diperoleh B R Mf(x) p dx C f p L p,λ Jadi didapat R λ p untuk suatu konstanta C ( { (2R) λ + k Mf(x) p B R. } (2 k R) n (2k+ R) λ C f p R λ L p,λ ) p C f p L p,λ Berdasarkan pada fakta keterbatasan fungsi maksimal M f di ruang Morrey, maka dapat dibuktikan suatu pernyataan teorema berikut, bahwa operator integral fraksional I α juga terbatas di ruang Morrey. Teorema 3.5 (Chiarenza-Frasca) Jika q p α n λ, 0 < α < n, < p < n α dan 0 λ < n αp. Maka terdapat C p,q > 0 sedemikian sehingga I α f L q,λ C p,q f L q,λ
12 38 Keterbatasan Operator Riesz di Ruang Morrey Bukti: Misalkan f L p,λ, dan f 0, maka untuk x R n dan r > 0 tuliskan I α f(x) : I (x) + I 2 (x), dengan I (x) : x y <R Untuk I (x) diperoleh I (x) x y <R f(y) x y n α dy, dan I 2(x) : f(y) x y n α dy C Sementara itu, untuk I 2 (x) diperoleh I 2 (x) x y R k x y R f(y) dy x y n α (2 k R) α Mf(x) dy CR α Mf(x) f(y) x y n α dy CRα n p + λ p f p,λ CR λ n α+ p f L p,λ Sehingga untuk setiap x R n dan R > 0 diperoleh ) I α f(x) C (R α λ n α+ Mf(x) + R p f L p,λ (2) > 0 dan mensubstitusikan- ( Mf(x) Selanjutnya dengan memilih R 0 f L p,λ nya ke dalam Ketaksamaan 2, sehingga didapat I α f(x) C (Mf(x)) n λ pα n λ f pα n λ ) p n λ Lp,λ C (Mf(x)) p q f q p q L p,λ Dengan menggunakan fakta bahwa fungsi maksimal terbatas di L p,λ, maka diperoleh ketaksamaan I α f L q,λ C f L p,λ untuk suatu konstanta C yang hanya tergantung pada p dan q. Perhatikan bahwa jika λ 0 maka L p,0 (R n ) L p (R n ). Ini berarti akan diperoleh kembali keterbatasan I α dari L p (R n ) ke L q (R n ). Sedangkan jika λ n, maka diperoleh L p,λ (R n ) L (R n ). Dalam hal λ n ini, keterbatasan operator I α dari L p (R n ) ke L q (R n ) menjadi tidak berlaku, seperti yang ditunjukan dalam ([2], halaman 9).
13 Gani Gunawan, Hendra Gunawan Kesimpulan Melalui operator dilasi yang dikenakan terhadap operator integral fraksional, dan dengan adanya fakta keterbatasan fungsi maksimal di ruang L p (R n ), diperoleh fakta bahwa untuk 0 < α < n, operator integral fraksional I α yang didefinisikan sebagai I α f(x) : Γ(α) R n f(y) dy x y n α merupakan operator terbatas dari L p (R n ) ke L q (R n ) dengan p q α n dan < p < q <. Persisnya kita mempunyai ketaksamaan I α f C p,q f p jika dan hanya jika p q α n dan < p < q <. Selanjutnya di ruang perumumannya, khususnya di ruang Morrey L p,λ, (R n ), dengan menggunakan ketaksamaan Fefferman-Stein diperoleh fakta bahwa operator maksimal juga terbatas di ruang perumumannya. Akibatnya dengan memanfaatkan fakta ini diperoleh hasil bahwa operator integral fraksional I α juga terbatas di ruang perumumannya, yaitu I α terbatas dari ruang L p,λ (R n ) ke L q,λ (R n ) dengan p q dan 0 λ < n αp. α n α Ucapan Terima Kasih. Kedua penulis berterima kasih kepada LPPM-ITB untuk dana Riset ITB Tahun 2006 No. 0004/K0.03.2/PL2..5/I/2006. Pustaka [] E. Nakai, Recent topics of fractional integrals, Departemen of Mathematics, Osaka Kyoiku University Kashiwara, Osaka , Japan. [2] E.M. Stein, Singular integrals and differentiability properties of functions, Princenton University Press, Princenton, N.J, 970. [3] E.M. Stein, Harmonic Analysis: real variable methods, orthogonality, and oscillatory integrals, Princenton University Press, Princenton, New Jersey, 993. [4] F. Chiarenza and M.Frasca, Morrey spaces and Hardy Littlewood maximal function, rend. Mat. 7, , 987.
14 40 Keterbatasan Operator Riesz di Ruang Morrey [5] G.B. Folland, Fourier analysis and its applications, Wadsworth & Brooks/Cole, Pacific Grove, CA, 992. [6] J.G. Cuerva and A.E. Gatto, Boundedness properties of fractional integral operators associated to non doubling measures, Mathematics Subject Classification, DePaul University, Spain, 99. [7] M. Loss and H. Elliot, Analysis, Graduate student in mathematics, volume 4, 200. [8] R. Fefferman, Maximal functions in analysis, The University of Chicago REU, 2005.
KETAKSAMAAN OLSEN UNTUK OPERATOR RIESZ YANG DIPERUMUM. Oleh. Hendra Gunawan* dan Yudi Soeharyadi. Institut Teknologi Bandung Bandung, Indonesia
 KETAKSAMAAN OLSEN UNTUK OPERATOR RIESZ YANG DIPERUMUM Oleh Hendra Gunawan* dan Yudi Soeharyadi Institut Teknologi Bandung Bandung, Indonesia dipresentasikan pada Konferensi Nasional Matematika XIII, di
KETAKSAMAAN OLSEN UNTUK OPERATOR RIESZ YANG DIPERUMUM Oleh Hendra Gunawan* dan Yudi Soeharyadi Institut Teknologi Bandung Bandung, Indonesia dipresentasikan pada Konferensi Nasional Matematika XIII, di
KETAKSAMAAN TIPE LEMAH UNTUK OPERATOR INTEGRAL FRAKSIONAL DI RUANG MORREY ATAS RUANG METRIK TAK HOMOGEN
 KETAKSAMAAN TIPE LEMAH UNTUK OPERATOR INTEGRAL FRAKSIONAL DI RUANG MORREY ATAS RUANG METRIK TAK HOMOGEN Idha Sihwaningrum Jurusan Matematika FMIPA Unsoed Email: idha.sihwaningrum@unsoed.ac.id Abstrak Pada
KETAKSAMAAN TIPE LEMAH UNTUK OPERATOR INTEGRAL FRAKSIONAL DI RUANG MORREY ATAS RUANG METRIK TAK HOMOGEN Idha Sihwaningrum Jurusan Matematika FMIPA Unsoed Email: idha.sihwaningrum@unsoed.ac.id Abstrak Pada
Fourier Analysis & Its Applications in PDEs - Part II
 Fourier Analysis & Its Applications in PDEs Hendra Gunawan http://personal.fmipa.itb.ac.id/hgunawan/ Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA WIDE 2010 5-6 August
Fourier Analysis & Its Applications in PDEs Hendra Gunawan http://personal.fmipa.itb.ac.id/hgunawan/ Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA WIDE 2010 5-6 August
KETERBATASAN OPERATOR INTEGRAL FRAKSIONAL PADA RUANG KUASI METRIK TAK HOMOGEN TERBOBOTI
 Seminar Nasional Matematika dan Aplikasinya 2 Oktober 207 Surabaya Universitas Airlangga KETERBATASAN OPERATOR INTEGRAL FRAKSIONAL PADA RUANG KUASI METRIK TAK HOMOGEN TERBOBOTI Mohammad Imam Utoyo Departemen
Seminar Nasional Matematika dan Aplikasinya 2 Oktober 207 Surabaya Universitas Airlangga KETERBATASAN OPERATOR INTEGRAL FRAKSIONAL PADA RUANG KUASI METRIK TAK HOMOGEN TERBOBOTI Mohammad Imam Utoyo Departemen
10. Transformasi Fourier
 10. Transformasi Fourier Dalam beberapa bab ke depan, kita akan membahas transformasi Fourier, sifatsifatnya, dan aplikasinya. Seperti halnya pada pembahasan deret Fourier, pendekatan yang diambil dalam
10. Transformasi Fourier Dalam beberapa bab ke depan, kita akan membahas transformasi Fourier, sifatsifatnya, dan aplikasinya. Seperti halnya pada pembahasan deret Fourier, pendekatan yang diambil dalam
12. Teorema Inversi Fourier dan Transformasi Fourier di L 2 (R)
 1. Teorema Inversi Fourier dan Transformasi Fourier di L (R) 1.1 Teorema Inversi Fourier Dari hasil hitung-hitungan kasar di awal bagian ke-10, kita ingin membuktikan bahwa, dalam kondisi tertentu, kita
1. Teorema Inversi Fourier dan Transformasi Fourier di L (R) 1.1 Teorema Inversi Fourier Dari hasil hitung-hitungan kasar di awal bagian ke-10, kita ingin membuktikan bahwa, dalam kondisi tertentu, kita
DASAR-DASAR TEORI RUANG HILBERT
 DASAR-DASAR TEORI RUANG HILBERT Herry P. Suryawan 1 Geometri Ruang Hilbert Definisi 1.1 Ruang vektor kompleks V disebut ruang hasilkali dalam jika ada fungsi (.,.) : V V C sehingga untuk setiap x, y, z
DASAR-DASAR TEORI RUANG HILBERT Herry P. Suryawan 1 Geometri Ruang Hilbert Definisi 1.1 Ruang vektor kompleks V disebut ruang hasilkali dalam jika ada fungsi (.,.) : V V C sehingga untuk setiap x, y, z
7. Transformasi Fourier
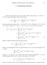 Pengantar Analisis Fourier dan eori Aproksimasi 33 7. ransformasi Fourier Pada bab sebelumnya kita telah melihat bahwa setiap fungsi f L 1 ([0, 1] L ([0, 1] dapat dinyatakan sebagai deret Fourier f(x =
Pengantar Analisis Fourier dan eori Aproksimasi 33 7. ransformasi Fourier Pada bab sebelumnya kita telah melihat bahwa setiap fungsi f L 1 ([0, 1] L ([0, 1] dapat dinyatakan sebagai deret Fourier f(x =
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
11. FUNGSI MONOTON (DAN FUNGSI KONVEKS)
 11. FUNGSI MONOTON (DAN FUNGSI KONVEKS) 11.1 Definisi dan Limit Fungsi Monoton Misalkan f terdefinisi pada suatu himpunan H. Kita katakan bahwa f naik pada H apabila untuk setiap x, y H dengan x < y berlaku
11. FUNGSI MONOTON (DAN FUNGSI KONVEKS) 11.1 Definisi dan Limit Fungsi Monoton Misalkan f terdefinisi pada suatu himpunan H. Kita katakan bahwa f naik pada H apabila untuk setiap x, y H dengan x < y berlaku
DASAR-DASAR ANALISIS MATEMATIKA
 (Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. December 11, 2007 Misalkan f terdefinisi pada suatu himpunan H. Kita katakan bahwa f naik pada H apabila
(Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. December 11, 2007 Misalkan f terdefinisi pada suatu himpunan H. Kita katakan bahwa f naik pada H apabila
Fourier Analysis & Its Applications in PDEs - Part I
 Fourier Analysis & Its Applications in PDEs Hendra Gunawan http://personal.fmipa.itb.ac.id/hgunawan/ Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA WIDE 2010 5-6 August
Fourier Analysis & Its Applications in PDEs Hendra Gunawan http://personal.fmipa.itb.ac.id/hgunawan/ Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA WIDE 2010 5-6 August
KETAKSAMAAN TIPE LEMAH UNTUK OPERATOR MAKSIMAL DI RUANG MORREY TAK HOMOGEN YANG DIPERUMUM
 JMP : Volume 4 Nomor 2, Desember 2012, hal. 265-270 KETAKSAMAAN TIPE LEMAH UNTUK OPERATOR MAKSIMAL DI RUANG MORREY TAK HOMOGEN YANG DIPERUMUM Sri Maryai Uiversitas Jederal Soedirma sri.maryai@usoed.ac.id
JMP : Volume 4 Nomor 2, Desember 2012, hal. 265-270 KETAKSAMAAN TIPE LEMAH UNTUK OPERATOR MAKSIMAL DI RUANG MORREY TAK HOMOGEN YANG DIPERUMUM Sri Maryai Uiversitas Jederal Soedirma sri.maryai@usoed.ac.id
11. Konvolusi. Misalkan f dan g fungsi yang terdefinisi pada R. Konvolusi dari f dan g adalah fungsi f g yang didefinisikan sebagai.
 11. Konvolusi Operasi konvolusi yang akan kita bahas di sini sebetulnya pernah kita jumpai pada pembahasan deret Fourier (ketika membuktikan kekonvergenan jumlah parsialnya). Operasi konvolusi merupakan
11. Konvolusi Operasi konvolusi yang akan kita bahas di sini sebetulnya pernah kita jumpai pada pembahasan deret Fourier (ketika membuktikan kekonvergenan jumlah parsialnya). Operasi konvolusi merupakan
BAB I PENDAHULUAN Latar Belakang Permasalahan
 BAB I PENDAHULUAN 1.1. Latar Belakang Permasalahan Ditinjau dari bidang ilmu pengetahuan, teori persamaan diferensial merupakan suatu cabang analisis matematika yang banyak dipakai dalam kehidupan nyata,
BAB I PENDAHULUAN 1.1. Latar Belakang Permasalahan Ditinjau dari bidang ilmu pengetahuan, teori persamaan diferensial merupakan suatu cabang analisis matematika yang banyak dipakai dalam kehidupan nyata,
0. Pendahuluan. 0.1 Notasi dan istilah, bilangan kompleks
 0. Pendahuluan Analisis Fourier mempelajari berbagai teknik menganalisis sebuah fungsi dengan menguraikannya sebagai deret atau integral fungsi tertentu (yang sifat-sifatnya telah kita kenal dengan baik,
0. Pendahuluan Analisis Fourier mempelajari berbagai teknik menganalisis sebuah fungsi dengan menguraikannya sebagai deret atau integral fungsi tertentu (yang sifat-sifatnya telah kita kenal dengan baik,
SIFAT P-KONVEKS PADA RUANG FUNGSI MUSIELAK-ORLICZ TYPE BOCHNER. Yulia Romadiastri
 Jurnal Matematika Murni dan Terapan εpsilon Vol. 07, No.01, 013, Hal. 1 1 SIFAT P-KONVEKS PADA RUANG FUNGSI MUSIELAK-ORLICZ TYPE BOCHNER Yulia Romadiastri Program Studi Tadris Matematika Fakultas Tarbiyah
Jurnal Matematika Murni dan Terapan εpsilon Vol. 07, No.01, 013, Hal. 1 1 SIFAT P-KONVEKS PADA RUANG FUNGSI MUSIELAK-ORLICZ TYPE BOCHNER Yulia Romadiastri Program Studi Tadris Matematika Fakultas Tarbiyah
BAB III OPERATOR LINEAR TERBATAS PADA RUANG HILBERT. Operator merupakan salah satu materi yang akan dibahas dalam fungsi
 BAB III OPERATOR LINEAR TERBATAS PADA RUANG HILBERT 3.1 Operator linear Operator merupakan salah satu materi yang akan dibahas dalam fungsi real yaitu suatu fungsi dari ruang vektor ke ruang vektor. Ruang
BAB III OPERATOR LINEAR TERBATAS PADA RUANG HILBERT 3.1 Operator linear Operator merupakan salah satu materi yang akan dibahas dalam fungsi real yaitu suatu fungsi dari ruang vektor ke ruang vektor. Ruang
Ruang Norm-n Berdimensi Hingga
 Jurnal Matematika Integratif. Vol. 3, No. 2 (207), pp. 95 04. p-issn:42-684, e-issn:2549-903 doi:0.2498/jmi.v3.n2.986.95-04 Ruang Norm-n Berdimensi Hingga Moh. Januar Ismail Burhan Jurusan Matematika dan
Jurnal Matematika Integratif. Vol. 3, No. 2 (207), pp. 95 04. p-issn:42-684, e-issn:2549-903 doi:0.2498/jmi.v3.n2.986.95-04 Ruang Norm-n Berdimensi Hingga Moh. Januar Ismail Burhan Jurusan Matematika dan
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
DASAR-DASAR ANALISIS MATEMATIKA
 (Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. December 26, 2007 Misalkan f kontinu pada interval [a, b]. Apakah masuk akal untuk membahas luas daerah
(Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. December 26, 2007 Misalkan f kontinu pada interval [a, b]. Apakah masuk akal untuk membahas luas daerah
9. Teori Aproksimasi
 44 Hendra Gunawan 9 Teori Aproksimasi Mulai bab ini tema kita adalah aproksimasi fungsi dan interpolasi Diberikan sebuah fungsi f, baik secara utuh ataupun hanya beberapilai di titik-titik tertentu saja,
44 Hendra Gunawan 9 Teori Aproksimasi Mulai bab ini tema kita adalah aproksimasi fungsi dan interpolasi Diberikan sebuah fungsi f, baik secara utuh ataupun hanya beberapilai di titik-titik tertentu saja,
ANALISIS AKIBAT INTEGRAL CAUCHY Ricky Antonius, Helmi, Yudhi INTISARI
 Buletin Ilmiah Mat. Stat. dan Terapannya (Bimaster) Volume 07, No. 1 (2018), hal 41-46. ANALISIS AKIBAT INTEGRAL CAUCHY Ricky Antonius, Helmi, Yudhi INTISARI Analisis kompleks salah satu cabang matematika
Buletin Ilmiah Mat. Stat. dan Terapannya (Bimaster) Volume 07, No. 1 (2018), hal 41-46. ANALISIS AKIBAT INTEGRAL CAUCHY Ricky Antonius, Helmi, Yudhi INTISARI Analisis kompleks salah satu cabang matematika
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
BARISAN SIMBOL DAN UKURAN INVARIAN FUNGSI MONOTON SEPOTONG-SEPOTONG KONTINU
 BARISAN SIMBOL DAN UKURAN INVARIAN FUNGSI MONOTON SEPOTONG-SEPOTONG KONTINU Rinurwati Jurusan Matematika FMIPA-ITS Jl. Arif Rahman Hakim Surabaya 60 Abstract. Let g [0 ] [0] is piecewise continuous monotone
BARISAN SIMBOL DAN UKURAN INVARIAN FUNGSI MONOTON SEPOTONG-SEPOTONG KONTINU Rinurwati Jurusan Matematika FMIPA-ITS Jl. Arif Rahman Hakim Surabaya 60 Abstract. Let g [0 ] [0] is piecewise continuous monotone
Karakteristik Operator Positif Pada Ruang Hilbert
 SEMINAR NASIONAL MATEMATIKA DAN PENDIDIKAN MATEMATIKA UNY 05 A - 4 Karakteristik Operator Positif Pada Ruang Hilbert Gunawan Fakultas Keguruan dan Ilmu Pendidikan, Universitas Muhammadiyah Purwokerto gunoge@gmailcom
SEMINAR NASIONAL MATEMATIKA DAN PENDIDIKAN MATEMATIKA UNY 05 A - 4 Karakteristik Operator Positif Pada Ruang Hilbert Gunawan Fakultas Keguruan dan Ilmu Pendidikan, Universitas Muhammadiyah Purwokerto gunoge@gmailcom
17. Transformasi Wavelet Kontinu dan Frame
 17. Transformasi Wavelet Kontinu dan Frame Pada 16 kita mempelajari basis ortonormal {e 2πimx g(x n)} dengan g = χ [,1). Transformasi f f(x)g(x n)e 2πimx dx, m, n Z, dikenal sebagai transformasi Fourier
17. Transformasi Wavelet Kontinu dan Frame Pada 16 kita mempelajari basis ortonormal {e 2πimx g(x n)} dengan g = χ [,1). Transformasi f f(x)g(x n)e 2πimx dx, m, n Z, dikenal sebagai transformasi Fourier
FUNGSIONAL LINEAR-2 DALAM RUANG NORM-2 2-LINEAR FUNCTIONALS IN 2-NORMED SPACE
 Jurnal Ilmu Matematika dan Terapan Maret 016 Volume 10 Nomor 1 Hal. 1 7 FUNGSIONAL LINEAR- DALAM RUANG NORM- Harmanus Batkunde 1, Meilin I. Tilukay dan F. Y. Rumlawang 3 1,,3 Jurusan Matematika FMIPA Universitas
Jurnal Ilmu Matematika dan Terapan Maret 016 Volume 10 Nomor 1 Hal. 1 7 FUNGSIONAL LINEAR- DALAM RUANG NORM- Harmanus Batkunde 1, Meilin I. Tilukay dan F. Y. Rumlawang 3 1,,3 Jurusan Matematika FMIPA Universitas
TEOREMA PEMBATASAN DIMENSI DUA. Hendra Gunawan Jurusan Matematika ITB Jl. Ganesha 10 Bandung
 TEOREMA PEMBATASAN IMENSI UA Henda Gunawan Juusan Matematika ITB Jl Ganesha Bandung Abstak alam makalah ini kami buktikan teoema embatasan dimensi dua dengan menggunakan ketaksamaan Babenko-Hausdoff-Young
TEOREMA PEMBATASAN IMENSI UA Henda Gunawan Juusan Matematika ITB Jl Ganesha Bandung Abstak alam makalah ini kami buktikan teoema embatasan dimensi dua dengan menggunakan ketaksamaan Babenko-Hausdoff-Young
FUNGSI DELTA DIRAC. Marwan Wirianto 1) dan Wono Setya Budhi 2)
 INTEGRAL, Vol. 1 No. 1, Maret 5 FUNGSI DELTA DIRAC Marwan Wirianto 1) dan Wono Setya Budhi ) 1) Jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Katolik Parahyangan, Bandung
INTEGRAL, Vol. 1 No. 1, Maret 5 FUNGSI DELTA DIRAC Marwan Wirianto 1) dan Wono Setya Budhi ) 1) Jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Katolik Parahyangan, Bandung
(MS.2) KEKONVERGENAN BARISAN FUNGSI TURUNAN BERORDE FRAKSIONAL
 (MS.2) KEKONVERGENAN BARISAN FUNGSI TURUNAN BERORDE FRAKSIONAL Endang Rusyaman, Kankan Parmikanti, Iin Irianingsih Jurusan Matematika FMIPA Universitas Padjadjaran Jl. Raya Bandung Sumedang Km 21 Jatinangor
(MS.2) KEKONVERGENAN BARISAN FUNGSI TURUNAN BERORDE FRAKSIONAL Endang Rusyaman, Kankan Parmikanti, Iin Irianingsih Jurusan Matematika FMIPA Universitas Padjadjaran Jl. Raya Bandung Sumedang Km 21 Jatinangor
METODE TRANSFORMASI DIFERENSIAL FRAKSIONAL UNTUK MENYELESAIKAN MASALAH STURM-LIOUVILLE FRAKSIONAL
 METODE TRANSFORMASI DIFERENSIAL FRAKSIONAL UNTUK MENYELESAIKAN MASALAH STURM-LIOUVILLE FRAKSIONAL oleh ASRI SEJATI M0110009 SKRIPSI ditulis dan diajukan untuk memenuhi sebagian persyaratan memperoleh gelar
METODE TRANSFORMASI DIFERENSIAL FRAKSIONAL UNTUK MENYELESAIKAN MASALAH STURM-LIOUVILLE FRAKSIONAL oleh ASRI SEJATI M0110009 SKRIPSI ditulis dan diajukan untuk memenuhi sebagian persyaratan memperoleh gelar
MINGGU KE-6 VARIABEL RANDOM DAN DISTRIBUSINYA
 MINGGU KE-6 VARIABEL RANDOM DAN DISTRIBUSINYA VARIABEL RANDOM Misalkan (Ω, A, P) ruang probabilitas dan R = {x < x < } dan B : Borel field pada R. Andaikan X : Ω R dan untuk setiap A R, kita definisikan
MINGGU KE-6 VARIABEL RANDOM DAN DISTRIBUSINYA VARIABEL RANDOM Misalkan (Ω, A, P) ruang probabilitas dan R = {x < x < } dan B : Borel field pada R. Andaikan X : Ω R dan untuk setiap A R, kita definisikan
BAB I PENDAHULUAN. Integral Lebesgue merupakan suatu perluasan dari integral Riemann.
 BAB I PENDAHULUAN 1.1 Latar Belakang Masalah Integral Lebesgue merupakan suatu perluasan dari integral Riemann. Sebagaimana telah diketahui, pengkonstruksian integral Riemann dilakukan dengan cara pemartisian
BAB I PENDAHULUAN 1.1 Latar Belakang Masalah Integral Lebesgue merupakan suatu perluasan dari integral Riemann. Sebagaimana telah diketahui, pengkonstruksian integral Riemann dilakukan dengan cara pemartisian
BAB III FUNGSI YOUNG DAN KOMPLEMEN YOUNG
 BAB III FUNGSI YOUNG DAN KOMPLEMEN YOUNG Pada bab ini, dibahas tentang definisi fungsi Young dengan domain real diperluas dan komplemennya. Sebelumnya, dalam studi deret Fourier, W. H. Young telah menganalisis
BAB III FUNGSI YOUNG DAN KOMPLEMEN YOUNG Pada bab ini, dibahas tentang definisi fungsi Young dengan domain real diperluas dan komplemennya. Sebelumnya, dalam studi deret Fourier, W. H. Young telah menganalisis
ANALISIS NUMERIK LANJUT. Hendra Gunawan, Ph.D. 2006/2007
 ANALISIS NUMERIK LANJUT Hendra Gunawan, Ph.D. 2006/2007 BAB I. RUANG LINEAR Pelajari definisi dan contoh: ruang linear (hal. 1-3); subruang (hal. 3); kombinasi linear (hal. 4); bebas/bergantung linear
ANALISIS NUMERIK LANJUT Hendra Gunawan, Ph.D. 2006/2007 BAB I. RUANG LINEAR Pelajari definisi dan contoh: ruang linear (hal. 1-3); subruang (hal. 3); kombinasi linear (hal. 4); bebas/bergantung linear
ANALISIS REAL. (Semester I Tahun ) Hendra Gunawan. August 18, Dosen FMIPA - ITB
 (Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. August 18, 2011 Kita telah mencatat sebelumnya bahwa supremum dan infimum suatu himpunan tidak harus merupakan anggota himpunan
(Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. August 18, 2011 Kita telah mencatat sebelumnya bahwa supremum dan infimum suatu himpunan tidak harus merupakan anggota himpunan
PENGANTAR ANALISIS FUNGSIONAL
 PENGANTAR ANALISIS FUNGSIONAL SUMANANG MUHTAR GOZALI KBK ANALISIS UNIVERSITAS PENDIDIKAN INDONESIA BANDUNG 2010 2 KATA PENGANTAR Bismillahirrahmanirrahim Segala puji bagi Allah Rabb semesta alam. Shalawat
PENGANTAR ANALISIS FUNGSIONAL SUMANANG MUHTAR GOZALI KBK ANALISIS UNIVERSITAS PENDIDIKAN INDONESIA BANDUNG 2010 2 KATA PENGANTAR Bismillahirrahmanirrahim Segala puji bagi Allah Rabb semesta alam. Shalawat
DEFINISI TIPE RIEMANN UNTUK INTEGRAL LEBESGUE 1. Drajad Maknawi 2 dan Muslich 3 Jurusan Matematika FMIPA UNS. Abstrak
 DEFINISI TIPE RIEMANN UNTUK INTEGRAL LEBESGUE 1 An-2 1. PENDAHULUAN Drajad Maknawi 2 dan Muslich 3 Jurusan Matematika FMIPA UNS Abstrak Tujuan dari tulisan ini adalah membahas tentang integral Lebesgue
DEFINISI TIPE RIEMANN UNTUK INTEGRAL LEBESGUE 1 An-2 1. PENDAHULUAN Drajad Maknawi 2 dan Muslich 3 Jurusan Matematika FMIPA UNS Abstrak Tujuan dari tulisan ini adalah membahas tentang integral Lebesgue
Regularitas Operator Potensial Layer Tunggal
 JMS Vol. No., al. 8-5, April 997 egularitas Operator Potensial Layer Tunggal Wono Setya Budi Jurusan Matematika, FMIPA Institut Teknologi Bandung Jl. Ganesa 0 Bandunng, 403 Abstrak egulitas operator =
JMS Vol. No., al. 8-5, April 997 egularitas Operator Potensial Layer Tunggal Wono Setya Budi Jurusan Matematika, FMIPA Institut Teknologi Bandung Jl. Ganesa 0 Bandunng, 403 Abstrak egulitas operator =
PERHITUNGAN NUMERIK DALAM MENENTUKAN KESTABILAN SOLITON CERAH ONSITE PADA PERSAMAAN SCHRÖDINGER NONLINIER DISKRIT DENGAN PENAMBAHAN POTENSIAL LINIER
 Jurnal Matematika UNAND Vol 3 No 3 Hal 68 75 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND PERHITUNGAN NUMERIK DALAM MENENTUKAN KESTABILAN SOLITON CERAH ONSITE PADA PERSAMAAN SCHRÖDINGER NONLINIER
Jurnal Matematika UNAND Vol 3 No 3 Hal 68 75 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND PERHITUNGAN NUMERIK DALAM MENENTUKAN KESTABILAN SOLITON CERAH ONSITE PADA PERSAMAAN SCHRÖDINGER NONLINIER
ANALISIS REAL. (Semester I Tahun ) Hendra Gunawan. September 12, Dosen FMIPA - ITB
 (Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. September 12, 2011 Teorema 11 pada Bab 3 memberi kita cara untuk menyelidiki kekonvergenan sebuah barisan tanpa harus mengetahui
(Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. September 12, 2011 Teorema 11 pada Bab 3 memberi kita cara untuk menyelidiki kekonvergenan sebuah barisan tanpa harus mengetahui
MASALAH INTERPOLASI 1-D DAN 2-D
 MASALAH INTERPOLASI 1-D DAN 2-D Hendra Gunawan ITB Bandung http://personal.fmipa.itb.ac.id/hgunawan/ Analysis and Geometry Group Bandung Institute of Technology Bandung, Indonesia Seminar Nasional Analisis
MASALAH INTERPOLASI 1-D DAN 2-D Hendra Gunawan ITB Bandung http://personal.fmipa.itb.ac.id/hgunawan/ Analysis and Geometry Group Bandung Institute of Technology Bandung, Indonesia Seminar Nasional Analisis
Tugas Statistika Matematika TEORI PELUANG
 Lusi Agustin 131810101004 Ria Ammelia Wahyu 131810101008 Atiqoh Hani R 131810101044 Tugas Statistika Matematika TEORI PELUANG Percobaan acak menjadi percobaan yang hasilnya tidak dapat diprediksi dengan
Lusi Agustin 131810101004 Ria Ammelia Wahyu 131810101008 Atiqoh Hani R 131810101044 Tugas Statistika Matematika TEORI PELUANG Percobaan acak menjadi percobaan yang hasilnya tidak dapat diprediksi dengan
KEKONVERGENAN LEMAH PADA RUANG HILBERT
 KEKONVERGENAN LEMAH PADA RUANG HILBERT Moch. Ramadhan Mubarak 1), Encum Sumiaty 2), Cece Kustiawan 3) 1), 2), 3) Departemen Pendidikan Matematika FPMIPA UPI *Surel: ramadhan.101110176@gmail.com ABSTRAK.
KEKONVERGENAN LEMAH PADA RUANG HILBERT Moch. Ramadhan Mubarak 1), Encum Sumiaty 2), Cece Kustiawan 3) 1), 2), 3) Departemen Pendidikan Matematika FPMIPA UPI *Surel: ramadhan.101110176@gmail.com ABSTRAK.
TEOREMA TITIK TETAP PADA RUANG NORM-n STANDAR. Shelvi Ekariani KK Analisis dan Geometri FMIPA ITB
 JMP : Volume 4 Nomor, Juni 0, hal. 69-77 TEOREMA TITIK TETAP PADA RUANG NORM-n STANDAR Shelvi Ekariani KK Analisis dan Geometri FMIPA ITB shelvi_ekariani@students.itb.ac.id Hendra Gunawan KK Analisis dan
JMP : Volume 4 Nomor, Juni 0, hal. 69-77 TEOREMA TITIK TETAP PADA RUANG NORM-n STANDAR Shelvi Ekariani KK Analisis dan Geometri FMIPA ITB shelvi_ekariani@students.itb.ac.id Hendra Gunawan KK Analisis dan
DASAR-DASAR TEORI PELUANG
 DASAR-DASAR TEORI PELUANG Herry P. Suryawan 1 Ruang Peluang Definisi 1.1 Diberikan himpunan tak kosong Ω. Aljabar-σ (σ-algebra pada Ω adalah koleksi subhimpunan A dari Ω dengan sifat (i, Ω A (ii jika A
DASAR-DASAR TEORI PELUANG Herry P. Suryawan 1 Ruang Peluang Definisi 1.1 Diberikan himpunan tak kosong Ω. Aljabar-σ (σ-algebra pada Ω adalah koleksi subhimpunan A dari Ω dengan sifat (i, Ω A (ii jika A
METODE DEKOMPOSISI ADOMIAN LAPLACE UNTUK SOLUSI PERSAMAAN DIFERENSIAL NONLINIER KOEFISIEN FUNGSI
 METODE DEKOMPOSISI ADOMIAN LAPLACE UNTUK SOLUSI PERSAMAAN DIFERENSIAL NONLINIER KOEFISIEN FUNGSI Yuni Yulida Program Studi Matematika FMIPA Unlam Universitas Lambung Mangkurat Jl. Jend. A. Yani km. 36
METODE DEKOMPOSISI ADOMIAN LAPLACE UNTUK SOLUSI PERSAMAAN DIFERENSIAL NONLINIER KOEFISIEN FUNGSI Yuni Yulida Program Studi Matematika FMIPA Unlam Universitas Lambung Mangkurat Jl. Jend. A. Yani km. 36
BAGIAN KEDUA. Fungsi, Limit dan Kekontinuan, Turunan
 BAGIAN KEDUA Fungsi, Limit dan Kekontinuan, Turunan 51 52 Hendra Gunawan Pengantar Analisis Real 53 6. FUNGSI 6.1 Fungsi dan Grafiknya Konsep fungsi telah dipelajari oleh Gottfried Wilhelm von Leibniz
BAGIAN KEDUA Fungsi, Limit dan Kekontinuan, Turunan 51 52 Hendra Gunawan Pengantar Analisis Real 53 6. FUNGSI 6.1 Fungsi dan Grafiknya Konsep fungsi telah dipelajari oleh Gottfried Wilhelm von Leibniz
Hendra Gunawan. KK Analisis & Geometri FMIPA-ITB. Bandung, Maret 2001 [Edisi Revisi II: Mei 2014]
![Hendra Gunawan. KK Analisis & Geometri FMIPA-ITB. Bandung, Maret 2001 [Edisi Revisi II: Mei 2014] Hendra Gunawan. KK Analisis & Geometri FMIPA-ITB. Bandung, Maret 2001 [Edisi Revisi II: Mei 2014]](/thumbs/72/67819562.jpg) Analisis Fourier dan Wavelet 1 Catatan Kuliah Analisis Fourier dan Wavelet Oleh Hendra Gunawan KK Analisis & Geometri FMIPA-ITB Bandung, Maret 2001 [Edisi Revisi II: Mei 2014] 1 2 Hendra Gunawan Daftar
Analisis Fourier dan Wavelet 1 Catatan Kuliah Analisis Fourier dan Wavelet Oleh Hendra Gunawan KK Analisis & Geometri FMIPA-ITB Bandung, Maret 2001 [Edisi Revisi II: Mei 2014] 1 2 Hendra Gunawan Daftar
Kelengkapan Ruang l pada Ruang Norm-n
 Jurnal Matematika, Statistika,& Komputasi Vol.... No... 20... Kelengkapan Ruang l pada Ruang Norm-n Meriam, Naimah Aris 2, Muh Nur 3 Abstrak Rumusan norm-n pada l merupakan perumuman dari rumusan norm-n
Jurnal Matematika, Statistika,& Komputasi Vol.... No... 20... Kelengkapan Ruang l pada Ruang Norm-n Meriam, Naimah Aris 2, Muh Nur 3 Abstrak Rumusan norm-n pada l merupakan perumuman dari rumusan norm-n
BEBERAPA KONSEP ORTOGONALITAS DI RUANG NORM
 Final Draft 1 Desember 2005 BEBERAPA KONSEP ORTOGONALITAS DI RUANG NORM Hendra Gunawan, Nursupiamin, dan Eder Kikianty Ortogonalitas merupakan salah satu konsep penting di ruang hasilkali dalam. Dalam
Final Draft 1 Desember 2005 BEBERAPA KONSEP ORTOGONALITAS DI RUANG NORM Hendra Gunawan, Nursupiamin, dan Eder Kikianty Ortogonalitas merupakan salah satu konsep penting di ruang hasilkali dalam. Dalam
Deret Binomial. Ayundyah Kesumawati. June 25, Prodi Statistika FMIPA-UII. Ayundyah (UII) Deret Binomial June 25, / 14
 Deret Binomial Ayundyah Kesumawati Prodi Statistika FMIPA-UII June 25, 2015 Ayundyah (UII) Deret Binomial June 25, 2015 1 / 14 Pendahuluan Deret Binomial Kita telah mengenal Rumus Binomial. Untuk bilangan
Deret Binomial Ayundyah Kesumawati Prodi Statistika FMIPA-UII June 25, 2015 Ayundyah (UII) Deret Binomial June 25, 2015 1 / 14 Pendahuluan Deret Binomial Kita telah mengenal Rumus Binomial. Untuk bilangan
BAB V KEKONVERGENAN BARISAN PADA DAN KETERKAITAN DENGAN. Pada subbab 4.1 telah dibahas beberapa sifat dasar yang berlaku pada koleksi
 BAB V KEKONVERGENAN BARISAN PADA DAN KETERKAITAN DENGAN Pada subbab 4.1 telah dibahas beberapa sifat dasar yang berlaku pada koleksi semua fungsi yang terintegralkan Lebesgue, 1. Sebagaimana telah dirumuskan
BAB V KEKONVERGENAN BARISAN PADA DAN KETERKAITAN DENGAN Pada subbab 4.1 telah dibahas beberapa sifat dasar yang berlaku pada koleksi semua fungsi yang terintegralkan Lebesgue, 1. Sebagaimana telah dirumuskan
Keterbatasan Lokal Suatu Operator Superposisi Pada Ruang Barisan Real. Lina Nurhayati, Universitas Sanggabuana
 Keterbatasan Lokal Suatu Operator Superposisi Pada Ruang Barisan Real Lina urhayati, Universitas Sanggabuana nurhayati_lina@yahoo.co.id Abstrak Misalkan P suatu operator superposisi terbatas dan T adalah
Keterbatasan Lokal Suatu Operator Superposisi Pada Ruang Barisan Real Lina urhayati, Universitas Sanggabuana nurhayati_lina@yahoo.co.id Abstrak Misalkan P suatu operator superposisi terbatas dan T adalah
KONVOLUSI DISTRIBUSI EKSPONENSIAL DENGAN PARAMETER BERBEDA
 Jurnal Matematika UNAND Vol. No. 4 Hal. 9 ISSN : 33 9 c Jurusan Matematika FMIPA UNAND KONVOLUSI DISTRIBUSI EKSPONENSIAL DENGAN PARAMETER BERBEDA MARNISYAH ANAS Program Studi Magister Matematika, Fakultas
Jurnal Matematika UNAND Vol. No. 4 Hal. 9 ISSN : 33 9 c Jurusan Matematika FMIPA UNAND KONVOLUSI DISTRIBUSI EKSPONENSIAL DENGAN PARAMETER BERBEDA MARNISYAH ANAS Program Studi Magister Matematika, Fakultas
Analisis Fourier dan Wavelet
 0 Hendra Gunawan Analisis Fourier dan Wavelet Hendra Gunawan KK Analisis & Geometri FMIPA-ITB Bandung, 2017 Analisis Fourier dan Wavelet 1 Daftar Isi Kata Pengantar 5 0 Pendahuluan 7 0.1 Notasi dan istilah,
0 Hendra Gunawan Analisis Fourier dan Wavelet Hendra Gunawan KK Analisis & Geometri FMIPA-ITB Bandung, 2017 Analisis Fourier dan Wavelet 1 Daftar Isi Kata Pengantar 5 0 Pendahuluan 7 0.1 Notasi dan istilah,
= = =
 = + + + = + + + = + +.. + + + + + + + + = + + + + ( ) + ( ) + + = + + + = + = 1,2,, = + + + + = + + + =, + + = 1,, ; = 1,, =, + = 1,, ; = 1,, = 0 0 0 0 0 0 0...... 0 0 0, =, + + + = 0 0 0 0 0 0 0 0 0....
= + + + = + + + = + +.. + + + + + + + + = + + + + ( ) + ( ) + + = + + + = + = 1,2,, = + + + + = + + + =, + + = 1,, ; = 1,, =, + = 1,, ; = 1,, = 0 0 0 0 0 0 0...... 0 0 0, =, + + + = 0 0 0 0 0 0 0 0 0....
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
SIFAT-SIFAT HIMPUNAN PROXIMINAL
 Prima: Jurnal Pendidikan Matematika Vol. 2, No. 1, Januari 2018, hal. 49-56 P-ISSN: 2579-9827, E-ISSN: 2580-2216 SIFAT-SIFAT HIMPUNAN PROXIMINAL Arta Ekayanti Universitas Muhammadiyah Ponorogo, Jl. Budi
Prima: Jurnal Pendidikan Matematika Vol. 2, No. 1, Januari 2018, hal. 49-56 P-ISSN: 2579-9827, E-ISSN: 2580-2216 SIFAT-SIFAT HIMPUNAN PROXIMINAL Arta Ekayanti Universitas Muhammadiyah Ponorogo, Jl. Budi
METODE DEKOMPOSISI ADOMIAN UNTUK MENYELESAIKAN PERMASALAHAN NILAI BATAS PADA PERSAMAAN DIFERENSIAL PARSIAL NONLINEAR ABSTRACT
 METODE DEKOMPOSISI ADOMIAN UNTUK MENYELESAIKAN PERMASALAHAN NILAI BATAS PADA PERSAMAAN DIFERENSIAL PARSIAL NONLINEAR Birmansyah 1, Khozin Mu tamar 2, M. Natsir 2 1 Mahasiswa Program Studi S1 Matematika
METODE DEKOMPOSISI ADOMIAN UNTUK MENYELESAIKAN PERMASALAHAN NILAI BATAS PADA PERSAMAAN DIFERENSIAL PARSIAL NONLINEAR Birmansyah 1, Khozin Mu tamar 2, M. Natsir 2 1 Mahasiswa Program Studi S1 Matematika
INFERENSI PARAMETER MEAN POPULASI NORMAL DENGAN METODE BAYESIAN OBYEKTIF
 INFERENSI PARAMETER MEAN POPULASI NORMAL DENGAN METODE BAYESIAN OBYEKTIF Adi Setiawan Program Studi Matematika Industri dan Statistika, Fakultas Sains dan Matematika Universitas Kristen Satya Wacana Jl
INFERENSI PARAMETER MEAN POPULASI NORMAL DENGAN METODE BAYESIAN OBYEKTIF Adi Setiawan Program Studi Matematika Industri dan Statistika, Fakultas Sains dan Matematika Universitas Kristen Satya Wacana Jl
13. Aplikasi Transformasi Fourier
 13. plikasi ransformasi Fourier Misal adalah operator linear pada fungsi yang terdefinisi pada R dengan sifat: jika [f(x] = g(x, maka [f(x + s] = g(x + s untuk setiap s R. Maka, fungsi f(x = e ax (a C
13. plikasi ransformasi Fourier Misal adalah operator linear pada fungsi yang terdefinisi pada R dengan sifat: jika [f(x] = g(x, maka [f(x + s] = g(x + s untuk setiap s R. Maka, fungsi f(x = e ax (a C
SIFAT SPEKTRAL DARI MASALAH STURM-LIOUVILLE FRAKSIONAL DENGAN POTENSIAL COULOMB
 SIFAT SPEKTRAL DARI MASALAH STURM-LIOUVILLE FRAKSIONAL DENGAN POTENSIAL COULOMB oleh NURUL KOMIYATUN M0110063 SKRIPSI ditulis dan diajukan untuk memenuhi sebagian persyaratan memperoleh gelar Sarjana Sains
SIFAT SPEKTRAL DARI MASALAH STURM-LIOUVILLE FRAKSIONAL DENGAN POTENSIAL COULOMB oleh NURUL KOMIYATUN M0110063 SKRIPSI ditulis dan diajukan untuk memenuhi sebagian persyaratan memperoleh gelar Sarjana Sains
Bab II Kajian Teori Copula
 Bab Kajian Teori Copula.1 Pendahuluan Copula Tesis ini mengacu pada terminologi copula sebagai fungsi yang menghubungkan fungsi distribusi multivariat terhadap fungsi distribusi marginal uniform. Misalkan
Bab Kajian Teori Copula.1 Pendahuluan Copula Tesis ini mengacu pada terminologi copula sebagai fungsi yang menghubungkan fungsi distribusi multivariat terhadap fungsi distribusi marginal uniform. Misalkan
0,1, Holder s continue function in rank of and. 0,1, fungsi kontinu Holder berpangkat-,
 JMP : Volume 4 Nomor 1, Juni 2012, hal 233-240 HUBUNGAN ANTARA NILAI KRITIS DERIVATI- DENGAN DIMENSI- DARI SUATU KURVA Supriyadi Wibowo Jurusan Matematika MIPA UNS Surakarta Email supriyadi_w@yahoocoid
JMP : Volume 4 Nomor 1, Juni 2012, hal 233-240 HUBUNGAN ANTARA NILAI KRITIS DERIVATI- DENGAN DIMENSI- DARI SUATU KURVA Supriyadi Wibowo Jurusan Matematika MIPA UNS Surakarta Email supriyadi_w@yahoocoid
FUNGSI REGULAR. Endang Cahya M.A 1 Jurusan Matematika FMIPA ITB Jl. Ganesa 10, Bandung, Indonesia
 FUNGSI REGULAR Endang Cahya M.A Jurusan Matematika FMIPA ITB Jl. Ganesa 0, Bandung, 403-Indonesia Abstrak Tulisan ini membahas bagaimana mengkonstruksi sebuah fungsi Regular dari suatu fungsi panharmonik,
FUNGSI REGULAR Endang Cahya M.A Jurusan Matematika FMIPA ITB Jl. Ganesa 0, Bandung, 403-Indonesia Abstrak Tulisan ini membahas bagaimana mengkonstruksi sebuah fungsi Regular dari suatu fungsi panharmonik,
MODIFIKASI METODE DEKOMPOSISI ADOMIAN UNTUK MENYELESAIKAN MASALAH NILAI AWAL SINGULAR PADA PERSAMAAN DIFERENSIAL BIASA ORDE DUA ABSTRACT
 MODIFIKASI METODE DEKOMPOSISI ADOMIAN UNTUK MENYELESAIKAN MASALAH NILAI AWAL SINGULAR PADA PERSAMAAN DIFERENSIAL BIASA ORDE DUA Kristiani Panjaitan 1, Syamsudhuha 2, Leli Deswita 2 1 Mahasiswi Program
MODIFIKASI METODE DEKOMPOSISI ADOMIAN UNTUK MENYELESAIKAN MASALAH NILAI AWAL SINGULAR PADA PERSAMAAN DIFERENSIAL BIASA ORDE DUA Kristiani Panjaitan 1, Syamsudhuha 2, Leli Deswita 2 1 Mahasiswi Program
Modul KALKULUS MULTIVARIABEL II
 Modul KALKULUS MULTIVARIABEL II Oleh Ayundyah Kesumawati, S.Si., M.Si. (Program Studi Statistika) FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS ISLAM INDONESIA 26 Daftar Isi Daftar Isi iv Daftar
Modul KALKULUS MULTIVARIABEL II Oleh Ayundyah Kesumawati, S.Si., M.Si. (Program Studi Statistika) FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS ISLAM INDONESIA 26 Daftar Isi Daftar Isi iv Daftar
BAB III INTEGRAL LEBESGUE. Pada bab sebelumnya telah disebutkan bahwa ruang dibangun oleh
 BAB III INTEGRAL LEBESGUE Pada bab sebelumnya telah disebutkan bahwa ruang dibangun oleh fungsi-fungsi terukur dan memenuhi sifat yang berkaitan dengan integral Lebesgue. Kajian mengenai keterukuran suatu
BAB III INTEGRAL LEBESGUE Pada bab sebelumnya telah disebutkan bahwa ruang dibangun oleh fungsi-fungsi terukur dan memenuhi sifat yang berkaitan dengan integral Lebesgue. Kajian mengenai keterukuran suatu
JURNAL FOURIER April 2017, Vol. 6, No. 1, ISSN X; E-ISSN
 JURNAL FOURIER Aril 7, Vol. 6, No., -6 ISSN 5-763X; E-ISSN 54-539 Kaitan Antara Ruang W m, () Sobolev dan Ruang L () Lebesgue Piit Pratii Rahayu Program Studi Matematika Fakultas Sains dan Teknologi, UIN
JURNAL FOURIER Aril 7, Vol. 6, No., -6 ISSN 5-763X; E-ISSN 54-539 Kaitan Antara Ruang W m, () Sobolev dan Ruang L () Lebesgue Piit Pratii Rahayu Program Studi Matematika Fakultas Sains dan Teknologi, UIN
16. Analisis Multi Resolusi
 16. Analisis Multi esolusi Esensi dari basis ortonormal yang dibangun oleh sebuah wavelet adalah sifat multi resolusi-nya, sehingga kita dapat menganalisis suatu signal pada berbagai frekuensi di suatu
16. Analisis Multi esolusi Esensi dari basis ortonormal yang dibangun oleh sebuah wavelet adalah sifat multi resolusi-nya, sehingga kita dapat menganalisis suatu signal pada berbagai frekuensi di suatu
KAJIAN OPERATOR ACCRETIVE DAN SIFAT KETERBATASAN PADA RUANG HILBERT
 Seminar Nasional Matematika dan Aplikasinya, 1 Oktober 017 KAJIAN OPERATOR ACCRETIVE DAN SIFAT KETERBATASAN PADA RUANG HILBERT Susilo Hariyantoe 1), Y.D Sumanto ), Solikhin 3), Abdul Aziz 1 Departemen
Seminar Nasional Matematika dan Aplikasinya, 1 Oktober 017 KAJIAN OPERATOR ACCRETIVE DAN SIFAT KETERBATASAN PADA RUANG HILBERT Susilo Hariyantoe 1), Y.D Sumanto ), Solikhin 3), Abdul Aziz 1 Departemen
BAB II PENGANTAR SOLUSI PERSOALAN FISIKA MENURUT PENDEKATAN ANALITIK DAN NUMERIK
 BAB II PENGANTAR SOLUSI PERSOALAN FISIKA MENURUT PENDEKATAN ANALITIK DAN NUMERIK Tujuan Instruksional Setelah mempelajari bab ini pembaca diharapkan dapat: 1. Menjelaskan cara penyelesaian soal dengan
BAB II PENGANTAR SOLUSI PERSOALAN FISIKA MENURUT PENDEKATAN ANALITIK DAN NUMERIK Tujuan Instruksional Setelah mempelajari bab ini pembaca diharapkan dapat: 1. Menjelaskan cara penyelesaian soal dengan
LAMPIRAN I. Alfabet Yunani
 LAMPIRAN I Alfabet Yunani Alha Α Nu Ν Beta Β Xi Ξ Gamma Γ Omicron Ο Delta Δ Pi Π Esilon Ε Rho Ρ Zeta Ζ Sigma Σ Eta Η Tau Τ Theta Θ Usilon Υ Iota Ι hi Φ, Kaa Κ Chi Χ Lambda Λ Psi Ψ Mu Μ Omega Ω LAMPIRAN
LAMPIRAN I Alfabet Yunani Alha Α Nu Ν Beta Β Xi Ξ Gamma Γ Omicron Ο Delta Δ Pi Π Esilon Ε Rho Ρ Zeta Ζ Sigma Σ Eta Η Tau Τ Theta Θ Usilon Υ Iota Ι hi Φ, Kaa Κ Chi Χ Lambda Λ Psi Ψ Mu Μ Omega Ω LAMPIRAN
SOLUSI NUMERIK PERSAMAAN INTEGRAL VOLTERRA-FREDHOLM NONLINEAR MENGGUNAKAN FUNGSI BASIS BARU ABSTRACT
 SOLUSI NUMERIK PERSAMAAN INTEGRAL VOLTERRA-FREDHOLM NONLINEAR MENGGUNAKAN FUNGSI BASIS BARU Vanny Octary 1 Endang Lily 2 1 Mahasiswa Program Studi S1 Matematika 2 Dosen Jurusan Matematika Fakultas Matematika
SOLUSI NUMERIK PERSAMAAN INTEGRAL VOLTERRA-FREDHOLM NONLINEAR MENGGUNAKAN FUNGSI BASIS BARU Vanny Octary 1 Endang Lily 2 1 Mahasiswa Program Studi S1 Matematika 2 Dosen Jurusan Matematika Fakultas Matematika
OPTIMISASI KONVEKS: Konsep-konsep
 OPTIMISASI KONVEKS: Konsep-konsep Caturiyati, M.Si 1 dan Himmawati Puji Lestari, M.Si 2 1,2 Jurdik Matematika FMIPA UNY 1 wcaturiyati@yahoo.com 2 himmawatipl@yahoo.com Abstrak Pada masalah optimisasi konveks
OPTIMISASI KONVEKS: Konsep-konsep Caturiyati, M.Si 1 dan Himmawati Puji Lestari, M.Si 2 1,2 Jurdik Matematika FMIPA UNY 1 wcaturiyati@yahoo.com 2 himmawatipl@yahoo.com Abstrak Pada masalah optimisasi konveks
Husna Arifah,M.Sc : Persamaan Bessel: Fungsi-fungsi Besel jenis Pertama
 Bentuk umum PD Bessel : x 2 y"+xy' +(x 2 υ 2 )y =...() Kita asumsikan bahwa parameter υ dalam () adalah bilangan riil dan tak negatif. Penyelesaian PD mempunyai bentuk : y(x) = x r m = a m x m = a m xm
Bentuk umum PD Bessel : x 2 y"+xy' +(x 2 υ 2 )y =...() Kita asumsikan bahwa parameter υ dalam () adalah bilangan riil dan tak negatif. Penyelesaian PD mempunyai bentuk : y(x) = x r m = a m x m = a m xm
Pengantar Statistika Matematika II
 Pengantar a Matematika II Atina Ahdika, S.Si., M.Si. Prodi a FMIPA Universitas Islam Indonesia March 20, 2017 atinaahdika.com t F Parameter adalah karakteristik dari populasi (misal θ) adalah karakteristik
Pengantar a Matematika II Atina Ahdika, S.Si., M.Si. Prodi a FMIPA Universitas Islam Indonesia March 20, 2017 atinaahdika.com t F Parameter adalah karakteristik dari populasi (misal θ) adalah karakteristik
II. TINJAUAN PUSTAKA. Turunan fungsi f adalah fungsi lain f (dibaca f aksen ) yang nilainya pada ( ) ( ) ( )
 II. TINJAUAN PUSTAKA 2.1 Definisi Turunan Turunan fungsi f adalah fungsi lain f (dibaca f aksen ) yang nilainya pada sebarang bilangan c adalah asalkan limit ini ada. Jika limit ini memang ada, maka dikatakan
II. TINJAUAN PUSTAKA 2.1 Definisi Turunan Turunan fungsi f adalah fungsi lain f (dibaca f aksen ) yang nilainya pada sebarang bilangan c adalah asalkan limit ini ada. Jika limit ini memang ada, maka dikatakan
FORMULA PENGGANTI METODE KOEFISIEN TAK TENTU ABSTRACT
 FORMULA PENGGANTI METODE KOEFISIEN TAK TENTU Syofia Deswita 1, Syamsudhuha 2, Agusni 2 1 Mahasiswa Program Studi S1 Matematika 2 Dosen Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas
FORMULA PENGGANTI METODE KOEFISIEN TAK TENTU Syofia Deswita 1, Syamsudhuha 2, Agusni 2 1 Mahasiswa Program Studi S1 Matematika 2 Dosen Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas
KETERBATASAN OPERATOR BESSEL-RIESZ DI RUANG LEBESGUE SKRIPSI
 KETERBATASAN OPERATOR BESSEL-RIESZ DI RUANG LEBESGUE SKRIPSI MOCHAMMAD FANDI ANSORI PROGRAM STUDI S1 MATEMATIKA DEPARTEMEN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI UNIVERSITAS AIRLANGGA 2016 KETERBATASAN
KETERBATASAN OPERATOR BESSEL-RIESZ DI RUANG LEBESGUE SKRIPSI MOCHAMMAD FANDI ANSORI PROGRAM STUDI S1 MATEMATIKA DEPARTEMEN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI UNIVERSITAS AIRLANGGA 2016 KETERBATASAN
Profesor Hendra Gunawan
 Majelis Guru Besar Institut Teknologi Bandung Pidato Ilmiah Guru Besar Institut Teknologi Bandung Profesor Hendra Gunawan Kontribusi dalam Matematika dan Pengembangan Ilmu dan Teknologi 26 Januari 2007
Majelis Guru Besar Institut Teknologi Bandung Pidato Ilmiah Guru Besar Institut Teknologi Bandung Profesor Hendra Gunawan Kontribusi dalam Matematika dan Pengembangan Ilmu dan Teknologi 26 Januari 2007
Konstruksi Matriks NonNegatif Simetri dengan Spektrum Bilangan Real
 J. Math. and Its Appl. ISSN: 189-605X Vol. 4, No. 1, May 007, 17 5 Konstruksi Matriks NonNegatif Simetri dengan Spektrum Bilangan Real Bambang Sugandi 1 dan Erna Apriliani 1 Jurusan Matematika, FMIPA Unibraw,
J. Math. and Its Appl. ISSN: 189-605X Vol. 4, No. 1, May 007, 17 5 Konstruksi Matriks NonNegatif Simetri dengan Spektrum Bilangan Real Bambang Sugandi 1 dan Erna Apriliani 1 Jurusan Matematika, FMIPA Unibraw,
Beberapa Sifat Operator Self Adjoint dalam Ruang Hilbert
 Vol 12, No 2, 153-159, Januari 2016 Beberapa Sifat Operator Self Adjoint dalam Ruang Hilbert Firman Abstrak Misalkan adalah operator linier dengan adalah ruang Hilbert Pada operator linier dikenal istilah
Vol 12, No 2, 153-159, Januari 2016 Beberapa Sifat Operator Self Adjoint dalam Ruang Hilbert Firman Abstrak Misalkan adalah operator linier dengan adalah ruang Hilbert Pada operator linier dikenal istilah
KONVOLUSI DARI PEUBAH ACAK BINOMIAL NEGATIF
 Jurnal Matematika UNAND Vol. 2 No. 3 Hal. 22 27 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND KONVOLUSI DARI PEUBAH ACAK BINOMIAL NEGATIF NUR ADE YANI Program Studi Magister Matematika, Fakultas Matematika
Jurnal Matematika UNAND Vol. 2 No. 3 Hal. 22 27 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND KONVOLUSI DARI PEUBAH ACAK BINOMIAL NEGATIF NUR ADE YANI Program Studi Magister Matematika, Fakultas Matematika
Kuliah PD. Gaya yang bekerj a pada suatu massa sama dengan laju perubahan momentum terhadap waktu.
 Kuliah PD Pertemuan ke-1: Motivasi: 1. Mekanika A. Hukum Newton ke-: Gaya yang bekerj a pada suatu massa sama dengan laju perubahan momentum terhadap waktu. Misalkan F: gaya, m: massa benda, a: percepatan,
Kuliah PD Pertemuan ke-1: Motivasi: 1. Mekanika A. Hukum Newton ke-: Gaya yang bekerj a pada suatu massa sama dengan laju perubahan momentum terhadap waktu. Misalkan F: gaya, m: massa benda, a: percepatan,
TRANSFORMASI FOURIER QUATERNION
 JIMT Vol. 10 No. 1 Juni 2013 (Hal. 83 88 ) Jurnal Ilmiah Matematika dan Terapan ISSN : 2450 766X TANSFOMASI FOUIE QUATENION esnawati Program Studi Matematika Jurusan Matematika FMIPA Universitas Tadulako
JIMT Vol. 10 No. 1 Juni 2013 (Hal. 83 88 ) Jurnal Ilmiah Matematika dan Terapan ISSN : 2450 766X TANSFOMASI FOUIE QUATENION esnawati Program Studi Matematika Jurusan Matematika FMIPA Universitas Tadulako
4.1 Sistem kuasi-linear hiperbolik. Sistem (hukum kekekalan) kuasi-linear mempunyai bentuk umum. t u + A α (u) xα u = b(u) (4.1.
 Bab 4 SISTEM KUASI-LINEAR 4. Sistem kuasi-linear hiperbolik Sistem (hukum kekekalan) kuasi-linear mempunyai bentuk umum t u + A α (u) xα u = b(u) (4..) α= u(x, 0) = u 0 (x) Jika u 0 adalah fungsi konstan,
Bab 4 SISTEM KUASI-LINEAR 4. Sistem kuasi-linear hiperbolik Sistem (hukum kekekalan) kuasi-linear mempunyai bentuk umum t u + A α (u) xα u = b(u) (4..) α= u(x, 0) = u 0 (x) Jika u 0 adalah fungsi konstan,
Pengantar Statistika Matematika II
 Bab 1: a FMIPA Universitas Islam Indonesia Parameter adalah karakteristik dari populasi (misal θ) adalah karakteristik dari sampel Akan dibahas konsep statistik dan distribusi sampling Parameter Misalkan
Bab 1: a FMIPA Universitas Islam Indonesia Parameter adalah karakteristik dari populasi (misal θ) adalah karakteristik dari sampel Akan dibahas konsep statistik dan distribusi sampling Parameter Misalkan
Pengaruh Waktu Tunda Yang Kecil Terhadap Stabilitas Eksponensial Seragam Suatu Sistem Persamaan Diferensial
 SEMINAR NASIONAL MATEMATIKA DAN PENDIDIKAN MATEMATIKA UNY 2015 Pengaruh Waktu Tunda Yang Kecil Terhadap Stabilitas Eksponensial Seragam Suatu Sistem Persamaan Diferensial Aloysius Joakim Fernandez Fakultas
SEMINAR NASIONAL MATEMATIKA DAN PENDIDIKAN MATEMATIKA UNY 2015 Pengaruh Waktu Tunda Yang Kecil Terhadap Stabilitas Eksponensial Seragam Suatu Sistem Persamaan Diferensial Aloysius Joakim Fernandez Fakultas
ELLIPTIC CURVE CRYPTOGRAPHY. Disarikan oleh: Dinisfu Sya ban ( )
 ELLIPTIC CURVE CRYPTOGRAPHY Disarikan oleh: Dinisfu Sya ban (0403100596) SEKOLAH TINGGI SANDI NEGARA BOGOR 007 A. Fungsi Elliptic Curves 1. Definisi Elliptic Curves Definisi 1. : Misalkan k merupakan field
ELLIPTIC CURVE CRYPTOGRAPHY Disarikan oleh: Dinisfu Sya ban (0403100596) SEKOLAH TINGGI SANDI NEGARA BOGOR 007 A. Fungsi Elliptic Curves 1. Definisi Elliptic Curves Definisi 1. : Misalkan k merupakan field
TRANSFORMASI LINIER PADA RUANG BANACH
 TRANSFORMASI LINIER PADA RUANG BANACH Nur Aeni, S.Si., M.Pd Jurusan Matematika, Fakultas Sains dan Teknologi, UINAM nuraeniayatullah@gmail.com ABSTRAK Info: Jurnal MSA Vol. 2 No. 1 Edisi: Januari Juni
TRANSFORMASI LINIER PADA RUANG BANACH Nur Aeni, S.Si., M.Pd Jurusan Matematika, Fakultas Sains dan Teknologi, UINAM nuraeniayatullah@gmail.com ABSTRAK Info: Jurnal MSA Vol. 2 No. 1 Edisi: Januari Juni
REFLEKSIVITAS PADA RUANG ORLICZ DENGAN KEKONVERGENAN RATA-RATA
 REFLEKSIVITAS PADA RUANG ORLICZ DENGAN KEKONVERGENAN RATA-RATA Mila Apriliani Utari, Encum Sumiaty, Sumanang Muchtar Departemen Pendidikan Matematika FPMIPA Universitas Pendidikan Indonesia *Coresponding
REFLEKSIVITAS PADA RUANG ORLICZ DENGAN KEKONVERGENAN RATA-RATA Mila Apriliani Utari, Encum Sumiaty, Sumanang Muchtar Departemen Pendidikan Matematika FPMIPA Universitas Pendidikan Indonesia *Coresponding
BAB 2 PERSAMAAN DIFFERENSIAL BIASA
 BAB 2 BIASA 2.1. KONSEP DASAR Persamaan Diferensial (PD) Biasa adalah persamaan yang mengandung satu atau beberapa penurunan y (varibel terikat) terhadap x (variabel bebas) yang tidak spesifik dan ditentukan
BAB 2 BIASA 2.1. KONSEP DASAR Persamaan Diferensial (PD) Biasa adalah persamaan yang mengandung satu atau beberapa penurunan y (varibel terikat) terhadap x (variabel bebas) yang tidak spesifik dan ditentukan
RUANG TOPOLOGI LEMBUT KABUR
 Jurnal Matematika UNAND Vol. 5 No. 2 Hal. 122 128 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND RUANG TOPOLOGI LEMBUT KABUR SRI NOVITA SARI Program Studi Matematika, Fakultas Matematika dan Ilmu Pengetahuan
Jurnal Matematika UNAND Vol. 5 No. 2 Hal. 122 128 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND RUANG TOPOLOGI LEMBUT KABUR SRI NOVITA SARI Program Studi Matematika, Fakultas Matematika dan Ilmu Pengetahuan
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
Variabel Banyak Bernilai Real 1 / 1
 Fungsi Variabel Banyak Bernilai Real Turunan Parsial dan Turunan Wono Setya Budhi KK Analisis dan Geometri, FMIPA ITB Variabel Banyak Bernilai Real 1 / 1 Turunan Parsial dan Turunan Usaha pertama untuk
Fungsi Variabel Banyak Bernilai Real Turunan Parsial dan Turunan Wono Setya Budhi KK Analisis dan Geometri, FMIPA ITB Variabel Banyak Bernilai Real 1 / 1 Turunan Parsial dan Turunan Usaha pertama untuk
Pengantar Statistika Matematik(a)
 Catatan Kuliah Pengantar Statistika Matematik(a) Statistika Lebih Dari Sekadar Matematika disusun oleh Khreshna I.A. Syuhada, MSc. PhD. Kelompok Keilmuan STATISTIKA - FMIPA Institut Teknologi Bandung 2014
Catatan Kuliah Pengantar Statistika Matematik(a) Statistika Lebih Dari Sekadar Matematika disusun oleh Khreshna I.A. Syuhada, MSc. PhD. Kelompok Keilmuan STATISTIKA - FMIPA Institut Teknologi Bandung 2014
Pengantar Statistika Matematika II
 Pengantar Statistika Matematika II Estimasi Titik dengan Metode Atina Ahdika, S.Si., M.Si. Prodi Statistika FMIPA Universitas Islam Indonesia May 9, 2017 atinaahdika.com Dalam pendekatan klasik, parameter
Pengantar Statistika Matematika II Estimasi Titik dengan Metode Atina Ahdika, S.Si., M.Si. Prodi Statistika FMIPA Universitas Islam Indonesia May 9, 2017 atinaahdika.com Dalam pendekatan klasik, parameter
