BAGIAN KEDUA. Fungsi, Limit dan Kekontinuan, Turunan
|
|
|
- Irwan Wibowo
- 6 tahun lalu
- Tontonan:
Transkripsi
1 BAGIAN KEDUA Fungsi, Limit dan Kekontinuan, Turunan 51
2 52 Hendra Gunawan
3 Pengantar Analisis Real FUNGSI 6.1 Fungsi dan Grafiknya Konsep fungsi telah dipelajari oleh Gottfried Wilhelm von Leibniz sejak akhir abad ke-17, namun definisi fungsi yang kita kenal sekarang berakar pada rumusan Leonhard Euler pada 1749, yang disempurnakan kemudian oleh Joseph Fourier pada 1822 dan Lejeune Dirichlet pada Sebuah fungsi dari himpunan A ke himpunan B adalah suatu aturan yang mengaitkan setiap x A dengan sebuah elemen tunggal y B, ditulis f : A B x y. Elemen y yang terkait dengan x disebut peta dari x (di bawah f) dan kita tulis y = f(x). Bila f(x) mempunyai rumus yang eksplisit, fungsi f sering dinyatakan sebagai persamaan y = f(x). Dalam buku ini, kita membatasi pembahasan kita pada fungsi dari A R ke B R, yakni fungsi bernilai real dengan peubah real. Dalam hal ini, kita dapat menggambar grafik fungsi f : A B sebagai grafik persamaan y = f(x) pada sistem koordinat Cartesius (lihat Gambar 6.1). Definisi di atas menjamin bahwa setiap garis vertikal yang memotong A akan memotong grafik tepat pada satu buah titik (tidak mungkin lebih). Jika f adalah sebuah fungsi dari A ke B dan H A, maka kita katakan bahwa f terdefinisi pada H. Himpunan terbesar pada mana f terdefinisi adalah A. Himpunan A dalam hal ini disebut sebagai daerah asal f. Sebagai contoh, sebuah barisan merupakan fungsi dengan daerah asal himpunan bilangan asli N.
4 54 Hendra Gunawan Gambar 6.1 Grafik sebuah fungsi Jika f terdefinisi pada H, maka kita definisikan peta dari H di bawah f sebagai f(h) := {f(x) : x H}. Untuk ilustrasi, lihat Gambar 6.2 di bawah ini. Dalam hal H = A, himpunan f(a) disebut sebagai daerah nilai f. Catat bahwa f(a) tidak harus sama dengan B. Gambar 6.2 Peta dari H di bawah f Contoh 1. Persamaan y = x 2 mendefinisikan sebuah fungsi dari R ke R. Untuk tiap x R terdapat tepat sebuah y R yang memenuhi aturan y = x 2. Amati bahwa, dalam Gambar 6.3 pada halaman berikut, setiap garis vertikal memotong
5 Pengantar Analisis Real 55 grafik y = x 2 tepat pada sebuah titik. Daerah asal fungsi ini adalah R dan daerah nilainya adalah [0, ). Peta dari ( 0.5, 1], misalnya, adalah [0, 1]. Gambar 6.3 Grafik persamaan y = x 2 Contoh 2. Persamaan y 2 = x tidak mendefinisikan fungsi dari [0, ) ke R. Untuk tiap x > 0 terdapat dua buah y R, yakni y = ± x, yang memenuhi aturan y 2 = x. Dalam Gambar 6.4, amati bahwa setiap garis vertikal yang memotong sumbu-x pada x 0 > 0 akan memotong grafik y 2 = x pada dua buah titik. Gambar 6.4 Grafik persamaan y 2 = x Contoh 3. Persamaan y 2 = x, y 0, mendefinisikan sebuah fungsi dari [0, ) ke [0, ). Untuk tiap x > 0 terdapat tepat sebuah y [0, ), yakni y = x, yang
6 56 Hendra Gunawan memenuhi aturan y 2 = x. Dalam Gambar 5.5, amati bahwa setiap garis vertikal yang memotong sumbu-x pada x 0 0 akan memotong grafik y 2 = x, y 0, tepat pada sebuah titik. Gambar 6.5 Grafik persamaan y 2 = x, y 0 Soal Latihan 1. Gambar grafik himpunan semua titik (x, y) sedemikian sehingga { 5 jika x 1 y = 2 jika x < 1 Jelaskan mengapa grafik tersebut merupakan grafik sebuah fungsi dari R ke R. Tentukan daerah nilainya. Tentukan pula peta dari [1, 2] di bawah fungsi tersebut. 2. Apakah persamaan x 2 + y 2 = 1 mendefinisikan sebuah fungsi dari [ 1, 1] ke [ 1, 1]? Jelaskan. 3. Apakah persamaan x 2 +y 2 = 1, y 0, mendefinisikan sebuah fungsi dari [ 1, 1] ke [0, 1]? Jelaskan. 4. Diketahui f terdefinisi pada H dan A, B H. Selidiki apakah f(a B) = f(a) f(b) dan f(a B) = f(a) f(b).
7 Pengantar Analisis Real Fungsi Polinom dan Fungsi Rasional Jika a 0, a 1,..., a n R, maka persamaan y = a 0 +a 1 x+ +a n x n mendefinisikan sebuah fungsi dari R ke R. Sembarang nilai x yang disubstitusikan ke ruas kanan akan memberi kita sebuah nilai y yang berkaitan dengannya. Untuk n N, fungsi ini dikenal sebagai polinom berderajat n asalkan a n 0. Untuk n = 0, fungsi konstan y = a 0 merupakan polinom berderajat 0. Misalkan P dan Q adalah fungsi polinom, dan S adalah himpunan semua bilangan x R dengan Q(x) 0. Maka, persamaan y = P (x) Q(x) mendefinisikan sebuah fungsi dari S ke R. Fungsi ini dikenal sebagai fungsi rasional. Contoh 4. Fungsi yang diberikan oleh persamaan y = x 3 3x 2 + 2x merupakan polinom berderajat 3 (atau polinom kubik ). Grafik fungsi ini dapat dilihat dalam Gambar 6.6. Perhatikan bahwa grafik memotong sumbu-x pada tiga buah titik (yang merupakan akar persamaan kubik x 3 3x 2 + 2x = 0). Gambar 6.6 Grafik fungsi y = x 3 3x 2 + 2x Contoh 5. Fungsi yang diberikan oleh persamaan y = x2 + 4 x 2 4
8 58 Hendra Gunawan merupakan polinom rasional. Daerah asalnya adalah {x : x ±2}. Grafiknya dapat dilihat dalam Gambar 6.7. Gambar 6.7 Grafik fungsi y = x2 +4 x 2 4 Soal Latihan 1. Tentukan daerah nilai fungsi polinom y = 4x 4x 2 dan sketsalah grafiknya. 2. Tentukan daerah asal fungsi rasional y = 1 x 1+x dan sketsalah grafiknya. 6.3 Operasi pada Fungsi; Fungsi Invers Jika H R, f, g : H R, dan λ R, maka kita definisikan f + g dan λf sebagai fungsi yang memenuhi aturan (f + g)(x) := f(x) + g(x), x H; (λf)(x) := λf(x), x H. Selain itu kita definisikan pula fg dan f/g sebagai (fg)(x) := f(x)g(x), x H; (f/g)(x) := f(x)/g(x), x H, g(x) 0. Sebagai contoh, jika f dan g adalah polinom, maka f/g merupakan fungsi rasional.
9 Pengantar Analisis Real 59 Misalkan A, B R, g : A B, dan f : B R. Maka kita definisikan fungsi komposisi f g : A R sebagai Perhatikan bahwa untuk tiap x A (f g)(x) := f(g(x)), x A. x g(x) f(g(x)). Di sini fungsi g beroperasi terlebih dahulu terhadap x, dan setelah itu fungsi f beroperasi terhadap g(x). Contoh 6. Misalkan f : R R didefinisikan sebagai dan g : R R didefinisikan sebagai f(x) = x2 1 x 2 + 1, x R, g(x) = x 2. Maka f g : R R adalah fungsi dengan aturan (f g)(x) = f(g(x)) = {g(x)}2 1 {g(x)} = x4 1 x Misalkan A dan B adalah himpunan dan f adalah fungsi dari A ke B. Ini berarti bahwa bahwa setiap anggota a A mempunyai sebuah peta tunggal b = f(a) B. Kita sebut f 1 fungsi invers dari f apabila f 1 merupakan fungsi dari B ke A dengan sifat x = f 1 (y) jika dan hanya jika y = f(x). Tidak semua fungsi mempunyai fungsi invers. Dari definisi di atas jelas bahwa f : A B mempunyai fungsi invers f 1 : B A jika dan hanya jika setiap b B merupakan peta dari sebuah anggota tunggal a A. Fungsi dengan sifat ini disebut sebagai suatu korespondensi 1 1 antara A dan B. Secara geometris, f : A B merupakan korespondensi 1 1 antara A dan B jika dan hanya jika setiap garis vertikal yang memotong A juga memotong grafik f tepat pada sebuah titik dan setiap garis horisontal yang memotong B juga akan memotong grafik f tepat pada sebuah titik. Kondisi pertama memastikan bahwa
10 60 Hendra Gunawan f merupakan fungsi, sementara kondisi kedua memastikan bahwa f 1 merupakan fungsi. Lihat Gambar 6.8 di bawah ini. Contoh 7. Fungsi f(x) = x merupakan korespondensi 1 1 antara [0, ) dan [0, ). Fungsi ini mempunyai fungsi invers, yaitu f 1 (x) = x 2, x 0. Gambar 6.8 Korespondensi 1 1 Soal Latihan 1. Misalkan f : [0, 1] [0, 1] didefinisikan sebagai f(x) = 1 x 1 + x, 0 x 1, dan g : [0, 1] [0, 1] didefinisikan sebagai g(x) = 4x 4x 2, 0 x 1. Tentukan aturan untuk f g dan g f. Apakah mereka sama? 2. Untuk fungsi f dan g pada Soal 1, tunjukkan bahwa f 1 ada sedangkan g 1 tidak ada. Tentukan aturan untuk f Diketahui g : A B merupakan suatu korespondensi 1 1 antara A dan B. Buktikan bahwa (g 1 g)(x) = x untuk tiap x A dan (g g 1 )(y) = y untuk tiap y B.
11 Pengantar Analisis Real Fungsi Terbatas Misalkan f terdefinisi pada H. Kita katakan bahwa f terbatas di atas pada H oleh suatu batas atas M apabila untuk tiap x H berlaku f(x) M. Ini setara dengan mengatakan bahwa himpunan f(h) = {f(x) : x H} terbatas di atas oleh M. Jika f terbatas di atas pada H, maka menurut Sifat Kelengkapan f(h) mempunyai supremum. Misalkan B := sup f(x) = sup f(h). x H Secara umum, belum tentu terdapat c H sehingga f(c) = B. Jika terdapat c H sehingga f(c) = B, maka B disebut sebagai nilai maksimum f pada H dan nilai maksimum ini tercapai di c. Untuk ilustrasi, lihat Gambar 6.9 di bawah ini. Gambar 6.9 Fungsi terbatas dan nilai maksimumnya Definisi fungsi terbatas di bawah dan nilai minimum dapat dirumuskan secara serupa. Jika f terbatas di atas dan juga di bawah pada himpunan H, maka f dikatakan terbatas pada H. Menurut Proposisi 2 pada Bab 1, f terbatas pada H jika dan hanya jika terdapat K > 0 sedemikian sehingga untuk tiap x H berlaku f(x) K.
12 62 Hendra Gunawan Contoh 8. Misalkan f : (0, ) R didefinisikan sebagai f(x) = 1 x, x > 0. Fungsi ini terbatas di bawah pada (0, ) dan inf f(x) = 0, namun f tidak mempunyai x>0 nilai minimum. Perhatikan pula bahwa f tidak terbatas di atas pada (0, ). Contoh 9. Misalkan f : [0, 1] [0, 1] didefinisikan oleh f(x) = 1 x. Fungsi ini terbatas pada [0, 1], mencapai nilai maksimumnya (yaitu 1) di 0, dan juga mencapai nilai minimumnya (yaitu 0) di 1. Soal Latihan 1. Selidiki apakah f : [0, 1] [0, 1] yang didefinisikan sebagai f(x) = 1 x 1 + x, 0 x 1, terbatas serta mencapai nilai maksimum dan minimumnya. 2. Selidiki apakah g : [0, 1] [0, 1] yang didefinisikan sebagai g(x) = 4x 4x 2, 0 x 1. terbatas serta mencapai nilai maksimum dan minimumnya. 3. Tunjukkan bahwa f(x) = 1 1+x 2 terbatas pada R. Apakah f mencapai nilai maksimum dan minimumnya? 4. Misalkan f dan g terbatas di atas pada H dan a R. Buktikan bahwa sup{a + f(x)} = a + sup f(x). x H x H sup x H {f(x) + g(x)} sup x H f(x) + sup x H g(x). Beri contoh bahwa kesamaan tidak harus berlaku.
13 Pengantar Analisis Real LIMIT DAN KEKONTINUAN 7.1 Limit Fungsi di Suatu Titik Diberikan sebuah fungsi f yang terdefinisi pada interval (a, b) kecuali mungkin di sebuah titik c (a, b), kita tertarik untuk mengamati nilai f(x) untuk x di sekitar c. Khususnya, kita bertanya: apakah f(x) menuju suatu bilangan tertentu bila x menuju c? Berikut ini adalah definisi limit sepihak, yaitu limit kiri dan limit kanan, di suatu titik. Misalkan f terdefinisi pada interval (a, c) dan L R. Kita katakan bahwa f menuju L bila x menuju c dari kiri, dan kita tulis atau f(x) L bila x c lim f(x) = L, x c apabila untuk setiap ɛ > 0 terdapat δ > 0 sedemikian sehingga jika c δ < x < c, maka f(x) L < ɛ. Misalkan f terdefinisi pada interval (c, b) dan M R. Kita katakan bahwa f menuju M bila x menuju c dari kanan, dan kita tulis atau f(x) M bila x c + lim f(x) = M, x c + apabila untuk setiap ɛ > 0 terdapat δ > 0 sedemikian sehingga jika c < x < c + δ, maka f(x) M < ɛ.
14 64 Hendra Gunawan Gambar 7.1 Limit Kiri f di c Bilangan L dan M disebut sebagai limit kiri dan limit kanan dari f di c. Nilai f(x) L (atau f(x) M ) menyatakan jarak antara f(x) dan L (atau jarak antara f(x) dan M), yang dapat kita interpretasikan sebagai kesalahan dalam menghampiri nilai L atau M dengan f(x) (atau sebaliknya menghampiri nilai f(x) dengan L atau M). Kesalahan ini dapat dibuat sekecil yang kita kehendaki dengan cara mengambil x sedekat-dekatnya ke c dari kiri atau kanan. Contoh 1. Misalkan f : R R adalah fungsi yang didefinisikan sebagai { 1 x, x 1; f(x) = 2x, x > 1. Maka, lim f(x) = 0 dan x 1 lim f(x) = 2. x 1 + Perhatikan bahwa nilai f(1) terdefinisi, yakni f(1) = 0. Misalkan f terdefinisi pada interval (a, b) kecuali mungkin di titik c (a, b), dan L R. Kita katakan bahwa f menuju ke L bila x menuju c, dan kita tuliskan f(x) L bila x c atau lim f(x) = L, x c
15 Pengantar Analisis Real 65 apabila untuk setiap ɛ > 0 terdapat δ > 0 sedemikian sehingga jika 0 < x c < δ, maka f(x) L < ɛ. Dalam hal ini, bilangan L disebut sebagai limit f di c, dan f dikatakan mempunyai limit L di c. Gambar 7.2 Limit f di c Perhatikan bahwa kondisi 0 < x c < δ setara dengan δ < x c < δ, x c. Jadi, 0 < x c < δ jika dan hanya jika x memenuhi salah satu dari dua pertaksamaan berikut: c δ < x < c atau c < x < c + δ. Sehubungan dengan itu, kita mempunyai proposisi berikut. Proposisi 2. lim x c f(x) = L jika dan hanya jika lim x c x c f(x) = L dan lim f(x) = L. + Menurut Proposisi 2, fungsi pada Contoh 1 tidak mempunyai limit di 1 karena limit kiri dan limit kanannya tidak sama. Contoh 3. Misalkan f(x) = x2 1 x 1. Fungsi ini terdefinisi pada (, 1) dan juga pada (1, ). Bila kita tinjau nilai f(x) untuk x < 1, maka kita dapatkan bahwa f(x) 2 bila x 1. Bila kita amati nilai f(x) untuk x > 1, maka kita dapatkan bahwa f(x) 2 bila x 1 +.
16 66 Hendra Gunawan Jadi, limit kiri dari f di c sama dengan limit kanannya, yaitu 2. Karena itu lim f(x) = 2. x c (Perhatikan bahwa pada contoh ini, f tidak terdefinisi di 1.) Proposisi 4. (i) lim x c k = k dan (ii) lim x c x = c. Bukti. (i) Diberikan ɛ > 0, pilih δ > 0 sembarang. Jika 0 < x c < δ, maka k k = 0 < ɛ. Ini membuktikan bahwa lim x c k = k. (ii) Diberikan ɛ > 0, pilih δ = ɛ. Jika 0 < x c < δ, maka x c < δ = ɛ. Ini membuktikan bahwa lim x c x = c. Soal Latihan 1. Misalkan n N. Buktikan, dengan menggunakan definisi, bahwa lim x 0 + x 1/n = Misalkan f : R R adalah fungsi yang didefinisikan sebagai 2x, x < 1; f(x) = 1, x = 1 3 x, x > 1. Buktikan, dengan menggunakan definisi, bahwa lim f(x) = 2 dan lim x 1 Simpulkan bahwa lim x 1 f(x) = 2. f(x) = 2. x Buktikan, dengan menggunakan definisi, bahwa lim x c (px + q) = pc + q. 4. Buktikan lim x c f(x) = 0 jika dan hanya jika lim x c f(x) = Buktikan jika f(x) g(x) h(x) untuk x di sekitar c dan lim f(x) = lim h(x) = x c x c L, maka lim g(x) = L. x c 6. Buktikan jika lim x c f(x) = L > 0, maka terdapat δ > 0 sehingga f(x) > 0 untuk c δ < x < c + δ, x c.
17 Pengantar Analisis Real Kekontinuan di Suatu Titik Dalam definisi lim x c f(x), nilai f di c sama sekali tidak diperhatikan. Kita hanya tertarik dengan nilai f(x) untuk x menuju c, bukan dengan nilai f di c. Jadi mungkin saja f mempunyai limit L di c sekalipun f tidak terdefinisi di titik c. Dalam hal f terdefinisi di c, dapat terjadi f(c) L. Misalkan f terdefinisi pada (a, b) dan c (a, b). Kita katakan bahwa f kontinu di titik c jika dan hanya jika lim f(x) = f(c). x c Berdasarkan Proposisi 2, f kontinu di c jika dan hanya jika untuk setiap ɛ > 0 terdapat δ > 0 sedemikian sehingga jika x c < δ, maka f(x) f(c) < ɛ. Secara intuitif, f kontinu di c berarti grafik fungsi f tidak terputus di c. Seperti halnya limit sepihak, kita juga mempunyai definisi kekontinuan sepihak. Jika f terdefinisi pada (a, c] dan lim f(x) = f(c), maka kita katakan bahwa f kontinu x c kiri di c. Jika f terdefinisi pada [c, b) dan lim f(x) = f(c), maka kita katakan bahwa x c + f kontinu kanan di c. Gambar 7.3 Fungsi Kontinu di Suatu Titik Contoh 5. (i) Untuk setiap n N, fungsi f(x) = x 1/n kontinu kanan di 0. (ii) Fungsi f(x) = px + q kontinu di setiap titik.
18 68 Hendra Gunawan Teorema 6. Misalkan f terdefinisi pada (a, b) kecuali mungkin di c (a, b). Maka, lim f(x) = L jika dan hanya jika, untuk setiap barisan x n di (a, b) dengan x n x c c (n N) dan lim x n = c, berlaku lim f(x n) = L. n n Catatan. Jika f kontinu di c, maka L = f(c) dan Teorema 6 menyatakan bahwa lim f(x n) = f ( lim x ) n ; n n yakni, limit dapat bertukar dengan f. Hasil serupa berlaku untuk limit kiri dan limit kanan. Dengan menggunakan Teorema 6, kekontinuan f(x) = px + q di sebarang titik c R dapat dibuktikan sebagai berikut. Misalkan x n adalah sebarang barisan yang konvergen ke c. Maka, menurut Proposisi 5 pada Bab 3, f(x n ) = px n + q pc + q = f(c), untuk n. Menurut akibat dari Teorema 6, f kontinu di c. Soal Latihan 1. Buktikan Teorema Buktikan bahwa f(x) = x kontinu di setiap c > Buktikan bahwa f(x) = x kontinu di setiap titik. 4. Misalkan f(x) = x untuk x rasional dan f(x) = x untuk x irrasional. Buktikan bahwa f kontinu hanya di c = Misalkan f terdefinisi pada (a, b) dan kontinu di suatu titik c (a, b). Buktikan jika f(c) > 0, maka terdapat δ > 0 sehingga f(x) > 0 untuk x (c δ, c + δ). 6. Konstruksi sebuah fungsi f : R R yang kontinu hanya di sebuah titik. 7.3 Sifat-sifat Limit dan Kekontinuan Proposisi 7. Misalkan f dan g terdefinisi pada interval (a, b) kecuali mungkin di c (a, b). Misalkan lim x c f(x) = L dan lim x c g(x) = M, dan λ, µ R. Maka
19 Pengantar Analisis Real 69 (i) lim[λf(x) + µg(x)] = λl + µm; x c (ii) lim f(x)g(x) = LM; x c f(x) (iii) lim x c g(x) = L M, asalkan M 0. Akibat 8. Jika f dan g kontinu di c, maka λf +µg, fg, dan f g g(c) 0). kontinu di c (asalkan Akibat 9. Fungsi polinom kontinu di setiap titik. Fungsi rasional kontinu di setiap titik dalam daerah asalnya. Bukti. Menurut Proposisi 4, f(x) = k dan g(x) = x kontinu di sebarang titik c R. Menurut Proposisi 7(ii), h(x) = x i kontinu di sebarang titik c R, untuk tiap i N. Akibatnya, menurut Proposisi 7(i), fungsi polinom p(x) = a n x n + a n 1 x n a 1 x + a 0 kontinu di setiap titik c R. Untuk membuktikan kekontinuan fungsi rasional di setiap titik dalam daerah asalnya, kita perlu menggunakan Proposisi 7(iii). Teorema 10. Jika g kontinu di c dan f kontinu di g(c), maka f g kontinu pada c. Bukti. Ambil ɛ > 0 sebarang. Karena f kontinu di b := g(c), maka terdapat δ > 0 sedemikian sehingga f(y) f(b) < ɛ untuk y b < δ. Selanjutnya, karena g kontinu di c, kita dapat memilih γ > 0 sedemikian sehingga g(x) g(c) < δ untuk x c < γ. Akibatnya, jika x c < γ, maka g(x) b = g(x) g(c) < δ, sehingga f g(x) f g(c) = f(g(x)) f(b) < ɛ. Ini berarti bahwa f g kontinu di c. Soal Latihan 1. Buktikan Proposisi 7.
20 70 Hendra Gunawan 2. Berikan contoh fungsi f dan g dengan lim f(x) tidak ada, lim g(x) ada, dan x 0 x 0 f(x)g(x) ada. Apakah ini bertentangan dengan Proposisi 7(ii) atau 7(iii)? lim x 0 3. Benar atau salah: Jika lim g(x) = L dan lim f(y) = M, maka lim f(g(x)) = x c y L x c M? 4. Buktikan jika lim x c g(x) = L dan f kontinu di L, maka lim x c f(g(x)) = f(l). 5. Kita katakan bahwa lim f(x) = + apabila, untuk setiap M > 0 terdapat x c + δ > 0 sehingga f(x) > M untuk c < x < c+δ. Buktikan bahwa lim x 1 = +. x 0 +
21 Pengantar Analisis Real FUNGSI KONTINU PADA INTERVAL 8.1 Kekontinuan pada Interval Secara geometris, f kontinu di suatu titik berarti bahwa grafiknya tidak terputus di titik tersebut. Serupa dengan itu, f kontinu pada suatu interval apabila grafiknya tidak terputus pada interval tersebut. Secara intuitif, f kontinu pada suatu interval apabila kita dapat menggambar grafik fungsi f pada interval tersebut tanpa harus mengangkat pena dari kertas. Secara formal, sebuah fungsi f dikatakan kontinu pada suatu interval buka I jika dan hanya jika f kontinu di setiap titik pada I. Fungsi f dikatakan kontinu pada interval tutup I = [a, b] jika dan hanya jika f kontinu di setiap titik c (a, b), kontinu kanan di a, dan kontinu kiri di b. (Lihat Gambar 8.1 dan 8.2.) Gambar 8.1 Grafik fungsi kontinu pada interval buka Contoh 1. Misalkan f : R R didefinisikan sebagai { x, x 1; f(x) = 3 2, x > 1
22 72 Hendra Gunawan Perhatikan bahwa f kontinu di setiap titik kecuali di c = 1. Namun f kontinu kiri di c = 1, dan karenanya f kontinu pada interval [0, 1]. Karena f tidak kontinu kanan di c = 1, maka f tidak kontinu pada interval [1, 2]. Gambar 8.2 Grafik fungsi kontinu pada interval tutup Proposisi 2. Misalkan f terdefinisi pada suatu interval I. Maka, f kontinu pada I jika dan hanya jika, untuk setiap x I dan setiap ɛ > 0 terdapat δ > 0 sedemikian sehingga f(x) f(y) < ɛ untuk y I dengan x y < δ. Contoh 3. (i) Fungsi f(x) = px + q kontinu pada sebarang interval I. (ii) Fungsi g(x) = x kontinu pada sebarang interval I. (iii) Fungsi h(x) = x kontinu pada sebarang interval I [0, ). Soal Latihan 1. Misalkan f : [0, 5] R didefinisikan sebagai f(x) = { 2x, 0 x < 1; 1, 1 x 5. Selidiki apakah f kontinu di setiap titik pada interval [0, 5]. Selidiki kekontinuan f pada interval [0, 1] dan pada interval [1, 5]. Sketsalah grafiknya.
23 Pengantar Analisis Real Buktikan bahwa fungsi f pada Soal 1 terbatas. Tentukan apakah ia mempunyai nilai maksimum dan nilai minimum. 3. Misalkan K > 0 dan f : I R adalah fungsi yang memenuhi f(x) f(y) K x y untuk setiap x, y I. Buktikan bahwa f kontinu pada I. 8.2 Sifat-sifat Fungsi Kontinu pada Interval Sebagai akibat dari Proposisi 8 dan Teorema 11 yang telah dibahas pada Bab 7, kita mempunyai Proposisi 4 dan Proposisi 6 di bawah ini. Proposisi 4. Misalkan f dan g kontinu pada suatu interval I dan λ, µ R. Maka λf + µg dan fg kontinu pada I. Juga, jika g 0, maka f g kontinu pada I. Contoh 5. (i) Setiap fungsi polinom kontinu pada sebarang interval. (ii) Setiap fungsi rasional kontinu pada sebarang interval dalam daerah asalnya. Sebagai contoh, f(x) = 1 x kontinu pada (0, ). (iii) Fungsi f(x) = x+ x kontinu pada sebarang interval I [0, ), karena f 1 (x) = x dan f 2 (x) = x kontinu pada sebarang interval I [0, ). Proposisi 6. Misalkan g : I J kontinu pada interval I dan f : J R kontinu pada interval J. Maka f g kontinu pada I. Contoh 7. (i) Fungsi h(x) = 1+x kontinu pada sebarang interval, karena f(x) = x dan g(x) = 1 + x kontinu pada sebarang interval. (ii) Fungsi h(x) = 1 x 1+ x Soal Latihan kontinu pada sebarang interval I [0, ). 1. Jelaskan mengapa fungsi berikut kontinu pada sebarang interval. f(x) = 1 1+ x. g(x) = 1 + x 2.
24 74 Hendra Gunawan 2. Misalkan f kontinu pada suatu interval I dan untuk setiap bilangan rasional r I berlaku f(r) = r 2. Buktikan bahwa f(x) = x 2 untuk setiap x I. 3. Misalkan f : [0, 1] [0, 1] adalah fungsi kontraktif, yakni memenuhi ketaksamaan f(x) f(y) C x y, x, y [0, 1], untuk suatu konstanta C dengan 0 < C < 1. Konstruksi barisan x n dengan x 1 I dan x n+1 = f(x n ), n N. Buktikan bahwa x n konvergen ke suatu L [0, 1], dan L = f(l). 8.3 Lebih jauh tentang Fungsi Kontinu pada Interval Sebagaimana telah disinggung dalam Bab 2, interval [a, b] yang tertutup dan terbatas merupakan himpunan kompak di R. Sekarang kita akan mempelajari keistimewaan yang dimiliki oleh fungsi kontinu pada interval kompak [a, b]. Teorema 8. Misalkan f kontinu pada interval [a, b]. Maka f([a, b]) juga merupakan suatu interval kompak. Teorema ini merupakan konsekuensi dari beberapa teorema berikut. Teorema 9. Misalkan f kontinu pada suatu interval I. Maka daerah nilainya, yaitu f(i), juga merupakan suatu interval. Teorema 10 (Teorema Nilai Antara). Misalkan f kontinu pada suatu interval I yang memuat a dan b. Jika u terletak di antara f(a) dan f(b), maka terdapat c di antara a dan b sedemikian sehingga f(c) = u. Catatan. Teorema 10 setara dengan Teorema 9. Oleh karena itu kita cukup membuktikan salah satu di antara mereka. Bukti Teorema 10. Tanpa mengurangi keumuman, asumsikan a < b dan f(a) < u < f(b). Tinjau himpunan H := {x [a, b] : f(x) < u}. Jelas bahwa H karena a H. Karena H juga terbatas, maka H mempunyai supremum, sebutlah c = sup H. Di sini a < c < b. Selanjutnya tinggal membuktikan bahwa f(c) = u, dengan menunjukkan bahwa tidak mungkin f(c) < u ataupun f(c) > u.
25 Pengantar Analisis Real 75 Andaikan f(c) < u. Karena f kontinu di c, maka terdapat δ > 0 sedemikian sehingga f ( c + 2) δ < u (?). Jadi c + δ 2 H. Ini bertentangan dengan fakta bahwa c = sup H. Sekarang andaikan f(c) > u. Sekali lagi, karena f kontinu di c, maka terdapat δ > 0 sedemikian sehingga f(x) > u untuk c δ < x c (?). Jadi tidak ada satu pun anggota H pada interval (c δ, c]. Ini juga bertentangan dengan fakta bahwa c = sup H. Teorema 11. Misalkan f kontinu pada interval [a, b]. Maka f terbatas pada [a, b]. Bukti. Misalkan f tak terbatas pada [a, b]. Maka terdapat suatu barisan x n di [a, b] sedemikian sehingga f(x n ) + untuk n. (1) Karena x n terbatas, maka menurut Teorema Bolzano - Weierstrass terdapat suatu sub-barisan x nk yang konvergen ke suatu titik c [a, b]. Tetapi f kontinu di c, sehingga f(x nk ) f(c) untuk k. Ini bertentangan dengan (1). Jadi mestilah f terbatas pada [a, b]. Teorema 12. Misalkan f kontinu pada interval [a, b]. Maka f mencapai nilai maksimum dan nilai minimum pada [a, b]. Bukti. Dari Teorema 11 kita tahu bahwa f terbatas pada [a, b]. Misalkan v := sup f([a, b]). Konstruksi barisan x n di [a, b] dengan f(x n ) v untuk n. Karena x n terbatas, terdapat sub-barisan x nk yang konvergen ke suatu titik c [a, b]. Namun kekontinuan di c mengakibatkan f(x nk ) f(c) untuk k. Jadi mestilah v = f(c), dan ini berarti bahwa v merupakan nilai maksimum. Serupa dengan itu, f juga mencapai nilai minimumnya. Contoh 13. Persamaan 10x 7 13x 5 1 = 0 mempunyai sebuah akar c ( 1, 0). Untuk menunjukkannya, misalkan f(x) = 10x 7 13x 5 1. Maka, f( 1) = 2 dan f(0) = 1. Karena f kontinu pada [ 1, 0] dan 0 terletak di antara f( 1) dan f(0), maka menurut Teorema Nilai Antara terdapat c ( 1, 0) sedemikian sehingga f(c) = 0. Bilangan c dalam hal ini merupakan akar persamaan di atas. Contoh 14. Misalkan f : [a, b] [a, b] kontinu pada [a, b]. Maka, terdapat c [a, b] sedemikian sehingga f(c) = c. [Bilangan c demikian disebut sebagai titik tetap f.] Perhatikan bahwa peta dari [a, b] merupakan himpunan bagian dari [a, b], sehingga f(a) a dan f(b) b. Sekarang tinjau g(x) = f(x) x, x [a, b]. Karena f
26 76 Hendra Gunawan kontinu pada [a, b], maka g juga kontinu pada [a, b]. Namun g(a) = f(a) a 0 dan g(b) = f(b) b 0. Menurut Teorema Nilai Antara, mestilah terdapat c [a, b] sedemikian sehingga g(c) = 0. Akibatnya f(c) = c. Soal Latihan 1. Lengkapi Bukti Teorema Nilai Antara, khususnya bagian yang diberi tanda tanya (?). 2. Buktikan bahwa setiap polinom berderajat ganjil mempunyai sedikitnya satu akar real. 3. Misalkan f kontinu pada suatu interval kompak I. Misalkan untuk setiap x I terdapat y I sedemikian sehingga f(y) 1 2 f(x). Buktikan bahwa terdapat suatu c I sedemikian sehingga f(c) = Kekontinuan Seragam Proposisi 2 menyatakan bahwa suatu fungsi f kontinu pada sebuah interval I jika dan hanya jika untuk setiap x I dan setiap ɛ > 0 terdapat δ > 0 sedemikian sehingga f(x) f(y) < ɛ untuk y I dengan x y < δ. Contoh berikut memperlihatkan bahwa secara umum nilai δ bergantung pada ɛ dan x. Contoh 16. Kita telah mengetahui bahwa f(x) = 1 x kontinu pada (0, 1]. Diberikan x (0, 1] dan ɛ > 0 sebarang, kita dapat memilih δ = min { x 2, } ɛx2 2 sedemikian sehingga untuk y (0, 1] dengan x y < δ berlaku 1 x 1 = x y = 1 y xy x 1 y x y < 1 x 2 x ɛx2 2 = ɛ. Perhatikan bahwa jika x menuju 0, maka δ akan menuju 0.
27 Pengantar Analisis Real 77 Dalam kasus tertentu, nilai δ hanya bergantung pada ɛ, tidak pada x. Hal ini terjadi pada, misalnya, f(x) = px + q, x R, dengan p 0. Diberikan ɛ > 0, kita dapat memilih δ = ɛ p sedemikian sehingga untuk x, y R dengan x y < δ. f(x) f(y) = p x y < ɛ merupakan kekontinuan seragam pada R. Kekontinuan f(x) = px + q dalam hal ini Fungsi f : I R dikatakan kontinu seragam pada I apabila untuk setiap ɛ > 0 terdapat δ > 0 sedemikian sehingga f(x) f(y) < ɛ untuk x, y I dengan x y < δ. Perhatikan bahwa dalam definisi di atas x dan y muncul setelah δ, yang mengindikasikan bahwa δ tidak bergantung pada x (dan y). Teorema 17. Fungsi f : I R tidak kontinu seragam pada I jika dan hanya jika terdapat ɛ 0 > 0 dan dua barisan x n dan y n di I sedemikian sehingga x n y n < 1 n dan f(x n ) f(y n ) ɛ 0 untuk setiap n N. Teorema berikut menyatakan bahwa kekontinuan pada interval kompak merupakan kekontinuan seragam. Teorema 18. Jika f kontinu pada [a, b], maka f kontinu seragam pada [a, b]. Bukti. Andaikan f tidak kontinu seragam pada [a, b]. Maka, menurut Teorema 17, terdapat ɛ 0 > 0 dan dua barisan x n dan y n di [a, b] sedemikian sehingga x n y n < 1 n dan f(x n) f(y n ) ɛ 0 untuk setiap n N. Karena x n terbatas di [a, b], maka menurut Teorema Bolzano-Weierstrass terdapat sub-barisan x nk yang konvergen, sebutlah ke c [a, b]. Karena x n y n < 1 n untuk setiap n N, maka sub-barisan y nk akan konvergen ke c juga. Selanjutnya, karena f kontinu di c, maka f(x nk ) dan f(y nk ) konvergen ke f(c). Akibatnya, f(x nk ) f(y nk ) 0 untuk k. Ini mustahil karena f(x n ) f(y n ) ɛ 0 untuk setiap n N.
28 78 Hendra Gunawan Soal Latihan 1. Contoh 16 memperlihatkan bahwa fungsi f(x) = 1 x tampaknya tidak kontinu seragam pada (0, 1]. Buktikan bahwa ia memang tidak kontinu seragam pada (0, 1]. 2. Selidiki apakah f(x) = x 2 kontinu seragam pada [0, ). 3. Buktikan jika fungsi f : I R memenuhi ketaksamaan f(x) f(y) K x y, x, y I, untuk suatu K > 0, maka f kontinu seragam pada I. 4. Buktikan bahwa f(x) = x kontinu seragam pada [0, ).
29 Pengantar Analisis Real TURUNAN 9.1 Turunan di Suatu Titik Diberikan sebuah fungsi, kita seringkali perlu mempelajari bagaimana nilai fungsi itu berubah terhadap peubahnya. Salah satu caranya adalah dengan menghitung turunan dari fungsi itu. Misalkan f terdefinisi pada suatu interval terbuka I yang memuat titik c. Maka, f dikatakan mempunyai turunan di titik c apabila limit f(x) f(c) lim x c x c ada, dan dalam hal ini nilai limit tersebut disebut turunan dari f di titik c, yang biasanya dilambangkan dengan f (c) atau Df(c). Jadi, untuk fungsi f yang mempunyai turunan di c, kita mempunyai f f(x) f(c) (c) = lim. x c x c Dengan mengganti x dengan c + h, kita peroleh f f(c + h) f(c) (c) = lim. h 0 h Catat bahwa f mempunyai turunan di c jika dan hanya jika terdapat suatu bilangan L = f (c) sedemikian sehingga f(c + h) f(c) Lh = ɛ(h) dengan ɛ(h) h 0 untuk h 0. Secara intuitif, sebuah fungsi f mempunyai turunan di titik c berarti bahwa grafik fungsi y = f(x) mempunyai garis singgung di titik (c, f(c)) dan gradien garis
30 80 Hendra Gunawan singgung tersebut adalah f (c). Untuk ilustrasi, lihat Gambar 9.1. Persamaan garis singgung pada grafik fungsi y = f(x) di titik (c, f(c)) dalam hal ini adalah y = f(c) + f (c)(x c). Persamaan ini merupakan hampiran linear untuk y = f(x). Jika x berubah dari c ke c + h, maka y akan bertambah kira-kira sebesar hf (c). Jadi, dengan mengetahui f, kita mengetahui bagaimana f berubah (bila x berubah). Sebagai catatan, masalah menentukan persamaan garis singgung pada kurva di titik tertentu pertama kali dipelajari oleh Rene Descartes pada 1620-an. Namun, kalkulus diferensial dan integral yang kita kenal sekarang ini ditemukan oleh Isaac Newton pada 1665 (namun dipublikasikan pada 1704) dan Gottfried Wilhelm von Leibniz pada Gambar 9.1 Grafik fungsi f yang mempunyai turunan di titik c Contoh 1. Misalkan f(x) = x 2 dan c = 1. Untuk memeriksa apakah f mempunyai turunan di 1, kita hitung f(x) f(1) x 2 1 lim = lim x 1 x 1 x 1 x 1 = lim (x + 1) = 2. x 1 Jadi f mempunyai turunan di 1, dengan f (1) = 2. Secara umum dapat ditunjukkan bahwa f(x) = x 2 mempunyai turunan di setiap titik c R, dengan f (c) = 2c. Fungsi f : c 2c disebut sebagai turunan dari f.
31 Pengantar Analisis Real 81 Contoh 2. Misalkan f(x) = x dan c = 0. Perhatikan bahwa f(h) f(0) h lim = lim h 0 h h 0 h tidak ada (?). Karena itu, f tidak mempunyai turunan di 0. Proposisi 3. Misalkan f terdefinisi pada suatu interval terbuka I yang memuat titik c. Jika f mempunyai turunan di c, maka f kontinu di c. Bukti. Perhatikan bahwa f(x) f(c) = f(x) f(c) x c untuk x c. Jadi f(x) f(c) untuk x c. (x c) f (c) 0 = 0 Dalam prakteknya, kita sering pula menggunakan kontraposisi dari Proposisi 3 yang menyatakan: jika f tidak kontinu di c, maka f tidak akan mempunyai turunan di c. Sebagai contoh, fungsi f : [0, 2] R yang didefinisikan sebagai { 2x, 0 x < 1; f(x) = 1, 1 x 2, tidak mungkin mempunyai turunan di 1 karena f tidak kontinu di titik tersebut. Catatan. Proposisi 3 menyatakan bahwa kekontinuan f di c merupakan syarat perlu bagi f untuk mempunyai turunan di c. Namun, Contoh 2 memperlihatkan bahwa kekontinuan f di c bukan merupakan syarat cukup untuk mempunyai turunan di c. Soal Latihan 1. Tentukan persamaan garis singgung pada kurva y = x 2 di titik (1, 1). 2. Tunjukkan bahwa f(x) = x 2 mempunyai turunan di setiap titik c R, dengan f (c) = 2c. 3. Diketahui f(x) = x x, x R. Selidiki apakah f mempunyai turunan di Berikan sebuah contoh fungsi f yang kontinu di 0 tetapi tidak mempunyai turunan di sana, selain f(x) = x. 5. Konstruksi sebuah fungsi f : R R yang mempunyai turunan hanya di sebuah titik.
32 82 Hendra Gunawan 6. Buktikan jika f mempunyai turunan di c, maka f f(c + h) f(c h) (c) = lim. h 0 2h Berikan sebuah contoh fungsi yang tidak mempunyai turunan di suatu titik namun limit di atas ada. 9.2 Sifat-sifat Dasar Turunan Teorema 4. Misalkan f dan g terdefinisi pada suatu interval terbuka I yang memuat titik c. Misalkan λ dan µ bilangan real sembarang. Jika f dan g mempunyai turunan di c, maka λf + µg, fg, dan f/g mempunyai turunan di c, dan (i) (λf + µg) (c) = λf (c) + µf (c); (ii) (fg) (c) = f (c)g(c) + f(c)g (c); (iii) ( f g ) (c) = f (c)g(c) f(c)g (c) g 2 (c) asalkan g(c) 0. Bukti. (i) Perhatikan bahwa [ ] 1 h[ λf(c + h) + ] µg(c [ + h) λf(c) ] µg(c) = λ f(c+h) f(c) + µ g(c+h) g(c) untuk h 0. h λf (c) + µg (c) (ii) Di sini kita mempunyai [ ] 1 h f(c + [ h)g(c + h) ] f(c)g(c) = g(c + h) f(c+h) f(c) + f(c) untuk h 0. (iii) Latihan. h g(c)f (c) + f(c)g (c), h [ g(c+h) g(c) Contoh 5. Misalkan n N dan f(x) = x n. Maka turunan dari f adalah f (x) = nx n 1. Fakta ini dapat dibuktikan secara induktif. Untuk n = 1 atau f(x) = x, jelas bahwa f (x) = 1. Sekarang misalkan pernyataan di atas benar untuk n = k, yakni jika h ]
33 Pengantar Analisis Real 83 f(x) = x k, maka f (x) = kx k 1. Maka, untuk n = k + 1 atau f(x) = x k+1, kita peroleh f (x) = D(x k.x) = D(x k ).x + x k.d(x) = kx k 1.x + x k = (k + 1)x k. Jadi, menurut Prinsip Induksi Matematika, pernyataan benar untuk setiap n N. Teorema 6 (Aturan Rantai). Misalkan g mempunyai turunan di c dan f mempunyai turunan di y = g(c). Maka, f g mempunyai turunan di c dan (f g) (c) = f (g(c))g (c). Bukti. Berdasarkan definisi turunan, (f g) (f g)(x) (f g)(c) f(g(x)) f(g(c)) (c) = lim = lim. x c x c x c x c Bila g(x) g(c) 0 pada suatu interval terbuka (c δ, c + δ), maka (f g) f(g(x)) f(g(c)) g(x) g(c) (c) = lim = f (g(c)) g (c). x c g(x) g(c) x c Namun, bila g konstan (misalnya), maka argumentasi di atas gugur. Untuk mengatasinya, definisikan h(y) := { f(y) f(g(c)) y g(c), y g(c), f (g(c)), y = g(c). Perhatikan bahwa h kontinu di g(c). Mengingat g kontinu di c, maka menurut Teorema 10 pada Bab 7, h g kontinu di c. Akibatnya (f g) f(g(x)) f(g(c)) g(x) g(c) (c) = lim = lim h(g(x)) = f (g(c)) g (c), x c x c x c x c sebagaimana yang kita harapkan. Soal Latihan 1. Buktikan Teorema 4 bagian (iii). 2. Misalkan n N dan f(x) = x n. Buktikan dengan menggunakan definisi bahwa f (x) = nx n 1.
34 84 Hendra Gunawan 3. Misalkan n N. Buktikan jika f(x) = x n (x 0), maka f (x) = nx n 1. jika f(x) = x 1/n (x > 0), maka f (x) = 1 n x1/n Buktikan bahwa untuk bilangan rasional r sembarang berlaku asalkan x > 0. D(x r ) = rx r 1 5. Misalkan f : R R mempunyai turunan di x. Buktikan jika f mempunyai invers f 1 : R R dan f 1 mempunyai turunan di y = f(x), maka Df 1 (y) = 1 Df(x). 9.3 Turunan Tingkat Tinggi Jika f mempunyai turunan di setiap titik dalam suatu interval terbuka I, maka kita katakan f mempunyai turunan pada I. Dalam hal ini turunan dari f, yaitu f, merupakan fungsi yang juga terdefinisi pada I. Selanjutnya kita dapat mendefinisikan turunan kedua dari f sebagai turunan dari f, yang nilainya di c adalah f f (x) f (c) (c) = lim, x c x c asalkan limit ini ada. Dapat diperiksa bahwa bila f mempunyai turunan kedua di c, maka f(c + h) f(c) hf (c) h2 2 f (c) = ɛ(h), dengan ɛ(h) h 2 0 untuk h 0. Turunan kedua dari f berkaitan dengan kecekungan grafik fungsi f. Jika f bernilai positif pada suatu interval, maka grafik fungsi f cekung ke atas pada interval tersebut. Sementara itu, jika f bernilai negatif pada suatu interval, maka grafik fungsi f cekung ke bawah pada interval tersebut. Dengan mengetahui f, kita juga mengetahui bagaimana f berubah.
35 Pengantar Analisis Real 85 Setelah menghitung turunan pertama dan kedua dari f, turunan ketiga dan seterusnya dapat didefinisikan secara serupa. Secara umum, f (n) (x) menyatakan turunan ke-n, n N, dari f. Contoh 7. Jika f(x) = 1 x, maka f (x) = 1 x 2 ; f (x) = 2 x 3 ; f (x) = 6 x 4 ; dan seterusnya. (Dapatkah anda menentukan rumus umum f (n) (x) untuk n N?) Bila f mempunyai turunan ke-n pada suatu interval yang memuat titik c, maka f dapat dihampiri oleh suatu polinom berderajat n 1 dan kesalahannya dapat ditaksir dengan turunan ke-n. Lihat Teorema Taylor pada bab berikutnya. Soal Latihan 1. Buktikan bila f mempunyai turunan kedua di c, maka dengan ɛ(h) h 2 0 untuk h 0. f(c + h) f(c) hf (c) h2 2 f (c) = ɛ(h), 2. Tentukan pada interval mana grafik fungsi f(x) = x 3 cekung ke atas dan pada interval mana ia cekung ke bawah. 3. Tentukan rumus umum turunan ke-n dari f(x) = 1 x. 4. Diketahui f(x) = x. Tentukan f (x), f (x), dan f (x). Tentukan rumus umum f (n) (x) untuk n N. 5. Misalkan p(x) adalah polinom berderajat n. Buktikan bahwa p (m) (x) = 0 untuk m > n. 6. Berikan sebuah contoh fungsi yang mempunyai turunan pertama tetapi tidak mempunyai turunan kedua di 0.
36 86 Hendra Gunawan 10. TEOREMA NILAI RATA-RATA 10.1 Maksimum dan Minimum Lokal Misalkan f terdefinisi pada suatu interval terbuka (a, b) dan c (a, b). Kita katakan bahwa f mencapai nilai maksimum lokal di c apabila f(x) f(c) untuk setiap x dalam suatu interval terbuka I yang memuat c. Titik c dalam hal ini disebut sebagai titik maksimum lokal. Nilai dan titik minimum lokal didefinisikan secara analog. Gambar 10.1 f mencapai nilai maksimum lokal di c Secara intuitif, f mencapai nilai maksimum lokal di c apabila grafiknya mempunyai sebuah puncak di atas titik c. Serupa dengan itu, f mencapai nilai minimum lokal di c apabila grafiknya mempunyai sebuah lembah di atas titik c.
37 Pengantar Analisis Real 87 Jika f(c) merupakan nilai maksimum f pada seluruh interval (a, b), maka tentunya f mencapai nilai maksimum lokal di c. Namun sebaliknya belum tentu benar, nilai maksimum lokal belum tentu merupakan nilai maksimum f. Contoh 1. Misalkan f : R R adalah fungsi yang didefinsikan sebagai { x + 2, x < 1, f(x) = x, x 1. Maka, f mencapai nilai maksimum lokal di 1, namun f( 1) = 1 bukan merupakan nilai maksimum f pada R. Demikian pula f mencapai nilai minimum lokal di 0, namun f(0) = 0 bukan merupakan nilai minimum f pada R. Teorema 2. Misalkan f mempunyai turunan pada (a, b) dan c (a, b). Jika f mencapai nilai maksimum atau minimum lokal di c, maka f (c) = 0. Bukti. Menurut definisi turunan, f(x) f(c) x c f (c) untuk x c. Misalkan f (c) > 0. Menurut Soal Latihan 7.1 No. 4, terdapat suatu δ > 0 sedemikian sehingga f(x) f(c) > 0 (2) x c untuk x (c δ, c + δ), x c. Sekarang misalkan x (c, c + δ) sembarang. Maka, x c > 0 dan (1) memberikan f(x) f(c) > 0 atau f(x) > f(c). Jadi f tidak mungkin mencapai nilai maksimum lokal di c. Selanjutnya misalkan x (c δ, c) sembarang. Maka, x c < 0 dan (1) memberikan f(x) f(c) < 0 atau f(x) < f(c). Jadi f juga tidak mungkin mencapai nilai minimum lokal di c. Hal serupa terjadi ketika f (c) < 0. Jadi, jika f (c) 0, maka f tidak akan mencapai nilai maksimum atau minimum lokal di c. Catatan. Kebalikan dari Teorema 2 tidak berlaku: jika f (c) = 0, belum tentu f mencapai nilai maksimum atau minimum lokal di c. Soal Latihan 1. Berikan sebuah contoh fungsi f yang terdefinisi pada ( 2, 2) dan mencapai nilai maksimum lokal di 1 tetapi f(1) bukan merupakan nilai maksimum f pada ( 2, 2).
38 88 Hendra Gunawan 2. Berikan sebuah contoh fungsi f yang mempunyai turunan nol di suatu titik tetapi f tidak mencapai nilai maksimum atau minimum lokal di titik tersebut Titik Stasioner Titik c dengan f (c) = 0 disebut titik stasioner f. Sebagaimana telah dicatat sebelumnya, tidak semua titik stasioner merupakan titik maksimum atau minimum lokal. Sebagai contoh, jika f(x) = x 3, maka f (x) = 3x 2, sehingga 0 merupakan titik stasioner. Namun, 0 bukan merupakan titik maksimum maupun minimum f. (Titik 0 dalam hal ini merupakan titik infleksi f, yaitu titik terjadinya perubahan kecekungan grafik fungsi f.) Situasi yang lebih parah dapat terjadi. Sebagai contoh, fungsi f(x) = x 2 sin 1 x untuk x 0 dan f(0) = 0 mempunyai turunan f (0) = 0 tetapi 0 bukan merupakan titik maksimum atau minimum lokal, ataupun titik infleksi. Gambar 10.2 Grafik fungsi f(x) = x 3 Teorema 3 (Teorema Rolle). Misalkan f kontinu pada [a, b] dan mempunyai turunan pada (a, b). Jika f(a) = f(b), maka f (c) = 0 untuk suatu c (a, b). Bukti. Karena f kontinu pada interval kompak [a, b], maka menurut sifat kekontinuan f mencapai nilai maksimum M di suatu titik c 1 [a, b] dan juga mencapai nilai minimum m di suatu titik c 2 [a, b].
39 Pengantar Analisis Real 89 Misalkan c 1 dan c 2 adalah titik-titik ujung [a, b]. Karena f(a) = f(b), maka m = M dan dengan demikian f konstan pada [a, b]. Akibatnya f (c) = 0 untuk setiap c (a, b). Jika c 1 bukan titik ujung [a, b], maka c 1 (a, b) dan f mencapai nilai maksimum lokal di c 1. Menurut Teorema 2, f (c 1 ) = 0. Hal serupa terjadi bila c 2 bukan titik ujung [a, b]. Soal Latihan 1. Diketahui f(x) = x x, x R. Tunjukkan bahwa 0 merupakan titik stasioner. Selidiki apakah f mencapai nilai maksimum atau minimum lokal di Beri contoh sebuah fungsi f yang terdefinisi pada [a, b], mempunyai turunan pada (a, b), dan f(a) = f(b), namun tidak ada c (a, b) dengan f (c) = Teorema Nilai Rata-rata dan Teorema Taylor Sebagai perumuman dari Teorema Rolle, kita mempunyai teorema berikut. Teorema 4 (Teorema Nilai Rata-rata). Misalkan f kontinu pada [a, b] dan mempunyai turunan pada (a, b). Maka untuk suatu c (a, b). f (c) = f(b) f(a) b a Catatan. Nilai f(b) f(a) b a disebut nilai rata-rata f pada [a, b]. Nilai ini sama dengan gradien ruas garis singgung yang menghubungkan titik (a, f(a)) dan (b, f(b)). Teorema Nilai Rata-rata menyatakan bahwa pada kurva y = f(x) terdapat suatu titik (c, f(c)) dengan gradien garis singgung sama dengan nilai rata-rata f pada [a, b]. Bukti Teorema 4. Misalkan F didefinisikan pada [a, b] sebagai F (x) = f(x) hx dengan h konstanta. Maka F kontinu pada [a, b] dan mempunyai turunan pada (a, b). Kita pilih konstanta h sedemikian sehingga F (a) = F (b), yakni h = f(b) f(a). b a
40 90 Hendra Gunawan Karena F memenuhi hipotesis Teorema Rolle, maka F (c) = 0 untuk suatu c (a, b). Namun sehingga teorema pun terbukti. F (c) = f (c) h = 0, Jika f mempunyai turunan di c, maka persamaan garis singgung pada kurva y = f(x) di titik (c, f(c)) adalah y = f(c) + (x c)f (c). Untuk x dekat c, nilai f(c) + (x c)f (c) merupakan hampiran yang baik untuk f(x). Namun seberapa besar kesalahan dalam penghampiran ini? Lebih jauh, misalkan f mempunyai turunan ke-(n 1) di c. Maka polinom P (x) = f(c) + (x c)f (c) + (x c)2 f (c) + + 2! (x c)n 1 f (n 1) (c) (n 1)! mempunyai turunan ke-k, k = 0, 1,..., n 1, yang sama dengan turunan ke-k dari f. Karena itu masuk akal untuk menghampiri f(x) dengan P (x) untuk x di sekitar c. Namun, sekali lagi, seberapa besar kesalahan dalam penghampiran ini. Teorema Taylor di bawah ini menjawab pertanyaan tersebut. Teorema 5 (Teorema Taylor). Misalkan f mempunyai turunan ke-n pada interval terbuka I yang memuat titik c. Maka, untuk setiap x I, berlaku f(x) = f(c) + (x c)f (c) + (x c)2 f (c) + + 2! dengan E n = 1 n! (x c)n f (n) (ξ) untuk suatu ξ di antara x dan c. Proof. Untuk t di antara x dan c, definisikan F (t) = f(x) f(t) (x t)f (t) (x c)n 1 f (n 1) (c) + E n (n 1)! (x t)n 1 f (n 1) (t). (n 1)! Perhatikan bahwa Sekarang definisikan F (t) = G(t) = F (t) (x t)n 1 f (n) (t). (n 1)! ( x t ) nf (c). x c
41 Pengantar Analisis Real 91 Maka, G(x) = G(c) = 0, sehingga menurut Teorema Rolle, terdapat ξ di antara x dan c sedemikian sehingga 0 = G (ξ) = F (ξ) + n(x ξ)n 1 (x ξ)n 1 (x c) n F (c) = f (n) n(x ξ)n 1 (ξ) + (n 1)! (x c) n F (c). Dari sini kita peroleh dan teorema pun terbukti. F (c) = (x c)n f (n) (ξ) n! Soal Latihan 1. Diketahui f(x) = x. Tentukan nilai rata-rata f pada [0, 4]. Tentukan c (0, 4) sedemikian sehingga f (c) sama dengan nilai rata-rata tersebut. 2. Misalkan f kontinu pada [a, b] dan mempunyai turunan pada (a, b). Buktikan jika f (x) = 0 untuk setiap x (a, b), maka f konstan pada [a, b]. 3. Misalkan f : R R mempunyai turunan di setiap titik dan f (x) = x 2 untuk setiap x R. Buktikan bahwa f(x) = 1 3 x3 + C, dengan C suatu konstanta. 4. Diketahui f : R R memenuhi ketaksamaan f(x) f(y) C x y p, x, y R, untuk suatu C > 0 dan p > 1. Buktikan bahwa f konstan. 5. Buktikan jika f mempunyai turunan kedua di c, maka f f(c + h) 2f(c) + f(c h) (c) = lim h 0 h 2. Berikan sebuah contoh fungsi yang tidak mempunyai turunan kedua di suatu titik namun limit di atas ada. 6. Misalkan c R dan n N. Buktikan dengan menggunakan Teorema Taylor bahwa (1 + c) n = 1 + nc + (Petunjuk. Tinjau f(x) = x n.) n(n 1) c c n. 2!
42 92 Hendra Gunawan 11. FUNGSI MONOTON (DAN FUNGSI KONVEKS) 11.1 Definisi dan Limit Fungsi Monoton Misalkan f terdefinisi pada suatu himpunan H. Kita katakan bahwa f naik pada H apabila untuk setiap x, y H dengan x < y berlaku f(x) f(y). Jika ketaksamaan < berlaku, maka kita katakan bahwa f naik sejati pada H. Definisi serupa dapat dirumuskan untuk fungsi turun dan turun sejati pada H. Fungsi naik atau turun disebut fungsi monoton. Fungsi yang naik dan turun sekaligus pada H mestilah konstan pada H. Contoh 1. (i) Fungsi f : R R yang didefinisikan sebagai f(x) = x 3 merupakan fungsi naik sejati pada R. (ii) Fungsi g : (0, ) R yang didefinisikan sebagai g(x) = 1 x turun sejati pada (0, ). merupakan fungsi Proposisi 2. Jika f naik pada [a, b], maka f mencapai nilai minimum di a dan nilai maksimum di b. Bukti. Misalkan a < x < b. Maka menurut definisi kita mempunyai f(a) f(x) f(b). Jadi f mencapai nilai minimum di a dan nilai maksimum di b. Sekarang kita akan membahas limit fungsi monoton. Untuk itu, kita perkenalkan notasi f(c ) = lim x c f(x)
43 Pengantar Analisis Real 93 Gambar 11.1(i) Grafik fungsi f(x) = x 3 Gambar 11.1(ii) Grafik fungsi g(x) = 1 x dan asalkan kedua limit ini ada. f(c+) = lim x c + f(x), Contoh 3. Misalkan f : R R didefinisikan sebagai { x, x 1; f(x) = 3 2, x > 1
44 94 Hendra Gunawan Maka, f(1 ) = 1 = f(1), sedangkan f(1+) = 3 2. Teorema 4. (i) Jika f naik dan terbatas di atas pada (a, b), maka f(b ) = sup f(x). x (a,b) (ii) Jika f naik dan terbatas di bawah pada (a, b), maka f(a+) = inf f(x). x (a,b) Bukti. (i) Misalkan M = sup x (a,b) f(x). Diberikan ɛ > 0 sembarang, kita harus mencari suatu δ > 0 sedemikian sehingga jika b δ < x < b, maka f(x) M < ɛ atau M ɛ < f(x) < M + ɛ. Ketaksamaan f(x) < M + ɛ selalu terpenuhi karena M merupakan batas atas untuk f pada (a, b). Selanjutnya, karena M ɛ bukan merupakan batas atas untuk f pada (a, b), maka terdapat suatu y (a, b) sedemikian sehingga M ɛ < f(y). Namun f naik pada (a, b), sehingga untuk setiap x yang memenuhi y < x < b berlaku Jadi, pilihlah δ = b y. (ii) Serupa dengan (i). M ɛ < f(y) f(x). Akibat 5. Misalkan f naik pada (a, b). Jika c (a, b), maka f(c ) dan f(c+) ada, dan untuk a < x < c < y < b. f(x) f(c ) f(c) f(c+) f(y) Soal Latihan 1. Buktikan Teorema 4 bagian (ii). Mulai dengan memisalkan m = inf x (a,b) f(x). 2. Buktikan jika f turun dan terbatas di bawah pada (a, b), maka f(b ) = inf f(x). x (a,b)
45 Pengantar Analisis Real 95 Gambar 11.2 Kasus f(c ) < f(c) < f(c+) 3. Buktikan jika f dan g naik (sejati) pada H, maka f + g naik (sejati) pada H. 4. Diketahui f(x) > 0 untuk setiap x H, dan g := 1 f. Buktikan jika f naik (sejati) pada H, maka g turun (sejati) pada H. 5. Diketahui f naik sejati pada A. Buktikan bahwa f merupakan korespondensi 1-1 antara A dan B := f(a), sehingga f 1 ada. Buktikan bahwa f 1 naik sejati pada B Fungsi Monoton yang Mempunyai Turunan Pada bagian ini kita akan membahas bagaimana kita dapat menyelidiki kemonotonan suatu fungsi melalui turunannya, bila fungsi tersebut mempunyai turunan. Persisnya, kita mempunyai teorema berikut. Teorema 6. Misalkan f kontinu pada [a, b] dan mempunyai turunan pada (a, b). (i) Jika f (x) 0 untuk tiap x (a, b), maka f naik pada [a, b]. Jika f (x) > 0 untuk tiap x (a, b), maka f naik sejati pada [a, b]. (ii) Jika f (x) 0 untuk tiap x (a, b), maka f turun pada [a, b]. Jika f (x) < 0 untuk tiap x (a, b), maka f turun sejati pada [a, b].
46 96 Hendra Gunawan Bukti. (i) Misalkan x dan y bilangan sembarang di [a, b] dengan x < y. Maka f memenuhi hipotesis Teorema Nilai Rata-rata pada [x, y] dan karenanya f (c) = f(y) f(x) y x untuk suatu c (x, y). Jika f (t) 0 untuk tiap t (a, b), maka f (c) 0 dan karenanya f(x) f(y). Jadi f naik pada [a, b]. Jika f (t) > 0 untuk tiap t (a, b), maka f (c) > 0 dan karenanya f(x) < f(y). Jadi f naik sejati pada [a, b]. (ii) Serupa dengan (i). Contoh 7. Misalkan f : R R didefinisikan sebagai f(x) = x(1 x). Turunannya adalah f (x) = 1 2x. Jadi f (x) 0 untuk x 1 2 dan f (x) 0 untuk x 1 2. Dengan demikian f naik pada (, 1 2 ] dan turun pada [ 1 2, ). Soal Latihan 1. Misalkan n N. Buktikan bahwa fungsi f : [0, ) R yang didefinisikan sebagai f(x) = (x + 1) 1/n x 1/n merupakan fungsi turun pada [0, ). 2. Misalkan f mempunyai turunan dan naik pada suatu interval terbuka I. Buktikan bahwa f (x) 0 untuk tiap x I. Jika f naik sejati pada I, apakah dapat disimpulkan bahwa f (x) > 0 untuk tiap x I? Jelaskan Invers Fungsi Monoton Menurut Soal 11.1 No. 5, fungsi f yang naik sejati pada A mendefinisikan suatu korespondensi 1-1 antara A dan B := f(a). Dalam hal ini f akan mempunyai invers f 1. Lebih jauh, f 1 naik sejati pada B.
47 Pengantar Analisis Real 97 Dalam kasus di mana f kontinu dan daerah asal f merupakan interval, sebutlah I, maka daerah nilainya juga merupakan suatu interval, sebutlah J = f(i) (Teorema 10 pada Bab 8). Lebih jauh, kita mempunyai teorema berikut. Teorema 8. Misalkan f : I J dengan I interval dan J = f(i). Jika f naik sejati dan kontinu pada I, maka f 1 : J I kontinu pada J. Bukti. Andaikan f 1 tidak kontinu di suatu titik d J. Asumsikan bahwa d bukan titik ujung J. Maka, mengingat f 1 naik sejati pada J, f 1 (d ) dan f 1 (d+) ada, dan f 1 (d ) < f 1 (d+). Sekarang misalkan c I sedemikian sehingga f 1 (d ) < c < f 1 (d+) dan c f 1 (d). Karena itu f(c) tidak terdefinisi (buatlah ilustrasinya!), dan ini bertentangan dengan hipotesis bahwa f terdefinisi pada I. Teorema 9. Misalkan I dan J interval, I dan J interval terbuka yang mempunyai titik ujung sama dengan titik ujung I dan J. Misalkan f : I J kontinu dan J = f(i). Jika f mempunyai turunan pada I dan f (x) > 0 untuk tiap x I, maka f 1 : J I ada dan kontinu pada J. Lebih jauh, f 1 mempunyai turunan pada J dan untuk tiap y J dan x = f 1 (y). (f 1 ) (y) = 1 f (x) Catatan. Bukti Teorema 9 dapat dilihat di [2]. Soal Latihan 1. Misalkan f : R R didefinisikan sebagai f(x) = 1 + x + x 3. Tunjukkan bahwa f mempunyai invers dan hitunglah nilai (f 1 ) ( 1). 2. Berikan sebuah contoh fungsi f : A R yang naik sejati dan kontinu pada A, tetapi f 1 tidak kontinu pada B = f(a). (Petunjuk. Himpunan A tentunya bukan suatu interval.)
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
10. TEOREMA NILAI RATA-RATA
 10. TEOREMA NILAI RATA-RATA 10.1 Maksimum dan Minimum Lokal Misalkan f terdefinisi pada suatu interval terbuka (a, b) dan c (a, b). Kita katakan bahwa f mencapai nilai maksimum lokal di c apabila f(x)
10. TEOREMA NILAI RATA-RATA 10.1 Maksimum dan Minimum Lokal Misalkan f terdefinisi pada suatu interval terbuka (a, b) dan c (a, b). Kita katakan bahwa f mencapai nilai maksimum lokal di c apabila f(x)
DASAR-DASAR ANALISIS MATEMATIKA
 (Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. November 19, 2007 Secara geometris, f kontinu di suatu titik berarti bahwa grafiknya tidak terputus
(Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. November 19, 2007 Secara geometris, f kontinu di suatu titik berarti bahwa grafiknya tidak terputus
11. FUNGSI MONOTON (DAN FUNGSI KONVEKS)
 11. FUNGSI MONOTON (DAN FUNGSI KONVEKS) 11.1 Definisi dan Limit Fungsi Monoton Misalkan f terdefinisi pada suatu himpunan H. Kita katakan bahwa f naik pada H apabila untuk setiap x, y H dengan x < y berlaku
11. FUNGSI MONOTON (DAN FUNGSI KONVEKS) 11.1 Definisi dan Limit Fungsi Monoton Misalkan f terdefinisi pada suatu himpunan H. Kita katakan bahwa f naik pada H apabila untuk setiap x, y H dengan x < y berlaku
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
DASAR-DASAR ANALISIS MATEMATIKA
 (Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. December 1, 2007 Diberikan sebuah fungsi yang terdefinisi pada interval (a, b) kecuali mungkin di
(Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. December 1, 2007 Diberikan sebuah fungsi yang terdefinisi pada interval (a, b) kecuali mungkin di
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
DASAR-DASAR ANALISIS MATEMATIKA
 (Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. December 11, 2007 Misalkan f terdefinisi pada suatu himpunan H. Kita katakan bahwa f naik pada H apabila
(Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. December 11, 2007 Misalkan f terdefinisi pada suatu himpunan H. Kita katakan bahwa f naik pada H apabila
MA3231. Pengantar Analisis Real. Hendra Gunawan, Ph.D. Semester II, Tahun
 MA3231 Pengantar Analisis Real Semester II, Tahun 2016-2017 Hendra Gunawan, Ph.D. Bab 7 Limit dan Kekontinuan 2 Isaac Newton (1643-1727) Isaac Newton adalah seorang fisikawan & matematikawan Inggris yang
MA3231 Pengantar Analisis Real Semester II, Tahun 2016-2017 Hendra Gunawan, Ph.D. Bab 7 Limit dan Kekontinuan 2 Isaac Newton (1643-1727) Isaac Newton adalah seorang fisikawan & matematikawan Inggris yang
MA3231. Pengantar Analisis Real. Hendra Gunawan, Ph.D. Semester II, Tahun
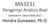 MA3231 Pengantar Analisis Real Semester II, Tahun 2016-2017 Hendra Gunawan, Ph.D. Bab 6 Fungsi 2 Rene Descartes (1596-1650) Rene Descartes adalah seorang filsuf & matematikawan Perancis, penemu sistem
MA3231 Pengantar Analisis Real Semester II, Tahun 2016-2017 Hendra Gunawan, Ph.D. Bab 6 Fungsi 2 Rene Descartes (1596-1650) Rene Descartes adalah seorang filsuf & matematikawan Perancis, penemu sistem
Analisis Riil II: Diferensiasi
 Definisi Turunan Definisi dan Teorema Aturan Rantai Fungsi Invers Definisi (Turunan) Misalkan I R sebuah interval, f : I R, dan c I. Bilangan riil L dikatakan turunan dari f di c jika diberikan sebarang
Definisi Turunan Definisi dan Teorema Aturan Rantai Fungsi Invers Definisi (Turunan) Misalkan I R sebuah interval, f : I R, dan c I. Bilangan riil L dikatakan turunan dari f di c jika diberikan sebarang
KALKULUS BAB II FUNGSI, LIMIT, DAN KEKONTINUAN. DEPARTEMEN TEKNIK KIMIA Universitas Indonesia
 KALKULUS BAB II FUNGSI, LIMIT, DAN KEKONTINUAN DEPARTEMEN TEKNIK KIMIA Universitas Indonesia BAB II. FUNGSI, LIMIT, DAN KEKONTINUAN Fungsi dan Operasi pada Fungsi Beberapa Fungsi Khusus Limit dan Limit
KALKULUS BAB II FUNGSI, LIMIT, DAN KEKONTINUAN DEPARTEMEN TEKNIK KIMIA Universitas Indonesia BAB II. FUNGSI, LIMIT, DAN KEKONTINUAN Fungsi dan Operasi pada Fungsi Beberapa Fungsi Khusus Limit dan Limit
Catatan Kuliah MA1123 Kalkulus Elementer I
 Catatan Kuliah MA1123 Kalkulus Elementer I Oleh Hendra Gunawan, Ph.D. Departemen Matematika ITB Sasaran Belajar Setelah mempelajari materi Kalkulus Elementer I, mahasiswa diharapkan memiliki (terutama):
Catatan Kuliah MA1123 Kalkulus Elementer I Oleh Hendra Gunawan, Ph.D. Departemen Matematika ITB Sasaran Belajar Setelah mempelajari materi Kalkulus Elementer I, mahasiswa diharapkan memiliki (terutama):
DASAR-DASAR ANALISIS MATEMATIKA
 (Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. December 6, 2007 Misalkan f terdefinisi pada suatu interval terbuka (a, b) dan c (a, b). Kita katakan
(Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. December 6, 2007 Misalkan f terdefinisi pada suatu interval terbuka (a, b) dan c (a, b). Kita katakan
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016. Hendra Gunawan
 MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 4.2 Sifat-Sifat Fungsi Kontinu Diberikan f dan g, keduanya terdefinisi pada himpunan A, kita definisikan f + g, f g, fg, f/g secara
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 4.2 Sifat-Sifat Fungsi Kontinu Diberikan f dan g, keduanya terdefinisi pada himpunan A, kita definisikan f + g, f g, fg, f/g secara
4 DIFERENSIAL. 4.1 Pengertian derivatif
 Diferensial merupakan topik yang cukup 'baru' dalam matematika. Dimulai sekitar tahun 1630 an oleh Fermat ketika menghadapi masalah menentukan garis singgung kurva, dan juga masalah menentukan maksimum
Diferensial merupakan topik yang cukup 'baru' dalam matematika. Dimulai sekitar tahun 1630 an oleh Fermat ketika menghadapi masalah menentukan garis singgung kurva, dan juga masalah menentukan maksimum
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
3 LIMIT DAN KEKONTINUAN
 Menurut Bartle dan Sherbet (1994), Analisis matematika secara umum dipahami sebagai tubuh matematika yang dibangun oleh berbagai konsep limit. Pada bab sebelumnya kita telah mempelajari limit barisan,
Menurut Bartle dan Sherbet (1994), Analisis matematika secara umum dipahami sebagai tubuh matematika yang dibangun oleh berbagai konsep limit. Pada bab sebelumnya kita telah mempelajari limit barisan,
4 DIFERENSIAL. 4.1 Pengertian derivatif
 Diferensial merupakan topik yang cukup 'baru' dalam matematika. Dimulai sekitar tahun 1630 an oleh Fermat ketika menghadapi masalah menentukan garis singgung kurva, dan juga masalah menentukan maksimum
Diferensial merupakan topik yang cukup 'baru' dalam matematika. Dimulai sekitar tahun 1630 an oleh Fermat ketika menghadapi masalah menentukan garis singgung kurva, dan juga masalah menentukan maksimum
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
16. BARISAN FUNGSI. 16.1 Barisan Fungsi dan Kekonvergenan Titik Demi Titik
 16. BARISAN FUNGSI 16.1 Barisan Fungsi dan Kekonvergenan Titik Demi Titik Bila pada bab-bab sebelumnya kita membahas fungsi sebagai sebuah objek individual, maka pada bab ini dan selanjutnya kita akan
16. BARISAN FUNGSI 16.1 Barisan Fungsi dan Kekonvergenan Titik Demi Titik Bila pada bab-bab sebelumnya kita membahas fungsi sebagai sebuah objek individual, maka pada bab ini dan selanjutnya kita akan
BAGIAN PERTAMA. Bilangan Real, Barisan, Deret
 BAGIAN PERTAMA Bilangan Real, Barisan, Deret 2 Hendra Gunawan Pengantar Analisis Real 3 0. BILANGAN REAL 0. Bilangan Real sebagai Bentuk Desimal Dalam buku ini pembaca diasumsikan telah mengenal dengan
BAGIAN PERTAMA Bilangan Real, Barisan, Deret 2 Hendra Gunawan Pengantar Analisis Real 3 0. BILANGAN REAL 0. Bilangan Real sebagai Bentuk Desimal Dalam buku ini pembaca diasumsikan telah mengenal dengan
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
3 LIMIT DAN KEKONTINUAN
 Menurut Bartle dan Sherbet (994), Analisis matematika secara umum dipahami sebagai tubuh matematika yang dibangun oleh berbagai konsep limit. Pada bab sebelumnya kita telah mempelajari limit barisan, kekonvergenan
Menurut Bartle dan Sherbet (994), Analisis matematika secara umum dipahami sebagai tubuh matematika yang dibangun oleh berbagai konsep limit. Pada bab sebelumnya kita telah mempelajari limit barisan, kekonvergenan
(b) M merupakan nilai minimum (mutlak) f apabila M f(x) x I..
 3. Aplikasi Turunan a. Nilai ekstrim Bagian ini dimulai dengan pengertian nilai ekstrim suatu fungsi yang mencakup nilai ekstrim maksimum dan nilai ekstrim minimum. Definisi 3. Diberikan fungsi f: I R,
3. Aplikasi Turunan a. Nilai ekstrim Bagian ini dimulai dengan pengertian nilai ekstrim suatu fungsi yang mencakup nilai ekstrim maksimum dan nilai ekstrim minimum. Definisi 3. Diberikan fungsi f: I R,
3 LIMIT DAN KEKONTINUAN
 Menurut Bartle dan Sherbet (1994), Analisis matematika secara umum dipahami sebagai tubuh matematika yang dibangun dari berbagai konsep limit. Pada bab sebelumnya kita telah mempelajari limit barisan,
Menurut Bartle dan Sherbet (1994), Analisis matematika secara umum dipahami sebagai tubuh matematika yang dibangun dari berbagai konsep limit. Pada bab sebelumnya kita telah mempelajari limit barisan,
FUNGSI KONTINU. sedemikian sehingga jika x adalah titik dari A (c), maka f (x) berada pada Vg (f (c)). (Lihat Gambar 5.1.1).
 FUNGSI KONTINU 51 FUNGSI KONTINU 511 Definisi A R, f: A R, dan c A Kita mengatakan bahwa f kontinu di c jika, diberi persekitaran Vg (f (c)) dari f (c) terdapat persekitaran (c) dari c sedemikian sehingga
FUNGSI KONTINU 51 FUNGSI KONTINU 511 Definisi A R, f: A R, dan c A Kita mengatakan bahwa f kontinu di c jika, diberi persekitaran Vg (f (c)) dari f (c) terdapat persekitaran (c) dari c sedemikian sehingga
Daftar Isi 3. BARISAN ANALISIS REAL. (Semester I Tahun ) Hendra Gunawan. Dosen FMIPA - ITB
 (Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. August 29, 2011 Dalam kisah Zeno tentang perlombaan lari antara Achilles dan seekor kura-kura, ketika Achilles mencapai
(Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. August 29, 2011 Dalam kisah Zeno tentang perlombaan lari antara Achilles dan seekor kura-kura, ketika Achilles mencapai
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016. Hendra Gunawan
 MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 5.3 Kalkulus Turunan Pada bagian ini kita akan membahas sejumlah aturan untuk diferensial dan aturan untuk turunan, yg mempunyai kemiripan
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 5.3 Kalkulus Turunan Pada bagian ini kita akan membahas sejumlah aturan untuk diferensial dan aturan untuk turunan, yg mempunyai kemiripan
Nilai mutlak pada definisi tersebut di interpretasikan untuk mengukur jarak dua
 II. LANDASAN TEORI 2.1 Limit Fungsi Definisi 2.1.1(Edwin J, 1987) Misalkan I interval terbuka pada R dan f: I R fungsi bernilai real. Secara matematis ditulis lim f(x) = l untuk suatu a I, yaitu nilai
II. LANDASAN TEORI 2.1 Limit Fungsi Definisi 2.1.1(Edwin J, 1987) Misalkan I interval terbuka pada R dan f: I R fungsi bernilai real. Secara matematis ditulis lim f(x) = l untuk suatu a I, yaitu nilai
Muhafzan TURUNAN. Muhafzan, Ph.D
 1 TURUNAN, Ph.D TURUNAN 3 1 Turunan Kita mulai diskusi ini dengan memperkenalkan denisi turunan suatu fungsi Denisi 1. Misalkan I R; f : I! R dan c 2 I: Bilangan L 2 R dikatakan merupakan turunan dari
1 TURUNAN, Ph.D TURUNAN 3 1 Turunan Kita mulai diskusi ini dengan memperkenalkan denisi turunan suatu fungsi Denisi 1. Misalkan I R; f : I! R dan c 2 I: Bilangan L 2 R dikatakan merupakan turunan dari
II. TINJUAN PUSTAKA. lim f(x) = L berarti bahwa bilamana x dekat tetapi sebelah kiri c 0 maka f(x)
 II. TINJUAN PUSTAKA 2.1. Limit Definisi lim f(x) = L, dan mengatakan limit f (x) ketika x mendekati a sama dengan L, jika dapat dibuat nilai f (x) sebarang yang dekat dengan L dengan cara mengambil nilai
II. TINJUAN PUSTAKA 2.1. Limit Definisi lim f(x) = L, dan mengatakan limit f (x) ketika x mendekati a sama dengan L, jika dapat dibuat nilai f (x) sebarang yang dekat dengan L dengan cara mengambil nilai
Definisi 4.1 Fungsi f dikatakan kontinu di titik a (continuous at a) jika dan hanya jika ketiga syarat berikut dipenuhi: (1) f(a) ada,
 Lecture 4. Limit B A. Continuity Definisi 4.1 Fungsi f dikatakan kontinu di titik a (continuous at a) jika dan hanya jika ketiga syarat berikut dipenuhi: (1) f(a) ada, (2) lim f(x) ada, (3) lim f(x) =
Lecture 4. Limit B A. Continuity Definisi 4.1 Fungsi f dikatakan kontinu di titik a (continuous at a) jika dan hanya jika ketiga syarat berikut dipenuhi: (1) f(a) ada, (2) lim f(x) ada, (3) lim f(x) =
Catatan Kuliah MA1123 KALKULUS ELEMENTER I BAB III. TURUNAN
 BAB III. TURUNAN Kecepatan Sesaat dan Gradien Garis Singgung Turunan dan Hubungannya dengan Kekontinuan Aturan Dasar Turunan Notasi Leibniz dan Turunan Tingkat Tinggi Penurunan Implisit Laju yang Berkaitan
BAB III. TURUNAN Kecepatan Sesaat dan Gradien Garis Singgung Turunan dan Hubungannya dengan Kekontinuan Aturan Dasar Turunan Notasi Leibniz dan Turunan Tingkat Tinggi Penurunan Implisit Laju yang Berkaitan
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
DASAR-DASAR ANALISIS MATEMATIKA
 (Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. December 26, 2007 Misalkan f kontinu pada interval [a, b]. Apakah masuk akal untuk membahas luas daerah
(Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. December 26, 2007 Misalkan f kontinu pada interval [a, b]. Apakah masuk akal untuk membahas luas daerah
ANALISIS REAL. (Semester I Tahun ) Hendra Gunawan. October 10, Dosen FMIPA - ITB
 (Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. October 10, 2011 Pemahaman yang baik tentang fungsi kontinu merupakan hal yang penting dalam analisis. Dalam optimisasi,
(Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. October 10, 2011 Pemahaman yang baik tentang fungsi kontinu merupakan hal yang penting dalam analisis. Dalam optimisasi,
Muhafzan FUNGSI KONTINU. Muhafzan, Ph.D
 1 FUNGSI KONTINU, Ph.D FUNGSI KONTINU 3 1 Kekontinuan Bab ini akan diawali dengan klas fungsi yang terpenting dalam analisis riil, yaitu klas fungsi-fungsi kontinu. Terlebih dahulu akan didenisikan gagasan
1 FUNGSI KONTINU, Ph.D FUNGSI KONTINU 3 1 Kekontinuan Bab ini akan diawali dengan klas fungsi yang terpenting dalam analisis riil, yaitu klas fungsi-fungsi kontinu. Terlebih dahulu akan didenisikan gagasan
Hendra Gunawan. 13 September 2013
 MA1101 MATEMATIKA 1A Hendra Gunawan Semester I, 2013/2014 13 September 2013 Latihan (Kuliah yang Lalu) sin t 1. Menggunakan fakta bahwa lim 1, t0 hitunglah: t 2 sin( 2 ) a. limsin t.cot 2t b. lim t 0 0
MA1101 MATEMATIKA 1A Hendra Gunawan Semester I, 2013/2014 13 September 2013 Latihan (Kuliah yang Lalu) sin t 1. Menggunakan fakta bahwa lim 1, t0 hitunglah: t 2 sin( 2 ) a. limsin t.cot 2t b. lim t 0 0
Bahan Diskusi/Tugas Kelompok Topik: Turunan Fungsi
 Jurusan Pendidikan Matematika FPMIPA Universitas Pendidikan Indonesia Bahan Diskusi/Tugas Kelompok Topik: Turunan Fungsi Definisi 1: Misalkan I R suatu interval, c I dan f : I R. Fungsi f disebut diferensiabel
Jurusan Pendidikan Matematika FPMIPA Universitas Pendidikan Indonesia Bahan Diskusi/Tugas Kelompok Topik: Turunan Fungsi Definisi 1: Misalkan I R suatu interval, c I dan f : I R. Fungsi f disebut diferensiabel
PENGANTAR ANALISIS REAL
 Seri Analisis dan Geometri No. 1 (2009), -15 158 (173 hlm.) PENGANTAR ANALISIS REAL Oleh Hendra Gunawan Edisi Pertama Bandung, Januari 2009 2000 Dewey Classification: 515-xx. Kata Kunci: Analisis matematika,
Seri Analisis dan Geometri No. 1 (2009), -15 158 (173 hlm.) PENGANTAR ANALISIS REAL Oleh Hendra Gunawan Edisi Pertama Bandung, Januari 2009 2000 Dewey Classification: 515-xx. Kata Kunci: Analisis matematika,
Matematika I: APLIKASI TURUNAN. Dadang Amir Hamzah. Dadang Amir Hamzah Matematika I Semester I / 70
 Matematika I: APLIKASI TURUNAN Dadang Amir Hamzah 2015 Dadang Amir Hamzah Matematika I Semester I 2015 1 / 70 Outline 1 Maksimum dan Minimum Dadang Amir Hamzah Matematika I Semester I 2015 2 / 70 Outline
Matematika I: APLIKASI TURUNAN Dadang Amir Hamzah 2015 Dadang Amir Hamzah Matematika I Semester I 2015 1 / 70 Outline 1 Maksimum dan Minimum Dadang Amir Hamzah Matematika I Semester I 2015 2 / 70 Outline
MA1201 KALKULUS 2A Do maths and you see the world
 Catatan Kuliah MA20 KALKULUS 2A Do maths and you see the world disusun oleh Khreshna I.A. Syuhada, MSc. PhD. Kelompok Keilmuan STATISTIKA - FMIPA Institut Teknologi Bandung 203 Catatan kuliah ini ditulis
Catatan Kuliah MA20 KALKULUS 2A Do maths and you see the world disusun oleh Khreshna I.A. Syuhada, MSc. PhD. Kelompok Keilmuan STATISTIKA - FMIPA Institut Teknologi Bandung 203 Catatan kuliah ini ditulis
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI 2.1 Latar Belakang Historis Fondasi dari integral pertama kali dideklarasikan oleh Cavalieri, seorang ahli matematika berkebangsaan Italia pada tahun 1635. Cavalieri menemukan bahwa
BAB II LANDASAN TEORI 2.1 Latar Belakang Historis Fondasi dari integral pertama kali dideklarasikan oleh Cavalieri, seorang ahli matematika berkebangsaan Italia pada tahun 1635. Cavalieri menemukan bahwa
F. RANCANGAN KEGIATAN BELAJAR MENGAJAR
 F. RANCANGAN KEGIATAN BELAJAR MENGAJAR No. (TIU) 1. Limit Fungsi Mahasiswa dapar memahami secara mendalam (deduktif) pengertian limit fungsi, definisi dan te-orema-teorema serta mampu menga-plikasikannya
F. RANCANGAN KEGIATAN BELAJAR MENGAJAR No. (TIU) 1. Limit Fungsi Mahasiswa dapar memahami secara mendalam (deduktif) pengertian limit fungsi, definisi dan te-orema-teorema serta mampu menga-plikasikannya
asimtot.wordpress.com BAB I PENDAHULUAN
 BAB I PENDAHULUAN. Latar Belakang Kalkulus Differensial dan Integral sangat luas penggunaannya dalam berbagai bidang seperti penentuan maksimum dan minimum. Suatu fungsi yang sering digunakan mahasiswa
BAB I PENDAHULUAN. Latar Belakang Kalkulus Differensial dan Integral sangat luas penggunaannya dalam berbagai bidang seperti penentuan maksimum dan minimum. Suatu fungsi yang sering digunakan mahasiswa
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016. Hendra Gunawan
 MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 3. Topologi Garis Bilangan Real 3.1 Teori Limit Limit, supremum, dan infimum Titik limit 3.2 Himpunan Buka dan Himpunan Tutup 3.3
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 3. Topologi Garis Bilangan Real 3.1 Teori Limit Limit, supremum, dan infimum Titik limit 3.2 Himpunan Buka dan Himpunan Tutup 3.3
FUNGSI dan LIMIT. 1.1 Fungsi dan Grafiknya
 FUNGSI dan LIMIT 1.1 Fungsi dan Grafiknya Fungsi : suatu aturan yang menghubungkan setiap elemen suatu himpunan pertama (daerah asal) tepat kepada satu elemen himpunan kedua (daerah hasil) fungsi Daerah
FUNGSI dan LIMIT 1.1 Fungsi dan Grafiknya Fungsi : suatu aturan yang menghubungkan setiap elemen suatu himpunan pertama (daerah asal) tepat kepada satu elemen himpunan kedua (daerah hasil) fungsi Daerah
BAB II TEOREMA NILAI RATA-RATA (TNR)
 BAB II TEOREMA NILAI RATA-RATA (TNR) Teorema nilai rata-rata menghubungkan nilai suatu fungsi dengan nilai derivatifnya (turunannya), dimana TNR merupakan salah satu bagian penting dalam kuliah analisis
BAB II TEOREMA NILAI RATA-RATA (TNR) Teorema nilai rata-rata menghubungkan nilai suatu fungsi dengan nilai derivatifnya (turunannya), dimana TNR merupakan salah satu bagian penting dalam kuliah analisis
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016. Hendra Gunawan
 MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 5. Kalkulus Diferensial 5.1 Konsep Turunan Beberapa Definisi yang Setara Kekontinuan dan Keterdiferensialan secara Kontinu 5.2 Sifat-Sifat
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 5. Kalkulus Diferensial 5.1 Konsep Turunan Beberapa Definisi yang Setara Kekontinuan dan Keterdiferensialan secara Kontinu 5.2 Sifat-Sifat
SISTEM BILANGAN RIIL DAN FUNGSI
 SISTEM BILANGAN RIIL DAN FUNGSI Matematika Juni 2016 Dosen : Dadang Amir Hamzah MATEMATIKA Juni 2016 1 / 67 Outline 1 Sistem Bilangan Riil Dosen : Dadang Amir Hamzah MATEMATIKA Juni 2016 2 / 67 Outline
SISTEM BILANGAN RIIL DAN FUNGSI Matematika Juni 2016 Dosen : Dadang Amir Hamzah MATEMATIKA Juni 2016 1 / 67 Outline 1 Sistem Bilangan Riil Dosen : Dadang Amir Hamzah MATEMATIKA Juni 2016 2 / 67 Outline
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016. Hendra Gunawan
 MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 4. Fungsi Kontinu 4.1 Konsep Kekontinuan Fungsi kontinu Limit fungsi dan limit barisan Prapeta himpunan buka 4.2 Sifat-Sifat Fungsi
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 4. Fungsi Kontinu 4.1 Konsep Kekontinuan Fungsi kontinu Limit fungsi dan limit barisan Prapeta himpunan buka 4.2 Sifat-Sifat Fungsi
ANALISIS REAL. (Semester I Tahun ) Hendra Gunawan. September 12, Dosen FMIPA - ITB
 (Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. September 12, 2011 Teorema 11 pada Bab 3 memberi kita cara untuk menyelidiki kekonvergenan sebuah barisan tanpa harus mengetahui
(Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. September 12, 2011 Teorema 11 pada Bab 3 memberi kita cara untuk menyelidiki kekonvergenan sebuah barisan tanpa harus mengetahui
BAB I DERIVATIF (TURUNAN)
 BAB I DERIVATIF (TURUNAN) Pada bab ini akan dipaparkan pengertian derivatif suatu fungsi, beberapa sifat aljabar derivatif, aturan rantai, dan derifativ fungsi invers. A. Pengertian Derivatif Pengertian
BAB I DERIVATIF (TURUNAN) Pada bab ini akan dipaparkan pengertian derivatif suatu fungsi, beberapa sifat aljabar derivatif, aturan rantai, dan derifativ fungsi invers. A. Pengertian Derivatif Pengertian
LIMIT DAN KEKONTINUAN
 LIMIT DAN KEKONTINUAN Departemen Matematika FMIPA IPB Bogor, 2012 (Departemen Matematika FMIPA IPB) Kalkulus I Bogor, 2012 1 / 37 Topik Bahasan 1 Limit Fungsi 2 Hukum Limit 3 Kekontinuan Fungsi (Departemen
LIMIT DAN KEKONTINUAN Departemen Matematika FMIPA IPB Bogor, 2012 (Departemen Matematika FMIPA IPB) Kalkulus I Bogor, 2012 1 / 37 Topik Bahasan 1 Limit Fungsi 2 Hukum Limit 3 Kekontinuan Fungsi (Departemen
DERIVATIVE Arum Handini primandari
 DERIVATIVE Arum Handini primandari INTRODUCTION Calculus adalah perubahan matematis, alat utama dalam studi perubahan adalah prosedur yang disebut differentiation (deferensial/turunan) Calculus dikembangkan
DERIVATIVE Arum Handini primandari INTRODUCTION Calculus adalah perubahan matematis, alat utama dalam studi perubahan adalah prosedur yang disebut differentiation (deferensial/turunan) Calculus dikembangkan
Hendra Gunawan. 2 Oktober 2013
 MA1101 MATEMATIKA 1A Hendra Gunawan Semester I, 2013/2014 2 Oktober 2013 Apa yang Telah Dipelajari pada Bab 2 2.1 Dua Masalah Satu Tema 2.2 Turunan 2.3 Aturan Turunan 2.4 Turunan Fungsi Trigonometri 2.5Aturan
MA1101 MATEMATIKA 1A Hendra Gunawan Semester I, 2013/2014 2 Oktober 2013 Apa yang Telah Dipelajari pada Bab 2 2.1 Dua Masalah Satu Tema 2.2 Turunan 2.3 Aturan Turunan 2.4 Turunan Fungsi Trigonometri 2.5Aturan
Matematika I : Limit. Dadang Amir Hamzah. Dadang Amir Hamzah Matematika I Semester I / 79
 Matematika I : Limit Dadang Amir Hamzah 2015 Dadang Amir Hamzah Matematika I Semester I 2015 1 / 79 Outline 1 limit Introduction to Limit Rigorous Study of Limits Limit Theorem Limit Involving Trigonometric
Matematika I : Limit Dadang Amir Hamzah 2015 Dadang Amir Hamzah Matematika I Semester I 2015 1 / 79 Outline 1 limit Introduction to Limit Rigorous Study of Limits Limit Theorem Limit Involving Trigonometric
= + atau = - 2. TURUNAN 2.1 Definisi Turunan fungsi f adalah fungsi yang nilainya di setiap bilangan sebarang c di dalam D f diberikan oleh
 JURUSAN PENDIDIKAN MATEMATIKA FPMIPA-UPI BANDUNG HAND OUT TURUNAN DAN DIFERENSIASI OLEH: FIRDAUS-UPI 0716 1. GARIS SINGGUNG 1.1 Definisi Misalkan fungsi f kontinu di c. Garis singgung ( tangent line )
JURUSAN PENDIDIKAN MATEMATIKA FPMIPA-UPI BANDUNG HAND OUT TURUNAN DAN DIFERENSIASI OLEH: FIRDAUS-UPI 0716 1. GARIS SINGGUNG 1.1 Definisi Misalkan fungsi f kontinu di c. Garis singgung ( tangent line )
Bab 16. LIMIT dan TURUNAN. Motivasi. Limit Fungsi. Fungsi Turunan. Matematika SMK, Bab 16: Limit dan Turunan 1/35
 Bab 16 Grafik LIMIT dan TURUNAN Matematika SMK, Bab 16: Limit dan 1/35 Grafik Pada dasarnya, konsep limit dikembangkan untuk mengerjakan perhitungan matematis yang melibatkan: nilai sangat kecil; Matematika
Bab 16 Grafik LIMIT dan TURUNAN Matematika SMK, Bab 16: Limit dan 1/35 Grafik Pada dasarnya, konsep limit dikembangkan untuk mengerjakan perhitungan matematis yang melibatkan: nilai sangat kecil; Matematika
SISTEM BILANGAN REAL
 DAFTAR ISI 1 SISTEM BILANGAN REAL 1 1.1 Sifat Aljabar Bilangan Real..................... 1 1.2 Sifat Urutan Bilangan Real..................... 6 1.3 Nilai Mutlak dan Jarak Pada Bilangan Real............
DAFTAR ISI 1 SISTEM BILANGAN REAL 1 1.1 Sifat Aljabar Bilangan Real..................... 1 1.2 Sifat Urutan Bilangan Real..................... 6 1.3 Nilai Mutlak dan Jarak Pada Bilangan Real............
ANALISIS REAL. (Semester I Tahun ) Hendra Gunawan. October 3, Dosen FMIPA - ITB
 (Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. October 3, 2011 6.3 Limit Sepihak, Limit di Tak Hingga, dan Limit Tak Hingga Bila sebelumnya kita mempelajari limit barisan,
(Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. October 3, 2011 6.3 Limit Sepihak, Limit di Tak Hingga, dan Limit Tak Hingga Bila sebelumnya kita mempelajari limit barisan,
ANALISIS REAL. (Semester I Tahun ) Hendra Gunawan. August 18, Dosen FMIPA - ITB
 (Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. August 18, 2011 Kita telah mencatat sebelumnya bahwa supremum dan infimum suatu himpunan tidak harus merupakan anggota himpunan
(Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. August 18, 2011 Kita telah mencatat sebelumnya bahwa supremum dan infimum suatu himpunan tidak harus merupakan anggota himpunan
TUJUAN INSTRUKSIONAL KHUSUS
 PREVIEW KALKULUS TUJUAN INSTRUKSIONAL KHUSUS Mahasiswa mampu: menyebutkan konsep-konsep utama dalam kalkulus dan contoh masalah-masalah yang memotivasi konsep tersebut; menjelaskan menyebutkan konsep-konsep
PREVIEW KALKULUS TUJUAN INSTRUKSIONAL KHUSUS Mahasiswa mampu: menyebutkan konsep-konsep utama dalam kalkulus dan contoh masalah-masalah yang memotivasi konsep tersebut; menjelaskan menyebutkan konsep-konsep
II. LANDASAN TEORI ( ) =
 II. LANDASAN TEORI 2.1 Fungsi Definisi 2.1.1 Fungsi Bernilai Real Fungsi bernilai real adalah fungsi yang domain dan rangenya adalah himpunan bagian dari real. Definisi 2.1.2 Limit Fungsi Jika adalah suatu
II. LANDASAN TEORI 2.1 Fungsi Definisi 2.1.1 Fungsi Bernilai Real Fungsi bernilai real adalah fungsi yang domain dan rangenya adalah himpunan bagian dari real. Definisi 2.1.2 Limit Fungsi Jika adalah suatu
BAB I LIMIT-LIMIT Limit-limit Fungsi
 .. Limit-it Fungsi BAB I LIMIT-LIMIT... Definisi. Misalkan A R. Suatu titik c R adalah titik cluster dari A jika setiap lingkungan-δ dari c, V δ (c) = (c-δ,c+δ), memuat paling sedikit satu titik dari A
.. Limit-it Fungsi BAB I LIMIT-LIMIT... Definisi. Misalkan A R. Suatu titik c R adalah titik cluster dari A jika setiap lingkungan-δ dari c, V δ (c) = (c-δ,c+δ), memuat paling sedikit satu titik dari A
Hendra Gunawan. 11 Oktober 2013
 MA1101 MATEMATIKA 1A Hendra Gunawan Semester I, 2013/2014 11 Oktober 2013 Latihan (Kuliah yang Lalu) Dengan memperhatikan: daerah asal dan daerahhasilnya, titik titik potong dengan sumbu koordinat, asimtot
MA1101 MATEMATIKA 1A Hendra Gunawan Semester I, 2013/2014 11 Oktober 2013 Latihan (Kuliah yang Lalu) Dengan memperhatikan: daerah asal dan daerahhasilnya, titik titik potong dengan sumbu koordinat, asimtot
Open Source. Not For Commercial Use
 Ringkasan Kalkulus 2, Untuk dipakai di ITB 1 Limit dan Kekontinuan Misalkan z = f(, y) fungsi dua peubah dan (a, b) R 2. Seperti pada limit fungsi satu peubah, limit fungsi dua peubah bertujuan untuk mengamati
Ringkasan Kalkulus 2, Untuk dipakai di ITB 1 Limit dan Kekontinuan Misalkan z = f(, y) fungsi dua peubah dan (a, b) R 2. Seperti pada limit fungsi satu peubah, limit fungsi dua peubah bertujuan untuk mengamati
Barisan dan Deret Agus Yodi Gunawan
 Barisan dan Deret Agus Yodi Gunawan Barisan. Definisi. Barisan tak hingga adalah suatu fungsi dengan daerah asalnya himpunan bilangan bulat positif dan daerah kawannya himpunan bilangan real. Notasi untuk
Barisan dan Deret Agus Yodi Gunawan Barisan. Definisi. Barisan tak hingga adalah suatu fungsi dengan daerah asalnya himpunan bilangan bulat positif dan daerah kawannya himpunan bilangan real. Notasi untuk
Hendra Gunawan. 18 September 2013
 MA1101 MATEMATIKA 1A Hendra Gunawan Semester I, 2013/2014 18 September 2013 Review: Teorema Nilai Antara Jika f kontinu pada [a,b],, f(a) < 0 dan f(b) > 0 (atau sebaliknya, f(a) > 0 dan f(b) < 0), maka
MA1101 MATEMATIKA 1A Hendra Gunawan Semester I, 2013/2014 18 September 2013 Review: Teorema Nilai Antara Jika f kontinu pada [a,b],, f(a) < 0 dan f(b) > 0 (atau sebaliknya, f(a) > 0 dan f(b) < 0), maka
Catatan Kuliah KALKULUS II BAB V. INTEGRAL
 BAB V. INTEGRAL Anti-turunan dan Integral TakTentu Persamaan Diferensial Sederhana Notasi Sigma dan Luas Daerah di Bawah Kurva Integral Tentu Teorema Dasar Kalkulus Sifat-sifat Integral Tentu Lebih Lanjut
BAB V. INTEGRAL Anti-turunan dan Integral TakTentu Persamaan Diferensial Sederhana Notasi Sigma dan Luas Daerah di Bawah Kurva Integral Tentu Teorema Dasar Kalkulus Sifat-sifat Integral Tentu Lebih Lanjut
MA5032 ANALISIS REAL
 (Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. August 16, 2011 Pada bab ini anda diasumsikan telah mengenal dengan cukup baik bilangan asli, bilangan bulat, dan bilangan
(Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. August 16, 2011 Pada bab ini anda diasumsikan telah mengenal dengan cukup baik bilangan asli, bilangan bulat, dan bilangan
Gambar 1. Gradien garis singgung grafik f
 D. URAIAN MATERI 1. Definisi dan Rumus-rumus Turunan Fungsi a. Definisi Turunan Sala satu masala yang mendasari munculnya kajian tentang turunan adala gradien garis singgung. Peratikan Gambar 1. f(c +
D. URAIAN MATERI 1. Definisi dan Rumus-rumus Turunan Fungsi a. Definisi Turunan Sala satu masala yang mendasari munculnya kajian tentang turunan adala gradien garis singgung. Peratikan Gambar 1. f(c +
Turunan Fungsi. h asalkan limit ini ada.
 Turunan Fungsi q Definisi Turunan Fungsi Misalkan fungsi f terdefinisi pada selang terbuka I yang memuat a. Turunan pertama fungsi f di =a ditulis f (a) didefinisikan dengan f ( a h) f ( a) f '( a) lim
Turunan Fungsi q Definisi Turunan Fungsi Misalkan fungsi f terdefinisi pada selang terbuka I yang memuat a. Turunan pertama fungsi f di =a ditulis f (a) didefinisikan dengan f ( a h) f ( a) f '( a) lim
BAB 5 TEOREMA SISA. Menggunakan aturan sukubanyak dalam penyelesaian masalah. Kompetensi Dasar
 Standar Kompetensi BAB 5 TEOREMA SISA Menggunakan aturan sukubanyak dalam penyelesaian masalah. Kompetensi Dasar Menggunakan algoritma pembagian sukubanyak untuk menentukan hasil bagi dan sisa pembagian
Standar Kompetensi BAB 5 TEOREMA SISA Menggunakan aturan sukubanyak dalam penyelesaian masalah. Kompetensi Dasar Menggunakan algoritma pembagian sukubanyak untuk menentukan hasil bagi dan sisa pembagian
11. Konvolusi. Misalkan f dan g fungsi yang terdefinisi pada R. Konvolusi dari f dan g adalah fungsi f g yang didefinisikan sebagai.
 11. Konvolusi Operasi konvolusi yang akan kita bahas di sini sebetulnya pernah kita jumpai pada pembahasan deret Fourier (ketika membuktikan kekonvergenan jumlah parsialnya). Operasi konvolusi merupakan
11. Konvolusi Operasi konvolusi yang akan kita bahas di sini sebetulnya pernah kita jumpai pada pembahasan deret Fourier (ketika membuktikan kekonvergenan jumlah parsialnya). Operasi konvolusi merupakan
Zulfaneti Yulia Haryono Rina F ebriana. Berbasis Penemuan Terbimbing = = D(sec x)= sec x tan x, ( + ) ( ) ( )=
 Zulfaneti Yulia Haryono Rina F ebriana Berbasis Penemuan Terbimbing = = D(sec x)= sec x tan x, ()= (+) () Penyusun Zulfaneti Yulia Haryono Rina Febriana Nama NIm : : Untuk ilmu yang bermanfaat Untuk Harapan
Zulfaneti Yulia Haryono Rina F ebriana Berbasis Penemuan Terbimbing = = D(sec x)= sec x tan x, ()= (+) () Penyusun Zulfaneti Yulia Haryono Rina Febriana Nama NIm : : Untuk ilmu yang bermanfaat Untuk Harapan
Fungsi dan Limit Fungsi 23. Contoh 5. lim. Buktikan, jika c 0, maka
 Contoh 5 Buktikan jika c 0 maka c c Analisis Pendahuluan Akan dicari bilangan 0 sedemikian sehingga apabila c untuk setiap 0. 0 c berlaku Perhatikan: c ( c)( c) c c c c Dapat dipilih c Bukti: c c c Ambil
Contoh 5 Buktikan jika c 0 maka c c Analisis Pendahuluan Akan dicari bilangan 0 sedemikian sehingga apabila c untuk setiap 0. 0 c berlaku Perhatikan: c ( c)( c) c c c c Dapat dipilih c Bukti: c c c Ambil
Memahami konsep dasar turunan fungsi dan menggunakan turunan fungsi pada
 5 TURUNAN JUMLAH PERTEMUAN : 4 PERTEMUAN TUJUAN INSTRUKSIONAL KHUSUS : Memahami konsep dasar turunan fungsi dan menggunakan turunan fungsi pada permasalahan yang ada Materi : 5.1 Pendahuluan Ide awal adanya
5 TURUNAN JUMLAH PERTEMUAN : 4 PERTEMUAN TUJUAN INSTRUKSIONAL KHUSUS : Memahami konsep dasar turunan fungsi dan menggunakan turunan fungsi pada permasalahan yang ada Materi : 5.1 Pendahuluan Ide awal adanya
2 BARISAN BILANGAN REAL
 2 BARISAN BILANGAN REAL Di sekolah menengah barisan diperkenalkan sebagai kumpulan bilangan yang disusun menurut "pola" tertentu, misalnya barisan aritmatika dan barisan geometri. Biasanya barisan dan
2 BARISAN BILANGAN REAL Di sekolah menengah barisan diperkenalkan sebagai kumpulan bilangan yang disusun menurut "pola" tertentu, misalnya barisan aritmatika dan barisan geometri. Biasanya barisan dan
Memahami konsep dasar turunan fungsi dan mengaplikasikan turunan fungsi pada
 5 TURUNAN JUMLAH PERTEMUAN : 4 PERTEMUAN TUJUAN INSTRUKSIONAL KHUSUS : Memahami konsep dasar turunan fungsi dan mengaplikasikan turunan fungsi pada permasalahan yang ada Materi : 5.1 Pendahuluan Ide awal
5 TURUNAN JUMLAH PERTEMUAN : 4 PERTEMUAN TUJUAN INSTRUKSIONAL KHUSUS : Memahami konsep dasar turunan fungsi dan mengaplikasikan turunan fungsi pada permasalahan yang ada Materi : 5.1 Pendahuluan Ide awal
MATEMATIKA TURUNAN FUNGSI
 MATEMATIKA TURUNAN FUNGSI lim h 0 f ( x h) f( x) h KELAS : XII IIS SEMESTER GANJIL SMA Santa Angela Bandung Tahun Pelajaran 017/018 XII IIS Semester 1 Tahun Pelajaran 017/018 PENGANTAR : TURUNAN FUNGSI
MATEMATIKA TURUNAN FUNGSI lim h 0 f ( x h) f( x) h KELAS : XII IIS SEMESTER GANJIL SMA Santa Angela Bandung Tahun Pelajaran 017/018 XII IIS Semester 1 Tahun Pelajaran 017/018 PENGANTAR : TURUNAN FUNGSI
BAB IV. PENGGUNAAN TURUNAN. Departemen Teknik Kimia Universitas Indonesia
 BAB IV. PENGGUNAAN TURUNAN Departemen Teknik Kimia Universitas Indonesia BAB IV. PENGGUNAAN TURUNAN Maksimum dan Minimum Kemonotonan dan Kecekungan Maksimum dan Minimum Lokal Masalah Maksimum dan Minimum
BAB IV. PENGGUNAAN TURUNAN Departemen Teknik Kimia Universitas Indonesia BAB IV. PENGGUNAAN TURUNAN Maksimum dan Minimum Kemonotonan dan Kecekungan Maksimum dan Minimum Lokal Masalah Maksimum dan Minimum
f (a) = laju perubahan y = f(x) pada x = a = turunan pertama y=f(x) pada x = a
 LEMBAR AKTIVITAS SISWA DIFFERENSIAL (TURUNAN) Nama Siswa : y f(a h) f(a) x (a h) a Kelas : Kompetensi Dasar (KURIKULUM 2013): 3.21 Memahami konsep turunan dengan menggunakan konteks matematik atau konteks
LEMBAR AKTIVITAS SISWA DIFFERENSIAL (TURUNAN) Nama Siswa : y f(a h) f(a) x (a h) a Kelas : Kompetensi Dasar (KURIKULUM 2013): 3.21 Memahami konsep turunan dengan menggunakan konteks matematik atau konteks
Daftar Isi 5. DERET ANALISIS REAL. (Semester I Tahun ) Hendra Gunawan. Dosen FMIPA - ITB September 26, 2011
 (Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. September 26, 2011 Diberikan sejumlah terhingga bilangan a 1,..., a N, kita dapat menghitung jumlah a 1 + + a N. Namun,
(Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. September 26, 2011 Diberikan sejumlah terhingga bilangan a 1,..., a N, kita dapat menghitung jumlah a 1 + + a N. Namun,
3 LIMIT DAN KEKONTINUAN
 Menurut Bartle dan Sherbet (1994), Analisis matematika secara umum dipahami sebagai tubuh matematika yang dibangun oleh berbagai konsep limit. Pada bab sebelumnya kita telah mempelajari limit barisan,
Menurut Bartle dan Sherbet (1994), Analisis matematika secara umum dipahami sebagai tubuh matematika yang dibangun oleh berbagai konsep limit. Pada bab sebelumnya kita telah mempelajari limit barisan,
Kalkulus II. Diferensial dalam ruang berdimensi n
 Kalkulus II Diferensial dalam ruang berdimensi n Minggu ke-9 DIFERENSIAL DALAM RUANG BERDIMENSI-n 1. Fungsi Dua Peubah atau Lebih 2. Diferensial Parsial 3. Limit dan Kekontinuan 1. Fungsi Dua Peubah atau
Kalkulus II Diferensial dalam ruang berdimensi n Minggu ke-9 DIFERENSIAL DALAM RUANG BERDIMENSI-n 1. Fungsi Dua Peubah atau Lebih 2. Diferensial Parsial 3. Limit dan Kekontinuan 1. Fungsi Dua Peubah atau
Kuliah 3: TURUNAN. Indah Yanti
 Kuliah 3: TURUNAN Indah Yanti Turunan Parsial DEFINISI Misalkan fungsi f: A R, dengan A R n adalah himpunan buka. Untuk setiap x = (x 1,..., x n ) A dan setiap j = 1,..., n limit f x j x 1,, x n f x 1,,
Kuliah 3: TURUNAN Indah Yanti Turunan Parsial DEFINISI Misalkan fungsi f: A R, dengan A R n adalah himpunan buka. Untuk setiap x = (x 1,..., x n ) A dan setiap j = 1,..., n limit f x j x 1,, x n f x 1,,
MAKALAH MATEMATIKA DASAR TURUNAN (DIFERENSIAL)
 MAKALAH MATEMATIKA DASAR TURUNAN (DIFERENSIAL) KATA PENGANTAR Puji dan Syukur kami panjatkan ke Hadirat Tuhan Yang Maha Esa, karena berkat limpahan Rahmat dan Karunia-nya sehingga kami dapat menyusun makalah
MAKALAH MATEMATIKA DASAR TURUNAN (DIFERENSIAL) KATA PENGANTAR Puji dan Syukur kami panjatkan ke Hadirat Tuhan Yang Maha Esa, karena berkat limpahan Rahmat dan Karunia-nya sehingga kami dapat menyusun makalah
BAB III Diferensial. Departemen Teknik Kimia Universitas Indonesia
 BAB III Diferensial Departemen Teknik Kimia Universitas Indonesia BAB III. TURUNAN Kecepatan Sesaat dan Gradien Garis Singgung Turunan dan Hubungannya dengan Kekontinuan Aturan Dasar Turunan Notasi Leibniz
BAB III Diferensial Departemen Teknik Kimia Universitas Indonesia BAB III. TURUNAN Kecepatan Sesaat dan Gradien Garis Singgung Turunan dan Hubungannya dengan Kekontinuan Aturan Dasar Turunan Notasi Leibniz
7. Transformasi Fourier
 Pengantar Analisis Fourier dan eori Aproksimasi 33 7. ransformasi Fourier Pada bab sebelumnya kita telah melihat bahwa setiap fungsi f L 1 ([0, 1] L ([0, 1] dapat dinyatakan sebagai deret Fourier f(x =
Pengantar Analisis Fourier dan eori Aproksimasi 33 7. ransformasi Fourier Pada bab sebelumnya kita telah melihat bahwa setiap fungsi f L 1 ([0, 1] L ([0, 1] dapat dinyatakan sebagai deret Fourier f(x =
Ringkasan Kalkulus 2, Untuk dipakai di ITB 1
 Ringkasan Kalkulus 2, Untuk dipakai di ITB Deret Tak Hingga Pada bagian ini akan dibicarakan penjumlahan berbentuk a +a 2 + +a n + dengan a n R Sebelumnya akan dibahas terlebih dahulu pengertian barisan
Ringkasan Kalkulus 2, Untuk dipakai di ITB Deret Tak Hingga Pada bagian ini akan dibicarakan penjumlahan berbentuk a +a 2 + +a n + dengan a n R Sebelumnya akan dibahas terlebih dahulu pengertian barisan
KALKULUS 1 HADI SUTRISNO. Pendidikan Matematika STKIP PGRI Bangkalan. Hadi Sutrisno/P.Matematika/STKIP PGRI Bangkalan
 KALKULUS 1 HADI SUTRISNO 1 Pendidikan Matematika STKIP PGRI Bangkalan BAB I PENDAHULUAN A. Sistem Bilangan Real Untuk mempelajari kalkulus kita terlebih dahulu perlu memahami bahasan tentang sistem bilangan
KALKULUS 1 HADI SUTRISNO 1 Pendidikan Matematika STKIP PGRI Bangkalan BAB I PENDAHULUAN A. Sistem Bilangan Real Untuk mempelajari kalkulus kita terlebih dahulu perlu memahami bahasan tentang sistem bilangan
LIMIT DAN KEKONTINUAN
 LIMIT DAN KEKONTINUAN Pengertian dan notasi dari it suatu fungsi, f() di suatu nilai = a diberikan secara intuitif berikut. Bila nilai f() mendekati L untuk nilai mendekati a dari arah kanan maka dikatakan
LIMIT DAN KEKONTINUAN Pengertian dan notasi dari it suatu fungsi, f() di suatu nilai = a diberikan secara intuitif berikut. Bila nilai f() mendekati L untuk nilai mendekati a dari arah kanan maka dikatakan
BARISAN BILANGAN REAL
 BAB 2 BARISAN BILANGAN REAL Di sekolah menengah barisan diperkenalkan sebagai kumpulan bilangan yang disusun menurut pola tertentu, misalnya barisan aritmatika dan barisan geometri. Biasanya barisan dan
BAB 2 BARISAN BILANGAN REAL Di sekolah menengah barisan diperkenalkan sebagai kumpulan bilangan yang disusun menurut pola tertentu, misalnya barisan aritmatika dan barisan geometri. Biasanya barisan dan
Variabel Banyak Bernilai Real 1 / 1
 Fungsi Variabel Banyak Bernilai Real Turunan Parsial dan Turunan Wono Setya Budhi KK Analisis dan Geometri, FMIPA ITB Variabel Banyak Bernilai Real 1 / 1 Turunan Parsial dan Turunan Usaha pertama untuk
Fungsi Variabel Banyak Bernilai Real Turunan Parsial dan Turunan Wono Setya Budhi KK Analisis dan Geometri, FMIPA ITB Variabel Banyak Bernilai Real 1 / 1 Turunan Parsial dan Turunan Usaha pertama untuk
SISTEM BILANGAN REAL
 DAFTAR ISI SISTEM BILANGAN REAL. Sifat Aljabar Bilangan Real......................2 Sifat Urutan Bilangan Real..................... 6.3 Nilai Mutlak dan Jarak Pada Bilangan Real.............4 Supremum
DAFTAR ISI SISTEM BILANGAN REAL. Sifat Aljabar Bilangan Real......................2 Sifat Urutan Bilangan Real..................... 6.3 Nilai Mutlak dan Jarak Pada Bilangan Real.............4 Supremum
INTEGRAL. disebut integral tak tentu dan f(x) disebut integran. = X n+1 + C, a = konstanta
 INTEGRAL Jika f(x) = F (x) adalah turunan pertama dari fungsi F(x) maka F(x) adalah antiturunan dari f(x)dan ditulis dengan F(x) = (dibaca integral f(x) terhadap x) = lambang integral, f(x) = integran.
INTEGRAL Jika f(x) = F (x) adalah turunan pertama dari fungsi F(x) maka F(x) adalah antiturunan dari f(x)dan ditulis dengan F(x) = (dibaca integral f(x) terhadap x) = lambang integral, f(x) = integran.
PAM 252 Metode Numerik Bab 2 Persamaan Nonlinier
 PAM 252 Metode Numerik Bab 2 Persamaan Nonlinier Mahdhivan Syafwan Jurusan Matematika FMIPA Universitas Andalas Semester Genap 2013/2014 1 Mahdhivan Syafwan Metode Numerik: Persamaan Nonlinier Solusi persamaan
PAM 252 Metode Numerik Bab 2 Persamaan Nonlinier Mahdhivan Syafwan Jurusan Matematika FMIPA Universitas Andalas Semester Genap 2013/2014 1 Mahdhivan Syafwan Metode Numerik: Persamaan Nonlinier Solusi persamaan
