DASAR-DASAR TEORI RUANG HILBERT
|
|
|
- Yanti Cahyadi
- 7 tahun lalu
- Tontonan:
Transkripsi
1 DASAR-DASAR TEORI RUANG HILBERT Herry P. Suryawan 1 Geometri Ruang Hilbert Definisi 1.1 Ruang vektor kompleks V disebut ruang hasilkali dalam jika ada fungsi (.,.) : V V C sehingga untuk setiap x, y, z V dan α C berlaku: (i) (x, x) > 0 dan (x, x) = 0 jika dan hanya jika x = 0 (ii) (x, y + z) = (x, y) + (x, z) (iii) (x, αy) = α(x, y) (iv) (x, y) = (y, x) Fungsi (.,.) disebut hasilkali dalam. Perhatikan bahwa (ii), (iii), dan (iv) berakibat (x, αy + βz) = α(x, y) + β(x, z) dan (αx, y) = α(x, y). Menurut definisi di atas hasilkali dalam bersifat linear terhadap komponen kedua dan bersifat konjugat linear terhadap komponen pertama. Contoh 1.2 Diberikan C n yaitu himpunan semua n-tupel bilangan kompleks. Untuk x = (x 1,..., x n ), y = (y 1,..., y n ) C n didefinisikan (x, y) = x j y j Contoh 1.3 Diberikan C[a, b] yaitu himpunan semua fungsi kontinu bernilai kompleks pada interval [a, b]. Untuk f, g C[a, b] didefinisikan (f, g) = b a j=1 f(x)g(x) dx Definisi 1.4 Dua vektor x dan y di dalam ruang hasilkali dalam V dikatakan ortogonal jika (x, y) = 0. Himpunan vektor {x i } V dikatakan himpunan ortonormal jika (x i, x i ) = 0 untuk setiap i dan (x i, x j ) = 0 jika i j. Selanjutnya dinotasikan x = (x, x). Akan diperlihatkan bahwa. merupakan norma pada V. Kita ingat kembali definisi norma. 1
2 Definisi 1.5 Ruang vektor kompleks V disebut ruang bernorma jika ada fungsi. : V R sehingga untuk setiap x, y V dan α C berlaku: (i) x 0 (ii) x = 0 jika dan hanya jika x = 0 (iii) αx = α x (iv) x + y x + y (ketaksamaan segitiga) Fungsi. disebut norma. Teorema 1.6 (Teorema Phytagoras) Diberikan {x n } m himpunan ortonormal di dalam ruang hasilkali dalam V. Maka untuk setiap x V, m x 2 = (x, x n ) 2 m + x (x n, x)x n Bukti. Tulis x sebagai ( m x = (x n, x)x n + x ) m (x n, x)x n. Dengan menggunakan sifat-sifat hasilkali dalam diperoleh bahwa m m (x n, x)x n dan x (x n, x)x n ortogonal. Oleh karena itu m 2 m (x, x) = (x n, x)x n + x 2 (x n, x)x n m = (x n, x) 2 m + x 2 (x n, x)x n Akibat 1.7 (Ketaksamaan Bessel) Diberikan {x n } m himpunan ortonormal di dalam ruang hasilkali dalam V. Maka untuk setiap x V m x 2 (x, x n ) 2 2
3 Akibat 1.8 (Ketaksamaan Schwarz) Jika x dan y dua vektor di dalam ruang hasilkali dalam V, maka (x, y) x y { } Bukti. Kasus y = 0 trivial, jadi diasumsikan y 0. Himpunan y y merupakan himpunan ortonormal, maka dengan menerapkan ketaksamaan Bessel pada sebarang x V diperoleh ( ) x 2 y 2 (x, y) 2 x, = y y 2 yakni diperoleh (x, y) x y. Ketaksamaan geometrik lain yang sangat berguna adalah hukum jajargenjang x + y 2 + x y 2 = 2 x y 2. Diingat bahwa setiap ruang bernorma merupakan ruang metrik. Teorema berikut menunjukkan bahwa setiap ruang hasilkali dalam merupakan ruang bernorma. Teorema 1.9 Setiap ruang hasilkali dalam V merupakan ruang bernorma dengan norma x = (x, x) 1/2. Bukti. Karena V adalah ruang vektor, maka tinggal diperiksa bahwa. memenuhi sifat-sifat norma. Disini hanya akan ditunjukkan bahwa ketaksamaan segitiga berlaku. Ambil x, y V, maka dengan menggunakan ketaksamaan Schwarz Jadi x + y 2 = (x, x) + (x, y) + (y, x) + (y, y) = (x, x) + 2R(x, y) + (y, y) (x, x) + 2 (x, y) + (y, y) (x, x) + 2(x, x) 1/2 (y, y) 1/2 + (y, y). x + y 2 ( x + y ) 2 dan terbuktilah ketaksamaan segitiga. Teorema ini menunjukkan bahwa di dalam ruang hasilkali dalam V terdapat metrik natural yang diinduksi oleh hasilkali dalam d(x, y) = (x y, x y). 3
4 Dengan menggunakan metrik ini kita dapat mendefinisikan konsep kekonvergenan, kelengkapan, dan kepadatan di dalam V. Khususnya, kita dapat melengkapkan V ke suatu ruang bernorma Ṽ dimana V tersisip secara isometrik sebagai subhimpunan padat. Catat bahwa Ṽ juga merupakan ruang hasilkali dalam sebab hasilkali dalam di V dapat diperluas ke Ṽ menggunakan sifat kekontinuan. Definisi 1.10 Ruang hasilkali dalam yang lengkap disebut ruang Hilbert. Ruang hasilkali dalam seringkali disebut ruang pra-hilbert. Definisi 1.11 Dua ruang Hilbert H 1 dan H 2 dikatakan isomorfik jika ada operator linear U dari H 1 pada H 2 sehingga (Ux, Uy) H2 = (x, y) H1 untuk setiap x, y H 1. Operator demikian dikatakan uniter. Contoh 1.12 Didefinisikan L 2 [a, b] adalah himpunan semua fungsi terukur bernilai kompleks pada interval hingga [a, b] yang memenuhi b a f(x) 2 dx <. Untuk f, g L 2 [a, b] didefinisikan hasilkali dalam (f, g) = b a f(x)g(x) dx Hasilkali dalam ini terdefinisi dengan baik sebab f(x)g(x) 1 2 f(x) g(x) 2 sehingga f(x)g(x) L 1 [a, b]. Dapat ditunjukkan bahwa L 2 [a, b] lengkap dan karenanya merupakan ruang Hilbert. Selain itu L 2 [a, b] merupakan lengkapan dari C[a, b] terhadap norma ( b 1/2 f = f(x) dx) 2. a Contoh 1.13 Didefinisikan l 2 adalah himpunan semua barisan bilangan kompleks {x n } yang memenuhi x n 2 dx < dengan hasilkali dalam ({x n }, {y n } ) = x n y n Pada subbab 3 akan diperlihatkan bahwa setiap ruang Hilbert berdimensi tak hingga yang memiliki subhimpunan terhitung yang padat isomorfik dengan l 2. Dalam konteks ini l 2 adalah contoh kanonik dari ruang Hilbert. 4
5 Contoh 1.14 Diketahui µ adalah ukuran Borel pada R n dan L 2 (R n, dµ) adalah himpunan semua fungsi terukur bernilai kompleks pada R n yang memenuhi R f(x) 2 dµ <. L 2 (R n, dµ) adalah ruang Hilbert terhadap n hasilkali dalam (f, g) = f(x)g(x) dµ R n Contoh 1.15 Misalkan (X, µ) adalah ruang ukuran dan H adalah ruang Hilbert. L 2 (X, dµ; H) menotasikan himpunan semua fungsi terukur pada X dengan nilai di H yang memenuhi f(x) 2 H dµ(x) <. X Himpunan ini merupakan ruang Hilbert terhadap hasilkali dalam (f, g) = (f(x), g(x)) H dµ(x) Contoh 1.16 (Jumlah langsung) Diberikan ruang Hilbert H 1 dan H 2. Himpunan X {(x, y) : x x H 1, y H 1 } merupakan ruang Hilbert terhadap hasilkali dalam ((x 1, y 1 ), (x 2, y 2 )) = (x 1, x 2 ) H1 + (y 1, y 2 ) H1. Ruang ini disebut jumlah langsung dari H 1 dan H 2, dan dinotasikan dengan H 1 H 2. Dua ukuran µ 1 dan µ 2 pada ruang M yang dilengkapi dengan aljabar-σ A dikatakan mutually singular jika ada A A dengan µ 1 (A) = 0 dan µ 2 (M \ A) = 0. Jika µ 1 dan µ 2 adalah dua ukuran Borel pada R yang mutually singular dan µ = µ 1 + µ 2, maka L 2 (R, dµ) isomorfik dengan L 2 (R, dµ 1 ) L 2 (R, dµ 2 ). Kita juga dapat mengkonstruksi jumlah langsung terhitung ruang Hilbert. Diberikan barisan ruang Hilbert {H n }. Misalkan H adalah himpunan semua barisan {x n } dengan x n H n yang memenuhi x n 2 H n <. Maka H adalah ruang Hilbert terhadap hasilkali dalam ({x n }, {y n } ) = (x n, y n ) Hn. 5
6 2 Teorema Representasi Riesz Salah satu cara untuk mengkonstruksi ruang Hilbert adalah dengan membatasi hasilkali dalam pada suatu subruang tertutup M dari ruang Hilbert H yang diberikan. Terhadap hasilkali dalam di H, M merupakan ruang Hilbert. Komplemen ortogonal dari M, dinotasikan dengan M, adalah himpunan semua vektor di H yang ortogonal terhadap M. Mudah ditunjukkan bahwa M merupakan subruang tertutup dari H. Jadi M merupakan ruang Hilbert. Catat bahwa M M = {0}. Teorema berikut menunjukkan bahwa terdapat vektor yang tegaklurus dengan setiap subruang proper tertutup, yakni H = M + M = {x + y : x M, y M }. Lema 2.1 Diketahui H ruang Hilbert, M subruang tertutup dari H, dan x H. Maka terdapat dengan tunggal z M yang jaraknya terdekat ke x. Bukti. Misalkan d = inf y M x y. Pilih barisan {y n } di M sehingga Maka y n x d. y n y m 2 = (y n x) (y m x) 2 = 2 y n x y m x 2 2x + y n + y m 2 = 2 y n x y m x 2 4 x 1 2 (y n + y m ) 2 2 y n x y m x 2 4d 2 2d 2 + 2d 2 4d 2 = 0 untuk m, n. Identitas kedua berasal dari hukum jajargenjang sementara ketaksamaan diperoleh dari fakta bahwa 1 2 (y n + y m ) M. Jadi {y n } adalah barisan Cauchy dan karena M tertutup, {y n } konvergen ke suatu elemen z M. Jadi diperoleh x z = d. Bukti ketunggalan ditinggalkan sebagai latihan. Teorema 2.2 (Teorema proyeksi) Diketahui H ruang Hilbert dan M subruang tertutup dari H. Maka setiap x H dapat dituliskan secara tunggal sebagai x = z + w dengan z M dan w M. 6
7 Bukti. Ambil x H. Maka menurut Lema 2.1 terdapat dengan tunggal z M dengan jarak terdekat ke x. Definisikan w = x z. Ambil y M dan t R. Jika d = x z, maka d 2 x (z + ty) 2 = w ty 2 = d 2 2tR(w, y) + t 2 y 2. Jadi, 2tR(w, y) + t 2 y 2 0 untuk setiap t, yang berakibat R(w, y) = 0. Secara analog dengan mengganti peranan t dengan ti diperoleh I(w, y) = 0. Jadi w M. Bukti ketunggalan untuk latihan. Teorema proyeksi memberikan isomorfisma natural antara M M dengan H melalui (z, w) z + w. Di dalam konteks isomorfisma ini kita tulis H = M M. Selanjutnya kita mengingat kembali pengertian dan sifat-sifat dasar operator linear terbatas di ruang bernorma. Definisi 2.3 Operator linear terbatas dari ruang bernorma (V 1,. 1 ) ke ruang bernorma (V 2,. 2 ) adalah pemetaan T : V 1 V 2 yang memenuhi untuk setiap u, v V 1 dan α, β C: (i) T (αu + βv) = αt u + βt v (ii) T u 2 C u 1, untuk suatu C > 0. Konstanta terkecil C yang memenuhi (ii) disebut norma dari T, ditulis T. Jadi T = inf{c : T v 2 C v 1 } = sup{ T u 2 : u 1 = 1}. Teorema 2.4 Diberikan T suatu operator linear dari suatu ruang bernorma ke ruang bernorma yang lain. Maka ketiga pernyataan berikut ekuivalen: (a) T kontinu di satu titik (b) T kontinu di setiap titik (c) T terbatas Teorema 2.5 Misalkan T operator linear terbatas dari ruang bernorma (V 1,. 1 ) ke ruang Banach (V 2,. 2 ). Maka T dapat diperluas secara tunggal ke operator linear terbatas T dari lengkapan V 1 ke (V 2,. 2 ). 7
8 Misalkan L(H 1, H 2 ) adalah himpunan semua operator linear terbatas dari ruang Hilbert H 1 ke ruang Hilbert H 2. Maka L(H 1, H 2 ) merupakan ruang Banach terhadap norma T = sup{ T x H2 : x H1 = 1}. Untuk bagian selanjutnya akan dibicarakan kasus khusus yakni untuk H 2 = C. Definisi 2.6 Ruang L(H, C) disebut ruang dual dari H dan dinotasikan dengan H. Anggota H disebut fungsional linear kontinu. Teorema berikut menyatakan bahwa setiap fungsional linear kontinu di dalam ruang Hilbert dapat dinyatakan sebagai hasilkali dalam. Teorema 2.7 (Teorema representasi Riesz) Untuk setiap T H, terdapat dengan tunggal y T H sehingga T x = (y T, x) untuk setiap x H. Lebih jauh y T H = T H. Bukti. Definisikan N := {x H : T x = 0}. Dengan menggunakan kekontinuan T, N merupakan subruang tertutup. Jika N = H, maka T x = 0 = (0, x) untuk setiap x. Selanjutnya diasumsikan N H. Menurut teorema proyeksi terdapat vektor tak nol x 0 N. Kita definisikan y T = T x 0 x 0 2 x 0. Akan diperlihatkan bahwa y T memiliki sifat yang diinginkan. Jika x N, maka T x = 0 = (y T, x). Selanjutnya apabila x = αx 0, maka T x = T (αx 0 ) = αt x 0 = (T x 0 x 0 2 x 0, αx 0 ) = (y T, αx 0 ). Karena fungsi-fungsi T dan (y T,.) bersifat linear dan bernilai sama pada N dan x 0, maka keduanya bernilai sama pada ruang yang dibangun oleh N dan x 0. Di lain pihak N dan x 0 membangun H sebab setiap elemen y H dapat ditulis sebagai ( y = y T y ) x 0 + T y x 0. T x 0 T x 0 Jadi T x = (y T, x) untuk setiap x H. Untuk bukti ketunggalan, misalkan T x = (z, x), maka z y T 2 = T (z y T ) T (z y T ) = 0. Jadi z = y T. Terakhir dibuktikan bahwa y T H = T H. Perhatikan bahwa T = sup{ T x : x 1} = sup{ (y T, x) : x 1} sup y T x = y T 8
9 dan ( T = sup{t x : x 1} T yt y T ) = ( y T, ) y T = y T. y T Ketaksamaan Schwarz memberikan bahwa konvers dari teorema representasi Riesz berlaku: setiap y H mendefinisikan sebuah fungsional linear kontinu T y pada H dengan T y x = (y, x). Subbab ini diakhiri dengan sebuah akibat penting dari teorema representasi Riesz. Akibat 2.8 Jika B(, ) sebuah fungsi dari H H ke C yang memenuhi untuk setiap x, y, z H, α, β C: (i) B(x, αy + βz) = αb(x, y) + βb(x, z) (ii) B(αx + βy, z) = αb(x, z) + βb(y, z) (iii) B(x, y) k x y untuk suatu k > 0, maka terdapat dengan tunggal operator linear terbatas A dari H ke H sehingga B(x, y) = (Ax, y) untuk setiap x, y H. Norma dari A adalah konstanta terkecil k sehingga (iii) berlaku. Bukti. Pilih suatu x tetap, maka (i) dan (iii) menunjukkan bahwa B(x, ) adalah fungsional linear kontinu pada H. Jadi teorema representasi Riesz menjamin adanya x H sehingga B(x, y) = (x, y) untuk setiap y H. Definisikan operator A dengan Ax = x. Mudah ditunjukkan bahwa A adalah operator linear kontinu dengan sifat yang diinginkan. 3 Basis Ortonormal Pada subbab ini kita akan memperluas konsep basis dari ruang vektor berdimensi hingga ke ruang Hilbert. Jika S adalah sebuah himpunan ortonormal di dalam ruang Hilbert H dan tidak ada himpunan ortonormal lain yang memuat S sebagai subhimpunan proper, maka S disebut basis ortonormal (sistem ortonormal lengkap) dari H. Teorema 3.1 Setiap ruang Hilbert tak nol H mempunyai basis ortonormal. 9
10 Bukti. Misalkan O adalah himpunan semua himpunan ortonormal di dalam H. Catat bahwa O (mengapa?). Selanjutnya didefinisikan relasi urutan pada O yaitu S 1 S 2 jika S 1 S 2. Diperoleh (O, ) merupakan himpunan terurut parsial. Ambil sebarang {S i } i I subhimpunan terurut linear dari O. Maka i I S i merupakan himpunan ortonormal yang memuat semua S i, dan karenanya merupakan batas atas untuk {S α } a I. Oleh karena itu menurut Lemma Zorn O memiliki elemen maksimal, yakni himpunan ortonormal yang tidak termuat secara proper di dalam setiap himpunan ortonormal yang lain. Teorema berikut memperlihatkan bahwa seperti halnya pada kasus ruang vektor berdimensi hingga setiap elemen dari ruang Hilbert dapat dinyatakan sebagai suatu kombinasi linear (mungkin tak hingga) dari elemen-elemen basis. Teorema 3.2 Diberikan H ruang Hilbert dan S = {x} α I ortonormal. Maka untuk setiap y H sebuah basis y = α I(x i, y)x i (1) dan y 2 = α I (x i, y) 2 (2) Kesamaan (1) berarti bahwa jumlahan di ruas kanan konvergen (tidak bergantung pada urutan α) ke y di H. Sebaliknya, jika α I c i 2 <, c α C, maka α I c αx α konvergen ke suatu elemen dari H. Bukti. Pada subbab 1 telah ditunjukkan (ketaksamaan Bessel) bahwa untuk setiap subhimpunan berhingga A A, α A (x α, y) 2 y 2. Jadi (x α, y) 0 untuk sejumlah paling banyak terhitung α di dalam A yang dapat kita urutkan sebagai α 1, α 2,.... Lebih jauh karena N j=1 (x α j, y) 2 naik monoton dan terbatas, maka konvergen untuk N. Misalkan maka untuk setiap n > m, y n y m 2 = y n = j=m+1 (x αj, y)x αj, j=1 (x αj, y)x αj 10 2 = j=m+1 (x αj, y) 2.
11 Jadi {y n } adalah barisan Cauchy dan karenanya konvergen ke suatu y H. Perhatikan bahwa (y y, x αl ) = lim y (x αj, y)x αj, x αl n dan jika α α l untuk suatu l maka (y y, x α ) = lim j=1 = (y, x αl ) (y, x αl ) = 0, n y (x αj, y)x αj, x α = 0. Oleh karena itu y y ortogonal dengan semua x α S. Mengingat bahwa S adalah sistem ortonormal lengkap maka haruslah y y = 0. Jadi y = lim yakni (1) berlaku. Lebih jauh n n j=1 j=1 (x αj, y)x αj, 2 0 = lim n y (x αj, y)x αj j=1 = lim y 2 (x αj, y) 2 = y 2 α I j=1 (x α, y) 2, yakni (2) berlaku. Bukti pernyataan konvers ditinggalkan sebagai latihan. Identitas (2) seringkali disebut sebagai identitas Parseval dan koefisien (x α, y) seringkali disebut sebagai koefisien Fourier dari y terhadap basis {x α }. Sekarang kita akan membicarakan suatu prosedur untuk mengkonstruksi sebuah himpunan ortonormal dari sebarang barisan vektor yang bebas linear. Prosedur ini dikenal sebagai ortogonalisasi Gram-Schmidt. Diberikan 11
12 barisan vektor yang bebas linear u 1, u 2,... dan kita definisikan w 1 = u 1, v 1 = w 1 w 1 w 2 = u 2 (v 1, u 2 )v 1, v 2 = w 2 w 2. n 1 w n = u n (v k, u n )v k, v n = w n w n. k=1 Himpunan {v j } merupakan sebuah himpunan ortonormal dan mempunyai sifat bahwa untuk setiap m, {u j } m j=1 dan {v j} m j=1 membangun ruang vektor yang sama. Khususnya, himpunan kombinasi linear berhingga dari v j, j = 1, 2,... sama dengan himpunan kombinasi linear berhingga dari u j, j = 1, 2,.... Sebagai contoh polinomial Legendre diperoleh dengan menerapkan proses Gram-Schmidt ke fungsi 1, x, x 2, x 3,... pada interval [ 1, 1] terhadap hasilkali dalam baku di L 2 [ 1, 1]. Definisi 3.3 Sebuah ruang metrik dikatakan separabel apabila memiliki subhimpunan terhitung yang padat. Sebagian besar ruang Hilbert yang muncul dalam penerapan bersifat separabel. Teorema berikut memberikan karakterisasi dari ruang Hilbert separabel. Teorema 3.4 Ruang Hilbert H separabel jika dan hanya jika H memiliki basis ortonormal S yang terhitung. Jika S berhingga dengan n elemen maka H isomorfik dengan C n. Jika S denumerabel maka H isomorfik dengan l 2 (contoh 1.13). Bukti. Misalkan H separabel dan {x n } suatu himpunan terhitung yang padat di dalam H. Dengan membuang beberapa x n kita dapat memperoleh subhimpunan {x nj } dari {x n } yang terdiri dari vektor-vektor bebas linear dimana ruang yang dibangun {x nj } sama dengan ruang yang dibangun oleh {x n } dan oleh karenanya {x nj } padat di dalam H. Dengan menerapkan prosedur Gram-Schmidt pada {x nj } kita memperoleh suatu sistem ortonormal lengkap yang terhitung. Sebaliknya, jika {y n } adalah sistem ortonormal lengkap dari ruang Hilbert H maka Teorema 3.2 mengakibatkan himpunan 12
13 kombinasi linear dari vektor-vektor di {y n } dengan koefisien rasional padat di H. Karena {y n } terhitung, maka H separabel. Misalkan H separabel dan {y n } adalah sistem ortonormal lengkap. Kita mendefinisikan pemetaan U : H l 2 dengan Ux = {(y n, x)}. Teorema 3.2 menunjukkan bahwa pemetaan ini terdefinisi dengan baik dan bersifat pada. Mudah diperlihatkan bahwa U uniter. Bukti bahwa H isomorfik dengan C n jika S berhingga dengan n elemen dilakukan dengan cara yang sejalan. Catat bahwa dalam kasus separabel, proses Gram-Schmidt memungkinkan kita untuk mengkonstruksi sebuah basis ortonormal tanpa menggunakan Lema Zorn. Terakhir di bagian ini akan diberikan sebuah contoh yang menunjukkan bagaimana ruang Hilbert muncul secara alami dari masalah di dalam analisis klasik. Jika f sebuah fungsi terintegral pada [0, ] maka dapat didefinisikan Deret c n = 1 n= 0 e inx f(x) dx. c n 1 e inx disebut deret Fourier dari f. Masalah klasik: untuk fungsi f yang mana dan dalam jenis kekonvergenan apa deret Fourier dari f konvergen ke f? Masalah ini mulai dipelajari oleh matematikawan Jean Baptiste Joseph Fourier sejak tahun 1811 dan terus berkembang sampai sekarang dalam cabang matematika modern yang disebut analisis harmonik atau analisis Fourier. Salah satu hasil klasik di dalam analisis Fourier adalah Teorema 3.5 Jika f fungsi periodik dengan periode dan terdiferensial kontinu, maka fungsi n n c n 1 e inx konvergen seragam ke f untuk n. Teorema di atas memberikan syarat cukup kekonvergenan seragam dari deret Fourier suatu fungsi. Namun demikian mencari kelas fungsi sehingga deret Fouriernya konvergen seragam atau konvergen titik demi titik merupakan masalah yang cukup sukar. Salah satu pemecahan persoalan ini adalah dengan menggunakan konsep kekonvergenan yang lain dan disinilah teori ruang Hilbert muncul. Himpunan fungsi { 1 e inx } n= merupakan himpunan 13
14 ortonormal di ruang L 2 [0, ]. Apabila himpunan ortonormal ini lengkap maka Teorema 3.2 memberikan kesimpulan untuk setiap fungsi f L 2 [0, ] berlaku 1 f(x) = lim c n e inx n n dengan kekonvergenan merupakan kekonvergenan terhadap norma L 2. Dapat dibuktikan bahwa { 1 e inx } n= merupakan sistem ortonormal lengkap. Kita akan membuktikan dengan memanfaatkan hasil klasik di atas (Teorema 3.5). Teorema 3.6 Jika f L 2 [0, ], maka n= c n 1 e inx konvergen ke f di dalam norma L 2 untuk n. Bukti. Dapat diperlihatkan bahwa fungsi terdiferensial kontinu yang periodik Cp[0, 1 ] padat di dalam L 2 [0, ]. Idenya adalah himpunan fungsi tangga padat di dalam L 2 [0, ]. Lebih jauh setiap fungsi tangga dapat dihampiri di dalam norma L 2 oleh suatu fungsi di dalam Cp[0, 1 ]. Detailnya ditinggalkan sebagai latihan. Untuk menunjukkan bahwa { 1 e inx } n= lengkap cukup ditunjukkan bahwa (e inx, g) = 0 untuk setiap n berakibat g = 0. Ambil sebarang f C 1 p[0, ], maka menurut Teorema 3.5 n c n 1 e inx f seragam dan karenanya juga di dalam norma L 2. Oleh karena itu ( ) 1 (f, g) = lim c n e inx, g = 0 n n jika (e inx, g) = 0 untuk setiap n. Jadi g ortogonal dengan semua fungsi f di dalam himpunan padat Cp[0, 1 ]. Hal ini berakibat g = 0. Jadi { 1 e inx } n= adalah sistem ortonormal lengkap dan menurut Teorema 3.2 deret Fourier dari setiap f L 2 [0, ] konvergen di dalam norma L 2 ke f. Teorema di atas menunjukkan bahwa konsep alami untuk kekonvergenan deret Fourier adalah kekonvergenan di dalam norma L 2. Hal ini juga mengilustrasikan salah satu dari prinsip dasar dari analisis fungsional yakni memilih sebuah ruang abstrak dan konsep kekonvergenan yang sesuai sehingga sebuah permasalahan dapat diselesaikan dengan mudah. 14
15 4 Hasilkali Tensor Di dalam subbab 1 dan 2 telah dibicarakan beberapa cara untuk membentuk ruang Hilbert baru dari sebuah ruang Hilbert (jumlah langsung dan subruang). Pada subbab ini akan dijelaskan hasilkali tensor H 1 H 2 dari dua ruang Hilbert H 1 dan H 2. Hasil ini dapat diperluas dengan mudah untuk mengkonstruksi hasilkali tensor H 1 H 2... H n dari sejumlah berhingga ruang Hilbert. Diberikan dua ruang Hilbert H 1 dan H 2. Untuk setiap h 1 H 1, h 2 H 2, h 1 h 2 menotasikan bentuk konjugat linear yang beraksi pada H 1 H 2 menurut (h 1 h 2 ) ϕ 1, ϕ 2 = (ϕ 1, h 1 )(ϕ 2, h 2 ). Definisikan E sebagai himpunan semua kombinasi linear berhingga dari semua bentuk konjugat linear yang dideskripsikan di atas. Selanjutnya didefinisikan hasilkali dalam (.,.) pada E dengan (h 1 h 2, g 1 g 2 ) = (h 1, g 1 )(h 2, g 2 ) dan kita dapat memperluas definisi ini untuk anggota E menggunakan kelinearan. Lema 4.1 Hasilkali dalam (.,.) di atas terdefinisi dengan baik dan bersifat definit positif. Bukti. Untuk menunjukkan (.,.) terdefinisi dengan baik kita harus menunjukkan bahwa (ϕ, ϕ ) tidak bergantung pada bentuk kombinasi linear berhingga yang membentuk ϕ dan ϕ. Untuk itu cukup ditunjukkan jika µ adalah jumlahan berhingga yang merupakan bentuk nol, maka (η, µ) = 0 untuk setiap η E. Misalkan η = N i=1 c i(f i g i ), maka ( N ) (η, µ) = c i (f i g i ), µ = = 0 i=1 N c i µ f i, g i i=1 karena µ adalah bentuk nol. Jadi (.,.) terdefinisi dengan baik. Selanjutnya, misalkan ϕ = M k=1 d k(η k µ k ), maka {η k } M k=1 dan {µ k} M k=1 berturut-turut membangun subruang M 1 H 1 dan M 2 H 2. Jika kita pilih {ω j } N 1 j=1 basis 15
16 ortonormal dari M 1 dan {ψ l } N 2 l=1 basis ortonormal dari M 2, maka kita dapat menyatakan setiap η k dalam ω j dan µ k dalam ψ l dan diperoleh N 1 N 2 ϕ = c jl (ω j ψ l ). j=1 l=1 Dari sini diperoleh N 1 N 2 N 1 N 2 (ϕ, ϕ) = c jl (ω j ψ l ), c st (ω s ψ t ) j=1 l=1 s=1 t=1 N 1 N 2 N 1 N 2 = c jl c st (ω j, ω s )(ψ l, ψ t ) j=1 l=1 s=1 t=1 N 1 N 2 = c jl 2. j=1 l=1 Jadi (ϕ, ϕ) = 0 berakibat c jl = 0 untuk semua j dan l. Ini berarti ϕ adalah bentuk nol. Terbukti (.,.) definit positif. Definisi 4.2 Hasilkali tensor H 1 H 2 dari H 1 dan H 2 didefinisikan sebagai lengkapan dari E terhadap hasilkali dalam (.,.) yang didefinisikan di atas. Teorema 4.3 Jika {ω k } adalah basis ortonormal dari H 1 dan {ψ l } adalah basis ortonormal dari H 2, maka {ω k ψ l } adalah basis ortonormal dari H 1 H 2 Bukti. Untuk penyederhanaan notasi, kita memperhatikan kasus dimana H 1 dan H 2 keduanya berdimensi tak hingga dan separabel. Mudah dilihat bahwa himpunan {ω k ψ l } ortonormal dan karenanya kita hanya perlu membuktikan bahwa E termuat di dalam ruang tertutup S yang dibangun oleh {ω k ψ l }. Ambil sebarang ω ψ E. Karena {ω k } dan {ψ l } adalah basis, maka ω = k c kω k dan ψ = l d lψ l dengan k c k 2 < dan l d l 2 <. Akibatnya l k c kd l 2 <. Jadi menurut Teorema 3.2 ada vektor µ = l k c kd l ω k ψ l di S. Dengan perhitungan langsung diperoleh ω ψ c k d l ω k ψ l 0 untuk M, N. k<m,l<n 16
17 5 Soal Latihan 1. Buktikan bahwa ruang barisan l 2 pada Contoh 1.13 merupakan ruang Hilbert. 2. Diberikan ruang hasilkali dalam kompleks H. Buktikan bahwa hasilkali dalam pada H dapat diperoleh dari norma, yakni berlaku identitas polarisasi (x, y) = 1 4 untuk setiap x, y H. (( x + y 2 x y 2) i ( x + iy 2 x iy 2)) 3. Buktikan bahwa ruang bernorma merupakan ruang hasilkali dalam jika dan hanya jika norma tersebut memenuhi hukum jajargenjang. 4. Diberikan ruang hasilkali dalam V dan {x n } N ortonormal di dalam V. Buktikan bahwa N x c n x n sebuah himpunan minimum dengan memilih c n = (x n, x). 5. Diberikan ruang Hilbert H dan subruang M dari H. Buktikan bahwa M adalah subruang tertutup dan M = ( M ). 6. Terapkan proses Gram-Schmidt terhadap fungsi-fungsi 1, x, x 2, x 3 pada interval [ 1, 1] terhadap hasilkali dalam baku di L 2 [ 1, 1] untuk memperoleh empat polinomial Legendre yang pertama. 7. Diberikan ruang Hilbert H dan subruang V dari H. Misalkan A sebuah operator linear dari H ke V sehingga x Ax V untuk setiap x H. Buktikan bahwa A kontinu dan idempoten. Buktikan juga bahwa V tertutup dan A adalah proyeksi ortogonal dari H pada V. 8. Tunjukkan bahwa bola satuan di dalam suatu ruang Hilbert berdimensi tak hingga memuat tak hingga banyaknya translasi yang saling asing dari sebuah bola dengan jari-jari
BAB 2 RUANG HILBERT. 2.1 Definisi Ruang Hilbert
 BAB 2 RUANG HILBERT Pokok pembicaraan kita dalam tugas akhir ini berpangkal pada teori ruang Hilbert. Untuk itu di bab ini akan diberikan definisi ruang Hilbert dan ciri-cirinya, separabilitas ruang Hilbert,
BAB 2 RUANG HILBERT Pokok pembicaraan kita dalam tugas akhir ini berpangkal pada teori ruang Hilbert. Untuk itu di bab ini akan diberikan definisi ruang Hilbert dan ciri-cirinya, separabilitas ruang Hilbert,
Analisis Fungsional. Oleh: Dr. Rizky Rosjanuardi, M.Si Jurusan Pendidikan Matematika UNIVERSITAS PENDIDIKAN INDONESIA
 Analisis Fungsional Oleh: Dr. Rizky Rosjanuardi, M.Si Jurusan Pendidikan Matematika UNIVERSITAS PENDIDIKAN INDONESIA Lingkup Materi Ruang Metrik dan Ruang Topologi Kelengkapan Ruang Banach Ruang Hilbert
Analisis Fungsional Oleh: Dr. Rizky Rosjanuardi, M.Si Jurusan Pendidikan Matematika UNIVERSITAS PENDIDIKAN INDONESIA Lingkup Materi Ruang Metrik dan Ruang Topologi Kelengkapan Ruang Banach Ruang Hilbert
BAB III KEKONVERGENAN LEMAH
 BAB III KEKONVERGENAN LEMAH Bab ini membahas inti kajian tugas akhir. Di dalamnya akan dibahas mengenai kekonvergenan lemah beserta sifat-sifat yang terkait dengannya. Sifatsifat yang dikaji pada bab ini
BAB III KEKONVERGENAN LEMAH Bab ini membahas inti kajian tugas akhir. Di dalamnya akan dibahas mengenai kekonvergenan lemah beserta sifat-sifat yang terkait dengannya. Sifatsifat yang dikaji pada bab ini
0. Pendahuluan. 0.1 Notasi dan istilah, bilangan kompleks
 0. Pendahuluan Analisis Fourier mempelajari berbagai teknik menganalisis sebuah fungsi dengan menguraikannya sebagai deret atau integral fungsi tertentu (yang sifat-sifatnya telah kita kenal dengan baik,
0. Pendahuluan Analisis Fourier mempelajari berbagai teknik menganalisis sebuah fungsi dengan menguraikannya sebagai deret atau integral fungsi tertentu (yang sifat-sifatnya telah kita kenal dengan baik,
PENGANTAR ANALISIS FUNGSIONAL
 PENGANTAR ANALISIS FUNGSIONAL SUMANANG MUHTAR GOZALI KBK ANALISIS UNIVERSITAS PENDIDIKAN INDONESIA BANDUNG 2010 2 KATA PENGANTAR Bismillahirrahmanirrahim Segala puji bagi Allah Rabb semesta alam. Shalawat
PENGANTAR ANALISIS FUNGSIONAL SUMANANG MUHTAR GOZALI KBK ANALISIS UNIVERSITAS PENDIDIKAN INDONESIA BANDUNG 2010 2 KATA PENGANTAR Bismillahirrahmanirrahim Segala puji bagi Allah Rabb semesta alam. Shalawat
ANALISIS NUMERIK LANJUT. Hendra Gunawan, Ph.D. 2006/2007
 ANALISIS NUMERIK LANJUT Hendra Gunawan, Ph.D. 2006/2007 BAB I. RUANG LINEAR Pelajari definisi dan contoh: ruang linear (hal. 1-3); subruang (hal. 3); kombinasi linear (hal. 4); bebas/bergantung linear
ANALISIS NUMERIK LANJUT Hendra Gunawan, Ph.D. 2006/2007 BAB I. RUANG LINEAR Pelajari definisi dan contoh: ruang linear (hal. 1-3); subruang (hal. 3); kombinasi linear (hal. 4); bebas/bergantung linear
BAB III OPERATOR LINEAR TERBATAS PADA RUANG HILBERT. Operator merupakan salah satu materi yang akan dibahas dalam fungsi
 BAB III OPERATOR LINEAR TERBATAS PADA RUANG HILBERT 3.1 Operator linear Operator merupakan salah satu materi yang akan dibahas dalam fungsi real yaitu suatu fungsi dari ruang vektor ke ruang vektor. Ruang
BAB III OPERATOR LINEAR TERBATAS PADA RUANG HILBERT 3.1 Operator linear Operator merupakan salah satu materi yang akan dibahas dalam fungsi real yaitu suatu fungsi dari ruang vektor ke ruang vektor. Ruang
UNIVERSITAS PENDIDIKAN INDONESIA
 Ruang Norm Sumanang Muhtar Gozali UNIVERSITAS PENDIDIKAN INDONESIA Definisi. Misalkan suatu ruang vektor atas. Norm pada didefinisikan sebagai fungsi. : yang memenuhi N1. 0 N2. 0 0 N3.,, N4.,, Kita dapat
Ruang Norm Sumanang Muhtar Gozali UNIVERSITAS PENDIDIKAN INDONESIA Definisi. Misalkan suatu ruang vektor atas. Norm pada didefinisikan sebagai fungsi. : yang memenuhi N1. 0 N2. 0 0 N3.,, N4.,, Kita dapat
BAB I PENDAHULUAN. 1.1 Latar Belakang
 BAB I PENDAHULUAN 1.1 Latar Belakang Dalam ilmu matematika, banyak pembahasan di bidang analisis dan topologi yang memerlukan pengertian ruang Hilbert. Ruang Hilbert merupakan konsep abstrak yang mendasari
BAB I PENDAHULUAN 1.1 Latar Belakang Dalam ilmu matematika, banyak pembahasan di bidang analisis dan topologi yang memerlukan pengertian ruang Hilbert. Ruang Hilbert merupakan konsep abstrak yang mendasari
8. Deret Fourier yang Diperumum dan Hampiran Terbaik di L 2 (a, b)
 8. Deret Fourier yang Diperumum dan Hampiran Terbaik di L (a, b) 8.1 Deret Fourier yang Diperumum Jika {ϕ n } 1 adalah basis ortonormal untuk L (a, b) dan f L (a, b), maka f, ϕ n disebut koefisien Fourier
8. Deret Fourier yang Diperumum dan Hampiran Terbaik di L (a, b) 8.1 Deret Fourier yang Diperumum Jika {ϕ n } 1 adalah basis ortonormal untuk L (a, b) dan f L (a, b), maka f, ϕ n disebut koefisien Fourier
9. Teori Aproksimasi
 44 Hendra Gunawan 9 Teori Aproksimasi Mulai bab ini tema kita adalah aproksimasi fungsi dan interpolasi Diberikan sebuah fungsi f, baik secara utuh ataupun hanya beberapilai di titik-titik tertentu saja,
44 Hendra Gunawan 9 Teori Aproksimasi Mulai bab ini tema kita adalah aproksimasi fungsi dan interpolasi Diberikan sebuah fungsi f, baik secara utuh ataupun hanya beberapilai di titik-titik tertentu saja,
dari ruang vektor berdimensi hingga V (dimana I adalah suatu himpunan indeks) disebut basis bagi V jika V = span(ψ) dan vektorvektor
 BAB 3 FRAME Sinyal kontinu dapat kita diskritisasi dengan menggunakan ekspansi vektor. Sifat yang paling esensial untuk melakukan hal tersebut adalah adanya operator yang menjamin bahwa ekspansi vektor
BAB 3 FRAME Sinyal kontinu dapat kita diskritisasi dengan menggunakan ekspansi vektor. Sifat yang paling esensial untuk melakukan hal tersebut adalah adanya operator yang menjamin bahwa ekspansi vektor
TINJAUAN PUSTAKA. Ruang metrik merupakan ruang abstrak, yaitu ruang yang dibangun oleh
 II. TINJAUAN PUSTAKA 2.1 Ruang Metrik Ruang metrik merupakan ruang abstrak, yaitu ruang yang dibangun oleh aksioma-aksioma tertentu. Ruang metrik merupakan hal yang fundamental dalam analisis fungsional,
II. TINJAUAN PUSTAKA 2.1 Ruang Metrik Ruang metrik merupakan ruang abstrak, yaitu ruang yang dibangun oleh aksioma-aksioma tertentu. Ruang metrik merupakan hal yang fundamental dalam analisis fungsional,
RENCANA KEGIATAN PERKULIAHAN Kode Mata Kuliah : MAA 526 Nama Mata Kuliah : Analisis Fungsional
 Ming gu ke RENCANA KEGIATAN PERKULIAHAN Kode Mata Kuliah : MAA 56 Nama Mata Kuliah : Analisis Fungsional T o p i k S u b T o p i k 1. Ruang Banach - Ruang metrik - Ruang vektor bernorm - Barisan di ruang
Ming gu ke RENCANA KEGIATAN PERKULIAHAN Kode Mata Kuliah : MAA 56 Nama Mata Kuliah : Analisis Fungsional T o p i k S u b T o p i k 1. Ruang Banach - Ruang metrik - Ruang vektor bernorm - Barisan di ruang
4.1 Algoritma Ortogonalisasi Gram-Schmidt yang Diperumum
 BAB 4 ORTOGONALISASI GRAM-SCHMIDT YANG DIPERUMUM Diberikan sebarang barisan hingga vektor di ruang Hilbert berdimensi hingga. Pada bab ini akan diberikan algoritma untuk menghitung frame Parseval pada
BAB 4 ORTOGONALISASI GRAM-SCHMIDT YANG DIPERUMUM Diberikan sebarang barisan hingga vektor di ruang Hilbert berdimensi hingga. Pada bab ini akan diberikan algoritma untuk menghitung frame Parseval pada
BAB I PENDAHULUAN. umum ruang metrik dan memperluas pengertian klasik dari ruang Euclidean R n, sehingga
 BAB I PENDAHULUAN 1.1 Latar Belakang dan Permasalahan Permulaan munculnya analisis fungsional didasari oleh permasalahan pada kurang memadainya metode analitik klasik pada fisika dan astronomi matematika.
BAB I PENDAHULUAN 1.1 Latar Belakang dan Permasalahan Permulaan munculnya analisis fungsional didasari oleh permasalahan pada kurang memadainya metode analitik klasik pada fisika dan astronomi matematika.
BAB III INTEGRAL LEBESGUE. Pada bab sebelumnya telah disebutkan bahwa ruang dibangun oleh
 BAB III INTEGRAL LEBESGUE Pada bab sebelumnya telah disebutkan bahwa ruang dibangun oleh fungsi-fungsi terukur dan memenuhi sifat yang berkaitan dengan integral Lebesgue. Kajian mengenai keterukuran suatu
BAB III INTEGRAL LEBESGUE Pada bab sebelumnya telah disebutkan bahwa ruang dibangun oleh fungsi-fungsi terukur dan memenuhi sifat yang berkaitan dengan integral Lebesgue. Kajian mengenai keterukuran suatu
BAB V KEKONVERGENAN BARISAN PADA DAN KETERKAITAN DENGAN. Pada subbab 4.1 telah dibahas beberapa sifat dasar yang berlaku pada koleksi
 BAB V KEKONVERGENAN BARISAN PADA DAN KETERKAITAN DENGAN Pada subbab 4.1 telah dibahas beberapa sifat dasar yang berlaku pada koleksi semua fungsi yang terintegralkan Lebesgue, 1. Sebagaimana telah dirumuskan
BAB V KEKONVERGENAN BARISAN PADA DAN KETERKAITAN DENGAN Pada subbab 4.1 telah dibahas beberapa sifat dasar yang berlaku pada koleksi semua fungsi yang terintegralkan Lebesgue, 1. Sebagaimana telah dirumuskan
BAB I PENDAHULUAN. Integral Lebesgue merupakan suatu perluasan dari integral Riemann.
 BAB I PENDAHULUAN 1.1 Latar Belakang Masalah Integral Lebesgue merupakan suatu perluasan dari integral Riemann. Sebagaimana telah diketahui, pengkonstruksian integral Riemann dilakukan dengan cara pemartisian
BAB I PENDAHULUAN 1.1 Latar Belakang Masalah Integral Lebesgue merupakan suatu perluasan dari integral Riemann. Sebagaimana telah diketahui, pengkonstruksian integral Riemann dilakukan dengan cara pemartisian
Ketaksamaan Cauchy-Schwarz, Ketaksamaan Bessel, dan Kesamaan Parseval di Ruang n-hasilkali Dalam Baku. Hendra Gunawan
 Ketaksamaan Cauchy-Schwarz, Ketaksamaan Bessel, dan Kesamaan Parseval di Ruang n-hasilkali Dalam Baku Hendra Gunawan Departemen Matematika, ITB, Bandung 40132 hgunawan@dns.math.itb.ac.id 1 Abstrak Beberapa
Ketaksamaan Cauchy-Schwarz, Ketaksamaan Bessel, dan Kesamaan Parseval di Ruang n-hasilkali Dalam Baku Hendra Gunawan Departemen Matematika, ITB, Bandung 40132 hgunawan@dns.math.itb.ac.id 1 Abstrak Beberapa
BAB II TEORI KODING DAN TEORI INVARIAN
 BAB II TEORI KODING DAN TEORI INVARIAN Pada bab 1 ini akan dibahas definisi kode, khususnya kode linier atas dan pencacah bobot Hammingnya. Di samping itu, akan dijelaskanan invarian, ring invarian dan
BAB II TEORI KODING DAN TEORI INVARIAN Pada bab 1 ini akan dibahas definisi kode, khususnya kode linier atas dan pencacah bobot Hammingnya. Di samping itu, akan dijelaskanan invarian, ring invarian dan
BAB III PEMBAHASAN. Bab III terbagi menjadi tiga sub-bab, yaitu sub-bab A, sub-bab B, dan subbab
 BAB III PEMBAHASAN Bab III terbagi menjadi tiga sub-bab, yaitu sub-bab A, sub-bab B, dan subbab C. Sub-bab A menjelaskan mengenai konsep dasar C[a, b] sebagai ruang vektor beserta contohnya. Sub-bab B
BAB III PEMBAHASAN Bab III terbagi menjadi tiga sub-bab, yaitu sub-bab A, sub-bab B, dan subbab C. Sub-bab A menjelaskan mengenai konsep dasar C[a, b] sebagai ruang vektor beserta contohnya. Sub-bab B
BAB V DUALITAS RUANG ORLICZ
 BAB V DUALITAS RUANG ORLICZ Karena ketaksamaan Holder yang telah dipelajari pada bab sebelumnya, Untuk sembarang h L θ, kita dapat mendefinisikan suatu fungsional linear kontinu l h yang memetakan L θ
BAB V DUALITAS RUANG ORLICZ Karena ketaksamaan Holder yang telah dipelajari pada bab sebelumnya, Untuk sembarang h L θ, kita dapat mendefinisikan suatu fungsional linear kontinu l h yang memetakan L θ
TINJAUAN PUSTAKA. Dalam bab ini akan dibahas beberapa konsep mendasar meliputi ruang vektor,
 II. TINJAUAN PUSTAKA Dalam bab ini akan dibahas beberapa konsep mendasar meliputi ruang vektor, ruang Bernorm dan ruang Banach, ruang barisan, operator linear (transformasi linear) serta teorema-teorema
II. TINJAUAN PUSTAKA Dalam bab ini akan dibahas beberapa konsep mendasar meliputi ruang vektor, ruang Bernorm dan ruang Banach, ruang barisan, operator linear (transformasi linear) serta teorema-teorema
Teorema Titik Tetap di Ruang Norm-2 Standar
 Teorema Titik Tetap di Ruang Norm- Standar Muh. Nur Universitas Hasanuddin Abstract Pada tulisan ini, akan dipelajari ruang norm- standar, yakni ruang hasil kali dalam yang dilengkapi dengan norm- standar.
Teorema Titik Tetap di Ruang Norm- Standar Muh. Nur Universitas Hasanuddin Abstract Pada tulisan ini, akan dipelajari ruang norm- standar, yakni ruang hasil kali dalam yang dilengkapi dengan norm- standar.
BAB I PENDAHULUAN. Misalkan diberikan suatu ruang vektor atas lapangan R atau C. Jika
 BAB I PENDAHULUAN 1.1 Latar Belakang Masalah Misalkan diberikan suatu ruang vektor atas lapangan R atau C. Jika dilengkapi dengan suatu norma., maka dikenal bahwa suatu ruang vektor bernorma. Kemudian
BAB I PENDAHULUAN 1.1 Latar Belakang Masalah Misalkan diberikan suatu ruang vektor atas lapangan R atau C. Jika dilengkapi dengan suatu norma., maka dikenal bahwa suatu ruang vektor bernorma. Kemudian
II. LANDASAN TEORI. Pada bab ini akan dijelaskan mengenai teori-teori yang berhubungan dengan
 II. LANDASAN TEORI Pada bab ini akan dijelaskan mengenai teori-teori yang berhubungan dengan penelitian ini sehingga dapat dijadikan sebagai landasan berfikir dalam melakukan penelitian dan akan mempermudah
II. LANDASAN TEORI Pada bab ini akan dijelaskan mengenai teori-teori yang berhubungan dengan penelitian ini sehingga dapat dijadikan sebagai landasan berfikir dalam melakukan penelitian dan akan mempermudah
BAB I PENDAHULUAN Latar Belakang Masalah
 BAB I PENDAHULUAN 1.1. Latar Belakang Masalah Ilmu Matematika merupakan salah satu cabang ilmu yang berperan penting dalam berbagai bidang. Salah satu cabang ilmu matematika yang banyak diperbincangkan
BAB I PENDAHULUAN 1.1. Latar Belakang Masalah Ilmu Matematika merupakan salah satu cabang ilmu yang berperan penting dalam berbagai bidang. Salah satu cabang ilmu matematika yang banyak diperbincangkan
TRANSFORMASI LINIER PADA RUANG BANACH
 TRANSFORMASI LINIER PADA RUANG BANACH Nur Aeni, S.Si., M.Pd Jurusan Matematika, Fakultas Sains dan Teknologi, UINAM nuraeniayatullah@gmail.com ABSTRAK Info: Jurnal MSA Vol. 2 No. 1 Edisi: Januari Juni
TRANSFORMASI LINIER PADA RUANG BANACH Nur Aeni, S.Si., M.Pd Jurusan Matematika, Fakultas Sains dan Teknologi, UINAM nuraeniayatullah@gmail.com ABSTRAK Info: Jurnal MSA Vol. 2 No. 1 Edisi: Januari Juni
BAB III FUNGSI TERUKUR LEBESGUE. Setelah dibahas mengenai ukuran Lebesgue dan beberapa sifatnya pada
 BAB III FUNGSI TERUKUR LEBESGUE Setelah dibahas mengenai ukuran Lebesgue dan beberapa sifatnya pada Bab II, selanjutnya pada bab ini akan dipelajari gagasan mengenai fungsi terukur Lebesgue. Gagasan mengenai
BAB III FUNGSI TERUKUR LEBESGUE Setelah dibahas mengenai ukuran Lebesgue dan beberapa sifatnya pada Bab II, selanjutnya pada bab ini akan dipelajari gagasan mengenai fungsi terukur Lebesgue. Gagasan mengenai
1 Mengapa Perlu Belajar Geometri Daftar Pustaka... 1
 Daftar Isi 1 Mengapa Perlu Belajar Geometri 1 1.1 Daftar Pustaka.................................... 1 2 Ruang Euclid 3 2.1 Geometri Euclid.................................... 8 2.2 Pencerminan dan Transformasi
Daftar Isi 1 Mengapa Perlu Belajar Geometri 1 1.1 Daftar Pustaka.................................... 1 2 Ruang Euclid 3 2.1 Geometri Euclid.................................... 8 2.2 Pencerminan dan Transformasi
17. Transformasi Wavelet Kontinu dan Frame
 17. Transformasi Wavelet Kontinu dan Frame Pada 16 kita mempelajari basis ortonormal {e 2πimx g(x n)} dengan g = χ [,1). Transformasi f f(x)g(x n)e 2πimx dx, m, n Z, dikenal sebagai transformasi Fourier
17. Transformasi Wavelet Kontinu dan Frame Pada 16 kita mempelajari basis ortonormal {e 2πimx g(x n)} dengan g = χ [,1). Transformasi f f(x)g(x n)e 2πimx dx, m, n Z, dikenal sebagai transformasi Fourier
BAB I PENDAHULUAN Latar Belakang Masalah
 BAB I PENDAHULUAN Pada bab ini akan dibahas mengenai latar belakang masalah, perumusan masalah, batasan masalah, maksud dan tujuan penulisan, tinjauan pustaka serta sistematika penulisan skirpsi ini. 1.1.
BAB I PENDAHULUAN Pada bab ini akan dibahas mengenai latar belakang masalah, perumusan masalah, batasan masalah, maksud dan tujuan penulisan, tinjauan pustaka serta sistematika penulisan skirpsi ini. 1.1.
ANALISIS REAL. (Semester I Tahun ) Hendra Gunawan. October 3, Dosen FMIPA - ITB
 (Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. October 3, 2011 6.3 Limit Sepihak, Limit di Tak Hingga, dan Limit Tak Hingga Bila sebelumnya kita mempelajari limit barisan,
(Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. October 3, 2011 6.3 Limit Sepihak, Limit di Tak Hingga, dan Limit Tak Hingga Bila sebelumnya kita mempelajari limit barisan,
BAB 4 KEKONSISTENAN PENDUGA DARI FUNGSI SEBARAN DAN FUNGSI KEPEKATAN WAKTU TUNGGU DARI PROSES POISSON PERIODIK DENGAN TREN FUNGSI PANGKAT
 29 BAB 4 KEKONSISTENAN PENDUGA DARI FUNGSI SEBARAN DAN FUNGSI KEPEKATAN WAKTU TUNGGU DARI PROSES POISSON PERIODIK DENGAN TREN FUNGSI PANGKAT 4.1 Perumusan Penduga Misalkan adalah proses Poisson nonhomogen
29 BAB 4 KEKONSISTENAN PENDUGA DARI FUNGSI SEBARAN DAN FUNGSI KEPEKATAN WAKTU TUNGGU DARI PROSES POISSON PERIODIK DENGAN TREN FUNGSI PANGKAT 4.1 Perumusan Penduga Misalkan adalah proses Poisson nonhomogen
SISTEM BILANGAN REAL
 DAFTAR ISI 1 SISTEM BILANGAN REAL 1 1.1 Sifat Aljabar Bilangan Real..................... 1 1.2 Sifat Urutan Bilangan Real..................... 6 1.3 Nilai Mutlak dan Jarak Pada Bilangan Real............
DAFTAR ISI 1 SISTEM BILANGAN REAL 1 1.1 Sifat Aljabar Bilangan Real..................... 1 1.2 Sifat Urutan Bilangan Real..................... 6 1.3 Nilai Mutlak dan Jarak Pada Bilangan Real............
Analisis Fourier dan Wavelet
 0 Hendra Gunawan Analisis Fourier dan Wavelet Hendra Gunawan KK Analisis & Geometri FMIPA-ITB Bandung, 2017 Analisis Fourier dan Wavelet 1 Daftar Isi Kata Pengantar 5 0 Pendahuluan 7 0.1 Notasi dan istilah,
0 Hendra Gunawan Analisis Fourier dan Wavelet Hendra Gunawan KK Analisis & Geometri FMIPA-ITB Bandung, 2017 Analisis Fourier dan Wavelet 1 Daftar Isi Kata Pengantar 5 0 Pendahuluan 7 0.1 Notasi dan istilah,
BAB I PENDAHULUAN 1.1 Latar Belakang
 1 BAB I PENDAHULUAN 1.1 Latar Belakang Pada awalnya deret Fourier diperkenalkan oleh Joseph Fourier pada tahun 1807 untuk memecahkan model masalah persamaan panas pada suatu lempeng logam (Fourier, 1878).
1 BAB I PENDAHULUAN 1.1 Latar Belakang Pada awalnya deret Fourier diperkenalkan oleh Joseph Fourier pada tahun 1807 untuk memecahkan model masalah persamaan panas pada suatu lempeng logam (Fourier, 1878).
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
Sifat Barisan Subhimpunan Tutup di Ruang Metrik yang Completion-nya adalah Ruang Atsuji
 Sifat Barisan Subhimpunan Tutup di Ruang Metrik yang Completion-nya adalah Ruang Atsuji Hendy Fergus A. Hura 1, Nora Hariadi 2, Suarsih Utama 3 1 Departemen Matematika, FMIPA UI, Kampus UI Depok, 16424,
Sifat Barisan Subhimpunan Tutup di Ruang Metrik yang Completion-nya adalah Ruang Atsuji Hendy Fergus A. Hura 1, Nora Hariadi 2, Suarsih Utama 3 1 Departemen Matematika, FMIPA UI, Kampus UI Depok, 16424,
yang Dibangun oleh Ukuran Bernilai Proyeksi
 SEMINAR NASIONAL MATEMATIKA DAN PENDIDIKAN MATEMATIKA UNY 2015 Integral pada A - 3 yang Dibangun oleh Ukuran Bernilai Proyeksi Arta Ekayanti dan Ch. Rini Indrati. FMIPA Universitas Gadjah Mada arta_ekayanti@ymail.com
SEMINAR NASIONAL MATEMATIKA DAN PENDIDIKAN MATEMATIKA UNY 2015 Integral pada A - 3 yang Dibangun oleh Ukuran Bernilai Proyeksi Arta Ekayanti dan Ch. Rini Indrati. FMIPA Universitas Gadjah Mada arta_ekayanti@ymail.com
Hendra Gunawan. KK Analisis & Geometri FMIPA-ITB. Bandung, Maret 2001 [Edisi Revisi II: Mei 2014]
![Hendra Gunawan. KK Analisis & Geometri FMIPA-ITB. Bandung, Maret 2001 [Edisi Revisi II: Mei 2014] Hendra Gunawan. KK Analisis & Geometri FMIPA-ITB. Bandung, Maret 2001 [Edisi Revisi II: Mei 2014]](/thumbs/72/67819562.jpg) Analisis Fourier dan Wavelet 1 Catatan Kuliah Analisis Fourier dan Wavelet Oleh Hendra Gunawan KK Analisis & Geometri FMIPA-ITB Bandung, Maret 2001 [Edisi Revisi II: Mei 2014] 1 2 Hendra Gunawan Daftar
Analisis Fourier dan Wavelet 1 Catatan Kuliah Analisis Fourier dan Wavelet Oleh Hendra Gunawan KK Analisis & Geometri FMIPA-ITB Bandung, Maret 2001 [Edisi Revisi II: Mei 2014] 1 2 Hendra Gunawan Daftar
7. Transformasi Fourier
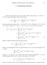 Pengantar Analisis Fourier dan eori Aproksimasi 33 7. ransformasi Fourier Pada bab sebelumnya kita telah melihat bahwa setiap fungsi f L 1 ([0, 1] L ([0, 1] dapat dinyatakan sebagai deret Fourier f(x =
Pengantar Analisis Fourier dan eori Aproksimasi 33 7. ransformasi Fourier Pada bab sebelumnya kita telah melihat bahwa setiap fungsi f L 1 ([0, 1] L ([0, 1] dapat dinyatakan sebagai deret Fourier f(x =
SIFAT P-KONVEKS PADA RUANG FUNGSI MUSIELAK-ORLICZ TYPE BOCHNER. Yulia Romadiastri
 Jurnal Matematika Murni dan Terapan εpsilon Vol. 07, No.01, 013, Hal. 1 1 SIFAT P-KONVEKS PADA RUANG FUNGSI MUSIELAK-ORLICZ TYPE BOCHNER Yulia Romadiastri Program Studi Tadris Matematika Fakultas Tarbiyah
Jurnal Matematika Murni dan Terapan εpsilon Vol. 07, No.01, 013, Hal. 1 1 SIFAT P-KONVEKS PADA RUANG FUNGSI MUSIELAK-ORLICZ TYPE BOCHNER Yulia Romadiastri Program Studi Tadris Matematika Fakultas Tarbiyah
BAB I PENDAHULUAN Latar Belakang Masalah
 BAB I PENDAHULUAN 1.1. Latar Belakang Masalah Pemetaan linear merupakan salah satu jenis pemetaan yang dikenal dalam bidang matematika, khususnya dalam bidang matematika analisis. Diberikan ruang vektor
BAB I PENDAHULUAN 1.1. Latar Belakang Masalah Pemetaan linear merupakan salah satu jenis pemetaan yang dikenal dalam bidang matematika, khususnya dalam bidang matematika analisis. Diberikan ruang vektor
EKSISTENSI TITIK TETAP DARI SUATU TRANSFORMASI LINIER PADA RUANG BANACH
 EKSISTENSI TITIK TETAP DARI SUATU TRANSFORMASI LINIER PADA RUANG BANACH Nur Aeni Prodi Matematika, Fakultas Sains dan Teknologi, UINAM nuraeniayatullah@gmailcom Info: Jurnal MSA Vol 3 No 1 Edisi: Januari
EKSISTENSI TITIK TETAP DARI SUATU TRANSFORMASI LINIER PADA RUANG BANACH Nur Aeni Prodi Matematika, Fakultas Sains dan Teknologi, UINAM nuraeniayatullah@gmailcom Info: Jurnal MSA Vol 3 No 1 Edisi: Januari
UNIVERSITAS GADJAH MADA. Bahan Ajar:
 UNIVERSITAS GADJAH MADA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM JURUSAN MATEMATIKA PROGRAM STUDI S1 MATEMATIKA Sekip Utara, Gedung Jurusan Matematika, Yogyakarta - 55281 Bahan Ajar: BAB POKOK BAHASAN
UNIVERSITAS GADJAH MADA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM JURUSAN MATEMATIKA PROGRAM STUDI S1 MATEMATIKA Sekip Utara, Gedung Jurusan Matematika, Yogyakarta - 55281 Bahan Ajar: BAB POKOK BAHASAN
DIAGONALISASI MATRIKS KOMPLEKS
 Buletin Ilmiah Mat Stat dan Terapannya (Bimaster) Volume 04, No 3 (2015), hal 337-346 DIAGONALISASI MATRIKS KOMPLEKS Heronimus Hengki, Helmi, Mariatul Kiftiah INTISARI Matriks kompleks merupakan matriks
Buletin Ilmiah Mat Stat dan Terapannya (Bimaster) Volume 04, No 3 (2015), hal 337-346 DIAGONALISASI MATRIKS KOMPLEKS Heronimus Hengki, Helmi, Mariatul Kiftiah INTISARI Matriks kompleks merupakan matriks
OPERATOR PADA RUANG BARISAN TERBATAS
 OPERATOR PADA RUANG BARISAN TERBATAS Muslim Ansori *,Tiryono 2, Suharsono S 2,Dorrah Azis 2 Jurusan Matematika FMIPA Universitas Lampung,2 Jln. Soemantri Brodjonegoro No Bandar Lampung email: ansomath@yahoo.com
OPERATOR PADA RUANG BARISAN TERBATAS Muslim Ansori *,Tiryono 2, Suharsono S 2,Dorrah Azis 2 Jurusan Matematika FMIPA Universitas Lampung,2 Jln. Soemantri Brodjonegoro No Bandar Lampung email: ansomath@yahoo.com
DASAR-DASAR TEORI PELUANG
 DASAR-DASAR TEORI PELUANG Herry P. Suryawan 1 Ruang Peluang Definisi 1.1 Diberikan himpunan tak kosong Ω. Aljabar-σ (σ-algebra pada Ω adalah koleksi subhimpunan A dari Ω dengan sifat (i, Ω A (ii jika A
DASAR-DASAR TEORI PELUANG Herry P. Suryawan 1 Ruang Peluang Definisi 1.1 Diberikan himpunan tak kosong Ω. Aljabar-σ (σ-algebra pada Ω adalah koleksi subhimpunan A dari Ω dengan sifat (i, Ω A (ii jika A
5. Sifat Kelengkapan Bilangan Real
 5. Sifat Kelengkapan Bilangan Real Sifat aljabar dan sifat urutan bilangan real telah dibahas sebelumnya. Selanjutnya, akan dijelaskan sifat kelengkapan bilangan real. Bilangan rasional ℚ juga memenuhi
5. Sifat Kelengkapan Bilangan Real Sifat aljabar dan sifat urutan bilangan real telah dibahas sebelumnya. Selanjutnya, akan dijelaskan sifat kelengkapan bilangan real. Bilangan rasional ℚ juga memenuhi
16. Analisis Multi Resolusi
 16. Analisis Multi esolusi Esensi dari basis ortonormal yang dibangun oleh sebuah wavelet adalah sifat multi resolusi-nya, sehingga kita dapat menganalisis suatu signal pada berbagai frekuensi di suatu
16. Analisis Multi esolusi Esensi dari basis ortonormal yang dibangun oleh sebuah wavelet adalah sifat multi resolusi-nya, sehingga kita dapat menganalisis suatu signal pada berbagai frekuensi di suatu
BAB III FUNGSI UJI DAN DISTRIBUSI
 BAB III FUNGSI UJI DAN DISTRIBUSI Bab ini membahas tentang fungsi uji dan distribusi di mana ruang yang memuat keduanya secara berturut-turut dinamakan ruang fungsi uji dan ruang distribusi. Ruang fungsi
BAB III FUNGSI UJI DAN DISTRIBUSI Bab ini membahas tentang fungsi uji dan distribusi di mana ruang yang memuat keduanya secara berturut-turut dinamakan ruang fungsi uji dan ruang distribusi. Ruang fungsi
BAB II KAJIAN PUSTAKA. Pada bab ini akan diberikan landasan teori tentang optimasi, fungsi, turunan,
 BAB II KAJIAN PUSTAKA Pada bab ini akan diberikan landasan teori tentang optimasi, fungsi, turunan, pemrograman linear, metode simpleks, teorema dualitas, pemrograman nonlinear, persyaratan karush kuhn
BAB II KAJIAN PUSTAKA Pada bab ini akan diberikan landasan teori tentang optimasi, fungsi, turunan, pemrograman linear, metode simpleks, teorema dualitas, pemrograman nonlinear, persyaratan karush kuhn
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MATERI ALJABAR LINEAR LANJUT RUANG VEKTOR
 MATERI ALJABAR LINEAR LANJUT RUANG VEKTOR Disusun oleh: Dwi Lestari, M.Sc email: dwilestari@uny.ac.id JURUSAN PENDIDIKAN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS NEGERI YOGYAKARTA
MATERI ALJABAR LINEAR LANJUT RUANG VEKTOR Disusun oleh: Dwi Lestari, M.Sc email: dwilestari@uny.ac.id JURUSAN PENDIDIKAN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS NEGERI YOGYAKARTA
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016. Hendra Gunawan
 MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 3. Topologi Garis Bilangan Real 3.1 Teori Limit Limit, supremum, dan infimum Titik limit 3.2 Himpunan Buka dan Himpunan Tutup 3.3
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 3. Topologi Garis Bilangan Real 3.1 Teori Limit Limit, supremum, dan infimum Titik limit 3.2 Himpunan Buka dan Himpunan Tutup 3.3
BAB III REPRESENTASI GELFAND-NAIMARK-SEGAL
 BAB III REPRESENTASI GELFAND-NAIMARK-SEGAL Pada bagian ini akan dibahas konsep yang terkait dengan representasi yaitu homomorfisma-*, representasi nondegenerate, representasi faithful, representasi siklik,
BAB III REPRESENTASI GELFAND-NAIMARK-SEGAL Pada bagian ini akan dibahas konsep yang terkait dengan representasi yaitu homomorfisma-*, representasi nondegenerate, representasi faithful, representasi siklik,
ANALISIS REAL. (Semester I Tahun ) Hendra Gunawan. September 12, Dosen FMIPA - ITB
 (Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. September 12, 2011 Teorema 11 pada Bab 3 memberi kita cara untuk menyelidiki kekonvergenan sebuah barisan tanpa harus mengetahui
(Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. September 12, 2011 Teorema 11 pada Bab 3 memberi kita cara untuk menyelidiki kekonvergenan sebuah barisan tanpa harus mengetahui
16. BARISAN FUNGSI. 16.1 Barisan Fungsi dan Kekonvergenan Titik Demi Titik
 16. BARISAN FUNGSI 16.1 Barisan Fungsi dan Kekonvergenan Titik Demi Titik Bila pada bab-bab sebelumnya kita membahas fungsi sebagai sebuah objek individual, maka pada bab ini dan selanjutnya kita akan
16. BARISAN FUNGSI 16.1 Barisan Fungsi dan Kekonvergenan Titik Demi Titik Bila pada bab-bab sebelumnya kita membahas fungsi sebagai sebuah objek individual, maka pada bab ini dan selanjutnya kita akan
4. Deret Fourier pada Interval Sebarang dan Aplikasi
 4. Deret Fourier pada Interval Sebarang dan Aplikasi Kita telah mempelajari bagaimana menguraikan fungsi periodik dengan periode 2 yang terdefinisi pada R sebagai deret Fourier. Deret trigonometri tersebut
4. Deret Fourier pada Interval Sebarang dan Aplikasi Kita telah mempelajari bagaimana menguraikan fungsi periodik dengan periode 2 yang terdefinisi pada R sebagai deret Fourier. Deret trigonometri tersebut
3 LIMIT DAN KEKONTINUAN
 Menurut Bartle dan Sherbet (1994), Analisis matematika secara umum dipahami sebagai tubuh matematika yang dibangun oleh berbagai konsep limit. Pada bab sebelumnya kita telah mempelajari limit barisan,
Menurut Bartle dan Sherbet (1994), Analisis matematika secara umum dipahami sebagai tubuh matematika yang dibangun oleh berbagai konsep limit. Pada bab sebelumnya kita telah mempelajari limit barisan,
SIFAT-SIFAT HIMPUNAN PROXIMINAL
 Prima: Jurnal Pendidikan Matematika Vol. 2, No. 1, Januari 2018, hal. 49-56 P-ISSN: 2579-9827, E-ISSN: 2580-2216 SIFAT-SIFAT HIMPUNAN PROXIMINAL Arta Ekayanti Universitas Muhammadiyah Ponorogo, Jl. Budi
Prima: Jurnal Pendidikan Matematika Vol. 2, No. 1, Januari 2018, hal. 49-56 P-ISSN: 2579-9827, E-ISSN: 2580-2216 SIFAT-SIFAT HIMPUNAN PROXIMINAL Arta Ekayanti Universitas Muhammadiyah Ponorogo, Jl. Budi
ABSTRAK 1 PENDAHULUAN
 EKSISTENSI SOLUSI LOKAL DAN KETUNGGALAN SOLUSI MASALAH NILAI AWAL PERSAMAAN DIFERENSIAL TUNDAAN Muhammad Abdulloh Mahin Manuharawati Matematika, Fakultas Ilmu Pengetahuan Alam Matematika, Universitas Negeri
EKSISTENSI SOLUSI LOKAL DAN KETUNGGALAN SOLUSI MASALAH NILAI AWAL PERSAMAAN DIFERENSIAL TUNDAAN Muhammad Abdulloh Mahin Manuharawati Matematika, Fakultas Ilmu Pengetahuan Alam Matematika, Universitas Negeri
SYARAT FRITZ JOHN PADA MASALAH OPTIMASI BERKENDALA KETAKSAMAAN. Caturiyati 1 Himmawati Puji Lestari 2. Abstrak
 Syarat Fritz John... (Caturiyati) SYARAT FRITZ JOHN PADA MASALAH OPTIMASI BERKENDALA KETAKSAMAAN Caturiyati 1 Himmawati Puji Lestari 2 1,2 Jurusan Pendidikan Matematika FMIPA UNY 1 wcaturiyati@yahoo.com
Syarat Fritz John... (Caturiyati) SYARAT FRITZ JOHN PADA MASALAH OPTIMASI BERKENDALA KETAKSAMAAN Caturiyati 1 Himmawati Puji Lestari 2 1,2 Jurusan Pendidikan Matematika FMIPA UNY 1 wcaturiyati@yahoo.com
Memahami definisi barisan tak hingga dan deret tak hingga, dan juga dapat menentukan
 4 BARISAN TAK HINGGA DAN DERET TAK HINGGA JUMLAH PERTEMUAN : 5 PERTEMUAN TUJUAN INSTRUKSIONAL KHUSUS : Memahami definisi barisan tak hingga dan deret tak hingga, dan juga dapat menentukan kekonvergenan
4 BARISAN TAK HINGGA DAN DERET TAK HINGGA JUMLAH PERTEMUAN : 5 PERTEMUAN TUJUAN INSTRUKSIONAL KHUSUS : Memahami definisi barisan tak hingga dan deret tak hingga, dan juga dapat menentukan kekonvergenan
TEOREMA TITIK TETAP BANACH
 TEOREMA TITIK TETAP BANACH Esih Sukaesih Abstrak Ruang Banach menjamin setiap barisan akan konvergen ke vektor di ruang tersebut. Barisan iterasi yang kontraktif menjamin bahwa barisan tersebut akan konvergen
TEOREMA TITIK TETAP BANACH Esih Sukaesih Abstrak Ruang Banach menjamin setiap barisan akan konvergen ke vektor di ruang tersebut. Barisan iterasi yang kontraktif menjamin bahwa barisan tersebut akan konvergen
TEOREMA TITIK TETAP PADA RUANG NORM-n STANDAR. Shelvi Ekariani KK Analisis dan Geometri FMIPA ITB
 JMP : Volume 4 Nomor, Juni 0, hal. 69-77 TEOREMA TITIK TETAP PADA RUANG NORM-n STANDAR Shelvi Ekariani KK Analisis dan Geometri FMIPA ITB shelvi_ekariani@students.itb.ac.id Hendra Gunawan KK Analisis dan
JMP : Volume 4 Nomor, Juni 0, hal. 69-77 TEOREMA TITIK TETAP PADA RUANG NORM-n STANDAR Shelvi Ekariani KK Analisis dan Geometri FMIPA ITB shelvi_ekariani@students.itb.ac.id Hendra Gunawan KK Analisis dan
KEKONVERGENAN LEMAH PADA RUANG HILBERT
 KEKONVERGENAN LEMAH PADA RUANG HILBERT Moch. Ramadhan Mubarak 1), Encum Sumiaty 2), Cece Kustiawan 3) 1), 2), 3) Departemen Pendidikan Matematika FPMIPA UPI *Surel: ramadhan.101110176@gmail.com ABSTRAK.
KEKONVERGENAN LEMAH PADA RUANG HILBERT Moch. Ramadhan Mubarak 1), Encum Sumiaty 2), Cece Kustiawan 3) 1), 2), 3) Departemen Pendidikan Matematika FPMIPA UPI *Surel: ramadhan.101110176@gmail.com ABSTRAK.
Beberapa Sifat Operator Self Adjoint dalam Ruang Hilbert
 Vol 12, No 2, 153-159, Januari 2016 Beberapa Sifat Operator Self Adjoint dalam Ruang Hilbert Firman Abstrak Misalkan adalah operator linier dengan adalah ruang Hilbert Pada operator linier dikenal istilah
Vol 12, No 2, 153-159, Januari 2016 Beberapa Sifat Operator Self Adjoint dalam Ruang Hilbert Firman Abstrak Misalkan adalah operator linier dengan adalah ruang Hilbert Pada operator linier dikenal istilah
6 Sistem Persamaan Linear
 6 Sistem Persamaan Linear Pada bab, kita diminta untuk mencari suatu nilai x yang memenuhi persamaan f(x) = 0. Pada bab ini, masalah tersebut diperumum dengan mencari x = (x, x,..., x n ) yang secara sekaligus
6 Sistem Persamaan Linear Pada bab, kita diminta untuk mencari suatu nilai x yang memenuhi persamaan f(x) = 0. Pada bab ini, masalah tersebut diperumum dengan mencari x = (x, x,..., x n ) yang secara sekaligus
13. Aplikasi Transformasi Fourier
 13. plikasi ransformasi Fourier Misal adalah operator linear pada fungsi yang terdefinisi pada R dengan sifat: jika [f(x] = g(x, maka [f(x + s] = g(x + s untuk setiap s R. Maka, fungsi f(x = e ax (a C
13. plikasi ransformasi Fourier Misal adalah operator linear pada fungsi yang terdefinisi pada R dengan sifat: jika [f(x] = g(x, maka [f(x + s] = g(x + s untuk setiap s R. Maka, fungsi f(x = e ax (a C
Karakteristik Operator Positif Pada Ruang Hilbert
 SEMINAR NASIONAL MATEMATIKA DAN PENDIDIKAN MATEMATIKA UNY 05 A - 4 Karakteristik Operator Positif Pada Ruang Hilbert Gunawan Fakultas Keguruan dan Ilmu Pendidikan, Universitas Muhammadiyah Purwokerto gunoge@gmailcom
SEMINAR NASIONAL MATEMATIKA DAN PENDIDIKAN MATEMATIKA UNY 05 A - 4 Karakteristik Operator Positif Pada Ruang Hilbert Gunawan Fakultas Keguruan dan Ilmu Pendidikan, Universitas Muhammadiyah Purwokerto gunoge@gmailcom
BAGIAN KEDUA. Fungsi, Limit dan Kekontinuan, Turunan
 BAGIAN KEDUA Fungsi, Limit dan Kekontinuan, Turunan 51 52 Hendra Gunawan Pengantar Analisis Real 53 6. FUNGSI 6.1 Fungsi dan Grafiknya Konsep fungsi telah dipelajari oleh Gottfried Wilhelm von Leibniz
BAGIAN KEDUA Fungsi, Limit dan Kekontinuan, Turunan 51 52 Hendra Gunawan Pengantar Analisis Real 53 6. FUNGSI 6.1 Fungsi dan Grafiknya Konsep fungsi telah dipelajari oleh Gottfried Wilhelm von Leibniz
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016. Hendra Gunawan
 MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 2.2 Sistem Bilangan Real sebagai Lapangan Terurut Operasi Aritmetika. Sifat-sifat dasar urutan dan aritmetika dari Sistem Bilangan
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 2.2 Sistem Bilangan Real sebagai Lapangan Terurut Operasi Aritmetika. Sifat-sifat dasar urutan dan aritmetika dari Sistem Bilangan
Catatan Kuliah MA1123 Kalkulus Elementer I
 Catatan Kuliah MA1123 Kalkulus Elementer I Oleh Hendra Gunawan, Ph.D. Departemen Matematika ITB Sasaran Belajar Setelah mempelajari materi Kalkulus Elementer I, mahasiswa diharapkan memiliki (terutama):
Catatan Kuliah MA1123 Kalkulus Elementer I Oleh Hendra Gunawan, Ph.D. Departemen Matematika ITB Sasaran Belajar Setelah mempelajari materi Kalkulus Elementer I, mahasiswa diharapkan memiliki (terutama):
1 SISTEM BILANGAN REAL
 1 SISTEM BILANGAN REAL Bilangan real sudah dikenal dengan baik sejak masih di sekolah menengah, bahkan sejak dari sekolah dasar. Namun untuk memulai mempelajari materi pada BAB ini anggaplah diri kita
1 SISTEM BILANGAN REAL Bilangan real sudah dikenal dengan baik sejak masih di sekolah menengah, bahkan sejak dari sekolah dasar. Namun untuk memulai mempelajari materi pada BAB ini anggaplah diri kita
MINGGU KE-6 VARIABEL RANDOM DAN DISTRIBUSINYA
 MINGGU KE-6 VARIABEL RANDOM DAN DISTRIBUSINYA VARIABEL RANDOM Misalkan (Ω, A, P) ruang probabilitas dan R = {x < x < } dan B : Borel field pada R. Andaikan X : Ω R dan untuk setiap A R, kita definisikan
MINGGU KE-6 VARIABEL RANDOM DAN DISTRIBUSINYA VARIABEL RANDOM Misalkan (Ω, A, P) ruang probabilitas dan R = {x < x < } dan B : Borel field pada R. Andaikan X : Ω R dan untuk setiap A R, kita definisikan
Bab 2 Fungsi Analitik
 Bab 2 Fungsi Analitik Bab 2 ini direncanakan akan disampaikan dalam 4 kali pertemuan, dengan perincian sebagai berikut: () Pertemuan I: Fungsi Kompleks dan Pemetaan. (2) Pertemuan II: Limit Fungsi, Kekontiuan,
Bab 2 Fungsi Analitik Bab 2 ini direncanakan akan disampaikan dalam 4 kali pertemuan, dengan perincian sebagai berikut: () Pertemuan I: Fungsi Kompleks dan Pemetaan. (2) Pertemuan II: Limit Fungsi, Kekontiuan,
DASAR-DASAR ANALISIS MATEMATIKA
 (Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. December 26, 2007 Misalkan f kontinu pada interval [a, b]. Apakah masuk akal untuk membahas luas daerah
(Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. December 26, 2007 Misalkan f kontinu pada interval [a, b]. Apakah masuk akal untuk membahas luas daerah
BAB I PENDAHULUAN. Analisis fungsional merupakan salah satu cabang dari kelompok analisis
 BAB I PENDAHULUAN 1.1 Latar Belakang Analisis fungsional merupakan salah satu cabang dari kelompok analisis yang membahas operator, operator linear dan sifat-sifatnya. Sebuah pemetaan antar ruang bernorm
BAB I PENDAHULUAN 1.1 Latar Belakang Analisis fungsional merupakan salah satu cabang dari kelompok analisis yang membahas operator, operator linear dan sifat-sifatnya. Sebuah pemetaan antar ruang bernorm
III. HASIL DAN PEMBAHASAN
 III. HASIL DAN PEMBAHASAN 3.1 Perumusan Masalah Misalkan adalah proses Poisson nonhomogen pada interval dengan fungsi intensitas yang tidak diketahui. Fungsi intensitas diasumsikan terintegralkan lokal
III. HASIL DAN PEMBAHASAN 3.1 Perumusan Masalah Misalkan adalah proses Poisson nonhomogen pada interval dengan fungsi intensitas yang tidak diketahui. Fungsi intensitas diasumsikan terintegralkan lokal
BAB II MATRIKS POSITIF. Pada bab ini akan dibahas mengenai Teorema Perron, yaitu teori hasil kontribusi
 BAB II MATRIKS POSITIF Pada bab ini akan dibahas mengenai Teorema Perron, yaitu teori hasil kontribusi dari seorang matematikawan German, Oskar Perron. Perron menerbitkan tulisannya tentang sifat-sifat
BAB II MATRIKS POSITIF Pada bab ini akan dibahas mengenai Teorema Perron, yaitu teori hasil kontribusi dari seorang matematikawan German, Oskar Perron. Perron menerbitkan tulisannya tentang sifat-sifat
BAB II TINJAUAN PUSTAKA
 5 BAB II TINJAUAN PUSTAKA A Matriks 1 Pengertian Matriks Definisi 21 Matriks adalah kumpulan bilangan bilangan yang disusun secara khusus dalam bentuk baris kolom sehingga membentuk empat persegi panjang
5 BAB II TINJAUAN PUSTAKA A Matriks 1 Pengertian Matriks Definisi 21 Matriks adalah kumpulan bilangan bilangan yang disusun secara khusus dalam bentuk baris kolom sehingga membentuk empat persegi panjang
BAB II TEORI DASAR. S, torus, topologi adalah suatu himpunan yang mempunyai topologi, yaitu koleksi dari
 BAB II TEORI DASAR Pada skripsi ini, akan dipelajari perbedaan sifat grup fundamental yang dimiliki beberapa ruang topologi, yaitu 2 S, torus, 2 P dan figure eight. Ruang topologi adalah suatu himpunan
BAB II TEORI DASAR Pada skripsi ini, akan dipelajari perbedaan sifat grup fundamental yang dimiliki beberapa ruang topologi, yaitu 2 S, torus, 2 P dan figure eight. Ruang topologi adalah suatu himpunan
1 SISTEM BILANGAN REAL
 Bilangan real sudah dikenal dengan baik sejak masih di sekolah menengah, bahkan sejak dari sekolah dasar. Namun untuk memulai mempelajari materi pada BAB ini anggaplah diri kita belum tahu apa-apa tentang
Bilangan real sudah dikenal dengan baik sejak masih di sekolah menengah, bahkan sejak dari sekolah dasar. Namun untuk memulai mempelajari materi pada BAB ini anggaplah diri kita belum tahu apa-apa tentang
PENGANTAR TOPOLOGI. Dosen Pengampu: Siti Julaeha, M.Si EDISI PERTAMA UNIVERSITAS ISLAM NEGERI SUNAN GUNUNG DJATI BANDUNG 2015
 PENGANTAR TOPOLOGI EDISI PERTAMA Dosen Pengampu: Siti Julaeha, M.Si UNIVERSITAS ISLAM NEGERI SUNAN GUNUNG DJATI BANDUNG 2015 by Matematika Sains 2012 UIN SGD, Copyright 2015 BAB 0. HIMPUNAN, RELASI, FUNGSI,
PENGANTAR TOPOLOGI EDISI PERTAMA Dosen Pengampu: Siti Julaeha, M.Si UNIVERSITAS ISLAM NEGERI SUNAN GUNUNG DJATI BANDUNG 2015 by Matematika Sains 2012 UIN SGD, Copyright 2015 BAB 0. HIMPUNAN, RELASI, FUNGSI,
PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI
 METODE TITIK-INTERIOR PADA PEMROGRAMAN KUADRATIK KONVEKS Skripsi Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains Program Studi Matematika Oleh: Fenny Basuki NIM: 831143 PROGRAM
METODE TITIK-INTERIOR PADA PEMROGRAMAN KUADRATIK KONVEKS Skripsi Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains Program Studi Matematika Oleh: Fenny Basuki NIM: 831143 PROGRAM
Kelengkapan Ruang l pada Ruang Norm-n
 Jurnal Matematika, Statistika,& Komputasi Vol.... No... 20... Kelengkapan Ruang l pada Ruang Norm-n Meriam, Naimah Aris 2, Muh Nur 3 Abstrak Rumusan norm-n pada l merupakan perumuman dari rumusan norm-n
Jurnal Matematika, Statistika,& Komputasi Vol.... No... 20... Kelengkapan Ruang l pada Ruang Norm-n Meriam, Naimah Aris 2, Muh Nur 3 Abstrak Rumusan norm-n pada l merupakan perumuman dari rumusan norm-n
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI Sebagai acuan penulisan penelitian ini diperlukan beberapa pengertian dan teori yang berkaitan dengan pembahasan. Dalam sub bab ini akan diberikan beberapa landasan teori berupa pengertian,
BAB II LANDASAN TEORI Sebagai acuan penulisan penelitian ini diperlukan beberapa pengertian dan teori yang berkaitan dengan pembahasan. Dalam sub bab ini akan diberikan beberapa landasan teori berupa pengertian,
UJI KONVERGENSI. Januari Tim Dosen Kalkulus 2 TPB ITK
 UJI KONVERGENSI Januari 208 Tim Dosen Kalkulus 2 TPB ITK Uji Integral Teorema 3 Jika + k= u k adalah deret dengan suku-suku tak negatif, dan jika ada suatu konstanta M sedemikian hingga s n = u + u 2 +
UJI KONVERGENSI Januari 208 Tim Dosen Kalkulus 2 TPB ITK Uji Integral Teorema 3 Jika + k= u k adalah deret dengan suku-suku tak negatif, dan jika ada suatu konstanta M sedemikian hingga s n = u + u 2 +
BAB II LANDASAN TEORI. selanjutnya sebagai bahan acuan yang mendukung tujuan penulisan. Materi-materi
 BAB II LANDASAN TEORI Pada bab ini akan dibahas tentang landasan teori yang digunakan pada bab selanjutnya sebagai bahan acuan yang mendukung tujuan penulisan. Materi-materi yang diuraikan berupa definisi-definisi
BAB II LANDASAN TEORI Pada bab ini akan dibahas tentang landasan teori yang digunakan pada bab selanjutnya sebagai bahan acuan yang mendukung tujuan penulisan. Materi-materi yang diuraikan berupa definisi-definisi
KEKONVERGENAN BARISAN DI RUANG HILBERT PADA PEMETAAN TIPE-NONSPREADING DAN NONEXPANSIVE
 Jurnal Matematika UNAND Vol. 2 No. 1 Hal. 42 51 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND KEKONVERGENAN BARISAN DI RUANG HILBERT PADA PEMETAAN TIPE-NONSPREADING DAN NONEXPANSIVE DEBI OKTIA HARYENI
Jurnal Matematika UNAND Vol. 2 No. 1 Hal. 42 51 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND KEKONVERGENAN BARISAN DI RUANG HILBERT PADA PEMETAAN TIPE-NONSPREADING DAN NONEXPANSIVE DEBI OKTIA HARYENI
3 LIMIT DAN KEKONTINUAN
 Menurut Bartle dan Sherbet (994), Analisis matematika secara umum dipahami sebagai tubuh matematika yang dibangun oleh berbagai konsep limit. Pada bab sebelumnya kita telah mempelajari limit barisan, kekonvergenan
Menurut Bartle dan Sherbet (994), Analisis matematika secara umum dipahami sebagai tubuh matematika yang dibangun oleh berbagai konsep limit. Pada bab sebelumnya kita telah mempelajari limit barisan, kekonvergenan
BAB 1 PENDAHULUAN. 1 ; untuk k = n 0 ; untuk k n. e [n]
![BAB 1 PENDAHULUAN. 1 ; untuk k = n 0 ; untuk k n. e [n] BAB 1 PENDAHULUAN. 1 ; untuk k = n 0 ; untuk k n. e [n]](/thumbs/68/58947103.jpg) BAB 1 PENDAHULUAN 1.1. Latar Belakang Barisan bilangan real adalah suatu fungsi bernilai real yang didefinisikan pada himpunan N = 0, 1, 2,.... Dengan kata lain, barisan bilangan real adalah suatu fungsi
BAB 1 PENDAHULUAN 1.1. Latar Belakang Barisan bilangan real adalah suatu fungsi bernilai real yang didefinisikan pada himpunan N = 0, 1, 2,.... Dengan kata lain, barisan bilangan real adalah suatu fungsi
BAHAN AJAR ANALISIS REAL 1. DOSEN PENGAMPU RINA AGUSTINA, S. Pd., M. Pd. NIDN
 BAHAN AJAR ANALISIS REAL 1 DOSEN PENGAMPU RINA AGUSTINA, S. Pd., M. Pd. NIDN. 0212088701 PENDIDIKAN MATEMATIKA FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN UNIVERSITAS MUHAMMADIYAH METRO 2015 1 KATA PENGANTAR
BAHAN AJAR ANALISIS REAL 1 DOSEN PENGAMPU RINA AGUSTINA, S. Pd., M. Pd. NIDN. 0212088701 PENDIDIKAN MATEMATIKA FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN UNIVERSITAS MUHAMMADIYAH METRO 2015 1 KATA PENGANTAR
KALKULUS MULTIVARIABEL II
 Pada Bidang Bentuk Vektor dari KALKULUS MULTIVARIABEL II (Minggu ke-9) Andradi Jurusan Matematika FMIPA UGM Yogyakarta, Indonesia Pada Bidang Bentuk Vektor dari 1 Definisi Daerah Sederhana x 2 Pada Bidang
Pada Bidang Bentuk Vektor dari KALKULUS MULTIVARIABEL II (Minggu ke-9) Andradi Jurusan Matematika FMIPA UGM Yogyakarta, Indonesia Pada Bidang Bentuk Vektor dari 1 Definisi Daerah Sederhana x 2 Pada Bidang
II. LANDASAN TEORI ( ) =
 II. LANDASAN TEORI 2.1 Fungsi Definisi 2.1.1 Fungsi Bernilai Real Fungsi bernilai real adalah fungsi yang domain dan rangenya adalah himpunan bagian dari real. Definisi 2.1.2 Limit Fungsi Jika adalah suatu
II. LANDASAN TEORI 2.1 Fungsi Definisi 2.1.1 Fungsi Bernilai Real Fungsi bernilai real adalah fungsi yang domain dan rangenya adalah himpunan bagian dari real. Definisi 2.1.2 Limit Fungsi Jika adalah suatu
Aljabar Linear Elementer
 BAB I RUANG VEKTOR Pada kuliah Aljabar Matriks kita telah mendiskusikan struktur ruang R 2 dan R 3 beserta semua konsep yang terkait. Pada bab ini kita akan membicarakan struktur yang merupakan bentuk
BAB I RUANG VEKTOR Pada kuliah Aljabar Matriks kita telah mendiskusikan struktur ruang R 2 dan R 3 beserta semua konsep yang terkait. Pada bab ini kita akan membicarakan struktur yang merupakan bentuk
BAB II TINJAUAN PUSTAKA
 4 BAB II TINJAUAN PUSTAKA Untuk mencapai tujuan penulisan penelitian diperlukan beberapa pengertian dan teori yang berkaitan dengan pembahasan. Dalam subbab ini akan diberikan beberapa teori berupa definisi,
4 BAB II TINJAUAN PUSTAKA Untuk mencapai tujuan penulisan penelitian diperlukan beberapa pengertian dan teori yang berkaitan dengan pembahasan. Dalam subbab ini akan diberikan beberapa teori berupa definisi,
