MES (Journal of Mathematics Education and Science) ISSN: PERSAMAAN DIFFERENSIAL EKSAK DENGAN FAKTOR INTEGRASI
|
|
|
- Sucianty Kusnadi
- 6 tahun lalu
- Tontonan:
Transkripsi
1 ES Jornal of athmatis Edation and Sin ISS: PERSAAA DIFFERESIAL EKSAK DEGA FAKTOR ITEGRASI Rosliana Sirgar Dosn Kooprtis Wil I Dpk FKIP-UISU Rosliana2012@ahoo.om Abstrak. Pnlitian ini brtjan ntk mngtahi hbngan prsamaan diffrnsial tak ksak dngan faktor intgrasi. kajian pnntan faktor intgrasi pada prsamaan difrnsial ksak dngan mnggnakan langkah-langkah pnlsaian dari prsamaan diffrnsial. Prsamaan difrnsial ksak mmiliki kass prsamaan difrnsial tak ksak di mana prsamaan difrnsial tak ksak ini dapat di bah mnjadi prsamaan difrnsial ksak. Dalam hal ini diprlkan konsp faktor intgrasi ntk mnlsaikanna shingga dari prsamaan difrnsial tak ksak dapat di bah mnjadi prsaman difrnsial ksak. Hasil pmbahasan dari pnlitian ini mmbktikan adana hbngan antara prsamaan difrnsial ksak dngan faktor intgrasi. Kata Kni: Prsamaan Diffrnsial Eksak Tak Eksak Faktor Intgrasi PEDAHULUA Prsamaan difrnsial adalah abang matmatika ang banak dignakan ntk mnjlaskan masalah-masalah fisis. asalah-masalah fisis trsbt dapat dimodlkan dalam prsamaan difrnsial. Pada prkmbangan ilm prsamaan difrnsial sbagai modl banak dijmpai dalam bidang-bidang sains tknologi tknik biologi konomi ilm sosial dmografi dan sbagaina. Prsamaan difrnsial dignakan sbagai alat ntk mngtahi klakan mapn sifat-sifat masalah ang ditinja. Karna it pnting skali mmplajari prsamaan difrnsial. Prll E.J mnatakan prsamaan diffrnsial adalah Smbarang prsamaan dngan ang tidak diktahi brpa sat fngsi dan daa ang mnakp trnan ata difrnsial dan fngsi tidak diktahi. Kmdian ia mmbri dfinisi formal dari prsamaan difrnsial ait: Andaikan = f trdfinisi di dan andaikan d didifrnsialkan dari prbahan bbas mnatakan prtambahan smbarang dari. Difrnsial ang brssaian dngan d dari prbahan bbas didifrnsialkan olh: d = f d. Pngrtian-pngrtian diffrnsial dapat didfnisikan sbagai brikt: Dfinisi 1.1: Prsamaan Difrnsial adalah sat prsamaan ang mlipti trnan fngsi dari sat ata lbih variabl trikat trhadap sat ata lbih variabl bbas. Bila ada sat fngsi F maka sat prsamaan difrnsial: d + d = 0 disbt ksak shingga df = d + d. Jika diktahi rms difrnsial df = F F F F d + d maka = ; = shinggan brlak ktntan = pada prsamaan difrnsial ksak. Ada bntk prsamaan difrnsial ang tak ksak ttapi bila dikalikan dngan sat fngsi trtnt maka akan diprolh sat prsamaan ang ksak. Pross trsbt dinamakan dngan faktor intgrasi. Faktor Intgrasi dilakkan dngan tjan sbagai brikt: a. Untk mngtahi bahwa adana hbngan antara prsamaan difrnsial ksak dan prsamaan difrnsial tak ksak dngan faktor intgral. b. Untk mngtahi sarat-sarat kksakan sat prsamaan difrnsial ksak. 68
2 Vol. 2 o. 1 Oktobr Untk mngtahi ara mnntkan faktor intgrasi pada prsamaan difrnsial ksak. d. Untk mngtahi pada saat kapan faktor intgrasi it dignakan. Pada prinsipna prsamaan difrnsial tak ksak dapat dibah mnjadi prsamaan difrnsial ksak. Dalam masalah ini diprlkan konsp faktor intgrasi ntk mnlsaikanna shingga prsamaan difrnsial tak ksak bisa mnjadi prsamaan difrnsial ksak. Dari masalah trsbt bagaimana mnlsaikan masalah pnntan faktor intgrasi pada prsamaan difrnsial ksak. PEBAHASA Prsamaan Difrnsial Eksak Dfinisi 1: Jika F sat fngsi dari da variabl ral dan F kontin pada trnan prtama pada domain D maka jmlah difrnsial df didfinisikan sbagai df = F d + F d ntk sma D. Dfinisi 2: Prsamaan d + d = 0 disbt difrnsial ksak pada domain D jika ada fngsi F dari da variabl maka sdmikian hingga ktntan trsbt sama dngan jmlah df ntk D. Ssaikan dfinisi 2 dngan prsamaan d + d = 0 diprolh = F = F Dfinisi 3: Apabila fngsi f = maka prsamaan difrnsial ord sat brbntk d + d = 0 1 disbt ksak shingga df = d + d 2 dari dfinisi prsamaan difrnsial ksak dan hbngan 1 dapat dilihat bahwa df = jadi dngan mngintgralkan ini diprolh bahwa solsi mm prsamaan difrnsial 1 adalah f =. Slanjtna dari dfinisi difrnsial total dan hbngan 2 dapat dilihat bahwa f f = dan = 3 Bila dan mmpnai trnan- trnan parsial ang kontin di bidang-bidang maka dari 3 diprolh = 2 f dan = 2 f Slanjtna bila f mmpnai trnan-trnan parsial k da ang kontin maka dari 4 diprolh = Sarat 5 mrpakan sarat prl agar prsamaan difrnsial 1 ksak. Dapat diprlihatkan bahwa sarat ini jga sarat kp shingga hbngan 3 dapat diprgnakan ntk mnntkan fngsi f = ang mrpakan solsi mm prsamaan difrnsial
3 Rosliana Sirgar Torma 1: Prsamaan d + d = 0 dngan kontin pada trnan prtamana C 1 D akan mmnhi kondisi brikt: 1. Bila d + d = 0 PD ksak di D maka ntk D 2. Sbalikna bila = d + d = 0 mrpakan PD ksak. = ntk D maka dikatakan Jika d + d mrpakan trnan total dari bbrapa fngsi F ; dan maka sat prsamaan difrnsial dngan bntk mm d + d = 0 adalah mrpakan sbah prsamaan difrnsial ksak dikatakan dmikian karna trnan parsial dari F adalah masing-masing trnan parsial trhadap dan. Trnan parsial ampran ord k da dari F ada dan kontin shingga F = F. Jadi jika sbah prsamaan difrnsial brbntk d + d = 0 adalah ksak maka =. Dapatlah ditnjkkan bahwa ini jga mrpakan sarat kp ntk kksakan ait = d + d = 0 adalah ksak. tod Pnlsaian Prsamaan Difrnsial Eksak Jika sbah prsamaan difrnsial adalah ksak maka pnlsaianna dapat diprolh dngan mtod brikt ini: 1. Intgralkanlah k mnggantikan ttapan pngintgralan biasa dngan sbah fngsi f dari. F = d = G + 2. Difrnsialkanlah F = G + f ang diprolh dari langkah prtama k dan bandingkanlah dngan dari prsamaan difrnsial ang akan dislsaikan ntk mndapatkan nilai f G + f = f = G 3. Intgralkanlah f k ntk mndapatkan f. fd = f Tidaklah prl ntk mnakp ttapan pngintgralan biasa karna ttapan it dinatakan pada langkah akhir dari pnlsaian. 4. Pnlsaian dari langkah-langkah prtama dan k tiga adalah: F = G + f + C = 0. Jlaslah pnlsaian it dapat jga diprolh dngan mngintgralkan trlbih dahl k. Prsamaan Difrnsial Tak Eksak Dalam bbrapa kass sat prsamaan difrnsial ang tak ksak dapat dijadikan ksak dngan mngalikanna dngan sat faktor faktor sprti it disbt faktor pngintgralan karna faktor it mmngkinkan prsamaan trsbt diintgralkan. Pada mmna mnntkan faktor pngintgralan ang ook ntk 70
4 Vol. 2 o. 1 Oktobr 2016 sbah prsamaan difrnsial trtnt bkanlah soal ang mdah namn dmikian dapatlah ditnjkkan bahwa ntk stiap prsamaan difrnsial linar ord prtama mmiliki faktor pngintgralan Pd. Faktor Intgrasi Intgrasi mrpakan pross kbalikan dari difrnsiasi. Apabila didifrnsiasikan maka dimlai dngan sat prnataan dan mlanjtkanna ntk mnari trnanna. Apabila diintgralkan maka dimlai dngan trnanna dan kmdian mnari prnataan asal intgral ini. Faktor intgrasi ini dignakan ntk mnlsaikan PD ord sat tak ksak. Langkah ang dimaksd adalah mrbah PD tak ksak mnjadi ksak. Bila maka dapat ditntkan μ sdmikian hingga μ d + μ d = 0 mrpakan PD ksak. Skarang bagaimana mnntkan dapatlah dignakan torma PD ksak. Bila prsamaan μ d + μ d = 0 ksak maka μ = μ μ + μ [ = μ μ ] = + μ μ μ = μ μ adalah mrpakan formla faktor intgrasi sara mm. mprtimbangkan prsamaan difrnsial biasa dalam bntk + P = Q di mana = adalah fngsi ang tidak diktahi dari P dan Q adalah fngsi ang dibrikan. tod faktor ang mngintgrasikan bkrja dngan mmtar sisi kiri k dalam bntk trnan dari sat prodk. Prtimbangkan fngsi kalikan k da sisi + P = Q olh : + P = Q diinginkan sisi kiri brada dalam bntk trnan dari sat prodk shingga + P = Q dapat ditlis sbagai = Q. Sisi kiri dalam = Q kini dapat trintgrasi dngan lbih mdah dngan mnggnakan torma dasar kalkls = Qd + C di mana C adalah konstan lihat konstanta smbarang intgrasi. Skarang dapat dipahkan ntk Qd + C = Tapi ntk mmahkan sara ksplisit ntk prl ditmkan ksprsi ntk. = Q mnggnakan prodk. = + = Q Idntifikasi istilah dalam + P = Q dan jlas bahwa F mmathi prsamaan difrnsial: = P ntk mndapatkan bagi k da blah pihak olh : 71
5 Rosliana Sirgar P = 0 Prsamaan P = 0 adalah dalam bntk drivativ logaritmik mmbrikan = Pd. Dapat dilihat bahwa mngalikan olh dan proprti = f sangat pnting dalam mmahkan prsamaan difrnsial ini. F disbt faktor intgrasi. Dalam matmatika sat faktor intgrasi adalah sat fngsi ang dipilih ntk mmfasilitasi pnlsaian trtnt ang mlibatkan prsamaan difrnsial. Hal ini biasana dignakan ntk mnlsaikan prsamaan difrnsial biasa ttapi jga dignakan dalam kalkls mltivariabl dalam hal ini sring mngalikan mlali olh faktor mngintgrasikan ang mmngkinkan sbah difrnsial tak ksak ntk dibat mnjadi sbah difrnsial ksak. Pnlsaian Prsamaan Difrnsial Eksak Sat prsamaan difrnsial ord sat brbntk d + d = 0. Jika ras kirina adalah difrnsial total ata difrnsial ksak ait d d d maka disbt prsamaan difrnsial ksak. Dari sat fngsi prsamaan difrnsial d + d =0 dapat ditlis dngan d = 0. Dngan pngintgralan akan diprolh pnlsaian mm dari g = f ang brbntk = Dngan mmbandingkan d + d = 0 dan d d d dapat diktahi bahwa d + d = 0 adalah prsamaan difrnsial ksak dari sat fngsi sdmikian hingga; a b isal dan trdfinisikan dan mmpnai trnan parsial prtama ang kontin dalam sat darah di bidang ang batas-batasna brpa krva ttp ang tidak mmpnai irisan mandiri slf-intrstions. Dari diprolh a 2 2 b dngan asmsi kontinitas dapat disimplkan bahwasana da trnan k da di atas adalah sama. Jadi 72
6 Vol. 2 o. 1 Oktobr 2016 sarat ini bkan hana prl ttapi jga kp ntk d + d mnjadi difrnsial total. Jika d + d = 0 ksak maka fngsi dapat ditmkan dngan prkiraan ata dngan ara sistmatis sprti brikt. Dari dngan pngintgralan trhadap diprolh: = d k Dalam pngintgralan ini dipandang sbagai sat konstan dan k brpran sbagai konstan intgrasi. Untk mnntkan k ditrnkan / dari dk = d k gnakan ntk mndapatkan kmdian d diintgralkan. Rms = d k diprolh dari dignakan rms dngan = d k ait = d l. Untk mnntkan l trnkan. Sara sama bisa ntk mndapatkan rms = d l ang mirip ntk mndapatkan dl/d kmdian diintgralkan. / dari = d l gnakan Hbngan Faktor Intgrasi Pada Prsamaan Difrnsial Eksak dan Prsamaan Difrnsial Tak Eksak. Tlah dibahas sblmna bahwa prsamaan difrnsial tak ksak dapat dibah mnjadi prsamaan difrnsial ksak ait dngan mngalikan k da ras prsamaan dngan sat fngsi ang disbt dngan faktor intgrasi. Akan ditntkan ara mnari faktor intgral ntk kjadian ang sangat khss ait ang mrpakan fngsi saja ata saja. isalkan prsamaan d + d = 0 mrpakan prsamaan difrnsial tak ksak dngan faktor intgral mrpakan fngsi saja misalkan v = v. Dngan dmikian vd + v = 0 mrpakan prsamaanprsamaan difrnsial ksak brarti; v v. ata dapat ditlis dv v v. d Dari prsamaan trsbt diprolh: 73
7 Rosliana Sirgar 74 v d dv Karna diktahi bahwa v mrpakan fngsi saja maka hars mrpakan fngsi saja shingga: d v ln. Slanjtna dngan jalan ang sama jika v mrpakan fngsi saja maka diprolh: d v ln Faktor intgrasi dignakan pada saat prsamaan difrnsial trsbt tak ksak ait shingga dignakanlah faktor intgrasi ntk mngbahna mnjadi prsamaan difrnsial ksak. Pada pnlsaian soal-soal mngnai faktor intgrasi ada 2 da hal ang hars diprhatikan ait: a. Pada soal-soal mngnai faktor intgrasi tlah diantmkan ata ditntkan jnis dari faktor-faktor intgrasina. isalna: mmpnai faktor intgrasi hana fngsi dari. mmpnai faktor intgrasi trgantng dari dan lain-lain. b. Pada soal-soal mngnai faktor intgrasi tidak diantmkan ata ditntkan faktor-faktor intgrasina jadi hars diari lagi jnis faktor ang ssai dngan soal trsbt. Dalam hal a dapat dimaskkan langsng jnis dari faktor intgrasina k dalam prsamaan: shingga harga faktor intgrasi dapat diprolh. Dalam hal b blm mmpnai rms ang tpat ntk langsng mmprolh jnis dan harga dari faktor intgrasi ang ssai. Ada ktntanktntan ntk mnari jnis dan harga dari faktor intgrasi. Ktntan-ktntan trsbt adalah sbagai brikt: 1. Bila faktor intgrasina hana trgantng dari maka: d d dan 0 shingga rms faktor intgrasi mnjadi:
8 Vol. 2 o. 1 Oktobr 2016 P d d 0 ata d. d Sbalikna bila sat soal dari trdapat fngsi adalah fngsi dari saja maka faktor intgrasi hana fngsi dari. 2. Bila faktor intgrasina hana trgantng dari maka 0 dan d d. Shingga rms faktor intgrasi mnjadi 0 ata d d d d. Sbalikna bila sat soal harga dari trdapat fngsi adalah sat fngsi dari saja maka faktor intgrasi hana fngsi dari. Pnlsaian Faktor Intgrasi Jika d 0 tak ksak maka dngan mmprbanak prsamaan d 0 dngan sat fngsi bisa dijadikan prsamaan difrnsial ksak shingga d d 0 adalah prsamaan difrnsial ksak shingga brlaklah: ata Dari prsamaan ini harga dapat diari. Stlah harga dimaskkan dalam prsamaan d d 0 trjadilah prsamaan difrnsial ksak. nari Faktor Intgrasi 1 Sat prsamaan difrnsial d 2d 0 adalah tidak ksak ttapi bila dikalikan dngan F = / maka akan diprolh prsamaan difrnsial ksak: 1 d 2d 0. Slanjtna bila dislsaikan maka akan diprolh ln 2. Hal ini mngilstrasikan bahwa kadang-kadang sat prsamaan difrnsial brbntk Pd + Qd = 0 adalah tidak ksak ttapi bisa dibat ksak dngan mngalikan dngan fngsi ang ook ang brbntk F 0. Fngsi ini disbt faktor intgrasi dari d + d = 0. Brdasarakan pngalaman faktor intgrasi bisa diprolh dngan mlakkan pmriksaan. Untk ini prl diingat bbrapa difrnsial sprti dalam ontoh 75
9 Rosliana Sirgar brikt. Dalam kass-kass khss ang pnting faktor intgrasi dapat ditntkan dngan ara ang sistmatis sprti ontoh brikt. Contoh 1: Slsaikan prsamaan difrnsial brikt : d-d = 0 Pnlsaian: Psamaan difrnsial d-d = 0 adalah bkan prsamaan difrnsial ksak. Sat faktor intgrasi ang ook adalah F = 1 2 shingga diprolh: d F d d d 0; 2 = Contoh 2: Tntkan faktor-faktor intgrasi ang lain dari prsamaan difrnsial pada ontoh 1. Pnlsaian: d dln d d 2 d d d d dartan 2 2 shingga fngsi-fngsi dan adalah faktor-faktor intgrasi dari prsamaan difrnsial d-d = 0. Pnlsaian ang brssaian dngan faktor-faktor intgral it brtrt-trt adalah: ln artan. K tiga pnlsaian trsbt sara snsial adalah sama karna masing-masing mnatakan klarga garis lrs ang mlali titik asal. Contoh 2 mngilstrasikan bahwa jika trdapat sat faktor intgral F dari prsamaan difrnsial = maka slal dapat diprolh faktor-faktor intgral ang lainna karna FPd + FQd adalah difrnsial d ntk sat fngsi dan ntk sbarang H. Difrnsial ang lain adalah HFPd + FQd = Hd. Ini mnnjkkan bahwa HF adalah faktor intgral ang lain dari =. Jika F faktor intgrasi ang lain dari = maka FPd + FQd = 0 adalah sat prsamaan difrnsial ksak. Jadi sarat kksakan mnjadi FP FQ. Hal ini lbih komplk daripada prsamaan d + d = 0 ang dislsaikan. Akan diamati sat faktor intgral ang hana brgantng pada sat 76
10 Vol. 2 o. 1 Oktobr 2016 P variabl katakan. Jadi FP FQ mnjadi F Dngan mmbagi dngan FQ dan pngrtan kmbali diprolh: 1 df 1 P Q. F d Q df Q Q F. d Kass Prsamaan Difrnsial Tak Eksak Prhatikan prsamaan difrnsial d-d=0. Trlihat bahwa = dan =- shingga / 1 ttapi / 1 Jadi prsamaan difrnsialna tak ksak. Dari = d k shingga d k = +k ' / k ini hars sama dngan =-. Hal ini tidak mngkin karna k hana fngsi dari saja. Jika dignakan = d l maka akan mnghasilkan hal ang sama. Untk mnlsaikan prsamaan difrnsial tak ksak ang dmikian ini diprlkan mtod lain. Jika sat prsamaan difrnsial it ksak maka dapat dibah mnjadi tak ksak dngan mmbagi dngan sat fngsi trtnt. Prsamaan Difrnsial ang Dibat Eksak prsamaan difrnsial mnggnakan faktor intgrasi d + d = 0 Prsamaan: tak ksak F = F F df = 0 d d 0 Prsamaan: tak ksak dan prsamaan F F df = 0 d d 0 adalah ksak dan k dana adalah idntik ang mmpnai solsi ang sama. Hal ini brarti kofisin dari d dan d dngan mmpnai prbandingan ang sama. F F mrpakan faktor intgrasi 77
11 Rosliana Sirgar F F.. Jadi prsamaan difrnsial ang tak ksak jika dikalikan dngan faktor intgrasina maka akan mnjadi ksak dan apabila tidak diktahi fngsi dari maka masalah ang timbl ait akan mngalami kslitan dalam mnntkan. Contoh 3: Tntkan solsi prsamaan difrnsial ksakna dngan fngsi dari diktahi: d + d = 0. Diktahi: faktor intgrasi fngsi dari Pnlsaian: Faktor intgrasi = = + 1 = 1 0 d + = 0 d d 0 d d = 0 mrpakan prsamaan difrnsial ksak Untk mnntkan : isal: P Q Karna Prsamaan Difrnsial Eksak jadi: P Q. 0 prsamaan difrnsial dngan variabl dapat dipisahkan d d- = 0 = ln di sini adalah smbarang konstanta ambil = 1 kmbali k prsamaan: d d 0. Dipriksa apakah trbkti bnar ksak: 78
12 Vol. 2 o. 1 Oktobr trbkti d F d F ' F ' ' d d ' d d D d F = D mrpakan solsi mm prsamaan difrnsial PEUTUP Brdasarkan hasil pmbahasan trsbt dapat diambil ksimplan sbagai brikt: 1. Hasil pmbahasan dapat mmbktikan adana hbngan antara prsamaan difrnsial ksak dngan faktor intgrasi. Kaitanna ait dalam prsamaan difrnsial tak ksak ang dalam hal ini faktor intgrasi dignakan ntk mngbah prsamaan difrnsial tak ksak mnjadi prsamaan difrnsial ksak. 2. Dikatakan prsamaan difrnsial ksak apabila mmnhi sarat brikt: 0 d d d. 3. Ada 2 da ara mnlsaikan PD ksak ait dngan mnggnakan prosdr dalam torma dan dngan tknik pnglompokan. 4. Faktor intgrasi dignakan pada saat prsamaan difrnsial trsbt tak ksak ait shingga dignakanlah faktor intgrasi ntk mngbahna mnjadi prsamaan difrnsial ksak. DAFTAR PUSTAKA Edwin J Prll. Dal Varbrg Kalkls dan Gomtri Analitis. Jilid II. Jakarta: Erlangga Gazali Wikaria Kalkls Lanjtan Edisi 2. Yogakarta: Graha Ilm. ababan S Bk atri Pokok Pndahlan Prsamaan Difrnsial Biasa. Jakarta: Karnika Prll E. J Kalkls dan Gomtri Analitis Jilid 1. Erlangga: Jakarta
13 Rosliana Sirgar Stwart Jams Kalkls. Jakarta: Erlangga Spranto J atmatika Untk Ekonomi dan Bisnis Bk 1 dan 2. Fakltas Ekonomi Univrsitas Indonsia: Jakarta Wah S. B Prsamaan Difrnsial Edisi 1. Yogakarta: Graha Ilm Wbr Jan E Analisis atmatika Pnrapan Bisnis dan Ekonomi Edisi k mpat-jilid 2. Jakarta: Erlangga 80
BAB II PERSAMAAN DIFFERENSIAL ORDO SATU
 BAB II PERSAAA DIERESIAL ORDO SATU Tjan Pmblajaran Bab. ini, mrpakan lanjtan dari pmbahasan PD bab, ait jnis-jnis prsamaan diffrnsial ordo sat dan ara-ara pnlsaianna. Diantarana adalah Prsamaan Trpisah,
BAB II PERSAAA DIERESIAL ORDO SATU Tjan Pmblajaran Bab. ini, mrpakan lanjtan dari pmbahasan PD bab, ait jnis-jnis prsamaan diffrnsial ordo sat dan ara-ara pnlsaianna. Diantarana adalah Prsamaan Trpisah,
8. FUNGSI TRANSENDEN
 8. FUNGSI TRANSENDEN 8. Fngsi Invrs Misalkan : D R dngan Dinisi 8. Fngsi = disbt sat-sat jika = v maka = v ata jika v maka v v ngsi = sat-sat ngsi =- sat-sat ngsi tidak sat-sat INF8 Kalkls Dasar Scara
8. FUNGSI TRANSENDEN 8. Fngsi Invrs Misalkan : D R dngan Dinisi 8. Fngsi = disbt sat-sat jika = v maka = v ata jika v maka v v ngsi = sat-sat ngsi =- sat-sat ngsi tidak sat-sat INF8 Kalkls Dasar Scara
BAB 2. TURUNAN PARSIAL
 BAB TURUNAN PARSIAL PENDAHULUAN Pada bagian ini akan dilajari rlasan kons trnan ngsi sat bah k trnan ngsi da bah ata lbih Stlah mmlajari bab ini anda akan daat: - Mnntkan trnan arsial ngsi da bah ata lbih
BAB TURUNAN PARSIAL PENDAHULUAN Pada bagian ini akan dilajari rlasan kons trnan ngsi sat bah k trnan ngsi da bah ata lbih Stlah mmlajari bab ini anda akan daat: - Mnntkan trnan arsial ngsi da bah ata lbih
PERTEMUAN-4 dan 5. [PD. Menggunakan faktor Integrasi] (1) ) Tidak Eksak (2)
![PERTEMUAN-4 dan 5. [PD. Menggunakan faktor Integrasi] (1) ) Tidak Eksak (2) PERTEMUAN-4 dan 5. [PD. Menggunakan faktor Integrasi] (1) ) Tidak Eksak (2)](/thumbs/53/32024190.jpg) ERTEUA- an 5. ang apat ibat Eksak [. nggnakan faktor Intgrasi] Jika: Tiak Eksak rsamaan tiak ksak an prsamaan aalah ksak an kana aalah intik ang mmpnai solsi ang sama. Hal ini brarti kofisin ari an ngan
ERTEUA- an 5. ang apat ibat Eksak [. nggnakan faktor Intgrasi] Jika: Tiak Eksak rsamaan tiak ksak an prsamaan aalah ksak an kana aalah intik ang mmpnai solsi ang sama. Hal ini brarti kofisin ari an ngan
Ringkasan Materi Kuliah METODE-METODE DASAR PERSAMAAN DIFERENSIAL ORDE SATU
 Ringkasan atri Kuliah ETODE-ETODE DASAR PERSAAAN DIFERENSIAL ORDE SATU Pndahuluan Prsamaan dirnsial adalah prsamaan ang mmuat turunan satu atau bbrapa) ungsi ang takdiktahui skipun prsamaan sprti itu harusna
Ringkasan atri Kuliah ETODE-ETODE DASAR PERSAAAN DIFERENSIAL ORDE SATU Pndahuluan Prsamaan dirnsial adalah prsamaan ang mmuat turunan satu atau bbrapa) ungsi ang takdiktahui skipun prsamaan sprti itu harusna
Universitas Indonusa Esa Unggul Fakultas Ilmu Komputer Teknik Informatika. Persamaan Diferensial Orde I
 Univrsitas Indonusa Esa Unggul Fakultas Ilmu Komputr Tknik Informatika Prsamaan Difrnsial Ord I Dfinisi Prsamaan Difrnsial Prsamaan difrnsial adalah suatu prsamaan ang mmuat satu atau lbih turunan fungsi
Univrsitas Indonusa Esa Unggul Fakultas Ilmu Komputr Tknik Informatika Prsamaan Difrnsial Ord I Dfinisi Prsamaan Difrnsial Prsamaan difrnsial adalah suatu prsamaan ang mmuat satu atau lbih turunan fungsi
8. Fungsi Logaritma Natural, Eksponensial, Hiperbolik
 8. Fungsi Logaritma Natural, Eksponnsial, Hiprbolik 8.. Fungsi Logarithma Natural. Sudaratno Sudirham Dfinisi. Logaritma natural adalah logaritma dngan mnggunakan basis bilangan. Bilangan ini, sprti halna
8. Fungsi Logaritma Natural, Eksponnsial, Hiprbolik 8.. Fungsi Logarithma Natural. Sudaratno Sudirham Dfinisi. Logaritma natural adalah logaritma dngan mnggunakan basis bilangan. Bilangan ini, sprti halna
TINJAUAN ULANG EKSPANSI ASIMTOTIK UNTUK MASALAH BOUNDARY LAYER
 TINJAUAN ULANG EKSPANSI ASIMTOTIK UNTUK MASALAH BOUNDARY LAYER HannaA Parhusip Cntr of Applid Mathmatics Program Studi Matmatika Industri dan Statistika Fakultas Sains dan Matmatika Univrsitas Kristn Sata
TINJAUAN ULANG EKSPANSI ASIMTOTIK UNTUK MASALAH BOUNDARY LAYER HannaA Parhusip Cntr of Applid Mathmatics Program Studi Matmatika Industri dan Statistika Fakultas Sains dan Matmatika Univrsitas Kristn Sata
BAB IV SIMULASI MODEL
 BAB IV SIMULASI MODEL Dalam Bab III tlah dilaskan sifat-sifat sistm dinamis dari modl k & t) = yˆ t) k t), =, srta modl k& t) = yˆ k t), k t)) k t) =, khssnya φ η) = 0. Skarang akan dibat simlasi modl
BAB IV SIMULASI MODEL Dalam Bab III tlah dilaskan sifat-sifat sistm dinamis dari modl k & t) = yˆ t) k t), =, srta modl k& t) = yˆ k t), k t)) k t) =, khssnya φ η) = 0. Skarang akan dibat simlasi modl
Integral Fungsi Eksponen, Fungsi Trigonometri, Fungsi Logaritma
 Modul Intgral Fungsi Eksponn, Fungsi Trigonomtri, Fungsi Logaritma Dr. Subanar D PENDAHULUAN alam mata kuliah Kalkulus I Anda tlah mngnal bahwa intgrasi adalah pross balikan dari difrnsiasi. Jadi untuk
Modul Intgral Fungsi Eksponn, Fungsi Trigonomtri, Fungsi Logaritma Dr. Subanar D PENDAHULUAN alam mata kuliah Kalkulus I Anda tlah mngnal bahwa intgrasi adalah pross balikan dari difrnsiasi. Jadi untuk
BAB I METODE NUMERIK SECARA UMUM
 BAB I METODE NUMERIK SECARA UMUM Aplikasi modl matmatika banyak muncul dalam brbagai disiplin ilmu pngtahuan, sprti isika, kimia, konomi, prsoalan rkayasa (tknik msin, sipil, lktro). Modl matmatika yang
BAB I METODE NUMERIK SECARA UMUM Aplikasi modl matmatika banyak muncul dalam brbagai disiplin ilmu pngtahuan, sprti isika, kimia, konomi, prsoalan rkayasa (tknik msin, sipil, lktro). Modl matmatika yang
Bab 6 Sumber dan Perambatan Galat
 Mtod Pnlitian Suradi Sirgar Bab 6 Sumbr dan Prambatan Galat 6. Sumbr galat. Data masukan, misal hasil pngukuran (galat bawaan). Slama komputasi (galat pross), galat ang timbul akibat komputasi 3. Galat
Mtod Pnlitian Suradi Sirgar Bab 6 Sumbr dan Prambatan Galat 6. Sumbr galat. Data masukan, misal hasil pngukuran (galat bawaan). Slama komputasi (galat pross), galat ang timbul akibat komputasi 3. Galat
PENDEKATAN FUNGSI EI SECARA NUMERIK
 PENDEKATAN FUNGSI EI SECARA NUMERIK TUGAS AKHIR Olh: SUKANTO NIM 40 Diajkan sbagai salah sat syarat ntk mndapatkan glar SARJANA TEKNIK pada Program Stdi Tknik Prminyakan PROGRAM STUDI TEKNIK PERMINYAKAN
PENDEKATAN FUNGSI EI SECARA NUMERIK TUGAS AKHIR Olh: SUKANTO NIM 40 Diajkan sbagai salah sat syarat ntk mndapatkan glar SARJANA TEKNIK pada Program Stdi Tknik Prminyakan PROGRAM STUDI TEKNIK PERMINYAKAN
II. LANDASAN TEORI. digunakan sebagai landasan teori pada penelitian ini. Teori dasar mengenai graf
 II. LANDASAN TEORI 2.1 Konsp Dasar Graf Pada bagian ini akan dibrikan konsp dasar graf dan dimnsi partisi graf yang digunakan sbagai landasan tori pada pnlitian ini. Tori dasar mngnai graf yang akan digunakan
II. LANDASAN TEORI 2.1 Konsp Dasar Graf Pada bagian ini akan dibrikan konsp dasar graf dan dimnsi partisi graf yang digunakan sbagai landasan tori pada pnlitian ini. Tori dasar mngnai graf yang akan digunakan
UJI KESELARASAN FUNGSI (GOODNESS-OF-FIT TEST)
 UJI CHI KUADRAT PENDAHULUAN Distribusi chi kuadrat mrupakan mtod pngujian hipotsa trhadap prbdaan lbih dari proporsi. Contoh: manajr pmasaran suatu prusahaan ingin mngtahui apakah prbdaan proporsi pnjualan
UJI CHI KUADRAT PENDAHULUAN Distribusi chi kuadrat mrupakan mtod pngujian hipotsa trhadap prbdaan lbih dari proporsi. Contoh: manajr pmasaran suatu prusahaan ingin mngtahui apakah prbdaan proporsi pnjualan
KARAKTERISASI ELEMEN IDEMPOTEN CENTRAL
 Jurnal Barkng Vol 5 No Hal 33 39 (0) KAAKTEISASI ELEMEN IDEMPOTEN CENTAL HENY W M PATTY, ELVINUS ICHAD PESULESSY, UDI WOLTE MATAKUPAN 3,,3 Staf Jurusan Matmatika FMIPA UNPATTI Jl Ir M Putuhna, Kampus Unpatti,
Jurnal Barkng Vol 5 No Hal 33 39 (0) KAAKTEISASI ELEMEN IDEMPOTEN CENTAL HENY W M PATTY, ELVINUS ICHAD PESULESSY, UDI WOLTE MATAKUPAN 3,,3 Staf Jurusan Matmatika FMIPA UNPATTI Jl Ir M Putuhna, Kampus Unpatti,
Aplikasi Integral. Panjang sebuah kurva w(y) sepanjang selang dapat ditemukan menggunakan persamaan
 Aplikasi Intgral Intgral dapat diaplikasikan k dalam banyak hal. Dari yang sdrhana, hingga aplikasi prhitungan yang sangat komplks. Brikut mrupakan aplikasi-aplikasi intgral yang tlah diklompokkan dalam
Aplikasi Intgral Intgral dapat diaplikasikan k dalam banyak hal. Dari yang sdrhana, hingga aplikasi prhitungan yang sangat komplks. Brikut mrupakan aplikasi-aplikasi intgral yang tlah diklompokkan dalam
Analisis Rangkaian Listrik
 Sudaryatno Sudirham Analisis Rangkaian Listrik Mnggunakan Transformasi Fourir - Sudaryatno Sudirham, Analisis Rangkaian Listrik (4) BAB Analisis Rangkaian Mnggunakan Transformasi Fourir Dngan pmbahasan
Sudaryatno Sudirham Analisis Rangkaian Listrik Mnggunakan Transformasi Fourir - Sudaryatno Sudirham, Analisis Rangkaian Listrik (4) BAB Analisis Rangkaian Mnggunakan Transformasi Fourir Dngan pmbahasan
BAB III LIMIT DAN FUNGSI KONTINU
 BAB III LIMIT DAN FUNGSI KONTINU Konsep it mempnyai peranan yang sangat penting di dalam kalkls dan berbagai bidang matematika. Oleh karena it, konsep ini sangat perl ntk dipahami. Meskipn pada awalnya
BAB III LIMIT DAN FUNGSI KONTINU Konsep it mempnyai peranan yang sangat penting di dalam kalkls dan berbagai bidang matematika. Oleh karena it, konsep ini sangat perl ntk dipahami. Meskipn pada awalnya
Materike April 2014
 Matrik-6 Pnggunaan Intgral Tak Tntu 10 April 014 Prsamaan Difrnsial dan Pnggunaanna Prsamaan difrnsial mngaitkan suatu fungsi dngan turunanna ( difrnsial Contoh ' ' '' ' Prsamaan Difrnsial dan Pnggunaanna
Matrik-6 Pnggunaan Intgral Tak Tntu 10 April 014 Prsamaan Difrnsial dan Pnggunaanna Prsamaan difrnsial mngaitkan suatu fungsi dngan turunanna ( difrnsial Contoh ' ' '' ' Prsamaan Difrnsial dan Pnggunaanna
Materi ke - 6. Penggunaan Integral Tak Tentu. 30 Maret 2015
 Matri k - 6 Pnggunaan Intgral Tak Tntu 30 Mart 015 Industrial Enginring UNS ko@uns.ac.id Prsamaan Difrnsial dan Pnggunaanna Prsamaan difrnsial mngaitkan suatu fungsi dngan turunanna difrnsial Contoh '
Matri k - 6 Pnggunaan Intgral Tak Tntu 30 Mart 015 Industrial Enginring UNS ko@uns.ac.id Prsamaan Difrnsial dan Pnggunaanna Prsamaan difrnsial mngaitkan suatu fungsi dngan turunanna difrnsial Contoh '
Presentasi 2. Isi: Solusi Persamaan Diferensial pada Saluran Transmisi
 Prsntasi Isi: Solusi Prsamaan Difrnsial pada Saluran Transmisi Rprsntasi sinyal dalam bntuk phasor Pmikiran Dasar Sinyal harmonis mudah untuk diturunkan dan diintgralkan Smua sinyal fungsi waktu bisa dirprsntasikan
Prsntasi Isi: Solusi Prsamaan Difrnsial pada Saluran Transmisi Rprsntasi sinyal dalam bntuk phasor Pmikiran Dasar Sinyal harmonis mudah untuk diturunkan dan diintgralkan Smua sinyal fungsi waktu bisa dirprsntasikan
METODE ITERASI KELUARGA CHEBYSHEV-HALLEY UNTUK MENYELESAIKAN PERSAMAAN NONLINEAR. Yuli Syafti Purnama 1 ABSTRACT
 METODE ITERASI KELUARGA CHEBYSHEV-HALLEY UNTUK MENYELESAIKAN PERSAMAAN NONLINEAR Yuli Syafti Purnama Mahasiswa Program Studi S Matmatika Fakultas Matmatika dan Ilmu Pngtahuan Alam Univrsitas Riau Kampus
METODE ITERASI KELUARGA CHEBYSHEV-HALLEY UNTUK MENYELESAIKAN PERSAMAAN NONLINEAR Yuli Syafti Purnama Mahasiswa Program Studi S Matmatika Fakultas Matmatika dan Ilmu Pngtahuan Alam Univrsitas Riau Kampus
Oleh : Bustanul Arifin K BAB IV HASIL PENELITIAN. Nama N Mean Std. Deviation Minimum Maximum X ,97 3,
 Kpdulian trhadap sanitasi lingkungan diprdiksi dari tingkat pndidikan ibu dan pndapatan kluarga pada kluarga sjahtra I klurahan Krtn kcamatan Lawyan kota Surakarta Olh : Bustanul Arifin K.39817 BAB IV
Kpdulian trhadap sanitasi lingkungan diprdiksi dari tingkat pndidikan ibu dan pndapatan kluarga pada kluarga sjahtra I klurahan Krtn kcamatan Lawyan kota Surakarta Olh : Bustanul Arifin K.39817 BAB IV
PELABELAN TOTAL SISI ANTI AJAIB SUPER (PTSAAS) PADA GABUNGAN GRAF BINTANG GANDA DAN LINTASAN
 JIMT ol. 9 No. 1 Juni 01 (Hal. 16 8) Jurnal Ilmiah Matmatika dan Trapan ISSN : 450 766X PELABELAN TOTAL SISI ANTI AJAIB SUPER (PTSAAS) PADA GABUNGAN GRAF BINTANG GANDA DAN LINTASAN Nurainun 1, S. Musdalifah,
JIMT ol. 9 No. 1 Juni 01 (Hal. 16 8) Jurnal Ilmiah Matmatika dan Trapan ISSN : 450 766X PELABELAN TOTAL SISI ANTI AJAIB SUPER (PTSAAS) PADA GABUNGAN GRAF BINTANG GANDA DAN LINTASAN Nurainun 1, S. Musdalifah,
Transformasi Peubah Acak (Lanjutan)
 Dpt. Statistika IPB, 0 Transormasi Pubah Acak Lanjutan B. Mtod Pnggantian Pubah Mtod ini mrupakan pngmbangan dari mtod ungsi sbaran. Misalkan diktahui kp bagi p.a. adalah x. Jika didinisikan p.a. lainna
Dpt. Statistika IPB, 0 Transormasi Pubah Acak Lanjutan B. Mtod Pnggantian Pubah Mtod ini mrupakan pngmbangan dari mtod ungsi sbaran. Misalkan diktahui kp bagi p.a. adalah x. Jika didinisikan p.a. lainna
Pembahasan Soal. Pak Anang SELEKSI MASUK UNIVERSITAS INDONESIA. Disertai TRIK SUPERKILAT dan LOGIKA PRAKTIS. Disusun Oleh :
 Pmbahasan Soal SELEKSI MASUK UNIVERSITAS INDONESIA Disrtai TRIK SUPERKILAT dan LOGIKA PRAKTIS Disusun Olh : Pak Anang Kumpulan SMART SOLUTION dan TRIK SUPERKILAT Pmbahasan Soal SIMAK UI 2011 Matmatika
Pmbahasan Soal SELEKSI MASUK UNIVERSITAS INDONESIA Disrtai TRIK SUPERKILAT dan LOGIKA PRAKTIS Disusun Olh : Pak Anang Kumpulan SMART SOLUTION dan TRIK SUPERKILAT Pmbahasan Soal SIMAK UI 2011 Matmatika
BAB IV HASIL PENELITIAN DAN PEMBAHASAN. Data penelitian diperoleh dari siswa kelas XII Jurusan Teknik Elektronika
 BAB IV HASIL PENELITIAN DAN PEMBAHASAN A. DESKRIPSI DATA Data pnlitian diprolh dari siswa klas XII Jurusan Tknik Elktronika Industri SMK Ma arif 1 kbumn. Data variabl pngalaman praktik industri, kmandirian
BAB IV HASIL PENELITIAN DAN PEMBAHASAN A. DESKRIPSI DATA Data pnlitian diprolh dari siswa klas XII Jurusan Tknik Elktronika Industri SMK Ma arif 1 kbumn. Data variabl pngalaman praktik industri, kmandirian
METODE ITERASI TANPA TURUNAN BERDASARKAN EKSPANSI TAYLOR UNTUK MENYELESAIKAN PERSAMAAN NONLINEAR ABSTRACT
 METODE ITERASI TANPA TURUNAN BERDASARKAN EKSPANSI TAYLOR UNTUK MENYELESAIKAN PERSAMAAN NONLINEAR E. Yuliani, M. Imran, S. Putra Mahasiswa Program Studi S Matmatika Laboratorium Matmatika Trapan, Jurusan
METODE ITERASI TANPA TURUNAN BERDASARKAN EKSPANSI TAYLOR UNTUK MENYELESAIKAN PERSAMAAN NONLINEAR E. Yuliani, M. Imran, S. Putra Mahasiswa Program Studi S Matmatika Laboratorium Matmatika Trapan, Jurusan
Diskritisasi Persamaan Difusi Permanen Satu Dimensi dengan Metode Volume Hingga Istiarto JTSL FT UGM
 Isiaro Jrsan Tknik Sipil dan Lingkngan FT UGM hp://isiaro.saff.gm.ac.id mail: isiaro@gm.ac.id DIFUSI PERMANEN SATU DIMENSI Diskriisasi Prsamaan Difsi Prmann Sa Dimnsi dngan Mod Volm Hingga Isiaro JTSL
Isiaro Jrsan Tknik Sipil dan Lingkngan FT UGM hp://isiaro.saff.gm.ac.id mail: isiaro@gm.ac.id DIFUSI PERMANEN SATU DIMENSI Diskriisasi Prsamaan Difsi Prmann Sa Dimnsi dngan Mod Volm Hingga Isiaro JTSL
Desain Kontrol Vibrasi Semi Aktif Reaksi Fixed Point Menggunakan Pengontrol H
 sain Kontrol Vibrasi Smi Aktif Raksi Fixd Point Mnggnakan Pngontrol H Strisno, idowati Jrsan Matmatika FMIPA UNIP ABSTRAK sain kontrol vibrasi strktr tip smi aktif raksi fixd point trdiri dari Massa, Pgas,
sain Kontrol Vibrasi Smi Aktif Raksi Fixd Point Mnggnakan Pngontrol H Strisno, idowati Jrsan Matmatika FMIPA UNIP ABSTRAK sain kontrol vibrasi strktr tip smi aktif raksi fixd point trdiri dari Massa, Pgas,
PERTEMUAN-2. Persamaan Diferensial Homogen. Persamaan diferensial yang unsur x dan y tidak dapat dipisah n. Contoh: 1.
 PERTEMUAN- Persamaan Diferensial Homogen Persamaan diferensial ang nsr dan tidak daat diisah n semana. F t, t) t. F, ) Contoh:. F, ) 7 F t, t) t F t, t) t t t 7t 7. F, ) Homogen derajat ). F, ) F t, t)
PERTEMUAN- Persamaan Diferensial Homogen Persamaan diferensial ang nsr dan tidak daat diisah n semana. F t, t) t. F, ) Contoh:. F, ) 7 F t, t) t F t, t) t t t 7t 7. F, ) Homogen derajat ). F, ) F t, t)
model pengukuran yang menunjukkan ukur Pengukuran dalam B. Model Mode sama indikator dan 1 Pag
 Modl Modl Pngukuran dalam Pmodlan Prsamaan Struktural Wahyu Widhiarso Fakultas Psikologi UGM Tulisan ini akan mmbahas bbrapa modl dalam SEM yang unik. Dikatakan unik karna jarang dipakai. Tulisan hanya
Modl Modl Pngukuran dalam Pmodlan Prsamaan Struktural Wahyu Widhiarso Fakultas Psikologi UGM Tulisan ini akan mmbahas bbrapa modl dalam SEM yang unik. Dikatakan unik karna jarang dipakai. Tulisan hanya
Analisis Dinamis Portal Bertingkat Banyak Multi Bentang Dengan Variasi Tingkat (Storey) Pada Tiap Bentang
 Analisis Dinamis Portal Brtingkat Banyak Multi Bntang Dngan Variasi Tingkat (Story) Pada Tiap Bntang Hiryco Manalip Rky Stnly Windah Jams Albrt Kaunang Univrsitas Sam Ratulangi Fakultas Tknik Jurusan Sipil
Analisis Dinamis Portal Brtingkat Banyak Multi Bntang Dngan Variasi Tingkat (Story) Pada Tiap Bntang Hiryco Manalip Rky Stnly Windah Jams Albrt Kaunang Univrsitas Sam Ratulangi Fakultas Tknik Jurusan Sipil
Hendra Gunawan. 29 November 2013
 MA1101 MATEMATIKA 1A Hndra Gunawan Smstr I, 013/014 9 Novmbr 013 Latihan (Kuliah yang Lalu) Ssorangygtingginya~1,60 m brdiri ditpiatastbing, mlihat lh k laut yang brada ~18,40 m di bawahnya. Pada saatitu
MA1101 MATEMATIKA 1A Hndra Gunawan Smstr I, 013/014 9 Novmbr 013 Latihan (Kuliah yang Lalu) Ssorangygtingginya~1,60 m brdiri ditpiatastbing, mlihat lh k laut yang brada ~18,40 m di bawahnya. Pada saatitu
MODUL PERKULIAHAN REKAYASA FONDASI 1. Penurunan Tanah pada Fondasi Dangkal. Fakultas Program Studi Tatap Muka Kode MK Disusun Oleh
 MODUL PERKULIAHAN REKAYASA FONDASI 1 Pnurunan Tanah pada Fondasi Dangkal Fakultas Program Studi Tatap Muka Kod MK Disusun Olh Tknik Prnanaan Tknik A41117AB dan Dsain Sipil 9 Abstrat Modul ini brisi bbrapa
MODUL PERKULIAHAN REKAYASA FONDASI 1 Pnurunan Tanah pada Fondasi Dangkal Fakultas Program Studi Tatap Muka Kod MK Disusun Olh Tknik Prnanaan Tknik A41117AB dan Dsain Sipil 9 Abstrat Modul ini brisi bbrapa
BAB 2 LANDASAN TEORI
 6 BAB LANDASAN TEORI Pada bab ini akan diuraikan mngnai tori dan trminologi graph, yaitu bntuk-bntuk khusus suatu graph. Di sini uga akan dilaskan mngnai minimum spanning tr, pmrograman 0-, dan aplikasi
6 BAB LANDASAN TEORI Pada bab ini akan diuraikan mngnai tori dan trminologi graph, yaitu bntuk-bntuk khusus suatu graph. Di sini uga akan dilaskan mngnai minimum spanning tr, pmrograman 0-, dan aplikasi
Pengembangan Hasil Kali Titik Pada Vektor
 Pengembangan Hasil Kali Titik Pada Vektor Swandi *, Sri Gemawati 2, Samsdhha 2 Mahasiswa Program Stdi Magister Matematika, Dosen Pendidikan Matematika Uniersitas Pasir Pengaraian 2 Dosen Jrsan Matematika
Pengembangan Hasil Kali Titik Pada Vektor Swandi *, Sri Gemawati 2, Samsdhha 2 Mahasiswa Program Stdi Magister Matematika, Dosen Pendidikan Matematika Uniersitas Pasir Pengaraian 2 Dosen Jrsan Matematika
BAB II TEORI DASAR 2.1 Pengertian Pasang Surut
 BAB II TEORI DASAR 2.1 Pngrtian Pasang Surut Pasang surut air laut (pasut) adalah pristiwa naik turunnya muka air scara priodik dngan rata-rata priodnya 12,4 jam (di bbrapa tmpat 24,8 jam) (Pond dan Pickard,
BAB II TEORI DASAR 2.1 Pngrtian Pasang Surut Pasang surut air laut (pasut) adalah pristiwa naik turunnya muka air scara priodik dngan rata-rata priodnya 12,4 jam (di bbrapa tmpat 24,8 jam) (Pond dan Pickard,
1. Proses Normalisasi
 BAB IV PEMBAHASAN A. Pr-Procssing Pross pngolahan signal PCG sblum dilakukan kstaksi dan klasifikasi adalah pr-procssing. Signal PCG untuk data training dan data tsting trdapat dalam lampiran 5 (halaman
BAB IV PEMBAHASAN A. Pr-Procssing Pross pngolahan signal PCG sblum dilakukan kstaksi dan klasifikasi adalah pr-procssing. Signal PCG untuk data training dan data tsting trdapat dalam lampiran 5 (halaman
Bab 1 Ruang Vektor. I. 1 Ruang Vektor R n. 1. Ruang berdimensi satu R 1 = R = kumpulan bilangan real Menyatakan suatu garis bilangan;
 Bab Ruang Vktor I. Ruang Vktor R n. Ruang brdimnsi satu R = R = kumpulan bilangan ral Mnyatakan suatu garis bilangan; -3 - - 0. Ruang brdimnsi dua R = bidang datar ; Stiap vktor di R dinyatakan sbagai
Bab Ruang Vktor I. Ruang Vktor R n. Ruang brdimnsi satu R = R = kumpulan bilangan ral Mnyatakan suatu garis bilangan; -3 - - 0. Ruang brdimnsi dua R = bidang datar ; Stiap vktor di R dinyatakan sbagai
PENENTUAN NILAI e/m ELEKTRON
 Pnntuan Nilai E/m Elktron 013 PENENTUAN NILAI /m ELEKTRON Intan Masruroh S, Anita Susanti, Rza Ruzuqi, Zaky Alam Laboratorium Fisika Radiasi, Dpartmn Fisika Fakultas Sains Dan Tknologi, Univrsitas Airlangga
Pnntuan Nilai E/m Elktron 013 PENENTUAN NILAI /m ELEKTRON Intan Masruroh S, Anita Susanti, Rza Ruzuqi, Zaky Alam Laboratorium Fisika Radiasi, Dpartmn Fisika Fakultas Sains Dan Tknologi, Univrsitas Airlangga
HASIL DAN PEMBAHASAN. Gambar 3 Proses penentuan perilaku api.
 6 yang diharapkan. Msin infrnsi disusun brdasarkan stratgi pnalaran yang akan digunakan dalam sistm dan rprsntasi pngtahuan. Msin infrnsi yang digunakan dalam pngmbangan sistm pakar ini adalah FIS. Implmntasi
6 yang diharapkan. Msin infrnsi disusun brdasarkan stratgi pnalaran yang akan digunakan dalam sistm dan rprsntasi pngtahuan. Msin infrnsi yang digunakan dalam pngmbangan sistm pakar ini adalah FIS. Implmntasi
MODEL PERSEDIAAN DETERMINISTIK DENGAN MEMPERTIMBANGKAN MASA KADALUARSA DAN PENURUNAN HARGA JUAL
 ISSN : 407 846 -ISSN : 460 846 MODEL PERSEDIAAN DETERMINISTIK DENGAN MEMPERTIMBANGKAN MASA KADALUARSA DAN PENURUNAN HARGA JUAL Chrish Rikardo *, Taufik Limansyah, Dharma Lsmono Magistr Tknik Industri,
ISSN : 407 846 -ISSN : 460 846 MODEL PERSEDIAAN DETERMINISTIK DENGAN MEMPERTIMBANGKAN MASA KADALUARSA DAN PENURUNAN HARGA JUAL Chrish Rikardo *, Taufik Limansyah, Dharma Lsmono Magistr Tknik Industri,
Pada gambar 2 merupakan luasan bidang dua dimensi telah mengalami regangan. Salah satu titik yang menjadi titik acuan adalah titik P.
 nurunan Kcpatan Glombang dan Glombang S Glombang sismik mrupakan gtaran yang mrambat pada mdium batuan dan mnmbus lapisan bumi. njalaran mnybabkan dformasi batuan.strss atau tkanan didfinisikan gaya prsatuan
nurunan Kcpatan Glombang dan Glombang S Glombang sismik mrupakan gtaran yang mrambat pada mdium batuan dan mnmbus lapisan bumi. njalaran mnybabkan dformasi batuan.strss atau tkanan didfinisikan gaya prsatuan
BAB V DISTRIBUSI PROBABILITAS DISKRIT
 BAB V DISTRIBUSI ROBABILITAS DISKRIT 5.. Distribusi Uniform Disrit Bila variabl aca X mmilii nilai,,... dngan probabilitas yang sama, maa distribusi uniform disrit dinyataan sbagai: f (, ) ;,,... paramtr
BAB V DISTRIBUSI ROBABILITAS DISKRIT 5.. Distribusi Uniform Disrit Bila variabl aca X mmilii nilai,,... dngan probabilitas yang sama, maa distribusi uniform disrit dinyataan sbagai: f (, ) ;,,... paramtr
DESAIN KONTROL VIBRASI SEMI AKTIF REAKSI FIXED POINT MENGGUNAKAN PENGONTROL H. Sutrisno 1 dan Widowati 2
 ESAIN KONTROL VIBRASI SEMI AKTIF REAKSI FIXE POINT MENGGUNAKAN PENGONTROL H Strisno dan idowati, Jrsan Matmatika FMIPA UNIP Jl. Prof. H. Sodarto, S.H., Tmbalang, Smarang. Abstrat. Th smi ativ fixd oint
ESAIN KONTROL VIBRASI SEMI AKTIF REAKSI FIXE POINT MENGGUNAKAN PENGONTROL H Strisno dan idowati, Jrsan Matmatika FMIPA UNIP Jl. Prof. H. Sodarto, S.H., Tmbalang, Smarang. Abstrat. Th smi ativ fixd oint
PENYELESAIAN LUAS BANGUN DATAR DAN VOLUME BANGUN RUANG DENGAN KONSEP DETERMINAN
 Bletin Ilmiah Math. Stat. dan Terapannya (Bimaster) Volme xx, No. x (tahn), hal xx xx. PENYELESAIAN LUAS BANGUN DATAR DAN VOLUME BANGUN RUANG DENGAN KONSEP DETERMINAN Doni Saptra, Helmi, Shantika Martha
Bletin Ilmiah Math. Stat. dan Terapannya (Bimaster) Volme xx, No. x (tahn), hal xx xx. PENYELESAIAN LUAS BANGUN DATAR DAN VOLUME BANGUN RUANG DENGAN KONSEP DETERMINAN Doni Saptra, Helmi, Shantika Martha
Online Jurnal of Natural Science, Vol.3(1): ISSN: March 2014
 Onlin Jurnal of Natural Scinc, ol.3(1): 65-74 ISSN: 338-0950 March 014 PELABELAN TOTAL SISI AJAIB SUPER (TSAS) PADA GABUNGAN GRAF ULAT BULU DAN BIPARTITE LENGKAP I W. Sudarsana 1, Fitria and S. Musdalifah
Onlin Jurnal of Natural Scinc, ol.3(1): 65-74 ISSN: 338-0950 March 014 PELABELAN TOTAL SISI AJAIB SUPER (TSAS) PADA GABUNGAN GRAF ULAT BULU DAN BIPARTITE LENGKAP I W. Sudarsana 1, Fitria and S. Musdalifah
SISTEM PENGOLAHAN ISYARAT. Kuliah 5 Transformasi Fourier
 TKE 403 SISTEM PENGOLAHAN ISYARAT Kuliah 5 Transformasi Fourir Bagian II Indah Susilawai, S.T., M.Eng. Program Sudi Tknik Elkro Fakulas Tknik dan Ilmu Kompur Univrsias Mrcu Buana Yogyakara 009 KULIAH 5
TKE 403 SISTEM PENGOLAHAN ISYARAT Kuliah 5 Transformasi Fourir Bagian II Indah Susilawai, S.T., M.Eng. Program Sudi Tknik Elkro Fakulas Tknik dan Ilmu Kompur Univrsias Mrcu Buana Yogyakara 009 KULIAH 5
RANCANG BANGUN PATCH RECTANGULAR ANTENNA 2.4 GHz DENGAN METODE PENCATUAN EMC (ELECTROMAGNETICALLY COUPLED)
 RANCANG BANGUN PATCH RECTANGULAR ANTENNA 2.4 GHz DENGAN METODE PENCATUAN EMC (ELECTROMAGNETICALLY COUPLED) Winny Friska Uli,Ali Hanafiah Ramb Konsntrasi Tknik Tlkomunikasi, Dpartmn Tknik Elktro Fakultas
RANCANG BANGUN PATCH RECTANGULAR ANTENNA 2.4 GHz DENGAN METODE PENCATUAN EMC (ELECTROMAGNETICALLY COUPLED) Winny Friska Uli,Ali Hanafiah Ramb Konsntrasi Tknik Tlkomunikasi, Dpartmn Tknik Elktro Fakultas
IDE - IDE DASAR MEKANIKA KUANTUM
 IDE - IDE DASAR MEKANIKA KUANTUM A. Radiasi Bnda Hitam 1. Hasil-Hasil Empiris Gambar 1. Grafik fungsi radiasi spktral bnda hitam smpurna a. Hukum Stfan Hukum Stfan dapat dituliskan sbagai total = f df
IDE - IDE DASAR MEKANIKA KUANTUM A. Radiasi Bnda Hitam 1. Hasil-Hasil Empiris Gambar 1. Grafik fungsi radiasi spktral bnda hitam smpurna a. Hukum Stfan Hukum Stfan dapat dituliskan sbagai total = f df
HUBUNGAN ANTARA KELOMPOK UMUR, JENIS KELAMIN DAN JENIS PEKERJAAN PADA PENDERITA HIV/AIDS DI KABUPATEN BANYUMAS
 18Novmbr 17 Tma 7: Ilmu-Ilmu Murni (Matmatika, Fisika, Kimia dan Biologi) HUBUNGAN ANTARA KELOMPOK UMUR, JENIS KELAMIN DAN JENIS PEKERJAAN PADA PENDERITA HIV/AIDS DI KABUPATEN BANYUMAS Olh Agung Prabowo
18Novmbr 17 Tma 7: Ilmu-Ilmu Murni (Matmatika, Fisika, Kimia dan Biologi) HUBUNGAN ANTARA KELOMPOK UMUR, JENIS KELAMIN DAN JENIS PEKERJAAN PADA PENDERITA HIV/AIDS DI KABUPATEN BANYUMAS Olh Agung Prabowo
II LANDASAN TEORI 2.1 Pengertian Opsi 2.2 Aset yang Mendasari Opsi 2.3 Nilai Opsi
 II LANDAAN EORI Pngrtian Opsi alah sat instrn rivatif yang pnyai potnsi ntk ikbangkan aalah opsi Pngrtian ari opsi aalah sat kontrak antara a pihak i ana salah sat pihak (sbagai pbli) pnyai hak ntk bli
II LANDAAN EORI Pngrtian Opsi alah sat instrn rivatif yang pnyai potnsi ntk ikbangkan aalah opsi Pngrtian ari opsi aalah sat kontrak antara a pihak i ana salah sat pihak (sbagai pbli) pnyai hak ntk bli
Tinjauan Termodinamika Sistem Partikel Tunggal Yang Terjebak Dalam Sebuah Sumur Potensial. Oleh. Saeful Karim
 Tinjauan Trmodinamika Sistm artikl Tunggal Yang Trjbak Dalam Sbua Sumur otnsial Ol Saful Karim Jurusan ndidikan Fisika Fakultas ndidikan Matmatika dan Ilmu ngtauan Alam Univrsitas ndidikan Indonsia 00
Tinjauan Trmodinamika Sistm artikl Tunggal Yang Trjbak Dalam Sbua Sumur otnsial Ol Saful Karim Jurusan ndidikan Fisika Fakultas ndidikan Matmatika dan Ilmu ngtauan Alam Univrsitas ndidikan Indonsia 00
Pertemuan XIV, XV VII. Garis Pengaruh
 ahan jar Statika ulyati, ST., T rtmuan X, X. Garis ngaruh. ndahuluan danya muatan hidup yang brgrak dari satu ujung k ujung lain pada suatu konstruksi disbut bban brgrak. isalkan ada sbuah kndaraan mlalui
ahan jar Statika ulyati, ST., T rtmuan X, X. Garis ngaruh. ndahuluan danya muatan hidup yang brgrak dari satu ujung k ujung lain pada suatu konstruksi disbut bban brgrak. isalkan ada sbuah kndaraan mlalui
FUNGSI DOMINASI ROMAWI PADA LINE GRAPH
 Bultin Ilmiah Mat. Stat. dan Trapannya (Bimastr) Volum 04, No. 2 (2015), hal 119 126. FUNGSI DOMINASI ROMAWI PADA LINE GRAPH Ysi Januarti, Mariatul Kiftiah, Nilamsari Kusumastuti INTISARI Himpunan D disbut
Bultin Ilmiah Mat. Stat. dan Trapannya (Bimastr) Volum 04, No. 2 (2015), hal 119 126. FUNGSI DOMINASI ROMAWI PADA LINE GRAPH Ysi Januarti, Mariatul Kiftiah, Nilamsari Kusumastuti INTISARI Himpunan D disbut
BAB 4 MODEL MATEMATIKA PENGARUH TERAPI OBAT TERHADAP DINAMIKA VIRUS HIV DALAM TUBUH
 BAB 4 MODEL MATEMATIKA PENGARUH TERAPI OBAT TERHADAP DINAMIKA VIRUS HIV DALAM TUBUH Sjak bbrapa ahun yang lalu, ilmuwan asal Amrika Marin Nowak dan Sbasian Bonhoffr mncoba mmplo daa dari pnliian oba ani-hiv.
BAB 4 MODEL MATEMATIKA PENGARUH TERAPI OBAT TERHADAP DINAMIKA VIRUS HIV DALAM TUBUH Sjak bbrapa ahun yang lalu, ilmuwan asal Amrika Marin Nowak dan Sbasian Bonhoffr mncoba mmplo daa dari pnliian oba ani-hiv.
ISOMORFISMA PADA GRAF P 4
 ISOMORFISMA PADA GRAF P Eka Adhistiasari, I Ktut Budayasa 2 Jurusan Matmatika, Fakultas Martmatika dan Ilmu Pngtahuan Alam, UNESA Kampus Ktintang 6023,Surabaya Email : tias-adhis@yahoocoid, ktutbudayasa@yahoocom
ISOMORFISMA PADA GRAF P Eka Adhistiasari, I Ktut Budayasa 2 Jurusan Matmatika, Fakultas Martmatika dan Ilmu Pngtahuan Alam, UNESA Kampus Ktintang 6023,Surabaya Email : tias-adhis@yahoocoid, ktutbudayasa@yahoocom
Transformasi Satu Peubah Acak (Lanjutan) Dr. Kusman Sadik, M.Si Departemen Statistika IPB, 2016
 Transformasi Satu Pubah Acak (Lanjutan) Dr. Kusman Sadik, M.Si Dpartmn Statistika IPB, 06 Transformasi Pubah Acak (Lanjutan) B. Mtod Pnggantian Pubah Mtod ini mrupakan pngmbangan dari mtod fungsi sbaran.
Transformasi Satu Pubah Acak (Lanjutan) Dr. Kusman Sadik, M.Si Dpartmn Statistika IPB, 06 Transformasi Pubah Acak (Lanjutan) B. Mtod Pnggantian Pubah Mtod ini mrupakan pngmbangan dari mtod fungsi sbaran.
BAB II TINJAUAN KEPUSTAKAAN
 BAB II TINJAUAN KEPUTAKAAN II.1 PENDAHULUAN Yild lin adalah suatu pmcahan yang dapat digunakan dalam plat bton dimana trjadinya tgangan llh dan rotasi scara plastis muncul. Tori ini dapat digunakan dalam
BAB II TINJAUAN KEPUTAKAAN II.1 PENDAHULUAN Yild lin adalah suatu pmcahan yang dapat digunakan dalam plat bton dimana trjadinya tgangan llh dan rotasi scara plastis muncul. Tori ini dapat digunakan dalam
MODEL MATEMATIKA WAKTU PENGOSONGAN TANGKI AIR
 Prosiding Seinar Nasional Penelitian, Pendidikan dan Penerapan MIPA Fakltas MIPA, Universitas Negeri Yogakarta, 6 Mei 9 MODEL MATEMATIKA WAKTU PENGOSONGAN TANGKI AIR Irawati, Kntjoro Adji Sidarto. Gr SMA
Prosiding Seinar Nasional Penelitian, Pendidikan dan Penerapan MIPA Fakltas MIPA, Universitas Negeri Yogakarta, 6 Mei 9 MODEL MATEMATIKA WAKTU PENGOSONGAN TANGKI AIR Irawati, Kntjoro Adji Sidarto. Gr SMA
Transformasi Satu Peubah Acak (Bagian II) Dr. Kusman Sadik, M.Si Departemen Statistika IPB, 2017
 Transformasi Satu Pubah Acak Bagian II) Dr. Kusman Sadik, M.Si Dpartmn Statistika IPB, 07 Transformasi Pubah Acak Lanjutan) B. Mtod Pnggantian Pubah Mtod ini mrupakan pngmbangan dari mtod fungsi sbaran.
Transformasi Satu Pubah Acak Bagian II) Dr. Kusman Sadik, M.Si Dpartmn Statistika IPB, 07 Transformasi Pubah Acak Lanjutan) B. Mtod Pnggantian Pubah Mtod ini mrupakan pngmbangan dari mtod fungsi sbaran.
Reduksi data gravitasi
 Modul 5 Rduksi data gravitasi Rduksi data gravitasi trdiri dari:. Rduksi g toritis. Rduksi fr air 3. Rduksi Bougur 4. Rduksi mdan/trrain. Rduksi g toritis Pnlaahan tntang konsp rduksi data gravitasi lbih
Modul 5 Rduksi data gravitasi Rduksi data gravitasi trdiri dari:. Rduksi g toritis. Rduksi fr air 3. Rduksi Bougur 4. Rduksi mdan/trrain. Rduksi g toritis Pnlaahan tntang konsp rduksi data gravitasi lbih
EKONOMETRIKA PERSAMAAN SIMULTAN
 EKONOMETRIKA PERSAMAAN SIMULTAN OLEH KELOMPOK 5 DEKI D. TAPATAB JUMASNI K. TANEO MERSY C. PELT DELFIANA N. ERO GERARDUS V. META ARMY A. MBATU SILVESTER LANGKAMANG FAKULTAS PERTANIAN UNIVERSITAS NUSA CENDANA
EKONOMETRIKA PERSAMAAN SIMULTAN OLEH KELOMPOK 5 DEKI D. TAPATAB JUMASNI K. TANEO MERSY C. PELT DELFIANA N. ERO GERARDUS V. META ARMY A. MBATU SILVESTER LANGKAMANG FAKULTAS PERTANIAN UNIVERSITAS NUSA CENDANA
DISTRIBUSI PROBABILITAS DARI TOTAL BIAYA PERAWATAN KOMPONEN
 DISTRIBUSI PROBABILITAS DARI TOTAL BIAYA PRAWATAN OMPONN Sono ABSTRACT Aril di h probabili diribion of h oal mainnan o of a omponn ovr a fini im horizon Th mainnan o i amd o b a fnion of h omponn lifim
DISTRIBUSI PROBABILITAS DARI TOTAL BIAYA PRAWATAN OMPONN Sono ABSTRACT Aril di h probabili diribion of h oal mainnan o of a omponn ovr a fini im horizon Th mainnan o i amd o b a fnion of h omponn lifim
Susda Heleni ABSTRACT. Keywords: Reciprocal Teaching, Cooperative Learning, STAD ABSTRAK
 PENERAPAN RECIPROCAL TEACHING DALAM MODEL PEMBELAJARAN KOOPERATIF TIPE STAD UNTUK MENINGKATKAN HASIL BELAJAR MAHASISWA PADA MATA KULIAH KALKULUS I THE IMPLEMENTATION OF RECIPROCAL TEACHING ON COOPERATIVE
PENERAPAN RECIPROCAL TEACHING DALAM MODEL PEMBELAJARAN KOOPERATIF TIPE STAD UNTUK MENINGKATKAN HASIL BELAJAR MAHASISWA PADA MATA KULIAH KALKULUS I THE IMPLEMENTATION OF RECIPROCAL TEACHING ON COOPERATIVE
Modifikasi Analytic Network Process Untuk Rekomendasi Pemilihan Handphone
 Modifikasi Analytic Ntwork Procss Untuk Rkomndasi Pmilihan Handphon Fry Dwi Hrmawan Jurusan Informatika Fakultas MIPA, Univrsitas Sblas Mart Surakarta frydh@yahoocom Ristu Saptono Jurusan Informatika Fakultas
Modifikasi Analytic Ntwork Procss Untuk Rkomndasi Pmilihan Handphon Fry Dwi Hrmawan Jurusan Informatika Fakultas MIPA, Univrsitas Sblas Mart Surakarta frydh@yahoocom Ristu Saptono Jurusan Informatika Fakultas
Direct Model Reference Adaptive Control (DMRAC) untuk Sistem Pengaturan Kecepatan Motor DC
 Dirct Modl Rfrnc Adativ ontrol (DMRA) ntk istm Pngatran Kcatan Motor D Widya Nila Vlayati (86) Laboratorim knik Pngatran Jrsan knik Elktro -, Kams Ktih, kolilo, rabaya 6 Email : vla@lct-ng.its.ac.id Abstrak
Dirct Modl Rfrnc Adativ ontrol (DMRA) ntk istm Pngatran Kcatan Motor D Widya Nila Vlayati (86) Laboratorim knik Pngatran Jrsan knik Elktro -, Kams Ktih, kolilo, rabaya 6 Email : vla@lct-ng.its.ac.id Abstrak
Pengaruh Posisi Pipa Segi Empat dalam Aliran Fluida Terhadap Perpindahan Panas
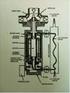 Pngaruh Posisi Pipa Sgi Empat dalam Aliran Fluida Trhadap Prpindahan Panas Kaprawi Jurusan Tknik Msin, Fakultas Tknik UNSRI, Palmbang E-mail: kaprawis@yahoo.com ABSTRAK Sbuah pipa brpnampang sgi mpat dipasang
Pngaruh Posisi Pipa Sgi Empat dalam Aliran Fluida Trhadap Prpindahan Panas Kaprawi Jurusan Tknik Msin, Fakultas Tknik UNSRI, Palmbang E-mail: kaprawis@yahoo.com ABSTRAK Sbuah pipa brpnampang sgi mpat dipasang
Tinjauan Termodinamika Pada Sistem Partikel Tunggal Yang Terjebak Dalam Sebuah Sumur Potensial
 injauan rmodinamika ada Sistm artikl unggal Yang rjbak Dalam Sbua Sumur otnsial Dngan mngmbangkan ubungan trmodinamik yang sdrana untuk pngumpulan partikl yang tunggal yang ditmpatkan pada dara potnsial.
injauan rmodinamika ada Sistm artikl unggal Yang rjbak Dalam Sbua Sumur otnsial Dngan mngmbangkan ubungan trmodinamik yang sdrana untuk pngumpulan partikl yang tunggal yang ditmpatkan pada dara potnsial.
ANALISA PENGARUH PACK CARBURIZING MENGGUNAKAN ARANG MLANDING UNTUK MENINGKATKAN SIFAT MEKANIS SPROKET SEPEDA MOTOR SUZUKI
 Analisa Pngaruh Pack Carburizing Mnggunakan Arang Mlanding (Mas ad dkk.) ANALISA PENGARUH PACK CARBURIZING MENGGUNAKAN ARANG MLANDING UNTUK MENINGKATKAN SIFAT MEKANIS SPROKET SEPEDA MOTOR SUZUKI Mas ad,
Analisa Pngaruh Pack Carburizing Mnggunakan Arang Mlanding (Mas ad dkk.) ANALISA PENGARUH PACK CARBURIZING MENGGUNAKAN ARANG MLANDING UNTUK MENINGKATKAN SIFAT MEKANIS SPROKET SEPEDA MOTOR SUZUKI Mas ad,
BAB NILAI EIGEN DAN VEKTOR EIGEN
 BAB 8 RUANG EIGEN Masalah nilai dan vkor ign banyak skali dijumpai dalam bidang rkayasa, spri maslah ksabilan sism, opimasi dngan SVD, komprsi pada pngolahan cira, dan lain-lain. Unuk lbih mmahami masalah
BAB 8 RUANG EIGEN Masalah nilai dan vkor ign banyak skali dijumpai dalam bidang rkayasa, spri maslah ksabilan sism, opimasi dngan SVD, komprsi pada pngolahan cira, dan lain-lain. Unuk lbih mmahami masalah
PENGENALAN ANGKA MELALUI PERMAINAN DADU DALAM PEMBELAJARAN MATEMATIKA PADA ANAK USIA 5-6 TAHUN
 PENGENALAN ANGKA MELALUI PERMAINAN DADU DALAM PEMBELAJARAN MATEMATIKA PADA ANAK USIA 5-6 TAHUN Mlania, Masluyah Suib, Dsni Yuniarni Pndidikan Guru Pndidikan Anak Usia Dini FKIP Untan, Pontianak Email :
PENGENALAN ANGKA MELALUI PERMAINAN DADU DALAM PEMBELAJARAN MATEMATIKA PADA ANAK USIA 5-6 TAHUN Mlania, Masluyah Suib, Dsni Yuniarni Pndidikan Guru Pndidikan Anak Usia Dini FKIP Untan, Pontianak Email :
PERKEMBANGAN TEORI ATOM & PENEMUAN PROTON, NEUTRON, ELEKTRON. Putri Anjarsari, S.Si., M.Pd
 PERKEMBANGAN TEORI ATOM & PENEMUAN PROTON, NEUTRON, ELEKTRON Putri Anjarsari, S.Si., M.Pd putri_anjarsari@uny.ac.id PERKEMBANGAN TEORI ATOM Dmokritus Dalton Thomson Ruthrford Bohr Mkanika glombang Dmokritus
PERKEMBANGAN TEORI ATOM & PENEMUAN PROTON, NEUTRON, ELEKTRON Putri Anjarsari, S.Si., M.Pd putri_anjarsari@uny.ac.id PERKEMBANGAN TEORI ATOM Dmokritus Dalton Thomson Ruthrford Bohr Mkanika glombang Dmokritus
Diferensial fungsi sederhana
 Diferensial fngsi sederhana Kaidah-kaidah diferensiasi 1. Diferensiasi konstanta Jika y = k, dimana k adalah konstanta, maka / = 0 contoh : y = 5 / = 0. Diferensiasi fngsi pangkat Jika y = n, dimana n
Diferensial fngsi sederhana Kaidah-kaidah diferensiasi 1. Diferensiasi konstanta Jika y = k, dimana k adalah konstanta, maka / = 0 contoh : y = 5 / = 0. Diferensiasi fngsi pangkat Jika y = n, dimana n
FUNGSI EKSPONEN, TRIGONOMETRI DAN HYPERBOLIK BAB I FUNGSI EKSPONEN
 BAB I FUNGSI EKSPONEN Dfinisi Fungsi ksponn aalah fungsi f yang mnntukan k. Rumusnya ialah f(. Fungsi ksponn ngan pubah bbas + yi ( an y bilangan ral aalah (cos y + i sin y. Dari finisi ini, jika : y 0
BAB I FUNGSI EKSPONEN Dfinisi Fungsi ksponn aalah fungsi f yang mnntukan k. Rumusnya ialah f(. Fungsi ksponn ngan pubah bbas + yi ( an y bilangan ral aalah (cos y + i sin y. Dari finisi ini, jika : y 0
PENENTUAN RUTE TERPENDEK DENGAN MENGGUNAKAN ALGORITMA CHEAPEST INSERTION HEURISTIC (STUDI KASUS: PT.
 Bultin Ilmiah Math. Stat. dan Trapannya (Bimastr) Volum 04, No. 3 (2015), hal 295 304. PENENTUAN RUTE TERPENDEK DENGAN MENGGUNAKAN ALGORITMA CHEAPEST INSERTION HEURISTIC (STUDI KASUS: PT. Wicaksana Ovrsas
Bultin Ilmiah Math. Stat. dan Trapannya (Bimastr) Volum 04, No. 3 (2015), hal 295 304. PENENTUAN RUTE TERPENDEK DENGAN MENGGUNAKAN ALGORITMA CHEAPEST INSERTION HEURISTIC (STUDI KASUS: PT. Wicaksana Ovrsas
MODUL PERKULIAHAN. Kalkulus. Fakultas Program Studi Tatap Muka Kode MK Disusun Oleh
 MODUL PERKULIAHAN Modl Standar ntk dignakan dalam Perkliahan di Universitas Merc Bana Fakltas Program Stdi Tatap Mka Kode MK Dissn Oleh Ilm Kompter Teknik Informatika 9 Abstract Matakliah Menjadi Dasar
MODUL PERKULIAHAN Modl Standar ntk dignakan dalam Perkliahan di Universitas Merc Bana Fakltas Program Stdi Tatap Mka Kode MK Dissn Oleh Ilm Kompter Teknik Informatika 9 Abstract Matakliah Menjadi Dasar
Deret Fourier, Transformasi Fourier dan DFT
 Drt Fourir, Transformasi Fourir dan DFT A. Drt Fourir Drt fourir adalah drt yang digunakan dalam bidang rkayasa. Drt ini prtama kali ditmukan olh sorang ilmuan prancis Jan-Baptist Josph Fourir (1768-18).
Drt Fourir, Transformasi Fourir dan DFT A. Drt Fourir Drt fourir adalah drt yang digunakan dalam bidang rkayasa. Drt ini prtama kali ditmukan olh sorang ilmuan prancis Jan-Baptist Josph Fourir (1768-18).
UJI PERFORMANCE MEJA GETAR SATU DERAJAT KEBEBASAN DENGAN METODE STFT
 UJI PERFORMANCE MEJA GETAR SATU DERAJAT KEBEBASAN DENGAN METODE STFT Jhon Malta (1) (1) Laboratorium Dinamika Struktur Jurusan Tknik Msin Fakultas Tknik Univrsitas Andalas, Padang. Email: jhonmalta@ft.unand.ac.id
UJI PERFORMANCE MEJA GETAR SATU DERAJAT KEBEBASAN DENGAN METODE STFT Jhon Malta (1) (1) Laboratorium Dinamika Struktur Jurusan Tknik Msin Fakultas Tknik Univrsitas Andalas, Padang. Email: jhonmalta@ft.unand.ac.id
BAB VI MODEL ELEKTRON BEBAS ( GAS FERMI )
 A VI MODL LKRON AS GAS RMI MARI 6.1. ltron bbas dalam satu dimnsi. 6.1.1.tingat nrgi 6.1..distribusi rmi-dirac 6.1..nrgi rmi 6.. ltron bbas dalam tiga dimnsi. 6..1.nrgi rmi untu tiga dimnsi. 6...cpatan
A VI MODL LKRON AS GAS RMI MARI 6.1. ltron bbas dalam satu dimnsi. 6.1.1.tingat nrgi 6.1..distribusi rmi-dirac 6.1..nrgi rmi 6.. ltron bbas dalam tiga dimnsi. 6..1.nrgi rmi untu tiga dimnsi. 6...cpatan
IV. Konsolidasi. Pertemuan VII
 Prtmuan VII IV. Konsolidasi IV. Pndahuluan. Konsolidasi adalah pross brkurangnya volum atau brkurangnya rongga pori dari tanah jnuh brpmabilitas rndah akibat pmbbanan. Pross ini trjadi jika tanah jnuh
Prtmuan VII IV. Konsolidasi IV. Pndahuluan. Konsolidasi adalah pross brkurangnya volum atau brkurangnya rongga pori dari tanah jnuh brpmabilitas rndah akibat pmbbanan. Pross ini trjadi jika tanah jnuh
ANALISIS KINERJA STRUKTUR PADA BANGUNAN BERTINGKAT BERATURAN DAN KETIDAK BERATURAN HORIZONTAL SESUAI SNI
 ANALISIS KINERJA STRUKTUR PADA BANGUNAN BERTINGKAT BERATURAN DAN KETIDAK BERATURAN HORIZONTAL SESUAI SNI 03-1726-2012 Hotma L Purba Jurusan Tknik Sipil,Univrsitas Sriwijaya Korspondnsi pnulis : hotmapurba@hotmail.com
ANALISIS KINERJA STRUKTUR PADA BANGUNAN BERTINGKAT BERATURAN DAN KETIDAK BERATURAN HORIZONTAL SESUAI SNI 03-1726-2012 Hotma L Purba Jurusan Tknik Sipil,Univrsitas Sriwijaya Korspondnsi pnulis : hotmapurba@hotmail.com
lim 0 h Jadi f (x) = k maka f (x)= 0 lim lim lim TURUNAN/DIFERENSIAL Definisi : Laju perubahan nilai f terhadap variabelnya adalah :
 TURUNAN/DIFERENSIAL Deinisi : Laj perbaan nilai teradap ariabelnya adala : y dy d lim = lim = 0 0 d d merpakan ngsi bar disebt trnan ngsi ata perbandingan dierensial, proses mencarinya disebt menrnkan
TURUNAN/DIFERENSIAL Deinisi : Laj perbaan nilai teradap ariabelnya adala : y dy d lim = lim = 0 0 d d merpakan ngsi bar disebt trnan ngsi ata perbandingan dierensial, proses mencarinya disebt menrnkan
BAB 2 DISTRIBUSI INDUK DAN DISTRIBUSI SAMPEL
 BAB DISTRIBUSI IDUK DA DISTRIBUSI SAMEL.. EDAHULUA Jika suatu bsaran mmiliki nilai ssungguhnya sdangkan hasil ukurnya adalah maka kita mngharapkan hasil pngamatan mndkati, namun knyataannya tidak slalu
BAB DISTRIBUSI IDUK DA DISTRIBUSI SAMEL.. EDAHULUA Jika suatu bsaran mmiliki nilai ssungguhnya sdangkan hasil ukurnya adalah maka kita mngharapkan hasil pngamatan mndkati, namun knyataannya tidak slalu
OPERASI GABUNGAN, JOIN, KOMPOSISI DAN HASIL KALI KARTESIAN PADA GRAF FUZZY SERTA KOMPLEMENNYA. Tina Anggitta Novia 1 dan Lucia Ratnasari 2
 OPERASI ABUNAN JOIN KOMPOSISI DAN HASIL KALI KARTESIAN PADA RAF FUZZY SERTA KOMPLEMENNYA Tina Anggitta Novia Lucia Ratnasari Program Studi Matmatika FMIPA UNDIP Jl Prof Sodarto SH Smarang 5075 Abstract
OPERASI ABUNAN JOIN KOMPOSISI DAN HASIL KALI KARTESIAN PADA RAF FUZZY SERTA KOMPLEMENNYA Tina Anggitta Novia Lucia Ratnasari Program Studi Matmatika FMIPA UNDIP Jl Prof Sodarto SH Smarang 5075 Abstract
BAB 3 PERSAMAAN DIFFERENSIAL UNTUK MENENTUKAN HARGA SUATU ASET TURUNAN
 BAB 3 PERSAMAAN DIFFERENSIAL UNTUK MENENTUKAN HARGA SUATU ASET TURUNAN Pmbahasan harga opsi idak dapa dilpaskan dari pmbahasan nang skurias lain yang brhubungan dngan haga opsi. Shingga prlu dibahas masalah
BAB 3 PERSAMAAN DIFFERENSIAL UNTUK MENENTUKAN HARGA SUATU ASET TURUNAN Pmbahasan harga opsi idak dapa dilpaskan dari pmbahasan nang skurias lain yang brhubungan dngan haga opsi. Shingga prlu dibahas masalah
(x, f(x)) P. x = h. Gambar 4.1. Gradien garis singgung didifinisikan sebagai limit y/ x ketika x mendekati 0, yakni
 Diktat Klia TK Matematika BAB TURUNAN Graien Garis Singgng Tinja seba krva = f() seperti iperliatkan paa Gambar Garis ang melali titik P(, f( )) an Q( +, f( + )) isebt tali bsr Graien tali bsr tersebt
Diktat Klia TK Matematika BAB TURUNAN Graien Garis Singgng Tinja seba krva = f() seperti iperliatkan paa Gambar Garis ang melali titik P(, f( )) an Q( +, f( + )) isebt tali bsr Graien tali bsr tersebt
Hasil Kali Titik. Dua Operasi Vektor. Sifat-sifat Hasil Kali Titik. oki neswan (fmipa-itb)
 oki neswan (fmipa-itb) Da Operasi Vektor Hasil Kali Titik Misalkan OAB adalah sebah segitiga, O (0; 0) ; A (a 1 ; a ) ; dan B (b 1 ; b ) : Maka panjang sisi OA; OB; dan AB maing-masing adalah q joaj =
oki neswan (fmipa-itb) Da Operasi Vektor Hasil Kali Titik Misalkan OAB adalah sebah segitiga, O (0; 0) ; A (a 1 ; a ) ; dan B (b 1 ; b ) : Maka panjang sisi OA; OB; dan AB maing-masing adalah q joaj =
KINETIKA SORPSI ION ZINK (II) PADA PARTIKEL GAMBUT
 Prosiding SNaPP2012 : Sains, Tknologi, dan Kshatan ISSN 2089-3582 KINETIKA SORPSI ION ZINK (II) PADA PARTIKEL GAMBUT 1 Munawar 1 Jurusan Tknik Kimia Politknik Ngri Lhoksumaw, Jl. B. Ach - Mdan Km. 280,
Prosiding SNaPP2012 : Sains, Tknologi, dan Kshatan ISSN 2089-3582 KINETIKA SORPSI ION ZINK (II) PADA PARTIKEL GAMBUT 1 Munawar 1 Jurusan Tknik Kimia Politknik Ngri Lhoksumaw, Jl. B. Ach - Mdan Km. 280,
SAMBUNGAN BALOK PENDUKUNG MOMEN
 BAB VI SABUNGAN BALOK ENDUKUNG OEN 1. TUJUAN ERKULIAHAN A. TUJUAN UU ERKULIAHAN (TU) Stlah mmplajari matri tntang sambungan balok pndukung momn, scara umum anda diharapkan : 1. ampu mnjlaskan pngrtian
BAB VI SABUNGAN BALOK ENDUKUNG OEN 1. TUJUAN ERKULIAHAN A. TUJUAN UU ERKULIAHAN (TU) Stlah mmplajari matri tntang sambungan balok pndukung momn, scara umum anda diharapkan : 1. ampu mnjlaskan pngrtian
ANALISIS NOSEL MOTOR ROKET RX LAPAN SETELAH DILAKUKAN PEMOTONGAN PANJANG DAN DIAMETER
 Analisis Nosl Motor Rokt RX-1 LAPAN... (Ahmad Jamaludin Fitroh, Sari) ANALISIS NOSEL MOTOR ROKET RX - 1 LAPAN SETELAH DILAKUKAN PEMOTONGAN PANJANG DAN DIAMETER Ahmad Jamaludin Fitroh, Sari Pnliti Pnliti
Analisis Nosl Motor Rokt RX-1 LAPAN... (Ahmad Jamaludin Fitroh, Sari) ANALISIS NOSEL MOTOR ROKET RX - 1 LAPAN SETELAH DILAKUKAN PEMOTONGAN PANJANG DAN DIAMETER Ahmad Jamaludin Fitroh, Sari Pnliti Pnliti
ANALISIS PEMANFAATAN CITRA SATELIT ALOS-PRISM
 ANALISIS PEMANFAATAN CITRA SATELIT ALOS-PRISM SEBAGAI DASAR PEMBUATAN PETA PENDAFTARAN TANAH (Studi Kasus : Dsa Babalan, Kcamatan Gabus, Kabupatn Pati) Pandu Sandy Utomo, Ir. Chatarina Nurdjati S., MT,
ANALISIS PEMANFAATAN CITRA SATELIT ALOS-PRISM SEBAGAI DASAR PEMBUATAN PETA PENDAFTARAN TANAH (Studi Kasus : Dsa Babalan, Kcamatan Gabus, Kabupatn Pati) Pandu Sandy Utomo, Ir. Chatarina Nurdjati S., MT,
Gambar IV.6. Gambaran kontur bidang sesar yang menggambarkan bentuk ramp-flat-ramp pada border fault di Sub-cekungan Kiri.
 Pada pta struktur waktu (Gambar IV.4) trlihat bntuk ssar utama yang cukup unik dibagian tngah. Bntuk ini dipngaruhi olh konfigurasi Batuan Dasar yang dihasilkan olh struktur brumur Pra-Trsir. Pada pta
Pada pta struktur waktu (Gambar IV.4) trlihat bntuk ssar utama yang cukup unik dibagian tngah. Bntuk ini dipngaruhi olh konfigurasi Batuan Dasar yang dihasilkan olh struktur brumur Pra-Trsir. Pada pta
ANALISIS AERODINAMIKA AIRFOIL DENGAN METODA INTERAKSI VISKOS TAK VISKOS QUASI - SIMULTAN
 Availabl onlin at Wbsit http://jornal.ndip.a.id/ind.php/rotasi ANALISIS ARODINAMIKA AIRFOIL DNGAN MTODA INTRAKSI VISKOS TAK VISKOS QUASI - SIMULTAN Ismoyo aryanto, Mnadi, Ahmad Widodo, Toni Prahasto Dpartmn
Availabl onlin at Wbsit http://jornal.ndip.a.id/ind.php/rotasi ANALISIS ARODINAMIKA AIRFOIL DNGAN MTODA INTRAKSI VISKOS TAK VISKOS QUASI - SIMULTAN Ismoyo aryanto, Mnadi, Ahmad Widodo, Toni Prahasto Dpartmn
SIMULASI DESAIN COOLING SYSTEM DAN RUNNER SYSTEM UNTUK OPTIMASI KUALITAS PRODUK TOP CASE
 SIMULASI DESAIN COOLING SYSTEM DAN RUNNER SYSTEM UNTUK OPTIMASI KUALITAS PRODUK TOP CASE Fabio Dwi Bagus Irawan 1,a, Cahyo Budiyantoro 1,b, Thoharudin 1,c 1 Program Studi Tknik Msin, Fakultas Tknik, Univrsitas
SIMULASI DESAIN COOLING SYSTEM DAN RUNNER SYSTEM UNTUK OPTIMASI KUALITAS PRODUK TOP CASE Fabio Dwi Bagus Irawan 1,a, Cahyo Budiyantoro 1,b, Thoharudin 1,c 1 Program Studi Tknik Msin, Fakultas Tknik, Univrsitas
Solusi Sistem Persamaan Linear Fuzzy
 Jrnal Matematika Vol. 16, No. 2, November 2017 ISSN: 1412-5056 / 2598-8980 http://ejornal.nisba.ac.id Diterima: 14/08/2017 Disetji: 20/10/2017 Pblikasi Online: 28/11/2017 Solsi Sistem Persamaan Linear
Jrnal Matematika Vol. 16, No. 2, November 2017 ISSN: 1412-5056 / 2598-8980 http://ejornal.nisba.ac.id Diterima: 14/08/2017 Disetji: 20/10/2017 Pblikasi Online: 28/11/2017 Solsi Sistem Persamaan Linear
REGRESI LINEAR & KORELASI. Elty Sarvia, ST., MT. Fakultas Teknik Jurusan Teknik Industri Universitas Kristen Maranatha Bandung REGRESI
 9/08/0 REGREI LINEAR & KORELAI Elty arvia, T., MT. Fakultas Tknik Jurusan Tknik Industri Univrsitas Kristn Maranatha Bandung REGREI jauh ini,kita hanya mmbuat statistik dngan satu variabl pada waktu trtntu,
9/08/0 REGREI LINEAR & KORELAI Elty arvia, T., MT. Fakultas Tknik Jurusan Tknik Industri Univrsitas Kristn Maranatha Bandung REGREI jauh ini,kita hanya mmbuat statistik dngan satu variabl pada waktu trtntu,
URUNAN PARSIAL. Definisi Jika f fungsi dua variable (x dan y) maka: atau f x (x,y), didefinisikan sebagai
 6 URUNAN PARSIAL Deinisi Jika ngsi da ariable maka: i Trnan parsial terhadap dinotasikan dengan ata dideinisikan sebagai ii Trnan parsial terhadap dinotasikan dengan ata dideinisikan sebagai Tentkan trnan
6 URUNAN PARSIAL Deinisi Jika ngsi da ariable maka: i Trnan parsial terhadap dinotasikan dengan ata dideinisikan sebagai ii Trnan parsial terhadap dinotasikan dengan ata dideinisikan sebagai Tentkan trnan
