BAB II PERSAMAAN KUADRAT DAN FUNGSI KUADRAT
|
|
|
- Surya Oesman
- 6 tahun lalu
- Tontonan:
Transkripsi
1 BAB II PERSAMAAN KUADRAT DAN FUNGSI KUADRAT 1. Menentukan koefisien persamaan kuadrat 2. Jenis-jenis akar persamaan kuadrat 3. Menyusun persamaan kuadrat yang akarnya diketahui 4. Fungsi kuadrat dan grafiknya 5. Menyelesaikan persamaan kuadrat dengan melengkapkan bentuk kuadrat 6. Merancang model matematika yang berkaitan dengan persamaan dan fungsi kuadrat. 36
2 LEMBAR KERJA SISWA 1 Mata pelajaran : Matematika Uraian Materi Pelajaran : Menentukan koefisisen persamaan kuadrat dan menentukan akar-akar persamaan kuadrat dengan pemfaktoran dan rumus abc. Kelas/Semester : X /Gasal Waktu : 2 45menit MATERI : A. MENENTUKAN KOEFISIEN PERSAMAAN KUADRAT Bentuk umum persamaan kuadrat a 2 + b + c =0,a, b, c bilangan real dan a 0. a disebut koefisien 2, b koefisien dan c konstanta. Tentukan koefisien persamaan kuadrat : a = 0 Jawab : a = 6, b = -7, dan c = 10 b. 5-2 = 0 Jawab : a = -1, b = 5, dan c = 0 c. 4 = 2/ Jawab : pada bentuk ini diubah ke bentuk kuadrat yang sudah baku 4-2/ = = = 0 d. p 2-3p 6 = 0 a =, b =., dan c =. Jawab : a = p, b =., dan c = Latihan 1 Tentukan koefisien persamaan kuadrat : = 0 37
3 = = = 6/ 5. 2/ = 3/(+1) m m = 0 7. (t-1) t = 0 B. MENENTUKAN AKAR-AKAR PERSAMAAN KUADRAT DENGAN MEMFAKTORKAN Tentukan akar-akar persamaan kuadrat dengan pemfaktoran a = 0 Jawab : = 0 (dua bilangan jika dikali 6 dan jika ditambah 5) ( - 6) ( + 1) = 0 6 = 0 atau + 1 = 0 = 6 atau = -1 b = 0 Jawab : = 0 (2 -.) (.- 3) = = 0 atau. 3 = 0 =. atau =. c = 0 Jawab : 4 2 = 0 (4 -.) ( - 0) = = 0 atau 0 = 0 =. atau =. 38
4 Latihan 2 Tentukan akar akar persamaan kuadrat dengan memfaktorkan = = = = m = 2m 2 6. p 2-3p 18 = 0 C. MENENTUKAN AKAR-AKAR PERSAMAAN KUADRAT DENGAN MENGGUNAKAN RUMUS ABC Akar-akar persamaan kuadrat a 2 +b + c = 0 dapat ditentukan dengan menggunakan rumus abc. -b ( b 2-4ac ) 1,2 = 2a Tentukan akar-akar persamaan kuadrat dengan rumus abc = 0 a = 1, b = 5, dan c = -6 Rumus : -b (b 2 4ac) -5 ( ) ,2 = = = 2a = = 1 atau 2 = =
5 Latihan 3 Tentukan akar-akar persamaan kuadrat dengan rumus abc = = = = 0 40
6 LEMBAR KERJA SISWA 2 Mata Pelajaran : Matematika Uraian Materi Pelajaran : Jenis-jenis akar-akar persamaan kuadrat dan jumlah dan hasil kali akar-akar persamaan kuadrat. Kelas / Semester : X / Gasal Waktu : 2 45 menit MATERI : A. JENIS - JENIS AKAR PERSAMAAN KUADRAT Persamaan kuadrat a 2 + b + c = 0 dengan a, b, c bilangan real dan a 0 akar-akar persamaan tersebut dapat ditentukan dengan rumus : -b ( b 2-4ac) 1,2 = 2a nilai b 2-4ac disebut nilai Diskriminan dan ditulis D Jenis-jenis akar-akar persamaan kuadrat dapat dilihat dari nilai diskriminannya. a. jika D > 0, akar-akar persamaan kuadrat nyata dan berbeda b. jika D = 0, akar-akar persamaan kuadrat nyata dan sama c. jika D < 0, akar-akar persamaan kuadrat tidak nyata atau imajiner Tentukan jenis-jenis akar-akar persamaan kuadrat : 1) = 0 a = 1, b = 2, c = 3 D = b 2 4 a c = = 4 12 = - 8 D < 0 maka akar akarnya tidak nyata atau imajiner 41
7 2). 2 + = 0 a =., b =.., c = D = b 2 4 a c =.. D 0, maka akar-akarnya.. 3) = 0 a =, b =., c = D = b 2 4 a c = D =.. 0, maka akar-akarnya.. Latihan Tentukan jenis-jenis akar-akar persamaan kuadrat : = = = p = 2p m 3 = 6/m B. MENENTUKAN JUMLAH DAN HASIL KALI AKAR-AKAR PERSAMAAN KUADRAT Persamaan kuadrat a 2 + b + c = 0 ; a, b, c bilangan real dan a 0 mempunyai akar - akar 1 dan 2. a. jumlah akar-akar persamaan kuadrat : = -b / a b. hasil kali akar-akar persamaan kuadrat : 1. 2 = c / a Persamaan kuadrat = 0 mempunyai akar-akar 1 dan 2. 42
8 a. 1 +2= -b / a = -(-7) / 2 = 7 / 2 b = c / a = - 4 / 2 = - 2 c = 2( ) = 2 ( -b/a ) = 2.( 7/2) = 7 d = = 9. (c/a) = 9. 2 = ( -b/a ) 7/2. e. 1 /1 + 1/2 = = = = = (c/a) -2. f. Ingat rumus ( a + b ) 2 = a 2 + 2ab + b 2 a 2 + b 2 = ( + ) 2 2ab = (1+ 2 ) = ( -b/a ) 2 2. (c/a) = (..) 2 2. ( ) = (-b/a) g. + = = = = (c/a)... h. (1 3) ( 2 3) = = (. +.) + 9 = (c/a) 3 (.) + 9 = 43
9 Latihan A. Persamaan kuadrat = 0, jika akar-akarnya 1dan 2 tentukan nilai : /1 + 1/2 7. (1 2) (2 2) B. Ulangi pertanyaan di atas untuk persamaan kuadrat 6 =
10 LEMBAR KERJA SISWA 3 Mata Pelajaran : Matematika Uraian Materi Pelajaran : Menyusun persamaan kuadrat yang akar-akarnya diketahui dan akar-akarnya simetris dengan akar-akar persamaan yang lain. Kelas / Semester : X / Gasal Waktu : 2 45 menit MATERI : A. MENYUSUN PERSAMAAN KUADRAT YANG AKAR AKARNYA DIKETAHUI Pada pembahasan yang lalu, akar-akar persamaan kuadrat dapat diperoleh dengan cara memfaktorkan. Persamaan kuadrat = 0 ( 6) ( + 1) = 0 ( 6 ) ( ( -1) ) = 0 = 6 atau = -1 Dengan cara membalik langkah-langkah diatas dapat disusun suatu persamaan kuadrat : = 6 atau = -1 ( 6 ) ( ( -1) ) = 0 ( 6 ) ( + 1 ) = 0 dijabarkan : = 0 a. Jika 1 dan 2 akar-akar suatu persamaan kuadrat maka dapat disusun persamaan kuadratnya yaitu : ( 1 ) ( 2 ) = 0 Persamaan kuadrat : ( 1) ( 2 ) = 0 dijabarkan : 45
11 = 0 2 ( ) = 0 Jumlah akar-akar hasil kali akar-akar b. Jika 1 dan 2 akar-akar suatu persamaan kuadrat maka dapat disusun persamaan kuadratnya yaitu : 2 ( ) + 1.2= 0 atau 2 ( jumlah akar-akar) + hasil kali akar-akar = 0 Susun persamaan kuadrat yang akar-akarnya diketahui 2 dan 5 Jawab : 1 = 2 dan 2= 5 cara 1. Persamaan kuadrat ( 1 ) ( 2 ) = 0 ( 2 ) ( 5 ) = = 0 cara 2. Persamaan kuadrat 2 ( jumlah akar-akar) + hasil kali akar-akar = 0 2 ( ) + (2. 5 ) = = 0 Latihan Susun persamaan kuadrat yang akar-akarnya diketahui 1. 3 dan 4 Jawab : 1 = -3 dan 2 = 4 persamaan kuadrat 2 ( ) + = = 0 2. ½ dan /3 dan 2/ dan
12 B. MENYUSUN PERSAMAAN KUADRAT YANG AKAR-AKARNYA SIMETRIS DENGAN AKAR-AKAR PERSAMAAN KUADRAT YANG LAIN Persamaan kuadrat I mempunyai akar-akar 1 dan 2 Persamaan kuadrat II mempunyai akar-akar y1 dan y2 Bentuk-bentuk simetris : 1. y1 = 1 + c dan y2 = 2 + c 2. y1 = 1 c dan y2 = 2 c 3. y1 = 1 / 1 dan y2 = 1 / 2 4. y1 = k. 1 dan y2 = k y1 = - 1 dan y2 = - 2 a. Susun persamaan kuadrat jika diketahui akar-akarnya 4 lebihnya akar-akar persamaan = 0 Jawab : Misal akar-akar persamaan kuadrat = 0 adalah 1 dan 2 Maka akar-akar persamaan kuadrat baru adalah y1 dan y2 y1 = = y1-4 = y 4 y2 = = y2-4 = y - 4 Nilai = y 4 disubtitusi ke persamaan = 0 diperoleh : ( y 4 ) 2 ( y 4 ) + 5 = 0 (y 2-8y + ) ( y - ) + 5 = 0 y 2 -.y +..= 0 Jadi persamaan kuadrat baru adalah mengganti variabel y dengan variabel adalah = 0 b. Diketahui persamaan kuadrat = 0, susun persamaan kuadrat jika akar-akarnya 1 dan Jawab : Misal akar-akar persamaan kuadrat = 0 adalah 1 dan 2 47
13 Maka akar-akar persamaan kuadrat baru adalah y1 dan y2 y1 = y2= =. =. 2 =. =. Nilai =.. subtitusi ke persamaan = 0 diperoleh : 2( ) 2 3 (..) + 1 = 0 2(.) (.) + 1 = 0 = 0 Jadi persamaan kuadrat baru adalah = 0 Latihan 1. Jika 1 dan 2 adalah akar-akar persamaan = 0, susunlah persamaan kuadrat baru yang akar-akarnya 31 dan Jika 1 dan 2 akar-akar persamaan = 0, susunlah persamaan kuadrat baru yang akar-akarnya 3 kurangnya dari akar-akar persamaan tersebut. 3. Susun persamaan kuadrat baru yang akar-akarnya berlawanan dengan akarakar persamaan = 0 4. Susun persamaan kuadrat baru yang akar-akarnya 1 1 dan jika 1dan 2 akar-akar persamaan kuadrat = 0 48
14 LEMBAR KERJA SISWA 4 Mata Pelajaran : Matematika Uraian Materi Pelajaran : Membuat grafik fungsi kuadrat Kelas / Semester : X / Gasal Waktu : 2 45 menit MATERI : FUNGSI KUADRAT DAN GRAFIKNYA Fungsi kuadrat dalam variabel mempunyai bentuk umum f() = a 2 + b + c Dengan a, b, c bilangan real dan a 0. Grafik fungsi kuadrat berbentuk parabola. Langkah-langkah menggambar grafik fungsi kuadrat : 1. Menentukan titik potong grafik dengan sumbu koordinat. a. titik potong dengan sumbu Titik potong grafik fungsi kuadrat f() = a 2 + b + c dengan sumbu diperoleh jika y = f() = 0, yaitu a 2 + b + c = 0, nilai yang memenuhi persamaan ini tergantung dari nilai diskriminan yaitu D = b 2 4ac jika D>0, maka persamaan kuadrat mempunyai dua akar real yang berbeda, sehingga grafik fungsi memotong di sumbu di dua titik. jika D = 0, maka persamaan kuadrat mempunyai dua akar real yang sama, sehingga grafik fungsi memotong di satu titik atau menyinggung sumbu. jika D<0, maka persamaan kuadrat tidak mempunyai akar real, sehingga grafik fungsi tidak memotong sumbu. Keadaan di atas dapat dilihat pada gambar di bawah ini : 49
15 y D>0, a>0 D=0, a>0 D<0, a>0 y y y D>0, a<0 y D=0, a<0 y D<0, a<0 b. titik potong dengan sumbu y Titik potong grafik fungsi kuadrat f() = a 2 + b + c = 0 dengan sumbu y diperoleh jika = 0, sehingga y = f() = c. jadi titik potongngrafik dengan sumbu y tergantung dari nilai c. > Jika c > 0, maka grafik memotong sumbu y positif > jika c = 0, maka grafik melalui titik asal (0,0) > jika c < 0, maka grafik memotong sumbu y negatif keadaan grafik dapat dilihat pada gambar di bawah ini : y c>0, a>0 c=0, a>0 c<0, a>0 y y (0,c) (0,0) (0,c) y y y c>0, a<0 c=0, a<0 c<0, a<0 (0,c) (0,0) (0,c) 50
16 2. Koordinat titik puncak Koordinat titik puncak fungsi kuadrat diperoleh dengan cara mengubah bentuk f() = a 2 + b + c menjadi bentuk kuadrat sempurna. f() = a 2 + b + c f() = 2 b D a, D = b 2 4ac 2a 4a jika a > 0, maka parabola terbuka ke atas, titik puncak adalah titik balik minimum, koordinat titik balik minimum b D, 2a 4a Jika a < 0, maka parabola terbuka ke bawah, titik puncak adalah titik balik b D maksimum, koordinat titik balik maksimum, 2a 4a 3. Persamaan sumbu simetri Koordinat titik puncak parabola fungsi f() = a 2 + b + c adalah b D,, 2a 4a karena sumbu simetri melalui titik puncak maka persamaan sumbu simetri parabola mempunyai rumus = b 2a Gambar grafik fungsi kuadrat f() = Jawab : F() = a. titik potong dengan sumbu koordinat - dengan sumbu, diperoleh jika y = 0,yaitu = 0 ( 4 ) ( + 2 ) = 0 = 4 atau = -2 jadi titik potongnya di (-2,0) dan (4,0) - dengan sumbu y, diperoleh jika = 0, yaitu : y = -8, jadi titik potongnya di (0, -8) 51
17 b. persamaan sumbu simetri b = 2a = 1 c. koordinat titik puncak b D P =, 2a 4a Karena a = 1 = ( 1, -9 ) a>0 maka titik puncak parabola merupakan titik balik minimum Gambar grafik : y P(1,-9) Latihan Untuk tiap fungsi di bawah ini, gambarlah grafiknya dengan menentukan koordinat titik potong dengan sumbu dan sumbu y, persamaan sumbu simetri, dan koordinat titik puncak. 1. f() = f() = f() = f() = f() =
18 LEMBAR KERJA SISWA 5 Mata Pelajaran : Matematika Uraian Materi Pelajaran : Akar akar persamaan kuadrat dengan melengkapkan bentuk kuadrat, sumbu simetri, titik puncak dengan melengkapkan bentuk kuadrat, dan fungsi kuadrat yang melalui tiga titik. Kelas / Semester : X / Gasal Waktu : 3 45 menit MATERI : A. MENYELESAIKAN PERSAMAAN KUADRAT DENGAN MELENGKAPKAN BENTUK KUADRAT Contoh-contoh bentuk kuadrat 1. 2 = = 0 = + 36 atau = = = 0 = + 16 atau = - 16 jika 2 = k, k 0 maka = + k atau = - k 3. ( - 2) 2 = 3 ( 2) = + 3 atau ( 2) = - 3 = atau = 2-3 jika ( + p) 2 = k, k 0, maka + p = + k atau + p = - k Untuk dapat menentukan nilai dari bentuk (+p) 2 = k maka bentuk persamaan kuadrat a 2 + b + c = 0 diubah ke bentuk (+p) 2 = k, cara ini disebut melengkapkan bentuk kuadrat. Tentukan himpunan penyelesaian dari persamaan kuadrat di bawah dengan melengkapkan bentuk kuadrat. a = 5 ruas kiri diubah menjadi bentuk kuadrat 53
19 ( 1) 2 = 5 1 = + 5 atau 1 = - 5 = atau = 1-5 HP = { 1 + 5, 1-5 } b = 15 Ruas kiri ubah menjadi bentuk kuadrat yaitu bagi koefisien, 14 dengan 2, kemudian kuadratkan hasilnya. ( + 14/2) 2 = 15 + (14/2) 2 (tambahkan 14/2 pada ruas kanan) ( + 7) 2 = 15 + (7)2 ( + 7 ) 2 = = 64 atau + 7 = - 64 = atau = -7 8 = 1 atau = -15 HP = { -15, 1 } c = -7 jika koefisien 2 1, maka persamaan kuadrat diubah sehingga koefisien 2 = = = -2-7 ( bagi dengan 5 pada kedua ruas) = -9/5 ( + 3/2 ) 2 = -9/5 + (3/2) 2 ( + 3/2) 2 = -9/5 + 9/4 + 3/2 = + 9/20 atau + 3/2 = - 9/20 = -3/2 + 9/20 atau = -3/2-9/20 =. atau = HP = {.., } 54
20 Latihan Tentukan penyelesaian persamaan kuadrat berikut dengan melengkapkan bentuk kuadrat = = = ( 1 ) = = 12 3 B. MENENTUKAN SUMBU SIMETRI, TITIK PUNCAK DENGAN MELENGKAPKAN BENTUK KUADRAT Fungsi kuadrat f() = a 2 + b + c dapat diubah ke y = a ( h) 2 + k Titik puncak dan persamaan sumbu simetri y = a( h) 2 + k dapat ditentukan tanpa menggambar grafiknya, yaitu : Koordinat titik puncak / titik ekstrem adalah titik (h, k) Persamaan sumbu simetri adalah = h Nilai ekstrem / nilai puncak adalah y = k Y ekstrem maksimum = y maks, jika a < 0 Y ekstrem minimum = y min, jika a > 0 Tentukan titik puncak, persamaan sumbu simetri dan nilai ekstrem pada fungsi kuadrat di bawah a. y = 3 ( + ½) 2-1/4 Jawab : titik puncak ( -1/2, -1/4 ) persamaan sumbu simetri = - 1/2 y min = - ¼ karena a > 0 b. y = - ( 3 ) Jawab : titik puncak (3, 4) persamaan sumbu simetri = 3 y maks = 4 karena a < 0 55
21 Latihan Tentukan titik puncak, persamaan sumbu simetri dan nilai ekstrem pada fungsi kuadrat di bawah. 1. y = - ( 4) y = 1/3 ( + 6) y = - ( + 5) 2 4. y = y = C. MENYUSUN FUNGSI KUADRAT JIKA TIGA TITIK SEBARANG DIKETAHUI Grafik fungsi kuadrat f() = a 2 + b + c, jika titik (, y) terletak pada grafik, maka untuk setiap nilai dan y memenuhi persamaan tersebut. a. Susun fungsi kuadrat melalui titik ( 1,2 ), ( 3,8 ) dan ( -2,8 ) misal persamaan grafik y = a 2 + b + c grafik melalui (1,2), subtitusi nilai = 1 dan y = 2 diperoleh a + b + c = 2 grafik melalui (3,8), subtitusi nilai = 3 dan y = 8 diperoleh 9a + 3b + c = 8 grafik melalui (-2,8), subtitusi nilai = -2 dan y = 8 diperoleh 4a 2b + c = 8 diperoleh sistem persamaan linier dengan tiga variabel : a + b + c = 2. (1) 9a + 3b + c = 8. (2) 4a 2b + c = 8. (3) b. Ubah persamaan linier tiga variabel menjadi persamaan linier dua variabel, dengan menghilangkan variabel c dari dua pasang persamaan linier tersebut. Dari persamaan (1) dan (2) hilangkan variabel c a + b + c = 2 9a + 3b + c = a - 2b = -6 4a + b = 3 (4) Dari persamaan (2) dan (3) hilangkan variabel c 56
22 9a + 3b + c = 8 4a 2b + c = 8-5a + 5b = 0 a + b = 0. (5) persamaan (4) dan (5) adalah persamaan linier dua variabel c. menentukan nilai a dan b dengan menghilangkan salah satu variabel pada persamaan (4) dan (5) 4a + b = 3 a + b = 0-3a = 3 a = 1 subtitusi a = 1 ke persamaan a + b = 0 didapat b = -1 untuk a = 1, b = -1 subtitusi ke persamaan (1) didapat a + b + c = c = 2 c = 2 jadi a = 1, b = -1 dan c = 2 maka f() = Latihan Susun fungsi kuadrat yang diketahui grafiknya melalui titik-titik 1. (0,-3), ( 2,-5) dan (-4,13) 2. (-2,0), (4,0) dan (0,-16) 3. (-3,0), (1,0) dan (-2,-6) 57
23 LEMBAR KERJA SISWA 6 Mata Pelajaran : Matematika Uraian Mata Pelajaran : Merancang model matematika yang berkaitan dengan persamaan dan fungsi kuadrat, menyelesaikan modelnya menafsirkan modelnya dan menafsirkan hasil yang diperoleh Kelas / Semester : X / Gasal Waktu : 2 45 menit MATERI : Dalam kehidupan sehari-hari maupun masalah dalam matematika sering dijumpai penggunaan persamaan kuadrat untuk menyelesaikannya. Biasanya masalah tersebut berbentuk kalimat, sehingga perlu sekali memahami dan menguasai bagaimana pemecahan masalah tersebut. Pemecahan masalah tersebut diselesaikan dengan 1. memahami soal sehingga mengetahui apa yang diketahui dan apa yang ditanyakan. 2. gunakan bantuan gambar serta keterangan keterangan pada gambarnya. 3. menyatakan atau mengubah dalam model matematika dalam variabel-variabel. 4. menyelesaikan persamaan pada langkah 3. Sisi miring suatu segitiga siku-siku adalah 34 cm, sedang panjang salah satu kakinya lebih panjang 14 cm dari panjang kaki lainnya. Tentukan panjang kedua kaki segitiga itu. Jawab : Gambar segitiga siku-siku serta keterangannya. C A X B Misal panjang AB =, > 0 AC = + 14 CB = 34 58
24 Dengan menggunakan pythagoras diperoleh : AB 2 + AC 2 = CB 2 X 2 + ( + 14) 2 = 34 2 X = = = 0 ( + 30) ( 16) = 0 = -30 atau = 16 karena > 0 maka = 16 jadi panjang AB = 16 cm dan AC = 30 cm Latihan 1. Misal, y bilangan-bilangan positif dan berlaku hubungan + y = 20, hasil perkalian kedua bilangan itu adalah 96. Tentukan bilangan-bilangan itu. 2. Selisih dua bilangan positif adalah 3, dan jumlah kebalikan kedua bilangan itu adalah ½, tentukan kedua bilangan itu. 3. Sepotong kawat panjang 60 cm akan dibuat menjadi sebuah segitiga siku-siku jika panjang sisi miringnya 25 cm. Tentukan luas segitiga tersebut. 4. Sebuah peluru dilemparkan vertikal ke atas sejauh h meter, setelah t detik dinyatakan oleh h = 64t 16t2. Tentukan waktu yang dibutuhkan bola untuk mencapai ketinggian 48 meter! 5. Sebuah persegi panjang mempunyai panjang tiga kali lebarnya. Jika lebarnya kurang dari 1 cm dan panjangnya bertambah 3 cm, maka luasnya 72 cm 2. Tentukan keliling persegi panjang tersebut. 6. Jumlah kuadrat tiga bilangan bulat yang berurutan adalah 110. Carilah bilangan tersebut. 7. Sebuah bilangan terdiri dari dua angka dimana angka puluhan adalah dua kali angka satuan. Jika nilai bilangan tersebut dikalikan jumlah angka-angkanya maka hasilnya adalah 63. Tentukan bilangan tersebut. 59
6 FUNGSI LINEAR DAN FUNGSI
6 FUNGSI LINEAR DAN FUNGSI KUADRAT 5.1. Fungsi Linear Pada Bab 5 telah dijelaskan bahwa fungsi linear merupakan fungsi yang variabel bebasnya paling tinggi berpangkat satu. Bentuk umum fungsi linear adalah
A. MENYELESAIKAN PERSAMAAN KUADRAT
A. MENYELESAIKAN PERSAMAAN KUADRAT STANDAR KOMPETENSI Memecahkan masalah yang berkaitan dengan fungsi, persamaan dan fungsi kuadrat serta pertidaksamaan kuadrat KOMPETENSI DASAR Menggunakan sifat dan aturan
PERSAMAAN, FUNGSI DAN PERTIDAKSAMAAN KUADRAT
LA - WB (Lembar Aktivitas Warga Belajar) PERSAMAAN, FUNGSI DAN PERTIDAKSAMAAN KUADRAT Oleh: Hj. ITA YULIANA, S.Pd, M.Pd MATEMATIKA PAKET C TINGKAT V DERAJAT MAHIR 1 SETARA KELAS X Created By Ita Yuliana
PERSAMAAN KUADRAT. Persamaan. Sistem Persamaan Linear
Persamaan Sistem Persamaan Linear PENGERTIAN Definisi Persamaan kuadrat adalah kalimat matematika terbuka yang memuat hubungan sama dengan yang pangkat tertinggi dari variabelnya adalah 2. Bentuk umum
BAB 1 PERSAMAAN. a) 2x + 3 = 9 a) 5 = b) x 2 9 = 0 b) = 12 c) x = 0 c) 2 adalah bilangan prima genap d) 3x 2 = 3x + 5
BAB PERSAMAAN Sifat Sifat Persamaan Persamaan adalah kalimat matematika terbuka yang menyatakan hubungan sama dengan. Sedangkan kesamaan adalah kalimat matematika tertutup yang menyatakan hubungan sama
LEMBAR KEGIATAN SISWA 1 PERSAMAAN KUADRAT
1 LEMBAR KEGIATAN SISWA 1 PERSAMAAN KUADRAT Masalah 1 : Pak Amat dan pak Aman masing-masing merahasiakan suatu bilangan real. Bilangan pak Aman lebih 11 daripada bilangan pak Amat. Dua kali bilangan pak
1. Akar-akar persamaan kuadrat 5x 2 3x + 1 = 0 adalah
1. Akar-akar persamaan kuadrat 5x 3x + 1 0 adalah A. imajiner B. kompleks C. nyata, rasional dan sama D. nyata dan rasional E. nyata, rasional dan berlainan. NOTE : D > 0, memiliki akar-akar riil dan berbeda
fungsi Dan Grafik fungsi
fungsi Dan Grafik fungsi Suatu fungsi adalah pemadanan dua himpunan tidak kosong dengan pasangan terurut (x, y) dimana tidak terdapat elemen kedua yang berbeda. Fungsi (pemetaan) himpunan A ke himpunan
matematika PEMINATAN Kelas X PERSAMAAN KUADRAT K-13 A. BENTUK UMUM PERSAMAAN KUADRAT
K-13 Kelas X matematika PEMINATAN PERSAMAAN KUADRAT TUJUAN PEMBELAJARAN Setelah mempelajari materi ini, kamu diharapkan memiliki kemampuan berikut. 1. Memahami definisi dan bentuk umum persamaan kuadrat..
King s Learning Be Smart Without Limits. (4) Grafik Fungsi kuadrat: (3) Titik lain (jika diperlukan) X Y. (4) Grafik Fungsi kuadrat:
Nama Siswa : LEMBAR AKTIVITAS SISWA FUNGSI KUADRAT - Hubungkan titik-titik tersebut sehingga terbentuk kurva atau grafik yang mulus. Kelas : A. FUNGSI KUADRAT Bentuk umum fungsi kuadrat adalah: y = f(x)
BAB IV PERTIDAKSAMAAN. 1. Pertidaksamaan Kuadrat 2. Pertidaksamaan Bentuk Pecahan 3. Pertidaksamaan Bentuk Akar 4. Pertidaksamaan Nilai Mutlak
BAB IV PERTIDAKSAMAAN 1. Pertidaksamaan Kuadrat. Pertidaksamaan Bentuk Pecahan 3. Pertidaksamaan Bentuk Akar 4. Pertidaksamaan Nilai Mutlak 86 LEMBAR KERJA SISWA 1 Mata Pelajaran : Matematika Uraian Materi
MATEMATIKA DASAR 16. Jika maka Jawab : E 17. Diketahui premis-premis sebagai berikut : 1) Jika maka 2) atau Jika adalah peubah pada himpunan bilangan real, nilai yang memenuhi agar kesimpulan dari kedua
FUNGSI. Riri Irawati, M.Kom 3 sks
FUNGSI Riri Irawati, M.Kom 3 sks Agenda 1. Sistem Koordinat Kartesius. Garis Lurus 3. Grafik persamaan Tujuan Agar mahasiswa dapat : Menggunakan sistem koordinat untuk menentukan titik-titik dan kurva-kurva.
Persamaan dan pertidaksamaan kuadrat BAB II
BAB II Misalkan a,b,c Є R dan a 0 maka persamaan yang berbentuk dinamakan persamaan kuadrat dalam peubah x. Dalam persamaan kuadrat ax bx c 0, a adalah koefisien dari x, b adalah koefisien dari x dan c
I. PETUNJUK: Untuk soal nomor 1 sampai dengan nomor, pilihlah salah satu jawaban yang paling tepat!
I. PETUNJUK: Untuk soal nomor sampai dengan nomor, pilihlah salah satu jawaban yang paling tepat!. Persamaan ( p + ) x ( p + ) x + ( p ) = 0, p, merupakan persamaan kuadrat dalam x untuk nilai p... p c.
y
Menyelesaikan Persamaan Kuadrat dengan Grafik Menyesaikan persamaan ax 2 +bx+c=0. Berarti menentukan nilai-nilai x bila f(x) = 0, dimana f(x) = ax 2 +bx+c. apabila grafik fungsi f(x) telah dilukis, maka
Persamaan dan Pertidaksamaan Linear
MATERI POKOK Persamaan dan Pertidaksamaan Linear MATERI BAHASAN : A. Persamaan Linear B. Pertidaksamaan Linear Modul.MTK X 0 Kalimat terbuka adalah kalimat matematika yang belum dapat ditentukan nilai
Materi Matematika Persamaan dan Pertidaksamaan kuadrat Persamaan Linear Persamaan Kuadrat Contoh : Persamaan Derajat Tinggi
Materi Matematika Persamaan dan Pertidaksamaan kuadrat Persamaan Linear Persamaan linear dengan n peubah adalah persamaan dengan bentuk : dengan adalah bilangan- bilangan real, dan adalah peubah. Secara
Fungsi Linear dan Fungsi Kuadrat
Modul 1 Fungsi Linear dan Fungsi Kuadrat Drs. Susiswo, M.Si. K PENDAHULUAN ompetensi umum yang diharapkan, setelah mempelajari modul ini, adalah Anda dapat memahami konsep tentang persamaan linear dan
(A) 3 (B) 5 (B) 1 (C) 8
. Turunan dari f ( ) = + + (E) 7 + +. Turunan dari y = ( ) ( + ) ( ) ( + ) ( ) ( + ) ( + ) ( + ) ( ) ( + ) (E) ( ) ( + ) 7 5 (E) 9 5 9 7 0. Jika f ( ) = maka f () = 8 (E) 8. Jika f () = 5 maka f (0) +
β α α β SOAL MATEMATIKA UNTUK SMA istiyanto.com Mari Berbagi Ilmu Dengan Yang Lain A. Persamaan Kuadrat dan Fungsi Kuadrat
A. Persamaan Kuadrat dan Fungsi Kuadrat 1. Salah satu akar persamaan kuadrat ( a 1) x + (3a 1) x 3a = 0 adalah 1, maka akar lainnya adalah.... Nilai m yang memenuhi agar persamaan kuadrat ( m + 1) x +
2. FUNGSI KUADRAT. , D = b 2 4ac
. FUNGSI KUADRAT A. Persamaan Kuadrat 1) Bentuk umum persamaan kuadrat : ax + bx + c =, a ) Akar akar persamaan kuadrat dapat dicari dengan memfaktorkan ataupun dengan rumus: x 1, b D, D = b 4ac a 3) Jumlah,
Matematika Ekonomi KUADRAT DAN FUNGSI RASIONAL (FUNGSI PECAH) GRAFIK FUNGSI KUADRAT BERUPA PARABOLA GRAFIK FUNGSI RASIONAL BERUPA HIPERBOLA
Fungsi Non Linier Diskripsi materi: -Harga ekstrim pada fungsi kuadrat 1 Fungsi non linier FUNGSI LINIER DAPT BERUPA FUNGSI KUADRAT DAN FUNGSI RASIONAL (FUNGSI PECAH) GRAFIK FUNGSI KUADRAT BERUPA PARABOLA
KELAS XI PROGRAM KEAHLIAN : BISNIS DAN MANAJEMEN & PARIWISATA SMK NEGERI 1 SURABAYA. BY : Drs. Abd. Salam, MM
KELAS XI PROGRAM KEAHLIAN : BISNIS DAN MANAJEMEN & PARIWISATA SMK NEGERI 1 SURABAYA BAHAN AJAR FUNGSI LINIER & KUADRAT SMK NEGERI 1 SURABAYA Halaman 1 BAB FUNGSI A. FUNGSI DAN RELASI Topik penting yang
Fungsi kuadrat. Hafidh munawir
Fungsi kuadrat Hafidh munawir Bentuk Umum Persamaan Kuadrat Bentuk umum atau Bentuk Baku persamaan kuadrat adalah: a + b + c = Dengan a,b,c R dan a serta adalah peubah (variabel) a merupakan koefisien
MAT 602 DASAR MATEMATIKA II
MAT 60 DASAR MATEMATIKA II Disusun Oleh: Dr. St. Budi Waluya, M. Sc Jurusan Pendidikan Matematika Program Pascasarjana Unnes 1 HIMPUNAN 1. Notasi Himpunan. Relasi Himpunan 3. Operasi Himpunan A B : A B
http://meetabied.wordpress.com Matematika X Semester 1 SMAN 1 Bone-Bone Kita dibentuk oleh sesuatu yang kita lakukan berulang kali. Keunggulan, bukan hasil dari satu tindakan, melainkan dari kebiasaan.
MADRASAH ALIYAH AL-MU AWANAH BEKASI SELATAN 2012
MODUL MATEMATIKA PERSIAPAN UJIAN NASIONAL 0 TAHUN AJARAN 0/0 MATERI PERSAMAAN KUADRAT DAN PERTIDAKSAMAAN KUADRAT UNTUK KALANGAN MA AL-MU AWANAH MADRASAH ALIYAH AL-MU AWANAH BEKASI SELATAN 0 Jalan RH. Umar
Matematika Proyek Perintis I Tahun 1980
Matematika Proyek Perintis I Tahun 980 MA-80-0 Di antara lima hubungan di bawah ini, yang benar adalah Jika B C dan B C, maka A C Jika A B dan C B, maka A C Jika B A dan C B, maka A C Jika A C dan C B,
MATERI PRASYARAT. ke y= f(x) =ax2 + bx +c
1 MATERI PRASYARAT A. Fungsi Kuadrat Bentuk umum : y= f(x) = ax 2 + bx +c dengan a 0. Langkah-langkah dalam menggambar grafik fungsi kuadrat y= f(x) = ax 2 + bx +c 1. Tentukan titik potong dengan sumbu
SOAL OLIMPIADE MATEMATIKA TINGKAT SMP PART 2. Departemen Matematika - Wardaya College MMXVIII-XII
SOAL OLIMPIADE MATEMATIKA TINGKAT SMP PART - Wardaya College MMXVIII-XII TIPE A. Andi dan Bobby berlari berlawanan arah dalam suatu lintasan melingkar. Keduanya berawal dari titik-titik yang saling berseberangan
SOAL-SOAL LATIHAN FUNGSI KUADRAT UJIAN NASIONAL
SAL-SAL LATIHAN FUNGSI KUADRAT UJIAN NASINAL Peserta didik memiliki kemampuan memahami konsep pada topik fungsi kuadrat. Peserta didik memilki kemampuan mengaplikan konsep kalkulus dalam masalah kontekstual
Mata Pelajaran MATEMATIKA Kelas X
Mata Pelajaran MATEMATIKA Kelas X SEKOLAH MENENGAH ATAS dan MADRASAH ALIYAH PG Matematika Kelas X 37 Bab 1 Bentuk Pangkat, Akar, dan Logaritma Nama Sekolah : SMA dan MA Mata Pelajaran : Matematika Kelas
2. PERSAMAAN, PERTIDAKSAMAAN DAN FUNGSI KUADRAT
2. PERSAMAAN, PERTIDAKSAMAAN DAN FUNGSI KUADRAT A. Persamaan Kuadrat 1) Bentuk umum persamaan kuadrat : ax 2 + bx + c =, a 2) Nilai determinan persamaan kuadrat : D = b 2 4ac 3) Akar-akar persamaan kuadrat
PERSAMAAN KUADRAT. Untuk suatu kuadrat sempurna x bx c, nilai c diperoleh dengan membagi koefisien x dengan 2, kemudian mengkuadratkan hasilnya.
PERSAMAAN KUADRAT Bab. Bentuk Umum : a b c 0, a 0, a, b, c Real Menyelesaikan ersamaan kuadrat :. dg. Memfaktorkan : a b c a ( a )( a q) q a q = a ( q) a dimana : b = + q dan c, Jika ac 0 dan q berbeda
Matematika Proyek Perintis I Tahun 1979
Matematika Proyek Perintis I Tahun 979 MA-79-0 Irisan himpunan : A = { x x < } dan himpunan B = { x < x < 8 } ialah himpunan A. { x x < 8 } { x x < } { x < x < 8 } { x < x < } { x < x } MA-79-0 Apabila
MAKALAH FUNGSI KUADRAT GRAFIK FUNGSI,&SISTEM PERSAMAAN KUADRAT
MAKALAH FUNGSI KUADRAT GRAFIK FUNGSI,&SISTEM PERSAMAAN KUADRAT Kelompok 3 : 1.Suci rachmawati (ekonomi akuntansi) 2.Fitri rachmad (ekonomi akuntansi) 3.Elif (ekonomi akuntansi) 4.Dewi shanty (ekonomi management)
1. Jika p dan q akar-akar persamaan. x 2 bx c 0 dan k konstanta real, maka
PERSAMAAAN DAN FUNGSI KUADRAT Bentuk umum persamaan kuadrat a + + c =0, a 0 Akar-akar persamaan : D = a D = 4ac Menyusun persamaan paraola y q = a ( p) Diskriminan (D = 4ac) Persamaan kuadrat memiliki.
PENERAPAN FAKTOR PRIMA DALAM MENYELESAIKAN BENTUK ALJABAR (Andi Syamsuddin*)
PENERAPAN FAKTOR PRIMA DALAM MENYELESAIKAN BENTUK ALJABAR (Andi Syamsuddin*) A. Faktor Prima Dalam tulisan ini yang dimaksud dengan faktor prima sebuah bilangan adalah pembagi habis dari sebuah bilangan
Materi Fungsi Linear Fungsi Variabel, koefisien, dan konstanta Variabel variabel bebas Koefisien Konstanta 1). Pengertian fungsi linier
Materi Fungsi Linear Admin 8:32:00 PM Duhh akhirnya nongol lagi... kali ini saya akan bahas mengenai pelajaran yang paling disukai oleh hampir seluruh warga dunia :v... MATEMATIKA, ya itu namanya. materi
PEMBAHASAN SOAL OLIMPIADE SAINS NASIONAL SMP SELEKSI TINGKAT KOTA/KABUPATEN TAHUN 2016 BIDANG MATEMATIKA
PEMBAHASAN OSK MATEMATIKA SMP TAHUN 06 PEMBAHASAN SOAL OLIMPIADE SAINS NASIONAL SMP SELEKSI TINGKAT KOTA/KABUPATEN TAHUN 06 BIDANG MATEMATIKA BAGIAN A: PILIHAN GANDA 07 (06 6) 05. Nilai dari adalah....
PERSAMAAN KUADRAT. AC 0 P DAN Q SAMA TANDA. 2. DG. MELENGKAPKAN BENTUK KUADRAT ( KUADRAT SEMPURNA ) :
PERSAMAAN KUADRAT. AC 0 P DAN Q SAMA TANDA.. DG. MELENGKAPKAN BENTUK KUADRAT ( KUADRAT SEMPURNA ) : Bab 3 PERSAMAAN KUADRAT 1. Bentuk Umum : ax bx c 0, a 0, a, b, c Re al Menyelesaikan persamaan kuadrat
Mata Pelajaran Wajib. Disusun Oleh: Ngapiningsih
Mata Pelajaran Wajib Disusun Oleh: Ngapiningsih Disklaimer Daftar isi Disklaimer Powerpoint pembelajaran ini dibuat sebagai alternatif guna membantu Bapak/Ibu Guru melaksanakan pembelajaran. Materi powerpoint
PERSAMAAN DAN FUNGSI KUADRAT
Materi W2e PERSAMAAN DAN FUNGSI KUADRAT Kelas X, Semester 1 E. Grafik Fungsi Kuadrat www.yudarwi.com E. Grafik Fungsi Kuadrat Grafik fungsi kuadrat f(x) = ax 2 + bx + c dapat dilukis dengan langkah-langkah
MBS - DTA. Sucipto UNTUK KALANGAN SENDIRI. SMK Muhammadiyah 3 Singosari
MBS - DTA Sucipto UNTUK KALANGAN SENDIRI SMK Muhammadiyah Singosari SERI : MBS-DTA FUNGSI STANDAR KOMPETENSI Siswa mampu memecahkan masalah yang berkaitan dengan fungsi, persamaan fungsi linear dan fungsi
A. DEFINISI DAN BENTUK UMUM SISTEM PERSAMAAN LINEAR KUADRAT
K-13 Kelas X matematika PEMINATAN SISTEM PERSAMAAN LINEAR KUADRAT TUJUAN PEMBELAJARAN Setelah mempelajari materi ini, kamu diharapkan memiliki kemampuan berikut. 1. Memahami definisi dan bentuk umum sistem
FUNGSI. A. Relasi dan Fungsi Contoh: Manakah yang merupakan fungsi/pemetaan dan manakah yang bukan fungsi? (i) (ii) (iii)
FUNGSI A. Relasi dan Fungsi Manakah yang merupakan fungsi/pemetaan dan manakah yang bukan fungsi? (i) (ii) (iii) Relasi himpunan A ke himpunan B adalah relasi yang memasangkan/mengkawankan/mengkorepodensikan
BAHAN AJAR PERSAMAAN GARIS SINGGUNG PADA KURVA
142 LAMPIRAN III BAHAN AJAR PERSAMAAN GARIS SINGGUNG PADA KURVA Pernahkan kamu melempar sebuah bola tenis atau bola voli ke atas? Apa lintasan yang terbuat dari lemparan bola tersebut ketika bola itu jatuh
MATEMATIKA DASAR TAHUN 1987
MATEMATIKA DASAR TAHUN 987 MD-87-0 Garis singgung pada kurva y di titik potong nya dengan sumbu yang absisnya positif mempunyai gradien 0 MD-87-0 Titik potong garis y + dengan parabola y + ialah P (5,
Matematika Semester IV
F U N G S I KOMPETENSI DASAR Mendeskripsikan perbedaan konsep relasi dan fungsi Menerapkan konsep fungsi linear Menggambar fungsi kuadrat Menerapkan konsep fungsi kuadrat Menerapkan konsep fungsi trigonometri
fungsi rasional adalah rasio dari dua polinomial. Secara umum,
fungsi rasional adalah rasio dari dua polinomial. Secara umum, Fungsi Rasional Fungsi rasional adalah fungsi yang memiliki bentuk Dengan p dan d merupakan polinomial dan d(x) 0. Domain dari V(x) adalah
Modul Matrikulasi, SMA Labschool Kebayoran 2017 Page 1
Modul : Grafik Fungsi Kuadrat Teori: Bagian bagian grafik fungsi kuadrat = a + b + c, a 0 Grafik fungsi kuadrat Titik ekstrim fungsi kuadrat = f () = a + b + c D = 0 Memiliki dua akar kembar Grafik fungsi
Prestasi itu diraih bukan didapat!!! SOLUSI SOAL
SELEKSI OLIMPIADE TINGKAT KABUPATEN/KOTA 008 TIM OLIMPIADE MATEMATIKA INDONESIA 009 Prestasi itu diraih bukan didapat!!! SOLUSI SOAL Bidang Matematika Disusun oleh : Olimpiade Matematika Tk Kabupaten/Kota
BEBERAPA FUNGSI KHUSUS
BEBERAPA FUNGSI KHUSUS ). Fungsi Konstan ). Fungsi Identitas 3). Fungsi Modulus 4). Fungsi Genap dan Fungsi Ganjil Fungsi genap jika f(x) = f(x), dan Fungsi ganjil jika f(x) = f(x) 5). Fungsi Tangga dan
OLIMPIADE SAINS TERAPAN NASIONAL SEKOLAH MENENGAH KEJURUAN TINGKAT PROPINSI JAWA TENGAH 2010 BIDANG MATEMATIKA TEKNOLOGI
OLIMPIADE SAINS TERAPAN NASIONAL SEKOLAH MENENGAH KEJURUAN TINGKAT PROPINSI JAWA TENGAH 2010 BIDANG MATEMATIKA TEKNOLOGI SESI III (ISIAN SINGKAT DAN ESSAY) WAKTU : 180 MENIT ============================================================
PERSAMAAN DAN PERTIDAKSAMAAN PERSAMAAN LINEAR
PERSAMAAN DAN PERTIDAKSAMAAN PERSAMAAN LINEAR Persamaan linear Bentuk umun persamaan linear satu vareabel Ax + b = 0 dengan a,b R ; a 0, x adalah vareabel Contoh: Tentukan penyelesaian dari 4x-8 = 0 Penyelesaian.
III. FUNGSI POLINOMIAL
III. FUNGSI POLINOMIAL 3. Pendahuluan A. Tujuan Setelah mempelajari bagian ini diharapkan mahasiswa dapat:. menuliskan bentuk umum fungsi polinomial;. menghitung nilai fungsi polinomial; 3. menuliskan
Modul Matematika 2012
Modul Matematika MINGGU V Pokok Bahasan : Fungsi Non Linier Sub Pokok Bahasan :. Pendahuluan. Fungsi kuadrat 3. Fungsi pangkat tiga. Fungsi Rasional 5. Lingkaran 6. Ellips Tujuan Instruksional Umum : Agar
SOAL DAN SOLUSI SIAP SBMPTN 2013 MATEMATIKA IPA
SOAL DAN SOLUSI SIAP SBMPTN 0 MATEMATIKA IPA. Jika 0 b a dan a b ab maka a+b = a - b (A) () (E) (B) (D) o o o o. cos 77 cos sin77 sin.... (A) cos 0 o (B) cos 70 o () sin 70 o (D) cos 0 o (E) sin 0 o. Dari
KONSEP DASAR FUNGSI DAN GRAFIK. Oleh : Agus Arwani, SE, M.Ag
KONSEP DASAR FUNGSI DAN GRAFIK Oleh : Agus Arwani, SE, M.Ag KONSEP DASAR FUNGSI DAN GRAFIK Definisi : Fungsi f : A B adalah suatu aturan yang mengaitkan (memadankan) setiap dengan tepat satu A y B Notasi
M. PRAHASTOMI M. S. SISTEM PERSAMAAN LINEAR. A. a = 2 dan b = 4 B. a = 2 dan b = 4 C. a = 2 dan b = 4 D. E. a = 2
SISTEM PERSAMAAN LINEAR M. PRAHASTOMI M. S. 0. MD-8-8 B C G E F A D H 6 7 8 6 Jika gradien garis AB = m, gradien garis CD = m, gradien garis EF = m dan gradien garis GH = m, maka... () m = () m = 0 ()
Institut Manajemen Telkom
Institut Manajemen Telkom Osa Omar Sharif JENIS JENIS FUNGSI1 JENIS JENIS FUNGSI 2 Jenis Fungsi Gambar 1. FUNGSI POLINOM mengandung banyak suku (polinom) dalam variabel bebas y = a 0 + a 1 x + a 2 x 2
SISTEM PERSAMAAN LINEAR, KUADRAT DAN PERTIDAKSAMAAN SATU VARIABEL
LA - WB (Lembar Aktivitas Warga Belajar) SISTEM PERSAMAAN LINEAR, KUADRAT DAN PERTIDAKSAMAAN SATU VARIABEL Oleh: Hj. ITA YULIANA, S.Pd, M.Pd MATEMATIKA PAKET C TINGKAT V DERAJAT MAHIR 1 SETARA KELAS X
Matematika: Persamaan Kuadrat 11/22/2011 PERSAMAAN KUADRAT. Oleh Syawaludin A. Harahap, MSc
Matematika: Persamaan Kuadrat //0 MATA KULIAH : MATEMATIKA KODE MATA KULIAH : UNM0.0 SKS : (-) ) PERSAMAAN KUADRAT Oleh Syawaludin A. Harahap, MSc UNIVERSITAS PADJADJARAN FAKULTAS PERIKANAN DAN ILMU KELAUTAN
PENGGUNAAN TURUNAN IKA ARFIANI, S.T.
PENGGUNAAN TURUNAN IKA ARFIANI, S.T. MASALAH MAKSIMUM DAN MINIMUM Misalkan f fungsi dua variable maka f dikatakan mencapai maksimum relatif di titik (a,b) jika terdapat kitaran dari (a,b) demikian sehingga
01. Perhatikan persegi panjang ABCD di bawah ini. Jika OA = 26 cm, maka panjang BO adalah... (A) 78 cm (B) 52 cm (C) 26 cm (D) 13 cm
0. Perhatikan persegi panjang ABCD di bawah ini. Jika OA = 26 cm, maka panjang BO adalah.... (A) 78 cm (B) 52 cm (C) 26 cm (D) 3 cm 02. Bangun di bawah ini merupakan bangun yang memiliki simetri putar
Prestasi itu diraih bukan didapat!!! SOLUSI SOAL
SELEKSI OLIMPIADE TINGKAT PROVINSI 009 TIM OLIMPIADE MATEMATIKA INDONESIA 00 Prestasi itu diraih bukan didapat!!! SOLUSI SOAL BAGIAN PERTAMA Disusun oleh : Solusi Olimpiade Matematika Tk Provinsi 009 Bagian
Solusi Pengayaan Matematika Edisi 3 Januari Pekan Ke-3, 2005 Nomor Soal: 21-30
Solusi Pengayaan Matematika Edisi 3 Januari Pekan Ke-3, 005 Nomor Soal: -30. Garis 5y 60 memotong sumbu X dan sumbu Y masing-masing di titik A dan B, sehingga OAB membentuk segitiga siku-siku. Sebuah lingkaran
PR ONLINE MATA UJIAN: MATEMATIKA IPA (KODE: A05) Petunjuk A digunakan untuk menjawab soal nomor 1 sampai dengan nomor 40.
PR ONLINE MATA UJIAN: MATEMATIKA IPA (KODE: A05) Petunjuk A digunakan untuk menjawab soal nomor sampai dengan nomor 0. 5. Jika a b 5, maka a + b = 5 (A). (C) 0. 0.. 7.. Nilai x yang memenuhi pertidaksamaan
Pengertian Fungsi. MA 1114 Kalkulus I 2
Fungsi Pengertian Fungsi Relasi : aturan yang mengawankan himpunan Fungsi Misalkan A dan B himpunan. Relasi biner dari A ke B merupakan suatu ungsi jika setiap elemen di dalam A dihubungkan dengan tepat
2. Suku-suku sejenis Suku-suku sejenis adalah suku-suku yang mempunyai variabel dan bilangan pangkat dari variabel tersebut sama.
A. OPERASI BENTUK ALJABAR 1. Pengertian suku, koefisien, variabel, dan konstanta bentuk aljabar Bentuk 8x + 17 merupakan bentuk aljabar dengan x sebagai variabel, 8 sebagai koefisien, dan 17 adalah konstant
Pertemuan ke 8. GRAFIK FUNGSI Diketahui fungsi f. Himpunan {(x,y): y = f(x), x D f } disebut grafik fungsi f.
Pertemuan ke 8 GRAFIK FUNGSI Diketahui fungsi f. Himpunan {(,y): y = f(), D f } disebut grafik fungsi f. Grafik metode yang paling umum untuk menyatakan hubungan antara dua himpunan yaitu dengan menggunakan
Hand out_x_fungsi kuadrat
STANDAR KOMPETENSI: Memecahkan masalah yang berkaitan dengan fungsi, persamaan dan fungsi kuadrat serta pertidaksamaan kuadrat. KOMPETENSI DASAR: Menggambar grafik fungsi aljabar sederhana dan fungsi kuadrat
SOAL-SOAL LATIHAN TURUNAN FUNGSI SPMB
SOL-SOL LTIHN TURUNN FUNGSI SPM 00-007. SPM Matematika asar Regional I 00 Kode 0 Garis singgung kurva di titik potongnya dengan sumbu yang absisnya postif y mempunyai gradien.. 9 8 7. SPM Matematika asar
PEMBAHASAN SOAL OSN MATEMATIKA SMP TINGKAT PROPINSI 2012 OLEH :SAIFUL ARIF, S.Pd (SMP NEGERI 2 MALANG)
PEMBAHASAN SOAL OSN MATEMATIKA SMP TINGKAT PROPINSI 0 OLEH :SAIFUL ARIF, S.Pd (SMP NEGERI MALANG) PEMBAHASAN SOAL OLIMPIADE SAINS NASIONAL SMP A. ISIAN SINGKAT SELEKSI TINGKAT PROPINSI TAHUN 0 BIDANG STUDI
PEMBAHASAN OSN MATEMATIKA SMP TINGKAT KABUPATEN TAHUN 2018 PROVINSI SULAWESI SELATAN
PEMBAHASAN OSN MATEMATIKA SMP TINGKAT KABUPATEN TAHUN 08 PROVINSI SULAWESI SELATAN 0. Pada suatu data terdapat 5 bilangan bulat positif. Bilangan terbesar pada data tersebut adalah 55. Median dari data
Soal Soal Latihan UKK
Sal Sal Latihan UKK. Jika p q 6 ; p dan q bilangan bulat, maka nilai p + q A. E.. Himpunan penyelesaian dari persamaan () A. E.. Diketahui bahwa. Maka nilai... A. E. 7 6. Diketahui bahwa dan merupakan
A. UNSUR - UNSUR ALJABAR
PENGERTIAN ALJABAR Bentuk ALJABAR adalah suatu bentuk matematika yang dalam penyajiannya memuat hurufhuruf untuk mewakili bilangan yang belum diketahui. Bentuk aljabar dapat dimanfaatkan untuk menyelesaikan
Fungsi. Pengertian Fungsi. Pengertian Fungsi ( ) ( )
Fungsi Pengertian Fungsi Relasi : aturan yang mengawankan/ mengkaitkan/ menugaskan himpunan Fungsi Misalkan A dan B himpunan. Relasi biner dari A ke B merupakan suatu ungsi jika setiap elemen di dalam
BEBERAPA MACAM FUNGSI DALAM ALJABAR
BEBEAA MACAM FUNGI DALAM ALJABA 1. Fungsi Komposisi Dari dua jenis fungsi f dan g kita dapat membentuk sebuah fungsi baru dengan menggunakan sistem operasi komposisi. operasi komposisi biasa dilambangkan
Kelas XI MIA Peminatan
Kelas Disusun : Markus Yuniarto, S.Si Tahun Pelajaran 017 018 Peta Konsep Glosarium Istilah Keterangan Lingkaran Himpunan titik-titik (pada bidang datar) yang memiliki jarak tetap terhadap suatu titik
Matematik Ekonom Fungsi nonlinear
1 FUNGSI Fungsi adalah hubungan antara 2 buah variabel atau lebih, dimana masing-masing dari dua variabel atau lebih tersebut saling pengaruh mempengaruhi. Variabel merupakan suatu besaran yang sifatnya
2.1 Soal Matematika Dasar UM UGM c. 1 d d. 3a + b. e. 3a + b. e. b + a b a
Soal - Soal UM UGM. Soal Matematika Dasar UM UGM 00. Jika x = 3 maka + 3 log 4 x =... a. b. c. d. e.. Jika x+y log = a dan x y log 8 = b dengan 0 < y < x maka 4 log (x y ) =... a. a + 3b ab b. a + b ab
8. Nilai x yang memenuhi 2 log 2 (4x -
1. Agar F(x) = (p - 2) x² - 2 (2p - 3) x + 5p - 6 bernilai positif untuk semua x, maka batas-batas nilai p p > l 2 < p < 3 p > 3 1 < p < 2 p < 1 atau p > 2 2. Fungsi kuadrat yang mempunyai nilai maksimum
Sistem Bilangan Real. Pendahuluan
Sistem Bilangan Real Pendahuluan Kalkulus didasarkan pada sistem bilangan real dan sifat-sifatnya. Sistem bilangan real adalah himpunan bilangan real yang disertai operasi penjumlahan dan perkalian sehingga
MATERI KALKULUS. y' = F'(x) = f(x), y'' = F''(x) = f'(x), y'''=f'''(x) = f''(x)= g'(x)= h(x) y1= f(x) y2 = g(x) y3 = h(x)
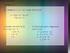Universitas Muhammadiyah Sukabumi Artikel Kalkulus Oleh : ardi meridian herdiansyah MATERI KALKULUS KALKULUS 1 MODUL 6 V. MAKSIMUM / MINIMUM ( EKSTREM FUNGSI ) 5.1. Pengertian Diketahui y = F(x) suatu
Untuk mencari akar-akar dari persamaan kuadrat, dapat menggunakan rumus :
RUMUS-RUMUS PERSAMAAN KUADRAT Bentuk umum: ax 2 + bx + c = 0, a 0 AKAR-AKAR PERSAMAAN KUADRAT Untuk mencari akar-akar dari persamaan kuadrat, dapat menggunakan rumus : X 1.2 = Dengan : D = b 2 4ac, dan
LEMBAR SOAL National Math Olympiad 3 RD PDIM UB 2014
PETUNJUK UNTUK PESERTA 1. Tuliskan nama lengkap, kelas, asal sekolah, alamat sekolah lengkap dengan nomor telepon, faximile, email sekolah dan nama guru Matematika di tempat yang telah disediakan.. Tes
Lingkaran adalah tempat kedudukan titik-titik pada bidang yang berjarak
4 Lingkaran 4.1. Persamaan Lingkaran Bentuk Baku. Lingkaran adalah tempat kedudukan titik-titik pada bidang yang berjarak tetap dari suatu titik tetap. Titik tetap dari lingkaran disebut pusat lingkaran,
MATEMATIKA EBTANAS TAHUN 1992
MATEMATIKA EBTANAS TAHUN 99 EBT-SMP-9-0 Diketahui: A = {m, a, d, i, u, n} dan B = {m, a, n, a, d, o} Diagram Venn dari kedua himpunan di atas A. m a d o a m o i e e I d u a a u n e m i d o m i d a u n
GAMBARAN UMUM SMA/MA. Hak Cipta pada Pusat Penilaian Pendidikan BALITBANG DEPDIKNAS 1
GAMBARAN UMUM Pada ujian nasional tahun pelajaran 006/007, bentuk tes Matematika tingkat berupa tes tertulis dengan bentuk soal pilihan ganda, sebanyak 0 soal dengan alokasi waktu 0 menit. Acuan yang digunakan
Pembahasan OSN Tingkat Provinsi Tahun 2012 Jenjang SMP Bidang Matematika
Pembahasan OSN Tingkat Provinsi Tahun 202 Jenjang SMP Bidang Matematika Bagian A : Soal Isian Singkat. Sebuah silinder memiliki tinggi 5 cm dan volume 20 cm 2. Luas permukaan bola terbesar yang mungkin
BAB II TINJAUAN PUSTAKA. tegak, perlu diketahui tentang materi-materi sebagai berikut.
BAB II TINJAUAN PUSTAKA Sebelum pembahasan mengenai irisan bidang datar dengan tabung lingkaran tegak, perlu diketahui tentang materi-materi sebagai berikut. A. Matriks Matriks adalah himpunan skalar (bilangan
Pola (1) (2) (3) Banyak segilima pada pola ke-15 adalah. A. 235 C. 255 B. 250 D Yang merupakan bilangan terbesar adalah. A. C. B. D.
SOAL SELEKSI AWAL 1. Suhu dalam sebuah lemari es adalah 15 o C di bawah nol. Pada saat mati listrik suhu dalam lemari es meningkat 2 o C setiap 120 detik. Jika listrik mati selama 210 detik, suhu dalam
UJIAN SARINGAN MASUK PERGURUAN TINGGI NEGERI MATEMATIKA DASAR FUNGSI KUADRAT. A. 1 B. 2 C. 3 D. 5 E. 7 Solusi: [D]
![UJIAN SARINGAN MASUK PERGURUAN TINGGI NEGERI MATEMATIKA DASAR FUNGSI KUADRAT. A. 1 B. 2 C. 3 D. 5 E. 7 Solusi: [D]](/thumbs/61/45428222.jpg "UJIAN SARINGAN MASUK PERGURUAN TINGGI NEGERI MATEMATIKA DASAR FUNGSI KUADRAT. A. 1 B. 2 C. 3 D. 5 E. 7 Solusi: [D]")
UJIAN SARINGAN MASUK PERGURUAN TINGGI NEGERI MATEMATIKA DASAR FUNGSI KUADRAT. SBMPTN MADAS 4 Jika fungsi f x a x x c menyinggung sumbu x di x, maka a A. B. C. D. 5 E. 7 Solusi: [D] 6 f x a x x c f ' x
KOTA - PROVINSI - NASIONAL TAHUN 2017 MATA PELAJARAN: MATEMATIKA
OLIMPIADE SAINS SMP/MTs TINGKAT KOTA - PROVINSI - NASIONAL TAHUN 07 MATA PELAJARAN: MATEMATIKA Mata Pelajaran : Matematika Jenjang : SMP/MTs MATA PELAJARAN PETUNJUK UMUM () Kerjakan soal ini dengan JUJUR,
A. Persamaan Kuadrat dan Fungsi Kuadrat. Salah satu akar persamaan kuadrat ( a ) (3a ) 3a 0 adalah, maka akar lainna adalah. Nilai m ang memenuhi agar persamaan kuadrat ( m ) (m ) ( m ) 0 mempunai dua
MA5032 ANALISIS REAL
(Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. August 16, 2011 Pada bab ini anda diasumsikan telah mengenal dengan cukup baik bilangan asli, bilangan bulat, dan bilangan
7. Himpunan penyelesaian dari 2(x 3) 4(2x + 3) adalah... a. x -1 c. X 1 e. x -3 b. x 1 d. x -3
. 4% uang Ani diberikan kepada adiknya dan 5% dari uang tersebut untuk membayar rekening listrik dan 5% untuk membayar rekening telpon, sisa uang Ani adalah Rp 4.,. Berapakah jumlah uang Ani a. Rp 4.,
Matematika EBTANAS Tahun 1986
Matematika EBTANAS Tahun 986 EBT-SMA-86- Bila diketahui A = { x x bilangan prima < }, B = { x x bilangan ganjil < }, maka eleman A B =.. 3 7 9 EBT-SMA-86- Bila matriks A berordo 3 dan matriks B berordo