2. Suku-suku sejenis Suku-suku sejenis adalah suku-suku yang mempunyai variabel dan bilangan pangkat dari variabel tersebut sama.
|
|
|
- Ade Jayadi
- 6 tahun lalu
- Tontonan:
Transkripsi
1 A. OPERASI BENTUK ALJABAR 1. Pengertian suku, koefisien, variabel, dan konstanta bentuk aljabar Bentuk 8x + 17 merupakan bentuk aljabar dengan x sebagai variabel, 8 sebagai koefisien, dan 17 adalah konstant Dari contoh sederhana tersebut, marilah kita definisikan istilah tersebut di atas. Suku adalah bentuk aljabar yang memuat koefisien, variabel, dan konstanta atau memuat koefisien dan variabel saj Variabel adalah suatu besaran matematika yang nilainya dapat berubah. Variabel dituliskan dalam bentuk huruf abjad (huruf kecil). c. Koefisien adalah bilangan yang diikuti oleh variabel Konstanta adalah bilangan yang tidak diikuti variabel. Suku-suku sejenis Suku-suku sejenis adalah suku-suku yang mempunyai variabel dan bilangan pangkat dari variabel tersebut sam Untuk lebih jelas memahami konsep suku-suku sejenis, perhatikan tabel berikut! Suku Sejenis / tidak sejenis Keterangan 18p dan 10p -9a dan 1a 9a dan 9b mn dan 8mn Suku sejenis Suku sejenis Suku tidak sejenis Suku tidak sejenis Variabel dan pangkat dari variabel sama Variabel dan pangkat dari variabel sama Variabelnya tidak sama Pangkat dari variabelnya tidak sama PENDALAMAN MATERI 1 BANYAK SUKU, KOEFISIEN, VARIABEL, DAN KONSTANTA. 1. Diketahui bentuk aljabar: a + b 7ab + 8. Tentukan: banyak suku, konstanta, c. koefisien untuk variabel. Diketahui bentuk aljabar: 17x - 8x + 69y 9xy 8. Tentukan: banyak suku, konstanta, c. variabel, koefisien untuk variabel y dan xy.. Diketahui bentuk aljabar: mn + n m + mn. Tentukan : banyak suku, konstanta, c. variabel, koefisien untuk variabel mn dan m.. Diketahui bentuk aljabar: pq p + q. Tentukan: banyak suku, konstanta, c. variabel, 1
2 5. Bentuk aljabar -c d + 17e. Tentukan : banyak suku, konstanta, c. variabel, koefisien untuk variabel c dan. Operasi Bentuk Aljabar Penjumlahan Dan Pengurangan Bentuk Aljabar Dua suku atau lebih dapat dilakukan operasi penjumlahan atau pengurangan apabila suku-suku tersebut merupakan suku-suku yang sejenis. Contoh : 1.1 1) p + p = 5p ) 8xy 6xy = xy ) x + 7x + 6x x = x + 6x + 7x x = 9x + x ) (1d + 5e) (8d e) = 1d + 5e -8d + e = 1d 8d + 5e + e = d + 7e 1. Sederhanakan! 6a 6 + a 7b + 1 9b c. 1x + 7x 8y + y -6x + y + 1x 5y e. 8ab + 15a ab 17a f. 8k + 99j 5k + 11j g. 0m + 8n + m 7n 10m + h. 5p + q + r p + 6q r +. Sederhanakan! (1a + 8) + (8a + 1) (b 7) (-a + 11) c. (j + k) + (8j + k) (x y) (8y + x) e. (5a b) (-6a 7b) f. (18h 5i + 8j) (h + i 6j) g. (9m 5n + 10k) (-6n 7m + k) h. (7a + 8 b 11) + (5b 10b ). Jumlahkan! 18h + dan 1h 5 m + n dan 5m + 7n c. 50a + 0b dan 10b 0a + 9 1f 6g + 7h dan 8g 11f 5h e. b + 15c -1 dengan c f. 8ab + b dengan ab b + 7 g. -1a b 8ab dengan 6ab + b h. 9c d + 1 dengan 10cd 1. Kurangkan! 8p + + 5q dari 1p + q 5-7h 18 dari + 17h c. 15v + w dengan 0v w + 8 5c + 78 dengan 5c + 58 e. 5x + y + 7 oleh x y + f. a 6b + oleh 8b 1a 5 g. -7ab + 6a 1 dari ab b + 1 h. a b + c dari -a + b c + 5 PENDALAMAN MATERI OPERASI PENJUMLAHAN DAN PENGURANGAN
3 5. Jika p = d d dan q = d + d, hitunglah (p + q) dan (p q) 6. Gambar pekarangan Pak Yasin membentuk huruf L seperti tampak pada gambar berikut. Tentukan keliling pekarangan Pak Yasin dalam p! Jika keliling pekarangan 56 cm, carilah nilai p! p p p Alas kandang ayam Pak Amin berbentuk persegi panjang. Panjang kandang (a + ) meter dan lebarnya (5a ) meter, sedangkan panjang kayu yang diperlukan untuk membuat alas adalah 90 meter. Tentukan : nilai a, ukuran kandang, c. luas kandang (dalam are). Perkalian bentuk aljabar 1) Perkalian suatu bilangan dengan dua suku Bentuk umum perkalian suatu bilangan dengan dua suku antara lain : k(p + q) = kp + kq k(p - q) = kp kq, dengan p, q variabel dan k konstant Contoh : 1. (x + y) = 6x + y (5x y) = 0x 1y c. -(a 7) = -a + 1 5a(a b) = 5a 5ab ) Perkalian antara dua suku Perkalian antara dua suku bentuk aljabar dapat dilakukan dengan menggunakan sifat distributif. Contoh : 1. (x + 5) ( x + ) = x(x + ) + 5(x + ) = 6x + 8x + 15x + 0 = 6x + x + 0 (y z) (8y 1) = y(8y 1) z(8y 1) = y y yz + z (a + b) (a + b 8) = a(a + b - 8) + b(a + b 8) = a + ab 8a + ab + b 8b = a + ab 8a 8b + b ) Perkalian istimewa Perkalian istimewa adalah perkalian yang hasil kalinya bersifat khusus. Beberapa perkalian istimewa : (a + b) = a + ab + b (a b) = a ab + b c. (a + b) (a b) = a b (a + b) (a ab + b ) = a + b e. (a b) ((a + ab + b ) = a b Contoh : 1. Jabarkan! (y + ) = y +.y. + = y + y + (x ) = x +.x.(-) + (-) = x 6x + 9 c. (p + 8) (p 8) = p - 8 = p 6 (x + 5) (x 5) = (x) - 5 = 9x - 5 e. (k + ) (k k + 9) = k + = k + 7 f. (m ) (m +m + 16) = m - = m 6
4 1. Sederhanakan 5(x + y) -5(q r) c. -(-8h 5i) 6(-c d) e. 5(m n) f. (8a + 5) + (6a + 10) g. 5(7c ) 9(c ) h. 10(m + 5) - 8(5m + 6). Jabarkan! (x + ) (x + ) (x ) (x + 5) c. (a 1) (a + ) (5p + 7q) (p + q) e. (8c 5d) (-c + d) f. (5d e + ) (d + ) g. (1x + 5) (5x y 6) h. (m n 6)(m + n+8). Jabarkan! (x + ) (y 8) c. (a ) (15b + c) e. (p + 5q) f. (5mn pq) g. (6abc + 7def) h. (1x y 5x y ) PENDALAMAN MATERI OPERASI PERKALIAN BENTUK ALJABAR. Jabarkan bentuk aljabar berikut dalam bentuk perkalian istimewa! a 5 b 11 c. 169 c h e. d 81e f. 9m 5n g. 100x 81y h. 1p q 5r s 5. Jabarkan bentuk aljabar berikut dalam bentuk perkalian istimewa! j + 7 k 8 c. 6 m n e. g + 16 f. h 79i g. 8a + 15b h. x y 6. Jabarkan dan sederhanakan bentuk-bentuk aljabar di bawah ini! (a + b) (5a + ab b ) c. (5x 1) (x ) (x + 5y) (x y) e. f. 11x p 1 y 1 p 5x 1 16p 1 y
5 7. Tentukan hasil perpangkatan di bawah ini! (a + 5) (x - 1) c. (x + y) 5 (a + b) 6 8. Jabarkan! (a + b + 5c) (c 6d + 10) c. (5m 7n k) (8x + 5y 1z) e. (6v + 5w + 1) (v w ) c. Pembagian bentuk aljabar Pada pembagian bentuk aljabar, jika pembagi merupakan suku satu maka hasil pembagian dapat ditentukan dengan cara seperti pembagian pada bilangan bulat, tetapi jika pembagi lebih dari satu suku maka dapat ditentukan dengan cara bersusun kebawah. Contoh: 1.5 Tentukan hasil bagi dari bentuk aljabar berikut! 18a : 9a b - b 1) : (b 1) Penyelesaian: 18a : 9a = a b - b 1) : (b 1) = b + 1 b +1 b 1 b b 1 b b b 1 b 1 0 PENDALAMAN MATERI OPERASI PEMBAGIAN BENTUK ALJABAR 1. Tentukan hasil pembagian bentuk aljabar berikut ini! 1a : 6 7b : 9b c. 0a b : ab 8c d : 8c d e. 8a b c : a bc f. m 8 n 7 : (6m n : 9mn) g. 100c 6 d 5 : (5c d : 9cd ) h. (18p 9 q 8 : p q) : (6p 8 q 5 : pq ) Ingat (a b : a c = a b c ) - -. Tentukan hasil pembagian bentuk aljabar berikut ini! (g + g + 1) : (g + 1) (h + 8h + ) : (h + ) c. (i + 11i 6) : (i 1) (5j + 15j + j + 6) : (j + ) e. (6k 8k 15k + 0) : (k ) f. (-a + 11a a 15) : (5 x) g. (b b b + b) : (b + b) h. (x 1) : (x + 1) 5
6 B. Pemfaktoran Bentuk Aljabar 1. Bentuk ap + aq Bentuk ap + aq dapat difaktorkan menjadi: ap + aq = a(p + q) ap aq = a(p q) Contoh : 1.6 Faktorkan bentuk aljabar berikut ini x + y = (x + y) a + 6b 1c = (a + b c) c. 8ab + 1abc 0ac = a(b + bc 5c). Selisih kuadrat Misalkan : (x + y) (x y) = x(x y) + y(x y) = x xy + (yx) y = x y Jadi faktor dari : x y = (x + y) (x y) Contoh : 1.7 Faktorkan bentuk aljabar berikuk ini : x 81 = (x + 9) (x 9) 16a 5 = (a + 5) (a 5) c. x 9y = (x + 7y) (x 7y) a 98 = (16a 9) = (a + 7) (a 7) e. 16c 65d = (c + 5d ) (c - 5d ) = (c + 5d ) (c + 5d) (c 5d) PENDALAMAN MATERI 5 PEMFAKTORAN BENTUK (ap+ aq) = a(p + q) dan a b = (a + b) (a b) 1. Faktorkan! 15x + 0 6y 1 c. 15a + 1b 51 a + 0b 8 e. x xy + 0xz f. 5a b + 10ab g. 15cd 51c d + 6cd h. 1m n 16mn 9n. Faktorkan! x 5 x 5 c. 81y 1 169x 11y e. 9a b 5c d f. 5y z 9a b g. (a + b) c h. (c + d) d. Faktorkan bentuk aljabar berilkut ini : 18p 10p 0 c. 8p 50q 80p 7q e. 0p q 5x y f. a b - c d g. 1a b c 00 h. 0c d 15c d 6
7 . Bentuk Kuadrat Bentuk kuadrat ax + bx + c, a = 1 Karena nilai a = 1, maka bentuk ax + bx + c menjadi x + bx + c. Misalkan faktor dari : x + bx + c = (x + p) (x + q). Kita coba lakukan perkalian pada ruas kanan untuk mencari hubungan antara kedua ruas x + bx + c = (x + p) (x + q) = x(x + q) + p(x + q) = x + qx + px + pq = x + (p + q)x + pq. Maka terdapat hubungan b, c terhadap p dan q. b = p + q c = p x q, Dengan p dan q merupakan sembarang bilangan. Contoh : 1.8 Faktorkan! x + 5x + 6 y + y 5 Penyelesaian : Cara Tidak Langsung Cara Langsung Keterangan X + 5x + 6 = x + (x + x) + 6 x + 5x + 6 = (x + ) (x + ) b= 5 danc = 6 = (x + x + (x + 6) = (x + ) (x + ) = x(x + ) + (x + ) 6 =(x + ) (x + ) Jadi p =, q= y + y 5= y + (7y 5y) 5 = (y + 7y) (5y + 5) = y(y + 7) 5(y + 7) = (y 5y) (y + 7) y + y 5 = (y +7) (y 5) b=, c= Jadi p= 7, q= -5 Bentuk kuadrat ax + bx + c, a 1 Maka : Misalkan bentuk faktor dari : ax + bx + c = a 1 (ax + p) (ax + q). ax + bx + c = a 1 (ax + p) (ax + q). a x + abx + ac = (ax + p) (ax + q) kedua ruas dikalikan a = ax(ax + q) + p(ax + q) ruas kanan dilakukan perkalian = a x + qax + pax + pq = a x + (p + q) ax + pq Dari informasi diatas, hubungana,b, pd an q adalah : b = p + q ac = p x q, Dengan p dan q sembarang bilangan Contoh : 1. 9 Faktorkan : 8y + 10y + penyelesaian : Cara tidak lansung Cara langsung Keterangan 8y + 10y + = = 8y + (y + 6y) + = (8y + y) + (6y + ) = y(y + 1) + (y + 1) = (y + ) (y + 1) 8y + 10y + = = 8 1 (8y + ) (8y + 6) = 8 1.(y + 1). (y + ) = (y + 1) (y + ) B = 10 = p + q c = 8x = = pq p= dan 6 q= 6 7
8 PENDALAMAN MATERI 6 MATERI PEMFAKTORAN BENTUK x + bx + c dan ax + bx + c, dengan a 0 1. Faktorkan bentuk-bentuk berikut ini. x + x + x + 8x + 1 c. y + y 8 y + 1y 51 e. p p 0 f. p 11p 60 g. k 9k + 60 h. k 68k Faktorkan bentuk-bentuk berikut ini. h 8hj + 1j h 11hj + j c. a + 10ab + 5b a 1ab + 6b e. c - 1cd - 51d f. c + 0cd + 5d g. d 0de + 00e h. m + 16mn +6n. Faktorkan bentuk-bentuk berikut ini. 10t + 17t + k + 7k c. 9a a b 11b 5 e. 10c + 17c + f. 10d d + 1 g. g + 1g 6 h. g + 11g. Sederhanakan dalam bentuk faktorisasi. (x + x + 1) (9x 1x + ) (x 5xy y ) + (x xy y ) 5. Sederhanakan, kemudian faktorkan bentuk-bentuk berikut ini. (5x y) + 80x 16y + 6 9( x+ y ) 0x 10y Sebuah bola dilempar vertikal ke atas. Tinggi bola (h meter) setelah t detik dinyatakan dengan rumus h = 8 + t t. Bila bola dilempar setelah 1,5 detik, tentukan tinggi bola! Jika h = 0, carilah nilai t! C. Pecahan Bentuk Aljabar 1. Operasi pecahan bentuk aljabar Penjumlahan dan pengurangan Dua pecahan bentuk aljabar dapat dilakukan penjumlahan atau pengurangan apabila penyebutnya sam Jika penyebut-penyebut dari pecahan tersebut tidak sama, samakan penyebut dengan menggunakan faktor persekutuan terkeci (KPK). Contoh : 1.10 Sederhanakanlah! x 5x a b 8
9 Penyelesaian : x 5x 1x 15x 9x b 15a b15a a b 6ab 6ab 6ab Perkalian Perkalian pecahan bentuk aljabar mengikuti ketentuan : a x b Contoh : 1.11 c ac, dengan a dan b 0. d bd a b 6ab x y 1 x 6y y 1 (ingat KPK (5 dan 7 adalah 5) y 1y 1 y 1 6y. x y 1 c. Pembagian Pembagian pecahan bentuk aljabar mengikuti ketentuan : a a 1 a :c x b b c bc b c ac a: ax c b b a c a d ad : x b d b c bc y Contoh : 1. 1 p: q p px q q 5a 10a6 5a 1a8 5a 7a : x x 1 7a 1a8 7a 10a6 7a 5a PENDALAMAN MATERI 7 OPERASI PECAHAN BENTUK ALJABAR (Evaluasi kemampuan pemahaman) 1. Sederhanakan operasi penjumlahan dan pengurangan di bawah ini! 8 a a d 1 d - 1 y y - 1 c. a 10 a 5 e. a a 1 a 1 9 x 5x x 5 x 8 9
10 . Sederhanakan perkalian pecahan dibawah ini. cd 16c c 8d a 6b b a 1 c. m mn m n m mn m n 1j j k k j k 6jk 8h h h 1 e. 9h h 1. Sederhanakan pembagian pecahan di bawah ini. c. e. ab b : 9a 18a 8a 7a b 16b : 9a a 9a 9a : 16a 5a 1c c d 8 c d : c c 18 c - q q q q q : q q 5. Menyederhanakan pecahan Suatu pecahan a b a (pembilang) dan b (penyebut) adalah 1. Contoh : 1. 1 Sederhanakan pecahan berikut ini. x 6 x x 5x 6 Penyelesaian : x 6 x x. x x x 5x 6 x x x dapat dikatakan sederhana, apabila faktor persekutuan x. 10
11 PENDALAMAN MATERI 8 MENYEDERHANAKAN PECAHAN 1. Sederhanakanlah. c. e. 51x y 17xy 6x y 8xy xy 5x 10xy 10x 0y 18x 9xy x y 1x 18y 15xy 8x 1xy 10x y. Sederhanakan bentuk pecahan di bawah ini. c. e. x x x x 6x 5 x 1x 5 x 7x 6 6x 1x 1 x 7x x x 1 x 6x 6 x 6. Ubahlah pecahan bersusun dibawah ini ke dalam bentuk yang paling sederhan c. 1 1 a b a b b a a b b a 1 1 b a a b c b c a 1 1 b c a a 5 b 5b a 11
FAKTORISASI SUKU ALJABAR
 1 FAKTORISASI SUKU ALJABAR Pernahkah kalian berbelanja di supermarket? Sebelum berbelanja, kalian pasti memperkirakan barang apa saja yang akan dibeli dan berapa jumlah uang yang harus dibayar. Kalian
1 FAKTORISASI SUKU ALJABAR Pernahkah kalian berbelanja di supermarket? Sebelum berbelanja, kalian pasti memperkirakan barang apa saja yang akan dibeli dan berapa jumlah uang yang harus dibayar. Kalian
A. UNSUR - UNSUR ALJABAR
 PENGERTIAN ALJABAR Bentuk ALJABAR adalah suatu bentuk matematika yang dalam penyajiannya memuat hurufhuruf untuk mewakili bilangan yang belum diketahui. Bentuk aljabar dapat dimanfaatkan untuk menyelesaikan
PENGERTIAN ALJABAR Bentuk ALJABAR adalah suatu bentuk matematika yang dalam penyajiannya memuat hurufhuruf untuk mewakili bilangan yang belum diketahui. Bentuk aljabar dapat dimanfaatkan untuk menyelesaikan
Jakarta,. Guru Mata Pelajaran Memeriksa / Mengetahui Kepala SMP NIP... NIP...
 Kompetensi Dasar : 2.1 Mengenali bentuk aljabar dan unsur-unsurnya. 2.2 Melakukan operasi pada bentuk aljabar. Indikator : 1. Menentukan variabel, koefisien, konstanta, dan suku sejenis. 2. Menentukan
Kompetensi Dasar : 2.1 Mengenali bentuk aljabar dan unsur-unsurnya. 2.2 Melakukan operasi pada bentuk aljabar. Indikator : 1. Menentukan variabel, koefisien, konstanta, dan suku sejenis. 2. Menentukan
Faktorisasi Suku Aljabar
 Bab 1 Tujuan Pembelajaran Setelah mempelajari bab ini siswa diharapkan mampu: Menjelaskan pengertian koe sien, variabel, konstanta, suku satu, suku dua, dan suku banyak; Menyelesaikan masalah operasi tambah,
Bab 1 Tujuan Pembelajaran Setelah mempelajari bab ini siswa diharapkan mampu: Menjelaskan pengertian koe sien, variabel, konstanta, suku satu, suku dua, dan suku banyak; Menyelesaikan masalah operasi tambah,
matematika PEMINATAN Kelas X PERSAMAAN KUADRAT K-13 A. BENTUK UMUM PERSAMAAN KUADRAT
 K-13 Kelas X matematika PEMINATAN PERSAMAAN KUADRAT TUJUAN PEMBELAJARAN Setelah mempelajari materi ini, kamu diharapkan memiliki kemampuan berikut. 1. Memahami definisi dan bentuk umum persamaan kuadrat..
K-13 Kelas X matematika PEMINATAN PERSAMAAN KUADRAT TUJUAN PEMBELAJARAN Setelah mempelajari materi ini, kamu diharapkan memiliki kemampuan berikut. 1. Memahami definisi dan bentuk umum persamaan kuadrat..
PERSAMAAN KUADRAT. Persamaan. Sistem Persamaan Linear
 Persamaan Sistem Persamaan Linear PENGERTIAN Definisi Persamaan kuadrat adalah kalimat matematika terbuka yang memuat hubungan sama dengan yang pangkat tertinggi dari variabelnya adalah 2. Bentuk umum
Persamaan Sistem Persamaan Linear PENGERTIAN Definisi Persamaan kuadrat adalah kalimat matematika terbuka yang memuat hubungan sama dengan yang pangkat tertinggi dari variabelnya adalah 2. Bentuk umum
3 OPERASI HITUNG BENTUK ALJABAR
 OPERASI HITUNG BENTUK ALJABAR Pada arena balap mobil, sebuah mobil balap mampu melaju dengan kecepatan (x + 10) km/jam selama 0,5 jam. Berapakah kecepatannya jika jarak yang ditempuh mobil tersebut 00
OPERASI HITUNG BENTUK ALJABAR Pada arena balap mobil, sebuah mobil balap mampu melaju dengan kecepatan (x + 10) km/jam selama 0,5 jam. Berapakah kecepatannya jika jarak yang ditempuh mobil tersebut 00
RENCANA PELAKSANAAN PEMBELAJARAN No : 1 Mata Pelajaran : Matematika Kelas / Semester : VIII /1
 RENCANA PELASANAAN PEMBELAJARAN No : 1 Mata Pelajaran : Matematika elas / Semester : V /1 Alokasi : 4 jam pelajaran A. Standar ompetensi : 1. Memahami bentuk aljabar, relasi, fungsi, dan persamaan garis
RENCANA PELASANAAN PEMBELAJARAN No : 1 Mata Pelajaran : Matematika elas / Semester : V /1 Alokasi : 4 jam pelajaran A. Standar ompetensi : 1. Memahami bentuk aljabar, relasi, fungsi, dan persamaan garis
BAB I OPERASI ALJABAR DAN PEMFAKTORAN BENTUK ALJABAR
 BAB I OPERASI ALJABAR DAN PEMFAKTORAN BENTUK ALJABAR Setelah mempelajari bab ini kamu diharapkan mampu melakukan operasi aljabar, beberapa alternatif penyelesaian yang dihadapi oleh siswa terkait dengan
BAB I OPERASI ALJABAR DAN PEMFAKTORAN BENTUK ALJABAR Setelah mempelajari bab ini kamu diharapkan mampu melakukan operasi aljabar, beberapa alternatif penyelesaian yang dihadapi oleh siswa terkait dengan
PENERAPAN FAKTOR PRIMA DALAM MENYELESAIKAN BENTUK ALJABAR (Andi Syamsuddin*)
 PENERAPAN FAKTOR PRIMA DALAM MENYELESAIKAN BENTUK ALJABAR (Andi Syamsuddin*) A. Faktor Prima Dalam tulisan ini yang dimaksud dengan faktor prima sebuah bilangan adalah pembagi habis dari sebuah bilangan
PENERAPAN FAKTOR PRIMA DALAM MENYELESAIKAN BENTUK ALJABAR (Andi Syamsuddin*) A. Faktor Prima Dalam tulisan ini yang dimaksud dengan faktor prima sebuah bilangan adalah pembagi habis dari sebuah bilangan
1. Variabel, Konstanta, dan Faktor Variabel Konstanta Faktor
 ALJABAR BENTUK ALJABAR adalah suatu bentuk matematika yang dalam penyajiannya memuat huruf-huruf untuk mewakili bilangan yang belum diketahui Bentuk aljabar dapat dimanfaatkan untuk menyelesaikan masalah
ALJABAR BENTUK ALJABAR adalah suatu bentuk matematika yang dalam penyajiannya memuat huruf-huruf untuk mewakili bilangan yang belum diketahui Bentuk aljabar dapat dimanfaatkan untuk menyelesaikan masalah
Bab 3. Persamaan Garis Lurus. Standar Kompetensi. Memahami bentuk aljabar,persamaan dan pertidaksamaan linier satu variabel.
 Bab Persamaan Garis Lurus Standar Kompetensi Memahami bentuk aljabar,persamaan dan pertidaksamaan linier satu variabel. Kompetensi Dasar 1.1. Mengenali bentuk aljabar dan unsur-unsurnya. 1.. Melakukan
Bab Persamaan Garis Lurus Standar Kompetensi Memahami bentuk aljabar,persamaan dan pertidaksamaan linier satu variabel. Kompetensi Dasar 1.1. Mengenali bentuk aljabar dan unsur-unsurnya. 1.. Melakukan
Bab. Faktorisasi Aljabar. A. Operasi Hitung Bentuk Aljabar B. Pemfaktoran Bentuk Aljabar C. Pecahan dalam Bentuk Aljabar
 Bab Sumber: Science Encylopedia, 997 Faktorisasi Aljabar Masih ingatkah kamu tentang pelajaran Aljabar? Di Kelas VII, kamu telah mengenal bentuk aljabar dan juga telah mempelajari operasi hitung pada bentuk
Bab Sumber: Science Encylopedia, 997 Faktorisasi Aljabar Masih ingatkah kamu tentang pelajaran Aljabar? Di Kelas VII, kamu telah mengenal bentuk aljabar dan juga telah mempelajari operasi hitung pada bentuk
Ely Purnamasari (2008.V.I.0019) Kd. Winda Mahayanti (2008.V.I.0027) Pend. Matematika IKIP PGRI BALI
 Ely Purnamasari (2008.V.I.0019) Kd. Winda Mahayanti (2008.V.I.0027) Pend. Matematika IKIP PGRI BALI Indikator Standar Kompetensi Mamahami dan dapat melakukan operasi bentuk aljabar, persamaan dan pertidaksamaan
Ely Purnamasari (2008.V.I.0019) Kd. Winda Mahayanti (2008.V.I.0027) Pend. Matematika IKIP PGRI BALI Indikator Standar Kompetensi Mamahami dan dapat melakukan operasi bentuk aljabar, persamaan dan pertidaksamaan
PERSAMAAN KUADRAT. AC 0 P DAN Q SAMA TANDA. 2. DG. MELENGKAPKAN BENTUK KUADRAT ( KUADRAT SEMPURNA ) :
 PERSAMAAN KUADRAT. AC 0 P DAN Q SAMA TANDA.. DG. MELENGKAPKAN BENTUK KUADRAT ( KUADRAT SEMPURNA ) : Bab 3 PERSAMAAN KUADRAT 1. Bentuk Umum : ax bx c 0, a 0, a, b, c Re al Menyelesaikan persamaan kuadrat
PERSAMAAN KUADRAT. AC 0 P DAN Q SAMA TANDA.. DG. MELENGKAPKAN BENTUK KUADRAT ( KUADRAT SEMPURNA ) : Bab 3 PERSAMAAN KUADRAT 1. Bentuk Umum : ax bx c 0, a 0, a, b, c Re al Menyelesaikan persamaan kuadrat
SELEKSI OLIMPIADE MATEMATIKA INDONESIA 2007 TINGKAT PROVINSI TAHUN Prestasi itu diraih bukan didapat!!!
 SELEKSI OLIMPIADE MATEMATIKA INDONESIA 007 TINGKAT PROVINSI TAHUN 006 Prestasi itu diraih bukan didapat!!! SOLUSI SOAL Bidang Matematika Bagian Pertama Disusun oleh : Solusi Olimpiade Matematika Tk Provinsi
SELEKSI OLIMPIADE MATEMATIKA INDONESIA 007 TINGKAT PROVINSI TAHUN 006 Prestasi itu diraih bukan didapat!!! SOLUSI SOAL Bidang Matematika Bagian Pertama Disusun oleh : Solusi Olimpiade Matematika Tk Provinsi
BENTUK-BENTUK ALJABAR
 BENTUK-BENTUK ALJABAR (Pembelajaran Matematika SMP) Oleh : H. Karso FPMIPA UPI A. Kalimat Matematika dalam Bentuk Aljabar Serta Unsur-unsurnya Dalam pelajaran matematika pengertian kalimat matematika dibedakan
BENTUK-BENTUK ALJABAR (Pembelajaran Matematika SMP) Oleh : H. Karso FPMIPA UPI A. Kalimat Matematika dalam Bentuk Aljabar Serta Unsur-unsurnya Dalam pelajaran matematika pengertian kalimat matematika dibedakan
Faktorisasi Bentuk Aljabar
 Faktorisasi Bentuk Aljabar Satuan Pendidikan Bidang Study Kelas / Semester : SMP. N 2 Jatipuro : MATEMATIKA : VIII / I 1. STANDAR KOMPETENSI Memahami bentuk aljabar. 2. KOMPETENSI DASAR 1.1 Melakukan operasi
Faktorisasi Bentuk Aljabar Satuan Pendidikan Bidang Study Kelas / Semester : SMP. N 2 Jatipuro : MATEMATIKA : VIII / I 1. STANDAR KOMPETENSI Memahami bentuk aljabar. 2. KOMPETENSI DASAR 1.1 Melakukan operasi
BAB II PERSAMAAN KUADRAT DAN FUNGSI KUADRAT
 BAB II PERSAMAAN KUADRAT DAN FUNGSI KUADRAT 1. Menentukan koefisien persamaan kuadrat 2. Jenis-jenis akar persamaan kuadrat 3. Menyusun persamaan kuadrat yang akarnya diketahui 4. Fungsi kuadrat dan grafiknya
BAB II PERSAMAAN KUADRAT DAN FUNGSI KUADRAT 1. Menentukan koefisien persamaan kuadrat 2. Jenis-jenis akar persamaan kuadrat 3. Menyusun persamaan kuadrat yang akarnya diketahui 4. Fungsi kuadrat dan grafiknya
ALJABAR. Al-Khwarizi adalah ahli matematika dan ahlli astronomi yang termasyur yang tinggal di bagdad(irak) pada permulaan abad ke-9
 ALJABAR Al-Khwarizi adalah ahli matematika dan ahlli astronomi yang termasyur yang tinggal di bagdad(irak) pada permulaan abad ke-9 Aljabar adalah salah satu cabang penting dalam matematika. Kata aljabar
ALJABAR Al-Khwarizi adalah ahli matematika dan ahlli astronomi yang termasyur yang tinggal di bagdad(irak) pada permulaan abad ke-9 Aljabar adalah salah satu cabang penting dalam matematika. Kata aljabar
PEMBINAAN TAHAP I CALON SISWA INVITATIONAL WORLD YOUTH MATHEMATICS INTERCITY COMPETITION (IWYMIC) 2010 MODUL ALJABAR
 PEMBINAAN TAHAP I CALON SISWA INVITATIONAL WORLD YOUTH MATHEMATICS INTERCITY COMPETITION (IWYMIC) 2010 MODUL ALJABAR DIREKTORAT JENDERAL MANAJEMEN PENDIDIKAN DASAR DAN MENENGAH DIREKTORAT PEMBINAAN SMP
PEMBINAAN TAHAP I CALON SISWA INVITATIONAL WORLD YOUTH MATHEMATICS INTERCITY COMPETITION (IWYMIC) 2010 MODUL ALJABAR DIREKTORAT JENDERAL MANAJEMEN PENDIDIKAN DASAR DAN MENENGAH DIREKTORAT PEMBINAAN SMP
Relasi, Fungsi, dan Transformasi
 Modul 1 Relasi, Fungsi, dan Transformasi Drs. Ame Rasmedi S. Dr. Darhim, M.Si. M PENDAHULUAN odul ini merupakan modul pertama pada mata kuliah Geometri Transformasi. Modul ini akan membahas pengertian
Modul 1 Relasi, Fungsi, dan Transformasi Drs. Ame Rasmedi S. Dr. Darhim, M.Si. M PENDAHULUAN odul ini merupakan modul pertama pada mata kuliah Geometri Transformasi. Modul ini akan membahas pengertian
Menyelesaikan Persamaan Kuadrat. 3. Rumus ABC ax² + bx + c = 0 X1,2 = ( [-b ± (b²-4ac)]/2a. Kemungkinan Jenis Akar Ditinjau Dari Nilai Diskriminan
![Menyelesaikan Persamaan Kuadrat. 3. Rumus ABC ax² + bx + c = 0 X1,2 = ( [-b ± (b²-4ac)]/2a. Kemungkinan Jenis Akar Ditinjau Dari Nilai Diskriminan Menyelesaikan Persamaan Kuadrat. 3. Rumus ABC ax² + bx + c = 0 X1,2 = ( [-b ± (b²-4ac)]/2a. Kemungkinan Jenis Akar Ditinjau Dari Nilai Diskriminan](/thumbs/52/29781394.jpg) Menyelesaikan Persamaan Kuadrat Bentuk umum : ax² + bx + c = 0 x variabel; a,b,c konstanta ; a 0 Menyelesaikan persamaan kuadrat berarti mencari harga x yang memenuhi persamaan kudrat (PK) tersebut (disebut
Menyelesaikan Persamaan Kuadrat Bentuk umum : ax² + bx + c = 0 x variabel; a,b,c konstanta ; a 0 Menyelesaikan persamaan kuadrat berarti mencari harga x yang memenuhi persamaan kudrat (PK) tersebut (disebut
matematika Wajib Kelas X PERSAMAAN LINEAR SATU VARIABEL K-13 A. DEFINISI PERSAMAAN LINEAR SATU VARIABEL
 K-3 Kelas X matematika Wajib PERSAMAAN LINEAR SATU VARIABEL TUJUAN PEMBELAJARAN Setelah mempelajari materi ini, kamu diharapkan memiliki kemampuan berikut.. Memahami definisi dan solusi persamaan linear
K-3 Kelas X matematika Wajib PERSAMAAN LINEAR SATU VARIABEL TUJUAN PEMBELAJARAN Setelah mempelajari materi ini, kamu diharapkan memiliki kemampuan berikut.. Memahami definisi dan solusi persamaan linear
LEMBAR KERJA SISWA. Semester Ganjil STANDAR ISI KTSP. Nama :... Kelas :... Sekolah :...
 LEMBAR KERJA SISWA Semester Ganjil Nama :... Kelas :... Sekolah :... STANDAR ISI KTSP Standar kompetensi : Memahami bentuk aljabar, persamaan dan pertidaksamaan linier dan satu variabel. Kompetensi dasar
LEMBAR KERJA SISWA Semester Ganjil Nama :... Kelas :... Sekolah :... STANDAR ISI KTSP Standar kompetensi : Memahami bentuk aljabar, persamaan dan pertidaksamaan linier dan satu variabel. Kompetensi dasar
MADRASAH ALIYAH AL-MU AWANAH BEKASI SELATAN 2012
 MODUL MATEMATIKA PERSIAPAN UJIAN NASIONAL 0 TAHUN AJARAN 0/0 MATERI PERSAMAAN KUADRAT DAN PERTIDAKSAMAAN KUADRAT UNTUK KALANGAN MA AL-MU AWANAH MADRASAH ALIYAH AL-MU AWANAH BEKASI SELATAN 0 Jalan RH. Umar
MODUL MATEMATIKA PERSIAPAN UJIAN NASIONAL 0 TAHUN AJARAN 0/0 MATERI PERSAMAAN KUADRAT DAN PERTIDAKSAMAAN KUADRAT UNTUK KALANGAN MA AL-MU AWANAH MADRASAH ALIYAH AL-MU AWANAH BEKASI SELATAN 0 Jalan RH. Umar
Standar Kompetensi : 1. Memahami bentuk aljabar, relasi, fungsi, dan persamaan garis lurus. Kompetensi Dasar : 1.1. Melakukan operasi aljabar
 Standar Kompetensi :. Memahami bentuk aljabar, relasi, fungsi, dan persamaan garis lurus. Kompetensi Dasar :.. Melakukan operasi aljabar A. PENGERTIAN KOEFISIEN, VARIABEL, KONSTANTA, SUKU SATU, SUKU DUA
Standar Kompetensi :. Memahami bentuk aljabar, relasi, fungsi, dan persamaan garis lurus. Kompetensi Dasar :.. Melakukan operasi aljabar A. PENGERTIAN KOEFISIEN, VARIABEL, KONSTANTA, SUKU SATU, SUKU DUA
Prestasi itu diraih bukan didapat!!! SOLUSI SOAL
 SELEKSI OLIMPIADE TINGKAT PROVINSI 013 TIM OLIMPIADE MATEMATIKA INDONESIA 014 Prestasi itu diraih bukan didapat!!! SOLUSI SOAL BAGIAN PERTAMA Disusun oleh : Solusi Olimpiade Matematika Tk Provinsi 013
SELEKSI OLIMPIADE TINGKAT PROVINSI 013 TIM OLIMPIADE MATEMATIKA INDONESIA 014 Prestasi itu diraih bukan didapat!!! SOLUSI SOAL BAGIAN PERTAMA Disusun oleh : Solusi Olimpiade Matematika Tk Provinsi 013
Bab 1. Faktorisasi Suku Aljabar. Standar Kompetensi. Memahami bentuk aljabar, relasi, fungsi, dan persamaan garis lurus.
 Bab 1 Faktorisasi Suku Aljabar Standar Kompetensi Memahami bentuk aljabar, relasi, fungsi, dan persamaan garis lurus. Kompetensi Dasar 1.1 Melakukan operasi aljabar. 1.2 Menguraikan bentuk aljabar ke dalam
Bab 1 Faktorisasi Suku Aljabar Standar Kompetensi Memahami bentuk aljabar, relasi, fungsi, dan persamaan garis lurus. Kompetensi Dasar 1.1 Melakukan operasi aljabar. 1.2 Menguraikan bentuk aljabar ke dalam
Soal Ulangan Umum Semester 1 Kelas VIII
 Soal Ulangan Umum Semester 1 Kelas VIII A. Berilah tanda silang (x) pada huruf a, b, c, d atau e di depan jawaban yang benar! 1. Salah satu factor dari x - xy 4y adalah cm a. (x - 4y)(x + 3y) b. (x + 4y)(x
Soal Ulangan Umum Semester 1 Kelas VIII A. Berilah tanda silang (x) pada huruf a, b, c, d atau e di depan jawaban yang benar! 1. Salah satu factor dari x - xy 4y adalah cm a. (x - 4y)(x + 3y) b. (x + 4y)(x
LEMBAR AKTIVITAS SISWA BENTUK PANGKAT (EKSPONEN)
 Nama Siswa Kelas PETA KONSEP: LEMBAR AKTIVITAS SISWA BENTUK PANGKAT (EKSPONEN) Latihan :. :. 3. A. PANGKAT BULAT POSITIF Jika a R dan bilangan bulat positif n, maka a n didefinisikan sbg berikut: a n =
Nama Siswa Kelas PETA KONSEP: LEMBAR AKTIVITAS SISWA BENTUK PANGKAT (EKSPONEN) Latihan :. :. 3. A. PANGKAT BULAT POSITIF Jika a R dan bilangan bulat positif n, maka a n didefinisikan sbg berikut: a n =
Matematika: Persamaan Kuadrat 11/22/2011 PERSAMAAN KUADRAT. Oleh Syawaludin A. Harahap, MSc
 Matematika: Persamaan Kuadrat //0 MATA KULIAH : MATEMATIKA KODE MATA KULIAH : UNM0.0 SKS : (-) ) PERSAMAAN KUADRAT Oleh Syawaludin A. Harahap, MSc UNIVERSITAS PADJADJARAN FAKULTAS PERIKANAN DAN ILMU KELAUTAN
Matematika: Persamaan Kuadrat //0 MATA KULIAH : MATEMATIKA KODE MATA KULIAH : UNM0.0 SKS : (-) ) PERSAMAAN KUADRAT Oleh Syawaludin A. Harahap, MSc UNIVERSITAS PADJADJARAN FAKULTAS PERIKANAN DAN ILMU KELAUTAN
SOLUSI SOAL OLIMPIADE SAINS NASIONAL SMP SELEKSI TINGKAT PROPINSI TAHUN 2015 BIDANG MATEMATIKA
 SOLUSI SOAL OLIMPIADE SAINS NASIONAL SMP SELEKSI TINGKAT PROPINSI TAHUN 015 BIDANG MATEMATIKA BAGIAN A: SOAL ISIAN SINGKAT 1. Banyak faktor persekutuan dari 1515 dan 530 yang merupakan bilangan genap positip
SOLUSI SOAL OLIMPIADE SAINS NASIONAL SMP SELEKSI TINGKAT PROPINSI TAHUN 015 BIDANG MATEMATIKA BAGIAN A: SOAL ISIAN SINGKAT 1. Banyak faktor persekutuan dari 1515 dan 530 yang merupakan bilangan genap positip
SOAL DAN SOLUSI PEREMPATFINAL KOMPETISI MATEMATIKA UNIVERSITAS TARUMANAGARA 2011
 SOAL DAN SOLUSI PEREMPATFINAL KOMPETISI MATEMATIKA UNIVERSITAS TARUMANAGARA 2011 (90menit) 1. Semua tripel (x, y, z) yang memenuhi bahwa salah satu bilangan jika ditambahkan dengan hasil kali kedua bilangan
SOAL DAN SOLUSI PEREMPATFINAL KOMPETISI MATEMATIKA UNIVERSITAS TARUMANAGARA 2011 (90menit) 1. Semua tripel (x, y, z) yang memenuhi bahwa salah satu bilangan jika ditambahkan dengan hasil kali kedua bilangan
Prestasi itu diraih bukan didapat!!! SOLUSI SOAL
 SELEKSI OLIMPIADE TINGKAT PROVINSI 2013 TIM OLIMPIADE MATEMATIKA INDONESIA 2014 Prestasi itu diraih bukan didapat!!! SOLUSI SOAL BAGIAN PERTAMA Disusun oleh : BAGIAN PERTAMA 1. ABC adalah segitiga sama
SELEKSI OLIMPIADE TINGKAT PROVINSI 2013 TIM OLIMPIADE MATEMATIKA INDONESIA 2014 Prestasi itu diraih bukan didapat!!! SOLUSI SOAL BAGIAN PERTAMA Disusun oleh : BAGIAN PERTAMA 1. ABC adalah segitiga sama
LAMPIRAN A : SILABUS KTSP KLS VII SEMESTER GANJIL KURIKULUM TINGKAT SATUAN PENDIDIKAN (KTSP) ANALISIS MATERI KOMPETENSI SISWA SMP (SILABUS)
 LAMPIRAN A : SILABUS KTSP KLS VII SEMESTER GANJIL SEKOLAH KELAS MATA PELAJARAN SEMESTER BILANGAN Standar Kompetensi KOMPETENSI DASAR 1.1 Melakukan operasi hitung bilangan bulat. : SMP : VII : MATEMATIKA
LAMPIRAN A : SILABUS KTSP KLS VII SEMESTER GANJIL SEKOLAH KELAS MATA PELAJARAN SEMESTER BILANGAN Standar Kompetensi KOMPETENSI DASAR 1.1 Melakukan operasi hitung bilangan bulat. : SMP : VII : MATEMATIKA
Pembahasan Soal SIMAK UI 2012 SELEKSI MASUK UNIVERSITAS INDONESIA. Disertai TRIK SUPERKILAT dan LOGIKA PRAKTIS. Matematika IPA
 Pembahasan Soal SIMAK UI 0 SELEKSI MASUK UNIVERSITAS INDONESIA Disertai TRIK SUPERKILAT dan LOGIKA PRAKTIS Matematika IPA Disusun Oleh : Pak Anang Kumpulan SMART SOLUTION dan TRIK SUPERKILAT Pembahasan
Pembahasan Soal SIMAK UI 0 SELEKSI MASUK UNIVERSITAS INDONESIA Disertai TRIK SUPERKILAT dan LOGIKA PRAKTIS Matematika IPA Disusun Oleh : Pak Anang Kumpulan SMART SOLUTION dan TRIK SUPERKILAT Pembahasan
FAQ ALJABAR SMP KELAS 7
 FAQ ALJABAR SMP KELAS 7 Pertanyaan yang Sering Ditanyakan Seputar Aljabar SMP Kelas 7 http://caramudahbelajarmatematika.com/ Cara Mudah Belajar Matematika Assalamualaikum Wr. Wb. Jumpa Lagi dengan Saya,
FAQ ALJABAR SMP KELAS 7 Pertanyaan yang Sering Ditanyakan Seputar Aljabar SMP Kelas 7 http://caramudahbelajarmatematika.com/ Cara Mudah Belajar Matematika Assalamualaikum Wr. Wb. Jumpa Lagi dengan Saya,
MA5032 ANALISIS REAL
 (Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. August 16, 2011 Pada bab ini anda diasumsikan telah mengenal dengan cukup baik bilangan asli, bilangan bulat, dan bilangan
(Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. August 16, 2011 Pada bab ini anda diasumsikan telah mengenal dengan cukup baik bilangan asli, bilangan bulat, dan bilangan
SMP kelas 9 - MATEMATIKA BAB 20. PYTHAGORASLatihan Soal km. 225 km. 250 km. 280 km
 SMP kelas 9 - MATEMATIKA BAB 20. PYTHAGORASLatihan Soal 20.1 1. Sebuah kapal berangkat dari pelabuhan ke arah utara sejauh 120 km, kemudian berbelok ke arah barat sejauh 160 km. Jarak terdekat kapal dari
SMP kelas 9 - MATEMATIKA BAB 20. PYTHAGORASLatihan Soal 20.1 1. Sebuah kapal berangkat dari pelabuhan ke arah utara sejauh 120 km, kemudian berbelok ke arah barat sejauh 160 km. Jarak terdekat kapal dari
BAHAN AJAR ANALISIS REAL 1 Matematika STKIP Tuanku Tambusai Bangkinang
 Pertemuan 2. BAHAN AJAR ANALISIS REAL Matematika STKIP Tuanku Tambusai Bangkinang 0. Bilangan Real 0. Bilangan Real sebagai bentuk desimal Pada pembahasan berikutnya kita diasumsikan telah mengetahui dengan
Pertemuan 2. BAHAN AJAR ANALISIS REAL Matematika STKIP Tuanku Tambusai Bangkinang 0. Bilangan Real 0. Bilangan Real sebagai bentuk desimal Pada pembahasan berikutnya kita diasumsikan telah mengetahui dengan
Mata Pelajaran Wajib. Disusun Oleh: Ngapiningsih
 Mata Pelajaran Wajib Disusun Oleh: Ngapiningsih Disklaimer Daftar isi Disklaimer Powerpoint pembelajaran ini dibuat sebagai alternatif guna membantu Bapak/Ibu Guru melaksanakan pembelajaran. Materi powerpoint
Mata Pelajaran Wajib Disusun Oleh: Ngapiningsih Disklaimer Daftar isi Disklaimer Powerpoint pembelajaran ini dibuat sebagai alternatif guna membantu Bapak/Ibu Guru melaksanakan pembelajaran. Materi powerpoint
BAB IV PERTIDAKSAMAAN. 1. Pertidaksamaan Kuadrat 2. Pertidaksamaan Bentuk Pecahan 3. Pertidaksamaan Bentuk Akar 4. Pertidaksamaan Nilai Mutlak
 BAB IV PERTIDAKSAMAAN 1. Pertidaksamaan Kuadrat. Pertidaksamaan Bentuk Pecahan 3. Pertidaksamaan Bentuk Akar 4. Pertidaksamaan Nilai Mutlak 86 LEMBAR KERJA SISWA 1 Mata Pelajaran : Matematika Uraian Materi
BAB IV PERTIDAKSAMAAN 1. Pertidaksamaan Kuadrat. Pertidaksamaan Bentuk Pecahan 3. Pertidaksamaan Bentuk Akar 4. Pertidaksamaan Nilai Mutlak 86 LEMBAR KERJA SISWA 1 Mata Pelajaran : Matematika Uraian Materi
II. M A T R I K S ... A... Contoh II.1 : Macam-macam ukuran matriks 2 A. 1 3 Matrik A berukuran 3 x 1. Matriks B berukuran 1 x 3
 11 II. M A T R I K S Untuk mencari pemecahan sistem persamaan linier dapat digunakan beberapa cara. Salah satu yang paling mudah adalah dengan menggunakan matriks. Dalam matematika istilah matriks digunakan
11 II. M A T R I K S Untuk mencari pemecahan sistem persamaan linier dapat digunakan beberapa cara. Salah satu yang paling mudah adalah dengan menggunakan matriks. Dalam matematika istilah matriks digunakan
KUMPULAN SOAL MATEMATIKA SMP KELAS 7
 KUMPULAN SOAL MATEMATIKA SMP KELAS 7 Dirangkum oleh Moch. Fatkoer Rohman Website: http://fatkoer.co.cc http://zonamatematika.co.cc Email: fatkoer@gmail.com EVALUASI MANDIRI A. SOAL PILIHAN GANDA. Pilih
KUMPULAN SOAL MATEMATIKA SMP KELAS 7 Dirangkum oleh Moch. Fatkoer Rohman Website: http://fatkoer.co.cc http://zonamatematika.co.cc Email: fatkoer@gmail.com EVALUASI MANDIRI A. SOAL PILIHAN GANDA. Pilih
Pembahasan Soal OSK SMA 2018 OLIMPIADE SAINS KABUPATEN/KOTA SMA OSK Matematika SMA. (Olimpiade Sains Kabupaten/Kota Matematika SMA)
 Pembahasan Soal OSK SMA 018 OLIMPIADE SAINS KABUPATEN/KOTA SMA 018 OSK Matematika SMA (Olimpiade Sains Kabupaten/Kota Matematika SMA) Disusun oleh: Pak Anang Pembahasan Soal OSK SMA 018 OLIMPIADE SAINS
Pembahasan Soal OSK SMA 018 OLIMPIADE SAINS KABUPATEN/KOTA SMA 018 OSK Matematika SMA (Olimpiade Sains Kabupaten/Kota Matematika SMA) Disusun oleh: Pak Anang Pembahasan Soal OSK SMA 018 OLIMPIADE SAINS
Faktorisasi Aljabar Linear
 Faktorisasi Aljabar Linear Click to here INTRO SEJARAH ISI QUIS PENUTUP FAKTORISASI ALJABAR TEAM SHINOBI PRAKATA INTRO SEJARAH ISI QUIS PENUTUP Puji syukur penulis panjatkan kepada Tuhan Yang Maha Esa
Faktorisasi Aljabar Linear Click to here INTRO SEJARAH ISI QUIS PENUTUP FAKTORISASI ALJABAR TEAM SHINOBI PRAKATA INTRO SEJARAH ISI QUIS PENUTUP Puji syukur penulis panjatkan kepada Tuhan Yang Maha Esa
PERSAMAAN, FUNGSI DAN PERTIDAKSAMAAN KUADRAT
 LA - WB (Lembar Aktivitas Warga Belajar) PERSAMAAN, FUNGSI DAN PERTIDAKSAMAAN KUADRAT Oleh: Hj. ITA YULIANA, S.Pd, M.Pd MATEMATIKA PAKET C TINGKAT V DERAJAT MAHIR 1 SETARA KELAS X Created By Ita Yuliana
LA - WB (Lembar Aktivitas Warga Belajar) PERSAMAAN, FUNGSI DAN PERTIDAKSAMAAN KUADRAT Oleh: Hj. ITA YULIANA, S.Pd, M.Pd MATEMATIKA PAKET C TINGKAT V DERAJAT MAHIR 1 SETARA KELAS X Created By Ita Yuliana
MSH1B3 LOGIKA MATEMATIKA Aljabar Boolean (Lanjutan)
 MSH1B3 LOGIKA MATEMATIKA Aljabar Boolean (Lanjutan) Dosen: Aniq A Rohmawati, M.Si TELKOM UNIVERSITY JALAN TELEKOMUNIKASI 1, BANDUNG, INDONESIA Latihan 1 Simplify the following Boolean functions using Boolean
MSH1B3 LOGIKA MATEMATIKA Aljabar Boolean (Lanjutan) Dosen: Aniq A Rohmawati, M.Si TELKOM UNIVERSITY JALAN TELEKOMUNIKASI 1, BANDUNG, INDONESIA Latihan 1 Simplify the following Boolean functions using Boolean
Pembahasan OSN Tingkat Provinsi Tahun 2012 Jenjang SMP Bidang Matematika
 Pembahasan OSN Tingkat Provinsi Tahun 202 Jenjang SMP Bidang Matematika Bagian A : Soal Isian Singkat. Sebuah silinder memiliki tinggi 5 cm dan volume 20 cm 2. Luas permukaan bola terbesar yang mungkin
Pembahasan OSN Tingkat Provinsi Tahun 202 Jenjang SMP Bidang Matematika Bagian A : Soal Isian Singkat. Sebuah silinder memiliki tinggi 5 cm dan volume 20 cm 2. Luas permukaan bola terbesar yang mungkin
GLOSSARIUM. A Akar kuadrat
 A Akar kuadrat GLOSSARIUM Akar kuadrat adalah salah satu dari dua faktor yang sama dari suatu bilangan. Contoh: 9 = 3 karena 3 2 = 9 Anggota Himpunan Suatu objek dalam suatu himpunan B Belahketupat Bentuk
A Akar kuadrat GLOSSARIUM Akar kuadrat adalah salah satu dari dua faktor yang sama dari suatu bilangan. Contoh: 9 = 3 karena 3 2 = 9 Anggota Himpunan Suatu objek dalam suatu himpunan B Belahketupat Bentuk
KOTA - PROVINSI - NASIONAL TAHUN 2017 MATA PELAJARAN: MATEMATIKA
 OLIMPIADE SAINS SMP/MTs TINGKAT KOTA - PROVINSI - NASIONAL TAHUN 07 MATA PELAJARAN: MATEMATIKA Mata Pelajaran : Matematika Jenjang : SMP/MTs MATA PELAJARAN PETUNJUK UMUM () Kerjakan soal ini dengan JUJUR,
OLIMPIADE SAINS SMP/MTs TINGKAT KOTA - PROVINSI - NASIONAL TAHUN 07 MATA PELAJARAN: MATEMATIKA Mata Pelajaran : Matematika Jenjang : SMP/MTs MATA PELAJARAN PETUNJUK UMUM () Kerjakan soal ini dengan JUJUR,
Prestasi itu diraih bukan didapat!!! SOLUSI SOAL
 SELEKSI OLIMPIADE TINGKAT KABUPATEN/KOTA 013 CALON TIM OLIMPIADE MATEMATIKA INDONESIA 014 Prestasi itu diraih bukan didapat!!! SOLUSI SOAL Bidang Matematika Disusun oleh : 1. 94 + 013 = a + b 013 = 61
SELEKSI OLIMPIADE TINGKAT KABUPATEN/KOTA 013 CALON TIM OLIMPIADE MATEMATIKA INDONESIA 014 Prestasi itu diraih bukan didapat!!! SOLUSI SOAL Bidang Matematika Disusun oleh : 1. 94 + 013 = a + b 013 = 61
= Tentukan jumlah dari : ( 1) ( jawaban boleh di faktorkan) 6. Tentukan semua penyelesaian system persamaan dari : =
 1. Diberikan polynomial f(x) = x n + a 1x n-1 +...+ a n-1 x + a 0 dengan koefisien a 1, a,...a n semua bilangan bulat dan ada 4 bilangan bulat berbeda a,b,c, dan d yang memenuhi f(a) = f(b) = f(c) = f(d)
1. Diberikan polynomial f(x) = x n + a 1x n-1 +...+ a n-1 x + a 0 dengan koefisien a 1, a,...a n semua bilangan bulat dan ada 4 bilangan bulat berbeda a,b,c, dan d yang memenuhi f(a) = f(b) = f(c) = f(d)
Jika persegi panjang ABCD di atas diketahui OA = 26 cm, maka panjang BO adalah... A. 78 cm. C. 26 cm B. 52 cm. D. 13 cm Kunci : C Penyelesaian :
 1. Jika persegi panjang ABCD di atas diketahui OA = 26 cm, maka panjang BO adalah... A. 78 cm C. 26 cm B. 52 cm D. 13 cm 2. Gambar disamping adalah persegi panjang. Salah satu sifat persegi panjang adalah
1. Jika persegi panjang ABCD di atas diketahui OA = 26 cm, maka panjang BO adalah... A. 78 cm C. 26 cm B. 52 cm D. 13 cm 2. Gambar disamping adalah persegi panjang. Salah satu sifat persegi panjang adalah
BAB 1 FAKTORISASI SUKU ALJABAR SOAL LATIHAN 1.1
 BAB 1 FAKTORISASI SUKU ALJABAR SOAL LATIHAN 1.1 BAB 1 FAKTORISASI SUKU ALJABAR SOAL LATIHAN 1.1 A. Pilihan Ganda 1. Bentuk x + x 48 jika difaktorkan adalah A. (x 6)(x 8) B. (x + 8)(x 6) C. (x 4)(x 1)
BAB 1 FAKTORISASI SUKU ALJABAR SOAL LATIHAN 1.1 BAB 1 FAKTORISASI SUKU ALJABAR SOAL LATIHAN 1.1 A. Pilihan Ganda 1. Bentuk x + x 48 jika difaktorkan adalah A. (x 6)(x 8) B. (x + 8)(x 6) C. (x 4)(x 1)
LAMPIRAN A. A1. Analisis kurikulum. A2. Skenario (jalan cerita) A3. Flowchart (alur) Permainan Pekerja Aljabar
 86 LAMPIRAN A A1. Analisis kurikulum A2. Skenario (jalan cerita) A3. Flowchart (alur) Permainan Pekerja Aljabar A. Materi, contoh soal dan soal latihan permainan materi operasi aljabar 87 ANALISIS KURIKULUM
86 LAMPIRAN A A1. Analisis kurikulum A2. Skenario (jalan cerita) A3. Flowchart (alur) Permainan Pekerja Aljabar A. Materi, contoh soal dan soal latihan permainan materi operasi aljabar 87 ANALISIS KURIKULUM
BILANGAN BERPANGKAT DAN BENTUK AKAR
 BILANGAN BERPANGKAT DAN BENTUK AKAR 1. Bilangan Berpangkat Sederhana Dalam kehidupan sehari-hari kita sering menemui perkalian bilangan-bilangan dengan faktorfaktor yang sama. Misalkan kita temui perkalian
BILANGAN BERPANGKAT DAN BENTUK AKAR 1. Bilangan Berpangkat Sederhana Dalam kehidupan sehari-hari kita sering menemui perkalian bilangan-bilangan dengan faktorfaktor yang sama. Misalkan kita temui perkalian
Jikax (2 x) = 57, maka jumlah semua bilangan bulat x yang memenuhi adalah A. -5 B. -1 C. 0 D. 1 E. 5
 Soal Babak Penyisihan OMITS 011 BAGIAN I. PILIHAN GANDA 1. Hasil kali sebarang bilangan rasional dengan sebarang bilangan irasional selalu merupakan anggota dari himpunan bilangan A. Bulat B. Asli C. Rasional
Soal Babak Penyisihan OMITS 011 BAGIAN I. PILIHAN GANDA 1. Hasil kali sebarang bilangan rasional dengan sebarang bilangan irasional selalu merupakan anggota dari himpunan bilangan A. Bulat B. Asli C. Rasional
BERBASIS PENDEKATAN KONTEKSTUAL. SMP/MT s. Kelas :... Sekolah :...
 BERBASIS PENDEKATAN KONTEKSTUAL MODUL MATEMATIKA ALJABAR SMP/MT s SMP/MT s Elvira Resa Krismasari Nama :... Kelas :... Sekolah :... Modul Matematika Aljabar Berbasis Pendekatan Kontekstual Untuk Siswa
BERBASIS PENDEKATAN KONTEKSTUAL MODUL MATEMATIKA ALJABAR SMP/MT s SMP/MT s Elvira Resa Krismasari Nama :... Kelas :... Sekolah :... Modul Matematika Aljabar Berbasis Pendekatan Kontekstual Untuk Siswa
PEMBAHASAN UN 2009/2010
 PEMBAHASAN UN 009/00. Konsep: Operasi Bilangan Real (Perbandingan Berbalik Nilai) Suatu pekerjaan dikerjakan orang dapat selesai 0 hari. Pekerjaan akan diselesaikan dalam waktu hari. Pekerja Hari 0 y y
PEMBAHASAN UN 009/00. Konsep: Operasi Bilangan Real (Perbandingan Berbalik Nilai) Suatu pekerjaan dikerjakan orang dapat selesai 0 hari. Pekerjaan akan diselesaikan dalam waktu hari. Pekerja Hari 0 y y
PENGEMBANGAN KISI-KISI UJIAN SEMESTER GANJIL TAHUN 2016/2017
 PENGEMBANGAN KISI-KISI UJIAN SEMESTER GANJIL TAHUN 2016/2017 Jenis Sekolah : SMP Waktu : 90 menit Mata Pelajaran : Matematika Banyak soal : 25/5 Kelas : VII Pembuat Soal : Tim Kurikulum : KTSP Bentuk Soal
PENGEMBANGAN KISI-KISI UJIAN SEMESTER GANJIL TAHUN 2016/2017 Jenis Sekolah : SMP Waktu : 90 menit Mata Pelajaran : Matematika Banyak soal : 25/5 Kelas : VII Pembuat Soal : Tim Kurikulum : KTSP Bentuk Soal
SOAL SELEKSI TINGKAT KOTA/KABUPATEN OLIMPIADE SAINS NASIONAL 2007 BIDANG MATEMATIKA SMP
 SOAL SELEKSI TINGKAT KOTA/KABUPATEN OLIMPIADE SAINS NASIONAL 27 BIDANG MATEMATIKA SMP A. SOAL PILIHAN GANDA. Urutan Bilangan-bilangan 2 5555, 5 2222, dan dari yang terkecil sampai yang terbesar adalah.
SOAL SELEKSI TINGKAT KOTA/KABUPATEN OLIMPIADE SAINS NASIONAL 27 BIDANG MATEMATIKA SMP A. SOAL PILIHAN GANDA. Urutan Bilangan-bilangan 2 5555, 5 2222, dan dari yang terkecil sampai yang terbesar adalah.
Bilangan Berpangkat. Pangkat Bulat Negatif. a bilangan real. bilangan bulat positif
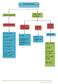 Pangkat sebenarnya Pangkat Tak sebenarnya Pangkat bulat positif Pangkat Bulat Negatif Pangkat Nol Pangkat pecaha a m x a n a m+n a m n an am (a m ) n a nxm p.a n + q. a m a n m n p + qa p.a n - q. a m
Pangkat sebenarnya Pangkat Tak sebenarnya Pangkat bulat positif Pangkat Bulat Negatif Pangkat Nol Pangkat pecaha a m x a n a m+n a m n an am (a m ) n a nxm p.a n + q. a m a n m n p + qa p.a n - q. a m
LAMPIRAN 1 DAFTAR NILAI SISWA
 LAMPIRAN LAMPIRAN 1 DAFTAR NILAI SISWA DAFTAR NILAI MATEMATIKA KELAS VIII A SEMESTER 1 SMP PANGUDI LUHUR TUNTANG NO NAMA Nilai Sebelum Tindakan Nilai Siklus 1 Nilai Siklus 2 1 R1 40 70 40 2 R2 45 58 90
LAMPIRAN LAMPIRAN 1 DAFTAR NILAI SISWA DAFTAR NILAI MATEMATIKA KELAS VIII A SEMESTER 1 SMP PANGUDI LUHUR TUNTANG NO NAMA Nilai Sebelum Tindakan Nilai Siklus 1 Nilai Siklus 2 1 R1 40 70 40 2 R2 45 58 90
MATEMATIKA. Jilid 2. SMP dan MTs Kelas VIII. J. Dris Tasari. PUSAT KURIKULUM PERBUKUAN Departemen Pendidikan Nasional
 Untuk Sekolah Menengah Pertama dan Madrasah Tsanawiyah MTMTIK Jilid SMP dan MTs Kelas VIII J. ris Tasari PUST KURIKULUM PRUKUN epartemen Pendidikan Nasional Hak cipta pada Kementerian Pendidikan Nasional.
Untuk Sekolah Menengah Pertama dan Madrasah Tsanawiyah MTMTIK Jilid SMP dan MTs Kelas VIII J. ris Tasari PUST KURIKULUM PRUKUN epartemen Pendidikan Nasional Hak cipta pada Kementerian Pendidikan Nasional.
SOAL DAN PEMBAHASAN OSN 2018 KABUPATEN SUMBA TIMUR NUSA TENGGARA TIMUR
 SOAL DAN PEMBAHASAN OSN 08 KABUPATEN SUMBA TIMUR NUSA TENGGARA TIMUR Oleh : SUKAMTO, S.Pd.,Gr Guru Matematika SMPN Kambata Mapambuhang. Suku keempat, suku ketujuh, suku kesepuluh, dan suku ke-00 suatu
SOAL DAN PEMBAHASAN OSN 08 KABUPATEN SUMBA TIMUR NUSA TENGGARA TIMUR Oleh : SUKAMTO, S.Pd.,Gr Guru Matematika SMPN Kambata Mapambuhang. Suku keempat, suku ketujuh, suku kesepuluh, dan suku ke-00 suatu
MODUL PENDALAMAN MATERI ESENSIAL DAN SULIT MATA PELAJARAN : MATEMATIKA ASPEK : ALJABAR
 MODUL PENDALAMAN MATERI ESENSIAL DAN SULIT MATA PELAJARAN : MATEMATIKA ASPEK : ALJABAR STANDAR KOMPETENSI LULUSAN 2. Memahami operasi bentuk aljabar, konsep persamaan dan pertidaksamaan linear, persamaan
MODUL PENDALAMAN MATERI ESENSIAL DAN SULIT MATA PELAJARAN : MATEMATIKA ASPEK : ALJABAR STANDAR KOMPETENSI LULUSAN 2. Memahami operasi bentuk aljabar, konsep persamaan dan pertidaksamaan linear, persamaan
RENCANA PELAKSANAN PEMBELAJARAN ( R P P ke - 1)
 RENCANA PELAKSANAN PEMBELAJARAN ( R P P ke - ) A. Identitas Sekolah : SMP Negeri Gerokgak Mata Pelajaran : Matematika Kelas / Semester : VIII (delapan ) / Ganjil Standar Kompetensi :. Memahami bentuk aljabar,
RENCANA PELAKSANAN PEMBELAJARAN ( R P P ke - ) A. Identitas Sekolah : SMP Negeri Gerokgak Mata Pelajaran : Matematika Kelas / Semester : VIII (delapan ) / Ganjil Standar Kompetensi :. Memahami bentuk aljabar,
2) Drs. Mustafa, M.Pd., selaku Kepala Dinas Pendidikan Kota Langsa.
 Ucapan Terima Kasih Syukur Alhamdulillah, akhirnya kami dapat menyelesaikan Lembar Kerja Siswa (LKS) Matematika untuk SMP/MTs Kelas VIII Semester 1 dengan bantuan berbagai pihak. Untuk itu, pada kesempatan
Ucapan Terima Kasih Syukur Alhamdulillah, akhirnya kami dapat menyelesaikan Lembar Kerja Siswa (LKS) Matematika untuk SMP/MTs Kelas VIII Semester 1 dengan bantuan berbagai pihak. Untuk itu, pada kesempatan
diunduh dari
 diunduh dari http://www.pustakasoal.com Pusat Perbukuan Departemen Pendidikan Nasional Hak ipta pada Departemen Pendidikan Nasional Dilindungi Undang-undang Hak ipta uku ini dibeli oleh Departemen Pendidikan
diunduh dari http://www.pustakasoal.com Pusat Perbukuan Departemen Pendidikan Nasional Hak ipta pada Departemen Pendidikan Nasional Dilindungi Undang-undang Hak ipta uku ini dibeli oleh Departemen Pendidikan
SMP / MTs Mata Pelajaran : Matematika
 Kunci Jawaban Latihan Soal Ujian Nasional 010 Sekolah Menengah Pertama / Madrasah Tsanawiyah SMP / MTs Mata Pelajaran : Matematika 1. Jawab: b Untuk menentukan hasil dari suatu akar telebih dahulu cari
Kunci Jawaban Latihan Soal Ujian Nasional 010 Sekolah Menengah Pertama / Madrasah Tsanawiyah SMP / MTs Mata Pelajaran : Matematika 1. Jawab: b Untuk menentukan hasil dari suatu akar telebih dahulu cari
Suku Banyak. A. Pengertian Suku Banyak B. Menentukan Nilai Suku Banyak C. Pembagian Suku Banyak D. Teorema Sisa E. Teorema Faktor
 Bab 5 Sumber: www.in.gr Setelah mempelajari bab ini, Anda harus mampu menggunakan konsep, sifat, dan aturan fungsi komposisi dalam pemecahan masalah; menggunakan konsep, sifat, dan aturan fungsi invers
Bab 5 Sumber: www.in.gr Setelah mempelajari bab ini, Anda harus mampu menggunakan konsep, sifat, dan aturan fungsi komposisi dalam pemecahan masalah; menggunakan konsep, sifat, dan aturan fungsi invers
SOAL MATEMATIKA - SMP
 SOAL MATEMATIKA - SMP OLIMPIADE SAINS NASIONAL TINGKAT KABUPATEN/KOTA KEMENTERIAN PENDIDIKAN DAN KEBUDAYAAN DIREKTORAT JENDERAL PENDIDIKAN DASAR DIREKTORAT PEMBINAAN SEKOLAH MENENGAH PERTAMA TAHUN 007
SOAL MATEMATIKA - SMP OLIMPIADE SAINS NASIONAL TINGKAT KABUPATEN/KOTA KEMENTERIAN PENDIDIKAN DAN KEBUDAYAAN DIREKTORAT JENDERAL PENDIDIKAN DASAR DIREKTORAT PEMBINAAN SEKOLAH MENENGAH PERTAMA TAHUN 007
Sifat 1 Untuksebarang bilangan rasional a tak nol dan sebarang bilangan bulat m dan n, berlaku a m. a m = a m + n
 Bilangan Berpangkat Kita ingat kembali bahwa untuk bilangan-bilangan cacah a, m, dan n dengan a 0, berlaku: 1 a m = a a a a (sebanyak m faktor) a m a n = a m + n a 0 = 1, di mana a 0 Notasi-notasi di atas
Bilangan Berpangkat Kita ingat kembali bahwa untuk bilangan-bilangan cacah a, m, dan n dengan a 0, berlaku: 1 a m = a a a a (sebanyak m faktor) a m a n = a m + n a 0 = 1, di mana a 0 Notasi-notasi di atas
UJIAN NASIONAL SMP/MTs
 UJIAN NASIONAL SMP/MTs Tahun Pelajaran 2007/2008 Mata Pelajaran Jenjang : Matematika : SMP/MTs MATA PELAJARAN Hari/Tanggal : Selasa, 6 Mei 2008 Jam : 08.00-10.00 WAKTU PELAKSANAAN PETUNJUK UMUM 1. Isikan
UJIAN NASIONAL SMP/MTs Tahun Pelajaran 2007/2008 Mata Pelajaran Jenjang : Matematika : SMP/MTs MATA PELAJARAN Hari/Tanggal : Selasa, 6 Mei 2008 Jam : 08.00-10.00 WAKTU PELAKSANAAN PETUNJUK UMUM 1. Isikan
PREDIKSI UN 2012 MATEMATIKA SMP
 Dibuat untuk persiapan menghadapi UN 2012 PREDIKSI UN 2012 MATEMATIKA SMP Lengkap dengan kisi-kisi dan pembahasan Mungkin (tidak) JITU 12 1. Menghitung hasil operasi tambah, kurang, kali dan bagi pada
Dibuat untuk persiapan menghadapi UN 2012 PREDIKSI UN 2012 MATEMATIKA SMP Lengkap dengan kisi-kisi dan pembahasan Mungkin (tidak) JITU 12 1. Menghitung hasil operasi tambah, kurang, kali dan bagi pada
SOAL DAN JAWABAN TENTANG NILAI MUTLAK. Tentukan himpunan penyelesaian dari persamaan nilai Mutlak di bawah ini.
 SOAL DAN JAWABAN TENTANG NILAI MUTLAK Tentukan himpunan penyelesaian dari persamaan nilai Mutlak di bawah ini. Jawaban: Bentuk-Bentuk persamaan nilai mutlak di atas dapat diselesaikan sebagai berikut.
SOAL DAN JAWABAN TENTANG NILAI MUTLAK Tentukan himpunan penyelesaian dari persamaan nilai Mutlak di bawah ini. Jawaban: Bentuk-Bentuk persamaan nilai mutlak di atas dapat diselesaikan sebagai berikut.
Semester 1 - Edisi v15
 KTSP Matematika SMP/MTs Kelas VIII-A P a g e Spesial Siswa Yoyo Apriyanto, S.Pd Diktat Matematika SMP/MTs Kelas VII-A Semester - Edisi v + Ringkasan Materi + Soal dan Pembahasan + Soal Uji Kompetensi Siswa
KTSP Matematika SMP/MTs Kelas VIII-A P a g e Spesial Siswa Yoyo Apriyanto, S.Pd Diktat Matematika SMP/MTs Kelas VII-A Semester - Edisi v + Ringkasan Materi + Soal dan Pembahasan + Soal Uji Kompetensi Siswa
a. 7x 2-5x + 3 = 0 a=, b=, c= b. 4x 2 + 2x = 0 a=, b=, c= e. 3k 2 = -7k a=, b=, c= f. 8n + 14n 2 = 5n +3 a=, b=, c= g. 2(x 2-5x)= x 2 + 3x a=, b=, c=
 Nama Siswa Kelas : : KOMPETENSI DASAR (KURIKULUM 2013): 9 Mendeskripsikan berbagai bentuk ekspresi yang dapat diubah menjadi persamaan kuadrat. 10 Mendeskripsikan persamaan dan fungsi kuadrat, memilih
Nama Siswa Kelas : : KOMPETENSI DASAR (KURIKULUM 2013): 9 Mendeskripsikan berbagai bentuk ekspresi yang dapat diubah menjadi persamaan kuadrat. 10 Mendeskripsikan persamaan dan fungsi kuadrat, memilih
2. Pembahasan: Aturan penjumlahan dan pengurangan pecahan dengan terlebih dahulu menyamakan penyebutnya.
 PEMBAHASAN SOAL MATEMATIKA 1. Pembahasan: Urutan pengoperasian bilangan bulat adalah: a. Perkalian, pembagian, penjumlahan, pengurangan b. Dalam hal perkalian dan pembagian, atau penjumlahan dan pengurangan
PEMBAHASAN SOAL MATEMATIKA 1. Pembahasan: Urutan pengoperasian bilangan bulat adalah: a. Perkalian, pembagian, penjumlahan, pengurangan b. Dalam hal perkalian dan pembagian, atau penjumlahan dan pengurangan
SOAL UJI COBA MATEMATIKA DKI JAKARTA 20 FEBRUARI 2018 D. 97
 SOAL UJI COBA MATEMATIKA DKI JAKARTA 0 FEBRUARI 08. Hasil dari 8 ( )adalah... A. B. 0 C. 8 D. 8. Hasil dari 5 - : adalah... A. B. C. D. 9 9. Hasil dari -./ - 0 A. B. z C. z D. z 5 -. adalah.... Hasil dari
SOAL UJI COBA MATEMATIKA DKI JAKARTA 0 FEBRUARI 08. Hasil dari 8 ( )adalah... A. B. 0 C. 8 D. 8. Hasil dari 5 - : adalah... A. B. C. D. 9 9. Hasil dari -./ - 0 A. B. z C. z D. z 5 -. adalah.... Hasil dari
Lingkaran adalah tempat kedudukan titik-titik pada bidang yang berjarak
 4 Lingkaran 4.1. Persamaan Lingkaran Bentuk Baku. Lingkaran adalah tempat kedudukan titik-titik pada bidang yang berjarak tetap dari suatu titik tetap. Titik tetap dari lingkaran disebut pusat lingkaran,
4 Lingkaran 4.1. Persamaan Lingkaran Bentuk Baku. Lingkaran adalah tempat kedudukan titik-titik pada bidang yang berjarak tetap dari suatu titik tetap. Titik tetap dari lingkaran disebut pusat lingkaran,
BAB II KETERBAGIAN. 1. Mahasiswa bisa memahami pengertian keterbagian. 2. Mahasiswa bisa mengidentifikasi bilangan prima
 BAB II KETERBAGIAN 2.1 Pendahuluan Pada pertemuan minggu ke-3, dan 4 ini dibahas konsep keterbagian, algoritma pembagian dan bilangan prima pada bilangan bulat. Relasi keterbagian pada himpunan semua bilangan
BAB II KETERBAGIAN 2.1 Pendahuluan Pada pertemuan minggu ke-3, dan 4 ini dibahas konsep keterbagian, algoritma pembagian dan bilangan prima pada bilangan bulat. Relasi keterbagian pada himpunan semua bilangan
SELEKSI OLIMPIADE TINGKAT KABUPATEN/KOTA TAHUN 2006 TIM OLIMPIADE MATEMATIKA INDONESIA TAHUN 2007
 SELEKSI OLIMPIADE TINGKAT KABUPATEN/KOTA TAHUN 006 TIM OLIMPIADE MATEMATIKA INDONESIA TAHUN 007 Bidang Matematika Waktu : 3,5 Jam DEPARTEMEN PENDIDIKAN NASIONAL DIREKTORAT JENDERAL MANAJEMEN PENDIDIKAN
SELEKSI OLIMPIADE TINGKAT KABUPATEN/KOTA TAHUN 006 TIM OLIMPIADE MATEMATIKA INDONESIA TAHUN 007 Bidang Matematika Waktu : 3,5 Jam DEPARTEMEN PENDIDIKAN NASIONAL DIREKTORAT JENDERAL MANAJEMEN PENDIDIKAN
1. BARISAN ARITMATIKA
 MATEMATIKA DASAR ARITMATIKA BARISAN ARITMATIKA 1. BARISAN ARITMATIKA Sering disebut barisan hitung, adalah barisan bilangan yang setiap sukunya diperoleh dari suku sebelumnya dengan menambah atau mengurangi
MATEMATIKA DASAR ARITMATIKA BARISAN ARITMATIKA 1. BARISAN ARITMATIKA Sering disebut barisan hitung, adalah barisan bilangan yang setiap sukunya diperoleh dari suku sebelumnya dengan menambah atau mengurangi
Kumpulan Soal Olimpiade Tingkat SMP dan Pembahasannya
 Kumpulan Soal Olimpiade Tingkat SMP dan Pembahasannya Nama : Ayu Dwi Asnantia Nim : 09320042 Soal Pilihan Ganda!! 1. Jika a + b = 1, b + c = 2, dan c + a = 3, maka a + b + c =... a. 2 b. 3 c. 4 d. 5 e.
Kumpulan Soal Olimpiade Tingkat SMP dan Pembahasannya Nama : Ayu Dwi Asnantia Nim : 09320042 Soal Pilihan Ganda!! 1. Jika a + b = 1, b + c = 2, dan c + a = 3, maka a + b + c =... a. 2 b. 3 c. 4 d. 5 e.
Matematika Teknik Dasar-2 4 Aljabar Vektor-1. Sebrian Mirdeklis Beselly Putra Teknik Pengairan Universitas Brawijaya
 Matematika Teknik Dasar-2 4 Aljabar Vektor-1 Sebrian Mirdeklis Beselly Putra Teknik Pengairan Universitas Brawijaya Kuantitas Skalar dan Vektor Kuantitas Fisis dibagi menjadi dua, yaitu: 1. Kuantitas skalar:
Matematika Teknik Dasar-2 4 Aljabar Vektor-1 Sebrian Mirdeklis Beselly Putra Teknik Pengairan Universitas Brawijaya Kuantitas Skalar dan Vektor Kuantitas Fisis dibagi menjadi dua, yaitu: 1. Kuantitas skalar:
matematika WAJIB Kelas X PERTIDAKSAMAAN LINEAR SATU VARIABEL K-13 A. PENDAHULUAN
 K-1 Kelas X matematika WAJIB PERTIDAKSAMAAN LINEAR SATU VARIABEL TUJUAN PEMBELAJARAN Setelah mempelajari materi ini, kamu diharapkan memiliki kemampuan berikut. 1. Memahami definisi pertidaksamaan linear
K-1 Kelas X matematika WAJIB PERTIDAKSAMAAN LINEAR SATU VARIABEL TUJUAN PEMBELAJARAN Setelah mempelajari materi ini, kamu diharapkan memiliki kemampuan berikut. 1. Memahami definisi pertidaksamaan linear
SOAL MATEMATIKA - SMP
 SOAL MATEMATIKA - SMP OLIMPIADE SAINS NASIONAL TINGKAT KABUPATEN/KOTA KEMENTERIAN PENDIDIKAN DAN KEBUDAYAAN DIREKTORAT JENDERAL PENDIDIKAN DASAR DIREKTORAT PEMBINAAN SEKOLAH MENENGAH PERTAMA TAHUN 200
SOAL MATEMATIKA - SMP OLIMPIADE SAINS NASIONAL TINGKAT KABUPATEN/KOTA KEMENTERIAN PENDIDIKAN DAN KEBUDAYAAN DIREKTORAT JENDERAL PENDIDIKAN DASAR DIREKTORAT PEMBINAAN SEKOLAH MENENGAH PERTAMA TAHUN 200
BIMBINGAN BELAJAR & KONSULTASI PENDIDIKAN SERI : MATEMATIKA SMA EKSPONEN. MARZAN NURJANAH, S.Pd.
 BIMBINGAN BELAJAR & KONSULTASI PENDIDIKAN SERI : MATEMATIKA SMA EKSPONEN MARZAN NURJANAH, S.Pd. Agenda Pengertian dan Sifat Eksponen Persamaan Eksponen Pertidaksamaan Eksponen Latihan Soal Agenda Pengertian
BIMBINGAN BELAJAR & KONSULTASI PENDIDIKAN SERI : MATEMATIKA SMA EKSPONEN MARZAN NURJANAH, S.Pd. Agenda Pengertian dan Sifat Eksponen Persamaan Eksponen Pertidaksamaan Eksponen Latihan Soal Agenda Pengertian
PAKET 2 CONTOH SOAL DAN PEMBAHASAN MATEMATIKA SMP/MTs
 PAKET CONTOH SOAL DAN PEMBAHASAN MATEMATIKA SMP/MTs 1. * Kemampuan yang diuji. Menghitung hasil operasi tambah, kurang, kali dan bagi pada bilangan bulat Menentukan hasil operasi campuran bilangan bulat.
PAKET CONTOH SOAL DAN PEMBAHASAN MATEMATIKA SMP/MTs 1. * Kemampuan yang diuji. Menghitung hasil operasi tambah, kurang, kali dan bagi pada bilangan bulat Menentukan hasil operasi campuran bilangan bulat.
Prestasi itu diraih bukan didapat!!! SOLUSI SOAL
 "We are the first of the fastest online solution of mathematics" 009 SELEKSI OLIMPIADE TINGKAT PROVINSI 008 TIM OLIMPIADE MATEMATIKA INDONESIA 009 Prestasi itu diraih bukan didapat!!! SOLUSI SOAL Bidang
"We are the first of the fastest online solution of mathematics" 009 SELEKSI OLIMPIADE TINGKAT PROVINSI 008 TIM OLIMPIADE MATEMATIKA INDONESIA 009 Prestasi itu diraih bukan didapat!!! SOLUSI SOAL Bidang
C. 30 Januari 2001 B. 29 Januari 2001
 1. Notasi pembentuk himpunan dari B = {1, 4, 9} adalah... A. B = {x x kuadrat tiga bilangan asli yang pertama} B. B = {x x bilangan tersusun yang kurang dari 10} C. B = {x x kelipatan bilangan 2 dan 3
1. Notasi pembentuk himpunan dari B = {1, 4, 9} adalah... A. B = {x x kuadrat tiga bilangan asli yang pertama} B. B = {x x bilangan tersusun yang kurang dari 10} C. B = {x x kelipatan bilangan 2 dan 3
Untuk mencari akar-akar dari persamaan kuadrat, dapat menggunakan rumus :
 RUMUS-RUMUS PERSAMAAN KUADRAT Bentuk umum: ax 2 + bx + c = 0, a 0 AKAR-AKAR PERSAMAAN KUADRAT Untuk mencari akar-akar dari persamaan kuadrat, dapat menggunakan rumus : X 1.2 = Dengan : D = b 2 4ac, dan
RUMUS-RUMUS PERSAMAAN KUADRAT Bentuk umum: ax 2 + bx + c = 0, a 0 AKAR-AKAR PERSAMAAN KUADRAT Untuk mencari akar-akar dari persamaan kuadrat, dapat menggunakan rumus : X 1.2 = Dengan : D = b 2 4ac, dan
SOAL SELEKSI TINGKAT KOTA/KABUPATEN OLIMPIADE SAINS NASIONAL 2007 BIDANG MATEMATIKA SMP
 SOL SELEKSI TINGKT KOT/KUPTEN OLIMPIE SINS NSIONL 7 ING MTEMTIK SMP. SOL PILIHN GN. Urutan ilangan-bilangan 5555, 5, dan dari yang terkecil sampai yang terbesar adalah. a. 5555, 5, dan b. 5,, dan 5555
SOL SELEKSI TINGKT KOT/KUPTEN OLIMPIE SINS NSIONL 7 ING MTEMTIK SMP. SOL PILIHN GN. Urutan ilangan-bilangan 5555, 5, dan dari yang terkecil sampai yang terbesar adalah. a. 5555, 5, dan b. 5,, dan 5555
SPMB 2004 Matematika Dasar Kode Soal
 SPMB 00 Matematika Dasar Kode Soal Doc. Name: SPMB00MATDAS999 Version : 0- halaman 0. Nilai x yang memenuhi persamaan : 3 x ( ) adalah. 0 - - 0. Dalam bentuk pangkat positif dan bentuk akar, x y x y...
SPMB 00 Matematika Dasar Kode Soal Doc. Name: SPMB00MATDAS999 Version : 0- halaman 0. Nilai x yang memenuhi persamaan : 3 x ( ) adalah. 0 - - 0. Dalam bentuk pangkat positif dan bentuk akar, x y x y...
HAPUS SALAH SATU BILANGAN DAN BERIKAN ALASAN, KENAPA BILANGAN ITU ANDA HAPUS.
 15, 20, 23, 25 HAPUS SALAH SATU BILANGAN DAN BERIKAN ALASAN, KENAPA BILANGAN ITU ANDA HAPUS. Dst. KESIMPULAN : (hubungkan dengan SIKAP yang harus Anda miliki untuk memilih dan memberikan alasan) PROBLEM
15, 20, 23, 25 HAPUS SALAH SATU BILANGAN DAN BERIKAN ALASAN, KENAPA BILANGAN ITU ANDA HAPUS. Dst. KESIMPULAN : (hubungkan dengan SIKAP yang harus Anda miliki untuk memilih dan memberikan alasan) PROBLEM
Modul 05 Persamaan Linear dan Persamaan Linear Simultan
 Modul 05 Persamaan Linear dan Persamaan Linear Simultan 5.1. Persamaan Linear Persamaan adalah pernyataan kesamaan antara dua ekspresi aljabar yang cocok untuk bilangan nilai variable tertentu atau variable
Modul 05 Persamaan Linear dan Persamaan Linear Simultan 5.1. Persamaan Linear Persamaan adalah pernyataan kesamaan antara dua ekspresi aljabar yang cocok untuk bilangan nilai variable tertentu atau variable
OLIMPIADE SAINS TERAPAN SMK PROPINSI JAWA TENGAH 2009
 OLIMPIADE SAINS TERAPAN SMK PROPINSI JAWA TENGAH 009 Mata pelajaran Matematika Teknologi Kerjasama Dengan FMIPA Universitas Diponegoro Dan Dinas Pendidikan Propinsi Jawa Tengah OLIMPIADE SAINS TERAPAN
OLIMPIADE SAINS TERAPAN SMK PROPINSI JAWA TENGAH 009 Mata pelajaran Matematika Teknologi Kerjasama Dengan FMIPA Universitas Diponegoro Dan Dinas Pendidikan Propinsi Jawa Tengah OLIMPIADE SAINS TERAPAN
