Kuliah Pengantar Kontrol Optimum dan Metode Numeriknya dalam Scilab
|
|
|
- Yulia Gunawan
- 6 tahun lalu
- Tontonan:
Transkripsi
1 Kuliah Pengantar Kontrol Optimum dan Metode Numeriknya dalam Scilab Effendi Syahril Agah D. Garnadi
2 Kuliah Pengantar Kontrol Optimum dan Metode Numeriknya dalam Scilab Effendi Syahril Agah D. Garnadi e-version : Versi : -.1
3 Contents 1 Pendahuluan Masalah Optimisasi Dinamis State Sistem Dinamis Peubah Kontrol Reachability, Controllability dan Observability Fungsional Objektif Kalkulus Variasi dan Kontrol Optimum Kalkulus Variasi Pendahuluan Fungsional Dan Variasi Syarat Perlu Untuk Optimum : Persamaan Euler Persamaan Euler Yang Lebih Umum Kasus Peubah banyak Kasus Fungsi f Memuat Turunan ke-n Kasus Khusus Persamaan Euler Fungsi f Tidak Memuat x Fungsi f Tidak Memuat t Fungsi f Tidak Memuat ẋ Masalah Variasi Dengan Kendala Kendala Titik Dan Persamaan Diferensial Kendala Isoperimetris Syarat Batas Dalam Masalah Variasi i
4 2.7.1 Dua Titik Ujung Tetap Dan Syarat Batas Natural Titik Ujung Bebas Syarat Cukup / Sufficiency Conditions Variasi Fungsional Syarat Legendre Syarat Jacobi Syarat Weierstrass untuk Ekstremal Kuat Syarat Legendre-Clebsch Syarat Cukup : Kasus khusus Kontrol Optimum : Pendekatan Kalkulus Variasi Formulasi Masalah Kontrol Optimum Syarat Perlu : Prinsip Maksimum Pontryagin Syarat Transversalitas Atau Syarat Batas Masalah Waktu Terminal T Tetap Masalah Waktu Terminal T Bebas Syarat Cukup Untuk Kontrol Optimum Current-Value Hamiltonian Beberapa contoh masalah nyata kontrol optimum Kontrol Variabel Berbatas Masalah Kontrol Optimum dengan Variabel State Berbatas Masalah Kontrol Optimum dengan Kendala Persamaan Masalah Kontrol Optimum dengan Variabel Kontrol Berbatas Kontrol Optimum Linier Soal-soal Latihan Soal-soal Kalkulus Variasi Soal-Soal Kontrol Optimum Soal-soal Ujian ii
5 Chapter 1 Pendahuluan 1.1 Masalah Optimisasi Dinamis Masalah pengalokasian optimum dari sumber daya yang terbatas yang memiliki alternatif penggunaannya, baik pada suatu titik waktu maupun pada jangka waktu tertentu, dapat melibatkan optimisasi statis maupun optimisasi dinamis. Pilihan antara mengurangi konsumsi masa kini dan konsumsi yang cukup untuk masa depan, merupakan masalah optimisasi dinamis. Suatu alat yang sangat penting dalam optimisasi dinamis adalah Kalkulus Variasi. Teknik kalkulus variasi ini telah diterapkan dalam masalah ekonomi sejak tahun Namun demikian, teknik kalkulus variasi memiliki keterbatasan, yang berarti tidak semua masalah dapat diselesaikan dengan teknik kalkulus variasi. Teknik kontrol optimum, mampu mengatasi keterbatasan yang dimiliki oleh teknik kalkulus variasi. Teknik kontrol optimum berkembang pesat sejak ditemukannya teknik program dynamis oleh Richard Bellman pada tahun 1957 dan prinsip maksimum oleh Pontryagin pada tahun Dengan penemuan tersebut, teknik kontrol optimum yang berkembang mempunyai 2 pendekatan, yaitu pendekatan program dinamis dan pendekatan prinsip maksimum. Dalam kuliah ini, digunakan pendekatan prinsip maksimum, karena lebih mudah dipahami. Pendekatan prinsip maksimum menggunakan teknik yang dikembangkan dalam kalkulus variasi. Oleh karena itu, pembahasan kuliah dimulai dengan pembahasan topik teknik kalkulus variasi. Dengan bekal teknik kalkulus variasi, pembahasan difokuskan pada teknik-teknik kontrol optimum. Secara sederhana, masalah kontrol optimum adalah memilih peubah kontrol u(t) diantara semua peubah kontrol yang admissible, yaitu kontrol yang membawa sistem dari state awal x(t ) pada waktu t kepada state terminal x(t ) pada waktu terminal T, demikian rupa sehingga memberikan nilai maksimum atau nilai minimum bagi fungsional objektif yang juga disebut sebagai indeks performance. 1
6 1.2 State Sistem Dinamis State atau keadaan sistem dinamis adalah koleksi dari bilangan x(t) (x 1 (t), x 2 (t),..., x n (t)) yang apabila diberikan suatu nilai pada waktu t = t, maka nilainya akan dapat ditentukan pada t t melalui pilihan vektor kontrol u(t) = (u 1 (t), u 2 (t),..., x r (t)). Bilangan x i (t) untuk (1 i n, t t T ) disebut sebagai peubah keadaan atau peubah state, dan ruang keadaan adalah ruang dimensi n yang memuat koordinat x i (t) (1 i n). Dengan cara yang sama, bilangan u i (t) untuk (1 i r t t T ) disebut sebagai peubah kontrol atau peubah kendali. Misalnya, x(t) dapat melambangkan peubah ekonomi, seperti GNP, konsumsi, investasi dan kondisi perekonomian lainnya, serta u(t) mewakili peubah kontrol, seperti kebijakan suku bunga, pengeluaran pemerintah, suplai uang dan instrumen ekonomi lainnya yang dapat dikendalikan. Keadaan atau state suatu sistem pada waktu t, yang disebut dengan sistem dinamis, direpresentasikan oleh sistem persamaan diferensial dalam hal masalah kontinyu, atau sistem persamaan beda untuk masalah diskret. Misalnya, (1.1) atau (1.2) ẋ(t) = f[x(t), u(t), t] x(k + 1) = f[x(k), u(k), k]. Sistem dinamis dapat berbentuk linier dan dapat pula berbentuk tak-linier, juga dapat berbentuk sistem autonomous (sistem tidak memuat t atau k) atau berbentuk sistem nonautonomous, dapat pula memiliki koefisien konstanta atau koefisien peubah pada persamaan diferensial atau persamaan beda. Sistem juga dapat berbentuk deterministik dan juga dapat berbentuk stokastik. Dalam kuliah ini hanya akan dibahas sistem deterministik. 1.3 Peubah Kontrol Sistem dinamis dikontrol atau dikendalikan oleh instrumen atau kontrol yang sesuai. Hanya kontrol yang admissible ( yaitu kontrol yang memenuhi persyaratan yang diberikan) saja yang perlu diperhatikan. Misalnya, jika u i (t) menyatakan proporsi pendapatan nasional yang ditabung untuk membentuk kapital di sektor i, (i = 1, 2,..., r) maka u i (t) 1, i, t dan r 1 u i (t) 1. Secara umum, kendala fisik ini dinyatakan dengan persyaratan bahwa peubah kontrol harus dipilih dari kumpulan kontrol-kontrol yang admissible, yang dilambangkan dengan Ω(u(t)), artinya, kontrol u(t) Ω(u(t)). Untuk ilustrasi di atas, Ω(u(t)) {u i (t) : u i (t) 1, r u i (t) 1} 1 Apabila u(t) hanya fungsi dari t, maka disebut kontrol open-loop, misalnya mengatur mesin cuci untuk berfungsi dalam jangka waktu tertentu. Apabila kontrol u(t) juga merupakan fungsi dari peubah state x(t), yaitu u(t) = u[x(t), t], maka disebut kontrol closed- 2
7 loop, misalnya pengeluaran pemerintah, u(t), merupakan fungsi dari GNP/PDB, x(t), dan waktu pemilu, t. 1.4 Reachability, Controllability dan Observability Suatu keadaan x 1 dikatakan dapat dicapai (reachable) dari sebarang keadaan x pada waktu t jika kontrol u 1 (T ) Ω(u(t)) dapat ditemukan demikian rupa sehingga x(u 1, x, t 1 ) = x 1 untuk waktu t 1 t. Koleksi dari semua x 1 tersebut disebut reachable states pada waktu t. Istilah controllability merujuk pada kenyataan bahwa beberapa state terminal x 1 dapat dicapai dari state awal x dengan pilihan kontrol u(t)yang tepat, u(t) Ω(u). Jadi, controllability merupakan syarat perlu untuk adanya suatu solusi. Observability adalah kemampuan untuk menentukan state awal x dari observasi data dan output. Output menyatakan hubungan antara peubah state dengan [eubah kontrol, misalnya y(t) = g[x(t), u(t), t]. Masalah observability hanya muncul jika output tidak dapat diukur secara eksplisit. 1.5 Fungsional Objektif Peubah kontrol u(t) harus dipilih dalam rangka memaksimumkan atau meminimumkan fungsional objektif J[u(t)], (fungsional objektif ini merupakan ukuran performance, makanya kadang-kadang juga disebut indeks performance) : (1.3) J[u(t)] = dengan f adalah fungsi bernilai riel. Jika fungsi t f (x(t), u(t), t)dt f (x, u, t) = π(x, p)e rt, atau f = u(c)e rt, maka fungsional J merupakan nilai kini (present value) dari profit π atau utilitas konsumsi yang terdiskon pada tingkat diskon r. Secara umum, terdapat 3 alternatif untuk menyajikan formulasi fungsional objektif ( 1.3), yaitu : 1. (Formulasi Bolza) Formulasi fungsional objektif bentuk Bolza merupakan formulasi yang lebih umum. (1.4) J[u(t)] = S[x(T ), T ] + t f (x(t), u(t), t)dt dengan f dan S adalah fungsi yang kontinu dan dapat diturunkan. Fungsi S[x(T ), T ] dikenal dengan fungsi scrap value pada waktu terminal T. 3
8 2. (Formulasi Lagrange ) Formulasi Lagrange merupakan bentuk khusus dari ( 1.4), dengan S[x(T ), T ] =, yaitu (1.5) J[u(t)] = t f(x(t), u(t), t)dt 3. (Formulasi Mayer) Formulasi Mayer ini juga merupakan bentuk khusus dari ( 1.4), dengan f(x(t), u(t), t) =, yaitu (1.6) J[u(t)] = S[x(T ), T ] Dengan pendefinisian kembali peubah-peubahnya, maka ke-3 alternatif di atas ekivalen. Misalnya, formulasi Bolza dapat dikonversikan menjadi formulasi Mayer dengan mendefinisikan peubah tambahan x n+1 (t) sebagai x n+1 (t) = t akan menghasilkan J = x n+1 (t) + S[x(T ), T ]. t f(x, u, τ)dτ, x n+1 (t ) = 1.6 Kalkulus Variasi dan Kontrol Optimum Dalam masalah kalkulus variasi dalam bentuk baku, tujuannya adalah untuk memaksimumkan atau meminimumkan fungsional objektif J[x(t)] = f (x(t), ẋ(t), t)dt dengan fungsi kendala atau tanpa kendala; fungsi kendala dapat berupa persamaan diferensial atau persamaan aljabar. Misalnya, ẋ = f(x(t), ẋ(t), t). Dalam bentuk baku, kontrol optimum mempunyai tujuan untuk memaksimumkan atau meminimumkan fungsional objektif J[u(t)] = f (x(t), u(t), t)dt dengan kendala persamaan diferensial ẋ = f(x(t), u(t), t). Apabila ẋ(t) = u(t), maka masalah kalkulus variasi sama saja dengan masalah kontrol optimum. Kenyataannya, masalah kontrol optimum dapat diselesaikan dengan teknik kalkulus variasi (persamaan Euler) dan sebaliknya prinsip Maksimum Pontryagin yang merupakan syarat perlu untuk adanya kontrol optimum dapat diperlakukan sebagai pengembangan dari kalkulus variasi. 4
9 Chapter 2 Kalkulus Variasi 2.1 Pendahuluan Kalkulus variasi merupakan cabang ilmu matematika yang berkaitan dengan pengoptimuman fungsional. Cabang ilmu ini telah mulai berkembang sejak ditemukannya masalah isoperimetris untuk pertamakalinya sekitar tahun 85 B.C. Akan tetapi, progres yang signifikan dalam cabang ilmu ini baru terjadi sekitar penghujung abad 17 melalui penemuan masalah brachitoschrone, yang solusinya diberikan oleh Newton, de l Hospital, John dan Jacob Bernoulli pada tahun Dalam bidang ekonomi, penggunaan kalkulus variasi sudah ada sejak tahun 192an, melalui karya Evans (1924 dan 193), Ramsey (1928) dan Hotelling (1931). Evans dan Roos berupaya untuk menemukan harga optimum untuk keseluruhan periode perencanaan, seperti memaksimumkan fungsional keuntungan dari monopolist. Sedangkan Ramsey ingin menemukan program penghematan yang meminimumkan perbedaan tingkat utilitas. Masalah penghematan optimum ini, yang memuat sumber inspirasi dalam teori pertumbuhan ekonomi yang optimum, diselesaikan dengan kalkulus variasi. Sementara itu Hotelling menggunakan kalkulus variasi dalam masalah penambangan optimum dari sumber daya alam. 2.2 Fungsional Dan Variasi Fungsional memainkan peranan penting dalam kalkulus variasi. Fungsional, misalnya norm x = x, atau misalnya J(x) = b a x(t)dt, adalah suatu aturan yang mengkaitkan tiap fungsi x R dengan suatu bilangan tunggal x atau J(x). Terdapat analogi antara fungsi dengan fungsional. Argumen dari fungsi merupakan peubah, misalnya x = x(t), sedangkan argumen dari fungsional merupakan fungsi, misalnya J(x(t)) = b a x(t)dt. Apabila fungsi secara lengkap dapat ditentukan manakala peubahnya diberikan nilai-nilai tertentu, maka 5
10 suatu fungsional secara lengkap ditentukan oleh pilihan fungsi tertentu dari sekumpulan fungsi yang admissible. Increment atau kenaikan dari argumen fungsi adalah dt = t t, sementara increment dari argumen fungsional, yang kita sebut dengan variasi dan dengan notasi δx merupakan selisih δx = x(t) x(t ). Dalam mempelajari fungsi, kita tertarik untuk menemukan titik yang memberikan ekstremum untuk fungsi, sedangkan dalam pembahasan fungsional kita tertarik untuk menemukan fungsi yang memberikan ekstremum untuk fungsional. Variasi dari fungsional J(x) adalah J(x) = J(x+δx) J(x). Dengan mengambil δx = h sebarang fungsi, maka dengan menggunakan perluasan deret Taylor, maka diperoleh J(x + δx) = = + sehingga diperoleh (2.1) = J(x) + f(x + h, ẋ + ḣ, t)dt f(x, h, t)dt + (hf x + ḣf ẋ)dt (h 2 f xx + 2hḣf xẋ + fẋẋ ḣ 2 )dt + O h 2 f(x, h, t)dt + J(h) = J(x + h) J(x) = φ(h) + Q(h) + O h 2 (h 2 f xx + 2hḣf xẋ + fẋẋ ḣ 2 )dt + O h 2, = δj(h) + δ 2 J(h) + O h 2 dengan φ(h) merupakan suku-suku linear dalam deret Taylor yang kita sebut dengan variasi pertama δj(h) dan Q(h) adalah suku-suku kuadrat yang mengindikasikan variasi kedua δ 2 J(h) dan O h 2 untuk h. Definisi 2.1 Fungsional J(x) dikatakan mencapai maksimum (minimum) lokal atau relatif sepanjang x (t) apabila J(x ) ( ), yaitu J(x ) J(x) (J(x ) J(x)) untuk semua fungsi-fungsi yang cukup dekat dengan x. Fungsional J(x) dikatakan mencapai maksimum (minimum) global sepanjang x (t) apabila J(x ) ( ), yaitu J(x ) J(x) (J(x ) J(x)) untuk semua fungsi x(t) x (t). 2.3 Syarat Perlu Untuk Optimum : Persamaan Euler Misalkan C[, T ] menyatakan kelas semua fungsi kontinu yang terdefinisi pada selang [, T ] dan C i [, T ] menyatakan semua fungsi yang didefinisikan di selang [, T ] dan memiliki turunan ke-i yang kontinu. Perhatikan masalah variasi dalam bentuk sederhana, (2.2) J(x) = 6 f(x, ẋ, t)dt
11 dengan titik ujung A(, x()) dan B(T, x(t )) adalah tetap, f(x, ẋ, t), x(t) C 2 [, T ] dan ẋ dx/dt dan x adalah fungsi bernilai skalar. Permasalahan adalah memilih fungsi x (t) diantara fungsi-fungsi admissible, yaitu semua fungsi x(t) C 2 [, T ] yang memiliki titik awal di A dan titik akhir di B yang memberikan nilai maksimum atau nilai minimum untuk fungsional J(x). Syarat perlu untuk adanya ekstremum adalah δj(x) =. Misalkan (2.3) δj(x) = g(t)h(t)dt dengan g(t) C[, T ] dan h(t) sebarang fungsi yang memenuhi h() = h(t ) =. Lema 2.1 ( Lema Dasar ) Misal g(t) C[, T ] dan S himpunan semua fungsi h(t) kontinu dan dapat diturunkan di [, T ] dan h() = h(t ) = dengan T adalah tetap. Jika (2.4) g(t)h(t)dt = untuk semua h S, maka g(t) = untuk semua t [, T ]. Bukti : Misalkan g(t), yaitu g(t) >, pada [, T ]. Dengan sifat kekontinuan, maka g(t) untuk suatu selang [a, b] [, T ], dengan < a < b < T. Misal h(t) (t a)(b t) untuk t [a, b] dan h(t) =, t [a, b]. Jelas bahwa h(t) memenuhi persyaratan lema. Tetapi, g(t)(t a)(b t)dt. Suatu kontradiksi. Dengan demikian, haruslah g(t) =. Teorema 2.1 Misalkan J(x) = f(x, ẋ, t)dt didefinisikan pada C [, T ] dan memenuhi syarat batas x() = x, x(t ) = x T. Maka syarat perlu bagi J(x) untuk memiliki ekstremum adalah fungsi x(t) memenuhi persamaan Euler: (2.5) f x d dt f ẋ =, atau dituliskan dalam bentuk penuh, yang disebut persamaan Euler-Lagrange : (2.6) f x fẋt f xẋ ẋ fẋẋ ẍ =. Bukti : Syarat perlu untuk ekstremum adalah δj(x) =, yaitu (2.7) δj = [f x (x, ẋ, t)h + fẋ(x, ẋ, t)ḣ]dt =, 7
12 dengan f x f(x, ẋ, t)/ x, fẋ f(x, ẋ, t)/ ẋ dan h(t) adalah fungsi displacement merupakan fungsi kontinu sebarang dan bersifat h() = = h(t ). Dengan melakukan integrasi bagian terhadap suku kedua, diperoleh ḣfẋ = hfẋ T = karena h() = = h(t ). Sehingga diperoleh (2.8) δj = ( d dt f ẋ)hdt ( d dt f ẋ)hdt (f x d dt f ẋ)hdt =, yang pada gilirannya dengan Lema Dasar memberikan persamaan Euler : f x d dt f ẋ =. Contoh 2.1 Tentukan ekstremum dari 1 (aẋ2 +bt)dt, diberikan x() =, x(1) = 2, a. Solusi : Fungsi integran adalah dalam bentuk f(ẋ) = aẋ 2 +bt. Persamaan Euler memberikan d/dt(2aẋ) =, atau ẍ =, karena a. Lakukan integrasi, maka diperoleh ẋ(t) = c dan x(t) = ct + d, dengan c dan d merupakan konstanta yang akan ditentukan nilanya dari syarat batas x() = dan x(1) = 2. Akhirnya diperoleh solusi yang merupakan garis lurus, yaitu x(t) = 2t. Contoh 2.2 Tentukan ekstremum dari 1 f(x, ẋ, t)dt, dengan fungsional objektif didefinisikan oleh f(x, ẋ, t) aẋ 2 + bx, dan persyaratan pada kedua titik ujung diberikan oleh x() = 1 dan x(1) = 5. Solusi : Fungsi f(x, ẋ, t) = aẋ 2 + bx. Maka persamaan Euler f x d f dt ẋ = akan memberikan b d 2aẋ =. Yang terakhir ini akan memberikan ẍ = b/(2a). Dengan melakukan integrasi dua dt kali, maka akan diperoleh solusi umum x(t) = b 4a t2 + k 1 t + k 2. Dengan menggunakan x() = 1 dan x(1) = 5, diperoleh k 1 = 25b/a, diperoleh solusi khusus x(t) = b 4a t2 + 25b/at + 1. k 2 = 1, sehingga 8
13 Contoh 2.3 Seorang produsen merencanakan produksi dalam rentang waktu [, 1]. Tingkat output pada waktu t = adalah nol dan tingkat output pada waktu terminal t = 1 adalah sebesar 1 satuan produksi. Tentukan tingkat output optimum x(t) apabila produsen dihadapkan pada harga pasar stabil, p = 4 satuan moneter dan fungsi ongkos total ẋ 2 + x 2 yang mengalami diskon pada tingkat suku bunga pasar r =, 2. Solusi : Fungsional objektif yang akan dimaksimumkan oleh investor adalah J(x) = 1 Persamaan Euler memberikan e,2t [4x (ẋ 2 + x 2 )]dt, x() =, x(1) = 1. f x d dt f ẋ = e,2t (4 2x) d dt e,2t ( 2ẋ) =, yaitu menghasilkan ẍ, 2ẋ x = 2. Solusi dari persamaan diferensial ini adalah x(t) = k 1 e λ 1t + k 2 e λ 2t + 2, dengan λ 1, λ 2 =, 1 ±, merupakan akar dari persamaan karakteristik λ 2, 2λ 1 =, dan 2 merupakan solusi dari persamaan diferensial tak homogen. Konstanta k 1 dan k 2 adalah konstanta integrasi yang dapat ditentukan dari syarat batas x() = dan x(1) = 1. Akhirnya diperoleh solusi khusus, yaitu x(t) = 3, 358e 1,15t 5, 358e,95t Persamaan Euler Yang Lebih Umum Kasus Peubah banyak Perhatikan fungsional objektif J(x) = f(x, ẋ, t)dt, dengan x = (x 1, x 2,..., x n ) dan ẋ = ( x 1, x 2,..., x n ). Maka, dengan melakukan integrasi bagian terhadap δj dan dengan menggunakan h i () = = h i (T ), i diperoleh : δj = = ( n h i f xi + 1 n h i f xi )dt = 1 (f xi d dt f x i )h i dt, h i (t). 9
14 Dengan menggunakan Lema Dasar, akan menghasilkan persamaan Euler (2.9) f xi d dt f x i =, i, atau dalam bentuk penuh, persamaan Euler-Lagrange (2.1) f xi f xi t f xi x i x i f xi x i ẍ i =, (1 i n). Contoh 2.4 Tentukan ekstremum untuk 1 ( x x e t )dt dengan syarat batas x 1 () = 1, x 1 (1) = 11 dan x 2 () = 2, x 2 (1) = 6. Solusi : Fungsi integran dalam bentuk f(x 1, x 2, x 1, x 2, t) = x x 2 2 +e t. Persamaan Euler memberikan f xi d dt f ẋ i = d dt 2ẋ i (i = 1, 2), yaitu ẍ i =, ẋ i = k i, dengan solusinya adalah persamaan linier x i (t) = k i (t)+c i, (i = 1, 2). Dengan menggunakan syarat batas, maka diperoleh solusi khusus x 1 (t) = t + 1, x 2 (t) =, 4t Kasus Fungsi f Memuat Turunan ke-n Perhatikan fungsional objektif dengan fungsi f memuat turunan ke-n, (n 1) (2.11) J(x) = f(t, x, ẋ, ẍ,..., x n )dt dengan titik ujung tetap x i () = x i, dan x i i (T ) = x T berturut-turut memberikan persyaratan h() = ḣ() =... = hn () =, dan h(t ) = = ḣ(t ) =... = hn (T ). Syarat perlu untuk adanya ekstremum bagi J(x) adalah (2.12) δj = (f x h + fẋḣ + fẍḧ f x nh n )dt =. Integrasi bagian terhadap suku kedua integran menghasilkan fẋḣdt = fẋh T = karena h() = = h(t ). ( d dt f ẋ)hdt ( d dt f ẋ)hdt 1
15 Integrasi bagian terhadap suku ketiga integran, dan mengulangi integrasi bagian sampai diperoleh suku yang memuat perkalian dengan fungsi h, diperoleh : fẍḧdt = fẍḣ T = d dt f ẍh T + = + ḣ d dt f ẍdt h d2 dt 2 f ẍdt. h d2 dt 2 f ẍdt Penggunaan integrasi bagian secara berulang terhadap suku-suku berikutnya dan dengan menggunakan syarat h() = = ḣ() = ḧ() =... = hn () dan h(t ) = = ḣ(t ) = ḧ(t ) =... = h n (T ), menghasilkan δj = (f x d dt f ẋ + d2 dt f 2 ẍ ( 1) n dn dt f n xn)hdt =. Dengan Lema Dasar, maka diperoleh persamaan Euler-Poisson : (2.13) f x d dt f ẋ + d2 dt 2 f ẍ ( 1) n dn dt n f x n =. Contoh 2.5 Tentukan ekstremum dari 1 (ẍ2 + ẋ + at 2 )dt, dengan x() =, ẋ() = 1, x(1) = 1, dan ẋ(1) = 1. Solusi : Fungsi objektif adalah f(ẍ, ẋ, x, t) = ẍ 2 + ẋ + at 2. Persamaan Euler-Poisson memberikan f x d dt f ẋ + d2 dt f 2 ẍ = d dt 1 + d2 2ẍ =, dt2 yang memberikan x (4) =. Dengan melakukan integrasi secara berulang, maka diperoleh solusi umum x(t) = k 1t k 2t k 3t + k 4, dengan konstanta integrasi k 1, k 2, k 3 dan k 4 ditentukan dari syarat batas yang diberikan. Maka akan diperoleh solusi atau ekstremal x(t) = t. 2.5 Kasus Khusus Persamaan Euler Fungsi f Tidak Memuat x Fungsional objektif adalah dalam bentuk J(x) = 11 f(ẋ, t)dt,
16 dengan f tidak memuat x secara ekslpisit. Persamaan Euler akan berbentuk d/dtfẋ =. Ini berarti bahwa fẋ = k, dengan k adalah konstanta. Ini merupakan persamaan diferensial ordo-1, dengan k merupakan konstanta sebarang. Solusinya diperoleh dengan melakukan integrasi ẋ. Jika f bergantung hanya pada ẋ, maka persamaan Euler menjadi d dt f ẋ = fẋẋ ẍ =. Hal ini terjadi hanya jika ẍ =, yang memberikan ẋ = c, dan x(t) = c 1 t + c 2, atau terjadi jika fẋẋ =. Jika fẋẋ memiliki akar nyata, dalam hal ini ẋ(t) = c, maka solusinya adalah x(t) = c 3 t + c 4. Terlihat bahwa manapun yang berlaku, solusi dari persamaan Euler berbentuk persamaan garis lurus x(t) = at + b. Contoh 2.6 Tentukan ekstremum untuk fungsional objektif J(x) = 1 (tẋ + ẋ2 )dt dengan syarat batas x() = 1, x(1) = 1. Solusi : Karena fungsi f(x, ẋ, t) = tẋ + ẋ 2 tidak memuat x, maka persamaan Euler menghasilkan d/dt(fẋ) = t + 2ẋ yang memberikan t + 2ẋ = konstanta, atau ẋ = 1/2t + k 1. Dengan melakukan integrasi secara langsung, diperoleh solusi umum : x(t) = 1 4 t2 + k 1 t + k 2. Dengan menggunakan syarat batas, diperoleh k 1 = 1/4, k 2 = 1, sehingga diperoleh solusi khusus : x(t) = 1 4 t t Fungsi f Tidak Memuat t Fungsional objektif dalam bentuk Persamaan Euler memberikan J(x) = f(x, ẋ)dt. f x d dt f ẋ = f x fẋx ẋ fẋẋ ẍ Kalikan dengan ẋ memberikan f x ẋ fẋx ẋ 2 fẋẋ ẋẍ d dt (f ẋf ẋ) =. Ini berarti bahwa f ẋfẋ = k. 12
17 2.5.3 Fungsi f Tidak Memuat ẋ Fungsional objektif dalam bentuk J(x) = f(x, t)dt. Persamaan Euler memberikan f x =. Ini bukan persamaan diferensial, tetapi secara umum merupakan persamaan aljabar tak linier. Umumnya, syarat batas tidak dapat dipenuhi, karena tidak ada konstanta integrasi. Dengan kata lain, solusi ada hanya jika kurva x = x(t) melewati titik batas. 2.6 Masalah Variasi Dengan Kendala Dalam masalah kalkulus variasi, kadangkala terdapat kendala tambahan yang disebabkan oleh kondisi fisik dari permasalahan. Ekstremum dari fungsional didefinisikan dalam kerangka kendala tersebut yang sering dikenal dengan sebutan ekstremum berkendala. Implikasi yang sangat penting dari kendala tersebut adalah variasi δx i bukan lagi merupakan sebarang sehingga Lema Dasar tidak dapat diterapkan. Untuk masalah seperti ini digunakan metoda substitusi atau yang lebih dikenal dengan sebutan pengali Lagrange. Akan dibahas kendala titik, kendala persamaan diferensial dan kendala isoperimetric Kendala Titik Dan Persamaan Diferensial Perhatikan masalah menentukan ekstremum fungsional (2.14) terhadap kendala (2.15) f(x, ẋ, t)dt g i (x, ẋ, t) =, (1 i r < n) dengan x merupakan vektor dimensi-n dan ẋ merupakan turunannya terhadap waktu t, serta f(x, ẋ, t) adalah fungsi bernilai skalar. Persamaan g i (x, ẋ, t) = disebut dengan kendala persamaan diferensial. Apabila g i (x, ẋ, t) tidak memuat ẋ maka g i (x, t) = disebut kendala titik. Definisikan fungsi Lagrange L sebagai berikut : (2.16) atau dalam bentuk skalar (2.17) L f(x, ẋ, t) + p.g i (x, ẋ, t) r L f(x, ẋ, t) + p i g i (x, ẋ, t) i=1 13
18 dengan x() = x dan x(t ) = x T. Definisikan fungsional objektif yang diperluas, J a sebagai berikut (2.18) Variasi δj a adalah (2.19) δj a = = J a L(x, ẋ, p, t)dt. (L x δx + Lẋδẋ + L p δp)dt [(L x d dt L ẋ)δx + L p δp]dt. Syarat perlu untuk adanya ekstremum adalah δj a = dan dipenuhinya kendala yang ada. In berarti bahwa persamaan Euler berikut harus dipenuhi, yaitu : (2.2) (2.21) L x d dt L ẋ =, L p d dt L ṗ =, dengan L x f x + g x p, dan Lẋ fẋ + gẋp, untuk kendala diferensial, dan Lẋ fẋ untuk kendala titik. Karena Lṗ = maka diperoleh L p = g =. Solusi, atau ekstremal akan diperoleh dengan menyelesaikan persamaan diferensial yang diberikan oleh persamaan Euler Kendala Isoperimetris Pada awalnya, masalah isoperimetric adalah masalah mencari kurva dengan panjangnya l yang melingkari daerah terbesar. Dalam perspektif yang lebih luas, masalah isoperimetric adalah masalah variasi dengan kendala yang diberikan dalam bentuk integral tentu yang mempunyai nilai tertentu. Secara matematis, masalah isoperimetric adalah masalah menentukan ekstremum dari fungsional objektif (2.22) terhadap kendala (2.23) dan (2.24) J(x) = f(x, ẋ, t)dt x i () = x i, x i (T ) = x it, (1 i n) g i (x, ẋ, t)dt = l i, (1 i r < n) dengan l i merupakan konstanta. Kendala ( 2.24) dinamakan kendala isoperimetric. Definisikan fungsi baru y i (t) t g i(x, ẋ, t)dt, dengan y i () =, dan y i (T ) = l i, (1 i r < n). Dengan menurunkan y i (t) terhadap waktu t maka diperoleh ẏ i (t) = g i (x, ẋ, t) atau g i ẏ i =. Dengan cara ini, kendala isoperimetric sudah ditransfer menjadi kendala 14
19 persamaan diferensial. Jadi, untuk menyelesaikannya, digunakan metode pengali Lagrange. Fungsional yang diperluas diberikan oleh (2.25) J a Persamaan Euler memberikan (2.26) (2.27) = F (x, ẋ, t)dt r [f(x, ẋ, t) + p i (t)(g i ẏ i )]dt i=1 F d x j dt ( F ) ẋ j = (1 i n) F d y j dt ( F ) ẏ j = (1 i r) Selanjutnya, solusi atau ekstremum akan diperoleh dengan menentukan solusi dari persamaan diferensial yang dibentuk oleh persamaan Euler. Contoh 2.7 Maksimumkan J(x) = ẋ2 dt, terhadap kendala x() = x, x(t ) = x T dengan T diberikan, dan (1 + x)dt = l, (l konstanta ). Solusi : Definisikan fungsi y(t) dengan y(t) t (1 + x)dt dengan y() =, y(t ) = l. Maka ẏ(t) = 1 + x(t), dan fungsi Lagrange diberikan oleh L = ẋ 2 + p(1 + x ẏ). Sehingga persamaan Euler memberikan 2ẍ = p, dengan solusinya adalah Syarat batas memberikan x() = x = b x(t) = p 4 t2 + at + b. x(t ) = x T = p 4 T 2 + at + b l = (1 + x)dt = Persamaan yang terakhir ini memberikan (1 + p 4 t2 + at + b)dt p = 12 T 3 (l a 2 T 2 (1 + b)t ). Persamaan di atas akan memberikan kontanta a, b dan p. 15
20 2.7 Syarat Batas Dalam Masalah Variasi Dua Titik Ujung Tetap Dan Syarat Batas Natural Perhatikan fungsional objektif (2.28) J(x) = f(x, ẋ, t)dt Syarat perlu terdapatnya ekstremum adalah δj =, dengan (2.29) δj = = (f x h + fẋḣ)dt (f x d dt f ẋ)hdt + hfẋ T =. Karena persamaan Euler harus dipenuhi, yaitu f x d dt f ẋ =, maka suku kedua pada persamaan ( 2.29) haruslah memenuhi (2.3) hfẋ T =. Jika titik awal A(, x ) dan titik terminal B(T, x T ) merupakan dua titik tetap, maka h() = = h(t ), atau X() = x, x(t ) = x T dan persamaan ( 2.3) dipenuhi. Permasalahan seperti ini dikenal dengan sebutan masalah dua titik ujung tetap. Apabila titik ujung x() dan x(t ) tidak diberikan, maka fungsi h(t) tidak lagi memenuhi h() = = h(t ). Sehingga untuk dapat terpenuhinya persyaratan ( 2.3) haruslah dipenuhi (2.31) fẋ = pada t = dan fẋ = pada t = T. Persyaratan ini dikenal dengan sebutan syarat batas natural. Persamaan ( 2.31) akan menentukan konstanta integrasi. Contoh 2.8 Perhatikan masalah brachistochrone yang meminimumkan fungsional objektif dengan T = 1 dan x() = 4. J(x) = 1/ (1 + ẋ 2 )dt, Solusi : Persamaan Euler memberikan ẍ =, yang memberikan solusi x(t) = at + b. Apabila x() = 4 dan T = 1, tetapi x(1) belum ditentukan, maka kita gunakan syarat fẋ t=1 =, yaitu ẋ(1) fẋ t=1 = =, (1 + ẋ 2 (1)) 1/2 memberikan ẋ(1) = a =. Sedangkan x() = 4 memberikan b = 4, sehingga diperoleh solusi khusus x(t) = 4. 16
21 2.7.2 Titik Ujung Bebas Perhatikan masalah menentukan ekstremum untuk fungsional objektif (2.32) J(x) = t f(x, ẋ, t)dt dengan t, T, x(t ) dan x(t ) semuanya belum diketahui. Untuk memudahkan pembahasan, misalkan t = dan x() = x adalah tetap, sedangkan T dan x(t ) adalah bebas. Variasi pertama adalah (2.33) δj = = (f x h + fẋḣ)dt + f(.) T δt (f x d dt f ẋ)hdt + hfẋ T + f(.) T δt Karena variasi pada titik ujung tidak mempengaruhi variasi dalam selang terbuka (, T ), maka syarat perlu untuk δj = adalah dipenuhinya persamaan Euler, yaitu (2.34) f x d dt f ẋ =. Akibatnya, persamaan ( 2.33) menjadi δj = fẋh T + f(.) T δt =. Dengan menggunakan informasi h(t ) = δx T ẋ(t )δt, menghasilkan Syarat Batas atau Syarat Transversalitas : (2.35) (f(.) T ẋfẋ T )δt + fẋ T δx T =. Syarat batas ini akan menentukan nilai T dan x T. Terdapat 2 kasus yang perlu diperhatikan. Kasus pertama apabila variasi δx T dan δt saling bebas. Akibatnya, koefisien dari δx T dan δt dalam persamaan ( 2.35) masing-masing sama dengan nol, yaitu (2.36) f(.) T ẋfẋ T =, dan fẋ T =, yang secara bersama menghasilkan (2.37) f(.) T = = fẋ T. Kasus kedua apabila titik ujung B(T, x T ) bergerak sepanjang kurva x(t) = g(t). Untuk kasus ini, maka δx T = ġ(t )δt. Dengan substitusi ini ke dalam persamaan ( 2.35) menghasilkan (2.38) (f(.) + [ġ(t ) ẋ(t )]fẋ) t=t δt =. Analisis yang sama berlaku pula untuk kasus titik awal bebas, yaitu apabila t dan x(t ) bebas. Secara umum, Syarat Transversalitas atau Syarat Batas ( 2.35) menjadi (2.39) [f(.) ẋfẋ]δt t=t t=t + fẋδx(t) t=t t=t =. 17
22 Dengan cara yang sama seperti analisis untuk satu titik ujung tetap, maka untuk kasus variasi δx T dan δt saling bebas, diperoleh (2.4) f(.) t=t t=t = = fẋ t=t t=t dan untuk kasus titik ujung bergerak sepanjang kurva g, akan diperoleh (2.41) [f(.) + (ġ ẋ)fẋ] t=t t=t δt =. Syarat Transversalitas di atas mencakup semua kasus yang ada, sebagai berikut : 1. Apabila kedua titik ujung terletak pada garis lurus t = t dan t = T, maka δt = = δt sehingga suku pertama dalam persamaan ( 2.39) menjadi nol dan persamaan ( 2.39) menjadi fẋδx(t) t=t t=t =. 2. Apabila titik ujung A dan B tetap, yaitu x(t ), x(t ) dan t dan T tetap, maka δt = = δt dan δx() = = δx(t ). Jadi kita mempunyai masalah dua titik ujung tetap, dan konstanta integrasi ditentukan oleh syarat batas pada titik A dan B. 3. Apabila x dan x T tetap, tetapi t dan T bebas, maka δx() = = δx(t ), tetapi δt dan δt. Persamaan ( 2.39) memberikan (f(.) ẋfẋ) t=t t=t =. 4. Titik ujung bebas, yaitu x, x T, t dan T semuanya bebas, maka Syarat Transversalitas ( 2.39) harus dipenuhi. Dalam hal ini, (f(.) ẋfẋ) t=t t=t =, dan fẋ t=t t=t =. 5. Titik ujung bebas, yaitu x(t ), x(t ), t dan T semuanya bebas, tetapi x(t ) dan x(t ) harus bergerak sepanjang kurva x(t ) = g 1 (t ) dan x(t ) = g 2 (T ). Maka konstanta integrasi akan ditentukan oleh [f + (ġ 1 ẋ)fẋ] t=t = dan f + (ġ 2 ẋ)fẋ] t=t =. 6. Kombinasi dari semua kasus-kasus di atas. 7. Kadangkala dalam masalah ekonomi, syarat yang diberikan pada titik ujung tidak selalu dalam bentuk suatu nilai, tapi dibatasi oleh suatu nilai. Misalnya, jumlah produksi x pada waktu terminal haruslah lebih besar dari suatu nilai. 18
23 Perhatikan masalah memaksimumkan fungsional objektif (2.42) Definisikan J(x) = t f(x, ẋ, t)dt, x(t ) = x, x(t ) x T, (x T diberikan, T tetap.). Maka syarat batas yang harus dipenuhi oleh masalah seperti ini adalah f ẋ t=t, (=, jika x(t ) > x T ). (2.43) (2.44) p(t) f/ ẋ, H f(x, ẋ, t) ẋfẋ f + pẋ. Syarat Transversalitas ( 2.39) dapat dituliskan dalam bentuk (2.45) (Hδt + pδx) t=t t=t =. Untuk kasus waktu awal t dan waktu terminal T bebas, maka H(t ) = = H(T ). Sedangkan untuk kasus x(t ) dan x(t ) belum ditentukan maka p(t ) = = p(t ). Syarat Batas dan Penentuan Konstanta Integrasi Kasus Substitusi Syarat Batas T dan x(t ) δx T = x () = x dua2nya ditentukan δt = x (T ) = x T x(t ) bebas δx(t ) x () = x T ditentukan δt = fẋi t=t = x(t ) = x T tetap δx T = x () = x T bebas δt x (T ) = x T H (f ẋfẋ) t=t = x(t ) dan T δx(t ) x () = x dua2nya belum ditentukan δt fẋ t=t = dan saling bebas H (f ẋfẋ) t=t = x(t ) dan T bebas ẋ(t ) = ġ(t )δt x () = x, x (T ) = g(t ) tetapi x(t ) = g(t ) δx i (T ) = ġ i (T )δt (f + (ġ(t ) ẋ(t ))fẋ) t=t = T tetap x T diberikan fẋ t=t, (=, x(t ) > x T ) x(t ) x T Contoh 2.9 Perhatikan masalah meminimumkan fungsional objektif J(x) dengan J(x) = 2 dengan x() dan x(2) belum ditentukan. (ẋ 2 + xẋ + 2ẋ + 4x)dt 19
24 Solusi : Persamaan Euler memberikan ẍ = 2, dengan solusinya adalah x(t) = t 2 + k 1 t + k 2. Konstanta k 1 dan k 2 akan ditentukan dari syarat fẋ = 2ẋ + x + 2 =, untuk t =, dan t = 2. Syarat di atas memberikan k 1 = 6, k 2 = 1. Sehingga diperoleh solusi x(t) = t 2 6t + 1. Contoh 2.1 Tentukan ekstremum untuk fungsional objektif J(x) = dengan setiap kasus kendala berikut : (x + ẋ 2 )dt 1. x() = 1, T = 2, x(2) = 1 ( dua titik ujung tetap ). 2. x() = 1, T = 2, x(2) bebas ( titik ujung bebas ). 3. x() = 1, x(t ) = 4, T bebas tetapi T > 2 ( waktu terminal bebas ). Solusi : Persamaan Euler memberikan 1 2ẍ =, yang memberikan solusi x(t) = 1 4 t2 + k 1 t + k 2, dengan konstanta k 1 dan k 2 akan ditentukan untuk setiap kasus sebagai berikut : 1. x() = 1 k 2 = 1, x(2) = 1 k 1 = 4, sehingga solusi adalah x(t) = 1 4 t2 + 4t x() = 1 k 2 = 1. Untuk menentukan k 1 gunakan fẋ = 2ẋ = pada t = T, yaitu ẋ(t ) =, memberikan k 1 = 1. Jadi, diperoleh solusi x(t) = 1 4 t2 t x() = 1 k 2 = 1. Untuk menentukan k 1 gunakan persyaratan (f ẋfẋ) t=t =, yang menghasilkan ẋ 2 (T ) + x(t ) =. Ini akan memberikan k 1 = ±1. Untuk k 1 = 1 T = 2. sedangkan untuk k 1 = 1 T = 6. Karena T > 2, maka haruslah k 1 = 1. Sehingga diperoleh solusi optimum adalah x(t) = 1 4 t2 t + 1, T = 6. 2
25 2.8 Syarat Cukup / Sufficiency Conditions Variasi Fungsional Perhatikan fungsional objektif (2.46) J(x) = Variasi total dari fungsional objektif adalah J(h) J(x + h) J(x) f(x, ẋ, t)dt. = (f x h + fẋḣ)dt + 1 (f xx h 2 + 2f xẋ hḣ 2 + fẋẋḣ2 )dt + O( h ) 2 δj(h) + δ 2 J(h) + O( h ) 2 = variasi pertama + variasi kedua + orde lebih tinggi dengan O( h ) 2 untuk h. Pada kurva ekstremum, δj(h) = dan J(h) harus memiliki tanda yang sama dengan tanda δ 2 J(h). Untuk memudahkan pembahasan, tuliskan variasi kedua sebagai berikut : (2.47) δ 2 J(h) = 1 2 (f xx h 2 + 2f xẋ hḣ + f ẋẋḣ2 )dt (P ḣ2 + Qh 2 )dt dengan P P (t) 1f 2 ẋẋ; Q Q(t) = 1(f 2 xx d f dt xẋ) dan dengan melakukan integrasi bagian maka diperoleh 2fxẋhḣdt = ( d f dt xẋ)h 2 dt. Untuk masalah meminimumkan, δ 2 J(h), dan untuk masalah memaksimumkan, δ 2 J(h). Untuk fokusnya, kita lihat masalah meminimumkan, dan untuk masalah memaksimumkan, tinggal mengganti tanda yang berlawanan. Akan dilihat kondisi-kondisi yang membuat δ 2 J(h). Akan ditunjukkan bahwa δ 2 J(h), jika dan hanya jika (P ḣ2 + Qh 2 ) untuk semua h(t) yang memenuhi h() = = h(t ). Fungsi h(t) yang memenuhi sifat ini bernilai kecil jika ḣ(t), t (, T ) juga bernilai kecil, tapi sebaliknya tidak berlaku. Apabila fungsi h(t) yang bersifat se[erti di atas dapat ditemukan demikian rupa sehingga h(t) kecil tetapi ḣ(t) besar untuk tin(, T ), maka P ḣ2 mendominasi Qh 2 dalam penentuan tanda dari δ 2 J(h), seperti yang ditunjukkan oleh lema dan teorema berikut Syarat Legendre Lema 2.2 Misalkan δ 2 J(h) = (P ḣ2 +Qh 2 )dt didefinisikan untuk fungsi h(t), yang memiliki sifat dapat diturunkan pada t (, T ) dan memenuhi h() = = h(t ). Maka syarat 21
26 perlu untuk δ 2 J(h) = (P ḣ2 +Qh 2 )dt adalah P (t), t (, T ). Ini disebut Syarat Legendre. Teorema 2.2 (Legendre). Syarat perlu bagi fungsional objektif J(x) = f(x, ẋ, t)dt dengan syarat pada titik ujung x() = x, x(t ) = x T untuk memiliki nilai minimum ( atau maksimum ) untuk semua kurva x = x(t) adalah dipenuhinya syarat Legendre P (t) untuk semua t (, T ). Teorema Legendre ini, sayangnya masih merupakan syarat perlu. Upaya Legendre untuk membuktikannya sebagai syarat cukup untuk optimum mengalami kegagalan Syarat Jacobi Upaya Legendre yang gagal, membawa kepada suatu persamaan diferensial linier ordo-2 dalam v, d (P v) + Qv =. dt Teorema 2.3 Perhatikan persamaan diferensial orde-2 (2.48) d (P v) + Qv =. dt Jika P > (< ) dan solusi v(t) untuk semua fungsi v(t) yang dapat diturunkan memenuhi sifat v() = = v(t ), maka δ 2 J > (< ) artinya nilai minimum ( atau nilai maksimum ) telah diperoleh. Ini disebut syarat perlu Jacobi Syarat Weierstrass untuk Ekstremal Kuat Teorema 2.4 Definisikan fungsi ekstra E dengan (2.49) E(x, ẋ, p, t) = f(x, ẋ, t) f(x, p, t) (ẋ p)f p dengan p(t, x) adalah fungsi kemiringan/ slope dari ekstremum yang melalui titik (t, x). Apabila Jacobi dipenuhi maka E untuk masalah memaksimumkan dan E untuk masalah meminimumkan. 22
27 2.8.5 Syarat Legendre-Clebsch Teorema 2.5 Fungsi ekstra E dapat disederhanakan menjadi (2.5) E (ẋ p)2 fẋẋ (t, x, q) 2! dengan q = θẋ + (1 θ)p, ( < θ < 1). Supaya x(t) mencapai minimum ( atau maksimum) adalah cukup dipenuhi syarat Legendre-Clebsch E ( ) yang berarti fẋẋ ( ), atau dalam bentuk yang lebih umum, matriks [fẋẋ ] merupakan semi-definit positif ( atau negatif ) dan syarat Jacobi dipenuhi untuk semua ẋ Syarat Cukup : Kasus khusus Teorema 2.6 (Mangasarian). Misalkan f(x, ẋ, t) merupakan fungsi yang dapat diturunkan dua kali dan concave/cembung ( convex/cekung) dalam x dan ẋ. Maka syarat perlu dan syarat cukup untuk x sebagai maksimum ( atau minimum ) dari fungsional J(x) = adalah dipenuhinya persamaan Euler dan x() = x, dan x(t ) = x T. f(x, ẋ, t)dt 23
28 Chapter 3 Kontrol Optimum : Pendekatan Kalkulus Variasi 3.1 Formulasi Masalah Kontrol Optimum Teori kontrol optimum berkembang secara pesat pada tahun 5-an, dengan adanya penemuan 2 metode penyelesaian masalah kontrol optimum, yaitu dynamic programming yang ditemukan oleh Richard Bellman (1957) dan maximum principle yang ditemukan oleh Pontryagin (1962). Dengan alasan kepraktisan, pembahasan akan difokuskan pada teknik maximum principle, yang dapat didekati dengan metode kalkulus variasi, terutama yang terkait dengan syarat perlu yang tertuang dalam persamaan Euler. Lagi pula, masalah kalkulus variasi dengan kendala persamaan differensial merupakan masalah kontrol optimum, dengan mengganti peubah ẋ dengan peubah kontrol u(t). Perhatikan suatu masalah ekonomi yang berkembang menurut waktu. Pada waktu t, sistem berada dalam keadaan atau kondisi (state), yang dapat diungkapkan dengan peubah keadaan (state variables) x 1 (t), x 2 (t),..., x n (t), atau dalam bentuk vektor x(t) R n. Dengan nilai t yang berbeda, vektor x(t) me-nempati posisi yang berbeda di ruang R n. Dalam hal ini, kita katakan bahwa sistem bergerak sepanjang suatu kurva di R n. Misalkan proses yang terjadi pada ekonomi (yang membuat x(t) bervariasi/bergerak) dapat dikendalikan atau dikontrol. Artinya, ada fungsi kontrol atau variable controls atau decision variables u 1 (t), u 2 (t),..., u k (t) atau dalam bentuk vektor u(t) R k, k n, yang mempengaruhi proses. [Contoh : pajak, tingkat suku bunga, alokasi investasi, dsb.] Tentunya kita harus mengetahui aturan/hukum/kaidah yang membentuk perilaku ekonomi sepanjang waktu, yang kita sebut dengan dinamika dari sistem. 24
29 Sistem yang akan kita lihat adalah sistem yang dibentuk oleh sistem persamaan differensial : (3.1) ẋ(t) = f(x(t), u(t), t) dengan f = (f 1, f 2,..., f n ), f i dan f i / x i adalah kontinu. Misal state dari sistem diketahui pada waktu t sehingga x(t ) = x, x R n. Jika dipilih kontrol u(t) = (u 1 (t), u 2 (t),..., u k (t)) R k yang terdefinisi untuk waktu t t, maka diperoleh sistem x(t). Jadi, x(t) merupakan respons terhadap kontrol u(t), sehingga kadangkadang dituliskan sebagai x u (t). Untuk setiap fungsi kontrol u(t) dan respons x u (t) atau disingkat x(t), dikaitkan suatu bilangan J yang didefinisikan oleh (3.2) J[u(t)] = S[x(T ), T ] + t f (x(t), u(t), t)dt dengan fungsi f adalah suatu fungsi yang diberikan dan S[x(T ), T ] merupakan fungsi scrap. Waktu akhir atau waktu terminal T tidak selalu harus tetap, dan x(t ) dapat saja memiliki batasan tertentu. Definisi 3.1 Misalkan U menyatakan kelas dari semua fungsi yang kontinu bagian. Masalah kontrol optimum (MKO) adalah masalah menentukan fungsi kontrol u (t) diantara fungsi admissible u(t) U yang membawa sistem dari state awal x kepada state akhir/terminal x T yang memenuhi kondisi akhir/terminal, melalui sistem (3.3) ẋ(t) = f(x(t), u(t), t) sehingga fungsional J mencapai nilai maksimum. Dengan kata lain, masalah kontrol optimum adalah masalah memaksimumkan fungsional objektif (3.4) max J[u(t)] = S[x(T ), T ] + f (x(t), u(t), t)dt u(t) U t terhadap kendala ẋ(t) = f(x(t), u(t), t), x(t ) = x, x(t) R n. 3.2 Syarat Perlu : Prinsip Maksimum Pontryagin Teorema 3.1 Misalkan u (t) sebagai kontrol admissible yang membawa state awal (x(t ), t ) kepada target state terminal (x(t ), T ), dengan x(t ) dan T secara umum tidak ditentukan. Misalkan x (t) merupakan trajektori dari sistem yang berkaitan dengan u (t). Supaya kontrol u (t) merupakan kontrol optimum adalah perlu terdapat fungsi vektor p (t), dan konstanta p demikian rupa sehingga 25
30 1. p (t) dan x (t) merupakan solusi dari sistem kanonik (3.5) (3.6) ẋ (t) = H p (x (t), u (t), p (t), t) ṗ (t) = H x (x (t), u (t), p (t), t) dengan fungsi Hamilton H diberikan oleh (3.7) H(x, u, p, t) = f (x(t), u(t), t) + p.f(x(t), u(t), t) dengan p H(x (t), u (t), p (t), t) H(x(t), u(t), p(t), t) 3. Semua syarat batas dipenuhi. Bukti : Untuk memudahkan pembahasan, ambil t = dan x() = x. Tuliskan fungsi scrap S[x(T ), T ] dalam bentuk (3.8) S[x(T ), T ] S[x, ] + d S[x(t), t]dt dt sehingga fungsional objektif J dalam persamaan ( 3.2) dapat ditulis dalam bentuk yang berikut : (3.9) (3.1) J[u(t)] = S[x, ] + = S[x, ] + [f (x(t), u(t), t) + d S(x(t), t)]dt t dt [f (.) + S t x ẋ + S t ]dt Suku S[x, ] dapat diabaikan untuk mempermudah pembahasan, karena x() = x sudah tetap, sehingga tidak mempengaruhi proses optimisasi. Tuliskan fungsional objektif yang diperluas J a (u) sebagai berikut (3.11) J a (u) = t L(x, ẋ, p, u, t)dt dengan fungsi L didefinisikan oleh (3.12) (3.13) L(x, ẋ, p, u, t) f (.) + p[f(.) ẋ] + S x ẋ + S t H(x, u, p, t) pẋ + S x ẋ + S t dengan H(x, u, p, t) f (x, u, t) + pf(x, u, t) merupakan fungsi Hamilton. 26
31 Dengan menggunakan syarat perlu untuk adanya ekstremum pada fungsional objektif yang diperluas, maka (3.14) (3.15) δj a (u) = [(L x d dt L ẋ)δx + L u δu + L p δp]dt + [Lẋδx + (L Lẋẋ)δt] t=t =. Karena persamaan Euler harus dipenuhi, maka haruslah (3.16) L x d dt L ẋ = H x + x (S xẋ + S t ) d dt (S x p) = H x + S xx ẋ + S xt S xx ẋ S xt + ṗ = H x + ṗ =. Ini memberikan (3.17) ṗ = H x Karena δu dan δp adalah sebarang dan saling bebas, maka haruslah L u = dan L p =. Dari pendefinisian fungsi L, maka sehingga diperoleh L u = H u, dan L p = f(.) ẋ = H p ẋ, (3.18) (3.19) H u = ẋ = f(x, u, t) = H p Syarat transversalitas atau syarat batas diberikan oleh suku-suku sisanya, yaitu (3.2) [Lẋδx + (L Lẋẋ)δt] t=t =. Tetapi Lẋ = S x p L Lẋẋ H pẋ + S x ẋ + S t ẋs x + ẋp = H + S t sehingga diperoleh syarat transversalitas atau syarat batas (3.21) (S x p)δx t=t + [H(t) + S t ]δt t=t =. Apabila x(t ) dan t dua-duanya belum ditentukan pula, maka syarat batas menjadi (3.22) (S x p)δx t=t t=t + [H(t) + S t ]δt t=t t=t = yang menghasilkan teorema Pontryagin. Catatan : 27
32 1. H(x (t), u (t), p (t), t) H(x(t), u(t), p(t), t) disebut dengan Prinsip Maksimum Pontryagin. Kondisi ini dipenuhi oleh H u = dan H uu <, untuk masalah yang kita bicarakan. Jika u U dan U himpunan tertutup, maka H u = tidak memiliki arti, kecuali maksimum dari H diberikan oleh bagian dalam (interior ) himpunan U. 2. Jika H fungsi monoton naik dalam peubah u, dan U tertutup, maka kontrol optimum adalah u imax untuk masalah memaksimumkan dan u imin untuk masalah meminimumkan. Jika H fungsi monoton turun, maka kontrol optimum adalah u imin untuk masalah memaksimumkan dan u imax untuk masalah meminimumkan. Hal ini juga berlaku apabila H adalah fungsi linier dalam u. Sehingga peubah kontrol optimum u i adalah kontinu bagian dan loncat dari satu vertex ke vertex lainnya. Ini adalah kasus khusus dari kontrol bang-bang. 3. H(x (t), u (t), p (t), t) H(x(t), u(t), p(t), t) juga mencakup syarat cukup. 4. Vektor p disebut juga vektor adjoint, memiliki peranan sebagai pengali Lagrange. Dalam masalah optimisasi dinamis, peubah atau vektor adjoint merupakan shadow price nilai marginal dari vektor atau peubah x, menunjukkan jumlah kenaikan/penurunan untuk setiap kenaikan/penurunan dalam nilai x pada waktu t yang berkontribusi terhadap fungsional objektif optimum J. Sedangkan ṗ mengindikasikan tingkat kenaikan (appresiasi untuk ṗ >,) atau penurunan ( depresiasi untuk ṗ < )dalam nilai dari tiap unit modal. 5. dh/dt = H/ t. 6. ṗ = H x, H u =, ẋ = H p memberikan syarat perlu untuk masalah yang dibicarakan. 7. Syarat batas diberikan oleh persamaan ( 3.22). Apabila fungsi scrap S =, maka persamaan ( 3.22) menjadi (3.23) p(t)δx(t) t=t t=t + H(t)δt t=t t=t =. Khususnya, apabila waktu awal t dan x(t ) telah ditentukan, sedangkan T dan x(t ) belum ditentukan, maka syarat batas menjadi p(t )δx(t ) + H(T )δt =. Contoh 3.1 Minimumkan fungsional objektif J(u(t)) = 1 (x + u 2 )dt dengan kendala ẋ(t) = u(t); x() =, x(1) bebas. 28
33 Solusi : Dalam masalah di atas, f (x, u, t) = x + u 2, fungsi f(x, u, t) = u(t). Maka fungsi Hamilton adalah sehingga diperoleh H(x, u, p, t) = f (x, u, t) + pf(x, u, t) = x + u 2 + p( u(t)) H u = 2u(t) p(t) u (t) = p(t)/2; H uu = 2 >. ṗ(t) = H x = 1, memberikan p(t) = t + k 1. Karena fungsi scrap S =, dan x(1) belum ditentukan ( dan T = 1), maka syarat batas p(1)δx(1) =, yang memberikan p(1) = 1 + k 1 =, yaitu k 1 = 1, dan p(t) = t + 1. Sistem dinamis menjadi yang memberikan solusi ẋ(t) = u(t) = p(t)/2 = 1 2 ( t + 1) = t 2 1 2, x(t) = t k 2 dengan k 2 =, karena x() =. Jadi solusi optimum adalah x (t) = t p (t) = t + 1 u (t) = t Contoh 3.2 Minimumkan fungsional objektif dengan kendala ẋ = u(t), x() = 1. J(u(t)) = 1 2 x(1) Solusi : Fungsi Hamilton adalah H = 1 2 u2 pu, sehingga H u = u p =. Ini memberikan u(t) = p(t); H uu = 1 >. ṗ = H x =. Ini memberikan p(t) = k, konstanta. Sedangkan ẋ = u = p memberikan 1 u 2 dt x(t) = pt + k 1 == pt + 1, karena x() = 1. Syarat batas p(1) = S x = x(1) memberikan p(1) = x(1) = p + 1, yaitu p (t) = 1 2. Sehingga diperoleh solusi optimum x (t) = 1 2 t + 1, p (t) = u (t) =
34 Perhatikan masalah kontrol optimum satu dimensi yang memaksimumkan fungsional objektif J (3.24) max J[u(t)] = f (x(t), u(t), t)dt u(t) U t terhadap kendala (3.25) ẋ(t) = f(x(t), u(t), t), x(t ) = x, T dan x T tetap dan salah satu dari syarat terminal berikut : 1. x(t ) = x T, 2. x(t ) x T, 3. x(t ) bebas dan kontrol u(t) U. Teorema 3.2 Syarat perlu untuk adanya kontrol optimum adalah (p, p(t)) (, ) dan (3.26) (3.27) (3.28) (3.29) H(x (t), u (t), p (t), t) H(x(t), u(t), p(t), t) ẋ (t) = H p (x (t), u (t), p (t), t) ṗ (t) = H x (x (t), u (t), p (t), t) p = 1 atau p =, dan syarat batas yang sesuai adalah : 1. p(t ) tanpa syarat, 2. p(t ) (= jika x (T ) > x(t )), 3. p(t ) =. 3.3 Syarat Transversalitas Atau Syarat Batas Perhatikan masalah kontrol optimum yang memaksimumkan fungsional objektif (3.3) max J[u(t)] = S[x(T ), T ] + f (x(t), u(t), t)dt u(t) U t 3
35 terhadap kendala (3.31) ẋ(t) = f(x(t), u(t), t), x(t ) = x, x(t) R n. Maka syarat transversalitas atau syarat batas diberikan oleh (3.32) (S x p) x t=t + [H + S t ] t t=t = Masalah Waktu Terminal T Tetap Dengan waktu terminal T tetap, maka δt =, dan persamaan ( 3.32) menjadi (3.33) (S x p) x t=t = Terdapat 3 kasus untuk masalah ini, yaitu : Kasus 1 : State terminal (akhir) tetap, x(t ) = x T. Untuk kasus ini, jelas bahwa δx(t ) =, dan persamaan ( 3.32) tidak memberikan informasi apa-apa. Malahan informasi tersebut tidak diperlukan, karena konstanta integrasi akan diberikan oleh x(t ) = x dan oleh x(t ) = x T. Kasus 2 : State Terminal Bebas. Untuk kasus ini, jelas bahwa δx(t ) sehingga diperoleh p(t ) = S x. Apabila tanpa S[x(T ), T ], yaitu S[x(T ), T ] =, maka syarat batas adalah p(t ) =. Kasus 3 : State Terminal berada pada manifold M[x(T ), T ] =. Apabila state terminal berada pada manifold M[x(T ), T ] = dengan M merupakan vektor, maka syarat batas menjadi (3.34) (R x p) x t=t = dengan (3.35) R[x(T ), T ] S[x(T ), T ] + µm[x(t ), T ] dengan µ merupakan pengali Lagrange. Jadi syarat batas atau syarat transversalitas menjadi p(t ) = R x Masalah Waktu Terminal T Bebas Syarat batas menjadi (3.36) (R x p) x t=t + [H + S t ] t t=t =. Terdapat 3 kasus untuk masalah ini, yaitu : Kasus 4 : State Terminal x(t ) = x T Tetap Jelas bahwa δx(t ) =, sehingga diperoleh (3.37) H(T ) + S t t=t =. 31
36 Apabila tanpa fungsi scrap, maka H(T ) =. Kasus 5 : State Terminal x(t ) Bebas, yaitu δx(t ). Maka syarat batas menjadi p(t ) = S x [x(t ), T ], dan H(T ) + S t t=t = Apabila fungsi scrap tidak ada, maka p(t ) = = H(T ). Kasus 6 : State Terminal Bebas, tapi memenuhi M[x(T ), T ] =. Maka syarat batas menjadi p(t ) = R x, H(T ) + R t t=t =, M[x(T ), T ] =. 32
37 Ringkasan Syarat Batas/Transversalitas Conditions Kontrol Optimum (S x p)δx t=t + [H(t) + S t ]δt t=t =. Kasus Substitusi Syarat Batas Waktu Terminal T tetap ( δt = ) x(t ) = x T tetap δx(t ) = x() = x, x(t ) = x T δt = (tidak ada batasan pada p(t )) x(t ) bebas δx(t ) x() = x yaitu δx(t ) δt = p(t ) = S x State terminal x(t ) δx(t ) x() = x berada pada M(x, t) = δt = p(t ) = S x + M xµ M(x(T ), T ) = Waktu Terminal T bebas ( δt ) x(t ) = x T tetap δx(t ) = x() = x δt x(t ) = x T H(T ) + S t = pada t = T x(t ) bebas δx(t ) x() = x δt p(t ) = S x [x(t ), T ] H(T ) + S t = pada t = T x(t ) tidak diberikan δx(t ) x() = x berada pada manifold δt p(t ) = R x S x + M x M(x(T ), T ) = H(T ) + R t = M = 3.4 Syarat Cukup Untuk Kontrol Optimum Syarat H(x (t), u (t), p (t), t) H(x(t), u(t), p(t), t) dalam Prinsip Maksimum Pontryagin sekaligus memberikan syarat cukup. Variasi total dari fungsional yang diperluas J a (u) adalah J a (u) J a (u) J a (u ) = δj a (u) + δ 2 J a (u) + O(u). Tanpa mempedulikan orde yang lebih tinggi O(u) dan pada saat ekstremum variasi pertama δj a (u) =, maka terlihat bahwa tanda dari J a (u) ditentukan oleh tanda dari variasi kedua δ 2 J a (u), yang harus bertanda tak-positif untuk maslah maksimum dan tak-negatif untuk masalah minimum. Dengan mengabaikan fungsi scrap, yaitu S(x(T ), t) =, maka variasi kedua δ 2 J a (u) diberikan oleh [ ][ ] T 2 δ 2 H 2 H J a (u) = 1/2 ( δx δu ) 2 x x u δx dt δu 2 H u x dengan H xx [δ 2 H/δx i δx j ], merupakan turunan dari H x terhadap x yang dihitung pada (x, p, u, t). Hal yang sama berlaku untuk H ux (= H xu ) dan H uu. 2 H 2 u 33
Kontrol Optimum. Prinsip Maksimum Pontryagin. Toni Bakhtiar. Departemen Matematika IPB. Februari 2014
 Kontrol Optimum Prinsip Maksimum Pontryagin Toni Bakhtiar Departemen Matematika IPB Februari 214 tbakhtiar@ipb.ac.id (IPB) MAT332 Kontrol Optimum Februari 214 1 / 25 Outline Masalah kontrol optimum Prinsip
Kontrol Optimum Prinsip Maksimum Pontryagin Toni Bakhtiar Departemen Matematika IPB Februari 214 tbakhtiar@ipb.ac.id (IPB) MAT332 Kontrol Optimum Februari 214 1 / 25 Outline Masalah kontrol optimum Prinsip
Kalkulus Variasi. Masalah Kalkulus Variasi, Fungsional Objektif, Variasi, Syarat Perlu Optimalitas. Toni Bakhtiar. Departemen Matematika IPB
 Kalkulus Variasi Masalah Kalkulus Variasi, Fungsional Objektif, Variasi, Syarat Perlu Optimalitas Toni Bakhtiar Departemen Matematika IPB Februari 2014 tbakhtiar@ipb.ac.id (IPB) MAT332 Kontrol Optimum
Kalkulus Variasi Masalah Kalkulus Variasi, Fungsional Objektif, Variasi, Syarat Perlu Optimalitas Toni Bakhtiar Departemen Matematika IPB Februari 2014 tbakhtiar@ipb.ac.id (IPB) MAT332 Kontrol Optimum
Masalah Kalkulus Variasi, Fungsional Objektif, Variasi, Syarat Perlu Optimalitas
 Masalah Kalkulus Variasi, Fungsional Objektif, Variasi, Syarat Perlu Optimalitas Slide II Toni Bakhtiar Departemen Matematika IPB February 2012 TBK (IPB) Kalkulus Variasi February 2012 1 / 37 Masalah Brachystochrone
Masalah Kalkulus Variasi, Fungsional Objektif, Variasi, Syarat Perlu Optimalitas Slide II Toni Bakhtiar Departemen Matematika IPB February 2012 TBK (IPB) Kalkulus Variasi February 2012 1 / 37 Masalah Brachystochrone
II LANDASAN TEORI. ii. Constant returns to scale, yaitu situasi di mana output meningkat sama banyaknya dengan porsi peningkatan input
 2 II LANDASAN EORI Pada bab ini akan diuraikan beberapa definisi dan teori penunjang yang akan digunakan dalam karya ilmiah ini. 2.1 Istilah Ekonomi Definisi 1 (Pertumbuhan Ekonomi) Pertumbuhan ekonomi
2 II LANDASAN EORI Pada bab ini akan diuraikan beberapa definisi dan teori penunjang yang akan digunakan dalam karya ilmiah ini. 2.1 Istilah Ekonomi Definisi 1 (Pertumbuhan Ekonomi) Pertumbuhan ekonomi
Kontrol Optimum. Syarat Transversalitas, Current-valued Hamiltonian. Toni Bakhtiar. Departemen Matematika IPB. Februari 2014
 Kontrol Optimum Syarat Transversalitas, Current-valued Hamiltonian Toni Bakhtiar Departemen Matematika IPB Februari 2014 tbakhtiar@ipb.ac.id (IPB) MAT332 Kontrol Optimum Februari 2014 1 / 37 Outline Syarat
Kontrol Optimum Syarat Transversalitas, Current-valued Hamiltonian Toni Bakhtiar Departemen Matematika IPB Februari 2014 tbakhtiar@ipb.ac.id (IPB) MAT332 Kontrol Optimum Februari 2014 1 / 37 Outline Syarat
Kalkulus Variasi. Persamaan Euler, Masalah Kalkulus Variasi Berkendala, Syarat Batas. Toni Bakhtiar. Departemen Matematika IPB.
 Kalkulus Variasi Persamaan Euler, Masalah Kalkulus Variasi Berkendala, Syarat Batas Toni Bakhtiar Departemen Matematika IPB Februari 214 tbakhtiar@ipb.ac.id (IPB) MAT332 Kontrol Optimum Februari 214 1
Kalkulus Variasi Persamaan Euler, Masalah Kalkulus Variasi Berkendala, Syarat Batas Toni Bakhtiar Departemen Matematika IPB Februari 214 tbakhtiar@ipb.ac.id (IPB) MAT332 Kontrol Optimum Februari 214 1
Kalkulus Variasi. Syarat Cukup, Masalah Kalkulus Variasi dengan Horizon Takhingga. Toni Bakhtiar. Departemen Matematika IPB.
 Kalkulus Variasi Syarat Cukup, Masalah Kalkulus Variasi dengan Horizon Takhingga Toni Bakhtiar Departemen Matematika IPB Februari 2014 tbakhtiar@ipb.ac.id (IPB) MAT332 Kontrol Optimum Februari 2014 1 /
Kalkulus Variasi Syarat Cukup, Masalah Kalkulus Variasi dengan Horizon Takhingga Toni Bakhtiar Departemen Matematika IPB Februari 2014 tbakhtiar@ipb.ac.id (IPB) MAT332 Kontrol Optimum Februari 2014 1 /
Kalkulus Variasi. Pendahuluan, Model Matematika, Keterkontrolan. Toni Bakhtiar. Departemen Matematika IPB. Februari 2014
 Kalkulus Variasi Pendahuluan, Model Matematika, Keterkontrolan Toni Bakhtiar Departemen Matematika IPB Februari 2014 tbakhtiar@ipb.ac.id (IPB) MAT332 Kontrol Optimum Februari 2014 1 / 42 Outline Beberapa
Kalkulus Variasi Pendahuluan, Model Matematika, Keterkontrolan Toni Bakhtiar Departemen Matematika IPB Februari 2014 tbakhtiar@ipb.ac.id (IPB) MAT332 Kontrol Optimum Februari 2014 1 / 42 Outline Beberapa
Selanjutnya didefinisikan fungsional objektif yang diperbesar (augmented) J ( u ) sebagai:
 LAMPIRAN Lampiran 1. Bukti Teorema 4 Diketahui masalah memaksimumkan: T J ( x) = S( x( T), T) + f ( x( t), u( t), t) dt (1) dengan kendala : x() t = f( x(), t u(),) t t dt () Misalkan x() = x, t =, sedangkan
LAMPIRAN Lampiran 1. Bukti Teorema 4 Diketahui masalah memaksimumkan: T J ( x) = S( x( T), T) + f ( x( t), u( t), t) dt (1) dengan kendala : x() t = f( x(), t u(),) t t dt () Misalkan x() = x, t =, sedangkan
Kontrol Optimum. MKO dengan Horizon Takhingga, Syarat Cukup. Toni Bakhtiar. Departemen Matematika IPB. Februari 2014
 Kontrol Optimum MKO dengan Horizon Takhingga, Syarat Cukup Toni Bakhtiar Departemen Matematika IPB Februari 2014 tbakhtiar@ipb.ac.id (IPB) MAT332 Kontrol Optimum Februari 2014 1 / 23 Outline MKO dengan
Kontrol Optimum MKO dengan Horizon Takhingga, Syarat Cukup Toni Bakhtiar Departemen Matematika IPB Februari 2014 tbakhtiar@ipb.ac.id (IPB) MAT332 Kontrol Optimum Februari 2014 1 / 23 Outline MKO dengan
Kontrol Optimum. MKO dengan Kendala pada Peubah Kontrol. Toni Bakhtiar. Departemen Matematika IPB. Februari 2017
 Kontrol Optimum MKO dengan Kendala pada Peubah Kontrol Toni Bakhtiar Departemen Matematika IPB Februari 2017 tbakhtiar@ipb.ac.id (IPB) MAT332 Kontrol Optimum Februari 2017 1 / 53 Outline MKO berkendala
Kontrol Optimum MKO dengan Kendala pada Peubah Kontrol Toni Bakhtiar Departemen Matematika IPB Februari 2017 tbakhtiar@ipb.ac.id (IPB) MAT332 Kontrol Optimum Februari 2017 1 / 53 Outline MKO berkendala
III HASIL DAN PEMBAHASAN
 7 III HASIL DAN PEMBAHASAN 3.1 Perumusan Model Pada bagian ini akan dirumuskan model pertumbuhan ekonomi yang mengoptimalkan utilitas dari konsumen dengan asumsi: 1. Terdapat tiga sektor dalam perekonomian:
7 III HASIL DAN PEMBAHASAN 3.1 Perumusan Model Pada bagian ini akan dirumuskan model pertumbuhan ekonomi yang mengoptimalkan utilitas dari konsumen dengan asumsi: 1. Terdapat tiga sektor dalam perekonomian:
Kontrol Optimum. MKO dengan Mixed Constraints dan Pure State Constraints. Toni Bakhtiar. Departemen Matematika IPB. Februari 2014
 Kontrol Optimum MKO dengan Mixed Constraints dan Pure State Constraints Toni Bakhtiar Departemen Matematika IPB Februari 2014 tbakhtiar@ipb.ac.id (IPB) MAT332 Kontrol Optimum Februari 2014 1 / 38 Outline
Kontrol Optimum MKO dengan Mixed Constraints dan Pure State Constraints Toni Bakhtiar Departemen Matematika IPB Februari 2014 tbakhtiar@ipb.ac.id (IPB) MAT332 Kontrol Optimum Februari 2014 1 / 38 Outline
Teori kendali. Oleh: Ari suparwanto
 Teori kendali Oleh: Ari suparwanto Minggu Ke-1 Permasalahan oleh : Ari Suparwanto Permasalahan Diberikan sistem dan sinyal referensi. Masalah kendali adalah menentukan sinyal kendali sehingga output sistem
Teori kendali Oleh: Ari suparwanto Minggu Ke-1 Permasalahan oleh : Ari Suparwanto Permasalahan Diberikan sistem dan sinyal referensi. Masalah kendali adalah menentukan sinyal kendali sehingga output sistem
BAB II PENGANTAR SOLUSI PERSOALAN FISIKA MENURUT PENDEKATAN ANALITIK DAN NUMERIK
 BAB II PENGANTAR SOLUSI PERSOALAN FISIKA MENURUT PENDEKATAN ANALITIK DAN NUMERIK Tujuan Instruksional Setelah mempelajari bab ini pembaca diharapkan dapat: 1. Menjelaskan cara penyelesaian soal dengan
BAB II PENGANTAR SOLUSI PERSOALAN FISIKA MENURUT PENDEKATAN ANALITIK DAN NUMERIK Tujuan Instruksional Setelah mempelajari bab ini pembaca diharapkan dapat: 1. Menjelaskan cara penyelesaian soal dengan
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI Pada bab ini akan dijelaskan mengenai teori teori yang berhubungan dengan pembahasan ini sehingga dapat dijadikan sebagai landasan berpikir dan akan mempermudah dalam hal pembahasan
BAB 2 LANDASAN TEORI Pada bab ini akan dijelaskan mengenai teori teori yang berhubungan dengan pembahasan ini sehingga dapat dijadikan sebagai landasan berpikir dan akan mempermudah dalam hal pembahasan
Kontrol Optimal Waktu Diskrit
 Kontrol Optimal Waktu Diskrit April 2012 () Kontrol Optimal (3 SKS) April 2012 1 / 18 Ekstrim Suatu Fungsional untuk Fungsi Skalar Dalam bagian ini, kita akan menentukan syarat perlu untuk optimisasi fungsional
Kontrol Optimal Waktu Diskrit April 2012 () Kontrol Optimal (3 SKS) April 2012 1 / 18 Ekstrim Suatu Fungsional untuk Fungsi Skalar Dalam bagian ini, kita akan menentukan syarat perlu untuk optimisasi fungsional
PENERAPAN PRINSIP MAKSIMUM PONTRYAGIN PADA SISTEM INVENTORI-PRODUKSI. Nurus Sa adah, Toni Bakhtiar, Farida Hanum
 PENERAPAN PRINSIP MAKSIMUM PONTRYAGIN PADA SISTEM INVENTORI-PRODUKSI Nurus Sa adah, Toni Bakhtiar, Farida Hanum Departemen Matematika FMIPA, Institut Pertanian Bogor Jl. Meranti, Kampus IPB Darmaga, Bogor
PENERAPAN PRINSIP MAKSIMUM PONTRYAGIN PADA SISTEM INVENTORI-PRODUKSI Nurus Sa adah, Toni Bakhtiar, Farida Hanum Departemen Matematika FMIPA, Institut Pertanian Bogor Jl. Meranti, Kampus IPB Darmaga, Bogor
II LANDASAN TEORI. Contoh. Ditinjau dari sistem yang didefinisikan oleh:
 5 II LANDASAN TEORI 2.1 Keterkontrolan Untuk mengetahui persoalan sistem kontrol mungkin tidak ada, jika sistem yang ditinjau tidak terkontrol. Walaupun sebagian besar sistem terkontrol ada, akan tetapi
5 II LANDASAN TEORI 2.1 Keterkontrolan Untuk mengetahui persoalan sistem kontrol mungkin tidak ada, jika sistem yang ditinjau tidak terkontrol. Walaupun sebagian besar sistem terkontrol ada, akan tetapi
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI Berikut ini adalah beberapa definisi dan teorema yang menjadi landasan dalam penentuan harga premi, fungsi permintaan, dan kesetimbangannya pada portfolio heterogen. 2.1 Percobaan
BAB II LANDASAN TEORI Berikut ini adalah beberapa definisi dan teorema yang menjadi landasan dalam penentuan harga premi, fungsi permintaan, dan kesetimbangannya pada portfolio heterogen. 2.1 Percobaan
KENDALI OPTIMAL PERMAINAN NON-KOOPERATIF KONTINU SKALAR DUA PEMAIN DENGAN STRATEGI NASH TUGAS AKHIR. Oleh : M.LUTHFI RUSYDI
 KENDALI OPTIMAL PERMAINAN NON-KOOPERATIF KONTINU SKALAR DUA PEMAIN DENGAN STRATEGI NASH TUGAS AKHIR Diajukan Sebagai Salah Satu Syarat untuk Memperoleh Gelar Sarjana Sains Pada Jurusan Matematika Oleh
KENDALI OPTIMAL PERMAINAN NON-KOOPERATIF KONTINU SKALAR DUA PEMAIN DENGAN STRATEGI NASH TUGAS AKHIR Diajukan Sebagai Salah Satu Syarat untuk Memperoleh Gelar Sarjana Sains Pada Jurusan Matematika Oleh
III PEMBAHASAN. untuk setiap di dan untuk setiap, dengan. (Peressini et al. 1988)
 4 untuk setiap di dan untuk setiap (Peressini et al 1988) Definisi 22 Teorema Deret Taylor Nilai hampiran f di x untuk fungsi di a (atau sekitar a atau berpusat di a) didefinisikan (Stewart 1999) 24 Kontrol
4 untuk setiap di dan untuk setiap (Peressini et al 1988) Definisi 22 Teorema Deret Taylor Nilai hampiran f di x untuk fungsi di a (atau sekitar a atau berpusat di a) didefinisikan (Stewart 1999) 24 Kontrol
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI Pada bab ini akan dibahas beberapa pengertian dari optimasi bersyarat dengan kendala persamaan menggunakan multiplier lagrange serta penerapannya yang akan digunakan sebagai landasan
BAB 2 LANDASAN TEORI Pada bab ini akan dibahas beberapa pengertian dari optimasi bersyarat dengan kendala persamaan menggunakan multiplier lagrange serta penerapannya yang akan digunakan sebagai landasan
BAB 2 LANDASAN TEORI
 6 BAB LANDASAN TEORI Pada bab ini akan dibahas beberapa konsep dasar ang akan digunakan sebagai landasan berpikir seperti beberapa teorema dan definisi ang berkaitan dengan penelitian ini. Dengan begitu
6 BAB LANDASAN TEORI Pada bab ini akan dibahas beberapa konsep dasar ang akan digunakan sebagai landasan berpikir seperti beberapa teorema dan definisi ang berkaitan dengan penelitian ini. Dengan begitu
OPTIMASI (Pemrograman Non Linear)
 OPTIMASI (Pemrograman Non Linear) 3 SKS PILIHAN Arrival Rince Putri, 013 1 Silabus I. Pendahuluan 1. Perkuliahan: Silabus, Referensi, Penilaian. Pengantar Optimasi 3. Riview Differential Calculus II. Dasar-Dasar
OPTIMASI (Pemrograman Non Linear) 3 SKS PILIHAN Arrival Rince Putri, 013 1 Silabus I. Pendahuluan 1. Perkuliahan: Silabus, Referensi, Penilaian. Pengantar Optimasi 3. Riview Differential Calculus II. Dasar-Dasar
BAB II KAJIAN PUSTAKA. pemrograman nonlinear, fungsi konveks dan konkaf, pengali lagrange, dan
 BAB II KAJIAN PUSTAKA Kajian pustaka pada bab ini akan membahas tentang pengertian dan penjelasan yang berkaitan dengan fungsi, turunan parsial, pemrograman linear, pemrograman nonlinear, fungsi konveks
BAB II KAJIAN PUSTAKA Kajian pustaka pada bab ini akan membahas tentang pengertian dan penjelasan yang berkaitan dengan fungsi, turunan parsial, pemrograman linear, pemrograman nonlinear, fungsi konveks
BAB II KAJIAN PUSTAKA
 BAB II KAJIAN PUSTAKA A. Efektivitas Efektivitas berasal dari kata efektif, yang merupakan kata serapan dari bahasa Inggris yaitu effective yang artinya berhasil. Menurut kamus ilmiah popular, efektivitas
BAB II KAJIAN PUSTAKA A. Efektivitas Efektivitas berasal dari kata efektif, yang merupakan kata serapan dari bahasa Inggris yaitu effective yang artinya berhasil. Menurut kamus ilmiah popular, efektivitas
Persamaan Diferensial Biasa
 Persamaan Diferensial Biasa Pendahuluan, Persamaan Diferensial Orde-1 Toni Bakhtiar Departemen Matematika IPB September 2012 Toni Bakhtiar (m@thipb) PDB September 2012 1 / 37 Pendahuluan Konsep Dasar Beberapa
Persamaan Diferensial Biasa Pendahuluan, Persamaan Diferensial Orde-1 Toni Bakhtiar Departemen Matematika IPB September 2012 Toni Bakhtiar (m@thipb) PDB September 2012 1 / 37 Pendahuluan Konsep Dasar Beberapa
BAB I PENDAHULUAN. keadaan dari suatu sistem. Dalam aplikasinya, suatu sistem kontrol memiliki tujuan
 BAB I PENDAHULUAN 11 Latar Belakang Masalah Sistem kontrol merupakan suatu alat untuk mengendalikan dan mengatur keadaan dari suatu sistem Dalam aplikasinya, suatu sistem kontrol memiliki tujuan atau sasaran
BAB I PENDAHULUAN 11 Latar Belakang Masalah Sistem kontrol merupakan suatu alat untuk mengendalikan dan mengatur keadaan dari suatu sistem Dalam aplikasinya, suatu sistem kontrol memiliki tujuan atau sasaran
BAB 2 TINJAUAN PUSTAKA. ini sehingga dapat dijadikan sebagai landasan berpikir dan akan mempermudah. dalam hal pembahasan hasil utama berikutnya.
 BAB 2 TINJAUAN PUSTAKA Pada bab ini akan dijelaskan mengenai teori-teori yang berhubungan dengan pembahasan ini sehingga dapat dijadikan sebagai landasan berpikir dan akan mempermudah dalam hal pembahasan
BAB 2 TINJAUAN PUSTAKA Pada bab ini akan dijelaskan mengenai teori-teori yang berhubungan dengan pembahasan ini sehingga dapat dijadikan sebagai landasan berpikir dan akan mempermudah dalam hal pembahasan
BAB II KAJIAN PUSTAKA. Pada bab ini akan diberikan landasan teori tentang optimasi, fungsi, turunan,
 BAB II KAJIAN PUSTAKA Pada bab ini akan diberikan landasan teori tentang optimasi, fungsi, turunan, pemrograman linear, metode simpleks, teorema dualitas, pemrograman nonlinear, persyaratan karush kuhn
BAB II KAJIAN PUSTAKA Pada bab ini akan diberikan landasan teori tentang optimasi, fungsi, turunan, pemrograman linear, metode simpleks, teorema dualitas, pemrograman nonlinear, persyaratan karush kuhn
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI 2.1 Aljabar Linear Definisi 2.1.1 Matriks Matriks A adalah susunan persegi panjang yang terdiri dari skalar-skalar yang biasanya dinyatakan dalam bentuk berikut: [ ] Definisi 2.1.2
BAB II LANDASAN TEORI 2.1 Aljabar Linear Definisi 2.1.1 Matriks Matriks A adalah susunan persegi panjang yang terdiri dari skalar-skalar yang biasanya dinyatakan dalam bentuk berikut: [ ] Definisi 2.1.2
Outline. Bagian 0: Motivasi. Bagian 1: Optimasi Taklinier Dasar dasar Teorema Karush Kuhn Tucker. Bagian 2: Sequential Quadratic Programming
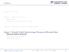 Outline Bagian 0: Motivasi Bagian 1: Optimasi Taklinier Dasar dasar Teorema Karush Kuhn Tucker Bagian 2: Sequential Quadratic Programming Bagian 3: Masalah Kendali Optimal dengan Persamaan Di erensial
Outline Bagian 0: Motivasi Bagian 1: Optimasi Taklinier Dasar dasar Teorema Karush Kuhn Tucker Bagian 2: Sequential Quadratic Programming Bagian 3: Masalah Kendali Optimal dengan Persamaan Di erensial
Integral Tak Tentu. Modul 1 PENDAHULUAN
 Modul 1 Integral Tak Tentu M PENDAHULUAN Drs. Hidayat Sardi, M.Si odul ini akan membahas operasi balikan dari penurunan (pendiferensialan) yang disebut anti turunan (antipendiferensialan). Dengan mengikuti
Modul 1 Integral Tak Tentu M PENDAHULUAN Drs. Hidayat Sardi, M.Si odul ini akan membahas operasi balikan dari penurunan (pendiferensialan) yang disebut anti turunan (antipendiferensialan). Dengan mengikuti
BAB II TINJAUAN PUSTAKA. kestabilan model predator-prey tipe Holling II dengan faktor pemanenan.
 BAB II TINJAUAN PUSTAKA Dalam bab ini akan dibahas mengenai dasar teori untuk menganalisis simulasi kestabilan model predator-prey tipe Holling II dengan faktor pemanenan. 2.1 Persamaan Diferensial Biasa
BAB II TINJAUAN PUSTAKA Dalam bab ini akan dibahas mengenai dasar teori untuk menganalisis simulasi kestabilan model predator-prey tipe Holling II dengan faktor pemanenan. 2.1 Persamaan Diferensial Biasa
I. PENDAHULUAN II. LANDASAN TEORI
 1 I PENDAHULUAN 11 Latar Belakang Perusahaan merupakan salah satu bagian penting dari sektor perekonomian suatu negara Apabila kondisi perekonomian suatu negara sedang membaik dan diikuti dengan perkembangan
1 I PENDAHULUAN 11 Latar Belakang Perusahaan merupakan salah satu bagian penting dari sektor perekonomian suatu negara Apabila kondisi perekonomian suatu negara sedang membaik dan diikuti dengan perkembangan
Bab II Teori Pendukung
 Bab II Teori Pendukung II.1 Sistem Autonomous Tinjau sistem persamaan differensial berikut, = dy = f(x, y), g(x, y), (2.1) dengan asumsi f dan g adalah fungsi kontinu yang mempunyai turunan yang kontinu
Bab II Teori Pendukung II.1 Sistem Autonomous Tinjau sistem persamaan differensial berikut, = dy = f(x, y), g(x, y), (2.1) dengan asumsi f dan g adalah fungsi kontinu yang mempunyai turunan yang kontinu
PENERAPAN TEORI KENDALI PADA MASALAH PROGRAM DINAMIK
 PENERAPAN TEORI KENDALI PADA MASALAH PROGRAM DINAMIK Pardi Affandi, Dewi A, Nur Salam Program Studi Matematika Universitas Lambung Mangkurat Jl Jend A Yani km 35, 8 Banjarbaru Email: pardi_affandi@yahoocom
PENERAPAN TEORI KENDALI PADA MASALAH PROGRAM DINAMIK Pardi Affandi, Dewi A, Nur Salam Program Studi Matematika Universitas Lambung Mangkurat Jl Jend A Yani km 35, 8 Banjarbaru Email: pardi_affandi@yahoocom
BAB II LANDASAN TEORI. selanjutnya sebagai bahan acuan yang mendukung tujuan penulisan. Materi-materi
 BAB II LANDASAN TEORI Pada bab ini akan dibahas tentang landasan teori yang digunakan pada bab selanjutnya sebagai bahan acuan yang mendukung tujuan penulisan. Materi-materi yang diuraikan berupa definisi-definisi
BAB II LANDASAN TEORI Pada bab ini akan dibahas tentang landasan teori yang digunakan pada bab selanjutnya sebagai bahan acuan yang mendukung tujuan penulisan. Materi-materi yang diuraikan berupa definisi-definisi
BAB 2 PROGRAM LINIER DAN TAK LINIER. Program linier (Linear programming) adalah suatu masalah matematika
 BAB 2 PROGRAM LINIER DAN TAK LINIER 2.1 Program Linier Program linier (Linear programming) adalah suatu masalah matematika yang mempunyai fungsi objektif dan kendala berbentuk linier untuk meminimalkan
BAB 2 PROGRAM LINIER DAN TAK LINIER 2.1 Program Linier Program linier (Linear programming) adalah suatu masalah matematika yang mempunyai fungsi objektif dan kendala berbentuk linier untuk meminimalkan
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI 2.1 Pemrograman Non Linier Pemrograman Non linier merupakan pemrograman dengan fungsi tujuannya saja atau bersama dengan fungsi kendala berbentuk non linier yaitu pangkat dari variabelnya
BAB 2 LANDASAN TEORI 2.1 Pemrograman Non Linier Pemrograman Non linier merupakan pemrograman dengan fungsi tujuannya saja atau bersama dengan fungsi kendala berbentuk non linier yaitu pangkat dari variabelnya
Modifikasi Kontrol untuk Sistem Tak Linier Input Tunggal-Output Tunggal
 Vol 7, No2, 118-123, Januari 2011 Modifikasi Kontrol untuk Sistem Tak Linier Input Tunggal-Output Tunggal Abstrak Dalam tulisan ini diuraikan sebuah kontrol umpan balik dinamik Dari kontrol yang diperoleh
Vol 7, No2, 118-123, Januari 2011 Modifikasi Kontrol untuk Sistem Tak Linier Input Tunggal-Output Tunggal Abstrak Dalam tulisan ini diuraikan sebuah kontrol umpan balik dinamik Dari kontrol yang diperoleh
BAB I DASAR-DASAR PEMODELAN MATEMATIKA DENGAN PERSAMAAN DIFERENSIAL
 BAB I DASAR-DASAR PEMODELAN MATEMATIKA DENGAN PERSAMAAN DIFERENSIAL Pendahuluan Persamaan diferensial adalah persamaan yang memuat diferensial Kita akan membahas tentang Persamaan Diferensial Biasa yaitu
BAB I DASAR-DASAR PEMODELAN MATEMATIKA DENGAN PERSAMAAN DIFERENSIAL Pendahuluan Persamaan diferensial adalah persamaan yang memuat diferensial Kita akan membahas tentang Persamaan Diferensial Biasa yaitu
BAB II TINJAUAN PUSTAKA
 BAB II TINJAUAN PUSTAKA 2.1 Transformasi Laplace Salah satu cara untuk menganalisis gejala peralihan (transien) adalah menggunakan transformasi Laplace, yaitu pengubahan suatu fungsi waktu f(t) menjadi
BAB II TINJAUAN PUSTAKA 2.1 Transformasi Laplace Salah satu cara untuk menganalisis gejala peralihan (transien) adalah menggunakan transformasi Laplace, yaitu pengubahan suatu fungsi waktu f(t) menjadi
Pertemuan Minggu ke Bidang Singgung, Hampiran 2. Maksimum dan Minimum 3. Metode Lagrange
 Pertemuan Minggu ke-11 1. Bidang Singgung, Hampiran 2. Maksimum dan Minimum 3. Metode Lagrange 1. BIDANG SINGGUNG, HAMPIRAN Tujuan mempelajari: memperoleh persamaan bidang singgung terhadap permukaan z
Pertemuan Minggu ke-11 1. Bidang Singgung, Hampiran 2. Maksimum dan Minimum 3. Metode Lagrange 1. BIDANG SINGGUNG, HAMPIRAN Tujuan mempelajari: memperoleh persamaan bidang singgung terhadap permukaan z
BAB 2 LANDASAN TEORI. 2.1 Program Dinamik
 5 BAB 2 LANDASAN TEORI 2.1 Program Dinamik Pemrograman dinamik adalah suatu teknik matematis yang biasanya digunakan untuk membuat suatu keputusan dari serangkaian keputusan yang saling berkaitan. Pemrograman
5 BAB 2 LANDASAN TEORI 2.1 Program Dinamik Pemrograman dinamik adalah suatu teknik matematis yang biasanya digunakan untuk membuat suatu keputusan dari serangkaian keputusan yang saling berkaitan. Pemrograman
BAB 2 TINJAUAN PUSTAKA
 BAB 2 TINJAUAN PUSTAKA 2.1 Optimasi Non-Linier Suatu permasalahan optimasi disebut nonlinier jika fungsi tujuan dan kendalanya mempunyai bentuk nonlinier pada salah satu atau keduanya. Optimasi nonlinier
BAB 2 TINJAUAN PUSTAKA 2.1 Optimasi Non-Linier Suatu permasalahan optimasi disebut nonlinier jika fungsi tujuan dan kendalanya mempunyai bentuk nonlinier pada salah satu atau keduanya. Optimasi nonlinier
BAB II LANDASAN TEORI. dalam penulisan skripsi ini. Teori-teori yang digunakan berupa definisi-definisi serta
 BAB II LANDASAN TEORI Pada bab ini akan diuraikan beberapa teori-teori yang digunakan sebagai acuan dalam penulisan skripsi ini. Teori-teori yang digunakan berupa definisi-definisi serta teorema-teorema
BAB II LANDASAN TEORI Pada bab ini akan diuraikan beberapa teori-teori yang digunakan sebagai acuan dalam penulisan skripsi ini. Teori-teori yang digunakan berupa definisi-definisi serta teorema-teorema
TE Sistem Linier. Sistem Waktu Kontinu
 TE 226 - Sistem Linier Jimmy Hasugian Electrical Engineering - Maranatha Christian University jimlecture@gmail.com - http://wp.me/p4scve-g Sistem Waktu Kontinu Jimmy Hasugian (MCU) Sistem Waktu Kontinu
TE 226 - Sistem Linier Jimmy Hasugian Electrical Engineering - Maranatha Christian University jimlecture@gmail.com - http://wp.me/p4scve-g Sistem Waktu Kontinu Jimmy Hasugian (MCU) Sistem Waktu Kontinu
SILABUS MATA KULIAH. Tujuan
 SILABUS MATA KULIAH NAMA MATAKULIAH KODE MATAKULIAH KREDIT/SKS SEMESTER DESKRIPSI TUJUAN UMUM PERKULIAHAN Matematika Ekonomi EKO 500 3 (3-0) 1 Kuliah ini terdiri dari tiga bagian pokok, yakni aljabar matriks,
SILABUS MATA KULIAH NAMA MATAKULIAH KODE MATAKULIAH KREDIT/SKS SEMESTER DESKRIPSI TUJUAN UMUM PERKULIAHAN Matematika Ekonomi EKO 500 3 (3-0) 1 Kuliah ini terdiri dari tiga bagian pokok, yakni aljabar matriks,
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI 2.1 Pemrograman Non linier Pemrograman non linier adalah suatu bentuk pemrograman yang berhubungan dengan suatu perencanaan aktivitas tertentu yang dapat diformulasikan dalam model
BAB 2 LANDASAN TEORI 2.1 Pemrograman Non linier Pemrograman non linier adalah suatu bentuk pemrograman yang berhubungan dengan suatu perencanaan aktivitas tertentu yang dapat diformulasikan dalam model
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI. Sistem Pendulum Terbalik Dalam penelitian ini diperhatikan sistem pendulum terbalik seperti pada Gambar di mana sebuah pendulum terbalik dimuat dalam motor yang bisa digerakkan.
BAB II LANDASAN TEORI. Sistem Pendulum Terbalik Dalam penelitian ini diperhatikan sistem pendulum terbalik seperti pada Gambar di mana sebuah pendulum terbalik dimuat dalam motor yang bisa digerakkan.
Catatan Kuliah MA1123 Kalkulus Elementer I
 Catatan Kuliah MA1123 Kalkulus Elementer I Oleh Hendra Gunawan, Ph.D. Departemen Matematika ITB Sasaran Belajar Setelah mempelajari materi Kalkulus Elementer I, mahasiswa diharapkan memiliki (terutama):
Catatan Kuliah MA1123 Kalkulus Elementer I Oleh Hendra Gunawan, Ph.D. Departemen Matematika ITB Sasaran Belajar Setelah mempelajari materi Kalkulus Elementer I, mahasiswa diharapkan memiliki (terutama):
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI 2.1 Arti dan Peranan Persediaan Merujuk pada penjelasan Herjanto (1999), persediaan dapat diartikan sebagai bahan atau barang yang disimpan yang akan digunakan untuk memenuhi tujuan
BAB 2 LANDASAN TEORI 2.1 Arti dan Peranan Persediaan Merujuk pada penjelasan Herjanto (1999), persediaan dapat diartikan sebagai bahan atau barang yang disimpan yang akan digunakan untuk memenuhi tujuan
BAB III APLIKASI METODE EULER PADA KAJIAN TENTANG GERAK Tujuan Instruksional Setelah mempelajari bab ini pembaca diharapkan dapat: 1.
 BAB III APLIKASI METODE EULER PADA KAJIAN TENTANG GERAK Tujuan Instruksional Setelah mempelajari bab ini pembaca diharapkan dapat: 1. Menentukan solusi persamaan gerak jatuh bebas berdasarkan pendekatan
BAB III APLIKASI METODE EULER PADA KAJIAN TENTANG GERAK Tujuan Instruksional Setelah mempelajari bab ini pembaca diharapkan dapat: 1. Menentukan solusi persamaan gerak jatuh bebas berdasarkan pendekatan
II LANDASAN TEORI 2.1 Sistem Persamaan Diferensial Definisi 1 [Sistem Persamaan Diferensial Linear (SPDL)]
![II LANDASAN TEORI 2.1 Sistem Persamaan Diferensial Definisi 1 [Sistem Persamaan Diferensial Linear (SPDL)] II LANDASAN TEORI 2.1 Sistem Persamaan Diferensial Definisi 1 [Sistem Persamaan Diferensial Linear (SPDL)]](/thumbs/63/48871975.jpg) II LANDASAN TEORI 2.1 Sistem Persamaan Diferensial Definisi 1 [Sistem Persamaan Diferensial Linear (SPDL)] Suatu sistem persamaan diferensial dinyatakan sebagai berikut: A adalah matriks koefisien konstan
II LANDASAN TEORI 2.1 Sistem Persamaan Diferensial Definisi 1 [Sistem Persamaan Diferensial Linear (SPDL)] Suatu sistem persamaan diferensial dinyatakan sebagai berikut: A adalah matriks koefisien konstan
BAB II TINJAUAN PUSTAKA. operasi yang mampu menyelesaikan masalah optimasi sejak diperkenalkan di
 BAB II TINJAUAN PUSTAKA 2.1 Pemrograman Linier (Linear Programming) Pemrograman linier (linear programming) merupakan salah satu teknik riset operasi yang mampu menyelesaikan masalah optimasi sejak diperkenalkan
BAB II TINJAUAN PUSTAKA 2.1 Pemrograman Linier (Linear Programming) Pemrograman linier (linear programming) merupakan salah satu teknik riset operasi yang mampu menyelesaikan masalah optimasi sejak diperkenalkan
BAB 2 PDB Linier Order Satu 2
 BAB Konsep Dasar BAB 2 PDB Linier Order Satu 2 BAB 3 Aplikasi PDB Order Satu 3 BAB 4 PDB Linier Order Dua 4 BAB 5 Aplikasi PDB Order Dua 5 BAB 6 Sistem PDB 6 BAB 7 PDB Nonlinier dan Kesetimbangan Dalam
BAB Konsep Dasar BAB 2 PDB Linier Order Satu 2 BAB 3 Aplikasi PDB Order Satu 3 BAB 4 PDB Linier Order Dua 4 BAB 5 Aplikasi PDB Order Dua 5 BAB 6 Sistem PDB 6 BAB 7 PDB Nonlinier dan Kesetimbangan Dalam
BAB II LANDASAN TEORI. Pada Bab Landasan Teori ini akan dibahas mengenai definisi-definisi, dan
 BAB II LANDASAN TEORI Pada Bab Landasan Teori ini akan dibahas mengenai definisi-definisi, dan teorema-teorema yang akan menjadi landasan untuk pembahasan pada Bab III nanti, diantaranya: fungsi komposisi,
BAB II LANDASAN TEORI Pada Bab Landasan Teori ini akan dibahas mengenai definisi-definisi, dan teorema-teorema yang akan menjadi landasan untuk pembahasan pada Bab III nanti, diantaranya: fungsi komposisi,
Bab 2 LANDASAN TEORI. 2.1 Pengantar Proses Stokastik
 Bab 2 LANDASAN TEORI Pada bab ini akan diberikan penjelasan singkat mengenai pengantar proses stokastik dan rantai Markov, yang akan digunakan untuk analisis pada bab-bab selanjutnya. 2.1 Pengantar Proses
Bab 2 LANDASAN TEORI Pada bab ini akan diberikan penjelasan singkat mengenai pengantar proses stokastik dan rantai Markov, yang akan digunakan untuk analisis pada bab-bab selanjutnya. 2.1 Pengantar Proses
PENDEKATAN KALKULUS VARIASIONAL PADA SISTEM KONTROL DAYA DORONG ROKET. Niken Madu Meta Jurusan Matematika, FMIPA UNS
 1 PENDEKATAN KALKULUS VARIASIONAL PADA SISTEM KONTROL DAYA DORONG ROKET Niken Madu Meta Jurusan Matematika, FMIPA UNS Abstrak. Kalkulus variasional adalah cabang dari kalkulus diferensial yang digunakan
1 PENDEKATAN KALKULUS VARIASIONAL PADA SISTEM KONTROL DAYA DORONG ROKET Niken Madu Meta Jurusan Matematika, FMIPA UNS Abstrak. Kalkulus variasional adalah cabang dari kalkulus diferensial yang digunakan
III RELAKSASI LAGRANGE
 III RELAKSASI LAGRANGE Relaksasi Lagrange merupakan salah satu metode yang terus dikembangkan dalam aplikasi pemrograman matematik. Sebagian besar konsep teoretis dari banyak aplikasi menggunakan metode
III RELAKSASI LAGRANGE Relaksasi Lagrange merupakan salah satu metode yang terus dikembangkan dalam aplikasi pemrograman matematik. Sebagian besar konsep teoretis dari banyak aplikasi menggunakan metode
Analisis Komponen Utama (Principal component analysis)
 Analisis Komponen Utama (Principal component analysis) A. LANDASAN TEORI Misalkan χ merupakan matriks berukuran nxp, dengan baris-baris yang berisi observasi sebanyak n dari p-variat variabel acak X. Analisis
Analisis Komponen Utama (Principal component analysis) A. LANDASAN TEORI Misalkan χ merupakan matriks berukuran nxp, dengan baris-baris yang berisi observasi sebanyak n dari p-variat variabel acak X. Analisis
PENGANTAR KALKULUS PEUBAH BANYAK. 1. Pengertian Vektor pada Bidang Datar
 PENGANTAR KALKULUS PEUBAH BANYAK ERIDANI 1. Pengertian Vektor pada Bidang Datar Misalkan R menyatakan sistem bilangan real, yaitu himpunan bilangan real yang dilengkapi dengan empat operasi baku (tambah,
PENGANTAR KALKULUS PEUBAH BANYAK ERIDANI 1. Pengertian Vektor pada Bidang Datar Misalkan R menyatakan sistem bilangan real, yaitu himpunan bilangan real yang dilengkapi dengan empat operasi baku (tambah,
Invers Transformasi Laplace
 Invers Transformasi Laplace Transformasi Laplace Domain Waktu Invers Transformasi Laplace Domain Frekuensi Jika mengubah sinyal analog kontinyu dari domain waktu menjadi domain frekuensi menggunakan transformasi
Invers Transformasi Laplace Transformasi Laplace Domain Waktu Invers Transformasi Laplace Domain Frekuensi Jika mengubah sinyal analog kontinyu dari domain waktu menjadi domain frekuensi menggunakan transformasi
BAB 2 TINJAUAN PUSTAKA
 BAB TINJAUAN PUSTAKA.1 Model Aliran Dua-Fase Nonekulibrium pada Media Berpori Penelitian ini merupakan kajian ulang terhadap penelitian yang telah dilakukan oleh Juanes (008), dalam tulisannya yang berjudul
BAB TINJAUAN PUSTAKA.1 Model Aliran Dua-Fase Nonekulibrium pada Media Berpori Penelitian ini merupakan kajian ulang terhadap penelitian yang telah dilakukan oleh Juanes (008), dalam tulisannya yang berjudul
I. Sistem Persamaan Diferensial Linier Orde 1 (Review)
 I. Sistem Persamaan Diferensial Linier Orde (Review) November 0 () I. Sistem Persamaan Diferensial Linier Orde (Review) November 0 / 6 Teori Umum Bentuk umum sistem persamaan diferensial linier orde satu
I. Sistem Persamaan Diferensial Linier Orde (Review) November 0 () I. Sistem Persamaan Diferensial Linier Orde (Review) November 0 / 6 Teori Umum Bentuk umum sistem persamaan diferensial linier orde satu
Model Matematika dari Sistem Dinamis
 Model Matematika dari Sistem Dinamis September 2012 () Model Matematika dari Sistem Dinamis September 2012 1 / 60 Pendahuluan Untuk analisis dan desain sistem kontrol, sistem sis harus dibuat model sisnya.
Model Matematika dari Sistem Dinamis September 2012 () Model Matematika dari Sistem Dinamis September 2012 1 / 60 Pendahuluan Untuk analisis dan desain sistem kontrol, sistem sis harus dibuat model sisnya.
APLIKASI FUNGSI LINIER DALAM BIDANG EKONOMI FUNGSI PERMINTAAN & PENAWARAN. Oleh : Agus Arwani, SE, M.Ag.
 APLIKASI FUNGSI LINIER DALAM BIDANG EKONOMI FUNGSI PERMINTAAN & PENAWARAN Oleh : Agus Arwani, SE, M.Ag. FUNGSI PERMINTAAN Q dx,t = ƒ (P x,t, P y,t, Y t, P e X,t+1,S t ) Dimana Q dx,t = Jumlah produk X
APLIKASI FUNGSI LINIER DALAM BIDANG EKONOMI FUNGSI PERMINTAAN & PENAWARAN Oleh : Agus Arwani, SE, M.Ag. FUNGSI PERMINTAAN Q dx,t = ƒ (P x,t, P y,t, Y t, P e X,t+1,S t ) Dimana Q dx,t = Jumlah produk X
SYARAT FRITZ JOHN PADA MASALAH OPTIMASI BERKENDALA KETAKSAMAAN. Caturiyati 1 Himmawati Puji Lestari 2. Abstrak
 Syarat Fritz John... (Caturiyati) SYARAT FRITZ JOHN PADA MASALAH OPTIMASI BERKENDALA KETAKSAMAAN Caturiyati 1 Himmawati Puji Lestari 2 1,2 Jurusan Pendidikan Matematika FMIPA UNY 1 wcaturiyati@yahoo.com
Syarat Fritz John... (Caturiyati) SYARAT FRITZ JOHN PADA MASALAH OPTIMASI BERKENDALA KETAKSAMAAN Caturiyati 1 Himmawati Puji Lestari 2 1,2 Jurusan Pendidikan Matematika FMIPA UNY 1 wcaturiyati@yahoo.com
BAB III TURUNAN DALAM RUANG DIMENSI-n
 BAB III TURUNAN DALAM RUANG DIMENSI-n 1. FUNGSI DUA PEUBAH ATAU LEBIH fungsi bernilai riil dari peubah riil, fungsi bernilai vektor dari peubah riil Fungsi bernilai riil dari dua peubah riil yakni, fungsi
BAB III TURUNAN DALAM RUANG DIMENSI-n 1. FUNGSI DUA PEUBAH ATAU LEBIH fungsi bernilai riil dari peubah riil, fungsi bernilai vektor dari peubah riil Fungsi bernilai riil dari dua peubah riil yakni, fungsi
BAB 2 TINJAUAN PUSTAKA
 BAB 2 TINJAUAN PUSTAKA Pada bab ini dibahas mengenai tinjauan pustaka yang digunakan dalam penelitian ini, khususnya yang diperlukan dalam Bab 3. Teori yang dibahas adalah teori yang mendukung pembentukan
BAB 2 TINJAUAN PUSTAKA Pada bab ini dibahas mengenai tinjauan pustaka yang digunakan dalam penelitian ini, khususnya yang diperlukan dalam Bab 3. Teori yang dibahas adalah teori yang mendukung pembentukan
PENGGUNAAN PENYELESAIAN PERSAMAAN ALJABAR RICCATI WAKTU DISKRIT PADA KENDALI OPTIMAL LINIER KUADRATIK
 J. Math. and Its Appl. ISSN: 1829-605X Vol. 12, No. 1, Mei 2015, 23 33 PENGGUNAAN PENYELESAIAN PERSAMAAN ALJABAR RICCATI WAKTU DISKRIT PADA KENDALI OPTIMAL LINIER KUADRATIK Dita Marsa Yuanita 1, Soleha
J. Math. and Its Appl. ISSN: 1829-605X Vol. 12, No. 1, Mei 2015, 23 33 PENGGUNAAN PENYELESAIAN PERSAMAAN ALJABAR RICCATI WAKTU DISKRIT PADA KENDALI OPTIMAL LINIER KUADRATIK Dita Marsa Yuanita 1, Soleha
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI Pada bab II ini dibahas teori-teori pendukung yang digunakan untuk pembahasan selanjutnya yaitu tentang Persamaan Nonlinier, Metode Newton, Aturan Trapesium, Rata-rata Aritmatik dan
BAB II LANDASAN TEORI Pada bab II ini dibahas teori-teori pendukung yang digunakan untuk pembahasan selanjutnya yaitu tentang Persamaan Nonlinier, Metode Newton, Aturan Trapesium, Rata-rata Aritmatik dan
PENGENDALIAN OPTIMAL DISTRIBUSI VAKSIN PADA MODEL EPIDEMIK RABIES DENGAN MASA KELAHIRAN PERIODIK
 PENDAHULUAN PENGENDALIAN OPTIMAL DISTRIBUSI VAKSIN PADA MODEL EPIDEMIK RABIES DENGAN MASA KELAHIRAN PERIODIK Oleh : Qurrotu Ainy Jufri (1210100072) Dosen Pembimbing : Drs. Kamiran, M.Si. Jurusan Matematika
PENDAHULUAN PENGENDALIAN OPTIMAL DISTRIBUSI VAKSIN PADA MODEL EPIDEMIK RABIES DENGAN MASA KELAHIRAN PERIODIK Oleh : Qurrotu Ainy Jufri (1210100072) Dosen Pembimbing : Drs. Kamiran, M.Si. Jurusan Matematika
Persamaan Diferensial Biasa
 Persamaan Diferensial Biasa Titik Tetap dan Sistem Linear Toni Bakhtiar Departemen Matematika IPB Oktober 2012 Toni Bakhtiar (m@thipb) PDB Oktober 2012 1 / 31 Titik Tetap SPD Mandiri dan Titik Tetap Tinjau
Persamaan Diferensial Biasa Titik Tetap dan Sistem Linear Toni Bakhtiar Departemen Matematika IPB Oktober 2012 Toni Bakhtiar (m@thipb) PDB Oktober 2012 1 / 31 Titik Tetap SPD Mandiri dan Titik Tetap Tinjau
Bab 2 LANDASAN TEORI
 17 Bab 2 LANDASAN TEORI 2.1 Aljabar Matriks 2.1.1 Definisi Matriks Matriks adalah suatu kumpulan angka-angka yang juga sering disebut elemen-elemen yang disusun secara teratur menurut baris dan kolom sehingga
17 Bab 2 LANDASAN TEORI 2.1 Aljabar Matriks 2.1.1 Definisi Matriks Matriks adalah suatu kumpulan angka-angka yang juga sering disebut elemen-elemen yang disusun secara teratur menurut baris dan kolom sehingga
MODUL MATEMATIKA XI IPA SUKU BANYAK SMA SANTA ANGELA TAHUN PELAJARAN SEMSTER GENAP
 MODUL MATEMATIKA XI IPA SUKU BANYAK SMA SANTA ANGELA TAHUN PELAJARAN 05 06 SEMSTER GENAP STANDAR KOMPETENSI 4. Menggunakan aturan sukubanyak dalam penyelesaian masalah. KOMPETENSI DASAR 4. Menggunakan
MODUL MATEMATIKA XI IPA SUKU BANYAK SMA SANTA ANGELA TAHUN PELAJARAN 05 06 SEMSTER GENAP STANDAR KOMPETENSI 4. Menggunakan aturan sukubanyak dalam penyelesaian masalah. KOMPETENSI DASAR 4. Menggunakan
Metode Simpleks (Simplex Method) Materi Bahasan
 Metode Simpleks (Simplex Method) Kuliah 03 TI2231 Penelitian Operasional I 1 Materi Bahasan 1 Rumusan Pemrograman linier dalam bentuk baku 2 Pemecahan sistem persamaan linier 3 Prinsip-prinsip metode simpleks
Metode Simpleks (Simplex Method) Kuliah 03 TI2231 Penelitian Operasional I 1 Materi Bahasan 1 Rumusan Pemrograman linier dalam bentuk baku 2 Pemecahan sistem persamaan linier 3 Prinsip-prinsip metode simpleks
a. untuk (n+1) genap: terjadi ekstrem, dan jika (ii) f (x ) > 0, maka f(x) mencapai minimum di titik x.
 Lecture I: Introduction A. Masalah Optimisasi Dalam kehidupan sehari-hari, manusia cenderung untuk berprinsip ekonomi, yaitu dengan sumber daya terbatas dapat memperoleh hasil sebanyak-banyaknya. Banyak
Lecture I: Introduction A. Masalah Optimisasi Dalam kehidupan sehari-hari, manusia cenderung untuk berprinsip ekonomi, yaitu dengan sumber daya terbatas dapat memperoleh hasil sebanyak-banyaknya. Banyak
METODE PSEUDO ARC-LENGTH DAN PENERAPANNYA PADA PENYELESAIAN SISTEM PERSAMAAN NONLINIER TERPARAMETERISASI
 Jurnal Matematika UNAND Vol. 5 No. 4 Hal. 9 17 ISSN : 233 291 c Jurusan Matematika FMIPA UNAND METODE PSEUDO ARC-LENGTH DAN PENERAPANNYA PADA PENYELESAIAN SISTEM PERSAMAAN NONLINIER TERPARAMETERISASI RAHIMA
Jurnal Matematika UNAND Vol. 5 No. 4 Hal. 9 17 ISSN : 233 291 c Jurusan Matematika FMIPA UNAND METODE PSEUDO ARC-LENGTH DAN PENERAPANNYA PADA PENYELESAIAN SISTEM PERSAMAAN NONLINIER TERPARAMETERISASI RAHIMA
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI 2.1 Latar Belakang Historis Fondasi dari integral pertama kali dideklarasikan oleh Cavalieri, seorang ahli matematika berkebangsaan Italia pada tahun 1635. Cavalieri menemukan bahwa
BAB II LANDASAN TEORI 2.1 Latar Belakang Historis Fondasi dari integral pertama kali dideklarasikan oleh Cavalieri, seorang ahli matematika berkebangsaan Italia pada tahun 1635. Cavalieri menemukan bahwa
PENGGUNAAN METODE DEKOMPOSISI ADOMIAN UNTUK MENYELESAIKAN PERMASALAHAN PADA KALKULUS VARIASI ABSTRACT
 PENGGUNAAN METODE DEKOMPOSISI ADOMIAN UNTUK MENYELESAIKAN PERMASALAHAN PADA KALKULUS VARIASI Febrian Lisnan, Asmara Karma 2 Mahasiswa Program Studi S Matematika 2 Dosen Jurusan Matematika Fakultas Matematika
PENGGUNAAN METODE DEKOMPOSISI ADOMIAN UNTUK MENYELESAIKAN PERMASALAHAN PADA KALKULUS VARIASI Febrian Lisnan, Asmara Karma 2 Mahasiswa Program Studi S Matematika 2 Dosen Jurusan Matematika Fakultas Matematika
Ilustrasi Persoalan Matematika
 Pendahuluan Persoalan yang melibatkan model matematika banyak muncul dalam berbagai disiplin ilmu pengetahuan, seperti dalam bidang fisika, kimia, ekonomi, atau pada persoalan rekayasa (engineering), seperti
Pendahuluan Persoalan yang melibatkan model matematika banyak muncul dalam berbagai disiplin ilmu pengetahuan, seperti dalam bidang fisika, kimia, ekonomi, atau pada persoalan rekayasa (engineering), seperti
BAB II LANDASAN TEORI. eigen dan vektor eigen, persamaan diferensial, sistem persamaan diferensial, titik
 BAB II LANDASAN TEORI Pada bab ini, akan dijelaskan landasan teori yang akan digunakan dalam bab selanjutnya sebagai bahan acuan yang mendukung dan memperkuat tujuan penelitian. Landasan teori yang dimaksud
BAB II LANDASAN TEORI Pada bab ini, akan dijelaskan landasan teori yang akan digunakan dalam bab selanjutnya sebagai bahan acuan yang mendukung dan memperkuat tujuan penelitian. Landasan teori yang dimaksud
BAB 2 OPTIMISASI KOMBINATORIAL. Masalah optimisasi merupakan suatu proses pencarian varibel bebas yang
 BAB 2 OPTIMISASI KOMBINATORIAL 2.1 Masalah Model Optimisasi Kombinatorial Masalah optimisasi merupakan suatu proses pencarian varibel bebas yang memenuhi kondisi atau batasan yang disebut kendala dari
BAB 2 OPTIMISASI KOMBINATORIAL 2.1 Masalah Model Optimisasi Kombinatorial Masalah optimisasi merupakan suatu proses pencarian varibel bebas yang memenuhi kondisi atau batasan yang disebut kendala dari
BAB 1 PENDAHULUAN. Kalkulus merupakan salah satu prestasi tertinggi dari kecerdasan manusia.
 BAB 1 PENDAHULUAN 1.1 Latar Belakang Kalkulus merupakan salah satu prestasi tertinggi dari kecerdasan manusia. Disiplin ilmu Matematika ini secara umum berasal dari penyelidikan oleh Isaac Newton (1642-1727)
BAB 1 PENDAHULUAN 1.1 Latar Belakang Kalkulus merupakan salah satu prestasi tertinggi dari kecerdasan manusia. Disiplin ilmu Matematika ini secara umum berasal dari penyelidikan oleh Isaac Newton (1642-1727)
KENDALI OPTIMAL PADA MODEL PERIKLANAN NERLOVE-ARROW DENGAN MENGGUNAKAN PRINSIP MAKSIMUM
 KENDALI OPTIMAL PADA MODEL PERIKLANAN NERLOVE-ARROW DENGAN MENGGUNAKAN PRINSIP MAKSIMUM Skripsi Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains Program Studi Matematika Oleh: Dewita
KENDALI OPTIMAL PADA MODEL PERIKLANAN NERLOVE-ARROW DENGAN MENGGUNAKAN PRINSIP MAKSIMUM Skripsi Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains Program Studi Matematika Oleh: Dewita
Catatan Kuliah KALKULUS II BAB V. INTEGRAL
 BAB V. INTEGRAL Anti-turunan dan Integral TakTentu Persamaan Diferensial Sederhana Notasi Sigma dan Luas Daerah di Bawah Kurva Integral Tentu Teorema Dasar Kalkulus Sifat-sifat Integral Tentu Lebih Lanjut
BAB V. INTEGRAL Anti-turunan dan Integral TakTentu Persamaan Diferensial Sederhana Notasi Sigma dan Luas Daerah di Bawah Kurva Integral Tentu Teorema Dasar Kalkulus Sifat-sifat Integral Tentu Lebih Lanjut
TE Sistem Linier. Sistem Waktu Kontinu
 TE 226 - Sistem Linier Jimmy Hasugian Electrical Engineering - Maranatha Christian University jimlecture@gmail.com - http://wp.me/p4scve-g Sistem Waktu Kontinu Jimmy Hasugian (MCU) Sistem Waktu Kontinu
TE 226 - Sistem Linier Jimmy Hasugian Electrical Engineering - Maranatha Christian University jimlecture@gmail.com - http://wp.me/p4scve-g Sistem Waktu Kontinu Jimmy Hasugian (MCU) Sistem Waktu Kontinu
Pertemuan Minggu ke Keterdiferensialan 2. Derivatif berarah dan gradien 3. Aturan rantai
 Pertemuan Minggu ke-10 1. Keterdiferensialan 2. Derivatif berarah dan gradien 3. Aturan rantai 1. Keterdiferensialan Pada fungsi satu peubah, keterdiferensialan f di x berarti keujudan derivatif f (x).
Pertemuan Minggu ke-10 1. Keterdiferensialan 2. Derivatif berarah dan gradien 3. Aturan rantai 1. Keterdiferensialan Pada fungsi satu peubah, keterdiferensialan f di x berarti keujudan derivatif f (x).
BAB 4 MODEL RUANG KEADAAN (STATE SPACE)
 BAB 4 MODEL RUANG KEADAAN (STATE SPACE) KOMPETENSI Kemampuan untuk menjelaskan pengertian tentang state space, menentukan nisbah alih hubungannya dengan persamaan ruang keadaan dan Mengembangkan analisis
BAB 4 MODEL RUANG KEADAAN (STATE SPACE) KOMPETENSI Kemampuan untuk menjelaskan pengertian tentang state space, menentukan nisbah alih hubungannya dengan persamaan ruang keadaan dan Mengembangkan analisis
Teori Dualitas dan Penerapannya (Duality Theory and Its Application)
 Teori Dualitas dan Penerapannya (Duality Theory and Its Application) Kuliah 6 TI2231 Penelitian Operasional I 1 Materi Bahasan 1 Teori dualitas 2 Metode simpleks dual TI2231 Penelitian Operasional I 2
Teori Dualitas dan Penerapannya (Duality Theory and Its Application) Kuliah 6 TI2231 Penelitian Operasional I 1 Materi Bahasan 1 Teori dualitas 2 Metode simpleks dual TI2231 Penelitian Operasional I 2
2.1 Soal Matematika Dasar UM UGM c. 1 d d. 3a + b. e. 3a + b. e. b + a b a
 Soal - Soal UM UGM. Soal Matematika Dasar UM UGM 00. Jika x = 3 maka + 3 log 4 x =... a. b. c. d. e.. Jika x+y log = a dan x y log 8 = b dengan 0 < y < x maka 4 log (x y ) =... a. a + 3b ab b. a + b ab
Soal - Soal UM UGM. Soal Matematika Dasar UM UGM 00. Jika x = 3 maka + 3 log 4 x =... a. b. c. d. e.. Jika x+y log = a dan x y log 8 = b dengan 0 < y < x maka 4 log (x y ) =... a. a + 3b ab b. a + b ab
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI 2.1 Pengantar Pada bab ini akan diuraikan beberapa landasan teori untuk menunjang penulisan skripsi ini. Uraian ini terdiri dari beberapa bagian yang akan dipaparkan secara terperinci
BAB 2 LANDASAN TEORI 2.1 Pengantar Pada bab ini akan diuraikan beberapa landasan teori untuk menunjang penulisan skripsi ini. Uraian ini terdiri dari beberapa bagian yang akan dipaparkan secara terperinci
II. LANDASAN TEORI ( ) =
 II. LANDASAN TEORI 2.1 Fungsi Definisi 2.1.1 Fungsi Bernilai Real Fungsi bernilai real adalah fungsi yang domain dan rangenya adalah himpunan bagian dari real. Definisi 2.1.2 Limit Fungsi Jika adalah suatu
II. LANDASAN TEORI 2.1 Fungsi Definisi 2.1.1 Fungsi Bernilai Real Fungsi bernilai real adalah fungsi yang domain dan rangenya adalah himpunan bagian dari real. Definisi 2.1.2 Limit Fungsi Jika adalah suatu
BAB III MODEL HIDDEN MARKOV KONTINU DENGAN PROSES OBSERVASI ZERO DELAY
 BAB III MODEL HIDDEN MARKOV KONTINU DENGAN PROSES OBSERVASI ZERO DELAY 3.1 State dan Proses Observasi Semua proses didefinisikan pada ruang peluang Ω,,. Misalkan ; adalah rantai Markov dengan state berhingga
BAB III MODEL HIDDEN MARKOV KONTINU DENGAN PROSES OBSERVASI ZERO DELAY 3.1 State dan Proses Observasi Semua proses didefinisikan pada ruang peluang Ω,,. Misalkan ; adalah rantai Markov dengan state berhingga
BAB PDB Linier Order Satu
 BAB 1 Konsep Dasar 1 BAB PDB Linier Order Satu BAB 3 Aplikasi PDB Order Satu 3 BAB 4 PDB Linier Order Dua Untuk memulai pembahasan ini terlebih dahulu akan ditinjau beberapa teorema tentang konsep umum
BAB 1 Konsep Dasar 1 BAB PDB Linier Order Satu BAB 3 Aplikasi PDB Order Satu 3 BAB 4 PDB Linier Order Dua Untuk memulai pembahasan ini terlebih dahulu akan ditinjau beberapa teorema tentang konsep umum
BAB 1 PENDAHULUAN Latar Belakang
 BAB 1 PENDAHULUAN 1.1. Latar Belakang Optimasi (Optimization) adalah aktivitas untuk mendapatkan hasil terbaik di dalam suatu keadaan yang diberikan. Tujuan akhir dari semua aktivitas tersebut adalah meminimumkan
BAB 1 PENDAHULUAN 1.1. Latar Belakang Optimasi (Optimization) adalah aktivitas untuk mendapatkan hasil terbaik di dalam suatu keadaan yang diberikan. Tujuan akhir dari semua aktivitas tersebut adalah meminimumkan
