BAB I MATRIKS. Aljabar matriks merupakan salah satu cabang matematika yang. dikembangkan oleh seorang matematikawan Inggris Arthur Cayley ( ).
|
|
|
- Yuliana Hermawan
- 7 tahun lalu
- Tontonan:
Transkripsi
1 BAB I MATRIKS Aljbr mtriks merupkn slh stu cbng mtemtik yng dikembngkn oleh seorng mtemtikwn Inggris Arthur Cyley (8 89) Mtriks berkembng kren pernnny dlm cbng-cbng Mtemtik linny, mislny bidng ekonomi, industri dn trnsportsi Dengn menggunkn mtriks, mk penyelesin sistem persmn liner kn lebih mudh diselesikn Pembhsn bb ini diwli dengn definisi mtriks dn opersi dsr mtriks yng sudh dikenl, nmun untuk pengenln sift-sift lebih lnjut penyjin mtriks kn menggunkn notsi mtriks untuk mempersingkt penulisn Meskipun mtriks ini bukn hl yng bru, kren sudh pernh diperoleh di SLTA, nmun dengn mengusi mteri dlm bb ini kn lebih mudh mengikuti pembhsn berikutny TIK : Setelh mempeljri mteri inidihrpkn mhsisw dpt: menjelskn opersi-opersi ljbr mtriks b menentukn bentuk eselon tereduksi sutu mtriks c menghitung nili determinn sutu mtriks d menentukn invers sutu mtriks
2 Opersi Aljbr Mtriks Definisi : Mtriks dlh sutu susunn segiempt siku-siku dri bilngnbilngn, susunn tersebut disjikn di dlm kurung besr tu kurung siku Bilngn-bilngn itu disebut entri tu elemen dri mtriks Bentuk umum sutu mtriks yng terdiri dri m bris dn n kolom dlh A m m n n mn tu A m m n n mn Bentuk mtriks tersebut dpt disjikn dengn notsi mtriks, yitu A ( ij ) dengn i,,,m dn j,,,n berturut-turut menunjukkn bris dn kolom dri mtriks A Sutu mtriks A yng terdiri dri m bris dn n kolom disebut mtriks berukurn mxn dn dilmbngkn dengn A mxn tu ( ij ) mxn, ditulis singkt A ( ij ) Dlm hl ini ij dinmkn elemen ke -ij dri mtriks A Mtriks A ( ij ) dengn mn diktkn sebgi mtriks persegi, elemen,,, nn disebut elemen digonl utm dri A Jumlhn elemen digonl utm disebut trce dri A Untuk dpt menggunkn mtriks perlu dikji opersi ljbr mtriks berikut Kesmn Mtriks Du buh mtriks A dn B diktkn sm, ditulis A B, jik A dn B berukurn sm dn elemen-elemen yng bersesuin (seletk ) dlh sm
3 Jik disjikn dlm notsi mtriks, A ( ij ) dn B ( ij ) ij b ij, untuk setip i,,,m dn j,,,n b mk A B jik Jik A x, B x, C x, dn D x mk A B, A C, B C, dn A D š Penjumlhn dn pengurngn mtriks Penjumlhn dn pengurngn du mtriks tu lebih, hny dpt dilkukn jik mtriks tersebut berukurn sm Penjumlhn tu pengurngn du mtriks didefinisikn sebgi penjumlhn tu pengurngn elemen yng bersesuin Jik A ) dn B b ), mk A + B ij + b ) dn A B ij b ) ( ij ( ij ( ij ( ij Jik 9 A dn B mk A + B, 9 B + A, A B, dn B A 6 6 š Sift : Jik A, B, dn C mtriks yng berukurn sm mk berlku: A + B B + A (Komuttif) b A + ( B + C) ( A + B) + C (Asositif) Pergndn mtriks dengn bilngn (sklr) Pergndn mtriks dengn sklr didefinisikn sebgi perklin sklr dengn setip elemen mtriks tersebut
4 Jik A ) dn k sebrng sklr, mk ka Ak k ) ( ij ( ij Jik 8 A, mk A dn A 6 š Pergndn mtriks Pergndn mtriks A dn B, dinotsikn AB, hny dpt dilkukn jik bnykny kolom mtriks A sm dengn bnykny bris mtriks B Jik A ) ( ij mxp dn B ( b ij ) pxn, mk AB C ( c ij ) mxn, dengn cij ikbkj p k Jik A dn B mk AB Mtriks BA tidk dpt diperoleh kren bnykny kolom dri B dlh sedngkn bnykny bris dri A dlh š Sift : Jik A, B, dn C mtriks sehingg opersi berikut berlku, mk : A ( B + C) AB + AC Distributif kiri ( B + C) A BA + CA Distributif knn b A( B C) AB AC Distributif kiri ( B C) A BA CA Distributif knn c A ( BC) ( AB) C Assositif
5 Jenis jenis Mtriks Beberp mtriks dengn elemen tertentu yng seringkli digunkn disjikn berikut Mtriks Nol Mtriks yng semu elemenny nol disebut mtriks nol, dinotsikn Mtriks, merupkn mtriks nol Sift : Untuk sebrng mtriks A yng ukurnny bersesuin sehingg opersi ljbr berikut dpt dilkukn, berlku : A + + A A b A A c A A d A A Mtriks Trnspos Trnspos dri mtriks A, dinotsikn dengn A tu A t, dlh mtriks yng kolom pertmny dlh bris pertm mtriks A, kolom keduny dlh bris kedu mtriks A, dn seterusny Jik t ( ij mxn mk A ( ji ) nxm A )
6 Jik A, B 7 mk t t A 7 dn B š Sift : Untuk sebrng mtriks A berlku : (A t ) t A b (ka) t ka t c (A + B) t A t + B t d (AB) t B t A t Mtriks Segitig Ats dn Mtriks Segitig Bwh Mtriks persegi yng semu elemen di bwh digonl utm bernili disebut mtriks segitig ts Begitu pul mtriks persegi yng semu elemen di ts digonl utm bernili disebut mtriks segitig bwh Jdi A ( ij ) nxn disebut mtriks segitig ts jik ij untuk i > j dn disebut mtriks segitig bwh jik ij untuk i < j Mtriks A dn B berturut-turut dlh mtriks segitig ts dn mtriks segitig bwh Mtriks Digonl Adlh mtriks persegi yng semu elemen-elemenny dlh nol keculi elemen pd digonl utm Jdi A ( ij ) nxn disebut mtriks digonl jik ij untuk i j 6
7 7, Mtriks Identits (Mtriks Stun) Mtriks digonl yng semu elemen digonl utmny sm dengn disebut mtriks identits, dinotsikn dengn I n tu I Dlm bentuk notsi mtriks, dituliskn ) ( ij I dengn ij, untuk ij dn ij, untuk i j, berlku untuk i,j,,,n I Sift : Untuk sebrng mtriks A yng berukurn nxn berlku I n AA I n A 6 Mtriks invers Mtriks B diktkn sebgi invers dri mtriks A jik AB BA I Dlm hl ini invers mtriks A dinotsikn A - Mtriks yng mempunyi invers disebut mtriks non singulr Jik A mk B dlh invers dri A sebb AB dn BA š Sift : ( A - ) - A b (AB ) - B - A -
8 7 Mtriks Simetris Sutu mtriks persegi A diktkn simetris jik A A t Jik A ( ij ) mk A diktkn simetris jik ij ji, untuk setip i,j Mtriks A dlh simetris sedngkn mtriks B tidk simetris Mengp? Untuk sebrng mtriks persegi A, mtriks A+A t merupkn mtriks simetris Mengp? 8 Mtriks Skew Simetris (Simetris Miring) Mtriks A diktkn simetris miring jik A t A Jik A ( ij ) mk A diktkn simetris miring jik ij ji, untuk setip i,j Mtriks A dlh mtriks simetris miring 9 Mtriks-mtriks persegi yng istimew - Jik A dn B mtriks-mtriks persegi sedemikin sehingg AB BA, mk A dn B disebut commute - Jik AB -BA, mk A dn B disebut Anti Commute - Mtriks A yng memenuhi A k+ A (k bilngn positif), disebut periodik 8
9 - Jik A A, mk A disebut mtriks Idempoten - Jik A k, dengn k bilngn bult positif terkecil mk A disebut mtriks nilpoten Dlm hl ini bilngn k disebut indeks nilpoten 6 Mtriks A dn B dlh Commute, sebb : 6 AB dn BA b Mtriks c Mtriks A dlh idempoten sebb A A M 6 dlh nilpoten berindeks, sebb M Opersi Bris Elementer Selin opersi ljbr mtriks yng sudh diperkenlkn pd subbb, d opersi lin yng dpt dikenkn pd sutu mtriks untuk mendptkn mtriks lin Opersi ini dinmkn opersi bris elementer kren dikenkn pd bris-bris sutu mtriks Opersi ini bnyk digunkn untuk menentukn penyelesin sistem persmn liner yng kn dibhs pd bb berikutny Opersi bris elementer meliputi tig bentuk, yitu : Menukr bris ke-i dn bris ke-j, dinytkn dengn B ij 9
10 b Menggndkn setip elemen bris ke i dengn sklr k, dinytkn dengn B i (k) c Menmbhkn k kli elemen-elemen bris ke-j (k sklr) kepd bris ke-i, dinytkn dengn B ij (k) Opersi semcm ini jug dpt dilkukn pd kolom, dengn notsi B dignti K, nmun untuk pembhsn ini opersi hny dikenkn pd bris sj Jik kit melkukn opersi bris elementer pd sutu mtriks untuk memperoleh mtriks yng lin, mtriks wl dn hsilny dihubungkn dengn tnd Dikethui mtriks A Jik bris ke- ditukr dengn bris ke-, diperoleh B Jik opersi K dikenkn pd A diperoleh b Jik bris ke- diklikn, diperoleh ) ( B 9 6 Jik opersi K () dikenkn pd A diperoleh
11 c Jik bris ke- diklikn - kemudin ditmbhkn ke bris ke-, diperoleh ) ( B Jik opersi K (-) dikenkn pd A diperoleh š Jik opersi bris elementer dikenkn pd mtriks identits kn diperoleh sutu mtriks yng khs Sebuh mtriks berukurn nxn disebut mtriks elementer jik mtriks tersebut dpt diperoleh dri mtriks stun I n dengn melkukn stu opersi bris elementer Kren d tig mcm opersi bris elementer, mk d mcm mtriks elementer : E ij, yitu mtriks yng didpt dri mtriks I jik bris ke-i ditukr dengn bris ke-j Dri I, diperoleh E, E ) k ( E i dlh mtriks yng didpt dri mtriks I jik bris ke-i digndkn dengn sklr k Dri I, diperoleh () E, ) ( E
12 Mtriks ) k ( E ij dlh mtriks yng didpt dri mtriks I jik bris ke-j digndkn dengn sklr k kemudin ditmbhkn ke bris ke-i Dri I, diperoleh ) ( E, ) ( E Sift-sift mtriks elementer: Jik mtriks A digndkn dri kiri dengn mtriks elementer E, mk EA dlh sutu mtriks bru yng diperoleh bil opersi bris elementer yng digunkn untuk memperoleh E dri I, diterpkn pd A Misl 7 A, E, () E, dn ) ( E 7 B 7, dn E A () B 7 9, dn () E A () B 7, dn () E A 7 7 š b Invers dri mtriks elementer jug merupkn mtriks elementer
13 Jik stu opersi bris elementer diterpkn pd I untuk menghsilkn E, mk terdpt opersi bris elementer yng bil diterpkn pd E kn menghsilkn I Berbgi kemungkinn opersi seperti di ts disjikn sebgi berikut Opersi bris pd I untuk Opersi bris pd E untuk menghsilkn E menghsilkn I Menukr bris ke-i dn bris ke-j (B ij ) Menukr bris ke-j dn bris ke-i (B ji ) Menggndkn bris ke -i dengn Menggndkn bris ke -i dengn /k sklr k (B i (k)) (B i (/k)) Menmbhkn k kli bris ke-j kepd Menmbhkn -k kli bris ke-j bris ke-i (B ij (k)) kepd bris ke-i (B ij (-k)) Opersi pd kolom knn merupkn invers (blikn) dri opersi pd kolom kiri Jik opersi pd kolom knn dikenkn pd I mk kn menghsilkn mtriks elementer, sebut sj E, yng menurut sift berlku EE I dn E E I Dengn demikin E dlh invers dri E Dri tbel di ts diperoleh : (E ij ) - E ji, (E i (k)) - E i (/k)) dn (E ij (k)) - E ij (-k) E E dn E E I E ( ) E ( ) / dn E (/) E () I
14 E ( ) E ( ) dn E (-) E () I š Kedu sift di ts penting untuk digunkn dlm teorem berikut Teorem : Jik A mtriks nonsingulr mk A dpt dinytkn sebgi hsil gnd mtriks-mtriks elementer Nytkn A sebgi hsil gnd mtriks-mtriks elementer Penyelesin : Kit dpt melkukn opersi bris elementer berhingg kli pd A smpi diperoleh mtriks I sebgi berikut A B (/ ) / B B ( ) / / C B () / D B ( ) I Menurut sift, tentu berlku : B E (/) A, C E (-)B, D E ()C, dn I E (-) D Dengn demikin diperoleh E (-) E () E (-) E (/) A I Kren mtriks elementer mempunyi invers mtriks elementer pul, mk A (E (/)) - (E (-) ) - (E ()) - (E (-)) - I E () E () E (-) E (-/) Jdi A / Bentuk perklin mtriks elementer ini tidk tunggl Periks bhw A E E E ()E () Dptkh kmu cri bentuk perklin yng lin? š
15 Definisi : Mtriks B diktkn ekivlen bris (row equivlent) dengn mtriks A, ditulis A ~ B, jik mtriks B dpt diperoleh dri mtriks A dengn berhingg bnyk opersi bris elementer Mengingt sift dri mtriks elementer, definisi di ts dpt pul dinytkn sebgi : mtriks B diktkn ekivlen bris dengn mtriks A jik terdpt mtriks-mtriks elementer E, E,,E p sehingg B E p E p- E A Contoh A dn B dlh ekivlen bris, kren B ( ) B ( ) š Sift : Jik A ekivlen bris dengn B, mk B ekivlen bris dengn A Jik A ekivlen bris dengn B dn B ekivlen bris dengn C, mk A ekivlen bris dengn C Definisi : Sutu mtriks diktkn dlm bentuk eselon bris (row-echelon form) jik memenuhi : Jik terdpt bris yng tidk semu elemenny nol, mk elemen pertm yng tidk nol dlh, dn disebut utm (pivot) b Jik terdpt bris yng semu elemenny nol, mk bris ini diletkkn pd bris pling bwh
16 6 c Pd sebrng du bris yng berurutn yng tidk semu elemenny nol, utm pd bris yng bwh terletk di sebelh knn dri utm bris di tsny dn Definisi : Sutu mtriks diktkn dlm bentuk eselon bris tereduksi (reduced row-echelon form) jik mtriks tersebut dlm bentuk eselon bris dn pd msing-msing kolom yng memut utm, elemen merupkn stu-stuny elemen yng tidk nol Contoh dn Definisi : Sutu mtriks diktkn dlm bentuk norml jik mtriks tersebut memut submtriks identits Ad jenis bentuk norml yitu : I p, Ip, [ ] p I, dn Ip dengn I p dlh mtriks identits Contoh Selin untuk menentukn bentuk eselon bris tereduksi, opersi bris elementer jug dpt digunkn untuk memperoleh invers dri sutu mtriks non singulr
17 Jik A dlh mtriks non singulr, mk dengn melkukn sebnyk berhingg kli opersi bris elementer pd mtriks [A I] (mtriks ini disebut perlusn dri mtriks A) kn didpt mtriks [I B] Mislkn untuk itu diperlukn n opersi bris elementer Kren A dibw ke I dn I dibw ke B, mk I E E E E na dn B E E E E ni Kren mtriks elementer mempunyi invers mk dri perklin yng pertm diperoleh n n ( n n n n A E E E E I sehingg AB E E E E )( E E E E ) I dn BA ( E En EnEn )( En E E E E En En ) I Ini berrti B dlh invers dri A, tu B A - Jik A mk invers dri A dpt ditentukn sebgi berikut Dibentuk mtriks [A I] Selnjutny dengn melkukn opersi bris berikut ini : B (-), B (-), B (/), B (/), B (-), B (), B (-), kn diperoleh mtriks : / / Jdi A - / / š Definisi : Rnk dri mtriks A dpt didefinisikn sebgi bnykny bris (kolom) tk nol dri bentuk eselon bris yng diperoleh dri mtriks A 7
18 Kren bnykny bris (kolom) tk nol sellu kurng dri minimum dintr bris dn kolom, mk rnk(a mxn) min {m, n} Crilh rnk dri mtriks A Jwb : Jik mtriks A dikeni opersi bris elementer B (/), B (-), B (-), B (-/), dn B () kit memperoleh / / / Jdi rnk(a) š Determinn Determinn sutu mtriks persegi sngt bnyk gunny dlm berbgi cbng mtemtik Sebgi contoh pd ljbr, determinn digunkn untuk mencri jwb n persmn liner dengn n vribel Ad du definisi determinn diliht dri segi pendektnny, pertm dengn pendektn klsik, yitu bertitik tolk pd fungsi permutsi, kedu dengn pendektn bukn klsik, yitu pd fungsi multiliner Pd pembhsn kli ini kit mendefinisikn determinn dengn pendektn klsik, yitu mellui fungsi permutsi Definisi : Permutsi bilngn sli, dinotsikn s, dlh susunn bilngnbilngn sli menurut sutu turn tnp menghilngkn tu mengulngi bilngn tersebut Himpunn semu permutsi dri n ditulis dengn S n 8
19 Permutsi dri brisn bilngn dn dlh (,) dn (,) Jdi S {(,), (,)} Permutsi dri bilngn,, dn dlh (,,), (,,), (,,), (,,), (,,), dn (,,) Jdi S {(,,), (,,), (,,), (,,), (,,), (,,)} Kit liht bhw bnykny permutsi bilngn dlh, bnykny permutsi bilngn dlh 6 Secr umum bnykny permutsi n bilngn dlh n! Penulisn permutsi k bilngn dlh (j,j,,j k) dengn ji jk untuk i k Definisi : Inversi pd sutu permutsi dlh terdptny bilngn yng lebih besr mendhului bilngn yng lebih kecil, tu j i > j k untuk i < k Pd permutsi (,,) terdpt inversi yitu mendhului Pd permutsi (,,) terdpt inversi yitu : mendhului, mendhului, dn mendhului Definisi : Jik jumlh inversi dri sutu permutsi dlh genp, mk disebut permutsi genp dn jik jumlh inversi sutu permutsi gnjil mk disebut permutsi gnjil Definisi : Tnd dri permutsi s, dinotsikn sgn(s), didefinisikn sebgi +, jik jumlh inversi σ genp sign( σ ), jik jumlh inversi σ gsl Jik s (,,) mk sgn(s) - Jik s (,,) mk sgn(s) - 9
20 Definisi : Determinn dri mtriks A nxn didefinisikn sebgi : det( A ) sgn( σ ) σ Sn j j j njn Jik A mk S {(,), (,)} dengn sgn(,) +, sgn(,) - sehingg det( A) Jik A mk S {(,,), (,,), (,,), ((,,), (,,),(,,)} dengn sgn(,,) +, sgn(,,) +, sgn(,,) +, sgn(,,) -, sgn(,,)-, dn sgn(,,) - Sehingg det(a) Apbil contoh tersebut diterpkn pd mtriks A dn B 6 mk det(a) - - dn det(b) š Dri definisi di ts, pbil A sutu mtriks segitig (ts tupun bwh) mk det(a) psti bernili nol sebb stu-stuny suku tidk nol dlh perklin elemen-elemen digonl utm Jdi jik A nxn ( ij ) mk det(a) nn Selnjutny sift-sift yng berlku pd determinn dlh : Nili determinn mtriks A sm dengn nili determinn trnsposeny, yitu det(a) det(a t )
21 Jik A mk A t Sehingg det( A) dn det( A t ) Jik setip elemen pd sutu bris tu kolom mtriks A bernili nol, mk det(a) B mk det(b) Jik mtriks A mempunyi du bris tu du kolom yng sm (elemen yng bersesuin bernili sm), mk det(a) C mk det(c) Jik mtriks B diperoleh dengn menukr du bris tu du kolom mtriks A mk det(b) - det(a) Mtriks A, det (A) Dengn menukr bris dn 6 bris mtriks A diperoleh mtriks C 6 dengn det(c)
22 Jik mtriks B diperoleh dengn menglikn stu bris tu stu kolom mtriks A dengn sklr k, mk det(b) kdet(a) Mtriks A 6, det (A) Dengn menglikn bris ke tig mtriks A dengn, diperoleh mtriks C 8 dengn det(c) Jik A, B, dn C mtriks yng identik (sm) keculi pd stu bris Pd bris yng tidk identik ini, bris mtriks C merupkn jumlhn dri bris mtriks A bris mtriks B, mk det(c) det(a) + det (B) Mislkn A 6, B 6, dn C 6 Mk det(a), det(b) det(c) Jik mtriks B diperoleh dri mtriks A dengn menmbh stu bris dengn k kli bris yng lin, mk det(b ) det(a)
23 Mislkn A 6 dn B Mk det(a), det(b) (-) - - (-)6 - Dri 7 sift di ts kit dpt mengubh sebrng mtriks menjdi mtriks segitig dengn opersi bris elementer jenis tersebut, tnp mengubh nili determinnny Misl A, dengn opersi B (-/) dilnjutkn B (-/8) diperoleh 6 mtriks B 8/ /, sehingg det(a) det(b ) / Ekspnsi Kofktor Definisi : Jik A dlh mtriks persegi mk minor dri elemen ij, dinytkn dengn M ij, dlh determinn tingkt (n-) yng diperoleh dengn mencoret bris ke i dn kolom ke j dri mtriks A Bilngn (-) i+j M ij, dinytkn dengn K ij, dinmkn kofktor entri ij
24 Misl A, mk M det dn K (-) + M Selnjutny M det - dn K (-) + M -( -) Secr sm diperoleh M -, M, M -, M -, M, M, dn M - Kemudin didpt K -, K -, K -, K, K, K, dn K - š Dri penghitungn kofktor elemen sutu mtriks kit dpt menghitung determinn dn invers dri sutu mtriks Definisi : Jik A ( ij ), mk determinn A didefinisikn sebgi : n det( A) ( ) M K (ekspnsi bris ke i), tu j n i+ j ij ij n ij j det( A) ( ) M K (ekspnsi kolom ke j) i i+ j ij ij n ij i ij ij Jik A mk det(a) K + K + K + + (-) Atu det(a) K + K + K (-) + (-) + (-6) + 8 Coblh hitung dengn ekspnsi kolom Definisi : Jik A ( ij ) mtriks persegi mk mtriks K ( ) š K ij dengn ij K dlh kofktor dri ij dinmkn mtriks kofktor dri A Trnspose dri mtriks kofktor disebut mtriks djoin dri A, dinotsikn dj(a)
25 Jik A, mk K, dn dj(a) Teorem : Jik A mtriks yng mempunyi invers mk ) ( ) det( A dj A A Jik A, mk A - / / Ltihn Diberikn mtriks A, B, C, D, E, [ ] F, G, dn [ ] H Mnkh di ntr opersi berikut yng dpt dilkukn? Jik dpt dilkukn tentukn hsilny, jik tidk dpt dilkukn berikn lsnny A + B b A + C c B - D d H - F e AB + FE f BA g ED - BA h BG + GH i HD - A t j F t + G t k (F + G) t l (AB) t
26 6 Berikn stu contoh mtriks simetris ukurn x Berikn stu contoh mtriks simetris miring A yng berukurn x Apkh A + A t jug simetris miring? Berikn lsnny Jik C dn D, hitunglh : C (C + D) b C + CD) c C (CD) d C D e (C - D)C f C - DC Lkukn opersi bris elementer B (-), B (), B, B (-), B (-),dn B () pd mtriks berikut A b B c C 6 Dptkn invers dri mtriks elementer berikut b c 7 Tentukn bentuk eselon bris dri mtriks berikut Cttlh opersi bris elementer yng dilkukn untuk mendptkn bentuk eselon brisny Dptkn pul bentuk eselon bris tereduksiny A b B c C
27 8 ll 7
BAB 10. MATRIKS DAN DETERMINAN
 Dessy Dwiynti, S.Si, MBA Mtemtik Ekonomi 1 BAB 10. MATRIKS DAN DETERMINAN 1. Pengertin mtriks Mtriks kumpuln bilngn yng disjikn secr tertur dlm bris dn kolom yng membentuk sutu persegi pnjng, sert termut
Dessy Dwiynti, S.Si, MBA Mtemtik Ekonomi 1 BAB 10. MATRIKS DAN DETERMINAN 1. Pengertin mtriks Mtriks kumpuln bilngn yng disjikn secr tertur dlm bris dn kolom yng membentuk sutu persegi pnjng, sert termut
M A T R I K S. Oleh: Dimas Rahadian AM, S.TP. M.Sc.
 M T R I K S Oleh Dims Rhdin M, S.TP. M.Sc Emil rhdindims@yhoo.com JURUSN ILMU DN TEKNOLOGI PNGN UNIVERSITS SEBELS MRET SURKRT DEFINISI... Mtriks dlh susunn bilngn berbentuk jjrn segi empt siku-siku yng
M T R I K S Oleh Dims Rhdin M, S.TP. M.Sc Emil rhdindims@yhoo.com JURUSN ILMU DN TEKNOLOGI PNGN UNIVERSITS SEBELS MRET SURKRT DEFINISI... Mtriks dlh susunn bilngn berbentuk jjrn segi empt siku-siku yng
Bab a. maka notasi determinan dari matriks A ditulis : det (A) atau. atau A.
 Bb DETERMINAN MATRIKS Determinn sutu mtriks dlh sutu fungsi sklr dengn domin mtriks bujur sngkr. Dengn kt lin, determinn merupkn pemetn dengn domin berup mtriks bujur sngkr, sementr kodomin berup sutu
Bb DETERMINAN MATRIKS Determinn sutu mtriks dlh sutu fungsi sklr dengn domin mtriks bujur sngkr. Dengn kt lin, determinn merupkn pemetn dengn domin berup mtriks bujur sngkr, sementr kodomin berup sutu
Aljabar Linear Elementer
 ljbr Liner Elementer M SKS Silbus : Bb I Mtriks dn Opersiny Bb II Determinn Mtriks Bb III Sistem Persmn Liner Bb IV Vektor di Bidng dn di Rung Bb V Rung Vektor Bb VI Rung Hsil Kli Dlm Bb VII Trnsformsi
ljbr Liner Elementer M SKS Silbus : Bb I Mtriks dn Opersiny Bb II Determinn Mtriks Bb III Sistem Persmn Liner Bb IV Vektor di Bidng dn di Rung Bb V Rung Vektor Bb VI Rung Hsil Kli Dlm Bb VII Trnsformsi
Kerjakan di buku tugas. Tentukan hasil operasi berikut. a. A 2 d. (A B) (A + B) b. B 2 e. A (B + B t ) c. A B f. A t (A t + B t ) Tes Mandiri
 Mmt Apliksi SMA Bhs Dikethui A = Tentukn hsil opersi berikut A c A A b A A d A Dikethui A = Tentukn hsil opersi berikut (A + B) c (B A) b A + AB + B d B BA + A Sol Terbuk Kerjkn di buku tugs Jik X = dn
Mmt Apliksi SMA Bhs Dikethui A = Tentukn hsil opersi berikut A c A A b A A d A Dikethui A = Tentukn hsil opersi berikut (A + B) c (B A) b A + AB + B d B BA + A Sol Terbuk Kerjkn di buku tugs Jik X = dn
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI Bb berikut ini kn disjikn mteri pendukung yng dpt membntu penulis untuk menyelesikn permslhn yng kn dibhs pd bb selnjutny. Adpun mteri pendukungny dlh pengertin mtriks, jenis-jenis
BAB II LANDASAN TEORI Bb berikut ini kn disjikn mteri pendukung yng dpt membntu penulis untuk menyelesikn permslhn yng kn dibhs pd bb selnjutny. Adpun mteri pendukungny dlh pengertin mtriks, jenis-jenis
Aljabar Linear Elementer
 ljbr Liner Elementer M3 3 SKS Silbus : Bb I Mtriks dn Opersiny Bb II Determinn Mtriks Bb III Sistem Persmn Liner Bb IV Vektor di Bidng dn di Rung Bb V Rung Vektor Bb VI Rung Hsil Kli Dlm Bb VII Trnsformsi
ljbr Liner Elementer M3 3 SKS Silbus : Bb I Mtriks dn Opersiny Bb II Determinn Mtriks Bb III Sistem Persmn Liner Bb IV Vektor di Bidng dn di Rung Bb V Rung Vektor Bb VI Rung Hsil Kli Dlm Bb VII Trnsformsi
DETERMINAN. Misalkan A adalah suatu matriks persegi. a) Jika A memiliki satu baris atau satu kolom bilangan nol, maka det(a) = 0.
 DETERMINAN Fungsi determinn dri sutu mtriks persegi A (dinotsikn dengn det(a) tu A ) didefinisikn sebgi jumlh dri semu hsil kli elementer bertnd dri A. Sementr, ngk tu bilngn dri det(a) disebut determinn
DETERMINAN Fungsi determinn dri sutu mtriks persegi A (dinotsikn dengn det(a) tu A ) didefinisikn sebgi jumlh dri semu hsil kli elementer bertnd dri A. Sementr, ngk tu bilngn dri det(a) disebut determinn
3.1 Permutasi. Secara umum, bilangan-bilangan pada {1, 2,, n} akan mempunyai n! permutasi
 BB Determinn . Permutsi Definisi Permutsi: (i) Sutu permutsi dri bilngn-bilngn bult {,,,, n} dlh penyusunn bilngn-bilngn tersebut dengn urutn tnp pengulngn. (ii) Brisn bilngn ( j, j,.., j n ) dimn j i
BB Determinn . Permutsi Definisi Permutsi: (i) Sutu permutsi dri bilngn-bilngn bult {,,,, n} dlh penyusunn bilngn-bilngn tersebut dengn urutn tnp pengulngn. (ii) Brisn bilngn ( j, j,.., j n ) dimn j i
PERTEMUAN - 1 JENIS DAN OPERASI MATRIKS
 PERTEMUN - JENIS DN OPERSI MTRIKS Pengertin Mtriks : merupkn sutu lt tu srn yng sngt mpuh untuk menyelesikn model-model liner. Definisi : Mtriks dlh susunn empt persegi pnjng tu bujur sngkr dri bilngn-bilngn
PERTEMUN - JENIS DN OPERSI MTRIKS Pengertin Mtriks : merupkn sutu lt tu srn yng sngt mpuh untuk menyelesikn model-model liner. Definisi : Mtriks dlh susunn empt persegi pnjng tu bujur sngkr dri bilngn-bilngn
BAB III MATRIKS
 BB III MTRIKS PENGERTIN MTRIKS Pengertin Mtriks Mtriks dlh susunn bilngn-bilngn ng berbentuk persegi tu persegi pnjng ng ditur dlm bris dn kolom Bentuk Umum Mtriks : i m i m i m j j j ij mj n n n in mn
BB III MTRIKS PENGERTIN MTRIKS Pengertin Mtriks Mtriks dlh susunn bilngn-bilngn ng berbentuk persegi tu persegi pnjng ng ditur dlm bris dn kolom Bentuk Umum Mtriks : i m i m i m j j j ij mj n n n in mn
Minggu ke 3 : Lanjutan Matriks
 inggu ke : Lnjutn triks Pokok Bhsn Sub Pokok Bhsn Tujun Instruksionl Umum Tujun Instruksionl Khusus : triks :. Trnsformsi Elementer. Trnsformsi Elementer pd bris dn kolom. triks Ekivlen. Rnk triks B. Determinn.
inggu ke : Lnjutn triks Pokok Bhsn Sub Pokok Bhsn Tujun Instruksionl Umum Tujun Instruksionl Khusus : triks :. Trnsformsi Elementer. Trnsformsi Elementer pd bris dn kolom. triks Ekivlen. Rnk triks B. Determinn.
SISTEM BILANGAN REAL. 1. Sifat Aljabar Bilangan Real
 SISTEM BILANGAN REAL Dlm terminologi Aljbr Abstrk, sistem bilngn rel disebut dengn field (lpngn) pd opersi penjumlhn dn perklin. Sutu opersi biner bis ditulis dengn sutu psngn terurut (, b) yng unik dri
SISTEM BILANGAN REAL Dlm terminologi Aljbr Abstrk, sistem bilngn rel disebut dengn field (lpngn) pd opersi penjumlhn dn perklin. Sutu opersi biner bis ditulis dengn sutu psngn terurut (, b) yng unik dri
det DEFINISI Jika A 0 disebut matriks non singular
 DETERINAN DEFINISI Untuk setip mtriks persegi (bujur sngkr), d stu bilngn tertentu yng disebut determinn Determinn dlh jumlh semu hsil kli elementer bertnd dri sutu mtriks bujur sngkr. Disimbolkn dengn:
DETERINAN DEFINISI Untuk setip mtriks persegi (bujur sngkr), d stu bilngn tertentu yng disebut determinn Determinn dlh jumlh semu hsil kli elementer bertnd dri sutu mtriks bujur sngkr. Disimbolkn dengn:
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI. Mtriks Definisi. (Anton, Howrd. ). Mtriks dlh sutu susunn bilngn berbentuk segi empt. Bilngn-bilngn dlm susunn itu disebut nggot dlm mtriks tersebut. Ukurn (size) sutu mtriks dinytkn
BAB II LANDASAN TEORI. Mtriks Definisi. (Anton, Howrd. ). Mtriks dlh sutu susunn bilngn berbentuk segi empt. Bilngn-bilngn dlm susunn itu disebut nggot dlm mtriks tersebut. Ukurn (size) sutu mtriks dinytkn
MATRIKS. Agustina Pradjaningsih, M.Si. Jurusan Matematika FMIPA UNEJ
 MTRIKS gustin Prdjningsih, M.Si. Jurusn Mtemtik FMIP UNEJ tinprdj.mth@gmil.com DEFINISI MTRIKS Sutu dftr bilngn-bilngn rel tu kompleks terdiri ts m bris dn n kolom, m dn n bilngn bult positip disebut mtriks
MTRIKS gustin Prdjningsih, M.Si. Jurusn Mtemtik FMIP UNEJ tinprdj.mth@gmil.com DEFINISI MTRIKS Sutu dftr bilngn-bilngn rel tu kompleks terdiri ts m bris dn n kolom, m dn n bilngn bult positip disebut mtriks
Topik: Matriks Dan Sistem Persamaan Linier
 Mt Kulih: Mtemtik Kode: TKF Topik: Mtriks Dn Sistem Persmn Linier MAT Kompetensi : Dpt menerpkn konsep-konsep mtriks dn sistem persmn linier dlm mempeljri konsep-konsep keteknikn pd mt kulih mt kulih progrm
Mt Kulih: Mtemtik Kode: TKF Topik: Mtriks Dn Sistem Persmn Linier MAT Kompetensi : Dpt menerpkn konsep-konsep mtriks dn sistem persmn linier dlm mempeljri konsep-konsep keteknikn pd mt kulih mt kulih progrm
Matriks. Pengertian. Lambang Matrik
 triks Pengertin Definisi: trik dlh susunn bilngn tu fungsi yng diletkkn ts bris dn kolom sert dipit oleh du kurung siku. Bilngn tu fungsi tersebut disebut entri tu elemen mtrik. mbng mtrik dilmbngkn dengn
triks Pengertin Definisi: trik dlh susunn bilngn tu fungsi yng diletkkn ts bris dn kolom sert dipit oleh du kurung siku. Bilngn tu fungsi tersebut disebut entri tu elemen mtrik. mbng mtrik dilmbngkn dengn
Universitas Esa Unggul
 ALJABAR LINIER DAN MATRIKS BHAN KULIAH DRA SURYARI PURNAMA, MM Universits Es Unggul Minggu I Mtriks Pokok Bhsn Sub Pokok Bhsn Tujun Instruksionl Umum Tujun Instruksionl Khusus : Pendhulun Mtriks : A. Pengertin
ALJABAR LINIER DAN MATRIKS BHAN KULIAH DRA SURYARI PURNAMA, MM Universits Es Unggul Minggu I Mtriks Pokok Bhsn Sub Pokok Bhsn Tujun Instruksionl Umum Tujun Instruksionl Khusus : Pendhulun Mtriks : A. Pengertin
BAB I. MATRIKS BAB II. DETERMINAN BAB III. INVERS MATRIKS BAB IV. PENYELESAIAN PERSAMAAN LINEAR SIMULTAN
 DFTR ISI BB I. MTRIKS BB II. DETERMINN BB III. INVERS MTRIKS BB IV. PENYELESIN PERSMN LINER SIMULTN BB I. MTRIKS Mtriks erup sekelompok ilngn yng disusun empt persegi dn ditsi tnd terdiri dri ris dn kolom
DFTR ISI BB I. MTRIKS BB II. DETERMINN BB III. INVERS MTRIKS BB IV. PENYELESIN PERSMN LINER SIMULTN BB I. MTRIKS Mtriks erup sekelompok ilngn yng disusun empt persegi dn ditsi tnd terdiri dri ris dn kolom
ALJABAR LINIER DAN MATRIKS MATRIKS (DETERMINAN, INVERS, TRANSPOSE)
 ALJABAR LINIER DAN MATRIKS MATRIKS (DETERMINAN, INVERS, TRANSPOSE) Mcm Mtriks Mtriks Nol () Mtriks yng semu entriny nol. Ex: Mtriks Identits (I) Mtriks persegi dengn entri pd digonl utmny dn pd tempt lin.
ALJABAR LINIER DAN MATRIKS MATRIKS (DETERMINAN, INVERS, TRANSPOSE) Mcm Mtriks Mtriks Nol () Mtriks yng semu entriny nol. Ex: Mtriks Identits (I) Mtriks persegi dengn entri pd digonl utmny dn pd tempt lin.
4. Perkalian Matriks. Riki 3 2 Fera 2 5. Data harga bolpoin dan buku (dinyatakan oleh matriks Q), yaitu
 Sift-Sift Perklin Sklr Mislkn dn b sklr, D dn H mtriks sebrng dengn ordo sm, mk berlku sift-sift sebgi berikut. D + H (D + H) 2. D + bd ( + b)d 3. (bd) (b)d 4. Perklin Mtriks Du buh mtriks tu lebih selin
Sift-Sift Perklin Sklr Mislkn dn b sklr, D dn H mtriks sebrng dengn ordo sm, mk berlku sift-sift sebgi berikut. D + H (D + H) 2. D + bd ( + b)d 3. (bd) (b)d 4. Perklin Mtriks Du buh mtriks tu lebih selin
 BAB ALJABAR MARIX Dlm pokok bhsn ini kn disjikn dsr-dsr opersi ljbr mtrix yng berhubungn dengn nlisis struktur dengn menggunkn metode mtrix kekkun (stiffness method)... Pengertin Mtrix Mtrix merupkn sutu
BAB ALJABAR MARIX Dlm pokok bhsn ini kn disjikn dsr-dsr opersi ljbr mtrix yng berhubungn dengn nlisis struktur dengn menggunkn metode mtrix kekkun (stiffness method)... Pengertin Mtrix Mtrix merupkn sutu
2.Matriks & Vektor (1)
 .triks & Vektor () t Kulih: ljbr Liner dn triks Semester Pendek T. / S Teknik Informtik Dosen Pengmpu: Heri Sismoro,.Kom. STIK IKO YOGYKRT Jl. Ringrod Utr Condong Ctur Yogykrt. Telp. 7 88 Fx 7-888 Website:
.triks & Vektor () t Kulih: ljbr Liner dn triks Semester Pendek T. / S Teknik Informtik Dosen Pengmpu: Heri Sismoro,.Kom. STIK IKO YOGYKRT Jl. Ringrod Utr Condong Ctur Yogykrt. Telp. 7 88 Fx 7-888 Website:
1. Pengertian Matriks
 BAB MATRIKS BAB MATRIKS. Pengertin Mtriks. Opersi Mtriks. Trnspose Sutu Mtriks. Kesmn Duh Buh Mtriks. Jenis-Jenis Mtriks. Trnsformsi Elementer 7. Rnk Mtriks . Pengertin Mtriks Mtriks dlh dftr ilngn yng
BAB MATRIKS BAB MATRIKS. Pengertin Mtriks. Opersi Mtriks. Trnspose Sutu Mtriks. Kesmn Duh Buh Mtriks. Jenis-Jenis Mtriks. Trnsformsi Elementer 7. Rnk Mtriks . Pengertin Mtriks Mtriks dlh dftr ilngn yng
A. PENGERTIAN B. DETERMINAN MATRIKS
 ATRIKS A. PENGERTIAN triks dlh sutu deretn elemen yng mementuk empt persegi pnjng, terdiri dri m ris dn n kolom. Elemen terseut dpt erentuk koefisien, ilngn tu simul. triks yng mempunyi m ris dn n kolom
ATRIKS A. PENGERTIAN triks dlh sutu deretn elemen yng mementuk empt persegi pnjng, terdiri dri m ris dn n kolom. Elemen terseut dpt erentuk koefisien, ilngn tu simul. triks yng mempunyi m ris dn n kolom
Matriks yang mempunyai jumlah baris sama dengan jumlah kolomnya disebut matriks bujur sangkar (square matrix). contoh :
 TRIKS. PENGERTIN triks dlh sutu deretn elemen yng mementuk empt persegi pnjng, terdiri dri m ris dn n kolom. Elemen terseut dpt erentuk koefisien, ilngn tu simul. triks yng mempunyi m ris dn n kolom diseut
TRIKS. PENGERTIN triks dlh sutu deretn elemen yng mementuk empt persegi pnjng, terdiri dri m ris dn n kolom. Elemen terseut dpt erentuk koefisien, ilngn tu simul. triks yng mempunyi m ris dn n kolom diseut
MATRIKS Definisi: Matriks Susunan persegi panjang dari bilangan-bilangan yang diatur dalam baris dan kolom. Matriks ditulis sebagai berikut (1)...
 MATRIKS Definisi: Mtriks Susunn persegi pnjng dri ilngn-ilngn yng ditur dlm ris dn kolom. Mtriks ditulis segi erikut ()... m... m... n... n......... mn Susunn dits diseut mtriks m x n kren memiliki m ris
MATRIKS Definisi: Mtriks Susunn persegi pnjng dri ilngn-ilngn yng ditur dlm ris dn kolom. Mtriks ditulis segi erikut ()... m... m... n... n......... mn Susunn dits diseut mtriks m x n kren memiliki m ris
MODUL 2 DETERMINAN DAN INVERS MATRIKS
 MODUL DETERMINN DN INVERS MTRIKS.. Determinn Definisi. (Determinn) Untuk setip mtriks berukurn n x n, yng dikitkn dengn sutu bilngn rel dengn sift tertentu dinmkn determinn, dengn notsi dri determinn mtriks
MODUL DETERMINN DN INVERS MTRIKS.. Determinn Definisi. (Determinn) Untuk setip mtriks berukurn n x n, yng dikitkn dengn sutu bilngn rel dengn sift tertentu dinmkn determinn, dengn notsi dri determinn mtriks
DETERMINAN DAN INVERS MATRIKS BLOK 2 2
 Buletin Ilmih Mth. Stt. dn Terpnny (Bimster) Volume 06, No. 3(2017), hl 193 202. DETERMINAN DAN INVERS MATRIKS BLOK 2 2 Ilhmsyh, Helmi, Frnsiskus Frn INTISARI Mtriks blok merupkn mtriks persegi yng diblok
Buletin Ilmih Mth. Stt. dn Terpnny (Bimster) Volume 06, No. 3(2017), hl 193 202. DETERMINAN DAN INVERS MATRIKS BLOK 2 2 Ilhmsyh, Helmi, Frnsiskus Frn INTISARI Mtriks blok merupkn mtriks persegi yng diblok
A x = b apakah solusi x
 MTRIKS INVERSI & SIFT-SIFTNY Bil, x, dlh sklr ilngn rel yng memenuhi x, mk x pil. Sekrng, untuk sistem persmn linier x pkh solusi x dpt diselesikn dengn x? Mtriks Identits Untuk sklr (rel numer dn ), mk.
MTRIKS INVERSI & SIFT-SIFTNY Bil, x, dlh sklr ilngn rel yng memenuhi x, mk x pil. Sekrng, untuk sistem persmn linier x pkh solusi x dpt diselesikn dengn x? Mtriks Identits Untuk sklr (rel numer dn ), mk.
METODE ALTERNATIF BARU UNTUK MENGHITUNG DETERMINAN MATRIKS ORDE 3 X 3
 METODE ALTERNATIF BARU UNTUK MENGHITUNG DETERMINAN MATRIKS ORDE 3 X 3 Glng Ismu Hndoko 1, M Ntsir 2, Sigit Sugirto 2 1 Mhsisw Progrm S1 Mtemtik 2 Dosen Jurusn Mtemtik Fkults Mtemtik dn Ilmu Pengethun Alm
METODE ALTERNATIF BARU UNTUK MENGHITUNG DETERMINAN MATRIKS ORDE 3 X 3 Glng Ismu Hndoko 1, M Ntsir 2, Sigit Sugirto 2 1 Mhsisw Progrm S1 Mtemtik 2 Dosen Jurusn Mtemtik Fkults Mtemtik dn Ilmu Pengethun Alm
Skew- Semifield dan Beberapa Sifatnya 1
 Skew- Semifield dn Beberp Siftny K r y t i Jurusn Pendidikn Mtemtik Fkults Mtemtik dn Ilmu Pengethun Alm Universits Negeri Yogykrt E-mil: ytiuny@yhoo.com Abstrk Sutu field ( lpngn ) F dlh struktur ljbr
Skew- Semifield dn Beberp Siftny K r y t i Jurusn Pendidikn Mtemtik Fkults Mtemtik dn Ilmu Pengethun Alm Universits Negeri Yogykrt E-mil: ytiuny@yhoo.com Abstrk Sutu field ( lpngn ) F dlh struktur ljbr
Matematika Lanjut 1. Onggo Wiryawan
 Mtemtik Lnjut 1 Onggo Wirywn Setip mtriks persegi tu bujur sngkr memiliki nili determinn Nili determinn sklr Mtriks Singulr= Mtriks yng determinnny bernili 0 Determinn & Invers - Onggo Wr 2 Mislkn A sutu
Mtemtik Lnjut 1 Onggo Wirywn Setip mtriks persegi tu bujur sngkr memiliki nili determinn Nili determinn sklr Mtriks Singulr= Mtriks yng determinnny bernili 0 Determinn & Invers - Onggo Wr 2 Mislkn A sutu
VEKTOR. 1. Pengertian Vektor adalah besaran yang memiliki besar (nilai) dan arah. Vektor merupakan sebuah ruas garis yang
 VEKTOR 1. Pengertin Vektor dlh besrn yng memiliki besr (nili dn rh. Vektor merupkn sebuh rus gris yng P berrh dn memiliki pnjng. Pnjng rus gris tersebut dlh pnjng vektor. Rus gris dri titik P dn berujung
VEKTOR 1. Pengertin Vektor dlh besrn yng memiliki besr (nili dn rh. Vektor merupkn sebuh rus gris yng P berrh dn memiliki pnjng. Pnjng rus gris tersebut dlh pnjng vektor. Rus gris dri titik P dn berujung
1) BENTUK UMUM DAN BAGIAN-BAGIAN PERSAMAAN KUADRAT Bentuk umum persamaan kuadrat adalah seperti di bawah ini:
 ) BENTUK UMUM DAN BAGIAN-BAGIAN PERSAMAAN KUADRAT Bentuk umum persmn kudrt dlh seperti di bwh ini: b c dengn, b, c bilngn dn riil Dimn, disebut sebgi koefisien dri b disebut sebgi koefisien dri c disebut
) BENTUK UMUM DAN BAGIAN-BAGIAN PERSAMAAN KUADRAT Bentuk umum persmn kudrt dlh seperti di bwh ini: b c dengn, b, c bilngn dn riil Dimn, disebut sebgi koefisien dri b disebut sebgi koefisien dri c disebut
Sistem Persamaan Linier
 b I Sistem Persmn Linier I Sistem Persmn Linier TUJUN PEMELJRN: Mhsisw memhmi konsep-konsep tentng sistem persmn linier, eksistensi dn keunikn sistem persmn linier, keunikn sistem persmn linier homogen,
b I Sistem Persmn Linier I Sistem Persmn Linier TUJUN PEMELJRN: Mhsisw memhmi konsep-konsep tentng sistem persmn linier, eksistensi dn keunikn sistem persmn linier, keunikn sistem persmn linier homogen,
Sistem Persamaan Linear Bagian 1
 Sistem Persmn Liner Bgin. SISTEM PERSAMAAN LINEAR PENGANTAR Dlm bgin ini kn kit perkenlkn istilh dsr dn kit bhs sebuh metode untuk memechkn sistem-sistem persmn liner. Sebuh gris dlm bidng xy secr ljbr
Sistem Persmn Liner Bgin. SISTEM PERSAMAAN LINEAR PENGANTAR Dlm bgin ini kn kit perkenlkn istilh dsr dn kit bhs sebuh metode untuk memechkn sistem-sistem persmn liner. Sebuh gris dlm bidng xy secr ljbr
LIMIT FUNGSI DAN KEKONTINUAN
 LIMIT FUNGSI DAN KEKONTINUAN RANGKUMAN MATERI Sebelum memsuki mteri, perhtikn himpunn-himpunn berikut: ) Himpunn bilngn sli:,,,4,5,.... b) Himpunn bilngn bult:...,,,0,,,.... p c) Himpunn bilngn rsionl:
LIMIT FUNGSI DAN KEKONTINUAN RANGKUMAN MATERI Sebelum memsuki mteri, perhtikn himpunn-himpunn berikut: ) Himpunn bilngn sli:,,,4,5,.... b) Himpunn bilngn bult:...,,,0,,,.... p c) Himpunn bilngn rsionl:
VEKTOR. Adri Priadana. ilkomadri.com
 VEKTOR Adri Pridn ilkomdri.com Pengertin Dlm Fisik dikenl du buh besrn, yitu 1. Besrn Sklr. Besrn Vektor Pengertin Besrn Sklr dlh sutu besrn yng hny mempunyi nili dn dinytkn dengn sutu bilngn tunggl diserti
VEKTOR Adri Pridn ilkomdri.com Pengertin Dlm Fisik dikenl du buh besrn, yitu 1. Besrn Sklr. Besrn Vektor Pengertin Besrn Sklr dlh sutu besrn yng hny mempunyi nili dn dinytkn dengn sutu bilngn tunggl diserti
1. Introduction. Aljabar Linear dan Matriks Semester Pendek TA 2009/2010 S1 Teknik Informatika. Mata Kuliah: Dosen Pengampu: Heri Sismoro, M.Kom.
 1. Introduction Mt Kulih: Aljbr Liner dn Mtriks Semester Pendek TA 9/1 S1 Teknik Informtik Dosen Pengmpu: Heri Sismoro, M.Kom. STMIK AMIKOM YOGYAKARTA Jl. Ringrod Utr Condong Ctur Yogykrt. Telp. 74 8841
1. Introduction Mt Kulih: Aljbr Liner dn Mtriks Semester Pendek TA 9/1 S1 Teknik Informtik Dosen Pengmpu: Heri Sismoro, M.Kom. STMIK AMIKOM YOGYAKARTA Jl. Ringrod Utr Condong Ctur Yogykrt. Telp. 74 8841
MATRIKS A. Pengertian, Notasi dan Bagian Dalam Matriks
 MATRIKS A. Pengertin, Notsi dn Bgin Dlm Mtriks Dlm kehidupn sehri-hri kit sering menemui dt tu informsi dlm entuk tel, seperti tel pertndingn sepkol, tel sensi kels, tel hrg tiket keret pi dn seginy..
MATRIKS A. Pengertin, Notsi dn Bgin Dlm Mtriks Dlm kehidupn sehri-hri kit sering menemui dt tu informsi dlm entuk tel, seperti tel pertndingn sepkol, tel sensi kels, tel hrg tiket keret pi dn seginy..
didefinisikan sebagai bilangan yang dapat ditulis dengan b
 1 PENDAHULUAN 1.1 Sistem Bilngn Rel Untuk mempeljri klkulus perlu memhmi hsn tentng system ilngn rel, kren klkulus didsrkn pd system ilngn rel dn siftsiftny. Sistem ilngn yng pling sederhn dlh ilngn sli,
1 PENDAHULUAN 1.1 Sistem Bilngn Rel Untuk mempeljri klkulus perlu memhmi hsn tentng system ilngn rel, kren klkulus didsrkn pd system ilngn rel dn siftsiftny. Sistem ilngn yng pling sederhn dlh ilngn sli,
BAB I PENDAHULUAN. A. Latar belakang
 BAB I PENDAHULUAN A. Ltr belkng Bnyk orng yng bernggpn bhw Mtemtik itu rumit, kren lsn itulh bnyk orng yng menghindri Mtemtik. Pdhl Mtemtik dpt kit jumpi di dlm kehidupn sehri-hri, dn mu tidk mu kit psti
BAB I PENDAHULUAN A. Ltr belkng Bnyk orng yng bernggpn bhw Mtemtik itu rumit, kren lsn itulh bnyk orng yng menghindri Mtemtik. Pdhl Mtemtik dpt kit jumpi di dlm kehidupn sehri-hri, dn mu tidk mu kit psti
Pengertian Matriks. B. Notasi Matriks. a 21 adalah elemen baris 2 kolom 1. Banyaknya baris : Banyaknya kolom : Ordo Matrik :
 MATRIKS Segi gmrn wl mengeni mteri mtriks mri kit ermti urin erikut ini. Dikethui dt hsil penjuln tiket penerngn tujun Medn dn Sury dri seuh gen tiket selm empt hri erturut-turut disjikn dlm tel erikut.
MATRIKS Segi gmrn wl mengeni mteri mtriks mri kit ermti urin erikut ini. Dikethui dt hsil penjuln tiket penerngn tujun Medn dn Sury dri seuh gen tiket selm empt hri erturut-turut disjikn dlm tel erikut.
Bilangan. Bilangan Nol. Bilangan Bulat (Z )
 Bilngn Bilngn Asli (N) (,2,, ) Bilngn Nol (0) Bilngn Negtif (,, 2, ) Bilngn Bult (Z ) Bilngn Pechn ( 2 ; 5 ; 5%; 6,82; ) 7 A. Bilngn Asli (N) Bilngn Asli dlh himpunn bilngn bult positif (nol tidk termsuk).
Bilngn Bilngn Asli (N) (,2,, ) Bilngn Nol (0) Bilngn Negtif (,, 2, ) Bilngn Bult (Z ) Bilngn Pechn ( 2 ; 5 ; 5%; 6,82; ) 7 A. Bilngn Asli (N) Bilngn Asli dlh himpunn bilngn bult positif (nol tidk termsuk).
NILAI EIGEN DAN VEKTOR EIGEN
 Pert 9 (mengjrkomputer.wordpress.com) NILAI EIGEN DAN VEKTOR EIGEN 9. Definisi Sebuh mtriks bujur sngkr dengn orde n n mislkn A, dn sebuh vektor kolom X. Vektor X dlh vektor dlm rung Euklidin n R yng dihubungkn
Pert 9 (mengjrkomputer.wordpress.com) NILAI EIGEN DAN VEKTOR EIGEN 9. Definisi Sebuh mtriks bujur sngkr dengn orde n n mislkn A, dn sebuh vektor kolom X. Vektor X dlh vektor dlm rung Euklidin n R yng dihubungkn
PENYELESAIAN SISTEM PERSAMAAN LINEAR DENGAN MENGGUNAKAN DETERMINAN (ATURAN CRAMER)
 PENYELESAIAN SISTEM PERSAMAAN LINEAR DENGAN MENGGUNAKAN DETERMINAN (ATURAN CRAMER) Dikethui system Persmn Linier x+ x + x = x+ x + x = x+ x + x = dlm entuk mtriks x x x Penyelesin Dengn Aturn Crmer dlh
PENYELESAIAN SISTEM PERSAMAAN LINEAR DENGAN MENGGUNAKAN DETERMINAN (ATURAN CRAMER) Dikethui system Persmn Linier x+ x + x = x+ x + x = x+ x + x = dlm entuk mtriks x x x Penyelesin Dengn Aturn Crmer dlh
Integral Tak Wajar. Ayundyah Kesumawati. March 25, Prodi Statistika FMIPA-UII
 Kesumwti Prodi Sttistik FMIPA-UII Mrch 25, 205 Sutu integrl tertentu b f (x)dx () diktkn wjr jik i memenuhi du syrt berikut: i. Bts integrsi dn b merupkn bilngn berhingg ii. fungsi f (x) terbts pd intervl
Kesumwti Prodi Sttistik FMIPA-UII Mrch 25, 205 Sutu integrl tertentu b f (x)dx () diktkn wjr jik i memenuhi du syrt berikut: i. Bts integrsi dn b merupkn bilngn berhingg ii. fungsi f (x) terbts pd intervl
MATRIKS. Menggunakan konsep matriks, vektor, dan transformasi dalam pemecahan masalah.
 MATRIKS Stndr Kompetensi : Menggunkn konsep mtriks, vektor, dn trnsformsi dlm pemechn mslh Kompetensi Dsr : Menggunkn sift-sift dn opersi mtriks untuk menentukn invers mtriks persegi Menggunkn determinn
MATRIKS Stndr Kompetensi : Menggunkn konsep mtriks, vektor, dn trnsformsi dlm pemechn mslh Kompetensi Dsr : Menggunkn sift-sift dn opersi mtriks untuk menentukn invers mtriks persegi Menggunkn determinn
Modul 1. Pendahuluan
 Modul Pendhulun.. Pengertin Mtriks Definisi. (Pengertin Mtriks) Mtriks didefinisikn sebgi sutu susunn bilngn berbentuk segiempt. Bilngnbilngn yng terdpt dlm susunn itu disebut elemen mtriks tersebut. Secr
Modul Pendhulun.. Pengertin Mtriks Definisi. (Pengertin Mtriks) Mtriks didefinisikn sebgi sutu susunn bilngn berbentuk segiempt. Bilngnbilngn yng terdpt dlm susunn itu disebut elemen mtriks tersebut. Secr
Matriks. Bab II. Motivasi. Tujuan Pembelajaran
 Mtriks Bb II Mtriks Sumber: Ensiklopedi Peljr, 999 Motivsi Secr umum mtriks merupkn sutu dftr yng berisi ngkngk dn ditulis di dlm tnd kurung. Dftr-dftr yng dpt ditulis dlm bentuk mtriks, mislny perolehn
Mtriks Bb II Mtriks Sumber: Ensiklopedi Peljr, 999 Motivsi Secr umum mtriks merupkn sutu dftr yng berisi ngkngk dn ditulis di dlm tnd kurung. Dftr-dftr yng dpt ditulis dlm bentuk mtriks, mislny perolehn
Catatan Kuliah 2 Matematika Ekonomi Memahami dan Menganalisa Aljabar Matriks (2)
 Cttn Kulih Mtemtik Ekonomi Memhmi dn Mengnlis ljbr Mtriks (). Vektor dn kr Krkteristik pbil dlh mtriks berordo n n dn X dlh vector n, kn dicri sklr λ R yng memenuhi persmn : X λ X tu ( λi) X gr X (solusiny
Cttn Kulih Mtemtik Ekonomi Memhmi dn Mengnlis ljbr Mtriks (). Vektor dn kr Krkteristik pbil dlh mtriks berordo n n dn X dlh vector n, kn dicri sklr λ R yng memenuhi persmn : X λ X tu ( λi) X gr X (solusiny
1. Matriks dan Jenisnya Definisi: Matrik A berukuran m x n ialah suatu susunan angka dalam persegi empat ukuran m x n, sebagai berikut:
 triks dn opersiny by yudiri ATRIKS DAN OPERASINYA. triks dn Jenisny Definisi: trik A berukurn x n ilh sutu susunn ngk dl persegi ept ukurn x n, sebgi berikut: A = n n n triks berukurn (ordo) x n. tu A
triks dn opersiny by yudiri ATRIKS DAN OPERASINYA. triks dn Jenisny Definisi: trik A berukurn x n ilh sutu susunn ngk dl persegi ept ukurn x n, sebgi berikut: A = n n n triks berukurn (ordo) x n. tu A
ALJABAR LINIER _1 Matrik. Ira Prasetyaningrum
 LJR LINIER _ Mtrik Ir Prsetyningrum DEFINISI MTRIKS pkh yng dimksud dengn Mtriks? kumpuln ilngn yng disjikn secr tertur dlm ris dn kolom yng mementuk sutu persegi pnjng, sert termut dintr sepsng tnd kurung.
LJR LINIER _ Mtrik Ir Prsetyningrum DEFINISI MTRIKS pkh yng dimksud dengn Mtriks? kumpuln ilngn yng disjikn secr tertur dlm ris dn kolom yng mementuk sutu persegi pnjng, sert termut dintr sepsng tnd kurung.
Vektor di R 2 dan R 3
 Vektor di R dn R Pengertin Vektor dlh besrn yng mempunyi besr dn rh Vektor digmbrkn oleh rus gris yng dilengkpi dengn nk pnh vektor dimuli dri titik wl (initil point) dn dikhiri oleh titik khir (terminl
Vektor di R dn R Pengertin Vektor dlh besrn yng mempunyi besr dn rh Vektor digmbrkn oleh rus gris yng dilengkpi dengn nk pnh vektor dimuli dri titik wl (initil point) dn dikhiri oleh titik khir (terminl
Hands Out Mata Kuliah: Aljabar Matriks (2 SKS) Dosen: Dra. Hj Ade Rohayati, M. Pd.
 Hnds Out Mt Kulih: Aljbr Mtriks ( SKS) Dosen: Dr. Hj Ade Rohyti, M. Pd. No. Indiktor Urin Mteri. menyebutkn definisi mtriks.. membut beberp contoh mtriks dengn menggunkn notsi yng tept.. menentukn ordo
Hnds Out Mt Kulih: Aljbr Mtriks ( SKS) Dosen: Dr. Hj Ade Rohyti, M. Pd. No. Indiktor Urin Mteri. menyebutkn definisi mtriks.. membut beberp contoh mtriks dengn menggunkn notsi yng tept.. menentukn ordo
Handout Mata Kuliah: Aljabar Matriks (2 SKS) Dosen: Dra. Hj Ade Rohayati, M. Pd.
 Hndout Mt Kulih: Aljbr Mtriks ( SKS) Dosen: Dr. Hj Ade Rohyti, M. Pd. No. Indiktor Urin Mteri. menyebutkn definisi mtriks.. membut beberp contoh mtriks dengn menggunkn notsi yng tept.. menentukn ordo dri
Hndout Mt Kulih: Aljbr Mtriks ( SKS) Dosen: Dr. Hj Ade Rohyti, M. Pd. No. Indiktor Urin Mteri. menyebutkn definisi mtriks.. membut beberp contoh mtriks dengn menggunkn notsi yng tept.. menentukn ordo dri
r x = 0. Koefisien-koefisien persamaan yang dihasilkan adalah analitik pada x = 0. Jadi dapat kita gunakan metode deret pangkat.
 Husn Arifh,M.Sc : Persmn Legendre Emil : husnrifh@uny.c.id Persmn diferensil Legendre (1) 1 x 2 y 2xy + n n + 1 y = 0 Prmeter n pd (1) dlh bilngn rill yng diberikn. Setip penyelesin dri (1) dinmkn fungsi
Husn Arifh,M.Sc : Persmn Legendre Emil : husnrifh@uny.c.id Persmn diferensil Legendre (1) 1 x 2 y 2xy + n n + 1 y = 0 Prmeter n pd (1) dlh bilngn rill yng diberikn. Setip penyelesin dri (1) dinmkn fungsi
matematika K-13 TEOREMA FAKTOR DAN OPERASI AKAR K e l a s
 K-3 mtemtik K e l s XI TEOREMA FAKTOR DAN OPERASI AKAR Tujun Pemeljrn Setelh mempeljri mteri ini, kmu dihrpkn memiliki kemmpun erikut.. Memhmi teorem fktor.. Menentukn kr dn fktor liner suku nyk dengn
K-3 mtemtik K e l s XI TEOREMA FAKTOR DAN OPERASI AKAR Tujun Pemeljrn Setelh mempeljri mteri ini, kmu dihrpkn memiliki kemmpun erikut.. Memhmi teorem fktor.. Menentukn kr dn fktor liner suku nyk dengn
III. Bab. Matriks. Di unduh dari: (www.bukupaket.com) Sumber buku : (bse.kemdikbud.go.id)
 Bb III Mtriks 79 Tujun Pembeljrn Setelh mempeljri bb ini, dihrpkn klin dpt. menjelskn ciri sutu mtriks;. menuliskn informsi dlm bentuk mtriks;. melkukn opersi ljbr ts du mtriks; 4. menentukn determinn
Bb III Mtriks 79 Tujun Pembeljrn Setelh mempeljri bb ini, dihrpkn klin dpt. menjelskn ciri sutu mtriks;. menuliskn informsi dlm bentuk mtriks;. melkukn opersi ljbr ts du mtriks; 4. menentukn determinn
MUH1G3/ MATRIKS DAN RUANG VEKTOR
 MUHG3/ MATRIKS DAN RUANG VEKTOR TIM DOSEN 3 Sistem Persmn Liner Sistem Persmn Liner Su Pokok Bhsn Pendhulun Solusi SPL dengn OBE Solusi SPL dengn Invers mtriks dn Aturn Crmmer SPL Homogen Beerp Apliksi
MUHG3/ MATRIKS DAN RUANG VEKTOR TIM DOSEN 3 Sistem Persmn Liner Sistem Persmn Liner Su Pokok Bhsn Pendhulun Solusi SPL dengn OBE Solusi SPL dengn Invers mtriks dn Aturn Crmmer SPL Homogen Beerp Apliksi
2. Paman mempunyai sebidang tanah yang luasnya 5 hektar. Tanah itu dibagikan kepada 3. Luas tanah yang diterima oleh mereka masing-masing = 5 :3 1
 . Hitunglh 7 5. : b. 5 : c. 8 : 6 d. 8 9 7 7 7 5 77 77 77. : c. 8 : 6 : 6 6 9 9 9 6 54 8 40 7 b. 5: 5 d. 4: 4: 4 6 8 7 95 Husein Tmpoms, Rumus-rumus Dsr Mtemtik 4 :. Pmn mempunyi sebidng tnh yng lusny
. Hitunglh 7 5. : b. 5 : c. 8 : 6 d. 8 9 7 7 7 5 77 77 77. : c. 8 : 6 : 6 6 9 9 9 6 54 8 40 7 b. 5: 5 d. 4: 4: 4 6 8 7 95 Husein Tmpoms, Rumus-rumus Dsr Mtemtik 4 :. Pmn mempunyi sebidng tnh yng lusny
Integral Kompleks (Bagian Kesatu)
 Integrl Kompleks (Bgin Kestu) Supm Jurusn Mtemtik, FMIPA UGM Yogykrt 55281, INDONESIA Emil:mspomo@yhoo.com, supm@ugm.c.id (Pertemun Minggu XI) Outline 1 Fungsi Bernili Kompleks 2 Lintsn tu Kontur 3 Integrl
Integrl Kompleks (Bgin Kestu) Supm Jurusn Mtemtik, FMIPA UGM Yogykrt 55281, INDONESIA Emil:mspomo@yhoo.com, supm@ugm.c.id (Pertemun Minggu XI) Outline 1 Fungsi Bernili Kompleks 2 Lintsn tu Kontur 3 Integrl
CHAPTER 1 EXPONENTS, ROOTS, AND LOGARITHMS
 CHAPTER EXPONENTS, ROOTS, AND LOGARITHMS Indiktor (penunjuk): Mengubh bentuk pngkt negtif ke pngkt positif dn seblikny. (4 jp) A. EXPONENTS. Definition (ketentun): Positive Integers Exponents n = x x...
CHAPTER EXPONENTS, ROOTS, AND LOGARITHMS Indiktor (penunjuk): Mengubh bentuk pngkt negtif ke pngkt positif dn seblikny. (4 jp) A. EXPONENTS. Definition (ketentun): Positive Integers Exponents n = x x...
Matriks. Modul 1 PENDAHULUAN
 Modul 1 Mtriks Dr. Whyu Widyt, M.Ec. S PENDAHULUAN ering kli kit berhdpn dengn mslh mencri solusi dri sistem persmn linier, tu mslh optimissi sutu fungsi dengn jumlh vribel yng bnyk. Mslh-mslh tersebut
Modul 1 Mtriks Dr. Whyu Widyt, M.Ec. S PENDAHULUAN ering kli kit berhdpn dengn mslh mencri solusi dri sistem persmn linier, tu mslh optimissi sutu fungsi dengn jumlh vribel yng bnyk. Mslh-mslh tersebut
BAB II LANDASAN TEORI. himpunan bilangan bulat dan diberi simbol dengan hurup besar B. Anggota
 BB II LNDSN EORI. Bilngn Bult Himpunn bilngn bilngn {..,-,-,-,,,,,..} disebut himpunn bilngn bult dn diberi simbol dengn hurup besr B. nggot nggot dri {-,-,-,..} disebut bilngn bilngn bult negtif. Definisi
BB II LNDSN EORI. Bilngn Bult Himpunn bilngn bilngn {..,-,-,-,,,,,..} disebut himpunn bilngn bult dn diberi simbol dengn hurup besr B. nggot nggot dri {-,-,-,..} disebut bilngn bilngn bult negtif. Definisi
b. Notasi vektor : - Vektor A dinotasikan a atau a atau PQ - Panjang vektor a dinotasikan a atau PQ
 BAB 4 VEKTOR Stndr Kompetensi: 3. Menggunkn konsep mtriks, vektor, dn trnsformsi Kompetensi Dsr: 3.4 Menggunkn sift-sift dn opersi ljbr vktor dlm pemechn mslh 3.5 Menggunkn sift-sift dn opersi perklin
BAB 4 VEKTOR Stndr Kompetensi: 3. Menggunkn konsep mtriks, vektor, dn trnsformsi Kompetensi Dsr: 3.4 Menggunkn sift-sift dn opersi ljbr vktor dlm pemechn mslh 3.5 Menggunkn sift-sift dn opersi perklin
TURUNAN FUNGSI. LA - WB (Lembar Aktivitas Warga Belajar) MATEMATIKA PAKET C TINGKAT VI DERAJAT MAHIR 2 SETARA KELAS XI
 LA - WB (Lembr Aktivits Wrg Beljr) TURUNAN FUNGSI Oleh: Hj. ITA YULIANA, S.Pd, M.Pd MATEMATIKA PAKET C TINGKAT VI DERAJAT MAHIR 2 SETARA KELAS XI Creted By It Yulin 33 Turunn Fungsi Kompetensi Dsr 1. Menggunkn
LA - WB (Lembr Aktivits Wrg Beljr) TURUNAN FUNGSI Oleh: Hj. ITA YULIANA, S.Pd, M.Pd MATEMATIKA PAKET C TINGKAT VI DERAJAT MAHIR 2 SETARA KELAS XI Creted By It Yulin 33 Turunn Fungsi Kompetensi Dsr 1. Menggunkn
RUANG VEKTOR (lanjut..)
 RUANG VEKTOR (Vector Spce) dn Rung Bgin (Subspce) 8/0/009 budi murtiys ums surkrt RUANG VEKTOR (VECTOR SPACE) Dikethui himpunn V dengn u, v, w V dn opersi i(+)b berlku dintr nggot-nggot t V. Dikethui Field
RUANG VEKTOR (Vector Spce) dn Rung Bgin (Subspce) 8/0/009 budi murtiys ums surkrt RUANG VEKTOR (VECTOR SPACE) Dikethui himpunn V dengn u, v, w V dn opersi i(+)b berlku dintr nggot-nggot t V. Dikethui Field
A. Kompetensi Dasar : Menyelesaikan sistem persamaan linear. B. Materi : 1. Sistem Persamaan Linear dan Matriks 2. Determinan
 (Oleh: Winit Sulndri, M.Si) A. Kompetensi Dsr : Menyelesikn sistem persmn liner B. Mteri :. Sistem Persmn Liner dn Mtriks. Determinn C. Indiktor :. Mendefinisikn persmn liner dn sistem persmn liner. Mengenl
(Oleh: Winit Sulndri, M.Si) A. Kompetensi Dsr : Menyelesikn sistem persmn liner B. Mteri :. Sistem Persmn Liner dn Mtriks. Determinn C. Indiktor :. Mendefinisikn persmn liner dn sistem persmn liner. Mengenl
DAFTAR ISI. DAFTAR ISI... iii
 DAFTAR ISI DAFTAR ISI... iii BAB I MATRIKS DAN OPERASINYA.... Konsepsi Mtriks.... Opersi Aljbr Mtriks.... Trnspose dri Sutu Mtriks... 5. Beberp Jenis Mtriks Khusus... 5.5 Trnsformsi Elementer... 8.6 Rnk
DAFTAR ISI DAFTAR ISI... iii BAB I MATRIKS DAN OPERASINYA.... Konsepsi Mtriks.... Opersi Aljbr Mtriks.... Trnspose dri Sutu Mtriks... 5. Beberp Jenis Mtriks Khusus... 5.5 Trnsformsi Elementer... 8.6 Rnk
SISTEM BILANGAN REAL. Purnami E. Soewardi. Direktorat Pembinaan Tendik Dikdasmen Ditjen GTK Kementerian Pendidikan dan Kebudayaan
 SISTEM BILANGAN REAL Purnmi E. Soewrdi Direktort Peminn Tendik Dikdsmen Ditjen GTK Kementerin Pendidikn dn Keudyn Himpunn Bilngn Asli (N) Bilngn sli dlh ilngn yng pertm kli dikenl dn digunkn oleh mnusi
SISTEM BILANGAN REAL Purnmi E. Soewrdi Direktort Peminn Tendik Dikdsmen Ditjen GTK Kementerin Pendidikn dn Keudyn Himpunn Bilngn Asli (N) Bilngn sli dlh ilngn yng pertm kli dikenl dn digunkn oleh mnusi
3. LIMIT DAN KEKONTINUAN
 3. LIMIT DAN KEKONTINUAN 1 3.1 Limit Fungsi di Stu Titik Pengertin it secr intuisi Perhtikn ungsi 1 1 Fungsi dits tidk terdeinisi di =1, kren di titik tersebut berbentuk 0/0. Tpi msih bis ditnykn berp
3. LIMIT DAN KEKONTINUAN 1 3.1 Limit Fungsi di Stu Titik Pengertin it secr intuisi Perhtikn ungsi 1 1 Fungsi dits tidk terdeinisi di =1, kren di titik tersebut berbentuk 0/0. Tpi msih bis ditnykn berp
Modul PELATIHAN GUIDE MATLAB UNTUK PEMBUATAN ANTARMUKA PEMBELAJARAN PERSAMAAN MATEMATIKA DAN GRAFIKNYA
 Modul PELATIHAN GUIDE MATLAB UNTUK PEMBUATAN ANTARMUKA PEMBELAJARAN PERSAMAAN MATEMATIKA DAN GRAFIKNYA PENGENALAN PROGRAM MATLAB MENGGUNAKAN OPERASI OPERASI MATRIKS Oleh : Nur Hdi Wrnto, S.Si Lbortorium
Modul PELATIHAN GUIDE MATLAB UNTUK PEMBUATAN ANTARMUKA PEMBELAJARAN PERSAMAAN MATEMATIKA DAN GRAFIKNYA PENGENALAN PROGRAM MATLAB MENGGUNAKAN OPERASI OPERASI MATRIKS Oleh : Nur Hdi Wrnto, S.Si Lbortorium
6. Himpunan Fungsi Ortogonal
 6. Himpunn Fungsi Ortogonl Mislkn f periodik dengn periode, dn mulus bgin demi bgin pd [ π, π]. Jik S f N (θ) = N n= N c ne inθ, n =,, 2,..., dlh jumlh prsil dri deret Fourier f, mk kit telh menunjukkn
6. Himpunn Fungsi Ortogonl Mislkn f periodik dengn periode, dn mulus bgin demi bgin pd [ π, π]. Jik S f N (θ) = N n= N c ne inθ, n =,, 2,..., dlh jumlh prsil dri deret Fourier f, mk kit telh menunjukkn
3. LIMIT DAN KEKONTINUAN. INF228 Kalkulus Dasar
 . LIMIT DAN KEKONTINUAN INF8 Klkulus Dsr . Limit Fungsi di Stu Titik Pengertin it secr intuisi Perhtikn ungsi Fungsi dits tidk terdeinisi di =, kren di titik tersebut berbentuk 0/0. Tpi msih bis ditnykn
. LIMIT DAN KEKONTINUAN INF8 Klkulus Dsr . Limit Fungsi di Stu Titik Pengertin it secr intuisi Perhtikn ungsi Fungsi dits tidk terdeinisi di =, kren di titik tersebut berbentuk 0/0. Tpi msih bis ditnykn
CONTOH SOLUSI BEBERAPA SOAL OLIMPIADE MATEMATIKA Oleh: Wiworo, S.Si, M.M. 3. Untuk k 2 didefinisikan bahwa a
 CONTOH SOLUSI BEBERAPA SOAL OLIMPIADE MATEMATIKA Oleh: Wiworo, S.Si, M.M. Dikethui bhw,. Untuk k didefinisikn bhw k k k. Tentukn jumlh tk hingg dri. Kit mislkn S S. Dengn demikin kit dpt menuliskn Kedu
CONTOH SOLUSI BEBERAPA SOAL OLIMPIADE MATEMATIKA Oleh: Wiworo, S.Si, M.M. Dikethui bhw,. Untuk k didefinisikn bhw k k k. Tentukn jumlh tk hingg dri. Kit mislkn S S. Dengn demikin kit dpt menuliskn Kedu
15. INTEGRAL SEBAGAI LIMIT
 15. INTEGRAL SEBAGAI LIMIT 15.1 Jumlh Riemnn Dlm kulih Klkulus pd thun pertm, integrl Riemnn bisny diperkenlkn sebgi limit dri jumlh Riemnn, tidk mellui integrl Riemnn ts dn integrl Riemnn bwh. Hl ini
15. INTEGRAL SEBAGAI LIMIT 15.1 Jumlh Riemnn Dlm kulih Klkulus pd thun pertm, integrl Riemnn bisny diperkenlkn sebgi limit dri jumlh Riemnn, tidk mellui integrl Riemnn ts dn integrl Riemnn bwh. Hl ini
Aljabar Linier & Matriks. Tatap Muka 3
 Aljbr Linier & Mtriks Ttp Muk Eliminsi Guss-Jordn Sistem persmn linier dengn n vribel dn m persmn secr umum dinytkn sbg: Sistem persmn linier tsb dpt dinytkn dlm bentuk mtriks sbb: A x X = b dengn A dlh
Aljbr Linier & Mtriks Ttp Muk Eliminsi Guss-Jordn Sistem persmn linier dengn n vribel dn m persmn secr umum dinytkn sbg: Sistem persmn linier tsb dpt dinytkn dlm bentuk mtriks sbb: A x X = b dengn A dlh
PELATIHAN INSTRUKTUR/PENGEMBANG SMU TANGGAL 28 JULI s.d. 10 AGUSTUS 2003 SUKU BANYAK. Oleh: Fadjar Shadiq, M.App.Sc.
 PELATIHAN INSTRUKTUR/PENGEMBANG SMU TANGGAL 8 JULI s.d. 0 AGUSTUS 00 SUKU BANYAK Oleh: Fdjr Shdiq, M.App.Sc. DEPARTEMEN PENDIDIKAN NASIONAL DIREKTORAT JENDERAL PENDIDIKAN DASAR DAN MENENGAH PUSAT PENGEMBANGAN
PELATIHAN INSTRUKTUR/PENGEMBANG SMU TANGGAL 8 JULI s.d. 0 AGUSTUS 00 SUKU BANYAK Oleh: Fdjr Shdiq, M.App.Sc. DEPARTEMEN PENDIDIKAN NASIONAL DIREKTORAT JENDERAL PENDIDIKAN DASAR DAN MENENGAH PUSAT PENGEMBANGAN
Aljabar Linear. Pertemuan 12_14 Aljabar Vektor (Perkalian vektor)
 Aljbr Liner Pertemun 12_14 Aljbr Vektor (Perklin vektor) Pembhsn Perklin vektor dengn sklr Rung vektor Perklin Vektor dengn Vektor: Dot Product - Model dot product - Sift dot product Pendhulun Penmbhn
Aljbr Liner Pertemun 12_14 Aljbr Vektor (Perklin vektor) Pembhsn Perklin vektor dengn sklr Rung vektor Perklin Vektor dengn Vektor: Dot Product - Model dot product - Sift dot product Pendhulun Penmbhn
Bab. Matriks. A. Pengertian dan Jenis. Matriks. B. Operasi Aljabar pada. Matriks
 Bb IV Sumber: www.gerrysckes.com Mtriks Pd bb sebelumny, And telh mempeljri persmn dn pertidksmn. Bentuk persmn dpt diubh ke bentuk mtriks untuk mempermudh dlm perhitungn, mislny pliksi berikut ini. Ti,
Bb IV Sumber: www.gerrysckes.com Mtriks Pd bb sebelumny, And telh mempeljri persmn dn pertidksmn. Bentuk persmn dpt diubh ke bentuk mtriks untuk mempermudh dlm perhitungn, mislny pliksi berikut ini. Ti,
LIMIT DAN KONTINUITAS
 LIMIT DAN KONTINUITAS Limit Fungsi di Stu Titik Pengertin it secr intuisi Perhtikn ungsi Fungsi dits tidk terdeinisi di =, kren di titik tersebut berbentuk 0/0. Tpi msih bis ditnykn berp nili jik mendekti
LIMIT DAN KONTINUITAS Limit Fungsi di Stu Titik Pengertin it secr intuisi Perhtikn ungsi Fungsi dits tidk terdeinisi di =, kren di titik tersebut berbentuk 0/0. Tpi msih bis ditnykn berp nili jik mendekti
PROBLEM SOLVING TERKAIT DENGAN KELAS X SEMESTER 1 PADA STANDAR KOMPETENSI (SK) 1.
 PROLEM SOLVING TERKIT DENGN KELS X SEMESTER PD STNDR KOMPETENSI (SK). LJR Memechkn mslh yng berkitn dengn bentuk pngkt, kr, dn logritm Oleh: Sigit Tri Guntoro. Du orng berselisih mengeni bnykny psngn bilngn
PROLEM SOLVING TERKIT DENGN KELS X SEMESTER PD STNDR KOMPETENSI (SK). LJR Memechkn mslh yng berkitn dengn bentuk pngkt, kr, dn logritm Oleh: Sigit Tri Guntoro. Du orng berselisih mengeni bnykny psngn bilngn
3. LIMIT DAN KEKONTINUAN
 . LIMIT DAN KEKONTINUAN . Limit Fungsi di Stu Titik Pengertin it secr intuisi Perhtikn ungsi Fungsi dits tidk terdeinisi di, kren di titik tersebut berbentuk 0/0. Tpi msih bis ditnykn berp nili jik mendekti
. LIMIT DAN KEKONTINUAN . Limit Fungsi di Stu Titik Pengertin it secr intuisi Perhtikn ungsi Fungsi dits tidk terdeinisi di, kren di titik tersebut berbentuk 0/0. Tpi msih bis ditnykn berp nili jik mendekti
BAB I PENDAHULUAN. Sebuah sistem sebarang yang terdiri dari m persamaan linear dengan n M M M M M
 BAB I PENDAHUUAN Sebuh sistem sebrng yng teriri ri m persmn liner engn n bilngn tk ikethui kn ituliskn sebgi : x + x +... + n x n = b x + x +... + n x n = b n x + n x +... + nn x n = b n imn x, x,...,
BAB I PENDAHUUAN Sebuh sistem sebrng yng teriri ri m persmn liner engn n bilngn tk ikethui kn ituliskn sebgi : x + x +... + n x n = b x + x +... + n x n = b n x + n x +... + nn x n = b n imn x, x,...,
BAB 1 PERSAMAAN DAN PERTIDAKSAMAAN. Standar Kompetensi Mahasiswa memahami konsep dasar sistem bilangan real (R)
 BAB PERSAMAAN DAN PERTIDAKSAMAAN Stndr Kompetensi Mhsisw memhmi konsep dsr sistem bilngn rel (R) sebgi semest untuk menentukn selesin persmn dn pertidksmn, dpt mengembngkn bentuk persmn dn pertidksmn yng
BAB PERSAMAAN DAN PERTIDAKSAMAAN Stndr Kompetensi Mhsisw memhmi konsep dsr sistem bilngn rel (R) sebgi semest untuk menentukn selesin persmn dn pertidksmn, dpt mengembngkn bentuk persmn dn pertidksmn yng
INTEGRAL FOURIER KED. Diasumsikan syarat-syarat berikut pada f(x): 1. f x memenuhi syarat Dirichlet pada setiap interval terhingga L, L.
 INTEGRAL FOURIER Disumsikn syrt-syrt berikut pd f(x):. f x memenuhi syrt Dirichlet pd setip intervl terhingg L, L.. f x dx konvergen, yitu f(x) dpt diintegrsikn secr mutlk dlm (, ). Selnjutny, Teorem integrl
INTEGRAL FOURIER Disumsikn syrt-syrt berikut pd f(x):. f x memenuhi syrt Dirichlet pd setip intervl terhingg L, L.. f x dx konvergen, yitu f(x) dpt diintegrsikn secr mutlk dlm (, ). Selnjutny, Teorem integrl
STRATEGI PENGAJARAN MATEMATIKA UNTUK MENENTUKAN AKAR-AKAR PERSAMAAN KUADRAT
 Jurnl Vol II. No., Mret 08, hlm. 9-95 vilble online t www.jurnl.un.c.id/indeks/jmp STRTEGI PENGJRN MTEMTIK UNTUK MENENTUKN KR-KR PERSMN KUDRT Indh Purnm Putri, Symsudhuh, Ihd Hsbiyti 3 Progrm Studi Mgister
Jurnl Vol II. No., Mret 08, hlm. 9-95 vilble online t www.jurnl.un.c.id/indeks/jmp STRTEGI PENGJRN MTEMTIK UNTUK MENENTUKN KR-KR PERSMN KUDRT Indh Purnm Putri, Symsudhuh, Ihd Hsbiyti 3 Progrm Studi Mgister
Definisi Vektor. Vektor adalah besaran yang mempunyai besar dan arah
 VEKTOR Definisi Vektor Vektor dlh esrn yng mempunyi esr dn rh Besr vektor rtiny pnjng vektor Arh vektor rtiny sudut yng dientuk dengn sumu X positif Vektor disjikn dlm entuk rus gris errh Gmr Vektor B
VEKTOR Definisi Vektor Vektor dlh esrn yng mempunyi esr dn rh Besr vektor rtiny pnjng vektor Arh vektor rtiny sudut yng dientuk dengn sumu X positif Vektor disjikn dlm entuk rus gris errh Gmr Vektor B
BAB I V E K T O R. 1.1 Pengertian
 Vektor BAB I V E K T O R Pengertin Bnyk kuntits fisik, seperti lus, pnjng, mss dn tempertur, dpt dijelskn secr lengkp pbil besrn kuntits tersebut telh diberikn Kuntits seperti ini dinmkn sklr Kulits fisik
Vektor BAB I V E K T O R Pengertin Bnyk kuntits fisik, seperti lus, pnjng, mss dn tempertur, dpt dijelskn secr lengkp pbil besrn kuntits tersebut telh diberikn Kuntits seperti ini dinmkn sklr Kulits fisik
Menerapkan konsep vektor dalam pemecahan masalah. Menerapkan konsep vektor pada bangun ruang
 VEKTOR PADA BIDANG SK : Menerpkn konsep vektor dlm pemechn mslh KD : Menerpkn konsep vektor pd bidng dtr Menerpkn konsep vektor pd bngun rung TUJUAN PELATIHAN: Pesert memiliki kemmpun untuk mengembngkn
VEKTOR PADA BIDANG SK : Menerpkn konsep vektor dlm pemechn mslh KD : Menerpkn konsep vektor pd bidng dtr Menerpkn konsep vektor pd bngun rung TUJUAN PELATIHAN: Pesert memiliki kemmpun untuk mengembngkn
MODUL 6. Materi Kuliah New_S1
 MODUL 6 Mteri Kulih New_S1 KULIAH 10 Spnning tree dn minimum spnning tree - Definisi spnning tree T diktkn spnning tree dri grph terhubung G bil T dlh sutu tree yng vertexvertexny sm dengn vertexny G dn
MODUL 6 Mteri Kulih New_S1 KULIAH 10 Spnning tree dn minimum spnning tree - Definisi spnning tree T diktkn spnning tree dri grph terhubung G bil T dlh sutu tree yng vertexvertexny sm dengn vertexny G dn
PERSAMAAN DAN PERTIDAKSAMAAN LOGARITMA
 K- Kels X mtemtik PEMINATAN PERSAMAAN DAN PERTIDAKSAMAAN LOGARITMA Tujun Pembeljrn Setelh mempeljri mteri ini, kmu dihrpkn memiliki kemmpun berikut.. Memhmi definisi persmn dn pertidksmn logritm.. Dpt
K- Kels X mtemtik PEMINATAN PERSAMAAN DAN PERTIDAKSAMAAN LOGARITMA Tujun Pembeljrn Setelh mempeljri mteri ini, kmu dihrpkn memiliki kemmpun berikut.. Memhmi definisi persmn dn pertidksmn logritm.. Dpt
DIKTAT MATA KULIAH ALJABAR LINEAR ELEMENTER (BAGIAN I) DISUSUN OLEH ABDUL JABAR, M.Pd
 DIKTAT MATA KULIAH ALJABAR LINEAR ELEMENTER (BAGIAN I) DISUSUN OLEH ABDUL JABAR, M.Pd JURUSAN/PROGRAM STUDI PENDIDIKAN MATEMATIKA STKIP PGRI BANJARMASIN MARET MUQADIMAH Alhmdulillh penyusun ucpkn ke hdirt
DIKTAT MATA KULIAH ALJABAR LINEAR ELEMENTER (BAGIAN I) DISUSUN OLEH ABDUL JABAR, M.Pd JURUSAN/PROGRAM STUDI PENDIDIKAN MATEMATIKA STKIP PGRI BANJARMASIN MARET MUQADIMAH Alhmdulillh penyusun ucpkn ke hdirt
,, % ,, % -0: 0 -0: 0! 2 % 26, &
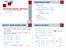 PERSAMAAN LINIER GAUSS-SIEDEL METHOD Simultneous Liner Equtions Oleh : Purwnto,S.Si Bentuk Umum x + x + 3 x 3 + + n x n = b Sebuh persmn linier dengn : n peubh : x, x, x 3,, x n n konstnt :,, 3,, n Contoh
PERSAMAAN LINIER GAUSS-SIEDEL METHOD Simultneous Liner Equtions Oleh : Purwnto,S.Si Bentuk Umum x + x + 3 x 3 + + n x n = b Sebuh persmn linier dengn : n peubh : x, x, x 3,, x n n konstnt :,, 3,, n Contoh
MATEMATIKA DASAR. Bab Bilangan Irasional dan Logaritma. Drs. Sumardi Hs., M.Sc. Modul ke: 02Fakultas FASILKOM. Program Studi Teknik Informatika
 MATEMATIKA DASAR Modul ke: 0Fkults FASILKOM Progrm Studi Teknik Informtik Bb Bilngn Irsionl dn Logritm Drs. Sumrdi Hs., M.Sc. Bgin Isi Bilngn Irsionl - Berbgi bentuk kr dn opersiny Logritm - Sift-sift
MATEMATIKA DASAR Modul ke: 0Fkults FASILKOM Progrm Studi Teknik Informtik Bb Bilngn Irsionl dn Logritm Drs. Sumrdi Hs., M.Sc. Bgin Isi Bilngn Irsionl - Berbgi bentuk kr dn opersiny Logritm - Sift-sift
POSET ( Partially Ordered Set ) Himpunan Terurut Parsial
 POSET ( Prtilly Ordered Set ) Himpunn Terurut Prsil Definisi Sutu relsi biner dinmkn sebgi sutu relsi pengurutn tk lengkp tu relsi pengurutn prsil ( prtil ordering reltion ) jik i bersift reflexive, ntisymmetric,
POSET ( Prtilly Ordered Set ) Himpunn Terurut Prsil Definisi Sutu relsi biner dinmkn sebgi sutu relsi pengurutn tk lengkp tu relsi pengurutn prsil ( prtil ordering reltion ) jik i bersift reflexive, ntisymmetric,
Materi IX A. Pendahuluan
 Mteri IX Tujun :. Mhsisw dpt memhmi vektor. Mhsisw mmpu mengunkn vektor dlm persoln sederhn 3. Mhsisw mengimplementsikn konsep vektor pd rngkin listrik. Pendhulun Sudh menjdi kesepktn umum hw untuk menentukn
Mteri IX Tujun :. Mhsisw dpt memhmi vektor. Mhsisw mmpu mengunkn vektor dlm persoln sederhn 3. Mhsisw mengimplementsikn konsep vektor pd rngkin listrik. Pendhulun Sudh menjdi kesepktn umum hw untuk menentukn
