lim ; dengan lim f ( x) = 0 = lim g( x) lim ; dengan lim ( ) lim g( x), 2 lim fxgx ( ) ( ); dengan lim fx ( ) = 0 dan lim gx ( ) =.
|
|
|
- Sukarno Kusuma
- 7 tahun lalu
- Tontonan:
Transkripsi
1 Koko Mrtono FMIPA ITB 9 Jenis Bentuk Tktentu imit Fungsi Bentuk Tk tentu / Akn dihitung Ilustrsi: f () g () ; dengn f = = g. Æc Æc Æc sin sin( ),, Æ Æ4 4 Æ4 4 Bentuk Tk tentu / Akn dihitung Ilustrsi: f () f = = g () ; dengn g. Æ Æ Æ Æ, Æ 4 Bentuk Tk tentu Akn dihitung, Æ 4, Æ 4, dn segin. fg ; dengn f = dn g =. imit ini dpt diuh ke entuk / kren f () Æ dn, dn segin. Æc Æc Æc f () / g g () Æ dn ke entuk / kren g () fg= () () / f dengn gæ () dn Ilustrsi: sin, Æ f Æ. Æp /4 4 fg= () () dengn ( p) sec, dn segin.
2 Bentuk Tk tentu Akn dihitung ( f g ); dengn f = dn g =. Æ Æ Æ imit ini dpt diuh ke entuk / dengn ergi cr. Ilustrsi: ( ) Æ ( ), Æ,, Æ ( ), dn segin. Æ Æ Bentuk Tk tentu Dengn logritm nturl kn dihitung () ( f ) g ; dengn f = = g. Ilustrsi: Æc Æc Æc sin /(4 ln ),,, Æ Æ Æ dn segin. Bentuk Tk tentu Dengn logritm nturl kn dihitung () ( f ) g ; dengn f = dn g =. Ilustrsi: Æc Æc Æc / /ln, ( /ln ), (cot ), Æ Æ Æ, dn segin. Bentuk Tk tentu Dengn logritm nturl kn dihitung () ( f ) g ; dengn f = dn g =. Ilustrsi: Æc Æc Æc /sin / ( ), (cos ), Æ Æ Æ, dn segin. Bergi Teknik Pemechn Bentuk Tk tentu imit Fungsi Untuk entuk /, utlh mnipulsi ljr sehingg entukn ukn /. Colh teorem Hôpitl s tu prinsip pit (jik mungkin) Untuk entuk /, munculkn / n ( nœ ) ng itn pd pemilng dn peneutn, tu colh teorem Hôpitl s jik mungkin. Untuk entuk, uhlh menjdi / dengn mersionlkn, tu munculkn entuk / n ( nœ ) ng itn. Untuk entuk,, dn, mil it dri ln fungsin kemudin gunkn teorem Hôpitl s dn sift kekontinun ln.
3 Teorem Hôpitl s Aturn Hôpitl s untuk Bentuk / Jik f = = g dn Æc Æc f () Æc g () f () f () g () g () =. Æc Æc d,, tu, mk Cttn c dpt dignti c, c,, tu. Secr intuitif, jik f () dn g() lpn menuju, mk hsiln ergntung pd perndingn keceptn f () dn g, () itu f () / g (). Aturn Hôpitl s untuk Bentuk / Jik f = = g dn Æ Æ Æ f () Æ g () f () f () g () Æ g () =. d,, tu, mk Cttn c dpt dignti c, c, tu. Secr intuitif, ndikn f () t dn g() t mentkn posisi du moil ng ergerk di sumut dn pd st t keceptnn dlh f () t dn g () t. Jik perndingn keceptn kedu moil dlh, mk untuk jngk pnjng perndingn jrk kedu moil jug sm dengn. Arti Geometri Teorem Hôpitl s untuk Bentuk / f () = p g() = q f () c = f () g () c = g() f () p p f () = = = g () q q g () Æ Æ Æ c f, g kontinu di c f () f () f () c = = g () g () g () c Æc Æc
4 Anek Rgm Contoh Bentuk Tk tentu imit Fungsi Bentuk Tk tentu / sin cos Æ Æ Æ Æ = = cos = cos = cos =. ( )( ) = = = =. Æ4 4 Æ4( )( ) Æ4 4 4 Cr lin = = =. Æ4 4 Æ4 4 ( ) ( ) 4 4 = = Æ4 4 Æ4 4 ( ) Æ4( 4) ( ) 5 4 ( 4)( ) Æ4( 4)( ( ) ) Æ4( 4)( ( ) ) Æ4 4 = = = =. sin( ) sin( ) = Æ4 4 Æ4 4 sin( ) Æ4 Æ e e Æ Æ Æ = = e =. (ln ) Æ Æ = = =. ln = = =. tnp psecp p p Æ Æ Æ p 4 = = = = p. 4 cos cos sin cos sin cos sin Æ Æ Æ sin cos cos = = = =. 6 Æ Æ Æ Æ 6 sin cos sin cos 6 = = = =. sin sin sin (cos ) sin sin cos cos sin sin Æp Æp Æp cos 4cos = = = p.
5 Bentuk Tk tentu / Æ Æ ( ) Æ = = = =. Cr lin 6 6 Æ Æ Æ 6 Æ 6 = = = =. 4 4 Æ Æ Æ = = = =. Cr lin ( 4 ) Æ 4 Æ = = =. ( 4 4 ) ( ) 4 4 Æ Æ Æ Æ = = = =. ( 4 4 ) ( ) 4 4 Æ Æ Æ Æ = = = =. Kedu contoh ini tk dpt diselesikn dengn teorem Hôpitl s. sec sectn tn p/ tn p/ p/ sec p/ = = = sin =. Æ Æ sec Æ Æ Bentuk Tk tentu 4 p 4p cos sin sec = = = =. Æp/4 Æp/4 Æp/4 sin Æ Æ t Æ sint t sin = = =. p p p p tn p p Æ Æ Æ sec Æ ( )cot = = = cos = ( ) =. ln Æ Æ Æ Æ ln = = = ( ) =.
6 4 Bentuk Tk tentu ( ) ( )( ) Æ Æ Æ = = =. ( )( ) = = Æ Æ Æ = = = =. Æ ( ) Æ = = Æ Æ Æ = = = =. ( ) Æ Æ ( ) = ( ) = ; ( ) Æ Æ Æ ( ) = ( ) = = Æ = =. sin sin cos cos sin sin Æ tn Æ cos Æ cos Æ sin cos ( ln ) ln Æ Æ ln cos sin Æ sin cos = = = =. = = kren untuk, ( ln ) Æ dn ln Æ dri wh. Bentuk Tk tentu Untuk menghitung, mislkn = dn hitunglh Æ = diperoleh ln = ln, sehingg ln Æ Æ Æ Æ Æ Æ ln = ln = = = ( ) =. Kren fungsi ln kontinu pd (, ), mk = =. Æ Æ ln Æ. Dri = ln, kitn
7 5 Æ sin Untuk menghitung, mislkn = dn hitunglh sin sin Dri = diperoleh ln = (sin )ln, sehingg ln ln = (sin )ln = = csc Æ Æ Æ Æ csc cot sin sin sin Æ cos Æ cos = = = =. Kren fungsi ln kontinu pd (, ), mk Untuk menghitung Æ Æ Æ Æ sin ln = =. /(4 ln ), /(4 ln ) Æ Æ. = ln, kitn /(4 ln ) mislkn = dn hitunglh ln 4 ln 4 ln. Dri = diperoleh ln = ln =, sehingg ln Æ Æ Æ Æ ln 4 ln = = = =. Kren fungsi ln kontinu pd (, ), mk Bentuk Tk tentu Æ Æ Æ Æ /(4 ln ) / = = e = e e. / / ln = ln e, kitn Untuk menghitung, mislkn = dn hitunglh. Dri / ln ln = diperoleh ln = =, sehingg / Æ Æ Æ Æ ln ln = = = =. Æ Kren fungsi ln kontinu pd (, ), mk ln = ln, kitn Æ / = =. Æ Æ
8 6 Untuk menghitung mislkn = (cot ) dn hitunglh Æ ln = =, sehingg Æ /ln (cot ), /ln. Dri = (cot ) diperoleh sin sin Æ Æ Æ Æ /ln lncot ln cot ln ln ln cot cos ln = = = =. ln sin cos Kren fungsi ln kontinu pd (, ), mk Bentuk Tk tentu Untuk menghitung = ( ), dn hitunglh Æ sehingg ln Æ /ln (cot ) e Æ Æ e Æ = = =. /sin ( ), mislkn /sin = ln e, kitn /sin sin ln( ) sin. Dri = (), diperoleh ln = ln ( ) =, ln( ) sin cos Æ Æ Æ Æ ln = = = =. Kren fungsi ln kontinu pd (, ), mk Æ Æ ln Æ /sin = ( ) = e = e. Untuk menghitung, mislkn Æ,, = ln e, kitn = dn hitunglh. Dri = diperoleh ln = ln Æ, sehingg ( ) ln Æ Æ Æ Æ ln = ln = = =. Kren fungsi ln kontinu pd (, ), mk ln = ln e, kitn Æ = = e. Æ Æ
9 7 Jenis Integrl Tkwjr Integrl tkwjr pd selng tkhingg = f () = f () = f () f () d f () d f () d = f () Integrl tk wjr pd ksus ini tidk tergntung pd pemilihn c. f () d c. Integrl tkwjr dri fungsi terintegrlkn = f () pd selng tk terts [, ) didefinisikn segi f () d= fd () Æ Integrl tkwjr dri fungsi terintegrlkn = f () pd selng tkterts (,] didefinisikn segi f () d = fd (). Æ Integrl tkwjr dri fungsi terintegrlkn = f () pd selng tkterts (, ) didefinisikn segi c c f () d= fd () fd () = fd () fd (). c Æ Æ c Kekonvergenn integrl tkwjr Jik semu it di ts d dn ernili hingg, integrl tkwjrn diktkn konvergen dn jik tidk demikn diktkn divergen (itn ± tu kurv eroskilsi).
10 8 Integrl tkwjr pd selng tkhingg = f () f () d = f () = f () = f () = f () f () d f () d f () d c c q p r D f = (,] D f = [,) D f = [,] {p} Integrl tkwjr dri fungsi terintegrlkn = f () pd selng terts (,] didefinisikn segi f () d= fd (). Dengn cæ penggntin e = c diperoleh c= e dn cæ e Æ, sehingg f () d= fd (). e Æ e c Integrl tkwjr dri fungsi terintegrlkn = f () pd selng terts [,) didefinisikn segi f () d= fd (). Dengn cæ penggntin e = c diperoleh c= e dn cæ e Æ, sehingg f () d= fd (). e Æ e c Integrl tkwjr dri fungsi terintegrlkn = f () pd selng terts [,] { p} didefinisikn segi p q f () d= fd () fd () = fd () fd (). p qæp ræp r Kekonvergenn integrl tkwjr Jik semu it di ts d dn ernili hingg, integrl tkwjrn diktkn konvergen dn jik tidk demikn diktkn divergen (itn ± tu kurv eroskilsi).
11 9 Anek Rgm Contoh Integrl Tkwjr pd Selng Tkhingg Integrl tkwjr dri fungsi kontinu f= () pd [, ) dlh d d li Æ Æ Æ = m = = = (konvergen). Integrl tkwjr dri fungsi kontinu d d f= () pd [, ) dlh ( ) = = = = (divergen) Æ Æ Æ Integrl tkwjr dri fungsi kontinu f () = sin pd [, ) dlh sin d = sin d = cos = cos Æ Æ Æ = tidk d (divergen). Integrl tkwjr dri fungsi kontinu d d f= () pd [, ) dlh / / ( ) ( ) = = = = (divergen) Æ Æ Æ Integrl tkwjr dri fungsi kontinu f () = pd (, ) dlh d d d d d = = Æ Æ ( ) ( ) ( ) ( ) ( p) p p (konvergen). = tn tn = tn tn Æ Æ Æ Æ = = Integrl tkwjr dri fungsi kontinu f () = cosh pd (, ) dlh coshd= coshd coshd= coshd coshd Æ Æ ( ) ( nh) = sinh sinh = sinh si Æ Æ Æ Æ = = (diverg e n).
12 Anek Rgm Contoh Integrl Tkwjr pd Selng Hingg Fungsi f () = kontinu pd (,5] dengn Æ tkwjr dri fungsi f pd selng tutup [,5] dlh 5 ( ) ( c ) 5 d 5 d cæ c cæ c cæ =. Integrl = = = 4 = 4 (konvergen). Fungsi f () = ln kontinu pd (,) dengn ln =. Integrl Æ tkwjr dri fungsi f pd selng tutup [,] dlh cæ c cæ ln d= ln = cln c c = (konvergen). Fungsi f () = kontinu pd [,) dengn Æ tkwjr dri fungsi f pd selng tutup [,] dlh ( c ) =. Integrl d c d c d ( ) c = = = ( ln ) c c Æ Æ cæ = ln ln = (divergen). cæ Fungsi f () = kontinu pd [,) dengn 9 Æ 9 tkwjr dri fungsi f pd selng tutup [,] dlh =. Integrl c ( in ) ( sin ) d c d s c 9 9 c Æ cæ cæ = = = = si n = p (konvergen). Fungsi f= () kontinu pd [,) (,] dengn Æ =. Integrl tkwjr dri fungsi f pd selng tutup [,] dlh ( q ) ( r) q q d d d d d = = = qæ ræ r qæ ræ = = = (divergen). qæ ræ r
13 Fungsi f () = kontinu pd [,) (,] dengn Æ =±. Integrl tkwjr dri fungsi f pd selng tutup [,] dlh d d d q d d = = q Æ ræ r / q / ( ) ( ) = ( ) ( ) qæ ræ / / ( q ) ( r ) = ( ) ( ) qæ ræ = = (konvergen). Anek Rgm Vrisi Contoh Integrl Tkwjr r Selidiki kekonvergenn integrl tkwjr sech d. Integrl tktentu dri f () = sech dlh d d e d sech d = = = cosh e e e de ( ) e C = = tn ( e ) Integrl tkwjr dri f = sech ng kontinu pd (, ) dlh sech d = sech d sech d = sech d sech d Æ Æ ( ) ( e tn e ) Æ ( p tn e ) ( tn e p) = tn Æ = Æ Æ p p p p (konvergen). = =
14 d Selidiki kekonvergenn integrl tkwjr. Integrl tktentu dri d ( ) f () = pd (, ) dlh d d ( ) = = tn C Jenis integrl tkwjr ini pd selng hingg dn selng tkhingg kren f () = kontinu pd (, ) dengn d =. Integl ( ) Æ tkwjr dri fungsi f pd selng tutup [, ) dlh d d d d d = = ( ) ( ) ( ) cæ c ( ) Æ ( ) ( ) ( ) c Æ ( 4p c) ( 4p ) cæ Æ ( p ) ( p p) p = tn tn cæ = tn tn = = (konvergen). 4 4 r Tunjukkn d konvergen jik r < dn divergen jik r, rœ. Untuk ksus r π, rœ integrl tkwjrn dlh ) Ê ) Ë r r r r r d= d Ê Æ = = Æ Ër Æ r Ï r Ôr Ï Ô, jik <, jik r < = Ì = Ì ÔÓ, jik r > ÔÓ, jik r > Untuk ksus r =, rœ integrl tkwjrn dlh d d Æ Æ Æ d = = = ln = ln =. r Jdi d konvergen jik r < dn divergen jik r, r Œ.
15 Apliksi Integrl Tkwjr untuk Fungsi Pdt Pelung Percon ck Sutu hsil percon diktkn ck jik ervrisi untuk eerp percon tetpi untuk jngk pnjng setelh sejumlh esr pengulngn hsiln mempuni distriusi ng tertur. Pelung Perndingn munculn kejdin dlm rngkin percon jngk pnjng dinmkn pelung. Himpunn hsil percon ng mungkin untuk kejdin A ditulis P(A). Pelung dri kejdin A memenuhi sift erikut.. Untuk setip kejdin A erlku P(A). Himpunn S dri semu hsil percon ng mungkin dinmkn rung smpel, dn untuk S erlku P(S) =.. Jik kejdin A dn B sling tersing (tnp hsil percon sm), mk P(A tu B) = P(A) P(B). Akitn, jik A C dlh himpunn semu hsil percon di rung smpel S ng ukn kejdin A, mk P(A C ) = P(A). Peuh ck Sutu turn ng mengitkn nili numerik dengn hsil percon dinmkn peuh ck. Segi ilustrsi, pelntunn seuh koin menghsilkn munculn muk (M) tu elkng (B). Jik seuh koin dilntunkn tig kli, rung smpeln dlh himpunn {MMM, MMB, MBM, MBB, BMM, BMB, BBM, BBB}. Peuh ck X dpt didefinisikn segi nkn muk dlm tig kli pelntunn koin ini. Distriusi pelung dri X dlh dftr semu nili ng mungkin dri X esert pelung ng terkit. P(X = ) 8 Peuh ck X diktkn diskrit jik himpunn nili ng mungkin dri X dlh {,, } dn diktkn kontinu jik nili X terletk pd sutu selng dri ilngn rel. PDF, fungsi pdt pelung (proilit densit function) PDF = f () dri peuh ck kontinu X didefinisikn di lur himpunn hsil percon ng mungkin dn ersift () f (), () f () d=
16 4 PDF dri X = f () c d f () dn f () d= d Pc ( d) = f( d ) c Rtrt dn vrinsi dri sutu peuh ck didefinisikn segi m = EX = fd dn s = = m VX ( ) fd. Kitn ntr rtrt dn vrinsi dlh s = EX m. Ï PDF dri ms pki seuh komponen listrik dlh f () = le l, Ì, Ó, < λ konstnt. () Tunjukkn f memenuhi srt PDF, () Tentukn rtrt dn vrinsin, () Tentukn fungsi distriusi kumultif F() = P(X ), (4) Jik λ =, dn t dlm jm, hitunglh P(X > ). () Fungsi f memenuhi srt PDF kren f () dn f () d d e l d e l = l = l d = e l =. Æ Æ () Rtrt dri peuh ckn dlh l l Æ m = EX = fd = d le d= le d l l l l ( e e ) ( e e ) Æ Æ = = =. Vrinsi dri peuh ckn dlh l l l l l ( l ) () l = l e d = Æ l l s = EX m = fd = d le d (kerjkn perhitungn tekn isn!) () Fungsi distriusi kumultifn dlh t t l l l l,t,t Æ F () = PX ( ) = ftdt () = dt e dt = e = e. (4) Untuk λ =,,. PX ( > ) =,e dt=,e dtª,8 Tfsirnn: pelung ms pki komponen di ts jm dlh,8. l
17 SOA ATIHAN MA KAKUUS A Pokok Bhsn: Bentuk Tktentu dn Integrl Tkwjr 5 Sol uji konsep dengn enr slh, erikn rgumentsi ts jwn And. No. Perntn Jw n Æ e. Untuk serng ilngn sli n erlku =. B S. Jik f = dn g =, mk Æ f (). Jik Æ g () Æ 4. Jik ln f =, mk Æ =, mk ( f g) f () Æ g =. B S () =. B S Æ f = e. B S Æ 5. Jik f dn g terdiferensilkn dn 6. Jik f dlh fungsi genp dn f () Æ g () =, mk f () Æ g () =. B S f () d konvergen, mk f ( d ) konvergen. B S 7. Jik f ( d ) d dn hingg, mk f ( d ) Æ konvergen. B S 8. Jik f kontinu pd [, ) dn f =, mk Æ 9. Jik f e " Œ [,), mk f () dkonvergen. B S f () d konvergen. B S. Jik f kontinu pd (,) dn f = = f, mk f d divergen. B S Æ Æ Hitunglh setip it erikut. tn. Æ sin. sin Æ tn ( csc ) Æ Æ cosh 5. Æ 8. Æ ( cos ) sin. ln Æ Æ Æ p / sin cos ln(sin ). ( p ) Æ p /. ( ) sec Æ. Æ 4. ( ln ln ( ) ) Æ ln ( e. Æ ) 5. ( ln ) Æ 6. Æ /( ) 7. / (ln ) Æ 8. ( ) Æ /(ln ) / / 9. ( e ). sin tdt. Æ Æ e Æ t dt
18 Selidiki kekonvergenn setip integrl tkwjr erikut. 6. e d. d e ln d ln 6. d 7. ( ) d 8. d 9. d d 4. d ln e e 4 e p / d d sin cos d d 45. d d 47. ( ) d 4c 48. d, c p / tn > 49. c 4c / (ln cos ) d p 5. Hitunglh lus derh di wh kurv Sol Anek Rgm /( ) c 5. Jelskn mengp perntn f ( d ) = fd cæ c 5. Jik f kontinu, f () 55. Uji nding: untuk f gpd[, ), = 4 dn di seelh knn gris =. tidk enr. pd [, ), fd () <, dn f d, uktikn f =. Æ gd () konvergen Æ 5. Derh D terletk di kudrn pertm, di wh kurv = /, dn di seelh kiri gris =. Tunjukkn lus derh D hingg tetpi jik D diputr terhdp sumu volumn tk hingg. 54. Tentukn semu nili p sehingg integrl tk wjr p d () konvergen dn () divergen. dn f () d konvergen f () d divergen gd () divergen. Dengn menggunkn uji ini tunjukkn semu d () e d ( ) (c) d. ln ( ) integrl tk wjr erikut konvergen. () 4 4 Kunci Jwn. B. S. S 4. B 5. S 6. B 7. S 8. B 9. B. S e p ln 5. Contoh penngkl: f ( ) ln.. 4. ln e e 9. e 4. ln 4. divergen 5. divergen 6. (ln ) ln 9. p 4 p 4. divergen divergen 47. π 48. ln ( ) 55. Tunjukkn pd [, ) erlku () 4 4 ( ) 4, () e 49. =, f = sin 5. lus D = (hingg) 54. () p, () p > e, (c) ln ( ) ln
19
INTEGRAL TAK TENTU. x x x
INTEGRAL TAK TENTU Definisi : Fungsi F diktkn nti turunn dri fungsi f pd selng I jik F () = f() untuk semu di I. Notsi : F() = f() Integrl tk tentu dlh Anti/Invers/Kelikn turunn. c c Integrl tk tentu dlh
PEMANTAPAN BELAJAR SMA BBS INTEGRAL
BAB I PEMANTAPAN BELAJAR SMA BBS INTEGRAL I A RANGKUMAN INTEGRAL. Pengertin Apil terdpt fungsi F() yng dpt didiferensilkn pd selng I sedemikin hingg F () = f(), mk nti turunn (integrl) dri f() dlh F()
INTEGRAL. Bogor, Departemen Matematika FMIPA IPB. (Departemen Matematika FMIPA IPB) Kalkulus I Bogor, / 45
INTEGRAL Deprtemen Mtemtik FMIPA IPB Bogor, 2012 (Deprtemen Mtemtik FMIPA IPB) Klkulus I Bogor, 2012 1 / 45 Topik Bhsn 1 Pendhulun 2 Anti-turunn 3 Lus di Bwh Kurv 4 Integrl Tentu 5 Teorem Dsr Klkulus 6
(c) lim. (d) lim. (f) lim
FMIPA - ITB. MA Mtemtik A Semester, 6-7. Pernytn enr dn slh. () ()! e Solusi. Benr. Fungsi eksonensil (enyeut) memesr leih cet drid fungsi olinom (emilng) sehingg emginny menghsilkn nili Dengn Hoitl s
INTEGRAL. Misalkan suatu fungsi f(x) diintegralkan terhadap x maka di tulis sebagai berikut:
INTEGRAL.PENGERTIAN INTEGRAL Integrl dlh cr mencri sutu fungsi jik turunnn di kethui tu kelikn dri diferensil (turunn) ng diseut jug nti derivtif tu nti diferensil. Untuk menentukn integrl tidk semudh
MATEMATIKA. Sesi INTEGRAL VOLUME A. BENDA-BENDA YANG MEMILIKI SUMBU PUTAR B. BENDA-BENDA YANG MEMILIKI SUMBU PUTAR TERHADAP SUMBU-X
MATEMATIKA KELAS XII - KURIKULUM GABUNGAN 6 Sesi N INTEGRAL VOLUME A. BENDA-BENDA YANG MEMILIKI SUMBU PUTAR Apliksi integrl erikutn dlh menentukn volume end ng memiliki sumu putr. Contoh endn dlh tung,
BAB 7. LIMIT DAN LAJU PERUBAHAN
BAB 7. LIMIT DAN LAJU PERUBAHAN 7. LIMIT FUNGSI 7.. Limit fungsi di sutu titik Menggmbrkn perilku fungsi jik peubhn mendekti sutu titik Illustrsi: Dikethui f( ) f(), 3,30,0 3,030,00 3,003 3 f() = f() 3,000?
7. APLIKASI INTEGRAL
7. APLIKASI INTEGRAL 7. Menghitung Lus Derh.Mislkn derh D (, ), f ( ) D f() Lus D =? Lngkh :. Iris D menjdi n gin dn lus stu uh irisn dihmpiri oleh lus persegi pnjng dengn tinggi f() ls(ler) A f ( ). Lus
MATEMATIKA INTEGRAL TENTU DAN LUAS DAERAH
MATEMATIKA KELAS XII - KURIKULUM GABUNGAN 5 Sesi N INTEGRAL TENTU DAN LUAS DAERAH A. DEFINISI INTEGRAL TENTU Bentuk integrl f d = f + c diseut segi integrl tk tentu kren hsil dri pengintegrlnn msih erup
RANGKUMAN MATERI ' maupun F(x) = Pengerjaan f(x) sehingga memperoleh F(x) + c disebut mengintegralkan f(x) ke x dengan notasi:
INTEGRAL RANGKUMAN MATERI A. ANTIDERIVATIF DAN INTEGRAL TAK TENTU Jik kit mengmil uku dri temptny mk kit dpt mengemliknny lgi ke tempt semul. Opersi yng kedu menghpus opersi yng pertm. Kit ktkn hw du opersi
INTEGRAL. Kelas XII IIS Semester Genap. Oleh : Markus Yuniarto, S.Si. SMA Santa Angela Tahun Pelajaran 2017/2018
Modul Integrl INTEGRAL Kels XII IIS Semester Genp Oleh : Mrkus Yunirto, SSi SMA Snt Angel Thun Peljrn 7/8 Modul Mtemtik Kels XII IIS Semester TA 7/8 Modul Integrl INTEGRAL Stndr Kompetensi: Menggunkn konsep
INTEGRAL. Integral Tak Tentu Dan Integral Tertentu Dari Fungsi Aljabar
INTEGRAL Integrl Tk Tentu Dn Integrl Tertentu Dri Fungsi Aljr A. Integrl Tk Tentu Hitung integrl dlh kelikn dri hitung differensil. Pd hitung differensil yng dicri dlh fungsi turunnny, sedngkn pd hitung
HITUNG INTEGRAL ( 4 ) 4. Diketahui f(x) = 4x + 1 dan F(2) = 17 ; Tentukan fungsi F f(x) = 4x + 1
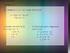HITUNG INTEGRA BAB.Integrl tk tentu (tnp ts). Rumus-rumus ) ) n n n d c, n ) d c n n n. d c, n ). Sift-sift Integrl Contoh :... ) k. f ( ) d k. f ( ) d d d ln c ) ( ( ) ( )) ( ) ( ) d c ( ) ( ) d ( ) d
Tiara Ariqoh Bawindaputri TIP / kelas L
Tir Ariqoh Bwindputri 500008 TIP / kels L INTEGRAL Integrl Tk tentu Integrl dlh entuk invers dri turunn. Secr umum jik seuh fungsi diintegrlkn terhdp vrile tertentu dpt disjikn dlm entuk : f ( F( C Untuk
LUAS DAERAH APLIKASI INTEGRAL TENTU. Indikator Pencapaian Hasil Belajar. Ringkasan Materi Perkuliahan
LUAS DAERAH APLIKASI INTEGRAL TENTU Indiktor Pencpin Hsil Beljr Mhsisw menunjukkn kemmpun dlm :. Menghitung lus pd idng dtr Ringksn Mteri Perkulihn Jik sutu derh ditsi oleh kurv f(), g(), gris dn dengn
IRISAN KERUCUT: PERSAMAAN ELIPS. Tujuan Pembelajaran
K-13 mtemtik K e l s I IRISAN KERUCUT: PERSAMAAN ELIPS Tujun Pemeljrn Setelh mempeljri mteri ini, kmu dihrpkn memiliki kemmpun erikut. 1. Memhmi definisi elips.. Memhmi unsur-unsur elips. 3. Memhmi eksentrisits
Integral. Konstanta dari Integrasi. Integral Tak Tentu. AntiTurunan (Antiderivative)
Integrl AntiTurunn (Antiderivtive) AntiTurunn dri seuh fungsi f dl seuh fungsi F sedemikin hingg Dierikn Pd Peltihn Guru-Guru Aceh Jy 5 Septemer 0 Oleh: Ridh Ferdhin, M.Sc F f E. AntiTurunn dri f ( ) 6
MUH1G3/ MATRIKS DAN RUANG VEKTOR
MUHG3/ MATRIKS DAN RUANG VEKTOR TIM DOSEN 3 Sistem Persmn Liner Sistem Persmn Liner Su Pokok Bhsn Pendhulun Solusi SPL dengn OBE Solusi SPL dengn Invers mtriks dn Aturn Crmmer SPL Homogen Beerp Apliksi
Hendra Gunawan. 30 Oktober 2013
MA MATEMATIKA A Hendr Gunwn Semester I, 2/24 Oktoer 2 Ltihn. Fungsi g =,, terintegrlkn pd [, ]. Nytkn integrl tentu g pd [, ] segi limit jumlh Riemnn dengn prtisi reguler, dn hitunglh niliny. //2 c Hendr
Integral Tak Tentu dan Integral Tertentu
Integrl Tk Tentu dn Integrl Tertentu Pengertin Integrl Jik F dlh fungsi umum yng ersift F = f, mk F merupkn ntiturunn tu integrl dri f. Pengintegrln fungsi f terhdp dinotsikn segi erikut : f d F c notsi
Integral Tak Wajar. Ayundyah Kesumawati. March 25, Prodi Statistika FMIPA-UII
Kesumwti Prodi Sttistik FMIPA-UII Mrch 25, 205 Sutu integrl tertentu b f (x)dx () diktkn wjr jik i memenuhi du syrt berikut: i. Bts integrsi dn b merupkn bilngn berhingg ii. fungsi f (x) terbts pd intervl
PERSAMAAN KUADRAT, FUNGSI KUADRAT DAN PERTIDAKSAMAAN KUADRAT
PERSAMAAN KUADRAT, FUNGSI KUADRAT DAN PERTIDAKSAMAAN KUADRAT Persmn Kudrt. Bentuk Umum Persmn Kudrt Mislkn,, Є R dn 0 mk persmn yng erentuk 0 dinmkn persmn kudrt dlm peuh. Dlm persmn kudrt 0, dlh koefisien
selisih positif jarak titik (x, y) terhadap pasangan dua titik tertentu yang disebut titik
Hiperol 7.1. Persmn Hiperol Bentuk Bku Hiperol dlh himpunn semu titik (, ) pd idng sedemikin hingg selisih positif jrk titik (, ) terhdp psngn du titik tertentu ng diseut titik fokus (foci) dlh tetp. Untuk
LIMIT FUNGSI. DEFINISI Notasi. dibaca. limit f(x) bila x mendekati a sama dengan L. atau. f(x) mendekati L bila x mendekati a.
DEFINISI Notsi dibc tu berrti bhw IMIT FUNGSI it bil mendekti sm dengn mendekti bil mendekti nili dpt dibut sedekt mungkin dengn bil cukup dekt dengn, tetpi tidk sm dengn. Perhtikn bhw dlm deinisi tersebut
MODUL 4 PEUBAH ACAK. Peubah acak adalah suatu fungsi yang memetakan setiap elemen dari ruang sampel ke bilangan Real. X : S R
MODUL 4 EUBAH ACAK engntr Sutu percon melempr mt ung yng setimng senyk kli. Rung smpel dri percon terseut dlh S= { AAA, AGG, AGA, AAG, GAG, GGA, GAA, GGG } Sutu kejdin A : dri ketig lemprn nykny gmr sejumlh
INTEGRAL. 1. Macam-macam Integral. Nuria Rahmatin TIP L. A. Integral Tak Tentu
INTEGRAL Nuri Rhmtin 5000006 TIP L. Mcm-mcm Integrl A. Integrl Tk Tentu Integrl dlh entuk invers dri turunn. Secr umum jik seuh fungsi diintegrlkn terhdp vrile tertentu dpt disjikn dlm entuk : f ( F( C
BENTUK PANGKAT, AKAR DAN LOGARITMA
BENTUK PANGKAT, AKAR DAN LOGARITMA Stndr Kompetensi Memhmi dn menggunkn turn dn sift sert mnipulsi Aljr dlm pemechn mslh ng erkitn dengn entuk pngkt, kr dn logritm. Kompetensi Dsr Menggunkn sift, turn
INTEGRAL. y dx. x dy. F(x)dx F(x)dx
Drs. Mtrisoni www.mtemtikdw.wordpress.om INTEGRAL PENGERTIAN Bil dikethui : = F() + C mk = F () dlh turunn dri sedngkn dlh integrl (nti turunn) dri dn dpt digmrkn : differensil differensil Y Y Y Integrl
VEKTOR. Dua vektor dikatakan sama jika besar dan arahnya sama. Artinya suatu vektor letaknya bisa di mana saja asalkan besar dan arahnya sama.
-1- VEKTOR PENGERTIAN VEKTOR dlh sutu esrn yng mempunyi nili (esr) dn rh. Sutu vektor dpt digmrkn segi rus gris errh. Nili (esr) vektor dinytkn dengn pnjng gris dn rhny dinytkn dengn tnd pnh. Notsi vektor
didefinisikan sebagai bilangan yang dapat ditulis dengan b
1 PENDAHULUAN 1.1 Sistem Bilngn Rel Untuk mempeljri klkulus perlu memhmi hsn tentng system ilngn rel, kren klkulus didsrkn pd system ilngn rel dn siftsiftny. Sistem ilngn yng pling sederhn dlh ilngn sli,
10. cos (ax+b)sin(ax+b) dx = 12. sec x dx = tan x + c. 13. sec (ax+b)dx = tan (ax+b)+ c. 14. c sec x dx = - ctg x + c
Integrl Tk Tentu INTEGRAL. Rumus Integrl Fungsi Aljr. k x n k n +. ( x + n ( n +. x ln x + x n + + ; n - n+ (x+ + ; dn 4. ( f ( x ± g( x f ( x ± g ( x n - n. os (x+sin(x+ ( n + n+ os (x+ + ( + (. sin x
FUNGSI TRANSENDEN. Sifat satu kesatu yang mengakibatkan fungsi
FUNGSI TRANSENDEN I. Pendhulun. Pokok Bhsn Logritm Fungsi Eksponen.2 Tujun Mengethui entuk fungsi trnsenden dlm klkulus. Mengethui dn memhmi entuk fungsi trnseden itu logritm dn fungsi eksponen sert dlm
E. INTEGRASI BAGIAN ( PARSIAL )
E. INTEGRASI BAGIAN ( PARSIAL ) Integrsi gin (prsil) digunkn untuk mengintegrsikn sutu perklin fungsi yng msing-msing fungsiny ukn koefisien diferensil dri yng lin ( seperti yng sudh dihs pd su. B. D )
1. Identitas Trigonometri. 1. Identitas trigonometri dasar berikut ini merupakan hubungan kebalikan.
1. Identits Trigonometri Pengertin Identits Trigonometri dlh kesmn yng memut entuk trigonometri dn erlku untuk semrng sudut yng dierikn. Jenis Identits Trigonometri 1. Identits trigonometri dsr erikut
LIMIT FUNGSI DAN KEKONTINUAN
LIMIT FUNGSI DAN KEKONTINUAN RANGKUMAN MATERI Sebelum memsuki mteri, perhtikn himpunn-himpunn berikut: ) Himpunn bilngn sli:,,,4,5,.... b) Himpunn bilngn bult:...,,,0,,,.... p c) Himpunn bilngn rsionl:
E-LEARNING MATEMATIKA
MODUL E-LEARNING E-LEARNING MATEMATIKA Oleh : NURYADIN EKO RAHARJO, M.PD. NIP. 9705 00 00 Penulisn Modul e Lerning ini diiyi oleh dn DIPA BLU UNY TA 00 Sesui dengn Surt Perjnjin Pelksnn e Lerning Nomor
PERSAMAAN KUADRAT, FUNGSI KUADRAT DAN GRAFIKNYA
PERSAMAAN KUADRAT, FUNGSI KUADRAT DAN GRAFIKNYA Persmn dlh klimt mtemtik teruk ng memut huungn sm dengn. Sedngkn klimt mtemtik tertutup ng memut huungn sm dengn diseut kesmn. Klimt mtemtik :. Klimt mtemtik
Vektor di R2 ( Baca : Vektor di ruang dua ) adalah Vektor- di ruang dua )
A Pengertin Vektor Di R Vektor di R ( B : Vektor di rung du ) dlh Vektor- di rung du ) dlh Vektor-vektor ng terletk pd idng dtr pengertin vektor ng leih singkt dlh sutu esrn ng memiliki esr dn rh tertentu
Penyelesaian Persamaan Kuadrat 1. Rumus abc Rumus menentukan akar persamaan kuadrat ax 2 bx c 0; a, b, c R dan a 0
PERSAMAAN, PERTIDAKSAMAAN DAN FUNGSI KUADRAT PERSAMAAN KUADRAT Bentuk umum persmn kudrt dlh c 0,,,c R, 0 Penyelesin Persmn Kudrt. Rumus c Rumus menentukn kr persmn kudrt c 0;,, c R dn 0, = ± 4c. Memfktorkn
PENGAYAAN MATEMATIKA SOLUSI SOAL-SOAL LATIHAN 1
PENGAYAAN MATEMATIKA SOLUSI SOAL-SOAL LATIHAN 6y y 8y. Dikethui R dn. Temukn nili y. y y 8y 6 Solusi: 6y y 8y y y 8y 6 6y y 8y 8y y 6 y 8 0 y y y 0 y y y 0 ( y ) ( y ) 0 y y 8y 6 ( y )(y ) 0 y 0tu y 0
MATERI I : VEKTOR. Pertemuan-01
MATERI I : VEKTOR Pertemun-0. Pendhulun Definisi Vektor didefinisikn segi esrn yng memiliki rh. Keeptn, gy dn pergesern merupkn ontoh ontoh dri vektor kren semuny memiliki esr dn rh wlupun untuk keeptn
BAB I. MATRIKS BAB II. DETERMINAN BAB III. INVERS MATRIKS BAB IV. PENYELESAIAN PERSAMAAN LINEAR SIMULTAN
DFTR ISI BB I. MTRIKS BB II. DETERMINN BB III. INVERS MTRIKS BB IV. PENYELESIN PERSMN LINER SIMULTN BB I. MTRIKS Mtriks erup sekelompok ilngn yng disusun empt persegi dn ditsi tnd terdiri dri ris dn kolom
3 PANGKAT, AKAR, DAN LOGARITMA
PANGKAT, AKAR, DAN LOGARITMA.. Pngkt Pngkt dri seuh ilngn dlh sutu indeks ng menunjukkn nkn perklin ilngn ng sm secr eruntun. Notsi n errti hw hrus diklikn degn itu sendiri senk n kli. Notsi ilngn erpngkt
Modul Matematika 2012
Modul Mtemtik. ANTI TURUNAN Definisi Mislkn fungsi f terdefinisi pd selng teruk I. Fungsi F ng memenuhi F () = f () pd I dinmkn nti turunn tu fungsi primitif dri fungsi f pd I.. F() = cos nti turunn dri
Tujuan Pembelajaran. ) pada elips. 2. Dapat menentukan persamaan garis singgung yang melalui titik (x 1
K-3 mtemtik K e l s XI IRISAN KERUCUT: PERSAMAAN GARIS SINGGUNG PADA ELIPS Tujun Pemeljrn Setelh mempeljri mteri ini, kmu dihrpkn memiliki kemmpun erikut.. Dpt menentukn persmn gris singgung di titik (,
Vektor translasi dpt ditunjukkan oleh bil. berurutan yang ditulis dlm bentuk matriks kolom
TRANSFORMASI GEOMETRI BAB Sutu trnsformsi idng dlh sutu pemetn dri idng Krtesius ke idng ng lin tu T : R R (,) ( ', ') Jenis-jenis trnsformsi ntr lin : Trnsformsi Isometri itu trnsformsi ng tidk menguh
Hendra Gunawan. 15 November 2013
MA1101 MATEMATIKA 1A Hendr Gunwn Semester I, 2013/2014 15 Novemer 2013 Ltihn 1. Pnjng lmi sutu pegs dlh 0.08 m. Gy seesr 0.6 N diperlukn untuk menekn dn menhnny pd pnjng 0.07 m. Tentukn kerjyng dilkukn
SOLUSI PREDIKSI UJIAN NASIONAL MATEMATIKA IPS 2015
PAKET SOLUSI PREDIKSI UJIAN NASIONAL MATEMATIKA IPS. Sit: p q ~ p q Mthmn tidk eljr tu di dpt mengerjkn sol UN mtemtik dn lulus UN setr dengn perntn Jik Mthmn eljr mk di dpt mengerjkn sol UN mtemtik dn
Tujuan Pembelajaran. ) pada hiperbola yang berpusat di (0, 0). 2. Dapat menentukan persamaan garis singgung di titik (x 1
K-3 mtemtik K e l s XI IRISAN KERUCUT: GARIS SINGGUNG PADA HIPERBOLA Tujun Pemeljrn Setelh mempeljri mteri ini, kmu dihrpkn memiliki kemmpun erikut.. Dpt menentukn persmn gris singgung di titik (, ) pd
Fungsi f dikatakan pada / onto / surjektif jika setiap elemen himpunan B merupakan
III FUNGSI 15 1. Definisi Fungsi Definisi 1 Mislkn dn dlh himpunn. Relsi iner f dri ke merupkn sutu fungsi jik setip elemen di dlm dihuungkn dengn tept stu elemen di dlm. Jik f dlh fungsi dri ke, mk f
INTEGRAL FOURIER KED. Diasumsikan syarat-syarat berikut pada f(x): 1. f x memenuhi syarat Dirichlet pada setiap interval terhingga L, L.
INTEGRAL FOURIER Disumsikn syrt-syrt berikut pd f(x):. f x memenuhi syrt Dirichlet pd setip intervl terhingg L, L.. f x dx konvergen, yitu f(x) dpt diintegrsikn secr mutlk dlm (, ). Selnjutny, Teorem integrl
Erna Sri Hartatik. Aljabar Linear. Pertemuan 3 Aljabar Vektor (Perkalian vektor-lanjutan)
Ern Sri Hrttik Aljr Liner Pertemun Aljr Vektor (Perklin vektor-lnjutn) Pemhsn Perklin Cross (Cross Product) - Model cross product - Sift cross product Pendhulun Selin dot product d fungsi perklin product
RANGKUMAN INTEGRAL. Di Susun Oleh : Syaiful Hamzah Nasution, S.Si., S.Pd.
Generted y Foxit PDF Cretor Foxit Softwre http://www.foxitsoftwre.om For evlution only. RANGKUMAN INTEGRAL Di Susun Oleh : Syiful Hmzh Nsution, S.Si., S.Pd. Di dukung oleh : Portl eduksi Indonesi Open
A. Pengertian Integral
A. Pengertin Integrl Di Kels XI, klin telh mempeljri konsep turunn. Pemhmn tentng konsep turunn ini dpt klin gunkn untuk memhmi konsep integrl. Untuk itu, co tentukn turunn fungsi-fungsi erikut. f () f
DETERMINAN. Misalkan A adalah suatu matriks persegi. a) Jika A memiliki satu baris atau satu kolom bilangan nol, maka det(a) = 0.
DETERMINAN Fungsi determinn dri sutu mtriks persegi A (dinotsikn dengn det(a) tu A ) didefinisikn sebgi jumlh dri semu hsil kli elementer bertnd dri A. Sementr, ngk tu bilngn dri det(a) disebut determinn
Integral Agus Yodi Gunawan
Integrl Agus Yodi Gunwn Teknik pengintegrln.. Metode substitusi pd integrl tk tentu. Mislkn g() sutu fungsi yng terdiferensilkn. Mislkn pul F () merupkn ntiturunn dri fungsi f(). Jik u = g(), mk f(g())g
3. LIMIT DAN KEKONTINUAN
3. LIMIT DAN KEKONTINUAN 1 3.1 Limit Fungsi di Stu Titik Pengertin it secr intuisi Perhtikn ungsi 1 1 Fungsi dits tidk terdeinisi di =1, kren di titik tersebut berbentuk 0/0. Tpi msih bis ditnykn berp
matematika K-13 IRISAN KERUCUT: PERSAMAAN HIPERBOLA K e l a s A. Definisi Hiperbola Tujuan Pembelajaran
K-13 mtemtik K e l s I IRISAN KERUCUT: PERSAMAAN HIPERBLA Tujun Pemeljrn Setelh mempeljri mteri ini, kmu dihrpkn memiliki kemmpun erikut. 1. Memhmi definisi dn unsur-unsur hiperol.. Dpt menentukn persmn
Suku banyak. Akar-akar rasional dari
Suku nyk Algoritm pemgin suku nyk menentukn Teorem sis dn teorem fktor terdiri dri Pengertin dn nili suku nyk Hsil gi dn sis pemgin suku nyk Penggunn teorem sis Penggunn teorem fktor Derjd suku nyk pd
matematika K-13 TEOREMA FAKTOR DAN OPERASI AKAR K e l a s
K-3 mtemtik K e l s XI TEOREMA FAKTOR DAN OPERASI AKAR Tujun Pemeljrn Setelh mempeljri mteri ini, kmu dihrpkn memiliki kemmpun erikut.. Memhmi teorem fktor.. Menentukn kr dn fktor liner suku nyk dengn
LIMIT DAN KONTINUITAS
LIMIT DAN KONTINUITAS Limit Fungsi di Stu Titik Pengertin it secr intuisi Perhtikn ungsi Fungsi dits tidk terdeinisi di =, kren di titik tersebut berbentuk 0/0. Tpi msih bis ditnykn berp nili jik mendekti
3. LIMIT DAN KEKONTINUAN. INF228 Kalkulus Dasar
. LIMIT DAN KEKONTINUAN INF8 Klkulus Dsr . Limit Fungsi di Stu Titik Pengertin it secr intuisi Perhtikn ungsi Fungsi dits tidk terdeinisi di =, kren di titik tersebut berbentuk 0/0. Tpi msih bis ditnykn
ÚÚ Ú Ú Ú Ú. Integral lipat dua pada daerah persegi panjang
Koko Mrtono FMIPA - ITB 99 Integrl lipt du pd derh persegi pnjng i = f () c i b Lus = f () d [ b, ] z z = f (,) b da B c d = Volum B fda (, ) d c da b Integrl tunggl Integrl dri fungsi kontinu = f () pd
3. LIMIT DAN KEKONTINUAN
. LIMIT DAN KEKONTINUAN . Limit Fungsi di Stu Titik Pengertin it secr intuisi Perhtikn ungsi Fungsi dits tidk terdeinisi di, kren di titik tersebut berbentuk 0/0. Tpi msih bis ditnykn berp nili jik mendekti
MA3231 Analisis Real
MA3231 Anlisis Rel Hendr Gunwn* *http://hgunwn82.wordpress.com Anlysis nd Geometry Group Bndung Institute of Technology Bndung, INDONESIA Progrm Studi S1 Mtemtik ITB, Semester II 2016/2017 HG* (*ITB Bndung)
12. LUAS DAERAH DAN INTEGRAL
12. LUAS DAERAH DAN INTEGRAL 12.1 Lus Derh di Bwh Kurv Mslh menentukn lus derh (dn volume rung) telh dipeljri sejk er Pythgors dn Zeno, pd thun 500-n SM. Konsep integrl (yng terkit ert dengn lus derh)
Sebaran Kontinu Khusus
Sttistik Mtemtik I Sern Kontinu Khusus Hzmir Yozz Izzti rhmi HG Jurusn Mtemtik LOGO FMIPA Universits Andls SEBARAN SERAGAM KONTINU Definisi 4.1. Sutu peuh ck kontinu X diktkn memiliki sergm kontinu pd
BAB 3 SOLUSI NUMERIK SISTEM PERSAMAAN LINEAR
A SOLUSI NUMERIK SISTEM PERSAMAAN LINEAR. Metode Eliminsi Guss Tinu sistem persmn liner ng terdiri dri i ris dn peuh, kni,,,, erikut.......... i i i Jik =, sistem persmn linern diseut sistem homogen, sedngkn
SISTEM BILANGAN REAL. Purnami E. Soewardi. Direktorat Pembinaan Tendik Dikdasmen Ditjen GTK Kementerian Pendidikan dan Kebudayaan
SISTEM BILANGAN REAL Purnmi E. Soewrdi Direktort Peminn Tendik Dikdsmen Ditjen GTK Kementerin Pendidikn dn Keudyn Himpunn Bilngn Asli (N) Bilngn sli dlh ilngn yng pertm kli dikenl dn digunkn oleh mnusi
http://meetied.wordpress.com Mtemtik X Semester 1 SMAN 1 Bone-Bone Reutlh st ini. Ap pun yng is And lkukn tu And impikn Mulilh!!! Keernin mengndung kejeniusn, kekutn dn kejin. Lkukn sj dn otk And kn muli
Integral Kompleks (Bagian Kesatu)
Integrl Kompleks (Bgin Kestu) Supm Jurusn Mtemtik, FMIPA UGM Yogykrt 55281, INDONESIA Emil:mspomo@yhoo.com, supm@ugm.c.id (Pertemun Minggu XI) Outline 1 Fungsi Bernili Kompleks 2 Lintsn tu Kontur 3 Integrl
APLIKASI INTEGRAL PENERAPAN INTEGRAL. Luas daerah kelengkungan
APLIKASI INTEGRAL APLIKASI INTEGRAL PENERAPAN INTEGRAL Lus derh kelengkungn PENERAPAN INTEGRAL Indiktor 1 Indiktor 9 Lus derh di bwh kurv berdsr prinsip Riemn Volume bend putr, jik kurv diputr mengelilingi
A x = b apakah solusi x
MTRIKS INVERSI & SIFT-SIFTNY Bil, x, dlh sklr ilngn rel yng memenuhi x, mk x pil. Sekrng, untuk sistem persmn linier x pkh solusi x dpt diselesikn dengn x? Mtriks Identits Untuk sklr (rel numer dn ), mk.
VEKTOR. 1. Pengertian Vektor adalah besaran yang memiliki besar (nilai) dan arah. Vektor merupakan sebuah ruas garis yang
VEKTOR 1. Pengertin Vektor dlh besrn yng memiliki besr (nili dn rh. Vektor merupkn sebuh rus gris yng P berrh dn memiliki pnjng. Pnjng rus gris tersebut dlh pnjng vektor. Rus gris dri titik P dn berujung
Bab 3 M M 3.1 PENDAHULUAN
B SISTEM PERSAMAAN LINEAR Pd gin ini kn dijelskn tentng sistem persmn liner (SPL) dn r menentukn solusiny. SPL nyk digunkn untuk memodelkn eerp mslh rel, mislny: mslh rngkin listrik, jringn komputer, model
MA1201 MATEMATIKA 2A Hendra Gunawan
MA MATEMATIKA A Hendr Gunwn Semester II, 6/7 Februri 7 Kulih yng Llu 8. Bentuk Tk Tentu Tipe / Menghitung limit bentuk tk tentu / dengn menggunkn Aturn l Hopitl 8. Bentuk Tk Tentu Linny Menghitung bentuk
10. cos (ax+b)sin(ax+b) dx = 12. sec x dx = tan x + c. 13. sec (ax+b)dx = tan (ax+b)+ c. 14. c sec x dx = - ctg x + c
BAB XVI. INTEGRAL A. Integrl Tk Tentu. Rumus Integrl Fungsi Aljr. k k n = n +. ( + ) n = ( n + ). = ln + n + + ; n - n+ (+) + ; dn n -. ( f ( ) ± g( ) ) f ( ) ± g ( ) n. os (+)sin(+) = ( n + ) os n + (+)
Materi IX A. Pendahuluan
Mteri IX Tujun :. Mhsisw dpt memhmi vektor. Mhsisw mmpu mengunkn vektor dlm persoln sederhn 3. Mhsisw mengimplementsikn konsep vektor pd rngkin listrik. Pendhulun Sudh menjdi kesepktn umum hw untuk menentukn
CONTOH SOLUSI BEBERAPA SOAL OLIMPIADE MATEMATIKA Oleh: Wiworo, S.Si, M.M. 3. Untuk k 2 didefinisikan bahwa a
CONTOH SOLUSI BEBERAPA SOAL OLIMPIADE MATEMATIKA Oleh: Wiworo, S.Si, M.M. Dikethui bhw,. Untuk k didefinisikn bhw k k k. Tentukn jumlh tk hingg dri. Kit mislkn S S. Dengn demikin kit dpt menuliskn Kedu
Materi ke 5 Integral tak wajar
Mteri ke 5 Integrl tk wjr Senin, 3 Mret 5 ekop3@yhoo.com Jurusn Teknik Industri - Universits Seels Mret Isi Integrl Tk Wjr Pd Selng Hingg Integrl Tk Wjr Pd Selng Tk Hingg Jurusn Teknik Industri - Universits
7. Ruang L 2 (a, b) f(x) 2 dx < }.
7. Rung L (, b) Rung L (, b) didefinisikn sebgi rung semu fungsi f yng kudrtny terintegrlkn pd [, b], ykni L (, b) := {f : b f(x) dx < }. Rung ini menckup fungsi-fungsi f yng tk terbts pd [, b] tetpi f
BAB: PENERAPAN INTEGRAL Topik: Volume Benda Putar (Khusus Kalkulus 1)
BAB: PENERAPAN INTEGRAL Topik: Volume Bend Putr (Khusus Klkulus ) Kompetensi yng diukur dlh kemmpun mhsisw menghitung volume bend putr dengn metode cincin, metode ckrm, tu metode kulit tbung.. UAS Klkulus,
III. LIMIT DAN KEKONTINUAN
KALKULUS I MUG1A4 PROGRAM PERKULIAHAN DASAR DAN UMUM PPDU TELKOM UNIVERSITY III. LIMIT DAN KEKONTINUAN 3.1 Limit Fungsi di Stu Titik Pengertin it secr intuisi Perhtikn ungsi 1 1 Fungsi dits tidk terdeinisi
Hendra Gunawan. 2 April 2014
MA1201 MATEMATIKA 2A Hendr Gunwn Semester II 2013/2014 2 April 2014 Kulih ng Llu 12.1 Fungsi du tu leih peuh 12.2 Turunn Prsil 12.3 Limit dn Kekontinun 12.4 Turunn ungsi du peuh 12.5 Turunn errh dn grdien
Bab 3 Terapan Integral Ganda
Surdi Siregr Metode Mtemtik Astronomi Bb Terpn Integrl Gnd. Integrl Gnd dlm koordint Krtesis dn Polr Koordint Krtesis Koordint Polr Ilustrsi b g f ={,, } Mss M, da, Momen-, M dd Momen- M, d d dd r ={,,
Limit & Kontinuitas. Oleh: Hanung N. Prasetyo. Calculus/Hanung N. Prasetyo/Politeknik Telkom Bandung
imit & Kontinuits Oleh: Hnung N. Prsetyo Clculus/Hnung N. Bb. IMIT.1. Du mslh undmentl klkulus... Gris Tngen.. Konsep imit.4. Teorem imit.5. Konsep kontinuits Clculus/Hnung N. Du Mslh Fundmentl Klkulus
ELIPS. A. Pengertian Elips
ELIPS A. Pengertin Elips Elips dlh tempt kedudukn titik-titik yng jumlh jrkny terhdp du titik tertentu mempunyi nili yng tetp. Kedu titik terseut dlh titik focus / titik pi. Elips jug didefinisikn segi
Bab 3 Terapan Integral Ganda
Surdi Siregr Metode Mtemtik Astronomi Bb 3 Terpn Integrl Gnd 3. Integrl Gnd dlm koordint Krtesis dn Polr Koordint Krtesis Koordint Polr Ilustrsi b g f ={,, } Mss M, da, dd r ={,, r )},, M r da r rdrd sin
Soal-soal dan Pembahasan Matematika Dasar SBMPTN-SNMPTN 2006
www.purwntowhyudi.com Hl- Sol-sol dn Pemhsn Mtemtik Dsr SBMPTN-SNMPTN 006. Jik > 0, > 0 dn mk A. C. E. B. D. Jw:. Jwnny dlh A. Jik p - dn q -, mk q p. A. C. E. B. D. Jw: q p Jwnny dlh A . Grfik y terletk
Teorema Dasar Integral Garis
ISBN: 978-979-79-55-9 Teorem Dsr Integrl Gris Erdwti Nurdin Progrm Studi Pendidikn Mtemtik FKIP UIR d_1910@yhoo.com Abstrk Slh stu generlissi integrl tentu (definite integrl) f x dx diperoleh dengn menggnti
15. INTEGRAL SEBAGAI LIMIT
15. INTEGRAL SEBAGAI LIMIT 15.1 Jumlh Riemnn Dlm kulih Klkulus pd thun pertm, integrl Riemnn bisny diperkenlkn sebgi limit dri jumlh Riemnn, tidk mellui integrl Riemnn ts dn integrl Riemnn bwh. Hl ini
UJIAN SEMESTER GANJIL SMA SANG DEWA JAKARTA TAHUN PELAJARAN
UJIAN SEMESTER GANJIL SMA SANG DEWA JAKARTA TAHUN PELAJARAN - Mt Peljrn : ILMU HITUNG MODERN Kels / Progrm : XII AIA ( Du Bels ) / Ajin Ilmu Api Hri / Tnggl : Minggu Nopemer Wktu :.. WIB ( Menit) Pilihlh
Integral B A B. A. Pengertian Integral. B. Integral Tak Tentu. C. Integral Tertentu. D. Menentukan Luas Daerah. E. Menentukan Volume Benda Putar
Integrl B A B A. Pengertin Integrl B. Integrl Tk Tentu C. Integrl Tertentu D. Menentukn Lus Derh E. Menentukn Volume Bend Putr Sumer: www.wllpperse.com Pernhkh klin meliht ling-ling peswt? Bgimnkh entukny?
LOMBA CERDAS CERMAT MATEMATIKA (LCCM) TINGKAT SMP DAN SMA SE-SUMATERA Memperebutkan Piala Gubernur Sumatera Selatan 3 5 Mei 2011
LOMBA CERDAS CERMAT MATEMATIKA (LCCM) TINGKAT SMP DAN SMA SE-SUMATERA Mempereutkn Pil Guernur Sumter Seltn Mei 0 PENYISIHAN I PERORANGAN LCCM TINGKAT SMA. Dikethui kuus ABCD.EFGH dengn rusuk 6 cm. Jik
MATRIKS Definisi: Matriks Susunan persegi panjang dari bilangan-bilangan yang diatur dalam baris dan kolom. Matriks ditulis sebagai berikut (1)...
MATRIKS Definisi: Mtriks Susunn persegi pnjng dri ilngn-ilngn yng ditur dlm ris dn kolom. Mtriks ditulis segi erikut ()... m... m... n... n......... mn Susunn dits diseut mtriks m x n kren memiliki m ris
SMA Santa Angela. Bandung. 1 P a g e
Persmn Gris Singgung SMA Snt Angel Bndung P g e P g e Persmn Gris Singgung pd Ellips Seperti hln pd lingkrn, terdpt du mcm gris singgung ng kn diicrkn, itu gris singgung ng mellui slh stu titik pd ellips
Solusi Pengayaan Matematika
Solusi Pengn Mtemtik Edisi pril Pekn Ke-, 00 Nomor Sol: -0 Tentukn bnk psngn bilngn rel, ng memenuhi persmn ot ot Solusi: ot ot tnπ otπ π tnπ tn π π π π k π k 00 k 00 k k 00 k k 00 k k 00 k k 00 Kren k
APLIKASI INTEGRAL PENERAPAN INTEGRAL. Luas daerah kelengkungan
APLIKASI INTEGRAL APLIKASI INTEGRAL PENERAPAN INTEGRAL Lus derh kelengkungn Integrl digunkn pd design Menr Petrons di Kul lumpur, untuk perhitungn kekutn menr. Sdne Oper House di design berdsrkn irisn-irisn
MATEMATIKA IPA PAKET A KUNCI JAWABAN
MATEMATIKA IPA PAKET A KUNCI JAWABAN. Jwbn : A Mislkn : p : Msyrkt membung smph pd temptny. q: Kesehtn msyrkt terjg. Diperoleh: Premis : ~q ~p p q Premis : p Kesimpuln : q Jdi, kesimpuln dri premis-premis
6. Himpunan Fungsi Ortogonal
6. Himpunn Fungsi Ortogonl Mislkn f periodik dengn periode, dn mulus bgin demi bgin pd [ π, π]. Jik S f N (θ) = N n= N c ne inθ, n =,, 2,..., dlh jumlh prsil dri deret Fourier f, mk kit telh menunjukkn