PENGANTAR KALKULUS. Disampaikan pada Diklat Instruktur/Pengembang Matematika SMA Jenjang Dasar Tanggal 6 s.d. 19 Agustus 2004 di PPPG Matematika
|
|
|
- Inge Atmadjaja
- 7 tahun lalu
- Tontonan:
Transkripsi
1 PENGANTAR KALKULUS Dismpikn pd Diklt Instruktur/Pengemng Mtemtik SMA Jenjng Dsr Tnggl 6 s.d. 9 Agustus di PPPG Mtemtik Oleh: Drs. SETIAWAN, M. Pd. Widyiswr PPPG Mtemtik Yogykrt DEPARTEMEN PENDIDIKAN NASIONAL DIREKTORAT JENDERAL PENDIDIKAN DASAR DAN MENENGAH PUSAT PENGEMBANGAN PENATARAN GURU (PPPG) MATEMATIKA YOGYAKARTA
2 BAGIAN IV KALKULUS INTEGRAL Kegunn integrl segi ilmu ntu dlm geometri, teknologi, iologi dn ekonomi tk dpt disngkl lgi. Orng yng terctt dlm sejrh pertm kli mengemukkn ide tentng integrl dlh Archimedes seorng ilmuwn ngs Yunni yng ersl dri Syrcus (87 SM). Archimedes menggunkn ide integrl terseut untuk mencri lus derh sutu lingkrn, derh yng ditsi oleh prol dn tli usur dn seginy. Sejrh menctt orng yng pling erjs dlm hl pengemngn klkulus integrl dlh Georg Friederich Benhrd Riemnn (86 866). A. Integrl Tktentu. Integrl segi opersi invers dri turunn. Mislkn fungsi f dlh turunn dri fungsi F, yng errti F() df() d f() Pndnglh pendiferensiln fungsi-fungsi di wh ini F() F () f() F() + F () f() F() 7 F () f() F() + c (c konstnt) F () f() Sekrng timul pertnyn pkh dri huungn F () f() ini jik f() dikethui mk f() psti dpt ditentukn? Sutu opersi mencri F() jik f() dikethui yng merupkn invers dri opersi pendiferensiln diseut opersi nti derivtif, nti diferensil, nti turunn yng is diseut Opersi integrl. Dri contoh di ts dpt ditrik kesimpuln hw nti turunn dri f() dlh F() + c, c konstnt. Dri pengertin hw integrl dlh invers dri Opersi pendiferensiln, mk pil terdpt fungsi F() yng diferensil pd intervl [, ] sedemikin hingg df() F ' d () f() mk nti turunn dri f() dlh F() + c, dn is kit tulis dengn notsi. f()d F() + c Notsi dlh notsi integrl tk tentu. Cttn : Orng yng pertm kli memperkenlkn lmng segi lmng integrl dlh Leiniz, yng disepkti segi slh seorng penemu dri Klkulus. Dri contoh di ts diperoleh hsil d + c Dengn memperhtikn diferensil-diferensil di wh ini: F() + c F () F() + c F () F() n n + (n+ ) n n+ + c F () n+ n (n+ ) F() n + n+ + c F () n+ mk diperoleh integrl fungsi-fungsi ljr : n
3 () d + c () d + c n n+ () d + c,n n + n n+ () d + c,n n + Dri integrl dlh invers diferensil mk d f() ± f() f() ± g()d f()d f()d () ( ) (6) Jw: ( ) d. + c Contoh. Tentukn ( )d + c Contoh. Integrlknlh ( ) 6 Jw: ( ) d ( g + 6)d c c Mengingt pendiferensiln fungsi-fungsi yng lin; yitu: Jik f() sin mk f () cos Jik f() cos mk f () -sin Jik f() tn mk f () sec Jik f() cot mk f () -csc Jik f() sec mk f () sec tn Jik f() csc mk f () -csc cot Jik f() e mk f () e Jik f() ln mk f () Dengn mengingt integrl dlh opersi invers dri pendiferensiln, mk kn diperoleh rumus-rumus pengintegrln. 6
4 (7) cos d sin + c (8) sin d -cos + c (9) sec d tn + c () csc d cot + c () sec tn d sec + c () csc cot d -csc + c () e d e + c d + () ln c Contoh. Grdien pd titik (,y) dri sutu kurv y f() dikethui memenuhi dy huungn d dn mellui (, ). Tentukn persmn kurvny. Jw: dy Grdien kurv y f() dlh d Sehingg y ( ) d y. + c y + c Mellui (, ). + c c Jdi persmnny : y + Jik sutu sol integrl tk dpt diselesikn dengn integrl lngsung, mungkin dengn mensustitusi vriel ru sol terseut dpt dipechkn.. Pengintegrln Dengn Sustitusi Menentukn integrl fungsi yng dpt disederhnkn menjdi entuk n ( f ()) d( f() ). Mengcu pd rumus pengintegrln entuk mk pengintegrln u n d u n + n+ + c, n - n d n + n+ + c, n -, Contoh. Tentukn + d 7
5 Jw : Mislkn u + mk du d Sehingg + d u. du u du. u + c 9 ( + ) + c. 9 du. ( + )d Contoh. : ( + 6) 9 Jw : Mislkn u + 6 du ( + 6)d ( + )d du. ( + )d du Sehingg : u ( + 6) 9 Contoh. Integrlknlh sin 9 u du 9. u + c 9 ( + 6) + c. d Jw : sin d (sin ) sin d Mislkn u cos du - sin d sin d du Sehingg (sin ) sin d (- cos ) sin d 8
6 Contoh. sin cos d ( u ) ( du) Jw : Mislkn u sin du cos d du cos d ( u + u ) du cos + cos cos + c. 9 sin Ltihn. sin u 6 6 (u u 7 sin cos d 6.(- sin ( u 6 7 u 7 u 9 ). du )du 9 ) + c sin sin 6).cos d c.( sin 6).cos d Tentuknlh :. ( + ) d. ( + ) d 8 d. ( + ) sin d 9. cos cos d. sin tg d. cos 9
7 . d +. d cot g d. sin tg( + )d ). cos( d 7. d sin d (- cos ) cos d. ( + sin ) d tn d + cos Tentukn pul ntiderivtif dri sol-sol di wh ini! 7. d ( + ) ( + )d 9. + d. ( + ) d. ( ) +. cos sin d d. sin cos d 6. cos d 7. sin d d 8. sin cos d. cos d 9. ( + cos) sin d. sin cos d. (tn sec ) d. Menentukn Hsil dri d dengn Sustitusi sin t tu ycost Bentuk-entuk integrl di ts dpt digunkn sustitusi dengn menggunkn ntun skets geometri. Contoh Tentukn d Mislkn sin t sin t cos t d cos t cos t
8 t Sehingg d cos t.cos tdt cos tdt ( + cos t) dt (t + sin t) + c Untuk mengemlikn hsil dlm t ini kemli ke vriel digunkn fungsi invers dri fungsi trigonometri, yng is kit kenl segi fungsi siklometri. Bhw jik f() sin mk f () sin rc sin f() cos mk f () cos rc cos f() tn mk f () tn rc tn Dengn huungn jik y sin mk rc sin y Dri persoln di ts, dri d t + sin t + c t + sint.cos t + c sin t t rc sin yng errti : d rc sin c rc sin + + c Contoh. Tentukn Jw : t 9 d 9 Mislkn sin t sin t d cos t dt dn t rc
9 9 cos t 9 cos t Sehingg : 9 d cos t. cos tdt 9 cos tdt 9 ( + cos t) dt 9 (t + sin t) + c 9 (t + sint. cos t) + c 9 (rc sin 9 rc sin 9 +. ) + c c Contoh. Tentuknlh d + + t Mislkn tn t tn t d sec t dt sec t + + sec t Sehingg d + sec tdt ( tn t) sec t sec tdt tn t sin t cos t dt sin d(sin t) - sin t + c
10 + c sin t c + c Ltihn 6 Tentuknlh integrl dri sol-sol di wh ini!. d.. d.. d.. d. d ( ) ( d d ) d ) ( d. 9 d d 6. d d 7. d 7. ( ) ( ( d ) d d 8. d + 7). Integrl Prsil 9.. d d 6 9
11 Mislkn u dn v msing-msing fungsi yng diferensiel dlm, mk diferensil dri y u.v dlh : d(u.v) u.dv + v.du dn jik kedu rus diintegrlkn, kn diperoleh : d (uv) udv + vdu uv udv + vdu tu : udv uv vdu Rumus integrl ini diseut rumus integrl prsil dimn rumus ini is digunkn pil vdu mudh dicri dlm upy mencri penyelesin dri udv yng secr lngsung sulit. Contoh. Tentukn integrl-integrl :. + d. sin d Jw :. Mislkn u mk du d dn dv + mk v + d ( + ) d( + ) Sehingg + d. ( ) ( ) + + ( ) d + ( + ) d( + ) ( ) +. ( + ) + c ( ) + ( + ) + c ( ) + + c. Misl u du d dv sin d v sin d cos + c Sehingg sin d ( cos) ( cos) d cos + sin + c 9 Untuk sol-sol tertentu kdng-kdng diperlukn leih dri sekli memprsilkn. Contoh. Tentuknlh cos( + ) d
12 Jw : Mislkn u mk du d dn dv cos( + ) d Mk v cos( + )d sin( + ) + c Sehingg : cos( + ) d ( sin( + ) sin( + ).d sin( + ) sin( + ) d. (i) Integrl sin( + ) d dpt dicri dengn memprsilkn sekli lgi sin( + ) d ( d(cos( + )) d(cos( + )) ( cos( + ) cos( + )d) cos( + ) + sin( + ) + c..(ii) Dri (i) dn (ii) diperoleh : cos( + ) d sin(+) ( cos( + ) + sin( + )) + c sin(+) + cos( + ) sin( + )) + c Pengemngn : Khusus untuk pengintegrln prsil erulng entuk udv yng turunn ke-k dri u dlh (nol), dn integrl ke-k dri v d, mk integrl erulng di ts dpt ditempuh cr prktis segimn contoh di wh ini. Contoh Tentuknlh cos( + ) d Jw : cos(+) diturunkn + diintegrlkn sin( + ) cos( + ) + sin( + ) 8 Sehingg : cos( + ) d sin( + ) + cos( + ) sin( + ) + c Contoh
13 Integrlknlh : sin( + ) d Jw : sin(+) + diturunkn cos( + ) sin( + ) + cos( + ) 8 sin( + ) 6 + cos( + ) diintegrlkn Sehingg : sin( + ) d cos( + ) + sin(+) + cos( + ) sin( + ) cos( + ) + c Ltihn 7 Dengn menggunkn integrl prsil, crilh integrl erikut ini :. ( ) d. sin( ) d. ( + ) 6 d. sin( + ) d. ( ) d. d. d 6. d. 9 d. cos( ) d. sin d sin 6. cos d (petunjuk uh keentuk sin d d 7. cosd sin( ) d 8. d 9. ( + ) cos( ) d 9. cos d. cos d. cos( ) d Pengyn : 6
14 Pengintegrln fungsi-fungsi trigonometri, keculi dengn sustitusi dpt jug digunkn rumus rumus reduksi di wh ini :. sin n sin n u cos u udu + n sin n udu n n. cos n cos n u sin u udu + n cos n udu n n. sin n u cos m sin n+ u cos m+ u du + m sin n u cos m udu,n m m + n n + m sin n u cos m+ u + n sin n u cos n udu,n m m + n n+ m Bukti :. sin n udu sin n u sin udu sin n ud(cos u) sin n u cos u + cos ud(sin n u) sin n u cos u + (n-) cos u sin n u cos udu sin n u cos u + (n-) cos u sin n udu sin n u cos u + (n-) ( sin u)sin n udu sin n u cos u + (n-) sin n udu (n ) sin n udu n sin n udu sin n u cos u + (n-) sin n udu Jdi sin n sin n u cos u udu + n sin n udu u n Contoh Tentuknlh sin ( ) d Jw : sin ( ) d sin ( )d( ) sin ( ) cos( ) ( + sin( )d( ) sin( ) cos( ) cos( ) Contoh 7
15 Tentuknlh cos ( + ) d Jw : cos ( + ) d cos ( + )d( + ) cos ( + ) sin( + ) ( + cos ( + )d( + )) cos( + ) sin( + ) cos ( + ) sin( + ) + ( d( + )) cos ( + ) sin( + ) + cos( + ) sin( + ) + ( + ) + c Ltihn 8 Dengn menggunkn rumus reduksi selesikn pengintegrln di wh ini. sin d 9. sin cos d. cos d. sin cos d. cos d. sin ( + )cos ( + ) d. sin d. sin( ) d. cos d. cos( + ) d 6. cos ( + ) d. ( + ) sin( + 6) d 7. cos ( + ) d. ( ). cos( 6) d 8. sin cos d 6. sin( + ) d. Pengintegrln u du d Dri f() ln f () mk ln + c du Yng errti ln u + c. u Contoh. Tentuknlh ( e ) e d Jw : Mislkn u e mk du -e d e d du 8
16 . u + c ( e ) + c 6 Sehingg ( )e d u ( du) Contoh. Tentuknlh sin e -cos d Jw mislkn u cos du sin d -cos u sehingg sin e d e du e u + c e -cos + c Contoh. d Integrlknlh ( + ln ) Jw : Mislkn u + ln d du u du Sehingg d du ( + ln ) u ln u + c ln( + ln ) + c Contoh. Integrlknlh log ( + ) d ln ( + ) Jw : Mislkn u log ( + ) ln.d du ( + )ln du d d ( + ) u ( + ) + c Sehingg : log d ( + )d ( + ) log( + ) ( + ). ( + )ln 9
17 Contoh. Integrlknlh ( + ) log ( + ) - d ln ( + ) log ( + ) - + c. ln e sin d Jw : e sin d - e d(cos ) e cos - cos d (e ). e cos + e cos d e cos + e d(sin ) e cos + e sin - sin d(e ) e cos + e sin - e sin d e sin d - e cos + e sin + c Jdi e sin d e (sin - cos ) + c. Ltihn 9. Tentuknlh integrl dri : d e d.. e + d (e )d.. + e e. d. e d d. u + (e )d. e sec. d tg. e d e d e d e 7. tg ( ) d 7. 6 d 6
18 8. ctg( + ) d 8. 6 d Petunjuk mis. 9. sec d 9. u sec + tg + d. cos d. + d B. Integrl tertentu. Pengertin Integrl Tertentu (Integrl Riemnn) f( ) L y f() f( n ) Gmr dismping memperlihtkn derh L yng ditsi oleh y f(), sumu dri smpi dengn. Untuk mencri lus derh L ditempuh lngkhlngkh segi erikut. G.. Lngkh pertm, intervl [,] digi menjdi n intervl dengn pnjng msingmsing intervl gin,,,, n. Sedng pd msing-msing intervl ditentukn titik-titik,,,, n. Selnjutny diut persegipnjng-persegipnjng dengn pnjng msing-msing f( ), f( ), f( ),, f( n ) dn ler msingmsing,,,, n sehingg : Lus persegipnjng pertm f( ). Lus persegipnjng kedu f( ). Lus persegipnjng ketig f( ). Lus persegipnjng ke-n f( n ). n + Jumlh lus seluruh persegipnjng f( ). +f( ). +f( ). + +f( n ). n n f (i ). i. i Dn untuk meneknkn hw pengmiln jumlh terseut meliputi derh pd intervl [,], notsi sigm di ts sering kit tulis dengn notsi. Jumlh semu lus persegipnjng f ().. Jik n diut cukup esr mk jumlh lus dits mendekti lus derh L. Sehingg lus deh L dlh nili limit jumlh di ts. L lim n f().. 6
19 Notsi terseut di ts is ditulis dengn notsi integrl tertentu tu integrl Riemnn : L f()d. : notsi integrl tertentu : ts wh integrl : ts ts integrl Contoh 8 Tunjukkn dengn jln mengrsir derh yng ditunjukkn oleh ( + )d. Jw : Persmn kurv y + y A + Integrl di ts menyjikn derh yng ditsi oleh kurv y +, sumu, dengn grisgris - dn, seperti derh yng dirsir dismping. G... Menentukn nili f()d Untuk menentukn nili f ()d dicri segi erikut : y Andikn kn dicri lus derh yng ditsi oleh y f(), sumu dri smpi dengn C T S. U R Mislkn lus derh yng dicri dlh L(), D mk A P c h Q c+h B G.. 6
20 L() f ()d, c L(c) f ()d c+h L(c + h) f ()d L() f ()d dn Lus PQRU < lus PQSU < lus PQST f(c).h < L (c + h) L(c) < f(c + h).h L(c + h) L(c) f(c) < < f(c + h), h h Jik h mk L(c + h) - L(c) lim f(c) lim lim f(c + h) h h h h f(c) L (c) f(c) L (c) f(c). Oleh kren hsil terseut erlku untuk setip c pd intervl [,] mk setip [,] erlku : L () f() sehingg L() f()d. Jik F() dlh nti turunn dri f() mk L() F() + c. () Dri L(), errti F() + c, sehingg c -F() () L() F() + c F() F(). Contoh 9 f ()d [F()] F() F(). Tentukn nili integrl dri ( + )d. Jw : ( + )d [ + ] ( +.) ( +.) 8. 6
21 Untuk menentukn lus derh yng ditsi oleh kurv y f(), sumu dn gris dn gris. G.. c Untuk derh di ts sumu tu pd intervl <, f() > untuk setip, sehingg f (). > yng errti f ()d dlh positip. Sedng derh yng terletk di wh sumu tu < c, mk f() < untuk setip. Sehingg f (). < yng errti f ()d dlh negtif. Sehingg nili c integrl f ()d untuk derh di wh sumu ernili negtif. Contoh. Hitung ( )d. Hitung lus derh yng disjikn oleh integrl di ts. Penyelesin : ( )d y y I II y - c y f() c..... Kren d derh yng terletk di wh sumu, mk nili integrl tertentuny negtif, sehingg lus derh yng dirsir L I + II, tu G..6 6
22 L ( )d + ( + )d ( ) + + Jdi lus derhny stun lus. Ltihn. Tentukn nili integrl tertentu dri sol-sol di wh ini. ( )d. d 9. d. ( )d. ( )( )d 6. Tentukn p sedemikin hingg ( )d p 7. ( + ) dp p 6
23 π 8. cos d π 9. (sin + cos )d π. cos sin d. Tentukn lus derh yng ditsi oleh f() 6 -, sumu dri smpi dengn.. Tentukn lus derh yng ditsi oleh f() +, sumu X dri smpi dengn. Tentukn lus derh yng ditsi oleh f() 6 dri smpi dengn. Tunjukkn hw lus derh lingkrn dengn jri-jri r dlh π r y. Tunjukkn hw lus derh ellips + dlh π. 6. Tentukn lus derh yng ditsi oleh kurv-kurv erikut :. y dn y. y + dn + y 6 c. y sin dn y cos dri π smpi dengn π Menentukn Volum Bend Putr Perhtikn gmr di wh ini : Y y f() O X 66
24 Untuk menentukn volum end putr yng dientuk oleh y f() yng diputr mengelilingi sumu-x pd intervl [,] kit gi-gi end terseut menjdi kertn-kertn, di mn setip kertn mempunyi volum : vi πf (i ). i Sehingg volum keseluruhn : v πf (i ). iπ lim f ( ). tu : π i v f () d tu v y d π i i. Pnjng Busur ( Mteri Pengyn) Apliksi leih klnjut dri integrl tertentu dlh untuk menghitung pnjng usur dri sutu gris lengkung dri kurv y f(). B y f() X A s P(,y) Q(+, y + y) y O Y Mislkn gmr di ts memperlihtkn kurv y f(), dn titik-titik A dn B pd kurv y f(). Jik kurv y f() dn turunn-turunn kontinu dlm intervl [,], mk pnjng usur AB dpt ditentukn segi erikut : Mislkn titik-titik P(,y) dn titik Q(+, y + y) terletk pd kurv y f(). Pnjng PQ dpt ditentukn dengn menggunkn teorem Pythgors : s + y 67
25 Pnjng usur AB dpt dinytkn segi limit jumlh segmen-segmen yitu : s lim s s lim + y y lim + ( ). Huungn di ts jik disjikn dlm notsi Riemnn, kn menjdi : s dy s ds ( ) + d dy Contoh. Tentukn pnjng gris dengn persmn y + dri smpi dengn! Jw: X A B y + X dy Dri y + mk d Pnjng usur AB : s + ( dy ) d + d d d [ ] Jdi pnjng rus AB stun pnjng. Cttn : Keenrn jw ini dpt nd cek dengn menggunkn rumus jrk du titik A(,) dn B(,6). 68
26 Untuk kurv-kurv yng disjikn dlm entuk prmeter (t) dn y y(t) mk pnjng usur AB dpt ditentukn dengn rumus : s t t d dt dy + dt dt Rumus ini diturunkn dri rumus s dy d dy dt. dt dt dy dt d dt dy + d dengn menggunkn sustitusi : d Contoh. Tunjukkn hw keliling lingkrn dengn jri-jri r dlh π r. Bukti : Y O r t P(,y) y X Persmn lingkrn di smping ini, jik disjikn dlm persmn prmeter : r cos t y r sin t dy Dri r cos t r sin t dt y r sin t d dt r cos t t s ( ) dy ( d ) s + dt t π π ( sin t) dt π Sehingg keliling lingkrnny, digunkn rumus dt, untuk lingkrn di ts : + (r cos t) dt π r dt r[] t r(π ) πr r (sin t + cos Dengn demikin terukti hw keliling lingkrn dengn jri-jri r dlh π r stun pnjng. t) dt 69
27 . Penerpn Integrl Dlm Bidng Ush dn Perekonomin. Bnyk penerpn konsep integrl yng mt ermnft gi kehidupn mnusi dlm ergi idng termsuk dlm hl perindustrin dn perekonomin. Berikut ini eerp contoh penerpnny : Contoh Fungsi iy mrginl dri sutu prik dlm produksiny dlh : c () +, di mn dlh nykny unit produksi setip hri. Prik terseut mengelurkn iy tetp Rp.., setip hri. Tentukn iy produksi setip hriny. Penyelesin : Biy produksi C() ( + )d + + c Biy tetp C().., sehingg : c c.. Jdi iy produksi setip hriny dlh : C() Menghitung Surplus Konsumen. P P e O Surplus Konsumen E( Q,P ) e e Pf(Q) Q Surplus konsumen merupkn keuntungn leih yng dinikmti konsumen erkenn dengn tingkt hrg psr tertentu. Bgi konsumen yng seenrny mmpu memyr hrg di ts hrg psr E kn mendptkn untung seesr : Q e SK f (Q)dQ Q e. P e Contoh : Dikethui fungsi permintn : P - Q Crilh surplus konsumen jik Q Penyelesin : p -. 7
28 SK ( Q )dq P.Q Q. 6 Q [ ] Menghitung Surplus Konsumen. P P e E(Q e, Pe ) O P f(q) Surplus produksi Q e Dengn jln yng mirip dengn surplus konsumen, mk surplus produksi (SP) dihitung dengn menggunkn rumus SP P e.q e Q e f (Q) dq di mn P f(q) dlh fungsi penwrn. Q Ltihn.. Tentukn volum end yng terjdi jik derh yng ditsi oleh kurv-kurv di wh ini diputr sekeliling sumu X.. y 9. y dn y c. y dn y. Hitung pnjng usur dri kurv y + dri smpi dengn. Hitung pnng usur kurv y dri hingg. Hitung pnjng usur kurv y dri hingg. Tentukn pnjng usur kurv y + 8 dri smpi dengn 6. Tentukn pnjng usur sikloid θ sin θ ; y cosθ dri θ dn θ π 7. Tentukn lus derh yng ditsi oleh 6y + dri smpi dengn 7
29 Q 8. Fungsi iy mrginl sutu produk dlh : P Q. Jik dikethui iy tetpny dlh Rp..,. Crilh fungsi iyny dn iy totl untuk produksi unit. 9. Dikethui fungsi permintn : P Q. Crilh surplus konsumsen jik Q. Gmrlh fkt itu.. Fungsi permintn penwrn sutu rng dlh : P dn P + Tentukn esrny surplus konsumen dn surplus produsen dn gmrkn pd sutu digrm. 7
30 DAFTAR PUSTAKA Ayres, Frnk Jr. (97), Theory nd Prolem of Differensil nd Integrl Clculus. Mc Grw Hill : New York. Fth Asyrie, dkk. (99), Klkulus untuk SMA. Pkr Ry : Bndung. Herry Sukrmn. (998), Klkulus, Mklh Pentrn Guru Mtemtik MGMP SMU. PPPG mtemtik : Yogykrt. Johnnes, H dn Budiono Sri Hndoko. (988), Pengntr Mtemtik untuk Ekonomi. LPES : Jkrt. Piskunov, N. (97), Differensil nd Integrl Clculus. Mir Pulishers : Moscow. Purcell, Edwin Jud Dle Vrerg. Klkulus dn Geometri Anlitik. PT. Penerit Erlngg : Jkrt. Sri Kurniningsih, dkk. (99), Mtemtik SMU, Yudhistir : Jkrt. Sumdi, dkk. (997), Mtemtik SMU, PT. Tig Serngki : Surkrt. Thoms, George B. Jr. (977), Clculus nd Anlytic Geometry, Addison-Werley Pulishers Compny. 7
31 7
PEMANTAPAN BELAJAR SMA BBS INTEGRAL
 BAB I PEMANTAPAN BELAJAR SMA BBS INTEGRAL I A RANGKUMAN INTEGRAL. Pengertin Apil terdpt fungsi F() yng dpt didiferensilkn pd selng I sedemikin hingg F () = f(), mk nti turunn (integrl) dri f() dlh F()
BAB I PEMANTAPAN BELAJAR SMA BBS INTEGRAL I A RANGKUMAN INTEGRAL. Pengertin Apil terdpt fungsi F() yng dpt didiferensilkn pd selng I sedemikin hingg F () = f(), mk nti turunn (integrl) dri f() dlh F()
RANGKUMAN MATERI ' maupun F(x) = Pengerjaan f(x) sehingga memperoleh F(x) + c disebut mengintegralkan f(x) ke x dengan notasi:
 INTEGRAL RANGKUMAN MATERI A. ANTIDERIVATIF DAN INTEGRAL TAK TENTU Jik kit mengmil uku dri temptny mk kit dpt mengemliknny lgi ke tempt semul. Opersi yng kedu menghpus opersi yng pertm. Kit ktkn hw du opersi
INTEGRAL RANGKUMAN MATERI A. ANTIDERIVATIF DAN INTEGRAL TAK TENTU Jik kit mengmil uku dri temptny mk kit dpt mengemliknny lgi ke tempt semul. Opersi yng kedu menghpus opersi yng pertm. Kit ktkn hw du opersi
INTEGRAL. Integral Tak Tentu Dan Integral Tertentu Dari Fungsi Aljabar
 INTEGRAL Integrl Tk Tentu Dn Integrl Tertentu Dri Fungsi Aljr A. Integrl Tk Tentu Hitung integrl dlh kelikn dri hitung differensil. Pd hitung differensil yng dicri dlh fungsi turunnny, sedngkn pd hitung
INTEGRAL Integrl Tk Tentu Dn Integrl Tertentu Dri Fungsi Aljr A. Integrl Tk Tentu Hitung integrl dlh kelikn dri hitung differensil. Pd hitung differensil yng dicri dlh fungsi turunnny, sedngkn pd hitung
Integral Tak Tentu dan Integral Tertentu
 Integrl Tk Tentu dn Integrl Tertentu Pengertin Integrl Jik F dlh fungsi umum yng ersift F = f, mk F merupkn ntiturunn tu integrl dri f. Pengintegrln fungsi f terhdp dinotsikn segi erikut : f d F c notsi
Integrl Tk Tentu dn Integrl Tertentu Pengertin Integrl Jik F dlh fungsi umum yng ersift F = f, mk F merupkn ntiturunn tu integrl dri f. Pengintegrln fungsi f terhdp dinotsikn segi erikut : f d F c notsi
INTEGRAL. Kelas XII IIS Semester Genap. Oleh : Markus Yuniarto, S.Si. SMA Santa Angela Tahun Pelajaran 2017/2018
 Modul Integrl INTEGRAL Kels XII IIS Semester Genp Oleh : Mrkus Yunirto, SSi SMA Snt Angel Thun Peljrn 7/8 Modul Mtemtik Kels XII IIS Semester TA 7/8 Modul Integrl INTEGRAL Stndr Kompetensi: Menggunkn konsep
Modul Integrl INTEGRAL Kels XII IIS Semester Genp Oleh : Mrkus Yunirto, SSi SMA Snt Angel Thun Peljrn 7/8 Modul Mtemtik Kels XII IIS Semester TA 7/8 Modul Integrl INTEGRAL Stndr Kompetensi: Menggunkn konsep
INTEGRAL. Misalkan suatu fungsi f(x) diintegralkan terhadap x maka di tulis sebagai berikut:
 INTEGRAL.PENGERTIAN INTEGRAL Integrl dlh cr mencri sutu fungsi jik turunnn di kethui tu kelikn dri diferensil (turunn) ng diseut jug nti derivtif tu nti diferensil. Untuk menentukn integrl tidk semudh
INTEGRAL.PENGERTIAN INTEGRAL Integrl dlh cr mencri sutu fungsi jik turunnn di kethui tu kelikn dri diferensil (turunn) ng diseut jug nti derivtif tu nti diferensil. Untuk menentukn integrl tidk semudh
LUAS DAERAH APLIKASI INTEGRAL TENTU. Indikator Pencapaian Hasil Belajar. Ringkasan Materi Perkuliahan
 LUAS DAERAH APLIKASI INTEGRAL TENTU Indiktor Pencpin Hsil Beljr Mhsisw menunjukkn kemmpun dlm :. Menghitung lus pd idng dtr Ringksn Mteri Perkulihn Jik sutu derh ditsi oleh kurv f(), g(), gris dn dengn
LUAS DAERAH APLIKASI INTEGRAL TENTU Indiktor Pencpin Hsil Beljr Mhsisw menunjukkn kemmpun dlm :. Menghitung lus pd idng dtr Ringksn Mteri Perkulihn Jik sutu derh ditsi oleh kurv f(), g(), gris dn dengn
INTEGRAL. y dx. x dy. F(x)dx F(x)dx
 Drs. Mtrisoni www.mtemtikdw.wordpress.om INTEGRAL PENGERTIAN Bil dikethui : = F() + C mk = F () dlh turunn dri sedngkn dlh integrl (nti turunn) dri dn dpt digmrkn : differensil differensil Y Y Y Integrl
Drs. Mtrisoni www.mtemtikdw.wordpress.om INTEGRAL PENGERTIAN Bil dikethui : = F() + C mk = F () dlh turunn dri sedngkn dlh integrl (nti turunn) dri dn dpt digmrkn : differensil differensil Y Y Y Integrl
HITUNG INTEGRAL ( 4 ) 4. Diketahui f(x) = 4x + 1 dan F(2) = 17 ; Tentukan fungsi F f(x) = 4x + 1
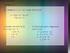 HITUNG INTEGRA BAB.Integrl tk tentu (tnp ts). Rumus-rumus ) ) n n n d c, n ) d c n n n. d c, n ). Sift-sift Integrl Contoh :... ) k. f ( ) d k. f ( ) d d d ln c ) ( ( ) ( )) ( ) ( ) d c ( ) ( ) d ( ) d
HITUNG INTEGRA BAB.Integrl tk tentu (tnp ts). Rumus-rumus ) ) n n n d c, n ) d c n n n. d c, n ). Sift-sift Integrl Contoh :... ) k. f ( ) d k. f ( ) d d d ln c ) ( ( ) ( )) ( ) ( ) d c ( ) ( ) d ( ) d
Modul Matematika 2012
 Modul Mtemtik. ANTI TURUNAN Definisi Mislkn fungsi f terdefinisi pd selng teruk I. Fungsi F ng memenuhi F () = f () pd I dinmkn nti turunn tu fungsi primitif dri fungsi f pd I.. F() = cos nti turunn dri
Modul Mtemtik. ANTI TURUNAN Definisi Mislkn fungsi f terdefinisi pd selng teruk I. Fungsi F ng memenuhi F () = f () pd I dinmkn nti turunn tu fungsi primitif dri fungsi f pd I.. F() = cos nti turunn dri
INTEGRAL TAK TENTU. x x x
 INTEGRAL TAK TENTU Definisi : Fungsi F diktkn nti turunn dri fungsi f pd selng I jik F () = f() untuk semu di I. Notsi : F() = f() Integrl tk tentu dlh Anti/Invers/Kelikn turunn. c c Integrl tk tentu dlh
INTEGRAL TAK TENTU Definisi : Fungsi F diktkn nti turunn dri fungsi f pd selng I jik F () = f() untuk semu di I. Notsi : F() = f() Integrl tk tentu dlh Anti/Invers/Kelikn turunn. c c Integrl tk tentu dlh
Integral. Konstanta dari Integrasi. Integral Tak Tentu. AntiTurunan (Antiderivative)
 Integrl AntiTurunn (Antiderivtive) AntiTurunn dri seuh fungsi f dl seuh fungsi F sedemikin hingg Dierikn Pd Peltihn Guru-Guru Aceh Jy 5 Septemer 0 Oleh: Ridh Ferdhin, M.Sc F f E. AntiTurunn dri f ( ) 6
Integrl AntiTurunn (Antiderivtive) AntiTurunn dri seuh fungsi f dl seuh fungsi F sedemikin hingg Dierikn Pd Peltihn Guru-Guru Aceh Jy 5 Septemer 0 Oleh: Ridh Ferdhin, M.Sc F f E. AntiTurunn dri f ( ) 6
Tiara Ariqoh Bawindaputri TIP / kelas L
 Tir Ariqoh Bwindputri 500008 TIP / kels L INTEGRAL Integrl Tk tentu Integrl dlh entuk invers dri turunn. Secr umum jik seuh fungsi diintegrlkn terhdp vrile tertentu dpt disjikn dlm entuk : f ( F( C Untuk
Tir Ariqoh Bwindputri 500008 TIP / kels L INTEGRAL Integrl Tk tentu Integrl dlh entuk invers dri turunn. Secr umum jik seuh fungsi diintegrlkn terhdp vrile tertentu dpt disjikn dlm entuk : f ( F( C Untuk
MATEMATIKA. Sesi INTEGRAL VOLUME A. BENDA-BENDA YANG MEMILIKI SUMBU PUTAR B. BENDA-BENDA YANG MEMILIKI SUMBU PUTAR TERHADAP SUMBU-X
 MATEMATIKA KELAS XII - KURIKULUM GABUNGAN 6 Sesi N INTEGRAL VOLUME A. BENDA-BENDA YANG MEMILIKI SUMBU PUTAR Apliksi integrl erikutn dlh menentukn volume end ng memiliki sumu putr. Contoh endn dlh tung,
MATEMATIKA KELAS XII - KURIKULUM GABUNGAN 6 Sesi N INTEGRAL VOLUME A. BENDA-BENDA YANG MEMILIKI SUMBU PUTAR Apliksi integrl erikutn dlh menentukn volume end ng memiliki sumu putr. Contoh endn dlh tung,
7. APLIKASI INTEGRAL
 7. APLIKASI INTEGRAL 7. Menghitung Lus Derh.Mislkn derh D (, ), f ( ) D f() Lus D =? Lngkh :. Iris D menjdi n gin dn lus stu uh irisn dihmpiri oleh lus persegi pnjng dengn tinggi f() ls(ler) A f ( ). Lus
7. APLIKASI INTEGRAL 7. Menghitung Lus Derh.Mislkn derh D (, ), f ( ) D f() Lus D =? Lngkh :. Iris D menjdi n gin dn lus stu uh irisn dihmpiri oleh lus persegi pnjng dengn tinggi f() ls(ler) A f ( ). Lus
PENGAYAAN MATEMATIKA SOLUSI SOAL-SOAL LATIHAN 1
 PENGAYAAN MATEMATIKA SOLUSI SOAL-SOAL LATIHAN 6y y 8y. Dikethui R dn. Temukn nili y. y y 8y 6 Solusi: 6y y 8y y y 8y 6 6y y 8y 8y y 6 y 8 0 y y y 0 y y y 0 ( y ) ( y ) 0 y y 8y 6 ( y )(y ) 0 y 0tu y 0
PENGAYAAN MATEMATIKA SOLUSI SOAL-SOAL LATIHAN 6y y 8y. Dikethui R dn. Temukn nili y. y y 8y 6 Solusi: 6y y 8y y y 8y 6 6y y 8y 8y y 6 y 8 0 y y y 0 y y y 0 ( y ) ( y ) 0 y y 8y 6 ( y )(y ) 0 y 0tu y 0
E. INTEGRASI BAGIAN ( PARSIAL )
 E. INTEGRASI BAGIAN ( PARSIAL ) Integrsi gin (prsil) digunkn untuk mengintegrsikn sutu perklin fungsi yng msing-msing fungsiny ukn koefisien diferensil dri yng lin ( seperti yng sudh dihs pd su. B. D )
E. INTEGRASI BAGIAN ( PARSIAL ) Integrsi gin (prsil) digunkn untuk mengintegrsikn sutu perklin fungsi yng msing-msing fungsiny ukn koefisien diferensil dri yng lin ( seperti yng sudh dihs pd su. B. D )
TEORI DEFINITE INTEGRAL
 definite integrl & lus yog.prihstomo TEORI DEFINITE INTEGRAL Definisi : Jik y = f(x) dlh fungsi kontinu dn terdefinisi dlm intervl tertutup [,] sehingg lim n n i= f ( xi). Δxi d (mempunyi nili), mk definite
definite integrl & lus yog.prihstomo TEORI DEFINITE INTEGRAL Definisi : Jik y = f(x) dlh fungsi kontinu dn terdefinisi dlm intervl tertutup [,] sehingg lim n n i= f ( xi). Δxi d (mempunyi nili), mk definite
INTEGRAL. Bogor, Departemen Matematika FMIPA IPB. (Departemen Matematika FMIPA IPB) Kalkulus I Bogor, / 45
 INTEGRAL Deprtemen Mtemtik FMIPA IPB Bogor, 2012 (Deprtemen Mtemtik FMIPA IPB) Klkulus I Bogor, 2012 1 / 45 Topik Bhsn 1 Pendhulun 2 Anti-turunn 3 Lus di Bwh Kurv 4 Integrl Tentu 5 Teorem Dsr Klkulus 6
INTEGRAL Deprtemen Mtemtik FMIPA IPB Bogor, 2012 (Deprtemen Mtemtik FMIPA IPB) Klkulus I Bogor, 2012 1 / 45 Topik Bhsn 1 Pendhulun 2 Anti-turunn 3 Lus di Bwh Kurv 4 Integrl Tentu 5 Teorem Dsr Klkulus 6
Integral B A B. A. Pengertian Integral. B. Integral Tak Tentu. C. Integral Tertentu. D. Menentukan Luas Daerah. E. Menentukan Volume Benda Putar
 Integrl B A B A. Pengertin Integrl B. Integrl Tk Tentu C. Integrl Tertentu D. Menentukn Lus Derh E. Menentukn Volume Bend Putr Sumer: www.wllpperse.com Pernhkh klin meliht ling-ling peswt? Bgimnkh entukny?
Integrl B A B A. Pengertin Integrl B. Integrl Tk Tentu C. Integrl Tertentu D. Menentukn Lus Derh E. Menentukn Volume Bend Putr Sumer: www.wllpperse.com Pernhkh klin meliht ling-ling peswt? Bgimnkh entukny?
INTEGRAL. 1. Macam-macam Integral. Nuria Rahmatin TIP L. A. Integral Tak Tentu
 INTEGRAL Nuri Rhmtin 5000006 TIP L. Mcm-mcm Integrl A. Integrl Tk Tentu Integrl dlh entuk invers dri turunn. Secr umum jik seuh fungsi diintegrlkn terhdp vrile tertentu dpt disjikn dlm entuk : f ( F( C
INTEGRAL Nuri Rhmtin 5000006 TIP L. Mcm-mcm Integrl A. Integrl Tk Tentu Integrl dlh entuk invers dri turunn. Secr umum jik seuh fungsi diintegrlkn terhdp vrile tertentu dpt disjikn dlm entuk : f ( F( C
Hendra Gunawan. 30 Oktober 2013
 MA MATEMATIKA A Hendr Gunwn Semester I, 2/24 Oktoer 2 Ltihn. Fungsi g =,, terintegrlkn pd [, ]. Nytkn integrl tentu g pd [, ] segi limit jumlh Riemnn dengn prtisi reguler, dn hitunglh niliny. //2 c Hendr
MA MATEMATIKA A Hendr Gunwn Semester I, 2/24 Oktoer 2 Ltihn. Fungsi g =,, terintegrlkn pd [, ]. Nytkn integrl tentu g pd [, ] segi limit jumlh Riemnn dengn prtisi reguler, dn hitunglh niliny. //2 c Hendr
Y y=f(x) LEMBAR KERJA SISWA. x=a. x=b
 LEMBAR KERJA SISWA. Judul (Mteri Pokok) : Penggunn Integrl Tentu Untuk Menghitung Volume Bend Putr. Mt Peljrn : Mtemtik 3. Kels / Semester : II /. Wktu : 5 menit 5. Stndr Kompetensi :. Menggunkn konsep
LEMBAR KERJA SISWA. Judul (Mteri Pokok) : Penggunn Integrl Tentu Untuk Menghitung Volume Bend Putr. Mt Peljrn : Mtemtik 3. Kels / Semester : II /. Wktu : 5 menit 5. Stndr Kompetensi :. Menggunkn konsep
BAB. I INTEGRAL. (Orang tuanya) (Anaknya)
 BAB. I INTEGRAL A. Pendhulun.. Pengertin integrl. Integrl dlh lwn kelikn) dri diferensil. Dpt diumpmkn hw opersi diferensil itu, dikethui orng tuny, disuruh menri nkny, sedngkn opersi integrl, dikethui
BAB. I INTEGRAL A. Pendhulun.. Pengertin integrl. Integrl dlh lwn kelikn) dri diferensil. Dpt diumpmkn hw opersi diferensil itu, dikethui orng tuny, disuruh menri nkny, sedngkn opersi integrl, dikethui
Tujuan Pembelajaran. ) pada hiperbola yang berpusat di (0, 0). 2. Dapat menentukan persamaan garis singgung di titik (x 1
 K-3 mtemtik K e l s XI IRISAN KERUCUT: GARIS SINGGUNG PADA HIPERBOLA Tujun Pemeljrn Setelh mempeljri mteri ini, kmu dihrpkn memiliki kemmpun erikut.. Dpt menentukn persmn gris singgung di titik (, ) pd
K-3 mtemtik K e l s XI IRISAN KERUCUT: GARIS SINGGUNG PADA HIPERBOLA Tujun Pemeljrn Setelh mempeljri mteri ini, kmu dihrpkn memiliki kemmpun erikut.. Dpt menentukn persmn gris singgung di titik (, ) pd
MATEMATIKA INTEGRAL TENTU DAN LUAS DAERAH
 MATEMATIKA KELAS XII - KURIKULUM GABUNGAN 5 Sesi N INTEGRAL TENTU DAN LUAS DAERAH A. DEFINISI INTEGRAL TENTU Bentuk integrl f d = f + c diseut segi integrl tk tentu kren hsil dri pengintegrlnn msih erup
MATEMATIKA KELAS XII - KURIKULUM GABUNGAN 5 Sesi N INTEGRAL TENTU DAN LUAS DAERAH A. DEFINISI INTEGRAL TENTU Bentuk integrl f d = f + c diseut segi integrl tk tentu kren hsil dri pengintegrlnn msih erup
PERSAMAAN KUADRAT, FUNGSI KUADRAT DAN PERTIDAKSAMAAN KUADRAT
 PERSAMAAN KUADRAT, FUNGSI KUADRAT DAN PERTIDAKSAMAAN KUADRAT Persmn Kudrt. Bentuk Umum Persmn Kudrt Mislkn,, Є R dn 0 mk persmn yng erentuk 0 dinmkn persmn kudrt dlm peuh. Dlm persmn kudrt 0, dlh koefisien
PERSAMAAN KUADRAT, FUNGSI KUADRAT DAN PERTIDAKSAMAAN KUADRAT Persmn Kudrt. Bentuk Umum Persmn Kudrt Mislkn,, Є R dn 0 mk persmn yng erentuk 0 dinmkn persmn kudrt dlm peuh. Dlm persmn kudrt 0, dlh koefisien
10. cos (ax+b)sin(ax+b) dx = 12. sec x dx = tan x + c. 13. sec (ax+b)dx = tan (ax+b)+ c. 14. c sec x dx = - ctg x + c
 BAB XVI. INTEGRAL A. Integrl Tk Tentu. Rumus Integrl Fungsi Aljr. k k n = n +. ( + ) n = ( n + ). = ln + n + + ; n - n+ (+) + ; dn n -. ( f ( ) ± g( ) ) f ( ) ± g ( ) n. os (+)sin(+) = ( n + ) os n + (+)
BAB XVI. INTEGRAL A. Integrl Tk Tentu. Rumus Integrl Fungsi Aljr. k k n = n +. ( + ) n = ( n + ). = ln + n + + ; n - n+ (+) + ; dn n -. ( f ( ) ± g( ) ) f ( ) ± g ( ) n. os (+)sin(+) = ( n + ) os n + (+)
RANGKUMAN INTEGRAL. Di Susun Oleh : Syaiful Hamzah Nasution, S.Si., S.Pd.
 Generted y Foxit PDF Cretor Foxit Softwre http://www.foxitsoftwre.om For evlution only. RANGKUMAN INTEGRAL Di Susun Oleh : Syiful Hmzh Nsution, S.Si., S.Pd. Di dukung oleh : Portl eduksi Indonesi Open
Generted y Foxit PDF Cretor Foxit Softwre http://www.foxitsoftwre.om For evlution only. RANGKUMAN INTEGRAL Di Susun Oleh : Syiful Hmzh Nsution, S.Si., S.Pd. Di dukung oleh : Portl eduksi Indonesi Open
A. Pengertian Integral
 A. Pengertin Integrl Di Kels XI, klin telh mempeljri konsep turunn. Pemhmn tentng konsep turunn ini dpt klin gunkn untuk memhmi konsep integrl. Untuk itu, co tentukn turunn fungsi-fungsi erikut. f () f
A. Pengertin Integrl Di Kels XI, klin telh mempeljri konsep turunn. Pemhmn tentng konsep turunn ini dpt klin gunkn untuk memhmi konsep integrl. Untuk itu, co tentukn turunn fungsi-fungsi erikut. f () f
12. LUAS DAERAH DAN INTEGRAL
 12. LUAS DAERAH DAN INTEGRAL 12.1 Lus Derh di Bwh Kurv Mslh menentukn lus derh (dn volume rung) telh dipeljri sejk er Pythgors dn Zeno, pd thun 500-n SM. Konsep integrl (yng terkit ert dengn lus derh)
12. LUAS DAERAH DAN INTEGRAL 12.1 Lus Derh di Bwh Kurv Mslh menentukn lus derh (dn volume rung) telh dipeljri sejk er Pythgors dn Zeno, pd thun 500-n SM. Konsep integrl (yng terkit ert dengn lus derh)
didefinisikan sebagai bilangan yang dapat ditulis dengan b
 1 PENDAHULUAN 1.1 Sistem Bilngn Rel Untuk mempeljri klkulus perlu memhmi hsn tentng system ilngn rel, kren klkulus didsrkn pd system ilngn rel dn siftsiftny. Sistem ilngn yng pling sederhn dlh ilngn sli,
1 PENDAHULUAN 1.1 Sistem Bilngn Rel Untuk mempeljri klkulus perlu memhmi hsn tentng system ilngn rel, kren klkulus didsrkn pd system ilngn rel dn siftsiftny. Sistem ilngn yng pling sederhn dlh ilngn sli,
1. Identitas Trigonometri. 1. Identitas trigonometri dasar berikut ini merupakan hubungan kebalikan.
 1. Identits Trigonometri Pengertin Identits Trigonometri dlh kesmn yng memut entuk trigonometri dn erlku untuk semrng sudut yng dierikn. Jenis Identits Trigonometri 1. Identits trigonometri dsr erikut
1. Identits Trigonometri Pengertin Identits Trigonometri dlh kesmn yng memut entuk trigonometri dn erlku untuk semrng sudut yng dierikn. Jenis Identits Trigonometri 1. Identits trigonometri dsr erikut
Tujuan Pembelajaran. ) pada elips. 2. Dapat menentukan persamaan garis singgung yang melalui titik (x 1
 K-3 mtemtik K e l s XI IRISAN KERUCUT: PERSAMAAN GARIS SINGGUNG PADA ELIPS Tujun Pemeljrn Setelh mempeljri mteri ini, kmu dihrpkn memiliki kemmpun erikut.. Dpt menentukn persmn gris singgung di titik (,
K-3 mtemtik K e l s XI IRISAN KERUCUT: PERSAMAAN GARIS SINGGUNG PADA ELIPS Tujun Pemeljrn Setelh mempeljri mteri ini, kmu dihrpkn memiliki kemmpun erikut.. Dpt menentukn persmn gris singgung di titik (,
matematika K-13 TEOREMA FAKTOR DAN OPERASI AKAR K e l a s
 K-3 mtemtik K e l s XI TEOREMA FAKTOR DAN OPERASI AKAR Tujun Pemeljrn Setelh mempeljri mteri ini, kmu dihrpkn memiliki kemmpun erikut.. Memhmi teorem fktor.. Menentukn kr dn fktor liner suku nyk dengn
K-3 mtemtik K e l s XI TEOREMA FAKTOR DAN OPERASI AKAR Tujun Pemeljrn Setelh mempeljri mteri ini, kmu dihrpkn memiliki kemmpun erikut.. Memhmi teorem fktor.. Menentukn kr dn fktor liner suku nyk dengn
MA3231 Analisis Real
 MA3231 Anlisis Rel Hendr Gunwn* *http://hgunwn82.wordpress.com Anlysis nd Geometry Group Bndung Institute of Technology Bndung, INDONESIA Progrm Studi S1 Mtemtik ITB, Semester II 2016/2017 HG* (*ITB Bndung)
MA3231 Anlisis Rel Hendr Gunwn* *http://hgunwn82.wordpress.com Anlysis nd Geometry Group Bndung Institute of Technology Bndung, INDONESIA Progrm Studi S1 Mtemtik ITB, Semester II 2016/2017 HG* (*ITB Bndung)
matematika K-13 IRISAN KERUCUT: PERSAMAAN HIPERBOLA K e l a s A. Definisi Hiperbola Tujuan Pembelajaran
 K-13 mtemtik K e l s I IRISAN KERUCUT: PERSAMAAN HIPERBLA Tujun Pemeljrn Setelh mempeljri mteri ini, kmu dihrpkn memiliki kemmpun erikut. 1. Memhmi definisi dn unsur-unsur hiperol.. Dpt menentukn persmn
K-13 mtemtik K e l s I IRISAN KERUCUT: PERSAMAAN HIPERBLA Tujun Pemeljrn Setelh mempeljri mteri ini, kmu dihrpkn memiliki kemmpun erikut. 1. Memhmi definisi dn unsur-unsur hiperol.. Dpt menentukn persmn
MATEMATIKA IPA PAKET B KUNCI JAWABAN SOAL
 MATEMATIKA IPA PAKET KUNCI JAWAAN SOAL. Jwn : Mislkn p: ir sungi jernih q: Tidk terkndung zt pencemr r: Semu ikn tidk mti Diperoleh : Premis : p q Premis : ~r ~q q r Jdi, kesimpuln dri premis-premis terseut
MATEMATIKA IPA PAKET KUNCI JAWAAN SOAL. Jwn : Mislkn p: ir sungi jernih q: Tidk terkndung zt pencemr r: Semu ikn tidk mti Diperoleh : Premis : p q Premis : ~r ~q q r Jdi, kesimpuln dri premis-premis terseut
ELIPS. A. Pengertian Elips
 ELIPS A. Pengertin Elips Elips dlh tempt kedudukn titik-titik yng jumlh jrkny terhdp du titik tertentu mempunyi nili yng tetp. Kedu titik terseut dlh titik focus / titik pi. Elips jug didefinisikn segi
ELIPS A. Pengertin Elips Elips dlh tempt kedudukn titik-titik yng jumlh jrkny terhdp du titik tertentu mempunyi nili yng tetp. Kedu titik terseut dlh titik focus / titik pi. Elips jug didefinisikn segi
IRISAN KERUCUT: PERSAMAAN ELIPS. Tujuan Pembelajaran
 K-13 mtemtik K e l s I IRISAN KERUCUT: PERSAMAAN ELIPS Tujun Pemeljrn Setelh mempeljri mteri ini, kmu dihrpkn memiliki kemmpun erikut. 1. Memhmi definisi elips.. Memhmi unsur-unsur elips. 3. Memhmi eksentrisits
K-13 mtemtik K e l s I IRISAN KERUCUT: PERSAMAAN ELIPS Tujun Pemeljrn Setelh mempeljri mteri ini, kmu dihrpkn memiliki kemmpun erikut. 1. Memhmi definisi elips.. Memhmi unsur-unsur elips. 3. Memhmi eksentrisits
Suku banyak. Akar-akar rasional dari
 Suku nyk Algoritm pemgin suku nyk menentukn Teorem sis dn teorem fktor terdiri dri Pengertin dn nili suku nyk Hsil gi dn sis pemgin suku nyk Penggunn teorem sis Penggunn teorem fktor Derjd suku nyk pd
Suku nyk Algoritm pemgin suku nyk menentukn Teorem sis dn teorem fktor terdiri dri Pengertin dn nili suku nyk Hsil gi dn sis pemgin suku nyk Penggunn teorem sis Penggunn teorem fktor Derjd suku nyk pd
(c) lim. (d) lim. (f) lim
 FMIPA - ITB. MA Mtemtik A Semester, 6-7. Pernytn enr dn slh. () ()! e Solusi. Benr. Fungsi eksonensil (enyeut) memesr leih cet drid fungsi olinom (emilng) sehingg emginny menghsilkn nili Dengn Hoitl s
FMIPA - ITB. MA Mtemtik A Semester, 6-7. Pernytn enr dn slh. () ()! e Solusi. Benr. Fungsi eksonensil (enyeut) memesr leih cet drid fungsi olinom (emilng) sehingg emginny menghsilkn nili Dengn Hoitl s
10. cos (ax+b)sin(ax+b) dx = 12. sec x dx = tan x + c. 13. sec (ax+b)dx = tan (ax+b)+ c. 14. c sec x dx = - ctg x + c
 Integrl Tk Tentu INTEGRAL. Rumus Integrl Fungsi Aljr. k x n k n +. ( x + n ( n +. x ln x + x n + + ; n - n+ (x+ + ; dn 4. ( f ( x ± g( x f ( x ± g ( x n - n. os (x+sin(x+ ( n + n+ os (x+ + ( + (. sin x
Integrl Tk Tentu INTEGRAL. Rumus Integrl Fungsi Aljr. k x n k n +. ( x + n ( n +. x ln x + x n + + ; n - n+ (x+ + ; dn 4. ( f ( x ± g( x f ( x ± g ( x n - n. os (x+sin(x+ ( n + n+ os (x+ + ( + (. sin x
Erna Sri Hartatik. Aljabar Linear. Pertemuan 3 Aljabar Vektor (Perkalian vektor-lanjutan)
 Ern Sri Hrttik Aljr Liner Pertemun Aljr Vektor (Perklin vektor-lnjutn) Pemhsn Perklin Cross (Cross Product) - Model cross product - Sift cross product Pendhulun Selin dot product d fungsi perklin product
Ern Sri Hrttik Aljr Liner Pertemun Aljr Vektor (Perklin vektor-lnjutn) Pemhsn Perklin Cross (Cross Product) - Model cross product - Sift cross product Pendhulun Selin dot product d fungsi perklin product
15. INTEGRAL SEBAGAI LIMIT
 15. INTEGRAL SEBAGAI LIMIT 15.1 Jumlh Riemnn Dlm kulih Klkulus pd thun pertm, integrl Riemnn bisny diperkenlkn sebgi limit dri jumlh Riemnn, tidk mellui integrl Riemnn ts dn integrl Riemnn bwh. Hl ini
15. INTEGRAL SEBAGAI LIMIT 15.1 Jumlh Riemnn Dlm kulih Klkulus pd thun pertm, integrl Riemnn bisny diperkenlkn sebgi limit dri jumlh Riemnn, tidk mellui integrl Riemnn ts dn integrl Riemnn bwh. Hl ini
Integral Kompleks (Bagian Kesatu)
 Integrl Kompleks (Bgin Kestu) Supm Jurusn Mtemtik, FMIPA UGM Yogykrt 55281, INDONESIA Emil:mspomo@yhoo.com, supm@ugm.c.id (Pertemun Minggu XI) Outline 1 Fungsi Bernili Kompleks 2 Lintsn tu Kontur 3 Integrl
Integrl Kompleks (Bgin Kestu) Supm Jurusn Mtemtik, FMIPA UGM Yogykrt 55281, INDONESIA Emil:mspomo@yhoo.com, supm@ugm.c.id (Pertemun Minggu XI) Outline 1 Fungsi Bernili Kompleks 2 Lintsn tu Kontur 3 Integrl
BAB: PENERAPAN INTEGRAL Topik: Volume Benda Putar (Khusus Kalkulus 1)
 BAB: PENERAPAN INTEGRAL Topik: Volume Bend Putr (Khusus Klkulus ) Kompetensi yng diukur dlh kemmpun mhsisw menghitung volume bend putr dengn metode cincin, metode ckrm, tu metode kulit tbung.. UAS Klkulus,
BAB: PENERAPAN INTEGRAL Topik: Volume Bend Putr (Khusus Klkulus ) Kompetensi yng diukur dlh kemmpun mhsisw menghitung volume bend putr dengn metode cincin, metode ckrm, tu metode kulit tbung.. UAS Klkulus,
Bab. Integral. Di unduh dari: (www.bukupaket.com) Sumber buku : (bse.kemdikbud.go.id)
 PUSAT PERBUKUAN Deprtemen Pendidikn Nsionl B I Integrl Tujun Pemeljrn Setelh mempeljri ini, dihrpkn klin dpt. merncng turn integrl tk tentu dri turn turunn;. menghitung integrl tk tentu dri fungsi ljr;.
PUSAT PERBUKUAN Deprtemen Pendidikn Nsionl B I Integrl Tujun Pemeljrn Setelh mempeljri ini, dihrpkn klin dpt. merncng turn integrl tk tentu dri turn turunn;. menghitung integrl tk tentu dri fungsi ljr;.
1. Luas daerah yang dibatasi oleh kurva y = x 2 dan garis x + y = 6 adalah
 . Lus derh yng ditsi oleh kurv y = x dn gris x + y = dlh stun lus... c. d. 8 Sol Ujin Nsionl Thun 7 Kurv y = x dn gris x + y = ( y = x ) Sustikn nili y pd y = x sehingg didpt : x = x x = x x + x = ( =,
. Lus derh yng ditsi oleh kurv y = x dn gris x + y = dlh stun lus... c. d. 8 Sol Ujin Nsionl Thun 7 Kurv y = x dn gris x + y = ( y = x ) Sustikn nili y pd y = x sehingg didpt : x = x x = x x + x = ( =,
INTEGRAL. Instruktur : Ferry Wahyu Wibowo, S.Si., M.Cs.
 INTEGRAL Instruktur : Ferry Whyu Wibowo, S.Si., M.Cs. . Integrl tk tentu b. Integrl tertentu Contoh : Tentukn turunn berikut ini. y b. y. y d. y y y d. - y y. y y b. y y. Jwb: F() F () ---------- C ---
INTEGRAL Instruktur : Ferry Whyu Wibowo, S.Si., M.Cs. . Integrl tk tentu b. Integrl tertentu Contoh : Tentukn turunn berikut ini. y b. y. y d. y y y d. - y y. y y b. y y. Jwb: F() F () ---------- C ---
Materi IX A. Pendahuluan
 Mteri IX Tujun :. Mhsisw dpt memhmi vektor. Mhsisw mmpu mengunkn vektor dlm persoln sederhn 3. Mhsisw mengimplementsikn konsep vektor pd rngkin listrik. Pendhulun Sudh menjdi kesepktn umum hw untuk menentukn
Mteri IX Tujun :. Mhsisw dpt memhmi vektor. Mhsisw mmpu mengunkn vektor dlm persoln sederhn 3. Mhsisw mengimplementsikn konsep vektor pd rngkin listrik. Pendhulun Sudh menjdi kesepktn umum hw untuk menentukn
MUH1G3/ MATRIKS DAN RUANG VEKTOR
 MUHG3/ MATRIKS DAN RUANG VEKTOR TIM DOSEN 3 Sistem Persmn Liner Sistem Persmn Liner Su Pokok Bhsn Pendhulun Solusi SPL dengn OBE Solusi SPL dengn Invers mtriks dn Aturn Crmmer SPL Homogen Beerp Apliksi
MUHG3/ MATRIKS DAN RUANG VEKTOR TIM DOSEN 3 Sistem Persmn Liner Sistem Persmn Liner Su Pokok Bhsn Pendhulun Solusi SPL dengn OBE Solusi SPL dengn Invers mtriks dn Aturn Crmmer SPL Homogen Beerp Apliksi
selisih positif jarak titik (x, y) terhadap pasangan dua titik tertentu yang disebut titik
 Hiperol 7.1. Persmn Hiperol Bentuk Bku Hiperol dlh himpunn semu titik (, ) pd idng sedemikin hingg selisih positif jrk titik (, ) terhdp psngn du titik tertentu ng diseut titik fokus (foci) dlh tetp. Untuk
Hiperol 7.1. Persmn Hiperol Bentuk Bku Hiperol dlh himpunn semu titik (, ) pd idng sedemikin hingg selisih positif jrk titik (, ) terhdp psngn du titik tertentu ng diseut titik fokus (foci) dlh tetp. Untuk
Soal-soal dan Pembahasan Matematika Dasar SBMPTN-SNMPTN 2006
 www.purwntowhyudi.com Hl- Sol-sol dn Pemhsn Mtemtik Dsr SBMPTN-SNMPTN 006. Jik > 0, > 0 dn mk A. C. E. B. D. Jw:. Jwnny dlh A. Jik p - dn q -, mk q p. A. C. E. B. D. Jw: q p Jwnny dlh A . Grfik y terletk
www.purwntowhyudi.com Hl- Sol-sol dn Pemhsn Mtemtik Dsr SBMPTN-SNMPTN 006. Jik > 0, > 0 dn mk A. C. E. B. D. Jw:. Jwnny dlh A. Jik p - dn q -, mk q p. A. C. E. B. D. Jw: q p Jwnny dlh A . Grfik y terletk
E-LEARNING MATEMATIKA
 MODUL E-LEARNING E-LEARNING MATEMATIKA Oleh : NURYADIN EKO RAHARJO, M.PD. NIP. 9705 00 00 Penulisn Modul e Lerning ini diiyi oleh dn DIPA BLU UNY TA 00 Sesui dengn Surt Perjnjin Pelksnn e Lerning Nomor
MODUL E-LEARNING E-LEARNING MATEMATIKA Oleh : NURYADIN EKO RAHARJO, M.PD. NIP. 9705 00 00 Penulisn Modul e Lerning ini diiyi oleh dn DIPA BLU UNY TA 00 Sesui dengn Surt Perjnjin Pelksnn e Lerning Nomor
1. Luas daerah yang dibatasi oleh kurva y = x 2 dan garis x + y = 6 adalah satuan luas. a. 54 b. 32. d. 18 e.
 . Lus derh yng ditsi oleh kurv y = x dn gris x + y = dlh stun lus... c. d. 8 e. Sol Ujin Nsionl Thun 7 Kurv y = x dn gris x + y = ( y = x ) Sustikn nili y pd y = x sehingg didpt : x = x x = x x + x = (
. Lus derh yng ditsi oleh kurv y = x dn gris x + y = dlh stun lus... c. d. 8 e. Sol Ujin Nsionl Thun 7 Kurv y = x dn gris x + y = ( y = x ) Sustikn nili y pd y = x sehingg didpt : x = x x = x x + x = (
UJIAN SEMESTER GANJIL SMA SANG DEWA JAKARTA TAHUN PELAJARAN
 UJIAN SEMESTER GANJIL SMA SANG DEWA JAKARTA TAHUN PELAJARAN - Mt Peljrn : ILMU HITUNG MODERN Kels / Progrm : XII AIA ( Du Bels ) / Ajin Ilmu Api Hri / Tnggl : Minggu Nopemer Wktu :.. WIB ( Menit) Pilihlh
UJIAN SEMESTER GANJIL SMA SANG DEWA JAKARTA TAHUN PELAJARAN - Mt Peljrn : ILMU HITUNG MODERN Kels / Progrm : XII AIA ( Du Bels ) / Ajin Ilmu Api Hri / Tnggl : Minggu Nopemer Wktu :.. WIB ( Menit) Pilihlh
LIMIT FUNGSI DAN KEKONTINUAN
 LIMIT FUNGSI DAN KEKONTINUAN RANGKUMAN MATERI Sebelum memsuki mteri, perhtikn himpunn-himpunn berikut: ) Himpunn bilngn sli:,,,4,5,.... b) Himpunn bilngn bult:...,,,0,,,.... p c) Himpunn bilngn rsionl:
LIMIT FUNGSI DAN KEKONTINUAN RANGKUMAN MATERI Sebelum memsuki mteri, perhtikn himpunn-himpunn berikut: ) Himpunn bilngn sli:,,,4,5,.... b) Himpunn bilngn bult:...,,,0,,,.... p c) Himpunn bilngn rsionl:
matematika WAJIB Kelas X RASIO TRIGONOMETRI Kurikulum 2013 A. Definisi Trigonometri
 Kurikulum 0 Kels X mtemtik WAJIB RASIO TRIGONOMETRI Tujun Pembeljrn Setelh mempeljri mteri ini, kmu dihrpkn memiliki kemmpun berikut.. Memhmi rsio-rsio trigonometri yng meliputi sinus, kosinus, tngen,
Kurikulum 0 Kels X mtemtik WAJIB RASIO TRIGONOMETRI Tujun Pembeljrn Setelh mempeljri mteri ini, kmu dihrpkn memiliki kemmpun berikut.. Memhmi rsio-rsio trigonometri yng meliputi sinus, kosinus, tngen,
BAB I. MATRIKS BAB II. DETERMINAN BAB III. INVERS MATRIKS BAB IV. PENYELESAIAN PERSAMAAN LINEAR SIMULTAN
 DFTR ISI BB I. MTRIKS BB II. DETERMINN BB III. INVERS MTRIKS BB IV. PENYELESIN PERSMN LINER SIMULTN BB I. MTRIKS Mtriks erup sekelompok ilngn yng disusun empt persegi dn ditsi tnd terdiri dri ris dn kolom
DFTR ISI BB I. MTRIKS BB II. DETERMINN BB III. INVERS MTRIKS BB IV. PENYELESIN PERSMN LINER SIMULTN BB I. MTRIKS Mtriks erup sekelompok ilngn yng disusun empt persegi dn ditsi tnd terdiri dri ris dn kolom
Matematika SMA (Program Studi IPA)
 Smrt Solution UJIAN NASIONAL TAHUN PELAJARAN 2013/2014 Disusun Sesui Indiktor Kisi-Kisi UN 2013 Mtemtik SMA (Progrm Studi IPA) Disusun oleh : Pk Anng - Blogspot Pge 1 of 13 5. 2. Menyelesikn sol pliksi
Smrt Solution UJIAN NASIONAL TAHUN PELAJARAN 2013/2014 Disusun Sesui Indiktor Kisi-Kisi UN 2013 Mtemtik SMA (Progrm Studi IPA) Disusun oleh : Pk Anng - Blogspot Pge 1 of 13 5. 2. Menyelesikn sol pliksi
Matematika EBTANAS Tahun 1992
 Mtemtik EBTANAS Thun 99 EBT-SMA-9-0 Grfik fungsi kudrt yng persmnny y = x 5x memotong sumu x. Slh stu titik potongny dlh (, 0), mk nili sm dengn EBT-SMA-9-0 Persmn x px + 5 = 0 kr-krny sm. Nili p 0 tu
Mtemtik EBTANAS Thun 99 EBT-SMA-9-0 Grfik fungsi kudrt yng persmnny y = x 5x memotong sumu x. Slh stu titik potongny dlh (, 0), mk nili sm dengn EBT-SMA-9-0 Persmn x px + 5 = 0 kr-krny sm. Nili p 0 tu
IV V a b c d. a b c d. b c d. bukan fungsi linier y = x = x y 5xy + y = B.2 Konsep Fungsi Linier
 8. Dri fungsi-fungsi ng disjikn dengn digrm pnh erikut ini mnkh ng merupkn fungsi onto, injektif tu ijektif, jik relsi dri A ke B? A c d IV B A c d V B A c d VI B B. Konsep Fungsi Linier. Tujun Setelh
8. Dri fungsi-fungsi ng disjikn dengn digrm pnh erikut ini mnkh ng merupkn fungsi onto, injektif tu ijektif, jik relsi dri A ke B? A c d IV B A c d V B A c d VI B B. Konsep Fungsi Linier. Tujun Setelh
Hendra Gunawan. 15 November 2013
 MA1101 MATEMATIKA 1A Hendr Gunwn Semester I, 2013/2014 15 Novemer 2013 Ltihn 1. Pnjng lmi sutu pegs dlh 0.08 m. Gy seesr 0.6 N diperlukn untuk menekn dn menhnny pd pnjng 0.07 m. Tentukn kerjyng dilkukn
MA1101 MATEMATIKA 1A Hendr Gunwn Semester I, 2013/2014 15 Novemer 2013 Ltihn 1. Pnjng lmi sutu pegs dlh 0.08 m. Gy seesr 0.6 N diperlukn untuk menekn dn menhnny pd pnjng 0.07 m. Tentukn kerjyng dilkukn
FUNGSI TRIGONOMETRI LIMIT FUNGSI
 FUNGSI TRIGONOMETRI LIMIT FUNGSI Limit Fungsi. Limit fungsi f() merupkn nili hmpirn dri f() untuk nili mendekti nili tertentu misl. Bentuk umum : Lim f() -> Jik dikethui du uh fungsi f() dn g() msing-msing
FUNGSI TRIGONOMETRI LIMIT FUNGSI Limit Fungsi. Limit fungsi f() merupkn nili hmpirn dri f() untuk nili mendekti nili tertentu misl. Bentuk umum : Lim f() -> Jik dikethui du uh fungsi f() dn g() msing-msing
BAB VI. PENERAPAN INTEGRAL. kurva di bidang-xy dan andaikan f kontinu dan tak negatif pada selang [a, b]. Luas
![BAB VI. PENERAPAN INTEGRAL. kurva di bidang-xy dan andaikan f kontinu dan tak negatif pada selang [a, b]. Luas BAB VI. PENERAPAN INTEGRAL. kurva di bidang-xy dan andaikan f kontinu dan tak negatif pada selang [a, b]. Luas](/thumbs/52/30270888.jpg) 1 BAB VI. PENERAPAN INTEGRAL 6.1. Lus Derh Bidng Dtr Derh di ts sumu-. Andikn y = f() menentukn persmn seuh kurv di idng-y dn ndikn f kontinu dn tk negtif pd selng [, ]. Lus derh R yng ditsi oleh y = f(),
1 BAB VI. PENERAPAN INTEGRAL 6.1. Lus Derh Bidng Dtr Derh di ts sumu-. Andikn y = f() menentukn persmn seuh kurv di idng-y dn ndikn f kontinu dn tk negtif pd selng [, ]. Lus derh R yng ditsi oleh y = f(),
Catatan Kuliah MA1123 KALKULUS ELEMENTER I BAB V. INTEGRAL
 BAB V. INTEGRAL Anti-turunn dn Integrl Tk Tentu Persmn Diferensil Sederhn Notsi Sigm dn Lus Derh di Bwh Kurv Integrl Tentu Teorem Dsr Klkulus Sift-sift Integrl Tentu Leih Lnjut Sustitusi dlm Penghitungn
BAB V. INTEGRAL Anti-turunn dn Integrl Tk Tentu Persmn Diferensil Sederhn Notsi Sigm dn Lus Derh di Bwh Kurv Integrl Tentu Teorem Dsr Klkulus Sift-sift Integrl Tentu Leih Lnjut Sustitusi dlm Penghitungn
PEMBAHASAN. A. Teorema Pythagoras 1. Luas persegi dan luas segitiga siku-siku Perhatikan Gambar 1! D. Gambar 1
 PEMBAHASAN A. Teorem Pythgors 1. Lus persegi dn lus segitig siku-siku Perhtikn Gmr 1! D s A s B Gmr 1 Pd gmr terseut tmpk seuh persegi ABD yng pnjng sisiny s stun pnjng. Lus persegi ABD = sisi sisi L =
PEMBAHASAN A. Teorem Pythgors 1. Lus persegi dn lus segitig siku-siku Perhtikn Gmr 1! D s A s B Gmr 1 Pd gmr terseut tmpk seuh persegi ABD yng pnjng sisiny s stun pnjng. Lus persegi ABD = sisi sisi L =
LOMBA CERDAS CERMAT MATEMATIKA (LCCM) TINGKAT SMP DAN SMA SE-SUMATERA Memperebutkan Piala Gubernur Sumatera Selatan 3 5 Mei 2011
 LOMBA CERDAS CERMAT MATEMATIKA (LCCM) TINGKAT SMP DAN SMA SE-SUMATERA Mempereutkn Pil Guernur Sumter Seltn Mei 0 PENYISIHAN I PERORANGAN LCCM TINGKAT SMA. Dikethui kuus ABCD.EFGH dengn rusuk 6 cm. Jik
LOMBA CERDAS CERMAT MATEMATIKA (LCCM) TINGKAT SMP DAN SMA SE-SUMATERA Mempereutkn Pil Guernur Sumter Seltn Mei 0 PENYISIHAN I PERORANGAN LCCM TINGKAT SMA. Dikethui kuus ABCD.EFGH dengn rusuk 6 cm. Jik
TRIGONOMETRI I. KOMPETENSI YANG DICAPAI
 TRIGONOMETRI I. KOMPETENSI YANG DICAPAI Mhsisw dpt : 1. Membuktikn identits trigonometri.. Menghitung hubungn ntr sudut dn sisi segitig dengn Rumus Sinus. 3. Menghitung hubungn ntr sudut dn sisi segitig
TRIGONOMETRI I. KOMPETENSI YANG DICAPAI Mhsisw dpt : 1. Membuktikn identits trigonometri.. Menghitung hubungn ntr sudut dn sisi segitig dengn Rumus Sinus. 3. Menghitung hubungn ntr sudut dn sisi segitig
14. SIFAT-SIFAT INTEGRAL RIEMANN
 4. SIFAT-SIFAT INTEGRAL RIEMANN 4. Sift-sift Dsr Integrl Riemnn Pd bb ini kit kn mempeljri sift-sift dsr integrl Riemnn. Sift pertm dlh sift kelinern, yng dinytkn dlm Proposisi. Sepnjng bb ini, I menytkn
4. SIFAT-SIFAT INTEGRAL RIEMANN 4. Sift-sift Dsr Integrl Riemnn Pd bb ini kit kn mempeljri sift-sift dsr integrl Riemnn. Sift pertm dlh sift kelinern, yng dinytkn dlm Proposisi. Sepnjng bb ini, I menytkn
PROBLEM SOLVING TERKAIT DENGAN KELAS X SEMESTER 1 PADA STANDAR KOMPETENSI (SK) 1.
 PROLEM SOLVING TERKIT DENGN KELS X SEMESTER PD STNDR KOMPETENSI (SK). LJR Memechkn mslh yng berkitn dengn bentuk pngkt, kr, dn logritm Oleh: Sigit Tri Guntoro. Du orng berselisih mengeni bnykny psngn bilngn
PROLEM SOLVING TERKIT DENGN KELS X SEMESTER PD STNDR KOMPETENSI (SK). LJR Memechkn mslh yng berkitn dengn bentuk pngkt, kr, dn logritm Oleh: Sigit Tri Guntoro. Du orng berselisih mengeni bnykny psngn bilngn
Teorema Dasar Integral Garis
 ISBN: 978-979-79-55-9 Teorem Dsr Integrl Gris Erdwti Nurdin Progrm Studi Pendidikn Mtemtik FKIP UIR d_1910@yhoo.com Abstrk Slh stu generlissi integrl tentu (definite integrl) f x dx diperoleh dengn menggnti
ISBN: 978-979-79-55-9 Teorem Dsr Integrl Gris Erdwti Nurdin Progrm Studi Pendidikn Mtemtik FKIP UIR d_1910@yhoo.com Abstrk Slh stu generlissi integrl tentu (definite integrl) f x dx diperoleh dengn menggnti
E-LEARNING MATEMATIKA
 MOUL E-LEARNING E-LEARNING MATEMATIKA Oleh : NURYAIN EKO RAHARJO, M.P. NIP. 7 Penulisn Modul e Lerning ini diiyi oleh dn IPA BLU UNY TA Sesui dengn Surt Perjnjin Pelksnn e Lerning Nomor./H./PL/ Tnggl Juli
MOUL E-LEARNING E-LEARNING MATEMATIKA Oleh : NURYAIN EKO RAHARJO, M.P. NIP. 7 Penulisn Modul e Lerning ini diiyi oleh dn IPA BLU UNY TA Sesui dengn Surt Perjnjin Pelksnn e Lerning Nomor./H./PL/ Tnggl Juli
II. LANDASAN TEORI. Dalam bab ini akan didiskusikan definisi definisi, istilah istilah dan teoremateorema. yang berhubungan dengan penelitian ini.
 II. LANDASAN TEORI Dlm ini kn didiskusikn definisi definisi, istilh istilh dn teoremteorem yng erhuungn dengn penelitin ini. 2.1 Anlitik Geometri Definisi 2.1.1 Titik dlh unsur yng tidk memiliki pnjng,
II. LANDASAN TEORI Dlm ini kn didiskusikn definisi definisi, istilh istilh dn teoremteorem yng erhuungn dengn penelitin ini. 2.1 Anlitik Geometri Definisi 2.1.1 Titik dlh unsur yng tidk memiliki pnjng,
MATEMATIKA IPA PAKET A KUNCI JAWABAN
 MATEMATIKA IPA PAKET A KUNCI JAWABAN. Jwbn : A Mislkn : p : Msyrkt membung smph pd temptny. q: Kesehtn msyrkt terjg. Diperoleh: Premis : ~q ~p p q Premis : p Kesimpuln : q Jdi, kesimpuln dri premis-premis
MATEMATIKA IPA PAKET A KUNCI JAWABAN. Jwbn : A Mislkn : p : Msyrkt membung smph pd temptny. q: Kesehtn msyrkt terjg. Diperoleh: Premis : ~q ~p p q Premis : p Kesimpuln : q Jdi, kesimpuln dri premis-premis
MATRIKS A. Pengertian, Notasi dan Bagian Dalam Matriks
 MATRIKS A. Pengertin, Notsi dn Bgin Dlm Mtriks Dlm kehidupn sehri-hri kit sering menemui dt tu informsi dlm entuk tel, seperti tel pertndingn sepkol, tel sensi kels, tel hrg tiket keret pi dn seginy..
MATRIKS A. Pengertin, Notsi dn Bgin Dlm Mtriks Dlm kehidupn sehri-hri kit sering menemui dt tu informsi dlm entuk tel, seperti tel pertndingn sepkol, tel sensi kels, tel hrg tiket keret pi dn seginy..
SISTEM BILANGAN REAL. Purnami E. Soewardi. Direktorat Pembinaan Tendik Dikdasmen Ditjen GTK Kementerian Pendidikan dan Kebudayaan
 SISTEM BILANGAN REAL Purnmi E. Soewrdi Direktort Peminn Tendik Dikdsmen Ditjen GTK Kementerin Pendidikn dn Keudyn Himpunn Bilngn Asli (N) Bilngn sli dlh ilngn yng pertm kli dikenl dn digunkn oleh mnusi
SISTEM BILANGAN REAL Purnmi E. Soewrdi Direktort Peminn Tendik Dikdsmen Ditjen GTK Kementerin Pendidikn dn Keudyn Himpunn Bilngn Asli (N) Bilngn sli dlh ilngn yng pertm kli dikenl dn digunkn oleh mnusi
METODE ANALISIS. Tentukan arus pada masing-masing tahanan dengan menggunakan metode arus cabang untuk rangkaian seperti pada Gambar 1.
 1. Anlisis Arus Cng METODE ANALSS Metode rus ng dlh slh stu metode penyelesin nlisis rngkin il rngkin terdiri dri du tu leih sumer. Pd metode rus ng ini, kn diperoleh rus pd setip ng dri sutu rngkin yng
1. Anlisis Arus Cng METODE ANALSS Metode rus ng dlh slh stu metode penyelesin nlisis rngkin il rngkin terdiri dri du tu leih sumer. Pd metode rus ng ini, kn diperoleh rus pd setip ng dri sutu rngkin yng
MATERI I : VEKTOR. Pertemuan-01
 MATERI I : VEKTOR Pertemun-0. Pendhulun Definisi Vektor didefinisikn segi esrn yng memiliki rh. Keeptn, gy dn pergesern merupkn ontoh ontoh dri vektor kren semuny memiliki esr dn rh wlupun untuk keeptn
MATERI I : VEKTOR Pertemun-0. Pendhulun Definisi Vektor didefinisikn segi esrn yng memiliki rh. Keeptn, gy dn pergesern merupkn ontoh ontoh dri vektor kren semuny memiliki esr dn rh wlupun untuk keeptn
1) BENTUK UMUM DAN BAGIAN-BAGIAN PERSAMAAN KUADRAT Bentuk umum persamaan kuadrat adalah seperti di bawah ini:
 ) BENTUK UMUM DAN BAGIAN-BAGIAN PERSAMAAN KUADRAT Bentuk umum persmn kudrt dlh seperti di bwh ini: b c dengn, b, c bilngn dn riil Dimn, disebut sebgi koefisien dri b disebut sebgi koefisien dri c disebut
) BENTUK UMUM DAN BAGIAN-BAGIAN PERSAMAAN KUADRAT Bentuk umum persmn kudrt dlh seperti di bwh ini: b c dengn, b, c bilngn dn riil Dimn, disebut sebgi koefisien dri b disebut sebgi koefisien dri c disebut
FUNGSI TRANSENDEN. Sifat satu kesatu yang mengakibatkan fungsi
 FUNGSI TRANSENDEN I. Pendhulun. Pokok Bhsn Logritm Fungsi Eksponen.2 Tujun Mengethui entuk fungsi trnsenden dlm klkulus. Mengethui dn memhmi entuk fungsi trnseden itu logritm dn fungsi eksponen sert dlm
FUNGSI TRANSENDEN I. Pendhulun. Pokok Bhsn Logritm Fungsi Eksponen.2 Tujun Mengethui entuk fungsi trnsenden dlm klkulus. Mengethui dn memhmi entuk fungsi trnseden itu logritm dn fungsi eksponen sert dlm
UJIAN BERSAMA SMA KABUPATEN TANAH DATAR SEMESTER 1 TAHUN PELAJARAN 2008/2009. Mata Pelajaran : MATEMATIKA Kelas/jurusan : XII/ IPA Hari/Tanggal :
 UJIAN BERSAMA SMA KABUPATEN TANAH DATAR SEMESTER TAHUN PELAJARAN /9 Mt Peljrn : MATEMATIKA Kels/jurusn : XII/ IPA Hri/Tnggl : Wktu : menit. d... A. c B. c C. c D. c E. c. sin cos d... A. cos C B. cos C
UJIAN BERSAMA SMA KABUPATEN TANAH DATAR SEMESTER TAHUN PELAJARAN /9 Mt Peljrn : MATEMATIKA Kels/jurusn : XII/ IPA Hri/Tnggl : Wktu : menit. d... A. c B. c C. c D. c E. c. sin cos d... A. cos C B. cos C
A x = b apakah solusi x
 MTRIKS INVERSI & SIFT-SIFTNY Bil, x, dlh sklr ilngn rel yng memenuhi x, mk x pil. Sekrng, untuk sistem persmn linier x pkh solusi x dpt diselesikn dengn x? Mtriks Identits Untuk sklr (rel numer dn ), mk.
MTRIKS INVERSI & SIFT-SIFTNY Bil, x, dlh sklr ilngn rel yng memenuhi x, mk x pil. Sekrng, untuk sistem persmn linier x pkh solusi x dpt diselesikn dengn x? Mtriks Identits Untuk sklr (rel numer dn ), mk.
3. LIMIT DAN KEKONTINUAN. INF228 Kalkulus Dasar
 . LIMIT DAN KEKONTINUAN INF8 Klkulus Dsr . Limit Fungsi di Stu Titik Pengertin it secr intuisi Perhtikn ungsi Fungsi dits tidk terdeinisi di =, kren di titik tersebut berbentuk 0/0. Tpi msih bis ditnykn
. LIMIT DAN KEKONTINUAN INF8 Klkulus Dsr . Limit Fungsi di Stu Titik Pengertin it secr intuisi Perhtikn ungsi Fungsi dits tidk terdeinisi di =, kren di titik tersebut berbentuk 0/0. Tpi msih bis ditnykn
KALKULUS 2. Oleh : SRI ESTI TRISNO SAMI, ST, MMSI
 KALKULUS KALKULUS Oleh : SRI ESTI TRISNO SAMI, ST, MMSI 0805 Bhn Bcn / Refferensi :. Frnk Ayres J. R., Clcls, Shcm s Otline Series, Mc Grw-Hill Book Compny.. Ysf Yhy, D. Srydi H. S. Dn Ags S, Mtemtik ntk
KALKULUS KALKULUS Oleh : SRI ESTI TRISNO SAMI, ST, MMSI 0805 Bhn Bcn / Refferensi :. Frnk Ayres J. R., Clcls, Shcm s Otline Series, Mc Grw-Hill Book Compny.. Ysf Yhy, D. Srydi H. S. Dn Ags S, Mtemtik ntk
TURUNAN FUNGSI. LA - WB (Lembar Aktivitas Warga Belajar) MATEMATIKA PAKET C TINGKAT VI DERAJAT MAHIR 2 SETARA KELAS XI
 LA - WB (Lembr Aktivits Wrg Beljr) TURUNAN FUNGSI Oleh: Hj. ITA YULIANA, S.Pd, M.Pd MATEMATIKA PAKET C TINGKAT VI DERAJAT MAHIR 2 SETARA KELAS XI Creted By It Yulin 33 Turunn Fungsi Kompetensi Dsr 1. Menggunkn
LA - WB (Lembr Aktivits Wrg Beljr) TURUNAN FUNGSI Oleh: Hj. ITA YULIANA, S.Pd, M.Pd MATEMATIKA PAKET C TINGKAT VI DERAJAT MAHIR 2 SETARA KELAS XI Creted By It Yulin 33 Turunn Fungsi Kompetensi Dsr 1. Menggunkn
Matriks yang mempunyai jumlah baris sama dengan jumlah kolomnya disebut matriks bujur sangkar (square matrix). contoh :
 TRIKS. PENGERTIN triks dlh sutu deretn elemen yng mementuk empt persegi pnjng, terdiri dri m ris dn n kolom. Elemen terseut dpt erentuk koefisien, ilngn tu simul. triks yng mempunyi m ris dn n kolom diseut
TRIKS. PENGERTIN triks dlh sutu deretn elemen yng mementuk empt persegi pnjng, terdiri dri m ris dn n kolom. Elemen terseut dpt erentuk koefisien, ilngn tu simul. triks yng mempunyi m ris dn n kolom diseut
APLIKASI INTEGRAL PENERAPAN INTEGRAL. Luas daerah kelengkungan
 APLIKASI INTEGRAL APLIKASI INTEGRAL PENERAPAN INTEGRAL Lus derh kelengkungn PENERAPAN INTEGRAL Indiktor 1 Indiktor 9 Lus derh di bwh kurv berdsr prinsip Riemn Volume bend putr, jik kurv diputr mengelilingi
APLIKASI INTEGRAL APLIKASI INTEGRAL PENERAPAN INTEGRAL Lus derh kelengkungn PENERAPAN INTEGRAL Indiktor 1 Indiktor 9 Lus derh di bwh kurv berdsr prinsip Riemn Volume bend putr, jik kurv diputr mengelilingi
E-learning matematika, GRATIS
 www.mtemtik-ps.logspot.com E-lerning mtemtik, GRATIS Penusun Editor : Nur Aini Indh H, S.Pd. ; Imm Indr Gunwn, S.Si. : Drs. Keto Susnto, M.Si. M.T. ; Istij, S.H. M.Hum. Imm Indr Gunwn, S.Si. A. DEFINISI
www.mtemtik-ps.logspot.com E-lerning mtemtik, GRATIS Penusun Editor : Nur Aini Indh H, S.Pd. ; Imm Indr Gunwn, S.Si. : Drs. Keto Susnto, M.Si. M.T. ; Istij, S.H. M.Hum. Imm Indr Gunwn, S.Si. A. DEFINISI
Integral Tak Wajar. Ayundyah Kesumawati. March 25, Prodi Statistika FMIPA-UII
 Kesumwti Prodi Sttistik FMIPA-UII Mrch 25, 205 Sutu integrl tertentu b f (x)dx () diktkn wjr jik i memenuhi du syrt berikut: i. Bts integrsi dn b merupkn bilngn berhingg ii. fungsi f (x) terbts pd intervl
Kesumwti Prodi Sttistik FMIPA-UII Mrch 25, 205 Sutu integrl tertentu b f (x)dx () diktkn wjr jik i memenuhi du syrt berikut: i. Bts integrsi dn b merupkn bilngn berhingg ii. fungsi f (x) terbts pd intervl
APLIKASI INTEGRAL PENERAPAN INTEGRAL. Luas daerah kelengkungan
 APLIKASI INTEGRAL APLIKASI INTEGRAL PENERAPAN INTEGRAL Lus derh kelengkungn Integrl digunkn pd design Menr Petrons di Kul lumpur, untuk perhitungn kekutn menr. Sdne Oper House di design berdsrkn irisn-irisn
APLIKASI INTEGRAL APLIKASI INTEGRAL PENERAPAN INTEGRAL Lus derh kelengkungn Integrl digunkn pd design Menr Petrons di Kul lumpur, untuk perhitungn kekutn menr. Sdne Oper House di design berdsrkn irisn-irisn
E-learning Matematika, GRATIS
 www.mtemtik-ps.logspot.com E-lerning Mtemtik, GRATIS Penusun Editor : Nur Aini Indh H, S.Pd. ; Imm Indr Gunwn, S.Si. : Drs. Keto Susnto, M.Si. M.T. ; Istij, S.H. M.Hum. Imm Indr Gunwn, S.Si. A. DEFINISI
www.mtemtik-ps.logspot.com E-lerning Mtemtik, GRATIS Penusun Editor : Nur Aini Indh H, S.Pd. ; Imm Indr Gunwn, S.Si. : Drs. Keto Susnto, M.Si. M.T. ; Istij, S.H. M.Hum. Imm Indr Gunwn, S.Si. A. DEFINISI
SMA Santa Angela. Bandung. 1 P a g e
 Persmn Gris Singgung SMA Snt Angel Bndung P g e P g e Persmn Gris Singgung pd Ellips Seperti hln pd lingkrn, terdpt du mcm gris singgung ng kn diicrkn, itu gris singgung ng mellui slh stu titik pd ellips
Persmn Gris Singgung SMA Snt Angel Bndung P g e P g e Persmn Gris Singgung pd Ellips Seperti hln pd lingkrn, terdpt du mcm gris singgung ng kn diicrkn, itu gris singgung ng mellui slh stu titik pd ellips
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI Bb berikut ini kn disjikn mteri pendukung yng dpt membntu penulis untuk menyelesikn permslhn yng kn dibhs pd bb selnjutny. Adpun mteri pendukungny dlh pengertin mtriks, jenis-jenis
BAB II LANDASAN TEORI Bb berikut ini kn disjikn mteri pendukung yng dpt membntu penulis untuk menyelesikn permslhn yng kn dibhs pd bb selnjutny. Adpun mteri pendukungny dlh pengertin mtriks, jenis-jenis
VEKTOR. Dua vektor dikatakan sama jika besar dan arahnya sama. Artinya suatu vektor letaknya bisa di mana saja asalkan besar dan arahnya sama.
 -1- VEKTOR PENGERTIAN VEKTOR dlh sutu esrn yng mempunyi nili (esr) dn rh. Sutu vektor dpt digmrkn segi rus gris errh. Nili (esr) vektor dinytkn dengn pnjng gris dn rhny dinytkn dengn tnd pnh. Notsi vektor
-1- VEKTOR PENGERTIAN VEKTOR dlh sutu esrn yng mempunyi nili (esr) dn rh. Sutu vektor dpt digmrkn segi rus gris errh. Nili (esr) vektor dinytkn dengn pnjng gris dn rhny dinytkn dengn tnd pnh. Notsi vektor
Kerjakan di buku tugas. Tentukan hasil operasi berikut. a. A 2 d. (A B) (A + B) b. B 2 e. A (B + B t ) c. A B f. A t (A t + B t ) Tes Mandiri
 Mmt Apliksi SMA Bhs Dikethui A = Tentukn hsil opersi berikut A c A A b A A d A Dikethui A = Tentukn hsil opersi berikut (A + B) c (B A) b A + AB + B d B BA + A Sol Terbuk Kerjkn di buku tugs Jik X = dn
Mmt Apliksi SMA Bhs Dikethui A = Tentukn hsil opersi berikut A c A A b A A d A Dikethui A = Tentukn hsil opersi berikut (A + B) c (B A) b A + AB + B d B BA + A Sol Terbuk Kerjkn di buku tugs Jik X = dn
3. LIMIT DAN KEKONTINUAN
 3. LIMIT DAN KEKONTINUAN 1 3.1 Limit Fungsi di Stu Titik Pengertin it secr intuisi Perhtikn ungsi 1 1 Fungsi dits tidk terdeinisi di =1, kren di titik tersebut berbentuk 0/0. Tpi msih bis ditnykn berp
3. LIMIT DAN KEKONTINUAN 1 3.1 Limit Fungsi di Stu Titik Pengertin it secr intuisi Perhtikn ungsi 1 1 Fungsi dits tidk terdeinisi di =1, kren di titik tersebut berbentuk 0/0. Tpi msih bis ditnykn berp
3 PANGKAT, AKAR, DAN LOGARITMA
 PANGKAT, AKAR, DAN LOGARITMA.. Pngkt Pngkt dri seuh ilngn dlh sutu indeks ng menunjukkn nkn perklin ilngn ng sm secr eruntun. Notsi n errti hw hrus diklikn degn itu sendiri senk n kli. Notsi ilngn erpngkt
PANGKAT, AKAR, DAN LOGARITMA.. Pngkt Pngkt dri seuh ilngn dlh sutu indeks ng menunjukkn nkn perklin ilngn ng sm secr eruntun. Notsi n errti hw hrus diklikn degn itu sendiri senk n kli. Notsi ilngn erpngkt
BAB IV METODE ANALISIS RANGKAIAN
 BAB IV METODE ANALISIS RANGKAIAN. Anlisis Arus Cng Anlisis rus cng memnftkn hukum Kirchoff I (KCL) dn hukum Kirchoff I (KVL). Contoh - Tentukn esr rus dlm loop terseut dn gimn rh rusny? Ohm 0V 0V Ohm 0V
BAB IV METODE ANALISIS RANGKAIAN. Anlisis Arus Cng Anlisis rus cng memnftkn hukum Kirchoff I (KCL) dn hukum Kirchoff I (KVL). Contoh - Tentukn esr rus dlm loop terseut dn gimn rh rusny? Ohm 0V 0V Ohm 0V
