BAB VI. PENERAPAN INTEGRAL. kurva di bidang-xy dan andaikan f kontinu dan tak negatif pada selang [a, b]. Luas
|
|
|
- Yanti Kusumo
- 7 tahun lalu
- Tontonan:
Transkripsi
1 1 BAB VI. PENERAPAN INTEGRAL 6.1. Lus Derh Bidng Dtr Derh di ts sumu-. Andikn y = f() menentukn persmn seuh kurv di idng-y dn ndikn f kontinu dn tk negtif pd selng [, ]. Lus derh R yng ditsi oleh y = f(), =, =, dn y = 0 dlh A(R) = f ( ) d Contoh 1: Tentuknlh lus derh R diwh kurv y = + di ntr = -1 dn =. y = - + Jw: A(R) = ( 1 + ) d = 5 5 [ ] = ( + ) ( ) = = 5,
2 Penyelesin dengn Derive: AreUnderCurve(f(),,,, y) dlh menggmr derh R yng ditsi grfik fungsi y = f() di ts sumu- di ntr = dn =. 1. Tulislh: AreUnderCurve( +,, -1,, y), enter, sm dengn. Klik icon gmr. Tulislh: A(R):= int( +,,-1,), enter. Klik icon sm dengn, llu proksimsi. Jdi lus derh R dlh A(R) = 5,1 Derh di wh sumu-. Andikn y = f() menentukn persmn seuh kurv di idng-y dn ndikn f kontinu dn tk negtif pd selng [, ]. Lus derh R yng ditsi oleh y = f(), =, =, dn y = 0 dlh A(R) = f ( ) d
3 Contoh : Tentuknlh lus derh R diwh kurv y = di ntr = - dn =. y = Jw: A(R) = ( ) d = 9 [ + ] = ( + 1) ( 8) = = 16, Penyelesin dengn Derive: AreOverCurve(f(),,,, y) dlh menggmr derh R yng ditsi grfik fungsi y = f() di wh sumu- di ntr = dn =. 1. Tulislh: AreOverCurve(,, -,, y), enter. Klik icon gmr. Tulislh: A(R):= int(,, -, ), enter. Klik icon sm dengn, llu proksimsi.
4 Jdi lus derh R dlh A(R) = 15/9 = 16,11. Derh di knn sumu-y. Andikn = f(y) menentukn persmn seuh kurv di idng-y dn ndikn f kontinu dn tk negtif pd selng [, ]. Lus derh R yng ditsi oleh = f(y), y =, y =, dn = 0 dlh A(R) = f ( y) dy Contoh : Tentuknlh lus derh R yng ditsi oleh kurv = y + cos(y) di ntr y = 0 dn y =.
5 5 = y + cos(y) Jw: A(R) = y + cos( y) dy = 0 y + [ sin( y)] 0 = 9 + sin() =,50 + 0,111 =,6 Penyelesin dengn Derive: AreUnderCurve(f(y), y,,, ) dlh menggmr derh R yng ditsi grfik fungsi = f(y) di knn sumu-y di ntr y = dn y =. 1. Tulislh: AreUnderCurve(y + cos(y), y, 0,, ), enter. Klik icon gmr. Tulislh: A(R):= int(y + cos(y), y, 0, ), enter. Klik icon sm dengn, llu proksimsi.
6 6 Jdi lus derh R dlh A(R) =,6 Derh di kiri sumu-y. Andikn = f(y) menentukn persmn seuh kurv di idng-y dn ndikn f kontinu dn tk negtif pd selng [, ]. Lus derh R yng ditsi oleh = f(y), y =, y =, dn = 0 dlh A(R) = - f ( y) dy AreOverCurve(f(y), y,,, ) dlh menggmr derh R yng ditsi grfik fungsi = f(y) di kiri sumu-y di ntr y = dn y =. Contoh : Tentukn lus derh R yng ditsi oleh = cos( y) y di ntr y = 1 dn y = (liht tugs kelompok)
7 7 Derh di ntr Du Kurv. Andikn kurv y = f() dn y = g() dengn f() g() pd selng [, ]. Lus yng ditsi oleh f() g(), =, = dlh ( f ( ) g( )) d Contoh 5: Tentuknlh lus derh di ntr kurv y = dn y = y = y = - Jw: A(R) = [ ] = ( 1 ) = = 0, ( ) d = 1 0 Penyelesin dengn Derive: AreBetweenCurves(f(), g(),,,, y) dlh menggmr derh R yng ditsi grfik fungsi y = f() dn y = g() di ntr = dn =. 1. Deklsikn: f():= dn g():=. Tulislh: AreBetweenCurves(,,, 0, 1, y)
8 8. Klik icon gmr. Tulislh: A:= int(f()-g(),, 0, 1), enter 5. Klik icon sm dengn, llu proksimsi. Jdi lus derh di ntr y = dn y = dlh 0,7. AreBetweenCurves(f(y), g(y), y,,, ) dlh menggmr derh R yng ditsi grfik fungsi = f(y) dn = g(y) di ntr y = dn y =. Tugs Kelompok 1. Konstruksi lngkh-lngkh menentukn lus derh R yng ditsi oleh = cos( y) y di ntr y = 1 dn =, Jw:,7.. Konstruksi lngkh-lngkh menentukn lus derh R yng ditsi oleh y = + di ntr = -1 dn =, Jw: /. Konstruksi lngkh-lngkh menentukn lus derh R yng ditsi oleh kurv y = dn y =. Jw: 15/
9 9 Sol-Sol Ltihn Gmrlh derh yng ditsi grfik persmn-persmn yng dikethui, kemudin tentuknlh lus derh yng terentuk. 1. y 1 =, y = 0, di ntr = 0 dn =. y = ( )( + ), y = 0, di ntr = 0 dn =. y = 1 ( 7), y = 0, di ntr = 0 dn =. y =, y = 0, di ntr = - dn = 5. y = ( )( + 1), y = 6. y =, y = 7. = 8y y, = 0 8. = y y, y = 0 9. y = 0, y + 1 = y = + 6, y =, dn y + = Tinjulh kurv y = untuk 1 6 () Hitunglh lus diwh kurv ini () Tentuknlh c sedemikin sehingg gris = c memgi du lus pd () sm esr (c) Tentuknlh d sedemikin sehingg gris y = d memgi du lus pd () sm esr
10 0 6.. Volume Bend Putr Apil seuh derh rt, yng terletk seluruhny pd stu sisi dri seuh gris tetp dlm idngny, diputr mengelilingi gris terseut, derh itu kn mementuk seuh end putr. Gris tetp diseut sumu end putr. Metode Ckrm Menentukn volume end yng dientuk oleh derh R yng ditsi kurv y = f(), =, = diputr mengelilingi sumu- dengn metode ckrm dlh V = π ( f ( ) ) d Contoh 6: Tentuknlh volume end putr yng dientuk oleh derh R yng ditsi oleh kurv y =, sumu-, dn gris = pil R diputr mengelilingi sumu-. Jw: V = π ( ) ) d = 0 0 π. d
11 1 16 = π[ ] 0 = π ( ) = 8π = 5, 1 Penyelesin dengn Derive Cr 1: Menggunkn rumus V= π ( f ( )) 1. Menggmr derh R: AreUnderCurve(,, 0,, y) enter. Klik icon gmr d. Deklrsikn: V:= π. int(,,0,) enter. Klik sm dengn, llu klik proksimsi Jdi volume end putr yng ditsi oleh kurv y =, sumu-, dn gris y = pil R diputr mengelilingi sumu- dlh V = 8 π = 5,1.
12 Cr : Volume_Of_Revolution(f(),, 1, ) dlh menghitung volume derh yng ditsi oleh y = f(), sumu-, di ntr = 1 dn = di putr mengelilingi sumu-. 1. Menggmr derh R: AreUnderCurve(,, 0,, y) enter. Klik icon gmr. Tuliskn: VOLUME_OF_REVOLUTION(,, 0, ) enter. Klik sm dengn, llu proksimsi
13 Menentukn volume end yng dientuk oleh derh R yng ditsi kurv = f(y), y =, y = diputr mengelilingi sumu-y dlh V = π ( f ( y) ) d Contoh 6: Tentuknlh volume end putr yng dientuk oleh derh R yng ditsi oleh kurv y =, sumu-y, dn gris y = pil R diputr mengelilingi sumu-y. Jw: V = π ( y ) d = 0 0 π /. y d = π[ y 5 / ] 0 = π ( ) = π = 11, Penyelesin dengn Derive Cr 1: Menggunkn rumus V= π ( f ( y)) 1. Menggmr derh R: AreUnderCurve( y, y, 0,, ) enter d
14 . Klik icon gmr. Deklrsikn: V:= π.int( y /, y,0,) enter. Klik sm dengn, llu klik proksimsi Cr : Volume_Of_Revolution(f(y), y, y1, y) dlh menghitung volume derh yng ditsi oleh = f(y), sumu-y, di ntr y = y1 dn y = y di putr mengelilingi sumu-y. 1. Menggmr derh R: AreUnderCurve(y 1/, y, 0,, ) enter. Klik icon gmr. Tuliskn: VOLUME_OF_REVOLUTION(y 1/, y, 0, ) enter. Klik sm dengn, llu proksimsi
15 5 Metode Cincin. Menentukn volume end yng dientuk oleh derh R yng ditsi kurv y = f() dn y = g() dengn f() g() dintr =, = diputr mengelilingi sumu- dengn metode cincin dlh V = π ( f ( ) g( ) ) d Contoh 7: Tentuknlh volume end putr yng dientuk oleh derh R yng ditsi oleh kurv y = dn y 8 = diputr mengelilingi sumu-.
16 6 y = y = 8 Jw: 5 8 V = π ( 8 8π ) d = π[ ] 0 = = 0, Penyelesin dengn Derive Menggunkn rumus V= π ( f ( ) g( ) d : 1. Deklrsikn f(): 8 dn g(): =. Tulislh: AreBetweenCurves( 8,,, 0,, y). Klik icon gmr. Deklrsikn: V:= π.int( f ( ) g( ),,0,) enter 5. Klik sm dengn, llu klik proksimsi
17 7 Jdi volume end putr yng ditsi oleh kurv y = 8 dn y = mengelilingi sumu- dlh V = 8 π /5 = 0,16. Tugs Kelompok: 1. Konstruksilh lngkh-lngkh mencri volume end putr yng dientuk oleh derh R yng ditsi oleh kurv pil R diputr mengelilingi sumu-y. = y, sumu-y, dn gris y =. Konstruksilh lngkh-lngkh mencri volume pd contoh 6, untuk R diputr mengelilingi sumu-y (Metode Kulit Tung). Gunkn:. Rumus V = π. f ( ) d. VOLUMEY_OF_REVOLUTION (y,, 0, )
18 8. Konstruksilh lngkh-lngkh mencri volume end putr dengn metode kulit tung diputr mengelilingi sumu y = c, c konstn. (Gunkn: rumus V= π (c ) y d ). Konstruksilh lngkh-lngkh mencri volume end putr yng dientuk oleh derh R yng ditsi oleh kurv y = dn y 8 = mengelilingi sumu-y. Sol-Sol Ltihn Dlm sol-sol (1-5) gmrlh derh R yng ditsi oleh grfik persmn, kemudin tentukn volume end putr yng terentuk pil R diputr mengelilingi sumu-. 1. y =, π =, y = 0. 1 y =, =, =, y = 0. y = 9, =, =, y = 0. = y, = 0, y = 1 5. = y + 1, = 0, y =, y = 0 Dlm sol-sol (-6) gmrlh derh R yng ditsi oleh grfik persmn, kemudin tentukn volume end putr yng terentuk pil R diputr mengelilingi sumu-y. 6. = y, = 0, y =
19 9 7. = y, = 0, y = 8. = y /, = 0, y = y =, = 1, =, y = y =, =, y = 0 Dlm sol-sol (11-1) gmrlh derh R yng ditsi oleh grfik persmn, kemudin tentukn volume end putr yng terentuk pil R diputr mengelilingi gris yng dierikn. 11. y =, = 5, y = 0 mengelilingi gris = 5 1. y = 9 ( 0), = 0, y = 0 mengelilingi gris = 1. = y, = 0, y = mengelilingi gris y = 1. = y + 1, = 0, y = 0, y = mengelilingi gris y =
20 Pnjng Kurv Bidng dn Lus Permukn Bend Putr Pnjng Kurv Kurv idng ditentukn sepsng persmn prmetrik = f(t), y = g(t), t, dengn fungsi f dn g kontinu pd selng terseut. Anggp t menytkn wktu, pil t ertmh dri ke mk (, y) menyelusuri sutu kurv di idng. Rumus pnjng kurv: L = f '( t) + g'( t) dt ; entuk prmetrik = f(t), y = g(t), dn t. Contoh 8: Crilh pnjng kurv = t +, y = t - 1 dengn 1 t Jw: d/dt = 6t, dy/dt = 6t L = f '( t) + g'( t) dt = ( 6t ) + (6t ) dt = 6 + t t dt = 6 t 1+ t dt Mislkn u = 1 + t mk du = t dt Untuk t = 1 diperoleh u = dn t = diperoleh u =17 Sehingg: 6 t 1+ t dt = 17 1 u du = [ u ] = (17 / - / ) = 1,5 / 17 Jdi pnjng kuv dlh 1,5 stun pnjng
21 51 PARA_ARC_LENGTH(v, t,, ) dlh menghitung pnjng kurv entuk prmetrik entuk vektor v = [(t), y(t)] dengn t. Cr 1 (menggunkn PARA_ARC_LENGTH(v, t,, ): 1. Tulislh: PARA_ARC_LENGTH([t +, t -1/], t, 1, ) enter.. Klik sm dengn, llu proksimsi Cr (menggunkn rumus): 1. Deklrsikn: f(t):= dif(t +, t) dn g(t):= dif( t 1/, t). Deklrsikn: L:=int( (f(t) + g(t) ), t, 1, ). Klik sm dengn, llu proksimsi
22 5 Rumus pnjng kurv: L = 1 + f '( ) d ; entuk y = f(), dn. Contoh 9: Crilh pnjng kurv / y = dri titik (1,1) ke titik (,8). Jw: dy/d = 1/ 9 L = 1 + f '( ) d = 1+ ( 1/ ) d = 1+ d Misl u = 1 + 9/ mk du = 9/ d 1 1
23 5 Untuk = 1 diperoleh u =1/ dn = diperoleh u = d = / u du = / 10 8 / / 1 [ u ] 1 / = [10 ] = 7,6 9 7 Penyelesin dengn Derive: ARC_LENGTH(f(),,, ) dlh menghitung pnjng kurv entuk y = f() dengn. Cr 1 (menggunkn ARC_LENGTH(f(),,, ): 1. Tulislh: ARC_LENGTH( /. Klik sm dengn, llu proksimsi,, 1, ) enter. Jdi pnjng kurvny dlh 7,6 Cr (menggunkn rumus): 1. Deklrsikn: f():=dif( /, )
24 5. Deklrsikn: L:=int( (1 + (f()) ),, 1, ). Klik sm dengn, llu proksimsi Tugs Kelompok:: Selesikn contoh 9 dengn menggunkn:. Rumus: L = 1 + f '( y) dy ; entuk = f(y), dn y.. Konstruksi dengn Derive
25 55 Lus Permukn Bend Putr Rumus lus permukn end putr: A = π g( t) f '( t) + g'( t) dt ; entuk prmetrik = f(t), y = g(t), t diputr mengelilingi sumu-. A = π f ( ) 1+ sumu-. f '( ) d ; entuk y = f(), dn diputr mengelilingi Are_Of_Revolution(f(),,, ) dlh menghitung lus permukn il y = f() ntr = dn = diputr mengelilingi sumu-. Arey_Of_Revolution(f(),,, ) dlh menghitung lus permukn il y = f() ntr = dn = diputr mengelilingi sumu-y. Contoh 10: Crilh lus permukn end putr il kurv mengelilingi sumu-. Jw: dy/d = 1/ y =, 0 diputr 1 A = π f ( ) 1+ f '( ) d = π 1+ ( ) d = π + 1 d 1 / = [ π.. ( + 1) ] 0 = 6, 18 Penyelesin dengn Derive: Cr 1 (menggunkn Are_Of_Revolution(f(),,, ) ): 1. Tulislh: Are_Of_Revolution(,, 0, ) enter. 0 0
26 56. Klik sm dengn, llu proksimsi Jdi lus permukn end putr dlh 6,18 Cr (menggunkn rumus): 1. Deklrsikn: f():= enter. Deklrsikn: g():=dif(f(), ) enter. Deklrsikn: A(R):= π.int( (1 + (g()) ),, 0, ). Klik sm dengn, llu proksimsi
27 57 Tugs Kelompok: 1. Konstruksilh lngkh-lngkh mencri pnjng kurv = y ; 0 y dlm du cr.. Konstruksilh lngkh-lngkh mencri lus permukn end putr il kurv / y =, 1 diputr mengelilingi sumu-y dlm du cr.. Konstruksilh lngkh-lngkh mencri lus permukn end putr il kurv = cos( t) y = sin( t), - t diputr mengelilingi sumu-.
28 58 Sol-sol Ltihn Crilh pnjng kurv-kuv yng dierikn 1. y =, dintr = 1 dn =. y = sin( ), dintr = 0 dn = π. y = +, dintr = 1 dn =. y =, dintr = 1/ dn = 5 5. y = ( / ), dintr = 1 dn = 8 6. y 1 = +, 16 y dintr y = dn y = 7. = sin( y), dintr y = 0 dn y = π 8. t = t, y = ; 0 t 1 9. = sin( t), y = cos( t) 5; 0 t π 10. = sin ( t), y = cos ( t); 0 t π Crilh lus permukn end putr yng terentuk il kurv-kurv: 11. y = 6, 0 1 mengelilingi sumu 1. y = 6, 0 1 mengelilingi sumu y 1. y = /, 1 7 mengelilingi sumu 1. y = /, 1 7 mengelilingi sumu y 15. = t, y = t, 0 1 mengelilingi sumu
29 Momen dn Pust Mss Momen Hsil kli mss m sutu prtikel dengn jrk errhny dri sutu titik (lengn tus) dinmkn momen prtikel terhdp titik terseut. Dengn kt lin Momen = pnjng lengn tus kli mss tu M = m m Gmr 1. Jdi, M m n i= 1 = = n i= 1 m i m i i Titik dinmkn pust mss (titik kesetimngn) Contoh 11: Mss seesr,, 6, dn 7 kilogrm msing-msing diletkkn pd titik-titik 0, 1,, dn sepnjng sumu-. Crilh pust mssny. Jw: (0)() + (1)() + ()(6) + ()(7) = = =,1 19 Distriusi mss yng kontinu sepnjng kwt dengn kepdtn di dlh δ() dlh
30 60 δ ( ) d M = = m δ ( ) d Contoh 1: Kepdtn δ() sepotong kwt di titik yng terletk sentimeter dri slh stu ujungny dlh δ() = grm/sentimeter. Tentukn pust mss kwt ntr = 0 dn = 10. Jw: =. d d = = 7,5 cm Tugs: Hitung contoh 1 di ts menggunkn derive Pust Mss (centroid) Are_Centroid(,,, y, f(), g()) dlh untuk menghitung pust mss derh R yng ditsi oleh dengn y = f() dn y = g(). Contoh 1: Tentuknlh pust mss derh R yng ditsi oleh 0 1, y =, dn y =. Penyelesin dengn Derive: 1. Gmr derh R: AreBetweenCurves(,,, 0, 1, y). Gmr pust mss: Are_Centroid(, 0, 1, y, (, ). Klik sm dengn, llu proksimsi
31 61 Jdi pust mss derh R dlh (0,8; 0,) Tugs: Hitunglh contoh 1 di ts dengn menggunkn rumus: = d g f d g f ) ( ) ( [ )] ( ) ( [ = d g f d g f y ) ( ) ( [ ] ) ( ) ( [
32 6 Sol-Sol Ltihn 1. Prtikel-prtikel ermss m 1 = 5, m = 7, dn m = 9 terletk di 1 =, = -, dn m = 1 sepnjng sutu gris. Crilh pust mssny.. Feni dn Wti ertny msing-msing 5 dn 15 kilogrm duduk pd ujungujung ppn yng pnjngny meter dengn titik tumpu di tengh-tengh ppn. Dimnkh Ari dengn ert 10 kilogrm hrus duduk gr ppn terseut dlm kedn setimng?. Sepotong kwt lurus pnjngny 7 stun mempunyi kepdtn δ() = pd seuh titik yng juhny -stun dri slh stu ujungny. Tentukn jrk dri ujung ini ke pust mss kwt. Dlm sol-sol -5, Mss-mss dn koordint-koordint sutu sistem prtikel dlm idng koordint dierikn. Tentuknlh momen dn pust mssny.., (1,1);, (7,1);, (-,-5); 6, (-1,0);, (,6) 5. 5, (-,); 6, (-,-);, (,5); 7, (,); 1, (7,-1) Dlm sol-sol 6-8, Crilh centroid derh yng dilingkupi oleh kurv yng dierikn dn utlh grfikny. 6. y =, y = 0 7. y =, y = 0, = 1 8. y =, y =, = 1 9. Untuk setip lmin homogen R1 dn R yng ditunjukkn dlm gmr, crilh m, M, M y,, dn y.
33 6 10. Untuk lmin homogen R yng ditunjukkn dlm gmr, crilh m, M, M y,, dn y.
Hendra Gunawan. 15 November 2013
MA1101 MATEMATIKA 1A Hendr Gunwn Semester I, 2013/2014 15 Novemer 2013 Ltihn 1. Pnjng lmi sutu pegs dlh 0.08 m. Gy seesr 0.6 N diperlukn untuk menekn dn menhnny pd pnjng 0.07 m. Tentukn kerjyng dilkukn
PEMANTAPAN BELAJAR SMA BBS INTEGRAL
BAB I PEMANTAPAN BELAJAR SMA BBS INTEGRAL I A RANGKUMAN INTEGRAL. Pengertin Apil terdpt fungsi F() yng dpt didiferensilkn pd selng I sedemikin hingg F () = f(), mk nti turunn (integrl) dri f() dlh F()
7. APLIKASI INTEGRAL
7. APLIKASI INTEGRAL 7. Menghitung Lus Derh.Mislkn derh D (, ), f ( ) D f() Lus D =? Lngkh :. Iris D menjdi n gin dn lus stu uh irisn dihmpiri oleh lus persegi pnjng dengn tinggi f() ls(ler) A f ( ). Lus
INTEGRAL. Misalkan suatu fungsi f(x) diintegralkan terhadap x maka di tulis sebagai berikut:
INTEGRAL.PENGERTIAN INTEGRAL Integrl dlh cr mencri sutu fungsi jik turunnn di kethui tu kelikn dri diferensil (turunn) ng diseut jug nti derivtif tu nti diferensil. Untuk menentukn integrl tidk semudh
LUAS DAERAH APLIKASI INTEGRAL TENTU. Indikator Pencapaian Hasil Belajar. Ringkasan Materi Perkuliahan
LUAS DAERAH APLIKASI INTEGRAL TENTU Indiktor Pencpin Hsil Beljr Mhsisw menunjukkn kemmpun dlm :. Menghitung lus pd idng dtr Ringksn Mteri Perkulihn Jik sutu derh ditsi oleh kurv f(), g(), gris dn dengn
MATEMATIKA. Sesi INTEGRAL VOLUME A. BENDA-BENDA YANG MEMILIKI SUMBU PUTAR B. BENDA-BENDA YANG MEMILIKI SUMBU PUTAR TERHADAP SUMBU-X
MATEMATIKA KELAS XII - KURIKULUM GABUNGAN 6 Sesi N INTEGRAL VOLUME A. BENDA-BENDA YANG MEMILIKI SUMBU PUTAR Apliksi integrl erikutn dlh menentukn volume end ng memiliki sumu putr. Contoh endn dlh tung,
MATEMATIKA INTEGRAL TENTU DAN LUAS DAERAH
MATEMATIKA KELAS XII - KURIKULUM GABUNGAN 5 Sesi N INTEGRAL TENTU DAN LUAS DAERAH A. DEFINISI INTEGRAL TENTU Bentuk integrl f d = f + c diseut segi integrl tk tentu kren hsil dri pengintegrlnn msih erup
selisih positif jarak titik (x, y) terhadap pasangan dua titik tertentu yang disebut titik
Hiperol 7.1. Persmn Hiperol Bentuk Bku Hiperol dlh himpunn semu titik (, ) pd idng sedemikin hingg selisih positif jrk titik (, ) terhdp psngn du titik tertentu ng diseut titik fokus (foci) dlh tetp. Untuk
INTEGRAL. Integral Tak Tentu Dan Integral Tertentu Dari Fungsi Aljabar
INTEGRAL Integrl Tk Tentu Dn Integrl Tertentu Dri Fungsi Aljr A. Integrl Tk Tentu Hitung integrl dlh kelikn dri hitung differensil. Pd hitung differensil yng dicri dlh fungsi turunnny, sedngkn pd hitung
10. cos (ax+b)sin(ax+b) dx = 12. sec x dx = tan x + c. 13. sec (ax+b)dx = tan (ax+b)+ c. 14. c sec x dx = - ctg x + c
BAB XVI. INTEGRAL A. Integrl Tk Tentu. Rumus Integrl Fungsi Aljr. k k n = n +. ( + ) n = ( n + ). = ln + n + + ; n - n+ (+) + ; dn n -. ( f ( ) ± g( ) ) f ( ) ± g ( ) n. os (+)sin(+) = ( n + ) os n + (+)
BAB: PENERAPAN INTEGRAL Topik: Volume Benda Putar (Khusus Kalkulus 1)
BAB: PENERAPAN INTEGRAL Topik: Volume Bend Putr (Khusus Klkulus ) Kompetensi yng diukur dlh kemmpun mhsisw menghitung volume bend putr dengn metode cincin, metode ckrm, tu metode kulit tbung.. UAS Klkulus,
INTEGRAL TAK TENTU. x x x
INTEGRAL TAK TENTU Definisi : Fungsi F diktkn nti turunn dri fungsi f pd selng I jik F () = f() untuk semu di I. Notsi : F() = f() Integrl tk tentu dlh Anti/Invers/Kelikn turunn. c c Integrl tk tentu dlh
INTEGRAL. y dx. x dy. F(x)dx F(x)dx
Drs. Mtrisoni www.mtemtikdw.wordpress.om INTEGRAL PENGERTIAN Bil dikethui : = F() + C mk = F () dlh turunn dri sedngkn dlh integrl (nti turunn) dri dn dpt digmrkn : differensil differensil Y Y Y Integrl
10. cos (ax+b)sin(ax+b) dx = 12. sec x dx = tan x + c. 13. sec (ax+b)dx = tan (ax+b)+ c. 14. c sec x dx = - ctg x + c
Integrl Tk Tentu INTEGRAL. Rumus Integrl Fungsi Aljr. k x n k n +. ( x + n ( n +. x ln x + x n + + ; n - n+ (x+ + ; dn 4. ( f ( x ± g( x f ( x ± g ( x n - n. os (x+sin(x+ ( n + n+ os (x+ + ( + (. sin x
Modul Matematika 2012
Modul Mtemtik. ANTI TURUNAN Definisi Mislkn fungsi f terdefinisi pd selng teruk I. Fungsi F ng memenuhi F () = f () pd I dinmkn nti turunn tu fungsi primitif dri fungsi f pd I.. F() = cos nti turunn dri
E. INTEGRASI BAGIAN ( PARSIAL )
E. INTEGRASI BAGIAN ( PARSIAL ) Integrsi gin (prsil) digunkn untuk mengintegrsikn sutu perklin fungsi yng msing-msing fungsiny ukn koefisien diferensil dri yng lin ( seperti yng sudh dihs pd su. B. D )
Matematika EBTANAS Tahun 1992
Mtemtik EBTANAS Thun 99 EBT-SMA-9-0 Grfik fungsi kudrt yng persmnny y = x 5x memotong sumu x. Slh stu titik potongny dlh (, 0), mk nili sm dengn EBT-SMA-9-0 Persmn x px + 5 = 0 kr-krny sm. Nili p 0 tu
RANGKUMAN MATERI ' maupun F(x) = Pengerjaan f(x) sehingga memperoleh F(x) + c disebut mengintegralkan f(x) ke x dengan notasi:
INTEGRAL RANGKUMAN MATERI A. ANTIDERIVATIF DAN INTEGRAL TAK TENTU Jik kit mengmil uku dri temptny mk kit dpt mengemliknny lgi ke tempt semul. Opersi yng kedu menghpus opersi yng pertm. Kit ktkn hw du opersi
INTEGRAL. Kelas XII IIS Semester Genap. Oleh : Markus Yuniarto, S.Si. SMA Santa Angela Tahun Pelajaran 2017/2018
Modul Integrl INTEGRAL Kels XII IIS Semester Genp Oleh : Mrkus Yunirto, SSi SMA Snt Angel Thun Peljrn 7/8 Modul Mtemtik Kels XII IIS Semester TA 7/8 Modul Integrl INTEGRAL Stndr Kompetensi: Menggunkn konsep
VEKTOR. Dua vektor dikatakan sama jika besar dan arahnya sama. Artinya suatu vektor letaknya bisa di mana saja asalkan besar dan arahnya sama.
-1- VEKTOR PENGERTIAN VEKTOR dlh sutu esrn yng mempunyi nili (esr) dn rh. Sutu vektor dpt digmrkn segi rus gris errh. Nili (esr) vektor dinytkn dengn pnjng gris dn rhny dinytkn dengn tnd pnh. Notsi vektor
1. Luas daerah yang dibatasi oleh kurva y = x 2 dan garis x + y = 6 adalah
. Lus derh yng ditsi oleh kurv y = x dn gris x + y = dlh stun lus... c. d. 8 Sol Ujin Nsionl Thun 7 Kurv y = x dn gris x + y = ( y = x ) Sustikn nili y pd y = x sehingg didpt : x = x x = x x + x = ( =,
PERSAMAAN KUADRAT, FUNGSI KUADRAT DAN PERTIDAKSAMAAN KUADRAT
PERSAMAAN KUADRAT, FUNGSI KUADRAT DAN PERTIDAKSAMAAN KUADRAT Persmn Kudrt. Bentuk Umum Persmn Kudrt Mislkn,, Є R dn 0 mk persmn yng erentuk 0 dinmkn persmn kudrt dlm peuh. Dlm persmn kudrt 0, dlh koefisien
1. Luas daerah yang dibatasi oleh kurva y = x 2 dan garis x + y = 6 adalah satuan luas. a. 54 b. 32. d. 18 e.
. Lus derh yng ditsi oleh kurv y = x dn gris x + y = dlh stun lus... c. d. 8 e. Sol Ujin Nsionl Thun 7 Kurv y = x dn gris x + y = ( y = x ) Sustikn nili y pd y = x sehingg didpt : x = x x = x x + x = (
Erna Sri Hartatik. Aljabar Linear. Pertemuan 3 Aljabar Vektor (Perkalian vektor-lanjutan)
Ern Sri Hrttik Aljr Liner Pertemun Aljr Vektor (Perklin vektor-lnjutn) Pemhsn Perklin Cross (Cross Product) - Model cross product - Sift cross product Pendhulun Selin dot product d fungsi perklin product
INTEGRAL. 1. Macam-macam Integral. Nuria Rahmatin TIP L. A. Integral Tak Tentu
INTEGRAL Nuri Rhmtin 5000006 TIP L. Mcm-mcm Integrl A. Integrl Tk Tentu Integrl dlh entuk invers dri turunn. Secr umum jik seuh fungsi diintegrlkn terhdp vrile tertentu dpt disjikn dlm entuk : f ( F( C
Integral. Konstanta dari Integrasi. Integral Tak Tentu. AntiTurunan (Antiderivative)
Integrl AntiTurunn (Antiderivtive) AntiTurunn dri seuh fungsi f dl seuh fungsi F sedemikin hingg Dierikn Pd Peltihn Guru-Guru Aceh Jy 5 Septemer 0 Oleh: Ridh Ferdhin, M.Sc F f E. AntiTurunn dri f ( ) 6
ELIPS. A. Pengertian Elips
ELIPS A. Pengertin Elips Elips dlh tempt kedudukn titik-titik yng jumlh jrkny terhdp du titik tertentu mempunyi nili yng tetp. Kedu titik terseut dlh titik focus / titik pi. Elips jug didefinisikn segi
HITUNG INTEGRAL ( 4 ) 4. Diketahui f(x) = 4x + 1 dan F(2) = 17 ; Tentukan fungsi F f(x) = 4x + 1
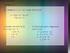HITUNG INTEGRA BAB.Integrl tk tentu (tnp ts). Rumus-rumus ) ) n n n d c, n ) d c n n n. d c, n ). Sift-sift Integrl Contoh :... ) k. f ( ) d k. f ( ) d d d ln c ) ( ( ) ( )) ( ) ( ) d c ( ) ( ) d ( ) d
IRISAN KERUCUT: PERSAMAAN ELIPS. Tujuan Pembelajaran
K-13 mtemtik K e l s I IRISAN KERUCUT: PERSAMAAN ELIPS Tujun Pemeljrn Setelh mempeljri mteri ini, kmu dihrpkn memiliki kemmpun erikut. 1. Memhmi definisi elips.. Memhmi unsur-unsur elips. 3. Memhmi eksentrisits
E-LEARNING MATEMATIKA
MODUL E-LEARNING E-LEARNING MATEMATIKA Oleh : NURYADIN EKO RAHARJO, M.PD. NIP. 9705 00 00 Penulisn Modul e Lerning ini diiyi oleh dn DIPA BLU UNY TA 00 Sesui dengn Surt Perjnjin Pelksnn e Lerning Nomor
APLIKASI INTEGRAL TENTU
APLIKASI INTEGRAL TENTU Apliksi Itegrl Tetu థ Lus ditr 2 kurv థ Volume ed dlm idg (deg metode ckrm d cici) థ Volume ed putr (deg metode kulit tug) థ Lus permuk ed putr థ Mome d pust mss 1 2 1. LUAS DIANTARA
PENGAYAAN MATEMATIKA SOLUSI SOAL-SOAL LATIHAN 1
PENGAYAAN MATEMATIKA SOLUSI SOAL-SOAL LATIHAN 6y y 8y. Dikethui R dn. Temukn nili y. y y 8y 6 Solusi: 6y y 8y y y 8y 6 6y y 8y 8y y 6 y 8 0 y y y 0 y y y 0 ( y ) ( y ) 0 y y 8y 6 ( y )(y ) 0 y 0tu y 0
Integral B A B. A. Pengertian Integral. B. Integral Tak Tentu. C. Integral Tertentu. D. Menentukan Luas Daerah. E. Menentukan Volume Benda Putar
Integrl B A B A. Pengertin Integrl B. Integrl Tk Tentu C. Integrl Tertentu D. Menentukn Lus Derh E. Menentukn Volume Bend Putr Sumer: www.wllpperse.com Pernhkh klin meliht ling-ling peswt? Bgimnkh entukny?
MATERI I : VEKTOR. Pertemuan-01
MATERI I : VEKTOR Pertemun-0. Pendhulun Definisi Vektor didefinisikn segi esrn yng memiliki rh. Keeptn, gy dn pergesern merupkn ontoh ontoh dri vektor kren semuny memiliki esr dn rh wlupun untuk keeptn
Penyelesaian Persamaan Kuadrat 1. Rumus abc Rumus menentukan akar persamaan kuadrat ax 2 bx c 0; a, b, c R dan a 0
PERSAMAAN, PERTIDAKSAMAAN DAN FUNGSI KUADRAT PERSAMAAN KUADRAT Bentuk umum persmn kudrt dlh c 0,,,c R, 0 Penyelesin Persmn Kudrt. Rumus c Rumus menentukn kr persmn kudrt c 0;,, c R dn 0, = ± 4c. Memfktorkn
UJIAN SEMESTER GANJIL SMA SANG DEWA JAKARTA TAHUN PELAJARAN
UJIAN SEMESTER GANJIL SMA SANG DEWA JAKARTA TAHUN PELAJARAN - Mt Peljrn : ILMU HITUNG MODERN Kels / Progrm : XII AIA ( Du Bels ) / Ajin Ilmu Api Hri / Tnggl : Minggu Nopemer Wktu :.. WIB ( Menit) Pilihlh
Y y=f(x) LEMBAR KERJA SISWA. x=a. x=b
LEMBAR KERJA SISWA. Judul (Mteri Pokok) : Penggunn Integrl Tentu Untuk Menghitung Volume Bend Putr. Mt Peljrn : Mtemtik 3. Kels / Semester : II /. Wktu : 5 menit 5. Stndr Kompetensi :. Menggunkn konsep
Tiara Ariqoh Bawindaputri TIP / kelas L
Tir Ariqoh Bwindputri 500008 TIP / kels L INTEGRAL Integrl Tk tentu Integrl dlh entuk invers dri turunn. Secr umum jik seuh fungsi diintegrlkn terhdp vrile tertentu dpt disjikn dlm entuk : f ( F( C Untuk
Catatan Kuliah MA1123 KALKULUS ELEMENTER I BAB V. INTEGRAL
BAB V. INTEGRAL Anti-turunn dn Integrl Tk Tentu Persmn Diferensil Sederhn Notsi Sigm dn Lus Derh di Bwh Kurv Integrl Tentu Teorem Dsr Klkulus Sift-sift Integrl Tentu Leih Lnjut Sustitusi dlm Penghitungn
Materi IX A. Pendahuluan
Mteri IX Tujun :. Mhsisw dpt memhmi vektor. Mhsisw mmpu mengunkn vektor dlm persoln sederhn 3. Mhsisw mengimplementsikn konsep vektor pd rngkin listrik. Pendhulun Sudh menjdi kesepktn umum hw untuk menentukn
[RUMUS CEPAT MATEMATIKA]
![[RUMUS CEPAT MATEMATIKA]](/thumbs/55/35374920.jpg "[RUMUS CEPAT MATEMATIKA]")
http://meetied.wordpress.com SMAN BoneBone, Luwu Utr, SulSel Keslhn teresr yng diut mnusi dlm kehidupnny dlh terusmenerus mers tkut hw merek kn melkukn keslhn (Elert Hud) [RUMUS CEPAT MATEMATIKA] Vektor
matematika K-13 IRISAN KERUCUT: PERSAMAAN HIPERBOLA K e l a s A. Definisi Hiperbola Tujuan Pembelajaran
K-13 mtemtik K e l s I IRISAN KERUCUT: PERSAMAAN HIPERBLA Tujun Pemeljrn Setelh mempeljri mteri ini, kmu dihrpkn memiliki kemmpun erikut. 1. Memhmi definisi dn unsur-unsur hiperol.. Dpt menentukn persmn
Jarak Titik, Garis dan Bidang dalam Ruang
Pge of Kegitn eljr. Tujun Pembeljrn Setelh mempeljri kegitn beljr, dihrpkn sisw dpt :. Menentukn jrk titik dn gris dlm rung b. Menentukn jrk titik dn bidng dlm rung c. Menentukn jrk ntr du gris dlm rung.
FUNGSI TRIGONOMETRI LIMIT FUNGSI
FUNGSI TRIGONOMETRI LIMIT FUNGSI Limit Fungsi. Limit fungsi f() merupkn nili hmpirn dri f() untuk nili mendekti nili tertentu misl. Bentuk umum : Lim f() -> Jik dikethui du uh fungsi f() dn g() msing-msing
TEORI DEFINITE INTEGRAL
definite integrl & lus yog.prihstomo TEORI DEFINITE INTEGRAL Definisi : Jik y = f(x) dlh fungsi kontinu dn terdefinisi dlm intervl tertutup [,] sehingg lim n n i= f ( xi). Δxi d (mempunyi nili), mk definite
UJIAN BERSAMA SMA KABUPATEN TANAH DATAR SEMESTER 1 TAHUN PELAJARAN 2008/2009. Mata Pelajaran : MATEMATIKA Kelas/jurusan : XII/ IPA Hari/Tanggal :
UJIAN BERSAMA SMA KABUPATEN TANAH DATAR SEMESTER TAHUN PELAJARAN /9 Mt Peljrn : MATEMATIKA Kels/jurusn : XII/ IPA Hri/Tnggl : Wktu : menit. d... A. c B. c C. c D. c E. c. sin cos d... A. cos C B. cos C
Bab 3 Terapan Integral Ganda
Surdi Siregr Metode Mtemtik Astronomi Bb 3 Terpn Integrl Gnd 3. Integrl Gnd dlm koordint Krtesis dn Polr Koordint Krtesis Koordint Polr Ilustrsi b g f ={,, } Mss M, da, dd r ={,, r )},, M r da r rdrd sin
Definisi Vektor. Vektor adalah besaran yang mempunyai besar dan arah
VEKTOR Definisi Vektor Vektor dlh esrn yng mempunyi esr dn rh Besr vektor rtiny pnjng vektor Arh vektor rtiny sudut yng dientuk dengn sumu X positif Vektor disjikn dlm entuk rus gris errh Gmr Vektor B
Bab 3 Terapan Integral Ganda
Surdi Siregr Metode Mtemtik Astronomi Bb Terpn Integrl Gnd. Integrl Gnd dlm koordint Krtesis dn Polr Koordint Krtesis Koordint Polr Ilustrsi b g f ={,, } Mss M, da, Momen-, M dd Momen- M, d d dd r ={,,
BAB 7. LIMIT DAN LAJU PERUBAHAN
BAB 7. LIMIT DAN LAJU PERUBAHAN 7. LIMIT FUNGSI 7.. Limit fungsi di sutu titik Menggmbrkn perilku fungsi jik peubhn mendekti sutu titik Illustrsi: Dikethui f( ) f(), 3,30,0 3,030,00 3,003 3 f() = f() 3,000?
PREDIKSI UJIAN NASIONAL TAHUN PELAJARAN
PREDIKSI UJIAN NASIONAL TAHUN PELAJARAN - Mt Peljrn Progrm : Mtemtik (MA) : IPA Petunjuk : Pilihlh slh stu jwn yng pling tept!. Dikethui: 5. Dikethui log = dn log = y. Nili log P : Hri tidk hujn tu Rudi
1) BENTUK UMUM DAN BAGIAN-BAGIAN PERSAMAAN KUADRAT Bentuk umum persamaan kuadrat adalah seperti di bawah ini:
) BENTUK UMUM DAN BAGIAN-BAGIAN PERSAMAAN KUADRAT Bentuk umum persmn kudrt dlh seperti di bwh ini: b c dengn, b, c bilngn dn riil Dimn, disebut sebgi koefisien dri b disebut sebgi koefisien dri c disebut
BAB. I INTEGRAL. (Orang tuanya) (Anaknya)
BAB. I INTEGRAL A. Pendhulun.. Pengertin integrl. Integrl dlh lwn kelikn) dri diferensil. Dpt diumpmkn hw opersi diferensil itu, dikethui orng tuny, disuruh menri nkny, sedngkn opersi integrl, dikethui
Parabola adalah tempat kedudukan titik-titik yang jaraknya ke satu titik tertentu sama dengan jaraknya ke sebuah garis tertentu (direktriks).
Prol dlh tempt kedudukn titik-titik ng jrkn ke stu titik tertentu sm dengn jrkn ke seuh gris tertentu (direktriks). Persmn Prol 1. Persmn Prol dengn Punck O(,) Perhtikn gmr erikut ini! PARABOLA g A P(,
Matematika Dasar VOLUME BENDA PUTAR
OLUME BENDA PUTAR Ben putr yng seerhn pt kit mil ontoh lh tung engn esr volume lh hsilkli lus ls ( lus lingkrn ) n tinggi tung. olume ri en putr ser umum pt ihitung ri hsilkli ntr lus ls n tinggi. Bil
LOMBA CERDAS CERMAT MATEMATIKA (LCCM) TINGKAT SMP DAN SMA SE-SUMATERA Memperebutkan Piala Gubernur Sumatera Selatan 3 5 Mei 2011
LOMBA CERDAS CERMAT MATEMATIKA (LCCM) TINGKAT SMP DAN SMA SE-SUMATERA Mempereutkn Pil Guernur Sumter Seltn Mei 0 PENYISIHAN I PERORANGAN LCCM TINGKAT SMA. Dikethui kuus ABCD.EFGH dengn rusuk 6 cm. Jik
METODE ANALISIS. Tentukan arus pada masing-masing tahanan dengan menggunakan metode arus cabang untuk rangkaian seperti pada Gambar 1.
1. Anlisis Arus Cng METODE ANALSS Metode rus ng dlh slh stu metode penyelesin nlisis rngkin il rngkin terdiri dri du tu leih sumer. Pd metode rus ng ini, kn diperoleh rus pd setip ng dri sutu rngkin yng
Vektor translasi dpt ditunjukkan oleh bil. berurutan yang ditulis dlm bentuk matriks kolom
TRANSFORMASI GEOMETRI BAB Sutu trnsformsi idng dlh sutu pemetn dri idng Krtesius ke idng ng lin tu T : R R (,) ( ', ') Jenis-jenis trnsformsi ntr lin : Trnsformsi Isometri itu trnsformsi ng tidk menguh
A. Pengertian Integral
A. Pengertin Integrl Di Kels XI, klin telh mempeljri konsep turunn. Pemhmn tentng konsep turunn ini dpt klin gunkn untuk memhmi konsep integrl. Untuk itu, co tentukn turunn fungsi-fungsi erikut. f () f
BAB I. MATRIKS BAB II. DETERMINAN BAB III. INVERS MATRIKS BAB IV. PENYELESAIAN PERSAMAAN LINEAR SIMULTAN
DFTR ISI BB I. MTRIKS BB II. DETERMINN BB III. INVERS MTRIKS BB IV. PENYELESIN PERSMN LINER SIMULTN BB I. MTRIKS Mtriks erup sekelompok ilngn yng disusun empt persegi dn ditsi tnd terdiri dri ris dn kolom
A 1P = PA 2 B 1P = PB 2 F 1P = PF 2 A 1A 2 B 1B 2 F 1 dan F 2 A 1 dan A 2 B 1 dan B 2 B 2
http://www.smkpeklongn.sch.id Elips A. Pengertin Elips Elips dlh tempt kedudukn titik-titik pd geometri dimensi yng memiliki jumlh jrk yng tetp terhdp du titik tertentu. Selnjutny du titik tertentu terseut
II. LANDASAN TEORI. Dalam bab ini akan didiskusikan definisi definisi, istilah istilah dan teoremateorema. yang berhubungan dengan penelitian ini.
II. LANDASAN TEORI Dlm ini kn didiskusikn definisi definisi, istilh istilh dn teoremteorem yng erhuungn dengn penelitin ini. 2.1 Anlitik Geometri Definisi 2.1.1 Titik dlh unsur yng tidk memiliki pnjng,
RENCANA PELAKSANAAN PEMBELAJARAN (RPP) : 2 jam tatap muka dan 2 jam tugas terstruktur
RENCANA PELAKSANAAN PEMBELAJARAN (RPP) Nm Sekolh : SMAN 78 JAKARTA Mt Peljrn : Mtemtik 4 Ben Beljr : 4 sks Aloksi wktu : 2 jm ttp muk dn 2 jm tugs terstruktur Aspek Stndr Kompetensi Kompetensi Dsr Indiktor
APLIKASI INTEGRAL PENERAPAN INTEGRAL. Luas daerah kelengkungan
APLIKASI INTEGRAL APLIKASI INTEGRAL PENERAPAN INTEGRAL Lus derh kelengkungn PENERAPAN INTEGRAL Indiktor 1 Indiktor 9 Lus derh di bwh kurv berdsr prinsip Riemn Volume bend putr, jik kurv diputr mengelilingi
VEKTOR. seperti AB, AB, a r, a, atau a.
VEKTOR I. KOMPETENSI YANG DICAPAI Mhsisw dpt :. Menggmr vektor dengn sistem vektor stun.. Menghitung perklin vektor. 3. Menghitung penmhn vektor dengn turn segitig, turn rn genng, dn turn poligon. 4. Menghitung
VECTOR DI BIDANG R 2 DAN RUANG R 3. Nurdinintya Athari (NDT)
VECTOR DI BIDANG R DAN RUANG R Nurdininty Athri (NDT) VEKTOR DI BIDANG (R ) DAN DI RUANG (R ) Pokok Bhsn :. Notsi dn Opersi Vektor. Perklin titik dn Proyeksi Ortogonl. Perklin silng dn Apliksiny Beerp
APLIKASI INTEGRAL TENTU
APLIKASI INTEGAL TENTU A. Lus Derh Bing t 1. Mislkn erh = x, y x, y f x. Lus? y = f(x) x Lngkh-lngkh: 1. Iris menji n gin ri lus stu uh irisn ihmpiri oleh lus persegi pnjng engn tinggi f(x). ls (ler) x
Bab 4 Transformasi Geometri
B 4 Trnsformsi Geometri TUJUAN PEMBELAJARAN Pem is memhmi konsep trnsformsi geometri -D dn -D : trnslsi, rotsi, Refleksi, her dn slling OUTCOME PEMBELAJARAN Pem is menghitung trnsformsi geometri -D ser
XIII. METODE ENERGI REGANGAN
[etode Energi Regngn] X. ETOE ENERG REGANGAN.. Konsep Energi Regngn Konsep energi regngn dijelskn seelumny pd tng yng terken en norml dn puntir. Konsep-konsep terseut kn dipki pd lenturn lok. Hny lok yng
didefinisikan sebagai bilangan yang dapat ditulis dengan b
1 PENDAHULUAN 1.1 Sistem Bilngn Rel Untuk mempeljri klkulus perlu memhmi hsn tentng system ilngn rel, kren klkulus didsrkn pd system ilngn rel dn siftsiftny. Sistem ilngn yng pling sederhn dlh ilngn sli,
1. Identitas Trigonometri. 1. Identitas trigonometri dasar berikut ini merupakan hubungan kebalikan.
1. Identits Trigonometri Pengertin Identits Trigonometri dlh kesmn yng memut entuk trigonometri dn erlku untuk semrng sudut yng dierikn. Jenis Identits Trigonometri 1. Identits trigonometri dsr erikut
VEKTOR. 1. Pengertian Vektor adalah besaran yang memiliki besar (nilai) dan arah. Vektor merupakan sebuah ruas garis yang
VEKTOR 1. Pengertin Vektor dlh besrn yng memiliki besr (nili dn rh. Vektor merupkn sebuh rus gris yng P berrh dn memiliki pnjng. Pnjng rus gris tersebut dlh pnjng vektor. Rus gris dri titik P dn berujung
PRINSIP DASAR SURVEYING
POKOK HSN : PRINSIP DSR SURVEYING Metri system, Dsr Mtemtik, Prinsip pengkurn : pengkurn jrk, pengkurn sudut dn pengukurn jrk dn sudut,.. Sistem Ukurn Jrk Unit pling dsr dlm sistem metrik dlh meter, dimn
MATEMATIKA IPA PAKET B KUNCI JAWABAN SOAL
MATEMATIKA IPA PAKET KUNCI JAWAAN SOAL. Jwn : Mislkn p: ir sungi jernih q: Tidk terkndung zt pencemr r: Semu ikn tidk mti Diperoleh : Premis : p q Premis : ~r ~q q r Jdi, kesimpuln dri premis-premis terseut
Bab. Vektor. A. Vektor B. Perkalian Vektor. Hasil yang harus Anda capai: menerapkan konsep besaran Fisika dan pengukurannya.
2 Sumer: Dsr-Dsr Foto Jurnlistik, 2003 esrn yng memiliki esr dn rh diseut esrn vektor. Keceptn merupkn slh stu esrn vektor. Vektor Hsil yng hrus nd cpi: menerpkn konsep esrn Fisik dn pengukurnny. Setelh
Hendra Gunawan. 2 April 2014
MA1201 MATEMATIKA 2A Hendr Gunwn Semester II 2013/2014 2 April 2014 Kulih ng Llu 12.1 Fungsi du tu leih peuh 12.2 Turunn Prsil 12.3 Limit dn Kekontinun 12.4 Turunn ungsi du peuh 12.5 Turunn errh dn grdien
Soal-soal dan Pembahasan Matematika Dasar SBMPTN-SNMPTN 2006
www.purwntowhyudi.com Hl- Sol-sol dn Pemhsn Mtemtik Dsr SBMPTN-SNMPTN 006. Jik > 0, > 0 dn mk A. C. E. B. D. Jw:. Jwnny dlh A. Jik p - dn q -, mk q p. A. C. E. B. D. Jw: q p Jwnny dlh A . Grfik y terletk
http://meetied.wordpress.com Mtemtik X Semester 1 SMAN 1 Bone-Bone Reutlh st ini. Ap pun yng is And lkukn tu And impikn Mulilh!!! Keernin mengndung kejeniusn, kekutn dn kejin. Lkukn sj dn otk And kn muli
SISTEM BILANGAN REAL. Purnami E. Soewardi. Direktorat Pembinaan Tendik Dikdasmen Ditjen GTK Kementerian Pendidikan dan Kebudayaan
SISTEM BILANGAN REAL Purnmi E. Soewrdi Direktort Peminn Tendik Dikdsmen Ditjen GTK Kementerin Pendidikn dn Keudyn Himpunn Bilngn Asli (N) Bilngn sli dlh ilngn yng pertm kli dikenl dn digunkn oleh mnusi
IRISAN KERUCUT. 1. Persamaan lingkaran dengan pusat (0,0) dan jari-jari r. Persamaan = TK titik T = =
IRISAN KERUCUT Bb 9 A. LINGKARAN. Persmn lingkrn dengn pust (0,0) dn jri-jri r 0 r T(x,y) X Persmn = TK titik T = { T / OT r } = = {( x, y) / r } {( x, y) / r }. Persmn lingkrn dengn pust (,b) dengn jri-jri
UNTUK MENDAPATKAN SOAL PREDIKSI SBMPTN 2015
-. UNTUK MENDAPATKAN SOAL PREDIKSI SBMPTN 015 SILAHKAN KLIK KUNJUNGI: WWW.E-SBMPTN.COM Ltihn Sol Fisik 1. Thun hy dlh stun dri... (A) jrk (D) momentum (B) keeptn (E) energi (C) wktu. Stu wtt hour sm dengn...
APLIKASI INTEGRAL PENERAPAN INTEGRAL. Luas daerah kelengkungan
APLIKASI INTEGRAL APLIKASI INTEGRAL PENERAPAN INTEGRAL Lus derh kelengkungn Integrl digunkn pd design Menr Petrons di Kul lumpur, untuk perhitungn kekutn menr. Sdne Oper House di design berdsrkn irisn-irisn
mengambil semua titik sample berupa titik ujung, yakni jumlah Riemann merupakan hampiran luas dari daerah dibawah kurva y = f (x) x i b x
B 4. Peerp Itegrl BAB 4. PENGGUNAAN INTEGRAL 4.. Lus re dtr Perhtik derh di wh kurv y = f () di tr du gris tegk = d = di ts sumu, deg f fugsi kotiu. Seperti pd s medefiisik itegrl tertetu, kit gi itervl
UJIAN BERSAMA SMA KABUPATEN TANAH DATAR SEMESTER 1 TAHUN PELAJARAN 2008/2009. Mata Pelajaran : MATEMATIKA Kelas/jurusan : XII/IPS Hari/Tanggal :
UJIN ERSM SM KUPTEN TNH DTR SEMESTER THUN PELJRN / Mt Peljrn : MTEMTIK Kels/jurusn : XII/IPS Hri/Tnggl : Wktu : menit Pilihlh slh stu jwn ng dinggp pling enr dn tept!. d c c c c. Jik F '( ) dn F () mk
Vektor di R2 ( Baca : Vektor di ruang dua ) adalah Vektor- di ruang dua )
A Pengertin Vektor Di R Vektor di R ( B : Vektor di rung du ) dlh Vektor- di rung du ) dlh Vektor-vektor ng terletk pd idng dtr pengertin vektor ng leih singkt dlh sutu esrn ng memiliki esr dn rh tertentu
Soal Latihan dan Pembahasan Dimensi Tiga
Sol Ltihn dn embhsn imensi ig i susun Oleh : Yuyun Somntri http://bimbingnbeljr.net/ i dukung oleh : ortl eduksi rtis Indonesi Open Knowledge nd duction http://oke.or.id utoril ini diperbolehkn untuk di
Tujuan Pembelajaran. ) pada hiperbola yang berpusat di (0, 0). 2. Dapat menentukan persamaan garis singgung di titik (x 1
K-3 mtemtik K e l s XI IRISAN KERUCUT: GARIS SINGGUNG PADA HIPERBOLA Tujun Pemeljrn Setelh mempeljri mteri ini, kmu dihrpkn memiliki kemmpun erikut.. Dpt menentukn persmn gris singgung di titik (, ) pd
2. A dan B titik-titik ujung sebuah terowongan yang dilihat dari C dengan sudut lihat
. Dikethui segitig ABC dengn sudut B= dn CT gris tinggi dri titik C. Jik BC = dn AT = mk tentukn AC! C A T B AC ( CT CT ) ( ). A dn B titik-titik ujung seuh terowongn yng diliht dri C dengn sudut liht
Limit & Kontinuitas. Oleh: Hanung N. Prasetyo. Calculus/Hanung N. Prasetyo/Politeknik Telkom Bandung
imit & Kontinuits Oleh: Hnung N. Prsetyo Clculus/Hnung N. Bb. IMIT.1. Du mslh undmentl klkulus... Gris Tngen.. Konsep imit.4. Teorem imit.5. Konsep kontinuits Clculus/Hnung N. Du Mslh Fundmentl Klkulus
MA1201 MATEMATIKA 2A Hendra Gunawan
MA1201 MATEMATIKA 2A Hendr Gunwn Semester II 2016/2017 31 Mret 2017 Kulih yng Llu 12.1 Fungsi du tu leih peuh 12.2 Turunn Prsil 12.3 Limit dn Kekontinun 12.4 Turunn ungsi du peuh 12.5 Turunn errh dn grdien
GEOMETRI PADA BIDANG: VEKTOR
GEOMETRI PADA BIDANG: VEKTOR A. Kurv Bidng: Representsi Prmetrik Sutu kurv bidng ditentukn oleh sepsng persmn prmetrik: x f () t, y f () t t dlm intervl I dengn f dn g kontinu pd intervl I. Secr umum,
UJIAN NASIONAL. Matematika (D10) PROGRAM STUDI IPA PAKET 1 (UTAMA) SELASA, 11 MEI 2004 Pukul
0-0 D0-P-0- DOKUMEN NEGARA SANGAT RAHASIA UJIAN NASIONAL TAHUN PELAJARAN 00/00 SMA/MA Mtemtik (D0) PROGRAM STUDI IPA PAKET (UTAMA) SELASA, MEI 00 Pukul 07.0 09.0 DEPARTEMEN PENDIDIKAN NASIONAL Hk Cipt
STATIKA (Reaksi Perletakan)
STTIK (Reksi erletkn) Meknik Rekys I Norm uspit, ST.MT. Tumpun Tumpun merupkn tempt perletkn konstruksi tu dukungn bgi konstruksi dlm meneruskn gy gyyng bekerj ke pondsi Dlm ilmu Meknik Rekys dikenl 3
Tujuan Pembelajaran. ) pada elips. 2. Dapat menentukan persamaan garis singgung yang melalui titik (x 1
K-3 mtemtik K e l s XI IRISAN KERUCUT: PERSAMAAN GARIS SINGGUNG PADA ELIPS Tujun Pemeljrn Setelh mempeljri mteri ini, kmu dihrpkn memiliki kemmpun erikut.. Dpt menentukn persmn gris singgung di titik (,
BAB 4 PERBANDINGAN, PROPORSI, DAN SKALA
BAB PERBANDINGAN, PROPORSI, DAN SKALA A. Perndingn. Perndingn dn Pechn Perndingn tu rsio ntr dn ditulis : dlh pechn, dengn syrt 0. Jdi, Jik k 0, mk :, dengn 0. Apil 0, mk : :. : k: k :. k k Menyederhnkn
1 B. Mengkonversi dari pecahan ke persen. 1 Operasi bilangan berpangkat. 2. Menyederhanakan bilangan berpangkat bentuk:
KISI KISI SOAL UJI COBA UJIAN NASIONAL MATA PELAJARAN MATEMATIKA TAHUN 009 / 00 MGMP MATEMATIKA SMK TEKNIK KABUPATEN KLATEN Bhn/ X / Opersi bilngn rel. Sisw dpt: A. Mengkonversi dri desiml ke persen B.
Fungsi f dikatakan pada / onto / surjektif jika setiap elemen himpunan B merupakan
III FUNGSI 15 1. Definisi Fungsi Definisi 1 Mislkn dn dlh himpunn. Relsi iner f dri ke merupkn sutu fungsi jik setip elemen di dlm dihuungkn dengn tept stu elemen di dlm. Jik f dlh fungsi dri ke, mk f
3. LIMIT DAN KEKONTINUAN
3. LIMIT DAN KEKONTINUAN 1 3.1 Limit Fungsi di Stu Titik Pengertin it secr intuisi Perhtikn ungsi 1 1 Fungsi dits tidk terdeinisi di =1, kren di titik tersebut berbentuk 0/0. Tpi msih bis ditnykn berp
Pertemuan : 1 Materi : Vektor Pada Bidang ( R 2 ), Bab I. Pendahuluan
Pertemun : 1 Mteri : Vektor Pd Bidng ( R 2 ), Bb I. Pendhulun Stndr Kompetensi : Setelh mengikuti perkulihn ini mhsisw dihrpkn dpt : 1. Memhmi kembli pengertin vektor, opersi pd vektor, dn sift-sift opersi
Integral Tak Wajar. Ayundyah Kesumawati. March 25, Prodi Statistika FMIPA-UII
Kesumwti Prodi Sttistik FMIPA-UII Mrch 25, 205 Sutu integrl tertentu b f (x)dx () diktkn wjr jik i memenuhi du syrt berikut: i. Bts integrsi dn b merupkn bilngn berhingg ii. fungsi f (x) terbts pd intervl