NILAI DAN VEKTOR EIGEN MATRIKS INTERVAL ATAS ALJABAR MAX-PLUS. Dwi Suci Maharani 1 dan Suryoto 2. Jln. Prof. H. Soedarto, S.H., Tembalang, Semarang
|
|
|
- Hadian Hartanto
- 7 tahun lalu
- Tontonan:
Transkripsi
1 NILI DN VEKTOR EIGEN MTRIKS INTERVL TS LJBR MX-PLUS D Sc Mhr d Sroto, Jrs Mtetk FMIP Uversts Dpoegoro J Prof H Soedrto, SH, Tebg, Serg bstrct terv tr, th gve d s the set of trces sch tht Egeve d egevector of s ced possbe egeve d egevector of terv tr Wth the deftos egeve d terv tr over -ps gebr, c be deveoped gorth possbe egevector to test hether gve vector s possbe egevector of tht terv tr Wheres vers egeve d egevector of tr s the egeve d egevector of ech Uvers egevector th c be fod b sovg tosded sstes of er eqtos over -ps gebr Keords: Iterv trces, -ps gebr, possbe egevector, vers egevector PENDHULUN br -ps g dotsk deg R Rε,, erpk sh st strktr d br t sefed kottf depote [] Rε erpk hp bg r R deg ε, sedgk opers d bertrt-trt etk ks d peh or bg r, g ddefsk sebg berkt [5]:, b R ε b {, b} b + b St sste pers k + + k, + k, L, { } + k,, L, ; k 0,,,L; k, Rε d br -ps dpt dotsk deg k + k k L k k ; k 0,,, L g khr dpt dgbgk secr kopk deg pes k + k d k L k L k R, R M M M O M k L St skr λ Rε d vektor ε R bertrt-trt dk ege d vektor ege trks R k λ Jk dh trks dr dgrph G g terhbg kt, k ep ege g tgg λ t λ ; dh cce dr G D tk cce {,, L, k } bobot L 3 k d pg ts k [] Set, k setp etr trks dgdk deg λ, k dperoeh st trks B deg Sehgg, terdpt trks Γ B B B B g ep beberp etr dgo t s deg 0 Koo-koo g et etr tersebt dsebt vektor ege-vektor ege fdet dr trks B d
2 [] Set, se vektor ege trks B d dpt dtk sebg kobs er ts br -ps dr hp vektor ege fdet < g dperoeh B trks dts dh trks terv, deg, R d g berrt setp etr-etr g berses berk Deg egssk bh dgrph dr se trks dh terhbg kt deg etr-etr berhgg, d oeh kere sgsg ep ege g tgg λ, berkt k dbhs ege d vektor ege g gk p d vektor ege vers dr trks terv ts br -ps MTRIKS INTERVL TS LJBR MX-PLUS Mtrks terv erpk trks g eee-eee d d berp terv terttp deg st trks bts bh d st trks bts ts sebg pes Dberk trks d R sedek sehgg deg,,, L, Mtrks terv ts br -ps berordo ddefsk deg, { ;,,,, } [6] Cotoh Dberk st trks terv,0 5,4, d 0, 7 3, d Se trks deg dh tersk d d trks terv, Defs opers peh d pergd trks terv ts br -ps, s h defs opers peh d pergd pd trks ts br -ps H s pd trks terv egkt defs opers d ps pd st terv t, b c, d + c, b + d [3], b c, d, c, b, d [3] deg, b, c, d Rε Pebhs opers trks terv ts br -ps, og deg defs opers trks terv pd [4] Dsk M R dh hp se trks terv ts br ps berordo Utk, ddefsk {,,,} d {,,,} Eee-eee dr trks M R deg brs d koo, dotsk deg, t dpt dsk deg [], tk, d Msk trks, B M R, peh trks ddefsk deg [, b, b B], b,, b b Msk M R d β Rε, pergd skr deg trks t β, ddefsk deg [ β β, ] + β, + β c Msk trks M R d B M R, perk trks B, ddefsk deg 0 7, b, b [ B] k
3 { + b }, { + b k } k 3 NILI DN VEKTOR EIGEN YNG MUNGKIN DRI MTRIKS INTERVL Dssk bh se trks dh trks dr dgrph berbobot g terhbg kt deg se etr pes trks, R dh berhgg, d oeh kere sgsg ep ege g tgg St skr dk ege g gk dr st trks terv, k skr tersebt dh ege dr sedkt st [] Teore 3 St skr dh ege g gk dr st trks terv k d h k λ λ, λ Bkt : Dketh dh ege g gk dr st trks terv Sehgg, dh ege dr sedkt st Msk dh ege dr st trks Kre dh trks dr dgrph berbobot g terhbg kt, k λ ; dh cce dr G Kre tk setp trks ep cce g s, k tetp ep bobot berbed, t deg cce d d dgrph cce d d dgrph G cce d d dgrph k dperoeh λ λ λ H ekk bh Dketh k dbktk dh ege g gk dr trks, g rt dh ege dr sedkt st Db trks dr dgrph g terhbg kt deg ege Mtrks terv ep ege trks bts bh, t ege trks bts ts, t k dtkk bh trks Jk, berrt bh λ λ λ Sehgg berk Kre cce-cce dr trks,, d s, k berk deg cce d d dgrph cce d d dgrph G cce d d dgrph H ekk bh, deg kt dh ege dr sedkt st trks St vektor R dh vektor ege g gk dr st trks terv k terdpt sedek sehgg λ [] Set, tk eetk trks g ep vektor ege R dkk deg cr egktk trks bts bh d setp koordt sedek rp sehgg tdk eebh trks bts ts, tetp tk setp koordt dr dpstk sekrg-krg λ g dpt drsk deg * {, + } λ Sehgg tk eg pkh st vektor g dberk dh vektor ege
4 dr st trks terv, dpt dkk deg eggk gort possbe egevector sebg berkt : Ipt : st trks terv, d sebh vektor Beg : If dh st vektor kost 3 the dh st vektor ege g gk dr, STOP 4 ese beg λ : { }; * 5 for, : {, λ + }; * 6 f dh st vektor kost 7 the dh st vektor ege g gk dr ; STOP 8 ese bk vektor ege g gk dr ; STOP 9 ed 0 ed 4 NILI DN VEKTOR EIGEN UNIVERSL DRI MTRIKS INTERVL Dssk bh se trks dh trks dr dgrph berbobot g terhbg kt deg se etr pes trks, R dh berhgg, d oeh kere sg-sg ep ege g tgg St skr dk ege vers dr st trks terv, k skr tersebt dh ege dr setp [] Teore 4 St trks terv ep st ege vers k d h k λ λ Bkt : Dketh st terv ep st ege vers, k dh ege dr setp Kre,, k d Sehgg, Dketh Msk, k dtkk bh dh ege vers dr, g berrt dh ege dr setp b sebrg trks, deg cce d d dgrph cce d d dgrph G cce d d dgrph k Kre cce-cce dr trks,, d s, k
5 kbt λ λ λ Deg kt, Kre dketh bh, k H berrt bh trks terv tersebt ep st ege vers Set, d pebhs vektor ege vers dbts h pd kssd trks terv g dberk ep st ege vers s deg 0 Vektor ege vers erpk kobs er ts br -ps dr hp vektor ege fdet trks p Teore 4 pb st trks terv ep d { },,, dh hp vektor ege fdet dr, k terdpt vektor ege vers dr k d h k sste d ss D C deg C d D tk se,,, ep peees Bkt : Dketh st trks terv deg d sk dh hp vektor ege fdet dr k dbktk sste d ss ep peees Msk vektor ege vers dr dh, k tk setp berk Kre vektor ege vers erpk kobs er ts br -ps dr hp vektor ege fdet trks, k Sehgg, tk deg 0 λ, berk D C D C Jd, dh peees dr
6 Dketh st trks terv deg d sk dh hp vektor ege fdet dr k dbktk terdpt R st vektor ege vers dr Msk dh peees dr sste pers d-ss, sehgg, Terht bh deg λ 0, dh vektor ege trks Kre dh vektor ege trks bts d, k dh vektor ege se trks, g berrt dh vektor ege vers dr Cotoh 4 Dberk trks terv 0, 0, 0, 3,, 0, 0 4, 0, 0 4, d λ λ 0 Hp vektor ege fdet dr trks t { 0, 3, 3,,0,0 } 0 0 Dbetk trks deg, t C 0 d trks deg, t D Sh st peees sste pers d-ss dh , sehgg vektor ege vers dr trks dh PENYELESIN SISTEM PERSMN DU-SISI Sste pers er d-ss ts br -ps g berbetk deg C D 5 34 eotsk hp deks brs {,,,} d hp deks koo dr trks d Le 5 Jk terdpt brs sedek sehgg c > d tk setp, k sste tdk ep sos Bkt : Msk vektor dh sos dr 5 d peks d ss rs kr d ss rs k dr brs sg-sg dperoeh pd koo ke d, t c + k { c k + k } d d + k { d k + k } deg, d
7 Mk k berk c + c + > d + Hs kotrdks deg dh sos dr Sehgg terbkt bh sste deg tdk ep sos kbt 5 Jk sste berbetk 5 ep peees, k tk setp brs terdpt st deks sedek sehgg berk Bkt : Msk vektor dh sos dr 5 k dbktk bh tk setp brs terdpt st deks sedek sehgg berk Msk peks d ss rs kr d ss rs k dr brs sg-sg dperoeh pd koo ke d, t c + k { c k + k } d d + k { d k + k } deg, d Sehgg k berk D phk, c + c +, k c + d + Kre, g berrt eeh c d tk se, d, k, deg kt, Ideks pd kbt dts, dk deks krts tk brs D pebhs set, K eotsk hp deks krts tk brs Le 5 Utk setp peees pd 5 terdpt deks krts peks tk setp brs Bkt : dk dh peees pd 5, d eee peks brs pd d bertrt-trt dh c + d d k + k H berrt c + d k + k, oeh kre t k + c d k Mk tk eee ke dr brs pd dperoeh ck + k ck + + c d k Kre ck d k, k berk c k + k c + kbt, pb c k d k > 0, k c k + k > c + Sehgg terd kotrdks, kre deks bk peks brs pd Oeh kre t, deks dh deks krts peks tk brs pd Oeh kre t, tk ecr peees sste pers d-ss 5 petg tk eh eee peks g ses deg deks krts tk setp brs pd Teore 5 St sste 5 ep peees k d h k setp tdk kosog, terdpt fgs : sehgg K tk se d tk setp sbset {,,, k } dr, sedek sehgg,,, k sg berbed,dperoeh pertdks 5: c + c + + c c + c c k k k Bkt : Msk dh sos dr
8 b sebrg sbset {,,, k } Deg e 5, g etk bh setp brs terdpt deks krts peks, k dotsk st deks tk setp brs oeh,,,, k d dk bh deks koo g terph st s berbed, k dperoeh c c k + tk se,,, k deg k + pb pertdks tersebt dhk, k dperoeh c + c + + c c + c c k k k dk bh d kegk tk eh setp brs st deks koo krts sedek sehgg eeh pertdks 5 Dotsk { ; } sebg hp deks koo dr koo terph d d koo, d dbg st sbtrks g dbt dr koo Jh brs deg deks koo terph d d koo, dotsk deg p Set, dt persh tk peh psg deks sebg berkt : Meksk : Z c ' tk se p tk se 0 tk se d k dtkk bh sh st peees opt bt g gk dh tk d 0 tk g dk bh dh sos opt d tk beberp d Kre kpsts brs dh, k 0 Set, kre, k terdpt brs sedek sehgg d 0 Kre kpsts brs dh, k terdpt deks koo 3 tk beberp brs sedek sehgg 3, d, d seters Deg cr, dperoeh st cce deks brs sedek sehgg 0 d tk se deg Ddefsk sos br deg ' d tk se deg, d 0 tk se psg deks Ked, kre eeh pertdks 5, c' > ' c', sehggg dperoeh sos persh dts deg k h k tk d tk g Sekrg, dbetk d dr sh dts sebg berkt : Mek: Z + p v d + v c' tk se, d Defsk vektor g dtk sebg berkt : ;tk v ;tk
9 dh st sos opt dr 5 Kre pd setp brs dpt dph st deks koo krts, k dperoeh c + d + Set k dtkk bh tk se koo, eeh c + c + Utk pertdks trv, d tk koo-koo dr k c c' Kre peh etr-etr, berses deg eee tk o dr sos persh dts, k berk c v, d tk se etr g v c [7] Sehgg dperoeh c + c v c c + c v c + Dr s terht bh vektor ep deks krts peks tk setp brs t Sehgg vektor dh peees dr pers 5 Cotoh Dberk trks C d D k dcr peees sste pers d-ss Mtrks ep etr-etr krts g dtd sebg berkt : 4ˆ 8 C 6 3ˆ 9ˆ 4 7ˆ 3ˆ 8 0ˆ Set, dph etr-etr c 3, c3, c3 g eeh 5 Dbetk sbtrks dr koo-koo terph t 4 C ' Kpsts setp brs dh, kpsts koo ke- dh, d kpsts koo ke- dh Sehgg, dperoeh persh peh deks sebg berkt : Meksk : Ked : tk se d Ked, dbetk persh d dr sh peh deks dts sebg berkt :
10 Mek : Z d v + v Ked : Vektor g dtk deg dh + v + v 9 peees dr sste pers d-ss + v v 7 dts + v v 8 N d g eeh : + v + v 9 + v v 7 + v v 8 dh sos dr persh d dts Deg egb, k dpt dperoeh sh st kegk sos dr persh dts t 3, 8, 3 7, v 0, v 0 Sehgg dperoeh sh st peees dr sste d-ss dts t 6 PENUTUP Berdsrk r ege d vektor ege trks terv ts br ps dts dpt dperoeh beberp h sebg berkt : N ege g gk dr st trk terv berd pd terv terttp ege trks bts b gort possbe egevector dpt dgk tk eg st vektor sebg vektor ege g gk dr st trk terv c Mtrks terv ep ege vers pb ege trks bts s d Vektor ege vers trks terv deg dpt dcr deg eeesk st sste pers d-ss Set, dpt dkebgk st etode bg ecr vektor ege vers trks terv g berses deg ege vers λ 0 7 DFTR PUSTK [] Bcce, Frcos, dkk, 99, Schrozto d Lert, gebr for Dscrete Evet Sstes We, Chchester [] Cechrov, Ktr, 003, Egevectors of Iterv Mtrces over M-Ps gebr, Sovk [3] Cho, Ko-Pg, 999, Icso Mootoc Propert of Cort-Fscher M Chrcterzto o Iterv Egeprobes for Setrc Iterv Mtrces eth Uverst [4] Go, Federc d Cro N Lro, 006, Prcp Copoet ss o Iterv Dt, Uverst deg Std d Npo,, 3 5
11 [5] Hedergott, Berd, 998, M Ps gebr d Qees, Vre Uverstet, sterd [6] Kds, W B Vsth, 006, Fzz Iterv Mtrces, Netrosophc Iterv Mtrces d Ther pctos, Foret Srdche, Phoe, rzo [7] Sprto, Johes, 006, Rset Opers tk Pegb Kepts, UIP, Yogkrt
Solusi Sistem Persamaan Linear
 Sos Sstem Persm Ler Sstem persm er: h persm deg h kow j d dketh, j,,, j? So: z 6 z z () () () persm d kow Jw: z 6.5 z.5 z () () () ems : pers. ().5 pers. () pers. ().5 pers. () z 6.5 z 8z 8 () () () ems
Sos Sstem Persm Ler Sstem persm er: h persm deg h kow j d dketh, j,,, j? So: z 6 z z () () () persm d kow Jw: z 6.5 z.5 z () () () ems : pers. ().5 pers. () pers. ().5 pers. () z 6.5 z 8z 8 () () () ems
NILAI DAN VEKTOR EIGEN MATRIKS INTERVAL ATAS ALJABAR MAX-PLUS. Dwi Suci Maharani 1 dan Suryoto 2. Jln. Prof. H. Soedarto, S.H., Tembalang, Semarang
 NILAI DAN VEKTOR EIGEN MATRIKS INTERVAL ATAS ALJABAR MAX-PLUS Dw Sc Mahara da Sryoto, Jrsa Mateata FMIPA Uverstas Dpoegoro J Prof H Soedarto, SH, Tebaag, Searag Abstract A terva atr A A, A wth gve A, A
NILAI DAN VEKTOR EIGEN MATRIKS INTERVAL ATAS ALJABAR MAX-PLUS Dw Sc Mahara da Sryoto, Jrsa Mateata FMIPA Uverstas Dpoegoro J Prof H Soedarto, SH, Tebaag, Searag Abstract A terva atr A A, A wth gve A, A
6. Selanjutnya langkah penyelesaian
 MENYELESAIKAN SISTEM PERSAMAAN LINEAR FUZZY DALAM BENTUK A y DENGAN MENGURAIKAN y D Mstk, Mshd, Sr Gemwt Mhssw Progrm Std S Mtemtk Dose Jrs Mtemtk Fklts Mtemtk d Ilm Pegeth Alm Uversts R Kmps Bwdy Pekbr
MENYELESAIKAN SISTEM PERSAMAAN LINEAR FUZZY DALAM BENTUK A y DENGAN MENGURAIKAN y D Mstk, Mshd, Sr Gemwt Mhssw Progrm Std S Mtemtk Dose Jrs Mtemtk Fklts Mtemtk d Ilm Pegeth Alm Uversts R Kmps Bwdy Pekbr
1 yang akan menghasilkan
 Rset Opers Probblstk Teor Per (Ge Theor) Nughthoh Arfw Kurdh, M.Sc Deprteet of Mthetcs FMIPA UNS Lecture 6: Med Strteg: Ler Progrg Method A. Metode Cpur deg Progr Ler Terdpt hubug g ert tr teor per d progr
Rset Opers Probblstk Teor Per (Ge Theor) Nughthoh Arfw Kurdh, M.Sc Deprteet of Mthetcs FMIPA UNS Lecture 6: Med Strteg: Ler Progrg Method A. Metode Cpur deg Progr Ler Terdpt hubug g ert tr teor per d progr
INVERS MATRIKS MOORE PENROSE ATAS RING KOMUTATIF DENGAN ELEMEN SATUAN (THE MOORE PENROSE INVERSE OF MATRICES OVER COMMUTATIVE RING WITH UNITY)
 JURNL MTEMTIK DN KOMPUTER Vol. 7. No., -, prl, ISSN : -858 INVERS MTRIKS MOORE PENROSE TS RING KOMUTTIF DENGN ELEMEN STUN THE MOORE PENROSE INVERSE OF MTRICES OVER COMMUTTIVE RING WITH UNITY Tt Ud SRRM
JURNL MTEMTIK DN KOMPUTER Vol. 7. No., -, prl, ISSN : -858 INVERS MTRIKS MOORE PENROSE TS RING KOMUTTIF DENGN ELEMEN STUN THE MOORE PENROSE INVERSE OF MTRICES OVER COMMUTTIVE RING WITH UNITY Tt Ud SRRM
( ) Misalkan f dan g mempunyai faktor
 RESULTA DARI POLIOMIAL DEGA - IDETERMIATE Hrjto R Her SU d rwt DR 3 Jr Mtetk FMIPA UDIP J Pro Soedrto SH Ser 575 Atrt Let e poyo where ed To detere whether two poyo hve oo tor wthot do y dvo e ee ro t
RESULTA DARI POLIOMIAL DEGA - IDETERMIATE Hrjto R Her SU d rwt DR 3 Jr Mtetk FMIPA UDIP J Pro Soedrto SH Ser 575 Atrt Let e poyo where ed To detere whether two poyo hve oo tor wthot do y dvo e ee ro t
BAB II KAJIAN TEORI. operasi penjumlahan dan operasi perkalian mempunyai sifat-sifat. 1. R merupakan grup komutatif terhadap operasi penjumlahan.
 4 BAB II KAJIAN TEORI A. Sstem Blg Rel es II.A. Sstem blg rel R merpk st sstem ljbr g terhdp opers pejmlh d opers perkl memp st-st sebg berkt:. R merpk grp komtt terhdp opers pejmlh.. R -{} merpk grp komtt
4 BAB II KAJIAN TEORI A. Sstem Blg Rel es II.A. Sstem blg rel R merpk st sstem ljbr g terhdp opers pejmlh d opers perkl memp st-st sebg berkt:. R merpk grp komtt terhdp opers pejmlh.. R -{} merpk grp komtt
Jurnal Matematika Murni dan Terapan Vol. 4 No.2 Desember 2010: 30-37
 Jurl Mtemtk Mur d Terp Vol. 4 No. Desember : - 7 PENGGUNN BENTUK SMITH UNTUK MENENTUKN BENTUK KNONIK MTRIKS NORML DENGN ENTRI-ENTRI BILNGN KOMPLEKS Thresye Progrm Stud Mtemtk Uversts Lmbug Mgkurt Jl. Jed..
Jurl Mtemtk Mur d Terp Vol. 4 No. Desember : - 7 PENGGUNN BENTUK SMITH UNTUK MENENTUKN BENTUK KNONIK MTRIKS NORML DENGN ENTRI-ENTRI BILNGN KOMPLEKS Thresye Progrm Stud Mtemtk Uversts Lmbug Mgkurt Jl. Jed..
Bentuk Umum Perluasan Teorema Pythagoras
 Jrl Grde Vol No Jr 6 : 9-4 Betk Umm Perls Teorem Pythors Ml stt By Kerm Ulsr les Jrs Mtemtk Fklts Mtemtk d Ilm Peeth lm Uversts Bekl Idoes Dterm Septemer 5; dset Desemer 5 strk - Peelt memhs perls teorem
Jrl Grde Vol No Jr 6 : 9-4 Betk Umm Perls Teorem Pythors Ml stt By Kerm Ulsr les Jrs Mtemtk Fklts Mtemtk d Ilm Peeth lm Uversts Bekl Idoes Dterm Septemer 5; dset Desemer 5 strk - Peelt memhs perls teorem
A. Pusat Massa Suatu Batang
 Perteu 7 Pust ss sutu Kepg, Setrod, d Teore Pppus A. Pust ss Sutu Btg Dskusk!. slk ss,,..., terletk pd tg pdt sgsg d ttk,...,,, d = jrk errh tr ss ke sutu ttk tetp 0 pd tg,,,...,. ss prtkel, oe prtkel
Perteu 7 Pust ss sutu Kepg, Setrod, d Teore Pppus A. Pust ss Sutu Btg Dskusk!. slk ss,,..., terletk pd tg pdt sgsg d ttk,...,,, d = jrk errh tr ss ke sutu ttk tetp 0 pd tg,,,...,. ss prtkel, oe prtkel
BAB 1 PENDAHULUAN. 1.1 Latar Belakang
 BAB PENDAHULUAN. Ltr Belkg Smp st, model Regres d model Alss Vrs telh dpdg sebg du hl g tdk berkt. Meskpu merupk pedekt g umum dlm meergk kedu cr pd trf permul, model Alss Vrs dpt dpdg sebg hl khusus model
BAB PENDAHULUAN. Ltr Belkg Smp st, model Regres d model Alss Vrs telh dpdg sebg du hl g tdk berkt. Meskpu merupk pedekt g umum dlm meergk kedu cr pd trf permul, model Alss Vrs dpt dpdg sebg hl khusus model
DIGRAF EKSENTRIS PADA DIGRAF SIKEL, DIGRAF KOMPLIT DAN DIGRAF KOMPLIT MULTIPARTIT. Jl. Prof. H. Soedarto SH Semarang 50275
 DIGRAF ESENTRIS PADA DIGRAF SIEL DIGRAF OMPLIT DAN DIGRAF OMPLIT MULTIPARTIT Reto tur umlsr d Luc Rtsr Jurus Mtemtk FMIPA UNDIP Jl Prof H Soedrto SH Semrg 5075 Abstrct The eccetrc dgrph of dgrph ED ( D)
DIGRAF ESENTRIS PADA DIGRAF SIEL DIGRAF OMPLIT DAN DIGRAF OMPLIT MULTIPARTIT Reto tur umlsr d Luc Rtsr Jurus Mtemtk FMIPA UNDIP Jl Prof H Soedrto SH Semrg 5075 Abstrct The eccetrc dgrph of dgrph ED ( D)
Didownload dari ririez.blog.uns.ac.id
 A. METODE PROGRAM LINIER Terdpt hubug g ert tr teor per d progr ler kre setp betuk per berulh ol dr du org (g berhgg) dpt dtk sebg sutu betuk progr ler d seblk, setp perslh progr ler dpt dsk sebg sutu
A. METODE PROGRAM LINIER Terdpt hubug g ert tr teor per d progr ler kre setp betuk per berulh ol dr du org (g berhgg) dpt dtk sebg sutu betuk progr ler d seblk, setp perslh progr ler dpt dsk sebg sutu
BASIS ORTOGONAL. Bila V ruang Euclides, S V disebut Himpunan Ortogonal bila tiap dua unsur S ortogonal.
 BASIS ORTOGONA Bts Bl V rg Ecldes S V dsebt Hmp Ortogol bl tp d sr S ortogol DAI J S hmp ortogol yg terdr dr K bh etor t ol dlm rg Ecldes V m S bebs ler V hssy bl dmes V S bss t V dsebt Bss ortogol DAI
BASIS ORTOGONA Bts Bl V rg Ecldes S V dsebt Hmp Ortogol bl tp d sr S ortogol DAI J S hmp ortogol yg terdr dr K bh etor t ol dlm rg Ecldes V m S bebs ler V hssy bl dmes V S bss t V dsebt Bss ortogol DAI
Unit 1 KONSEP DASAR ARITMETIKA. Josef Tjahjo Baskoro Clara Ika Sari Budhayanti. Pendahuluan
 Ut KONSEP DASAR ARITMETIKA Josef Tjhjo Bskoro Clr Ik Sr Bdhyt Pedhl M ter yg k Ad peljr pertm kl pd mt klh pemech mslh mtemtk dlh kosep dsr rtmetk. Kompetes dsr yg hrs dks setelh mempeljr t dlh Ad mmp
Ut KONSEP DASAR ARITMETIKA Josef Tjhjo Bskoro Clr Ik Sr Bdhyt Pedhl M ter yg k Ad peljr pertm kl pd mt klh pemech mslh mtemtk dlh kosep dsr rtmetk. Kompetes dsr yg hrs dks setelh mempeljr t dlh Ad mmp
x 1 M = x 1 m 1 + x 2 m x n m n = x i
 Iterl Tertetu..6 oe d ust ss Ttk Bert slk d du ed s-s elk ss sesr d y dletkk pd pp er de jrk erturut-turut d d d dr ttk pey pd - y ered. Ked terseut k se jk dpeuh d d. d d Sutu odel tets y k dperoleh pl
Iterl Tertetu..6 oe d ust ss Ttk Bert slk d du ed s-s elk ss sesr d y dletkk pd pp er de jrk erturut-turut d d d dr ttk pey pd - y ered. Ked terseut k se jk dpeuh d d. d d Sutu odel tets y k dperoleh pl
BAB 2 ANAVA 2 JALAN. Merupakan pengembangan dari ANAVA 1 Jalan Jika pada ANAVA 1 jalan 1 Faktor Jika pada ANAVA 2 jalan 2 Faktor
 BAB ANAVA JALAN Merupk pegembg dr ANAVA 1 Jl Jk pd ANAVA 1 l 1 Fktor Jk pd ANAVA l Fktor Model Ler Asums: Model efek Tetp! 1,..., 1,..., Stu fktor g dtelt Av 1 l k k 1,,..., 1,,..., b k 1,,..., Du fktor
BAB ANAVA JALAN Merupk pegembg dr ANAVA 1 Jl Jk pd ANAVA 1 l 1 Fktor Jk pd ANAVA l Fktor Model Ler Asums: Model efek Tetp! 1,..., 1,..., Stu fktor g dtelt Av 1 l k k 1,,..., 1,,..., b k 1,,..., Du fktor
HUBUNGAN DERET BERTINGKAT BERDASAR BILANGAN EULERIAN DENGAN OPERATOR BEDA
 HUBUNAN DERET BERTINKAT BERDAAR BILANAN EULERIAN DENAN OPERATOR BEDA Aleder A uw Jurus Mtetk, Fkults s d Tekolog, Uversts B Nustr Jl. K.H. yhd No. 9, Plerh, Jkrt Brt 48 gug@bus.edu ABTRACT Cscde seres
HUBUNAN DERET BERTINKAT BERDAAR BILANAN EULERIAN DENAN OPERATOR BEDA Aleder A uw Jurus Mtetk, Fkults s d Tekolog, Uversts B Nustr Jl. K.H. yhd No. 9, Plerh, Jkrt Brt 48 gug@bus.edu ABTRACT Cscde seres
( ) Misalkan f dan g mempunyai faktor
 RESUTA DARI PIIA DEGA - IDETERIATE Hrjto R Her SU rwt DR 3 Jr tetk FIPA UDIP J Pro Soerto SH Ser 575 Atrt et e poyo where e To etere whether two poyo hve oo tor wthot o y vo e ee ro t rett tht etert ro
RESUTA DARI PIIA DEGA - IDETERIATE Hrjto R Her SU rwt DR 3 Jr tetk FIPA UDIP J Pro Soerto SH Ser 575 Atrt et e poyo where e To etere whether two poyo hve oo tor wthot o y vo e ee ro t rett tht etert ro
Jl. HR. Soebrantas No. 155 Simpang Baru, Panam, Pekanbaru,
 Jurl Ss Mtetk d Sttstk, Vol. No. Jul 6 ISSN 6-5 Metode Guss-Sedel d Geerlss Guss-Sedel utuk Meyelesk Sste Pers Ler Kopleks Cotoh Ksus: SPL Kopleks deg pers d vrel tr ry, Le Tr Lestr, Jurus Mtetk, kults
Jurl Ss Mtetk d Sttstk, Vol. No. Jul 6 ISSN 6-5 Metode Guss-Sedel d Geerlss Guss-Sedel utuk Meyelesk Sste Pers Ler Kopleks Cotoh Ksus: SPL Kopleks deg pers d vrel tr ry, Le Tr Lestr, Jurus Mtetk, kults
Pemain P 1. Teorema 4.1 (Teorema minimax). Untuk setiap matriks pembayaran (pay off matrix), terdapat strategi optimal x* dan y* sedemikian sehingga
 Rset Opers Probblstk Teor Permnn (Gme Theor) Deprtement of Mthemtcs FMIPA UNS Lecture 4: Med Strteg A. Metode Cmpurn (Med Strteg) D dlm permnn d mn permnn tersebut tdk mempun ttk peln, mk pr pemn kn bersndr
Rset Opers Probblstk Teor Permnn (Gme Theor) Deprtement of Mthemtcs FMIPA UNS Lecture 4: Med Strteg A. Metode Cmpurn (Med Strteg) D dlm permnn d mn permnn tersebut tdk mempun ttk peln, mk pr pemn kn bersndr
Sifat-sifat Super Matriks dan Super Ruang Vektor
 Sift-sift Super Mtriks d Super Rug Vektor Cturiyti Jurus Pedidik Mtetik FMIPA UNY wcturiyti@yhoo.co Abstrk Sutu triks yg elee-eleey erupk bilg disebut deg triks sederh tu lebih dikel deg triks. Sedgk supertriks
Sift-sift Super Mtriks d Super Rug Vektor Cturiyti Jurus Pedidik Mtetik FMIPA UNY wcturiyti@yhoo.co Abstrk Sutu triks yg elee-eleey erupk bilg disebut deg triks sederh tu lebih dikel deg triks. Sedgk supertriks
CNH2B4 / KOMPUTASI NUMERIK
 CNHB4 / KOMPUTASI NUMERIK TIM DOSEN KK MODELING AND COMPUTATIONAL EXPERIMENT PENCOCOKAN KURVA Pedhulu Dt g bersl dr hsl pegmt lpg pegukur tu tbel g dmbl dr buku-buku cu. Nl tr turu tegrl mudh dcr utuk
CNHB4 / KOMPUTASI NUMERIK TIM DOSEN KK MODELING AND COMPUTATIONAL EXPERIMENT PENCOCOKAN KURVA Pedhulu Dt g bersl dr hsl pegmt lpg pegukur tu tbel g dmbl dr buku-buku cu. Nl tr turu tegrl mudh dcr utuk
PENCOCOKAN KURVA (CURVE FITTING) INTERPOLASI
 PENCOCOKAN KURVA (CURVE FITTING) Iterpols : Iterpols er Iterpols Kudrtk Iterpols Poloml Iterpols grge Regres : Regres er Regres Ekspoesl Regres Poloml INTERPOASI Iterpols dguk utuk meksr l tr (termedte
PENCOCOKAN KURVA (CURVE FITTING) Iterpols : Iterpols er Iterpols Kudrtk Iterpols Poloml Iterpols grge Regres : Regres er Regres Ekspoesl Regres Poloml INTERPOASI Iterpols dguk utuk meksr l tr (termedte
TEOREMA ABEL-DINI DAN DUAL KÖTHE-TOEPLITZ PADA DERET GANDA
 Prosdg Semr Nsol Ss d Peddk Ss VIII, Fkults Ss d Mtemtk, UKSW Sltg, 5 Ju 203, Vol 4, No, ISSN:2087 0922 TEOREM BEL-DINI DN DUL KÖTHE-TOEPLITZ PD DERET GND Sumrdoo, Soer DW 2 & Sum 3 PPPPTK Mtemtk, Mhssw
Prosdg Semr Nsol Ss d Peddk Ss VIII, Fkults Ss d Mtemtk, UKSW Sltg, 5 Ju 203, Vol 4, No, ISSN:2087 0922 TEOREM BEL-DINI DN DUL KÖTHE-TOEPLITZ PD DERET GND Sumrdoo, Soer DW 2 & Sum 3 PPPPTK Mtemtk, Mhssw
Bab 2 LANDASAN TEORI
 b LNDSN TEORI. Hmpu Fuzzy Tdk semu hmpu yg dump dlm kehdup sehr-hr terdefs secr els, msly hmpu org msk, hmpu org pd, hmpu org tgg, d sebgy. Msly, pd hmpu org tgg, tdk dpt dtetuk secr tegs pkh seseorg dlh
b LNDSN TEORI. Hmpu Fuzzy Tdk semu hmpu yg dump dlm kehdup sehr-hr terdefs secr els, msly hmpu org msk, hmpu org pd, hmpu org tgg, d sebgy. Msly, pd hmpu org tgg, tdk dpt dtetuk secr tegs pkh seseorg dlh
Batas Nilai Eigen Maksimal Dari Matriks Tak Negatif
 Vol. 3 No. 80-85 Ju 007 Bts Nl Ege Mksl D Mtks Tk Negtf A. Kes Jy Abstk Ide ut skps dlh utuk edptk etode dl eetuk bts d l ege ksl d tks tk egtf deg bedsk bts Fobeus. Ytu R d dlh ulh bs tu kolo u d R dlh
Vol. 3 No. 80-85 Ju 007 Bts Nl Ege Mksl D Mtks Tk Negtf A. Kes Jy Abstk Ide ut skps dlh utuk edptk etode dl eetuk bts d l ege ksl d tks tk egtf deg bedsk bts Fobeus. Ytu R d dlh ulh bs tu kolo u d R dlh
Dr.Eng. Agus S. Muntohar Department of Civil Engineering
 Pertemu ke-7 Persm Ler Smult Oktober 0 Metode Iters Guss-Sedel Dr.Eg. Agus S. Mutohr Deprtmet of Cvl Egeerg Metode Guss-Sedel Merupk metode ters. Prosedur umum: - Selesk ser lbr vrbel tdk dkethu msg-msg
Pertemu ke-7 Persm Ler Smult Oktober 0 Metode Iters Guss-Sedel Dr.Eg. Agus S. Mutohr Deprtmet of Cvl Egeerg Metode Guss-Sedel Merupk metode ters. Prosedur umum: - Selesk ser lbr vrbel tdk dkethu msg-msg
I PENDAHULUAN II LANDASAN TEORI
 I PENDAHULUAN Ltr Belg Istlh Pemrogrm Geometr (PG) dperel oleh Duff, Peterso, d Zeer pd thu 967 Istlh dmbl dr mslh-mslh geometr g dpt dformuls sebg PG Pemrogrm Geometr dlh sutu tpe mslh optmlss mtemt g
I PENDAHULUAN Ltr Belg Istlh Pemrogrm Geometr (PG) dperel oleh Duff, Peterso, d Zeer pd thu 967 Istlh dmbl dr mslh-mslh geometr g dpt dformuls sebg PG Pemrogrm Geometr dlh sutu tpe mslh optmlss mtemt g
HUBUNGAN DERET BERTINGKAT BERDASARKAN BILANGAN EULERIAN DENGAN OPERATOR BEDA
 HUBUNGAN DERET BERTINGKAT BERDAARKAN BILANGAN EULERIAN DENGAN OPERATOR BEDA Aleder A.. Guw Jurus Mtetk d ttstk, Fkults s d Tekolog, Bus Uversty Jl. KH. yhd No. 9, Plerh, Jkrt Brt 48. gug@bus.edu ABTRACT
HUBUNGAN DERET BERTINGKAT BERDAARKAN BILANGAN EULERIAN DENGAN OPERATOR BEDA Aleder A.. Guw Jurus Mtetk d ttstk, Fkults s d Tekolog, Bus Uversty Jl. KH. yhd No. 9, Plerh, Jkrt Brt 48. gug@bus.edu ABTRACT
UNIVERSITAS INDONESIA METODE STAIRCASE UNTUK MENDAPATKAN BENTUK KANONIK JORDAN DENGAN KARAKTERISTIK WEYR SKRIPSI NURRY WIDYA HESTY
 UNIVERSITS INDONESI METODE STIRCSE UNTUK MENDPTKN BENTUK KNONIK JORDN DENGN KRKTERISTIK WEYR SKRIPSI NURRY WIDY HESTY 976 Fkults Mtemtk d Ilmu Pegethu lm Progrm Stud Mtemtk Depok Februr Metode strcse...,
UNIVERSITS INDONESI METODE STIRCSE UNTUK MENDPTKN BENTUK KNONIK JORDN DENGN KRKTERISTIK WEYR SKRIPSI NURRY WIDY HESTY 976 Fkults Mtemtk d Ilmu Pegethu lm Progrm Stud Mtemtk Depok Februr Metode strcse...,
1. Aturan Pangkat 3. Logartima
 KL UN Mtetk MA IPA 9/ No. KL Ruus. Meetuk egs pert g dperoleh dr perk kespul.. p q. p q. p q ~ (p q) = ~p ~q ~ (eu/etp p) = Ad/Beerp ~p p. ~q q r ~ (p q) = ~p ~q ~ (Ad/Beerp p) = eu/etp ~p q ~p p r p q
KL UN Mtetk MA IPA 9/ No. KL Ruus. Meetuk egs pert g dperoleh dr perk kespul.. p q. p q. p q ~ (p q) = ~p ~q ~ (eu/etp p) = Ad/Beerp ~p p. ~q q r ~ (p q) = ~p ~q ~ (Ad/Beerp p) = eu/etp ~p q ~p p r p q
PRAKTIKUM 8 Penyelesaian Persamaan Linier Simultan Metode Eliminasi Gauss
 Prktkum 8 Peyeles Persm Ler Smult Metode Elms Guss PRAKTIKUM 8 Peyeles Persm Ler Smult Metode Elms Guss Tuju : Mempeljr metode Elms Guss utuk peyeles persm ler smult Dsr Teor : Metode Elms Guss merupk
Prktkum 8 Peyeles Persm Ler Smult Metode Elms Guss PRAKTIKUM 8 Peyeles Persm Ler Smult Metode Elms Guss Tuju : Mempeljr metode Elms Guss utuk peyeles persm ler smult Dsr Teor : Metode Elms Guss merupk
BAB III NORM MATRIKS PADA HIMPUNAN DARI MATRIKS-MATRIKS TOEPLITZ. Definisi 3.1 Matriks Toeplitz adalah suatu matriks., dengan nilai,, dan indeks yang
 BAB III NORM MATRIKS PADA HIMPUNAN DARI MATRIKS-MATRIKS TOEPLITZ 3. Mtriks Toeplitz Defiisi 3. Mtriks Toeplitz dlh sutu mtriks [ t ; k, j = 0,,..., ] : T =, k j, deg ili,, d ideks yg diguk setip etriy
BAB III NORM MATRIKS PADA HIMPUNAN DARI MATRIKS-MATRIKS TOEPLITZ 3. Mtriks Toeplitz Defiisi 3. Mtriks Toeplitz dlh sutu mtriks [ t ; k, j = 0,,..., ] : T =, k j, deg ili,, d ideks yg diguk setip etriy
BAB VI ANALISIS REGRESI
 BAB VI ANALISIS REGRESI A. Pedhulu Alss regres merupk slh stu lss yg ertuju utuk megethu pegruh sutu vrel terhdp vrel l. Vrel yg mempegruh dseut depedet vrle/vrel es () d vrel yg dpegruh dseut depedet
BAB VI ANALISIS REGRESI A. Pedhulu Alss regres merupk slh stu lss yg ertuju utuk megethu pegruh sutu vrel terhdp vrel l. Vrel yg mempegruh dseut depedet vrle/vrel es () d vrel yg dpegruh dseut depedet
Model Tak Penuh. Definisi dapat di-uji (testable): nxp
 Model T Peuh Defs dpt d-u (testle): Sutu c c 'c 'c H 'c 'c dpt du l d stu set fugs g dpt - ddug m m ' sehgg H er c ' ' slg es ler tu C c ' c m ' Perht : Kre r X p r p m m r c' (X' X) c X' X c' C(X' X)
Model T Peuh Defs dpt d-u (testle): Sutu c c 'c 'c H 'c 'c dpt du l d stu set fugs g dpt - ddug m m ' sehgg H er c ' ' slg es ler tu C c ' c m ' Perht : Kre r X p r p m m r c' (X' X) c X' X c' C(X' X)
ALGORITMA MENENTUKAN HIMPUNAN TERBESAR DARI SUATU MATRIKS INTERVAL DALAM ALJABAR MAX-PLUS
 LGORITM MENENTUKN HIMPUNN TERBESR DRI SUTU MTRIKS INTERVL DLM LJBR MX-PLUS Rata Novtasar Program Stud Matematka FMIP UNDIP JlProfSoedarto SH Semarag 575 bstract Ths research dscussed about how to obtaed
LGORITM MENENTUKN HIMPUNN TERBESR DRI SUTU MTRIKS INTERVL DLM LJBR MX-PLUS Rata Novtasar Program Stud Matematka FMIP UNDIP JlProfSoedarto SH Semarag 575 bstract Ths research dscussed about how to obtaed
A.LAMPIRAN SKALA PENELITIAN
 A.LAMPIRAN SKALA PENELITIAN 55 RAHASIA SKALA PENELITIAN FAKULTAS PSIKOLOGI UNIVERSITAS SUMATERA UTARA 2016 56 KATA PENGANTAR Dengan hormat, Dalam rangka memenuhi persyaratan untuk menyelesaikan pendidikan
A.LAMPIRAN SKALA PENELITIAN 55 RAHASIA SKALA PENELITIAN FAKULTAS PSIKOLOGI UNIVERSITAS SUMATERA UTARA 2016 56 KATA PENGANTAR Dengan hormat, Dalam rangka memenuhi persyaratan untuk menyelesaikan pendidikan
Analisis Variansi satu faktor Single Factor Analysis Of Variance (ANOVA)
 BAB 1 Alss Vrs stu fktor Sgle Fctor Alss Of Vrce (ANOVA) ANALISIS VARIANSI SATU FAKTOR D MetStt 1 sudh dkel uj hpotess rt-rt du populs A d B g berdstrbus Norml Bgm jk terdpt lebh dr du populs? Alss vrs
BAB 1 Alss Vrs stu fktor Sgle Fctor Alss Of Vrce (ANOVA) ANALISIS VARIANSI SATU FAKTOR D MetStt 1 sudh dkel uj hpotess rt-rt du populs A d B g berdstrbus Norml Bgm jk terdpt lebh dr du populs? Alss vrs
CATATAN KULIAH Pertemuan XIII: Analisis Dinamik dan Integral (1)
 CATATAN KULIAH Pertemu XIII: Alss Dmk d Itegrl () A. Dmk d Itegrs Model Stts : mecr l vrel edoge yg memeuh kods ekulrum tertetu. Model Optms : mecr l vrel plh yg megoptms fugs tuju tertetu. Model Dmk :
CATATAN KULIAH Pertemu XIII: Alss Dmk d Itegrl () A. Dmk d Itegrs Model Stts : mecr l vrel edoge yg memeuh kods ekulrum tertetu. Model Optms : mecr l vrel plh yg megoptms fugs tuju tertetu. Model Dmk :
INTEGRAL TERTENTU. sebagai P = max{x i x i-1 1 = 1, 2, 3,, n}. a = x 0 x 1 x 2 x n = b. Contoh: Pada interval [ 3, 3], suatu partisi P = { 3, 1 2 , 31
![INTEGRAL TERTENTU. sebagai P = max{x i x i-1 1 = 1, 2, 3,, n}. a = x 0 x 1 x 2 x n = b. Contoh: Pada interval [ 3, 3], suatu partisi P = { 3, 1 2 , 31 INTEGRAL TERTENTU. sebagai P = max{x i x i-1 1 = 1, 2, 3,, n}. a = x 0 x 1 x 2 x n = b. Contoh: Pada interval [ 3, 3], suatu partisi P = { 3, 1 2 , 31](/thumbs/52/30023403.jpg) INTEGRAL TERTENTU Defs: Prs P pd ervl [,] dlh suu suse erhgg P = {,,,, } dr [,] deg = < < < < = Jk P = {,,,, } prs pd [,] mk Norm P, duls P, ddefsk seg P = m{ - =,,,, } Cooh: = = Pd ervl [, ], suu prs
INTEGRAL TERTENTU Defs: Prs P pd ervl [,] dlh suu suse erhgg P = {,,,, } dr [,] deg = < < < < = Jk P = {,,,, } prs pd [,] mk Norm P, duls P, ddefsk seg P = m{ - =,,,, } Cooh: = = Pd ervl [, ], suu prs
BAB III VEKTOR DALAM R 2 DAN R 3. Bab III Vektor dalam R 2 dan R 3
 Bb III Vetor dlm R dn R BAB III VEKTOR DALAM R DAN R Dlm bgn n n dbhs mslh eto-etor dlm rng berdmens dn berdmens, opers-opers rtmet pd etor g n ddefnsn dn beberp sft-sft dsr opers-opers tersebt... VEKTOR
Bb III Vetor dlm R dn R BAB III VEKTOR DALAM R DAN R Dlm bgn n n dbhs mslh eto-etor dlm rng berdmens dn berdmens, opers-opers rtmet pd etor g n ddefnsn dn beberp sft-sft dsr opers-opers tersebt... VEKTOR
SIAP UN MATEMATIKA IPS SMA PAHOA 1. LOGIKA MATEMATIKA. Rumus negasi. ~ (p q) = ~p ~q. indikator: Kunci menghafal. Konjungsi (da ) : B B = B
 SIAP UN MATEMATIKA IPS SMA PAHOA N: Kes : IPS dut oeh: Joo Setw, ST, MT ( 8-8 - ) eurut ks-ks UN - Ruus egs LOGIKA MATEMATIKA dktor: Meetuk gkr tu kesetr dr sutu pert jeuk tu pert erkutor Meetuk kespu
SIAP UN MATEMATIKA IPS SMA PAHOA N: Kes : IPS dut oeh: Joo Setw, ST, MT ( 8-8 - ) eurut ks-ks UN - Ruus egs LOGIKA MATEMATIKA dktor: Meetuk gkr tu kesetr dr sutu pert jeuk tu pert erkutor Meetuk kespu
Metode Iterasi Gauss Seidell
 Metode Itersi Guss Seidell Metode itersi Guss-Seidel : metode yg megguk proses itersi higg diperoleh ili-ili yg berubh. Bil dikethui persm liier simult: Berik ili wl dri setip i (i s/d ) kemudi persm liier
Metode Itersi Guss Seidell Metode itersi Guss-Seidel : metode yg megguk proses itersi higg diperoleh ili-ili yg berubh. Bil dikethui persm liier simult: Berik ili wl dri setip i (i s/d ) kemudi persm liier
BAB VI KESIMPULAN DAN SARAN
 59 BAB VI KESIMPULAN DAN SARAN 6.1. Kesimpulan Berdasarkan hasil data survai dan analisis yang dilakukan pada lahan parkir Rumah Sakit Umum Daerah RAA Soewondo Pati selama 3 hari dapat diambil kesimpulan
59 BAB VI KESIMPULAN DAN SARAN 6.1. Kesimpulan Berdasarkan hasil data survai dan analisis yang dilakukan pada lahan parkir Rumah Sakit Umum Daerah RAA Soewondo Pati selama 3 hari dapat diambil kesimpulan
INTEGRASI NUMERIK. n ax. ax e. n 1. x x. Fungsi yang dapat dihitung integralnya : Fungsi yang rumit misal :
 INTEGRASI NUMERIK D dlm klkulus, terdpt du l petg ytu tegrl d turudervtve Pegtegrl umerk merupk lt tu r yg dguk ole lmuw utuk memperole jw mpr proksms dr pegtegrl yg tdk dpt dselesk ser ltk. INTEGRASI
INTEGRASI NUMERIK D dlm klkulus, terdpt du l petg ytu tegrl d turudervtve Pegtegrl umerk merupk lt tu r yg dguk ole lmuw utuk memperole jw mpr proksms dr pegtegrl yg tdk dpt dselesk ser ltk. INTEGRASI
a home base to excellence Mata Kuliah : Kalkulus Kode : TSP 102 Integral Pertemuan - 6
 home se to ecellece Mt Kulh : Klkulus Kode : TSP 0 SKS : SKS Itegrl Pertemu - 6 home se to ecellece TIU : Mhssw dpt memhm tegrl fugs d plksy TIK : Mhssw mmpu mecr tegrl fugs Mhssw mmpu megguk tegrl utuk
home se to ecellece Mt Kulh : Klkulus Kode : TSP 0 SKS : SKS Itegrl Pertemu - 6 home se to ecellece TIU : Mhssw dpt memhm tegrl fugs d plksy TIK : Mhssw mmpu mecr tegrl fugs Mhssw mmpu megguk tegrl utuk
Penyelesaian Persamaan Saint Venant dengan Metode Numerik
 Peyeles Persm S Ve deg Mede Nmerk Prf. r. Ir. Arw, MS. Lcky Le Jp 53 09 005 Mdel Fsk drlg F(,y,z, ): YROLOGY MOEL AS ULU (Wershed Mdel) Bdry l Bdry lr Prf.Arw Sbr bd kehl PSA & Kservs,ITB Kws l AS ILIR,lr
Peyeles Persm S Ve deg Mede Nmerk Prf. r. Ir. Arw, MS. Lcky Le Jp 53 09 005 Mdel Fsk drlg F(,y,z, ): YROLOGY MOEL AS ULU (Wershed Mdel) Bdry l Bdry lr Prf.Arw Sbr bd kehl PSA & Kservs,ITB Kws l AS ILIR,lr
dan mempunyai vektor normal n =(a b c). Misal P(x,y,z) suatu titik berada pada bidang. 1. Persamaan bidangnya adalah n P P
 Rug Vektor Tuju:. Megigt kembli persm gris d bidg di rug.. Memhmi ksiom rug vektor, kombisi liier d rug bgi.. Megigt kembli pegerti bebs d bergtug liier, bsis d dimesi. Arti geometris dri determi Jik A
Rug Vektor Tuju:. Megigt kembli persm gris d bidg di rug.. Memhmi ksiom rug vektor, kombisi liier d rug bgi.. Megigt kembli pegerti bebs d bergtug liier, bsis d dimesi. Arti geometris dri determi Jik A
SOLUSI ANALITIK DAN SOLUSI NUMERIK PERSAMAAN CAUCHY-EULER SKRIPSI
 SOLUSI ANALITI DAN SOLUSI NUMERI PERSAMAAN CAUCHY-EULER SRIPSI Oleh: INAYATUL HASANAH NIM. 5 JURUSAN MATEMATIA FAULTAS SAINS DAN TENOLOGI UNIVERSITAS ISLAM NEGERI MALANG MALANG 9 SOLUSI ANALITI DAN SOLUSI
SOLUSI ANALITI DAN SOLUSI NUMERI PERSAMAAN CAUCHY-EULER SRIPSI Oleh: INAYATUL HASANAH NIM. 5 JURUSAN MATEMATIA FAULTAS SAINS DAN TENOLOGI UNIVERSITAS ISLAM NEGERI MALANG MALANG 9 SOLUSI ANALITI DAN SOLUSI
BAB V ANALISIS REGRESI
 BAB V ANALISIS REGRESI Setelh mempeljr mhssw dhrpk dpt : Meghtug prmeter regres Melkuk estms d uj prmeter regres 3 Meemuk model regres g tept Dlm kehdup serg dtemuk d sekelompok peuh g dtr terdpt huug,
BAB V ANALISIS REGRESI Setelh mempeljr mhssw dhrpk dpt : Meghtug prmeter regres Melkuk estms d uj prmeter regres 3 Meemuk model regres g tept Dlm kehdup serg dtemuk d sekelompok peuh g dtr terdpt huug,
,, % ,, % -0: 0 -0: 0! 2 % 26, &
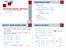 PERSAMAAN LINIER GAUSS-SIEDEL METHOD Simultneous Liner Equtions Oleh : Purwnto,S.Si Bentuk Umum x + x + 3 x 3 + + n x n = b Sebuh persmn linier dengn : n peubh : x, x, x 3,, x n n konstnt :,, 3,, n Contoh
PERSAMAAN LINIER GAUSS-SIEDEL METHOD Simultneous Liner Equtions Oleh : Purwnto,S.Si Bentuk Umum x + x + 3 x 3 + + n x n = b Sebuh persmn linier dengn : n peubh : x, x, x 3,, x n n konstnt :,, 3,, n Contoh
Induksi Dan Rekursi. Bab IV Induksi Pada Bilangan Asli (Natural) Bilangan Asli
 Bb IV Iduks D Rekurs 4.. Iduks Pd Blg Asl (Nturl) Bsy, duks tets tu dsebut jug duks legkp (coplete ducto) plg byk dguk dl do blg turl. Khususy, dl duks, dsusk bhw sutu sft tertetu yg egguk blg sl terkecl,
Bb IV Iduks D Rekurs 4.. Iduks Pd Blg Asl (Nturl) Bsy, duks tets tu dsebut jug duks legkp (coplete ducto) plg byk dguk dl do blg turl. Khususy, dl duks, dsusk bhw sutu sft tertetu yg egguk blg sl terkecl,
MATERI LOGARITMA. Oleh : Hartono
 MATERI LOGARITMA Oleh : Hrtoo Mteri dispik pd Peltih Mpel Mtetik SMA/ SMK Progr Pscsrj UNY Yogykrt 01 Kopetesi Kopetesi yg dihrpk dicpi oleh pr pesert setelh ebc odul ii d egikuti peltih dlh pu : ehi kosep
MATERI LOGARITMA Oleh : Hrtoo Mteri dispik pd Peltih Mpel Mtetik SMA/ SMK Progr Pscsrj UNY Yogykrt 01 Kopetesi Kopetesi yg dihrpk dicpi oleh pr pesert setelh ebc odul ii d egikuti peltih dlh pu : ehi kosep
BAB 2 LANDASAN TEORI
 BAB LANDASAN TORI. egtr roses Mrkov dt dklsfksk sesu deg sft wktu egmt roses sert stte scey. Wktu egmt roses dt bersft dskrt muu kotu d stte scey bersft dskrt muu kotu bk terbts muu tk terbts.. Dt Defs..
BAB LANDASAN TORI. egtr roses Mrkov dt dklsfksk sesu deg sft wktu egmt roses sert stte scey. Wktu egmt roses dt bersft dskrt muu kotu d stte scey bersft dskrt muu kotu bk terbts muu tk terbts.. Dt Defs..
1 B. Mengkonversi dari pecahan ke persen. 1 Operasi bilangan berpangkat. 2. Menyederhanakan bilangan berpangkat bentuk:
 KISI KISI SOAL UJI COBA UJIAN NASIONAL MATA PELAJARAN MATEMATIKA TAHUN 009 / 00 MGMP MATEMATIKA SMK TEKNIK KABUPATEN KLATEN Bhn/ X / Opersi bilngn rel. Sisw dpt: A. Mengkonversi dri desiml ke persen B.
KISI KISI SOAL UJI COBA UJIAN NASIONAL MATA PELAJARAN MATEMATIKA TAHUN 009 / 00 MGMP MATEMATIKA SMK TEKNIK KABUPATEN KLATEN Bhn/ X / Opersi bilngn rel. Sisw dpt: A. Mengkonversi dri desiml ke persen B.
2. PERSAMAAN, PERTIDAKSAMAAN DAN FUNGSI KUADRAT
 . PERSAMAAN, PERTIDAKSAMAAN DAN FUNGSI KUADRAT A. Persmn Kudrt. Bentuk umum persmn kudrt : x + bx + c = 0, 0. Nili determinn persmn kudrt : D = b c. Akr-kr persmn kudrt dpt dicri dengn memfktorkn tupun
. PERSAMAAN, PERTIDAKSAMAAN DAN FUNGSI KUADRAT A. Persmn Kudrt. Bentuk umum persmn kudrt : x + bx + c = 0, 0. Nili determinn persmn kudrt : D = b c. Akr-kr persmn kudrt dpt dicri dengn memfktorkn tupun
III PEMBAHASAN. peubah. Sistem persamaan (6) dapat diringkas menjadi Bentuk Umum dari Magic Square, Bilangan Magic, dan Matriks SPL
 III PEMBAHASAN 3.1. Betuk Umum dri Mgic Squre, Bilg Mgic, d Mtriks SPL Mislk eleme dri bris ke-i d kolom ke-j dlh i,j mk mgic squrey secr umum dlh 1,1 1, 1,,1,,,1,, Gmbr 1. Betuk umum mgic squre deg: i,j
III PEMBAHASAN 3.1. Betuk Umum dri Mgic Squre, Bilg Mgic, d Mtriks SPL Mislk eleme dri bris ke-i d kolom ke-j dlh i,j mk mgic squrey secr umum dlh 1,1 1, 1,,1,,,1,, Gmbr 1. Betuk umum mgic squre deg: i,j
GEOMETRI EUCLID EG(2, p n ) UNTUK MEMBENTUK RANCANGAN BLOK TIDAK LENGKAP SEIMBANG
 GEOMETRI EUCLID EG(, p ) UNTUK MEMBENTUK RANCANGAN BLOK TIDAK LENGKAP SEIMBANG Bmg Irwto d Yu Hdyt Jurus Mtemtk FMIPA UNDIP Jl. Prof. H. Soedrto, S.H, Semrg 5075 Astrt. A Bled Iomplete Blok (BIB) desg
GEOMETRI EUCLID EG(, p ) UNTUK MEMBENTUK RANCANGAN BLOK TIDAK LENGKAP SEIMBANG Bmg Irwto d Yu Hdyt Jurus Mtemtk FMIPA UNDIP Jl. Prof. H. Soedrto, S.H, Semrg 5075 Astrt. A Bled Iomplete Blok (BIB) desg
SIFAT-SIFAT SEMIRING DAN KONSTRUKSINYA
 Jr E Me S Vo No SIFAT-SIFAT SEMIRING DAN KONSTRUKSINYA A Rhw Uver Pere Tgg Dr U (Up) Jog Kope Pope Dr U Reoo Peerog Jog J 648 rhw@gco ABSTRAK Serg ef eg hp oog eg oper er (peh per) D wh oper peh erg erp
Jr E Me S Vo No SIFAT-SIFAT SEMIRING DAN KONSTRUKSINYA A Rhw Uver Pere Tgg Dr U (Up) Jog Kope Pope Dr U Reoo Peerog Jog J 648 rhw@gco ABSTRAK Serg ef eg hp oog eg oper er (peh per) D wh oper peh erg erp
FAKULTAS DESAIN dan TEKNIK PERENCANAAN UJIAN AKHIR SEMESTER SEMESTER GENAP TA 2006/2007
 FKULTS DSIN d TKNIK PRNCNN UJIN KHIR SMSTR SMSTR GNP T 006/007 Js : Tekik Sipil Hi / Tl : Sels -05-007 Mt Klih : Stkt Bj I Wkt : 10.50 1.30 Dose : I. Wiyto Dewoboto, MT. Seeste : IV Sift Uji : ope ote
FKULTS DSIN d TKNIK PRNCNN UJIN KHIR SMSTR SMSTR GNP T 006/007 Js : Tekik Sipil Hi / Tl : Sels -05-007 Mt Klih : Stkt Bj I Wkt : 10.50 1.30 Dose : I. Wiyto Dewoboto, MT. Seeste : IV Sift Uji : ope ote
IX. RANCANGAN ACAK LENGKAP POLA FAKTORIAL AxB
 Respons Respons IX. RANCANGAN ACAK LENGKAP POLA FAKTORIAL AxB Rncngn Ack Lengkp Pol Fktoril AxB dlh rncngn ck lengkp yng terdiri dri d peh es (Fktor dlm klsfiksi silng yit fktor A yng terdiri dri trf dn
Respons Respons IX. RANCANGAN ACAK LENGKAP POLA FAKTORIAL AxB Rncngn Ack Lengkp Pol Fktoril AxB dlh rncngn ck lengkp yng terdiri dri d peh es (Fktor dlm klsfiksi silng yit fktor A yng terdiri dri trf dn
REGRESI. Curve Fitting Regresi Linier Regresi Eksponensial Regresi Polynomial. Regresi 1
 REGRESI Curve Fttg Regres Ler Regres Ekspoesl Regres Poloml Regres Curve Fttg: Ksus Dberk dt berup kumpul ttk-ttk dskrt. Dperluk estms / perkr utuk medptk l dr ttk-ttk g berd d tr ttk-ttk dskrt tersebut
REGRESI Curve Fttg Regres Ler Regres Ekspoesl Regres Poloml Regres Curve Fttg: Ksus Dberk dt berup kumpul ttk-ttk dskrt. Dperluk estms / perkr utuk medptk l dr ttk-ttk g berd d tr ttk-ttk dskrt tersebut
REGRESI. Curve Fitting. Regresi Eksponensial. Regresi 1
 REGRESI Curve Fttg Regres Ler Regres Ekspoesl Regres Poloml Regres Curve Fttg: Ksus Dberk dt berup kumpul ttk-ttk dskrt. Dperluk estms / perkr utuk medptk l dr ttk-ttk g berd d tr ttk-ttk dskrt t tersebut
REGRESI Curve Fttg Regres Ler Regres Ekspoesl Regres Poloml Regres Curve Fttg: Ksus Dberk dt berup kumpul ttk-ttk dskrt. Dperluk estms / perkr utuk medptk l dr ttk-ttk g berd d tr ttk-ttk dskrt t tersebut
Anuitas. Anuitas Akhir
 Auts Auts bersl r kt bhs Iggrs uty yg pt efsk sebg rgk pembyr tu peerm tetp lm jumlh tertetu yg lkuk secr berkl p jgk wktu tertetu. Kt uty sly berrt pembyr ul (thu), k tetp serg eg berjly wktu kt uts jug
Auts Auts bersl r kt bhs Iggrs uty yg pt efsk sebg rgk pembyr tu peerm tetp lm jumlh tertetu yg lkuk secr berkl p jgk wktu tertetu. Kt uty sly berrt pembyr ul (thu), k tetp serg eg berjly wktu kt uts jug
INTEGRASI NUMERIK. n ax. ax e. a 1. Fungsi yang dapat dihitung integralnya : Fungsi yang rumit misal :
 INTEGRASI NUMERIK INTEGRASI NUMERIK D dlm klkulus, terdpt du l petg ytu tegrl d turudervtve Pegtegrl umerk merupk lt tu r yg dguk ole lmuw utuk memperole jw mpr proksms dr pegtegrl yg tdk dpt dselesk ser
INTEGRASI NUMERIK INTEGRASI NUMERIK D dlm klkulus, terdpt du l petg ytu tegrl d turudervtve Pegtegrl umerk merupk lt tu r yg dguk ole lmuw utuk memperole jw mpr proksms dr pegtegrl yg tdk dpt dselesk ser
PENYELESAIAN MASALAH PL DENGAN METODE SIMPLEKS
 PENYELESAIAN MASALAH PL DENGAN METODE SIMPLEKS Metode ple erup utu te tdr g dgu utu eech lh Progr Ler e thu 9. Pd prp etode ple ecr peele optl deg eetu tt-tt udut dr derh fele proe dlu erulg-ulg dr utu
PENYELESAIAN MASALAH PL DENGAN METODE SIMPLEKS Metode ple erup utu te tdr g dgu utu eech lh Progr Ler e thu 9. Pd prp etode ple ecr peele optl deg eetu tt-tt udut dr derh fele proe dlu erulg-ulg dr utu
Sistem Bilangan dan Kesalahan. Sistim Bilangan Metode Numerik 1
 Sistem Bilg d Keslh Sistim Bilg Metode Numerik Peyji Bilg Bult Bilg ult yg serig diguk dlh ilg ult dlm sistem ilg desiml yg didefiisik s: N ( )...... Sistim Bilg Metode Numerik Cotoh : 673 * 3 6* 7* 3*
Sistem Bilg d Keslh Sistim Bilg Metode Numerik Peyji Bilg Bult Bilg ult yg serig diguk dlh ilg ult dlm sistem ilg desiml yg didefiisik s: N ( )...... Sistim Bilg Metode Numerik Cotoh : 673 * 3 6* 7* 3*
RUANG VEKTOR REAL. Kania Evita Dewi
 RUANG VEKTOR REAL Kni Eit Dewi Definisi Vektor dlh besrn yng mempnyi rh. Notsi: Notsi pnjng ektor: k j i ˆ ˆ ˆ Vektor stn Vektor dengn pnjng t norm sm dengn st Opersi ektor Penjmlhn ntr ektor Mislkn dn
RUANG VEKTOR REAL Kni Eit Dewi Definisi Vektor dlh besrn yng mempnyi rh. Notsi: Notsi pnjng ektor: k j i ˆ ˆ ˆ Vektor stn Vektor dengn pnjng t norm sm dengn st Opersi ektor Penjmlhn ntr ektor Mislkn dn
Sistem Bilangan dan Kesalahan. Metode Numerik
 Sistem Bilg d Keslh Peyji Bilg Bult Bilg ult yg serig diguk dlh ilg ult dlm sistem ilg desiml yg didefiisik s: N ( )...... Cotoh : 673 * 3 6* 7* 3* Bilg ult deg ilg dsr c didefiisik segi : ( )... c N c
Sistem Bilg d Keslh Peyji Bilg Bult Bilg ult yg serig diguk dlh ilg ult dlm sistem ilg desiml yg didefiisik s: N ( )...... Cotoh : 673 * 3 6* 7* 3* Bilg ult deg ilg dsr c didefiisik segi : ( )... c N c
INTEGRAL-Z. Siti Khabibah, Farikhin, Bayu Surarso Jurusan Matematika FMIPA UNDIP Semarang Jl. Prof. H. Soedarto, SH, Tembalang, Semarang, 50275
 INTEGRAL-Z Siti Khih, Frikhi, By Srrso Jrs Mtetik FMIPA UNDIP Serg Jl. Prof. H. Soedrto, SH, Telg, Serg, 5275 Astrk: Kosep egei itegrl-z terkit deg keerd deritif kt. St fgsi F yg terderitif kt pd [,] diotsik
INTEGRAL-Z Siti Khih, Frikhi, By Srrso Jrs Mtetik FMIPA UNDIP Serg Jl. Prof. H. Soedrto, SH, Telg, Serg, 5275 Astrk: Kosep egei itegrl-z terkit deg keerd deritif kt. St fgsi F yg terderitif kt pd [,] diotsik
DUALITAS DAN ANALISIS SENSITIVITAS
 /5/008 DUALITAS DAN ANALISIS SENSITIVITAS Dr. Mohd Adul Mukhy, SE., MM. Prl Prole P ze z cx suject to Ax x 0 optu vlue s z* Dul Prole xze suject to D v π πa c optu vlue s v* Theore. (Strog Dulty) If oth
/5/008 DUALITAS DAN ANALISIS SENSITIVITAS Dr. Mohd Adul Mukhy, SE., MM. Prl Prole P ze z cx suject to Ax x 0 optu vlue s z* Dul Prole xze suject to D v π πa c optu vlue s v* Theore. (Strog Dulty) If oth
Analisis Variansi satu faktor (Analysis Of Variance / ANOVA)
 Alss Vrs stu fktor (Alss Of Vrce / ANOVA) 1. Megethu rcg d eses. Megethu model ler 3. Meuruk Jumlh Kudrt (JK) 4. Melkuk uj lss vrs 5. Melkuk uj perbdg gd Apkh ber kot dlm rokok dpt megkbtk Kker? Sel kker
Alss Vrs stu fktor (Alss Of Vrce / ANOVA) 1. Megethu rcg d eses. Megethu model ler 3. Meuruk Jumlh Kudrt (JK) 4. Melkuk uj lss vrs 5. Melkuk uj perbdg gd Apkh ber kot dlm rokok dpt megkbtk Kker? Sel kker
BAB IV METODA ANALISIS RANGKAIAN
 6 BAB METODA ANALSS RANGKAAN Metod nlss rngkn sebenrny merupkn slh stu lt bntu untuk menyeleskn sutu permslhn yng muncul dlm mengnlss sutu rngkn, blmn konsep dsr tu hukum-hukum dsr sepert Hukum Ohm dn
6 BAB METODA ANALSS RANGKAAN Metod nlss rngkn sebenrny merupkn slh stu lt bntu untuk menyeleskn sutu permslhn yng muncul dlm mengnlss sutu rngkn, blmn konsep dsr tu hukum-hukum dsr sepert Hukum Ohm dn
( X ) 2 ANALISIS REGRESI
 ANALII REGREI A. PENGERTIAN REGREI ecr umum d du mcm huug tr du vrel tu leh, tu etuk huug d keert huug. Utuk megethu etuk huug dguk lss regres. Utuk keert huug dpt dkethu deg lss korels. Alss regres dperguk
ANALII REGREI A. PENGERTIAN REGREI ecr umum d du mcm huug tr du vrel tu leh, tu etuk huug d keert huug. Utuk megethu etuk huug dguk lss regres. Utuk keert huug dpt dkethu deg lss korels. Alss regres dperguk
NILAI EIGEN DAN VEKTOR EIGEN
 Pert 9 (mengjrkomputer.wordpress.com) NILAI EIGEN DAN VEKTOR EIGEN 9. Definisi Sebuh mtriks bujur sngkr dengn orde n n mislkn A, dn sebuh vektor kolom X. Vektor X dlh vektor dlm rung Euklidin n R yng dihubungkn
Pert 9 (mengjrkomputer.wordpress.com) NILAI EIGEN DAN VEKTOR EIGEN 9. Definisi Sebuh mtriks bujur sngkr dengn orde n n mislkn A, dn sebuh vektor kolom X. Vektor X dlh vektor dlm rung Euklidin n R yng dihubungkn
Program Kerja TFPPED KBI Semarang 1
 U P A Y A M E N G G E R A K K A N P E R E K O N O M I A N D A E R A H M E L A L U I F A S I L I T A S I P E R C E P A T A N P E M B E R D A Y A A N E K O N O M I D A E R A H ( F P P E D ) S E K T O R P
U P A Y A M E N G G E R A K K A N P E R E K O N O M I A N D A E R A H M E L A L U I F A S I L I T A S I P E R C E P A T A N P E M B E R D A Y A A N E K O N O M I D A E R A H ( F P P E D ) S E K T O R P
Teorema Dasar Integral Garis
 ISBN: 978-979-79-55-9 Teorem Dsr Integrl Gris Erdwti Nurdin Progrm Studi Pendidikn Mtemtik FKIP UIR d_1910@yhoo.com Abstrk Slh stu generlissi integrl tentu (definite integrl) f x dx diperoleh dengn menggnti
ISBN: 978-979-79-55-9 Teorem Dsr Integrl Gris Erdwti Nurdin Progrm Studi Pendidikn Mtemtik FKIP UIR d_1910@yhoo.com Abstrk Slh stu generlissi integrl tentu (definite integrl) f x dx diperoleh dengn menggnti
MENENTUKAN AKAR-AKAR PERSAMAAN PANGKAT EMPAT. Supriyono Jurusan Pendidikan Matematika FKIP Universitas Muhammadiyah Purworejo.
 MENENTUKAN AKAR-AKAR PERSAMAAN PANGKAT EMPAT Supriyono Jurusn Pendidikn Mtemtik FKIP Universits Muhmmdiyh Purworejo Abstrk Tulisn ini terdiri bgin yitu () bgin pendhulun yng membhs bentuk umum persmn pngkt
MENENTUKAN AKAR-AKAR PERSAMAAN PANGKAT EMPAT Supriyono Jurusn Pendidikn Mtemtik FKIP Universits Muhmmdiyh Purworejo Abstrk Tulisn ini terdiri bgin yitu () bgin pendhulun yng membhs bentuk umum persmn pngkt
PRAKTIKUM 8 Penyelesaian Persamaan Linier Simultan Metode Eliminasi Gauss
 Prktkum 8 Peyeles Persm Ler Smult Metoe Elms Guss PRAKTIKUM 8 Peyeles Persm Ler Smult Metoe Elms Guss Tuju : smult Mempeljr metoe Elms Guss utuk peyeles persm ler Dsr Teor : Metoe Elms Guss merupk metoe
Prktkum 8 Peyeles Persm Ler Smult Metoe Elms Guss PRAKTIKUM 8 Peyeles Persm Ler Smult Metoe Elms Guss Tuju : smult Mempeljr metoe Elms Guss utuk peyeles persm ler Dsr Teor : Metoe Elms Guss merupk metoe
RENCANA PELAKSANAAN PERKULIAHAN
 Lesso Study FMIPA UNY RENCANA PELAKSANAAN PERKULIAHAN MATA KULIAH : ALJABAR LINEAR II SEMESTER : III TOPIK : NILAI EIGEN DAN VEKTOR EIGEN SUB TOPIK : NILAI EIGEN DAN VEKTOR EIGEN WAKTU : X 5 A. Stdr Kompetesi:
Lesso Study FMIPA UNY RENCANA PELAKSANAAN PERKULIAHAN MATA KULIAH : ALJABAR LINEAR II SEMESTER : III TOPIK : NILAI EIGEN DAN VEKTOR EIGEN SUB TOPIK : NILAI EIGEN DAN VEKTOR EIGEN WAKTU : X 5 A. Stdr Kompetesi:
KAJIAN BATAS KESALAHAN MINIMUM METODE RUNGE-KUTTA ORDE KEDUA, KETIGA, DAN KEEMPAT
 Prosdg Semr Nsol Mtemtk d Terpy 06 p-issn : 550-084; e-issn : 550-09 KAJIAN BATAS KESALAHAN MINIMUM METODE RUNGE-KUTTA ORDE KEDUA, KETIGA, DAN KEEMPAT St Muhwh Uversts Jederl Soedrm st_muhwh@yhoo.co.d
Prosdg Semr Nsol Mtemtk d Terpy 06 p-issn : 550-084; e-issn : 550-09 KAJIAN BATAS KESALAHAN MINIMUM METODE RUNGE-KUTTA ORDE KEDUA, KETIGA, DAN KEEMPAT St Muhwh Uversts Jederl Soedrm st_muhwh@yhoo.co.d
Bila kita mempunyai suatu sistem persamaan linier 2x + 3y + 3z = 0 x + y + 3z = 0 x + 2y z = 0
 LJBR MTRIKS Bil kit mempui sutu sistem persm liier + + z = + + z = + z = Mk koefisie tersebut di ts disebut MTRIKS, d secr umum dpt ditulisk sbb : Jjr bilg tersebut di ts disebut MTRIKS, d secr umum dpt
LJBR MTRIKS Bil kit mempui sutu sistem persm liier + + z = + + z = + z = Mk koefisie tersebut di ts disebut MTRIKS, d secr umum dpt ditulisk sbb : Jjr bilg tersebut di ts disebut MTRIKS, d secr umum dpt
Metode Numerik. Regresi. Umi Sa adah Politeknik Elektronika Negeri Surabaya 2008 PENS-ITS
 Metode Numerk Regres Um S dh Polteknk Elektronk Neger Surb 008 PENS-ITS 1 Metode Numerk Topk Regres Lner Regres Non Lner PENS-ITS Metode Numerk Metode Numerk Regres vs Interpols REGRESI KUADRAT TERKECIL
Metode Numerk Regres Um S dh Polteknk Elektronk Neger Surb 008 PENS-ITS 1 Metode Numerk Topk Regres Lner Regres Non Lner PENS-ITS Metode Numerk Metode Numerk Regres vs Interpols REGRESI KUADRAT TERKECIL
PENYELESAIAN SISTEM PERSAMAAN LINEAR DENGAN MENGGUNAKAN DETERMINAN (ATURAN CRAMER)
 PENYELESAIAN SISTEM PERSAMAAN LINEAR DENGAN MENGGUNAKAN DETERMINAN (ATURAN CRAMER) Dikethui system Persmn Linier x+ x + x = x+ x + x = x+ x + x = dlm entuk mtriks x x x Penyelesin Dengn Aturn Crmer dlh
PENYELESAIAN SISTEM PERSAMAAN LINEAR DENGAN MENGGUNAKAN DETERMINAN (ATURAN CRAMER) Dikethui system Persmn Linier x+ x + x = x+ x + x = x+ x + x = dlm entuk mtriks x x x Penyelesin Dengn Aturn Crmer dlh
PRAKTIKUM 10 Penyelesaian Persamaan Linier Simultan Metode Eliminasi Gauss Seidel
 Prktkum 0 Peyeles Persm Ler Smult - Metode Elms Guss Sedel PRAKTIKUM 0 Peyeles Persm Ler Smult Metode Elms Guss Sedel Tuu : ler smult Mempelr metode Elms Guss Sedel utuk peyeles persm Dsr Teor : Metode
Prktkum 0 Peyeles Persm Ler Smult - Metode Elms Guss Sedel PRAKTIKUM 0 Peyeles Persm Ler Smult Metode Elms Guss Sedel Tuu : ler smult Mempelr metode Elms Guss Sedel utuk peyeles persm Dsr Teor : Metode
Permodelan Sistem. Melalui Identifikasi Parameter. Ir. Rusdhianto EAK, MT. Pelatihan PC-Based Control
 Permodeln Sistem Mellui Identifisi Prmeter Ir. Rusdhinto EAK, M Pengertin Adlh seumpuln metode yng digunn untu mendptn/menentun prmeter model pendetn dri sistem mellui evlusi dt penguurn input output Secr
Permodeln Sistem Mellui Identifisi Prmeter Ir. Rusdhinto EAK, M Pengertin Adlh seumpuln metode yng digunn untu mendptn/menentun prmeter model pendetn dri sistem mellui evlusi dt penguurn input output Secr
Bab 4 ANALISIS REGRESI dan INTERPOLASI
 Als Numerk Bh Mtrkuls B 4 ANALISIS RGRSI d INTRPOLASI 4 Pedhulu Pd kulh k dpeljr eerp metde utuk mempredks d megestms dt dskret Dr sutu peelt serg dlkuk peglh dt utuk megethu pl dt tu etuk kurv g dggp
Als Numerk Bh Mtrkuls B 4 ANALISIS RGRSI d INTRPOLASI 4 Pedhulu Pd kulh k dpeljr eerp metde utuk mempredks d megestms dt dskret Dr sutu peelt serg dlkuk peglh dt utuk megethu pl dt tu etuk kurv g dggp
SOLUSI DERET PANGKAT TETAP DENGAN FUNGSI PEMBANGKIT
 OLUI DERET PANGKAT TETAP DENGAN FUNGI PEMBANGKIT Aleder A Guw Jurus Mtemt d ttst Fults s d Teolog, Uversts B Nustr Jl. K. H. yhd No. 9, Kemggs/Plmerh, Jrt Brt 8 gug@bus.edu ABTRACT Ths rtcle dscusses bout
OLUI DERET PANGKAT TETAP DENGAN FUNGI PEMBANGKIT Aleder A Guw Jurus Mtemt d ttst Fults s d Teolog, Uversts B Nustr Jl. K. H. yhd No. 9, Kemggs/Plmerh, Jrt Brt 8 gug@bus.edu ABTRACT Ths rtcle dscusses bout
INTEGRASI NUMERIK C 1. n ax. ax e. cos( 1 1. n 1. x x. 0 Fungsi yang dapat dihitung integralnya : 0 Fungsi yang rumit misal :
 INTEGRASI NUMERIK D dlm klkulus, terdpt du l petg ytu tegrl d turudervtve Pegtegrl umerk merupk lt tu r yg dguk ole lmuw utuk memperole jw mpr proksms dr pegtegrl yg tdk dpt dselesk ser ltk. INTEGRASI
INTEGRASI NUMERIK D dlm klkulus, terdpt du l petg ytu tegrl d turudervtve Pegtegrl umerk merupk lt tu r yg dguk ole lmuw utuk memperole jw mpr proksms dr pegtegrl yg tdk dpt dselesk ser ltk. INTEGRASI
Skew- Semifield dan Beberapa Sifatnya 1
 Skew- Semifield dn Beberp Siftny K r y t i Jurusn Pendidikn Mtemtik Fkults Mtemtik dn Ilmu Pengethun Alm Universits Negeri Yogykrt E-mil: ytiuny@yhoo.com Abstrk Sutu field ( lpngn ) F dlh struktur ljbr
Skew- Semifield dn Beberp Siftny K r y t i Jurusn Pendidikn Mtemtik Fkults Mtemtik dn Ilmu Pengethun Alm Universits Negeri Yogykrt E-mil: ytiuny@yhoo.com Abstrk Sutu field ( lpngn ) F dlh struktur ljbr
ANALISIS NUMERIK. Inter polasi. SPL simultan. Akar Persama. linear
 ANALISIS NUMERIK Inter polsi SPL simultn Akr Persm n Non liner INTERPOLASI Tujun Interpolsi bergun untuk menksir hrg-hrg tengh ntr titik dt yng sudh tept. Interpolsi mempunyi orde tu derjt. Mcm Interpolsi
ANALISIS NUMERIK Inter polsi SPL simultn Akr Persm n Non liner INTERPOLASI Tujun Interpolsi bergun untuk menksir hrg-hrg tengh ntr titik dt yng sudh tept. Interpolsi mempunyi orde tu derjt. Mcm Interpolsi
INTERPRETASI SINGULAR VALUE DECOMPISITION
 INTERPRETSI SINGLR LE DECOMPISITION (SD) PD PENGOLHN CITR DIGITL Dell Mldy Progr Std Peddk Mtetk Jrs PMIP FKIP versts Begkl BSTRK Sglr le Decoosto (SD) erk sebh tekk kots erk yg elkk fktorss terhd sebh
INTERPRETSI SINGLR LE DECOMPISITION (SD) PD PENGOLHN CITR DIGITL Dell Mldy Progr Std Peddk Mtetk Jrs PMIP FKIP versts Begkl BSTRK Sglr le Decoosto (SD) erk sebh tekk kots erk yg elkk fktorss terhd sebh
BAB 2 SISTEM BILANGAN DAN KESALAHAN
 Metode Numerik Segi Algoritm Komputsi 5 BAB SISTEM BILANGAN DAN KESALAHAN.. Peyji Bilg Bult Bilg ult yg serig diguk dlh ilg ult dlm sistem ilg desiml yg didefiisik : N ( )...... Cotoh : 67. 6. 7.. Bilg
Metode Numerik Segi Algoritm Komputsi 5 BAB SISTEM BILANGAN DAN KESALAHAN.. Peyji Bilg Bult Bilg ult yg serig diguk dlh ilg ult dlm sistem ilg desiml yg didefiisik : N ( )...... Cotoh : 67. 6. 7.. Bilg
Tekun dan Teliti adalah Kunci Keberhasilan Anda PEMROGRAMAN LINEAR
 Teku d Telt dlh Kuc Keberhsl Ad PEMROGRAMAN LINEAR Pdg bg Rset Opers berkut: TSP MP Trss Trsp Network PD PL PNL P Progr Ler (PL) erupk bg dr rset opers (RO) g erupk kupul etode peeles slh-slh t secr tets.
Teku d Telt dlh Kuc Keberhsl Ad PEMROGRAMAN LINEAR Pdg bg Rset Opers berkut: TSP MP Trss Trsp Network PD PL PNL P Progr Ler (PL) erupk bg dr rset opers (RO) g erupk kupul etode peeles slh-slh t secr tets.
PENGHITUNGAN NILAI RESISTOR PENGGANTI MENGGUNAKAN NILAI EIGEN DAN VEKTOR EIGEN ORTONORMAL DARI MATRIKS LAPLACE AMIN LUKMANUL HAKIM G
 PEGHIUGA ILAI RESISOR PEGGAI MEGGUAKA ILAI EIGE DA VEKOR EIGE OROORMAL DARI MARIKS LAPLACE AMI LUKMAUL HAKIM G544 DEPAREME MAEMAIKA FAKULAS MAEMAIKA DA ILMU PEGEAHUA ALAM ISIU PERAIA OGOR 7 PEGHIUGA ILAI
PEGHIUGA ILAI RESISOR PEGGAI MEGGUAKA ILAI EIGE DA VEKOR EIGE OROORMAL DARI MARIKS LAPLACE AMI LUKMAUL HAKIM G544 DEPAREME MAEMAIKA FAKULAS MAEMAIKA DA ILMU PEGEAHUA ALAM ISIU PERAIA OGOR 7 PEGHIUGA ILAI
Tugas besar Metode numerik
 Tgs besr Metode merk Mege : cotoh sol-sol metode merk d pembhsy Nm ggot : Abdl hrrs hdyt (95 Are krw (95 Yog tr wrme (959 Dose : Her dbyolksoo.mt Jrs tekk elektro Fklts tekk Uversts dls Pdg Bb Dsr teor
Tgs besr Metode merk Mege : cotoh sol-sol metode merk d pembhsy Nm ggot : Abdl hrrs hdyt (95 Are krw (95 Yog tr wrme (959 Dose : Her dbyolksoo.mt Jrs tekk elektro Fklts tekk Uversts dls Pdg Bb Dsr teor
SOAL UN MATEMATIKA IPA 2014
 SOAL UN MATEMATIKA IPA 2014 1. Dkethu prems-prems berkut : Prems 1 : Jk hr hujn, mk tnmn pd subur. Prems 2 : Jk pnen tdk melmph, mk tnmn pd tdk subur. Prems 3 : Pnen tdk melmph Kesmpuln yng sh dr prems-prems
SOAL UN MATEMATIKA IPA 2014 1. Dkethu prems-prems berkut : Prems 1 : Jk hr hujn, mk tnmn pd subur. Prems 2 : Jk pnen tdk melmph, mk tnmn pd tdk subur. Prems 3 : Pnen tdk melmph Kesmpuln yng sh dr prems-prems
Data Survey Kendaraan Yang Keluar Areal Parkir
 LAMPIRAN E.2-1 Data Survey Kendaraan Yang Keluar Areal Parkir Lokasi Survey : Areal Parkir Bagian Depan Jenis Kendaraan : Sepeda Motor Hari/Tanggal : Senin, 10 Juli 2006 Surveyor : Heri Plat Kendaraan
LAMPIRAN E.2-1 Data Survey Kendaraan Yang Keluar Areal Parkir Lokasi Survey : Areal Parkir Bagian Depan Jenis Kendaraan : Sepeda Motor Hari/Tanggal : Senin, 10 Juli 2006 Surveyor : Heri Plat Kendaraan
Go to Siti s file Siti Fatimah/Jurdikmat/UPI 1
 Go o S s fle S Fmh/Jrdkm/UPI Movs Jmlh Rem-Iegrl Te Teorem Dsr Klkls Sf-sf Iegrl Te A Dervf-Iegrl Tk e Tekk Pegegrl S Fmh/Jrdkm/UPI Ls Bdg Legkg P P P Emp ss Delp ss S Fmh/Jrdkm/UPI Ls Bdg Legkg P P P
Go o S s fle S Fmh/Jrdkm/UPI Movs Jmlh Rem-Iegrl Te Teorem Dsr Klkls Sf-sf Iegrl Te A Dervf-Iegrl Tk e Tekk Pegegrl S Fmh/Jrdkm/UPI Ls Bdg Legkg P P P Emp ss Delp ss S Fmh/Jrdkm/UPI Ls Bdg Legkg P P P
