BAB 5 PERSAMAAN DIFERENSIAL HOMOGEN ORDE TINGGI
|
|
|
- Susanto Yohanes Darmali
- 7 tahun lalu
- Tontonan:
Transkripsi
1 BAB 5 PESAMAAN DIFEENSIA HOMOGEN ODE TINGGI 5. Pendhulun Metode penyelesn persmn dferensl orde stu dn du yng telh dbhs dpt dpergunkn untuk persmn dferensl homogen untuk orde n dengn persmn krkterstk sepert d bwh n : n n n n s s s... ns ns n (5.) menurut teorem dsr ljbr menytkn bhw sebuh persmn dferensl orde n yng memlk kr-kr sebnyk n dmn kr-kr n bs ddpt dengn cr memfktorkn Persmn (73) sebg berkut : (s s)(s s )...(s s n ) (5.) dmn setp kr s, s,, s n kn menmbulkn fktor st K dlm penyelesnny, dmn jumlh semu fktor kn membentuk penyelesn persmn dferensl, sehngg penyelesn sutu persmn dferensl homogen untuk orde n, kn memlk bentuk mslkn sebg berkut : s t s t s K s K K n... K n (5.3) sehngg yng menjd permslhn dlm penyelesn persmn dferensl homogen orde n dlh mencr kr-kr dr persmn krkterstk persmn dferensl tersebut. Akn tetp d beberp penyerdhn dlm mencr kr-kr persmn n kren koefsen-koefsen Persmn (5.) dlh koefsen rl dn postf, hl n dsebbkn koefsen-koefsen n terbentuk dr prmeter rngkn, ytu, dn C, dn kren, dn C dnggp rl dn postf, mk koefsen dr Persmn (5.) menjd rl dn postf jug. Ad tg kemungknn yng bs terjd pd kr-kr dr persmn krkterstk tersebut :. Akr-kr persmn krkterstk merupkn kr yng rl.. Akr-kr persmn krkterstk merupkn kr yng mjner. 3. Akr-kr persmn krkterstk merupkn kr yng kompleks.
2 5. Persmn Krkterstk Orde Stu Mslkn persmn krkterstk berbentuk sebg berkut : s (5.4) mk kr persmn n dlh : s mk kr n sellu rl dn negtf kren dn sellu rl dn postf. (5.5) 5.3 Persmn Krkterstk Orde Du Mslkn persmn krkterstk berbentuk sebg berkut : s s (5.6) s s mk kr-kr Persmn (5.7) n dlh : s,s 4.. (5.7) (5.8) dsn kr-kr n bs rl, mjner tu kompleks dn klu kr-krny kompleks hruslh merupkn kompleks sekwn/konjugs. 5.4 Persmn Krkterstk Orde Tg Akr-kr persmn krkterstk merupkn sepsng, sepsng kr-kr kompleks sekwn, tupun setdk-tdkny stu krny hrus rl dn yng duny lnny, bs kedu-duny rl tu psngn konjugs kr-kr sekwn. 5.5 Persmn Krkterstk Orde Empt Dlm hl n d beberp kemungknn :. Ke-empt krny rl b. Du rl dn sepsng kompleks sekwn c. Du psng kr kompleks sekwn 3
3 Ad beberp turn dpt dpergunkn yng berhubungn dengn kr-kr tersebut, ytu :. Apbl kr-krny kompleks sekwn, mk krny dlm bentuk psngn sekwn.. Blmn persmn krkterstk ber-orde gnjl, plng sedkt stu kr rl dn ssny bs rl tu dlm psngn kompleks sekwn. 3. Blmn persmn krkterstk ber-orde genp, kr-krny bs rl tu psngn kompleks sekwn. Sebg rngksny, sebuh persmn dengn orde berppun dpt dfktorkn menurut kr-krny, dmn kr-kr menentukn pnyelesn dferensl homogen sebg jumlh penyelesn orde pertm tu orde kedu yng telh dbhs sebelumny. 5.6 Penyelesn Persmn Dferensl Tdk Homogen Sebgmn telh dkethu bhw sutu persmn dferensl dktkn tdk homogen pbl rus knn dr persmn tersebut tdk nol, kn tetp sm dengn fungs pemks (forcng functon) tu beberp turunny. Dlm mengnls persmn demkn, yng perlu dmt bhw penyelesn persmn dferensl homogen yng bersngkutn dlh bgn dr penyelesn persmn dferensl tk homogen. Sebg lustrs perhtkn persmn tdk homogen lner orde du d bwh n : d d 7 v(t) (5.9) penyelesn persmn tdk homogen n mengndung sebgn dr penyelesn persmn homogen. Mslkn v(t) =. mk persmn n memlk kr-kr s = - dn s = -5, sehngg penyelesn lengkp dr persmn n dlh : c K. K. 3t (5.) Sendny beberp fungs p yng kn dcr memenuh persmn tdk homogen Persmn (5.9), sehngg ( p + c ) jug merupkn penyelesn dr persmn tdk 4
4 homogen dr Persmn (5.9), kren dengn mensubsttus K t. tu K 3t. kedlm Persmn (5.9) tdk kn menmbh ppun kerus knn dr Persmn. Sehngg dpt dktkn penyelesn persmn dferensl tdk homogen mengndung penyelesn dr persmn dferensl homogen, dmn bgn n dsebut sebg fungs komplementer dn ssny merupkn bgn prtkulr ntegrl, sehngg totl penyelesn dr persmn dferensl tdk homogen dberkn oleh : = p + c (5.) Adpun persmn dferensl dlm rngkn lstrk suku v(t) pd persmn dferensl dlh gy penggerk tu turunny. Adpun tpe bentuk gelombng sebg fungs penggerk pd rngkn lstrk dlh mslny v(t) dpt berup :. Sutu konstnt. Berbentuk sn ωt ; cos ωt ; Kt 3. Perkln dr suku-suku tersebut 4. Kombns lner untuk mendptkn gelombng sku-sku, puls dn sebgny. Adpun beberp metode yng dpt dpergunkn untuk mencr prtkulr ntegrl, klu fungs penggerk merupkn sepert yng dmksud d ts, mk metode koefsen tk-tentu (method of underemned coeffcent) dpt dpergunkn. Bsny pd penggunn metode koefsen tk-tentu mellu lngkh-lngkh :. Plh fungs percobn dr semu bentuk yng mungkn bs memenuh persmn dferensl sepert pd Tbel 5... Setp fungs percobn dtnd koefsen tk-tentu. 3. Jumlh semu fungs percobn dsubsttuskn kedlm persmn dferensl, kn dperoleh seperngkt persmn ljbr lner dengn menymkn koefsenkoefsen fungs yng sm dlm persmn yng dhslkn dr hsl substtus tersebut. 4. Koefsen-koefsen tk-tentu, dtentukn oleh pemechn seperngkt persmn ljbr tersebut. Klu sutu fungs percobn tdk menghslkn sutu penyelesn, mk koefsenny dlh nol. 5
5 Tbel 5. Plhn Penyelesn Percobn Fktor Dlm v(t) * ) Plhn Bg Integrl Khusus ** ). (konstnt) A. t n B t n + B t n- + + B n- t + B n 3. ε mt Cε mt 4. 3 cos ωt 5. 4 sn ωt D cos ωt + E snωt 6. 5.t n.ε mt cos ωt ( F t n + F t n- + + F n- t + F n ) ε mt cos ωt t n.ε mt sn ωt ( G t n + G t n- + + G n- t + G n ) ε mt sn ωt * ) Blmn v(t) terdr dr jumlh beberp suku, mk ntegrl khusus yng tept dlh jumlh ntegrl khusus bersesun/pdnn msng-msng suku tu sendr-sendr. ** ) Blmn sebuh suku dr ntegrl yng dcob mnpun yng terter dlm kolom n telh merupkn bgn fungs komplementer dr persmn yng dberkn, mk perlu ddkn modfks plhn yng dtunjukn dengn menglknny dengn t sebelum dgunkn. Bl suku yng demkn muncul sebnyk m kl dlm funs komplementer, mk plhn yng dtunjukn hrus dklkn dengn t m. Dlm menggunkn Tbel 5., d beberp lngkh yng perlu dperhtkn :. Tentukn fungs komplementer c. Kemudn bndngkn setp bgn fungs komplementer dengn bentuk v(t). Aturn pd Tbel 5., dmodfks blmn kedu fngs n memlk suku-suku dengn bentuk mtemtk yng sm.. Tulskn bentuk ntegrl khusus yng dcob, dengn menggunkn Tbel 5.. Setp penyelesn yng dcob yng berbed hrus dberkn koefsen huruf yng berbed, dn semu fungs yng sm hrus dgbungkn. 3. Substtuskn hsl penyelesn yng dcob kedlm persmn dferensl, dn dengn menymkn koefsen dr semu suku yng sm, bentuk seperngktn persmn ljbr dlm koefsen yng tk-tentu. 6
6 4. Crlh koefsen tk-tentu dn dengn demkn ntegrl khusus ddpt, koefsenkoefsen n hrus dnytkn dlm prmeter rngkn dn gy penggerk/sumber, dn tdk d konstnt sembrng dlm ntegrl khusus. Setelh ntegrl khusus dperoleh, mk penyelesn totl ddpt dengn menjumlhkn fungs komplementer dengn ntegrl khusus, dn bl dperlukn penyelesn khusus, mk konstnt sembrng dr fungs komplementer ( c ) bs dhtung dengn menggunkn konds wl. Perlu dperhtkn, konds wl hrus sellu dterpkn pd penyelesn totl dn jngn hny pd fungs komplementer sj kecul p =. [bl v(t) = ] 5.7 esponse Ser Dengn Input Fungs Eksponensl ngkn d bwh n dengn sumber tegngn berbentuk : v Gmbr 5. ngkn ser dengn sumber fungs ekponensl Dmn edn α dlh merupkn konstnt, dn pd st t =, sklr dtutup, mk yng dperlukn dlh bentuk persmn. Dengn menggunkn hukum tegngn Krchhoff dpt dtulskn : d d mk persmn krkterstkny dlh :.. sehngg penyelesn komplementer dlh : t (5.) (5.3) A. (5.4) 7
7 mk melht ke Tbel 5., penyelesn yng dcob dlh : c K (5.5) p A. (5.6) dmn A dlh merupkn koefsen tk-tentu, mk untuk = p, Persmn (5.3) menjd:.a..a.. (5.7). Blmn :, mk dr Persmn (5.7) dperoleh : A (5.8) sehngg klu Persmn (5.8) n dsubttuskn ke dlm Persmn (5.6) dperoleh : sehngg penyelesn lengkpny dlh : K. p. = p + c t. dmn konstnt sembrng K dpt dtentukn dr konds wl. (5.9). Blmn, mk bentuk persmn yng dcob dlh : mk Persmn (5.3) menjd : dn dperoleh : mk : A( p At. ) At A (5.) (5.) (5.) 8
8 sehngg penyelesn lengkpny : p t. (5.3) = p + c K. t t K. t dmn konstnt sembrng K dpt dtentukn dr konds wl. (5.4) Contoh : Perhtkn rngkn d bwh n : Crlh bentuk persmn rus. Jwb : Adpun persmn tegngn pd rngkn setelh sklr dtutup dlh : mk persmn krkterstk : d sehngg penyelesn komplementer : d.. s + = t t () Penyelesn ntegrl khusus : c K 9
9 p A terlht bentukny tdk sm dengn fungs komplementer, mk substtuskn kedlm Persmn () untuk = p : t A t A t A = Sehngg penyelesn ntegrl khusus dlh : t p sehngg penyelesn lengkp : = p + c t t K (b) kren rus pd yng tdk dpt berubh dengn seketk, mk pd t =, tu t = + rus () =, sehngg Persmn (b) menjd : K K = -.. Mk persmn rus pd rngkn setelh sklr dtutup dlh : t Amp. Contoh : ngkn sepert berkut : Crlh bentuk persmn rus I setelh sklr dtutup. Jwb : Persmn tegngn pd rngkn setelh sklr dtutup dlh :
10 mk persmn krkterstk : d d sehngg penyelesn komplementer : s + = () c K terlht bentukpersmn tegngn sm dengn fungs komplementer, mk ntegrl khusus yng dcob dlh : p At blmn Persmn () untuk = p, mk dperoleh : mk : mk penyelesn lengkp : At( ) A p A = 4 4t At 4 = p + c K 4t (b) kren rus pd yng tdk dpt berubh dengn seketk, mk pd t =, tu t = + rus pd rngkn dlh nol, sehngg Persmn (b) menjd : K K = Mk persmn rus pd rngkn setelh sklr dtutup dlh : 4t Amp. 5.8 Sol thn
11 . Sutu sumber tegngn = volt (dc) dpsngkn ke sutu rngkn ser C dmn = 9 Ω ; = H dn C =,5 F. Crlh bentuk umum persmn rus yng menglr pd rngkn dn penyelesn prtkulr dr. Asumskn kpstor sebelumny tnp mutn.. Sutu sumber tegngn v 4 volt pd st t = dhubungkn ke rngkn ser yng terdr dr =,5 Ω dn =,5 H. Dengn mengbkn konds wl, crlh penyelesn prtkulr rus yng menglr pd rngkn.,5t 3. Sutu sumber tegngn v 3 pd st t = dhubungkn ke rngkn ser = 3 Ω dn = 6 H. Dengn mengnsumskn konds wl mk berp besr rus pd rngkn n setelh terhubung dengn sumber tegngn selm 5 detk dn bgmn bentuk persmn tegngn pd setelh terhubung dengn sumber tegngn tersebut. 4. Sutu sumber tegngn v pd st t = dhubungkn ke rngkn ser = 4 Ω dn = H. Dengn mengbkn semu konds wl, berp besr tegngn pd setelh sumber tegngn terhubung ke rngkn selm,5 detk.
BAB IV METODA ANALISIS RANGKAIAN
6 BAB METODA ANALSS RANGKAAN Metod nlss rngkn sebenrny merupkn slh stu lt bntu untuk menyeleskn sutu permslhn yng muncul dlm mengnlss sutu rngkn, blmn konsep dsr tu hukum-hukum dsr sepert Hukum Ohm dn
Pemain P 1. Teorema 4.1 (Teorema minimax). Untuk setiap matriks pembayaran (pay off matrix), terdapat strategi optimal x* dan y* sedemikian sehingga
Rset Opers Probblstk Teor Permnn (Gme Theor) Deprtement of Mthemtcs FMIPA UNS Lecture 4: Med Strteg A. Metode Cmpurn (Med Strteg) D dlm permnn d mn permnn tersebut tdk mempun ttk peln, mk pr pemn kn bersndr
Koefisien Regresi / persamaan regresi linier digunakan untuk meramalkan / mengetahui besarnya pengaruh variabel X terhadap variabel Y
REGRESI Koefsen Regres / persmn regres lner dgunkn untuk mermlkn / mengethu esrny pengruh vrel terhdp vrel Vrel yng mempengruh ddlm nlss regres dseut vrel predktor ( ) Vrel yng dpengruh dseut vrel krterum
Metode Numerik. Regresi. Umi Sa adah Politeknik Elektronika Negeri Surabaya 2008 PENS-ITS
Metode Numerk Regres Um S dh Polteknk Elektronk Neger Surb 008 PENS-ITS 1 Metode Numerk Topk Regres Lner Regres Non Lner PENS-ITS Metode Numerk Metode Numerk Regres vs Interpols REGRESI KUADRAT TERKECIL
MATEMATIKA TEKNIK 2 3 SKS TEKNIK ELEKTRO UDINUS
MATEMATIKA TEKNIK SKS TEKNIK ELEKTRO UDINUS Integrl Fungs Kompleks 4 INTEGRAL FUNGSI KOMPLEKS Sepert hlny dlm fungs rl, dlm fungs kompleks jug dkenl stlh ntegrl fungs kompleks sert sft-sftny Sft kenltkn
VEKTOR. 1. Pengertian Vektor adalah besaran yang memiliki besar (nilai) dan arah. Vektor merupakan sebuah ruas garis yang
VEKTOR 1. Pengertin Vektor dlh besrn yng memiliki besr (nili dn rh. Vektor merupkn sebuh rus gris yng P berrh dn memiliki pnjng. Pnjng rus gris tersebut dlh pnjng vektor. Rus gris dri titik P dn berujung
1) BENTUK UMUM DAN BAGIAN-BAGIAN PERSAMAAN KUADRAT Bentuk umum persamaan kuadrat adalah seperti di bawah ini:
) BENTUK UMUM DAN BAGIAN-BAGIAN PERSAMAAN KUADRAT Bentuk umum persmn kudrt dlh seperti di bwh ini: b c dengn, b, c bilngn dn riil Dimn, disebut sebgi koefisien dri b disebut sebgi koefisien dri c disebut
ANALISIS OPTIMASI. Oleh Muhiddin Sirat*)
ANALISIS OPTIMASI Oleh Muhddn Srt*) I. PENDAHULUAN D tnju dr seg ekonom, sumber terjdny mslh ekonom yng dhdp msyrkt berwl dr kebutuhn mnus yng tdk terbts, dln phk sumber-sumber ekonom sngt terbts. Untuk
Teorema Gauss. Garis Gaya oleh muatan negatip. Garis gaya listrik. Garis gaya oleh sebuah muatan titik. Sebuah muatan negatip
Gs Gy Lstk Konsep fluks Teoem Guss Teoem Guss Penggunn Teoem Guss Medn oleh mutn ttk Medn oleh kwt pnjng tk behngg Medn lstk oleh plt lus tk behngg Medn lstk oleh bol solto dn kondukto Medn lstk oleh slnde
Menentukan Statistik Pengujian Untuk Eksperimen Faktorial dengan Dua Kali Pembatasan Pengacakan. Oleh : Enny Supartini
Menentukn Sttstk Pengujn Untuk Ekspermen Fktorl dengn Du Kl Pembtsn Pengckn Oleh : Enny Suprtn Jurusn Sttstk FMIPA Unversts Pdjdjrn Bndung e-ml : rthn@yhoo.com Abstrk Dlm ekspermen fktorl pbl pengckn tdk
BAB 6 FITTING DATA ˆ (6.1) (6.2) (6.3) =. Nilai akan. akan minimum jika. minimum. Misal. 0. Jika ini dikerjakan maka akan diperoleh nilai
BAB 6 FITTIG DATA Atu dseut dengn penookn dt tu menentukn kurv terk ng mellu set dt (sekumpuln dt) dengn keslhn mnmum. Ukurn keslhn dlh E (root men squre, kr kudrt rt-rt). Ad eerp mm pol fttng dt: menurut
5. INDUKSI MAGNETIK. A. Medan Magnetik
5. INDUKSI MAGNETIK Setelh mempeljr modul n, dhrpkn And dpt memhm konsep nduks mgnetk secr umum. Secr lebh khusus, And dhrpkn dpt : Mendeskrpskn hsl percobn Hns Chrstn Oersted tentng pengertn nduks mgnetk.
BAB I PENDAHULUAN. Universitas Sumatera Utara
BAB I PENDAHULUAN 1.1 Ltr Belkng Dlm teor permnn dkenl orng kembl setelh munculny kry bersm yng gemlng dr John Von Neumn dn V Mergenstern pd thun 1944 dengn judul Theory of Gmes nd economc behvor. Teor
2. PERSAMAAN, PERTIDAKSAMAAN DAN FUNGSI KUADRAT
. PERSAMAAN, PERTIDAKSAMAAN DAN FUNGSI KUADRAT A. Persmn Kudrt. Bentuk umum persmn kudrt : x + bx + c = 0, 0. Nili determinn persmn kudrt : D = b c. Akr-kr persmn kudrt dpt dicri dengn memfktorkn tupun
FISIKA. Sesi INDUKSI MAGNETIK A. KAWAT LURUS BERARUS
FISIKA KELAS XII IPA - KURIKULUM GABUNGAN 07 Ses NGAN INDUKSI MAGNETIK Pd bd kesembln bels, Hns Chrstn Oersted (777-85) membuktkn keterktn ntr gejl lstrk dn gejl kemgnetn. Oersted mengmt st jrum kmps dtempelkn
Bab a. maka notasi determinan dari matriks A ditulis : det (A) atau. atau A.
Bb DETERMINAN MATRIKS Determinn sutu mtriks dlh sutu fungsi sklr dengn domin mtriks bujur sngkr. Dengn kt lin, determinn merupkn pemetn dengn domin berup mtriks bujur sngkr, sementr kodomin berup sutu
Aljabar Linear dan Matriks (Transformasi Linier dan Matriks) Instruktur : Ferry Wahyu Wibowo, S.Si., M.Cs.
ljr Lner dn Mtrks (Trnsforms Lner dn Mtrks) Instruktur : Ferry Whyu Wowo SS MCs Penjumlhn Perkln Sklr dn Perkln Mtrks j : unsur dr mtrks d rs dn kolom j Defns Du mtrks dlh sm jk keduny mempuny ukurn yng
DETERMINAN. Misalkan A adalah suatu matriks persegi. a) Jika A memiliki satu baris atau satu kolom bilangan nol, maka det(a) = 0.
DETERMINAN Fungsi determinn dri sutu mtriks persegi A (dinotsikn dengn det(a) tu A ) didefinisikn sebgi jumlh dri semu hsil kli elementer bertnd dri A. Sementr, ngk tu bilngn dri det(a) disebut determinn
ANALISIS NUMERIK. Inter polasi. SPL simultan. Akar Persama. linear
ANALISIS NUMERIK Inter polsi SPL simultn Akr Persm n Non liner INTERPOLASI Tujun Interpolsi bergun untuk menksir hrg-hrg tengh ntr titik dt yng sudh tept. Interpolsi mempunyi orde tu derjt. Mcm Interpolsi
1. HUKUM SAMBUNGAN KIRCHOFF (HUKUM KIRCHOFF I) 2. HUKUM CABANG KIRCHOFF (HUKUM KIRCHOFF II)
MATA KULIAH KODE MK Dosen : FISIKA DASAR II : EL-22 : Dr. Budi Mulynti, MSi Pertemun ke-6 CAKUPAN MATERI. HUKUM SAMBUNGAN KIRCHOFF (HUKUM KIRCHOFF I) 2. HUKUM CABANG KIRCHOFF (HUKUM KIRCHOFF II) SUMBER-SUMBER:.
matematika K-13 TEOREMA FAKTOR DAN OPERASI AKAR K e l a s
K-3 mtemtik K e l s XI TEOREMA FAKTOR DAN OPERASI AKAR Tujun Pemeljrn Setelh mempeljri mteri ini, kmu dihrpkn memiliki kemmpun erikut.. Memhmi teorem fktor.. Menentukn kr dn fktor liner suku nyk dengn
3. LIMIT DAN KEKONTINUAN. INF228 Kalkulus Dasar
. LIMIT DAN KEKONTINUAN INF8 Klkulus Dsr . Limit Fungsi di Stu Titik Pengertin it secr intuisi Perhtikn ungsi Fungsi dits tidk terdeinisi di =, kren di titik tersebut berbentuk 0/0. Tpi msih bis ditnykn
3. LIMIT DAN KEKONTINUAN
. LIMIT DAN KEKONTINUAN . Limit Fungsi di Stu Titik Pengertin it secr intuisi Perhtikn ungsi Fungsi dits tidk terdeinisi di, kren di titik tersebut berbentuk 0/0. Tpi msih bis ditnykn berp nili jik mendekti
KAJIAN TENTANG SKEMA BEDA HINGGA KOMPAK ORDE-4
KAJIA TETAG SKEA BEDA HIGGA KOPAK ORDE-4 Eko Prsety Budn Abstrct : Fourth order compct fnte-dfference scheme s bsed on low-storge Runge-Kutt schemes for temporl dscretzton nd fourth order compct fnte-dfference
FISIKA BESARAN VEKTOR
K-3 Kels X FISIKA BESARAN VEKTOR TUJUAN PEMBELAJARAN Setelh mempeljri mteri ini, kmu dihrpkn memiliki kemmpun berikut.. Memhmi pengertin besrn vektor.. Mengusi konsep penjumlhn vektor dengn berbgi metode.
Matematika SKALU Tahun 1978
Mtemtik SKALU Thun 978 MA-78-0 Persmn c + b + = 0, mempunyi kr-kr dn, mk berlku A. + = b B. + = c C. = c = c = c MA-78-0 Akr dri persmn 5 - = 7 + dlh A. B. C. 4 5 MA-78-0 Hrg dri log b. b log c. c log
3. LIMIT DAN KEKONTINUAN
3. LIMIT DAN KEKONTINUAN 1 3.1 Limit Fungsi di Stu Titik Pengertin it secr intuisi Perhtikn ungsi 1 1 Fungsi dits tidk terdeinisi di =1, kren di titik tersebut berbentuk 0/0. Tpi msih bis ditnykn berp
PRAKTIKUM 6 Penyelesaian Persamaan Linier Simultan Metode Eliminasi Gauss Jordan
Prtum 6 Penyelesn Persmn Lner Smultn - Metode Elmns Guss Jordn PRAKTIKUM 6 Penyelesn Persmn Lner Smultn Metode Elmns Guss Jordn. Tujun : Mempeljr metode Elmns Guss Jordn untu penyelesn persmn lner smultn.
Kerjakan di buku tugas. Tentukan hasil operasi berikut. a. A 2 d. (A B) (A + B) b. B 2 e. A (B + B t ) c. A B f. A t (A t + B t ) Tes Mandiri
Mmt Apliksi SMA Bhs Dikethui A = Tentukn hsil opersi berikut A c A A b A A d A Dikethui A = Tentukn hsil opersi berikut (A + B) c (B A) b A + AB + B d B BA + A Sol Terbuk Kerjkn di buku tugs Jik X = dn
MODEL PENJADWALAN BATCH PADA FLOWSHOP DUA TAHAP DENGAN VARIASI JUMLAH PART UNTUK MEMINIMASI TOTAL ACTUAL FLOW TIME
MODEL PEJADWALA BATCH PADA LOWSHOP DUA TAHAP DEGA VARIASI JUMLAH PART UTUK MEMIIMASI TOTAL ACTUAL LOW TIME Prty Poer Surydhn Industrl Engneerng Study Progrm, Industrl Engneerng culty, Telkom Unversty prty@telkomunversty.c.d
SISTEM BILANGAN REAL. 1. Sifat Aljabar Bilangan Real
SISTEM BILANGAN REAL Dlm terminologi Aljbr Abstrk, sistem bilngn rel disebut dengn field (lpngn) pd opersi penjumlhn dn perklin. Sutu opersi biner bis ditulis dengn sutu psngn terurut (, b) yng unik dri
LIMIT DAN KONTINUITAS
LIMIT DAN KONTINUITAS Limit Fungsi di Stu Titik Pengertin it secr intuisi Perhtikn ungsi Fungsi dits tidk terdeinisi di =, kren di titik tersebut berbentuk 0/0. Tpi msih bis ditnykn berp nili jik mendekti
CONTOH SOLUSI BEBERAPA SOAL OLIMPIADE MATEMATIKA Oleh: Wiworo, S.Si, M.M. 3. Untuk k 2 didefinisikan bahwa a
CONTOH SOLUSI BEBERAPA SOAL OLIMPIADE MATEMATIKA Oleh: Wiworo, S.Si, M.M. Dikethui bhw,. Untuk k didefinisikn bhw k k k. Tentukn jumlh tk hingg dri. Kit mislkn S S. Dengn demikin kit dpt menuliskn Kedu
Aljabar Linear Elementer
ljbr Liner Elementer M SKS Silbus : Bb I Mtriks dn Opersiny Bb II Determinn Mtriks Bb III Sistem Persmn Liner Bb IV Vektor di Bidng dn di Rung Bb V Rung Vektor Bb VI Rung Hsil Kli Dlm Bb VII Trnsformsi
BAB II LANDASAN TEORI
BAB II LANDASAN TEORI Bb berikut ini kn disjikn mteri pendukung yng dpt membntu penulis untuk menyelesikn permslhn yng kn dibhs pd bb selnjutny. Adpun mteri pendukungny dlh pengertin mtriks, jenis-jenis
SOAL UN MATEMATIKA IPA 2014
SOAL UN MATEMATIKA IPA 2014 1. Dkethu prems-prems berkut : Prems 1 : Jk hr hujn, mk tnmn pd subur. Prems 2 : Jk pnen tdk melmph, mk tnmn pd tdk subur. Prems 3 : Pnen tdk melmph Kesmpuln yng sh dr prems-prems
BAB 1 PENDAHULUAN. 1.1 Latar Belakang
BAB PENDAHULUAN. Ltr Belkg Smp st, model Regres d model Alss Vrs telh dpdg sebg du hl g tdk berkt. Meskpu merupk pedekt g umum dlm meergk kedu cr pd trf permul, model Alss Vrs dpt dpdg sebg hl khusus model
BAB 2 LANDASAN TEORI
BAB LANDASAN TEORI. Persmn Smultn Persmn smultn tmbul hmpr dsetp cbng mtemtk, dlm beberp hl, persmn n tmbul lngsung dr perumusn mul dr persolnny, ddlm hl ln penyelesn dr persmn merupkn bgn dr pengerjn
r x = 0. Koefisien-koefisien persamaan yang dihasilkan adalah analitik pada x = 0. Jadi dapat kita gunakan metode deret pangkat.
Husn Arifh,M.Sc : Persmn Legendre Emil : husnrifh@uny.c.id Persmn diferensil Legendre (1) 1 x 2 y 2xy + n n + 1 y = 0 Prmeter n pd (1) dlh bilngn rill yng diberikn. Setip penyelesin dri (1) dinmkn fungsi
INTEGRAL. Bogor, Departemen Matematika FMIPA IPB. (Departemen Matematika FMIPA IPB) Kalkulus I Bogor, / 45
INTEGRAL Deprtemen Mtemtik FMIPA IPB Bogor, 2012 (Deprtemen Mtemtik FMIPA IPB) Klkulus I Bogor, 2012 1 / 45 Topik Bhsn 1 Pendhulun 2 Anti-turunn 3 Lus di Bwh Kurv 4 Integrl Tentu 5 Teorem Dsr Klkulus 6
Aljabar Linear Elementer
ljbr Liner Elementer M3 3 SKS Silbus : Bb I Mtriks dn Opersiny Bb II Determinn Mtriks Bb III Sistem Persmn Liner Bb IV Vektor di Bidng dn di Rung Bb V Rung Vektor Bb VI Rung Hsil Kli Dlm Bb VII Trnsformsi
Integral Tak Wajar. Ayundyah Kesumawati. March 25, Prodi Statistika FMIPA-UII
Kesumwti Prodi Sttistik FMIPA-UII Mrch 25, 205 Sutu integrl tertentu b f (x)dx () diktkn wjr jik i memenuhi du syrt berikut: i. Bts integrsi dn b merupkn bilngn berhingg ii. fungsi f (x) terbts pd intervl
Penyelesaian Persamaan Kuadrat 1. Rumus abc Rumus menentukan akar persamaan kuadrat ax 2 bx c 0; a, b, c R dan a 0
PERSAMAAN, PERTIDAKSAMAAN DAN FUNGSI KUADRAT PERSAMAAN KUADRAT Bentuk umum persmn kudrt dlh c 0,,,c R, 0 Penyelesin Persmn Kudrt. Rumus c Rumus menentukn kr persmn kudrt c 0;,, c R dn 0, = ± 4c. Memfktorkn
MUH1G3/ MATRIKS DAN RUANG VEKTOR
MUHG3/ MATRIKS DAN RUANG VEKTOR TIM DOSEN 3 Sistem Persmn Liner Sistem Persmn Liner Su Pokok Bhsn Pendhulun Solusi SPL dengn OBE Solusi SPL dengn Invers mtriks dn Aturn Crmmer SPL Homogen Beerp Apliksi
MODEL POTENSIAL 1 DIMENSI
MODEL POTENSIAL 1 DIMENSI 1. Sumur Potensil Tk Berhingg Kit tinju prtikel bermss m dengn energi positif, berd dlm sumur potensil stu dimensi dengn dinding potensil tk berhingg dn potensil didlmny nol,
. = Arah induksi magnet tegak lurus bidang gambar menuju pembaca x = Arah induksi magnet tegak lurus bidang gambar menjauhi pembaca
7.7 MEDAN MAGNET INDUKSI Gejl Kemgnetn : Medn Mgnet dlh rungn yng memberkn gy mgnet kepd bend-bend dn mutn lstrk yng bergerk dsektrny. Adny medn mgnet dnytkn dengn grs-grs gy mgnet ( grs nduks ) Apbl membentuk
BAB: PENERAPAN INTEGRAL Topik: Volume Benda Putar (Khusus Kalkulus 1)
BAB: PENERAPAN INTEGRAL Topik: Volume Bend Putr (Khusus Klkulus ) Kompetensi yng diukur dlh kemmpun mhsisw menghitung volume bend putr dengn metode cincin, metode ckrm, tu metode kulit tbung.. UAS Klkulus,
PERSAMAAN DAN PERTIDAKSAMAAN LOGARITMA
K- Kels X mtemtik PEMINATAN PERSAMAAN DAN PERTIDAKSAMAAN LOGARITMA Tujun Pembeljrn Setelh mempeljri mteri ini, kmu dihrpkn memiliki kemmpun berikut.. Memhmi definisi persmn dn pertidksmn logritm.. Dpt
Menerapkan konsep vektor dalam pemecahan masalah. Menerapkan konsep vektor pada bangun ruang
VEKTOR PADA BIDANG SK : Menerpkn konsep vektor dlm pemechn mslh KD : Menerpkn konsep vektor pd bidng dtr Menerpkn konsep vektor pd bngun rung TUJUAN PELATIHAN: Pesert memiliki kemmpun untuk mengembngkn
Equation 1. ( ) i. Equation 2
Predks Defleks Jngk Pnjng Deforms pd elemen-elemen pregngn kn berubh sejln dengn wku sebg kb rngkk dn susu beon ser relkss egngn pd bj. Defleks elemen-elemen pregngn dp dhung secr relf erhdp sebuh dum,
PRAKTIKUM 9 Penyelesaian Persamaan Linier Simultan Metode Eliminasi Gauss Jordan
Prtum 9 Penyelesn Persmn Lner Smultn - Metode Elmns Guss Jordn PRAKTIKUM 9 Penyelesn Persmn Lner Smultn Metode Elmns Guss Jordn Tujun : lner smultn Mempeljr metode Elmns Guss Jordn untu penyelesn persmn
10/21/2011 POKOK BAHASAN MODEL DATAMINING DEFINISI KATEGORI DALAM DATA MINING. Definisi Kategori Model Naïve Bayesian k-nearest Neighbor Clustering
0//0 POKOK BAHASAN Defns Ktegor Model Nïve Byesn k-nerest Neghbor Clusterng MODEL DATAMINING Bhn Kulh : Topk Khusus DEFINISI DEFINISI Mnng : proses tu ush untuk mendptkn sedkt brng berhrg dr sejumlh besr
PenerapanTeori Respons Butir Dalam Penyetaran Tes. Kana Hidayati Jurusan Pendidikan Matematika FMIPA UNY ABSTRAK
PenerpnTeor Respons Butr Dlm Penyetrn Tes Kn Hdyt Jurusn Penddkn Mtemtk FMIPA UNY ABSTRAK Penyetrn tes perlu dlkukn khususny bg kegtn pengujn dlm skl besr yng memperspkn lebh dr stu perngkt tes mengngt
ξ. Elemen elemen dari ruang vektor
KEGITN BELJR REPRESENTSI MTRIKS Rung Hlbert "ξ" Menurut nots drc Vektor Ket dn Vektor Br Setp elemen tu vektor ddlm rung hlbert dsebut vektor ket tu ket Ket menurut nots drc dnytkn dengn smbol " " Supy
Two-Stage Nested Design
Mteri #13 TIN309 DESAIN EKSPERIMEN Two-Stge Nested Design Nested design dlh slh stu ksus dri desin multi fktor dimn level dri slh stu fktor (misl: fktor B) serup tpi tidk identik untuk setip level yng
LIMIT FUNGSI DAN KEKONTINUAN
LIMIT FUNGSI DAN KEKONTINUAN RANGKUMAN MATERI Sebelum memsuki mteri, perhtikn himpunn-himpunn berikut: ) Himpunn bilngn sli:,,,4,5,.... b) Himpunn bilngn bult:...,,,0,,,.... p c) Himpunn bilngn rsionl:
Kegiatan Belajar 5. Aturan Sinus. Kegiatan 5.1
Pge of 8 Kegitn eljr 5. Tujun Pembeljrn Setelh mempeljri kegitn beljr 5, dihrpkn sisw dpt. Menentukn unsur-unsur segitig dengn turn sinus b. Menentukn unsur-unsur segitig dengn turn kosinus. Menghitung
PERSAMAAN KUADRAT, FUNGSI KUADRAT DAN PERTIDAKSAMAAN KUADRAT
PERSAMAAN KUADRAT, FUNGSI KUADRAT DAN PERTIDAKSAMAAN KUADRAT Persmn Kudrt. Bentuk Umum Persmn Kudrt Mislkn,, Є R dn 0 mk persmn yng erentuk 0 dinmkn persmn kudrt dlm peuh. Dlm persmn kudrt 0, dlh koefisien
PERTEMUAN - 1 JENIS DAN OPERASI MATRIKS
PERTEMUN - JENIS DN OPERSI MTRIKS Pengertin Mtriks : merupkn sutu lt tu srn yng sngt mpuh untuk menyelesikn model-model liner. Definisi : Mtriks dlh susunn empt persegi pnjng tu bujur sngkr dri bilngn-bilngn
b. Notasi vektor : - Vektor A dinotasikan a atau a atau PQ - Panjang vektor a dinotasikan a atau PQ
BAB 4 VEKTOR Stndr Kompetensi: 3. Menggunkn konsep mtriks, vektor, dn trnsformsi Kompetensi Dsr: 3.4 Menggunkn sift-sift dn opersi ljbr vktor dlm pemechn mslh 3.5 Menggunkn sift-sift dn opersi perklin
BAB ALJABAR MARIX Dlm pokok bhsn ini kn disjikn dsr-dsr opersi ljbr mtrix yng berhubungn dengn nlisis struktur dengn menggunkn metode mtrix kekkun (stiffness method)... Pengertin Mtrix Mtrix merupkn sutu
III. LIMIT DAN KEKONTINUAN
KALKULUS I MUG1A4 PROGRAM PERKULIAHAN DASAR DAN UMUM PPDU TELKOM UNIVERSITY III. LIMIT DAN KEKONTINUAN 3.1 Limit Fungsi di Stu Titik Pengertin it secr intuisi Perhtikn ungsi 1 1 Fungsi dits tidk terdeinisi
PROBLEM SOLVING TERKAIT DENGAN KELAS X SEMESTER 1 PADA STANDAR KOMPETENSI (SK) 1.
PROLEM SOLVING TERKIT DENGN KELS X SEMESTER PD STNDR KOMPETENSI (SK). LJR Memechkn mslh yng berkitn dengn bentuk pngkt, kr, dn logritm Oleh: Sigit Tri Guntoro. Du orng berselisih mengeni bnykny psngn bilngn
LUAS DENGAN PARTISI SEGITIGA UNTUK FUNGSI CEKUNG
Posdng Semt05 dng MIPA BKS-PTN Bt Unvests Tnjungpu Pontnk Hl 7 - LUAS DENGAN PARTISI SEGITIGA UNTUK FUNGSI CEKUNG Jun Lest Nengsh *, Symsudhuh, Lel Deswt Juusn Mtemtk Unvests Ru, Ru jun.lest@gml.om, Kmpus
INTEGRAL FOURIER KED. Diasumsikan syarat-syarat berikut pada f(x): 1. f x memenuhi syarat Dirichlet pada setiap interval terhingga L, L.
INTEGRAL FOURIER Disumsikn syrt-syrt berikut pd f(x):. f x memenuhi syrt Dirichlet pd setip intervl terhingg L, L.. f x dx konvergen, yitu f(x) dpt diintegrsikn secr mutlk dlm (, ). Selnjutny, Teorem integrl
PERSAMAAN KUADRAT, FUNGSI KUADRAT DAN GRAFIKNYA
PERSAMAAN KUADRAT, FUNGSI KUADRAT DAN GRAFIKNYA Persmn dlh klimt mtemtik teruk ng memut huungn sm dengn. Sedngkn klimt mtemtik tertutup ng memut huungn sm dengn diseut kesmn. Klimt mtemtik :. Klimt mtemtik
15. INTEGRAL SEBAGAI LIMIT
15. INTEGRAL SEBAGAI LIMIT 15.1 Jumlh Riemnn Dlm kulih Klkulus pd thun pertm, integrl Riemnn bisny diperkenlkn sebgi limit dri jumlh Riemnn, tidk mellui integrl Riemnn ts dn integrl Riemnn bwh. Hl ini
RUMUS HERON DAN RUMUS BRAHMAGUPTA
RUMUS HERON DAN RUMUS BRAHMAGUPTA Sumrdyono, M.Pd. Topik lus bngun dtr telh dipeljri sejk di Sekolh Dsr hingg SMA. Bil di SD, dipeljri lus segitig dn beberp bngun segiempt mk di SMP dipeljri lebih lnjut
2. Paman mempunyai sebidang tanah yang luasnya 5 hektar. Tanah itu dibagikan kepada 3. Luas tanah yang diterima oleh mereka masing-masing = 5 :3 1
. Hitunglh 7 5. : b. 5 : c. 8 : 6 d. 8 9 7 7 7 5 77 77 77. : c. 8 : 6 : 6 6 9 9 9 6 54 8 40 7 b. 5: 5 d. 4: 4: 4 6 8 7 95 Husein Tmpoms, Rumus-rumus Dsr Mtemtik 4 :. Pmn mempunyi sebidng tnh yng lusny
TURUNAN FUNGSI. LA - WB (Lembar Aktivitas Warga Belajar) MATEMATIKA PAKET C TINGKAT VI DERAJAT MAHIR 2 SETARA KELAS XI
LA - WB (Lembr Aktivits Wrg Beljr) TURUNAN FUNGSI Oleh: Hj. ITA YULIANA, S.Pd, M.Pd MATEMATIKA PAKET C TINGKAT VI DERAJAT MAHIR 2 SETARA KELAS XI Creted By It Yulin 33 Turunn Fungsi Kompetensi Dsr 1. Menggunkn
Matriks yang mempunyai jumlah baris sama dengan jumlah kolomnya disebut matriks bujur sangkar (square matrix). contoh :
TRIKS. PENGERTIN triks dlh sutu deretn elemen yng mementuk empt persegi pnjng, terdiri dri m ris dn n kolom. Elemen terseut dpt erentuk koefisien, ilngn tu simul. triks yng mempunyi m ris dn n kolom diseut
BAB I. MATRIKS BAB II. DETERMINAN BAB III. INVERS MATRIKS BAB IV. PENYELESAIAN PERSAMAAN LINEAR SIMULTAN
DFTR ISI BB I. MTRIKS BB II. DETERMINN BB III. INVERS MTRIKS BB IV. PENYELESIN PERSMN LINER SIMULTN BB I. MTRIKS Mtriks erup sekelompok ilngn yng disusun empt persegi dn ditsi tnd terdiri dri ris dn kolom
Jarak Titik, Garis dan Bidang dalam Ruang
Pge of Kegitn eljr. Tujun Pembeljrn Setelh mempeljri kegitn beljr, dihrpkn sisw dpt :. Menentukn jrk titik dn gris dlm rung b. Menentukn jrk titik dn bidng dlm rung c. Menentukn jrk ntr du gris dlm rung.
CATATAN KULIAH Pertemuan XI: Optimasi Tanpa Kendala dan Aplikasinya (Fungsi dengan Variabel 2 atau Lebih) II. = dx
CATATAN KULIA ertemun XI: Optms Tnp Kendl dn Aplksny (Fungs dengn Vrel tu Leh) II A. Fungs Tujun dengn Leh dr Du Vrel Bentuk Umum Fungs Vrel : z( ) Derensl Totl Orde Stu: Derensl Totl Orde Du: Derensl
A. PENGERTIAN B. DETERMINAN MATRIKS
ATRIKS A. PENGERTIAN triks dlh sutu deretn elemen yng mementuk empt persegi pnjng, terdiri dri m ris dn n kolom. Elemen terseut dpt erentuk koefisien, ilngn tu simul. triks yng mempunyi m ris dn n kolom
Deret Fourier. (Pertemuan X) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya
TKS 47 Mtemtik III Deret Fourier (Pertemun X) Dr. AZ Jurusn Teknik Sipil Fkults Teknik Universits Brwijy Pendhulun Deret Fourier ditemukn oleh ilmun Perncis, Jen Bptiste Joseph Fourier (768-83) yng menytkn
det DEFINISI Jika A 0 disebut matriks non singular
DETERINAN DEFINISI Untuk setip mtriks persegi (bujur sngkr), d stu bilngn tertentu yng disebut determinn Determinn dlh jumlh semu hsil kli elementer bertnd dri sutu mtriks bujur sngkr. Disimbolkn dengn:
STRATEGI PENGAJARAN MATEMATIKA UNTUK MENENTUKAN AKAR-AKAR PERSAMAAN KUADRAT
Jurnl Vol II. No., Mret 08, hlm. 9-95 vilble online t www.jurnl.un.c.id/indeks/jmp STRTEGI PENGJRN MTEMTIK UNTUK MENENTUKN KR-KR PERSMN KUDRT Indh Purnm Putri, Symsudhuh, Ihd Hsbiyti 3 Progrm Studi Mgister
BAB 10. MATRIKS DAN DETERMINAN
Dessy Dwiynti, S.Si, MBA Mtemtik Ekonomi 1 BAB 10. MATRIKS DAN DETERMINAN 1. Pengertin mtriks Mtriks kumpuln bilngn yng disjikn secr tertur dlm bris dn kolom yng membentuk sutu persegi pnjng, sert termut
BABAK PENYISIHAN AMSO JENJANG SMA PEMBAHASAN BABAK PENYISIHAN AMSO
. Jwbn : C 8 3 8 6 3 3 3 6 BABAK PENYISIHAN AMSO JENJANG SMA PEMBAHASAN BABAK PENYISIHAN AMSO. Jwbn : C Tig bilngn prim pertm yng lebih besr dri 0 dlh 3, 9, dn 6. Mk 3 + 9 + 6 = 73. Jdi, jumlh tig bilngn
12. LUAS DAERAH DAN INTEGRAL
12. LUAS DAERAH DAN INTEGRAL 12.1 Lus Derh di Bwh Kurv Mslh menentukn lus derh (dn volume rung) telh dipeljri sejk er Pythgors dn Zeno, pd thun 500-n SM. Konsep integrl (yng terkit ert dengn lus derh)
VEKTOR. Adri Priadana. ilkomadri.com
VEKTOR Adri Pridn ilkomdri.com Pengertin Dlm Fisik dikenl du buh besrn, yitu 1. Besrn Sklr. Besrn Vektor Pengertin Besrn Sklr dlh sutu besrn yng hny mempunyi nili dn dinytkn dengn sutu bilngn tunggl diserti
BAB III VEKTOR DALAM R 2 DAN R 3. Bab III Vektor dalam R 2 dan R 3
Bb III Vetor dlm R dn R BAB III VEKTOR DALAM R DAN R Dlm bgn n n dbhs mslh eto-etor dlm rng berdmens dn berdmens, opers-opers rtmet pd etor g n ddefnsn dn beberp sft-sft dsr opers-opers tersebt... VEKTOR
Matriks. Pengertian. Lambang Matrik
triks Pengertin Definisi: trik dlh susunn bilngn tu fungsi yng diletkkn ts bris dn kolom sert dipit oleh du kurung siku. Bilngn tu fungsi tersebut disebut entri tu elemen mtrik. mbng mtrik dilmbngkn dengn
MATRIKS. Agustina Pradjaningsih, M.Si. Jurusan Matematika FMIPA UNEJ
MTRIKS gustin Prdjningsih, M.Si. Jurusn Mtemtik FMIP UNEJ tinprdj.mth@gmil.com DEFINISI MTRIKS Sutu dftr bilngn-bilngn rel tu kompleks terdiri ts m bris dn n kolom, m dn n bilngn bult positip disebut mtriks
BAB 7. LIMIT DAN LAJU PERUBAHAN
BAB 7. LIMIT DAN LAJU PERUBAHAN 7. LIMIT FUNGSI 7.. Limit fungsi di sutu titik Menggmbrkn perilku fungsi jik peubhn mendekti sutu titik Illustrsi: Dikethui f( ) f(), 3,30,0 3,030,00 3,003 3 f() = f() 3,000?
Dr.Eng. Agus S. Muntohar Department of Civil Engineering
Pertemu ke-7 Persm Ler Smult Oktober 0 Metode Iters Guss-Sedel Dr.Eg. Agus S. Mutohr Deprtmet of Cvl Egeerg Metode Guss-Sedel Merupk metode ters. Prosedur umum: - Selesk ser lbr vrbel tdk dkethu msg-msg
MA3231 Analisis Real
MA3231 Anlisis Rel Hendr Gunwn* *http://hgunwn82.wordpress.com Anlysis nd Geometry Group Bndung Institute of Technology Bndung, INDONESIA Progrm Studi S1 Mtemtik ITB, Semester II 2016/2017 HG* (*ITB Bndung)
f 1 f 2 f 3 η(t) α(f 2 ) a(f 1 ) 2a(f) Metode Least Square untuk Analisis Harmonik
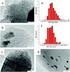Meode Les Squre unuk nlss Hrmonk Secr umum meode Les Squre mencr koefsen seuh rumus yng dhrpkn dp mendek suu gel d lpngn semksml mungkn. Dengn demkn meode n sellu erpsngn dengn seuh model persmn yng dusulkn
12 Langkah Penyelesaian Pendekatan
Meto Elemen Hngg Dlm Hrulk B 4 Dsr eu: Lngkh Penyelesn Penektn Ir. Djoko Luknnto, M.S., Ph.D. mlto:luknnto@ugm.. Revew (hl.96) Anlss yng utuhkn: Û(;) hrus r Integrs Resul rter Optms p R(;) untuk menentukn
Materi V. Determianan dinotasikan berupa pembatas dua gris lurus,
Mteri V Tujun : 1. Mhsisw dpt mengenli determinn.. Mhsisw dpt merubh persmn linier menjdi persmn determinn.. Mhsisw menelesikn determinn ordo du. Mhsisw mmpu menelesikn determinn ordo tig. Mhsisw mengethui
Solusi Pengayaan Matematika Edisi 4 Januari Pekan Ke-4, 2007 Nomor Soal: 31-40
Solusi Pengn Mtemtik Edisi 4 Jnuri Pekn Ke-4, 007 Nomor Sol: -40. Diberikn persmn 8 9 4 8 007 dn b, dengn b. Angk stun dri b dlh. A. B. C. D. 7 E. 9 Persmn 8 9 4 8 8 9 4 8 9 4 8 8 8 9 8 4 8 8 8 0 0 b tu
Universitas Esa Unggul
ALJABAR LINIER DAN MATRIKS BHAN KULIAH DRA SURYARI PURNAMA, MM Universits Es Unggul Minggu I Mtriks Pokok Bhsn Sub Pokok Bhsn Tujun Instruksionl Umum Tujun Instruksionl Khusus : Pendhulun Mtriks : A. Pengertin
BAB II LANDASAN TEORI
BAB II LANDASAN TEORI. Mtriks Definisi. (Anton, Howrd. ). Mtriks dlh sutu susunn bilngn berbentuk segi empt. Bilngn-bilngn dlm susunn itu disebut nggot dlm mtriks tersebut. Ukurn (size) sutu mtriks dinytkn
Skew- Semifield dan Beberapa Sifatnya 1
Skew- Semifield dn Beberp Siftny K r y t i Jurusn Pendidikn Mtemtik Fkults Mtemtik dn Ilmu Pengethun Alm Universits Negeri Yogykrt E-mil: ytiuny@yhoo.com Abstrk Sutu field ( lpngn ) F dlh struktur ljbr
PENDAHULUAN. 1993). Pada penelitian ini menggunakan rancangan acak kelompok dengan model liniear aditif ditulis sebagai berikut: Latar belakang
PENDAHULUAN Ltr belkng Anlss rgm memerlukn sums yng kett, slh stuny sums kehomogenn rgm. Pdhl bnyk ksus d lpngn yng ggl dlm memenuh sums n. Dlm percobn multloks serng terjd ketdkhomogenn rgm pd fktor loks
BAB III. PERANCANGAN ANTENA BRICK 2,4 GHz
BAB III PERANCANGAN ANTENA BRICK, GHZ BAB III PERANCANGAN ANTENA BRICK, GHz 3. Pernnn Anten Brik Bb ini menjelskn proses pernnn nten brik denn melkukn beberp perhitunn yn terdiri dri beberp prmeter yn
Soal-soal dan Pembahasan Matematika Dasar SBMPTN-SNMPTN 2006
www.purwntowhyudi.com Hl- Sol-sol dn Pemhsn Mtemtik Dsr SBMPTN-SNMPTN 006. Jik > 0, > 0 dn mk A. C. E. B. D. Jw:. Jwnny dlh A. Jik p - dn q -, mk q p. A. C. E. B. D. Jw: q p Jwnny dlh A . Grfik y terletk
Integral Tak Tentu dan Integral Tertentu
Integrl Tk Tentu dn Integrl Tertentu Pengertin Integrl Jik F dlh fungsi umum yng ersift F = f, mk F merupkn ntiturunn tu integrl dri f. Pengintegrln fungsi f terhdp dinotsikn segi erikut : f d F c notsi
matematika K-13 IRISAN KERUCUT: PERSAMAAN HIPERBOLA K e l a s A. Definisi Hiperbola Tujuan Pembelajaran
K-13 mtemtik K e l s I IRISAN KERUCUT: PERSAMAAN HIPERBLA Tujun Pemeljrn Setelh mempeljri mteri ini, kmu dihrpkn memiliki kemmpun erikut. 1. Memhmi definisi dn unsur-unsur hiperol.. Dpt menentukn persmn