Bab 1 Vektor. A. Pendahuluan
|
|
|
- Utami Chandra
- 7 tahun lalu
- Tontonan:
Transkripsi
1 Bab 1 Vektor A. Pendahuluan Dalam mata kuliah Listrik Magnet A, maupun mata kuliah Listrik Magnet B sebagaii lanjutannya, penyajian konsep dan pemecahan masalah akan banyak memerlukan pengetahuan tentang vektor, mecakup gradien skalar, divergensi dan rotasi vektor, integral garis, integral permukaan, teorema Stokes, teorema divergensi Gauss, dan penyajiannya dalam beragam sistem koordinat. Oleh karena itu, sebelum membahas tentang masalah kelistrikan dan kemagnetan dalam mata kuliah ini, pokok bahasan tentang vector ini perlu diberikan terlebih dahulu. Meskipun materi yang ada dalam pokok bahasan ini cukup banyak materi ini diharapkan dapat diselesaikan dalam waktu yang relatif cukup singkat. Hal ini demikian karena mata kuliah-mata kuliah yang menjadi prasyarat mata kuliah ini semestinya sudah menyediakan pengetahuan yang cukup, khususnya tentang vektor, untuk dapat mengikuti mata kuliah ini dengan baik; jadi ini hanya sebagai semacam review. Setelah mengikuti kuliah pokok bahasan ini, mahasiswa diharapkan dapat mengkalkulasi gradien skalar, divergensi dan rotasi suatu vektor, integral garis dan integral permukaan, serta menggunakan teorema divergensi dan teorema Stokes, dapat menyatakan hubunganhubungan antara sistem-sistem koordinat Cartesian, Silinder dan Bola, dapat menyatakan suatu vektor, vektor letak, elemen volume, gradien skalar, divergensi dan rotasi vektor, serta Laplacian dalam ketiga sistem koordinat tersebut. B. Penyajian 1.1 Definisi Vektor, Vektor Satuan, dan Komponen Vektor Definisi Vektor Vektor adalah besaran yang memiliki nilai (magnitude) dan arah (direction). Di sini, vektor dilambangkan oleh sebuah huruf atau karakter dengan tanda panah di atasnya, seperti, yang besar atau nilainya ditulis sebagai = A. Sebuah vektor digambarkan sebagai sebuah anak panah (Gambar 1.1). Contoh besaran vektor: medan listrik, medan magnet, gaya, dll. Skalar adalah besaran yang hanya memiliki nilai, seperti massa benda m. Universits Gadjah Mada 1
2 Gambar 1.1 Sebuah vektor digambar sebagai sebuah anak panah. Dua buah vektor dikatakan sama jika keduanya memiliki nilai dan arah yang sama. Vektor negatif (atau negatif vektor ) adalah vektor yang sama besar tetapi berlawanan arah dengan vektor. Vektor-vektor patuh pada aturan penjumlahan seperti ditunjukkan oleh Gambar 1.2, yang menunjukkan bahwa (1-1) Pengurangan vektor dengan vektor lainnya tidak lain adalah penjumlahan vektor dengan negative vektor lain tadi (Gambar 4), yaitu ( ) (1-2) Vektor Satuan Vektor satuan adalah vektor yang besarnya satu (tanpa satuan); sebagai contoh ditulis sebagai (besarnya =1), yaitu vektor satuan dalam arah vektor (Gambar 1.4). Dengan demikian: Universits Gadjah Mada 2
3 Vektor-vektor satuan dalam sistem koordinat Cartesian (SKC) di sini adalah,, dan berturut-turut dalam arah sumbu x, sumbu y, dan sumbu z positif. Komponen Vektor Jika vektor digambar dalam SKC (Gambar 1.5), maka ia dapat ditulis sebagai atau Di sini,, dan adalah vektor-vektor komponen dari vektor ; sedangkan,, dan disebut komponen-komponen vektor. Besar (nilai) vektor dinyatakan dengan komponen-komponennya: Universits Gadjah Mada 3
4 Sudut Arah Vektor Sebuah vektor dalam SKC membetuk sudut-sudut α, β, dan berturut-turut terhadap sumbu-sumbu x, y dan z (Gambar 1.6.a). Sudut-sudut α, β, dan ini disebut sudut arah vektor. Gambar 1.6.b memperlihatkan bidang yang dibentuk oleh vektor dengan sumbu x, sudut arah α, serta komponen A x (gambar serupa untuk bidang-bidang yang dibentuk oleh vektor dengan sumbu x dan sumbu y). Dari Gambar 1.6.b diperoleh cosinus-cosinus arah vektor : sehingga berlaku hubungan: Dapat ditulis bahwa: Universits Gadjah Mada 4
5 Komponen-komponen vektor satuan merupakan cosinus-cosinus arah vektor. Penjumlahan Vektor dalam SKC Ditinjau jumlahan vektor dalam bidang xy (2 dimensi), seperti ditunjukkan oleh Gambar 1.7. Vektor hasil jumlahan: Dengan Untuk penjumlahan dalam 3 dimensi: dengan Universits Gadjah Mada 5
6 1.2 Vektor Letak Vektor letak ( sering ditulis sebagai ) menunjukkan letak suatu titik di dalam ruang (sistem koordinat), berpangkal di titik asal O dan berujung di titik yang ditinjau. Anggap bahwa di dalam sistem koordinat Cartesian (lihat Gambar 1.8): - letak titik P(x, y, z) : - letak titik P (x, y, z ) : Vektor letak P relative terhadap P (Gambar 1.8): atau Jarak antara P dan P adalah Vektor letak P relative terhadap P adalah Jadi diperoleh bahwa Universits Gadjah Mada 6
7 1.3 Perkalian dengan Vektor Perkalian Skalar dengan Vektor Perkalian skalar s dengan vektor, ditulis sebagai s atau s, merupakan jumlahan s buah vektor, yaitu sebuah vektor yang besarnya kali, arahnya sama dengan arah jika s positif, berlawanan arah dengan arah jika s negatif. Perkalian Titik (Dot Product) Perkalian titik atau dot product disebut juga sebagai perkalian skalar atau scalar product, yaitu perkalian dua vektor yang menghasilkan sebuah skalar. Perkalian titik antara vektor-vektor dan didefinisikan sebagai dengan adalah sudut kecil yang dibentuk oleh kedua vektor dan (lihat Gambar 1.9). Berlaku bahwa Jika dan saling tegak lurus (ortogonal), maka Perkalian titik suatu vektor dengan dirinya sendiri : Perkalian titik antara vektor-vektor satuan dalam SKC: sehingga Universits Gadjah Mada 7
8 Jika adalah vektor satuan dalam suatu arah, dan A e adalah komponen vektor dalam arah tersebut, maka berlaku bahwa (lihat Gambar 1.10) Perkalian Silang (Cross Product) Perkalian silang atau cross product disebut juga perkalian vektor atau vector product, yaitu perkalian dua vektor yang menghasilkan vektor baru. Perkalian silang antara vektor-vektor dan didefinisikan sebagai dengan dengan adalah sudut kecil yang dibentuk oleh kedua vektor dan (lihat Gambar 1.11) dan vektor memiliki arah yang tegak lurus terhadap bidang yang dibentuk oleh kedua vektor dan sesuai dengan aturan tangan kanan ; Nilai AB sin ini sama dengan luas jajaran genjang dengan sisi-sisi vektor dan. Universits Gadjah Mada 8
9 Berlaku bahwa Jika searah dengan,maka. Jadi Perkalian silang antara vektor-vektor satuan dalam SKC: Sehingga Yang dapat diungkapkan dalam bentuk determinan sebagai Berlaku pula : 1.4 Diferensiasi Vektor terhadap Skalar Suatu vektor sebagai fungsi kontinyu dari variabel skalar s dapat ditulis sebagai Universits Gadjah Mada 9
10 Diferensial (turunan) terhadap s: Sebagai contoh: - vektor letak sebagai fungsi waktu : ( ) ( ) ( ) ( ) - kecepatan : ( ) ( ) ( ) ( ) ( ) Dapat ditulis bahwa: 1.5 GradienSkalar Ditinjau besaran skalar u sebagai fungsi letak: u = u(x, y, z); Besaran skalar ini disebut medan skalar contoh: suhu ruangan. Anggap bahwa (Gambar 1.12): - Di titik P(x, y, z), nilai skalar u adalah u(x, y, z); - Di titik lain P (x,y,z ), dengan x = x + dx, y = y + dy, z = z + dz, nilai skalar u adalah u (x,y,z ) = u(x,y,z) + du Jadi, dari titik P ke titik P ada pergeseran yang menyebabkan perubahan scalar dari u menjadi u = u + du. Kenyataannya du dapat diungkapkan sebagai Dengan diferensial parsial dievaluasi di titik P. Di lain pihak Universits Gadjah Mada 10
11 Dengan demikian dapat ditulis bahwa Dengan Persamaan (1-34), yaitu ungkapan, disebut gradien skalar u, atau singkatnya gradien u (grad u), yang definisi umumnya diberikan oleh persamaan (1-33); ia memiliki sifat sebagai vektor. Jadi, gradien skalar merupakan besaran yang akan memberikan perubahan skalar jika di- dot -kan dengan pergeseran. Ditinjau suatu permukaan dengan nilai u tetap. Pergeseran sepanjang permukaan ini tidak mengubah nilai skalar u (du = 0) (lihat Gambar 1.13). Dengan demikian. berarti tegak lurus terhadap. Jadi, tegak lurus terhadap permukaan yang memiliki u tetap. Universits Gadjah Mada 11
12 Sekarang dianggap pergeseran membentuk sudut terhadap seperti ditunjukkan oleh Gambar 1.14, maka. Dengan demikian, du akan maksimum jika = 0, yaitu jika searah dengan yang tegak lurus terhadap permukaan dengan u tetap. Jadi, arah gradien skalar menunjukkan arah ke mana laju perubahan skalar bernilai maksimum. Ditinjau sebagai contoh u = y 2 x. Dapat ditulis bahwa y 2 = x + u, yaitu parabola-parabola dengan u tetap. Untuk : Untuk : Untuk : Ketiga parabola ini ditunjukkan oleh Gambar Vektor satuan yang tegak lurus suatu permukaan di suatu titik disebut vektor normal. Mengingat bahwa juga tegak lurus permukaan dengan u tetap, maka searah dengan, dan kita dapat menuliskan bahwa Vektor normal permukaan parabola dengan u = -2 adalah Dan di titik (3,1) adalah Universits Gadjah Mada 12
13 Jadi, terlihat pada Gambar 1.15, bahwa arah lebih besar (lebih positif). (searah dengan ) menuju ke skalar u yang 1.6 Divergensi dan Rotasi Vektor Komponen-komponen vektor dapat bergantung pada letak, misalnya A x = A x (x, y, z). Jadi, dapat berbeda arah dan/atau besarnya di tempat-tempat yang berbeda. Ditulis : dengan adalah vektor letak. Vektor ini disebut medan vektor. Dari persamaan (1-34) diperoleh operator nabla atau operator del: yang memiliki sifat vektor. Yang dinamakan sebagai divergensi (atau ditulis juga sebagai div ) adalah sedangkan rotasi (atau ditulis juga sebagai curl atau rot ) adalah atau dalam bentuk determinan: Operator Laplacian: bekerja pada skalar: bekerja pada vektor: Universits Gadjah Mada 13
14 Berlaku pula 1.7 Integral Garis Dibayangkan kita bergerak dari titik awal P i (x i,y i, z i ) ke titik P f (x f, y f, z f ) melalui lintasan sepanjang kurva C di dalam medan vektor (Gambar 1.16). Lintasan ini dapat dipandang sebagai jumlahan sejumlah vektor pergeseran infinitesimal sepanjang kurva C. Integral garis sepanjang kurva C merupakan hasil evaluasi vektor di tiap, yaitu komponen sepanjang dikalikan dengan, tidak lain adalah A cos ds =, kemudian semuanya dijumlahkan; ini ditulis sebagai: Jika lintasan integrasi berupa kurva tertutup, seperti lingkaran, titik awal berimpit dengan titik akhir, maka integral garis ditulis sebagai: yang disebut sirkulasi, dapat bernilai nol atau tak nol bergantung pada. Jika adalah vektor letak tiap titik pada kurva C, maka, sehingga Perhatian: Di sini, dx, dy, dan dz tidaklah saling bebas karena x, y, dan z dihubungkan oleh persamaan lintasan (kurva C); demikian juga dengan A x, A y, dan A z. Contoh: Diketahui medan vektor :, dan lintasan berupa parabola antara Universits Gadjah Mada 14
15 (0,0,0) dan (2,,0). Dengan demikian, lintasan terletak di bidang xy, yaitu bidang z = 0, dan berarti z tetap atau dz =0, sehingga Karena, maka dan, sehingga 1.8 Integral Permukaan Sebelum membahas tentang integral permukaan, bahasan tentang vektor elemen luasan perlu diuraikan terlebih dahulu. Vektor Elemen Luasan Pada Gambar 1.17, da adalah elemen luasan infinitesimal sedemikian sehingga berbentuk datar (tidak harus horisontal). Vektor elemen luasan ini adalah Dengan adalah vektor normal elemen luasan da. Ada dua arah yang mungkin yang saling berlawanan sehingga perlu ada kesepakatan; ada 2 kasus. Kasus I da merupakan bagian dari suatu permukaan terbuka yang dibatasi oleh kurva tertutup C. Dalam kasus ini kita perlu memilih atau menentukan arah lintasan pada kurva C tersebut, kemudian menggunakan aturan tangan kanan untuk menentukan arah (Gambar 1.18). Universits Gadjah Mada 15
16 Kasus II: da merupakan bagian dari suatu permukaan tertutup. Dalam hal ini tidak ada kurva C; permukaan ini membagi ruang menjadi dalam dan luar. Arah senantiasa dipilih dari dalam ke luar. Jika ungkapan dan digabung, maka dapat ditulis bahwa dengan - adalah komponen-x dari, proyeksi da pada bidang yz; - adalah komponen-y dari, proyeksi da pada bidang xz; - adalah komponen-z dari, proyeksi da pada bidang xy. Dapat ditunjukkan bahwa: ( + digunakan jika < 90, - jika > 90 ), ( + digunakan jika < 90, - jika > 90 ), (1-50) ( + digunakan jika < 90, - jika > 90 ). Integral Permukaan Ditinjau suatu permukaan S yang berada di dalam medan vektor (Gambar 1.19). Elemen luasan pada permukaan ini adalah da; vektor elemen luasannya adalah. Universits Gadjah Mada 16
17 Di tiap elemen luasan da pada S, komponen dalam arah, yaitu A cos, dikalikan dengan, kemudian semuanya dijumlahkan, hasilnya disebut sebagai integral permukaan pada S ; ditulis: Integral permukaan ini disebut juga sebagai fluks yang melewati permukaan S. Jika permukaan S merupakan permukaan tertutup, maka integral permukaan ditulis sebagai yang dapat bernilai nol atau tak nol bergantung pada. Dalam SKC, dan, sehingga Ingat: dx, dy, dan dz tidak saling bebas, demikian juga dengan,, dan. Contoh: Diketahui permukaan S berupa seperempat piringan Iingkaran berjejari b yang berpusat di O (titik asal SKC) di kuadran I pada bidang xy berada dalam medan vektor, seperti ditunjukkan oleh Gambar Persamaan lingkaran ini adalah. Permukaan S pada bidang xy, maka dapat merupakan atau. Anggap dipilih =, maka da = da z = dxdy. Dengan demikian, integral permukaan: Universits Gadjah Mada 17
18 1.9 Teorema Divergensi Gauss dan Teorema Stokes Teorema Divergensi Gauss Ditinjau suatu ruang V (volumenya V) yang dibatasi oleh suatu permukaan tertutup S (contoh: bola, kubus, dli) berada dalam medan vektor. Teorema divergensi Gauss diungkapkan secara matematik sebagai dengan adalah elemen volume. Teorema ini menghubungkan integral permukaan suatu medan vektor dengan integral volume divergensi medan vektor tersebut. Integral permukaan hanya bergantung pada nilai di permukaan; integral volume memerlukan pengetahuan tentang, bukan tentang di seluruh volume. Teorema ini berlaku juga untuk ruang yang dibatasi oleh lebih dari satu permukaan tertutup. Teorema Stokes Ditinjau suatu permukaan terbuka S sembarang yang dibatasi oleh suatu kurva tertutup C berada dalam medan vektor (Gambar 1.21). Teorema Stokes diungkapkan secara matematik sebagai: Teorema ini menghubungkan integral garis suatu medan vektor pada suatu lintasan tertutup dengan integral permukaan rotasi medan vektor tersebut pada permukaan yang dibatasi oleh lintasan tertutup tersebut. Arah ditentukan oleh arah lintasan pada kurva C dan dengan menggunakan aturan tangan kanan. Untuk kurva-kurva tertutup C yang sama dan permukaan-permukaan S 1 dan S 2 yang berbeda, maka Universits Gadjah Mada 18
19 Teorema ini berlaku juga untuk permukaan yang dibatasi oleh lebih dari satu kurva tertutup; contoh permukaan yang dibatasi oleh dua kurva tertutup ditunjukkan oleh Gambar Vektor dalam Sistem Koordinat Silinder dan Bola Vektor dalam Sistem Koordinat Silinder (SKS) Letak titik dalam SKS ditentukan oleh koordinat ( ). Hubungan SKS dengan SKC ditunjukkan oleh Gambar 1.23 Variabel merupakan jarak dari sumbu z. Variabel merupakan sudut m( Ukur dari sumbu x positif). Variabel merupakan jarak dari bidang xy. Hubungan koordinat SKS dengan koordinat SKC: Universits Gadjah Mada 19
20 Vector-vektor satuan dalam SKS, yaitu dan saling tegak lurus: Arah senantiasa tetap, sedangkan arah dan berbeda-beda di titik-titik yang berbeda. Hubungan vector-vektor satuan dalam SKS dan SKC: Diferensial vektor satuan dalam SKS: Dalam SKS, ungkapan suatu vektor adalah sedangkan ungkapan vektor letak adalah Ungkapan vektor pergeseran infinitesimal adalah atau Jika medan skalar ( ), maka Mengingat bahwa, maka gradien skalar dalam SKS: dan operator nabla dalam SKS: Universits Gadjah Mada 20
21 Komponen-komponen vector elemen luasan dalam SKS : Elemen volume dalam SKS (Gambar 1.24) Volume total: Divergensi vektor dalam SKS: Rotasi vektor dalam SKS: Laplacian dalam SKS: Vektor dalam Sistem Koordinat Bola (SKB) Letak titik dalam SKB ditentukan oleh koordinat ( ). Hubungan SKB dengan SKC ditunjukkan oleh Gambar Variabel r adalah jarak dari pusat sistem koordinat. Variabel adalah sudut yang diukur dari sumbu z positif ` Variabel adalah sudut yang diukur dari sumbu x positif Universits Gadjah Mada 21
22 Hubungan koordinat SKB dengan koordinat SKC : Vektor-vektor satuan dalam SKB, yaitu,, dan, saling tegak lurus: Arah masing-masing vektor satuan,, dan berbeda-beda di titik-titik yang berbeda. Hubungan vektor-vektor satuan dalam SKB dan SKC: Universits Gadjah Mada 22
23 Diferensial vektor-vektor satuan dalam SKB: Dalam SKB, ungkapan suatu vektor adalah Sedangkan ungkapan vektor letak adalah Ungkapan vektor pergeseran infinitesimal adalah, atau Komponen-komponen vektor elemen luasan dalam SKB: Elemen volume dalam SKB (Gambar 1.26): Universits Gadjah Mada 23
24 Volume total Jika medan skalar ( ) maka Mengingat bahwa, maka gradien skalar dalam SKS: dan operator nabla dalam SKB: Divergensi vektor dalam SKB: Rotasi vektor dalam SKB: Laplacian dalam SKB: C. Penutup Setelah mempelajari pokok bahasan ini, mahasiswa diharapkan dapat menyelesaikan soalsoal latihan berikut ini. 1. Carilah vektor letak relatif titik P(2, -2, 3) terhadap titik P (-3, 1, 4)! Tentukan sudutsudut arah! 2. Diketahui dan. Carilah komponen sepanjang arah! Universits Gadjah Mada 24
25 3. Diketahui persamaan suatu kelompok ellipsoida sebagai. Carilah vektor satuan normal di tiap titik di permukaan tiap ellipsoida ini! 4. Diketahui medan vektor. Hitunglah secara langsung fluks yang melewati permukaan balok yang memiliki sisi-sisi a, b, dan c seperti ditunjukkan oleh Gambar 1.27! Hitunglah pada seluruh volume balok tersebut, dan bandingkan hasil-hasil yang diperoleh! 5. Diketahui medan vektor dengan,, dan adalah tetapan-tetapan. Hitunglah secara langsung integral pada lintasan tertutup dalam bidang xy seperti ditunjukkan oleh Gambar 1.28! Kurva lengkung adalah parabola y 2 = kx dengan k adalah tetapan. Hitunglah integral permukaan pada seluruh luasan S yang dibatasi oleh kurva C, dan bandingkan hasil-hasil yang diperoleh! 6. Diketahui dengan a, b, dan c adalah tetapan-tetapan. Apakah merupakan vektor yang tetap (konstan)? Carilah dan! Carilah komponenkomponen dalam SKC (x, y, z) dan SKB ( )! 7. Carilah untuk vektor letak yang diungkapkan dalam SKC, SKS, dan SKB! Universits Gadjah Mada 25
26 8. Diketahui vector, carilah integral garisnya pada lintasan tertutup seperti yang ditunjukkan oleh Gambar Kurva lengkung merupakan busur lingkaran berjejari r 0 yang berpusat di titik asal O. Cari juga integral permukaan pada luasan yang dibatasi oleh kurva tertutup tadi, dan bandingkan hasil-hasil yang diperoleh! 9. Dengan menerapkan teorema divergensi pada kasus khusus adalah vektor tetap dan sembarang, tunjukkan bahwan luasan vektor total suatu permukaan tertutup adalah nol, yaitu! Serupa dengannya, tunjukkan bahwa! Daftar Pustaka 1. Wangsness, R.K., 1979, Electromagnetic Fields, John Wiley & Sons, New York Universits Gadjah Mada 26
Bab 4 Hukum Gauss. A. Pendahuluan
 Bab 4 Hukum Gauss A. Pendahuluan Pada pokok bahasan ini, disajikan tentang hukum Gauss yang memberikan fluks medan listrik yang melewati suatu permukaan tertutup yang melingkupi suatu distribusi muatan.
Bab 4 Hukum Gauss A. Pendahuluan Pada pokok bahasan ini, disajikan tentang hukum Gauss yang memberikan fluks medan listrik yang melewati suatu permukaan tertutup yang melingkupi suatu distribusi muatan.
Bab 3 Medan Listrik. A. Pendahuluan
 Bab 3 Medan Listrik A. Pendahuluan Pada pokok bahasan ini, akan disajikan tentang medan listrik, baik konsep maupun cara memperolehnya dari beragam distribusi muatan, baik distribusi muatan diskrit (sistem
Bab 3 Medan Listrik A. Pendahuluan Pada pokok bahasan ini, akan disajikan tentang medan listrik, baik konsep maupun cara memperolehnya dari beragam distribusi muatan, baik distribusi muatan diskrit (sistem
Bab 5 Potensial Skalar. A. Pendahuluan
 Bab 5 Potensial Skalar A. Pendahuluan Pada pokok bahasan terdahulu medan listrik merupakan besaran vektor yang memberikan informasi lengkap tentang efek-efek elektrostatik. Secara substansial informasi
Bab 5 Potensial Skalar A. Pendahuluan Pada pokok bahasan terdahulu medan listrik merupakan besaran vektor yang memberikan informasi lengkap tentang efek-efek elektrostatik. Secara substansial informasi
ANALISIS VEKTOR. Aljabar Vektor. Operasi vektor
 ANALISIS VEKTOR Aljabar Vektor Operasi vektor Besaran yang memiliki nilai dan arah disebut dengan vektor. Contohnya adalah perpindahan, kecepatan, percepatan, gaya, dan momentum. Sementara itu, besaran
ANALISIS VEKTOR Aljabar Vektor Operasi vektor Besaran yang memiliki nilai dan arah disebut dengan vektor. Contohnya adalah perpindahan, kecepatan, percepatan, gaya, dan momentum. Sementara itu, besaran
BESARAN VEKTOR. Gb. 1.1 Vektor dan vektor
 BAB 1 BESARAN VEKTOR Tujuan Pembelajaran 1. Menjelaskan definisi vektor, dan representasinya dalam sistem koordinat cartesius 2. Menjumlahkan vektor secara grafis dan dengan vektor komponen 3. Melakukan
BAB 1 BESARAN VEKTOR Tujuan Pembelajaran 1. Menjelaskan definisi vektor, dan representasinya dalam sistem koordinat cartesius 2. Menjumlahkan vektor secara grafis dan dengan vektor komponen 3. Melakukan
9.1. Skalar dan Vektor
 ANALISIS VEKTOR 9.1. Skalar dan Vektor Skalar Satuan yang ditentukan oleh besaran Contoh: panjang, voltase, temperatur Vektor Satuan yang ditentukan oleh besaran dan arah Contoh: gaya, velocity Vektor
ANALISIS VEKTOR 9.1. Skalar dan Vektor Skalar Satuan yang ditentukan oleh besaran Contoh: panjang, voltase, temperatur Vektor Satuan yang ditentukan oleh besaran dan arah Contoh: gaya, velocity Vektor
Teorema Divergensi, Teorema Stokes, dan Teorema Green
 TEOREMA DIVERGENSI, STOKES, DAN GREEN Materi pokok pertemuan ke 13: 1. Teorema divergensi Gauss URAIAN MATERI Untuk memudahkan perhitungan seringkali dibutuhkan penyederhanaan bentuk integral yang berdasarkan
TEOREMA DIVERGENSI, STOKES, DAN GREEN Materi pokok pertemuan ke 13: 1. Teorema divergensi Gauss URAIAN MATERI Untuk memudahkan perhitungan seringkali dibutuhkan penyederhanaan bentuk integral yang berdasarkan
BAB 1 BESARAN VEKTOR. A. Representasi Besaran Vektor
 BAB 1 BESARAN VEKTOR TUJUAN PEMBELAJARAN 1. Menjelaskan definisi vektor, dan representasinya dalam sistem koordinat cartesius 2. Menjumlahan vektor secara grafis dan matematis 3. Melakukan perkalian vektor
BAB 1 BESARAN VEKTOR TUJUAN PEMBELAJARAN 1. Menjelaskan definisi vektor, dan representasinya dalam sistem koordinat cartesius 2. Menjumlahan vektor secara grafis dan matematis 3. Melakukan perkalian vektor
Bab 2 Hukum Coulomb A. Pendahuluan
 Bab 2 Hukum Coulomb A. Pendahuluan Pada pokok bahasan ini disajikan tentang hukum Coulomb, yaitu hukum dasar yang mengatur tentang gaya interaksi (gaya Coulomb) antara muatan-muatan yang terpisah pada
Bab 2 Hukum Coulomb A. Pendahuluan Pada pokok bahasan ini disajikan tentang hukum Coulomb, yaitu hukum dasar yang mengatur tentang gaya interaksi (gaya Coulomb) antara muatan-muatan yang terpisah pada
Program Studi Teknik Mesin S1
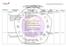 SATUAN ACARA PERKULIAHAN MATA KULIAH : MATEMATIKA TEKNIK 2 KODE/SKS : IT042227 / 2 SKS Pertemuan Pokok Bahasan dan TIU 1 Pendahuluan Mahasiswa mengerti tentang mata kuliah Matematika Teknik 2 : bahan ajar,
SATUAN ACARA PERKULIAHAN MATA KULIAH : MATEMATIKA TEKNIK 2 KODE/SKS : IT042227 / 2 SKS Pertemuan Pokok Bahasan dan TIU 1 Pendahuluan Mahasiswa mengerti tentang mata kuliah Matematika Teknik 2 : bahan ajar,
Catatan Kuliah FI2101 Fisika Matematik IA
 Khairul Basar atatan Kuliah FI2101 Fisika Matematik IA Semester I 2015-2016 Fakultas Matematika dan Ilmu Pengetahuan Alam Institut Teknologi Bandung Bab 6 Analisa Vektor 6.1 Perkalian Vektor Pada bagian
Khairul Basar atatan Kuliah FI2101 Fisika Matematik IA Semester I 2015-2016 Fakultas Matematika dan Ilmu Pengetahuan Alam Institut Teknologi Bandung Bab 6 Analisa Vektor 6.1 Perkalian Vektor Pada bagian
Bab 1 : Skalar dan Vektor
 Bab 1 : Skalar dan Vektor 1.1 Skalar dan Vektor Istilah skalar mengacu pada kuantitas yang nilainya dapat diwakili oleh bilangan real tunggal (positif atau negatif). x, y dan z kita gunakan dalam aljabar
Bab 1 : Skalar dan Vektor 1.1 Skalar dan Vektor Istilah skalar mengacu pada kuantitas yang nilainya dapat diwakili oleh bilangan real tunggal (positif atau negatif). x, y dan z kita gunakan dalam aljabar
dengan vektor tersebut, namun nilai skalarnya satu. Artinya
 1. Pendahuluan Penggunaan besaran vektor dalam kehidupan sehari-hari sangat penting mengingat aplikasi besaran vektor yang luas. Mulai dari prinsip gaya, hingga bidang teknik dalam memahami konsep medan
1. Pendahuluan Penggunaan besaran vektor dalam kehidupan sehari-hari sangat penting mengingat aplikasi besaran vektor yang luas. Mulai dari prinsip gaya, hingga bidang teknik dalam memahami konsep medan
VEKTOR. Gambar 1.1 Gambar 1.2 Gambar 1.3. Liduina Asih Primandari, S.Si., M.Si.
 VEKTOR 1 A. Definisi vektor Beberapa besaran Fisika dapat dinyatakan dengan sebuah bilangan dan sebuah satuan untuk menyatakan nilai besaran tersebut. Misal, massa, waktu, suhu, dan lain lain. Namun, ada
VEKTOR 1 A. Definisi vektor Beberapa besaran Fisika dapat dinyatakan dengan sebuah bilangan dan sebuah satuan untuk menyatakan nilai besaran tersebut. Misal, massa, waktu, suhu, dan lain lain. Namun, ada
Aljabar Vektor. Sesi XI Vektor 12/4/2015
 Mata Kuliah : Matematika Rekayasa Lanjut Kode MK : TKS 8105 Pengampu : Achfas Zacoeb Sesi XI Vektor e-mail : zacoeb@ub.ac.id www.zacoeb.lecture.ub.ac.id Hp. 081233978339 Aljabar Vektor Vektor juga memiliki
Mata Kuliah : Matematika Rekayasa Lanjut Kode MK : TKS 8105 Pengampu : Achfas Zacoeb Sesi XI Vektor e-mail : zacoeb@ub.ac.id www.zacoeb.lecture.ub.ac.id Hp. 081233978339 Aljabar Vektor Vektor juga memiliki
VEKTOR. Besaran skalar (scalar quantities) : besaran yang hanya mempunyai nilai saja. Contoh: jarak, luas, isi dan waktu.
 VEKTOR Kata vektor berasal dari bahasa Latin yang berarti "pembawa" (carrier), yang ada hubungannya dengan "pergeseran" (diplacement). Vektor biasanya digunakan untuk menggambarkan perpindahan suatu partikel
VEKTOR Kata vektor berasal dari bahasa Latin yang berarti "pembawa" (carrier), yang ada hubungannya dengan "pergeseran" (diplacement). Vektor biasanya digunakan untuk menggambarkan perpindahan suatu partikel
Universitas Gadjah Mada 1
 I. Nama Mata Kuliah : LISTRIK MAGNET A II. Kode / SKS : MSF-2411 / 2 III. Prasyarat : - Mekanika B (MSF-2128)** - Fisika Matematik IA (MSF-2010A)** (** harus pernah ditempuh meskipun tidak lulus) IV. Status
I. Nama Mata Kuliah : LISTRIK MAGNET A II. Kode / SKS : MSF-2411 / 2 III. Prasyarat : - Mekanika B (MSF-2128)** - Fisika Matematik IA (MSF-2010A)** (** harus pernah ditempuh meskipun tidak lulus) IV. Status
BAB I VEKTOR DALAM BIDANG
 BAB I VEKTOR DALAM BIDANG I. KURVA BIDANG : Penyajian secara parameter Suatu kurva bidang ditentukan oleh sepasang persamaan parameter. ; dalam I dan kontinue pada selang I, yang pada umumnya sebuah selang
BAB I VEKTOR DALAM BIDANG I. KURVA BIDANG : Penyajian secara parameter Suatu kurva bidang ditentukan oleh sepasang persamaan parameter. ; dalam I dan kontinue pada selang I, yang pada umumnya sebuah selang
BAB II VEKTOR DAN GERAK DALAM RUANG
 BAB II VEKTOR DAN GERAK DALAM RUANG 1. KOORDINAT CARTESIUS DALAM RUANG DIMENSI TIGA SISTEM TANGAN KANAN SISTEM TANGAN KIRI RUMUS JARAK,,,, 16 Contoh : Carilah jarak antara titik,, dan,,. Solusi :, Persamaan
BAB II VEKTOR DAN GERAK DALAM RUANG 1. KOORDINAT CARTESIUS DALAM RUANG DIMENSI TIGA SISTEM TANGAN KANAN SISTEM TANGAN KIRI RUMUS JARAK,,,, 16 Contoh : Carilah jarak antara titik,, dan,,. Solusi :, Persamaan
Matematika Dasar INTEGRAL PERMUKAAN
 Matematika asar INTEGRAL PERMUKAAN Misal suatu permukaan yang dinyatakan dengan persamaan z = f( x,y ) dan merupakan proyeksi pada bidang XOY. Bila diberikan lapangan vektor F( x,y,z ) = f( x,y,z ) i +
Matematika asar INTEGRAL PERMUKAAN Misal suatu permukaan yang dinyatakan dengan persamaan z = f( x,y ) dan merupakan proyeksi pada bidang XOY. Bila diberikan lapangan vektor F( x,y,z ) = f( x,y,z ) i +
fi5080-by-khbasar BAB 1 Analisa Vektor 1.1 Notasi dan Deskripsi
 BB 1 nalisa Vektor Vektor, dibedakan dari skalar, adalah suatu besaran yang memiliki besar dan arah. rtinya untuk mendeskripsikan suatu besaran vektor secara lengkap perlu disampaikan informasi tentang
BB 1 nalisa Vektor Vektor, dibedakan dari skalar, adalah suatu besaran yang memiliki besar dan arah. rtinya untuk mendeskripsikan suatu besaran vektor secara lengkap perlu disampaikan informasi tentang
BAB II V E K T O R. Untuk menyatakan arah vektor diperlukan sistem koordinat.
 .. esaran Vektor Dan Skalar II V E K T O R da beberapa besaran fisis yang cukup hanya dinyatakan dengan suatu angka dan satuan yang menyatakan besarnya saja. da juga besaran fisis yang tidak cukup hanya
.. esaran Vektor Dan Skalar II V E K T O R da beberapa besaran fisis yang cukup hanya dinyatakan dengan suatu angka dan satuan yang menyatakan besarnya saja. da juga besaran fisis yang tidak cukup hanya
Selain besaran pokok dan turunan, besaran fisika masih dapat dibagi atas dua kelompok lain yaitu besaran skalar dan besaran vektor
 Selain besaran pokok dan turunan, besaran fisika masih dapat dibagi atas dua kelompok lain yaitu besaran skalar dan besaran vektor Besaran skalar adalah besaran yang hanya memiliki nilai saja. Contoh :
Selain besaran pokok dan turunan, besaran fisika masih dapat dibagi atas dua kelompok lain yaitu besaran skalar dan besaran vektor Besaran skalar adalah besaran yang hanya memiliki nilai saja. Contoh :
Program Studi Pendidikan Matematika STKIP PGRI SUMBAR
 INTEGRASI VEKTOR Materi pokok pertemuan ke 11: 1. Integral Biasa 2. Integral Garis URAIAN MATERI Sebelum masuk ke integral garis, Anda pelajari dulu mengenai integral biasa dari vektor. Integral Biasa
INTEGRASI VEKTOR Materi pokok pertemuan ke 11: 1. Integral Biasa 2. Integral Garis URAIAN MATERI Sebelum masuk ke integral garis, Anda pelajari dulu mengenai integral biasa dari vektor. Integral Biasa
Bab 6 Konduktor dalam Medan Elektrostatik. 1. Pendahuluan
 Bab 6 Konduktor dalam Medan Elektrostatik 1. Pendahuluan Pada pokok bahasan terdahulu tentang hukum Coulomb, telah diasumsikan bahwa daerah di antara muatan-muatan merupakan ruang hampa. Di sini akan dibahas
Bab 6 Konduktor dalam Medan Elektrostatik 1. Pendahuluan Pada pokok bahasan terdahulu tentang hukum Coulomb, telah diasumsikan bahwa daerah di antara muatan-muatan merupakan ruang hampa. Di sini akan dibahas
Gradien, Divergensi, dan Curl
 GRADIEN, DIVERGENSI, DAN CURL Materi pokok pertemuan ke 8 : 1. Operator Del 2. Gradien 3. Turunan berarah URAIAN MATERI Operator Del Operator del merupakan operator pada diferensial vektor yang disimbolkan
GRADIEN, DIVERGENSI, DAN CURL Materi pokok pertemuan ke 8 : 1. Operator Del 2. Gradien 3. Turunan berarah URAIAN MATERI Operator Del Operator del merupakan operator pada diferensial vektor yang disimbolkan
BESARAN SKALAR DAN VEKTOR. Besaran Skalar. Besaran Vektor. Sifat besaran fisis : Skalar Vektor
 PERTEMUAN II VEKTOR BESARAN SKALAR DAN VEKTOR Sifat besaran fisis : Skalar Vektor Besaran Skalar Besaran yang cukup dinyatakan oleh besarnya saja (besar dinyatakan oleh bilangan dan satuan). Contoh : waktu,
PERTEMUAN II VEKTOR BESARAN SKALAR DAN VEKTOR Sifat besaran fisis : Skalar Vektor Besaran Skalar Besaran yang cukup dinyatakan oleh besarnya saja (besar dinyatakan oleh bilangan dan satuan). Contoh : waktu,
Diferensial Vektor. (Pertemuan V) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya
 TKS 4007 Matematika III Diferensial Vektor (Pertemuan V) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya Operator Del Operator del merupakan operator pada diferensial vektor yang disimbolkan
TKS 4007 Matematika III Diferensial Vektor (Pertemuan V) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya Operator Del Operator del merupakan operator pada diferensial vektor yang disimbolkan
Pertemuan : 4 Materi : Fungsi Bernilai Vektor dan Gerak Sepanjang Kurva Bab II. Diferensial Kalkulus Dari Vektor
 Pertemuan : 4 Materi : Fungsi Bernilai Vektor dan Gerak Sepanjang Kurva Bab II. Diferensial Kalkulus Dari Vektor Standar Kompetensi : Setelah mengikuti perkuliahaan ini mahasiswa diharapkan dapat : 1.
Pertemuan : 4 Materi : Fungsi Bernilai Vektor dan Gerak Sepanjang Kurva Bab II. Diferensial Kalkulus Dari Vektor Standar Kompetensi : Setelah mengikuti perkuliahaan ini mahasiswa diharapkan dapat : 1.
ALJABAR LINEAR DAN MATRIKS. MODUL 10 Kalkulus Vektor. Zuhair Jurusan Teknik Informatika Universitas Mercu Buana Jakarta 2007 年 12 月 30 日 ( 日 )
 ALJABAR LINEAR DAN MATRIKS MODUL 10 Kalkulus Vektor Zuhair Jurusan Teknik Informatika Universitas Mercu Buana Jakarta 2007 年 12 月 30 日 ( 日 ) Kalkulus Vektor Kalkulus vektor (vector calculus) atau sering
ALJABAR LINEAR DAN MATRIKS MODUL 10 Kalkulus Vektor Zuhair Jurusan Teknik Informatika Universitas Mercu Buana Jakarta 2007 年 12 月 30 日 ( 日 ) Kalkulus Vektor Kalkulus vektor (vector calculus) atau sering
Arahnya diwakili oleh sudut yang dibentuk oleh A dengan ketigas umbu koordinat,
 VEKTOR Dalam mempelajari fisika kita selalu berhubungan dengan besaran, yaitu sesuatu yang dapat diukur dan dioperasikan. da besaran yang cukup dinyatakan dengan nilai (harga magnitude) dan satuannya saja,
VEKTOR Dalam mempelajari fisika kita selalu berhubungan dengan besaran, yaitu sesuatu yang dapat diukur dan dioperasikan. da besaran yang cukup dinyatakan dengan nilai (harga magnitude) dan satuannya saja,
Dr. Ramadoni Syahputra Jurusan Teknik Elektro FT UMY
 SISTEM-SISTEM KOORDINAT Dr. Ramadoni Syahputra Jurusan Teknik Elektro FT UMY Sistem Koordinat Kartesian Dalam sistem koordinat Kartesian, terdapat tiga sumbu koordinat yaitu sumbu x, y, dan z. Suatu titik
SISTEM-SISTEM KOORDINAT Dr. Ramadoni Syahputra Jurusan Teknik Elektro FT UMY Sistem Koordinat Kartesian Dalam sistem koordinat Kartesian, terdapat tiga sumbu koordinat yaitu sumbu x, y, dan z. Suatu titik
Suryadi Siregar Metode Matematika Astronomi 2
 Suryadi Siregar Metode Matematika Astronomi Bab 4 Integral Garis dan Teorema Green 4. Integral Garis Definisi : Misal suatu lintasan dalam ruang dimensi m pada interval [a,b]. Andaikan adalah medan vektor
Suryadi Siregar Metode Matematika Astronomi Bab 4 Integral Garis dan Teorema Green 4. Integral Garis Definisi : Misal suatu lintasan dalam ruang dimensi m pada interval [a,b]. Andaikan adalah medan vektor
BAB II LANDASAN TEORI. A. Tinjauan Pustaka. 1. Vektor
 BAB II LANDASAN TEORI A. Tinjauan Pustaka 1. Vektor Ada beberapa besaran fisis yang cukup hanya dinyatakan dengan suatu angka dan satuan yang menyatakan besarnya saja. Ada juga besaran fisis yang tidak
BAB II LANDASAN TEORI A. Tinjauan Pustaka 1. Vektor Ada beberapa besaran fisis yang cukup hanya dinyatakan dengan suatu angka dan satuan yang menyatakan besarnya saja. Ada juga besaran fisis yang tidak
Pengantar KULIAH MEDAN ELEKTROMAGNETIK MATERI I ANALISIS VEKTOR DAN SISTEM KOORDINAT
 KULIAH MEDAN ELEKTROMAGNETIK Pengantar Definisi Arsitektur MATERI I ANALISIS VEKTOR DAN SISTEM KOORDINAT Operasional Sinkronisasi Kesimpulan & Saran Muhamad Ali, MT Http://www.elektro-uny.net/ali Pengantar
KULIAH MEDAN ELEKTROMAGNETIK Pengantar Definisi Arsitektur MATERI I ANALISIS VEKTOR DAN SISTEM KOORDINAT Operasional Sinkronisasi Kesimpulan & Saran Muhamad Ali, MT Http://www.elektro-uny.net/ali Pengantar
Pertemuan : 9 Materi : Teorema Green Bab IV. Teorema Green, Teorema Divergensi Gauss, dan Teorema Stokes
 Pertemuan : 9 Materi : Teorema Green Bab IV. Teorema Green, Teorema Divergensi Gauss, dan Teorema Stokes Standar Kompetensi : 1. Memahami Teorema Green Kompetensi Dasar : 1. Menyebutkan kembali pengertian
Pertemuan : 9 Materi : Teorema Green Bab IV. Teorema Green, Teorema Divergensi Gauss, dan Teorema Stokes Standar Kompetensi : 1. Memahami Teorema Green Kompetensi Dasar : 1. Menyebutkan kembali pengertian
Integral Vektor. (Pertemuan VII) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya
 TK 47 Matematika III Integral Vektor (Pertemuan VII) Dr. AZ Jurusan Teknik ipil Fakultas Teknik Universitas Brawijaya Teorema Gauss Definisi : Jika V adalah volume yang dibatasi oleh suatu permukaan tertutup
TK 47 Matematika III Integral Vektor (Pertemuan VII) Dr. AZ Jurusan Teknik ipil Fakultas Teknik Universitas Brawijaya Teorema Gauss Definisi : Jika V adalah volume yang dibatasi oleh suatu permukaan tertutup
VII III II VIII HAND OUT PERKULIAHAN GEOMETRI ANALITIK
 HAND OUT PERKULIAHAN GEOMETRI ANALITIK A. Sistem Koordinat Tegak Lurus Suatu sistem koordinat tegak lurus disebut juga dengan sistem koordinat cartesian. Di dalam ruang, terdapat tiga buah garis lurus
HAND OUT PERKULIAHAN GEOMETRI ANALITIK A. Sistem Koordinat Tegak Lurus Suatu sistem koordinat tegak lurus disebut juga dengan sistem koordinat cartesian. Di dalam ruang, terdapat tiga buah garis lurus
Vektor Ruang 2D dan 3D
 Vektor Ruang 2D dan D Besaran Skalar (Tidak mempunyai arah) Vektor (Mempunyai Arah) Vektor Geometris Skalar (Luas, Panjang, Massa, Waktu dan lain - lain), merupakan suatu besaran yang mempunyai nilai mutlak
Vektor Ruang 2D dan D Besaran Skalar (Tidak mempunyai arah) Vektor (Mempunyai Arah) Vektor Geometris Skalar (Luas, Panjang, Massa, Waktu dan lain - lain), merupakan suatu besaran yang mempunyai nilai mutlak
4.4. KERAPATAN FLUKS LISTRIK
 4.4. KERAPATAN FLUKS LISTRIK Misalkan D adalah suatu medan vektor baru yang tidak bergantung pada medium dan didefinisikan oleh Didefinisikan fluks listrik dalam D sebagai Dalam satuan SI, satu garis fluks
4.4. KERAPATAN FLUKS LISTRIK Misalkan D adalah suatu medan vektor baru yang tidak bergantung pada medium dan didefinisikan oleh Didefinisikan fluks listrik dalam D sebagai Dalam satuan SI, satu garis fluks
VEKTOR. Oleh : Musayyanah, S.ST, MT
 VEKTOR Oleh : Musayyanah, S.ST, MT 1 2.1 ESRN SKLR DN VEKTOR Sifat besaran fisis : esaran Skalar Skalar Vektor esaran yang cukup dinyatakan oleh besarnya saja (besar dinyatakan oleh bilangan dan satuan).
VEKTOR Oleh : Musayyanah, S.ST, MT 1 2.1 ESRN SKLR DN VEKTOR Sifat besaran fisis : esaran Skalar Skalar Vektor esaran yang cukup dinyatakan oleh besarnya saja (besar dinyatakan oleh bilangan dan satuan).
Dosen Pengampu : Puji Andayani, S.Si, M.Si, M.Sc
 KALKULUS III Teorema Integral (Stokes Theorem) Dosen Pengampu : Puji Andayani, S.Si, M.Si, M.Sc 1 Stokes Theorem Review : Pada pembahasan sebelumnya, kepadatan sirkulasi atau curl pada bidang dua dimensi
KALKULUS III Teorema Integral (Stokes Theorem) Dosen Pengampu : Puji Andayani, S.Si, M.Si, M.Sc 1 Stokes Theorem Review : Pada pembahasan sebelumnya, kepadatan sirkulasi atau curl pada bidang dua dimensi
FISIKA UNTUK UNIVERSITAS OLEH
 FISIKA UNTUK UNIVERSITAS OLEH BAB I VEKTOR Pendahuluan B esaran adalah segala sesuatu yang dapat diukur dan dinyatakan dalam bentuk angkaangka. Besaran fisika dapat dibagi menjadi besaran pokok dan besaran
FISIKA UNTUK UNIVERSITAS OLEH BAB I VEKTOR Pendahuluan B esaran adalah segala sesuatu yang dapat diukur dan dinyatakan dalam bentuk angkaangka. Besaran fisika dapat dibagi menjadi besaran pokok dan besaran
Modul 6 berisi pengertian integral garis (kurva), sifat-sifat dan penerapannya. Pengintegralan sepanjang kurva, kita harus memperhatikan arah kurva,
 ix T Tinjauan Mata Kuliah ujuan mempelajari mata kuliah ini adalah agar Anda memiliki kemampuan dalam menjelaskan aljabar vektor, turunan dan integral fungsi vektor, serta mampu menerapkannya dalam geometri
ix T Tinjauan Mata Kuliah ujuan mempelajari mata kuliah ini adalah agar Anda memiliki kemampuan dalam menjelaskan aljabar vektor, turunan dan integral fungsi vektor, serta mampu menerapkannya dalam geometri
BAB II V E K T O R. Drs. Pristiadi Utomo, M.Pd. FISIKA KELAS X Drs. Pristiadi Utomo, M.Pd. Drs. Pristiadi Utomo, M.Pd. 52
 FISIKA KELAS X Drs. Pristiadi Utomo, M.Pd. BAB II V E K T O R Pernahkah Kamu naik pesawat terbang? Antara penumpang dan pilot dan copilot di ruang kemudi dipisah dengan sekat. Tujuannya agar pilot dapat
FISIKA KELAS X Drs. Pristiadi Utomo, M.Pd. BAB II V E K T O R Pernahkah Kamu naik pesawat terbang? Antara penumpang dan pilot dan copilot di ruang kemudi dipisah dengan sekat. Tujuannya agar pilot dapat
4.3. MEDAN LISTRIK OLEH DISTRIBUSI MUATAN KONTINYU
 4.3. MEDAN LISTRIK OLEH DISTRIBUSI MUATAN KONTINYU Selain muatan berbentuk titik, dimungkinkan juga distribusi muatan kontinyu dalam bentuk garis, permukaan atau volume seperti yang ditunjukkan pada Gambar
4.3. MEDAN LISTRIK OLEH DISTRIBUSI MUATAN KONTINYU Selain muatan berbentuk titik, dimungkinkan juga distribusi muatan kontinyu dalam bentuk garis, permukaan atau volume seperti yang ditunjukkan pada Gambar
Vektor. Vektor memiliki besaran dan arah. Beberapa besaran fisika yang dinyatakan dengan vektor seperti : perpindahan, kecepatan dan percepatan.
 Vektor Vektor memiliki besaran dan arah. Beberapa besaran fisika yang dinyatakan dengan vektor seperti : perpindahan, kecepatan dan percepatan. Skalar hanya memiliki besaran saja, contoh : temperatur,
Vektor Vektor memiliki besaran dan arah. Beberapa besaran fisika yang dinyatakan dengan vektor seperti : perpindahan, kecepatan dan percepatan. Skalar hanya memiliki besaran saja, contoh : temperatur,
Medan Elektromagnetik 3 SKS. M. Hariansyah Program Studi Teknik Elektro Fakultas Teknik Universitas Ibn Khaldun Bogor
 Medan Elektromagnetik 3 SKS M. Hariansyah Program Studi Teknik Elektro Fakultas Teknik Universitas Ibn Khaldun Bogor 2 0 1 4 Medan Elektromagnetik I -Referensi: WILLIAM H HAYT Materi Kuliah -Analisa Vektor
Medan Elektromagnetik 3 SKS M. Hariansyah Program Studi Teknik Elektro Fakultas Teknik Universitas Ibn Khaldun Bogor 2 0 1 4 Medan Elektromagnetik I -Referensi: WILLIAM H HAYT Materi Kuliah -Analisa Vektor
MODUL PEMBELAJARAN KALKULUS II. ALFIANI ATHMA PUTRI ROSYADI, M.Pd
 MODUL PEMBELAJARAN KALKULUS II ALFIANI ATHMA PUTRI ROSYADI, M.Pd IDENTITAS MAHASISWA NAMA : KLS/NIM :. KELOMPOK:. Daftar Isi Kata Pengantar Peta Konsep Materi. BAB I Analisis Vektor a. Vektor Pada Bidang.6
MODUL PEMBELAJARAN KALKULUS II ALFIANI ATHMA PUTRI ROSYADI, M.Pd IDENTITAS MAHASISWA NAMA : KLS/NIM :. KELOMPOK:. Daftar Isi Kata Pengantar Peta Konsep Materi. BAB I Analisis Vektor a. Vektor Pada Bidang.6
Mata Kuliah : ELEKTROMAGNETIKA I Kode Kuliah : FEG2C3 Semester : Genap 2014/2015 Kredit : 3 SKS
 Mata Kuliah : ELEKTROMAGNETIKA I Kode Kuliah : FEG2C3 Semester : Genap 2014/2015 Kredit : 3 SKS Minggu Pokok 1 Analisis Vektor dan Sistem Koordinat a. Konsep vektor : - definisi dan arti, notasi/simbol
Mata Kuliah : ELEKTROMAGNETIKA I Kode Kuliah : FEG2C3 Semester : Genap 2014/2015 Kredit : 3 SKS Minggu Pokok 1 Analisis Vektor dan Sistem Koordinat a. Konsep vektor : - definisi dan arti, notasi/simbol
BESARAN VEKTOR B A B B A B
 Besaran Vektor 8 B A B B A B BESARAN VEKTOR Sumber : penerbit cv adi perkasa Perhatikan dua anak yang mendorong meja pada gambar di atas. Apakah dua anak tersebut dapat mempermudah dalam mendorong meja?
Besaran Vektor 8 B A B B A B BESARAN VEKTOR Sumber : penerbit cv adi perkasa Perhatikan dua anak yang mendorong meja pada gambar di atas. Apakah dua anak tersebut dapat mempermudah dalam mendorong meja?
Perkalian Titik dan Silang
 PERKALIAN TITIK DAN SILANG Materi pokok pertemuan ke 3: 1. Perkalian titik URAIAN MATERI Perkalian Titik Perkalian titik dari dua buah vektor dan dinyatakan oleh (baca: titik ). Untuk lebih jelas, berikut
PERKALIAN TITIK DAN SILANG Materi pokok pertemuan ke 3: 1. Perkalian titik URAIAN MATERI Perkalian Titik Perkalian titik dari dua buah vektor dan dinyatakan oleh (baca: titik ). Untuk lebih jelas, berikut
Ruang Vektor Euclid R 2 dan R 3
 Ruang Vektor Euclid R 2 dan R 3 Kuliah Aljabar Linier Semester Ganjil 2015-2016 MZI Fakultas Informatika Telkom University FIF Tel-U September 2015 MZI (FIF Tel-U) Ruang Vektor R 2 dan R 3 September 2015
Ruang Vektor Euclid R 2 dan R 3 Kuliah Aljabar Linier Semester Ganjil 2015-2016 MZI Fakultas Informatika Telkom University FIF Tel-U September 2015 MZI (FIF Tel-U) Ruang Vektor R 2 dan R 3 September 2015
BESARAN, SATUAN & DIMENSI
 BESARAN, SATUAN & DIMENSI Defenisi Apakah yang dimaksud dengan besaran? Besaran : segala sesuatu yang dapat diukur dan dinyatakan dengan angka (kuantitatif). Apakah yang dimaksud dengan satuan? Satuan
BESARAN, SATUAN & DIMENSI Defenisi Apakah yang dimaksud dengan besaran? Besaran : segala sesuatu yang dapat diukur dan dinyatakan dengan angka (kuantitatif). Apakah yang dimaksud dengan satuan? Satuan
Matematika II : Vektor. Dadang Amir Hamzah
 Matematika II : Vektor Dadang Amir Hamzah sumber : http://www.whsd.org/uploaded/faculty/tmm/calc front image.jpg 2016 Dadang Amir Hamzah Matematika II Semester II 2016 1 / 24 Outline 1 Pendahuluan Dadang
Matematika II : Vektor Dadang Amir Hamzah sumber : http://www.whsd.org/uploaded/faculty/tmm/calc front image.jpg 2016 Dadang Amir Hamzah Matematika II Semester II 2016 1 / 24 Outline 1 Pendahuluan Dadang
IKIP BUDI UTOMO MALANG. Analytic Geometry TEXT BOOK. Alfiani Athma Putri Rosyadi, M.Pd
 IKIP BUDI UTOMO MALANG Analytic Geometry TEXT BOOK Alfiani Athma Putri Rosyadi, M.Pd 2012 DAFTAR ISI 1 VEKTOR 1.1 Vektor Pada Bidang... 4 1.2 Vektor Pada Ruang... 6 1.3 Operasi Vektor.. 8 1.4 Perkalian
IKIP BUDI UTOMO MALANG Analytic Geometry TEXT BOOK Alfiani Athma Putri Rosyadi, M.Pd 2012 DAFTAR ISI 1 VEKTOR 1.1 Vektor Pada Bidang... 4 1.2 Vektor Pada Ruang... 6 1.3 Operasi Vektor.. 8 1.4 Perkalian
Diferensial Vektor. (Pertemuan II) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya
 TKS 4007 Matematika III Diferensial Vektor (Pertemuan II) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya Definisi Secara Grafis : Dari gambar di samping, ada sebuah anak panah yang berawal
TKS 4007 Matematika III Diferensial Vektor (Pertemuan II) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya Definisi Secara Grafis : Dari gambar di samping, ada sebuah anak panah yang berawal
Keep running VEKTOR. 3/8/2007 Fisika I 1
 VEKTOR 3/8/007 Fisika I 1 BAB I : VEKTOR Besaran vektor adalah besaran yang terdiri dari dua variabel, yaitu besar dan arah. Sebagai contoh dari besaran vektor adalah perpindahan. Sebuah besaran vektor
VEKTOR 3/8/007 Fisika I 1 BAB I : VEKTOR Besaran vektor adalah besaran yang terdiri dari dua variabel, yaitu besar dan arah. Sebagai contoh dari besaran vektor adalah perpindahan. Sebuah besaran vektor
Program Studi Pendidikan Matematika STKIP PGRI SUMBAR
 VEKTOR DAN SKALAR Materi pokok pertemuan ke I: 1. Vektor dan skalar 2. Komponen vektor 3. Operasi dasar aljabar vektor URAIAN MATERI Masih ingatkah Anda tentang vektor? Apa beda vektor dengan skalar? Ya,
VEKTOR DAN SKALAR Materi pokok pertemuan ke I: 1. Vektor dan skalar 2. Komponen vektor 3. Operasi dasar aljabar vektor URAIAN MATERI Masih ingatkah Anda tentang vektor? Apa beda vektor dengan skalar? Ya,
BAB VI INTEGRAL LIPAT
 BAB VI INTEGRAL LIPAT 6.1 Pendahuluan Pada kalkulus dan fisika dasar, kita melihat sejumlah pemakaian integral misal untuk mencari luasan, volume, massa, momen inersia, dsb.nya. Dalam bab ini kita ingin
BAB VI INTEGRAL LIPAT 6.1 Pendahuluan Pada kalkulus dan fisika dasar, kita melihat sejumlah pemakaian integral misal untuk mencari luasan, volume, massa, momen inersia, dsb.nya. Dalam bab ini kita ingin
Vektor di Bidang dan di Ruang
 Vektor di Bidang dan di Ruang 4.1. Pengertian, notasi,dan operasi pada ektor Vektor merupakan istilah untuk menyatakan besaran yang mempunyai arah. Secara geometris, ektor dinyakan dengan segmen-segmen
Vektor di Bidang dan di Ruang 4.1. Pengertian, notasi,dan operasi pada ektor Vektor merupakan istilah untuk menyatakan besaran yang mempunyai arah. Secara geometris, ektor dinyakan dengan segmen-segmen
Gambar 1-1. Garis berarah D adalah pergeseran titik dari P 1 ke P 2. Gambar 1-2. Pergeseran F adalah resultan dari pergeseran D dan pergeseran E.
 ab 1 Vektor Dalam mempelajari kelistrikan dan kemagnetan, kita selalu bekerja dengan besaran-besaran ang perlu dideskripsikan dengan besar (magnitude) dan arahna (direction). esaran seperti ini disebut
ab 1 Vektor Dalam mempelajari kelistrikan dan kemagnetan, kita selalu bekerja dengan besaran-besaran ang perlu dideskripsikan dengan besar (magnitude) dan arahna (direction). esaran seperti ini disebut
VEKTOR YUSRON SUGIARTO
 VEKTOR YUSRON SUGIARTO Jurusan Keteknikan Pertanian FTP UB 2013 2 3 B E S A R A N Skalar besaran yang hanya memiliki besar (panjang/nilai) Vektor memiliki besar dan arah Massa Waktu Kecepatan Percepatan
VEKTOR YUSRON SUGIARTO Jurusan Keteknikan Pertanian FTP UB 2013 2 3 B E S A R A N Skalar besaran yang hanya memiliki besar (panjang/nilai) Vektor memiliki besar dan arah Massa Waktu Kecepatan Percepatan
DIKTAT KULIAH KALKULUS PEUBAH BANYAK (IE-308)
 DIKTAT KULIAH (IE-308) BAB 7 INTEGRAL PERMUKAAN Diktat ini digunakan bagi mahasiswa Jurusan Teknik Industri Fakultas Teknik Universitas Kristen Maranatha Ir. Rudy Wawolumaja M.Sc JURUSAN TEKNIK INDUSTRI
DIKTAT KULIAH (IE-308) BAB 7 INTEGRAL PERMUKAAN Diktat ini digunakan bagi mahasiswa Jurusan Teknik Industri Fakultas Teknik Universitas Kristen Maranatha Ir. Rudy Wawolumaja M.Sc JURUSAN TEKNIK INDUSTRI
Diferensial Vektor. (Pertemuan V) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya
 TKS 4007 Matematika III Diferensial Vektor (Pertemuan V) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya Operator Del Operator del merupakan operator pada diferensial vektor yang disimbolkan
TKS 4007 Matematika III Diferensial Vektor (Pertemuan V) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya Operator Del Operator del merupakan operator pada diferensial vektor yang disimbolkan
DIKTAT KULIAH KALKULUS PEUBAH BANYAK (IE-308)
 DIKTAT KULIAH (IE-308) BAB 6 INTEGRAL GARIS Diktat ini digunakan bagi mahasiswa Jurusan Teknik Industri Fakultas Teknik Universitas Kristen Maranatha Ir. Rudy Wawolumaja M.Sc JURUSAN TEKNIK INDUSTRI -
DIKTAT KULIAH (IE-308) BAB 6 INTEGRAL GARIS Diktat ini digunakan bagi mahasiswa Jurusan Teknik Industri Fakultas Teknik Universitas Kristen Maranatha Ir. Rudy Wawolumaja M.Sc JURUSAN TEKNIK INDUSTRI -
VEKTOR YUSRON SUGIARTO
 VEKTOR YUSRON SUGIARTO Jurusan Keteknikan Pertanian FTP UB 2012 2 3 B E S A R A N Skalar besaran yang hanya memiliki besar (panjang/nilai) massa, waktu, suhu, panjang, luas, volum Vektor memiliki besar
VEKTOR YUSRON SUGIARTO Jurusan Keteknikan Pertanian FTP UB 2012 2 3 B E S A R A N Skalar besaran yang hanya memiliki besar (panjang/nilai) massa, waktu, suhu, panjang, luas, volum Vektor memiliki besar
VEKTOR A. Vektor Vektor B. Penjumlahan Vektor R = A + B
 Amran Shidik MATERI FISIKA KELAS X 11/13/2016 VEKTOR A. Vektor Vektor adalah jenis besaran yang mempunyai nilai dan arah. Besaran yang termasuk besaran vektor antara lain perpindahan, gaya, kecepatan,
Amran Shidik MATERI FISIKA KELAS X 11/13/2016 VEKTOR A. Vektor Vektor adalah jenis besaran yang mempunyai nilai dan arah. Besaran yang termasuk besaran vektor antara lain perpindahan, gaya, kecepatan,
a menunjukkan jumlah satuan skala relatif terhadap nol pada sumbu X Gambar 1
 1. Koordinat Cartesius Sistem koordinat Cartesius terdiri dari dua garis yang saling tegak lurus yang disebut sumbu Sumbu horizontal disebut sumbu X dan sumbu vertikal disebut sumbu Y Tiap sumbu mempunyai
1. Koordinat Cartesius Sistem koordinat Cartesius terdiri dari dua garis yang saling tegak lurus yang disebut sumbu Sumbu horizontal disebut sumbu X dan sumbu vertikal disebut sumbu Y Tiap sumbu mempunyai
BAB II BESARAN VEKTOR
 BAB II BESARAN VEKTOR.1. Besaran Skalar Dan Vektor Dalam fisika, besaran dapat dibedakan menjadi dua kelompok yaitu besaran skalar dan besaran vektor. Besaran skalar adalah besaran yang dinyatakan dengan
BAB II BESARAN VEKTOR.1. Besaran Skalar Dan Vektor Dalam fisika, besaran dapat dibedakan menjadi dua kelompok yaitu besaran skalar dan besaran vektor. Besaran skalar adalah besaran yang dinyatakan dengan
SEMESTER 3 ANALISIS VEKTOR PROGRAM STUDI PENDIDIKAN MATEMATIKA FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN UNIVERSITAS MUHAMMADIYAH SURAKARTA
 SEMESTER 3 ANALISIS VEKTOR PROGRAM STUDI PENDIDIKAN MATEMATIKA FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN UNIVERSITAS MUHAMMADIYAH SURAKARTA Sks : 2 sks Dosen : Sri Rejeki Nomor Telepon: 085725313171 E mail
SEMESTER 3 ANALISIS VEKTOR PROGRAM STUDI PENDIDIKAN MATEMATIKA FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN UNIVERSITAS MUHAMMADIYAH SURAKARTA Sks : 2 sks Dosen : Sri Rejeki Nomor Telepon: 085725313171 E mail
VEKTOR. 45 O x PENDAHULUAN PETA KONSEP. Vektor di R 2. Vektor di R 3. Perkalian Skalar Dua Vektor. Proyeksi Ortogonal suatu Vektor pada Vektor Lain
 VEKTOR y PENDAHULUAN PETA KONSEP a Vektor di R 2 Vektor di R 3 Perkalian Skalar Dua Vektor o 45 O x Proyeksi Ortogonal suatu Vektor pada Vektor Lain Soal-Soal PENDAHULUAN Dalam ilmu pengetahuan kita sering
VEKTOR y PENDAHULUAN PETA KONSEP a Vektor di R 2 Vektor di R 3 Perkalian Skalar Dua Vektor o 45 O x Proyeksi Ortogonal suatu Vektor pada Vektor Lain Soal-Soal PENDAHULUAN Dalam ilmu pengetahuan kita sering
BAB 1 Vektor. Fisika. Tim Dosen Fisika 1, Ganjil 2016/2017 Program Studi S1 - Teknik Telekomunikasi Fakultas Teknik Elektro - Universitas Telkom
 A 1 Vektor Fisika Tim Dosen Fisika 1, Ganjil 2016/2017 Program Studi S1 - Teknik Telekomunikasi Fakultas Teknik Elektro - Universitas Telkom Sub Pokok ahasan Definisi Vektor Penjumlahan Vektor Vektor Satuan
A 1 Vektor Fisika Tim Dosen Fisika 1, Ganjil 2016/2017 Program Studi S1 - Teknik Telekomunikasi Fakultas Teknik Elektro - Universitas Telkom Sub Pokok ahasan Definisi Vektor Penjumlahan Vektor Vektor Satuan
Program Studi Pendidikan Matematika STKIP PGRI SUMBAR
 DIFERENSIASI VEKTOR Materi pokok pertemuan ke 5 : 1. Turunan biasa fungsi vektor URAIAN MATERI Fungsi Vektor Jika sembarang nilai skalar t dikaitkan dengan suatu vektor, maka bisa dinyatakan sebagai fungsi
DIFERENSIASI VEKTOR Materi pokok pertemuan ke 5 : 1. Turunan biasa fungsi vektor URAIAN MATERI Fungsi Vektor Jika sembarang nilai skalar t dikaitkan dengan suatu vektor, maka bisa dinyatakan sebagai fungsi
Integral Garis. Sesi XIII INTEGRAL 12/7/2015
 2//25 Mata Kuliah : Matematika Rekayasa Lanjut Kode MK : TK 85 Pengampu : Achfas Zacoeb esi XIII INTEGRAL e-mail : zacoeb@ub.ac.id www.zacoeb.lecture.ub.ac.id Hp. 823398339 Integral Garis Dari Gambar.,
2//25 Mata Kuliah : Matematika Rekayasa Lanjut Kode MK : TK 85 Pengampu : Achfas Zacoeb esi XIII INTEGRAL e-mail : zacoeb@ub.ac.id www.zacoeb.lecture.ub.ac.id Hp. 823398339 Integral Garis Dari Gambar.,
Outline Vektor dan Garis Koordinat Norma Vektor Hasil Kali Titik dan Proyeksi Hasil Kali Silang. Geometri Vektor. Kusbudiono. Jurusan Matematika
 Jurusan Matematika 1 Nopember 2011 1 Vektor dan Garis 2 Koordinat 3 Norma Vektor 4 Hasil Kali Titik dan Proyeksi 5 Hasil Kali Silang Definisi Vektor Definisi Jika AB dan CD ruas garis berarah, keduanya
Jurusan Matematika 1 Nopember 2011 1 Vektor dan Garis 2 Koordinat 3 Norma Vektor 4 Hasil Kali Titik dan Proyeksi 5 Hasil Kali Silang Definisi Vektor Definisi Jika AB dan CD ruas garis berarah, keduanya
Vektor di ruang dimensi 2 dan ruang dimensi 3
 Vektor di ruang dimensi 2 dan ruang dimensi 3 Maulana Malik 1 (maulana.malik@sci.ui.ac.id) 1 Departemen Matematika FMIPA UI Kampus Depok UI, Depok 16424 2014/2015 1/21 maulana.malik@sci.ui.ac.id Vektor
Vektor di ruang dimensi 2 dan ruang dimensi 3 Maulana Malik 1 (maulana.malik@sci.ui.ac.id) 1 Departemen Matematika FMIPA UI Kampus Depok UI, Depok 16424 2014/2015 1/21 maulana.malik@sci.ui.ac.id Vektor
A x pada sumbu x dan. Pembina Olimpiade Fisika davitsipayung.com. 2. Vektor. 2.1 Representasi grafis sebuah vektor
 . Vektor.1 Representasi grafis sebuah vektor erdasarkan nilai dan arah, besaran dibagi menjadi dua bagian aitu besaran skalar dan besaran vektor. esaran skalar adalah besaran ang memiliki nilai dan tidak
. Vektor.1 Representasi grafis sebuah vektor erdasarkan nilai dan arah, besaran dibagi menjadi dua bagian aitu besaran skalar dan besaran vektor. esaran skalar adalah besaran ang memiliki nilai dan tidak
Analisis Vektor. Ramadoni Syahputra Jurusan Teknik Elektro FT UMY
 Analisis Vektor Ramadoni Syahputra Jurusan Teknik Elektro FT UMY Analisis Vektor Analisis vektor meliputi bidang matematika dan fisika sekaligus dalam pembahasannya Skalar dan Vektor Skalar Skalar ialah
Analisis Vektor Ramadoni Syahputra Jurusan Teknik Elektro FT UMY Analisis Vektor Analisis vektor meliputi bidang matematika dan fisika sekaligus dalam pembahasannya Skalar dan Vektor Skalar Skalar ialah
B. Pengertian skalar dan vektor Dalam mempelajari dasar-dasar fisika, terdapat beberapa macam kuantitas kelompok besaran yaitu Vektor dan Skalar.
 ANALISIS VEKTOR A. Deskripsi Materi ini akan membahas tentang pengertian, sifat, operasi dan manipulasi besaran fisik scalar dan vector. Pada pembahasan materi medan elektromagnetik berikutna akan melibatkan
ANALISIS VEKTOR A. Deskripsi Materi ini akan membahas tentang pengertian, sifat, operasi dan manipulasi besaran fisik scalar dan vector. Pada pembahasan materi medan elektromagnetik berikutna akan melibatkan
BAB II TINJAUAN PUSTAKA. tegak, perlu diketahui tentang materi-materi sebagai berikut.
 BAB II TINJAUAN PUSTAKA Sebelum pembahasan mengenai irisan bidang datar dengan tabung lingkaran tegak, perlu diketahui tentang materi-materi sebagai berikut. A. Matriks Matriks adalah himpunan skalar (bilangan
BAB II TINJAUAN PUSTAKA Sebelum pembahasan mengenai irisan bidang datar dengan tabung lingkaran tegak, perlu diketahui tentang materi-materi sebagai berikut. A. Matriks Matriks adalah himpunan skalar (bilangan
B.1. Menjumlah Beberapa Gaya Sebidang Dengan Cara Grafis
 BAB II RESULTAN (JUMLAH) DAN URAIAN GAYA A. Pendahuluan Pada bab ini, anda akan mempelajari bagaimana kita bekerja dengan besaran vektor. Kita dapat menjumlah dua vektor atau lebih dengan beberapa cara,
BAB II RESULTAN (JUMLAH) DAN URAIAN GAYA A. Pendahuluan Pada bab ini, anda akan mempelajari bagaimana kita bekerja dengan besaran vektor. Kita dapat menjumlah dua vektor atau lebih dengan beberapa cara,
VEKTOR. Makalah ini ditujukkan untuk Memenuhi Tugas. Disusun Oleh : PRODI TEKNIK SIPIL FAKULTAS TEKNIK SIPIL DAN PERENCANAAN
 VEKTOR Makalah ini ditujukkan untuk Memenuhi Tugas Disusun Oleh : 1. Chrisnaldo noel (12110024) 2. Maria Luciana (12110014) 3. Rahmat Fatoni (121100) PRODI TEKNIK SIPIL FAKULTAS TEKNIK SIPIL DAN PERENCANAAN
VEKTOR Makalah ini ditujukkan untuk Memenuhi Tugas Disusun Oleh : 1. Chrisnaldo noel (12110024) 2. Maria Luciana (12110014) 3. Rahmat Fatoni (121100) PRODI TEKNIK SIPIL FAKULTAS TEKNIK SIPIL DAN PERENCANAAN
Pesawat Terbang. gaya angkat. gaya berat
 Sumber: www.staralliance.com Pesawat Terbang Terbayangkah kalian dengan teknologi pesawat terbang? Alat transportasi ini diciptakan dengan teknologi yang canggih. Salah satunya adalah saat merancang konstruksi
Sumber: www.staralliance.com Pesawat Terbang Terbayangkah kalian dengan teknologi pesawat terbang? Alat transportasi ini diciptakan dengan teknologi yang canggih. Salah satunya adalah saat merancang konstruksi
BAB I ANALISIS VEKTOR
 BAB I ANALISIS VEKTOR A. Deskripsi Materi ini akan membahas tentang pengertian, sifat, operasi dan manipulasi besaran fisik scalar dan vector. Pada pembahasan materi medan elektromagnetik berikutna akan
BAB I ANALISIS VEKTOR A. Deskripsi Materi ini akan membahas tentang pengertian, sifat, operasi dan manipulasi besaran fisik scalar dan vector. Pada pembahasan materi medan elektromagnetik berikutna akan
Kalkulus Multivariabel I
 Penerapan Integral Lipat-Dua Atina Ahdika,.i, M.i tatistika FMIPA Universitas Islam Indonesia 214 Penerapan Integral Lipat-Dua Penerapan Integral Lipat-Dua Penerapan lain dari integral lipat-dua antara
Penerapan Integral Lipat-Dua Atina Ahdika,.i, M.i tatistika FMIPA Universitas Islam Indonesia 214 Penerapan Integral Lipat-Dua Penerapan Integral Lipat-Dua Penerapan lain dari integral lipat-dua antara
Integral yang berhubungan dengan kepentingan fisika
 Integral yang berhubungan dengan kepentingan fisika 14.1 APLIKASI INTEGRAL A. Usaha Dan Energi Hampir semua ilmu mekanika ditemukan oleh Issac newton kecuali konsep energi. Energi dapat muncul dalam berbagai
Integral yang berhubungan dengan kepentingan fisika 14.1 APLIKASI INTEGRAL A. Usaha Dan Energi Hampir semua ilmu mekanika ditemukan oleh Issac newton kecuali konsep energi. Energi dapat muncul dalam berbagai
BINOVATIF LISTRIK DAN MAGNET. Hani Nurbiantoro Santosa, PhD.
 BINOVATIF LISTRIK DAN MAGNET Hani Nurbiantoro Santosa, PhD hanisantosa@gmail.com 2 BAB 2 MEDAN LISTRIK DAN HUKUM GAUSS Pendahuluan, Distribusi Muatan Kontinu, Mencari Medan Listrik Menggunakan Integral,
BINOVATIF LISTRIK DAN MAGNET Hani Nurbiantoro Santosa, PhD hanisantosa@gmail.com 2 BAB 2 MEDAN LISTRIK DAN HUKUM GAUSS Pendahuluan, Distribusi Muatan Kontinu, Mencari Medan Listrik Menggunakan Integral,
BAB I TEGANGAN DAN REGANGAN
 BAB I TEGANGAN DAN REGANGAN.. Tegangan Mekanika bahan merupakan salah satu ilmu yang mempelajari/membahas tentang tahanan dalam dari sebuah benda, yang berupa gaya-gaya yang ada di dalam suatu benda yang
BAB I TEGANGAN DAN REGANGAN.. Tegangan Mekanika bahan merupakan salah satu ilmu yang mempelajari/membahas tentang tahanan dalam dari sebuah benda, yang berupa gaya-gaya yang ada di dalam suatu benda yang
DIKTAT MATEMATIKA II
 DIKTT MTEMTIK II (VEKTOR) Drs.. NN PURNWN, M.T JURUSN PENDIDIKN TEKNIK MESIN FKULTS PENDIDIKN TEKNOLOGI DN KEJURUN UNIVERSITS PENDIDIKN INDONESI 004 VEKTOR I. PENDHULUN 1.1. PENGERTIN Sepotong garis berarah
DIKTT MTEMTIK II (VEKTOR) Drs.. NN PURNWN, M.T JURUSN PENDIDIKN TEKNIK MESIN FKULTS PENDIDIKN TEKNOLOGI DN KEJURUN UNIVERSITS PENDIDIKN INDONESI 004 VEKTOR I. PENDHULUN 1.1. PENGERTIN Sepotong garis berarah
Program Studi Teknik Mesin S1
 SATUAN ACARA PERKULIAHAN MATA KULIAH : KALKULUS 3 KODE / SKS : IT042219 / 2 SKS Pertemuan Pokok Bahasan dan TIU Geometri pada bidang, vektor vektor pada bidang : pendekatan secara geometrik dan secara
SATUAN ACARA PERKULIAHAN MATA KULIAH : KALKULUS 3 KODE / SKS : IT042219 / 2 SKS Pertemuan Pokok Bahasan dan TIU Geometri pada bidang, vektor vektor pada bidang : pendekatan secara geometrik dan secara
1. Akar-akar persamaan 2x² + px - q² = 0 adalah p dan q, p - q = 6. Nilai pq =... A. 6 B. -2 C. -4 Kunci : E Penyelesaian : D. -6 E.
 1. Akar-akar persamaan 2x² + px - q² = 0 adalah p dan q, p - q = 6. Nilai pq =... A. 6-2 -4 Kunci : E -6-8 2. Himpunan penyelesaian sistem persamaan Nilai 6x 0.y 0 =... A. 1 Kunci : C 6 36 3. Absis titik
1. Akar-akar persamaan 2x² + px - q² = 0 adalah p dan q, p - q = 6. Nilai pq =... A. 6-2 -4 Kunci : E -6-8 2. Himpunan penyelesaian sistem persamaan Nilai 6x 0.y 0 =... A. 1 Kunci : C 6 36 3. Absis titik
KINEMATIKA GERAK 1 PERSAMAAN GERAK
 KINEMATIKA GERAK 1 PERSAMAAN GERAK Posisi titik materi dapat dinyatakan dengan sebuah VEKTOR, baik pada suatu bidang datar maupun dalam bidang ruang. Vektor yang dipergunakan untuk menentukan posisi disebut
KINEMATIKA GERAK 1 PERSAMAAN GERAK Posisi titik materi dapat dinyatakan dengan sebuah VEKTOR, baik pada suatu bidang datar maupun dalam bidang ruang. Vektor yang dipergunakan untuk menentukan posisi disebut
8. Nilai x yang memenuhi 2 log 2 (4x -
 1. Agar F(x) = (p - 2) x² - 2 (2p - 3) x + 5p - 6 bernilai positif untuk semua x, maka batas-batas nilai p p > l 2 < p < 3 p > 3 1 < p < 2 p < 1 atau p > 2 2. Fungsi kuadrat yang mempunyai nilai maksimum
1. Agar F(x) = (p - 2) x² - 2 (2p - 3) x + 5p - 6 bernilai positif untuk semua x, maka batas-batas nilai p p > l 2 < p < 3 p > 3 1 < p < 2 p < 1 atau p > 2 2. Fungsi kuadrat yang mempunyai nilai maksimum
Geometri pada Bidang, Vektor
 Jurusan Matematika FMIPA Unsyiah September 9, 2011 Secara geometrik, vektor pada bidang dapat digambarkan sebagai ruas garis berarah (anak panah). Panjang dari anak panah merepresentasikan besaran (magnitude)
Jurusan Matematika FMIPA Unsyiah September 9, 2011 Secara geometrik, vektor pada bidang dapat digambarkan sebagai ruas garis berarah (anak panah). Panjang dari anak panah merepresentasikan besaran (magnitude)
MATRIKS & TRANSFORMASI LINIER
 MATRIKS & TRANSFORMASI LINIER Oleh : SRI ESTI TRISNO SAMI, ST, MMSI 082334051324 Daftar Referensi : 1. Kreyzig Erwin, Advance Engineering Mathematic, Edisi ke-7, John wiley,1993 2. Spiegel, Murray R, Advanced
MATRIKS & TRANSFORMASI LINIER Oleh : SRI ESTI TRISNO SAMI, ST, MMSI 082334051324 Daftar Referensi : 1. Kreyzig Erwin, Advance Engineering Mathematic, Edisi ke-7, John wiley,1993 2. Spiegel, Murray R, Advanced
Perkuliahan Fisika Dasar II FI-331. Oleh Endi Suhendi 1
 Perkuliahan Fisika Dasar II FI-331 Oleh Endi Suhendi 1 Menu hari ini: Silabus Review Matematik Oleh Endi Suhendi 2 Silabus Identitas Mata Kuliah Nama mata kuliah : Fisika Dasar II Kode mata kuliah : FI-331
Perkuliahan Fisika Dasar II FI-331 Oleh Endi Suhendi 1 Menu hari ini: Silabus Review Matematik Oleh Endi Suhendi 2 Silabus Identitas Mata Kuliah Nama mata kuliah : Fisika Dasar II Kode mata kuliah : FI-331
SISTEM KOORDINAT VEKTOR. Tri Rahajoeningroem, MT T. Elektro - UNIKOM
 SISTEM KOORDINAT VEKTOR Tri Rahajoeningroem, MT T. Elektro - UNIKOM Tujuan Pembelajaran Mahasiswa dapat memahami koordinat vektor Mahasiswa dapat menggunakan sistem koordinat vektor untuk menyelesaikan
SISTEM KOORDINAT VEKTOR Tri Rahajoeningroem, MT T. Elektro - UNIKOM Tujuan Pembelajaran Mahasiswa dapat memahami koordinat vektor Mahasiswa dapat menggunakan sistem koordinat vektor untuk menyelesaikan
Rudi Susanto, M.Si VEKTOR
 Rudi Susanto, M.Si VEKTOR ESRN SKLR DN VEKTOR esaran Skalar esaran yang cukup dinyatakan oleh besarnya saja (besar dinyatakan oleh bilangan dan satuan). Contoh Catatan : waktu, suhu, volume, laju, energi
Rudi Susanto, M.Si VEKTOR ESRN SKLR DN VEKTOR esaran Skalar esaran yang cukup dinyatakan oleh besarnya saja (besar dinyatakan oleh bilangan dan satuan). Contoh Catatan : waktu, suhu, volume, laju, energi
Pengantar Teknologi dan Aplikasi Elektromagnetik. Dr. Ramadoni Syahputra Jurusan Teknik Elektro FT UMY
 Pengantar Teknologi dan Aplikasi Elektromagnetik Dr. Ramadoni Syahputra Jurusan Teknik Elektro FT UMY Kelistrikan dan Kemagnetan Tanpa listrik dan magnet, maka dalam kehidupan jaman sekarang: tanpa motor
Pengantar Teknologi dan Aplikasi Elektromagnetik Dr. Ramadoni Syahputra Jurusan Teknik Elektro FT UMY Kelistrikan dan Kemagnetan Tanpa listrik dan magnet, maka dalam kehidupan jaman sekarang: tanpa motor
