DIKTAT KULIAH KALKULUS PEUBAH BANYAK (IE-308)
|
|
|
- Iwan Widjaja
- 7 tahun lalu
- Tontonan:
Transkripsi
1 DIKTAT KULIAH (IE-308) BAB 7 INTEGRAL PERMUKAAN Diktat ini digunakan bagi mahasiswa Jurusan Teknik Industri Fakultas Teknik Universitas Kristen Maranatha Ir. Rudy Wawolumaja M.Sc JURUSAN TEKNIK INDUSTRI - FAKULTAS TEKNIK UNIVERSITAS KRISTEN MARANATHA BANDUNG 2012 Diktat ini disusun berdasarkan Calculus III oleh Paul Dawkins, Lamar University dengan penyesuaian berupa penerjemahan, pengurangan dan penambahan dari sumber-sumber lainnya.
2 Bab 7. INTEGRAL PERMUKAAN 7.1. Permukaan Parametrik Sebelum membahas integral permukaan, maka akan dibahas terlebih dulu bagaimana menuliskan persamaan suatu permukaan dalam bentuk parameter atau bagaimana memparameterisasi (parameterize) suatu permukaan. Dalam melakukan parameterisasi suatu kurva, nilai t dalam interval kedalam diambil dan dimasukkan Menghasilkan vektor posisi untuk setiap titik pada kurva yang dimaksud. Demikian juga dengan permukaan, untuk setiap titik, dimasukkan kedalam persamaan,, dalam ruang 2 dimensi D diambil dan Menghasilkan vector posisi untuk tiap titik pada permukaan S yang dimaksud. Bentuk diatas adalah representasi parametric dari permukaan S. Persamaan parametric / parametric equations dari suatu permukaan adalah setiap komponen dari representasi parametric (vector) yang dituliskan sebagai, Contoh Tentukan permukaan apakah yang dinyatakan oleh representasi parametric Solution Sehingga didapat persamaan, Dalam bab Permukaan Quadric ini adalah permukaan sebuah cone yang terbuka sepanjang sumbu - x. Bagaimana halnya bila diberikan suatu bentuk permukaan dan diminta untuk menuliskan dalam bentuk representasi parametric. Contoh Dapatkan representasi parametric dari permukaan berikut ini, (a) elliptic paraboloid. (b) elliptic paraboloid (c) Bola. (d) Silender. (a) Elliptic paraboloid. Karena permukaan dalam bentuk sebagai berikut, yang ada didepan bidang yz. maka dapat dengan cepat ditulis persamaan parametric Rudy Wawolumaja- Universitas Kristen Maranatha Halaman 170
3 Sehingga vector representasi parametric didapat, (b) Elliptic paraboloid yang berada didepan bidang- yz. Persoalan sama dengan contoh 2b dengan pembatasan, sehingga bentuk vector parametris nya sama dengan contoh 2b, Pembatasan bahwa permukaan ada didepan bidang-yz berarti,. Sehingga, 5y 2 + 2z atau 5y 2 + 2z 2 10 (c) Bola. Dalam koordinat bola, persamaan sebuah bola dengan radius a adalah, Sehingga persamaan bola dalam soal diatas dalam koordinat bola adalah. Dan dengan rumus konversi dari koordinat Cartesian ke koordinat bola, Sehingga representasi parametric dari permukaan bola diatas adalah, Dengan batasan, (d) Silender. Dalam koordinat silendris, persamaan diatas adalah. Dan dengan rumus konversi koordinat Cartesian ke koordinat Sehingga representasi parametrik dari silender diatas adalah, Dengan batasan Secara umum setiap fungsi permukaan dapat dinyatakan dalam bentuk representasi parametric sebagai berikut, Mencari bidang singgung pada suatu permukaan parametrik. Misal diketahui suatu permukaan parametric S, Dicari bidang singgung pada permukaan S diatas. Rudy Wawolumaja- Universitas Kristen Maranatha Halaman 171
4 Bila maka adalah orthogonal pada permukaan S. adalah vektor normal yang akan digunakan untuk merumuskan persamaan bidang singgung. Contoh Cari persamaan bidang singgung pada permukaan, Pada titik. Jawab Let s first compute. Here are the two individual vectors. Perkalian silang, yang merupakan vector normal adalah, Titik (2, 2, 3) pada berarti Didapat dua kemungkinan nilai v. Dengan memasukkan nilai u kepersamaan ke 3, didapat nilai v yang dipakai, yaitu Sehingga, dengan dan, didapat vector normal adalah, Bidang singgung adalah, Mencari luas permukaan parametric S, Untuk mencari luas permukaan parametric S, Dibutuhkan vektor. Luas permukaan S pada range yaitu titik-titik pada daerah D adalah, Contoh Cari luas permukaan potongan bola radius 4 yang terletak didalam silinder dan diatas bidang - xy. Rudy Wawolumaja- Universitas Kristen Maranatha Halaman 172
5 Bentuk parameterisasi dari permukaan bola adalah, Perlu ditentukan daerah pembatas D, batasan jangkauan adalah, Untuk menentukan batasan jangkauan., dilakukan substitusi persamaan silinder kedalam persamaan bola untuk mendapatkan niloai z dimana bola dan silinder beririsan. Karena salah satu syarat bahwa potongan bola terletak diatas bidang-xy, maka nilai z yang diambil adalah :. Radius bola =4,. Sehingga batas jangkauan (range) adalah, 0 φ π 3 Langkah berikut menentukan. Nilai absolute (magnitude) : Sehingga luas permukaan yang dicari, A = 16 sin φ da D 2π 0 π = 3 16 sin φ dφ dθ 0 π 2π 3 = 16 cos φ 0 dθ 0 2π = 8 dθ 0 = 16π Rudy Wawolumaja- Universitas Kristen Maranatha Halaman 173
6 7.2. Integral Permukaan / Surface Integrals Berikut adalah gambar sketsa dari permukaan S, dalam ruang tiga dimensi. Gambar 7.1. Permukaan S terletak diatas daerah D yang terletak dibidang- xy. Dalam gambar contoh diatas, daerah S dan D dipilih berbentuk persegi empat, namun sebenarnya dapat berbentuk lainnya. Juga permukaan S dapat terletak didepan D, dimana D terletak di bidang-yz atau bidang-xz. Bagaimana menghitung integral permukaan (surface integral) ditentukan oleh permukaan yang diberikan. Pada dasarnya ada dua metoda yang dapat digunakan. Metoda Pertama, Integral permukaan dimana permukaan S adalah, sehingga : Bentuk integral yang ada disebelah kiri tanda samadengan (=) adalah integral permukaan, sedangkan bentuk integral yang ada disisi kanan adalah bentuk baku integral ganda. Integral permukaan menggunakan ds sedangkan integral ganda menggunakan da. Rumus yang serupa juga diterapkan untuk permukaan dibawah. (dimana D ada di bidang- xz) dan (dimana D ada dibidang-yz). Rumus tersebut akan ditunjukkan dalam contoh soal Metoda kedua, untuk menghitung integral permukaan dimana permukaan dalam bentuk parameterisasi. Sehingga integral permukaan adalah, Dimana D adalah jangkauan (range) dari parameter. Rudy Wawolumaja- Universitas Kristen Maranatha Halaman 174
7 Bila rumus metoda kedua diterapkan pada permukaan yang diparameterisasi menjadi, Dan karena, Maka metoda 2 akan menghasilkan rumusan metoda 1, sehingga pada prinsipnya kedua metoda diatas adalah sama. Contoh Hitung dimana S adalah potongan bidang yang terletak didepan bidang- yz. Solusi Bidang permukaan S adalah potongan bidang permukaan yang terletak didepan bidang-yz, sehingga persamaan permukaan S dapat dituliskan dalam bentuk, yaitu Selanjutnya perlu ditetapkan D. Berikut adalah gambar sketsa dari permukaan S. Sedangkan gambar sketsa dari daerah D. Gambar 7.2. Gambar 7.3. Persamaan garis miring segitiga diatas yang merupakan irisan permukaan S dengan bidang-yz didapat dengan memasukkan x = 0 kedalam persamaan permukaan. Dan untuk jangkauan y dan z didapat, Dengan menggunakan rumus pertama integral permukaan didapat, Rudy Wawolumaja- Universitas Kristen Maranatha Halaman 175
8 Sehingga untuk penerapan persoalan diatas, didapat : Contoh Hitung dimana S adalah potongan atas setengah bola dengan radius 2. Solusi Parameterisasi dari bola adalah : Karena permukaan adalah potongan atas setengah bola, maka Untuk mendapatkan : Rudy Wawolumaja- Universitas Kristen Maranatha Halaman 176
9 Sehingga, Karena dalam range antara 0 dan π maka sin φ selalu positif sehingga tanda absolute dapat 2 dihilangkan, maka integral permukaan menjadi, Dengan merubah z kedalam koordinat bola, didapat integral permukaan menjadi integral ganda : Contoh Hitung dimana S adalah potongan silinder yang terletak antara dan. Solusi Bentuk parameterisasi dari silinder adalah, Jangkauan (range) parameter adalah, Untuk mendapatkan : Sehingga integral permukaan adalah, Rudy Wawolumaja- Universitas Kristen Maranatha Halaman 177
10 Contoh Hitung dimana S adalah permukaan yang dibatasi oleh silinder, dasarnya adalah cakram pada bidang- xy dan bagian atas adalah bidang. Solusi Gambar sketsa permukaan adalah, Gambar 7.4. Karena permukaan S terdiri dari sisi ( S 1 ), tutup ( S 2 ) dan dasar ( S 3 ), maka Integral permukaan menjadi, Sehingga perhitungan integral permukaan dilakukan satu persatu : : The Cylinder Parameterisasi silinder dan adalah, Sehingga integral permukaan silinder adalah, Rudy Wawolumaja- Universitas Kristen Maranatha Halaman 178
11 : Bidang yang merupakan tutup dari silinder Dalam kasus ini tidak perlu dilakukan parameterisasi, akan digunakan metoda pertama integral permukaan. Persamaan bidang adalah dengan radius berpusat dititik 0. Sehingga,. Dan untuk permukaan ini, daerah D adalah cakram adalah luas daerah D dan D adalah cakram dengan radius perhitungan integral, jadi didapat sehingga tidak usah dilakukan : Bidang yang merupakan dasar dari silinder Persamaan bidang dasar silinder adalah berpusat di titik 0 (origin). Sehingga dan D adalah cakram dengan radius Rudy Wawolumaja- Universitas Kristen Maranatha Halaman 179
12 Perhitungan akhir integral permukaan menjadi, Rudy Wawolumaja- Universitas Kristen Maranatha Halaman 180
13 7.3. Integral Permukaan Medan Vektor Seperti halnya dalam integral garis, orientasi kurva berpengaruh pada hasil perhitungan, demikian juga untuk integral permukaan orientasi permukaan berpengaruh pada hasil perhitungan. Pada suatu permukaan setiap titik mempunyai dua unit vektor normal, yaitu and. Pilihan unit vector yang mana yang dipilih untuk mewakili permukaan akan mempengaruhi orientasi dari permukaan. Untuk permukaan dibuat perjanjian (konvensi) untuk orientasi permukaan. Definisi : 1. Suatu permukaan dikatakan tertutup, apabila permukaan tersebut merupakan pembatas (boundary) dari suatu benda pejal E, contoh permukaan bola merupakan permukaan tertutup yang membatasi volume bola, atau kerak bumi merupakan permukaan tertutup yang membatasi bola dunia. 2. Suatu permukaan tertutup S memiliki orientasi positif, bila dipilih himpunan unit vektor normal yang mempunyai arah keluar dari daerah volume E. Dan orientasi negatif bila arah vektor normalnya mengarah kedalam daerah volume E yang diliputi permukaan tersebut, Misal suatu fungsi. Dan suatu fungsi baru dimana, Fungsi baru tersebut memenuhi persamaan. merupakan orthogonal ( normal) terhadap permukaan. Untuk mendapatkan unit vektor normal, Untuk fungsi dalam bentuk ) adalah selalu positif dan selalu mengarah keatas. Proses yang sama dilakukan untuk permukaan dalam bentuk diatas komponen vektor normal pada arah z (dinyatakan oleh (sehingga ) atau untuk permukaan dalam bentuk (sehingga ). Untuk permukaan yang dinyatakan dalam bentuk parametrik (vektor) seperti, Maka vektor adalah normal terhadap bidang singgung pada titik tertentu, dan dengan itu akan juga normal terhadap permukaan dimaksud pada titik tertentu tersebut. Sehingga unit normal vektor, Rudy Wawolumaja- Universitas Kristen Maranatha Halaman 181
14 Dan untuk setiap permukaan baik (atau atau ) dapat dinyatakan di parameterisasi kedalam bentuk vektor dan dengan mudah dapat dicari unit vektor normal nya. Berikut bentuk integral permukaan untuk medan vektor terhadap permukaan S. Misal medan vektor dengan unit vektor normal, maka integral permukaan atas permukaan S adalah, Bentuk diatas sering disebut flux menembus S. Misal suatu permukaan dan medan vektor dan orientasi positif adalah keatas, maka dengan assumsi ini maka, Bila diberikan permukaan tidak dalam bentuk permukaan, maka akan ada 6 kemungkinan integral. Dua untuk masing-masing permukaan, dan. Untuk setiap permukaan ada dua bentuk pernyataan unit vektor normal yang sebenarnya keduanya adalah identik. Dengan menggunakan unit vektor normal, maka kerumitan perhitungan adanya akar dapat dihindari. Dan sebenarnya bentuk akar adalah, Sehingga dengan menggunakan notasi gradient, akan menjadi lebih sederhana. Rumus integral permukaan atas permukaan yang diberikan dalam bentuk parametrik. Rudy Wawolumaja- Universitas Kristen Maranatha Halaman 182
15 Contoh Hitung dimana dan S adalah permukaan suatu paraboloid, dan cakram pada., S berorientasi positif. Solusi Cakram dalam soal ini adalah tutup dari paraboloid, sehingga didapat permukaan yang tertutup. Adanya permukaan tertutup penting, karena S berorientasi positif dan menurut konvensi yang telah di definisikan maka semua unit vektor normal akan mengarah keluar daerah yang dibatasi oleh S. Berikut gambar sketsa permukaan S, Gambar 7.5. Paraboloid dinyatakan oleh dan cakram dinyatakan oleh. Dan supaya unit vektor pada paraboloid mengarah keluar maka akan mengarah kearah negatif y. Sebaliknya supaya unit vektor normal pada cakram mengarah keluar maka akan mengarah kearah positif y. Karena permukaan S terdiri dari dua permukaan, maka perhitungan integral permukaan dilakukan pada setiap permukaan dan hasil akhirnya adalah penjumlahan keduanya. Untuk paraboloid, permukaan diberikan dalam bentuk sebagai, sehingga dapat dinyatakan Vektor gradient fungsi diatas adalah, Vektor gradient diatas memiliki komponen y positif, artinya mengarah ke y positif, sedangkan dari interpretasi gambar sketsa diatas, dibutuhkan unit vektor normal yang mengarah y negatif agar memenuhi syarat arah keluar dari daerah tertutup. Jadi unit vektor normal adalah, Perhitungan integral lipat atas : Paraboloid Rudy Wawolumaja- Universitas Kristen Maranatha Halaman 183
16 Persamaan permukaan dimasukkan kedalam perhitungan integral diatas dan daerah D adalah cakram dengan 1 pada bidang- xz, sehingga perhitungan akanmenjadi lebih mudah bila dilakukan dengan menggunakan koordinat polar. Berikut konversi ke koordinat polar, Perhitungan integral menjadi, Perhitungan integral lipat atas permukaan : Tutup Paraboloid yang adalah cakram Permukaan tutup paraboloid berupa cakram tidak lain adalah potongan bidang yang ada didepan cakram dengan radius 1 pada bidang- xz (bayangkan cakram pada bidang xz diproyeksikan pada bidang y =1). Dan karena orientasi permukaan disyaratkan positif, maka unit vektor normal mengarah keluar permukaan tertutup artinya orthogonal terhadap bidang y=1, yaitu paralel terhadap sumbu-y dan berarah positif, yaitu Sehingga, Dengan memasukkan nilai y=1 didapat, Dan, Sehingga, Karena D adalah cakram dengan radius 1, maka integral diatas adalah luas cakram daerah D, Rudy Wawolumaja- Universitas Kristen Maranatha Halaman 184
17 Sehingga hasil akhir adalah, Contoh Hitung dimana dan S adalah potongan atas setengah bola dan cakram yang terletak pada bidang. Permukaan S berorientasi positif. Solusi Berikut adalah gambar sketsa dari permukaan S, Gambar 7.6. adalah permukaan bola dan adalah dasar / tutup bawah dari potongan atas setengah bola yang berbentuk cakram. Dari gambar diatas, disimpulkan unit vektor normal permukaan bola memiliki komponen z arah positif, sedangkan untuk unit vektor normal dasar permukaan memiliki komponen z arah negatif. Perhitungan Integral dilakukan dua tahap, pertama terhadap Parameterisasi permukaan : Setengah Bola Atas yang berupa bola adalah, Karena permukaan berupa setengah bola bagian atas, maka Langkah berikutnya adalah menentukan. Besaran (magnitude) dari vektor perkalian silang integral nanti akan tercoret sendirinya. tidak perlu dicari, karena dari rumus Rudy Wawolumaja- Universitas Kristen Maranatha Halaman 185
18 Dari range didapat nilai sine dan cosine keduanya adalah positif, sehingga agar hasil akan memiliki komponen z negatif, sedangkan untuk memenuhi syarat orientasi permukaan tertutup S positif, maka komponen z harus positif, sehingga Karena, Maka, Sehingga, : Tutup dasar permukaan setengah bola atas Permukaan adalah cakram yang terletak pada bidang sehingga persamaan permukaan ini adalah. Maka unit vektor normal adalah, Dibutuhkan nilai negatif, agar memenuhi syarat orientasi positif permukaan S. Sehingga, Dengan memasukkan, Hasil akhir adalah penjumlahan, Rudy Wawolumaja- Universitas Kristen Maranatha Halaman 186
19 Interpretasi fisis dari integral permukaan adalah dalam aplikasi mekanika fluida. Jika adalah medan vektor kecepatan fluida, maka integral permukaan merepresentasikan volume fluida yang mengalir melalui S per unit waktu (yaitu per detik, per menit atau jam) dengan kata lain debit dari aliran fluida. Rudy Wawolumaja- Universitas Kristen Maranatha Halaman 187
20 7.4. Teorema Stokes Bila Teorema Green menyatakan hubungan integral garis dengan integral ganda atas suatu daerah. Maka Teorema Stokes menyatakan hubungan antara integral garis dengan integral permukaan. Berikut adalah gambar suatu permukaan S, lintasan C dengan arah panah sebagai orientasi. Gambar 7.7. Mengelilingi ujung dasar permukaan adalah kurva C. Kurva ini dinamakan kurva pembatas ( boundary curve). Orientasi permukaan S akan menentukan orientasi positif kurva C. Untuk mendapatkan orientasi positif kurva C, bayangkan kita berjalan sepanjang kurva. Sementara berjalan, bila kepala kita menunjuk arah sama dengan unit vektor normal dan permukaan ada disebelah kiri, maka kita berjalan dalam arah positif pada kurva C. Teorema Stokes Bila S adalah permukaan rata yang berorientasi dan dibatasi oleh kurva C yang sederhana, tertutup dan rata dan berorientasi positif. Bila adalah medan vektor, maka Contoh Gunakan teorema Stokes untuk menghitung dimana dan S adalah potongan yang terletak diatas bidang. Orientasi S adalah keatas. Solusi Berikut gambar sketsa permukaan. Gambar 7.8. Rudy Wawolumaja- Universitas Kristen Maranatha Halaman 188
21 Kurva pembatas (boundary curve) C adalah irisan permukaan dengan bidang dan kurva tersebut adalah 1 = 5 - x 2 y 2 x 2 + y 2 = 4 pada z =1 Jadi kurva pembatas C adalah lingkaran dengan radius 2 yang terletak dibidang. Parameterisasi kurva ini, Dengan menggunakan Teorema Stokes, Sehingga, Contoh Gunakan Teorema Stokes untuk menghitung dimana dan C adalah segitiga dengan titik ujung, dan dan mempunyai arah rotasi berlawanan dengan jarum jam. Solusi Berikut adalah gambar sketsa permukaan S, kurva pembatas C dan orientasi C. Orientasi permukaan adalah keatas. Rudy Wawolumaja- Universitas Kristen Maranatha Halaman 189
22 Gambar 7.9. Orientasi kurva menentukan orientasi permukaan dan sebaliknya. Persamaan bidang adalah, Dengan menggunakan Teorema Stokes, didapat Gradient f mempunyai arah keatas, jadi arah untuk unit vektor normal sudah cocok. Berikut gambar sketsa, D daerah terletak di bidang xy, Gambar Persamaan sisi miring didapat dengan memasukkan kedalam persamaan bidang. Sehingga ketidaksamaan (range) yang men definisikan D adalah, Sehingga dengan memasukkan z = 1 x y, didapat Rudy Wawolumaja- Universitas Kristen Maranatha Halaman 190
23 Hasil akhir, Rudy Wawolumaja- Universitas Kristen Maranatha Halaman 191
24 7.5. Teorema Divergence Bila E adalah wilayah benda pejal sederhana dan S adalah permukaan pembatas (boundary surface) dari E berorientasi positif. adalah medan vektor dengan komponen vektor yang memiliki turunan parsial pertama yang kontinu, maka Teorema Divergence menyatakan hubungan integral permukaan dengan integral lipat tiga. Contoh Gunakan teorema divergence untuk menghitung dimana dan permukaan pembatas terdiri dari 3 permukaan,, disebelah atas,, pada sisi dan permukaan dasar. Solusi Berikut gambar sketsa permukaan. Gambar Dari bentuk benda diatas, maka paling tepat digunakan koordinat silendris, sehingga batas jangkauan (range) adalah, Rudy Wawolumaja- Universitas Kristen Maranatha Halaman 192
25 Rudy Wawolumaja- Universitas Kristen Maranatha Halaman 193
DIKTAT KULIAH KALKULUS PEUBAH BANYAK (IE-308)
 DIKTAT KULIAH (IE-308) BAB 5 INTEGRAL LIPAT Diktat ini digunakan bagi mahasiswa Jurusan Teknik Industri Fakultas Teknik Universitas Kristen Maranatha Ir. Rudy Wawolumaja M.Sc JURUSAN TEKNIK INDUSTRI -
DIKTAT KULIAH (IE-308) BAB 5 INTEGRAL LIPAT Diktat ini digunakan bagi mahasiswa Jurusan Teknik Industri Fakultas Teknik Universitas Kristen Maranatha Ir. Rudy Wawolumaja M.Sc JURUSAN TEKNIK INDUSTRI -
DIKTAT KULIAH KALKULUS PEUBAH BANYAK (IE-308)
 DIKTAT KULIAH (IE-308) BAB 6 INTEGRAL GARIS Diktat ini digunakan bagi mahasiswa Jurusan Teknik Industri Fakultas Teknik Universitas Kristen Maranatha Ir. Rudy Wawolumaja M.Sc JURUSAN TEKNIK INDUSTRI -
DIKTAT KULIAH (IE-308) BAB 6 INTEGRAL GARIS Diktat ini digunakan bagi mahasiswa Jurusan Teknik Industri Fakultas Teknik Universitas Kristen Maranatha Ir. Rudy Wawolumaja M.Sc JURUSAN TEKNIK INDUSTRI -
DIKTAT KULIAH KALKULUS PEUBAH BANYAK (IE-308)
 DIKTAT KULIAH (IE-308) BAB 3 TURUNAN PARSIAL Diktat ini digunakan bagi mahasiswa Jurusan Teknik Industri Fakultas Teknik Universitas Kristen Maranatha Ir. Rudy Wawolumaja M.Sc JURUSAN TEKNIK INDUSTRI -
DIKTAT KULIAH (IE-308) BAB 3 TURUNAN PARSIAL Diktat ini digunakan bagi mahasiswa Jurusan Teknik Industri Fakultas Teknik Universitas Kristen Maranatha Ir. Rudy Wawolumaja M.Sc JURUSAN TEKNIK INDUSTRI -
DIKTAT KULIAH KALKULUS PEUBAH BANYAK (IE-308)
 DIKTAT KULIAH (IE-308) BAB 2 RUANG 3 DIMENSI Diktat ini digunakan bagi mahasiswa Jurusan Teknik Industri Fakultas Teknik Universitas Kristen Maranatha Ir. Rudy Wawolumaja M.Sc JURUSAN TEKNIK INDUSTRI -
DIKTAT KULIAH (IE-308) BAB 2 RUANG 3 DIMENSI Diktat ini digunakan bagi mahasiswa Jurusan Teknik Industri Fakultas Teknik Universitas Kristen Maranatha Ir. Rudy Wawolumaja M.Sc JURUSAN TEKNIK INDUSTRI -
DIKTAT KULIAH KALKULUS PEUBAH BANYAK (IE-308)
 DIKTAT KULIAH (IE-308) BAB 1. PENDAHULUAN Diktat ini digunakan bagi mahasiswa Jurusan Teknik Industri Fakultas Teknik Universitas Kristen Maranatha Ir. Rudy Wawolumaja M.Sc JURUSAN TEKNIK INDUSTRI - FAKULTAS
DIKTAT KULIAH (IE-308) BAB 1. PENDAHULUAN Diktat ini digunakan bagi mahasiswa Jurusan Teknik Industri Fakultas Teknik Universitas Kristen Maranatha Ir. Rudy Wawolumaja M.Sc JURUSAN TEKNIK INDUSTRI - FAKULTAS
Pertemuan : 9 Materi : Teorema Green Bab IV. Teorema Green, Teorema Divergensi Gauss, dan Teorema Stokes
 Pertemuan : 9 Materi : Teorema Green Bab IV. Teorema Green, Teorema Divergensi Gauss, dan Teorema Stokes Standar Kompetensi : 1. Memahami Teorema Green Kompetensi Dasar : 1. Menyebutkan kembali pengertian
Pertemuan : 9 Materi : Teorema Green Bab IV. Teorema Green, Teorema Divergensi Gauss, dan Teorema Stokes Standar Kompetensi : 1. Memahami Teorema Green Kompetensi Dasar : 1. Menyebutkan kembali pengertian
Teorema Divergensi, Teorema Stokes, dan Teorema Green
 TEOREMA DIVERGENSI, STOKES, DAN GREEN Materi pokok pertemuan ke 13: 1. Teorema divergensi Gauss URAIAN MATERI Untuk memudahkan perhitungan seringkali dibutuhkan penyederhanaan bentuk integral yang berdasarkan
TEOREMA DIVERGENSI, STOKES, DAN GREEN Materi pokok pertemuan ke 13: 1. Teorema divergensi Gauss URAIAN MATERI Untuk memudahkan perhitungan seringkali dibutuhkan penyederhanaan bentuk integral yang berdasarkan
DIKTAT KULIAH KALKULUS PEUBAH BANYAK (IE-308)
 DIKTAT KULIAH (IE-308) BAB 4 PENERAPAN TURUNAN PARSIAL Diktat ini digunakan bagi mahasiswa Jurusan Teknik Industri Fakultas Teknik Universitas Kristen Maranatha Ir. Rudy Wawolumaja M.Sc JURUSAN TEKNIK
DIKTAT KULIAH (IE-308) BAB 4 PENERAPAN TURUNAN PARSIAL Diktat ini digunakan bagi mahasiswa Jurusan Teknik Industri Fakultas Teknik Universitas Kristen Maranatha Ir. Rudy Wawolumaja M.Sc JURUSAN TEKNIK
Catatan Kuliah FI2101 Fisika Matematik IA
 Khairul Basar atatan Kuliah FI2101 Fisika Matematik IA Semester I 2015-2016 Fakultas Matematika dan Ilmu Pengetahuan Alam Institut Teknologi Bandung Bab 6 Analisa Vektor 6.1 Perkalian Vektor Pada bagian
Khairul Basar atatan Kuliah FI2101 Fisika Matematik IA Semester I 2015-2016 Fakultas Matematika dan Ilmu Pengetahuan Alam Institut Teknologi Bandung Bab 6 Analisa Vektor 6.1 Perkalian Vektor Pada bagian
Bab 1 Vektor. A. Pendahuluan
 Bab 1 Vektor A. Pendahuluan Dalam mata kuliah Listrik Magnet A, maupun mata kuliah Listrik Magnet B sebagaii lanjutannya, penyajian konsep dan pemecahan masalah akan banyak memerlukan pengetahuan tentang
Bab 1 Vektor A. Pendahuluan Dalam mata kuliah Listrik Magnet A, maupun mata kuliah Listrik Magnet B sebagaii lanjutannya, penyajian konsep dan pemecahan masalah akan banyak memerlukan pengetahuan tentang
Dosen Pengampu : Puji Andayani, S.Si, M.Si, M.Sc
 KALKULUS III Teorema Integral (Green s Theorem) Dosen Pengampu : Puji Andayani, S.Si, M.Si, M.Sc 1 Kurva Tertutup Sederhana, Daerah Terhubung sederhana dan Berganda Suatu kurva tertutup sederhana adalah
KALKULUS III Teorema Integral (Green s Theorem) Dosen Pengampu : Puji Andayani, S.Si, M.Si, M.Sc 1 Kurva Tertutup Sederhana, Daerah Terhubung sederhana dan Berganda Suatu kurva tertutup sederhana adalah
Program Studi Pendidikan Matematika STKIP PGRI SUMBAR
 INTEGRASI VEKTOR Materi pokok pertemuan ke 11: 1. Integral Biasa 2. Integral Garis URAIAN MATERI Sebelum masuk ke integral garis, Anda pelajari dulu mengenai integral biasa dari vektor. Integral Biasa
INTEGRASI VEKTOR Materi pokok pertemuan ke 11: 1. Integral Biasa 2. Integral Garis URAIAN MATERI Sebelum masuk ke integral garis, Anda pelajari dulu mengenai integral biasa dari vektor. Integral Biasa
BAB II VEKTOR DAN GERAK DALAM RUANG
 BAB II VEKTOR DAN GERAK DALAM RUANG 1. KOORDINAT CARTESIUS DALAM RUANG DIMENSI TIGA SISTEM TANGAN KANAN SISTEM TANGAN KIRI RUMUS JARAK,,,, 16 Contoh : Carilah jarak antara titik,, dan,,. Solusi :, Persamaan
BAB II VEKTOR DAN GERAK DALAM RUANG 1. KOORDINAT CARTESIUS DALAM RUANG DIMENSI TIGA SISTEM TANGAN KANAN SISTEM TANGAN KIRI RUMUS JARAK,,,, 16 Contoh : Carilah jarak antara titik,, dan,,. Solusi :, Persamaan
KALKULUS MULTIVARIABEL II
 Pada Bidang Bentuk Vektor dari KALKULUS MULTIVARIABEL II (Minggu ke-9) Andradi Jurusan Matematika FMIPA UGM Yogyakarta, Indonesia Pada Bidang Bentuk Vektor dari 1 Definisi Daerah Sederhana x 2 Pada Bidang
Pada Bidang Bentuk Vektor dari KALKULUS MULTIVARIABEL II (Minggu ke-9) Andradi Jurusan Matematika FMIPA UGM Yogyakarta, Indonesia Pada Bidang Bentuk Vektor dari 1 Definisi Daerah Sederhana x 2 Pada Bidang
Program Studi Teknik Mesin S1
 SATUAN ACARA PERKULIAHAN MATA KULIAH : KALKULUS 3 KODE / SKS : IT042219 / 2 SKS Pertemuan Pokok Bahasan dan TIU Geometri pada bidang, vektor vektor pada bidang : pendekatan secara geometrik dan secara
SATUAN ACARA PERKULIAHAN MATA KULIAH : KALKULUS 3 KODE / SKS : IT042219 / 2 SKS Pertemuan Pokok Bahasan dan TIU Geometri pada bidang, vektor vektor pada bidang : pendekatan secara geometrik dan secara
Kalkulus Multivariabel I
 dan Gradien dan Gradien Statistika FMIPA Universitas Islam Indonesia dan Gradien Turunan-turunan parsial f x (x, y) dan f y (x, y) mengukur laju perubahan (dan kemiringan garis singgung) pada arah sejajar
dan Gradien dan Gradien Statistika FMIPA Universitas Islam Indonesia dan Gradien Turunan-turunan parsial f x (x, y) dan f y (x, y) mengukur laju perubahan (dan kemiringan garis singgung) pada arah sejajar
SIFAT-SIFAT INTEGRAL LIPAT
 TUGAS KALKULUS LANJUT SIFAT-SIFAT INTEGAL LIPAT Oleh: KAMELIANI 46 JUUSAN MATEMATIKA FAKULTAS MATEMATIKA AN ILMU PENGETAHUAN ALAM UNIVESITAS NEGEI MAKASSA 4 SIFAT-SIFAT INTEGAL LIPAT A. SIFAT-SIFAT INTEGAL
TUGAS KALKULUS LANJUT SIFAT-SIFAT INTEGAL LIPAT Oleh: KAMELIANI 46 JUUSAN MATEMATIKA FAKULTAS MATEMATIKA AN ILMU PENGETAHUAN ALAM UNIVESITAS NEGEI MAKASSA 4 SIFAT-SIFAT INTEGAL LIPAT A. SIFAT-SIFAT INTEGAL
Dosen Pengampu : Puji Andayani, S.Si, M.Si, M.Sc
 KALKULUS III Teorema Integral (Stokes Theorem) Dosen Pengampu : Puji Andayani, S.Si, M.Si, M.Sc 1 Stokes Theorem Review : Pada pembahasan sebelumnya, kepadatan sirkulasi atau curl pada bidang dua dimensi
KALKULUS III Teorema Integral (Stokes Theorem) Dosen Pengampu : Puji Andayani, S.Si, M.Si, M.Sc 1 Stokes Theorem Review : Pada pembahasan sebelumnya, kepadatan sirkulasi atau curl pada bidang dua dimensi
ANALISIS VEKTOR. Aljabar Vektor. Operasi vektor
 ANALISIS VEKTOR Aljabar Vektor Operasi vektor Besaran yang memiliki nilai dan arah disebut dengan vektor. Contohnya adalah perpindahan, kecepatan, percepatan, gaya, dan momentum. Sementara itu, besaran
ANALISIS VEKTOR Aljabar Vektor Operasi vektor Besaran yang memiliki nilai dan arah disebut dengan vektor. Contohnya adalah perpindahan, kecepatan, percepatan, gaya, dan momentum. Sementara itu, besaran
BAB 1 BESARAN VEKTOR. A. Representasi Besaran Vektor
 BAB 1 BESARAN VEKTOR TUJUAN PEMBELAJARAN 1. Menjelaskan definisi vektor, dan representasinya dalam sistem koordinat cartesius 2. Menjumlahan vektor secara grafis dan matematis 3. Melakukan perkalian vektor
BAB 1 BESARAN VEKTOR TUJUAN PEMBELAJARAN 1. Menjelaskan definisi vektor, dan representasinya dalam sistem koordinat cartesius 2. Menjumlahan vektor secara grafis dan matematis 3. Melakukan perkalian vektor
Soal-Soal dan Pembahasan Matematika IPA SNMPTN 2012 Tanggal Ujian: 13 Juni 2012
 Soal-Soal dan Pembahasan Matematika IPA SNMPTN 01 Tanggal Ujian: 13 Juni 01 1. Lingkaran (x + 6) + (y + 1) 5 menyinggung garis y 4 di titik... A. ( -6, 4 ). ( -1, 4 ) E. ( 5, 4 ) B. ( 6, 4) D. ( 1, 4 )
Soal-Soal dan Pembahasan Matematika IPA SNMPTN 01 Tanggal Ujian: 13 Juni 01 1. Lingkaran (x + 6) + (y + 1) 5 menyinggung garis y 4 di titik... A. ( -6, 4 ). ( -1, 4 ) E. ( 5, 4 ) B. ( 6, 4) D. ( 1, 4 )
MODUL PEMBELAJARAN KALKULUS II. ALFIANI ATHMA PUTRI ROSYADI, M.Pd
 MODUL PEMBELAJARAN KALKULUS II ALFIANI ATHMA PUTRI ROSYADI, M.Pd IDENTITAS MAHASISWA NAMA : KLS/NIM :. KELOMPOK:. Daftar Isi Kata Pengantar Peta Konsep Materi. BAB I Analisis Vektor a. Vektor Pada Bidang.6
MODUL PEMBELAJARAN KALKULUS II ALFIANI ATHMA PUTRI ROSYADI, M.Pd IDENTITAS MAHASISWA NAMA : KLS/NIM :. KELOMPOK:. Daftar Isi Kata Pengantar Peta Konsep Materi. BAB I Analisis Vektor a. Vektor Pada Bidang.6
Kalkulus II. Institut Teknologi Kalimantan
 Tim Dosen Kalkulus II Tahun Persiapan Bersama Institut Kalkulus Teknologi II Kalimantan January 31, () 2018 1 / 71 Kalkulus II Tim Dosen Kalkulus II Tahun Persiapan Bersama Institut Teknologi Kalimantan
Tim Dosen Kalkulus II Tahun Persiapan Bersama Institut Kalkulus Teknologi II Kalimantan January 31, () 2018 1 / 71 Kalkulus II Tim Dosen Kalkulus II Tahun Persiapan Bersama Institut Teknologi Kalimantan
Soal-Soal dan Pembahasan Matematika IPA SNMPTN 2012 Tanggal Ujian: 13 Juni 2012
 Soal-Soal dan Pembahasan Matematika IPA SNMPTN 01 Tanggal Ujian: 13 Juni 01 1. Lingkaran (x + 6) + (y + 1) 5 menyinggung garis y 4 di titik... A. ( -6 4 ). ( -1 4 ) E. ( 5 4 ) B. ( 6 4) D. ( 1 4 ) BAB
Soal-Soal dan Pembahasan Matematika IPA SNMPTN 01 Tanggal Ujian: 13 Juni 01 1. Lingkaran (x + 6) + (y + 1) 5 menyinggung garis y 4 di titik... A. ( -6 4 ). ( -1 4 ) E. ( 5 4 ) B. ( 6 4) D. ( 1 4 ) BAB
Ringkasan Kalkulus 2, Untuk dipakai di ITB 1. Integral Lipat Dua Atas Daerah Persegipanjang
 ingkasan Kalkulus 2, Untuk dipakai di ITB 1 Integral Lipat Dua Atas Daerah Persegipanjang Perhatikan fungsi z = f(x, y) pada = {(x, y) : a x b, c y d} Bentuk partisi P atas daerah berupa n buah persegipanjang
ingkasan Kalkulus 2, Untuk dipakai di ITB 1 Integral Lipat Dua Atas Daerah Persegipanjang Perhatikan fungsi z = f(x, y) pada = {(x, y) : a x b, c y d} Bentuk partisi P atas daerah berupa n buah persegipanjang
BESARAN VEKTOR. Gb. 1.1 Vektor dan vektor
 BAB 1 BESARAN VEKTOR Tujuan Pembelajaran 1. Menjelaskan definisi vektor, dan representasinya dalam sistem koordinat cartesius 2. Menjumlahkan vektor secara grafis dan dengan vektor komponen 3. Melakukan
BAB 1 BESARAN VEKTOR Tujuan Pembelajaran 1. Menjelaskan definisi vektor, dan representasinya dalam sistem koordinat cartesius 2. Menjumlahkan vektor secara grafis dan dengan vektor komponen 3. Melakukan
1.1 Fungsi Dua Peubah Atau Lebih 1.2 Turunan Parsial Fungsi Dua Peubah atau Lebih
 ] 1 Pada Bab 1 ini akan dibahas antara lain sebagai berikut. 1.1 Fungsi Dua Peubah Atau Lebih 1.2 Turunan Parsial Fungsi Dua Peubah atau Lebih Tema sentral dari bab ini adalah kalkulus dari fungsi peubah
] 1 Pada Bab 1 ini akan dibahas antara lain sebagai berikut. 1.1 Fungsi Dua Peubah Atau Lebih 1.2 Turunan Parsial Fungsi Dua Peubah atau Lebih Tema sentral dari bab ini adalah kalkulus dari fungsi peubah
AFTAR ISI KATA PENGANTAR... i DAFTAR ISI... iii SOAL - SOAL... 2 PEMBAHASAN... 19
 DAFTAR ISI KATA PENGANTAR... i DAFTAR ISI... iii SOAL - SOAL... UTS Genap 009/00... UTS Ganjil 009/00... UTS Genap 008/009... 5 UTS Pendek 008/009... 6 UTS 007/008... 8 UTS 006/007... 9 UTS 005/006...
DAFTAR ISI KATA PENGANTAR... i DAFTAR ISI... iii SOAL - SOAL... UTS Genap 009/00... UTS Ganjil 009/00... UTS Genap 008/009... 5 UTS Pendek 008/009... 6 UTS 007/008... 8 UTS 006/007... 9 UTS 005/006...
Pertemuan Minggu ke Keterdiferensialan 2. Derivatif berarah dan gradien 3. Aturan rantai
 Pertemuan Minggu ke-10 1. Keterdiferensialan 2. Derivatif berarah dan gradien 3. Aturan rantai 1. Keterdiferensialan Pada fungsi satu peubah, keterdiferensialan f di x berarti keujudan derivatif f (x).
Pertemuan Minggu ke-10 1. Keterdiferensialan 2. Derivatif berarah dan gradien 3. Aturan rantai 1. Keterdiferensialan Pada fungsi satu peubah, keterdiferensialan f di x berarti keujudan derivatif f (x).
Matematika Dasar INTEGRAL PERMUKAAN
 Matematika asar INTEGRAL PERMUKAAN Misal suatu permukaan yang dinyatakan dengan persamaan z = f( x,y ) dan merupakan proyeksi pada bidang XOY. Bila diberikan lapangan vektor F( x,y,z ) = f( x,y,z ) i +
Matematika asar INTEGRAL PERMUKAAN Misal suatu permukaan yang dinyatakan dengan persamaan z = f( x,y ) dan merupakan proyeksi pada bidang XOY. Bila diberikan lapangan vektor F( x,y,z ) = f( x,y,z ) i +
SRI REDJEKI KALKULUS I
 SRI REDJEKI KALKULUS I KLASIFIKASI BILANGAN RIIL n Bilangan yang paling sederhana adalah bilangan asli : n 1, 2, 3, 4, 5,. n n Bilangan asli membentuk himpunan bagian dari klas himpunan bilangan yang lebih
SRI REDJEKI KALKULUS I KLASIFIKASI BILANGAN RIIL n Bilangan yang paling sederhana adalah bilangan asli : n 1, 2, 3, 4, 5,. n n Bilangan asli membentuk himpunan bagian dari klas himpunan bilangan yang lebih
Integral lipat dua BAB V INTEGRAL LIPAT 5.1. DEFINISI INTEGRAL LIPAT DUA. gambar 5.1 Luasan di bawah permukaan
 BAB V INTEGRAL LIPAT 5.1. DEFINISI INTEGRAL LIPAT DUA gambar 5.1 Luasan di bawah permukaan 61 Pada Matematika Dasar I telah dipelajari integral tertentu b f ( x) dx yang dapat didefinisikan, apabila f
BAB V INTEGRAL LIPAT 5.1. DEFINISI INTEGRAL LIPAT DUA gambar 5.1 Luasan di bawah permukaan 61 Pada Matematika Dasar I telah dipelajari integral tertentu b f ( x) dx yang dapat didefinisikan, apabila f
MA1201 MATEMATIKA 2A Hendra Gunawan
 MA101 MATEMATIKA A Hendra Gunawan Semester II, 016/017 10 Maret 01 Kuliah ang Lalu 10.1- Parabola, Elips, dan Hiperbola 10.4 Persamaan Parametrik Kurva di Bidang 10.5 Sistem Koordinat Polar 11.1 Sistem
MA101 MATEMATIKA A Hendra Gunawan Semester II, 016/017 10 Maret 01 Kuliah ang Lalu 10.1- Parabola, Elips, dan Hiperbola 10.4 Persamaan Parametrik Kurva di Bidang 10.5 Sistem Koordinat Polar 11.1 Sistem
Suryadi Siregar Metode Matematika Astronomi 2
 Suryadi Siregar Metode Matematika Astronomi Bab 4 Integral Garis dan Teorema Green 4. Integral Garis Definisi : Misal suatu lintasan dalam ruang dimensi m pada interval [a,b]. Andaikan adalah medan vektor
Suryadi Siregar Metode Matematika Astronomi Bab 4 Integral Garis dan Teorema Green 4. Integral Garis Definisi : Misal suatu lintasan dalam ruang dimensi m pada interval [a,b]. Andaikan adalah medan vektor
Dosen Pengampu : Puji Andayani, S.Si, M.Si, M.Sc
 KALKULUS III Teorema Integral Dosen Pengampu : Puji Andayani, S.Si, M.Si, M.Sc 1 INTEGRAL GARIS Integral Garis pada Fungsi Skalar Definisi : Jika f didefinisikan pada kurva diberikan secara parametrik
KALKULUS III Teorema Integral Dosen Pengampu : Puji Andayani, S.Si, M.Si, M.Sc 1 INTEGRAL GARIS Integral Garis pada Fungsi Skalar Definisi : Jika f didefinisikan pada kurva diberikan secara parametrik
UJIAN NASIONAL DINAS PENDIDIKAN DKI JAKARTA SMA/MA
 B Matematika IPA SMA/MA TRYOUT UJIAN NASIONAL DINAS PENDIDIKAN DKI JAKARTA SMA/MA TAHUN PELAJARAN 04/05 MATEMATIKA IPA Hasil Kerja Sama dengan Matematika IPA SMA/MA Mata Pelajaran : Matematika IPA Jenjang
B Matematika IPA SMA/MA TRYOUT UJIAN NASIONAL DINAS PENDIDIKAN DKI JAKARTA SMA/MA TAHUN PELAJARAN 04/05 MATEMATIKA IPA Hasil Kerja Sama dengan Matematika IPA SMA/MA Mata Pelajaran : Matematika IPA Jenjang
Program Studi Teknik Mesin S1
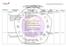 SATUAN ACARA PERKULIAHAN MATA KULIAH : MATEMATIKA TEKNIK 2 KODE/SKS : IT042227 / 2 SKS Pertemuan Pokok Bahasan dan TIU 1 Pendahuluan Mahasiswa mengerti tentang mata kuliah Matematika Teknik 2 : bahan ajar,
SATUAN ACARA PERKULIAHAN MATA KULIAH : MATEMATIKA TEKNIK 2 KODE/SKS : IT042227 / 2 SKS Pertemuan Pokok Bahasan dan TIU 1 Pendahuluan Mahasiswa mengerti tentang mata kuliah Matematika Teknik 2 : bahan ajar,
Bagian 4 Terapan Differensial
 Bagian 4 Terapan Differensial Dalam bagian 4 Terapan Differensial, kita akan mempelajari materi bagaimana konsep differensial dapat dipergunakan untuk mengatasi persoalan yang terjadi di sekitar kita.
Bagian 4 Terapan Differensial Dalam bagian 4 Terapan Differensial, kita akan mempelajari materi bagaimana konsep differensial dapat dipergunakan untuk mengatasi persoalan yang terjadi di sekitar kita.
Hendra Gunawan. 5 Maret 2014
 MA101 MATEMATIKA A Hendra Gunawan Semester II, 013/014 5 Maret 014 Kuliah yang Lalu 10.1 Parabola, aboa, Elips, danhiperbola a 10.4 Persamaan Parametrik Kurva di Bidang 10.5 SistemKoordinatPolar 11.1 Sistem
MA101 MATEMATIKA A Hendra Gunawan Semester II, 013/014 5 Maret 014 Kuliah yang Lalu 10.1 Parabola, aboa, Elips, danhiperbola a 10.4 Persamaan Parametrik Kurva di Bidang 10.5 SistemKoordinatPolar 11.1 Sistem
Integral Vektor. (Pertemuan VII) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya
 TK 47 Matematika III Integral Vektor (Pertemuan VII) Dr. AZ Jurusan Teknik ipil Fakultas Teknik Universitas Brawijaya Teorema Gauss Definisi : Jika V adalah volume yang dibatasi oleh suatu permukaan tertutup
TK 47 Matematika III Integral Vektor (Pertemuan VII) Dr. AZ Jurusan Teknik ipil Fakultas Teknik Universitas Brawijaya Teorema Gauss Definisi : Jika V adalah volume yang dibatasi oleh suatu permukaan tertutup
Kalkulus Multivariabel I
 Integral Lipat-Dua dalam Koordinat Kutub Statistika FMIPA Universitas Islam Indonesia Terdapat beberapa kurva tertentu pada suatu bidang yang lebih mudah dijelaskan dengan menggunakan koordinat Kutub.
Integral Lipat-Dua dalam Koordinat Kutub Statistika FMIPA Universitas Islam Indonesia Terdapat beberapa kurva tertentu pada suatu bidang yang lebih mudah dijelaskan dengan menggunakan koordinat Kutub.
Kinematika. 1 Kinematika benda titik: posisi, kecepatan, percepatan
 ekan #1 Kinematika Mekanika membahas gerakan benda-benda fisis. Kita akan memulai pembahasan kinematika benda titik. Kinematika aitu topik ang membahas deskripsi gerak benda-benda tanpa memperhatikan penebab
ekan #1 Kinematika Mekanika membahas gerakan benda-benda fisis. Kita akan memulai pembahasan kinematika benda titik. Kinematika aitu topik ang membahas deskripsi gerak benda-benda tanpa memperhatikan penebab
MA1201 MATEMATIKA 2A Hendra Gunawan
 MA101 MATEMATIKA A Hendra Gunawan Semester II, 016/017 1 Maret 017 Bab Sebelumnya 9.1 Barisan Tak Terhingga 9. Deret Tak Terhingga 9.3 Deret Positif: Uji Integral 9.4 Deret Positif: Uji Lainnya 9.5 Deret
MA101 MATEMATIKA A Hendra Gunawan Semester II, 016/017 1 Maret 017 Bab Sebelumnya 9.1 Barisan Tak Terhingga 9. Deret Tak Terhingga 9.3 Deret Positif: Uji Integral 9.4 Deret Positif: Uji Lainnya 9.5 Deret
Ringkasan Kalkulus 2, Untuk dipakai di ITB 1. Integral Lipat Dua Atas Daerah Persegipanjang
 ingkasan Kalkulus 2, Untuk dipakai di ITB 1 Integral Lipat Dua Atas Daerah Persegipanjang Perhatikan fungsi z = f(x,y) pada = {(x,y) : a x b, c y d} Bentuk partisi P atas daerah berupa n buah persegipanjang
ingkasan Kalkulus 2, Untuk dipakai di ITB 1 Integral Lipat Dua Atas Daerah Persegipanjang Perhatikan fungsi z = f(x,y) pada = {(x,y) : a x b, c y d} Bentuk partisi P atas daerah berupa n buah persegipanjang
Persamaan Parametrik
 oki neswan (fmipa-itb) Persamaan Parametrik Kita telah lama terbiasa dengan kurva yang dide nisikan oleh sebuah persamaan yang menghubungkan koordinat x dan y: Contohnya persamaan eksplisit seperti y x
oki neswan (fmipa-itb) Persamaan Parametrik Kita telah lama terbiasa dengan kurva yang dide nisikan oleh sebuah persamaan yang menghubungkan koordinat x dan y: Contohnya persamaan eksplisit seperti y x
Geometri dalam Ruang, Vektor
 Prodi Matematika FMIPA Unsyiah July 11, 2011 Koordinat Cartesius: Tiga garis koordinat yang saling tegak lurus (sumbu x, sumbu y dan sumbvu z); Titik nol ketiga garis berada pada titik O yang sama yang
Prodi Matematika FMIPA Unsyiah July 11, 2011 Koordinat Cartesius: Tiga garis koordinat yang saling tegak lurus (sumbu x, sumbu y dan sumbvu z); Titik nol ketiga garis berada pada titik O yang sama yang
TURUNAN, EKSTRIM, BELOK, MINIMUM DAN MAKSIMUM
 TURUNAN, EKSTRIM, BELOK, MINIMUM DAN MAKSIMUM Fungsi f dikatakan mencapai maksimum mutlak di c jika f c f x untuk setiap x I. Di sini f c dinamakan nilai maksimum mutlak. Dan c, f c dinamakan titik maksimum
TURUNAN, EKSTRIM, BELOK, MINIMUM DAN MAKSIMUM Fungsi f dikatakan mencapai maksimum mutlak di c jika f c f x untuk setiap x I. Di sini f c dinamakan nilai maksimum mutlak. Dan c, f c dinamakan titik maksimum
Hendra Gunawan. 8 November 2013
 MA1101 MATEMATIKA 1A Hendra Gunawan Semester I, 013/014 8 November 013 Apa yang Telah Dipelajari pada Bab 4 1. Notasi Sigma dan Luas Daerah di Bawah Kurva. Jumlah Riemann dan Integral Tentu 3. Teorema
MA1101 MATEMATIKA 1A Hendra Gunawan Semester I, 013/014 8 November 013 Apa yang Telah Dipelajari pada Bab 4 1. Notasi Sigma dan Luas Daerah di Bawah Kurva. Jumlah Riemann dan Integral Tentu 3. Teorema
Integral Garis. Sesi XIII INTEGRAL 12/7/2015
 2//25 Mata Kuliah : Matematika Rekayasa Lanjut Kode MK : TK 85 Pengampu : Achfas Zacoeb esi XIII INTEGRAL e-mail : zacoeb@ub.ac.id www.zacoeb.lecture.ub.ac.id Hp. 823398339 Integral Garis Dari Gambar.,
2//25 Mata Kuliah : Matematika Rekayasa Lanjut Kode MK : TK 85 Pengampu : Achfas Zacoeb esi XIII INTEGRAL e-mail : zacoeb@ub.ac.id www.zacoeb.lecture.ub.ac.id Hp. 823398339 Integral Garis Dari Gambar.,
TUJUAN INSTRUKSIONAL KHUSUS
 PREVIEW KALKULUS TUJUAN INSTRUKSIONAL KHUSUS Mahasiswa mampu: menyebutkan konsep-konsep utama dalam kalkulus dan contoh masalah-masalah yang memotivasi konsep tersebut; menjelaskan menyebutkan konsep-konsep
PREVIEW KALKULUS TUJUAN INSTRUKSIONAL KHUSUS Mahasiswa mampu: menyebutkan konsep-konsep utama dalam kalkulus dan contoh masalah-masalah yang memotivasi konsep tersebut; menjelaskan menyebutkan konsep-konsep
Soal dan Solusi Materi Elektrostatika
 P Soal dan Solusi Materi Elektrostatika 1. Tentukan medan listrik pada jarak z di atas salah satu ujung kawat sepanjang L yang membawa muatan berdistribusi seragam dengan rapat muatan, seperti gambar berikut
P Soal dan Solusi Materi Elektrostatika 1. Tentukan medan listrik pada jarak z di atas salah satu ujung kawat sepanjang L yang membawa muatan berdistribusi seragam dengan rapat muatan, seperti gambar berikut
Dinamika Rotasi, Statika dan Titik Berat 1 MOMEN GAYA DAN MOMEN INERSIA
 Dinamika Rotasi, Statika dan Titik Berat 1 MOMEN GAYA DAN MOMEN INERSIA Dalam gerak translasi gaya dikaitkan dengan percepatan linier benda, dalam gerak rotasi besaran yang dikaitkan dengan percepatan
Dinamika Rotasi, Statika dan Titik Berat 1 MOMEN GAYA DAN MOMEN INERSIA Dalam gerak translasi gaya dikaitkan dengan percepatan linier benda, dalam gerak rotasi besaran yang dikaitkan dengan percepatan
Pada integral diatas, dalam mencari penyelesaiannya, pertama diintegralkan terlebih dahulu terhadap x kemudian diintegralkan lagi terhadap y.
 PENDAHULUAN Pada bagian ini akan dibahas perluasan integral tertentu ke bentuk integral lipat dua dari fungsi dua peubah Akan dibahas bentukbentuk integral lipat dalam koordinat kartesius koordinat kutub
PENDAHULUAN Pada bagian ini akan dibahas perluasan integral tertentu ke bentuk integral lipat dua dari fungsi dua peubah Akan dibahas bentukbentuk integral lipat dalam koordinat kartesius koordinat kutub
Kalkulus Peubah Banyak Modul Pembelajaran. January UNIVERSITAS MUHAMMADIYAH MALANG ALFIANI ATHMA PUTRI ROSYADI, M.Pd
 Kalkulus Peubah Banyak Modul Pembelajaran January UNIVERSITAS MUHAMMADIYAH MALANG ALFIANI ATHMA PUTRI ROSYADI, M.Pd IDENTITAS MAHASISWA NAMA : KLS/NIM :. KELOMPOK:. A l f i a n i A t h m a P u t r i R
Kalkulus Peubah Banyak Modul Pembelajaran January UNIVERSITAS MUHAMMADIYAH MALANG ALFIANI ATHMA PUTRI ROSYADI, M.Pd IDENTITAS MAHASISWA NAMA : KLS/NIM :. KELOMPOK:. A l f i a n i A t h m a P u t r i R
A + ( B + C ) = ( A + B ) + C
 VEKTOR ANALISIS 1.1. Skalar dan Vektor Istilah skalar mengacu pada sebuah jumlah yang nilai dapat diwakili oleh satu ( positif atau negatif ) nomor asli. x, y, dan z yang kami gunakan dalam dasar aljabar
VEKTOR ANALISIS 1.1. Skalar dan Vektor Istilah skalar mengacu pada sebuah jumlah yang nilai dapat diwakili oleh satu ( positif atau negatif ) nomor asli. x, y, dan z yang kami gunakan dalam dasar aljabar
Solusi: [Jawaban E] Solusi: [Jawaban D]
![Solusi: [Jawaban E] Solusi: [Jawaban D] Solusi: [Jawaban E] Solusi: [Jawaban D]](/thumbs/56/38103387.jpg) SOLUSI SMA/MA MATEMATIKA Program Studi IPA Kerjasama UNIVERSITAS GUNADARMA dengan Dinas Pendidikan Provinsi DKI Jakarta, Kota/Kabupaten BODETABEK, Tangerang Selatan, Karawang, Serang, Pandeglang, dan Cilegon
SOLUSI SMA/MA MATEMATIKA Program Studi IPA Kerjasama UNIVERSITAS GUNADARMA dengan Dinas Pendidikan Provinsi DKI Jakarta, Kota/Kabupaten BODETABEK, Tangerang Selatan, Karawang, Serang, Pandeglang, dan Cilegon
Dr. Ramadoni Syahputra Jurusan Teknik Elektro FT UMY
 SISTEM-SISTEM KOORDINAT Dr. Ramadoni Syahputra Jurusan Teknik Elektro FT UMY Sistem Koordinat Kartesian Dalam sistem koordinat Kartesian, terdapat tiga sumbu koordinat yaitu sumbu x, y, dan z. Suatu titik
SISTEM-SISTEM KOORDINAT Dr. Ramadoni Syahputra Jurusan Teknik Elektro FT UMY Sistem Koordinat Kartesian Dalam sistem koordinat Kartesian, terdapat tiga sumbu koordinat yaitu sumbu x, y, dan z. Suatu titik
VEKTOR. Besaran skalar (scalar quantities) : besaran yang hanya mempunyai nilai saja. Contoh: jarak, luas, isi dan waktu.
 VEKTOR Kata vektor berasal dari bahasa Latin yang berarti "pembawa" (carrier), yang ada hubungannya dengan "pergeseran" (diplacement). Vektor biasanya digunakan untuk menggambarkan perpindahan suatu partikel
VEKTOR Kata vektor berasal dari bahasa Latin yang berarti "pembawa" (carrier), yang ada hubungannya dengan "pergeseran" (diplacement). Vektor biasanya digunakan untuk menggambarkan perpindahan suatu partikel
RENCANA PEMBELAJARAN 1. POKOK BAHASAN : KINEMATIKA
 RENCANA PEMBELAJARAN 1. POKOK BAHASAN : KINEMATIKA A. Sistem koordinat (SK) Secara umum, sistem koordinat merupakan cara menyatakan posisi dalam ruang, dinyatakan dalam variabel ruang. Dalam ruang D-2,
RENCANA PEMBELAJARAN 1. POKOK BAHASAN : KINEMATIKA A. Sistem koordinat (SK) Secara umum, sistem koordinat merupakan cara menyatakan posisi dalam ruang, dinyatakan dalam variabel ruang. Dalam ruang D-2,
Kalkulus II. Diferensial dalam ruang berdimensi n
 Kalkulus II Diferensial dalam ruang berdimensi n Minggu ke-9 DIFERENSIAL DALAM RUANG BERDIMENSI-n 1. Fungsi Dua Peubah atau Lebih 2. Diferensial Parsial 3. Limit dan Kekontinuan 1. Fungsi Dua Peubah atau
Kalkulus II Diferensial dalam ruang berdimensi n Minggu ke-9 DIFERENSIAL DALAM RUANG BERDIMENSI-n 1. Fungsi Dua Peubah atau Lebih 2. Diferensial Parsial 3. Limit dan Kekontinuan 1. Fungsi Dua Peubah atau
BAB I TEGANGAN DAN REGANGAN
 BAB I TEGANGAN DAN REGANGAN.. Tegangan Mekanika bahan merupakan salah satu ilmu yang mempelajari/membahas tentang tahanan dalam dari sebuah benda, yang berupa gaya-gaya yang ada di dalam suatu benda yang
BAB I TEGANGAN DAN REGANGAN.. Tegangan Mekanika bahan merupakan salah satu ilmu yang mempelajari/membahas tentang tahanan dalam dari sebuah benda, yang berupa gaya-gaya yang ada di dalam suatu benda yang
BAB II TINJAUAN PUSTAKA. tegak, perlu diketahui tentang materi-materi sebagai berikut.
 BAB II TINJAUAN PUSTAKA Sebelum pembahasan mengenai irisan bidang datar dengan tabung lingkaran tegak, perlu diketahui tentang materi-materi sebagai berikut. A. Matriks Matriks adalah himpunan skalar (bilangan
BAB II TINJAUAN PUSTAKA Sebelum pembahasan mengenai irisan bidang datar dengan tabung lingkaran tegak, perlu diketahui tentang materi-materi sebagai berikut. A. Matriks Matriks adalah himpunan skalar (bilangan
BINOVATIF LISTRIK DAN MAGNET. Hani Nurbiantoro Santosa, PhD.
 BINOVATIF LISTRIK DAN MAGNET Hani Nurbiantoro Santosa, PhD hanisantosa@gmail.com 2 BAB 2 MEDAN LISTRIK DAN HUKUM GAUSS Pendahuluan, Distribusi Muatan Kontinu, Mencari Medan Listrik Menggunakan Integral,
BINOVATIF LISTRIK DAN MAGNET Hani Nurbiantoro Santosa, PhD hanisantosa@gmail.com 2 BAB 2 MEDAN LISTRIK DAN HUKUM GAUSS Pendahuluan, Distribusi Muatan Kontinu, Mencari Medan Listrik Menggunakan Integral,
KINEMATIKA. Fisika. Tim Dosen Fisika 1, ganjil 2016/2017 Program Studi S1 - Teknik Telekomunikasi Fakultas Teknik Elektro - Universitas Telkom
 KINEMATIKA Fisika Tim Dosen Fisika 1, ganjil 2016/2017 Program Studi S1 - Teknik Telekomunikasi Fakultas Teknik Elektro - Universitas Telkom Sasaran Pembelajaran Indikator: Mahasiswa mampu mencari besaran
KINEMATIKA Fisika Tim Dosen Fisika 1, ganjil 2016/2017 Program Studi S1 - Teknik Telekomunikasi Fakultas Teknik Elektro - Universitas Telkom Sasaran Pembelajaran Indikator: Mahasiswa mampu mencari besaran
Bab 1 : Skalar dan Vektor
 Bab 1 : Skalar dan Vektor 1.1 Skalar dan Vektor Istilah skalar mengacu pada kuantitas yang nilainya dapat diwakili oleh bilangan real tunggal (positif atau negatif). x, y dan z kita gunakan dalam aljabar
Bab 1 : Skalar dan Vektor 1.1 Skalar dan Vektor Istilah skalar mengacu pada kuantitas yang nilainya dapat diwakili oleh bilangan real tunggal (positif atau negatif). x, y dan z kita gunakan dalam aljabar
BAB IV HASIL PENELITIAN DAN PEMBAHASAN
 BAB IV HASIL PENELITIAN DAN PEMBAHASAN A. HASIL PENELITIAN 1. Hasil Pengembangan Produk Penelitian ini merupakan penelitian pengembangan yang bertujuan untuk mengembangkan produk berupa Skema Pencapaian
BAB IV HASIL PENELITIAN DAN PEMBAHASAN A. HASIL PENELITIAN 1. Hasil Pengembangan Produk Penelitian ini merupakan penelitian pengembangan yang bertujuan untuk mengembangkan produk berupa Skema Pencapaian
GEOMETRI ANALIT DI R3
 GEOMETRI ANALIT DI R3 1. Persamaan berderajat pertama dengan tiga variabel di Persamaan yang berbentuk Ax + By + Cz + D = 0, (3*) dengan A, B, C, D merupakan bilangan real dan A, B, C tak bersama-sama
GEOMETRI ANALIT DI R3 1. Persamaan berderajat pertama dengan tiga variabel di Persamaan yang berbentuk Ax + By + Cz + D = 0, (3*) dengan A, B, C, D merupakan bilangan real dan A, B, C tak bersama-sama
Matematika EBTANAS Tahun 2001
 Matematika EBTANAS Tahun 00 EBT-SMA-0-0 Luas maksimum persegipanjang OABC pada gambar adalah satuan luas satuan luas C B(,y) satuan luas + y = satuan luas satuan luas O A EBT-SMA-0-0 Diketahui + Maka nilai
Matematika EBTANAS Tahun 00 EBT-SMA-0-0 Luas maksimum persegipanjang OABC pada gambar adalah satuan luas satuan luas C B(,y) satuan luas + y = satuan luas satuan luas O A EBT-SMA-0-0 Diketahui + Maka nilai
G. Minimum Lokal dan Global Berikut diberikan definisi minimum local (relatif) dan minimum global (mutlak) dari fungsi dua variabel.
 G. Minimum Lokal dan Global Berikut diberikan definisi minimum local (relatif) dan minimum global (mutlak) dari fungsi dua variabel. Definisi. (i) Suatu fungsi f(x, y) memiliki minimum lokal pada titik
G. Minimum Lokal dan Global Berikut diberikan definisi minimum local (relatif) dan minimum global (mutlak) dari fungsi dua variabel. Definisi. (i) Suatu fungsi f(x, y) memiliki minimum lokal pada titik
PEMBAHASAN KISI-KISI SOAL UAS KALKULUS PEUBAH BANYAK (TA 2015/2016)
 PEMBAHAAN KII-KII OAL UA KALKULU PEUBAH BANYAK (TA 5/6) Arini oesatyo Putri DEEMBER 3, 5 UNIVERITA ILAM NEGERI UNAN GUNUNG DJATI BANDUNG Pembahasan oal Kisi-Kisi UA Kalkulus Peubah Banyak Tahun Ajaran
PEMBAHAAN KII-KII OAL UA KALKULU PEUBAH BANYAK (TA 5/6) Arini oesatyo Putri DEEMBER 3, 5 UNIVERITA ILAM NEGERI UNAN GUNUNG DJATI BANDUNG Pembahasan oal Kisi-Kisi UA Kalkulus Peubah Banyak Tahun Ajaran
Koordinat Kartesius, Koordinat Tabung & Koordinat Bola. Tim Kalkulus II
 Koordinat Kartesius, Koordinat Tabung & Koordinat Bola Tim Kalkulus II Koordinat Kartesius Sistem Koordinat 2 Dimensi Sistem koordinat kartesian dua dimensi merupakan sistem koordinat yang terdiri dari
Koordinat Kartesius, Koordinat Tabung & Koordinat Bola Tim Kalkulus II Koordinat Kartesius Sistem Koordinat 2 Dimensi Sistem koordinat kartesian dua dimensi merupakan sistem koordinat yang terdiri dari
Kuliah 2: FUNGSI MULTIVARIABEL. Indah Yanti
 Kuliah 2: FUNGSI MULTIVARIABEL Indah Yanti Definisi Dasar Perhatikan fungsi f: A R n R m : x f x n = m = 1 fungsi bernilai riil satu variabel n = 1, m > 1 fungsi bernilai vektor satu variabel n > 1, m
Kuliah 2: FUNGSI MULTIVARIABEL Indah Yanti Definisi Dasar Perhatikan fungsi f: A R n R m : x f x n = m = 1 fungsi bernilai riil satu variabel n = 1, m > 1 fungsi bernilai vektor satu variabel n > 1, m
VEKTOR. Oleh : Musayyanah, S.ST, MT
 VEKTOR Oleh : Musayyanah, S.ST, MT 1 2.1 ESRN SKLR DN VEKTOR Sifat besaran fisis : esaran Skalar Skalar Vektor esaran yang cukup dinyatakan oleh besarnya saja (besar dinyatakan oleh bilangan dan satuan).
VEKTOR Oleh : Musayyanah, S.ST, MT 1 2.1 ESRN SKLR DN VEKTOR Sifat besaran fisis : esaran Skalar Skalar Vektor esaran yang cukup dinyatakan oleh besarnya saja (besar dinyatakan oleh bilangan dan satuan).
PEMBAHASAN UN SMA TAHUN PELAJARAN 2009/2010 MATEMATIKA PROGRAM STUDY IPA
 PEMBAHASAN UN SMA TAHUN PELAJARAN 009/010 MATEMATIKA PROGRAM STUDY IPA PEMBAHAS : 1. Sigit Tri Guntoro, M.Si.. Jakim Wiyoto, S.Si. 3. Marfuah, M.T. 4. Rohmitawati, S.Si. PPPPTK MATEMATIKA 010 1. Perhatikan
PEMBAHASAN UN SMA TAHUN PELAJARAN 009/010 MATEMATIKA PROGRAM STUDY IPA PEMBAHAS : 1. Sigit Tri Guntoro, M.Si.. Jakim Wiyoto, S.Si. 3. Marfuah, M.T. 4. Rohmitawati, S.Si. PPPPTK MATEMATIKA 010 1. Perhatikan
( ) 2. Nilai x yang memenuhi log 9. Jadi 4x 12 = 3 atau x = 3,75
 Here is the Problem and the Answer. Diketahui premis premis berikut! a. Jika sebuah segitiga siku siku maka salah satu sudutnya 9 b. Jika salah satu sudutnya 9 maka berlaku teorema Phytagoras Ingkaran
Here is the Problem and the Answer. Diketahui premis premis berikut! a. Jika sebuah segitiga siku siku maka salah satu sudutnya 9 b. Jika salah satu sudutnya 9 maka berlaku teorema Phytagoras Ingkaran
Pengantar KULIAH MEDAN ELEKTROMAGNETIK MATERI I ANALISIS VEKTOR DAN SISTEM KOORDINAT
 KULIAH MEDAN ELEKTROMAGNETIK Pengantar Definisi Arsitektur MATERI I ANALISIS VEKTOR DAN SISTEM KOORDINAT Operasional Sinkronisasi Kesimpulan & Saran Muhamad Ali, MT Http://www.elektro-uny.net/ali Pengantar
KULIAH MEDAN ELEKTROMAGNETIK Pengantar Definisi Arsitektur MATERI I ANALISIS VEKTOR DAN SISTEM KOORDINAT Operasional Sinkronisasi Kesimpulan & Saran Muhamad Ali, MT Http://www.elektro-uny.net/ali Pengantar
BAB III TURUNAN DALAM RUANG DIMENSI-n
 BAB III TURUNAN DALAM RUANG DIMENSI-n 1. FUNGSI DUA PEUBAH ATAU LEBIH fungsi bernilai riil dari peubah riil, fungsi bernilai vektor dari peubah riil Fungsi bernilai riil dari dua peubah riil yakni, fungsi
BAB III TURUNAN DALAM RUANG DIMENSI-n 1. FUNGSI DUA PEUBAH ATAU LEBIH fungsi bernilai riil dari peubah riil, fungsi bernilai vektor dari peubah riil Fungsi bernilai riil dari dua peubah riil yakni, fungsi
syarat tertentu yang diberikan. Atau bisa juga diartikan sebagai lintasan dari sebuah
 2 Tempat Kedudukan dan Persamaan 2.1. Tempat Kedudukan Tempat kedudukan (locus) adalah himpunan titik-titik yang memenuhi suatu syarat tertentu yang diberikan. Atau bisa juga diartikan sebagai lintasan
2 Tempat Kedudukan dan Persamaan 2.1. Tempat Kedudukan Tempat kedudukan (locus) adalah himpunan titik-titik yang memenuhi suatu syarat tertentu yang diberikan. Atau bisa juga diartikan sebagai lintasan
Listrik Statik. Agus Suroso
 Listrik Statik Agus Suroso Muatan Listrik Ada dua macam: positif dan negatif. Sejenis tolak menolak, beda jenis tarik menarik. Muatan fundamental e =, 60 0 9 Coulomb. Atau, C = 6,5 0 8 e. Atom = proton
Listrik Statik Agus Suroso Muatan Listrik Ada dua macam: positif dan negatif. Sejenis tolak menolak, beda jenis tarik menarik. Muatan fundamental e =, 60 0 9 Coulomb. Atau, C = 6,5 0 8 e. Atom = proton
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI 2.1 Latar Belakang Historis Fondasi dari integral pertama kali dideklarasikan oleh Cavalieri, seorang ahli matematika berkebangsaan Italia pada tahun 1635. Cavalieri menemukan bahwa
BAB II LANDASAN TEORI 2.1 Latar Belakang Historis Fondasi dari integral pertama kali dideklarasikan oleh Cavalieri, seorang ahli matematika berkebangsaan Italia pada tahun 1635. Cavalieri menemukan bahwa
Ringkasan Kalkulus 2, Untuk dipakai di ITB 36
 Ringkasan Kalkulus 2, Untuk dipakai di ITB 36 Irisan Kerucut animation 1 animation 2 Irisan kerucut adalah kurva ang terbentuk dari perpotongan antara sebuah kerucut dengan bidang datar. Kurva irisan ini
Ringkasan Kalkulus 2, Untuk dipakai di ITB 36 Irisan Kerucut animation 1 animation 2 Irisan kerucut adalah kurva ang terbentuk dari perpotongan antara sebuah kerucut dengan bidang datar. Kurva irisan ini
Kalkulus Multivariabel I
 Integral Lipat-Dua dalam Koordinat Kutub Atina Ahdika, S.Si, M.Si Statistika FMIPA Universitas Islam Indonesia 214 / 2 Integral Lipat-Dua dalam Koordinat Kutub Terdapat beberapa kurva tertentu pada suatu
Integral Lipat-Dua dalam Koordinat Kutub Atina Ahdika, S.Si, M.Si Statistika FMIPA Universitas Islam Indonesia 214 / 2 Integral Lipat-Dua dalam Koordinat Kutub Terdapat beberapa kurva tertentu pada suatu
SOAL&PEMBAHASAN MATEMATIKATKDSAINTEK SBMPTN. yos3prens.wordpres.com
 SOAL&PEMBAHASAN MATEMATIKATKDSAINTEK SBMPTN 05 yosprens.wordpres.com SOAL DAN PEMBAHASAN MATA UJI MATEMATIKA TKD SAINTEK SBMPTN 05 Berikut ini 5 soal mata uji matematika beserta pembahasannya yang diujikan
SOAL&PEMBAHASAN MATEMATIKATKDSAINTEK SBMPTN 05 yosprens.wordpres.com SOAL DAN PEMBAHASAN MATA UJI MATEMATIKA TKD SAINTEK SBMPTN 05 Berikut ini 5 soal mata uji matematika beserta pembahasannya yang diujikan
Modul 6 berisi pengertian integral garis (kurva), sifat-sifat dan penerapannya. Pengintegralan sepanjang kurva, kita harus memperhatikan arah kurva,
 ix T Tinjauan Mata Kuliah ujuan mempelajari mata kuliah ini adalah agar Anda memiliki kemampuan dalam menjelaskan aljabar vektor, turunan dan integral fungsi vektor, serta mampu menerapkannya dalam geometri
ix T Tinjauan Mata Kuliah ujuan mempelajari mata kuliah ini adalah agar Anda memiliki kemampuan dalam menjelaskan aljabar vektor, turunan dan integral fungsi vektor, serta mampu menerapkannya dalam geometri
2. Memahami dan mampu menyelesaikan Permasalahan yang berkaitan dengan vektor di Ruang Tiga, yaitu Persamaan Bidang
 TUJUAN EMBELAJARAN Agar pembaca memahami tentang Sistem Koordinat Kartesian beserta fungsinya yaitu titik, jarak dua titik, persamaan bola serta Vektor dalam ruang dimensi tiga beserta aplikasinya yaitu
TUJUAN EMBELAJARAN Agar pembaca memahami tentang Sistem Koordinat Kartesian beserta fungsinya yaitu titik, jarak dua titik, persamaan bola serta Vektor dalam ruang dimensi tiga beserta aplikasinya yaitu
MATEMATIKA TEKNIK II BILANGAN KOMPLEKS
 MATEMATIKA TEKNIK II BILANGAN KOMPLEKS 2 PENDAHULUAN SISTEM BILANGAN KOMPLEKS REAL IMAJINER RASIONAL IRASIONAL BULAT PECAHAN BULAT NEGATIF CACAH ASLI 0 3 ILUSTRASI Carilah akar-akar persamaan x 2 + 4x
MATEMATIKA TEKNIK II BILANGAN KOMPLEKS 2 PENDAHULUAN SISTEM BILANGAN KOMPLEKS REAL IMAJINER RASIONAL IRASIONAL BULAT PECAHAN BULAT NEGATIF CACAH ASLI 0 3 ILUSTRASI Carilah akar-akar persamaan x 2 + 4x
10 Grafik Sudut Deviasi Bangun Datar
 10 Grafik Sudut Deviasi Bangun Datar Kita telah mempelajari bagaimana menghitung besar sudut belok di setiap titik pada tepi suatu bangun datar. Satu hal yang menarik tentang lingkaran adalah bahwa besar
10 Grafik Sudut Deviasi Bangun Datar Kita telah mempelajari bagaimana menghitung besar sudut belok di setiap titik pada tepi suatu bangun datar. Satu hal yang menarik tentang lingkaran adalah bahwa besar
sebagai, dan dua buah variabel dan dapat digunakan untuk memparameterisasi sebuah permukaan sebagai
 BAB II MANIFOLD DIFFERENSIABEL 2.1 Definisi Manifold [13] Manifold adalah generalisasi dari ide-ide yang familiar tentang kurva dan permukaan pada ruang Euclidean. Sebuah kurva pada ruang Euclidean berdimensi
BAB II MANIFOLD DIFFERENSIABEL 2.1 Definisi Manifold [13] Manifold adalah generalisasi dari ide-ide yang familiar tentang kurva dan permukaan pada ruang Euclidean. Sebuah kurva pada ruang Euclidean berdimensi
UJIAN NASIONAL DINAS PENDIDIKAN DKI JAKARTA SMA/MA
 A Matematika IPA SMA/MA TRYOUT UJIAN NASIONAL DINAS PENDIDIKAN DKI JAKARTA SMA/MA TAHUN PELAJARAN 04/05 MATEMATIKA IPA Hasil Kerja Sama dengan Matematika IPA SMA/MA Mata Pelajaran : Matematika IPA Jenjang
A Matematika IPA SMA/MA TRYOUT UJIAN NASIONAL DINAS PENDIDIKAN DKI JAKARTA SMA/MA TAHUN PELAJARAN 04/05 MATEMATIKA IPA Hasil Kerja Sama dengan Matematika IPA SMA/MA Mata Pelajaran : Matematika IPA Jenjang
Pertemuan : 4 Materi : Fungsi Bernilai Vektor dan Gerak Sepanjang Kurva Bab II. Diferensial Kalkulus Dari Vektor
 Pertemuan : 4 Materi : Fungsi Bernilai Vektor dan Gerak Sepanjang Kurva Bab II. Diferensial Kalkulus Dari Vektor Standar Kompetensi : Setelah mengikuti perkuliahaan ini mahasiswa diharapkan dapat : 1.
Pertemuan : 4 Materi : Fungsi Bernilai Vektor dan Gerak Sepanjang Kurva Bab II. Diferensial Kalkulus Dari Vektor Standar Kompetensi : Setelah mengikuti perkuliahaan ini mahasiswa diharapkan dapat : 1.
BAB II V E K T O R. Untuk menyatakan arah vektor diperlukan sistem koordinat.
 .. esaran Vektor Dan Skalar II V E K T O R da beberapa besaran fisis yang cukup hanya dinyatakan dengan suatu angka dan satuan yang menyatakan besarnya saja. da juga besaran fisis yang tidak cukup hanya
.. esaran Vektor Dan Skalar II V E K T O R da beberapa besaran fisis yang cukup hanya dinyatakan dengan suatu angka dan satuan yang menyatakan besarnya saja. da juga besaran fisis yang tidak cukup hanya
Program Perkuliahan Dasar Umum Sekolah Tinggi Teknologi Telkom Integral Lipat Tiga
 Program Perkuliahan Dasar Umum Sekolah Tinggi Teknologi Telkom Integral Lipat Tiga [MA4] Integral Lipat Tiga pada Balok ( k, k, k ) B B k k 7/6/7 [MA 4]. Partisi balok B menjadi n bagian; B, B,, B k,,
Program Perkuliahan Dasar Umum Sekolah Tinggi Teknologi Telkom Integral Lipat Tiga [MA4] Integral Lipat Tiga pada Balok ( k, k, k ) B B k k 7/6/7 [MA 4]. Partisi balok B menjadi n bagian; B, B,, B k,,
SILABUS. 1 / Silabus Matematika XII-IA. : 1.Menggunakan konsep integral dalam pemecahan masalah. Nilai Karakter
 SILABUS Satuan Pendidikan Mata Pelajaran Kelas/semester Reference Standar Kompetensi : SMA Negeri 5 Surabaya : : XII/1 : BSNP / CIE : 1.Menggunakan konsep integral dalam pemecahan masalah Kompetensi Dasar
SILABUS Satuan Pendidikan Mata Pelajaran Kelas/semester Reference Standar Kompetensi : SMA Negeri 5 Surabaya : : XII/1 : BSNP / CIE : 1.Menggunakan konsep integral dalam pemecahan masalah Kompetensi Dasar
SISTEM KOORDINAT SISTEM TRANSFORMASI KOORDINAT RG091521
 SISTEM KOORDINAT SISTEM TRANSFORMASI KOORDINAT RG091521 SISTEM KOORDINAT SISTEM TRANSFORMASI KOORDINAT RG091521 Sistem Koordinat Parameter SistemKoordinat Koordinat Kartesian Koordinat Polar Sistem Koordinat
SISTEM KOORDINAT SISTEM TRANSFORMASI KOORDINAT RG091521 SISTEM KOORDINAT SISTEM TRANSFORMASI KOORDINAT RG091521 Sistem Koordinat Parameter SistemKoordinat Koordinat Kartesian Koordinat Polar Sistem Koordinat
KARTU SOAL UJIAN NASIONAL MADRASAH ALIYAH NEGERI PANGKALPINANG
 Jumlah 50 Bentuk Pilihan Ganda Standar Kompetensi : Menggunakan logika matematika dalam pemecahan masalah yang berkaitan dengan pernyataan majemuk dan pernyataan berkuantor Kompetensi Dasar : Menggunakan
Jumlah 50 Bentuk Pilihan Ganda Standar Kompetensi : Menggunakan logika matematika dalam pemecahan masalah yang berkaitan dengan pernyataan majemuk dan pernyataan berkuantor Kompetensi Dasar : Menggunakan
IKIP BUDI UTOMO MALANG. Analytic Geometry TEXT BOOK. Alfiani Athma Putri Rosyadi, M.Pd
 IKIP BUDI UTOMO MALANG Analytic Geometry TEXT BOOK Alfiani Athma Putri Rosyadi, M.Pd 2012 DAFTAR ISI 1 VEKTOR 1.1 Vektor Pada Bidang... 4 1.2 Vektor Pada Ruang... 6 1.3 Operasi Vektor.. 8 1.4 Perkalian
IKIP BUDI UTOMO MALANG Analytic Geometry TEXT BOOK Alfiani Athma Putri Rosyadi, M.Pd 2012 DAFTAR ISI 1 VEKTOR 1.1 Vektor Pada Bidang... 4 1.2 Vektor Pada Ruang... 6 1.3 Operasi Vektor.. 8 1.4 Perkalian
Materi UTS. Matematika Optimisasi. Semester Gasal Pengajar: Hazrul Iswadi
 Materi UTS Matematika Optimisasi Semester Gasal 6-7 Pengajar: Hazrul Iswadi Daftar Isi Pendahuluan...hal Pertemuan...hal - Pertemuan...hal - 9 Pertemuan...hal - 5 Pertemuan 4...hal 6 - Pertemuan 5...hal
Materi UTS Matematika Optimisasi Semester Gasal 6-7 Pengajar: Hazrul Iswadi Daftar Isi Pendahuluan...hal Pertemuan...hal - Pertemuan...hal - 9 Pertemuan...hal - 5 Pertemuan 4...hal 6 - Pertemuan 5...hal
ALJABAR LINEAR DAN MATRIKS. MODUL 10 Kalkulus Vektor. Zuhair Jurusan Teknik Informatika Universitas Mercu Buana Jakarta 2007 年 12 月 30 日 ( 日 )
 ALJABAR LINEAR DAN MATRIKS MODUL 10 Kalkulus Vektor Zuhair Jurusan Teknik Informatika Universitas Mercu Buana Jakarta 2007 年 12 月 30 日 ( 日 ) Kalkulus Vektor Kalkulus vektor (vector calculus) atau sering
ALJABAR LINEAR DAN MATRIKS MODUL 10 Kalkulus Vektor Zuhair Jurusan Teknik Informatika Universitas Mercu Buana Jakarta 2007 年 12 月 30 日 ( 日 ) Kalkulus Vektor Kalkulus vektor (vector calculus) atau sering
PEMBAHASAN UN SMA TAHUN PELAJARAN 2009/2010 MATEMATIKA PROGRAM STUDI IPA
 PEMBAHASAN UN SMA TAHUN PELAJARAN 009/00 MATEMATIKA PROGRAM STUDI IPA PEMBAHAS :. Sigit Tri Guntoro, M.Si.. Jakim Wiyoto, S.Si. 3. Marfuah, M.T. 4. Rohmitawati, S.Si. PPPPTK MATEMATIKA 00 . Perhatikan
PEMBAHASAN UN SMA TAHUN PELAJARAN 009/00 MATEMATIKA PROGRAM STUDI IPA PEMBAHAS :. Sigit Tri Guntoro, M.Si.. Jakim Wiyoto, S.Si. 3. Marfuah, M.T. 4. Rohmitawati, S.Si. PPPPTK MATEMATIKA 00 . Perhatikan
MA5032 ANALISIS REAL
 (Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. August 16, 2011 Pada bab ini anda diasumsikan telah mengenal dengan cukup baik bilangan asli, bilangan bulat, dan bilangan
(Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. August 16, 2011 Pada bab ini anda diasumsikan telah mengenal dengan cukup baik bilangan asli, bilangan bulat, dan bilangan
