KETIDAK-KOMPLITAN GEODESIK SEBAGAI INDIKATOR SINGULARITAS RUANG - WAKTU
|
|
|
- Devi Sudjarwadi
- 7 tahun lalu
- Tontonan:
Transkripsi
1 SKRIPSI KETIDAK-KOMPLITAN GEODESIK SEBAGAI INDIKATOR SINGULARITAS RUANG - WAKTU Romy Hanang Setya Budhi 99/128946/PA/07864 Departemen Pendidikan Nasional Universitas Gadjah Mada Fakultas Matematika dan Ilmu Pengetahuan Alam Yogyakarta 2005
2 SKRIPSI KETIDAK-KOMPLITAN GEODESIK SEBAGAI INDIKATOR SINGULARITAS RUANG - WAKTU Romy Hanang Setya Budhi 99/128946/PA/07864 Sebagai salah satu syarat untuk memperoleh derajat Sarjana S1 Program Studi Fisika pada Jurusan Fisika Departemen Pendidikan Nasional Universitas Gadjah Mada Fakultas Matematika dan Ilmu Pengetahuan Alam Yogyakarta 2005
3 SKRIPSI KETIDAK-KOMPLITAN GEODESIK SEBAGAI INDIKATOR SINGULARITAS RUANG - WAKTU Romy Hanang Setya Budhi 99/128946/PA/07864 Dinyatakan lulus ujian skripsi oleh tim penguji pada tanggal 11 Juli 2005 Tim Penguji Dr.rer.nat. M. Farchani Rosyid Pembimbing I Dr. H. Karyono, SU. Penguji I Dr. Mirza Satriawan Penguji II
4 Karya ini kupersembahkan buat Robb-ku tercinta yang menjanjikan kejayaan bagi orang - orang yang berjalan di jalannya. Juga kepada para sahabatku yang telah terbang di seberang jalan. Hari ini kuturut langkah kalian, tapi suatu saat kelak akan kuretas jalan baru yang lebih baik dari sekarang. iii
5 (Al Quran) ini adalah penerang bagi seluruh manusia dan petunjuk serta pelajaran bagi orang - orang yang bertakwa. Janganlah kamu bersikap lemah dan janganlah (pula) kamu bersedih hati, padahal kamulah orang - orang yang paling tinggi (derajatnya) jika kamu orang - orang yang beriman. (Ali Imran : ) Hai orang - orang yang beriman, jika datang kepadamu orang fasik yang membawa berita, maka periksalah dengan teliti agar kamu tidak menimpakan suatu musibah pada suatu kaum tanpa mengetahui keadaannya yang menyebabkan kamu menyesal atas perbuatan itu. (Al-Hujurat : 6) iv
6 PRAKATA Segala puji bagi Allah robb sekalian alam yang tiada ilah selain-nya, yang menciptakan dan mengatur segala sesuatu sesuai dengan kehendak-nya. Dia lah yang menganugerahkan nikmat akal kepada manusia agar dengannya digunakan sebagai penimbang. Juga semoga kesejahteraan dan keselamatan terlimpah kepada hamba dan Rasul-Nya yaitu Rasullullah SAW dan keluarganya, beserta sahabat dan orangorang yang mengikuti Beliau sampai akhir jaman. Penulis patut bersyukur kepada Allah ta ala, karena hanya atas kehendak- Nya saja tulisan ini dapat diselesaikan. Juga atas bantuan berbagai pihak yang telah memberikan dukungan kepada kami, tidak lupa penulis mengucapkan terima kasih yang sedalam-dalamnya. Ucapan terima kasih ini kami tujukan kepada: 1. Ayah dan Ibu tercinta, yang selalu memberikan kepercayaan penuh dan selalu mendukung setiap langkah kami. 2. Dr. rer. nat. M. Farchani Rosyid, yang telah dengan sabar membimbing kami sedari awal. Membukakan wacana - wacana baru dan memulihkan warna dasar yang hampir hilang pada diri kami dan memberikan ruang seluas - luasnya untuk mengekspresikan diri. 3. Dra, Dwi Satya Palupi, M.Si, yang telah banyak memberikan dorongan moril kepada kami terutama pada awal - awal penulisan. 4. Semua staf program studi fisika yang telah membimbing selama masa perkuliahan. 5. Teman-teman kami fisika angkatan 1999 dan teman-teman diskusi pada kelaskelas teori dan kelas matematik yang telah berkenan berbagi pustaka dan men diskusikan banyak hal dengan kami. v
7 vi 6. Dan semua pihak yang belum disebutkan di atas tetapi telah terlibat dalam pro ses penulisan ini. Akhirnya, penulis berharap agar tulisan ini dapat menyumbangkan sesuatu pada dunia fisika teori. Penulis menyadari bahwa tidak ada manusia yang lepas dari kealpaan, oleh karena itu kami mohon maaf atas kesalahan yang ada dalam tulisan ini. Yogyakarta, 4 Juli 2005 Penulis
8 DAFTAR ISI Halaman Judul i Halaman Pengesahan ii Halaman Persembahan iii Halaman Motto iv PRAKATA v INTISARI xi I PENDAHULUAN 1 1. Latar Belakang Tujuan Penulisan Ruang Lingkup Kajian II ANALISIS PADA MANIFOLD LICIN 4 1. Manifold Licin Vektor Singgung, Kovektor dan Tensor Pada Manifold Kongruensi dan Derivatif Lie Koneksi dan Kelengkungan Pada Manifold Manifold Pseudo-Riemannan Submanifold Teorema Frobenius Integrasi Pada Manifold vii
9 viii III TEORI RELATIVITAS UMUM Manifold Ruang-Waktu Medan - Medan Materi Syarat Energi Sedikit Tentang Singularitas Contoh Singularitas Pada Beberapa Solusi Medan Einstein a. Ruang Schwarzschild b. Ruang Robertson - Walker Singularitas: Pendefinisian dan Pemecahannya IV SIGNIFIKANSI KELENGKUNGAN Variasi Geodesik Titik - Titik Berkonjugasi Pada geodesik Titik Fokal Submanifold Sepanjang Geodesik Variasi Fungsional Panjang dan Energi Kurva Titik Konjugasi Pada Geodesik Komplit V STRUKTUR KAUSAL PADA RUANG-WAKTU Orientabilitas Waktu Kondisi - Kondisi Kausalitas Wilayah Kegayutan Sifat Kausalitas Stabil Pada Ruang waktu Yang Hiperbolis Global Eksistensi Geodesik Pada Ruang-waktu yang Kausal VI SINGULARITAS RUANG - WAKTU 136 VIIPENUTUP Kesimpulan
10 ix 2. Saran A RUANG TOPOLOGIS Identifikasi Topologi dan Pemetaan Kontinyu Interior, Klosure dan Bounderi Ruang Hausdorff Ketersambungan Kekompakan
11 DAFTAR GAMBAR II.1 {(U α, φ α )} dan {(U β, φ β )} saling C - rukun apabila φ α φ 1 β φ β φ 1 α masing - masing merupakan pemetaan licin dan III.1 Perluasan Kruskal untuk ruang-waktu Schwarzschild IV.1 Lingkaran besar (great circle) atau lingkaran yang melalui kutub - kutub permukaan bola S 2 merupakan geodesik. Geodesik - geodesik yang berasal dari suatu titik akan bertemu kembali pada kutub yang berlawanan dengannya. Oleh karena itu, kutub-kutub S 2 merupakan dua titik yang saling berkonjugasi IV.2 Titik γ(b) menjadi titik fokal dari submanifold Σ di bawah medan variasi ξ V.1 Sifat Lipschitzan setiap kurva kausal V.2 Bidang ruang Minkowski (R 2, dx 0 dx 0 + dx 1 dx 1 ) yang dibatasi oleh batas-batas x 0 = 1 dan x 0 = 0 dapat mempunyai kurva bakwaktu tertutup ketika batas - batasnya saling disambung membentuk ruang-waktu S 1 R V.3 D + S dan H + (S) dari himpunan akronal S yang mengandung bagian null dan bagian bak-ruang pada ruang Minkowski yang sebagian daerahnya dibuang x
12 INTISARI KETIDAK-KOMPLITAN GEODESIK SEBAGAI INDIKATOR SINGULARITAS RUANG - WAKTU Oleh : Romy Hanang Setya Budhi 99/128946/PA/07864 Telah dilakukan kajian singularitas pada ruang-waktu relativitas umum melalui studi ketidak-komplitan geodesik pada sembarang manifold Lorentzian. Ditunjukkan bahwa ruang-waktu yang memenuhi syarat energi tertentu, mempunyai struktur kausalitas global yang realistis secara fisis dan mempunyai subhimpunan yang memenuhi syarat topologis tertentu akan selalu mengijinkan geodesik kausal yang tidak komplit. Kajian singularitas pada manifold Lorentzian berdimensi empat akan menghasilkan singularitas pada ruang-waktu relativitas umum. xi
13 xii ABSTRACT GEODESICS INCOMPLETENESS AS INDICATION OF THE SPACETIME SINGULARITY By Romy Hanang Setya Budhi 99/128946/PA/07864 The spacetime singularity of general relativity in the general Lorentzian manifolds has been studied through the geodesics incompleteness concept. Every spacetime which is required to satisfy certain energy condition, having realistic global causality structure and contain subset which is required by certain topological condition will admit incomplete causal geodesics. So, the dimension restriction on the four is just singularity in the general relativity spacetime.
14 BAB I PENDAHULUAN 1. Latar Belakang Dalam upaya menyingkap kaidah yang dianut oleh fenomena - fenomena alamiah, kalangan fisikawan teori mengajukan berbagai macam model hukum alam berdasarkan data - data empiris yang telah dimiliki. Sejauh ini dikenal tiga macam pemodelan yaitu model fisis, model matematis dan model metafisis. Dalam prakteknya, model - model matematis lebih operasional sehingga lebih banyak dimanfaatkan dalam sains daripada model lainnya. Model - model hukum alam sesungguhnya tidak identik dengan hukum alam sendiri. Model - model tersebut hanyalah merupakan pendekatan (aproksimasi), oleh karena itu derajat akurasi suatu model sangat berkaitan dengan kedekatannya terhadap hukum alam yang dimodelkan. Gejala alamiah mempunyai struktur yang sangat kompleks sehingga sangat sulit menyajikan gambaran fenomena - fenomena alamiah secara utuh. Diperlukan proses eleminasi terhadap hal - hal yang tidak relefan pada fenomena alamiah yang akan dimodelkan. Proses eleminasi tersebut disebut sebagai proses idealisasi. Idealisasi suatu gejala alamiah akan menghasilkan sistem fisis, yaitu gejala alamiah yang telah mengalami pereduksian secara proporsional. Selanjutnya yang dimaksud dengan model matematik adalah hasil penafsiran terhadap suatu sistem fisis secara matematis sebagai proses semantika matematisnya. Kedekatan suatu model dengan gejala - gejalah alamiah yang diwakili tentu saja sa ngat bergantung dengan proses idealisasi yang dilakukan. Makin sedikit hal - hal yang dieleminasi, semakin akurat model tersebut. Hanya saja hal ini harus dibayar mahal dengan kompleksitas matematis (Mathematical Complexity) yang lebih abstrak, lebih 1
15 2 general dan lebih formal. Relasi yang sangat kuat antara matematika dengan fisika dapat dilihat pada penggunaan geometri differensial pada relativitas umum, hampir - hampir antara keduanya tidak dapat saling dibedakan. Postulat-postulat dalam fisika dalam pemodelan dapat dianggap sebagai aksioma - aksioma dalam cabang matematika yang digunakan sebagai model [Kriele, 2001]. Hanya saja penggunaan geometri differensial dalam relativitas umum masih terlihat kurang optimal. Seperti dapat dilihat pada buku-buku teks relativitas yang ditemukan pada perpustakaan - perpustakaan di lingkungan kampus UGM, sebagian besar masih membatasi pada penggunaan geometri differensial berbasis koordinat atau berbahasa lokal sehingga sering melibatkan diskusi tentang efek perubahan sistem koordinat pada objek - objek tensor yang sebenarnya hanya dapat dilakukan pada saat domain antara kedua sistem koordinat saling bersesuaian yaitu saat jacobian transformasinya tidak lenyap [Isham, 1999]. Oleh karena itu, seringkali sifat-sifat global suatu model tidak dapat dilihat secara memadai. Untuk mengantisipasi masalah tersebut, diperlukan pembahasan yang tidak gayut terhadap sistem koordinat yang dipakai. Geometri diffferensial yang memakai sudut pandang ini biasa disebut sebagai geometri differensial modern atau analisa global. Analisa global, sekarang ini mempunyai lapangan aplikasi yang luas. Semisal dalam mekanika klasik, medan Yang - Mills, model sigma nonlinear, teori supersting, quantum gravity dan sistem medan nonlinear pada teori partikel elementer modern. Berkaitan dengan masalah singularitas dan eksistensinya dalam teori relati vitas umum, Hawking dan Ellis telah mendiskusikannya secara panjang lebar dalam bukunya: "The large scale structure of space-time". Pengaruh analisa global dalam buku tersebut terasa sangat kental. Hanya saja, pembatasan pembahasan hanya pada manifold Lorentzian berdimensi empat agak mengurangi selera pada penikmat matematika. Oleh karena itu, dengan tetap mengikuti ide utama dalam pendefinisian
16 3 singularitas: ketidak-komplitan geodesik, penulis berusaha menyajikan ulang permasalahan singularitas pada manifold Lorentzian berdimensi sembarang yang meme nuhi syarat - syarat ruang-waktu relativitas umum. 2. Tujuan Penulisan Adapun tujuan yang hendak dicapai dalam skripsi ini adalah : 1. Merumuskan model ruang-waktu relativitas umum dalam geometri differensial global. 2. Mendiskusikan kemungkinan menunjukkan eksistensi singularitas melalui konsep ketidak-komplitan geodesik kausal pada ruang-waktu relativitas umum. 3. Mendiskusikan kemungkinan perluasan topik - topik bahasan ke sembarang manifold Lorentzian sehingga dengan demikian dapat diterapkan pada bidang lain yang memakai area matematik yang sama. Memakai sudut pandang ini, singularitas pada ruang-waktu relativitas umum hanyalah merupakan pemba tasan bidang kajian pada manifold lorentzian yang berdimensi empat. 3. Ruang Lingkup Kajian Kajian skripsi ini dititikberatkan pada aplikasi analisa global dalam memodelkan singularitas dalam ruang-waktu. Oleh karenanya bahasa penyampaian yang digunakan akan lebih banyak menggunakan bahasa formal matematika. Untuk beberapa kajian yang sudah terlalu familiar dalam buku -buku teks geometri diffe rensial modern, pembuktian - pembuktian akan sesedikit mungkin diberikan. Perlu ditekankan pula bahwa topik kajian ini adalah ruang-waktu yang masih diasumsikan kontinyu dan tidak memperhitungkan efek kuantum padanya.
17 BAB II ANALISIS PADA MANIFOLD LICIN Pada bab ini akan dipaparkan fakta - fakta geometri differensial secukupnya yang diperlukan dalam pembahasan manifold ruang-waktu. Fakta - fakta geometris ini muncul secara alamiah sebagai akibat bahwa ruang-waktu merupakan manifold licin. Sebagian besar notasi pada bab ini diambil dari [Kriele, 2001]. Karena topik - topik ini sangat umum dijumpai pada buku - buku teks geometri differensial maka bukti - bukti sesedikit mungkin ditampilkan. 1. Manifold Licin Sebelumnya akan diperkenalkan pemetaan proyeksi dari R n ke R yang dilambangkan dengan P i. P i ( x 1,, x n) := x i (II.1) Untuk setiap (x 1,, x n ) R n. Definisi II.1 ( Fungsi licin) Pemetaan f: U R n R m dikatakan kontinyu jika f i (p) := P i f(p); i = 1, 2,, m semuanya kontinyu untuk setiap p U. f dikatakan licin atau C - differentiabel pada U jika setiap f i mempunyai turunan parsial untuk semua orde pada U terhadap sistem koordinat pada R n. Definisi II.1 di atas sama saja dengan mengatakan bahwa f licin jika determinan Jacobiannya pada setiap titik p U yang didefinisikan sebagai 4
18 5 f (p) = [D i f j (p)] = D 1 f 1 D n f D 1 f m D n f m (p) (II.2) dengan D i f j := f j x i, tidak lenyap untuk 1 i n dan 1 j m. Selanjutnya C - differentiabel akan disebut licin atau differensiabel saja. Definisi II.2 (Manifold topologis berdimensi m ) Manifold X adalah ruang topologis yang Hausdorff, tersambung dan berbasis tercacah (countable basis) serta terdapat homeomorfisme φ p : U x W R m, p X dengan U p X adalah lingkungan bagi p dan W subhimpunan terbuka di R m. Selanjutnya φ disebut pemetaan koordinat, x i = P i φ(p) disebut fungsi koordinat di p dan pasangan (U p, φ p ) disebut sistem koordinat di p X Definisi II.3 (Struktur licin) Struktur licin (C - structure) pada manifold topologis X adalah himpunan semua sistem koordinat U = {(U α, φ α )} sedemikian rupa memenuhi 1. U α merupakan liput (cover) bagi X, yaitu dipenuhi α U α = X, α A, A = 1, 2, Untuk setiap pasangan α, β A,{(U α, φ α )} dan {(U β, φ β )} saling C - rukun (C -compatible), yaitu φ α φ 1 β pemetaan licin. dan φ β φ 1 α masing - masing merupakan 3. U maksimal menurut kriteria 2, dalam artian jika (U, φ) suatu sistem koordinat pada X yang memenuhi sifat C - rukun dengan setiap unsur di U maka (U, φ) U
19 6 Gambar II.1: {(U α, φ α )} dan {(U β, φ β )} saling C - rukun apabila φ α φ 1 β φ β φ 1 α masing - masing merupakan pemetaan licin. dan Definisi II.4 ( Manifold licin ) Manifold licin adalah manifold topologis yang dilengkapi dengan suatu struktur licin. Selanjutnya, manifold licin akan cukup disebut sebagai manifold saja dan akan dilambangkan dengan M. Dengan demikian suatu manifold topologis dapat mempunyai lebih dari satu manifold licin atau tidak ada sama sekali, tergantung dari seberapa banyak struktur licin yang bisa dibangun padanya. Sebagai contoh, permukaan bola di ruang R n+1 yaitu S n, (ditunjukkan oleh John Milnor) mempunyai 28 struktur licin yang berbeda untuk n = 7, 2 struktur untuk n = 10 dan 992 struktur untuk n = 11 [Qoquereauex, 1988]. Berikut ini akan diberikan beberapa contoh untuk menentukan suatu himpunan adalah suatu manifold atau bukan 1. Ruang Eucledian R n dilengkapi sruktur licin U = (R n, I d ) dengan I d : R n R n pemetaan identitas adalah suatu manifold.
20 7 2. Titik - titik (x, y) di R 2 yang memenuhi y = a x 0 0 x 0 b x o adalah himpunan yang bukan manifold karena tidak tersambung dan tidak Hausdorff di x = Permukaan bola berjari - jari satu satuan S m dilengkapi dengan struktur licin {(S m {n}, P n ), (S m {s}, P s )} dengan {n} = {(0, 0,, 1)} dan {s} = {(0, 0,, 1)} dan P n, P s masing - masing projeksi stereografik dari {n} dan {s}, merupakan manifold. 4. Permukaan kubus di R n yang dibangkitkan oleh metrik d k = n i=i x i bukanlah manifold licin karena tidak terdapat homeomorfisme dengan R m saat diambil x j = d k. 5. Subhimpunan terbuka V dari M dengan struktur licin U V = {( V U α, φ α V Uα ) (Uα, φ α ) U } dengan φ α V Uα pemetaan φ α yang dibatasi pada V U α dan U adalah struktur licin pada M, merupakan manifold yang disebut submanifold terbuka dari M. 6. Grup linier umum yaitu himpunan G l (n, R) yang beranggotakan semua matriks n n nonsingular berunsur riil merupakan manifold sebagai akibat adanya diffeomorfisme dengan R {0} melalui fungsi determinan.
21 8 Definisi II.5 ( Pemetaan licin) Diandaikan M dan N manifold licin. Jika F : M N adalah pemetaan dari mani fold M ke manifold N, maka wakilan lokal menurut sistem koordinat (U, φ) di M dan (V, ψ) di N adalah ψ F φ 1 : φ (U) ψ (V ). F dikatakan licin di p M jika terdapat wakilan lokal bagi F yang licin di p. F dikatakan licin jika F licin pada setiap titik p M. Keberadaan struktur licin menjamin differensiabilitas pemetaan antar manifold terjadi secara global sebagai akibat sifat maksimal yang dimiliki oleh struktur licin pada kedua manifold. Dalam hal ini jika F licin, bijektif dan F 1 juga licin, maka F disebut diffeomorfisme dan kedua manifold dikatakan saling saling diffeomorfis. Diffeomorfisme adalah relasi ekuivalen antar manifold, dalam artian setiap manifold yang saling diffeomorfis mempunyai struktur yang sama dan bisa saling menggantikan. 2. Vektor Singgung, Kovektor dan Tensor Pada Manifold Konsep vektor singgung (tangent vector) erat kaitannya dengan pendefinisian pergeseran infinitisimal pada suatu titik suatu manifold. Pada permukaan di ruang R n, ruang singgung adalah subruang linier dari R n yang ortogonal dengan vektor normal permukaan. Hanya saja manifold tidak selalu terbenam dalam ruang R n, dengan demikian pendefinisian ruang singgung perlu mengambil esensi yang lebih dalam dari ruang vektor. Pendefinisian ini biasanya diambil dari konsep turunan berarah dari suatu fungsi dan vektor kecepatan dari kurva singgung. Dari konsep turunan berarah (directional derivative) dari fungsi bernilai riil, v dikatakan turunan berarah dari f di titik p jika dipenuhi v(f) = f(p) v sehingga dapat dikatakan vektor singgung adalah fungsional licin bernilai riil yang bekerja pada fungsi f. Jika M manifold, himpunan fungsi bernilai riil licin pada M hendak ditu
22 9 liskan sebagai C (M). Dilengkapi perkalian dan penjumlahan fungsi yaitu f + g (p) := f(p) + g(p) dan f g(p) := f(p)g(p), C (M) membentuk aljabar komutatif di atas lapangan riil. C (M) bisa dipersempit menjadi C (p) yaitu himpunan semua kelas ekuivalensi dari C (M) di suatu lingkungan p yaitu U p melalui relasi ekuivalen f = g f(q) = g(q), q U p. Kelas - kelas ekuivalensi ini biasa disebut sebagai benih ( germ ). Definisi II.6 ( Vektor singgung ) Jika M manifold dan p M, yang disebut sebagai vektor singgung pada p adalah fungsional bernilai riil v: C (p) R sedemikian rupa memenuhi sifat 1. ( Linieritas) v(af + bg) = av(f) + bv(g) 2. (Leibnizan) v(fg)(p) = v(f)g(p) + f(p)v(g) a, b R; f, g C (p) Vektor singgung pada p M membentuk ruang vektor di atas lapangan riil dengan operasi penjumlahan dan perkalian yang didefinisikan sebagai (v + w)(f) = v(f) + w(f), (av)(f) = av(f); a R, f C (p). Selanjutnya ruang vektor singgung pada p akan ditulis sebagai T p M. Definisi II.7 Misalkan I adalah interval terbuka pada R. Pemetaan licin α: I M disebut kurva licin pada M. Jika diambil t I dan p α(t 0 ) dapat didefinisikan pemetaan α(t 0 ): C (p) R sebagai α(t 0 )(f) := d (f α)(t dt 0); f C (p). α(t 0 ) menyatakan vektor kecepatan α di t 0 atau vektor singgung kurva α di titik t 0. Karena α(t 0 ) memenuhi syarat Leibnizan dan linearitas terhadap aljabar C (p) maka jelas bahwa α (t 0 ) T p M
23 10 Teorema II.1 Jika (U, φ) adalah sistem koordinat pada p M, dengan fungsi koordinat x i = P i φ; i = 1, 2,, m maka { / x i } p yang didefinisikan sebagai / x i p (f) = / x i (f φ 1 )(φ(p)) merupakan basis bagi T p M, sehingga dimensi T p M = dimensi M. Basis ruang singgung yang berhubungan sistem koordinat ini disebut sebagai basis Gaussan. Selanjutnya dapat difahami bahwa ruang singgung yang dibangun oleh derivatif pada aljabar C (p) dan vektor singgung kurva - kurva licin di suatu titik tak bisa dibedakan melalui kaitan isomorfisme v(f)(p) := d/dt(f α) t=t0 = α(to)(f) Teorema II.2 Jika F pemetaan licin dari manifold M dan N maka dapat diimbas suatu pemetaan F p : T p M T F (p) N yang didefinisikan oleh F p (v)(g) := v(g F ); g C (F (p)) dan merupakan isomorfisme jika dan hanya jika dapat ditemukan diffeomorfisme lokal antara lingkungan p dan lingkungan F (p). Pemetaan yang diimbas ini biasa disebut sebagai differensial dari pemetaan F di p atau push forward. Jika kemudian terdapat pemetaan licin G dari manifold N ke manifold O maka akan dipenuhi aturan komposisi atau dalil rantai (G F ) p = G F (p) F p Tentu saja apabila terdapat diffeomorfisme diantara M dan N, differensial pemetaan F akan menyebabkan ruang singgung pada M diimpor keseluruhan ke N sehingga yang mungkin adalah bahwa jika dua manifold saling diffeomorfis maka dimensi keduanya sama tetapi tidak selalu sebaliknya. Misalkan pada titik p M ditemukan sistem koordinat (U, φ) dan (V, ψ), berdasarkan teorema II.1 dapat disusun basis pada T p M yang berbentuk { / x i } menurut (U, φ) dan { / x j} menurut (V, ψ). Untuk setiap v Tp M dapat di nyatakan sebagai kombinasi linier kedua basis v = m v i / x i = i=1 m v j / x j j=1 (II.3)
24 11 Dengan menganggap ψ φ 1 sebagai pemetaan antar manifold, maka dapat ditunjukkan adanya aturan transformasi komponen vektor singgung yang berbentuk v j = m v i x j/ x i i=1 (II.4) Vektor singgung dalam buku - buku teks fisika biasa disebut sebagai vektor kontrava rian. Jika f C (p) maka dengan menggunakan teorema II.2 dapat disusun pemetaan f p : T p M T f(p) R, v f p (v) yang diberikan oleh f p (v)(x) = v(x f) (II.5) v T p M. Karena T f(p) R dibentang oleh basis tunggal / x f(p) diperoleh f p (v) = v(f) / x f(p) (II.6) Melalui pemetaan ini dapat disusun fungsional linier yang bekerja pada T p M df p : T p M R df p (v) := v(f); v T p M yang linier pada T p M. Definisi II.8 Kovektor atau vektor kovarian adalah suatu pemetaan linier ω: T p M R. Himpunan semua kovektor pada p merupakan ruang jodoh (dual space) dari T p M dan dinyatakan dengan T p M.
25 12 Dapat mudah dilihat bahwa df adalah unsur dari T p M. Jika df dan dg elemen T p M, maka dapat didefinisikan operasi (αdf + βdg) (v) := αv(f) + βv(g); α, β R; v T p M. Dalam suatu sistem koordinat lokal {x 1,..., x n }, dapat ditemukan / x i p T p M yang tindakannya terhadap x j dinyatakan sebagai / x i p (x j ) = dx i ( / x i p ) = δ j i. Hal ini menunjukkan bahwa dxi p membentuk basis pada T p M yang disebut basis jodoh (dual basis) bagi basis / x i p. Simpulan II.1 Tp M merupakan ruang vektor riil dengan basis pada suatu koordinat lokal {x 1,..., x n }, mempunyai basis } {dx i p. Dengan demikian dimensi (T p M) = dimensi ( T p M ) = dimensi(m). Perilaku unsur - unsur di T p M yang diimbas oleh pemetaan kontinyu antar manifold dinyatakan oleh teorema berikut Teorema II.3 Jika F : M N suatu pemetaan licin, dapat diimbas suatu pemetaan F f(p) : T f(p) N T p M yang disebut pull back berikut F f(p) (θ) (v) p := θ (F p v) F (p) θ T f(p) N ; v T pm. Apabila G: N O licin, maka pemetaan licin G F mengimbas komposisi (G F ) G F (p) = F F (p) G G F (p) Seperti halnya pada sembarang ruang vektor V yang bersama ruang vektor jodohnya dapat disusun ruang tensor pada ruang vektor tersebut, maka pada T p M dapat disusun ruang tensor padanya. Berikut ini didefinisikan tensor pada sembarang ruang vektor V, jadi untuk mengetahui tensor pada p M cukup dilakukan pergantian V = T p M.
26 13 Definisi II.9 (Tensor) Misalkan V ruang vektor di atas lapangan K dan V menyatakan ruang vektor jodohnya. Tensor - (s, r) pada ruang vektor V adalah suatu pemetaan θ: V }. {{.. V } V }. {{.. V } K s faktor r faktor yang linier pada setiap argumennya. θ disebut sebagai tensor tipe (s, r) atau tensor r kontravarian dan s kovarian. Ruang yang beranggotakan semua tensor (s, r) di nyatakan sebagai T r s (V ). Didefinisikan untuk kondisi khusus T 0 0 (V ) := K. Sebagai contoh ruang tensor adalah T 0 1 (V ) = V dan T 1 0 (V ) = V. Oleh karena itu dalam konteks ruang tensor, kadang ruang singgung dan jodohnya masing - masing biasa dinyatakan dengan T 0 1 (V ) dan T 1 0 (V ). Di antara dua tensor dengan tipe berbeda mungkin untuk dikombinasikan menjadi tensor tipe yang lebih tinggi melalui operasi produk tensor Definisi II.10 (Produk tensor) Andaikan θ T r s (V ) dan ψ T q p (V ). Produk tensor θ ψ adalah tensor θ ψ T r+q s+p (V ) yang memenuhi θ ψ ( v 1,..., v s, w 1,..., w p, υ 1,..., υ r, ω 1,..., ω q) := θ ( v 1,..., v s, υ 1,..., υ r) ψ ( w 1,..., w p, ω 1,..., ω q) untuk semua v, w V dan υ, ω V. Dapat dibuktikan bahwa produk tensor ini bersifat assosiatif. Berbekal operasi perkalian terhadap skalar (aθ) ( v 1,..., v s, υ 1,..., υ r) := a.θ ( v 1,..., v s, υ 1,..., υ r)
27 14 serta jumlahan θ+ψ ( v 1,..., v s, υ 1,..., υ r) := θ ( v 1,..., v s, υ 1,..., υ r) +ψ ( v 1,..., v s, υ 1,..., υ r) maka jelas bahwa T r s (V ) merupakan ruang vektor diatas lapangan K. Jika {e 1,..., e n } basis pada V dan {θ 1,..., θ n } basis jodohnya, maka basis pada T r s (V ) dapat diungkapkan sebagai { θ i 1... θ is e j1... ej r } (II.7) i 1,..., i s, j 1,..., j r {1,..., n} ; n = dimensi(v ) Setiap unsur ψ T r s (v) dapat dinyatakan dalam jumlahan linier basis di atas ψ = ψ j 1...j r i 1...j s θ i 1... θ is e j1... ej r (II.8) dengan ψ j 1...j r i 1...j s := ψ ( e i1,..., e is, θ j 1,..., θ jr) (II.9) Hal ini berarti T r s (V ) merupakan ruang vektor di atas K dengan dimensi n r+s. Ungkapan pada persamaan II.9 biasa disebut sebagai komponen tensor menurut basis II.7. Berikut ini didefinisikan beberapa operasi penting pada tensor 1. Kontraksi Misalkan ψ Ts r (V ) dan {e 1,..., e n },{θ 1,..., θ n } pasangan basis, dapat didefinisikan operasi kontraksi antara ˆr kontravarian dan ŝ kovarian pada ψ sebagai C ˆr ŝ ψ ( v 1,..., v s 1, υ 1,..., υ r 1)
28 15 := ψ v 1,..., e }{{} i,..., v s 1, υ 1,..., θ i argumen ke ŝ }{{} argumen ke ˆr,..., υ r 1 (II.10) Operasi ini bebas terhadap pemilihan basis. Dapat dilihat, aksi operasi kontraksi pada suatu tensor adalah menurunkan indeks atas dan indeks bawahnya masing - masing satu. Misalkan φ T r s (V ) dan ψ T p q (V ), terhadap produk tensor kontraksi bersifat ( C ˆrŝ φ ) ψ = C ˆr ŝ (φ ψ) ) φ (C ˆpˆq ψ = C r+ˆp s+ˆq (φ ψ) 2. Simetrisasi dan antisimetrisasi Misalkan ψ T 0 p (V ) sembarang permutasi 1 σ p S p didefinisikan σ p ψ (v 1,..., v p ) := ψ ( ) v σp(1),..., v σp(p) kemudian (a) Simetrisasi dari T 0 p (V ) dinyatakan sebagai Sym: T 0 p (V ) T 0 p (V ) 1 Permutasi merupakan pemetaan σ p : {i 1,..., i p } {i 1,..., i p }; σ p {i 1,..., i p } = { i σp(1),..., i σp(p)}. himpunan semua permutasi seperti ini membentuk struktur grup S p yang homeomorfis dengan grup ({ 1, 1},.) melalui Sign(σ p ) = 1 untuk permutasi genap dan untuk permutasi ganjil Sign(σ p ) = 1
29 16 Sym(ψ) = 1/p! σ p S p σ p ψ (II.11) (b) Antisimetrisasidari T 0 p (V ) dinyatakan sebagai Alt: T 0 p (V ) T 0 p (V ) Alt(ψ) = 1/p! σ p S p Sign(σ p )σ p ψ (II.12) Tensor ψ Tp 0 (V ) dikatakan simetris jika ψ = Symψ dan antisimetris jika ψ = Altψ. Pendefinisian yang sama dapat dilakukan untuk simetrisasi dan antisimetrisasi pada ψ T p 0. Simetrisasi ψ Tp 0 bila diungkapkan dalam komponen basis dinyatakan dengan lambang ψ (i1,...,i p) dan untuk antrisimetrisasinya dinyatakan dengan ψ [i1,...,i p]. Jika diinginkan beberapa suku tidak diikutkan dalam permutasi, bisa diberikan tanda pada suku tersebut. Cacah permutasinya berkurang menurut beberapa banyak suku tetap tersebut. Sebagai contoh misalkan ψ T 0 4 maka ψ (i, j, k,l) = 1/2! [ψ ijkl + ψ ljki ]. Ruang tensor T 0 p (V ) antisimetris memegang peranan penting dalam analisis manifold licin, di antaranya dalam teori integrasi dan teori sistem differensial. Definisi II.11 (Forma-p) Tensor ψ T 0 p (V ) dengan sifat Altψ = ψ akan disebut dengan forma-p. Ruang vektor yang beranggotakan semua forma-p dinyatakan dengan Λ p (V ) = Alt ( T 0 p (V ) ). Produk tensor mengimbas produk yang disebut sebagai produk eksterior ( wedge product) : Λ p (V ) Λ q (V ) Λ p+q (V ) (ω, η) ω η := (p + q)! Alt (ω η) p!q!
30 { θ i 1 θ ip} 1 i 1 < <i p n 17 yang bersifat bilinear assosiatif dan antisimetris. Dengan memakai produk eksterior dimungkinkan untuk menyusun basis pada ruang Λ p (V ) menggunakan unsur - unsur V. Berikut ini disajikan lemma yang memudahkan pengungkapan unsur ruang Λ p (V ) dalam basisnya. Lemma II.1 Misalkan ω 1,, ω p V dan σ p S p 1. ω 1 ω p = sign(σ p )ω σp(1) ω σp(p) 2. ω 1 ω p = σ p S p sign(σ p )ω σp(1) ω σp(p) 3. ω 1 ω p = 0 jika dan hanya jika ω 1,, ω p gayut linier. Teorema II.4 Jika {e 1,, e n }, {θ 1,, θ n } pasangan basis jodoh maka himpunan membentuk basis pada ruang Λ p (V ). Dengan demikian dimensi Λ p (V ) = ( n p) = n! (n p)!p! Di samping produk eksterior yang berguna untuk mengkombinasikan beberapa forma, dapat disusun operasi yang menurunkan indeks jenisnya. Operasi ini disebut produk interior (interior product) yang merupakan pemetaan : V Λ p (V ) Λ p 1 (V ) (v, ω) v ω : (ω 1,, ω p 1 ) ω(v, ω 1,, ω p 1 ) dan didefinisikan untuk p = 0, v ω = 0. Kemudian akan dikenalkan medan tensor pada manifold yaitu suatu pemetaan yang bernilai tensor. Berbagai struktur geometris dan fisis dapat memakai konsep ini sebagai model.
31 18 Definisi II.12 (Medan tensor) Ruang vektor yang beranggotakan semua pemetaan licin φ: M Ts r (T p M) p M dengan φ(p) T r s (T p M) ; p M disebut sebagai medan tensor - (r, s) dan akan dinyatakan dengan T r s (M). Suatu medan tensor T 1 0 (M) biasa disebut sebagai medan vektor karena pertitiknya berhubungan dengan vektor singgung, kemudian medan tensor T 0 1 (M) biasa disebut sebagai medan kovektor karena pertitiknya berhubungan dengan kovektor, sedangkan medan tensor T 0 p (M) yang antisimetris pada setiap pertukaran indeksnya biasa disebut sebagai forma differensial tipe-p atau cukup disebut forma-p, dengan forma-0 sebagai fungsi pada manifold dan forma-1 sebagai medan kovektor. Suatu U M yang berhubungan dengan sistem koordinat {x i } menyebabkan ruang tensor T r s (T p M) dibentang oleh basis yang diperoleh dari produk tensor { / x i } dan {dx i } pada setiap p U. Dengan demikian jelas dapat dibentuk medan vektor basis yang dihasilkan dari sistem koordinat Gaussan pada U. Misalkan φ suatu medan tensor, maka ungkapannya dalam sistem koordinat lokal dapat dituliskan sebagai φ(p) = φ i 1...i r j 1...j s (p)dx j 1... dx js / x i1... / x ir (II.13) Berikut ini disajikan lemma yang memudahkan identifikasi medan tensor pada manifold [Lee, 1997] Lemma II.2 (Lemma karakterisasi medan tensor)
32 19 Suatu pemetaan φ: T0 1 (M)... T0 1 (M) T1 0 (M)... T1 0 (M) C (M) }{{}}{{} s faktor r faktor merupakan medan tensor anggota T r s (M) jika dan hanya jika multilinier atas C (M). Juga pemetaan φ: T0 1 (M)... T0 1 (M) T1 0 (M)... T1 0 (M) }{{}}{{} s faktor r faktor T 1 0 (M) diimbas oleh medan tensor anggota Ts r+1 (M) jika dan hanya jika multilinier atas C (M) Teorema II.2 dan II.3 dapat diperluas pemakaiannya pada tensor sembarang. Misalkan g: M N suatu diffeomorfisme lokal dan ψ T r s (N ), didefinisikan pemetaan pull back yang memetakan setiap elemen T r s (N ) ke T r s (M) sebagai g ψ(v 1,..., v s, ω 1,..., ω s ) := ψ ( (g (v 1 )),..., (g (v s )), (g 1 ) (ω 1 ),..., (g 1 ) (ω s ) ) (II.14) sedangkan push forward pada ˆψ T r s (M) untuk dibawa ke T r s (N ) didefinisikan sebagai g ˆψ = ( g 1 ) ˆψ (II.15) Lemma II.3 Untuk setiap diffeomorfisme lokal g: M N dan semua medan tensor φ, ψ T r s (M) dipenuhi sifat g (αψ + βφ) = αg ψ + βg φ g (φ ψ) = g φ g ψ
33 20 g C ˆr ŝ ψ = C ˆr ŝ g ψ Misalkan M manifold licin berdimensi-n, himpunan Ts r M = p M T s r (T p M) secara alamiah membawa struktur licin yang diimbas dari M. Andaikan (U α, ϕ α ) sitim koordinat pada titik p, dapat didefinisikan pemetaan ψ α : Ts r (T p M) ϕ α (U) R nr n s p M φ p (ϕ α (p), (φ i 1,,i r (α)j 1,,j s )) di mana φ i 1,,i r (α)j 1,,j s merupakan komponen tensor φ p menurut ϕ α (p). Jelas bahwa setiap ψ q T r s (T q M) berada pada paling sedikit satu di antara himpunan - himpunan T r s U = p U α T r s (T p M). Apabila sistem koordinat (U α, ϕ α ) dinyatakan dengan (x 1,, x n ) dan (U β, ϕ β ) dengan (y 1,, y n ), setiap vektor singgung v T p M dapat dituliskan dengan v = n i=1 vi α i x = n i=1 vi β i y dengan transformasi antar komponen kooardinat vα j = n i=1 vi (ϕ α (ϕ β ) 1 ) j β y i atau dengan kata lain v α = Dϕ αβ (v β ) dengan Dϕ αβ menyatakan (ϕ α (ϕ β ) 1 ). Begitu juga dengan forma-1 ω, komponen - komponennya akan terhubung melalui ω α = ω β D(ϕ αβ ) 1. Dengan argumentasi yang sama, komponen komponen tensor φ i 1,,i r (α)j 1,,j s dan φ i 1,,i r (β)j 1,,j s terhubung melalui φ k 1,,k r (α)l 1,,l s = 1 i 1,,ir n 1 j 1,,js n φ i 1,,i r (β)j 1,,j s (Dϕ αβ ) k 1 i 1 (Dϕ αβ ) kr i r (D(ϕ αβ ) 1 ) j 1 l1 (D(ϕ αβ ) 1 ) js l s Oleh karena itu komponen - komponen φ α dan φ β dari tensor φ p menurut (U α, ϕ α ) dan (U β, ϕ β ) terhubung oleh isomorphisme linier D αβ. Dengan demikian pemetaan ψ α ψ 1 β : ψ β(t r s U α T r s U β ) ψ α (T r s U α T r s U β )
34 21 (y, (φ β )) ψ α ψ 1 β (y, (φ β)) = (ϕ αβ (y), D αβ (ϕ β )) merupakan diffeomorfisme. Hal ini berarti himpunan T r s M secara alamiah merupakan manifold licin berdimensi n r+s. Manifold ini biasa disebut sebagai bundel tensor (tensor bundle). Bundel tensor T M = T 1 0 M disebut sebagai bundel singgung (tangent bundle), sedangkan bundel tensor T M = T 0 1 M disebut sebagai bundel kotangen (cotangent bundle). Bundel tensor adalah salah satu contoh dari suatu bundel vektor atas suatu manifold, yaitu manifold licin E bersama dengan pemetaan surjektif licin π: E M yang memenuhi: 1. Untuk setiap p M, himpunan E p = π 1 (p) E (disebut fiber E atas p) memiliki suatu struktur ruang vektor riil. 2. Untuk setiap p M, terdapat lingkungan U dari p di M dan suatu diffeomorfisme Φ: π 1 (U) U R k sedemikian rupa sehingga diagram berikut komutatif: Φ π 1 (U) U R k π π 1 U dengan π 1 menyatakan proyeksi ke faktor pertama π 1 (p, v) = p. Pembatasan Φ atas E p merupakan isomorfisme linier dari E p ke {p} R k = R k Manifold E biasa disebut sebagai ruang total dari bundel, M sebagai basis dan π sebagai proyeksinya. Untuk lebih ringkasnya, bundel vektor E atas basis M dengan proyeksi π akan dilambangkan dengan (E, π, M). Setiap pemetaan Φ seperti yang terdefinisi diatas disebut sebagai trivialisasi lokal atas U, Jika terdapat suatu trivialisasi lokal yang terdefinisi pada seluruh manifold basis M (disebut trivialisasi
35 22 global), dikatakan E menjadi bundel trivial. Jika U M terbuka, dapat dibuktikan pembatasan proyeksi E U = π 1 (U) juga merupakan bundel vektor. Pemetaan kontinyu σ: M E sedemikian rupa sehingga π σ = Id M disebut sebagai section dari E. Zero section merupakan ζ: M E yang didefinisikan oleh ζ(p) = 0 E p untuk setiap p M. Sebagai suatu pemetaan, support dari section σ didefinisikan sebagai klosure dari himpunan {p M σ(p) 0}. Pada bundel tensor, section merupakan bahasa lain untuk mengungkapkan medan tensor pada manifold basis. Himpunan section {σ 1,, σ k } sedemikian rupa sehingga span {σ 1 (p),, σ k (p)} = E p untuk setiap p U M dikatakan sebagai suatu kerangka (frame) pada E. 3. Kongruensi dan Derivatif Lie Pada setiap kurva licin, dapat selalu dibangun medan vektor sepanjang kurva dengan nilai - nilainya pada titik sepanjang kurva berupa vektor singgung. Hal sebaliknya apakah bisa terjadi?. Teorema berikut menjamin keberadaannya [Kriele, 2001]. Teorema II.5 Misalkan M manifold licin, V medan vektor pada M. Pada setiap p M terdapat suatu I R dan kurva licin γ p : I M yang memenuhi kondisi γ p (0) = p dan γ(t) = V γ(t) Jika V p 0 maka terdapat suatu lingkungan U dari (0, p) R M sedemikian rupa sehingga pemetaan F : U M; (t, q) F t (q) = γ q (t) dapat didefinisikan dengan baik. Pemetaan q F t (q) merupakan suatu diffeomorfisme lokal untuk setiap t dengan inverse diberikan oleh F t. Jika t, s cukup kecil akan dipenuhi F t F s = F t s. Kurva γ seperti di atas disebut sebagai kurva integral dari medan vektor V, sedangkan F t disebut sebagai aliran (flow) atau kongruensi dari V. Dengan
36 23 demikian, dapat dikatakan bahwa setiap medan vektor dapat selalu membangkitkan kongruansi atau himpunan kurva licin yang tidak saling beririsan dan melalui setiap titik pada lingkungan lokal tertentu. Diffeomorphime lokal pada aliran suatu medan vektor dapat digunakan untuk membangun derivasi suatu medan tensor 2. Definisi II.13 ( Derivatif Lie) Misalkan p M, ψ medan tensor, U medan vektor dan F t aliran dari U, derivatif Lie ψ oleh U dinyatakan dalam L U ψ(x) := dengan (d/dt) t=0 menyatakan derivatif biasa. (( ) ) d Ft ψ (p) dt t=0 Derivatif lie berguna dalam mengukur perubahan ψ sepanjang U. Dengan memakai lemma II.3 dapat mudah dibuktikan bahwa derivatif lie merupakan suatu derivasi. Apabila diterapkan pada fungsi licin f dan medan vektor V diperoleh L U f = U(f) (II.16) 2 Derivasi adalah suatu pemetaan D yang memetakan medan - medan tensor ke medan - medan tensor dengan sifat - sifat D (T r s (M)) T r s (M) D (φ ψ) = D (φ) ψ + φ D (ψ) D komut terhadap kontraksi. Dua derivasi dikatakan bersesuaian jika mereka bersesuaian terhadap medan - medan vektor dan fungsi. Jika D, D, ˆD derivasi maka komutator [ D, ˆD ] := D ˆD ˆD D juga merupakan derivasi. Dipenuhi pula identitas Jacobi [ [ ]] [ [ D, ˆD, D + D, D, ˆD ]] [ [ ]] + ˆD, D, D = 0
37 24 (L U V )(f) = U V (f)f V U(f) (II.17) Mengingat medan vektor dapat dipandang sebagai derivasi di atas fungsi licin, maka persamaan II.17 bisa dipandang sebagai komutator pada medan vektor. Kita nyatakan [U, V ] = L U V. Identitas Jacobi pada medan vektor berakibat dipenuhinya relasi L [U,V ] = [L U, L V ]. Dua medan vektor U dan V dikatakan rukun jika derivatif lie-nya lenyap, secara geometri dapat ditafsirkan bahwa aliran antara keduanya saling rukun. Sebagai contoh, medan basis koordinat yaitu himpunan medan vektor yang menjadi basis ortogonal bagi sembarang medan vektor pada suatu lingkungan, merupakan salah satu himpunan medan vektor yang saling rukun. Pada teori fisika konsep tentang derivatif Lie berguna untuk menyatakan konsep tentang invariansi medan tensor di bawah aksi medan vektor tertentu [Schutz, 1980]. Medan tensor ψ invarian di bawah U jika L U ψ = 0 yaitu saat F t ψ = ψ. Yang menarik di sini, himpunan semua medan vektor yang menyebabkan medan tensor ψ ternyata membentuk aljabar Lie yaitu ruang vektor yang tunduk di bawah operasi komutasi. Kita bisa memilih unsur-unsur pada aljabar Lie tersebut yang saling bebas linier. Karena pada setiap aljabar Lie dapat ditemukan subset medan koordinat Gaussan yang membentangnya, maka penentuan medan vektor bebas linier dari aljabar Lie tersebut sama saja dengan menentukan sistem koordinat yang medan basis koordinatnya membuat ψ invarian. 4. Koneksi dan Kelengkungan Pada Manifold Dalam sembarang manifold, untuk menentukan turunan suatu medan vektor dilakukan dengan membandingkan nilai medan vektor tersebut di suatu titik dengan nilainya di titik yang lain. Oleh karena itu masalahnya adalah bagaimana membandingkan dua vektor singgung yang hidup dalam ruang singgung yang berbeda. Diperlukan suatu cara untuk membandingkan nilai medan vektor pada tempat yang berbeda atau secara mudahnya diperlukan suatu koneksi (connection) antara ruang singgung.
38 25 Definisi II.14 (Koneksi) Koneksi adalah suatu pemetaan : T 1 0 (M) T 1 0 (M) T 1 0 (M) (U, V ) = U V sedemikian rupa sehingga memenuhi sifat - sifat : 1. U V linier atas C (M) pada U fu+gw V = f U V + g W V ; f, g C (M) 2. U V linier atas R pada V U (av + bw ) = a U V + b U W ; a, b R 3. memenuhi aturan produk U fv = U(f)V + f U V ; f C (M) Torsi dari adalah medan tensor (U, V ) T or(u, V ) = U V V U [U, V ] koneksi dikatakan bebas torsi jika dipenuhi T or = 0. Biasanya U V disebut turunan kovarian V sepanjang U. Pada suatu titik p, nilai U V hanya bergantung pada nilai U di p dan nilai V di sekitar p yaitu U V p =
39 26 Up V. Oleh karena itu dapat ditafsirkan sebagai turunan V sepanjang arah vektor singgung U p. Dalam sistem koordinat lokal, misalkan kita nyatakan / x i := xi dan xi xj := Γ k ij xk maka suatu koneksi yang bebas torsi memenuhi sifat Γ k ij = Γ k ji. Komponen koneksi Γ a bc biasa disebut simbol Christoffel. Transformasi Γc ab antar sistem koordinat koordinat lokal { x i } ke {x i } memenuhi Γ e df = xe 2 x h x h x f x + xe x a x b d x h x d x Γ c f ab (II.18) Dengan memakai persamaan ini apabila diketahui suatu sistem koordinat tertentu pada manifold, dapat selalu ditemukan sistem koordinat lokal lain dengan Γ c ab = 0. Misalnya saja apabila suatu sistem koordinat lokal { x a } mempunyai Γ c ab, transformasi sistem koordinat kuadratik berbentuk x a = x a +1/2A a bc xb x c dengan A a bc simetris pada b dan c akan menyebabkan dipenuhinya persamaan Γ c ab = Γ c ab +Ac ab, dengan demikian ) pemiliahan A c ab ( Γc = ab akan menyebabkan Γ c ab = 0 pada sistem koordinat lokal {x a }. Sembarang medan vektor U, V akan memenuhi U V = ( ) U i xi V j xj = ( ) U i xi V j xj = U [( i xi V j) ] xj + V j Γ k ij xk = U [ i xi V k + V j Γij] k xk (II.19) Menggunakan lemma karakterisasi tensor, U V dapat dipandang sebagai V (U,.) dengan V T 1 1 (M). Oleh karena itu, merupakan pemetaan T 1 0 M T 1 1 M. Pemetaan ini disebut sebagai turunan kovarian pada medan vektor. Secara lokal, V dapat dituliskan sebagai V = V i ;j dx j xi dengan V i ;j = xi V k + V j Γ k ij. Karena f = df, maka turunan kovarian pada suatu medan kovektor juga dapat
40 27 didefinisikan. Misalkan diambil ω T 0 1 dengan ω(v ) = f, maka diperoleh U f = U ω(v ) = ω(v, U). Ungkapan lokalnya dinyatakan dengan ω = ω i;j dx i dx j dengan ω i;j = xi ω j + ω k Γ k ij. Adanya turunan kovarian pada fungsi, medan vektor dan medan kovektor memungkinkan untuk mendefinisikan turunan kovarian pada sembarang medan tensor. Perluasan sebagai turunan kovarian pada sembarang medan tensor dapat dilakukan dengan memakai sifat - sifat derivasi pada catatan kaki (2) Lemma II.4 (Tindakan koneksi atas medan tensor) Misalkan (M, ) manifold dengan koneksi, akan terdapat perluasan tunggal untuk jika dikenakan pada medan tensor sembarang : T r s (M) T r s+1 (M) ; ψ ψ yang diberikan oleh ψ(u, V 1,, V s, ω 1,, ω r ) = U ψ(v 1,, V s, ω 1,, ω r ) Pada ruang medan forma-p, yaitu Ω p (M ω T 0 p (M), Alt(ω) = ω ) dapat disusun pemetaan tunggal yang dapat digunakan untuk menaikkan indek medan forma. Pemetaan ini disebut turunan eksterior (exterior derivative). d: Ω p (M Ω p+1 (M; ω dω yang secara lokal dinyatakan dengan dω = d(ω i1 i p ) dx i 1 dx ip 1 i 1 < <i p n
41 28 yang memenuhi sifat 1. d d = 0, 2. d(ω η) = dω η + ( 1) p ω dη untuk semua ω Ω p (M) dan η Ω q (M), 3. Untuk f Ω 0 (M), df berhubungan dengan differensial biasa pada fungsi 4. Komutatif terhadap pull back: F (dω) = d(f ω). Dari sifat terakhir berakibat dipenuhinya hubungan L V dω = dl V ω. Oleh karena itu, derivatif Lie sembarang medan forma dapat dinyatakan sebagai L V ω = V dω + d(v dω). Hubungan ini memungkinkan untuk mengungkapkan turunan eksterior dalam bahasa yang bebas koordinat. Proposisi II.1 Misalkan ω Ω p (M) dan V 0,, V p medan vektor. Maka turunan eksterior dari ω dapat dinyatakan dengan dω(v 0,, V p ) = = p ( 1) i L Vi (ω(v 0,, ˆV i,, V p )) i=0 + 0 i<j p ( 1) i+j ω(l Vi V j, V 0, ˆV i,, ˆV j,, V p ) p ( 1) i V i (ω(v 0,, ˆV i,, V p )) i=0 + 0 i<j p ( 1) i+j ω([v i, V j ], V 0, ˆV i,, ˆV j,, V p ) dimana tanda ˆ (.) menyatakan medan vektor dibuang. Telah disebutkan di atas bahwa nilai turunan kovarian pada suatu titik hanya bergantung pada nilai medan vektor pada lingkungan titik tersebut. Dapat dilakukan pembatasan lingkungan pada medan vektor, misalnya saja pembatasan hanya pada sepanjang kurva. Pada kondisi tersebut, medan vektor yang bersesuaian dikatakan
42 29 sebagai medan vektor sepanjang kurva. selanjutnya didefinisikan turunan kovarian sepanjang kurva. Definisi II.15 Misalkan koneksi, t γ(t) suatu kurva dan t V (t) medan vektor sepanjang kurva γ didefinisikan 1. Turunan kovarian V sepanjang kurva γ dinyatakan sebagai V (t) = γ(t) V (t) = ( d dt V a (t) + Γ a bc V c (t) γ b (t) ) a. Medan vektor V (t) dikatakan mengalami transport paralel sepanjang γ jika γ(t) V (t) = 0 2. Kurva prageodesik merupakan kurva γ yang memenuhi sifat γ γ γ, suatu prageodesik dikatakan geodesik apabila γ γ = 0 3. Geodesik dikatakan komplit jika didefinisikan pada semua t R Setiap prageodesik dapat dijadikan geodesik dengan mengganti parameter kurvanya. Misalkan parameter prageodesik dinyatakan dengan t, maka dengan mengganti parameter menjadi t = at + b akan diperoleh geodesik. parameter pengganti ini disebut sebagai parameter affine (affine parameter). Poin 1 pada definisi di atas menunjukkan bahwa pada setiap medan vektor selalu bisa ditemukan suatu kurva menurut suatu koneksi sedemikian rupa menurut kurva tersebut medan vektor sepanjang kurva terlihat parallel. Simpulan II.2 Geodesik merupakan kurva paling lurus menurut koneksinya. Karena kelurusan geodesik tersebut, maka pada teori relativitas, geodesik digunakan untuk model lintasan gerak materi yang tidak dipercepat atau bebar dari pengaruh luar. Secara lokal persamaan geodesik dapat dinyatakan dengan sistem persamaan orde dua γ a + Γ a bc γb γ c = 0, yang penyelesaiannya dapat diperoleh dengan mereduksi
43 30 persaman tersebut menjadi dua sistem persamaan differensial orde satu d dt γa = v a dan d dt va = Γ a bc vb v c. Dengan demikian penyelesaiannya ditentukan dengan syarat batas {(p, v) p M, v T p M}. Hal ini berarti, pada setiap titik pada manifold dapat dibangun berkas - berkas geodesik yang secara tepat ditentukan oleh setiap vektor singgung pada titik tersebut. Masing - masing berkas geodesik ini dilambangkan γ v dengan v menyatakan kecepatan geodesik pada titik p. Definisi II.16 Misalkan (M, ) manifold dengan koneksi. Pemetaan exp p : T p M M; v exp p (v) := γ v (1) disebut sebagai pemetaan eksponensial dari. Pemetaan ini bersifat licin dan homogen: exp p (tv) = γ tv (1) = γ v (t). Pemetaan ini merupakan diffeomorfisme antara lingkungan terbuka pada T p M yang memuat vektor nol dan suatu lingkungan terbuka di M. Ambil Ũ lingkungan terbuka titik 0 di T p M dan U lingkungan terbuka titik p, misalkan ṽ = d (tv) dt t=0 T 0 T p M maka (exp p ) (ṽ) = ( d dt p(tv)) t=0 exp = ( d tv(1)) dt t=0 γ = ( d v(t)) dt t=0 γ = v Dengan demikian (exp p ) isomorfis, karena itu exp p suatu diffeomorfisme. Jika diambil {e 1,, e n } sebagai basis pada T p M dan menyatakan v = v i e i, dapat diperoleh lingkungan dari 0 T p M yang berbentuk B { r (0) = v } n a=1 (va ) 2 < r. Pemetaan exp p : B r (0) B r (p) := exp p ( B r (0)) merupakan diffeomorfisme untuk r yang cukup kecil. Menggunakan diffeomorfisme ini, dapat didefinisikan suatu sistem koordinat x a (q) := (exp 1 p (q)) a pada B r (p). Koordinat ini disebut sebagai sistem koordinat normal. Bersama dengan sistem koordinat normal, B r (p) disebut sebagai lingkungan normal dari titik p. Dapat dilihat, karena γ = 0 pada lingkungan normal, maka komponen simbol Christoffel Γ a bc = 0. Karena pada setiap titik selalu dapat
44 31 ditemukan lingkungan normalnya, maka dapat diatur suatu lingkungan yang menyebabkan setiap titiknya dihubungkan oleh geodesik tunggal yang sepenuhnya berada di dalam lingkungan tersebut. Lingkungan seperti ini disebut sebagai lingkungan normal konvek atau cukup disebut sebagai lingkungan konvek. Dalam lingkungan konvek, geodesik berperan sebagai garis lurus tunggal yang menghubungkan setiap titik dalam lingkungan tersebut dan tetap di dalamnya sehingga bersesuaian dengan ide tentang lingkungan konvek yang dikenal dalam ruang R n. Jika didefinisikan V W = V W 1 T or(v, W ) dengan koneksi sem- 2 barang dan T or adalah torsi dari. Dapat diketahui bahwa T or(w, W ) = 0 untuk semua W, sehingga dan mempunyai geodesik yang sama. Tapi jika kita tambahkan sembarang S T 1 2 (M) yang anti simetris pada bagian kovariannya pada, T or menurut + S memenuhi T or = 2S 0. Oleh karena itu dapat disimpulkan bahwa untuk setiap koneksi, selalu terdapat koneksi bebas torsi tunggal yang mempunyai geodesik yang sama dengannya. Berikutnya didefinisikan kuantitas pada sembarang manifold yang memberikan ukuran yang membedakannya dengan ruang R n. Pada manifold R n dipenuhi hubungan X Y Z Y X Z = [X,Y ] Z untuk X, Y, Z sembarang medan vektor. Dengan hubungan seperti ini kita nyatakan bahwa R n bersifat datar dan persamaan diatas dianggap sebagai kriteria kedataran. Secara umum tidak setiap manifold memenuhi kriteria kedataran, sehingga tidak dapat dikatakan datar. Akan terdapat suatu medan tensor R: T 0 1 (M) T 0 1 (M) T 0 1 (M) T 0 1 (M) yang didefinisikan sebagai R (U, V ) W = U V W V U W [U,V ] W (II.20)
sebagai, dan dua buah variabel dan dapat digunakan untuk memparameterisasi sebuah permukaan sebagai
 BAB II MANIFOLD DIFFERENSIABEL 2.1 Definisi Manifold [13] Manifold adalah generalisasi dari ide-ide yang familiar tentang kurva dan permukaan pada ruang Euclidean. Sebuah kurva pada ruang Euclidean berdimensi
BAB II MANIFOLD DIFFERENSIABEL 2.1 Definisi Manifold [13] Manifold adalah generalisasi dari ide-ide yang familiar tentang kurva dan permukaan pada ruang Euclidean. Sebuah kurva pada ruang Euclidean berdimensi
Teori Relativitas. Mirza Satriawan. December 23, Pengantar Kelengkungan. M. Satriawan Teori Relativitas
 Teori Relativitas Mirza Satriawan December 23, 2010 Pengantar Kelengkungan Quiz 1 Apakah basis vektor dalam sistem koordinat melengkung selalu konstan? 2 Dalam sistem koordinat apakah basis vektornya selalu
Teori Relativitas Mirza Satriawan December 23, 2010 Pengantar Kelengkungan Quiz 1 Apakah basis vektor dalam sistem koordinat melengkung selalu konstan? 2 Dalam sistem koordinat apakah basis vektornya selalu
PENENTUAN MEDAN GRAVITASI EINSTEIN DALAM RUANG MINKOWSKI MENGGUNAKAN SIMBOL CHRISTOFFEL JENIS I DAN II SKRIPSI MELLY FRIZHA
 PENENTUAN MEDAN GRAVITASI EINSTEIN DALAM RUANG MINKOWSKI MENGGUNAKAN SIMBOL CHRISTOFFEL JENIS I DAN II SKRIPSI Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains MELLY FRIZHA
PENENTUAN MEDAN GRAVITASI EINSTEIN DALAM RUANG MINKOWSKI MENGGUNAKAN SIMBOL CHRISTOFFEL JENIS I DAN II SKRIPSI Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains MELLY FRIZHA
BAB 2 TINJAUAN PUSTAKA
 BAB 2 TINJAUAN PUSTAKA 2.1 Teori Relativitas Einstein Relativitas merupakan subjek yang penting yang berkaitan dengan pengukuran (pengamatan) tentang di mana dan kapan suatu kejadian terjadi dan bagaimana
BAB 2 TINJAUAN PUSTAKA 2.1 Teori Relativitas Einstein Relativitas merupakan subjek yang penting yang berkaitan dengan pengukuran (pengamatan) tentang di mana dan kapan suatu kejadian terjadi dan bagaimana
DASAR-DASAR TEORI RUANG HILBERT
 DASAR-DASAR TEORI RUANG HILBERT Herry P. Suryawan 1 Geometri Ruang Hilbert Definisi 1.1 Ruang vektor kompleks V disebut ruang hasilkali dalam jika ada fungsi (.,.) : V V C sehingga untuk setiap x, y, z
DASAR-DASAR TEORI RUANG HILBERT Herry P. Suryawan 1 Geometri Ruang Hilbert Definisi 1.1 Ruang vektor kompleks V disebut ruang hasilkali dalam jika ada fungsi (.,.) : V V C sehingga untuk setiap x, y, z
Bab 2. Geometri Riemann dan Persamaan Ricci Flow. 2.1 Geometri Riemann Manifold Riemannian
 Bab 2 Geometri Riemann dan Persamaan Ricci Flow 2.1 Geometri Riemann Geometri Riemann pertama kali dikemukakan secara general oleh Bernhard Riemann pada abad ke 19. Pada bagian ini akan diberikan penjelasan
Bab 2 Geometri Riemann dan Persamaan Ricci Flow 2.1 Geometri Riemann Geometri Riemann pertama kali dikemukakan secara general oleh Bernhard Riemann pada abad ke 19. Pada bagian ini akan diberikan penjelasan
PRISMA FISIKA, Vol. I, No. 3 (2013), Hal ISSN :
 PRISMA FISIKA, Vol. I, No. (01), Hal. 1-17 ISSN : 7-804 Aplikasi Persamaan Einstein Hyperbolic Geometric Flow Pada Lintasan Cahaya di Alam Semesta Risko 1, Hasanuddin 1, Boni Pahlanop Lapanporo 1, Azrul
PRISMA FISIKA, Vol. I, No. (01), Hal. 1-17 ISSN : 7-804 Aplikasi Persamaan Einstein Hyperbolic Geometric Flow Pada Lintasan Cahaya di Alam Semesta Risko 1, Hasanuddin 1, Boni Pahlanop Lapanporo 1, Azrul
Teori Relativitas. Mirza Satriawan. December 7, Fluida Ideal dalam Relativitas Khusus. M. Satriawan Teori Relativitas
 Teori Relativitas Mirza Satriawan December 7, 2010 Fluida Ideal dalam Relativitas Khusus Quiz 1 Tuliskan perumusan kelestarian jumlah partikel dengan memakai vektor-4 fluks jumlah partikel. 2 Tuliskan
Teori Relativitas Mirza Satriawan December 7, 2010 Fluida Ideal dalam Relativitas Khusus Quiz 1 Tuliskan perumusan kelestarian jumlah partikel dengan memakai vektor-4 fluks jumlah partikel. 2 Tuliskan
1 Mengapa Perlu Belajar Geometri Daftar Pustaka... 1
 Daftar Isi 1 Mengapa Perlu Belajar Geometri 1 1.1 Daftar Pustaka.................................... 1 2 Ruang Euclid 3 2.1 Geometri Euclid.................................... 8 2.2 Pencerminan dan Transformasi
Daftar Isi 1 Mengapa Perlu Belajar Geometri 1 1.1 Daftar Pustaka.................................... 1 2 Ruang Euclid 3 2.1 Geometri Euclid.................................... 8 2.2 Pencerminan dan Transformasi
BAB I PENDAHULUAN. 1.1 Latar Belakang Permasalahan
 1 BAB I PENDAHULUAN 1.1 Latar Belakang Permasalahan Upaya para fisikawan, khususnya fisikawan teoretik untuk mengungkap fenomena alam adalah dengan diajukannya berbagai macam model hukum alam berdasarkan
1 BAB I PENDAHULUAN 1.1 Latar Belakang Permasalahan Upaya para fisikawan, khususnya fisikawan teoretik untuk mengungkap fenomena alam adalah dengan diajukannya berbagai macam model hukum alam berdasarkan
Teori Dasar Gelombang Gravitasi
 Bab 2 Teori Dasar Gelombang Gravitasi 2.1 Gravitasi terlinearisasi Gravitasi terlinearisasi merupakan pendekatan yang memadai ketika metrik ruang waktu, g ab, terdeviasi sedikit dari metrik datar, η ab
Bab 2 Teori Dasar Gelombang Gravitasi 2.1 Gravitasi terlinearisasi Gravitasi terlinearisasi merupakan pendekatan yang memadai ketika metrik ruang waktu, g ab, terdeviasi sedikit dari metrik datar, η ab
BAB III TENSOR. Berdasarkan uraian bab sebelumnya yang telah menjelaskan beberapa
 BAB III TENSOR Berdasarkan uraian bab sebelumnya yang telah menjelaskan beberapa istilah dan materi pendukung yang berkaitan dengan tensor, pada bab ini akan dijelaskan pengertian dasar dari tensor. Tensor
BAB III TENSOR Berdasarkan uraian bab sebelumnya yang telah menjelaskan beberapa istilah dan materi pendukung yang berkaitan dengan tensor, pada bab ini akan dijelaskan pengertian dasar dari tensor. Tensor
SOLUSI PERSAMAAN RICCI FLOW UNTUK RUANG EMPAT DIMENSI BERSIMETRI SILINDER
 SOLUSI PERSAMAAN RICCI FLOW UNTUK RUANG EMPAT DIMENSI BERSIMETRI SILINDER SKRIPSI Oleh Sudarmadi NIM 061810201112 JURUSAN FISIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS JEMBER 2012 SOLUSI
SOLUSI PERSAMAAN RICCI FLOW UNTUK RUANG EMPAT DIMENSI BERSIMETRI SILINDER SKRIPSI Oleh Sudarmadi NIM 061810201112 JURUSAN FISIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS JEMBER 2012 SOLUSI
Bab 2. Persamaan Einstein dan Ricci Flow. 2.1 Geometri Riemann
 Bab 2 Persamaan Einstein dan Ricci Flow 2.1 Geometri Riemann Sebuah himpunan M disebut sebagai manifold jika tiap titik Q dalam M memiliki lingkungan terbuka S yang dapat dipetakan 1-1 melalui sebuah pemetaan
Bab 2 Persamaan Einstein dan Ricci Flow 2.1 Geometri Riemann Sebuah himpunan M disebut sebagai manifold jika tiap titik Q dalam M memiliki lingkungan terbuka S yang dapat dipetakan 1-1 melalui sebuah pemetaan
Bagian 2 Matriks dan Determinan
 Bagian Matriks dan Determinan Materi mengenai fungsi, limit, dan kontinuitas akan kita pelajari dalam Bagian Fungsi dan Limit. Pada bagian Fungsi akan mempelajari tentang jenis-jenis fungsi dalam matematika
Bagian Matriks dan Determinan Materi mengenai fungsi, limit, dan kontinuitas akan kita pelajari dalam Bagian Fungsi dan Limit. Pada bagian Fungsi akan mempelajari tentang jenis-jenis fungsi dalam matematika
9. Teori Aproksimasi
 44 Hendra Gunawan 9 Teori Aproksimasi Mulai bab ini tema kita adalah aproksimasi fungsi dan interpolasi Diberikan sebuah fungsi f, baik secara utuh ataupun hanya beberapilai di titik-titik tertentu saja,
44 Hendra Gunawan 9 Teori Aproksimasi Mulai bab ini tema kita adalah aproksimasi fungsi dan interpolasi Diberikan sebuah fungsi f, baik secara utuh ataupun hanya beberapilai di titik-titik tertentu saja,
BAB II TEORI KODING DAN TEORI INVARIAN
 BAB II TEORI KODING DAN TEORI INVARIAN Pada bab 1 ini akan dibahas definisi kode, khususnya kode linier atas dan pencacah bobot Hammingnya. Di samping itu, akan dijelaskanan invarian, ring invarian dan
BAB II TEORI KODING DAN TEORI INVARIAN Pada bab 1 ini akan dibahas definisi kode, khususnya kode linier atas dan pencacah bobot Hammingnya. Di samping itu, akan dijelaskanan invarian, ring invarian dan
PRISMA FISIKA, Vol. I, No. 1 (2013), Hal ISSN : Analisis Lintasan Foton Dalam Ruang-Waktu Schwarzschild
 Analisis Lintasan Foton Dalam Ruang-Waktu Schwarzschild Urai astri lidya ningsih 1, Hasanuddin 1, Joko Sampurno 1, Azrul Azwar 1 1 Program Studi Fisika, FMIPA, Universitas Tanjungpura; e-mail: nlidya14@yahoo.com
Analisis Lintasan Foton Dalam Ruang-Waktu Schwarzschild Urai astri lidya ningsih 1, Hasanuddin 1, Joko Sampurno 1, Azrul Azwar 1 1 Program Studi Fisika, FMIPA, Universitas Tanjungpura; e-mail: nlidya14@yahoo.com
Menuju Mekanika Kuantum Relativistik Melalui Aljabar Clifford
 Prosiding Seminar Nasional Penelitian, Pendidikan, dan Penerapan MIPA Fakultas MIPA, Universitas Negeri Yogyakarta, 16 Mei 2009 Intisari Menuju Mekanika Kuantum Relativistik Melalui Aljabar Clifford Romy
Prosiding Seminar Nasional Penelitian, Pendidikan, dan Penerapan MIPA Fakultas MIPA, Universitas Negeri Yogyakarta, 16 Mei 2009 Intisari Menuju Mekanika Kuantum Relativistik Melalui Aljabar Clifford Romy
Teori Medan Klasik. USSR Academy of Sciences. Miftachul Hadi. Applied Mathematics for Biophysics Group. Physics Research Centre LIPI
 Teori Medan Klasik L. D. Landau 1, E. M. Lifshitz 2 1,2 Institute of Physical Problems USSR Academy of Sciences Miftachul Hadi Applied Mathematics for Biophysics Group Physics Research Centre LIPI Puspiptek,
Teori Medan Klasik L. D. Landau 1, E. M. Lifshitz 2 1,2 Institute of Physical Problems USSR Academy of Sciences Miftachul Hadi Applied Mathematics for Biophysics Group Physics Research Centre LIPI Puspiptek,
Analisis Fungsional. Oleh: Dr. Rizky Rosjanuardi, M.Si Jurusan Pendidikan Matematika UNIVERSITAS PENDIDIKAN INDONESIA
 Analisis Fungsional Oleh: Dr. Rizky Rosjanuardi, M.Si Jurusan Pendidikan Matematika UNIVERSITAS PENDIDIKAN INDONESIA Lingkup Materi Ruang Metrik dan Ruang Topologi Kelengkapan Ruang Banach Ruang Hilbert
Analisis Fungsional Oleh: Dr. Rizky Rosjanuardi, M.Si Jurusan Pendidikan Matematika UNIVERSITAS PENDIDIKAN INDONESIA Lingkup Materi Ruang Metrik dan Ruang Topologi Kelengkapan Ruang Banach Ruang Hilbert
Matriks biasanya dituliskan menggunakan kurung dan terdiri dari baris dan kolom: A =
 Bab 2 cakul fi080 by khbasar; sem1 2010-2011 Matriks Dalam BAB ini akan dibahas mengenai matriks, sifat-sifatnya serta penggunaannya dalam penyelesaian persamaan linier. Matriks merupakan representasi
Bab 2 cakul fi080 by khbasar; sem1 2010-2011 Matriks Dalam BAB ini akan dibahas mengenai matriks, sifat-sifatnya serta penggunaannya dalam penyelesaian persamaan linier. Matriks merupakan representasi
BAB 2 TINJAUAN PUSTAKA
 BAB 2 TINJAUAN PUSTAKA Hukum gravitasi Newton mampu menerangkan fenomena benda-benda langit yang dipengaruhi oleh gaya gravitasi antar benda. Namun, hukum gravitasi Newton ini tidak sesuai dengan teori
BAB 2 TINJAUAN PUSTAKA Hukum gravitasi Newton mampu menerangkan fenomena benda-benda langit yang dipengaruhi oleh gaya gravitasi antar benda. Namun, hukum gravitasi Newton ini tidak sesuai dengan teori
Stephen Hawking. Muhammad Farchani Rosyid
 Stephen Hawking Muhammad Farchani Rosyid Kelompok Penelitian Kosmologi, Astrofisika, Partikel, dan Fisika Matematik (KAMP), Laboratorium Fisika Atom dan Inti, Jurusan Fisika FMIPA, Universitas Gadjah Mada,
Stephen Hawking Muhammad Farchani Rosyid Kelompok Penelitian Kosmologi, Astrofisika, Partikel, dan Fisika Matematik (KAMP), Laboratorium Fisika Atom dan Inti, Jurusan Fisika FMIPA, Universitas Gadjah Mada,
SILABUS PENGALAMAN BELAJAR ALOKASI WAKTU
 SILABUS Mata Pelajaran : Matematika Satuan Pendidikan : SMA Ungguan BPPT Darus Sholah Jember kelas : XII IPA Semester : Ganjil Jumlah Pertemuan : 44 x 35 menit (22 pertemuan) STANDAR 1. Menggunakan konsep
SILABUS Mata Pelajaran : Matematika Satuan Pendidikan : SMA Ungguan BPPT Darus Sholah Jember kelas : XII IPA Semester : Ganjil Jumlah Pertemuan : 44 x 35 menit (22 pertemuan) STANDAR 1. Menggunakan konsep
BAB II TINJAUAN PUSTAKA. tegak, perlu diketahui tentang materi-materi sebagai berikut.
 BAB II TINJAUAN PUSTAKA Sebelum pembahasan mengenai irisan bidang datar dengan tabung lingkaran tegak, perlu diketahui tentang materi-materi sebagai berikut. A. Matriks Matriks adalah himpunan skalar (bilangan
BAB II TINJAUAN PUSTAKA Sebelum pembahasan mengenai irisan bidang datar dengan tabung lingkaran tegak, perlu diketahui tentang materi-materi sebagai berikut. A. Matriks Matriks adalah himpunan skalar (bilangan
Ruang Vektor Euclid R 2 dan R 3
 Ruang Vektor Euclid R 2 dan R 3 Kuliah Aljabar Linier Semester Ganjil 2015-2016 MZI Fakultas Informatika Telkom University FIF Tel-U September 2015 MZI (FIF Tel-U) Ruang Vektor R 2 dan R 3 September 2015
Ruang Vektor Euclid R 2 dan R 3 Kuliah Aljabar Linier Semester Ganjil 2015-2016 MZI Fakultas Informatika Telkom University FIF Tel-U September 2015 MZI (FIF Tel-U) Ruang Vektor R 2 dan R 3 September 2015
Pengantar Topologi - MK : Prinsip Matematika
 Pengantar Topologi - MK : Prinsip Matematika Topologi merupakan kajian pemetaan dari suatu obyek dalam ruang baik dalam struktur global maupun dalam struktur lokal yang lebih halus. Dapat dikatakan bahwa
Pengantar Topologi - MK : Prinsip Matematika Topologi merupakan kajian pemetaan dari suatu obyek dalam ruang baik dalam struktur global maupun dalam struktur lokal yang lebih halus. Dapat dikatakan bahwa
1/32 FISIKA DASAR (TEKNIK SIPIL) KINEMATIKA. menu. Mirza Satriawan. Physics Dept. Gadjah Mada University Bulaksumur, Yogyakarta
 1/32 FISIKA DASAR (TEKNIK SIPIL) KINEMATIKA Mirza Satriawan Physics Dept. Gadjah Mada University Bulaksumur, Yogyakarta email: mirza@ugm.ac.id Definisi KINEMATIKA Kinematika adalah cabang ilmu fisika yang
1/32 FISIKA DASAR (TEKNIK SIPIL) KINEMATIKA Mirza Satriawan Physics Dept. Gadjah Mada University Bulaksumur, Yogyakarta email: mirza@ugm.ac.id Definisi KINEMATIKA Kinematika adalah cabang ilmu fisika yang
Aljabar Linier. Kuliah
 Aljabar Linier Kuliah 10 11 12 Materi Kuliah Transformasi Linier Kernel dan Image dari Transformasi Linier isomorfisma Teorema Rank plus Nullity 1/11/2014 Yanita FMIPA Matematika Unand 2 Transformasi Linier
Aljabar Linier Kuliah 10 11 12 Materi Kuliah Transformasi Linier Kernel dan Image dari Transformasi Linier isomorfisma Teorema Rank plus Nullity 1/11/2014 Yanita FMIPA Matematika Unand 2 Transformasi Linier
Aljabar Linear dan Matriks (Persamaan Linear dan Vektor) Instruktur : Ferry Wahyu Wibowo, S.Si., M.Cs.
 Aljabar Linear dan Matriks (Persamaan Linear dan Vektor) Instruktur : Ferry Wahyu Wibowo, S.Si., M.Cs. . Matriks dan Sistem Persamaan Linear Definisi Persamaan dalam variabel dan y dapat ditulis dalam
Aljabar Linear dan Matriks (Persamaan Linear dan Vektor) Instruktur : Ferry Wahyu Wibowo, S.Si., M.Cs. . Matriks dan Sistem Persamaan Linear Definisi Persamaan dalam variabel dan y dapat ditulis dalam
Bab IV Gravitasi Braneworld IV.1 Pendahuluan
 Bab IV Gravitasi Braneworld IV.1 Pendahuluan Pada Bab III, telah diperoleh sebuah deskripsi teori efektif 4-dimensi dari teori 5- dimensi dengan cara mengkompaktifikasi pada orbifold dalam kerangka kerja
Bab IV Gravitasi Braneworld IV.1 Pendahuluan Pada Bab III, telah diperoleh sebuah deskripsi teori efektif 4-dimensi dari teori 5- dimensi dengan cara mengkompaktifikasi pada orbifold dalam kerangka kerja
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI 2.1 Aljabar Linear Definisi 2.1.1 Matriks Matriks A adalah susunan persegi panjang yang terdiri dari skalar-skalar yang biasanya dinyatakan dalam bentuk berikut: [ ] Definisi 2.1.2
BAB II LANDASAN TEORI 2.1 Aljabar Linear Definisi 2.1.1 Matriks Matriks A adalah susunan persegi panjang yang terdiri dari skalar-skalar yang biasanya dinyatakan dalam bentuk berikut: [ ] Definisi 2.1.2
BIFURKASI TRANSKRITIKAL PADA SISTEM DINAMIK SKRIPSI
 BIFURKASI TRANSKRITIKAL PADA SISTEM DINAMIK SKRIPSI Diajukan kepada Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Yogyakarta untuk memenuhi sebagian persyaratan guna memperoleh gelar
BIFURKASI TRANSKRITIKAL PADA SISTEM DINAMIK SKRIPSI Diajukan kepada Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Yogyakarta untuk memenuhi sebagian persyaratan guna memperoleh gelar
Soal-Soal dan Pembahasan Matematika IPA SNMPTN 2012 Tanggal Ujian: 13 Juni 2012
 Soal-Soal dan Pembahasan Matematika IPA SNMPTN 01 Tanggal Ujian: 13 Juni 01 1. Lingkaran (x + 6) + (y + 1) 5 menyinggung garis y 4 di titik... A. ( -6, 4 ). ( -1, 4 ) E. ( 5, 4 ) B. ( 6, 4) D. ( 1, 4 )
Soal-Soal dan Pembahasan Matematika IPA SNMPTN 01 Tanggal Ujian: 13 Juni 01 1. Lingkaran (x + 6) + (y + 1) 5 menyinggung garis y 4 di titik... A. ( -6, 4 ). ( -1, 4 ) E. ( 5, 4 ) B. ( 6, 4) D. ( 1, 4 )
BUKU DIKTAT ANALISA VARIABEL KOMPLEKS. OLEH : DWI IVAYANA SARI, M.Pd
 BUKU DIKTAT ANALISA VARIABEL KOMPLEKS OLEH : DWI IVAYANA SARI, M.Pd i DAFTAR ISI BAB I. BILANGAN KOMPLEKS... 1 I. Bilangan Kompleks dan Operasinya... 1 II. Operasi Hitung Pada Bilangan Kompleks... 1 III.
BUKU DIKTAT ANALISA VARIABEL KOMPLEKS OLEH : DWI IVAYANA SARI, M.Pd i DAFTAR ISI BAB I. BILANGAN KOMPLEKS... 1 I. Bilangan Kompleks dan Operasinya... 1 II. Operasi Hitung Pada Bilangan Kompleks... 1 III.
Himpunan dan Fungsi. Modul 1 PENDAHULUAN
 Modul 1 Himpunan dan Fungsi Dr Rizky Rosjanuardi P PENDAHULUAN ada modul ini dibahas konsep himpunan dan fungsi Pada Kegiatan Belajar 1 dibahas konsep-konsep dasar dan sifat dari himpunan, sedangkan pada
Modul 1 Himpunan dan Fungsi Dr Rizky Rosjanuardi P PENDAHULUAN ada modul ini dibahas konsep himpunan dan fungsi Pada Kegiatan Belajar 1 dibahas konsep-konsep dasar dan sifat dari himpunan, sedangkan pada
Metrik Finsler Pseudo-Konveks Kuat pada Bundel Vektor Holomorfik
 Metrik Finsler Pseudo-Konveks Kuat pada Bundel Vektor Holomorfik Haripamyu FMIPA Universitas Andalas Email: harpamyu@gmail.com Jenizon FMIPA Universitas Andalas Email: jenizon@gmail.com I Made Arnawa FMIPA
Metrik Finsler Pseudo-Konveks Kuat pada Bundel Vektor Holomorfik Haripamyu FMIPA Universitas Andalas Email: harpamyu@gmail.com Jenizon FMIPA Universitas Andalas Email: jenizon@gmail.com I Made Arnawa FMIPA
BAB II PENGANTAR SOLUSI PERSOALAN FISIKA MENURUT PENDEKATAN ANALITIK DAN NUMERIK
 BAB II PENGANTAR SOLUSI PERSOALAN FISIKA MENURUT PENDEKATAN ANALITIK DAN NUMERIK Tujuan Instruksional Setelah mempelajari bab ini pembaca diharapkan dapat: 1. Menjelaskan cara penyelesaian soal dengan
BAB II PENGANTAR SOLUSI PERSOALAN FISIKA MENURUT PENDEKATAN ANALITIK DAN NUMERIK Tujuan Instruksional Setelah mempelajari bab ini pembaca diharapkan dapat: 1. Menjelaskan cara penyelesaian soal dengan
Aljabar Linear Elementer
 BAB I RUANG VEKTOR Pada kuliah Aljabar Matriks kita telah mendiskusikan struktur ruang R 2 dan R 3 beserta semua konsep yang terkait. Pada bab ini kita akan membicarakan struktur yang merupakan bentuk
BAB I RUANG VEKTOR Pada kuliah Aljabar Matriks kita telah mendiskusikan struktur ruang R 2 dan R 3 beserta semua konsep yang terkait. Pada bab ini kita akan membicarakan struktur yang merupakan bentuk
BAB 2 KAJIAN PUSTAKA DAN LANDASAN TEORI. Dalam beberapa tahun terakhir, model graph secara statistik telah diaplikasikan
 BAB 2 KAJIAN PUSTAKA DAN LANDASAN TEORI Dalam beberapa tahun terakhir, model graph secara statistik telah diaplikasikan dengan baik pada aplikasi pengenalan suara, pengolahan citra (Willsky, 2002 dan Choi
BAB 2 KAJIAN PUSTAKA DAN LANDASAN TEORI Dalam beberapa tahun terakhir, model graph secara statistik telah diaplikasikan dengan baik pada aplikasi pengenalan suara, pengolahan citra (Willsky, 2002 dan Choi
UNIVERSITAS GADJAH MADA. Bahan Ajar:
 UNIVERSITAS GADJAH MADA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM JURUSAN MATEMATIKA PROGRAM STUDI S1 MATEMATIKA Sekip Utara, Gedung Jurusan Matematika, Yogyakarta - 55281 Bahan Ajar: BAB POKOK BAHASAN
UNIVERSITAS GADJAH MADA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM JURUSAN MATEMATIKA PROGRAM STUDI S1 MATEMATIKA Sekip Utara, Gedung Jurusan Matematika, Yogyakarta - 55281 Bahan Ajar: BAB POKOK BAHASAN
SILABUS. tentu. Menentukan integral tentu dengan menggunakan sifat-sifat integral. Menyelesaikan masalah
 SILABUS Nama Sekolah : SMA PGRI 1 AMLAPURA Mata Pelajaran : MATEMATIKA Kelas/Program : XII / IPA Semester : 1 STANDAR KOMPETENSI: 1. Menggunakan konsep integral dalam pemecahan masalah. KOMPETENSI DASAR
SILABUS Nama Sekolah : SMA PGRI 1 AMLAPURA Mata Pelajaran : MATEMATIKA Kelas/Program : XII / IPA Semester : 1 STANDAR KOMPETENSI: 1. Menggunakan konsep integral dalam pemecahan masalah. KOMPETENSI DASAR
Kemudian, diterapkan pengortonormalan terhadap x 2 dan x 3 pada persamaan (1), sehingga diperoleh
 SOLUSI VAKUM PERSAMAAN MEDAN EINSTEIN UNTUK BENDA SIMETRI AKSIAL STASIONER MENGGUNAKAN PERSAMAAN ERNST Aldytia Gema Sukma 1, Drs. Bansawang BJ, M.Si, Dr. Tasrief Surungan, M.Sc 3 Universitas Hasanuddin,
SOLUSI VAKUM PERSAMAAN MEDAN EINSTEIN UNTUK BENDA SIMETRI AKSIAL STASIONER MENGGUNAKAN PERSAMAAN ERNST Aldytia Gema Sukma 1, Drs. Bansawang BJ, M.Si, Dr. Tasrief Surungan, M.Sc 3 Universitas Hasanuddin,
BAB I PENDAHULUAN 1.1 Latar Belakang Masalah
 BAB I PENDAHULUAN 1.1 Latar Belakang Masalah Mekanika geometrik merupakan bidang kajian yang membahas subyek-subyek seperti persamaan diferensial, kalkulus variasi, analisis vektor dan tensor, aljabar
BAB I PENDAHULUAN 1.1 Latar Belakang Masalah Mekanika geometrik merupakan bidang kajian yang membahas subyek-subyek seperti persamaan diferensial, kalkulus variasi, analisis vektor dan tensor, aljabar
BAB 1 PENDAHULUAN. 1.1 Latar Belakang Masalah
 BAB 1 PENDAHULUAN Perkembangan fisika teoritik melalui Teori Relativitas Umum (TRU) yang dikemukakan oleh Albert Einstein sudah sangat pesat dan cukup baik dalam mendeskripsikan ataupun memprediksi fenomena-fenomena
BAB 1 PENDAHULUAN Perkembangan fisika teoritik melalui Teori Relativitas Umum (TRU) yang dikemukakan oleh Albert Einstein sudah sangat pesat dan cukup baik dalam mendeskripsikan ataupun memprediksi fenomena-fenomena
MODUL PEMBELAJARAN ANALISIS VARIABEL KOMPLEKS 2/22/2012 IKIP BUDI UTOMO MALANG ALFIANI ATHMA PUTRI ROSYADI
 MODUL PEMBELAJARAN ANALISIS VARIABEL KOMPLEKS 2/22/2012 IKIP BUDI UTOMO MALANG ALFIANI ATHMA PUTRI ROSYADI IDENTITAS MAHASISWA NAMA NPM KELOMPOK : : : DAFTAR ISI Kata Pengantar Daftar Isi BAB I Bilangan
MODUL PEMBELAJARAN ANALISIS VARIABEL KOMPLEKS 2/22/2012 IKIP BUDI UTOMO MALANG ALFIANI ATHMA PUTRI ROSYADI IDENTITAS MAHASISWA NAMA NPM KELOMPOK : : : DAFTAR ISI Kata Pengantar Daftar Isi BAB I Bilangan
Vektor. Vektor memiliki besaran dan arah. Beberapa besaran fisika yang dinyatakan dengan vektor seperti : perpindahan, kecepatan dan percepatan.
 Vektor Vektor memiliki besaran dan arah. Beberapa besaran fisika yang dinyatakan dengan vektor seperti : perpindahan, kecepatan dan percepatan. Skalar hanya memiliki besaran saja, contoh : temperatur,
Vektor Vektor memiliki besaran dan arah. Beberapa besaran fisika yang dinyatakan dengan vektor seperti : perpindahan, kecepatan dan percepatan. Skalar hanya memiliki besaran saja, contoh : temperatur,
BAB II VEKTOR DAN GERAK DALAM RUANG
 BAB II VEKTOR DAN GERAK DALAM RUANG 1. KOORDINAT CARTESIUS DALAM RUANG DIMENSI TIGA SISTEM TANGAN KANAN SISTEM TANGAN KIRI RUMUS JARAK,,,, 16 Contoh : Carilah jarak antara titik,, dan,,. Solusi :, Persamaan
BAB II VEKTOR DAN GERAK DALAM RUANG 1. KOORDINAT CARTESIUS DALAM RUANG DIMENSI TIGA SISTEM TANGAN KANAN SISTEM TANGAN KIRI RUMUS JARAK,,,, 16 Contoh : Carilah jarak antara titik,, dan,,. Solusi :, Persamaan
ISTIYANTO.COM. memenuhi persamaan itu adalah B. 4 4 C. 4 1 PERBANDINGAN KISI-KISI UN 2009 DAN 2010 SMA IPA
 PERBANDINGAN KISI-KISI UN 009 DAN 00 SMA IPA Materi Logika Matematika Kemampuan yang diuji UN 009 UN 00 Menentukan negasi pernyataan yang diperoleh dari penarikan kesimpulan Menentukan negasi pernyataan
PERBANDINGAN KISI-KISI UN 009 DAN 00 SMA IPA Materi Logika Matematika Kemampuan yang diuji UN 009 UN 00 Menentukan negasi pernyataan yang diperoleh dari penarikan kesimpulan Menentukan negasi pernyataan
LAMPIRAN A. Ringkasan Relativitas Umum
 LAMPIRAN A Ringkasan Relativitas Umum Besaran fisika harus invarian terhadap semua kerangka acuan. Kalimat tersebut merupakan prinsip relativitas khusus yang pertama. Salah satu besaran yang harus invarian
LAMPIRAN A Ringkasan Relativitas Umum Besaran fisika harus invarian terhadap semua kerangka acuan. Kalimat tersebut merupakan prinsip relativitas khusus yang pertama. Salah satu besaran yang harus invarian
Aljabar Linier Sistem koordinat, dimensi ruang vektor dan rank
 Aljabar Linier Sistem koordinat, dimensi ruang vektor dan rank khozin mu tamar 9 Oktober 2014 PERTEMUAN-4 : SISTEM KOORDINAT, DIMEN- SI RUANG VEKTOR DAN RANK 1. Sistem koordinat (a) Ketunggalan scalar
Aljabar Linier Sistem koordinat, dimensi ruang vektor dan rank khozin mu tamar 9 Oktober 2014 PERTEMUAN-4 : SISTEM KOORDINAT, DIMEN- SI RUANG VEKTOR DAN RANK 1. Sistem koordinat (a) Ketunggalan scalar
BAB III FUNGSI UJI DAN DISTRIBUSI
 BAB III FUNGSI UJI DAN DISTRIBUSI Bab ini membahas tentang fungsi uji dan distribusi di mana ruang yang memuat keduanya secara berturut-turut dinamakan ruang fungsi uji dan ruang distribusi. Ruang fungsi
BAB III FUNGSI UJI DAN DISTRIBUSI Bab ini membahas tentang fungsi uji dan distribusi di mana ruang yang memuat keduanya secara berturut-turut dinamakan ruang fungsi uji dan ruang distribusi. Ruang fungsi
Catatan Kuliah FI2101 Fisika Matematik IA
 Khairul Basar atatan Kuliah FI2101 Fisika Matematik IA Semester I 2015-2016 Fakultas Matematika dan Ilmu Pengetahuan Alam Institut Teknologi Bandung Bab 6 Analisa Vektor 6.1 Perkalian Vektor Pada bagian
Khairul Basar atatan Kuliah FI2101 Fisika Matematik IA Semester I 2015-2016 Fakultas Matematika dan Ilmu Pengetahuan Alam Institut Teknologi Bandung Bab 6 Analisa Vektor 6.1 Perkalian Vektor Pada bagian
Geometri di Bidang Euclid
 Modul 1 Geometri di Bidang Euclid Dr. Wono Setya Budhi G PENDAHULUAN eometri merupakan ilmu pengetahuan yang sudah lama, mulai dari ribuan tahun yang lalu. Berpikir secara geometris dari satu bentuk ke
Modul 1 Geometri di Bidang Euclid Dr. Wono Setya Budhi G PENDAHULUAN eometri merupakan ilmu pengetahuan yang sudah lama, mulai dari ribuan tahun yang lalu. Berpikir secara geometris dari satu bentuk ke
UNIVERSITAS GADJAH MADA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM JURUSAN MATEMATIKA PROGRAM STUDI S1 MATEMATIKA Sekip Utara, Yogyakarta
 UNIVERSITAS GADJAH MADA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM JURUSAN MATEMATIKA PROGRAM STUDI S1 MATEMATIKA Sekip Utara, Yogyakarta Bahan Ajar: BAB POKOK BAHASAN I MODUL ATAS RING Direncanakan
UNIVERSITAS GADJAH MADA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM JURUSAN MATEMATIKA PROGRAM STUDI S1 MATEMATIKA Sekip Utara, Yogyakarta Bahan Ajar: BAB POKOK BAHASAN I MODUL ATAS RING Direncanakan
Pertama, daftarkan kedua himpunan vektor: himpunan yang merentang diikuti dengan himpunan yang bergantung linear, perhatikan:
 Dimensi dari Suatu Ruang Vektor Jika suatu ruang vektor V memiliki suatu himpunan S yang merentang V, maka ukuran dari sembarang himpunan di V yang bebas linier tidak akan melebihi ukuran dari S. Teorema
Dimensi dari Suatu Ruang Vektor Jika suatu ruang vektor V memiliki suatu himpunan S yang merentang V, maka ukuran dari sembarang himpunan di V yang bebas linier tidak akan melebihi ukuran dari S. Teorema
09. Mata Pelajaran Matematika
 09. Mata Pelajaran Matematika A. Latar Belakang Matematika merupakan ilmu universal yang mendasari perkembangan teknologi modern, mempunyai peran penting dalam berbagai disiplin dan mengembangkan daya
09. Mata Pelajaran Matematika A. Latar Belakang Matematika merupakan ilmu universal yang mendasari perkembangan teknologi modern, mempunyai peran penting dalam berbagai disiplin dan mengembangkan daya
Bab 4 RUANG VEKTOR. 4.1 Ruang Vektor
 Bab RUANG VEKTOR. Ruang Vektor DEFINISI.. Suatu ruang vektor (V, +,, F) atas field (F, +), ditulis singkat V(F), adalah suatu himpunan tak kosong V dengan elemenelemennya disebut vektor, yang dilengkapi
Bab RUANG VEKTOR. Ruang Vektor DEFINISI.. Suatu ruang vektor (V, +,, F) atas field (F, +), ditulis singkat V(F), adalah suatu himpunan tak kosong V dengan elemenelemennya disebut vektor, yang dilengkapi
Soal UN 2009 Materi KISI UN 2010 Prediksi UN 2010
 PREDIKSI UN 00 SMA IPA BAG. (Berdasar buku terbitan Istiyanto: Bank Soal Matematika-Gagas Media) Logika Matematika Soal UN 009 Materi KISI UN 00 Prediksi UN 00 Menentukan negasi pernyataan yang diperoleh
PREDIKSI UN 00 SMA IPA BAG. (Berdasar buku terbitan Istiyanto: Bank Soal Matematika-Gagas Media) Logika Matematika Soal UN 009 Materi KISI UN 00 Prediksi UN 00 Menentukan negasi pernyataan yang diperoleh
II. KONSEP DASAR GRUP. abstrak (abstract algebra). Sistem aljabar (algebraic system) terdiri dari suatu
 II KONSEP DASAR GRUP Suatu cabang matematika yang mempelajari struktur aljabar dinamakan aljabar abstrak abstract algebra Sistem aljabar algebraic system terdiri dari suatu himpunan obyek satu atau lebih
II KONSEP DASAR GRUP Suatu cabang matematika yang mempelajari struktur aljabar dinamakan aljabar abstrak abstract algebra Sistem aljabar algebraic system terdiri dari suatu himpunan obyek satu atau lebih
VEKTOR. Makalah ini ditujukkan untuk Memenuhi Tugas. Disusun Oleh : PRODI TEKNIK SIPIL FAKULTAS TEKNIK SIPIL DAN PERENCANAAN
 VEKTOR Makalah ini ditujukkan untuk Memenuhi Tugas Disusun Oleh : 1. Chrisnaldo noel (12110024) 2. Maria Luciana (12110014) 3. Rahmat Fatoni (121100) PRODI TEKNIK SIPIL FAKULTAS TEKNIK SIPIL DAN PERENCANAAN
VEKTOR Makalah ini ditujukkan untuk Memenuhi Tugas Disusun Oleh : 1. Chrisnaldo noel (12110024) 2. Maria Luciana (12110014) 3. Rahmat Fatoni (121100) PRODI TEKNIK SIPIL FAKULTAS TEKNIK SIPIL DAN PERENCANAAN
DAFTAR ISI. HALAMAN JUDUL... i HALAMAN PERSETUJUAN... II HALAMAN PENGESAHAN... III KATA PENGANTAR... IV DAFTAR ISI... V BAB I PENDAHULUAN...
 DAFTAR ISI HALAMAN JUDUL... i HALAMAN PERSETUJUAN... II HALAMAN PENGESAHAN... III KATA PENGANTAR... IV DAFTAR ISI... V BAB I PENDAHULUAN... 1 A. LATAR BELAKANG MASALAH... 1 B. PEMBATASAN MASALAH... 2 C.
DAFTAR ISI HALAMAN JUDUL... i HALAMAN PERSETUJUAN... II HALAMAN PENGESAHAN... III KATA PENGANTAR... IV DAFTAR ISI... V BAB I PENDAHULUAN... 1 A. LATAR BELAKANG MASALAH... 1 B. PEMBATASAN MASALAH... 2 C.
dengan vektor tersebut, namun nilai skalarnya satu. Artinya
 1. Pendahuluan Penggunaan besaran vektor dalam kehidupan sehari-hari sangat penting mengingat aplikasi besaran vektor yang luas. Mulai dari prinsip gaya, hingga bidang teknik dalam memahami konsep medan
1. Pendahuluan Penggunaan besaran vektor dalam kehidupan sehari-hari sangat penting mengingat aplikasi besaran vektor yang luas. Mulai dari prinsip gaya, hingga bidang teknik dalam memahami konsep medan
Soal-Soal dan Pembahasan SNMPTN Matematika IPA Tahun Pelajaran 2010/2011 Tanggal Ujian: 01 Juni 2011
 Soal-Soal dan Pembahasan SNMPTN Matematika IPA Tahun Pelajaran 00/0 Tanggal Ujian: 0 Juni 0. Diketahui vektor u = (a, -, -) dan v = (a, a, -). Jika vektor u tegak lurus pada v, maka nilai a adalah... A.
Soal-Soal dan Pembahasan SNMPTN Matematika IPA Tahun Pelajaran 00/0 Tanggal Ujian: 0 Juni 0. Diketahui vektor u = (a, -, -) dan v = (a, a, -). Jika vektor u tegak lurus pada v, maka nilai a adalah... A.
BAB II DASAR TEORI. 2.1 Teori Relativitas Umum Einstein
 BAB II DASAR TEORI Sebagaimana telah diketahui dalam kinematika relativistik, persamaanpersamaannya diturunkan dari dua postulat relativitas. Dua kerangka inersia yang bergerak relatif satu dengan yang
BAB II DASAR TEORI Sebagaimana telah diketahui dalam kinematika relativistik, persamaanpersamaannya diturunkan dari dua postulat relativitas. Dua kerangka inersia yang bergerak relatif satu dengan yang
44. Mata Pelajaran Matematika untuk Sekolah Menengah Atas (SMA)/ Madrasah Aliyah (MA)
 44. Mata Pelajaran Matematika untuk Sekolah Menengah Atas (SMA)/ Madrasah Aliyah (MA) A. Latar Belakang Matematika merupakan ilmu universal yang mendasari perkembangan teknologi modern, mempunyai peran
44. Mata Pelajaran Matematika untuk Sekolah Menengah Atas (SMA)/ Madrasah Aliyah (MA) A. Latar Belakang Matematika merupakan ilmu universal yang mendasari perkembangan teknologi modern, mempunyai peran
II. TINJAUAN PUSTAKA. nyata (fenomena-fenomena alam) ke dalam bagian-bagian matematika yang. disebut dunia matematika (mathematical world).
 5 II. TINJAUAN PUSTAKA 2.1. Pemodelan Matematika Definisi pemodelan matematika : Pemodelan matematika adalah suatu deskripsi dari beberapa perilaku dunia nyata (fenomena-fenomena alam) ke dalam bagian-bagian
5 II. TINJAUAN PUSTAKA 2.1. Pemodelan Matematika Definisi pemodelan matematika : Pemodelan matematika adalah suatu deskripsi dari beberapa perilaku dunia nyata (fenomena-fenomena alam) ke dalam bagian-bagian
Kata Pengantar. Puji syukur kehadirat Yang Maha Kuasa yang telah memberikan pertolongan hingga modul ajar ini dapat terselesaikan.
 i Kata Pengantar Puji syukur kehadirat Yang Maha Kuasa yang telah memberikan pertolongan hingga modul ajar ini dapat terselesaikan. Modul ajar ini dimaksudkan untuk membantu penyelenggaraan kuliah jarak
i Kata Pengantar Puji syukur kehadirat Yang Maha Kuasa yang telah memberikan pertolongan hingga modul ajar ini dapat terselesaikan. Modul ajar ini dimaksudkan untuk membantu penyelenggaraan kuliah jarak
SOLUSI STATIK PERSAMAAN MEDAN EINSTEIN UNTUK RUANG VAKUM BERSIMETRI SILINDER DAN PERSAMAAN GERAK PARTIKEL JATUH BEBAS DARI SOLUSI TERSEBUT
 SOLUSI STATIK PERSAMAAN MEDAN EINSTEIN UNTUK RUANG VAKUM BERSIMETRI SILINDER DAN PERSAMAAN GERAK PARTIKEL JATUH BEBAS DARI SOLUSI TERSEBUT SKRIPSI Oleh A.Syaiful Lutfi NIM 081810201005 JURUSAN FISIKA FAKULTAS
SOLUSI STATIK PERSAMAAN MEDAN EINSTEIN UNTUK RUANG VAKUM BERSIMETRI SILINDER DAN PERSAMAAN GERAK PARTIKEL JATUH BEBAS DARI SOLUSI TERSEBUT SKRIPSI Oleh A.Syaiful Lutfi NIM 081810201005 JURUSAN FISIKA FAKULTAS
BAB III PEREDUKSIAN RUANG INDIVIDU DENGAN ANALISIS KOMPONEN UTAMA. Analisis komponen utama adalah metode statistika multivariat yang
 BAB III PEREDUKSIAN RUANG INDIVIDU DENGAN ANALISIS KOMPONEN UTAMA Analisis komponen utama adalah metode statistika multivariat yang bertujuan untuk mereduksi dimensi data dengan membentuk kombinasi linear
BAB III PEREDUKSIAN RUANG INDIVIDU DENGAN ANALISIS KOMPONEN UTAMA Analisis komponen utama adalah metode statistika multivariat yang bertujuan untuk mereduksi dimensi data dengan membentuk kombinasi linear
Bab 1 : Skalar dan Vektor
 Bab 1 : Skalar dan Vektor 1.1 Skalar dan Vektor Istilah skalar mengacu pada kuantitas yang nilainya dapat diwakili oleh bilangan real tunggal (positif atau negatif). x, y dan z kita gunakan dalam aljabar
Bab 1 : Skalar dan Vektor 1.1 Skalar dan Vektor Istilah skalar mengacu pada kuantitas yang nilainya dapat diwakili oleh bilangan real tunggal (positif atau negatif). x, y dan z kita gunakan dalam aljabar
Definisi Jumlah Vektor Jumlah dua buah vektor u dan v diperoleh dari aturan jajaran genjang atau aturan segitiga;
 BAB I VEKTOR A. DEFINISI VEKTOR 1). Pada mulanya vektor adalah objek telaah dalam ilmu fisika. Dalam ilmu fisika vektor didefinisikan sebagai sebuah besaran yang mempunyai besar dan arah seperti gaya,
BAB I VEKTOR A. DEFINISI VEKTOR 1). Pada mulanya vektor adalah objek telaah dalam ilmu fisika. Dalam ilmu fisika vektor didefinisikan sebagai sebuah besaran yang mempunyai besar dan arah seperti gaya,
Soal-Soal dan Pembahasan Matematika IPA SNMPTN 2012 Tanggal Ujian: 13 Juni 2012
 Soal-Soal dan Pembahasan Matematika IPA SNMPTN 01 Tanggal Ujian: 13 Juni 01 1. Lingkaran (x + 6) + (y + 1) 5 menyinggung garis y 4 di titik... A. ( -6 4 ). ( -1 4 ) E. ( 5 4 ) B. ( 6 4) D. ( 1 4 ) BAB
Soal-Soal dan Pembahasan Matematika IPA SNMPTN 01 Tanggal Ujian: 13 Juni 01 1. Lingkaran (x + 6) + (y + 1) 5 menyinggung garis y 4 di titik... A. ( -6 4 ). ( -1 4 ) E. ( 5 4 ) B. ( 6 4) D. ( 1 4 ) BAB
09. Mata Pelajaran Matematika
 09. Mata Pelajaran Matematika A. Latar Belakang Matematika merupakan ilmu universal yang mendasari perkembangan teknologi modern, mempunyai peran penting dalam berbagai disiplin dan mengembangkan daya
09. Mata Pelajaran Matematika A. Latar Belakang Matematika merupakan ilmu universal yang mendasari perkembangan teknologi modern, mempunyai peran penting dalam berbagai disiplin dan mengembangkan daya
VEKTOR. Besaran skalar (scalar quantities) : besaran yang hanya mempunyai nilai saja. Contoh: jarak, luas, isi dan waktu.
 VEKTOR Kata vektor berasal dari bahasa Latin yang berarti "pembawa" (carrier), yang ada hubungannya dengan "pergeseran" (diplacement). Vektor biasanya digunakan untuk menggambarkan perpindahan suatu partikel
VEKTOR Kata vektor berasal dari bahasa Latin yang berarti "pembawa" (carrier), yang ada hubungannya dengan "pergeseran" (diplacement). Vektor biasanya digunakan untuk menggambarkan perpindahan suatu partikel
Perluasan Model Statik Black Hole Schwartzchild
 Perluasan Model Statik Black Hole Schwartzchild Abd Mujahid Hamdan Fakultas Sains dan Teknologi UIN Ar-raniry, Banda Aceh, Indonesia mujahid@ar-raniry.ac.id Abstrak: Telah dilakukan perluasan model black
Perluasan Model Statik Black Hole Schwartzchild Abd Mujahid Hamdan Fakultas Sains dan Teknologi UIN Ar-raniry, Banda Aceh, Indonesia mujahid@ar-raniry.ac.id Abstrak: Telah dilakukan perluasan model black
Program Studi Teknik Mesin S1
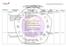 SATUAN ACARA PERKULIAHAN MATA KULIAH : MATEMATIKA TEKNIK 2 KODE/SKS : IT042227 / 2 SKS Pertemuan Pokok Bahasan dan TIU 1 Pendahuluan Mahasiswa mengerti tentang mata kuliah Matematika Teknik 2 : bahan ajar,
SATUAN ACARA PERKULIAHAN MATA KULIAH : MATEMATIKA TEKNIK 2 KODE/SKS : IT042227 / 2 SKS Pertemuan Pokok Bahasan dan TIU 1 Pendahuluan Mahasiswa mengerti tentang mata kuliah Matematika Teknik 2 : bahan ajar,
Tentang Sistem Mekanik Dengan Kendala Tak Holonomik
 4 Rosyid, Tentang Sistem Mekanik Dengan Kendala Tentang Sistem Mekanik Dengan Kendala Tak Holonomik M. F. Rosyid Kelompok Penelitian Kosmologi, Astrofisika, dan Fisika Matematik (KAM), Laboratorium Fisika
4 Rosyid, Tentang Sistem Mekanik Dengan Kendala Tentang Sistem Mekanik Dengan Kendala Tak Holonomik M. F. Rosyid Kelompok Penelitian Kosmologi, Astrofisika, dan Fisika Matematik (KAM), Laboratorium Fisika
Teori Ensambel. Bab Rapat Ruang Fase
 Bab 2 Teori Ensambel 2.1 Rapat Ruang Fase Dalam bagian sebelumnya, kita telah menghitung sifat makroskopis dari suatu sistem terisolasi dengan nilai E, V dan N tertentu. Sekarang kita akan membangun suatu
Bab 2 Teori Ensambel 2.1 Rapat Ruang Fase Dalam bagian sebelumnya, kita telah menghitung sifat makroskopis dari suatu sistem terisolasi dengan nilai E, V dan N tertentu. Sekarang kita akan membangun suatu
uiopasdfghjklzxcvbnmqwertyuiopasd fghjklzxcvbnmqwertyuiopasdfghjklzx wertyuiopasdfghjklzxcvbnmqwertyui opasdfghjklzxcvbnmqwertyuiopasdfg
 uiopasdfghjklzxcvbnmqwertyuiopasd Qwertyuiopasdfghjklzxcvbnmqwerty cvbnmqwertyuiopasdfghjklzxcvbnmq fghjklzxcvbnmqwertyuiopasdfghjklzx wertyuiopasdfghjklzxcvbnmqwertyui opasdfghjklzxcvbnmqwertyuiopasdfg
uiopasdfghjklzxcvbnmqwertyuiopasd Qwertyuiopasdfghjklzxcvbnmqwerty cvbnmqwertyuiopasdfghjklzxcvbnmq fghjklzxcvbnmqwertyuiopasdfghjklzx wertyuiopasdfghjklzxcvbnmqwertyui opasdfghjklzxcvbnmqwertyuiopasdfg
Bab 1 Vektor. A. Pendahuluan
 Bab 1 Vektor A. Pendahuluan Dalam mata kuliah Listrik Magnet A, maupun mata kuliah Listrik Magnet B sebagaii lanjutannya, penyajian konsep dan pemecahan masalah akan banyak memerlukan pengetahuan tentang
Bab 1 Vektor A. Pendahuluan Dalam mata kuliah Listrik Magnet A, maupun mata kuliah Listrik Magnet B sebagaii lanjutannya, penyajian konsep dan pemecahan masalah akan banyak memerlukan pengetahuan tentang
TURUNAN DALAM RUANG DIMENSI-n
 TURUNAN DALAM RUANG DIMENSI-n A. Fungsi Dua Variabel atau Lebih Dalam subbab ini, fungsi dua variabel atau lebih dikaji dari tiga sudut pandang: secara verbal (melalui uraian dalam kata-kata) secara aljabar
TURUNAN DALAM RUANG DIMENSI-n A. Fungsi Dua Variabel atau Lebih Dalam subbab ini, fungsi dua variabel atau lebih dikaji dari tiga sudut pandang: secara verbal (melalui uraian dalam kata-kata) secara aljabar
BAB III TURUNAN DALAM RUANG DIMENSI-n
 BAB III TURUNAN DALAM RUANG DIMENSI-n 1. FUNGSI DUA PEUBAH ATAU LEBIH fungsi bernilai riil dari peubah riil, fungsi bernilai vektor dari peubah riil Fungsi bernilai riil dari dua peubah riil yakni, fungsi
BAB III TURUNAN DALAM RUANG DIMENSI-n 1. FUNGSI DUA PEUBAH ATAU LEBIH fungsi bernilai riil dari peubah riil, fungsi bernilai vektor dari peubah riil Fungsi bernilai riil dari dua peubah riil yakni, fungsi
Transformasi Laplace Peninjauan kembali variabel kompleks dan fungsi kompleks Variabel kompleks Fungsi Kompleks
 Transformasi Laplace Metode transformasi Laplace adalah suatu metode operasional yang dapat digunakan secara mudah untuk menyelesaikan persamaan diferensial linear. Dengan menggunakan transformasi Laplace,
Transformasi Laplace Metode transformasi Laplace adalah suatu metode operasional yang dapat digunakan secara mudah untuk menyelesaikan persamaan diferensial linear. Dengan menggunakan transformasi Laplace,
BAB II TINJAUAN PUSTAKA
 1.4. Hipotesis 1. Model penampang hamburan Galster dan Miller memiliki perbedaan mulai kisaran energi 0.3 sampai 1.0. 2. Model penampang hamburan Galster dan Miller memiliki kesamaan pada kisaran energi
1.4. Hipotesis 1. Model penampang hamburan Galster dan Miller memiliki perbedaan mulai kisaran energi 0.3 sampai 1.0. 2. Model penampang hamburan Galster dan Miller memiliki kesamaan pada kisaran energi
Integral lipat dua BAB V INTEGRAL LIPAT 5.1. DEFINISI INTEGRAL LIPAT DUA. gambar 5.1 Luasan di bawah permukaan
 BAB V INTEGRAL LIPAT 5.1. DEFINISI INTEGRAL LIPAT DUA gambar 5.1 Luasan di bawah permukaan 61 Pada Matematika Dasar I telah dipelajari integral tertentu b f ( x) dx yang dapat didefinisikan, apabila f
BAB V INTEGRAL LIPAT 5.1. DEFINISI INTEGRAL LIPAT DUA gambar 5.1 Luasan di bawah permukaan 61 Pada Matematika Dasar I telah dipelajari integral tertentu b f ( x) dx yang dapat didefinisikan, apabila f
BAB II TINJAUAN PUSTAKA
 BAB II TINJAUAN PUSTAKA 2.1 Teori Gravitasi Newton Mengapa planet, bulan dan matahari memiliki bentuk mendekati bola? Mengapa satelit bumi mengelilingi bumi 90 menit, sedangkan bulan memerlukan waktu 27
BAB II TINJAUAN PUSTAKA 2.1 Teori Gravitasi Newton Mengapa planet, bulan dan matahari memiliki bentuk mendekati bola? Mengapa satelit bumi mengelilingi bumi 90 menit, sedangkan bulan memerlukan waktu 27
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI Sebagai acuan penulisan penelitian ini diperlukan beberapa pengertian dan teori yang berkaitan dengan pembahasan. Dalam sub bab ini akan diberikan beberapa landasan teori berupa pengertian,
BAB II LANDASAN TEORI Sebagai acuan penulisan penelitian ini diperlukan beberapa pengertian dan teori yang berkaitan dengan pembahasan. Dalam sub bab ini akan diberikan beberapa landasan teori berupa pengertian,
BAB 1 OPERASI PADA HIMPUNAN BAHAN AJAR STRUKTUR ALJABAR, BY FADLI
 BAB 1 OPERASI PADA HIMPUNAN Tujuan Instruksional Umum : Setelah mengikuti pokok bahasan ini mahasiswa dapat menggunakan operasi pada himpunan untuk memecahkan masalah dan mengidentifikasi suatu himpunan
BAB 1 OPERASI PADA HIMPUNAN Tujuan Instruksional Umum : Setelah mengikuti pokok bahasan ini mahasiswa dapat menggunakan operasi pada himpunan untuk memecahkan masalah dan mengidentifikasi suatu himpunan
BAB III PEMODELAN PERSAMAAN INTEGRAL PADA ALIRAN FLUIDA
 BAB III PEMODELAN PERSAMAAN INTEGRAL PADA ALIRAN FLUIDA 3.1 Deskripsi Masalah Permasalahan yang dibahas di dalam Tugas Akhir ini adalah mengenai aliran fluida yang mengalir keluar melalui sebuah celah
BAB III PEMODELAN PERSAMAAN INTEGRAL PADA ALIRAN FLUIDA 3.1 Deskripsi Masalah Permasalahan yang dibahas di dalam Tugas Akhir ini adalah mengenai aliran fluida yang mengalir keluar melalui sebuah celah
BAB I PENDAHULUAN. 1.1 Latar Belakang Masalah
 BAB I PENDAHULUAN 1.1 Latar Belakang Masalah Elektromagnetika merupakan cabang fisika yang menjadi tonggak munculnya teori-teori fisika modern dan banyak diterapkan dalam perkembangan teknologi saat ini,
BAB I PENDAHULUAN 1.1 Latar Belakang Masalah Elektromagnetika merupakan cabang fisika yang menjadi tonggak munculnya teori-teori fisika modern dan banyak diterapkan dalam perkembangan teknologi saat ini,
Pengantar Vektor. Besaran. Vektor (Mempunyai Arah) Skalar (Tidak mempunyai arah)
 Pengantar Vektor Besaran Skalar (Tidak mempunyai arah) Vektor (Mempunyai Arah) Vektor Geometris Skalar (Luas, Panjang, Massa, Waktu dan lain - lain), merupakan suatu besaran yang mempunyai nilai mutlak
Pengantar Vektor Besaran Skalar (Tidak mempunyai arah) Vektor (Mempunyai Arah) Vektor Geometris Skalar (Luas, Panjang, Massa, Waktu dan lain - lain), merupakan suatu besaran yang mempunyai nilai mutlak
BAB III PEMBAHASAN. Dalam tesis ini akan dibahas definisi alajabar klasik dan definisi aljabar
 4 BAB III PEMBAHASAN 3. Aljabar atas Lapangan Dalam tesis ini akan dibahas definisi alajabar klasik dan definisi aljabar melalui karakterisasi hasilkali tensor. Berikutnya akan ditunjukkan bahwa setiap
4 BAB III PEMBAHASAN 3. Aljabar atas Lapangan Dalam tesis ini akan dibahas definisi alajabar klasik dan definisi aljabar melalui karakterisasi hasilkali tensor. Berikutnya akan ditunjukkan bahwa setiap
51. Mata Pelajaran Matematika Kelompok Teknologi, Kesehatan dan Pertanian untuk Sekolah Menengah Kejuruan (SMK)/Madrasah Aliyah Kejuruan (MAK) A.
 51. Mata Pelajaran Matematika Kelompok Teknologi, Kesehatan dan Pertanian untuk Sekolah Menengah Kejuruan (SMK)/Madrasah Aliyah Kejuruan (MAK) A. Latar Belakang Matematika merupakan ilmu universal yang
51. Mata Pelajaran Matematika Kelompok Teknologi, Kesehatan dan Pertanian untuk Sekolah Menengah Kejuruan (SMK)/Madrasah Aliyah Kejuruan (MAK) A. Latar Belakang Matematika merupakan ilmu universal yang
Variabel Banyak Bernilai Real 1 / 1
 Fungsi Variabel Banyak Bernilai Real Turunan Parsial dan Turunan Wono Setya Budhi KK Analisis dan Geometri, FMIPA ITB Variabel Banyak Bernilai Real 1 / 1 Turunan Parsial dan Turunan Usaha pertama untuk
Fungsi Variabel Banyak Bernilai Real Turunan Parsial dan Turunan Wono Setya Budhi KK Analisis dan Geometri, FMIPA ITB Variabel Banyak Bernilai Real 1 / 1 Turunan Parsial dan Turunan Usaha pertama untuk
BIFURKASI HOPF PADA SISTEM PREDATOR PREY DENGAN FUNGSI RESPON TIPE II
 BIFURKASI HOPF PADA SISTEM PREDATOR PREY DENGAN FUNGSI RESPON TIPE II SKRIPSI Diajukan kepada Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Yogyakarta untuk Memenuhi Sebagian Persyaratan
BIFURKASI HOPF PADA SISTEM PREDATOR PREY DENGAN FUNGSI RESPON TIPE II SKRIPSI Diajukan kepada Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Yogyakarta untuk Memenuhi Sebagian Persyaratan
perpindahan, kita peroleh persamaan differensial berikut :
 1.1 Pengertian Persamaan Differensial Banyak sekali masalah terapan (dalam ilmu teknik, ilmu fisika, biologi, kimia, sosial, dan lain-lain), yang telah dirumuskan dengan model matematika dalam bentuk persamaan
1.1 Pengertian Persamaan Differensial Banyak sekali masalah terapan (dalam ilmu teknik, ilmu fisika, biologi, kimia, sosial, dan lain-lain), yang telah dirumuskan dengan model matematika dalam bentuk persamaan
Solusi Khusus Persamaan Ricci Flow untuk Metrik Axisimetrik Empat Dimensi
 Solusi Khusus Persamaan Ricci Flow untuk Metrik Axisimetrik Empat Dimensi Laporan Tugas Akhir Diajukan untuk memenuhi persyaratan kelulusan pendidikan tingkat S1 di Program Studi Fisika ITB oleh: FIKI
Solusi Khusus Persamaan Ricci Flow untuk Metrik Axisimetrik Empat Dimensi Laporan Tugas Akhir Diajukan untuk memenuhi persyaratan kelulusan pendidikan tingkat S1 di Program Studi Fisika ITB oleh: FIKI
KINEMATIKA GERAK 1 PERSAMAAN GERAK
 KINEMATIKA GERAK 1 PERSAMAAN GERAK Posisi titik materi dapat dinyatakan dengan sebuah VEKTOR, baik pada suatu bidang datar maupun dalam bidang ruang. Vektor yang dipergunakan untuk menentukan posisi disebut
KINEMATIKA GERAK 1 PERSAMAAN GERAK Posisi titik materi dapat dinyatakan dengan sebuah VEKTOR, baik pada suatu bidang datar maupun dalam bidang ruang. Vektor yang dipergunakan untuk menentukan posisi disebut
