sebuah cara baru belajar Kalkulus dengan komputer
|
|
|
- Sucianty Sanjaya
- 6 tahun lalu
- Tontonan:
Transkripsi
1 Kalkulus dengan Maple sebuah cara baru belajar Kalkulus dengan komputer Oleh : Rosihan Ari Yuana
2 Daftar Isi DAFTAR ISI...II DAFTAR GAMBAR...IV DAFTAR TABEL...V DAFTAR LAMPIRAN...VI KATA PENGANTAR... VII PENGENALAN MAPLE...9 PENGENALAN IDE MAPLE...9 BEKERJA DENGAN WORKSHEET MAPLE...10 OPERASI DASAR ARITMATIK MAPLE...1 OPERATOR DASAR ARITMATIK...1 TINGKAT PRESEDENSI...13 ASSIGNMENT...14 FUNGSI (PEMETAAN)...15 PENDEFINISIAN FUNGSI...15 EVALUASI FUNGSI...18 GRAFIK FUNGSI...0 FUNGSI IMPLISIT...3 FUNGSI GENAP DAN FUNGSI GANJIL...35 OPERASI ALJABAR FUNGSI...37 KOMPOSISI FUNGSI...40 FUNGSI INVERS...41 MENGGAMBAR GRAFIK FUNGSI INVERS...43 PENDEKATAN FUNGSI DENGAN INTERPOLASI...44 SOAL-SOAL LATIHAN...47 LIMIT FUNGSI...5 PERHITUNGAN LIMIT DENGAN FUNCTION...56 CALCULUS1 STUDENT PACKAGE UNTUK LIMIT...58 KEKONTINUAN...66 APLIKASI LIMIT...70 SOAL-SOAL LATIHAN...76 TURUNAN...80 FUNGSI TERDIFERENSIAL...83 FUNCTION DIFF UNTUK TURUNAN...84 CALCULUS1 STUDENT PACKAGE UNTUK TURUNAN...85 ATURAN RANTAI (CHAIN RULE)...89 TURUNAN IMPLISIT...93 TURUNAN ORDE TINGGI...94 ii
3 TURUNAN PARSIAL...96 TEOREMA ROLLE...98 TEOREMA NILAI RATA-RATA APLIKASI TURUNAN SOAL-SOAL LATIHAN INTEGRAL INTEGRAL TENTU INTEGRAL TAK TENTU CALCULUS1 STUDENT PACKAGE UNTUK INTEGRAL MENCARI INTEGRAL TENTU DENGAN METODE PENDEKATAN INTEGRAL LIPAT PENERAPAN INTEGRAL SOAL-SOAL LATIHAN DAFTAR PUSTAKA LAMPIRAN DAFTAR INDEKS CONTACT PERSON: iii
4 Daftar Gambar Gambar -1. Tampilan IDE Maple...10 Gambar 4-1. Grafik fungsi f(x) = x-1... Gambar 4-. Grafik fungsi y = sin(x)...5 Gambar 4-3. Grafik fungsi y=sin(x) dan y=cos(x)...6 Gambar 4-4. Menu option properti grafik...7 Gambar 4-5. Grafik fungsi dari data diskrit...8 Gambar 4-6. Grafik fungsi dari data diskrit dengan style=point...8 Gambar 4-7. Grafik fungsi f(x,y) = sin(x) cos(y)...9 Gambar 4-8. Grafik fungsi r = 1 + sin(t) dalam koordinat polar...31 Gambar 4-9. Grafik x + y = Gambar Grafik ( x y ) 5( x y ) Gambar Grafik ( + ) = 5( ) + =...34 x y x y yang diperbaiki...35 Gambar 4-1. Grafik fungsi y = x...36 Gambar Grafik fungsi y = x Gambar Grafik f(x)=sin(x) dan inversnya...44 Gambar Grafik pendekatan f(x) dengan Spline derajad Gambar 5-1. Grafik f ( x) ( x 3 )/( x 1) = dan garis singgungnya...73 Gambar 5-. Garis singgung f(x) = sin(x)+1 di titik x= Gambar 6-1. Grafik y=x 4 +3x 3 -x +6 beserta turunannya...81 Gambar 6-. Grafik y = 4x 3 +9x -4x memotong sumbu x di 3 titik...8 Gambar 6-3. Grafik y = 3x 3-4x beserta turunannya...83 Gambar 6-4. Grafik f(x)=x 4-3x +1 dan titik yang bergradien nol Gambar 6-5. Visualisasi teorema nilai rata-rata pada f(x)=sin(x)+cos(x) dalam selang [0,5] Gambar 6-6. Grafik posisi, kecepatan, dan percepatan partikel Gambar 6-7. Grafik f(x) = x 3-3x +1 pada selang [-½, 4] Gambar 6-8. Grafik fungsi f(x) = x- sin(x) Gambar 6-9. Grafik fungsi f(x) = x /3 (6-x) 1/ Gambar Grafik fungsi f(x) = 0.5x 4 -x 3 +4x Gambar Grafik fungsi f(x) = x/(x +4) pada interval [-6,6] Gambar 6-1. Grafik fungsi f(x) = x 3 x Gambar Grafik S(θ) pada interval [0.5, 1.] Gambar 7-1. Visualisasi Jumlahan Riemann untuk f(x)=sin(x) dengan 0 partisi pada [0,5].. 13 Gambar 7-. Visualisasi Jumlahan Riemann untuk f(x)=sin(x) dengan 50 partisi pada [0,5].. 13 Gambar 7-3. Visualisasi metode trapezoid dengan 10 partisi Gambar 7-4. Plot kurva y=x dan y=x-x Gambar 7-5. Plot kurva y = x/ x + 1 dan y = x x Gambar 7-6. Plot kurva y =3x+7 dany=x Gambar 7-7. Kurva y=x untuk x=0 4 diputar pada sumbu x Gambar 7-8. Kurva y=x untuk x=0 4 diputar pada sumbu y Gambar 7-9. Daerah yang dibatasi kurva y=6x-x dan y=x Gambar Daerah antara kurva y=6x-x dan y=x diputar pada sumbu x Gambar Daerah di bawah kurva y = x untuk x= Gambar 7-1. Daerah yang dibatasi kurva y=x, y=3x, dan y= iv
5 Daftar Tabel Tabel 4-1. Operator dasar aritmatika...1 Tabel 5-1. Fungsi-fungsi transenden dalam Maple...17 Tabel 6-1. Aturan dalam pencarian limit...59 Tabel 6-. Aturan limit terkait untuk fungsi transenden...60 Tabel 7-1. Aturan dalam mencari turunan...86 Tabel 7-. Aturan turunan fungsi transenden...87 Tabel 8-1. Aturan teknik pengintegralan Tabel 8-. Aturan pengintegralan terkait dengan bentuk fungsi dasar v
6 Daftar Lampiran Lampiran 1. Option plot dua dimensi Lampiran. Option Plot Tiga Dimensi vi
7 Kata Pengantar Puji syukur penulis panjatkan ke hadirat Tuhan Yang Maha Esa karena hanya atas limpahan rahmat dan karunianya penulis dapat menyelesaikan buku Kalkulus dengan Maple ini dengan sebaik-baiknya. Penyusunan buku ini merupakan upaya kami untuk ikut serta meningkatkan kualitas pendidikan bangsa Indonesia, terutama bidang Matematika. Matematika seringkali dianggap suatu hal yang menakutkan di kalangan siswa sekolah karena identik dengan banyak rumus, harus selalu bergelut dengan angka, perhitungan yang sangat rumit bahkan seringkali dirasa sangat abstrak sehingga dirasa kurang ada manfaatnya dalam kehidupan sehari-hari. Padahal tidak demikian halnya. Matematika merupakan suatu ilmu sains yang sangat menarik dan banyak sekali manfaatnya dalam kehidupan sehari-hari di sekitar kita. Apabila seseorang menguasai Matematika maka ia akan menguasai banyak pengetahuan di luar Matematika itu sendiri. Hal ini dikarenakan Matematika merupakan mother of science yang di dalamnya melatih seseorang untuk berpikir logis, kritis dan dinamis. Sebagai salah satu upaya untuk membuat Matematika sebagai suatu hal yang menarik adalah mengkaitkannya dengan teknologi. Dengan menggunakan teknologi, pembelajaran Matematika dapat dilakukan dengan mudah, selain itu kita tidak perlu direpotkan lagi dengan perhitungan matematis secara manual yang terkadang kurang teliti atau kurang akurat. Maple merupakan suatu software yang kemampuannya tidak hanya sebagai alat hitung (tool for computing) seperti halnya kalkulator tangan biasa, namun lebih jauh dari itu Maple juga dapat digunakan sebagai alat pembelajaran (tool for learning), khususnya Matematika. Dengan dasar di atas itulah, mengapa buku ini penulis buat. Buku ini memfokuskan bagaimana menggunakan Maple sebagai alat hitung dan alat pembelajaran Matematika khususnya Kalkulus. Untuk dapat mempergunakan buku ini, disarankan para pembaca mempergunakan minimal Maple 7, karena di dalam buku ini akan dibahas pula beberapa perintah atau paket yang tidak terdapat dalam Maple sebelum rilis 7. Harapan penulis dengan hadirnya buku ini adalah semakin tertariknya minat masyarakat terutama siswa sekolah dalam mempelajari Matematika khususnya Kalkulus. Selain itu, dengan adanya buku ini diharapkan para pengajar juga dapat melakukan inovasi dalam mengajarkan konsep Kalkulus. Demi kesempurnaan buku ini, penulis sangat mengharapkan kritik, saran, dan masukan dari para pembaca yang dapat disampaikan melalui vii
8 Selain menggunakan , para pembaca dapat juga berdiskusi menggunakan Yahoo Messenger dengan id penulis adalah rosihanari. viii
9 Bab 1 Pengenalan Maple Maple merupakan salah satu software aplikasi yang dapat digunakan untuk perhitungan matematika dan sains. Beberapa kelebihannya antara lain bahwa Maple dapat digunakan untuk menyelesaikan persoalan-persoalan dalam bidang matematika seperti aljabar, kalkulus, matematika diskrit, numerik dan masih banyak lagi yang lain. Selain itu dalam Maple juga tersedia fasilitas untuk membuat grafik baik dua dimensi maupun tiga dimensi. Grafik yang dihasilkan dapat dipindah ke dalam dokumen lain. Kelebihan Maple yang lain adalah dapat mendukung pemrograman. Dengan demikian, program dalam bentuk fungsi-fungsi baru untuk penggunaan yang bersifat khusus dapat dibuat. Perintah-perintah dasar Maple sangat sederhana dan mudah dipahami oleh pengguna pemula sekalipun, sehingga Maple cocok digunakan tidak hanya untuk komputasi sains melainkan juga dapat dimanfaatkan untuk proses pemahaman dan pembelajaran matema-tika serta sains. Dengan proses perhitungan dan visualisasi grafik dalam Maple akan dapat memudahkan siswa dalam memahami konsepkonsep dasar matematika. Maple dibuat dan dikembangkan oleh Waterloo Maple inc. Maple dapat diinstal dalam komputer bersistem operasi Windows maupun Macintosh. Pengenalan IDE Maple Dalam subbab ini akan diperkenalkan IDE (Integrated Development Environment) atau lingkungan dari Maple. Gambar 3-1 menunjukkan tampilan lingkungan Maple.
10 10 Pengenalan Maple Gambar 3-1. Tampilan IDE Maple Secara garis besar lingkungan Maple terdiri dari menu utama, toolbar, dan juga worksheet. Bagian worksheet inilah nantinya digunakan untuk menuliskan perintahperintah Maple untuk perhitungan matematika. Dalam Maple juga terdapat fasilitas palette untuk memudahkan pengguna dalam menuliskan perintah maupun simbol-simbol matematis. Beberapa jenis palette yang tersedia adalah symbol palette, expression palette, dan matrix palette. Symbol palette digunakan untuk menuliskan simbol-simbol matematika, expression palette digunakan untuk memudahkan dalam menuliskan ekspresi matematika misalnya integral, deret sigma, bentuk akar dan sebagainya, sedangkan matrix palette digunakan untuk memudahkan pengguna dalam menuliskan matriks. Sebagai dokumentasi, perintah-perintah yang telah dituliskan dalam worksheet dapat disimpan ke dalam file. Secara default, ekstensi file worksheet yang disimpan adalah *.mws (maple worksheet). Untuk proses penyimpanan worksheet langkahnya adalah sebagai berikut: 1. Klik menu FILE pada menu utama. Klik submenu SAVE atau SAVE AS.. 3. Arahkan folder tempat file worksheet akan disimpan dan beri nama file worksheetnya pada bagian FILE NAME 4. Klik OK Bekerja dengan Worksheet Maple Seperti yang telah dijelaskan sebelumnya bahwa worksheet adalah tempat dituliskannya perintah-perintah Maple. Perintah Maple dituliskan di sebelah kanan dari tanda prompt (>).
11 Kalkulus dengan Maple 11 Sebagai contoh, misalkan akan dicari hasil penjumlahan 3+4, maka perintah Maplenya adalah: > 3+4; Selanjutnya tekan ENTER. Setelah tombol ENTER ditekan, maka dibawah perintah tersebut akan tampak hasil output penjumlahan kedua bilangan yaitu 7. Perhatikan perintah yang telah diberikan, khususnya pada akhir dari perintah yang diberikan tanda titik koma (;). Apabila di bagian akhir perintah tidak diberikan tanda titik koma, maka akan terjadi kesalahan yang ditandai dengan munculnya pesan Warning, premature end of input. Selain tanda titik koma, dapat pula diberikan tanda titik dua (:). Apabila di akhir perintah diberikan tanda tersebut, maka hasil output perintah tidak ditampilkan, namun hanya disimpan di dalam memori komputer. Selain dengan menuliskan perintah atau ekspresinya langsung, dapat juga digunakan expression palette. Cara penggunaannya adalah: 1. Klik VIEW pada menu utama. Pilih PALETTES 3. Beri tanda cek pada EXPRESSION PALETTE. Setelah itu akan muncul palette yang di dalamnya tersedia beberapa jenis ekspresi matematika. 4. Pilih ekspresi a+b (penjumlahan) dan selanjutnya Maple akan menampilkan > (%?+%?); 5. Tanda %? adalah tempat menuliskan operand yang akan dijumlahkan. Isilah tanda %? pertama dengan 3. Tekan tombol TAB untuk pindah ke tanda %? kedua dan isilah dengan 4. Selanjutnya tekan ENTER Selain perintah untuk perhitungan matematika, dapat pula diberikan teks yang tidak akan diproses oleh Maple. Untuk membuat teks, caranya adalah dengan mengklik tombol bertuliskan T pada toolbar. Selanjutnya teks yang diinginkan dapat dituliskan. Sedangkan untuk mengembalikan ke bentuk prompt (>) kembali, klik tombol prompt (di sebelah kanan tombol T pada toolbar).
12 1 Operasi Dasar Aritmatik Maple Bab Operasi Dasar Aritmatik Maple Sebelum membahas lebih lanjut penggunaan Maple untuk keperluan perhitungan kalkulus, terlebih dahulu diberikan penjelasan mengenai operasi dasar aritmatik dalam Maple. Pembahasan hal ini meliputi operator dasar aritmatik, tingkat presedensi operator aritmatik dan assignment (pemberian nilai pada variabel). Operator Dasar Aritmatik Tabel 4-1 menjelaskan beberapa operator dasar aritmatik yang sering digunakan dalam Maple. Operator-operator yang disajikan dalam tabel tersebut dapat dikombinasikan satu sama lain. Sebagai contoh misalkan akan dicari hasil perhitungan 3+4*(-)-4/. Perintah Maplenya adalah: > 3+4*(-)-4/; yang akan dihasilkan 7. Kenapa 7? Mengapa tidak 9? Jawaban pertanyaan ini terkait dengan tingkat presedensi dari operator aritmatik yang akan dibahas berikut ini. Operator Makna Contoh + Penjumlahan > 3+7; (akan dihasilkan 10) - Pengurangan > 3-7; (akan dihasilkan 4) * Perkalian > 3*7; (akan dihasilkan 1) / Pembagian > 1/3; (akan dihasilkan 4) ^ atau ** Pangkat > ^3; atau > **3; (keduanya akan menghasilkan 8) mod Modulo (sisa hasil bagi) > 6 mod 4; (akan menghasilkan ) Tabel 4-1. Operator dasar aritmatika
13 Kalkulus dengan Maple 13 Tingkat Presedensi Tingkat presedensi dari suatu operator menunjukan prioritas operator dikerjakan/dievaluasi. Semakin tinggi tingkat presedensi operator maka operator tersebut lebih diprioritaskan untuk dikerjakan lebih dahulu. Berikut ini disajikan urutan tingkat presedensi operator aritmatik mulai dari tertinggi sampai terendah (mulai dari kiri). (^, **), (*,/), (+,-), mod Operator-operator yang ada dalam kurung memiliki tingkat presendensi yang sama, misalnya ^ dengan **, + dengan -. Apabila dalam suatu perintah operasi aritmatik Maple terdapat beberapa operator yang memiliki tingkat presedensi yang sama, maka akan didahulukan operasi yang melibatkan operator yang terletak di sebelah kirinya. Misalnya operasi yang telah diberikan sebelumnya yaitu > 3+4*(-)-4/; Dalam operasi yang diberikan di atas, operator * dan / memiliki tingkat presedensi yang lebih tinggi daripada + dan -, sehingga * dan / dikerjakan lebih dahulu daripada + dan -. Namun, di antara operator * dan / manakah yang akan dikerjakan Maple lebih dahulu? Seperti yang terlihat pada operasi tersebut, bahwa * terletak di sebelah kiri dari /, maka 4*(-) dikerjakan lebih dahulu kemudian 4/. Setelah kedua operasi dikerjakan dan diperoleh hasilnya yaitu 8 dan barulah operasi + dan dikerjakan. Dalam hal ini operasi + dikerjakan lebih dahulu karena terletak di sebelah kiri pengurangan, sehingga 3+(-8) dikerjakan lebih dahulu dan hasilnya barulah dikurangkan dengan atau -5-. Dengan demikian diperoleh hasil 7. Tingkat presedensi suatu operator dapat dinaikkan, misalnya operator penjumlahan dapat diubah untuk lebih diprioritaskan daripada perkalian. Untuk menaikkan tingkat presedensi suatu operator dapat dilakukan dengan menambahkan tanda kurung. Misalnya > (3+4)*((-)-4)/; Dari operasi ini akan dihasilkan 1. Dalam operasi tersebut, operasi penjumlahan lebih diprioritaskan daripada perkalian dan pembagian, demikian pula untuk operasi pengurangannya. Akan tetapi operasi penjumlahan lebih didahulukan daripada pengurangannya karena terletak di sebelah kiri pengurangan.
14 14 Operasi Dasar Aritmatik Maple Assignment Proses assignment merupakan pemberian nilai pada suatu variabel untuk disimpan pada alamat tertentu pada memori komputer yang suatu saat dapat digunakan atau dipanggil kembali. Nilai yang diassign pada suatu variabel dapat berupa konstanta maupun berasal dari suatu operasi. Sintaks untuk assignment dalam Maple adalah > variabel := nilai; Sebagai contoh, berikut ini diberikan beberapa perintah assignment pada Maple. > a := 5; > b := -34; > c := *a+b; Perintah pertama berfungsi untuk mengassign variabel a dengan nilai 5. Perintah kedua untuk mengassign variabel b dengan 34, sedangkan yang perintah ketiga mengassign variabel c yang nilainya merupakan hasil operasi a+b yaitu -4.
15 Kalkulus dengan Maple 15 Bab 3 Fungsi (pemetaan) Dalam matematika, suatu fungsi (pemetaan) didefinisikan sebagai suatu relasi dari himpunan A ke himpunan B yang dalam hal ini setiap anggota dari A direlasikan dengan tepat satu anggota B. Apabila dinyatakan dalam notasi, misalkan f adalah suatu fungsi yang memetakan himpunan A ke B, maka notasinya adalah f : A B Pendefinisian Fungsi Salah satu contoh fungsi adalah ( x) = 3 x + 4 f. Fungsi tersebut memetakan bilangan real ke bilangan real juga. Selanjutnya, bagaimana cara mendefinisikan fungsi dalam Maple? Dalam Maple, fungsi di atas dapat didefinisikan dengan cara: > f := (x) -> 3*x+4; Sintaks secara umum untuk mendefinisikan suatu fungsi dalam Maple adalah sebagai berikut: > nama_fungsi := (variabel) -> operasi; Berikut ini beberapa contoh bagaimana mendefinisikan fungsi ke dalam Maple baik fungsi satu variabel atau lebih. Contoh: Definisikan fungsi-fungsi berikut ini ke dalam Maple! 1. f ( x) = 5x 10
16 16 Fungsi (pemetaan). ( ) g x = x + x + 3. f ( x) 3 7 x 1, x > 0 = x, x 0 4. g( x) = x 3 5. h( x) 4x 3 = x 1 6. g( x, y) = xy + x h( x, y) = 4x x y + 5xy + 8y 8. f ( x, y) = x y + xy Penyelesaian: 1. > f := (x) -> 5*x-10;. > g := (x) -> -3*x^ + *x + 7; 3. > f := (x) -> piecewise(x>0,*x-1,x<=0,-x); 4. > g := (x) -> sqrt(*x-3); atau > g := (x) -> (*x-3)^(1/); 5. > h := (x) -> (4*x-3)/(x-1); 6. > g := (x,y) -> *x*y+x^; 7. > h := (x,y) -> 4*x^3 *x^*y + 5*x*y^ + 8*y^3; 8. > f := (x,y) -> abs(x-y) + x*y^; Selain bentuk fungsi-fungsi seperti yang telah diberikan, dalam kalkulus dikenal juga beberapa bentuk fungsi transenden seperti fungsi logaritma, eksponensial, trigonometri dan hiperbolik. Tabel 5-1 menjelaskan bagaimana mendefinisikan fungsifungsi tersebut dengan Maple.
17 Kalkulus dengan Maple 17 Catatan: khusus untuk fungsi-fungsi trigonometri nilai x adalah dalam radian. Selanjutnya akan diberikan contoh bagaimana mendefinisikan fungsi dengan bentuk transenden menggunakan Maple. Sintaks a^x surd(x,n) exp(x) ln(x) log[n](x) log10(x) sin(x) cos(x) tan(x) csc(x) sec(x) cot(x) sinh(x) cosh(x) tanh(x) csch(x) sech(h) coth(x) Makna Eksponensial a x, a konstan Pangkat pecahan (x 1/n ), n bilangan bulat. Eksponensial e x, e bilangan natural Logaritma natural Logaritma bilangan pokok n, n bilangan asli Logaritma bilangan pokok 10 Sinus x Cosinus x Tangen x Cosecan x Secan x Cotangen x Sinus hiperbolik x Cosinus hiperbolik x Tangen hiperbolik x Cosecan hiperbolik x Secan hiperbolik x Cotangen hiperbolik x Tabel 5-1. Fungsi-fungsi transenden dalam Maple
18 18 Fungsi (pemetaan) Contoh: Definisikan fungsi-fungsi berikut ini dalam Maple: 1. f ( x) = x e x. g( x) = xsin ( x + 1) sin ( x) 3. f ( x) = 3x + ln( x + ) log ( x) ( ) ( ) 4. ( ) ( ) g x, y = log sin x 5 sinh xy Penyelesaian: 1. > f := (x) -> 3^x + exp(x-1);. > g := (x) -> x*sin(x+1)-sin(x)^; 3. > f := (x) -> 3*x^ + ln(x^+)-log10(x); atau > f := (x) -> 3*x^ + ln(x^+)-log[10](x); 4. g := (x,y) -> log[](sin(x-5)^)-sinh(x*y); Evaluasi Fungsi Misalkan sudah diketahui suatu fungsi f ( x ), selanjutnya dapat dicari nilai fungsi untuk x tertentu. Sebagai contoh diberikan fungsi f ( x) = x + 3x 1 dan akan dicari nilai fungsi untuk x=1 atau f(1). Dari perhitungan manual diperoleh f ( 1) = = 3. Maple dapat mendukung proses evaluasi fungsi (mencari nilai fungsi). Selanjutnya akan diberikan beberapa contoh bagaimana mengevaluasi fungsi menggunakan Maple. Contoh: Dengan menggunakan Maple tentukan nilai fungsi berikut ini pada titik yang diberikan. f x 1. ( ) 3 = x, pada x = -3
19 Kalkulus dengan Maple 19. ( ) g x x x 3. f ( x) = 3 + 4, pada x = 5 x, x > 1 =, pada x = 0 x + 3, x 1 4. f ( x, y) cos( x) sin ( x y) = + +, pada x =.3 dan y = 1 Penyelesaian: 1. > f := (x) -> *x-3; > f(-3); hasil dari perintah tersebut diperoleh f ( 3) adalah 9.. > g := (x) -> x^ 3*x + 4; > g(5); hasil g ( 5) akan diperoleh > f := (x) -> piecewise(x>1,x-,x<=1,-x+3); > f(0); Nilai f ( 0) berdasarkan perhitungan tersebut diperoleh 3 4. > f := (x,y) -> cos(x)+*sin(x+y); > f(.3, 1); dengan menggunakan Maple diperoleh nilai f (.3, 1) adalah Beberapa kasus evaluasi fungsi dalam Maple dari fungsi yang telah didefinisikan sebelumnya terkadang tidak memberikan hasil seperti yang diharapkan (hasil tampilan hanya dalam bentuk simbolik). Sebagai gambaran, diberikan contoh fungsi f x = sin x + cos x, dan akan dievaluasi nilai fungsi tersebut pada x=. ( ) ( ) ( ) Apabila digunakan perintah Maple seperti di bawah ini, > f := (x) -> sin(x) + cos(x); > f();
20 0 Fungsi (pemetaan) maka Maple akan menghasilkan sin ( ) + cos( ). Di sini nilai sin ( ) dan cos( ) masing-masing tidak dihitung nilainya (dalam numerik), sehingga nilai fungsi f ( ) masih dinyatakan dalam simbol. Kasus semacam ini muncul karena nilai x bukan dalam bentuk floating point. Untuk menyatakan nilai x dalam floating point, caranya dengan menambahkan digit desimal pada nilai x yang akan dievaluasi. Dengan demikian perintah f ( ) ; diubah menjadi (.0) f ; Hal itu bukan satu-satunya cara untuk menghindari munculnya hasil perhitungan dalam bentuk simbol. Cara lain adalah dengan memberikan perintah evalf() seperti yang ditunjukkan di bawah ini. > f := (x) -> sin(x) + cos(x); > evalf(f()); Tingkat presisi (digit) hasil perhitungan Maple dapat diatur. Secara default Maple menampilkan hasil perhitungan dalam 10 digit presisi. Hal ini tampak pada soal no. (4) dari contoh sebelumnya yaitu dari hasil Untuk mengubah digit presisi perintahnya adalah > Digits := n; dengan n adalah bilangan asli Perintah di atas diberikan sebelum operasi perhitungan dilakukan. Misalnya untuk hasil perhitungan soal no. (4) akan ditampilkan dalam 7 digit presisi, maka perintahnya: > Digits := 7; > f := (x,y) -> cos(x)+*sin(x+y); > f(.3, 1); dan diperoleh hasil Grafik Fungsi Salah satu kelebihan Maple adalah tersedianya fasilitas untuk membuat grafik suatu fungsi baik berdimensi maupun 3, serta fungsi parametrik. Selain itu, grafik juga dapat disajikan dalam bentuk koordinat kutub (polar). Efek-efek animasi juga dapat diberikan pada grafik supaya lebih menarik.
21 Kalkulus dengan Maple 1 Grafik Fungsi Dimensi Diberikan suatu fungsi y f ( x) =, apabila fungsi ini akan dibuat dibuat grafiknya menggunakan Maple, maka digunakan perintah plot dengan sintaks perintahnya adalah: > plot(f(x), x=a..b, option1, option,...); dengan x=a..b adalah batas nilai x untuk grafik yang akan dibuat pada selang [a, b]. Sedangkan parameter option adalah properti asesoris grafik. Option ini bersifat optional (tidak harus dituliskan). Berikut ini beberapa contoh penggunaan perintah Maple untuk membuat grafik fungsi dalam dimensi: Contoh: Gambarlah grafik fungsi-fungsi di bawah ini: 1. y = x 1, untuk x [-3, 3]. y x x = 3 + 7, untuk x [-10,10] 3. y sin( x) cos( x) = +, untuk x [-5,8] 4. x, x > 1 y =, untuk x [0, 7] x + 3, x 1 Penyelesaian: 1. > plot(*x-1, x = -3..3); cara lain dapat dilakukan dengan mendefinisikan fungsinya terlebih dahulu. > f := (x) -> *x-1; > plot(f(x),x=-3..3); dari perintah tersebut diperoleh grafik seperti pada Gambar 5-1
22 Fungsi (pemetaan) Gambar 5-1. Grafik fungsi f(x) = x-1 kedua cara yang telah diberikan dapat juga dilakukan pada contoh-contoh berikutnya.. > plot(x^-3*x+7,x= ); 3. > plot(sin(x)+*cos(x),x=-5..8); 4. > plot(piecewise(x>1,x-,x<=1,-x+3),x=0..7); Apabila diinginkan untuk ditambahkan option pada perintah plot, maka berikut ini beberapa perintah option yang sering digunakan. 1. color=warna Perintah ini digunakan untuk memberi warna grafik. Beberapa warna yang dapat dipilih antara lain aquamarine black blue navy coral cyan brown gold green gray grey khaki magenta maroon orange pink plum red sienna tan turquoise violet wheat white yellow
23 Kalkulus dengan Maple 3 Sebagai contoh misalkan suatu grafik diberi warna merah muda, maka dapat ditambahkan perintah Color = pink. filled=true,false Option ini untuk memberi warna pada daerah antara kurva grafik dengan sumbu x. Nilai dari parameter filled dapat diberi true atau false. Apabila bernilai true maka daerah antara kurva dengan sumbu x diberi warna, sedangkan apabila bernilai false maka daerahnya tidak diberi warna 3. labels=[string1, string] Perintah ini digunakan untuk memberi nama label pada sumbu x dan y. Parameter string1 dan string pada perintah dapat diganti dengan suatu kata (diapit dengan dengan tanda petik dua ("). Misalnya untuk nama sumbu-x nya diberi nama dengan "nilai x" dan sumbu-y nya dengan "nilai y", maka perintahnya labels=["nilai x","nilai y"] 4. legend=string Suatu grafik dapat diberi keterangan berupa legenda untuk menjelaskan makna grafik tersebut. Parameter string pada perintah diganti dengan keterangan yang menjelaskan makna suatu grafik. Sebagai contoh misalkan diberikan suatu grafik fungsi sinus dan selanjutnya akan dibuat keterangan legenda pada grafik, maka dapat ditambahkan perintah legend = "Grafik sinus" 5. linestyle=jenisgaris Perintah linestyle digunakan untuk memilih bentuk garis yang membentuk kurva grafik. Beberapa pilihan bentuk garis yang dapat digunakan antara lain: a. SOLID (berbentuk garisnya utuh) b. DOT (berbentuk titik-titik) c. DASH (berbentuk garis putus-putus) d. DASHDOT (berbentuk gabungan garis putus-putus dan titik)
24 4 Fungsi (pemetaan) 6. style=s Perintah ini digunakan untuk mengatur tampilan grafik apakah disajikan dalam bentuk titik-titik terhubung ataukah tidak terhubung. Nilai s dapat diganti dengan LINE untuk mendapatkan grafik dengan titik terhubung, atau POINT untuk grafik dengan titik tidak terhubung. Secara default, style dalam Maple adalah LINE. 7. symbol=jenis simbol Option ini digunakan untuk menentukan bentuk titik pada suatu grafik. Option ini akan terlihat efeknya apabila grafik fungsinya dibuat dari sekumpulan titiktitik yang tidak kontinyu. Beberapa jenis simbol yang dapat dipilih antara lain BOX, CROSS, CIRCLE, POINT, and DIAMOND. 8. title=string Perintah title digunakan untuk memberi judul grafik yang akan tampak di bagian atas grafik, dengan nilai string adalah judul yang ingin dituliskan dalam bentuk string. 9. thickness=n Tingkat ketebalan garis suatu grafik fungsi dapat ditentukan dengan option ini. Nilai n dapat diisi dengan bilangan antara 0 s/d 15. Semakin besar nilai n, maka semakin tebal garisnya. 10. view = [xmin..xmax, ymin..ymax] Perintah view dapat digunakan untuk mengatur koordinat-koordinat maksimum dan minimum yang ditampilkan pada grafik. Nilai-nilai xmin, xmax, ymin dan ymax diganti dengan nilai-nilai yang diinginkan. Selain option yang telah disebutkan tersebut, masih banyak option lain yang dapat digunakan. Secara lengkap, option untuk plot dapat dilihat pada bagian Lampiran 1 buku ini. Contoh: Buatlah grafik fungsi y sin( x) = pada x [0, 3π] dengan warna kurva biru, bertitel "Grafik Fungsi Sinus" dan beri nama label sumbu-x dengan "Nilai x", sumbu-y dengan "Nilai y".
25 Kalkulus dengan Maple 5 Penyelesaian: > plot(sin(x),x=0..3*pi, color=blue, title="grafik Fungsi Sinus", labels=["nilai x", "nilai y"]); Hasil dari perintah tersebut akan diperoleh suatu grafik seperti tampak pada Gambar 5-. Gambar 5-. Grafik fungsi y = sin(x) Beberapa buah grafik fungsi juga dapat digabung dalam satu bidang gambar. Biasanya hal ini digunakan untuk memudahkan perban-dingan sifat fungsi-fungsi melalui pengamatan grafik. Untuk membuat grafik yang semacam ini masih menggunakan perintah plot, akan tetapi ada sedikit perbedaan dalam sintaks. sebelumnya Berikut ini adalah sintaksnya: > plot([fungsi 1, fungsi,...], domain, option); dengan parameter domain adalah batas nilai pada domain untuk fungsi-fungsi yang akan digambar. Contoh: Buatlah grafik fungsi y = sin( x) dan y cos( x) = pada domain x = 0 s/d 3π dalam satu bidang gambar. Sertakan option yaitu untuk grafik sinus diberi warna biru, dan cosinus diberi warna hijau. Selain itu juga diberi legend untuk masing-masing fungsi.
26 6 Fungsi (pemetaan) Penyelesaian: > plot([sin(x), cos(x)],x=0..3*pi,title = "Grafik Fungsi Sinus dan Cosinus", color=[blue, green], labels=["nilai x", "nilai y"], legend = ["Grafik y=sin(x)","grafik y=cos(x)"]); dan hasilnya tampak pada Gambar 5-3. Gambar 5-3. Grafik fungsi y=sin(x) dan y=cos(x) Dengan cara yang hampir sama, dapat pula dibuat 3 atau lebih grafik fungsi pada satu bidang gambar. Sebagai catatan bahwa untuk menambahkan option grafik tidak harus diberikan dalam perintah plot. Meskipun dalam perintah plot tidak diberikan option, namun properti dari grafik tetap dapat diberikan dengan melakukan klik kanan pada grafik kemudian pilih properti yang diinginkan. Adapun tampilan menu properti dari hasil klik kanan tersebut sebagaimana tampak pada Gambar 5-4 berikut ini
27 Kalkulus dengan Maple 7 Gambar 5-4. Menu option properti grafik Grafik suatu fungsi dapat pula dibuat hanya dari beberapa titik saja (data diskrit), seperti contoh kasus berikut ini. Contoh: Diberikan nilai suatu fungsi f ( x ) untuk x tertentu seperti tersaji pada tabel berikut ini x f(x) Selanjutnya buatlah grafik dari data tersebut menggunakan Maple dengan garis terhubung. Penyelesaian: > plot([[,10],[3,1.5],[4,14],[6,15.6],[7,16],[9,18]]); dan hasilnya ditunjukkan seperti Gambar 5-5.
28 8 Fungsi (pemetaan) Gambar 5-5. Grafik fungsi dari data diskrit Secara default, Maple akan menghubungkan titik-titik data dengan suatu garis. Perintah tersebut dapat ditambahkan option style = POINT untuk mendapatkan grafik dengan titik-titik yang tidak terhubung. > plot([[,10],[3,1.5],[4,14],[6,15.6],[7,16],[9,18]], style=point); Gambar 5-6 menunjukkan output dari perintah yang telah diberikan. Gambar 5-6. Grafik fungsi dari data diskrit dengan style=point
29 Kalkulus dengan Maple 9 Grafik Fungsi 3 Dimensi Selain grafik fungsi dalam dimensi, Maple dapat pula digunakan untuk menggambar grafik fungsi 3 dimensi untuk fungsi-fungsi yang memiliki variabel. Diberikan fungsi z f ( x, y) =. Apabila grafik fungsi tersebut akan digambar menggunakan Maple, maka digunakan perintah plot3d dengansintaks perintahnya adalah: > plot3d(f(x,y), x=a..b, y=c..d); Contoh: Buatlah grafik fungsi f ( x, y) sin( x) cos( y) = pada x [0,5] dan y [-,4] Penyelesaian: > plot3d(sin(x)*cos(y), x=0..5, y=-..4); dan hasilnya tampak pada Gambar 5-7. Gambar 5-7. Grafik fungsi f(x,y) = sin(x) cos(y) Hasil grafik fungsi berbentuk 3 dimensi ini dapat diubah-ubah sudut pandangnya sesuai yang diinginkan. Caranya adalah dengan men-drag grafiknya dan digesergeser sampai pada sudut pandang yang diinginkan. Seperti halnya grafik dimensi,
30 30 Fungsi (pemetaan) properti dari grafik 3 dimensi juga dapat diubah dengan mengklik kanan hasil grafik kemudian pilih properti yang diinginkan. Untuk menampilkan nama sumbu dari grafik 3 dimensi, caranya adalah klik kanan pada grafik, kemudian pilih AXES, pilih jenis tampilan sumbu yang diinginkan (BOXED, FRAMED, atau NORMAL). Bagaimana dengan menggabungkan beberapa grafik fungsi 3 dimensi dalam satu bidang gambar? Caranya hampir sama dengan grafik fungsi dimensi. Misalkan akan dibuat grafik f(x, y) dan g(x, y) dalam satu bidang gambar dengan x [a,b] dan y [c,d], perintahnya adalah > plot3d([f(x,y),g(x,y)],x=a..b,y=c..d); Beberapa option grafik dapat ditambahkan pada perintah plot3d. Secara lengkap, option-option tersebut dapat dilihat pada bagian Lampiran. Grafik Fungsi dalam Koordinat Polar Dengan Maple juga dapat dibuat grafik dalam koordinat kutub (polar). Misalkan r t dalam sistem koordinat polar untuk domain t [a,b]. Untuk diberikan fungsi ( ) membuat grafiknya dengan Maple, perintahnya adalah: > with(plots): > polarplot(r(t),t=a..b) Perintah polarplot dapat dijalankan apabila paket (package) bernama plots telah dipanggil. Oleh karena itu sebelum menggunakan perintah polarplot, paket plots harus dipanggil terlebih dahulu dengan perintah with(plots): Contoh: Buatlah grafik fungsi r ( t) 1 sin( t) = +, untuk t [0,π] dalam koordinat polar. Penyelesaian: > with(plots); > polarplot(1+sin(t),t=0..*pi);
31 Kalkulus dengan Maple 31 Hasil dari perintah di atas akan diperoleh grafik seperti yang ditunjukkan pada Gambar 5-8. Apabila akan dibuat grafik koordinat polar lagi, maka perintah with(plots): tidak perlu dituliskan kembali. Beberapa option untuk plot dalam koordinat polat juga dapat ditambahkan. Option tersebut juga sama dengan option untuk perintah plot yang secara detail dapat dilihat pada bagian Lampiran 1. Gambar 5-8. Grafik fungsi r = 1 + sin(t) dalam koordinat polar Efek Animasi pada Grafik Grafik fungsi dimensi dalam Maple juga dapat dibuat dalam bentuk animasi. Efek animasi yang muncul memvisualisasikan proses membuat grafik melalui penggabungan titik demi titik. Perintah untuk membuat efek animasi dari suatu grafik fungsi dimensi adalah: > with(plots): > animatecurve(f, domain, option); dengan F adalah fungsi yang akan dibuat grafik animasinya, domain adalah batas nilai untuk domainnya, dan option adalah properti dari grafik yang macamnya sama dengan option pada perintah plot. Sebagai contoh, akan dibuat grafik fungsi y sin( x) animasi. Perintahnya adalah: = pada x [0,π] dengan efek
32 3 Fungsi (pemetaan) > with(plots): > animatecurve(sin(x),x=0..*pi); Setelah perintah tersebut diberikan, Maple tidak langsung menampilkan efek animasi pada grafik. Untuk menjalankan efek animasinya dengan melakukan klik kanan pada grafik, selanjutnya pilih menu animation, dan terakhir pilih play. Kecepatan efek animasi dapat diatur dengan memberikan option frames = n. Perintah option ini menunjukkan banyak frame yang akan dibuat. Secara default, nilai n pada adalah 16. Semakin besar nilai n, maka semakin lambat kecepatan efek animasinya. Sebagai gambaran, apabila ditambahkan perintah option frames dengan n = 100 pada grafik sinus maka perintahnya menjadi > animatecurve(sin(x),x=0..*pi, frames = 100); Apabila efek animasi grafik dari hasil perintah di atas dijalankan, maka akan tampak kecepatan animasi yang sedikit lebih lambat dari grafik sebelumnya. Beberapa option untuk animatecurve juga dapat diberikan. Option tersebut sama dengan option pada perintah plot yang secara detail dapat dilihat pada Lampiran 1. Fungsi Implisit Bentuk-bentuk fungsi yang dibahas sampai pokok bahasan ini dinyatakan dalam satu y = f x. Namun beberapa fungsi dapat variabel secara eksplisit dalam bentuk ( ) didefinisikan secara implisit oleh suatu kaitan antara x dan y. Sebagai contoh adalah 3 fungsi berbentuk x + y = 16 atau x + y = 4xy. Dalam beberapa kasus dimungkinkan fungsi-fungsi implisit dapat dipecah menjadi sebuah atau beberapa fungsi eksplisit. Misalnya fungsi implisit berbentuk x + y = 16 dapat dipecah menjadi buah fungsi eksplisit dalam x, yaitu y = 16 x dan y = 16 x. Apabila grafik fungsi implisit x + y = 16 digambar, maka akan diperoleh grafik berbentuk lingkaran, karena setengah lingkaran atas berasal dari grafik y = 16 x dan setengah yang bawah berasal dari y = 16 x. Grafik fungsi implisit sebenarnya dapat dibuat dengan perintah plot. Akan tetapi harus terlebih dahulu diuraikan dan dinyatakan dalam fungsi eksplisit dalam x, seperti halnya fungsi yang menghasilkan lingkaran tersebut. Tentu saja hal ini akan membutuhkan banyak waktu. Untuk memudahkan hal itu, Maple menyediakan function khusus untuk menggambar grafik fungsi-fungsi implisit. Sintaksnya adalah
33 Kalkulus dengan Maple 33 > with(plots): > implicitplot(fungsi,x=a..b,y=m..n); Perintah implicitplot juga menggunakan paket plots. Nilai-nilai a, b, m, dan n adalah paramater yang merupakan batas-batas untuk nilai x dan y untuk fungsi yang akan digambar. Contoh: Gambarlah grafik fungsi x + y = 16, pada x [-10,10] dan y [-10,10]. Penyelesaian: > with(plots): > implicitplot(x^+y^=16,x= ,y= ); Perintah ini akan menghasilkan grafik seperti pada Gambar 5-9 Gambar 5-9. Grafik x + y = 16 Pada gambar yang telah muncul, tampak bahwa nilai x dan y antara [-4,4], padahal dalam perintah dituliskan [-10,10]. Hal tersebut menggambarkan bahwa fungsi hanya terdefinisi untuk nilai x dan y pada interval [-4,4].
34 34 Fungsi (pemetaan) Contoh: Gambarlah grafik fungsi ( x y ) 5( x y ) + =, untuk x dan y [-4, 4] Penyelesaian: > with(plots): > implicitplot(*(x^+y^)^=5*(x^-y^),x=-4..4, y=-4..4); Hasil perintah ini tampak pada Gambar 5-10 Gambar Grafik ( x + y ) = 5( x y ) Tampak pada gambar bahwa untuk (0,0) tidak dilewati oleh grafik. Padahal seharusnya titik tersebut dilewati, karena untuk titik (0,0) persamaan yang diberikan akan terpenuhi. Hal ini disebabkan jumlah titik-titik pada grafik plot kurang banyak. Secara default, jumlah minimum titik yang digambar pada Maple adalah 50 buah. Sehingga, untuk memperoleh hasil grafik yang lebih baik, jumlah titik harus ditambah. Untuk mengubah jumlah titik-titik plot, digunakan option numpoints. Berikut ini perintah implicitplot yang sudah diubah jumlah titiknya menjadi > implicitplot(*(x^+y^)^=5*(x^-y^),x=-4..4, y=-4..4, numpoints=1000); dan hasilnya tampak pada Gambar 5-11.
35 Kalkulus dengan Maple 35 Gambar Grafik ( + ) = 5( ) x y x y yang diperbaiki Option numpoints juga dapat ditambahkan pada perintah plot yang telah dibahas sebelumnya. Seperti halnya perintah plot, dengan perintah implicitplot juga dapat dibuat beberapa grafik fungsi implisit dalam satu bidang gambar (koordinat). Adapun caranya sama dengan ketika digunakan perintah plot. Secara umum, option yang digunakan pada implicitplot adalah sama dengan option untuk plot (lihat Lampiran 1). Fungsi Genap dan Fungsi Ganjil Secara teori, jika fungsi f memenuhi f ( x) = f ( x) untuk setiap bilangan x di dalam domain, maka f disebut fungsi genap. Selain itu ditinjau dari sudut pandang geometri, suatu fungsi genap dapat dilihat dari grafik fungsinya yaitu simetris terhadap sumbu y. Berikut ini beberapa contoh penentuan apakah suatu fungsi termasuk fungsi genap atau bukan dengan Maple. Contoh: Diberikan fungsi f ( x) tersebut merupakan fungsi genap. = x. Dengan menggunakan Maple, tunjukkan bahwa fungsi
36 36 Fungsi (pemetaan) Penyelesaian: Langkah penyelesaiannya adalah: > f := (x) -> x^; > f(-x); Dari perintah ini akan tampak bahwa bentuk f ( x ) akan sama dengan f ( x) yaitu x. Selanjutnya akan dilihat dari sudut pandang geometri, yaitu dengan membuat grafik fungsi ( ) f x. Dengan menggunakan Maple, diperoleh grafik fungsi f ( x ) seperti pada Gambar 5-1. Dari Gambar 5-1 tampak bahwa grafik y=x simetris terhadap sumbu y. Selain fungsi genap, terdapat pula fungsi ganjil. Jika suatu fungsi f memenuhi f x = f x untuk semua x dalam domain, maka f disebut fungsi ganjil. ( ) ( ) Gambar 5-1. Grafik fungsi y = x. Seperti halnya fungsi genap, karakteristik fungsi ganjil juga dapat dilihat dari grafik. Grafik fungsi ganjil simetris dengan titik asal (0,0). Jika telah dipunyai grafik f untuk x 0, maka grafik untuk x < 0 diperoleh dengan memutar 180 o terhadap titik (0,0).
37 Kalkulus dengan Maple 37 Contoh: Diberikan fungsi f ( x) tersebut termasuk fungsi ganjil. 3 = x. Dengan menggunakan Maple tunjukkan bahwa fungsi Penyelesaian: > f := (x) -> x^3; > -f(x); > f(-x); Hasil dari perintah yang telah diberikan akan tampak bahwa f ( x) = f ( x) yaitu x 3 3, dengan demikian f ( x) = x termasuk fungsi ganjil. Sedangkan grafik fungsinya ditunjukkan pada Gambar Gambar Grafik fungsi y = x 3. Tampak bahwa grafik fungsi simetris pada titik (0,0) dengan kata lain, grafik fungsi f untuk x < 0 dapat diperoleh dengan memutar grafik f untuk x 0 sebesar 180 o. Operasi Aljabar Fungsi Operasi aljabar yang meliputi penjumlahan, pengurangan, perkalian, dan pembagian dapat diterapkan pada suatu fungsi. Misalkan diberikan fungsi f(x) dan g(x), maka dapat dituliskan operasi aljabar untuk kedua fungsi sebagai berikut: 1. ( f + g)( x) = f ( x) + g( x)
38 38 Fungsi (pemetaan). ( f g)( x) = f ( x) g( x) 3. ( f. g)( x) = f ( x). g( x) f g 4. ( x) = ( ) ( ) f x g x Sebagai ilustrasi dapat diambil contoh misalkan diberikan f ( x) g( x) = x + 1, maka operasi aljabar kedua fungsi adalah sebagai berikut: 1. ( f + g)( x) = x + x + 1 = 3x + 1. ( )( ) ( ) f g x = x x + 1 = x 1 3. ( )( ) ( ) f. g x = x x + 1 = x + x f g 4. ( x) x = x + 1 = x dan Selanjutnya misalkan diketahui dua buah fungsi, bagaimana cara menentukan operasi aljabar pada kedua fungsi tersebut menggunakan Maple? Berikut ini adalah contohnya. Contoh: Diketahui fungsi f ( x) = 5x + 8 dan g( x) kedua fungsi menggunakan Maple! = x 1. Tentukan hasil operasi aljabar Penyelesaian: Langkah pertama adalah mendefinisikan kedua fungsi dalam Maple. > f := (x) -> 5*x+8; > g := (x) -> x^ 1; Langkah selanjutnya adalah mencari operasi aljabar kedua fungsi.
39 Kalkulus dengan Maple 39 Sintaks secara umum untuk melakukan operasi aljabar dua buah fungsi adalah > (fungsi1 operator fungsi) (variabel); dengan catatan bahwa fungsi1 dan fungsi sudah didefinisikan sebelumnya. Sehingga untuk contoh yang diberikan, berikut ini adalah perintah-perintah Maple untuk mencari operasi aljabar kedua fungsi f dan g. > (f + g) (x); Maple akan memberikan hasil x +5x + 7. > (f - g) (x); Hasilnya adalah -x + 5x +9 > (f * g) (x); Diperoleh hasil (5x + 8)(x - 1). Untuk menjabarkan hasil tersebut tambahkan perintah > expand(%); Perintah di atas dituliskan setelah operasi perkalian fungsi. Perintah expand(%) digunakan untuk menjabarkan hasil perhitungan yang baru saja diperoleh. > (f /g) (x); 5x + 8 Perintah ini akan menghasilkan x 1. Contoh yang diberikan ini menjelaskan bagaimana mencari fungsi-fungsi baru sebagai hasil dari operasi aljabar dua buah fungsi. Selanjutnya bagaimana cara mengevaluasi fungsi baru tersebut pada suatu titik tertentu menggunakan Maple? Berikut ini adalah contoh yang akan membahasnya.
40 40 Fungsi (pemetaan) Contoh: 3 Diberikan fungsi f ( x) = x + 8 dan g( x) x x 9 Maple tentukan ( f g)( x) dan selanjutnya tentukan nilai ( f g)( x) = +. Dengan menggunakan untuk x =.6. Penyelesaian: > f := (x) -> -x + 8; > g := (x) -> -x^3 *x^ + 9; > (f - g) (x); Hasil ( f g)( x) diperoleh x 3 + x x - 1. Selanjutnya akan ditentukan nilai ( f g)( x) untuk x =.6 yaitu > (f - g) (.6); Perhitungan di atas akan dihasilkan Komposisi Fungsi Secara teori, komposisi dua buah fungsi f ( x ) dan g( x ) didefinisikan oleh ( f g)( x) = f ( g( x) ). Untuk mencari komposisi dari dua fungsi juga dapat menggunakan Maple. Diberikan fungsi f ( x ) dan g( x ). Selanjutnya akan dicari ( f g)( x) maka sintaks perintahnya: > g) (x); dengan Maple, dengan f ( x ) dan g( x ) telah didefinisikan terlebih dahulu. Contoh: Diketahui f ( x) = x + 1 dan g( x) x hasil komposisi ( f g)( x) dan ( g f )( x) =. Selanjutnya akan dicari fungsi baru sebagai dengan Maple.
41 Kalkulus dengan Maple 41 Penyelesaian: > f := (x) -> *x+1; > g:= (x) -> x^; > g) (x); Dari perintah ini akan diperoleh fungsi hasil komposisi ( f g)( x) adalah x -1. Dapat pula dicari ( g f )( x), yaitu dengan cara: > f) (x); yang akan menghasilkan (x+1) sebagai fungsi komposisinya. Nilai evaluasi fungsi komposisi pada x tertentu dapat juga dicari. Misalnya pada g f x pada x =, maka perintahnya: contoh tersebut, akan dicari nilai ( )( ) > f) (); dan hasilnya diperoleh 5. Bagaimana dengan komposisi dari 3 buah fungsi, katakanlah f ( x ), g( x ), dan h( x )? Pada prinsipnya sama dengan komposisi fungsi. Misalkan sebelumnya sudah didefinisikan fungsi f ( x ), g( x ), dan h ( x ) pada Maple, dan akan dicari ( f g h)( x) maka perintahnya: > h)(x); Fungsi Invers Secara teori dikatakan bahwa misalkan f ( x ) adalah fungsi satu-satu dan g( x ) adalah fungsi invers dari f ( x ), maka akan berlaku ( f g)( x) = x 1 g( x ) dapat dinotasikan dengan f ( x).. Dalam hal ini
42 4 Fungsi (pemetaan) Dalam Maple tidak ada perintah khusus untuk mencari fungsi invers. Oleh karena itu f x digunakan konsep teori tersebut yaitu dengan untuk mencari fungsi invers ( ) mencari g( x ) sebagai penyelesaian dari persamaan ( )( ) f g x = x. Contoh: Misalkan diberikan suatu fungsi f ( x) dari f ( x ) dengan Maple. 3x + = x 1. Selanjutnya akan dicari fungsi invers Penyelesaian: Langkah penyelesaiannya adalah > f := (x) -> (3*x+)/(*x-1); > finv := (x) -> g)(x) = x, g(x)); > finv(x); Perintah baris pertama untuk mendefinisikan fungsi f(x). Sedangkan perintah baris f g x = x, yang dalam hal ini mencari kedua adalah menyelesaikan persamaan ( )( ) g(x) dan selanjutnya dinyatakan dalam finv(x). Dengan demikian finv(x) merupakan fungsi invers dari f(x). Perintah ketiga adalah untuk menampilkan fungsi inversnya. Hasil dari pencarian sebelumnya diperoleh fungsi invers dari f(x) adalah 1 ( ) + x f x =. 3 + x Untuk mengecek hasil yang telah diperoleh, akan dicari nilai fungsi invers pada x tertentu dan selanjutnya nilai fungsi invers dipetakan pada f. Dari hasil pemetaan seharusnya akan diperoleh nilai x kembali. Berikut ini perintah Maple untuk melakukan hal tersebut. Sebagai contoh nilai x yang diambil adalah 1. > x := 1; > hasil := finv(x); > f(hasil); Dari perintah yang diberikan, akan terlihat bahwa nilai dari variabel hasil yang merupakan nilai invers adalah 5. Selanjutnya nilai hasil tersebut dipetakan oleh f yang sudah diperoleh sebelumnya dan dihasilkan 1 sama dengan nilai x mula-mula.
43 Kalkulus dengan Maple 43 Menggambar Grafik Fungsi Invers Dalam Maple telah tersedia perintah khusus untuk menggambar grafik fungsi invers dari suatu fungsi. Perintah ini terdapat dalam Calculus1 Student Package. Berikut ini adalah sintaks perintahnya. > with(student[calculus1]): > InversePlot(f(x),x=a..b,option); Perintah tersebut akan menampilkan grafik fungsi f(x) pada selang [a, b] dan juga fungsi inversnya. Beberapa option yang dapat diberikan pada perintah InversePlot: antara lain - showfunction = true atau false Option ini digunakan untuk menentukan tampil atau tidaknya grafik f(x). Default dari option ini adalah bernilai true (grafik f(x) ditampilkan) - showinverse = true atau false Option ini digunakan untuk menentukan tampil atau tidaknya grafik invers f(x). Default dari option ini adalah bernilai true (grafik invers f(x) ditampilkan) - showline = true atau false Apabila showline=true, maka akan tampil garis y=x berupa titik-titik pada grafik output yang merupakan pemisah antara grafik f(x) dengan inversnya. Secara default, option ini adalah true. - title = string Option ini digunakan untuk mengubah title grafik dengan suatu string tertentu. Contoh: Gambarlah grafik fungsi f(x) = sin(x) pada interval [0,π ] beserta inversnya. Penyelesaian: > with(student[calculus1]): > f := x -> sin(x); > InversePlot(f(x),x=0..*Pi,title="Grafik y=sin(x) dan inversnya");
44 44 Fungsi (pemetaan) Perintah tersebut akan menghasilkan grafik pada Gambar Gambar Grafik f(x)=sin(x) dan inversnya Pendekatan Fungsi dengan Interpolasi Dalam kehidupan sehari-hari banyak hal yang dijumpai dalam bentuk data yang bersifat diskrit. Sebagai contoh, misalnya dalam hal masalah kependudukan. Mengingat biaya dan tenaga, sangatlah tidak mungkin untuk melakukan sensus penduduk setiap tahun. Oleh karena itu sensus hanya dapat dilakukan pada kurun waktu tertentu. Misalnya pada tahun 1900 diketahui jumlah penduduk suatu daerah adalah x orang. Sepuluh tahun berikutnya (tahun 1910) diketahui jumlahnya menjadi y, dan seterusnya. Apabila data yang diperoleh bersifat diskrit (tidak kontinu) seperti contoh yang telah diberikan, maka akan terdapat permasalahan yaitu bagaimana menentukan jumlah penduduk pada tahun-tahun ketika sensus tidak diadakan. Penyelesaian dari masalah tersebut yaitu dengan melakukan pendekatan fungsi. Cara ini dilakukan dengan mengkonstruksi suatu fungsi kontinu pada selang tertentu yang mendekati titik-titik data yang diketahui. Berdasarkan fungsi kontinu yang dikonstruksi dapat diketahui nilai fungsi pada titik data yang belum diketahui. Metode inilah yang dinamakan interpolasi. Dalam teori interpolasi terdapat lebih dari satu metode yang dapat dipilih. Beberapa diantaranya adalah spline, dan polinomial. Maple mendukung metode-metode interpolasi yang terdapat dalam paket CurveFitting. Berikut adalah sintaks perintah untuk memanggil paket tersebut: > with(curvefitting):
45 Kalkulus dengan Maple 45 Selanjutnya akan dibahas setiap metode yang dapat digunakan. Dalam hal ini misalkan diketahui titik-titik data x dan y (dalam bentuk list, array atau matriks), yang masing-masing dinotasikan dengan xdata dan ydata, maka berikut ini adalah perintah penggunaan metode yang diinginkan untuk interpolasi : Spline Sintaks perintahnya adalah: > Spline(xdata, ydata, v, dgr); Dengan parameter v adalah variabel yang digunakan untuk pendekatan fungsi, sedangkan dgr adalah derajad dari polinomial fungsi pendekatan yang diinginkan. Contoh: Diketahui titik-titik data sebagai berikut: x y=f(x) Tentukan fungsi pendekatan f(x) untuk data-data tersebut menggunakan metode Spline derajad 1. Gambarkan grafik fungsi pendekatan f(x), selanjutnya tentukan perkiraan nilai f(x) untuk x = 0.5! Penyelesaian: > f:= x -> Spline([0.1,0.3,0.6,0.7,1], [.5,.7,3.6,3.9,4.],x,degree=1); > f(x); > plot(f(x),x= ); > f(0.5); Dengan menggunakan perintah Spline akan diperoleh hasil pendekatan f(x) adalah
46 46 Fungsi (pemetaan) ( ) f x x, x < x, x < x, x < x, otherwise Sedangkan plot grafik pendekatan f(x) akan diperoleh sebagai berikut (lihat Gambar 5-15) Gambar Grafik pendekatan f(x) dengan Spline derajad 1. Adapun hasil pendekatan untuk f(0.5) adalah sekitar 3.3. Polinomial Beberapa metode yang termasuk interpolasi polinomial adalah Lagrange dan selisih terbagi Newton. Berikut ini adalah sintaks perintahnya: > PolynomialInterpolation(xdata, ydata, v, option); dengan v adalah variabel untuk fungsi pendekatan dan option dapat dipilih metode interpolasi polinomialnya. Apabila diinginkan menggunakan metode Lagrange, maka optionnya adalah form = Lagrange. Sedangkan untuk metode selisih terbagi Newton optionnya adalah form = Newton. Contoh: Perhatikan data pada contoh sebelumnya (kasus Spline). Tentukan pendekatan fungsi f(x) dengan metode Lagrange. Tentukan pula nilai pendekatan untuk f(0.5).
47 Kalkulus dengan Maple 47 Penyelesaian: > f := x -> PolynomialInterpolation([0.1,0.3,0.6,0.7,1], [.5,.7,3.6,3.9,4.], x, form=lagrange); > f(x); > f(0.5); Perintah tersebut akan menampilkan polinomial pendekatan f(x) yaitu ( ) ( 0.3)( 0.6)( 0.7)( 1) ( x 0.1)( x 0.6)( x 0.7)( x 1) ( x 0.1)( x 0.3)( x 0.7)( x 1) ( x 0.1)( x 0.3)( x 0.6)( x 1) ( x 0.1)( x 0.3)( x 0.6)( x 0.7) f x x x x x sedangkan nilai pendekatan untuk f(0.5) adalah Soal-soal latihan 1. Definisikan fungsi di bawah ini dan tentukan nilai fungsinya untuk nilai x atau y yang telah diketahui a. f ( x) 3 b. ( ) = x, untuk x = -10 f x x x c. f ( x) 6 = + 1, untuk x = 5 = x, untuk x =.5 d. g( x) = x + x 3 3x 1, untuk x = /3 1, x 1 g x = 3x +, 1 < x < 1, untuk x = 3 7 x, x 1 e. ( ) Petunjuk: Gunakan perintah berikut untuk mendefinisikan fungsinya piecewise(x<=-1,-1,x>=1,7-*x,3x+); sin( x) f. g( x) e cos( x 1) = +, untuk x = 3π
48 48 Fungsi (pemetaan), log ln x =, untuk x = 5 dan y =3 y g. f ( x y) ( x) h. f ( x, y) = x + y xy ( x + y) cos, untuk x = -3 dan y = 5. Sebuah batu dilemparkan ke dalam kolam dan menciptakan suatu riak melingkar yang bergerak ke arah luar pada kecepatan 60 cm/dt. Definisikan jari-jari r dari lingkaran ini sebagai fungsi dari waktu t (dalam detik) dengan Maple. Selanjutnya tentukan berapa jari-jari lingkaran riak tersebut (dalam cm) setelah 10 detik batu dilemparkan? 3. Di negara tertentu, pajak penghasilan dipungut dengan ketentuan sebagai berikut. Bebas pajak sampai penghasilan sebesar $ Pajak sebesar 10% dikenakan pada penghasilan yang berkisar $ s/d $ Sedangkan Pajak 15% dikenakan pada penghasilan lebih dari $ Definisikan fungsi besar pajak tersebut dengan menggunakan Maple, kemudian tentukan berapa besar pajak yang dipungut dari penghasilan sebesar $14.000? dan $6.000? 4. Gambarkan grafik fungsi-fungsi berikut ini a. y = x 5, pada x [5, 0] b. y = x + x, pada x [-10, 10] c. x y = + 5x + 6, pada x [-5, 3/4] x + d. y cos( x 5) sin( x ) e. = + +, pada x [0, 5π] x +, x > =,, pada x [-5, 5.5] 1, x y x x f. r ( t) t sin( t) = +, pada t [0, π] (sajikan dalam koordinat polar) g. r ( t) 1 cos( t) sin ( t) =, pada t [0, 4π] (sajikan dalam koordinat polar) h. f ( x) = x + 3x 5 dan g( x) ln( x) 10] x i. f ( x) = cos dan g( x) 1 sin( x) π, π]. = pada satu bidang gambar untuk x [, = + pada satu bidang gambar untuk x [-
49 Kalkulus dengan Maple 49 j. f ( x, y) sin ( x y) cos( x) k. ( ) = +, pada x [0, 3π] dan y [0, π] f x, y = x + y + 3xy, pada x [-3/5, 5] dan y [-3/5, 5] l. f ( x, y) x + y = x + x y + 3xy + y 3 3, pada x [1, 7/3] dan y [1, 7/3] 5. Gambarkan grafik fungsi ( ) 4 f x x cx x bagaimana grafik berubah pada waktu c berubah. 6. Gambarkan grafik fungsi f ( x) bagaimana pengaruh perubahan nilai c pada grafik! = + + untuk beberapa nilai c. Amatilah = 1 + cx untuk beberapa nilai c. Jelaskan x 7. Grafik dengan persamaan y = disebut kurva hidung peluru. Gambarkan c x grafik dari persamaan tersebut untuk beberapa nilai c. Amatilah mengapa grafik yang muncul dinamakan kurva hidung peluru? Apa yang terjadi pada grafik apabila nilai c bertambah besar? 8. Dalam soal ini akan ditinjau fungsi dalam bentuk f ( x) 1/ x n bilangan positif. a. Gambarkan grafik fungsi y = 1/ x dan y =, dengan n 3 = 1/ x pada bidang yang sama, dengan batas grafik untuk x dan y masing-masing adalah [-3,3] dan [-3,3]. b. Gambarkan grafik fungsi y = 1/ x dan y 4 = 1/ x pada bidang yang sama, dengan batas grafik untuk x dan y masing-masing adalah [-3,3] dan [-3,3]. c. Gambarkan semua grafik pada (a) dan (b) pada satu bidang yang sama, dengan batas grafik x dan y masing-masing [-1,3] dan [-1,3]. d. Apa kesimpulan yang dapat diambil dari grafik-grafik tersebut? 9. Jarak yang ditempuh sebuah mobil diberikan seperti pada tabel t (detik) d (meter) a. Gunakan data yang telah diberikan untuk mensketsakan grafik fungsi d ( t ) b. Berdasarkan garfik dari (a), kira-kira berapa jarak yang sudah ditempuh mobil setelah 5.5 detik?
50 50 Fungsi (pemetaan) 10. Carilah f + g, f g, f. g, dan f / g dari fungsi-fungsi berikut ini 3 a. f ( x) = x + x dan g( x) b. f ( x) = 1 + x dan g( x) 1 = 3x 1 = x 11. Tentukan f g, g f, g g dan f f dari fungsi-fungsi berikut ini c. f ( x) = x 1, g( x) d. f ( x) = 1/ x, ( ) 1 x 1 e. f ( x) =, g ( x ) = x 3 g x x x = + = x 1 x + 1 f. f ( x) = sin ( x), g( x) 1 = x g. f ( x) = x 1, g( x) 1 = x 1. Dengan menggunakan operasi fungsi dan grafik, tentukan apakah fungsi-fungsi di bawah ini termasuk fungsi genap atau ganjil ataukah bukan keduanya. a. f ( x) b. f ( x) c. ( ) = x = x 3 f x = x + x d. ( ) g x = x 4x e. ( ) 4 3 g x = x x f. ( ) g x = x + x g. g( x) = cos( x) h. h( x) = 1 + sin( x) i. h( x) = cos( x ) 13. Tentukan fungsi invers dan gambarlah grafik fungsi invers tersebut dari fungsifungsi berikut ini a. f ( x) = 4x + 7
51 Kalkulus dengan Maple 51 b. f ( x) c. f ( x) d. g( x) = x x x = 5 x = 5 4x e. g( x) = + 5 f. h( x) 1 + e = 1 e x x 3 x g. h( x) = ln ( x + 4) h. ( ) h x = 10 x 14. Rumus C = 5 ( F 3) menyatakan suhu Celcius (C) sebagai fungsi dari suhu 9 Fahrenheit (F). Tentukan rumus untuk fungsi invers dari C, dan berikan interpretasinya! 15. Jika suatu populasi bakteri pada awalnya 100 buah dan menjadi berlipat ganda setiap 3 jam, maka banyaknya bakteri setelah t jam dirumuskan dengan f t = 100. t /3 ( ) a. Tentukan invers fungsi f ( t ) dan jelaskan artinya! b. Kapan populasi akan mencapai ?
52 5 Limit Fungsi Bab 4 Limit Fungsi Istilah limit dalam bahasa Inggris berarti mendekati. Sesuai dengan kata mendekati, jika dikatakan bahwa x mendekati artinya nilai x hanya mendekati nilai, tapi tidak pernah bernilai. Misalkan f adalah suatu fungsi dalam x dan L adalah bilangan real ( ) lim f x = L x a diartikan untuk x mendekati a, nilai f ( x ) mendekati L. Suatu fungsi dikatakan mempunyai limit di titik x=a jika limit dari kiri maupun dari f x untuk x yang kanan x=a bernilai sama. Limit dari kiri maksudnya adalah nilai ( ) mendekati a dari kiri (x<a). Limit dari kanan maksudnya adalah nilai f ( x ) untuk x yang mendekati a dari kanan (x>a). Untuk mempermudah penulisan, nilai x mendekati a dari kiri dituliskan x a - dan nilai x mendekati a dari kanan dituliskan x a +. Dengan demikian secara intuitif, nilai limit fungsi f ( x ) dapat dicari dengan mencari nilai fungsi tersebut di titik-titik sekitar x=a baik dari kiri maupun dari kanan. Sehingga konsep ini dapat dituliskan sebagai berikut: Jika lim f ( x) = L dan lim f ( x) = L, maka lim ( ) x a + x a f x = L x a Pada contoh berikut ini akan dijelaskan bagaimana mencari nilai limit fungsi secara intuitif menggunakan Maple. Contoh: Dengan menentukan nilai x+3 untuk x disekitar, tentukan lim( x 3) x +.
53 Kalkulus dengan Maple 53 Penyelesaian: Untuk menentukan limit fungsi dari soal yang diberikan, maka terlebih dahulu dipilih titik-titik secara sebarang di sekitar x = baik dari kiri maupun dari kanan. Berikut ini titik-titik x yang dipilih: x = 1.9, 1.95, 1.96, 1.99, 1.995, (dari kiri atau x < ) x =.10,.09,.05,.01,.005,.001 (dari kanan atau x > ) Dengan menggunakan Maple, selanjutnya akan dicari nilai x+3 untuk setiap titik tersebut. > f := (x) -> *x+3; > x1 := Array([1.90, 1.95, 1.96, 1.99, 1.995, 1.999]): > x := Array([.10,.09,.05,.01,.005,.001]): > n1 := ArrayNumElems(x1): > n := ArrayNumElems(x): > y1 := Array(1..n1): > y := Array(1..n): > for i from 1 to n1 do y1[i] := evalf(f(x1[i])): end do: > for i from 1 to n do y[i] := evalf(f(x[i])): end do: > y1; > y; Keterangan: Perintah pada baris kedua dan ketiga digunakan untuk mendefinisikan x1 sebagai titik-titik di sebelah kiri dan x sebagai titik-titik di sebelah kanan. Baris keempat dan kelima digunakan untuk menghitung jumlah titik data dari x1 dan x. Selanjutnya pada baris keenam dan ketujuh digunakan untuk mendefinisikan y1 dan y yang masing-masing nantinya akan digunakan untuk menyimpan nilai fungsi untuk x1 dan x. Sedangkan proses perhitungan nilai fungsi untuk setiap x1 dan x dilakukan pada baris kedelapan dan kesembilan. Dua baris terakhir menampilkan hasil y1 dan y. Dari perhitungan diperoleh y1 = [6.80, 6.90, 6.9, 6.98, 6.990, 6.998] dan y = [7.0, 7.18, 7.10, 7.0, 7.01, 7.00] atau jika hasil tersebut disajikan dalam bentuk tabel maka diperoleh
54 54 Limit Fungsi x f(x) dan x f(x) Tampak dari hasil yang diperoleh bahwa untuk x mendekati dari kiri diperoleh nilai f x semakin mendekati 7 begitu pula dari kanan. Dengan demikian ( ) ( x ) lim + 3 = 7. x Contoh: x x Diberikan fungsi f ( x) =. Tentukan lim f ( x) x 0. Penyelesaian: Untuk menyelesaikan limit fungsi tersebut, dapat dipilih nilai x sebagai berikut x = -, -1.95, -1.5, -1, -0.5, -0.1, -0.05, -0.01, , (untuk x < 0) dan x =, 1.7, 1.5, 1, 0.5, 0.1, 0.05, 0.01, 0.005, (untuk x > 0) Selanjutnya akan dicari nilai f(x) untuk semua x. > f := (x) -> (sqrt(x^+5)-3)/x^; > x1 := Array([-, -1.95, -1.5, -1, -0.5, -0.1, -0.05, -0.01, , ]):
55 Kalkulus dengan Maple 55 > x := Array([, 1.7, 1.5, 1, 0.5, 0.1, 0.05, 0.01, 0.005, 0.001]): > n1 := ArrayNumElems(x1): > n := ArrayNumElems(x): > y1 := Array(1..n1): > y := Array(1..n): > for i from 1 to n1 do y1[i] := evalf(f(x1[i])): end do: > for i from 1 to n do y[i] := evalf(f(x[i])): end do: > y1; > y; Dari perintah-perintah tersebut akan diperoleh nilai y1 dan y yang semakin lim f x = mendekati sekitar Dengan demikian ( ) x 0 Contoh: Diberikan fungsi ( ) f x x 1, x > 0 =. x, x 0 Selanjutnya akan ditentukan nilai limit f ( x ) untuk x mendekati 0. Penyelesaian: Dapat dipilih nilai-nilai x dari yang mendekati 0 dari kiri maupun kanan sebagai berikut: x = -, -1.5, -1, -0.5, -0.1, -0.05, -0.01, , , (untuk x < 0) x = 1, 0.5, 0.1, 0.05, 0.01, 0.005, 0.001, , (untuk x > 0) Perintah Maple untuk mencari nilai f ( x ) pada titik-titik tersebut adalah > f := (x) -> piecewise(x>0,*x-1, x<=0, -x); > x1 := Array([-, -1.5, -1, -0.5, -0.1, -0.05, -0.01, , , ]): > x := Array([1, 0.5, 0.1, 0.05, 0.01, 0.005, 0.001, , ]): > n1 := ArrayNumElems(x1): > n := ArrayNumElems(x):
56 56 Limit Fungsi > y1 := Array(1..n1): > y := Array(1..n): > for i from 1 to n1 do y1[i] := evalf(f(x1[i])): end do: > for i from 1 to n do y[i] := evalf(f(x[i])): end do: > y1; > y; Dari hasil perhitungan akan tampak bahwa untuk nilai y1 (nilai fungsi untuk titik-titik x yang mendekati 0 dari kiri) semakin mendekati 0 (hasil perhitungan tidak disajikan di sini), sedangkan y (nilai fungsi untuk titik-titik x yang mendekati 0 dari kanan) f x tidak memiliki limit di x = 0 semakin mendekati 1. Dengan demikian fungsi ( ) karena limit kiri dan kanan dari 0 tidak sama. Perhitungan Limit Dengan Function Cara perhitungan limit fungsi yang telah diberikan menggunakan konsep dasar limit yaitu dengan melihat langsung nilai fungsi di titik-titik persekitaran. Meskipun demikian Maple juga menyediakan function khusus untuk mencari limit secara cepat. Sintaks perintah Maple untuk mencari lim ( ) x a f x adalah sebagai berikut: > limit(f(x), x=a, dir ); dengan f(x) adalah fungsi yang telah didefinisikan sebelumnya, a adalah titik yang akan dicari limit fungsinya, sedangkan dir dapat diganti dengan left atau right yang masing-masing menunjukkan arah limit dari kiri atau kanan. Penggunaan dir adalah optional. Apabila dir tidak diberikan, maka Maple akan langsung mencari nilai limit fungsi. Berikut ini akan diberikan beberapa contoh penggunaan function tersebut untuk menentukan limit fungsi. Contoh: Tentukan lim( x 1) x 1. Penyelesaian: > f := (x) -> x^-1;
57 Kalkulus dengan Maple 57 > limit(f(x),x=1,left); > limit(f(x),x=1,right); Perintah kedua untuk mencari limit f ( x ) untuk x 1 -. Sedangkan yang ketiga untuk untuk mencari limit f ( x ) untuk x 1 +. Dari kedua arah limit, akan diperoleh hasil limit yang sama yaitu 0. Dengan demikian limit f ( x ) untuk x 1 adalah 0. Selanjutnya akan ditunjukkan bahwa nilai limit sebenarnya dari f ( x ) untuk x 1 (tanpa mencari nilai limit dari kiri maupun kanan) dengan Maple adalah juga 0. > limit(f(x),x=1); Hasil perintah tersebut akan menunjukkan 0. Dengan demikian akan diperoleh hasil limit yang sama apabila digunakan konsep limit kiri dan kanan. Contoh: Tinjau kembali limit fungsi ( ) f x x 1, x > 0 = x, x 0 untuk x mendekati 0 pada contoh sebelumnya. Dengan menggunakan perintah limit pada Maple, tunjukkan bahwa nilai limit fungsinya tidak ada. Penyelesaian: > f := (x) -> piecewise(x>0,*x-1, x<=0, -x); > limit(f(x),x=0); Perintah tersebut memberikan hasil undefined yang berarti nilai limitnya tidak ada atau tidak terdefinisi. Hasil yang sama juga akan diperoleh apabila digunakan konsep limit kiri dan kanan. > limit(f(x),x=0,left); > limit(f(x),x=0,right);
58 58 Limit Fungsi Dari hasil tersebut akan tampak bahwa limit kiri adalah 0 dan limit kanan adalah 1. Dengan demikian benar bahwa limit fungsi f ( x ) untuk x 0 tidak ada karena limit kiri dan kanan tidak sama. Contoh: 3 x + x 1 Tentukan lim. x 3 x + 4 Penyelesaian: > f := (x) -> (*x^3+*x^-1)/(x^3+4); > limit(f(x),x=infinity); Perintah infinity pada perintah di atas bermakna tak hingga. Dari perhitungan tersebut akan diperoleh nilai limit adalah. Calculus1 Student Package untuk Limit Dalam Maple terdapat suatu paket untuk komputasi kalkulus yang bernama Calculus1 Student Package. Paket ini membantu siswa dan pengajar untuk mempelajari konsep-konsep dasar Kalkulus yang salah satunya adalah tentang limit. Pemakai paket ini dapat belajar bagaimana mencari limit suatu fungsi secara langkahperlangkah menggunakan aturan-aturan limit yang berlaku. Untuk menggunakan paket ini, terlebih dahulu harus diberikan perintah berikut ini guna aktifasi. > with(student:-calculus1): > infolevel[student] := 1: Dalam menyelesaikan dan mencari nilai limit, terlebih dahulu harus mengetahui beberapa aturan limit sebagaimana terdapat pada Tabel 6-1:
59 Kalkulus dengan Maple 59 Nama Aturan Notasi Deskripsi constant constantmultiple difference identity power product quotient `c*` `-` `^` `^` `*` `/` limc = c x a ( ) = lim ( ) limcf x c f x x a x a ( ) ( ) = ( ) ( ) lim f x g x lim f x lim g x x a x a x a lim x = a x a lim f x ( ) n ( ) lim f ( x) x a x a lim f x n =, n bilangan real ( ) g ( ) ( x ) = lim f ( x) x a x a lim g ( x ) x a ( ) ( ) = ( ) ( ) lim f x g x lim f x lim g x x a x a x a ( ) ( ) f x lim x a g x ( ) lim f x x a = lim g x x a ( ) sum `+` lim f ( x) + g( x) = lim f ( x) + lim g( x) x a x a x a Tabel 6-1. Aturan dalam pencarian limit Sintaks secara umum untuk penyelesaian limit menggunakan Maple dengan calculus student package adalah > Rule[nama aturan](ekspresi); Untuk nama aturan pada sintaks dapat dipilih dari tabel tersebut (kolom pertamapaling kiri), dan nama aturan dapat diganti dengan notasi yang terkait (kolom kedua). Apabila fungsi dalam bentuk transenden seperti halnya telah dijelaskan di Bab, maka nama aturan dapat diganti dengan perintah yang terkait dengan bentuk/nama fungsinya (lihat Tabel 6-).
60 60 Limit Fungsi Nama Aturan Deskripsi sin lim sin( x) = sin( lim x) x c x c cos lim cos( x) = cos( lim x) x c x c tan lim tan ( x) = tan( lim x) x c x c csc lim csc( x) = csc( lim x) x c x c sec lim sec( x) = sec( lim x) x c x c cot lim cot( x) = cot( lim x) x c x c sinh lim sinh ( x) = sinh ( lim x) x c x c cosh lim cosh ( x) = cosh( lim x) x c x c tanh lim tanh ( x) = tanh( lim x) x c x c csch lim csch ( x) = csch ( lim x) x c x c sech lim sech ( x) = sech ( lim x) x c x c coth lim coth ( x) = coth ( lim x) exp x c x c lim x c lim e x = e x x c ln lim ln( x) = ln( lim x) x c x c Tabel 6-. Aturan limit terkait untuk fungsi transenden Contoh: Dengan menggunakan Calculus student package, tentukan lim( 4 x 3x ) x 1 +.
61 Kalkulus dengan Maple 61 Penyelesaian: > with(student:-calculus1): > infolevel[student] := 1: > f := (x) -> 4+x-3*x^; Langkah pertama dalam menyelesaikan limit tersebut dapat diterapkan dengan aturan penjumlahan (sum) > Rule[sum](Limit(f(x), x=1)); atau > Rule[`+`](Limit(f(x), x=1)); Dengan diterapkannya aturan penjumlahan ini maka Maple akan menampilkan ( + x x ) = + x + ( x ) lim 4 3 lim 4 lim lim 3 x 1 x 1 x 1 x 1 Perhatikan, bahwa penulisan huruf L pada perintah limit di atas menggunakan huruf besar. Langkah kedua, dari ruas kanan persamaan terakhir yang dihasilkan dapat diterapkan aturan constant. > Rule[constant](%); hasil perintah tersebut adalah ( + x x ) = + x + ( x ) lim lim lim 3 x 1 x 1 x 1 Tanda % pada perintah yang dituliskan digunakan untuk memproses hasil perhitungan terakhir sebelumnya. Langkah ketiga dapat digunakan aturan identity > Rule[identity](%); Hasilnya diperoleh
62 6 Limit Fungsi ( + x x ) = + ( x ) lim lim 3 x 1 x 1 Langkah keempat digunakan aturan constantmultiple > Rule[constantmultiple](%); dan diperoleh ( ) lim 4 + x 3x = 5 3lim x x 1 x 1 Langkah kelima digunakan aturan power (pangkat) > Rule[power](%); dan diperoleh ( + x x ) = ( x) lim lim x 1 x 1 Terakhir, langkah keenam adalah kembali digunakan aturan identity > Rule[identity](%); dan akhirnya diperoleh hasil. Dengan demikian ( x x ) lim =. Urutan tahap-tahap penyelesaian untuk mencari nilai limit pada kasus ini tidak harus sama seperti tersebut dan demikian pula untuk kasus-kasus yang lain. Urutan langkah penyelesaian tergantung proses cara berpikir pemakai untuk menyelesaikannya. Apabila pemilihan aturan tidak tepat, maka Maple akan memberitahukan pemakai dengan pernyataan Rule[nama aturan] does not apply. Selain aturan-aturan yang telah digunakan sebelumnya, dapat pula dipilih aturan L- Hopital. Aturan ini dapat digunakan untuk mencari lim f ( x )/ g ( x ) dengan x a f x / g x = / untuk x=a. ketentuan bahwa ( )/ ( ) 0/0 Dengan aturan L-Hopital berlaku x 1 f x g x = atau ( ) ( )
63 Kalkulus dengan Maple 63 ( ) ( ) ( ) ( ) f x f ' x lim = lim x a g x x a g ' x Apabila f '( x) / g' ( x) masih berbentuk 0/0 atau / untuk x = a, maka f '( ) g'( x ) akan diturunkan lagi, dan begitu seterusnya. Adapun perintah Maple untuk menggunakan aturan L-Hopital adalah x dan > Rule[lhopital,f(x)](ekspresi); Contoh: x Tentukan lim x 3 + x 1. x 3 Penyelesaian: Perhatikan bahwa bentuk fungsi yang akan dicari limitnya berbentuk 0/0 untuk x=3, sehingga dapat diterapkan aturan L-Hopital. Perintah Maplenya adalah > with(student:-calculus1): > infolevel[student] := 1: > f := (x) -> x^+x-1; > g := (x) -> x-3; > Rule[lhopital,f(x)](Limit(f(x)/g(x),x=3)); Dengan penerapan aturan L-Hopital diperoleh hasil x + x 1 lim = lim x + 1 x 3 x 3 x 3 Selanjutnya dapat diterapkan aturan sum (penjumlahan) > Rule[sum](%); dan diperoleh x + x 1 lim = lim x + lim 1 x 3 x 3 x 3 x 3
64 64 Limit Fungsi Aturan berikutnya yang dapat dipilih adalah constantmultiple, kemudian identity dan terakhir constant. > Rule[constantmultiple](%); > Rule[identity](%); > Rule[constant](%); Dari perintah terakhir tersebut dapat diketahui bahwa nilai x + x 1 lim = 7 x 3 x 3 Contoh: Tentukan lim e x 3 x sin x. cos x Penyelesaian: > with(student:-calculus1): > infolevel[student] := 1: > f := (x) -> exp(*x)*sin(x)/cos(*x); Langkah pertama dapat dilakukan aturan product > Rule[product](Limit(f(x),x=3)); sehingga diperoleh x ( )( ) sin x 1 = cosx cosx x lim e lim e lim sin x lim x 3 x 3 x 3 x 3 Selanjutnya hasil tersebut dapat dikenakan operasi eksponensial (exp). > Rule[exp](%);
65 Kalkulus dengan Maple 65 ( ) sin x 1 = cosx cosx x lim x x 3 lim e e lim sin x lim x 3 x 3 x 3 > Rule[constantmultiple](%) ( ) sin x 1 = cosx cosx x lim x x 3 lim e e lim sin x lim x 3 x 3 x 3 > Rule[identity](%); ( ) sin x 1 = cosx cosx x lim e 6 e lim sin x lim x 3 x 3 x 3 Hasil tersebut dapat dikenakan aturan sinus (sin). > Rule[sin](%); dan diperoleh sin x 1 = ( ) cosx cosx x lim e 6 e sin 3 lim x 3 x 3 > Rule[quotient](%); sin x lim e = e sin 3 x 3 cosx ( ) lim 1 lim cosx x 3 x 6 x 3 > Rule[constant](%); sin x ( sin 3) 6 x lim e = x 3 cos x lim cos x 3 e x Selanjutnya hasil tersebut dapat dikenakan aturan cosinus (cos). > Rule[cos](%); sin x ( sin 3) 6 x lim e = x 3 cos x cos lim x 3 e ( x)
66 66 Limit Fungsi > Rule[constantmultiple](%); sin x ( sin 3) 6 x lim e = x 3 cos x cos lim x 3 e ( x) > Rule[identity](%); 6 x sin x e sin 3 lim e = x 3 cos x cos6 Dengan demikian nilai limitnya adalah e 6 sin 3. cos6 Kekontinuan Suatu fungsi f dikatakan kontinu pada x=a apabila memenuhi ketiga syarat berikut ini 1. f ( x) terdefinisi di x = a. lim ( ) x a f x ada 3. lim ( ) = ( ) f x f a x a Hal tersebut mengatakan bahwa f kontinu di a jika f(x) mendekati f(a) ketika x mendekati a. Dengan demikian, sebuah fungsi kontinu f mempunyai sifat bahwa perubahan kecil pada x hanya menghasilkan perubahan kecil dari f(x). Beberapa kejadian dalam kehidupan sehari-hari yang dapat dikaitkan dengan kekontinuan misalnya perpindahan atau kecepatan mesin yang bervariasi secara kontinu seiring dengan waktu. Sedangkan secara geometri, sebuah fungsi yang kontinu dapat dibayangkan ketika menggambar grafik yang tidak putus/tanpa mengangkat pena. Selanjutnya akan diberikan contoh bagaimana menguji kekontinuan fungsi pada suatu titik menggunakan Maple. Contoh:. Diberikan fungsi ( ) f x x x =. x
67 Kalkulus dengan Maple 67 Dengan menggunakan Maple selidikah apakah f(x) kontinu pada x=1. Penyelesaian: > f := (x) -> (x^-x-)/(x-); > f(1); Dari perhitungan tersebut diperoleh nilai f(1) =. Selanjutnya akan dicari lim f ( x) x 1. > limit(f(x),x=1); Maple akan memberikan hasil limitnya adalah. Dengan demikian lim f ( x) f ( 1) sehingga dapat dikatakan f(x) kontinu pada x=1. x 1 =, Contoh: Diberikan fungsi yang sama seperti pada contoh sebelumnya, selidikah apakah f(x) kontinu pada x = atau tidak. Penyelesaian: > f := (x) -> (x^-x-)/(x-); > f(); Dari hasil perhitungan akan tampak bahwa f() tidak terdefinisi. Apabila dicari nilai lim f x, maka akan diperoleh hasil 3. Meskipun nilai limitnya ada, akan tetapi x ( ) syarat pertama untuk kekontinuan tidak terpenuhi. Dengan demikian dapat dikatakan bahwa f(x) tidak kontinu pada x=1
68 68 Limit Fungsi Contoh: Diberikan fungsi ( ) f x x x, x = x. 1, x = Tentukan apakah fungsi tersebut kontinu pada x=. Penyelesaian: > f := (x) -> piecewise(x=,1,(x^-x-)/(x-)); > f(); > limit(f(x),x=); Berdasarkan perintah tersebut, akan diperoleh nilai f() = 1 dan limitnya adalah 3. Meskipun f() dan limitnya terdefinisi, akan tetapi syarat ketiga untuk kekontinuan lim f x f. Dengan demikian f(x) tidak kontinu di x=. tidak terpenuhi atau ( ) ( ) x Contoh-contoh yang telah diberikan menjelaskan bagaimana mengetahui kekontinuan suatu fungsi pada titik tertentu. Selain itu kekontinuan suatu fungsi pada selang/interval tertentu juga dapat diketahui dengan Maple. Sintaks untuk mengetahui kekontinuan suatu fungsi pada selang/interval tertentu dengan Maple adalah > iscont(f(x),x=a..b,option); dengan nilai a dan b adalah batas interval, sedangkan option dapat diisi closed maupun open. Misalkan nilai a=1 dan nilai b=3 serta option yang dipilih adalah closed, maka perintah ini digunakan untuk mengetahui kekontinuan f(x) pada selang tertutup [1,3]. Sedangkan apabila option dipilih open, maka intervalnya terbuka [1,3). Option tidak harus disertakan. Akan tetapi apabila option tidak disertakan, maka dianggap sebagai selang terbuka [a,b). Perintah iscont akan menghasilkan pernyataan true atau false. Apabila hasilnya true, maka f(x) kontinu pada interval. Sedangkan apabila false, maka f(x) tidak kontinu.
69 Kalkulus dengan Maple 69 Contoh: Diketahui fungsi ( ) f x Tentukan kekontinuan f(x) pada selang [0,4]. x x, x = x. 1, x = Penyelesaian: Pada contoh sebelumnya telah dibahas bahwa f(x) tidak kontinu pada x=. Karena x= termasuk dalam selang [0,4], maka f(x) tidak kontinu pada selang tersebut. Hal ini akan kembali ditunjukkan dengan menggunakan perintah iscont. > f := (x) -> piecewise(x=,1,(x^-x-)/(x-)); > iscont(f(x),x=1..4, closed ); Perintah iscont akan menghasilkan false yang berarti bahwa f(x) tidak kontinu pada [1,4]. Dalam Maple juga terdapat function untuk mencari titik-titik dimana f(x) tidak kontinu untuk semua x bilangan real. Sintaksnya adalah > discont(f(x),x); Output/hasil dari perintah discont berupa himpunan titik-titik x dimana f(x) tidak kontinu. Contoh: Tentukan titik-titik x dimana fungsi f ( x) 1/ ( x ) = tidak kontinu.
70 70 Limit Fungsi Penyelesaian: > f := (x) -> 1/(x-); > discont(f(x),x); dari perintah tersebut akan dihasilkan {}, yang artinya f(x) tidak kontinu untuk x=. Contoh: Tentukan titik-titik x dimana fungsi f ( x) tan( x) = tidak kontinu. Penyelesaian: > f := (x) -> tan(x); > discont(f(x),x); Hasil perintah yang telah diberikan akan menghasilkan 1 { π _ Z1 + π }. Perhatikan bahwa pada hasil yang telah diperoleh terdapat notasi _Z1~. Makna dari _Zn~ secara umum (n=1,, 3,...) adalah bahwa notasi tersebut dapat diganti untuk semua bilangan bulat. Sehingga f(x) tidak kontinu pada titik-titik {, 3 π + 1 π, π + 1 π, π + 1 π, 1 π, π + 1 π, π + 1 π, } Selain notasi _Zn~, kadang-kadang dalam Maple juga muncul notasi yang lain seperti _NNn~ dan _Bn~. Notasi _NNn~ bermakna bahwa notasi ini dapat diganti dengan bilangan bulat non negatif, sedangkan _Bn~ dapat diganti dengan bilangan biner 0 atau 1. Aplikasi Limit Pada pokok bahasan ini akan diuraikan pengaplikasian limit pada beberapa masalah perhitungan.
71 Kalkulus dengan Maple 71 Masalah Garis Singgung Limit dapat diaplikasikan untuk mencari gradien/kemiringan garis singgung suatu grafik fungsi di titik tertentu. Gradien garis singgung (m) dari suatu fungsi f(x) pada titik P(a, f(a)) dirumuskan ( ) ( ) f x f a m = lim x a x a ( ) ( ) f a + h f a atau m = lim h 0 h Contoh: Diketahui fungsi f(x) = 4/x. Tentukan gradien garis singgung grafik fungsi tersebut di titik (4,1). Penyelesaian: Dengan menggunakan konsep limit yang digunakan untuk mencari gradien garis singgung, maka perintah Maple nya: > f := (x) -> 4/x; > limit((f(x)-f(4))/(x-4),x=4); atau > limit((f(4+h)-f(4))/h,h=0); Dari perhitungan limit tersebut akan diperoleh 1/4. Dengan demikian gradien garis singgung grafik fungsi f(x) di titik (4,1) adalah 1/4. Contoh: Diketahui fungsi f(x) = ( x 3 )/( x 1). Tentukan gradien garis singgung grafik fungsi tersebut di titik ( 1, 5 ).
72 7 Limit Fungsi Penyelesaian: > f := (x) -> sqrt((x-3)/(x-1)); > limit((f(x)-f(1/))/(x-1/),x=1/); atau > limit((f(1/+h)-f(1/))/h,h=0); Kedua perhitungan limit ini akan menghasilkan 4 5 /5. Sehingga gradien garis singgung grafik fungsi f(x) di titik ( 1/, 5 ) adalah 4 5 /5. Selanjutnya untuk memberikan visualisasi grafik fungsi f(x) dan garis singgungnya, perintah yang telah diberikan dapat dimodifikasi kembali. Sebelum membuat grafik garis singgungnya, terlebih dahulu harus diketahui persamaan garis singgungnya. Persamaan garis singgung fungsi f(x) di titik (a, b) dirumuskan y b = m (x - a) atau y = m (x - a) + b, dengan m adalah gradien persamaan garis singgungnya. Sehingga perintah untuk membuat grafik fungsi f(x) dan garis singgungnya di titik ( 1/, 5 ) adalah: > f := (x) -> sqrt((x-3)/(x-1)); > m := limit((f(x)-f(1/))/(x-1/),x=1/); > plot([f(x),m*(x-1/)+sqrt(5)],x=-3..5,color=[red,blue], legend=["grafik f(x)", "Grafik persamaan garis singgung"]); Perintah ini akan menghasilkan output seperti yang tampak pada Gambar 6-1
73 Kalkulus dengan Maple 73 Gambar 6-1. Grafik f ( x) ( x 3 )/( x 1) = dan garis singgungnya Dalam Maple juga tersedia perintah khusus yang dapat digunakan untuk menggambar grafik persamaan garis yang menyinggung grafik f(x) di titik tertentu secara cepat. Perintah ini termasuk dalam paket Calculus1 Student Package. Sintaks perintahnya: > with(student[calculus1]): > Tangent(fungsi, titik singgung,output = plot); Berikut ini adalah contoh penggunaan perintah untuk menggambar garis yang menyinggung f(x) = sin(x)+1 di titik x=1. > with(student[calculus1]): > f := (x) -> sin(x)+1; > Tangent(f(x), x=1,output = plot); Perintah tersebut menghasilkan grafik yang tampak pada Gambar 6- berikut
74 74 Limit Fungsi Gambar 6-. Garis singgung f(x) = sin(x)+1 di titik x=1 Keterangan: The tangent at... mempunyai arti garis singgung di titik... Apabila Maple tidak mendukung Calculus1 Student Package, maka perintah DerivativePlot tidak bisa digunakan. Alternatif lain adalah dengan menggunakan perintah showtangent yang sintaksnya adalah: > with(student); > showtangent(fungsi, titik singgung); Berikut ini contoh penggunaan perintah showtangent untuk menggambar garis singgung f(x) = x +5 di titik x=. > with(student): > f := (x) -> x^+5; > showtangent(f(x),x=);
75 Kalkulus dengan Maple 75 Masalah Kecepatan/Laju Secara umum, andaikan suatu benda bergerak sepanjang garis lurus sesuai dengan persamaan gerak s=f(t), dengan s adalah perpindahan dan f(t) adalah fungsi terhadap waktu. Pada selang waktu dari t=a sampai t=a+h perubahan posisi benda adalah f(a+h)-f(a), sehingga kecepatan rata-rata benda pada selang waktu tersebut dirumuskan Kecepatan rata-rata = ( + ) ( ) f a h f a h. Sekarang andaikan akan dihitung kecepatan rata-rata pada selang waktu yang semakin pendek (h mendekati 0), maka kecepatan sesaat v(a) pada saat t=a dinyatakan sebagai ( ) v a = ( + ) ( ) h 0 f a lim h f a Dengan demikian kecepataan sesaat benda pada t=a sama dengan kemiringan garis singgung grafik f(t) di titik (a, f(a)). h Contoh: Sebuah bola dilemparkan ke udara pada kecepatan 40 kaki/detik dan ketinggiannya (dalam kaki) setelah t detik diberikan oleh y(t) = 40t-16t. Dengan menggunakan Maple dan konsep limit, tentukan kecepatan bola ketika t = detik. Tentukan pula arah bola pada saat itu Penyelesaian: > y := (t) -> 40*t-16*t^; > limit((y(+h)-y())/h,h=0); Hasil limit akan diperoleh 4, artinya bahwa kecepatan bola ketika t= adalah 4 kaki/detik. Tanda negatif bermakna bahwa bola sedang bergerak ke bawah. Aplikasi limit untuk menentukan kecepatan sesaat tidak hanya terkait dengan benda yang bergerak. Kecepatan sesaat juga dapat terkait misalnya kecepatan perubahan suhu terhadap waktu, kecepatan suatu reaksi kimia, laju perubahan biaya produksi suatu barang dan lain-lain.
76 76 Limit Fungsi Soal-soal Latihan 1. Secara intuitif, tentukan perkiraan nilai limit di bawah ini, kemudian bandingkan hasil perkiraan limit tersebut dengan nilai limit sebenarnya yang diperoleh dari penggunaan function limit dalam Maple. a. lim x 4x 1 x x 1 b. lim x 1 3 x 1 c. d. e. lim x + x 1 x + 3x x 5 lim x 5 x 5 lim t 1 3 t 1 t 1 1 cos x f. lim x 0 x g. h. cos x 1 lim sin x x 0 x 6 lim x 0 x x 5. Diketahui fungsi ( ) f x x x + x < =, 1 3 x, x 1 Secara intuitif, tentukan perkiraan nilai limit lim f ( x) x 1, kemudian bandingkan hasil perkiraan limit tersebut dengan nilai limit sebenarnya yang diperoleh dari penggunaan function limit dalam Maple. 6. Diketahui fungsi ( ) x, x < 0 =,0 < 8 x, x > f x x x
77 Kalkulus dengan Maple 77 Secara intuitif, tentukan perkiraan nilai limit di bawah ini, kemudian bandingkan hasil perkiraan limit tersebut dengan nilai limit sebenarnya yang diperoleh dari penggunaan function limit dalam Maple. a. lim f ( x) x 0 b. lim f ( x) x 1 c. lim f ( x) x 7. Dengan menggunakan Calculus1 Student Package untuk limit, tentukan limit berikut ini a. lim( 5x x + 3) x 4 b. lim( x 3 + )( x 5x) x 3 x c. lim x 1 x + 4x 3 d. e. x lim x 1 x x 6 + x lim t + 3t + 6 t 1 cosx f. lim x 0 sin x g. e x 3e x lim x 1 sin 4 x 8. Carilah nilai limit di bawah ini x + 4 a. lim x x x + 5 b. 3 lim 7x + 4x x 3 x x + 3 c. lim x x 1 x + 8x d. ( 1 x)( + x) ( + x)( x) lim x 1 3
78 78 Limit Fungsi e. lim( x + 1 x 1) x f. 1 lim xsin x x 9. Jelaskan mengapa fungsi-fungsi berikut tidak kontinu pada titik yang diberikan. a. f ( x) = 1 ( x 1), pada x = 1 b. f ( x) c. f ( x) x 1 =, pada x = -1 x + 1 d. f ( x) = x x 8, x 4 = x 4, pada x = 4 3, x = 4 1 x, x, pada x= x x, x > 10. Dengan menggunakan perintah iscont, tentukan kekontinuan fungsi-fungsi berikut pada selang yang diberikan. f x a. ( ) = b. f ( x) x c. f ( x) tan x, pada selang [-5, 0] + 5x + 6 sin x =, pada selang [0,π) x + 1 = x, pada selang [0,10] d. f ( x) sin ( cos( sin x) ) e. ( ) =, pada selang [1, ) x + 1, x 1 h x = 3 x, 1 < x < 1, pada selang [-,0] x 1, x Dengan menggunakan perintah discont, tentukan ada tidaknya titik-titik diskontinu (pada semua bilangan real x) untuk semua fungsi pada no. 7! 1. Tentukan kemiringan garis singgung pada grafik fungsi berikut ini di titik yang diketahui dan tentukan pula persamaan garis singgungnya a. y = x + x di titik (-3,3)
79 Kalkulus dengan Maple 79 b. y = 1-x-3x di titik (-,-7) c. y = 1 x di titik (4,1/) x d. y = di titik (0,0) 1 x e. y = sin x π di titik (, 1) 1 cos x 13. Gambarkan grafik fungsi pada no.9 beserta persamaan garis singgungnya pada titik yang telah diberikan. 14. Sebuah anak panah ditembakkan ke atas menuju sebuah sasaran yang berada pada ketinggian 500 m dengan kecepatan 58 m/detik. Ketinggian anak panah setelah t detik adalah h(t) = 58t-0.83t. a. Tentukan kecepatan anak panah setelah 1 detik! b. Kapan anak panah mengenai sasaran? c. Dengan kecepatan berapa anak panah mengenai sasaran? 15. Sebuah tangki berbentuk silinder berisi galon air yang dapat dikosongkan melalui bawah tangki dalam waktu 60 menit (1 jam). Hukum Torricelli menyatakan volume air yang masih tersisa dalam tangki tersebut setelah t menit adalah ( ) V t t = , untuk 0 t 60 a. Tentukan laju aliran air ke luar tangki (laju perubahan sesaat V terhadap t) sebagai fungsi dari t. b. Tentukan volume air yang tersisa dalam tangki dan laju aliran air ke luar tangki setelah t=0, 10, 0, 30, 40, 50, dan 60 menit. c. Berdasarkan jawaban b, kapan laju aliran air terbesar dan terkecil?
80 80 Turunan Bab 5 Turunan Pada bab sebelumnya telah dibahas mengenai limit. Turunan suatu fungsi mempunyai hubungan erat dengan limit. Turunan suatu fungsi y=f(x) yang dinotasikan dengan f (x) atau dy didefinisikan sebagai berikut dx f ' ( x) dy = = dx ( + ) ( ) h 0 f x lim h f x Definisi di atas sama dengan pembahasan bab sebelumnya pada pokok permasalahan pencarian gradien garis singgung. Oleh karena itu turunan suatu fungsi dapat ditafsirkan secara geometri merupakan kemiringan persamaan garis singgung grafik fungsi y=f(x) di titik (x, f(x)). Berikut ini contoh pencarian turunan fungsi dan gradien pada titik tertentu menggunakan konsep limit dengan Maple. h Contoh: Tentukan turunan fungsi ( ) f x x x x 4 3 = Kemudian tentukan pula gradien persamaan garis singgung grafik fungsi tersebut di titik (1,-4). Penyelesaian: > f := (x) -> x^4+3*x^3-*x^+6; > f_turunan := (x) -> limit((f(x+h)-f(x))/h,h=0); Dari perhitungan tersebut diperoleh hasil 4x 3 +9x -4x. Dengan demikian f (x) = 4x 3 +9x - 4x. Selanjutnya akan dicari gradien persamaan garis singgung di titik (1,-4). Untuk mencari gradiennya berarti mencari nilai f (1). > f_turunan(1);
81 Kalkulus dengan Maple 81 dan akan diperoleh 9. Dengan demikian gradien persamaan garis singgung grafik f(x) di titik (1,-4) adalah 9. Apabila f(x) dan f (x) digambar pada satu bidang gambar yang sama, dengan perintah > plot([f(x),f_turunan(x)], x=-5..3,color=[red,blue],legend=["grafik f(x)","grafik f (x) "]); maka akan diperoleh grafik pada Gambar 7-1 Gambar 7-1. Grafik y=x 4 +3x 3 -x +6 beserta turunannya Pada gambar tampak bahwa selang dimana grafik f (x) bernilai negatif, maka grafik f(x) nya turun. Sedangkan selang dimana grafik f (x) bernilai positif, maka grafik f(x) nya naik. Selanjutnya nilai x di mana f (x) = 0 (memotong sumbu x) menunjukkan bahwa gradien persamaan garis singgung f(x) di titik x tersebut adalah 0 (garis singgungnya mendatar/horizontal). Untuk mencari nilai x dimana f (x)=0, dapat digunakan perintah solve > solve(f_turunan(x)=0,x); dan diperoleh penyelesaian 0, +,
82 8 Turunan atau supaya diperoleh penyelesaian dalam bentuk floating point dapat digunakan perintah > solve(f_turunan(x)=0.0,x); sehingga diperoleh penyelesaian 0, 0.380, Dengan demikian pada ketiga nilai x tersebut gradien garis singgungnya adalah 0. Secara sekilas pada Gambar 7-1 tidak tampak 3 titik perpotongan grafik f (x) dengan sumbu x. Untuk memperjelas gambaran hal ini, perintah plot dapat dimodifikasi dengan memperkecil interval x nya, misalnya [-.8,0.5]. > plot([f(x),f_turunan(x)],x= , color=[red,blue],legend=["grafik f(x)", "Grafik f (x)"]); Sehingga diperoleh grafik sebagaimana tampak pada Gambar 7- Dengan menggunakan Calculus1 Student Package dalam Maple, dapat dengan mudah dan cepat dibuat grafik f(x) beserta f (x) pada interval tertentu [a, b]. Sintaks perintahnya: > with(student[calculus1]): > DerivativePlot(fungsi, x=a..b); Gambar 7-. Grafik y = 4x 3 +9x -4x memotong sumbu x di 3 titik
83 Kalkulus dengan Maple 83 Sebagai contoh, akan digambar grafik f(x) = 3x 3-4x dan turunannya pada interval [-,3]. Perintahnya sebagai berikut: > with(student[calculus1]): > f := (x) -> 3*x^3-4*x; > DerivativePlot(f(x), x=-..3); dan outputnya akan diperoleh grafik seperti pada gambar berikut (Gambar 7-3) Gambar 7-3. Grafik y = 3x 3-4x beserta turunannya Keterangan 1 st derivative mempunyai arti grafik turunan f(x). Fungsi Terdiferensial Suatu fungsi f dikatakan terdiferensial (diferensiabel) di x=a apabila f (a) ada. Berikut ini contoh bagaimana menentukan apakah suatu fungsi diferensiabel atau tidak. Contoh: Selidikilah apakah fungsi f(x) = x diferensiabel di x=1? Bagaimana dengan x=0?
84 84 Turunan Penyelesaian: > f := (x) -> abs(x); > f_turunan := (x) -> limit((f(x+h)-f(x))/h,h=0); > f_turunan(1); Dari perhitungan tersebut diperoleh hasil f_turunan(1) atau f (1) bernilai 1. Dengan demikian f (1) ada, sehingga f(x) diferensiabel di x=1. Selanjutnya hal yang sama akan diselidiki untuk x=0. > f_turunan(0); Ternyata perintah ini menghasilkan undefined atau tidak terdefinisi. Dengan demikian f(x) tidak diferensiabel di x=0. Function diff untuk Turunan Jika setiap kali mencari turunan suatu fungsi menggunakan konsep evaluasi limit, maka hal ini dapat menjadi terlalu lama. Untuk mempercepat perhitungan turunan, Maple menyediakan function khusus yang dapat digunakan untuk mencari turunan suatu fungsi. Function yang dimaksud adalah diff. Sintaks perintah diff adalah: > diff(fungsi, x) Function diff digunakan untuk mencari turunan fungsi terhadap x. Contoh: Dengan menggunakan perintah diff, tentukan turunan dari fungsi f(x) = x -3x+9. Penyelesaian: > f := (x) -> *x^-3*x+9; > diff(f(x),x);
85 Kalkulus dengan Maple 85 Dari perhitungan akan diperoleh 4x-3. Contoh: Tentukan turunan dari fungsi f(t) = sin t. t 1 Penyelesaian: > f := (t) -> sin(*t)/(t-1); > diff(f(t),t); Maple akan memberikan hasil cos t sin t t 1 1 ( t ). Calculus1 Student Package untuk Turunan Seperti halnya limit yang telah dibahas pada bab sebelumnya, Maple juga menyediakan paket pembelajaran bagaimana menentukan turunan suatu fungsi menggunakan aturan-aturan dasar. Sebelum membahas lebih lanjut tentang hal ini, terlebih dahulu akan diberikan aturan-aturan dasar tersebut (lihat Tabel 7-1). Sintaks secara umum untuk pembelajaran dalam penyelesaian turunan menggunakan Maple dengan Calculus1 student package adalah > Rule[nama aturan](ekspresi); Untuk nama aturan pada sintaks yang akan digunakan dapat dipilih dari tabel, atau nama aturan dapat diganti dengan notasi yang terkait. Apabila fungsi yang akan dicari turunannya adalah dalam bentuk transenden seperti halnya telah dijelaskan di Bab, maka nama aturan dapat diganti dengan perintah yang terkait dengan bentuk fungsinya. Untuk lebih jelasnya, lihat Tabel 7- tentang aturan turunan fungsi transenden.
86 86 Turunan Nama Aturan Notasi Deskripsi constant constant multiple difference identity power product quotient sum `c*` `-` `^` `^` `*` `/` `+` d c dx = 0, dengan c adalah suatu konstanta d d cf x c f x dx dx ( ) = ( ) d f x g x d f x d g x dx dx dx d x 1 dx = d x dx ( ) ( ) = ( ) ( ) n nx n 1 =, n bilangan real d f ( x ) g ( x ) = dx d d g x f x f x g x dx dx ( ) ( ) + ( ) ( ) d d g x f x f x g x d f ( x) = dx dx dx g( x) g( x) ( ) ( ) ( ) ( ) d f x g x d f x d g x dx dx dx ( ) + ( ) = ( ) + ( ) Tabel 7-1. Aturan dalam mencari turunan
87 Kalkulus dengan Maple 87 Nama Aturan sin cos Deskripsi d sin x = cos x dx d cosx = sin x dx tan d tan x = sec x dx csc sec cot d csc x = cscx cot x dx d secx = sec x tan x dx d cot 1 cot dx ( x) = ( x) exp d e x e x = dx ln d 1 ln x = dx x sinh cosh d sinh x = cosh x dx d cosh x = sinh x dx tanh d tanh x = 1 tanh x dx csch sech d csc h x = csc h x coth x dx d sech x = sech x tanh x dx coth d coth x = 1 coth x dx Tabel 7-. Aturan turunan fungsi transenden
88 88 Turunan Contoh: Dengan menggunakan Calculus1 Student Package, tentukan turunan dari fungsi f(x) = 3sin x x + 9 x. Penyelesaian: > with(student[calculus1]): > infolevel[calculus1] := 1: > f := (x) -> (3*sin(x)-x^+9)/(x-); Berikut ini langkah-langkah penyelesaian yang dapat dipilih dari aturan tersebut. > Rule[`/`](Diff(f(x),x)); d d ( 3sin x x + 9) ( x ) ( 3sin x x + 9) ( x ) d 3sin x x + 9 dx dx = dx x ( x ) > Rule[`-`](%); d d d d 3sin 9 x x + ( x ) ( 3sin x x + 9) ( x ) d 3sin x x + 9 dx dx dx dx = dx x ( x ) > Rule[constantmultiple](%); d x x dx x = 3sin + 9 d d d d x x ( x ) ( x x ) ( x ) dx dx dx dx 3 sin + 9 3sin + 9 > Rule[sin](%); ( x )
89 Kalkulus dengan Maple 89 d d d 3 cos x 9 x + ( x ) ( 3sin x x + 9) ( x ) d 3sin x x + 9 dx dx dx = dx x ( x ) > Rule[power](%); d d 3 cos x x + 9 ( x ) ( 3sin x x + 9) ( x ) d 3sin x x + 9 dx dx = dx x ( x ) > Rule[constant](%); d ( 3 cos x)( x ) ( 3sin x x + 9) ( x ) d 3sin x x + 9 dx = dx x ( x ) > Rule[`-`](%); d d ( 3 cos x x)( x ) ( 3sin x x + 9) x + ( ) d 3sin x x + 9 dx dx = dx x ( x ) > Rule[identity](%); d ( 3 cos x x )( x ) ( 3sin x x + 9) 1 + ( ) d 3sin x x + 9 dx = dx x x > Rule[constant](%); ( )( ) ( ) ( ) d 3sin x x + 9 x x x x x = dx x x 3 cos 3sin + 9 Aturan Rantai ( (Chain Rule) Jika fungsi f dan g keduanya dapat diturunkan dan F adalah fungsi komposisi yang didefinisikan dengan F(x) = f(g(x)), maka F dapat diturunkan menjadi F dalam bentuk F (x) = f (g(x)) g (x) Dalam Calculus1 Student Package juga terdapat Rule yang terkait dengan aturan rantai ini. Untuk menggunakan aturan rantai tersebut digunakan perintah
90 90 Turunan chain. Aturan ini biasanya diterapkan pada fungsi yang memiliki bentuk dasar seperti pada Tabel 7-1 dan Tabel 7-, misalnya fungsi-fungsi berbentuk f(x) = sin(x+), yang memiliki bentuk dasar sama seperti aturan sin, f(x) = (x+3) 3, yang memiliki bentuk dasar sama dengan aturan Power, f(x) = e x-7, yang memiliki bentuk dasar sama dengan aturan exp, dan lain sebagainya. Contoh: Dengan menggunakan Calculus1 Student Package,tentukan turunan dari ( ) ( ) f x = sin x + 3x 1 x + 1. Penyelesaian: Berikut ini adalah urutan langkah penyelesaian yang dapat dipilih > with(student[calculus1]): > infolevel[calculus1] := 1: > f := (x) -> sin(x^+3*x-1)-sqrt(x+1); > Rule[`-`](Diff(f(x),x)); akan diperoleh ( ( ) ) ( ) d d d sin x + 3x 1 x + 1 = sin x + 3x 1 x + 1 dx dx dx d dx Selanjutnya akan dicoba mencari sin ( x 3x 1) aturan sin. + secara langsung menggunakan > Rule[sin](%); Setelah perintah tersebut dijalankan akan muncul peringatan Rule [sin] is not valid or does not apply. Ternyata Maple tidak bisa langsung menentukan hasil turunannya. Langkah yang harus diambil adalah menggunakan aturan rantai untuk d mencari turunan sin ( x + 3x 1) dx > Rule[chain](%);
91 Kalkulus dengan Maple 91 d dx ( sin( x + 3x 1) x + 1) d d d = sin (_ X) ( x 3x 1) x 1 d X + + dx dx _ _ X= x + 3x 1 > Rule[sin](%); ( sin( x + 3x 1) x + 1) d dx d d = cos( x + 3x 1) ( x + 3x 1) x + 1 dx dx > Rule[`+`](%); ( sin( x + 3x 1) x + 1) d dx d d d d = cos( x + 3x 1) ( x ) + ( 3x) + ( 1) x + 1 dx dx dx dx > Rule[power](%); ( sin ( x + 3x 1) x + 1) d dx d d d = cos( x + 3x 1) x + ( 3x) + ( 1) x + 1 dx dx dx > Rule[constantmultiple](%); ( sin( x + 3x 1) x + 1) d dx d d d = cos( x + 3x 1) x + 3 x + ( 1) x + 1 dx dx dx > Rule[identity](%); ( sin( x + 3x 1) x + 1) d dx d d = cos( x + 3x 1) x ( 1) x + 1 dx dx > Rule[constant](%);
92 9 Turunan d dx ( ( ) ) ( )( ) d sin x + 3x 1 x + 1 = cos x + 3x 1 x + 3 x + 1 dx Selanjutnya akan dicari d dx x + 1 dengan menggunakan aturan rantai, karena memiliki bentuk dasar aturan Power dengan pangkat ½. > Rule[chain](%); d dx ( sin( x + 3x 1) x + 1) d d = cos( x + 3x 1)( x + 3 ) _ X ( x + 1) d _ X dx _ X= x+ 1 > Rule[power](%); d d 1 dx ( sin( x + 3x 1) x + 1) = cos( x + 3x 1)( x + 3 ) dx x + 1 > Rule[`+`](%); d ( sin( x + 3x 1) x + 1) dx d d 1 1 x + dx dx = cos( x + 3x 1)( x + 3 ) x + 1 ( x + 1) > Rule[identity](%); 1 d 1 d 1 + ( sin( 3 1) 1) cos( dx x + x x + = x + 3x 1)( x + 3 ) dx x + 1 > Rule[constant](%); d dx ( sin( x 3x 1) x 1) cos( x 3x 1)( x 3) + + = + + x + 1 1
93 Kalkulus dengan Maple 93 Turunan Implisit Bagaimana dengan turunan fungsi-fungsi berbentuk implisit? Dan bagaimana cara mendapatkan turunannya? Secara teoritis, turunannya dapat dicari dengan aturan berantai. Namun, untuk memudahkan pengguna, Maple juga menyediakan function untuk mencari turunan fungsi implisit. Apabila diketahui fungsi implisit f dalam bentuk eksplisit x dan y, maka perintah untuk mencari dy/dx dengan Maple adalah > implicitdiff(f, y, x) Sedangkan kebalikannya, apabila akan dicari turunan dx/dy, maka perintahnya > implicitdiff(f, x, y); Contoh: Tentukan dy/dx dari x +y = 9. Tentukan pula dx/dy dari fungsi implisit tersebut! Penyelesaian: Terlebih dahulu didefinisikan fungsi implisit f > f := x^+y^=9; selanjutnya dicari dy/dx dengan perintah > implicitdiff(f,y,x); dan diperoleh hasil x. y Fungsi implisit tidak harus didefinisikan terlebih dahulu seperti halnya contoh ini. Fungsi implisit yang akan dicari turunannya langsung dapat diletakkan dalam implicitdiff.
94 94 Turunan > implicitdiff(x^+y^=9,y,x); Selanjutnya untuk mencari dx/dy, perintahnya > implicitdiff(f,x,y); atau > implicitdiff(x^+y^=9,x,y); Kedua perintah tersebut akan sama-sama menghasilkan y x Contoh: Tentukan dy/dx dan dx/dy dari x +y =6xy. Penyelesaian: > f := x^+y^=6*x*y; > implicitdiff(f, y, x); dan hasil yang akan diperoleh adalah dy x 3y = dx y + 3x > implicitdiff(f, x, y); Sedangkan untuk dx/dy diperoleh hasil dx y 3x =. dy x + 3y Turunan Orde Tinggi Jika y=f(x) merupakan fungsi yang diturunkan, maka turunannya (f ) juga merupakan fungsi, yang dalam hal ini f sering disebut turunan pertama dari f. Selanjutnya f
95 Kalkulus dengan Maple 95 kemungkinan dapat diturunkan lagi yang turunannya dinotasikan dengan f (turunan kedua dari f) dan seterusnya. Seringkali f juga dinotasikan dengan d y / dx dalam notasi Leibniz. Dengan menggunakan Maple, dapat pula dicari turunan kedua, ketiga, keempat, dan seterusnya dari suatu fungsi. Adapun sintaks perintahnya adalah sebagai berikut: > diff(f, x$n); Perintah tersebut adalah sintaks untuk mencari turunan ke-n terhadap x dari fungsi f. Contoh: Tentukan turunan kedua dari f(x) = sin(x)! Tentukan pula f (3) (x) dan f (4) (x). Penyelesaian: > f := (x) -> sin(*x); Perintah untuk mencari turunan keduanya adalah > diff(f(x),x$); diperoleh hasil 4sin(x). Turunan ketiganya adalah > diff(f(x),x$3); dan diperoleh hasil 8cos(x). > diff(f(x),x$4); Untuk turunan keempat diperoleh hasil 16sin(x).
96 96 Turunan Turunan n Parsial Misalkan diketahui suatu fungsi dengan variabel yaitu f(x,y), turunan parsialnya adalah f x (turunan parsial terhadap x) dan f y (turunan parsial terhadap y) didefinisikan oleh f f x y ( x y) ( +, ) (, ) f x h y f x y, = lim h 0 h ( x y) (, + ) (, ) f x y h f x y, = lim h 0 h Dari definisi tersebut dapat dilihat bahwa apabila akan ditentukan f x, y dipandang tetap/konstan. Begitu pula sebaliknya, apabila akan ditentukan f y, x dipandang sebagai suatu konstanta. Hal ini berlaku pula untuk fungsi-fungsi dengan 3 variabel atau lebih. Dengan Maple kita dapat mencari turunan parsial secara langsung yang caranya sama dengan mencari turunan fungsi satu variabel. Contoh: Diketahui fungsi multivariabel sebagai berikut ( ) = + dan g( x, y, z) f x x x y y Tentukan f x, f y, g x, g y, g z! sin( xy) 3 = + x yz z Penyelesaian: > f := (x,y) -> x^3+*x^*y^3-y^3; > g := (x,y,z) -> sin(x*y)/z+x^*y*z^3; Dua perintah berikut digunakan untuk mencari f x dan f y > diff(f(x,y),x); > diff(f(x,y),y); Kedua perintah tersebut menghasilkan
97 Kalkulus dengan Maple 97 x 3 (, ) = dan f ( x, y) = 6x y 3y f x y x y x Sedangkan tiga perintah berturut-turut berikut ini digunakan untuk mencari g x, g y, dan g z. y > diff(g(x,y,z),x); > diff(g(x,y,z),y); > diff(g(x,y,z),z); dan akan diperoleh cos( xy) y 3 gx ( x, y, z) = + z yx z cos( xy) x 3 gy ( x, y, z) = + z x z ( xy) sin gz ( x, y, z) = + 3z yx z Dalam turunan parsial juga terdapat turunan order tinggi. Misalkan suatu fungsi multivariabel f diturunkan dua kali terhadap x, dinotasikan dengan f xx. Sedangkan apabila diberikan notasi f xy, maka bermakna bahwa f diturunkan parsial terhadap x kemudian terhadap y. Berikut ini contoh mencari turunan parsial order tinggi. Contoh: Diketahui fungsi ( ) f x, y, z = xy z 4x y + z Tentukan f xx, f xyx, f yyy, f xxy, f xyz.setelah itu tentukan f xyz(,1,4). Penyelesaian: > f := (x,y,z) -> x*y^4*z^5-4*x^*y^3+z^5; Perintah berikut untuk mencari f xx
98 98 Turunan > diff(f(x,y,z),x$); Sedangkan perintah di bawah ini untuk mencari f xyx > diff(f(x,y,z),x,y,x); Tiga perintah berikut berturut-turut untuk mencari f yyy, f xxy dan f xyz. > diff(f(x,y,z),y$3); > diff(f(x,y,z),x$,y); > diff(f(x,y,z),x,y,z); Untuk mencari f xyz(,1,4) dapat dilakukan melalui cara berikut ini. > der := (x,y,z) -> diff(f(x,y,z),x,y,z); > eval(der(x,y,z),{x=,y=1,z=4}); Perintah eval digunakan untuk mengevaluasi fungsi (hasil turunan) dengan nilai variabel yang telah ditentukan. Teorema Rolle Misalkan suatu benda bergerak dengan posisi s=f(t), pada waktu t tertentu. Apabila benda berada pada posisi yang sama pada dua waktu yang berbeda katakanlah t=a dan t=b (sehingga f(a)=f(b)), maka akan terdapat suatu saat yaitu t=c, dimana c di antara a dan b yang menyebabkan f (c)=0 atau kecepatannya menjadi nol. Atau secara umum dapat pula dikatakan bahwa terdapat c sedemikan hingga gradien f(t) di x=c sama dengan nol. Keadaan tersebut dapat kita lihat sehari-hari misalnya ketika suatu benda dilempar ke atas secara vertikal. Dalam hal ini kecepatan sama dengan nol ketika benda mencapai ketinggian maksimum. Hal yang telah disebutkan ini merupakan penerapan teorema Rolle, yang secara lengkap dinyatakan sebagai: Misalkan f adalah fungsi yang memenuhi tiga syarat berikut ini 1. f kontinu pada selang tertutup [a, b]. f terdiferensial pada selang terbuka (a, b)
99 Kalkulus dengan Maple f(a) = f(b) Maka terdapat suatu bilangan c dalam (a, b) sedemikian hingga f (c) =0. Untuk memvisualisasikan teorema Rolle ini, Maple telah menyediakan perintah khusus. Perintah ini terdapat dalam Calculus1 Student Package. Adapun perintahnya berikut: > with(student[calculus1]): > RollesTheorem(f(x),x=a..b,option); dengan a dan b menyatakan selang (a, b), dan option dapat dituliskan perintahperintah berikut ini: - output = plot atau points Apabila dipilih output=plot, maka Maple akan menampilkan visualisasi teorema ini dalam bentuk grafik. Pada grafik ini akan ditampilkan titik-titik dimana gradiennya 0 (ditunjukkan dengan garis mendatar). Sedangkan apabila output=points, maka hasil yang tampak hanyalah nilai-nilai c dalam selang (a, b) sedemikian hingga f (c) = 0. Default dari option ini adalah output=plot. - numeric = true atau false Option ini hanya digunakan ketika dipilih output=points. Apabila numeric=true, maka titik-titik yang dihasilkan ditampilkan dalam bentuk floating point, sedangkan apabila false dalam bentuk eksak. Defaultnya adalah numeric=false. - title = string Option ini digunakan untuk mengubah title dari grafik. Contoh: Diketahui ( ) f x x x sedemikian hingga f (x)=0. 4 = Tunjukkan bahwa dalam selang (-,) terdapat x Penyelesaian: Kita akan mencoba menerapkan soal tersebut dengan teorema Rolle. Perintahnya adalah:
100 100 Turunan > with(student[calculus1]): > f := x -> x^4-3*x^+1; > RollesTheorem(f(x),x=-..); atau > RollesTheorem(f(x),x=-..,output=plot); Perintah yang telah diberikan ini akan dihasilkan grafik yang menunjukkan adanya titik x sedemikian hingga f (x)=0. Perhatikan Gambar 7-4 berikut Gambar 7-4. Grafik f(x)=x 4-3x +1 dan titik yang bergradien nol Pada gambar yang dihasilkan tampak bahwa terdapat 3 buah titik yang bergradien nol atau f (x)=0. Untuk mengetahui lebih jelas berapakah nilai titik-titik tersebut, dapat digunakan perintah berikut. > RollesTheorem(f(x),x=-..,output=points,numeric=true); dan akan diperoleh hasil x= , x=0, dan x= Apabila selang dalam contoh tersebut diubah menjadi (-1,), maka Maple akan menunjukkan kesalahan, yaitu: Error, (in Student:-Calculus1:-RollesTheorem) Rolle's theorem on the interval [a, b] requires that the function `f` satisfies f(a) = f(b) yang artinya bahwa terdapat syarat dalam teorema Rolle tidak terpenuhi yaitu f(a) = f(b) dalam hal ini f(-1) f().
101 Kalkulus dengan Maple 101 Sedangkan untuk kasus yang lain, misalkan diketahui f(x)= x untuk x [-,]. Dalam kasus ini, teorema Rolle juga tidak berlaku. Apabila digunakan Maple, maka akan tampil kesalahan Error, (in Student:-Calculus1:-RollesTheorem) Rolle's theorem requires the function to be differentiable on the open interval (a, b) Error tersebut menyatakan bahwa f(x) tidak terdiferensial pada selang (a, b). Teorema Nilai Rata-rata Teorema ini mengatakan bahwa misalkan f adalah fungsi yang memenuhi hipotesis berikut: 1. f kontinu pada selang tertutup [a,b]. f terdiferensial pada selang terbuka (a, b) maka terdapat bilangan c dalam (a, b) sedemikian hingga f ' ( c) = ( ) f ( a) f b b a atau f ( b) f ( a) f '( c)( b a) =. Secara geometri, teorema ini dapat dikatakan bahwa terdapat paling tidak satu titik pada interval (a, b) yang gradien garis singgungnya sama dengan gradien garis tali busur yang menghubungkan (a, f(a)) dan (b, f(b)). Dalam Maple terdapat perintah yang mampu memvisualisasikan penerapan teorema ini. Seperti halnya teorema Rolle, perintah ini juga terdapat dalam Calculus1 Student Package. Berikut ini adalah sintaksnya: > with(student[calculus1]): > MeanValueTheorem(f(x),x=a..b,option); Adapun parameter (termasuk option) pada perintah tersebut sama dengan perintah RollesTheorem. Contoh: Diketahui fungsi f ( x) sin ( x) cos( x) = +. Tunjukkan dengan menggunakan grafik bahwa pada selang [0,5] terdapat titik yang gradien garis singgungnya sama dengan gradien garis yang menghubungkan titik (0, f(0)) dan (5, f(5)). Tentukan kedua titik tersebut dan gradiennya.
102 10 Turunan Penyelesaian: Kita akan gunakan perintah MeanValueTheorem. Berikut ini perintahnya. > f := x -> sin(x)+cos(x); > with(student[calculus1]): > MeanValueTheorem(f(x),x=0..5); Perintah di atas akan menghasilkan grafik seperti pada Gambar 7-5. Pada gambar tersebut tampak dua buah titik (ditandai dengan lingkaran kecil), yaitu di titik sekitar x=1 dan x=3. Dua titik ini memiliki gradien garis singgung yang sejajar dengan gradien garis yang menghubungkan titik (0, f(0)) dan (5, f(5)) yang digambarkan sebagai garis putus-putus berwarna biru. Selanjutnya akan ditentukan nilai x yang memenuhi teorema nilai rata-rata dengan menggunakan perintah berikut ini > c = MeanValueTheorem(f(x),x=0..5,output=points, numerik=true); yang akan menghasilkan c = [ , ]. Kedua titik itulah yang memenuhi teorema nilai rata-rata. Sedangkan gradien garis singgung pada titik tersebut dapat dicari dengan perintah berikut. > eval(diff(f(x),x),x=c[1]); atau > eval(diff(f(x),x),x=c[]); Kedua perintah ini akan menghasilkan gradien yang sama yaitu
103 Kalkulus dengan Maple 103 Gambar 7-5. Visualisasi teorema nilai rata-rata pada f(x)=sin(x)+cos(x) dalam selang [0,5] Seperti halnya perintah pada RollesTheorem, pada perintah MeanValueTheorem inipun akan memberikan pesan kesalahan (error) apabila terdapat hipotesis yang tidak dipenuhi. Aplikasi Turunan Pada subbab ini akan dibahas mengenai aplikasi turunan. Bagaimana pengaruh turunan terhadap bentuk grafik fungsi, serta bagaimana menentukan titik minimum dan maksimum fungsi, menentukan titik balik fungsi merupakan bentuk- bentuk aplikasi turunan. Beberapa aplikasi terkait dengan permasalahan sehari-hari yang sering dijumpai, misalnya kelajuan, bagaimana meminimumkan biaya suatu proses dan lain-lain, juga akan dibahas. Kecepatan/Laju Permasalahan kecepatan/laju sebenarnya sudah dibahas pada pokok bahasan limit. Pada dasarnya ada kaitan limit untuk perhitungan kecepatan dengan turunan. Pandang kembali konsep limit untuk kecepatan sesaat untuk benda yang bergerak. Kecepatan v pada saat t=a dinyatakan sebagai ( ) v a = ( + ) ( ) h 0 f a lim h f a Apabila diperhatikan limit tersebut, maka sebenarnya v(a) = f (a). Sehingga secara umum kecepatan sesaat pada waktu t atau v(t) merupakan turunan dari f(t) atau f (t), dengan f(t) adalah fungsi yang menyatakan jarak benda pada saat t. h
104 104 Turunan Konsep turunan juga dapat digunakan untuk mencari percepatan sesaat. Percepatan didefinisikan sebagai laju perubahan sesaat kecepatan terhadap waktu, yang dinotasikan dengan a(t). Dari definisi tersebut, percepatan dapat dinyatakan dengan ( ) = '( ) = ''( ) a t v t f t dengan kata lain, percepatan merupakan turunan kedua dari fungsi jarak f(t). Apabila v(t)>0 maka benda bergerak maju dan apabila v(t) < 0 maka benda bergerak mundur. Sedangkan untuk v(t) = 0, benda tidak bergerak sama sekali (diam). Selanjutnya apabila a(t) > 0, maka pergerakan benda mengalami percepatan, sedangkan a(t) < 0 benda mengalami perlambatan. Untuk a(t) = 0, kecepatan benda tetap/konstan. Konsep kecepatan dan percepatan ini tidak hanya diterapkan pada suatu benda yang bergerak, namun juga dapat diterapkan pada permasalahan yang lain. Contoh: Posisi sebuah partikel diberikan oleh persamaan f(t) = t 3-6t +9t, dengan t dalam satuan detik dan f(t) dalam meter. 1. Tentukan kecepatan partikel pada saat t = 10. Kapan (pada saat t berapa) partikel berhenti 3. Carilah percepatan setelah 6 detik 4. Gambarkan grafik fungsi posisi f(t), kecepatan, dan percepatan untuk 0 t 7 5. Berdasarkan grafik dari d, kapan partikel bertambah cepat dan kapan bertambah lambat? Penyelesaian: > f := (t) -> t^3-6*t^+9*t; Akan dicari terlebih dahulu v(t) yaitu kecepatan sesaat pada waktu t detik. > v := (t) -> diff(f(t),t); > v(t);
105 Kalkulus dengan Maple 105 Dari perhitungan tersebut diperoleh v(t) = 3t -1t+9 Selanjutnya akan dicari v(10). > eval(v(t),t=10); dan diperoleh hasil 189. Dengan demikian kecepatan partikel pada saat 10 detik adalah 189 meter/detik. Suatu benda akan berhenti apabila v(t) = 0. Sehingga untuk menentukan kapan partikel berhenti berarti mencari nilai t sedemikian hingga v(t) = 0. Dengan menggunakan perintah berikut ini > solve(v(t)=0,t); akan dihasilkan 1 dan 3. Dengan demikian partikel akan berhenti ketika t=1 detik dan t=3 detik. Percepatan pada saat t=6 detik dicari dengan perintah berikut ini > a := (t) -> diff(v(t),t); atau > a := (t) -> diff(f(t),t$); kemudian dihitung a(t) pada saat t=6. > a(t); > eval(a(t),t=6); dan diperoleh hasil 4. Dengan demikian percepatan partikel pada saat 6 detik adalah 4 m/detik. Berikutnya akan digambar grafik fungsi f(t), v(t), dan a(t) untuk 0 t 7. > plot([f(t),v(t),a(t)],t=0..7, legend=[ "f(t)", "v(t)","a(t)"], color=[red,blue,magenta]);
106 106 Turunan dan dihasilkan grafik seperti pada Gambar 7-6 Gambar 7-6. Grafik posisi, kecepatan, dan percepatan partikel Sebuah benda bergerak bertambah cepat atau tidak, dapat dilihat dari grafik v(t) maupun a(t) nya. Benda bertambah cepat apabila v(t) dan a(t) sama-sama positif atau v(t) dan a(t) sama-sama negatif. Pada grafik terlihat bahwa partikel bertambah cepat pada selang 1 < t < serta t > 3. Sedangkan benda bergerak bertambah lambat apabila v(t) positif dan a(t) negatif atau v(t) negatif dan a(t) positif. Pada grafik tersebut tampak bahwa partikel bertambah lambat pada selang 0 t < 1 serta pada < t < 3. Contoh: Besarnya muatan Q dalam satuan Coulomb (C) yang melewati sebuah titik dalam kabel sampai waktu t (dalam detik) diberikan oleh Q(t) = t 3 -t +6t+. Carilah besarnya arus listrik (dalam Ampere) pada waktu t = 0.5 detik dan 1 detik. Penyelesaian: Menurut hukum fisika, arus listrik yang mengalir pada saat t detik atau I(t) merupakan besar laju perubahan muatan pada saat t. Dengan demikian I(t) = Q (t). > Q := (t) -> t^3-*t^+6*t+; > i := (t) -> diff(q(t),t);
107 Kalkulus dengan Maple 107 Selanjutnya akan ditentukan I(0.5) dan I(1). > eval(i(t),t=0.5); > eval(i(t), t=1); Dari dua perhitungan tersebut diperoleh hasil untuk t=0.5, arus listrik yang mengalir sebesar 4.75 Ampere dan untuk t=1 sebesar 5 Ampere. Nilai Maksimum dan Minimum Dengan menggunakan konsep turunan, nilai maksimum dan minimum suatu fungsi dalam selang interval tertentu dapat dicari. Sebelum membahas lebih lanjut tentang bagaimana menentukan nilai maksimum dan minimum fungsi, terlebih dahulu dibahas mengenai nilai kritis. Definisi nilai kritis adalah sebagai berikut: Nilai kritis c dari suatu fungsi f merupakan bilangan dalam daerah asal f sedemikian hingga f (c) = 0 atau f (c) tidak ada. Dalam Maple tersedia function untuk mencari nilai kritis suatu fungsi. Function tersebut tersedia dalam Calculus1 Student Package. Sintaksnya adalah > with(student[calculus1]): > CriticalPoints(fungsi,[interval],[option]); Penggunaan parameter interval pada perintah CriticalPoints sifatnya optional. Parameter ini ditambahkan apabila diinginkan mencari nilai kritis pada suatu interval tertentu. Hasil nilai kritis dapat dinyatakan dalam bentuk floating point. Apabila hal ini diinginkan, maka tambahkan perintah numeric = true pada bagian option. Secara default, nilai kritis yang ditampilkan dalam bentuk eksak. Berikut ini akan diberikan contoh bagaimana menentukan nilai kritis suatu fungsi menggunakan Maple. Contoh: Diberikan fungsi f(x) = x 3/4 (x-7). Tentukan nilai kritis fungsi tersebut!
108 108 Turunan Penyelesaian: > f := (x) -> x^(3/4)*(x-7); > with(student[calculus1]): > CriticalPoints(f(x)); Dari hasil perintah terakhir, diperoleh [0, 3], artinya nilai kritisnya adalah x=0 dan x=3. Contoh: Diberikan fungsi f(x) seperti pada contoh sebelumnya. Tentukan nilai kritis fungsi pada interval [1, 5]. Penyelesaian: > f := (x) -> x^(3/4)*(x-7); > with(student[calculus1]): > CriticalPoints(f(x),x=1..5); dan hasilnya akan diperoleh [3], artinya nilai kritis pada interval tersebut hanya ada satu yaitu x=3. Setelah dijelaskan bagaimana mencari nilai kritis suatu fungsi, selanjutnya akan dibahas bagaimana mencari nilai minimum dan maksimum fungsi. Secara teori, pencarian nilai-nilai kritis dapat dilakukan dengan metode selang tertutup. Metode ini menyatakan bahwa untuk mencari nilai maksimum dan minimum mutlak suatu fungsi kontinu f pada selang tertutup [a, b] dilakukan dengan cara: 1. Dicari nilai fungsi pada nilai kritis f pada selang [a, b]. Dicari nilai fungsi pada titik ujung selang (dalam hal ini pada a dan b). 3. Nilai maksimum mutlak pada selang [a, b] adalah nilai f tertinggi dari langkah 1 dan. Sedangkan nilai minimum mutlak pada selang [a, b] adalah nilai f terendah dari langkah 1 dan. Contoh: Tentukan nilai maksimum dan minimum mutlak fungsi f(x) = x 3-3x +1 pada selang [- ½, 4].
109 Kalkulus dengan Maple 109 Penyelesaian: Terlebih dahulu dicari nilai kritis fungsi pada selang tersebut. > f := (x) -> x^3-3*x^+1; > with(student[calculus1]): > CriticalPoints(f(x),x=-1/..4); Berdasarkan perintah di atas, diperoleh nilai kritis adalah x=0 dan x=. Selanjutnya dicari nilai fungsi pada nilai kritisnya. > f(0); > f(); dan diperoleh hasil f(0) = 1, dan f() = -3. Akan dicari juga nilai fungsi pada batas tepi interval yaitu untuk x=-½ dan x=4. > f(-1/); > f(4); yang hasilnya adalah f(-½ ) = 1/8 dan f(4) = 17. Berdasarkan perhitungan tersebut, maka dapat disimpulkan bahwa nilai maksimum mutlak adalah f(4)=17 dan minimumnya adalah f()= -3. Sebagai gambaran, dapat dilihat pada grafik fungsi pada Gambar 7-7. > plot(f(x),x=-1/..4);
110 110 Turunan Gambar 7-7. Grafik f(x) = x 3-3x +1 pada selang [-½, 4] Pada gambar grafik di atas tampak bahwa titik minimum terletak di x=, dengan f() = -3 dan maksimumnya terletak pada x=4 dengan f(4) = 17. Contoh: Diberikan fungsi f(x) = x- sin(x). Tentukan nilai maksimum dan minimum mutlak pada interval [0,π]. Penyelesaian: > f := (x) -> x-*sin(*x); > with(student[calculus1]): > CriticalPoints(f(x),x=0..*Pi); Hasil perintah tersebut akan diperoleh 4 buah nilai kritis yaitu x = arccos + π, x = arccos + π, dan x = arccos 4, 1 1 x = arccos + π. 4 Apabila diinginkan tampilan nilai kritis dalam floating point, maka ditambahkan option pada perintah terakhir, menjadi > CriticalPoints(f(x),x=0..*Pi, numeric=true);
111 Kalkulus dengan Maple 111 dan diperoleh hasil x= ,.48534, , Supaya mempermudah evaluasi fungsi pada nilai-nilai kritis tersebut, maka sebaiknya nilai-nilai kritis disimpan dalam suatu array. Dengan menggunakan array, dapat dengan mudah memanggil nilai-nilai kritis melalui nomor urutan array nya saja. Untuk menyimpan hasil nilai-nilai kritis dalam sebuah array, perintah terakhir diubah menjadi > nilai_kritis := Array(): > nilai_kritis := CriticalPoints(f(x),x=0..*Pi, numeric=true); Perintah pertama digunakan untuk mendefinisikan variabel nilai_kritis sebagai array. Sedangkan perintah kedua bertujuan menyimpan nilai-nilai kritis dalam variabel nilai_kritis tadi. Perintah tersebut akan menampilkan nilai_kritis = [ ,.48534, , ] Selanjutnya akan dicari nilai fungsi pada setiap nilai kritisnya. > f(nilai_kritis[1]); Perintah di atas digunakan untuk mencari nilai f( ) dan diperoleh hasil sekitar Sedangkan di bawah ini perintah untuk mencari nilai f(.48534) > f(nilai_kritis[]); hasilnya adalah f(.48534) Kemudian berturut-turut di bawah ini perintah untuk mencari f( ) dan f(5.6417) > f(nilai_kritis[3]); > f(nilai_kritis[4]); dari perhitungan diperoleh hasil f( ) dan f(5.6417) Selanjutnya akan dicari nilai fungsi pada tepi interval yaitu pada x=0 dan x=π.
112 11 Turunan > f(0); > f(*pi); kedua perintah tersebut diperoleh f(0) = 0 dan f(π) = π. Alangkah baiknya untuk f(π) dinyatakan dalam bentuk floating point supaya dapat dibandingkan dengan nilai fungsi pada nilai kritis. > evalf(%); dan diperoleh hasil f(π) Berdasarkan hasil perhitungan nilai fungsinya, terlihat bahwa untuk sekitar x = memiliki nilai fungsi terbesar, dan sekitar x = memiliki nilai fungsi terkecil. Dengan demikian f(5.6417) merupakan nilai maksimum dan f( ) merupakan nilai minimum fungsi. Sebagai ilustrasi, berikut ini grafik fungsi f(x) pada selang [0, π]. Lihat Gambar 7-8. Gambar 7-8. Grafik fungsi f(x) = x- sin(x) Dari gambar tersebut memang terlihat bahwa nilai maksimum mutlak fungsi terletak pada x antara 5 dan 6. Melalui perhitungan sebelumnya diperkirakan sekitar x= Sedangkan nilai minimum mutlak fungsi terletak pada x antara 0 dan 1, yang berdasarkan perhitungan sebelumnya diperkirakan sekitar
113 Kalkulus dengan Maple 113 Fungsi Naik dan Fungsi Turun Nilai x dimana suatu grafik fungsi f(x) naik atau turun dapat diketahui dengan menggunakan konsep turunan. Pada contoh sebelumnya dalam bab ini sudah digambarkan bahwa grafik fungsi f(x) akan turun apabila f (x) bernilai negatif (f (x) < 0). Sedangkan apabila f (x) > 0, maka grafik f(x) akan naik. Contoh: Diberikan fungsi f(x) = x /3 (6-x) 1/3. Tentukan nilai x sedemikian hingga f(x) naik atau turun! Penyelesaian: > f := (x) -> surd(x^,3) *surd(6-x,3); Berikutnya akan dicari penyelesaian untuk x dari f (x) > 0, yaitu nilai x yang menyebabkan f(x) naik. > solve(diff(f(x),x)>0,{x}); perintah tersebut menghasilkan output {x < 4, 0 < x} atau dengan kata lain 0 < x < 4. Kemudian akan dicari penyelesaian untuk x dari f (x) <0, yaitu nilai x yang menyebabkan f(x) turun. > solve(diff(f(x),x)<0,{x}); dan diperoleh hasil {x < 0}, {4 < x, x < 6}, dan {6 < x} atau dengan kata lain diperoleh hasil x < 0, 4 < x < 6, dan x > 6. Untuk memberikan gambaran hal ini, akan digambar grafik fungsi f(x), misalnya untuk domain [-10,10]. > plot(f(x),x= );
114 114 Turunan dan diperoleh grafik seperti pada Gambar 7-9 Gambar 7-9. Grafik fungsi f(x) = x /3 (6-x) 1/3 Berdasarkan ilustrasi grafik tersebut, tampak bahwa untuk x < 0 nilai f(x) turun, kemudian naik untuk 0 < x < 4, turun kembali pada 4 < x < 6 dan x > 6. Titik Balik Grafik Fungsi Diberikan suatu fungsi f(x). Misalkan a adalah nilai kritis dari f(x), maka titik (a, f(a)) dinamakan titik balik. Pada titik inilah terjadi perubahan arah grafik fungsi. Adapun jenis titik balik ada 3 macam, yaitu titik balik maksimum, minimum, dan titik belok. Untuk lebih jelasnya, perhatikan grafik fungsi f(x) = 0.5x 4 -x 3 +4x pada interval [-,6] pada Gambar Pada gambar tersebut terlihat memiliki titik balik yang terletak pada x=0, x=, dan x=4. Untuk x=0 dan x=4 titik balik yang ada dinamakan titik balik minimum karena untuk x < 0 menyebabkan f(x) turun (demikian pula untuk x < 4) dan untuk x > 0 menyebabkan f(x) naik, begitu pula untuk x > 4. Sedangkan pada x= titik baliknya dinamakan titik balik maksimum karena untuk x < menyebabkan f(x) naik dan untuk x > membuat f(x) turun.
115 Kalkulus dengan Maple 115 Gambar Grafik fungsi f(x) = 0.5x 4 -x 3 +4x Misalkan pada x=a terdapat titik balik. Apabila untuk x<a menyebabkan f(x) naik dan untuk x>a menyebabkan f(x) juga naik, maka x=a dinamakan titik belok. Begitu pula apabila untuk x<a menyebabkan f(x) turun dan untuk x>a nilai f(x) juga turun, maka x=a juga dinamakan titik belok. Berikut ini diberikan contoh menentukan titik balik dan jenisnya menggunakan Maple. Contoh: Tentukan titik balik dan jenisnya dari f ( x) = x x + 4. Penyelesaian: Langkah pertama adalah mencari nilai kritis dari fungsi. > f := (x) -> x/(x^+4); > solve(diff(f(x),x)=0,x); Dari perintah tersebut akan diperoleh hasil dan, artinya titik balik fungsi ada di x=- dan x=. Selanjutnya untuk menentukan jenis titik balik di x=-, pilih sebarang nilai x pada interval x<- dan pada interval <x<. Misalkan pada interval x<- dipilih x =-3 dan untuk interval <x< dipilih x=1. Selanjutnya akan dicari nilai f (x) untuk kedua nilai x. Dengan menggunakan perintah berikut ini
116 116 Turunan > eval(diff(f(x),x),x=-3); akan dihasilkan 5/169 atau dengan kata lain f (x) bernilai negatif (f (x) < 0). Artinya f(x) turun untuk x<-. > eval(diff(f(x),x),x=1); Hasilnya akan diperoleh 3/5 sehingga f (x) positif, artinya untuk f(x) naik. <x< fungsi Dengan demikian dapat disimpulkan bahwa x=- terdapat titik balik minimum, lebih tepatnya pada titik (-, -1/4). Berikutnya untuk x=. Pilih sebarang nilai x pada <x< dan pada x>. Misalkan pada <x< dipilih x=0 dan pada x> dipilih 4. Selanjutnya akan dicari nilai f (x) untuk kedua nilai x. > eval(diff(f(x),x),x=0); > eval(diff(f(x),x),x=4); Dari perhitungan tersebut, nilai f (x) untuk x=0 adalah positif (1/4). Dengan demikian untuk <x< nilai f(x) adalah naik. Sedangkan untuk x=4, diperoleh nilai f (x)=- 3/100. Sehingga dapat dikatakan pada x>, nilai f(x) turun. Berdasarkan perhitungan, maka dapat disimpulkan bahwa di x= terdapat titik balik maksimum tepatnya pada titik (,1/4) Untuk menguji kebenaran perolehan kedua titik balik, dapat dilihat grafik fungsinya. Perhatikan Gambar 7-11.
117 Kalkulus dengan Maple 117 Gambar Grafik fungsi f(x) = x/(x +4) pada interval [-6,6] Pada Gambar 7-11 tampak bahwa titik balik minimum terletak pada x=-, dan titik balik maksimum pada x=. Contoh: Tentukan titik balik dan jenisnya untuk f(x) = x 3 x 4. Penyelesaian: Terlebih dahulu akan dicari nilai kritis dari f(x). > f := (x) -> *x^3-x^4; > solve(diff(f(x),x)=0,x); Berdasarkan hasil perhitungan diperoleh bahwa titik balik terletak pada x=0 dan x=3/. Berikutnya akan ditentukan jenis titik balik di kedua titik ini. Pilih sebarang nilai x pada x < 0. Dalam hal ini, dapat dipilih x = -3. Selanjutnya pilih x pada 0 < x < 3/, misalnya dipilih x = 1. Nilai f (x) pada kedua nilai x tersebut akan ditentukan. > eval(diff(f(x),x),x=-3); > eval(diff(f(x),x),x=1);
118 118 Turunan Nilai f (x) pada perhitungan di atas akan dihasilkan 16 untuk x=-3 atau f (x) > 0. Dengan demikian untuk x < 0 nilai f(x) naik. Sedangkan untuk x=1, nilai f (x) = atau f (x) > 0. Dalam hal ini untuk 0 < x < 3/ nilai f(x) juga naik. Sehingga berdasarkan keterangan yang diperoleh dapat disimpulkan pada x=0 terdapat titik belok, lebih tepatnya pada titik (0,0). Selanjutnya akan ditentukan jenis titik balik yang ada di x=3/. Pilih sebarang x pada 0 < x < 3/, misalnya x=1/ dan sebarang x pada x > 3/, misalnya x=5. Dengan cara yang sama akan diperoleh hasil bahwa titik balik pada x=3/ merupakan titik balik maksimum tepatnya pada titik (3/, 7/16). Sebagai pembanding, dapat dilihat gambar grafik dari fungsi ini pada Gambar 7-1. Gambar 7-1. Grafik fungsi f(x) = x 3 x 4 Optimisasi Aplikasi turunan yang terkait dengan optimisasi ini merupakan pengembangan dari pencarian nilai maksimum dan minimum yang telah dibahas di subbab sebelumnya. Pada subbab ini, pencarian nilai maksimum dan minimum akan diaplikasikan pada permasalahan kehidupan sehari-hari. Kasus 1. Perhatikan gambar berikut ini. 6 cm
119 Kalkulus dengan Maple 119 Berapakah luas maksimum persegi panjang yang terbentuk jika kedua titik sudutnya terletak pada keliling setengah lingkaran yang berjari-jari 6cm, dan salah satu sisinya berimpit dengan diameter lingkaran? Penyelesaian: Terlebih dahulu misalkan panjang persegi panjang adalah a cm dan lebarnya b cm. R b cm a cm Dengan R adalah jarak antara titik tengah diameter lingkaran dengan salah satu titik sudut persegi panjang, atau dengan kata lain R adalah jari-jari setengah lingkaran. Dari gambar tersebut diperoleh: a a a R = b + 36 = b + b = 36 Dengan demikian luas persegi panjang adalah a L = a. b = a 36 Selanjutnya untuk mencari nilai maksimum L, terlebih dahulu dicari nilai kritis dari L. Berikut ini adalah perintah Maplenya. > L := (a) -> a*sqrt(36-(a/)^); > solve(diff(l(a),a)=0,a); Dari perhitungan tersebut diperoleh hasil nilai kritisnya adalah a= 6 dan a= 6. Akan tetapi ukuran panjang tidak mungkin bernilai negatif, sehingga untuk a=- 6 dapat diabaikan. Dengan demikian dapat diketahui bahwa untuk mendapatkan luas persegi panjang maksimum maka panjangnya harusnya 6 cm. Sedangkan luas maksimumnya sendiri dapat dicari dengan perintah Maple > L(6*sqrt());
120 10 Turunan dan diperoleh hasil 18. Jadi luas maksimum persegi panjang adalah 18 cm. Kasus. Sebuah perahu A meninggalkan sebuah dermaga pada pukul dan berlayar menuju selatan dengan kecepatan 0 km/jam. Perahu lain katakanlah B menuju ke timur pada kecepatan 15 km/jam dan mencapai dermaga yang sama pukul Tentukan pada pukul berapa kedua perahu itu paling berdekatan dan berapa jarak yang paling berdekatan tersebut? Penyelesaian: Ilustrasi kasus ini dapat digambarkan sebagai berikut Kapal B dermaga R Kapal A Dengan R adalah jarak antara kedua kapal. Pada kasus ini, ketika kapal A baru berangkat (pukul 14.00), maka posisi kapal B berjarak 15 km dari dermaga (mengingat satu jam berikutnya yaitu jam kapal B sampai di dermaga dengan kecepatan 15 km/jam). Jarak yang ditempuh kapal B setelah t jam adalah 15t km. Dengan demikian perubahan jarak kapal B dari dermaga sejak pukul adalah 15-15t km. Sedangkan perubahan jarak kapal A dari dermaga sejak pukul adalah 0t km. Sehingga ilustrasi kasus tersebut dapat digambarkan sebagai berikut
121 Kalkulus dengan Maple 11 Kapal B 15-15t km dermaga R 0t km Kapal A Dengan menggunakan teorema Pythagoras, dapat ditentukan jarak antara kedua kapal yaitu ( ) ( 0 ) R = t + t Sehingga jarak kedua kapal paling berdekatan adalah ekuivalen dengan mencari minimum dari R. Berikut ini adalah perintah Maplenya. > R := (t) -> sqrt((15-15*t)^ + (0*t)^); > solve(diff(r(t),t)=0,t); Berdasarkan perhitungan diperoleh hasil bahwa nilai kritis adalah t = 9/5. Dengan kata lain, kedua kapal paling berdekatan setelah 9/5 jam atau 1 menit 36 detik. Sehingga kedua kapal berada paling berdekatan pada pukul 14.1 lebih 36 detik. Sedangkan jarak R dapat dicari dengan perintah > R(9/5); dan diperoleh hasil 1. Jadi kedua kapal berada paling berdekatan pada jarak 1 km. Kasus 3. Dalam suatu sarang lebah, setiap sel berupa prisma segienam beraturan yang terbuka pada satu ujung dengan sudut trihedral pada sudut yang lainnya. Perhatikan gambar berikut ini.
122 1 Turunan θ h s Dipercaya bahwa lebah membentuk sel sarangnya dalam suatu cara sehingga dapat meminimumkan luas permukaan sel. Hal ini dilakukan oleh lebah untuk meminimumkan jumlah lilin yang digunakan untuk membangun sel. Berdasarkan ilmu geometri, luas permukaan sel (S) dapat dirumuskan sebagai berikut: 3 3 S = sh s θ + s 6 cot 3 csc dengan s adalah panjang sisi segienam dan h adalah tinggi sel. Keduanya adalah konstanta. 1. Tentukan ds/dθ. Berapa seharusnya sudut (θ) yang lebih disenangi lebah? 3. Tentukan luas permukaan minimum sel lebah (dalam s dan h) 4. Gambar grafik S untuk s=0.5 cm dan h=.5 cm 5. pada θ [0.5,1.]. Ingat, bahwa dalam hal ini θ dalam satuan radian. θ Penyelesaian: 1. Berikut ini adalah perintah untuk mencari ds/dθ > S:=(teta)->6*s*h-3/*s^*ctg(teta)+ 3/*sqrt(3)*s^*csc(teta); > Derv := (teta) -> diff(s(teta),teta); perintah tersebut akan menghasilkan cot θ s 3 cscθ cotθ ds/dθ = s ( )
123 Kalkulus dengan Maple 13. Dalam hal ini, akan dicari nilai θ sedemikian S minimum. Sehingga dalam mencari θ, terlebih dahulu akan dicari nilai kritis dari S. Dengan menggunakan perintah berikut > nilaikritis := evalf(solve(derv(teta)=0),teta); akan diperoleh hasil nilaikritis = ( , ); Artinya bahwa telah diperoleh buah nilai kritis. Apabila kedua nilaikritis dikonversi ke dalam derajad, maka perintahnya: > sudut1 := nilaikritis[1]*180/pi; > sudut := nilaikritis[]*180/pi; Dua perintah di atas akan menghasilkan buah sudut dalam derajad, yaitu o dan o. Dalam hal ini untuk sudut negatif tidak mungkin, sehingga untuk mendapatkan luas permukaan minimum, besar θ adalah sekitar o. 3. Luas permukaan sel S dapat dicari dengan perintah berikut > evalf(s(nilaikritis[1])); dan akan diperoleh hasil luas permukaan S adalah 6sh s. 4. Berikut ini adalah perintah plot untuk menggambar grafik S Untuk s=0.5 cm dan h=.5 cm > s := 0.5; > h :=.5; > plot(s(teta),teta= ); dan perintah tersebut akan menghasilkan grafik seperti berikut (Gambar 7-13)
124 14 Turunan Gambar Grafik S(θ) pada interval [0.5, 1.] Dari Gambar 7-13 tampak bahwa nilai minimum S berada di sekitar θ = 0.95 hal ini mendukung hasil perhitungan soal b. Soal-soal Latihan 1. Dengan menggunakan definisi turunan, tentukan f (x) berikut ini. a. ( ) f x = 1 + x x b. f ( x) x = 3x c. f ( x) = 1 6x 1 3x 4x 3 d. f ( x) = e. f ( x) = x + 1 f. f ( x) = x + sin( x) g. f ( x) = 3e + e x h. f ( x) xsin = x e cos ( x) ( x). Tentukan gradien pada x=3 dari semua fungsi f(x) yang ada pada soal no. 1
125 Kalkulus dengan Maple Gambarlah grafik fungsi f (x) dari f(x) yang ada pada soal no. 1 dengan dan tanpa menggunakan perintah DerivativePlot. 4. Tunjukkan bahwa f ( x) x 6 sketsa grafiknya. = tidak diferensiabel di x=6. Carilah f (x) dan buat 5. Dengan menggunakan perintah diff, tentukan turunan fungsi-fungsi berikut ini a. f ( x) = ( 16x) 3 g x 1 = x + x b. ( ) 1 f x = 5x + x + x c. ( ) h x = x 4x d. ( ) e. g( x) 4 3/4 5/3 x 3x x = x f. G( s) = ( s + s + 1)( s + ) g. f ( t) = ( 3t 14) 15 ( t + 4t ) h. H ( t) = 3 t ( t + ) B C K t A t t i. ( ) = + + j. g( x) = x x + k. h( x) = x + x + x l. ( ) x 1 x s = + sin s s F s e + m. H ( x) = tan( sin x + cos x) n. P( x) ( x ) ( x ) 1 + tan + = 1 tan Gunakan Calculus 1 Student Package untuk mencari turunan dari fungsifungsi yang ada di soal no. 6.f sampai 6.n.
126 16 Turunan 7. Carilah titik pada kurva y = x 3 x x + 1 yang garis singgungnya mendatar! 8. Carilah semua titik dari fungsi ( ) mendatar! f x sin x sin x = + yang garis singgungnya 9. Tunjukkan bahwa kurva y = 6x 3 + 5x 3 tidak mempunyai garis singgung yang gradiennya Carilah persamaan garis singgung pada kurva berikut ini di titik yang diberikan a. b. x y =, (1,1) x + 1 x y =, (4,0.4) x + 1 c. y = x + x x, (1,) 11. Kurva y=1/(1+x ) disebut kurva sihir Maria Agnesi. Carilah persamaan garis singgung pada kurva ini di titik (-1, 0.5). Selanjutnya gambarlah grafik y dan garis singgung di titik tersebut dalam satu bidang grafik. 1. Kurva y=x/(1+x ) disebut kurva serupa ular. Carilah persamaan garis singgung pada kurva ini di titik (3, 0.3). Selanjutnya gambarlah grafik y dan garis singgung di titik tersebut dalam satu bidang grafik. 13. Pada x berapakah fungsi f(x) berikut terdiferensial? ( ) 1 x jika x < 1 = jika x jika x > 1 f x x x Tentukan pula f (x) dan buat sketsa grafik f(x) dan f (x). 14. Jika persamaan gerak partikel diberikan oleh s = Acos( ωt + δ ) dengan ω dan δ adalah suatu konstanta, maka partikel tersebut dikatakan mengalami gerak harmonis sederhana. a. Carilah kecepatan [artikel pada waktu t b. Kapan kecepatannya sama dengan 0? 15. Bintang-bintang bernama Chepeid adalah bintang yang kecemerlangannya berganti-ganti (bertambah dan berku-rang). Diantara bintang-bintang tersebut yang paling dapat dilihat dengan mudah adalah Delta Chepei yang kecemerlangannya dirumuskan oleh
127 Kalkulus dengan Maple 17 ( ) = sin ( πt/5.4) B t dengan t diukur dalam satuan hari. a. carilah laju perubahan kecemerlangan setelah t hari b. carilah laju perubahan kecemerlangan setelah 5 hari 16. Carilah persamaan garis singgung pada kurva berikut ini pada titik yang diberikan a. y x = 1, (-5, -9/4) 16 9 b. y x + = 1, (-1, 4 ) 9 36 c. y x 3 ( 3 x) =, (1,) d. x y ( y 1) ( 4 y ) = +, (0,-) 17. Kurva dengan persamaan y =x +3x disebut kubik Tschirnhausen. Carilah persamaan garis singgung kurva di titik (1,-). Selanjutnya gambarkan kurva dan garis singgung di titik tersebut. Tentukan pula titik pada kurva dimana garis singgungnya mendatar. 18. Lampu jalan dipasang pada puncak tiang setinggi 5 kaki. Seorang pejalan kaki yang tingginya 6 kaki berjalan menjauhi tiang tersebut dengan kecepatan 5 kaki/detik sepanjang garis lurus. Seberapa cepat ujung bayangan bergerak sewaktu orang tersebut berada sejauh 40 kaki dari tiang? 19. Volume suatu kubus bertambah pada laju 35 cm 3 /menit. Berapa cepat luas permukaan kubus bertambah pada waktu panjang sisi 40 cm? 0. Volume 1 kg air pada suhu T antara 0 o C sampai dengan 30 o C dirumuskan dengan V = T T T 3 Carilah suhu T yang menyebabkan air mencapai volume maksimum! 1. Model untuk harga suatu makanan antara tahun 1984 dan 1994 diberikan oleh rumus ( ) P t = t t t + t t
128 18 Turunan dengan t diukur dalam tahun terhitung mulai tahun 1985, sehingga 0 t 10 dan satuan P(t) adalah dalam dollar. Tentukan harga makanan terendah dalam kurun waktu tersebut!. Carilah nilai kritis, maksimum dan minimum lokal, titik balik, dan selang dimana f(x) turun atau naik dari fungsi-fungsi f(x) berikut ini. Selanjutnya bandingkan hasil perhitungan tersebut dengan grafik fungsinya. a. ( ) 3 f x = x 3x 15x b. ( ) f x = x x + c. f ( x) = x x + d. f ( x) = x 1/3 ( x + 4) /3 e. f ( x) x = x + 5 x Carilah luas persegi panjang maksimum yang dapat diletakkan dalam segitiga siku-siku dengan panjang alas 4 cm dan tinggi 3 cm. Kedua sisi-sisi persegi panjang terletak pada sisi alas dan tinggi segitiga! 4. Sebuah kaleng silinder tanpa tutup dibuat untuk menampung V cm 3 cairan. Carilah ukuran kaleng (jari-jari dan tinggi) sedemikian hingga meminimumkan biaya baja untuk membuat kaleng tersebut! 5. Sebuah talang penampung air hujan dibangun dari lembaran seng yang memiliki lebar 30 cm dengan menekuk sepertiga lebar senga ke atas pada masing-masing sisi sebesar sudut θ (perhatikan gambar berikut). θ θ 10 cm 10 cm 10 cm Tentukan θ sedemikian hingga diperoleh bentuk talang yang dapat menampung air dalam jumlah maksimum?
129 Kalkulus dengan Maple 19 Bab 6 Integral Integral Tentu Secara matematis, integral tentu adalah sebagai berikut: Misalkan f fungsi kontinu yang didefinisikan untuk a x b. Selanjutnya interval x = b a / n. [a,b] dibagi menjadi n subinterval yang sama dengan lebar ( ) Dimisalkan x 0 (=a), x 1, x,, x n(=b) adalah titik-titik ujung subinterval tersebut dan dipilih titik-titik x 1*, x *,, x n* pada setiap subinterval sehingga x i* terletak pada setiap selang [x I-1, x i], maka definisi integral tentu f dari a sampai b adalah Jumlahan b a n * ( ) lim ( i ) f x dx = f x x n i = 1 ( i ) n f x * i= 1 yang muncul pada definisi integral tentu dinamakan jumlahan Riemann. Pada subbab ini akan dibahas bagaimana menentukan integral tentu dengan menggunakan konsep jumlahan Riemann dan juga perintah khusus dalam Maple untuk menghitung integral tentu. Jumlahan Riemann Jumlahan Riemann ini menghitung integral tentu secara pendekatan. Nilai integral tentu f(x) dari [a, b] dihitung dengan mencari luas seluruh persegi panjang yang ada antara garis kurva dan sumbu x. Dalam Maple telah tersedia perintah untuk memvisualisasikan jumlahan Riemann ini secara grafis dan juga menghitung nilai integral tentu tersebut. Perintah ini terdapat dalam Calculus1 Student Package. Adapun sintaks perintahnya adalah x > with(student[calculus1]): > RiemannSum(f(x), x = a..b, option)
130 130 Integral Perintah di atas digunakan untuk menghitung jumlahan Riemann suatu fungsi f(x) dengan batas kiri a dan batas kanan b menggunakan metode tertentu (jenis metode ditambahkan pada option). Adapun pada option dapat ditambahkan perintahperintah sebagai berikut - method = left, right, midpoint, upper, lower, atau random Perintah ini digunakan untuk menentukan metode yang digunakan dalam perhitungan jumlahan Riemann. Beberapa alternatif pilihan metode yang dapat digunakan adalah: a. method = left, metode ini memilih x * i yaitu titik di paling kiri subinterval b. method = right, metode ini memilih x * i yaitu titik di paling kanan subinterval c. method = midpoint, metode ini memilih x * i yaitu titik di tengah subinterval. Metode ini adalah sebagai default dari perintah RiemannSum, sehingga apabila option method tidak disertakan, maka metode inilah yang digunakan oleh Maple. d. method = upper, metode ini memilih x * i yaitu titik yang paling besar nilai fungsinya dalam subinterval e. method = lower, metode ini memilih fungsinya dalam subinterval * x i yaitu titik yang paling kecil nilai f. method = random, metode ini memilih x * i secara random dalam subinterval - output = value, plot, sum, animation Perintah dalam option ini digunakan untuk menentukan output yang ingin ditampilkan setelah perintah RiemannSum ini diberikan. Berikut ini beberapa jenis output yang dapat dipilih a. output = value, digunakan untuk menampilkan output dalam bentuk hasil pendekatan jumlahan Riemann (default) b. output = plot, digunakan untuk menampilkan output dalam bentuk grafik yang memvisualisasikan jumlahan Riemann. c. output = sum, digunakan untuk menampilkan output dalam bentuk formulasi jumlahan ( i ) n * i= 1 f x x. d. output = animation, digunakan untuk menampilkan output dalam bentuk animasi.
131 Kalkulus dengan Maple partition = n Option ini digunakan untuk menentukan jumlah partisi /subinterval dalam interval [a, b]. Secara default jumlah partisi adalah 10. Sedangkan apabila ingin mempartisi interval menjadi 0 subinterval, maka tambahkan perintah partition=0 pada option ini. - Title = string Judul/title dari visualisasi dapat diatur menggunakan option ini. Contoh: Tentukan integral tentu dari 5 sin( x) dx 0 dengan jumlahan Riemann menggunakan 0 partisi/subinterval. Metode yang digunakan adalah titik kiri (left). Tampilkan pula visualisasi secara grafis jumlahan Riemann ini. Penyelesaian: > f := x -> sin(x); > with(student[calculus1]): > RiemannSum(f(x), x = 0..5, partition=0, method=left, output=value); > evalf(%); Perintah diatas akan menghasilkan Nilai tersebut adalah nilai pendekatan dari integral tentu f(x)=sin(x) dengan batas bawah 0 dan batas atas 5 dengan 0 partisi. Berikutnya, kita akan memvisualisasikan jumlahan Riemann untuk kasus ini. > RiemannSum(f(x), x = 0..5, partition=0, method=left, output=plot,title= Jumlahan Riemann f(x)=sin x ); Selanjutnya akan diperoleh grafik seperti pada Gambar 8-1.
132 13 Integral Gambar 8-1. Visualisasi Jumlahan Riemann untuk f(x)=sin(x) dengan 0 partisi pada [0,5] Pada gambar tersebut terlihat bahwa interval [0,5] dibagi menjadi 0 partisi. Nilai pendekatan integral tentu diperoleh dengan menjumlahkan luasan persegi panjangpersegi panjang yang dibatasi oleh kurva dengan sumbu x. Bagaimana apabila jumlah partisi diperbanyak? Bandingkan Gambar 8-1 dengan Gambar 8- berikut ini yang menggunakan jumlah partisi 50. Gambar 8-. Visualisasi Jumlahan Riemann untuk f(x)=sin(x) dengan 50 partisi pada [0,5] Dari gambar tersebut tampak bahwa semakin banyak partisi, maka luasan semua persegi panjang semakin mendekati luasan bidang yang dibatasi kurva dengan sumbu x. Dengan demikian semakin banyak partisi yang diambil maka hasil pendekatan integral tentu semakin mendekati eksaknya. Pertanyaannya sekarang adalah bagaimana menentukan hasil eksak dari integral tentu f(x) dengan batas integrasi a sampai b? Secara definisi yang sudah dijelaskan
133 Kalkulus dengan Maple 133 sebelumnya, kita dapat menghitungnya dengan Maple. Berikut ini adalah urutan perintahnya. > with(student[calculus1]): > RiemannSum(f(x), x = a..b, partition=n,output=sum); > limit(%,n=infinity); Perintah kedua digunakan untuk mencari formula jumlahan Riemaan dengan partisi sejumlah n. Selanjutnya formula Riemann yang telah diperoleh dicari limitnya untuk n. Untuk perintah terakhir tersebut dapat pula diubah menjadi > evalf(limit(%,n=infinity)); untuk menyatakan hasil integral tentu dalam bentuk floating point. Contoh: Dengan menggunakan perhitungan sesuai dengan definisi integral tentu, tentukan Penyelesaian: 3π π ( ) x cos x dx > with(student[calculus1]): > f := x -> x*cos(x); > RiemannSum(f(x), x = Pi..3*Pi, partition=n,output=sum); > limit(%,n=infinity); Secara perhitungan, hasil integral tentu untuk contoh ini adalah 0. Menghitung Integral Tentu Selain cara perhitungan integral menggunakan definisi, dalam Maple juga terdapat perintah yang lebih praktis untuk perhitungan integral tentu. Berikut ini adalah sintaks untuk menghitung integral tentu f(x) dengan batas integrasi a sampai b adalah: > int(f(x),x=a..b);
134 134 Integral Contoh: Tentukan nilai integral tentu berikut ini 1. 7 x dx x x e sin x dx 5 1/3 3/ 3. ( + 1) x x dx 4. 8 f ( x) dx dengan f ( x) 0 x, x < 4 = x, x 4 Penyelesaian: 1. > int(x/(x-3),x=4..7); dan akan diperoleh hasil 3+ln() atau dalam floating point.. > evalf(int(exp(x)*sin(x),x=-1..4)); Hasil integrasinya akan diperoleh > evalf(int(surd(x^3,)*surd(x+1,3),x=..5)); dan hasilnya adalah > f := x -> piecewise(x<4,x,x>=4,x^); > int(f(x),x=0..8); Hasil integrasinya adalah 47/3 atau
135 Kalkulus dengan Maple 135 Integral Tak Tentu Integral tak tentu dari suatu fungsi merupakan kebalikan dari turunan/derivatif sehingga integral tak tentu ini juga disebut anti derivatif. Misalkan F(x) adalah suatu fungsi dan f(x) merupakan derivatif dari F(x) tersebut, maka integral tak tentu dari f(x) dinotasikan sebagai f x dx ( ) = F ( x ) Maple juga menyediakan perintah untuk mencari integral tak tentu ini. Perintahnya mirip dengan pencarian integral tentu. Misalkan akan dicari integral f(x) terhadap x, maka sintaks perintahnya adalah: > int(f(x),x); Contoh: Tentukan integral berikut 1. ( x + ) sin dx. ( t cos ) t dt 3. x + dx x /3 1 Penyelesaian: 1. > f := x -> (x+)^; > int(f(x),x); Hasilnya akan diperoleh ( x + ) 3 3. > int(sin(t)-cos(t),t); Hasil integralnya adalah cos ( t) sin ( t )
136 136 Integral 3. > int(x^(/3)+1/x,x); Hasilnya adalah 3x 5 5/3 + ln ( x ) Calculus1 lus1 Student Package untuk Integral Dalam subbab ini akan dibahas mengenai bagaimana mencari integral dengan menggunakan Calculus1 Student Package. Meskipun Maple telah menyediakan perintah untuk mencari integral dengan cepat seperti yang dibahas sebelumnya, namun sangatlah perlu untuk mempelajari teknik pengintegralan, terutama bagi para siswa yang sedang mempelajari kalkulus integral. Cara penggunaan Calculus1 Student Package untuk mencari integral hampir sama dengan mencari limit dan turunan seperti yang telah dibahas di bab sebelumnya. Sebagai awal untuk menggunakan paket ini, berikut adalah perintah untuk aktifasinya. > with(student:-calculus1): > infolevel[student] := 1: Sedangkan tabel berikut ini menampilkan beberapa aturan yang dapat diberikan dalam teknik pengintegralan.
137 Kalkulus dengan Maple 137 Nama Aturan Notasi Deskripsi constant c dx = cx constantmultiple `c*` ( ) = ( ) cf x dx c f x dx ' diff Diff f ( x) dx = f ( x ) difference `-` ( ) ( ) identity ( ) = ( ) ( ) f x g x dx f x dx g x dx x x dx = partialfractions ( ) = ( ( ) + ( ) + ) 1 f x dx R x R x dx dengan ( ) ( ) R x + R x + adalah pecahan partial dari f(x). 1 n+ 1 power `^` n x x dx = n + 1 change revert parts Menyelesaikan integrasi dengan substitusi. Mengembalikan perubahan substitusi variabel Menyelesaikan integrasi menggunakan teknik integral parsial. solve ( ) '( ) f x g x dx = ( ) ( ) ( ) '( ) f x g x g x f x dx sum `+` ( ( ) ( )) Menyelesaikan integrasi secara aljabar apabila dijumpai bentuk integral yang sama lebih dari sekali. Biasanya sering digunakan untuk integrasi parsial. f x + g x dx = ( ) + ( ) f x dx g x dx Tabel 8-1. Aturan teknik pengintegralan Selain aturan tersebut, terdapat pula aturan yang terkait dengan bentuk dasar fungsi. Perhatikan tabel berikut ini.
138 138 Integral Nama Aturan sin Deskripsi sin x dx = cos x cos cosx dx = sin x tan tan x dx = ln ( cos x ) csc csc x dx = ln( csc x + cot x ) sec sec x dx = ln( sec x + tan x ) cot cot x dx = ln ( sin x ) sinh sinh = cosh cosh = tanh tanh x dx = ln( cosh x ) csch sech = ln tanh x x dx tanh sech x dx = arctan ( sinh x ) coth coth x dx = ln ( sinh x ) ln ln x dx = xln x x x exp e dx = e x Tabel 8-. Aturan pengintegralan terkait dengan bentuk fungsi dasar Contoh: Dengan menggunakan Calculus1 Student Package, tentukan integral berikut ini. sin x dx 1. x ( )
139 Kalkulus dengan Maple 139. ( x + 1) x e dx 3. sin ( + 1) x+ 1 x e dx 4. 3x 1 1 dx 3x x x Penyelesaian: > with(student:-calculus1): > infolevel[student] := 1: 1. Misalkan f ( x) = xsin( x ) > f := x -> *x*sin(x); Sebagai langkah pertama dapat digunakan aturan constantmultipe > Rule[constantmultiple](Int(f(x),x)); ( ) = ( ) xsin x dx xsin x dx (*) Selanjutnya dapat digunakan aturan integral parsial (parts). Misalkan akan dicari ( ) '( ) = ( ) ( ) ( ) '( ) f x g x dx f x g x g x f x dx dengan integral parsial, maka penulisan aturan ini adalah Rule[parts,f(x),g(x)]. Untuk integral (*) tersebut, dapat dipilih f(x)=x dan g(x) = -cos(x). > Rule[parts,x,-cos(x)](%);
140 140 Integral Hasilnya adalah ( ) = ( ) ( ) xsin x dx x cos x cos x dx Kembali diberikan aturan constantmultiple. > Rule[constantmultiple](%); diperoleh hasil ( ) = ( ) + ( ) xsin x dx x cos x cos x dx Selanjutnya integral terakhir yang diperoleh dapat diselesaikan dengan aturan cosinus (cos). > Rule[cos](%); ( ) = ( ) + ( ) x sin x dx x cos x sin x Demikianlah hasil integral dari contoh pertama ini.. Misalkan ( ) ( 1) f x = x + e x > f := (x+1)^*exp(x); Sebagai langkah pertama dapat dimisalkan u = x+1. > Rule[change,u=x+1](Int(g(x),x));
141 Kalkulus dengan Maple 141 ( u ) ( + 1) = x 1 e x dx e u du Langkah berikutnya akan diterapkan aturan integral parsial dengan memilih f(u) = u dan g(u)=e u-1. > Rule[parts,u^,exp(u-1)](%); ( ) ( ) ( ) = u u x e x dx e u e udu > Rule[constantmultiple](%); ( ) ( ) ( ) = u u x e x dx e u e udu Selanjutnya diterapkan aturan integral parsial kembali dengan mengambil f(u)=u dan g(u)=e u-1 > Rule[parts,u,exp(u-1)](%); ( 1) ( 1) ( 1) ( + 1) = u u + u x e x dx e u e u e du Langkah berikutnya dapat dimisalkan y=u-1. > Rule[change,y=u-1](%); ( 1) ( 1) ( ) u u x y e x + 1 dx = e u e u + e dy
142 14 Integral Bentuk terakhir tersebut dijumpai integral dalam bentuk dasar eksponen, sehingga langkah berikutnya dapat diterapkan aturan exp. > Rule[exp](%); ( 1) ( 1) ( ) u u x e x + 1 dx = e u e u + e y Setelah tidak ada lagi bentuk integral, langkah berikutnya adalah menyatakan y sebagai u-1 kembali. > Rule[revert](%); ( u 1) ( u 1) ( u 1) ( + 1) = + x e x dx e u e u e Perintah berikut digunakan untuk menyatakan kembali u sebagai x-1. > Rule[revert](%); ( 1) x x x e x + dx = e x + e f x x e 3. Misalkan ( ) = sin ( + 1) x+ 1 > f := x -> sin(*x+1)*exp(*x+1); Sebagai langkah awal, dapat kita misalkan u = x+1. > Rule[change,u=*x+1](Int(h(x),x));
143 Kalkulus dengan Maple 143 ( ) ( x+ + ) = ( ) u sin x 1 e dx sin u e du 1 1 > Rule[constantmultiple](%); ( ) ( x+ + ) = ( ) u sin x 1 e dx sin u e du 1 1 Selanjutnya digunakan integral parsial dengan f(u)=sin(u) dan g(u)=exp(u). > Rule[parts,sin(u),exp(u)](%); ( ) ( x+ 1 ) 1 u 1 u sin x + 1 e dx = sin( u) e cos( u) e du Kembali digunakan integral parsial dengan f(u)=cos(u) dan g(u)=exp(u) > Rule[parts,cos(u),exp(u)](%); ( ) ( x+ 1 ) 1 u 1 u 1 u sin x + 1 e dx = sin( u) e cos( u) e + sin ( u) e du > Rule[constantmultiple](%); ( ) ( x+ 1 ) 1 u 1 u 1 u sin x + 1 e dx = sin( u) e cos( u) e sin ( u) e du Karena dijumpai kembali bentuk integral yang sama dengan langkah di awal yaitu sin ( ) u u e du, maka dapat digunakan aturan solve. > Rule[solve](%);
144 144 Integral ( ) ( + 1 ) 1 ( ) ( = + ) 1 sin x 1 e dx sin x 1 e cos( u) e 4 4 x x u Selanjutnya u dinyatakan kembali ke x+1. > Rule[revert](%); 1 1 sin 1 sin 1 cos ( ) ( x + 1 ) ( ) ( x = + ) ( + ) ( x + 1 x e dx x e x e ) 4. Misalkan f ( x) 3x 1 1 = 3x x x > f := x -> (3*x-1)/(3*x^-*x+1)-1/(5-3*x); Sebagai langkah awal, kita pilih aturan difference. > Rule[difference](Int(j(x),x)); 3x 1 1 3x 1 1 dx dx dx x = ( + ) 3x x 1 x ( 3x x + 1) Untuk integral bagian pertama dapat dimisalkan u=3x -x+1. > Rule[change,u=3*x^-*x+1](%); 3x dx = du + dx 5 3x u 5 3x ( + ) 3x x 1
145 Kalkulus dengan Maple 145 > Rule[constantmultiple](%); 3x dx du dx 5 3x u 5 3x = ( + ) 3x x 1 Selanjutnya digunakan aturan power. > Rule[power](%); 3x dx = dx x u 5 3x ( 3x x + 1) > Rule[constantmultiple](%); 3x dx = 5 3 dx x u 5 3x ( 3x x + 1) Untuk integral bagian kedua, dapat dimisalkan v=5-3x. > Rule[change,v=5-3*x](%); 3x dx = dv x u 3v ( 3x x + 1) > Rule[constantmultiple](%);
146 146 Integral 3x dx = dv x u v ( 3x x + 1) Untuk integral bagian kedua, selanjutnya digunakan aturan power > Rule[power](%); 3x dx = + ln 5 3x u 3 ( 3x x + 1) ( v) Perintah di bawah ini untuk menyatakan kembali v sebagai 5-3x. > Rule[revert](%); 3x dx = + ln x u 3 ( 3x x + 1) ( x) Sedangkan langkah berikut ini untuk menyatakan kembali u sebagai 3x -x+1. > Rule[revert](%); 3x dx = + ln x 6x 4x + 3 ( 3x x + 1) ( x) Mencari Integral Tentu dengan Metode Pendekatan Tidak semua fungsi yang terintegral dapat diintegralkan dengan mudah secara eksak dengan aturan-aturan yang ada. Beberapa fungsi sangat sulit untuk dicari integralnya.
147 Kalkulus dengan Maple 147 Oleh karena itu diperlukan metode numerik untuk mencari pendekatan hasil integrasi. Terdapat beberapa metode untuk mencari pendekatan integral tentu, diantaranya adalah metode trapezoid, Newton Cotes, metode Simpson, dan metode Simpson 3/8. Maple menyediakan perintah untuk mencari pendekatan integral tentu dengan metode tersebut. Selain itu, dapat pula dihasilkan visualisasi implementasi metode secara grafis. Berikut ini adalah sintaks penulisan perintah untuk mencari pendekatan integral tentu b a ( ) f x dx menggunakan Maple. > with(student[calculus1]): > ApproximateInt(f(x),x=a..b,option) Bagian option dapat dituliskan beberapa perintah berikut ini: - Method = newtoncotes[n], simpson, simpson[3/8], trapezoid Option ini digunakan untuk menentukan metode yang digunakan untuk mencari pendekatan integrasinya. Parameter N dalam newtoncotes dapat diisi bilangan bulat positif yang menyatakan order yang akan dipilih. - Output = sum, value, plot, animation Apabila output=sum yang dipilih, maka akan dihasilkan pendekatan integrasi tentu dalam bentuk/format jumlahan. Sedangkan apabila dipilih value, maka akan dihasilkan nilai hasil pendekatannya. Untuk menampilkan visualisasi grafis dari metode yang dipilih, digunakan output=plot. Output= animation akan menghasilkan visualisasi dalam bentuk animasi. - Partition = n Option ini menyatakan jumlah partisi/subinterval dalam interval [a, b]. - Title = string Title dari grafik visualisasi dapat diubah dengan option ini.
148 148 Integral Contoh: Tentukan pendekatan integral berikut ini. 0 x e dx menggunakan metode: 1. Trapezoid dengan 10 partisi/subinterval. Simpson dengan 1 partisi/subinterval 3. Simpson 3/8 dengan 15 partisi/subinterval Penyelesaian: Integral tersebut sangat sulit dicari penyelesaian eksaknya. Oleh karena itu dibutuhkan metode penyelesaian secara numerik. > f := x -> exp(x^); > with(student[calculus1]): 1. > ApproximateInt(f(x), x=0.., partition=10, method=trapezoid, output=plot, title="pendekatan Integral dengan M. Trapezoid"); Perintah tersebut menghasilkan grafik visualisasi penerapan metode trapezoid untuk mencari pendekatan integral pada contoh ini (lihat Gambar 8-3). Sedangkan perintah berikut digunakan untuk mencari hasil pendekatan integrasinya.
149 Kalkulus dengan Maple 149 Gambar 8-3. Visualisasi metode trapezoid dengan 10 partisi > ApproximateInt(f(x), x=0.., partition=10, method=trapezoid, output=value); > evalf(%); Adapun hasil pendekatan integrasinya akan diperoleh > ApproximateInt(f(x), x=0.., partition=1, method=simpson, output=plot, title="pendekatan Integral dengan M. Simpson"); > ApproximateInt(f(x), x=0.., partition=1, method=simpson, output=value); > evalf(%); 3. > ApproximateInt(f(x), x=0.., partition=15, method=simpson[3/8], output=plot, title="pendekatan Integral dengan M. Simpson 3/8"); > ApproximateInt(f(x), x=0.., partition=15, method=simpson[3/8], output=value); > evalf(%); Dalam penggunaan metode pendekatan integrasi tersebut, semakin banyak partisi yang diambil maka hasil pendekatannya juga semakin baik.
150 150 Integral Penggunaan metode pendekatan tertentu juga akan berpengaruh pada hasil. Secara teori numerik, metode simpson atau simpson 3/8 lebih baik daripada metode trapezoid. Hal ini dapat ditunjukkan dengan mengambil jumlah partisi yang sama untuk kedua metode, kemudian dibandingkan error penyelesaian pendekatannya yaitu selisih penyelesaian pendekatan dengan nilai sebenarnya/ eksak, apabila penyelesaian eksaknya sudah diketahui). Integral Lipat Misalkan diketahui fungsi dua variabel f(x, y). Fungsi ini akan diintegralkan terhadap x (dengan menganggap y tetap). Selanjutnya hasil integral akan diintegralkan kembali terhadap x (dengan menganggap y tetap). Hal tersebut merupakan integral lipat dua yang dinotasikan sebagai atau f ( x, y) dy dx (, ) f x y dy dx Dengan menggunakan Maple, dapat dengan mudah menentukan integral lipat baik untuk fungsi dua variabel atau lebih. Berikut ini adalah beberapa contoh penggunaannya. Contoh: Tentukan integral lipat berikut 4 1. ( x y + ) x y dx dy 3. ( + ) ( x 4 ) xy z x y z dzdy dx xy dy dx Penyelesaian: 1. > f := (x,y) -> *x^*y+x^4*y; > int(f(x,y),x); > int(%,y);
151 Kalkulus dengan Maple 151 Perintah kedua tersebut digunakan untuk mencari integral f(x, y) terhadap x dan dihasilkan x y + x y 3 5 Selanjutnya hasil integral yang diperoleh diintegralkan kembali terhadap y, sehingga akan dihasilkan 1 1 x 3 y + x 5 y > int(x*y^3*z^+x^*y-z,z); > int(%,y); > int(%,x); Hasil integral lipat tiga tersebut akan diperoleh x y 4 z 3 + x 3 y z z xy > int(x^-4*x*y,y=..3); > int(%,x=0..1); Hasil integral akan diperoleh 14/3. Penerapan Integral Pada subbab berikut ini akan dibahas mengenai penerapan integral dalam mencari luas daerah yang dibatasi kurva, menentukan volume dan luas permukaan benda putar, serta panjang busur suatu kurva. Luasan Daerah yang dibatasi Kurva Seperti telah dibahas pada pembahasan sebelumnya bahwa integral tentu suatu fungsi y=f(x) dari x=a b merupakan luas daerah yang dibatasi kurva y=f(x) dengan sumbu x untuk x=a sampai x=b. Berdasarkan konsep tersebut, integral dapat digunakan untuk mencari luasan yang dibatasi oleh beberapa kurva.
152 15 Integral Luas suatu daerah A yang dibatasi oleh kurva y=f(x), y=g(x), dan garis x=a, x=b dengan f dan g kontinu serta f(x) g(x) untuk semua x pada selang [a, b] adalah b a ( ) ( ) A = f x g x dx Selanjutnya akan diberikan beberapa contoh permasalahan penghitungan luas daerah dengan menggunakan Maple. Contoh: Tentukan luas daerah yang dibatasi oleh kurva y=x dan y=x-x. Penyelesaian: Untuk memudahkan penyelesaian, sebelumnya akan digambar dahulu daerah yang dimaksud. > f1 := x -> x^; > f := x -> *x-x^; > plot([f1(x),f(x)],x=0..1.5,color=[red,blue], legend=["y=x^","y=x-x^"]); Gambar 8-4. Plot kurva y=x dan y=x-x Pada grafik terlihat ada titik perpotongan. Titik-titik tersebut ditentukan dengan perintah berikut ini.
153 Kalkulus dengan Maple 153 > titikpot := evalf(solve(f1(x)=f(x),x)); dan diperoleh hasil bahwa kedua kurva berpotongan di x=0 dan x=1. Sehingga berdasarkan Gambar 8-4, daerah yang dimaksud adalah daerah yang dibatasi kedua kurva dengan batas x=0 sampai x=1. Dalam hal ini f(x) f1(x). Perintah dalam Maple untuk penyelesaiannya adalah: > Luas := int(f(x)-f1(x),x=titikpot[1]..titikpot[]); Dari perhitungan tersebut akan diketahui bahwa luas yang dibatasi kurva y=x dan y=x-x adalah 1/3 satuan luas. Contoh: 4 Carilah luas daerah yang dibatasi oleh kurva y = x/ x + 1 dan y = x x. Penyelesaian: Terlebih dahulu akan digambar plot kedua kurva. > f1 := x -> x/(x^+1)^(1/); > f := x -> x^4-x; > plot([f1(x),f(x)],x=0..1.5, color=[red,blue], legend=["y=x/(x^+1)^(1/)","y=x^4-x"]); Pada Gambar 8-5 tampak bahwa f1(x) f(x) dan kedua kurva berpotongan di dua titik yang masing-masing akan ditentukan berikut ini.
154 154 Integral 4 Gambar 8-5. Plot kurva y = x/ x + 1 dan y = x x > titikpot := evalf(solve(f1(x)=f(x),x)); Apabila perintah tersebut dijalankan, maka akan diperoleh penyelesaian sebagai berikut 0, I, I, Dari hasil yang telah diperoleh, tampak bahwa untuk penyelesaian real x hanya pada penyelesaian pertama dan keempat, sedangkan yang lain adalah imajiner. Oleh karena itu kedua kurva berpotongan di x=0 dan x= Perhitungan Maple untuk menentukan luasnya adalah > Luas := int(f1(x)-f(x),x=titikpot[1]..titikpot[4]); Berdasarkan perhitungan tersebut, diperoleh luas daerah yang dibatasi kedua kurva adalah satuan luas. Contoh : Carilah luas daerah yang dibatasi kurva y=x- dan y =3x+7.
155 Kalkulus dengan Maple 155 Penyelesaian: Perintah di bawah ini digunakan untuk menggambar kedua kurva. > with(plots): > Gb1 := implicitplot(y^=3*x+7,x=-3..10, y=-3..8,color=red): > Gb := plot(x-,x=-3..10,color=blue): > plots[display]({gb1,gb}); Keterangan: Perintah plots[display](); digunakan untuk menampilkan beberapa grafik yang dihasilkan dari perintah yang berbeda dalam satu bidang gambar. Adapun gambar kedua kurva seperti tampak pada Gambar 8-6. Gambar 8-6. Plot kurva y =3x+7 dany=x- Pada Gambar 8-6 terlihat bahwa y =3x+7 bukanlah suatu fungsi dalam x. Akan tetapi dalam hal ini y =3x+7 dapat dinyatakan sebagai fungsi dalam y, yaitu f 1(y) = (y -7)/3. Selanjutnya kita nyatakan pula y=x- sebagai fungsi dalam y, yaitu f (y)=y+. > f1 := y -> (y^-7)/3; > f := y -> y+; Berikutnya akan dicari dua titik perpotongan kedua kurva di y.
156 156 Integral > titikpot := evalf(solve(f1(y)=f(y),y)); Perintah ini akan menghasilkan titik potong kedua kurva di y= dan y= Pada Gambar 8-6 juga tampak bahwa f (y) f 1(y), sehingga luas daerah yang dibatasi kedua kurva adalah > Luas := int(f(y)-f1(y),y=titikpot[]..titikpot[1]); dan hasilnya adalah satuan luas. Volume Benda Putar Misalkan diketahui suatu kurva y=f(x) pada selang [a, b] yang kontinu pada selang tersebut. Apabila daerah antara kurva dan sumbu x diputar 360 o maka akan diperoleh sebuah benda pejal bervolume. Dalam subbab selanjutnya berikut ini akan dibahas bagaimana menggambar benda putar serta menghitung volumenya menggunakan Maple. Menggambar Volume Benda Putar Untuk menggambar benda putar dengan Maple, dapat menggunakan Calculus1 Student Package. Dalam paket ini terdapat perintah VolumeOfRevolution(). Adapun sintaksnya adalah: > with(student[calculus1]): > VolumeOfRevolution(f(x),x=a..b,option); Perintah tersebut digunakan untuk menggambar benda putar yang diperoleh dengan memutar daerah antara kurva y=f(x) yang dibatasi oleh x=a sampai x=b. Adapun option yang dapat diberikan antara lain: - axis=horizontal,vertical Option ini digunakan untuk menentukan sumbu putar dari benda pejal. Apabila diinginkan sumbu putarnya adalah sumbu x, maka axis=horizontal. Sedangkan apabila sumbu y maka axis=vertical. - output=value, plot, integral
157 Kalkulus dengan Maple 157 Supaya perintah tersebut dapat menampilkan visualisasi benda putar yang diinginkan, maka option output dipilih plot. Apabila hanya diinginkan menampilkan besarnya volume, maka output=value. Sedangkan output=integral dipilih apabila ingin menampilkan formulasi integral yang menyatakan perhitungan besarnya volume benda putar tersebut. - title=string Title dari plot benda putar dapat diubah melalui option ini. Contoh: Diketahui daerah yang dibatasi kurva y=x (untuk x=0 sampai dengan 4) dan sumbu x. Sebuah benda pejal diperoleh dengan memutar daerah tersebut pada sumbu x. Gambarlah benda pejal tersebut. Selanjutnya gambar pula benda pejal yang diperoleh dengan memutar daerah tersebut pada sumbu y. Penyelesaian: > f := x -> x^; > with(student[calculus1]): > VolumeOfRevolution(f(x),x=0..4,output=plot, title="kurva y=x^ diputar pada sumbu x", axis=horizontal); dan hasilnya akan diperoleh seperti pada Gambar 8-7.
158 158 Integral Gambar 8-7. Kurva y=x untuk x=0 4 diputar pada sumbu x Selanjutnya apabila diputar pada sumbu y, maka perintahnya > VolumeOfRevolution(f(x),x=0..4,output=plot,title="Kurva y=x^ diputar pada sumbu y",axis=vertical); hasilnya tampak pada Gambar 8-8. Gambar 8-8. Kurva y=x untuk x=0 4 diputar pada sumbu y Gambar 8-8 tersebut memperlihatkan dari atas benda pejal yang diperoleh. Garis merah pada gambar menunjukkan kurva y=x. Bagaimana dengan benda pejal yang diperoleh dari daerah diantara dua kurva yang diputar? Untuk lebih jelasnya perhatikan contoh berikut ini. Contoh: Sebuah daerah dibatasi oleh kurva y=6x-x dan y=x (pada kuadran I). Daerah tersebut diputar pada sumbu x dan terbentuklah benda pejal. Gambarkan benda pejal yang terbentuk tersebut.
159 Kalkulus dengan Maple 159 Penyelesaian: Sebagai ilustrasi perhatikan Gambar 8-9 berikut yang menunjukkan daerah yang dibatasi kurva y=6x-x dan y=x. Gambar 8-9. Daerah yang dibatasi kurva y=6x-x dan y=x Catatan: Gambar yang muncul di atas dihasilkan oleh perintah berikut ini. > Gb1:=plot([x,6*x-x^],x=0..6, color=[white,blue],filled=true): > Gb:=plot(6*x-x^,x=0..6,color=black): > Gb3:=plot(x,x=0..6,color=black): > plots[display]({gb1,gb,gb3}); Untuk menggambar benda pejal yang dihasilkan dengan memutar daerah pada Gambar 8-9, dengan terlebih dahulu harus diketahui batas kanan x pada daerah tersebut yang merupakan titik potong antara kedua kurva. Berikut ini adalah perintah Maple untuk mencari titik potong kedua kurva. > solve(6*x-x^=x,x); dan diperoleh hasil bahwa kedua kurva berpotongan di x=0 dan x=5. Sehingga dari hasil ini telah diketahui bahwa batas kanan dari daerah antara kedua kurva adalah x=5.
160 160 Integral Dengan demikian, selanjutnya dapat digambar benda pejal yang diinginkan. > f := x -> 6*x-x^; > g := x -> x; > with(student[calculus1]): > VolumeOfRevolution(f(x),g(x),x=0..5,output=plot, title="kurva antara y=6x-x^ dan y=x diputar pada sumbu x", axis=horizontal); dan akhirnya diperoleh tampilan seperti pada Gambar Gambar Daerah antara kurva y=6x-x dan y=x diputar pada sumbu x Perhitungan Volume Benda Putar Misalkan S sebuah benda pejal yang diperoleh dengan memutar daerah di bawah kurva y=f(x) antara x=a b di sekeliling sumbu x, maka volumenya (V) adalah b V f x dx = π a Sedangkan apabila S diperoleh dengan memutar daerah di bawah kurva x=f(y) antara y=a b di sekeliling sumbu y, volumenya adalah ( )
161 Kalkulus dengan Maple 161 b V f y dy = π a Selanjutnya bagaimana dengan daerah yang diputar dibatasi dengan dua buah kurva? Misalkan S diperoleh dengan memutar daerah yang dibatasi kurva y=f 1(x) dan y=f (x) dengan f 1(x) f (x) pada x=a sampai x=b disekeliling sumbu x, volumenya adalah b ( ) π ( 1 ( ) ( )) V = f x f x dx a Sedangkan apabila S diperoleh dengan memutar daerah yang dibatasi kurva x=f 1(y) dan x=f (y) dengan f 1(y) f (y) pada y=a sampai y=b di sekeliling sumbu y, volumenya adalah b π ( 1 ( ) ( )) V = f y f y dy a Rumus perhitungan volume benda putar di atas menggunakan metode cincin anulus. Keterangan lebih lanjut mengenai metode ini dapat dibaca di beberapa buku referensi kalkulus. Contoh: Tentukan volume benda pejal yang diperoleh dengan memutar daerah yang ada di bawah kurva y = x untuk x= 0 di sekeliling sumbu x. Tentukan pula volume daerah apabila diputar disekeliling sumbu y. Penyelesaian: Perhatikan Gambar 8-11 yang merupakan penampang/ daerah yang akan diputar di sekeliling sumbu x. Daerah yang dimaksud berada di bawah kurva y = =0. x dengan x
162 16 Integral Gambar Daerah di bawah kurva y = x untuk x=0 Sehingga volume benda pejal yang diperoleh dengan memutar daerah tersebut di sekeliling sumbu x adalah > f := x -> sqrt(x); > Vol := int(pi*f(x)^,x=0..); Dari perhitungan di atas, akan diperoleh volumenya adalah π satuan volume. Bagaimana volumenya apabila daerah tersebut diputar di sekeliling sumbu y? Apabila dipandang dari sumbu y, maka daerah pada Gambar 8-11 dibatasi oleh kurva x=f 1(y)=y dan x=f (y)= yang dalam hal ini f (y) f 1(y). Sebelum menghitung volumenya, terlebih dahulu akan ditentukan titik perpotongan kedua kurva di titik y. > f1 := y -> y^; > f := y -> ; > titikpot := solve(f1(y)=f(y),y); Dari perhitungan di atas akan diperoleh titik perpotongannya di y= dan y=. Dalam hal ini titik potong yang dipilih adalah y=.sehingga volumenya adalah > Vol := evalf(int(pi*(f(y)^-f1(y)^), y=0..titikpot[1]));
PRAKTIKUM MAPLE 4 KALKULUS LANJUTAN
 11 Fungsi Implisit PRAKTIKUM MAPLE 4 KALKULUS LANJUTAN Pada pembelajaran praktikum 3, diajarkan fungsi eksplisit dalam bentuk y = f(x). Sekarang bagaimana menuliskan fungsi apabila dalam bentuk implisit?
11 Fungsi Implisit PRAKTIKUM MAPLE 4 KALKULUS LANJUTAN Pada pembelajaran praktikum 3, diajarkan fungsi eksplisit dalam bentuk y = f(x). Sekarang bagaimana menuliskan fungsi apabila dalam bentuk implisit?
BAB I PENDAHULUAN 1 BAB I PENDAHULUAN
 BAB I PENDAHULUAN 1 BAB I PENDAHULUAN 1.1. Apakah Maple itu? Maple adalah suatu program interaktif yang mengintegrasikan kemampuan komputasi baik numerik ataupun simbolik, visualisasi (grafik) dan pemrograman.
BAB I PENDAHULUAN 1 BAB I PENDAHULUAN 1.1. Apakah Maple itu? Maple adalah suatu program interaktif yang mengintegrasikan kemampuan komputasi baik numerik ataupun simbolik, visualisasi (grafik) dan pemrograman.
Perbandingan trigonometri sin x merupakan relasi yang memetakan setiap x tepat satu nilai sin x yang dinyatakan dengan notasi f : x sinx
 MENGGAMBAR GRAFIK FUNGSI TRIGONOMETRI Perbandingan trigonometri dari suatu sudut tertentu terdapat tepat satu nilai dari sinus, kosinus dan tangens dari sudut tersebut. Sehingga perbandingan trigonometri
MENGGAMBAR GRAFIK FUNGSI TRIGONOMETRI Perbandingan trigonometri dari suatu sudut tertentu terdapat tepat satu nilai dari sinus, kosinus dan tangens dari sudut tersebut. Sehingga perbandingan trigonometri
TUJUAN INSTRUKSIONAL KHUSUS
 PREVIEW KALKULUS TUJUAN INSTRUKSIONAL KHUSUS Mahasiswa mampu: menyebutkan konsep-konsep utama dalam kalkulus dan contoh masalah-masalah yang memotivasi konsep tersebut; menjelaskan menyebutkan konsep-konsep
PREVIEW KALKULUS TUJUAN INSTRUKSIONAL KHUSUS Mahasiswa mampu: menyebutkan konsep-konsep utama dalam kalkulus dan contoh masalah-masalah yang memotivasi konsep tersebut; menjelaskan menyebutkan konsep-konsep
FUNGSI DAN GRAFIK FUNGSI
 FUNGSI DAN GRAFIK FUNGSI Apabila suatu besaran y memiliki nilai yang tergantung dari nilai besaran lain x, maka dikatakan bahwa besaran y tersebut merupakan fungsi besaran x. secara umum ditulis: y= f(x)
FUNGSI DAN GRAFIK FUNGSI Apabila suatu besaran y memiliki nilai yang tergantung dari nilai besaran lain x, maka dikatakan bahwa besaran y tersebut merupakan fungsi besaran x. secara umum ditulis: y= f(x)
FUNGSI Matematika Industri I
 FUNGSI TIP FTP UB Pokok Bahasan Memproses bilangan Komposisi fungsi dari fungsi Jenis fungsi Fungsi trigonometrik Fungsi eksponensial dan logaritmik Fungsi ganjil dan fungsi genap Pokok Bahasan Memproses
FUNGSI TIP FTP UB Pokok Bahasan Memproses bilangan Komposisi fungsi dari fungsi Jenis fungsi Fungsi trigonometrik Fungsi eksponensial dan logaritmik Fungsi ganjil dan fungsi genap Pokok Bahasan Memproses
Pengantar Mathematica
 Pengantar Mathematica Hazrul Iswadi Departemen MIPA Ubaya Seminar Internal pada hari Sabtu 22 Juli 2006 Sari: Pengantar Mathematica ini bertujuan memperkenalkan operasi-operasi dasar yang dilakukan ketika
Pengantar Mathematica Hazrul Iswadi Departemen MIPA Ubaya Seminar Internal pada hari Sabtu 22 Juli 2006 Sari: Pengantar Mathematica ini bertujuan memperkenalkan operasi-operasi dasar yang dilakukan ketika
FUNGSI dan LIMIT. 1.1 Fungsi dan Grafiknya
 FUNGSI dan LIMIT 1.1 Fungsi dan Grafiknya Fungsi : suatu aturan yang menghubungkan setiap elemen suatu himpunan pertama (daerah asal) tepat kepada satu elemen himpunan kedua (daerah hasil) fungsi Daerah
FUNGSI dan LIMIT 1.1 Fungsi dan Grafiknya Fungsi : suatu aturan yang menghubungkan setiap elemen suatu himpunan pertama (daerah asal) tepat kepada satu elemen himpunan kedua (daerah hasil) fungsi Daerah
FAKULTAS TEKNIK UNIVERSITAS NEGERI YOGYAKARTA
 No. LSKD/EKO/DEL221/01 Revisi : 02 Tgl : - Hal 1 dari 12 1. Kompetensi Setelah melakukan praktik, mahasiswa diharapkan memiliki kompetensi: dapat memahami input, output dan grafik pada. 2. Sub Kompetensi
No. LSKD/EKO/DEL221/01 Revisi : 02 Tgl : - Hal 1 dari 12 1. Kompetensi Setelah melakukan praktik, mahasiswa diharapkan memiliki kompetensi: dapat memahami input, output dan grafik pada. 2. Sub Kompetensi
Tugas Praktikum Matematika Dasar I Ringkasan Materi Maple
 Tugas Praktikum Matematika Dasar I Ringkasan Materi Maple Nama : YULI ARDIKA PRIHATAMA NIM : K2308062 Prodi : Pendidikan Fisika Kelas/Angkatan : B/2008 PENDAHULUAN Maple adalah sebuah software yang biasa
Tugas Praktikum Matematika Dasar I Ringkasan Materi Maple Nama : YULI ARDIKA PRIHATAMA NIM : K2308062 Prodi : Pendidikan Fisika Kelas/Angkatan : B/2008 PENDAHULUAN Maple adalah sebuah software yang biasa
BAB II OPERASI DASAR MAPLE
 BAB II OPERASI DASAR MAPLE 7 BAB II OPERASI DASAR MAPLE.1. Fungsi Maple mempunyai library fungsi yang sangat besar. Secara sintak, fungsi adalah tipe ekspresi. Fungsi-fungsi mempunyai nama dengan nol atau
BAB II OPERASI DASAR MAPLE 7 BAB II OPERASI DASAR MAPLE.1. Fungsi Maple mempunyai library fungsi yang sangat besar. Secara sintak, fungsi adalah tipe ekspresi. Fungsi-fungsi mempunyai nama dengan nol atau
PENGGUNAAN GEOGEBRA PADA PEMBELAJARAN MATEMATIKA
 PENGGUNAAN GEOGEBRA PADA PEMBELAJARAN MATEMATIKA Tugas Mata Kuliah Pengembangan Pembelajaran Matematika berbasis ICT Dosen Pengampu Dr. Dwijanto, M.S. Oleh: Purwanti Wahyuningsih (0401514014) Franky Martion
PENGGUNAAN GEOGEBRA PADA PEMBELAJARAN MATEMATIKA Tugas Mata Kuliah Pengembangan Pembelajaran Matematika berbasis ICT Dosen Pengampu Dr. Dwijanto, M.S. Oleh: Purwanti Wahyuningsih (0401514014) Franky Martion
Definisi 4.1 Fungsi f dikatakan kontinu di titik a (continuous at a) jika dan hanya jika ketiga syarat berikut dipenuhi: (1) f(a) ada,
 Lecture 4. Limit B A. Continuity Definisi 4.1 Fungsi f dikatakan kontinu di titik a (continuous at a) jika dan hanya jika ketiga syarat berikut dipenuhi: (1) f(a) ada, (2) lim f(x) ada, (3) lim f(x) =
Lecture 4. Limit B A. Continuity Definisi 4.1 Fungsi f dikatakan kontinu di titik a (continuous at a) jika dan hanya jika ketiga syarat berikut dipenuhi: (1) f(a) ada, (2) lim f(x) ada, (3) lim f(x) =
PRAKTIKUM 1 PENGENALAN PROGRAM APLIKASI MATEMATIKA MAPLE 7
 PRAKTIKUM 1 PENGENALAN PROGRAM APLIKASI MATEMATIKA MAPLE 7 1. MINGGU KE : 1 2. PERALATAN : LCD, E-LEARNING 3. SOFTWARE : MAPLE 4. TUJUAN Mahasiswa dapat: Mengaktifkan Maple. Mengetahui lingkungan Maple.
PRAKTIKUM 1 PENGENALAN PROGRAM APLIKASI MATEMATIKA MAPLE 7 1. MINGGU KE : 1 2. PERALATAN : LCD, E-LEARNING 3. SOFTWARE : MAPLE 4. TUJUAN Mahasiswa dapat: Mengaktifkan Maple. Mengetahui lingkungan Maple.
RANGKUMAN MATERI FUNGSI KOMPOSISI DAN FUNGSI INVERS
 RANGKUMAN MATERI FUNGSI KOMPOSISI DAN FUNGSI INVERS Diajukan untuk Memenuhi Tugas Mata Kuliah Matematika Sekolah Dosen Pembina: Dr. Tatag Yuli Eko Siswono, M.Pd. Universitas Negeri Surabaya Oleh Siti Rohmawati
RANGKUMAN MATERI FUNGSI KOMPOSISI DAN FUNGSI INVERS Diajukan untuk Memenuhi Tugas Mata Kuliah Matematika Sekolah Dosen Pembina: Dr. Tatag Yuli Eko Siswono, M.Pd. Universitas Negeri Surabaya Oleh Siti Rohmawati
Catatan Kuliah MA1123 Kalkulus Elementer I
 Catatan Kuliah MA1123 Kalkulus Elementer I Oleh Hendra Gunawan, Ph.D. Departemen Matematika ITB Sasaran Belajar Setelah mempelajari materi Kalkulus Elementer I, mahasiswa diharapkan memiliki (terutama):
Catatan Kuliah MA1123 Kalkulus Elementer I Oleh Hendra Gunawan, Ph.D. Departemen Matematika ITB Sasaran Belajar Setelah mempelajari materi Kalkulus Elementer I, mahasiswa diharapkan memiliki (terutama):
Menurut jenisnya, fungsi dapat dibedakan menjadi (1) Fungsi aljabar (2) Fungsi transenden
 Lecture 3. Function (B) A. Macam-macam Fungsi Menurut jenisnya, fungsi dapat dibedakan menjadi (1) Fungsi aljabar (2) Fungsi transenden Fungsi aljabar dibedakan menjadi (1) Fungsi rasional (a) Fungsi konstan
Lecture 3. Function (B) A. Macam-macam Fungsi Menurut jenisnya, fungsi dapat dibedakan menjadi (1) Fungsi aljabar (2) Fungsi transenden Fungsi aljabar dibedakan menjadi (1) Fungsi rasional (a) Fungsi konstan
KATA PENGANTAR. Penulis. Raizal Dzil Wafa M.
 i KATA PENGANTAR Buku ini dibuat untuk memudahkan siapa saja yang ingin belajar MATLAB terutama bagi yang baru mengenal MATLAB. Buku ini sangat cocok untuk pemula terutama untuk pelajar yang sedang menempuh
i KATA PENGANTAR Buku ini dibuat untuk memudahkan siapa saja yang ingin belajar MATLAB terutama bagi yang baru mengenal MATLAB. Buku ini sangat cocok untuk pemula terutama untuk pelajar yang sedang menempuh
2016 SRIWIJ MODUL PRAKTIKUM ALJABAR LINIER PENDIDIKAN MATEMATIKA FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN 2016 SRIWIJAYA
 2016 SRIWIJ MODUL PRAKTIKUM ALJABAR LINIER PENDIDIKAN MATEMATIKA FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN 2016 SRIWIJAYA KATA PENGANTAR Assalamu alaikum warahmatullahi wabarakatuh Puji syukur kehadirat Allah
2016 SRIWIJ MODUL PRAKTIKUM ALJABAR LINIER PENDIDIKAN MATEMATIKA FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN 2016 SRIWIJAYA KATA PENGANTAR Assalamu alaikum warahmatullahi wabarakatuh Puji syukur kehadirat Allah
BAGIAN 1 SINTAK DASAR MATLAB
 BAGIAN 1 SINTAK DASAR MATLAB Pada bagian 1 ini, akan diuraikan tentang bagaimana mendefinisikan data, operasi data dan teknik mengakses data pada Matlab. Untuk lebih memahami, pembaca sebaiknya mecobanya
BAGIAN 1 SINTAK DASAR MATLAB Pada bagian 1 ini, akan diuraikan tentang bagaimana mendefinisikan data, operasi data dan teknik mengakses data pada Matlab. Untuk lebih memahami, pembaca sebaiknya mecobanya
BAB IV. OPERATOR DAN STATEMENT
 BAB IV. OPERATOR DAN STATEMENT A. Pengantar Operator Operator merupakan simbol yang biasa dilibatkan dalam program untuk melakukan suatu operasi atau manipulasi, misalnya untuk: - menjumlahkan dua nilai
BAB IV. OPERATOR DAN STATEMENT A. Pengantar Operator Operator merupakan simbol yang biasa dilibatkan dalam program untuk melakukan suatu operasi atau manipulasi, misalnya untuk: - menjumlahkan dua nilai
KALKULUS 1. Oleh : SRI ESTI TRISNO SAMI, ST, MMSI /
 Oleh : SRI ESTI TRISNO SAMI, ST, MMSI 08125218506 / 082334051234 E-mail : sriestits2@gmail.com Bahan Bacaan / Refferensi : 1. Frank Ayres J. R., Calculus, Shcaum s Outline Series, Mc Graw-Hill Book Company.
Oleh : SRI ESTI TRISNO SAMI, ST, MMSI 08125218506 / 082334051234 E-mail : sriestits2@gmail.com Bahan Bacaan / Refferensi : 1. Frank Ayres J. R., Calculus, Shcaum s Outline Series, Mc Graw-Hill Book Company.
BAB II KAJIAN TEORI. pada penulisan bab III. Materi yang diuraikan berisi tentang definisi, teorema, dan
 BAB II KAJIAN TEORI Pada bab ini akan dibahas beberapa hal yang digunakan sebagai landasan pada penulisan bab III. Materi yang diuraikan berisi tentang definisi, teorema, dan beberapa kajian matematika,
BAB II KAJIAN TEORI Pada bab ini akan dibahas beberapa hal yang digunakan sebagai landasan pada penulisan bab III. Materi yang diuraikan berisi tentang definisi, teorema, dan beberapa kajian matematika,
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI 2.1 Latar Belakang Historis Fondasi dari integral pertama kali dideklarasikan oleh Cavalieri, seorang ahli matematika berkebangsaan Italia pada tahun 1635. Cavalieri menemukan bahwa
BAB II LANDASAN TEORI 2.1 Latar Belakang Historis Fondasi dari integral pertama kali dideklarasikan oleh Cavalieri, seorang ahli matematika berkebangsaan Italia pada tahun 1635. Cavalieri menemukan bahwa
A B A B. ( a ) ( b )
 BAB. FUNGSI A. Relasi dan Fungsi Misalkan A dan B dua himpunan tak kosong. Relasi T dari himpunan A ke B adalah himpunan bagian dari A B. Jadi relasi A ke B merupakan himpunan (,y), dengan pada himpunan
BAB. FUNGSI A. Relasi dan Fungsi Misalkan A dan B dua himpunan tak kosong. Relasi T dari himpunan A ke B adalah himpunan bagian dari A B. Jadi relasi A ke B merupakan himpunan (,y), dengan pada himpunan
LIMIT DAN KEKONTINUAN
 LIMIT DAN KEKONTINUAN Departemen Matematika FMIPA IPB Bogor, 2012 (Departemen Matematika FMIPA IPB) Kalkulus I Bogor, 2012 1 / 37 Topik Bahasan 1 Limit Fungsi 2 Hukum Limit 3 Kekontinuan Fungsi (Departemen
LIMIT DAN KEKONTINUAN Departemen Matematika FMIPA IPB Bogor, 2012 (Departemen Matematika FMIPA IPB) Kalkulus I Bogor, 2012 1 / 37 Topik Bahasan 1 Limit Fungsi 2 Hukum Limit 3 Kekontinuan Fungsi (Departemen
BAB III MENGGAMBAR GRAFIK
 BAB III MENGGAMBAR GRAFIK 15 BAB III MENGGAMBAR GRAFIK 3.1. Grafik Dua Dimensi Menggambar fungsi dengan satu variabel pada Maple dilakukan dengan perintah plot. Perintah ini hanya dapat digunakan untuk
BAB III MENGGAMBAR GRAFIK 15 BAB III MENGGAMBAR GRAFIK 3.1. Grafik Dua Dimensi Menggambar fungsi dengan satu variabel pada Maple dilakukan dengan perintah plot. Perintah ini hanya dapat digunakan untuk
Matematika I: Turunan. Dadang Amir Hamzah. Dadang Amir Hamzah Matematika I Semester I / 61
 Matematika I: Turunan Dadang Amir Hamzah 2015 Dadang Amir Hamzah Matematika I Semester I 2015 1 / 61 Outline 1 Garis Singgung Dadang Amir Hamzah Matematika I Semester I 2015 2 / 61 Outline 1 Garis Singgung
Matematika I: Turunan Dadang Amir Hamzah 2015 Dadang Amir Hamzah Matematika I Semester I 2015 1 / 61 Outline 1 Garis Singgung Dadang Amir Hamzah Matematika I Semester I 2015 2 / 61 Outline 1 Garis Singgung
KALKULUS BAB II FUNGSI, LIMIT, DAN KEKONTINUAN. DEPARTEMEN TEKNIK KIMIA Universitas Indonesia
 KALKULUS BAB II FUNGSI, LIMIT, DAN KEKONTINUAN DEPARTEMEN TEKNIK KIMIA Universitas Indonesia BAB II. FUNGSI, LIMIT, DAN KEKONTINUAN Fungsi dan Operasi pada Fungsi Beberapa Fungsi Khusus Limit dan Limit
KALKULUS BAB II FUNGSI, LIMIT, DAN KEKONTINUAN DEPARTEMEN TEKNIK KIMIA Universitas Indonesia BAB II. FUNGSI, LIMIT, DAN KEKONTINUAN Fungsi dan Operasi pada Fungsi Beberapa Fungsi Khusus Limit dan Limit
MODUL I MENGENAL MATLAB
 MODUL I MENGENAL MATLAB TUJUAN Mahasiswa dapat mengenal MATLAB Mahasiswa dapat menggunakan fungsi Help Mahasiswa dapat menggunakan operasi pada MATLAB TEORI Gambaran sederhana tentang MATLAB adalah sebuah
MODUL I MENGENAL MATLAB TUJUAN Mahasiswa dapat mengenal MATLAB Mahasiswa dapat menggunakan fungsi Help Mahasiswa dapat menggunakan operasi pada MATLAB TEORI Gambaran sederhana tentang MATLAB adalah sebuah
MAKALAH MATEMATIKA DASAR TURUNAN (DIFERENSIAL)
 MAKALAH MATEMATIKA DASAR TURUNAN (DIFERENSIAL) KATA PENGANTAR Puji dan Syukur kami panjatkan ke Hadirat Tuhan Yang Maha Esa, karena berkat limpahan Rahmat dan Karunia-nya sehingga kami dapat menyusun makalah
MAKALAH MATEMATIKA DASAR TURUNAN (DIFERENSIAL) KATA PENGANTAR Puji dan Syukur kami panjatkan ke Hadirat Tuhan Yang Maha Esa, karena berkat limpahan Rahmat dan Karunia-nya sehingga kami dapat menyusun makalah
Bagian 2 Matriks dan Determinan
 Bagian Matriks dan Determinan Materi mengenai fungsi, limit, dan kontinuitas akan kita pelajari dalam Bagian Fungsi dan Limit. Pada bagian Fungsi akan mempelajari tentang jenis-jenis fungsi dalam matematika
Bagian Matriks dan Determinan Materi mengenai fungsi, limit, dan kontinuitas akan kita pelajari dalam Bagian Fungsi dan Limit. Pada bagian Fungsi akan mempelajari tentang jenis-jenis fungsi dalam matematika
SISTEM BILANGAN RIIL DAN FUNGSI
 SISTEM BILANGAN RIIL DAN FUNGSI Matematika Juni 2016 Dosen : Dadang Amir Hamzah MATEMATIKA Juni 2016 1 / 67 Outline 1 Sistem Bilangan Riil Dosen : Dadang Amir Hamzah MATEMATIKA Juni 2016 2 / 67 Outline
SISTEM BILANGAN RIIL DAN FUNGSI Matematika Juni 2016 Dosen : Dadang Amir Hamzah MATEMATIKA Juni 2016 1 / 67 Outline 1 Sistem Bilangan Riil Dosen : Dadang Amir Hamzah MATEMATIKA Juni 2016 2 / 67 Outline
MODUL PETUNJUK PRAKTIKUM KALKULUS I. OLEH : Drs. J. V. A. Tambelu, M.Pd Dra. T. A. S. Rembet, M.Sc Navel O. Mangelep, S.Pd
 MODUL PETUNJUK PRAKTIKUM KALKULUS I OLEH : Drs. J. V. A. Tambelu, M.Pd Dra. T. A. S. Rembet, M.Sc Navel O. Mangelep, S.Pd UNIVERSITAS NEGERI MANADO FAKULTAS MATEMATIKA DAN ILMU PENGETAHUANN ALAM JURUSAN
MODUL PETUNJUK PRAKTIKUM KALKULUS I OLEH : Drs. J. V. A. Tambelu, M.Pd Dra. T. A. S. Rembet, M.Sc Navel O. Mangelep, S.Pd UNIVERSITAS NEGERI MANADO FAKULTAS MATEMATIKA DAN ILMU PENGETAHUANN ALAM JURUSAN
BERKENALAN DENGAN MAXIMA
 BERKENALAN DENGAN MAXIMA Muda Nurul K. Saat ini ada banyak software open source yang bisa dimanfaatkan untuk pembelajaran matematika., diantaranya adalah Maxima. Maxima merupakan salah satu software open
BERKENALAN DENGAN MAXIMA Muda Nurul K. Saat ini ada banyak software open source yang bisa dimanfaatkan untuk pembelajaran matematika., diantaranya adalah Maxima. Maxima merupakan salah satu software open
Bil Riil. Bil Irasional. Bil Bulat - Bil Bulat 0 Bil Bulat + maka bentuk umum bilangan kompleks adalah
 ANALISIS KOMPLEKS Pendahuluan Bil Kompleks Bil Riil Bil Imaginer (khayal) Bil Rasional Bil Irasional Bil Pecahan Bil Bulat Sistem Bilangan Kompleks Bil Bulat - Bil Bulat 0 Bil Bulat + Untuk maka bentuk
ANALISIS KOMPLEKS Pendahuluan Bil Kompleks Bil Riil Bil Imaginer (khayal) Bil Rasional Bil Irasional Bil Pecahan Bil Bulat Sistem Bilangan Kompleks Bil Bulat - Bil Bulat 0 Bil Bulat + Untuk maka bentuk
2.1 Soal Matematika Dasar UM UGM c. 1 d d. 3a + b. e. 3a + b. e. b + a b a
 Soal - Soal UM UGM. Soal Matematika Dasar UM UGM 00. Jika x = 3 maka + 3 log 4 x =... a. b. c. d. e.. Jika x+y log = a dan x y log 8 = b dengan 0 < y < x maka 4 log (x y ) =... a. a + 3b ab b. a + b ab
Soal - Soal UM UGM. Soal Matematika Dasar UM UGM 00. Jika x = 3 maka + 3 log 4 x =... a. b. c. d. e.. Jika x+y log = a dan x y log 8 = b dengan 0 < y < x maka 4 log (x y ) =... a. a + 3b ab b. a + b ab
KALKULUS INTEGRAL 2013
 KALKULUS INTEGRAL 0 PENDAHULUAN A. DESKRIPSI MATA KULIAH Isi pokok mata kuliah ini memuat pemahaman tentang: () Anti turunan: pengertian anti turunan, teorema-teorema, dan teknik anti turunan, () Integral
KALKULUS INTEGRAL 0 PENDAHULUAN A. DESKRIPSI MATA KULIAH Isi pokok mata kuliah ini memuat pemahaman tentang: () Anti turunan: pengertian anti turunan, teorema-teorema, dan teknik anti turunan, () Integral
PENGGUNAAN EKSTRAPOLASI UNTUK MENYELESAIKAN FUNGSI INTEGRAL TENTU NIRSAL
 PENGGUNAAN EKSTRAPOLASI UNTUK MENYELESAIKAN FUNGSI INTEGRAL TENTU NIRSAL Dosen Tetap Yayasan Universitas Cokroaminoto Palopo E-Mail: nirsal_uncpftkom@yahoo.co.id Abstrak Tujuan penelitian ini adalah untuk
PENGGUNAAN EKSTRAPOLASI UNTUK MENYELESAIKAN FUNGSI INTEGRAL TENTU NIRSAL Dosen Tetap Yayasan Universitas Cokroaminoto Palopo E-Mail: nirsal_uncpftkom@yahoo.co.id Abstrak Tujuan penelitian ini adalah untuk
UNIVERSITAS NEGERI YOGYAKARTA FAKULTAS MIPA RENCANA PELAKSANAAN PEMBELAJARAN
 UNIVERSITAS NEGERI YOGYAKARTA FAKULTAS MIPA RENCANA PELAKSANAAN PEMBELAJARAN 1. Fakultas/Program Studi : MIPA/Pendidikan Matematika. Mata Kuliah/Kode : Aplikasi Komputer/MAT33 3. Jumlah SKS : Teori = Praktek
UNIVERSITAS NEGERI YOGYAKARTA FAKULTAS MIPA RENCANA PELAKSANAAN PEMBELAJARAN 1. Fakultas/Program Studi : MIPA/Pendidikan Matematika. Mata Kuliah/Kode : Aplikasi Komputer/MAT33 3. Jumlah SKS : Teori = Praktek
BAB IV HASIL PENELITIAN DAN PEMBAHASAN
 BAB IV HASIL PENELITIAN DAN PEMBAHASAN A. HASIL PENELITIAN 1. Hasil Pengembangan Produk Penelitian ini merupakan penelitian pengembangan yang bertujuan untuk mengembangkan produk berupa Skema Pencapaian
BAB IV HASIL PENELITIAN DAN PEMBAHASAN A. HASIL PENELITIAN 1. Hasil Pengembangan Produk Penelitian ini merupakan penelitian pengembangan yang bertujuan untuk mengembangkan produk berupa Skema Pencapaian
PENGERTIAN FUNGSI JENIS-JENIS FUNGSI PENGGAMBARAN GRAFIK FUNGSI
 FUNGSI PENGERTIAN FUNGSI JENIS-JENIS FUNGSI PENGGAMBARAN GRAFIK FUNGSI PENGERTIAN FUNGSI Sebuah fungsi f dari himpunan A ke himpunan B adalah suatu aturan yang memasangkan setiap X anggota A dengan tepat
FUNGSI PENGERTIAN FUNGSI JENIS-JENIS FUNGSI PENGGAMBARAN GRAFIK FUNGSI PENGERTIAN FUNGSI Sebuah fungsi f dari himpunan A ke himpunan B adalah suatu aturan yang memasangkan setiap X anggota A dengan tepat
SATUAN ACARA PEMBELAJARAN (SAP)
 SATUAN ACARA PEMBELAJARAN (SAP) Mata Kuliah Kode Mata Kuliah SKS Durasi Pertemuan Pertemuan ke : Kalkulus : TSP-102 : 3 (tiga) : 150 menit : 1 (Satu) A. Kompetensi: a. Umum : Mahasiswa dapat menggunakan
SATUAN ACARA PEMBELAJARAN (SAP) Mata Kuliah Kode Mata Kuliah SKS Durasi Pertemuan Pertemuan ke : Kalkulus : TSP-102 : 3 (tiga) : 150 menit : 1 (Satu) A. Kompetensi: a. Umum : Mahasiswa dapat menggunakan
Turunan. Ayundyah Kesumawati. January 8, Prodi Statistika FMIPA-UII. Ayundyah Kesumawati (UII) Turunan January 8, / 15
 Turunan Ayundyah Kesumawati Prodi Statistika FMIPA-UII January 8, 2015 Ayundyah Kesumawati (UII) Turunan January 8, 2015 1 / 15 Sub Materi Turunan : a. Turunan Fungsi b. Turunan Tingkat Tinggi c. Teorema
Turunan Ayundyah Kesumawati Prodi Statistika FMIPA-UII January 8, 2015 Ayundyah Kesumawati (UII) Turunan January 8, 2015 1 / 15 Sub Materi Turunan : a. Turunan Fungsi b. Turunan Tingkat Tinggi c. Teorema
MATEMATIKA TEKNIK DASAR-I FUNGSI-2 SEBRIAN MIRDEKLIS BESELLY PUTRA TEKNIK PENGAIRAN
 MATEMATIKA TEKNIK DASAR-I FUNGSI-2 SEBRIAN MIRDEKLIS BESELLY PUTRA TEKNIK PENGAIRAN FUNGSI Perhatikan relasi {(x,y) x, y R; y=x 2 } Untuk tiap-tiap nilai x dalam wilayahnya, relasi itu hanya menyatakan
MATEMATIKA TEKNIK DASAR-I FUNGSI-2 SEBRIAN MIRDEKLIS BESELLY PUTRA TEKNIK PENGAIRAN FUNGSI Perhatikan relasi {(x,y) x, y R; y=x 2 } Untuk tiap-tiap nilai x dalam wilayahnya, relasi itu hanya menyatakan
SOAL-SOAL dan PEMBAHASAN UN MATEMATIKA SMA/MA IPA TAHUN PELAJARAN 2011/2012
 SOAL-SOAL dan PEMBAHASAN UN MATEMATIKA SMA/MA IPA TAHUN PELAJARAN 0/0. Akar-akar persamaan kuadrat x +ax - 40 adalah p dan q. Jika p - pq + q 8a, maka nilai a... A. -8 B. -4 C. 4 D. 6 E. 8 BAB III Persamaan
SOAL-SOAL dan PEMBAHASAN UN MATEMATIKA SMA/MA IPA TAHUN PELAJARAN 0/0. Akar-akar persamaan kuadrat x +ax - 40 adalah p dan q. Jika p - pq + q 8a, maka nilai a... A. -8 B. -4 C. 4 D. 6 E. 8 BAB III Persamaan
MODUL 1. Teori Bilangan MATERI PENYEGARAN KALKULUS
 MODUL 1 Teori Bilangan Bilangan merupakan sebuah alat bantu untuk menghitung, sehingga pengetahuan tentang bilangan, mutlak diperlukan. Pada modul pertama ini akan dibahas mengenai bilangan (terutama bilangan
MODUL 1 Teori Bilangan Bilangan merupakan sebuah alat bantu untuk menghitung, sehingga pengetahuan tentang bilangan, mutlak diperlukan. Pada modul pertama ini akan dibahas mengenai bilangan (terutama bilangan
FAKULTAS TEKNIK UNIVERSITAS NEGERI YOGYAKARTA LAB SHEET 1 (TEKNIK KOMPUTASI)
 No. LSKD/EKO/DEL221/01 Revisi : 03 Tgl : 30/10/2012 Hal 1 dari 8 1. Kompetensi Setelah melakukan praktik, mahasiswa diharapkan memiliki kompetensi dapat memahami operasi matematika sederhana pada Matlab.
No. LSKD/EKO/DEL221/01 Revisi : 03 Tgl : 30/10/2012 Hal 1 dari 8 1. Kompetensi Setelah melakukan praktik, mahasiswa diharapkan memiliki kompetensi dapat memahami operasi matematika sederhana pada Matlab.
Pertemuan ke 8. GRAFIK FUNGSI Diketahui fungsi f. Himpunan {(x,y): y = f(x), x D f } disebut grafik fungsi f.
 Pertemuan ke 8 GRAFIK FUNGSI Diketahui fungsi f. Himpunan {(,y): y = f(), D f } disebut grafik fungsi f. Grafik metode yang paling umum untuk menyatakan hubungan antara dua himpunan yaitu dengan menggunakan
Pertemuan ke 8 GRAFIK FUNGSI Diketahui fungsi f. Himpunan {(,y): y = f(), D f } disebut grafik fungsi f. Grafik metode yang paling umum untuk menyatakan hubungan antara dua himpunan yaitu dengan menggunakan
KED INTEGRAL JUMLAH PERTEMUAN : 2 PERTEMUAN TUJUAN INSTRUKSIONAL KHUSUS: Materi : 7.1 Anti Turunan. 7.2 Sifat-sifat Integral Tak Tentu KALKULUS I
 7 INTEGRAL JUMLAH PERTEMUAN : 2 PERTEMUAN TUJUAN INSTRUKSIONAL KHUSUS: Memahami konsep dasar integral, teorema-teorema, sifat-sifat, notasi jumlah, fungsi transenden dan teknik-teknik pengintegralan. Materi
7 INTEGRAL JUMLAH PERTEMUAN : 2 PERTEMUAN TUJUAN INSTRUKSIONAL KHUSUS: Memahami konsep dasar integral, teorema-teorema, sifat-sifat, notasi jumlah, fungsi transenden dan teknik-teknik pengintegralan. Materi
Rencana Pembelajaran
 Learning Outcome Rencana Pembelajaran Setelah mengikuti proses pembelajaran ini, diharapkan mahasiswa dapat ) Menentukan nilai turunan suatu fungsi di suatu titik ) Menentukan nilai koefisien fungsi sehingga
Learning Outcome Rencana Pembelajaran Setelah mengikuti proses pembelajaran ini, diharapkan mahasiswa dapat ) Menentukan nilai turunan suatu fungsi di suatu titik ) Menentukan nilai koefisien fungsi sehingga
Matematika SMA (Program Studi IPA)
 Smart Solution UJIAN NASIONAL TAHUN PELAJARAN 0/0 Disusun Sesuai Indikator Kisi-Kisi UN 0 Matematika SMA (Program Studi IPA) Disusun oleh : Hario Pamungkas 4.. Menyelesaikan persamaan trigonometri. Nilai
Smart Solution UJIAN NASIONAL TAHUN PELAJARAN 0/0 Disusun Sesuai Indikator Kisi-Kisi UN 0 Matematika SMA (Program Studi IPA) Disusun oleh : Hario Pamungkas 4.. Menyelesaikan persamaan trigonometri. Nilai
KALKULUS 1 HADI SUTRISNO. Pendidikan Matematika STKIP PGRI Bangkalan. Hadi Sutrisno/P.Matematika/STKIP PGRI Bangkalan
 KALKULUS 1 HADI SUTRISNO 1 Pendidikan Matematika STKIP PGRI Bangkalan BAB I PENDAHULUAN A. Sistem Bilangan Real Untuk mempelajari kalkulus kita terlebih dahulu perlu memahami bahasan tentang sistem bilangan
KALKULUS 1 HADI SUTRISNO 1 Pendidikan Matematika STKIP PGRI Bangkalan BAB I PENDAHULUAN A. Sistem Bilangan Real Untuk mempelajari kalkulus kita terlebih dahulu perlu memahami bahasan tentang sistem bilangan
III HASIL DAN PEMBAHASAN
 Fungsi periodizer kutub tersebut dapat dituliskan pula sebagai: p θ, N, θ 0 = π N N.0 n= n sin Nn θ θ 0. () f p θ, N, θ 0 = π N N j= j sin Nj θ θ 0 diperoleh dengan menyubstitusi variabel θ pada f θ =
Fungsi periodizer kutub tersebut dapat dituliskan pula sebagai: p θ, N, θ 0 = π N N.0 n= n sin Nn θ θ 0. () f p θ, N, θ 0 = π N N j= j sin Nj θ θ 0 diperoleh dengan menyubstitusi variabel θ pada f θ =
BAB I DASAR-DASAR PEMODELAN MATEMATIKA DENGAN PERSAMAAN DIFERENSIAL
 BAB I DASAR-DASAR PEMODELAN MATEMATIKA DENGAN PERSAMAAN DIFERENSIAL Pendahuluan Persamaan diferensial adalah persamaan yang memuat diferensial Kita akan membahas tentang Persamaan Diferensial Biasa yaitu
BAB I DASAR-DASAR PEMODELAN MATEMATIKA DENGAN PERSAMAAN DIFERENSIAL Pendahuluan Persamaan diferensial adalah persamaan yang memuat diferensial Kita akan membahas tentang Persamaan Diferensial Biasa yaitu
FUNGSI. Sesi XI 12/4/2015
 Mata Kuliah : Matematika Rekayasa Lanjut Kode MK : TKS 8105 Pengampu : Achfas Zacoeb Sesi XI FUNGSI dan GRAFIK e-mail : zacoeb@ub.ac.id www.zacoeb.lecture.ub.ac.id Hp. 081233978339 FUNGSI Secara intuitif,
Mata Kuliah : Matematika Rekayasa Lanjut Kode MK : TKS 8105 Pengampu : Achfas Zacoeb Sesi XI FUNGSI dan GRAFIK e-mail : zacoeb@ub.ac.id www.zacoeb.lecture.ub.ac.id Hp. 081233978339 FUNGSI Secara intuitif,
Pengenalan Geogebra. Oleh: Hazrul Iswadi. Disampaikan pada seminar internal Departemen MIPA. Tanggal 10 September 2011
 Pengenalan Geogebra Oleh: Hazrul Iswadi Disampaikan pada seminar internal Departemen MIPA Tanggal 10 September 2011 Departemen MIPA Universitas Surabaya A. Apa itu GeoGebra? GeoGebra adalah software gratis
Pengenalan Geogebra Oleh: Hazrul Iswadi Disampaikan pada seminar internal Departemen MIPA Tanggal 10 September 2011 Departemen MIPA Universitas Surabaya A. Apa itu GeoGebra? GeoGebra adalah software gratis
5 F U N G S I. 1 Matematika Ekonomi
 5 F U N G S I Pemahaman tentang konsep fungsi sangat penting dalam mempelajari ilmu ekonomi, mengingat kajian ekonomi banyak bekerja dengan fungsi. Fungsi dalam matematika menyatakan suatu hubungan formal
5 F U N G S I Pemahaman tentang konsep fungsi sangat penting dalam mempelajari ilmu ekonomi, mengingat kajian ekonomi banyak bekerja dengan fungsi. Fungsi dalam matematika menyatakan suatu hubungan formal
Modul 2016 KATA PENGANTAR
 KATA PENGANTAR Kita tahu bahwa dewasa ini pperkembangan dari teknologi sangatlah pesat, sehingga apapun saat ini selalu berkaitan dengan yang namanya teknologi. Teknologi juga tidak hanya dipahami oleh
KATA PENGANTAR Kita tahu bahwa dewasa ini pperkembangan dari teknologi sangatlah pesat, sehingga apapun saat ini selalu berkaitan dengan yang namanya teknologi. Teknologi juga tidak hanya dipahami oleh
KATA PENGANTAR. Malang, 20 Januari 2015 Penulis. DR Suhartono M.Kom
 KATA PENGANTAR Assalamu alaikum Wr. Wb. Alhamdulillahirabbil Alamin penulis haturkan kehadirat Allah SWT yang telah memberikan rahmat, hidayah, dan ridha-nya, sehingga penulis dapat menyelesaikan buku
KATA PENGANTAR Assalamu alaikum Wr. Wb. Alhamdulillahirabbil Alamin penulis haturkan kehadirat Allah SWT yang telah memberikan rahmat, hidayah, dan ridha-nya, sehingga penulis dapat menyelesaikan buku
Antiremed Kelas 12 Matematika
 Antiremed Kelas Matematika Integral - Latihan Ulangan Doc. Name: ARMAT098 Version : 0 0 halaman 0. f (x)=x +x+ maka f(x) =... x +x +x +c x +x +x+c x - x +x+c x +x +x+c x - x +x+c 0. 0. 0. 0 x +c x c x
Antiremed Kelas Matematika Integral - Latihan Ulangan Doc. Name: ARMAT098 Version : 0 0 halaman 0. f (x)=x +x+ maka f(x) =... x +x +x +c x +x +x+c x - x +x+c x +x +x+c x - x +x+c 0. 0. 0. 0 x +c x c x
Matematika I: APLIKASI TURUNAN. Dadang Amir Hamzah. Dadang Amir Hamzah Matematika I Semester I / 70
 Matematika I: APLIKASI TURUNAN Dadang Amir Hamzah 2015 Dadang Amir Hamzah Matematika I Semester I 2015 1 / 70 Outline 1 Maksimum dan Minimum Dadang Amir Hamzah Matematika I Semester I 2015 2 / 70 Outline
Matematika I: APLIKASI TURUNAN Dadang Amir Hamzah 2015 Dadang Amir Hamzah Matematika I Semester I 2015 1 / 70 Outline 1 Maksimum dan Minimum Dadang Amir Hamzah Matematika I Semester I 2015 2 / 70 Outline
Artikel BERKENALAN DENGAN MAXIMA
 Artikel BERKENALAN DENGAN MAXIMA Oleh Muda Nurul Khikmawati PUSAT PENGEMBANGAN DAN PEMBERDAYAAN PENDIDIK DAN TENAGA KEPENDIDIKAN (PPPPTK) MATEMATIKA 2010 Abstrak Maxima merupakan salah satu software open
Artikel BERKENALAN DENGAN MAXIMA Oleh Muda Nurul Khikmawati PUSAT PENGEMBANGAN DAN PEMBERDAYAAN PENDIDIK DAN TENAGA KEPENDIDIKAN (PPPPTK) MATEMATIKA 2010 Abstrak Maxima merupakan salah satu software open
atau y= f(x) = ax 2 + bx + c (3.17) y= f(x) = a 2 x + a 0 x 2 + a 1
 i. Fungsi kuadrat - Penyelesaian fungsi kuadrat dengan pemfaktoran Fungsi kuadrat adalah fungsi polinomial yang mempunyai derajad dua dan mempunyai bentuk umum : y= f(x) = a 2 x 2 + a 1 x + a 0 atau y=
i. Fungsi kuadrat - Penyelesaian fungsi kuadrat dengan pemfaktoran Fungsi kuadrat adalah fungsi polinomial yang mempunyai derajad dua dan mempunyai bentuk umum : y= f(x) = a 2 x 2 + a 1 x + a 0 atau y=
ISTIYANTO.COM. memenuhi persamaan itu adalah B. 4 4 C. 4 1 PERBANDINGAN KISI-KISI UN 2009 DAN 2010 SMA IPA
 PERBANDINGAN KISI-KISI UN 009 DAN 00 SMA IPA Materi Logika Matematika Kemampuan yang diuji UN 009 UN 00 Menentukan negasi pernyataan yang diperoleh dari penarikan kesimpulan Menentukan negasi pernyataan
PERBANDINGAN KISI-KISI UN 009 DAN 00 SMA IPA Materi Logika Matematika Kemampuan yang diuji UN 009 UN 00 Menentukan negasi pernyataan yang diperoleh dari penarikan kesimpulan Menentukan negasi pernyataan
Matematika I: Turunan. Dadang Amir Hamzah. Dadang Amir Hamzah Matematika I Semester I / 75
 Matematika I: Turunan Dadang Amir Hamzah 2015 Dadang Amir Hamzah Matematika I Semester I 2015 1 / 75 Outline 1 Garis Singgung Dadang Amir Hamzah Matematika I Semester I 2015 2 / 75 Outline 1 Garis Singgung
Matematika I: Turunan Dadang Amir Hamzah 2015 Dadang Amir Hamzah Matematika I Semester I 2015 1 / 75 Outline 1 Garis Singgung Dadang Amir Hamzah Matematika I Semester I 2015 2 / 75 Outline 1 Garis Singgung
BAB II AKAR-AKAR PERSAMAAN
 BAB II AKAR-AKAR PERSAMAAN 2.1 PENDAHULUAN Salah satu masalah yang sering terjadi pada bidang ilmiah adalah masalah untuk mencari akar-akar persamaan berbentuk : = 0 Fungsi f di sini adalah fungsi atau
BAB II AKAR-AKAR PERSAMAAN 2.1 PENDAHULUAN Salah satu masalah yang sering terjadi pada bidang ilmiah adalah masalah untuk mencari akar-akar persamaan berbentuk : = 0 Fungsi f di sini adalah fungsi atau
1 Sistem Bilangan Real
 Learning Outcome Rencana Pembelajaran Setelah mengikuti proses pembelajaran ini, diharapkan mahasiswa dapat ) Menentukan solusi pertidaksamaan aljabar ) Menyelesaikan pertidaksamaan dengan nilai mutlak
Learning Outcome Rencana Pembelajaran Setelah mengikuti proses pembelajaran ini, diharapkan mahasiswa dapat ) Menentukan solusi pertidaksamaan aljabar ) Menyelesaikan pertidaksamaan dengan nilai mutlak
Matematika EBTANAS Tahun 1986
 Matematika EBTANAS Tahun 986 EBT-SMA-86- Bila diketahui A = { x x bilangan prima < }, B = { x x bilangan ganjil < }, maka eleman A B =.. 3 7 9 EBT-SMA-86- Bila matriks A berordo 3 dan matriks B berordo
Matematika EBTANAS Tahun 986 EBT-SMA-86- Bila diketahui A = { x x bilangan prima < }, B = { x x bilangan ganjil < }, maka eleman A B =.. 3 7 9 EBT-SMA-86- Bila matriks A berordo 3 dan matriks B berordo
Analisis Riil II: Diferensiasi
 Definisi Turunan Definisi dan Teorema Aturan Rantai Fungsi Invers Definisi (Turunan) Misalkan I R sebuah interval, f : I R, dan c I. Bilangan riil L dikatakan turunan dari f di c jika diberikan sebarang
Definisi Turunan Definisi dan Teorema Aturan Rantai Fungsi Invers Definisi (Turunan) Misalkan I R sebuah interval, f : I R, dan c I. Bilangan riil L dikatakan turunan dari f di c jika diberikan sebarang
TRANSFORMASI GEOMETRI ROTASI BERBANTUAN SOFTWARE GEOGEBRA
 ISSN : 2460 7797 e-issn : 2614 8234 Website : jurnal.umj.ac.id/index.php/fbc Email : fibonacci@umj.ac.id Jurnal Pendidikan Matematika dan Matematika TRANSFORMASI GEOMETRI ROTASI BERBANTUAN SOFTWARE GEOGEBRA
ISSN : 2460 7797 e-issn : 2614 8234 Website : jurnal.umj.ac.id/index.php/fbc Email : fibonacci@umj.ac.id Jurnal Pendidikan Matematika dan Matematika TRANSFORMASI GEOMETRI ROTASI BERBANTUAN SOFTWARE GEOGEBRA
MODUL PRAKTIKUM ALJABAR LINIER
 2012 MODUL PRAKTIKUM ALJABAR LINIER LABORATORIUM MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM NIVERSITAS NEGERI GORONTALO KATA PENGANTAR Penuntun Praktikum dirancang untuk memberikan tuntunan
2012 MODUL PRAKTIKUM ALJABAR LINIER LABORATORIUM MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM NIVERSITAS NEGERI GORONTALO KATA PENGANTAR Penuntun Praktikum dirancang untuk memberikan tuntunan
FUNGSI DAN MODEL. Bogor, Departemen Matematika FMIPA IPB. (Departemen Matematika FMIPA IPB) Kalkulus I Bogor, / 63
 FUNGSI DAN MODEL Departemen Matematika FMIPA IPB Bogor, 2012 (Departemen Matematika FMIPA IPB) Kalkulus I Bogor, 2012 1 / 63 Topik Bahasan 1 Fungsi 2 Jenis-jenis Fungsi 3 Fungsi Baru dari Fungsi Lama 4
FUNGSI DAN MODEL Departemen Matematika FMIPA IPB Bogor, 2012 (Departemen Matematika FMIPA IPB) Kalkulus I Bogor, 2012 1 / 63 Topik Bahasan 1 Fungsi 2 Jenis-jenis Fungsi 3 Fungsi Baru dari Fungsi Lama 4
3. FUNGSI DAN GRAFIKNYA
 3. FUNGSI DAN GRAFIKNYA 3.1 Pengertian Relasi Misalkan A dan B suatu himpunan. anggota A dikaitkan dengan anggota B berdasarkan suatu hubungan tertentu maka diperoleh suatu relasi dari A ke B. : A = {1,
3. FUNGSI DAN GRAFIKNYA 3.1 Pengertian Relasi Misalkan A dan B suatu himpunan. anggota A dikaitkan dengan anggota B berdasarkan suatu hubungan tertentu maka diperoleh suatu relasi dari A ke B. : A = {1,
Zulfaneti Yulia Haryono Rina F ebriana. Berbasis Penemuan Terbimbing = = D(sec x)= sec x tan x, ( + ) ( ) ( )=
 Zulfaneti Yulia Haryono Rina F ebriana Berbasis Penemuan Terbimbing = = D(sec x)= sec x tan x, ()= (+) () Penyusun Zulfaneti Yulia Haryono Rina Febriana Nama NIm : : Untuk ilmu yang bermanfaat Untuk Harapan
Zulfaneti Yulia Haryono Rina F ebriana Berbasis Penemuan Terbimbing = = D(sec x)= sec x tan x, ()= (+) () Penyusun Zulfaneti Yulia Haryono Rina Febriana Nama NIm : : Untuk ilmu yang bermanfaat Untuk Harapan
Ringkasan Kalkulus 2, Untuk dipakai di ITB 1
 Ringkasan Kalkulus 2, Untuk dipakai di ITB Deret Tak Hingga Pada bagian ini akan dibicarakan penjumlahan berbentuk a +a 2 + +a n + dengan a n R Sebelumnya akan dibahas terlebih dahulu pengertian barisan
Ringkasan Kalkulus 2, Untuk dipakai di ITB Deret Tak Hingga Pada bagian ini akan dibicarakan penjumlahan berbentuk a +a 2 + +a n + dengan a n R Sebelumnya akan dibahas terlebih dahulu pengertian barisan
PLOT plot(y) menggambar garis yang didefinisikan oleh titik Y vs indeksnya (Y bil real) Contoh : >>Y = [ ]; >>plot(y)
![PLOT plot(y) menggambar garis yang didefinisikan oleh titik Y vs indeksnya (Y bil real) Contoh : >>Y = [ ]; >>plot(y) PLOT plot(y) menggambar garis yang didefinisikan oleh titik Y vs indeksnya (Y bil real) Contoh : >>Y = [ ]; >>plot(y)](/thumbs/56/38275649.jpg) MATERI 7 GRAFIK 2 DIMENSI PLOT plot(y) menggambar garis yang didefinisikan oleh titik Y vs indeksnya (Y bil real) >>Y = [1 3 5 4 7 0 9 8 2]; >>plot(y) plot(x,y) menggambar garis yang didefinisikan oleh
MATERI 7 GRAFIK 2 DIMENSI PLOT plot(y) menggambar garis yang didefinisikan oleh titik Y vs indeksnya (Y bil real) >>Y = [1 3 5 4 7 0 9 8 2]; >>plot(y) plot(x,y) menggambar garis yang didefinisikan oleh
Soal UN 2009 Materi KISI UN 2010 Prediksi UN 2010
 PREDIKSI UN 00 SMA IPA BAG. (Berdasar buku terbitan Istiyanto: Bank Soal Matematika-Gagas Media) Logika Matematika Soal UN 009 Materi KISI UN 00 Prediksi UN 00 Menentukan negasi pernyataan yang diperoleh
PREDIKSI UN 00 SMA IPA BAG. (Berdasar buku terbitan Istiyanto: Bank Soal Matematika-Gagas Media) Logika Matematika Soal UN 009 Materi KISI UN 00 Prediksi UN 00 Menentukan negasi pernyataan yang diperoleh
Modul Praktikum Kalkulus II dengan Menggunakan Matlab
 Modul Praktikum Kalkulus II dengan Menggunakan Matlab disusun oleh : Arif Muchyidin, S.Si., M.Si. NIP. 19830806 201101 1 009 TADRIS MATEMATIKA INSTITUT AGAMA ISLAM NEGERI SYEKH NURJATI CIREBON 2016 KATA
Modul Praktikum Kalkulus II dengan Menggunakan Matlab disusun oleh : Arif Muchyidin, S.Si., M.Si. NIP. 19830806 201101 1 009 TADRIS MATEMATIKA INSTITUT AGAMA ISLAM NEGERI SYEKH NURJATI CIREBON 2016 KATA
Dasar-dasar MATLAB. by Jusak Irawan, STIKOM Surabaya
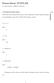 Dasar-dasar MATLAB by Jusak Irawan, STIKOM Surabaya Perintah-Perintah Dasar MATLAB akan memberikan respons secara langsung terhadap ekspresi apapun yang diketikkan pada editor MATLAB. Sebagai contoh: >>
Dasar-dasar MATLAB by Jusak Irawan, STIKOM Surabaya Perintah-Perintah Dasar MATLAB akan memberikan respons secara langsung terhadap ekspresi apapun yang diketikkan pada editor MATLAB. Sebagai contoh: >>
PERBANDINGAN BEBERAPA METODE NUMERIK DALAM MENGHITUNG NILAI PI
 PERBANDINGAN BEBERAPA METODE NUMERIK DALAM MENGHITUNG NILAI PI Perbandingan Beberapa Metode Numerik dalam Menghitung Nilai Pi Aditya Agung Putra (13510010)1 Program Studi Teknik Informatika Sekolah Teknik
PERBANDINGAN BEBERAPA METODE NUMERIK DALAM MENGHITUNG NILAI PI Perbandingan Beberapa Metode Numerik dalam Menghitung Nilai Pi Aditya Agung Putra (13510010)1 Program Studi Teknik Informatika Sekolah Teknik
GARIS BESAR PROGRAM PEMBELAJARAN (GBPP) UNIVERSITAS DIPONEGORO
 GARIS BESAR PROGRAM PEMBELAJARAN (GBPP) UNIVERSITAS DIPONEGORO SPMI- UNDIP GBPP xx.xx.xx xx Revisi ke Tanggal Dikaji Ulang Oleh Dikendalikan Oleh Disetujui Oleh Ketua Program Studi GPM DekanFakultas. UNIVERSITAS
GARIS BESAR PROGRAM PEMBELAJARAN (GBPP) UNIVERSITAS DIPONEGORO SPMI- UNDIP GBPP xx.xx.xx xx Revisi ke Tanggal Dikaji Ulang Oleh Dikendalikan Oleh Disetujui Oleh Ketua Program Studi GPM DekanFakultas. UNIVERSITAS
BAB II PENGANTAR SOLUSI PERSOALAN FISIKA MENURUT PENDEKATAN ANALITIK DAN NUMERIK
 BAB II PENGANTAR SOLUSI PERSOALAN FISIKA MENURUT PENDEKATAN ANALITIK DAN NUMERIK Tujuan Instruksional Setelah mempelajari bab ini pembaca diharapkan dapat: 1. Menjelaskan cara penyelesaian soal dengan
BAB II PENGANTAR SOLUSI PERSOALAN FISIKA MENURUT PENDEKATAN ANALITIK DAN NUMERIK Tujuan Instruksional Setelah mempelajari bab ini pembaca diharapkan dapat: 1. Menjelaskan cara penyelesaian soal dengan
CONTOH SOAL DAN PEMBAHASAN PERSIAPAN UN 2014
 CONTOH SOAL DAN PEMBAHASAN PERSIAPAN UN 04 DISUSUN OLEH AHMAD THOHIR MA FUTUHIYAH JEKETRO GUBUG GROBOGAN JATENG KATA PENGANTAR Tulisan yang sangat sederhana ini berisi kisi-kisi UN 0 disertai contoh soal
CONTOH SOAL DAN PEMBAHASAN PERSIAPAN UN 04 DISUSUN OLEH AHMAD THOHIR MA FUTUHIYAH JEKETRO GUBUG GROBOGAN JATENG KATA PENGANTAR Tulisan yang sangat sederhana ini berisi kisi-kisi UN 0 disertai contoh soal
WORKSHOP DAN PELATIHAN MATLAB : PENUNJANG PEMBELAJARAN MATEMATIKA DI SMU DALAM RANGKA IMPLEMENTASI CONTEXTUAL TEACHING LEARNING ABSTRAK
 WORKSHOP DAN PELATIHAN MATLAB : PENUNJANG PEMBELAJARAN MATEMATIKA DI SMU DALAM RANGKA IMPLEMENTASI CONTEXTUAL TEACHING LEARNING Tim Pengabdi:. Agus Maman Abadi. Dhoriva UW. Sri Andayani 4. Karyati 5. Caturiyati
WORKSHOP DAN PELATIHAN MATLAB : PENUNJANG PEMBELAJARAN MATEMATIKA DI SMU DALAM RANGKA IMPLEMENTASI CONTEXTUAL TEACHING LEARNING Tim Pengabdi:. Agus Maman Abadi. Dhoriva UW. Sri Andayani 4. Karyati 5. Caturiyati
Bab 16. LIMIT dan TURUNAN. Motivasi. Limit Fungsi. Fungsi Turunan. Matematika SMK, Bab 16: Limit dan Turunan 1/35
 Bab 16 Grafik LIMIT dan TURUNAN Matematika SMK, Bab 16: Limit dan 1/35 Grafik Pada dasarnya, konsep limit dikembangkan untuk mengerjakan perhitungan matematis yang melibatkan: nilai sangat kecil; Matematika
Bab 16 Grafik LIMIT dan TURUNAN Matematika SMK, Bab 16: Limit dan 1/35 Grafik Pada dasarnya, konsep limit dikembangkan untuk mengerjakan perhitungan matematis yang melibatkan: nilai sangat kecil; Matematika
Pembahasan Matematika IPA SIMAK UI 2009
 Pembahasan Matematika IPA SIMAK UI 2009 Kode 924 Oleh Kak Mufidah 1. Diketahui fungsi. Agar fungsi tersebut senantiasa berada di bawah sumbu x, maka nilai m yang mungkin adalah Agar fungsi tersebut senantiasa
Pembahasan Matematika IPA SIMAK UI 2009 Kode 924 Oleh Kak Mufidah 1. Diketahui fungsi. Agar fungsi tersebut senantiasa berada di bawah sumbu x, maka nilai m yang mungkin adalah Agar fungsi tersebut senantiasa
SKL 1 Soal logika matematika dalam pemecahan masalah Menentukan ingkaran atau kesetaraan dari pernyataan majemuk
 SKL Soal 0-0 No. KOMPETENSI INDIKATOR 0. M e n g g u n a k a n Menentukan penarikan kesimpulan dari beberapa premis logika matematika dalam pemecahan masalah Menentukan ingkaran atau kesetaraan dari pernyataan
SKL Soal 0-0 No. KOMPETENSI INDIKATOR 0. M e n g g u n a k a n Menentukan penarikan kesimpulan dari beberapa premis logika matematika dalam pemecahan masalah Menentukan ingkaran atau kesetaraan dari pernyataan
PRAKTIKUM 13 PENYELESAIAN PERSAMAAN ALJABAR
 PRAKTIKUM 13 PENYELESAIAN PERSAMAAN ALJABAR Dalam bab ini kita akan menggunakan Matlab untuk menyelesaikan persamaan aljabar. Kita akan mulai dengan menyelesaikan persamaan sederhana (persamaan dengan
PRAKTIKUM 13 PENYELESAIAN PERSAMAAN ALJABAR Dalam bab ini kita akan menggunakan Matlab untuk menyelesaikan persamaan aljabar. Kita akan mulai dengan menyelesaikan persamaan sederhana (persamaan dengan
F U N G S I A R U M H A N D I N I P R I M A N D A R I
 F U N G S I A R U M H A N D I N I P R I M A N D A R I DEFINISI Fungsi adalah suatu aturan yang memetakan setiap anggota himpunan A pada tepat satu anggota himpunan B. Dimana: Himpunan A disebut domain
F U N G S I A R U M H A N D I N I P R I M A N D A R I DEFINISI Fungsi adalah suatu aturan yang memetakan setiap anggota himpunan A pada tepat satu anggota himpunan B. Dimana: Himpunan A disebut domain
SPMB 2004 Matematika Dasar Kode Soal
 SPMB 00 Matematika Dasar Kode Soal Doc. Name: SPMB00MATDAS999 Version : 0- halaman 0. Nilai x yang memenuhi persamaan : 3 x ( ) adalah. 0 - - 0. Dalam bentuk pangkat positif dan bentuk akar, x y x y...
SPMB 00 Matematika Dasar Kode Soal Doc. Name: SPMB00MATDAS999 Version : 0- halaman 0. Nilai x yang memenuhi persamaan : 3 x ( ) adalah. 0 - - 0. Dalam bentuk pangkat positif dan bentuk akar, x y x y...
DERET FOURIER DAN APLIKASINYA DALAM FISIKA
 Matakuliah: Fisika Matematika DERET FOURIER DAN APLIKASINYA DALAM FISIKA Di S U S U N Oleh : Kelompok VI DEWI RATNA PERTIWI SITEPU (8176175004) RIFKA ANNISA GIRSANG (8176175014) PENDIDIKAN FISIKA REGULER
Matakuliah: Fisika Matematika DERET FOURIER DAN APLIKASINYA DALAM FISIKA Di S U S U N Oleh : Kelompok VI DEWI RATNA PERTIWI SITEPU (8176175004) RIFKA ANNISA GIRSANG (8176175014) PENDIDIKAN FISIKA REGULER
PRAKTIKUM 2 PENGENALAN PROGRAM APLIKASI MATEMATIKA MAPLE 7
 PRAKTIKUM PENGENALAN PROGRAM APLIKASI MATEMATIKA MAPLE 7. MINGGU KE :. PERALATAN : LCD, E-LEARNING. SOFTWARE : MAPLE. TUJUAN Mahasiswa dapat: Menggunakan konstanta, bilangan kompleks, bilangan dasar (basis),
PRAKTIKUM PENGENALAN PROGRAM APLIKASI MATEMATIKA MAPLE 7. MINGGU KE :. PERALATAN : LCD, E-LEARNING. SOFTWARE : MAPLE. TUJUAN Mahasiswa dapat: Menggunakan konstanta, bilangan kompleks, bilangan dasar (basis),
Soal dan Pembahasan UN Matematika SMA IPA Tahun 2013
 Soal dan Pembahasan UN Matematika SMA IPA Tahun 013 LOGIKA MATEMATIKA p siswa rajin belajar ; q mendapat nilai yang baik r siswa tidak mengikuti kegiatan remedial ~ r siswa mengikut kegiatan remedial Premis
Soal dan Pembahasan UN Matematika SMA IPA Tahun 013 LOGIKA MATEMATIKA p siswa rajin belajar ; q mendapat nilai yang baik r siswa tidak mengikuti kegiatan remedial ~ r siswa mengikut kegiatan remedial Premis
Kelompok Mata Kuliah : MKU Program Studi/Program : Teknik Tenaga Elektrik/S1 Status Mata Kuliah : Wajib Prasyarat : - : Aip Saripudin, M.T.
 DESKRIPSI MATA KULIAH TK-... Matematika Dasar: S1, 3 SKS, Semester I Mata kuliah ini merupakan kuliah dasar. Selesai mengikuti perkuliahan ini mahasiswa diharapkan mampu memahami konsep-konsep matematika
DESKRIPSI MATA KULIAH TK-... Matematika Dasar: S1, 3 SKS, Semester I Mata kuliah ini merupakan kuliah dasar. Selesai mengikuti perkuliahan ini mahasiswa diharapkan mampu memahami konsep-konsep matematika
MA1201 MATEMATIKA 2A Hendra Gunawan
 MA1201 MATEMATIKA 2A Hendra Gunawan Semester II, 2016/2017 15 Maret 2017 Kuliah yang Lalu 10.1-2 Parabola, Elips, dan Hiperbola 10.4 Persamaan Parametrik Kurva di Bidang 10.5 Sistem Koordinat Polar 11.1
MA1201 MATEMATIKA 2A Hendra Gunawan Semester II, 2016/2017 15 Maret 2017 Kuliah yang Lalu 10.1-2 Parabola, Elips, dan Hiperbola 10.4 Persamaan Parametrik Kurva di Bidang 10.5 Sistem Koordinat Polar 11.1
PREDIKSI UAN MATEMATIKA SESUAI KISI-KISI PEMERINTAH
 PREDIKSI UAN MATEMATIKA SESUAI KISI-KISI PEMERINTAH. Apabila P dan q kalimat pernyataan, di mana ~p q kalimat bernilai salah, maka kalimat yang benar berikut ini, kecuali (d) p q (~p ~q) (~p ~q) ~ (~p
PREDIKSI UAN MATEMATIKA SESUAI KISI-KISI PEMERINTAH. Apabila P dan q kalimat pernyataan, di mana ~p q kalimat bernilai salah, maka kalimat yang benar berikut ini, kecuali (d) p q (~p ~q) (~p ~q) ~ (~p
SRI REDJEKI KALKULUS I
 SRI REDJEKI KALKULUS I KLASIFIKASI BILANGAN RIIL n Bilangan yang paling sederhana adalah bilangan asli : n 1, 2, 3, 4, 5,. n n Bilangan asli membentuk himpunan bagian dari klas himpunan bilangan yang lebih
SRI REDJEKI KALKULUS I KLASIFIKASI BILANGAN RIIL n Bilangan yang paling sederhana adalah bilangan asli : n 1, 2, 3, 4, 5,. n n Bilangan asli membentuk himpunan bagian dari klas himpunan bilangan yang lebih
SMA/MA MATEMATIKA FISIKA KIMIA BIOLOGI BAHASA INDONESIA BAHASA INGGRIS
 PREDIKSI UJIAN NASIONAL SMA/MA MATEMATIKA FISIKA KIMIA BIOLOGI BAHASA INDONESIA BAHASA INGGRIS SEMOGA SUKSES PAKET PREDIKSI UJIAN NASIONAL SMA/MA Mata Pelajaran : MATEMATIKA Tanggal : - Waktu : MENIT PETUNJUK
PREDIKSI UJIAN NASIONAL SMA/MA MATEMATIKA FISIKA KIMIA BIOLOGI BAHASA INDONESIA BAHASA INGGRIS SEMOGA SUKSES PAKET PREDIKSI UJIAN NASIONAL SMA/MA Mata Pelajaran : MATEMATIKA Tanggal : - Waktu : MENIT PETUNJUK
