Profesor Hendra Gunawan
|
|
|
- Handoko Hartono
- 6 tahun lalu
- Tontonan:
Transkripsi
1 Majelis Guru Besar Institut Teknologi Bandung Pidato Ilmiah Guru Besar Institut Teknologi Bandung Profesor Hendra Gunawan Kontribusi dalam Matematika dan Pengembangan Ilmu dan Teknologi 26 Januari 2007 Balai Pertemuan Ilmiah ITB Hak Cipta Ada pada Penulis
2 Kata Pengantar Pertama-tama saya ucapkan terima kasih yang sebesar-besarnya kepada Majelis Guru Besar Institut Teknologi Bandung yang telah memberi kesempatan kepada saya untuk menyampaikan naskah Pidato Ilmiah ini di hadapan sidang pleno Majelis Guru Besar Institut Teknologi Bandung yang terhormat. Bagian awal buku Pidato Ilmiah ini saya isi dengan sejarah singkat perkembangan matematika, baik di dunia maupun di Indonesia. Pada dua bagian berikutnya saya paparkan kontribusi saya dalam matematika, khususnya dalam analisis Fourier, analisis fungsional, dan potensi aplikasinya. Hasil renungan mengenai posisi dan peran matematika dan matematikawan dalam pengembangan ilmu dan teknologi serta sejumlah harapan saya kemukakan pula pada bagian penutup buku ini. Selain merupakan bentuk pertanggungjawaban akademis dan komitmen saya sebagai seorang yang baru menduduki jabatan guru besarnya, buku Pidato Ilmiah ini saya persembahkan pula dalam rangka mengenang Profesor Moedomo ( ) guru, pembimbing, dan mentor saya sejak saya masih mahasiswa, menjadi dosen, hingga saat saya mengajukan usulan kenaikan jabatan terakhir pada Tanpa jasa beliau, saya takkan mungkin berhasil seperti sekarang. iii
3 Daftar Isi Kata Pengantar iii 1. Prolog: Menelusuri Sejarah 1 2. Kontribusi dalam Analisis Fourier (dan PDP) 7 3. Kontribusi dalam Analisis Fungsional (dan Geometri) Epilog: Renungan dan Harapan 39 Ucapan Terima Kasih 45 Daftar Pustaka 46 Curriculum Vitae 51 iv
4 Majelis Guru Besar Institut Teknologi Bandung Pidato Ilmiah Guru Besar Institut Teknologi Bandung Profesor Hendra Gunawan Kontribusi dalam Matematika dan Pengembangan Ilmu dan Teknologi 26 Januari 2007 Balai Pertemuan Ilmiah ITB Hak Cipta Ada pada Penulis
5 Kata Pengantar Pertama-tama saya ucapkan terima kasih yang sebesar-besarnya kepada Majelis Guru Besar Institut Teknologi Bandung yang telah memberi kesempatan kepada saya untuk menyampaikan naskah Pidato Ilmiah ini di hadapan sidang pleno Majelis Guru Besar Institut Teknologi Bandung yang terhormat. Bagian awal buku Pidato Ilmiah ini saya isi dengan sejarah singkat perkembangan matematika, baik di dunia maupun di Indonesia. Pada dua bagian berikutnya saya paparkan kontribusi saya dalam matematika, khususnya dalam analisis Fourier, analisis fungsional, dan potensi aplikasinya. Hasil renungan mengenai posisi dan peran matematika dan matematikawan dalam pengembangan ilmu dan teknologi serta sejumlah harapan saya kemukakan pula pada bagian penutup buku ini. Selain merupakan bentuk pertanggungjawaban akademis dan komitmen saya sebagai seorang yang baru menduduki jabatan guru besarnya, buku Pidato Ilmiah ini saya persembahkan pula dalam rangka mengenang Profesor Moedomo ( ) guru, pembimbing, dan mentor saya sejak saya masih mahasiswa, menjadi dosen, hingga saat saya mengajukan usulan kenaikan jabatan terakhir pada Tanpa jasa beliau, saya takkan mungkin berhasil seperti sekarang. 2
6 Daftar Isi Kata Pengantar iii 1. Prolog: Menelusuri Sejarah 1 2. Kontribusi dalam Analisis Fourier (dan PDP) 7 3. Kontribusi dalam Analisis Fungsional (dan Geometri) Epilog: Renungan dan Harapan 39 Ucapan Terima Kasih 45 Daftar Pustaka 46 Curriculum Vitae 51 3
7 1. Prolog: Menelusuri Sejarah Matematika, menurut catatan sejarah, telah lahir sejak jaman Mesir Kuno, kira-kira lima ribu tahun yang lalu. Sekitar empat ribu tahun yang lampau, bangsa Babilonia telah menggunakan geometri sebagai basis perhitungan astronomis, sementara bangsa Mesir telah mengenal tripel Pythagoras dan menggunakannya untuk membuat sudut siku. Tiga ribuan tahun yang lalu sifat-sifat segitiga siku-siku juga telah dikenal oleh bangsa Cina. Namun, bangsa Yunani Kuno-lah yang telah mengembangkan matematika secara sistematis sebagai ilmu sejak dua ribu lima ratusan tahun yang lalu. Dalil pertama tentang segitiga siku-siku dalam lingkaran dibuktikan oleh Thales ( SM), dan dalil tentang ketiga sisi segitiga siku-siku yang dipelajari di sekolah hingga sekarang ini dibuktikan oleh Pythagoras ( SM). Matematikawan Yunani Kuno lainnya yang terkenal melalui karyanya adalah Eudoxus ( SM), Euclid ( SM), Archimedes ( SM), dan Hipparcus ( SM). Euclid, khususnya, menulis lima belas jilid buku geometri berjudul Elements, yang menjadi standar buku matematika hingga sekarang. Sementara itu Archimedes menulis buku The Method dan terkenal dengan teriakannya Eureka! [lihat A.D. Aczel, 1996]. 4
8 Halaman judul buku Euclid Elements, terjemahan bahasa Inggris pada 1570 [difoto dari J. Gullberg, 1997] 5
9 Menurut The Timetables of History [B. Grun, 1963], buku pertama tentang aljabar ditulis oleh Diophantus dari Alexandria pada tahun 250-an. Sekitar tahun 595, bilangan desimal telah dikenal di India. Pada tahun 630-an, matematikawan India Brahmagupta ( ) telah mengenal konsep bilangan negatif dan nol serta mengembangkan metode untuk menyelesaikan persamaan kuadrat. Pada tahun 750, matematika dikembangkan di Spanyol Arab dan karya Euclid Elements diterjemahkan ke bahasa Arab. Pada tahun 820-an, matematikawan Persia Muhammad Ibnu Musa al Khowarizmi ( ) menulis buku Al Jabr Wa l Muqabalah yang memperkenalkan istilah aljabar. Notasi aritmetika yang kita kenal sekarang ini dibawa ke Eropa oleh bangsa Arab pada tahun 975. Selama abad pertengahan, tidak banyak perkembangan dalam matematika, kecuali pengenalan lambang bilangan Arab di Eropa oleh Fibonacci ( ) dalam Liber Abaci pada Namun demikian, sejumlah universitas didirikan di Eropa pada masa itu. Matematika mulai dipelajari kembali secara intensif pada jaman Renaissance di Eropa, sekitar abad ke-17. Beberapa matematikawan masa itu yang terkenal melalui karyanya adalah René Descartes ( ), Pierre de Fermat ( ), Isaac Newton ( ), Gottfried von Leibniz ( ), Jacob Bernoulli ( ), Johann Bernoulli ( ), Daniel Bernoulli ( ), 6
10 Leonhard Euler ( ), Jean Le Rond d Alembert ( ), Pierre Simon Laplace ( ), Jean Baptiste Joseph Fourier ( ), dan Karl Friedrich Gauss ( ). Dalam kata pengantarnya untuk buku Mathematics: From the Birth of Numbers [J. Gullberg, 1997], P. Hilton menyatakan bahwa matematika lahir dan berkembang karena adanya keinginan manusia untuk mensistematisasikan pengalaman hidupnya, menatanya dan membuatnya mudah dimengerti, supaya dapat meramalkan dan bila memungkinkan mengendalikan peristiwa yang akan terjadi pada masa depan. Bila naluri engineers adalah merekayasa alam dan naluri scientists adalah memahami alam dan mencari tahu apa yang sesungguhnya terjadi, maka naluri matematikawan adalah menstrukturkan proses pemahaman tersebut dengan mencari kesamaan pola di antara berbagai fenomena [I. Stewart, 1995]. Hingga sekarang, cabang-cabang utama matematika, di antaranya logika, kombinatorika, aljabar, teori bilangan, geometri, analisis, teori peluang, statistika, analisis numerik, matematika komputasi, teori kontrol, optimisasi, fisika matematik, dan biologi matematika, telah berkembang jauh dan banyak diaplikasikan dalam bidang lainnya, terutama dalam bidang-bidang yang memerlukan analisis kuantitatif seperti sains, engineering, ekonomi, dan kedokteran. 7
11 Aplikasi matematika di dunia industri dapat dijumpai dalam sektor manufacturing, desain produk, pengelolaan lingkungan, dan sains informasi (khususnya bio-informatics) [Society for Industrial and Applied Mathematics, 1996]. Dibandingkan dengan keadaan di negara lain, pengembangan dan pemanfaatan matematika di Indonesia jauh tertinggal. Matematika mulai ditekuni oleh bangsa Indonesia pada abad 20. Doktor matematika pertama dari Indonesia adalah Dr. G.S.S.J. Ratu Langie (alm.), atau lebih dikenal sebagai Dr. Sam Ratulangi, yang meraih gelar doktornya pada 1919 dari University of Zürich, dengan disertasinya yang berjudul Kurven-Systeme in vollständigen Figuren. Hampir 40 tahun kemudian, Profesor Handali mendapat gelar doktornya dari FIPIA-UI Bandung pada 1957, dengan disertasinya yang berjudul On the Zeros of Polynomials of the Form βf(z) zf (z). Pada 1959, Profesor Moedomo (alm.) meraih gelar doktornya dari University of Illinois, dengan disertasinya yang berjudul A Representation Theory for the Laplace Transform of Vector-Valued Functions. Paper pertama karya putra Indonesia, yang terekam di Mathematical Reviews (American Mathematical Society), adalah paper Moedomo dan J.J. Uhl Jr. Radon-Nikodym theorems for the Bochner and Pettis integrals, yang dipublikasikan di Pacific Journal of Mathematics pada
12 Di antara cabang-cabang utama matematika, analisis termasuk cabang terbesar, yang meliputi analisis real (termasuk teori ukuran dan integral), analisis kompleks, analisis Fourier, analisis fungsional, persamaan diferensial biasa, persamaan diferensial parsial, persamaan integral, sistem dinamik, topologi, teori operator, dan aljabar operator. Untuk menekuni cabang ini, KBK Analisis dibentuk pada 1979 di Departemen Matematika ITB. Pada akhir 2005, KBK Analisis dan KBK Geometri bergabung menjadi KK Analisis dan Geometri, yang saat itu beranggotakan 12 dosen, 7 di antaranya bergelar doktor. Pada pertengahan 2006, Drs. E. Hutahaean, M.Si. pensiun, sehingga anggotanya sekarang tinggal 11 dosen. Selain merupakan salah satu KK pendukung utama Program Studi Matematika di ITB, KK Analisis dan Geometri termasuk kelompok yang aktif dalam penelitian dan pengabdian kepada masyarakat. Saya termasuk peneliti aktif dalam area analisis Fourier (modern) dan analisis fungsional. Gelar doktor saya diperoleh dari University of New South Wales, Australia, pada tahun 1992, dengan disertasi berjudul Maximal Functions and Harmonic Analysis. Pada bagian berikutnya akan diuraikan kontribusi saya dalam analisis Fourier dan analisis fungsional, keterkaitannya dengan persamaan diferensial dan geometri, dan potensi aplikasinya. 9
13 2. Kontribusi dalam Analisis Fourier (dan PDP) Sebelum saya paparkan hasil-hasil penelitian saya selama ini, ijinkan saya untuk menyampaikan secara ringkas lahirnya analisis Fourier serta kaitannya dengan berbagai cabang matematika dan bidang ilmu lainnya, sambil bernostalgia tentang materi kuliah yang saya dapatkan dari Profesor M. Ansjar pada 1980-an. Analisis Fourier klasik pada mulanya berkembang dalam upaya mempelajari deret dan integral Fourier. Deret trigonometri yang kita kenal sekarang sebagai deret Fourier pertama kali diperkenalkan oleh D. Bernoulli pada tahun 1750-an, ketika ia mengkaji persamaan diferensial parsial untuk sebuah dawai bergetar utt = c 2.uxx dengan syarat batas u(0,t) = u(l,t) = 0 untuk setiap t dan syarat awal u(x,0) = f(x) dan ut(x,0) = 0. Di sini c adalah konstanta, L menyatakan panjang dawai, f(x) adalah bentuk awal dawai, u = u(x,t) menyatakan simpangan vertikal dawai pada posisi x dan waktu t, dan uxx dan utt menyatakan turunan parsial kedua u terhadap x dan terhadap t. Persamaan diferensial parsial ini merupakan persamaan gelombang dimensi-1. 10
14 Bernoulli menemukan bahwa untuk f(x) = sin(kπx/l), fungsi u(x,t) = sin(kπx/l).cos(ckπt/l) merupakan solusi untuk setiap bilangan bulat positif k. (Di sini u(x,t) mempunyai interpretasi musikal sebagai suara yang dihasilkan oleh dawai. Pada masa itu, matematika dan musik mempunyai hubungan yang mesra, seperti pada era Pythagoras.) Karena persamaan di atas termasuk persamaan diferensial parsial linear, kombinasi linear dari solusi-solusi tadi juga merupakan solusi. Bernoulli menyimpulkan bahwa u( x, t) ak sin( kx / L)cos( ckt / L) k 1 memenuhi persamaan dengan syarat awal f ( x) ak sin( k x / L). k 1 Bernoulli juga menyatakan bahwa ia telah mendapat semua solusi tanpa penjelasan tentang koefisien ak. Temuan Bernoulli ini langsung disanggah oleh L. Euler. Menurut Euler, bagaimana mungkin sebarang fungsi f(x) yang terdefinisi pada selang [0,L] dengan f(0) = f(l) = 0 dapat dinyatakan sebagai deret tak hingga sinus, yakni f ( x) ak sin( k x / L). k 1 11
15 Euler menganggap bahwa hal ini absurd karena deret sinus memiliki sifat khusus, yakni ganjil dan periodik dengan periode 2L, sesuatu yang tak dimiliki oleh, misalnya, f(x) = x(l x). Euler, dan secara independen d Alembert, pada saat itu telah menemukan solusi dalam bentuk yang berbeda, yakni u(x,t) = ½ [f*(x + ct) + f*(x ct)] dengan f* menyatakan perluasan dari f pada seluruh garis R sehingga f* ganjil dan periodik dengan periode 2L. Mengingat sin( / )cos( / ) 1 k k k x L ckt L 2 sin( ( x ct) sin( ( x ct ), solusi Bernoulli dianggap kasus khusus dari solusi temuannya. L L Bernoulli tidak dapat menjawab dengan baik sanggahan Euler. Ia hanya mengulang argumennya bahwa persamaan f ( x) ak sin( k x / L) k 1 dapat dipandang sebagai suatu sistem aljabar yang terdiri dari tak hingga persamaan linear dengan tak hingga peubah. Kelemahan utama argumennya adalah bahwa ia tak dapat memberikan rumus untuk koefisien ak dalam f. Rumus itu akhirnya ditemukan oleh Euler beberapa tahun sesudahnya, namun Euler tidak mempelajari lebih lanjut relevansinya karena ia telah menolak gagasan Bernoulli sebelumnya. 12
16 Setengah abad kemudian, tepatnya pada 1807, Fourier berhasil mengembangkan apa yang kita kenal sekarang sebagai deret Fourier. Ketika itu ia tertarik dengan persamaan panas atau persamaan difusi ut(x,t) = c 2.uxx(x,t) dengan u(x,t) menyatakan suhu kawat yang panjangnya L pada posisi x dan waktu t, dengan syarat batas dan syarat awal u(0,t) = u(l,t) = 0 dan u(x,0) = f(x). Dengan menuliskan f sebagai deret k 1 f ( x) a sin( k x / L), Fourier k menemukan solusi u( x, t) k 1 a k c k t kx exp sin 2. L L Namun, tak seperti Bernoulli, Fourier memberikan rumus untuk koefisien ak dalam f, yakni a k 2 L L 0 f ( x)sin( k x / L) dx [lihat Strichartz, 2000]. Bermula dari penemuan Fourier inilah anak-cabang matematika yang dikenal sebagai analisis Fourier lahir. Tidak hanya itu, banyak gagasan dasar dan hasil dalam matematika yang dikembangkan oleh sejumlah matematikawan ketika mereka mempelajari deret Fourier. Sebagai contoh, konsep fungsi modern diperkenalkan oleh P.G.L. Dirichlet ( ) ketika ia mempelajari kekonvergenan 13
17 deret Fourier; demikian pula teori distribusi dikembangkan olehnya dalam rangka mempelajari transformasi Fourier. Konsep integral Riemann dan integral Lebesgue diperkenalkan oleh G.F.B. Riemann ( ) dan H. Lebesgue ( ) juga dalam studi analisis Fourier. Contoh lainnya, bilangan ordinal dan kardinal tak hingga dikembangkan oleh G. Cantor ( ) dalam upayanya memecahkan suatu masalah analisis real yang melibatkan deret trigonometri [lihat G. Weiss, 1965]. Bila pada awalnya analisis Fourier dikembangkan untuk memecahkan masalah fisis tertentu, analisis Fourier kini mempunyai banyak aplikasi, tidak hanya dalam matematika tetapi juga dalam bidang ilmu lainnya, sebutlah misalnya dalam teori bilangan [lihat E.M. Stein & R. Sharkarchi, 2003], teori peluang, dan analisis signal di fisika, teknik elektro, dan kedokteran [lihat G.B. Folland, 1996, dan M.A. Pinsky, 2002]. Sejalan dengan perkembangan anak-cabang matematika dan bidang ilmu lainnya, analisis Fourier kini telah berkembang semakin jauh. Dalam buku-buku teks terkini, deret Fourier untuk fungsi periodik f dengan periode 1 didefinisikan sebagai c e 2ikx, k k 14
18 dengan rumus koefisien c k 1 0 f 2ikx ( x) e dx. Sementara itu, transformasi Fourier dari fungsi f yang terintegralkan Lebesgue pada R didefinisikan sebagai dengan rumus inversi Ff ( ) f ( x) f ( x) e Ff ( ) e 2ix 2ix dx, d. Baik deret maupun transformasi Fourier mempunyai interpretasi penting dalam analisis signal. Bila f menyatakan signal pada domain waktu, maka Ff menyatakan signal yang sama pada domain frekuensi. Analisis signal f dalam hal ini dapat dilakukan melalui transformasi Fourier-nya, yaitu Ff. Pendekatan baru banyak dilakukan dalam studi analisis Fourier, misalnya melalui pemahaman analisis fungsional abstrak. Perkembangan ini tentu saja diikuti oleh penemuan-penemuan baru, yang akhirnya melahirkan analisis Fourier modern. Dalam analisis Fourier modern, berbagai operator integral selain transformasi Fourier, sebutlah transformasi Hilbert, operator konvolusi, operator maksimal, operator integral singular, dan operator integral fraksional, 15
19 juga menjadi bahan kajian utama. Permasalahan sentral berkenaan dengan operator-operator tersebut adalah: apakah mereka terbatas dari suatu ruang fungsi ke ruang fungsi lainnya? Sebagai contoh, kita tahu bahwa transformasi Fourier merupakan isometri (yakni, mengawetkan energi) di ruang Lebesgue L 2, dan secara umum ia terbatas dari L p ke L q, yakni memenuhi ketaksamaan Ff q C p, q f p, untuk 1 p 2 dan 1/q = 1 1/p. (Catatan: Ruang Lebesgue L p (X) p p beranggotakan fungsi f dengan f ( ) p f x dx. ) X 1 Beberapa operator yang dipelajari dalam analisis Fourier terkait erat dengan persamaan-persamaan diferensial klasik seperti persamaan gelombang, persamaan panas, dan persamaan Poisson. Keterbatasan sebuah operator dalam hal ini setara dengan kekontinuan operator, yang terkait dengan regularitas operator tersebut. Bila operator itu terkait dengan suatu persamaan diferensial, maka keterbatasannya menentukan well-posedness persamaan diferensial tersebut. Pengetahuan tentang keterbatasan operator yang terkait dengan suatu persamaan diferensial atau persamaan integral seringkali diperlukan ketika kita harus menghampiri solusi persamaan tersebut secara numerik. 16
20 2.1 Operator Maksimal Kiprah penelitian saya dalam analisis Fourier berawal ketika saya menempuh program doktor di UNSW, Sydney, pada tahun , di bawah bimbingan Professor M. Cowling. Topik penelitian saya ketika itu adalah mengenai operator maksimal yang diperumum di R n dan di grup Lie. Operator maksimal pertama kali dipelajari oleh G.H. Hardy dan J.E. Littlewood pada tahun Dalam notasi sekarang, operator maksimal M didefinisikan sebagai operator yang memetakan fungsi f : R n R ke fungsi Mf : R n R, dengan 1 Mf ( x) : sup r0 B( x, r) B( x, r) f ( y) dy. Hardy dan Littlewood membuktikan bahwa operator ini terbatas dari L p ke L p, untuk 1 < p. Sebagai akibat dari keterbatasan operator maksimal M, kita mempunyai Teorema Diferensiasi Lebesgue, yang menyatakan bahwa 1 lim r0 B( x, r) B( x, r) f ( y) dy f ( x) hampir di mana-mana [lihat E.M. Stein, 1970]. Selain itu, fungsi maksimal Hardy-Littlewood Mf dapat dipakai untuk menaksir operator konvolusi yang memetakan f ke Kf = kt * f, yakni 17
21 Kf ( x) k ( y) f ( x y) dy, R n t dengan kernel radial kt(y) = t -n k1(y/t). Ini merupakan hasil penting mengingat solusi persamaan diferensial klasik seperti persamaan panas ut = Δu dengan u(x,0) = f(x) merupakan bentuk konvolusi u(x,t) = Ht * f(x) dengan kernel panas H1(x) = 2 e (4 ) x / 4 n / 2 [lihat Pinsky, 2002]. Pada 1976, Stein mempelajari operator maksimal sperikal MS, yakni M S f ( x) sup f ( x r ) d, r 0 1 n S dengan S n-1 menyatakan permukaan bola satuan di R n dan dσ adalah ukuran permukaan pada S n-1 dengan massa total 1. Stein membuktikan bahwa operator ini terbatas dari L p ke L p, n/(n-1) < p, untuk n 3. Hasil ini dibuktikan kembali oleh M. Cowling dan G. Mauceri pada 1979 dengan menggunakan transformasi Mellin. Keterbatasan operator MS dari L p ke L p, 2 < p, untuk n = 2, dibuktikan oleh J. Bourgain pada (Bourgain mendapatkan Fields Medal pada 1994, di antaranya untuk temuannya tentang operator maksimal sperikal MS di R 2.) Pada 1986, Cowling dan Mauceri mendefinisikan operator maksimal Mφ yang terkait dengan distribusi φ pada R n, 18
22 M f ( x) sup * f ( x), r0 dengan φr(x) = r -n φ(x/r). Jika φ adalah ukuran permukaan pada S n-1, maka Mφ adalah operator maksimal sperikal yang telah dipelajari oleh Stein sebelumnya. Cowling dan Mauceri (dan secara independen J.L. Rubio de Francia) membuktikan teorema berikut. r Teorema [Cowling-Mauceri; Rubio de Francia]. Jika φ mempunyai support kompak di R n dan memenuhi Fφ(rσ) C(1 + r) -α, r > 0, σ = 1, untuk suatu α > ½, maka Mφ terbatas di L 2. Dengan menggunakan transformasi Mellin, saya berhasil membuktikan keterbatasan Mφ untuk distribusi φ yang berbeda. Teorema. Jika φ mempunyai support kompak di R n dan memenuhi Fφ(rσ) C(1 + r) -ε dan δrfφ(rσ) C(1 + r) -1-ε, r > 0, σ = 1, untuk suatu ε > 0, maka Mφ terbatas di L 2. Hasil ini dipublikasikan di Bollettino della Unione Matematica Italiana pada 1993, yang merupakan paper kedua saya. Paper pertama saya adalah tentang keterbatasan operator maksimal yang diperumum di grup Lie, yang dipublikasikan di Pacific Journal of Mathematics pada (Karena terlalu teknis, saya tidak menampilkannya di 19
23 sini.) Sebuah spin-off dari hasil penelitian tentang keterbatasan operator maksimal di grup Lie adalah metode alternatif penentuan bobot dominan dasar dari suatu sistem akar untuk aljabar Lie, yang papernya terbit pada Pada , dengan dana hibah Program Dosen Muda dari DIKTI, saya mempelajari ketaksamaan berbobot untuk operator maksimal sperikal. Salah satu hasilnya adalah teorema berikut. Teorema. Untuk n 3 dan n/(n-1) < p 2, ketaksamaan berbobot M S f C p f p w,,, p, w berlaku untuk w di Ap dan 0 δ < [p(n-1) n]/[n(p-1)]. Di sini f p p, w ) n R 1/ p f ( x) w( x dx dan Ap adalah kelas bobot w yang memenuhi ketaksamaan 1 B B 1 w( x) dx B B w( x) 1/( p1) dx p1 C [lihat Stein, 1993]. Hasil di atas dipublikasikan di Bulletin of Australian Mathematical Society pada Hasil lainnya dipublikasikan di jurnal berbeda pada Untuk hasil-hasil penelitian ini, saya mendapat hibah publikasi dan juga hibah perjalanan dari DIKTI untuk mempresentasikannya di konferensi di Taiwan pada
24 Pada 2002, Cowling, J. Garcia-Cuerva, dan saya mempublikasikan hasil tentang fungsi maksimal fraksional yang berkaitan dengan rataan sperikal di Bulletin of Australian Mathematical Society. 2.2 Operator Integral Singular (-Δ) -iu/2 Keterkaitan antara operator maksimal, operator maksimal sperikal, dan persamaan gelombang dimensi-n, dapat dijelaskan melalui operator Laplace, yaitu operator diferensial n Δ = x j1 2 2 j. Diilhami oleh rumus F(-Δf)(ξ) = 2πξ 2 Ff(ξ), kita definisikan (-Δ) α/2 untuk sebarang eksponen α melalui F[(-Δ) α/2 f](ξ) = 2πξ α Ff(ξ). Khususnya, untuk α = -iu dengan u 0, kita mempunyai operator Iiu = (-Δ) -iu/2, yang dipelajari oleh A. Sikora dan J. Wright pada Operator Iiu dapat dikenali sebagai operator integral singular Iiuf = Kiu * f, dengan kernel Kiu(x) = c(n,u). x -n+iu. Di sini F(Kiu)(ξ) = 2πξ -iu, dan karena itu Iiu memenuhi kesamaan Parseval I iu f 2 f 2, yakni Iiu merupakan suatu isometri di L 2. Lebih jauh, dapat dibuktikan bahwa Iiu terbatas di L p. 21
25 n / pn / 2 Teorema. I f C (1 u ) f, untuk 1 < p <. iu p p p Dengan menggunakan metode dekomposisi atomik, dapat dibuktikan bahwa operator Iiu juga terbatas dari ruang Hardy H p ke ruang Lebesgue L p untuk 0 < p 1, sebagaimana telah saya publikasikan di Bulletin of Australian Mathematical Society pada Ketaksamaan untuk Iiu dapat digunakan untuk menaksir operator maksimal Mψ,L yang didefinisikan sebagai Mψ,Lf = sup ( tl) f, t0 di mana L adalah operator positif self-adjoint Lf n j, k 1 j a jk k f, dengan ajk = akj terdiferensialkan tak hingga kali, sementara ψ = ψα adalah fungsi yang terdefinisi pada R ix ( ) (1 x ) e dx 1 dan ψ(tl) didefinisikan dengan bantuan teori spektral ixtl ( tl) (1 x ) e dx 1,. Perhatikan bahwa ψ0(λ) = cos(λ) dan ψ1(λ) = 2sin() terkait erat dengan persamaan gelombang dimensi-n utt = Δu, dengan syarat 22
26 awal u(x,0) = g(x), ut(x,0) = f(x), yang solusinya mempunyai transformasi Fourier sin( 2 t) Fu(ξ,t) = Fg(ξ) cos( 2πξ t) + Ff(ξ). 2 Selanjutnya, dengan ketaksamaan untuk Iiu, diperoleh hasil berikut. Teorema. Jika L = (-Δ) 1/2, maka Mψ,L terbatas di L p untuk (a) Re(α) > n/p n/2 + ½, 1 < p 2, dan (b) Re(α) > n/2 n/p + 2/p ½, 2 < p. Jika L = (-Δ) 1/2, maka untuk α = (n+1)/2 operator Mψ,L tak lain adalah operator maksimal Hardy-Littlewood, sementara untuk α = (n-1)/2 ia tak lain adalah operator maksimal sperikal yang dipelajari oleh Stein. Hasil di atas telah dibuktikan oleh Stein pada Saya dan A. Sikora membuktikannya kembali dengan menggunakan ketaksamaan untuk Iiu dan teori spektral pada Sebagai akibat dari teorema di atas, kita mempunyai taksiran untuk M yang terkait dengan solusi persamaan gelombang utt = Δu 1 / 2 1,( ) dengan syarat awal Cauchy u(x,0) = 0 dan ut(x,0) = f(x). Persisnya, kita mempunyai ketaksamaan u(, t) sup t0 t p C p f p, 23
27 untuk 2n/(n+1) < p (jika n 3) atau 2n/(n+1) < p < 2(n-2)/(n-3) (jika n 4). Hasil pengamatan ini saya tulis bersama dengan W. Setya-Budhi dan kami publikasikan di Jurnal Matematika dan Sains pada Operator Integral Fraksional (-Δ) -α/2 Untuk 0 < α < n, operator Iα := (-Δ) -α/2 merupakan operator konvolusi dengan kernel c(n,α). x -n+α, yang lebih dikenal sebagai operator integral fraksional atau potensial Riesz: I f ( y) f ( x) c( n, ) n x y n R dy. Sekitar tahun 1930, Hardy dan Littlewood (dan secara independen Sobolev) membuktikan ketaksamaan untuk 1 < p < n/α, 1/q = 1/p α/n. I f q CP, q f p, Secara umum, pengintegralan menghasilkan fungsi yang lebih mulus. Ketaksamaan Hardy-Littlewood-Sobolev menyatakan bahwa operator integral fraksional Iα memetakan fungsi di L p ke fungsi di L q yang secara lokal berderajat α lebih baik. Untuk α = 2, operator I2 = (-Δ) -1 merupakan invers (lemah) dari operator Laplace. Dari 24
28 ketaksamaan Hardy-Littlewood-Sobolev, kita peroleh hampiran untuk solusi persamaan Poisson (-Δ)u = f di R n dengan n 3, yakni u q C p, q f p, untuk 1 < p < n/2, 1/q = 1/p 2/n. Pada 1970-an, D.R. Adams membuktikan keterbatasan operator Iα dari ruang Morrey L p,λ ke ruang L q,λ, yakni I f P, C p, q f p,, untuk 1 < p < n/α, 0 λ < n αp, dan 1/q = 1/p α/(n λ). (Catatan: 1 p f di L p,λ p (X) berarti f sup ( ) p., f y dy Jika λ = 0, BB( x, r) r B maka L p,λ = L p.) Hasil ini dibuktikan kembali oleh F. Chiarenza dan M. Frasca pada 1987, dan diperluas ke ruang Morrey yang diperumum oleh E. Nakai pada Pada awal tahun 2000-an, Nakai mempelajari keterbatasan operator integral fraksional yang diperumum ( x y ) I f ( x) : f ( y) dy, n n x y dengan : R + R +, di ruang Morrey yang diperumum R L p, : f : f p, sup BB( a, r) 1 1 ( r) B B f ( y) p dy 1/ p. dengan φ : R + R +. 25
29 Jika (t) = t α, maka I = Iα; dan jika φ(r) = r (λ-n)/p, maka L p,φ = L p,λ. Secara umum, fungsi (dan juga φ) harus memenuhi persyaratan tertentu, khususnya doubling condition: 1 2 r s 1 2 C ( r) C. ( s) Hasil Nakai dikembangkan lebih lanjut oleh Eridani pada (Eridani mendapat gelar doktor, dengan predikat cum laude, dari FMIPA-ITB pada 2005.) Dengan menggunakan teknik pemilahan integral, dekomposisi diadik dan memanfaatkan keterbatasan operator maksimal Hardy- Littlewood, saya memperoleh hasil berikut, yang dipublikasikan di Journal of the Indonesian Mathematical Society pada (Dekomposisi diadik merupakan teknik dasar yang telah lama dikenal oleh peneliti analisis Fourier sebelum teori wavelet dan konsep analisis multiresolusi berkembang pada 1980-an.) Teorema. Jika dan φ memenuhi doubling condition, φ surjektif, memenuhi r ( t) t p dt C. ( r) p dan r ( t) ( t) ( t) ( r) t t p / q dt dt C. ( r), r 0 r untuk 1 < p < q <, maka I terbatas dari L p,φ ke L q,ψ, dengan ψ = φ p/q. 0, 26
30 Pada 2004, Eridani, Gunawan, dan Nakai memperluas hasil ini dan mempublikasikannya di Scientiae Mathematicae Japonicae. Pada 2005, saya diundang sebagai pembicara tamu pada Asian Mathematical Conference IV di Singapura, untuk menyampaikan hasil penelitian tentang operator integral fraksional yang diperumum. 2.4 Rencana ke Depan Pada 2006, dengan dana Riset ITB, saya dan beberapa rekan mempelajari keterbatasan operator W. I, dengan W menyatakan operator perkalian. Untuk (t) = t α, subjek ini dipelajari oleh P. Olsen pada 1995 serta K. Kurata, S. Nishigaki, dan S. Sugano pada 1999, dalam rangka memahami perilaku solusi suatu persamaan Schrödinger. Hasil yang kami peroleh telah dikirimkan ke sebuah jurnal internasional. Dalam beberapa tahun ke depan, penelitian tentang operator integral fraksional yang diperumum dan ketaksamaan Olsen masih akan dilakukan. Dalam jangka pendek, keterbatasannya di ruang tak-homogen akan dipelajari. Beberapa peneliti telah bergerak ke arah itu, namun yang dikaji oleh mereka adalah operator integral fraksional Iα. Kami dalam hal ini akan menggarap operator integral fraksional yang diperumum I. Penelitian ini akan dilaksanakan bersama dengan Dr. Eridani dari Unair dan melibatkan seorang mahasiswa program doktor. 27
31 3. Kontribusi dalam Analisis Fungsional (dan Geometri) Berpikir dan bekerja abstrak adalah ciri matematikawan. Bekerja abstrak berarti bekerja dengan intisari atau esensi dari objek-objek yang diamati. (Pelukis seperti Picasso pun memfokuskan dirinya pada esensi dari objek lukisannya.) Meng-abstrak dapat pula diibaratkan meng-angkasa. Dengan mengangkasa, seseorang mempunyai cakrawala yang lebih luas. Itu yang telah kita lihat pada bagian sebelumnya: dengan mempelajari operator maksimal Mψ,L, misalnya, kita telah mempelajari operator maksimal Hardy-Littlewood, operator maksimal sperikal Stein, dan perilaku persamaan gelombang sekaligus. Sekali tepuk banyak nyamuk! Kecenderungan untuk mempelajari topik-topik dalam analisis, terutama analisis Fourier, persamaan diferensial, dan persamaan integral, secara abstrak sebagaimana yang dilakukan oleh V. Volterra ( ), D. Hilbert ( ), E.I. Fredholm ( ), M.R. Frechet ( ), dan F. Riesz ( ) pada awal abad ke-20, telah memicu lahirnya sebuah anak-cabang matematika yang kita kenal sekarang sebagai analisis fungsional. Aksioma-aksioma ruang bernorma diperkenalkan pertama kali oleh Riesz ketika ia mempelajari operator di ruang fungsi kontinu 28
32 C[a,b] pada 1918, namun abstraksinya dirumuskan oleh S. Banach ( ) dalam disertasinya pada Perluasannya untuk ruang bernorma atas lapangan bilangan kompleks C dikembangkan oleh N. Wiener ( ) pada 1923 [lihat W. Rudin, 1973]. Perlunya bekerja di suatu ruang tertentu dengan norma tertentu dapat dijelaskan sebagai berikut. Misalkan kita ingin mengetahui apakah persamaan diferensial orde-1 dy/dx = f(x,y) dengan syarat awal y(x0) = y0 mempunyai solusi; dan bila terdapat solusi, apakah ia tunggal. Untuk itu kita mengubahnya menjadi persamaan integral y(x) = y0 + x x0 f ( t, y( t)) dt. Persamaan integral ini dapat dinyatakan secara singkat sebagai y(x) = Ty(x), dengan T menyatakan operator integral Ty(x) = y0 + x x0 f ( t, y( t)) dt. Fungsi y(x) yang memenuhi persamaan di atas tak lain merupakan titik tetap operator T. Sekilas tampak tidak mudah mencari titik tetap tersebut. Jika kita coba substitusikan sebarang fungsi y0(x) ke 29
33 dalam persamaan di atas, maka kecil kemungkinannya Ty0(x) = y0(x). Jika itu terjadi, maka kita telah menyelesaikan masalah nilai awal di atas. Secara umum, kita akan peroleh sebuah fungsi lain, sebutlah y1(x), yang mungkin jauh dari y0(x). Namun (blink!), bagaimana kalau kita substitusikan y1(x) sekarang, untuk mendapatkan fungsi lain lagi, sebutlah y2(x). Jika kita lakukan ini terusmenerus, maka akan kita dapatkan iterasi Picard yn(x) = Tyn-1(x), n = 1, 2, 3, Di sini kita berharap bahwa barisan yn(x) konvergen ke suatu fungsi y(x), yang merupakan solusi persamaan yang sedang kita cari. Harapan ini akan terkabul apabila y(x) kontinu dan Tyn(x) konvergen ke Ty(x). Permasalahannya sekarang adalah: apakah artinya yn(x) konvergen ke y(x) dan sifat apakah yang harus dimiliki oleh T agar Tyn(x) konvergen ke Ty(x)? Dalam konteks seperti inilah kita perlu bekerja dalam ruang tertentu yang dilengkapi dengan konsep jarak atau norma tertentu. Sebelum saya paparkan hasil-hasil penelitian saya dalam analisis fungsional (dan aplikasinya dalam geometri), terlebih dahulu saya harus menyajikan materi kuliah yang pernah saya dapat dari Profesor Moedomo dan Drs. E. Hutahaean, M.Si., khususnya tentang ruang bernorma dan ruang hasilkali dalam. 30
34 Ruang bernorma adalah ruang vektor X (atas lapangan F = R atau C) yang dilengkapi dengan norma : X R yang bersifat (a) x 0 x X ; x 0 jika dan hanya jika x = 0; (b) cx c. x c F, x X ; (c) x y x y x, y X. Contoh ruang bernorma adalah R n 2 2 dengan x x... x. 1 n Contoh lainnya adalah ruang Lebesgue L p (R) yang beranggotakan 1/ p p fungsi f : R C dengan f p ( ). f x dx R Di ruang bernorma X, barisan (xn) dikatakan konvergen ke x apabila x n x 0 untuk n. Barisan (xn) disebut barisan Cauchy jika m n x x 0 untuk m, n. Jika setiap barisan Cauchy di X merupakan barisan yang konvergen (ke suatu x di X), maka X merupakan ruang yang lengkap dan disebut ruang Banach. Jika T : X X merupakan operator terbatas dan (yn) konvergen ke y, maka (Tyn) konvergen ke Ty. Lebih jauh, jika X merupakan ruang Banach dan T : X X bersifat kontraktif, yakni terdapat C < 1 sehingga Tx Ty C x y x, y X, maka T mempunyai titik tetap (yang tunggal). 31
35 Selanjutnya, ruang hasilkali dalam adalah ruang vektor X yang dilengkapi dengan hasilkali dalam (.,. ) : X X X yang bersifat (a) (x,x) 0; (x,x) = 0 jika dan hanya jika x = 0; (b) (x,y) = (y,x)*; (c) (cx,y) = c(x,y); (d) (x,y+z) = (x,y) + (x,z). [Catatan. Untuk bilangan kompleks, z* berarti z konjugat.] Contoh ruang hasilkali dalam adalah C n dengan hasilkali dalam (x,y) = x1y1* + + xnyn*. Contoh lainnya adalah ruang l 2 yang beranggotakan barisan x = (xk) dengan hasilkali dalam x, y) x y. k Di ruang ( * k k 2 hasilkali dalam, dapat didefinisikan norma x ( x, x) 1/. Ruang hasilkali dalam yang lengkap disebut ruang Hilbert. Konsep ruang bernorma dan ruang hasilkali dalam merupakan pangkal analisis fungsional. Materi selanjutnya mencakup ruang fungsi tertentu (khususnya ruang Lebesgue), operator linear (terbatas dan tak terbatas), dan teori spektral, yang tidak dapat saya jelaskan semuanya di sini. Pada bagian sebelumnya, kita telah melihat aplikasi sejumlah konsep analisis fungsional dalam analisis Fourier modern. Aplikasi analisis fungsional dapat pula dijumpai dalam persamaan diferensial, persamaan integral, analisis numerik, statistika, teori kontrol, riset operasi, fisika, dan engineering science pada umumnya [lihat N. Young, 1988]. 32
36 3.1 Ruang Bernorma-n dan Ruang Hasilkali Dalam-n Pada awal tahun 2000, melalui Dr. Mashadi dari Universitas Riau, saya berkenalan dengan konsep ruang bernorma-2, yang merupakan pengembangan dari ruang bernorma. Bila di ruang bernorma ada konsep jarak atau panjang, maka di ruang bernorma-2 kita dibekali dengan konsep luas. Konsep ruang bernorma-2 pertama kali diperkenalkan oleh S. Gähler pada 1960-an. Dengan segera kita dapat memperumum pola ini dan merumuskan konsep ruang bernorma-n. Terkait dengan konsep ini, pada akhir 1980-an, A. Misiak mengembangkan konsep ruang hasilkali dalam-n. Untuk kemudahan notasi, selanjutnya kita akan membatasi diri pada ruang vektor atas lapangan real yang berdimensi sekurangkurangnya n. Ruang bernorma-n adalah ruang vektor X yang dilengkapi dengan norma-n,..., : X n R yang bersifat (a) x 1,..., xn 0 x1,..., x bergantung linear; n (b) x1,..., x x,..., x untuk tiap permutasi {i1,,in} dari {1,,n}; n i 1 i n (c) cx, x2,..., xn c. x1,..., x untuk tiap bilangan real c; 1 n (d) x x1 ', x2,..., xn x1, x2,..., xn x1 ', x2,..., x 1 n Jika X dilengkapi dengan hasilkali dalam (.,. ), maka x,..., x :=. 1 n det[(xi,xj)] ½ merupakan norma-n pada X. Secara geometris, nilai 33
37 1 n x,..., x dapat ditafsirkan sebagai volume paralelpipedium berdimensi-n yang direntang oleh x1,, xn di X. Ruang hasilkali dalam-n adalah ruang vektor X yang dilengkapi dengan hasilkali dalam-n (.,..,,. ) : X n+1 R yang bersifat (a) (x1,x1 x2,,xn) 0; (x1,x1 x2,,xn) = 0 x1,, xn bergantung linear; (b) x, x x,..., x ) ( x, x x,..., x ) untuk tiap permutasi {i1,,in} ( n i1 i1 i 2 in dari {1,,n}; (c) (x0,x1 x2,,xn) = (x1,x0 x2,,xn) (c) (cx0,x1 x2,,xn) = c(x0,x1 x2,,xn) untuk tiap bilangan real c; (d) (x0+x0,x1 x2,,xn) = (x0,x1 x2,,xn) + (x0,x1 x2,,xn). Jika X dilengkapi dengan hasilkali dalam (.,. ), maka X dapat pula dilengkapi dengan hasilkali dalam-n x, x 0 1 x 2,..., x n ( x ( x2, x1 ) ( x2, x2 ) ( x2, xn ) :. ( x 0 n, x ) 1, x ) 1 Perhatikan bahwa untuk x0 = x1, (x1,x1 x2,,xn) = det[(xi,xj)]. Secara umum, di ruang hasilkali dalam-n dapat didefinisikan norma-n 1 n n ( x ( x 0 n, x, x 2 x,..., x ( x, x x,..., x ) 1/. Ketaksamaan segitiganya merupakan akibat dari ketaksamaan Cauchy-Schwarz 2 2 ) ) ( x ( x 0 n, x, x n n ) ) ( x0, x1 x2,..., xn ) x0, x2,..., xn. x1, x2,..., xn. 34
38 Lebih jauh, dapat dibuktikan bahwa kesamaan pada ketaksamaan Cauchy-Schwarz berlaku jika dan hanya jika x0, x1, x2,, xn bergantung linear. Hasil penelitian saya tentang hasilkali dalam-n, norma-n, dan ketaksamaan Cauchy-Schwarz telah dipublikasikan di Scientiae Mathematicae Japonicae pada Generalisasi dari ketaksamaan Bessel dan kesamaan Parseval di ruang hasilkali dalamn juga saya peroleh dan telah dipublikasikan di Periodica Mathematica Hungarica pada 2002 (namun tidak saya tampilkan di sini karena terlalu teknis). Bila di ruang hasilkali dalam kita dapat mendefinisikan hasilkali dalam-n sebagaimana dirumuskan di atas, maka di ruang hasilkali dalam-n kita dapat pula mendefinisikan hasilkali dalam. Teorema. Misalkan (X, (.,..,,. )) adalah ruang hasilkali dalam-n. Maka, untuk sebarang himpunan {a1,, an} yang bebas linear, ( x, y) : merupakan hasilkali dalam pada X. ( x, y a,..., i2 i ) { i 2,..., i } {1,..., n} n a n Hasil ini mengatakan bahwa ruang hasilkali dalam-n yang diperkenalkan oleh Misiak sesungguhnya merupakan ruang hasilkali dalam. Hasil penelitian ini telah dipublikasikan di Soochow Journal of Mathematics pada Hasil serupa untuk ruang bernorma-n, 35
39 baik untuk kasus umum maupun khusus, telah dipublikasikan di International Journal of Mathematics and Mathematical Sciences dan Bulletin of Australian Mathematical Society pada Ketaksamaan Cauchy-Schwarz yang Diperumum dan Sudut antara Dua Subruang di Ruang Hasilkali Dalam Dengan hasil-hasil yang saya peroleh, kajian tentang ruang bernorma-n dan ruang hasilkali dalam-n pada dasarnya sudah berakhir, karena hampir semuanya dapat dikembalikan ke kerangka ruang bernorma dan ruang hasilkali dalam. Namun, masih ada yang menarik untuk dipelajari berkaitan dengan ketaksamaan Cauchy-Schwarz dan interpretasi geometrisnya. Persisnya, masih sekitar tahun 2000-an, saya tertarik dengan generalisasi dari ketaksamaan Cauchy-Schwarz yang dirumuskan oleh S. Kurepa pada 1966 sebagai berikut. Teorema [Kurepa]. Misalkan (X, (.,. )) ruang hasilkali dalam, {u1,, un} dan {v1,, vn} dua himpunan sebarang di X. Maka, kita mempunyai det[(ui,vj)] 2 det[(ui,uj)].det[(vi,vj)] dan kesamaan berlaku jika dan hanya jika subruang yang direntang oleh {u1,, un} termuat dalam subruang yang direntang oleh {v1,, vn} atau sebaliknya. 36
40 Pada 2001, I.B. Risteski dan K.G. Trenčevski merumuskan generalisasinya untuk himpunan {u1,, un} dan {v1,, vm} dengan m n, dalam rangka mendefinisikan sudut antara dua subruang yang direntang oleh kedua himpunan tersebut. Persisnya, mereka membuktikan ketaksamaan det(mm T ) det[(ui,uj)].det[(vk,vl)] dengan M := [(ui,vk)]. Namun, pada 2003, saya, O. Neswan, dan W. Setya-Budhi, menemukan bahwa ketaksamaan ini hanya berlaku untuk kasus m = n, tidak untuk m > n. Sebagai contoh, di R 3, ambil U = span{u} dengan u = (1,0,0), dan V = span{v1,v2} dengan v1 = (½,½,0) dan v2 = (½,-½,½). Maka det(mm T ) = (u,v1) 2 + (u,v2) 2 = ½, sementara det[(u,u)].det[(vk,vl)] = 3/8. Tidak terlalu sulit bagi kami untuk menemukan kesalahan mereka pada pembuktian ketaksamaan di atas. Namun, untuk memperbaikinya, kami perlu kembali ke esensi sudut antara dua subruang, yang terkait erat dengan ketaksamaan tersebut. Misalnya, sudut θ antara subruang U = span{u} dan V = span{v1,, vm} di ruang hasilkali dalam X diberikan oleh rumus 2 2 ( u, uv ) cos, 2 2 u u dengan uv menyatakan vektor proyeksi u terhadap V. V 37
41 Jika kita tuliskan u = uv + u V dengan u V menyatakan komplemen ortogonal u terhadap V, maka rumus ini setara dengan 2 u cos V 2 u Jadi, nilai cos θ sama dengan rasio panjang vektor proyeksi u terhadap V dan panjang vektor u. Secara umum, untuk berbagai kasus yang dikenal, kami mengamati bahwa nilai cosinus sudut yang dibentuk oleh subruang U = span{u1,, un} dan V = span{v1,, vm} dengan m n senantiasa sama dengan rasio volume paralelpipedium berdimensi-n yang direntang oleh vektor proyeksi u1,, un terhadap V dan volume paralelpipedium berdimensi-n yang direntang oleh u1,, un. Berdasarkan pengamatan inilah kami pada akhirnya dapat memperbaiki kesalahan Risteski dan Trenčevski dan merumuskan sudut antara dua subruang di ruang hasilkali dalam, sebagaimana telah kami publikasikan di Beiträge zur Algebra und Geometrie pada Teorema. Misalkan {u1,, un} dan {v1,, vm} dua himpunan bebas linear di X, dengan m n. Maka, kita mempunyai det M ~ T M det[(ui,uj)].det n [(vk,vl)], ~ dengan M := [(ui,vk)] dan M : [( u, v v,..., v )] dengan {i2(k),, i k i2 ( k ) im ( k ) im(k)} = {1, 2,, m}\{k}, k = 1, 2,, m; dan kesamaan berlaku jika dan 38
42 hanya jika subruang yang direntang oleh {u1,, un} termuat dalam subruang yang direntang oleh {v1,, vm}. Lebih jauh, ~ T det MM cos 2 : n det[( u, u )].det [( v i j k, v )] mendefinisikan sudut θ antara subruang yang direntang oleh {u1,, un} dan subruang yang direntang oleh {v1,, vm}. l Rumus ini mencakup rumus sudut antara dua garis, sudut antara garis dan subruang, serta sudut antara dua subruang berdimensi sama yang tersirat dalam Teorema Kurepa. Lagi-lagi, sekali tepuk banyak nyamuk! Lebih jauh, jika {u1,, un} dan {v1,, vm} bersifat ortonormal, maka sudut antara kedua subruangnya terkait erat dengan sudut kanonik atau sudut utama sebagaimana dijelaskan oleh Risteski dan Trenčevski dalam teorema berikut. Teorema [Risteski & Trenčevski]. Misalkan {u1,, un} dan {v1,, vm} ortonormal, dan θ1 θn sudut kanonik antara U = span{u1,, un} dan V = span{v1,, vm} yang didefinisikan secara rekursif: cos 1 cos i1 max uu, u 1 vv, v 1 max max ( u, v) ( u, v ) uu i, u 1 vv i, v 1 max ( u, v) ( u dengan Ui menyatakan komplemen ortogonal dari ui terhadap Ui-1 dan Vi menyatakan komplemen ortogonal dari vi terhadap Vi-1 (dengan U0 = U dan V0 = V). Maka cos 2 θ = cos 2 θ1 cos 2 θn. 1 1 i1, v i1 ) 39
43 Statistikawan menggunakan sudut kanonik sebagai ukuran ketergantungan sejumlah peubah acak terhadap sejumlah peubah acak lainnya. Untuk n = 2, khususnya, nilai cos θ merupakan hasilkali korelasi maksimum dan korelasi minimum antara u di U dengan penaksir terbaiknya di V, sebagaimana dinyatakan oleh teorema berikut (yang dapat dibuktikan hanya dengan kalkulus elementer). Teorema. Untuk n = 2, cos θ = max max ( u, v) min max ( u, v). uu, u 1 vv, v 1 uu, u 1 vv, v 1 Untuk n sebarang, saya dan Neswan dapat membuktikan teorema berikut dengan menggunakan pengetahuan aljabar linear elementer dan kalkulus peubah banyak. Teorema. Nilai cos θ sama dengan hasilkali semua nilai kritis fungsi f(u) = max ( u, v), u U, u 1. vv, v 1 Teorema. Nilai cos θ sama dengan volume paralelpipedium berdimensin yang direntang oleh vektor projv(ui), i = 1,, n. Hasil ini kami publikasikan di Journal of the Indonesian Mathematical Society pada Penelitian tentang sudut antara dua subruang didanai oleh Sub-Proyek QUE Matematika ITB. 40
44 3.3 Rencana ke Depan Dalam beberapa tahun terakhir, saya dan rekan telah mempelajari pula konsep ortogonalitas di ruang bernorma-n dan ruang hasilkali dalam-n. Ke depan, mengingat bahwa hasil-hasil yang diperoleh banyak bersentuhan dengan geometri, saya berencana untuk mempelajari aljabar geometrik, dalam rangka meng-abstrak lebih jauh, dengan harapan mempunyai cakrawala yang lebih luas. Selain itu, kami juga akan mulai mengkaji area aplikasi analisis fungsional, khususnya dalam analisis numerik. Penelitian pertama ke arah itu adalah tentang interpolasi yang meminimumkan fungsional tertentu (seperti kurvatur atau energi secara umum). Sebagai ilustrasi, diberikan n buah titik (x1,c1), (x2,c2),..., (xn,cn), dengan a = x1 < x2 <... < xn = b, permasalahannya adalah bagaimana mencari fungsi terdiferensialkan (dua kali atau lebih) pada selang [a,b] yang melalui n titik tersebut dan memiliki kurvatur minimum. Selain konsep-konsep analisis fungsional, konsep-konsep analisis Fourier juga diperlukan untuk memecahkan masalah ini. Penelitian ini akan dilaksanakan bersama dengan Dr. A.R. Alghofari dari Unibraw dan seorang mahasiswa program doktor Unpad. 41
45 4. Epilog: Renungan dan Harapan Dihitung mulai dari Dr. Sam Ratulangi, Indonesia kini memiliki hampir 100 doktor matematika, tersebar di sejumlah perguruan tinggi di Indonesia (31 di antaranya dosen aktif di ITB). Jumlah ini kira-kira sama dengan jumlah total doktor matematika di NUS dan NTU Singapura. Namun, dalam hal produktivitas riset, kita jauh tertinggal. Per Desember 2006 tercatat hanya 163 paper karya matematikawan Indonesia yang dipublikasikan di berbagai jurnal yang dipantau oleh Mathematical Reviews. Jumlah ini sudah termasuk 52 paper yang terbit di Journal of the Indonesian Mathematical Society (Majalah Ilmiah Himpunan Matematika Indonesia) sejak tahun (Sebagai pembanding, Singapura telah membukukan 4741 paper di Mathematical Reviews.) Sebanyak 112 di antara 163 paper tadi adalah karya matematikawan ITB. Paper karya Profesor Moedomo, dan beberapa paper karya Profesor S.M. Nababan dan Profesor Edy Soewono yang terbit dari awal 1970-an hingga awal 1990-an, juga terekam di Mathematical Reviews, namun tidak membawa nama ITB ataupun Indonesia. Bila paper-paper tersebut dihitung, maka jumlah total paper matematikawan ITB mencapai 150-an dan jumlah total paper matematikawan Indonesia mungkin mencapai 200-an. (Sebagai pembanding lainnya, Malaysia per Desember 2006 telah membukukan 701 paper di Mathematical Reviews.) 42
46 Dari statistik sederhana ini, kita dapat menyimpulkan bahwa perkembangan matematika di Indonesia masih jauh tertinggal dari negara-negara lainnya. Bukan hanya karena jumlah matematikawan di Indonesia belum mencapai critical mass, tetapi produktivitasnya juga rendah. Selain itu, penelitian dalam bidang dasar seperti matematika belum (dan mungkin tidak akan pernah) menjadi prioritas. Untuk mendapatkan hibah penelitian, sebagian dosen matematika terpaksa menjual diri dengan menampilkan judul berbau fisika, teknologi informasi, atau industri, karena bidang-bidang itulah yang diprioritaskan baik oleh DIKTI maupun Menristek. Kelak, ketika dana hibah diperoleh, output-nya entah termasuk karya matematika atau bukan, dipublikasikan atau tidak, seringkali tidak dipertanyakan. Pada kenyataannya, jumlah paper matematika hasil penelitian yang didanai oleh DIKTI atau Menristek dan dipublikasikan di jurnal internasional bisa dihitung dengan jari. Sebagian besar paper yang terekam di Mathematical Reviews dan membawa nama institusinya di Indonesia adalah buah proyek cinta, meminjam istilah Profesor Maman A. Djauhari. Sebagian besar lainnya dihasilkan ketika si penulis menempuh program doktornya di luar negeri. Untuk bertahan dan tetap berkarya dalam kondisi seperti ini diperlukan niat dan tekad yang kuat. Selain itu, jaringan dengan pe- 43
47 neliti di luar negeri mutlak diperlukan. Dengan jaringan yang saya miliki, misalnya, saya beberapa kali diundang dan dibiayai untuk berkunjung ke universitas di luar negeri. Permasalahannya adalah bahwa saya tidak dapat dengan mudah mengundang dan membiayai kolega dari luar negeri untuk berkunjung ke ITB, karena keterbatasan dana yang ada. Fasilitas dan dukungan dari institusi setempat, sekecil apapun, sangat berarti. Manfaat dana Riset ITB yang dikucurkan oleh LPPM sejak 2004, misalnya, dapat dirasakan baik oleh para dosen maupun ITB sendiri, dan cepat atau lambat buahnya dapat dinikmati bersama. Namun, dalam struktur organisasi yang baru di ITB, peran KK dan juga komunikasi dan sinergi antar-kk saat ini masih jauh dari optimal. Selain masih ada kebingungan dengan penulisan alamat dan terjemahan KK dalam bahasa Inggris, tembok departemen terasa masih ada sekalipun departemen sudah dihapus. Sebagai contoh, dalam struktur sekarang sebetulnya tidak ada lagi sekat di antara dosen matematika dan dosen fisika, kecuali gedungnya terpisah. Namun, seberapa seringkah dalam setahun terakhir komunikasi ilmiah terjalin di antara kedua komunitas? Lalu, bila kita tengok kurikulum kedua Program Studi Matematika dan Fisika, seberapa banyakkah irisannya? Tidakkah janggal bila irisannya hanya sejumlah matakuliah tahun pertama? 44
48 Komunikasi, apalagi sinergi, rupanya memang tidak mudah. Di milis Dosen ITB, seorang dosen teknik pernah mengatakan bahwa matematikawan dan scientists perlu mendukung para engineers untuk memecahkan permasalahan dalam engineering, jangan menekuni sains hanya untuk sains. Tanggapan saya waktu itu adalah OK, saya menguasai analisis Fourier dan analisis fungsional, apa yang bisa saya bantu? Saya sungguh berharap para engineers dapat menguraikan permasalahannya cukup rinci sehingga jelas dukungan matematika (dan sains) apa yang diperlukan oleh mereka. Sayangnya, tidak ada tanggapan lebih lanjut hingga saat ini. Sebagian rekan lainnya di ITB berpandangan bahwa sains untuk sains tidak perlu dicegah. Menurut mereka, banyak penemuan yang pada awalnya bersifat sains untuk sains berdampak positif pada bidang lain di kemudian hari. Di antara para matematikawan sendiri, konon ada matematika murni dan matematika terapan, walaupun sesungguhnya proses yang dilakukan oleh para matematikawan terapan tidaklah banyak berbeda dengan yang dilakukan oleh matematikawan murni. Yang seringkali berbeda adalah sumber permasalahannya: yang satu muncul ketika mempelajari matematika itu sendiri, sementara yang lainnya dipicu oleh masalah nyata dari bidang lain. G. Gonnet mengilustrasikan keterkaitan antarcabang matematika 45
49 dan penerapannya sebagai rantai makanan. Sebagai contoh, dalam suatu rantai makanan, ada yang harus menggarap sawah, memilih bibit, menanam dan menuai padi, memberi makan ternak, mengangkut dan memasarkan, dan akhirnya kita semua dapat menikmati semur daging di rumah. Setiap tahap memerlukan tahap sebelumnya dan menopang tahap selanjutnya. Jadi, bila kita ingin hidup di dunia yang kian bergantung pada teknologi yang semakin canggih seperti sekarang ini, kita harus menjaga semua mata rantai yang ada termasuk yang paling teoritis sekalipun. Bila tidak ada yang menggarap sawah, dalam beberapa tahun kita mungkin takkan dapat menikmati semur daging lagi! Dan bila tidak ada yang menekuni matematika murni, dalam beberapa tahun kita mungkin takkan pernah mendengar penemuan teknologi baru lagi. Bila kita telusuri kemajuan teknologi di Eropa dan negara-negara maju lainnya, maka kita akan melihat bahwa mereka memang pantas menikmatinya karena mereka telah menanam bibitnya sebelumnya. Pada jaman Renaissance di Eropa, penelitian lebih banyak dilakukan di akademi kerajaan, bukannya di universitas. Sebagian area penelitian bersifat terapan, namun sebagian lainnya lebih bersifat murni, alias riset untuk riset. Pihak Kerajaan (baca: 46
50 Pemerintah) mendanai secara generous penelitian murni, di antaranya bidang matematika, demi pengembangan pengetahuan manusia. Singkat kata, matematikawan dan scientists pada jaman itu tidak mengalami kesulitan dana dan dapat mendedikasikan waktu sepenuhnya untuk mengembangkan ilmu. Karena itu, matematika dan sains berkembang subur dan berbuah! Jelaslah kiranya sekarang mengapa teknologi hasil karya putra bangsa merupakan barang langka di Indonesia, karena matematika (dan mungkin sains juga) yang seharusnya dikembangkan untuk menopang pengembangan teknologi baru belum terlalu berkembang. Selain komunitas matematikawan yang belum terlalu kuat dan pendanaan untuk penelitian dalam matematika yang kurang memadai, komunikasi dan sinergi di antara komunitas matematika, sains dan engineering belum terbangun. Bila masalahnya sudah begitu gamblang, solusinya pun sesungguhnya amat jelas: penelitian dalam bidang matematika (dan sains) mau tidak mau harus digalakkan dan didukung, dan untuk itu komunitas matematikawan khususnya harus diperkuat. Selain itu, komunikasi dan sinergi antar-komunitas harus dibangun. Di ITB khususnya, adanya Advanced Research Program yang bergulir baru-baru ini, bila terealisasi kelak, harus kita manfaatkan bersama untuk membangun sinergi dan melompat maju! 47
51 Ucapan Terima Kasih Pertama, ucapan terima kasih penulis tujukan kepada Papah (alm.) dan Mamah atas didikan dan kasih-sayangnya, dan kepada Istri tercinta, Ita Ananta, serta anak-anak tersayang, Rubio dan Viola, atas dukungan, pengertian, dan kesabarannya. Penulis juga berhutang-budi kepada Prof. Moedomo (alm.), Prof. Michael Cowling (UNSW), Drs. E. Hutahaean, M.Si., Dr. Wono Setya-Budhi, yang telah memperkenalkan analisis kepada penulis; dan juga kepada Prof. A. Arifin (alm.), Prof. M. Ansjar, Prof. S.M. Nababan, Prof. Eiichi Nakai (Osaka), Dr. Bana G. Kartasasmita, Drs. I Nyoman Susila, M.Sc., Prof. Maman A. Djauhari, yang telah membagikan ilmunya. Kepada beberapa kolega yang sering berdiskusi dengan penulis, khususnya Prof. Edy Soewono, Dr. Iwan Pranoto, Dr. Oki Neswan, Dr. Andonowati, Prof. Edy Tri Baskoro, Dr. Yudi Soeharyadi, Dr. Theo Tuwankotta, dan seluruh anggota KK Analisis dan Geometri serta rekan lainnya di eks-departemen Matematika ITB, penulis ucapkan terima kasih. Secara khusus penulis berterima kasih kepada Prof. Wiranto Arismunandar dan Prof. Bambang Hidayat yang sedikit banyak telah mempengaruhi penulis dalam kehidupan akademis. Ucapan terima kasih penulis sampaikan pula kepada Prof. Deny Juanda Puradimaja, Dr. Satria Bijaksana, dan Dr. Sri Widiyantoro, atas komunikasi yang telah terjalin selama ini. Akhirnya, penulis tak lupa menyampaikan terima kasih dan penghargaan yang setinggi-tingginya kepada para pejabat eksekutif dan normatif serta karyawan di ITB periode , yang tak dapat disebutkan namanya satu per satu. 48
52 Daftar Pustaka A.D. Aczel (1996), Fermat s Last Theorem, Four Walls Eight Windows, New York. D.R. Adams (1975), A note on Riesz potentials, Duke Math. J. 42, J. Bourgain (1986), Averages in the plane over convex curves and maximal operators, J. Analyse Math. 47, F. Chiarenza and M. Frasca (1987), Morrey spaces and Hardy- Littlewood maximal functions, Rend. Mat. 7, M. Cowling, J. Garcia-Cuerva, and H. Gunawan (2002), Weighted estimates for fractional maximal functions related to spherical means, Bull. Austral. Math. Soc. 66, M. Cowling and G. Mauceri (1979), On maximal functions, Rend. Sem. Mat. Fis. Milano 49, (1986), Inequalities for some maximal functions. II, Trans. Amer. Math. Soc. 296, Eridani (2002), On the boundedness of a generalized fractional integral on generalized Morrey spaces, Tamkang J. Math. 33, Eridani and H. Gunawan (2005), Stummel class and Morrey spaces, Southeast Asian Bull. Math. 29, Eridani, H. Gunawan, and E. Nakai (2004), On generalized fractional integral operators, Sci. Math. Jpn. 60, G.B. Folland (1992), Fourier Analysis and Its Applications, Brooks/ Cole, Pacific Grove. S. Gähler (1964), Lineare 2-normietre räume, Math. Nachr.28,
53 G. Gonnet (1994), artikel di Zürich Intelligencer, International Congress of Mathematicians. B. Grun (1991), The Timetables of History, 3 rd ed., Simon & Schuster, New York. J. Gullberg (1997), Mathematics: From the Birth of Numbers, W.W. Norton & Company, New York. H. Gunawan (1991), Maximal Functions and Harmonic Analysis, Ph.D. Thesis, University of New South Wales, Sydney. [Abstrak terbit pada 1993 di Bull. Austral. Math. Soc. 47, 351.] (1992), A generalization of maximal functions on compact semi-simple Lie groups, Pacific J. Math. 156, (1993), L 2 estimates for some maximal functions, Boll. Un. Mat. Ital. B (7) 7, (1996), On weighted estimates for Stein's maximal function, Bull. Austral. Math. Soc. 54, (1997), On finding the fundamental dominant weights of a root system, Southeast Asian Bull. Math. 21, (1998), Some weighted estimates for Stein's maximal function, Bull. Malaysian Math. Soc. 21, (2001), The space of p-summable sequences and its natural n-norm, Bull. Austral. Math. Soc. 64, (2001), An inner product that makes a set of vectors orthonormal, Austral. Math. Soc. Gazette 28, (2002), On n-inner products, n-norms, and the Cauchy-Schwarz inequality, Sci. Math. Jpn. 55, (2002), A generalization of Bessel s inequality and Parseval s identity, Periodica Math. Hungarica 44, (2002), Inner products on n-inner product spaces, Soochow J. Math. 28,
54 (2002), On convergence in n-inner product spaces, Bull. Malaysian. Math. Sci. Sc. 25, (2002), Some weighted estimates for imaginary powers of the Laplace operator, Bull. Austral. Math. Soc. 65, (2003), A note on generalized fractional integral operators, J. Indones. Math. Soc. 9, (2005), Generalized fractional integral operators and their modified versions, Proceedings of Fourth Asian Mathematical Conference, Singapore. H. Gunawan, G. Gunawan, Y. Soeharyadi, and Eridani (2006), Generalized fractional integral operators and Olsen inequalities, Preprint. H. Gunawan, E. Kikianty, Mashadi, S. Gemawati, dan I. Sihwaningrum (2006), Orthogonality in n-normed spaces, Preprint. H. Gunawan and Mashadi (2001), On finite-dimensional 2-normed spaces, Soochow J. Math. 27, (2001), On n-normed spaces, Int. J. Math. Math. Sci. 27, H. Gunawan, Mashadi, S. Gemawati, Nursupiamin, and I. Sihwaningrum (2006), Orthogonality in 2-normed spaces revisited, Univ. Beograd. Publ. Elektrotehn. Fak. Ser. Mat. 17, H. Gunawan and O. Neswan (2005), On angles between subspaces of inner product spaces, J. Indones. Math. Soc. 11, H. Gunawan, O. Neswan, and W. Setya-Budhi (2005), A formula for angles between subspaces of inner product spaces, Beiträge Alg. Geom. 46, H. Gunawan dan W. Setya-Budhi (2004), On the behavior of the solution of the wave equation, Jurnal Matematika dan Sains 9,
55 H. Gunawan, W. Setya-Budhi, Mashadi, S. Gemawati (2005), On volumes of n-dimensional parallelepiped in l p spaces, Univ. Beograd. Publ. Elektrotehn. Fak. Ser. Mat. 16, H. Gunawan and A. Sikora (2002), On maximal operators associated to Laplace operators, Research Report. G.H. Hardy and J.E. Littlewood (1927), Some properties of fractional integrals. I, Mat. Zeit. 27, (1930), A maximal theorem with function-theoretic applications, Acta Mat. 54, K. Kurata, S. Nishigaki, and S. Sugano (1999), Boundedness of integral operators on generalized Morrey spaces and its application to Schrödinger operators, Proc. Amer. Math. Soc. 128, S. Kurepa (1966), On the Buniakowsky-Cauchy-Schwarz inequality, Glas. Mat. III Ser. 1, 21, A. Misiak (1989), n-inner product spaces, Math. Nachr. 140, E. Nakai (1994), Hardy-Littlewood maximal operator, singular integral operators and the Riesz potentials on generalized Morrey spaces, Math. Nachr. 166, (2002), On generalized fractional integrals, Taiwan. J. Math. 5, (2002), On generalized fractional integrals on the weak Orlicz spaces, BMOφ, the Morrey spaces and the Campanato spaces, in Function Spaces, Interpolation Theory and Related Topics (Lund, 2000), , de Gruyter, Berlin. P.J. Olsen (1995), Fractional integration, Morrey spaces, and a Schrödinger operator, Comm. Partial Diff. Equation 20, M.A. Pinsky (2002), Introduction to Fourier Analysis and Wavelets, Brooks/Cole, Pacific Grove. 52
56 I.B. Risteski and K.G. Trenčevski (2001), Principal values and principal subspaces of two subspaces of vector spaces with inner product, Beiträge Alg. Geom. 42, J.L. Rubio de Francia (1986), Maximal functions and Fourier transforms, Duke Math J. 53, W. Rudin (1973), Functional Analysis, Tata McGraw-Hill Publishing Company, New Delhi. A. Sikora and J. Wright (2001), Imaginary powers of Laplace operators, Proc. Amer. Math. Soc. 129, S.L. Sobolev (1938), On a theorem in functional analysis, Mat. Sob. 46, Society for Industrial and Applied Mathematics (1996), SIAM Report on Mathematics in Industry, Philadelphia. E.M. Stein (1970), Singular Integrals and Differentiability Properties of Functions, Princeton University Press, Princeton (1976), Maximal functions: spherical means, Proc. Nat. Acad. Sci. USA 73, (1993), Harmonic Analysis, Princeton University Press, Princeton. E.M. Stein and R. Shakarchi (2003), Fourier Analysis, Princeton University Press, Princeton. I. Stewart (1995), Nature s Numbers, A Phoenix Paperback. R.S. Strichartz (2000), The Way of Analysis, Jones & Bartlett Publishers, Sudbury, G. Weiss (1965), Harmonic Analysis, MAA Studies in Mathematics (I.I Hirschman, Jr., Ed.), Prentice-Hall. N. Young (1988), An Introduction to Hilbert Space Theory, Cambridge University Press, Cambridge. 53
57 Curriculum Vitae N a m a : Hendra Gunawan Tempat & Tgl. Lahir : Bandung, 29 Des 1964 Nama Istri & Anak : Ir. Ita Ananta, MAppSc. Alamat Kantor Rubio Gunawan Viola Ananta : FMIPA ITB Jl. Ganesa 10 Bandung Riwayat Pendidikan : Ph.D., School of Mathematics, UNSW, Sydney : Sarjana, Jurusan Matematika, ITB, Bandung Riwayat Pekerjaan/Jabatan : Guru Besar pada FMIPA-ITB : Lektor Kepala pada FMIPA-ITB 2000 : Lektor pada FMIPA-ITB : Lektor Muda pada FMIPA ITB : Asisten Ahli pada FMIPA-ITB : Asisten Ahli Madya pada FMIPA-ITB : Tutor pada School of Mathematics, UNSW, Sydney 1987 : Asisten pada Fakultas Teknik, Unpar Penugasan di Lingkungan ITB : Anggota Majelis Guru Besar ITB : Anggota Satgas Akreditasi & Asesmen Internal SPM-ITB : Anggota Senat FMIPA-ITB : Anggota Komisi Program Pascasarjana FMIPA-ITB : Ketua Gugus Kendali Mutu FMIPA-ITB : Ketua KK Analisis dan Geometri, FMIPA-ITB 54
SUKSES BELAJAR KALKULUS
 SUKSES BELAJAR KALKULUS Hendra Gunawan, Ph.D. Bandung, 14 Maret 2007 BELAJAR =? proses menumbuhkembangkan pengetahuan dan/atau keterampilan, dengan/melalui pengalaman, pengamatan, mencoba melakukan, praktek/latihan,
SUKSES BELAJAR KALKULUS Hendra Gunawan, Ph.D. Bandung, 14 Maret 2007 BELAJAR =? proses menumbuhkembangkan pengetahuan dan/atau keterampilan, dengan/melalui pengalaman, pengamatan, mencoba melakukan, praktek/latihan,
KETAKSAMAAN OLSEN UNTUK OPERATOR RIESZ YANG DIPERUMUM. Oleh. Hendra Gunawan* dan Yudi Soeharyadi. Institut Teknologi Bandung Bandung, Indonesia
 KETAKSAMAAN OLSEN UNTUK OPERATOR RIESZ YANG DIPERUMUM Oleh Hendra Gunawan* dan Yudi Soeharyadi Institut Teknologi Bandung Bandung, Indonesia dipresentasikan pada Konferensi Nasional Matematika XIII, di
KETAKSAMAAN OLSEN UNTUK OPERATOR RIESZ YANG DIPERUMUM Oleh Hendra Gunawan* dan Yudi Soeharyadi Institut Teknologi Bandung Bandung, Indonesia dipresentasikan pada Konferensi Nasional Matematika XIII, di
DASAR-DASAR TEORI RUANG HILBERT
 DASAR-DASAR TEORI RUANG HILBERT Herry P. Suryawan 1 Geometri Ruang Hilbert Definisi 1.1 Ruang vektor kompleks V disebut ruang hasilkali dalam jika ada fungsi (.,.) : V V C sehingga untuk setiap x, y, z
DASAR-DASAR TEORI RUANG HILBERT Herry P. Suryawan 1 Geometri Ruang Hilbert Definisi 1.1 Ruang vektor kompleks V disebut ruang hasilkali dalam jika ada fungsi (.,.) : V V C sehingga untuk setiap x, y, z
0. Pendahuluan. 0.1 Notasi dan istilah, bilangan kompleks
 0. Pendahuluan Analisis Fourier mempelajari berbagai teknik menganalisis sebuah fungsi dengan menguraikannya sebagai deret atau integral fungsi tertentu (yang sifat-sifatnya telah kita kenal dengan baik,
0. Pendahuluan Analisis Fourier mempelajari berbagai teknik menganalisis sebuah fungsi dengan menguraikannya sebagai deret atau integral fungsi tertentu (yang sifat-sifatnya telah kita kenal dengan baik,
SUKSES BELAJAR KALKULUS
 SUKSES BELAJAR KALKULUS Hendra Gunawan, Ph.D. 31 Agustus & 7 September 2007 BELAJAR =? proses menumbuhkembangkan pengetahuan dan/atau keterampilan, dengan/melalui pengalaman, pengamatan, mencoba melakukan,
SUKSES BELAJAR KALKULUS Hendra Gunawan, Ph.D. 31 Agustus & 7 September 2007 BELAJAR =? proses menumbuhkembangkan pengetahuan dan/atau keterampilan, dengan/melalui pengalaman, pengamatan, mencoba melakukan,
Fourier Analysis & Its Applications in PDEs - Part II
 Fourier Analysis & Its Applications in PDEs Hendra Gunawan http://personal.fmipa.itb.ac.id/hgunawan/ Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA WIDE 2010 5-6 August
Fourier Analysis & Its Applications in PDEs Hendra Gunawan http://personal.fmipa.itb.ac.id/hgunawan/ Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA WIDE 2010 5-6 August
Keterbatasan Operator Riesz di Ruang Morrey
 J. Math. and Its Appl. ISSN: 829-605X Vol. 3, No., May 2006, 27 40 Keterbatasan Operator Riesz di Ruang Morrey Gani Gunawan, Hendra Gunawan Departemen Matematika FMIPA ITB Abstrak Dengan menggunakan transformasi
J. Math. and Its Appl. ISSN: 829-605X Vol. 3, No., May 2006, 27 40 Keterbatasan Operator Riesz di Ruang Morrey Gani Gunawan, Hendra Gunawan Departemen Matematika FMIPA ITB Abstrak Dengan menggunakan transformasi
BAB 2 RUANG HILBERT. 2.1 Definisi Ruang Hilbert
 BAB 2 RUANG HILBERT Pokok pembicaraan kita dalam tugas akhir ini berpangkal pada teori ruang Hilbert. Untuk itu di bab ini akan diberikan definisi ruang Hilbert dan ciri-cirinya, separabilitas ruang Hilbert,
BAB 2 RUANG HILBERT Pokok pembicaraan kita dalam tugas akhir ini berpangkal pada teori ruang Hilbert. Untuk itu di bab ini akan diberikan definisi ruang Hilbert dan ciri-cirinya, separabilitas ruang Hilbert,
MATEMATIKA BUKAN SEKADAR BERHITUNG
 MATEMATIKA BUKAN SEKADAR BERHITUNG Oleh Hendra Gunawan * Selama ini masih banyak orang yang menganggap bahwa matematika tidaklah lebih daripada sekadar berhitung dan bermain dengan angka-angka. Anggapan
MATEMATIKA BUKAN SEKADAR BERHITUNG Oleh Hendra Gunawan * Selama ini masih banyak orang yang menganggap bahwa matematika tidaklah lebih daripada sekadar berhitung dan bermain dengan angka-angka. Anggapan
Geometri di Bidang Euclid
 Modul 1 Geometri di Bidang Euclid Dr. Wono Setya Budhi G PENDAHULUAN eometri merupakan ilmu pengetahuan yang sudah lama, mulai dari ribuan tahun yang lalu. Berpikir secara geometris dari satu bentuk ke
Modul 1 Geometri di Bidang Euclid Dr. Wono Setya Budhi G PENDAHULUAN eometri merupakan ilmu pengetahuan yang sudah lama, mulai dari ribuan tahun yang lalu. Berpikir secara geometris dari satu bentuk ke
RENCANA KEGIATAN PERKULIAHAN Kode Mata Kuliah : MAA 526 Nama Mata Kuliah : Analisis Fungsional
 Ming gu ke RENCANA KEGIATAN PERKULIAHAN Kode Mata Kuliah : MAA 56 Nama Mata Kuliah : Analisis Fungsional T o p i k S u b T o p i k 1. Ruang Banach - Ruang metrik - Ruang vektor bernorm - Barisan di ruang
Ming gu ke RENCANA KEGIATAN PERKULIAHAN Kode Mata Kuliah : MAA 56 Nama Mata Kuliah : Analisis Fungsional T o p i k S u b T o p i k 1. Ruang Banach - Ruang metrik - Ruang vektor bernorm - Barisan di ruang
Fourier Analysis & Its Applications in PDEs - Part I
 Fourier Analysis & Its Applications in PDEs Hendra Gunawan http://personal.fmipa.itb.ac.id/hgunawan/ Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA WIDE 2010 5-6 August
Fourier Analysis & Its Applications in PDEs Hendra Gunawan http://personal.fmipa.itb.ac.id/hgunawan/ Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA WIDE 2010 5-6 August
ANALISIS NUMERIK LANJUT. Hendra Gunawan, Ph.D. 2006/2007
 ANALISIS NUMERIK LANJUT Hendra Gunawan, Ph.D. 2006/2007 BAB I. RUANG LINEAR Pelajari definisi dan contoh: ruang linear (hal. 1-3); subruang (hal. 3); kombinasi linear (hal. 4); bebas/bergantung linear
ANALISIS NUMERIK LANJUT Hendra Gunawan, Ph.D. 2006/2007 BAB I. RUANG LINEAR Pelajari definisi dan contoh: ruang linear (hal. 1-3); subruang (hal. 3); kombinasi linear (hal. 4); bebas/bergantung linear
Matematikawan Abad XVII-XIX yang Membuat Perubahan. Hendra Gunawan 2016
 Matematikawan Abad XVII-XIX yang Membuat Perubahan Hendra Gunawan 2016 Galileo Galilei (1564-1642) Galileo Galilei adalah seorang astronom, fisikawan & matematikawan Italia yang terkenal dengan ucapannya
Matematikawan Abad XVII-XIX yang Membuat Perubahan Hendra Gunawan 2016 Galileo Galilei (1564-1642) Galileo Galilei adalah seorang astronom, fisikawan & matematikawan Italia yang terkenal dengan ucapannya
13. Aplikasi Transformasi Fourier
 13. plikasi ransformasi Fourier Misal adalah operator linear pada fungsi yang terdefinisi pada R dengan sifat: jika [f(x] = g(x, maka [f(x + s] = g(x + s untuk setiap s R. Maka, fungsi f(x = e ax (a C
13. plikasi ransformasi Fourier Misal adalah operator linear pada fungsi yang terdefinisi pada R dengan sifat: jika [f(x] = g(x, maka [f(x + s] = g(x + s untuk setiap s R. Maka, fungsi f(x = e ax (a C
Catatan Kuliah MA1123 Kalkulus Elementer I
 Catatan Kuliah MA1123 Kalkulus Elementer I Oleh Hendra Gunawan, Ph.D. Departemen Matematika ITB Sasaran Belajar Setelah mempelajari materi Kalkulus Elementer I, mahasiswa diharapkan memiliki (terutama):
Catatan Kuliah MA1123 Kalkulus Elementer I Oleh Hendra Gunawan, Ph.D. Departemen Matematika ITB Sasaran Belajar Setelah mempelajari materi Kalkulus Elementer I, mahasiswa diharapkan memiliki (terutama):
BAGIAN KEDUA. Fungsi, Limit dan Kekontinuan, Turunan
 BAGIAN KEDUA Fungsi, Limit dan Kekontinuan, Turunan 51 52 Hendra Gunawan Pengantar Analisis Real 53 6. FUNGSI 6.1 Fungsi dan Grafiknya Konsep fungsi telah dipelajari oleh Gottfried Wilhelm von Leibniz
BAGIAN KEDUA Fungsi, Limit dan Kekontinuan, Turunan 51 52 Hendra Gunawan Pengantar Analisis Real 53 6. FUNGSI 6.1 Fungsi dan Grafiknya Konsep fungsi telah dipelajari oleh Gottfried Wilhelm von Leibniz
BAB I PENDAHULUAN. umum ruang metrik dan memperluas pengertian klasik dari ruang Euclidean R n, sehingga
 BAB I PENDAHULUAN 1.1 Latar Belakang dan Permasalahan Permulaan munculnya analisis fungsional didasari oleh permasalahan pada kurang memadainya metode analitik klasik pada fisika dan astronomi matematika.
BAB I PENDAHULUAN 1.1 Latar Belakang dan Permasalahan Permulaan munculnya analisis fungsional didasari oleh permasalahan pada kurang memadainya metode analitik klasik pada fisika dan astronomi matematika.
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI 2.1 Latar Belakang Historis Fondasi dari integral pertama kali dideklarasikan oleh Cavalieri, seorang ahli matematika berkebangsaan Italia pada tahun 1635. Cavalieri menemukan bahwa
BAB II LANDASAN TEORI 2.1 Latar Belakang Historis Fondasi dari integral pertama kali dideklarasikan oleh Cavalieri, seorang ahli matematika berkebangsaan Italia pada tahun 1635. Cavalieri menemukan bahwa
MATEMATIKA. Hendra Gunawan
 MENULIS SKRIPSI MATEMATIKA Hendra Gunawan 26 Maret 2011 MATEMATIKA BUKAN BARU LAHIR KEMARIN 2 ±4000 tahun y.l. bangsa Babilonia telah menggunakan geometri sebagai basis perhitungan astronomis. Bangsa Mesir
MENULIS SKRIPSI MATEMATIKA Hendra Gunawan 26 Maret 2011 MATEMATIKA BUKAN BARU LAHIR KEMARIN 2 ±4000 tahun y.l. bangsa Babilonia telah menggunakan geometri sebagai basis perhitungan astronomis. Bangsa Mesir
Implementasi Metode Jumlah Riemann untuk Mendekati Luas Daerah di Bawah Kurva Suatu Fungsi Polinom dengan Divide and Conquer
 Implementasi Metode Jumlah Riemann untuk Mendekati Luas Daerah di Bawah Kurva Suatu Fungsi Polinom dengan Divide and Conquer Dewita Sonya Tarabunga - 13515021 Program Studi Tenik Informatika Sekolah Teknik
Implementasi Metode Jumlah Riemann untuk Mendekati Luas Daerah di Bawah Kurva Suatu Fungsi Polinom dengan Divide and Conquer Dewita Sonya Tarabunga - 13515021 Program Studi Tenik Informatika Sekolah Teknik
BAGIAN PERTAMA. Bilangan Real, Barisan, Deret
 BAGIAN PERTAMA Bilangan Real, Barisan, Deret 2 Hendra Gunawan Pengantar Analisis Real 3 0. BILANGAN REAL 0. Bilangan Real sebagai Bentuk Desimal Dalam buku ini pembaca diasumsikan telah mengenal dengan
BAGIAN PERTAMA Bilangan Real, Barisan, Deret 2 Hendra Gunawan Pengantar Analisis Real 3 0. BILANGAN REAL 0. Bilangan Real sebagai Bentuk Desimal Dalam buku ini pembaca diasumsikan telah mengenal dengan
PENGANTAR ANALISIS REAL
 Seri Analisis dan Geometri No. 1 (2009), -15 158 (173 hlm.) PENGANTAR ANALISIS REAL Oleh Hendra Gunawan Edisi Pertama Bandung, Januari 2009 2000 Dewey Classification: 515-xx. Kata Kunci: Analisis matematika,
Seri Analisis dan Geometri No. 1 (2009), -15 158 (173 hlm.) PENGANTAR ANALISIS REAL Oleh Hendra Gunawan Edisi Pertama Bandung, Januari 2009 2000 Dewey Classification: 515-xx. Kata Kunci: Analisis matematika,
KELOMPOK MATA KULIAH FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM (FMIPA)
 KELOMPOK MATA KULIAH FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM (FMIPA) 2 Deskripsi Mata Kuliah 2017/2018 2. KELOMPOK MATA KULIAH FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM 2.1 Kelompok Mata Kuliah
KELOMPOK MATA KULIAH FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM (FMIPA) 2 Deskripsi Mata Kuliah 2017/2018 2. KELOMPOK MATA KULIAH FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM 2.1 Kelompok Mata Kuliah
KETAKSAMAAN TIPE LEMAH UNTUK OPERATOR INTEGRAL FRAKSIONAL DI RUANG MORREY ATAS RUANG METRIK TAK HOMOGEN
 KETAKSAMAAN TIPE LEMAH UNTUK OPERATOR INTEGRAL FRAKSIONAL DI RUANG MORREY ATAS RUANG METRIK TAK HOMOGEN Idha Sihwaningrum Jurusan Matematika FMIPA Unsoed Email: idha.sihwaningrum@unsoed.ac.id Abstrak Pada
KETAKSAMAAN TIPE LEMAH UNTUK OPERATOR INTEGRAL FRAKSIONAL DI RUANG MORREY ATAS RUANG METRIK TAK HOMOGEN Idha Sihwaningrum Jurusan Matematika FMIPA Unsoed Email: idha.sihwaningrum@unsoed.ac.id Abstrak Pada
7. Transformasi Fourier
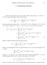 Pengantar Analisis Fourier dan eori Aproksimasi 33 7. ransformasi Fourier Pada bab sebelumnya kita telah melihat bahwa setiap fungsi f L 1 ([0, 1] L ([0, 1] dapat dinyatakan sebagai deret Fourier f(x =
Pengantar Analisis Fourier dan eori Aproksimasi 33 7. ransformasi Fourier Pada bab sebelumnya kita telah melihat bahwa setiap fungsi f L 1 ([0, 1] L ([0, 1] dapat dinyatakan sebagai deret Fourier f(x =
Analisis Fourier dan Wavelet
 0 Hendra Gunawan Analisis Fourier dan Wavelet Hendra Gunawan KK Analisis & Geometri FMIPA-ITB Bandung, 2017 Analisis Fourier dan Wavelet 1 Daftar Isi Kata Pengantar 5 0 Pendahuluan 7 0.1 Notasi dan istilah,
0 Hendra Gunawan Analisis Fourier dan Wavelet Hendra Gunawan KK Analisis & Geometri FMIPA-ITB Bandung, 2017 Analisis Fourier dan Wavelet 1 Daftar Isi Kata Pengantar 5 0 Pendahuluan 7 0.1 Notasi dan istilah,
MASALAH INTERPOLASI 1-D DAN 2-D
 MASALAH INTERPOLASI 1-D DAN 2-D Hendra Gunawan ITB Bandung http://personal.fmipa.itb.ac.id/hgunawan/ Analysis and Geometry Group Bandung Institute of Technology Bandung, Indonesia Seminar Nasional Analisis
MASALAH INTERPOLASI 1-D DAN 2-D Hendra Gunawan ITB Bandung http://personal.fmipa.itb.ac.id/hgunawan/ Analysis and Geometry Group Bandung Institute of Technology Bandung, Indonesia Seminar Nasional Analisis
MA1201 KALKULUS 2A Do maths and you see the world
 Catatan Kuliah MA20 KALKULUS 2A Do maths and you see the world disusun oleh Khreshna I.A. Syuhada, MSc. PhD. Kelompok Keilmuan STATISTIKA - FMIPA Institut Teknologi Bandung 203 Catatan kuliah ini ditulis
Catatan Kuliah MA20 KALKULUS 2A Do maths and you see the world disusun oleh Khreshna I.A. Syuhada, MSc. PhD. Kelompok Keilmuan STATISTIKA - FMIPA Institut Teknologi Bandung 203 Catatan kuliah ini ditulis
4 DIFERENSIAL. 4.1 Pengertian derivatif
 Diferensial merupakan topik yang cukup 'baru' dalam matematika. Dimulai sekitar tahun 1630 an oleh Fermat ketika menghadapi masalah menentukan garis singgung kurva, dan juga masalah menentukan maksimum
Diferensial merupakan topik yang cukup 'baru' dalam matematika. Dimulai sekitar tahun 1630 an oleh Fermat ketika menghadapi masalah menentukan garis singgung kurva, dan juga masalah menentukan maksimum
9. Teori Aproksimasi
 44 Hendra Gunawan 9 Teori Aproksimasi Mulai bab ini tema kita adalah aproksimasi fungsi dan interpolasi Diberikan sebuah fungsi f, baik secara utuh ataupun hanya beberapilai di titik-titik tertentu saja,
44 Hendra Gunawan 9 Teori Aproksimasi Mulai bab ini tema kita adalah aproksimasi fungsi dan interpolasi Diberikan sebuah fungsi f, baik secara utuh ataupun hanya beberapilai di titik-titik tertentu saja,
Analisis Fungsional. Oleh: Dr. Rizky Rosjanuardi, M.Si Jurusan Pendidikan Matematika UNIVERSITAS PENDIDIKAN INDONESIA
 Analisis Fungsional Oleh: Dr. Rizky Rosjanuardi, M.Si Jurusan Pendidikan Matematika UNIVERSITAS PENDIDIKAN INDONESIA Lingkup Materi Ruang Metrik dan Ruang Topologi Kelengkapan Ruang Banach Ruang Hilbert
Analisis Fungsional Oleh: Dr. Rizky Rosjanuardi, M.Si Jurusan Pendidikan Matematika UNIVERSITAS PENDIDIKAN INDONESIA Lingkup Materi Ruang Metrik dan Ruang Topologi Kelengkapan Ruang Banach Ruang Hilbert
Hendra Gunawan. KK Analisis & Geometri FMIPA-ITB. Bandung, Maret 2001 [Edisi Revisi II: Mei 2014]
![Hendra Gunawan. KK Analisis & Geometri FMIPA-ITB. Bandung, Maret 2001 [Edisi Revisi II: Mei 2014] Hendra Gunawan. KK Analisis & Geometri FMIPA-ITB. Bandung, Maret 2001 [Edisi Revisi II: Mei 2014]](/thumbs/72/67819562.jpg) Analisis Fourier dan Wavelet 1 Catatan Kuliah Analisis Fourier dan Wavelet Oleh Hendra Gunawan KK Analisis & Geometri FMIPA-ITB Bandung, Maret 2001 [Edisi Revisi II: Mei 2014] 1 2 Hendra Gunawan Daftar
Analisis Fourier dan Wavelet 1 Catatan Kuliah Analisis Fourier dan Wavelet Oleh Hendra Gunawan KK Analisis & Geometri FMIPA-ITB Bandung, Maret 2001 [Edisi Revisi II: Mei 2014] 1 2 Hendra Gunawan Daftar
4. Deret Fourier pada Interval Sebarang dan Aplikasi
 4. Deret Fourier pada Interval Sebarang dan Aplikasi Kita telah mempelajari bagaimana menguraikan fungsi periodik dengan periode 2 yang terdefinisi pada R sebagai deret Fourier. Deret trigonometri tersebut
4. Deret Fourier pada Interval Sebarang dan Aplikasi Kita telah mempelajari bagaimana menguraikan fungsi periodik dengan periode 2 yang terdefinisi pada R sebagai deret Fourier. Deret trigonometri tersebut
BAB III OPERATOR LINEAR TERBATAS PADA RUANG HILBERT. Operator merupakan salah satu materi yang akan dibahas dalam fungsi
 BAB III OPERATOR LINEAR TERBATAS PADA RUANG HILBERT 3.1 Operator linear Operator merupakan salah satu materi yang akan dibahas dalam fungsi real yaitu suatu fungsi dari ruang vektor ke ruang vektor. Ruang
BAB III OPERATOR LINEAR TERBATAS PADA RUANG HILBERT 3.1 Operator linear Operator merupakan salah satu materi yang akan dibahas dalam fungsi real yaitu suatu fungsi dari ruang vektor ke ruang vektor. Ruang
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
BAB 1 PENDAHULUAN. Kalkulus merupakan salah satu prestasi tertinggi dari kecerdasan manusia.
 BAB 1 PENDAHULUAN 1.1 Latar Belakang Kalkulus merupakan salah satu prestasi tertinggi dari kecerdasan manusia. Disiplin ilmu Matematika ini secara umum berasal dari penyelidikan oleh Isaac Newton (1642-1727)
BAB 1 PENDAHULUAN 1.1 Latar Belakang Kalkulus merupakan salah satu prestasi tertinggi dari kecerdasan manusia. Disiplin ilmu Matematika ini secara umum berasal dari penyelidikan oleh Isaac Newton (1642-1727)
PENGANTAR MATEMATIKA TEKNIK 1. By : Suthami A
 PENGANTAR MATEMATIKA TEKNIK 1 By : Suthami A MATEMATIKA TEKNIK 1??? MATEMATIKA TEKNIK 1??? MATEMATIKA TEKNIK Matematika sebagai ilmu dasar yang digunakan sebagai alat pemecahan masalah di bidang keteknikan
PENGANTAR MATEMATIKA TEKNIK 1 By : Suthami A MATEMATIKA TEKNIK 1??? MATEMATIKA TEKNIK 1??? MATEMATIKA TEKNIK Matematika sebagai ilmu dasar yang digunakan sebagai alat pemecahan masalah di bidang keteknikan
PENGANTAR ANALISIS FUNGSIONAL
 PENGANTAR ANALISIS FUNGSIONAL SUMANANG MUHTAR GOZALI KBK ANALISIS UNIVERSITAS PENDIDIKAN INDONESIA BANDUNG 2010 2 KATA PENGANTAR Bismillahirrahmanirrahim Segala puji bagi Allah Rabb semesta alam. Shalawat
PENGANTAR ANALISIS FUNGSIONAL SUMANANG MUHTAR GOZALI KBK ANALISIS UNIVERSITAS PENDIDIKAN INDONESIA BANDUNG 2010 2 KATA PENGANTAR Bismillahirrahmanirrahim Segala puji bagi Allah Rabb semesta alam. Shalawat
8. Deret Fourier yang Diperumum dan Hampiran Terbaik di L 2 (a, b)
 8. Deret Fourier yang Diperumum dan Hampiran Terbaik di L (a, b) 8.1 Deret Fourier yang Diperumum Jika {ϕ n } 1 adalah basis ortonormal untuk L (a, b) dan f L (a, b), maka f, ϕ n disebut koefisien Fourier
8. Deret Fourier yang Diperumum dan Hampiran Terbaik di L (a, b) 8.1 Deret Fourier yang Diperumum Jika {ϕ n } 1 adalah basis ortonormal untuk L (a, b) dan f L (a, b), maka f, ϕ n disebut koefisien Fourier
BAB I PENDAHULUAN Latar Belakang Permasalahan
 BAB I PENDAHULUAN 1.1. Latar Belakang Permasalahan Ditinjau dari bidang ilmu pengetahuan, teori persamaan diferensial merupakan suatu cabang analisis matematika yang banyak dipakai dalam kehidupan nyata,
BAB I PENDAHULUAN 1.1. Latar Belakang Permasalahan Ditinjau dari bidang ilmu pengetahuan, teori persamaan diferensial merupakan suatu cabang analisis matematika yang banyak dipakai dalam kehidupan nyata,
BAB III KEKONVERGENAN LEMAH
 BAB III KEKONVERGENAN LEMAH Bab ini membahas inti kajian tugas akhir. Di dalamnya akan dibahas mengenai kekonvergenan lemah beserta sifat-sifat yang terkait dengannya. Sifatsifat yang dikaji pada bab ini
BAB III KEKONVERGENAN LEMAH Bab ini membahas inti kajian tugas akhir. Di dalamnya akan dibahas mengenai kekonvergenan lemah beserta sifat-sifat yang terkait dengannya. Sifatsifat yang dikaji pada bab ini
KELOMPOK MATA KULIAH FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM (FMIPA)
 KELOMPOK MATA KULIAH FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM (FMIPA) 2 Deskripsi Mata Kuliah 2014 2. KELOMPOK MATA KULIAH FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM 2.1 Kelompok Mata Kuliah Matematika
KELOMPOK MATA KULIAH FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM (FMIPA) 2 Deskripsi Mata Kuliah 2014 2. KELOMPOK MATA KULIAH FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM 2.1 Kelompok Mata Kuliah Matematika
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016. Hendra Gunawan
 MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan Matematika & Analisis Real Matematika berurusan dengan gagasan, yang mungkin merupakan abstraksi atau sari dari sesuatu yang terdapat
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan Matematika & Analisis Real Matematika berurusan dengan gagasan, yang mungkin merupakan abstraksi atau sari dari sesuatu yang terdapat
Kegiatan Belajar 1 HAKIKAT MATEMATIKA
 Kegiatan Belajar 1 HAKIKAT MATEMATIKA A. Pengantar Matematika merupakan salah satu bidang studi yang dijarkan di SD. Seorang guru SD yang akan mengajarkan matematika kepada siswanya, hendaklah mengetahui
Kegiatan Belajar 1 HAKIKAT MATEMATIKA A. Pengantar Matematika merupakan salah satu bidang studi yang dijarkan di SD. Seorang guru SD yang akan mengajarkan matematika kepada siswanya, hendaklah mengetahui
BUKU DIKTAT ANALISA VARIABEL KOMPLEKS. OLEH : DWI IVAYANA SARI, M.Pd
 BUKU DIKTAT ANALISA VARIABEL KOMPLEKS OLEH : DWI IVAYANA SARI, M.Pd i DAFTAR ISI BAB I. BILANGAN KOMPLEKS... 1 I. Bilangan Kompleks dan Operasinya... 1 II. Operasi Hitung Pada Bilangan Kompleks... 1 III.
BUKU DIKTAT ANALISA VARIABEL KOMPLEKS OLEH : DWI IVAYANA SARI, M.Pd i DAFTAR ISI BAB I. BILANGAN KOMPLEKS... 1 I. Bilangan Kompleks dan Operasinya... 1 II. Operasi Hitung Pada Bilangan Kompleks... 1 III.
Kelompok Mata Kuliah : MKU Program Studi/Program : Pendidikan Teknik Elektro/S1 Status Mata Kuliah : Wajib. : Aip Saripudin, M.T.
 DESKIPSI MATA KULIAH EL-121 Matematika Teknik I: S1, 3 SKS, Semester II Mata kuliah ini merupakan kuliah lanjut. Selesai mengikuti perkuliahan ini mahasiswa diharapkan mampu memahami konsep-konsep matematika
DESKIPSI MATA KULIAH EL-121 Matematika Teknik I: S1, 3 SKS, Semester II Mata kuliah ini merupakan kuliah lanjut. Selesai mengikuti perkuliahan ini mahasiswa diharapkan mampu memahami konsep-konsep matematika
BAB II KAJIAN TEORI. pada penulisan bab III. Materi yang diuraikan berisi tentang definisi, teorema, dan
 BAB II KAJIAN TEORI Pada bab ini akan dibahas beberapa hal yang digunakan sebagai landasan pada penulisan bab III. Materi yang diuraikan berisi tentang definisi, teorema, dan beberapa kajian matematika,
BAB II KAJIAN TEORI Pada bab ini akan dibahas beberapa hal yang digunakan sebagai landasan pada penulisan bab III. Materi yang diuraikan berisi tentang definisi, teorema, dan beberapa kajian matematika,
4. Deret Fourier pada Interval Sebarang dan Aplikasi
 8 Hendra Gunawan 4. Deret Fourier pada Interval Sebarang dan Aplikasi Kita telah mempelajari bagaimana menguraikan fungsi periodik dengan periode 2 yang terdefinisi pada R sebagai deret Fourier. Deret
8 Hendra Gunawan 4. Deret Fourier pada Interval Sebarang dan Aplikasi Kita telah mempelajari bagaimana menguraikan fungsi periodik dengan periode 2 yang terdefinisi pada R sebagai deret Fourier. Deret
BAB I PENDAHULUAN Latar Belakang Masalah
 BAB I PENDAHULUAN 1.1. Latar Belakang Masalah Ilmu Matematika merupakan salah satu cabang ilmu yang berperan penting dalam berbagai bidang. Salah satu cabang ilmu matematika yang banyak diperbincangkan
BAB I PENDAHULUAN 1.1. Latar Belakang Masalah Ilmu Matematika merupakan salah satu cabang ilmu yang berperan penting dalam berbagai bidang. Salah satu cabang ilmu matematika yang banyak diperbincangkan
digunakan untuk menyelesaikan integral seperti 3
 Bab Teknik Pengintegralan BAB TEKNIK PENGINTEGRALAN Rumus-rumus dasar integral tak tertentu yang diberikan pada bab hanya dapat digunakan untuk mengevaluasi integral dari fungsi sederhana dan tidak dapat
Bab Teknik Pengintegralan BAB TEKNIK PENGINTEGRALAN Rumus-rumus dasar integral tak tertentu yang diberikan pada bab hanya dapat digunakan untuk mengevaluasi integral dari fungsi sederhana dan tidak dapat
KALKULUS BAB II FUNGSI, LIMIT, DAN KEKONTINUAN. DEPARTEMEN TEKNIK KIMIA Universitas Indonesia
 KALKULUS BAB II FUNGSI, LIMIT, DAN KEKONTINUAN DEPARTEMEN TEKNIK KIMIA Universitas Indonesia BAB II. FUNGSI, LIMIT, DAN KEKONTINUAN Fungsi dan Operasi pada Fungsi Beberapa Fungsi Khusus Limit dan Limit
KALKULUS BAB II FUNGSI, LIMIT, DAN KEKONTINUAN DEPARTEMEN TEKNIK KIMIA Universitas Indonesia BAB II. FUNGSI, LIMIT, DAN KEKONTINUAN Fungsi dan Operasi pada Fungsi Beberapa Fungsi Khusus Limit dan Limit
PDP linear orde 2 Agus Yodi Gunawan
 PDP linear orde 2 Agus Yodi Gunawan Pada bagian ini akan dipelajari tiga jenis persamaan diferensial parsial (PDP) linear orde dua yang biasa dijumpai pada masalah-masalah dunia nyata, yaitu persamaan
PDP linear orde 2 Agus Yodi Gunawan Pada bagian ini akan dipelajari tiga jenis persamaan diferensial parsial (PDP) linear orde dua yang biasa dijumpai pada masalah-masalah dunia nyata, yaitu persamaan
Ayundyah Kesumawati. April 29, Prodi Statistika FMIPA-UII. Deret Tak Terhingga. Ayundyah. Barisan Tak Hingga. Deret Tak Terhingga
 Kesumawati Prodi Statistika FMIPA-UII April 29, 2015 Akar Barisan a 1, a 2, a 3, a 4,... adalah susunan bilangan-bilangan real yang teratur, satu untuk setiap bilangan bulat positif. adalah fungsi yang
Kesumawati Prodi Statistika FMIPA-UII April 29, 2015 Akar Barisan a 1, a 2, a 3, a 4,... adalah susunan bilangan-bilangan real yang teratur, satu untuk setiap bilangan bulat positif. adalah fungsi yang
TINJAUAN PUSTAKA. Ruang metrik merupakan ruang abstrak, yaitu ruang yang dibangun oleh
 II. TINJAUAN PUSTAKA 2.1 Ruang Metrik Ruang metrik merupakan ruang abstrak, yaitu ruang yang dibangun oleh aksioma-aksioma tertentu. Ruang metrik merupakan hal yang fundamental dalam analisis fungsional,
II. TINJAUAN PUSTAKA 2.1 Ruang Metrik Ruang metrik merupakan ruang abstrak, yaitu ruang yang dibangun oleh aksioma-aksioma tertentu. Ruang metrik merupakan hal yang fundamental dalam analisis fungsional,
Rumus eksplisit untuk sudut antara dua subruang dari suatu ruang hasilkali dalam 1. Hendra Gunawan 2
 Rumus eksplisit untuk sudut antara dua subruang dari suatu ruang hasilkali dalam 1 Hendra Gunawan 2 Departemen Matematika Institut Teknologi Bandung Bandung 40132, Indonesia 1 Dipresentasikan pada Konferensi
Rumus eksplisit untuk sudut antara dua subruang dari suatu ruang hasilkali dalam 1 Hendra Gunawan 2 Departemen Matematika Institut Teknologi Bandung Bandung 40132, Indonesia 1 Dipresentasikan pada Konferensi
BAB III PEMBAHASAN. Bab III terbagi menjadi tiga sub-bab, yaitu sub-bab A, sub-bab B, dan subbab
 BAB III PEMBAHASAN Bab III terbagi menjadi tiga sub-bab, yaitu sub-bab A, sub-bab B, dan subbab C. Sub-bab A menjelaskan mengenai konsep dasar C[a, b] sebagai ruang vektor beserta contohnya. Sub-bab B
BAB III PEMBAHASAN Bab III terbagi menjadi tiga sub-bab, yaitu sub-bab A, sub-bab B, dan subbab C. Sub-bab A menjelaskan mengenai konsep dasar C[a, b] sebagai ruang vektor beserta contohnya. Sub-bab B
Analisis Real. Johan Matheus Tuwankotta 1. December 3,
 Analisis Real Johan Matheus Tuwankotta December 3, 200 Departemen Matematika, FMIPA, Institut Teknologi Bandung, jl. Ganesha no. 0, Bandung, Indonesia. mailto:theo@dns.math.itb.ac.id 2 Daftar Isi Sistem
Analisis Real Johan Matheus Tuwankotta December 3, 200 Departemen Matematika, FMIPA, Institut Teknologi Bandung, jl. Ganesha no. 0, Bandung, Indonesia. mailto:theo@dns.math.itb.ac.id 2 Daftar Isi Sistem
Bab 2 Fungsi Analitik
 Bab 2 Fungsi Analitik Bab 2 ini direncanakan akan disampaikan dalam 4 kali pertemuan, dengan perincian sebagai berikut: () Pertemuan I: Fungsi Kompleks dan Pemetaan. (2) Pertemuan II: Limit Fungsi, Kekontiuan,
Bab 2 Fungsi Analitik Bab 2 ini direncanakan akan disampaikan dalam 4 kali pertemuan, dengan perincian sebagai berikut: () Pertemuan I: Fungsi Kompleks dan Pemetaan. (2) Pertemuan II: Limit Fungsi, Kekontiuan,
SATUAN ACARA PERKULIAHAN MATA KULIAH KALKULUS LANJUT A (S1 / TEKNIK INFORMATIKA ) KODE / SKS KD
 SATUAN ACARA PERKULIAHAN MATA KULIAH KALKULUS LANJUT A (S1 / TEKNIK INFORMATIKA ) KODE / SKS KD-045315 Mingg u Ke Pokok Bahasan dan TIU Sub-pokok Bahasan dan Sasaran Belajar Cara Pengajaran Media Tugas
SATUAN ACARA PERKULIAHAN MATA KULIAH KALKULUS LANJUT A (S1 / TEKNIK INFORMATIKA ) KODE / SKS KD-045315 Mingg u Ke Pokok Bahasan dan TIU Sub-pokok Bahasan dan Sasaran Belajar Cara Pengajaran Media Tugas
4 Jasa Besar Euclid. 4 Jasa Besar Euclid 19
 4 Jasa Besar Euclid Kota Alexandria (Al-Iskandariya), yang terletak di pantai utara Mesir, dibangun oleh Alexander Agung pada tahun 322 SM, menyaingi kota Athena. Pada tahun 300 SM, Raja Ptolemy I Soter
4 Jasa Besar Euclid Kota Alexandria (Al-Iskandariya), yang terletak di pantai utara Mesir, dibangun oleh Alexander Agung pada tahun 322 SM, menyaingi kota Athena. Pada tahun 300 SM, Raja Ptolemy I Soter
= + atau = - 2. TURUNAN 2.1 Definisi Turunan fungsi f adalah fungsi yang nilainya di setiap bilangan sebarang c di dalam D f diberikan oleh
 JURUSAN PENDIDIKAN MATEMATIKA FPMIPA-UPI BANDUNG HAND OUT TURUNAN DAN DIFERENSIASI OLEH: FIRDAUS-UPI 0716 1. GARIS SINGGUNG 1.1 Definisi Misalkan fungsi f kontinu di c. Garis singgung ( tangent line )
JURUSAN PENDIDIKAN MATEMATIKA FPMIPA-UPI BANDUNG HAND OUT TURUNAN DAN DIFERENSIASI OLEH: FIRDAUS-UPI 0716 1. GARIS SINGGUNG 1.1 Definisi Misalkan fungsi f kontinu di c. Garis singgung ( tangent line )
UNIVERSITAS PENDIDIKAN INDONESIA
 Ruang Norm Sumanang Muhtar Gozali UNIVERSITAS PENDIDIKAN INDONESIA Definisi. Misalkan suatu ruang vektor atas. Norm pada didefinisikan sebagai fungsi. : yang memenuhi N1. 0 N2. 0 0 N3.,, N4.,, Kita dapat
Ruang Norm Sumanang Muhtar Gozali UNIVERSITAS PENDIDIKAN INDONESIA Definisi. Misalkan suatu ruang vektor atas. Norm pada didefinisikan sebagai fungsi. : yang memenuhi N1. 0 N2. 0 0 N3.,, N4.,, Kita dapat
BAB I PENDAHULUAN. 1.1 Latar Belakang
 BAB I PENDAHULUAN 1.1 Latar Belakang Dalam ilmu matematika, banyak pembahasan di bidang analisis dan topologi yang memerlukan pengertian ruang Hilbert. Ruang Hilbert merupakan konsep abstrak yang mendasari
BAB I PENDAHULUAN 1.1 Latar Belakang Dalam ilmu matematika, banyak pembahasan di bidang analisis dan topologi yang memerlukan pengertian ruang Hilbert. Ruang Hilbert merupakan konsep abstrak yang mendasari
Aplikasi Persamaan Bessel Orde Nol Pada Persamaan Panas Dua dimensi
 JURNAL FOURIER Oktober 2013, Vol. 2, No. 2, 113-123 ISSN 2252-763X Aplikasi Persamaan Bessel Orde Nol Pada Persamaan Panas Dua dimensi Annisa Eki Mulyati dan Sugiyanto Program Studi Matematika Fakultas
JURNAL FOURIER Oktober 2013, Vol. 2, No. 2, 113-123 ISSN 2252-763X Aplikasi Persamaan Bessel Orde Nol Pada Persamaan Panas Dua dimensi Annisa Eki Mulyati dan Sugiyanto Program Studi Matematika Fakultas
SOAL-SOAL dan PEMBAHASAN UN MATEMATIKA SMA/MA IPA TAHUN PELAJARAN 2011/2012
 SOAL-SOAL dan PEMBAHASAN UN MATEMATIKA SMA/MA IPA TAHUN PELAJARAN 0/0. Akar-akar persamaan kuadrat x +ax - 40 adalah p dan q. Jika p - pq + q 8a, maka nilai a... A. -8 B. -4 C. 4 D. 6 E. 8 BAB III Persamaan
SOAL-SOAL dan PEMBAHASAN UN MATEMATIKA SMA/MA IPA TAHUN PELAJARAN 0/0. Akar-akar persamaan kuadrat x +ax - 40 adalah p dan q. Jika p - pq + q 8a, maka nilai a... A. -8 B. -4 C. 4 D. 6 E. 8 BAB III Persamaan
OSN Guru Matematika SMA (Olimpiade Sains Nasional)
 ocsz Pembahasan Soal OSN Guru 2012 OLIMPIADE SAINS NASIONAL KHUSUS GURU MATEMATIKA SMA OSN Guru Matematika SMA (Olimpiade Sains Nasional) Disusun oleh: Pak Anang Halaman 2 dari 26 PEMBAHASAN SOAL OLIMPIADE
ocsz Pembahasan Soal OSN Guru 2012 OLIMPIADE SAINS NASIONAL KHUSUS GURU MATEMATIKA SMA OSN Guru Matematika SMA (Olimpiade Sains Nasional) Disusun oleh: Pak Anang Halaman 2 dari 26 PEMBAHASAN SOAL OLIMPIADE
FUNGSI KHUSUS FSK 20238/2 SKS
 FUNGSI KHUSUS FSK 20238/2 SKS 0.5-0.5 0 Dosen: Dr. Muhammad Hikam Re@GHzLD -4 0 24 y -2-2 0 x 2-4 GHxL 4 2-4 -2 2 4 x -2-4 Muhammad Hikam Pekerjaan Permanen: Staf Pengajar (Lektor Kepala) Fisika FMIPA
FUNGSI KHUSUS FSK 20238/2 SKS 0.5-0.5 0 Dosen: Dr. Muhammad Hikam Re@GHzLD -4 0 24 y -2-2 0 x 2-4 GHxL 4 2-4 -2 2 4 x -2-4 Muhammad Hikam Pekerjaan Permanen: Staf Pengajar (Lektor Kepala) Fisika FMIPA
Ketaksamaan Cauchy-Schwarz, Ketaksamaan Bessel, dan Kesamaan Parseval di Ruang n-hasilkali Dalam Baku. Hendra Gunawan
 Ketaksamaan Cauchy-Schwarz, Ketaksamaan Bessel, dan Kesamaan Parseval di Ruang n-hasilkali Dalam Baku Hendra Gunawan Departemen Matematika, ITB, Bandung 40132 hgunawan@dns.math.itb.ac.id 1 Abstrak Beberapa
Ketaksamaan Cauchy-Schwarz, Ketaksamaan Bessel, dan Kesamaan Parseval di Ruang n-hasilkali Dalam Baku Hendra Gunawan Departemen Matematika, ITB, Bandung 40132 hgunawan@dns.math.itb.ac.id 1 Abstrak Beberapa
PREDIKSI UN 2014 MATEMATIKA IPA
 NAMA : KELAS : 1. Kisi-Kisi: Logika Matematika Diketahui 3 Premis, Premis Menggunakan kesetaraan, dan penarikan MP atau MT PREDIKSI UN 2014 MATEMATIKA IPA 3. Kisi-Kisi: Materi Ekponen Éksponen pecahan,3
NAMA : KELAS : 1. Kisi-Kisi: Logika Matematika Diketahui 3 Premis, Premis Menggunakan kesetaraan, dan penarikan MP atau MT PREDIKSI UN 2014 MATEMATIKA IPA 3. Kisi-Kisi: Materi Ekponen Éksponen pecahan,3
17. Transformasi Wavelet Kontinu dan Frame
 17. Transformasi Wavelet Kontinu dan Frame Pada 16 kita mempelajari basis ortonormal {e 2πimx g(x n)} dengan g = χ [,1). Transformasi f f(x)g(x n)e 2πimx dx, m, n Z, dikenal sebagai transformasi Fourier
17. Transformasi Wavelet Kontinu dan Frame Pada 16 kita mempelajari basis ortonormal {e 2πimx g(x n)} dengan g = χ [,1). Transformasi f f(x)g(x n)e 2πimx dx, m, n Z, dikenal sebagai transformasi Fourier
Soal Ujian Komprehensif
 Soal Ujian Komprehensif Bahan ujian komprehensif memuat konsep-konsep penting pada bidang: Kalkulus, dan Matriks / Aljabar Linear. Logika, Soal ujian disediakan secara terbuka, dapat diperoleh setiap saat
Soal Ujian Komprehensif Bahan ujian komprehensif memuat konsep-konsep penting pada bidang: Kalkulus, dan Matriks / Aljabar Linear. Logika, Soal ujian disediakan secara terbuka, dapat diperoleh setiap saat
Bilangan Kompleks. Anwar Mutaqin. Program Studi Pendidikan Matematika UNTIRTA
 Bilangan Kompleks Anwar Mutaqin Program Studi Pendidikan Matematika UNTIRTA DAFTAR ISI 1 BILANGAN KOMPLEKS 1 1.1 Eksistensi Bilangan Kompleks.................... 1 1.2 Operasi Aritmatika..........................
Bilangan Kompleks Anwar Mutaqin Program Studi Pendidikan Matematika UNTIRTA DAFTAR ISI 1 BILANGAN KOMPLEKS 1 1.1 Eksistensi Bilangan Kompleks.................... 1 1.2 Operasi Aritmatika..........................
PIDATO ILMIAH. HENDRA GUNAWAN, Ph.D.
 PIDATO ILMIAH HENDRA GUNAWAN, Ph.D. Garis Besar Pidato Mengapa perlu rumus sudut antara dua subruang Bagaimana memperoleh rumus tersebut (dari rumus-rumus lain yang telah dikenal sebelumnya) Bagaimana
PIDATO ILMIAH HENDRA GUNAWAN, Ph.D. Garis Besar Pidato Mengapa perlu rumus sudut antara dua subruang Bagaimana memperoleh rumus tersebut (dari rumus-rumus lain yang telah dikenal sebelumnya) Bagaimana
BAB III INDUKSI MATEMATIKA
 BAB III INDUKSI MATEMATIKA BAB III INDUKSI MATEMATIKA 3.1 Pendahuluan Dalam bidang matematika tidak jarang ditemui pola-pola induktif yang melibatkan himpunan indeks berupa himpunan bilangan asli atau
BAB III INDUKSI MATEMATIKA BAB III INDUKSI MATEMATIKA 3.1 Pendahuluan Dalam bidang matematika tidak jarang ditemui pola-pola induktif yang melibatkan himpunan indeks berupa himpunan bilangan asli atau
Variabel Banyak Bernilai Real 1 / 1
 Fungsi Variabel Banyak Bernilai Real Turunan Parsial dan Turunan Wono Setya Budhi KK Analisis dan Geometri, FMIPA ITB Variabel Banyak Bernilai Real 1 / 1 Turunan Parsial dan Turunan Usaha pertama untuk
Fungsi Variabel Banyak Bernilai Real Turunan Parsial dan Turunan Wono Setya Budhi KK Analisis dan Geometri, FMIPA ITB Variabel Banyak Bernilai Real 1 / 1 Turunan Parsial dan Turunan Usaha pertama untuk
DERET FOURIER. n = bilangan asli (1,2,3,4,5,.) L = pertemuan titik. Bilangan-bilangan untuk,,,, disebut koefisien fourier dari f(x) dalam (-L,L)
 DERET FOURIER Bila f adalah fungsi periodic yang berperioda p, maka f adalah fungsi periodic. Berperiode n, dimana n adalah bilangan asli positif (+). Untuk setiap bilangan asli positif fungsi yang didefinisikan
DERET FOURIER Bila f adalah fungsi periodic yang berperioda p, maka f adalah fungsi periodic. Berperiode n, dimana n adalah bilangan asli positif (+). Untuk setiap bilangan asli positif fungsi yang didefinisikan
Pengantar Statistika Matematik(a)
 Catatan Kuliah Pengantar Statistika Matematik(a) Statistika Lebih Dari Sekadar Matematika disusun oleh Khreshna I.A. Syuhada, MSc. PhD. Kelompok Keilmuan STATISTIKA - FMIPA Institut Teknologi Bandung 2014
Catatan Kuliah Pengantar Statistika Matematik(a) Statistika Lebih Dari Sekadar Matematika disusun oleh Khreshna I.A. Syuhada, MSc. PhD. Kelompok Keilmuan STATISTIKA - FMIPA Institut Teknologi Bandung 2014
Catatan Kuliah MA1123 KALKULUS ELEMENTER I BAB III. TURUNAN
 BAB III. TURUNAN Kecepatan Sesaat dan Gradien Garis Singgung Turunan dan Hubungannya dengan Kekontinuan Aturan Dasar Turunan Notasi Leibniz dan Turunan Tingkat Tinggi Penurunan Implisit Laju yang Berkaitan
BAB III. TURUNAN Kecepatan Sesaat dan Gradien Garis Singgung Turunan dan Hubungannya dengan Kekontinuan Aturan Dasar Turunan Notasi Leibniz dan Turunan Tingkat Tinggi Penurunan Implisit Laju yang Berkaitan
Penerapan Turunan Fungsi Dalam Bidang Kimia
 Penerapan Turunan Fungsi Dalam Bidang Kimia Kelompok 2 Asmiladita Pridilla Athiya Salma Avira Yunita Besafina Hanan Dicky Syahreza Dwi Bhakti Kusuma PERSAMAAN DIFERENSIAL DAN APLIKASINYA DALAM KIMIA A.
Penerapan Turunan Fungsi Dalam Bidang Kimia Kelompok 2 Asmiladita Pridilla Athiya Salma Avira Yunita Besafina Hanan Dicky Syahreza Dwi Bhakti Kusuma PERSAMAAN DIFERENSIAL DAN APLIKASINYA DALAM KIMIA A.
Analisis Instruksional (AI) dan Silabus. MAT100 Pengantar Matematika. Program Studi S-1 Matematika Departemen Matematika Institut Pertanian Bogor
 Analisis Instruksional (AI) dan Silabus MAT100 Pengantar Matematika Program Studi S-1 Matematika Departemen Matematika Institut Pertanian Bogor ANALISIS INSTRUKSIONAL (AI) DAN SILABUS MATA KULIAH MAT100
Analisis Instruksional (AI) dan Silabus MAT100 Pengantar Matematika Program Studi S-1 Matematika Departemen Matematika Institut Pertanian Bogor ANALISIS INSTRUKSIONAL (AI) DAN SILABUS MATA KULIAH MAT100
MA5032 ANALISIS REAL
 (Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. August 16, 2011 Pada bab ini anda diasumsikan telah mengenal dengan cukup baik bilangan asli, bilangan bulat, dan bilangan
(Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. August 16, 2011 Pada bab ini anda diasumsikan telah mengenal dengan cukup baik bilangan asli, bilangan bulat, dan bilangan
KONSEP DASAR PERSAMAAN DIFERENSIAL
 KONSEP DASAR PERSAMAAN DIFERENSIAL A. PENGERTIAN PERSAMAAN DIFERENSIAL Dalam pelajaran kalkulus, kita telah berkenalan dan mengkaji berbagai macam metode untuk mendiferensialkan suatu fungsi (dasar). Sebagai
KONSEP DASAR PERSAMAAN DIFERENSIAL A. PENGERTIAN PERSAMAAN DIFERENSIAL Dalam pelajaran kalkulus, kita telah berkenalan dan mengkaji berbagai macam metode untuk mendiferensialkan suatu fungsi (dasar). Sebagai
RPS MATA KULIAH KALKULUS 1B
 RPS MATA KULIAH KALKULUS 1B CAPAIAN PEMBELAJARAN MATA KULIAH: 1. Mempunyai pengetahuan dibidang matematika, statistika, komputasi (algoritma), dan pengetahuan dasar dalam menyelesaikan permasalahan dibidang
RPS MATA KULIAH KALKULUS 1B CAPAIAN PEMBELAJARAN MATA KULIAH: 1. Mempunyai pengetahuan dibidang matematika, statistika, komputasi (algoritma), dan pengetahuan dasar dalam menyelesaikan permasalahan dibidang
Soal dan Pembahasan UN Matematika SMA IPA Tahun 2013
 Soal dan Pembahasan UN Matematika SMA IPA Tahun 013 LOGIKA MATEMATIKA p siswa rajin belajar ; q mendapat nilai yang baik r siswa tidak mengikuti kegiatan remedial ~ r siswa mengikut kegiatan remedial Premis
Soal dan Pembahasan UN Matematika SMA IPA Tahun 013 LOGIKA MATEMATIKA p siswa rajin belajar ; q mendapat nilai yang baik r siswa tidak mengikuti kegiatan remedial ~ r siswa mengikut kegiatan remedial Premis
Barisan dan Deret Agus Yodi Gunawan
 Barisan dan Deret Agus Yodi Gunawan Barisan. Definisi. Barisan tak hingga adalah suatu fungsi dengan daerah asalnya himpunan bilangan bulat positif dan daerah kawannya himpunan bilangan real. Notasi untuk
Barisan dan Deret Agus Yodi Gunawan Barisan. Definisi. Barisan tak hingga adalah suatu fungsi dengan daerah asalnya himpunan bilangan bulat positif dan daerah kawannya himpunan bilangan real. Notasi untuk
16. Analisis Multi Resolusi
 16. Analisis Multi esolusi Esensi dari basis ortonormal yang dibangun oleh sebuah wavelet adalah sifat multi resolusi-nya, sehingga kita dapat menganalisis suatu signal pada berbagai frekuensi di suatu
16. Analisis Multi esolusi Esensi dari basis ortonormal yang dibangun oleh sebuah wavelet adalah sifat multi resolusi-nya, sehingga kita dapat menganalisis suatu signal pada berbagai frekuensi di suatu
BIODATA KETUA PENELITI
 BIODATA KETUA PENELITI A. IDENTITAS DIRI 1. Nama Lengkap (dengan : Dr. Rizky Rosjanuardi, M.Si. gelar) 2. Jenis Kelamin : L 3. Jabatan Fungsional : Lektor Kepala 4. NIP/NIK/Identitas Lainnya : 196901191993031001
BIODATA KETUA PENELITI A. IDENTITAS DIRI 1. Nama Lengkap (dengan : Dr. Rizky Rosjanuardi, M.Si. gelar) 2. Jenis Kelamin : L 3. Jabatan Fungsional : Lektor Kepala 4. NIP/NIK/Identitas Lainnya : 196901191993031001
BARISAN BILANGAN REAL
 BAB 2 BARISAN BILANGAN REAL Di sekolah menengah barisan diperkenalkan sebagai kumpulan bilangan yang disusun menurut pola tertentu, misalnya barisan aritmatika dan barisan geometri. Biasanya barisan dan
BAB 2 BARISAN BILANGAN REAL Di sekolah menengah barisan diperkenalkan sebagai kumpulan bilangan yang disusun menurut pola tertentu, misalnya barisan aritmatika dan barisan geometri. Biasanya barisan dan
BAB I PENDAHULUAN 1.1 Latar Belakang
 1 BAB I PENDAHULUAN 1.1 Latar Belakang Pada awalnya deret Fourier diperkenalkan oleh Joseph Fourier pada tahun 1807 untuk memecahkan model masalah persamaan panas pada suatu lempeng logam (Fourier, 1878).
1 BAB I PENDAHULUAN 1.1 Latar Belakang Pada awalnya deret Fourier diperkenalkan oleh Joseph Fourier pada tahun 1807 untuk memecahkan model masalah persamaan panas pada suatu lempeng logam (Fourier, 1878).
BAB III INDUKSI MATEMATIKA
 3.1 Pendahuluan BAB III INDUKSI MATEMATIKA Dalam bidang matematika tidak jarang ditemui pola-pola induktif yang melibatkan himpunan indeks berupa himpunan bilangan asli atau bulat seperti barisan atau
3.1 Pendahuluan BAB III INDUKSI MATEMATIKA Dalam bidang matematika tidak jarang ditemui pola-pola induktif yang melibatkan himpunan indeks berupa himpunan bilangan asli atau bulat seperti barisan atau
II. TINJAUAN PUSTAKA. Turunan fungsi f adalah fungsi lain f (dibaca f aksen ) yang nilainya pada ( ) ( ) ( )
 II. TINJAUAN PUSTAKA 2.1 Definisi Turunan Turunan fungsi f adalah fungsi lain f (dibaca f aksen ) yang nilainya pada sebarang bilangan c adalah asalkan limit ini ada. Jika limit ini memang ada, maka dikatakan
II. TINJAUAN PUSTAKA 2.1 Definisi Turunan Turunan fungsi f adalah fungsi lain f (dibaca f aksen ) yang nilainya pada sebarang bilangan c adalah asalkan limit ini ada. Jika limit ini memang ada, maka dikatakan
REDUNDANSI FRAME DAN PENGARUHNYA PADA DEKOMPOSISI FUNGSI DI RUANG HILBERT
 Page 1 of 33 REDUNDANSI FRAME DAN PENGARUHNYA PADA DEKOMPOSISI FUNGSI DI RUANG HILBERT SUZYANNA NRP.1208 201 002 July 13, 2010 ABSTRAK Page 2 of 33 Konsep frame di ruang hasil kali dalam dapat dipandang
Page 1 of 33 REDUNDANSI FRAME DAN PENGARUHNYA PADA DEKOMPOSISI FUNGSI DI RUANG HILBERT SUZYANNA NRP.1208 201 002 July 13, 2010 ABSTRAK Page 2 of 33 Konsep frame di ruang hasil kali dalam dapat dipandang
TEOREMA TITIK TETAP DI RUANG BARISAN p-summable DALAM NORM-n
 TEOREMA TITIK TETAP DI RUANG BARISAN p-summable DALAM NORM-n Anwar Mutaqin dan Indiana Marethi Program Studi Pendidikan Matematika Fakultas Keguruan dan Ilmu Pendidikan Universitas Sultan Ageng Tirtayasa
TEOREMA TITIK TETAP DI RUANG BARISAN p-summable DALAM NORM-n Anwar Mutaqin dan Indiana Marethi Program Studi Pendidikan Matematika Fakultas Keguruan dan Ilmu Pendidikan Universitas Sultan Ageng Tirtayasa
Teorema Titik Tetap di Ruang Norm-2 Standar
 Teorema Titik Tetap di Ruang Norm- Standar Muh. Nur Universitas Hasanuddin Abstract Pada tulisan ini, akan dipelajari ruang norm- standar, yakni ruang hasil kali dalam yang dilengkapi dengan norm- standar.
Teorema Titik Tetap di Ruang Norm- Standar Muh. Nur Universitas Hasanuddin Abstract Pada tulisan ini, akan dipelajari ruang norm- standar, yakni ruang hasil kali dalam yang dilengkapi dengan norm- standar.
PROYEKSI ORTOGONAL PADA RUANG HILBERT. Skripsi
 PROYEKSI ORTOGONAL PADA RUANG HILBERT Skripsi Diajukan Kepada Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Yogyakarta untuk Memenuhi Sebagian Persyaratan Guna Memenuhi Gelar Sarjana
PROYEKSI ORTOGONAL PADA RUANG HILBERT Skripsi Diajukan Kepada Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Yogyakarta untuk Memenuhi Sebagian Persyaratan Guna Memenuhi Gelar Sarjana
Archimedes dan Taksiran Bilangan π
 Bersains, Vol. 1, No. 7 (Juli 2015) Archimedes dan Taksiran Bilangan π Hendra Gunawan Beri saya tempat untuk bertumpu, dan saya akan angkat Bumi ini. Demikian ujar Archimedes dari Syracusa (287 212 SM),
Bersains, Vol. 1, No. 7 (Juli 2015) Archimedes dan Taksiran Bilangan π Hendra Gunawan Beri saya tempat untuk bertumpu, dan saya akan angkat Bumi ini. Demikian ujar Archimedes dari Syracusa (287 212 SM),
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
FUNGSI DELTA DIRAC. Marwan Wirianto 1) dan Wono Setya Budhi 2)
 INTEGRAL, Vol. 1 No. 1, Maret 5 FUNGSI DELTA DIRAC Marwan Wirianto 1) dan Wono Setya Budhi ) 1) Jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Katolik Parahyangan, Bandung
INTEGRAL, Vol. 1 No. 1, Maret 5 FUNGSI DELTA DIRAC Marwan Wirianto 1) dan Wono Setya Budhi ) 1) Jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Katolik Parahyangan, Bandung
MA1121 Pengantar Matematika
 Catatan Kuliah MA1121 Pengantar Matematika Oleh Hendra Gunawan KK Analisis & Geometri FMIPA-ITB Bandung, Desember 2005 0 PENGANTAR Matakuliah MA1121 Pengantar Matematika I merupakan jembatan antara matematika
Catatan Kuliah MA1121 Pengantar Matematika Oleh Hendra Gunawan KK Analisis & Geometri FMIPA-ITB Bandung, Desember 2005 0 PENGANTAR Matakuliah MA1121 Pengantar Matematika I merupakan jembatan antara matematika
