Persamaan Lingkaran. Pusat Jari-jari Pusat. Jari-jari Menentukan persamaan lingkaran atau garis singgung lingkaran. Persamaan Lingkaran
Ukuran: px
Mulai penontonan dengan halaman:

Download "Persamaan Lingkaran. Pusat Jari-jari Pusat. Jari-jari Menentukan persamaan lingkaran atau garis singgung lingkaran. Persamaan Lingkaran"

Transkripsi

1 2. 5. Menentukan persamaan lingkaran atau garis singgung lingkaran. Persamaan Lingkaran Persamaan Lingkaran () () Bentuk Umum 0 dibagi (2) Pusat Jari-jari Pusat (,), Jumlah kuadrat pusat dikurangi Jari-jari

2 Persamaan Garis Singgung (PGS) Lingkaran PGS Lingkaran di titik (, ) pada lingkaran PGS Lingkaran dengan gradien Pangkat dua menjadi perkalian dua faktor. Pangkat satu menjadi setengah penjumlahan. Ingat pola persamaan garis lurus Lalu perhatikan gambar berikut! () ( )() ( ) Karena ada dua PGS Lingkaran bergradien, maka PGS tersebut adalah dimana PGS lingkaran di titik (, ) pada lingkaran pusat di (0,0) dan jari-jari PGS lingkaran di titik (, ) pada lingkaran pusat di (0,0) dan jari-jari ( )()( )() PGS lingkaran di titik (, ) pada lingkaran dengan bentuk umum 0 PGS dengan gradien dari lingkaran pusat (0,0) dan jari-jari 1 PGS dengan gradien dari lingkaran pusat (,) dan jari-jari ()() 1 ( ) ( )0 Catatan Tambahan: Ingat juga tentang konsep jarak titik (, ) ke garis 0: PGS lingkaran pusat (, ) jari-jari yang sejajar dengan garis 0: PGS lingkaran pusat (, ) jari-jari yang tegak lurus dengan garis 0:

3 PGS Lingkaran di titik (, ) yang berada di luar lingkaran (,) (0,0) (, ) Titik Singgung (,) Diperoleh PGS Persamaan Lingkaran (dalam variabel,). Substitusi titik (, ) ke PGS, lalu substitusi PGS ke persamaan lingkaran Diperoleh dua titik Singgung (, ) dan (, ) Substitusikan ke PGS di langkah kedua Selesai Cari gradien PGS tersebut menggunakan rumus PGS dengan gradien tertentu. PGS akan diperoleh dengan mensubstitusi titik di luar lingkaran tersebut dan nilai gradien. Selesai.

4 Contoh Soal: Tentukan persamaan garis singgung lingkaran di titik (5,5) yang menyinggung lingkaran 10! (,) PGS menyinggung titik tertentu di lingkaran. Misal titik singgung tersebut (,). Artinya titik (,)tersebut berada (0,0) baik di PGS maupun lingkaran. (5,5) Sehingga, diperoleh PGS lingkaran dan persamaan lingkaran dalam variabel dan. Perhatikan bahwa (,) berada di lingkaran, maka: PGS lingkaran di titik (,) adalah Persamaan lingkaran dengan pusat (0,0) dan melewati titik (,) adalah Karena PGS melewati (5,5) maka bila kita substitusikan (,) ke PGS akan diperoleh: Dari persamaan lingkaran 10 dan 2, substitusikan ke persamaan lingkaran diperoleh: (2) 10 (44 ) (1)(3)0 1 atau 3 Dari 1 atau 3 akan diperoleh nilai, yaitu: Jadi dua titik singgung tersebut adalah (,) dan (,). Sehingga PGS lingkaran pada titik (,) dan (,) adalah: 310 dan 310. Lingkaran 10 adalah lingkaran dengan titik pusat (0, 0) dan jari-jari 10. Cari nilai gradien PGS tersebut dengan mensubstitusikan titik (5,5) dan jari-jari 10 ke dalam rumus: 1 5(5) (kuadratkan kedua ruas) (31)(3)0 1 atau 3 3 Jadi, persamaan garis singgung melalui (5,5) dan gradien ( ) (5) 310 Persamaan garis singgung melalui (5,5) dan gradien 3 ( ) 53(5) 10

5 Tipe Soal Sering Muncul pada Bab Lingkaran: Menentukan pusat dan jari-jari lingkaran Perhatikan pola persamaan lingkaran yang ada pada soal! Contoh: 1. Diberikan persamaan lingkaran 25, maka pusat dan jari-jari lingkaran adalah. (0) (0) 25 Pusat di (0, 0) dan jari-jari Diberikan persamaan lingkaran (3) (4) 25, maka pusat dan jari-jari lingkaran adalah. (3) (4) 25 Pusat di (3, -4) dan jari-jari Diberikan persamaan lingkaran 24200, maka pusat dan jari-jari lingkaran adalah dibagi (-2) Maka pusat (1,2), dan jari-jari adalah (1) (2) (20)

6 Menentukan persamaan lingkaran Seringkali tidak diketahui jari-jari lingkaran. Misal diketahui pusat lingkaran (,) dan lingkaran menyinggung sumbu X, maka. Misal diketahui pusat lingkaran (,) dan lingkaran menyinggung sumbu Y, maka. Seringkali juga jari-jari diperoleh dengan menggunakan rumus jarak titik ke garis. Bila diketahui pusat lingkaran dan garis singgung lingkaran, maka jari-jari lingkaran adalah jarak titik pusat ke garis singgung. Contoh: 1. Persamaan lingkaran dengan pusat (5,1) dan jari-jari 3 adalah. Persamaan lingkaran dengan pusat (,) dengan jari-jari : () () (5) (1) 9 atau diubah ke bentuk umum persamaan lingkaran: (5) (1) Persamaan lingkaran dengan pusat di (3, 2) yang menyinggung sumbu X adalah. (3) (2) Persamaan lingkaran dengan pusat di (1, 2) yang menyinggung sumbu Y adalah. (1) (2) (1) Persamaan lingkaran yang berpusat di (1, 4) dan menyinggung garis 3420 adalah. Pusat (, )(1,4) Garis 3420, dengan 3,4,dan 2. Persamaan lingkaran dengan pusat (, ) menyinggung garis 0 adalah: () () (1) (4) 3(1)4(4)

7 Menentukan persamaan garis singgung lingkaran n pada titik yang terletak di lingkaran. Ingat konsep PGS dapat dilihat dari bentuk persamaan lingkarannya. Pangkat dua diubah menjadi perkalian dua faktor. Pangkat satu, diubah menjadi setengah penjumlahan. Contoh: 1. Persamaan garis singgung lingkaran 25 di titik (4, 3) adalah. 4 dan 3 Ingat, ganti menjadi, dan menjadi Sehingga persamaan garis singgungnya adalah: Persamaan garis singgung lingkaran (1) (4) 25 di titik (2, 0) adalah. 2 dan 0 Ingat, ganti menjadi, dan menjadi. (1) (4) 25 ( 1)(1)( 4)(4)25 Sehingga persamaan garis singgungnya adalah: (21)(1)(04)(4)25 (3)(1)(4)(4) Persamaan garis singgung lingkaran di titik (7, 1) adalah. 7 dan 1 Ingat, ganti menjadi, dan menjadi Sehingga persamaan garis singgungnya adalah: 73(7)2(1)

8 Menentukan persamaan garis singgung lingkaran n pada titik yang terletak di luar lingkaran. 1. Persamaan garis singgung lingkaran 9 di titik (1, 3) adalah. Lingkaran pusat (0, 0) dan jari-jari 3. Cek apakah titik (1, 3) berada di dalam atau di luar lingkaran (?). 9(1) (3) 109 (maka titik berada di luar lingkaran) Gunakan rumus berikut: 1 3(1) (kuadratkan kedua ruas) (43)0 0 atau 3 4 Melalui (1,3) dan gradien 0 ( ) 30(1) 3 Melalui (1,3) dan gradien ( ) (1)

9 Menentukan persamaan garis singgung lingkaran n yang sejajar atau tegak lurus terhadap sebuah garis. 1. Persamaan garis singgung lingkaran (3) (5) 80 yang sejajar dengan garis 250 adalah. Trik Superkilat: Sesuaikan sejajar apa nggak? PGS lingkaran pusat (, ) jari-jari yang sejajar dengan garis 0: Masukkan substitusikan pusat Rumus substitusikan jari-jari dan koefisien Lingkaran pusat (3, 5) dan jari-jari 80 PGS yang sejajar 250 adalah 2 juga!!! 2(5)2(3) 80 1 (2) Salah satu persamaan garis singgung lingkaran yang tegak lurus garis 26 adalah. Trik Superkilat: Lingkaran pusat (2, 4) jari-jari 5 PGS yang sejajar 26 adalah 2 harus diubah menjadi 2!!! 22(2)(4) 5 (2) (1) dan 25

10 Pembahasan TRIK SUPERKILAT pada contoh soal yang serupa pada UN 2012 kemarin: Lingkaran L ( + 1) + ( y 3) = 9 x memotong garis y = 3. Garis singgung lingkaran yang melalui titik potong antara lingkaran dan garis tersebut adalah... A. x = 2 dan x = 4 Memotong garis 3 PGS lingkaran B. x = 2 dan x = 2 3 (1) (33) 9 ( )()( )() C. x = 2 dan x = 4 (1) 9 13 (4,3) (41)(1)09 D. x = 2 dan x = 4 13 atau E. x = 8 dan x = 10 Gunakan sketsa lingkaran 4 Jadi titik potongnya di (4,3) dan (2,3) 2 4 (2,3) (21)(1) Lingkaran L ( + 1) + ( y 3) = 9 x memotong garis y = 3. Garis singgung lingkaran yang melalui titik potong antara lingkaran dan garis tersebut adalah... A. x = 2 dan x = 4 Memotong garis 3 PGS lingkaran B. x = 2 dan x = 2 3 (1) (33) 9 ( )()( )() C. x = 2 dan x = 4 (1) 9 D. x = 2 dan x = 4 13 (4,3) (41)(1)09 E. x = 8 dan x = atau Gunakan sketsa lingkaran 4 Jadi titik potongnya di (4,3) dan (2,3) 2 4 (2,3) (21)(1)

dokumen-dokumen yang mirip

Matematika SMA (Program Studi IPA)

Matematika SMA (Program Studi IPA) Smart Solution UJIAN NASIONAL TAHUN PELAJARAN 2012/2013 Disusun Sesuai Indikator Kisi-Kisi UN 2013 Matematika SMA (Program Studi IPA) Disusun oleh : Pak Anang 2. 5. Menentukan persamaan lingkaran atau

Lebih terperinci

c. 2 d Jika suatu garis mempunyai persamaan 2x + y + 4 = 0, maka gradiennya adalah a. 2 b. ½ c. 2 d. ½

c. 2 d Jika suatu garis mempunyai persamaan 2x + y + 4 = 0, maka gradiennya adalah a. 2 b. ½ c. 2 d. ½ 1 SOAL LATIHAN UH MATEMATIKA PERSAMAAN GARIS LURUS KELAS 8 SMP I. Pilihan Ganda GRADIEN (m) 1. Persamaan garis y = x, maka gradiennya adalah a. b. 4 c. d.. Persamaan garis y = x, maka gradiennya adalah

Lebih terperinci

matematika KTSP & K-13 GARIS SINGGUNG LINGKARAN K e a s A. Definisi Garis Singgung Lingkaran Tujuan Pembelajaran

matematika KTSP & K-13 GARIS SINGGUNG LINGKARAN K e a s A. Definisi Garis Singgung Lingkaran Tujuan Pembelajaran KTSP & K-3 matematika K e l a s XI GARIS SINGGUNG LINGKARAN Tujuan Pembelajaran Setelah mempelajari materi ini, kamu diharapkan memiliki kemampuan berikut.. Memahami definisi garis singgung lingkaran..

Lebih terperinci

MODUL 8 FUNGSI LINGKARAN & ELLIPS

MODUL 8 FUNGSI LINGKARAN & ELLIPS MODUL 8 FUNGSI LINGKARAN & ELLIPS 8.1. LINGKARAN A. PERSAMAAN LINGKARAN DENGAN PUSAT PADA TITIK ASAL DAN JARI-JARI R Persamaan lingkaran dengan pusat (0,0) dan jari jari R adalah : x 2 + y 2 = R 2 B. PERSAMAAN

Lebih terperinci

6 FUNGSI LINEAR DAN FUNGSI

6 FUNGSI LINEAR DAN FUNGSI 6 FUNGSI LINEAR DAN FUNGSI KUADRAT 5.1. Fungsi Linear Pada Bab 5 telah dijelaskan bahwa fungsi linear merupakan fungsi yang variabel bebasnya paling tinggi berpangkat satu. Bentuk umum fungsi linear adalah

Lebih terperinci

LINGKARAN. Lingkaran. pusat lingkaran diskriminan posisi titik posisi garis garis kutub gradien. sejajar tegak lurus persamaan lingkaran

LINGKARAN. Lingkaran. pusat lingkaran diskriminan posisi titik posisi garis garis kutub gradien. sejajar tegak lurus persamaan lingkaran LINGKARAN Persamaan Persamaan garis singgung lingkaran Persamaan lingkaran berpusat di (0, 0) dan (a, b) Kedudukan titik dan garis terhadap lingkaran Merumuskan persamaan garis singgung yang melalui suatu

Lebih terperinci

Pertemuan 2 KOORDINAT CARTESIUS

Pertemuan 2 KOORDINAT CARTESIUS Kalkulus Pertemuan 2 KOORDINAT CARTESIUS Koordinat Cartesius 1 2 3 Jarak y Hitunglah jarak dari A(3,-5) ke B(4,2) A(3,-5) maka x 1 = 3 dan y 1 = -5 B(4,9) maka x 2 = 4 dan y 2 = 2 sehingga d(a, B) = (x

Lebih terperinci

Matematika IPA (MATEMATIKA TKD SAINTEK)

Matematika IPA (MATEMATIKA TKD SAINTEK) Pembahasan Soal SBMPTN 2016 SELEKSI BERSAMA MASUK PERGURUAN TINGGI NEGERI Disertai TRIK SUPERKILAT dan LOGIKA PRAKTIS Matematika IPA (MATEMATIKA TKD SAINTEK) Kumpulan SMART SOLUTION dan TRIK SUPERKILAT

Lebih terperinci

LINGKARAN 2. A. Kedudukan titik dan Garis terhadap Lingkaran 11/18/2015. Peta Konsep. A. Kedudukan Titik dan Garis Terhadap. Lingkaran.

LINGKARAN 2. A. Kedudukan titik dan Garis terhadap Lingkaran 11/18/2015. Peta Konsep. A. Kedudukan Titik dan Garis Terhadap. Lingkaran. /8/205 Peta Konsep Jurnal Materi MIPA Peta Konsep Lingkaran Daftar Hadir MateriA LINGKARAN 2 Kelas XI, Semester 3 Berpusat di O(0, 0) Berpusat di P(a, b) A. Kedudukan Titik dan Garis Terhadap Lingkaran

Lebih terperinci

Persamaan Garis singgung Melalui titik (x 1, y 1 ) diluar lingkaran. Pusat Lingkaran (a, b) Persamaan Garis singgung. Jari Jari r.

Persamaan Garis singgung Melalui titik (x 1, y 1 ) diluar lingkaran. Pusat Lingkaran (a, b) Persamaan Garis singgung. Jari Jari r. PERSAMAAN LINGKARAN Pusat Lingkaran (0, 0) Melalui titik (x, y ) pada lingkaran Jika diketahui gradient m xx y mx r yy r m x y r Persamaan Garis singgung Melalui titik (x, y ) diluar lingkaran Jari Jari

Lebih terperinci

1. Salah satu persamaan garis singgung lingkaran ( x 2 )² + ( y + 1 )² =13 di titik yang berabsis 1 adalah. a. 3x 2y 3 = 0 b. 3x 2y 5 = 0 c.

1. Salah satu persamaan garis singgung lingkaran ( x 2 )² + ( y + 1 )² =13 di titik yang berabsis 1 adalah. a. 3x 2y 3 = 0 b. 3x 2y 5 = 0 c. . Salah satu persamaan garis singgung lingkaran ( x )² + ( y + )² =3 di titik yang berabsis adalah. a. 3x y 3 = 0 b. 3x y 5 = 0 c. 3x + y 9 = 0 d. 3x + y + 9 = 0 e. 3x + y + 5 = 0 Soal Ujian Nasional tahun

Lebih terperinci

fungsi Dan Grafik fungsi

fungsi Dan Grafik fungsi fungsi Dan Grafik fungsi Suatu fungsi adalah pemadanan dua himpunan tidak kosong dengan pasangan terurut (x, y) dimana tidak terdapat elemen kedua yang berbeda. Fungsi (pemetaan) himpunan A ke himpunan

Lebih terperinci

Kelas XI MIA Peminatan

Kelas XI MIA Peminatan Kelas Disusun : Markus Yuniarto, S.Si Tahun Pelajaran 017 018 Peta Konsep Glosarium Istilah Keterangan Lingkaran Himpunan titik-titik (pada bidang datar) yang memiliki jarak tetap terhadap suatu titik

Lebih terperinci

Smart Solution TAHUN PELAJARAN 2012/201 /2013. (Program Studi IPA) Disusun Sesuai Indikator Kisi-Kisi UN Disusun oleh : Pak Anang

Smart Solution TAHUN PELAJARAN 2012/201 /2013. (Program Studi IPA) Disusun Sesuai Indikator Kisi-Kisi UN Disusun oleh : Pak Anang Smart Solution TAHUN PELAJARAN 0/0 /0 Disusun Sesuai Indikator Kisi-Kisi UN 0 (Program Studi IPA) Disusun oleh : Pak Anang SMART SOLUTION dan TRIK SUPERKILAT UN Matematika SMA Program IPA Per Indikator

Lebih terperinci

PERSAMAAN GARIS SINGGUNG PARABOLA

PERSAMAAN GARIS SINGGUNG PARABOLA 1 KEGIATAN BELAJAR 11 PERSAMAAN GARIS SINGGUNG PARABOLA Setelah mempelajari kegiatan belajar 11 ini, mahasiswa diharapkan mampu Menentukan Persamaan Garis Singgung Parabola, Titik dan Garis Polar Pada

Lebih terperinci

BAB XI PERSAMAAN GARIS LURUS

BAB XI PERSAMAAN GARIS LURUS BAB XI PERSAMAAN GARIS LURUS A. Pengertian Pesamaan Garis Lurus Persamaan garis lurus adalah suatu fungsi yang apabila digambarkan ke dalam bidang Cartesius akan berbentuk garis lurus. Garis lurus ini

Lebih terperinci

4. Persamaan garis lingkaran yang berpusat di ( 1,4 ) dan menyinggung garis 3x 4y 2 = 0 adalah.

4. Persamaan garis lingkaran yang berpusat di ( 1,4 ) dan menyinggung garis 3x 4y 2 = 0 adalah. . Salah satu persamaan garis singgung lingkaran ( x )² + ( y + )² =3 di titik yang berabsis adalah. a. 3x y 3 = 0 b. 3x y 5 = 0 c. 3x + y 9 = 0 d. 3x + y + 9 = 0 e. 3x + y + 5 = 0 Langkah : Substitusi

Lebih terperinci

PEMBAHASAN DAN KUNCI JAWABAN UN MATEMATIKA SMA 2011 PAKET 12 PLUS TRIK SUPERKILAT DAN LOGIKA PRAKTIS (By Pak Anang

PEMBAHASAN DAN KUNCI JAWABAN UN MATEMATIKA SMA 2011 PAKET 12 PLUS TRIK SUPERKILAT DAN LOGIKA PRAKTIS (By Pak Anang 1. Bentuk sederhana dari A. LOGIKA PRAKTIS: PEMBAHASAN DAN KUNCI JAWABAN UN MATEMATIKA SMA 2011 PAKET 12 PLUS TRIK SUPERKILAT DAN LOGIKA PRAKTIS (By Pak Anang http://www.facebook.com/pak.anang ) Pembilang

Lebih terperinci

2. Di antara bilangan-bilangan berikut, hanya ada satu yang habis membagi , yaitu. c. 1 d.

2. Di antara bilangan-bilangan berikut, hanya ada satu yang habis membagi , yaitu. c. 1 d. Halaman: 1 1. Akar pangkat empat dari 4 adalah a. 4 b. 4 c. 4 d. 4 2. Di antara bilangan-bilangan berikut, hanya ada satu yang habis membagi 100 000 064, yaitu a. 10404 b. 10408 c. 10804 d. 10808 3. Banyaknya

Lebih terperinci

FUNGSI. Riri Irawati, M.Kom 3 sks

FUNGSI. Riri Irawati, M.Kom 3 sks FUNGSI Riri Irawati, M.Kom 3 sks Agenda 1. Sistem Koordinat Kartesius. Garis Lurus 3. Grafik persamaan Tujuan Agar mahasiswa dapat : Menggunakan sistem koordinat untuk menentukan titik-titik dan kurva-kurva.

Lebih terperinci

Matematika Ekonomi KUADRAT DAN FUNGSI RASIONAL (FUNGSI PECAH) GRAFIK FUNGSI KUADRAT BERUPA PARABOLA GRAFIK FUNGSI RASIONAL BERUPA HIPERBOLA

Matematika Ekonomi KUADRAT DAN FUNGSI RASIONAL (FUNGSI PECAH) GRAFIK FUNGSI KUADRAT BERUPA PARABOLA GRAFIK FUNGSI RASIONAL BERUPA HIPERBOLA Fungsi Non Linier Diskripsi materi: -Harga ekstrim pada fungsi kuadrat 1 Fungsi non linier FUNGSI LINIER DAPT BERUPA FUNGSI KUADRAT DAN FUNGSI RASIONAL (FUNGSI PECAH) GRAFIK FUNGSI KUADRAT BERUPA PARABOLA

Lebih terperinci

RINGKASAN IRISAN KERUCUT (PARABOLA, ELIPS, DAN HIPERBOLA)

RINGKASAN IRISAN KERUCUT (PARABOLA, ELIPS, DAN HIPERBOLA) RINGKASAN IRISAN KERUCUT (PARABOLA, ELIPS, DAN HIPERBOLA) Matematika15.wordpress.com NAMA: KELAS: RINGKASAN IRISAN KERUCUT (PARABOLA, ELIPS, DAN HIPERBOLA) PENGERTIAN IRISAN KERUCUT Bangun Ruang Kerucut

Lebih terperinci

Pembahasan Soal SBMPTN 2014 SELEKSI BERSAMA MASUK PERGURUAN TINGGI NEGERI. Disertai TRIK SUPERKILAT dan LOGIKA PRAKTIS

Pembahasan Soal SBMPTN 2014 SELEKSI BERSAMA MASUK PERGURUAN TINGGI NEGERI. Disertai TRIK SUPERKILAT dan LOGIKA PRAKTIS Pembahasan Soal SBMPTN 2014 SELEKSI BERSAMA MASUK PERGURUAN TINGGI NEGERI Disertai TRIK SUPERKILAT dan LOGIKA PRAKTIS Matematika IPA (MATEMATIKA TKD SAINTEK) Distributed By : WWW.E-SBMPTN.COM Kumpulan

Lebih terperinci

FUNGSI. A. Relasi dan Fungsi Contoh: Manakah yang merupakan fungsi/pemetaan dan manakah yang bukan fungsi? (i) (ii) (iii)

FUNGSI. A. Relasi dan Fungsi Contoh: Manakah yang merupakan fungsi/pemetaan dan manakah yang bukan fungsi? (i) (ii) (iii) FUNGSI A. Relasi dan Fungsi Manakah yang merupakan fungsi/pemetaan dan manakah yang bukan fungsi? (i) (ii) (iii) Relasi himpunan A ke himpunan B adalah relasi yang memasangkan/mengkawankan/mengkorepodensikan

Lebih terperinci

RINGKASAN IRISAN KERUCUT (PARABOLA, ELIPS, DAN HIPERBOLA)

RINGKASAN IRISAN KERUCUT (PARABOLA, ELIPS, DAN HIPERBOLA) NAMA: KELAS: PENGERTIAN IRISAN KERUCUT Bangun Ruang Kerucut yang dipotong oleh sebuah bidang datar. RINGKASAN IRISAN KERUCUT (PARABOLA, ELIPS, DAN HIPERBOLA) Macam-macam Irisan Kerucut: 1. Parabola 2.

Lebih terperinci

PERSAMAAN GARIS LURUS

PERSAMAAN GARIS LURUS PERSAMAAN GARIS LURUS A. Menggambar grafik garis lurus Langkah langkah mengambar grafik persamaan garis lurus sama dengan langkahlangkah membuat grafik pada sistim koordinat. Gambarlah grafik persamaan

Lebih terperinci

Solusi dan Penyelesaian. Persamaan Lingkaran. Solusi 6. (a) m = 8 (b) m = ±2 (c*) m = 1 (d*) m > 10. (b) di luar lingkaran (c) di dalam lingkaran

Solusi dan Penyelesaian. Persamaan Lingkaran. Solusi 6. (a) m = 8 (b) m = ±2 (c*) m = 1 (d*) m > 10. (b) di luar lingkaran (c) di dalam lingkaran Solusi dan Penyelesaian Persamaan Lingkaran # Ralat Soal --- tidak ada --- Bagian A Solusi Solusi 1. (a) x 2 + y 2 = 13 (b) x 2 + y 2 = 1 5 Solusi 2. (a) (x + 1) 2 + (y 2) 2 = 9 (b*) tidak ada persamaan

Lebih terperinci

FUNGSI DAN PERSAMAAN LINEAR. EvanRamdan

FUNGSI DAN PERSAMAAN LINEAR. EvanRamdan FUNGSI DAN PERSAMAAN LINEAR TEORI FUNGSI Fungsi yaitu hubungan matematis antara suatu variabel dengan variabel lainnya. Unsur-unsur pembentukan fungsi yaitu variabel (terikat dan bebas), koefisien dan

Lebih terperinci

Matematika IPA (MATEMATIKA TKD SAINTEK)

Matematika IPA (MATEMATIKA TKD SAINTEK) Pembahasan Soal SBMPTN 2014 SELEKSI BERSAMA MASUK PERGURUAN TINGGI NEGERI Disertai TRIK SUPERKILAT dan LOGIKA PRAKTIS Matematika IPA (MATEMATIKA TKD SAINTEK) Disusun Oleh : Pak Anang (http://pak-anang.blogspot.com)

Lebih terperinci

Solusi Pengayaan Matematika Edisi 3 Januari Pekan Ke-3, 2005 Nomor Soal: 21-30

Solusi Pengayaan Matematika Edisi 3 Januari Pekan Ke-3, 2005 Nomor Soal: 21-30 Solusi Pengayaan Matematika Edisi 3 Januari Pekan Ke-3, 005 Nomor Soal: -30. Garis 5y 60 memotong sumbu X dan sumbu Y masing-masing di titik A dan B, sehingga OAB membentuk segitiga siku-siku. Sebuah lingkaran

Lebih terperinci

K13 Antiremed Kelas 11 Matematika Peminatan

K13 Antiremed Kelas 11 Matematika Peminatan K13 Antiremed Kelas 11 Matematika Peminatan Persiapan UAS 1 Doc. Name: K13AR11MATPMT01UAS Version : 015-11 halaman 1 01. Sukubanyak f() = 3 + + 3- dapat ditulis sebagai. f() = [( + ) - 3] + f() = [( -

Lebih terperinci

Solusi Pengayaan Matematika

Solusi Pengayaan Matematika Solusi Pengaaan Matematika Edisi Januari Pekan Ke-, 006 Nomor Soal: 1-0 1. Melalui (0, 0) buatlah garis-garis ang memotong lingkaran 0 pada dua titik. Carilah tempat kedudukan pertengahan ke dua titik.

Lebih terperinci

GEOMETRI ANALITIK BIDANG & RUANG

GEOMETRI ANALITIK BIDANG & RUANG HANDOUT (BAHAN AJAR) GEOMETRI ANALITIK BIDANG & RUANG Sofyan Mahfudy IAIN Mataram KATA PENGANTAR Alhamdulillah puji syukur kepada Alloh Ta ala yang dengan rahmat dan karunia-nya penulis dapat menyelesaikan

Lebih terperinci

(x- x 1. Contoh soal: jawab: x 2 + y 2 = 2 2 x 2 + y 2 = 4. x 2 + y 2 = 4. jawab: (x 5) 2 + (y 2) 2 = 4 2

(x- x 1. Contoh soal: jawab: x 2 + y 2 = 2 2 x 2 + y 2 = 4. x 2 + y 2 = 4. jawab: (x 5) 2 + (y 2) 2 = 4 2 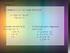LINGKRN (x- x ) (x- x ) + (y- y ) (y- y ) = 0 Contoh soal: Pengertian : Lingkaran adalah tepat kedudukan titik-titik yang berjarak konstan/saa terhadap sebuah titik tertentu. Sebuah titik tertentu itu

Lebih terperinci

MBS - DTA. Sucipto UNTUK KALANGAN SENDIRI. SMK Muhammadiyah 3 Singosari

MBS - DTA. Sucipto UNTUK KALANGAN SENDIRI. SMK Muhammadiyah 3 Singosari MBS - DTA Sucipto UNTUK KALANGAN SENDIRI SMK Muhammadiyah Singosari SERI : MBS-DTA FUNGSI STANDAR KOMPETENSI Siswa mampu memecahkan masalah yang berkaitan dengan fungsi, persamaan fungsi linear dan fungsi

Lebih terperinci

Pembahasan Matematika IPA SIMAK UI 2009

Pembahasan Matematika IPA SIMAK UI 2009 Pembahasan Matematika IPA SIMAK UI 2009 Kode 924 Oleh Kak Mufidah 1. Diketahui fungsi. Agar fungsi tersebut senantiasa berada di bawah sumbu x, maka nilai m yang mungkin adalah Agar fungsi tersebut senantiasa

Lebih terperinci

BEBERAPA FUNGSI KHUSUS

BEBERAPA FUNGSI KHUSUS BEBERAPA FUNGSI KHUSUS ). Fungsi Konstan ). Fungsi Identitas 3). Fungsi Modulus 4). Fungsi Genap dan Fungsi Ganjil Fungsi genap jika f(x) = f(x), dan Fungsi ganjil jika f(x) = f(x) 5). Fungsi Tangga dan

Lebih terperinci

Wardaya College. Tes Simulasi Ujian Nasional SMA Berbasis Komputer. Mata Pelajaran Matematika Tahun Ajaran 2017/2018

Wardaya College. Tes Simulasi Ujian Nasional SMA Berbasis Komputer. Mata Pelajaran Matematika Tahun Ajaran 2017/2018 Tes Simulasi Ujian Nasional SMA Berbasis Komputer Mata Pelajaran Matematika Tahun Ajaran 07/08 -. Jika diketahui x = 8, y = 5 dan z = 8, maka nilai dari x y z adalah.... (a) 0 (b) 00 (c) 500 (d) 750 (e)

Lebih terperinci

PERSAMAAN GARIS SINGGUNG ELLIPS

PERSAMAAN GARIS SINGGUNG ELLIPS 1 KEGIATAN BELAJAR 13 PERSAMAAN GARIS SINGGUNG ELLIPS Setelah mempelajari kegiatan belajar 13 ini, mahasiswa diharapkan mampu Menentukan Persamaan Garis Singgung Elips, Titik Singung dan Garis Pada kegiatan

Lebih terperinci

Pembahasan Soal SIMAK UI 2012 SELEKSI MASUK UNIVERSITAS INDONESIA. Disertai TRIK SUPERKILAT dan LOGIKA PRAKTIS. Matematika IPA

Pembahasan Soal SIMAK UI 2012 SELEKSI MASUK UNIVERSITAS INDONESIA. Disertai TRIK SUPERKILAT dan LOGIKA PRAKTIS. Matematika IPA Pembahasan Soal SIMAK UI 0 SELEKSI MASUK UNIVERSITAS INDONESIA Disertai TRIK SUPERKILAT dan LOGIKA PRAKTIS Matematika IPA Disusun Oleh : Pak Anang Kumpulan SMART SOLUTION dan TRIK SUPERKILAT Pembahasan

Lebih terperinci

LINGKARAN. Lingkaran merupakan tempat kedudukan titik-titik yang berjarak sama terhadap titik tertentu. Perhatikan gambar berikut.

LINGKARAN. Lingkaran merupakan tempat kedudukan titik-titik yang berjarak sama terhadap titik tertentu. Perhatikan gambar berikut. LINGKARAN Lingkaran merupakan tempat kedudukan titik-titik ang berjarak sama terhadap titik tertentu. Perhatikan gambar berikut. r P Titik P disebut pusat, sedangkan Jarak P ke lingkaran dinamakan jari-jari.

Lebih terperinci

KURVA DAN PENCOCOKAN KURVA. Matematika Industri 1 TIP FTP UB

KURVA DAN PENCOCOKAN KURVA. Matematika Industri 1 TIP FTP UB KURVA DAN PENCOCOKAN KURVA TIP FTP UB Pokok Bahasan Pendahuluan Kurva-kurva standar Asimtot Penggambaran kurva secara sistematis, jika persamaan kurvanya diketahui Pencocokan kurva Metode kuadrat terkecil

Lebih terperinci

SMAN Bone-Bone, Luwu Utara, Sul-Sel Dan bahwa setiap pengalaman mestilah dimasukkan ke dalam kehidupan, guna memperkaya kehidupan itu sendiri. Karena tiada kata akhir untuk belajar seperti juga tiada kata

Lebih terperinci

MATEMATIKA DASAR TAHUN 1987

MATEMATIKA DASAR TAHUN 1987 MATEMATIKA DASAR TAHUN 987 MD-87-0 Garis singgung pada kurva y di titik potong nya dengan sumbu yang absisnya positif mempunyai gradien 0 MD-87-0 Titik potong garis y + dengan parabola y + ialah P (5,

Lebih terperinci

PERSAMAAN GARIS SINGGUNG HIPERBOLA

PERSAMAAN GARIS SINGGUNG HIPERBOLA 1 KEGIATAN BELAJAR 15 PERSAMAAN GARIS SINGGUNG HIPERBOLA Setelah mempelajari kegiatan belajar 15 ini, mahasiswa diharapkan mampu: 1. Menemukan Persamaan Garis Singgung Hiperbola, Titik Singung dan Garis

Lebih terperinci

SEKOLAH MENENGAH PERTAMA (SMP) NEGERI 103 JAKARTA

SEKOLAH MENENGAH PERTAMA (SMP) NEGERI 103 JAKARTA PEMERINTAH PROVINSI DAERAH KHUSUS IBUKOTA JAKARTA DINAS PENDIDIKAN SEKOLAH MENENGAH PERTAMA (SMP) NEGERI 103 JAKARTA SEKOLAH STANDAR NASIONAL (SSN) Jl. RA Fadillah Komp. Kopassus Cijantung Telp. 8400005,

Lebih terperinci

KISI-KISI UJIAN SEKOLAH

KISI-KISI UJIAN SEKOLAH KISI-KISI UJIAN SEKOLAH Matematika SEKOLAH MENENGAH PERTAMA DAERAH KHUSUS IBUKOTA (DKI) JAKARTA TAHUN PELAJARAN 2012-2013 KISI KISI PENULISAN SOAL UJIAN SEKOLAH TAHUN PELAJARAN 2012-2013 Jenjang : SMP

Lebih terperinci

A18 MATEMATIKA. Pak Anang. Rabu, 18 April 2012 ( ) Pembahasan soal oleh

A18 MATEMATIKA. Pak Anang. Rabu, 18 April 2012 ( ) Pembahasan soal oleh DOKUMEN NEGARA A8 MATEMATIKA SMA/MA IPA MATEMATIKA SMA/MA IPA Pak Anang http://pakhttp://pak-anang.blogspot.com MATEMATIKA Rabu, 8 April 0 (08.00 0.00) A-MAT-ZD-M-0/0 Hak Cipta pada Pusat Penilaian Pendidikan-BALITBANG-KEMDIKBUD

Lebih terperinci

MATERI PRASYARAT. ke y= f(x) =ax2 + bx +c

MATERI PRASYARAT. ke y= f(x) =ax2 + bx +c 1 MATERI PRASYARAT A. Fungsi Kuadrat Bentuk umum : y= f(x) = ax 2 + bx +c dengan a 0. Langkah-langkah dalam menggambar grafik fungsi kuadrat y= f(x) = ax 2 + bx +c 1. Tentukan titik potong dengan sumbu

Lebih terperinci

SOAL-SOAL LATIHAN TURUNAN FUNGSI SPMB

SOAL-SOAL LATIHAN TURUNAN FUNGSI SPMB SOL-SOL LTIHN TURUNN FUNGSI SPM 00-007. SPM Matematika asar Regional I 00 Kode 0 Garis singgung kurva di titik potongnya dengan sumbu yang absisnya postif y mempunyai gradien.. 9 8 7. SPM Matematika asar

Lebih terperinci

Matematika EBTANAS Tahun 1986

Matematika EBTANAS Tahun 1986 Matematika EBTANAS Tahun 986 EBT-SMA-86- Bila diketahui A = { x x bilangan prima < }, B = { x x bilangan ganjil < }, maka eleman A B =.. 3 7 9 EBT-SMA-86- Bila matriks A berordo 3 dan matriks B berordo

Lebih terperinci

Pembahasan soal oleh MATEMATIKA. Rabu, 18 April 2012 ( )

Pembahasan soal oleh MATEMATIKA. Rabu, 18 April 2012 ( ) DOKUMEN NEGARA Pembahasan soal oleh http://pak-anang.blogspot.com A8 MATEMATIKA SMA/MA IPA MATEMATIKA SMA/MA IPA Perpustakaan SMAN Wonogiri MATEMATIKA Rabu, 8 April 0 (08.00 0.00) A-MAT-ZD-M-0/0 Hak Cipta

Lebih terperinci

Penerapan Turunan MAT 4 D. PERSAMAAN GARIS SINGGUNG KURVA A. PENDAHULUAN B. DALIL L HÔPITAL C. PERSAMAAN PADA KINEMATIKA GERAK TURUNAN. materi78.co.

Penerapan Turunan MAT 4 D. PERSAMAAN GARIS SINGGUNG KURVA A. PENDAHULUAN B. DALIL L HÔPITAL C. PERSAMAAN PADA KINEMATIKA GERAK TURUNAN. materi78.co. Penerapan Turunan A. PENDAHULUAN Turunan dapat digunakan untuk: 1) Perhitungan nilai limit dengan dalil l Hôpital 2) Menentukan persamaan fungsi kecepatan dan percepatan dari persamaan fungsi posisi )

Lebih terperinci

Silabus. Kegiatan Pembelajaran Instrumen. Tugas individu.

Silabus. Kegiatan Pembelajaran Instrumen. Tugas individu. Silabus Jenjang : SMP dan MTs Mata Pelajaran : Matematika Kelas : VIII Semester : 1 Standar Kompetensi : ALJABAR 1. Memahami bentuk aljabar, relasi, fungsi, dan garis lurus. Kompetensi Dasar Materi Ajar

Lebih terperinci

SOAL DAN PEMBAHASAN OSN MATEMATIKA SMP 2012 TINGKAT PROVINSI (BAGIAN A : ISIAN SINGKAT)

SOAL DAN PEMBAHASAN OSN MATEMATIKA SMP 2012 TINGKAT PROVINSI (BAGIAN A : ISIAN SINGKAT) SOAL DAN PEMBAHASAN OSN MATEMATIKA SMP 2012 TINGKAT PROVINSI (BAGIAN A : ISIAN SINGKAT) BAGIAN A : ISIAN SINGKAT 1. Sebuah silinder memiliki tinggi dan volume. Luas permukaan bola terbesar yang mungkin

Lebih terperinci

Modul Matematika XI MIA Semester 1 Lingkaran

Modul Matematika XI MIA Semester 1 Lingkaran Lingkaran XI MIA 017/018 Modul Matematika XI MIA Semester 1 Lingkaran Oleh : Markus Yuniarto, S.Si 1 Tahun Pelajaran 017/018 SMA Santa Angela Jl. Merdeka No. Bandung Lingkaran XI MIA 017/018 Peta Konsep

Lebih terperinci

2. Memahami dan mampu menyelesaikan Permasalahan yang berkaitan dengan vektor di Ruang Tiga, yaitu Persamaan Bidang

2. Memahami dan mampu menyelesaikan Permasalahan yang berkaitan dengan vektor di Ruang Tiga, yaitu Persamaan Bidang TUJUAN EMBELAJARAN Agar pembaca memahami tentang Sistem Koordinat Kartesian beserta fungsinya yaitu titik, jarak dua titik, persamaan bola serta Vektor dalam ruang dimensi tiga beserta aplikasinya yaitu

Lebih terperinci

Modul Matematika XI IPA Semester 1 Lingkaran

Modul Matematika XI IPA Semester 1 Lingkaran Modul Matematika XI IPA Semester 1 Lingkaran Oleh : Markus Yuniarto, S.Si Tahun Pelajaran 015 016 SMA Santa Angela Jl. Merdeka No. 4 Bandung Lingkaran XI IPA Sem 1/014-015 4 Peta Konsep Persamaan Lingkaran

Lebih terperinci

Lingkaran adalah tempat kedudukan titik-titik pada bidang yang berjarak

Lingkaran adalah tempat kedudukan titik-titik pada bidang yang berjarak 4 Lingkaran 4.1. Persamaan Lingkaran Bentuk Baku. Lingkaran adalah tempat kedudukan titik-titik pada bidang yang berjarak tetap dari suatu titik tetap. Titik tetap dari lingkaran disebut pusat lingkaran,

Lebih terperinci

PERSAMAAN HIPERBOLA KEGIATAN BELAJAR 14

PERSAMAAN HIPERBOLA KEGIATAN BELAJAR 14 1 KEGIATAN BELAJAR 14 PERSAMAAN HIPERBOLA Setelah mempelajari kegiatan belajar 14 ini, mahasiswa diharapkan mampu: 1. Menentukan Persamaan Hiperbola 2. Melukis Persamaan Hiperbola Sebelumnya anda telah

Lebih terperinci

4. SISTEM PERSAMAAN DAN PERTIDAKSAMAAN

4. SISTEM PERSAMAAN DAN PERTIDAKSAMAAN 4. SISTEM PERSAMAAN DAN PERTIDAKSAMAAN 4.1 Persamaan Garis a. Bentuk umum persamaan garis Garis lurus yang biasa disebut garis merupakan kurva yang paling sederhana dari semua kurva. Misalnya titik A(2,1)

Lebih terperinci

MATEMATIKA BISNIS FUNGSI LINIER

MATEMATIKA BISNIS FUNGSI LINIER MODUL MATEMATIKA BISNIS 2 FUNGSI LINIER Definisi Fungsi linier adalah fungsi paling sederhana karena hanya mempunyai satu variabel bebas dan berpangkat satu pada variabel tersebut, atau dengan kata lain

Lebih terperinci

Fungsi Linear dan Fungsi Kuadrat

Fungsi Linear dan Fungsi Kuadrat Modul 1 Fungsi Linear dan Fungsi Kuadrat Drs. Susiswo, M.Si. K PENDAHULUAN ompetensi umum yang diharapkan, setelah mempelajari modul ini, adalah Anda dapat memahami konsep tentang persamaan linear dan

Lebih terperinci

KELAS XI PROGRAM KEAHLIAN : BISNIS DAN MANAJEMEN & PARIWISATA SMK NEGERI 1 SURABAYA. BY : Drs. Abd. Salam, MM

KELAS XI PROGRAM KEAHLIAN : BISNIS DAN MANAJEMEN & PARIWISATA SMK NEGERI 1 SURABAYA. BY : Drs. Abd. Salam, MM KELAS XI PROGRAM KEAHLIAN : BISNIS DAN MANAJEMEN & PARIWISATA SMK NEGERI 1 SURABAYA BAHAN AJAR FUNGSI LINIER & KUADRAT SMK NEGERI 1 SURABAYA Halaman 1 BAB FUNGSI A. FUNGSI DAN RELASI Topik penting yang

Lebih terperinci

2. Tentukan persamaan garis yang melalui titik P (x 1,y 1,z 1 ) dan R (x 2,y 2,z 2 ) seperti yang ditunjukkan pada gambar. Z P Q R

2. Tentukan persamaan garis yang melalui titik P (x 1,y 1,z 1 ) dan R (x 2,y 2,z 2 ) seperti yang ditunjukkan pada gambar. Z P Q R . Jika dan vektor-vektor tak kolinear dan A = ( x + 4y ) + ( 2x + y + ) dan B = ( y 2x + 2 ) + ( 2x 3y -), maka carilah nilai x dan y sehingga 3A = 2B. Penyelesian: 3A = 2 B 3(x + 4y ) +3 ( 2x + y + )b

Lebih terperinci

Persamaan dan Pertidaksamaan Linear

Persamaan dan Pertidaksamaan Linear MATERI POKOK Persamaan dan Pertidaksamaan Linear MATERI BAHASAN : A. Persamaan Linear B. Pertidaksamaan Linear Modul.MTK X 0 Kalimat terbuka adalah kalimat matematika yang belum dapat ditentukan nilai

Lebih terperinci

OSN Guru Matematika SMA

OSN Guru Matematika SMA z Pembahasan Soal OLIMPIADE SAINS NASIONAL KHUSUS GURU MATEMATIKA SMA OSN Guru Matematika SMA (Olimpiade Sains Nasional) Disusun oleh: Pak Anang Halaman 2 dari 26 PEMBAHASAN SOAL OLIMPIADE GURU MATEMATIKA

Lebih terperinci

LINGKARAN. Bab. Di unduh dari : Bukupaket.com

LINGKARAN. Bab. Di unduh dari : Bukupaket.com Bab 9 LINGKARAN A. KOMPETENSI DASAR DAN PENGALAMAN BELAJAR Kompetensi Dasar Setelah mengikuti pembelajaran lingkaran siswa mampu: 1. Mendeskripsikan konsep persamaan lingkaran dan menganalisis sifat garis

Lebih terperinci

Notasi turunan. Penggunaan turunan. 6. Menggunakan konsep limit fungsi dan turunan fungsi dalam pemecahan masalah.

Notasi turunan. Penggunaan turunan. 6. Menggunakan konsep limit fungsi dan turunan fungsi dalam pemecahan masalah. Turunan fungsi adalah fungsi lain dari suatu fungsi sebelumnya misalkan fungsi f menjadi f' TURUNAN Notasi turunan y' atau f'(x) atau dy/dx fungsi naik Penggunaan turunan fungsi turun persamaan garis singgung

Lebih terperinci

A. MENYELESAIKAN PERSAMAAN KUADRAT

A. MENYELESAIKAN PERSAMAAN KUADRAT A. MENYELESAIKAN PERSAMAAN KUADRAT STANDAR KOMPETENSI Memecahkan masalah yang berkaitan dengan fungsi, persamaan dan fungsi kuadrat serta pertidaksamaan kuadrat KOMPETENSI DASAR Menggunakan sifat dan aturan

Lebih terperinci

B. 30 X + 10 Y 300; 20 X + 20 Y 400; X 0, Y 0 C. 10 X + 30 Y 300; 20 X + 20 Y 400, X 0, Y 0 D. 10 X + 30 Y 300, 20 X + 20 Y 400, X 0, Y 0

B. 30 X + 10 Y 300; 20 X + 20 Y 400; X 0, Y 0 C. 10 X + 30 Y 300; 20 X + 20 Y 400, X 0, Y 0 D. 10 X + 30 Y 300, 20 X + 20 Y 400, X 0, Y 0 BIDANG STUDI : MATEMATIKA 1. Harga 3 kg pepaya dan 5 kg jeruk adalah Rp 13.000, sedangkan harga 4 kg papaya dan 3 kg jeruk adalah Rp 10.000, maka harga 2 kg papaya dan 4 kg jeruk adalah. A. Rp 10.000 B.

Lebih terperinci

APLIKASI TURUNAN ALJABAR. Tujuan Pembelajaran. ) kemudian menyentuh bukit kedua pada titik B(x 2

APLIKASI TURUNAN ALJABAR. Tujuan Pembelajaran. ) kemudian menyentuh bukit kedua pada titik B(x 2 Kurikulum 3/6 matematika K e l a s XI APLIKASI TURUNAN ALJABAR Tujuan Pembelajaran Setelah mempelajari materi ini, kamu diharapkan memiliki kemampuan berikut.. Dapat menerapkan aturan turunan aljabar untuk

Lebih terperinci

(x- x 1. Contoh soal: jawab: x 2 + y 2 = 2 2 x 2 + y 2 = 4. x 2 + y 2 = 4. jawab: (x 5) 2 + (y 2) 2 = 4 2

(x- x 1. Contoh soal: jawab: x 2 + y 2 = 2 2 x 2 + y 2 = 4. x 2 + y 2 = 4. jawab: (x 5) 2 + (y 2) 2 = 4 2 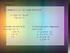BB XI. LINGKRN (x- x ) (x- x ) + (y- y ) (y- y ) 0 Contoh soal: Pengertian : Lingkaran adalah tepat kedudukan titik-titik yang berjarak konstan/saa terhadap sebuah titik tertentu. Sebuah titik tertentu

Lebih terperinci

fungsi rasional adalah rasio dari dua polinomial. Secara umum,

fungsi rasional adalah rasio dari dua polinomial. Secara umum, fungsi rasional adalah rasio dari dua polinomial. Secara umum, Fungsi Rasional Fungsi rasional adalah fungsi yang memiliki bentuk Dengan p dan d merupakan polinomial dan d(x) 0. Domain dari V(x) adalah

Lebih terperinci

CONTOH SOAL MATEMATIKA KELAS 8 PERSAMAAN GARIS LURUS

CONTOH SOAL MATEMATIKA KELAS 8 PERSAMAAN GARIS LURUS CONTOH SOAL MATEMATIKA KELAS 8 PERSAMAAN GARIS LURUS 1. Diketahui titik-titik pada bidang koordinat Cartesius sebagai berikut. a. (10, 5) c. ( 7, 3) e. ( 4, 9) b. (2, 8) d. (6, 1) Tentukan absis dan ordinat

Lebih terperinci

MODUL 2 GARIS LURUS. Mesin Antrian Bank

MODUL 2 GARIS LURUS. Mesin Antrian Bank 1 MODUL 2 GARIS LURUS Gambar 4. 4 Mesin Antrian Bank Persamaan garis lurus sangat berperan penting terhadap kemajuan teknologi sekarang ini. Bagi programmer handal, banyak aplikasi yang membutuhkan persamaan

Lebih terperinci

MATEMATIKA EKONOMI 1 FUNGSI DAN GRAFIK. DOSEN Fitri Yulianti, SP, MSi.

MATEMATIKA EKONOMI 1 FUNGSI DAN GRAFIK. DOSEN Fitri Yulianti, SP, MSi. MATEMATIKA EKONOMI 1 FUNGSI DAN GRAFIK DOSEN Fitri Yulianti, SP, MSi. Fungsi Fungsi merupakan hubungan antara dua variabel atau lebih. Variabel dibedakan : 1. Variabel bebas yaitu variabel yang besarannya

Lebih terperinci

PERSAMAAN GARIS LURUS

PERSAMAAN GARIS LURUS 1 KEGIATAN BELAJAR 3 PERSAMAAN GARIS LURUS Setelah mempelajari kegiatan belajar 3 ini, mahasiswa diharapkan mampu: 1. menentukan persamaan gradien garis lurus, 2. menentukan persamaan vektoris dan persamaan

Lebih terperinci

Materi Fungsi Linear Fungsi Variabel, koefisien, dan konstanta Variabel variabel bebas Koefisien Konstanta 1). Pengertian fungsi linier

Materi Fungsi Linear Fungsi Variabel, koefisien, dan konstanta Variabel variabel bebas Koefisien Konstanta 1). Pengertian fungsi linier Materi Fungsi Linear Admin 8:32:00 PM Duhh akhirnya nongol lagi... kali ini saya akan bahas mengenai pelajaran yang paling disukai oleh hampir seluruh warga dunia :v... MATEMATIKA, ya itu namanya. materi

Lebih terperinci

(A) 3 (B) 5 (B) 1 (C) 8

(A) 3 (B) 5 (B) 1 (C) 8 . Turunan dari f ( ) = + + (E) 7 + +. Turunan dari y = ( ) ( + ) ( ) ( + ) ( ) ( + ) ( + ) ( + ) ( ) ( + ) (E) ( ) ( + ) 7 5 (E) 9 5 9 7 0. Jika f ( ) = maka f () = 8 (E) 8. Jika f () = 5 maka f (0) +

Lebih terperinci

Langkah Penyelesaian Example 1) Tentukan nilai awal x 0 2) Hitung f(x 0 ) kemudian cek konvergensi f(x 0 ) 3) Tentukan fungsi f (x), kemudian hitung f

Langkah Penyelesaian Example 1) Tentukan nilai awal x 0 2) Hitung f(x 0 ) kemudian cek konvergensi f(x 0 ) 3) Tentukan fungsi f (x), kemudian hitung f METODE NEWTON RAPHSON (1) METODE NEWTON RAPHSON Solusi Persamaan Non Linier Oleh : Metode Newton-Raphson merupakan salah satu metode terbuka untuk menentukan solusi akar dari persamaan non linier, dengan

Lebih terperinci

SILABUS KURIKULUM BERBASIS KOMPETENSI FAKULTAS TARBIYAH BANJARMASIN

SILABUS KURIKULUM BERBASIS KOMPETENSI FAKULTAS TARBIYAH BANJARMASIN SILABUS KURIKULUM BERBASIS KOMPETENSI FAKULTAS TARBIYAH BANJARMASIN 1. Mata Kuliah / Kode : Geometri Analitik/ PMK 708 2. Jumlah SKS : 3 SKS 3. Jurusan / Program Studi : TMIPA / Tadris Matematika 4. Tujuan

Lebih terperinci

Modul Statistika Kelas XII SMKN 1 Stabat. Lingkaran. Elips

Modul Statistika Kelas XII SMKN 1 Stabat. Lingkaran. Elips IR Lingkaran Elips 1 Smk n 1 stabat IRISAN KERUCUT Disusun Oleh : Dian Septiana 07144110049 Dalam PPL-T Unimed SMK N 1 Stabat SEKOLAH MENENGAH KEJURUAN NEGERI 1 STABAT LANGKAT 010 KATA PENGANTAR Puji syukur

Lebih terperinci

(x- x 1. Contoh soal: jawab: x 2 + y 2 = 2 2 x 2 + y 2 = 4. x 2 + y 2 = 4. jawab: (x 5) 2 + (y 2) 2 = 4 2

(x- x 1. Contoh soal: jawab: x 2 + y 2 = 2 2 x 2 + y 2 = 4. x 2 + y 2 = 4. jawab: (x 5) 2 + (y 2) 2 = 4 2 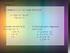BB XI. LINGKRN (x- x ) (x- x ) + (y- y ) (y- y ) = 0 Contoh soal: Pengertian : Lingkaran adalah tepat kedudukan titik-titik yang berjarak konstan/saa terhadap sebuah titik tertentu. Sebuah titik tertentu

Lebih terperinci

MATEMATIKA EKONOMI DAN BISNIS. Nuryanto.ST.,MT

MATEMATIKA EKONOMI DAN BISNIS. Nuryanto.ST.,MT MATEMATIKA EKONOMI DAN BISNIS Fungsi Dalam ilmu ekonomi, kita selalu berhadapan dengan variabel-variabel ekonomi seperti harga, pendapatan nasional, tingkat bunga, dan lainlain. Hubungan kait-mengkait

Lebih terperinci

Pertemuan Minggu ke Keterdiferensialan 2. Derivatif berarah dan gradien 3. Aturan rantai

Pertemuan Minggu ke Keterdiferensialan 2. Derivatif berarah dan gradien 3. Aturan rantai Pertemuan Minggu ke-10 1. Keterdiferensialan 2. Derivatif berarah dan gradien 3. Aturan rantai 1. Keterdiferensialan Pada fungsi satu peubah, keterdiferensialan f di x berarti keujudan derivatif f (x).

Lebih terperinci

Lingkaran. A. Persamaan Lingkaran B. Persamaan Garis Singgung Lingkaran

Lingkaran. A. Persamaan Lingkaran B. Persamaan Garis Singgung Lingkaran Bab Sumber: www.panebiancod.com Setelah mempelajari bab ini, Anda harus mampu merumuskan persamaan lingkaran dan menggunakannya dalam pemecahan masalah; menentukan persamaan garis singgung pada lingkaran

Lebih terperinci

PEMBAHASAN UN SMA TAHUN PELAJARAN 2009/2010 MATEMATIKA PROGRAM STUDY IPA

PEMBAHASAN UN SMA TAHUN PELAJARAN 2009/2010 MATEMATIKA PROGRAM STUDY IPA PEMBAHASAN UN SMA TAHUN PELAJARAN 009/010 MATEMATIKA PROGRAM STUDY IPA PEMBAHAS : 1. Sigit Tri Guntoro, M.Si.. Jakim Wiyoto, S.Si. 3. Marfuah, M.T. 4. Rohmitawati, S.Si. PPPPTK MATEMATIKA 010 1. Perhatikan

Lebih terperinci

Pendahuluan. 1.1 Latar Belakang

Pendahuluan. 1.1 Latar Belakang Pendahuluan 1.1 Latar elakang Geometri datar, merupakan studi tentang titik, garis, sudut, dan bangun-bangun geometri yang terletak pada sebuah bidang datar. erbagai mekanisme peralatan dalam kehidupan

Lebih terperinci

IRISAN DUA LINGKARAN. Tujuan Pembelajaran. ). Segmen garis dari P ke Q disebut sebagai tali busur. Tali busur ini memotong tegak lurus garis C 1

IRISAN DUA LINGKARAN. Tujuan Pembelajaran. ). Segmen garis dari P ke Q disebut sebagai tali busur. Tali busur ini memotong tegak lurus garis C 1 K- matematika K e l a s I IRISAN DUA LINGKARAN Tujuan Pembelajaran Setelah mempelajari materi ini, kamu diharapkan memiliki kemampuan berikut.. Dapat menentukan persamaan dan panjang tali busur dua lingkaran

Lebih terperinci

JAWABAN PERSIAPAN UKD-5 APLIKASI TURUNAN. 1. Tentukan pers garis singgung (PGS) pada kurva. 2. Tentukan pers garis normal (PGN) pada kurva

JAWABAN PERSIAPAN UKD-5 APLIKASI TURUNAN. 1. Tentukan pers garis singgung (PGS) pada kurva. 2. Tentukan pers garis normal (PGN) pada kurva JAWABAN PERSIAPAN UKD-5 APLIKASI TURUNAN. Tentukan pers garis singgung (PGS) pada kurva y 4x % 7x + 5 di titik (, ) x y 4( ) % 7( ) + 5 oke y 5 8x 7 m 8( ) 7 5 y 5(x + ) y 5x 5 y 5x +. Tentukan pers garis

Lebih terperinci

A. PERSAMAAN GARIS LURUS

A. PERSAMAAN GARIS LURUS A. PERSAMAAN GARIS LURUS Persamaan garis lurus adalah hubungan nilai x dan nilai y yang terletak pada garis lurus serta dapat di tulis px + qy = r dengan p, q, r bilangan real dan p, q 0. Persamaan dalam

Lebih terperinci

abcde dengan a, c, e adalah bilangan genap dan b, d adalah bilangan ganjil? A B C D E. 3000

abcde dengan a, c, e adalah bilangan genap dan b, d adalah bilangan ganjil? A B C D E. 3000 Hal. 1 / 7 METHODIST-2 EDUCATION EXPO LOMBA SAINS PLUS ANTAR PELAJAR TINGKAT SMA SE-SUMATERA UTARA TAHUN 2015 BIDANG WAKTU : MATEMATIKA : 120 MENIT PETUNJUK : 1. Pilihlah jawaban yang benar dan tepat.

Lebih terperinci

Bab 1. Irisan Kerucut

Bab 1. Irisan Kerucut Tahun Ajaran 01 01-013/Genap Bab 1. Irisan Kerucut e=0 e 1 A. Lingkaran Persamaan Lingkaran yang berpusat di titik (0,0) Pada segitiga siku-siku, siku, menurut dalil phytagoras berlaku : c =

Lebih terperinci

KONSEP DASAR FUNGSI DAN GRAFIK. Oleh : Agus Arwani, SE, M.Ag

KONSEP DASAR FUNGSI DAN GRAFIK. Oleh : Agus Arwani, SE, M.Ag KONSEP DASAR FUNGSI DAN GRAFIK Oleh : Agus Arwani, SE, M.Ag KONSEP DASAR FUNGSI DAN GRAFIK Definisi : Fungsi f : A B adalah suatu aturan yang mengaitkan (memadankan) setiap dengan tepat satu A y B Notasi

Lebih terperinci

TEOREMA SISA 1. Nilai Sukubanyak Tugas 1

TEOREMA SISA 1. Nilai Sukubanyak Tugas 1 TEOREMA SISA 1. Nilai Sukubanyak Apa yang dimaksud sukubanyak (polinom)? Ingat kembali bentuk linear seperti 2x + 1 atau bentuk kuadrat 2x 2-3x + 5 dan juga bentuk pangkat tiga 2x 3 x 2 + x 7. Bentuk-bentuk

Lebih terperinci

PERSAMAAN BAKU PARABOLA DAN PERSAMAAN GARIS SINGGUNG PARABOLA MAKALAH

PERSAMAAN BAKU PARABOLA DAN PERSAMAAN GARIS SINGGUNG PARABOLA MAKALAH PERSAMAAN BAKU PARABOLA DAN PERSAMAAN GARIS SINGGUNG PARABOLA MAKALAH Dibuat untuk Memenuhi Tugas Mata Kuliah Geometri Analitik Ruang yang diampu oleh M. Khoridatul Huda, S. Pd., M. Si. Oleh: TMT 5E Kelompok

Lebih terperinci

LINGKARAN. A. PERSAMAAN LINGKARAN B. PERSAMAAN GARIS SINGGUNG LINGKARAN

LINGKARAN. A. PERSAMAAN LINGKARAN B. PERSAMAAN GARIS SINGGUNG LINGKARAN LINGKARAN. A. PERSAMAAN LINGKARAN B. PERSAMAAN GARIS SINGGUNG LINGKARAN 4 ia nc o3 D.c om Bab r: w be Su m. pa ww ne b Lingkaran Setelah mempelajari bab ini, Anda harus mampu merumuskan persamaan lingkaran

Lebih terperinci

(D) 2 x < 2 atau x > 2 (E) x > Kurva y = naik pada

(D) 2 x < 2 atau x > 2 (E) x > Kurva y = naik pada f =, maka fungsi f naik + 1 pada selang (A), 0 (D), 1. Jika ( ) (B) 0, (E) (C),,. Persamaan garis singgung kurva lurus + = 0 adalah (A) + = 0 (B) + = 0 (C) + + = 0 (D) + = 0 (E) + + = 0 = ang sejajar dengasn

Lebih terperinci

Matematika Dasar NILAI EKSTRIM

Matematika Dasar NILAI EKSTRIM NILAI EKSTRIM Misal diberikan kurva f( ) dan titik ( a,b ) merupakan titik puncak ( titik maksimum atau minimum ). Maka garis singgung kurva di titik ( a,b ) akan sejajar sumbu X atau [ ] mempunyai gradien

Lebih terperinci
2024 © DocPlayer.info Pengaturan dan alat privasi | Ketentuan | Tanggapan