II. TINJAUAN PUSTAKA. kromatik lokasi pada suatu graf sebagai landasan teori pada penelitian ini
|
|
|
- Iwan Irawan
- 7 tahun lalu
- Tontonan:
Transkripsi
1 5 II. TINJAUAN PUSTAKA Pada bagian ini akan diberikan konsep dasar graf, graf pohon dan bilangan kromatik lokasi pada suatu graf sebagai landasan teori pada penelitian ini 2.1 KONSEP DASAR GRAF Konsep dasar mengenai graf yang akan digunakan dalam penelitian ini diambil dari Deo (1989). Graf G adalah himpunan terurut (V(G), E(G)), dengan V(G) menyatakan himpunan titik dari G dengan, dan menyatakan himpuanan sisi yaitu pasangan tak terurut dari. Banyaknya himpunan titik disebut orde dari graf G. Misalkan v dan w adalah titik pada graf G, jika v dan w dihubungkan oleh sisi e, maka v dan w dikatakan bertetangga (adjacent), sedangkan titik v dan w dikatakan menempel (incident) dengan sisi e, demikian juga sisi e dikatakan menempel dengan titik v dan w. Himpunan tetangga (Neigborhood) dari suatu titik v, dinotasikan dengan N(v) adalah himpunan titik-titik yang bertetangga dengan v. v 1 v 2 e 1 e 3 e 5 e 4 e 2 e 7 v 3 e 6 v 4 v 5 Gambar 2. Contoh graf dengan 5 titik dan 7 sisi
2 6 Pada Gambar 2 graf (V, E), dan. Titik bertetangga dengan titik dan sedangkan dan menempel dengan dan. Sebaliknya, sisi menempel pada titik dan titik.. Derajat suatu titik v pada graf G adalah banyaknya sisi yang menempel pada titik v, dinotasikan dengan d(v). Daun (pendant vertex) adalah titik yang berderajat 1. Pada Gambar 2,,, dan adalah daun karena berderajat satu. Pada graf G, jika x = uv adalah garis pada graf G dan w bukan sebuah titik pada graf G, maka x disubdivisi oleh titik w pada graf G, apabila titik w ditempatkan / ditambahkan pada garis x, sehingga terbentuk garis uw dan wv ( Harary, 1994) v v w u u Gambar 3. Graf G dan Graf G yang telah disubdivisi Loop adalah sisi yang memiliki titik awal dan titik akhir yang sama. Sisi paralel adalah sisi yang memiliki dua titik ujung yang sama. Graf yang tidak mempunyai sisi ganda atau loop disebut graf sederhana. Graf pada Gambar 2 bukan merupakan graf sederhana karena pada graf tersebut terdapat loop, yaitu pada titik.
3 7 Pada graf terhubung G, jarak diantara dua titik x dan y adalah panjang lintasan terpendek diantara kedua titik tersebut, dinotasikan dengan d(x, y). Istilah lain yang sering muncul pada pembahasan graf adalah jalan (walk), lintasan (path) dan sirkuit (circuit). Jalan (walk) adalah barisan berhingga dari titik dan sisi dimulai dan diakhiri sedemikian sehingga setiap sisi menempel dengan titik sebelum dan sesudahnya. Contoh jalan berdasarkan Gambar 2 adalah. Lintasan (path) adalah jalan yang melewati titik yang berbeda-beda. Graf G dikatakan graf terhubung jika terdapat lintasan yang menghubungkan setiap dua titik yang berbeda. Pada Gambar 2 contoh lintasan adalah. Sirkuit (circuit) adalah lintasan tertutup (closed path), yaitu lintasan yang memiliki titik awal dan titik akhir yang sama. Sirkuit dibedakan menjadi dua macam, yaitu sirkuit genap dan sirkuit ganjil. Sirkuit genap adalah sirkuit dengan banyaknya titik genap, dan sirkuit ganjil adalah sirkuit dengan banyaknya titik ganjil. Contoh sirkuit berdasarkan gambar pada Gambar 2. adalah. Lemma yang menyatakan kaitan antara jumlah derajat semua titik pada suatu graf G dengan banyak sisinya adalah sebagai berikut;
4 8 Lemma 2.1 (Deo, 1989) Misalkan G(V,E) adalah graf terhubung dengan, maka : Sebagai contoh pada graf Gambar 2 adalah = 3 = 14 = dua kali jumlah sisi. Teorema 2.1 (Deo, 1989) Untuk sembarang graf G, banyaknya titik yang berderajat ganjil, selalu genap. Bukti : Misalkan V genap dan V ganjil masing masing adalah himpunan simpul yang berderajat genap dan himpunan simpul yang berderajat ganjil pada G(V,E). Maka persamaan dapat ditulis sebagi berikut : Karena untuk setiap, maka suku pertama dari ruas kanan persamaan harus bernilai genap. Ruas kiri Persamaan (2.1.1) juga harus bernilai genap. Nilai genap pada ruas kiri hanya benar bila suku kedua dari ruas kanan juga harus genap. Karena untuk setiap, maka banyaknya titik di dalam harus genap agar jumlah seluruh derajatnya bernilai genap. Jadi banyaknya titik yang berderajat ganjil selalu genap.
5 9 2.2 GRAF POHON Graf pohon (tree) adalah suatu graf terhubung yang tidak memuat siklus. Suatu graf yang setiap titiknya mempunyai derajat satu disebut daun (pendant vertex). v 6 v 7 v 8 v 9 v 11 v 5 v 3 v 4 v 2 v 1 Gambar 4. Contoh pohon G dengan 11 titik Pada Gambar 3, graf merupakan graf pohon karena graf tersebut merupakan graf terhubung dan tidak memuat siklus. Titik disebut pendant vertex atau daun. Gabungan dari beberapa pohon disebut hutan (forest). Gambar 5. Contoh hutan (forest) Selanjutnya, akan diberikan definisi beberapa kelas graf pohon. Suatu graf bintang K 1,n (star) adalah suatu graf terhubung yang mempunyai satu titik berderajat n yang disebut pusat dan titik lainnya berderajat satu (Chartrand dkk., 1998).
6 10 Gambar 6. Contoh graf bintang K 1,6 Graf pohon disebut graf bintang ganda (double star) jika graf pohon tersebut mempunyai tepat dua titik x dan y berderajat lebih dari satu. Jika x dan y berturut-turut berderajat a+1 dan b+1, dinotasikan dengan S a,b, (Chartrand dkk., 1998) Gambar 7. Contoh graf bintang ganda S 3,4 Graf ulat (caterpillar graf) adalah graf pohon yang memiliki sifat apabila dihapus semua daunnya akan menghasilkan lintasan (Chartrand dkk., 1998). Gambar 8. Contoh graf ulat Misalkan untuk setiap dan. Graf amalgamasi bintang tak seragam,, untuk adalah graf pohon yang
7 11 diperoleh dengan menyatukan sebuah daun dari setiap graf. Titik penyatuan tersebut dikatakan sebagai titik pusat dari, dinotasikan dengan x. Titik titik yang berjarak 1 dari titik pusat disebut dengan titik antara, dinotasikan dengan untuk. Titik daun ke-j dari titik dinotasikan dengan untuk (Carlson, 2006). Gambar 9. Contoh graf amalgamasi bintang tak seragam Graf amalgamasi bintang seragam, adalah amalgamasi dari k buah graf bintang K1,m bila, untuk setiap i (Asmiati dkk., 2011). Gambar 10. Contoh graf amalgamasi bintang Graf pohon pisang, adalah graf yang diperoleh dari n buah graf bintang dengan cara menghubungkan sebuah daun dari setiap ke suatu titik baru (Chen dkk.(1997)).
8 12 Gambar 11. Contoh graf pohon pisang Graf kembang api seragam, adalah graf yang diperoleh dari n buah graf bintang dengan cara menghubungkan sebuah daun dari setiap melalui sebuah lintasan (Chen dkk.(1997)). Gambar 12.Contoh graf kembang api Selanjutnya diberikan beberapa teorema mengenai graf pohon sebagai berikut : Teorema 2.2 (Harsfield dan Ringel, 1994) Jika adalah pohon dengan titik (vertex ) dan sisi (edge), maka. Bukti: Jika adalah pohon dengan satu sisi maka teorema benar untuk. Asumsikan teorema benar untuk semua pohon dengan sisi kurang dari, artinya untuk, maka. Misal pohon dengan sisi. Pilih satu lintasan terpanjang di dari ke. Titik harus berderajat, karena kalau tidak lintasan akan menjadi lebih panjang atau terbentuk siklus di. Selanjutnya buang
9 13 titik, akibatnya sisi terhubung dengan titik terbuang. Sehingga, pohon terbentuk dengan dan sisi dengan asumsi diperoleh atau. Teorema 2.3 (Harsfield dan Ringel, 1994) Graf adalah pohon jika dan hanya jika ada terdapat tepat satu lintasan di antara kedua titik tersebut. Bukti: ( >) Akan ditunjukkan graf adalah pohon maka ada terdapat tepat satu lintasan di antara kedua titik. Asumsikan adalah pohon, misal dan titik-titik di, maka pohon dapat dihubungkan lintasan ke. Anggaplah terdapat dua lintasan dari ke, dan Jika adalah jarak dari, selanjutnya sampai ditemukan suatu titik yang terdapat dalam yang juga ada dalam. Maka akan terdapat siklus. Jika, maka dapat dilihat pada. Untuk beberapa,, karena ada dua lintasan sebagai asumsi. Selanjutnya mulai dari sampai ditemukan suatu titik yang ada dalam yang juga ada dalam dan selanjutnya pindah ke kembali ke, dan akan didapatkan siklus lagi. Tetapi ada dua adalah pohon, sehingga tidak ada siklus. Jadi asumsi bahwa lintasan salah.
10 14 (< ) Akan ditunjukkan ada terdapat tepat satu lintasan di antara kedua titik maka graf adalah pohon. Asumsikan adalah graf dengan tepat satu lintasan di antara dua titik. Pertama perhatikan terhubung. Anggaplah bahwa memuat siklus. Jelas bahwa ada dua lintasan dari ke. Ini kontradiksi, karena mempunyai tepat satu lintasan di antara dua titik. Jadi graf tidak memuat siklus dan adalah pohon. 2.3 Bilangan Kromatik Lokasi Graf Bilangan kromatik lokasi graf pertama kali dikaji oleh Chartrand dkk.(2002). Konsep ini merupakan pengembangan dari konsep dimensi partisi dan pewarnaan graf. Pewarnaan titik pada graf adalah dengan syarat untuk setiap titik bertetangga harus memiliki warna yang berbeda. Minimum banyaknya warna yang digunakan untuk pewarnaan titik pada graf G disebut bilangan kromatik, yang dinotasikan dengan. Berikut ini diberikan definisi bilangan kromatik lokasi graf yang diambil dari Chartrand dkk.(2002). Misalkan c suatu pewarnaan titik pada graf G dengan untuk u dan v yang bertetangga di G. Misalkan himpunan titik titik yang diberi warna i, yang selanjutnya disebut kelas warna, maka adalah himpunan yang terdiri dari kelas kelas warna dari V(G). Kode warna dari v adalah k-pasang terurut,..., dengan = min untuk. Jika setiap
11 15 G mempunyai kode warna yang berbeda, maka c disebut pewarnaan lokasi G. Banyaknya warna minimum yang digunakan untuk pewarnaan lokasi disebut bilangan kromatik lokasi dari G, dan dinotasikan dengan. Karena setiap pewarnaan lokasi juga merupakan suatu pewarnaan, maka. Berikut ini Chartrand dkk.(2002) telah memberikan teorema dasar dari bilangan kromatik lokasi suatu graf. Teorema 2.4 (Chartrand dkk, 2002) Misalkan c adalah pewarnaan pada graf terhubung G. Jika u dan v adalah dua titik yang berbeda di G sedemikian sehingga d(u,w)=d(v,w) untuk setiap, maka. Secara khusus, jika u dan v titik titik yang tidak bertetangga di G sedemikian sehingga, maka. Bukti : misalkan c adalah suatu pewarnaan lokasi pada graf terhubung G dan misalkan adalah partisi dari titik titik G ke dalam kelas warna. Untuk suatu titik, andaikan sedemikian sehingga titik u dan v berada dalam kelas warna yang sama, misalkan dari. Akibatnya. Karena untuk setiap, maka untuk setiap,. Akibatnya, sehingga c bukan pewarnaan lokasi. Jadi Akibat dari teorema tersebut, dapat ditentukan batas bawah trivial bilangan kromatik lokasi graf.
12 16 Akibat 2.1 (Chartrand dkk, 2002) Misalkan G adalah graf terhubung dengan satu titik yang bertetangga dengan k daun, maka. Bukti : Misalkan v adalah satu titik yang bertetangga dengan k daun di G. Berdasarkan Teorema 2.4, setiap pewarnaan lokasi di G mempunyai warna yang berbeda untuk setiap,. Karena v bertetangga dengan semua maka v harus mempunyai warna yang berbeda dengan semua daun. Akibatnya,. Selanjutnya, akan diberikan contoh menentukan bilangan kromatik lokasi pada suatu graf G seperti Gambar 13 berikut ini : Gambar 13. Pewarnaan lokasi minimum pada graf G Diberikan graf G seperti terlihat pada Gambar 13 akan ditentukan terlebih dahulu batas bawah bilangan kromatik lokasi dari graf G. Karena terdapat titik yang memiliki 3 daun, maka berdasarkan Akibat 2.1,. (2.1.2) Selanjutnya, akan ditentukan batas atas bilangan kromatik lokasi graf G. Titik titik pada dipartisi sebagai berikut : ; ; ;. Kode warnanya adalah ; ; ; ;
13 17 ; ; ; ; Karena kode warna semua titik di berbeda, maka pewarnaan tersebut merupakan pewarnaan lokasi. Jadi, (2.1.3) Berdasarkan Persamaan (2.1.2) dan (2.1.3) diperoleh. Teorema 2.5 (Chartrand dkk, 2002) Misalkan k adalah derajat maksimum di graf G, maka. Bukti : Misalkan v adalah satu titik yang berderajat maksimum k daun x 1, x 2,...x k di G. Berdasarkan Teorema 2.4 dan Akibat 2.1, setiap pewarnaan lokasi di G mempunyai warna yang berbeda setiap x i, i = 1, 2, 3,...,k. Karena v berderajat maksimum k dengan x i, maka v harus mempunyai warna yang berbeda dengan semua daun x i. Akibatnya, Berikut ini akan diberikan bilangan kromatik lokasi beberapa kelas graf sederhana. Teorema 2.6 (Chartrand dkk, 2002) Bilangan kromatik lokasi graf lintasan adalah 3. Bukti : Perhatikan bahwa dan. Jelaslah bahwa untuk. Berdasarkan Teorema 2.5, dengan k derajat titik maksimum. Karena pada, maka. Akibatnya. Jadi terbukti.
14 v 1 v 2 v 3 v 4 v 5 v 6 u n-1 u n Gambar 14. Pewarnaan lokasi minimum pada graf lintasan Teorema 2.7 (Chartrand dkk, 2002) Untuk bilangan bulat a dan b dengan dan. Bukti : Berdasarkan Akibat 2.4, diperoleh batas bawah yaitu. Selanjutnya, akan ditentukan batas atasnya yaitu. Misalkan c adalah pewarnaan titik menggunakan (b+1) warna sebagaimana terlihat pada Gambar 14. Perhatikan bahwa kode warna dari setiap titik berbeda, akibatnya c adalah pewarnaan lokasi. Jadi Gambar 15. Pewarnaan lokasi minimum pada Chartrand dkk. (2003) telah mendapatkan bentuk graf pohon berorde yang memiliki bilangan kromatik lokasi dari 3 sampai n, kecuali n-1, sebagaimana torema berikut ini.
15 19 Teorema 2.8 (Chartrand dkk, 2002) Terdapat Pohon berorde yang mempunyai bilangan kromatik k jika dan hanya jika. Bukti : Misalkan. Untuk k = 3, misalkan T = P n ; untuk k = n, misalkan T = K 1,n-1. Sehingga diasumsikan bahwa 4 k n-2. Misalkan T didapat dari lintasan P n-k+1 : v 1, v 2,..., v n-k+1 dengan menambahkan k-1 titik baru u 1, u 2,..., u k-1 dan hubungkan setiap u i, untuk 1 i k 1 (lihat Gambar 16). Jadi adalah pewarnaan lokasi,. Berdasarkan Akibat 2.1,, maka Pewarnaan Teorema 2.8 dapat diberikan sebagai berikut : Gambar 16. Pohon T berorde n dengan Selanjutnya akan diberikan beberapa definisi tentang titik dominan dan clear path yang diambil dari Asmiati dkk. (2012). Misalkan c adalah k-pewarnaan lokasi pada graf G(V,E) dan misalkan adalah partisi dari V(G) yang diinduksi oleh c. Titik v V(G) dikatakan suatu titik dominan jika, jika v. Suatu lintasan yang menghubungkan dua titik dominan di graf G disebut clear path, jika semua titik internalnya bukan merupakan titik dominan.
16 20 Gambar 17. Graf G dengan 3 titik dominan Titik dominan pada Gambar 17 adalah v2, v4, dan v7. Clear path pada Gambar 17 adalah lintasan yang menghubungkan v4 dan v7 dimana tidak terdapat titik dominan dalam titik internalnya. Karena graf G pada Gambar 17 mempunyai bilangan kromatik lokasi tiga, maka panjang clear path dari graf G ganjil. Lemma 2.1 (Asmiati dkk. 2012) Diberikan graf G dengan maka terdapat paling banyak k titik dominan di G dan masing-masing titik dominan memiliki warna yang berbeda. Bukti : Misalkan v G merupakan titik dominan dan G adalah graf terhubung, maka untuk v dan untuk v. Karena, maka kelas partisi memuat k kelas warna, katakan dan setiap x G memiliki kode warna yang berbeda. Oleh karena itu, G paling banyak memuat sebanyak k titik dominan dan masing masing titik dominan pada G memiliki kode warna yang berbeda. Lemma 2.2 (Asmiati dkk. 2012) Misalkan graf G dengan, maka panjang dari setiap clear path di G adalah ganjil.
17 21 Bukti : Misalkan G adalah graf terhubung dan P adalah clear path yang menghubungkan 2 titik dominan x dan y di G. Asumsikan c(x) = 1 dan c(y)=2. Karena P adalah clear path maka warna dari titik titik didalamnya harus 1 dan 2 berturut-turut. Misalkan x dan y akan membentuk barisan alternating. Karena banyaknya titik dalam clear path P harus genap, maka panjang P ganjil. Lemma 2.3 (Asmiati dkk. 2012) Misalkan G adalah graf terhubung dengan Jika G memuat 3 titik dominan, maka terdapat 3 titik dominan dalam suatu lintasan. Bukti : Misalkan G adalah graf terhubung dan x, y dan z adalah tiga titik dominan dari graf G. P adalah lintasan yang menghubungkan x dan z. Asumsikan y tidak terdapat dalam lintasan P. Karena G adalah graf terhubung maka terdapat titik dalam u, sehingga u memiliki jarak terpendek (dibandingkan dengan titik dalam lainnya) ke y. Lintasan L1 menghubungkan x ke u kemudian ke y. Sehingga lintasan L1 adalah clear path. Oleh karena itu, panjangnya lintasan tersebut adalah ganjil. Sekarang, pertimbangkan lintasan L2 yang menghubungkan y ke u kemudian ke z. Maka, L2 merupakan clear path. Oleh karena itu, panjangnya adalah ganjil. Kedua fakta tersebut menyatakan panjang dari lintasan yang menghubungkan x ke u ditambah dengan panjang lintasan yang menghubungkan u ke z panjangnya adalah genap, kontradiksi. Selanjutnya Asmiati (2012) telah mendapatkan bilangan kromatik lokasi graf kembang api tak seragam. Graf kembang api tak seragam, diperoleh
18 22 dari n buah graf bintang, i dengan cara menghubungkan sebuah daun dari setiap melalui sebuah lintasan. Misalkan V ( ) = { x i,, l ij ǀ i = 1,2,..., n; j=1,2,...,k i -2} dan E )={x i x i+1 ǀ i = 1,2,..., n -1} {x i,, m i l ij ǀ i = 1,2,..., n; j=1,2,...,k i -2}. Jika k maks = maks {k 1, k 2,..., k n } maka subgraf disebut sebagai subgraf bintang maksimum pada graf kembang api. Dalam hal terdapat p buah subgraf, maka masing-masing subgraf, dari kiri ke kanan, dinotasikan dengan, dengan 1 i p. Definisi 2.1 Misalkan dan, dengan 1 i j m. Jika sehingga 1., dengan titik pusat dari atau 2., dengan dan berturut-turut adalah titik pusat dari yang berbeda, maka subgraf dan disebut subgraf bintang berjarak sama. Teorema 2.9. (Asmiati, 2012) Misalkan adalah subgraf bintang maksimum dari dan p menyatakan banyaknya subgraf Maka, untuk bilangan kromatik lokasi graf kembang api adalah
19 23 k maks 1, jika p k maks 1, = k maks, jika p > k maks 1. Bukti : Kasus 1. Akan ditentukan batas bawah trivial untuk p k maks 1. Karena banyaknya daun pada subgraf maksimal adalah k maks 2, maka berdasarkan Akibat 2.1, L ( ) k maks 1, untuk p k maks 1. Akan ditunjukkan bahwa kode warna semua titik di ), untuk p k maks 1 berbeda. Pandang sebarang dua daun berbeda u ЄV( ЄV( dengan c(u) = c(v). Jika k i = k j = k maks maka, karena terbedakan pada ordinat dari warna m i = m j. Jika salah satu dari k i atau k j adalah k maks, misalnya k i = k maks dan k j < k maks, maka kode warna dari u danv terbedakan pada warna daun di yang tidak termuat di Berdasarkan berdasarkan semua kasus diatas, dapat disimpulkan bahwa kode warna dari semua titik di, untuk p k maks 1 berbeda. Jadi L ( ) = k maks 1 untuk p k maks 1. Kasus 2. Akan ditentukan batas bawah trivial untuk p > k maks 1. Berdasarkan Akibat 2.1, diperoleh L ( ) k maks 1. Tetapi, akan ditunjukkan bahwa k maks 1 warna tidaklah cukup untuk mewarnai. Untuk kontradiksi, andaikan
20 24 terdapat pewarnaan- (k maks 1) lokasi c pada untuk p > k maks 1. Karena p > k maks 1, maka terdapat i, j, i j, sedemikian sehingga {c(l ih )ǀ h = 1, 2,..., k maks 2}= {c(l jl )ǀ l = 1, 2,..., k maks 2}. Akibatnya, kode warna dari m i dan m j akan sama, suatu kontradiksi. Selanjutnya, akan ditentukan batas atas dari untuk p > k maks 1. Untuk menunjukkan k maks, pandang pewarnaan lokasi c pada sebagai berikut: c(x i ) = 1 jika i ganjil dan c(x i ) = 3 jika i genap; c(m 1 ) = k maks dan c(m i ) = 2 untuk i lainnya; Jika A = {1, 2,..., k maks }, didefinisikan: A\ {1, k maks } jika i = 1, {c(l ij )ǀ l = 1, 2,..., k maks 2} = A\ {2, k maks } lainnya. Mudah untuk menunjukkan bahwa kode warna semua titik di untuk p > k maks 1 berbeda. Akibatnya, c merupakan pewarnaan lokasi. Jadi = k maks, untuk p > k maks 1.
TINJAUAN PUSTAKA. Pada bab ini akan dijelaskan beberapa konsep dasar teori graf dan dimensi partisi
 II. TINJAUAN PUSTAKA Pada bab ini akan dijelaskan beberapa konsep dasar teori graf dan dimensi partisi pada suatu graf sebagai landasan teori pada penelitian ini.. Konsep Dasar Graf Pada bagian ini akan
II. TINJAUAN PUSTAKA Pada bab ini akan dijelaskan beberapa konsep dasar teori graf dan dimensi partisi pada suatu graf sebagai landasan teori pada penelitian ini.. Konsep Dasar Graf Pada bagian ini akan
II. KONSEP DASAR GRAF DAN GRAF POHON. Graf G adalah himpunan terurut ( V(G), E(G)), dengan V(G) menyatakan
 II. KONSEP DASAR GRAF DAN GRAF POHON 2.1 Konsep Dasar Graf Teori dasar mengenai graf yang akan digunakan dalam penelitian ini diambil dari Deo (1989). Graf G adalah himpunan terurut ( V(G), E(G)), dengan
II. KONSEP DASAR GRAF DAN GRAF POHON 2.1 Konsep Dasar Graf Teori dasar mengenai graf yang akan digunakan dalam penelitian ini diambil dari Deo (1989). Graf G adalah himpunan terurut ( V(G), E(G)), dengan
KONSEP DASAR GRAF DAN GRAF POHON. Pada bab ini akan dijabarkan teori graf dan bilangan kromatik lokasi pada suatu graf
 II. KONSEP DASAR GRAF DAN GRAF POHON Pada bab ini akan dijabarkan teori graf dan bilangan kromatik lokasi pada suatu graf sebagai landasan teori pada penelitian ini. 2.1 Konsep Dasar Graf Pada bagian ini
II. KONSEP DASAR GRAF DAN GRAF POHON Pada bab ini akan dijabarkan teori graf dan bilangan kromatik lokasi pada suatu graf sebagai landasan teori pada penelitian ini. 2.1 Konsep Dasar Graf Pada bagian ini
III. BILANGAN KROMATIK LOKASI GRAF. Bilangan kromatik lokasi graf pertama kali dikaji oleh Chartrand dkk.(2002). = ( ) {1,2,3,, } dengan syarat
 III. BILANGAN KROMATIK LOKASI GRAF Bilangan kromatik lokasi graf pertama kali dikaji oleh Chartrand dkk.00). Konsep ini merupakan pengembangan dari konsep dimensi partisi dan pewarnaan graf. Pewarnaan
III. BILANGAN KROMATIK LOKASI GRAF Bilangan kromatik lokasi graf pertama kali dikaji oleh Chartrand dkk.00). Konsep ini merupakan pengembangan dari konsep dimensi partisi dan pewarnaan graf. Pewarnaan
BAB II TINJAUAN PUSTAKA. kromatik lokasi sebagai landasan teori dari penelitian ini.
 BAB II TINJAUAN PUSTAKA Pada bab ini akan diberikan beberapa konsep dasar teori graf dan bilangan kromatik lokasi sebagai landasan teori dari penelitian ini. 2.1 Konsep Dasar Graf Beberapa konsep dasar
BAB II TINJAUAN PUSTAKA Pada bab ini akan diberikan beberapa konsep dasar teori graf dan bilangan kromatik lokasi sebagai landasan teori dari penelitian ini. 2.1 Konsep Dasar Graf Beberapa konsep dasar
LANDASAN TEORI. Pada bab ini akan diberikan beberapa konsep dasar teori graf dan bilangan. kromatik lokasi sebagai landasan teori pada penelitian ini.
 6 II. LANDASAN TEORI Pada bab ini akan diberikan beberapa konsep dasar teori graf dan bilangan kromatik lokasi sebagai landasan teori pada penelitian ini. 2.1 Konsep Dasar Graf Pada sub bab ini akan diberikan
6 II. LANDASAN TEORI Pada bab ini akan diberikan beberapa konsep dasar teori graf dan bilangan kromatik lokasi sebagai landasan teori pada penelitian ini. 2.1 Konsep Dasar Graf Pada sub bab ini akan diberikan
v 3 e 2 e 4 e 6 e 3 v 4
 5 II. TINJAUAN PUSTAKA Pada bab ini akan diberikan beberapa konsep dasar teori graf dan dimensi partisi graf sebagai landasan teori dari penelitian ini... Konsep Dasar Graf Pada bagian ini akan diberikan
5 II. TINJAUAN PUSTAKA Pada bab ini akan diberikan beberapa konsep dasar teori graf dan dimensi partisi graf sebagai landasan teori dari penelitian ini... Konsep Dasar Graf Pada bagian ini akan diberikan
TINJAUAN PUSTAKA. Pada bagian ini akan diberikan konsep dasar graf dan bilangan kromatik lokasi pada
 II. TINJAUAN PUSTAKA Pada bagian ini akan diberikan konsep dasar graf dan bilangan kromatik lokasi pada suatu graf sebagai landasan teori penelitian ini. 2. Konsep Dasar Graf Teori dasar mengenai graf
II. TINJAUAN PUSTAKA Pada bagian ini akan diberikan konsep dasar graf dan bilangan kromatik lokasi pada suatu graf sebagai landasan teori penelitian ini. 2. Konsep Dasar Graf Teori dasar mengenai graf
III. BILANGAN KROMATIK LOKASI GRAF. ini merupakan pengembangan dari konsep dimensi partisi dan pewarnaan graf.
 III BILANGAN KROMATIK LOKASI GRAF Bilangan kromatik lokasi graf pertama kali dikaji oleh Chartrand dkk 00) Konsep ini merupakan pengembangan dari konsep dimensi partisi pewarnaan graf Pewarnaan titik pada
III BILANGAN KROMATIK LOKASI GRAF Bilangan kromatik lokasi graf pertama kali dikaji oleh Chartrand dkk 00) Konsep ini merupakan pengembangan dari konsep dimensi partisi pewarnaan graf Pewarnaan titik pada
KLASIFIKASI GRAF PETERSEN BERBILANGAN KROMATIK LOKASI EMPAT ATAU LIMA
 KLASIFIKASI GRAF PETERSEN BERBILANGAN KROMATIK LOKASI EMPAT ATAU LIMA (Tesis) Oleh : Devriyadi Saputra S NPM. 1427031001 MAGISTER MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG
KLASIFIKASI GRAF PETERSEN BERBILANGAN KROMATIK LOKASI EMPAT ATAU LIMA (Tesis) Oleh : Devriyadi Saputra S NPM. 1427031001 MAGISTER MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG
2. TINJAUAN PUSTAKA. Chartrand dan Zhang (2005) yaitu sebagai berikut: himpunan tak kosong dan berhingga dari objek-objek yang disebut titik
 2. TINJAUAN PUSTAKA 2.1 Konsep Dasar Graf Pada bagian ini akan diberikan konsep dasar graf yang diambil dari buku Chartrand dan Zhang (2005) yaitu sebagai berikut: Suatu Graf G adalah suatu pasangan himpunan
2. TINJAUAN PUSTAKA 2.1 Konsep Dasar Graf Pada bagian ini akan diberikan konsep dasar graf yang diambil dari buku Chartrand dan Zhang (2005) yaitu sebagai berikut: Suatu Graf G adalah suatu pasangan himpunan
BILANGAN KROMATIK LOKASI DARI GRAF ULAT
 Jurnal Matematika UNAND Vol. 5 No. 1 Hal. 1 6 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND BILANGAN KROMATIK LOKASI DARI GRAF ULAT AIDILLA DARMAWAHYUNI, NARWEN Program Studi Matematika, Fakultas Matematika
Jurnal Matematika UNAND Vol. 5 No. 1 Hal. 1 6 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND BILANGAN KROMATIK LOKASI DARI GRAF ULAT AIDILLA DARMAWAHYUNI, NARWEN Program Studi Matematika, Fakultas Matematika
KARAKTERISASI GRAF POHON DENGAN BILANGAN KROMATIK LOKASI 3
 Jurnal Matematika UNAND Vol. 5 No. 2 Hal. 71 77 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND KARAKTERISASI GRAF POHON DENGAN BILANGAN KROMATIK LOKASI 3 FAIZAH, NARWEN Program Studi Matematika, Fakultas
Jurnal Matematika UNAND Vol. 5 No. 2 Hal. 71 77 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND KARAKTERISASI GRAF POHON DENGAN BILANGAN KROMATIK LOKASI 3 FAIZAH, NARWEN Program Studi Matematika, Fakultas
BILANGAN KROMATIK LOKASI GRAF TAK TERHUBUNG DARI GRAF BINTANG GANDA DAN SUBDIVISINYA. (Skripsi) Oleh SITI NURAZIZAH
 BILANGAN KROMATIK LOKASI GRAF TAK TERHUBUNG DARI GRAF BINTANG GANDA DAN SUBDIVISINYA (Skripsi) Oleh SITI NURAZIZAH FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG BANDAR LAMPUNG 2017
BILANGAN KROMATIK LOKASI GRAF TAK TERHUBUNG DARI GRAF BINTANG GANDA DAN SUBDIVISINYA (Skripsi) Oleh SITI NURAZIZAH FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG BANDAR LAMPUNG 2017
II. TINJAUAN PUSTAKA. Pada bab ini akan diberikan beberapa konsep dasar dalam teori graf dan teknik
 II. TINJAUAN PUSTAKA Pada bab ini akan diberikan beberapa konsep dasar dalam teori graf dan teknik pencacahan dalam bentuk definisi dan teorema yang berhubungan dengan penelitian yang akan dilakukan. 2.1
II. TINJAUAN PUSTAKA Pada bab ini akan diberikan beberapa konsep dasar dalam teori graf dan teknik pencacahan dalam bentuk definisi dan teorema yang berhubungan dengan penelitian yang akan dilakukan. 2.1
MA3051 Pengantar Teori Graf. Semester /2014 Pengajar: Hilda Assiyatun
 MA3051 Pengantar Teori Graf Semester 1 2013/2014 Pengajar: Hilda Assiyatun Bab 1: Graf dan subgraf Graf G : tripel terurut VG, E G, ψ G ) V G himpunan titik (vertex) E G himpunan sisi (edge) ψ G fungsi
MA3051 Pengantar Teori Graf Semester 1 2013/2014 Pengajar: Hilda Assiyatun Bab 1: Graf dan subgraf Graf G : tripel terurut VG, E G, ψ G ) V G himpunan titik (vertex) E G himpunan sisi (edge) ψ G fungsi
ALTERNATIF PEMBUKTIAN DAN PENERAPAN TEOREMA BONDY. Hasmawati Jurusan Matematika, Fakultas Mipa Universitas Hasanuddin
 ALTERNATIF PEMBUKTIAN DAN PENERAPAN TEOREMA BONDY Hasmawati Jurusan Matematika, Fakultas Mipa Universitas Hasanuddin hasma_ba@yahoo.com Abstract Graf yang memuat semua siklus dari yang terkecil sampai
ALTERNATIF PEMBUKTIAN DAN PENERAPAN TEOREMA BONDY Hasmawati Jurusan Matematika, Fakultas Mipa Universitas Hasanuddin hasma_ba@yahoo.com Abstract Graf yang memuat semua siklus dari yang terkecil sampai
II. TINJAUAN PUSTAKA. Graf G adalah suatu struktur (V,E) dengan V(G) = {v 1, v 2, v 3,.., v n } himpunan
 5 II. TINJAUAN PUSTAKA Definisi 2.1 Graf (Deo,1989) Graf G adalah suatu struktur (V,E) dengan V(G) = {v 1, v 2, v 3,.., v n } himpunan tak kosong dengan elemen-elemennya disebut vertex, sedangkan E(G)
5 II. TINJAUAN PUSTAKA Definisi 2.1 Graf (Deo,1989) Graf G adalah suatu struktur (V,E) dengan V(G) = {v 1, v 2, v 3,.., v n } himpunan tak kosong dengan elemen-elemennya disebut vertex, sedangkan E(G)
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI Dalam bab ini dipaparkan beberapa hasil penelitian yang dilakukan para peneliti sebelumnya, pengertian dasar graf, operasi-operasi pada graf, kelas-kelas graf dan dimensi partisi
BAB II LANDASAN TEORI Dalam bab ini dipaparkan beberapa hasil penelitian yang dilakukan para peneliti sebelumnya, pengertian dasar graf, operasi-operasi pada graf, kelas-kelas graf dan dimensi partisi
I. PENDAHULUAN. Perkembangan ilmu pengetahuan dan teknologi sampai saat ini terus
 1 I. PENDAHULUAN 1.1 Latar Belakang Perkembangan ilmu pengetahuan dan teknologi sampai saat ini terus mengalami kemajuan. Salah satunya adalah cabang ilmu matematika yang sampai saat ini mengalami perkembangan
1 I. PENDAHULUAN 1.1 Latar Belakang Perkembangan ilmu pengetahuan dan teknologi sampai saat ini terus mengalami kemajuan. Salah satunya adalah cabang ilmu matematika yang sampai saat ini mengalami perkembangan
Bab 2 TEORI DASAR. 2.1 Graf
 Bab 2 TEORI DASAR Pada bab ini akan dipaparkan beberapa definisi dasar dalam Teori Graf yang kemudian dilanjutkan dengan definisi bilangan kromatik lokasi, serta menyertakan beberapa hasil penelitian sebelumnya.
Bab 2 TEORI DASAR Pada bab ini akan dipaparkan beberapa definisi dasar dalam Teori Graf yang kemudian dilanjutkan dengan definisi bilangan kromatik lokasi, serta menyertakan beberapa hasil penelitian sebelumnya.
BILANGAN KROMATIK LOKASI UNTUK GRAF AMALGAMASI BINTANG
 Jurnal Matematika UNAND Vol. 2 No. 1 Hal. 6 13 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND BILANGAN KROMATIK LOKASI UNTUK GRAF AMALGAMASI BINTANG FADHILAH SYAMSI Program Studi Matematika, Pascasarjana
Jurnal Matematika UNAND Vol. 2 No. 1 Hal. 6 13 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND BILANGAN KROMATIK LOKASI UNTUK GRAF AMALGAMASI BINTANG FADHILAH SYAMSI Program Studi Matematika, Pascasarjana
Suatu graf G adalah pasangan himpunan (V, E), dimana V adalah himpunan titik
 BAB II DASAR TEORI 2.1 Teori Dasar Graf 2.1.1 Graf dan Graf Sederhana Suatu graf G adalah pasangan himpunan (V, E), dimana V adalah himpunan titik yang tak kosong dan E adalah himpunan sisi. Untuk selanjutnya,
BAB II DASAR TEORI 2.1 Teori Dasar Graf 2.1.1 Graf dan Graf Sederhana Suatu graf G adalah pasangan himpunan (V, E), dimana V adalah himpunan titik yang tak kosong dan E adalah himpunan sisi. Untuk selanjutnya,
BILANGAN KROMATIK LOKASI UNTUK GRAF POHON n-ary LENGKAP
 Jurnal Matematika UNAND Vol. VI No. 1 Hal. 90 96 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND BILANGAN KROMATIK LOKASI UNTUK GRAF POHON n-ary LENGKAP AFIFAH DWI PUTRI, NARWEN Program Studi Matematika,
Jurnal Matematika UNAND Vol. VI No. 1 Hal. 90 96 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND BILANGAN KROMATIK LOKASI UNTUK GRAF POHON n-ary LENGKAP AFIFAH DWI PUTRI, NARWEN Program Studi Matematika,
Penerapan Teorema Bondy pada Penentuan Bilangan Ramsey Graf Bintang Terhadap Graf Roda
 Vol. 9, No.2, 114-122, Januari 2013 Penerapan Teorema Bondy pada Penentuan Bilangan Ramsey Graf Bintang Terhadap Graf Roda Hasmawati 1 Abstrak Graf yang memuat semua siklus dari yang terkecil sampai ke
Vol. 9, No.2, 114-122, Januari 2013 Penerapan Teorema Bondy pada Penentuan Bilangan Ramsey Graf Bintang Terhadap Graf Roda Hasmawati 1 Abstrak Graf yang memuat semua siklus dari yang terkecil sampai ke
BAB 2 GRAF PRIMITIF. 2.1 Definisi Graf
 BAB 2 GRAF PRIMITIF Pada Bagian ini akan dijelaskan beberapa definisi dan teorema terkait graf, matriks adjency, terhubung, primitifitas, dan scrambling index sebagai landasan teori yang menjadi acuan
BAB 2 GRAF PRIMITIF Pada Bagian ini akan dijelaskan beberapa definisi dan teorema terkait graf, matriks adjency, terhubung, primitifitas, dan scrambling index sebagai landasan teori yang menjadi acuan
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI 2.1 Teori Graf 2.1.1 Defenisi Graf Suatu graf G adalah suatu himpunan berhingga tak kosong dari objek-objek yang disebut verteks (titik/simpul) dengan suatu himpunan yang anggotanya
BAB 2 LANDASAN TEORI 2.1 Teori Graf 2.1.1 Defenisi Graf Suatu graf G adalah suatu himpunan berhingga tak kosong dari objek-objek yang disebut verteks (titik/simpul) dengan suatu himpunan yang anggotanya
Sebuah graf sederhana G adalah pasangan terurut G = (V, E) dengan V adalah
 BAB II KAJIAN TEORI II.1 Teori-teori Dasar Graf II.1.1 Definisi Graf Sebuah graf sederhana G adalah pasangan terurut G = (V, E) dengan V adalah himpunan tak kosong dari titik graf G, dan E, himpunan sisi
BAB II KAJIAN TEORI II.1 Teori-teori Dasar Graf II.1.1 Definisi Graf Sebuah graf sederhana G adalah pasangan terurut G = (V, E) dengan V adalah himpunan tak kosong dari titik graf G, dan E, himpunan sisi
BAB II Graf dan Pelabelan Total Sisi-Ajaib Super
 BAB II Graf dan Pelabelan Total Sisi-Ajaib Super 2.1 Graf dan Beberapa Definisi Dasar Graf G=(V,E) didefinisikan sebagai pasangan terurut himpunan berhingga dan tak hampa V dan himpunan E. Himpunan V dinamakan
BAB II Graf dan Pelabelan Total Sisi-Ajaib Super 2.1 Graf dan Beberapa Definisi Dasar Graf G=(V,E) didefinisikan sebagai pasangan terurut himpunan berhingga dan tak hampa V dan himpunan E. Himpunan V dinamakan
Konsep Dasar dan Tinjauan Pustaka
 Bab II Konsep Dasar dan Tinjauan Pustaka Pembahasan bilangan Ramsey pada bab-bab berikutnya menggunakan definisi, notasi, dan konsep dasar teori graf yang sesuai dengan rujukan Chartrand dan Lesniak (1996),
Bab II Konsep Dasar dan Tinjauan Pustaka Pembahasan bilangan Ramsey pada bab-bab berikutnya menggunakan definisi, notasi, dan konsep dasar teori graf yang sesuai dengan rujukan Chartrand dan Lesniak (1996),
BAB II TINJAUAN PUSTAKA. sepasang titik. Himpunan titik di G dinotasikan dengan V(G) dan himpunan
 5 BAB II TINJAUAN PUSTAKA A. Teori Graf 1. Dasar-dasar Graf Graf G didefinisikan sebagai pasangan himpunan (V, E) ditulis dengan notasi G = (V, E), dimana V adalah himpunan titik yang tidak kosong (vertex)
5 BAB II TINJAUAN PUSTAKA A. Teori Graf 1. Dasar-dasar Graf Graf G didefinisikan sebagai pasangan himpunan (V, E) ditulis dengan notasi G = (V, E), dimana V adalah himpunan titik yang tidak kosong (vertex)
PENGERTIAN GRAPH. G 1 adalah graph dengan V(G) = { 1, 2, 3, 4 } E(G) = { (1, 2), (1, 3), (2, 3), (2, 4), (3, 4) } Graph 2
 PENGERTIAN GRAPH 1. DEFINISI GRAPH Graph G adalah pasangan terurut dua himpunan (V(G), E(G)), V(G) himpunan berhingga dan tak kosong dari obyek-obyek yang disebut himpunan titik (vertex) dan E(G) himpunan
PENGERTIAN GRAPH 1. DEFINISI GRAPH Graph G adalah pasangan terurut dua himpunan (V(G), E(G)), V(G) himpunan berhingga dan tak kosong dari obyek-obyek yang disebut himpunan titik (vertex) dan E(G) himpunan
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI 2.1 Konsep Dasar Teori Graph 2.1.1 Graph Tak Berarah dan Digraph Suatu Graph Tak Berarah (Undirected Graph) merupakan kumpulan dari titik yang disebut verteks dan segmen garis yang
BAB II LANDASAN TEORI 2.1 Konsep Dasar Teori Graph 2.1.1 Graph Tak Berarah dan Digraph Suatu Graph Tak Berarah (Undirected Graph) merupakan kumpulan dari titik yang disebut verteks dan segmen garis yang
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI Pada bab ini akan diberikan beberapa definisi dan konsep dasar dalam teori graf dan pelabelan graf yang akan digunakan pada bab selanjutnya. 2.1 Definisi dan Istilah Dalam Teori Graf
BAB II LANDASAN TEORI Pada bab ini akan diberikan beberapa definisi dan konsep dasar dalam teori graf dan pelabelan graf yang akan digunakan pada bab selanjutnya. 2.1 Definisi dan Istilah Dalam Teori Graf
Graf dan Operasi graf
 6 Bab II Graf dan Operasi graf Dalam subbab ini akan diberikan konsep dasar, definisi dan notasi pada teori graf yang dipergunakan dalam penulisan disertasi ini. Konsep dasar tersebut ditulis sesuai dengan
6 Bab II Graf dan Operasi graf Dalam subbab ini akan diberikan konsep dasar, definisi dan notasi pada teori graf yang dipergunakan dalam penulisan disertasi ini. Konsep dasar tersebut ditulis sesuai dengan
II.TINJAUAN PUSTAKA. Pada bab ini akan dijelaskan tentang definisi serta konsep-konsep yang mendukung
 II.TINJAUAN PUSTAKA Pada bab ini akan dijelaskan tentang definisi serta konsep-konsep yang mendukung dalam penelitian ini. 2.1. Konsep Dasar Teori Graf Graf G didefinisikan sebagai pasangan himpunan terurut
II.TINJAUAN PUSTAKA Pada bab ini akan dijelaskan tentang definisi serta konsep-konsep yang mendukung dalam penelitian ini. 2.1. Konsep Dasar Teori Graf Graf G didefinisikan sebagai pasangan himpunan terurut
3.1 Beberapa Nilai Dimensi Partisi pada Suatu Graf. Dalam dimensi partisi suatu graf, terdapat kelas graf yang nilai dimensi partisinya
 BAB III DIMENSI PARTISI n 1 3.1 Beberapa Nilai Dimensi Partisi pada Suatu Graf Dalam dimensi partisi suatu graf, terdapat kelas graf yang nilai dimensi partisinya cukup mudah atau sederhana. Kelas graf
BAB III DIMENSI PARTISI n 1 3.1 Beberapa Nilai Dimensi Partisi pada Suatu Graf Dalam dimensi partisi suatu graf, terdapat kelas graf yang nilai dimensi partisinya cukup mudah atau sederhana. Kelas graf
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI Dalam bab ini dipaparkan beberapa hasil penelitian yang dilakukan para peneliti sebelumnya, pengertian dasar graf, operasi-operasi pada graf, kelas-kelas graf dan dimensi partisi
BAB II LANDASAN TEORI Dalam bab ini dipaparkan beberapa hasil penelitian yang dilakukan para peneliti sebelumnya, pengertian dasar graf, operasi-operasi pada graf, kelas-kelas graf dan dimensi partisi
BAB II TINJAUAN PUSTAKA
 BAB II TINJAUAN PUSTAKA 2.1 Graf (Graph) Graf G didefinisikan sebagai pasangan himpunan (V, E) yang dinotasikan dalam bentuk G = {V(G), E(G)}, dimana V(G) adalah himpunan vertex (simpul) yang tidak kosong
BAB II TINJAUAN PUSTAKA 2.1 Graf (Graph) Graf G didefinisikan sebagai pasangan himpunan (V, E) yang dinotasikan dalam bentuk G = {V(G), E(G)}, dimana V(G) adalah himpunan vertex (simpul) yang tidak kosong
BAB 2 GRAF PRIMITIF. 2.1 Definisi Graf
 BAB 2 GRAF PRIMITIF Pada bab ini akan dijelaskan beberapa konsep dasar seperti definisi dan teorema yang dijadikan landasan teori dalam penelitian ini. Konsep dasar tersebut berkaitan dengan definisi graf,
BAB 2 GRAF PRIMITIF Pada bab ini akan dijelaskan beberapa konsep dasar seperti definisi dan teorema yang dijadikan landasan teori dalam penelitian ini. Konsep dasar tersebut berkaitan dengan definisi graf,
BAB II TINJAUAN PUSTAKA. Pada bab ini akan diberikan definisi dan teorema yang berhubungan dengan
 BAB II TINJAUAN PUSTAKA Pada bab ini akan diberikan definisi dan teorema yang berhubungan dengan penelitian yang dilakukan. 2.1. Konsep Dasar Graf Graf G didefinisikan sebagai pasangan himpunan terurut
BAB II TINJAUAN PUSTAKA Pada bab ini akan diberikan definisi dan teorema yang berhubungan dengan penelitian yang dilakukan. 2.1. Konsep Dasar Graf Graf G didefinisikan sebagai pasangan himpunan terurut
ALTERNATIF PEMBUKTIAN PENGEMBANGAN TEOREMA DIRAC UNTUK GRAF BERORDE KURANG ATAU SAMA DENGAN SEPULUH
 ALTERNATIF PEMBUKTIAN PENGEMBANGAN TEOREMA DIRAC UNTUK GRAF BERORDE KURANG ATAU SAMA DENGAN SEPULUH Hasmawati, Jusmawati Massalesse, Hendra, Muhamad Hasbi Jurusan Matematika FMIPA Universitas Hasanudin
ALTERNATIF PEMBUKTIAN PENGEMBANGAN TEOREMA DIRAC UNTUK GRAF BERORDE KURANG ATAU SAMA DENGAN SEPULUH Hasmawati, Jusmawati Massalesse, Hendra, Muhamad Hasbi Jurusan Matematika FMIPA Universitas Hasanudin
Bilangan Ramsey untuk Graf Bintang Genap Terhadap Roda Genap
 Vol.4, No., 49-53, Januari 08 Bilangan Ramsey untuk Graf Bintang Genap erhadap Roda Genap Hasmawati Abstrak Untuk sebarang graf G dan H, bilangan Ramsey R(G,H) adalah bilangan asli terkecil n sedemikian
Vol.4, No., 49-53, Januari 08 Bilangan Ramsey untuk Graf Bintang Genap erhadap Roda Genap Hasmawati Abstrak Untuk sebarang graf G dan H, bilangan Ramsey R(G,H) adalah bilangan asli terkecil n sedemikian
GRAF AMALGAMASI POHON BERBILANGAN KROMATIK LOKASI EMPAT
 GRAF AMALGAMASI POHON BERBILANGAN KROMATIK LOKASI EMPAT ASMIATI, FITRIANI Jurusan Matematika, FMIPA Universitas Lampung Jl. Prof. Soemantri Brojonegoro No.1 Gedong Meneng, Bandar Lampung Email : asmiati308@yahoo.com;
GRAF AMALGAMASI POHON BERBILANGAN KROMATIK LOKASI EMPAT ASMIATI, FITRIANI Jurusan Matematika, FMIPA Universitas Lampung Jl. Prof. Soemantri Brojonegoro No.1 Gedong Meneng, Bandar Lampung Email : asmiati308@yahoo.com;
TINJAUAN PUSTAKA. Pada bab ini akan diberikan beberapa definisi, istilah istilah yang berhubungan dengan materi
 II. TINJAUAN PUSTAKA Pada bab ini akan diberikan beberapa definisi, istilah istilah yang berhubungan dengan materi yang akan dihasilkan pada penelitian ini. 2.1 Beberapa Definisi dan Istilah 1. Graf (
II. TINJAUAN PUSTAKA Pada bab ini akan diberikan beberapa definisi, istilah istilah yang berhubungan dengan materi yang akan dihasilkan pada penelitian ini. 2.1 Beberapa Definisi dan Istilah 1. Graf (
BILANGAN KROMATIK LOKASI UNTUK GRAF C n K m, DENGAN n 3 DAN m 1
 Jurnal Matematika UNAND Vol. 2 No. 1 Hal. 37 41 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND BILANGAN KROMATIK LOKASI UNTUK GRAF C n K m, DENGAN n 3 DAN m 1 MERY ANGGRAINI, NARWEN Program Studi Matematika,
Jurnal Matematika UNAND Vol. 2 No. 1 Hal. 37 41 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND BILANGAN KROMATIK LOKASI UNTUK GRAF C n K m, DENGAN n 3 DAN m 1 MERY ANGGRAINI, NARWEN Program Studi Matematika,
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI Bab ini terdiri dari tiga subbab. Subbab pertama adalah tinjauan pustaka yang memuat hasil penelitian yang dilakukan oleh peneliti sebelumnya dalam bidang dimensi metrik. Subbab kedua
BAB II LANDASAN TEORI Bab ini terdiri dari tiga subbab. Subbab pertama adalah tinjauan pustaka yang memuat hasil penelitian yang dilakukan oleh peneliti sebelumnya dalam bidang dimensi metrik. Subbab kedua
BAB 2 GRAF PRIMITIF. Gambar 2.1. Contoh Graf
 BAB 2 GRAF PRIMITIF Pada bagian ini akan dijelaskan mengenai definisi graf, istilah-istilah dalam graf, matriks ketetanggaan, graf terhubung, primitivitas graf, dan scrambling index. 2.1 Definisi Graf
BAB 2 GRAF PRIMITIF Pada bagian ini akan dijelaskan mengenai definisi graf, istilah-istilah dalam graf, matriks ketetanggaan, graf terhubung, primitivitas graf, dan scrambling index. 2.1 Definisi Graf
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI Pada bab ini akan dijelaskan himpunan dan beberapa definisi yang berkaitan dengan himpunan, serta konsep dasar dan teori graf yang akan digunakan pada bab selanjutnya. 2.1 Himpunan
BAB 2 LANDASAN TEORI Pada bab ini akan dijelaskan himpunan dan beberapa definisi yang berkaitan dengan himpunan, serta konsep dasar dan teori graf yang akan digunakan pada bab selanjutnya. 2.1 Himpunan
Struktur dan Organisasi Data 2 G R A P H
 G R A P H Graf adalah : Himpunan V (Vertex) yang elemennya disebut simpul (atau point atau node atau titik) Himpunan E (Edge) yang merupakan pasangan tak urut dari simpul, anggotanya disebut ruas (rusuk
G R A P H Graf adalah : Himpunan V (Vertex) yang elemennya disebut simpul (atau point atau node atau titik) Himpunan E (Edge) yang merupakan pasangan tak urut dari simpul, anggotanya disebut ruas (rusuk
STUDI BILANGAN PEWARNAAN λ-backbone PADA GRAF SPLIT DENGAN BACKBONE SEGITIGA
 STUDI BILANGAN PEWARNAAN λ-backbone PADA GRAF SPLIT DENGAN BACKBONE SEGITIGA Anis Kamilah Hayati NIM : 13505075 Program Studi Teknik Informatika, Sekolah Teknik Elektro dan Informatika, Institut Teknologi
STUDI BILANGAN PEWARNAAN λ-backbone PADA GRAF SPLIT DENGAN BACKBONE SEGITIGA Anis Kamilah Hayati NIM : 13505075 Program Studi Teknik Informatika, Sekolah Teknik Elektro dan Informatika, Institut Teknologi
BAB 2 DEGREE CONSTRAINED MINIMUM SPANNING TREE. Pada bab ini diberikan beberapa konsep dasar seperti beberapa definisi dan teorema
 BAB 2 DEGREE CONSTRAINED MINIMUM SPANNING TREE Pada bab ini diberikan beberapa konsep dasar seperti beberapa definisi dan teorema sebagai landasan berfikir dalam melakukan penelitian ini dan akan mempermudah
BAB 2 DEGREE CONSTRAINED MINIMUM SPANNING TREE Pada bab ini diberikan beberapa konsep dasar seperti beberapa definisi dan teorema sebagai landasan berfikir dalam melakukan penelitian ini dan akan mempermudah
Graph. Rembang. Kudus. Brebes Tegal. Demak Semarang. Pemalang. Kendal. Pekalongan Blora. Slawi. Purwodadi. Temanggung Salatiga Wonosobo Purbalingga
 TEORI GRAPH Graph Graph Graph digunakan untuk merepresentasikan objek-objek diskrit dan hubungan antara objek-objek tersebut. Gambar berikut ini sebuah graph yang menyatakan peta jaringan jalan raya yang
TEORI GRAPH Graph Graph Graph digunakan untuk merepresentasikan objek-objek diskrit dan hubungan antara objek-objek tersebut. Gambar berikut ini sebuah graph yang menyatakan peta jaringan jalan raya yang
KAITAN ANTARA DIMENSI METRIK DAN DIMENSI PARTISI PADA SUATU GRAF. (Skripsi) Oleh GIOVANNY THEOTISTA
 KAITAN ANTARA DIMENSI METRIK DAN DIMENSI PARTISI PADA SUATU GRAF (Skripsi) Oleh GIOVANNY THEOTISTA JURUSAN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG 2016 ABSTRAK STUDI
KAITAN ANTARA DIMENSI METRIK DAN DIMENSI PARTISI PADA SUATU GRAF (Skripsi) Oleh GIOVANNY THEOTISTA JURUSAN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG 2016 ABSTRAK STUDI
BAB 2 LANDASAN TEORI. yang tak kosong yang anggotanya disebut vertex, dan E adalah himpunan yang
 BAB 2 LANDASAN TEORI 2.1 Konsep Dasar Graf Definisi 2.1.1 Sebuah graf G adalah pasangan (V,E) dengan V adalah himpunan yang tak kosong yang anggotanya disebut vertex, dan E adalah himpunan yang anggotanya
BAB 2 LANDASAN TEORI 2.1 Konsep Dasar Graf Definisi 2.1.1 Sebuah graf G adalah pasangan (V,E) dengan V adalah himpunan yang tak kosong yang anggotanya disebut vertex, dan E adalah himpunan yang anggotanya
BILANGAN KROMATIK LOKASI UNTUK GRAF KEMBANG API F n,2 DAN F n,3 DENGAN n 2
 Jurnal Matematika UNAND Vol. 3 No. 4 Hal. 49 53 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND BILANGAN KROMATIK LOKASI UNTUK GRAF KEMBANG API F n,2 DAN F n,3 DENGAN n 2 ANDRE SAPUTRA Program Studi
Jurnal Matematika UNAND Vol. 3 No. 4 Hal. 49 53 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND BILANGAN KROMATIK LOKASI UNTUK GRAF KEMBANG API F n,2 DAN F n,3 DENGAN n 2 ANDRE SAPUTRA Program Studi
Dasar-Dasar Teori Graf. Sistem Informasi Universitas Gunadarma 2012/2013
 Dasar-Dasar Teori Graf Sistem Informasi Universitas Gunadarma 2012/2013 Teori Graf Teori Graf mulai dikenal saat matematikawan kebangsaan Swiss bernama Leonhard Euler, yang berhasil mengungkapkan Misteri
Dasar-Dasar Teori Graf Sistem Informasi Universitas Gunadarma 2012/2013 Teori Graf Teori Graf mulai dikenal saat matematikawan kebangsaan Swiss bernama Leonhard Euler, yang berhasil mengungkapkan Misteri
BAB II KAJIAN PUSTAKA
 BAB II KAJIAN PUSTAKA A. Logika Fuzzy Logika fuzzy pertama kali dikembangkan oleh Prof. Lotfi A. Zadeh, seorang peneliti dari Universitas California, pada tahun 1960-an. Logika fuzzy dikembangkan dari
BAB II KAJIAN PUSTAKA A. Logika Fuzzy Logika fuzzy pertama kali dikembangkan oleh Prof. Lotfi A. Zadeh, seorang peneliti dari Universitas California, pada tahun 1960-an. Logika fuzzy dikembangkan dari
BAB 2 TINJAUAN PUSTAKA
 BAB 2 TINJAUAN PUSTAKA Pada bagian ini akan dijelaskan beberapa konsep dasar yang berkaitan dengan permasalahan, seperti definisi dan teorema yang dijadikan landasan dalam penelitian ini. 2.1 Graf Graf
BAB 2 TINJAUAN PUSTAKA Pada bagian ini akan dijelaskan beberapa konsep dasar yang berkaitan dengan permasalahan, seperti definisi dan teorema yang dijadikan landasan dalam penelitian ini. 2.1 Graf Graf
Bab 2. Teori Dasar. 2.1 Definisi Graf
 Bab 2 Teori Dasar Pada bagian ini diberikan definisi-definisi dasar dalam teori graf berikut penjabaran mengenai kompleksitas algoritma beserta contohnya yang akan digunakan dalam tugas akhir ini. Berikut
Bab 2 Teori Dasar Pada bagian ini diberikan definisi-definisi dasar dalam teori graf berikut penjabaran mengenai kompleksitas algoritma beserta contohnya yang akan digunakan dalam tugas akhir ini. Berikut
BAB 2. Konsep Dasar. 2.1 Definisi graf
 BAB 2 Konsep Dasar 21 Definisi graf Suatu graf G = (V(G), E(G)) didefinisikan sebagai pasangan himpunan 2 titik V(G) dan himpunan sisi E(G) dengan V(G) dan E(G) [ VG ( )] Sebagai contoh, graf G 1 = (V(G
BAB 2 Konsep Dasar 21 Definisi graf Suatu graf G = (V(G), E(G)) didefinisikan sebagai pasangan himpunan 2 titik V(G) dan himpunan sisi E(G) dengan V(G) dan E(G) [ VG ( )] Sebagai contoh, graf G 1 = (V(G
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI 2.1 Konsep Dasar Graf Definisi 2.1.1 Sebuah graf didefinisikan sebagai pasangan terurut himpunan dimana: 1. adalah sebuah himpunan tidak kosong yang berhingga yang anggotaanggotanya
BAB 2 LANDASAN TEORI 2.1 Konsep Dasar Graf Definisi 2.1.1 Sebuah graf didefinisikan sebagai pasangan terurut himpunan dimana: 1. adalah sebuah himpunan tidak kosong yang berhingga yang anggotaanggotanya
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI Sebelum memulai pembahasan lebih lanjut, pertama-tama haruslah dijelaskan apa yang dimaksud dengan traveling salesman problem atau dalam bahasa Indonesia disebut sebagai persoalan
BAB 2 LANDASAN TEORI Sebelum memulai pembahasan lebih lanjut, pertama-tama haruslah dijelaskan apa yang dimaksud dengan traveling salesman problem atau dalam bahasa Indonesia disebut sebagai persoalan
Bilangan Ramsey untuk Kombinasi Bintang dan Beberapa Graf Tertentu
 Bab III Bilangan Ramsey untuk Kombinasi Bintang dan Beberapa Graf Tertentu Kajian penentuan bilangan Ramsey untuk bintang dan bintang telah tuntas, dilakukan Burr dkk. (1973). Penentuan bilangan Ramsey
Bab III Bilangan Ramsey untuk Kombinasi Bintang dan Beberapa Graf Tertentu Kajian penentuan bilangan Ramsey untuk bintang dan bintang telah tuntas, dilakukan Burr dkk. (1973). Penentuan bilangan Ramsey
PENGETAHUAN DASAR TEORI GRAF
 PENGETAHUAN DASAR TEORI GRAF 1 Sejarah Singkat dan Beberapa Pengertian Dasar Teori Graf Teori graf lahir pada tahun 1736 melalui makalah tulisan Leonard Euler seorang ahli matematika dari Swiss. Euler
PENGETAHUAN DASAR TEORI GRAF 1 Sejarah Singkat dan Beberapa Pengertian Dasar Teori Graf Teori graf lahir pada tahun 1736 melalui makalah tulisan Leonard Euler seorang ahli matematika dari Swiss. Euler
Graf Ajaib (Super) dengan Sisi Pendan
 54 Bab IV Graf Ajaib (Super) dengan Sisi Pen Pada bab ini disajikan metode untuk membentuk graf ajaib (super) baru dari graf ajaib (super) yang sudah diketahui. Berdasarkan metode tersebut diperoleh graf
54 Bab IV Graf Ajaib (Super) dengan Sisi Pen Pada bab ini disajikan metode untuk membentuk graf ajaib (super) baru dari graf ajaib (super) yang sudah diketahui. Berdasarkan metode tersebut diperoleh graf
Bab 2. Landasan Teori. 2.1 Konsep Dasar
 Bab 2 Landasan Teori Pada bab ini akan diuraikan konsep dasar dan teori graf yang berhubungan dengan topik penelitian ini, termasuk didalamnya mengenai pelabelan total tak teratur titik dan total vertex
Bab 2 Landasan Teori Pada bab ini akan diuraikan konsep dasar dan teori graf yang berhubungan dengan topik penelitian ini, termasuk didalamnya mengenai pelabelan total tak teratur titik dan total vertex
DIMENSI PARTISI DARI GRAF ULAT
 Jurnal Matematika UNAND Vol. 5 No. 3 Hal. 1 6 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND DIMENSI PARTISI DARI GRAF ULAT FADHILA TURRAHMAH, BUDI RUDIANTO Program Studi Matematika, Fakultas Matematika
Jurnal Matematika UNAND Vol. 5 No. 3 Hal. 1 6 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND DIMENSI PARTISI DARI GRAF ULAT FADHILA TURRAHMAH, BUDI RUDIANTO Program Studi Matematika, Fakultas Matematika
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI Dalam bab ini dipaparkan beberapa hasil penelitian yang dilakukan para peneliti sebelumnya, pengertian dasar graf, operasi-operasi pada graf, kelaskelas graf, dan dimensi metrik pada
BAB II LANDASAN TEORI Dalam bab ini dipaparkan beberapa hasil penelitian yang dilakukan para peneliti sebelumnya, pengertian dasar graf, operasi-operasi pada graf, kelaskelas graf, dan dimensi metrik pada
Graf dan Analisa Algoritma. Pertemuan #01 - Dasar-Dasar Teori Graf Universitas Gunadarma 2017
 Graf dan Analisa Algoritma Pertemuan #01 - Dasar-Dasar Teori Graf Universitas Gunadarma 2017 Who Am I? Stya Putra Pratama, CHFI, EDRP Pendidikan - Universitas Gunadarma S1-2007 Teknik Informatika S2-2012
Graf dan Analisa Algoritma Pertemuan #01 - Dasar-Dasar Teori Graf Universitas Gunadarma 2017 Who Am I? Stya Putra Pratama, CHFI, EDRP Pendidikan - Universitas Gunadarma S1-2007 Teknik Informatika S2-2012
I.1 Latar Belakang Masalah
 Bab I Pendahuluan I.1 Latar Belakang Masalah Teori Ramsey adalah suatu area penelitian dalam teori graf yang sedang berkembang pesat dan mempunyai banyak aplikasi. Dalam makalah Rosta (2004) disebutkan
Bab I Pendahuluan I.1 Latar Belakang Masalah Teori Ramsey adalah suatu area penelitian dalam teori graf yang sedang berkembang pesat dan mempunyai banyak aplikasi. Dalam makalah Rosta (2004) disebutkan
LANDASAN TEORI. Bab Konsep Dasar Graf. Definisi Graf
 Bab 2 LANDASAN TEORI 2.1. Konsep Dasar Graf Definisi Graf Suatu graf G terdiri atas himpunan yang tidak kosong dari elemen elemen yang disebut titik atau simpul (vertex), dan suatu daftar pasangan vertex
Bab 2 LANDASAN TEORI 2.1. Konsep Dasar Graf Definisi Graf Suatu graf G terdiri atas himpunan yang tidak kosong dari elemen elemen yang disebut titik atau simpul (vertex), dan suatu daftar pasangan vertex
Teori Dasar Graf (Lanjutan)
 Teori Dasar Graf (Lanjutan) MATRIKS DAN GRAF Untuk menyelesaikan suatu permasalahan model graf dengan bantuan komputer, maka graf tersebut disajikan dalam bentuk matriks. Matriks-matriks yang dapat menyajikan
Teori Dasar Graf (Lanjutan) MATRIKS DAN GRAF Untuk menyelesaikan suatu permasalahan model graf dengan bantuan komputer, maka graf tersebut disajikan dalam bentuk matriks. Matriks-matriks yang dapat menyajikan
DIMENSI PARTISI PADA GRAPH HASIL KORONA C m K n. Oleh : Yogi Sindy Prakoso ( ) JURUSAN MATEMATIKA. Company
 DIMENSI PARTISI PADA GRAPH HASIL KORONA C m K n Oleh : Yogi Sindy Prakoso (1206100015) JURUSAN MATEMATIKA Company FAKULTAS MATEMATIKA Click to DAN add ILMU subtitle PENGETAHUAN ALAM INSTITUT TEKNOLOGI
DIMENSI PARTISI PADA GRAPH HASIL KORONA C m K n Oleh : Yogi Sindy Prakoso (1206100015) JURUSAN MATEMATIKA Company FAKULTAS MATEMATIKA Click to DAN add ILMU subtitle PENGETAHUAN ALAM INSTITUT TEKNOLOGI
BILANGAN KROMATIK LOKASI DARI GRAF HUTAN LINIER H t
 Jurnal Matematika UNAND Vol. 5 No. 4 Hal. 18 22 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND BILANGAN KROMATIK LOKASI DARI GRAF HUTAN LINIER H t SHERLY AFRI ASTUTI, ZULAKMAL Program Studi Matematika,
Jurnal Matematika UNAND Vol. 5 No. 4 Hal. 18 22 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND BILANGAN KROMATIK LOKASI DARI GRAF HUTAN LINIER H t SHERLY AFRI ASTUTI, ZULAKMAL Program Studi Matematika,
INTRODUCTION TO GRAPH THEORY LECTURE 2
 INTRODUCTION TO GRAPH THEORY LECTURE Operasi-Operasi Pada Graph Union Misal G dan H adalah dua graph yang saling asing. Union G H adalah graph dengan V(G H)=V(G) V(H) dan E(G H)=E(G) E(H). Join Join dari
INTRODUCTION TO GRAPH THEORY LECTURE Operasi-Operasi Pada Graph Union Misal G dan H adalah dua graph yang saling asing. Union G H adalah graph dengan V(G H)=V(G) V(H) dan E(G H)=E(G) E(H). Join Join dari
Pewarnaan Total Pada Graf Outerplanar
 JURNAL TEKNIK POMITS Vol. 1, No. 1, (2013) 1-6 1 Pewarnaan Total Pada Graf Outerplanar Prihasto.B Sumarno Jurusan Matematika, Fakultas Matematika Ilmu Pengetahuan Alam, Institut Teknologi Sepuluh Nopember
JURNAL TEKNIK POMITS Vol. 1, No. 1, (2013) 1-6 1 Pewarnaan Total Pada Graf Outerplanar Prihasto.B Sumarno Jurusan Matematika, Fakultas Matematika Ilmu Pengetahuan Alam, Institut Teknologi Sepuluh Nopember
I. PENDAHULUAN. Teori graf merupakan salah satu bidang matematika yang memiliki banyak. terapan di berbagai bidang sampai saat ini.
 1 I. PENDAHULUAN 1.1 Latar Belakang Teori graf merupakan salah satu bidang matematika yang memiliki banyak terapan di berbagai bidang sampai saat ini. Graf digunakan untuk merepresentasikan objek-objek
1 I. PENDAHULUAN 1.1 Latar Belakang Teori graf merupakan salah satu bidang matematika yang memiliki banyak terapan di berbagai bidang sampai saat ini. Graf digunakan untuk merepresentasikan objek-objek
BAB I PENDAHULUAN 1.1 Latar Belakang Masalah
 BAB I PENDAHULUAN. Latar Belakang Masalah Seiring perkembangan zaman, maka perkembangan ilmu pengetahuan berkembang pesat, begitu pula dengan ilmu matematika. Salah satu cabang ilmu matematika yang memiliki
BAB I PENDAHULUAN. Latar Belakang Masalah Seiring perkembangan zaman, maka perkembangan ilmu pengetahuan berkembang pesat, begitu pula dengan ilmu matematika. Salah satu cabang ilmu matematika yang memiliki
BILANGAN KROMATIK LOKASI GRAF POHON DAN KARAKTERISASI GRAF DENGAN BILANGAN KROMATIK LOKASI 3 DISERTASI ASMIATI
 BILANGAN KROMATIK LOKASI GRAF POHON DAN KARAKTERISASI GRAF DENGAN BILANGAN KROMATIK LOKASI 3 DISERTASI Karya tulis sebagai salah satu syarat untuk memperoleh gelar Doktor dari Institut Teknologi Bandung
BILANGAN KROMATIK LOKASI GRAF POHON DAN KARAKTERISASI GRAF DENGAN BILANGAN KROMATIK LOKASI 3 DISERTASI Karya tulis sebagai salah satu syarat untuk memperoleh gelar Doktor dari Institut Teknologi Bandung
BAB III PELABELAN KOMBINASI
 1 BAB III PELABELAN KOMBINASI 3.1 Konsep Pelabelan Kombinasi Pelabelan kombinasi dari suatu graf dengan titik dan sisi,, graf G, disebut graf kombinasi jika terdapat fungsi bijektif dari ( himpunan titik
1 BAB III PELABELAN KOMBINASI 3.1 Konsep Pelabelan Kombinasi Pelabelan kombinasi dari suatu graf dengan titik dan sisi,, graf G, disebut graf kombinasi jika terdapat fungsi bijektif dari ( himpunan titik
BAB I PENDAHULUAN 1.1 Latar Belakang
 BAB I PENDAHULUAN 1.1 Latar Belakang Matematika adalah salah satu ilmu yang banyak memberikan dasar bagi berkembangnya ilmu pengetahuan dan teknologi. Seiring dengan kemajuan dan perkembangan teknologi,
BAB I PENDAHULUAN 1.1 Latar Belakang Matematika adalah salah satu ilmu yang banyak memberikan dasar bagi berkembangnya ilmu pengetahuan dan teknologi. Seiring dengan kemajuan dan perkembangan teknologi,
PENENTUAN BANYAKNYA GRAF TERHUBUNG BERLABEL BERORDE LIMA TANPA GARIS PARALEL. (Skripsi) Oleh Eni Zuliana
 PENENTUAN BANYAKNYA GRAF TERHUBUNG BERLABEL BERORDE LIMA TANPA GARIS PARALEL (Skripsi) Oleh Eni Zuliana FAKULTAS MATEMATIKA DAN ILMU PEGETAHUAN ALAM UNIVERSITAS LAMPUNG BANDAR LAMPUNG 2016 ABSTRAK PENENTUAN
PENENTUAN BANYAKNYA GRAF TERHUBUNG BERLABEL BERORDE LIMA TANPA GARIS PARALEL (Skripsi) Oleh Eni Zuliana FAKULTAS MATEMATIKA DAN ILMU PEGETAHUAN ALAM UNIVERSITAS LAMPUNG BANDAR LAMPUNG 2016 ABSTRAK PENENTUAN
BILANGAN KROMATIK LOKASI DARI GRAF P m P n, K m P n, DAN K m K n
 Jurnal Matematika UNAND Vol. 2 No. 1 Hal. 14 22 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND BILANGAN KROMATIK LOKASI DARI GRAF P m P n, K m P n, DAN K m K n MARIZA WENNI Program Studi Matematika,
Jurnal Matematika UNAND Vol. 2 No. 1 Hal. 14 22 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND BILANGAN KROMATIK LOKASI DARI GRAF P m P n, K m P n, DAN K m K n MARIZA WENNI Program Studi Matematika,
BILANGAN KROMATIK LOKASI UNTUK JOIN DARI DUA GRAF
 Jurnal Matematika UNAND Vol. 2 No. 1 Hal. 23 31 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND BILANGAN KROMATIK LOKASI UNTUK JOIN DARI DUA GRAF YULI ERITA Program Studi Matematika, Pascasarjana Fakultas
Jurnal Matematika UNAND Vol. 2 No. 1 Hal. 23 31 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND BILANGAN KROMATIK LOKASI UNTUK JOIN DARI DUA GRAF YULI ERITA Program Studi Matematika, Pascasarjana Fakultas
Mizan Ahmad, Tri Atmojo Kusmayadi Program Studi Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sebelas Maret. 1.
 DIMENSI PARTISI PADA GRAF C m K n, GRAF C m [P n ], DAN GRAF t-fold WHEEL Mizan Ahmad, Tri Atmojo Kusmayadi Program Studi Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sebelas Maret
DIMENSI PARTISI PADA GRAF C m K n, GRAF C m [P n ], DAN GRAF t-fold WHEEL Mizan Ahmad, Tri Atmojo Kusmayadi Program Studi Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sebelas Maret
Teori Dasar Graf (Lanjutan)
 Teori Dasar Graf (Lanjutan) ATRIKS DAN GRAF Untuk menyelesaikan suatu permasalahan model graf dengan bantuan komputer, maka graf tersebut disajikan dalam bentuk matriks. atriks-matriks yang dapat menyajikan
Teori Dasar Graf (Lanjutan) ATRIKS DAN GRAF Untuk menyelesaikan suatu permasalahan model graf dengan bantuan komputer, maka graf tersebut disajikan dalam bentuk matriks. atriks-matriks yang dapat menyajikan
BILANGAN KROMATIK LOKASI PADA GRAF KNESER. ( Skripsi ) Oleh. Muhammad Haidir Alam
 BILANGAN KROMATIK LOKASI PADA GRAF KNESER ( Skripsi ) Oleh Muhammad Haidir Alam FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG BANDAR LAMPUNG 2016 ABSTRAK BILANGAN KROMATIK LOKASI PADA
BILANGAN KROMATIK LOKASI PADA GRAF KNESER ( Skripsi ) Oleh Muhammad Haidir Alam FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG BANDAR LAMPUNG 2016 ABSTRAK BILANGAN KROMATIK LOKASI PADA
I. LANDASAN TEORI. Seperti yang telah dipaparkan pada bab sebelumnya, teori graf merupakan salah satu ilmu
 I. LANDASAN TEORI Seperti yang telah dipaparkan pada bab sebelumnya, teori graf merupakan salah satu ilmu matematika yang mempresentasikan suatu objek berupa vertex (titik) dan edge (garis), edge merupakan
I. LANDASAN TEORI Seperti yang telah dipaparkan pada bab sebelumnya, teori graf merupakan salah satu ilmu matematika yang mempresentasikan suatu objek berupa vertex (titik) dan edge (garis), edge merupakan
Pertemuan 12. Teori Graf
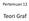 Pertemuan 2 Teori Graf Derajat Definisi Misalkan adalah titik dalam suatu Graf G. Derajat titik (simbol d()) adalah jumlah garis yang berhubungan dengan titik dan garis suatu loop dihitung dua kali. Derajat
Pertemuan 2 Teori Graf Derajat Definisi Misalkan adalah titik dalam suatu Graf G. Derajat titik (simbol d()) adalah jumlah garis yang berhubungan dengan titik dan garis suatu loop dihitung dua kali. Derajat
BILANGAN RAMSEY UNTUK GRAF BINTANG S n DAN GRAF RODA W m
 BILANGAN RAMSEY UNTUK GRAF BINTANG S n DAN GRAF RODA W m ISNAINI RAMADHANI Program Studi Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Andalas Padang, Kampus UNAND Limau Manis
BILANGAN RAMSEY UNTUK GRAF BINTANG S n DAN GRAF RODA W m ISNAINI RAMADHANI Program Studi Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Andalas Padang, Kampus UNAND Limau Manis
Discrete Mathematics & Its Applications Chapter 10 : Graphs. Fahrul Usman Institut Teknologi Bandung Pengajaran Matematika
 Discrete Mathematics & Its Applications Chapter 10 : Graphs Fahrul Usman Institut Teknologi Bandung Pengajaran Matematika 16/12/2015 2 Sub Topik A. Graf dan Model Graf B. Terminologi Dasar Graf dan Jenis
Discrete Mathematics & Its Applications Chapter 10 : Graphs Fahrul Usman Institut Teknologi Bandung Pengajaran Matematika 16/12/2015 2 Sub Topik A. Graf dan Model Graf B. Terminologi Dasar Graf dan Jenis
`BAB II LANDASAN TEORI
 `BAB II LANDASAN TEORI Landasan teori yang digunakan sebagai materi pendukung untuk menyelesaikan permasalahan yang dibahas dalam Bab IV adalah teori graf, subgraf, subgraf komplit, graf terhubung, graf
`BAB II LANDASAN TEORI Landasan teori yang digunakan sebagai materi pendukung untuk menyelesaikan permasalahan yang dibahas dalam Bab IV adalah teori graf, subgraf, subgraf komplit, graf terhubung, graf
BAB III MATCHING. Sebelum membahas lebih jauh mengenai optimal assignment problem dan
 BAB III MATCHING Sebelum membahas lebih jauh mengenai optimal assignment problem dan cara penyelesaiannya, pada bab ini akan dibahas mengenai definisi matching dan matching pada graf bipartit, karena penyelesaian
BAB III MATCHING Sebelum membahas lebih jauh mengenai optimal assignment problem dan cara penyelesaiannya, pada bab ini akan dibahas mengenai definisi matching dan matching pada graf bipartit, karena penyelesaian
HAND OUT MATA KULIAH TEORI GRAF (MT 424) JILID SATU. Oleh: Kartika Yulianti, S.Pd., M.Si.
 HAND OUT MATA KULIAH TEORI GRAF (MT 424) JILID SATU Oleh: Kartika Yulianti, S.Pd., M.Si. JURUSAN PENDIDIKAN MATEMATIKA FAKULTAS PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS PENDIDIKAN INDONESIA
HAND OUT MATA KULIAH TEORI GRAF (MT 424) JILID SATU Oleh: Kartika Yulianti, S.Pd., M.Si. JURUSAN PENDIDIKAN MATEMATIKA FAKULTAS PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS PENDIDIKAN INDONESIA
MIDDLE PADA BEBERAPA GRAF KHUSUS
 PELABELAN DAN PEMBENTUKAN GRAF MIDDLE PADA BEBERAPA GRAF KHUSUS skripsi disajikan sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains Program Studi Matematika oleh Meliana Deta Anggraeni 4111409019
PELABELAN DAN PEMBENTUKAN GRAF MIDDLE PADA BEBERAPA GRAF KHUSUS skripsi disajikan sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains Program Studi Matematika oleh Meliana Deta Anggraeni 4111409019
Gambar 6. Graf lengkap K n
 . Jenis-jenis Graf Tertentu Ada beberapa graf khusus yang sering dijumpai. Beberapa diantaranya adalah sebagai berikut. a. Graf Lengkap (Graf Komplit) Graf lengkap ialah graf sederhana yang setiap titiknya
. Jenis-jenis Graf Tertentu Ada beberapa graf khusus yang sering dijumpai. Beberapa diantaranya adalah sebagai berikut. a. Graf Lengkap (Graf Komplit) Graf lengkap ialah graf sederhana yang setiap titiknya
SIFAT SIFAT GRAF YANG MEMUAT SEMUA SIKLUS Nur Rohmah Oktaviani Putri * CHARACTERISTIC OF THE GRAPH THAT CONTAINS ALL CYCLES Nur Rohmah Oktaviani Putri
 SIFAT SIFAT GRAF YANG MEMUAT SEMUA SIKLUS Nur Rohmah Oktaviani Putri * Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Hasanuddin CHARACTERISTIC OF THE GRAPH THAT CONTAINS
SIFAT SIFAT GRAF YANG MEMUAT SEMUA SIKLUS Nur Rohmah Oktaviani Putri * Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Hasanuddin CHARACTERISTIC OF THE GRAPH THAT CONTAINS
II. LANDASAN TEORI. Ide Leonard Euler di tahun 1736 untuk menyelesaikan masalah jembatan
 4 II. LANDASAN TEORI Ide Leonard Euler di tahun 1736 untuk menyelesaikan masalah jembatan Konisberg yang kemudian menghasilkan konsep graf Eulerian merupakan awal dari lahirnya teori graf. Euler mengilustrasikan
4 II. LANDASAN TEORI Ide Leonard Euler di tahun 1736 untuk menyelesaikan masalah jembatan Konisberg yang kemudian menghasilkan konsep graf Eulerian merupakan awal dari lahirnya teori graf. Euler mengilustrasikan
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI Untuk menjelaskan pelabelan analytic mean pada graf bayangan dari graf bintang K 1,n dan graf bayangan dari graf bistar B n,n perlu adanya beberapa teori dasar yang akan menunjang
BAB II LANDASAN TEORI Untuk menjelaskan pelabelan analytic mean pada graf bayangan dari graf bintang K 1,n dan graf bayangan dari graf bistar B n,n perlu adanya beberapa teori dasar yang akan menunjang
