2. TINJAUAN PUSTAKA. Chartrand dan Zhang (2005) yaitu sebagai berikut: himpunan tak kosong dan berhingga dari objek-objek yang disebut titik
|
|
|
- Johan Pranata
- 7 tahun lalu
- Tontonan:
Transkripsi
1 2. TINJAUAN PUSTAKA 2.1 Konsep Dasar Graf Pada bagian ini akan diberikan konsep dasar graf yang diambil dari buku Chartrand dan Zhang (2005) yaitu sebagai berikut: Suatu Graf G adalah suatu pasangan himpunan (V, E) dimana V(G) adalah himpunan tak kosong dan berhingga dari objek-objek yang disebut titik (vertex), dan E(G) adalah himpunan dari pasangan tak terurut dari titik-titik berbeda di V yang disebut sisi (edge). Sebuah sisi yang menghubungkan pasangan titik yang sama atau bisa disebut juga sebuah sisi yang berawal dan berakhir dengan pada titik yang sama disebut dengan gelang (loop). Dua atau lebih sisi yang mempunyai titik-titik ujung yang sama disebut dengan sisi paralel. Jika sebuah graf G yang di dalamnya tidak terdapat gelang dan sisi paralel disebut graf sederhana. Pada Gambar 1 contoh loop adalah e 1 dan sisi paralel adalah e 3, e 5. 4
2 Gambar 1. Graf dengan titik terasing, gelang dan sisi paralel. Suatu jalan (walk) dalam graf G adalah suatu barisan berhingga dari titik dan sisi secara bergantian yang dimulai dan diakhiri dengan titik sehingga setiap sisi yang menempel dengan titik sebelum dan sesudahnya, dimana sebuah sisi hanya dilalui satu kali. Di dalam suatu jalan pada sebuah graf dapat terjadi bahwa satu titik dilalui lebih dari satu kali. Pada umumnya penulisan barisan jalan biasanya mengikutsertakan sisinya, tetapi boleh juga tidak. Dapat juga sebuah jalan dimulai dan diakhiri oleh titik yang sama, jalan yang demikian disebut dengan jalan tertutup (close walk). Sebaliknya sebuah jalan yang tidak tertutup disebut jalan terbuka (open walk). Pada Gambar 1 contoh jalan terbuka adalah v 1, e 2, v 2, e 3, v 3, e 3, v 2, e 2 dan jalan tertutup adalah v 1, e 2, v 2, e 3, v 3, e 3, v 2, e 2, v 1. Sebuah jalan terbuka yang di dalamnya tidak ada titik yang muncul lebih dari sekali disebut dengan lintasan (path). Pada Gambar 1 lintasan yaitu v 1, e 2, v 2, e 4, v 3, e 6, v 4, e 8. Jalan yang semua sisi di dalam setiap barisan harus berbeda disebut jejak (trail). jejak tertutup adalah suatu trail dengan titik awal dan titik akhir yang sama. 5
3 Pada Gambar 1 contoh jejak yaitu v 1, e 2, v 2, e 7, v 4, e 8. Sebuah lintasan yang tertutup disebut sirkuit. Pada Gambar 1 sirkuit yaitu v 2, e 4, v 3, e 6, v 4, e 7, v 2. Dua buah titik pada graf tak berarah G dikatakan bertetangga (adjacent) bila keduanya terhubung langsung dengan sebuah sisi. Dengan kata lain, v j bertetangga dengan v k jika (v j, v k ) adalah sebuah sisi dari graf. Untuk sebarang sisi e = (v j, v k ), sisi e dikatakan menempel (incident) dengan titik v j dan v k. Pada Gambar 1 v 1 bertetangga dengan v 4, e 6 menempel pada v 3 dan v 4. Titik yang tidak memiliki sisi yang menempel dengannya atau tidak bertetangga dengan titik lainnya disebut dengan titik terasing. Pada Gambar 1 titik terasing yaitu v 5. Derajat (degree) dari sebuah titik v i dalam graf G adalah banyaknya sisi yang menempel pada v i, dengan gelang dihitung dua kali. Bila jumlah sisi yang menempel dengan jumlah titik v i adalah n maka derajat dari v i adalah n sehingga d(v i ) = n. Pada Gambar 1 derajat dari titik v 4 yaitu tiga. Jumlah derajat semua titik pada suatu graf adalah genap, yaitu dua kali banyaknya sisi pada graf tersebut. Dengan kata lain, jika G = (V, E), maka d(v) = v V 2 E. 2.2 Kelas-kelas Graf Pada bagian ini akan diberikan kelas-kelas graf yang diambil dari buku Aldous dan Wilson (2000) yaitu sebagai berikut: 6
4 Graf lengkap ialah graf sederhana yang setiap titiknya bertetangga dengan semua titik lainnya. Graf lengkap dengan n titik dilambangkan dengan K n. Jumlah sisi pada graf lengkap yang terdiri dari n titik adalah n(n 1). 2 Gambar 2. Graf lengkap K 1, K 2, K 3, K 4, K 5 dan K 6. Graf lingkaran adalah graf sederhana yang setiap titiknya berderajat dua. Graf lingkaran dengan n titik dilambangkan dengan C n. Gambar 3. Graf lingkaran C 1, C 2, C 3 dan C 4. Graf lintasan ialah graf yang terdiri dari satu lintasan. Graf lintasan dengan n titik dinotasikan dengan P n. Graf G yang himpunan titiknya dapat dipisah menjadi dua himpunan bagian V 1 dan V 2, sedemikian sehingga setiap sisi pada G menghubungkan sebuah 7
5 titik di V 1 ke sebuah titik di V 2 disebut graf bipartit dan dinyatakan sebagai G = (V 1, V 2 ). Apabila G graf sederhana dan bipartit dengan partisi V 1, V 2 sedemikian sehingga setiap titik di V 1 bertetangga dengan setiap titik di V 2 maka G disebut graf bipartit lengkap. Graf pohon ialah graf terhubung yang tidak mengandung sirkuit. Karena merupakan graf terhubung maka graf pohon selalu terdapat jalur yang menghubungkan setiap dua titik. Salah satu contoh dari graf pohon yaitu graf bintang. Graf bintang adalah graf pohon dengan satu titik pusat yang terhubung dengan n daun. Graf bintang dinotasikan dengan K 1,n. 2.3 Dimensi Metrik Dimensi Metrik adalah kardinalitas minimum himpunan pemisah (resolving set) pada G. Misalkan u dan v adalah titik-titik dalam graf terhubung G maka jarak d(u, v) adalah panjang lintasan terpendek antara u dan v pada G. Untuk himpunan terurut W = {w 1, w 2, w 3,, w k } dari titik-titik dalam graf terhubung G dan titik v V(G), representasi dari v terhadap W adalah kvektor (pasangan k-tuple) r(v W) = (d(v, w 1 ), d(v, w 2 ),, d(v, w k )). Jika r(v W) untuk setiap titik v V(G) berbeda, maka W disebut himpunan pemisah dari V(G). Himpunan pemisah dengan kardinalitas minimum (basis metrik), dan kardinalitas dari basis metrik tersebut dinamakan dimensi metrik dari G dinotasikan dim(g) (Chartrand, dkk, 1999). 8
6 Berikut ini akan diberikan contoh dimensi metrik pada suatu graf Gambar 4. Graf dengan 4 titik dan 5 sisi. Ambil W = {v 1 }, representasi titiknya adalah r(v 1 W) = (0), r(v 3 W) = (2), r(v 2 W) = (1), r(v 4 W) = (1). Karena ada representasi titik yang sama untuk W = {v 1 }, maka W = {v 1 } bukan himpunan pemisah dan juga bukan merupakan basis metrik. Sehingga banyaknya anggota W = {v 1 } tidak dapat dikatakan sebagai dimensi metrik. Oleh karena itu, ambil W yang lain. Ambil W = {v 1, v 2 }, representasi titiknya adalah r(v 1 W) = (0,1), r(v 3 W) = (2,1), r(v 2 W) = (1,0), r(v 4 W) = (1,1). Karena representasi semua titik berbeda untuk W = {v 1, v 2 }, maka W = {v 1, v 2 } merupakan himpunan pemisah dari basis metrik. Selain itu, banyaknya anggota basis ini merupakan yang paling minimum sehingga banyaknya anggota W = {v 1, v 2 } dapat dinyatakan sebagai dimensi metrik dari graf tersebut (Chartrand, dkk, 2000). 9
v 3 e 2 e 4 e 6 e 3 v 4
 5 II. TINJAUAN PUSTAKA Pada bab ini akan diberikan beberapa konsep dasar teori graf dan dimensi partisi graf sebagai landasan teori dari penelitian ini... Konsep Dasar Graf Pada bagian ini akan diberikan
5 II. TINJAUAN PUSTAKA Pada bab ini akan diberikan beberapa konsep dasar teori graf dan dimensi partisi graf sebagai landasan teori dari penelitian ini... Konsep Dasar Graf Pada bagian ini akan diberikan
LANDASAN TEORI. Pada bab ini akan diberikan beberapa konsep dasar teori graf dan bilangan. kromatik lokasi sebagai landasan teori pada penelitian ini.
 6 II. LANDASAN TEORI Pada bab ini akan diberikan beberapa konsep dasar teori graf dan bilangan kromatik lokasi sebagai landasan teori pada penelitian ini. 2.1 Konsep Dasar Graf Pada sub bab ini akan diberikan
6 II. LANDASAN TEORI Pada bab ini akan diberikan beberapa konsep dasar teori graf dan bilangan kromatik lokasi sebagai landasan teori pada penelitian ini. 2.1 Konsep Dasar Graf Pada sub bab ini akan diberikan
TINJAUAN PUSTAKA. Pada bagian ini akan diberikan konsep dasar graf dan bilangan kromatik lokasi pada
 II. TINJAUAN PUSTAKA Pada bagian ini akan diberikan konsep dasar graf dan bilangan kromatik lokasi pada suatu graf sebagai landasan teori penelitian ini. 2. Konsep Dasar Graf Teori dasar mengenai graf
II. TINJAUAN PUSTAKA Pada bagian ini akan diberikan konsep dasar graf dan bilangan kromatik lokasi pada suatu graf sebagai landasan teori penelitian ini. 2. Konsep Dasar Graf Teori dasar mengenai graf
TINJAUAN PUSTAKA. Pada bab ini akan dijelaskan beberapa konsep dasar teori graf dan dimensi partisi
 II. TINJAUAN PUSTAKA Pada bab ini akan dijelaskan beberapa konsep dasar teori graf dan dimensi partisi pada suatu graf sebagai landasan teori pada penelitian ini.. Konsep Dasar Graf Pada bagian ini akan
II. TINJAUAN PUSTAKA Pada bab ini akan dijelaskan beberapa konsep dasar teori graf dan dimensi partisi pada suatu graf sebagai landasan teori pada penelitian ini.. Konsep Dasar Graf Pada bagian ini akan
BAB 2 LANDASAN TEORI. yang tak kosong yang anggotanya disebut vertex, dan E adalah himpunan yang
 BAB 2 LANDASAN TEORI 2.1 Konsep Dasar Graf Definisi 2.1.1 Sebuah graf G adalah pasangan (V,E) dengan V adalah himpunan yang tak kosong yang anggotanya disebut vertex, dan E adalah himpunan yang anggotanya
BAB 2 LANDASAN TEORI 2.1 Konsep Dasar Graf Definisi 2.1.1 Sebuah graf G adalah pasangan (V,E) dengan V adalah himpunan yang tak kosong yang anggotanya disebut vertex, dan E adalah himpunan yang anggotanya
BAB II TINJAUAN PUSTAKA. kromatik lokasi sebagai landasan teori dari penelitian ini.
 BAB II TINJAUAN PUSTAKA Pada bab ini akan diberikan beberapa konsep dasar teori graf dan bilangan kromatik lokasi sebagai landasan teori dari penelitian ini. 2.1 Konsep Dasar Graf Beberapa konsep dasar
BAB II TINJAUAN PUSTAKA Pada bab ini akan diberikan beberapa konsep dasar teori graf dan bilangan kromatik lokasi sebagai landasan teori dari penelitian ini. 2.1 Konsep Dasar Graf Beberapa konsep dasar
II. KONSEP DASAR GRAF DAN GRAF POHON. Graf G adalah himpunan terurut ( V(G), E(G)), dengan V(G) menyatakan
 II. KONSEP DASAR GRAF DAN GRAF POHON 2.1 Konsep Dasar Graf Teori dasar mengenai graf yang akan digunakan dalam penelitian ini diambil dari Deo (1989). Graf G adalah himpunan terurut ( V(G), E(G)), dengan
II. KONSEP DASAR GRAF DAN GRAF POHON 2.1 Konsep Dasar Graf Teori dasar mengenai graf yang akan digunakan dalam penelitian ini diambil dari Deo (1989). Graf G adalah himpunan terurut ( V(G), E(G)), dengan
Suatu graf G adalah pasangan himpunan (V, E), dimana V adalah himpunan titik
 BAB II DASAR TEORI 2.1 Teori Dasar Graf 2.1.1 Graf dan Graf Sederhana Suatu graf G adalah pasangan himpunan (V, E), dimana V adalah himpunan titik yang tak kosong dan E adalah himpunan sisi. Untuk selanjutnya,
BAB II DASAR TEORI 2.1 Teori Dasar Graf 2.1.1 Graf dan Graf Sederhana Suatu graf G adalah pasangan himpunan (V, E), dimana V adalah himpunan titik yang tak kosong dan E adalah himpunan sisi. Untuk selanjutnya,
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI Dalam bab ini dipaparkan beberapa hasil penelitian yang dilakukan para peneliti sebelumnya, pengertian dasar graf, operasi-operasi pada graf, kelas-kelas graf dan dimensi partisi
BAB II LANDASAN TEORI Dalam bab ini dipaparkan beberapa hasil penelitian yang dilakukan para peneliti sebelumnya, pengertian dasar graf, operasi-operasi pada graf, kelas-kelas graf dan dimensi partisi
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI Dalam bab ini dipaparkan beberapa hasil penelitian yang dilakukan para peneliti sebelumnya, pengertian dasar graf, operasi-operasi pada graf, kelaskelas graf, dan dimensi metrik pada
BAB II LANDASAN TEORI Dalam bab ini dipaparkan beberapa hasil penelitian yang dilakukan para peneliti sebelumnya, pengertian dasar graf, operasi-operasi pada graf, kelaskelas graf, dan dimensi metrik pada
II. TINJAUAN PUSTAKA. kromatik lokasi pada suatu graf sebagai landasan teori pada penelitian ini
 5 II. TINJAUAN PUSTAKA Pada bagian ini akan diberikan konsep dasar graf, graf pohon dan bilangan kromatik lokasi pada suatu graf sebagai landasan teori pada penelitian ini 2.1 KONSEP DASAR GRAF Konsep
5 II. TINJAUAN PUSTAKA Pada bagian ini akan diberikan konsep dasar graf, graf pohon dan bilangan kromatik lokasi pada suatu graf sebagai landasan teori pada penelitian ini 2.1 KONSEP DASAR GRAF Konsep
BAB II LANDASAN TEORI
 15 BAB II LANDASAN TEORI 2.1 Konsep Dasar Graf Definisi 2.1.1 Graf Sebuah graf G adalah pasangan (V,E) dengan V adalah himpunan yang tak kosong yang anggotanya disebut vertex, dan E adalah himpunan yang
15 BAB II LANDASAN TEORI 2.1 Konsep Dasar Graf Definisi 2.1.1 Graf Sebuah graf G adalah pasangan (V,E) dengan V adalah himpunan yang tak kosong yang anggotanya disebut vertex, dan E adalah himpunan yang
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI Bab ini terdiri dari tiga subbab. Subbab pertama adalah tinjauan pustaka yang memuat hasil penelitian yang dilakukan oleh peneliti sebelumnya dalam bidang dimensi metrik. Subbab kedua
BAB II LANDASAN TEORI Bab ini terdiri dari tiga subbab. Subbab pertama adalah tinjauan pustaka yang memuat hasil penelitian yang dilakukan oleh peneliti sebelumnya dalam bidang dimensi metrik. Subbab kedua
KONSEP DASAR GRAF DAN GRAF POHON. Pada bab ini akan dijabarkan teori graf dan bilangan kromatik lokasi pada suatu graf
 II. KONSEP DASAR GRAF DAN GRAF POHON Pada bab ini akan dijabarkan teori graf dan bilangan kromatik lokasi pada suatu graf sebagai landasan teori pada penelitian ini. 2.1 Konsep Dasar Graf Pada bagian ini
II. KONSEP DASAR GRAF DAN GRAF POHON Pada bab ini akan dijabarkan teori graf dan bilangan kromatik lokasi pada suatu graf sebagai landasan teori pada penelitian ini. 2.1 Konsep Dasar Graf Pada bagian ini
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI Dalam bab ini dipaparkan beberapa hasil penelitian yang dilakukan para peneliti sebelumnya, pengertian dasar graf, operasi-operasi pada graf, kelas-kelas graf dan dimensi partisi
BAB II LANDASAN TEORI Dalam bab ini dipaparkan beberapa hasil penelitian yang dilakukan para peneliti sebelumnya, pengertian dasar graf, operasi-operasi pada graf, kelas-kelas graf dan dimensi partisi
TINJAUAN PUSTAKA. Pada bab ini akan diberikan beberapa definisi, istilah istilah yang berhubungan dengan materi
 II. TINJAUAN PUSTAKA Pada bab ini akan diberikan beberapa definisi, istilah istilah yang berhubungan dengan materi yang akan dihasilkan pada penelitian ini. 2.1 Beberapa Definisi dan Istilah 1. Graf (
II. TINJAUAN PUSTAKA Pada bab ini akan diberikan beberapa definisi, istilah istilah yang berhubungan dengan materi yang akan dihasilkan pada penelitian ini. 2.1 Beberapa Definisi dan Istilah 1. Graf (
Graph. Rembang. Kudus. Brebes Tegal. Demak Semarang. Pemalang. Kendal. Pekalongan Blora. Slawi. Purwodadi. Temanggung Salatiga Wonosobo Purbalingga
 TEORI GRAPH Graph Graph Graph digunakan untuk merepresentasikan objek-objek diskrit dan hubungan antara objek-objek tersebut. Gambar berikut ini sebuah graph yang menyatakan peta jaringan jalan raya yang
TEORI GRAPH Graph Graph Graph digunakan untuk merepresentasikan objek-objek diskrit dan hubungan antara objek-objek tersebut. Gambar berikut ini sebuah graph yang menyatakan peta jaringan jalan raya yang
BAB II TINJAUAN PUSTAKA
 BAB II TINJAUAN PUSTAKA 2.1 Graf (Graph) Graf G didefinisikan sebagai pasangan himpunan (V, E) yang dinotasikan dalam bentuk G = {V(G), E(G)}, dimana V(G) adalah himpunan vertex (simpul) yang tidak kosong
BAB II TINJAUAN PUSTAKA 2.1 Graf (Graph) Graf G didefinisikan sebagai pasangan himpunan (V, E) yang dinotasikan dalam bentuk G = {V(G), E(G)}, dimana V(G) adalah himpunan vertex (simpul) yang tidak kosong
BAB II TINJAUAN PUSTAKA. Pada bab ini akan diberikan definisi dan teorema yang berhubungan dengan
 BAB II TINJAUAN PUSTAKA Pada bab ini akan diberikan definisi dan teorema yang berhubungan dengan penelitian yang dilakukan. 2.1. Konsep Dasar Graf Graf G didefinisikan sebagai pasangan himpunan terurut
BAB II TINJAUAN PUSTAKA Pada bab ini akan diberikan definisi dan teorema yang berhubungan dengan penelitian yang dilakukan. 2.1. Konsep Dasar Graf Graf G didefinisikan sebagai pasangan himpunan terurut
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI 2.1 Teori Graf 2.1.1 Defenisi Graf Suatu graf G adalah suatu himpunan berhingga tak kosong dari objek-objek yang disebut verteks (titik/simpul) dengan suatu himpunan yang anggotanya
BAB 2 LANDASAN TEORI 2.1 Teori Graf 2.1.1 Defenisi Graf Suatu graf G adalah suatu himpunan berhingga tak kosong dari objek-objek yang disebut verteks (titik/simpul) dengan suatu himpunan yang anggotanya
II. TINJAUAN PUSTAKA. Graf G adalah suatu struktur (V,E) dengan V(G) = {v 1, v 2, v 3,.., v n } himpunan
 5 II. TINJAUAN PUSTAKA Definisi 2.1 Graf (Deo,1989) Graf G adalah suatu struktur (V,E) dengan V(G) = {v 1, v 2, v 3,.., v n } himpunan tak kosong dengan elemen-elemennya disebut vertex, sedangkan E(G)
5 II. TINJAUAN PUSTAKA Definisi 2.1 Graf (Deo,1989) Graf G adalah suatu struktur (V,E) dengan V(G) = {v 1, v 2, v 3,.., v n } himpunan tak kosong dengan elemen-elemennya disebut vertex, sedangkan E(G)
MA3051 Pengantar Teori Graf. Semester /2014 Pengajar: Hilda Assiyatun
 MA3051 Pengantar Teori Graf Semester 1 2013/2014 Pengajar: Hilda Assiyatun Bab 1: Graf dan subgraf Graf G : tripel terurut VG, E G, ψ G ) V G himpunan titik (vertex) E G himpunan sisi (edge) ψ G fungsi
MA3051 Pengantar Teori Graf Semester 1 2013/2014 Pengajar: Hilda Assiyatun Bab 1: Graf dan subgraf Graf G : tripel terurut VG, E G, ψ G ) V G himpunan titik (vertex) E G himpunan sisi (edge) ψ G fungsi
Dasar-Dasar Teori Graf. Sistem Informasi Universitas Gunadarma 2012/2013
 Dasar-Dasar Teori Graf Sistem Informasi Universitas Gunadarma 2012/2013 Teori Graf Teori Graf mulai dikenal saat matematikawan kebangsaan Swiss bernama Leonhard Euler, yang berhasil mengungkapkan Misteri
Dasar-Dasar Teori Graf Sistem Informasi Universitas Gunadarma 2012/2013 Teori Graf Teori Graf mulai dikenal saat matematikawan kebangsaan Swiss bernama Leonhard Euler, yang berhasil mengungkapkan Misteri
DIMENSI METRIK PADA HASIL OPERASI KORONA DUA BUAH GRAF
 JURNAL BUANA MATEMATIKA Vol 7, No 2, Tahun 2017 ISSN 2088-3021 (media cetak) ISSN 2598-8077 (media online) DIMENSI METRIK PADA HASIL OPERASI KORONA DUA BUAH GRAF Silviana Maya P 1, Syarifuddin N Kapita
JURNAL BUANA MATEMATIKA Vol 7, No 2, Tahun 2017 ISSN 2088-3021 (media cetak) ISSN 2598-8077 (media online) DIMENSI METRIK PADA HASIL OPERASI KORONA DUA BUAH GRAF Silviana Maya P 1, Syarifuddin N Kapita
II. TINJAUAN PUSTAKA. Pada bab ini akan diberikan beberapa konsep dasar dalam teori graf dan teknik
 II. TINJAUAN PUSTAKA Pada bab ini akan diberikan beberapa konsep dasar dalam teori graf dan teknik pencacahan dalam bentuk definisi dan teorema yang berhubungan dengan penelitian yang akan dilakukan. 2.1
II. TINJAUAN PUSTAKA Pada bab ini akan diberikan beberapa konsep dasar dalam teori graf dan teknik pencacahan dalam bentuk definisi dan teorema yang berhubungan dengan penelitian yang akan dilakukan. 2.1
II.TINJAUAN PUSTAKA. Pada bab ini akan dijelaskan tentang definisi serta konsep-konsep yang mendukung
 II.TINJAUAN PUSTAKA Pada bab ini akan dijelaskan tentang definisi serta konsep-konsep yang mendukung dalam penelitian ini. 2.1. Konsep Dasar Teori Graf Graf G didefinisikan sebagai pasangan himpunan terurut
II.TINJAUAN PUSTAKA Pada bab ini akan dijelaskan tentang definisi serta konsep-konsep yang mendukung dalam penelitian ini. 2.1. Konsep Dasar Teori Graf Graf G didefinisikan sebagai pasangan himpunan terurut
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI 2.1 Konsep Dasar Teori Graph 2.1.1 Graph Tak Berarah dan Digraph Suatu Graph Tak Berarah (Undirected Graph) merupakan kumpulan dari titik yang disebut verteks dan segmen garis yang
BAB II LANDASAN TEORI 2.1 Konsep Dasar Teori Graph 2.1.1 Graph Tak Berarah dan Digraph Suatu Graph Tak Berarah (Undirected Graph) merupakan kumpulan dari titik yang disebut verteks dan segmen garis yang
Graf dan Analisa Algoritma. Pertemuan #01 - Dasar-Dasar Teori Graf Universitas Gunadarma 2017
 Graf dan Analisa Algoritma Pertemuan #01 - Dasar-Dasar Teori Graf Universitas Gunadarma 2017 Who Am I? Stya Putra Pratama, CHFI, EDRP Pendidikan - Universitas Gunadarma S1-2007 Teknik Informatika S2-2012
Graf dan Analisa Algoritma Pertemuan #01 - Dasar-Dasar Teori Graf Universitas Gunadarma 2017 Who Am I? Stya Putra Pratama, CHFI, EDRP Pendidikan - Universitas Gunadarma S1-2007 Teknik Informatika S2-2012
LOGIKA DAN ALGORITMA
 LOGIKA DAN ALGORITMA DASAR DASAR TEORI GRAF Kelahiran Teori Graf Sejarah Graf : masalah jembatan Königsberg (tahun 736) C A D B Gbr. Masalah Jembatan Königsberg Graf yang merepresentasikan jembatan Königsberg
LOGIKA DAN ALGORITMA DASAR DASAR TEORI GRAF Kelahiran Teori Graf Sejarah Graf : masalah jembatan Königsberg (tahun 736) C A D B Gbr. Masalah Jembatan Königsberg Graf yang merepresentasikan jembatan Königsberg
BAB II TINJAUAN PUSTAKA. sepasang titik. Himpunan titik di G dinotasikan dengan V(G) dan himpunan
 5 BAB II TINJAUAN PUSTAKA A. Teori Graf 1. Dasar-dasar Graf Graf G didefinisikan sebagai pasangan himpunan (V, E) ditulis dengan notasi G = (V, E), dimana V adalah himpunan titik yang tidak kosong (vertex)
5 BAB II TINJAUAN PUSTAKA A. Teori Graf 1. Dasar-dasar Graf Graf G didefinisikan sebagai pasangan himpunan (V, E) ditulis dengan notasi G = (V, E), dimana V adalah himpunan titik yang tidak kosong (vertex)
BAB 2 LANDASAN TEORI. 2.1 Penugasan Sebagai Masalah Matching Bobot Maksimum Dalam Graf Bipartisi Lengkap Berlabel
 BAB 2 LANDASAN TEORI 2.1 Penugasan Sebagai Masalah Matching Bobot Maksimum Dalam Graf Bipartisi Lengkap Berlabel Teori Dasar Graf Graf G adalah pasangan himpunan (V,E) di mana V adalah himpunan dari vertex
BAB 2 LANDASAN TEORI 2.1 Penugasan Sebagai Masalah Matching Bobot Maksimum Dalam Graf Bipartisi Lengkap Berlabel Teori Dasar Graf Graf G adalah pasangan himpunan (V,E) di mana V adalah himpunan dari vertex
Jln. Perintis Kemerdekaan, Makassar, Indonesia, Kode Pos BASIS FOR DETERMINING THE WHEEL GRAPH
 PENETUAN BASIS BAGI GRAF RODA Nur Ulfah Dwiyanti Obed 1*), Nurdin 2), Amir Kamal Amir 3) 1 Jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Hasanuddin Jln. Perintis Kemerdekaan,
PENETUAN BASIS BAGI GRAF RODA Nur Ulfah Dwiyanti Obed 1*), Nurdin 2), Amir Kamal Amir 3) 1 Jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Hasanuddin Jln. Perintis Kemerdekaan,
III. BILANGAN KROMATIK LOKASI GRAF. ini merupakan pengembangan dari konsep dimensi partisi dan pewarnaan graf.
 III BILANGAN KROMATIK LOKASI GRAF Bilangan kromatik lokasi graf pertama kali dikaji oleh Chartrand dkk 00) Konsep ini merupakan pengembangan dari konsep dimensi partisi pewarnaan graf Pewarnaan titik pada
III BILANGAN KROMATIK LOKASI GRAF Bilangan kromatik lokasi graf pertama kali dikaji oleh Chartrand dkk 00) Konsep ini merupakan pengembangan dari konsep dimensi partisi pewarnaan graf Pewarnaan titik pada
BAB II LANDASAN TEORI
 5 BAB II LANDASAN TEORI.1 Sejarah Graf Menurut catatan sejarah, masalah jembatan KÖnigsberg adalah masalah yang pertama kali menggunakan graf (tahun 1736). Di kota KÖnigsberg (sebelah timur Negara bagian
5 BAB II LANDASAN TEORI.1 Sejarah Graf Menurut catatan sejarah, masalah jembatan KÖnigsberg adalah masalah yang pertama kali menggunakan graf (tahun 1736). Di kota KÖnigsberg (sebelah timur Negara bagian
3.1 Beberapa Nilai Dimensi Partisi pada Suatu Graf. Dalam dimensi partisi suatu graf, terdapat kelas graf yang nilai dimensi partisinya
 BAB III DIMENSI PARTISI n 1 3.1 Beberapa Nilai Dimensi Partisi pada Suatu Graf Dalam dimensi partisi suatu graf, terdapat kelas graf yang nilai dimensi partisinya cukup mudah atau sederhana. Kelas graf
BAB III DIMENSI PARTISI n 1 3.1 Beberapa Nilai Dimensi Partisi pada Suatu Graf Dalam dimensi partisi suatu graf, terdapat kelas graf yang nilai dimensi partisinya cukup mudah atau sederhana. Kelas graf
Dimensi Metrik Graf Pohon Bentuk Tertentu
 Dimensi Metrik Graf Pohon Bentuk Tertentu Angga Budi Permana 1207100008 Dosen Pembimbing : Dr. Darmaji, S.Si, M.T. Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Institut Teknologi Sepuluh
Dimensi Metrik Graf Pohon Bentuk Tertentu Angga Budi Permana 1207100008 Dosen Pembimbing : Dr. Darmaji, S.Si, M.T. Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Institut Teknologi Sepuluh
I. PENDAHULUAN. Teori graf merupakan salah satu bidang matematika yang memiliki banyak. terapan di berbagai bidang sampai saat ini.
 1 I. PENDAHULUAN 1.1 Latar Belakang Teori graf merupakan salah satu bidang matematika yang memiliki banyak terapan di berbagai bidang sampai saat ini. Graf digunakan untuk merepresentasikan objek-objek
1 I. PENDAHULUAN 1.1 Latar Belakang Teori graf merupakan salah satu bidang matematika yang memiliki banyak terapan di berbagai bidang sampai saat ini. Graf digunakan untuk merepresentasikan objek-objek
PENGETAHUAN DASAR TEORI GRAF
 PENGETAHUAN DASAR TEORI GRAF 1 Sejarah Singkat dan Beberapa Pengertian Dasar Teori Graf Teori graf lahir pada tahun 1736 melalui makalah tulisan Leonard Euler seorang ahli matematika dari Swiss. Euler
PENGETAHUAN DASAR TEORI GRAF 1 Sejarah Singkat dan Beberapa Pengertian Dasar Teori Graf Teori graf lahir pada tahun 1736 melalui makalah tulisan Leonard Euler seorang ahli matematika dari Swiss. Euler
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI Untuk menjelaskan pelabelan analytic mean pada graf bayangan dari graf bintang K 1,n dan graf bayangan dari graf bistar B n,n perlu adanya beberapa teori dasar yang akan menunjang
BAB II LANDASAN TEORI Untuk menjelaskan pelabelan analytic mean pada graf bayangan dari graf bintang K 1,n dan graf bayangan dari graf bistar B n,n perlu adanya beberapa teori dasar yang akan menunjang
DIMENSI METRIK DAN DIAMETER DARI GRAF ULAT C m, n
 JURNAL BUANA MATEMATIKA Vol 6, No 1, Tahun 2016 DIMENSI METRIK DAN DIAMETER DARI GRAF ULAT C m, n Restu Ria Wantika Pendidikan Matematika, Fakultas Keguruan dan Ilmu Pendidikan, Universitas PGRI Adi Buana
JURNAL BUANA MATEMATIKA Vol 6, No 1, Tahun 2016 DIMENSI METRIK DAN DIAMETER DARI GRAF ULAT C m, n Restu Ria Wantika Pendidikan Matematika, Fakultas Keguruan dan Ilmu Pendidikan, Universitas PGRI Adi Buana
Graph. Politeknik Elektronika Negeri Surabaya
 Graph Politeknik Elektronika Negeri Surabaya Pengantar Teori graph merupakan pokok bahasan yang memiliki banyak penerapan. Graph digunakan untuk merepresentasikan obyek-obyek diskrit dan hubungan antar
Graph Politeknik Elektronika Negeri Surabaya Pengantar Teori graph merupakan pokok bahasan yang memiliki banyak penerapan. Graph digunakan untuk merepresentasikan obyek-obyek diskrit dan hubungan antar
PENGERTIAN GRAPH. G 1 adalah graph dengan V(G) = { 1, 2, 3, 4 } E(G) = { (1, 2), (1, 3), (2, 3), (2, 4), (3, 4) } Graph 2
 PENGERTIAN GRAPH 1. DEFINISI GRAPH Graph G adalah pasangan terurut dua himpunan (V(G), E(G)), V(G) himpunan berhingga dan tak kosong dari obyek-obyek yang disebut himpunan titik (vertex) dan E(G) himpunan
PENGERTIAN GRAPH 1. DEFINISI GRAPH Graph G adalah pasangan terurut dua himpunan (V(G), E(G)), V(G) himpunan berhingga dan tak kosong dari obyek-obyek yang disebut himpunan titik (vertex) dan E(G) himpunan
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI Sebelum memulai pembahasan lebih lanjut, pertama-tama haruslah dijelaskan apa yang dimaksud dengan traveling salesman problem atau dalam bahasa Indonesia disebut sebagai persoalan
BAB 2 LANDASAN TEORI Sebelum memulai pembahasan lebih lanjut, pertama-tama haruslah dijelaskan apa yang dimaksud dengan traveling salesman problem atau dalam bahasa Indonesia disebut sebagai persoalan
GRAF. V3 e5. V = {v 1, v 2, v 3, v 4 } E = {e 1, e 2, e 3, e 4, e 5 } E = {(v 1,v 2 ), (v 1,v 2 ), (v 1,v 3 ), (v 2,v 3 ), (v 3,v 3 )}
 GRAF Graf G(V,E) didefinisikan sebagai pasangan himpunan (V,E), dengan V adalah himpunan berhingga dan tidak kosong dari simpul-simpul (verteks atau node). Dan E adalah himpunan berhingga dari busur (vertices
GRAF Graf G(V,E) didefinisikan sebagai pasangan himpunan (V,E), dengan V adalah himpunan berhingga dan tidak kosong dari simpul-simpul (verteks atau node). Dan E adalah himpunan berhingga dari busur (vertices
LANDASAN TEORI. Bab Konsep Dasar Graf. Definisi Graf
 Bab 2 LANDASAN TEORI 2.1. Konsep Dasar Graf Definisi Graf Suatu graf G terdiri atas himpunan yang tidak kosong dari elemen elemen yang disebut titik atau simpul (vertex), dan suatu daftar pasangan vertex
Bab 2 LANDASAN TEORI 2.1. Konsep Dasar Graf Definisi Graf Suatu graf G terdiri atas himpunan yang tidak kosong dari elemen elemen yang disebut titik atau simpul (vertex), dan suatu daftar pasangan vertex
Penerapan Teori Graf untuk Mencari Eksentrik Digraf dari Graf Star, Graf Double Star dan Graf Komplit Bipartit
 Penerapan Teori Graf untuk Mencari Eksentrik Digraf dari Graf Star, Graf Double Star dan Graf Komplit Bipartit Ivan Saputra 13505091 Program Studi Teknik Informatika, Institut Teknologi Bandung Jl. Ganesha
Penerapan Teori Graf untuk Mencari Eksentrik Digraf dari Graf Star, Graf Double Star dan Graf Komplit Bipartit Ivan Saputra 13505091 Program Studi Teknik Informatika, Institut Teknologi Bandung Jl. Ganesha
Bab 2 LANDASAN TEORI
 Bab LANDASAN TEORI Pada bab ini akan dijelaskan mengenai teori teori yang berhubungan dengan penelitian sehingga dapat dijadikan sebagai landasan berfikir dalam melakukan penelitian dan akan mempermudah
Bab LANDASAN TEORI Pada bab ini akan dijelaskan mengenai teori teori yang berhubungan dengan penelitian sehingga dapat dijadikan sebagai landasan berfikir dalam melakukan penelitian dan akan mempermudah
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI Pada bab ini akan diberikan beberapa definisi dan konsep dasar dalam teori graf dan pelabelan graf yang akan digunakan pada bab selanjutnya. 2.1 Definisi dan Istilah Dalam Teori Graf
BAB II LANDASAN TEORI Pada bab ini akan diberikan beberapa definisi dan konsep dasar dalam teori graf dan pelabelan graf yang akan digunakan pada bab selanjutnya. 2.1 Definisi dan Istilah Dalam Teori Graf
II. LANDASAN TEORI. Ide Leonard Euler di tahun 1736 untuk menyelesaikan masalah jembatan
 4 II. LANDASAN TEORI Ide Leonard Euler di tahun 1736 untuk menyelesaikan masalah jembatan Konisberg yang kemudian menghasilkan konsep graf Eulerian merupakan awal dari lahirnya teori graf. Euler mengilustrasikan
4 II. LANDASAN TEORI Ide Leonard Euler di tahun 1736 untuk menyelesaikan masalah jembatan Konisberg yang kemudian menghasilkan konsep graf Eulerian merupakan awal dari lahirnya teori graf. Euler mengilustrasikan
EKSENTRIK DIGRAF DARI GRAF-GRAF KHUSUS
 EKSENTRIK DIGRAF DARI GRAF-GRAF KHUSUS Sulistyo Unggul Wicaksono NIM : 13503058 Program Studi Teknik Informatika, Institut Teknologi Bandung Jl. Ganesha 10, Bandung E-mail: if13058@students.if.itb.ac.id
EKSENTRIK DIGRAF DARI GRAF-GRAF KHUSUS Sulistyo Unggul Wicaksono NIM : 13503058 Program Studi Teknik Informatika, Institut Teknologi Bandung Jl. Ganesha 10, Bandung E-mail: if13058@students.if.itb.ac.id
KLASIFIKASI GRAF PETERSEN BERBILANGAN KROMATIK LOKASI EMPAT ATAU LIMA
 KLASIFIKASI GRAF PETERSEN BERBILANGAN KROMATIK LOKASI EMPAT ATAU LIMA (Tesis) Oleh : Devriyadi Saputra S NPM. 1427031001 MAGISTER MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG
KLASIFIKASI GRAF PETERSEN BERBILANGAN KROMATIK LOKASI EMPAT ATAU LIMA (Tesis) Oleh : Devriyadi Saputra S NPM. 1427031001 MAGISTER MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG
I. PENDAHULUAN. Perkembangan ilmu pengetahuan dan teknologi sampai saat ini terus
 1 I. PENDAHULUAN 1.1 Latar Belakang Perkembangan ilmu pengetahuan dan teknologi sampai saat ini terus mengalami kemajuan. Salah satunya adalah cabang ilmu matematika yang sampai saat ini mengalami perkembangan
1 I. PENDAHULUAN 1.1 Latar Belakang Perkembangan ilmu pengetahuan dan teknologi sampai saat ini terus mengalami kemajuan. Salah satunya adalah cabang ilmu matematika yang sampai saat ini mengalami perkembangan
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI 2.1 Konsep Dasar Graf Definisi 2.1.1 Sebuah graf didefinisikan sebagai pasangan terurut himpunan dimana: 1. adalah sebuah himpunan tidak kosong yang berhingga yang anggotaanggotanya
BAB 2 LANDASAN TEORI 2.1 Konsep Dasar Graf Definisi 2.1.1 Sebuah graf didefinisikan sebagai pasangan terurut himpunan dimana: 1. adalah sebuah himpunan tidak kosong yang berhingga yang anggotaanggotanya
SIFAT SIFAT GRAF YANG MEMUAT SEMUA SIKLUS Nur Rohmah Oktaviani Putri * CHARACTERISTIC OF THE GRAPH THAT CONTAINS ALL CYCLES Nur Rohmah Oktaviani Putri
 SIFAT SIFAT GRAF YANG MEMUAT SEMUA SIKLUS Nur Rohmah Oktaviani Putri * Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Hasanuddin CHARACTERISTIC OF THE GRAPH THAT CONTAINS
SIFAT SIFAT GRAF YANG MEMUAT SEMUA SIKLUS Nur Rohmah Oktaviani Putri * Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Hasanuddin CHARACTERISTIC OF THE GRAPH THAT CONTAINS
III. BILANGAN KROMATIK LOKASI GRAF. Bilangan kromatik lokasi graf pertama kali dikaji oleh Chartrand dkk.(2002). = ( ) {1,2,3,, } dengan syarat
 III. BILANGAN KROMATIK LOKASI GRAF Bilangan kromatik lokasi graf pertama kali dikaji oleh Chartrand dkk.00). Konsep ini merupakan pengembangan dari konsep dimensi partisi dan pewarnaan graf. Pewarnaan
III. BILANGAN KROMATIK LOKASI GRAF Bilangan kromatik lokasi graf pertama kali dikaji oleh Chartrand dkk.00). Konsep ini merupakan pengembangan dari konsep dimensi partisi dan pewarnaan graf. Pewarnaan
G r a f. Pendahuluan. Oleh: Panca Mudjirahardjo. Graf digunakan untuk merepresentasikan objek-objek diskrit dan hubungan antara objek-objek tersebut.
 G r a f Oleh: Panca Mudjirahardjo Pendahuluan Graf digunakan untuk merepresentasikan objek-objek diskrit dan hubungan antara objek-objek tersebut. 1 Pendahuluan Jaringan jalan raya di propinsi Jawa Tengah
G r a f Oleh: Panca Mudjirahardjo Pendahuluan Graf digunakan untuk merepresentasikan objek-objek diskrit dan hubungan antara objek-objek tersebut. 1 Pendahuluan Jaringan jalan raya di propinsi Jawa Tengah
KAITAN ANTARA DIMENSI METRIK DAN DIMENSI PARTISI PADA SUATU GRAF. (Skripsi) Oleh GIOVANNY THEOTISTA
 KAITAN ANTARA DIMENSI METRIK DAN DIMENSI PARTISI PADA SUATU GRAF (Skripsi) Oleh GIOVANNY THEOTISTA JURUSAN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG 2016 ABSTRAK STUDI
KAITAN ANTARA DIMENSI METRIK DAN DIMENSI PARTISI PADA SUATU GRAF (Skripsi) Oleh GIOVANNY THEOTISTA JURUSAN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG 2016 ABSTRAK STUDI
BAB 2 GRAF PRIMITIF. 2.1 Definisi Graf
 BAB 2 GRAF PRIMITIF Pada Bagian ini akan dijelaskan beberapa definisi dan teorema terkait graf, matriks adjency, terhubung, primitifitas, dan scrambling index sebagai landasan teori yang menjadi acuan
BAB 2 GRAF PRIMITIF Pada Bagian ini akan dijelaskan beberapa definisi dan teorema terkait graf, matriks adjency, terhubung, primitifitas, dan scrambling index sebagai landasan teori yang menjadi acuan
DIMENSI METRIK PADA GRAF LINTASAN, GRAF KOMPLIT, GRAF SIKEL, GRAF BINTANG DAN GRAF BIPARTIT KOMPLIT
 DIMENSI METRIK PADA GRAF LINTASAN, GRAF KOMPLIT, GRAF SIKEL, GRAF BINTANG DAN GRAF BIPARTIT KOMPLIT Septiana Eka R. Jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam,Universitas Negeri
DIMENSI METRIK PADA GRAF LINTASAN, GRAF KOMPLIT, GRAF SIKEL, GRAF BINTANG DAN GRAF BIPARTIT KOMPLIT Septiana Eka R. Jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam,Universitas Negeri
Bab 2 TEORI DASAR. 2.1 Graf
 Bab 2 TEORI DASAR Pada bab ini akan dipaparkan beberapa definisi dasar dalam Teori Graf yang kemudian dilanjutkan dengan definisi bilangan kromatik lokasi, serta menyertakan beberapa hasil penelitian sebelumnya.
Bab 2 TEORI DASAR Pada bab ini akan dipaparkan beberapa definisi dasar dalam Teori Graf yang kemudian dilanjutkan dengan definisi bilangan kromatik lokasi, serta menyertakan beberapa hasil penelitian sebelumnya.
BAB II KAJIAN PUSTAKA
 BAB II KAJIAN PUSTAKA A. Logika Fuzzy Logika fuzzy pertama kali dikembangkan oleh Prof. Lotfi A. Zadeh, seorang peneliti dari Universitas California, pada tahun 1960-an. Logika fuzzy dikembangkan dari
BAB II KAJIAN PUSTAKA A. Logika Fuzzy Logika fuzzy pertama kali dikembangkan oleh Prof. Lotfi A. Zadeh, seorang peneliti dari Universitas California, pada tahun 1960-an. Logika fuzzy dikembangkan dari
BAB 2 BEBERAPA ISTILAH DARI GRAPH
 BAB 2 BEBERAPA ISTILAH DARI GRAPH Pada bab ini akan dibahas beberapa konsep dan terminologi dalam graph yang akan dipergunakan sebagai landasan berpikir dalam melakukan penelitian ini. Juga akan dibahas
BAB 2 BEBERAPA ISTILAH DARI GRAPH Pada bab ini akan dibahas beberapa konsep dan terminologi dalam graph yang akan dipergunakan sebagai landasan berpikir dalam melakukan penelitian ini. Juga akan dibahas
Eksentrik Digraf dari Graf Star, Graf Double Star, dan Graf Komplit Bipartit
 Eksentrik Digraf dari Graf Star, Graf Double Star, dan Graf Komplit Bipartit Charles Hariyadi Jurusan Teknik Informatika, Institut Teknologi Bandung Bandung if15105@students.if.itb.ac.id(13505105) Abstrak
Eksentrik Digraf dari Graf Star, Graf Double Star, dan Graf Komplit Bipartit Charles Hariyadi Jurusan Teknik Informatika, Institut Teknologi Bandung Bandung if15105@students.if.itb.ac.id(13505105) Abstrak
PENENTUAN BILANGAN DOMINASI SISI PADA GRAF HASIL OPERASI PRODUK TENSOR
 TESIS - SM 142501 PENENTUAN BILANGAN DOMINASI SISI PADA GRAF HASIL OPERASI PRODUK TENSOR ROBIATUL ADAWIYAH NRP 1214 201 019 DOSEN PEMBIMBING Dr. Darmaji, S.Si., M.T. PROGRAM MAGISTER JURUSAN MATEMATIKA
TESIS - SM 142501 PENENTUAN BILANGAN DOMINASI SISI PADA GRAF HASIL OPERASI PRODUK TENSOR ROBIATUL ADAWIYAH NRP 1214 201 019 DOSEN PEMBIMBING Dr. Darmaji, S.Si., M.T. PROGRAM MAGISTER JURUSAN MATEMATIKA
ALTERNATIF PEMBUKTIAN DAN PENERAPAN TEOREMA BONDY. Hasmawati Jurusan Matematika, Fakultas Mipa Universitas Hasanuddin
 ALTERNATIF PEMBUKTIAN DAN PENERAPAN TEOREMA BONDY Hasmawati Jurusan Matematika, Fakultas Mipa Universitas Hasanuddin hasma_ba@yahoo.com Abstract Graf yang memuat semua siklus dari yang terkecil sampai
ALTERNATIF PEMBUKTIAN DAN PENERAPAN TEOREMA BONDY Hasmawati Jurusan Matematika, Fakultas Mipa Universitas Hasanuddin hasma_ba@yahoo.com Abstract Graf yang memuat semua siklus dari yang terkecil sampai
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI Pada bab ini akan dijelaskan himpunan dan beberapa definisi yang berkaitan dengan himpunan, serta konsep dasar dan teori graf yang akan digunakan pada bab selanjutnya. 2.1 Himpunan
BAB 2 LANDASAN TEORI Pada bab ini akan dijelaskan himpunan dan beberapa definisi yang berkaitan dengan himpunan, serta konsep dasar dan teori graf yang akan digunakan pada bab selanjutnya. 2.1 Himpunan
Sebuah graf sederhana G adalah pasangan terurut G = (V, E) dengan V adalah
 BAB II KAJIAN TEORI II.1 Teori-teori Dasar Graf II.1.1 Definisi Graf Sebuah graf sederhana G adalah pasangan terurut G = (V, E) dengan V adalah himpunan tak kosong dari titik graf G, dan E, himpunan sisi
BAB II KAJIAN TEORI II.1 Teori-teori Dasar Graf II.1.1 Definisi Graf Sebuah graf sederhana G adalah pasangan terurut G = (V, E) dengan V adalah himpunan tak kosong dari titik graf G, dan E, himpunan sisi
BILANGAN KROMATIK LOKASI UNTUK GRAF POHON n-ary LENGKAP
 Jurnal Matematika UNAND Vol. VI No. 1 Hal. 90 96 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND BILANGAN KROMATIK LOKASI UNTUK GRAF POHON n-ary LENGKAP AFIFAH DWI PUTRI, NARWEN Program Studi Matematika,
Jurnal Matematika UNAND Vol. VI No. 1 Hal. 90 96 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND BILANGAN KROMATIK LOKASI UNTUK GRAF POHON n-ary LENGKAP AFIFAH DWI PUTRI, NARWEN Program Studi Matematika,
DIMENSI METRIK PENGEMBANGAN GRAF KINCIR POLA K 1 + mk 3
 J. Math. and Its Appl. ISSN: 1829-605X Vol. 8, No. 2, November 2011, 17 22 DIMENSI METRIK PENGEMBANGAN GRAF KINCIR POLA K 1 + mk 3 Suhud Wahyudi, Sumarno, Suharmadi Jurusan Matematika, FMIPA ITS Surabaya
J. Math. and Its Appl. ISSN: 1829-605X Vol. 8, No. 2, November 2011, 17 22 DIMENSI METRIK PENGEMBANGAN GRAF KINCIR POLA K 1 + mk 3 Suhud Wahyudi, Sumarno, Suharmadi Jurusan Matematika, FMIPA ITS Surabaya
DIMENSI PARTISI PADA GRAF ANTIPRISMA, GRAF MONGOLIAN TENT, DAN GRAF STACKED BOOK
 DIMENSI PARTISI PADA GRAF ANTIPRISMA, GRAF MONGOLIAN TENT, DAN GRAF STACKED BOOK oleh TIA APRILIANI M0112086 SKRIPSI ditulis dan diajukan untuk memenuhi sebagian persyaratan memperoleh gelar Sarjana Sains
DIMENSI PARTISI PADA GRAF ANTIPRISMA, GRAF MONGOLIAN TENT, DAN GRAF STACKED BOOK oleh TIA APRILIANI M0112086 SKRIPSI ditulis dan diajukan untuk memenuhi sebagian persyaratan memperoleh gelar Sarjana Sains
Penerapan Teorema Bondy pada Penentuan Bilangan Ramsey Graf Bintang Terhadap Graf Roda
 Vol. 9, No.2, 114-122, Januari 2013 Penerapan Teorema Bondy pada Penentuan Bilangan Ramsey Graf Bintang Terhadap Graf Roda Hasmawati 1 Abstrak Graf yang memuat semua siklus dari yang terkecil sampai ke
Vol. 9, No.2, 114-122, Januari 2013 Penerapan Teorema Bondy pada Penentuan Bilangan Ramsey Graf Bintang Terhadap Graf Roda Hasmawati 1 Abstrak Graf yang memuat semua siklus dari yang terkecil sampai ke
Graf. Matematika Diskrit. Materi ke-5
 Graf Materi ke-5 Pendahuluan Graf digunakan untuk merepresentasikan objek-objek diskrit dan hubungan antara objek-objek tersebut. Gambar di bawah ini sebuah graf yang menyatakan peta jaringan jalan raya
Graf Materi ke-5 Pendahuluan Graf digunakan untuk merepresentasikan objek-objek diskrit dan hubungan antara objek-objek tersebut. Gambar di bawah ini sebuah graf yang menyatakan peta jaringan jalan raya
HAND OUT MATA KULIAH TEORI GRAF (MT 424) JILID SATU. Oleh: Kartika Yulianti, S.Pd., M.Si.
 HAND OUT MATA KULIAH TEORI GRAF (MT 424) JILID SATU Oleh: Kartika Yulianti, S.Pd., M.Si. JURUSAN PENDIDIKAN MATEMATIKA FAKULTAS PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS PENDIDIKAN INDONESIA
HAND OUT MATA KULIAH TEORI GRAF (MT 424) JILID SATU Oleh: Kartika Yulianti, S.Pd., M.Si. JURUSAN PENDIDIKAN MATEMATIKA FAKULTAS PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS PENDIDIKAN INDONESIA
BAB II TINJAUAN PUSTAKA. elemen-elemennya disebut dengan vertex (titik/node), sedangkan E yang mungkin kosong
 BAB II TINJAUAN PUSTAKA A. Graf Graf G adalah suatu struktur (V, E) dimana V merupakan himpunan tak kosong dengan elemen-elemennya disebut dengan vertex (titik/node), sedangkan E yang mungkin kosong merupakan
BAB II TINJAUAN PUSTAKA A. Graf Graf G adalah suatu struktur (V, E) dimana V merupakan himpunan tak kosong dengan elemen-elemennya disebut dengan vertex (titik/node), sedangkan E yang mungkin kosong merupakan
oleh BANGKIT JOKO WIDODO M SKRIPSI ditulis dan diajukan untuk memenuhi sebagian persyaratan memperoleh gelar Sarjana Sains Matematika
 DIMENSI METRIK PADA GRAF SUN, GRAF HELM DAN GRAF DOUBLE CONES oleh BANGKIT JOKO WIDODO M0109015 SKRIPSI ditulis dan diajukan untuk memenuhi sebagian persyaratan memperoleh gelar Sarjana Sains Matematika
DIMENSI METRIK PADA GRAF SUN, GRAF HELM DAN GRAF DOUBLE CONES oleh BANGKIT JOKO WIDODO M0109015 SKRIPSI ditulis dan diajukan untuk memenuhi sebagian persyaratan memperoleh gelar Sarjana Sains Matematika
DIGRAF EKSENTRIK DARI GRAF STAR DAN GRAF WHEEL
 DIGRAF EKSENTRIK DARI GRAF STAR DAN GRAF WHEEL skripsi disajikan sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains Program Studi Matematika oleh Rido Oktosa 4150406504 JURUSAN MATEMATIKA FAKULTAS
DIGRAF EKSENTRIK DARI GRAF STAR DAN GRAF WHEEL skripsi disajikan sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains Program Studi Matematika oleh Rido Oktosa 4150406504 JURUSAN MATEMATIKA FAKULTAS
TEORI GRAF UNIVERSITAS MUHAMMADIYAH JEMBER ILHAM SAIFUDIN PROGRAM STUDI TEKNIK INFORMATIKA FAKULTAS TEKNIK. Selasa, 13 Desember 2016
 PROGRAM STUDI TEKNIK INFORMATIKA FAKULTAS TEKNIK UNIVERSITAS MUHAMMADIYAH JEMBER TEORI GRAF ILHAM SAIFUDIN Selasa, 13 Desember 2016 Universitas Muhammadiyah Jember Pendahuluan 1 OUTLINE 2 Definisi Graf
PROGRAM STUDI TEKNIK INFORMATIKA FAKULTAS TEKNIK UNIVERSITAS MUHAMMADIYAH JEMBER TEORI GRAF ILHAM SAIFUDIN Selasa, 13 Desember 2016 Universitas Muhammadiyah Jember Pendahuluan 1 OUTLINE 2 Definisi Graf
Konsep. Graph adalah suatu diagram yang memuat informasi tertentu. Contoh : Struktur organisasi
 GRPH 1 Konsep Graph adalah suatu diagram yang memuat informasi tertentu. Contoh : Struktur organisasi 2 Contoh Graph agan alir pengambilan mata kuliah 3 Contoh Graph Peta 4 5 Dasar-dasar Graph Suatu graph
GRPH 1 Konsep Graph adalah suatu diagram yang memuat informasi tertentu. Contoh : Struktur organisasi 2 Contoh Graph agan alir pengambilan mata kuliah 3 Contoh Graph Peta 4 5 Dasar-dasar Graph Suatu graph
Graf. Program Studi Teknik Informatika FTI-ITP
 Graf Program Studi Teknik Informatika FTI-ITP Pendahuluan Graf digunakan untuk merepresentasikan objek-objek diskrit dan hubungan antara objek-objek tersebut. Gambar di bawah ini sebuah graf yang menyatakan
Graf Program Studi Teknik Informatika FTI-ITP Pendahuluan Graf digunakan untuk merepresentasikan objek-objek diskrit dan hubungan antara objek-objek tersebut. Gambar di bawah ini sebuah graf yang menyatakan
DIMENSI PARTISI PADA GRAPH HASIL KORONA C m K n. Oleh : Yogi Sindy Prakoso ( ) JURUSAN MATEMATIKA. Company
 DIMENSI PARTISI PADA GRAPH HASIL KORONA C m K n Oleh : Yogi Sindy Prakoso (1206100015) JURUSAN MATEMATIKA Company FAKULTAS MATEMATIKA Click to DAN add ILMU subtitle PENGETAHUAN ALAM INSTITUT TEKNOLOGI
DIMENSI PARTISI PADA GRAPH HASIL KORONA C m K n Oleh : Yogi Sindy Prakoso (1206100015) JURUSAN MATEMATIKA Company FAKULTAS MATEMATIKA Click to DAN add ILMU subtitle PENGETAHUAN ALAM INSTITUT TEKNOLOGI
Graf dan Operasi graf
 6 Bab II Graf dan Operasi graf Dalam subbab ini akan diberikan konsep dasar, definisi dan notasi pada teori graf yang dipergunakan dalam penulisan disertasi ini. Konsep dasar tersebut ditulis sesuai dengan
6 Bab II Graf dan Operasi graf Dalam subbab ini akan diberikan konsep dasar, definisi dan notasi pada teori graf yang dipergunakan dalam penulisan disertasi ini. Konsep dasar tersebut ditulis sesuai dengan
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI.. Definisi Graf Secara matematis, graf G didefinisikan sebagai pasangan himpunan (V,E) ditulis dengan notasi G = (V, E), yang dalam hal ini: V = himpunan tidak-kosong dari simpul-simpul
BAB II LANDASAN TEORI.. Definisi Graf Secara matematis, graf G didefinisikan sebagai pasangan himpunan (V,E) ditulis dengan notasi G = (V, E), yang dalam hal ini: V = himpunan tidak-kosong dari simpul-simpul
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI 2.1 Terminologi graf Tereminologi termasuk istilah yang berkaitan dengan graf. Di bawah ini akan dijelaskan beberapa definisi yang sering dipakai terminologi. 2.1.1 Graf Definisi
BAB II LANDASAN TEORI 2.1 Terminologi graf Tereminologi termasuk istilah yang berkaitan dengan graf. Di bawah ini akan dijelaskan beberapa definisi yang sering dipakai terminologi. 2.1.1 Graf Definisi
DIMENSI METRIK PADA BEBERAPA KELAS GRAF
 DIMENSI METRIK PADA BEBERAPA KELAS GRAF oleh DWI RIA KARTIKA M0112025 SKRIPSI ditulis dan diajukan untuk memenuhi sebagian persyaratan memperoleh gelar Sarjana Sains Matematika FAKULTAS MATEMATIKA DAN
DIMENSI METRIK PADA BEBERAPA KELAS GRAF oleh DWI RIA KARTIKA M0112025 SKRIPSI ditulis dan diajukan untuk memenuhi sebagian persyaratan memperoleh gelar Sarjana Sains Matematika FAKULTAS MATEMATIKA DAN
Struktur dan Organisasi Data 2 G R A P H
 G R A P H Graf adalah : Himpunan V (Vertex) yang elemennya disebut simpul (atau point atau node atau titik) Himpunan E (Edge) yang merupakan pasangan tak urut dari simpul, anggotanya disebut ruas (rusuk
G R A P H Graf adalah : Himpunan V (Vertex) yang elemennya disebut simpul (atau point atau node atau titik) Himpunan E (Edge) yang merupakan pasangan tak urut dari simpul, anggotanya disebut ruas (rusuk
DIMENSI METRIK PADA GRAF LOLLIPOP, GRAF MONGOLIAN TENT, DAN GRAF GENERALIZED JAHANGIR
 DIMENSI METRIK PADA GRAF LOLLIPOP, GRAF MONGOLIAN TENT, DAN GRAF GENERALIZED JAHANGIR oleh ARDINA RIZQY RACHMASARI M0112013 SKRIPSI ditulis dan diajukan untuk memenuhi sebagian persyaratan memperoleh gelar
DIMENSI METRIK PADA GRAF LOLLIPOP, GRAF MONGOLIAN TENT, DAN GRAF GENERALIZED JAHANGIR oleh ARDINA RIZQY RACHMASARI M0112013 SKRIPSI ditulis dan diajukan untuk memenuhi sebagian persyaratan memperoleh gelar
Mizan Ahmad, Tri Atmojo Kusmayadi Program Studi Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sebelas Maret. 1.
 DIMENSI PARTISI PADA GRAF C m K n, GRAF C m [P n ], DAN GRAF t-fold WHEEL Mizan Ahmad, Tri Atmojo Kusmayadi Program Studi Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sebelas Maret
DIMENSI PARTISI PADA GRAF C m K n, GRAF C m [P n ], DAN GRAF t-fold WHEEL Mizan Ahmad, Tri Atmojo Kusmayadi Program Studi Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sebelas Maret
BILANGAN KROMATIK LOKASI DARI GRAF ULAT
 Jurnal Matematika UNAND Vol. 5 No. 1 Hal. 1 6 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND BILANGAN KROMATIK LOKASI DARI GRAF ULAT AIDILLA DARMAWAHYUNI, NARWEN Program Studi Matematika, Fakultas Matematika
Jurnal Matematika UNAND Vol. 5 No. 1 Hal. 1 6 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND BILANGAN KROMATIK LOKASI DARI GRAF ULAT AIDILLA DARMAWAHYUNI, NARWEN Program Studi Matematika, Fakultas Matematika
Kode MK/ Matematika Diskrit
 Kode MK/ Matematika Diskrit TEORI GRAF 1 8/29/2014 Cakupan Himpunan, Relasi dan fungsi Kombinatorial Teori graf Pohon (Tree) dan pewarnaan graf 2 8/29/2014 1 TEORI GRAF Tujuan Mahasiswa memahami konsep
Kode MK/ Matematika Diskrit TEORI GRAF 1 8/29/2014 Cakupan Himpunan, Relasi dan fungsi Kombinatorial Teori graf Pohon (Tree) dan pewarnaan graf 2 8/29/2014 1 TEORI GRAF Tujuan Mahasiswa memahami konsep
`BAB II LANDASAN TEORI
 `BAB II LANDASAN TEORI Landasan teori yang digunakan sebagai materi pendukung untuk menyelesaikan permasalahan yang dibahas dalam Bab IV adalah teori graf, subgraf, subgraf komplit, graf terhubung, graf
`BAB II LANDASAN TEORI Landasan teori yang digunakan sebagai materi pendukung untuk menyelesaikan permasalahan yang dibahas dalam Bab IV adalah teori graf, subgraf, subgraf komplit, graf terhubung, graf
Pertemuan 12. Teori Graf
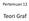 Pertemuan 2 Teori Graf Derajat Definisi Misalkan adalah titik dalam suatu Graf G. Derajat titik (simbol d()) adalah jumlah garis yang berhubungan dengan titik dan garis suatu loop dihitung dua kali. Derajat
Pertemuan 2 Teori Graf Derajat Definisi Misalkan adalah titik dalam suatu Graf G. Derajat titik (simbol d()) adalah jumlah garis yang berhubungan dengan titik dan garis suatu loop dihitung dua kali. Derajat
merupakan himpunan sisi-sisi tidak berarah pada. (Yaoyuenyong et al. 2002)
 dari elemen graf yang disebut verteks (node, point), sedangkan, atau biasa disebut (), adalah himpunan pasangan tak terurut yang menghubungkan dua elemen subset dari yang disebut sisi (edge, line). Setiap
dari elemen graf yang disebut verteks (node, point), sedangkan, atau biasa disebut (), adalah himpunan pasangan tak terurut yang menghubungkan dua elemen subset dari yang disebut sisi (edge, line). Setiap
PENENTUAN DIMENSI METRIK GRAF HELM
 PENENTUAN DIMENSI METRIK GRAF HELM SKRIPSI Oleh : DIAN FIRMAYASARI S NIM : H 111 08 011 JURUSAN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS HASANUDDIN MAKASSAR 2012 PENENTUAN DIMENSI
PENENTUAN DIMENSI METRIK GRAF HELM SKRIPSI Oleh : DIAN FIRMAYASARI S NIM : H 111 08 011 JURUSAN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS HASANUDDIN MAKASSAR 2012 PENENTUAN DIMENSI
DIMENSI PARTISI DARI GRAF ULAT
 Jurnal Matematika UNAND Vol. 5 No. 3 Hal. 1 6 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND DIMENSI PARTISI DARI GRAF ULAT FADHILA TURRAHMAH, BUDI RUDIANTO Program Studi Matematika, Fakultas Matematika
Jurnal Matematika UNAND Vol. 5 No. 3 Hal. 1 6 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND DIMENSI PARTISI DARI GRAF ULAT FADHILA TURRAHMAH, BUDI RUDIANTO Program Studi Matematika, Fakultas Matematika
BAB 2 GRAF PRIMITIF. 2.1 Definisi Graf
 BAB 2 GRAF PRIMITIF Pada bab ini akan dijelaskan beberapa konsep dasar seperti definisi dan teorema yang dijadikan landasan teori dalam penelitian ini. Konsep dasar tersebut berkaitan dengan definisi graf,
BAB 2 GRAF PRIMITIF Pada bab ini akan dijelaskan beberapa konsep dasar seperti definisi dan teorema yang dijadikan landasan teori dalam penelitian ini. Konsep dasar tersebut berkaitan dengan definisi graf,
I. LANDASAN TEORI. Seperti yang telah dipaparkan pada bab sebelumnya, teori graf merupakan salah satu ilmu
 I. LANDASAN TEORI Seperti yang telah dipaparkan pada bab sebelumnya, teori graf merupakan salah satu ilmu matematika yang mempresentasikan suatu objek berupa vertex (titik) dan edge (garis), edge merupakan
I. LANDASAN TEORI Seperti yang telah dipaparkan pada bab sebelumnya, teori graf merupakan salah satu ilmu matematika yang mempresentasikan suatu objek berupa vertex (titik) dan edge (garis), edge merupakan
ALTERNATIF PEMBUKTIAN PENGEMBANGAN TEOREMA DIRAC UNTUK GRAF BERORDE KURANG ATAU SAMA DENGAN SEPULUH
 ALTERNATIF PEMBUKTIAN PENGEMBANGAN TEOREMA DIRAC UNTUK GRAF BERORDE KURANG ATAU SAMA DENGAN SEPULUH Hasmawati, Jusmawati Massalesse, Hendra, Muhamad Hasbi Jurusan Matematika FMIPA Universitas Hasanudin
ALTERNATIF PEMBUKTIAN PENGEMBANGAN TEOREMA DIRAC UNTUK GRAF BERORDE KURANG ATAU SAMA DENGAN SEPULUH Hasmawati, Jusmawati Massalesse, Hendra, Muhamad Hasbi Jurusan Matematika FMIPA Universitas Hasanudin
Gambar8.1. Contoh Graf
 MATERI 10 Definisi Graf Diagram yang memuat informasi tertentu dan dilambangkan dengan suatu keterhubungan antar titik. Menggambarkan berbagai macam struktur yang ada, misalnya: struktur organisasi, rute
MATERI 10 Definisi Graf Diagram yang memuat informasi tertentu dan dilambangkan dengan suatu keterhubungan antar titik. Menggambarkan berbagai macam struktur yang ada, misalnya: struktur organisasi, rute
BAB III PELABELAN KOMBINASI
 1 BAB III PELABELAN KOMBINASI 3.1 Konsep Pelabelan Kombinasi Pelabelan kombinasi dari suatu graf dengan titik dan sisi,, graf G, disebut graf kombinasi jika terdapat fungsi bijektif dari ( himpunan titik
1 BAB III PELABELAN KOMBINASI 3.1 Konsep Pelabelan Kombinasi Pelabelan kombinasi dari suatu graf dengan titik dan sisi,, graf G, disebut graf kombinasi jika terdapat fungsi bijektif dari ( himpunan titik
BAB I PENDAHULUAN. himpunan bagian bilangan cacah yang disebut label. Pertama kali diperkenalkan
 1 BAB I PENDAHULUAN 1.1. Latar Belakang Pelabelan graf merupakan suatu topik dalam teori graf. Objek kajiannya berupa graf yang secara umum direpresentasikan oleh titik dan sisi serta himpunan bagian bilangan
1 BAB I PENDAHULUAN 1.1. Latar Belakang Pelabelan graf merupakan suatu topik dalam teori graf. Objek kajiannya berupa graf yang secara umum direpresentasikan oleh titik dan sisi serta himpunan bagian bilangan
