OPTIMASI FUNGSI MULTI VARIABEL DENGAN METODE UNIVARIATE. Dwi Suraningsih (M ), Marifatun (M ), Nisa Karunia (M )
|
|
|
- Hartono Sanjaya
- 6 tahun lalu
- Tontonan:
Transkripsi
1 OPTIMASI FUNGSI MULTI VARIABEL DENGAN METODE UNIVARIATE Dwi Suraningsih (M2, Marifatun (M53, Nisa Karunia (M6 I. Pendahuluan Latar Belakang. Dalam kehidupan sehari-hari disa maupun tidak, sebenarnya manusia selalu melakukan opimasi untuk memenuhi kebutuhan hidupnya. Akan tetapi, optimasi yang dilakukan oleh masyarakat awam lebih banyak didasar oleh intuisi pada teori optimasi yang kita pelajari di bangku sekolah. Optimasi merupakan masalah yang berhubungan dengan keputusan terbaik, maksimum, minimum dan memberikan cara penentuan solusi yang memuaskan. Fungsi multivariabel yaitu fungsi yang mengandung lebih satu macam variabel bebas. Nilai-nilai ekstrim (maksimum/minimum sebuah fungsi multivariabel dapat dengan menggunakan konsep diferensial parsial. Pada umumnya pemodelan nonlinear tanpa kendala berbentuk: minimumkan: (,,,. Atau Pada masalah optimasi untuk fungsi lebih satu variabel, masalah minimisasi mempunyai bentuk: minimumkan ( dengan. Masalah maksimisasi dapat ditinjau lewat metode minimisasi karena: maksimum ( minimum( (. dimana (,,, adalah fungsi objektif. Pada permasalahan program nonlinear tanpa kendala, kondisi penting untuk x* agar menjadi lokal minimum (,,,. a. (,,,. dapat diturunkan (differensiable pada x*. b. ( sebuah titik stationer (stationery point pada x*. c. definit positif (kondisi untuk maksimum adalah sama, kecuali matriks Hessian ( f(x* harus definit negatif. Pada beberapa kasus tertentu, kondisi di atas dulit dipenuhi meskipun ( tetap mempunyai titik optimum. Dalam hal ini dapat digunakan metode unconstrained optimization technique. Metode unconstrained optimization technique dibagi menjadi dua yaitu metode penyelidikan langsung dan metode gradien. Dalam hal ini hanya akan dibahas mengenai metode penyelidikan langsung (metode Univariata/One At A Time. Perumusan Masalah. Berdasarkan latar belakang yang telah disampaikan dapat dirumuskan masalah sebagai berikut :. bagaimana algoritma atau langkah-langkah dalam metode Univariate dan 2. bagaimana menerapkan metode Univariate dalam suatu kasus. Tujuan. Tujuan penulisan makalah ini adalah. menjelaskan algoritma atau langkah-langkah dalam metode Univariate dan 2. menerapkan metode Univariate dalam suatu kasus.
2 2. Pembahasan Metode Univariate. Dalam metode Univariate, perubahan dilakukan pada satu variabel tahap bertahap dengan menganggap variabel lainnya tetap. Mula mula variabel pertama dirubah pada titik awal untuk mendapat titik. Kemudian sebagai titik awal dipakai untuk merubah variabel kedua untuk mendapatkan dengan menganggap variabel pertama, ketiga, dan seterusnya tetap. Proses ini dilanjutkan sampai didapat dalam perubahan variabel ke. Dan satu siklus proses iterasi telah selesai. Prosedur ini dilanjutkan sampai tidak ada lagi perubahan fungsiobjektif untuk arah satu siklus. {Skema iterasi unconstrained minimization methods terlampir} Algoritma Algoritma atau langkah langkah metode ini dapat dinyatakan sebagai :. Menentukan titik awal dengan 2. Menentukan arah pencarian (descent direction (,,,,,, 2, (,,,,,, 2, (,,,,, 2, 3, dengan adalah banyaknya variabel fungsi (,,,. Misal: jika diketahui suatu fungsi (,,, maka 3. Berarti,,,, dan seterusnya berulang sampai iterasi berhenti. 3. Menentukan apakah berkurang dalam arah atau. Dalam langkah ini, perlu diambil panjang dan menghitung : ( ( ( Jika <, maka adalah arah yang tepat untuk meminimumkan. Jika <, maka adalah arah yang tepat untuk meminimumkan. 4. Menentukan optimum panjang langkah dengan meminimumkan fungsi ( ±. Di mana nilai adalah nilai minimum fungsi tersebut. Catatan : Pemakaian tanda atau pada fungsi ( ± bergantung pada atau yang merupakan arah penurunan nilai fungsi obyektif. Minimum dengan menggunakan konsep minimum lokal yaitu ( dan ( > yang berarti merupakan titik minimum. 5. Mencari ± dan ( 6. Mengambil nilai baru untuk dan kembali ke langkah 2. Hal ini dilanjutkan sampai tak ada perubahan yang berarti nilai fungsi objektif atau dengan kata lain iterasi STOP ketika nilai > dan >.
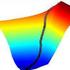
3 Contoh Kasus Minimumkan (, 2 2. menggunakan metode univariate. dengan titik awal (, dan Penyelesaian: {Gambar Plot dan Contour Plot terlampir} Iterasi k Step : titik awal (, ( (,.2 > ( (,.9996 < ( adalah arah yang tepat untuk meminimumkan Step 4 : menentukan optimum panjang dengan meminimumkan ( (, 2 min 2 4 Karena Step 5 : ambil ( Iterasi k Step : titik awal >, maka adalah titik minimum..25 dan (. ( 4 (.25, (.25 ( (.,,.399 <.99 > adalah arah yang tepat untuk meminimumkan. Step 4 : menentukan optimum panjang dengan meminimumkan ( (.25,.5.25 min.5.25 ( karena ( Step 5 : ambil Iterasi k 2 Step : titik awal.75 (2.5 2 >, maka.75 titik minimum..25 dan ( (.25,.75 ( > (.723 < ( adalah arah yang tepat untuk meminimumkan Step 4 : menentukan optimum panjang dengan meminimumkan.
4 ( min 2 4 (.25, Step 5 : ambil Iterasi k 3 Step : titik awal dan.75 ( (.625,.75 ( ( (.625, < (.625, > ( adalah arah yang tepat untuk meminimumkan (penyelesain arah positif Step 4 : menentukan optimum panjang dengan meminimumkan ( sehingga Step 5 : menghitung Iterasi k 4 Step : titik awal (.625,.25 (.938 (.65, > ( (.635, < ( adalah arah yang tepat untuk meminimumkan (penyelesaian arah negatif Step 4 : menentukan optimum panjang dengan meminimumkan ( sehingga.875 (.825,.25. Iterasi k 5 Step : titik awal ( -.825,.25 (.7969 (.825, < ( (.825, > ( adalah arah yang tepat untuk meminimumkan (penyelesaian arah positif (.825,.325 Iterasi k 6 Step : titik awal (.825,.325 (.2484
5 (.825, > ( (.8225, < ( adalah arah yang tepat untuk meminimumkan (penyelesaian arah negatif (.9625,.325 Iterasi k 7 Step : titik awal (.9625,.325 ( (.9625, < ( (.9625, > ( adalah arah yang tepat untuk meminimumkan (penyelesaian arah positif (.9625,.4625 Iterasi k 8 Step : titik awal (.9625,.4625 (.242 (.89625, > ( (.9625, < ( adalah arah yang tepat untuk meminimumkan (penyelesaian arah negatif (.95325,.4625 Iterasi k 9 Step : titik awal (.95325,.4625 (.2456 (.95325, < ( (.95325, > ( adalah arah yang tepat untuk meminimumkan (penyelesaian arah positif (.95325,.4533 Iterasi k Step : titik awal x( ,.4533 U (.2478 (.94325, > ( (.96325, < (
6 (penyelesaian arah negatif ( ,.4533 Iterasi k Step : titik awal ( ,.4533 (.2489 ( , < ( (.96325, > ( (penyelesaian arah positif ( , Iterasi k 2 Step : titik awal ( , ( ( , > ( ( , < ( (penyelesaian arah negatif ( , Iterasi k 3 Step : titik awal ( , ( ( , < ( ( , > ( (penyelesaian arah positif ( , Iterasi k 4 Step : titik awal ( , ( ( , > ( ( , < ( (penyelesaian arah negatif.
7 (.9944, Iterasi k 5 Step : titik awal (.9944, ( (.9944, < ( (.9944, > ( (penyelesaian arah positif (.9944, Iterasi k 6 Step : titik awal (.9944,.4944 (.2499 (.9844, > ( (.44, < ( (penyelesaian arah negatif (., Iterasi k 7 Step : titik awal (.,.4944 ( (., < ( (., > ( (penyelesaian arah positif (.,.5. Iterasi k 8 Step : titik awal (.,.5 (.25 (., > ( (., > ( Iterasi STOP. Sehingga (.,.5 dan (.25
8 ( Minimumkan (, (. menggunakan metode univariate. Penyelesaian: {Gambar Plot terlampir} Iterasi k Step : menentukan titik awal (, Step 2 : menentukan arah pencarian dengan titik awal (, dan ( (.,.8 > ( (.,.2 > ( Iterasi STOP, sehingga (, dan (
9 3. Penutup Kesimpulan. Kesimpulan yang dapat diambil pembahasan adalah: Algoritma metode Univariate dapat dinyatakan sebagai:. Menentukan titik awal dengan 2. Menentukan arah pencarian (descent direction (,,,,,, 2, (,,,,,, 2, (,,,,, 2, 3, dengan adalah banyaknya variabel fungsi (,,,. Misal : jika diketahui suatu fungsi (,,, maka 3. Berarti,,,, dan seterusnya berulang sampai iterasi berhenti. 3. Menentukan apakah berkurang dalam arah atau. Dalam langkah ini, perlu diambil panjang dan menghitung : ( ( ( Jika <, maka adalah arah yang tepat untuk meminimumkan. Jika <, maka adalah arah yang tepat untuk meminimumkan. 4. Menentukan optimum panjang langkah dengan meminimumkan fungsi ( ±. Di mana nilai adalah nilai minimum fungsi tersebut. Catatan : Pemakaian tanda atau pada fungsi ( ± bergantung pada atau yang merupakan arah penurunan nilai fungsi obyektif. Minimum dengan menggunakan konsep minimum lokal ( dan ( > yang berarti yaitu merupakan titik minimum. 5. Mencari ± dan ( 6. Mengambil nilai baru untuk dan kembali ke langkah 2. Hal ini dilanjutkan sampai tak ada perubahan yang berarti nilai fungsi objektif atau dengan kata lain iterasi STOP ketika nilai > dan >. Dari contoh kasus, minimum dengan (.,.5 dan (.25. Sedangkan contoh kasus 2, minimum dengan (, dan (.
10 LAMPIRAN LAMPIRAN Ambil k Tentukan ( Tentukan vektor baru Ambil dan STOP ya Tentukan ( Ambil kk Kekonvergenan dipenuhi? tidak Skema. Iterasi unconstrained minimization methods Gambar. Plot fungsi (, 2 2 sebelum iterasi.
11 Gambar 2. Contour plot fungsi (, iterasi. Gambar 3. Contour plot fungsi (, Gambar 4. Plot fungsi (, ( ( sebelum setelah iterasi. sebelum iterasi.
OPTIMASI FUNGSI MULTIVARIABLE TANPA KENDALA DENGAN METODE NEWTON
OPTIMASI FUNGSI MULTIVARIABLE TANPA KENDALA DENGAN METODE NEWTON Susi Ranangga [M008067], Aeroni Dwijayanti [M008078] Hamdani Citra P. [M0003], Nafi Nur Khasana [M00058]. Pendahuluan Dalam kehidupan sehari-hari
BAB 1 PENDAHULUAN. 1.1 Latar Belakang
BAB 1 PENDAHULUAN 1.1 Latar Belakang Dalam kehidupan sehari-hari baik disadari maupun tidak, optimasi selalu dilakukan untuk memenuhi kebutuhan. Tetapi optimasi yang dilakukan masyarakat awam lebih banyak
BAB 1 PENDAHULUAN. 1.1 Latar Belakang
BAB 1 PENDAHULUAN 1.1 Latar Belakang Dalam kehidupan sehari-hari baik disadari maupun tidak, sebenarnya orang selalu melakukan optimasi untuk memenuhi kebutuhannya. Tetapi optimasi yang dilakukan masyarakat
BAB 2 LANDASAN TEORI
BAB 2 LANDASAN TEORI Pada bab ini akan dijelaskan mengenai teori teori yang berhubungan dengan pembahasan ini sehingga dapat dijadikan sebagai landasan berpikir dan akan mempermudah dalam hal pembahasan
BAB I PENDAHULUAN. adalah optimasi digunakan untuk memaksimalkan keuntungan yang akan diraih
BAB I PENDAHULUAN 1.1 Latar Belakang Masalah Dalam kehidupan sehari-hari, baik disadari maupun tidak disadari, manusia sebenarnya telah melakukan upaya optimasi untuk memenuhi kebutuhan hidupnya. Akan
BAB 2 TINJAUAN PUSTAKA
BAB 2 TINJAUAN PUSTAKA 2.1 Optimasi Non-Linier Suatu permasalahan optimasi disebut nonlinier jika fungsi tujuan dan kendalanya mempunyai bentuk nonlinier pada salah satu atau keduanya. Optimasi nonlinier
BAB II KAJIAN PUSTAKA. Pada bab ini akan diberikan landasan teori tentang optimasi, fungsi, turunan,
BAB II KAJIAN PUSTAKA Pada bab ini akan diberikan landasan teori tentang optimasi, fungsi, turunan, pemrograman linear, metode simpleks, teorema dualitas, pemrograman nonlinear, persyaratan karush kuhn
METODE STEEPEST DESCENT
METODE STEEPEST DESCENT DENGAN UKURAN LANGKAH BARU UNTUK PENGOPTIMUMAN NIRKENDALA D. WUNGGULI 1, B. P. SILALAHI 2, S. GURITMAN 3 Abstrak Metode steepest descent adalah metode gradien sederhana untuk pengoptimuman.
Dr. Ir. Bib Paruhum Silalahi, M.Kom
Metode Descent Oleh : Andaikan fungsi tujuan kita adalah minf(x);x R n. Secara umum f(x) dapat berupa fungsi nonlinear. Metode-metode descent adalah metode iteratif untuk memperoleh solusi pendekatan dari
BAB 2 LANDASAN TEORI
BAB 2 LANDASAN TEORI 2.1 Pemrograman Non linier Pemrograman non linier adalah suatu bentuk pemrograman yang berhubungan dengan suatu perencanaan aktivitas tertentu yang dapat diformulasikan dalam model
Konvergensi Global Metode Spectral Conjugate Descent yang Baru Menggunakan Pencarian Garis Armijo yang Termodifikasi
42 ISSN 2302-7290 Vol. 2 No. 2, April 2014 Konvergensi Global Metode Spectral Conjugate Descent yang Baru Menggunakan Pencarian Garis Armijo yang Termodifikasi Global Convergence of the New Spectral Conjugate
SYARAT FRITZ JOHN PADA MASALAH OPTIMASI BERKENDALA KETAKSAMAAN. Caturiyati 1 Himmawati Puji Lestari 2. Abstrak
Syarat Fritz John... (Caturiyati) SYARAT FRITZ JOHN PADA MASALAH OPTIMASI BERKENDALA KETAKSAMAAN Caturiyati 1 Himmawati Puji Lestari 2 1,2 Jurusan Pendidikan Matematika FMIPA UNY 1 wcaturiyati@yahoo.com
Syarat Fritz John pada Masalah Optimasi Berkendala Ketaksamaan. Caturiyati 1 Himmawati Puji Lestari 2. Abstrak
Syarat Fritz John pada Masalah Optimasi Berkendala Ketaksamaan Caturiyati 1 Himmawati Puji Lestari 2 1,2 Jurusan Pendidikan Matematika FMIPA UNY 1 wcaturiyati@yahoo.com 2 himmawatipl@yahoo.com Abstrak
METODE STEEPEST DESCENT
METODE STEEPEST DESCENT Dosen Pengampu: Rukmono Budi Utomo M.Sc. Disusun Oleh : Linna Tri Lestari 6A1 1384202140 Diajukan sebagai tugas Ujian Akhir Semester UAS Metode Numerik UNIVERSITAS MUHAMMADIYAH
BAB 1 PENDAHULUAN. 1.1 Latar Belakang
BAB 1 PENDAHULUAN 1.1 Latar Belakang Zaman yang semakin berkembang membuat persoalan semakin kompleks, tidak terkecuali persoalan yang melibatkan persoalan matematika. Dalam pemecahannya, matematika memegang
BAB I PENDAHULUAN 1.1. Latar Belakang
BAB I PENDAHULUAN 1.1. Latar Belakang Saat ini semakin banyak permasalahan pada kehidupan sehari-hari yang memerlukan pendekatan optimisasi dalam penyelesaiannya. Sebagai contoh, misalkan sebuah perusahaan
OPTIMISASI NONLINEAR MULTIVARIABEL TANPA KENDALA DENGAN METODE DAVIDON FLETCHER POWELL
OPTIMISASI NONLINEAR MULTIVARIABEL TANPA KENDALA DENGAN METODE DAVIDON FLETCHER POWELL SKRIPSI Untuk Memenuhi Sebagian Persyaratan Guna Memperoleh Derajat Sarjana S-1 Program Studi Matematika Disusun oleh
BAB 1 PENDAHULUAN. 1.1 Latar Belakang
1 BAB 1 PENDAHULUAN 1.1 Latar Belakang Tidak semua permasalahan matematis atau perhitungan dapat diselesaikan dengan mudah. Bahkan dalam prinsip matematik, dalam memandang permasalahan, terlebih dahulu
kita menggunakan variabel semu untuk memulai pemecahan, dan meninggalkannya setelah misi terpenuhi
Lecture 4: (B) Supaya terdapat penyelesaian basis awal yang fisibel, pada kendala berbentuk = dan perlu ditambahkan variabel semu (artificial variable) pada ruas kiri bentuk standarnya, untuk siap ke tabel
METODE NUMERIK ARAH KONJUGASI
METODE NUMERIK ARAH KONJUGASI 14 Mei 2016 Diajukan untuk Memenuh Tugas Ujian Akhir Semester Mata kuliah Metode Numerik Dosen Pengampu Bapak Rukmono Budi Utomo,M.Sc Nur Aliyah 1384202043 6A1 Fakultas Keguruan
ALGORITMA MODIFIKASI BROYDEN-FLETCHER-GOLDFARB-SHANNO (MBFGS) PADA PERMASALAHAN OPTIMASI
ALGORITMA MODIFIKASI BROYDEN-FLETCHER-GOLDFARB-SHANNO (MBFGS) PADA PERMASALAHAN OPTIMASI Nama Mahasiswa : Rahmawati Erma.S. NRP : 1208100030 Jurusan : Matematika Dosen Pembimbing : 1. Subchan, M.Sc, Ph.D
BAB II LANDASAN TEORI
BAB II LANDASAN TEORI 2.1 Program Linear Program Linear adalah suatu cara yang digunakan untuk menyelesaikan masalah optimasi suatu model linear dengan berbagai kendala yang dihadapinya. Masalah program
BAB 2 LANDASAN TEORI
BAB 2 LANDASAN TEORI Pada bab ini akan dibahas beberapa pengertian dari optimasi bersyarat dengan kendala persamaan menggunakan multiplier lagrange serta penerapannya yang akan digunakan sebagai landasan
METODE PENGALI LAGRANGE DAN APLIKASINYA DALAM BIDANG EKONOMI SKRIPSI RAHMAD HIDAYAT
METODE PENGALI LAGRANGE DAN APLIKASINYA DALAM BIDANG EKONOMI SKRIPSI RAHMAD HIDAYAT 110803018 DEPARTEMEN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA MEDAN 2015 METODE
BAB I PENDAHULUAN. dilakukan masyarakat awam lebih banyak dilandasi oleh insting daripada teori
1 BAB I PENDAHULUAN 1.1 Latar Belakang Masalah Dalam kehidupan sehari-hari disadari atau tidak, sebenarnya orang selalu melakukan optimasi untuk memenuhi kebutuhannya. Tetapi optimasi yang dilakukan masyarakat
METODE NUMERIK STEEPEST DESCENT
METODE NUMERIK STEEPEST DESCENT 1 Juni 2016 Ujian Akhir Semester Untuk memenuhi ujian alhir semester mata kuliah metode numerik Selvi Kusdwi Lestari (1384202138 6A1 Pendidikan Matematika Fakultas Keguruan
BAB 3 PEMBAHASAN. 3.1 Pemodelan Nonlinear Multivariabel Tak Berkendala. Pada umumnya pemodelan nonlinear tanpa kendala berbentuk:
BAB 3 PEMBAHASAN Sebelum membahas Algoritma FletcherPowell, terlebih dahulu akan dibahas bentuk umum pemodelan nonlinear multivariabel tak berkendala. 3. Pemodelan Nonlinear Multivariabel ak Berkendala
III RELAKSASI LAGRANGE
III RELAKSASI LAGRANGE Relaksasi Lagrange merupakan salah satu metode yang terus dikembangkan dalam aplikasi pemrograman matematik. Sebagian besar konsep teoretis dari banyak aplikasi menggunakan metode
BAB 2 LANDASAN TEORI
BAB 2 LANDASAN TEORI 2.1 Pemrograman Non Linier Pemrograman Non linier merupakan pemrograman dengan fungsi tujuannya saja atau bersama dengan fungsi kendala berbentuk non linier yaitu pangkat dari variabelnya
BAB 2 TINJAUAN PUSTAKA. ini sehingga dapat dijadikan sebagai landasan berpikir dan akan mempermudah. dalam hal pembahasan hasil utama berikutnya.
BAB 2 TINJAUAN PUSTAKA Pada bab ini akan dijelaskan mengenai teori-teori yang berhubungan dengan pembahasan ini sehingga dapat dijadikan sebagai landasan berpikir dan akan mempermudah dalam hal pembahasan
BAB III PEMBAHASAN. digunakan untuk membentuk fungsi tujuan dari masalah pemrograman nonlinear
BAB III PEMBAHASAN Pada bab ini akan dijelaskan tentang konsep dasar metode kuadrat terkecil yang digunakan untuk membentuk fungsi tujuan dari masalah pemrograman nonlinear dan langkah-langkah penyelesaiannya
BAB VI. DUALITAS DAN ANALISIS POSTOPTIMAL
BAB VI. DUALITAS DAN ANALISIS POSTOPTIMAL HUBUNGAN PRIMAL-DUAL Dual adalah permasalahan PL yang diturunkan secara matematik dari primal PL tertentu. Setiap permasalahan primal selalu mempunyai pasangan
METODE STEEPEST DESCENT DENGAN UKURAN LANGKAH BARU UNTUK PENGOPTIMUMAN NIRKENDALA DJIHAD WUNGGULI
1 METODE STEEPEST DESCENT DENGAN UKURAN LANGKAH BARU UNTUK PENGOPTIMUMAN NIRKENDALA DJIHAD WUNGGULI SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR BOGOR 2015 2 3 PERNYATAAN MENGENAI TESIS DAN SUMBER INFORMASI
BAB 2 KAJIAN PUSTAKA. Menurut Asghar (2000), secara garis besar masalah optimisasi terbagi dalam beberapa tipe berikut:
BAB 2 KAJIAN PUSTAKA 2.1 Masalah Optimisasi dan Program Non Linier Menurut Asghar (2000), secara garis besar masalah optimisasi terbagi dalam beberapa tipe berikut: 1. Masalah optimisasi tanpa kendala.
ARAH KONJUGAT. dibuat guna memenuhi tugas UAS Mata Kuliah Metode Numerik Dosen: Rukmono Budi Utomo M.Sc. 4 juni Dadang Supriadi A2
ARAH KONJUGAT dibuat guna memenuhi tugas UAS Mata Kuliah Metode Numerik Dosen: Rukmono Budi Utomo M.Sc. 4 juni 2016 Dadang Supriadi 1384202098 6A2 UNIVERSITAS MUHAMMADIYAH TANGERANG FAKULTAS KEGURUAN ILMU
OPTIMASI TANAMAN PANGAN DI KOTA MAGELANG DENGAN PEMROGRAMAN KUADRATIK DAN METODE FUNGSI PENALTI EKSTERIOR
40 Jurnal Matematika Vol 6 No 2 Tahun 2017 OPTIMASI TANAMAN PANGAN DI KOTA MAGELANG DENGAN PEMROGRAMAN KUADRATIK DAN METODE FUNGSI PENALTI EKSTERIOR OPTIMIZATION OF FOOD CROPS IN MAGELANG WITH QUADRATIC
BAB 2 TINJAUAN PUSTAKA
BAB 2 TINJAUAN PUSTAKA 2.1 Program Stokastik Keputusan adalah suatu kesimpulan dari suatu proses untuk memilih tindakan yang terbaik dari sejumlah alternatif yang ada, sedangkan pengambilan keputusan adalah
BAB I PENDAHULUAN. yang dikemukakan oleh George Dantzig pada tahun Linear Programming (LP) adalah perencanaan aktivitas-aktivitas untuk
BAB I PENDAHULUAN 1.1 Latar Belakang Program Linear adalah suatu alat yang digunakan untuk menyelesaikan masalah optimasi suatu model linear dengan keterbatasan-keterbatasan sumber daya yang tersedia.
METODE NUMERIK ROSENBERG
METODE NUMERIK ROSENBERG Mata Kuliah : Metode Numerik Dosen Pengampu : Rukmono Budi Utomo, M.Sc Disusun Oleh : Rizka Apriyanti 6 A1 13840080 PROGRAM STUDI PENDIDIKAN MATEMATIKA FAKULTAS KEGURUAN DAN ILMU
What Is Greedy Technique
1 What Is Greedy Technique A technique constructing a solution through a sequence of steps, on each step it suggests a greedy grab of the best alternative available in the hope that a sequence of locally
METODE SEQUENTIAL QUADRATIC PROGRAMMING (SQP) PADA OPTIMASI NONLINIER BERKENDALA SKRIPSI
METODE SEQUENTIAL QUADRATIC PROGRAMMING (SQP) PADA OPTIMASI NONLINIER BERKENDALA SKRIPSI Diajukan sebagai salah satu syarat untuk memperoleh gelar Sarjana Program Strata Satu (S1) pada Program Studi Matematika
I PENDAHULUAN II LANDASAN TEORI
1 I PENDAHULUAN 1.1 Latar Belakang Kamar darurat (Emergency Room/ER) adalah tempat yang sangat penting peranannya pada rumah sakit. Aktivitas yang cukup padat mengharuskan kamar darurat selalu dijaga oleh
MATA KULIAH RISET OPERASIONAL
MATA KULIAH RISET OPERASIONAL [KODE/SKS : KK023311/ 2 SKS] METODE SIMPLEKS Pengubahan ke dalam bentuk baku Untuk menyempurnakan metode grafik. Diperkenalkan oleh : George B Dantzig Ciri ciri : 1. Semua
BAB 2 PROGRAM LINIER DAN TAK LINIER. Program linier (Linear programming) adalah suatu masalah matematika
BAB 2 PROGRAM LINIER DAN TAK LINIER 2.1 Program Linier Program linier (Linear programming) adalah suatu masalah matematika yang mempunyai fungsi objektif dan kendala berbentuk linier untuk meminimalkan
BAB I PENDAHULUAN. pembangunan konstruksi bangunan lebih ekonomis. artinya desain yang kuat strukturnya dan anggarannya paling kecil.
1 BAB I PENDAHULUAN A. Latar Belakang Masalah Penggunaan beton prategang pada bangunan konstruksi sipil pada masa sekarang menjadi hal yang lazim. Konstruksi dengan menggunakan beton prategang memungkinkan
II LANDASAN TEORI. suatu fungsi dalam variabel-variabel. adalah suatu fungsi linear jika dan hanya jika untuk himpunan konstanta,.
II LANDASAN TEORI Pada pembuatan model penjadwalan pertandingan sepak bola babak kualifikasi Piala Dunia FIFA 2014 Zona Amerika Selatan, diperlukan pemahaman beberapa teori yang digunakan di dalam penyelesaiannya,
Model umum metode simpleks
Model umum metode simpleks Fungsi Tujuan: Z C X C 2 X 2 C n X n S S 2 S n = NK FungsiPembatas: a X + a 2 X 2 + + a n X n + S + S 2 + + S n = b a 2 X + a 22 X 2 + + a 2n X n + S + S 2 + + S n = b 2 a m
Bab 4 SOLUSI PENGAMBILAN KEPUTUSAN. 4.1 Masalah Pengambilan Keputusan Markov dengan Pendekatan Program Linier
Bab 4 SOLUSI PENGAMBILAN KEPUTUSAN Pada bab ini akan dibahas mengenai masalah pengambilan keputusan Markov pada pengelolaan mata kuliah MA1122 Kalkulus I dengan pendekatan program linier, solusi dari masalah
BAB II KAJIAN PUSTAKA. pemrograman nonlinear, fungsi konveks dan konkaf, pengali lagrange, dan
BAB II KAJIAN PUSTAKA Kajian pustaka pada bab ini akan membahas tentang pengertian dan penjelasan yang berkaitan dengan fungsi, turunan parsial, pemrograman linear, pemrograman nonlinear, fungsi konveks
BAB II LANDASAN TEORI
BAB II LANDASAN TEORI Berikut ini adalah beberapa definisi dan teorema yang menjadi landasan dalam penentuan harga premi, fungsi permintaan, dan kesetimbangannya pada portfolio heterogen. 2.1 Percobaan
Kata Pengantar. Medan, 11 April Penulis
Kata Pengantar Puji syukur penulis panjatkan kepada Tuhan YME, bahwa penulis telah menyelesaikan tugas mata kuliah Matematika dengan membahas Numerical Optimization atau Optimasi Numerik dalam bentuk makalah.
TUGAS AKHIR ALGORITMA MODIFIKASI BROYDEN-FLETCHER-GOLDFARB- SHANNO (MBFGS) PADA PERMASALAHAN OPTIMASI
TUGAS AKHIR ALGORITMA MODIFIKASI BROYDEN-FLETCHER-GOLDFARB- SHANNO (MBFGS) PADA PERMASALAHAN OPTIMASI (ALGORITHM OF MODIFIED BROYDEN-FLETCHER-GOLDFARB- SHANNO (MBFGS ) FOR OPTIMIZATION PROBLEM ) Oleh:
I PENDAHULUAN II LANDASAN TEORI
I PENDAHULUAN 1.1 Latar Belakang Semakin tingginya mobilitas penduduk di suatu negara terutama di kota besar tentulah memiliki banyak permasalahan, mulai dari kemacetan yang tak terselesaikan hingga moda
Metode Simpleks dalam Bentuk Tabel (Simplex Method in Tabular Form) Materi Bahasan
Metode Simpleks dalam Bentuk Tabel (Simplex Method in Tabular Form) Kuliah 04 TI2231 Penelitian Operasional I 1 Materi Bahasan 1 Metode simpleks dalam bentuk tabel 2 Pemecahan untuk masalah minimisasi
BAB 1 PENDAHULUAN Latar Belakang
BAB 1 PENDAHULUAN 1.1. Latar Belakang Pengoptimalan merupakan ilmu Matematika terapan dan bertujuan untuk mencapai suatu titik optimum. Dalam kehidupan sehari-hari, baik disadari maupun tidak, sebenarnya
PERBANDINGAN METODE TRUST-REGION DENGAN METODE NEWTON-RAPHSON PADA OPTIMASI FUNGSI NON LINIER TANPA KENDALA
PERBANDINGAN METODE TRUST-REGION DENGAN METODE NEWTON-RAPHSON PADA OPTIMASI FUNGSI NON LINIER TANPA KENDALA Yully Estiningsih 1, Farikhin, Nikken Prima Puspita 3 1,,3 Jurusan Matematika FSM Universitas
Alur/flowchart perhitungan kimia komputasi
Austrian Indonesian Centre (AIC) for Computational Chemistry Jurusan Kimia - FMIPA Universitas Gadjah Mada (UGM) KIMIA KOMPUTASI Proses Optimisasi i i Geometri Drs. Iqmal Tahir, M.Si. Austrian-Indonesian
Bab 2 LANDASAN TEORI. 2.1 Pengantar Proses Stokastik
Bab 2 LANDASAN TEORI Pada bab ini akan diberikan penjelasan singkat mengenai pengantar proses stokastik dan rantai Markov, yang akan digunakan untuk analisis pada bab-bab selanjutnya. 2.1 Pengantar Proses
I PENDAHULUAN II LANDASAN TEORI
I PENDAHULUAN 1.1 Latar Belakang Sukarelawan adalah seseorang atau sekelompok orang yang secara ikhlas karena panggilan nuraninya memberikan apa yang dimilikinya tanpa mengharapkan imbalan. Sukarelawan
ALGORITMA GENETIKA PADA PEMROGRAMAN LINEAR DAN NONLINEAR
Buletin Ilmiah Mat. Stat. dan Terapannya (Bimaster) Volume 5, No. 03(2016), hal 265 274. ALGORITMA GENETIKA PADA PEMROGRAMAN LINEAR DAN NONLINEAR Abdul Azis, Bayu Prihandono, Ilhamsyah INTISARI Optimasi
PROGRAM LINEAR: METODE SIMPLEX
PROGRAM LINEAR: METODE SIMPLEX Latar Belakang Sulitnya menggambarkan grafik berdimensi banyak atau kombinasi lebih dari dua variabel. Metode grafik tidak mungkin dapat dilakukan untuk menyelesaikan masalah
METODE SEQUENTIAL QUADRATIC PROGRAMMING (SQP) UNTUK MENYELESAIKAN PERSOALAN NONLINEAR BERKENDALA SKRIPSI YANI
METODE SEQUENTIAL QUADRATIC PROGRAMMING (SQP) UNTUK MENYELESAIKAN PERSOALAN NONLINEAR BERKENDALA SKRIPSI YANI 070803040 DEPARTEMEN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA
OPTIMASI (Pemrograman Non Linear)
OPTIMASI (Pemrograman Non Linear) 3 SKS PILIHAN Arrival Rince Putri, 013 1 Silabus I. Pendahuluan 1. Perkuliahan: Silabus, Referensi, Penilaian. Pengantar Optimasi 3. Riview Differential Calculus II. Dasar-Dasar
TIN102 - Pengantar Teknik Industri Materi #10 Ganjil 2015/2016 TIN102 PENGANTAR TEKNIK INDUSTRI
Materi #10 TIN102 PENGANTAR TEKNIK INDUSTRI Pendahuluan 2 Permasalahan pemrograman dinamis secara umum memiliki proses keputusan yang bersifat multi tahapan (multi-stage). I1 D1 I2 D2 In Dn R1 R2 Rn 6623
Oleh: Dimas Avian Maulana Dosen Pembimbing: Subchan, Ph.D
Oleh: Dimas Avian Maulana-1207100045 Dosen Pembimbing: Subchan, Ph.D Robot mobil adalah salah satu contoh dari wahana nir awak (WaNA) yang dapat dikendalikan dari jauh atau memiliki sistem pengendali otomatis
METODE STEEPEST DESCENT DALAM PENGOPTIMUMAN FUNGSI DAN PENERAPANNYA MENGGUNAKAN APLIKASI ANDROID ALFI AINI
METODE STEEPEST DESCENT DALAM PENGOPTIMUMAN FUNGSI DAN PENERAPANNYA MENGGUNAKAN APLIKASI ANDROID ALFI AINI DEPARTEMEN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR BOGOR
OPTIMASI BIAYA PRODUKSI PADA HOME INDUSTRY SUSU KEDELAI MENGGUNAKAN PENDEKATAN PENGALI LAGRANGE DAN PEMROGRAMAN KUADRATIK TUGAS AKHIR SKRIPSI
OPTIMASI BIAYA PRODUKSI PADA HOME INDUSTRY SUSU KEDELAI MENGGUNAKAN PENDEKATAN PENGALI LAGRANGE DAN PEMROGRAMAN KUADRATIK TUGAS AKHIR SKRIPSI Diajukan kepada Fakultas Matematika dan Ilmu Pengetahuan Alam
BAB IV. METODE SIMPLEKS
BAB IV. METODE SIMPLEKS Penentuan solusi optimal menggunakan simpleks didasarkan pada teknik eliminasi Gauss Jordan. Penentuan solusi optimal dilakukan dengan memeriksa titik ekstrim (ingat kembali solusi
Pemrograman Linier (4)
Pemrograman Linier (4) Metode dua fase Ahmad Sabri Universitas Gunadarma, Indonesia Sesuai dengan namanya, metode dua fase menyelesaikan problem PL dalam dua tahap (fase): 1 Ubah model PL ke dalam bentuk
Modifikasi Kontrol untuk Sistem Tak Linier Input Tunggal-Output Tunggal
Vol 7, No2, 118-123, Januari 2011 Modifikasi Kontrol untuk Sistem Tak Linier Input Tunggal-Output Tunggal Abstrak Dalam tulisan ini diuraikan sebuah kontrol umpan balik dinamik Dari kontrol yang diperoleh
BAB II METODE SIMPLEKS
BAB II METODE SIMPLEKS 2.1 Pengantar Salah satu teknik penentuan solusi optimal yang digunakan dalam pemrograman linier adalah metode simpleks. Penentuan solusi optimal menggunakan metode simpleks didasarkan
PROGRAM LINEAR. tersebut. Dua macam fungsi Program Linear: tujuan perumusan masalah
PROGRAM LINEAR Program linear adalah salah satu model matematika yang digunakan untuk menyelesaikan masalah optimisasi, yaitu memaksimumkan atau meminimumkan fungsi tujuan yang bergantung pada sejumlah
BAB II TINJAUAN PUSTAKA. operasi yang mampu menyelesaikan masalah optimasi sejak diperkenalkan di
BAB II TINJAUAN PUSTAKA 2.1 Pemrograman Linier (Linear Programming) Pemrograman linier (linear programming) merupakan salah satu teknik riset operasi yang mampu menyelesaikan masalah optimasi sejak diperkenalkan
Staff Pengajar Jurusan Teknik Mesin, FT-Universitas Sebelas Maret Surakarta
DESAIN OPTIMASI UNGSI TAK LINIER MENGGUNAKAN METODE PENYELIDIKAN IBONACCI Yemi Kuswardi Nurul Muhayat Abstract: optimum design is an action to design the best product based on the problem. Theoretically,
METODE REDUCED-GRADIENT PADA OPTIMASI NONLINIER BERKENDALA PERTIDAKSAMAAN NONLINIER SKRIPSI. Oleh : Normayati Sumanto J2A
METODE REDUCED-GRADIENT PADA OPTIMASI NONLINIER BERKENDALA PERTIDAKSAMAAN NONLINIER SKRIPSI Oleh : Normayati Sumanto J2A 005 037 PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU
DIFERENSIAL FUNGSI MAJEMUK
DIFERENSIAL FUNGSI MAJEMUK Tujuan Instruktusional : Memahami diferensiasi untuk fungsi-fungsi yang mengandung lebih dari satu macam variabel bebas Daftar Materi Pembahasan : 1. Diferensiasi parsial 2.
Bab 1 PENDAHULUAN. 1.1 Latar Belakang
Bab 1 PENDAHULUAN 1.1 Latar Belakang Dewasa ini, manusia sering dihadapi oleh permasalahan melibatkan optimasi tujuan ganda (multi-objective), contohnya dalam hal perencanaan atau peramalan pasar yang
sejumlah variabel keputusan; fungsi yang akan dimaksimumkan atau diminimumkan disebut sebagai fungsi objektif, Ax = b, dengan = dapat
sejumlah variabel keputusan; fungsi yang akan dimaksimumkan atau diminimumkan disebut sebagai fungsi objektif nilai variabel-variabel keputusannya memenuhi suatu himpunan kendala yang berupa persamaan
MATEMATIKA EKONOMI DAN BISNIS MINGGU XII
MATEMATIKA EKONOMI DAN BISNIS MINGGU XII OPTIMASI FUNGSI MULTIVARIAT TANPA DAN DENGAN KENDALA Prepared by : W. Roianto ROFI KONDISI MAKSIMUM DAN MINIMUM RELATIF DEFINISI Fungsi y = (,,, n ) maksimum relati
BAB 1 PENDAHULUAN Latar Belakang
BAB 1 PENDAHULUAN 1.1. Latar Belakang Optimasi (Optimization) adalah aktivitas untuk mendapatkan hasil terbaik di dalam suatu keadaan yang diberikan. Tujuan akhir dari semua aktivitas tersebut adalah meminimumkan
FUNGSI ACKLEY DAN PENCARIAN NILAI OPTIMUMNYA MENGGUNAKAN ALGORITMA STROBERI. Muhamad Fadilah Universitas Jenderal Soedirman
Prosiding Seminar Nasional Matematika dan Terapannya 06 p-issn : 550-0384; e-issn : 550-039 FUNGSI ACKLEY DAN PENCARIAN NILAI OPTIMUMNYA MENGGUNAKAN ALGORITMA STROBERI Muhamad Fadilah Universitas Jenderal
OPTIMASI PEMROGRAMAN KUADRATIK KONVEKS DENGAN MENGGUNAKAN METODE PRIMAL-DUAL PATH-FOLLOWING
OPIMASI PEMROGRAMAN KUADRAIK KONVEKS DENGAN MENGGUNAKAN MEODE PRIMAL-DUAL PAH-FOLLOWING Raras yasnurita ), Wiwik Anggraeni ), Rully Soelaiman 3) ) Jurusan Sistem Informasi 3) Jurusan eknik Informatika
1. Fungsi Objektif z = ax + by
Nilai Optimum Suatu Fungsi Objektif, Program Linear, Fungsi Objektif, Cara Menentukan, Contoh Soal, Rumus, Pembahasan, Metode Uji Titik Sudut, Metode Garis Selidik, Matematika Nilai Optimum Suatu Fungsi
BAB 1 PENDAHULUAN. 1.1 Latar Belakang
BAB 1 PENDAHULUAN 1.1 Latar Belakang Metode Pengali Lagrange adalah sebuah konsep populer dalam menangani permasalahan optimasi untuk program-program nonlinier. Sesuai namanya, konsep ini dikemukakan oleh
OPTIMASI BERSYARAT DENGAN KENDALA PERSAMAAN MENGGUNAKAN MULTIPLIER LAGRANGE SERTA PENERAPANNYA SKRIPSI SANDRA RIZAL
OPTIMASI BERSYARAT DENGAN KENDALA PERSAMAAN MENGGUNAKAN MULTIPLIER LAGRANGE SERTA PENERAPANNYA SKRIPSI SANDRA RIZAL 060803016 DEPARTEMEN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS
Implementasi Algoritma Greedy pada Permainan Ludo
Implementasi Algoritma Greedy pada Permainan Ludo Sylvia Juliana, 13515070 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl, Ganesha 10 Bandung 40132,
BAB II KAJIAN PUSTAKA. Berikut diberikan landasan teori mengenai Teori Portofolio, Turunan
BAB II KAJIAN PUSTAKA Berikut diberikan landasan teori mengenai Teori Portofolio, Turunan Parsial, Supremum dan Infimum, Himpunan Konveks, Program Nonlinear, Matriks Definit Positif dan Definit Negatif,
PENGGUNAAN ALGORITMA NONLINEAR PROGRAMMING UNTUK MENGOPTIMALKAN PARAMETER DALAM METODE PEMULUSAN EKSPONENSIAL SATU PARAMETER
PENGGUNAAN ALGORITMA NONLINEAR PROGRAMMING UNTUK MENGOPTIMALKAN PARAMETER DALAM METODE PEMULUSAN EKSPONENSIAL SATU PARAMETER Nama Mahasiswa : Eka Novi Nurhidayati NRP : 1208 100 040 Jurusan : Matematika
BAB I DASAR SISTEM OPTIMASI
BAB I DASAR SISTEM OPTIMASI. Pendahuluan Teknik optimasi merupakan suatu cara yang dilakukan untuk memberikan hasil terbaik yang diinginkan. Teknik optimasi ini banyak memberikan menfaat dalam mengambil
METODE TWO-POINT STEPSIZE GRADIENT DAN METODE MODIFIKASI TWO-POINT STEPSIZE GRADIENT UNTUK MENYELESAIKAN OPTIMALISASI TANPA KENDALA RIZKI OKTAVIANI
METODE TWO-POINT STEPSIZE GRADIENT DAN METODE MODIFIKASI TWO-POINT STEPSIZE GRADIENT UNTUK MENYELESAIKAN OPTIMALISASI TANPA KENDALA RIZKI OKTAVIANI DEPARTEMEN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN
Matematika Bisnis (Linear Programming-Metode Grafik Minimisasi) Dosen Febriyanto, SE, MM.
(Linear Programming-Metode Grafik Minimisasi) Dosen Febriyanto, SE, MM. www.febriyanto79.wordpress.com - Linear Programming Linear programing (LP) adalah salah satu metode matematis yang digunakan untuk
OPTIMASI PARAMETER α DAN γ DALAM PEMULUSAN EKSPONENSIAL DUA PARAMETER DENGAN METODE MODIFIKASI GOLDEN SECTION
OPTIMASI PARAMETER α DAN γ DALAM PEMULUSAN EKSPONENSIAL DUA PARAMETER DENGAN METODE MODIFIKASI GOLDEN SECTION NILA YUWIDA 1208100015 Dosen Pembimbing : Dra. Nuri Wahyuningsih, M.Kes Drs. Lukman Hanafi,
BAB I PENDAHULUAN. 1.1 Latar Belakang
BAB I PENDAHULUAN 1.1 Latar Belakang Assignment problem yang biasa dibentuk dengan matriks berbobot merupakan salah satu masalah dalam dunia teknik informatika, dimana masalah ini merupakan masalah yang
KAJIAN DISKRETISASI DENGAN METODE GALERKIN SEMI DISKRET TERHADAP EFISIENSI SOLUSI MODEL RAMBATAN PANAS TANPA SUKU KONVEKSI
KAJIAN DISKRETISASI DENGAN METODE GALERKIN SEMI DISKRET TERHADAP EFISIENSI SOLUSI MODEL RAMBATAN PANAS TANPA SUKU KONVEKSI Suhartono dan Solikhin Zaki Jurusan Matematika FMIPA UNDIP Abstrak Penelitian
Taufiqurrahman 1
PROGRAM LINEAR: METODE SIMPLEX Latar Belakang Sulitnya menggambarkan grafik berdimensi banyak atau kombinasi lebih dari dua variabel. Metode grafik tidak mungkin dapat dilakukan untuk menyelesaikan masalah
ANALISIS POSTOPTIMAL/SENSITIVITAS
ANALISIS POSTOPTIMAL/SENSITIVITAS Dalam sub bab ini kita akan mempelajari apakah solusi optimal akan berubah jika terjadi perubahan parameter model awal. Jika solusi optimal berubah, dapatkah kita menghitung
Pemodelan Programasi Linier dan Solusi Manual Model Assignment
Pemodelan Programasi Linier dan Solusi Manual Model Assignment week 08 W. Rofianto, ST, MSi Model Transportasi Kota 1 2 3 4 Pabrik 1 $ 2 /ton $ 3 /ton $ 1.5 /ton $ 2.5 /ton 900 Pabrik 2 $ 4 /ton $ 3.5
Hendra Gunawan. 4 April 2014
MA1201 MATEMATIKA 2A Hendra Gunawan Semester II, 2013/2014 4 April 2014 Kuliah yang Lalu 12.1 Fungsi dua (atau lebih) peubah 12.2 Turunan Parsial 12.3 Limit dan Kekontinuan 12.4 Turunan fungsi dua peubah
DAFTAR ISI... HALAMAN JUDUL... HALAMAN PENGESAHAN... HALAMAN PERNYATAAN... HALAMAN PERSEMBAHAN... PRAKATA... DAFTAR LAMBANG... DAFTAR GAMBAR...
DAFTAR ISI Halaman HALAMAN JUDUL... HALAMAN PENGESAHAN... HALAMAN PERNYATAAN... HALAMAN PERSEMBAHAN... PRAKATA... DAFTAR ISI... DAFTAR LAMBANG... DAFTAR GAMBAR... DAFTAR TABEL... INTISARI... ABSTRACT...
BAB 2 LANDASAN TEORI
BAB 2 LANDASAN TEORI 2.1 Sistem Pendukung Keputusan Sebuah aplikasi berupa Sistem Pendukung Keputusan (Decision Support System) mulai dikembangkan pada tahun 1970. Decision Support Sistem (DSS) dengan