ALJABAR MAX-PLUS BILANGAN KABUR (Fuzzy Number Max-Plus Algebra) INTISARI ABSTRACT
|
|
|
- Yuliani Liana Budiono
- 6 tahun lalu
- Tontonan:
Transkripsi
1 M. And Rhudito, dkk., Aljabar Max-Plus Bilangan Kabur ALJABAR MAX-PLUS BILANGAN KABUR (Fuzz Nuber Max-Plus Algebra) M. And Rudhito, Sri Wahuni 2, Ari Suparwanto 2 dan F. Susilo 3 Jurusan Pendidikan Mateatika dan IPA, Universitas Sanata Dhara, Yogakarta rudhito@staff.usd.ac.id 2 Jurusan Mateatika FMIPA Universitas Gadjah Mada, Yogakarta swahuni@ug.ac.id, ari_arwanto@ahoo.co 3 Jurusan Mateatika, Universitas Sanata Dhara,Yogakarta fsusilo@staff.usd.ac.id INTISARI Makalah ini ebahas suatu aljabar hipunan seua bilangan kabur (fuzz nuber) ang dilengkapi dengan operasi axiu dan penjulahan. Aljabar ini erupakan perluasan aljabar ax-plus elalui aljabar ax-plus interval dan Teorea Dekoposisi dala hipunan kabur. Dapat ditunjukkan operasi axiu dan penjulahan ang didefinisikan elalui potongan-alfa tertutup dala hipunan seua bilangan kabur tersebut. Selanjutna hipunan seua bilangan kabur ang dilengkapi dengan operasi axiu dan penjulahan tersebut erupakan seiring idepoten koutatif. Kata-kata kunci: seiring, idepoten, aljabar ax-plus, bilangan kabur. ABSTRACT This paper discussed an algebra of the set of all fuzz nuber that copleted b axiu and addition operation. This algebra is an extension of ax-plus algebra through interval ax-plus algebra and Decoposition Theore in fuzz set. The finding show that axiu and addition operation through alpha-cut is closed in this set of all fuzz nuber. Furtherore, the set of all fuzz nuber that copleted b axiu and addition operation is a coutative idepotent seiring. Kewords : seiring, idepotent, ax-plus algebra, fuzz nuber 53
2 Berkala MIPA, 8(2), Mei LATAR BELAKANG Aljabar ax-plus (hipunan R {}, dengan R adalah hipunan seua bilangan real, ang dilengkapi dengan operasi axiu dan penjulahan) telah digunakan untuk eodelkan dan enganalisis jaringan untuk waktu aktifitas deterinistik. Dala asalah peodelan dan analisa suatu jaringan di ana waktu aktifitasna belu diketahui dengan pasti, waktu aktifitas jaringan diodelkan dala suatu bilangan kabur (fuzz nuber). Akhir-akhir ini telah berkebang peodelan jaringan ang elibatkan bilangan kabur. Peodelan dan analisa suatu siste jaringan ang elibatkan bilangan kabur, sejauh penulis ketahui, belu ada ang enggunakan pendekatan aljabar ax-plus. Dengan pendekatan ini aka akan diperlukan pebahasan engenai suatu aljabar dengan eleeneleenna berupa bilangan kabur dengan operasi axiu dan penjulahan ang didefinisikan di dalana. Aljabar ini diharapkan dapat eberikan landasan analisa jaringan dengan waktu aktifitas kabur elalui pendekatan aljabar ax-plus. Konsep-konsep dasar aljabar ax-plus secara lengkap telah dibahas dala Bacelli, et al. (200), di ana aljabar ax-plus erupakan seifield aitu seiring koutatif ang setiap eleen taknolna epunai invers terhadap operasi perkalian. Operasi-operasi aritatika seperti +,,, /, ax dan in pada bilangan kabur pada uuna didefinisikan dengan enggunakan Prinsip Perluasan (Extension Principle) dan dengan enggunakan potongan- (-cut) ang didasarkan pada Teorea Dekoposisi. Hal ini dapat dilihat dala Zieran, H.J. (99) Lee, K.H. (2005) dan Susilo, F. (2006). Dala Susilo, F. (2006) ditegaskan bahwa setiap bilangan kabur dapat dinatakan secara tunggal dengan enggunakan potongan--na. Karena potongan- suatu bilangan kabur berupa interval tertutup aka operasi-operasi aritatika pada bilangan kabur dapat dinatakan enggunakan operasi-operasi aritatika interval tertutup. Ditegaskan juga dala Susilo, F. (2006) bahwa operasi bilangan kabur dengan enggunakan Prinsip Perluasan dan dengan enggunakan potongan- adalah ekivalen. Pebahasan engenai seiring telah dikebangkan ke dala Analisis Interval Idepoten oleh Litvinov, G.L., Sobolevskii, A.N. (200). Analisis Interval Idepoten ini ebahas seiring dengan eleen-eleenna berupa interval tertutup. Dala literatur di atas dikatakan bahwa hipunan seua interval tertutup dala suatu seiring idepoten juga erupakan seiring idepoten dengan operasi ang bersesuaian. Ditunjukkan juga bahwa sifatsifat ang diiliki seiring juga diiliki oleh seiring hipunan seua interval tertutup tersebut. Dengan eperhatikan hasil-hasil di atas, aljabar ax-plus dapat diperluas ke dala aljabar ax-plus interval, di ana eleen-eleenna berupa interval tertutup dala aljabar ax-plus tersebut. Selanjutna dengan engabil pengoperasian axiu dan penjulahan bilangan kabur elalui potongan--na, akan dapat dikebangkan struktur aljabar ax-plus bilangan kabur. Terlebih dahulu akan ditinjau beberapa konsep dasar dan hasil dala aljabar ax-plus, hipunan kabur dan bilangan kabur ang enjadi landasan pebahasan aljabar ax-plus bilangan kabur. 2. TINJAUAN TEORI 2. Aljabar Max-Plus Dala bagian ini ditinjau konsep dasar aljabar ax-plus. Pebahasan selengkapna dapat dilihat pada Baccelli et.al (200), Rudhito A (2003) dan Schutter (996). Suatu seiring (S,, ) adalah suatu hipunan tak kosong S ang dilengkapi 54
3 M. And Rhudito, dkk., Aljabar Max-Plus Bilangan Kabur dengan dua operasi biner dan, ang eenuhi aksioa berikut: i) (S, ) adalah seigrup koutatif dengan eleen netral 0, aitu a, b, c S, (a b) c = a (b c), a b = b a, a 0 = a. ii) (S, ) adalah seigrup dengan eleen satuan, aitu a, b, c S, (a b) c = a (b c), a = a = a, iii) Eleen netral 0 erupakan eleen penerap terhadap operasi, aitu a S, a 0 = 0 a = 0. iv) Operasi distributif terhadap, aitu a, b, c S, (a b) c = (a c) (b c), a (b c) = (a b) (a c). Seiring (S,, ) dikatakan idepoten jika operasi bersifat idepoten, aitu a S : a a =a, dan dikatakan koutatif jika operasi bersifat koutatif. Suatu seiring koutatif (S,, ) disebut seifield jika setiap eleen tak netralna epunai invers terhadap operasi. Jika (S, + ) erupakan seigrup koutatif idepoten aka relasi ang didefinisikan pada S dengan x x + = erupakan urutan parsial pada S. Operasi dan dikatakan konsisten terhadap urutan dala S bhb jika x, aka x + z + z dan x z z, x,, z S. Dapat ditunjukkan bahwa dala seiring idepoten (S, +, ) operasi + dan konsisten terhadap urutan dala S. Seiring (S,, ) dengan eleen netral 0 dikatakan tidak euat pebagi nol bhb jika x = 0 aka x = 0 atau = 0, x, S. Diberikan R := R { } dengan R adalah hipunan seua bilangan real dan : =. Pada R didefinisikan operasi berikut: a,b R, a b := ax(a, b) dan a b : = a b. Dapat ditunjukkan bahwa (R,, ) erupakan seiring idepoten koutatif dengan eleen netral = dan eleen satuan e = 0. Lebih lanjut (R,, ) erupakan seifield, aitu bahwa 55 (R,, ) erupakan seiring koutatif di ana untuk setiap a R terdapat a sehingga berlaku a (a) = 0. Keudian (R,, ) disebut dengan aljabar axplus, ang selanjutna cukup dituliskan dengan R ax. Karena (R ax, ) erupakan seigrup koutatif idepoten, aka relasi ang didefinisikan pada R ax dengan x x = erupakan urutan parsial pada R ax. Lebih lanjut relasi ini erupakan urutan total pada R ax. Karena R ax erupakan seiring idepoten, aka operasi dan konsisten terhadap urutan, aitu a, b, c R ax, jika a aka a c b c, dan a c b c. Aljabar ax-plus R ax tidak euat pebagi nol aitu x, R berlaku: jika x = aka x = atau =. 2.2 Hipunan dan Bilangan Kabur Berikut ditinjau pengertian dan konsep dasar hipunan dan bilangan kabur. Uraian lebih lengkap dapat dilihat dala Zierann, H.J., (99), Lee, K.H. (2005) dan Susilo, F. (2006). Suatu hipunan A dala seesta X dapat dinatakan dengan fungsi karakteristik A : X {0, } ang didefinisikan dengan aturan, jika x A A (x) = untuk setiap x X. 0, jika x A Hipunan kabur K ~ dala seesta X dinatakan sebagai hipunan pasangan terurut K ~ = {(x, K ~ (x)) x X }, di ana K ~ adalah fungsi keanggotaan hipunan kabur K ~, ang erupakan suatu peetaan dari seesta X ke interval tertutup [0, ]. Pendukung (port) suatu hipunan kabur K ~, dilabangkan dengan pend( K ~ ) adalah hipunan tegas (crisp) ang euat seua anggota seesta ang epunai derajat keanggotaan taknol dala K ~, aitu pend( K ~ ) = {xx K ~ (x) 0}. Tinggi
4 Berkala MIPA, 8(2), Mei 2008 (height) suatu hipunan kabur K ~, dilabang-kan dengan tinggi( K ~ ), didefinisikan sebagai tinggi( K ~ ) = { ~ K (x)}. Suatu hipunan kabur K ~ xx dikatakan noral jika tinggi( K ~ ) =. Gabungan dua buah hipunan kabur K ~ dan L ~ adalah hipunan kabur K ~ L ~ dengan fungsi keanggotaan (x) = ax{ ~ (x), K L ~ (x)} untuk K ~ L ~ setiap x X. Sedangkan irisan dua buah hipunan kabur K ~ dan L ~ adalah hipunan kabur K ~ L ~ dengan fungsi keanggotaan K ~ L ~ (x) = in{ ~ (x), K L ~ (x)}, untuk ~ setiap x X. Jika K,..., K ~ n adalah hipunan-hipunan kabur berturut-turut dala seesta X,..., X n, aka hasilkali ~ Cartesius K... K ~ n adalah hipunan kabur dala X... X n dengan fungsi keanggotaan ~ ~ (x,..., x n ) = K in{ ~ (x),..., K... K n K ~ n (x)}. Untuk suatu bilangan [0, ], potongan- suatu hipunan kabur K ~, ang dilabangkan dengan pot ( K ~ ) = K, adalah hipunan crisp (tegas) ang euat seua eleen seesta dengan derajat keanggotaan dala K ~ lebih besar atau saa dengan, ang didefinisikan sebagai K = {xx K ~ (x) }. Salah satu sifat potongan- suatu hipunan kabur K ~ 2 adalah jika 2 aka K K,ang disebut dengan sifat tersarang (nested). Suatu hipunan kabur K ~ dikatakan konveks jika K konveks [0, ]. Teorea (Teorea Dekoposisi) Jika K adalah potongan- hipunan kabur K ~ dala seesta X dan K ~ adalah hipunan kabur dala X dengan fungsi keanggotaan K ~ K (x) = K (x), di ana adalah fungsi karakteristik hipunan K, aka K ~ = [0,] K ~ Bukti: Susilo, F. (2006, pp ). Teorea 2 (Teorea Representasi) Jika { K }, [0, ] adalah keluarga hipunan dala seesta X ang eenuhi sifat tersarang (nested), aitu jika aka berlaku K K,, [0, ], aka terdapat dengan tunggal hipunan kabur L ~ dala seesta X sedeikian hingga L = K, [0, ]. Bukti: Didefinisikan hipunan kabur L ~ dala seesta X ang fungsi keanggotaanna ang didefinisikan dengan (x) =. Abil sebarang [0, L ~ xk ]. Abil sebarang x L akan ditunjukkan bahwa x K. Karena x L, aka L ~ (x) =. Karena sifat tersarang aka xk K K = K, dengan = xk =, aka x K = xk K dan. Karena K, sehingga x K. Jadi L K untuk setiap [0, ]. Abil sebarang [0, ]. Abil sebarang x K akan ditunjukkan bahwa x L. Karena x K dan sifat tersarang, aka. Menurut xk definisi L ~ diperoleh L ~ (x), sehingga terbukti x L. Jadi K L, untuk setiap [0, ]. Dengan deikan terbukti bahwa K = L. Andaikan terdapat hipunan kabur M ~ dala seesta X sedeikian hingga M = K, [0, ]. Karena K = L, [0, ], aka 56
5 M. And Rhudito, dkk., Aljabar Max-Plus Bilangan Kabur berakibat M = L, [0, ], sehingga = M ~, ang berarti M~ = L ~. Jadi L ~ terbukti terdapat dengan tunggal hipunan kabur L ~ dala seesta X sedeikian hingga L = K, [0, ]. Berikut ditinjau engenai Prinsip Perluasan dala hipunan kabur. Misalkan f adalah fungsi dari X... X n ke Y, dan K ~,..., K ~ n adalah hipunan-hipunan kabur berturut-turut dala seesta X,..., X n. Fungsi f dapat diperluas enjadi fungsi bernilai kabur ~ f : F(X... X n ) F(Y), di ana F(X... X n ) dan F(Y) berturutturut adalah hipunan kuasa kabur dari seesta X... X n dan Y, dengan aturan sebagai berikut. Untuk setiap hipunan kabur K ~... K ~ n F(X... X n ), ~ f ( K ~... K ~ n ) adalah hipunan kabur dala F(Y) dengan fungsi keanggotaan ~ () = f ( K ~... K ~ n ) in{ ( ),..., ( )} K ~ x K ~ xn n f ( x,..., xn ) jika ( x,..., xn) X... X n, f ( x,..., xn). 0 jika( x,..., xn) X... X n, f ( x,..., xn) Bilangan kabur a ~ didefinisikan sebagai hipunan kabur dala seesta R ang eenuhi sifat berikut: i) noral, aitu a ii) (0, ], a adalah interval tertutup 57 dala R, aitu a, a a R dengan a sedeikian sehingga a = [ a, a ] = {x R a x a }. iii) pend( a ~ ) terbatas. Untuk = 0, didefinisikan bahwa a 0 = [inf(pend( a ~ )), (pend( a ~ ))]. Karena setiap interval tertutup dala R adalah konveks aka a konveks [0, ], sehingga a ~ konveks. Suatu bilangan kabur titik a ~ adalah bilangan kabur dengan fungsi keanggotaan a ~ (x) =, jika x a. 0, lainna Salah satu tipe bilangan kabur ang sederhana adalah bilangan kabur segitiga. Bilangan kabur segitiga a ~, ang dilabangkan dengan BKS(a, a, a 2 ), adalah suatu bilangan kabur dengan fungsi keanggotaan x a, a x a a a a ~ (x) = a2 x, a x a2 a2 a 0, lainna di ana a a atau a a 2. Napak bahwa potongan- a ~ di atas adalah a = [(a a ) + a, (a 2 a) + a 2 ] dan pend( a ~ ) = (a, a 2 ). Dua bilangan kabur a ~ dan b ~ dikatakan saa jika a ~ = b ~. Karena a ~ = b ~ aka berlaku a = b, [0, ]. Sebalikna enurut Teorea Dekoposisi jika a = b, [0, ], aka a ~ b ~ deikan dapat dikatakan bahwa a ~ =b ~ jika dan hana jika a = b, [0, ]. Operasi-operasi aritatika bilangan kabur dapat didefinisikan dengan enggunakan prinsip perluasan atau dengan enggunakan potongan-. Dengan enggunakan prinsip perluasan didefinisikan operasi-operasi bilangan kabur berikut. Misalkan a ~ dan b ~ adalah bilangan-bilangan kabur. i) Maksiu a ~ dan b ~, aitu a ~ ~ b ~ adalah hipunan kabur dengan fungsi keanggotaan: ~ b ~ (z) = z x in{ a ~ (x), b ~ ( )}. ii) Penjulahan a ~ dan b ~, aitu a ~ ~ b ~ adalah hipunan kabur dengan fungsi a ~
6 Berkala MIPA, 8(2), Mei 2008 keanggotaan: a ~ ~ b ~ (z) = ) z x in{ a ~ (x), b ~ ( )}. Sedangkan dengan enggunakan potongan- didefinisikan operasi-operasi bilangan kabur berikut. Misalkan a ~ dan b ~ adalah bilangan-bilangan kabur. dengan a = [ a, a ]dan b = [ b, b ], di ana a dan a berturut-turut adalah batas bawah dan batas atas interval a, sedangkan untuk b dan b analog, i') Maksiu a ~ dan b ~, aitu a ~ ~ b ~ adalah hipunan kabur dengan potongan--na adalah interval [ a a b ], untuk setiap [0, ]. ii') Penjulahan a ~ dan b ~, aitu a ~ ~ b ~ adalah hipunan kabur dengan potongan--na adalah interval [ a setiap [0, ]. 3. CARA PENELITIAN a b ], untuk Penelitian ini erupakan penelitian ang didasarkan pada studi literatur ang eliputi kajian-kajian secara teoritis. Terlebih dahulu akan dikaji aljabar axplus interval, ang erupakan perluasan aljabar ax-plus, di ana eleeneleena berupa interval-interval. Hasil pebahasan ini akan digunakan sebagai dasar pebahasan aljabar ax-plus bilangan kabur elalui potongan--na ang berupa interval. Selanjutna dengan eperhatikan struktur aljabar ax-plus interval, akan dikonstruksikan dan diselidiki aljabar ax-plus bilangan kabur. 4. HASIL DAN PEMBAHASAN Pebahasan aljabar ax-plus ini didasarkan pada analisis idepoten interval dala Litvinov, G.L., Sobolevskii, A.N. (200) Definisi Misalkan S adalah hipunan terurut parsial dengan relasi. Suatu interval (tertutup) dala S adalah hipunan bagian S ang berbentuk x = [ x, x ] = {xs x x x } dengan x dan x S berturut-turut disebut batas bawah dan batas atas interval [ x, x ]. Misalkan x dan adalah interval dala S. Perhatikan bahwa interval x jika dan hana jika x x. Secara khusus x = jika dan hana jika x = dan x =. Sebuah interval dengan x dengan x = x erepresentasi suatu eleen dala S. Contoh Telah diketahui bahwa R ax erupakan hipunan terurut parsial dengan relasi. Interval dala R ax berbentuk x = [ x, x ] = { x R ax x x x }. Bilangan x R ax dapat dinatakan dengan enggunakan interval x = [x, x]. Interval dala R ax isalna [2, 3], [4, ], [0, 0] = 0, [, ] = dan sebagaina. Diberikan (S, +, ) adalah suatu seiring idepoten dan tidak euat pebagi nol, dengan eleen netral 0. Didefinisikan I(S) = { x = [ x, x ] x, x S, 0 x x } {[0, 0]}. Pada I(S) didefinisikan operasi dan dengan x = [ x +, x + ] dan x = [ x, x ], x, I(S). Dapat ditunjukkan bahwa operasi ang didefinisikan di atas terdefinisi dengan baik (well defined), aitu eenuhi sarat tertutup dan bernilai tunggal. Teorea 3 Diberikan (S, +, ) adalah suatu seiring idepoten dan tidak euat pebagi nol, dengan eleen netral 58
7 M. And Rhudito, dkk., Aljabar Max-Plus Bilangan Kabur 0. (I(S),, ) erupakan seiring idepoten dengan eleen netral 0 I = [0, 0] dan eleen satuan I = [, ]. Bukti: Bahwa I(S) tertutup terhadap operasi dan sudah dijelaskan pada penjelasan setelah pendefinisian operasi interval di atas. Selanjutna karena operasioperasi dan pada (I(S),) didefinisikan koponen dei koponen dari S, aka sifat-sifat pada (I(S),, ) engikuti seluruh sifat-sifat pada (S, +,) ang erupakan seiring idepoten, dengan eleen netral 0 dan eleen satuan. Dengan deikian terbukti bahwa (I(S),, ) erupakan seiring idepoten koutatif dengan eleen netral 0 I = [0, 0] dan eleen satuan I = [, ]. Contoh 2 Telah diketahui (R,, ) erupakan seiring idepoten dan tidak euat pebagi nol, dengan eleen netral. Didefinisikan I(R) = {x = [ x, x ] x, x R, x x }{[, ]}. Pada I(R) didefinisikan operasi dan aitu x = [ x, x ] dan x = [ x, x ], x, I(R). Misalna [, ] [, 3] = [, 3] dan [, ] [, 3] = [0, 4]. Menurut Teorea 3 di atas (I(R),, ) erupakan seiring idepoten dengan eleen netral = [, ] dan eleen satuan 0 = [0, 0]. Lebih lanjut karena (R,, ) erupakan seiring idepoten koutatif, aka (I(R),, ) erupakan seiring idepoten koutatif. Selanjutna (I(R),, ) disebut dengan aljabar axplus interval ang cukup dituliskan dengan I(R) ax. Teorea 4 x, I(R) ax berlaku bahwa i. [ x, x ] = x dan ii. [ x, x ] = x, di ana x = {t R ax t = x, x x, } dan x = {t R ax t = x, x x, }. Bukti: i) Abil sebarang t x dan isalkan x x dan sedeikian hingga t = x. Karena x dan adalah interval, aka x x x dan. Karena operasi konsisten terhadap urutan, aka x x x, sehingga x [ x, x ]. Jadi x [ x, x ]. Abil sebarang t [ x, x ], aka x t x. Andaikan t x, aka x x dan berlaku t x, karena urutan dala R ax erupakan urutan total, berarti bahwa t x atau t x. Karena x x dan aka t x atau t x, sehingga terjadi kontradiksi. Jadi t x, ang berarti [ x, x ] x. Dengan deikan terbukti [ x, x ] = x. ii) Analog dengan pebuktian i) di atas. Berikut diberikan teorea ang enunjuk-kan bahwa operasi axiu bilangan kabur dengan enggunakan prinsip perluasan dan dengan enggunakan potongan- adalah ekivalen. Teorea 5 Diberikan dua buah bilangan kabur a ~ dan b ~ dengan potongan--na berturut-turut adalah a = [ a, a ] dan b = [ b ]. Maxiu a ~ dan b ~, aitu a ~ ~ b ~ adalah hipunan kabur dengan 59
8 Berkala MIPA, 8(2), Mei 2008 fungsi z x keanggotaan (z) = a ~ ~ b ~ in{ a ~ (x), ()} jika dan hana jika (a b) = [ a b, b ~ a b ]. Bukti: () Abil sebarang bilangan real z (a b), aka (z) ( a ~ ~ b ~ ). Andaikan z [ a a b ], aka untuk setiap x dan dengan x = z berlaku x [ a, a ] atau [ b, b ]. Hal ini berarti a ~ (x) atau b ~ () ang berakibat ~ (z) = a ~ b ~ z x in{ a ~ (x), b ~ ( )}, sehingga terjadi kontradiksi. Jadi z [ a (a b) [ a a b ], ang berarti a b ]. Abil sebarang bilangan real z [ a a b ]. Karena enurut Teorea 4, [ a a b ] = a b = {z R ax z = x, x a, b } aka terdapat x [ a, a ] dan [ b, b ] sedeikian sehingga x + = z. Hal ini berarti bahwa a ~ (x) dan b ~ ( ). Jadi (z) = a ~ ~ b ~ z x in{ a ~ (x), b ~ ( )}, aitu bahwa z (a b), ang berarti [ a a b ] (a b). Dengan deikian terbukti bahwa (a b) = [ a a b ]. () Andaikan (a b) = [ a b ]. Menurut Teorea, [ b ] = a a a a b = {zr ax z = x, x a, b }. Perhatikan bahwa a dan b dapat dipandang sebagai hipunan kabur dengan fungsi keanggotaanna berturutturut adalah fungsi karakteristik a dan b. Keudian enurut prinsip perluasan diperoleh (z) = a b in{ a (x), b ()}. Misalkan a ~ ~ z x b ~ = c ~, aka (a b) = c. Selanjutna enurut Teorea Dekoposisi diperoleh c ~ (z) = c ~ (z) = ax x[ 0, ] c ~ (z) [ 0, ] dengan c ~, adalah hipunan kabur dala R dengan fungsi keanggotaan c ~ (z) = (z). Karena (a b) = a b, ( a b) aka (z) = in{ a ~ (x), ()}(z) = c ~ zx zx in{ a ~ (x), ~ b ()}(z) = b ~ in zx { a ~ (x), ~ b ()}. Sehingga c ~ (z) = ax x[ 0, ] in { a ~ (x), ~ b ()} = zx in{ ax zx zx x[ 0, ] a ~ in{ diperoleh zx a ~ [ 0, ] (x), bahwa in{ a ~ (x), (x), b ~ ax x[ 0, ] ~ b ()} = ~ b ()}. Jadi [0,] (z) = a ~ ~ b ~ ( )}. Teorea di atas juga berlaku untuk operasi penjulahan, dengan bukti ang analog. Dala pebahasan selanjutna, operasi axiu dan penjulahan bilangan kabur akan didefinisikan elalui potongan--na. Teorea 6 Untuk bilangan kabur a ~ dan b ~ berlaku pend( a ~ ~ b ~ ) = pend( a ~ ) pend( b ~ ) di ana pend( a ~ ) pend( b ~ ) = {x x pend( a ~ ) dan pend( b ~ )}. Bukti: Abil sebarang bilangan real z pend( a ~ ~ b ~ ), aka ~ b ~ (z) 0. Andaikan z pend( a ~ ) pend( b ~ ), aka untuk setiap x dan dengan x = z berlaku x pend( a ~ ) atau pend( b ~ ). Hal ini berarti a ~ (x) 0 atau b ~ ( ) 0 a ~ ang berakibat a ~ ~ b ~ (z) = ) 60
9 M. And Rhudito, dkk., Aljabar Max-Plus Bilangan Kabur in{ a ~ (x), b ~ ( )} 0, sehingga zx terjadi kontradiksi. Jadi z pend( a ~ ) pend( b ~ ), ang berarti pend( a ~ ~ b ~ ) pend( a ~ ) pend( b ~ ). Abil sebarang bilangan real z pend( a ~ ) end( b ~ ), aka terdapat x pend( a ~ ) dan pend( b ~ ) sedeikian sehingga x + = z. Hal ini berarti bahwa (x) 0 dan b ~ ( ) 0. Akibatna a ~ (z) = ~ ~ a ~ b ) z x in{ a ~ (x), b ~ ()} 0, aitu bahwa z pend( a ~ ) pend( b ~ ). Jadi pend( a ~ ) pend( b ~ ) pend( a ~ ~ b ~ ). Dengan deikian terbukti bahwa pend( a ~ ~ b ~ ) = pend( a ~ ) pend( b ~ ). Teorea di atas juga berlaku untuk operasi aksiu, dengan bukti ang analog. Selanjutna diperoleh bahwa (a b) 0 = [inf(pend ( a ~ ~ b ~ )), (pend ( a ~ ~ b ~ ))] = [inf (pend( a ~ ) pend(b ~ )), (pend( a ~ ) pend(b ~ ))] = [inf(pend( a ~ )) inf(pend(b ~ ), (pend( a ~ ))(pend(b ~ ))] = [inf(pend( a ~ )), (pend( a ~ ))] [inf(pend(b ~ )),(pend( b ~ ))]= a 0 b 0. Dengan cara ang analog dapat juga diperoleh bahwa (a b) 0 = a 0 b 0. Suatu keluarga interval [a (), a 2 ()] dikatakan tersarang (nested) jika untuk aka berlaku [a (), a 2 ()] [a (), a 2 ()],, [0, ]. Berikut diberikan suatu hasil ang eberikan sarat bahwa suatu keluarga interval erupakan potongan- suatu bilangan kabur. Akibat 7 Jika keluarga interval {[a (), a 2 ()]} [0, ] eenuhi sifat i) [a (), a 2 ()], ii) [a (), a 2 ()] tersarang dan iii) [a (0), a 2 (0)] terbatas, 6 aka terdapat dengan tunggal bilangan kabur a ~ sedeikian hingga [a (), a 2 ()] = a, [0, ]. Bukti: Dari sifat ii) di atas, enurut Teorea 2 jelas bahwa terdapat dengan tunggal hipunan kabur a ~ sedeikian hingga [a (), a 2 ()] = a, [0, ]. Selanjutna dari sifat i) dan iii) di atas, enurut definisi bilangan kabur, jelas bahwa a ~ erupakan bilangan kabur. Untuk eperoleh fungsi keanggotaan hasil operasi pada bilangan kabur seperti di atas, dapat dengan enggunakan Teorea Dekoposisi. Potongan-potongan- ang didefinisikan pada operasi di atas eenuhi sarat sebagai keluarga potongan- dari suatu bilangan kabur, aitu i) Potongan-potongan- hasil operasi di atas berupa interval dala I(R) ax. Hal ini dipenuhi, karena a a dan b aka enurut sifat kekonsistenan urutan terhadap operasi dan dapat disipulkan ( a b ) b ) ( a b ) dan ( a ( a b ). ii) Karena a ~ dan b ~ adalah bilangan kabur, aka [ a, a ] dan [ b, b ] sehingga [ a b, a b ]. iii) Potongan-potongan- hasil operasi di atas berupa keluarga interval tersarang dala I(R) ax. Hal ini dapat ditunjukkan sebagai berikut. Karena a ~ dan b ~ erupakan bilangan kabur, aka berlaku: jika aka a a dan b b, aitu a b a b a b a dan b. Karena dala R ax operasi dan konsisten terhadap urutan,
10 Berkala MIPA, 8(2), Mei 2008 aka a b a b a a b b dan a b a b a b a, [0, ]. iv) Karena a ~ dan b ~ adalah bilangan 0 0 kabur, aka aka [ a, a ] dan 0 0 [ b ] asing-asing terbatas, sehingga 0 [ a b 0, 0 a b 0 ] juga terbatas. Selanjutna dengan enggunakan Teorea Dekoposisi diperoleh bahwa a ~ ~ b ~ = c ~ = c, di ana c ~ adalah hipunan [0,] kabur dala R dengan fungsi keanggotaan c ~ (x) = (x) ( a b), di ana adalah fungsi karakteristik ( ab) hipunan (a b). Deikian juga untuk operasi ~ dapat dilakukan dengan cara ang analog. Contoh 3 Diberikan dua buah bilangan kabur segitiga a ~ = BKS(a, a, a 2 ) dan b ~ =BKS(b, b, b 2 ), aka a = [ a, a ] = [(aa ) + a, (a 2 a) +a 2 ] dan b = [ b, b ] = [(bb ) + b, (b 2 b) + b 2 ]. Keudian potongan- dari a ~ ~ b ~ dan a ~ ~ b ~ berturut-turut adalah [((aa ) + a ) ((bb ) + b ), ((a 2 a) +a 2 ) ((b 2 b) + b 2 )] dan [((aa ) + a ) ((bb ) + b ), ((a 2 a) + a 2 ) ((b 2 b) + b 2 )]. Perhatikan bahwa untuk potongan- dari a ~ ~ b ~ berlaku [((aa ) + a ) ((bb ) + b ), ((a 2 a) + a 2 ) ((b 2 b) + b 2 )] = [(a+b) (a +b ) + (a +b ), ((a 2 +b 2 ) (a+b) + (a 2 +b 2 )], sehingga a ~ ~ b ~ = BKS((a +b ), (a+b), (a 2 + b 2 )). Sedangkan untuk (a ~ b)), jika a b dan a aka (a ~ b)) = b, aitu a ~ ~ b ~ = b ~. Salah satu keungkinan ang lain dari relasi antara a, a, b diberikan dala Contoh 4 berikut. Contoh 4 Misalkan a ~ = BKS(2,3, 4) dan b ~ = BKS(,4,5), aka a = [(32) + 2, (43) + 4] = [+2, +4] dan b = [(4) +, (54) + 5] = [3+, + 5]. Dengan enggunakan progra MATLAB berikut diberikan grafik fungsi keanggotaan dari a ~, b ~ (Gabar bagian atas) dan batas-batas potongan- dari a ~ ~ b ~ dan a ~ ~ b ~ untuk = 0, 0., 0.2,..., (Gabar bagian bawah). Gabar. Grafik Fungsi Keanggotaan Hasil Operasi BKS(2, 3, 4) dan BKS(, 4, 5). Keterangan Gabar : : a ~,. : b ~, a ~ ~ b ~. + : a ~ ~ b ~, * : Dengan eperhatikan gabar di atas dan bahwa titik potong a ~ (x) = x2 dan b ~ (x) = x adalah (2.5, 0.5), aka diperoleh 3 62
11 M. And Rhudito, dkk., Aljabar Max-Plus Bilangan Kabur a ~ ~ b ~ (x) = 0 x 2 x 3 5 x 0, x 2, 2 x 2, 5, 2, 5 x 4., 4 x 5, x 5 Seentara itu a ~ ~ b ~ = BKS(3, 7, 9). Dari Contoh 4 di atas napak bahwa hasil operasi axiu dua buah bilangan kabur segitiga tidak selalu erupakan bilangan kabur segitiga. Diberikan F(R) ~ := F(R) { ~ } dengan F(R) adalah hipunan seua bilangan kabur dan ~ := {}, dengan = [,], [0, ]. Pada (F(R)) ~ didefinisikan operasi aksiu ~ dan penjulahan ~, seperti pada bagian 2.2. di atas. Teorea 8 Struktur aljabar (F(R) ~, ~, ~ ) adalah seiring idepoten koutatif. Bukti: Operasi ang didefinisikan di atas terdefinisi dengan baik, aitu eenuhi sarat tertutup dan bernilai tunggal. Akan ditunjukkan untuk operasi ~, sedangkan untuk operasi ~ dapat dilakukan dengan cara ang analog. Untuk sarat ketertutupan dijelaskan sebagai berikut. Abil sebarang bilangan kabur a ~ dan b ~ F(R) ~. i) Karena a ~ dan b ~ erupakan bilangan kabur, aka a ~ dan b ~ noral, aitu bahwa a dan b. Hal ini berarti x a, x b R sedeikian hingga berlaku a x a a dan b x b b. Karena sifat kekonsistenan urutan terhadap operasi aka berlaku ( a b ) (x a x b ) ( a b ). Jadi [ a. Jadi a ~ ~ b ~ noral. a b ] = (a b) ii) Karena a ~ dan b ~ erupakan bilangan kabur, aka (0, ], a, b erupakan interval tertutup dala R. Menurut sifat ketertutupan operasi pada interval, [ a a b ] erupakan interval tertutup dala R, (0, ]. iii) Karena a ~ dan b ~ erupakan bilangan kabur, aka pend( a ~ ) dan pend( b ~ ) terbatas, sehingga berlaku pend( a ~ ) a 0 = [inf(pend( a ~ )), (pend( a ~ ))] dan pend( b ~ ) b 0 = [inf(pend(b ~ )), (pend( b ~ ))]. Dengan deikian enurut penjelasan pada bagian 2.2 di atas, pend( a ~ ~ b ~ ) = pend( a ~ ) pend(b ~ ) a 0 b 0 = (a b) 0 = [inf(pend( a ~ )) inf(pend( b ~ ), (pend( a ~ )) (pend(b ~ ))]. Jadi terbukti bahwa pend( a ~ ~ b ~ ) terbatas. Berdasarkan i), ii) dan iii) di atas dapat disipulkan bahwa operasi ~ ang didefinisikan di atas tertutup dala F(R). Ketunggalan hasil operasi di atas dapat dijelaskan sebagai berikut. Akan ditunjukkan ketunggalan untuk operasi ~, sedangkan untuk operasi ~ analog. Abil sebarang bilangan kabur a ~, b ~, c ~ dan d ~ F(R) sedeikian hingga a ~ = c ~ dan b ~ = d ~. Karena a ~ = c ~ dan b ~ = d ~, aka a = c dan b = d, [0, ] ang berarti [ a, a ] = [ c, c ] dan [ b, b ] = [ d, d d, a b = ] atau b = a = c, a = c, b = d. Hal ini berakibat bahwa c d dan c d aitu bahwa [ a = [ c d, c d a a b = b ] ], [0, ]. Jadi 63
12 Berkala MIPA, 8(2), Mei 2008 a ~ ~ b ~ = c ~ ~ d ~, ang berarti hasil operasi tersebut tunggal. Selanjutna karena potongan- suatu bilangan kabur berupa interval dala I(R ), dan enurut Contoh 2, (I(R ),, ) erupakan seiring idepoten koutatif, aka (F(R) ~, ~, ~ ) erupakan seiring idepoten koutatif, dengan eleen netral ~ = {} dan eleen satuan e ~ = {0}, dengan e = [0, 0], [0, ]). Seiring idepoten koutatif F(R) ax := (F(R), ~, ~ ) di atas disebut aljabar ax-plus bilangan kabur, atau secara singkat cukup dituliskan dengan F(R) ax. 5. KESIMPULAN DAN SARAN Dari pebahasan di atas dapat disipulkan bahwa operasi axiu dan penjulahan ang didefinisikan elalui potongan- tertutup dala hipunan seua bilangan kabur tersebut. Selanjutna hipunan seua bilangan kabur ang dilengkapi dengan operasi axiu dan penjulahan tersebut erupakan seiring idepoten koutatif. Untuk penelitian selanjutna dapat dilakukan pebahasan perluasan operasioperasi di atas ke dala operasi axiu dan penjulahan untuk atriks atas bilangan kabur beserta struktur-struktur aljabar ang enertaina. DAFTAR PUSTAKA Bacelli, F., et al Snchronization and Linearit. John Wile & Sons. New York. Lee, K.H First Course on Fuzz Theor and Applications. Spinger- Verlag. Berlin. Litvinov, G.L., Sobolevskii, A.N Idepotent Interval Anasis and Optiization Probles. Reliab. Coput., 7, (200); arxiv: ath.sc/ Rudhito, And Siste Linear Max- Plus Waktu-Invariant. Tesis: Progra Pascasarjana Universitas Gadjah Mada. Yogakarta. Schutter, B. De., 996, Max-Algebraic Sste Theor for Discrete Event Sstes, PhD thesis Departeent of Electrical Enginering Katholieke Universiteit Leuven, Leuven. Susilo, F Hipunan dan Logika Kabur serta Aplikasina. Edisi kedua. Graha Ilu. Yogakarta. Zierann, H.J., 99. Fuzz Set Theor and Its Applications. Kluwer Acadeic Publishers. Boston. 64
Sistem Linear Max-Plus Interval Waktu Invariant
 Siste Linear Max-Plus Interval Waktu Invariant A 11 M. Andy udhito Progra Studi Pendidikan Mateatika FKIP Universitas Sanata Dhara Paingan Maguwoharjo Yogyakarta eail: arudhito@yahoo.co.id Abstrak elah
Siste Linear Max-Plus Interval Waktu Invariant A 11 M. Andy udhito Progra Studi Pendidikan Mateatika FKIP Universitas Sanata Dhara Paingan Maguwoharjo Yogyakarta eail: arudhito@yahoo.co.id Abstrak elah
ISBN:
 POSIDING SEMINA NASIONAL P e n e l i t i a n, P e n d i d i k a n, d a n P e n e r a p a n M I P A Tanggal 18 Mei 2013, FMIPA UNIVESITAS NEGEI YOGYAKATA ISBN: 978 979-96880 7-1 Bidang: Mateatika dan Pendidikan
POSIDING SEMINA NASIONAL P e n e l i t i a n, P e n d i d i k a n, d a n P e n e r a p a n M I P A Tanggal 18 Mei 2013, FMIPA UNIVESITAS NEGEI YOGYAKATA ISBN: 978 979-96880 7-1 Bidang: Mateatika dan Pendidikan
BENTUK NORMAL SMITH DAN MATRIKS BAIK KIRI/KANAN
 BENTUK NORMAL SMITH DAN MATRIKS BAIK KIRI/KANAN Yuiati (yui@ail.ut.ac.id) Universitas Terbuka ABSTRACT The Sith noral for and left good atrix have been known in atrix theore. Any atrix over the principal
BENTUK NORMAL SMITH DAN MATRIKS BAIK KIRI/KANAN Yuiati (yui@ail.ut.ac.id) Universitas Terbuka ABSTRACT The Sith noral for and left good atrix have been known in atrix theore. Any atrix over the principal
DISTRIBUSI DUA PEUBAH ACAK
 0 DISTRIBUSI DUA PEUBAH ACAK Dala hal ini akan dibahas aca-aca fungsi peluang atau fungsi densitas ang berkaitan dengan dua peubah acak, aitu distribusi gabungan, distribusi arginal, distribusi bersarat,
0 DISTRIBUSI DUA PEUBAH ACAK Dala hal ini akan dibahas aca-aca fungsi peluang atau fungsi densitas ang berkaitan dengan dua peubah acak, aitu distribusi gabungan, distribusi arginal, distribusi bersarat,
Bab III S, TORUS, Sebelum mempelajari perbedaan pada grup fundamental., dan figure eight terlebih dahulu akan dipelajari sifat dari grup
 GRUP FUNDAMENTAL PADA Bab III S, TORUS, P dan FIGURE EIGHT Sebelu epelajari perbedaan pada grup fundaental S, Torus, P, dan figure eight terlebih dahulu akan dipelajari sifat dari grup fundaental asing-asing
GRUP FUNDAMENTAL PADA Bab III S, TORUS, P dan FIGURE EIGHT Sebelu epelajari perbedaan pada grup fundaental S, Torus, P, dan figure eight terlebih dahulu akan dipelajari sifat dari grup fundaental asing-asing
Perbandingan Bilangan Dominasi Jarak Satu dan Dua pada Graf Hasil Operasi Comb
 Perbandingan Bilangan Doinasi Jarak Satu dan Dua pada Graf Hasil Operasi Cob Reni Uilasari 1) 1) Jurusan Teknik Inforatika, Fakultas Teknik, Universitas Muhaadiyah Jeber Eail : 1) reniuilasari@gailco ABSTRAK
Perbandingan Bilangan Doinasi Jarak Satu dan Dua pada Graf Hasil Operasi Cob Reni Uilasari 1) 1) Jurusan Teknik Inforatika, Fakultas Teknik, Universitas Muhaadiyah Jeber Eail : 1) reniuilasari@gailco ABSTRAK
Diberikan sebarang relasi R dari himpunan A ke B. Invers dari R yang dinotasikan dengan R adalah relasi dari B ke A sedemikian sehingga
 Departent of Matheatics FMIPA UNS Lecture 3: Relation C A. Universal, Epty, and Equality Relations Diberikan sebarang hipunan A. Maka A A dan erupakan subset dari A A dan berturut-turut disebut relasi
Departent of Matheatics FMIPA UNS Lecture 3: Relation C A. Universal, Epty, and Equality Relations Diberikan sebarang hipunan A. Maka A A dan erupakan subset dari A A dan berturut-turut disebut relasi
BAB III m BAHASAN KONSTRUKSI GF(3 ) dalam penelitian ini dapat dilakukan dengan mengacu pada konsep perluasan filed pada Bab II bagian 2.8.
 BAB III BAHASAN KONSTRUKSI GF( ) Untuk engonstruksi GF( ) dala penelitian ini dapat dilakukan dengan engacu pada konsep perluasan filed pada Bab II bagian 28 Karena adalah bilangan pria, aka berdasarkan
BAB III BAHASAN KONSTRUKSI GF( ) Untuk engonstruksi GF( ) dala penelitian ini dapat dilakukan dengan engacu pada konsep perluasan filed pada Bab II bagian 28 Karena adalah bilangan pria, aka berdasarkan
SIFAT-SIFAT OPERASI ARITMATIKA, DETERMINAN DAN INVERS PADA MATRIKS INTERVAL TUGAS AKHIR. Oleh : NURSUKAISIH
 SIFAT-SIFAT OPERASI ARITMATIKA DETERMINAN DAN INVERS PADA MATRIKS INTERVAL TUGAS AKHIR Diajukan Sebagai Salah Satu Syarat untuk Meperoleh Gelar Sarjana Sains pada Jurusan Mateatika Oleh : NURSUKAISIH 0854003938
SIFAT-SIFAT OPERASI ARITMATIKA DETERMINAN DAN INVERS PADA MATRIKS INTERVAL TUGAS AKHIR Diajukan Sebagai Salah Satu Syarat untuk Meperoleh Gelar Sarjana Sains pada Jurusan Mateatika Oleh : NURSUKAISIH 0854003938
KEBERADAAN SOLUSI PERSAMAAN DIOPHANTIN MATRIKS POLINOMIAL DAN PENYELESAIANNYA MENGGUNAKAN TITIK-TITIK INTERPOLASI
 KEBERADAAN SOLUSI PERSAMAAN DIOPHANTIN MATRIKS POLINOMIAL DAN PENYELESAIANNYA MENGGUNAKAN TITIK-TITIK INTERPOLASI Laila Istiani R. Heri Soelistyo Utoo 2, 2 Progra Studi Mateatika Jurusan Mateatika FMIPA
KEBERADAAN SOLUSI PERSAMAAN DIOPHANTIN MATRIKS POLINOMIAL DAN PENYELESAIANNYA MENGGUNAKAN TITIK-TITIK INTERPOLASI Laila Istiani R. Heri Soelistyo Utoo 2, 2 Progra Studi Mateatika Jurusan Mateatika FMIPA
Pelabelan Total Super (a,d) - Sisi Antimagic Pada Graf Crown String (Super (a,d)-edge Antimagic Total Labeling of Crown String Graph )
 1 Pelabelan Total Super (a,d) - Sisi Antiagic Pada Graf Crown String (Super (a,d)-edge Antiagic Total Labeling of Crown String Graph ) Enin Lutfi Sundari, Dafik, Slain Pendidikan Mateatika, Fakultas Keguruan
1 Pelabelan Total Super (a,d) - Sisi Antiagic Pada Graf Crown String (Super (a,d)-edge Antiagic Total Labeling of Crown String Graph ) Enin Lutfi Sundari, Dafik, Slain Pendidikan Mateatika, Fakultas Keguruan
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI 2.1. Konsep Dasar Graph Sebelu sapai pada pendefinisian asalah network flow, terlebih dahulu pada bagian ini akan diuraikan engenai konsep-konsep dasar dari odel graph dan representasinya
BAB 2 LANDASAN TEORI 2.1. Konsep Dasar Graph Sebelu sapai pada pendefinisian asalah network flow, terlebih dahulu pada bagian ini akan diuraikan engenai konsep-konsep dasar dari odel graph dan representasinya
ANALISIS HOMOTOPI DALAM PENYELESAIAN SUATU MASALAH TAKLINEAR
 ANALISIS HOMOTOPI DALAM PENYELESAIAN SUATU MASALAH TAKLINEAR JAHARUDDIN Departeen Mateatika, Fakultas Mateatika dan Iu Pengetahuan Ala, Institut Pertanian Bogor Jln. Meranti, Kapus IPB Draaga, Bogor 1668,
ANALISIS HOMOTOPI DALAM PENYELESAIAN SUATU MASALAH TAKLINEAR JAHARUDDIN Departeen Mateatika, Fakultas Mateatika dan Iu Pengetahuan Ala, Institut Pertanian Bogor Jln. Meranti, Kapus IPB Draaga, Bogor 1668,
Hubungan Antara Turunan Parsial dan Kekontinuan Pada Fungsi Dua Peubah
 Jurnal EKSPONENSIAL Volue Noor Mei ISSN 85-789 Hubungan Antara Turunan Parsial dan Kekontinuan Pada Fungsi Dua Peuba Relationsip Between Partial Derivatives and Continuit on te Function o Two Variables
Jurnal EKSPONENSIAL Volue Noor Mei ISSN 85-789 Hubungan Antara Turunan Parsial dan Kekontinuan Pada Fungsi Dua Peuba Relationsip Between Partial Derivatives and Continuit on te Function o Two Variables
PENJUMLAHAN MOMENTUM SUDUT
 PENJUMAHAN MOMENTUM SUDUT A. Penjulahan Moentu Sudut = + Gabar.9. Penjulahan oentu angular secara klasik. Dua vektor oentu angular dan dijulahkan enghasilkan Jika oentu angular elektron pertaa adalah dan
PENJUMAHAN MOMENTUM SUDUT A. Penjulahan Moentu Sudut = + Gabar.9. Penjulahan oentu angular secara klasik. Dua vektor oentu angular dan dijulahkan enghasilkan Jika oentu angular elektron pertaa adalah dan
Definisi 3.3: RUANG SAMPEL KONTINU Ruang sampel kontinu adalah ruang sampel yang anggotanya merupakan interval pada garis bilangan real.
 0 RUANG SAMPEL Kita akan eperoleh ruang sapel, jika kita elakukan suatu eksperien atau percobaan. Eksperien disini erupakan eksperien acak. Misalnya kita elakukan suatu eksperien yang diulang beberapa
0 RUANG SAMPEL Kita akan eperoleh ruang sapel, jika kita elakukan suatu eksperien atau percobaan. Eksperien disini erupakan eksperien acak. Misalnya kita elakukan suatu eksperien yang diulang beberapa
POLINOMIAL ATAS ALJABAR MAX-PLUS INTERVAL
 POLINOMIAL ATAS ALJABAR MAX-PLUS INTERVAL A-4 Harry Nugroho 1, Effa Marta R 2, Ari Wardayani 3 1,2,3 Program Studi Matematika Universitas Jenderal Soedirman 1 harry_nugroho92@yahoo.com 2 marta_effa, 3
POLINOMIAL ATAS ALJABAR MAX-PLUS INTERVAL A-4 Harry Nugroho 1, Effa Marta R 2, Ari Wardayani 3 1,2,3 Program Studi Matematika Universitas Jenderal Soedirman 1 harry_nugroho92@yahoo.com 2 marta_effa, 3
Soal-Soal dan Pembahasan Matematika IPA SBMPTN/SNMPTN 2008
 Soal-Soal dan Pebahasan Mateatika IPA SBMPTN/SNMPTN 008. Diketahui fungsi-fungsi f dan g dengan f(x) g(x) x - x untuk setiap bilangan real x. Jika g(), f ' () f(), dan g ' () f(), aka g ' () A. C. 0 E.
Soal-Soal dan Pebahasan Mateatika IPA SBMPTN/SNMPTN 008. Diketahui fungsi-fungsi f dan g dengan f(x) g(x) x - x untuk setiap bilangan real x. Jika g(), f ' () f(), dan g ' () f(), aka g ' () A. C. 0 E.
BAB III ESTIMASI PARAMETER PADA MODEL REGRESI LOGISTIK 2-LEVEL. Model hirarki 2-level merupakan model statistik yang digunakan untuk
 BAB III ESTIMASI PARAMETER PADA MODEL REGRESI LOGISTIK -LEVEL Model hirarki -level erupakan odel statistik ang digunakan untuk enganalisis data ang bersarang, atau data ang epunai struktur hirarki -level.
BAB III ESTIMASI PARAMETER PADA MODEL REGRESI LOGISTIK -LEVEL Model hirarki -level erupakan odel statistik ang digunakan untuk enganalisis data ang bersarang, atau data ang epunai struktur hirarki -level.
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI 2. Graf Graf G= (V G,E G ) adalah suatu siste yang terdiri dari hipunan berhingga tak kosong V G dari objek yang dinaakan titik (ertex) dan hipunan E G, pasangan tak berurut dari
BAB II LANDASAN TEORI 2. Graf Graf G= (V G,E G ) adalah suatu siste yang terdiri dari hipunan berhingga tak kosong V G dari objek yang dinaakan titik (ertex) dan hipunan E G, pasangan tak berurut dari
BAHASAN ALGORITME ARITMETIK GF(3 ) Telah dijelaskan sebelumnya bahwa dalam mengonstruksi field GF(3 )
 BAB IV BAHASAN ALGORITME ARITMETIK GF(3 ) Telah dijelaskan sebelunya bahwa dala engonstruksi field GF(3 ) diperoleh dari perluasan field 3 dengan eilih polinoial priitif berderajat atas 3 yang dala hal
BAB IV BAHASAN ALGORITME ARITMETIK GF(3 ) Telah dijelaskan sebelunya bahwa dala engonstruksi field GF(3 ) diperoleh dari perluasan field 3 dengan eilih polinoial priitif berderajat atas 3 yang dala hal
I. PENDAHULUAN. Konsep teori graf diperkenalkan pertama kali oleh seorang matematikawan Swiss,
 I. PENDAHULUAN. Latar Belakang Konsep teori graf diperkenalkan pertaa kali oleh seorang ateatikawan Swiss, Leonard Euler pada tahun 736, dala perasalahan jebatan Konigsberg. Teori graf erupakan salah satu
I. PENDAHULUAN. Latar Belakang Konsep teori graf diperkenalkan pertaa kali oleh seorang ateatikawan Swiss, Leonard Euler pada tahun 736, dala perasalahan jebatan Konigsberg. Teori graf erupakan salah satu
J M A. Jurnal Matematika dan Aplikasinya. Journal of Mathematics and Its Applications. Volume 7, No. 1 Juli 2008 ISSN : X
 DEPARTEMEN MATEMATIKA F MIPA - INSTITUT PERTANIAN BOGOR ISSN : 1412-677X Journal of Matheatics and Its Applications J M A Jurnal Mateatika dan Aplikasinya Volue 7, No. 1 Juli 28 Alaat Redaksi : Departeen
DEPARTEMEN MATEMATIKA F MIPA - INSTITUT PERTANIAN BOGOR ISSN : 1412-677X Journal of Matheatics and Its Applications J M A Jurnal Mateatika dan Aplikasinya Volue 7, No. 1 Juli 28 Alaat Redaksi : Departeen
Penentuan Akar-Akar Sistem Persamaan Tak Linier dengan Kombinasi Differential Evolution dan Clustering
 Jurnal Kubik, Volue No. ISSN : 338-0896 Penentuan Akar-Akar Siste Persaaan Tak Linier dengan Kobinasi Differential Evolution dan Clustering Jaaliatul Badriyah Jurusan Mateatika, Universitas Negeri Malang
Jurnal Kubik, Volue No. ISSN : 338-0896 Penentuan Akar-Akar Siste Persaaan Tak Linier dengan Kobinasi Differential Evolution dan Clustering Jaaliatul Badriyah Jurusan Mateatika, Universitas Negeri Malang
PERHITUNGAN INTEGRAL FUNGSI REAL MENGGUNAKAN TEKNIK RESIDU
 PERHITUNGAN INTEGRAL FUNGSI REAL MENGGUNAKAN TEKNIK RESIDU Warsito (warsito@ail.ut.ac.id) Universitas Terbuka ABSTRAT A function f ( x) ( is bounded and continuous in (, ), so the iproper integral of rational
PERHITUNGAN INTEGRAL FUNGSI REAL MENGGUNAKAN TEKNIK RESIDU Warsito (warsito@ail.ut.ac.id) Universitas Terbuka ABSTRAT A function f ( x) ( is bounded and continuous in (, ), so the iproper integral of rational
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI Untuk encaai tujuan enelitian, dierlukan beberaa engertian dan teori yang relevan dengan ebahasan. Dala bab ini akan diberikan beberaa teori berua definisi, teorea, auun lea yang
BAB II LANDASAN TEORI Untuk encaai tujuan enelitian, dierlukan beberaa engertian dan teori yang relevan dengan ebahasan. Dala bab ini akan diberikan beberaa teori berua definisi, teorea, auun lea yang
Bilangan Kromatik Lokasi n Amalgamasi Bintang yang dihubungkan oleh suatu Lintasan
 Jurnal Mateatika Integratif. Vol. 13, No. 2 (2017), pp. 115 121. p-issn:1412-6184, e-issn:2549-903 doi:10.24198/ji.v13.n2.11891.151-121 Bilangan Kroatik Lokasi n Aalgaasi Bintang yang dihubungkan oleh
Jurnal Mateatika Integratif. Vol. 13, No. 2 (2017), pp. 115 121. p-issn:1412-6184, e-issn:2549-903 doi:10.24198/ji.v13.n2.11891.151-121 Bilangan Kroatik Lokasi n Aalgaasi Bintang yang dihubungkan oleh
III HASIL DAN PEMBAHASAN
 7 III HASIL DAN PEMBAHASAN 3. Analisis Metode Dala penelitian ini akan digunakan etode hootopi untuk enyelesaikan persaaan Whitha-Broer-Koup (WBK), yaitu persaaan gerak bagi perabatan gelobang pada perairan
7 III HASIL DAN PEMBAHASAN 3. Analisis Metode Dala penelitian ini akan digunakan etode hootopi untuk enyelesaikan persaaan Whitha-Broer-Koup (WBK), yaitu persaaan gerak bagi perabatan gelobang pada perairan
MATHunesa Jurnal Ilmiah Matematika Volume 3 No.6 Tahun 2017 ISSN
 MATHunesa Jurnal Iliah Mateatika Volue 3 No.6 Tahun 2017 ISSN 2301-9115 SIFAT-SIFAT TURUNAN MUTLAK FUNGSI PADA RUANG METRIK Wicitra Diah Kusua (S1 Mateatika, Fakultas Mateatika dan Ilu Pengetahuan Ala,
MATHunesa Jurnal Iliah Mateatika Volue 3 No.6 Tahun 2017 ISSN 2301-9115 SIFAT-SIFAT TURUNAN MUTLAK FUNGSI PADA RUANG METRIK Wicitra Diah Kusua (S1 Mateatika, Fakultas Mateatika dan Ilu Pengetahuan Ala,
BAB I PENDAHULUAN. segi kuantitas dan kualitasnya. Penambahan jumlah konsumen yang tidak di ikuti
 BAB I PENDAHULUAN 1.1 Latar Belakang Air erupakan kebutuhan yang penting bagi kehidupan anusia. Manusia tidak dapat elanjutkan kehidupannya tanpa penyediaan air yang cukup dala segi kuantitas dan kualitasnya.
BAB I PENDAHULUAN 1.1 Latar Belakang Air erupakan kebutuhan yang penting bagi kehidupan anusia. Manusia tidak dapat elanjutkan kehidupannya tanpa penyediaan air yang cukup dala segi kuantitas dan kualitasnya.
matematika K-13 PEMBAGIAN HORNER DAN TEOREMA SISA K e l a s
 i K- ateatika K e l a s XI PEMBAGIAN HORNER DAN TEOREMA SISA Tujuan Peelajaran Setelah epelajari ateri ini, kau diharapkan eiliki keapuan erikut.. Menguasai konsep peagian suku anyak dengan etode Horner..
i K- ateatika K e l a s XI PEMBAGIAN HORNER DAN TEOREMA SISA Tujuan Peelajaran Setelah epelajari ateri ini, kau diharapkan eiliki keapuan erikut.. Menguasai konsep peagian suku anyak dengan etode Horner..
MENENTUKAN NILAI EIGEN DAN VEKTOR EIGEN MATRIKS INTERVAL TUGAS AKHIR
 MENENTUKAN NILAI EIGEN DAN VEKTOR EIGEN MATRIKS INTERVAL TUGAS AKHIR Diajukan sebagai Salah Satu Syarat untuk Memperoleh Gelar Sarjana Sains pada Jurusan Matematika oleh DEVI SAFITRI 10654004470 FAKULTAS
MENENTUKAN NILAI EIGEN DAN VEKTOR EIGEN MATRIKS INTERVAL TUGAS AKHIR Diajukan sebagai Salah Satu Syarat untuk Memperoleh Gelar Sarjana Sains pada Jurusan Matematika oleh DEVI SAFITRI 10654004470 FAKULTAS
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI 2.1 Data dan Variabel 2.1.1 Data Pengertian data enurut Webster New World Dictionary adalah things known or assued, yang berarti bahwa data itu sesuatu yang diketahui atau dianggap.
BAB II LANDASAN TEORI 2.1 Data dan Variabel 2.1.1 Data Pengertian data enurut Webster New World Dictionary adalah things known or assued, yang berarti bahwa data itu sesuatu yang diketahui atau dianggap.
MENENTUKAN EIGEN PROBLEM ALJABAR MAX-PLUS
 MENENTUKAN EIGEN PROBLEM ALJABAR MAX-PLUS SKRIPSI Diajukan Kepada Fakultas Sains dan Teknologi Universitas Islam Negeri Sunan Kalijaga Yogyakarta untuk Memenuhi Sebagian Syarat Memperoleh Gelar Sarjana
MENENTUKAN EIGEN PROBLEM ALJABAR MAX-PLUS SKRIPSI Diajukan Kepada Fakultas Sains dan Teknologi Universitas Islam Negeri Sunan Kalijaga Yogyakarta untuk Memenuhi Sebagian Syarat Memperoleh Gelar Sarjana
TEOREMA ELIMINASI CUT PADA SISTEM LOGIKA FL gc DAN FL w,gc
 Jurnal Mateatika Vol 0 No Agustus 007:39-4 ISSN: 40-858 TEOREMA ELIMINASI CUT PAA SISTEM LOGIKA FL gc AN FL wgc Bayu Surarso Jurusan Mateatika FMIPA UNIP Jl Prof H Soedarto SH Tebalang Searang 5075 Abstract
Jurnal Mateatika Vol 0 No Agustus 007:39-4 ISSN: 40-858 TEOREMA ELIMINASI CUT PAA SISTEM LOGIKA FL gc AN FL wgc Bayu Surarso Jurusan Mateatika FMIPA UNIP Jl Prof H Soedarto SH Tebalang Searang 5075 Abstract
DAFTAR ISI. HALAMAN JUDUL... i HALAMAN PERSETUJUAN... II HALAMAN PENGESAHAN... III KATA PENGANTAR... IV DAFTAR ISI... V BAB I PENDAHULUAN...
 DAFTAR ISI HALAMAN JUDUL... i HALAMAN PERSETUJUAN... II HALAMAN PENGESAHAN... III KATA PENGANTAR... IV DAFTAR ISI... V BAB I PENDAHULUAN... 1 A. LATAR BELAKANG MASALAH... 1 B. PEMBATASAN MASALAH... 2 C.
DAFTAR ISI HALAMAN JUDUL... i HALAMAN PERSETUJUAN... II HALAMAN PENGESAHAN... III KATA PENGANTAR... IV DAFTAR ISI... V BAB I PENDAHULUAN... 1 A. LATAR BELAKANG MASALAH... 1 B. PEMBATASAN MASALAH... 2 C.
SOAL UJIAN SELEKSI CALON PESERTA OLIMPIADE SAINS NASIONAL 2013 TINGKAT PROPINSI
 SOAL UJIAN SELEKSI CALON PESERTA OLIMPIADE SAINS NASIONAL 013 TINGKAT PROPINSI FISIKA Waktu : 3,5 ja KEMENTERIAN PENDIDIKAN DAN KEBUDAYAAN DIREKTORAT JENDERAL PENDIDIKAN MENENGAH DIREKTORAT PEMBINAAN SEKOLAH
SOAL UJIAN SELEKSI CALON PESERTA OLIMPIADE SAINS NASIONAL 013 TINGKAT PROPINSI FISIKA Waktu : 3,5 ja KEMENTERIAN PENDIDIKAN DAN KEBUDAYAAN DIREKTORAT JENDERAL PENDIDIKAN MENENGAH DIREKTORAT PEMBINAAN SEKOLAH
2-EKSPONEN DIGRAPH DWIWARNA ASIMETRIK DENGAN DUA CYCLE YANG BERSINGGUNGAN
 Bulletin of Matheatics Vol. 03 No. 0 (20) pp. 39 48. 2-EKSPONEN DIGRAPH DWIWARNA ASIMETRIK DENGAN DUA CYCLE YANG BERSINGGUNGAN Mardiningsih Saib Suwilo dan Indra Syahputra Abstract. Let D asyetric two-coloured-digraph
Bulletin of Matheatics Vol. 03 No. 0 (20) pp. 39 48. 2-EKSPONEN DIGRAPH DWIWARNA ASIMETRIK DENGAN DUA CYCLE YANG BERSINGGUNGAN Mardiningsih Saib Suwilo dan Indra Syahputra Abstract. Let D asyetric two-coloured-digraph
MAKALAH SISTEM BASIS DATA
 MAKALAH SISTEM BASIS DATA (Entity Relationship Diagra (ERD) Reservasi Hotel) Disusun Oleh : Yulius Dona Hipa (16101055) Agustina Dau (15101635) Arsenia Weni (16101648) PROGRAM STUDI TEKNIK INFORMARIKA
MAKALAH SISTEM BASIS DATA (Entity Relationship Diagra (ERD) Reservasi Hotel) Disusun Oleh : Yulius Dona Hipa (16101055) Agustina Dau (15101635) Arsenia Weni (16101648) PROGRAM STUDI TEKNIK INFORMARIKA
FAMILI BARU DARI METODE ITERASI ORDE TIGA UNTUK MENYELESAIKAN PERSAMAAN NONLINEAR DENGAN AKAR GANDA ABSTRACT
 FAMILI BARU DARI METODE ITERASI ORDE TIGA UNTUK MENYELESAIKAN PERSAMAAN NONLINEAR DENGAN AKAR GANDA Elvi Syahriah 1, Khozin Mu taar 2 1,2 Progra Studi S1 Mateatika Jurusan Mateatika Fakultas Mateatika
FAMILI BARU DARI METODE ITERASI ORDE TIGA UNTUK MENYELESAIKAN PERSAMAAN NONLINEAR DENGAN AKAR GANDA Elvi Syahriah 1, Khozin Mu taar 2 1,2 Progra Studi S1 Mateatika Jurusan Mateatika Fakultas Mateatika
GELANGGANG ARTIN. Kata Kunci: Artin ring, prim ideal, maximal ideal, nilradikal.
 Jurnal Matematika UNAND Vol. 2 No. 2 Hal. 108 114 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND GELANGGANG ARTIN IMELDA FAUZIAH, NOVA NOLIZA BAKAR, ZULAKMAL Program Studi Matematika, Fakultas Matematika
Jurnal Matematika UNAND Vol. 2 No. 2 Hal. 108 114 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND GELANGGANG ARTIN IMELDA FAUZIAH, NOVA NOLIZA BAKAR, ZULAKMAL Program Studi Matematika, Fakultas Matematika
ANALISIS PERUBAHAN LUASAN AREAL PERTANAMAN DAERAH IRIGASI UPT-1 SUNGAI PAKU BERDASARKAN DEBIT AIR PADA SALURAN PRIMER BENDUNGAN SUNGAI PAKU
 NLISIS PERUBHN LUSN REL PERTNMN DERH IRIGSI UPT- SUNGI PKU BERDSRKN DEBIT IR PD SLURN PRIMER BENDUNGN SUNGI PKU Virgo Trisep Haris, Lusi Dwi Putri, Universitas Lancang Kuning, Pekanbaru E-ail:lusidwiputri@unilak.ac.id
NLISIS PERUBHN LUSN REL PERTNMN DERH IRIGSI UPT- SUNGI PKU BERDSRKN DEBIT IR PD SLURN PRIMER BENDUNGN SUNGI PKU Virgo Trisep Haris, Lusi Dwi Putri, Universitas Lancang Kuning, Pekanbaru E-ail:lusidwiputri@unilak.ac.id
PENGGUNAAN METODE HOMOTOPI PADA MASALAH PERAMBATAN GELOMBANG INTERFACIAL
 PENGGUNAAN METODE HOMOTOPI PADA MASALAH PERAMBATAN GELOMBANG INTERFACIAL JAHARUDDIN Departeen Mateatika Fakultas Mateatika Ilu Pengetahuan Ala Institut Pertanian Bogor Jl Meranti, Kapus IPB Daraga, Bogor
PENGGUNAAN METODE HOMOTOPI PADA MASALAH PERAMBATAN GELOMBANG INTERFACIAL JAHARUDDIN Departeen Mateatika Fakultas Mateatika Ilu Pengetahuan Ala Institut Pertanian Bogor Jl Meranti, Kapus IPB Daraga, Bogor
PENGUJIAN ALAT UKUR DAYA DIJITAL MENGGUNAKAN PIRANTI STANDAR YOKOGAWA CA71. Hari Prijanto *)
 Buletin Pengelolaan Reaktor uklir. Vol. 7 o. Oktober 00: 5-0 PEGUJIA ALAT UKUR DAYA DIJITAL MEGGUAKA PIRATI STADAR YOKOGAWA CA7 Hari Prijanto *) ABSTRAK PEGUJIA ALAT UKUR DAYA DIJITAL MEGGUAKA PIRATI STADAR
Buletin Pengelolaan Reaktor uklir. Vol. 7 o. Oktober 00: 5-0 PEGUJIA ALAT UKUR DAYA DIJITAL MEGGUAKA PIRATI STADAR YOKOGAWA CA7 Hari Prijanto *) ABSTRAK PEGUJIA ALAT UKUR DAYA DIJITAL MEGGUAKA PIRATI STADAR
PEMILIHAN KRITERIA DALAM PEMBUATAN KARTU KREDIT DENGAN MENGGUNAKAN METODE FUZZY AHP
 E-Jurnal Mateatika Vol. 3, No. Januari 204, 25-32 ISSN: 2303-75 PEMILIHAN KRITERIA DALAM PEMBUATAN KARTU KREDIT DENGAN MENGGUNAKAN METODE FUZZY AHP JOKO HADI APRIANTO, G. K. GANDHIADI 2, DESAK PUTU EKA
E-Jurnal Mateatika Vol. 3, No. Januari 204, 25-32 ISSN: 2303-75 PEMILIHAN KRITERIA DALAM PEMBUATAN KARTU KREDIT DENGAN MENGGUNAKAN METODE FUZZY AHP JOKO HADI APRIANTO, G. K. GANDHIADI 2, DESAK PUTU EKA
Konstruksi Kode Cross Bifix Bebas Ternair Untuk Panjang Ganjil
 Prosiding SI MaNIs (Seinar Nasional Integrasi Mateatika dan Nilai Islai) Vol.1, No.1, Juli 017, Hal. 1-5 p-issn: 580-4596; e-issn: 580-460X Halaan 1 Konstruksi Kode Cross Bifix Bebas Ternair Untuk Panjang
Prosiding SI MaNIs (Seinar Nasional Integrasi Mateatika dan Nilai Islai) Vol.1, No.1, Juli 017, Hal. 1-5 p-issn: 580-4596; e-issn: 580-460X Halaan 1 Konstruksi Kode Cross Bifix Bebas Ternair Untuk Panjang
USAHA DAN ENERGI DALAM ELEKTROSTATIKA
 USAHA DAN ENERGI DALAM ELEKTROSTATIKA Usaha untuk Meindahkan Muatan Usaha adalah kerja yang dilakukan oleh gaya F untuk eindahkan uatan dari satu tepat ke tepat lainnya. = (1) Jika kita hendak eindahkan
USAHA DAN ENERGI DALAM ELEKTROSTATIKA Usaha untuk Meindahkan Muatan Usaha adalah kerja yang dilakukan oleh gaya F untuk eindahkan uatan dari satu tepat ke tepat lainnya. = (1) Jika kita hendak eindahkan
Elliptic Curve Digital Signature Algorithm (ECDSA) Departemen Teknik Informatika ITB
 Elliptic Curve Digital Algorith (ECDSA) Departeen Teknik Inforatika ITB And Triwinarko Laboratoriu Ilu dan Rekaasa Koputasi Departeen Teknik Inforatika, Institut Teknologi Bandung Jl. Ganesha 0, Bandung
Elliptic Curve Digital Algorith (ECDSA) Departeen Teknik Inforatika ITB And Triwinarko Laboratoriu Ilu dan Rekaasa Koputasi Departeen Teknik Inforatika, Institut Teknologi Bandung Jl. Ganesha 0, Bandung
Membelajarkan Geometri dengan Program GeoGebra
 Mebelajarkan Geoetri dengan Progra GeoGebra Oleh : Jurusan Pendidikan Mateatika FMIPA UNY Yogyakarta Eail: ali_uny73@yahoo.co ABSTRAK Peanfaatan teknologi koputer dengan berbagai progranya dala pebelajaran
Mebelajarkan Geoetri dengan Progra GeoGebra Oleh : Jurusan Pendidikan Mateatika FMIPA UNY Yogyakarta Eail: ali_uny73@yahoo.co ABSTRAK Peanfaatan teknologi koputer dengan berbagai progranya dala pebelajaran
A-7 KEBEBASAN LINEAR DALAM ALJABAR MAX-PLUS INTERVAL
 PROSIDING ISBN : 978-979-16353-9-4 A-7 KEBEBASAN LINEAR DALAM ALJABAR MAX-PLUS INTERVAL Siswanto 1, Aditya NR 2, Supriyadi W 3 1,2,3 Jurusan Matematika FMIPA UNS 1 sismipauns@yahoocoid, 2 adityanurrochma@yahoocom,
PROSIDING ISBN : 978-979-16353-9-4 A-7 KEBEBASAN LINEAR DALAM ALJABAR MAX-PLUS INTERVAL Siswanto 1, Aditya NR 2, Supriyadi W 3 1,2,3 Jurusan Matematika FMIPA UNS 1 sismipauns@yahoocoid, 2 adityanurrochma@yahoocom,
Unit 2 KONSEP DASAR ALJABAR. Clara Ika Sari Pendahuluan
 Unit KONSEP DASAR ALJABAR Clara Ika Sari Pendahuluan P ada unit ini kita akan mempelajari beberapa konsep dasar dalam aljabar seperti persamaan dan pertidaksamaan ang berbentuk linear dan kuadrat, serta
Unit KONSEP DASAR ALJABAR Clara Ika Sari Pendahuluan P ada unit ini kita akan mempelajari beberapa konsep dasar dalam aljabar seperti persamaan dan pertidaksamaan ang berbentuk linear dan kuadrat, serta
MATRIKS DALAM LABORATORIUM oleh : Sugata Pikatan
 Kristal no.12/april/1995 1 MATRIKS DALAM LABORATORIUM oleh : Sugata Pikatan Di dala ateatika anda pasti sudah pernah berhadapan dengan sebuah siste persaaan linier. Cacah persaaan yang berada di dala siste
Kristal no.12/april/1995 1 MATRIKS DALAM LABORATORIUM oleh : Sugata Pikatan Di dala ateatika anda pasti sudah pernah berhadapan dengan sebuah siste persaaan linier. Cacah persaaan yang berada di dala siste
PENENTUAN JADWAL PRODUKSI PADA SISTEM PRODUKSI TIPE ASSEMBLY DI PERUSAHAAN ROTI GANEP SOLO MENGGUNAKAN ALJABAR MAKS-PLUS
 PENENTUAN JADWAL PRODUKSI PADA SISTEM PRODUKSI TIPE ASSEMBLY DI PERUSAHAAN ROTI GANEP SOLO MENGGUNAKAN ALJABAR MAKS-PLUS Galih Gusti Suryaning Akbar, Siswanto, dan Santoso Budi Wiyono Program Studi Matematika
PENENTUAN JADWAL PRODUKSI PADA SISTEM PRODUKSI TIPE ASSEMBLY DI PERUSAHAAN ROTI GANEP SOLO MENGGUNAKAN ALJABAR MAKS-PLUS Galih Gusti Suryaning Akbar, Siswanto, dan Santoso Budi Wiyono Program Studi Matematika
MATHunesa (Volume 3 No 3) 2014
 MATHunesa (Volue 3 No 3) 014 KODE SSRS (SUBSPACE SUBCODES OF REED-SOLOMON) Afifatus Sholihah Jurusan Mateatika Fakultas Mateatika dan Ilu Pengetahuan Ala Universitas Negeri Surabaya e-ail: afif165@yail.co
MATHunesa (Volue 3 No 3) 014 KODE SSRS (SUBSPACE SUBCODES OF REED-SOLOMON) Afifatus Sholihah Jurusan Mateatika Fakultas Mateatika dan Ilu Pengetahuan Ala Universitas Negeri Surabaya e-ail: afif165@yail.co
BAB I PENDAHULUAN. dalam skala prioritas pembangunan nasional dan daerah di Indonesia
 BAB I PENDAHULUAN A. Latar Belakang Masalah Pebangunan ekonoi erupakan asalah penting bagi suatu negara, untuk itu sejak awal pebangunan ekonoi endapat tepat penting dala skala prioritas pebangunan nasional
BAB I PENDAHULUAN A. Latar Belakang Masalah Pebangunan ekonoi erupakan asalah penting bagi suatu negara, untuk itu sejak awal pebangunan ekonoi endapat tepat penting dala skala prioritas pebangunan nasional
BAB 2 LANDASAN TEORI
 BAB LANDASAN TEORI. Beberapa Defenisi Pada analisa keputusan, si pebuat keputusan selalu doinan terhadap penjabaran seluruh alternatif yang terbuka, eperkirakan konsequensi yang perlu dihadapi pada setiap
BAB LANDASAN TEORI. Beberapa Defenisi Pada analisa keputusan, si pebuat keputusan selalu doinan terhadap penjabaran seluruh alternatif yang terbuka, eperkirakan konsequensi yang perlu dihadapi pada setiap
Penyelesaian Algortima Pattern Generation dengan Model Arc-Flow pada Cutting Stock Problem (CSP) Satu Dimensi
 Penyelesaian Algortia Pattern Generation dengan Model Arc-Flow pada Cutting Stock Proble (CSP) Satu Diensi Putra BJ Bangun, Sisca Octarina, Rika Apriani Jurusan Mateatika Fakultas MIPA Universitas Sriwijaya
Penyelesaian Algortia Pattern Generation dengan Model Arc-Flow pada Cutting Stock Proble (CSP) Satu Diensi Putra BJ Bangun, Sisca Octarina, Rika Apriani Jurusan Mateatika Fakultas MIPA Universitas Sriwijaya
II LANDASAN TEORI 2.1 Persamaan Dasar Fluida
 4 II LANDASAN TEORI Dala bab ini akan diberikan eori-eori yang berkaian dengan peneliian ini. Teori-eori ersebu elipui persaaan dasar fluida yang akan disarikan dari Billingha dan King [7], dan Wiha [8].
4 II LANDASAN TEORI Dala bab ini akan diberikan eori-eori yang berkaian dengan peneliian ini. Teori-eori ersebu elipui persaaan dasar fluida yang akan disarikan dari Billingha dan King [7], dan Wiha [8].
Perbandingan Mean Squared Error (MSE) Metode Prasad-Rao dan Jiang-Lahiri-Wan Pada Pendugaan Area Kecil
 Vol. 2, 2017 Perbandingan Mean Squared Error (MSE) Metode Prasad-Rao dan Jiang-Lahiri-Wan Pada Pendugaan Area Kecil Widiarti 1*, Rifa Raha Pertiwi 2, & Agus Sutrisno 3 Jurusan Mateatika, Fakultas Mateatika
Vol. 2, 2017 Perbandingan Mean Squared Error (MSE) Metode Prasad-Rao dan Jiang-Lahiri-Wan Pada Pendugaan Area Kecil Widiarti 1*, Rifa Raha Pertiwi 2, & Agus Sutrisno 3 Jurusan Mateatika, Fakultas Mateatika
KAJIAN METODE ZILLMER, FULL PRELIMINARY TERM, DAN PREMIUM SUFFICIENCY DALAM MENENTUKAN CADANGAN PREMI PADA ASURANSI JIWA DWIGUNA
 Jurnal Mateatika UNAND Vol. 3 No. 4 Hal. 160 167 ISSN : 2303 2910 c Jurusan Mateatika FMIPA UNAND KAJIAN METODE ZILLMER, FULL PRELIMINARY TERM, DAN PREMIUM SUFFICIENCY DALAM MENENTUKAN CADANGAN PREMI PADA
Jurnal Mateatika UNAND Vol. 3 No. 4 Hal. 160 167 ISSN : 2303 2910 c Jurusan Mateatika FMIPA UNAND KAJIAN METODE ZILLMER, FULL PRELIMINARY TERM, DAN PREMIUM SUFFICIENCY DALAM MENENTUKAN CADANGAN PREMI PADA
Persamaan Schrödinger dalam Matriks dan Uraian Fungsi Basis
 Bab 2 Persaaan Schrödinger dala Matriks dan Uraian Fungsi Basis 2.1 Matriks Hailtonian dan Fungsi Basis Tingkat-tingkat energi yang diizinkan untuk sebuah elektron dala pengaruh operator Hailtonian Ĥ dapat
Bab 2 Persaaan Schrödinger dala Matriks dan Uraian Fungsi Basis 2.1 Matriks Hailtonian dan Fungsi Basis Tingkat-tingkat energi yang diizinkan untuk sebuah elektron dala pengaruh operator Hailtonian Ĥ dapat
PEMILIHAN PERINGKAT TERBAIK FESTIVAL KOOR MENGGUNAKAN METODE TOPSIS
 Seinar Nasional Teknologi Inforasi dan Kounikasi 01 (SENTIKA 01 ISSN: 089-981 Yogyakarta, 8 Maret 01 PEMILIHAN PERINGKAT TERBAIK FESTIAL KOOR MENGGUNAKAN METODE TOPSIS Sauel Manurung 1 1Progra Studi Teknik
Seinar Nasional Teknologi Inforasi dan Kounikasi 01 (SENTIKA 01 ISSN: 089-981 Yogyakarta, 8 Maret 01 PEMILIHAN PERINGKAT TERBAIK FESTIAL KOOR MENGGUNAKAN METODE TOPSIS Sauel Manurung 1 1Progra Studi Teknik
BAB 3 ALJABAR MAX-PLUS. beberapa sifat khusus yang selanjutnya akan dibuktikan bahwa sifat-sifat tersebut
 BAB 3 ALJABAR MAX-PLUS Sebelum membahas Aljabar Max-Plus, akan diuraikan terlebih dahulu beberapa sifat khusus yang selanjutnya akan dibuktikan bahwa sifat-sifat tersebut dipenuhi oleh suatu Aljabar Max-Plus.
BAB 3 ALJABAR MAX-PLUS Sebelum membahas Aljabar Max-Plus, akan diuraikan terlebih dahulu beberapa sifat khusus yang selanjutnya akan dibuktikan bahwa sifat-sifat tersebut dipenuhi oleh suatu Aljabar Max-Plus.
HALAMAN PENGESAHAN PROPOSAL PENELITIAN DOSEN YUNOR
 HALAMAN PENGESAHAN PROPOSAL PENELITIAN DOSEN YUNOR. Judul Penelitian : Identifikasi Sifat-Sifat Nilai Eigen dan Vektor Eigen Matriks atas Aljabar Max-Plus..Ketua Pelaksana : a. Nama : Musthofa, M.Sc b.
HALAMAN PENGESAHAN PROPOSAL PENELITIAN DOSEN YUNOR. Judul Penelitian : Identifikasi Sifat-Sifat Nilai Eigen dan Vektor Eigen Matriks atas Aljabar Max-Plus..Ketua Pelaksana : a. Nama : Musthofa, M.Sc b.
STRUKTUR ALJABAR: RING
 STRUKTUR ALJABAR: RING BAHAN AJAR Oleh: Rippi Maya Program Studi Magister Pendidikan Matematika Sekolah Tinggi Keguruan dan Ilmu Pendidikan (STKIP) SILIWANGI - Bandung 2016 1 Pada grup telah dipelajari
STRUKTUR ALJABAR: RING BAHAN AJAR Oleh: Rippi Maya Program Studi Magister Pendidikan Matematika Sekolah Tinggi Keguruan dan Ilmu Pendidikan (STKIP) SILIWANGI - Bandung 2016 1 Pada grup telah dipelajari
Sistem Pendukung Keputusan Untuk Pengadaan Fasilitas Hotel Menggunakan Metode TOPSIS
 Jurnal Siste Inforasi Bisnis 0(0) On-line : http://ejournal.undip.ac.id/inde.php/jsinbis Siste Pendukung Keputusan Untuk Pengadaan Fasilitas Hotel Menggunakan Metode TOPSIS Susi Hendartie a,*, Bau Surarso
Jurnal Siste Inforasi Bisnis 0(0) On-line : http://ejournal.undip.ac.id/inde.php/jsinbis Siste Pendukung Keputusan Untuk Pengadaan Fasilitas Hotel Menggunakan Metode TOPSIS Susi Hendartie a,*, Bau Surarso
BAB I PENDAHULUAN. pembangunan di bidang-bidang lain, seperti sosial, politik, dan budaya. perbedaan antara yang kaya dengan yang miskin.
 BAB I PENDAHULUAN A. Latar Belakang Masalah Pebangunan ekonoi erupakan asalah penting bagi suatu negara, untuk itu sejak awal pebangunan ekonoi endapat tepat penting dala skala prioritas pebangunan nasional
BAB I PENDAHULUAN A. Latar Belakang Masalah Pebangunan ekonoi erupakan asalah penting bagi suatu negara, untuk itu sejak awal pebangunan ekonoi endapat tepat penting dala skala prioritas pebangunan nasional
GETARAN PEGAS SERI-PARALEL
 1 GETARAN PEGAS SERI-PARALEL I. Tujuan Percobaan 1. Menentukan konstanta pegas seri, paralel dan seri-paralel (gabungan). 2. Mebuktikan Huku Hooke. 3. Mengetahui hubungan antara periode pegas dan assa
1 GETARAN PEGAS SERI-PARALEL I. Tujuan Percobaan 1. Menentukan konstanta pegas seri, paralel dan seri-paralel (gabungan). 2. Mebuktikan Huku Hooke. 3. Mengetahui hubungan antara periode pegas dan assa
PERMANEN DAN DOMINAN SUATU MATRIKS ATAS ALJABAR MAX-PLUS INTERVAL
 PERMANEN DAN DOMINAN SUATU MATRIKS ATAS ALJABAR MAX-PLUS INTERVAL Siswanto Jurusan Matematika FMIPA UNS sis.mipauns@yahoo.co.id Abstrak Misalkan R himpunan bilangan real. Aljabar Max-Plus adalah himpunan
PERMANEN DAN DOMINAN SUATU MATRIKS ATAS ALJABAR MAX-PLUS INTERVAL Siswanto Jurusan Matematika FMIPA UNS sis.mipauns@yahoo.co.id Abstrak Misalkan R himpunan bilangan real. Aljabar Max-Plus adalah himpunan
PENYELESAIAN SISTEM PERSAMAAN LINEAR DUA SISI DALAM ALJABAR MAX-PLUS BILANGAN FUZZY
 PENYELESAIAN SISTEM PERSAMAAN LINEAR DUA SISI DALAM ALJABAR MAX-PLUS BILANGAN FUZZY Any Muanalifah August 9, 2010 Latar Belakang Latar Belakang Teori himpunan fuzzy berkembang pesat saat ini. Banyak sekali
PENYELESAIAN SISTEM PERSAMAAN LINEAR DUA SISI DALAM ALJABAR MAX-PLUS BILANGAN FUZZY Any Muanalifah August 9, 2010 Latar Belakang Latar Belakang Teori himpunan fuzzy berkembang pesat saat ini. Banyak sekali
PENGENDALIAN MUTU PRODUKSI BERAT SEMEN PT. SEMEN PADANG DENGAN BAGAN KENDALI SHEWHART DAN ROBUST
 Jurnal Mateatika UNAND Vol. 5 No. 1 Hal. 74 81 ISSN : 2303 2910 c Jurusan Mateatika FMIPA UNAND PENGENDALIAN MUTU PRODUKSI BERAT SEMEN PT. SEMEN PADANG DENGAN BAGAN KENDALI SHEWHART DAN ROBUST RELIGEA
Jurnal Mateatika UNAND Vol. 5 No. 1 Hal. 74 81 ISSN : 2303 2910 c Jurusan Mateatika FMIPA UNAND PENGENDALIAN MUTU PRODUKSI BERAT SEMEN PT. SEMEN PADANG DENGAN BAGAN KENDALI SHEWHART DAN ROBUST RELIGEA
KELUARGA METODE ITERASI ORDE EMPAT UNTUK MENCARI AKAR GANDA PERSAMAAN NONLINEAR ABSTRACT
 KELUARGA METODE ITERASI ORDE EMPAT UNTUK MENCARI AKAR GANDA PERSAMAAN NONLINEAR Kiki Reski Ananda 1 Khozin Mu taar 2 12 Progra Studi S1 Mateatika Jurusan Mateatika Fakultas Mateatika dan Ilu Pengetahuan
KELUARGA METODE ITERASI ORDE EMPAT UNTUK MENCARI AKAR GANDA PERSAMAAN NONLINEAR Kiki Reski Ananda 1 Khozin Mu taar 2 12 Progra Studi S1 Mateatika Jurusan Mateatika Fakultas Mateatika dan Ilu Pengetahuan
Bab 2 Tinjauan Pustaka
 5 Bab 2 Tinjauan Pustaka 2.1. Definisi Penjadwalan Penjadwalan adalah kegiatan pengalokasian suber-suber atau esin-esin yang ada untuk enjalankan sekupulan tugas dala jangka waktu tertentu. (Baker,1974).
5 Bab 2 Tinjauan Pustaka 2.1. Definisi Penjadwalan Penjadwalan adalah kegiatan pengalokasian suber-suber atau esin-esin yang ada untuk enjalankan sekupulan tugas dala jangka waktu tertentu. (Baker,1974).
Relasi dan Fungsi. Panca Mudjirahardjo, ST.MT. Relasi dan fungsi
 Relasi dan Fungsi Panca Mudjirahardjo, ST.MT. Relasi dan fungsi Definisi Menyatakan relasi Sifat-sifat relasi biner Kobinasi relasi Koposisi relasi Relasi n-ary Definsi Definisi: Relasi biner R antara
Relasi dan Fungsi Panca Mudjirahardjo, ST.MT. Relasi dan fungsi Definisi Menyatakan relasi Sifat-sifat relasi biner Kobinasi relasi Koposisi relasi Relasi n-ary Definsi Definisi: Relasi biner R antara
MODEL SKEDUL MIGRASI DAN APLIKASINYA DALAM PROYEKSI PENDUDUK MULTIREGIONAL MUSLIMAH
 MODEL SKEDUL MIGRASI DAN APLIKASINYA DALAM PROYEKSI PENDUDUK MULTIREGIONAL MUSLIMAH SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR BOGOR 2008 PERNYATAAN MENGENAI TESIS DAN SUMBER INFORMASI Dengan ini saya
MODEL SKEDUL MIGRASI DAN APLIKASINYA DALAM PROYEKSI PENDUDUK MULTIREGIONAL MUSLIMAH SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR BOGOR 2008 PERNYATAAN MENGENAI TESIS DAN SUMBER INFORMASI Dengan ini saya
BAB IV GENERATOR BILANGAN RANDOM
 BAB IV GENERATOR BILANGAN RANDOM 4.1. Generator Bilangan Rando dan Fungsi Distribusi Pada siulasi seringkali dibutuhkan bilangan-bilangan yang ewakili keadaan siste yang disiulasikan. Biasanya, kegiatan
BAB IV GENERATOR BILANGAN RANDOM 4.1. Generator Bilangan Rando dan Fungsi Distribusi Pada siulasi seringkali dibutuhkan bilangan-bilangan yang ewakili keadaan siste yang disiulasikan. Biasanya, kegiatan
OPERATOR SELF ADJOINT PADA RUANG HILBERT
 OPERATOR SELF ADJOINT PADA RUANG HILBERT Gunawan Universitas Muhammadiah Purwokerto, gun.oge@gmail.om Abstrat. In this artile, will disuss definition, examples, algebra properties, and some harateristi
OPERATOR SELF ADJOINT PADA RUANG HILBERT Gunawan Universitas Muhammadiah Purwokerto, gun.oge@gmail.om Abstrat. In this artile, will disuss definition, examples, algebra properties, and some harateristi
BENTUK GELOMBANG AC SINUSOIDAL
 BENTUK GELOMBANG AC SINUSOIDAL. PENDAHULUAN Pada bab sebelunya telah dibahas rangkaian resistif dengan tegangan dan arus dc. Bab ini akan eperkenalkan analisis rangkaian ac diana isyarat listriknya berubah
BENTUK GELOMBANG AC SINUSOIDAL. PENDAHULUAN Pada bab sebelunya telah dibahas rangkaian resistif dengan tegangan dan arus dc. Bab ini akan eperkenalkan analisis rangkaian ac diana isyarat listriknya berubah
KONSTRUKSI ALGORITME ARITMETIK GF(3 m ) DENGAN OPERASI DIBANGKITKAN DARI SIFAT GRUP SIKLIK I L H A M
 KONSTRUKSI ALGORITME ARITMETIK GF(3 ) DENGAN OPERASI DIBANGKITKAN DARI SIFAT GRUP SIKLIK I L H A M SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR BOGOR 2009 PERNYATAAN MENGENAI TESIS DAN SUMBER INFORMASI
KONSTRUKSI ALGORITME ARITMETIK GF(3 ) DENGAN OPERASI DIBANGKITKAN DARI SIFAT GRUP SIKLIK I L H A M SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR BOGOR 2009 PERNYATAAN MENGENAI TESIS DAN SUMBER INFORMASI
I. Aljabar Himpunan Handout Analisis Riil I (PAM 351)
 I. Aljabar Himpunan Aljabar Himpunan Dalam bab ini kita akan menyajikan latar belakang yang diperlukan untuk mempelajari analisis riil. Dua alat utama analisis riil, yakni aljabar himpunan dan fungsi,
I. Aljabar Himpunan Aljabar Himpunan Dalam bab ini kita akan menyajikan latar belakang yang diperlukan untuk mempelajari analisis riil. Dua alat utama analisis riil, yakni aljabar himpunan dan fungsi,
IMPLEMENTASI PANORAMIC IMAGE MOSAIC DENGAN METODE 8 PARAMETER PERSPECTIVE TRANSFORMATION
 IMPLEMENTSI PNORMIC IMGE MOSIC DENGN METODE 8 PRMETER PERSPECTIVE TRNSFORMTION Rud dipranata, Hendra Litoo, Cherr G. Ballangan Teknik Inforatika, Fakultas Teknologi Industri, Universitas Kristen Petra
IMPLEMENTSI PNORMIC IMGE MOSIC DENGN METODE 8 PRMETER PERSPECTIVE TRNSFORMTION Rud dipranata, Hendra Litoo, Cherr G. Ballangan Teknik Inforatika, Fakultas Teknologi Industri, Universitas Kristen Petra
BAB 4. HASIL DAN PEMBAHASAN
 BAB 4. HASIL DAN PEMBAHASAN Analisa pelat lantai gedung rawat inap RSUD Surodinawan Kota Mojokerto dengan enggunakan teori garis leleh ebutuhkan beberapa tahap perhitungan dan analsis aitu perhitungan
BAB 4. HASIL DAN PEMBAHASAN Analisa pelat lantai gedung rawat inap RSUD Surodinawan Kota Mojokerto dengan enggunakan teori garis leleh ebutuhkan beberapa tahap perhitungan dan analsis aitu perhitungan
BAB III PEMODELAN SISTEM DINAMIK PLANT. terbuat dari acrylic tembus pandang. Saluran masukan udara panas ditandai dengan
 BAB III PEMODELAN SISTEM DINAMIK PLANT 31 Kriteria rancangan plant Diensi plant yang dirancang berukuran 40cx60cx50c, dinding terbuat dari acrylic tebus pandang Saluran asukan udara panas ditandai dengan
BAB III PEMODELAN SISTEM DINAMIK PLANT 31 Kriteria rancangan plant Diensi plant yang dirancang berukuran 40cx60cx50c, dinding terbuat dari acrylic tebus pandang Saluran asukan udara panas ditandai dengan
UNIVERSITAS GADJAH MADA. Bahan Ajar:
 UNIVERSITAS GADJAH MADA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM JURUSAN MATEMATIKA PROGRAM STUDI S1 MATEMATIKA Sekip Utara, Gedung Jurusan Matematika, Yogyakarta - 55281 Bahan Ajar: BAB / POKOK BAHASAN
UNIVERSITAS GADJAH MADA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM JURUSAN MATEMATIKA PROGRAM STUDI S1 MATEMATIKA Sekip Utara, Gedung Jurusan Matematika, Yogyakarta - 55281 Bahan Ajar: BAB / POKOK BAHASAN
UNIVERSITAS GADJAH MADA. Bahan Ajar:
 UNIVERSITAS GADJAH MADA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM JURUSAN MATEMATIKA PROGRAM STUDI S1 MATEMATIKA Sekip Utara, Gedung Jurusan Matematika, Yogyakarta - 55281 Bahan Ajar: BAB POKOK BAHASAN
UNIVERSITAS GADJAH MADA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM JURUSAN MATEMATIKA PROGRAM STUDI S1 MATEMATIKA Sekip Utara, Gedung Jurusan Matematika, Yogyakarta - 55281 Bahan Ajar: BAB POKOK BAHASAN
BAB I PENDAHULUAN Latar Belakang Masalah
 BAB I PENDAHULUAN 1.1. Latar Belakang Masalah Sistem kejadian diskrit (Discrete-Event System) merupakan suatu sistem yang state space nya berbentuk diskret, sistem yang keadaannya berubah hanya pada waktu
BAB I PENDAHULUAN 1.1. Latar Belakang Masalah Sistem kejadian diskrit (Discrete-Event System) merupakan suatu sistem yang state space nya berbentuk diskret, sistem yang keadaannya berubah hanya pada waktu
SYARAT PERLU LAPANGAN PEMISAH. Bambang Irawanto Jurusan Matematika FMIPA UNDIP. Abstact. Keywords : extension fields, elemen algebra
 JURNAL MATEMATIKA DAN KOMPUTER Vol 4 No 2, 65-70, Agustus 2001, ISSN : 1410-8518 SYARAT PERLU LAPANGAN PEMISAH Bambang Irawanto Jurusan Matematika FMIPA UNDIP Abstact Field is integral domain and is a
JURNAL MATEMATIKA DAN KOMPUTER Vol 4 No 2, 65-70, Agustus 2001, ISSN : 1410-8518 SYARAT PERLU LAPANGAN PEMISAH Bambang Irawanto Jurusan Matematika FMIPA UNDIP Abstact Field is integral domain and is a
(x- x 1. Contoh soal: jawab: x 2 + y 2 = 2 2 x 2 + y 2 = 4. x 2 + y 2 = 4. jawab: (x 5) 2 + (y 2) 2 = 4 2
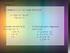 LINGKRN (x- x ) (x- x ) + (y- y ) (y- y ) = 0 Contoh soal: Pengertian : Lingkaran adalah tepat kedudukan titik-titik yang berjarak konstan/saa terhadap sebuah titik tertentu. Sebuah titik tertentu itu
LINGKRN (x- x ) (x- x ) + (y- y ) (y- y ) = 0 Contoh soal: Pengertian : Lingkaran adalah tepat kedudukan titik-titik yang berjarak konstan/saa terhadap sebuah titik tertentu. Sebuah titik tertentu itu
TITIK DAN SISI PENUTUP MINIMAL PADA GRAF BINTANG
 TITIK DAN SISI PENUTUP MINIMAL PADA GRAF BINTANG DAN GRAF RODA Nurul Hijriyah ) dan Wahyu H. Irawan ) ) Mahasiswa Pascasarjana Jurusan Mateatika Universitas Brawijaya Malang ) Jurusan Mateatika UIN Maulana
TITIK DAN SISI PENUTUP MINIMAL PADA GRAF BINTANG DAN GRAF RODA Nurul Hijriyah ) dan Wahyu H. Irawan ) ) Mahasiswa Pascasarjana Jurusan Mateatika Universitas Brawijaya Malang ) Jurusan Mateatika UIN Maulana
BAB III UJI STATISTIK PORTMANTEAU DALAM VERIFIKASI MODEL RUNTUN WAKTU
 BAB III UJI STATISTIK PORTMANTEAU DALAM VERIFIKASI MODEL RUNTUN WAKTU Salah satu langkah yang paling penting dala ebangun suatu odel runtun waktu adalah dari diagnosisnya dengan elakukan peeriksaan apakah
BAB III UJI STATISTIK PORTMANTEAU DALAM VERIFIKASI MODEL RUNTUN WAKTU Salah satu langkah yang paling penting dala ebangun suatu odel runtun waktu adalah dari diagnosisnya dengan elakukan peeriksaan apakah
IV. METODE PENELITIAN
 IV. METODE PENELITIAN 4.1 Lokasi dan Waktu Penelitian Penelitian ini dilakukan di PT Tirta Ala Seesta. Perusahaan tersebut berlokasi di Desa Ciburayut, Kecaatan Cigobong, Kabupaten Bogor. Peilihan objek
IV. METODE PENELITIAN 4.1 Lokasi dan Waktu Penelitian Penelitian ini dilakukan di PT Tirta Ala Seesta. Perusahaan tersebut berlokasi di Desa Ciburayut, Kecaatan Cigobong, Kabupaten Bogor. Peilihan objek
0,1,2,3,4. (e) Perhatikan jawabmu pada (a) (d). Tuliskan kembali sifat-sifat yang kamu temukan dalam. 5. a b c d
 1 Pada grup telah dipelajari himpunan dengan satu operasi. Sekarang akan dipelajari himpunan dengan dua operasi. Ilustrasi 1.1 Perhatikan himpunan 0,1,2,3,4. (a) Apakah grup terhadap operasi penjumlahan?
1 Pada grup telah dipelajari himpunan dengan satu operasi. Sekarang akan dipelajari himpunan dengan dua operasi. Ilustrasi 1.1 Perhatikan himpunan 0,1,2,3,4. (a) Apakah grup terhadap operasi penjumlahan?
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI.1. Uu Transforator erupakan suatu alat listrik yang engubah tegangan arus bolak balik dari satu tingkat ke tingkat yang lain elalui suatu gandengan agnet dan berdasarkan prinsip-prinsip
BAB II LANDASAN TEORI.1. Uu Transforator erupakan suatu alat listrik yang engubah tegangan arus bolak balik dari satu tingkat ke tingkat yang lain elalui suatu gandengan agnet dan berdasarkan prinsip-prinsip
MATEMATIKA BISNIS BAB 2 FUNGSI LINIER
 MATEMATIKA BISNIS BAB FUNGSI LINIER Hikmah Agustin, S.P.,MM DEFINISI FUNGSI Fungsi adalah hubungan matematis antara suatu variabel dengan variabel lainna. Unsur-unsur pembentukan fungsi : 1. Variabel Variabel
MATEMATIKA BISNIS BAB FUNGSI LINIER Hikmah Agustin, S.P.,MM DEFINISI FUNGSI Fungsi adalah hubungan matematis antara suatu variabel dengan variabel lainna. Unsur-unsur pembentukan fungsi : 1. Variabel Variabel
JMP : Volume 4 Nomor 2, Desember 2012, hal MODUL FAKTOR YANG DIBENTUK DARI SUBMODUL Z 2. Ari Wardayani
 JMP : Volume 4 Nomor, Desember 01, hal. 79-88 MODUL FAKTOR YANG DIBENTUK DARI SUBMODUL Z PADA MODUL R ATAS GAUSSIAN INTEGERS Ari Wardaani Universitas Jenderal Soedirman ariwardaani@ahoo.co.id ABSTRACT.
JMP : Volume 4 Nomor, Desember 01, hal. 79-88 MODUL FAKTOR YANG DIBENTUK DARI SUBMODUL Z PADA MODUL R ATAS GAUSSIAN INTEGERS Ari Wardaani Universitas Jenderal Soedirman ariwardaani@ahoo.co.id ABSTRACT.
A-10 OPTIMISASI JADWAL PEMESANAN BAKPIA PATHOK JAYA 25 DAERAH ISTIMEWA YOGYAKARTA DENGAN SISTEM LINEAR MAX-PLUS WAKTU INVARIANT
 A-10 OPIMISASI JADWAL PEMESANAN BAKPIA PAHOK JAYA 25 DAERAH ISIMEWA YOGYAKARA DENGAN SISEM LINEAR MAX-PLUS WAKU INVARIAN Mustofa Arifin 1 dan Musthofa 2 1 Mahasiswa Program Studi Matematika Jurusan Pendidikan
A-10 OPIMISASI JADWAL PEMESANAN BAKPIA PAHOK JAYA 25 DAERAH ISIMEWA YOGYAKARA DENGAN SISEM LINEAR MAX-PLUS WAKU INVARIAN Mustofa Arifin 1 dan Musthofa 2 1 Mahasiswa Program Studi Matematika Jurusan Pendidikan
Uji Rank Mann-Whitney Dua Tahap
 Statistika, Vol. 7 No., 55 60 Mei 007 ji Rank Mann-Whitney Dua Tahap Teti Sofia Yanti Dosen Jurusan Statistika FMIPA NISBA. Abstrak ji rank Mann-Whitney adalah salah satu bentuk pengujian dala analisis
Statistika, Vol. 7 No., 55 60 Mei 007 ji Rank Mann-Whitney Dua Tahap Teti Sofia Yanti Dosen Jurusan Statistika FMIPA NISBA. Abstrak ji rank Mann-Whitney adalah salah satu bentuk pengujian dala analisis
BAB I Sekilas tentang Teori-teori sebagai Dasar Program Linear
 BAB I Sekilas tentang Teori-teori sebagai Dasar Program Linear. Himpunan konveks Sebuah himpunan X dalam R n disebut himpunan konveks apabila memenuhi sifat berikut: jika diberikan sebarang dua titik x
BAB I Sekilas tentang Teori-teori sebagai Dasar Program Linear. Himpunan konveks Sebuah himpunan X dalam R n disebut himpunan konveks apabila memenuhi sifat berikut: jika diberikan sebarang dua titik x
Matriks atas Aljabar Max-Plus Interval
 Jural Natur Idoesia 13(2), Februari 211: 94-99 94 ISSN 141-9379, Jural Natur Keputusa Idoesia Akreditasi 13(2): No 94-99 65a/DIKTI/Kep/28 Rudhito, et al Matriks atas Aljabar Max-Plus Iterval Marcellius
Jural Natur Idoesia 13(2), Februari 211: 94-99 94 ISSN 141-9379, Jural Natur Keputusa Idoesia Akreditasi 13(2): No 94-99 65a/DIKTI/Kep/28 Rudhito, et al Matriks atas Aljabar Max-Plus Iterval Marcellius
PENGARUH POSISI BEBAN DAN MOMEN INERSIA TERHADAP PUTARAN KRITIS PADA MODEL POROS MESIN KAPAL
 PENGARUH POSISI BEBAN DAN MOMEN INERSIA TERHADAP PUTARAN KRITIS PADA MODEL POROS MESIN KAPAL Waris Wibowo Staf Pengajar Akadei Mariti Yogyakarta (AMY) ABSTRAK Penelitian ini bertujuan untuk endapatkan
PENGARUH POSISI BEBAN DAN MOMEN INERSIA TERHADAP PUTARAN KRITIS PADA MODEL POROS MESIN KAPAL Waris Wibowo Staf Pengajar Akadei Mariti Yogyakarta (AMY) ABSTRAK Penelitian ini bertujuan untuk endapatkan
