BAB 2 LANDASAN TEORI
|
|
|
- Liani Pranoto
- 6 tahun lalu
- Tontonan:
Transkripsi
1 BAB 2 LANDASAN TEORI 2. Probabilitas Probabilitas adalah suatu nilai untuk mengukur tingkat kemungkinan terjadinya suatu peristiwa (event) akan terjadi di masa mendatang yang hasilnya tidak pasti (uncertain event). Probabilitas dinyatakan antara (nol) sampai (satu) atau dalam persentase. Probabilitas menunjukkan peristiwa yang tidak mungkin terjadi, sedangkan probabilitas menunjukkan peristiwa yang pasti terjadi. P(A) =,99 artinya probabilitas bahwa kejadian A akan terjadi sebesar 99 % dan probabilitas A tidak terjadi adalah sebesar %. Ada tiga hal penting dalam rangka membicarakan probabilitas, yaitu percobaan (experiment), ruang sampel (sample space) dan kejadian (event). Percobaan (experiment) adalah pengamatan terhadap beberapa aktivitas atau proses yang memungkinkan timbulnya paling sedikit 2 (dua) peristiwa tanpa memperhatikan peristiwa mana yang akan terjadi. Contoh : Kegiatan melempar mata uang akan menghasilkan peristiwa muncul gambar atau angka, kegiatan jual beli saham akan menghasilkan peristiwa membeli atau menjual, perubahan harga-harga akan menghasilkan peristiwa inflasi atau deflasi, pertandingan sepak bola akan menghasilkan peristiwa menang, kalah atau seri. Kegiatan-kegiatan yang menimbulkan peristiwa tersebut dikenal sebagai percobaan.
2 Ruang sampel (sample space) atau semesta (universe) merupakan himpunan dari semua hasil (outcome) yang mungkin dari suatu percobaan (experiment). Jadi ruang sampel adalah seluruh kemungkinan peristiwa yang akan terjadi akibat adanya suatu percobaan atau kegiatan. Dari kegiatan diatas dapat diperoleh hasil sebagai berikut : Tabel 2. Percobaan dan Hasil PERCOBAAN RUANG SAMPEL Melempar Mata Uang (gambar, angka) Perdagangan Saham (menjual, membeli) Perubahan Angka (inflasi, deflasi) Pertandingan Sepak Bola (menang, kalah, seri) Kejadian (event) adalah kumpulan dari satu atau lebih hasil yang terjadi pada sebuah percobaan atau kegiatan. Kejadian menunjukkan hasil yang terjadi dari suatu percobaan. Dalam setiap percobaan atau kegiatan hanya ada satu hasil. Pada kegiatan jual beli saham, kalau tidak membeli berarti menjual. Pada perubahan harga terjadi inflasi atau deflasi. Dua peristiwa tersebut tidak dapat terjadi bersamaan. Pada pertandingan sepak bola juga hanya terjadi satu peristiwa, apakah klub sepak bola tersebut menang, kalah atau seri. Tidak mungkin dalam suatu pertandingan sepak bola, misalnya Persipura dan PSM, hasilnya adalah Persipura menang juga kalah. Peristiwa yang mungkin adalah Persipura menang, Persipura kalah, atau seri. Urutan antara percobaan, ruang sampel dan peristiwa yaitu: Tabel 2.2 Urutan Percobaan, Hasil dan Peristiwa Percobaan/ Kegiatan Pertandingan sepak bola antara PSMS VS PSM di Stadion Teladan, Medan, 7 Februari 2 Ruang Sampel PSMS Menang PSMS Kalah Seri, PSMS tidak menang dan tidak kalah Kejadian/ Peristiwa PSMS Menang
3 Nilai probabilitas dapat dihitung berdasarkan nilai hasil observasi (sifatnya subyektif) tau berdasarkan pertimbangan pembuat keputusan atau tenaga ahli dalam bidangnya secara subyektif. Besarnya nilai kemungkinan bagi munculnya suatu kejadian adalah selalu diantara (nol) dan (satu). Pernyataan ini dapat ditulis sebagai P(A), dimana P(A) menyatakan nilai kemungkinan bagi munculnya kejadian A. Jika suatu percobaan dapat menghasilkan N macam hasil yang berkemungkinan sama (equally likely) dan jika tepat terdapat sebanyak n hasil yang berkaitan dengan kejadian A, maka probabilitas kejadian A adalah : P(A) = n N Contoh: Didalam kegiatan pengendalian mutu produk, ada buah barang yang diperiksa, ternyata ada 2 buah barang yang cacat atau rusak. Kalau kebetulan diambil secara acak satu saja, berapa probabilitasnya bahwa barang yang diambil adalah barang yang rusak. Dari soal diketahui bahwa: N = buah barang n = 2 buah barang yang rusak A = barang yang diambil secara acak Jadi, probabilitas memperoleh barang yang rusak adalah : P(A) = n N P(A) = 2 =.2 Jika n=, berarti tidak ada barang yang rusak. P(A)= N =, kejadian ini disebut impossible event (tidak mungkin terjadi) tetapi jika N= berarti semua barang rusak P(A)= =, kejadian ini disebut dengan sure event (pasti terjadi).
4 2.2 Operasi-Operasi Dalam Kejadian Ada beberapa operasi-operasi dalam kejadian yaitu: gabungan (union), irisan (intersection), komplemen (complement), selisih dan kejadian majemuk Gabungan (Union) Gabungan dua kejadian A dan B, dinyatakan dengan A B, merupakan kejadian yang mengandung semua elemen yang termasuk A atau B atau keduanya. A B = {x : x A atau x B} Jika digambarkan pada diagram Venn maka daerah yang diarsir merupakan himpunan A B. Gambar 2. Gabungan Irisan (Intersection) Irisan dua kejadian A dan B, dinyatakan dengan A B, merupakan kejadian yang elemen-elemennya merupakan anggota dari A dan B. A B = {x : x A dan x B } Jika digambarkan pada diagram Venn maka daerah yang diarsir merupakanhimpunan A B.
5 Gambar 2.2 Irisan Komplemen (Complament) Komplemen dari kejadian A, dinyatakan dengan Ac, adalah kejadian dari elemenelemen yang merupakan anggota semesta tetapi bukan anggota A. Ac = {x : x S, x A} Jika digambarkan pada diagram Venn maka daerah yang diarsir merupakan himpunan Ac. Gambar 2.3 Komplemen Selisih Selisih kejadian B dari kejadian A dinyatakan dengan A B adalah kejadian dari elemen-elemen yang merupakan anggota dari A tetapi bukan anggota dari B. A B = {x : x A, x B}
6 Jika digambarkan pada diagram Venn maka daerah yang diarsir merupakan himpunan A - B. Gambar 2.4 selisih Kejadian Majemuk. Bila A dan B mutually exclusive (kejadian yang terpisah), maka : P(A B) = P(A) + P(B) 2. Bila A dan B dua kejadian sembarang, maka : P(A B) = P(A) + P(B) P(A B) 3. Bila K kejadian yaitu A,A 2,...A i,...a k yang mutually exclusive dan membentuk kejadian A, maka : P(A)=P(A A 2 A i A k ) P(A) = k P(A) = P(A i ) i= 4. Bila A dan B independent (bebas), maka : P(A B) = P(A)P(B) 5. Bila A dan B dependent (tidak bebas), maka :
7 P(A B) = P(A)P(B A) P(A B) = P(B)P(A B), dimana P(A), P(B). 2.3 Probabilitas Bersyarat Peluang terjadinya suatu kejadian A bila diketahui bahwa kejadian B telah terjadi disebut peluang bersyarat dan dinyatakan dengan P(A B). P(A B) P(A B) = P(B) Sama halnya dengan peluang terjadinya suatu kejadian B bila diketaui bahwa kejadian A telah terjadi dan dinyatakan dengan P(B A). P(A B) P(B A) = P(A) Dengan mengkombinasikan kedua persamaan maka diperoleh : P(A B) = P(A B)P(A B)P(A) P(A B) = P(A B) P(B) = P(A B)P(A) P(B) P(A B) P(A B) = P(B) Contoh: Dari 9 nama, terdapat 5 orang pria dengan status 46 orang bekerja, sedangkan 4 orang lagi tidak bekerja, dan 4 orang wanita dengan status 4 orang bekerja sedangkan 26 orang lagi tidak bekerja. Berapa probabilitas terpilihnya pria dengan status telah bekerja? A = pria terpilih B = orang yang terpilih berstatus bekerja
8 P(B) = 6 9 = 2/3 P(B A) = 46 9 = 23/45 P(A B) = 23/45 2/3 = 23/3 Dari perhitungan diatas maka diperoleh kemungkinan bahwa nama yang terpilih adalah pria dengan status bekerja adalah sebesar,77 atau 77%. 2.4 TITIK SAMPEL Titik sampel (sample point) merupakan tiap anggota atau elemen dari ruang sampel. Jika suatu operasi dapat dilakukan dengan n cara, dan bila untuk setiap cara ini operasi kedua dapat dilakukan dengan n 2 cara, dan bila untuk setiap cara ini operasi ketiga dapat dilakukan dengan n 3 cara, dst, maka deretan k operasi dapat dilakukan dengan n, n 2,, n k cara. Contoh: Tiga buah koin (uang logam) dilemparkan sekali. Banyaknya titik sampel dalam ruang sampel? Koin I dapat menghasilkan 2 hasil yang mungkin, muka (M) atau belakang (B) Koin II dapat menghasilkan 2 hasil yang mungkin, M atau B Koin III dapat menghasilkan 2 hasil yang mungkin, M atau B Jumlah titik sampel yang dihasilkan = (2) (2) (2) = Kombinasi (Combbination) Kombinasi merupakan susunan dari suatu himpunan obyek yang dapat dibentuk tanpa memperhatikan urutan. Kombinasi berkaitan dengan penentuan banyaknya cara
9 memilih r obyek dari sejumlah n obyek tanpa memperhatikan urutannya. Kombinasi merupakan sekatan dengan dua sel, sel pertama berisi r obyek yang dipilih dan (n r) obyek sisanya. Jumlah kombinasi dari n obyek yang berlainan jika diambil sebanyak r. C r n = n! r! (n r)! Contoh: Suatu kelas terdiri atas 4 pria dan 3 wanita Banyaknya panitia yang dibentuk yang beranggotakan 2 pria dan wanita? Banyaknya cara memilih 2 dari 4 pria = C 2 4 = 4! 2!(4 2)! = 6 Banyaknya cara memilih dari 3 wanita = C 3 = 3!!(3 )! = 3 Banyaknya panitia yang dapat dibentuk = (6) (3) = Permutasi (Permutation) Permutasi merupakan susunan dari suatu himpunan obyek yang dapat dibentuk yang memperhatikan urutan. Banyaknya permutasi n obyek berlainan adalah n! Banyaknya permutasi n obyek berlainan bila diambil r sekaligus P r n = permutasi n benda berlainan yang disusun melingkar adalah (n )!. n! r!(n r)!. Banyaknya Banyaknya permutasi yang berlainan dari n obyek bila n adalah jumlah obyek jenis pertama, n 2 adalah jumlah obyek jenis kedua,..., n k jumlah obyek ke-k adalah: n! n! n 2! n k!. Banyaknya cara menyekat n obyek dalam r sel bila masing-masing berisi n obyek pada sel pertama, n 2 obyek pada sel kedua, dan seterusnya adalah : n! n!n 2! n k! dengan n + n n r = n.
10 2.5 Distribusi Probabilitas Diskrit Penyajian distribusi probabilitas dalam bentuk grafis, tabel atau melalui rumusan tidak masalah, yang ingin dilukiskan adalah perilaku (kelakuan) perubah acak tersebut. Sering di menjumpai, pengamatan yang dihasilkan melalui percobaan statistik yang berbeda mempunyai bentuk kelakuan umum yang sama. Oleh karena itu perubah acak diskrit yang berkenaan dengan percobaan tersebut dapat dilukiskan dengan distribusi probabilitas yang sama, dan dapat dinyatakan dengan rumus yang sama. Dalam banyak praktek yang sering di jumpai, hanya memerlukan beberapa distribusi probabilitas yang penting untuk menyatakan banyak perubah acak diskrit Distribusi Seragam Distribusi probabilitas yang paling sederhana adalah yang semua perubah acaknya mempunyai probabilitas yang sama. Distribusi ini disebut distribusi probabilitas seragam diskrit. Jika perubah acak X mendapat nilai x, x 2,, x k dengan probabilitas yang sama, maka distribusi probabilitas diskrit diberikan oleh: f(x; k) = k, untuk x = x, x 2,, x k Lambang f(x;k) sebagai pengganti f(x), yang menunjukan bahwa distribusi seragam tersebut bergantung pada parameter x.
11 /k X X2 X3 Xk Gambar 2.5 Distribusi Seragam Rata-rata dan varians dari distribusi seragam diskrit adalah : μ = k i=k x i k 2 = k i= (x i μ)2 k Contoh: Sebuah dadu seimbang dilemparkan satu kali, maka tiap unsur dalam ruang sampel S={, 2,3 4, 5, 6}. Muncul dengan probabilitas /6. Jadi jika X menyatakan mata dadu yang muncul, maka X terdistribusi peluang seragam (uniform) yakni f(x;6)=/6, untuk x =, 2, 3, 4, 5, Distribusi Binomial Suatu percobaan yang terdiri atas beberapa usaha, tiap-tiap usaha, memberikan hasil yang dapat dikelompokan menjadi 2-kategori yaitu sukses atau gagal, dan tiap-tiap ulangan percobaan bebas satu sama lainnya. Probabilitas kesuksesan tidak berubah dari percobaan satu ke percobaan lainnya. Proses ini disebut proses Bernoulli. Jadi proses Bernoulli harus memenuhi persyaratan berikut:. Percobaan terdiri atas n-eksperimen yang berulang 2. Tiap-tiap eksperimen memberikan hasil yang dapat dikelompokan menjadi 2- kategori, sukses atau gagal 3. Peluang kesuksesan dinyatakan dengan p, tidak berubah dari satu eksperimen ke eksperimen berikutnya. 4. Tiap eksperimen bebas dengan eksperimen lainnya.
12 Jadi proses Bernoulli adalah suatu proses dengan ciri-ciri eksperimen berlangsung n kali dan tiap eksperimen berlangsung dalam cara dan kondisi yang sama. Untuk setiap eksperimen hanya ada 2 (dua) kejadian yang mungkin terjadi, dimana 2 (dua) kejadian tersebut adalah saling asing dan juga independent satu sama lain. Biasanya 2 (dua) kejadian tersebut dinotasikan sebagai kejadian sukses dan kejadian gagal. Probabilitas sukses dilambangkan dengan p, sedangkan probabilitas gagal dilambangkan dengan q, dan p + q =. Dari proses tersebut, yang di definisikan sebagai variabel adalah munculnya kejadian sukses, yang dilambangkan dengan x. Untuk distribusi Binomial semacam itu, bisa dihitung probabilitas x sukses akan muncul dalam n percobaan tersebut dengan rumus : F(x) = P(x, n; p) = C x n )p x q n x = n! x! (n x)! px q n x Dengan: x = munculnya sukses yang ingin di hitung n = jumlah eksperimen p = probabilitas sukses dalam tiap eksperimen q = probabilitas gagal dalam tiap eksperimen = p n-x = jumlah gagal dalam n eksperimen Distribusi binomial mempunyai nilai rata-rata µ = np dan nilai simpangan baku = npq Nilai Harapan Distribusi Binomial Untuk mencari rata-rata (µ) digunakan Rumus : E(X) = np (p + q) n = np() n = np Jadi ekspektasi dari distribusi binomial adalah np.
13 2.5.4 Variansi Distribusi Binomial Var (X) = E[X 2 ] (E[X]) 2 E[X] 2 = n(n )p 2 q n 2 + (n 2)pq n p n 2 + np = n(n )p 2 (q + p) n 2 + np = n(n )p n + np Jadi, Var (X) = E[X 2 ] (E[X]) 2 = n(n )p 2 + np n 2 p 2 = np(-p) = npq Jadi, varian dari distribusi binomial adalah npq. 2.6 DISTRIBUSI NORMAL Distribusi probailitas kontinyu yang terpenting di bidang statistik adalah distribusi Normal. Grafiknya disebut kurva normal, berbentuk lonceng. Distribusi ini ditemukan Karl Friedrich Gauss ( ) yang juga disebut distribusi Gauss. Perubah acak X yang bentuknya seperti lonceng disebut perubah acak normal dengan persamaan matematik distribusi probabilitas yang bergantung paramerter µ (mean) dan (simpangan baku). Dinyatakan n(x,µ, ) Gabar 2.6 Kurva Normal
14 Fungsi padat perubah acak normal X, dengan rata-rata µ dan simpangan baku dinyatakan sebagai : Dengan : µ = mean n(x; μ; ) 2π e = simpangan baku π = 3, e = 2, x μ 2, untuk < x < Luas daerah kurva normal antara x = a dan x = b dinyatakan sebagai berikut: b P(a x b) = f(x)dx a b = a 2π e 2 x μ 2 dx a b 2 4 Gambar 2.7 Luas Derah P(a < x < b) = Luas Daerah Diarsir 2.6. Nilai Harapan Variabel acak Normal E(X) = xf(x)dx
15 = x = 2π xe /2( z = x μ x = 2π = 2π = 2π x μ x 2π e /2( )2 dx x μ x )2 dx ; z + μ x = x ; dz = dx ; dx = dz (z + μ x )e 2 z2 dz (z + μ x )e 2 z2 dz z e 2 z2 dz + μ x 2π e 2 z2 dz untuk, z untuk, 2π = e 2 z2 dz = z 2π ( ze 2 z2 dz + ze 2 z2 dz) y = 2 z2 ; dy = zdz ; dz = dy z = 2π e y dy + e y dy dy e y z = e y dy = [e y ] dimana, Akibatnya, lim e y = ; maka e y dy = y 2π z e 2 z2 dz = ( + ) = 2π untuk, μ x 2π e 2 z2 dz = μ x 2π ( e 2 z2 dz + e 2 z2 dz) y = 2 z2 z = 2π dy = zdz dz = dy z = μ x 2π dy e y z + dy e y z )
16 = μ x 2π ( 2 y 2e y dy + = μ x 2π 2π 2 + 2π 2 = μ x 2 y 2e y dy) Sehingga : E[X] = 2π E[X] = + μ x = μ x z e 2 z2 dz + μ x 2π e 2 z2 dz Variansi Variabel Acak Normal Var (X) = E[X 2 ] (E[X]) 2 E[X 2 ] = x 2 x μ x 2π e /2( )2 dx = 2π x2 e /2( z = x μ x x μ x )2 dx z + μ x = x dz = dx dx = dz = 2π (z + μ x )2 e 2 z2 dz = 2π (z2 + 2zμ x + μ x ) 2 e 2 z2 dz = 2π z2 e 2 z2 dz + 2π 2zμ x e 2 z2 dz + 2π μ x 2 e 2 z2 dz = 2 2π z2 e 2 z2 dz + 2zμ x 2π z e 2 z2 dz + e 2 z2 dz
17 = 2 2π z2 e 2 z2 dz + + 2π ( 2π) = 2 2π z2 e 2 z2 dz + μ x 2 μ x 2 untuk, 2 2 2π z2 e 2 z2 dz = 2π z2 e 2 z2 dz + z 2 e 2 z2 dz y = 2 z 2 z = 2y dy = zdz dz = dy z = dy 2y 2π z2 e 2 z2 dz = 2π dy dy 2ye y + 2ye y 2y 2y 2 = 2 2π 2 2 y 2e y dy + 2 y 2e y dd 2y 2y = 2 2π 2 2 ᴦ ᴦ 2 = 2 2π 2π 2 + 2π 2 = 2 Sehingga : E[X 2 ] = 2 + μ x 2 Maka : Var(X) = E[X 2 ] (E[X]) 2 = 2 + μ x 2 μ x 2 = 2
18 2.6.3 Distribusi Normal Standar Keluarga distribusi normal memiliki jumlah yang banyak sekali, akibat pengaruh rata-rata dan simpangan baku. Akan tetapi, untuk mencari probabilitas suatu interval dari variabel random kontinu dapat di permudah dengan menggunakan bantuan distribusi normal standard. Distribusi normal standard adalah distribusi normal yang memiliki rata-rata (μ)= dan simpangan baku ( ) =. Bentuk fungsinya adalah : f(z) = 2π e 2 z2 Untuk mengubah distribusi normal umum menjadi distribusi normal standard di gunakan nilai Z (standard units). Bentuk rumusnya adalah: X μ Z = Dengan : Z = Skor Z atau nilai normal baku X = Nilai dari suatu pengamatan atau pengukuran µ = nilai rata-rata hitung suatu distribusi = standar deviasi suatu distribusi Nilai Z (standard units) adalah angka atau indeks yang menyatakan penyimpangan suatu nilai variabel random (X) dari rata-rata (µ ) dihitung dalam satuan simpangan baku ( ) Sifat-sifat Normal Standar Sifat-sifat penting dalam distribusi normal standard yaitu:
19 ) Grafiknya selalu ada di atas sumbu datar x 2) Bentuknya simetrik terhadap x = µ 3) Mempunyai satu modus, jadi kurva unimodal, tercapai pada x = µ 4) Grafiknya mendekati (berasimtutkan) sumbu datar x di mulai dari x = µ + 3 ke kanan dan x = µ 3 ke kiri 5) Luas daerah grafik selalu sama dengan satu unit persegi. Untuk tiap pasang µ dan, sifat-sifat di atas selalu di penuhi, hanya bentuk kurvanya saja yang berlainan. Jika makin besar, kurvanya makin rendah (platikurtik) dan untuk makin kecil, kurvanya makin tinggi (leptokurtik). Gambar 2.8 Distribusi Kurva Normal dengan μ Sama dan Berbeda Pada Gambar 2.8 menunjukkan bentuk distribusi dan kurva normal dengan nilai tengah sama dan standart deviasi yang berbeda. Kurva normal demikian mempunyai μ = Md = Mo yang sama, namun mempunyai yang berbeda. Semakin besar, maka kurva semakin pendek dan semakin tinggi nilai, maka semakin runcing. Oleh sebab itu, yang tinggi menunjukkan bahwa nilai data semakin menyebar dari nilai tengahnya (μ). Sebaliknya apabila semakin rendah, maka nilai semakin mengelompok pada nilai tengahnya, sehingga parameter nilai tengah menjadi indikator yang baik bagi ukuran populasi.
20 Gambar 2.9 Distribusi Kurva Normal dengan μ Berbeda dan Sama Pada Gambar 2.9 menunjukkan bentuk distribusi probabilitas dan kurva normal dengan μ berbeda dan sama, mempunyai jarak antara kurva yang berbeda, namun bentuk kurva tetap sama. Hal demikian bisa terjadi karena kemampuan antar populasi berbeda, namun setiap populasi mempunyai keragaman yang hampir sama. Gambar 2. Distribusi Kurva Normal dengan µ dan Berbeda Pada Gambar 2. menunjukkan bentuk distribusi probabilitas dan kurva normal dengan μ berbeda dan berbeda. Kurva yang demikian mempunyai titik pusat yang berbeda pada sumbu mendatar dan bentuk kurva berbeda karena mempunyai setandart deviasi yang berbeda. Kurva demikian relatif banyak terjadi, karena antarpopulasi terdapat perbedaan kemampuan, disamping itu di dalam setiap populasi juga terdapat perbedaan, atau setiap populasi juga mempunyai keragaman yang berbeda.
21 2.7 Menghampiri Distribusi Binomial Dengan Distribusi Normal Sebagaimana distribusi poisson sebagai penghampir distribusi binomial, maka distribusi binomial dapat juga dihampiri dengan distribusi normal. Penghampiran ini atas dasar teori asimtotik, yaitu dengan memisalkan banyak pengamatan n dan p tetap. Atas dasar pemisalan ini maka : f(x) = P(X = x) = n! x! (n x)! px ( p) n x Pendekatan distribusi normal ini dapat di gunakan untuk pendekatan distribusi binomial, dengan memenuhi beberapa syarat, yaitu : a. Jumlah pengamatan relatif besar (n 3), dan nilai dari np 5 dan n(-p) 5, dimana n = jumlah data dan p adalah probabilitas sukses. b. Memenuhi syarat binomial yaitu mempunyai peristiwa hanya 2 (dua), antara percobaan bersifat independent, probabilitas sukses dan gagal sama untuk semua percobaan dan data merupakan hasil perhitungan. c. Rumus nilai normal untuk mendekati binomial adalah : Z = X np npq d. Faktor korelasi diperlukan dari binomial yang acak diskrit menjadi normal yang kontinu dengan menambah atau mengurang,5 terhadap nilai X.
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI 2.1 Teori Probabilitas (Peluang) Probabilitas adalah suatu nilai untuk mengukur tingkat kemungkinan terjadinya suatu peristiwa (event) akan terjadi di masa mendatang yang hasilnya
BAB 2 LANDASAN TEORI 2.1 Teori Probabilitas (Peluang) Probabilitas adalah suatu nilai untuk mengukur tingkat kemungkinan terjadinya suatu peristiwa (event) akan terjadi di masa mendatang yang hasilnya
Bab 2 DISTRIBUSI PELUANG
 Bab 2 DISTRIBUSI PELUANG PENDAHULUAN Setiap peristiwa akan mempunyai peluangnya masingmasing, dan peluang terjadinya peristiwa itu akan mempunyai penyebaran yang mengikuti suatu pola tertentu yang di sebut
Bab 2 DISTRIBUSI PELUANG PENDAHULUAN Setiap peristiwa akan mempunyai peluangnya masingmasing, dan peluang terjadinya peristiwa itu akan mempunyai penyebaran yang mengikuti suatu pola tertentu yang di sebut
Ruang Sampel, Titik Sampel dan Kejadian
 Dasar Dasar robabilitas DSR DSR ROILITS Ruang Sampel, Titik Sampel dan Kejadian Ruang sampel (sample space atau semesta (universe merupakan himpunan dari semua hasil (outcome yang mungkin dari suatu percobaan
Dasar Dasar robabilitas DSR DSR ROILITS Ruang Sampel, Titik Sampel dan Kejadian Ruang sampel (sample space atau semesta (universe merupakan himpunan dari semua hasil (outcome yang mungkin dari suatu percobaan
STATISTIKA. Muhamad Nursalman Pendilkom/Ilkom UPI
 STATISTIKA Muhamad Nursalman Pendilkom/Ilkom UPI 1 Daftar Isi Bab 1 Peluang Bab Peubah Acak Bab 3 Distribusi Peluang Diskret Bab 4 Distribusi Peluang Kontinu Bab 5 Fungsi Peubah Acak Bab 6 Teori Penaksiran
STATISTIKA Muhamad Nursalman Pendilkom/Ilkom UPI 1 Daftar Isi Bab 1 Peluang Bab Peubah Acak Bab 3 Distribusi Peluang Diskret Bab 4 Distribusi Peluang Kontinu Bab 5 Fungsi Peubah Acak Bab 6 Teori Penaksiran
PROBABILITAS (PELUANG) PENGERTIAN PROBABILITAS
 PROBABILITAS (PELUANG) PENGERTIAN PROBABILITAS Dalam kehidupan sehari-hari kita sering mendengar dan menggunakan kata probabilitas (peluang). Kata ini mengisyaratkan bahwa kita berhadapan dengan sesuatu
PROBABILITAS (PELUANG) PENGERTIAN PROBABILITAS Dalam kehidupan sehari-hari kita sering mendengar dan menggunakan kata probabilitas (peluang). Kata ini mengisyaratkan bahwa kita berhadapan dengan sesuatu
KONSEP DASAR PROBABILITAS DAN DISTRIBUSI PROBABILITAS LELY RIAWATI, ST, MT.
 KONSEP DASAR PROBABILITAS DAN DISTRIBUSI PROBABILITAS LELY RIAWATI, ST, MT. EKSPERIMEN suatu percobaan yang dapat diulang-ulang dengan kondisi yang sama CONTOH : Eksperimen : melempar dadu 1 kali Hasilnya
KONSEP DASAR PROBABILITAS DAN DISTRIBUSI PROBABILITAS LELY RIAWATI, ST, MT. EKSPERIMEN suatu percobaan yang dapat diulang-ulang dengan kondisi yang sama CONTOH : Eksperimen : melempar dadu 1 kali Hasilnya
Kumpulan pasangan nilai-nilai dari variabel acak X dengan probabilitas nilai-nilai variabel random X, yaitu P(X=x) disebut distribusi probabilitas X
 Kumpulan pasangan nilai-nilai dari variabel acak X dengan probabilitas nilai-nilai variabel random X, yaitu P(X=) disebut distribusi probabilitas X (distribusi X) Diskrit Seragam Binomial Hipergeometrik
Kumpulan pasangan nilai-nilai dari variabel acak X dengan probabilitas nilai-nilai variabel random X, yaitu P(X=) disebut distribusi probabilitas X (distribusi X) Diskrit Seragam Binomial Hipergeometrik
Statistika Farmasi
 Bab 3: Distribusi Data Statistika FMIPA Universitas Islam Indonesia Distribusi Data Teori dalam statistika berkaitan dengan peluang Konsep dasar peluang tersebut berkaitan dengan peluang distribusi, yaitu
Bab 3: Distribusi Data Statistika FMIPA Universitas Islam Indonesia Distribusi Data Teori dalam statistika berkaitan dengan peluang Konsep dasar peluang tersebut berkaitan dengan peluang distribusi, yaitu
BAB II TINJAUAN TEORITIS. Menurut Darnius, O (2006, Hal : 53) simulasi dapat diartikan sebagai suatu
 BAB II TINJAUAN TEORITIS 2.1 Pendahulauan Menurut Darnius, O (2006, Hal : 53) simulasi dapat diartikan sebagai suatu rekayasa suatu model logika ilmiah untuk melihat kebenaran/kenyataan model tersebut.
BAB II TINJAUAN TEORITIS 2.1 Pendahulauan Menurut Darnius, O (2006, Hal : 53) simulasi dapat diartikan sebagai suatu rekayasa suatu model logika ilmiah untuk melihat kebenaran/kenyataan model tersebut.
PENGANTAR PROBABILITAS STATISTIKA UNIPA SBY
 PENGANTAR PROBABILITAS GANGGA ANURAGA POKOK BAHASAN Konsep dasar probabilitas Teori himpunan Permutasi Kombinasi Koefisien binomial Koefisien multinomial Probabilitas Aksioma probabilitas Probabilitas
PENGANTAR PROBABILITAS GANGGA ANURAGA POKOK BAHASAN Konsep dasar probabilitas Teori himpunan Permutasi Kombinasi Koefisien binomial Koefisien multinomial Probabilitas Aksioma probabilitas Probabilitas
DISTRIBUSI TEORITIS. P(M) = p = probabilitas untuk mendapat bola merah (sukses) 30
 DISTRIBUSI TEORITIS Distribusi teoritis merupakan alat bagi kita untuk menentukan apa yang dapat kita harapkan, apabila asumsi-asumsi yang kita buat benar. Distribusi teoritis memungkinkan para pembuat
DISTRIBUSI TEORITIS Distribusi teoritis merupakan alat bagi kita untuk menentukan apa yang dapat kita harapkan, apabila asumsi-asumsi yang kita buat benar. Distribusi teoritis memungkinkan para pembuat
MODUL II DISTRIBUSI PELUANG DISKRIT DAN KONTINU
 DISTRIBUSI PELUANG DISKRIT DAN KONTINU A. TUJUAN PRAKTIKUM Melalui praktikum Modul II ini diharapkan praktikan dapat: 1. Mengenal jenis dan karakteristik dari beberapa distribusi peluang. 2. Menguji dan
DISTRIBUSI PELUANG DISKRIT DAN KONTINU A. TUJUAN PRAKTIKUM Melalui praktikum Modul II ini diharapkan praktikan dapat: 1. Mengenal jenis dan karakteristik dari beberapa distribusi peluang. 2. Menguji dan
Kompetens n i s : Mahasiswa mam a pu p menjel enj a el s a ka k n gejala ekonomi dengan meng guna k n a konsep probabil i i l t i as
 Kompetensi: Mahasiswa mampu menjelaskan gejala ekonomi dengan menggunakan konsep probabilitas Hal. 9- Penelitian itu Penuh Kemungkinan (tdk pasti) Mengubah Saya tidak yakin Menjadi Saya yakin akan sukses
Kompetensi: Mahasiswa mampu menjelaskan gejala ekonomi dengan menggunakan konsep probabilitas Hal. 9- Penelitian itu Penuh Kemungkinan (tdk pasti) Mengubah Saya tidak yakin Menjadi Saya yakin akan sukses
BAB II DISTRIBUSI PROBABILITAS
 BAB II DISTRIBUSI PROBABILITAS.1. VARIABEL RANDOM Definisi 1: Variabel random adalah suatu fungsi yang memetakan ruang sampel (S) ke himpunan bilangan Real (R), dan ditulis X : S R Contoh (Variabel random)
BAB II DISTRIBUSI PROBABILITAS.1. VARIABEL RANDOM Definisi 1: Variabel random adalah suatu fungsi yang memetakan ruang sampel (S) ke himpunan bilangan Real (R), dan ditulis X : S R Contoh (Variabel random)
BAB 1 PENDAHULUAN. Universitas Sumatera Utara
 BAB 1 PENDAHULUAN 1.1 Latar Belakang Dalam teori probabilitas dan statistika, distribusi binomial adalah distribusi probabilitas diskret jumlah keberhasilan dalam n percobaan ya/tidak (berhasil/gagal)
BAB 1 PENDAHULUAN 1.1 Latar Belakang Dalam teori probabilitas dan statistika, distribusi binomial adalah distribusi probabilitas diskret jumlah keberhasilan dalam n percobaan ya/tidak (berhasil/gagal)
Nilai harapan suatu variabel acak x ditulis E (x) didefinisikan E (x) = Σ x. f (x) Var (x) = σ x 2 = E [ x E (x) ] 2 = E (x 2 ) { E (x) } 2
![Nilai harapan suatu variabel acak x ditulis E (x) didefinisikan E (x) = Σ x. f (x) Var (x) = σ x 2 = E [ x E (x) ] 2 = E (x 2 ) { E (x) } 2 Nilai harapan suatu variabel acak x ditulis E (x) didefinisikan E (x) = Σ x. f (x) Var (x) = σ x 2 = E [ x E (x) ] 2 = E (x 2 ) { E (x) } 2](/thumbs/52/30023529.jpg) Pertemuan ke- 4 BAB III POPULASI, SAMPEL & DISTRIBUSI TEORITIS VARIABEL DISKRIT DAN FUNGSI PROBABILITAS 3.1 Variabel Random atau Variabel Acak Variabel yang nilainya merupakan suatu bilangan yang ditentukan
Pertemuan ke- 4 BAB III POPULASI, SAMPEL & DISTRIBUSI TEORITIS VARIABEL DISKRIT DAN FUNGSI PROBABILITAS 3.1 Variabel Random atau Variabel Acak Variabel yang nilainya merupakan suatu bilangan yang ditentukan
Distribusi Diskrit dan Kontinu yang Penting. Oleh Azimmatul Ihwah
 Distribusi Diskrit dan Kontinu yang Penting Oleh Azimmatul Ihwah Distribusi Diskrit Fungsi probabilitas dari variabel random diskrit dapat dinyatakan dalam formula matematik tertentu yang dinamakan fungsi
Distribusi Diskrit dan Kontinu yang Penting Oleh Azimmatul Ihwah Distribusi Diskrit Fungsi probabilitas dari variabel random diskrit dapat dinyatakan dalam formula matematik tertentu yang dinamakan fungsi
STATISTICS. Oleh: Hanung N. Prasetyo DISTRIBUSI NORMAL WEEK 6 TELKOM POLTECH/HANUNG NP
 STATISTICS WEEK 6 Oleh: Hanung N. Prasetyo DISTRIBUSI NORMAL Pengantar: Dalam pokok bahasan disini memuat beberapa distribusi kontinyu yang sangat penting di bidang statistika. diantaranya distribusi normal.
STATISTICS WEEK 6 Oleh: Hanung N. Prasetyo DISTRIBUSI NORMAL Pengantar: Dalam pokok bahasan disini memuat beberapa distribusi kontinyu yang sangat penting di bidang statistika. diantaranya distribusi normal.
Model dan Simulasi Universitas Indo Global Mandiri
 Model dan Simulasi Universitas Indo Global Mandiri Nomor random >> angka muncul secara acak (random/tidak terurut) dengan probabilitas untuk muncul yang sama. Probabilitas/Peluang merupakan ukuran kecenderungan
Model dan Simulasi Universitas Indo Global Mandiri Nomor random >> angka muncul secara acak (random/tidak terurut) dengan probabilitas untuk muncul yang sama. Probabilitas/Peluang merupakan ukuran kecenderungan
PS-02 HUKUM-HUKUM PROBABILITAS. Nur Hayati, S.ST, MT Yogyakarta, Februari 2016
 PS-02 HUKUM-HUKUM PROBABILITAS Nur Hayati, S.ST, MT Yogyakarta, Februari 2016 Ruang Sampel Kejadian Hukum Probabilitas Pokok Bahasan Ruang Sampel Pengertian Ruang Sampel dan Titik Sampel Ruang Sampel adalah
PS-02 HUKUM-HUKUM PROBABILITAS Nur Hayati, S.ST, MT Yogyakarta, Februari 2016 Ruang Sampel Kejadian Hukum Probabilitas Pokok Bahasan Ruang Sampel Pengertian Ruang Sampel dan Titik Sampel Ruang Sampel adalah
KAJIAN TENTANG PENDEKATAN DISTRIBUSI BINOMIAL OLEH DISTRIBUSI NORMAL SKRIPSI MUSTAFA KEMAL RAMBE
 KAJIAN TENTANG PENDEKATAN DISTRIBUSI BINOMIAL OLEH DISTRIBUSI NORMAL SKRIPSI MUSTAFA KEMAL RAMBE 090823073 DEPARTEMEN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
KAJIAN TENTANG PENDEKATAN DISTRIBUSI BINOMIAL OLEH DISTRIBUSI NORMAL SKRIPSI MUSTAFA KEMAL RAMBE 090823073 DEPARTEMEN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
Tugas Kelompok. Mata Kuliah Metodologi Penelitian Kuantitatif. Judul Makalah Revisi DISTRIBUSI PELUANG
 Tugas Kelompok Mata Kuliah Metodologi Penelitian Kuantitatif Judul Makalah Revisi DISTRIBUSI PELUANG Kajian Buku Pengantar Statistika Pengarang Nana Sudjana Tugas dibuat untuk memenuhi tugas mata kuliah
Tugas Kelompok Mata Kuliah Metodologi Penelitian Kuantitatif Judul Makalah Revisi DISTRIBUSI PELUANG Kajian Buku Pengantar Statistika Pengarang Nana Sudjana Tugas dibuat untuk memenuhi tugas mata kuliah
DISTRIBUSI PROBABILITAS (PELUANG)
 DISTRIBUSI PROBABILITAS (PELUANG) Distribusi Probabilitas (Peluang) Distribusi? Probabilitas? Distribusi Probabilitas? JURUSAN PENDIDIKAN FISIKA FPMIPA UNIVERSITAS PENDIDIKAN INDONESIA Distribusi = sebaran,
DISTRIBUSI PROBABILITAS (PELUANG) Distribusi Probabilitas (Peluang) Distribusi? Probabilitas? Distribusi Probabilitas? JURUSAN PENDIDIKAN FISIKA FPMIPA UNIVERSITAS PENDIDIKAN INDONESIA Distribusi = sebaran,
STK 511 Analisis statistika. Materi 3 Sebaran Peubah Acak
 STK 511 Analisis statistika Materi 3 Sebaran Peubah Acak 1 Konsep Peluang 2 Peluang Peluang dapat diartikan sebagai ukuran kemungkinan terjadinya suatu kejadian Untuk memahami peluang diperlukan pemahaman
STK 511 Analisis statistika Materi 3 Sebaran Peubah Acak 1 Konsep Peluang 2 Peluang Peluang dapat diartikan sebagai ukuran kemungkinan terjadinya suatu kejadian Untuk memahami peluang diperlukan pemahaman
Hidup penuh dengan ketidakpastian
 BAB 2 Probabilitas Hidup penuh dengan ketidakpastian Tidak mungkin bagi kita untuk dapat mengatakan dengan pasti apa yang akan terjadi dalam 1 menit ke depan tapi Probabilitas akan memprediksikan masa
BAB 2 Probabilitas Hidup penuh dengan ketidakpastian Tidak mungkin bagi kita untuk dapat mengatakan dengan pasti apa yang akan terjadi dalam 1 menit ke depan tapi Probabilitas akan memprediksikan masa
STATISTIK PERTEMUAN VI
 STATISTIK PERTEMUAN VI 1. TEORI PENDUKUNG 1.1 Pendahuluan 1. Variabel acak 1.3 Distribusi variabel acak diskrit 1.4 Distribusi variabel acak kontinu 1.5 Distribusi multivariat 1.1 Pendahuluan Definisi
STATISTIK PERTEMUAN VI 1. TEORI PENDUKUNG 1.1 Pendahuluan 1. Variabel acak 1.3 Distribusi variabel acak diskrit 1.4 Distribusi variabel acak kontinu 1.5 Distribusi multivariat 1.1 Pendahuluan Definisi
MATERI STATISTIK II. Genrawan Hoendarto
 MATERI STATISTIK II Teori Probabilitas Variabel Acak dan Nilai Harapan Distribusi Teoritis Distribusi Sampling Pengujian Hipotesis Regresi dan Korelasi Linear Sederhana Statistik Nonparametrik Daftar Pustaka
MATERI STATISTIK II Teori Probabilitas Variabel Acak dan Nilai Harapan Distribusi Teoritis Distribusi Sampling Pengujian Hipotesis Regresi dan Korelasi Linear Sederhana Statistik Nonparametrik Daftar Pustaka
PENS. Probability and Random Process. Topik 5. Beberapa jenis Distribusi Variabel Acak. Prima Kristalina April 2015
 Program Pasca Sarjana Terapan Politeknik Elektronika Negeri Surabaya Probability and Random Process Topik 5. Beberapa jenis Distribusi Variabel Acak Prima Kristalina April 215 1 Outline 1. Beberapa macam
Program Pasca Sarjana Terapan Politeknik Elektronika Negeri Surabaya Probability and Random Process Topik 5. Beberapa jenis Distribusi Variabel Acak Prima Kristalina April 215 1 Outline 1. Beberapa macam
Contoh: Aturan Penjumlahan. Independen. P(A dan B) = P(A) x P(B)
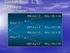 Aturan Penjumlahan Mutually Exclusive: Kemungkinan terjadi peristiwa A dan B: P(A atau B)= P(A)+P(B) Not Mutually Exclusive: Kemungkinan terjadi peristiwa A dan B: P(Aatau B): P(A)+P(B) P(A dan B) Contoh:
Aturan Penjumlahan Mutually Exclusive: Kemungkinan terjadi peristiwa A dan B: P(A atau B)= P(A)+P(B) Not Mutually Exclusive: Kemungkinan terjadi peristiwa A dan B: P(Aatau B): P(A)+P(B) P(A dan B) Contoh:
DISTRIBUSI TEORITIS. Variabel Acak Distribusi Teoritis Binomial Normal
 DISTRIBUSI TEORITIS DISTRIBUSI TEORITIS Variabel Acak Distribusi Teoritis Binomial Normal Variabel acak adalah sebuah besaran yang merupakan hasil dari percobaan acak yang secara untung-untungan, dapat
DISTRIBUSI TEORITIS DISTRIBUSI TEORITIS Variabel Acak Distribusi Teoritis Binomial Normal Variabel acak adalah sebuah besaran yang merupakan hasil dari percobaan acak yang secara untung-untungan, dapat
STK511 Analisis Statistika. Pertemuan 3 Sebaran Peluang Peubah Acak
 STK511 Analisis Statistika Pertemuan 3 Sebaran Peluang Peubah Acak Beberapa Konsep Dasar Percobaan statistika: kegiatan yang hasil akhir keluarannya tidak diketahui di awal, tetapi kemungkinan-kemungkinannya
STK511 Analisis Statistika Pertemuan 3 Sebaran Peluang Peubah Acak Beberapa Konsep Dasar Percobaan statistika: kegiatan yang hasil akhir keluarannya tidak diketahui di awal, tetapi kemungkinan-kemungkinannya
BAB 3 Teori Probabilitas
 BAB 3 Teori Probabilitas A. HIMPUNAN a. Penulisan Hipunan Cara Pendaftaran Cara Pencirian 1) A = {a,i,u,e,o} 1) A = {X: x huruf vokal } 2) B = {1,2,3,4,5} menghasilkan data diskrit 2) B = {X: 1 x 2} menghasilkan
BAB 3 Teori Probabilitas A. HIMPUNAN a. Penulisan Hipunan Cara Pendaftaran Cara Pencirian 1) A = {a,i,u,e,o} 1) A = {X: x huruf vokal } 2) B = {1,2,3,4,5} menghasilkan data diskrit 2) B = {X: 1 x 2} menghasilkan
Materi #2 TIN315 Pemeliharaan dan Rekayasa Keandalan Genap 2015/2016
 #2 PROBABILITAS 2.1. Pendahuluan Kata probabiliitas sering dipakai jika kehilangan sentuhan dalam mengimplikasikan bahwa suatu kejadian yang mempunyai peluang yang bagus akan terjadi. Dalam hal ini penilaian
#2 PROBABILITAS 2.1. Pendahuluan Kata probabiliitas sering dipakai jika kehilangan sentuhan dalam mengimplikasikan bahwa suatu kejadian yang mempunyai peluang yang bagus akan terjadi. Dalam hal ini penilaian
BAHAN AJAR STATISTIKA DASAR Matematika STKIP Tuanku Tambusai Bangkinang 4. BEBERAPA DISTRIBUSI PELUANG DISKRET
 Pertemuan 7. BAHAN AJAR STATISTIKA DASAR Matematika STKIP Tuanku Tambusai Bangkinang 4. BEBERAPA DISTRIBUSI PELUANG DISKRET 4. Pendahuluan 4.2 Distribusi seragam diskret 4.3 Distribusi binomial dan multinomial
Pertemuan 7. BAHAN AJAR STATISTIKA DASAR Matematika STKIP Tuanku Tambusai Bangkinang 4. BEBERAPA DISTRIBUSI PELUANG DISKRET 4. Pendahuluan 4.2 Distribusi seragam diskret 4.3 Distribusi binomial dan multinomial
CIRI-CIRI DISTRIBUSI NORMAL
 DISTRIBUSI NORMAL CIRI-CIRI DISTRIBUSI NORMAL Berbentuk lonceng simetris terhadap x = μ distribusi normal atau kurva normal disebut juga dengan nama distribusi Gauss, karena persamaan matematisnya ditemukan
DISTRIBUSI NORMAL CIRI-CIRI DISTRIBUSI NORMAL Berbentuk lonceng simetris terhadap x = μ distribusi normal atau kurva normal disebut juga dengan nama distribusi Gauss, karena persamaan matematisnya ditemukan
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI 2.1 Distribusi Normal Salah satu distribusi frekuensi yang paling penting dalam statistika adalah distribusi normal. Distribusi normal berupa kurva berbentuk lonceng setangkup yang
BAB 2 LANDASAN TEORI 2.1 Distribusi Normal Salah satu distribusi frekuensi yang paling penting dalam statistika adalah distribusi normal. Distribusi normal berupa kurva berbentuk lonceng setangkup yang
Distribusi Peluang. Kuliah 6
 Distribusi Peluang Kuliah 6 1. Diskrit 1. Bernoulli 2. Binomial 3. Poisson Distribution 2. Kontinu 1. Normal (Gaussian) 2. t 3. F 4. Chi Kuadrat Distribusi Peluang 1.1. Distribusi Bernoulli Distribusi
Distribusi Peluang Kuliah 6 1. Diskrit 1. Bernoulli 2. Binomial 3. Poisson Distribution 2. Kontinu 1. Normal (Gaussian) 2. t 3. F 4. Chi Kuadrat Distribusi Peluang 1.1. Distribusi Bernoulli Distribusi
Pertemuan ke Nilai Harapan (Mean atau Rata rata) dan Varians Distribusi Kontinu
 Pertemuan ke 5 4.1 Nilai Harapan (Mean atau Rata rata) dan Varians Distribusi Kontinu Fungsi Probabilitas dengan variabel kontinu terdiri dari : 1. Distribusi Normal 2. Distribusi T 3. Distribusi Chi Kuadrat
Pertemuan ke 5 4.1 Nilai Harapan (Mean atau Rata rata) dan Varians Distribusi Kontinu Fungsi Probabilitas dengan variabel kontinu terdiri dari : 1. Distribusi Normal 2. Distribusi T 3. Distribusi Chi Kuadrat
Nilai Harapan / Nilai Ekspektasi
 EKSPEKTASI Misalkan sebuah eksperimen menghasilkan k peristiwa, dan peluang masing-masing peristiwa P 1, P, P k dan untuk tiap peristiwa terdapat satuan (bobot d 1, d d k ) maka ekspektasi eksperimen itu
EKSPEKTASI Misalkan sebuah eksperimen menghasilkan k peristiwa, dan peluang masing-masing peristiwa P 1, P, P k dan untuk tiap peristiwa terdapat satuan (bobot d 1, d d k ) maka ekspektasi eksperimen itu
Peubah acak X yang berdistribusi normal dengan rataan sebagai: 2 ) X ~ N(,
 0 DISTRIBUSI NORMAL UMUM Distribusi normal umum ini merupakan distribusi dari peubah acak kontinu yang paling banyak sekali dipakai sebagai pendekatan yang baik dari distribusi lainnya dengan persyaratan
0 DISTRIBUSI NORMAL UMUM Distribusi normal umum ini merupakan distribusi dari peubah acak kontinu yang paling banyak sekali dipakai sebagai pendekatan yang baik dari distribusi lainnya dengan persyaratan
Bab 3 Pengantar teori Peluang
 Bab 3 Pengantar teori Peluang Istilah peluang atau kemungkinan, sering kali diucapkan atau didengar. Sebagai contoh ketika manajer dari sebuah klub sepak bola ditanya wartawan tentang hasil pertandingan
Bab 3 Pengantar teori Peluang Istilah peluang atau kemungkinan, sering kali diucapkan atau didengar. Sebagai contoh ketika manajer dari sebuah klub sepak bola ditanya wartawan tentang hasil pertandingan
KONSEP DASAR PROBABILITAS
 KONSEP DASAR PROBABILITAS 1 OUTLINE BAGIAN II Probabilitas dan Teori Keputusan Konsep-Konsep Dasar Probabilitas Distribusi Probabilitas Diskrit Pengertian Probabilitas dan Manfaat Probabilitas Pendekatan
KONSEP DASAR PROBABILITAS 1 OUTLINE BAGIAN II Probabilitas dan Teori Keputusan Konsep-Konsep Dasar Probabilitas Distribusi Probabilitas Diskrit Pengertian Probabilitas dan Manfaat Probabilitas Pendekatan
DISTRIBUSI PELUANG.
 DISTRIBUSI PELUANG readonee@yahoo.com Distribusi? Peluang? Distribusi Peluang? Distribusi = sebaran, pencaran, susunan data Peluang : Ukuran/derajat ketidakpastian suatu peristiwa Distribusi Peluang adalah
DISTRIBUSI PELUANG readonee@yahoo.com Distribusi? Peluang? Distribusi Peluang? Distribusi = sebaran, pencaran, susunan data Peluang : Ukuran/derajat ketidakpastian suatu peristiwa Distribusi Peluang adalah
Pengantar Proses Stokastik
 Bab 1: Dasar-Dasar Probabilitas Statistika FMIPA Universitas Islam Indonesia 2015 Percobaan adalah kegiatan yang menghasilkan keluaran/hasil yang mungkin secara acak. Contoh: pelemparan sebuah dadu. Ruang
Bab 1: Dasar-Dasar Probabilitas Statistika FMIPA Universitas Islam Indonesia 2015 Percobaan adalah kegiatan yang menghasilkan keluaran/hasil yang mungkin secara acak. Contoh: pelemparan sebuah dadu. Ruang
DISTRIBUSI TEORITIS DISTRIBUSI TEORITIS
 DISTRIBUSI TEORITIS DISTRIBUSI TEORITIS Variabel Acak Distribusi Teoritis Binomial Normal 1 Variabel acak adalah sebuah besaran yang merupakan hasil dari percobaan acak yang secara untung-untungan, dapat
DISTRIBUSI TEORITIS DISTRIBUSI TEORITIS Variabel Acak Distribusi Teoritis Binomial Normal 1 Variabel acak adalah sebuah besaran yang merupakan hasil dari percobaan acak yang secara untung-untungan, dapat
Statistika (MMS-1403)
 Statistika (MMS-1403) Dr. Danardono, MPH danardono@ugm.ac.id Program Studi Statistika Jurusan Matematika FMIPA UGM Materi dan Jadual Minggu ke- Pokok Bahasan Sub Pokok Bahasan 1. Pendahuluan 1 Perkuliahan
Statistika (MMS-1403) Dr. Danardono, MPH danardono@ugm.ac.id Program Studi Statistika Jurusan Matematika FMIPA UGM Materi dan Jadual Minggu ke- Pokok Bahasan Sub Pokok Bahasan 1. Pendahuluan 1 Perkuliahan
Metode Statistika (STK 211) Pertemuan ke-5
 Metode Statistika (STK 211) Pertemuan ke-5 rrahmaanisa@apps.ipb.ac.id Memahami definisi dan aplikasi peubah acak (peubah acak sebagai fungsi, peubah acak diskrit dan kontinu) Memahami sebaran peubah acak
Metode Statistika (STK 211) Pertemuan ke-5 rrahmaanisa@apps.ipb.ac.id Memahami definisi dan aplikasi peubah acak (peubah acak sebagai fungsi, peubah acak diskrit dan kontinu) Memahami sebaran peubah acak
DISTRIBUSI PROBABILITAS DISKRIT TEORITIS 2. Distribusi Hipergeometrik
 DISTRIBUSI PROBABILITAS DISKRIT TEORITIS 2 TI2131 TEORI PROBABILITAS MINGGU KE-10 Distribusi Hipergeometrik Eksperimen hipergeometrik memiliki karakteristik sebagai berikut: 1. sebuah sampel random berukuran
DISTRIBUSI PROBABILITAS DISKRIT TEORITIS 2 TI2131 TEORI PROBABILITAS MINGGU KE-10 Distribusi Hipergeometrik Eksperimen hipergeometrik memiliki karakteristik sebagai berikut: 1. sebuah sampel random berukuran
STATISTIK PERTEMUAN III
 STATISTIK PERTEMUAN III OUTLINE PERTEMUAN III BAGIAN II Probabilitas dan Teori Keputusan Konsep-Konsep Dasar Probabilitas Distribusi Probabilitas Diskrit Pengertian Probabilitas dan Manfaat Probabilitas
STATISTIK PERTEMUAN III OUTLINE PERTEMUAN III BAGIAN II Probabilitas dan Teori Keputusan Konsep-Konsep Dasar Probabilitas Distribusi Probabilitas Diskrit Pengertian Probabilitas dan Manfaat Probabilitas
BAB 8 DISTRIBUSI PELUANG DISKRIT
 BAB 8 DISTRIBUSI PELUANG DISKRIT A. Peluang Peluang atau yang sering disebut sebagai probabilitas dapat dipandang sebagai cara untuk mengungkapkan ukuran ketidakpastian/ ketidakyakinan/ kemungkinan suatu
BAB 8 DISTRIBUSI PELUANG DISKRIT A. Peluang Peluang atau yang sering disebut sebagai probabilitas dapat dipandang sebagai cara untuk mengungkapkan ukuran ketidakpastian/ ketidakyakinan/ kemungkinan suatu
STATISTIKA LINGKUNGAN
 STATISTIKA LINGKUNGAN TEORI PROBABILITAS Probabilitas -pendahuluan Statistika deskriptif : menggambarkan data Statistik inferensi kesimpulan valid dan perkiraan akurat ttg populasi dengan mengobservasi
STATISTIKA LINGKUNGAN TEORI PROBABILITAS Probabilitas -pendahuluan Statistika deskriptif : menggambarkan data Statistik inferensi kesimpulan valid dan perkiraan akurat ttg populasi dengan mengobservasi
STATISTIKA UNIPA SURABAYA
 MATEMATIKA STATISTIKA (MATHEMATICAL STATISTICS) GANGGA ANURAGA Materi : Distribusi variabel random Teori Himpunan Fungsi Himpunan Fungsi Himpunan Peluang Variabel Random Fungsi Kepadatan Peluang Fungsi
MATEMATIKA STATISTIKA (MATHEMATICAL STATISTICS) GANGGA ANURAGA Materi : Distribusi variabel random Teori Himpunan Fungsi Himpunan Fungsi Himpunan Peluang Variabel Random Fungsi Kepadatan Peluang Fungsi
Pengantar Proses Stokastik
 Bab 1: Dasar-Dasar Probabilitas Atina Ahdika, S.Si, M.Si Statistika FMIPA Universitas Islam Indonesia Ruang Sampel dan Kejadian Ruang Sampel dan Kejadian Ruang Sampel dan Kejadian Percobaan adalah kegiatan
Bab 1: Dasar-Dasar Probabilitas Atina Ahdika, S.Si, M.Si Statistika FMIPA Universitas Islam Indonesia Ruang Sampel dan Kejadian Ruang Sampel dan Kejadian Ruang Sampel dan Kejadian Percobaan adalah kegiatan
Haryoso Wicaksono, S.Si., M.M., M.Kom. 26
 Distribusi probabilita kontinu, yaitu apabila random variabel yang digunakan kontinu. Probabilita dihitung untuk nilai dalam suatu interval tertentu. Probabilita di suatu titik = 0. Probabilita untuk random
Distribusi probabilita kontinu, yaitu apabila random variabel yang digunakan kontinu. Probabilita dihitung untuk nilai dalam suatu interval tertentu. Probabilita di suatu titik = 0. Probabilita untuk random
DISTRIBUSI PROBABILITAS
 BAB 7 DISTRIBUSI PROBABILITAS Kompetensi Menjelaskan distribusi probabilitas Indikator 1. Menjelaskan distribusi hipergeometris 2. Menjelaskan distribusi binomial 3. Menjelaskan distribusi multinomial
BAB 7 DISTRIBUSI PROBABILITAS Kompetensi Menjelaskan distribusi probabilitas Indikator 1. Menjelaskan distribusi hipergeometris 2. Menjelaskan distribusi binomial 3. Menjelaskan distribusi multinomial
28/09/2012 SAMPLE SPACE, SAMPLE POINTS, EVENTS. ω Ω
 SAMPLE SPACE, SAMPLE POINTS, EVENTS Sample space,ω, Ω adalah sekumpulan semua sample points,ω, ω yang mungkin; dimana ω Ω Contoh 1. Melemparkan satu buah koin:ω={gambar,angka} Contoh 2. Menggelindingkan
SAMPLE SPACE, SAMPLE POINTS, EVENTS Sample space,ω, Ω adalah sekumpulan semua sample points,ω, ω yang mungkin; dimana ω Ω Contoh 1. Melemparkan satu buah koin:ω={gambar,angka} Contoh 2. Menggelindingkan
Pert 3 PROBABILITAS. Rekyan Regasari MP
 Pert 3 PROBABILITAS Rekyan Regasari MP Berapakah kemungkinan sebuah koin yang dilempar akan menghasilkan gambar angka Berapakah kemungkinan gedung ini akan runtuh Berapakah kemungkinan seorang kreditur
Pert 3 PROBABILITAS Rekyan Regasari MP Berapakah kemungkinan sebuah koin yang dilempar akan menghasilkan gambar angka Berapakah kemungkinan gedung ini akan runtuh Berapakah kemungkinan seorang kreditur
BAB 2 TINJAUAN TEORITIS. Menurut Open Darnius (2006, hal: 53) simulasi dapat diartikan sebagai suatu
 xiv BAB 2 TINJAUAN TEORITIS 2.1 Pendahuluan Menurut Open Darnius (2006, hal: 53) simulasi dapat diartikan sebagai suatu rekayasa dari suatu model secara logika ilmiah merupakan suatu metode alternatif
xiv BAB 2 TINJAUAN TEORITIS 2.1 Pendahuluan Menurut Open Darnius (2006, hal: 53) simulasi dapat diartikan sebagai suatu rekayasa dari suatu model secara logika ilmiah merupakan suatu metode alternatif
Peubah Acak. 14-Sep-07 TPADF (Kelas Ganjil/ Rahmat) Lecture 2 page 1
 Peubah Acak 14-Sep-07 TPADF (Kelas Ganjil/ Rahmat) Lecture 2 page 1 Definisi Peubah Acak Peubah acak adalah peubah yang mengkarakterisasikan setiap elemen dalam ruang sampel dengan suatu bilangan real.
Peubah Acak 14-Sep-07 TPADF (Kelas Ganjil/ Rahmat) Lecture 2 page 1 Definisi Peubah Acak Peubah acak adalah peubah yang mengkarakterisasikan setiap elemen dalam ruang sampel dengan suatu bilangan real.
Bagian 2. Probabilitas. Struktur Probabilitas. Probabilitas Subyektif. Metode Frekuensi Relatif Kejadian untuk Menentukan Probabilitas
 Probabilitas Bagian Probabilitas A) = peluang (probabilitas) bahwa kejadian A terjadi 0 < A) < 1 A) = 0 artinya A pasti terjadi A) = 1 artinya A tidak mungkin terjadi Penentuan nilai probabilitas: Metode
Probabilitas Bagian Probabilitas A) = peluang (probabilitas) bahwa kejadian A terjadi 0 < A) < 1 A) = 0 artinya A pasti terjadi A) = 1 artinya A tidak mungkin terjadi Penentuan nilai probabilitas: Metode
Probabilitas. Tujuan Pembelajaran
 Probabilitas 1 Tujuan Pembelajaran 1.Menjelaskan Eksperimen, Hasil,, Ruang Sampel, & Peluang 2. Menjelaskan bagaimana menetapkan peluang 3. Menggunakan Tabel Kontingensi, Diagram Venn, atau Diagram Tree
Probabilitas 1 Tujuan Pembelajaran 1.Menjelaskan Eksperimen, Hasil,, Ruang Sampel, & Peluang 2. Menjelaskan bagaimana menetapkan peluang 3. Menggunakan Tabel Kontingensi, Diagram Venn, atau Diagram Tree
Distribusi Normal. Statistika (MAM 4137) Syarifah Hikmah JS
 Distribusi Normal Statistika (MAM 4137) Syarifah Hikmah JS Outline Kurva normal Luas daerah di bawah kurva normal Penerapan sebaran normal DISTRIBUSI NORMAL model distribusi kontinyu yang paling penting
Distribusi Normal Statistika (MAM 4137) Syarifah Hikmah JS Outline Kurva normal Luas daerah di bawah kurva normal Penerapan sebaran normal DISTRIBUSI NORMAL model distribusi kontinyu yang paling penting
By : Refqi Kemal Habib
 BAB I PENDAHULUAN A. Dasar Teori Peluang atau kebolehjadian atau dikenal juga sebagai probabilitas adalah cara untuk mengungkapkan pengetahuan atau kepercayaan bahwa suatu kejadian akan berlaku atau telah
BAB I PENDAHULUAN A. Dasar Teori Peluang atau kebolehjadian atau dikenal juga sebagai probabilitas adalah cara untuk mengungkapkan pengetahuan atau kepercayaan bahwa suatu kejadian akan berlaku atau telah
KONSEP DASAR PROBABILITAS OLEH : RIANDY SYARIF
 KONSEP DASAR PROBABILITAS OLEH : RIANDY SYARIF Definisi Probabilitas adalah suatu ukuran tentang kemungkinan suatu peristiwa (event) akan terjadi dimasa mendatang. Probabilitas dinyatakan antara 0 s/d
KONSEP DASAR PROBABILITAS OLEH : RIANDY SYARIF Definisi Probabilitas adalah suatu ukuran tentang kemungkinan suatu peristiwa (event) akan terjadi dimasa mendatang. Probabilitas dinyatakan antara 0 s/d
Misalkan terdapat eksperimen. S disebut ruang sampel, adalah himpunan semua kemungkinan hasil dari eksperimen.
 Peluang Peluang dan Kejadian Peluang Bersyarat Peubah Acak dan Nilai Harapan Kovarian dan Korelasi 1.1 PELUANG DAN KEJADIAN Misalkan terdapat eksperimen. S disebut ruang sampel, adalah himpunan semua kemungkinan
Peluang Peluang dan Kejadian Peluang Bersyarat Peubah Acak dan Nilai Harapan Kovarian dan Korelasi 1.1 PELUANG DAN KEJADIAN Misalkan terdapat eksperimen. S disebut ruang sampel, adalah himpunan semua kemungkinan
DISTRIBUSI NORMAL. Pertemuan 3. Distribusi Normal_M. Jainuri, M.Pd 1
 DISTRIBUSI NORMAL Pertemuan 3 1 Distribusi Normal Pertama kali diperkenalkan oleh Abraham de Moivre (1733). De Moivre menemukan persamaan matematika untuk kurva normal yang menjadi dasar dalam banyak teori
DISTRIBUSI NORMAL Pertemuan 3 1 Distribusi Normal Pertama kali diperkenalkan oleh Abraham de Moivre (1733). De Moivre menemukan persamaan matematika untuk kurva normal yang menjadi dasar dalam banyak teori
KAJIAN TENTANG PENDEKATAN DISTRIBUSI BINOMIAL OLEH DISTRIBUSI NORMAL SKRIPSI RIDWAN NASUTION
 KAJIAN TENTANG PENDEKATAN DISTRIBUSI BINOMIAL OLEH DISTRIBUSI NORMAL SKRIPSI RIDWAN NASUTION 060823034 DEPARTEMEN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA MEDAN
KAJIAN TENTANG PENDEKATAN DISTRIBUSI BINOMIAL OLEH DISTRIBUSI NORMAL SKRIPSI RIDWAN NASUTION 060823034 DEPARTEMEN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA MEDAN
Probabilitas dan Statistika Distribusi Peluang Kontinyu 1. Adam Hendra Brata
 Probabilitas dan Statistika Distribusi Peluang Kontinyu 1 Adam Hendra Brata Variabel Acak Kontinyu - Variabel Acak Kontinyu Suatu variabel yang memiliki nilai pecahan didalam range tertentu Distribusi
Probabilitas dan Statistika Distribusi Peluang Kontinyu 1 Adam Hendra Brata Variabel Acak Kontinyu - Variabel Acak Kontinyu Suatu variabel yang memiliki nilai pecahan didalam range tertentu Distribusi
Statistika (MMS-1001)
 Statistika (MMS-1001) Dr. Danardono, MPH danardono@ugm.ac.id Program Studi Statistika Jurusan Matematika FMIPA UGM Materi dan Jadual Tatap Muka Pokok Bahasan Sub Pokok Bahasan 1. Statistika Deskriptif
Statistika (MMS-1001) Dr. Danardono, MPH danardono@ugm.ac.id Program Studi Statistika Jurusan Matematika FMIPA UGM Materi dan Jadual Tatap Muka Pokok Bahasan Sub Pokok Bahasan 1. Statistika Deskriptif
Peubah Acak. Bab 4. Definisi 4.1 Peubah acak adalah suatu fungsi dari ruang contoh ke bilangan nyata, f : S R
 Bab 4 Peubah Acak Definisi 4. Peubah acak adalah suatu fungsi dari ruang contoh ke bilangan nyata, f : S R Contoh 4. Jika Y adalah peubah acak banyaknya sisi muka yang muncul pada pelemparan tiga sisi
Bab 4 Peubah Acak Definisi 4. Peubah acak adalah suatu fungsi dari ruang contoh ke bilangan nyata, f : S R Contoh 4. Jika Y adalah peubah acak banyaknya sisi muka yang muncul pada pelemparan tiga sisi
25/09/2013. Konsep Peubah Acak. Metode Statistika (STK211) Peubah Acak Diskret. Kuis. Tipe Peubah Acak
 Konsep Peubah Acak Metode Statistika (STK11) Pertemuan V Konsep Peubah Acak dan Sebaran Peluang (Random Variable Concept and Probability Distribution) Peubah acak merupakan suatu fungsi yang memetakan
Konsep Peubah Acak Metode Statistika (STK11) Pertemuan V Konsep Peubah Acak dan Sebaran Peluang (Random Variable Concept and Probability Distribution) Peubah acak merupakan suatu fungsi yang memetakan
Statistika (MMS-1001)
 Statistika (MMS-1001) Dr. Danardono, MPH danardono@ugm.ac.id Program Studi Statistika Jurusan Matematika FMIPA UGM Materi dan Jadual Tatap Muka Pokok Bahasan Sub Pokok Bahasan 1. Statistika Deskriptif
Statistika (MMS-1001) Dr. Danardono, MPH danardono@ugm.ac.id Program Studi Statistika Jurusan Matematika FMIPA UGM Materi dan Jadual Tatap Muka Pokok Bahasan Sub Pokok Bahasan 1. Statistika Deskriptif
Peubah Acak (Lanjutan)
 Learning Outcomes 13 April 2014 Learning Outcomes Learning Outcome Outline Mahasiswa dapat mengerti dan menentukan peubah acak diskret Mahasiswa dapat memahami dan menghitung nilai harapan Mahasiswa dapat
Learning Outcomes 13 April 2014 Learning Outcomes Learning Outcome Outline Mahasiswa dapat mengerti dan menentukan peubah acak diskret Mahasiswa dapat memahami dan menghitung nilai harapan Mahasiswa dapat
15Ilmu. Uji t-student dan Uji Z (Distribusi Normal)
 Modul ke: Fakultas 15Ilmu Komunikasi Uji t-student dan Uji Z (Distribusi Normal) Untuk sebaran distribusi sampel kecil, dikembangkan suatu distribusi khusus yang disebut distribusi t atau t-student Dra.
Modul ke: Fakultas 15Ilmu Komunikasi Uji t-student dan Uji Z (Distribusi Normal) Untuk sebaran distribusi sampel kecil, dikembangkan suatu distribusi khusus yang disebut distribusi t atau t-student Dra.
BAB 2 TINJAUAN PUSTAKA
 BAB 2 TINJAUAN PUSTAKA 2.1 Data Data adalah bentuk jamak dari datum, yang dapat diartikan sebagai informasi yang diterima yang bentuknya dapat berupa angka, kata-kata, atau dalam bentuk lisan dan tulisan
BAB 2 TINJAUAN PUSTAKA 2.1 Data Data adalah bentuk jamak dari datum, yang dapat diartikan sebagai informasi yang diterima yang bentuknya dapat berupa angka, kata-kata, atau dalam bentuk lisan dan tulisan
PELUANG DAN PEUBAH ACAK
 PELUANG DAN PEUBAH ACAK Materi 3 - STK511 Analisis Statistika October 3, 2017 Okt, 2017 1 Konsep Peluang 2 Pendahuluan Kejadian di dunia: pasti (deterministik) atau tidak pasti (probabilistik) Contoh kejadian
PELUANG DAN PEUBAH ACAK Materi 3 - STK511 Analisis Statistika October 3, 2017 Okt, 2017 1 Konsep Peluang 2 Pendahuluan Kejadian di dunia: pasti (deterministik) atau tidak pasti (probabilistik) Contoh kejadian
MA2181 Analisis Data - U. Mukhaiyar 1
 DISTRIBUSI KONTINU Uniform Normal Gamma & Eksponensial MA 2181 Analisis Data Utriweni Mukhaiyar September 20 By NN 2008 DISTRIBUSI UNIFORM Distribusi kontinu yang paling sederhana Notasi: X ~ U (a,b) f.k.p:
DISTRIBUSI KONTINU Uniform Normal Gamma & Eksponensial MA 2181 Analisis Data Utriweni Mukhaiyar September 20 By NN 2008 DISTRIBUSI UNIFORM Distribusi kontinu yang paling sederhana Notasi: X ~ U (a,b) f.k.p:
Probabilitas metode ilmiah yang dikembangkan untuk menyelesaikan persoalan yang berhubungan dengan ketidakpastian (uncertaint).
 PROBSTAT (MUG2D3) III. PROBABILITAS (PROBABILITY) 3.1 Probabilitas dan Statistika 3.2 Konsep Probabilitas a. Pengertian: Eksperimen, Ruang Contoh, Titik Contoh, Event. b. Operasi dalam Himpunan - Komplemen
PROBSTAT (MUG2D3) III. PROBABILITAS (PROBABILITY) 3.1 Probabilitas dan Statistika 3.2 Konsep Probabilitas a. Pengertian: Eksperimen, Ruang Contoh, Titik Contoh, Event. b. Operasi dalam Himpunan - Komplemen
THEORY. By: Hanung N. Prasetyo PEUBAH ACAK TELKOM POLYTECHNIC/HANUNGNP
 THEORY By: Hanung N. Prasetyo PEUBAH ACAK Variabel acak adalah suatu variabel yang nilainya bisa berapa saja Variabel acak merupakan deskripsi numerik dari outcome beberapa percobaan / eksperimen VARIABEL
THEORY By: Hanung N. Prasetyo PEUBAH ACAK Variabel acak adalah suatu variabel yang nilainya bisa berapa saja Variabel acak merupakan deskripsi numerik dari outcome beberapa percobaan / eksperimen VARIABEL
DISTRIBUSI KONTINU. Utriweni Mukhaiyar
 DISTRIBUSI KONTINU Uniform Normal Gamma & Eksponensial MA 2081 Statistika ti tik Dasar Utriweni Mukhaiyar Maret 2012 By NN 2008 Distribusi Uniform Distribusi kontinu yang paling sederhana Notasi: X ~ U
DISTRIBUSI KONTINU Uniform Normal Gamma & Eksponensial MA 2081 Statistika ti tik Dasar Utriweni Mukhaiyar Maret 2012 By NN 2008 Distribusi Uniform Distribusi kontinu yang paling sederhana Notasi: X ~ U
KONSEP PROBABILITAS & DISTRIBUSI PROBABILITAS
 KONSEP PROBABILITAS & DISTRIBUSI PROBABILITAS 5 Pengendalian Kualitas Debrina Puspita Andriani Teknik Industri Universitas Brawijaya e- Mail : debrina@ub.ac.id Blog : hbp://debrina.lecture.ub.ac.id/ 2
KONSEP PROBABILITAS & DISTRIBUSI PROBABILITAS 5 Pengendalian Kualitas Debrina Puspita Andriani Teknik Industri Universitas Brawijaya e- Mail : debrina@ub.ac.id Blog : hbp://debrina.lecture.ub.ac.id/ 2
Jenis Distribusi. 1. Distribusi Probabilitas 2. Distribusi Binomial (Bernaulli) 3. Distribusi Multinomial 4. Distribusi Normal (Gauss)
 Ir Tito Adi Dewanto Jenis Distribusi 1. Distribusi Probabilitas 2. Distribusi Binomial (Bernaulli) 3. Distribusi Multinomial 4. Distribusi Normal (Gauss) Pengantar Kunci aplikasi probabilitas dalam statistik
Ir Tito Adi Dewanto Jenis Distribusi 1. Distribusi Probabilitas 2. Distribusi Binomial (Bernaulli) 3. Distribusi Multinomial 4. Distribusi Normal (Gauss) Pengantar Kunci aplikasi probabilitas dalam statistik
MA2082 BIOSTATISTIKA Bab 3 Peubah Acak dan Distribusi
 MA2082 BIOSTATISTIKA Bab 3 Peubah Acak dan Distribusi Orang Biologi Tidak Anti Statistika Silabus Silabus dan Tujuan Konsep peubah acak, fungsi peluang (probability density function), fungsi distribusi
MA2082 BIOSTATISTIKA Bab 3 Peubah Acak dan Distribusi Orang Biologi Tidak Anti Statistika Silabus Silabus dan Tujuan Konsep peubah acak, fungsi peluang (probability density function), fungsi distribusi
Probabilitas dan Statistika Ruang Sampel. Adam Hendra Brata
 dan Statistika Ruang Adam Hendra Brata adalah suatu ilmu untuk memprediksi suatu kejadian (event) atau dapat disebut peluang suatu kejadian berdasarkan pendekatan matematis. Dengan ilmu probabilitas, kita
dan Statistika Ruang Adam Hendra Brata adalah suatu ilmu untuk memprediksi suatu kejadian (event) atau dapat disebut peluang suatu kejadian berdasarkan pendekatan matematis. Dengan ilmu probabilitas, kita
Pengantar Proses Stokastik
 Bab 1: Dasar-Dasar Probabilitas Statistika FMIPA Universitas Islam Indonesia Peluang Percobaan adalah kegiatan yang menghasilkan keluaran/hasil yang mungkin secara acak. Contoh: pelemparan sebuah dadu.
Bab 1: Dasar-Dasar Probabilitas Statistika FMIPA Universitas Islam Indonesia Peluang Percobaan adalah kegiatan yang menghasilkan keluaran/hasil yang mungkin secara acak. Contoh: pelemparan sebuah dadu.
OUT LINE. Distribusi Probabilitas Normal. Pengertian Distribusi Probabilitas Normal. Distribusi Probabilitas Normal Standar
 3 OUT LINE Pengertian Distribusi Probabilitas Normal Distribusi Probabilitas Normal Distribusi Probabilitas Normal Standar Penerapan Distribusi Probabilitas Normal Standar Pendekatan Normal Terhadap Binomial
3 OUT LINE Pengertian Distribusi Probabilitas Normal Distribusi Probabilitas Normal Distribusi Probabilitas Normal Standar Penerapan Distribusi Probabilitas Normal Standar Pendekatan Normal Terhadap Binomial
Bab 9. Peluang Diskrit
 Bab 9. Peluang Diskrit Topik Definisi Peluang Diskrit Sifat Peluang Diskrit Probabilitas terbatas Konsep Teori Himpunan pada Peluang Diskrit Probabilitas Kejadian Majemuk A B dan A B DuaKejadianSalingLepas
Bab 9. Peluang Diskrit Topik Definisi Peluang Diskrit Sifat Peluang Diskrit Probabilitas terbatas Konsep Teori Himpunan pada Peluang Diskrit Probabilitas Kejadian Majemuk A B dan A B DuaKejadianSalingLepas
Hubungan antara kejadian dengan ruang contohnya Representasi secara grafis untuk mengilustrasikan logical relations di antara kejadian kejadian
 Diagram Venn. Hubungan antara kejadian dengan ruang contohnya Representasi secara grafis untuk mengilustrasikan logical relations di antara kejadian kejadian S = Himpunan bilangan asli A = Himpunan bilangan
Diagram Venn. Hubungan antara kejadian dengan ruang contohnya Representasi secara grafis untuk mengilustrasikan logical relations di antara kejadian kejadian S = Himpunan bilangan asli A = Himpunan bilangan
Pengantar Proses Stokastik
 Bab 1: Dasar-Dasar Probabilitas Statistika FMIPA Universitas Islam Indonesia Peluang Percobaan adalah kegiatan yang menghasilkan keluaran/hasil yang mungkin secara acak. Contoh: pelemparan sebuah dadu.
Bab 1: Dasar-Dasar Probabilitas Statistika FMIPA Universitas Islam Indonesia Peluang Percobaan adalah kegiatan yang menghasilkan keluaran/hasil yang mungkin secara acak. Contoh: pelemparan sebuah dadu.
Distribusi Peluang Teoritis. Titik-titik contoh di dalam Ruang Sampel (S) dapat disajikan dalam bentuk numerik/bilangan.
 Distribusi Peluang Teoritis. Pendahuluan Titik-titik contoh di dalam Ruang Sampel (S) dapat disajikan dalam bentuk numerik/bilangan. Peubah Acak Fungsi yang mendefinisikan titik-titik contoh dalam ruang
Distribusi Peluang Teoritis. Pendahuluan Titik-titik contoh di dalam Ruang Sampel (S) dapat disajikan dalam bentuk numerik/bilangan. Peubah Acak Fungsi yang mendefinisikan titik-titik contoh dalam ruang
KONSEP DASAR PROBABILITAS
 KONSEP DASAR PROBABILITAS Definisi: Probabilitas adalah peluang suatu kejadian Manfaat: Manfaat mengetahui probabilitas adalah membantu pengambilan keputusan yang tepat, karena kehidupan di dunia tidak
KONSEP DASAR PROBABILITAS Definisi: Probabilitas adalah peluang suatu kejadian Manfaat: Manfaat mengetahui probabilitas adalah membantu pengambilan keputusan yang tepat, karena kehidupan di dunia tidak
LAB MANAJEMEN DASAR MODUL STATISTIKA 1
 LAB MANAJEMEN DASAR MODUL STATISTIKA 1 Nama : NPM/Kelas : Fakultas/Jurusan : Hari dan Shift Praktikum : Fakultas Ekonomi Universitas Gunadarma Kelapa dua E531 1 UKURAN STATISTIK Pendahuluan Ukuran statistik
LAB MANAJEMEN DASAR MODUL STATISTIKA 1 Nama : NPM/Kelas : Fakultas/Jurusan : Hari dan Shift Praktikum : Fakultas Ekonomi Universitas Gunadarma Kelapa dua E531 1 UKURAN STATISTIK Pendahuluan Ukuran statistik
DISTRIBUSI PROBABILITAS
 DISTRIBUSI PROBABILITAS DISTRIBUSI PROBABILITAS Peluang terjadinya nilai variabel random X yang meliputi semua nilai ditentukan melalui distribusi peluang. Distribusi peluang suatu variabel random X adalah
DISTRIBUSI PROBABILITAS DISTRIBUSI PROBABILITAS Peluang terjadinya nilai variabel random X yang meliputi semua nilai ditentukan melalui distribusi peluang. Distribusi peluang suatu variabel random X adalah
MK Statistik Bisnis 2 MultiVariate. Haryoso Wicaksono, S.Si., M.M., M.Kom. 1
 Haryoso Wicaksono, S.Si., M.M., M.Kom. 1 Descriptive Statistics mengandung metoda dan prosedur yang digunakan untuk pengumpulan, pengorganisasian, presentasi dan memberikan karakteristik terhadap himpunan
Haryoso Wicaksono, S.Si., M.M., M.Kom. 1 Descriptive Statistics mengandung metoda dan prosedur yang digunakan untuk pengumpulan, pengorganisasian, presentasi dan memberikan karakteristik terhadap himpunan
HARAPAN MATEMATIK. Nur Hayati, S.ST, MT Yogyakarta, Maret 2016
 HARAPAN MATEMATIK Nur Hayati, S.ST, MT Yogyakarta, Maret 2016 Pendahuluan Rata-rata perubah acak X atau rata-rata distribusi peluang X ditulis x atau. Dalam statistik rata-rata ini disebut harapan matematik
HARAPAN MATEMATIK Nur Hayati, S.ST, MT Yogyakarta, Maret 2016 Pendahuluan Rata-rata perubah acak X atau rata-rata distribusi peluang X ditulis x atau. Dalam statistik rata-rata ini disebut harapan matematik
Harapan Matematik. Bahan Kuliah II2092 Probabilitas dan Statistik Oleh: Rinaldi Munir Sekolah Teknik Elektro dan Informatika ITB
 Harapan Matematik Bahan Kuliah II09 Probabilitas dan Statistik Oleh: Rinaldi Munir Sekolah Teknik Elektro dan Informatika ITB 1 Definisi Harapan Matematik Satu konsep yang penting di dalam teori peluang
Harapan Matematik Bahan Kuliah II09 Probabilitas dan Statistik Oleh: Rinaldi Munir Sekolah Teknik Elektro dan Informatika ITB 1 Definisi Harapan Matematik Satu konsep yang penting di dalam teori peluang
DISTRIBUSI DISKRIT KHUSUS
 DISTRIBUSI DISKRIT KHUSUS U N I F O R M ( S E R A G A M ) B E R N O U L L I B I N O M I A L P O I S S O N MA 4085 Pengantar Statistika 26 Februari 2013 Utriweni Mukhaiyar M U L T I N O M I A L H I P E
DISTRIBUSI DISKRIT KHUSUS U N I F O R M ( S E R A G A M ) B E R N O U L L I B I N O M I A L P O I S S O N MA 4085 Pengantar Statistika 26 Februari 2013 Utriweni Mukhaiyar M U L T I N O M I A L H I P E
DISTRIBUSI BINOMIAL STKIP SILIWANGI BANDUNG LUVY S ZANTHY KAPSEL SMA
 DISTRIBUSI BINOMIAL STKIP SILIWANGI BANDUNG LUVY S ZANTHY KAPSEL SMA 1 LUVY S. ZANTHY KAPSEL SMA 2 LUVY S. ZANTHY KAPSEL SMA 3 Distribusi Binomial O Dalam suatu percobaan statistik sering dijumpai pengulangan
DISTRIBUSI BINOMIAL STKIP SILIWANGI BANDUNG LUVY S ZANTHY KAPSEL SMA 1 LUVY S. ZANTHY KAPSEL SMA 2 LUVY S. ZANTHY KAPSEL SMA 3 Distribusi Binomial O Dalam suatu percobaan statistik sering dijumpai pengulangan
BAB II PROBABILITAS Ruang sampel (sample space)
 BAB II ROBABILITAS 2.1. Ruang sampel (sample space) Data diperoleh baik dari pengamatan kejadian yang tak dapat dikendalikan atau dari percobaan yang dikendalikan dalam laboratorium. Untuk penyederhanaan
BAB II ROBABILITAS 2.1. Ruang sampel (sample space) Data diperoleh baik dari pengamatan kejadian yang tak dapat dikendalikan atau dari percobaan yang dikendalikan dalam laboratorium. Untuk penyederhanaan
PEUBAH ACAK. Materi 4 - STK211 Metode Statistika. October 2, Okt, Department of Statistics, IPB. Dr. Agus Mohamad Soleh
 PEUBAH ACAK Materi 4 - STK211 Metode Statistika October 2, 2017 Okt, 2017 1 Pendahuluan Pernahkah bertanya, mengapa dalam soal ujian penerimaan mahasiswa baru, jika jawaban benar diberi nilai 4, salah
PEUBAH ACAK Materi 4 - STK211 Metode Statistika October 2, 2017 Okt, 2017 1 Pendahuluan Pernahkah bertanya, mengapa dalam soal ujian penerimaan mahasiswa baru, jika jawaban benar diberi nilai 4, salah
