LAPORAN PENELITIAN EFISIENSI ALGORITME ARITMETIK ( ) DENGAN OPERASI DIBANGKITKAN DARI SIFAT GRUP SIKLIK PADA KRIPTOGRAFI KURVA ELIPTIK
|
|
|
- Erlin Halim
- 6 tahun lalu
- Tontonan:
Transkripsi
1 LAPORAN PENELITIAN EFISIENSI ALGORITME ARITMETIK ( ) DENGAN OPERASI DIBANGKITKAN DARI SIFAT GRUP SIKLIK PADA KRIPTOGRAFI KURVA ELIPTIK Oleh : Dra. Eleonora Dwi W., M.Pd Ahmadi, M.Si FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN UNIVERSITAS PANCASAKTI TEGAL 2012
2
3
4
5
6
7 BAB I PENDAHULUAN Masalah keamanan merupakan salah satu aspek penting dari sebuah sistem informasi. Untuk menjamin keamanan sebuah informasi yang bersifat rahasia diperlukan suatu teknik pengamanan baik secara fisik maupun non fisik. Salah satu teknik pengamanan secara non fisik yaitu dengan mengenkripsi informasi rahasia menggunakan teknik kriptografi. Kriptografi secara terminologi dasarnya terdiri dari dua tipe yaitu kriptografi simetrik dan kriptografi asimetrik atau sering disebut sebagai kriptografi kunci publik. Kunci simetris adalah jenis kriptografi yang paling umum digunakan. Kunci untuk membuat pesan yang disandikan sama dengan kunci untuk membuka pesan yang disandikan itu. Jadi pembuat pesan dan penerimanya harus memiliki kunci yang sama persis. Siapapun yang memiliki kunci tersebut termasuk pihak-pihak yang tidak diinginkan dapat membuat dan membongkar rahasia ciphertext. Contoh algoritme kunci simetris yang terkenal adalah DES (Data Encryption Standard). Karya ini menjadi alat keamanan komersial elektronik di banyak institusi keuangan di seluruh dunia hingga pertengahan tahun 1990-an. DES secara DES tak aman sejak juli Walaupun demikian DES telah melandasi prinsip-prinsip sandi simetrik modern yang dewasa ini muncul produk-produk penggantinya seperti : AES (Advanced Encryption Standard), Blowfish, 3DES, RC5, dan lain sebagainya. Kunci asimetrik merupakan pasangan kunci kriptografi yang salah satunya digunakan untuk proses enkripsi dan yang satu lagi untuk dekripsi. Semua orang yang mendapatkan kunci publik dapat menggunakannya untuk mengenkripsikan suatu pesan,data ataupun informasi, sedangkan hanya satu orang saja yang memiliki rahasia tertentu dalam hal ini kunci privat untuk melakukan pembongkaran terhadap sandi yang dikirim untuknya. Pada algoritme kunci publik ini, semua orang dapat mengenkripsi data dengan memakai kunci publik penerima yang telah diketahui secara umum. Akan tetapi data yang telah terenkripsi tersebut hanya dapat didekripsi dengan menggunakan kunci privat
8 2 yang hanya diketahui oleh penerima. Contoh algoritme terkenal yang menggunakan kunci asimetrik adalah skema RSA yang ditemukan oleh Rivest, Shamir, dan Adleman pada tahun Skema ini didasarkan pada problem matematika yang sulit, yaitu pemecahan masalah faktorisasi integer besar. Bentuk praktis skema kunci publik lainnya ditemukan oleh ElGamal pada tahun Skema ini didasarkan pada pemecahan problem logaritma diskret. Keamanan algoritme ini sangat tergantung pada pemilihan bilangan prima p. Semakin besar p maka algoritme ini akan semakin aman, akan tetapi semakin besar pula beban komputasi yang digunakan. Oleh karena itu pada masa sekarang, orang sudah mulai mencari alternatif lain untuk menggantikan aritmetik modular diantaranya aritmetik yang dibangkitkan struktur finite field ( ), kurva eliptik kriptografi, dan hipereliptik kriptografi. Teori finite field mulai diperkenalkan pada abad ke tujuh dan abad ke delapan, dengan tokoh matematikanya Pierre de Fermat ( ) dan Leonhard Euler ( ) dengan kontribusinya pada khusus teori struktur finite field. Teori secara umum tentang finite field mulai dikerjakan oleh Carl Friedrich Gauss ( ) dan Evariste Galois ( ), teori ini banyak dikembangkan dalam dunia aplikasi matematika, komputer, dan teori komunikasi. 2
9 3 BAB II TINJAUAN PUSTAKA Untuk mencapai tujuan penulisan penelitian diperlukan beberapa pengertian dan teori yang berkaitan dengan pembahasan. Dalam subbab ini akan diberikan beberapa teori berupa definisi, lemma, dan teorema yang berkaitan dengan pembahasan Teori Grup Definisi 3.1. Struktur aljabar, tertutup terhadap operasi biner disebut grup jika memenuhi aksioma-aksioma berikut: a) Operasi biner bersifat asosiatif: a b c a b c, untuk setiap a, b, c G. b) Terdapat unsur identitas e G, untuk * pada G sehingga berlaku a e e a a untuk setiap a G. c) Untuk setiap a G ada unsur disebut invers a terhadap operasi *). a G 1 sehingga 1 1 a a a a e. ( a -1 Grup G disebut grup komutatif atau grup abelian jika operasi * bersifat komutatif yaitu: a b b a, untuk semua a, b G. Grup berhingga yaitu grup yang kardinalitasnya berhingga. Dalam hal ini kardinalitas suatu grup G disebut dengan order dari G, dinotasikan ord G atau O G atau G. Definisi 3.2. Jika H himpunan bagian atas grup G adalah grup di bawah operasi G, maka H subgrup dari G. Teorema 3.3. (Uji satu langkah) Misalkan G grup dan H himpunan bagian yang tak kosong atas G. Maka H adalah subgrup atas G jika H tertutup di bawah operasi pembagian; yaitu jika. bilamana, Teorema 3.4. (Uji dua langkah) Misalkan G grup dan H himpunan bagian tak kosong atas G. Maka, H disebut subgrup dari G jika. bilamana, 3
10 (tertutup terhadap perkalian), dan bilamana (tertutup terhadap invers) Sebagai contoh, Z dan Q merupakan subgrup dari R terhadap operasi +. Tentu saja Z Q R dan masing-masing merupakan grup terhadap operasi yang sama yaitu +. Misal G sembarang grup, a G, dan n bilangan bulat positif, maka: a n : aa... a, n kali n a : a a... a, dan = (a n ) -1 a 0 : n kali e. Jika ada bilangan bulat tidak nol m sedemikian sehingga dari unsur a, notasi sedemikian sehingga sehingga n a m a 4 e, maka order Oa, didefinisikan sebagai bilangan bulat positif terkecil n n a e. Jika tidak ada bilangan bulat tidak nol n sedemikian e, maka dikatakan a mempunyai order di tak hingga (infinity). Ringkasan 3.5. Berikut ini 3 sifat dasar yang berkaitan dengan pengertian order. 1. Jika Oa n, maka ada tepat n kuasa dari a (power of a) yang masingmasing berbeda, yaitu 0 2 n 1 a e, a, a,..., a. 2. Jika Oa tak hingga, maka semua kuasa dari a berbeda. Artinya, jika r dan s yaitu dua bilangan bulat yang berbeda, maka 3. Misalkan a yaitu unsur dari grup G dan Oa a r s a. n. Maka t a e jika dan hanya jika t yaitu kelipatan dari n (t kelipatan n artinya ada bilangan bulat q sehingga t=nq). Definisi 3.6. Misalkan H subgrup dari grup G. Himpunan bagian = {h h } atas G disebut koset kiri atas H memuat. Sedangkan himpunan bagian = {h h } atas G disebut koset kanan atas H memuat. Teorema 3.7. (Teorema Lagrange) Misalkan H subgrup dari grup berhingga G. Maka order dari H adalah pembagi dari order G. Teorema 3.8. Order dari unsur grup berhingga G membagi order G. 4
11 5 Jika H merupakan subgrup dari grup G, indeks dari H di dalam G diartikan sebagai jumlah koset dari H di dalam G, notasinya G : H. sedangkan G : H G H 3.2. Grup Siklik Grup G disebut siklik jika dan hanya jika ada unsur a G (a disebut generator) sehingga n G a a n Z. Dalam kasus G grup aditif, dapat ditulis G a na n Z. Ringkasan 3.9. (Sifat-sifat Grup Siklik) 1. Jika grup G berorder n, maka G siklik jika dan hanya jika ada a G sehingga Oa n. 2. Setiap grup siklik yaitu abelian. 3. Setiap subgrup dari grup siklik adalah siklik. 4. Jika G a dan b G, maka O b O a. 5. Jika G yaitu grup siklik berorder n dan suatu bilangan bulat k n, maka ada b G sehingga Ob k. 6. Misalkan G yaitu grup abelian berorder mn dengan m dan n prima relatif. Jika G mempunyai suatu unsur a dengan G yaitu grup siklik dengan G ab. Oa m dan b dengan Ob n, maka 7. r a yaitu generator dari G a dengan G n jika dan hanya jika r dan n prima relatif Grup Homomorfisme dan Isomorphisme Misal G dan H grup. Suatu homomorfisma (grup) dari G ke H yaitu suatu fungsi f : G H sedemikian sehingga untuk sembarang a dan b di dalam G, f a f b f ab. 5
12 6 Bayangan (Imej) dari f, dinotasikan Im f, yaitu Kernel dari f, dinotasikan ker f, yaitu Im f f G f x x G. ker f x G f x e (secara implisit e yaitu unsur identitas dari f). Sifat-sifat dasar homomorfisma dinyatakan dalam Ringkasan berikut ini. Ringkasan (Sifat-sifat Dasar Homomorfisma) Misalkan G dan H yaitu grup, f : G H homomorfisma, maka sifat-sifat berikut dipenuhi. 1. f e e. 2. ( ) = (()) untuk setiap a G. 3. Im f merupakan subgrup dari H. 4. ker f merupakan subgrup dari G. Jika homomorfisme yang bijektif, maka f disebut isomorfisme Ring Struktur aljabar dengan dua operasi biner yang paling umum yaitu Ring. Definisi Ring R adalah himpunan dengan dua operasi + dan x (disebut dengan penjumlahan dan perkalian) yang memenuhi aksioma-aksioma berikut: a. R, adalah grup abelian b. Operasi adalah asosiatif : () = () untuk setiap a, b, c R. c. Berlaku hukum distributif atas R : Untuk setiap a, b, c R memenuhi ( + ) = () + () dan ( + ) = () + () Ring R disebut komutatif jika perkaliannya bersifat komutatif. Ring R disebut mempunyai unsur kesatuan jika terdapat unsur 1 dengan 1 = 1 =, Definisi Unsur bukan nol dari Ring komutatif R disebut pembagi nol jika ada unsur bukan nol sehingga. = 0 Definisi Ring komutatif dengan unsur kesatuan 1 disebut daerah integral jika tidak memuat pembagi nol 6
13 Definisi Karakteristik Ring R adalah sekurang-kurangnya integer positif sehingga = 0 untuk setiap. Jika tidak ada, R disebut berkarakteristik 0. Teorema Karakteristik daerah integral adalah 0 atau prima. Teorema Di dalam sembarang Daerah Integral D dengan karakteristik p, p p p a b a b untuk semua unsur, a b D. Definisi Field adalah suatu Ring komutatif, ada unsur kesatuan 1 dan setiap unsur tak nolnya mempunyai invers (multiplikatif) Teorema Daerah integral yang berhingga adalah field. Akibat Untuk setiap bilangan prima p, Ring Z p integer modulo p, adalah field Definisi SubRing A dari Ring R disebut ideal dari R jika untuk setiap dan setiap, dan. Teorema Misal R Ring, I R, I tidak kosong. Himpunan bagian I disebut ideal jika memenuhi: a., ( ) b. dan dan. Untuk setiap Ring R, {0} dan R adalah ideal atas R. Ideal {0} disebut ideal trivial. Misalkan R Ring komutatif dengan unsur kesatuan 1 dan. Suatu himpunan = { } merupakan ideal. Ideal yang demikian disebut ideal utama yang dibangun oleh. Definisi Suatu ideal I atas Ring komutatif R disebut ideal prima atas R jika, dan sehingga dan. Suatu ideal B atas Ring komutatif R disebut ideal maksimal atas R jika B adalah ideal atas R dan maka B = A atau B = R. Misalkan Ring R dan I merupakan ideal dari R. Karena R merupakan grup terhadap penjumlahan dan I subgrup dari R, maka Ring faktor / dapat ditulis sebagai = { + }. Teorema Misal R Ring komutatif dengan unsur kesatuan 1. I ideal maksimal dari R. Maka R I adalah field jika dan hanya jika I ideal maksimal. 7 7
14 8 Definisi Suatu homomorfisma dari Ring R ke Ring ' R yaitu suatu fungsi f : R R ' yang memenuhi,, berlaku : a. f a b f a f b, dan b. f ab f a f b. Jika f surjektif, maka Kernel dari f didefinisikan dan range dari f didefinisikan ' R disebut bayangan homomorfik dari R. f x R f x ker 0, ran f f x x R. Jika f homomorfisma yang bijektif, maka f disebut isomorfisma. Dalam hal ini R dan ' R dikatakan isomorfik, dinotasikan Teorema Misal f x R f x f : R R ker 0 merupakan ideal dari R. ' Ring homomorfisma. Maka Teorema R I merupakan bayangan homomorfik dari R. Teorema (Teorema dasar homomorfisme) Misalkan ' f : R R merupakan epimorfisme, dan misalkan K yaitu kernel dari f. Maka / Ring Polinomial Misalkan R Ring komutatif dengan unsur kesatuan, dan x simbol yang tak tetap. Setiap ekspresi berbentuk disebut polinomial dalam x dengan. Polinomial dalam x dapat ditulis dengan (), (), (), dan lain-lain. Misal () = = merupakan sembarang polinomial, derajat dari polinomial () yaitu bilangan terbesar n sehingga koefisien dari bukan nol dan dinotasikan dengan deg (). Polinomial () = yang semua koefisiennya nol disebut polinomial nol, dan dinotasikan dengan () = 0. Jika polinomial () =, maka () berderajat nol dan disebut polinomial konstan. Misalkan () = dan 8
15 9 () = Operasi penjumlahan dan perkalian polinomial didefinisikan sebagai berikut : () + () = ( + ) + ( + ) + + ( + ) + + Dimana = 0 > = 0 >, (). () = Dimana, = , untuk k = 0,, m+n Jika R Ring, maka [] menotasikan himpunan semua polinomial dalam x yang koefisiennya ada di R dengan operasi penjumlahan dan perkalian seperti yang didefinisikan sebelumnya. Teorema Misal R Ring komutatif dengan unsur kesatuan 1. Maka R[x] merupakan Ring komutatif dengan unsur kesatuan 1. Teorema Jika R adalah daerah integral, maka R[x] adalah daerah integral. Definisi Suatu polinomial () [] irredusibel atas F bila f(x) tidak dapat dinyatakan sebagai perkalian (), h() dimana (), h() [] keduanya berderajat lebih rendah dari f(x). Teorema Misal F field dan Ring polinomial F x. Jika f x, g( x) F x dengan g x 0, maka ada polinomial unik q x, r( x) F x sehingga dengan r x 0 atau derajat r x derajat g x f ( x) q x g x r x. Teorema Misal F field, I ideal tak nol di F[x], dan unsur () []. Ideal = () jika dan hanya jika () merupakan polinomial tak nol berderajat terendah di I. Teorema Semua ideal dari [] merupakan ideal utama Teorema Misal F field dan () []. () ideal maksimal jika dan hanya jika () irredusibel atas F. Teorema () ideal maksimal jika dan hanya jika []/ () field Perluasan Field Definisi Jika E field yang memuat subfield F, maka E disebut perluasan field dari F. Definisi Misal E perluasan field dari field F dan c E. c disebut algebraic atas F jika f c 0 untuk f x F x yang tak nol. 9
16 10 F E c Gambar 1. Perluasan Field F Definisi Misal E perluasan field dari field F dan c E algebraic atas F. Polinomial monik p x merupakan polinomial irredusibel dengan akar c atas F dinotasikan dengan irr c, F dan derajat dari polinomial irredusibel dengan akar c atas F dinotasikan dengan deg c, F Teorema Misal F subfield dari field E, c E dan x tak tentu (indeterminate). Pemetaan : c F x E yang didefinisikan dengan n c f x f c dimana f x a0 a1 x... anx, f x F x merupakan homomorfisma. Homomorfisma c disebut homomorfisma evaluasi dan berlaku c x c serta c a a, a F. Kernel atas homomorfisma merupakan himpunan semua polinomial () sehingga () = (()) = 0. Jadi, kernel( ) berisi semua polinomial () [] sehingga c merupakan akar dari (). Misalkan kernel( ) dinotasikan sebagai, menurut Teorema 2.25 kernel untuk setiap homomorfisma merupakan ideal, sehingga merupakan ideal dari F[x]. Menurut Teorema 2.33 setiap ideal dari F[x] merupakan ideal utama. Karena merupakan ideal utama dan berdasarkan Teorema 2.32, ( ()), = () = {()() () []} dengan () polinomial berderajat terendah. Dengan Definisi 2.30 mudah untuk membuktikan bahwa () merupakan polinomial irredusibel. Misalkan () = (). h(). Sehingga 0 = () = (). h(), () = 0 atau () = 0 dimana (), h(). Hal ini tidaklah mungkin, karena () merupakan polinomial berderajat terendah di dalam. Sehingga (), h() merupakan polinomial berderajat lebih tinggi dari (). Maka menurut Definisi 2.30, () merupakan polinomial irredusibel. Karena setiap konstanta pengali dari () ada di maka 10
17 () monik. Sehingga dapat disimpulkan bahwa () merupakan polinomial minimum dari c atas F. Lalu bagaimana dengan Range dari? Range = { (()) () []} = {() () []} Dari penjelasan di atas diperoleh : [] () merupakan epimorfisme, = () dengan ()polinomial irredusibel. Dengan menggunakan Teorema dasar homomorfisme, maka []/ () (). Menurut Teorema 2.34, jika () polinomial irredusibel maka () merupakan ideal maksimal. Dan berdasarkan Teorema 2.35 dapat disimpulkan bahwa []/ () merupakan field. Karena []/ () (), maka () juga merupakan field. Teorema Misal F field dan p x polinomial tak konstan di suatu perluasan field E dari F dan unsur c di E sehingga c akar dari F x. Ada p x. Definisi 3.41 V himpunan, F field, operasi di V yaitu penjumlahan dan perkalian skalar. V disebut ruang vektor atas F jika memenuhi aksioma berikut: 1. Untuk setiap a, b V terdapat tunggal c V sehingga tertutup terhadap penjumlahan: a b c. 2. Untuk setiap a, b, c V a b c a b c. bersifat asosiatif: 3. Terdapat tunggal identitas 0V, untuk setiap a V a 0 0 a a. 4. Untuk setiap a V terdapat tunggal invers b V a b b a 0, b a. 5. Untuk setiap a, b V bersifat komutatif: a b b a. 6. Untuk setiap k F dan setiap a V terdapat tunggal b V tertutup terhadap perkalian: ka b. 7. Untuk setiap k F dan setiap a, b V k a b ka kb. 8. Untuk setiap k, l F dan setiap a V 9. Untuk setiap k, l F dan setiap a V, k l a ka la.,., kl a k la sehingga sehingga sehingga
18 Untuk setiap a V, 1a a ; 1 unsur identitas di F,. Definisi Misal E perluasan field dari field F. Jika E ruang vektor atas F berdimensi hingga n, maka E disebut perluasan hingga berderajat n atas F. Derajat E atas F sama dengan n dinotasikan E : F n. Definisi Jika field E dibangun oleh unsur satu c atas field F: E F c, maka E disebut perluasan tunggal dari F dan unsur c disebut unsur primitif atau akar primitif untuk perluasan. Teorema Misal deg c, F n, n 1. Setiap unsur dari E F c dengan c E algebraic atas F, dan 1 n1 0 1 n1 dalam bentuk b b c... b c, dimana b F x. E F c dapat dinyatakan secara unik Teorema Derajat dari () atas F sama dengan derajat dari polinomial minimum dari c atas F. Sebagai contoh, i merupakan akar dari polinomial irredusibel + 1 atas R[x]. + 1 mempunyai derajat 2, menurut Teorema 2.44, [(): ] = 2 dengan basisnya {1, i}. Setiap unsur dalam R[i] merupakan kombinasi linear dari 1 dan i yang berbentuk + dimana,. dan dinotasikan dengan () = { +, }. Teorema Misalkan () [] merupakan polinomial irredusibel berderajat m, maka []/ () adalah finite field berderajat. Operasi penjumlahan polinomial dan operasi perkalian polinomial dilakukan dalam modulo (). Teorema Misal E perluasan field dari field F dan c E algebraic atas F. Jika deg c, F 1,,..., 2 n 1 c c c. n, maka F c ruang vektor atas F berdimensi-n dengan basis Lemma Misal {,,, } basis dari ruang vektor K atas F dan {,,, } basis dari ruang vektor E atas K. Maka himpunan perkalian, merupakan basis dari ruang vektor E atas field F. i 12
19 13 BAB III TUJUAN DAN MANFAAT PENELITIAN 3.1. Tujuan Penelitian Dalam penelitian ini peneliti mencoba mengkonstruksi algoritme aritmetik (5 ) didasarkan pada sifat bahwa (5 ) merupakan grup siklik yang dibangkitkan dari akar primitif. Selain itu, peneliti ingin mengukur tingkat efisiensi algoritme hasil konstruksi Manfaat Penelitian 1. Manfaat teoritis Manfaat yang bisa didapat dari penelitian ini adalah memberikan pemahaman baru bahwa materi kuliah aljabar abstrak dapat diaplikasikan ke dalam dunia komputer diantaranya ilmu kriptografi 2. Manfaat Praktis Manfaat dari penelitian ini adalah : a. Algoritme hasil konstruksi dapat dipakai pada operasi pembuatan kunci dalam ilmu kriptografi b. Algoritme hasil konstruksi diharapkan mampu memberikan keamanan yang lebih baik dari algoritme-algoritme sebelumnya. 13
20 14 BAB IV METODE PENELITIAN 4.1 Kerangka Pemikiran Dari permasalahan di atas, maka peneliti mencoba menyelesaikan permasalahan tersebut dengan alur seperti pada Gambar 3.1 berikut : Definisikan fungsi polinomial primitif f ( x) F x Cari akar 0 f Tentukan Basis dan F Konstruksi Finite Field: F F x f ( x) Gambar 3.1: Diagram Alur Kerangka 4.2. Konstruksi Finite Field GF(5 m ) Dalam melakukan konstruksi finite field GF(5 m ), yang akan dilakukan adalah sebagai berikut : Langkah 1. Pilih polinomial irredusibel berderajat 5 atas Z 5, f(x) Z 5 [x]. Polinomial f(x) membentuk field Z 5 [x]/f(x). Kenapa kita memilih polinomial irredusibel? karena dengan memilih polinomial irredusibel maka ada jaminan bahwa Z 5 [x]/f(x) merupakan field. Hal ini dijamin oleh proposisi 31. Langkah 2. Berdasarkan teorema 62, definisikan : (5 ) = { Ζ } 14
21 15 Ambil sembarang (), () (5 ); () = () = Operasi penjumlahan; () + () = ( + ) + ( + ) + + ( + ) ( + ), ( + ),..., ( + ) Ζ Operasi perkalian; () () = (). () ( ()) Langkah 3. Berdasarkan teorema 63, GF(5 m ) mempunyai sifat grup siklik, sehingga GF(5 m ) dapat ditulis dengan 1,,,,. Setelah kita dapat mengetes irredusibel, kemudian dibuat algoritma membangun polynomial primitif yang kemudian dipilih polynomial primitif yang untuk komputasi baik. Teorema berikut menjelaskan bagaimana cara mendapatkan polynomial primitif secara komputasi Teorema 3.1. Misal p adalah bilangan prima dan misalkan factor-faktor prima yang berbeda dari p m 1 adalah r 1, r 2,, r t maka polynomial irredusibel () = Ζ (x) adalah primitf jika dan hanya jika, 1 berlaku 1 (). Langkah 4. Mengkonstruksi aritmetika finite field melalui representasi intejer yang diperoleh dari representasi polinomial primitif pada langkah 3. Setelah melakukan konstruksi aritmetika finite field, kemudian mengetes algoritma yang diperoleh dari segi kecepatan dan kapasitas memori. Untuk melakukan hal tersebut digunakan notasi Big-O atau notasi Asymptotic. 15
22 BAB V HASIL DAN PEMBAHASAN 5.1. Pembahasan Teorema dan Lemma yang Dibutuhkan Dalam Konstruksi Aritmetik GF (5 m ) Teori finite field mulai diperkenalkan pada abad ke tujuh dan abad ke delapan, dengan tokoh matematikanya Pierre de Fermat ( ) dan Leonhard Euler ( ) dengan kontribusinya pada khusus teori struktur finite field. Teori secara umum tentang finite field mulai dikerjakan oleh Carl Friedrich Gauss ( ) dan Evariste Galois ( ), teori ini banyak dikembangkan dalam dunia aplikasi matematika, komputer, dan teori komunikasi. Dalam melakukan konstruksi finite field (5 ), langkah pertama yang dilakukan adalah dengan memilih polinomial irredusibel berderajat 5 atas Z, misalkan () ϵ Z [x]. Kenapa kita memilih polinomial irredusibel f(x)? karena dengan memilih polinomial irredusibel f(x), menurut Teorema 2.35 []/ () merupakan field. Menurut Teorema 2.39 []/ () (), sehingga menurut Teorema 2.44 []/ () dapat ditulis sebagai { + + +,,, }. Langkah selanjutnya mengetes apakah polinomial irredusibel f(x) tersebut mempunyai akar atau tidak. Hasilnya dipergunakan untuk mengkonstruksi perluasan field F. Teorema berikut menjelaskan bahwa []/ () () (5 ). Teorema 5.1. Misal px yaitu polinomial irredusibel berderajat n atas ( ) = + + +,,, merupakan field. Z p. Bukti: Diketahui px yaitu polinomial irredusibel berderajat m atas Z p. Misalkan : [] ( ) yaitu fungsi yang didefinisikan () = () (). Fungsi f dibawah operasi dan merupakan homomorfisma karena ( () + ()) = ( () + ()) () = ( () ()) + ( () ()) = ( ()) + ( ()) 16
23 17 ( (). ()) = ( (). ()) () = ( () ()). ( () ()) = ( ()). ( ()) Fungsi f surjektif karena ambil () () ( ) terdapat () [] sedemikian hingga (()) = () () Kernel dari f yaitu () = () []() = 0 = {() [} () () = 0} = () Karena fungsi f homomorfisma dan surjektif maka f epimorfisma. Selanjutnya dengan memandang Teorema Dasar homomorfisma maka []/ () ( ). Menurut Teorema 2.35 F x p x field maka terbukti ( ) juga field. Akibat dari teorema di atas, maka []/ () () (5 ) sehingga diperoleh representasi (5 ) sebagai berikut. 1. field (5 ) = { + + +,,, } 2. field (5 ) dapat dipandang sebagai ruang vektor atas berdimensi m dengan basis standar {1,,,, }. 3. field GF(5 m ) dapat dipandang sebagai vektor dengan koordinatnya {,,, }, sehingga kita dapat menulis (5 ) = {[,,, ],,, }. himpunan Misal diberikan field hingga (5 ) dan didefinisikan (5 ) yaitu unsur-unsur (5 ) yang bukan nol dan dinotasikan dengan (5 )\{0}. Dua teorema berikut menjelaskan bahwa (5 ) merupakan grup siklik multiplikatif dan mempunyai generator c yang merupakan unsur primitif dari (5 ). Teorema 5.2. ( ) merupakan grup siklik multiplikatif ber order 1. Bukti: Dari Definisi field ( ) merupakan grup multiplikatif. Misal ( ) Karena ( ) ber order 1 maka i c mempunyai paling banyak 1 nilai yang berbeda. r Z dengan 1 1 sedemikian sehingga
24 18 c r i c c c c c c i r i i i i c c 1 c r i i (Sifat Assosiatif) r c 1. Dapat disimpulkan r Z minimum sehingga Oc r. Pilih c sehingga r sebesar mungkin. Akan ditunjukkan order l dari sembarang ( ) a yaitu membagi r. Untuk sembarang prima, misal r r ' dan b l l ' dimana r ' dan l ' tidak dapat dibagi oleh. Maka a c mempunyai order r ', sini diperoleh b l ' mempunyai order b, dan a l ' c mempunyai order b r '. Dari a atau r tidak maksimal. Dapat disimpulkan setiap pangkat prima pembagi dari l juga pembagi dari r dan l r. Maka setiap ( ) r r memenuhi persamaan x 1 0. Artinya x 1 dapat dibagi oleh x F*. Karena 1 ( ), 1 tetapi 1 maka diperoleh = 1. Sehingga diperoleh 1 p n x x 1 dan.( ) =,,,,, = 1 F* Teorema 5.5. Sembarang ( ) memuat suatu unsur primitif. Bukti: primitif atau akar Misal ( ) field berhingga berorder. Ambil c sebagai generator grup siklik ( ). Dari Definisi 2.43 maka c merupakan unsur primitif atau akar primitif. Karena (5 ) merupakan grup siklik multiplikatif, maka terdapat (5 ) sehingga (5 ) = = 1,,,...,. Sebagai akibatnya (5 ) = 0, 1,,,...,. Tabel berikut ini menunjukkan adanya hubungan antara representasi elemen primitif, representasi basis polinomial, dan representasi integer dalam (5 ) yang dibangun oleh polinomial primitif () = + + 2
25 19 Tabel 1. finite field ( ) No. Elemen primitif Representasi Basis Integer =
26 20 Kenapa kita perlu membahas polinomial minimum? Karena polinomial minimum menjamin bahwa polinomial tersebut adalah irredusibel dan jika berunsur primitif merupakan polinomial primitif. polinomial primitif inilah yang akan kita gunakan dalam mengkonstruksi algoritme aritmetik (5 ). Definisi 5.4. polinomial minimum M x dari c atas monik berderajat terendah dengan koefisien dari Z p merupakan polinomial Z p sehingga M c 0. Teorema 5.5. Misalkan m(x) adalah polinomial minimum dengan unsur α dalam finite field GF(p m ). Maka (i) (ii) (iii) (iv) (v) Bukti : m(x) irredusibel jika α akar dari polinomial f(x) dengan koefisien didalam GF (p), maka m(x) membagi f(x) m(x) membagi derajat () Polinomial minimum berunsur primitif dari ( ) yang berderajat m merupakan polinomial primitif. (i) Jika m(x) redusibel, maka () = ()(). Sebagai akibatnya () = 0. Karena tidak memuat pembagi nol, maka () = 0 atau () = 0. Hal ini kontradiksi dengan Definisi 5.4. Sehingga dapat disimpulkan bahwa () polinomial irredusibel. (ii) Dengan menggunakan algoritma pembagian, () = ()() + (), dimana derajat dari () lebih rendah daripada derajat (). Karena () = () = 0, () = 0. Dan karena derajat dari () lebih rendah daripada derajat (), maka () 0. (iii) Dari pembuktian sifat (ii) terbukti m(x) membagi (iv) Karena ( ) dan ( ) ruang vektor berdimensi m atas (). Ada + 1 sembarang anggota yaitu {1,,, } yang tak bebas linear = 0 dan terdapat = {1, 2,, } sehingga (). Maka merupakan polinomial berderajat yang mempunyai akar c sehingga derajat ()
27 21 (v) Misal ( ) unsur primitif. Menurut sifat 1, polinomial minimum () berderajat d merupakan polinomial irredusibel. Dengan Teorema 5.1, gunakan () untuk membangun field F ber order. Karena F memuat c dan semua unsur dari ( ), maka. Selanjutnya menurut sifat 4, derajat (), mengakibatkan = Dua teorema berikut menegaskan tentang eksistensi dan ketunggalan dari finite field (5 ). Teorema 5.6. Semua field hingga ber order adalah isomorfik. Bukti: Misal F dan G field ber order. Misal () polinomial minimum dari dan () polinomial minimum lain dari dan F G. Menurut Teorema 5.3, F G merupakan unsur primitif atau akar primitif dari F dan dari G, dan dengan Teorema merupakan polinomial primitif. Dengan Teorema 5.5.3,. (). Dan dari Teorema 5.5.4, derajat () sehingga dengan Teorema 5.1, field F dan G dapat dianggap memuat semua polinomial dalam dan berderajat n 1, yaitu memuat polinomial modulo (). Maka dapat dikatakan pemetaan merupakan isomorfima pemetaan F G. Teorema 5.7. Untuk sembarang p prima dan bilangan bulat 1, maka ada tunggal field ber order yang dinotasikan dengan ( ). Bukti: Misal ( ). perluasan field hingga dari ().. Untuk = 1, GF p Z p. Untuk > 1 bentuk F GF p 1. Akan dibuktikan ( ) field yang memuat semua akar dari. Misal f1 x faktor irredusibel berderajat 2 dari atas F 1. Menurut Teorema 5.1 dengan menggunakan p x f x Misal dapat diperoleh field baru F 2. 1 f2 x faktor irredusibel berderajat 2 dari atas F 2. Menurut Teorema 5.1 dengan menggunakan p x f x dapat diperoleh field baru F 3..sampai diperoleh field F r yang unik, memuat semua akar dari. 2
28 22 Sehingga diperoleh: () = = () () () Berikut ini merupakan Teorema dan Lemma sub field dari ( ). s r Lemma 5.8. Jika n, r, s bilangan bulat dengan n 1, r 1, s 1, maka n 1 n 1 jika dan hanya jika s r. Bukti: Misal r Qs R dimana 0 R s. r Qs R Qs r n 1 n 1 R n 1 n 1 n s s s s n 1 n 1 n 1 n 1. Qs s Maka n 1 selalu dapat dibagi dengan n 1. Teorema 5.9. r s i) GF p memuat sub field (isomorfik dengan ) GF p jika dan hanya jika s r. r s ii) Jika c GF p, maka c GF p jika dan hanya jika s p c c. Untuk Bukti: i) ) sembarang field jika 2 c s Misal c GF p s p 1 O c c, maka c yaitu 0 atau 1. merupakan unsur primitif maka s p 1 c 1 sehingga s r r Karena GF p sub field GF p maka c GF p sehingga r p 1 c 1. Berdasarkan sifat dasar ketiga dalam Ringkasan 2.3, maka p s r 1 p 1 dan selanjutnya dengan Lemma 5.11 mengakibatkan s r. s ) Misal c GF p merupakan unsur primitif maka s p 1 c 1 sehingga s p 1 O c s r. Dengan Lemma 5.11, karena s r diperoleh p 1 p 1. s r Karena p 1 p 1 r sehingga c GF p s r dan GF p sub field. GF p akibatnya s p 1 c 1
29 23 ii) ) r s Diketahui c GF p, maka c GF p s unsur c GF p memenuhi s p c c. r ) Misalkan c GF p dan diketahui r s field GF p maka c GF p. s p c. Dari Teorema Fermat setiap s c. Dari i) karena GF p sub = = 0 ( 1) = 0. Karena merupakan Daerah Integral dan tidak memuat pembagi nol diperoleh c 0 atau. 1 = 0 = 1 Dari teorema di atas, kita bisa mengetahui bahwa sub field dari (5 ) adalah (5 ), (5 ), (5 ), (5 ), (5 ), dan (5). Secara jelas dapat digambarkan sebagai berikut : (5 ) (5 ) (5 ) (5 ) (5 ) Untuk mencari polinomial monik dan irredusibel dalam (5 ) digunakan teorema berikut ini. Teorema = perkalian semua polinomial monik, irredusibel atas Z p yang derajatnya membagi m. Bukti: ) Misal Untuk kasus M x polinomial irredusibel atas M x membuat field, maka (5) Gambar 2. Subfield dari (5 ) x trivial. Asumsi M x Z p berderajat d, dimana. x. Gunakan M x untuk M x merupakan polinomial minimum. Misalkan () = dan dari Teorema5.5.3: (). Dengan memandang Lemma
30 24 5.8, karena maka 1 1 dan 1 1. Oleh karena itu (). ) Misal M x pembagi dari, polinomial irredusibel, dan berderajat d. Akan ditunjukkan. Asumsi. () () 1 1. Gunakan d untuk membuat field GF p ber order d M x dan GF p d d p. Misal c GF p merupakan unsur primitif dapat dinyatakan 2 d d 1 M x akar dari a a c a c... a c (*) (menurut Teorema 2.44) Karena c akar dari M x maka () = 0 = 0 =. =. = 1. Dari (*) dan Teorema 2.16: p p p a b a b maka diperoleh = 0 = = = 1. d n Berdasarkan sifat dasar ketiga dalam Ringkasan 2.5 maka p 1 p 1. Selanjutnya dengan Lemma 5.8 diperoleh d n. Dari teorema di atas kita dapat mencari polinomial irredusibel dan polinomial monik dalam (5 ) sebagai berikut : Untuk = 1 () = = + 4 = ( + 4) = ( + 1)( + 4) Untuk = 2 = ( + 2)( + 3)( + 1)( + 4) () = = + 4 = ( + 4) Dan seterusnya = ( + 1)( + 4) = ( + 2)( + 3)( + 1)( + 4) = ( + 3)( )( + 2)( )( + 2) ( + 3)( + 1)( + 4) = ( + 2)( + 3)( + 1)( + 1)( + 4)( + 3) ( + 2)( )( )( + + 1) ( )( + + 2)( )
31 25 Untuk memeriksa bahwa polinomial yang diperoleh merupakan polinomial irredusibel dan polinomial primitif digunakan dua teorema berikut ini. Teorema Jika p adalah prima dan m adalah intejer positif, maka berlaku : 1) Produk dari semua polinomial irredusibel monik dalam Ζ p [x] yang derajatnya membagi m atau faktor dari m sama dengan. 2) Misalkan f(x) adalah polinomial berderajat m dalam Ζ p [x], maka f(x) irredusibel atas Ζ p [x] jika dan hanya jika (), = 1, untuk setiap 1 Bukti : 1) Misalkan f(x) polinomial irredusibel atas Ζ p berderajat m, dimana. Untuk kasus f(x) = x trivial. Asumsi (). Gunakan f(x) untuk membuat field GF(p m ), maka f(x) merupakan polinomial minimum. Misalkan () = dan dari Teorema maka () 1. Dengan memandang Lemma 5.8 dan karena maka 1 1 dan 1 1. Dengan demikian (). Sebaliknya misalkan f(x) pembagi dari, polinomial irredusibel dan berderajat m. Akan ditunjukkan bahwa. Asumsi () () 1. Gunakan f(x) untuk membuat field GF(p m ) ber order p m. Misalkan ( ) adalah akar dari f(x) dan ( ) merupakan unsur primitif maka menurut Teorema 2.43 dapat dinyatakan sebagai = (*). Karena α adalah akar dari f(x), maka () = 0 = 0 =. =. = 1. Dari (*) dan Teorema 2.17 maka ( + ) = + sehingga diperoleh : = 0 =. =. = 1 Berdasarkan sifat ketiga pada Ringkasan 2.5 maka 1 1. Selanjutnya berdasarkan Lemma 5.8 maka diperoleh. 2) Berdasarkan Teorema ), bahwa setiap intejer positif 1, maka polinomial adalah produk dari semua irredusibel monik berderajat membagi k. Jadi (, ()) adalah pasti produk dari semua faktor linear f(x). Jika f(x) tidak mempunyai faktor linear maka (, ())
32 26 adalah pasti produk dari semua faktor irredusibel quadratik dari f(x). Jika f(x) tidak irredusibel maka harus dapat dibagi oleh beberapa polinomial irredusibel berderajat paling banyak /2 dan jika g(x) adalah faktor irredusibel dari f(x) berderajat minimum (misalkan k), maka /2. Jadi (, ()) 1. Hal ini kontradiksi dengan pengandaian. Sebaliknya jika f(x) adalah irredusibel, maka, () = 1, untuk setiap 1. Jadi untuk mengetes f(x) adalah irredusibel, hal ini cukup dites, () = 1 untuk setiap intejer positif 1. Dengan demikian dapat disimpulkan bahwa f(x) adalah irredusibel Teorema Misalkan p adalah bilangan prima dan misalkan mempunyai faktor-faktor prima yang berbeda dari p m -1 adalah r 1, r 2,, r t maka polinomial irredusibel ()()[] adalah 1 berlaku 1( ()) Bukti : primitif jika dan hanya jika untuk setiap Misalkan p adalah bilangan prima dan misalkan faktorisasi dari 1 adalah r 1, r 2,, r t, dimana r 1, r 2,, r t adalah polinomial irredusibel atas GF(p)[x]. Akan dibuktikan bahwa jika x adalah unsur primitif atas GF(p m )* maka berlaku 1 () untuk setiap 1 Misalkan d dinotasikan order dari x. Kita tahu bahwa d adalah pembagi dari 1 dan x adalah primitif jika dan hanya jika = 1. Pertama, andaikan bahwa 1( ()) untuk beberapa i, maka jelas bahwa 1/ sehingga pasti 1. Sebaliknya, andaikan bahwa 1 () untuk 1 dan juga 1. Karena d adalah pembagi dari 1 dan < 1 maka terdapat polinomial irredusibel r i dimana 1 sedemikian sehingga r i adalah pembagi dari ( 1)/. Tetapi ini berakibat bahwa d adalah pembagi ( 1)/. Dengan demikian 1( ()). Hal ini kontradiksi dengan pernyataan bahwa 1 ()
33 5.2. Konstruksi Algoritme Aritmetik GF(5 m ) Seperti yang telah dijelaskan dalam Bab III, bahwa (5 ) dapat direpresentasikan ke dalam bentuk polinomial dan vektor. Demi kemudahan komputasi dalam penelitian ini digunakan representasi vector. Berikut ini diberikan ilustrasi operasi penjumlahan dengan representasi vektor. Misalkan diberikan vektor = (0, 1, 2, 3) sebagai representasi dari () = dan vektor = (2, 2, 3, 1) sebagai reprentasi dari () = dalam (5 ), maka + = (0, 1, 2, 3) + (2, 2, 3, 1) = (0 + 2) 5, ( 1 + 2) 5, ( 2 + 3) 5, ( 3 + 1) 5 = (2, 3, 0, 4). Untuk mengkonstruksi aritmetik GF (5 m ) dalam penelitian ini langkah pertamanya adalah dengan memilih polinomial primitif berderajat m atas Z 5, misal () [] dimana () = sehingga diperoleh unsur primitif α dengan M(α) = 0. Kemudian, tentukan basis dari GF(5 m ) sebagai ruang vektor atas Z 5, yaitu {1, α 1, α 2,, α m-1 }. Dengan demikian, diperoleh himpunan (5 ) = { + +,,, (5)}. Kemudian semua unsur dari (5 ) direpresentasikan ke dalam bentuk ruang vektor berdimensi m atas. Tabel berikut ini menunjukkan adanya hubungan antara representasi elemen primitif, representasi basis polinomial, representasi vektor penta, dan representasi integer dalam (5 ) yang dibangun oleh polinomial primitif () = Tabel 2. Representasi finite field ( ) No. Elemen primitif Representasi Basis Vektor penta Integer (0, 0) 0 2 = 1 1 (1, 0) 1 3 (0, 1) (3, 4) (2, 4) 22
34 (2, 3) (4, 4) (2, 0) (0, 2) (1, 3) (4, 3) (4, 1) (3, 3) (4, 0) (0, 4) (2, 1) (3, 1) (3, 2) (1, 1) (3, 0) (0, 3) (4, 2) (1, 2) (1, 4) (2, 2) 12 Bagaimana memilih polinomial primitif? Sebagaimana telah dijelaskan sebelumnya, polynomial primitif adalah polinomial irredusibel yang akarnya adalah generator dari GF(5)*. Oleh karena itu, diperlukan pemilihan polinomial irredusibel terlebih dahulu. Sesuai dengan Teorema 3.14, diperoleh Algoritme pengetesan polinomial irredusibel sebagai berikut :
35 29 Algoritme 5.1. Pengetesan polinomial irredusibel Deskripsi : Mengetes Vektor Apakah Irredusibel atau Redusibel Input : Vektor A Output : True atau False 1. a = banyaknya unsur A 1, = (/2) dibulatkan ke bawah 2. W = [0, 1] 3. Untuk I dari 1 sampai m, lakukan secara berulang : 3.1. W = W pangkat 5 modulo A 3.2. U= Jumlahkan W dengan [0, 4] menggunakan algoritme H = FPB(U,A) 3.4. h = banyaknya unsur H 3.5. jika h > 1, maka return(false) 4. Return (True) Setelah kita mendapatkan polinomial irredusibel, kemudian memeriksa apakah polinomial irredusibel yang didapatkan tersebut merupakan polinomial primitif atau bukan. Untuk memeriksa polinomial irredusibel adalah primitif, digunakan Algoritme 5.2. Berdasarkan Teorema 3.15 diperoleh Algoritme 5.2 sebagai berikut : Algoritme 5.2. Pengetesan polinomial primitif Deskripsi : Mengetes Vektor Irredusibel Apakah Primitif atau Bukan Input : Vektor A Output : True atau False 1. m = banyaknya unsur A 1, h = 5 m 1 2. F = faktorkan h 3. a = banyaknya unsur F 4. Untuk i dari 1 sampai a, lakukan secara berulang 4.1. k = h/i 4.2. H = [0, 1] pangkat k modulo A 4.3. Jika H = [1], maka return(false) 5. Return(True)
36 30 Untuk mempercepat komputasi, dipilih polinomial primitif yang bersuku terkecil. Hal ini sangatlah beralasan, sebab operasi pada finite field (5 ) dilakukan dalam modulo f(x), dimana f(x) merupakan polinomial primitif. Dengan memilih polinomial primitif bersuku terkecil akan mengakibatkan proses komputasi yang dijalankan lebih cepat dibandingkan dengan menggunakan polinomial primitif biasa. Adapun polinomial primitif yang sudah diperoleh dapat dilihat di Lampiran I Penjumlahan Polinomial Seperti telah dijelaskan di atas, solusi yang digunakan di sini dengan menggunakan representasi vektor penta. Misal diberikan dua sembarang fungsi polinomial () = + + dan () = + + maka bentuk field penjumlahannya adalah sebagai berikut : () + () = ( + ) + ( + ) + +( + ) Fungsi polinomial a(x) direpresentasikan sebagai vektor penta = [,,, ], sedangkan fungsi polinomial b(x) sebagai vektor = [,,, ]. Operasi penjumlahan yang digunakan di sini yaitu instruksi xor. Sebagai contoh, diberikan sembarang fungsi polinomial () = dan () = 2 +. Maka bentuk representasi vektor penta (): = [3, 2, 2, 0, 4] dan bentuk representasi vektor penta (): = [2, 0, 0, 0, 1]. Untuk menghemat pemakaian ruang yang besar dalam komputasi, maka dilakukan reduksi nol pada vektor A atau B. Pada contoh di atas, vektor A dan vektor B memiliki elemen yang sama, maka penjumlahannya sebagai berikut : C = A + B = [(3+2) mod 5, (2+0) mod 5, (2+0) mod 5, (0+0) mod 5, (4+1) mod 5] = [0, 2, 2, 0, 0]. Setelah diperoleh Vektor C, kemudian dilakukan reduksi nol sehingga : = [0, 2, 2].
37 31 Algoritme 5.3. Penjumlahan polinomial Deskripsi : Menambahkan vektor A dan B dalam modulo 5 Input : Vektor = [,,, ], vektor = [,,, ], dan intejer positif m Output : Vektor = [,,, ] 1. Tentukan vektor A, dan vektor B 2. Jika = [0], maka C = B 3. Jika B= [0], maka C = A 4. Jika s=t, maka 4.1. = {[( + ) 5, ( + ) 5,, ( + ) 5]} 4.2. Lakukan reduksi nol dengan menggunakan algoritme Jika s < t, maka 5.1. = {[( + ) 5, ( + ) 5,, 5]} Lainnya = {[( + ) 5, ( + ) 5,, 5]} 6. Return (C) Pembentukan Algoritme 5.3. ini didasarkan pada Teorema Keistimewaan Algoritme ini adalah pada setiap melakukan operasi selalu melibatkan Algoritme Reduksi Nol. Algoritme Reduksi Nol dapat mengurangi jumlah operasi pada konstruksi algoritme-algoritme aritmetik berikutnya sehingga secara otomatis akan mampu mempercepat proses komputasi. Hal ini mengakibatkan banyaknya operasi pada Algoritme 5.4 ini dapat diminimalkan sehingga akan mempercepat proses komputasinya. Algoritme 5.5. Algoritme Reduksi Nol Deskripsi : Mereduksi nol pada posisi sebelah kanan Input : Vektor T dan bilangan posotof t. Output : Vektor 1. T = R, t = banyaknya unsur T 2. Untuk j selama T[t] = 0 dan t >1, lakukan berulang 2.1. Ganti unsur ke-j dari vektor T dengan himpunan kosong 2.2. t = t Return (R)
38 32 Algoritme Reduksi Nol di atas jika digunakan pada sebuah algoritme dapat mengurangi jumlah operasi pada algoritme itu sendiri sehingga secara otomatis akan mampu mempercepat proses komputasi. Cara kerja Algoritme ini adalah menghilangkan anggota sebuah vektor yang terletak di sebelah kanan dan bernilai nol Perkalian Polinomial Dua algoritme berikut ini yaitu Algoritme 5.5 dan Algoritme 5.6 digunakan untuk menunjang Algoritme Perkalian sehingga proses komputasi yang digunakan akan lebih baik daripada melakukan perkalian biasa. Algoritme 5.5. Kelipatan vektor Deskripsi : Mengalikan vektor A dengan skalar n Input : Vektor = [,,, ], dan intejer positif {0, 1,..., 4} Output : Vektor 1. Jika n = 0, maka return([0]) 2. Jika n = 1, maka return(a) 3. Selainnya = ( ) 5 4. Return (C) Algoritme 5.5 ini sangatlah baik karena hanya melibatkan perkalian vektor dengan skalar.
39 33 Algoritme 5.6. Geser satu Deskripsi : Menggeser vektor A satu langkah Input Output : Vektor = [,,, ], dan intejer positif : Vektor 1. L = DatP[m] 2. t = banyaknya unsur vektor A 3. Jika t < m, maka tambahkan 0 di sebelah kiri pada vektor A, selainnya : 4. Tambahkan 0 di sebelah kiri pada vektor A yang telah direduksi pada unsur ke-m 5. Lakukan reduksi nol menggunakan Algoritme Lipatkan vektor L dengan unsur ke-t pada vektor A menggunakan Algoritme Jumlahkan hasil dari langkah ke-5 dengan hasil dari langkah ke-6 menggunakan Algoritme Return(C) Keistimewaan dari algoritme ini adalah hanya mengubah strukturnya saja dan menggeser bersifat konstan. Oleh karena itu apabila digunakan pada suatu algoritme akan mempercepat algoritme tersebut. Dan selanjutnya algoritme ini akan digunakan dalam Algoritme Perkalian. Misalkan diberikan dua sembarang fungsi polinomial () = + + dan () = + + serta diberikan fungsi polinomial primitif p(x) sehingga bentuk field perkalian dengan modulo yaitu (). () = h() () dimana h() = ( 0. 0 ) + ( ) Pada Algoritme 5.7, proses pertama yang dilakukan adalah mengetes apakah kedua vektor mempunyai unsur yang sama ataukah berbeda. Jika kedua vektor mempunyai unsur yang berbeda, maka vektor yang mempunyai unsur yang lebih banyak ditempatkan sebagai vektor pertama. Hal ini bertujuan agar proses
40 34 perhitungan dalam komputasinya lebih sedikit. Selanjutnya pada algoritme ini melibatkan algoritme kelipatan vektor, algoritme geser satu, dan algoritme penjumlahan. Algoritme 5.7. Perkalian Polinomial Deskripsi : Mengalikan dua vektor, kemudian hasil perkaliannya dimoduluskan dengan vektor primitif P Input : Vektor = [,,, ], vektor = [,,, ], dan intejer positif m Output : Vektor = [,,, ] dan c = nops(r). 1. Tentukan vektor A, vektor B, s = banyaknya unsur A, dan t = banyaknya unsur B 2. Jika = [0], atau B= [0], maka return([0]) 3. Jika s < t, maka 3.1. S=B, T=A, a=s, s=t, t=a 3.2. R= Lipatkan vektor T dengan (op(1,s)) menggunakan algoritme Untuk j dari 1 sampai (s 1 ), lakukan T = Lakukan Geser satu dengan algoritme V = Lipatkan vektor T dengan (op(j+1,s)) menggunakan algoritme R = Jumlahkan vektor R dan V dengan menggunakan algoritme 5.4 secara rekursif 4. Return (R) Pembentukan Algoritme 5.7. ini didasarkan pada Teorema Karena pada algoritme ini melibatkan Algoritme Kelipatan Vektor, Algoritme Geser Satu, dan Algoritme Penjumlahan yang melibatkan Algoritme Reduksi Nol maka dapat dikatakan bahwa algoritme ini cukup baik karena tidak membutuhkan ruang yang cukup besar dan proses komputasinya cukup cepat.
41 Invers Polinomial Untuk menunjukkan bahwa setiap elemen tak nolnya mempunyai invers, diambil [()] []/ () dengan [) 0]. Karena [1] merupakan elemen identitas terhadap operasi perkalian, maka akan ditunjukkan bahwa terdapat [h()] []/ () sedemikian hingga [()]. [h()] = [1] atau (). h() 1 (). Karena f(x) merupakan polinomial irredusibel dan f(x) tidak membagi (), maka (), () = 1. Akibatnya terdapat polinomial s(x) dan t(x) sedemikian hingga (). () + ()() = 1 atau (). () 1( ()). Jadi diperoleh bahwa [()]. [()] = [1] sehingga [()] = [()]. Untuk menentukan invers dari vekrtor A dapat menggunakan Algoritme Algoritme ini didasarkan pada Definisi Algoritme 5.8 dan Algoritme 5.9 digunakan untuk mendukung Algoritme Invers Polinomial. Algoritme 5.8. Negasi vektor Deskripsi : Mengubah vektor A dengan negasinya Input : Vektor = [,,, ], Output : Vektor = [,,, ] 1. Petakan unsur x pada vektor A dengan x 2. Return (C) Algoritme ini digunakan untuk memperoleh invers penjumlahan dari masingmasing anggotanya. Adapun invers dari masing masing anggotanya adalah sebagai berikut : 1 inversnya 4, karena 1+4 = 0 2 inversnya 3, karena 2+3 = 0 3 inversnya 2, karena 3+2 = 0 4 inversnya 1, karena 4+1 = 0
42 36 Algoritme 5.9. Pembagian polinomial tanpa modulo m Deskripsi : Membagi dua polinomial tanpa modulo m Input : Vektor dan vektor Output : Vektor = [, ] dimana vektor Q sebagai hasil pembagian dan vektor R sebagai sisa pembagian 1. Jika S=[0], maka false 2. R=T; Q=[0]; r = banyaknya unsur T; s = banyaknya unsur S; g = unsur ke-s dari vektor S 3. Jika s = 1, maka 3.1. Q = lipatkan vektor R dengan operan S 3.2. R = [0] 3.3. Return ([Q, R]) 4. Untuk i selama, lakukan 4.1. k = r s; t = unsur ke-r dari vektor R 4.2. h = ( t*g) mod jika k = 0, maka K = lipatkan vektor S dengan h Q = jumlahkan vektor Q dengan [h] 4.4. Selainnya H = lipatkan vektor S dengan h K = [seq(0,j=1..k),op(h)] Q = jumlahkan (Q,[seq(0,j=1..k),h]) 5. K = negasikan vektor K 6. R = jumlahkan vektor K dan vektor R 7. Return ([Q, R]) Algoritme Pembagian di atas merupakan pembagian seperti biasa yang tidak melibatkan polinomial primitif () sebagai modulonya. Algoritme ini sangat baik karena operasi-operasi yang digunakan menggunakan operasi penjumlahan dan operasi kelipatan vektor.
43 37 Algoritme Invers Polinomial Deskripsi : Invers polinomial dari suatu bilangan bulat m Input : Vektor = [,,, ], dan intejer positif m Output : Vektor = [h, h,, h ] dan r = nops(c). 1. S = Negatifkan vektor (DatP(m)) menggunakan algoritme Jika = [0], maka salah 3. Jika banyaknya unsur T = 1, maka return (T) 4. RA = [op(s), seq(0, j = 1 (m t)), 1]; RB = T; QA = [0]; QB = [1]; 5. L = Bagi vektor RA dan RB menggunakan algoritme RA = RB 7. RB = Operan kedua dari L 8. Untuk i selama RB tidak nol, maka lakukan langkah berikut berulang-ulang 8.1. Tmp = QA; QA = QB 8.2. H = Kalikan vektor QB dengan op(1,l) menggunakan algoritme R = Negasikan vektor H menggunakan algoritme QB = Jumlahkan vektor Tmp dengan vektor R menggunakan algoritme L = Lakukan pembagian vektor RA dengan vektor RB menggunakan algoritme RA = RB; RB = operan kedua dari L 9. H = Lipatkan vektor QB dengan op(ra) menggunakan algoritme Return (H) Pada Algoritme 5.10, proses pertama yang dilakukan adalah negatifkan vektor dalam DatP(m) yang berfungsi sebagai polinomial primitif menggunakan Algoritme 5.8. Proses kedua adalah gabungkan vektor dalam DatP(m), vektor QA, dan vektor QB ke dalam vektor RA yang kemudian gunakan Algoritme 5.9
44 38 untuk menentukan vektor L, yaitu membagi vektor RA dengan vektor RB. Proses selanjutnya adalah selama sisa pembagiannya tidak nol, maka lakukan secara berulang-ulang dengan menggunakan Algoritme operasi rutin yaitu berturut-turut Algoritme 5.7 dan Algoritme 5.8 yang kemudian jumlahkan dengan menggunakan Algoritme 5.5. Proses yang terakhir adalah gunakan Algoritme 5.5 untuk menentukan vektor H. Algoritme Invers Polinomial ini digunakan untuk menghitung invers perkalian, karena (5 ) merupakan grup siklik multiplikatif. Algoritme ini dapat dikatakan sangat baik secara komputasi dikarenakan didalamnya melibatkan Algoritme Perkalian Polinomial, Algoritme Penjumlahan Polinomial, dan Algoritme Kelipatan Vektor. Algoritme-algoritme tersebut selalu melibatkan proses reduksi nol, geser satu, dan polinomial primitif yang digunakan sebagai modulonya menggunakan polinomial primitif yang bersuku kecil Pembagian Polinomial Misalkan diberikan dua sembarang fungsi polinomial () = + + dan () = + +. Fungsi polinomial a(x) direpresentasikan sebagai vektor penta = [,,, ], sedangkan fungsi polinomial b(x) sebagai vektor = [,,, ]. Berdasarkan Teorema 2.31, maka kita dapat membuat Algoritme pembagian polinomial (Algoritme 5.5). Pada Algoritme 5.5, langkah pertama adalah menginverskan vektor B dengan Algoritme 5.10, kemudian kalikan vektor A dengan invers vektor B dengan menggunakan Algoritme 5.7 sehingga diperoleh hasil yang diinginkan. Algoritme Pembagian Polinomial Deskripsi : Membagi dua polinomial dengan modulo m Input : Vektor = [,,, ], vektor = [,,, ], dan intejer positif m Output : Vektor = [,,, ] 1. ib = Inverskan vektor B menggunakan algoritme Kalikan vektor A dengan vektor ib menggunakan algoritme Return (C)
45 39 Algoritme Pembagian Polinomial ini hanya melibatkan Algoritme Invers Polinomial dan Perkalian Polinomial yang didalamnya melibatkan operasi reduksi nol dan kelipatan vektor yang tentunya membutuhkan ruang yang sedikit dan berakibat pada semakin cepatnya proses komputasi yang dijalankan Eksponen Polinomial Aritmetik eksponen polinomial dalam Algoritme 5.12 berfungsi untuk mengalikan dua fungsi polinomial atau lebih dengan modulo m. Yang menjadi kekuatan dari Algoritme 5.12 ini adalah bahwa finite field (5 ) dibentuk dari sifat grup siklik. Algoritme Eksponen Polinomial Deskripsi : Mengeksponensialkan polinomial dalam modulo m Input : Vektor = [,,, ], intejer x dan intejer positif m Output : Vektor = [h, h,, h ] 1. p = 5 m 1 2. k = moduluskan (x, p) menggunakan Algoritme Jika 0, maka 3.1. X = konversi nilai k dalam basis 2; t = banyaknya unsur X 3.2. G = A; H = [1] 3.3. Jika X 1 = 1, maka H = G 3.4. Untuk i mulai dari 2 sampai t, lakukan G = kalikan vektor G dengan G menggunakan Algoritme Jika X i = 1, maka H = kalikan vektor H dengan G menggunakan Algoritme n = -k 5. X = konversi nilai n dalam basis 2; t = banyaknya unsur X 6. G = inverskan vektor A dengan Algoritme 5.10; H = [1] 7. Jika x 1 = 1 maka H = G 8. Untuk i mulai dari 2 sampai dengan t, lakukan 8.1. G = kalikan vektor G dengan G menggunakan Algoritme Jika X i = 1, maka H = kalikan vektor H dengan G menggunakan Algoritme Return (H) Misalkan sembarang polinomial () = direpresentasikan dalam bentuk vektor = [,,, ] dan barisan basis dua = [,,, ] dimana [0, 1] serta polinomial primitif () berderajat m. Derajat maksimal dari polinomial di sini berlaku sebagai modulus yaitu (5 1),
BAB II TINJAUAN PUSTAKA
 4 BAB II TINJAUAN PUSTAKA Untuk mencapai tujuan penulisan penelitian diperlukan beberapa pengertian dan teori yang berkaitan dengan pembahasan. Dalam subbab ini akan diberikan beberapa teori berupa definisi,
4 BAB II TINJAUAN PUSTAKA Untuk mencapai tujuan penulisan penelitian diperlukan beberapa pengertian dan teori yang berkaitan dengan pembahasan. Dalam subbab ini akan diberikan beberapa teori berupa definisi,
PERNYATAAN MENGENAI TESIS DAN SUMBER INFORMASI
 PERNYATAAN MENGENAI TESIS DAN SUMBER INFORMASI Dengan ini saya menyatakan bahwa tesis Konstruksi Algoritme Aritmetik (5 ) Dengan Operasi Dibangkitkan Dari Sifat Grup siklik adalah karya saya dengan arahan
PERNYATAAN MENGENAI TESIS DAN SUMBER INFORMASI Dengan ini saya menyatakan bahwa tesis Konstruksi Algoritme Aritmetik (5 ) Dengan Operasi Dibangkitkan Dari Sifat Grup siklik adalah karya saya dengan arahan
BAB II TINJAUAN PUSTAKA
 BAB II TINJAUAN PUSTAKA Pada bab ini dituliskan beberapa aspek teoritis sebagai landasan teori dalam penelitian ini yaitu teori bilangan, bilangan bulat modulo?, struktur aljabar dan masalah logaritma
BAB II TINJAUAN PUSTAKA Pada bab ini dituliskan beberapa aspek teoritis sebagai landasan teori dalam penelitian ini yaitu teori bilangan, bilangan bulat modulo?, struktur aljabar dan masalah logaritma
BAB II TINJAUAN PUSTAKA
 BAB II TINJAUAN PUSTAKA Pada bab ini dituliskan beberapa aspek teoritis berupa definisi teorema sifat-sifat yang berhubungan dengan teori bilangan integer modulo aljabar abstrak masalah logaritma diskret
BAB II TINJAUAN PUSTAKA Pada bab ini dituliskan beberapa aspek teoritis berupa definisi teorema sifat-sifat yang berhubungan dengan teori bilangan integer modulo aljabar abstrak masalah logaritma diskret
BAB III PEMBAHASAN TEOREMA DAN LEMMA YANG DIBUTUHKAN DALAM KONSTRUKSI ARITMETIK GF(5m)
 BAB III PEMBAHASAN TEOREMA DAN LEMMA YANG DIBUTUHKAN DALAM KONSTRUKSI ARITMETIK GF5m) Teori finite field mulai diperkenalkan pada abad ke tujuh dan abad ke delapan dengan tokoh matematikanya Pierre de
BAB III PEMBAHASAN TEOREMA DAN LEMMA YANG DIBUTUHKAN DALAM KONSTRUKSI ARITMETIK GF5m) Teori finite field mulai diperkenalkan pada abad ke tujuh dan abad ke delapan dengan tokoh matematikanya Pierre de
BAB II KAJIAN TEORI. definisi mengenai grup, ring, dan lapangan serta teori-teori pengkodean yang
 BAB II KAJIAN TEORI Pada Bab II ini berisi kajian teori. Di bab ini akan dijelaskan beberapa definisi mengenai grup, ring, dan lapangan serta teori-teori pengkodean yang mendasari teori kode BCH. A. Grup
BAB II KAJIAN TEORI Pada Bab II ini berisi kajian teori. Di bab ini akan dijelaskan beberapa definisi mengenai grup, ring, dan lapangan serta teori-teori pengkodean yang mendasari teori kode BCH. A. Grup
BAB III HASIL DAN PEMBAHASAN
 BAB III HASIL DAN PEMBAHASAN Pada bab ini akan dijelaskan hal-hal yang berhubungan dengan masalah dan bagaimana mengeksplorasinya dengan logaritma diskret pada menggunakan algoritme Exhaustive Search Baby-Step
BAB III HASIL DAN PEMBAHASAN Pada bab ini akan dijelaskan hal-hal yang berhubungan dengan masalah dan bagaimana mengeksplorasinya dengan logaritma diskret pada menggunakan algoritme Exhaustive Search Baby-Step
PERNYATAAN MENGENAI TESIS DAN SUMBER INFORMASI
 PERNYATAAN MENGENAI TESIS DAN SUMBER INFORMASI Dengan ini saya menyatakan bahwa tesis Konstruksi Algoritme Aritmetik (5 ) Dengan Operasi Dibangkitkan Dari Sifat Grup siklik adalah karya saya dengan arahan
PERNYATAAN MENGENAI TESIS DAN SUMBER INFORMASI Dengan ini saya menyatakan bahwa tesis Konstruksi Algoritme Aritmetik (5 ) Dengan Operasi Dibangkitkan Dari Sifat Grup siklik adalah karya saya dengan arahan
STRUKTUR ALJABAR: RING
 STRUKTUR ALJABAR: RING BAHAN AJAR Oleh: Rippi Maya Program Studi Magister Pendidikan Matematika Sekolah Tinggi Keguruan dan Ilmu Pendidikan (STKIP) SILIWANGI - Bandung 2016 1 Pada grup telah dipelajari
STRUKTUR ALJABAR: RING BAHAN AJAR Oleh: Rippi Maya Program Studi Magister Pendidikan Matematika Sekolah Tinggi Keguruan dan Ilmu Pendidikan (STKIP) SILIWANGI - Bandung 2016 1 Pada grup telah dipelajari
II. TINJAUAN PUSTAKA. Pada bab ini akan diuraikan mengenai konsep teori grup, teorema lagrange dan
 II. TINJAUAN PUSTAKA Pada bab ini akan diuraikan mengenai konsep teori grup, teorema lagrange dan autokomutator yang akan digunakan dalam penelitian. Pada bagian pertama ini akan dibahas tentang teori
II. TINJAUAN PUSTAKA Pada bab ini akan diuraikan mengenai konsep teori grup, teorema lagrange dan autokomutator yang akan digunakan dalam penelitian. Pada bagian pertama ini akan dibahas tentang teori
BAB II TINJAUAN PUSTAKA
 6 BAB II TINJAUAN PUSTAKA A. Fungsi Definisi A.1 Diberikan A dan B adalah dua himpunan yang tidak kosong. Suatu cara atau aturan yang memasangkan atau mengaitkan setiap elemen dari himpunan A dengan tepat
6 BAB II TINJAUAN PUSTAKA A. Fungsi Definisi A.1 Diberikan A dan B adalah dua himpunan yang tidak kosong. Suatu cara atau aturan yang memasangkan atau mengaitkan setiap elemen dari himpunan A dengan tepat
BAB I PENDAHULUAN. Penyampaian pesan dapat dilakukan dengan media telephone, handphone,
 BAB I PENDAHULUAN. Latar Belakang Sekarang ini teknologi untuk berkomunikasi sangatlah mudah. Penyampaian pesan dapat dilakukan dengan media telephone, handphone, internet, dan berbagai macam peralatan
BAB I PENDAHULUAN. Latar Belakang Sekarang ini teknologi untuk berkomunikasi sangatlah mudah. Penyampaian pesan dapat dilakukan dengan media telephone, handphone, internet, dan berbagai macam peralatan
EKSPLORASI MASALAH LOGARITMA DISKRET PADA FINITE FIELD ( ) Y A N A
 EKSPLORASI MASALAH LOGARITMA DISKRET PADA FINITE FIELD ( ) Y A N A SEKOLAH PASCA SARJANA INSTITUT PERTANIAN BOGOR BOGOR 2009 PERNYATAAN MENGENAI TUGAS AKHIR DAN SUMBER INFORMASI Dengan ini saya menyatakan
EKSPLORASI MASALAH LOGARITMA DISKRET PADA FINITE FIELD ( ) Y A N A SEKOLAH PASCA SARJANA INSTITUT PERTANIAN BOGOR BOGOR 2009 PERNYATAAN MENGENAI TUGAS AKHIR DAN SUMBER INFORMASI Dengan ini saya menyatakan
BAB II LANDASAN TEORI. yang mendasari pembahasan pada bab-bab berikutnya. Beberapa definisi yang
 BAB II LANDASAN TEORI Pada bab ini akan diberikan beberapa definisi, penjelasan, dan teorema yang mendasari pembahasan pada bab-bab berikutnya. Beberapa definisi yang diberikan diantaranya adalah definisi
BAB II LANDASAN TEORI Pada bab ini akan diberikan beberapa definisi, penjelasan, dan teorema yang mendasari pembahasan pada bab-bab berikutnya. Beberapa definisi yang diberikan diantaranya adalah definisi
0,1,2,3,4. (e) Perhatikan jawabmu pada (a) (d). Tuliskan kembali sifat-sifat yang kamu temukan dalam. 5. a b c d
 1 Pada grup telah dipelajari himpunan dengan satu operasi. Sekarang akan dipelajari himpunan dengan dua operasi. Ilustrasi 1.1 Perhatikan himpunan 0,1,2,3,4. (a) Apakah grup terhadap operasi penjumlahan?
1 Pada grup telah dipelajari himpunan dengan satu operasi. Sekarang akan dipelajari himpunan dengan dua operasi. Ilustrasi 1.1 Perhatikan himpunan 0,1,2,3,4. (a) Apakah grup terhadap operasi penjumlahan?
BAB I PENDAHULUAN. Struktur aljabar merupakan suatu himpunan tidak kosong yang dilengkapi
 1 BAB I PENDAHULUAN 1.1 Latar Belakang Struktur aljabar merupakan suatu himpunan tidak kosong yang dilengkapi dengan aksioma dan suatu operasi biner. Teori grup dan ring merupakan konsep yang memegang
1 BAB I PENDAHULUAN 1.1 Latar Belakang Struktur aljabar merupakan suatu himpunan tidak kosong yang dilengkapi dengan aksioma dan suatu operasi biner. Teori grup dan ring merupakan konsep yang memegang
SEKILAS TENTANG KONSEP. dengan grup faktor, dan masih banyak lagi. Oleh karenanya sebelum
 Bab I. Sekilas Tentang Konsep Dasar Grup antonius cp 2 1. Tertutup, yakni jika diambil sebarang dua elemen dalam G maka hasil operasinya juga akan merupakan elemen G dan hasil tersebut adalah tunggal.
Bab I. Sekilas Tentang Konsep Dasar Grup antonius cp 2 1. Tertutup, yakni jika diambil sebarang dua elemen dalam G maka hasil operasinya juga akan merupakan elemen G dan hasil tersebut adalah tunggal.
III PEMBAHASAN. enkripsi didefinisikan oleh mod dan menghasilkan siferteks c.
 enkripsi didefinisikan oleh mod dan menghasilkan siferteks c 3 Algoritme 3 Dekripsi Untuk menemukan kembali m dari c, B harus melakukan hal-hal berikut a Menggunakan kunci pribadi a untuk menghitung mod
enkripsi didefinisikan oleh mod dan menghasilkan siferteks c 3 Algoritme 3 Dekripsi Untuk menemukan kembali m dari c, B harus melakukan hal-hal berikut a Menggunakan kunci pribadi a untuk menghitung mod
II. TINJAUAN PUSTAKA. Pengkajian pertama, diulas tentang definisi grup yang merupakan bentuk dasar
 II. TINJAUAN PUSTAKA 2.1 Grup Pengkajian pertama, diulas tentang definisi grup yang merupakan bentuk dasar dari suatu ring dan modul. Definisi 2.1.1 Diberikan himpunan dan operasi biner disebut grup yang
II. TINJAUAN PUSTAKA 2.1 Grup Pengkajian pertama, diulas tentang definisi grup yang merupakan bentuk dasar dari suatu ring dan modul. Definisi 2.1.1 Diberikan himpunan dan operasi biner disebut grup yang
BAB II TEORI DASAR. untuk setiap e G. 4. G mengandung balikan. Untuk setiap a G, terdapat b G sehingga a b =
 BAB II TEORI DASAR 2.1. Group Misalkan operasi biner didefinisikan untuk elemen-elemen dari himpunan G. Maka G adalah grup dengan operasi * jika kondisi di bawah ini terpenuhi : 1. G tertutup terhadap.
BAB II TEORI DASAR 2.1. Group Misalkan operasi biner didefinisikan untuk elemen-elemen dari himpunan G. Maka G adalah grup dengan operasi * jika kondisi di bawah ini terpenuhi : 1. G tertutup terhadap.
DAFTAR ISI. HALAMAN JUDUL... i HALAMAN PERSETUJUAN... II HALAMAN PENGESAHAN... III KATA PENGANTAR... IV DAFTAR ISI... V BAB I PENDAHULUAN...
 DAFTAR ISI HALAMAN JUDUL... i HALAMAN PERSETUJUAN... II HALAMAN PENGESAHAN... III KATA PENGANTAR... IV DAFTAR ISI... V BAB I PENDAHULUAN... 1 A. LATAR BELAKANG MASALAH... 1 B. PEMBATASAN MASALAH... 2 C.
DAFTAR ISI HALAMAN JUDUL... i HALAMAN PERSETUJUAN... II HALAMAN PENGESAHAN... III KATA PENGANTAR... IV DAFTAR ISI... V BAB I PENDAHULUAN... 1 A. LATAR BELAKANG MASALAH... 1 B. PEMBATASAN MASALAH... 2 C.
EKSPLORASI MASALAH LOGARITMA DISKRET PADA FINITE FIELD?????? SALAMIA
 EKSPLORASI MASALAH LOGARITMA DISKRET PADA FINITE FIELD SALAMIA SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR BOGOR 2009 PERYATAAN MENGENAI TESIS DAN SUMBER INFORMASI Dengan ini saya menyatakan bahwa tesis
EKSPLORASI MASALAH LOGARITMA DISKRET PADA FINITE FIELD SALAMIA SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR BOGOR 2009 PERYATAAN MENGENAI TESIS DAN SUMBER INFORMASI Dengan ini saya menyatakan bahwa tesis
Antonius C. Prihandoko
 Antonius C. Prihandoko Didanai oleh Proyek DIA-BERMUTU 2009 PROGRAM STUDI PENDIDIKAN MATEMATIKA Jurusan Pendidikan MIPA Fakultas Keguruan Dan Ilmu Pendidikan Universitas Jember Prakata Puji syukur ke hadirat
Antonius C. Prihandoko Didanai oleh Proyek DIA-BERMUTU 2009 PROGRAM STUDI PENDIDIKAN MATEMATIKA Jurusan Pendidikan MIPA Fakultas Keguruan Dan Ilmu Pendidikan Universitas Jember Prakata Puji syukur ke hadirat
TINJAUAN PUSTAKA. Pada bab ini akan diberikan beberapa definisi teori pendukung dalam proses
 II. TINJAUAN PUSTAKA Pada bab ini akan diberikan beberapa definisi teori pendukung dalam proses penelitian untuk penyelesaian persamaan Diophantine dengan relasi kongruensi modulo m mengenai aljabar dan
II. TINJAUAN PUSTAKA Pada bab ini akan diberikan beberapa definisi teori pendukung dalam proses penelitian untuk penyelesaian persamaan Diophantine dengan relasi kongruensi modulo m mengenai aljabar dan
II. TINJAUAN PUSTAKA. Pada bab ini diberikan beberapa definisi mengenai teori grup yang mendukung. ke. Untuk setiap, dinotasikan sebagai di
 II. TINJAUAN PUSTAKA Pada bab ini diberikan beberapa definisi mengenai teori grup yang mendukung proses penelitian. 2.1 Teori Grup Definisi 2.1.1 Operasi Biner Suatu operasi biner pada suatu himpunan adalah
II. TINJAUAN PUSTAKA Pada bab ini diberikan beberapa definisi mengenai teori grup yang mendukung proses penelitian. 2.1 Teori Grup Definisi 2.1.1 Operasi Biner Suatu operasi biner pada suatu himpunan adalah
BAB 2 LANDASAN TEORI. Universitas Sumatera Utara
 5 BAB 2 LANDASAN TEORI 2.1 Kriptografi Kriptografi adalah ilmu yang mempelajari bagaimana mengirim pesan secara rahasia sehingga hanya orang yang dituju saja yang dapat membaca pesan rahasia tersebut.
5 BAB 2 LANDASAN TEORI 2.1 Kriptografi Kriptografi adalah ilmu yang mempelajari bagaimana mengirim pesan secara rahasia sehingga hanya orang yang dituju saja yang dapat membaca pesan rahasia tersebut.
BAB I PENDAHULUAN. A. Latar Belakang. Struktur aljabar merupakan salah satu bidang kajian dalam matematika
 1 BAB I PENDAHULUAN A. Latar Belakang Struktur aljabar merupakan salah satu bidang kajian dalam matematika yang dikembangkan untuk menunjang pemahaman mengenai struktur bilangan. Struktur atau sistem aljabar
1 BAB I PENDAHULUAN A. Latar Belakang Struktur aljabar merupakan salah satu bidang kajian dalam matematika yang dikembangkan untuk menunjang pemahaman mengenai struktur bilangan. Struktur atau sistem aljabar
BAB III. Standard Kompetensi. 3. Mahasiswa dapat menjelaskan pengertian homomorfisma ring dan menggunakannya dalam kehidupan sehari-hari.
 BAB III Standard Kompetensi 3. Mahasiswa dapat menjelaskan pengertian homomorfisma ring menggunakannya dalam kehidupan sehari-hari. Kompetensi Dasar: Mahasiswa diharapkan dapat 3.1 Menyebutkan definisi
BAB III Standard Kompetensi 3. Mahasiswa dapat menjelaskan pengertian homomorfisma ring menggunakannya dalam kehidupan sehari-hari. Kompetensi Dasar: Mahasiswa diharapkan dapat 3.1 Menyebutkan definisi
PENGANTAR PADA TEORI GRUP DAN RING
 Handout MK Aljabar Abstract PENGANTAR PADA TEORI GRUP DAN RING Disusun oleh : Drs. Antonius Cahya Prihandoko, M.App.Sc, Ph.D e-mail: antoniuscp.ilkom@unej.ac.id Staf Pengajar Pada Program Studi Sistem
Handout MK Aljabar Abstract PENGANTAR PADA TEORI GRUP DAN RING Disusun oleh : Drs. Antonius Cahya Prihandoko, M.App.Sc, Ph.D e-mail: antoniuscp.ilkom@unej.ac.id Staf Pengajar Pada Program Studi Sistem
Struktur Aljabar I. Pada bab ini disajikan tentang pengertian. grup, sifat-sifat dasar grup, ordo grup dan elemennya, dan konsep
 GRUP Bab ini merupakan awal dari bagian pertama materi utama perkuliahan Struktur Aljabar I. Pada bab ini disajikan tentang pengertian grup, sifat-sifat dasar grup, ordo grup dan elemennya, dan konsep
GRUP Bab ini merupakan awal dari bagian pertama materi utama perkuliahan Struktur Aljabar I. Pada bab ini disajikan tentang pengertian grup, sifat-sifat dasar grup, ordo grup dan elemennya, dan konsep
G a a = e = a a. b. Berdasarkan Contoh 1.2 bagian b diperoleh himpunan semua bilangan bulat Z. merupakan grup terhadap penjumlahan bilangan.
 2. Grup Definisi 1.3 Suatu grup < G, > adalah himpunan tak-kosong G bersama-sama dengan operasi biner pada G sehingga memenuhi aksioma- aksioma berikut: a. operasi biner bersifat asosiatif, yaitu a, b,
2. Grup Definisi 1.3 Suatu grup < G, > adalah himpunan tak-kosong G bersama-sama dengan operasi biner pada G sehingga memenuhi aksioma- aksioma berikut: a. operasi biner bersifat asosiatif, yaitu a, b,
PERNYATAAN MENGENAI TESIS DAN SUMBER INFORMASI
 PERNYATAAN MENGENAI TESIS DAN SUMBER INFORMASI Dengan ini saya menyatakan bahwa tesis Konstruksi Algoritme Aritmetik (5 ) Dengan Operasi Dibangkitkan Dari Sifat Grup siklik adalah karya saya dengan arahan
PERNYATAAN MENGENAI TESIS DAN SUMBER INFORMASI Dengan ini saya menyatakan bahwa tesis Konstruksi Algoritme Aritmetik (5 ) Dengan Operasi Dibangkitkan Dari Sifat Grup siklik adalah karya saya dengan arahan
UNIVERSITAS GADJAH MADA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM JURUSAN MATEMATIKA PROGRAM STUDI S1 MATEMATIKA Sekip Utara, Yogyakarta
 UNIVERSITAS GADJAH MADA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM JURUSAN MATEMATIKA PROGRAM STUDI S1 MATEMATIKA Sekip Utara, Yogyakarta Bahan Ajar: BAB POKOK BAHASAN I MODUL ATAS RING Direncanakan
UNIVERSITAS GADJAH MADA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM JURUSAN MATEMATIKA PROGRAM STUDI S1 MATEMATIKA Sekip Utara, Yogyakarta Bahan Ajar: BAB POKOK BAHASAN I MODUL ATAS RING Direncanakan
BAB III m BAHASAN KONSTRUKSI GF(3 ) dalam penelitian ini dapat dilakukan dengan mengacu pada konsep perluasan filed pada Bab II bagian 2.8.
 BAB III BAHASAN KONSTRUKSI GF( ) Untuk engonstruksi GF( ) dala penelitian ini dapat dilakukan dengan engacu pada konsep perluasan filed pada Bab II bagian 28 Karena adalah bilangan pria, aka berdasarkan
BAB III BAHASAN KONSTRUKSI GF( ) Untuk engonstruksi GF( ) dala penelitian ini dapat dilakukan dengan engacu pada konsep perluasan filed pada Bab II bagian 28 Karena adalah bilangan pria, aka berdasarkan
I PENDAHULUAN II LANDASAN TEORI. Latar Belakang Berawal dari definisi grup periodik yaitu misalkan grup, jika terdapat unsur (nonidentitas)
 I PENDAHULUAN Latar Belakang Berawal dari definisi grup periodik yaitu misalkan grup, jika terdapat unsur (nonidentitas) di sehingga., maka disebut grup periodik dan disebut periode dari. Serta fakta bahwa
I PENDAHULUAN Latar Belakang Berawal dari definisi grup periodik yaitu misalkan grup, jika terdapat unsur (nonidentitas) di sehingga., maka disebut grup periodik dan disebut periode dari. Serta fakta bahwa
BAB IV KURVA ELIPTIK DAN ID BASED CRYPTOSYSTEM
 BAB IV KURVA ELIPTIK DAN ID BASED CRYPTOSYSTEM 4.1. Kurva Eliptik Misalkan p adalah bilangan prima yang lebih besar dari 3. Sebuah kurva eliptik atas lapangan hingga dengan ukuran p dinotasikan dengan
BAB IV KURVA ELIPTIK DAN ID BASED CRYPTOSYSTEM 4.1. Kurva Eliptik Misalkan p adalah bilangan prima yang lebih besar dari 3. Sebuah kurva eliptik atas lapangan hingga dengan ukuran p dinotasikan dengan
Keberlakuan Teorema pada Beberapa Struktur Aljabar
 PRISMA 1 (2018) https://journal.unnes.ac.id/sju/index.php/prisma/ Keberlakuan Teorema pada Beberapa Struktur Aljabar Mashuri, Kristina Wijayanti, Rahayu Budhiati Veronica, Isnarto Jurusan Matenmatika FMIPA
PRISMA 1 (2018) https://journal.unnes.ac.id/sju/index.php/prisma/ Keberlakuan Teorema pada Beberapa Struktur Aljabar Mashuri, Kristina Wijayanti, Rahayu Budhiati Veronica, Isnarto Jurusan Matenmatika FMIPA
BAB I PENDAHULUAN. Ada beberapa materi yang terdapat pada aljabar abstrak, salah satu materi
 1 BAB I PENDAHULUAN 1.1. Latar Belakang Ada beberapa materi yang terdapat pada aljabar abstrak, salah satu materi tersebut adalah modul. Untuk membahas pengertian tentang suatu modul harus dimengerti lebih
1 BAB I PENDAHULUAN 1.1. Latar Belakang Ada beberapa materi yang terdapat pada aljabar abstrak, salah satu materi tersebut adalah modul. Untuk membahas pengertian tentang suatu modul harus dimengerti lebih
BAB II KERANGKA TEORITIS. komposisi biner atau lebih dan bersifat tertutup. A = {x / x bilangan asli} dengan operasi +
 5 BAB II KERANGKA TEORITIS 2.1 Struktur Aljabar Struktur aljabar adalah salah satu mata kuliah dalam jurusan matematika yang mempelajari tentang himpunan (sets), proposisi, kuantor, relasi, fungsi, bilangan,
5 BAB II KERANGKA TEORITIS 2.1 Struktur Aljabar Struktur aljabar adalah salah satu mata kuliah dalam jurusan matematika yang mempelajari tentang himpunan (sets), proposisi, kuantor, relasi, fungsi, bilangan,
BAB 2 LANDASAN TEORI. Pada bab ini dibahas landasan teori yang akan digunakan untuk menentukan ciri-ciri dari polinomial permutasi atas finite field.
 BAB 2 LANDASAN TEORI Pada bab ini dibahas landasan teori yang akan digunakan untuk menentukan ciri-ciri dari polinomial permutasi atas finite field. Hal ini dimulai dengan memberikan pengertian dari group
BAB 2 LANDASAN TEORI Pada bab ini dibahas landasan teori yang akan digunakan untuk menentukan ciri-ciri dari polinomial permutasi atas finite field. Hal ini dimulai dengan memberikan pengertian dari group
BAB I Ring dan Ring Bagian
 BAB I Ring dan Ring Bagian Sistem bilangan yang telah dikenal seperti bilangan bulat, bilangan rasional dan bilangan kompleks mempunyai dua operasi yang didefinisikan padanya yaitu penjumlahan dan pergandaan.
BAB I Ring dan Ring Bagian Sistem bilangan yang telah dikenal seperti bilangan bulat, bilangan rasional dan bilangan kompleks mempunyai dua operasi yang didefinisikan padanya yaitu penjumlahan dan pergandaan.
UNIVERSITAS GADJAH MADA. Bahan Ajar:
 UNIVERSITAS GADJAH MADA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM JURUSAN MATEMATIKA PROGRAM STUDI S1 MATEMATIKA Sekip Utara, Gedung Jurusan Matematika, Yogyakarta - 55281 Bahan Ajar: BAB / POKOK BAHASAN
UNIVERSITAS GADJAH MADA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM JURUSAN MATEMATIKA PROGRAM STUDI S1 MATEMATIKA Sekip Utara, Gedung Jurusan Matematika, Yogyakarta - 55281 Bahan Ajar: BAB / POKOK BAHASAN
Kriteria Struktur Aljabar Modul Noetherian dan Gelanggang Noetherian
 Kriteria Struktur Aljabar Modul Noetherian dan Gelanggang Noetherian Rio Yohanes 1, Nora Hariadi 2, Kiki Ariyanti Sugeng 3 Departemen Matematika, FMIPA UI, Kampus UI Depok, 16424, Indonesia rio.yohanes@sci.ui.ac.id,
Kriteria Struktur Aljabar Modul Noetherian dan Gelanggang Noetherian Rio Yohanes 1, Nora Hariadi 2, Kiki Ariyanti Sugeng 3 Departemen Matematika, FMIPA UI, Kampus UI Depok, 16424, Indonesia rio.yohanes@sci.ui.ac.id,
II. TINJAUAN PUSTAKA. Pada bab ini akan diberikan konsep dasar (pengertian) tentang bilangan sempurna,
 3 II. TINJAUAN PUSTAKA Pada bab ini akan diberikan konsep dasar (pengertian) tentang bilangan sempurna, square free, keterbagian bilangan bulat, modulo, bilangan prima, ideal, daerah integral, ring quadratic.
3 II. TINJAUAN PUSTAKA Pada bab ini akan diberikan konsep dasar (pengertian) tentang bilangan sempurna, square free, keterbagian bilangan bulat, modulo, bilangan prima, ideal, daerah integral, ring quadratic.
BAB II TINJAUAN PUSTAKA
 BAB II TINJAUAN PUSTAKA Pada bagian ini dipaparkan dasar-dasar yang akan digunakan pada bagian pembahasan dari skripsi ini. Tinjauan yang dilakukan dengan memaparkan definisi mengenai himpunan fuzzy, struktur
BAB II TINJAUAN PUSTAKA Pada bagian ini dipaparkan dasar-dasar yang akan digunakan pada bagian pembahasan dari skripsi ini. Tinjauan yang dilakukan dengan memaparkan definisi mengenai himpunan fuzzy, struktur
ELLIPTIC CURVE CRYPTOGRAPHY. Disarikan oleh: Dinisfu Sya ban ( )
 ELLIPTIC CURVE CRYPTOGRAPHY Disarikan oleh: Dinisfu Sya ban (0403100596) SEKOLAH TINGGI SANDI NEGARA BOGOR 007 A. Fungsi Elliptic Curves 1. Definisi Elliptic Curves Definisi 1. : Misalkan k merupakan field
ELLIPTIC CURVE CRYPTOGRAPHY Disarikan oleh: Dinisfu Sya ban (0403100596) SEKOLAH TINGGI SANDI NEGARA BOGOR 007 A. Fungsi Elliptic Curves 1. Definisi Elliptic Curves Definisi 1. : Misalkan k merupakan field
II. LANDASAN TEORI. Pada bagian ini akan dikaji konsep operasi biner dan ring yang akan digunakan
 II. LANDASAN TEORI Pada bagian ini akan dikaji konsep operasi biner dan ring yang akan digunakan dalam pembahasan penelitian ini. Untuk lebih mudah memahami, akan diberikan beberapa contoh. Berikut ini
II. LANDASAN TEORI Pada bagian ini akan dikaji konsep operasi biner dan ring yang akan digunakan dalam pembahasan penelitian ini. Untuk lebih mudah memahami, akan diberikan beberapa contoh. Berikut ini
ABSTRACT. Keywords: arithmetic, cyclic group, GF(5 ), primitive polynomial, cryptography.
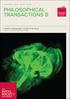 ABSTRACT AHMADI. The Construction of Arithmetic Algorithms GF(5 m ) Generated by Cyclic Grou Proerties. Suervised by SUGI GURITMAN and NUR ALIATININGTYAS. To construct a crytograhic algorithm, many arithmetic
ABSTRACT AHMADI. The Construction of Arithmetic Algorithms GF(5 m ) Generated by Cyclic Grou Proerties. Suervised by SUGI GURITMAN and NUR ALIATININGTYAS. To construct a crytograhic algorithm, many arithmetic
II. TINJAUAN PUSTAKA. Pada bab ini akan diberikan konsep dasar (pengertian) tentang bilangan sempurna,
 II. TINJAUAN PUSTAKA Pada bab ini akan diberikan konsep dasar (pengertian) tentang bilangan sempurna, square free, keterbagian bilangan bulat, modulo, bilangan prima, daerah integral, ring bilangan bulat
II. TINJAUAN PUSTAKA Pada bab ini akan diberikan konsep dasar (pengertian) tentang bilangan sempurna, square free, keterbagian bilangan bulat, modulo, bilangan prima, daerah integral, ring bilangan bulat
STRUKTUR ALJABAR II. Materi : 1. Ring 2. Sub Ring, Ideal, Ring Faktor 3. Daerah Integral, dan Field.
 STRUKTUR ALJABAR II Materi : 1. Ring 2. Sub Ring, Ideal, Ring Faktor 3. Daerah Integral, dan Field RING (GELANGGANG) Ring adalah himpunan G yang tidak kosong dan berlaku dua oprasi biner (penjumlahan dan
STRUKTUR ALJABAR II Materi : 1. Ring 2. Sub Ring, Ideal, Ring Faktor 3. Daerah Integral, dan Field RING (GELANGGANG) Ring adalah himpunan G yang tidak kosong dan berlaku dua oprasi biner (penjumlahan dan
Diktat Kuliah. Oleh:
 Diktat Kuliah TEORI GRUP Oleh: Dr. Adi Setiawan UNIVERSITAS KRISTEN SATYA WACANA SALATIGA 2015 Kata Pengantar Aljabar abstrak atau struktur aljabar merupakan suatu mata kuliah yang menjadi kurikulum nasional
Diktat Kuliah TEORI GRUP Oleh: Dr. Adi Setiawan UNIVERSITAS KRISTEN SATYA WACANA SALATIGA 2015 Kata Pengantar Aljabar abstrak atau struktur aljabar merupakan suatu mata kuliah yang menjadi kurikulum nasional
II. KONSEP DASAR GRUP. abstrak (abstract algebra). Sistem aljabar (algebraic system) terdiri dari suatu
 II KONSEP DASAR GRUP Suatu cabang matematika yang mempelajari struktur aljabar dinamakan aljabar abstrak abstract algebra Sistem aljabar algebraic system terdiri dari suatu himpunan obyek satu atau lebih
II KONSEP DASAR GRUP Suatu cabang matematika yang mempelajari struktur aljabar dinamakan aljabar abstrak abstract algebra Sistem aljabar algebraic system terdiri dari suatu himpunan obyek satu atau lebih
UNIVERSITAS GADJAH MADA. Bahan Ajar:
 UNIVERSITAS GADJAH MADA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM JURUSAN MATEMATIKA PROGRAM STUDI S1 MATEMATIKA Sekip Utara, Gedung Jurusan Matematika, Yogyakarta - 55281 Bahan Ajar: BAB POKOK BAHASAN
UNIVERSITAS GADJAH MADA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM JURUSAN MATEMATIKA PROGRAM STUDI S1 MATEMATIKA Sekip Utara, Gedung Jurusan Matematika, Yogyakarta - 55281 Bahan Ajar: BAB POKOK BAHASAN
BAB III PERLUASAN INTEGRAL
 BAB III PERLUASAN INTEGRAL Pembahasan pada bab ini termuat pada ruang lingkup perluasan uniter atas suatu ring komutatif. Jika adalah suatu ring, maka yang dimaksud adalah suatu ring yang komutatif dan
BAB III PERLUASAN INTEGRAL Pembahasan pada bab ini termuat pada ruang lingkup perluasan uniter atas suatu ring komutatif. Jika adalah suatu ring, maka yang dimaksud adalah suatu ring yang komutatif dan
II. TINJAUAN PUSTAKA. Pada bab ini akan diuraikan teori grup dan teori ring yang akan digunakan dalam
 II. TINJAUAN PUSTAKA Pada bab ini akan diuraikan teori grup dan teori ring yang akan digunakan dalam penelitian. Pada bagian pertama akan dibahas mengenai teori grup. 2.1 Grup Dalam struktur aljabar, himpunan
II. TINJAUAN PUSTAKA Pada bab ini akan diuraikan teori grup dan teori ring yang akan digunakan dalam penelitian. Pada bagian pertama akan dibahas mengenai teori grup. 2.1 Grup Dalam struktur aljabar, himpunan
PENGERTIAN RING. A. Pendahuluan
 Pertemuan 13 PENGERTIAN RING A. Pendahuluan Target yang diharapkan dalam pertemuan ke 13 ini (pertemuan pertama tentang teori ring) adalah mahasiswa dapat : a. membedakan suatu struktur aljabar merupakan
Pertemuan 13 PENGERTIAN RING A. Pendahuluan Target yang diharapkan dalam pertemuan ke 13 ini (pertemuan pertama tentang teori ring) adalah mahasiswa dapat : a. membedakan suatu struktur aljabar merupakan
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI Sebagai acuan penulisan penelitian ini diperlukan beberapa pengertian dan teori yang berkaitan dengan pembahasan. Dalam sub bab ini akan diberikan beberapa landasan teori berupa pengertian,
BAB II LANDASAN TEORI Sebagai acuan penulisan penelitian ini diperlukan beberapa pengertian dan teori yang berkaitan dengan pembahasan. Dalam sub bab ini akan diberikan beberapa landasan teori berupa pengertian,
BAB II DASAR TEORI. membahas tentang penerapan skema tanda tangan Schnorr pada pembuatan tanda
 BAB II DASAR TEORI Pada Bab II ini akan disajikan beberapa teori yang akan digunakan untuk membahas tentang penerapan skema tanda tangan Schnorr pada pembuatan tanda tangan digital yang meliputi: keterbagian
BAB II DASAR TEORI Pada Bab II ini akan disajikan beberapa teori yang akan digunakan untuk membahas tentang penerapan skema tanda tangan Schnorr pada pembuatan tanda tangan digital yang meliputi: keterbagian
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI Pada bab ini akan dijelaskan menenai teori teori yan berhubunan denan penelitian sehina dapat dijadikan sebaai landasan berfikir dalam melakukan penelitian dan akan mempermudah dalam
BAB 2 LANDASAN TEORI Pada bab ini akan dijelaskan menenai teori teori yan berhubunan denan penelitian sehina dapat dijadikan sebaai landasan berfikir dalam melakukan penelitian dan akan mempermudah dalam
TEORI GRUP SUMANANG MUHTAR GOZALI KBK ALJABAR & ANALISIS
 TEORI GRUP SUMANANG MUHTAR GOZALI KBK ALJABAR & ANALISIS UNIVERSITAS PENDIDIKAN INDONESIA BANDUNG 2010 2 KATA PENGANTAR Bismillahirrahmanirrahim Segala puji bagi Allah Rabb semesta alam. Shalawat serta
TEORI GRUP SUMANANG MUHTAR GOZALI KBK ALJABAR & ANALISIS UNIVERSITAS PENDIDIKAN INDONESIA BANDUNG 2010 2 KATA PENGANTAR Bismillahirrahmanirrahim Segala puji bagi Allah Rabb semesta alam. Shalawat serta
II. TINJAUAN PUSTAKA. modul yang akan digunakan dalam pembahasan hasil penelitian.
 II. TINJAUAN PUSTAKA Pada bab ini akan diberikan konsep dasar (pengertian) tentang grup, ring, dan modul yang akan digunakan dalam pembahasan hasil penelitian. 2.1 Ring Sebelum didefinisikan pengertian
II. TINJAUAN PUSTAKA Pada bab ini akan diberikan konsep dasar (pengertian) tentang grup, ring, dan modul yang akan digunakan dalam pembahasan hasil penelitian. 2.1 Ring Sebelum didefinisikan pengertian
LECTURE NOTES MATEMATIKA DISKRIT. Disusun Oleh : Dra. D. L. CRISPINA PARDEDE, DEA.
 LECTURE NOTES MATEMATIKA DISKRIT Disusun Oleh : Dra. D. L. CRISPINA PARDEDE, DEA. JURUSAN TEKNIK INFORMATIKA UNIVERSITAS GUNADARMA PONDOK CINA, MARET 2004 0 DAFTAR ISI DAFTAR ISI... 1 BAB I STRUKTUR ALJABAR...
LECTURE NOTES MATEMATIKA DISKRIT Disusun Oleh : Dra. D. L. CRISPINA PARDEDE, DEA. JURUSAN TEKNIK INFORMATIKA UNIVERSITAS GUNADARMA PONDOK CINA, MARET 2004 0 DAFTAR ISI DAFTAR ISI... 1 BAB I STRUKTUR ALJABAR...
PROTOKOL PERTUKARAN KUNCI BERBASIS KRIPTOSISTEM KUNCI PUBLIK ELGAMAL RESTU AULIYA
 PROTOKOL PERTUKARAN KUNCI BERBASIS KRIPTOSISTEM KUNCI PUBLIK ELGAMAL RESTU AULIYA DEPARTEMEN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR 2016 PERNYATAAN MENGENAI
PROTOKOL PERTUKARAN KUNCI BERBASIS KRIPTOSISTEM KUNCI PUBLIK ELGAMAL RESTU AULIYA DEPARTEMEN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR 2016 PERNYATAAN MENGENAI
Volume 9 Nomor 1 Maret 2015
 Volume 9 Nomor 1 Maret 015 Jurnal Ilmu Matematika dan Terapan Maret 015 Volume 9 Nomor 1 Hal. 1 10 KARAKTERISASI DAERAH DEDEKIND Elvinus R. Persulessy 1, Novita Dahoklory 1, Jurusan Matematika FMIPA Universitas
Volume 9 Nomor 1 Maret 015 Jurnal Ilmu Matematika dan Terapan Maret 015 Volume 9 Nomor 1 Hal. 1 10 KARAKTERISASI DAERAH DEDEKIND Elvinus R. Persulessy 1, Novita Dahoklory 1, Jurusan Matematika FMIPA Universitas
Bab 3 Gelanggang Polinom Miring
 Bab 3 Gelanggang Polinom Miring Dalam bab ini akan dibahas mengenai Gelanggang Poliom Miring mulai dengan bentuk yang sederhana (satu variabel) sampai ke bentuk yang lebih kompleks (banyak variabel) berikut
Bab 3 Gelanggang Polinom Miring Dalam bab ini akan dibahas mengenai Gelanggang Poliom Miring mulai dengan bentuk yang sederhana (satu variabel) sampai ke bentuk yang lebih kompleks (banyak variabel) berikut
BAB I PENDAHULUAN. diperhatikan, yaitu : kerahasiaan, integritas data, autentikasi dan non repudiasi.
 BAB I PENDAHULUAN 1.1 Latar Belakang Pada proses pengiriman data (pesan) terdapat beberapa hal yang harus diperhatikan, yaitu : kerahasiaan, integritas data, autentikasi dan non repudiasi. Oleh karenanya
BAB I PENDAHULUAN 1.1 Latar Belakang Pada proses pengiriman data (pesan) terdapat beberapa hal yang harus diperhatikan, yaitu : kerahasiaan, integritas data, autentikasi dan non repudiasi. Oleh karenanya
UNIVERSITAS GADJAH MADA. Bahan Ajar:
 UNIVERSITAS GADJAH MADA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM JURUSAN MATEMATIKA PROGRAM STUDI S1 MATEMATIKA Sekip Utara, Gedung Jurusan Matematika, Yogyakarta - 55281 Bahan Ajar: BAB POKOK BAHASAN
UNIVERSITAS GADJAH MADA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM JURUSAN MATEMATIKA PROGRAM STUDI S1 MATEMATIKA Sekip Utara, Gedung Jurusan Matematika, Yogyakarta - 55281 Bahan Ajar: BAB POKOK BAHASAN
SYARAT PERLU LAPANGAN PEMISAH. Bambang Irawanto Jurusan Matematika FMIPA UNDIP. Abstact. Keywords : extension fields, elemen algebra
 JURNAL MATEMATIKA DAN KOMPUTER Vol 4 No 2, 65-70, Agustus 2001, ISSN : 1410-8518 SYARAT PERLU LAPANGAN PEMISAH Bambang Irawanto Jurusan Matematika FMIPA UNDIP Abstact Field is integral domain and is a
JURNAL MATEMATIKA DAN KOMPUTER Vol 4 No 2, 65-70, Agustus 2001, ISSN : 1410-8518 SYARAT PERLU LAPANGAN PEMISAH Bambang Irawanto Jurusan Matematika FMIPA UNDIP Abstact Field is integral domain and is a
KRIPTOGRAFI KURVA ELIPTIK ELGAMAL UNTUK PROSES ENKRIPSI-DEKRIPSI CITRA DIGITAL BERWARNA
 JURNAL SAINS DAN SENI POMITS Vol. 1, No. 1, (2014) 1-6 1 KRIPTOGRAFI KURVA ELIPTIK ELGAMAL UNTUK PROSES ENKRIPSI-DEKRIPSI CITRA DIGITAL BERWARNA Gestihayu Romadhoni F. R, Drs. Daryono Budi Utomo, M.Si
JURNAL SAINS DAN SENI POMITS Vol. 1, No. 1, (2014) 1-6 1 KRIPTOGRAFI KURVA ELIPTIK ELGAMAL UNTUK PROSES ENKRIPSI-DEKRIPSI CITRA DIGITAL BERWARNA Gestihayu Romadhoni F. R, Drs. Daryono Budi Utomo, M.Si
KRIPTOGRAFI KURVA ELIPTIK ELGAMAL UNTUK PROSES ENKRIPSI- DEKRIPSI CITRA DIGITAL BERWARNA
 SEMINAR HASIL TUGAS AKHIR KRIPTOGRAFI KURVA ELIPTIK ELGAMAL UNTUK PROSES ENKRIPSI- DEKRIPSI CITRA DIGITAL BERWARNA Elliptic Curve ElGamal Cryptography For Encvryption- Decryption Process of Colored Digital
SEMINAR HASIL TUGAS AKHIR KRIPTOGRAFI KURVA ELIPTIK ELGAMAL UNTUK PROSES ENKRIPSI- DEKRIPSI CITRA DIGITAL BERWARNA Elliptic Curve ElGamal Cryptography For Encvryption- Decryption Process of Colored Digital
STRUKTUR ALJABAR: GRUP
 STRUKTUR ALJABAR: GRUP BAHAN AJAR Oleh: Rippi Maya Program Studi Pendidikan Matematika Sekolah Tinggi Keguruan dan Ilmu Pendidikan (STKIP) SILIWANGI Bandung 2016 1 A. Pendahuluan Ilustrasi 1.1: Perhatikan
STRUKTUR ALJABAR: GRUP BAHAN AJAR Oleh: Rippi Maya Program Studi Pendidikan Matematika Sekolah Tinggi Keguruan dan Ilmu Pendidikan (STKIP) SILIWANGI Bandung 2016 1 A. Pendahuluan Ilustrasi 1.1: Perhatikan
BAB II TINJAUAN PUSTAKA
 5 BAB II TINJAUAN PUSTAKA A Matriks 1 Pengertian Matriks Definisi 21 Matriks adalah kumpulan bilangan bilangan yang disusun secara khusus dalam bentuk baris kolom sehingga membentuk empat persegi panjang
5 BAB II TINJAUAN PUSTAKA A Matriks 1 Pengertian Matriks Definisi 21 Matriks adalah kumpulan bilangan bilangan yang disusun secara khusus dalam bentuk baris kolom sehingga membentuk empat persegi panjang
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI Sebelum kita membahas mengenai uji primalitas, terlebih dahulu kita bicarakan beberapa definisi yang diperlukan serta beberapa teorema dan sifat-sifat yang penting dalam teori bilangan
BAB 2 LANDASAN TEORI Sebelum kita membahas mengenai uji primalitas, terlebih dahulu kita bicarakan beberapa definisi yang diperlukan serta beberapa teorema dan sifat-sifat yang penting dalam teori bilangan
BAB 2 LANDASAN TEORI
 5 BAB 2 LANDASAN TEORI Struktur Aljabar Struktur aljabar adalah ilmu yang mempelajari suatu sistem aljabar dengan satu atau lebih operasi biner yang diberlakukan pada sistem aljabar tersebut. Struktur
5 BAB 2 LANDASAN TEORI Struktur Aljabar Struktur aljabar adalah ilmu yang mempelajari suatu sistem aljabar dengan satu atau lebih operasi biner yang diberlakukan pada sistem aljabar tersebut. Struktur
ALJABAR ABSTRAK ( TEORI GRUP DAN TEORI RING ) Dr. Adi Setiawan, M. Sc
 ALJABAR ABSTRAK ( TEORI GRUP DAN TEORI RING ) Dr. Adi Setiawan, M. Sc PROGRAM STUDI MATEMATIKA FAKULTAS SAINS DAN MATEMATIKA UNIVERSITAS KRISTEN SATYA WACANA SALATIGA 2011 0 KATA PENGANTAR Aljabar abstrak
ALJABAR ABSTRAK ( TEORI GRUP DAN TEORI RING ) Dr. Adi Setiawan, M. Sc PROGRAM STUDI MATEMATIKA FAKULTAS SAINS DAN MATEMATIKA UNIVERSITAS KRISTEN SATYA WACANA SALATIGA 2011 0 KATA PENGANTAR Aljabar abstrak
STRUKTUR ALJABAR 1. Kristiana Wijaya
 STRUKTUR ALJABAR 1 Kristiana Wijaya i ii Daftar Isi Judul Daftar Isi i iii 1 Himpunan 1 2 Partisi dan Relasi Ekuivalen 3 3 Grup 6 4 Koset Dan Teorema Lagrange, Homomorphisma Grup Dan Grup Faktor 11 Indeks
STRUKTUR ALJABAR 1 Kristiana Wijaya i ii Daftar Isi Judul Daftar Isi i iii 1 Himpunan 1 2 Partisi dan Relasi Ekuivalen 3 3 Grup 6 4 Koset Dan Teorema Lagrange, Homomorphisma Grup Dan Grup Faktor 11 Indeks
JURNAL MATEMATIKA DAN KOMPUTER Vol. 4. No. 2, 65-70, Agustus 2001, ISSN : SYARAT PERLU LAPANGAN PEMISAH
 JURNAL MATEMATIKA DAN KOMPUTER Vol 4 No 2, 65-70, Agustus 2001, ISSN : 1410-8518 SYARAT PERLU LAPANGAN PEMISAH Bambang Irawanto Jurusan Matematika FMIPA UNDIP Abstact Field is integral domain and is a
JURNAL MATEMATIKA DAN KOMPUTER Vol 4 No 2, 65-70, Agustus 2001, ISSN : 1410-8518 SYARAT PERLU LAPANGAN PEMISAH Bambang Irawanto Jurusan Matematika FMIPA UNDIP Abstact Field is integral domain and is a
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI Sejak tiga abad yang lalu, pakar-pakar matematika telah menghabiskan banyak waktu untuk mengeksplorasi dunia bilangan prima. Banyak sifat unik dari bilangan prima yang menakjubkan.
BAB 2 LANDASAN TEORI Sejak tiga abad yang lalu, pakar-pakar matematika telah menghabiskan banyak waktu untuk mengeksplorasi dunia bilangan prima. Banyak sifat unik dari bilangan prima yang menakjubkan.
BAB 2 LANDASAN TEORI. Berikut ini akan dijelaskan pengertian, tujuan dan jenis kriptografi.
 BAB 2 LANDASAN TEORI 2.1. Kriptografi Berikut ini akan dijelaskan pengertian, tujuan dan jenis kriptografi. 2.1.1. Pengertian Kriptografi Kriptografi (cryptography) berasal dari bahasa Yunani yang terdiri
BAB 2 LANDASAN TEORI 2.1. Kriptografi Berikut ini akan dijelaskan pengertian, tujuan dan jenis kriptografi. 2.1.1. Pengertian Kriptografi Kriptografi (cryptography) berasal dari bahasa Yunani yang terdiri
PENGANTAR GRUP. Yus Mochamad Cholily Jurusan Pendidikan Matematika Universitas Muhammadiyah Malang
 PENGANTAR GRUP Yus Mochamad Cholily Jurusan Pendidikan Matematika Universitas Muhammadiyah Malang email:ymcholily@gmail.com March 18, 2013 1 Daftar Isi 1 Tujuan 3 2 Pengantar Grup 3 3 Sifat-sifat Grup
PENGANTAR GRUP Yus Mochamad Cholily Jurusan Pendidikan Matematika Universitas Muhammadiyah Malang email:ymcholily@gmail.com March 18, 2013 1 Daftar Isi 1 Tujuan 3 2 Pengantar Grup 3 3 Sifat-sifat Grup
Tujuan Instruksional Umum : Setelah mengikuti pokok bahasan ini mahasiswa dapat mengidentifikasi dan mengenal sifat-sifat dasar suatu Grup
 BAB 3 DASAR DASAR GRUP Tujuan Instruksional Umum : Setelah mengikuti pokok bahasan ini mahasiswa dapat mengidentifikasi dan mengenal sifat-sifat dasar suatu Grup Tujuan Instruksional Khusus : Setelah diberikan
BAB 3 DASAR DASAR GRUP Tujuan Instruksional Umum : Setelah mengikuti pokok bahasan ini mahasiswa dapat mengidentifikasi dan mengenal sifat-sifat dasar suatu Grup Tujuan Instruksional Khusus : Setelah diberikan
HASIL KALI TENSOR: KONSTRUKSI, EKSISTENSI DAN KAITANNYA DENGAN BARISAN EKSAK
 HASIL KALI TENSO: KONSTUKSI, EKSISTENSI AN KAITANNYA ENGAN BAISAN EKSAK Samsul Arifin samsul_arifin@mail.ugm.ac.id Mahasiswa S Matematika FMIPA UGM alam tulisan ini akan dibahas mengenai konstruksi hasil
HASIL KALI TENSO: KONSTUKSI, EKSISTENSI AN KAITANNYA ENGAN BAISAN EKSAK Samsul Arifin samsul_arifin@mail.ugm.ac.id Mahasiswa S Matematika FMIPA UGM alam tulisan ini akan dibahas mengenai konstruksi hasil
KRIPTOSISTEM KURVA ELIPS (ELLIPTIC CURVE CRYPTOSYSTEM) Disarikan oleh: Dinisfu Sya ban ( )
 KRIPTOSISTEM KURVA ELIPS (ELLIPTIC CURVE CRYPTOSYSTEM) Disarikan oleh: Dinisfu Sya ban (040100596) SEKOLAH TINGGI SANDI NEGARA BOGOR 007 PENDAHULUAN Pada tahun 1985, Neil Koblitz dan Viktor Miller secara
KRIPTOSISTEM KURVA ELIPS (ELLIPTIC CURVE CRYPTOSYSTEM) Disarikan oleh: Dinisfu Sya ban (040100596) SEKOLAH TINGGI SANDI NEGARA BOGOR 007 PENDAHULUAN Pada tahun 1985, Neil Koblitz dan Viktor Miller secara
GRUP MONOTETIK TOPOLOGI DISKRIT BERHINGGA PADA DUALITAS PONTRYAGIN
 Saintia Matematika Vol. 1, No. 6 (2013), pp. 591 602. GRUP MONOTETIK TOPOLOGI DISKRIT BERHINGGA PADA DUALITAS PONTRYAGIN L.F.D. Bali, Tulus, Mardiningsih Abstrak. Dalam teori grup topologi kompak lokal,
Saintia Matematika Vol. 1, No. 6 (2013), pp. 591 602. GRUP MONOTETIK TOPOLOGI DISKRIT BERHINGGA PADA DUALITAS PONTRYAGIN L.F.D. Bali, Tulus, Mardiningsih Abstrak. Dalam teori grup topologi kompak lokal,
BAB II LANDASAN TEORI. bilangan bulat dan mengandung berbagai masalah terbuka yang dapat dimengerti
 BAB II LANDASAN TEORI A. Teori Bilangan Teori bilangan adalah cabang dari matematika murni yang mempelajari sifat-sifat bilangan bulat dan mengandung berbagai masalah terbuka yang dapat dimengerti sekalipun
BAB II LANDASAN TEORI A. Teori Bilangan Teori bilangan adalah cabang dari matematika murni yang mempelajari sifat-sifat bilangan bulat dan mengandung berbagai masalah terbuka yang dapat dimengerti sekalipun
II. TINJAUAN PUSTAKA. Diberikan himpunan dan operasi biner disebut grup yang dinotasikan. (i), untuk setiap ( bersifat assosiatif);
 II. TINJAUAN PUSTAKA 2.1 Grup Pengkajian pertama, diulas tentang definisi Grup yang merupakan bentuk dasar dari suatu ring dan modul. Definisi 2.1.1 Diberikan himpunan dan operasi biner disebut grup yang
II. TINJAUAN PUSTAKA 2.1 Grup Pengkajian pertama, diulas tentang definisi Grup yang merupakan bentuk dasar dari suatu ring dan modul. Definisi 2.1.1 Diberikan himpunan dan operasi biner disebut grup yang
BAB 2 TINJAUAN PUSTAKA
 BAB TINJAUAN PUSTAKA.1 Kriptografi Kriptografi pada awalnya dijabarkan sebagai ilmu yang mempelajari bagaimana menyembunyikan pesan. Namun pada pengertian modern kriptografi adalah ilmu yang bersandarkan
BAB TINJAUAN PUSTAKA.1 Kriptografi Kriptografi pada awalnya dijabarkan sebagai ilmu yang mempelajari bagaimana menyembunyikan pesan. Namun pada pengertian modern kriptografi adalah ilmu yang bersandarkan
DASAR-DASAR ALJABAR MODERN: TEORI GRUP & TEORI RING
 DASAR-DASAR ALJABAR MODERN: TEORI GRUP & TEORI RING Dr. Adi Setiawan, M.Sc G R A F I K A Penerbit Tisara Grafika SALATIGA 2014 Katalog Dalam Terbitan 512.24 ADI Adi Setiawan d Dasar-dasar aljabar modern:
DASAR-DASAR ALJABAR MODERN: TEORI GRUP & TEORI RING Dr. Adi Setiawan, M.Sc G R A F I K A Penerbit Tisara Grafika SALATIGA 2014 Katalog Dalam Terbitan 512.24 ADI Adi Setiawan d Dasar-dasar aljabar modern:
ARITMETIK RING POLINOMIAL UNTUK KONSTRUKSI FUNGSI HASH BERBASIS LATIS IDEAL
 ARITMETIK RING POLINOMIAL UNTUK KONSTRUKSI FUNGSI HASH BERBASIS LATIS IDEAL S. Guritman 1, N. Aliatiningtyas 2, T. Wulandari 3, M. Ilyas 4 Abstrak Sebagai hasil awal dari penelitian konstruksi fungsi hash
ARITMETIK RING POLINOMIAL UNTUK KONSTRUKSI FUNGSI HASH BERBASIS LATIS IDEAL S. Guritman 1, N. Aliatiningtyas 2, T. Wulandari 3, M. Ilyas 4 Abstrak Sebagai hasil awal dari penelitian konstruksi fungsi hash
BAB II TINJAUAN PUSTAKA
 BAB II TINJAUAN PUSTAKA 2.1. Kriptografi Kriptografi secara etimologi berasal dari bahasa Yunani kryptos yang artinya tersembunyi dan graphien yang artinya menulis, sehingga kriptografi merupakan metode
BAB II TINJAUAN PUSTAKA 2.1. Kriptografi Kriptografi secara etimologi berasal dari bahasa Yunani kryptos yang artinya tersembunyi dan graphien yang artinya menulis, sehingga kriptografi merupakan metode
Bab 2: Kriptografi. Landasan Matematika. Fungsi
 Bab 2: Kriptografi Landasan Matematika Fungsi Misalkan A dan B adalah himpunan. Relasi f dari A ke B adalah sebuah fungsi apabila tiap elemen di A dihubungkan dengan tepat satu elemen di B. Fungsi juga
Bab 2: Kriptografi Landasan Matematika Fungsi Misalkan A dan B adalah himpunan. Relasi f dari A ke B adalah sebuah fungsi apabila tiap elemen di A dihubungkan dengan tepat satu elemen di B. Fungsi juga
UNIVERSITAS GADJAH MADA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM JURUSAN MATEMATIKA PROGRAM STUDI S1 MATEMATIKA Sekip Utara, Yogyakarta
 UNIVERSITAS GADJAH MADA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM JURUSAN MATEMATIKA PROGRAM STUDI S1 MATEMATIKA Sekip Utara, Yogyakarta Bahan Ajar: BAB POKOK BAHASAN III MODUL BEBAS, PENGENOL, DAN
UNIVERSITAS GADJAH MADA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM JURUSAN MATEMATIKA PROGRAM STUDI S1 MATEMATIKA Sekip Utara, Yogyakarta Bahan Ajar: BAB POKOK BAHASAN III MODUL BEBAS, PENGENOL, DAN
TUGAS ALJABAR. RESUME GRUP, GRUP PERMUTASI, RING, dan RING POLINOMIAL. oleh. WAYAN RUMITE NRP Kelas: A. Dosen Pengampu MK:
 TUGAS ALJABAR RESUME GRUP, GRUP PERMUTASI, RING, dan RING POLINOMIAL oleh WAYAN RUMITE NRP 1213201037 Kelas: A Dosen Pengampu MK: Dr. SUBIONO, M.Sc. PROGRAM PASCASARJANA MATEMATIKA FAKULTAS MATEMATIKA
TUGAS ALJABAR RESUME GRUP, GRUP PERMUTASI, RING, dan RING POLINOMIAL oleh WAYAN RUMITE NRP 1213201037 Kelas: A Dosen Pengampu MK: Dr. SUBIONO, M.Sc. PROGRAM PASCASARJANA MATEMATIKA FAKULTAS MATEMATIKA
3 HASIL DAN PEMBAHASAN
 3 HASIL DAN PEMBAHASAN 3.1 Formulasi Masalah Sejauh ini telah diperkenalkan bahwa terdapat tiga parameter yang terkait dengan konstruksi suatu kode, yaitu panjang, dimensi, dan jarak minimum. Jika C adalah
3 HASIL DAN PEMBAHASAN 3.1 Formulasi Masalah Sejauh ini telah diperkenalkan bahwa terdapat tiga parameter yang terkait dengan konstruksi suatu kode, yaitu panjang, dimensi, dan jarak minimum. Jika C adalah
BAB II KAJIAN TEORI. Himpunan merupakan suatu kumpulan obyek-obyek yang didefinisikan. himpunan bilangan prima kurang dari 12 yaitu A = {2,3,5,7,11}.
 BAB II KAJIAN TEORI A. Lapangan Berhingga Himpunan merupakan suatu kumpulan obyek-obyek yang didefinisikan dengan jelas pada suatu batasan-batasan tertentu. Contoh himpunan hewan berkaki empat H4 ={sapi,
BAB II KAJIAN TEORI A. Lapangan Berhingga Himpunan merupakan suatu kumpulan obyek-obyek yang didefinisikan dengan jelas pada suatu batasan-batasan tertentu. Contoh himpunan hewan berkaki empat H4 ={sapi,
MATHunesa Jurnal Ilmiah Matematika Volume 2 No.6 Tahun 2017 ISSN
 MATHunesa Jurnal Ilmiah Matematika Volume 2 No.6 Tahun 2017 ISSN 2301-9115 GRAF TOTAL SUATU MODUL BERDASARKAN SUBMODUL SINGULER Dian Ambarsari (S1 Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam,
MATHunesa Jurnal Ilmiah Matematika Volume 2 No.6 Tahun 2017 ISSN 2301-9115 GRAF TOTAL SUATU MODUL BERDASARKAN SUBMODUL SINGULER Dian Ambarsari (S1 Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam,
Jurnal Matematika Murni dan Terapan Vol. 4 No. 2 Desember 2010: IDEAL MAKSIMAL DAN IDEAL PRIMA NEAR-RING
 IDEAL MAKSIMAL DAN IDEAL PRIMA NEAR-RING Saman Abdurrahman Program Studi Matematika Universitas Lambung Mangkurat Jl. Jend. A. Yani km 35, 8 Banjarbaru ABSTRAK Penelitian ini membahas ideal near-ring yang
IDEAL MAKSIMAL DAN IDEAL PRIMA NEAR-RING Saman Abdurrahman Program Studi Matematika Universitas Lambung Mangkurat Jl. Jend. A. Yani km 35, 8 Banjarbaru ABSTRAK Penelitian ini membahas ideal near-ring yang
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI 2.1 Teori Bilangan 2.1.1 Keterbagian Jika a dan b Z (Z = himpunan bilangan bulat) dimana b 0, maka dapat dikatakan b habis dibagi dengan a atau b mod a = 0 dan dinotasikan dengan
BAB II LANDASAN TEORI 2.1 Teori Bilangan 2.1.1 Keterbagian Jika a dan b Z (Z = himpunan bilangan bulat) dimana b 0, maka dapat dikatakan b habis dibagi dengan a atau b mod a = 0 dan dinotasikan dengan
SILLABUS PENILAIAN JENIS. SOAL Tes Tulis Uraian 4x50 David SD & Richard MF (1991) Abstract Algebra. Prentice Hall, Inc. Herstein, I.
 SILLABUS Mata Kuliah : & Ring Fakultas /Jurusan : FTIK /TMT Semester : 4 & 5 SKS : 3 & 3 Standar Kompetensi : Mahasiswa mampu memahami fungsi & operasi, grup & subgroup, grup permutasi, order grup, grup
SILLABUS Mata Kuliah : & Ring Fakultas /Jurusan : FTIK /TMT Semester : 4 & 5 SKS : 3 & 3 Standar Kompetensi : Mahasiswa mampu memahami fungsi & operasi, grup & subgroup, grup permutasi, order grup, grup
BAB 2 LANDASAN TEORI Interaksi Manusia dan Komputer. interaktif untuk digunakan oleh manusia. Golden Rules of Interaction Design, yaitu:
 BAB 2 LANDASAN TEORI 2.1 Teori Umum 2.1.1 Interaksi Manusia dan Komputer Interaksi manusia dan komputer adalah ilmu yang berhubungan dengan perancangan, evaluasi, dan implementasi sistem komputer interaktif
BAB 2 LANDASAN TEORI 2.1 Teori Umum 2.1.1 Interaksi Manusia dan Komputer Interaksi manusia dan komputer adalah ilmu yang berhubungan dengan perancangan, evaluasi, dan implementasi sistem komputer interaktif
