MODIFIKASI STEPSIZE PADA METODE STEEPEST DESCENT DALAM PENGOPTIMUMAN FUNGSI: KASUS FUNGSI KUADRATIK DIAGONAL FACHRIADI FADHILLAH

Transkripsi

1 MODIFIKASI STEPSIZE PADA METODE STEEPEST DESCENT DALAM PENGOPTIMUMAN FUNGSI: KASUS FUNGSI KUADRATIK DIAGONAL FACHRIADI FADHILLAH DEPARTEMEN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR BOGOR 2014

2

3 PERNYATAAN MENGENAI SKRIPSI DAN SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA* Dengan ini saya menyatakan bahwa skripsi berjudul Modifikasi Stepsize pada Metode Steepest Descent dalam Pengoptimuman Fungsi: Kasus Fungsi Kuadratik Diagonal adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir skripsi ini. Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor. Bogor, Desember 2014 Fachriadi Fadhillah NIM G

4 ABSTRAK FACHRIADI FADHILLAH. Modifikasi Stepsize pada Metode Steepest Descent dalam Pengoptimuman Fungsi: Kasus Fungsi Kuadratik Diagonal. Dibimbing oleh BIB PARUHUM SILALAHI dan MUHAMMAD ILYAS. Metode steepest descent adalah salah satu metode untuk menemukan titik optimum suatu fungsi tanpa kendala. Metode ini menggunakan stepsize yang diperoleh dari pencarian exact line. Metode ini mungkin menuju ke titik optimum dengan lambat. Beberapa penelitian telah dilakukan untuk mengatasi kelemahan ini dengan mengubah stepsize. Beberapa stepsize baru antara lain dikembangkan oleh Ya-xiang Yuan, Barzilai, dan Borwein. Karya ilmiah ini membandingkan waktu penyelesaian dan banyaknya iterasi untuk metode steepest descent, metode Yaxiang Yuan, dan metode Barzilai-Borwein dalam menyelesaikan suatu permasalahan pengoptimuman tanpa kendala untuk kasus fungsi kuadratik diagonal. Hasil numerik yang diperoleh menunjukan bahwa metode Ya-xiang Yuan dapat menemukan titik optimum hanya dengan tiga iterasi saja untuk fungsi dengan dua variabel. Selanjutnya metode Ya-xiang Yuan sangat efisien untuk masalah dengan dimensi kecil, sedangkan metode Barzilai-Borwein menunjukan hasil yang lebih baik untuk masalah dengan dimensi besar. Kata kunci: Modifikasi stepsize, Pengoptimuman fungsi tanpa kendala, Steepest descent ABSTRACT FACHRIADI FADHILLAH. A Stepsize Modification for Steepest Descent Method in Optimization of a Function: a Diagonal Quadratic Function Case. Supervised by BIB PARUHUM SILALAHI and MUHAMMAD ILYAS. The steepest descent is one of the methods for unconstrained optimization. This method uses stepsize which is obtained by using exact line searches. The exact line searches along steepest descent direction may found the optimum point slowly. A number of researches have been conducted for solving this weakness by changing the stepsize. Some new stepsizes were developed by Ya-xiang Yuan, Barzilai, and Borwein. In this paper, the execution times and the number of iterations of the steepest descent method, the Ya-xiang Yuan method, and the Barzilai-Borwein method will be compared in solving an unconstrained optimization for diagonal quadratic function case. Numerical results showed that the Ya-xiang Yuan method can find the optimum point within three iterations for two variables functions. Furthermore, the Ya-xiang Yuan method is the most efficient for small scale problems, while the Barzilai-Borwein method showed better results for large scale problems. Keywords: Optimization of unconstrained function, Steepest descent, Stepsize modification

5 MODIFIKASI STEPSIZE PADA METODE STEEPEST DESCENT DALAM PENGOPTIMUMAN FUNGSI: KASUS FUNGSI KUADRATIK DIAGONAL Skripsi sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains pada Departemen Matematika DEPARTEMEN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR BOGOR FACHRIADI 2014 FADHILLAH

6

7 Judul Skripsi : Modifikasi Stepsize pada Metode Steepest Descent dalam Pengoptimuman Fungsi: Kasus Fungsi Kuadratik Diagonal Nama : Fachriadi Fadhillah NIM : G Disetujui oleh Dr Ir Bib Paruhum Silalahi, MKom Pembimbing I Muhammad Ilyas, MSi MSc Pembimbing II Diketahui oleh Dr Toni Bakhtiar, MSc Ketua Departemen Tanggal Lulus:

8 PRAKATA Puji dan syukur penulis panjatkan kepada Allah subhanahu wa ta ala atas segala karunia-nya sehingga karya ilmiah ini berhasil diselesaikan. Judul karya ilmiah ini adalah Modifikasi Stepsize pada Metode Steepest Descent dalam Pengoptimuman Fungsi: Kasus Fungsi Kuadratik Diagonal. Terima kasih penulis ucapkan kepada Bapak Dr Ir Bib Paruhum Silalahi, Mkom dan Bapak Muhammad Ilyas, Msi MSc selaku pembimbing, serta Bapak Ruhiyat, SSi MSi yang telah banyak memberi saran, motivasi, dan bimbingan dalam penulisan karya ilmiah ini, serta kepada seluruh staf Departemen Matematika. Terima kasih juga penulis ucapkan kepada Bapak Chairul Chaniago, Ibu Radiah Azita, Rully Novriansyah, Redyan Febriansyah, Yoanka Khairunissa, Risya Ari Purnama, Tinneke Hakim Putri, Voira Alyssa Febriansyah, serta seluruh keluarga, atas segala doa dan kasih sayangnya. Ucapan terima kasih juga penulis berikan kepada para sahabat Erjodi Cahyo, Aisatul Mustaqimah, Intan Nabilla, Adi Kiswanto, Rayfan Ambrian, Laras Febi Amelia, Fachri Aditya, Annisyia Zarina, Zeta Fadilla, Annisa Primanitasari, Kiki Septiani, Gerry Kristian, Diah Putri Pertiwi, Chika Katelia, Nena Apriliana, seluruh mahasiswa Departemen Matematika Angkatan 45, 46, 47, 48, dan 49 serta teman-teman sekalian di luar Departemen Matematika baik di dalam Institut Pertanian Bogor maupun di luar Institut Pertanian Bogor atas kritik, saran, dan doanya selama pembuatan karya ilmiah ini. Semoga karya ilmiah ini bermanfaat. Bogor, Desember 2014 Fachriadi Fadhillah

9 DAFTAR ISI DAFTAR TABEL vi DAFTAR GAMBAR vi DAFTAR LAMPIRAN vi PENDAHULUAN 1 Latar Belakang 1 Tujuan Penelitian 1 TINJAUAN PUSTAKA 2 HASIL DAN PEMBAHASAN 2 Metode Ya-xiang Yuan 2 Metode Barzilai Borwein 6 Hasil Numerik 7 Algoritme Ya-xiang Yuan 7 Algoritme Steepest Descent 7 Algoritme Barzilai-Borwein 8 SIMPULAN 12 DAFTAR PUSTAKA 12 LAMPIRAN 13 RIWAYAT HIDUP 30

10 DAFTAR TABEL 1 Hasil untuk fungsi dua variabel 8 2 Hasil untuk fungsi tiga variabel 9 3 Hasil untuk fungsi sepuluh variabel 9 4 Hasil untuk fungsi 25 variabel 10 DAFTAR GAMBAR 1 Perbandingan waktu metode Ya-xiang Yuan, metode BB, dan metode steepest descent 11 2 Perbandingan banyak iterasi metode Ya-xiang Yuan, metode BB, dan metode steepest descent 11 DAFTAR LAMPIRAN 1 Metode Ya-xiang Yuan untuk dua variabel 13 2 Metode Ya-xiang Yuan untuk tiga variabel 14 3 Metode Ya-xiang Yuan untuk sepuluh variabel 16 4 Metode Ya-xiang Yuan untuk 25 variabel 18 5 Metode steepest descent untuk dua variabel 20 6 Metode steepest descent untuk tiga variabel 21 7 Metode steepest descent untuk sepuluh variabel 22 8 Metode steepest descent untuk 25 variabel 23 9 Metode BB untuk dua variabel Metode BB untuk tiga variabel Metode BB untuk sepuluh variabel Metode BB untuk 25 variabel 28

11 1 PENDAHULUAN Latar Belakang Permasalahan mengenai pengoptimuman adalah mencari penyelesaian terbaik dari suatu masalah. Masalah yang ditemui terdiri atas fungsi tujuan dan kendala yang dapat berupa fungsi linear maupun nonlinear. Terdapat beberapa metode untuk menyelesaikan masalah pengoptimuman dengan kelebihan dan kekurangan yang berbeda untuk masing-masing metode. Salah satu metode yang digunakan dalam masalah pengoptimuman bersifat iteratif, yaitu dimulai dari titik awal x 1 yang sudah ditentukan, kemudian bergerak ke titik x 2 hingga titik x n, yaitu titik yang mendekati atau sama dengan nilai optimal. Metode-metode tersebut dapat diklasifikasikan ke dalam dua kelompok, yaitu metode dengan menggunakan gradien dan metode tanpa menggunakan gradien. Untuk metode dengan menggunakan gradien, diperlukan syarat fungsi tujuan terturunkan. Contoh metode dengan menggunakan gradien yaitu metode steepest descent, metode Newton, dan metode conjugate gradien. Contoh metode tanpa menggunakan gradien yaitu metode Rosenbrock dan metode Nelder-Mead (Klerk et al. 2005). Masalah yang digunakan pada karya ilmiah ini adalah masalah pengoptimuman nonlinear tanpa kendala, yaitu mencari nilai x yang meminimumkan suatu fungsi f(x) dan metode yang digunakan adalah metode steepest descent. Metode steepest descent bergerak dengan langkah-langkah yang saling tegak lurus. Tepatnya, jika {x i } adalah barisan steepest descent untuk fungsi f(x), maka untuk setiap bilangan asli i 0, vektor yang menghubungkan x i 1 dengan x i tegak lurus dengan vektor yang menghubungkan x i dengan x i+1. Perlu diketahui, pencarian dengan arah steepest descent untuk menuju ke suatu titik mungkin berjalan dengan lambat (Yuan 2006). Metode steepest descent memerlukan iterasi yang banyak untuk menemukan solusi minimum karena gerak langkahnya yang berliku-liku (zigzag). Barzilai dan Borwein (1988) berusaha menyempurnakan metode ini dengan mengubah stepsize. Pada karya ilmiah ini akan dibahas tentang modifikasi metode steepest descent dengan mengubah stepsize. Algoritme yang baru ini akan menempatkan stepsize yang baru pada iterasi genap sedangkan pada setiap iterasi ganjil tetap menggunakan stepsize pada steepest descent. Algoritme ini didasarkan pada artikel yang ditulis oleh Yuan (2006). Setelah itu akan dilakukan simulasi sebagai perbandingan dengan metode steepest descent dan metode BB. Pengolahan data dilakukan dengan menggunakan bantuan software MATLAB R2010a. Tujuan Penelitian Penulisan karya ilmiah ini bertujuan untuk: 1. Merekonstruksi penggunaan stepsize baru pada metode steepest descent. 2. Membandingkan waktu penyelesaian dan banyaknya iterasi yang dilakukan pada metode steepest descent yang telah dimodifikasi, Barzilai dan Borwein, dan steepest descent.

12 2 TINJAUAN PUSTAKA Metode steepest descent adalah metode gradien sederhana untuk pengoptimuman tanpa kendala: min x Rⁿ f(x), dengan f(x) adalah fungsi kontinu dan terturunkan di R n. Metode ini memiliki bentuk sebagai berikut: x k+1 = x k + α k ( g k ), dengan g k = g(x k ) = f(x k ) adalah vektor gradien dari f(x) di x k dan α k > 0 adalah stepsize. Arah pencarian dalam metode ini berbanding terbalik dengan arah gradien, yaitu dengan arah menurun tercuram (steepest descent), sehingga metode ini diberi nama steepest descent. Arah curam menurun yang diterapkan dalam metode ini sendiri dipercaya merupakan arah terbaik dalam artian metode ini dapat mengurangi fungsi objektif sebanyak mungkin. Stepsize α k dapat diperoleh dengan pencarian exact line: α k = argmin{f(x k + a( g k ))}. Metode steepest descent selalu konvergen. Secara teori metode ini tidak akan berhenti atau akan terus melakukan iterasi sampai kriteria penghentian terpenuhi. Namun, untuk kasus yang sangat sederhana saat fungsi objektif f(x) merupakan fungsi kuadrat konveks sempurna, yaitu: f(x) = g T x xt Hx, dengan g R n, H R n n simetris dan definit positif. Asumsikan kita menggunakan stepsize yang didapat dari pencarian exact line, metode ini dapat membutuhkan waktu yang cukup lama untuk memperoleh hasil (Yuan 2006). HASIL DAN PEMBAHASAN Metode Ya-xiang Yuan Untuk analisis pada bab ini, diasumsikan bahwa fungsi objektif adalah sebagai berikut: f(x) = g T x xt Hx,

13 dengan g R n dan H R n n simetris dan definit positif. Pada dasarnya, metode baru ini adalah pengembangan dari metode steepest descent. Dapat dilihat pada metode baru ini pencarian exact line harus dilakukan pada iterasi terakhir sebelum algoritme berhasil menemukan solusinya. Diasumsikan pula bahwa digunakan pencarian exact line pada iterasi pertama supaya kita tidak menghindari keberuntungan apabila ada kasus di mana algoritme dapat menemukan solusi pada iterasi pertama. Oleh karena itu, dibuatlah algoritme sebagai berikut: 3 x 2 = x 1 α 1 g 1 x 3 = x 2 α 2 g 2 x 4 = x 3 α 3 g 3, di mana α 1 dan α 3 didapat dari pencarian exact line dan x 4 adalah solusi. Perlu dicari formula untuk α 2 sehingga x 4 akan menjadi nilai minimum dari fungsi objektif. Metode ini disebut metode Ya-xiang Yuan. Untuk mempermudah analisis, dipelajari kasus di mana g 1 dan g 2 adalah dua buah sumbu. Sesuai dengan pencarian exact line pada iterasi pertama, gradien g 1 dan g 2 adalah ortogonal. Oleh karena itu kita dapat menampilkan semua vektor x sebagai kombinasi linear dari g 1 dan g 2. Misalkan diberikan fungsi: f(x 2 + t g 1 + u g 2 ) = ( 0 T g 1 g 2 g 2 ) ( t u ) g T 1 Hg g T 1 Hg 2 2 (t g1 u )T ( 2 g1 g 2 g T 1 Hg 2 g T ) ( t 2 Hg 2 u ). g1 g 2 g2 2 Berdasarkan pencarian exact line pada iterasi pertama, diperoleh α 1 = g 1 2 / g 1 T Hg 1 dan g 1 T Hg 2 = g 2 2 /α 1 yang diperoleh dari: x k+1 = x k α k g k f(x k+1) = f(x k α k g k ) f (x k+1 ) = f (x k α k g k ). Karena α k = argmin {f(x k α k g k )}, diperlukan syarat f (x k+1 ) = 0 sehingga: f (x k α k g k ) = 0 f (x k α k g k ) T g k = 0 (g + H(x k α k g k )) T (g + Hx) = 0 (g + H x α k H(g k ) T (g + Hx) = 0 (g + Hx) T (g + Hx) + α k (g + Hx) T H(g + Hx) = 0

14 4 g k T g k + α k g k T Hg k = 0 α k g k T Hg k = g k T g k α k = g k T g k g T k Hg k α k = g k 2 g k T Hg k. Dengan menggunakan notasi α 2 = g 2 2 /g 2 T Hg 2, didapat bahwa: f(x 2 + t g 1 + u g 2 ) = ( 0 T g 1 g 2 g 2 ) ( t u ) 1 g (t a1 a u )T ( 1 g 1 ) ( t g 2 1 u ). a 1 g 1 a2 Oleh karena itu, dapat diketahui nilai minimum dari fungsi objektifnya adalah: u ) = g 1 g 2 g 1 2 /a 2 g 2 2 /a ( g 2 1 g 1 ), ( t yang diperoleh dari: df dt = 0 2t a 2u g 2 1 a 1 g 1 = 0 2t g 1 2u g 2 = 0 t g 1 u g 2 = 0 (1) df du = 0 g 2 + u a 2 t g 2 a 1 g 1 = 0 ta 2 g 2 + ua 1 g 1 = a 1 a 2 g 1 g 2. (2) Kemudian dilakukan eliminasi pada persamaan (1) dan (2)

15 (1) * a 2 g 2 ta 2 g 1 g 2 ua 2 g 2 2 = 0 (3) (2) * g 1 ta 2 g 1 g 2 + ua 1 g 1 2 = a 1 a 2 g 1 2 g 2 (4) (3) + (4) ua 1 g 1 2 ua 2 g 2 2 = a 1 a 2 g 1 2 g 2 u = a 1 a 2 g 1 2 g 2 a 1 g 1 2 a 2 g 2 2 u = Subtitusikan u ke persamaan (1) diperoleh: t = g 1 2 g 2 g 1 2 a g a 1 g 1 g 2 2 g 1 2 a g a Untuk mendapatkan x 4 = x 2 + t g 1 + g 1 u g 2, perlu diketahui bahwa arah g 2 gradien g 3 paralel terhadap vektor residual x 4 x 3. Untuk itu, diperlukan dua arah: dan ( t u ) ( 0 α 2 g 2 ) ( 0 1 g 2 g 2 ) + ( a1 a 1 g 1 0 ) ( g 2 1 α 2 g 2 ) a 1 g 1 a2 adalah dua buah arah yang paralel. Dua arah tersebut paralel terhadap masingmasing: dan g 2 ( g 1 α 2 ( g 1 2 g 2 2 )/ g α 2 α 1 ) 1 ( α 2 g 2 /α 1 g 1 1 α 2 /α 2 ). Dapat diasumsikan: g 2 ( g 1 α 2 ( g 1 2 g 2 2 )/ g α 2 α 1 ) = λ (α 2 g 2 /α 1 g 1 ) 1 α 2 /α 2 1

16 6 untuk λ R. Berdasarkan baris pertama didapatkan λ = α 1 g 1 /α 2. Kemudian nilai λ tersebut disubtitusikan ke baris kedua pada persamaan di atas sehingga diperoleh: Persamaan di atas ekuivalen dengan: 1 α 2 ( 1 α g α 1 g 1 2) = α 1 α α 1 2 α 2. ( 1 α 1 α 2 g 2 2 (α 1 g 1 ) 2) α 2 2 ( 1 α 1 1 α 2 ) α = 0. (3) Karena H definit positif, diketahui bahwa: Γ = 1 α 1 α 2 g 2 2 (α 1 g 1 ) 2 > 0. Dari persamaan (3) diperoleh dua solusi positif untuk α 2 yaitu: (1 α 1 +1 α 2 )± (1 α 1 +1 α 2 ) 2 4Γ 2Γ Dari dua solusi tersebut dipilih nilai yang lebih kecil dan dapat dituliskan sebagai berikut:. α 2 = 2 (1 α 1 1 α 2 ) 2 +4 g 2 2 s α 1 +1 α 2, dengan s 1 = x 2 x 1 = α 1 g 1. α 2 inilah yang disebut stepsize baru dan kemudian akan diaplikasikan ke dalam metode hasil modifikasi steepest descent. Metode Barzilai-Borwein Gagasan utama dari metode Barzilai-Borwein ini adalah dengan menggunakan hasil pada iterasi sebelumnya untuk menentukan stepsize. Metode ini kemudian dikenal dengan metode BB. Iterasi yang digunakan adalah sebagai berikut: x k+1 = x k D k g k, di mana D k = λ k I. Metode ini memiliki dua buah stepsize: λ k = s T k 1 s k 1 T s k 1 y k 1

17 7 dan λ k = s T k 1 y k 1 T, y k 1 y k 1 dengan s k 1 = x k x k 1 dan y k 1 = g k g k 1. Pada karya ilmiah ini hanya digunakan satu buah stepsize yaitu: λ k = s k 1 T s k 1. s T k 1 y k 1 Hasil Numerik Algoritme yang digunakan pada karya ilmiah ini adalah sebagai berikut: Algoritme Ya-xiang Yuan Step 1 Masukan titik awal x 1. 0< ε 1. Hitung g 1, Tetapkan k=1. Step 2 Hitung stepsize dengan pencarian exact line α 2k 1 ; Tetapkan x 2k = x 2k 1 α 2k 1 g 2k 1 Step 3 Jika g(x 2k ) ε maka berhenti; Step 4 Hitung stepsize dengan pencarian exact line α 2k, Tetapkan α 2k = dan 2 (1 α 2k 1 1 α 2k ) g 2k 2 s 2k α 2k α 2k Jika g 2k+1 ε maka berhenti; Step 5 k=k+1, kembali ke Step 2. x 2k+1 = x 2k α 2k g 2k Algoritme Steepest Descent Step 1 Masukan titik awal x 0. 0< ε 1. Hitung g 1, Tetapkan k=0. Step 2 Hitung stepsize dengan pencarian exact line α k ; Tetapkan Step 3 Jika g(x k ) ε maka berhenti; Step 4 k=k+1, kembali ke Step 2. x k+1 = x k α k g k

18 8 Algoritme Barzilai-Borwein Step 1. Diberikan x 0 εr n, 0< ε 1. Tetapkan k=0. Step 2. Jika g k ε, stop; lainnya d k = g k. Step 3. Jika k=0, menentukan λ 0 dengan pencarian exact line; selainnya dengan menghitung λ k dengan λ k = s T k 1 Step 4. Tentukan x k+1 = x k + λ k d k. Step 5. k = k + 1, kembali ke Step 2. s k 1 st. k 1 y k 1 Fungsi yang digunakan adalah fungsi kuadratik diagonal, yaitu fungsi yang dibangkitkan secara acak dengan ketentuan sebagai berikut: f(x) = (x x ) T diag(σ 1,, σ n )(x x ). x R n. Jumlah variabel yang digunakan dilambangkan dengan n di mana nilai n=2,3,10,25. Vektor x i (i = 1,, n) [ 5,5] yang dipilih secara acak. Diberikan σ n = cond(10,100) dan σ i (i = 1,, n) di mana nilainya diperoleh secara acak dengan interval [1, σ n ]. Untuk semua kasus diberikan titik awal adalah vektor nol (0,...,0) T dan kriteria penghentian adalah g k Untuk setiap kasus, dilakukan lima kali pengulangan. Tabel 1 Hasil untuk fungsi dua variabel Ya-xiang Yuan Steepest Descent BB n σ n Iterasi Waktu (s) Iterasi Waktu (s) Iterasi Waktu (s) , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , Rata-rata 3 0, ,8 0, ,6 0, Untuk fungsi dengan dua variabel, metode Ya-xiang Yuan hanya membutuhkan maksimal tiga iterasi untuk menemukan solusi minimumnya (Tabel 1). Metode ini memiliki waktu yang paling cepat dan banyaknya iterasi paling sedikit dibandingkan metode BB dan steepest descent.

19 9 Tabel 2 Hasil untuk fungsi tiga variabel Ya-xiang Yuan Steepest Descent BB n σ n Iterasi Waktu (s) Iterasi Waktu (s) Iterasi Waktu (s) , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , Rata-rata 8,3 0, ,4 2, ,9 0, Untuk fungsi dengan tiga variabel, metode Ya-xiang Yuan memiliki waktu yang paling cepat dan banyaknya iterasi paling sedikit dibandingkan metode BB dan steepest descent. Pada salah satu percobaan, metode Ya-xiang Yuan dan metode BB menghasilkan banyak iterasi yang sama yaitu sebesar sembilan iterasi, namun waktu yang dibutuhkan metode Ya-xiang Yuan lebih cepat daripada metode BB (Tabel 2). Berdasarkan nilai rata-rata, metode Ya-xiang Yuan dan BB hanya membutuhkan waktu kurang dari satu sekon untuk menemukan solusi, sedangkan metode steepest descent membutuhkan waktu lebih dari dua sekon. Tabel 3 Hasil untuk fungsi sepuluh variabel Ya-xiang Yuan Steepest Descent BB n σ n Iterasi Waktu (s) Iterasi Waktu (s) Iterasi Waktu (s) , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , Rata-rata 28,6 2, ,3 7, ,2 2, Untuk fungsi dengan sepuluh variabel, metode BB memiliki waktu yang paling cepat dan banyaknya iterasi paling sedikit dibandingkan metode Ya-xiang Yuan dan steepest descent. Pada salah satu percobaan, metode Ya-xiang Yuan dan metode BB menghasilkan banyaknya iterasi yang sama yaitu sebesar 17 iterasi, namun waktu yang dibutuhkan metode BB lebih cepat daripada metode Ya-xiang Yuan (Tabel 3). Berdasarkan nilai rata-rata, metode BB membutuhkan waktu

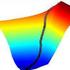
20 10 sekitar dua sekon untuk menemukan solusi minimumnya, metode Ya-xiang Yuan membutuhkan waktu hampir tiga sekon, dan metode steepest descent membutuhkan waktu sekitar tujuh sekon. Tabel 4 Hasil untuk fungsi 25 variabel Ya-xiang Yuan Steepest Descent BB n σ n Iterasi Waktu (s) Iterasi Waktu (s) Iterasi Waktu (s) , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , Rata-rata 46,7 11, ,4 28, ,4 7, Untuk fungsi dengan 25 variabel, metode BB memiliki waktu yang paling cepat dan banyaknya iterasi paling sedikit dibandingkan metode Ya-xiang Yuan dan steepest descent. Pada salah satu percobaan, metode Ya-xiang Yuan dan metode BB menghasilkan banyaknya iterasi yang sama yaitu sebesar 33 iterasi, namun waktu yang dibutuhkan metode BB lebih cepat daripada metode Ya-xiang Yuan (Tabel 4). Berdasarkan nilai rata-rata, metode BB membutuhkan waktu sekitar tujuh sekon untuk menemukan solusi minimumnya, metode Ya-xiang Yuan membutuhkan waktu sekitar 11 sekon, dan metode steepest descent membutuhkan waktu sekitar 28 sekon Perbandingan waktu eksekusi dan banyaknya iterasi untuk metode Ya-xiang Yuan, metode BB, dan metode steepest descent dalam bentuk grafik, ditunjukkan pada Gambar 1 dan Gambar 2. Untuk fungsi dengan dua dan tiga variabel, metode Ya-xiang Yuan memiliki waktu yang paling cepat untuk menemukan solusi dibandingkan metode BB dan steepest descent, sedangkan untuk fungsi dengan sepuluh dan 25 variabel, metode BB memiliki waktu yang paling cepat untuk menemukan solusi dibandingkan metode Ya-xiang Yuan dan steepest descent. Metode steepest descent memiliki waktu yang paling lambat dibandingkan metode BB dan Ya-xiang Yuan baik untuk fungsi dengan dua, tiga, sepuluh, maupun 25 variabel (Gambar 1).

21 11 30, , Waktu (s) 20, , , , , Ya-xiang Yuan 0, , , , SD 0, , , , BB 0, , , , Gambar 1 Perbandingan waktu metode Ya-xiang Yuan, metode BB, dan metode steepest descent Banyak Iterasi Ya-xiang Yuan 3 8,3 28,6 46,7 SD 10,8 36,4 71,3 148,4 BB 6,6 11,9 24,2 39,4 Gambar 2 Perbandingan banyak iterasi metode Ya-xiang Yuan, metode BB, dan metode steepest descent Untuk fungsi dengan dua dan tiga variabel, metode Ya-xiang Yuan memiliki iterasi paling sedikit dibandingkan metode BB dan steepest descent, sedangkan untuk fungsi dengan sepuluh dan 25 variabel, metode BB memiliki iterasi paling sedikit dibandingkan metode Ya-xiang Yuan dan steepest descent. Metode steepest descent memiliki banyaknya iterasi yang paling besar dibandingkan metode BB dan Yaxiang Yuan baik untuk fungsi dengan dua, tiga, sepuluh, maupun 25 variabel (Gambar 2).

22 12 SIMPULAN Modifikasi dengan memberikan stepsize baru yang dilakukan pada metode Ya-xiang Yuan dapat menemukan solusi suatu masalah nonlinear tanpa kendala dengan waktu yang lebih cepat dan jumlah iterasi yang lebih sedikit dibandingkan metode Barzilai-Borwein dan metode steepest descent untuk masalah dimensi kecil. Hasil percobaan bahkan menunjukan bahwa metode Ya-xiang Yuan dapat menemukan nilai minimum dengan tiga iterasi saja untuk fungsi dua variabel. Untuk masalah dengan dimensi yang besar, metode Barzilai-Borwein memberikan kinerja yang lebih baik dibandingkan metode Ya-xiang Yuan maupun metode steepest descent. DAFTAR PUSTAKA Barzilai J, Borwein JM Two point step size gradient methods. IMA J Numer Anal 8(1): doi: /imanum/ Klerk E, Roos C, Terlaky T Optimization. Delft(ND): Delft University of Technology. Yuan, Y A new stepsize for the steepest descent method. Journal of Computational Mathematics 24(2):

23 13 Lampiran 1 Metode Ya-xiang Yuan untuk dua variabel clear; clc; tic; syms x1 x2 v2=[x1,x2]; xb=randi([-5,5],2,1); b=randi(100,1,2); B=diag(b); f1=v2+xb.'; f=expand(f1*b*f1.') x = [x1 x2]; y = [0 0]; tol = 10^(-6); gradien = jacobian(f,x) a = jacobian(gradien,x); A = subs(a,x,y) g = -subs(gradien,x,y) Set_alpha=[]; set_ls=[]; k=1; while norm(g)>tol if (mod(k,2)==1) alfa = g*g'/(g*a*g'); y1 = y(k,:)+alfa*g; y = [y; y1] Set_alpha=[Set_alpha single(alfa)]; k = k+1; g = -subs(gradien,{x1,x2},{y(k,1),y(k,2)}) A = subs(a,{x1 x2},{y(k,1),y(k,2)}); nilai = subs(f,{x1,x2},{y(k,1),y(k,2)}); uji = norm(g); else alfa = g*g'/(g*a*g'); Set_alpha=[Set_alpha single(alfa)]; s =y(k,:)- y(k-1,:); L1 = sqrt((1/set_alpha(k-1)- 1/Set_alpha(k)).^2+4*g*g'/(s*s')); L2 = 1/Set_alpha(k-1)+1/Set_alpha(k); alfa_new = single(2/(l1+l2)); set_ls=[set_ls;alfa_new]; y1 = y(k,:)+ alfa_new*g; y = [y; y1] k = k+1; g = -subs(gradien,{x1,x2},{y(k,1),y(k,2)}) A = subs(a,{x1 x2},{y(k,1),y(k,2)}); nilai = subs(f,{x1,x2},{y(k,1),y(k,2)}); uji = norm(g); end end toc; iterasi = k-1 uji_konvergensi = norm(g);

24 14 Lampiran 2 Metode Ya-xiang Yuan untuk tiga variabel clear; clc; tic; syms x1 x2 x3 v2=[x1,x2,x3]; xb=randi([-5,5],3,1); b=randi(100,1,3); B=diag(b); f1=v2+xb.'; f=expand(f1*b*f1.') x = [x1 x2 x3]; y = [0 0 0]; tol = 10^(-6); gradien = jacobian(f,x) a = jacobian(gradien,x); A = subs(a,x,y); g = -subs(gradien,x,y) Set_alpha=[]; set_ls=[]; k=1; while norm(g)>tol if (mod(k,2)==1) L = g*g'/(g*a*g'); y1 = y(k,:)+l*g; y = [y; y1]; Set_alpha=[Set_alpha single(l)]; k = k+1; g = -subs(gradien,{x1,x2,x3},{y(k,1),y(k,2),y(k,3)}); A = subs(a,{x1 x2 x3},{y(k,1),y(k,2),y(k,3)}); hasil = subs(f,{x1,x2,x3},{y(k,1),y(k,2),y(k,3)}); else L = g*g'/(g*a*g'); Set_alpha=[Set_alpha single(l)]; s =y(k,:)- y(k-1,:); L1 = sqrt((1/set_alpha(k-1)- 1/Set_alpha(k)).^2+4*g*g'/(s*s')); L2 = 1/Set_alpha(k-1)+1/Set_alpha(k); LS = single(2/(l1+l2)); set_ls=[set_ls;ls]; y1 = y(k,:)+ LS*g; y = [y; y1] ; k = k+1; g = -subs(gradien,{x1,x2,x3},{y(k,1),y(k,2),y(k,3)}); A = subs(a,{x1 x2 x3},{y(k,1),y(k,2),y(k,3)}); hasil = subs(f,{x1,x2,x3},{y(k,1),y(k,2),y(k,3)}); end end y toc; iterasi = k-1 uji_konvergensi = norm(g);

25 hasil; F = subs(f,{x1,x2,x3},{y(end,1),y(end,2),y(end,3)}); 15

26 16 Lampiran 3 Metode Ya-xiang Yuan untuk sepuluh variabel clear; clc; tic; syms x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 v2=[x1,x2,x3,x4,x5,x6,x7,x8,x9,x10]; xb=randi([-5,5],10,1); b=randi(100,1,10); B=diag(b); f1=v2+xb.'; f=expand(f1*b*f1.') x = [x1 x2 x3 x4 x5 x6 x7 x8 x9 x10]; y = [ ]; tol = 10^(-8) gradien = jacobian(f,x) a = jacobian(gradien,x); A = subs(a,x,y) g = -subs(gradien,x,y) Set_alpha=[]; set_ls=[]; k=1; while norm(g)>tol if (mod(k,2)==1) alfa = g*g'/(g*a*g') y1 = y(k,:)+alfa*g y = [y; y1] Set_alpha=[Set_alpha single(alfa)] k = k+1; g = - subs(gradien,x,{y(k,1),y(k,2),y(k,3),y(k,4),y(k,5),y(k,6),y(k,7),y (k,8),y(k,9),y(k,10)}) A = subs(a,x,{y(k,1),y(k,2),y(k,3),y(k,4),y(k,5),y(k,6),y(k,7),y(k,8), y(k,9),y(k,10)}) nilai = subs(f,x,{y(k,1),y(k,2),y(k,3),y(k,4),y(k,5),y(k,6),y(k,7),y(k,8), y(k,9),y(k,10)}) uji = norm(g) else alfa = g*g'/(g*a*g') Set_alpha=[Set_alpha single(alfa)] s =y(k,:)- y(k-1,:) L1 = sqrt((1/set_alpha(k-1)- 1/Set_alpha(k)).^2+4*g*g'/(s*s')) L2 = 1/Set_alpha(k-1)+1/Set_alpha(k) alfa_new = single(2/(l1+l2)) set_ls=[set_ls;alfa_new] y1 = y(k,:)+ alfa_new*g y = [y; y1] k = k+1; g = - subs(gradien,x,{y(k,1),y(k,2),y(k,3),y(k,4),y(k,5),y(k,6),y(k,7),y (k,8),y(k,9),y(k,10)})

27 A = subs(a,x,{y(k,1),y(k,2),y(k,3),y(k,4),y(k,5),y(k,6),y(k,7),y(k,8), y(k,9),y(k,10)}) nilai = subs(f,x,{y(k,1),y(k,2),y(k,3),y(k,4),y(k,5),y(k,6),y(k,7),y(k,8), y(k,9),y(k,10)}) uji = norm(g) 17 end end y iterasi = k-1 f toc;

28 18 Lampiran 4 Metode Ya-xiang Yuan untuk 25 variabel clear; clc; tic; syms x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11 x12 x13 x14 x15 x16 x17 x18 x19 x20 x21 x22 x23 x24 x25 v2=[x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,x14,x15,x16,x17,x18,x19,x20,x21,x22,x23,x24,x25]; xb=randi([-5,5],25,1); b=randi(100,1,25); B=diag(b); f1=v2+xb.'; f=expand(f1*b*f1.') x = [x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11 x12 x13 x14 x15 x16 x17 x18 x19 x20 x21 x22 x23 x24 x25]; y = [ ]; tol = 10^(-6) gradien = jacobian(f,x) a = jacobian(gradien,x); A = subs(a,x,y) g = -subs(gradien,x,y) Set_alpha=[]; set_ls=[]; k=1; while norm(g)>tol if (mod(k,2)==1) alfa = g*g'/(g*a*g') y1 = y(k,:)+alfa*g y = [y; y1] Set_alpha=[Set_alpha single(alfa)] k = k+1; g = - subs(gradien,x,{y(end,1),y(end,2),y(end,3),y(end,4),y(end,5),y(end,6),y(end,7),y(end,8),y(end,9),y(end,10),y(end,11),y(end,12),y(end,13),y(end,14),y(end,15),y(end,16),y(end,17),y(end,18),y(end,19),y (end,20),y(end,21),y(end,22),y(end,23),y(end,24),y(end,25)}) A = subs(a,x,{y(k,1),y(k,2),y(k,3),y(k,4),y(k,5),y(k,6),y(k,7),y(k,8), y(k,9),y(k,10),y(k,11),y(k,12),y(k,13),y(k,14),y(k,15),y(k,16),y(k,17),y(k,18),y(k,19),y(k,20),y(k,21),y(k,22),y(k,23),y(k,24),y(k,2 5)}) nilai = subs(f,x,{y(k,1),y(k,2),y(k,3),y(k,4),y(k,5),y(k,6),y(k,7),y(k,8), y(k,9),y(k,10),y(k,11),y(k,12),y(k,13),y(k,14),y(k,15),y(k,16),y(k,17),y(k,18),y(k,19),y(k,20),y(k,21),y(k,22),y(k,23),y(k,24),y(k,2 5)}) uji = norm(g) else alfa = g*g'/(g*a*g') Set_alpha=[Set_alpha single(alfa)] s =y(k,:)- y(k-1,:) L1 = sqrt((1/set_alpha(k-1)- 1/Set_alpha(k)).^2+4*g*g'/(s*s')) L2 = 1/Set_alpha(k-1)+1/Set_alpha(k) alfa_new = single(2/(l1+l2))

29 19 set_ls=[set_ls;alfa_new] y1 = y(k,:)+ alfa_new*g y = [y; y1] k = k+1; g = - subs(gradien,x,{y(k,1),y(k,2),y(k,3),y(k,4),y(k,5),y(k,6),y(k,7),y (k,8),y(k,9),y(k,10),y(k,11),y(k,12),y(k,13),y(k,14),y(k,15),y(k,1 6),y(k,17),y(k,18),y(k,19),y(k,20),y(k,21),y(k,22),y(k,23),y(k,24),y(k,25)}) A = subs(a,x,{y(k,1),y(k,2),y(k,3),y(k,4),y(k,5),y(k,6),y(k,7),y(k,8), y(k,9),y(k,10),y(k,11),y(k,12),y(k,13),y(k,14),y(k,15),y(k,16),y(k,17),y(k,18),y(k,19),y(k,20),y(k,21),y(k,22),y(k,23),y(k,24),y(k,2 5)}) nilai = subs(f,x,{y(k,1),y(k,2),y(k,3),y(k,4),y(k,5),y(k,6),y(k,7),y(k,8), y(k,9),y(k,10),y(k,11),y(k,12),y(k,13),y(k,14),y(k,15),y(k,16),y(k,17),y(k,18),y(k,19),y(k,20),y(k,21),y(k,22),y(k,23),y(k,24),y(k,2 5)}) uji = norm(g) end end y iterasi = k-1 f toc;

30 20 Lampiran 5 Metode steepest descent untuk dua variabel Contoh: clear clc tic syms x1 x2 lambda f = 32*x1^2-192*x1 + 93*x2^2-186*x ; x = [x1 x2]; x0 = [0,0]; tol = 10^(-6); %Hitung Gradien f(x1,x2); Gradien = jacobian(f,x) S_cek = subs(f,[x1 x2],{x0(1),x0(2)}) %Subtitusi Gradien f(x0,y0) k = 0; N = []; N =[N; x0(1) x0(2)]; S = subs(gradien,[x1 x2],{x0(1),x0(2)}) while norm(s) > tol LGM = lambda*(-s); y0 = x0+lgm; fsub = subs(f,[x1,x2],{y0(1),y0(2)}); difsub = diff(fsub,lambda); Lsub = solve(difsub,lambda); LM = min(single(lsub)); y0 = subs(y0,lambda,lm); k = k+1; N = [N;y0(1) y0(2)]; x0 = y0; S = subs(gradien,[x1 x2],{x0(1),x0(2)}); %L(k) = LM end iterasi = k N toc clf(figure(1)) figure(1) ezcontour(f,[-1,4],[-1,4]) grid on hold on plot(n(:,1),n(:,2),'-ko','linewidth',2,... 'MarkerEdgeColor','k',... 'MarkerFaceColor','g',... 'MarkerSize',3) axis square

31 21 Lampiran 6 Metode steepest descent untuk tiga variabel Contoh: clear clc tic syms x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 lambda f = 6*x1^2 + 24*x1 + 10*x2^2-80*x2 + 7*x3^2 + 28*x ; x = [x1 x2 x3]; x0 = [0,0,0]; tol = 10^(-6); %Hitung Gradien f(x1,x2); Gradien = jacobian(f,x) S_cek = subs(f,x,{x0(1),x0(2),x0(3)}) %Subtitusi Gradien f(x0,y0) k = 0; N = []; N =[N; x0(1) x0(2) x0(3)]; S = subs(gradien,x,{x0(1),x0(2),x0(3)}) while norm(s) > tol LGM = lambda*(-s); y0 = x0+lgm; fsub = subs(f,x,{y0(1),y0(2),y0(3)}); difsub = diff(fsub,lambda); Lsub = solve(difsub,lambda); LM = min(single(lsub)); y0 = subs(y0,lambda,lm); k = k+1; N = [N;y0(1) y0(2) y0(3)]; x0 = y0; S = subs(gradien,x,{x0(1),x0(2),x0(3)}); %L(k) = LM end iterasi = k N toc

32 22 Lampiran 7 Metode steepest descent untuk sepuluh variabel Contoh: clear clc tic syms x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 lambda f = 68*x1^2-408*x1 + 70*x2^ *x2 + 7*x3^2-28*x ; x = [x1 x2 x3 x4 x5 x6 x7 x8 x9 x10]; x0 = [0,0,0,0,0,0,0,0,0,0]; tol = 10^(-6); %Hitung Gradien f(x1,x2); Gradien = jacobian(f,x) S_cek = subs(f,x,{x0(1),x0(2),x0(3)}) %Subtitusi Gradien f(x0,y0) k = 0; N = []; N =[N; x0(1) x0(2) x0(3) x0(4) x0(5) x0(6) x0(7) x0(8) x0(9) x0(10)]; S = subs(gradien,x,{x0(1),x0(2),x0(3),x0(4),x0(5),x0(6),x0(7),x0(8),x0 (9),x0(10)}) while norm(s) > tol LGM = lambda*(-s); y0 = x0+lgm; fsub = subs(f,x,{y0(1),y0(2),y0(3),y0(4),y0(5),y0(6),y0(7),y0(8),y0(9),y0 (10)}); difsub = diff(fsub,lambda); Lsub = solve(difsub,lambda); LM = min(single(lsub)); y0 = subs(y0,lambda,lm); k = k+1; N = [N;y0(1) y0(2) y0(3) y0(4) y0(5) y0(6) y0(7) y0(8) y0(9) y0(10)]; x0 = y0; S = subs(gradien,x,{x0(1),x0(2),x0(3),x0(4),x0(5),x0(6),x0(7),x0(8),x0 (9),x0(10)}); %L(k) = LM end iterasi = k N toc

33 23 Lampiran 8 Metode steepest descent untuk 25 variabel Contoh: clear clc tic syms x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11 x12 x13 x14 x15 x16 x17 x18 x19 x20 x21 x22 x23 x24 x25 lambda f = 38*x1^2-152*x1 + 41*x10^2 + 82*x *x11^ *x *x12^2-56*x12 + 7*x13^2 + 9*x14^2 + 36*x *x15^ *x *x16^ *x *x17^2-310*x17 + 2*x18^2 + 8*x *x19^2-108*x *x2^ *x2 + 10*x20^2-20*x *x21^2-120*x *x22^ *x *x23^2-344*x *x24^2-588*x *x25^2-232*x *x3^2-228*x3 + 40*x4^ *x4 + 40*x5^ *x5 + 52*x6^2-104*x6 + 66*x7^2 + 96*x8^ *x8 + 73*x9^ *x ; x = [x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11 x12 x13 x14 x15 x16 x17 x18 x19 x20 x21 x22 x23 x24 x25]; x0 = [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]; tol = 10^(-6); %Hitung Gradien f(x1,x2); Gradien = jacobian(f,x) S_cek = subs(f,x,{x0(1),x0(2),x0(3),x0(4),x0(5),x0(6),x0(7),x0(8),x0(9),x0 (10),x0(11),x0(12),x0(13),x0(14),x0(15),x0(16),x0(17),x0(18),x0(19 ),x0(20),x0(21),x0(22),x0(23),x0(24),x0(25)}) %Subtitusi Gradien f(x0,y0) k = 0; N = []; N =[N; x0(1) x0(2) x0(3) x0(4) x0(5) x0(6) x0(7) x0(8) x0(9) x0(10) x0(11) x0(12) x0(13) x0(14) x0(15) x0(16) x0(17) x0(18) x0(19) x0(20) x0(21) x0(22) x0(23) x0(24) x0(25)] S = subs(gradien,x,{x0(1),x0(2),x0(3),x0(4),x0(5),x0(6),x0(7),x0(8),x0 (9),x0(10),x0(11),x0(12),x0(13),x0(14),x0(15),x0(16),x0(17),x0(18),x0(19),x0(20),x0(21),x0(22),x0(23),x0(24),x0(25)}) while norm(s) > tol LGM = lambda*(-s); y0 = x0+lgm; fsub = subs(f,x,{y0(1),y0(2),y0(3),y0(4),y0(5),y0(6),y0(7),y0(8),y0(9),y0 (10),y0(11),y0(12),y0(13),y0(14),y0(15),y0(16),y0(17),y0(18),y0(19 ),y0(20),y0(21),y0(22),y0(23),y0(24),y0(25)}); difsub = diff(fsub,lambda); Lsub = solve(difsub,lambda); LM = min(single(lsub)); y0 = subs(y0,lambda,lm); k = k+1; N = [N;y0(1) y0(2) y0(3) y0(4) y0(5) y0(6) y0(7) y0(8) y0(9) y0(10) y0(11) y0(12) y0(13) y0(14) y0(15) y0(16) y0(17) y0(18) y0(19) y0(20) y0(21) y0(22) y0(23) y0(24) y0(25)] x0 = y0; S = subs(gradien,x,{x0(1),x0(2),x0(3),x0(4),x0(5),x0(6),x0(7),x0(8),x0 (9),x0(10),x0(11),x0(12),x0(13),x0(14),x0(15),x0(16),x0(17),x0(18),x0(19),x0(20),x0(21),x0(22),x0(23),x0(24),x0(25)}); end

34 24 N iterasi = k toc

35 25 Lampiran 9 Metode BB untuk dua variabel Contoh: clear; clc; tic; syms x1 x2 f = 26*x1^2-52*x1 + 41*x2^2-328*x x = [x1 x2] y = [0 0] tol = 10^(-6) gradien = jacobian(f,x) g = single(-subs(gradien,{x1,x2},{y(1,1),y(1,2)})) a = jacobian(gradien,x) A = subs(a,{x1 x2},{y(1,1),y(1,2)}) F = subs(f,{x1,x2},{y(1,1),y(1,2)}) set_f = [F] set_g = [g] k=1 while norm(g)>tol if mod(k,2)==1 L = g*g'/(g*a*g') y1 = y(end,:)+l*g y = [y; y1] g = single(-subs(gradien,{x1,x2},{y(end,1),y(end,2)})) F = subs(f,{x1,x2},{y(end,1),y(end,2)}) set_f = [set_f;f] set_g = [set_g;g] else sk =y(end,:)-y(end-1,:) yk =set_g(end,:)-set_g(end-1,:) L = -sk*sk'/(sk*yk') y1 = y(end,:)+ L*set_g(end,:) y = [y; y1] g = single(-subs(gradien,{x1,x2},{y(end,1),y(end,2)})) F = subs(f,{x1,x2},{y(end,1),y(end,2)}) set_f = [set_f;f] set_g = [set_g;g] end k = k+1; end y toc; iterasi = k-1

36 26 Lampiran 10 Metode BB untuk tiga variabel Contoh: clear; clc; tic; syms x1 x2 x3 f = 68*x1^2-408*x1 + 70*x2^ *x2 + 7*x3^2-28*x x = [x1 x2 x3] y = [0 0 0] tol = 10^(-6) gradien = jacobian(f,x) g = single(-subs(gradien,{x1,x2,x3},{y(1,1),y(1,2),y(1,3)})) a = jacobian(gradien,x) A = subs(a,{x1 x2 x3},{y(1,1),y(1,2),y(1,3)}) F = subs(f,{x1,x2,x3},{y(1,1),y(1,2),y(1,3)}) set_f = [F] set_g = [g] k=1 while norm(g)>tol if mod(k,2)==1 L = g*g'/(g*a*g') y1 = y(end,:)+l*g y = [y; y1] g = single(- subs(gradien,{x1,x2,x3},{y(end,1),y(end,2),y(end,3)})) F = subs(f,{x1,x2,x3},{y(end,1),y(end,2),y(end,3)}) set_f = [set_f;f] set_g = [set_g;g] else sk =y(end,:)-y(end-1,:) yk =set_g(end,:)-set_g(end-1,:) L = -sk*sk'/(sk*yk') y1 = y(end,:)+ L*set_g(end,:) y = [y; y1] g = single(- subs(gradien,{x1,x2,x3},{y(end,1),y(end,2),y(end,3)})) F = subs(f,{x1,x2,x3},{y(end,1),y(end,2),y(end,3)}) set_f = [set_f;f] set_g = [set_g;g] end k = k+1; end y toc; iterasi = k-1

37 27 Lampiran 11 Metode BB untuk sepuluh variabel Contoh: clear; clc; tic; syms x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 f = 28*x1^2-56*x1 + 23*x10^ *x *x2^2-136*x2 + 66*x3^ *x3 + 17*x4^ *x4 + 12*x5^2-72*x5 + 50*x6^2 + 96*x7^2-192*x7 + 35*x8^ *x8 + 59*x9^ *x x = [x1 x2 x3 x4 x5 x6 x7 x8 x9 x10] y = [0,0,0,0,0,0,0,0,0,0] tol = 10^(-6) gradien = jacobian(f,x) g = single(-subs(gradien,x,y)) a = jacobian(gradien,x) A = subs(a,x,y) F = subs(f,x,y) set_f = [F] set_g = [g] k=1 while norm(g)>tol if mod(k,2)==1 L = g*g'/(g*a*g') y1 = y(end,:)+l*g y = [y; y1] g = single(- subs(gradien,x,{y(end,1),y(end,2),y(end,3),y(end,4),y(end,5),y(end,6),y(end,7),y(end,8),y(end,9),y(end,10)})) F = subs(f,x,{y(end,1),y(end,2),y(end,3),y(end,4),y(end,5),y(end,6),y( end,7),y(end,8),y(end,9),y(end,10)}) set_f = [set_f;f] set_g = [set_g;g] else sk =y(end,:)-y(end-1,:) yk =set_g(end,:)-set_g(end-1,:) L = -sk*sk'/(sk*yk') y1 = y(end,:)+ L*set_g(end,:) y = [y; y1] g = single(- subs(gradien,x,{y(end,1),y(end,2),y(end,3),y(end,4),y(end,5),y(end,6),y(end,7),y(end,8),y(end,9),y(end,10)})) F = subs(f,x,{y(end,1),y(end,2),y(end,3),y(end,4),y(end,5),y(end,6),y( end,7),y(end,8),y(end,9),y(end,10)}) set_f = [set_f;f] set_g = [set_g;g] end k = k+1; end y toc; iterasi = k-1

38 28 Lampiran 12 Metode BB untuk 25 variabel Contoh: clear; clc; tic; syms x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11 x12 x13 x14 x15 x16 x17 x18 x19 x20 x21 x22 x23 x24 x25 f = 38*x1^2-152*x1 + 41*x10^2 + 82*x *x11^ *x *x12^2-56*x12 + 7*x13^2 + 9*x14^2 + 36*x *x15^ *x *x16^ *x *x17^2-310*x17 + 2*x18^2 + 8*x *x19^2-108*x *x2^ *x2 + 10*x20^2-20*x *x21^2-120*x *x22^ *x *x23^2-344*x *x24^2-588*x *x25^2-232*x *x3^2-228*x3 + 40*x4^ *x4 + 40*x5^ *x5 + 52*x6^2-104*x6 + 66*x7^2 + 96*x8^ *x8 + 73*x9^ *x x = [x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11 x12 x13 x14 x15 x16 x17 x18 x19 x20 x21 x22 x23 x24 x25] y = [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0] tol = 10^(-6) gradien = jacobian(f,x) g = single(-subs(gradien,x,y)) a = jacobian(gradien,x) A = subs(a,x,y) F = subs(f,x,y) set_f = [F] set_g = [g] k=1 while norm(g)>tol if mod(k,2)==1 L = g*g'/(g*a*g') y1 = y(end,:)+l*g y = [y; y1] g = single(- subs(gradien,x,{y(end,1),y(end,2),y(end,3),y(end,4),y(end,5),y(end,6),y(end,7),y(end,8),y(end,9),y(end,10),y(end,11),y(end,12),y(end,13),y(end,14),y(end,15),y(end,16),y(end,17),y(end,18),y(end,19),y (end,20),y(end,21),y(end,22),y(end,23),y(end,24),y(end,25)})) F = subs(f,x,{y(end,1),y(end,2),y(end,3),y(end,4),y(end,5),y(end,6),y( end,7),y(end,8),y(end,9),y(end,10),y(end,11),y(end,12),y(end,13),y (end,14),y(end,15),y(end,16),y(end,17),y(end,18),y(end,19),y(end,2 0),y(end,21),y(end,22),y(end,23),y(end,24),y(end,25)}) set_f = [set_f;f] set_g = [set_g;g] else sk =y(end,:)-y(end-1,:) yk =set_g(end,:)-set_g(end-1,:) L = -sk*sk'/(sk*yk') y1 = y(end,:)+ L*set_g(end,:) y = [y; y1] g = single(- subs(gradien,x,{y(end,1),y(end,2),y(end,3),y(end,4),y(end,5),y(end,6),y(end,7),y(end,8),y(end,9),y(end,10),y(end,11),y(end,12),y(end,13),y(end,14),y(end,15),y(end,16),y(end,17),y(end,18),y(end,19),y (end,20),y(end,21),y(end,22),y(end,23),y(end,24),y(end,25)}))

39 F = subs(f,x,{y(end,1),y(end,2),y(end,3),y(end,4),y(end,5),y(end,6),y( end,7),y(end,8),y(end,9),y(end,10),y(end,11),y(end,12),y(end,13),y (end,14),y(end,15),y(end,16),y(end,17),y(end,18),y(end,19),y(end,2 0),y(end,21),y(end,22),y(end,23),y(end,24),y(end,25)}) set_f = [set_f;f] set_g = [set_g;g] end k = k+1; end y toc; iterasi = k-1 29

40 30 RIWAYAT HIDUP Penulis dilahirkan di Jakarta pada tanggal 21 November 1992 dari ayah H. Chairul Chaniago dan ibu Hj. Radiah Azita. Penulis adalah putra keempat dari empat bersaudara. Tahun 2010 penulis lulus dari SMA Negeri 47 Jakarta dan pada tahun yang sama penulis lulus seleksi masuk Institut Pertanian Bogor (IPB) melalui jalur Undangan Seleksi Masuk IPB (USMI) dan diterima di Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam. Selama mengikuti perkuliahan, penulis pernah aktif sebagai anggota Organisasi Mahasiswa Daerah (OMDA) Jakarta Community. Penulis juga pernah aktif sebagai asisten pengajar di bimbingan belajar Matematika Kumon. Penulis juga aktif sebagai wakil ketua Futsal Kaskus Tangerang Selatan. Selain itu penulis juga pernah aktif di Futsal Matematika, Sepakbola Matematika, Atletik Matematika, Futsal FMIPA, dan Sepakbola TPB 47. Beberapa prestasi yang diraih oleh penulis antara lain ialah Juara 2 Sepakbola Olimpiade Mahasiswa IPB (OMI) tahun 2011, Juara 2 Futsal Sport Competition and Art Festival on Mipa Faculty (SPIRIT) tahun 2012, Juara 2 Sepakbola SPIRIT tahun 2012, Juara 1 Sepakbola SPIRIT tahun 2013, Juara 3 Estafet Pria SPIRIT 2013, dan Juara 2 Estafet Pria SPIRIT tahun 2014.