III PEMBAHASAN. μ v. r 3. μ h μ h r 4 r 5

Transkripsi

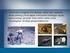
1 III PEMBAHASAN 3.1 Perumusan Model Model yang akan dibahas dalam karya ilmiah ini adalah model SIDRS (Susceptible Infected Dormant Removed Susceptible) dari penularan penyakit malaria dalam suatu populasi. Dalam model ini terdapat tiga populasi yang berbeda yaitu rentan S(t), terinfeksi I(t), dan sembuh R(t). S(t) digunakan untuk mewakili jumlah orang yang belum terinfeksi oleh penyakit pada waktu t, atau mereka yang rentan terhadap penyakit. I(t) menunjukkan jumlah individu yang telah terinfeksi oleh penyakit dan mampu menyebarkan penyakit kepada mereka yang masuk dalam kategori rentan. R(t) digunakan untuk menunjukkan banyaknya orang-orang yang telah terinfeksi dan kemudian pulih dari penyakit. Secara skematik, diagram alur model SIDRS pada penularan penyakit malaria dalam suatu populasi ditunjukkan pada diagram kompartemen di bawah (Gambar 1). Misalkan jumlah populasi pada waktu t dinyatakan dengan N = N h (t). Populasi ini dibagi menjadi empat kelas yaitu populasi rentan S = (t), populasi terinfeksi I = (t), populasi yang dorman D = (t) dan populasi yang sembuh R = (t). Total populasi dinyatakan dengan N h = Individu yang lahir digolongkan ke kelas rentan ( ) dengan laju kelahiran sebesar C. Individu yang berada di kelas rentan akan mengalami kematian dengan laju kematian sebesar, atau masuk ke kelas terinfeksi ( ) karena terjangkit plasmodium falciparum ( ) dan plasmodium vivax ( ). Laju penularan individu dari kelas rentan ( ) ke kelas Dorman ( ) karena terjangkit plasmodium vivax namun tidak terlihat gejala sebesar. Selanjutnya individu yang berada di kelas terinfeksi akan mati dengan laju kematian sebesar, atau sembuh dan masuk ke kelas rentan karena tidak adanya sistem kekebalan tubuh dengan laju atau sembuh dengan laju penyembuhan sebesar sehingga dimasukkan ke kelas sembuh ( ). Kemudian individu di kelas sembuh akan mati dengan laju kematian sebesar, atau menjadi rentan kembali karena sistem kekebalan tubuh dapat hilang sehingga kembali masuk ke kelas rentan dengan laju hilangnya kekebalan tubuh sebesar. Individu yang berada pada kelas Dorman ( ) akan mengalami kematian dengan laju atau sewaktu-waktu dapat kehilangan kekebalan tubuh dan masuk ke kelas terinfeksi dengan laju r 3 atau sembuh namun kehilangan kekebalan tubuh dengan laju r 4 dan menjadi rentan kembali sehingga siap untuk terinfeksi. A µ v μ v r r N h r r αr 2 r 3 μ h μ h μ h μ h r 4 r 5 Gambar 1 Diagram model penularan penyakit malaria pada manusia (yang dibagi dalam empat kelas,,, dan ) dan populasi vektor (yang dibagi dalam dua kelas dan ) Selain itu, pada diagram kompartemen di atas (Gambar 1) terdapat diagram alur yang menjelaskan populasi vektor yang membawa virus malaria. Diagram ini akan menunjukkan 2

2 5 kelas yang berbeda yakni kelas rentan S = (t) yakni ditujukan kepada populasi vektor yang masih steril dari virus malaria dan kelas infeksi I = (t) yaitu ditujukan kepada vektor yang sudah terinfeksi oleh virus malaria. Total populasi vektor dinyatakan dengan N V = +. Vektor yang lahir digolongkan ke dalam populasi rentan ( ) dengan laju kelahiran A. Vektor yang berada di kelas rentan akan mengalami kematian dengan laju μ v, atau masuk ke kelas terinfeksi ( ) dengan laju. Selanjutnya vektor yang berada pada kelas terinfeksi akan mengalami kematian dengan laju μ v. Laju perubahan populasi manusia atau vektor pada suatu kelas ialah jumlah manusia atau vektor yang masuk dalam kelas tersebut dikurangi dengan jumlah manusia atau vektor yang meninggalkan kelas tersebut. Penjelasan di atas dapat dituliskan dalam bentuk persamaan-persamaan berikut: I h A di mana µ h adalah laju kematian populasi µ v adalah laju kematian vektor adalah laju penularan P.falciparum dari nyamuk ke tubuh manusia adalah laju penularan P.vivax dari nyamuk ke tubuh manusia adalah laju penularan P.falciparum dari tubuh manusia ke tubuh nyamuk adalah laju penularan P.vivax dari tubuh manusia ke tubuh nyamuk adalah laju kelahiran populasi N h α adalah total banyaknya populasi adalah rasio dorman manusia yang terinfeksi adalah tingkat dimana seseorang terinfeksi P.falciparum adalah tingkat dimana seseorang terinfeksi P.vivax adalah tingkat dimana manusia tidak aktif namun akan kambuh kembali adalah laju pemulihan manusia yang dorman oleh P.vivax adalah tingkat pemulihan manusia dan akan menjadi manusia yang rentan adalah laju pemulihan manusia dari infeksi P.falciparum adalah laju pemulihan manusia dari infeksi P.vivax (t) adalah banyaknya vektor rentan (t) adalah banyaknya vektor menular Selanjutnya untuk mempermudah dalam menganalisis, normalkan atau sederhanakan persamaan (3.1)-(3.6) dengan mendefinisikan variabel baru:.,,,, akhirnya diperoleh persamaan: t 1 1 (3.7) (3.8) (t) (3.9) (t) + 1 (3.10)

3 6 dengan kondisi s h +i h +d h +r h =1 dan s v +i v =1, dan,, Selanjutnya akan dicari titik tetap untuk persamaan (3.7), (3.8), (3.9), dan (3.10) yang kemudian akan dianalisis kestabilan di sekitar titik tetap tersebut serta dinamika populasinya. 3.2 Titik Tetap Analisis titik tetap pada SPD sering digunakan untuk menentukan suatu solusi konstan. Titik tetap dari persamaan akan diperoleh dengan menetapkan s h(t) = 0, i h(t)= 0, d h(t) = 0 dan i v (t) 0 sehingga diperoleh persamaanpersamaan di bawah ini: 1 1 ) (i) (ii) (iii) (iv) Dengan menyelesaikan keempat persamaan di atas secara serentak akan diperoleh dua titik tetap yaitu titik tetap tanpa penyakit dan titik tetap endemik. 3.3 Titik Tetap tanpa Penyakit Titik tetap tanpa penyakit merupakan kondisi dimana semua individu sehat dan tetap sehat tiap waktu dengan kata lain tidak terdapat penyakit. Titik tetap ini diperoleh ketika banyaknya vektor yang terinfeksi sama dengan nol ( 0) yang didapat dari persamaan (iv), kemudian 0 disubstitusi ke persamaan (i), (ii), dan (iii) maka akan diperoleh nilai,, dan sehingga diperoleh titik tetap dari persamaan-persamaan (3.7), (3.8), (3.9), dan (3.10) yaitu 1,0,0, Titik Tetap Endemik Pada titik tetap endemik akan menghasilkan solusi nontrivial. Di sini titik tetap endemik merupakan kondisi dimana penyakit masih terdapat di dalam populasi vektor dan manusia. Dari persamaan (19), (20), (21), dan (22) diperoleh titik tetap endemik E 1 = (s h *,i h *,d h *,i v *) dengan s h * = i h * = d h * = i v * = 3.5. Analisis Kestabilan Titik Tetap Misalkan persamaan (3.7)-(3.10) dituliskan sebagai berikut : s h(t) = A(s h, i h, d h, i v ) i h(t) = B(s h, i h, d h, i v ) d h(t)= C(s h, i h, d h, i v ) i v(t) = D(s h, i h, d h, i v ) Dari persamaan di atas dapat diperoleh matriks Jacobi. J 0 = = dengan, J = { } untuk I = 1, 2, 3, 4 dan j =1, 2, 3, Kestabilan Titik Tetap tanpa Penyakit Pelinearan pada titik tetap akan menghasilkan matriks Jacobi sebagai berikut: J 0 = dengan μ 0 μ

4 7 0 μ μ Nilai eigen akan diperoleh dengan menyelesaikan persamaan karakteristik det J 0. Persamaan karakteristik dari J adalah (+µ + ) ( t t t ) = 0 sehingga diperoleh salah satu nilai eigen dari J yaitu = µ r dan nilai eigen yang lainnya diperoleh dari akar polinomial dimana, t 2 = 2μ μ t 1 = μ μ μ 2μ r r r r 1 α r r r r r r r r t 0 = μ 1 μ μ r r 1 α r r r r r r r dengan, R 0 = (*) Karena semua parameter yang terlibat positif maka t 0, 0, dan t 0 sehingga kestabilan di titik bergantung pada nilai. Kondisi 0 akan terpenuhi ketika R 0 < 1 maka titik tetap stabil dan sebaliknya kondisi 0 tidak dipenuhi ketika R 0 > 1 maka titik tetap sadel. Kondisi stabil yang dipenuhi ketika R 0 < 1 dimana R 0 merupakan bilangan reproduksi dasar virus dalam populasi, sehingga ketika 1 merupakan kondisi stabil asimtotik karena virus malaria tidak dapat bertahan dalam populasi. Sebaliknya, ketika 1 merupakan kondisi tidak stabil karena virus malaria dapat bertahan dan meningkat dalam populasi. Sehingga menurut kriteria Routh-Hurwitz, titik E 0 stabil Kestabilan Titik Tetap Endemik Pelinearan pada titik tetap akan menghasilkan matriks Jacobi sebagai berikut: J 1 = dengan μ = 0 μ Untuk memperoleh nilai eigen digunakan persamaan karakteristik det J 0. Persamaan karakteristik dari J adalah w w w w 0 dan nilai eigennya diperoleh dari akar polinomial p( λ ) = λ 4 +w 3 λ 3 + w 2 λ 2 + w 1 λ + w 0 = 0. Karena semua parameter yang terlibat positif maka w 0, 0, 0 dan dengan menggunakan software Mathematica dibuktikan w sehingga menurut Routh-Hurwitz, titik stabil. Berikut ini adalah tabel kondisi kestabilan dari kedua titik tetap yang diperoleh. Tabel 1 Kondisi kestabilan titik tetap. Kondisi 1 Simpul stabil Spiral Tidak stabil 1 Sadel Spiral stabil Dari Tabel 1 dapat dilihat bahwa kondisi kestabilan dari titik tetap yang diperoleh saling bertentangan. Ketika titik tetap yang pertama stabil, titik tetap yang kedua tidak stabil dan ketika titik tetap yang pertama tidak stabil, titik tetap yang kedua stabil.

5 8 3.6 Dinamika Populasi Penularan Malaria Untuk mengamati pengaruh masuknya virus malaria ke dalam populasi manusia maupun vektor pada waktu tertentu maka diperlukan kurva bidang solusi yang menunjukkan hubungan banyaknya populasi dengan variabel waktu. Hal ini membutuhkan nilai awal untuk semua parameter dan variabel. Pada proses penggambarannya diambil nilai awal populasi nyamuk atau vektor yang terinfeksi adalah 5% dari total populasi nyamuk. Dalam karya ilmiah ini dianalisis dinamika populasi untuk dua kondisi yaitu 1 di mana populasi akan stabil karena penyakit hilang dari populasi dan 1 di mana penyakit bertahan dalam populasi dan meningkat menjadi wabah Dinamika Populasi untuk 1 Proses penggambarannya dengan menggunakan Mathematica 7 yang dievaluasi ketika ditetapkan μ h = per hari yang sesuai dengan harapan hidup yang sesungguhnya dari 65 tahun untuk manusia, dan μ V = 1/30, yang sesuai dengan harapan hidup dari 30 hari untuk nyamuk Anopheles. Nilainilai = 1/20 per hari dan = 1/14 per hari, sesuai dengan waktu yang dibutuhkan orang manusia yang terinfeksi dengan P. falciparum dan P.vivax untuk meninggalkan kelas terinfeksi dan menjadi rentan kembali, yaitu 20 hari untuk P. falciparum dan 14 hari untuk P. vivax. Nilai-nilai = 1/365 per hari, = 1/(2*365) per hari sesuai dengan waktu yang dibutuhkan orang yang terinfeksi P.vivax untuk meninggalkan kelas dorman, yaitu 1 tahun untuk memasuki kelas yang terinfeksi, dan 2 tahun untuk memasuki kelas rentan. Nilai =1/(3*365) per hari sesuai dengan 3 tahun bagi orang-orang yang terinfeksi dengan P.vivax akan kehilangan sistem imun. Nilai-nilai = 1 / 30 per hari, = 1 / 25 per hari sesuai dengan waktu yang dibutuhkan orang-orang yang terinfeksi P.falciparum dan P.vivax untuk pulih, yakni 30 hari untuk P.falciparum dan 25 hari untuk P.vivax, α = 5. Untuk mendapatkan titik tetap pada keadaan bebas penyakit yang stabil lokal, kita menetapkan masing-masing,,, sama dengan 25, 24, 3 dan 2. Untuk nilai 1 dilakukan analisis untuk tiga kondisi yang berbeda dengan mengubah nilai (laju kematian vektor) dan α (rasio dorman manusia yang terinfeksi) seperti yang ditunjukkan pada tabel berikut. Tabel 2 Simulasi terhadap Ro < 1. μ v a.. Kondisi dipenuhi ketika = 33 dan α = 5. Dengan menggunakan nilai parameter yang telah ditetapkan, diperoleh gambar dinamika populasi Gambar 2 Dinamika populasi,., dan Pada gambar di bawah ini akan dilakukan simulasi populasi S h terhadap waktu t dengan mengubah nilai parameter dan Gambar 3 Dinamika populasi s h terhadap waktu t. = 25 = 24 = 45 = 56 = 60 = 75

6 9 b.. Kondisi dipenuhi ketika rasio jumlah manusia yang terinfeksi virus tetap dengan α = 5 dan laju kematian murni pada vektor dinaikkan menjadi sehingga diperoleh gambar dinamika populasi Gambar 4 Dinamika populasi,., dan Pada gambar di bawah ini akan dilakukan simulasi populasi S h terhadap waktu t dengan mengubah nilai parameter dan. = 25 = 24 = 45 = 56 = 60 = Gambar 5 Dinamika populasi s h terhadap waktu t. c.. Kondisi dipenuhi ketika rasio jumlah manusia yang terinfeksi virus diturunkan menjadi α = 0065 dan laju kematian murni pada vektor tetap 33 sehingga diperoleh gambar dinamika populasi Gambar 6 Dinamika populasi,., dan Pada Gambar 2, Gambar 4 dan Gambar 6 dapat dilihat bahwa kurva S h stabil naik menuju satu, namun pada kurva I h stabil turun menuju ke nol. Hal ini berarti bahwa banyaknya manusia yang terinfeksi akan mengurangi banyaknya manusia yang rentan karena total populasi dianggap konstan. Penurunan pada kurva mengakibatkan penurunan pada kurva I h, hal ini dikarenakan semakin sedikit jumlah nyamuk yang terinfeksi sehingga jumlah manusia yang terinfeksi pun semakin sedikit. Pada kurva D h dapat kita lihat awalnya mengalami sedikit kenaikan dan kemudian stabil turun menuju kepunahan. Hal ini berarti semakin sedikit jumlah nyamuk yang terinfeksi sehingga jumlah manusia yang dorman pun semakin sedikit. Pada Gambar 2, Gambar 4 dan Gambar 6 dilakukan simulasi dengan mengubah nilai parameter dan α. Jika nilai semakin besar maka jumlah manusia yang rentan akan semakin besar dan jika nilai semakin kecil maka akan terjadi penurunan pada jumlah manusia rentan. Jika nilai α semakin besar maka jumlah manusia rentan akan semakin kecil. Gambar 3 dan Gambar 5 menunjukkan hubungan populasi S h Ketiga kurva di atas dibandingkan berdasarkan nilai dan yang berbeda yaitu = 25 dan = 24, = 45 dan = 56, = 60 dan = 75. Dari kurva di atas dapat dilihat bahwa manusia yang rentan mengalami terus penaikan yang tajam menuju satu yang artinya menuju kestabilan. Semakin besar nilai dan, kurva akan mengalami penaikan yang datar, artinya laju manusia yang rentan

7 10 ketika = 45 dan = 56 lebih kecil dari laju manusia rentan ketika = 25 dan = 24 dan laju manusia rentan ketika = 60 dan = 75 lebih kecil dari laju manusia rentan ketika = 25, = 24 dan = 45, = 56. Ini berarti bahwa ketika laju penularan Plasmodium falciparum dan Plasmodium vivax dari nyamuk ke tubuh manusia meningkat dan mengakibatkan banyaknya manusia yang rentan menurun Dinamika Populasi untuk 1 Proses penggambarannya dengan menggunakan Mathematica 7 yang dievaluasi ketika ditetapkan μ h = per hari yang sesuai dengan harapan hidup yang sesungguhnya dari 65 tahun untuk manusia, dan μ V = 1/120, yang sesuai dengan harapan hidup dari 30 hari untuk nyamuk Anopheles. Nilainilai = 1/20 per hari dan = 1/14 per hari, sesuai dengan waktu yang dibutuhkan orang manusia yang terinfeksi dengan P. falciparum dan P.vivax untuk meninggalkan kelas terinfeksi dan menjadi rentan kembali, yaitu 20 hari untuk P. falciparum dan 14 hari untuk P. vivax. Nilai-nilai = 1/365 per hari, = 1/(2*365) per hari sesuai dengan waktu yang dibutuhkan orang yang terinfeksi P.vivax untuk meninggalkan kelas dorman, yaitu 1 tahun untuk memasuki kelas yang terinfeksi, dan 2 tahun untuk memasuki kelas rentan. Nilai =1/(3*365) per hari sesuai dengan 3 tahun bagi orang-orang yang terinfeksi dengan P.vivax akan kehilangan sistem imun. Nilai-nilai = 1 / 30 per hari, = 1 / 25 per hari sesuai dengan waktu yang dibutuhkan orang-orang yang terinfeksi P.falciparum dan P.vivax untuk pulih, yakni 30 hari untuk P.falciparum dan 25 hari untuk P.vivax, α = Untuk mendapatkan titik tetap pada keadaan endemik yang stabil lokal, kita menetapkan masingmasing,,, sama dengan 0.14, 0.1, 0.15 dan 0.1. Untuk nilai 1 dilakukan analisis untuk tiga kondisi yang berbeda dengan mengubah nilai (laju kematian vektor) dan α (rasio dorman manusia yang terinfeksi) seperti yang ditunjukkan pada tabel berikut. Tabel 3 Simulasi terhadap Ro > μ v a.. Kondisi dipenuhi ketika = 084 dan α = Dengan menggunakan nilai parameter yang telah ditetapkan, diperoleh gambar dinamika populasi Gambar 7 Dinamika populasi,., dan Pada gambar di bawah ini akan dilakukan simulasi populasi S h terhadap waktu t dengan mengubah nilai parameter dan = 0.14 = 0.1 = 5 = 2 = 0.56 = 4 Gambar 8 Dinamika populasi s h terhadap waktu t.

8 11 b.. Kondisi dipenuhi ketika = 042 dan α = Dengan menggunakan nilai parameter yang telah ditetapkan, diperoleh gambar dinamika populasi Gambar 9 Dinamika populasi,., dan Pada gambar di bawah ini akan dilakukan simulasi populasi S h terhadap waktu t dengan mengubah nilai parameter dan = 0.14 = 0.1 = 5 = 2 = 0.56 = 4 Gambar 10 Dinamika populasi s h terhadap waktu t. c.. Kondisi dipenuhi ketika = 084 dan α = Dengan menggunakan nilai parameter yang telah ditetapkan, diperoleh gambar dinamika populasi Gambar 11 Dinamika populasi,., dan Gambar 7, Gambar 9 dan Gambar 11 menunjukkan hubungan antara S h, I h, D h, dan Kurva S h terus menurun menjauhi satu dan kurva I h dan D h naik menjauhi nol serta kurva terus naik mendekati satu dan turun kembali namun bertahan pada titik kesetimbangannya, ini menunjukkan bahwa kurva S h, I h, D h, dan menjauhi 1,0,0,0 yang menandakan bahwa titik tetap tanpa penyakit tidak stabil pada 1 sedangkan titik tetap endemik menjadi stabil di mana keempat kurva dapat dilihat menuju kestabilan titik tetap. Ini menunjukkan kondisi ketika penyakit dapat bertahan pada populasi. Gambar 8 dan Gambar 10 merupakan dinamika populasi S h Ketiga kurva tersebut dibandingkan berdasarkan nilai nilai dan yang berbeda yaitu 0.14 dan 0.1, 5 dan 0,22, 0.56 dan 4 Semakin besar nilai, kurva terlihat semakin signifikan ke bawah sebelum kemudian menuju kestabilan. Laju manusia yang rentan ketika 5 dan 2 lebih kecil dari laju manusia rentan ketika 0.14 dan 0.1 dan laju manusia rentan ketika 0.56 dan 4 lebih kecil dari laju manusia rentan ketika 0.14 dan 0.1 dan 5 dan 2. Ini berarti bahwa semakin besar laju penularan Plasmodium falciparum dan Plasmodium vivax dari nyamuk ke tubuh manusia dan maka laju manusia yang rentan semakin kecil. Berikut akan dibandingkan ketika populasi awal nyamuk yang terinfeksi 5% dengan ketika populasi awal nyamuk yang terinfeksi 50%. Ketika populasi awal nyamuk yang terinfeksi

9 12 5% dari total populasi nyamuk 0 5 maka populasi manusia yang rentan adalah 100% dari total populasi manusia 0 1, sehingga kondisi awal lainnya 0 0 dan 0 0. Ketika populasi awal nyamuk yang terinfeksi 50% dari total populasi nyamuk maka populasi manusia yang rentan adalah 100% dari total populasi manusia 0 1 sehingga kondisi awal yang lainnya 0 0 dan 0 0. Berikut akan dibandingkan dinamika populasi dan pengaruhnya terhadap populasi manusia ketika populasi awal vektor yang terinfeksi 5% dan 50% dari total populasi vektor untuk R 0 < 1 dan R 0 > 1. Gambar 12 Dinamika populasi ketika vektor terinfeksi 5% terhadap waktu t untuk R 0 < 1. Gambar 13 Dinamika populasi ketika vektor terinfeksi 50% terhadap waktu t untuk R 0 < Gambar 14 Dinamika populasi ketika vektor terinfeksi 5% terhadap waktu t untuk R 0 > 1. Pada Gambar 12 dan Gambar 13 dapat dilihat bahwa kurva nyamuk yang terinfeksi 5% lebih curam dibandingkan 50%. Hal ini dikarenakan nyamuk yang terinfeksi 50% lebih banyak menginfeksi manusia dibandingkan 5%. Sehingga pada kurva infeksi 50% garis kurva manusia rentan lebih datar dibanding pada kurva infeksi 5% yang cenderung lebih tajam kenaikannya. Dengan kata lain banyaknya nyamuk yang terinfeksi mempengaruhi jumlah manusia yang terinfeksi atau tertular. Semakin Gambar 15 Dinamika populasi ketika vektor terinfeksi 50% terhadap waktu t untuk R 0 > 1. banyak nyamuk yang terinfeksi semakin banyak pula manusia yang terinfeksi. Berbeda halnya pada Gambar 14 dan Gambar 15 dapat dilihat bahwa kurva nyamuk yang terinfeksi 50% lebih curam dibandingkan 5%. Peningkatan banyaknya manusia yang terinfeksi lebih cepat terjadi pada nyamuk yang terinfeksi 50%. Hal ini dikarenakan nyamuk yang terinfeksi 50% lebih banyak menginfeksi manusia dibandingkan 5%.