Fungsi Analitik (Bagian Ketiga)
|
|
|
- Sri Sanjaya
- 7 tahun lalu
- Tontonan:
Transkripsi
1 Fungsi Analitik (Bagian Ketiga) Supama Jurusan Matematika, FMIPA UGM Yogyakarta 55281, INDONESIA (Pertemuan Minggu VI)
2 Outline 1 Persamaan Cauchy-Riemann 2 Persamaan Cauchy-Riemann di Dalam Sistem Koordinat Kutub
3 Persamaan Cauchy-Riemann Pada pertemuan yang lalu telah disebutkan bahwa apabila f (z) ada, maka f kontinu di titik z. Hal itu berarti bahwa syarat perlu agar f (z) ada, adalah kekontinuan f. Pada bagian ini akan ditunjukkan bahwa disamping kekontinuan, ada syarat perlu lain agar f (z) ada. Hal itu dinyatakan di dalam teorema berikut ini.
4 Persamaan Cauchy-Riemann Theorem Diberikan f (z) = u(x, y) + iv(x, y) dan z 0 = x 0 + iy 0 D f. Jika f (z 0 ) ada, maka u dan v mempunyai turunan partial tingkat pertama di titik (x 0, y 0 ) dan di titik tersebut berlaku persamaan Cauchy-Riemann, yaitu u x (x 0, y 0 ) = v y (x 0, y 0 ) dan u y (x 0, y 0 ) = v x (x 0, y 0 ) Selanjutnya, f (z 0 ) = u x (x 0, y 0 ) + iv x (x 0, y 0 )
5 Persamaan Cauchy-Riemann Teorema di atas menjelaskan bahwa persamaan Cauchy-Riemann merupakan syarat perlu agar suatu fungsi f mempunyai turunan di suatu titik, misalkan z 0. Oleh karena itu, persamaan Cauchy-Riemann sering dipakai untuk menentukan kapan suatu fungsi tak mempunyai turunan.
6 Contoh Example Pada Contoh terdahulu telah ditunjukkan bahwa f (z) = z 2 tidak mempunyai turunan di setiap z 0. Dengan menggunakan persamaan Cauchy-Riemann, hal ini dapat ditunjukkan sebagai berikut: Karena f (z) = z 2 = x 2 + y 2 maka u(x, y) = x 2 + y 2 dan v(x, y) = 0, sehingga u x = 2x, u y = 2y, v x = 0, dan v y = 0 Jelas bahwa di titik (x, y) (0, 0), persamaan Cauchy-Riemann tak dipenuhi. Jadi, menurut Teorema di atas f tak mempunyai turunan di setiap z 0.
7 Persamaan Cauchy-Riemann Bagaimana kebalikan Teorema di atas? Apabila di titik (x 0, y 0 ) persamaan Cauchy-Riemann dipenuhi, apakah f (z 0 ) ada? Untuk dapat menjawabnya, perhatikan contoh berikut ini.
8 Contoh Example Diberikan fungsi f dengan x 2 (1+i)+2y 2 (i 1) x+2y, z 0 f (z) = 0, z = 0 Akan ditunjukkan f (0) tidak ada.
9 Perhatikan bahwa f (z) f (0) z = x 2 (1 + i) + 2y 2 (i 1) (x + 2y)(x + iy) Untuk z 0 di sepanjang garis y = 0, f (z) f (0) x 2 (1 + i) lim = lim z 0 z x 0 x 2 = 1 + i sedangkan di sepanjang garis y = x, f (z) f (0) x 2 (3i 1) lim = lim z 0 z y 0 3x 2 (1 + i) = 3i i Karena nilai limit tidak tunggal, maka f (0) tidak ada.
10 Namun demikian, karena x 2 2y 2 x+2y, (x, y) (0, 0) u(x, y) = 0, (x, y) = (0, 0) dan x 2 +2y 2 x+2y, (x, y) (0, 0) v(x, y) = 0, (x, y) = (0, 0)
11 maka u x (0, 0) = u(x, 0) u(0, 0) lim = 1, x 0 x u y (0, 0) = u(0, y) u(0, 0) lim = 1, y 0 y v x (0, 0) = v(x, 0) v(0, 0) lim = 1, dan x 0 x v y (0, 0) = v(0, y) v(0, 0) lim = 1 y 0 y Jadi, persamaan Cauchy-Riemann dipenuhi di (0, 0).
12 Persamaan Cauchy-Riemann Dari Contoh di atas dapat diambil suatu kesimpulan bahwa persamaan Cauchy-Riemann hanyalah merupakan syarat perlu agar suatu fungsi mempunyai turunan, belum merupakan syarat cukup. Artinya, meskipun suatu fungsi memenuhi persamaan Cauchy-Riemann di titik (x 0, y 0 ), maka belum tentu fungsi tersebut mempunyai turunan di titik z 0. Namun demikian, dengan menambahkan syarat-syarat kontinu maka dapat disusun suatu syarat cukup agar suatu fungsi mempunyai turunan di suatu titik. Hal itu dinyatakan di dalam teorema berikut ini.
13 Persamaan Cauchy-Riemann Theorem Diketahui fungsi f (z) = u(x, y) + iv(x, y) terdefinisikan pada suatu persekitaran titik z 0 = x 0 + iy 0. Jika u x, u y, v x, dan v y ada di seluruh persekitaran tersebut dan masing-masing kontinu di titik (x 0, y 0 ), serta di titik tersebut berlaku persamaan Cauchy-Riemann, yaitu u x (x 0, y 0 ) = v y (x 0, y 0 ) dan u y (x 0, y 0 ) = v x (x 0, y 0 ), maka f (z 0 ) ada. Lebih lanjut, f (z 0 ) = u x (x 0, y 0 ) + iv x (x 0, y 0 )
14 Contoh Example Tunjukkan bahwa f (z) = z mempunyai turunan di setiap z, dan tentukan f (z). Penyelesaian: Nyatakan maka diperoleh f (z) = z = (x 2 y 2 + 1) + i2xy u(x, y) = x 2 y dan v(x, y) = 2xy sehingga u x (x, y) = 2x, v x (x, y) = 2y, u y (x, y) = 2y, v y (x, y) = 2x.
15 Mudah dipahami bahwa masing-masing turunan partial u dan v kontinu di setiap (x, y) dan di titik tersebut berlaku persamaan Cauchy-Riemann u x (x, y) = v y (x, y) dan u y (x, y) = v x (x, y) Jadi, menurut Teorema terdahulu f (z) ada dan f (z) = u x (x, y) + iv x (x, y) = 2x + i2y = 2z.
16 Contoh Example Tentukan titik-titik dimana f (z) = x 3 4i(y 1) 3 mempunyai turunan. Selanjutnya, tentukan f ( 2 + 2i) dan f (2 + 3i). Penyelesaian: Turunan partial u dan v berturut-turut adalah u x (x, y) = 3x 2, v x (x, y) = 0, u y (x, y) = 0, v y (x, y) = 12(y 1) 2,
17 dan karena masing-masing berupa polinomial maka u x, u y, v x, dan v y semua kontinu di setiap (x, y). Selanjutnya, karena persamaan Cauchy-Riemann hanya dipenuhi apabila 3x 2 = 12(y 1) 2 x = 2(y 1) atau x = 2(y 1) maka f (z) ada pada A = {z = x + iy : x = 2(y 1) atau x = 2(y 1)}, dan menurut Teorema terdahulu f (z) = 3x 2 = 12(y 1) 2 Akhirnya, karena 2 + 2i A, maka f ( 2 + 2i) = 12, dan karena 2 + 3i / A, maka f (2 + 3i) tidak ada.
18 Pada pertemuan terdahulu telah dijelaskan, apabila z 0 maka z dapat dinyatakan ke dalam bentuk kutub z = r(cos θ + i sin θ) dengan r = z dan θ = arg z. Selain itu, diterangkan pula hubungan antara (x, y) dengan (r, θ), yaitu x = r cos θ dan y = r sin θ (1) Jadi, apabila diberikan fungsi f (z) = u(x, y) + iv(x, y), maka berdasarkan (1), u dan v masing-masing dapat dipandang sebagai fungsi (r, θ).
19 Selanjutnya, menggunakan aturan rantai, diperoleh u r v r = u x x r, = v x x r, Dari persamaan (2) dan (3), diperoleh u θ = u x, dan x θ (2) v θ = v x x θ (3) u r = u x cos θ + u y sin θ, u θ = u x r sin θ + u y r cos θ,(4) v r = v x cos θ + v y sin θ, v θ = v x r sin θ + v y r cos θ (5)
20 Apabila di titik (x 0, y 0 ) = (r 0, θ 0 ) berlaku persamaan Cauchy-Riemann, yaitu u x (x 0, y 0 ) = v y (x 0, y 0 ) dan u y (x 0, y 0 ) = v x (x 0, y 0 ), (6) maka di titik tersebut persamaan (5) akan menjadi v r = u y cos θ + u x sin θ, v θ = u y r sin θ + u x r cos θ (7) Selanjutnya, dari (4) dan (7), diperoleh u r (r 0, θ 0 ) = 1 r v θ(r 0, θ 0 ) dan 1 r u θ(r 0, θ 0 ) = v r (r 0, θ 0 ) (8)
21 Persamaan (8) adalah persamaan Cauchy-Riemann di dalam sistem koordinat kutub. Persamaan pertama di dalam (4) dan (5) bersama-sama dengan (6) menghasilkan u x = u r cos θ + v t sin θ dan v x = u r sin θ + v r cos θ (9) Jadi, apabila f mempunyai turunan di z 0 = r 0 (cos θ 0 + i sin θ 0 ), maka menurut Teorema terdahulu dan persamaan (9) f (z 0 ) = u x (x 0, y 0 ) + iv x (x 0, y 0 ) = {u r (r 0, θ 0 ) cos θ 0 + v r (r 0, θ 0 ) sin θ 0 } +i{ u r (r 0, θ 0 ) sin θ 0 + v r (r 0, θ 0 ) cos θ 0 } = {u r (r 0, θ 0 ) + iv r (r 0, θ 0 )}{cos θ 0 i sin θ 0 }
22 Dengan demikian, apabila Teorema 4 dinyatakan kembali dengan menggunakan koordinat kutub, maka diperoleh Theorem Diketahui fungsi f (z) = u(r, θ) + iv(r, θ) terdefinisikan di suatu persekitaran titik (tak nol) z 0 = r 0 (cos θ 0 + i sin θ 0 ). Jika u dan v mempunyai turunan partial tingkat pertama pada persekitaran tersebut dan masing-masing kontinu di titik (r 0, θ 0 ) serta di titik tersebut berlaku persamaan Cauchy-Riemann, maka f (z 0 ) ada. Lebih lanjut, f (z 0 ) = {u r (r 0, θ 0 ) + iv r (r 0, θ 0 )}{cos θ 0 i sin θ 0 }
23 Contoh Example Tunjukkan bahwa d( 1 z ) dz = 1 z 2. Bukti: Karena z 0, maka dapat dimisalkan z = r(cos θ + i sin θ), sehingga Jadi, dalam hal ini f (z) = 1 z = 1 (cos θ i sin θ) r u(r, θ) = 1 r cos θ dan v(r, θ) = 1 r sin θ
24 Berturut-turut diperoleh u r = 1 r 2 cos θ, u θ = 1 sin θ, r v r = 1 sin θ, r 2 v θ = 1 r cos θ Mudah dilihat bahwa di sebarang titik z = (r, θ) 0, u r, u θ, v r, dan v θ kontinu dan di titik tersebut berlaku persamaan Cauchy-Riemann. Jadi, f (z) ada dan f (z) = (u r + iv r )(cos θ i sin θ) = ( 1 r 2 cos θ + i 1 sin θ)(cos θ i sin θ) r 2 = 1 r 2 {(cos2 θ sin 2 θ) i(sin θ cos θ + cos θ sin θ)} = 1 r 2 (cos 2θ i sin 2θ) = 1 (r(cos θ + i sin θ)) 2 = 1 z 2.
Fungsi Analitik (Bagian Pertama)
 Fungsi Analitik (Bagian Pertama) Supama Jurusan Matematika, FMIPA UGM Yogyakarta 55281, INDONESIA Email:maspomo@yahoo.com, supama@ugm.ac.id (Pertemuan Minggu IV) Outline 1 Fungsi Variabel Kompleks 2 Pemetaan/Transformasi/Mappings
Fungsi Analitik (Bagian Pertama) Supama Jurusan Matematika, FMIPA UGM Yogyakarta 55281, INDONESIA Email:maspomo@yahoo.com, supama@ugm.ac.id (Pertemuan Minggu IV) Outline 1 Fungsi Variabel Kompleks 2 Pemetaan/Transformasi/Mappings
Fungsi Analitik (Bagian Keempat)
 Fungsi Analitik (Bagian Keempat) Supama Jurusan Matematika, FMIPA UGM Yogyakarta 55281, INDONESIA Email:maspomo@yahoo.com, supama@ugm.ac.id (Pertemuan Minggu VII) Outline 1 Fungsi Analitik 2 Fungsi Analitik
Fungsi Analitik (Bagian Keempat) Supama Jurusan Matematika, FMIPA UGM Yogyakarta 55281, INDONESIA Email:maspomo@yahoo.com, supama@ugm.ac.id (Pertemuan Minggu VII) Outline 1 Fungsi Analitik 2 Fungsi Analitik
Fungsi Analitik (Bagian Kedua)
 Fungsi Analitik (Bagian Kedua) Supama Jurusan Matematika, FMIPA UGM Yogyakarta 5528, INDONESIA Email:maspomo@yahoo.com, supama@ugm.ac.id (Pertemuan Minggu V) Outline Limit Menuju Tak Hingga 2 Fungsi Kontinu
Fungsi Analitik (Bagian Kedua) Supama Jurusan Matematika, FMIPA UGM Yogyakarta 5528, INDONESIA Email:maspomo@yahoo.com, supama@ugm.ac.id (Pertemuan Minggu V) Outline Limit Menuju Tak Hingga 2 Fungsi Kontinu
Bab 2 Fungsi Analitik
 Bab 2 Fungsi Analitik Bab 2 ini direncanakan akan disampaikan dalam 4 kali pertemuan, dengan perincian sebagai berikut: () Pertemuan I: Fungsi Kompleks dan Pemetaan. (2) Pertemuan II: Limit Fungsi, Kekontiuan,
Bab 2 Fungsi Analitik Bab 2 ini direncanakan akan disampaikan dalam 4 kali pertemuan, dengan perincian sebagai berikut: () Pertemuan I: Fungsi Kompleks dan Pemetaan. (2) Pertemuan II: Limit Fungsi, Kekontiuan,
Sistem Bilangan Kompleks (Bagian Kedua)
 Sistem Bilangan Kompleks (Bagian Kedua) Supama Jurusan Matematika, FMIPA UGM Yogyakarta 55281, INDONESIA Email:maspomo@yahoo.com, supama@ugm.ac.id (Pertemuan Minggu II) Outline 1 Penyajian Secara Geometris
Sistem Bilangan Kompleks (Bagian Kedua) Supama Jurusan Matematika, FMIPA UGM Yogyakarta 55281, INDONESIA Email:maspomo@yahoo.com, supama@ugm.ac.id (Pertemuan Minggu II) Outline 1 Penyajian Secara Geometris
Sistem Bilangan Kompleks (Bagian Pertama)
 Sistem Bilangan Kompleks (Bagian Pertama) Supama Jurusan Matematika, FMIPA UGM Yogyakarta 55281, INDONESIA Email:maspomo@yahoo.com, supama@ugm.ac.id (Pertemuan Minggu I) Outline 1 Pendahuluan 2 Pengertian
Sistem Bilangan Kompleks (Bagian Pertama) Supama Jurusan Matematika, FMIPA UGM Yogyakarta 55281, INDONESIA Email:maspomo@yahoo.com, supama@ugm.ac.id (Pertemuan Minggu I) Outline 1 Pendahuluan 2 Pengertian
Integral Kompleks (Bagian Kedua)
 Integral Kompleks (Bagian Kedua) Supama Jurusan Matematika, FMIPA UGM Yogyakarta 55281, INDONESIA Email:maspomo@yahoo.com, supama@ugm.ac.id (Pertemuan Minggu XII) Outline 1 Antiderivatif 2 Antiderivatif
Integral Kompleks (Bagian Kedua) Supama Jurusan Matematika, FMIPA UGM Yogyakarta 55281, INDONESIA Email:maspomo@yahoo.com, supama@ugm.ac.id (Pertemuan Minggu XII) Outline 1 Antiderivatif 2 Antiderivatif
Fungsi Elementer (Bagian Kedua)
 Fungsi Elementer (Bagian Kedua) Supama Jurusan Matematika, FMIPA UGM Yogyakarta 55281, INDONESIA Email:maspomo@yahoo.com, supama@ugm.ac.id (Pertemuan Minggu IX) Outline 1 Fungsi Hiperbolik 2 sin(iz) =
Fungsi Elementer (Bagian Kedua) Supama Jurusan Matematika, FMIPA UGM Yogyakarta 55281, INDONESIA Email:maspomo@yahoo.com, supama@ugm.ac.id (Pertemuan Minggu IX) Outline 1 Fungsi Hiperbolik 2 sin(iz) =
MATEMATIKA TEKNIK 1 3 SKS TEKNIK ELEKTRO UDINUS
 MATEMATIKA TEKNIK 1 3 SKS TEKNIK ELEKTRO UDINUS 1 BAB II FUNGSI LIMIT DAN KEKONTINUAN Sebelum dibahas mengenai fungsi kompleks, maka perlu dipelajari konsep-konsep topologi yang akan digunakan pada fungsi
MATEMATIKA TEKNIK 1 3 SKS TEKNIK ELEKTRO UDINUS 1 BAB II FUNGSI LIMIT DAN KEKONTINUAN Sebelum dibahas mengenai fungsi kompleks, maka perlu dipelajari konsep-konsep topologi yang akan digunakan pada fungsi
MODUL ANALISIS VARIABEL KOMPLEKS
 1 MODUL ANALISIS VARIABEL KOMPLEKS Oleh: DIDIK HERMANTO, M. Pd. STKIP PGRI BANGKALAN PRODI S1PENDIDIKAN MATEMATIKA 2014 2 BAB I BILANGAN KOMPLEKS A. PENGERTIAN BILANGAN KOMPLEKS Bilangan kompleks merupakan
1 MODUL ANALISIS VARIABEL KOMPLEKS Oleh: DIDIK HERMANTO, M. Pd. STKIP PGRI BANGKALAN PRODI S1PENDIDIKAN MATEMATIKA 2014 2 BAB I BILANGAN KOMPLEKS A. PENGERTIAN BILANGAN KOMPLEKS Bilangan kompleks merupakan
Bab 1 Sistem Bilangan Kompleks
 Bab 1 Sistem Bilangan Kompleks Bab 1 ini direncanakan akan disampaikan dalam 3 kali pertemuan, dengan perincian sebagai berikut: (1) Pertemuan I: Pengertian bilangan kompleks, Sifat-sifat aljabat, dan
Bab 1 Sistem Bilangan Kompleks Bab 1 ini direncanakan akan disampaikan dalam 3 kali pertemuan, dengan perincian sebagai berikut: (1) Pertemuan I: Pengertian bilangan kompleks, Sifat-sifat aljabat, dan
Kuliah 2: FUNGSI MULTIVARIABEL. Indah Yanti
 Kuliah 2: FUNGSI MULTIVARIABEL Indah Yanti Definisi Dasar Perhatikan fungsi f: A R n R m : x f x n = m = 1 fungsi bernilai riil satu variabel n = 1, m > 1 fungsi bernilai vektor satu variabel n > 1, m
Kuliah 2: FUNGSI MULTIVARIABEL Indah Yanti Definisi Dasar Perhatikan fungsi f: A R n R m : x f x n = m = 1 fungsi bernilai riil satu variabel n = 1, m > 1 fungsi bernilai vektor satu variabel n > 1, m
MATEMATIKA TEKNIK 1 3 SKS TEKNIK ELEKTRO UDINUS
 MATEMATIKA TEKNIK 1 3 SKS TEKNIK ELEKTRO UDINUS 1 BAB III. TURUNAN 3.1 Definisi Turunan Diberikan fungsi f yang didefinisikan pada daerah D dan z D. Jika diketahui bahwa nilai lim zz f(z) z f(z z ) ada,
MATEMATIKA TEKNIK 1 3 SKS TEKNIK ELEKTRO UDINUS 1 BAB III. TURUNAN 3.1 Definisi Turunan Diberikan fungsi f yang didefinisikan pada daerah D dan z D. Jika diketahui bahwa nilai lim zz f(z) z f(z z ) ada,
BUKU DIKTAT ANALISA VARIABEL KOMPLEKS. OLEH : DWI IVAYANA SARI, M.Pd
 BUKU DIKTAT ANALISA VARIABEL KOMPLEKS OLEH : DWI IVAYANA SARI, M.Pd i DAFTAR ISI BAB I. BILANGAN KOMPLEKS... 1 I. Bilangan Kompleks dan Operasinya... 1 II. Operasi Hitung Pada Bilangan Kompleks... 1 III.
BUKU DIKTAT ANALISA VARIABEL KOMPLEKS OLEH : DWI IVAYANA SARI, M.Pd i DAFTAR ISI BAB I. BILANGAN KOMPLEKS... 1 I. Bilangan Kompleks dan Operasinya... 1 II. Operasi Hitung Pada Bilangan Kompleks... 1 III.
ANALISA VARIABEL KOMPLEKS
 ANALISA VARIABEL KOMPLEKS Oleh: BUDI NURACHMAN, IR BAB I BILANGAN KOMPLEKS Dengan memiliki sistem bilangan real R saja kita tidak dapat menelesaikan persamaan +=0. Jadi disamping bilangan real kita perlu
ANALISA VARIABEL KOMPLEKS Oleh: BUDI NURACHMAN, IR BAB I BILANGAN KOMPLEKS Dengan memiliki sistem bilangan real R saja kita tidak dapat menelesaikan persamaan +=0. Jadi disamping bilangan real kita perlu
Sistem Bilangan Kompleks (Bagian Ketiga)
 Sistem Bilaga Kompleks (Bagia Ketiga) Supama Jurusa Matematika, FMIPA UGM Yogyakarta 55281, INDONESIA Email:maspomo@yahoo.com, supama@ugm.ac.id (Pertemua Miggu III) Outlie 1 Akar Bilaga Kompleks 2 Akar
Sistem Bilaga Kompleks (Bagia Ketiga) Supama Jurusa Matematika, FMIPA UGM Yogyakarta 55281, INDONESIA Email:maspomo@yahoo.com, supama@ugm.ac.id (Pertemua Miggu III) Outlie 1 Akar Bilaga Kompleks 2 Akar
Turunan dalam Ruang berdimensi n
 Jurusan Matematika FMIPA Unsyiah October 13, 2011 Andaikan f adalah fungsi dengan peubah x dan y. Jika y dijaga agar tetap konstan, misalkan y = y 0 maka f(x, y 0 ) adalah fungsi dengan peubah tunggal
Jurusan Matematika FMIPA Unsyiah October 13, 2011 Andaikan f adalah fungsi dengan peubah x dan y. Jika y dijaga agar tetap konstan, misalkan y = y 0 maka f(x, y 0 ) adalah fungsi dengan peubah tunggal
Bab II Fungsi Kompleks
 Bab II Fungsi Kompleks Variabel kompleks z secara fisik ditentukan oleh dua variabel lain, yakni bagian realnya x dan bagian imajinernya y, sehingga dituliskan z z(x,y). Oleh sebab itu fungsi variabel
Bab II Fungsi Kompleks Variabel kompleks z secara fisik ditentukan oleh dua variabel lain, yakni bagian realnya x dan bagian imajinernya y, sehingga dituliskan z z(x,y). Oleh sebab itu fungsi variabel
Fungsi Gamma. Pengantar Matematika Teknik Kimia. Muthia Elma
 Fungsi Gamma Pengantar Matematika Teknik Kimia Muthia Elma Fungsi Gamma Defenisi Merupakan salah satu fungsi khusus yang biasanya disajikan dalam pembahasan kalkulus tingkat lanjut Dalam aplikasinya fungsi
Fungsi Gamma Pengantar Matematika Teknik Kimia Muthia Elma Fungsi Gamma Defenisi Merupakan salah satu fungsi khusus yang biasanya disajikan dalam pembahasan kalkulus tingkat lanjut Dalam aplikasinya fungsi
Bab 3 Fungsi Elementer
 Bab 3 Fungsi Elementer Bab 3 ini direncanakan akan disampaikan dalam 3 kali pertemuan, dengan perincian sebagai berikut: (1) Pertemuan I: Fungsi Eksponensial dan sifat-sifatnya, Fungsi Trigonometri. ()
Bab 3 Fungsi Elementer Bab 3 ini direncanakan akan disampaikan dalam 3 kali pertemuan, dengan perincian sebagai berikut: (1) Pertemuan I: Fungsi Eksponensial dan sifat-sifatnya, Fungsi Trigonometri. ()
BAB I BILANGAN KOMPLEKS
 BAB I BILANGAN KOMPLEKS. Pengertian Bilangan Kompleks Pada awal perkuliahan bilangan real (R), kita telah mempelajari bilangan real beserta sifat-sifatnya. Sekarang kita akan melanjutkan perkuliahan pada
BAB I BILANGAN KOMPLEKS. Pengertian Bilangan Kompleks Pada awal perkuliahan bilangan real (R), kita telah mempelajari bilangan real beserta sifat-sifatnya. Sekarang kita akan melanjutkan perkuliahan pada
II. TINJAUAN PUSTAKA. variabel x, sehingga nilai y bergantung pada nilai x. Adanya relasi kebergantungan
 II. TINJAUAN PUSTAKA 2.1 Persamaan Diferensial Differential Equation Fungsi mendeskripsikan bahwa nilai variabel y ditentukan oleh nilai variabel x, sehingga nilai y bergantung pada nilai x. Adanya relasi
II. TINJAUAN PUSTAKA 2.1 Persamaan Diferensial Differential Equation Fungsi mendeskripsikan bahwa nilai variabel y ditentukan oleh nilai variabel x, sehingga nilai y bergantung pada nilai x. Adanya relasi
CATATAN KULIAH FUNGSI KOMPLEKS. oleh Dr. Wuryansari Muharini Kusumawinahyu, M.Si.
 ATATAN KULIAH FUNGSI KOMPLEKS oleh Dr. Wuryansari Muharini Kusumawinahyu, M.Si. PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM 2014 Daftar Isi 1 Bilangan Kompleks
ATATAN KULIAH FUNGSI KOMPLEKS oleh Dr. Wuryansari Muharini Kusumawinahyu, M.Si. PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM 2014 Daftar Isi 1 Bilangan Kompleks
Bilangan Kompleks. Anwar Mutaqin. Program Studi Pendidikan Matematika UNTIRTA
 Bilangan Kompleks Anwar Mutaqin Program Studi Pendidikan Matematika UNTIRTA DAFTAR ISI 1 BILANGAN KOMPLEKS 1 1.1 Eksistensi Bilangan Kompleks.................... 1 1.2 Operasi Aritmatika..........................
Bilangan Kompleks Anwar Mutaqin Program Studi Pendidikan Matematika UNTIRTA DAFTAR ISI 1 BILANGAN KOMPLEKS 1 1.1 Eksistensi Bilangan Kompleks.................... 1 1.2 Operasi Aritmatika..........................
Kalkulus Multivariabel I
 dan Gradien dan Gradien Statistika FMIPA Universitas Islam Indonesia dan Gradien Turunan-turunan parsial f x (x, y) dan f y (x, y) mengukur laju perubahan (dan kemiringan garis singgung) pada arah sejajar
dan Gradien dan Gradien Statistika FMIPA Universitas Islam Indonesia dan Gradien Turunan-turunan parsial f x (x, y) dan f y (x, y) mengukur laju perubahan (dan kemiringan garis singgung) pada arah sejajar
KALKULUS MULTIVARIABEL II
 Definisi KALKULUS MULTIVARIABEL II (Minggu ke-7) Andradi Jurusan Matematika FMIPA UGM Yogyakarta, Indonesia Definisi 1 Definisi 2 ontoh Soal Definisi Integral Garis Fungsi f K R 2 R di Sepanjang Kurva
Definisi KALKULUS MULTIVARIABEL II (Minggu ke-7) Andradi Jurusan Matematika FMIPA UGM Yogyakarta, Indonesia Definisi 1 Definisi 2 ontoh Soal Definisi Integral Garis Fungsi f K R 2 R di Sepanjang Kurva
Kalkulus Multivariabel I
 Keterdiferensialan Statistika FMIPA Universitas Islam Indonesia Fungsi y = f (x) terdiferensialkan di titik x 0 jika f (x 0 + h) f (x 0 ) lim = f (x 0 ) h 0 ( h ) f (x0 + h) f (x 0 ) lim f (x 0 ) = 0 h
Keterdiferensialan Statistika FMIPA Universitas Islam Indonesia Fungsi y = f (x) terdiferensialkan di titik x 0 jika f (x 0 + h) f (x 0 ) lim = f (x 0 ) h 0 ( h ) f (x0 + h) f (x 0 ) lim f (x 0 ) = 0 h
Kalkulus Multivariabel I
 Integral Lipat-Dua dalam Koordinat Kutub Atina Ahdika, S.Si, M.Si Statistika FMIPA Universitas Islam Indonesia 214 / 2 Integral Lipat-Dua dalam Koordinat Kutub Terdapat beberapa kurva tertentu pada suatu
Integral Lipat-Dua dalam Koordinat Kutub Atina Ahdika, S.Si, M.Si Statistika FMIPA Universitas Islam Indonesia 214 / 2 Integral Lipat-Dua dalam Koordinat Kutub Terdapat beberapa kurva tertentu pada suatu
Sistem Bilangan Kompleks
 Modul Sistem Bilangan Kompleks Drs. Hidayat Sardi, M.Si. M PENDAHULUAN odul ini akan membahas bilangan kompleks, sistemnya dan arti geometri dari bilangan kompleks. Untuk itu Anda dianggap telah paham
Modul Sistem Bilangan Kompleks Drs. Hidayat Sardi, M.Si. M PENDAHULUAN odul ini akan membahas bilangan kompleks, sistemnya dan arti geometri dari bilangan kompleks. Untuk itu Anda dianggap telah paham
ANALISIS AKIBAT INTEGRAL CAUCHY Ricky Antonius, Helmi, Yudhi INTISARI
 Buletin Ilmiah Mat. Stat. dan Terapannya (Bimaster) Volume 07, No. 1 (2018), hal 41-46. ANALISIS AKIBAT INTEGRAL CAUCHY Ricky Antonius, Helmi, Yudhi INTISARI Analisis kompleks salah satu cabang matematika
Buletin Ilmiah Mat. Stat. dan Terapannya (Bimaster) Volume 07, No. 1 (2018), hal 41-46. ANALISIS AKIBAT INTEGRAL CAUCHY Ricky Antonius, Helmi, Yudhi INTISARI Analisis kompleks salah satu cabang matematika
Kalkulus Multivariabel I
 Integral Lipat-Dua dalam Koordinat Kutub Statistika FMIPA Universitas Islam Indonesia Terdapat beberapa kurva tertentu pada suatu bidang yang lebih mudah dijelaskan dengan menggunakan koordinat Kutub.
Integral Lipat-Dua dalam Koordinat Kutub Statistika FMIPA Universitas Islam Indonesia Terdapat beberapa kurva tertentu pada suatu bidang yang lebih mudah dijelaskan dengan menggunakan koordinat Kutub.
, maka., maka 1 = 1 +1 <3 1 < = 10 3 =1
 LATIHAN 4.1 1. Tentukan sebuah kondisi pada 1 yang akan menjamin bahwa : a. 1 < Penyelesaian: Kita perhatikan 1 = 1 +1
LATIHAN 4.1 1. Tentukan sebuah kondisi pada 1 yang akan menjamin bahwa : a. 1 < Penyelesaian: Kita perhatikan 1 = 1 +1
Kurikulum 2013 Antiremed Kelas 11 Matematika
 Kurikulum 03 Antiremed Kelas Matematika Turunan Fungsi dan Aplikasinya Soal Doc. Name: K3ARMATPMT060 Version: 05-0 halaman 0. Jika f(x) = 8x maka f (x). (A) 8x (B) 8x (C) 6x (D) 6x (E) 4x 0. Diketahui
Kurikulum 03 Antiremed Kelas Matematika Turunan Fungsi dan Aplikasinya Soal Doc. Name: K3ARMATPMT060 Version: 05-0 halaman 0. Jika f(x) = 8x maka f (x). (A) 8x (B) 8x (C) 6x (D) 6x (E) 4x 0. Diketahui
MATEMATIKA TEKNIK II BILANGAN KOMPLEKS
 MATEMATIKA TEKNIK II BILANGAN KOMPLEKS 2 PENDAHULUAN SISTEM BILANGAN KOMPLEKS REAL IMAJINER RASIONAL IRASIONAL BULAT PECAHAN BULAT NEGATIF CACAH ASLI 0 3 ILUSTRASI Carilah akar-akar persamaan x 2 + 4x
MATEMATIKA TEKNIK II BILANGAN KOMPLEKS 2 PENDAHULUAN SISTEM BILANGAN KOMPLEKS REAL IMAJINER RASIONAL IRASIONAL BULAT PECAHAN BULAT NEGATIF CACAH ASLI 0 3 ILUSTRASI Carilah akar-akar persamaan x 2 + 4x
BAB 3. LIMIT DAN KEKONTINUAN FUNGSI
 BAB. LIMIT DAN KEKONTINUAN FUNGSI A. Definisi it Sebelum mendefinisikan it, terlebih dahulu perhatikan gambar berikut! y L + ε ε ε f() f() - L L f() - L f() L - ε c - δ c c + δ c- -c δ δ Gambar. Dari gambar
BAB. LIMIT DAN KEKONTINUAN FUNGSI A. Definisi it Sebelum mendefinisikan it, terlebih dahulu perhatikan gambar berikut! y L + ε ε ε f() f() - L L f() - L f() L - ε c - δ c c + δ c- -c δ δ Gambar. Dari gambar
TURUNAN FUNGSI. dy (y atau f (x) atau ) dx. Hal-hal yang perlu diingat untuk menyelesaikan turunan fungsi aljabar adalah :
 TURUNAN FUNGSI dy (y atau f () atau ) d Hal-hal yang perlu diingat untuk menyelesaikan turunan fungsi aljabar adalah :. ( a + b) = ( a + ab + b ). ( a b) = ( a ab + b ) m n m n. a = a 4. a m = a m m m.
TURUNAN FUNGSI dy (y atau f () atau ) d Hal-hal yang perlu diingat untuk menyelesaikan turunan fungsi aljabar adalah :. ( a + b) = ( a + ab + b ). ( a b) = ( a ab + b ) m n m n. a = a 4. a m = a m m m.
LIMIT DAN KEKONTINUAN
 LIMIT DAN KEKONTINUAN Departemen Matematika FMIPA IPB Bogor, 2012 (Departemen Matematika FMIPA IPB) Kalkulus I Bogor, 2012 1 / 37 Topik Bahasan 1 Limit Fungsi 2 Hukum Limit 3 Kekontinuan Fungsi (Departemen
LIMIT DAN KEKONTINUAN Departemen Matematika FMIPA IPB Bogor, 2012 (Departemen Matematika FMIPA IPB) Kalkulus I Bogor, 2012 1 / 37 Topik Bahasan 1 Limit Fungsi 2 Hukum Limit 3 Kekontinuan Fungsi (Departemen
BILANGAN KOMPLEKS. Muhammad Hajarul Aswad Pendidikan Matematika Institut Agama Islam Negeri (IAIN) Palopo. Aswad
 4. Kompleks Kojugate (Sekawan) 5. Bentuk Polar & Eksponensial Bilangan Kompleks BILANGAN KOMPLEKS Muhammad Hajarul Aswad Pendidikan Matematika Institut Agama Islam Negeri (IAIN) Palopo 6. Perkalian & Pembagian
4. Kompleks Kojugate (Sekawan) 5. Bentuk Polar & Eksponensial Bilangan Kompleks BILANGAN KOMPLEKS Muhammad Hajarul Aswad Pendidikan Matematika Institut Agama Islam Negeri (IAIN) Palopo 6. Perkalian & Pembagian
Bil Riil. Bil Irasional. Bil Bulat - Bil Bulat 0 Bil Bulat + maka bentuk umum bilangan kompleks adalah
 ANALISIS KOMPLEKS Pendahuluan Bil Kompleks Bil Riil Bil Imaginer (khayal) Bil Rasional Bil Irasional Bil Pecahan Bil Bulat Sistem Bilangan Kompleks Bil Bulat - Bil Bulat 0 Bil Bulat + Untuk maka bentuk
ANALISIS KOMPLEKS Pendahuluan Bil Kompleks Bil Riil Bil Imaginer (khayal) Bil Rasional Bil Irasional Bil Pecahan Bil Bulat Sistem Bilangan Kompleks Bil Bulat - Bil Bulat 0 Bil Bulat + Untuk maka bentuk
LIMIT DAN KONTINUITAS. Arum Handini Primandari
 LIMIT DAN KONTINUITAS Arum Handini Primandari Jika sebuah fungsi yang terdefinisi pada suatu selang buka yang memuat a, kecuali di a sendiri, maka kita katakan bahwa limit f(x) untuk x mendekati a adalah
LIMIT DAN KONTINUITAS Arum Handini Primandari Jika sebuah fungsi yang terdefinisi pada suatu selang buka yang memuat a, kecuali di a sendiri, maka kita katakan bahwa limit f(x) untuk x mendekati a adalah
LUAS DAERAH DI BAWAH KURVA SUATU FUNGSI
 LUAS DAERAH DI BAWAH KURVA SUATU FUNGSI Afrizal, S.Pd, M.PMat Matematika MAN Kampar Juli 2010 Afrizal, S.Pd, M.PMat (Matematika) Luas Daerah Dibawah Kurva Juli 2010 1 / 29 Outline Outline 1 Limit dan Turunan
LUAS DAERAH DI BAWAH KURVA SUATU FUNGSI Afrizal, S.Pd, M.PMat Matematika MAN Kampar Juli 2010 Afrizal, S.Pd, M.PMat (Matematika) Luas Daerah Dibawah Kurva Juli 2010 1 / 29 Outline Outline 1 Limit dan Turunan
4. Deret Fourier pada Interval Sebarang dan Aplikasi
 4. Deret Fourier pada Interval Sebarang dan Aplikasi Kita telah mempelajari bagaimana menguraikan fungsi periodik dengan periode 2 yang terdefinisi pada R sebagai deret Fourier. Deret trigonometri tersebut
4. Deret Fourier pada Interval Sebarang dan Aplikasi Kita telah mempelajari bagaimana menguraikan fungsi periodik dengan periode 2 yang terdefinisi pada R sebagai deret Fourier. Deret trigonometri tersebut
1 Nama Anggota 1:Darul Afandi ( ) Jawaban soal No 40. -
 Universitas Jember Jurusan Matematika - FMIPA MAM 56 Deadline: Wednesday, 9 ; :55 Analisis Kompleks Tugas Template Jawaban Nama Kelompok: Group J Nama Anggota:. Darul Afandi (8). Wahyu Nikmatus Sholihah
Universitas Jember Jurusan Matematika - FMIPA MAM 56 Deadline: Wednesday, 9 ; :55 Analisis Kompleks Tugas Template Jawaban Nama Kelompok: Group J Nama Anggota:. Darul Afandi (8). Wahyu Nikmatus Sholihah
UJI KONVERGENSI. Januari Tim Dosen Kalkulus 2 TPB ITK
 UJI KONVERGENSI Januari 208 Tim Dosen Kalkulus 2 TPB ITK Uji Integral Teorema 3 Jika + k= u k adalah deret dengan suku-suku tak negatif, dan jika ada suatu konstanta M sedemikian hingga s n = u + u 2 +
UJI KONVERGENSI Januari 208 Tim Dosen Kalkulus 2 TPB ITK Uji Integral Teorema 3 Jika + k= u k adalah deret dengan suku-suku tak negatif, dan jika ada suatu konstanta M sedemikian hingga s n = u + u 2 +
Pertemuan ke-10: UJI PERBANDINGAN, DERET BERGANTI TANDA, KEKONVERGENAN MUTLAK, UJI RASIO, DAN UJI AKAR
 Pertemuan ke-0: UJI PERBANDINGAN, DERET BERGANTI TANDA, KEKONVERGENAN MUTLAK, UJI RASIO, DAN UJI AKAR Departemen Matematika FMIPA IPB Bogor, 205 (Departemen Matematika FMIPA IPB) Kalkulus II Bogor, 205
Pertemuan ke-0: UJI PERBANDINGAN, DERET BERGANTI TANDA, KEKONVERGENAN MUTLAK, UJI RASIO, DAN UJI AKAR Departemen Matematika FMIPA IPB Bogor, 205 (Departemen Matematika FMIPA IPB) Kalkulus II Bogor, 205
OPERATOR PADA RUANG BARISAN TERBATAS
 OPERATOR PADA RUANG BARISAN TERBATAS Muslim Ansori *,Tiryono 2, Suharsono S 2,Dorrah Azis 2 Jurusan Matematika FMIPA Universitas Lampung,2 Jln. Soemantri Brodjonegoro No Bandar Lampung email: ansomath@yahoo.com
OPERATOR PADA RUANG BARISAN TERBATAS Muslim Ansori *,Tiryono 2, Suharsono S 2,Dorrah Azis 2 Jurusan Matematika FMIPA Universitas Lampung,2 Jln. Soemantri Brodjonegoro No Bandar Lampung email: ansomath@yahoo.com
BAB 5 PENGGUNAAN TURUNAN
 Diktat Kuliah TK Matematika BAB 5 PENGGUNAAN TURUNAN 5. Nilai Ekstrim Fungsi Nilai ekstrim fungsi adalah nilai yang berkaitan dengan maksimum atau minimum fungsi tersebut. Ada dua jenis nilai ekstrim,
Diktat Kuliah TK Matematika BAB 5 PENGGUNAAN TURUNAN 5. Nilai Ekstrim Fungsi Nilai ekstrim fungsi adalah nilai yang berkaitan dengan maksimum atau minimum fungsi tersebut. Ada dua jenis nilai ekstrim,
PERSAMAAN DIFERENSIAL I PERSAMAAN DIFERENSIAL BIASA
 PERSAMAAN DIFERENSIAL I PERSAMAAN DIFERENSIAL BIASA Persamaan Diferensial Biasa 1. PDB Tingkat Satu (PDB) 1.1. Persamaan diferensial 1.2. Metode pemisahan peubah dan PD koefisien fungsi homogen 1.3. Persamaan
PERSAMAAN DIFERENSIAL I PERSAMAAN DIFERENSIAL BIASA Persamaan Diferensial Biasa 1. PDB Tingkat Satu (PDB) 1.1. Persamaan diferensial 1.2. Metode pemisahan peubah dan PD koefisien fungsi homogen 1.3. Persamaan
TURUNAN. Ide awal turunan: Garis singgung. Kemiringan garis singgung di titik P: lim. Definisi
 TURUNAN Ide awal turunan: Garis singgung Tali busur c +, f c + Garis singgung c, f c c P h c+h f c + f c Kemiringan garis singgung di titik P: f c + f c lim Definisi Turunan fungsi f adalah fungsi lain
TURUNAN Ide awal turunan: Garis singgung Tali busur c +, f c + Garis singgung c, f c c P h c+h f c + f c Kemiringan garis singgung di titik P: f c + f c lim Definisi Turunan fungsi f adalah fungsi lain
Kalkulus Multivariabel I
 dan Fungsi Implisit dan Fungsi Implisit Statistika FMIPA Universitas Islam Indonesia dan Fungsi Implisit Ingat kembali aturan rantai pada fungsi satu peubah! Jika y = f (x(t)), di mana baik f maupun t
dan Fungsi Implisit dan Fungsi Implisit Statistika FMIPA Universitas Islam Indonesia dan Fungsi Implisit Ingat kembali aturan rantai pada fungsi satu peubah! Jika y = f (x(t)), di mana baik f maupun t
LIMIT DAN KEKONTINUAN
 LIMIT DAN KEKONTINUAN 10.1 PENDAHULUAN Sebelum mambahas it fungsi di suatu titik terlebih dahulu kita akan mengamati perilaku suatu fungsi bila peubahnya mendekati suatu bilangan ril c tertentu. Misal
LIMIT DAN KEKONTINUAN 10.1 PENDAHULUAN Sebelum mambahas it fungsi di suatu titik terlebih dahulu kita akan mengamati perilaku suatu fungsi bila peubahnya mendekati suatu bilangan ril c tertentu. Misal
MATEMATIKA TEKNIK 1 3 SKS TEKNIK ELEKTRO UDINUS
 MATEMATIKA TEKNIK 3 SKS TEKNIK ELEKTRO UDINUS BAB I BILANGAN KOMPLEKS Dengan memiliki sistem bilangan real R saja kita tidak dapat menelesaikan persamaan +=0. Jadi disamping bilangan real kita perlu bilangan
MATEMATIKA TEKNIK 3 SKS TEKNIK ELEKTRO UDINUS BAB I BILANGAN KOMPLEKS Dengan memiliki sistem bilangan real R saja kita tidak dapat menelesaikan persamaan +=0. Jadi disamping bilangan real kita perlu bilangan
LIMIT FUNGSI. A. Menentukan Limit Fungsi Aljabar A.1. Limit x a Contoh A.1: Contoh A.2 : 2 4)
 LIMIT FUNGSI A. Menentukan Limit Fungsi Aljabar A.. Limit a Contoh A.:. ( ) 3 Contoh A. : 4 ( )( ) ( ) 4 Latihan. Hitunglah nilai it fungsi-fungsi berikut ini. a. (3 ) b. ( 4) c. ( 4) d. 0 . Hitunglah
LIMIT FUNGSI A. Menentukan Limit Fungsi Aljabar A.. Limit a Contoh A.:. ( ) 3 Contoh A. : 4 ( )( ) ( ) 4 Latihan. Hitunglah nilai it fungsi-fungsi berikut ini. a. (3 ) b. ( 4) c. ( 4) d. 0 . Hitunglah
Bab 16. LIMIT dan TURUNAN. Motivasi. Limit Fungsi. Fungsi Turunan. Matematika SMK, Bab 16: Limit dan Turunan 1/35
 Bab 16 Grafik LIMIT dan TURUNAN Matematika SMK, Bab 16: Limit dan 1/35 Grafik Pada dasarnya, konsep limit dikembangkan untuk mengerjakan perhitungan matematis yang melibatkan: nilai sangat kecil; Matematika
Bab 16 Grafik LIMIT dan TURUNAN Matematika SMK, Bab 16: Limit dan 1/35 Grafik Pada dasarnya, konsep limit dikembangkan untuk mengerjakan perhitungan matematis yang melibatkan: nilai sangat kecil; Matematika
TRANSFORMASI LINIER (Kajian Fungsi antar Ruang Vektor)
 Outline TRANSFORMASI LINIER (Kajian Fungsi antar Ruang Vektor) Drs. Antonius Cahya Prihandoko, M.App.Sc PS. Pendidikan Matematika PS. Sistem Informasi University of Jember Indonesia Jember, 2009 Outline
Outline TRANSFORMASI LINIER (Kajian Fungsi antar Ruang Vektor) Drs. Antonius Cahya Prihandoko, M.App.Sc PS. Pendidikan Matematika PS. Sistem Informasi University of Jember Indonesia Jember, 2009 Outline
Variabel Banyak Bernilai Real 1 / 1
 Fungsi Variabel Banyak Bernilai Real Turunan Parsial dan Turunan Wono Setya Budhi KK Analisis dan Geometri, FMIPA ITB Variabel Banyak Bernilai Real 1 / 1 Turunan Parsial dan Turunan Usaha pertama untuk
Fungsi Variabel Banyak Bernilai Real Turunan Parsial dan Turunan Wono Setya Budhi KK Analisis dan Geometri, FMIPA ITB Variabel Banyak Bernilai Real 1 / 1 Turunan Parsial dan Turunan Usaha pertama untuk
BAB II FUNGSI ANALITIK
 BAB II FUNGSI ANALITIK Sekarang kita akan mempelajari ungsi dari variabel kompleks dan pengembanganna dalam teori dierensial. Sebagai awal dari bab ini kita mulai dari ungsi analitik, ang mana sangat berperan
BAB II FUNGSI ANALITIK Sekarang kita akan mempelajari ungsi dari variabel kompleks dan pengembanganna dalam teori dierensial. Sebagai awal dari bab ini kita mulai dari ungsi analitik, ang mana sangat berperan
: 6. Menggunakan konsep limit fungsi dan turunan fungsi dalam pemecahan masalah.
 Latar belakang penyusunan: Lembar kerja siswa ini kami susun sebagai salah satu sumber belajar untuk siswa agar dapat dipelajari dengan lebih mudah. Kami menyajikan materi dalam modul ini berusaha mengacu
Latar belakang penyusunan: Lembar kerja siswa ini kami susun sebagai salah satu sumber belajar untuk siswa agar dapat dipelajari dengan lebih mudah. Kami menyajikan materi dalam modul ini berusaha mengacu
SIFAT KELENGKAPAN RUANG METRIK BERNILAI KOMPLEKS
 Prosiding Seminar Nasional Matematika dan Pembelajarannya. Jurusan Matematika, FMIPA UM. 13 Agustus 016 SIFAT KELENGKAPAN RUANG METRIK BERNILAI KOMPLEKS Dahliatul Hasanah FMIPA Universitas Negeri Malang
Prosiding Seminar Nasional Matematika dan Pembelajarannya. Jurusan Matematika, FMIPA UM. 13 Agustus 016 SIFAT KELENGKAPAN RUANG METRIK BERNILAI KOMPLEKS Dahliatul Hasanah FMIPA Universitas Negeri Malang
Matematika
 Fungsi dan Kekontinuan D3 Analis Kimia FMIPA Universitas Islam Indonesia Ilustrasi 1 Nol mutlak, yaitu temperatur T C di mana semua aktivitas molekular berhenti, dapat didekati namun tidak pernah dapat
Fungsi dan Kekontinuan D3 Analis Kimia FMIPA Universitas Islam Indonesia Ilustrasi 1 Nol mutlak, yaitu temperatur T C di mana semua aktivitas molekular berhenti, dapat didekati namun tidak pernah dapat
Koordinat Polar (Ch )
 Koordinat Polar (Ch.10.-10.) O (the pole) ray (polar axis) Dalam beberapa hal, lebih mudah mencari lokasi/posisi suatu titik dengan menggunakan koordinat polar. Koordinat polar menunjukkan posisi relatif
Koordinat Polar (Ch.10.-10.) O (the pole) ray (polar axis) Dalam beberapa hal, lebih mudah mencari lokasi/posisi suatu titik dengan menggunakan koordinat polar. Koordinat polar menunjukkan posisi relatif
Matematika I: Turunan. Dadang Amir Hamzah. Dadang Amir Hamzah Matematika I Semester I / 61
 Matematika I: Turunan Dadang Amir Hamzah 2015 Dadang Amir Hamzah Matematika I Semester I 2015 1 / 61 Outline 1 Garis Singgung Dadang Amir Hamzah Matematika I Semester I 2015 2 / 61 Outline 1 Garis Singgung
Matematika I: Turunan Dadang Amir Hamzah 2015 Dadang Amir Hamzah Matematika I Semester I 2015 1 / 61 Outline 1 Garis Singgung Dadang Amir Hamzah Matematika I Semester I 2015 2 / 61 Outline 1 Garis Singgung
Geometri pada Bidang, Vektor
 Prodi Matematika FMIPA Unsyiah September 9, 2011 Melalui pendekatan aljabar, vektor u dinyatakan oleh pasangan berurutan u 1, u 2. Disini digunakan notasi u 1, u 2 bukan (u 1, u 2 ) karena notasi (u 1,
Prodi Matematika FMIPA Unsyiah September 9, 2011 Melalui pendekatan aljabar, vektor u dinyatakan oleh pasangan berurutan u 1, u 2. Disini digunakan notasi u 1, u 2 bukan (u 1, u 2 ) karena notasi (u 1,
Teknik pengintegralan: Integral parsial (Integral by part)
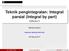 Teknik pengintegralan: Integral parsial (Integral by part) Kalkulus 2 Nanang Susyanto Departemen Matematika FMIPA UGM 06 Februari 2017 NS (FMIPA UGM) Teknik pengintegralan 06/02/2017 1 / 14 Mari mengingat
Teknik pengintegralan: Integral parsial (Integral by part) Kalkulus 2 Nanang Susyanto Departemen Matematika FMIPA UGM 06 Februari 2017 NS (FMIPA UGM) Teknik pengintegralan 06/02/2017 1 / 14 Mari mengingat
Dr. Ramadoni Syahputra Jurusan Teknik Elektro FT UMY
 SISTEM-SISTEM KOORDINAT Dr. Ramadoni Syahputra Jurusan Teknik Elektro FT UMY Sistem Koordinat Kartesian Dalam sistem koordinat Kartesian, terdapat tiga sumbu koordinat yaitu sumbu x, y, dan z. Suatu titik
SISTEM-SISTEM KOORDINAT Dr. Ramadoni Syahputra Jurusan Teknik Elektro FT UMY Sistem Koordinat Kartesian Dalam sistem koordinat Kartesian, terdapat tiga sumbu koordinat yaitu sumbu x, y, dan z. Suatu titik
4. Deret Fourier pada Interval Sebarang dan Aplikasi
 8 Hendra Gunawan 4. Deret Fourier pada Interval Sebarang dan Aplikasi Kita telah mempelajari bagaimana menguraikan fungsi periodik dengan periode 2 yang terdefinisi pada R sebagai deret Fourier. Deret
8 Hendra Gunawan 4. Deret Fourier pada Interval Sebarang dan Aplikasi Kita telah mempelajari bagaimana menguraikan fungsi periodik dengan periode 2 yang terdefinisi pada R sebagai deret Fourier. Deret
KALKULUS BAB II FUNGSI, LIMIT, DAN KEKONTINUAN. DEPARTEMEN TEKNIK KIMIA Universitas Indonesia
 KALKULUS BAB II FUNGSI, LIMIT, DAN KEKONTINUAN DEPARTEMEN TEKNIK KIMIA Universitas Indonesia BAB II. FUNGSI, LIMIT, DAN KEKONTINUAN Fungsi dan Operasi pada Fungsi Beberapa Fungsi Khusus Limit dan Limit
KALKULUS BAB II FUNGSI, LIMIT, DAN KEKONTINUAN DEPARTEMEN TEKNIK KIMIA Universitas Indonesia BAB II. FUNGSI, LIMIT, DAN KEKONTINUAN Fungsi dan Operasi pada Fungsi Beberapa Fungsi Khusus Limit dan Limit
Matematika I : Limit. Dadang Amir Hamzah. Dadang Amir Hamzah Matematika I Semester I / 79
 Matematika I : Limit Dadang Amir Hamzah 2015 Dadang Amir Hamzah Matematika I Semester I 2015 1 / 79 Outline 1 limit Introduction to Limit Rigorous Study of Limits Limit Theorem Limit Involving Trigonometric
Matematika I : Limit Dadang Amir Hamzah 2015 Dadang Amir Hamzah Matematika I Semester I 2015 1 / 79 Outline 1 limit Introduction to Limit Rigorous Study of Limits Limit Theorem Limit Involving Trigonometric
Open Source. Not For Commercial Use
 Ringkasan Kalkulus 2, Untuk dipakai di ITB 1 Limit dan Kekontinuan Misalkan z = f(, y) fungsi dua peubah dan (a, b) R 2. Seperti pada limit fungsi satu peubah, limit fungsi dua peubah bertujuan untuk mengamati
Ringkasan Kalkulus 2, Untuk dipakai di ITB 1 Limit dan Kekontinuan Misalkan z = f(, y) fungsi dua peubah dan (a, b) R 2. Seperti pada limit fungsi satu peubah, limit fungsi dua peubah bertujuan untuk mengamati
KALKULUS MULTIVARIABEL II
 KALKULUS MULTIVARIABEL II Integral Garis Medan Vektor dan (Minggu ke-8) Andradi Jurusan Matematika FMIPA UGM Yogyakarta, Indonesia 1 Integral Garis Medan Vektor 2 Terkait Lintasan Teorema Fundamental untuk
KALKULUS MULTIVARIABEL II Integral Garis Medan Vektor dan (Minggu ke-8) Andradi Jurusan Matematika FMIPA UGM Yogyakarta, Indonesia 1 Integral Garis Medan Vektor 2 Terkait Lintasan Teorema Fundamental untuk
Aplikasi Persamaan Bessel Orde Nol Pada Persamaan Panas Dua dimensi
 JURNAL FOURIER Oktober 2013, Vol. 2, No. 2, 113-123 ISSN 2252-763X Aplikasi Persamaan Bessel Orde Nol Pada Persamaan Panas Dua dimensi Annisa Eki Mulyati dan Sugiyanto Program Studi Matematika Fakultas
JURNAL FOURIER Oktober 2013, Vol. 2, No. 2, 113-123 ISSN 2252-763X Aplikasi Persamaan Bessel Orde Nol Pada Persamaan Panas Dua dimensi Annisa Eki Mulyati dan Sugiyanto Program Studi Matematika Fakultas
Catatan Kuliah MA1123 KALKULUS ELEMENTER I BAB III. TURUNAN
 BAB III. TURUNAN Kecepatan Sesaat dan Gradien Garis Singgung Turunan dan Hubungannya dengan Kekontinuan Aturan Dasar Turunan Notasi Leibniz dan Turunan Tingkat Tinggi Penurunan Implisit Laju yang Berkaitan
BAB III. TURUNAN Kecepatan Sesaat dan Gradien Garis Singgung Turunan dan Hubungannya dengan Kekontinuan Aturan Dasar Turunan Notasi Leibniz dan Turunan Tingkat Tinggi Penurunan Implisit Laju yang Berkaitan
K13 Revisi Antiremed Kelas 11 Matematika
 K3 Revisi Antiremed Kelas Matematika Turunan - Latihan Soal Doc. Name: RK3ARMATWJB080 Version: 06- halaman 0. Jika f(x) = 8x maka f'(x) =. (A) 8x (B) 8x (C) 6x (D) 6x (E) 4x 0. Diketahui y = sin ( π x),
K3 Revisi Antiremed Kelas Matematika Turunan - Latihan Soal Doc. Name: RK3ARMATWJB080 Version: 06- halaman 0. Jika f(x) = 8x maka f'(x) =. (A) 8x (B) 8x (C) 6x (D) 6x (E) 4x 0. Diketahui y = sin ( π x),
TURUNAN DALAM RUANG DIMENSI-n
 TURUNAN DALAM RUANG DIMENSI-n A. Fungsi Dua Variabel atau Lebih Dalam subbab ini, fungsi dua variabel atau lebih dikaji dari tiga sudut pandang: secara verbal (melalui uraian dalam kata-kata) secara aljabar
TURUNAN DALAM RUANG DIMENSI-n A. Fungsi Dua Variabel atau Lebih Dalam subbab ini, fungsi dua variabel atau lebih dikaji dari tiga sudut pandang: secara verbal (melalui uraian dalam kata-kata) secara aljabar
Definisi 4.1 Fungsi f dikatakan kontinu di titik a (continuous at a) jika dan hanya jika ketiga syarat berikut dipenuhi: (1) f(a) ada,
 Lecture 4. Limit B A. Continuity Definisi 4.1 Fungsi f dikatakan kontinu di titik a (continuous at a) jika dan hanya jika ketiga syarat berikut dipenuhi: (1) f(a) ada, (2) lim f(x) ada, (3) lim f(x) =
Lecture 4. Limit B A. Continuity Definisi 4.1 Fungsi f dikatakan kontinu di titik a (continuous at a) jika dan hanya jika ketiga syarat berikut dipenuhi: (1) f(a) ada, (2) lim f(x) ada, (3) lim f(x) =
FUNGSI VARIABEL KOMPLEKS. Oleh: Endang Dedy
 FUNGSI VARIABEL KOMPLEKS Oleh: Endang Dedy Diskusikan! Sistem Bilangan Kompleks 1 Perhatikan definisi berikut: Bilangan kompleks adalah suatu bilangan yang didefinisikan dengan =+iy,, y R dan i 1.Coba
FUNGSI VARIABEL KOMPLEKS Oleh: Endang Dedy Diskusikan! Sistem Bilangan Kompleks 1 Perhatikan definisi berikut: Bilangan kompleks adalah suatu bilangan yang didefinisikan dengan =+iy,, y R dan i 1.Coba
KALKULUS MULTIVARIABEL II
 Pada Bidang Bentuk Vektor dari KALKULUS MULTIVARIABEL II (Minggu ke-9) Andradi Jurusan Matematika FMIPA UGM Yogyakarta, Indonesia Pada Bidang Bentuk Vektor dari 1 Definisi Daerah Sederhana x 2 Pada Bidang
Pada Bidang Bentuk Vektor dari KALKULUS MULTIVARIABEL II (Minggu ke-9) Andradi Jurusan Matematika FMIPA UGM Yogyakarta, Indonesia Pada Bidang Bentuk Vektor dari 1 Definisi Daerah Sederhana x 2 Pada Bidang
Vektor di ruang dimensi 2 dan ruang dimensi 3
 Vektor di ruang dimensi 2 dan ruang dimensi 3 Maulana Malik 1 (maulana.malik@sci.ui.ac.id) 1 Departemen Matematika FMIPA UI Kampus Depok UI, Depok 16424 2014/2015 1/21 maulana.malik@sci.ui.ac.id Vektor
Vektor di ruang dimensi 2 dan ruang dimensi 3 Maulana Malik 1 (maulana.malik@sci.ui.ac.id) 1 Departemen Matematika FMIPA UI Kampus Depok UI, Depok 16424 2014/2015 1/21 maulana.malik@sci.ui.ac.id Vektor
Menggunakan Kurva Ketinggian Memahami Mengapa Fungsi Tidak Memiliki Limit di (0,0)
 oki neswan FMIPA-ITB Menggunakan Kurva Ketinggian Memahami Mengapa Fungsi Tidak Memiliki Limit di (0,0) Contoh 1 Salah satu fungsi digunakan berbagai buku kalkulus sebagai contoh fungsi yang tidak mempunyai
oki neswan FMIPA-ITB Menggunakan Kurva Ketinggian Memahami Mengapa Fungsi Tidak Memiliki Limit di (0,0) Contoh 1 Salah satu fungsi digunakan berbagai buku kalkulus sebagai contoh fungsi yang tidak mempunyai
Matematika Teknik Dasar-2 3 Bilangan Kompleks - 2. Sebrian Mirdeklis Beselly Putra Teknik Pengairan Universitas Brawijaya
 Matematika Teknik Dasar-2 3 Bilangan Kompleks - 2 Sebrian Mirdeklis Beselly Putra Teknik Pengairan Universitas Brawijaya Rekap Dari materi sebelumnya telah dipelajari operasi dalam bilangan kompleks (penambahan,
Matematika Teknik Dasar-2 3 Bilangan Kompleks - 2 Sebrian Mirdeklis Beselly Putra Teknik Pengairan Universitas Brawijaya Rekap Dari materi sebelumnya telah dipelajari operasi dalam bilangan kompleks (penambahan,
L A M P I R A N. M e t o d e p e n y e b a r a n k u e s i o n e r d i l a k u k a n u n t u k m e n g e t a h u i c u s t o m e r i n s i g h t
 L A M P I R A N M e t o d e p e n y e b a r a n k u e s i o n e r d i l a k u k a n u n t u k m e n g e t a h u i c u s t o m e r i n s i g h t d a l a m p e m b u a t a n b i s n i s m o d e l i n i.
L A M P I R A N M e t o d e p e n y e b a r a n k u e s i o n e r d i l a k u k a n u n t u k m e n g e t a h u i c u s t o m e r i n s i g h t d a l a m p e m b u a t a n b i s n i s m o d e l i n i.
DIKTAT KALKULUS MULTIVARIABEL I
 DIKTAT KALKULUS MULTIVARIABEL I Oleh Atina Ahdika, S.Si, M.Si Ayundyah Kesumawati, S.Si, M.Si (Program Studi Statistika) FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS ISLAM INDONESIA 214/215
DIKTAT KALKULUS MULTIVARIABEL I Oleh Atina Ahdika, S.Si, M.Si Ayundyah Kesumawati, S.Si, M.Si (Program Studi Statistika) FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS ISLAM INDONESIA 214/215
Persamaan Diferensial Biasa
 Persamaan Diferensial Biasa Pendahuluan, Persamaan Diferensial Orde-1 Toni Bakhtiar Departemen Matematika IPB September 2012 Toni Bakhtiar (m@thipb) PDB September 2012 1 / 37 Pendahuluan Konsep Dasar Beberapa
Persamaan Diferensial Biasa Pendahuluan, Persamaan Diferensial Orde-1 Toni Bakhtiar Departemen Matematika IPB September 2012 Toni Bakhtiar (m@thipb) PDB September 2012 1 / 37 Pendahuluan Konsep Dasar Beberapa
Deret Binomial. Ayundyah Kesumawati. June 25, Prodi Statistika FMIPA-UII. Ayundyah (UII) Deret Binomial June 25, / 14
 Deret Binomial Ayundyah Kesumawati Prodi Statistika FMIPA-UII June 25, 2015 Ayundyah (UII) Deret Binomial June 25, 2015 1 / 14 Pendahuluan Deret Binomial Kita telah mengenal Rumus Binomial. Untuk bilangan
Deret Binomial Ayundyah Kesumawati Prodi Statistika FMIPA-UII June 25, 2015 Ayundyah (UII) Deret Binomial June 25, 2015 1 / 14 Pendahuluan Deret Binomial Kita telah mengenal Rumus Binomial. Untuk bilangan
Bagian 7 Koordinat Kutub
 Bagian 7 Koordinat Kutub Bagian 7 Koordinat Kutub mempelajari bagaimana teknik integrasi yang telah Anda pelajari dalam bagian sebelumnya dapat digunakan untuk menyelesaikan soal yang berhubungan dengan
Bagian 7 Koordinat Kutub Bagian 7 Koordinat Kutub mempelajari bagaimana teknik integrasi yang telah Anda pelajari dalam bagian sebelumnya dapat digunakan untuk menyelesaikan soal yang berhubungan dengan
BILANGAN KOMPLEKS. Dimana cara penyelesaiannya dengan menggunakan rumus abc, yang menghasilkan dua akar sekaligus ..(4)
 BILANGAN KOMPLEKS A. Pengertian Bilangan Kompleks Himpunan bilangan yang terbesar di dalam matematika adalah himpunan bilangan komleks. Himpunan bilangan riil yang kita pakai sehari-hari merupakan himpunan
BILANGAN KOMPLEKS A. Pengertian Bilangan Kompleks Himpunan bilangan yang terbesar di dalam matematika adalah himpunan bilangan komleks. Himpunan bilangan riil yang kita pakai sehari-hari merupakan himpunan
Ruang Hasil Kali Dalam
 Ruang Hasil Kali Dalam Hasil Kali Dalam dan Norm Wono Setya Budhi KKAG FMIPA ITB v 0.1 Maret 2015 Wono Setya Budhi (KKAG FMIPA ITB) Ruang Hasil Kali Dalam v 0.1 Maret 2015 1 / 12 Pada bab ini kita akan
Ruang Hasil Kali Dalam Hasil Kali Dalam dan Norm Wono Setya Budhi KKAG FMIPA ITB v 0.1 Maret 2015 Wono Setya Budhi (KKAG FMIPA ITB) Ruang Hasil Kali Dalam v 0.1 Maret 2015 1 / 12 Pada bab ini kita akan
Pada integral diatas, dalam mencari penyelesaiannya, pertama diintegralkan terlebih dahulu terhadap x kemudian diintegralkan lagi terhadap y.
 PENDAHULUAN Pada bagian ini akan dibahas perluasan integral tertentu ke bentuk integral lipat dua dari fungsi dua peubah Akan dibahas bentukbentuk integral lipat dalam koordinat kartesius koordinat kutub
PENDAHULUAN Pada bagian ini akan dibahas perluasan integral tertentu ke bentuk integral lipat dua dari fungsi dua peubah Akan dibahas bentukbentuk integral lipat dalam koordinat kartesius koordinat kutub
BAB I DASAR-DASAR PEMODELAN MATEMATIKA DENGAN PERSAMAAN DIFERENSIAL
 BAB I DASAR-DASAR PEMODELAN MATEMATIKA DENGAN PERSAMAAN DIFERENSIAL Pendahuluan Persamaan diferensial adalah persamaan yang memuat diferensial Kita akan membahas tentang Persamaan Diferensial Biasa yaitu
BAB I DASAR-DASAR PEMODELAN MATEMATIKA DENGAN PERSAMAAN DIFERENSIAL Pendahuluan Persamaan diferensial adalah persamaan yang memuat diferensial Kita akan membahas tentang Persamaan Diferensial Biasa yaitu
SRI REDJEKI KALKULUS I
 SRI REDJEKI KALKULUS I KLASIFIKASI BILANGAN RIIL n Bilangan yang paling sederhana adalah bilangan asli : n 1, 2, 3, 4, 5,. n n Bilangan asli membentuk himpunan bagian dari klas himpunan bilangan yang lebih
SRI REDJEKI KALKULUS I KLASIFIKASI BILANGAN RIIL n Bilangan yang paling sederhana adalah bilangan asli : n 1, 2, 3, 4, 5,. n n Bilangan asli membentuk himpunan bagian dari klas himpunan bilangan yang lebih
KONSTRUKSI PERSAMAAN GARIS LURUS MELALUI ANALISIS VEKTORIS DALAM RUANG BERDIMENSI DUA
 Prosiding Seminar Nasional Volume 02, Nomor 1 ISSN 2443-1109 KONSTRUKSI PERSAMAAN GARIS LURUS MELALUI ANALISIS VEKTORIS DALAM RUANG BERDIMENSI DUA Rio Fabrika Pasandaran 1, Patmaniar 2 Universitas Cokroaminoto
Prosiding Seminar Nasional Volume 02, Nomor 1 ISSN 2443-1109 KONSTRUKSI PERSAMAAN GARIS LURUS MELALUI ANALISIS VEKTORIS DALAM RUANG BERDIMENSI DUA Rio Fabrika Pasandaran 1, Patmaniar 2 Universitas Cokroaminoto
BARISAN BILANGAN REAL
 BAB 2 BARISAN BILANGAN REAL Di sekolah menengah barisan diperkenalkan sebagai kumpulan bilangan yang disusun menurut pola tertentu, misalnya barisan aritmatika dan barisan geometri. Biasanya barisan dan
BAB 2 BARISAN BILANGAN REAL Di sekolah menengah barisan diperkenalkan sebagai kumpulan bilangan yang disusun menurut pola tertentu, misalnya barisan aritmatika dan barisan geometri. Biasanya barisan dan
SUSUNAN KOORDINAT BAGIAN-1. Oleh: Fitria Khasanah, M. Pd
 SUSUNAN KOORDINAT BAGIAN-1 Oleh: Fitria Khasanah, M. Pd Program Studi Pendidikan Matematika Fakultas Keguruan dan Ilmu Pendidikan Universitas PGRI Yogyakarta 2010 Letak Suatu Titik pada Garis Lurus O g
SUSUNAN KOORDINAT BAGIAN-1 Oleh: Fitria Khasanah, M. Pd Program Studi Pendidikan Matematika Fakultas Keguruan dan Ilmu Pendidikan Universitas PGRI Yogyakarta 2010 Letak Suatu Titik pada Garis Lurus O g
DIKTAT KALKULUS MULTIVARIABEL I
 DIKTAT KALKULUS MULTIVARIABEL I Oleh Atina Ahdika, S.Si, M.Si Ayundyah Kesumawati, S.Si, M.Si (Program Studi Statistika) FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS ISLAM INDONESIA 214/215
DIKTAT KALKULUS MULTIVARIABEL I Oleh Atina Ahdika, S.Si, M.Si Ayundyah Kesumawati, S.Si, M.Si (Program Studi Statistika) FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS ISLAM INDONESIA 214/215
x Lingkaran satuan, adalah lingkaran berjari-jari satu dan berpusat di titik asal, direprentasikan dengan z = 1.
 Bab. Fungsi Kmpleks BAB. FUNGSI KOMPLEKS Sebelum membahas ungsi kmpleks,berikut ini diberikan beberapa knsep dan istilah ang akan banak digunakan dalam pembahasan selanjutna.. Daerah di bidang kmpleks
Bab. Fungsi Kmpleks BAB. FUNGSI KOMPLEKS Sebelum membahas ungsi kmpleks,berikut ini diberikan beberapa knsep dan istilah ang akan banak digunakan dalam pembahasan selanjutna.. Daerah di bidang kmpleks
Hendra Gunawan. 25 September 2013
 MA1101 MATEMATIKA 1A Hendra Gunawan Semester I, 2013/2014 25 September 2013 Kuis 1 (Kuliah yang Lalu) 1. Selesaikan pertaksamaan 2x 3 < x. 2. Diketahui i f(x) ) = x 2 sin (1/x) untuk x 0 dan f(0) = 0.
MA1101 MATEMATIKA 1A Hendra Gunawan Semester I, 2013/2014 25 September 2013 Kuis 1 (Kuliah yang Lalu) 1. Selesaikan pertaksamaan 2x 3 < x. 2. Diketahui i f(x) ) = x 2 sin (1/x) untuk x 0 dan f(0) = 0.
Kuliah 3: TURUNAN. Indah Yanti
 Kuliah 3: TURUNAN Indah Yanti Turunan Parsial DEFINISI Misalkan fungsi f: A R, dengan A R n adalah himpunan buka. Untuk setiap x = (x 1,..., x n ) A dan setiap j = 1,..., n limit f x j x 1,, x n f x 1,,
Kuliah 3: TURUNAN Indah Yanti Turunan Parsial DEFINISI Misalkan fungsi f: A R, dengan A R n adalah himpunan buka. Untuk setiap x = (x 1,..., x n ) A dan setiap j = 1,..., n limit f x j x 1,, x n f x 1,,
a home base to excellence Mata Kuliah : Kalkulus Kode : TSP 102 Turunan Pertemuan - 3
 a home base to ecellence Mata Kuliah : Kalkulus Kode : TSP 102 SKS : 3 SKS Turunan Pertemuan - 3 a home base to ecellence TIU : Mahasiswa dapat memahami turunan unsi dan aplikasinya TIK : Mahasiswa mampu
a home base to ecellence Mata Kuliah : Kalkulus Kode : TSP 102 SKS : 3 SKS Turunan Pertemuan - 3 a home base to ecellence TIU : Mahasiswa dapat memahami turunan unsi dan aplikasinya TIK : Mahasiswa mampu
Discrete Time Dynamical Systems
 Discrete Time Dynamical Systems Sheet 1 and Solution (1) Tentukan titik tetap dari fungsi berikut. (a) f(x) = x x (b) f(x) = 2x + bx (c) f(x) = e (a) Titik tetap f memenuhi persamaan f(x) = x x x = x x
Discrete Time Dynamical Systems Sheet 1 and Solution (1) Tentukan titik tetap dari fungsi berikut. (a) f(x) = x x (b) f(x) = 2x + bx (c) f(x) = e (a) Titik tetap f memenuhi persamaan f(x) = x x x = x x
UJIAN TENGAH SEMESTER KALKULUS I
 UJIAN TENGAH SEMESTER KALKULUS I Senin, 9 April 001 Waktu :,5 jam 1. Tentukan dy dx jika (a) y 5x (x + 1) (b) y cos x.. Dengan menggunakan de nisi turunan, tentukan f 0 (x) untuk fungsi f berikut f (x)
UJIAN TENGAH SEMESTER KALKULUS I Senin, 9 April 001 Waktu :,5 jam 1. Tentukan dy dx jika (a) y 5x (x + 1) (b) y cos x.. Dengan menggunakan de nisi turunan, tentukan f 0 (x) untuk fungsi f berikut f (x)
