Metode Numerik Roosenberg

Transkripsi

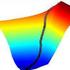
1 Metode Numerik Roosenberg Rukmono Budi Utomo, M.Sc. Prodi S1 Pendikan Matematika UMT May 4, 2016

2 Metode Numerik Roosenberg Metode Numerik Roosenberg Algoritma Roosenberg Contoh Penyelesaian Masalah Optimisasi dengan Roosenberg Penyelesaian Dengan Analitik Biografi Author

3 Metode Numerik Roosenberg Metode Numerik Roosenberg merupakan salah satu metode numerik yang dapat digunakan untuk menyelesaikan masalah optimisasi, yakni menentukan nilai X = {x 1, x 2 } R 2 yang meminimalkan atau memaksimalkan Z = F (X )

4 Metode Numerik Roosenberg Metode Numerik Roosenberg merupakan salah satu metode numerik yang dapat digunakan untuk menyelesaikan masalah optimisasi, yakni menentukan nilai X = {x 1, x 2 } R 2 yang meminimalkan atau memaksimalkan Z = F (X ) Metode untuk menyelesaikan masalah optimisasi ini juga dapat menggunakan metode aksial,stepest Descent,Hook and Jeeve, Arah Konjugasi atau atau Newton 2

5 Metode Numerik Roosenberg Metode Numerik Roosenberg merupakan salah satu metode numerik yang dapat digunakan untuk menyelesaikan masalah optimisasi, yakni menentukan nilai X = {x 1, x 2 } R 2 yang meminimalkan atau memaksimalkan Z = F (X ) Metode untuk menyelesaikan masalah optimisasi ini juga dapat menggunakan metode aksial,stepest Descent,Hook and Jeeve, Arah Konjugasi atau atau Newton 2 Tentu saja setiap metode numerik memilki algoritma yang berbeda dengan kecepatan tingkat efektivitas pencarian O (Big Oh)yang berbeda serta tingkat kesalahan yang berbeda pula

6 Algoritma Roosenberg Algoritma Algoritma Roosenberg dapat dijelaskan sebagai berikut: Diberikan fungsi Z = F (x 1, x 2 ) dan akan ditentukan nilai X = {x 1.x 2 } yang meminimalkan atau memaksimumkan nilai Z = F (x 1, x 2 ) tersebut

7 Algoritma Roosenberg Algoritma Algoritma Roosenberg dapat dijelaskan sebagai berikut: Diberikan fungsi Z = F (x 1, x 2 ) dan akan ditentukan nilai X = {x 1.x 2 } yang meminimalkan atau memaksimumkan nilai Z = F (x 1, x 2 ) tersebut

8 Algoritma Roosenberg Algoritma Algoritma Roosenberg dapat dijelaskan sebagai berikut: Diberikan fungsi Z = F (x 1, x 2 ) dan akan ditentukan nilai X = {x 1.x 2 } yang meminimalkan atau memaksimumkan nilai Z = F (x 1, x 2 ) tersebut Ambil sembarang titik awal X 1 = {x 1, x 2 } R 2

9 Algoritma Roosenberg Algoritma Algoritma Roosenberg dapat dijelaskan sebagai berikut: Diberikan fungsi Z = F (x 1, x 2 ) dan akan ditentukan nilai X = {x 1.x 2 } yang meminimalkan atau memaksimumkan nilai Z = F (x 1, x 2 ) tersebut Ambil sembarang titik awal X 1 = {x 1, x 2 } R 2 Tetapkan ɛ > 0 suatu konstanta postif yang menunjukkan kesalahan yang ditoleransi

10 Algoritma Roosenberg Algoritma Algoritma Roosenberg dapat dijelaskan sebagai berikut: Diberikan fungsi Z = F (x 1, x 2 ) dan akan ditentukan nilai X = {x 1.x 2 } yang meminimalkan atau memaksimumkan nilai Z = F (x 1, x 2 ) tersebut Ambil sembarang titik awal X 1 = {x 1, x 2 } R 2 Tetapkan ɛ > 0 suatu konstanta postif yang menunjukkan kesalahan yang ditoleransi Tentukan arah pencarian direction d 1 = (1, 0) dan d 2 = (0, 1)

11 Algoritma Roosenberg Algoritma Algoritma Roosenberg dapat dijelaskan sebagai berikut: Diberikan fungsi Z = F (x 1, x 2 ) dan akan ditentukan nilai X = {x 1.x 2 } yang meminimalkan atau memaksimumkan nilai Z = F (x 1, x 2 ) tersebut Ambil sembarang titik awal X 1 = {x 1, x 2 } R 2 Tetapkan ɛ > 0 suatu konstanta postif yang menunjukkan kesalahan yang ditoleransi Tentukan arah pencarian direction d 1 = (1, 0) dan d 2 = (0, 1) Cari λ k dengan cara λ k = minz(x k + λ k d k )

12 Algoritma Roosenberg Algoritma Algoritma Roosenberg dapat dijelaskan sebagai berikut: Diberikan fungsi Z = F (x 1, x 2 ) dan akan ditentukan nilai X = {x 1.x 2 } yang meminimalkan atau memaksimumkan nilai Z = F (x 1, x 2 ) tersebut Ambil sembarang titik awal X 1 = {x 1, x 2 } R 2 Tetapkan ɛ > 0 suatu konstanta postif yang menunjukkan kesalahan yang ditoleransi Tentukan arah pencarian direction d 1 = (1, 0) dan d 2 = (0, 1) Cari λ k dengan cara λ k = minz(x k + λ k d k ) nilai X k+1 ditentukan dengan X k+1 = X k + d k

13 Algoritma Roosenberg Algoritma Algoritma Roosenberg dapat dijelaskan sebagai berikut: Diberikan fungsi Z = F (x 1, x 2 ) dan akan ditentukan nilai X = {x 1.x 2 } yang meminimalkan atau memaksimumkan nilai Z = F (x 1, x 2 ) tersebut Ambil sembarang titik awal X 1 = {x 1, x 2 } R 2 Tetapkan ɛ > 0 suatu konstanta postif yang menunjukkan kesalahan yang ditoleransi Tentukan arah pencarian direction d 1 = (1, 0) dan d 2 = (0, 1) Cari λ k dengan cara λ k = minz(x k + λ k d k ) nilai X k+1 ditentukan dengan X k+1 = X k + d k Iterasi stop ketika norm X k+1 X k < ɛ

14 lanjutan Perlu diperhatikan bahwa tidak seperti metode aksial dengan d k = (1, 0) untuk arah ganjil dan d 2k = (0, 1) untuk arah genap, dalam metode Roosenberg ini d 2k+1 = untuk k ganjil dan d 2k = b k b k untuk k genap b k b k

15 lanjutan Perlu diperhatikan bahwa tidak seperti metode aksial dengan d k = (1, 0) untuk arah ganjil dan d 2k = (0, 1) untuk arah genap, dalam metode Roosenberg ini d 2k+1 = untuk k ganjil dan d 2k = Dengan b k = λ k d k + λ k+1 d k+1 b k b k untuk k genap b k b k

16 Contoh Penggunaan Roosenberg Tentukan nilai X = {x 1, x 2 } yang meminimalkan Z(x 1, x 2 ) = 2x x 2 2 3x 1 x 2 dengan menggunakan metode Roosenberg dengan toleransi kesalahan ɛ = 0.01 Solusi Ambil sembarang titik awal X 1 = {0, 1} R 2

17 Contoh Penggunaan Roosenberg Tentukan nilai X = {x 1, x 2 } yang meminimalkan Z(x 1, x 2 ) = 2x x 2 2 3x 1 x 2 dengan menggunakan metode Roosenberg dengan toleransi kesalahan ɛ = 0.01 Solusi Ambil sembarang titik awal X 1 = {0, 1} R 2 Arah pencarian d 1 = (1, 0) dan d 2 = (0, 1) serta ɛ = 0.01

18 Contoh Penggunaan Roosenberg Tentukan nilai X = {x 1, x 2 } yang meminimalkan Z(x 1, x 2 ) = 2x x 2 2 3x 1 x 2 dengan menggunakan metode Roosenberg dengan toleransi kesalahan ɛ = 0.01 Solusi Ambil sembarang titik awal X 1 = {0, 1} R 2 Arah pencarian d 1 = (1, 0) dan d 2 = (0, 1) serta ɛ = 0.01 nilai λ 1 dapat dicari sebagai berikut λ 1 = min Z ( X 1 + λ 1 d 1 ) = min Z ((0, 1) + λ 1 (1, 0)) = min Z (λ 1, 1)

19 lanjutan Derivatifkan Z(0, 1) dan sama dengankan nol, sehingga diperoleh λ 1 = 3 4. Berdasarkan hal tersebut ( ) 3 X 2 = X 1 + λ 1 d 1 = 4, 1

20 lanjutan Derivatifkan Z(0, 1) dan sama dengankan nol, sehingga diperoleh λ 1 = 3 4. Berdasarkan hal tersebut ( ) 3 X 2 = X 1 + λ 1 d 1 = 4, 1 karena norm X 2 X 1 = 3 4 dilanjutkan > 0.01 = ɛ,maka iterasi

21 lanjutan Derivatifkan Z(0, 1) dan sama dengankan nol, sehingga diperoleh λ 1 = 3 4. Berdasarkan hal tersebut ( ) 3 X 2 = X 1 + λ 1 d 1 = 4, 1 karena norm X 2 X 1 = 3 4 > 0.01 = ɛ,maka iterasi dilanjutkan Dengan cara serupa diperoleh λ 2 = 1 2 dan X 3 = { 3 4, 1 2 } dengan norm X 3 X 2 = 1 2 > 0.01 = ɛ, jadi iterasi dilanjutkan

22 lanjutan Untuk mencari X 4, diperlukan d 3 dan nilai d 3 disini adalah 0 (Dapat dicek dengan d 2k+1 = b k b k ) dan apabila dicari nilai d 4 diperoleh nilai d 4 = ( , 13 ). Hal ini dapat dicek dengan d 2k = b k b k

23 lanjutan Untuk mencari X 4, diperlukan d 3 dan nilai d 3 disini adalah 0 (Dapat dicek dengan d 2k+1 = b k b k ) dan apabila dicari nilai d 4 diperoleh nilai d 4 = ( , 13 ). Hal ini dapat dicek dengan d 2k = b k b k Dengan demikian nilai X 4 adalah X 4 = ( 3 4, 1 2 )

24 lanjutan Untuk mencari X 4, diperlukan d 3 dan nilai d 3 disini adalah 0 (Dapat dicek dengan d 2k+1 = b k b k ) dan apabila dicari nilai d 4 diperoleh nilai d 4 = ( , 13 ). Hal ini dapat dicek dengan d 2k = b k b k Dengan demikian nilai X 4 adalah X 4 = ( 3 4, 1 2 ) Dengan norm X 4 X 3 = 0 < 0.01 = ɛ, iterasi stop.

25 lanjutan Untuk mencari X 4, diperlukan d 3 dan nilai d 3 disini adalah 0 (Dapat dicek dengan d 2k+1 = b k b k ) dan apabila dicari nilai d 4 diperoleh nilai d 4 = ( , 13 ). Hal ini dapat dicek dengan d 2k = b k b k Dengan demikian nilai X 4 adalah X 4 = ( 3 4, 1 2 ) Dengan norm X 4 X 3 = 0 < 0.01 = ɛ, iterasi stop. Dengan demikian iterasi berhenti, sehingga nilai X yang meminimalkan fungsi Z dalam soal ini adalah X 4 = { 3 4, 1 2 }

26 lanjutan Untuk mencari X 4, diperlukan d 3 dan nilai d 3 disini adalah 0 (Dapat dicek dengan d 2k+1 = b k b k ) dan apabila dicari nilai d 4 diperoleh nilai d 4 = ( , 13 ). Hal ini dapat dicek dengan d 2k = b k b k Dengan demikian nilai X 4 adalah X 4 = ( 3 4, 1 2 ) Dengan norm X 4 X 3 = 0 < 0.01 = ɛ, iterasi stop. Dengan demikian iterasi berhenti, sehingga nilai X yang meminimalkan fungsi Z dalam soal ini adalah X 4 = { 3 4, 1 2 } Catatan Perlu diperhatikan bahwa, karena norm X 4 X 3 = 0 < 0.01 = ɛhal ini mengindikasikan kesalahan perhitungan numerik eror ɛ = 0 yang mengindikasikan bahwa solusi numerik juga merupakan solusi analitiknya.

27 Penyelesaian Dengan Analitik Diketahu Z(x 1, x 2 ) = 2x x 2 2 3x 1 x 2 dan akan ditentukan nilai X = {x 1, x 2 } yang meminimumkan fungsi Z = F (x 1, x 2 ) tersebut

28 Penyelesaian Dengan Analitik Diketahu Z(x 1, x 2 ) = 2x x 2 2 3x 1 x 2 dan akan ditentukan nilai X = {x 1, x 2 } yang meminimumkan fungsi Z = F (x 1, x 2 ) tersebut Solusi Z x 1 = 4x 1 3; Z x 2 = 2x 2 1

29 Penyelesaian Dengan Analitik Diketahu Z(x 1, x 2 ) = 2x x 2 2 3x 1 x 2 dan akan ditentukan nilai X = {x 1, x 2 } yang meminimumkan fungsi Z = F (x 1, x 2 ) tersebut Solusi Z = 4x 1 3; Z = 2x 2 1 x 1 x 2 Karena Z X 1 = 0 dan juga kerena Z X 2 = 0, maka diperoleh x 1 = 3 4 dan x 2 = 1 2

30 Penyelesaian Dengan Analitik Diketahu Z(x 1, x 2 ) = 2x x 2 2 3x 1 x 2 dan akan ditentukan nilai X = {x 1, x 2 } yang meminimumkan fungsi Z = F (x 1, x 2 ) tersebut Solusi Karena Z X 1 dan x 2 = 1 2 lebih lanjut Z = 4x 1 3; Z = 2x 2 1 x 1 x 2 = 0 dan juga kerena Z X 2 = 0, maka diperoleh x 1 = Z x 1 2 = 4; 2 Z x 2 2 = 2

31 Penyelesaian Dengan Analitik Diketahu Z(x 1, x 2 ) = 2x x 2 2 3x 1 x 2 dan akan ditentukan nilai X = {x 1, x 2 } yang meminimumkan fungsi Z = F (x 1, x 2 ) tersebut Solusi Karena Z X 1 dan x 2 = 1 2 lebih lanjut Z = 4x 1 3; Z = 2x 2 1 x 1 x 2 = 0 dan juga kerena Z X 2 = 0, maka diperoleh x 1 = Z x 1 2 = 4; 2 Z x 2 2 = 2

32 lanjutan karena 2 Z = 4 > 0 dan 2 Z ( 2 Z ) ( 2 Z x1 2 x1 2 x1 2 x 1 x 2 ) 2 = 8 > 0, maka terbukti bahwa titik { 3 4, 1 2 } merupakan titik yang meminimumkan fungsi Z = {x 1, x 2 } dalam soal ini. Q.E.D

33 Sekilas Tentang Penulis Rukmono Budi Utomo lahir di Tangerang, 26 September 1991 dan merupakan anak ke-2 dari 2 bersaudara. Penulis menamatkan sekolah antara lain: S1 Matematika Undip (2013) S2 Matematika UGM (2015) Saat ini penulis merupakan dosen di prodi pendidikan matematika Universitas Muhammadiyah Tangerang (UMT) sekaligus mahasiswa program Doktoral Matematika ITB. Kontak : , [email protected]