(b) M merupakan nilai minimum (mutlak) f apabila M f(x) x I..
|
|
|
- Yenny Pranoto
- 6 tahun lalu
- Tontonan:
Transkripsi
1 3. Aplikasi Turunan a. Nilai ekstrim Bagian ini dimulai dengan pengertian nilai ekstrim suatu fungsi yang mencakup nilai ekstrim maksimum dan nilai ekstrim minimum. Definisi 3. Diberikan fungsi f: I R, I R, dan M = f(c) untuk suatu c I. (a) M merupakan nilai maksimum (mutlak) f apabila M f(x) x I. (b) M merupakan nilai minimum (mutlak) f apabila M f(x) x I.. (c) Nilai maksimum dan minimum suatu fungsi disebut nilai ekstrim (mutlak) fungsi tersebut. Contoh 9. Dipunyai fungsi f: R R, f(x) = (x 1) 2. Sketsa grafik f dapat dilihat pada gambar berikut. Y f O (1,0) Gambar 3. Grafik f(x) = (x 1) 2. Intuisi: f(1) = 0 merupakan nilai minimum f(x). Bukti: Ambil sembarang x R. Jelas (x 1) 2 0 f(x) f(1). Jadi f(1) f(x) x R. Jadi f(1) = 0 merupakan nilai minimum f. Contoh 10. Dipunyai fungsi f: R R, f(x) = (x 2) Sketsa grafik f dapat dilihat pada gambar berikut.
2 Y (2,1) O (1,0) (3,0) (0, 3) f Gambar 4. Grafik f(x) = (x 2) Intuisi: f(2) = 1 merupakan nilai maksimum f. Bukti: Ambil sembarang x R. Jelas (x 2) 2 0 (x 2) f(x) f(2). Jadi f(2) f(x) x R. Jadi f(2) = 1 merupakan nilai maksimum f. Sekarang perhatikan fungsi f: R R, f(x) = { x2, x 1 2 x, x > 1. Sketsa grafik f dapat dilihat pada gambar berikut. Y 1 O 1 2 Gambar 5. Grafik f dengan f(x) = { x2, x 1 2 x, x > 1. Pada Gambar 5 terlihat bahwa terdapat suatu selang sehingga f(0) = 0 merupakan nilai minimum f akan tetapi masih ada nilai f(x) yang kurang dari 0. Demikian juga terdapat suatu selang sehingga nilai f(1) = 1 merupakan nilai maksimum f akan tetapi masih ada nilai f(x) yang lebih dari 1. Nilai f(0) = 0 disebut nilai minimum relatif f dan nilai f(1) = 1 disebut nilai maksimum relatif f. Berdasarkan f 2
3 kenyataan ini dapat didefinisikan konsep tentang nilai ekstrim relatif suatu fungsi sebagai berikut. Definisi 4. Dipunyai fungsi f: I R, I R. (a) Jika terdapat suatu selang buka D I yang memuat c sehingga berlaku f(c) f(x) x D, maka f(c) disebut nilai maksimum relatif f. (b) Jika terdapat suatu selang buka D I yang memuat c sehingga berlaku f(c) f(x) x D, maka f(c) disebut nilai minimum relatif f. Contoh 11. Dari fungsi f pada Gambar 5, tunjukkan bahwa (a) f(0) = 0 merupakan nilai minimum relatif f dan (b) f(1) = 1 merupakan nilai maksimum relatif f. Bukti: Dipunyai f: R R, f(x) = { x2, x 1 2 x, x > 1. (a) Pilih δ = 1 4. Bangun D = (0 1 4, ) = ( 1 4, 1 4 ). Ambil sembarang x D. Jelas 1 4 < x < 1 4. Kasus 1 < x < 0: 4 Jelas 0 < x 2 < 1 16 f(0) < f(x) < Kasus 0 x < 1 4 : Jelas 0 x 2 < 1 16 f(0) f(x) < Jadi terdapat selang buka D R sehingga f(0) f(x) x D. Jadi f(0) = 0 merupakan nilai minimum relatif f. (b) Pilih δ = 1 4. Bangun D = (1 1 4, ) = (3 4, 5 4 ). Ambil sembarang x D. Jelas 3 4 < x <
4 Kasus 3 < x 1: 4 Jelas 9 < 16 x2 1 9 < f(x) f(1). 16 Kasus 1 < x < 5 4 : Jelas 1 > x > > 2 x > 3 4 f(1) > f(x) > 3 4. Jadi terdapat selang buka D R sehingga f(1) f(x) x D. Jadi f(1) = 1 merupakan nilai maksimum relatif f. Catatan: Nilai ekstrim mutlak suatu fungsi juga merupakan nilai ekstrim relatif. Berikut ini disajikan suatu bilangan yang penting untuk menentukan nilai ekstrim relatif. Bilangan tersebut disebut bilangan kritis yang merupakan calon kuat nilai ekstrim. Definisi 5. Dipunyai fungsi f: I R, I R, dan c I. Jika f (c) = 0 atau f (c) tidak ada maka c disebut bilangan kritis f. Contoh 12. Dipunyai f: R R, f(x) = x 2 4x + 8. Periksa apakah f mempunyai nilai ekstrim. Penyelesaian: Jelas f (x) = 0 d(x2 4x + 8) = 0 2x 4 = 0 x = 2. Jelas x = 2 merupakan bilangan kritis f dan Jelas f(2) = Ambil sembarang x R. Jelas f(2) f(x) = 4 x 2 + 4x 8 = (x 2) 2 0. Jadi f(2) f(x) x R. Jadi f(2) = 4 suatu nilai minimum mutlak f. Berikut ini disajikan suatu teorema eksistensi nilai ekstrim suatu fungsi. Teorema 12. Jika fungsi f kontinu pada selang tutup [a, b] maka fungsi f memiliki nilai minimum dan maksimum mutlak. 4
5 Dari Definisi 5 dan Teorema 12 dapat dirumuskan Teorema terkait dengan bilangan kritis sebagai berikut. Teorema 13. Jika f terdefinisi pada suatu selang I yang memuat titik c. Jika f(c) adalah suatu nilai ekstrim maka c haruslah merupakan bilangan kritis fungsi f dan c memenuhi salah satu dari berikut ini. (a) c merupakan titik ujung I, (b) c merupakan titik stationer f (f (c) = 0), (c) c merupakan titik singular f (f (c) tidak ada). Teorema Rolle merupakan teorema tentang eksistensi suatu titik di domain suatu fungsi yang turunan fungsi di titik itu sama dengan nol. Berikut disajikan Teorema Rolle. Teorema 14. (Teorema Rolle) Dipunyai fungsi f: [a, b] R. Jika (1) f kontinu pada [a, b], (2) f mempunyai turunan pada (a, b), dan (3) f(a) = f(b) maka terdapat titik c (a, b) sehingga f (c) = 0. Berikut ini disajikan teorema yang lebih umum dari Teorema Rolle yang disebut dengan teorema nilai rata-rata (TNR). Teorema 15. (Teorema Nilai Rata-rata) Dipunyai fungsi f: [a, b] R. Jika f kontinu pada [a, b] dan f mempunyai turunan pada (a, b) maka terdapat titik c (a, b) sehingga f (c) = f(b) f(a). b a (a) Nilai f(b) f(a) b a B(b, f(b)) merupakan talibusur AB dengan A(a, f(a)) dan 5
6 (b) Jika f memenuhi kondisi teorema ini maka terdapat suatu garis singgung yang memiliki gradien sama dengan gradien talibusur AB. Interpretasi geometri tersebut dapat dilihat pada gambar berikut ini. Y s B f(b) f f(a) A O a b Gambar 6. Interpretasi teorema nilai rata-rata b. Kemonotonan grafik fungsi Pada bagian ini akan disajikan konsep tentang naik atau turunnya fungsi kaitannya dengan turunan fungsi itu dan uji turunan pertama untuk eksrim relatif suatu fungsi. Berikut diberikan definisi naik turunnya grafik fungsi. Definisi 6. Dipunyai fungsi f: I R, I R. (a) Grafik fungsi f dikatakan naik pada I apabila x 1, x 2 I, x 1 < x 2 f(x 1 ) < f(x 2 ). (b) Grafik fungsi f dikatakan turun pada I apabila x 1, x 2 I, x 1 < x 2 f(x 1 ) > f(x 2 ). Kaitan antara naik-turunnya fungsi dengan turunan fungsi diberikan pada Teorema berikut. Teorema 16. Dipunyai f: I R, I R, dan f (x) ada untuk setiap x I kecuali mungkin di titik-titik ujungnya. (i) Jika f (x) > 0 untuk setiap x I yang bukan di titik ujung maka grafik f naik pada I. (ii) Jika f (x) < 0 untuk setiap x I yang bukan di titik ujung maka grafik f turun pada I. 6
7 Berikut ini disajikan langkah-langkah untuk menentukan selang terbesar di mana grafik f naik atau turun: (1) tentukan bilangan kritis untuk f, (2) tentukan selang-selang dalam domain f berdasarkan bilanganbilangan kritis dan nilai-nilai x sehingga f tak terdefinisi, dan (3) manfaatkan Teorema 16. Contoh 13. Dipunyai fungsi f: R {1} R dengan f(x) = x2. Tentukan di mana grafik f naik dan turun. Penyelesaian: Jelas f tak terdefinisi di x = 1 dan f (x) = d( x2 x 1 ) x 1 = x(x 2) (x 1) 2. Jelas f (1) tidak ada dan f (x) = 0 x(x 2) (x 1) 2 = 0 x = 0 x = 2. Karena f tak terdefinisi di x = 1, maka bilangan kritis f hanya 0 dan 2. Bangun selang-selang (, 0), (0,1), (1,2), dan (2, + ). Kasus x (, 0): Jelas x < 0, (x 2) < 0, dan (x 2) 2 > 0. Jadi f (x) = x(x 2) (x 1) 2 > 0. Jadi grafik f naik pada (, 0). Kasus x (0, 1): Jelas 0 < x < 1 2 < x 2 < 1 dan (x 1) 2 > 0. f (x) < 0. Jadi grafik f turun pada (0, 1). Kasus x (1, 2): Jelas 1 < x < 2 1 < x 2 < 0 dan (x 1) 2 > 0. f (x) < 0. Jadi grafik f turun pada (1, 2). Kasus x (2, + ): Jadi Jadi 7
8 Jelas x > 2. Jadi (x 2) > 0 dan (x 1) 2 > 0. Jadi f (x) > 0. Jadi grafik f naik pada (2, + ). Berikut ini disajikan suatu teorema untuk menguji nilai ekstrim relatif suatu fungsi yang dikenal dengan Uji Turunan Pertama. Teorema 17. (Uji Turunan Pertama) Dipunyai fungsi f: I R, I R, dan c I suatu bilangan kritis untuk f. Jika f (x) ada pada selang (c h, c + h) untuk suatu h > 0 kecuali mungkin di titik c sendiri maka f(c) ekstrim relatif jika dan hanya jika tanda f (x) berganti tanda di x = c. Secara khusus dinyatakan sebagai berikut: (1) Jika f (x) > 0 untuk x < c dan f (x) < 0 untuk x > c maka f(c) suatu maksimum relatif. (2) Jika f (x) < 0 untuk x < c dan f (x) > 0 untuk x > c maka f(c) suatu minimum relatif. (3) Jika f (x) tidak berganti tanda di x = c maka f(c) bukan suatu Contoh 14. maksimum ataupun minimum relatif. Dipunyai fungsi f: R R yang diberikan oleh f(x) = 4x 2 4x 4. Tentukan nilai ekstrim fungsi f. Penyelesaian: Jelas f (x) = d[f(x)] = d(4x2 4x 4 ) Jelas f (x) = 0 8x(x 2x 2 ) x = 0 x = 2 2 Jadi bilangan kritis f adalah 2 2, 0, dan. 2 2 Uji turunan pertama di x = 2 2 : x ( 2 2 ) 2 2 ( 2 2 ) + f (x) + 0 f(x) Maks. Rel. f = 8x 16x 3 = 8x(x 2x 2 ). x =
9 Jadi f ( 2 ) = 1 suatu maksimum relatif f. 2 Uji turunan pertama di x = 0: x (0) 0 (0) + f (x) 0 + f(x) Min. Rel. f Jadi f(0) = 0 suatu minimum relatif f. Uji turunan pertama di x = 2 2 : x ( 2 2 ) 2 2 ( 2 2 ) + f (x) + 0 f(x) Maks. Rel. f Jadi f ( 2 ) = 1 suatu maksimum relatif f. 2 Skestas grafik f: 1 f O Gambar 7. Sketsa grafik f dengan f(x) = 4x 2 4x 4. c. Kecekungan grafik fungsi Setelah mempelajari naik turunnya grafik fungsi, selanjutnya akan disajikan materi terkait kecekungan grafik fungsi. Gambar-gambar berikut memberikan beberapa gambaran kecekungan pada beberapa nilai ekstrim. 9
10 Y B f A C Gambar 8. Fungsi f mempunyai maksimum di B dan minimum di A dan C. Akan tetapi cekung ke atas di kiri A dan di kanan C. Y B g A C Gambar 9. Fungsi g mempunyai maksimum di B dan minimum di A dan C. Akan tetapi cekung ke atas di antara A dan B dan di antara B dan C. Definisi kecekungan grafik fungsi diberikan berikut ini. Definisi 7. Dipunyai fungsi f: I R, I R, f kontinu pada I, dan f (x) ada pada I kecuali mungkin di titik-titik ujungnya. (a) Grafik fungsi f dikatakan cekung ke atas pada I apabila f merupakan fungsi naik pada I. (b) Grafik fungsi f dikatakan cekung ke bawah pada I apabila f merupakan fungsi turun pada I. Berikut ini disajikan teorema yang mengaitkan kecekungan grafik suatu fungsi dengan nilai turunan kedua fungsi tersebut. 10
11 Teorema 18. Dipunyai fungsi f: I R, I R, f kontinu pada I, dan f (x) ada pada I kecuali mungkin di titik-titik ujungnya. (a) Grafik f cekung ke atas pada I apabila f (x) > 0 untuk setiap x I yang bukan titik ujung I. (b) Grafik f cekung ke bawah pada I apabila f (x) < 0 untuk setiap x I yang bukan titik ujung I. Apabila fungsi f mempunyai turunan dan f kontinu, Teorema 17 mengisyaratkan langkah-langkah untuk menentukan selang di mana grafik fungsi f cekung ke atas atau ke bawah. Langkah-langkah tersebut yaitu: (1) Tentukan bilangan c sehingga f (c) = 0 atau f (c) tidak ada. (2) Bangun selang berdasarkan temuan titik c pada butir (1). (3) Periksa tanda f (x) pada selang-selang itu. Seperti dalam mencari selang-selang di mana f naik atau turun, juga diperhatikan bilangan c dengan f (c) = 0 atau f (c) tidak ada. Titiktitik pada grafik f yang memisahkan kurva dengan kecekungan berbeda disebut titik infleksi. Berikut teorema yang mengaitkan turunan kedua suatu fungsi dengan nilai ekstrim relatif fungsi tersebut. Teorema 19. (Uji Turunan Kedua) Dipunyai fungsi f: I R, I R, dan a I. Jika f (x) dan f (x) ada pada I maka: (a) f (a) < 0 f(a) suatu maksimum relatif f, (b) f (a) > 0 f(a) suatu minimum relatif f, dan (c) f (a) = 0 tidak ada kesimpulan 11
12 Contoh 15. Dipunyai fungsi f: R R yang diberikan oleh f(x) = 4x 2 4x 4. Pada Contoh 13 telah ditunjukkan bahwa f ( 2 ) = 1 = f ( 2 ) merupakan 2 2 maksimum relatif f, dan f(0) = 0 merupakan suatu minimum relatif f. Pada contoh kali ini akan digunakan uji turunan kedua. Jelas f (x) = d[f(x)] f (x) = d[f (x)] = d(4x2 4x 4 ) = d(8x 16x3 ) = 8x 16x 3 dan = 8 48x 2. Jelas f ( 2 ) < 0 dan 2 f ( 2 2 ) < 0, berakibat f ( ) = 1 = f ( merupakan maksimum relatif f. Jelas f (0) > 0 berakibat f(0) = 0 merupakan minimum relatif f. 2 ) d. Masalah maksimum minimum Berdasarkan teori-teori yang telah dipelajari sebelumnya, diberikan langkah-langkah dalam menyelesaikan masalah-masalah yang berkaitan dengan turunan terutama masalah maksimum dan minimum. Langkahlangkah ini dapat dikembangkan sesuai dengan karakteristik permasalah yang hendak diselesaikan. Adapun langkah-langkah yang dimaksud adalah sebagai berikut: Langkah 1. Buatlah gambaran umum dari persoalan dan identifikasi variabel-variabel penting beserta satuan/besarannya. Langkah 2. Tuliskan rumus dari fungsi tujuannya apakah meminimumkan atau memaksimumkan. Langkah 3. Gunakan kondisi dalam masalah untuk mengeliminasi variabel sehingga fungsi tujuan menjadi fungsi dengan satu variabel. Langkah 4. Tentukan bilangan kritis (titik ujung selang, titik stationer, titik singular). 12
13 Langkah 5. Substitusikan bilangan kritis ke fungsi tujuan atau gunakan uji turunan pertama atau uji turunan kedua untuk menentukan maksimum dan minimum dari fungsi tujuan tersebut. Contoh 16. Temukan suatu persegipanjang yang ukuran luas daerahnya 64cm 2 dan ukuran kelilingnya minimum. Penyelesaian: Tulis x: ukuran panjang persegipanjang (cm), y: ukuran lebar persegipanjang (cm), A: ukuran luas daerah persegipanjang (cm 2 ), dan K: ukuran keliling persegipanjang (cm). Karena x dan y menyatakan ukuran panjang dan lebar maka x 0 dan y 0. Dari soal diperoleh A = 64 xy = 64 y = 64 x. Jelas K(x) = 2(x + y) = 2 (x + 64 ). Jelas x 0. Jelas K (x) = 0 d[2(x+64 x )] Jadi titik kritis K adalah x = 8. Uji turunan pertama di x = 8: x (8) 8 (8) + f (x) 0 + f(x) Min. Rel. x = 0 2 (1 64 x2) x = 8 x = 8. Jadi Persegipanjang yang ukuran luasnya 64cm 2 dan ukuran kelilingnya minimum merupakan persegi dengan ukuran 8cm. 13
TURUNAN, EKSTRIM, BELOK, MINIMUM DAN MAKSIMUM
 TURUNAN, EKSTRIM, BELOK, MINIMUM DAN MAKSIMUM Fungsi f dikatakan mencapai maksimum mutlak di c jika f c f x untuk setiap x I. Di sini f c dinamakan nilai maksimum mutlak. Dan c, f c dinamakan titik maksimum
TURUNAN, EKSTRIM, BELOK, MINIMUM DAN MAKSIMUM Fungsi f dikatakan mencapai maksimum mutlak di c jika f c f x untuk setiap x I. Di sini f c dinamakan nilai maksimum mutlak. Dan c, f c dinamakan titik maksimum
BAB IV. PENGGUNAAN TURUNAN. Departemen Teknik Kimia Universitas Indonesia
 BAB IV. PENGGUNAAN TURUNAN Departemen Teknik Kimia Universitas Indonesia BAB IV. PENGGUNAAN TURUNAN Maksimum dan Minimum Kemonotonan dan Kecekungan Maksimum dan Minimum Lokal Masalah Maksimum dan Minimum
BAB IV. PENGGUNAAN TURUNAN Departemen Teknik Kimia Universitas Indonesia BAB IV. PENGGUNAAN TURUNAN Maksimum dan Minimum Kemonotonan dan Kecekungan Maksimum dan Minimum Lokal Masalah Maksimum dan Minimum
KED PENGGUNAAN TURUNAN
 6 PENGGUNAAN TURUNAN JUMLAH PERTEMUAN : 1 PERTEMUAN TUJUAN INSTRUKSIONAL KHUSUS : Menerapkan konsep dasar turunan fungsi dalam menentukan karakteristik grafik fungsi dan menggambarkan grafik Materi : 6.1
6 PENGGUNAAN TURUNAN JUMLAH PERTEMUAN : 1 PERTEMUAN TUJUAN INSTRUKSIONAL KHUSUS : Menerapkan konsep dasar turunan fungsi dalam menentukan karakteristik grafik fungsi dan menggambarkan grafik Materi : 6.1
Hendra Gunawan. 2 Oktober 2013
 MA1101 MATEMATIKA 1A Hendra Gunawan Semester I, 2013/2014 2 Oktober 2013 Apa yang Telah Dipelajari pada Bab 2 2.1 Dua Masalah Satu Tema 2.2 Turunan 2.3 Aturan Turunan 2.4 Turunan Fungsi Trigonometri 2.5Aturan
MA1101 MATEMATIKA 1A Hendra Gunawan Semester I, 2013/2014 2 Oktober 2013 Apa yang Telah Dipelajari pada Bab 2 2.1 Dua Masalah Satu Tema 2.2 Turunan 2.3 Aturan Turunan 2.4 Turunan Fungsi Trigonometri 2.5Aturan
5. Aplikasi Turunan MA1114 KALKULUS I 1
 5. Aplikasi Turunan MA4 KALKULUS I 5. Menggambar grafik fungsi Informasi yang dibutuhkan: A. Titik potong dengan sumbu dan sumbu y B. Asimtot fungsi C. Kemonotonan Fungsi D. Ekstrim Fungsi E. Kecekungan
5. Aplikasi Turunan MA4 KALKULUS I 5. Menggambar grafik fungsi Informasi yang dibutuhkan: A. Titik potong dengan sumbu dan sumbu y B. Asimtot fungsi C. Kemonotonan Fungsi D. Ekstrim Fungsi E. Kecekungan
PENGGUNAAN TURUNAN. Maksimum dan Minimum. Definisi. Andaikan S, daerah asal f, memuat titik c. Kita katakan bahwa:
 PENGGUNAAN TURUNAN Maksimum dan Minimum Andaikan S, daerah asal f, memuat titik c. Kita katakan bahwa: 1. f c adalah nilai maksimum f pada S jika f c f x untuk semua x di S;. f c adalah nilai minimum f
PENGGUNAAN TURUNAN Maksimum dan Minimum Andaikan S, daerah asal f, memuat titik c. Kita katakan bahwa: 1. f c adalah nilai maksimum f pada S jika f c f x untuk semua x di S;. f c adalah nilai minimum f
10. TEOREMA NILAI RATA-RATA
 10. TEOREMA NILAI RATA-RATA 10.1 Maksimum dan Minimum Lokal Misalkan f terdefinisi pada suatu interval terbuka (a, b) dan c (a, b). Kita katakan bahwa f mencapai nilai maksimum lokal di c apabila f(x)
10. TEOREMA NILAI RATA-RATA 10.1 Maksimum dan Minimum Lokal Misalkan f terdefinisi pada suatu interval terbuka (a, b) dan c (a, b). Kita katakan bahwa f mencapai nilai maksimum lokal di c apabila f(x)
G. Minimum Lokal dan Global Berikut diberikan definisi minimum local (relatif) dan minimum global (mutlak) dari fungsi dua variabel.
 G. Minimum Lokal dan Global Berikut diberikan definisi minimum local (relatif) dan minimum global (mutlak) dari fungsi dua variabel. Definisi. (i) Suatu fungsi f(x, y) memiliki minimum lokal pada titik
G. Minimum Lokal dan Global Berikut diberikan definisi minimum local (relatif) dan minimum global (mutlak) dari fungsi dua variabel. Definisi. (i) Suatu fungsi f(x, y) memiliki minimum lokal pada titik
TKS 4003 Matematika II. Nilai Ekstrim. (Extreme Values) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya
 TKS 4003 Matematika II Nilai Ekstrim (Extreme Values) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya Pendahuluan Jika diberikan suatu fungsi f dan daerah asal S seperti gambar di samping.
TKS 4003 Matematika II Nilai Ekstrim (Extreme Values) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya Pendahuluan Jika diberikan suatu fungsi f dan daerah asal S seperti gambar di samping.
KALKULUS I MUG1A4 PROGRAM PERKULIAHAN DASAR DAN UMUM (PPDU) TELKOM UNIVERSITY V. APLIKASI TURUNAN
 KALKULUS I MUGA4 PROGRAM PERKULIAHAN DASAR DAN UMUM (PPDU) TELKOM UNIVERSITY V. APLIKASI TURUNAN MENGGAMBAR GRAFIK FUNGSI A. Titik potong dengan sumbu dan sumbu y B. Asimtot ungsi Deinisi : Asimtot ungsi
KALKULUS I MUGA4 PROGRAM PERKULIAHAN DASAR DAN UMUM (PPDU) TELKOM UNIVERSITY V. APLIKASI TURUNAN MENGGAMBAR GRAFIK FUNGSI A. Titik potong dengan sumbu dan sumbu y B. Asimtot ungsi Deinisi : Asimtot ungsi
Catatan Kuliah MA1123 KALKULUS ELEMENTER I BAB III. TURUNAN
 BAB III. TURUNAN Kecepatan Sesaat dan Gradien Garis Singgung Turunan dan Hubungannya dengan Kekontinuan Aturan Dasar Turunan Notasi Leibniz dan Turunan Tingkat Tinggi Penurunan Implisit Laju yang Berkaitan
BAB III. TURUNAN Kecepatan Sesaat dan Gradien Garis Singgung Turunan dan Hubungannya dengan Kekontinuan Aturan Dasar Turunan Notasi Leibniz dan Turunan Tingkat Tinggi Penurunan Implisit Laju yang Berkaitan
Matematika I: APLIKASI TURUNAN. Dadang Amir Hamzah. Dadang Amir Hamzah Matematika I Semester I / 70
 Matematika I: APLIKASI TURUNAN Dadang Amir Hamzah 2015 Dadang Amir Hamzah Matematika I Semester I 2015 1 / 70 Outline 1 Maksimum dan Minimum Dadang Amir Hamzah Matematika I Semester I 2015 2 / 70 Outline
Matematika I: APLIKASI TURUNAN Dadang Amir Hamzah 2015 Dadang Amir Hamzah Matematika I Semester I 2015 1 / 70 Outline 1 Maksimum dan Minimum Dadang Amir Hamzah Matematika I Semester I 2015 2 / 70 Outline
BAB 5 PENGGUNAAN TURUNAN
 Diktat Kuliah TK Matematika BAB 5 PENGGUNAAN TURUNAN 5. Nilai Ekstrim Fungsi Nilai ekstrim fungsi adalah nilai yang berkaitan dengan maksimum atau minimum fungsi tersebut. Ada dua jenis nilai ekstrim,
Diktat Kuliah TK Matematika BAB 5 PENGGUNAAN TURUNAN 5. Nilai Ekstrim Fungsi Nilai ekstrim fungsi adalah nilai yang berkaitan dengan maksimum atau minimum fungsi tersebut. Ada dua jenis nilai ekstrim,
DASAR-DASAR ANALISIS MATEMATIKA
 (Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. December 6, 2007 Misalkan f terdefinisi pada suatu interval terbuka (a, b) dan c (a, b). Kita katakan
(Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. December 6, 2007 Misalkan f terdefinisi pada suatu interval terbuka (a, b) dan c (a, b). Kita katakan
5.1 Menggambar grafik fungsi
 5. Aplikasi Turunan 5. Menggambar graik ungsi Inormasi yang dibutuhkan: A. Titik potong dengan sumbu dan sumbu y B. Asimtot ungsi Deinisi 5.: Asimtot ungsi adalah garis lurus yang didekati oleh graik ungsi.
5. Aplikasi Turunan 5. Menggambar graik ungsi Inormasi yang dibutuhkan: A. Titik potong dengan sumbu dan sumbu y B. Asimtot ungsi Deinisi 5.: Asimtot ungsi adalah garis lurus yang didekati oleh graik ungsi.
Matematika Dasar NILAI EKSTRIM
 NILAI EKSTRIM Misal diberikan kurva f( ) dan titik ( a,b ) merupakan titik puncak ( titik maksimum atau minimum ). Maka garis singgung kurva di titik ( a,b ) akan sejajar sumbu X atau [ ] mempunyai gradien
NILAI EKSTRIM Misal diberikan kurva f( ) dan titik ( a,b ) merupakan titik puncak ( titik maksimum atau minimum ). Maka garis singgung kurva di titik ( a,b ) akan sejajar sumbu X atau [ ] mempunyai gradien
11. FUNGSI MONOTON (DAN FUNGSI KONVEKS)
 11. FUNGSI MONOTON (DAN FUNGSI KONVEKS) 11.1 Definisi dan Limit Fungsi Monoton Misalkan f terdefinisi pada suatu himpunan H. Kita katakan bahwa f naik pada H apabila untuk setiap x, y H dengan x < y berlaku
11. FUNGSI MONOTON (DAN FUNGSI KONVEKS) 11.1 Definisi dan Limit Fungsi Monoton Misalkan f terdefinisi pada suatu himpunan H. Kita katakan bahwa f naik pada H apabila untuk setiap x, y H dengan x < y berlaku
TEOREMA UJI TURUNAN. Agustina Pradjaningsih, M.Si. Jurusan Matematika FMIPA UNEJ
 TEOREMA UJI TURUNAN Agustina Pradjaningsih, M.Si. Jurusan Matematika FMIPA UNEJ agustina.mipa@unej.ac.id UJI TURUNAN I-ekstrim relati Andaikan kontinu pada selang (a,b), yang memuat titik kritis c : (i)
TEOREMA UJI TURUNAN Agustina Pradjaningsih, M.Si. Jurusan Matematika FMIPA UNEJ agustina.mipa@unej.ac.id UJI TURUNAN I-ekstrim relati Andaikan kontinu pada selang (a,b), yang memuat titik kritis c : (i)
TERAPAN TURUNAN. Bogor, Departemen Matematika FMIPA IPB. (Departemen Matematika FMIPA IPB) Kalkulus I Bogor, / 61
 TERAPAN TURUNAN Departemen Matematika FMIPA IPB Bogor, 2012 (Departemen Matematika FMIPA IPB) Kalkulus I Bogor, 2012 1 / 61 Topik Bahasan 1 Nilai Maksimum dan Minimum 2 Teorema Nilai Rataan (TNR) 3 Turunan
TERAPAN TURUNAN Departemen Matematika FMIPA IPB Bogor, 2012 (Departemen Matematika FMIPA IPB) Kalkulus I Bogor, 2012 1 / 61 Topik Bahasan 1 Nilai Maksimum dan Minimum 2 Teorema Nilai Rataan (TNR) 3 Turunan
Turunan Fungsi. h asalkan limit ini ada.
 Turunan Fungsi q Definisi Turunan Fungsi Misalkan fungsi f terdefinisi pada selang terbuka I yang memuat a. Turunan pertama fungsi f di =a ditulis f (a) didefinisikan dengan f ( a h) f ( a) f '( a) lim
Turunan Fungsi q Definisi Turunan Fungsi Misalkan fungsi f terdefinisi pada selang terbuka I yang memuat a. Turunan pertama fungsi f di =a ditulis f (a) didefinisikan dengan f ( a h) f ( a) f '( a) lim
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
PENGGUNAAN TURUNAN. Agustina Pradjaningsih, M.Si. Jurusan Matematika FMIPA UNEJ
 PENGGUNAAN TURUNAN Agustina Pradjaningsih, M.Si. Jurusan Matematika FMIPA UNEJ agustina.mipa@unej.a.id Pada materi sebelumnya telah dijelaskan bahwa Teorema Nilai Rata-Rata (TNR dierensial) memegang peranan
PENGGUNAAN TURUNAN Agustina Pradjaningsih, M.Si. Jurusan Matematika FMIPA UNEJ agustina.mipa@unej.a.id Pada materi sebelumnya telah dijelaskan bahwa Teorema Nilai Rata-Rata (TNR dierensial) memegang peranan
Aplikasi Turunan. Diadaptasi dengan tambahan dari slide Bu Puji Andayani, S.Si, M.Si, M.Sc
 Aplikasi Turunan Diadaptasi dengan tambahan dari slide Bu Puji Andayani, S.Si, M.Si, M.Sc 1 Menggambar Grafik Fungsi Informasi yang dibutuhkan: A. Titik potong dengan sumbu dan sumbu y B. Asimtot fungsi
Aplikasi Turunan Diadaptasi dengan tambahan dari slide Bu Puji Andayani, S.Si, M.Si, M.Sc 1 Menggambar Grafik Fungsi Informasi yang dibutuhkan: A. Titik potong dengan sumbu dan sumbu y B. Asimtot fungsi
a home base to excellence Mata Kuliah : Kalkulus Kode : TSP 102 Turunan Pertemuan - 4
 a home base to excellence Mata Kuliah : Kalkulus Kode : TSP 102 SKS : 3 SKS Turunan Pertemuan - 4 a home base to excellence TIU : Mahasiswa dapat memahami turunan fungsi dan aplikasinya TIK : Mahasiswa
a home base to excellence Mata Kuliah : Kalkulus Kode : TSP 102 SKS : 3 SKS Turunan Pertemuan - 4 a home base to excellence TIU : Mahasiswa dapat memahami turunan fungsi dan aplikasinya TIK : Mahasiswa
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
BAGIAN KEDUA. Fungsi, Limit dan Kekontinuan, Turunan
 BAGIAN KEDUA Fungsi, Limit dan Kekontinuan, Turunan 51 52 Hendra Gunawan Pengantar Analisis Real 53 6. FUNGSI 6.1 Fungsi dan Grafiknya Konsep fungsi telah dipelajari oleh Gottfried Wilhelm von Leibniz
BAGIAN KEDUA Fungsi, Limit dan Kekontinuan, Turunan 51 52 Hendra Gunawan Pengantar Analisis Real 53 6. FUNGSI 6.1 Fungsi dan Grafiknya Konsep fungsi telah dipelajari oleh Gottfried Wilhelm von Leibniz
Nilai Ekstrim. (Extreme Values)
 TKS 4003 Matematika II Nilai Ekstrim (Extreme Values) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya Pendahuluan Jika terdapat suatu hasil pengukuran seperti pada Gambar 1, dimana pengukuran
TKS 4003 Matematika II Nilai Ekstrim (Extreme Values) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya Pendahuluan Jika terdapat suatu hasil pengukuran seperti pada Gambar 1, dimana pengukuran
UJIAN TENGAH SEMESTER KALKULUS I
 UJIAN TENGAH SEMESTER KALKULUS I Senin, 9 April 001 Waktu :,5 jam 1. Tentukan dy dx jika (a) y 5x (x + 1) (b) y cos x.. Dengan menggunakan de nisi turunan, tentukan f 0 (x) untuk fungsi f berikut f (x)
UJIAN TENGAH SEMESTER KALKULUS I Senin, 9 April 001 Waktu :,5 jam 1. Tentukan dy dx jika (a) y 5x (x + 1) (b) y cos x.. Dengan menggunakan de nisi turunan, tentukan f 0 (x) untuk fungsi f berikut f (x)
Definisi. Fungsi f(x) dikatakan monoton naik pada interval I jika untuk ( ) ( ) x < x f x > f x, x, x I. monoton turun pada interval I jika untuk
 Definisi. Fungsi f(x) dikatakan monoton naik pada interval I jika untuk x < x f x < f x, x, x I ( ) ( ) 1 1 1 monoton turun pada interval I jika untuk x < x f x > f x, x, x I. ( ) ( ) 1 1 1 Fungsi monoton
Definisi. Fungsi f(x) dikatakan monoton naik pada interval I jika untuk x < x f x < f x, x, x I ( ) ( ) 1 1 1 monoton turun pada interval I jika untuk x < x f x > f x, x, x I. ( ) ( ) 1 1 1 Fungsi monoton
Bahan Diskusi/Tugas Kelompok Topik: Turunan Fungsi
 Jurusan Pendidikan Matematika FPMIPA Universitas Pendidikan Indonesia Bahan Diskusi/Tugas Kelompok Topik: Turunan Fungsi Definisi 1: Misalkan I R suatu interval, c I dan f : I R. Fungsi f disebut diferensiabel
Jurusan Pendidikan Matematika FPMIPA Universitas Pendidikan Indonesia Bahan Diskusi/Tugas Kelompok Topik: Turunan Fungsi Definisi 1: Misalkan I R suatu interval, c I dan f : I R. Fungsi f disebut diferensiabel
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI 2.1 Latar Belakang Historis Fondasi dari integral pertama kali dideklarasikan oleh Cavalieri, seorang ahli matematika berkebangsaan Italia pada tahun 1635. Cavalieri menemukan bahwa
BAB II LANDASAN TEORI 2.1 Latar Belakang Historis Fondasi dari integral pertama kali dideklarasikan oleh Cavalieri, seorang ahli matematika berkebangsaan Italia pada tahun 1635. Cavalieri menemukan bahwa
TKS 4003 Matematika II. Nilai Ekstrim. (Extreme Values) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya
 TKS 4003 Matematika II Nilai Ekstrim (Extreme Values) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya Fungsi Dua Peubah Bila untuk setiap pasangan (x,y) dari harga harga dua peubah bebas
TKS 4003 Matematika II Nilai Ekstrim (Extreme Values) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya Fungsi Dua Peubah Bila untuk setiap pasangan (x,y) dari harga harga dua peubah bebas
5. Aplikasi Turunan 1
 5. Aplikasi Turunan 5. Menggambar graik ungsi Inormasi yang dibutuhkan: A. Titik potong dengan sumbu dan sumbu y B. Asimtot ungsi Deinisi 5.: Asimtot ungsi adalah garis lurus yang didekati oleh graik ungsi.
5. Aplikasi Turunan 5. Menggambar graik ungsi Inormasi yang dibutuhkan: A. Titik potong dengan sumbu dan sumbu y B. Asimtot ungsi Deinisi 5.: Asimtot ungsi adalah garis lurus yang didekati oleh graik ungsi.
Gambar 1. Gradien garis singgung grafik f
 D. URAIAN MATERI 1. Definisi dan Rumus-rumus Turunan Fungsi a. Definisi Turunan Sala satu masala yang mendasari munculnya kajian tentang turunan adala gradien garis singgung. Peratikan Gambar 1. f(c +
D. URAIAN MATERI 1. Definisi dan Rumus-rumus Turunan Fungsi a. Definisi Turunan Sala satu masala yang mendasari munculnya kajian tentang turunan adala gradien garis singgung. Peratikan Gambar 1. f(c +
BAB II TEOREMA NILAI RATA-RATA (TNR)
 BAB II TEOREMA NILAI RATA-RATA (TNR) Teorema nilai rata-rata menghubungkan nilai suatu fungsi dengan nilai derivatifnya (turunannya), dimana TNR merupakan salah satu bagian penting dalam kuliah analisis
BAB II TEOREMA NILAI RATA-RATA (TNR) Teorema nilai rata-rata menghubungkan nilai suatu fungsi dengan nilai derivatifnya (turunannya), dimana TNR merupakan salah satu bagian penting dalam kuliah analisis
MATEMATIKA II. Turunan dan Aplikasinya. Rudi Prihandoko. March 9, 2017 ver 0.6
 MATEMATIKA II Turunan dan Aplikasinya Rudi Prihandoko March 9, 2017 ver 0.6 KUIS I KUIS Misalkan ABCDE adalah NIM Anda. Misalkan pula f(x) = (Ax2 + Bx + C) 2 Ax 2 + Dx + E adalah suatu fungsi rasional.
MATEMATIKA II Turunan dan Aplikasinya Rudi Prihandoko March 9, 2017 ver 0.6 KUIS I KUIS Misalkan ABCDE adalah NIM Anda. Misalkan pula f(x) = (Ax2 + Bx + C) 2 Ax 2 + Dx + E adalah suatu fungsi rasional.
Bagian 4 Terapan Differensial
 Bagian 4 Terapan Differensial Dalam bagian 4 Terapan Differensial, kita akan mempelajari materi bagaimana konsep differensial dapat dipergunakan untuk mengatasi persoalan yang terjadi di sekitar kita.
Bagian 4 Terapan Differensial Dalam bagian 4 Terapan Differensial, kita akan mempelajari materi bagaimana konsep differensial dapat dipergunakan untuk mengatasi persoalan yang terjadi di sekitar kita.
PENERAPAN TURUNAN MAT 4 D. PERSAMAAN GARIS SINGGUNG KURVA A. PENDAHULUAN B. DALIL L HÔPITAL C. PERSAMAAN PADA KINEMATIKA GERAK TURUNAN. MATERI78.
 PENERAPAN TURUNAN MAT 4 D. PERSAMAAN GARIS SINGGUNG KURVA A. PENDAHULUAN B. DALIL L HÔPITAL C. PERSAMAAN PADA KINEMATIKA GERAK TURUNAN. MATERI78.CO MAT 4 materi78.co.nr Penerapan Turunan A. PENDAHULUAN
PENERAPAN TURUNAN MAT 4 D. PERSAMAAN GARIS SINGGUNG KURVA A. PENDAHULUAN B. DALIL L HÔPITAL C. PERSAMAAN PADA KINEMATIKA GERAK TURUNAN. MATERI78.CO MAT 4 materi78.co.nr Penerapan Turunan A. PENDAHULUAN
King s Learning Be Smart Without Limits. (4) Grafik Fungsi kuadrat: (3) Titik lain (jika diperlukan) X Y. (4) Grafik Fungsi kuadrat:
 Nama Siswa : LEMBAR AKTIVITAS SISWA FUNGSI KUADRAT - Hubungkan titik-titik tersebut sehingga terbentuk kurva atau grafik yang mulus. Kelas : A. FUNGSI KUADRAT Bentuk umum fungsi kuadrat adalah: y = f(x)
Nama Siswa : LEMBAR AKTIVITAS SISWA FUNGSI KUADRAT - Hubungkan titik-titik tersebut sehingga terbentuk kurva atau grafik yang mulus. Kelas : A. FUNGSI KUADRAT Bentuk umum fungsi kuadrat adalah: y = f(x)
Penerapan Turunan MAT 4 D. PERSAMAAN GARIS SINGGUNG KURVA A. PENDAHULUAN B. DALIL L HÔPITAL C. PERSAMAAN PADA KINEMATIKA GERAK TURUNAN. materi78.co.
 Penerapan Turunan A. PENDAHULUAN Turunan dapat digunakan untuk: 1) Perhitungan nilai limit dengan dalil l Hôpital 2) Menentukan persamaan fungsi kecepatan dan percepatan dari persamaan fungsi posisi )
Penerapan Turunan A. PENDAHULUAN Turunan dapat digunakan untuk: 1) Perhitungan nilai limit dengan dalil l Hôpital 2) Menentukan persamaan fungsi kecepatan dan percepatan dari persamaan fungsi posisi )
BEBERAPA FUNGSI KHUSUS
 BEBERAPA FUNGSI KHUSUS ). Fungsi Konstan ). Fungsi Identitas 3). Fungsi Modulus 4). Fungsi Genap dan Fungsi Ganjil Fungsi genap jika f(x) = f(x), dan Fungsi ganjil jika f(x) = f(x) 5). Fungsi Tangga dan
BEBERAPA FUNGSI KHUSUS ). Fungsi Konstan ). Fungsi Identitas 3). Fungsi Modulus 4). Fungsi Genap dan Fungsi Ganjil Fungsi genap jika f(x) = f(x), dan Fungsi ganjil jika f(x) = f(x) 5). Fungsi Tangga dan
Hendra Gunawan. 13 September 2013
 MA1101 MATEMATIKA 1A Hendra Gunawan Semester I, 2013/2014 13 September 2013 Latihan (Kuliah yang Lalu) sin t 1. Menggunakan fakta bahwa lim 1, t0 hitunglah: t 2 sin( 2 ) a. limsin t.cot 2t b. lim t 0 0
MA1101 MATEMATIKA 1A Hendra Gunawan Semester I, 2013/2014 13 September 2013 Latihan (Kuliah yang Lalu) sin t 1. Menggunakan fakta bahwa lim 1, t0 hitunglah: t 2 sin( 2 ) a. limsin t.cot 2t b. lim t 0 0
Analisis Riil II: Diferensiasi
 Definisi Turunan Definisi dan Teorema Aturan Rantai Fungsi Invers Definisi (Turunan) Misalkan I R sebuah interval, f : I R, dan c I. Bilangan riil L dikatakan turunan dari f di c jika diberikan sebarang
Definisi Turunan Definisi dan Teorema Aturan Rantai Fungsi Invers Definisi (Turunan) Misalkan I R sebuah interval, f : I R, dan c I. Bilangan riil L dikatakan turunan dari f di c jika diberikan sebarang
UJIAN PERTAMA KALKULUS/KALKULUS I SEMESTER PENDEK 2004 SABTU, 17 JULI (2 JAM)
 Tentukan (jika ada) UJIAN PERTAMA KALKULUS/KALKULUS I SEMESTER PENDEK 2004 SABTU, 17 JULI (2 JAM) 1. Dengan menggunakan de nisi turunan, tentukan f 0 () bila f() = 2 + 4. 2. Tentukan: (a) d d (p + sin
Tentukan (jika ada) UJIAN PERTAMA KALKULUS/KALKULUS I SEMESTER PENDEK 2004 SABTU, 17 JULI (2 JAM) 1. Dengan menggunakan de nisi turunan, tentukan f 0 () bila f() = 2 + 4. 2. Tentukan: (a) d d (p + sin
TURUNAN FUNGSI TRIGONOMETRI
 SOAL-JAWAB MATEMATIKA PEMINATAN TURUNAN FUNGSI TRIGONOMETRI Soal Jika f ( ) sin cos tan maka f ( 0) Ingatlah rumus-rumus turunan trigonometri: y sin y cos y cos y sin y tan y sec Karena maka f ( ) sin
SOAL-JAWAB MATEMATIKA PEMINATAN TURUNAN FUNGSI TRIGONOMETRI Soal Jika f ( ) sin cos tan maka f ( 0) Ingatlah rumus-rumus turunan trigonometri: y sin y cos y cos y sin y tan y sec Karena maka f ( ) sin
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
LIMIT KED. Perhatikan fungsi di bawah ini:
 LIMIT Perhatikan fungsi di bawah ini: f x = x2 1 x 1 Perhatikan gambar di samping, untuk nilai x = 1 nilai f x tidak ada. Tetapi jikakita coba dekati nilai x = 1 dari sebelah kiri dan kanan maka dapat
LIMIT Perhatikan fungsi di bawah ini: f x = x2 1 x 1 Perhatikan gambar di samping, untuk nilai x = 1 nilai f x tidak ada. Tetapi jikakita coba dekati nilai x = 1 dari sebelah kiri dan kanan maka dapat
Rencana Pembelajaran
 Learning Outcome Rencana Pembelajaran Setelah mengikuti proses pembelajaran ini, diharapkan mahasiswa dapat ) Menentukan nilai turunan suatu fungsi di suatu titik ) Menentukan nilai koefisien fungsi sehingga
Learning Outcome Rencana Pembelajaran Setelah mengikuti proses pembelajaran ini, diharapkan mahasiswa dapat ) Menentukan nilai turunan suatu fungsi di suatu titik ) Menentukan nilai koefisien fungsi sehingga
Hendra Gunawan. 4 Oktober 2013
 MA1101 MATEMATIKA 1A Hendra Gunawan Semester I, 2013/2014 4 Oktober 2013 Latihan (Kuliah yg Lalu) 1. Tentukan pada selang mana grafik fungsi f(x) = x 3 2x 2 + x + 1 naik atau turun. Tentukan pula pada
MA1101 MATEMATIKA 1A Hendra Gunawan Semester I, 2013/2014 4 Oktober 2013 Latihan (Kuliah yg Lalu) 1. Tentukan pada selang mana grafik fungsi f(x) = x 3 2x 2 + x + 1 naik atau turun. Tentukan pula pada
UJIAN TENGAH SEMESTER KALKULUS I Senin, 5 Maret 1999 Waktu : 2,5 jam
 UJIAN TENGAH SEMESTER KALKULUS I Senin, 5 Maret 999 Waktu :,5 jam SETIAP NOMOR MEMPUNYAI BOBOT 0. Misalkan diketahui fungsi f dengan ; 0 f() = ; < 0 Gunakan de nisi turunan untuk memeriksa aakah f 0 (0)
UJIAN TENGAH SEMESTER KALKULUS I Senin, 5 Maret 999 Waktu :,5 jam SETIAP NOMOR MEMPUNYAI BOBOT 0. Misalkan diketahui fungsi f dengan ; 0 f() = ; < 0 Gunakan de nisi turunan untuk memeriksa aakah f 0 (0)
AFTAR ISI KATA PENGANTAR... i DAFTAR ISI... iii SOAL - SOAL... 2 PEMBAHASAN... 19
 DAFTAR ISI KATA PENGANTAR... i DAFTAR ISI... iii SOAL - SOAL... UTS Genap 009/00... UTS Ganjil 009/00... UTS Genap 008/009... 5 UTS Pendek 008/009... 6 UTS 007/008... 8 UTS 006/007... 9 UTS 005/006...
DAFTAR ISI KATA PENGANTAR... i DAFTAR ISI... iii SOAL - SOAL... UTS Genap 009/00... UTS Ganjil 009/00... UTS Genap 008/009... 5 UTS Pendek 008/009... 6 UTS 007/008... 8 UTS 006/007... 9 UTS 005/006...
asimtot.wordpress.com BAB I PENDAHULUAN
 BAB I PENDAHULUAN. Latar Belakang Kalkulus Differensial dan Integral sangat luas penggunaannya dalam berbagai bidang seperti penentuan maksimum dan minimum. Suatu fungsi yang sering digunakan mahasiswa
BAB I PENDAHULUAN. Latar Belakang Kalkulus Differensial dan Integral sangat luas penggunaannya dalam berbagai bidang seperti penentuan maksimum dan minimum. Suatu fungsi yang sering digunakan mahasiswa
BAHAN AJAR PERSAMAAN GARIS SINGGUNG PADA KURVA
 142 LAMPIRAN III BAHAN AJAR PERSAMAAN GARIS SINGGUNG PADA KURVA Pernahkan kamu melempar sebuah bola tenis atau bola voli ke atas? Apa lintasan yang terbuat dari lemparan bola tersebut ketika bola itu jatuh
142 LAMPIRAN III BAHAN AJAR PERSAMAAN GARIS SINGGUNG PADA KURVA Pernahkan kamu melempar sebuah bola tenis atau bola voli ke atas? Apa lintasan yang terbuat dari lemparan bola tersebut ketika bola itu jatuh
TURUNAN FUNGSI. dy (y atau f (x) atau ) dx. Hal-hal yang perlu diingat untuk menyelesaikan turunan fungsi aljabar adalah :
 TURUNAN FUNGSI dy (y atau f () atau ) d Hal-hal yang perlu diingat untuk menyelesaikan turunan fungsi aljabar adalah :. ( a + b) = ( a + ab + b ). ( a b) = ( a ab + b ) m n m n. a = a 4. a m = a m m m.
TURUNAN FUNGSI dy (y atau f () atau ) d Hal-hal yang perlu diingat untuk menyelesaikan turunan fungsi aljabar adalah :. ( a + b) = ( a + ab + b ). ( a b) = ( a ab + b ) m n m n. a = a 4. a m = a m m m.
Catatan Kuliah KALKULUS II BAB V. INTEGRAL
 BAB V. INTEGRAL Anti-turunan dan Integral TakTentu Persamaan Diferensial Sederhana Notasi Sigma dan Luas Daerah di Bawah Kurva Integral Tentu Teorema Dasar Kalkulus Sifat-sifat Integral Tentu Lebih Lanjut
BAB V. INTEGRAL Anti-turunan dan Integral TakTentu Persamaan Diferensial Sederhana Notasi Sigma dan Luas Daerah di Bawah Kurva Integral Tentu Teorema Dasar Kalkulus Sifat-sifat Integral Tentu Lebih Lanjut
KALKULUS BAB II FUNGSI, LIMIT, DAN KEKONTINUAN. DEPARTEMEN TEKNIK KIMIA Universitas Indonesia
 KALKULUS BAB II FUNGSI, LIMIT, DAN KEKONTINUAN DEPARTEMEN TEKNIK KIMIA Universitas Indonesia BAB II. FUNGSI, LIMIT, DAN KEKONTINUAN Fungsi dan Operasi pada Fungsi Beberapa Fungsi Khusus Limit dan Limit
KALKULUS BAB II FUNGSI, LIMIT, DAN KEKONTINUAN DEPARTEMEN TEKNIK KIMIA Universitas Indonesia BAB II. FUNGSI, LIMIT, DAN KEKONTINUAN Fungsi dan Operasi pada Fungsi Beberapa Fungsi Khusus Limit dan Limit
LIMIT DAN KEKONTINUAN
 LIMIT DAN KEKONTINUAN Pengertian dan notasi dari it suatu fungsi, f() di suatu nilai = a diberikan secara intuitif berikut. Bila nilai f() mendekati L untuk nilai mendekati a dari arah kanan maka dikatakan
LIMIT DAN KEKONTINUAN Pengertian dan notasi dari it suatu fungsi, f() di suatu nilai = a diberikan secara intuitif berikut. Bila nilai f() mendekati L untuk nilai mendekati a dari arah kanan maka dikatakan
BAB I SISTEM BILANGAN REAL
 BAB I SISTEM BILANGAN REAL A. Sistem Bilangan Real Sistem bilangan real sangat erat kaitannya dengan kalkulus. Sebagian dari kalkulus berdasar pada sifat-sifat sistem bilangan real, sehingga sistem bilangan
BAB I SISTEM BILANGAN REAL A. Sistem Bilangan Real Sistem bilangan real sangat erat kaitannya dengan kalkulus. Sebagian dari kalkulus berdasar pada sifat-sifat sistem bilangan real, sehingga sistem bilangan
Definisi 4.1 Fungsi f dikatakan kontinu di titik a (continuous at a) jika dan hanya jika ketiga syarat berikut dipenuhi: (1) f(a) ada,
 Lecture 4. Limit B A. Continuity Definisi 4.1 Fungsi f dikatakan kontinu di titik a (continuous at a) jika dan hanya jika ketiga syarat berikut dipenuhi: (1) f(a) ada, (2) lim f(x) ada, (3) lim f(x) =
Lecture 4. Limit B A. Continuity Definisi 4.1 Fungsi f dikatakan kontinu di titik a (continuous at a) jika dan hanya jika ketiga syarat berikut dipenuhi: (1) f(a) ada, (2) lim f(x) ada, (3) lim f(x) =
BAB V PENERAPAN DIFFERENSIASI
 BAB V PENERAPAN DIFFERENSIASI 5.1 Persamaan garis singgung Bentuk umum persamaan garis adalah = m + n, dimana m adalah koeffisien arah atau kemiringan garis dan n adalah penggal garis. Sekarang perhatikan
BAB V PENERAPAN DIFFERENSIASI 5.1 Persamaan garis singgung Bentuk umum persamaan garis adalah = m + n, dimana m adalah koeffisien arah atau kemiringan garis dan n adalah penggal garis. Sekarang perhatikan
BAB III TURUNAN DALAM RUANG DIMENSI-n
 BAB III TURUNAN DALAM RUANG DIMENSI-n 1. FUNGSI DUA PEUBAH ATAU LEBIH fungsi bernilai riil dari peubah riil, fungsi bernilai vektor dari peubah riil Fungsi bernilai riil dari dua peubah riil yakni, fungsi
BAB III TURUNAN DALAM RUANG DIMENSI-n 1. FUNGSI DUA PEUBAH ATAU LEBIH fungsi bernilai riil dari peubah riil, fungsi bernilai vektor dari peubah riil Fungsi bernilai riil dari dua peubah riil yakni, fungsi
Pertemuan Minggu ke Bidang Singgung, Hampiran 2. Maksimum dan Minimum 3. Metode Lagrange
 Pertemuan Minggu ke-11 1. Bidang Singgung, Hampiran 2. Maksimum dan Minimum 3. Metode Lagrange 1. BIDANG SINGGUNG, HAMPIRAN Tujuan mempelajari: memperoleh persamaan bidang singgung terhadap permukaan z
Pertemuan Minggu ke-11 1. Bidang Singgung, Hampiran 2. Maksimum dan Minimum 3. Metode Lagrange 1. BIDANG SINGGUNG, HAMPIRAN Tujuan mempelajari: memperoleh persamaan bidang singgung terhadap permukaan z
KALKULUS I TEOREMA NILAI RATAAN (Mean Value Theorem) SUTRIANI HIDRI Matematika B
 KALKULUS I TEOREMA NILAI RATAAN (Mean Value Theorem) SUTRIANI HIDRI Matematika B 1111140010 JURUSAN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS NEGERI MAKASSAR 2011 Teorema Nilai
KALKULUS I TEOREMA NILAI RATAAN (Mean Value Theorem) SUTRIANI HIDRI Matematika B 1111140010 JURUSAN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS NEGERI MAKASSAR 2011 Teorema Nilai
SATUAN ACARA PERKULIAHAN MATA KULIAH: KALKULUS 1 ; 3 SKS OLEH: FIRDAUS-0716 TUJUAN INSTRUKSIONAL KHUSUS Sistem Bilangan Real
 JURUSAN PENDIDIKAN MATEMATIKA FPMIPA UPI BANDUNG SESI POKOK DAN SUB POKOK BAHASAN TUJUAN INSTRUKSIONAL UMUM SATUAN ACARA PERKULIAHAN MATA KULIAH: KALKULUS 1 ; 3 SKS OLEH: FIRDAUS-0716 TUJUAN INSTRUKSIONAL
JURUSAN PENDIDIKAN MATEMATIKA FPMIPA UPI BANDUNG SESI POKOK DAN SUB POKOK BAHASAN TUJUAN INSTRUKSIONAL UMUM SATUAN ACARA PERKULIAHAN MATA KULIAH: KALKULUS 1 ; 3 SKS OLEH: FIRDAUS-0716 TUJUAN INSTRUKSIONAL
Catatan Kuliah MA1123 Kalkulus Elementer I
 Catatan Kuliah MA1123 Kalkulus Elementer I Oleh Hendra Gunawan, Ph.D. Departemen Matematika ITB Sasaran Belajar Setelah mempelajari materi Kalkulus Elementer I, mahasiswa diharapkan memiliki (terutama):
Catatan Kuliah MA1123 Kalkulus Elementer I Oleh Hendra Gunawan, Ph.D. Departemen Matematika ITB Sasaran Belajar Setelah mempelajari materi Kalkulus Elementer I, mahasiswa diharapkan memiliki (terutama):
UJIAN TENGAH SEMESTER KALKULUS/KALKULUS1
 Jurusan Matematika FMIPA IPB UJIAN TENGAH SEMESTER KALKULUS/KALKULUS1 Sabtu, 4 Maret 003 Waktu : jam SETIAP NOMOR MEMPUNYAI BOBOT 10 1. Tentukan: (a) (b) x sin x x + 1 ; x (cos (x 1)) :. Diberikan fungsi
Jurusan Matematika FMIPA IPB UJIAN TENGAH SEMESTER KALKULUS/KALKULUS1 Sabtu, 4 Maret 003 Waktu : jam SETIAP NOMOR MEMPUNYAI BOBOT 10 1. Tentukan: (a) (b) x sin x x + 1 ; x (cos (x 1)) :. Diberikan fungsi
DERIVATIVE Arum Handini primandari
 DERIVATIVE Arum Handini primandari INTRODUCTION Calculus adalah perubahan matematis, alat utama dalam studi perubahan adalah prosedur yang disebut differentiation (deferensial/turunan) Calculus dikembangkan
DERIVATIVE Arum Handini primandari INTRODUCTION Calculus adalah perubahan matematis, alat utama dalam studi perubahan adalah prosedur yang disebut differentiation (deferensial/turunan) Calculus dikembangkan
JAWABAN PERSIAPAN UKD-5 APLIKASI TURUNAN. 1. Tentukan pers garis singgung (PGS) pada kurva. 2. Tentukan pers garis normal (PGN) pada kurva
 JAWABAN PERSIAPAN UKD-5 APLIKASI TURUNAN. Tentukan pers garis singgung (PGS) pada kurva y 4x % 7x + 5 di titik (, ) x y 4( ) % 7( ) + 5 oke y 5 8x 7 m 8( ) 7 5 y 5(x + ) y 5x 5 y 5x +. Tentukan pers garis
JAWABAN PERSIAPAN UKD-5 APLIKASI TURUNAN. Tentukan pers garis singgung (PGS) pada kurva y 4x % 7x + 5 di titik (, ) x y 4( ) % 7( ) + 5 oke y 5 8x 7 m 8( ) 7 5 y 5(x + ) y 5x 5 y 5x +. Tentukan pers garis
TUJUAN INSTRUKSIONAL KHUSUS
 PREVIEW KALKULUS TUJUAN INSTRUKSIONAL KHUSUS Mahasiswa mampu: menyebutkan konsep-konsep utama dalam kalkulus dan contoh masalah-masalah yang memotivasi konsep tersebut; menjelaskan menyebutkan konsep-konsep
PREVIEW KALKULUS TUJUAN INSTRUKSIONAL KHUSUS Mahasiswa mampu: menyebutkan konsep-konsep utama dalam kalkulus dan contoh masalah-masalah yang memotivasi konsep tersebut; menjelaskan menyebutkan konsep-konsep
Silabus. Sekolah : : 2. Menentukan Komposisi Dua Fungsi Dan Invers Suatu Fungsi. Kegiatan Pembelajaran. Kompetensi Dasar.
 Silabus Sekolah : Mata Pelajaran : Matematika Kelas/Program : XI/ Ilmu Sosial Semester : II (Genap) Standar Kompetensi : 2. Menentukan Komposisi Dua Fungsi Dan Invers Suatu Fungsi : 35 x 45 Menit Kompetensi
Silabus Sekolah : Mata Pelajaran : Matematika Kelas/Program : XI/ Ilmu Sosial Semester : II (Genap) Standar Kompetensi : 2. Menentukan Komposisi Dua Fungsi Dan Invers Suatu Fungsi : 35 x 45 Menit Kompetensi
Pertemuan 6 APLIKASI TURUNAN
 Kalkulus Pertemuan 6 APLIKASI TURUNAN Menggambar Grafik Fungsi : Gambarlah grafik dari fungsi berikut! 4 f ( ) Beberapa informasi yang diperlukan untuk mengambar grafik dari fungsi tersebut adalah sebagai
Kalkulus Pertemuan 6 APLIKASI TURUNAN Menggambar Grafik Fungsi : Gambarlah grafik dari fungsi berikut! 4 f ( ) Beberapa informasi yang diperlukan untuk mengambar grafik dari fungsi tersebut adalah sebagai
MAKALAH PENGGUNAAN TURUNAN DALAM BIDANG KESEHATAN DAN FARMASI. Dibuat untuk memenuhi tugas Matematika Dosen: Andes Safarandes, S,Pd. M.
 MAKALAH PENGGUNAAN TURUNAN DALAM BIDANG KESEHATAN DAN FARMASI Dibuat untuk memenuhi tugas Matematika Dosen: Andes Safarandes, S,Pd. M.Pd Disusun Oleh: Kelompok 2 Siti Hufi Hutami Eni Nuraeni Dewanta Arya
MAKALAH PENGGUNAAN TURUNAN DALAM BIDANG KESEHATAN DAN FARMASI Dibuat untuk memenuhi tugas Matematika Dosen: Andes Safarandes, S,Pd. M.Pd Disusun Oleh: Kelompok 2 Siti Hufi Hutami Eni Nuraeni Dewanta Arya
Model Optimisasi dan Pemrograman Linear
 Modul Model Optimisasi dan Pemrograman Linear Prof. Dr. Djati Kerami Dra. Denny Riama Silaban, M.Kom. S PENDAHULUAN ebelum membuat rancangan penyelesaian masalah dalam bentuk riset operasional, kita harus
Modul Model Optimisasi dan Pemrograman Linear Prof. Dr. Djati Kerami Dra. Denny Riama Silaban, M.Kom. S PENDAHULUAN ebelum membuat rancangan penyelesaian masalah dalam bentuk riset operasional, kita harus
METODE NUMERIK TKM4104. Kuliah ke-3 SOLUSI PERSAMAAN NONLINIER 1
 METODE NUMERIK TKM4104 Kuliah ke-3 SOLUSI PERSAMAAN NONLINIER 1 SOLUSI PERSAMAAN NONLINIER Metode pengurung (Bracketing Method) Metode Konvergen Mulai dengan terkaan awal yang mengurung atau memuat akar
METODE NUMERIK TKM4104 Kuliah ke-3 SOLUSI PERSAMAAN NONLINIER 1 SOLUSI PERSAMAAN NONLINIER Metode pengurung (Bracketing Method) Metode Konvergen Mulai dengan terkaan awal yang mengurung atau memuat akar
Turunan Fungsi dan Aplikasinya
 Bab 8 Sumber: www.duniacyber.com Turunan Fungsi dan Aplikasinya Setelah mempelajari bab ini, Anda harus mampu menggunakan konsep, sifat, dan aturan dalam perhitungan turunan fungsi; menggunakan turunan
Bab 8 Sumber: www.duniacyber.com Turunan Fungsi dan Aplikasinya Setelah mempelajari bab ini, Anda harus mampu menggunakan konsep, sifat, dan aturan dalam perhitungan turunan fungsi; menggunakan turunan
Open Source. Not For Commercial Use
 Ringkasan Kalkulus 2, Untuk dipakai di ITB 1 Limit dan Kekontinuan Misalkan z = f(, y) fungsi dua peubah dan (a, b) R 2. Seperti pada limit fungsi satu peubah, limit fungsi dua peubah bertujuan untuk mengamati
Ringkasan Kalkulus 2, Untuk dipakai di ITB 1 Limit dan Kekontinuan Misalkan z = f(, y) fungsi dua peubah dan (a, b) R 2. Seperti pada limit fungsi satu peubah, limit fungsi dua peubah bertujuan untuk mengamati
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI Pada bab ini akan dibahas beberapa pengertian dari optimasi bersyarat dengan kendala persamaan menggunakan multiplier lagrange serta penerapannya yang akan digunakan sebagai landasan
BAB 2 LANDASAN TEORI Pada bab ini akan dibahas beberapa pengertian dari optimasi bersyarat dengan kendala persamaan menggunakan multiplier lagrange serta penerapannya yang akan digunakan sebagai landasan
SATUAN ACARA PERKULIAHAN PROGRAM KOMPETENSI GANDA DEPAG S1 KEDUA PROGRAM STUDI PENDIDIKAN MATEMATIKA
 SATUAN ACARA PERKULIAHAN PROGRAM GANDA DEPAG S1 DUA PROGRAM STUDI PENDIDIKAN MATEMATIKA 1. PROGRAM STUDI : Pendidikan Matematika 2. MATA KULIAH/SEMESTER : Kalkulus/2 3. PRASYARAT : -- 4. JENJANG / SKS
SATUAN ACARA PERKULIAHAN PROGRAM GANDA DEPAG S1 DUA PROGRAM STUDI PENDIDIKAN MATEMATIKA 1. PROGRAM STUDI : Pendidikan Matematika 2. MATA KULIAH/SEMESTER : Kalkulus/2 3. PRASYARAT : -- 4. JENJANG / SKS
AB = c, AC = b dan BC = a, maka PQ =. 1
 Soal-Soal dan Pembahasan Matematika IPA SNMPTN 9. Jika a, b, maka pernyataan di bawah ini yang benar adalah A. B. a b ab C. ab b a D. ab ab E. ab ab ab b a karena pada jawaban terdapat ab maka selesaikan
Soal-Soal dan Pembahasan Matematika IPA SNMPTN 9. Jika a, b, maka pernyataan di bawah ini yang benar adalah A. B. a b ab C. ab b a D. ab ab E. ab ab ab b a karena pada jawaban terdapat ab maka selesaikan
Kelompok Mata Kuliah : MKU Program Studi/Program : Teknik Tenaga Elektrik/S1 Status Mata Kuliah : Wajib Prasyarat : - : Aip Saripudin, M.T.
 DESKRIPSI MATA KULIAH TK-... Matematika Dasar: S1, 3 SKS, Semester I Mata kuliah ini merupakan kuliah dasar. Selesai mengikuti perkuliahan ini mahasiswa diharapkan mampu memahami konsep-konsep matematika
DESKRIPSI MATA KULIAH TK-... Matematika Dasar: S1, 3 SKS, Semester I Mata kuliah ini merupakan kuliah dasar. Selesai mengikuti perkuliahan ini mahasiswa diharapkan mampu memahami konsep-konsep matematika
Kalkulus Multivariabel I
 Maksimum, Minimum, dan Statistika FMIPA Universitas Islam Indonesia Titik Kritis Misalkan p = (x, y) adalah sebuah titik peubah dan p 0 = (x 0, y 0 ) adalah sebuah titik tetap pada bidang berdimensi dua
Maksimum, Minimum, dan Statistika FMIPA Universitas Islam Indonesia Titik Kritis Misalkan p = (x, y) adalah sebuah titik peubah dan p 0 = (x 0, y 0 ) adalah sebuah titik tetap pada bidang berdimensi dua
ANALISIS REAL. (Semester I Tahun ) Hendra Gunawan. October 10, Dosen FMIPA - ITB
 (Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. October 10, 2011 Pemahaman yang baik tentang fungsi kontinu merupakan hal yang penting dalam analisis. Dalam optimisasi,
(Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. October 10, 2011 Pemahaman yang baik tentang fungsi kontinu merupakan hal yang penting dalam analisis. Dalam optimisasi,
Kuliah 3: TURUNAN. Indah Yanti
 Kuliah 3: TURUNAN Indah Yanti Turunan Parsial DEFINISI Misalkan fungsi f: A R, dengan A R n adalah himpunan buka. Untuk setiap x = (x 1,..., x n ) A dan setiap j = 1,..., n limit f x j x 1,, x n f x 1,,
Kuliah 3: TURUNAN Indah Yanti Turunan Parsial DEFINISI Misalkan fungsi f: A R, dengan A R n adalah himpunan buka. Untuk setiap x = (x 1,..., x n ) A dan setiap j = 1,..., n limit f x j x 1,, x n f x 1,,
MATEMATIKA TURUNAN FUNGSI
 MATEMATIKA TURUNAN FUNGSI lim h 0 f ( x h) f( x) h KELAS : XI IPS SEMESTER : (DUA) SMA Santa Angela Bandung Tahun Pelajaran 015-016 XI IPS Semester Tahun Pelajaran 015 016 PENGANTAR : TURUNAN FUNGSI Modul
MATEMATIKA TURUNAN FUNGSI lim h 0 f ( x h) f( x) h KELAS : XI IPS SEMESTER : (DUA) SMA Santa Angela Bandung Tahun Pelajaran 015-016 XI IPS Semester Tahun Pelajaran 015 016 PENGANTAR : TURUNAN FUNGSI Modul
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
4 DIFERENSIAL. 4.1 Pengertian derivatif
 Diferensial merupakan topik yang cukup 'baru' dalam matematika. Dimulai sekitar tahun 1630 an oleh Fermat ketika menghadapi masalah menentukan garis singgung kurva, dan juga masalah menentukan maksimum
Diferensial merupakan topik yang cukup 'baru' dalam matematika. Dimulai sekitar tahun 1630 an oleh Fermat ketika menghadapi masalah menentukan garis singgung kurva, dan juga masalah menentukan maksimum
LEMBAR KERJA SISWA (LKS) Pertemuan I
 186 LAMPIRAN V LKS 1 LEMBAR KERJA SISWA (LKS) Pertemuan I Nama : Kelas : Mata Pelajaran Materi Pokok Standar kompetensi : Matematika : Persamaan Garis Singgung Kurva : Menggunakan konsep limit fungsi dan
186 LAMPIRAN V LKS 1 LEMBAR KERJA SISWA (LKS) Pertemuan I Nama : Kelas : Mata Pelajaran Materi Pokok Standar kompetensi : Matematika : Persamaan Garis Singgung Kurva : Menggunakan konsep limit fungsi dan
Kelompok Mata Kuliah : MKU Program Studi/Program : Pendidikan Teknik Elektro/S1 Status Mata Kuliah : Wajib Prasyarat : - : Aip Saripudin, M.T.
 DESKRIPSI MATA KULIAH TK-301 Matematika: S1, 3 SKS, Semester I Mata kuliah ini merupakan kuliah dasar. Selesai mengikuti perkuliahan ini mahasiswa diharapkan mampu memahami konsep-konsep matematika dan
DESKRIPSI MATA KULIAH TK-301 Matematika: S1, 3 SKS, Semester I Mata kuliah ini merupakan kuliah dasar. Selesai mengikuti perkuliahan ini mahasiswa diharapkan mampu memahami konsep-konsep matematika dan
PENGGUNAAN TURUNAN IKA ARFIANI, S.T.
 PENGGUNAAN TURUNAN IKA ARFIANI, S.T. MASALAH MAKSIMUM DAN MINIMUM Misalkan f fungsi dua variable maka f dikatakan mencapai maksimum relatif di titik (a,b) jika terdapat kitaran dari (a,b) demikian sehingga
PENGGUNAAN TURUNAN IKA ARFIANI, S.T. MASALAH MAKSIMUM DAN MINIMUM Misalkan f fungsi dua variable maka f dikatakan mencapai maksimum relatif di titik (a,b) jika terdapat kitaran dari (a,b) demikian sehingga
MATERI KALKULUS. y' = F'(x) = f(x), y'' = F''(x) = f'(x), y'''=f'''(x) = f''(x)= g'(x)= h(x) y1= f(x) y2 = g(x) y3 = h(x)
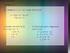 Universitas Muhammadiyah Sukabumi Artikel Kalkulus Oleh : ardi meridian herdiansyah MATERI KALKULUS KALKULUS 1 MODUL 6 V. MAKSIMUM / MINIMUM ( EKSTREM FUNGSI ) 5.1. Pengertian Diketahui y = F(x) suatu
Universitas Muhammadiyah Sukabumi Artikel Kalkulus Oleh : ardi meridian herdiansyah MATERI KALKULUS KALKULUS 1 MODUL 6 V. MAKSIMUM / MINIMUM ( EKSTREM FUNGSI ) 5.1. Pengertian Diketahui y = F(x) suatu
DIFERENSIAL FUNGSI SEDERHANA
 DIFERENSIAL FUNGSI SEDERHANA Salah satu metoe yang cukup penting alam matematika aalah turunan (iferensial). Sejalan engan perkembangannya aplikasi turunan telah banyak igunakan untuk biang-biang rekayasa
DIFERENSIAL FUNGSI SEDERHANA Salah satu metoe yang cukup penting alam matematika aalah turunan (iferensial). Sejalan engan perkembangannya aplikasi turunan telah banyak igunakan untuk biang-biang rekayasa
Turunan Fungsi dan Aplikasinya
 Bab 8 Sumber: www.duniacyber.com Turunan Fungsi dan Aplikasinya Setelah mempelajari bab ini, Anda harus mampu menggunakan konsep, siat, dan aturan dalam perhitungan turunan ungsi; menggunakan turunan untuk
Bab 8 Sumber: www.duniacyber.com Turunan Fungsi dan Aplikasinya Setelah mempelajari bab ini, Anda harus mampu menggunakan konsep, siat, dan aturan dalam perhitungan turunan ungsi; menggunakan turunan untuk
Hendra Gunawan. 11 Oktober 2013
 MA1101 MATEMATIKA 1A Hendra Gunawan Semester I, 2013/2014 11 Oktober 2013 Latihan (Kuliah yang Lalu) Dengan memperhatikan: daerah asal dan daerahhasilnya, titik titik potong dengan sumbu koordinat, asimtot
MA1101 MATEMATIKA 1A Hendra Gunawan Semester I, 2013/2014 11 Oktober 2013 Latihan (Kuliah yang Lalu) Dengan memperhatikan: daerah asal dan daerahhasilnya, titik titik potong dengan sumbu koordinat, asimtot
BAB V. PENGGUNAAN TURUNAN
 BAB V. PENGGUNAAN TURUNAN (Pertemuan ke 9 & 10) PENDAHULUAN Diskripsi singkat Pada bab ini ang dibahas adalah tentang nilai maksimum dan minimum, kemonotonan dan kean kurva, serta maksimum dan minimum
BAB V. PENGGUNAAN TURUNAN (Pertemuan ke 9 & 10) PENDAHULUAN Diskripsi singkat Pada bab ini ang dibahas adalah tentang nilai maksimum dan minimum, kemonotonan dan kean kurva, serta maksimum dan minimum
F. RANCANGAN KEGIATAN BELAJAR MENGAJAR
 F. RANCANGAN KEGIATAN BELAJAR MENGAJAR No. (TIU) 1. Limit Fungsi Mahasiswa dapar memahami secara mendalam (deduktif) pengertian limit fungsi, definisi dan te-orema-teorema serta mampu menga-plikasikannya
F. RANCANGAN KEGIATAN BELAJAR MENGAJAR No. (TIU) 1. Limit Fungsi Mahasiswa dapar memahami secara mendalam (deduktif) pengertian limit fungsi, definisi dan te-orema-teorema serta mampu menga-plikasikannya
FUNGSI. A. Relasi dan Fungsi Contoh: Manakah yang merupakan fungsi/pemetaan dan manakah yang bukan fungsi? (i) (ii) (iii)
 FUNGSI A. Relasi dan Fungsi Manakah yang merupakan fungsi/pemetaan dan manakah yang bukan fungsi? (i) (ii) (iii) Relasi himpunan A ke himpunan B adalah relasi yang memasangkan/mengkawankan/mengkorepodensikan
FUNGSI A. Relasi dan Fungsi Manakah yang merupakan fungsi/pemetaan dan manakah yang bukan fungsi? (i) (ii) (iii) Relasi himpunan A ke himpunan B adalah relasi yang memasangkan/mengkawankan/mengkorepodensikan
DASAR-DASAR ANALISIS MATEMATIKA
 (Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. December 11, 2007 Misalkan f terdefinisi pada suatu himpunan H. Kita katakan bahwa f naik pada H apabila
(Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. December 11, 2007 Misalkan f terdefinisi pada suatu himpunan H. Kita katakan bahwa f naik pada H apabila
APLIKASI TURUNAN ALJABAR. Tujuan Pembelajaran. ) kemudian menyentuh bukit kedua pada titik B(x 2
 Kurikulum 3/6 matematika K e l a s XI APLIKASI TURUNAN ALJABAR Tujuan Pembelajaran Setelah mempelajari materi ini, kamu diharapkan memiliki kemampuan berikut.. Dapat menerapkan aturan turunan aljabar untuk
Kurikulum 3/6 matematika K e l a s XI APLIKASI TURUNAN ALJABAR Tujuan Pembelajaran Setelah mempelajari materi ini, kamu diharapkan memiliki kemampuan berikut.. Dapat menerapkan aturan turunan aljabar untuk
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016. Hendra Gunawan
 MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 4.2 Sifat-Sifat Fungsi Kontinu Diberikan f dan g, keduanya terdefinisi pada himpunan A, kita definisikan f + g, f g, fg, f/g secara
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 4.2 Sifat-Sifat Fungsi Kontinu Diberikan f dan g, keduanya terdefinisi pada himpunan A, kita definisikan f + g, f g, fg, f/g secara
f (a) = laju perubahan y = f(x) pada x = a = turunan pertama y=f(x) pada x = a
 LEMBAR AKTIVITAS SISWA DIFFERENSIAL (TURUNAN) Nama Siswa : y f(a h) f(a) x (a h) a Kelas : Kompetensi Dasar (KURIKULUM 2013): 3.21 Memahami konsep turunan dengan menggunakan konteks matematik atau konteks
LEMBAR AKTIVITAS SISWA DIFFERENSIAL (TURUNAN) Nama Siswa : y f(a h) f(a) x (a h) a Kelas : Kompetensi Dasar (KURIKULUM 2013): 3.21 Memahami konsep turunan dengan menggunakan konteks matematik atau konteks
