Modul Matematika 2012
|
|
|
- Widya Sasmita
- 9 tahun lalu
- Tontonan:
Transkripsi
1 Modul Matematika 0 Minggu ke dan MAKSIMISASI ATAU MINIMISASI (MAXIMIZATION ATAU MINIMIZATION) : A FREE OPTIMUM. Pengertian dan persyaratan Global maximum atau global minimum, Relative maximum atau relative minimum : Dengan ungsi dari (satu) independent variable y = (x) Dependent variable dari ungsi merupakan the objective unction yaitu obyek dari maksimisasi (maximization) atau minimisasi (minimization). Maximization atau minimization menetapkan angka atau bilangan dari independent variables sehingga diperoleh angka atau nilai the objective unction atau dependent variable tertinggi (maximum) atau terendah (minimum). Karena itu, independent variables juga disebut sebagai choice variables. Istilah : Baik global maximum atau minimum, maupun relative maximum atau minimum, disebut extremum. Titik extremum disebut stationary point. Sedangkan angka atau nilai extremum dari ungsi atau dependent variable atau the objective unction disebut a critical value atau stationary value. Selain itu, the slope dari the objective unction pada titik extremum adalah 0 (nol). Suryari Purnama
2 Modul Matematika 0 Diagram G.4. : Extremum Fungsi y = (x) y (a) (b) y A z = g(w) E C B h = k(m) G 0 x D y M (c) q = s(u) y = (x) N F 0 x 0 x Global (absolute) maximum adalah titik atau angka tertinggi dari the objective unction atau dependent variable. Contoh, titik A pada ungsi z = g(w) di bawah. Sedangkan, global (absolute) minimum merupakan titik atau angka terendah. Contoh titik B pada ungsi h = k(m) di atas. Relative (local) maximum adalah titik atau angka maximum di sekitar titik itu pada the objective unction. Sedangkan, relative (local) minimum adalah titik atau angka minimum di sekitar titik itu pada the objective unction. Diantara 4 extremums pada Diagram G.4. (b) di atas, maka : Titik E adalah a global (absolute or ree) maximum, sedangkan titik G adalah local (relative) maximum. Titik F adalah a global minimum, sedangkan titk D adalah local minimum. Suryari Purnama
3 Modul Matematika 0 Persyaratan untuk extremum dan inlection point : Dengan ungsi dari (satu) independent variable) y = (x) PERSYARATAN EXTREMUM (Global/Absolute and Local/Relative) Maximum Minimum Inlection Point Necessary Condition, or, First Order Condition (FOC) (First Derivative Condition) 0 = 0 = 0 Suiciet Condition, or, Second Order Condition = (SOC) (Second Derivative Condition) : *) a. SOC necessary b. SOC suicient.. < 0 > 0 ) ) = 0 ) * ) SOC bahwa negative (< 0) / positi (> 0) pada nilai kritikal (the critical value) x 0 adalah cukup (suicient) untuk relative maximum/relative minimum, merupakan hal yang tidak perlu (necessary). Oleh karena itu, kehati-hatian diperlukan atas dasar kenyataan bahwa relative maximum/relative minimum dapat terjadi tidak hanya apabila negative (< 0) / positi (> 0), tetapi juga apabila = 0. Dengan demikian, SOC necessary harus dinyatakan dengan weak inequalities 0) / 0. Lihat C & W (Book ) Ch. 9 hal 35. Ingat :. Untuk the irst derivative : a. > 0 berarti nilai ungsi (the value o the unction) akan meningkat. b. > 0 berarti nilai ungsi (the value o the unction) akan menurun... Untuk the second derivative : a. > 0 berarti the slope o the unction or the curve akan meningkat. b. > 0 berarti the slope o the unction or the curve akan meningkat. Catatan : Titik M dan N pada Diagram G.4. (c) di atas, tidak dapat dianggap extremum karena pada kedua titik itu ungsi g = s(u) tidak kontinyu sehingga tidak terdapat derivati dari ungsi g. Titik inleksi (inlection point) adalah titik dimana tidak terdapat extremum (maximum atau minimum). Suryari Purnama 3
4 Modul Matematika 0 Diagram G.5. : Inlection point pada ungsi y = (x) dan y = g (x) (a) (b) y y = (x) y y = g(x) slope + slope + J slope = 0 K slope + slope + 0 x 0 x dy dy = dy dy = 0 J x 0 x Penjelasan inlection point : Pada Diagram G.5di atas, titik J dan K disebut inlection point karena tanda slope tidak berubah dari sebelum ke sesudah titik J atau K : Pada diagram G.5. (a), walaupun mempunyai ungsi (x) derivati pada titik J = 0 atau = 0, yang juga digambarkan dengan slope pada titik J = 0. Tetapi tanda slope atau derivati tetap sama positi (slope +) baik sebelum dan sesudah titik J dan J. Padahal syarat titik J menjadi extremum, apabila tanda slope berubah dari sebelum ke sesudah titik extremum J. Apabila titik J minimum, maka tanda slope berubah dari negati untuk sebelum titik J menjadi positi untuk setelah titik J. Atau sebaliknya, apabila titik J. Pada Diagram G.5. (b) di atas, derivati atau slope ungsi g(x) pada titik K tertinggi maximum (tidak sama dengan 0 (nol)) seperti terlihat pada titik K. Tetapi slope atau derivati atau sebelum titik K naik (+) tajam dan setelah titik K tetap naik (+) tetapi dengan melandai atau menurun.. Contoh Maximisasi dan Minimisasi dengan ungsi dari (satu) Independent variable Minimisasi dari ungsi y = (x) = 4 x x dimana kurva berbentuk U (U-shaped curve) Suryari Purnama 4
5 Modul Matematika 0 Syarat : The irst order condition (FOC) atau necessary condition : dy / 8x Maka : 8 x = berarti x = ⅛ The second order condition (SOC) atau suicient condition : d y // 8 > 0 d y // Karena SOC terpenuhi yaitu > 0 atau 0 tapi pisiti, maka nilai minimum dari ungsi atau dependent variable (the stationary value pada x = ⅛, yaitu y = 4. (⅛) ⅛ =. 3. Maksimisasi dan minimisasi dengan ungsi dari (dua) atau lebih independent variables Fungsi z = (x, y) FOC : Persyaratan FOC untuk Extermum bagi ungsi dengan independent variable z = (x, y) Maximum Minimum FOC dz = 0 untuk setiap nilai atau angka atau dy 0 atau hanya salah satu = 0, sehingga berarti : x = 0 dan y = 0 dz = 0 untuk setiap nilai atau angka dan dy 0 atau hanya salah satu = 0, sehingga berarti : x = 0 dan y = 0 dz = (The irst) total dierential dari ungsi z = (x, y) dz z z dy x ydy, dimana : x y x = z = the partial derivative ungsi z terhadap independent variable x x y = z = the partial derivative ungsi z terhadap independent variable y y Dengan FOC yaitu dz = 0 dan dan dy 0 sehingga partial derivatives x dan y = 0, maka angka atau nilai variabel x dan y diperoleh. 0 6 Untuk lebih dari (dua) independent variables FOC dan SOC diormulasikan dengan menggunakan matriks dan vectors, pada kuliah mendatang. Suryari Purnama 5
6 SOC : Persyaratan SOC untuk Extermum bagi ungsi dengan independent variable Maximum Modul Matematika 0 Minimum SOC necessary d z 0 D z 0 d z < 0 berarti jika (i) * : xx < 0, yy < 0, serta xx yy > ( xy ) xx yy > ( xy ) SOC suicient ( dz) ( dz) * Karena : d z d( dz) dy x y d z d( dz) = ( x ydy) ( x ydy) dy = x y = ( dy) ( dy dy= Catatan d z > 0 berarti jika (i) * : xx > 0, yy > 0, serta xx xy yx yy ) = xx xydy yxdy yydy = = xx xydy yydy atau mempunyai angka atau nilai yang sama xy seperti didalilkan oleh Young s theorem. Contoh : z = 8 x 3 + xy 3 x + y + FOC : x = 4 x + y 6 x = 0 dan y = x + y = 0 yx dengan substitusi, maka diperoleh angka x dan y : x = 0 berarti y = 0; x = 3 berarti y = 3 SOC : Dengan x = 0 dan y = 0, maka : xx = 48 x 6 = 6 (< 0); yy = (> 0), { xx yy = } < {( xy ) = () = 4} Jadi SOC tidak terpenuhi dengan x = 0 dan y = 0 baik untuk maximum maupun minimum Dengan x = 3 dan y = 3, maka : xx = 48 x 6 = 0 ( > 0); yy = (> 0), { xx yy = 0} > {( xy ) = () = 4} Suryari Purnama 6
7 Modul Matematika 0 Jadi SOC terpenuhi dengan x = 3 nilai atau angka z = dan y = 3, sehingga Contoh : z = x + ey e x e y FOC : x = e x = 0 dan y = e + e y = 0 dengan substitusi, maka diperoleh hanya angka x dan y : x = 0 berarti y = ½ SOC : Dengan x = 0 dan y = ½, maka : xx = e x = (< 0); yy = 4 e y = 4 e (< 0), { xx yy = 4} > {( xy ) = (0) = 0} Jadi SOC terpenuhi dengan x = 0 dan y = ½, sehingga nilai atau angka z = 0 + e e 0 e = G.. A CONSTRAINED OPTIMIZATION : OPTIMISASI, ATAU, MAKSIMISASI ATAU MINIMISASI DENGAN BATASAN TERTENTU. Pengertian a constrained opmization Pada G.3. tentang maksimisasi (maximization) dan minimisasi (minimization) atau extremum tanpa batasan tertentu (a constraint), disebut a ree optimum. Pada G.4. ini tentang maximization dan minimization atau extremum dengan suatu batasan tertentu (a constraint atau subject to), disebut a constraint optimization. The constraint juga disebut, restraint, side relation, subsidiary condition, yang berungsi membatasi (subject to) domain dari ungsi dan berarti akhirnya terhadap range dari ungsi itu sendiri (the objective unction). Diagram perbedaan a ree optimum dan a constrained optimum pada C&W (book ) Ch. hal Suryari Purnama 7
8 . Penyelesaian a constrained optimum dengan dua cara Modul Matematika 0 The objective unction : U = x x + x A constraint or subject to : 4 x + x = 60 Penyelesaian atas dasar cara a ree optimum seperti pada G.3. di atas Dari the constraint (a linear unction) 4 x + x = 60 diperoleh x = 30 x Maka the objective unction hanya dengan variable x menjadi : U = x (30 x ) + x = 3 x x Kemudian cari dan buktikan extremum dalam hal ini maximum atas dasar persyaratan the ree optimum seperti pada G.3. di atas : U = 3 4 x = 0 diperoleh x = 8 dan x = 4 sehingga U = = + 6 = 8 U = 8 maksimum karena U = 4 (< 0) sehingga SOC untuk maksimum terpenuhi. Penyelesaian dengan Lagrange Multiplier method Esensi dari the Lagrange multiplier method adalah agar cara the ree optimum dapat diaplikasikan pada the constrained optimum. Untuk itu perlu dibentuk the Lagrangian unction yang menyatukan the objective unction dan the constrained unction dengan the Lagrange (undermined) multiplier λ (the Greek letter lambda). Dengan contoh ungsi-ungsi di atas, maka the Lagrangian unction Z : Max. (maximize) : U = x x + x S.t. (subject to) : 4 x + x = 60 Z = Z (x, x, λ) = x x + x + λ {60 (4 x + x )} FOC : Z = Z = Z λ = Z = x λ = 0 x Z x = x λ = 0 Z = 60 4 x x = 0 Untuk lebih dari (dua) independent variables FOC dan SOC diormulasikan dengan menggunakan matriks dan vectors, pada kuliah mendatang. Suryari Purnama 8
9 Modul Matematika 0 Penyelesaian 3 persamaan FOC di atas dengan substitusi menghasilkan : x = 8, x = 4, λ = 4, sehingga Z = x x + x + λ {60 (4 x + x )} = 8 U = x x + x = = 8 Catatan : Dengan demikian apabila angka x dan x menyebabkan angka ungsi constraint benar sebesar 60, yaitu 4 x + x = 60, maka terlepas dari apapun angka λ ungsi dan angka Z = U = x x + x dan yang berarti ungsi λ {60 (4 x + x )} pada bagian akhir ungsi Z menjadi hilang. SOC : Akan dijelaskan dengan menggunakan matriks dan vectors. Bentuk umum penyelesaian dengan the Lagrangian unction The objective unction : z = (x, y) Subject to the constraint : g (x, y) = c The Lagrangian unction : Z = (x, y) + λ {c g (x, y)} FOC : Z x = x λ g x = 0 Z y = y λ g y = 0 Z λ = c g (x, y) = 0 SOC : Akan dijelaskan dengan menggunakan matriks dan vectors. Suryari Purnama 9
MATEMATIKA EKONOMI DAN BISNIS MINGGU XII
 MATEMATIKA EKONOMI DAN BISNIS MINGGU XII OPTIMASI FUNGSI MULTIVARIAT TANPA DAN DENGAN KENDALA Prepared by : W. Roianto ROFI KONDISI MAKSIMUM DAN MINIMUM RELATIF DEFINISI Fungsi y = (,,, n ) maksimum relati
MATEMATIKA EKONOMI DAN BISNIS MINGGU XII OPTIMASI FUNGSI MULTIVARIAT TANPA DAN DENGAN KENDALA Prepared by : W. Roianto ROFI KONDISI MAKSIMUM DAN MINIMUM RELATIF DEFINISI Fungsi y = (,,, n ) maksimum relati
Optimisasi dengan batasan persamaan (Optimization with equality constraints) Mengapa batasan relevan dalam kajian ekonomi?
 Optimisasi dengan batasan persamaan (Optimization with equality constraints) Mengapa batasan relevan dalam kajian ekonomi? Masalah ekonomi timbul karena kelangkaan (scarcity). Kelangkaan menyebabkan keputusan
Optimisasi dengan batasan persamaan (Optimization with equality constraints) Mengapa batasan relevan dalam kajian ekonomi? Masalah ekonomi timbul karena kelangkaan (scarcity). Kelangkaan menyebabkan keputusan
Derivatif Parsial (Fungsi Multivariat)
 Derivatif Parsial (Fungsi Multivariat) week 12 W. Rofianto, ST, MSi FUNGSI MULTIVARIAT Fungsi dapat memiliki lebih dari satu variabel bebas. Fungsi demikian biasanya disebut sebagai fungsi multivariat.
Derivatif Parsial (Fungsi Multivariat) week 12 W. Rofianto, ST, MSi FUNGSI MULTIVARIAT Fungsi dapat memiliki lebih dari satu variabel bebas. Fungsi demikian biasanya disebut sebagai fungsi multivariat.
EKONOMI PRODUKSI. PERTEMUAN KEDELAPAN: MAKSIMISASI TERKENDALA (Lanjutan)
 EKONOMI PRODUKSI Kode PTE-4103 PERTEMUAN KEDELAPAN: MAKSIMISASI TERKENDALA (Lanjutan) Rini Dwiastuti 2007 Sub-pokok Bahasan (Lanjutan) 7. Constrained Revenue Max. 8. Second Order Condition 9. Interpretation
EKONOMI PRODUKSI Kode PTE-4103 PERTEMUAN KEDELAPAN: MAKSIMISASI TERKENDALA (Lanjutan) Rini Dwiastuti 2007 Sub-pokok Bahasan (Lanjutan) 7. Constrained Revenue Max. 8. Second Order Condition 9. Interpretation
Catatan Kuliah 7 Memahami dan Menganalisa Optimisasi Sederhana Tanpa Kendala dengan Satu Variabel Keputusan
 Catatan Kuliah 7 Memahami dan Menganalisa Optimisasi Sederhana Tanpa Kendala dengan Satu Variabel Keputusan Optimisasi Ilmu ekonomi adalah ilmu yang mempelajari bagaimana melakukan penelitian yang terbaik
Catatan Kuliah 7 Memahami dan Menganalisa Optimisasi Sederhana Tanpa Kendala dengan Satu Variabel Keputusan Optimisasi Ilmu ekonomi adalah ilmu yang mempelajari bagaimana melakukan penelitian yang terbaik
Prosiding Matematika ISSN:
 Prosiding Matematika ISSN: 2460-6464 Optimisasi Fungsi Nonlinier Dua Variabel Bebas dengan Satu Kendala Pertidaksamaan Menggunakan Syarat Kuhn-Tucker Optimization of Nonlinear Function of Two Independent
Prosiding Matematika ISSN: 2460-6464 Optimisasi Fungsi Nonlinier Dua Variabel Bebas dengan Satu Kendala Pertidaksamaan Menggunakan Syarat Kuhn-Tucker Optimization of Nonlinear Function of Two Independent
9/26/2008 EKONOMI PRODUKSI. Kode PTE-4103 PERTEMUAN KEENAM: MAKSIMISASI 2 INPUT
 EKONOMI PRODUKSI Kode PTE-4103 PERTEMUAN KEENAM: MAKSIMISASI 2 INPUT Rini Dwiastuti 2007 1 1. Introduction Sub-pokok Bahasan 2. The Maximum of a Function 3. Maximizing a Profit Function with Two Input
EKONOMI PRODUKSI Kode PTE-4103 PERTEMUAN KEENAM: MAKSIMISASI 2 INPUT Rini Dwiastuti 2007 1 1. Introduction Sub-pokok Bahasan 2. The Maximum of a Function 3. Maximizing a Profit Function with Two Input
DIKTAT KULIAH KALKULUS PEUBAH BANYAK (IE-308)
 DIKTAT KULIAH (IE-308) BAB 4 PENERAPAN TURUNAN PARSIAL Diktat ini digunakan bagi mahasiswa Jurusan Teknik Industri Fakultas Teknik Universitas Kristen Maranatha Ir. Rudy Wawolumaja M.Sc JURUSAN TEKNIK
DIKTAT KULIAH (IE-308) BAB 4 PENERAPAN TURUNAN PARSIAL Diktat ini digunakan bagi mahasiswa Jurusan Teknik Industri Fakultas Teknik Universitas Kristen Maranatha Ir. Rudy Wawolumaja M.Sc JURUSAN TEKNIK
Modul 6. Ekonomi Produksi Pertanian. Program Studi Agribisnis Fakultas Pertanian Universitas Brawijaya
 Modul 6 Ekonomi Produksi Pertanian Program Studi Agribisnis Fakultas Pertanian Universitas Brawijaya VI. MAKSIMALISASI PADA KASUS DUA INPUT Deskripsi Materi Pembelajaran: Bab ini menjelaskan konsep dasar
Modul 6 Ekonomi Produksi Pertanian Program Studi Agribisnis Fakultas Pertanian Universitas Brawijaya VI. MAKSIMALISASI PADA KASUS DUA INPUT Deskripsi Materi Pembelajaran: Bab ini menjelaskan konsep dasar
CATATAN KULIAH #5&6 Optimasi Tanpa Kendala dengan Lebih dari Satu Variabel
 CATATAN KULIAH #5&6 Optimasi Tanpa Kendala dengan Lebih dari Satu Variabel Sumber: Alpha C. Chiang, Fundamental Methods of Mathematical Economics, Ch.11 5.1 Pendahuluan Pada kuliah sebelumnya, optimasi
CATATAN KULIAH #5&6 Optimasi Tanpa Kendala dengan Lebih dari Satu Variabel Sumber: Alpha C. Chiang, Fundamental Methods of Mathematical Economics, Ch.11 5.1 Pendahuluan Pada kuliah sebelumnya, optimasi
CATATAN KULIAH Pertemuan VIII: Optimasi Tanpa Kendala dan Aplikasinya (Fungsi dengan Satu Variabel)
 CATATAN KULIAH Pertemuan VIII: Optimasi Tanpa Kendala dan Aplikasinya (Fungsi dengan Satu Variabel) A. Nilai Optimum dan Nilai Ekstrem Ekuilibrium Tujuan vs. Ekuilibrium Non-Tujuan:. Ekuilibrium Non-Tujuan:
CATATAN KULIAH Pertemuan VIII: Optimasi Tanpa Kendala dan Aplikasinya (Fungsi dengan Satu Variabel) A. Nilai Optimum dan Nilai Ekstrem Ekuilibrium Tujuan vs. Ekuilibrium Non-Tujuan:. Ekuilibrium Non-Tujuan:
MODUL 2 OPTIMISASI OPTIMISASI EKONOMI EKONOMI. SRI SULASMIYATI, S.Sos, M.AP. Ari Darmawan, Dr., S.AB, M.AB
 MODUL 2 OPTIMISASI OPTIMISASI EKONOMI EKONOMI SRI SULASMIYATI, S.Sos, M.AP Ari Darmawan, Dr., S.AB, M.AB [email protected] Pendahuluan Adanya kebutuhan manusia yang tidak terbatas dan terbatasnya
MODUL 2 OPTIMISASI OPTIMISASI EKONOMI EKONOMI SRI SULASMIYATI, S.Sos, M.AP Ari Darmawan, Dr., S.AB, M.AB [email protected] Pendahuluan Adanya kebutuhan manusia yang tidak terbatas dan terbatasnya
Modul 5. Teori Perilaku Produsen
 Modul 5. Teori Perilaku Produsen A. Deskripsi Modul Seorang produsen atau pengusaha dalam melakukan proses produksi untuk mencapai tujuannya harus menentukan dua macam keputusan: berapa output yang harus
Modul 5. Teori Perilaku Produsen A. Deskripsi Modul Seorang produsen atau pengusaha dalam melakukan proses produksi untuk mencapai tujuannya harus menentukan dua macam keputusan: berapa output yang harus
OPTIMASI: DIFERENSIAL PARSIAL MATEMATIKA T E L K O M U N I V E R S I T Y
 OPTIMASI: DIFERENSIAL PARSIAL MATEMATIKA T E L K O M U N I V E R S I T Y DIFERENSIAL PARSIAL Fungsi yang mengandung satu variabel bebas hanya akan memiliki satu macam turunan. apabila y = f(x) maka turunannya
OPTIMASI: DIFERENSIAL PARSIAL MATEMATIKA T E L K O M U N I V E R S I T Y DIFERENSIAL PARSIAL Fungsi yang mengandung satu variabel bebas hanya akan memiliki satu macam turunan. apabila y = f(x) maka turunannya
V. TEORI PERILAKU PRODUSEN
 Kardono -nuhfil V. TEORI PERILAKU PRODUSEN 5.. Fungsi Produksi Seorang produsen atau pengusaha dalam melakukan proses produksi untuk mencapai tujuannya harus menentukan dua macam keputusan: ) berapa output
Kardono -nuhfil V. TEORI PERILAKU PRODUSEN 5.. Fungsi Produksi Seorang produsen atau pengusaha dalam melakukan proses produksi untuk mencapai tujuannya harus menentukan dua macam keputusan: ) berapa output
BAB 1 PENDAHULUAN. 1.1 Latar Belakang
 BAB 1 PENDAHULUAN 1.1 Latar Belakang Dalam kehidupan sehari-hari baik disadari maupun tidak, sebenarnya orang selalu melakukan optimasi untuk memenuhi kebutuhannya. Tetapi optimasi yang dilakukan masyarakat
BAB 1 PENDAHULUAN 1.1 Latar Belakang Dalam kehidupan sehari-hari baik disadari maupun tidak, sebenarnya orang selalu melakukan optimasi untuk memenuhi kebutuhannya. Tetapi optimasi yang dilakukan masyarakat
III. KERANGKA TEORITIS
 III. KERANGKA TEORITIS 3.. Penurunan Fungsi Produksi Pupuk Perilaku produsen pupuk adalah berusaha untuk memaksimumkan keuntungannya. Jika keuntungan produsen dinotasikan dengan π, total biaya (TC) terdiri
III. KERANGKA TEORITIS 3.. Penurunan Fungsi Produksi Pupuk Perilaku produsen pupuk adalah berusaha untuk memaksimumkan keuntungannya. Jika keuntungan produsen dinotasikan dengan π, total biaya (TC) terdiri
S1- MATEMATIKA I BAHAN 7 TURUNAN FUNGSI (DERIVATIVES OR DIFFERENTIATIONS)
 S1- MATEMATIKA I BAHAN 7 TURUNAN FUNGSI (DERIVATIVES OR DIFFERENTIATIONS) LANJUTAN TURUNAN FUNGSI (DERIVATIVE OR DIFFERENTIATION) : PARTIAL DERIVATIVE, TOTAL DIFFERENTIAL, TOTAL DERIVATIVE 1/15 Bahan 7.1.
S1- MATEMATIKA I BAHAN 7 TURUNAN FUNGSI (DERIVATIVES OR DIFFERENTIATIONS) LANJUTAN TURUNAN FUNGSI (DERIVATIVE OR DIFFERENTIATION) : PARTIAL DERIVATIVE, TOTAL DIFFERENTIAL, TOTAL DERIVATIVE 1/15 Bahan 7.1.
EKONOMI PRODUKSI PERTEMUAN KETUJUH: MAKSIMISASI TERKENDALA
 EKONOMI PRODUKSI Kode PTE-4103 PERTEMUAN KETUJUH: MAKSIMISASI TERKENDALA Rini Dwiastuti 2007 Sub-Pokok Bahasan 1. Introduction 2. The Budget Constraint 3. The Budget Constraint and the Isoquant Map g q
EKONOMI PRODUKSI Kode PTE-4103 PERTEMUAN KETUJUH: MAKSIMISASI TERKENDALA Rini Dwiastuti 2007 Sub-Pokok Bahasan 1. Introduction 2. The Budget Constraint 3. The Budget Constraint and the Isoquant Map g q
MAKALAH EKONOMI MANAJERIAL
 MAKALAH EKONOMI MANAJERIAL TEKNIK OPTIMASI MAKALAH INI DISUSUN UNTUK MEMENUHI TUGAS MATA KULIAH EKONOMI MANAJERIAL SEMESTER V DOSEN PENGAMPU : Dr. Supawi Pawenang, SE, MM NAMA : KHANIF ASFIROTUN NIM :
MAKALAH EKONOMI MANAJERIAL TEKNIK OPTIMASI MAKALAH INI DISUSUN UNTUK MEMENUHI TUGAS MATA KULIAH EKONOMI MANAJERIAL SEMESTER V DOSEN PENGAMPU : Dr. Supawi Pawenang, SE, MM NAMA : KHANIF ASFIROTUN NIM :
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI 2.1 Himpunan Fuzzy Tidak semua himpunan yang dijumpai dalam kehidupan sehari-hari terdefinisi secara jelas, misalnya himpunan orang miskin, himpunan orang pandai, himpunan orang tinggi,
BAB 2 LANDASAN TEORI 2.1 Himpunan Fuzzy Tidak semua himpunan yang dijumpai dalam kehidupan sehari-hari terdefinisi secara jelas, misalnya himpunan orang miskin, himpunan orang pandai, himpunan orang tinggi,
PERTEMUAN KETIGA: MAKSIMISASI PROFIT DG SATU INPUT & SATU OUTPUT
 EKONOMI PRODUKSI Kode PTE-4103 PERTEMUAN KETIGA: MAKSIMISASI PROFIT DG SATU INPUT & SATU OUTPUT Rini Dwiastuti 2007 Sub-pokok Bahasan 1. Total Physical Product versus Total Value 2. Total Factor or Resource
EKONOMI PRODUKSI Kode PTE-4103 PERTEMUAN KETIGA: MAKSIMISASI PROFIT DG SATU INPUT & SATU OUTPUT Rini Dwiastuti 2007 Sub-pokok Bahasan 1. Total Physical Product versus Total Value 2. Total Factor or Resource
CATATAN KULIAH Pertemuan V: Analisis Komparatif Statik dan Konsep Derivatif
 CATATAN KULIAH Pertemuan V: Analisis Komparati Statik dan Konsep Derivati A. Pengertian Komparati Statik dan Konsep Derivati Analisis Statis (ekuilibrium)yang dipelajari dalam bab yang lalu, mempunyai
CATATAN KULIAH Pertemuan V: Analisis Komparati Statik dan Konsep Derivati A. Pengertian Komparati Statik dan Konsep Derivati Analisis Statis (ekuilibrium)yang dipelajari dalam bab yang lalu, mempunyai
METODE PENGALI LAGRANGE DAN APLIKASINYA DALAM BIDANG EKONOMI SKRIPSI RAHMAD HIDAYAT
 METODE PENGALI LAGRANGE DAN APLIKASINYA DALAM BIDANG EKONOMI SKRIPSI RAHMAD HIDAYAT 110803018 DEPARTEMEN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA MEDAN 2015 METODE
METODE PENGALI LAGRANGE DAN APLIKASINYA DALAM BIDANG EKONOMI SKRIPSI RAHMAD HIDAYAT 110803018 DEPARTEMEN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA MEDAN 2015 METODE
Bagian 2 Turunan Parsial
 Bagian Turunan Parsial Bagian Turunan Parsial mempelajari bagaimana teknik dierensiasi diterapkan untuk ungsi dengan dua variabel atau lebih. Teknik dierensiasi ini tidak hana akan diterapkan untuk ungsi-ungsi
Bagian Turunan Parsial Bagian Turunan Parsial mempelajari bagaimana teknik dierensiasi diterapkan untuk ungsi dengan dua variabel atau lebih. Teknik dierensiasi ini tidak hana akan diterapkan untuk ungsi-ungsi
DIKTAT KULIAH KALKULUS PEUBAH BANYAK (IE-308)
 DIKTAT KULIAH (IE-308) BAB 3 TURUNAN PARSIAL Diktat ini digunakan bagi mahasiswa Jurusan Teknik Industri Fakultas Teknik Universitas Kristen Maranatha Ir. Rudy Wawolumaja M.Sc JURUSAN TEKNIK INDUSTRI -
DIKTAT KULIAH (IE-308) BAB 3 TURUNAN PARSIAL Diktat ini digunakan bagi mahasiswa Jurusan Teknik Industri Fakultas Teknik Universitas Kristen Maranatha Ir. Rudy Wawolumaja M.Sc JURUSAN TEKNIK INDUSTRI -
Kontrol Optimum. MKO dengan Horizon Takhingga, Syarat Cukup. Toni Bakhtiar. Departemen Matematika IPB. Februari 2014
 Kontrol Optimum MKO dengan Horizon Takhingga, Syarat Cukup Toni Bakhtiar Departemen Matematika IPB Februari 2014 [email protected] (IPB) MAT332 Kontrol Optimum Februari 2014 1 / 23 Outline MKO dengan
Kontrol Optimum MKO dengan Horizon Takhingga, Syarat Cukup Toni Bakhtiar Departemen Matematika IPB Februari 2014 [email protected] (IPB) MAT332 Kontrol Optimum Februari 2014 1 / 23 Outline MKO dengan
D. OPTIMISASI EKONOMI DENGAN KENDALA - Optimisasi dengan metode substitusi - Optimisasi dengan metode pengali lagrange
 OPTIMISASI EKONOMI Ari Darmawan, Dr. S.AB, M.AB Email: [email protected] A. PENDAHULUAN B. TEKNIK OPTIMISASI EKONOMI C. OPTIMISASI EKONOMI TANPA KENDALA - Hubungan Antara Nilai Total, Rata-rata
OPTIMISASI EKONOMI Ari Darmawan, Dr. S.AB, M.AB Email: [email protected] A. PENDAHULUAN B. TEKNIK OPTIMISASI EKONOMI C. OPTIMISASI EKONOMI TANPA KENDALA - Hubungan Antara Nilai Total, Rata-rata
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI Pada bab ini akan dibahas beberapa pengertian dari optimasi bersyarat dengan kendala persamaan menggunakan multiplier lagrange serta penerapannya yang akan digunakan sebagai landasan
BAB 2 LANDASAN TEORI Pada bab ini akan dibahas beberapa pengertian dari optimasi bersyarat dengan kendala persamaan menggunakan multiplier lagrange serta penerapannya yang akan digunakan sebagai landasan
III. KERANGKA PEMIKIRAN. fungsi permintaan, persamaan simultan, elastisitas, dan surplus produsen.
 III. KERANGKA PEMIKIRAN 3.1. Kerangka Pemikiran Teoritis Komponen utama pasar beras mencakup kegiatan produksi dan konsumsi. Penelitian ini menggunakan persamaan simultan karena memiliki lebih dari satu
III. KERANGKA PEMIKIRAN 3.1. Kerangka Pemikiran Teoritis Komponen utama pasar beras mencakup kegiatan produksi dan konsumsi. Penelitian ini menggunakan persamaan simultan karena memiliki lebih dari satu
Model umum metode simpleks
 Model umum metode simpleks Fungsi Tujuan: Z C X C 2 X 2 C n X n S S 2 S n = NK FungsiPembatas: a X + a 2 X 2 + + a n X n + S + S 2 + + S n = b a 2 X + a 22 X 2 + + a 2n X n + S + S 2 + + S n = b 2 a m
Model umum metode simpleks Fungsi Tujuan: Z C X C 2 X 2 C n X n S S 2 S n = NK FungsiPembatas: a X + a 2 X 2 + + a n X n + S + S 2 + + S n = b a 2 X + a 22 X 2 + + a 2n X n + S + S 2 + + S n = b 2 a m
BAB 2 MODEL OPTIMISASI. 1. Pengertian 2. Kendala Model Optimisasi 3. Formulasi Model Optimisasi
 BAB 2 MODEL OPTIMISASI 1. Pengertian 2. Kendala Model Optimisasi 3. Formulasi Model Optimisasi 1 PENGERTIAN OPTIMISASI Model Optimisasi menghasilkan jawaban optimal (solusi optimal) untuk permasalahan
BAB 2 MODEL OPTIMISASI 1. Pengertian 2. Kendala Model Optimisasi 3. Formulasi Model Optimisasi 1 PENGERTIAN OPTIMISASI Model Optimisasi menghasilkan jawaban optimal (solusi optimal) untuk permasalahan
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI 2.1 Pemrograman Non linier Pemrograman non linier adalah suatu bentuk pemrograman yang berhubungan dengan suatu perencanaan aktivitas tertentu yang dapat diformulasikan dalam model
BAB 2 LANDASAN TEORI 2.1 Pemrograman Non linier Pemrograman non linier adalah suatu bentuk pemrograman yang berhubungan dengan suatu perencanaan aktivitas tertentu yang dapat diformulasikan dalam model
Bab 2. Penggambaran Grafik Canggih
 Bab Penggambaran Graik Canggih 1. Graik Fungsi Naik/Turun Syarat graik ungsi naik pada sub interval bila pada sub interval tersebut y' Syarat graik ungsi turun pada sub interval bila pada sub interval
Bab Penggambaran Graik Canggih 1. Graik Fungsi Naik/Turun Syarat graik ungsi naik pada sub interval bila pada sub interval tersebut y' Syarat graik ungsi turun pada sub interval bila pada sub interval
FUNGSI GRIEWANK DAN PENENTUAN NILAI OPTIMUMNYA MENGGUNAKAN ALGORITMA STROBERI. Tri Nadiani Solihah
 Prosiding Seminar Nasional Matematika dan Terapannya 2016 p-issn : 2550-0384; e-issn : 2550-0392 FUNGSI GRIEWANK DAN PENENTUAN NILAI OPTIMUMNYA MENGGUNAKAN ALGORITMA STROBERI Tri Nadiani Solihah [email protected]
Prosiding Seminar Nasional Matematika dan Terapannya 2016 p-issn : 2550-0384; e-issn : 2550-0392 FUNGSI GRIEWANK DAN PENENTUAN NILAI OPTIMUMNYA MENGGUNAKAN ALGORITMA STROBERI Tri Nadiani Solihah [email protected]
kita menggunakan variabel semu untuk memulai pemecahan, dan meninggalkannya setelah misi terpenuhi
 Lecture 4: (B) Supaya terdapat penyelesaian basis awal yang fisibel, pada kendala berbentuk = dan perlu ditambahkan variabel semu (artificial variable) pada ruas kiri bentuk standarnya, untuk siap ke tabel
Lecture 4: (B) Supaya terdapat penyelesaian basis awal yang fisibel, pada kendala berbentuk = dan perlu ditambahkan variabel semu (artificial variable) pada ruas kiri bentuk standarnya, untuk siap ke tabel
PENYELESAIAN MODEL LINEAR PROGRAMMING SECARA MATEMATIK (METODE SIMPLEKS)
 Maximize or Minimize Subject to: Z = f (x,y) g (x,y) = c S1 60 4 2 1 0 S2 48 2 4 0 1 Zj 0-8 -6 0 0 PENYELESAIAN MODEL LINEAR PROGRAMMING SECARA MATEMATIK (METODE SIMPLEKS) Prof. Dr. Ir. ZULKIFLI ALAMSYAH,
Maximize or Minimize Subject to: Z = f (x,y) g (x,y) = c S1 60 4 2 1 0 S2 48 2 4 0 1 Zj 0-8 -6 0 0 PENYELESAIAN MODEL LINEAR PROGRAMMING SECARA MATEMATIK (METODE SIMPLEKS) Prof. Dr. Ir. ZULKIFLI ALAMSYAH,
TKS 4003 Matematika II. Nilai Ekstrim. (Extreme Values) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya
 TKS 4003 Matematika II Nilai Ekstrim (Extreme Values) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya Fungsi Dua Peubah Bila untuk setiap pasangan (x,y) dari harga harga dua peubah bebas
TKS 4003 Matematika II Nilai Ekstrim (Extreme Values) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya Fungsi Dua Peubah Bila untuk setiap pasangan (x,y) dari harga harga dua peubah bebas
MENENTUKAN MODEL KOEFISIEN REGRESI MULTIPLE VARIABEL DENGAN MENGGUNAKAN MAKSIMUM LIKELIHOOD SKRIPSI BENNY SOFYAN SAMOSIR
 MENENTUKAN MODEL KOEFISIEN REGRESI MULTIPLE VARIABEL DENGAN MENGGUNAKAN MAKSIMUM LIKELIHOOD SKRIPSI BENNY SOFYAN SAMOSIR 080823004 DEPARTEMEN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS
MENENTUKAN MODEL KOEFISIEN REGRESI MULTIPLE VARIABEL DENGAN MENGGUNAKAN MAKSIMUM LIKELIHOOD SKRIPSI BENNY SOFYAN SAMOSIR 080823004 DEPARTEMEN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS
ESTIMASI PARAMETER PADA MULTIPLE REGRESI MENGGUNAKAN MAKSIMUM LIKELIHOOD SKRIPSI SITI MAISAROH RITONGA
 ESTIMASI PARAMETER PADA MULTIPLE REGRESI MENGGUNAKAN MAKSIMUM LIKELIHOOD SKRIPSI SITI MAISAROH RITONGA 070823013 DEPARTEMEN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA
ESTIMASI PARAMETER PADA MULTIPLE REGRESI MENGGUNAKAN MAKSIMUM LIKELIHOOD SKRIPSI SITI MAISAROH RITONGA 070823013 DEPARTEMEN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA
BAB II TINJAUAN PUSTAKA. operasi yang mampu menyelesaikan masalah optimasi sejak diperkenalkan di
 BAB II TINJAUAN PUSTAKA 2.1 Pemrograman Linier (Linear Programming) Pemrograman linier (linear programming) merupakan salah satu teknik riset operasi yang mampu menyelesaikan masalah optimasi sejak diperkenalkan
BAB II TINJAUAN PUSTAKA 2.1 Pemrograman Linier (Linear Programming) Pemrograman linier (linear programming) merupakan salah satu teknik riset operasi yang mampu menyelesaikan masalah optimasi sejak diperkenalkan
Catatan Kuliah 10 Memahami dan Menganalisa Optimasi dengan Kendala Persamaan
 Catatan Kuliah 10 Memahami dan Menanalisa Optimasi denan Kendala Persamaan 1. Metode Larane Multiplier Misal diberikan masalah optimisasi sbb : OF : U =, st.: (, ) Selanjutna akan dipelajari baaimana mencari
Catatan Kuliah 10 Memahami dan Menanalisa Optimasi denan Kendala Persamaan 1. Metode Larane Multiplier Misal diberikan masalah optimisasi sbb : OF : U =, st.: (, ) Selanjutna akan dipelajari baaimana mencari
ISSN: Vol. 2 No. 1 Januari 2013
 ISSN: 2303-1751 Vol. 2 No. 1 Januari 2013 e-jurnal Matematika Vol. 2, No. 1, Januari 2013, 19-23 ISSN: 2303-1751 PENENTUAN KEUNTUNGAN MAKSIMUM PADA PENJUALAN OLAHAN TAPE DENGAN MENGGUNAKAN METODE LAGRANGE
ISSN: 2303-1751 Vol. 2 No. 1 Januari 2013 e-jurnal Matematika Vol. 2, No. 1, Januari 2013, 19-23 ISSN: 2303-1751 PENENTUAN KEUNTUNGAN MAKSIMUM PADA PENJUALAN OLAHAN TAPE DENGAN MENGGUNAKAN METODE LAGRANGE
Turunan dalam Ruang berdimensi n
 Jurusan Matematika FMIPA Unsyiah October 13, 2011 Andaikan f adalah fungsi dengan peubah x dan y. Jika y dijaga agar tetap konstan, misalkan y = y 0 maka f(x, y 0 ) adalah fungsi dengan peubah tunggal
Jurusan Matematika FMIPA Unsyiah October 13, 2011 Andaikan f adalah fungsi dengan peubah x dan y. Jika y dijaga agar tetap konstan, misalkan y = y 0 maka f(x, y 0 ) adalah fungsi dengan peubah tunggal
LINDO. Lindo dapat digunakan sampai dengan 150 kendala dan 300 variabel
 LINDO Pegertian: Lindo (Linear Interactive Discrete Optimize) adalah paket program siap pakai yang digunakan untuk memecahkan masalah linear, integer dan quadratic programming. Kemampuan: Lindo dapat digunakan
LINDO Pegertian: Lindo (Linear Interactive Discrete Optimize) adalah paket program siap pakai yang digunakan untuk memecahkan masalah linear, integer dan quadratic programming. Kemampuan: Lindo dapat digunakan
OPTIMISASI EKONOMI. Dr. Muh. Yunanto, MM. Kuliah Minggu ke-2
 OPTIMISASI EKONOMI Dr. Muh. Yunanto, MM. Kuliah Minggu ke-2 BAB II Berbagai Teknik Optimasi dan Peralatan Manajemen Baru Metode Dalam Mengambarkan hub Ekonomi Hubungan ekonomi dapat digambarkan dalam bentuk
OPTIMISASI EKONOMI Dr. Muh. Yunanto, MM. Kuliah Minggu ke-2 BAB II Berbagai Teknik Optimasi dan Peralatan Manajemen Baru Metode Dalam Mengambarkan hub Ekonomi Hubungan ekonomi dapat digambarkan dalam bentuk
BAB 1 PENDAHULUAN. 1.1 Latar Belakang
 BAB 1 PENDAHULUAN 1.1 Latar Belakang Zaman yang semakin berkembang membuat persoalan semakin kompleks, tidak terkecuali persoalan yang melibatkan persoalan matematika. Dalam pemecahannya, matematika memegang
BAB 1 PENDAHULUAN 1.1 Latar Belakang Zaman yang semakin berkembang membuat persoalan semakin kompleks, tidak terkecuali persoalan yang melibatkan persoalan matematika. Dalam pemecahannya, matematika memegang
PENENTUAN KEUNTUNGAN MAKSIMUM PADA PENJUALAN OLAHAN TAPE DENGAN MENGGUNAKAN METODE LAGRANGE (Studi Kasus: UD. Sari Madu)
 PENENTUAN KEUNTUNGAN MAKSIMUM PADA PENJUALAN OLAHAN TAPE DENGAN MENGGUNAKAN METODE LAGRANGE (Studi Kasus: UD. Sari Madu) FEMY AYU ASTITI 1, NI MADE ASIH 2, I NYOMAN WIDANA 3 1, 2, 3 Jurusan Matematika
PENENTUAN KEUNTUNGAN MAKSIMUM PADA PENJUALAN OLAHAN TAPE DENGAN MENGGUNAKAN METODE LAGRANGE (Studi Kasus: UD. Sari Madu) FEMY AYU ASTITI 1, NI MADE ASIH 2, I NYOMAN WIDANA 3 1, 2, 3 Jurusan Matematika
Kalkulus Multivariabel I
 Maksimum, Minimum, dan Statistika FMIPA Universitas Islam Indonesia Titik Kritis Misalkan p = (x, y) adalah sebuah titik peubah dan p 0 = (x 0, y 0 ) adalah sebuah titik tetap pada bidang berdimensi dua
Maksimum, Minimum, dan Statistika FMIPA Universitas Islam Indonesia Titik Kritis Misalkan p = (x, y) adalah sebuah titik peubah dan p 0 = (x 0, y 0 ) adalah sebuah titik tetap pada bidang berdimensi dua
BENTUK DUAL MASALAH SOCP NORMA SATU
 BENTUK DUAL MASALAH SOCP NORMA SATU Caturiyati 1, Ch. Rini Indrati 2, Lina Aryati 3 1 Mahasiswa Program Doktor Matematika FMIPA UGM dan Dosen Jurusan Pendidikan Matematika FMIPA UNY, 2,3 Dosen Jurusan
BENTUK DUAL MASALAH SOCP NORMA SATU Caturiyati 1, Ch. Rini Indrati 2, Lina Aryati 3 1 Mahasiswa Program Doktor Matematika FMIPA UGM dan Dosen Jurusan Pendidikan Matematika FMIPA UNY, 2,3 Dosen Jurusan
PERTEMUAN KESEBELAS: Maximization in a Two-Output Setting
 EKONOMI PRODUKSI Kode PTE-4103 PERTEMUAN KESEBELAS: Maximization in a Two-Output Setting Rini Dwiastuti 2007 Sub-Pokok Bahasan: 1. The Family of Product Transformation Function 2. Maximization of Output
EKONOMI PRODUKSI Kode PTE-4103 PERTEMUAN KESEBELAS: Maximization in a Two-Output Setting Rini Dwiastuti 2007 Sub-Pokok Bahasan: 1. The Family of Product Transformation Function 2. Maximization of Output
Kontrol Optimum. MKO dengan Mixed Constraints dan Pure State Constraints. Toni Bakhtiar. Departemen Matematika IPB. Februari 2014
 Kontrol Optimum MKO dengan Mixed Constraints dan Pure State Constraints Toni Bakhtiar Departemen Matematika IPB Februari 2014 [email protected] (IPB) MAT332 Kontrol Optimum Februari 2014 1 / 38 Outline
Kontrol Optimum MKO dengan Mixed Constraints dan Pure State Constraints Toni Bakhtiar Departemen Matematika IPB Februari 2014 [email protected] (IPB) MAT332 Kontrol Optimum Februari 2014 1 / 38 Outline
OPTIMASI (Pemrograman Non Linear)
 OPTIMASI (Pemrograman Non Linear) 3 SKS PILIHAN Arrival Rince Putri, 013 1 Silabus I. Pendahuluan 1. Perkuliahan: Silabus, Referensi, Penilaian. Pengantar Optimasi 3. Riview Differential Calculus II. Dasar-Dasar
OPTIMASI (Pemrograman Non Linear) 3 SKS PILIHAN Arrival Rince Putri, 013 1 Silabus I. Pendahuluan 1. Perkuliahan: Silabus, Referensi, Penilaian. Pengantar Optimasi 3. Riview Differential Calculus II. Dasar-Dasar
MATEMATIKA EKONOMI ( FUNGSI LINIER, GRAFIK FUNGSI DAN SISTEM PERSAMAAN LINIER )
 MATEMATIKA EKONOMI ( FUNGSI LINIER, GRAFIK FUNGSI DAN SISTEM PERSAMAAN LINIER ) KELOMPOK 2 1. UMAR ATTAMIMI (01212043) 2. SITI WASI ATUL MUFIDA (01212096) 3. DEVI PRATNYA. P. (01212078) 4. POPPY MERLIANA
MATEMATIKA EKONOMI ( FUNGSI LINIER, GRAFIK FUNGSI DAN SISTEM PERSAMAAN LINIER ) KELOMPOK 2 1. UMAR ATTAMIMI (01212043) 2. SITI WASI ATUL MUFIDA (01212096) 3. DEVI PRATNYA. P. (01212078) 4. POPPY MERLIANA
BAB LINEAR PROGRAMMING : METODE GRAFIK PENDAHULUAN PENDAHULUAN
 PENDAHULUAN BAB 1 LINEAR PROGRAMMING : METODE GRAFIK PENDAHULUAN inear programming adalah suatu teknis matematika yang dirancang untuk membantu manajer dalam merencanakan dan membuat keputusan dalam mengalokasikan
PENDAHULUAN BAB 1 LINEAR PROGRAMMING : METODE GRAFIK PENDAHULUAN inear programming adalah suatu teknis matematika yang dirancang untuk membantu manajer dalam merencanakan dan membuat keputusan dalam mengalokasikan
Masalah Kalkulus Variasi, Fungsional Objektif, Variasi, Syarat Perlu Optimalitas
 Masalah Kalkulus Variasi, Fungsional Objektif, Variasi, Syarat Perlu Optimalitas Slide II Toni Bakhtiar Departemen Matematika IPB February 2012 TBK (IPB) Kalkulus Variasi February 2012 1 / 37 Masalah Brachystochrone
Masalah Kalkulus Variasi, Fungsional Objektif, Variasi, Syarat Perlu Optimalitas Slide II Toni Bakhtiar Departemen Matematika IPB February 2012 TBK (IPB) Kalkulus Variasi February 2012 1 / 37 Masalah Brachystochrone
MA1201 MATEMATIKA 2A Hendra Gunawan
 MA1201 MATEMATIKA 2A Hendra Gunawan Semester II, 2016/2017 15 Maret 2017 Kuliah yang Lalu 10.1-2 Parabola, Elips, dan Hiperbola 10.4 Persamaan Parametrik Kurva di Bidang 10.5 Sistem Koordinat Polar 11.1
MA1201 MATEMATIKA 2A Hendra Gunawan Semester II, 2016/2017 15 Maret 2017 Kuliah yang Lalu 10.1-2 Parabola, Elips, dan Hiperbola 10.4 Persamaan Parametrik Kurva di Bidang 10.5 Sistem Koordinat Polar 11.1
LINEAR PROGRAMMING-1
 /5/ LINEAR PROGRAMMING- DR.MOHAMMAD ABDUL MUKHYI, SE., MM METODE KUANTITATIF Perumusan PL Ada tiga unsur dasar dari PL, ialah:. Fungsi Tujuan. Fungsi Pembatas (set ketidak samaan/pembatas strukturis) 3.
/5/ LINEAR PROGRAMMING- DR.MOHAMMAD ABDUL MUKHYI, SE., MM METODE KUANTITATIF Perumusan PL Ada tiga unsur dasar dari PL, ialah:. Fungsi Tujuan. Fungsi Pembatas (set ketidak samaan/pembatas strukturis) 3.
Dualitas Dalam Model Linear Programing
 Maximize or Minimize Z = f (x,y) Subject to: g (x,y) = c Dualitas Dalam Model Linear Programing Prof. Dr. Ir. ZULKIFLI ALAMSYAH, M.Sc. Program Studi Agribisnis Fakultas Pertanian Universitas Jambi KONSEP
Maximize or Minimize Z = f (x,y) Subject to: g (x,y) = c Dualitas Dalam Model Linear Programing Prof. Dr. Ir. ZULKIFLI ALAMSYAH, M.Sc. Program Studi Agribisnis Fakultas Pertanian Universitas Jambi KONSEP
TURUNAN DALAM RUANG DIMENSI-n
 TURUNAN DALAM RUANG DIMENSI-n A. Fungsi Dua Variabel atau Lebih Dalam subbab ini, fungsi dua variabel atau lebih dikaji dari tiga sudut pandang: secara verbal (melalui uraian dalam kata-kata) secara aljabar
TURUNAN DALAM RUANG DIMENSI-n A. Fungsi Dua Variabel atau Lebih Dalam subbab ini, fungsi dua variabel atau lebih dikaji dari tiga sudut pandang: secara verbal (melalui uraian dalam kata-kata) secara aljabar
Metode Simpleks (Simplex Method) Materi Bahasan
 Metode Simpleks (Simplex Method) Kuliah 03 TI2231 Penelitian Operasional I 1 Materi Bahasan 1 Rumusan Pemrograman linier dalam bentuk baku 2 Pemecahan sistem persamaan linier 3 Prinsip-prinsip metode simpleks
Metode Simpleks (Simplex Method) Kuliah 03 TI2231 Penelitian Operasional I 1 Materi Bahasan 1 Rumusan Pemrograman linier dalam bentuk baku 2 Pemecahan sistem persamaan linier 3 Prinsip-prinsip metode simpleks
0,1, Holder s continue function in rank of and. 0,1, fungsi kontinu Holder berpangkat-,
 JMP : Volume 4 Nomor 1, Juni 2012, hal 233-240 HUBUNGAN ANTARA NILAI KRITIS DERIVATI- DENGAN DIMENSI- DARI SUATU KURVA Supriyadi Wibowo Jurusan Matematika MIPA UNS Surakarta Email supriyadi_w@yahoocoid
JMP : Volume 4 Nomor 1, Juni 2012, hal 233-240 HUBUNGAN ANTARA NILAI KRITIS DERIVATI- DENGAN DIMENSI- DARI SUATU KURVA Supriyadi Wibowo Jurusan Matematika MIPA UNS Surakarta Email supriyadi_w@yahoocoid
Dualitas Dalam Model Linear Programing
 Maximize or Minimize Z = f (x,y) Subject to: g (x,y) = c Dualitas Dalam Model Linear Programing Prof. Dr. Ir. ZULKIFLI ALAMSYAH, M.Sc. Program Studi Agribisnis Fakultas Pertanian Universitas Jambi KONSEP
Maximize or Minimize Z = f (x,y) Subject to: g (x,y) = c Dualitas Dalam Model Linear Programing Prof. Dr. Ir. ZULKIFLI ALAMSYAH, M.Sc. Program Studi Agribisnis Fakultas Pertanian Universitas Jambi KONSEP
Matematika Bisnis (Linear Programming-Metode Grafik Minimisasi) Dosen Febriyanto, SE, MM.
 (Linear Programming-Metode Grafik Minimisasi) Dosen Febriyanto, SE, MM. www.febriyanto79.wordpress.com - Linear Programming Linear programing (LP) adalah salah satu metode matematis yang digunakan untuk
(Linear Programming-Metode Grafik Minimisasi) Dosen Febriyanto, SE, MM. www.febriyanto79.wordpress.com - Linear Programming Linear programing (LP) adalah salah satu metode matematis yang digunakan untuk
Nilai Ekstrim. (Extreme Values)
 TKS 4003 Matematika II Nilai Ekstrim (Extreme Values) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya Pendahuluan Jika terdapat suatu hasil pengukuran seperti pada Gambar 1, dimana pengukuran
TKS 4003 Matematika II Nilai Ekstrim (Extreme Values) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya Pendahuluan Jika terdapat suatu hasil pengukuran seperti pada Gambar 1, dimana pengukuran
ANALISIS KARAKTERISTIK FUNGSI LAGRANGE DALAM MENYELESAIKAN PERMASALAHAN OPTIMASI BERKENDALA SKRIPSI THERESIA M. MANIK
 ANALISIS KARAKTERISTIK FUNGSI LAGRANGE DALAM MENYELESAIKAN PERMASALAHAN OPTIMASI BERKENDALA SKRIPSI THERESIA M. MANIK 120803069 DEPARTEMEN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSTITAS
ANALISIS KARAKTERISTIK FUNGSI LAGRANGE DALAM MENYELESAIKAN PERMASALAHAN OPTIMASI BERKENDALA SKRIPSI THERESIA M. MANIK 120803069 DEPARTEMEN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSTITAS
RISET OPERASIONAL MINGGU KE-2. Disusun oleh: Nur Azifah., SE., M.Si. Linier Programming: Formulasi Masalah dan Model
 RISET OPERASIONAL MINGGU KE- Linier Programming: Formulasi Masalah dan Model Disusun oleh: Nur Azifah., SE., M.Si Pengertian Linear Programming Linear Programming (LP) adalah salah satu teknik riset operasi
RISET OPERASIONAL MINGGU KE- Linier Programming: Formulasi Masalah dan Model Disusun oleh: Nur Azifah., SE., M.Si Pengertian Linear Programming Linear Programming (LP) adalah salah satu teknik riset operasi
Fungsi Linier & Grafik Fungsi Aplikasi dalam Ekonomi
 Fungsi Linier & Grafik Fungsi Aplikasi dalam Ekonomi Diskripsi materi: -Bentuk umum dari fungsi linier dan menggambarkan grafik fungsi linier -Menentukan koefisien arah/ Kemiringan -Cara-cara pembentukan
Fungsi Linier & Grafik Fungsi Aplikasi dalam Ekonomi Diskripsi materi: -Bentuk umum dari fungsi linier dan menggambarkan grafik fungsi linier -Menentukan koefisien arah/ Kemiringan -Cara-cara pembentukan
Teori Dualitas dan Penerapannya (Duality Theory and Its Application)
 Teori Dualitas dan Penerapannya (Duality Theory and Its Application) Kuliah 6 TI2231 Penelitian Operasional I 1 Materi Bahasan 1 Teori dualitas 2 Metode simpleks dual TI2231 Penelitian Operasional I 2
Teori Dualitas dan Penerapannya (Duality Theory and Its Application) Kuliah 6 TI2231 Penelitian Operasional I 1 Materi Bahasan 1 Teori dualitas 2 Metode simpleks dual TI2231 Penelitian Operasional I 2
PERBANDINGAN ANALISIS SENSITIVITAS MENGGUNAKAN PARTISI OPTIMAL DAN BASIS OPTIMAL PADA OPTIMASI LINEAR MIRNA SARI DEWI
 PERBANDINGAN ANALISIS SENSITIVITAS MENGGUNAKAN PARTISI OPTIMAL DAN BASIS OPTIMAL PADA OPTIMASI LINEAR MIRNA SARI DEWI DEPARTEMEN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN
PERBANDINGAN ANALISIS SENSITIVITAS MENGGUNAKAN PARTISI OPTIMAL DAN BASIS OPTIMAL PADA OPTIMASI LINEAR MIRNA SARI DEWI DEPARTEMEN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN
Kalkulus Variasi. Masalah Kalkulus Variasi, Fungsional Objektif, Variasi, Syarat Perlu Optimalitas. Toni Bakhtiar. Departemen Matematika IPB
 Kalkulus Variasi Masalah Kalkulus Variasi, Fungsional Objektif, Variasi, Syarat Perlu Optimalitas Toni Bakhtiar Departemen Matematika IPB Februari 2014 [email protected] (IPB) MAT332 Kontrol Optimum
Kalkulus Variasi Masalah Kalkulus Variasi, Fungsional Objektif, Variasi, Syarat Perlu Optimalitas Toni Bakhtiar Departemen Matematika IPB Februari 2014 [email protected] (IPB) MAT332 Kontrol Optimum
Respect, Professionalism, & Entrepreneurship. Mata Kuliah : Kalkulus Kode : CIV Turunan. Pertemuan 3, 4, 5, 6, 7
 Mata Kuliah : Kalkulus Kode : CIV - 101 SKS : 3 SKS Turunan Pertemuan 3, 4, 5, 6, 7 Kemampuan Akhir ang Diharapkan Mahasiswa mampu : - menjelaskan arti turunan ungsi - mencari turunan ungsi - menggunakan
Mata Kuliah : Kalkulus Kode : CIV - 101 SKS : 3 SKS Turunan Pertemuan 3, 4, 5, 6, 7 Kemampuan Akhir ang Diharapkan Mahasiswa mampu : - menjelaskan arti turunan ungsi - mencari turunan ungsi - menggunakan
ABSTRAK. Latar Belakang Masalah
 Derivatif Untuk Menyelesaikan Optimisasi Berkendala Dalam Bisnis Dan Ekonomi (Derivative for Solvin Constrained Optimization in Business and Economics) Nurul Yaqin, M.Sc. Dosen pada Jurusan Sistem Informasi
Derivatif Untuk Menyelesaikan Optimisasi Berkendala Dalam Bisnis Dan Ekonomi (Derivative for Solvin Constrained Optimization in Business and Economics) Nurul Yaqin, M.Sc. Dosen pada Jurusan Sistem Informasi
JENIS JENIS FUNGSI 2. Gambar. Jenis Fungsi. mengandung banyak suku (polinom) dalam variabel bebas y = a 0 + a 1 x + a 2 x a n x n
 Telkom University Alamanda JENIS JENIS FUNGSI1 JENIS JENIS FUNGSI 2 Jenis Fungsi Gambar 1. FUNGSI POLINOM mengandung banyak suku (polinom) dalam variabel bebas y = a 0 + a 1 x + a 2 x 2 + + a n x n 2.
Telkom University Alamanda JENIS JENIS FUNGSI1 JENIS JENIS FUNGSI 2 Jenis Fungsi Gambar 1. FUNGSI POLINOM mengandung banyak suku (polinom) dalam variabel bebas y = a 0 + a 1 x + a 2 x 2 + + a n x n 2.
OPTIMISASI PEMROGRAMAN CEMBUNG MENGGUNAKAN SYARAT KUHN-TUCKER SKRIPSI
 OPTIMISASI PEMROGRAMAN CEMBUNG MENGGUNAKAN SYARAT KUHN-TUCKER SKRIPSI Diajukan kepada Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Yogyakarta untuk Memenuhi Sebagian Persyaratan Guna
OPTIMISASI PEMROGRAMAN CEMBUNG MENGGUNAKAN SYARAT KUHN-TUCKER SKRIPSI Diajukan kepada Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Yogyakarta untuk Memenuhi Sebagian Persyaratan Guna
MATEMATIKA SISTEM INFORMASI 2 [KODE/SKS : IT / 2 SKS]
![MATEMATIKA SISTEM INFORMASI 2 [KODE/SKS : IT / 2 SKS] MATEMATIKA SISTEM INFORMASI 2 [KODE/SKS : IT / 2 SKS]](/thumbs/62/47223020.jpg) MATA KULIAH MATEMATIKA SISTEM INFORMASI 2 [KODE/SKS : IT011215 / 2 SKS] LINIER PROGRAMMING Formulasi Masalah dan Pemodelan Pengertian Linear Programming Linear Programming (LP) adalah salah satu teknik
MATA KULIAH MATEMATIKA SISTEM INFORMASI 2 [KODE/SKS : IT011215 / 2 SKS] LINIER PROGRAMMING Formulasi Masalah dan Pemodelan Pengertian Linear Programming Linear Programming (LP) adalah salah satu teknik
Fungsi Analitik (Bagian Keempat)
 Fungsi Analitik (Bagian Keempat) Supama Jurusan Matematika, FMIPA UGM Yogyakarta 55281, INDONESIA Email:[email protected], [email protected] (Pertemuan Minggu VII) Outline 1 Fungsi Analitik 2 Fungsi Analitik
Fungsi Analitik (Bagian Keempat) Supama Jurusan Matematika, FMIPA UGM Yogyakarta 55281, INDONESIA Email:[email protected], [email protected] (Pertemuan Minggu VII) Outline 1 Fungsi Analitik 2 Fungsi Analitik
BAB I DASAR-DASAR PEMODELAN MATEMATIKA DENGAN PERSAMAAN DIFERENSIAL
 BAB I DASAR-DASAR PEMODELAN MATEMATIKA DENGAN PERSAMAAN DIFERENSIAL Pendahuluan Persamaan diferensial adalah persamaan yang memuat diferensial Kita akan membahas tentang Persamaan Diferensial Biasa yaitu
BAB I DASAR-DASAR PEMODELAN MATEMATIKA DENGAN PERSAMAAN DIFERENSIAL Pendahuluan Persamaan diferensial adalah persamaan yang memuat diferensial Kita akan membahas tentang Persamaan Diferensial Biasa yaitu
OPTIMASI DENGAN METODE DAKIAN TERCURAM
 OPTIMASI DENGAN METODE DAKIAN TERCURAM Marwan Jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Syiah Kuala, Jln. Syekh Abdur Rauf No. 3 Darussalam, Banda Aceh 23111 email:
OPTIMASI DENGAN METODE DAKIAN TERCURAM Marwan Jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Syiah Kuala, Jln. Syekh Abdur Rauf No. 3 Darussalam, Banda Aceh 23111 email:
Catatan Kuliah 9 Memahami dan Menganalisa Optimisasi Tanpa Kendala dengan 2 atau Lebih Variabel Keputusan
 Catatan Kuliah 9 Memahami dan Menganalisa Optimisasi Tanpa Kendala dengan atau Lebih Variabel Keputusan 1. Kondisi Turunan Pertama Perhatikan kembali optimisasi dengan 1 variabel bebas, aitu : z = ( )
Catatan Kuliah 9 Memahami dan Menganalisa Optimisasi Tanpa Kendala dengan atau Lebih Variabel Keputusan 1. Kondisi Turunan Pertama Perhatikan kembali optimisasi dengan 1 variabel bebas, aitu : z = ( )
G. Minimum Lokal dan Global Berikut diberikan definisi minimum local (relatif) dan minimum global (mutlak) dari fungsi dua variabel.
 G. Minimum Lokal dan Global Berikut diberikan definisi minimum local (relatif) dan minimum global (mutlak) dari fungsi dua variabel. Definisi. (i) Suatu fungsi f(x, y) memiliki minimum lokal pada titik
G. Minimum Lokal dan Global Berikut diberikan definisi minimum local (relatif) dan minimum global (mutlak) dari fungsi dua variabel. Definisi. (i) Suatu fungsi f(x, y) memiliki minimum lokal pada titik
Tugas Tersturtur Mata Kuliah Ekonomi Manajerial. Resume Bab Optimasi Ekonomi. Kelompok 2
 Tugas Tersturtur Mata Kuliah Ekonomi Manajerial Resume Bab Optimasi Ekonomi Kelompok 2 1. Pupun Sofiyati 115030201111037 2. Isty Puji H 115030205111004 3. Della Herlita 115030207111046 Fakultas Ilmu Administrasi
Tugas Tersturtur Mata Kuliah Ekonomi Manajerial Resume Bab Optimasi Ekonomi Kelompok 2 1. Pupun Sofiyati 115030201111037 2. Isty Puji H 115030205111004 3. Della Herlita 115030207111046 Fakultas Ilmu Administrasi
Open Source. Not For Commercial Use
 Ringkasan Kalkulus 2, Untuk dipakai di ITB 1 Limit dan Kekontinuan Misalkan z = f(, y) fungsi dua peubah dan (a, b) R 2. Seperti pada limit fungsi satu peubah, limit fungsi dua peubah bertujuan untuk mengamati
Ringkasan Kalkulus 2, Untuk dipakai di ITB 1 Limit dan Kekontinuan Misalkan z = f(, y) fungsi dua peubah dan (a, b) R 2. Seperti pada limit fungsi satu peubah, limit fungsi dua peubah bertujuan untuk mengamati
MATEMATIKA EKONOMI. Telkom University
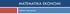 MATEMATIKA EKONOMI Telkom University Diferensial Parsial Diferensial parsial Nilai ekstrim: maksimum dan minimum Diferensial Parsial y = f(x,z) = x 3 +5z 2 4x 2 z 6xz 2 +8z 7 f x (x,z) = 3x 2 8xz 6z 2
MATEMATIKA EKONOMI Telkom University Diferensial Parsial Diferensial parsial Nilai ekstrim: maksimum dan minimum Diferensial Parsial y = f(x,z) = x 3 +5z 2 4x 2 z 6xz 2 +8z 7 f x (x,z) = 3x 2 8xz 6z 2
Kontrol Optimum. MKO dengan Kendala pada Peubah Kontrol. Toni Bakhtiar. Departemen Matematika IPB. Februari 2017
 Kontrol Optimum MKO dengan Kendala pada Peubah Kontrol Toni Bakhtiar Departemen Matematika IPB Februari 2017 [email protected] (IPB) MAT332 Kontrol Optimum Februari 2017 1 / 53 Outline MKO berkendala
Kontrol Optimum MKO dengan Kendala pada Peubah Kontrol Toni Bakhtiar Departemen Matematika IPB Februari 2017 [email protected] (IPB) MAT332 Kontrol Optimum Februari 2017 1 / 53 Outline MKO berkendala
Matematika I: APLIKASI TURUNAN. Dadang Amir Hamzah. Dadang Amir Hamzah Matematika I Semester I / 70
 Matematika I: APLIKASI TURUNAN Dadang Amir Hamzah 2015 Dadang Amir Hamzah Matematika I Semester I 2015 1 / 70 Outline 1 Maksimum dan Minimum Dadang Amir Hamzah Matematika I Semester I 2015 2 / 70 Outline
Matematika I: APLIKASI TURUNAN Dadang Amir Hamzah 2015 Dadang Amir Hamzah Matematika I Semester I 2015 1 / 70 Outline 1 Maksimum dan Minimum Dadang Amir Hamzah Matematika I Semester I 2015 2 / 70 Outline
PENERAPAN MODEL PROGRAM LINIER PRIMAL-DUAL DALAM MENGOPTIMALKAN PRODUKSI MINYAK GORENG PADA PT PACIFIC PALMINDO INDUSTRI SKRIPSI
 PENERAPAN MODEL PROGRAM LINIER PRIMAL-DUAL DALAM MENGOPTIMALKAN PRODUKSI MINYAK GORENG PADA PT PACIFIC PALMINDO INDUSTRI SKRIPSI SARAH MARINA GULTOM 080803064 DEPARTEMEN MATEMATIKA FAKULTAS MATEMATIKA
PENERAPAN MODEL PROGRAM LINIER PRIMAL-DUAL DALAM MENGOPTIMALKAN PRODUKSI MINYAK GORENG PADA PT PACIFIC PALMINDO INDUSTRI SKRIPSI SARAH MARINA GULTOM 080803064 DEPARTEMEN MATEMATIKA FAKULTAS MATEMATIKA
BAB VI PROGRAMA LINIER : DUALITAS DAN ANALISIS SENSITIVITAS
 BAB VI PROGRAMA LINIER : DUALITAS DAN ANALISIS SENSITIVITAS 6.1 Teori Dualitas Teori dualitas merupakan salah satu konsep programa linier yang penting dan menarik ditinjau dari segi teori dan praktisnya.
BAB VI PROGRAMA LINIER : DUALITAS DAN ANALISIS SENSITIVITAS 6.1 Teori Dualitas Teori dualitas merupakan salah satu konsep programa linier yang penting dan menarik ditinjau dari segi teori dan praktisnya.
Pertemuan Minggu ke Bidang Singgung, Hampiran 2. Maksimum dan Minimum 3. Metode Lagrange
 Pertemuan Minggu ke-11 1. Bidang Singgung, Hampiran 2. Maksimum dan Minimum 3. Metode Lagrange 1. BIDANG SINGGUNG, HAMPIRAN Tujuan mempelajari: memperoleh persamaan bidang singgung terhadap permukaan z
Pertemuan Minggu ke-11 1. Bidang Singgung, Hampiran 2. Maksimum dan Minimum 3. Metode Lagrange 1. BIDANG SINGGUNG, HAMPIRAN Tujuan mempelajari: memperoleh persamaan bidang singgung terhadap permukaan z
PENYELESAIAN MODEL LINEAR PROGRAMMING SECARA GRAFIK
 Maximize or Minimize 2X 1 = 8 X 2 Z = f (x,y) Subject to: 5 D C g (x,y) = c 3X 2 = 15 0 Daerah feasible A 4 B 6X 1 + 5X 2 = 30 X 1 PENYELESAIAN MODEL LINEAR PROGRAMMING SECARA GRAFIK Prof. Dr. Ir. ZULKIFLI
Maximize or Minimize 2X 1 = 8 X 2 Z = f (x,y) Subject to: 5 D C g (x,y) = c 3X 2 = 15 0 Daerah feasible A 4 B 6X 1 + 5X 2 = 30 X 1 PENYELESAIAN MODEL LINEAR PROGRAMMING SECARA GRAFIK Prof. Dr. Ir. ZULKIFLI
MODUL MATEMATIKA II. Oleh: Dr. Eng. LILYA SUSANTI
 MODUL MATEMATIKA II Oleh: Dr. Eng. LILYA SUSANTI DEPARTEMEN RISET TEKNOLOGI DAN PENDIDIKAN TINGGI UNIVERSITAS BRAWIJAYA FAKULTAS TEKNIK JURUSAN TEKNIK SIPIL KATA PENGANTAR Puji sukur kehadirat Allah SWT
MODUL MATEMATIKA II Oleh: Dr. Eng. LILYA SUSANTI DEPARTEMEN RISET TEKNOLOGI DAN PENDIDIKAN TINGGI UNIVERSITAS BRAWIJAYA FAKULTAS TEKNIK JURUSAN TEKNIK SIPIL KATA PENGANTAR Puji sukur kehadirat Allah SWT
Persamaan Diferensial Biasa
 Persamaan Diferensial Biasa Pendahuluan, Persamaan Diferensial Orde-1 Toni Bakhtiar Departemen Matematika IPB September 2012 Toni Bakhtiar (m@thipb) PDB September 2012 1 / 37 Pendahuluan Konsep Dasar Beberapa
Persamaan Diferensial Biasa Pendahuluan, Persamaan Diferensial Orde-1 Toni Bakhtiar Departemen Matematika IPB September 2012 Toni Bakhtiar (m@thipb) PDB September 2012 1 / 37 Pendahuluan Konsep Dasar Beberapa
Modul Matematika MINGGU 4. g. Titik Potong fungsi linier
 MINGGU 4 Pokok Bahasan Sub Pokok Bahasan Tujuan Instruksional Umum : Hubungan dan : 1. Hubungan 2. a. Pengertian fungsi b. Jenis-jenis fungsi c. Diagram fungsi d. Pengertian fungsi linier e. Penggambaran
MINGGU 4 Pokok Bahasan Sub Pokok Bahasan Tujuan Instruksional Umum : Hubungan dan : 1. Hubungan 2. a. Pengertian fungsi b. Jenis-jenis fungsi c. Diagram fungsi d. Pengertian fungsi linier e. Penggambaran
BAB 1 PENDAHULUAN. 1.1 Latar Belakang
 BAB 1 PENDAHULUAN 1.1 Latar Belakang Dalam kehidupan sehari-hari baik disadari maupun tidak, optimasi selalu dilakukan untuk memenuhi kebutuhan. Tetapi optimasi yang dilakukan masyarakat awam lebih banyak
BAB 1 PENDAHULUAN 1.1 Latar Belakang Dalam kehidupan sehari-hari baik disadari maupun tidak, optimasi selalu dilakukan untuk memenuhi kebutuhan. Tetapi optimasi yang dilakukan masyarakat awam lebih banyak
A. Distribusi Gabungan
 HANDOUT PERKULIAHAN Mata Kuliah : Statistika Matematika Pertemuan Ke : 5 Pokok Bahasan : Distibusi Dua peubah Acak URAIAN POKOK PERKULIAHAN A. Distribusi Gabungan Definisi 1: Peubah Acak Berdimensi Dua
HANDOUT PERKULIAHAN Mata Kuliah : Statistika Matematika Pertemuan Ke : 5 Pokok Bahasan : Distibusi Dua peubah Acak URAIAN POKOK PERKULIAHAN A. Distribusi Gabungan Definisi 1: Peubah Acak Berdimensi Dua
KURVA DAN PENCOCOKAN KURVA. Matematika Industri 1 TIP FTP UB
 KURVA DAN PENCOCOKAN KURVA TIP FTP UB Pokok Bahasan Pendahuluan Kurva-kurva standar Asimtot Penggambaran kurva secara sistematis, jika persamaan kurvanya diketahui Pencocokan kurva Metode kuadrat terkecil
KURVA DAN PENCOCOKAN KURVA TIP FTP UB Pokok Bahasan Pendahuluan Kurva-kurva standar Asimtot Penggambaran kurva secara sistematis, jika persamaan kurvanya diketahui Pencocokan kurva Metode kuadrat terkecil
DUALITAS. Obyektif 1. Memahami penyelesaian permasalahan dual 2. Mengerti Interpretasi Ekonomi permasalahan dual
 DUALITAS 3 Obyektif 1. Memahami penyelesaian permasalahan dual 2. Mengerti Interpretasi Ekonomi permasalahan dual Istilah dualitas menunjuk pada kenyataan bahwa setiap Program Linier terdiri atas dua bentuk
DUALITAS 3 Obyektif 1. Memahami penyelesaian permasalahan dual 2. Mengerti Interpretasi Ekonomi permasalahan dual Istilah dualitas menunjuk pada kenyataan bahwa setiap Program Linier terdiri atas dua bentuk
LINIEAR PROGRAMMING MATEMATIKA BISNIS ANDRI HELMI M, S.E., M.M.
 LINIEAR PROGRAMMING MATEMATIKA BISNIS ANDRI HELMI M, S.E., M.M. INTRODUCTION Masalah keputusan yang biasa dihadapi para analis adalah alokasi optimum sumber daya yang langka. Sumber daya dapat berupa modal,
LINIEAR PROGRAMMING MATEMATIKA BISNIS ANDRI HELMI M, S.E., M.M. INTRODUCTION Masalah keputusan yang biasa dihadapi para analis adalah alokasi optimum sumber daya yang langka. Sumber daya dapat berupa modal,
PROGRAM LINEAR. Dasar Matematis
 PROGRAM LINEAR Dasar Matematis PROGRAM LINIER adalah suatu teknik optimalisasi dimana variabel-variabelnya linier. Metode ini dipakai pada saat kita dihadapkan pada beberapa pilihan dengan batasan-batasan
PROGRAM LINEAR Dasar Matematis PROGRAM LINIER adalah suatu teknik optimalisasi dimana variabel-variabelnya linier. Metode ini dipakai pada saat kita dihadapkan pada beberapa pilihan dengan batasan-batasan
A. Distribusi Gabungan
 HANDOUT PERKULIAHAN Mata Kuliah Pokok Bahasan : Statistika Matematika : Distibusi Dua peubah Acak URAIAN POKOK PERKULIAHAN A. Distribusi Gabungan Definisi 1: Peubah Acak Berdimensi Dua Jika S merupakan
HANDOUT PERKULIAHAN Mata Kuliah Pokok Bahasan : Statistika Matematika : Distibusi Dua peubah Acak URAIAN POKOK PERKULIAHAN A. Distribusi Gabungan Definisi 1: Peubah Acak Berdimensi Dua Jika S merupakan
