Induksi Matematika. Metode pembuktian untuk pernyataan perihal bilangan bulat adalah induksi matematik.

Transkripsi

1 Induksi Matematika Metode pembuktian untuk pernyataan perihal bilangan bulat adalah induksi matematik. Misalkan p(n) adalah pernyataan yang menyatakan: Jumlah bilangan bulat positif dari 1 sampai n adalah n(n + 1)/2. Buktikan bahwa p(n) benar! Contoh lainnya: 1. Setiap bilangan bulat positif n (n 2) dapat dinyatakan sebagai perkalian dari (satu atau lebih) bilangan prima. 2. Untuk semua n 1, n 3 + 2n adalah kelipatan Untuk membayar biaya pos sebesar n sen dolar (n 8) selalu dapat digunakan hanya perangko 3 sen dan 5 sen dolar. 4. Di dalam sebuah pesta, setiap tamu berjabat tangan dengan tamu lainnya hanya sekali. Jika ada n orang tamu maka jumlah jabat tangan yang terjadi adalah n(n +1)/2. 5. Banyaknya himpunan bagian yang dapat dibentuk dari sebuah himpunan yang beranggotakan n elemen adalah 2 n Induksi matematik merupakan teknik pembuktian yang baku di dalam matematika. Melalui induksi matematik kita dapat mengurangi langkah-langkah pembuktian bahwa semua bilangan bulat termasuk ke dalam suatu himpunan kebenaran dengan hanya sejumlah langkah terbatas. Prinsip Induksi Sederhana. Misalkan p(n) adalah pernyataan perihal bilangan bulat positif dan kita ingin membuktikan bahwa p(n) benar untuk semua bilangan bulat positif n. Untuk membuktikan pernyataan ini, kita hanya perlu menunjukkan bahwa:

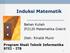
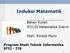
2 1. p(1) benar, dan 2. untuk semua bilangan bulat positif n 1, jika p(n) benar maka p(n + 1) juga benar. Langkah 1 dinamakan basis induksi, sedangkan langkah 2 dinamakan langkah induksi. Langkah induksi berisi asumsi (andaian) yang menyatakan bahwa p(n) benar. Asumsi tersebut dinamakan hipotesis induksi. Bila kita sudah menunjukkan kedua langkah tersebut benar maka kita sudah membuktikan bahwa p(n) benar untuk semua bilangan bulat positif n. Gambar 4.1 Efek domino Contoh 1. Gunakan induksi matematik untuk membuktikan bahwa 1(1!) + 2(2!) + + n(n!) = (n + 1)! 1 Contoh 2. Gunakan induksi matematik untuk membuktikan bahwa jumlah n buah bilangan ganjil positif pertama adalah n 2. Penyelesaian: (i) Basis induksi: Untuk n = 1, jumlah satu buah bilangan ganjil positif pertama adalah 1 2 = 1. Ini benar karena jumlah satu buah bilangan ganjil positif pertama adalah 1. (ii) Langkah induksi: Andaikan untuk n 1 pernyataan

3 (2n 1) = n 2 adalah benar (hipotesis induksi) [catatlah bahwa bilangan ganjil positif ke-n adalah (2n 1)]. Kita harus memperlihatkan bahwa (2n 1) + (2n + 1) = (n + 1) 2 juga benar. Hal ini dapat kita tunjukkan sebagai berikut: (2n 1) + (2n + 1) = [ (2n 1)] + (2n + 1) = n 2 + (2n + 1) = n 2 + 2n + 1 = (n + 1) 2 Karena langkah basis dan langkah induksi keduanya telah diperlihatkann benar, maka jumlah n buah bilangan ganjil positif pertama adalah n 2. Prinsip Induksi yang Dirampatkan Misalkan p(n) adalah pernyataan perihal bilangan bulat dan kita ingin membuktikan bahwa p(n) benar untuk semua bilangan bulat menunjukkan bahwa: 1. p(n0) benar, dan n n0. Untuk membuktikan ini, kita hanya perlu 2. untuk semua bilangan bulat n n0, jika p(n) benar maka p(n+1) juga benar. Contoh 3. Untuk semua bilangan bulat tidak-negatif n, buktikan dengan induksi matematik bahwa n = 2 n+1-1 Penyelesaian: (i) Basis induksi. Untuk n = 0 (bilangan bulat tidak negatif pertama), kita peroleh:

4 2 0 = Ini jelas benar, sebab 2 0 = 1 = = = 2-1 = 1 (ii) Langkah induksi. Andaikan bahwa untuk semua bilangan bulat tidak-negatif n, n = 2 n+1-1 adalah benar (hipotesis induksi). Kita harus menunjukkan bahwa n + 2 n+1 = 2 (n+1) juga benar. Ini kita tunjukkan sebagai berikut: n + 2 n+1 = ( n ) + 2 n+1 = (2 n+1-1) + 2 n+1 (dari hipotesis induksi) = (2 n n+1 ) - 1 = (2. 2 n+1 ) - 1 = 2 n+2-1 = 2 (n+1) Karena langkah 1 dan 2 keduanya telah diperlihatkan benar, maka untuk semua bilangan bulat tidak-negatif n, terbukti bahwa n = 2 n+1-1

5 Contoh 4. Buktikan dengan induksi matematik bahwa pada sebuah himpunan beranggotakan n elemen, banyaknya himpunan bagian yang dapat dibentuk dari himpunan tersebut adalah 2 n. Contoh 5. Buktikan pernyataan Untuk membayar biaya pos sebesar n sen (n 8) selalu dapat digunakan hanya perangko 3 sen dan perangko 5 sen benar. Penyelesaian: (i) Basis induksi. Untuk membayar biaya pos 8 sen dapat digunakan 1 buah perangko 3 sen dan 1 buah perangka 5 sen saja. Ini jelas benar. (ii) Langkah induksi. Andaikan bahwa untuk membayar biaya pos sebesar n (n 8) sen dapat digunakan perangko 3 sen dan 5 sen (hipotesis induksi). Kita harus menunjukkan bahwa untuk membayar biaya pos sebesar n + 1 sen juga dapat menggunakan perangko 3 sen dan perangko 5 sen. Ada dua kemungkinan yang perlu diperiksa: (a) (b) Kemungkinan pertama, misalkan kita membayar biaya pos senilai n sen dengan sedikitnya satu perangko 5 sen. Dengan mengganti satu buah perangko 5 sen dengan dua buah perangko 3 sen, akan diperoleh susunan perangko senilai n + 1 sen. Kemungkinan kedua, jika tidak ada perangko 5 sen yang digunakan, biaya pos senilai n sen menggunakan perangko 3 sen semuanya. Karena n 8, setidaknya harus digunakan tiga buah perangko 3 sen. Dengan mengganti tiga buah perangko 3 sen dengan 2 buah perangko 5 sen, akan dihasilkan nilai perangko n + 1 sen. Contoh 6. Sebuah ATM (Anjungan Tunai Mandiri) hanya menyediakan pecahan uang Rp ,- dan Rp , -. Kelipatan uang berapakah yang dapat dikeluarkan oleh ATM tersebut? Buktikan jawaban anda dengan induksi matematik.

6 Prinsip Induksi Kuat Misalkan p(n) adalah pernyataan perihal bilangan bulat dan kita ingin membuktikan bahwa p(n) benar untuk semua bilangan bulat menunjukkan bahwa: 1. p(n0) benar, dan n n0. Untuk membuktikan ini, kita hanya perlu 2. untuk semua bilangan bulat n n0, jika p(n0 ), p(n0+1),, p(n) benar maka p(n+1) juga benar. Contoh 7. Bilangan bulat positif disebut prima jika dan hanya jika bilangan bulat tersebut habis dibagi dengan 1 dan dirinya sendiri. Kita ingin membuktikan bahwa setiap bilangan bulat positif n (n 2) dapat dinyatakan sebagai perkalian dari (satu atau lebih) bilangan prima. Buktikan dengan prinsip induksi kuat. Penyelesaian: Basis induksi. Jika n = 2, maka 2 sendiri adalah bilangan prima dan di sini 2 dapat dinyatakan sebagai perkalian dari satu buah bilangan prima, yaitu dirinya sendiri. Langkah induksi. Misalkan pernyataan bahwa bilangan 2, 3,, n dapat dinyatakan sebagai perkalian (satu atau lebih) bilangan prima adalah benar (hipotesis induksi). Kita perlu menunjukkan bahwa n + 1 juga dapat dinyatakan sebagai perkalian bilangan prima. Ada dua kemungkinan nilai n + 1: (a) (b) Jika n + 1 sendiri bilangan prima, maka jelas ia dapat dinyatakan sebagai perkalian satu atau lebih bilangan prima. Jika n + 1 bukan bilangan prima, maka terdapat bilangan bulat positif a yang membagi habis n + 1 tanpa sisa. Dengan kata lain, (n + 1)/ a = b atau (n + 1) = ab

7 yang dalam hal ini, 2 a b n. Menurut hipotesis induksi, a dan b dapat dinyatakan sebagai perkalian satu atau lebih bilangan prima. Ini berarti, n + 1 jelas dapat dinyatakan sebagai perkalian bilangan prima, karena n + 1 = ab. Karena langkah (i) dan (ii) sudah ditunjukkan benar, maka terbukti bahwa setiap bilangan bulat positif n (n 2) dapat dinyatakan sebagai perkalian dari (satu atau lebih) bilangan prima. Contoh 8. [LIU85] Teka-teki susun potongan gambar (jigsaw puzzle) terdiri dari sejumlah potongan (bagian) gambar (lihat Gambar 4.2). Dua atau lebih potongan dapat disatukan untuk membentuk potongan yang lebih besar. Lebih tepatnya, kita gunakan istilah blok bagi satu potongan gambar. Blok-blok dengan batas yang cocok dapat disatukan membentuk blok yang lain yang lebih besar. Akhirnya, jika semua potongan telah disatukan menjadi satu buah blok, teka-teki susun gambar itu dikatakan telah dipecahkan. Menggabungkan dua buah blok dengan batas yang cocok dihitung sebagai satu langkah. Gunakan prinsip induksi kuat untuk membuktikan bahwa untuk suatu teka-teki susun gambar dengan n potongan, selalu diperlukan n - 1 langkah untuk memecahkan teki-teki itu. Penyelesaian:

8 (i) Basis induksi. Untuk teka-teki susun gambar dengan satu potongan, tidak diperlukan langkah apa-apa untuk memecahkan teka-teki itu. (ii) Langkah induksi. Misalkan pernyataan bahwa untuk teka-teki dengan n potongan (n = 1, 2, 3,, k) diperlukan sejumlah n 1 langkah untuk memecahkan teka-teki itu adalah benar (hipotesis induksi). Kita harus membuktikan bahwa untuk n + 1 potongan diperlukan n langkah. Bagilah n + 1 potongan menjadi dua buah blok satu dengan n1 potongan dan satu lagi dengan n2 potongan, dan n1 + n2 = n + 1. Untuk langkah terakhir yang memecahkan teka-teki ini, dua buah blok disatukan sehingga membentuk satu blok besar. Menurut hipotesis induksi, diperlukan n1-1 langkah untuk menyatukan blok yang satu dan n2 1 langkah untuk menyatukan blok yang lain. Digabungkan dengan langkah terakhir yang menyatukan kedua blok tersebut, maka banyaknya langkah adalah (n1-1) + (n2 1) + 1 langkah terakhir = (n1 + n2) = n = n. Karena langkah (i) dan (ii) sudah diperlihatkan benar maka terbukti bahwa suatu teka-teki susun gambar dengan n potongan, selalu diperlukan n - 1 langkah untuk memecahkan teki-teki itu. Contoh 9. Tunjukkan apa yang salah dari pembuktian di bawah ini yang menyimpulkan bahwa semua kuda berwarna sama? Misalkan P(n) adalah pernyataan bahwa semua kuda di dalam sebuah himpunan berwarna sama (i) Basis induksi: jika kuda di dalam himpunan hanya seekor, jelaslah P(1) benar. (ii) Langkah induksi: andaikan bahwa semua kuda di dalam himpunan n ekor kuda berwarna sama adalah benar. Tinjau untuk himpunan dengan n + 1 kuda; nomori kuda-kuda tersebut dengan 1, 2, 3,, n, n+1. Tinjau dua himpunan, yaitu n ekor kuda yang pertama (1, 2, n) harus berwarna sama, dan n ekor kuda yang terakhir (2, 3,, n, n+1) juga harus berwarna

9 sama. Karena himpunan n kuda pertama dan himpunan n kuda terakhir beririsan, maka semua n+1 kuda harus berwarna sama. Ini membuktikan bahwa P(n+1) benar. Penyelesaian: langkah induksi tidak benar jika n + 1 = 2, sebab dua himpunan (yang masingmasing beranggotakan n = 1 elemen) tidak beririsan. Contoh 10. Temukan kesalahan dalam pembuktian berikut. Kita ingin membuktikan bahwa a n = 1 untuk semua bilangan bulat tak-negatif n bilamana a adalah bilangan riil tidak-nol. Kita akan membuktikan ini dengan prinsip induksi kuat. (i) Basis induksi. Untuk n = 0, jelas a 0 = 1 adalah benar sesuai definisi a 0. (ii) Langkah induksi. Misalkan pernyataan tersebut benar untuk 0, 1, 2,, n, yaitu a 0 = 1, a 1 = 1, a 2 = 1,, a n = 1. Kita ingin memperlihatkan bahwa a (n+1) = 1. Untuk menunjukkan hal ini, maka a n 1 n a. a n 1 a n 1 1 (dari hipotesis induksi) 1 = 1 Penyelesaian: Kesalahan terjadi pada langkah induksi, karena untuk n = 0 kita tidak dapat menghitung a. a 1 1 a 1 a? sebab nilai a 1 tidak terdapat dalam hipotesis induksi.

10 Bentuk Induksi Secara Umum Relasi biner "<" pada himpunan X dikatakan terurut dengan baik (atau himpunan X dikatakan terurut dengan baik dengan "<") bila memiliki properti berikut: (i) Diberikan x, y, z X, jika x < y dan y < z, maka x < z. (ii) Diberikan x, y X. Salah satu dari kemungkinan ini benar: x < y atau y < x atau x = y. (iii) Jika A adalah himpunan bagian tidak kosong dari X, terdapat elemen x A sedemikian sehingga x y untuk semua y A. Dengan kata lain, setiap himpunan bagian tidak kosong dari X mengandung "elemen terkecil". Misalkan X terurut dengan baik oleh "<", dan p(x) adalah pernyataan perihal elemen x dari X. Kita ingin membuktikan bahwa p(x) benar untuk semua x X. Untuk membuktikan ini, kita hanya perlu menunjukkan bahwa: 1. p(x0) benar, yang dalam hal ini x0 adalah elemen terkecil di dalam X, dan 2. untuk semua x > x0 di dalam X, jika p(y) benar untuk semua y < x, maka p(x) juga benar. Contoh 11. Tinjau barisan bilangan yang didefinisikan sebagai berikut:

11 S m, n S S 0 m 1, n m, n jika m 0 dan n 0 jika n 0 jika n 0 Sebagai contoh, S0,0 = 0 S1, 0 = S0,0 + 1 = = 1 S0, 1 = S0,0 + 1 = 1 S1, 1 = S1,0 + 1 = = 2 S2, 0 = S1,0 + 1 = 2 S2, 1 = S2,0 + 1 = 3, Buktikanlah dengan induksi matematik bahwa untuk pasangan tidak negatif m dan n, Sm, n = m + n. Penyelesaian: Basis induksi. Karena (0, 0) adalah elemen terkecil di dalam X, maka S0,0 = = 0. Ini benar dari definisi S0,0. Langkah induksi. Buktikan untuk semua (m, n) > (0, 0) di dalam X bahwa jika Sm',n' = m' + n' benar untuk semua (m', n') < (m, n) maka Sm, n = m + n juga benar. Andaikan bahwa Sm, n = m + n benar untuk semua (m, n ) < (m,n). Ini adalah hipotesis induksi. Kita perlu menunjukkan bahwa Sm,n = m + n, baik untuk n = 0 atau n 0. Kasus 1: Jika n = 0, maka dari definisi Sm,n = Sm-1,n + 1. Karena (m-1, n) < (m, n), maka dari hipotesis induksi, Sm-1, n = (m 1) + n sehingga Sm,n = Sm-1,n + 1 = (m 1) + n + 1 = m + n. Kasus 2: Jika n 0, maka dari definisi Sm,n = Sm,n Karena (m, n-1) < (m, n), maka dari hipotesis induksi,

12 Sm, n-1 = m + (n 1) sehingga Sm, n = Sm, n = m + (n 1) + 1 = m + n. HIMPUNAN Pada materi ini akan dibahas tentang definisi dari himpunan, keanggotaan suatu himpunan, operasi himpunan dan beberapa jenis himpunan. 1.a Definisi dan Keanggotaan Suatu Himpunan Himpunan (set) merupakan sekumpulan objek-objek yang berbeda yang dapat didefinisikan dengan jelas. Objek di dalam himpunan dinamakan unsur atau anggota himpunan. Keanggotaan suatu himpunan dinyatakan oleh notasi. A = {x, y, z} x A : x merupakan anggota himpunan A. w A : w bukan merupakan anggota himpunan A. Ada beberapa cara dalam menyatakan himpunan, yaitu : a. Mencacahkan anggotanya (Enumerasi). Dengan cara ini, himpunan tersebut dinyatakan dengan menyebutkan semua anggota himpunannya di dalam suatu kurung kurawal ({}). - Himpunan empat bilangan ganjil pertama: A = {1, 3, 5, 7}. - Himpunan lima bilangan prima pertama: B = {2, 3, 5, 7, 11}. - Himpunan bilangan asli yang kurang dari 50 : C = {1, 2,, 50} - Himpunan bilangan bulat ditulis sebagai {, -2, -1, 0, 1, 2, }. b. Menggunakan simbol standar (baku) Suatu himpunan dapat dinyatakan dalam suatu simbol standar (baku) yang telah diketahui secara umum oleh masyarakat (ilmiah). N = himpunan bilangan alami (natural) = { 1, 2, }

13 Z = himpunan bilangan bulat = {, -2, -1, 0, 1, 2, } Q = himpunan bilangan rasional R = himpunan bilangan riil C = himpunan bilangan kompleks Himpunan yang universal (semesta pembicaraan) dinotasikan dengan U. Misalkan U = {1, 2, 3, 4, 5} dan A = {1, 3, 5} merupakan himpunan bagian dari U c. Menuliskan kriteria (syarat) keanggotaan himpunan Suatu himpunan dapat dinyatakan dengan cara menuliskan kriteria (syarat) keanggotaan himpunan tersebut. Himpunan ini dinotasinya sebagai berikut : { x syarat yang harus dipenuhi oleh x } (i) A adalah himpunan bilangan asli yang kecil dari 10 A = { x x 10 dan x N } atau A = { x N x 10 } yang ekivalen dengan A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} (ii) M = { x x adalah mahasiswa yang mengambil kuliah matematika diskrit} Atau M = { x adalah mahasiswa ia mengambil kuliah matematika diskrit} d. Menggunakan Diagram Venn Suatu himpunan dapat dinyatakan dengan cara menuliskan anggotanya dalam suatu gambar (diagram) yang dinamakan diagram venn. Misalkan U = {1, 2,, 7, 8}, A = {1, 2, 3, 5} dan B = {2, 5, 6, 8}.

14 Diagram Venn: Terkait dengan masalah keanggotaan, suatu himpunan dapat dinyatakan sebagai anggota himpunan lain. a. Misalkan, M = { mahasiswa STT GARUT } M1 = { mahasiswa anggota HIMATIF} M2 = { mahasiswa anggota HIMAKOM} M3 = { mahasiswa anggota HIMASIP} M4 = { mahasiswa anggota HIMATI } Dengan demikian, M = { M1, M2, M3, M4,} b. Bila P1 = {x, y}, P 2 = { {x, y} } atau P 2 ={P1}, Sementara itu, P3 = {{{x, y}}}, maka x P1 dan y P 2, sehingga P1 P2, sedangkan P1 P3, tetapi P2 P3 Jumlah unsur dalam suatu himpunan dinamakan kardinalitas dari himpunan tersebut. Misalkan, untuk menyatakan kardinalitas himpunan A ditulis dengan notasi: n(a) atau A (i) B = { x x merupakan bilangan prima yang lebih kecil dari 10 }, atau B = {2, 3, 5, 7 } maka B = 4 (ii) A = {a, {a}, {{a}} }, maka A = 3 Jika suatu himpunan tidak mempunyai anggota, dengan kata lain dengan kardinalitas himpunan tersebut sama dengan nol maka himpunan tersebut dinamakan himpunan kosong (null set). Notasi dari suatu himpunan kosong adalah : atau {} (i) P = {Mahasiswa Teknik Industri STT Garut yang pernah ke Mars},

15 maka n(p) = 0 Jadi P = (ii) A = {x akar persamaan kuadrat x = 0 dan x R}, maka n(a) = 0 Jadi A = {} (iii) B = {{ }} dapat juga ditulis sebagai B = { }. Jadi B bukan himpunan kosong karena ia memuat satu unsur yaitu himpunan kosong. Himpunan A dikatakan himpunan bagian (subset) dari himpunan B jika dan hanya jika setiap unsur A merupakan unsur dari B. Dalam hal ini, B dikatakan superset dari A. Notasi himpunan bagian : A B atau A B Contoh: (i) N Z R C (ii) {2, 3, 5} {2, 3, 5} Untuk setiap himpunan A berlaku hal-hal sebagai berikut: (a) A adalah himpunan bagian dari A itu sendiri (yaitu, A A). (b) Himpunan kosong merupakan himpunan bagian dari A ( A). (c) Jika A B dan B C, maka A C A dan A A, maka dan A disebut himpunan bagian tak sebenarnya (improper subset) dari himpunan A. Pernyataan A B berbeda dengan A B : A B : A adalah himpunan bagian dari B tetapi A B. Yang demikian, A merupakan himpunan bagian sebenarnya (proper subset) dari B. Misalkan A = {1, 2, 3}. {1} dan {2, 3} merupakan proper subset dari A.

16 Himpunan kuasa (power set) dari himpunan A merupakan suatu himpunan yang unsurunsurnya merupakan semua himpunan bagian dari A, termasuk himpunan kosong dan himpunan A sendiri. Himpunan kuasa dinotasikan oleh P(A). Jumlah anggota (kardinal) dari suatu himpunan kuasa bergantung pada kardinal himpunan asal. Misalkan, kardinalitas himpunan A adalah m, maka P(A) = 2 m. Jika A = { x, y }, maka P(A) = {, { x }, { y }, { x, y }} Himpunan kuasa dari himpunan kosong adalah P( ) = { }, sementara itu himpunan kuasa dari himpunan { } adalah P({ }) = {, { }}. Pernyataan A B digunakan untuk menyatakan bahwa A adalah himpunan bagian (subset) dari B yang memungkinkan A = B. Dua buah himpunan dikatakan sama jika memenuhi kondisi berikut : A = B jika dan hanya jika setiap unsur A merupakan unsur B dan sebaliknya setiap unsur B merupakan unsur A. Untuk menyatakan A = B, yang perlu dibuktikan adalah A adalah himpunan bagian dari B dan B merupakan himpunan bagian dari A. Jika tidak demikian, maka A B. atau A = B A B dan B A (i) Jika A = { 0, 1 } dan B = { x x (x 1) = 0 }, maka A = B (ii) Jika A = { 3, 5, 8, 5 } dan B = {5, 3, 8 }, maka A = B (iii) Jika A = { 3, 5, 8, 5 } dan B = {3, 8}, maka A B Untuk tiga buah himpunan, A, B, dan C berlaku aksioma berikut:

17 (a) A = A, B = B, dan C = C (b) Jika A = B, maka B = A (c) Jika A = B dan B = C, maka A = C Dua buah himpunan dikatakan ekivalen jika masing-masing mempunyai kardinalitas yang sama. Misalkan, himpunan A adalah ekivalen dengan himpunan B berarti kardinal dari himpunan A dan himpunan B adalah sama, notasi yang digunakan adalah : A ~ B Misalkan A = { 2, 3, 5, 7 } dan B = { a, b, c, d }, maka A ~ B sebab A = B = 4 Dua himpunan A dan B dikatakan saling lepas (disjoint) jika keduanya tidak memiliki unsur yang sama. Notasi yang digunakan adalah A // B. Jika A = { x x N, x < 10 } dan B = { 11, 12, 13, 14, 15 }, maka A // B 1.b Operasi Himpunan Ada beberapa operasi himpunan yang perlu diketahui, yaitu : irisan, gabungan, komplemen, selisih dan beda setangkup. a. Irisan (intersection) Irisan antara dua buah himpunan dinotasikan oleh tanda. Misalkan A dan B adalah himpunan yang tidak saling lepas, maka A B = { x x A dan x B } Jika dinyatakan dalam bentuk diagram Venn adalah : 1. Misalkan A = {2, 3, 5, 7, 11} dan B = {3, 6, 9, 12}, maka A B = {3}

18 2. Misalkan A adalah himpunan mahasiswi TI STT Garut dan B merupakan himpunan wanita lanjut usia (50 tahun ke atas) maka A B =. Hal ini berarti A dan B adalah saling lepas atau A // B. b. Gabungan (union) Gabungan antara dua buah himpunan dinotasikan oleh tanda. Misalkan A dan B adalah himpunan, maka A B = { x x A atau x B } (i) Jika A = { 2, 3, 5, 7} dan B = { 1, 2, 3, 4, 5 }, maka A B = { 1, 2, 3, 4, 5, 7} (ii) A = A c. Komplemen (complement) Komplemen dari suatu himpunan merupakan unsur -unsur yang ada pada himpunan universal (semesta pembicaraan ) kecuali anggota himpunan tersebut. Misalkan A merupakan himpunan yang berada pada semesta pembicaraan U, maka komplemen dari himpunan A dinotasikan oleh : -A = { x x U dan x A } Misalkan U = { 1, 2, 3,, 9 }, jika A = {1, 3, 7, 9}, maka -A = {2, 4, 5, 6, 8} jika A = { x U x habis dibagi dua }, maka -A= { 1, 3, 5, 7, 9 } A = himpunan mahasiswa STT GARUT B = himpunan mahasiswa yang tinggal di Asrama C = himpunan mahasiswa angkatan 2012 D = himpunan mahasiswa yang mengambil matematika diskrit

19 E = himpunan mahasiswa yang membawa motor untuk pergi ke kampus a. Pernyataan Semua mahasiswa STT GARUT angkatan 2012 yang membawa motor untuk pergi ke kampus dapat dinyatakan dalam notasi operasi himpunan sebagai berikut : (A C) E b. Pernyataan Semua mahasiswa STT GARUT yang tinggal di asrama dan tidak mengambil matematika diskrit dapat dinyatakan dalam notasi operasi himpunan sebagai berikut : A B -D c. Pernyataan semua mahasiswa angkatan 2012 yang tidak tinggal di asrama atau tidak membawa motor untuk pergi ke kampus dapat dinyatakan dalam notasi operasi himpunan sebagai berikut : C (-B -E) d. Selisih (difference) Selisih antara dua buah himpunan dinotasikan oleh tanda. Misalkan A dan B adalah himpunan, maka selisih A dan B dinotasikan oleh A B = { x x A dan x B } = A - B Jika A = { 1, 2, 3,, 10 } dan B = { 2, 3, 5, 7}, maka A B = { 1, 4, 6, 8, 9 } dan B A = e. Beda Setangkup (Symmetric Difference) Beda setangkup antara dua buah himpunan dinotasikan oleh tanda.

20 Misalkan A dan B adalah himpunan, maka beda setangkup antara A dan B dinotasikan oleh : A B = (A B) (A B) = (A B) (B A) Jika dinyatakan dalam bentuk diagram Venn adalah :Notasi: Jika A = { 2, 3, 5, 7} dan B = { 1, 2, 3, 4, 5 }, maka A B = { 1, 4, 7 } Beda setangkup memenuhi sifat-sifat berikut: (a) A B = B A (b) (A B ) C = A (B C ) (hukum komutatif) (hukum asosiatif) f. Perkalian Kartesian (cartesian product) Perkalian kartesian antara dua buah himpunan dinotasikan oleh tanda. Misalkan A dan B adalah himpunan, maka perkalian kartesian antara A dan B dinotasikan oleh : A B = {(a, b) a A dan b B } (i) Misalkan C = {1, 2, 3}, dan D = { a, b }, maka C D = { (1, a), (1, b), (2, a), (2, b), (3, a), (3, b) } (ii) Misalkan A = B = himpunan semua bilangan riil, maka A B = himpunan semua titik di bidang datar Misalkan ada dua himpunan dengan kardinalitas berhingga, maka kardinalitas himpunan hasil dari suatu perkalian kartesian antara dua himpunan tersebut adalah perkalian antara kardinalitas

21 masing-masing himpunan. Dengan demikian, jika A dan B merupakan himpunan berhingga, maka: A B = A. B. Pasangan terurut (a, b) berbeda dengan (b, a), dengan kata lain (a, b) (b, a). Dengan argumen ini berarti perkalian kartesian tidak komutatif, yaitu A B B A dimana A atau B bukan himpunan kosong. Jika A = atau B =, maka A B = B A = Hukum-hukum yang berlaku untuk operasi himpunan adalah sebagai berikut : 1. Hukum identitas: A = A A U = A 2. Hukum null/dominasi: A = A U = U 3. Hukum komplemen: A -A = U A -A = 4. Hukum idempoten: A A = A A A = A 5. Hukum involusi: ( A)= A

22 6. Hukum penyerapan (absorpsi): A (A B) = A A (A B) = A 7. Hukum komutatif: A B = B A A B = B A 8. Hukum asosiatif: A (B C) = (A B) C A (B C) = (A B) C 9. Hukum distributif: A (B C) = (A B) (A C) A (B C) = (A B) (A C) 10. Hukum De Morgan: A B = A B A B = A B 11. Hukum komplemen (- ) = U (-U) = 1.c Prinsip Dualitas Prinsip dualitas mengemukakan bahwa dua konsep yang berbeda dapat dipertukarkan namun tetap memberikan jawaban yang benar. Contoh 24 : AS kemudi mobil di kiri depan

23 Indonesia kemudi mobil di kanan depan Peraturan: (a) di Amerika Serikat, mobil harus berjalan di bagian kanan jalan, pada jalan yang berlajur banyak, lajur kiri untuk mendahului, bila lampu merah menyala, mobil belok kanan boleh langsung (b) di Indonesia, mobil harus berjalan di bagian kiri jalan, pada jalur yang berlajur banyak, lajur kanan untuk mendahului, bila lampu merah menyala, mobil belok kiri boleh langsung Prinsip dualitas pada kasus diatas adalah: Konsep kiri dan kanan dapat dipertukarkan pada kedua negara tersebut sehingga peraturan yang berlaku di Amerika Serikat menjadi berlaku pula di Inggris. (Prinsip Dualitas pada Himpunan). Misalkan S adalah suatu kesamaan (identity) yang melibatkan himpunan dan operasi-operasi seperti,, dan komplemen. Jika S* merupakan kesamaan yang berupa dual dari S maka dengan mengganti,, U, U, sedangkan komplemen dibiarkan seperti semula, maka operasi-operasi tersebut pada kesamaan S* juga benar. Tabel 1.c Dualitas dari Hukum Aljabar Himpunan 1. Hukum identitas:a = A Dualnya:A U = A 2. Hukum null/dominasi:a = Dualnya:A U = U 3. Hukum komplemen :A A = U Dualnya:A A= 4. Hukum idempoten :A A = A Dualnya:A A = A 5. Hukum penyerapan :A (A B) = Dualnya:A (A B) = A A 6. Hukum komutatif :A B = B A Dualnya:A B = B A 7. Hukum asosiatif :A (B C) = (A Dualnya:A (B C) = (A B) C B) C 8. Hukum distributif :A (B Dualnya:A (B C) = (A B) (A C)=(A B) (A C) C) 9. Hukum De Morgan:BA = A B Dualnya:BA = A B

24 10. Hukum 0/1 = U Dualnya:U = 1.d Prinsip Inklusi-Ekslusi Berapa banyak anggota didalam gabungan dua buah himpunan A dan B? Penggabungan dua buah menghasilkan dua buah himpunan baru yang elemen-elemenya berasal dari himpunan A dan himpunan B. Himpunan A dan himpunan B mungkin saja memiliki elemen-elemen yang sama. Banyaknya elemen bersama antara A dan B adalah A B. Setiap unsur yang sama itu telah dihitung dua kali, sekali pada A dan sekali pada B, meskipun ia seharusnya dianggap sebagai satu buah elemen didalam A B, karena itu, jumlah elemen hasil penghubungan seharusnya adalah jumlah elemen dimasing-masing himpunan dikurangi dengan jumlah elemen didalam irisannya, atau A B = A + B - A B. Prinsip ini dikenal dengan nama prinsip inklusi-eksklusi. 1.e Partisi

25 Tinjau sekumpulan mahasiswa di sebuah kelas. Bagaimana caranya agar dosen membagi (partisi) himpunan ini? Dosen dapat membagi menjadi beberapa buah himpunan bagian, yang dalam hal ini setiap himpunan bagian mungkin berisi 1 orang mahasiswa, 2 orang mahasiswa, dan seterusnya, bahkan kosong. Tidak ada mahasiswa yang sama berada dalam dua atau lebih himpunan bagian yang berbeda. Gabungan dari seluruh himpunan bagian itu adalah seluruh mahasiswa dalam kelas. Definisi Partisi dari sebuah himpunan A adalah sekumpulan himpunan bagian tidak kosong A1,A2..dari A sedemikian sehingga : (a) A1 A2. = A, dan (b) Himpunan bagian Ai saling lepas; yaitu Ai Aj = Ø untuk i j Misalkan A = { 1, 2, 3, 4, 5, 6, 7, 8}, maka { {1},{2, 3, 4},{7, 8},{5, 6}} adalah partisi A. Catatlah bahwa partisi membagi himpunan A menjadi beberapa buah blok. Pada contoh diatas, himpunan A dibagi menjadi 4 buah blok, yaitu {1},{2, 3, 4},{7, 8}, dan {5, 6}. Jika himpunan A terbatas jumlah elemennya, maka jumlah blok yang dapat dibentuk tidak lebih besar dari A. 1.f Multiset Dari definisi himpunan, himpunan adalah kumpulan elemen yang berbeda. Namun pada beberapa situasi, adakalanya elemen himpunan tidak seluruhnya berbeda, misalnya himpunan nama-nama mahasiswa di sebuah kelas. Nama-nama mahasiswa di dalam sebuah kelas mungkin ada yang sama, karena itu ada perulangan elemen yang sama di dalam himpunan tersebut. Himpunan yang elemennya boleh berulang (tidak harus berbeda) disebut himpunanganda atau multiset.contohnya, {1, 1, 1, 2, 2, 3}, {2, 2, 2}, {2, 3, 4}, {} adalah himpunan ganda. Multiplisitas dari suatu elemen pada multiset adalah jumlah kemunculan elemen tersebut pada multiset. Sebagai contoh: Jika M = { 0, 1, 01, 1, 0, 001, 0001, 00001, 0, 0, 1}, maka multiplisitas elemen 0 adalah 4. Himpunan merupakan contoh khusus dari suatu multiset, yang dalam hal ini multiplisitas dari setiap elemennya adalah 0 atau 1.Kardinalitas dari suatu multiset didefinisikan sebagai kardinalitas himpunan padanannya, dengan mengasumsikan elemen-elemen di dalam multiset semua berbeda.