IV. MATRIKS PEMADANAN MAKSIMAL

Transkripsi

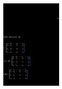
1 {(1,),(2,4),(,1),(4,2)} yang berarti pada periode ke dua yaitu baris ke tiga pada kolom pertama, agen 1 dipasangkan dengan agen. Lalu pada kolom dua agen 2 dipasangkan dengan agen 4, pada kolom berikutnya yaitu kolom tiga agen dipasangkan dengan agen 1 dan kolom empat agen 4 dipasangkan dengan agen 2. Selanjutnya pada periode yaitu periode ke tiga diperoleh pemadanan {(1,4),(2,),(,2),(4,1)} artinya pada periode ke tiga yaitu baris ke empat pada kolom pertama agen 1 dipasangkan dengan agen 4, pada kolom dua agen 2 dipasangkan dengan agen, pada kolom tiga agen dipasangkan dengan agen 2, dan pada kolom empat agen 4 dipasangkan dengan agen 1. Matriks pemadanan maksimal menjelaskan pemasangan di antara n agen dengan tidak ada agen yang bertemu dengan pasangan yang sama lagi. Perlu diketahui bahwa semua matriks pemadanan maksimal sembarang dengan n genap adalah bujursangkar latin yang memenuhi batasan tambahan bahwa setiap baris adalah involusi dari baris pertama. Hal ini merupakan kasus khusus karena tidak semua bujursangkar latin memenuhi sifat involusi. Contoh 14 Misal diberiakan matriks bujursangkar latin berikut dengan populasi 1,2,, Perhatikan matriks bujursangkar latin pada Contoh 14 di atas, pada baris ke dua diperoleh pemadanan {(1,2),(2,),(,4),(4,1)} yang artinya pada baris ke dua ini pada kolom satu agen 1 dipasangkan dengan agen 2 tetapi pada kolom dua agen 2 tidak dipasangkan dengan agen 1 melainkan dengan agen, hal ini bertentangan dengan sifat involusi sehingga matriks bujursangkar latin pada Contoh 14 ini bukan merupakan matriks pemadanan. Untuk popolasi X saat jumlah agen n ganjil matriks pemadanan maksimal bukan merupakan bujursangkar latin karena matriks pemadanan maksimal memiliki baris sebanyak 1. Perlu diingat pada Definisi 8 merupakan matriks pemadanan jika pada saat n ganjil maka dalam setiap kolom j agen j muncul paling banyak dua kali dan entri lainnya pada kolom tersebut seluruhnya berbeda yaitu agen X\{j}. Hal ini mengakibatkan jika n ganjil maka dengan mengeliminasi baris pertama dari matriks dapat diperoleh matriks bujursangkar latin. Contoh 15 Misal n=, didapatkan matriks pemadanan maksimal. Jika baris pertama dari dieliminasi, maka diperoleh bujursangkar latin L = L = IV. MATRIKS PEMADANAN MAKSIMAL Bagian ini akan membahas eksistensi matriks pemadanan maksimal untuk sebarang populasi terbatas yang kemudian akan diperlihatkan bagaimana membentuk matriks pemadanan yang maksimal. Andaikan terdapat X populasi yang terdiri atas dua grup, sebut saja grup A dan grup B. Setiap grup memiliki anggota yang sama banyaknya misalkan n anggota. Untuk lebih mudahnya diinterpretasikan setiap grup tersusun atas agen yang homogen, sebagai contohnya, grup pembeli dan grup penjual. Tujuan selanjutnya adalah memasangkan tepat satu kali setiap agen dari A dengan agen dari B, jadi setiap agen dari satu grup dipadankan dengan agen pada grup lainnya dalam keadaan mutlak saling asing, artinya setiap agen dipadankan dengan agen lainnya tepat satu kali dan dalam setiap periode pemadanan setiap agen yang diperoleh adalah maksimal artinya semua agen memperoleh pasangannya masingmasing. Perlu diingat bahwa kaidah pemadanan ini dapat menghasilkan paling bayak n periode dari pemadanan, karena setiap agen dapat berpasangan dengan paling banyak n agen

2 dari grup lainnya. Permasalahan di sini adalah bagaimana membentuk pemadanan maksimal yang diharapkan dan bagaimana cara sistematis untuk memperoleh pemadanan yang maksimal tersebut. Dalam hal ini kita menggambarkan dalam sebuah matriks yang sebelumnya sudah disebutkan sebagai matriks pemadanan maksimal. Terdapat dua hal yang diperoleh dari permasalahan di atas. Pertama hal tersebut menetapkan bahwa agen dipasangkan dalam keadaan mutlak saling asing paling banyak n kali. Ke dua diperoleh prosedur untuk membentuk kaidah pemadanan pada sembarang populasi. Misal dinotasikan X = AuB berarti dan, dengan kata lain X adalah union disjoint dari A dan B. Lema 1 Andaikan 1,..., dan 1,...,2, maka matriks M(A,B) berukuran L n 1 n n+ 1 n+ 2 L 2n 1 2n n+ 1 n+ 2 L 2n 1 2n 1 2 L n 1 n M( A, B) = n+ 2 n+ L 2n n+ 1 n 1 L n 2 n 1 M M O M M M M O M M 2n n+ 1 L 2n 2 2n 1 2 L n 1 adalah matriks pemadanan dari populasi X=AuB sedemikian sehingga setiap agen di A adalah pasangan yang terpadankan dengan setiap agen di B. [Aliprantis, et al 2006] Bukti Notasi M(A,B) menggambarkan di mana agen pada himpunan A dipadankan dengan agen pada himpunan B dengan tidak memasangkan dengan dirinya sendiri. Andaikan adalah bujursangkar latin dari himpunan 1,...,2 yang dibangun berdasarkan konstruksi bujursangkar latin #1 pada Bab II, dan melambangkan bujursangkar latin dari himpunan 1,..., yang dibangun berdasarkan konstruksi bujursangkar latin #2. Sehingga dengan demikian diperoleh matriks 1... n n n M( A, B) = + L ( B) L ( A). Dengan demikian M(A,B) adalah matriks pemadanan yang sesuai untuk populasi X = Perlu diperhatikan pada matriks pemadanan M(A,B) yang diperoleh dari Lema 1 bukan merupakan matriks pemadanan yang maksimal, karena matriks M(A,B) tidak menggambarkan pemadanan antar agen dalam himpunan itu sendiri melainkan pemadanan antar agen pada himpunan A dan B saja. Yang perlu diingat juga berdasarkan Definisi 8, matriks pemadanan maksimal M berukuran di mana saat n ganjil maka 1 dan saat n genap maka. Untuk lebih jelas lihat Contoh 16 berikut. Contoh 16 Andai 1,..,8 dengan 1,2,,4 dan 5,6,7,8. Maka berdasarkan Lema 1 di atas diperoleh matriks berikut M( A, B ) = Perhatikan matriks pada Contoh 16 di atas, terlihat bahwa matriks pemadanan M(A,B) yang terbentuk dari populasi 1,..,8 di mana 8. Matriks pemadanan M(A,B) yang terbentuk tidak berukuran seperti yang didasarkan pada Definisi 8 sehingga dapat disimpulkan matriks pemadanan M(A,B) yang diperoleh tidaklah maksimal. Selanjutnya akan dibahas prosedur untuk mendapatkan matriks pemadanan maksimal

3 yang diinginkan untuk memadankan setiap agen yang ada pada populasi yang terbatas. Teorema 1 Setiap populasi yang terbatas mempunyai matriks pemadanan maksimal. [Aliprantis, et al 2006] Bukti Pembuktian dari teorema ini terdiri atas dua bagian. Pada bagian pertama, akan ditunjukkan eksistensi matriks pemadanan maksimal untuk sebarang populasi ganjil, dan pada bagian kedua akan ditunjukkan eksistensi dari matriks pemadanan maksimal untuk sebarang populasi genap. Sekarang akan dibuktikan untuk bagian yang pertama untuk populasi ganjil. Misalkan diberikan populasi 1,.,, di mana n ganjil. Dengan menggunakan konstruksi bujursangkar latin pada Bab II maka diperoleh bujursangkar latin L, sedemikian sehingga diperoleh matriks berukuran 1 sebagai berikut: 1 2 L n 2 n 1 n n n 1 n 2 L 2 1 n 1 n 2 n L 2 1 n 1... n n = n 2 n n 4 L 1 n n 1 = L M M M O M M M 2 1 n L n n 1 L 4 2 Matriks tersebut merupakan matriks pemadanan maksimal untuk populasi X di mana n ganjil. Pada bagian ke dua untuk populasi genap, andaikan diberikan populasi 1,.,2, dan misalkan banyaknya populasi X adalah 2 2, di mana p dan k adalah bilangan natural dengan p bilangan ganjil. Untuk menyelesaikannya dipandang dalam dua kasus. Pertama jika populasi 2 2 dibagi menjadi dua populasi n yang sama banyak sebut saja menjadi populasi agen A dan agen B maka masing-masing populasi agen pada A dan B memiliki banyak anggota n dengan n genap. Kedua kasus di mana jika 2 2 dibagi menjadi dua populasi n yang sama banyak juga maka masing-masing populasi A dan B memiliki anggota n dengan n ganjil. Sekarang akan dibahas terlebih dahulu untuk kasus yang pertama Kasus 1 : p = 1 Sehingga diperoleh populasi banyaknya X adalah 2 2. Akan dibuktikan adanya matriks pemadanan maksimal dengan menggunakan induksi matematika pada k. Basis induksi: Untuk 1, maka 2 2 sehingga diperoleh matriks = 2 1 maksimal untuk populasi 2 2. Hipotesis Induksi: Anggap benar untuk sehingga 2 2 terdapat matriks pemadanan maksimal. Langkah Induksi Akan dibuktikan benar terdapat matriks pemadanan maksimal untuk 1 sehingga 2 2. Untuk membuktikannya misalkan 1,,2 = AuB di mana 1,,2 dan 2 1,,2. Dari hipotesis induksi diketahui bahwa terdapat matriks pemadanan maksimal berukuran 2 2 untuk 2 2. Sehingga terdapat matriks pemadanan maksimal untuk populasi 1,,2 dan matriks pemadanan maksimal untuk populasi 2 1,,2. Berdasarkan Lema 1 maka diperoleh ( ) ( ) A B + 1 = ( B) ( A) maksimal untuk populasi 1,,2 =

4 Selanjutnya akan dibahas keberadaan matriks pemadanan maksimal untuk kasus yang ke dua. Kasus 2 : 1 Dalam kasus dipilih 2 2, dan untuk membuktikannya masih dapat menggunakan induksi matematika pada k. Basis Induksi Untuk k=1, maka diperoleh 2 2, akibatnya 1,,2. Misalkan X = AuB dengan 1,, dan 1,,2 di mana A dan B masing-masing memiliki p agen. Misalkan dan adalah bujursangkar latin (p-1) x p yang dibentuk dengan menghapus baris pertama dari dan. Selanjutnya perlu diingat bahwa p ganjil. Andaikan dan merupakan matriks pemadanan maksimal 1 untuk A dan B yang dapat dibuat berdasarkan Definisi 8. Perlu diingat juga, pada Definisi 8 diketahui bahwa jika n ganjil maka dalam setiap kolom j agen j muncul paling banyak dua kali. Kemunculan agen j untuk yang ke dua kalinya ini disebut titik tetap di mana pada periode ini agen j dipasangkan dengan dirinya sendiri. Untuk membuat supaya hal ini tidak terjadi maka dapat dilakukan dengan cara menukar titik tetap tersebut dengan titik tetap pada matriks pemadanan lainnya. Untuk lebih jelas titik tetap yang terdapat pada matriks pemadanan maksimal ditukar dengan titik tetap yang ada pada matriks pemadanan maksimal pada. Untuk mengetahui letak titik tetap yang dimaksud, misalkan saja melambangkan yang dibulatkan ke integer yang lebih besar, dan 2 1. Sehingga diperoleh tabel untuk mencari titik tetap untuk setiap baris j dari dan berikut. Tabel 2 Titik tetap. Baris k j = 2k 1,., j = 2k + 1 1,.., 1 p (k 1) 2p - (k - 1) Lalu misalkan dan adalah matrik pemadanan maksimal yang diperoleh dengan menukar titik-titik tetap dari dan dalam setiap periode (baris). Sebagai contoh misalkan agent 1 yang muncul pada entri (p+1,1) dari yang dipasangkan dengan dirinya sendiri dengan kata lain tidak memiliki pasangan pada baris tersebut sementara itu agen 1 yang juga muncul pada entri 1,1 dari juga tidak memiliki pasangan pada baris tersebut, maka dengan menukar agen 1 pada baris tersebut dari dengan agen p+1 pada baris yang sama dari. Dengan prosedur yang serupa untuk agen-agen lainnya sehingga diperoleh matriks pemadanan maksimal dan. Lalu berdasarkan Lema 1, maka diperoleh matriks 2p x 2p sebagai berikut maksimal dari populasi 1,.,2. Hipotesisi Induksi Misalkan terdapat matriks pemadanan maksimal untuk populasi 2n = 2 h p, di mana. Langkah Induksi Sekarang akan diperlihatkan bahwa terdapat matriks pemadanan maksimal untuk populasi X pada saat 1 sehingga populasi 2n = 2 h+1 p. Untuk membuktikannya misalkan 1,,2 = AuB di mana 1,,2 dan 2 1,,2. Dari hipotesis induksi diketahui bahwa terdapat matriks pemadanan maksimal berukuran 2 2 untuk 2 2. Sehingga terdapat matriks pemadanan maksimal untuk populasi 1,,2 dan matriks pemadanan maksimal untuk populasi 2 1,,2. Berdasarkan Lema 1 maka diperoleh ( ) ( ) A B + 1 = ( B) ( A)

5 maksimal untuk populasi 1,,2 = Teorema 1 menunjukkan eksistensi dari matriks pemadanan maksimal untuk sembarang populasi terbatas dan pada beberapa kasus menyediakan algoritma untuk membangun matriks pemadanan maksimal pada populasi yang terbatas. Untuk lebih jelas perhatikan contoh-contoh berikut. Contoh 17 Misal populasi yang ganjil dengan. Maka matriks pemadanan maksimal yang diperoleh adalah = Perhatikan matriks pada Contoh 17 di atas agen 1 muncul dua kali pada kolom pertama, kemunculan agen 1 pada baris selain baris pertama dalam Contoh 17 pada baris terakhir (ke empat) ini yang disebut sebagai titik tetap pada matriks pemadanan maksimal. Contoh 18 Misalkan diberikan populasi genap 1,2,,4,5,6, di mana k=1 dan p=. Misalkan 1,2, dan 4,5,6. Sehingga diperoleh matriks pemadanan maksimal untuk A dan B sebagai berikut ( A) =, ( B) = Selanjutnya dengan menukar titik-titik tetap pada dan akan diperoleh matriks pemadanan maksimal untuk A dan B berikut ' ( A) =, ' ( ) B = Kemudian ingat kembali, berdasarkan defnisi dari dan, maka diperoleh matriks L ( A) 1 = 2 1 dan L ( B) 1 = Dengan demikian matriks 6 6 ' ' ( A) ( B) 6 = + L ( B) 1 L ( A) = adalah matriks pemadanan maksimal dari populasi X. V. PENERAPAN DALAM BIDANG EKONOMI Dalam percobaan ekonomi matriks pemadanan ini dapat dikaitkan untuk mencari pemadanan di antara pelaku ekonomi. Misalkan saja penjual dan pembeli. Andaikan akan dijalankan percobaan untuk memasangkan penjual dan pembeli. Andaikan juga hanya terdapat delapan subyek yang terkumpul yang terdiri dari empat penjual dan empat pembeli. Selanjutnya akan dipasangkan masing-masing subyek sedemikian rupa sehingga setiap pembeli dapat bertemu setiap penjual tepat satu kali untuk paling banyak dalam empat periode. Yang perlu diingat pemadanan yang dilakukan harus dalam keadaan mutlak saling asing, di mana setiap penjual dipadankan dengan pembeli tepat satu kali, dan dalam setiap periode pemadanan antara penjual dan pembeli yang diperoleh maksimal artinya semua penjual dan pembeli memperoleh pasangan. Dengan demikian tujuannya adalah meminimalkan interaksi berulang. Pemilihan secara acak dari semua kemungkinan pasangan yang muncul akan mengakibatkan tidak diperolehnya tujuan tersebut, dan peluang bahwa pemadanan yang dilakukan dalam keadaan mutlak saling asing