Sistem Bilangan Real
|
|
|
- Yuliani Chandra
- 7 tahun lalu
- Tontonan:
Transkripsi
1 TUGAS I ANALISIS REAL I Sistem Bilangan Real Tugas 1 Analisis Real I Disusun oleh : Nariswari Setya D. Kartini Marvina Puspito M M M JURUSAN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SEBELAS MARET SURAKARTA
2 LATIHAN BAGIAN Buktikan bahwa jika, maka (a) += + (b) = (a) Diketahui += + Berdasarkan Teorema (b) diperoleh bahwa += 1+ maka dapat dibuktikan bahwa 1+= 1+ 1 = + Jadi, terbukti += + (b) Diketahui = Berdasarkan Teorema (b) dan (d) maka dapat dibuktikan bahwa, = 1 1 Jadi, terbukti = = 1 1 = 1 1 = 1 1 =1 = 7. Jika, sehingga =, buktikan bahwa = atau = Diketahui: aa =bb Maka = =0 +=0 +=0 ++ =0+ ++ =0+ +0=0+ = Jadi, terbukti = atau = 8. Gunakan argument seperti Teorema untuk menunjukkan bahwa tidak ada bilangan rasional sehingga =8. Andaikan terdapat bilangan rasional sehingga =8. 2 =0 + +=0+ + +=0+ +0=0+ =
3 Oleh karena itu terdapat bilangan bulat dan dengan 0 sehingga =8. Tanpa mengurangi keumuman dapat diasumsikan bahwa dan bilangan positif dengan faktor persekutuan terbesar adalah 1. Karena =2, maka bilangan bulat genap. Akibatnya juga bilangan bulat genap. Karena jika bilangan bulat ganjil, maka juga bilangan bulat ganjil. Karena 8 bukan faktor persekutuan dari dan, maka bilangan bilangan bulat ganjil. Selanjutnya, karena bilangan bulat genap, maka =8 untuk suatu N. Akibatnya 8 =. Jadi, bilangan bulat genap, sehingga juga bilangan bulat genap. Terdapat kontradiksi bahwa adalah bilangan asli yang genap sekaligus ganjil. Jadi pengandaian salah. Terbukti bahwa tidak ada bilangan rasional sehingga = Jika bilangan prima, buktikan bahwa bilangan irrassional. Andaikan bilangan rasional, maka bisa dibentuk dimana a,b N, 2 = = =..(1) 2 merupakan kelipatan p, maka a kelipatan p. =, N maka 2 = p 2 x 2..(2) Dari persamaan (1) dan (2) maka diperoleh p b 2 = p 2 x 2 2 = b 2 b 2 merupakan kelipatan p, maka b kelipatan p. b = p y, y Z maka berlaku = = merupakan faktor persekutuan. Kontradiksi dengan pengandaian. Jadi, terbukti bahwa bilangan irrasional. 15. Misalkan A dan B himpunan bagian dari R dan didefinisikan operasi operasi (+) dan (.) dengan +=+ dan.= dan Untuk sembarang A,B dan C himpunan bagian dari R, buktikan bahwa : (a) R+R=R R=R (b) Jika A, maka A A = (c) A. = (d) Jika A B, maka A + C + (e) A.(B + C). B + A. C. Berikan contoh untuk menunjukkan bahwa kesamaan tidak harus terjadi. 3
4 (f) Jika A. C = B. C apakah A = B? (a) Diketahui R+R=R R=R Dimana A, B dan C R R+R=R R, R maka + R R R=R R, R maka R Jadi,terbukti R+R=R R=R (b) Diketahui jika A, maka A A = Dengan menggunakan Aksioma (A4), untuk setiap A R, terdapat A R sehingga A + (- A) = 0 A A = 0 Jadi, Jika A, maka A A =. (c) Diketahui A. =. = dan b }, Karena merupakan suatu himpunan yang tidak memiliki anggota, maka tidak dapat ditemukan sehingga. Jadi,terbukti. =. (d) Diketahui jika A B maka A + C B + C. A + C B + C A + C C B + C C A + (C C) B +( C C) (assosiatif) A + 0 B + 0 (aksioma (A4)) A B (Aksioma (A3)) Jadi,terbukti jika A B maka A + C B + C (e) Diketahui A. (B + C) A. B + A. C Dengan Aksioma 1.1.1(D) yaitu sifat distribusi perkalian terhadap penjumlahan maka A. B + A. C A. B + A. C Jadi, terbukti untuk A. (B + C) A. B + A. C (f) Diketahui jika A. C = B. C Dengan teorema 1.1.3(b) maka.c.a=.c.b 1.=1. = Contoh : misal A = 1, B = 2 4
5 A. C = B. C 1. 0 = = 0 Jadi, kesamaan tersebut tidak harus terjadi ketika C = 0. LATIHAN BAGIAN Jika < dan c < d, buktikan bahwa ad + bc < ac + bd Akan dibuktikan bahwa ad + bc < ac + bd Jika < dan c < d maka dan, sehingga dengan aksioma (b) maka diperoleh >0 +>+ +<+ Jadi, terbukti ad + bc < ac + bd 6. Jika,, buktikan bahwa + =0 jika dan hanya jika ==0 + =0 Andaikan 0, maka >0 atau <0 0, maka >0 atau <0 Menurut Teorema 1.2.5(a), maka >0, >0 Sehingga + >0, berarti pengandaian salah. Jadi, =0 dan =0 =0 dan =0 + =0 Jadi, terbukti bahwa + =0 jika dan hanya jika ==0 9. Tunjukkan bahwa jika <0 dan <0, maka < Diambil sembarang, Dengan menggunakan Teorema 1.2.6(a), jika < maka +<+ untuk,, R. Dari yang diketahui <0 yang berarti dan jika = maka Sehingga + (1) +<+ +<+0 +< 5
6 Dan dengan menggunakan Teorema (d) jika b <0, maka <0. Akibatnya (2) Dari akibat (1) dan (2), dengan menggunakan sifat urutan diperoleh Yang berarti <. Jadi,terbukti jika <0 dan <0, maka < 13. Misalkan, R dan berlaku + untuk setiap >0. (a) Tunjukkan bahwa. (b) Tunjukkan bahwa dalam kasus ini tidak mungkin <. (a) Akan dibuktikan jika, R berlaku + untuk setiap >0 Andaikan > Misalkan = maka >0. Sehingga diperoleh < Hal ini kontradiksi dengan yang diketahui, jadi seharusnya Jadi, terbukti bahwa (b) Akan dibuktikan bahwa dalam kasus ini tidak mungkin <. Andaikan dalam kasus ini mungkin <. Misalkan = maka >0. Sehingga diperoleh < Hal ini kontradiksi dengan yang diketahui, jadi dalam kasus ini tidak mungkin < 15. (a) Jika 0<<1, tunjukkan bahwa 0< <<1 (b) Jika <1, tunjukkan bahwa 1<< (a) Diketahui 0<<1, akan dibuktikan 0< <<1 Misal = dengan > = = >0 Karena >, akibatnya > Dapat ditulis > sehingga terbukti bahwa 0< <<1 6
7 (b) Akan dibuktikan jika <1 maka 1<< Misal =,> = = >0. Karena > dan > maka >. Dengan kata lain <. Sehingga terbukti bahwa jika >1 maka 1<< 22. Misalkan >0 untuk =1,2,,. Buktikan bahwa Perhatikan ketaksamaan Cauchy Dengan menggunakan ketaksamaan Cauchy dimana >0 dan >0, maka Dengan mengambil = dan = Terbukti Jadi, dengan induksi terbukti >0, k = 1,,n maka LATIHAN BAGIAN Jika, R, tunjukkan bahwa + = + jika dan hanya jika 0 Bukti : Akan ditunjukkan a + b < a + b dan a + b < a + b. Menurut teorema untuk sembarang bilangan real a, b berlaku a + b < a + b. Menurut teorema jika ab > 0 maka berlaku a > 0 dan b > 0 atau a < 0 dan b< 0. Untuk a > 0 dan b > 0, maka a + b = a+b dan a + b = a+b (1) Untuk a< 0 dan b< 0, maka a + b = ( a + b) = a+b dan a + b = -(a) +(-b)= - (a+b).(2) Dari persamaan (1) dan (2) diperoleh kesimpulan 7
8 a + b < a + b karena a + b < a + b dan a + b < a + b Jadi, terbukti bahwa a + b = a + b jika dan hanya jika ab > 0 7. Jika <1, tunjukkan bahwa < +1 Diketahui <1 maka diperoleh <1 dan <1 > 1 Sehingga, 1< <1 1+<<1+ 1+ <<1+ Menurut teorema (b) maka diperoleh 1+ <<1+ 1+ <<1+ Dengan teorema (d) diperoleh <1+ Jadi,terbukti < Jika >0 dan 3 <6+, buktikan bahwa 9 <6+. Diketahui >0 dan 3 <6+ Maka 3 < berarti < 3< < 3< 3 <<3+ 3 < <3+ =9 6+ < <9+6+ = <9+6+ karena >0 9<6+ 9 <6+ Jadi, terbukti jika >0 dan 3 < maka 9 <6+. 8
9 LATIHAN BAGIAN Misalkan = dan =1 (a) Jika = [ 1,1], tentukan sup A. (b) Jika = [ 1,1], tentukan sup B. (c) Jika =+ [ 1,1], tentukan sup C. (d) Apakah sup A + sup B = sup C? Mengapa? (a) = maka supremum dari = [ 1,1] adalah pada x = 1 sehingga 1=1 (b) =1 maka supremum dari = [ 1,1] adalah pada x = 0 sehingga 0=1 0 =1 (c) =, =1 Misal +=h=+1 maka supremum dari C adalah pada x = sehingga h = +1 = (d) sup A + sup B = 1+1 = 2 sup C = karena 2, maka sup A + sup B sup C Karena fungsi C merupakan sebuah fungsi yang terbentuk dari penggabungan fungsi A dan B maka fungsi C menghasilkan nilai supremum yang berbeda dari penjumlahan supremum A dan B. 9. Misalkan himpunan tak kosong dan terbatas di atas. Buktikan bahwa memuat anggota terbesarnya jika dan hanya jika memuat supremumnya. Akan dibuktikan S memuat anggota terbesarnya jika dan hanya jika S memuat supremumnya. 1) Akan dibuktikan jika S memuat anggota terbesar maka S memuat supremumnya. Misal merupakan anggota terbesar, artinya, maka merupakan batas atas. Menurut theorema (Setiap himpunan tak kosong didalam R yang mempunyai batas atas selalu mempunyai supremum di dalam R) karena S memuat batas atas maka S mempunyai supremum. Jadi, terbukti. 2) Akan dibuktikan jika S memuat supremum maka S memuat anggota terbesar. Misal = sup S artinya, dan jika <, < Ambil >0 maka terdapat sehingga <. Dapat disimpulkan bahwa merupakan batas atas. Sehingga terbukti S memuat anggota terbesar. 9
10 Jadi, dari pembukti 1) dan 2) terbukti bahwa S memuat anggota terbesarnya jika dan hanya jika S memuat supremumnya. 11. Misalkan S himpunan tak kosong dan terbatas. Jika > 0 dan >,,,. Buktikan bahwa S memuat anggota terbesar. (Petunjuk: gunakan latihan 9 dan 10) Diketahui > 0 dan >,,, Akan dibuktikan S memuat anggota terbesar LATIHAN BAGIAN Tunjukkan bahwa sup N}= 3 4. Akan ditunjukkan bahwa sup 3 1/4 N}=3/4., N <, N sehingga (dengan sifat Archimedes) 10
11 < < =, 3 1/4 N} Dengan demikian terbukti bahwa sup 3 1/4 N}=3/4. 6. Misalkan himpunan tak kosong terbatas di dalam, untuk didefinisikan = }. (b) Jika <0 buktikan bahwa: inf=asup dan sup=ainf Akan dibuktikan jika <0 maka inf= sup dan sup= inf Misal : = sup. Artinya : 1),. Karena <0 maka diperoleh, jadi merupakan batas bawah untuk. Dengan demikian sup. 2) Untuk sebarang batas atas. Karena <0 maka,. Akibatnya,. Sehingga dapat diambil kesimpulan merupakan batas bawah dari himpunan Jadi = sup atau. Dengan demikian sup Disimpulkan bahwa inf= atau bisa ditulis inf= sup Misal : = inf. Artinya : 1),. Karena <0 maka diperoleh, jadi merupakan batas atas untuk. Dengan demikian inf 2) Untuk sebarang batas bawah. Karena <0 maka,. Akibatnya,. Sehingga dapat diambil kesimpulan merupakan batas atas dari himpunan Jadi = inf atau. Dengan demikian inf. Disimpulkan bahwa sup= atau bisa ditulis sup = inf 7. Misalkan, R adalah dua himpunan terbatas dalam R. Didefinisikan =, } Buktikan bahwa C terbatas dalam R, dan nyatakan sub C dalam batas dari A dan B. Akan dibuktikan terbatas dalam R 11
12 i). Misal merupakan batas atas dari, artinya, dan misalkan merupakan batas atas dari, artinya,. Sehingga artinya merupakan batas atas C,Karena,. Jadi, terbatas atas dalam R. ii). Misal merupakan batas bawah artinya, dan misalkan merupakan batas bawah dari, artinya,. Sehingga artinya merupakan batas bawah C, Karena,. Jadi, terbatas bawah dalam R Dari i) dan ii) terbukti bahwa terbatas dalam R sup C dalam batas dari A dan B : Misal : = sup i)., ii). <, sehingga < Maka sup C =, <, sehingga < 8. Misalkan, R dua himpunan tak kosong yang terbatas di atas dalam R. Tunjukkan bahwa terbatas atas dan sup =sup,sup} Akan ditunjukkan terbatas diatas. i). Dari yang diketahui A terbatas atas dalam R, misalkan R. merupakan batas atas dari A jika,. ii). Dari yang diketahui B terbatas atas dalam R, misalkan R. merupakan batas atas dari B jika,. Dari i) dan ii) dapat disimpulan R atau R merupakan batas atas dari karena berlaku atau. Sehingga terbukti bahwa terbatas diatas. Akan ditunjukkan sup = maks {sup A,sup B}. Andaikan sup = min {sup A,sup B} Misalkan: sup A =, sup B = dan < = sup B i)., ii). <, sehingga < sup = min {sup A,sup B} =, maka = sehingga. 12
13 Hal ini kontradiksi dengan konsep supremum dimana,. Oleh karena itu pengandaian harus dibalik. Jadi, terbukti bahwa sup = maks{sup A,sup B}. 9. Buktikan bahwa untuk sembarang dua bilangan real <, terdapat bilangan irrasional berbentuk + 3 yang terletak diantar dan, dengan bilangan rasional. Akan dibuktikan bahwa untuk sembarang dua bilangan real <, terdapat + 3 dengan bilangan rasional sehingga <+ 3<. Karena < maka jelas bahwa 2 6< 2 6. Berdasarkan theorema (Kerapatan bilangan irrasional) pada bilangan real 2 6 dan 2 6., diperoleh bilangan irrasional 2 sehingga, 2 6< 2< << << 3 <+ 3< Dengan demikian terbukti bahwa untuk sembarang dua bilangan real <, terdapat + 3 dengan bilangan rasional sehingga <+ 3<. 10. Misalkan rapat dalam R dan, tunjukkan bahwa <= rapat dalam berarti, dengan < terdapat sehingga << Akan dibuktikan sup <= i)., untuk setiap ii). <, < Karena dari sifat kerapatan terdapat sehingga << maka benar bahwa sehingga < jadi <= 13
ANALISIS REAL. (Semester I Tahun ) Hendra Gunawan. August 18, Dosen FMIPA - ITB
 (Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. August 18, 2011 Kita telah mencatat sebelumnya bahwa supremum dan infimum suatu himpunan tidak harus merupakan anggota himpunan
(Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. August 18, 2011 Kita telah mencatat sebelumnya bahwa supremum dan infimum suatu himpunan tidak harus merupakan anggota himpunan
II. SISTEM BILANGAN RIIL. Handout Analisis Riil I (PAM 351)
 II. SISTEM BILANGAN RIIL Handout Analisis Riil I (PAM 351) Sifat Aljabar (Aksioma Lapangan) dari Bilangan Riil Bagian ini akan membicarakan struktur aljabar bilangan riil dengan terlebih dahulu memberikan
II. SISTEM BILANGAN RIIL Handout Analisis Riil I (PAM 351) Sifat Aljabar (Aksioma Lapangan) dari Bilangan Riil Bagian ini akan membicarakan struktur aljabar bilangan riil dengan terlebih dahulu memberikan
SISTEM BILANGAN REAL
 DAFTAR ISI 1 SISTEM BILANGAN REAL 1 1.1 Sifat Aljabar Bilangan Real..................... 1 1.2 Sifat Urutan Bilangan Real..................... 6 1.3 Nilai Mutlak dan Jarak Pada Bilangan Real............
DAFTAR ISI 1 SISTEM BILANGAN REAL 1 1.1 Sifat Aljabar Bilangan Real..................... 1 1.2 Sifat Urutan Bilangan Real..................... 6 1.3 Nilai Mutlak dan Jarak Pada Bilangan Real............
BAHAN AJAR ANALISIS REAL 1. DOSEN PENGAMPU RINA AGUSTINA, S. Pd., M. Pd. NIDN
 BAHAN AJAR ANALISIS REAL 1 DOSEN PENGAMPU RINA AGUSTINA, S. Pd., M. Pd. NIDN. 0212088701 PENDIDIKAN MATEMATIKA FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN UNIVERSITAS MUHAMMADIYAH METRO 2015 1 KATA PENGANTAR
BAHAN AJAR ANALISIS REAL 1 DOSEN PENGAMPU RINA AGUSTINA, S. Pd., M. Pd. NIDN. 0212088701 PENDIDIKAN MATEMATIKA FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN UNIVERSITAS MUHAMMADIYAH METRO 2015 1 KATA PENGANTAR
1 SISTEM BILANGAN REAL
 1 SISTEM BILANGAN REAL Bilangan real sudah dikenal dengan baik sejak masih di sekolah menengah, bahkan sejak dari sekolah dasar. Namun untuk memulai mempelajari materi pada BAB ini anggaplah diri kita
1 SISTEM BILANGAN REAL Bilangan real sudah dikenal dengan baik sejak masih di sekolah menengah, bahkan sejak dari sekolah dasar. Namun untuk memulai mempelajari materi pada BAB ini anggaplah diri kita
KONSTRUKSI SISTEM BILANGAN
 KONSTRUKSI SISTEM BILANGAN KEVIN MANDIRA LIMANTA 1. Konstruksi Aljabar 1.1. Bilangan Natural. Himpunan bilangan paling primitif adalah bilangan natural N, yang dicacah dengan aturan sebagai berikut: (1)
KONSTRUKSI SISTEM BILANGAN KEVIN MANDIRA LIMANTA 1. Konstruksi Aljabar 1.1. Bilangan Natural. Himpunan bilangan paling primitif adalah bilangan natural N, yang dicacah dengan aturan sebagai berikut: (1)
Keterbagian Pada Bilangan Bulat
 Latest Update: March 8, 2017 Pengantar Teori Bilangan (Bagian 1): Keterbagian Pada Bilangan Bulat Muhamad Zaki Riyanto Program Studi Matematika Fakultas Sains dan Teknologi UIN Sunan Kalijaga Yogyakarta
Latest Update: March 8, 2017 Pengantar Teori Bilangan (Bagian 1): Keterbagian Pada Bilangan Bulat Muhamad Zaki Riyanto Program Studi Matematika Fakultas Sains dan Teknologi UIN Sunan Kalijaga Yogyakarta
1 SISTEM BILANGAN REAL
 Bilangan real sudah dikenal dengan baik sejak masih di sekolah menengah, bahkan sejak dari sekolah dasar. Namun untuk memulai mempelajari materi pada BAB ini anggaplah diri kita belum tahu apa-apa tentang
Bilangan real sudah dikenal dengan baik sejak masih di sekolah menengah, bahkan sejak dari sekolah dasar. Namun untuk memulai mempelajari materi pada BAB ini anggaplah diri kita belum tahu apa-apa tentang
5. Sifat Kelengkapan Bilangan Real
 5. Sifat Kelengkapan Bilangan Real Sifat aljabar dan sifat urutan bilangan real telah dibahas sebelumnya. Selanjutnya, akan dijelaskan sifat kelengkapan bilangan real. Bilangan rasional ℚ juga memenuhi
5. Sifat Kelengkapan Bilangan Real Sifat aljabar dan sifat urutan bilangan real telah dibahas sebelumnya. Selanjutnya, akan dijelaskan sifat kelengkapan bilangan real. Bilangan rasional ℚ juga memenuhi
Contoh-contoh soal induksi matematika
 Contoh-contoh soal induksi matematika Buktikan bahwa 2 n > n + 20 untuk setiap bilangan bulat n 5. (i) Basis induksi : Untuk n = 5, kita peroleh 2 5 > 5 + 20 adalah suatu pernyataan yang benar. (ii) Langkah
Contoh-contoh soal induksi matematika Buktikan bahwa 2 n > n + 20 untuk setiap bilangan bulat n 5. (i) Basis induksi : Untuk n = 5, kita peroleh 2 5 > 5 + 20 adalah suatu pernyataan yang benar. (ii) Langkah
SISTEM BILANGAN REAL
 DAFTAR ISI SISTEM BILANGAN REAL. Sifat Aljabar Bilangan Real......................2 Sifat Urutan Bilangan Real..................... 6.3 Nilai Mutlak dan Jarak Pada Bilangan Real.............4 Supremum
DAFTAR ISI SISTEM BILANGAN REAL. Sifat Aljabar Bilangan Real......................2 Sifat Urutan Bilangan Real..................... 6.3 Nilai Mutlak dan Jarak Pada Bilangan Real.............4 Supremum
KALKULUS 1 UNTUK MAHASISWA CALON GURU MATEMATIKA OLEH: DADANG JUANDI, DKK PROGRAM STUDI PENDIDIKAN MATEMATIKA FPMIPA UNIVERSITAS PENDIDIKAN INDONESIA
 KALKULUS UNTUK MAHASISWA 9 CALON GURU MATEMATIKA OLEH: DADANG JUANDI, DKK PROGRAM STUDI PENDIDIKAN MATEMATIKA FPMIPA UNIVERSITAS PENDIDIKAN INDONESIA BAB I PENDAHULUAN. Sistem Bilangan Real Dalam Uraian
KALKULUS UNTUK MAHASISWA 9 CALON GURU MATEMATIKA OLEH: DADANG JUANDI, DKK PROGRAM STUDI PENDIDIKAN MATEMATIKA FPMIPA UNIVERSITAS PENDIDIKAN INDONESIA BAB I PENDAHULUAN. Sistem Bilangan Real Dalam Uraian
B I L A N G A N 1.1 SKEMA DARI HIMPUNAN BILANGAN. Bilangan Kompleks. Bilangan Nyata (Riil) Bilangan Khayal (Imajiner)
 1 B I L A N G A N 1.1 SKEMA DARI HIMPUNAN BILANGAN Bilangan Kompleks Bilangan Nyata (Riil) Bilangan Khayal (Imajiner) Bilangan Rasional Bilangan Irrasional Bilangan Pecahan Bilangan Bulat Bilangan Bulat
1 B I L A N G A N 1.1 SKEMA DARI HIMPUNAN BILANGAN Bilangan Kompleks Bilangan Nyata (Riil) Bilangan Khayal (Imajiner) Bilangan Rasional Bilangan Irrasional Bilangan Pecahan Bilangan Bulat Bilangan Bulat
Pengantar : Induksi Matematika
 Pengantar : Induksi Matematika Analisis Real /2 SKS/ Ega Gradini, M.Sc Induksi Matematika adalah cara standar dalam membuktikan bahwa sebuah pernyataan tertentu berlaku untuk setiap bilangan asli. Pembuktian
Pengantar : Induksi Matematika Analisis Real /2 SKS/ Ega Gradini, M.Sc Induksi Matematika adalah cara standar dalam membuktikan bahwa sebuah pernyataan tertentu berlaku untuk setiap bilangan asli. Pembuktian
Pembahasan Soal-Soal Latihan 1.1
 Pembahasan Soal-Soal Latihan. Oleh : Fendi Alfi Fauzi Anda pasti masih ingat bagaimana memanipulasi bilangan, tetapi tidak ada salahnya untuk mengulang kembali sejenak. Dalam Soal-soal 0, sederhanakanlah
Pembahasan Soal-Soal Latihan. Oleh : Fendi Alfi Fauzi Anda pasti masih ingat bagaimana memanipulasi bilangan, tetapi tidak ada salahnya untuk mengulang kembali sejenak. Dalam Soal-soal 0, sederhanakanlah
Metode pembuktian untuk proposisi yang berkaitan dengan bilangan bulat adalah induksi matematik.
 Induksi Matematika Metode pembuktian untuk proposisi yang berkaitan dengan bilangan bulat adalah induksi matematik. Contoh: 1. Buktikan bahwa jumlah n bilangan bilangan bulat positif pertama adalah n(n
Induksi Matematika Metode pembuktian untuk proposisi yang berkaitan dengan bilangan bulat adalah induksi matematik. Contoh: 1. Buktikan bahwa jumlah n bilangan bilangan bulat positif pertama adalah n(n
1 SISTEM BILANGAN REAL
 Bilangan real sudah dikenal dengan baik sejak masih di sekolah menengah, bahkan sejak dari sekolah dasar. Namun untuk memulai mempelajari materi pada BAB ini anggaplah diri kita belum tahu apa-apa tentang
Bilangan real sudah dikenal dengan baik sejak masih di sekolah menengah, bahkan sejak dari sekolah dasar. Namun untuk memulai mempelajari materi pada BAB ini anggaplah diri kita belum tahu apa-apa tentang
Prestasi itu diraih bukan didapat!!! SOLUSI SOAL
 SELEKSI OLIMPIADE TINGKAT PROVINSI 009 TIM OLIMPIADE MATEMATIKA INDONESIA 00 Prestasi itu diraih bukan didapat!!! SOLUSI SOAL BAGIAN PERTAMA Disusun oleh : Solusi Olimpiade Matematika Tk Provinsi 009 Bagian
SELEKSI OLIMPIADE TINGKAT PROVINSI 009 TIM OLIMPIADE MATEMATIKA INDONESIA 00 Prestasi itu diraih bukan didapat!!! SOLUSI SOAL BAGIAN PERTAMA Disusun oleh : Solusi Olimpiade Matematika Tk Provinsi 009 Bagian
BAGIAN PERTAMA. Bilangan Real, Barisan, Deret
 BAGIAN PERTAMA Bilangan Real, Barisan, Deret 2 Hendra Gunawan Pengantar Analisis Real 3 0. BILANGAN REAL 0. Bilangan Real sebagai Bentuk Desimal Dalam buku ini pembaca diasumsikan telah mengenal dengan
BAGIAN PERTAMA Bilangan Real, Barisan, Deret 2 Hendra Gunawan Pengantar Analisis Real 3 0. BILANGAN REAL 0. Bilangan Real sebagai Bentuk Desimal Dalam buku ini pembaca diasumsikan telah mengenal dengan
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016. Hendra Gunawan
 MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 3. Topologi Garis Bilangan Real 3.1 Teori Limit Limit, supremum, dan infimum Titik limit 3.2 Himpunan Buka dan Himpunan Tutup 3.3
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 3. Topologi Garis Bilangan Real 3.1 Teori Limit Limit, supremum, dan infimum Titik limit 3.2 Himpunan Buka dan Himpunan Tutup 3.3
PEMBAHASAN. Teorema 1. Tidak ada bilangan asli N yang lebih besar dari semua bilangan bulat lainnya.
 PEMAHAAN 1. Pengertian Kontradiksi Kontradiksi adalah dua pernyataan yang bernilai salah untuk setiap nilai kebenaran dari setiap komponen-komponennya. 2. Pembuktian dengan Kontradiksi Kontradiksi merupakan
PEMAHAAN 1. Pengertian Kontradiksi Kontradiksi adalah dua pernyataan yang bernilai salah untuk setiap nilai kebenaran dari setiap komponen-komponennya. 2. Pembuktian dengan Kontradiksi Kontradiksi merupakan
Oleh: Naning Sutriningsih
 Oleh: Naning Sutriningsih SEKOLAH TINGGI KEGURUAN DAN ILMU PENDIDIKAN (STKIP) MUHAMMADIYAH PRINGSEWU LAMPUNG 0 KATA PENGANTAR Syukur Alhamdulillah penulis panjatkan ke-hadirat Allah Rabbul Alamin, atas
Oleh: Naning Sutriningsih SEKOLAH TINGGI KEGURUAN DAN ILMU PENDIDIKAN (STKIP) MUHAMMADIYAH PRINGSEWU LAMPUNG 0 KATA PENGANTAR Syukur Alhamdulillah penulis panjatkan ke-hadirat Allah Rabbul Alamin, atas
Coba amati apakah sifat ini mempunyai signifikansi dalam sistem bilangan real.
 TUGAS ANREAL BAB Dosen: Julan HERNADI SELESAIKAN SOAL-SOAL BERIKUT SEKUAT KEMAMPUAN YANG ANDA MI- LIKI. WALAUPUN DALAM KETERBATASAN INTELIGENSI, COBALAH BERUSAHA LEBIH KERAS DALAM BELAJAR.. Jelaskan peran
TUGAS ANREAL BAB Dosen: Julan HERNADI SELESAIKAN SOAL-SOAL BERIKUT SEKUAT KEMAMPUAN YANG ANDA MI- LIKI. WALAUPUN DALAM KETERBATASAN INTELIGENSI, COBALAH BERUSAHA LEBIH KERAS DALAM BELAJAR.. Jelaskan peran
1 Preliminaries The Algebra of Sets... 3
 Contents 1 Preliminaries 3 1.1 The Algebra of Sets............................ 3 2 Bilangan Riil 5 2.1 Sifat-sifat Aljabar dari R......................... 5 2.1.1 Sifat Aljabar dari R........................
Contents 1 Preliminaries 3 1.1 The Algebra of Sets............................ 3 2 Bilangan Riil 5 2.1 Sifat-sifat Aljabar dari R......................... 5 2.1.1 Sifat Aljabar dari R........................
BAB III KEKONVERGENAN LEMAH
 BAB III KEKONVERGENAN LEMAH Bab ini membahas inti kajian tugas akhir. Di dalamnya akan dibahas mengenai kekonvergenan lemah beserta sifat-sifat yang terkait dengannya. Sifatsifat yang dikaji pada bab ini
BAB III KEKONVERGENAN LEMAH Bab ini membahas inti kajian tugas akhir. Di dalamnya akan dibahas mengenai kekonvergenan lemah beserta sifat-sifat yang terkait dengannya. Sifatsifat yang dikaji pada bab ini
BAHAN AJAR TEORI BILANGAN. DOSEN PENGAMPU RINA AGUSTINA, S. Pd., M. Pd. NIDN
 BAHAN AJAR TEORI BILANGAN DOSEN PENGAMPU RINA AGUSTINA, S. Pd., M. Pd. NIDN. 0212088701 PENDIDIKAN MATEMATIKA FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN UNIVERSITAS MUHAMMADIYAH METRO 2015 KATA PENGANTAR ب
BAHAN AJAR TEORI BILANGAN DOSEN PENGAMPU RINA AGUSTINA, S. Pd., M. Pd. NIDN. 0212088701 PENDIDIKAN MATEMATIKA FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN UNIVERSITAS MUHAMMADIYAH METRO 2015 KATA PENGANTAR ب
F. RANCANGAN KEGIATAN BELAJAR MENGAJAR
 F. RANCANGAN KEGIATAN BELAJAR MENGAJAR No. (TIU) : 1. Pendahuluan Mahasiswa dapat memahami pengertian dan konsep himpunan, fungsi dan induksi matematik, mampu menerapkannya dalam penyelesaian soal dan
F. RANCANGAN KEGIATAN BELAJAR MENGAJAR No. (TIU) : 1. Pendahuluan Mahasiswa dapat memahami pengertian dan konsep himpunan, fungsi dan induksi matematik, mampu menerapkannya dalam penyelesaian soal dan
BAB II DASAR TEORI. Di dalam BAB II ini akan dibahas materi yang menjadi dasar teori pada
 BAB II DASAR TEORI Di dalam BAB II ini akan dibahas materi yang menjadi dasar teori pada pembahasan BAB III, mulai dari definisi sampai sifat-sifat yang merupakan konsep dasar untuk mempelajari Fungsi
BAB II DASAR TEORI Di dalam BAB II ini akan dibahas materi yang menjadi dasar teori pada pembahasan BAB III, mulai dari definisi sampai sifat-sifat yang merupakan konsep dasar untuk mempelajari Fungsi
BAHAN AJAR ANALISIS REAL 1 Matematika STKIP Tuanku Tambusai Bangkinang
 Pertemuan 2. BAHAN AJAR ANALISIS REAL Matematika STKIP Tuanku Tambusai Bangkinang 0. Bilangan Real 0. Bilangan Real sebagai bentuk desimal Pada pembahasan berikutnya kita diasumsikan telah mengetahui dengan
Pertemuan 2. BAHAN AJAR ANALISIS REAL Matematika STKIP Tuanku Tambusai Bangkinang 0. Bilangan Real 0. Bilangan Real sebagai bentuk desimal Pada pembahasan berikutnya kita diasumsikan telah mengetahui dengan
MA5032 ANALISIS REAL
 (Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. August 16, 2011 Pada bab ini anda diasumsikan telah mengenal dengan cukup baik bilangan asli, bilangan bulat, dan bilangan
(Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. August 16, 2011 Pada bab ini anda diasumsikan telah mengenal dengan cukup baik bilangan asli, bilangan bulat, dan bilangan
Prestasi itu diraih bukan didapat!!! SOLUSI SOAL
 "We are the first of the fastest online solution of mathematics" 009 SELEKSI OLIMPIADE TINGKAT PROVINSI 008 TIM OLIMPIADE MATEMATIKA INDONESIA 009 Prestasi itu diraih bukan didapat!!! SOLUSI SOAL Bidang
"We are the first of the fastest online solution of mathematics" 009 SELEKSI OLIMPIADE TINGKAT PROVINSI 008 TIM OLIMPIADE MATEMATIKA INDONESIA 009 Prestasi itu diraih bukan didapat!!! SOLUSI SOAL Bidang
Induksi Matematika. Fitriyanti Mayasari
 Induksi Matematika Fitriyanti Mayasari Pendahuluan Induksi Matematika merupakan salah satu cara yang dapat digunakan untuk membuktikan pernyataan-pernyataan yang menegaskan bahwa suatu p(n) adalah benar
Induksi Matematika Fitriyanti Mayasari Pendahuluan Induksi Matematika merupakan salah satu cara yang dapat digunakan untuk membuktikan pernyataan-pernyataan yang menegaskan bahwa suatu p(n) adalah benar
Induksi 1 Matematika
 Induksi 1 Matematika Metode pembuktian untuk pernyataan perihal bilangan bulat adalah induksi matematik. Contoh : p(n): Jumlah bilangan bulat positif dari 1 sampai n adalah n(n + 1)/2. Buktikan p(n) benar!
Induksi 1 Matematika Metode pembuktian untuk pernyataan perihal bilangan bulat adalah induksi matematik. Contoh : p(n): Jumlah bilangan bulat positif dari 1 sampai n adalah n(n + 1)/2. Buktikan p(n) benar!
Metode pembuktian untuk pernyataan perihal bilangan bulat adalah induksi matematik.
 Induksi Matematik 1 Metode pembuktian untuk pernyataan perihal bilangan bulat adalah induksi matematik. Contoh : p(n): Jumlah bilangan bulat positif dari 1 sampai n adalah n(n + 1)/2. Buktikan p(n) benar!
Induksi Matematik 1 Metode pembuktian untuk pernyataan perihal bilangan bulat adalah induksi matematik. Contoh : p(n): Jumlah bilangan bulat positif dari 1 sampai n adalah n(n + 1)/2. Buktikan p(n) benar!
DASAR-DASAR ANALISIS MATEMATIKA
 (Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. December 11, 2007 Misalkan f terdefinisi pada suatu himpunan H. Kita katakan bahwa f naik pada H apabila
(Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. December 11, 2007 Misalkan f terdefinisi pada suatu himpunan H. Kita katakan bahwa f naik pada H apabila
G a a = e = a a. b. Berdasarkan Contoh 1.2 bagian b diperoleh himpunan semua bilangan bulat Z. merupakan grup terhadap penjumlahan bilangan.
 2. Grup Definisi 1.3 Suatu grup < G, > adalah himpunan tak-kosong G bersama-sama dengan operasi biner pada G sehingga memenuhi aksioma- aksioma berikut: a. operasi biner bersifat asosiatif, yaitu a, b,
2. Grup Definisi 1.3 Suatu grup < G, > adalah himpunan tak-kosong G bersama-sama dengan operasi biner pada G sehingga memenuhi aksioma- aksioma berikut: a. operasi biner bersifat asosiatif, yaitu a, b,
1 INDUKSI MATEMATIKA
 1 INDUKSI MATEMATIKA Induksi Matematis Induksi matematis merupakan teknik pembuktian yang baku di dalam matematika. Melalui induksi matematis maka dapat mengurangi langkah-langkah pembuktian bahwa semua
1 INDUKSI MATEMATIKA Induksi Matematis Induksi matematis merupakan teknik pembuktian yang baku di dalam matematika. Melalui induksi matematis maka dapat mengurangi langkah-langkah pembuktian bahwa semua
INF-104 Matematika Diskrit
 Jurusan Informatika FMIPA Unsyiah February 13, 2012 Apakah Matematika Diskrit Itu? Matematika diskrit: cabang matematika yang mengkaji objek-objek diskrit. Apa yang dimaksud dengan kata diskrit (discrete)?
Jurusan Informatika FMIPA Unsyiah February 13, 2012 Apakah Matematika Diskrit Itu? Matematika diskrit: cabang matematika yang mengkaji objek-objek diskrit. Apa yang dimaksud dengan kata diskrit (discrete)?
II. LANDASAN TEORI. Secara umum, apabila α bilangan bulat dan b bilangan bulat positif, maka ada
 II. LANDASAN TEORI Pada bilangan ini diterangkan materi yang berkaitan dengan penelitian, diantaranya konsep bilangan sempurna, bilangan bulat, bilangan prima,faktor bilangan bulat dan kekongruenan. 2.1
II. LANDASAN TEORI Pada bilangan ini diterangkan materi yang berkaitan dengan penelitian, diantaranya konsep bilangan sempurna, bilangan bulat, bilangan prima,faktor bilangan bulat dan kekongruenan. 2.1
Diktat Kuliah. Oleh:
 Diktat Kuliah TEORI GRUP Oleh: Dr. Adi Setiawan UNIVERSITAS KRISTEN SATYA WACANA SALATIGA 2015 Kata Pengantar Aljabar abstrak atau struktur aljabar merupakan suatu mata kuliah yang menjadi kurikulum nasional
Diktat Kuliah TEORI GRUP Oleh: Dr. Adi Setiawan UNIVERSITAS KRISTEN SATYA WACANA SALATIGA 2015 Kata Pengantar Aljabar abstrak atau struktur aljabar merupakan suatu mata kuliah yang menjadi kurikulum nasional
SELEKSI OLIMPIADE MATEMATIKA INDONESIA 2006 TINGKAT PROVINSI TAHUN Prestasi itu diraih bukan didapat!!!
 SELEKSI OLIMPIADE MATEMATIKA INDONESIA 006 TINGKAT PROVINSI TAHUN 005 Prestasi itu diraih bukan didapat!!! SOLUSI SOAL Bidang Matematika Bagian Pertama Disusun oleh : Solusi Olimpiade Matematika Tk Provinsi
SELEKSI OLIMPIADE MATEMATIKA INDONESIA 006 TINGKAT PROVINSI TAHUN 005 Prestasi itu diraih bukan didapat!!! SOLUSI SOAL Bidang Matematika Bagian Pertama Disusun oleh : Solusi Olimpiade Matematika Tk Provinsi
1 SISTEM BILANGAN REAL
 Pertemuan Standar kompetensi: mahasiswa memahami cara membangun sistem bilangan real, aturan dan sifat-sifat dasarnya. Kompetensi dasar Memahami aksioma atau sifat aljabar bilangan real Memahami fakta-fakta
Pertemuan Standar kompetensi: mahasiswa memahami cara membangun sistem bilangan real, aturan dan sifat-sifat dasarnya. Kompetensi dasar Memahami aksioma atau sifat aljabar bilangan real Memahami fakta-fakta
Tujuan Instruksional Umum : Setelah mengikuti pokok bahasan ini mahasiswa dapat mengidentifikasi dan memahami konsep dari Semigrup dan Monoid
 BAB 2 SEMIGRUP DAN MONOID Tujuan Instruksional Umum : Setelah mengikuti pokok bahasan ini mahasiswa dapat mengidentifikasi dan memahami konsep dari Semigrup dan Monoid Tujuan Instruksional Khusus : Setelah
BAB 2 SEMIGRUP DAN MONOID Tujuan Instruksional Umum : Setelah mengikuti pokok bahasan ini mahasiswa dapat mengidentifikasi dan memahami konsep dari Semigrup dan Monoid Tujuan Instruksional Khusus : Setelah
Pengantar Teori Bilangan
 Pengantar Teori Bilangan Kuliah 2 2/2/2014 Yanita, FMIPA Matematika Unand 1 Materi Kuliah 2 Teori Pembagian dalam Bilangan Bulat Algoritma Pembagian Pembagi Persekutuan Terbesar 2/2/2014 2 Algoritma Pembagian
Pengantar Teori Bilangan Kuliah 2 2/2/2014 Yanita, FMIPA Matematika Unand 1 Materi Kuliah 2 Teori Pembagian dalam Bilangan Bulat Algoritma Pembagian Pembagi Persekutuan Terbesar 2/2/2014 2 Algoritma Pembagian
A. PRINSIP INDUKSI SEDERHANA
 INDUKSI MATEMATIK Induksi matematik adalah merupakan teknik pembuktian yang baku di dalam Matematika. Induksi matematik digunakan untuk membuktikan pernyataan yang khusus menyangkut bilangan bulat positif.
INDUKSI MATEMATIK Induksi matematik adalah merupakan teknik pembuktian yang baku di dalam Matematika. Induksi matematik digunakan untuk membuktikan pernyataan yang khusus menyangkut bilangan bulat positif.
MA2111 PENGANTAR MATEMATIKA Semester I, Tahun 2015/2016. Hendra Gunawan
 MA2111 PENGANTAR MATEMATIKA Semester I, Tahun 2015/2016 Hendra Gunawan 3 DEFINISI DAN PERISTILAHAN MATEMATIKA (c) Hendra Gunawan (2015) 2 Ingat PROPOSISI Ini? Proposisi. Jika segitiga siku-siku XYZ dengan
MA2111 PENGANTAR MATEMATIKA Semester I, Tahun 2015/2016 Hendra Gunawan 3 DEFINISI DAN PERISTILAHAN MATEMATIKA (c) Hendra Gunawan (2015) 2 Ingat PROPOSISI Ini? Proposisi. Jika segitiga siku-siku XYZ dengan
PENGERTIAN RING. A. Pendahuluan
 Pertemuan 13 PENGERTIAN RING A. Pendahuluan Target yang diharapkan dalam pertemuan ke 13 ini (pertemuan pertama tentang teori ring) adalah mahasiswa dapat : a. membedakan suatu struktur aljabar merupakan
Pertemuan 13 PENGERTIAN RING A. Pendahuluan Target yang diharapkan dalam pertemuan ke 13 ini (pertemuan pertama tentang teori ring) adalah mahasiswa dapat : a. membedakan suatu struktur aljabar merupakan
BAB III SUB BARISAN DAN TEOREMA BOLZANO-WEIERSTRASS
 BAB III SUB BARISAN DAN TEOREMA BOLZANO-WEIERSTRASS Dalam bab ini akan kita bahas pengertian tentang sub barisan dari barisan bilangan real, yang lebih umum dibandingkan ekor suatu barisan, serta dapat
BAB III SUB BARISAN DAN TEOREMA BOLZANO-WEIERSTRASS Dalam bab ini akan kita bahas pengertian tentang sub barisan dari barisan bilangan real, yang lebih umum dibandingkan ekor suatu barisan, serta dapat
SOAL DAN PENYELESAIAN RING
 SOAL DAN PENYELESAIAN RING 1. Misalkan P himpunan bilangan bulat kelipatan 3. Tunjukan bahwa dengan operasi penjumlahan dan perkalian pada himpunan bilangan bulat, P membentuk ring komutatif. Jawaban:
SOAL DAN PENYELESAIAN RING 1. Misalkan P himpunan bilangan bulat kelipatan 3. Tunjukan bahwa dengan operasi penjumlahan dan perkalian pada himpunan bilangan bulat, P membentuk ring komutatif. Jawaban:
Pembahasan OSN Matematika SMA Tahun 2013 Seleksi Tingkat Provinsi. Tutur Widodo. Bagian Pertama : Soal Isian Singkat
 Pembahasan OSN Matematika SMA Tahun 013 Seleksi Tingkat Provinsi Tutur Widodo Bagian Pertama : Soal Isian Singkat 1. Diberikan tiga lingkaran dengan radius r =, yang saling bersinggungan. Total luas dari
Pembahasan OSN Matematika SMA Tahun 013 Seleksi Tingkat Provinsi Tutur Widodo Bagian Pertama : Soal Isian Singkat 1. Diberikan tiga lingkaran dengan radius r =, yang saling bersinggungan. Total luas dari
METODA PEMBUKTIAN DALAM MATEMATIKA
 1 1 Program Studi Pend Matematika FKIP UM Ponorogo January 12, 2011 Jenis Pernyataan dalam Matematika Denisi (Denition) Kesepakatan mengenai pegertian suatu istilah. Teorema (Theorem) Pernyataan yang dapat
1 1 Program Studi Pend Matematika FKIP UM Ponorogo January 12, 2011 Jenis Pernyataan dalam Matematika Denisi (Denition) Kesepakatan mengenai pegertian suatu istilah. Teorema (Theorem) Pernyataan yang dapat
TUGAS ANALISIS REAL OLEH KELOMPOK V KELAS VI A MATEMATIKA FAKULTAS PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM IKIP MATARAM
 Supremum dan Infimum TUGAS ANALISIS REAL OLEH KELOMPOK V KELAS VI A MATEMATIKA ANGGOTA : 1. ADESUHANDI (06 221 008) 2. ABDUSSALIM (06 221 006) 3. WAN SYAFRADINATA (07 221 299) 4. WIWIN WIDIARTI (07 221
Supremum dan Infimum TUGAS ANALISIS REAL OLEH KELOMPOK V KELAS VI A MATEMATIKA ANGGOTA : 1. ADESUHANDI (06 221 008) 2. ABDUSSALIM (06 221 006) 3. WAN SYAFRADINATA (07 221 299) 4. WIWIN WIDIARTI (07 221
BAB I NOTASI, KONJEKTUR, DAN PRINSIP
 BAB I NOTASI, KONJEKTUR, DAN PRINSIP Kompetensi yang akan dicapai setelah mempelajari bab ini adalah sebagai berikut. (1) Dapat memberikan sepuluh contoh notasi dalam teori bilangan dan menjelaskan masing-masing
BAB I NOTASI, KONJEKTUR, DAN PRINSIP Kompetensi yang akan dicapai setelah mempelajari bab ini adalah sebagai berikut. (1) Dapat memberikan sepuluh contoh notasi dalam teori bilangan dan menjelaskan masing-masing
BAB II KAJIAN TEORI. memahami sifat-sifat dari barisan fungsi. Pada bab ini akan diuraikan materimateri
 BAB II KAJIAN TEORI Analisis kekonvergenan pada barisan fungsi, apakah barisan fungsi itu? Apakah berbeda dengan barisan pada umumnya? Tentunya sebelum membahas mengenai barisan fungsi, apa saja jenis
BAB II KAJIAN TEORI Analisis kekonvergenan pada barisan fungsi, apakah barisan fungsi itu? Apakah berbeda dengan barisan pada umumnya? Tentunya sebelum membahas mengenai barisan fungsi, apa saja jenis
MATEMATIKA EKONOMI 1 HIMPUNAN BILANGAN. Dosen : Fitri Yulianti, SP. MSi
 MATEMATIKA EKONOMI 1 HIMPUNAN BILANGAN Dosen : Fitri Yulianti, SP. MSi Skema Himpunan Kompleks Real Rasional Bulat Cacah Asli Genap Ganjil Prima Komposit Nol Bulat Negatif Pecahan Irasional Imajiner Pengertian
MATEMATIKA EKONOMI 1 HIMPUNAN BILANGAN Dosen : Fitri Yulianti, SP. MSi Skema Himpunan Kompleks Real Rasional Bulat Cacah Asli Genap Ganjil Prima Komposit Nol Bulat Negatif Pecahan Irasional Imajiner Pengertian
BAB I PENDAHULUAN. Kata topologi berasal dari bahasa yunani yaitu topos yang artinya tempat
 1 BAB I PENDAHULUAN 1.1. Latar Belakang Masalah Kata topologi berasal dari bahasa yunani yaitu topos yang artinya tempat dan logos yang artinya ilmu merupakan cabang matematika yang bersangkutan dengan
1 BAB I PENDAHULUAN 1.1. Latar Belakang Masalah Kata topologi berasal dari bahasa yunani yaitu topos yang artinya tempat dan logos yang artinya ilmu merupakan cabang matematika yang bersangkutan dengan
MA2111 PENGANTAR MATEMATIKA Semester I, Tahun 2015/2016. Hendra Gunawan
 MA2111 PENGANTAR MATEMATIKA Semester I, Tahun 2015/2016 Hendra Gunawan 9-10 METODE KONTRADIKSI & METODE KONTRAPOSISI (c) Hendra Gunawan (2015) 2 Metode Pembuktian Lainnya Pada bab-bab sebelumnya kita telah
MA2111 PENGANTAR MATEMATIKA Semester I, Tahun 2015/2016 Hendra Gunawan 9-10 METODE KONTRADIKSI & METODE KONTRAPOSISI (c) Hendra Gunawan (2015) 2 Metode Pembuktian Lainnya Pada bab-bab sebelumnya kita telah
BAB 1. PENDAHULUAN. Bab ini akan membahas sekilas mengenai konsep-konsep yang berkaitan dengan himpunan dan fungsi.
 BAB PENDAHULUAN Bab ini akan membahas sekilas mengenai konsep-konsep yang berkaitan dengan himpunan dan fungsi Himpunan Real Ada beberapa notasi himpunan yang sering digunakan dalam Analisis () merupakan
BAB PENDAHULUAN Bab ini akan membahas sekilas mengenai konsep-konsep yang berkaitan dengan himpunan dan fungsi Himpunan Real Ada beberapa notasi himpunan yang sering digunakan dalam Analisis () merupakan
Perhatikan skema sistem bilangan berikut. Bilangan. Bilangan Rasional. Bilangan pecahan adalah bilangan yang berbentuk a b
 2 SISTEM BILANGAN Perhatikan skema sistem bilangan berikut Bilangan Bilangan Kompleks Bilangan Real Bilangan Rasional Bilangan Irasional Bilangan Bulat Bilangan Pecahan Bilangan bulat adalah bilangan yang
2 SISTEM BILANGAN Perhatikan skema sistem bilangan berikut Bilangan Bilangan Kompleks Bilangan Real Bilangan Rasional Bilangan Irasional Bilangan Bulat Bilangan Pecahan Bilangan bulat adalah bilangan yang
Himpunan dari Bilangan-Bilangan
 Program Studi Pendidikan Matematika STKIP YPM Bangko October 22, 2014 1 Khususnya dalam analisis, maka yang teristimewa penting adalah himpunan dari bilangan-bilangan riil, yang dinyatakan dengan R. Himpunan
Program Studi Pendidikan Matematika STKIP YPM Bangko October 22, 2014 1 Khususnya dalam analisis, maka yang teristimewa penting adalah himpunan dari bilangan-bilangan riil, yang dinyatakan dengan R. Himpunan
METODA PEMBUKTIAN DALAM MATEMATIKA
 1 1 Program Studi Pend Matematika FKIP UM Ponorogo October 29, 2011 Jenis Pernyataan dalam Matematika Denisi (Denition) Kesepakatan mengenai pegertian suatu istilah. Teorema (Theorem) Pernyataan yang dapat
1 1 Program Studi Pend Matematika FKIP UM Ponorogo October 29, 2011 Jenis Pernyataan dalam Matematika Denisi (Denition) Kesepakatan mengenai pegertian suatu istilah. Teorema (Theorem) Pernyataan yang dapat
ALJABAR ABSTRAK ( TEORI GRUP DAN TEORI RING ) Dr. Adi Setiawan, M. Sc
 ALJABAR ABSTRAK ( TEORI GRUP DAN TEORI RING ) Dr. Adi Setiawan, M. Sc PROGRAM STUDI MATEMATIKA FAKULTAS SAINS DAN MATEMATIKA UNIVERSITAS KRISTEN SATYA WACANA SALATIGA 2011 0 KATA PENGANTAR Aljabar abstrak
ALJABAR ABSTRAK ( TEORI GRUP DAN TEORI RING ) Dr. Adi Setiawan, M. Sc PROGRAM STUDI MATEMATIKA FAKULTAS SAINS DAN MATEMATIKA UNIVERSITAS KRISTEN SATYA WACANA SALATIGA 2011 0 KATA PENGANTAR Aljabar abstrak
II. LANDASAN TEORI ( ) =
 II. LANDASAN TEORI 2.1 Fungsi Definisi 2.1.1 Fungsi Bernilai Real Fungsi bernilai real adalah fungsi yang domain dan rangenya adalah himpunan bagian dari real. Definisi 2.1.2 Limit Fungsi Jika adalah suatu
II. LANDASAN TEORI 2.1 Fungsi Definisi 2.1.1 Fungsi Bernilai Real Fungsi bernilai real adalah fungsi yang domain dan rangenya adalah himpunan bagian dari real. Definisi 2.1.2 Limit Fungsi Jika adalah suatu
PENGENALAN KONSEP-KONSEP DALAM RING MELALUI PENGAMATAN Disampaikan dalam Lecture Series on Algebra Universitas Andalas Padang, 29 September 2017
 PENGENALAN KONSEP-KONSEP DALAM RING MELALUI PENGAMATAN Disampaikan dalam Lecture Series on Algebra Universitas Andalas Padang, 29 September 2017 Indah Emilia Wijayanti Departemen Matematika FMIPA Universitas
PENGENALAN KONSEP-KONSEP DALAM RING MELALUI PENGAMATAN Disampaikan dalam Lecture Series on Algebra Universitas Andalas Padang, 29 September 2017 Indah Emilia Wijayanti Departemen Matematika FMIPA Universitas
Pertemuan 1 HIMPUNAN. a.himpunan Kosong Ǿ adalah himpunan yang mempunyai nol anggota(tidak mempunyai elemen.)
 Pertemuan 1 HIMPUNAN 1.3.1. Definisi a.himpunan Kosong Ǿ adalah himpunan yang mempunyai nol anggota(tidak mempunyai elemen.) b. Misalkan nєν Himpunan S dikatakan mempunyai n anggota jika ada suatu fungsi
Pertemuan 1 HIMPUNAN 1.3.1. Definisi a.himpunan Kosong Ǿ adalah himpunan yang mempunyai nol anggota(tidak mempunyai elemen.) b. Misalkan nєν Himpunan S dikatakan mempunyai n anggota jika ada suatu fungsi
MA3231. Pengantar Analisis Real. Hendra Gunawan, Ph.D. Semester II, Tahun
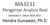 MA3231 Pengantar Analisis Real Semester II, Tahun 2016-2017 Hendra Gunawan, Ph.D. Bab 1 Sifat Kelengkapan Bilangan Real 2 1.1 Paradoks Zeno ACHILLES TORTOISE 0 1 1½ Sumber: skeptic.com 1 1 1... 1 2 4 8?
MA3231 Pengantar Analisis Real Semester II, Tahun 2016-2017 Hendra Gunawan, Ph.D. Bab 1 Sifat Kelengkapan Bilangan Real 2 1.1 Paradoks Zeno ACHILLES TORTOISE 0 1 1½ Sumber: skeptic.com 1 1 1... 1 2 4 8?
Lembar Kerja Mahasiswa 1: Teori Bilangan
 Lembar Kerja Mahasiswa 1: Teori Bilangan N a m a : NIM/Kelas : Waktu Kuliah : Kompetensi Dasar dan Indikator: 1. Memahami pengertian faktor dan kelipatan bilangan bulat. a) Menuliskan denisi faktor suatu
Lembar Kerja Mahasiswa 1: Teori Bilangan N a m a : NIM/Kelas : Waktu Kuliah : Kompetensi Dasar dan Indikator: 1. Memahami pengertian faktor dan kelipatan bilangan bulat. a) Menuliskan denisi faktor suatu
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016. Hendra Gunawan
 MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 4.2 Sifat-Sifat Fungsi Kontinu Diberikan f dan g, keduanya terdefinisi pada himpunan A, kita definisikan f + g, f g, fg, f/g secara
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 4.2 Sifat-Sifat Fungsi Kontinu Diberikan f dan g, keduanya terdefinisi pada himpunan A, kita definisikan f + g, f g, fg, f/g secara
III. BILANGAN KROMATIK LOKASI GRAF. ini merupakan pengembangan dari konsep dimensi partisi dan pewarnaan graf.
 III BILANGAN KROMATIK LOKASI GRAF Bilangan kromatik lokasi graf pertama kali dikaji oleh Chartrand dkk 00) Konsep ini merupakan pengembangan dari konsep dimensi partisi pewarnaan graf Pewarnaan titik pada
III BILANGAN KROMATIK LOKASI GRAF Bilangan kromatik lokasi graf pertama kali dikaji oleh Chartrand dkk 00) Konsep ini merupakan pengembangan dari konsep dimensi partisi pewarnaan graf Pewarnaan titik pada
TEORI KETERBAGIAN.
 TEORI KETERBAGIAN 1 ALGORITMA PEMBAGIAN Teorema 2.1: (Algoritma Pembagian) Diberikan bilangan bulat a dan b, dengan b > 0, maka ada bilangan bulat tunggal q dan r yang memenuhi a = qb + r, 0 r < b. Bilangan
TEORI KETERBAGIAN 1 ALGORITMA PEMBAGIAN Teorema 2.1: (Algoritma Pembagian) Diberikan bilangan bulat a dan b, dengan b > 0, maka ada bilangan bulat tunggal q dan r yang memenuhi a = qb + r, 0 r < b. Bilangan
BAB 6 RING (GELANGGANG) BAHAN AJAR STRUKTUR ALJABAR, BY FADLI
 BAB 6 RING (GELANGGANG) Tujuan Instruksional Umum : Setelah mengikuti pokok bahasan ini mahasiswa dapat mengenal dan mengaplikasikan sifat-sifat suatu Ring, Integral Domain dan Field Tujuan Instruksional
BAB 6 RING (GELANGGANG) Tujuan Instruksional Umum : Setelah mengikuti pokok bahasan ini mahasiswa dapat mengenal dan mengaplikasikan sifat-sifat suatu Ring, Integral Domain dan Field Tujuan Instruksional
II. TINJAUAN PUSTAKA. Pada bab ini akan dibahas konsep-konsep yang mendasari konsep representasi
 5 II. TINJAUAN PUSTAKA Pada bab ini akan dibahas konsep-konsep yang mendasari konsep representasi penjumlahan dua bilangan kuadrat sempurna. Seperti, teori keterbagian bilangan bulat, bilangan prima, kongruensi
5 II. TINJAUAN PUSTAKA Pada bab ini akan dibahas konsep-konsep yang mendasari konsep representasi penjumlahan dua bilangan kuadrat sempurna. Seperti, teori keterbagian bilangan bulat, bilangan prima, kongruensi
BAB I INDUKSI MATEMATIKA
 BAB I INDUKSI MATEMATIKA 1.1 Induksi Matematika Induksi matematika adalah suatu metode yang digunakan untuk memeriksa validasi suatu pernyataan yang diberikan dalam suku-suku bilangan asli. Dalam pembahasan
BAB I INDUKSI MATEMATIKA 1.1 Induksi Matematika Induksi matematika adalah suatu metode yang digunakan untuk memeriksa validasi suatu pernyataan yang diberikan dalam suku-suku bilangan asli. Dalam pembahasan
BAB 1. PENDAHULUAN KALKULUS
 BAB. PENDAHULUAN KALKULUS (Himpunan,selang, pertaksamaan, dan nilai mutlak) Pembicaraan kalkulus didasarkan pada sistem bilangan nyata. Sebagaimana kita ketahui sistem bilangan nyata dapat diklasifikasikan
BAB. PENDAHULUAN KALKULUS (Himpunan,selang, pertaksamaan, dan nilai mutlak) Pembicaraan kalkulus didasarkan pada sistem bilangan nyata. Sebagaimana kita ketahui sistem bilangan nyata dapat diklasifikasikan
II. TINJAUAN PUSTAKA. Pada bab ini akan diberikan konsep dasar (pengertian) tentang bilangan sempurna,
 II. TINJAUAN PUSTAKA Pada bab ini akan diberikan konsep dasar (pengertian) tentang bilangan sempurna, square free, keterbagian bilangan bulat, modulo, bilangan prima, daerah integral, ring bilangan bulat
II. TINJAUAN PUSTAKA Pada bab ini akan diberikan konsep dasar (pengertian) tentang bilangan sempurna, square free, keterbagian bilangan bulat, modulo, bilangan prima, daerah integral, ring bilangan bulat
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
BAB I TEORI KETERBAGIAN DALAM BILANGAN BULAT
 BAB I TEORI KETERBAGIAN DALAM BILANGAN BULAT. Pendahuluan Well-Ordering Principle Jika S himpunan bagian dari himpunan bilangan bulat positif yang tidak kosong, maka S memiliki sebuah unsur terkecil. Unsur
BAB I TEORI KETERBAGIAN DALAM BILANGAN BULAT. Pendahuluan Well-Ordering Principle Jika S himpunan bagian dari himpunan bilangan bulat positif yang tidak kosong, maka S memiliki sebuah unsur terkecil. Unsur
II. TINJAUAN PUSTAKA. Pada bagian ini diterangkan materi yang berkaitan dengan penelitian, diantaranya konsep
 II. TINJAUAN PUSTAKA Pada bagian ini diterangkan materi yang berkaitan dengan penelitian, diantaranya konsep bilangan bulat, bilangan prima,modular, dan kekongruenan. 2.1 Bilangan Bulat Sifat Pembagian
II. TINJAUAN PUSTAKA Pada bagian ini diterangkan materi yang berkaitan dengan penelitian, diantaranya konsep bilangan bulat, bilangan prima,modular, dan kekongruenan. 2.1 Bilangan Bulat Sifat Pembagian
CHAPTER 5 INDUCTION AND RECURSION
 CHAPTER 5 INDUCTION AND RECURSION 5.1 MATHEMATICAL INDUCTION Jumlah n Bilangan Ganjil Positif 1 = 1 1 + 3 = 4 1 + 3 + 5 = 9 1 + 3 + 5 + 7 = 16 1 + 3 + 5 + 7 + 9 = 25 Tebakan: Jumlah dari n bilangan ganjil
CHAPTER 5 INDUCTION AND RECURSION 5.1 MATHEMATICAL INDUCTION Jumlah n Bilangan Ganjil Positif 1 = 1 1 + 3 = 4 1 + 3 + 5 = 9 1 + 3 + 5 + 7 = 16 1 + 3 + 5 + 7 + 9 = 25 Tebakan: Jumlah dari n bilangan ganjil
1. GRUP. Definisi 1.1 (Operasi Biner) Diketahui G himpunan dan ab, G. Operasi biner pada G merupakan pengaitan
 1. GRUP Definisi 1.1 (Operasi Biner) Diketahui G himpunan dan ab, G. Operasi biner pada G merupakan pengaitan pasangan elemen ( ab, ) pada G, yang memenuhi dua kondisi berikut: 1. Setiap pasangan elemen
1. GRUP Definisi 1.1 (Operasi Biner) Diketahui G himpunan dan ab, G. Operasi biner pada G merupakan pengaitan pasangan elemen ( ab, ) pada G, yang memenuhi dua kondisi berikut: 1. Setiap pasangan elemen
CHAPTER 5 INDUCTION AND RECURSION
 CHAPTER 5 INDUCTION AND RECURSION 5.1 MATHEMATICAL INDUCTION Jumlah n Bilangan Ganjil Positif 1 = 1 1 + 3 = 4 1 + 3 + 5 = 9 1 + 3 + 5 + 7 = 16 1 + 3 + 5 + 7 + 9 = 25 Tebakan: Jumlah dari n bilangan ganjil
CHAPTER 5 INDUCTION AND RECURSION 5.1 MATHEMATICAL INDUCTION Jumlah n Bilangan Ganjil Positif 1 = 1 1 + 3 = 4 1 + 3 + 5 = 9 1 + 3 + 5 + 7 = 16 1 + 3 + 5 + 7 + 9 = 25 Tebakan: Jumlah dari n bilangan ganjil
OLIMPIADE MATEMATIKA SLTP TINGKAT KABUPATEN KOTA 2006
 OLIMPIADE MATEMATIKA SLTP TINGKAT KABUPATEN KOTA 00 SOAL PILIHAN GANDA. Jumlah dua bilangan bulat yang berbeda adalah. Jika hasil bagi kedua bilangan tersebut adalah juga bilangan bulat, maka salah satu
OLIMPIADE MATEMATIKA SLTP TINGKAT KABUPATEN KOTA 00 SOAL PILIHAN GANDA. Jumlah dua bilangan bulat yang berbeda adalah. Jika hasil bagi kedua bilangan tersebut adalah juga bilangan bulat, maka salah satu
DASAR-DASAR ANALISIS MATEMATIKA
 (Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. December 26, 2007 Misalkan f kontinu pada interval [a, b]. Apakah masuk akal untuk membahas luas daerah
(Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. December 26, 2007 Misalkan f kontinu pada interval [a, b]. Apakah masuk akal untuk membahas luas daerah
CATATAN KULIAH ANALISIS REAL LANJUT
 CATATAN KULIAH ANALISIS REAL LANJUT May 26, 203 A Lecture Note Acknowledgement of Sources For all ideas taken from other sources (books, articles, internet), the source of the ideas is mentioned in the
CATATAN KULIAH ANALISIS REAL LANJUT May 26, 203 A Lecture Note Acknowledgement of Sources For all ideas taken from other sources (books, articles, internet), the source of the ideas is mentioned in the
Pembagi Persekutuan Terbesar dan Teorema Bezout
 Latest Update: March 10, 2017 Pengantar Teori Bilangan (Bagian 3): Pembagi Persekutuan Terbesar dan Teorema Bezout M. Zaki Riyanto Program Studi Matematika Fakultas Sains dan Teknologi UIN Sunan Kalijaga
Latest Update: March 10, 2017 Pengantar Teori Bilangan (Bagian 3): Pembagi Persekutuan Terbesar dan Teorema Bezout M. Zaki Riyanto Program Studi Matematika Fakultas Sains dan Teknologi UIN Sunan Kalijaga
RUMUS-RUMUS TAUTOLOGI. (Minggu ke-5 dan 6)
 RUMUS-RUMUS TAUTOLOGI (Minggu ke-5 dan 6) 1 1 Rumus-rumus tautologi Rumus 1.1 (Komutatif) 1. p q q p 2. p q q p Bukti: p q p q q p T T T T T F F F F T F F F F F F 2 Rumus 1.2 (Distributif) 1. p (q r) (p
RUMUS-RUMUS TAUTOLOGI (Minggu ke-5 dan 6) 1 1 Rumus-rumus tautologi Rumus 1.1 (Komutatif) 1. p q q p 2. p q q p Bukti: p q p q q p T T T T T F F F F T F F F F F F 2 Rumus 1.2 (Distributif) 1. p (q r) (p
PENGANTAR ANALISIS REAL
 Seri Analisis dan Geometri No. 1 (2009), -15 158 (173 hlm.) PENGANTAR ANALISIS REAL Oleh Hendra Gunawan Edisi Pertama Bandung, Januari 2009 2000 Dewey Classification: 515-xx. Kata Kunci: Analisis matematika,
Seri Analisis dan Geometri No. 1 (2009), -15 158 (173 hlm.) PENGANTAR ANALISIS REAL Oleh Hendra Gunawan Edisi Pertama Bandung, Januari 2009 2000 Dewey Classification: 515-xx. Kata Kunci: Analisis matematika,
METODA PEMBUKTIAN DALAM MATEMATIKA
 METODA PEMBUKTIAN DALAM MATEMATIKA Dr. Julan HERNADI & Uki Suhendar, S.Pd (Asrul dan Enggar) Program Studi Pendidikan Matematika FKIP Unmuh Ponorogo Pertemuan 8 FONDASI MATEMATIKA Matematika Bukan Sekedar
METODA PEMBUKTIAN DALAM MATEMATIKA Dr. Julan HERNADI & Uki Suhendar, S.Pd (Asrul dan Enggar) Program Studi Pendidikan Matematika FKIP Unmuh Ponorogo Pertemuan 8 FONDASI MATEMATIKA Matematika Bukan Sekedar
UNIVERSITAS GADJAH MADA. Bahan Ajar:
 UNIVERSITAS GADJAH MADA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM JURUSAN MATEMATIKA PROGRAM STUDI S1 MATEMATIKA Sekip Utara, Gedung Jurusan Matematika, Yogyakarta - 55281 Bahan Ajar: BAB / POKOK BAHASAN
UNIVERSITAS GADJAH MADA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM JURUSAN MATEMATIKA PROGRAM STUDI S1 MATEMATIKA Sekip Utara, Gedung Jurusan Matematika, Yogyakarta - 55281 Bahan Ajar: BAB / POKOK BAHASAN
MA3231. Pengantar Analisis Real. Hendra Gunawan, Ph.D. Semester II, Tahun
 MA3231 Pengantar Analisis Real Semester II, Tahun 2016-2017 Hendra Gunawan, Ph.D. Tentang Mata Kuliah MA3231 Mata kuliah ini merupakan mata kuliah wajib bagi mahasiswa program studi S1 Matematika, dengan
MA3231 Pengantar Analisis Real Semester II, Tahun 2016-2017 Hendra Gunawan, Ph.D. Tentang Mata Kuliah MA3231 Mata kuliah ini merupakan mata kuliah wajib bagi mahasiswa program studi S1 Matematika, dengan
Pertemuan 3 METODE PEMBUKTIAN
 Pertemuan 3 METODE PEMBUKTIAN Metode Pembuktian Petunjuk umum dalam pembuktian Langkah-langkah untuk melakukan pembuktian adalah sebagai berikut: 1. Tulislah teorema yang akan dibuktikan 2. Tandailah permulaan
Pertemuan 3 METODE PEMBUKTIAN Metode Pembuktian Petunjuk umum dalam pembuktian Langkah-langkah untuk melakukan pembuktian adalah sebagai berikut: 1. Tulislah teorema yang akan dibuktikan 2. Tandailah permulaan
PENDAHULUAN INDUKSI MATEMATIKA Di dalam Matematika, sebuah pernyataan atau argumen dan bahkan sebuah rumus sekalipun tidak hanya sekedar dibaca.
 PENDAHULUAN INDUKSI MATEMATIKA Di dalam Matematika, sebuah pernyataan atau argumen dan bahkan sebuah rumus sekalipun tidak hanya sekedar dibaca. Karena hampir semua rumus dan hukum yang berlaku tidak tercipta
PENDAHULUAN INDUKSI MATEMATIKA Di dalam Matematika, sebuah pernyataan atau argumen dan bahkan sebuah rumus sekalipun tidak hanya sekedar dibaca. Karena hampir semua rumus dan hukum yang berlaku tidak tercipta
OSN MATEMATIKA SMA Hari 1 Soal 1. Buktikan bahwa untuk sebarang bilangan asli a dan b, bilangan. n = F P B(a, b) + KP K(a, b) a b
 OSN MATEMATIKA SMA Hari 1 Soal 1. Buktikan bahwa untuk sebarang bilangan asli a dan b, bilangan adalah bilangan bulat genap tak negatif. n = F P B(a, b + KP K(a, b a b Solusi. Misalkan d = F P B(a, b,
OSN MATEMATIKA SMA Hari 1 Soal 1. Buktikan bahwa untuk sebarang bilangan asli a dan b, bilangan adalah bilangan bulat genap tak negatif. n = F P B(a, b + KP K(a, b a b Solusi. Misalkan d = F P B(a, b,
PENERAPAN FAKTOR PRIMA DALAM MENYELESAIKAN BENTUK ALJABAR (Andi Syamsuddin*)
 PENERAPAN FAKTOR PRIMA DALAM MENYELESAIKAN BENTUK ALJABAR (Andi Syamsuddin*) A. Faktor Prima Dalam tulisan ini yang dimaksud dengan faktor prima sebuah bilangan adalah pembagi habis dari sebuah bilangan
PENERAPAN FAKTOR PRIMA DALAM MENYELESAIKAN BENTUK ALJABAR (Andi Syamsuddin*) A. Faktor Prima Dalam tulisan ini yang dimaksud dengan faktor prima sebuah bilangan adalah pembagi habis dari sebuah bilangan
BAB III INTEGRAL LEBESGUE. Pada bab sebelumnya telah disebutkan bahwa ruang dibangun oleh
 BAB III INTEGRAL LEBESGUE Pada bab sebelumnya telah disebutkan bahwa ruang dibangun oleh fungsi-fungsi terukur dan memenuhi sifat yang berkaitan dengan integral Lebesgue. Kajian mengenai keterukuran suatu
BAB III INTEGRAL LEBESGUE Pada bab sebelumnya telah disebutkan bahwa ruang dibangun oleh fungsi-fungsi terukur dan memenuhi sifat yang berkaitan dengan integral Lebesgue. Kajian mengenai keterukuran suatu
DASAR-DASAR ALJABAR MODERN: TEORI GRUP & TEORI RING
 DASAR-DASAR ALJABAR MODERN: TEORI GRUP & TEORI RING Dr. Adi Setiawan, M.Sc G R A F I K A Penerbit Tisara Grafika SALATIGA 2014 Katalog Dalam Terbitan 512.24 ADI Adi Setiawan d Dasar-dasar aljabar modern:
DASAR-DASAR ALJABAR MODERN: TEORI GRUP & TEORI RING Dr. Adi Setiawan, M.Sc G R A F I K A Penerbit Tisara Grafika SALATIGA 2014 Katalog Dalam Terbitan 512.24 ADI Adi Setiawan d Dasar-dasar aljabar modern:
TIM OLIPIADE MATEMATIKA INDONESIA. Olimpade Sains Propinsi 2013 Marking Scheme Uraian
 TIM OLIPIADE MATEMATIKA INDONESIA Olimpade Sains Propinsi 203 Marking Scheme Uraian 26 Juni 203 Daftar Isi I Isian Singkat 2 Jawaban 3 II Uraian 4 2 Soal 5 2. Jawab.....................................
TIM OLIPIADE MATEMATIKA INDONESIA Olimpade Sains Propinsi 203 Marking Scheme Uraian 26 Juni 203 Daftar Isi I Isian Singkat 2 Jawaban 3 II Uraian 4 2 Soal 5 2. Jawab.....................................
METODA PEMBUKTIAN DALAM MATEMATIKA
 METODA PEMBUKTIAN DALAM MATEMATIKA Dr. Julan HERNADI & Uki Suhendar, S.Pd (Asrul dan Enggar) Program Studi Pendidikan Matematika FKIP Unmuh Ponorogo Pertemuan 8 FONDASI MATEMATIKA Matematika Bukan Sekedar
METODA PEMBUKTIAN DALAM MATEMATIKA Dr. Julan HERNADI & Uki Suhendar, S.Pd (Asrul dan Enggar) Program Studi Pendidikan Matematika FKIP Unmuh Ponorogo Pertemuan 8 FONDASI MATEMATIKA Matematika Bukan Sekedar
MA5032 ANALISIS REAL
 (Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. August 17, 2011 Zeno, seorang filsuf dan matematikawan Yunani Kuno (490-435 SM), mengemukakan sebuah paradoks tentang suatu
(Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. August 17, 2011 Zeno, seorang filsuf dan matematikawan Yunani Kuno (490-435 SM), mengemukakan sebuah paradoks tentang suatu
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI Sejak tiga abad yang lalu, pakar-pakar matematika telah menghabiskan banyak waktu untuk mengeksplorasi dunia bilangan prima. Banyak sifat unik dari bilangan prima yang menakjubkan.
BAB 2 LANDASAN TEORI Sejak tiga abad yang lalu, pakar-pakar matematika telah menghabiskan banyak waktu untuk mengeksplorasi dunia bilangan prima. Banyak sifat unik dari bilangan prima yang menakjubkan.
