MODUL 4: Nondeterministic Finite Automata

Transkripsi

1 MODUL 4: Nondeterministic Finite Automata Slide dari 2

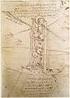
2 FA DENGAN NONDETERMINISME Disamping ini merupakan FA dari suatu bahasa regular dalam {,} * dengan ekspresi regular (+) *. p, q s, u r t Slide 2 dari 2

3 FA kah diagram berikut ini? Bukan, karena tidak memenuhi beberapa sifat FA! q 2 q q q 4 q 3 adanya status-status yang tidak memiliki transisi untuk kedua kemungkinan simbol, adanya status-status yang memiliki > transisi untuk simbol yang sama. Slide 3 dari 2

4 Namun menggambarkan secara lebih eksplisit ekspresi regular (+) *. Loop q -q -q menunjukkan pengulangan loop q -q 2 -q 3 -q menunjukkan pengulangan adanya simbol di akhir string. Dipandang sebagai recognizer, terdapat ketidak pastian langkah transisi berikutnya untuk dijalani. Misalnya simbol pertama maka ada dua pilihan. Slide 4 dari 2

5 Definisi NFA Suatu Nondeterministic Finite Automaton (NFA) adalah 5-tuple M = (Q, Σ, q, A, δ). Q adalah himpunan status, Σ adalah alfabet, q adalah status inisial, A adalah himpunan status terima dan δ fungsi transisi sebagai berikut. δ: Q Σ 2 Q Slide 5 dari 2

6 Definisi Fungsi Perluasan Transisi d * Modul 4: Nondeterministic Finite Automatar Pada setiap NFA M = (Q, Σ, q, A, δ) fungsi δ * : Q Σ * 2 Q didefinisikan sbb. Untuk setiap q Q maka δ * (q, Λ) = {q}. Untuk setiap y Σ *, a Σ, dan q Q, maka δ * ( q, ya) = p δ U * δ( p, a) ( q, y) Slide 6 dari 2

7 Dalam bentuk diagram dapat digambarkan sbb. δ * (q,y) a δ * (q,ya) q a a a y Slide 7 dari 2

8 NFA Sebagai Mesin Pengenal Bahasa Regular M = (Q, Σ, q, A, δ) suatu NFA, String x diterima oleh M bila δ * (q, x) A. Bahasa L dikenal oleh M adalah L(M) himpunan seluruh string yang diterima oleh M. Untuk bahasa L Σ *, L dikenali oleh M jika dan hanya jika L = L(M). Slide 8 dari 2

9 Contoh M = (Q, Σ, q, A, δ) suatu NFA, dengan Q = {q, q, q 2, q 3 }, Σ = {, }, A = {q 3 }, dan δ dinyatakan dalam tabel disamping ini. Modul 4: Nondeterministic Finite Automatar q δ (q, ) δ (q, ) Q {q } {q, q } q {q 2 } {q 2 } q 2 {q 3 } {q 3 } q 3 Dalam bentuk diagram digambarkan sbb., q q, q, 2 q 3 Slide 9 dari 2

10 Bahasa yang dikenal NFA tsb memiliki ekspresi regular (+) * (+) 2. Bahasa tsb dikenal juga sebagai L n = {x * simbol ke n dari kanan adalah } dengan kasus n = 3. Slide dari 2

11 Apakah NFA lebih powerful daripada FA? (Note: powerful dalam hal kemampuan penerimaannya terhadap suatu bahasa) Ternyata tidak! Suatu bahasa yang dikenali oleh NFA akan dapat dikenali pula oleh suatu FA (walaupun dengan diagram transisi yang lebih rumit). Slide dari 2

12 Konversi NFA ke FA Untuk setiap NFA M = (Q, Σ, q, A, δ) yang menerima bahasa L Σ, akan terdapat FA M = (Q, Σ, q, A, δ ) yang juga menerima L. Q = 2 Q q = {q } untuk q Q dan a Σ, maka δ ( q, a) = δ( p, a) U p q A = {q Q q A } Slide 2 dari 2

13 Note: Status-status q Q (dari M ) mrpk status yang dinamai sesuai himpunan status 2 Q. Contoh: Dari Q = {A, B, C} dibentuk Q = {, {A}, { B}, {C}, {A, B}, {A, C}, {B, C}, {A, B, C}}. Dalam hal ini {A} atau {A, B, C} merupakan nama-nama status anggota Q. Untuk menyederhanakan kadang-kadang ditulis tanpa notasi kurung dan koma. Contoh: Q = {, A, B, C, AB, AC, BC, ABC} Slide 3 dari 2

14 Kesimpulan: δ * (q, x) = δ * (q, x) Modul 4: Nondeterministic Finite Automatar (Ingat: δ * dan δ * berasal dari dua definisi yang berbeda, yang pertama dari FA dan yang kedua dari NFA). dibuktikan dengan induksi matematis sbb. Untuk x = Λ, δ * (q, x) = δ * (q, Λ) = q = {q } δ * (q, x) = δ * (q, Λ) = {q } Slide 4 dari 2

15 Asumsi δ * (q, x) = δ * (q, x) terpenuhi, akan dibuktikan untuk a Σ apakah juga δ * (q, xa) = δ * (q, xa) terpenuhi. Menurut definisi δ * (q, xa) = δ (δ * (q, x), a). Sementara, δ (δ * (q, x), a) = δ (δ * (q, x), a) = δ( p, a) = δ * (q, xa). Maka terbukti. p δ U * ( q, x) Slide 5 dari 2

16 Contoh: NFA untuk bahasa regular dengan ekspresi regular (+) * (+) 2 akan dicari FA ybs. Dari Q = {q, q, q 2, q 3 }, Q = {, {q }, {q },, {q, q }, } semua kemung. subset dari Q. Namun tidak semua status akan digunakan. Status inisial {q } Himp. status menerima = {{q 3 }, {q, q 3 }, {q, q 3 }, } -- semua subset yang berisi q 3 karena q 3 status menerima di NFA. Slide 6 dari 2

17 δ diperoleh secara bertahap mulai dari {q } δ ({q }, ) = {q } δ ({q }, ) = {q, q } Lalu dari {q, q } diperoleh δ ({q, q }, ) = δ ({q }, ) δ ({q }, ) ={q } {q 2 } = {q, q 2 } δ ({q, q }, ) = δ ({q }, ) δ ({q }, ) ={q, q } {q 2 } = {q, q, q 2 } Lalu dari {q, q 2 } diperoleh δ ({q, q 2 }, ) = δ ({q }, ) δ ({q 2 }, ) Slide 7 dari 2

18 = {q } {q 3 } = {q, q 3 } δ ({q, q 2 }, ) = δ ({q }, ) δ ({q 2 }, ) ={q, q } {q 3 } = {q, q, q 3 } Lalu dari {q, q, q 2 } diperoleh δ ({q, q, q 2 }, ) = {q } {q 2 } {q 3 } = {q, q 2, q 3 } δ ({q, q, q 2 }, ) = {q, q } {q 2 } {q 3 } = {q, q, q 2, q 3 } dst hanya 8 status yang digunakan. Slide 8 dari 2

19 q q q q q 2 q q q Note: {q, q 3 }, {q, q, q 2 }, {q, q, q 3 }, {q, q 2, q 3 }, {q, q, q 2, q 3 } tidak digunakan karena tidak pernah tercapai dari {q }. Slide 9 dari 2 q q 3 q q q 3 q q 2 q 3 q q q 2 q

20 Contoh: NFA di awal pembahasan untuk mengenali bahasa regular dengan ekspresi (+) * Modul 4: Nondeterministic Finite Automatar q 2 q q q 4 q 3 Slide 2 dari 2

21 Bila dikonversi ke FA menghasilkan tabel/diagram transisi sbb (yang persis seperti FA ybs). q δ (q, ) δ (q, ) {q } {q 4 } {q, q 2 } {q 4 } {q, q 2 } {q, q 3 } {q, q 3 } {q, q 4 } {q, q 2 } {q, q 4 } {q 4 } {q, q 2 } q 4, q, q q 2 q q 4 q q 3 Slide 2 dari 2