BAB I PENDAHULUAN 1.1 Kegunaan Metode Sampling 1.2 Tahap-Tahap dalam Survei Sampel 1. Tujuan survei.
|
|
|
- Erlin Lie
- 7 tahun lalu
- Tontonan:
Transkripsi
1 BAB I PENDAHULUAN 1.1 Kegunaan Metode Sampling Pengambilan sampel dari suatu survei telah menjadi sesuatu yang besar kegunaannya dalam kehidupan. Sebuah sampel terdiri sejumlah bola lampu dalam satu periode waktu produksi dapat memberikan gambaran kualitas dari seluruh bola lampu yang diproduksi dalam periode waktu tersebut. Tingkat sosial ekonomi keluarga atau rumah tangga dari sejumlah keluarga yang diambil dari seluruh keluarga yang tinggal di sebuah kota dapat menggambarkan tingkat sosial ekonomi seluruh keluarga yang tinggal di kota tersebut. Sebuah jajak pendapat terhadap sejumlah calon pemilih pada Pilkada disuatu kabupaten dapat memberikan ramalan siapa calon kepala daerah yang akan terpilih pada Pilkada yang akan datang. Gambaran atau ramalan seperti tersebut diatas akan sangat bermanfaat bagi setiap yang berkompeten untuk mengambil sikap atau tindakan sesuai dengan kepentingannya. Dalam survei sampel, sampel diambil dari populasi, kemudian dihitung nilai statistik guna menarik inferensi tentang parameter populasi. Pemilihan jenis sampel yang sesuai serta metode estimasi yang tepat akan memberikan hasil yang optimum dengan keakuratan yang tinggi. Keuntungan atau manfaat penggunaan metode survei sampel adalah antara lain, mengurangi biaya, memberikan kecepatan yang lebih besar, cakupan lebih besar, dan tingkat ketelitian sesuai dengan yang diinginkan. 1.2 Tahap-Tahap dalam Survei Sampel Tahapan-tahapan yang perlu dilakukan daalam sebuah survei sampel ada 11 tahap, yaitu : 1. Tujuan survei. Merupakan pernyataan yang jelas tentang maksud dan tujuan survei. Tanpa tujuan yang jelas, keputusan yang dapat diambil akan melenceng dengan tujuannya. 1
2 2. Populasi yang akan diambil sampelnya. Populasi adalah himpunan seluruh obyek penelitian yang mengandung paramater-parameter yang akan dicari. Sampel adalah himpunan bagian dari populasi tersebut. Dari sampel yang diambil, ditetapkan statistikstatistik estimator untuk parameter-parameter tersebut. 3. Data yang dikumpulkan. Data atau informasi yang dikumpulkan harus sesuai dengan tujuan survei. 4. Tingkat ketelitian yang diinginkan. Kesimpulan dalam estimasi selalu mengandung ketidakpastian yang dapat diukur dengan probabilitas. Kesalahan dalam estimasi dengan probabilitas tertentu dapat diperkecil dengan memperbesar sampel. 5. Metode pengukuran. Suatu survei dapat dilaksanakan dengan menggunakan kuesioner disertai wawancara atau dikirimkan lewat media komunikasi kepada responden, seperti pos atau telepon. Selanjutnya dari isian kuesioner yang masuk kembali disusun ringkasan dalam bentuk tabel-tabel. 6. Kerangka atau frame. Sebelum pengambilan sampel, populasi dibagi dalam bagian-bagian yang disebut unit pengambilan sampel atau unit. Dalam pengambilan sampel penduduk sebuah kota, unit dapat berupa orang, atau berupa keluarga, atau berupa semua penduduk yang tinggal di tiap rukun tetangga. Daftar unit pengambilan sampel ini disebut kerangka. 7. Pemilihan sampel. Perlu ditetapkan jenis sampel yang akan diambil, sesuai dengan keadaan, serta ukuran sampel yang disesuaikan dengan tingkat ketelitian. 8. Uji pendahuluan. Perlu sekali dilakukan uji coba terhadap kuesioner dalam lingkup yang lebih kecil, guna mendeteksi kemungkinana adanya kesulitan responden dalam jawabannya. 2
3 9. Organisasi lapangan. Perlu antisipasi masalah-masalah administrasi dan pelatihan terhadap tenaga-tenaga pencacah. 10. Ringkasan dan analisis data. Dari jawaban kuesioner, perlu dilakukan editing untuk menghindari salah catat atau kesalahan lainnya. Perlu diputuskan prosedur pengisian atau penghitungan apabila jawaban untuk pertanyaan tertentu tidak diisi oleh beberapa responden. 11. Keterangan yang bermanfaat untuk survei mendatang. Semakin banyak informasi yang dapat dikumpulkan akan semakin mudah memperoleh sampel yang memberikan perkiraan yang akurat. Setiap sampel yang lengkap merupakan petunjuk yang baik untuk perbaikan pengambilan sampel yang akan datang. Pengambilan sampel membutuhkan perhatian pada seluruh tahap tersebut, karena pelaksanaan yang buruk pada tahap tertentu dapat menyebabkan gagalnya suatu survei. Teori pengambilan sampel mencoba mengembangkan jenis sampel dan metode estimasi atau perkiraan dengan tujuan memperoleh hasil yang efisien, biaya yang lebih kecil namun keakuratannya tinggi. Jenis-jenis sanpel yang dikembangkan adalah sampel-sampel yang diambil dengan kaidah probabilitas. 1.3 Sifat-Sifat Baik Untuk Sebuah Estimator Misalkan sebuah populasi mempunyai parameter. Dari sampel yang diambil dari populasi tersebut misalkan suatu statistik estimator untuk. Selanjutnya misalkan seluruhnya terdapat K sampel-sampel yang mungkin terambil dari populasi tersebut dan masing-masing akan terambil dengan probabilitas. Maka mean atau ekspektasi atau nilai harapan dari adalah : 3
4 dengan adalah nilai pada sampel ke-k. Variansi dari didefinisikan dengan : Rata-rata kuadrat kesalahan dari didefinisikan dengan Statistik estimator dikatakan tak bias untuk parameter jika E( ) =, dikatakan konsisten untuk jika sama dengan pada sampel yang berhimpitan dengan populasi dan dikatakan efisien jika V( ) adalah terkecil diantara semua estimator untuk. Sifat-sifat tak bias, konsisten dan efisien adalah sifat-sifat baik yang mungkin dimiliki oleh sebuah estimator. Dengan sifat-sifat tersebut keakuratan yang tinggi dari sebuah estimator dapat diperoleh. Jika tak bias untuk, maka E( ) =, dan ini berakibat RKK( ) = V( ). Tetapi jika bias untuk, maka E( ), dan RKK ( ) V( ). Deviasi standar dari, ditulis, didefinisikan sebagai akar dari variansinya. Kesalahan standar dari, ditulis S( ) adalah akar dari RKK( ). Jadi =, S( ) = dalam kasus tak bias untuk maka = S( ) 4
5 1.4 Bias dan Pengaruhnya. Bias dari suatu estimator untuk, ditulis B( ), didefinisikan dengan B( ) = E( ) Jika m = E( ) dan tak bias untuk, maka m =, dan B( ) = 0. Tetapi jika bias untuk, maka m dan B( ) = m 0 Untuk sampel berukuran besar, distribusi dari statistik estimator akan mendekati normal dengan mean E( ) dan variansi V( ). Pada kasus tak bias untuk, maka E( ) = dan P( 1,96 + 1,96 ) = 0,95 Tetapi pada kasus bias untuk, maka E( )= m dan P( 1,96 m + 1,96 ) = 0,95 Kedua grafik distribusi tersebut pada kasus tak bias dan kasus bias adalah sebagai berikut, 0,025 1,96 1,96 0,95 Kasus 0,025 Kasus tak bias untuk (Gambar 1) bias untuk dengan E( ) = m> (Gambar 2) m Jika kesalahan dalam estimasi didefinisikan sebagai nilai mutlak dari selisih dengan, yaitu, maka pada kasus tak bias, 5
6 P ( >1,96 ) = 0,05 ( daerah diarsir dalam gambar 1), dan pada kasus bias untuk dengan E( ) = m >, nilai P ( > 1,96 ) >0,05 (daerah diarsir dalam gambar 2). Sebagai contoh, untuk B( ) = m = (0,1), maka P ( > 1,96 ) = P( < 1,96 ) + P( > 1,96 ) = P( < 2,06) + P( > 1,86) = 0, ,0314 = 0,0511 Demikian pula, untuk B( ) = m = (0,1), maka P ( >1,96 ) = P( < 1,86) + P( > 2,06) = 0, ,0197 = 0,0511 Dan untuk B( ) = (0,6) atau B( ) = (0,6), akan diperoleh P ( > 1,96 ) = 0, ,0869 = 0,0921 Jadi, ketika kita menyangka tak bias untuk, maka probabilitas terjadi kesalahan estimasi yang melebihi 1,96 hanya kita sangka sebesar 0,05. Tetapi jika kenyataannya bias untuk, maka nilai sebenarnya probabilitas tersebut adalah lebih dari 0,05. Dan nilai probabilitas tersebut semakin besar untuk B( ) yang semakin besar. Jadi adanya bias mengakibatkan semakin besar probabilitas terjadinya kesalahan dalam estimasi dan hal ini tentu saja akan mengurangi keakuratan dalam estimasi. Dengan adanya pengaruh bias terhadap keakuratan hasil estimasi tersebut, maka pengetahuan tentang sifat bias atau tak biasnya suatu estimator diperlukan sekali. Dari hasil diatas, jika estimator untuk dan B( ) (0,1), maka 6
7 P ( > 1,96 ) 0,0511 jauh berubah dan lebih besar dari 0,05. Tetapi jika B( ) (0,1), maka P ( >1,96 ) < 0,0511,tak jauh beda dengan 0,05. Jadi jika bias untuk namun B( ) kecil yaitu kurang dari (0,1), maka pengaruhnya kecil, dan bias tersebut dapat diabaikan. 1.5 Rata-Rata Kuadrat Kesalahan Dari definisi rata-rata kuadrat kesalahan, RKK ( ), diperoleh hubungan antara RKK ( ), V( ) dan B( ) sebagai berikut, RKK ( ) = E ( = E(( m) + (m ) = E ( = V( ) + (B( ) Jika tak bias untuk, maka B( ) = 0 dan RKK ( ) = V( ). Untuk membandingkan dua buah estimator dan, digunakan kesalahan standar dari kedua estimator tersebut, yaitu ( ) dan ( ), yang nilainya ( ) =, ( ) = pada keadaan umum dan ( ) =, ( ) = jika dan tak bias untuk, nilai kesalahan standar yang lebih kecil menunjukkan keakuratan yang lebih tinggi. Berikut ini diberikan ilustrasi visual tentang bias dan kesalahan standar. Misalkan terdapat 4 jenis senapan yang harus dipilih salah satu yang akan memberikan hasil tembakan yang tepat dan keakuratan yang tinggi. Setiap senapan dicoba sebanyak 8 kali tembakan dengan target titik pusat sebuah papan lingkaran yang radiusnya sama. Misalkan hasil tembakan 4 jenis senapan tersebut sebagai berikut, 7
8 X X X X X X X X X X X X X X X X Senapan 1 Senapan 2 X X X X X X X X X X X X X X Senapan 3 Senapan 4 Hasil tembakan senapan 1 memberikan gambaran bias (tembakan melenceng) dengan kesalahan standar yang tinggi (keakuratan rendah), senapan 2 tak bias dengan kesalahan standar yang tinggi, senapan 3 bias namun kesalahan standarnya rendah dan senapan 4 tak bias dengan kesalahan standar rendah. Dalam kasus real target bukan merupakan titik, namun merupakan bidang yang kecil. Jadi urutan senapan dimulai yang terbaik adalah: 4, 3, 2, 1 dan pilihan terbaik adalah senapan 4. 8
9 BAB II SAMPLING RANDOM SEDERHANA 2.1 Pengambilan Sampel Random Sederhana Ditentukan sebuah populasi berukuran N, yaitu banyaknya anggota atau unit populasi adalah N. Dari populasi ini akan diambil sampel berukuran n, yaitu sampel dengan anggota atau unit sebanyak n. Jika pengambilan tanpa pengembalian, maka terdapat sampel-sampel yang mungkin terambil. Jika pengambilan dilakukan dengan pengembalian maka terdapat sampel-sampel yang mungkin terambil. Sebuah sampel disebut sampel random sederhana jika setiap sampel yang mungkin terambil, diperoleh dengan probabilitas sama. Jadi, pada pengambilan tanpa pengembalian, jika setiap sampel yang mungkin terambil diperoleh dengan probabilitas : maka sampel yang diperoleh adalah sampel random sederhana. Pada pengambilan dengan pengembalian, sebuah sampel random sederhana akan diperoleh dengan probabilitas : Dalam pembahasan selanjutnya, akan dibatasi pada sampel random sederhana yang diambil tanpa pengembalian. Sebagai contoh, dari populasi berukuran 8 akan diambil sampel random sederhana berukuran 3. Maka terdapat : sampel-sampel yang mungkin terambil, masing-masing terpilih dengan probabilitas. 9
10 Pengambilan sampel random sederhana dapat dilakukan antara lain dengan menggunakan Tabel bilangan-bilangan random. 2.2 Definisi dan Notasi Unit-unit populasi berukuran N, ditulis dengan notasi atau lambang :. Parameter-parameter populasi ditulis dengan notasi huruf kapital, yaitu : Total populasi, Y, didefinisikan : Mean atau rata-rata populasi,, didefinisikan : Variansi populasi, ada dua definisi yang harus dibedakan, ditulis dengan notasi dan, Dalam pembahasan selanjutnya akan digunakan untuk menyatakan variansi populasi. Rumus lain untuk, = 10
11 atau = Deviasi standar dari populasi adalah, yaitu akar dari variansi. Statistik-statistik sampel, ditulis dengan notasi huruf-huruf kecil. Unit-unit sampel random sederhana berukuran n, ditulis dengan notasi : Mean atau rata-rata sampel,, didefinisikan Variansi sampel,, didefinisikan : = Rumus lain untuk, = atau = Deviasi standar sampel adalah akar dari variansi sampel, ditulis s. 11
12 2.3 Sifat-Sifat Estimator Mean dan Total Serta Variansinya Dari sebuah populasi berukuran N, misalkan, Y dan adalah mean, total dan variansinya. Nilai parameter-parameter tersebut tidak diketahui. Dengan sampling random sederhana berukuran n, akan dipelajari estimator dari masingmasing parameter tersebut yang ditulis :, dan beserta sifat-sifatnya. Dipelajari pula variansi dari dan variansi dari yang ditulis, V( ) dan V(Y) Dalam sampling random sederhana berukuran n, estimator dari adalah, estimator dari Y adalah N dan estimator dari adalah. Jadi, = N dan Teorema 2.1 Dalam sampling random sederhana berukuran n yang diambil dari populasi berukuran N, mean sampel,, adalah suatu estimator tak bias untuk mean populasi. Bukti : Dalam sampling ini terdapat sampel-sampel yang mungkin terambil, masingmasing akan terpilih dengan probabilitas. Misalkan adalah mean sampel ke-k, k =1,2,..., maka dengan adalah unit k-i di dalam sampel ke-k, i=1, 2,..., n. Setiap unit tertentu,, dalam populasi, i=1,2,...n, 12
13 dalam jumlahan : akan memberikan kontribusi sebesar jika berada dalam sampel ke-k dan tidak memberikan kontribusi atau kontribusinya nol, jika tak berada dalam sampel ke-k. Dari seluruh sampel yang mungkin terambil, banyaknya sampel yang memuat unit tertentu tersebut adalah. Jadi kontribusi dalam jumlahan : Jadi secara umum sebarang unit ke-i dalam populasi akan memberikan kontribusi sebesar dalam jumlahan tersebut, sehingga Terbukti bahwa adalah tak bias untuk. Akibatnya, karena Y = N, maka adalah tak bias untuk Y. Variansi dari yang ditulis V( ) = V( ) dan rumus umumnya dapat diperoleh dan dijabarkan dari definisi, Teorema 2.2 Dalam sampling random sederhana berukuran n yang diambil dari populasi berukuran N dengan variansi, variansi mean sampel, V( ), memenuhi rumus V( ) = (. 13
14 Bukti : Dalam jumlahan pertama, yaitu setiap unit populasi,, memberikan kontribusi sebesar, Jadi Dalam jumlahan kedua, yaitu, setiap pasang unit populasi, dan dengan j > i, memberikan kontribusi sebesar. 14
15 Jadi = = 0 (N 1) = (N 1) = Jadi V( ) = = V( ) sering ditulis dengan rumus V( ) = (1 f ) dengan f = dan disebut fraksi sampel. Kesalahan standar dari, = 2.4 Koreksi Pada Populasi yang Berhingga Jika ukuran populasi, N, sangat besar terhadap ukuran sampel, n, maka fraksi sampel, f =, mendekati nol. Dalam kasus seperti ini rumus variansi dari menjadi V( ) =, ( tanpa faktor (1 f) ), dan kesalahan standar dari menjadi 15
16 = Demikian pula, V( ) dan menjadi V( ) =, (tanpa faktor (1 f)), dan = Faktor (1 f) dalam rumus-rumusv( ) dan V( ) disebut faktor koreksi pada populasi yang berhingga yang dalam bahasa Inggris, finite population correction, ditulis fpc. Faktor fpc berperan memberikan koreksi pada V( ) maupun V( ) pada kasus populasi berhingga, apabila fraksi sampel, f, tidak terlalu kecil. Jadi, jika f sangat kecil maka fpc diabaikan dan jika f tak terlalu kecil maka fpc tak diabaikan. Dalam praktek biasanya fpc diabaikan jika f < 5 %. 2.5 Estimasi Kesalahan Standar Dalam praktek, variansi populasi, pada umumnya tidak diketahui. Pengetahuan tentang nilai, jika ada biasanya hanya melalui asumsi atau anggapan saja. Akibatnya V( ), V( ),, dan tak dapat diperoleh nilainya. Perlu ada estimasi untuk variansi dan kesalahan standar dari dan. Estimasi untuk V( ) akan ditulis atau v ( ) Estimasi untuk V( ) akan ditulis atau v( Estimasi untuk akan ditulis s( ) Estimasi untuk akan ditulis s( ) Teorema 2.3 Dalam sampling random sederhana berukuran n yang diambil dari populasi berukuran N, variansi sampel,, adalah suatu estimator tak bias untuk variansi populasi Bukti : dapat ditulis 16
17 Jadi = ( N 1) = ( nn n N+n) = Ini berarti tak bias untuk Berdasarkan teorema 2.3, dengan mengganti diganti dalam rumus untuk V( ) dan V( ) diperoleh hasil, dan = v ( ) = (1 f), tak bias untuk V( ) = (1 f) tak bias untuk V( ) Dalam praktek variansi dari dihitung dengan menggunakan rumus estimasi, yaitu, = v ( ) = (1 f) Demikian pula variansi dari dihitung dengan rumus estimasinya, 17
18 = v( = (1 f) Dan selanjutnya kesalahan standar dari dihitung dengan rumus s( = s Dan kesalahan standar dari dihitung dengan rumus s( ) = Ns 2.6 Batas-Batas Konfidensi Untuk sampel berukuran besar, mean sampel,, berdistribusi mendekati normal dengan mean dan variansi V( ) yang estimasinyav( ). Berdasarkan distribusi tersebut diperoleh batas-batas konfidensi ( 1 ) untuk adalah, = -, = + atau = -, = + bila fpc dapat diabaikan. Nilai dan disebut batas konfidensi bawah dan batas konfidensi atas untuk, dan berlaku P( ) = ( 1 ) Demikian pula batas-batas konfidensi ( 1- ) untuk Y adalah = N( ), = N( ) atau = N( ), = N( ) bila fpc dapat diabaikan. 2.7 Estimator Rasio Dalam suatu survei sampel, kadang-kadang paramater yang akan diestimasi adalah rasio dari dua parameter yang berbeda. Sebagai contoh, jika Y adalah total 18
19 biaya hidup per bulan dan tangga di kota K, maka rasio, adalah total penghasilan per bulan seluruh rumah yang didefinisikan = menunjukkan proporsi atau persentase dari penghasilan rumah tangga yang dibelanjakan untuk keperluan biaya hidup. Selanjutnya jika adalah total banyaknya anggota seluruh rumah tangga di kota K, maka rasio yang didefinisikan = menunjukkan mean penghasilan per bulan per anggota rumah tangga di kota K. Kiranya perlu kejelian untuk dapat membedakan interpretasi = dengan dalam contoh ini, menunjukkan mean penghasilan per bulan per rumah tangga dari seluruh rumah tangga di kota K. Dalam contoh ini pula, parameter apakah yang menyatakan : mean biaya hidup per bulan per anggota rumah tangga di kota K? Dan parameter apakah yang menyatakan : mean biaya hidup per bulan per rumah tangga di kota K? Misalkan unit-unit populasi berbentuk pasangan,, i =1,2,..., N, dan misalkan =, =, Parameter rasio, R, didefinisikan 19
20 R = atau R = Dalam pasal ini, dengan sampling random sederhana berukuran n akan dipelajari estimator untuk R beserta sifatnya. Misalkan adalah unit-unit sampel dalam sampling random sederhana berukuran n. Maka dan Merupakan estimator tak bias untuk dan. Jadi beralasan untuk menggunakan = sebagai estimator untuk R. Estimator,, bersifat bias untuk R, karena E ( ) R. Jadi RKK( = E E = V( ) Namun jika ukuran sampel, n, besar, maka mendekati tak bias untuk R dengan variansi seperti yang dinyatakan dalam teorema berikut, Teorema 2.4 Dalam sampling random sederhana berukuran n,, jika n besar maka mendekati tak bias untuk R dan variansinya Lambang artinya mendekati. Bukti : R =, =, untuk n besar, 20
21 = R = Sehingga E( ) E ( = ( E( ) E( ) ) = 0, jadi mendekati tak bias untuk R. Selanjutnya V( ) = E E E = adalah mean sampel dari = R dengan mean populasi Jadi V( ) = (1 f ) = = (1 f ) Dalam praktek rumus pendekatan variansi, V( ), pada kasus n besar, nilai V( ) tidak dapat diperoleh, sehingga diperlukan estimasinya. Estimator tak bias untuk V( ) adalah, ) = v( ) = Jika dalaam rumus ini nilai tidak diketahui, dapat diganti dengan. Selanjutnya kesalahan standar dari adalah, s( = = Untuk maksud penghitungan dapat dipakai rumus lain untuk pada kasus n besar, = 21
22 Pada kasus tidak diketahui, diganti dengan, dan kasus fraksi sampel kecil, fpc,( 1 ), dapat diabaikan dalam penghitungan. 2.8 Estimasi Mean dan Total Sub-Populasi Dalam beberapa survei, kadang-kadang estimasi dilakukan untuk parameter-parameter bagian dari populasi atau sub-populasi. Jadi, sampling dilakukan pada populasi guna mengestimasi paramater-parameter sub-populasi. Sub-populasi tersebut dinamakan domain penelitian. Dalam survei rumah tangga misalnya, estimasi diinginkan untuk paramater rumah tangga yang memiliki anak usia balita atau estimasi parameter rumah tangga yang masuk kategori pra sejahtera Dalam pasal ini parameter-parameter yang akan diestimasi adalah mean dan total sub-populasi. Misalkan sub-populasi atau domain penelitian ke-j mempunyai ukuran dan dalam sampling random sederhana berukuran n, terdapat berasal dari sub-populasi tersebut. Misalkan unit sampel yang adalah unit-unit subpopulasi. Maka total sub-populasi tersebut adalah, dan meannya adalah, Serta variansi sub-populasi adalah, = = Misalkan adalah unit-unit dalam sampling random sederhana berukuran n, yang berasal dari sub-populasi. Maka mean unit-unit tersebut 22
23 dan variansinya, = Dari seluruh sampel berukuran n dengan tertentu, n, probabilitas diperoleh unit-unit spesifik dari unit sub-populasi adalah, = Nilai probabilitas ini memberi gambaran seolah-olah sampling random sederhana berukuran diambil dari sub-populasi berukuran. Berdasarkan hasil-hasil di muka maka estimator tak bias untuk mean sub-populasi,, adalah, dengan variansi, V( ; =, dan kesalahan standarnya, Dalam praktek, variansi dan kesalahan standar dari dihitung dengan rumus estimasinya, yaitu, = v( ) = ( ) s( ) = = kecuali jika diketahui, Untuk mengestimasi total sub-populasi,, perlu ditinjau pengetahuan tentang ukuran sub-populasi,, dalam kasus 1 dan kasus 2 berikut : Kasus 1, diketahui. 23
24 Estimator tak bias untuk adalah dengan variansi, dan kesalahan standarnya V ( = = ( 1 ) = = Estimasi untuk variansi dan kesalahan standar dari adalah ) = v( = ( s( ) = Kasus 2, tidak diketahui. Estimator untuk total sub-populasi dalam kasus ini diperoleh demikian : Untuk setiap unit populasi,, didefinisikan dengan Maka total dalam populasi adalah memenuhi, Mean dalam sampel berukuran n adalah merupakan estimator tak bias untuk. Jadi estimator tak bias untuk adalah 24
25 dengan variansi, V( ) = V( ) = (1 f) dengan Kesalahan standar dari adalah, Penghitungan variansi dan kesalahan standar dari dalam praktek digunakan rumus estimasinya, yaitu, ) = v( ) = (1 f) s( ) = = Dari kasus 1 dan kasus 2 diatas, jika diketahui maka terdapat dua buah estimator untuk total sub-populasi,, yang dapat digunakan yaitu, = dan = N dan jika tidak diketahui, hanya estimator yang dapat digunakan. Apabila terdapat dua atau lebih estimator untuk suatu parameter, yang dipilih adalah estimator dengan kesalahan standar yang terkecil, yang berarti memiliki keakuratan yang tertinggi. Soal-soal latihan : 1. Sebuah kota mempunyai 50 buah hotel dengan kamar sebanyak 1500 buah. Sebuah sampel random sederhana 5 buah jotel diketahui jumlah kamar dan timgkat hunian ( persen kamar terisi saat musim liburan ) 25
26 No Hotel Jumlah Kamar Tingkat Hunian % % % % % a. Estimasikanlah mean tingkat hunian seluruh hotel di kota tersebut saat musim liburan. b. Jika tiap kamar rata-rata terisi 2 orang tamu (bagi kamar yang terisi), estimasikanlah total jumlah tamu yang tinggal diseluruh hotel di kota tersebut saat musim liburan. 2. Sebuah Kabupaten dihuni rumah tangga (rt), dan diketahui 500 rt diantaranya memiliki sapi. Sebuah sampel random sederhana terdiri 250 rt diketahui distribusi banyaknya sapi yang dimiliki sebagai berikut : Banyaknya sapi Banyaknya rumah tangga a. Dari seluruh rumah tangga pemilik sapi di Kabupaten tersebut, estimasikanlah total banyaknya rt yang sapinya lebih dari 2 ekor, (berikanlah dua buah nilai estimasi), dan hitunglah kesalahan standarnya masing-masing. b. Berikanlah dua buah estimasi untuk total banyaknya sapi yang dimiliki seluruh rumah tangga di Kabupaten tersebut, dan hitung variansi masingmasing. 26
27 3. Sebuah sampel random sederhana 50 orang mahasiswa FMIPA diketahui terdapat 28 orang dari jurusan Matematika, 8 orang dari jurusan Fisika dan yang lainnya dari jurusan Kimia. Dari sampel random tersebut, diperoleh data IPK mahasiswa Fisika sebagai berikut : 3,14 2,98 3,57 2,81 2,97 3,36 3,05 2,52 Diketahui pula total mahasiswa FMIPA 1700 orang, terdiri 675 orang dari jurusan Matematika, 550 orang dari jurusan Fisika, dan yang lainnya dari jurusan Kimia. a. Estimasikanlah mean IPK seluruh mahasiswa jurusan Fisika FMIPA, dan hitunglah pula kesalahan standarnya. b. Berikanlah dua buah nilai estimasi total IPK seluruh mahasiswa jurusan Fisika FMIPA, dan hitunglah dari masing-masing estimasi tersebut nilai kesalahan standarnya. 4. Populasi berukuran 5 unit dengan nilai sebagai berikut : 7, 10, 2, 11, 20. Diperhatikan sampel random sederhana berukuran 3, dan dua buah estimator bagi total populasi, Y sebagai berikut : Estimator pertama, = 5, estimator kedua yang didefinisikan: a. Daftarkanlah seluruh sampel yang mungkin terambil, dan hitunglah dan dari masing-masing sampel. b. Tunjukkanlah bahwa dan masing-masing merupakan estimator tak bias bagi Y. c. Hitunglah variansi dari dan. d. Untuk nilai k berapakah V( mencapai minimum? Hitunglah pula ( ). 27
28 5. Suatu sampel random sederhana berukuran 50 dengan mean diambil dari sebuah populasi berukuran 1000 dengan variansi Dari sampel tersebut diambil sub-sampel random sederhana berukuran 30 dengan mean. Misalkan adalah mean dari 20 unit sampel sisanya. Hitunglah : a. V( ) b. V( ) c. Kov(, ) 28
29 BAB III SAMPLING RANDOM SEDERHANA UNTUK PROPORSI 3.1 Karakteristik Kualitatif Dalam survei sampel, kadang-kadang parameter yang akan diestimasi adalah total banyak unitt, proporsi atau persentase unit populasi yang mempunyai karakteristik atau sifat tertentu. Dalam survei rumah tangga misalnya, ingin diestimasi berapa total banyaknya rumah tangga yang berhak mendapatkan bantuan dalam Program Sosial Pemerintah dari seluruh rumah tangga yang tinggaldi kota K. Hal ini diperlukan sekali untuk menetapkan anggaran yang perlu disediakan dalam program tersebut untuk seluruh rumah tangga di kota K. Dari pengamatan sejumlah komponen tertentu dari hasil produksi, diinginkan untuk mengetahui berapa persentase komponen-komponen yang cacat dari seluruh hasil produksi tersebut. Dari seluruh mahasiswa di sebuah universitas yang menggunakan ponsel, ingin diestimasi proporsi dan total banyaknya mahasiswa yang ponselnya merk M. Hasil pencacahan terhadap setiap unit sampel dijawab dengan ya ( berhak mendapatkan; cacat; memakai merk M ) atau tidak. Dengan demikian setiap unit akan masuk kedalam salah satu dari 2 kelas klasifikasi, sebut saja kelas C dan kelas. Misalkan N adalah ukuran populasi, A adalah total banyaknya unit populasi yang masuk kelas C dan P adalah proporsi atau persentase unit populasi yang masuk kelas C, yaitu P =. Parameter P dan A tidak diketahui nilainya dan dalam bab ini akan dipelajari statistik estimator untuk parameter-parameter tersebut beserta sifat-sifatnya. 3.2 Estimator Untuk Proporsi dan Total Banyak Unit Serta Variansinya. Dalam sampling random sederhana berukuran n, misalkan aadalah banyaknya unit sampel yang masuk kelas C, dan p adalah proporsi unit sampel yang masuk kelas C, yaitu p =. Maka diperoleh teorema berikut : 29
30 Teorema 3.1 Proporsi sampel, p =, adalah estimator yang tak bias untuk proporsi populasi, P =, dengan variansi V(p) = E(p P = ( ), dengan Q = 1 P Bukti : Untuk setiap unit dalam populasi didefinisikan = 1, jika masuk kelas C dan = 0, jika unit masuk kelas. Maka untuk nilai-nilai populasi ini, total populasi, dan mean populasi, = = = P Mean untuk sampelnya, = = = p dengan demikian total banyak unit populasi yang masuk kelas C dapat dipandang atau merupakan total populasi khusus yaitu populasi yang nilai unit-unitnya 1 atau 0, dan proporsi populasi adalah mean dari populasi tersebut. Berdasarkan Teorema 2.1, maka p tak bias untuk P. Untuk populasi tersebut, sehingga = ( NP N ) = PQ, dengan Q =1 P 30
31 Secara sama, untuk sampel, diperoleh = pq, dengan q = 1 p. Dan berdasarkan teorema 2.2 diperoleh bukti, V(p) = V( ) = = = ( ) Dari teorema 2.3, = adalah estimator tak bias untuk =, jadi estimator tak bias untuk V(p) adalah, (p) =v(p) = = = ( ) Karena A = NP, maka estimator tak bias untuk A adalah = Np dengan variansi, V( ) = V(p) = PQ Estimator tak bias untuk V( ) adalah ( ) = v ( ) = v(p) = pq Dari rumus-rumus diatas, jelas bahwa dalam terapan V(p) dan V( ) tidak dapat dihitung nilainya, karena memuat parameter P yang tidak diketahui nilainya, dan justru akan diestimasi. Maka variansi dari p dan variansi dari dihitung dari rumus estimatornya saja, yaitu v(p) dan v( ). Rumus lain untuk v(p) dan v( ) adalah v(p) = (1 f) v( ) = (1 f) Dari rumus ini, jika faktor koreksi dapat diabaikan maka v(p) dan v( ) menjadi, v(p) =, v( ) = 31
32 3.3 Pengaruh Nilai Proporsi P Pada Kesalahan Standar Dari rumus V(p) dimuka, V(p) =, jika faktor koreksi diabaikan, maka V(p) =, dan kesalahan standarnya, = Nilai PQ dan untuk beberapa nilai P seperti dalam tabel berikut ( P dalam persen ), P PQ Nilai maksimum adalah 50 % dicapai pada nilai P = 50 %. Pada selang 30 % P 0,70 % nilai tak jauh berubah dari 50 %, tetapi pada selang P < 30 % atau P > 70 %, nilai akan jauh berubah dari 50 %. Untuk P = 50 %, keinginan untuk mendapatkan kesalahan standar dari estimasi, = 5 %, diperlukan sampel sebesar n =100. Dan n = 100 ini tidak berubah banyak untuk 40 % P 60 %. Jika diinginkan kesalahan yang lebih kecil lagi pada nilai P dalam selang tersebut, misalnya kesalahan standar sebesar 2 %, maka ukuran sampel yang diperlukan jauh meningkat menjadi 625. Ini berarti untuk nilai P sekitar 50 %, untuk menurunkan kesalahan standar dari 5 % menjadi 2 %, diperlukan penambahan ukuran sampel dari 100 menjadi 625. Pada kondisi sebaliknya, untuk n tetap, kesalahan standar dari p sekitar untuk 40 % P 60 %, tidak banyak berubah yang berarti tidak besar 32
33 pengaruhnya terhadap V(p). Namun jika P < 30 % atau P > 70 %, maka pengaruhnya terhadap V(p) sangat besar. 3.4 Batas-Batas Konfidensi Dalam sampling random sederhana berukuran n yang diambil dari populasi berukuran N, banyaknya unit sampel yang masuk kelas C yaitu a, berdistribusi hipergeometrik dengan distribusi probabilitas, P(a = ) =, = 0, 1, 2,..., n dan pada populasi yang berukuran sangat besar, distribusi dari a akan mendekati Binomial, P(a = ) = Pendekatan selanjutnya, jika ukuran sampel relatif besar, maka distribusi dari a akan mendekati normal dengan mean, E(a) = np dan variansi v(a) = v(p). Dalam keadaan ini pula, p berdistribusi mendekati normal dengan mean, E(p) = P dan variansi v(p). Berdasarkan distribusi ini, diperoleh batas-batas konfidensi (1 ) untuk P, yaitu : = p, = p + Batas-batas konfidensi ( 1 ) untuk A adalah =N, =N Batas-batas konfidensi tersebut berlaku untuk sampel berukuran besar. 3.5 Klasifikasi ke Dalam Lebih Dari Dua Kelas Dalam sebuah survei, seringkali responden diminta memilih salah satu dari beberapa (lebih dari dua) jawaban yang tersedia. Maka hasil pencacahan unit-unit sampel akan terklasifikasi lebih dari dua kelas. Pertanyaan kepada mahasiswa tentang merk motor yang dipakai ke tempat kuliah dengan jawaban pilihan: 33
34 Honda, Yamaha, Suzuki, dll. Maka klasifikasi yang terjadi adalah 4 kelas. Pertanyaan berapa jumlah anggota rumah tangga Anda? Jawaban yang masuk adalah 1, 2, 3, 4, 5, lebih dari 5. Disini terjadi klasifikasi ke dalam 6 kelas. Pertanyaan, siapa calon yang akan Anda pilih dalam Pilkada yang akan datang diantara tiga calon yang sudah ditetapkan? Unit atau jawaban akan terklasifikasi ke dalam 3 kelas. Jika terjadi klasifikasi unit ke dalam lebih dari dua kelas, maka permasalahan yang harus diselesaikan dapat berupa, (a) Estimasi proporsi unit populasi yang masuk kelas C. (b) Estimasi total banyaknya unit populasi yang masuk kelas C. (c) Estimasi proporsi unit sub-populasi yang masuk kelas C. (d) Estimasi total banyaknya unit sub-populasi yang masuk kelas C. Sebagai contoh, misalkan di kota Baru beredar 7 merk sabun cuci dalam pasaran, yaitu merk,,,,,,. Merk, dan adalah produk pabrik K, merk dan adalah produk pabrik L, dan adalah produk pabrik yang lainnya. Dalam sampling random sederhana, terdiri n rumah tangga yang diambil dari seluruh ( N ) rumah tangga yang tinggal di kota Baru tersebut, kita diminta menyelesaikan masalah estimasi beberapa parameter, yaitu : (1) Proporsi rumah tangga pemakai merk, dari seluruh rumah tangga di kota Baru. (2) Total banyaknya rumah tangga di kota Baru yang memakai merk produk pabrik L (3) Proporsi rumah tangga pemakai merk dari seluruh rumah tangga pemakai produk pabrik K di kota Baru. (4) Total banyaknya rumah tangga pemakai merk atau di kota Baru. Penyelesaian masalah : (1) Dengan mendefinisikan kelas C sebagai kelas rumah tangga pemakai merk, maka (1) merupakan masalah estimasi proporsi unit populasi yang masuk kelas C. 34
35 (2) Dengan mendefinisikan kelas C sebagai kelas rumah tangga pemakai merk produk L maka (2) merupakam masalah estimasi total banyaknya unit populasi yang masuk kelas C. Adanya informasi yang lebih banyak seperti misalnya informasi tentang total banyaknya rumah tangga pemakai merk produk K dan L, maka (2) dapat dipandang sebagai masalah estimasi total banyaknya unit sub-populasi yang masuk kelas C, dengan memandang informasi tersebut sebagai ukuran sub-populasi. (3) Dengan mendefinisikan kelas C sebagai kelas rumah tangga pemakai merk dan seluruh rumah tangga pemakai produk pabrik K sebagai subpopulasi, maka (3) merupakan masalah estimasi proporsi unit sub-populasi yang masuk kelas C. (4) Dengan mendefinisikan kelas C sebagai kelas rumah tangga pemakai merk atau, maka (4) merupakan masalah estimasi total banyaknya unit populasi yang masuk kelas C. Dengan informasi yang lebih seperti yang tersebut dalam (2), maka (4) dapat dipandang sebagai masalah estimasi total banyaknya unit sub-populasi yang masuk kelas C. Adanya informasi yang lebih banyak seperti yang tersebut dalam penyelesaian masalah (2) dan (4), menjadikan masalah estimasi total banyaknya unit yang masuk kelas C memiliki estimator yang tidak tunggal. Masing-masing masalah (2) dan (4) di atas mempunyai dua buah estimator dan kita dapat menunjuk estimator manakah yang lebih akurat berdasarkan nilai kesalahan standarnya. Misalkan unit-unit populasi diklasifikasikan ke dalam salah satu dari k kelas, yaitu kelas,,,.... Misalkan N adalah ukuran populasi, adalah total banyaknya unit populasi yang masuk kelas, dengan tidak diketahui, maka, = + = N Dengan sampling random sederhana berukuran n, akan dipelajari masalah estimasi untuk beberapa parameter, yaitu seperti misalnya, 35
36 (1) Estimasi untuk (2) Estimasi untuk (3) Estimasi untuk (4) Estimasi untuk (5) Estimasi untuk (6) Estimasi untuk + (7) Estimasi untuk + Misalkan dari sampel yang diambil diperoleh banyaknya unit sampel yang masuk kelas adalah ; i = 1, 2, 3,...k Maka Berdasarkan pembahasan dimuka bahwa p adalah estimator tak bias untuk P dengan estimasi variansi tak biasnya, v(p) = (1 f) dan adalah estimator tak bias untuk A dengan estimasi variansi tak biasnya, v( ) = (1 f) maka diperoleh hasil-hasil sebagai berikut, (1) Estimator tak bias untuk adalah p =, dengan estimasi variansi tak biasnya v( ) = v(p) = (1 f), dengan p = (2) Estimator tak bias untuk adalah p = dengan variansi tak biasnya v( ) = v(p) = (1 f), dengan p = 36
37 (3) Dengan memandang gabungan kelas, dan sebagai subpopulasi atau domain penelitian, estimator tak bias untuk adalah, =, dengan = dengan estimasi variansi tak biasnya, v( ) = v( ) = (1 ), dengan = dan =. (4) Dengan memandang hal yang sama seperti dalam (3), estimator tak bias untuk adalah = dengan =, dengan estimasi variansi tak biasnya v( ) = v( ) = (1 ), dengan = dan =. Hasil-hasil estimasi dalam (5), (6) dan (7), jika = diketahui nilainya, maka ada dua buah estimator, tetapi jika tak diketahui nilainya, hanya ada sebuah estimator hasilnya sebagai berikut, (5) Jika = diketahui, maka estimator tak bias untuk adalah : Pertama ; =, dengan = dan =, dengan estimasi variansi v( ) = v( ) = (1 ) Kedua ; = Np, dengan p = dan dengan estimasi variansi v( ) = v(p) = (1 f) (6) Jika = diketahui, maka estimator tak bias untuk ( ) adalah, 37
38 Pertama ; = dengan = dan =, dengan estimasi variansi, v( ) = v( ) = (1 ) Kedua ; = Np, dengan p = dan dengan estimasi variansi v( ) = v(p) = (1 f) (7) Jika = diketahui maka estimator tak bias untuk ( ) adalah seperti pada (6) dengan = dan p = dalam masalah estimasi (5), (6) dan (7) jika tidak diketahui maka hanya estimator kedua yang dapat digunakan. Soal-soal latihan : 1. Unit-unit sebuah populasi diklasifikasikan ke dalam kelas-kelas,, dan. Misalkan adalah banyaknya unit populasi yang masuk kelas, i =1, 2, 3, 4 ; dan =. Nilai dan tidak diketahui. Dari populasi ini diambil sampel random sederhana berukuran n dan misalkan adalah banyaknya unit sampel yang masuk kelas. a) Tentukan estimator untuk dan tuliskanlah rumus variansinya. b) Tentukan estimator untuk dan tuliskanlah variansinya. c) Jika nilai diketahui, tentukanlah dua buah estimator untuk dan tuliskanlah masing-masing variansinya. 2. Sebuah kota dihuni rumah tangga, dengan mata pencaharian pokok diklasifikasikan : petani, pedagang, peg. Swasta dan PNS. Sebuah sampel random yang terdiri 800 rumah tangga yang diambil dari kota tersebut diketahui mata pencaharian pokok mereka sbb : petani 350 rt, pedagang 200 rt, peg. Swasta 175 rt, dan PNS 75 rt. Diketahui total banyaknya 38
39 rumah tangga dengan mata pencaharian pokok peg. Swasta atau PNS adalah 3200 rt. a) Estimasikanlah proporsi banyaknya rumah tangga dengan mata pencaharian pokok petani di kota tersebut dan hitunglah pula kesalahan standarnya. b) Berikanlah dua buah nilai estimasi untuk total banyaknya rumah tangga dengan mata pencaharian pokok pedagang di kota tersebut (berapa rt) dan hitunglah pula kesalahan standar dari masing-masing estimasi tersebut. 3. Terkait dengan program wajib belajar 9 tahun,akan diestimasi total banyaknya penduduk kota K yang saat ini berusia antara 6 th dan 16 th. Sebuah sampel random sederhana terdiri 200 rumah tangga diketahui distribusi banyaknya anak yang berusia antara 6 th dan 16 th dalam rumah tangga tersebut sbb : Banyaknya anak usia Banyaknya rumah tangga antara 6 th dan 16 th Diketahui kota K dihuni 3000 rumah tangga, dengan 2000 rumah tangga diantaranya mempunyai anak (anggota rt) yang berusia antara 6 th dan 16 th. Estimasikanlah total banyaknya rumah tangga kota K yang punya anak usia 6 th-16 th lebih dari 2 orang (dua estimasi). Estimasikan pula total banyaknya penduduk kota K ( berikan 2 estimasi ) yang berusia antara 6 th dan 16 th. Hitunglah pula kesalahan standar masing-masing estimasi tersebut. 39
40 4. Dari seluruh mahasiswa Universitas U diketahui 5000 orang mahasiswa memiliki ponsel dan 600 orang diantara mereka harga ponselnya lebih dari Rp ,-. Sebuah sampel random sederhana terdiri 300 orang mahasiswa pemilik ponsel dari universitas tersebut diketahui merk ponsel dan harganya sbb: Harga Merk Merk Merk Merk Lain Tak lebih dari Rp ,- Lebih dari Rp , a. Dari seluruh mahasiswa Universitas U, estimasikanlah total banyaknya mahasiswa pemilik ponsel Merk dan hitung pula kesalahan standarnya. b. Dari seluruh mahasiswa pemilik ponsel Merk, estimasikanlah proporsi mahasiswa yang harga ponselnya tak lebih dari Rp ,- c. Dari seluruh mahasiswa pemilik ponsel yang harganya tak lebih dari Rp ,-, estimasikanlah proporsi mahasiswa pemilik ponsel Merk dan hitung pula kesalahan standarnya. d. Berikanlah dua buah estimasi untuk total banyaknya mahasiswa Universitas U pemilik ponsel Merk yang harganya tak lebih dari Rp ,- dan hitunglah variansi dari masing-masing estimasi tersebut. 5. Estimator tak bias bagi V(p) = adalah v(p) = pq. Jadi (p) = adalah bias bagi V(p). Tentukanlah besarnya bias tersebut, B( (p)). 40
41 BAB IV ESTIMASI UKURAN SAMPEL 4.1 Analisis Masalah dan Spesifikasi Ketelitian Dalam setiap rancangan survei sampel, penentuan ukuran sampel merupakan tahap yang harus dilewati. Ukuran sampel yang diambil akan berhubungan langsung dengan biaya dan waktu. Semakin besar sampel diambil, akan semakin besar pula biaya dan waktu yang diperlukan. Bagaimana hubungan ukuran sampel dengan spesifikasi ketelitian? Spesifikasi ketelitian dalam estimasi merupakan pernyataan ketelitian yang diinginkan dalam estimasi tersebut. Pernyataan ini dapat berupa keakuratan yang diinginkan yang dapat dinyatakan dengan atau melalui kesalahan standar dari estimatornya. Ketelitian yang diinginkan dapat pula dinyatakan melalui tingkat kesalahan dalam estimasi yang masih dapat ditoleransi yang terjadi pada tingkat keyakinan atau probabilitas tertentu. Tingkat kesalahan tersebut harus ditetapkan dengan baik sesuai bidang penerapan estimasi tersebut. Jika diinginkan ketelitian yang tinggi, maka tingkat kesalahan harus ditetapkan dengan nilai yang kecil. 4.2 Rumus Untuk n Dalam Sampling Untuk Proporsi Dalam sampling random sederhana untuk proporsi, misalkan tingkat kesalahan estimasi yang masih dapat ditoleransi adalah d pada tingkat keyakinan atau tingkat konfidensi 1, Ini berarti, P( p P d ) = 1 Dengan menganggap p berdistribusi normal dengan mean, E(p) = P dan variansi V(p) =, maka diperoleh hubungan antara n dan d yaitu, d = Penyelesaian untuk n menghasilkan, 41
42 n = Untuk penggunaan praktis, sebuah perkiraan awal p diperlukan untuk mengganti P dalam rumus di atas sehingga n dapat dihitung. Perkiraan awal p ini dapat diperoleh dengan mengambil sampel awal dan menghitung nilai p dalam sampel tersebut atau menggunakan perkiraan lainnya, misalnya dari hasil survei yang lampau. Dengan nilai perkiraan awal p tersebut, estimasi pertama ukuran sampel adalah, = Jika < 5%, ambil n =. Namun jika 5%, maka ukuran sampel yang diambil, n = = Kesalahan relatif sebuah estimator untuk didefinisikan dengan koefisien variasi dari didefiniskan dengan Misalkan dalam estimasi total banyak unit populasi yang masuk kelas C, yaitu A = NP, kesalahan relatif dalam estimasi diinginkan tidak lebih dari r pada tingkat konfidensi 1. Maka, P( r) = 1 P( p P rp) = 1 Dari hasil di muka, dengan mengganti d dengan rp diperoleh, = dengan p adalah perkiraan awal untuk P. 42
43 4.3 Rumus Untuk n Dengan Data Kontinu Dalam estimasi mean atau total populasi, atau Y, sering diinginkan sebuah kesalahan relatif tidak lebih dari r dalam estimasinya. Jadi, P( r) = 1. Dengan menganggap berdistribusi normal dengan mean dan variansi V( ), maka, r = dengan penyelesaian untuk n n = Estimasi pertama, = Jika < 5 %, ukuran sampel yang diambil n =, dan jika 5%, maka n = = Kadang-kadang sampel yang akan diambil diinginkan agar mempunyai nilai koefisien variasi tertentu. Sebagai misal, untuk mengestimasi, diinginkan agar estimatornya mempunyai nilai koefisien variasi kv =, maka = ; = ; n = Estimasi pertama, = dengan C =, kuadrat dari koefisien variasi. Dalam rumus penghitungan ukuran sampel di atas, sampel awal diambil untuk sekedar memperoleh perkiraan untuk P atau, yang digunakan untuk menghitung dan menetapkan n, dan sampel awal tersebut tak digunakan lagi dalam 43
44 sampling selanjutnya. Dalam praktek metode ini jarang sekali dipakai karena akan memperlambat penyelesaian survei. Metode lain diberikan oleh Cox dan Stein, yaitu dengan mengkombinasikan sampel awal atau sampel pertama yang diambil berukuran, dengan unit-unit tambahan yang diambil dari populasi dan menjadikan ukuran sampel menjadi n. Estimator untuk P atau dari kombinasi sampel tersebut akan berubah sifatnya menjadi bias. Dengan menambahkan estimasi dari bias pada estimator yang bersangkutan akan didapat estimator baru yang tak bias untuk P dan. Hasilnya diberikan dalam rumus-rumus berikut : a) Sampling untuk dengan koefisien variasi ditetapkan kv =. Diambil sampel awal atau sampel pertama berukuran, selanjutnya dihitung mean dan variansinya dan. Dengan menganggap y berdistribusi normal, ambil unit-unit tambahan sehingga ukuran sampel menjadi, n = ( 1 + 8C + + ) Mean sampel akhir,, merupakan estimator yang bias untuk. Ambil estimator yang baru untuk yaitu : = (1 2C) b) Sampling untuk dengan variasi ditetapkan V. Ambil unit-unit tambahan untuk membuat ukuran sampel menjadi, n = (1 + ) c) Sampling untuk P dengan variansi ditetapkan V Misalkan adalah estimasi untuk P dari sampel pertama. Ambil unit-unit tambahan sehingga ukuran sampel menjadi, 44
45 n = + + Proporsi dalam sampel akhir, p, merupakan estimator yang bias untuk P. Untuk menghilangkan bias tersebut gunakan estimator baru untuk P yaitu, = p + d) Sampling untuk P dengan koefisien variasi ditetapkan kv = Ambil unit-unit tambahan untuk membuat ukuran sampel menjadi, n = + + proporsi dalam sampel akhir, p, merupakan estimator yang bias untuk P, dan untuk menghilangkannya, digunakan estimator baru, = p dalam rumus-rumus untuk (a), (b), (c) dan (d) diatas, dianggap < n. Unit-unit tambahan diambil untuk menjadikan sampel tersebut menjadi berukuran n. Jadi sampel baru berukuran n merupakan gabungan sampel pertama dengan unit-unit tambahan tersebut. Soal-soal latihan : 1. Fakultas Teknik mempunyai mahasiswa sebanyak 2800 orang. Sebuah sampel random sederhana akan diambil dari mahasiswa fakultas tersebut guna mengestimasi total banyaknya mahasiswa yang tinggal di tempat kos. Kesalahan estimasi diinginkan tidak lebih dari 50 orang pada tingkat konfidensi 95 %. Berapa ukuran sampel yang harus diambil jika estimasi untuk banyaknya mahasiswa yang tinggal di tempat kos adalah 500 orang? 2. Wilayah Kecamatan Duren merupakan penghasil buah durian. Hampir di setiap halaman rumah tangga tertanam pohon durian. Guna mengestimasi 45
46 total banyaknya pohon durian yang tumbuh di kecamatan tersebut akan digunakan sampling random sederhana, terdiri beberapa rumah tangga. Hasil estimasi nanti diinginkan memiliki koefisien variasi 0,18. Telah diambil sampel pertama berukuran 60 rumah tangga dan diperoleh mean banyaknya pohon tiap rumah tangga 4,8 dan deviasi standar 7,1. Tentukan ukuran sampel yang harus diambil, n. Selanjutnya jika dari sampel tersebut diperoleh Y = 8604 pohon. Tentukan estimasi akhir total banyaknya pohon durian di kecamatan Duren. 46
47 BAB V SAMPLING RANDOM BERSTRATA 5.1 Pengambilan Sampel Random Berstrata Untuk mengambil sampel random berstrata dari populasi berukuran N, mula-mula populasi dibagi menjadi beberapa bagian yang masing-masing berukuran,,..., unit. Bagian-bagian populasi tersebut dinamakan strata atau lapisan, dan tidak boleh overlap, sehingga, = N dengan L = banyaknya strata. Untuk memperoleh manfaat, nilai, h = 1,2,...,L harus diketahui. Jika strata-strata sudah ditentukan, sebuah sampel diambil dari masing-masing strata secara random dan independen gabungan dari seluruh sampel yang diambil dari setiap strata disebut sampel random berstrata. Jadi, jika adalah ukuran sampel dari strata ke-h, h =1,2,...,L dan n adalah ukuran sampel random berstrata, maka < n untuk setiap h, dan Nilai-nilai = n, h = 1,2,...,L disebut alokasi sampel. Stratifikasi atau pembagian populasi menjadi sejumlah strata, adalah sebuah teknik biasa, namun ada beberapa prinsip atau alasan mengapa hal tersebut dilakukan. Alasan dimaksud antara lain : 1) Jika dalam estimasi diinginkan ketelitian atau keakuratan pada bagianbagian dari populasi, per lakukan bagian-bagian tersebut sebagai subpopulasi dan selanjutnya dipandang sebagai strata. 2) Administrasi yang baik dapat menarik manfaat dari stratifikasi. Sebagai contoh sebuah pusat agensi dapat menggunakan kantor-kantor cabang sebagai strata. Lebih konkritnya misalnya, hasil UNAS SMA di wilayah sebuah kantor Diknas di kota K dapat menggunakan hasil UNAS semua siswa di seluruh SMA di wilayah kota tersebut. Semua siswa peserta UNAS di setiap SMA tersebut dipandang sebagai strata. 47
48 3) Masalah sampling dapat berbeda diantara bagian-bagian populasi. Perbedaan itu dapat berupa biaya per unit sampling, dapat pula berupa adat atau kebiasaan responden. Sebuah survei yang berpusat di kota Yogyakarta pada populasi rumah tangga yang tinggal di provinsi DIY, biaya per unit sampling di kota Yogyakarta, dan 4 kabupaten lainnya, Sleman, Bantul, Kulonprogo dan Gunung Kidul dapat berbeda. Responden yang tinggal di rumah dinas mempunyai adat kebiasaan yang berbeda dengan responden yang tinggal di rumah-rumah biasa. 5.2 Definisi dan Notasi Misalkan N adalah ukuran populasi, dan adalah ukuran strata ke-h, h = 1,2,3,...L. Unit-unit strata ke-h ditulis dengan lambang,,...,. Total strata ke-h dan mean strata ke-h ditulis dan adalah, = Variansi strata ke-h, ditulis adalah, atau Dalam sampling random berstrata berukuran n, misalkan adalah alokasi sampel pada strata ke-h. Mean dan variansi sampel dari strata ke-h ditulis dan adalah : dan 48
49 atau Nilai disebut bobot strata dan = disebut fraksi sampel dari strata ke-h. 5.3 Sifat-Sifat Estimator Mean dan Total Serta Variansinya Dalam sampling random berstrata, estimator untuk total populasi, Y, ditulis dengan adalah : dan estimator untuk mean populasi,, ditulis atau adalah : Rumus-rumus estimator tersebut diperoleh dengan alasan sebagai berikut. Mean sampel dari strata ke-h,, adalah estimator tak bias untuk, sehingga tak bias untuk. Karena Y =, maka tak bias untuk Y dan selanjutnya tak bias untuk. Variansi dari diberikan dalam teorema berikut. Teorema 5.1 Dalam sampling random berstrata, variansi dari adalah, Bukti : 49
50 Karena tak bias untuk, maka menurut teorema 2.2, V( ) = = ( 1 ) dan karena sampel-sampel dari setiap strata independen, maka, dari teorema 5.1 akan diperoleh variansi dari, yaitu, V( ) = V(N ) = V( ) Dalam kasus faktor koreksi, fpc, dapat diabaikan maka, dan Ada beberapa alokasi sampel yang mempunyai sifat tertentu yaitu alokasi sama untuk setiap strata dan alokasi proporsional. Sampling random berstrata dikatakan mempunyai alokasi sama, jika nilai sama untuk semua h, dan dikatakan mempunyai alokasi proporsional jika sebanding dengan ukuran strata. Jadi dalam alokasi sama, = dan dalam alokasi proporsional, = n. Rumus variansi dari dalam alokasi proporsional mempunyai bentuk yang lebih sederhana yaitu, 50
51 Nilai V( ) tidak bergantung pada n, tetapi bergantung pada alokasi sampel. Meskipun ukuran sampel, n, sama, tetapi jika alokasinya berbeda akan menghasilkan variansi yang berbeda. Sebuah pertanyaan yang menarik adalah, jika n ditetapkan, alokasi manakah yang akan menghasilkan V( ) minimum? Masalah ini akan dipelajari dalam pasal Estimasi Variansi dan Batas-Batas Konfidensi Dalam sampling random berstrata estimator dan selalu dapat dihitung nilainya, tetapi variansinya dalam terapan umumnya tidak dapat dihitung karena memuat parameter yang tidak diketahui nilainya. Oleh karena itu diperlukan estimasi untuk V( ). Berdasarkan teorema 2.3, diperoleh bahwa adalah estimator tak bias untuk. Jadi estimator tak bias untuk V( ) adalah, dan estimator tak bias untuk V( ) adalah, Dalam terapan variansi dari estimator untuk mean dan variansi dari estimator untuk total populasi dihitung dengan rumus-rumus yang terakhir ini. Jika ukuran sampel, besar maka akan berdistribusi mendekati normal dengan mean dan variansi v( ). Dari distribusi ini batas-batas konfidensi (1 ) untuk adalah, dan batas-batas konfidensi (1 ) untuk Y adalah, = 51
PENAKSIRAN RATAAN DAN VARIANSPOPULASI PADA SAMPEL ACAK TERSTRATIFIKA DENGAN AUXILIARY VARIABLE
 Vol. 12, No. 1, 9-18, Juli 2015 PENAKSIRAN RATAAN DAN VARIANSPOPULASI PADA SAMPEL ACAK TERSTRATIFIKA DENGAN AUXILIARY VARIABLE Raupong, M. Saleh AF, Hasruni Satya Taruma Abstrak Penaksiran rataan dan variansi
Vol. 12, No. 1, 9-18, Juli 2015 PENAKSIRAN RATAAN DAN VARIANSPOPULASI PADA SAMPEL ACAK TERSTRATIFIKA DENGAN AUXILIARY VARIABLE Raupong, M. Saleh AF, Hasruni Satya Taruma Abstrak Penaksiran rataan dan variansi
Statistika (MMS-1403)
 Statistika (MMS-1403) Dr. Danardono, MPH danardono@ugm.ac.id Program Studi Statistika Jurusan Matematika FMIPA UGM MMS-1403 p.1/93 Distribusi Sampling Statistik Populasi: himpunan keseluruhan obyek yang
Statistika (MMS-1403) Dr. Danardono, MPH danardono@ugm.ac.id Program Studi Statistika Jurusan Matematika FMIPA UGM MMS-1403 p.1/93 Distribusi Sampling Statistik Populasi: himpunan keseluruhan obyek yang
BAB 6 PENAKSIRAN PARAMETER
 BAB 6 PENAKSIRAN PARAMETER Bab 6 PENAKSIRAN PARAMETER Standar Kompetensi : Setelah mengikuti kuliah ini, mahasiswa dapat memahami hubungan nilai sampel dan populasi dan menentukan distribusi sampling yang
BAB 6 PENAKSIRAN PARAMETER Bab 6 PENAKSIRAN PARAMETER Standar Kompetensi : Setelah mengikuti kuliah ini, mahasiswa dapat memahami hubungan nilai sampel dan populasi dan menentukan distribusi sampling yang
KONSISTENSI ESTIMATOR
 KONSISTENSI ESTIMATOR TUGAS STATISTIKA MATEMATIKA II Oleh 1. Wahyu Nikmatus S. (121810101010) 2. Vivie Aisyafi F. (121810101050) 3. Rere Figurani A. (121810101052) 4. Dwindah Setiari W. (121810101054)
KONSISTENSI ESTIMATOR TUGAS STATISTIKA MATEMATIKA II Oleh 1. Wahyu Nikmatus S. (121810101010) 2. Vivie Aisyafi F. (121810101050) 3. Rere Figurani A. (121810101052) 4. Dwindah Setiari W. (121810101054)
Sampling, Estimasi dan Uji Hipotesis
 Sampling, Estimasi dan Uji Hipotesis Tujuan Pembelajaran Memahami perlunya suatu sampling (pengambilan sampel) serta keuntungan- keuntungan melakukannya Menjelaskan pengertian sampel acak untuk sampling
Sampling, Estimasi dan Uji Hipotesis Tujuan Pembelajaran Memahami perlunya suatu sampling (pengambilan sampel) serta keuntungan- keuntungan melakukannya Menjelaskan pengertian sampel acak untuk sampling
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI 2.1 Regresi Linier Sederhana Dalam beberapa masalah terdapat dua atau lebih variabel yang hubungannya tidak dapat dipisahkan karena perubahan nilai suatu variabel tidak selalu terjadi
BAB 2 LANDASAN TEORI 2.1 Regresi Linier Sederhana Dalam beberapa masalah terdapat dua atau lebih variabel yang hubungannya tidak dapat dipisahkan karena perubahan nilai suatu variabel tidak selalu terjadi
DISTRIBUSI PROBABILITAS DISKRIT TEORITIS 2. Distribusi Hipergeometrik
 DISTRIBUSI PROBABILITAS DISKRIT TEORITIS 2 TI2131 TEORI PROBABILITAS MINGGU KE-10 Distribusi Hipergeometrik Eksperimen hipergeometrik memiliki karakteristik sebagai berikut: 1. sebuah sampel random berukuran
DISTRIBUSI PROBABILITAS DISKRIT TEORITIS 2 TI2131 TEORI PROBABILITAS MINGGU KE-10 Distribusi Hipergeometrik Eksperimen hipergeometrik memiliki karakteristik sebagai berikut: 1. sebuah sampel random berukuran
MODUL TEORI ESTIMASI ATAU MENAKSIR TEORI ESTIMASI ATAU MENAKSIR
 TEORI ESTIMASI ATAU MENAKSIR MODUL 9 TEORI ESTIMASI ATAU MENAKSIR. Pendahuluan Untuk menginginkan mengumpulkan populasi kita lakukan dengan statistik berdasarkan data yang diambil secara sampling yang
TEORI ESTIMASI ATAU MENAKSIR MODUL 9 TEORI ESTIMASI ATAU MENAKSIR. Pendahuluan Untuk menginginkan mengumpulkan populasi kita lakukan dengan statistik berdasarkan data yang diambil secara sampling yang
BAB 2 TINJAUAN PUSTAKA
 BAB 2 TINJAUAN PUSTAKA Pada bab ini akan dibahas tinjauan pustaka yang akan digunakan untuk tesis ini, yang selanjutnya akan diperlukan pada bab 3. Yang akan dibahas dalam bab ini adalah metode bootstrap
BAB 2 TINJAUAN PUSTAKA Pada bab ini akan dibahas tinjauan pustaka yang akan digunakan untuk tesis ini, yang selanjutnya akan diperlukan pada bab 3. Yang akan dibahas dalam bab ini adalah metode bootstrap
BAB IV INFERENSI STATISTIK SATU POPULASI SEMBARANG
 BAB IV INFERENSI STATISTIK SATU POPULASI SEMBARANG Bab ini akan membahas inferensi statistik terhadap mean suatu populasi sembarang dan proporsi suatu populasi dikotomi/binomial. Ukuran sampel random yang
BAB IV INFERENSI STATISTIK SATU POPULASI SEMBARANG Bab ini akan membahas inferensi statistik terhadap mean suatu populasi sembarang dan proporsi suatu populasi dikotomi/binomial. Ukuran sampel random yang
BAB I PENDAHULUAN. melalui pos. Ada beberapa keuntungan yang dapat diperoleh, diantaranya
 BAB I PENDAHULUAN 1.1 Latar Belakang Masalah Dalam melakukan survei, seringkali digunakan angket yang dikirimkan melalui pos. Ada beberapa keuntungan yang dapat diperoleh, diantaranya adalah hemat biaya,
BAB I PENDAHULUAN 1.1 Latar Belakang Masalah Dalam melakukan survei, seringkali digunakan angket yang dikirimkan melalui pos. Ada beberapa keuntungan yang dapat diperoleh, diantaranya adalah hemat biaya,
APLIKASI RAPID SURVEY
 Materi Rapid Survey FIKes - UMMU Iswandi, SKM - 1 APLIKASI RAPID SURVEY A. Pengertian Rapid Survai Survai merupakan kegiatan atau usaha pengumpulan informasi dari sebagian populasi yang dianggap dapat
Materi Rapid Survey FIKes - UMMU Iswandi, SKM - 1 APLIKASI RAPID SURVEY A. Pengertian Rapid Survai Survai merupakan kegiatan atau usaha pengumpulan informasi dari sebagian populasi yang dianggap dapat
BAB VI INFERENSI STATISTIK DUA POPULASI SEMBARANG
 BAB VI INFERENSI STATISTIK DUA POPULASI SEMBARANG Bab ini membahas inferensi statistik selisih dua mean populasi sembarang dan selisih dua proporsi populasi dikotomi/binomial. Untuk membahas hal tersebut
BAB VI INFERENSI STATISTIK DUA POPULASI SEMBARANG Bab ini membahas inferensi statistik selisih dua mean populasi sembarang dan selisih dua proporsi populasi dikotomi/binomial. Untuk membahas hal tersebut
Metoda Penelitian TEKNIK SAMPLING
 Metoda Penelitian TEKNIK SAMPLING Jika Cukup Sesendok Tak Perlu Semangkok Dasar pemikiran Data yang dipergunakan dalam suatu penelitian belum tentu merupakan keseluruhan dari suatu populasi karena beberapa
Metoda Penelitian TEKNIK SAMPLING Jika Cukup Sesendok Tak Perlu Semangkok Dasar pemikiran Data yang dipergunakan dalam suatu penelitian belum tentu merupakan keseluruhan dari suatu populasi karena beberapa
: Purnomo Satria NIM : PENDISKRIPSIAN DATA
 Nama : Purnomo Satria PENDISKRIPSIAN DATA NIM : 1133467162 1. Pendahuluan Dalam suatu penelitian kadang-kadang seorang peneliti menemui kesulitan dalam menyajikan sejumlah besar data statistik dalam bentuk
Nama : Purnomo Satria PENDISKRIPSIAN DATA NIM : 1133467162 1. Pendahuluan Dalam suatu penelitian kadang-kadang seorang peneliti menemui kesulitan dalam menyajikan sejumlah besar data statistik dalam bentuk
BAB 8 DISTRIBUSI PELUANG DISKRIT
 BAB 8 DISTRIBUSI PELUANG DISKRIT A. Peluang Peluang atau yang sering disebut sebagai probabilitas dapat dipandang sebagai cara untuk mengungkapkan ukuran ketidakpastian/ ketidakyakinan/ kemungkinan suatu
BAB 8 DISTRIBUSI PELUANG DISKRIT A. Peluang Peluang atau yang sering disebut sebagai probabilitas dapat dipandang sebagai cara untuk mengungkapkan ukuran ketidakpastian/ ketidakyakinan/ kemungkinan suatu
BAB 2 LANDASAN TEORI. Definisi 1 Himpunan semua hasil yang mungkin dari suatu percobaan disebut ruang sampel dan dinyatakan dengan S.
 BAB 2 LANDASAN TEORI 2.1 Ruang Sampel dan Kejadian Definisi 1 Himpunan semua hasil yang mungkin dari suatu percobaan disebut ruang sampel dan dinyatakan dengan S. Tiap hasil dalam ruang sampel disebut
BAB 2 LANDASAN TEORI 2.1 Ruang Sampel dan Kejadian Definisi 1 Himpunan semua hasil yang mungkin dari suatu percobaan disebut ruang sampel dan dinyatakan dengan S. Tiap hasil dalam ruang sampel disebut
Bab 5 Distribusi Sampling
 Bab 5 Distribusi Sampling Pendahuluan Untuk mempelajari populasi kita memerlukan sampel yang diambil dari populasi yang bersangkutan. Meskipun kita dapat mengambil lebih dari sebuah sampel berukuran n
Bab 5 Distribusi Sampling Pendahuluan Untuk mempelajari populasi kita memerlukan sampel yang diambil dari populasi yang bersangkutan. Meskipun kita dapat mengambil lebih dari sebuah sampel berukuran n
STATISTICS WEEK 7. By: Hanung N. Prasetyo POLTECH TELKOM/HANUNG NP
 STATISTICS WEEK 7 By: Hanung N. Prasetyo Ada macam, sampel probabilitas dan non probabilitas. Sampel probabilitas ada empat teknik yang semuanya dapat dilakukan dengan pengembalian atau tanpa pengembalian,
STATISTICS WEEK 7 By: Hanung N. Prasetyo Ada macam, sampel probabilitas dan non probabilitas. Sampel probabilitas ada empat teknik yang semuanya dapat dilakukan dengan pengembalian atau tanpa pengembalian,
Margin of Error. 3. Convidence interval (selang kepercayaan)
 Margin of Error Raihan Budiwaskito (18209003) Program Studi Sistem dan Teknologi Informasi Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132, Indonesia raihanwaskito@itb.ac.id
Margin of Error Raihan Budiwaskito (18209003) Program Studi Sistem dan Teknologi Informasi Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132, Indonesia raihanwaskito@itb.ac.id
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI 2.1 Himpunan Fuzzy Tidak semua himpunan yang dijumpai dalam kehidupan sehari-hari terdefinisi secara jelas, misalnya himpunan orang miskin, himpunan orang pandai, himpunan orang tinggi,
BAB 2 LANDASAN TEORI 2.1 Himpunan Fuzzy Tidak semua himpunan yang dijumpai dalam kehidupan sehari-hari terdefinisi secara jelas, misalnya himpunan orang miskin, himpunan orang pandai, himpunan orang tinggi,
STATISTIKA. Muhamad Nursalman Pendilkom/Ilkom UPI
 STATISTIKA Muhamad Nursalman Pendilkom/Ilkom UPI 1 Daftar Isi Bab 1 Peluang Bab Peubah Acak Bab 3 Distribusi Peluang Diskret Bab 4 Distribusi Peluang Kontinu Bab 5 Fungsi Peubah Acak Bab 6 Teori Penaksiran
STATISTIKA Muhamad Nursalman Pendilkom/Ilkom UPI 1 Daftar Isi Bab 1 Peluang Bab Peubah Acak Bab 3 Distribusi Peluang Diskret Bab 4 Distribusi Peluang Kontinu Bab 5 Fungsi Peubah Acak Bab 6 Teori Penaksiran
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI 2.1 Distribusi Normal Salah satu distribusi frekuensi yang paling penting dalam statistika adalah distribusi normal. Distribusi normal berupa kurva berbentuk lonceng setangkup yang
BAB 2 LANDASAN TEORI 2.1 Distribusi Normal Salah satu distribusi frekuensi yang paling penting dalam statistika adalah distribusi normal. Distribusi normal berupa kurva berbentuk lonceng setangkup yang
DISTRIBUSI PROBABILITAS (PELUANG)
 DISTRIBUSI PROBABILITAS (PELUANG) Distribusi Probabilitas (Peluang) Distribusi? Probabilitas? Distribusi Probabilitas? JURUSAN PENDIDIKAN FISIKA FPMIPA UNIVERSITAS PENDIDIKAN INDONESIA Distribusi = sebaran,
DISTRIBUSI PROBABILITAS (PELUANG) Distribusi Probabilitas (Peluang) Distribusi? Probabilitas? Distribusi Probabilitas? JURUSAN PENDIDIKAN FISIKA FPMIPA UNIVERSITAS PENDIDIKAN INDONESIA Distribusi = sebaran,
BAB II DISTRIBUSI PROBABILITAS
 BAB II DISTRIBUSI PROBABILITAS.1. VARIABEL RANDOM Definisi 1: Variabel random adalah suatu fungsi yang memetakan ruang sampel (S) ke himpunan bilangan Real (R), dan ditulis X : S R Contoh (Variabel random)
BAB II DISTRIBUSI PROBABILITAS.1. VARIABEL RANDOM Definisi 1: Variabel random adalah suatu fungsi yang memetakan ruang sampel (S) ke himpunan bilangan Real (R), dan ditulis X : S R Contoh (Variabel random)
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI.1 Peubah Acak dan Distribusinya.1.1 Peubah Acak Definisi.1: Peubah acak adalah suatu fungsi yang menghubungkan sebuah bilangan real dengan setiap unsur di dalam ruang contoh, (Walpole
BAB II LANDASAN TEORI.1 Peubah Acak dan Distribusinya.1.1 Peubah Acak Definisi.1: Peubah acak adalah suatu fungsi yang menghubungkan sebuah bilangan real dengan setiap unsur di dalam ruang contoh, (Walpole
8/29/2014. Kode MK/ Nama MK. Matematika Diskrit 2 8/29/2014
 Kode MK/ Nama MK Matematika Diskrit 1 8/29/2014 2 8/29/2014 1 Cakupan Himpunan, Relasi dan fungsi Kombinatorial Teori graf Pohon (Tree) dan pewarnaan graf 3 8/29/2014 3 KOMBINATORIAL Tujuan 1.Mahasiswa
Kode MK/ Nama MK Matematika Diskrit 1 8/29/2014 2 8/29/2014 1 Cakupan Himpunan, Relasi dan fungsi Kombinatorial Teori graf Pohon (Tree) dan pewarnaan graf 3 8/29/2014 3 KOMBINATORIAL Tujuan 1.Mahasiswa
1. PENGERTIAN. Manfaat Sampling :
 1. PENGERTIAN Sampel adalah sebagian dari anggota populasi yang dipilih dengan cara tertentu yang akan diteliti sifat-sifatnya dalam penelitian. Nilai-nilai yang berasal dari data sampel dinamakan dengan
1. PENGERTIAN Sampel adalah sebagian dari anggota populasi yang dipilih dengan cara tertentu yang akan diteliti sifat-sifatnya dalam penelitian. Nilai-nilai yang berasal dari data sampel dinamakan dengan
6. Teori Estimasi. EL2002-Probabilitas dan Statistik. Dosen: Andriyan B. Suksmono
 6. Teori Estimasi EL2002-Probabilitas dan Statistik Dosen: Andriyan B. Suksmono Pendahuluan Inferensi statistik adalah metoda untuk menarik inferensi atau membuat generalisasi dari suatu populasi. Ada
6. Teori Estimasi EL2002-Probabilitas dan Statistik Dosen: Andriyan B. Suksmono Pendahuluan Inferensi statistik adalah metoda untuk menarik inferensi atau membuat generalisasi dari suatu populasi. Ada
ARUMEGA ZAREFAR, SE.,M.Ak.,Akt.,CA
 STATISTIK ARUMEGA ZAREFAR, SE.,M.Ak.,Akt.,CA http://arumega.staff.unri.ac.id/ arumegazarefar.ca@gmail.com Arti statistik Kumpulan data dalam bentuk angka maupun bukan angka yang disusun dalam bentuk tabel
STATISTIK ARUMEGA ZAREFAR, SE.,M.Ak.,Akt.,CA http://arumega.staff.unri.ac.id/ arumegazarefar.ca@gmail.com Arti statistik Kumpulan data dalam bentuk angka maupun bukan angka yang disusun dalam bentuk tabel
BAB I PENDAHULUAN. Dalam suatu penelitian, seringkali tidak mungkin untuk melakukan
 BAB I PENDAHULUAN 1.1 LATAR BELAKANG MASALAH Dalam suatu penelitian, seringkali tidak mungkin untuk melakukan pengamatan pada semua elemen populasi. Karena itu, perlu dilakukan pengambilan sampel yang
BAB I PENDAHULUAN 1.1 LATAR BELAKANG MASALAH Dalam suatu penelitian, seringkali tidak mungkin untuk melakukan pengamatan pada semua elemen populasi. Karena itu, perlu dilakukan pengambilan sampel yang
SATUAN ACARA PERKULIAHAN MATA KULIAH STATISTIKA dan PROBABILITAS (MI) KODE / SKS : KK /2 SKS
 Minggu Pokok Bahasan ke dan TIU 1 1. Tehnik Penarikan Sampling pengertian kegunaan sampling, tehnik yang dapat digunakan serta pemahaman terhadap keempat tehnik tersebut. Sub Pokok Bahasan dan Sasaran
Minggu Pokok Bahasan ke dan TIU 1 1. Tehnik Penarikan Sampling pengertian kegunaan sampling, tehnik yang dapat digunakan serta pemahaman terhadap keempat tehnik tersebut. Sub Pokok Bahasan dan Sasaran
Distribusi Sampling 6.2. Debrina Puspita Andriani /
 6. Debrina Puspita Andriani E-mail : debrina.ub@gmail.com / debrina@ub.ac.id Outline Pengertian dan Konsep Dasar Distribusi Sampling Distribusi Sampling Mean Distribusi Sampling Proporsi Distribusi Sampling
6. Debrina Puspita Andriani E-mail : debrina.ub@gmail.com / debrina@ub.ac.id Outline Pengertian dan Konsep Dasar Distribusi Sampling Distribusi Sampling Mean Distribusi Sampling Proporsi Distribusi Sampling
BAB III KOMBINATORIK
 37 BAB III KOMBINATORIK Persoalan kombinatorik bukan merupakan persoalan yang baru dalam kehidupan nyata. Banyak persoalan kombinatorik yang sederhana telah diselesaiakan dalam masyarakat. Misalkan, saat
37 BAB III KOMBINATORIK Persoalan kombinatorik bukan merupakan persoalan yang baru dalam kehidupan nyata. Banyak persoalan kombinatorik yang sederhana telah diselesaiakan dalam masyarakat. Misalkan, saat
BAB II LANDASAN TEORI. ilmiah. Pencacahan atau pengukuran karakteristik suatu objek kajian yang
 BAB II LANDASAN TEORI 2.1 Konsep Dasar Peluang Pada dasarnya statistika berkaitan dengan penyajian dan penafsiran hasil yang berkemungkinan (hasil yang belum dapat ditentukan sebelumnya) yang muncul dalam
BAB II LANDASAN TEORI 2.1 Konsep Dasar Peluang Pada dasarnya statistika berkaitan dengan penyajian dan penafsiran hasil yang berkemungkinan (hasil yang belum dapat ditentukan sebelumnya) yang muncul dalam
STK 511 Analisis statistika. Materi 3 Sebaran Peubah Acak
 STK 511 Analisis statistika Materi 3 Sebaran Peubah Acak 1 Konsep Peluang 2 Peluang Peluang dapat diartikan sebagai ukuran kemungkinan terjadinya suatu kejadian Untuk memahami peluang diperlukan pemahaman
STK 511 Analisis statistika Materi 3 Sebaran Peubah Acak 1 Konsep Peluang 2 Peluang Peluang dapat diartikan sebagai ukuran kemungkinan terjadinya suatu kejadian Untuk memahami peluang diperlukan pemahaman
BAB II TINJAUAN TEORITIS. Menurut Darnius, O (2006, Hal : 53) simulasi dapat diartikan sebagai suatu
 BAB II TINJAUAN TEORITIS 2.1 Pendahulauan Menurut Darnius, O (2006, Hal : 53) simulasi dapat diartikan sebagai suatu rekayasa suatu model logika ilmiah untuk melihat kebenaran/kenyataan model tersebut.
BAB II TINJAUAN TEORITIS 2.1 Pendahulauan Menurut Darnius, O (2006, Hal : 53) simulasi dapat diartikan sebagai suatu rekayasa suatu model logika ilmiah untuk melihat kebenaran/kenyataan model tersebut.
BAB I PENDAHULUAN 1.1. Latar Belakang Permasalahan
 BAB I PENDAHULUAN 1.1. Latar Belakang Permasalahan Estimasi fungsi survival atau biasa disebut regresi fungsi survival merupakan bagian penting dari analisis survival. Estimasi ini biasa digunakan dalam
BAB I PENDAHULUAN 1.1. Latar Belakang Permasalahan Estimasi fungsi survival atau biasa disebut regresi fungsi survival merupakan bagian penting dari analisis survival. Estimasi ini biasa digunakan dalam
II. LANDASAN TEORI. 2. P bersifat aditif tak hingga, yaitu jika dengan. 2.1 Ruang Contoh, Kejadian dan Peluang
 II. LANDASAN TEORI 2.1 Ruang Contoh, Kejadian dan Peluang Dalam suatu percobaan sering kali diperlukan pengulangan yang dilakukan dalam kondisi yang sama. Semua kemungkinan hasil yang akan muncul akan
II. LANDASAN TEORI 2.1 Ruang Contoh, Kejadian dan Peluang Dalam suatu percobaan sering kali diperlukan pengulangan yang dilakukan dalam kondisi yang sama. Semua kemungkinan hasil yang akan muncul akan
Probabilitas dan Statistika Distribusi Peluang Diskrit 2. Adam Hendra Brata
 Probabilitas dan Statistika Distribusi Peluang Diskrit 2 Adam Hendra Brata Distribusi Hipergeometrik Distribusi Hipergeometrik Jika sampling dilakukan tanpa pengembalian dari kejadian sampling yang diambil
Probabilitas dan Statistika Distribusi Peluang Diskrit 2 Adam Hendra Brata Distribusi Hipergeometrik Distribusi Hipergeometrik Jika sampling dilakukan tanpa pengembalian dari kejadian sampling yang diambil
statistika untuk penelitian
 statistika untuk penelitian Kelompok Ilmiah Remaja (KIR) Delayota Experiment Team (D Expert) 2013 Freeaninationwallpaper.blogspot.com Apa itu Statistika? Statistika adalah ilmu yang mempelajari cara pengumpulan,
statistika untuk penelitian Kelompok Ilmiah Remaja (KIR) Delayota Experiment Team (D Expert) 2013 Freeaninationwallpaper.blogspot.com Apa itu Statistika? Statistika adalah ilmu yang mempelajari cara pengumpulan,
matematika DISTRIBUSI VARIABEL ACAK DAN DISTRIBUSI BINOMIAL K e l a s A. Penarikan Sampel dari Suatu Populasi Kurikulum 2013 Tujuan Pembelajaran
 Kurikulum 20 matematika K e l a s XI DISTRIBUSI VARIABEL ACAK DAN DISTRIBUSI BINOMIAL Tujuan Pembelajaran Setelah mempelajari materi ini, kamu diharapkan memiliki kemampuan berikut.. Memahami perbedaan
Kurikulum 20 matematika K e l a s XI DISTRIBUSI VARIABEL ACAK DAN DISTRIBUSI BINOMIAL Tujuan Pembelajaran Setelah mempelajari materi ini, kamu diharapkan memiliki kemampuan berikut.. Memahami perbedaan
Statistika Farmasi
 Bab 3: Distribusi Data Statistika FMIPA Universitas Islam Indonesia Distribusi Data Teori dalam statistika berkaitan dengan peluang Konsep dasar peluang tersebut berkaitan dengan peluang distribusi, yaitu
Bab 3: Distribusi Data Statistika FMIPA Universitas Islam Indonesia Distribusi Data Teori dalam statistika berkaitan dengan peluang Konsep dasar peluang tersebut berkaitan dengan peluang distribusi, yaitu
(ESTIMASI/ PENAKSIRAN)
 ESTIMASI PENDAHULUAN Karena adanya berbagai alasan seperti banyaknya individu dalam populasi amatan, maka penelitian keseluruhan terhadap populasi tersebut tidaklah ekonomis, baik tenaga, waktu, maupun
ESTIMASI PENDAHULUAN Karena adanya berbagai alasan seperti banyaknya individu dalam populasi amatan, maka penelitian keseluruhan terhadap populasi tersebut tidaklah ekonomis, baik tenaga, waktu, maupun
Estimasi dan Uji Hipotesis
 Modul 7 Estimasi dan Uji Hipotesis Bambang Prastyo, S.Sos. PENDAHULUAN pa yang akan Anda lakukan setelah Anda selesai melakukan penelitian? A Tentunya Anda akan mengambil suatu kesimpulan. Nah seperti
Modul 7 Estimasi dan Uji Hipotesis Bambang Prastyo, S.Sos. PENDAHULUAN pa yang akan Anda lakukan setelah Anda selesai melakukan penelitian? A Tentunya Anda akan mengambil suatu kesimpulan. Nah seperti
PENARIKAN SAMPEL & PENDUGAAN PARAMETER
 PENARIKAN SAMPEL & PENDUGAAN PARAMETER Arti Penarikan Sampel Populasi ( Universe) adalah totalitas dari semua objek atau individu yang memiliki karakteristik tertentu, jelas dan lengkap yang akan diteliti
PENARIKAN SAMPEL & PENDUGAAN PARAMETER Arti Penarikan Sampel Populasi ( Universe) adalah totalitas dari semua objek atau individu yang memiliki karakteristik tertentu, jelas dan lengkap yang akan diteliti
BAB 2 TINJAUAN PUSTAKA
 BAB 2 TINJAUAN PUSTAKA 2.1 Data Data adalah bentuk jamak dari datum, yang dapat diartikan sebagai informasi yang diterima yang bentuknya dapat berupa angka, kata-kata, atau dalam bentuk lisan dan tulisan
BAB 2 TINJAUAN PUSTAKA 2.1 Data Data adalah bentuk jamak dari datum, yang dapat diartikan sebagai informasi yang diterima yang bentuknya dapat berupa angka, kata-kata, atau dalam bentuk lisan dan tulisan
PENGUJIAN HIPOTESIS 1
 PENGUJIAN HIPOTESIS 1 Pengertian Pengujian Hipotesis From: BAHASA YUNANI HUPO THESIS Lemah, kurang, di bawah Teori, proposisi, atau pernyataan yang disajikan sebagai bukti Hipotesis suatu pernyataan yang
PENGUJIAN HIPOTESIS 1 Pengertian Pengujian Hipotesis From: BAHASA YUNANI HUPO THESIS Lemah, kurang, di bawah Teori, proposisi, atau pernyataan yang disajikan sebagai bukti Hipotesis suatu pernyataan yang
Syllabus Statistika Dasar Semester Ganjil 2012/2013 Prodi Informatika FMIPA Unsyiah
 Syllabus Statistika Dasar Semester Ganjil 2012/2013 Prodi Informatika FMIPA Unsyiah Nama mata kuliah Statistika Dasar SKS 3 (2 1) Kode INF-201 Prasyarat Matematika Dasar 1 Dosen Pengasuh Kelas A : DR.
Syllabus Statistika Dasar Semester Ganjil 2012/2013 Prodi Informatika FMIPA Unsyiah Nama mata kuliah Statistika Dasar SKS 3 (2 1) Kode INF-201 Prasyarat Matematika Dasar 1 Dosen Pengasuh Kelas A : DR.
II. TINJAUAN PUSTAKA. Ruang sampel S adalah himpunan semua hasil dari suatu percobaan. Kejadian E
 5 II. TINJAUAN PUSTAKA 2.1 Konsep Dasar Peluang Ruang sampel S adalah himpunan semua hasil dari suatu percobaan. Kejadian E adalah himpunan bagian dari ruang sampel. Peluang suatu kejadian P(E) adalah
5 II. TINJAUAN PUSTAKA 2.1 Konsep Dasar Peluang Ruang sampel S adalah himpunan semua hasil dari suatu percobaan. Kejadian E adalah himpunan bagian dari ruang sampel. Peluang suatu kejadian P(E) adalah
MA2082 BIOSTATISTIKA Bab 3 Peubah Acak dan Distribusi
 MA2082 BIOSTATISTIKA Bab 3 Peubah Acak dan Distribusi Orang Biologi Tidak Anti Statistika Silabus Silabus dan Tujuan Konsep peubah acak, fungsi peluang (probability density function), fungsi distribusi
MA2082 BIOSTATISTIKA Bab 3 Peubah Acak dan Distribusi Orang Biologi Tidak Anti Statistika Silabus Silabus dan Tujuan Konsep peubah acak, fungsi peluang (probability density function), fungsi distribusi
BAB I PENDAHULUAN 1.1 Latar Belakang
 BAB I PENDAHULUAN 1.1 Latar Belakang Analisis statistika pada dasarnya merupakan suatu analisis terhadap sampel yang kemudian hasilnya akan digeneralisasi untuk menggambarkan suatu karakteristik populasi.
BAB I PENDAHULUAN 1.1 Latar Belakang Analisis statistika pada dasarnya merupakan suatu analisis terhadap sampel yang kemudian hasilnya akan digeneralisasi untuk menggambarkan suatu karakteristik populasi.
Distribusi Peluang Teoritis
 Distribusi Peluang Teoritis 1. Pendahuluan Titik-titik contoh di dalam Ruang Sampel (S) dapat disajikan dalam bentuk numerik/bilangan.. Peubah Acak Fungsi yang mendefinisikan titik-titik contoh dalam ruang
Distribusi Peluang Teoritis 1. Pendahuluan Titik-titik contoh di dalam Ruang Sampel (S) dapat disajikan dalam bentuk numerik/bilangan.. Peubah Acak Fungsi yang mendefinisikan titik-titik contoh dalam ruang
DASAR-DASAR ANALISIS MATEMATIKA
 (Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. December 26, 2007 Misalkan f kontinu pada interval [a, b]. Apakah masuk akal untuk membahas luas daerah
(Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: hgunawan@math.itb.ac.id. December 26, 2007 Misalkan f kontinu pada interval [a, b]. Apakah masuk akal untuk membahas luas daerah
BAB IV. DISTRIBUSI PROBABILITAS DISKRIT
 BAB IV. DISTRIBUSI PROBABILITAS DISKRIT A. Variabel random diskrit. Variabel random diskrit X adalah : Cara memberi nilai angka pada setiap elemen ruang sampel X(a) : Ukuran karakteristik tertentu dari
BAB IV. DISTRIBUSI PROBABILITAS DISKRIT A. Variabel random diskrit. Variabel random diskrit X adalah : Cara memberi nilai angka pada setiap elemen ruang sampel X(a) : Ukuran karakteristik tertentu dari
Hidup penuh dengan ketidakpastian
 BAB 2 Probabilitas Hidup penuh dengan ketidakpastian Tidak mungkin bagi kita untuk dapat mengatakan dengan pasti apa yang akan terjadi dalam 1 menit ke depan tapi Probabilitas akan memprediksikan masa
BAB 2 Probabilitas Hidup penuh dengan ketidakpastian Tidak mungkin bagi kita untuk dapat mengatakan dengan pasti apa yang akan terjadi dalam 1 menit ke depan tapi Probabilitas akan memprediksikan masa
TINJAUAN PUSTAKA ( ) ( ) ( )
 TINJAUAN PUSTAKA Penarikan Contoh Acak Berlapis Penarikan contoh acak berlapis adalah suatu rancangan penarikan contoh acak yang membagi N unit dari populasi ke dalam L strata yang tidak saling tumpang
TINJAUAN PUSTAKA Penarikan Contoh Acak Berlapis Penarikan contoh acak berlapis adalah suatu rancangan penarikan contoh acak yang membagi N unit dari populasi ke dalam L strata yang tidak saling tumpang
Bab 2 LANDASAN TEORI
 17 Bab 2 LANDASAN TEORI 2.1 Aljabar Matriks 2.1.1 Definisi Matriks Matriks adalah suatu kumpulan angka-angka yang juga sering disebut elemen-elemen yang disusun secara teratur menurut baris dan kolom sehingga
17 Bab 2 LANDASAN TEORI 2.1 Aljabar Matriks 2.1.1 Definisi Matriks Matriks adalah suatu kumpulan angka-angka yang juga sering disebut elemen-elemen yang disusun secara teratur menurut baris dan kolom sehingga
ANALISIS DATA SECARA RANDOM PADA APLIKASI MINITAB DENGAN MENGGUNAKAN DISTRIBUSI PELUANG
 LAPORAN RESMI PRAKTIKUM PENGANTAR METODE STATISTIKA MODUL 3 ANALISIS DATA SECARA RANDOM PADA APLIKASI MINITAB DENGAN MENGGUNAKAN DISTRIBUSI PELUANG Oleh : Diana Nafkiyah 1314030028 Nilamsari Farah Millatina
LAPORAN RESMI PRAKTIKUM PENGANTAR METODE STATISTIKA MODUL 3 ANALISIS DATA SECARA RANDOM PADA APLIKASI MINITAB DENGAN MENGGUNAKAN DISTRIBUSI PELUANG Oleh : Diana Nafkiyah 1314030028 Nilamsari Farah Millatina
STATISTIKA MATEMATIKA KELAS XI MIA
 STATISTIKA MATEMATIKA KELAS XI MIA STATISTIKA Matematika Kelas XI MIA 90 80 70 60 50 40 30 20 10 0 East West North 1st Qtr 2nd Qtr 3rd Qtr 4th Qtr Disusun oleh : Markus Yuniarto, S.Si Tahun Pelajaran 2016
STATISTIKA MATEMATIKA KELAS XI MIA STATISTIKA Matematika Kelas XI MIA 90 80 70 60 50 40 30 20 10 0 East West North 1st Qtr 2nd Qtr 3rd Qtr 4th Qtr Disusun oleh : Markus Yuniarto, S.Si Tahun Pelajaran 2016
BAB III METODE PENELITIAN
 BAB III METODE PENELITIAN 3.1 Variabel Penelitian Penelitian ini menggunakan satu definisi variabel operasional yaitu ratarata temperatur bumi periode tahun 1880 sampai dengan tahun 2012. 3.2 Jenis dan
BAB III METODE PENELITIAN 3.1 Variabel Penelitian Penelitian ini menggunakan satu definisi variabel operasional yaitu ratarata temperatur bumi periode tahun 1880 sampai dengan tahun 2012. 3.2 Jenis dan
BAB I PENDAHULUAN. dapat dianggap mendekati normal dengan mean μ = μ dan variansi
 BAB I PENDAHULUAN 1.1 Latar Belakang Masalah Matematika merupakan salah satu cabang ilmu pengetahuan yang melambangkan kemajuan zaman. Oleh karena itu matematika banyak digunakan oleh cabang ilmu lain
BAB I PENDAHULUAN 1.1 Latar Belakang Masalah Matematika merupakan salah satu cabang ilmu pengetahuan yang melambangkan kemajuan zaman. Oleh karena itu matematika banyak digunakan oleh cabang ilmu lain
DISTRIBUSI PROBABILITAS
 BAB 7 DISTRIBUSI PROBABILITAS Kompetensi Menjelaskan distribusi probabilitas Indikator 1. Menjelaskan distribusi hipergeometris 2. Menjelaskan distribusi binomial 3. Menjelaskan distribusi multinomial
BAB 7 DISTRIBUSI PROBABILITAS Kompetensi Menjelaskan distribusi probabilitas Indikator 1. Menjelaskan distribusi hipergeometris 2. Menjelaskan distribusi binomial 3. Menjelaskan distribusi multinomial
Mendefinisikan arti dari terminologi-terminologi penting dalam statistika Memahami dan menjelaskan peranan statistik dan penerapannya di bidang
 Tujuan Pembelajaran Mendefinisikan arti dari terminologi-terminologi penting dalam statistika Memahami dan menjelaskan peranan statistik dan penerapannya di bidang teknik Menjelaskan langkah-langkah dasar
Tujuan Pembelajaran Mendefinisikan arti dari terminologi-terminologi penting dalam statistika Memahami dan menjelaskan peranan statistik dan penerapannya di bidang teknik Menjelaskan langkah-langkah dasar
BAB II TINJAUAN PUSTAKA. Dalam bab ini dibahas tentang matriks, metode pengganda Lagrange, regresi
 BAB II TINJAUAN PUSTAKA Dalam bab ini dibahas tentang matriks, metode pengganda Lagrange, regresi linear, metode kuadrat terkecil, restriksi linear, multikolinearitas, regresi ridge, uang primer, dan koefisien
BAB II TINJAUAN PUSTAKA Dalam bab ini dibahas tentang matriks, metode pengganda Lagrange, regresi linear, metode kuadrat terkecil, restriksi linear, multikolinearitas, regresi ridge, uang primer, dan koefisien
PENERAPAN METODE JACKKNIFE TERHAPUS-1 PADA PENGOLAHAN DATA METODE QUICK COUNT
 PENERAPAN METODE JACKKNIFE TERHAPUS-1 PADA PENGOLAHAN DATA METODE QUICK COUNT Joko Sungkono* dan Udiyono* Abstrak: Secara statistik, metode quick count merupakan suatu proses estimasi parameter proporsi
PENERAPAN METODE JACKKNIFE TERHAPUS-1 PADA PENGOLAHAN DATA METODE QUICK COUNT Joko Sungkono* dan Udiyono* Abstrak: Secara statistik, metode quick count merupakan suatu proses estimasi parameter proporsi
Statistika (MMS-1001)
 Statistika (MMS-1001) Dr. Danardono, MPH danardono@ugm.ac.id Program Studi Statistika Jurusan Matematika FMIPA UGM Materi dan Jadual Tatap Muka Pokok Bahasan Sub Pokok Bahasan 1. Statistika Deskriptif
Statistika (MMS-1001) Dr. Danardono, MPH danardono@ugm.ac.id Program Studi Statistika Jurusan Matematika FMIPA UGM Materi dan Jadual Tatap Muka Pokok Bahasan Sub Pokok Bahasan 1. Statistika Deskriptif
Statistika (MMS-1001)
 Statistika (MMS-1001) Dr. Danardono, MPH danardono@ugm.ac.id Program Studi Statistika Jurusan Matematika FMIPA UGM Materi dan Jadual Tatap Muka Pokok Bahasan Sub Pokok Bahasan 1. Statistika Deskriptif
Statistika (MMS-1001) Dr. Danardono, MPH danardono@ugm.ac.id Program Studi Statistika Jurusan Matematika FMIPA UGM Materi dan Jadual Tatap Muka Pokok Bahasan Sub Pokok Bahasan 1. Statistika Deskriptif
MODUL II DISTRIBUSI PELUANG DISKRIT DAN KONTINU
 DISTRIBUSI PELUANG DISKRIT DAN KONTINU A. TUJUAN PRAKTIKUM Melalui praktikum Modul II ini diharapkan praktikan dapat: 1. Mengenal jenis dan karakteristik dari beberapa distribusi peluang. 2. Menguji dan
DISTRIBUSI PELUANG DISKRIT DAN KONTINU A. TUJUAN PRAKTIKUM Melalui praktikum Modul II ini diharapkan praktikan dapat: 1. Mengenal jenis dan karakteristik dari beberapa distribusi peluang. 2. Menguji dan
ANALISIS PENAKSIRAN REGRESI LINIER PADA SAMPLING KELOMPOK
 ANALISIS PENAKSIRAN REGRESI LINIER PADA SAMPLING KELOMPOK ARTIKEL Oleh ISWAHYUDI JOKO S, S.Si, M.Pd PROGRAM STUDI PENDIDIKAN MATEMATIKA FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN UNIVERSITAS MUHAMMADIYANEGERI
ANALISIS PENAKSIRAN REGRESI LINIER PADA SAMPLING KELOMPOK ARTIKEL Oleh ISWAHYUDI JOKO S, S.Si, M.Pd PROGRAM STUDI PENDIDIKAN MATEMATIKA FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN UNIVERSITAS MUHAMMADIYANEGERI
Studi dan Implementasi Integrasi Monte Carlo
 Studi dan Implementasi Integrasi Monte Carlo Firdi Mulia - 13507045 1 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132, Indonesia
Studi dan Implementasi Integrasi Monte Carlo Firdi Mulia - 13507045 1 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132, Indonesia
BAB II KAJIAN TEORI. hasil percobaan yang berbeda dan masing-masing mempunyai. itu menyusun kejadian, maka probabilitas kejadian
 BAB II KAJIAN TEORI A. Probabilitas Teorema 2.1 (Walpole, 1992) Probabilitas menunjukan suatu percobaan mempunyai hasil percobaan yang berbeda dan masing-masing mempunyai kemungkinan yang sama untuk terjadi,
BAB II KAJIAN TEORI A. Probabilitas Teorema 2.1 (Walpole, 1992) Probabilitas menunjukan suatu percobaan mempunyai hasil percobaan yang berbeda dan masing-masing mempunyai kemungkinan yang sama untuk terjadi,
REVIEW BIOSTATISTIK DESKRIPTIF
 REVIEW BIOSTATISTIK DESKRIPTIF POKOK BAHASAN 1. Konsep statistik deskriptif 2. Data dan variabel 3. Nilai Tengah (Ukuran Pusat), posisi dan variasi) pada data tunggal dan kelompok 4. Penyajian data 5.
REVIEW BIOSTATISTIK DESKRIPTIF POKOK BAHASAN 1. Konsep statistik deskriptif 2. Data dan variabel 3. Nilai Tengah (Ukuran Pusat), posisi dan variasi) pada data tunggal dan kelompok 4. Penyajian data 5.
Materi Kuliah: Statistik Inferensial
 TEORI PENDUGAAN STATISTIK Prof. Dr. Almasdi Syahza, SE., MP Email: asyahza@yahoo.co.id 1 Teori Statistik Titik Parameter Interval Teori Statistik Titik Parameter Interval 3 1 PENDUGA TUNGGAL SEBAGAI FUNGSI
TEORI PENDUGAAN STATISTIK Prof. Dr. Almasdi Syahza, SE., MP Email: asyahza@yahoo.co.id 1 Teori Statistik Titik Parameter Interval Teori Statistik Titik Parameter Interval 3 1 PENDUGA TUNGGAL SEBAGAI FUNGSI
BAB III METODE PENELITIAN. penelitian kuantitatif melalui analisis regresi linier berganda. Menurut. menguji hipotesis yang akan ditetapkan.
 BAB III METODE PENELITIAN Metode yang digunakan dalam penelitian ini adalah metode penelitian kuantitatif melalui analisis regresi linier berganda. Menurut sugiyono (2008:8) metode kuantitatif diartikan
BAB III METODE PENELITIAN Metode yang digunakan dalam penelitian ini adalah metode penelitian kuantitatif melalui analisis regresi linier berganda. Menurut sugiyono (2008:8) metode kuantitatif diartikan
PROBABILITAS &STATISTIK. Oleh: Kholistianingsih, S.T., M.Eng.
 PROBABILITAS &STATISTIK ke-1 Oleh: Kholistianingsih, S.T., M.Eng. KONTRAK PEMBELAJARAN UAS : 35% UTS : 35% TUGAS : 20% KEHADIRAN :10% SEMUA KOMPONEN HARUS ADA KEHADIRAN 0 NILAI MAKS D PEUBAH DAN GRAFIK
PROBABILITAS &STATISTIK ke-1 Oleh: Kholistianingsih, S.T., M.Eng. KONTRAK PEMBELAJARAN UAS : 35% UTS : 35% TUGAS : 20% KEHADIRAN :10% SEMUA KOMPONEN HARUS ADA KEHADIRAN 0 NILAI MAKS D PEUBAH DAN GRAFIK
STATISTIKA FAI SKS
 STATISTIKA FAI 1201 3 SKS DESKRIPSI SINGKAT : Mata kuliah ini adalah mata kuliah yang mengajarkan tentang peranan statistika dalam teori probabilitas, aplikasi distribusi probabilitas diskrit, aplikasi
STATISTIKA FAI 1201 3 SKS DESKRIPSI SINGKAT : Mata kuliah ini adalah mata kuliah yang mengajarkan tentang peranan statistika dalam teori probabilitas, aplikasi distribusi probabilitas diskrit, aplikasi
KONSEP DASAR PROBABILITAS DAN DISTRIBUSI PROBABILITAS LELY RIAWATI, ST, MT.
 KONSEP DASAR PROBABILITAS DAN DISTRIBUSI PROBABILITAS LELY RIAWATI, ST, MT. EKSPERIMEN suatu percobaan yang dapat diulang-ulang dengan kondisi yang sama CONTOH : Eksperimen : melempar dadu 1 kali Hasilnya
KONSEP DASAR PROBABILITAS DAN DISTRIBUSI PROBABILITAS LELY RIAWATI, ST, MT. EKSPERIMEN suatu percobaan yang dapat diulang-ulang dengan kondisi yang sama CONTOH : Eksperimen : melempar dadu 1 kali Hasilnya
Catatan Kuliah AK5161 Matematika Keuangan Aktuaria Insure and Invest! Dosen: Khreshna I.A. Syuhada, MSc. PhD.
 Catatan Kuliah AK5161 Matematika Keuangan Aktuaria Insure and Invest! Dosen: Khreshna I.A. Syuhada, MSc. PhD. Kelompok Keilmuan Statistika - FMIPA Institut Teknologi Bandung 2014 1 Tentang AK5161 Matematika
Catatan Kuliah AK5161 Matematika Keuangan Aktuaria Insure and Invest! Dosen: Khreshna I.A. Syuhada, MSc. PhD. Kelompok Keilmuan Statistika - FMIPA Institut Teknologi Bandung 2014 1 Tentang AK5161 Matematika
Distribusi Probabilitas Diskrit: Geometrik Hipergeometrik
 Distribusi Probabilitas Diskrit: Geometrik Hipergeometrik 4.3 Debrina Puspita Andriani E-mail : debrina.ub@gmail.com / debrina@ub.ac.id 2 Outline Distribusi Geometrik Distribusi Hipergeometrik Distribusi
Distribusi Probabilitas Diskrit: Geometrik Hipergeometrik 4.3 Debrina Puspita Andriani E-mail : debrina.ub@gmail.com / debrina@ub.ac.id 2 Outline Distribusi Geometrik Distribusi Hipergeometrik Distribusi
I. PENDAHULUAN II. TINJAUAN PUSTAKA
 I. PENDAHULUAN 1.1 Latar Belakang Pada masa sekarang, ditengah berkembangnya dunia industri tentunya terdapat berbagai permasalahan dalam bidang-bidang keindustrian. Permasalahan-permasalahan yang biasa
I. PENDAHULUAN 1.1 Latar Belakang Pada masa sekarang, ditengah berkembangnya dunia industri tentunya terdapat berbagai permasalahan dalam bidang-bidang keindustrian. Permasalahan-permasalahan yang biasa
BAB 2 TINJAUAN PUSTAKA
 BAB TINJAUAN PUSTAKA.1 Perkiraan Variansi Tipe SYG Perkiraan Ŷ tidak bias secara bersyarat untuk perkiraan tahap Ŷ1 = s 1 ẏ i, sebagai sampel tahap pertama s 1, dimana ẏ i = y i π 1i = d 1i y i. Sebagai
BAB TINJAUAN PUSTAKA.1 Perkiraan Variansi Tipe SYG Perkiraan Ŷ tidak bias secara bersyarat untuk perkiraan tahap Ŷ1 = s 1 ẏ i, sebagai sampel tahap pertama s 1, dimana ẏ i = y i π 1i = d 1i y i. Sebagai
BAB I PENDAHULUAN Latar Belakang Masalah
 BAB I PENDAHULUAN Pada bab ini akan diberikan pendahuluan sebelum menginjak pembahasan pokok. Pendahuluan ini meliputi latar belakang masalah, rumusan masalah, tujuan dan manfaat penelitian, tinjauan pustaka,
BAB I PENDAHULUAN Pada bab ini akan diberikan pendahuluan sebelum menginjak pembahasan pokok. Pendahuluan ini meliputi latar belakang masalah, rumusan masalah, tujuan dan manfaat penelitian, tinjauan pustaka,
Materi Kuliah: Statistik Inferensial
 TEORI PENDUGAAN STATISTIK Prof. Dr. Almasdi Syahza, SE., MP Email: asyahza@yahoo.co.id 1 Teori Statistik Pengujian Hipotesa Besar Pengujian Hipotesa Kecil Memilih Ukuran Teori Statistik Pengujian Hipotesa
TEORI PENDUGAAN STATISTIK Prof. Dr. Almasdi Syahza, SE., MP Email: asyahza@yahoo.co.id 1 Teori Statistik Pengujian Hipotesa Besar Pengujian Hipotesa Kecil Memilih Ukuran Teori Statistik Pengujian Hipotesa
MODUL 2 APROKSIMASI. Disusun oleh: Ani Ismayani S.Pd
 MODUL 2 APROKSIMASI Disusun oleh: Ani Ismayani S.Pd KEGIATAN BELAJAR a. Tujuan Kegiatan Belajar Setelah mempelajari uraian kegiatan belajar ini, diharapkan Anda dapat: 1) Menerapkan konsep kesalahan pengukuran
MODUL 2 APROKSIMASI Disusun oleh: Ani Ismayani S.Pd KEGIATAN BELAJAR a. Tujuan Kegiatan Belajar Setelah mempelajari uraian kegiatan belajar ini, diharapkan Anda dapat: 1) Menerapkan konsep kesalahan pengukuran
HASIL DAN PEMBAHASAN. (a) (b) (c)
 5 b. Analisis data daya tahan dengan metode semiparametrik, yaitu menggunakan regresi hazard proporsional. Analisis ini digunakan untuk melihat pengaruh peubah penjelas terhadap peubah respon secara simultan.
5 b. Analisis data daya tahan dengan metode semiparametrik, yaitu menggunakan regresi hazard proporsional. Analisis ini digunakan untuk melihat pengaruh peubah penjelas terhadap peubah respon secara simultan.
BAB III ANALISIS FAKTOR. berfungsi untuk mereduksi dimensi data dengan cara menyatakan variabel asal
 BAB III ANALISIS FAKTOR 3.1 Definisi Analisis faktor Analisis faktor adalah suatu teknik analisis statistika multivariat yang berfungsi untuk mereduksi dimensi data dengan cara menyatakan variabel asal
BAB III ANALISIS FAKTOR 3.1 Definisi Analisis faktor Analisis faktor adalah suatu teknik analisis statistika multivariat yang berfungsi untuk mereduksi dimensi data dengan cara menyatakan variabel asal
BAB II TINJAUAN PUSTAKA. satu peubah prediktor dengan satu peubah respon disebut analisis regresi linier
 BAB II TINJAUAN PUSTAKA 2.1 Analisis Regresi Linier Berganda Analisis regresi pertama kali dikembangkan oleh Sir Francis Galton pada abad ke-19. Analisis regresi dengan satu peubah prediktor dan satu peubah
BAB II TINJAUAN PUSTAKA 2.1 Analisis Regresi Linier Berganda Analisis regresi pertama kali dikembangkan oleh Sir Francis Galton pada abad ke-19. Analisis regresi dengan satu peubah prediktor dan satu peubah
Metode kuantitatif: Randomisasi 12 O K TO BER 2016
 Metode kuantitatif: Randomisasi PANJI FO RTUNA H ADI SO EMARTO M ETO DE, AP LI K ASI DAN M ANAJEM EN P ENELI TIAN K ESM AS S2 I K M FK UP 12 O K TO BER 2016 Random selection vs random allocation Dua jenis
Metode kuantitatif: Randomisasi PANJI FO RTUNA H ADI SO EMARTO M ETO DE, AP LI K ASI DAN M ANAJEM EN P ENELI TIAN K ESM AS S2 I K M FK UP 12 O K TO BER 2016 Random selection vs random allocation Dua jenis
BAB 5 PENENTUAN POPULASI DAN SAMPEL PENELITIAN. Populasi adalah wilayah generalisasi yang terdiri atas obyek atau
 BAB 5 PENENTUAN POPULASI DAN SAMPEL PENELITIAN 5.1. Populasi dan Sampel Populasi adalah wilayah generalisasi yang terdiri atas obyek atau subyek yang memiliki kuantitas atau kualitas tertentu yang ditentukan
BAB 5 PENENTUAN POPULASI DAN SAMPEL PENELITIAN 5.1. Populasi dan Sampel Populasi adalah wilayah generalisasi yang terdiri atas obyek atau subyek yang memiliki kuantitas atau kualitas tertentu yang ditentukan
BAB 1 PENDAHULUAN. Universitas Sumatera Utara
 BAB 1 PENDAHULUAN 1.1 Latar Belakang Dalam teori probabilitas dan statistika, distribusi binomial adalah distribusi probabilitas diskret jumlah keberhasilan dalam n percobaan ya/tidak (berhasil/gagal)
BAB 1 PENDAHULUAN 1.1 Latar Belakang Dalam teori probabilitas dan statistika, distribusi binomial adalah distribusi probabilitas diskret jumlah keberhasilan dalam n percobaan ya/tidak (berhasil/gagal)
BAB I PENDAHULUAN. 1.1 Latar Belakang Masalah
 BAB I PENDAHULUAN 1.1 Latar Belakang Masalah Kebutuhan akan informasi yang cepat, tepat dan akurat sangatlah mutlak, terutama dalam era globalisasi dalam skala luas maupun era otonomi daerah dalam lingkup
BAB I PENDAHULUAN 1.1 Latar Belakang Masalah Kebutuhan akan informasi yang cepat, tepat dan akurat sangatlah mutlak, terutama dalam era globalisasi dalam skala luas maupun era otonomi daerah dalam lingkup
FORMAT LAPORAN MODUL V DISTRIBUSI SAMPLING
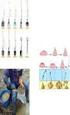 FORMAT LAPORAN MODUL V DISTRIBUSI SAMPLING ABSTRAK ABSTRACT KATA PENGANTAR DAFTAR ISI DAFTAR TABEL DAFTAR GAMBAR DAFTAR LAMPIRAN BAB I PENDAHULUAN (kata pengantar) 1.1 Latar Belakang 1.2 Tujuan Penulisan
FORMAT LAPORAN MODUL V DISTRIBUSI SAMPLING ABSTRAK ABSTRACT KATA PENGANTAR DAFTAR ISI DAFTAR TABEL DAFTAR GAMBAR DAFTAR LAMPIRAN BAB I PENDAHULUAN (kata pengantar) 1.1 Latar Belakang 1.2 Tujuan Penulisan
STATISTIKA UNIPA SURABAYA
 MATEMATIKA STATISTIKA (MATHEMATICAL STATISTICS) GANGGA ANURAGA Materi : Distribusi variabel random Teori Himpunan Fungsi Himpunan Fungsi Himpunan Peluang Variabel Random Fungsi Kepadatan Peluang Fungsi
MATEMATIKA STATISTIKA (MATHEMATICAL STATISTICS) GANGGA ANURAGA Materi : Distribusi variabel random Teori Himpunan Fungsi Himpunan Fungsi Himpunan Peluang Variabel Random Fungsi Kepadatan Peluang Fungsi
BAB III METODOLOGI POLLING
 BAB III METODOLOGI POLLING A. TEKNIK PENARIKAN SAMPEL Karena polling ingin membuat generalisasi agar hasilnya dapat menggambarkan pendapat publik secara keseluruhan, maka sampel yang harus diambil adalah
BAB III METODOLOGI POLLING A. TEKNIK PENARIKAN SAMPEL Karena polling ingin membuat generalisasi agar hasilnya dapat menggambarkan pendapat publik secara keseluruhan, maka sampel yang harus diambil adalah
II. TINJAUAN PUSTAKA. Dalam proses penelitian untuk mengkaji karakteristik penduga GMM pada data
 5 II. TINJAUAN PUSTAKA Dalam proses penelitian untuk mengkaji karakteristik penduga GMM pada data panel ini, penulis menggunakan definisi, teorema dan konsep dasar yang berkaitan dengan pendugaan parameter,
5 II. TINJAUAN PUSTAKA Dalam proses penelitian untuk mengkaji karakteristik penduga GMM pada data panel ini, penulis menggunakan definisi, teorema dan konsep dasar yang berkaitan dengan pendugaan parameter,
DISTRIBUSI TEORITIS. P(M) = p = probabilitas untuk mendapat bola merah (sukses) 30
 DISTRIBUSI TEORITIS Distribusi teoritis merupakan alat bagi kita untuk menentukan apa yang dapat kita harapkan, apabila asumsi-asumsi yang kita buat benar. Distribusi teoritis memungkinkan para pembuat
DISTRIBUSI TEORITIS Distribusi teoritis merupakan alat bagi kita untuk menentukan apa yang dapat kita harapkan, apabila asumsi-asumsi yang kita buat benar. Distribusi teoritis memungkinkan para pembuat
Bab 2 DISTRIBUSI PELUANG
 Bab 2 DISTRIBUSI PELUANG PENDAHULUAN Setiap peristiwa akan mempunyai peluangnya masingmasing, dan peluang terjadinya peristiwa itu akan mempunyai penyebaran yang mengikuti suatu pola tertentu yang di sebut
Bab 2 DISTRIBUSI PELUANG PENDAHULUAN Setiap peristiwa akan mempunyai peluangnya masingmasing, dan peluang terjadinya peristiwa itu akan mempunyai penyebaran yang mengikuti suatu pola tertentu yang di sebut
BAB I PENGANTAR STATISTIK DAN ANALISIS DATA
 BAB I PENGANTAR STATISTIK DAN ANALISIS DATA 1.1. Pengertian: Statistik inferensial, Sampel, Populasi, Disain eksperimen Pada awal tahun 1980 dan berlanjut sampai abad 1, industri di Amerika menekankan
BAB I PENGANTAR STATISTIK DAN ANALISIS DATA 1.1. Pengertian: Statistik inferensial, Sampel, Populasi, Disain eksperimen Pada awal tahun 1980 dan berlanjut sampai abad 1, industri di Amerika menekankan
Distribusi Probabilitas Diskret Teoritis
 Distribusi robabilitas Diskret Teoritis Distribusi robabilitas Teoritis Diskret Distribusi seragam diskret (discrete uniform distribution) Distribusi hipergeometris (hypergeometric distribution) Distribusi
Distribusi robabilitas Diskret Teoritis Distribusi robabilitas Teoritis Diskret Distribusi seragam diskret (discrete uniform distribution) Distribusi hipergeometris (hypergeometric distribution) Distribusi
