LU DECOMPOSITION (FAKTORISASI MATRIK)
|
|
|
- Devi Salim
- 9 tahun lalu
- Tontonan:
Transkripsi
1 LU DECOMPOSITION (FAKTORISASI MATRIK) Dr. Eng. Supriyanto, M.Sc Lab. Komputer, Departemen Fisika, Universitas Indonesia atau 5 Februari 2005 Pada semua catatan yang terdahulu, telah diulas secara panjang lebar bahwa sistem persamaan linear dapat dicari solusinya secara langsung dengan metode eliminasi gauss. Namun perlu juga diketahui bahwa eliminasi gauss bukan satu-satunya metode dalam mencari solusi sistem persamaan linear, misalnya ada metode matrik inversi seperti yang dijelaskan pada catatan yang paling terakhir. Terlepas dari masalah in-efisiensi penyelesaiannya, yang jelas metode invers matrik bisa digunakan untuk menyelesaikan sistem persamaan linear. Nah, pada catatan kali ini, saya ingin mengetengahkan sebuah metode yang lain untuk menyelesaikan sistem persamaan linear, yaitu metode faktorisasi matrik yang umum dikenal sebagai LU-decomposition. Metode ini sekaligus menjadi pengantar menuju metode Singular Value Decomposition, (SVD), suatu metode yang saat ini paling handal dalam menyelesaikan sistem persamaan linear dan merupakan bagian dari metode least square. Seperti biasa, kita berasumsi bahwa sistem persamaan linear dapat dinyatakan dalam operasi matrik Ax = b (1) Pada metode LU-decomposition, matrik A difaktorkan menjadi matrik L dan matrik U, dimana dimensi atau ukuran matrik L dan U harus sama dengan dimensi matrik A. Atau 1
2 dengan kata lain, hasil perkalian matrik L dan matrik U adalah matrik A, A = LU (2) sehingga persamaan (1) menjadi LUx = b Langkah penyelesaian sistem persamaan linear dengan metode LU-decomposition, diawali dengan menghadirkan vektor y dimana, Ux = y (3) Langkah tersebut tidak bermaksud untuk menghitung vektor y, melainkan untuk menghitung vektor x. Artinya, sebelum persamaan (3) dieksekusi, nilai-nilai yang menempati elemen-elemen vektor y harus sudah diketahui. Lalu bagaimana cara memperoleh vektor y? Begini caranya, Ly = b (4) Kesimpulannya, metode LU-decomposition dilakukan dengan tiga langkah sebagai berikut: Melakukan faktorisasi matrik A menjadi matrik L dan matrik U A = LU. Menghitung vektor y dengan operasi matrik Ly = b. Ini adalah proses forwardsubstitution atau substitusi-maju. Menghitung vektor x dengan operasi matrik Ux = y. Ini adalah proses backwardsubstitution atau substitusi-mundur. Metode LU-decomposition bisa dibilang merupakan modifikasi dari eliminasi gauss, karena beberapa langkah yang mesti dibuang pada eliminasi gauss, justru harus dipakai oleh LU-decomposition. Untuk lebih jelasnya, perhatikan contoh berikut ini. Diketahui sistem persamaan linear sebagai berikut P 1 : x = 4 P 2 : 2x 1 + x 3 + = 1 P 3 : 3x 1 x = -3 P 4 : x x 3 = 4 2
3 Sistem tersebut dapat dinyatakan dalam operasi matrik Ax = y, x x 3 = (5) Pada metode eliminasi gauss, matrik A dikonversi menjadi matrik triangular melalui urutan operasi-operasi berikut: (P 2 2P 1 ) (P 2 ), (P 3 3P 1 ) (P 3 ), (P 4 ( 1)P 1 ) (P 4 ), (P 3 4P 2 ) (P 3 ), (P 4 ( 3)P 2 ) (P 4 ). Disisi lain, vektor b ikut berubah nilainya menyesuaikan proses triangularisasi, x x 3 = 7 13 (6) Lain halnya dengan metode LU-decomposition dimana vektor b tidak mengalami perubahan. Yang berubah hanya matrik A saja, yaitu menjadi matrik L dan matrik U, A = LU A = = Jadi matrik L dan U masing-masing adalah L = U = Coba bandingkan matrik U di atas dengan matrik hasil triangularisasi dari metode eliminasi gauss pada persamaan (6), sama persis bukan? Jadi, cara memperoleh matrik U adalah dengan proses triangularisasi! Lantas, bagaimana cara memperoleh matrik L? Begini caranya: (1) elemen-elemen diagonal matrik L diberi nilai 1 (Asal tahu saja, cara ini dikenal dengan metode Doolittle). (2) elemen-elemen matrik L yang berada di atas elemen-elemen diagonal diberi nilai 0. (3) sedangkan, elemen-elemen matrik L yang berada di bawah elemen-elemen diagonal diisi dengan faktor pengali yang digunakan pada 3
4 proses triangularisasi eliminasi gauss. Misalnya pada operasi (P 2 2P 1 ) (P 2 ), maka faktor pengalinya adalah 2; pada operasi (P 3 3P 1 ) (P 3 ), maka faktor pengalinya adalah 3, dan seterusnya. Inilah letak perbedaannya, seluruh faktor pengali tersebut sangat dibutuhkan pada metode LU-decomposition untuk membentuk matrik L. Padahal dalam metode eliminasi gauss, seluruh faktor pengali tersebut tidak dimanfaatkan alias dibuang begitu saja. Disisi lain, vektor b tidak mengalami proses apapun sehingga nilainya tetap. Jadi, proses konversi matrik pada metode LU-decomposition hanya melibatkan matrik A saja! Setelah langkah faktorisasi matrik A dilalui, maka operasi matrik pada persamaan (5) menjadi, x x 3 = 1 (7) Langkah berikutnya adalah menentukan vektor y, dimana Ly = b, y y y 3 = Dengan proses substitusi-maju, elemen-elemen vektor y dapat ditentukan, y 1 = 4, 2y 1 + y 2 = 1, 3y 1 +4y 2 + y 3 = 3, y 1 3y 2 + y 4 = 4 maka diperoleh y 1 =4, y 2 = 7, y 3 =13, y 4 = 13. Langkah terakhir adalah proses substitusi-mundur untuk menghitung vektor x, dimana Ux = y, x x 3 = y 4
5 Melalui proses ini, yang pertama kali didapat solusinya adalah, kemudian x 3, lalu diikuti, dan akhirnya x 1. = 1 x 3 = 1 3 (13 13)=0 = ( x 3 )=2 x 1 = 4 3 = 1 akhirnya diperoleh solusi x 1 = 1, =2, x 3 =0, dan y 4 =1. Demikianlah contoh penyelesaian sistem persamaan linear dengan metode LU-decomposition. Sekali matrik A difaktorkan, maka vektor b bisa diganti nilainya sesuai dengan sistem persamaan linear yang lain, misalnya seluruh nilai di ruas kanan diganti menjadi P 1 : x = 8 P 2 : 2x 1 + x 3 + = 7 P 3 : 3x 1 x = 14 P 4 : x x 3 = -7 Dalam operasi matrik menjadi x 1 x 3 = (8) Perhatikan baik-baik! Matrik A sama persis dengan contoh sebelumnya. Perbedaannya hanya pada vektor b. Selanjutnya, dengan metode LU-decomposition, persamaan (8) menjadi x 1 x 3 = Silakan anda lanjutkan proses perhitungannya dengan mencari vektor y sesuai contoh yang telah diberikan sebelumnya. Pada akhirnya akan diperoleh solusi sebagai berikut: x 1 =3, = 1, x 3 =0, dan y 4 =2. 5 (9)
6 Sekarang saatnya saya tunjukkan algoritma metode LU decomposition. Algoritma ini dibuat untuk menyelesaikan sistem persamaan linear, dengan cara menfaktorkan matrik A =(a ij ) berukuran n x n menjadi matrik L =(l ij ) dan matrik U =(u ij ) dengan ukuran yang sama. Algoritma LU-decomposition yang anda lihat sekarang merupakan modifikasi dari algoritma eliminasi gauss. Silakan anda periksa langkah-langkah mana saja yang telah mengalami modifikasi! Tapi asal tahu saja bahwa ini bukan satu-satunya algoritma untuk mendapatkan matrik LU. Sejauh yang saya tahu, ada algoritma lain untuk tujuan yang sama, dimana algoritma tersebut membutuhkan matrik permutasi untuk menggeser elemen pivot yang bernilai nol agar terhindar dari singular. Nah, sedangkan algoritma yang akan anda baca saat ini, sama sekali tidak berurusan dengan matrik permutasi. Algoritma ini cuma memanfaatkan trik tukar posisi yang sudah pernah dibahas di awalawal catatan khususnya ketika membahas konsep eliminasi gauss. Satu lagi yang harus saya sampaikan juga adalah bahwa dalam algoritma ini, elemenelemen matrik L dan matrik U digabung jadi satu dan menggantikan seluruh elemenelemen matrik A. Perhatian! cara ini jangan diartikan sebagai perkalian matrik L dan matrik U menjadi matrik A kembali. Cara ini dimaksudkan untuk menghemat memori komputer. Suatu aspek yang tidak boleh diabaikan oleh para programer. Marilah kita simak algoritmanya bersama-sama! INPUT: dimensi n; nilai elemen a ij, 1 i, j n; nilai elemen b i. OUTPUT: solusi x 1,,x 3,..., x n atau pesan kesalahan yang mengatakan bahwa faktorisasi tidak mungkin dilakukan. Langkah 1: Inputkan konstanta-konstanta dari sistem persamaan linear kedalam elemen-elemen matrik A dan vektor b, seperti berikut ini: a 11 a a 1n a 21 a a 2n A = b =... a n1 a n2... a nn b 1 b 2. b n (10) Langkah 2: Untuk i =1,..., n 1, lakukan Langkah 3 sampai Langkah 5. Langkah 3: Definisikan p sebagai integer dimana i p n. Lalu pastikan bahwa a pi 0. Langkah dilakukan bila ditemukan elemen diagonal yang bernilai nol (a ii =0). Ketika ada elemen diagonal yang bernilai nol, maka 6
7 program harus mencari dan memeriksa elemen-elemen yang tidak bernilai nol dalam kolom yang sama dengan kolom tempat elemen diagonal tersebut berada. Jadi saat proses ini berlangsung, integer i (indeks dari kolom) dibuat konstan, sementara integer p (indeks dari baris) bergerak dari p = i sampai p = n. Bila ternyata setelah mencapai elemen paling bawah dalam kolom tersebut, yaitu saat p = n tetap didapat nilai a pi =0, maka sebuah pesan dimunculkan: sistem persamaan linear tidak memiliki solusi yang unik. Lalu program berakhir: STOP. Langkah 4: Namun jika sebelum integer p mencapai nilai p = n sudah diperoleh elemen yang tidak sama dengan nol (a pi 0), maka bisa dipastikan p i. Jika p i maka lakukan proses pertukaran (P p ) (P i ). Langkah 5: Untuk j = i +1,.., n, lakukan Langkah 6 dan Langkah 7. Langkah 6: Tentukan m ji, m ji = a ji a ii Langkah 7: Lakukan proses triangularisasi, (P j m ji P i ) (P j ) Langkah 8: Nilai m ji disimpan ke a ji, a ji = m ji Langkah 9: Nilai b 1 dicopy ke y 1, lalu lakukan substitusi-maju. Untuk i =2,..., n tentukan x i, y 1 = b 1 i 1 y i = b i a ij y j Langkah 10: Lakukan proses substitusi-mundur, dimulai dengan menentukan x n, Untuk i = n 1,..., 1 tentukan x i, j=1 x n = a n,n+1 a nn x i = a i,n+1 n j=i+1 a ijx j a ii 7
8 Langkah 11: Diperoleh solusi yaitu x 1,,..., x n. Algoritma telah dijalankan dengan sukses. STOP. Algoritma di atas telah diimplementasi kedalam program yang ditulis dengan bahasa Fortran. Program tersebut sudah berhasil dikompilasi dengan visual fortran (windows) dan g77 (debian-linux). Inilah programnya: DIMENSION A(10,11), B(10), Y(10), X(10) REAL MJI WRITE(*,*) WRITE(*,*) ==> FAKTORISASI MATRIK: LU DECOMPOSITION <== C LANGKAH 1: MEMASUKAN NILAI ELEMEN-ELEMEN MATRIK A DAN VEKTOR B WRITE (*, (1X,A) ) JUMLAH PERSAMAAN? READ (*,*) N MASUKAN ELEMEN-ELEMEN MATRIK A DO 50 I = 1,N DO 60 J = 1,N WRITE (*, (1X,A,I2,A,I2,A) ) A(,I,,,J, ) = READ (*,*) A(I,J) 60 CONTINUE WRITE (*, (1X,A,I2,A) ) B(,I, )? READ (*,*) B(I) 50 CONTINUE C MENAMPILKAN MATRIK A WRITE (*, (1X,A) ) MATRIK A: DO 110 I = 1,N WRITE (*,6) (A(I,J),J=1,N) 110 CONTINUE C LANGKAH 2: MEMERIKSA ELEMEN-ELEMEN PIVOT NN = N-1 8
9 DO 10 I=1,NN C LANGKAH 3: MENDEFINISIKAN P P = I 100 IF (ABS(A(P,I)).GE.1.0E-20.OR. P.GT.N) GOTO 200 P = P+1 GOTO IF(P.EQ.N+1)THEN C MENAMPILKAN PESAN TIDAK DAPAT DIFAKTORKAN WRITE(*,8) GOTO 400 END IF C LANGKAH 4: PROSES TUKAR POSISI IF(P.NE.I) THEN DO 20 JJ=1,N C = A(I,JJ) A(I,JJ) = A(P,JJ) A(P,JJ) = C 20 CONTINUE END IF C LANGKAH 5: PERSIAPAN PROSES TRIANGULARISASI JJ = I+1 DO 30 J=JJ,N C LANGKAH 6: TENTUKAN MJI MJI = A(J,I)/A(I,I) C LANGKAH 7: PROSES TRIANGULARISASI DO 40 K=JJ,N A(J,K) = A(J,K)-MJI*A(I,K) 40 CONTINUE C LANGKAH 8: MENYIMPAN MJI KE A(J,I) A(J,I) = MJI 30 CONTINUE 10 CONTINUE C MENAMPILKAN MATRIK LU WRITE (*, (1X,A) ) MATRIK LU: 9
10 DO 120 I = 1,N WRITE (*,6) (A(I,J),J=1,N) 120 CONTINUE C LANGKAH 9: SUBSTITUSI-MAJU Y(1) = B(1) DO 15 I=2,N SUM = 0.0 DO 16 J=1,I-1 SUM = SUM+A(I,J)*Y(J) 16 CONTINUE Y(I) = B(I)-SUM 15 CONTINUE C MENAMPILKAN VEKTOR Y WRITE (*, (1X,A) ) VEKTOR Y: DO 138 I = 1,N WRITE (*,6) Y(I) 138 CONTINUE C LANGKAH 10: SUBSTITUSI-MUNDUR X(N) = Y(N)/A(N,N) DO 24 K=1,N-1 I = N-K JJ = I+1 SUM = 0.0 DO 26 KK=JJ,N SUM = SUM+A(I,KK)*X(KK) 26 CONTINUE X(I) = (Y(I)-SUM)/A(I,I) 24 CONTINUE C LANGKAH 11: MENAMPILKAN SOLUSI DAN SELESAI WRITE (*, (1X,A) ) SOLUSI: DO 18 I = 1,N WRITE (*, (1X,A,I2,A,F14.8) ) X(,I, ) =,X(I) 10
11 18 CONTINUE WRITE(*,*) WRITE(*,*) SELESAI --> SUKSES WRITE(*,*) 400 CONTINUE 6 FORMAT(1X,5(F14.8)) 8 FORMAT(1X, TIDAK DAPAT DIFAKTORKAN ) END Demikianlah, sekarang kita punya tiga buah algoritma untuk memecahkan problem sistem persamaan linear, yaitu eliminasi gauss, invers matrik, dan lu-decomposition. Diantara ketiga-nya, eliminasi gauss adalah algoritma yang paling simpel dan efisien. Dia hanya butuh proses triangularisasi dan substitusi-mundur untuk mendapatkan solusi. Sedangkan dua algoritma yang lainnya membutuhkan proses-proses tambahan untuk mendapatkan solusi yang sama. Saya cukupkan sementara sampai disini. Insya Allah akan saya sambung lagi dilain waktu. Kalau ada yang mau didiskusikan, silakan hubungi saya melalui . 11
SISTEM PERSAMAAN LINEAR DAN ELIMINASI GAUSS
 SISTEM PERSAMAAN LINEAR DAN ELIMINASI GAUSS Dr. Eng. Supriyanto, M.Sc Lab. Komputer, Departemen Fisika, Universitas Indonesia email: [email protected] atau [email protected] 5 Februari 2005 Abstract
SISTEM PERSAMAAN LINEAR DAN ELIMINASI GAUSS Dr. Eng. Supriyanto, M.Sc Lab. Komputer, Departemen Fisika, Universitas Indonesia email: [email protected] atau [email protected] 5 Februari 2005 Abstract
INVERS MATRIK DAN ELIMINASI GAUSS
 INVERS MATRIK DAN ELIMINASI GAUSS Dr. Eng. Supriyanto, M.Sc Lab. Komputer, Departemen Fisika, Universitas Indonesia email: [email protected] atau [email protected] 5 Februari 2005 Secara umum, sistem
INVERS MATRIK DAN ELIMINASI GAUSS Dr. Eng. Supriyanto, M.Sc Lab. Komputer, Departemen Fisika, Universitas Indonesia email: [email protected] atau [email protected] 5 Februari 2005 Secara umum, sistem
Komputasi untuk Sains dan Teknik
 Komputasi untuk Sains dan Teknik Dr. Eng. Supriyanto, M.Sc Edisi I Laboratorium Jaringan Komputer Departemen Fisika-FMIPA Univeristas Indonesia 2006 Untuk Muflih Syamil dan Hasan Azmi... Mottoku : Tenang,
Komputasi untuk Sains dan Teknik Dr. Eng. Supriyanto, M.Sc Edisi I Laboratorium Jaringan Komputer Departemen Fisika-FMIPA Univeristas Indonesia 2006 Untuk Muflih Syamil dan Hasan Azmi... Mottoku : Tenang,
METODE ITERASI DALAM SISTEM PERSAMAAN LINEAR
 METODE ITERASI DALAM SISTEM PERSAMAAN LINEAR Penulis: Dr. Eng. Supriyanto, M.Sc, email: [email protected] Staf Lab. Komputer, Departemen Fisika, Universitas Indonesia Penulisan vektor-kolom Sebelum
METODE ITERASI DALAM SISTEM PERSAMAAN LINEAR Penulis: Dr. Eng. Supriyanto, M.Sc, email: [email protected] Staf Lab. Komputer, Departemen Fisika, Universitas Indonesia Penulisan vektor-kolom Sebelum
Komputasi untuk Sains dan Teknik
 Komputasi untuk Sains dan Teknik Supriyanto Suparno ( Website: http://supriyanto.fisika.ui.edu ) ( Email: [email protected] atau [email protected] ) Edisi II Revisi terakhir tgl: 12 Februari 2008 Departemen
Komputasi untuk Sains dan Teknik Supriyanto Suparno ( Website: http://supriyanto.fisika.ui.edu ) ( Email: [email protected] atau [email protected] ) Edisi II Revisi terakhir tgl: 12 Februari 2008 Departemen
Komputasi untuk Sains dan Teknik
 Komputasi untuk Sains dan Teknik Supriyanto Suparno ( Website: http://supriyanto.fisika.ui.edu ) ( Email: [email protected] atau [email protected] ) Edisi II Revisi terakhir tgl: 28 April 2008 Departemen
Komputasi untuk Sains dan Teknik Supriyanto Suparno ( Website: http://supriyanto.fisika.ui.edu ) ( Email: [email protected] atau [email protected] ) Edisi II Revisi terakhir tgl: 28 April 2008 Departemen
BAB 1 PENDAHULUAN. Sebuah garis dalam bidang xy secara aljabar dapat dinyatakan oleh persamaan yang berbentuk
 BAB 1 PENDAHULUAN 1.1 Latar belakang Sebagian besar dari sejarah ilmu pengetahuan alam adalah catatan dari usaha manusia secara kontinu untuk merumuskan konsep-konsep yang dapat menguraikan permasalahan
BAB 1 PENDAHULUAN 1.1 Latar belakang Sebagian besar dari sejarah ilmu pengetahuan alam adalah catatan dari usaha manusia secara kontinu untuk merumuskan konsep-konsep yang dapat menguraikan permasalahan
6 Sistem Persamaan Linear
 6 Sistem Persamaan Linear Pada bab, kita diminta untuk mencari suatu nilai x yang memenuhi persamaan f(x) = 0. Pada bab ini, masalah tersebut diperumum dengan mencari x = (x, x,..., x n ) yang secara sekaligus
6 Sistem Persamaan Linear Pada bab, kita diminta untuk mencari suatu nilai x yang memenuhi persamaan f(x) = 0. Pada bab ini, masalah tersebut diperumum dengan mencari x = (x, x,..., x n ) yang secara sekaligus
REGRESI LINEAR DAN ELIMINASI GAUSS
 REGRESI LINEAR DAN ELIMINASI GAUSS Penulis: Supriyanto, email: [email protected] Staf Lab. Komputer, Departemen Fisika, Universitas Indonesia Diketahui data eksperimen tersaji dalam tabel berikut ini
REGRESI LINEAR DAN ELIMINASI GAUSS Penulis: Supriyanto, email: [email protected] Staf Lab. Komputer, Departemen Fisika, Universitas Indonesia Diketahui data eksperimen tersaji dalam tabel berikut ini
Komputasi untuk Sains dan Teknik -Dalam Matlab-
 Komputasi untuk Sains dan Teknik -Dalam Matlab- Supriyanto Suparno ( Website: http://supriyanto.fisika.ui.edu ) ( Email: [email protected] atau [email protected] ) Edisi III Revisi terakhir tgl: 25
Komputasi untuk Sains dan Teknik -Dalam Matlab- Supriyanto Suparno ( Website: http://supriyanto.fisika.ui.edu ) ( Email: [email protected] atau [email protected] ) Edisi III Revisi terakhir tgl: 25
Solusi Sistem Persamaan Linear Ax = b
 Solusi Sistem Persamaan Linear Ax = b Kie Van Ivanky Saputra April 27, 2009 K V I Saputra (Analisis Numerik) Kuliah Sistem Persamaan Linier c April 27, 2009 1 / 9 Review 1 Substitusi mundur pada sistem
Solusi Sistem Persamaan Linear Ax = b Kie Van Ivanky Saputra April 27, 2009 K V I Saputra (Analisis Numerik) Kuliah Sistem Persamaan Linier c April 27, 2009 1 / 9 Review 1 Substitusi mundur pada sistem
PENDAHULUAN A. Latar Belakang 1. Metode Langsung Metode Langsung Eliminasi Gauss (EGAUSS) Metode Eliminasi Gauss Dekomposisi LU (DECOLU),
 PENDAHULUAN A. Latar Belakang Persoalan yang melibatkan model matematika banyak muncul dalam berbagai disiplin ilmu pengetahuan, seperti dalam bidang fisika, kimia, ekonomi, atau pada persoalan rekayasa.
PENDAHULUAN A. Latar Belakang Persoalan yang melibatkan model matematika banyak muncul dalam berbagai disiplin ilmu pengetahuan, seperti dalam bidang fisika, kimia, ekonomi, atau pada persoalan rekayasa.
PAM 252 Metode Numerik Bab 3 Sistem Persamaan Linier
 PAM 252 Metode Numerik Bab 3 Sistem Persamaan Linier Mahdhivan Syafwan Jurusan Matematika FMIPA Universitas Andalas Semester Genap 2013/2014 1 Mahdhivan Syafwan Metode Numerik: Sistem Persamaan Linier
PAM 252 Metode Numerik Bab 3 Sistem Persamaan Linier Mahdhivan Syafwan Jurusan Matematika FMIPA Universitas Andalas Semester Genap 2013/2014 1 Mahdhivan Syafwan Metode Numerik: Sistem Persamaan Linier
BAB II ISI ( ) (sumber:
 BAB II ISI A. Permasalahan yang Diberikan Soal saudara dalam UTS ini harus terus digunakan untuk mengerjakan tugas proyek ini, yaitu: prediksi sifat-sifat tekanan uap murni suatu fluida hidrokarbon sebagai
BAB II ISI A. Permasalahan yang Diberikan Soal saudara dalam UTS ini harus terus digunakan untuk mengerjakan tugas proyek ini, yaitu: prediksi sifat-sifat tekanan uap murni suatu fluida hidrokarbon sebagai
BAB 4 PENYELESAIAN SISTEM PERSAMAAN LINEAR
 BAB 4 PENYELESAIAN SISTEM PERSAMAAN LINEAR A. Latar Belakang Persoalan yang melibatkan model matematika banyak muncul dalam berbagai disiplin ilmu pengetahuan, seperti dalam bidang fisika, kimia, ekonomi,
BAB 4 PENYELESAIAN SISTEM PERSAMAAN LINEAR A. Latar Belakang Persoalan yang melibatkan model matematika banyak muncul dalam berbagai disiplin ilmu pengetahuan, seperti dalam bidang fisika, kimia, ekonomi,
PAM 252 Metode Numerik Bab 3 Sistem Persamaan Linier
 PAM 252 Metode Numerik Bab 3 Sistem Persamaan Linier Mahdhivan Syafwan Jurusan Matematika FMIPA Universitas Andalas Semester Genap 2016/2017 1 Mahdhivan Syafwan Metode Numerik: Sistem Persamaan Linier
PAM 252 Metode Numerik Bab 3 Sistem Persamaan Linier Mahdhivan Syafwan Jurusan Matematika FMIPA Universitas Andalas Semester Genap 2016/2017 1 Mahdhivan Syafwan Metode Numerik: Sistem Persamaan Linier
03-Pemecahan Persamaan Linier (2)
 -Pemecahan Persamaan Linier () Dosen: Anny Yuniarti, M.Comp.Sc Gasal - Anny Agenda Bagian : Matriks Invers Bagian : Eliminasi = Faktorisasi: A = LU Bagian : Transpos dan Permutasi Anny Bagian MATRIKS INVERS
-Pemecahan Persamaan Linier () Dosen: Anny Yuniarti, M.Comp.Sc Gasal - Anny Agenda Bagian : Matriks Invers Bagian : Eliminasi = Faktorisasi: A = LU Bagian : Transpos dan Permutasi Anny Bagian MATRIKS INVERS
BAB 4 Sistem Persamaan Linear. Sistem m persamaan linear dalam n variabel LG=C adalah himpunan persamaan linear
 BAB 4 Sistem Persamaan Linear berbentuk Sistem m persamaan linear dalam n variabel LG=C adalah himpunan persamaan linear Dengan koefisien dan adalah bilangan-bilangan yang diberikan. Sistem ini disebut
BAB 4 Sistem Persamaan Linear berbentuk Sistem m persamaan linear dalam n variabel LG=C adalah himpunan persamaan linear Dengan koefisien dan adalah bilangan-bilangan yang diberikan. Sistem ini disebut
MATRIK DAN KOMPUTASI
 MATRIK DAN KOMPUTASI Penulis: Supriyanto, email: [email protected] Staf Lab. Komputer, Departemen Fisika, Universitas Indonesia Fukuoka, 5 Feb 2005 Catatan ini bermaksud menjelaskan secara singkat
MATRIK DAN KOMPUTASI Penulis: Supriyanto, email: [email protected] Staf Lab. Komputer, Departemen Fisika, Universitas Indonesia Fukuoka, 5 Feb 2005 Catatan ini bermaksud menjelaskan secara singkat
BAB I PENDAHULUAN Latar Belakang Masalah
 BAB I PENDAHULUAN 1.1. Latar Belakang Masalah Suatu matriks A C m n dikatakan memiliki faktorisasi LU jika matriks tersebut dapat dinyatakan sebagai A = LU dengan L C m m matriks invertibel segitiga bawah
BAB I PENDAHULUAN 1.1. Latar Belakang Masalah Suatu matriks A C m n dikatakan memiliki faktorisasi LU jika matriks tersebut dapat dinyatakan sebagai A = LU dengan L C m m matriks invertibel segitiga bawah
Metode Matriks Balikan
 Metode Matriks Balikan MisalkanA -1 adalahmatriksbalikandaria. Sistempersamaan lanjar Ax = b dapat diselesaikan sebagai berikut: Ax= b A -1 Ax= A -1 b I x= A -1 b (A -1 A = I ) x= A -1 b Cara penyelesaiandenganmengalikanmatriksa
Metode Matriks Balikan MisalkanA -1 adalahmatriksbalikandaria. Sistempersamaan lanjar Ax = b dapat diselesaikan sebagai berikut: Ax= b A -1 Ax= A -1 b I x= A -1 b (A -1 A = I ) x= A -1 b Cara penyelesaiandenganmengalikanmatriksa
SCRIPT PERSAMAAN CRAMER
 SCRIPT PERSAMAAN CRAMER Program ; Uses crt; var a11,a12,a13,a21,a22,a23,a31,a32,a33,c1,c2,c3 : integer; D, Dx, Dy, Dz, x, y, z: real; Begin clrscr; writeln ('PENYELESAIAN PERS ALJABAR LINEAR':50); writeln
SCRIPT PERSAMAAN CRAMER Program ; Uses crt; var a11,a12,a13,a21,a22,a23,a31,a32,a33,c1,c2,c3 : integer; D, Dx, Dy, Dz, x, y, z: real; Begin clrscr; writeln ('PENYELESAIAN PERS ALJABAR LINEAR':50); writeln
Metode Matematika untuk Geofisika
 Metode Matematika untuk Geofisika Supriyanto Suparno ( Website: http://supriyanto.fisika.ui.ac.id ) ( Email: [email protected] atau [email protected] ) Edisi I Revisi terakhir tgl: Desember 009 Departemen
Metode Matematika untuk Geofisika Supriyanto Suparno ( Website: http://supriyanto.fisika.ui.ac.id ) ( Email: [email protected] atau [email protected] ) Edisi I Revisi terakhir tgl: Desember 009 Departemen
Sistem Persamaan Aljabar Linier
 Sistem Persamaan Aljabar Linier Dimana: a ij = koefisien konstanta; x j = unknown ; b j = konstanta; n = banyaknya persamaan Metode-Metode untuk menyelesaikan Sistem Persamaan Aljabar Linier: 1. Metode
Sistem Persamaan Aljabar Linier Dimana: a ij = koefisien konstanta; x j = unknown ; b j = konstanta; n = banyaknya persamaan Metode-Metode untuk menyelesaikan Sistem Persamaan Aljabar Linier: 1. Metode
02-Pemecahan Persamaan Linier (1)
 -Pemecahan Persamaan Linier () Dosen: Anny Yuniarti, M.Comp.Sc Gasal - Anny Agenda Bagian : Vektor dan Persamaan Linier Bagian : Teori Dasar Eliminasi Bagian 3: Eliminasi Menggunakan Matriks Bagian 4:
-Pemecahan Persamaan Linier () Dosen: Anny Yuniarti, M.Comp.Sc Gasal - Anny Agenda Bagian : Vektor dan Persamaan Linier Bagian : Teori Dasar Eliminasi Bagian 3: Eliminasi Menggunakan Matriks Bagian 4:
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI 2.1 Sistem Persamaan Linier Sistem Persamaan dengan m persamaan dan n bilangan tak diketahui ditulis dengan : Dimana x 1, x 2, x n : bilangan tak diketahui a,b : konstanta Jika SPL
BAB 2 LANDASAN TEORI 2.1 Sistem Persamaan Linier Sistem Persamaan dengan m persamaan dan n bilangan tak diketahui ditulis dengan : Dimana x 1, x 2, x n : bilangan tak diketahui a,b : konstanta Jika SPL
SISTEM PERSAMAAN LINEAR ( BAGIAN II )
 SISTEM PERSAMAAN LINEAR ( BAGIAN II ) D. FAKTORISASI MATRIKS D2 2. METODE ITERASI UNTUK MENYELESAIKAN SPL D3 3. NILAI EIGEN DAN VEKTOR EIGEN D4 4. POWER METHOD Beserta contoh soal untuk setiap subbab 2
SISTEM PERSAMAAN LINEAR ( BAGIAN II ) D. FAKTORISASI MATRIKS D2 2. METODE ITERASI UNTUK MENYELESAIKAN SPL D3 3. NILAI EIGEN DAN VEKTOR EIGEN D4 4. POWER METHOD Beserta contoh soal untuk setiap subbab 2
Matriks - Definisi. Sebuah matriks yang memiliki m baris dan n kolom disebut matriks m n. Sebagai contoh: Adalah sebuah matriks 2 3.
 MATRIKS Pokok Bahasan Matriks definisi Notasi matriks Matriks yang sama Panambahan dan pengurangan matriks Perkalian matriks Transpos suatu matriks Matriks khusus Determinan suatu matriks bujursangkar
MATRIKS Pokok Bahasan Matriks definisi Notasi matriks Matriks yang sama Panambahan dan pengurangan matriks Perkalian matriks Transpos suatu matriks Matriks khusus Determinan suatu matriks bujursangkar
STATEMENT FORMAT, DATA, PARAMETER, SPESIFIKASI DAN PENGERJAAN. Kuliah ke-3
 STATEMENT FORMAT, DATA, PARAMETER, SPESIFIKASI DAN PENGERJAAN Kuliah ke-3 1 PROGRAM FORTRAN STATEMENT FORMAT Bentuk umum penulisan statement FORMAT adalah ; < label statement > FORMAT Penjelasan
STATEMENT FORMAT, DATA, PARAMETER, SPESIFIKASI DAN PENGERJAAN Kuliah ke-3 1 PROGRAM FORTRAN STATEMENT FORMAT Bentuk umum penulisan statement FORMAT adalah ; < label statement > FORMAT Penjelasan
MODUL 3 FAKTORISASI LU, PARTISI MATRIK DAN FAKTORISASI QR
 MODUL 3 FAKTORISASI LU, PARTISI MATRIK DAN FAKTORISASI QR KOMPETENSI: 1. Memahami penggunaan faktorisasi LU dalam penyelesaian persamaan linear.. Memahami penggunaan partisi matrik dalam penyelesaian persamaan
MODUL 3 FAKTORISASI LU, PARTISI MATRIK DAN FAKTORISASI QR KOMPETENSI: 1. Memahami penggunaan faktorisasi LU dalam penyelesaian persamaan linear.. Memahami penggunaan partisi matrik dalam penyelesaian persamaan
MATRIKS. Matematika. FTP UB Mas ud Effendi. Matematika
 MATRIKS FTP UB Mas ud Effendi Pokok Bahasan Transpos suatu matriks Matriks khusus Determinan suatu matriks bujursangkar Invers suatu matriks bujursangkar Penyelesaian set persamaan linier Nilai-eigen dan
MATRIKS FTP UB Mas ud Effendi Pokok Bahasan Transpos suatu matriks Matriks khusus Determinan suatu matriks bujursangkar Invers suatu matriks bujursangkar Penyelesaian set persamaan linier Nilai-eigen dan
Interpolasi Cubic Spline
 Interpolasi Cubic Spline Dr. Eng. Supriyanto, M.Sc Lab. Komputer, Departemen Fisika, Universitas Indonesia email: [email protected] atau [email protected] December 13, 2006 Figure 1: Fungsi f(x) dengan
Interpolasi Cubic Spline Dr. Eng. Supriyanto, M.Sc Lab. Komputer, Departemen Fisika, Universitas Indonesia email: [email protected] atau [email protected] December 13, 2006 Figure 1: Fungsi f(x) dengan
MATRIKS Matematika Industri I
 MATRIKS TIP FTP UB Mas ud Effendi Pokok Bahasan Matriks definisi Notasi matriks Matriks yang sama Panambahan dan pengurangan matriks Perkalian matriks Transpos suatu matriks Matriks khusus Determinan suatu
MATRIKS TIP FTP UB Mas ud Effendi Pokok Bahasan Matriks definisi Notasi matriks Matriks yang sama Panambahan dan pengurangan matriks Perkalian matriks Transpos suatu matriks Matriks khusus Determinan suatu
PERBANDINGAN KOMPLEKSITAS ALGORITMA METODE-METODE PENYELESAIAN SISTEM PERSAMAAN LANJAR
 PERBANDINGAN KOMPLEKSITAS ALGORITMA METODE-METODE PENYELESAIAN SISTEM PERSAMAAN LANJAR Achmad Dimas Noorcahyo NIM 3508076 Program Studi Teknik Informatika, Institut Teknologi Bandung Jalan Ganeca 0, Bandung
PERBANDINGAN KOMPLEKSITAS ALGORITMA METODE-METODE PENYELESAIAN SISTEM PERSAMAAN LANJAR Achmad Dimas Noorcahyo NIM 3508076 Program Studi Teknik Informatika, Institut Teknologi Bandung Jalan Ganeca 0, Bandung
Bab 7 Sistem Pesamaan Linier. Oleh : Devie Rosa Anamisa
 Bab 7 Sistem Pesamaan Linier Oleh : Devie Rosa Anamisa Pendahuluan Bentuk umum dari aljabar linier sebagai berikut: a11x1 + a12a 12X2 +... + a1na 1nXn = b1b a21x1 + a22a 22X2 +... + a2na 2nXn = b2b...............
Bab 7 Sistem Pesamaan Linier Oleh : Devie Rosa Anamisa Pendahuluan Bentuk umum dari aljabar linier sebagai berikut: a11x1 + a12a 12X2 +... + a1na 1nXn = b1b a21x1 + a22a 22X2 +... + a2na 2nXn = b2b...............
Pertemuan 1 Sistem Persamaan Linier dan Matriks
 Matriks & Ruang Vektor Pertemuan Sistem Persamaan Linier dan Matriks Start Matriks & Ruang Vektor Outline Materi Pengenalan Sistem Persamaan Linier (SPL) SPL & Matriks Matriks & Ruang Vektor Persamaan
Matriks & Ruang Vektor Pertemuan Sistem Persamaan Linier dan Matriks Start Matriks & Ruang Vektor Outline Materi Pengenalan Sistem Persamaan Linier (SPL) SPL & Matriks Matriks & Ruang Vektor Persamaan
MATRIKS Matematika Industri I
 MATRIKS TIP FTP UB Mas ud Effendi Pokok Bahasan Matriks definisi Notasi matriks Matriks yang sama Panambahan dan pengurangan matriks Perkalian matriks Transpos suatu matriks Matriks khusus Determinan suatu
MATRIKS TIP FTP UB Mas ud Effendi Pokok Bahasan Matriks definisi Notasi matriks Matriks yang sama Panambahan dan pengurangan matriks Perkalian matriks Transpos suatu matriks Matriks khusus Determinan suatu
Part II SPL Homogen Matriks
 Part II SPL Homogen Matriks SPL Homogen Bentuk Umum SPL homogen dalam m persamaan dan n variabel x 1, x 2,, x n : a 11 x 1 + a 12 x 2 + + a 1n x n = 0 a 21 x 1 + a 22 x 2 + + a 2n x n = 0 a m1 x 1 + a
Part II SPL Homogen Matriks SPL Homogen Bentuk Umum SPL homogen dalam m persamaan dan n variabel x 1, x 2,, x n : a 11 x 1 + a 12 x 2 + + a 1n x n = 0 a 21 x 1 + a 22 x 2 + + a 2n x n = 0 a m1 x 1 + a
Lampiran 1 Pembuktian Teorema 2.3
 LAMPIRAN 16 Lampiran 1 Pembuktian Teorema 2.3 Sebelum membuktikan Teorema 2.3, terlebih dahulu diberikan beberapa definisi yang berhubungan dengan pembuktian Teorema 2.3. Definisi 1 (Matriks Eselon Baris)
LAMPIRAN 16 Lampiran 1 Pembuktian Teorema 2.3 Sebelum membuktikan Teorema 2.3, terlebih dahulu diberikan beberapa definisi yang berhubungan dengan pembuktian Teorema 2.3. Definisi 1 (Matriks Eselon Baris)
BAB X MATRIK DAN SISTEM PERSAMAAN LINIER SIMULTAN
 1 BAB X MATRIK DAN SISTEM PERSAMAAN LINIER SIMULTAN Pembahasan berikut ini akan meninjau salah satu implementasi operasi matrik untuk menyelesaikan sistem persamaan linier simultan. Selain menggunakan
1 BAB X MATRIK DAN SISTEM PERSAMAAN LINIER SIMULTAN Pembahasan berikut ini akan meninjau salah satu implementasi operasi matrik untuk menyelesaikan sistem persamaan linier simultan. Selain menggunakan
BAB I PENDAHULUAN. 3) Untuk mengetahui apa yang dimaksud dengan invers matriks. 4) Untuk mengetahui apa yang dimaksud dengan determinan matriks
 1.1 LATAR BELAKANG BAB I PENDAHULUAN Teori matriks merupakan salah satu cabang ilmu aljabar linier yang menjadi pembahasan penting dalam ilmu matematika. Sejalan dengan perkembangan ilmu pengetahuan, aplikasi
1.1 LATAR BELAKANG BAB I PENDAHULUAN Teori matriks merupakan salah satu cabang ilmu aljabar linier yang menjadi pembahasan penting dalam ilmu matematika. Sejalan dengan perkembangan ilmu pengetahuan, aplikasi
Solusi Persamaan Linier Simultan
 Solusi Persamaan Linier Simultan Obyektif : 1. Mengerti penggunaan solusi persamaan linier 2. Mengerti metode eliminasi gauss. 3. Mampu menggunakan metode eliminasi gauss untuk mencari solusi 1. Sistem
Solusi Persamaan Linier Simultan Obyektif : 1. Mengerti penggunaan solusi persamaan linier 2. Mengerti metode eliminasi gauss. 3. Mampu menggunakan metode eliminasi gauss untuk mencari solusi 1. Sistem
Syarif Abdullah (G ) Matematika Terapan FMIPA Institut Pertanian Bogor.
 Syarif Abdullah (G551150381) Matematika Terapan FMIPA Institut Pertanian Bogor e-mail: [email protected] 25 Maret 2016 Ringkasan Kuliah ke-6 Analisis Numerik (16 Maret 2016) Materi : System
Syarif Abdullah (G551150381) Matematika Terapan FMIPA Institut Pertanian Bogor e-mail: [email protected] 25 Maret 2016 Ringkasan Kuliah ke-6 Analisis Numerik (16 Maret 2016) Materi : System
BAB 4 : SISTEM PERSAMAAN LINIER
 BAB 4 : SISTEM PERSAMAAN LINIER 4.1 PERSAMAAN LINIER Misalnya x 2 Matematika analitik membicarakan ilmu ukur secara aljabar. Garis lurus pada bidang x 1 dan x 2 dapat dinyatakan sebagai persamaan a 1 x
BAB 4 : SISTEM PERSAMAAN LINIER 4.1 PERSAMAAN LINIER Misalnya x 2 Matematika analitik membicarakan ilmu ukur secara aljabar. Garis lurus pada bidang x 1 dan x 2 dapat dinyatakan sebagai persamaan a 1 x
Minggu II Lanjutan Matriks
 Minggu II Lanjutan Matriks Pokok Bahasan Sub Pokok Bahasan Tujuan Instruksional Umum Tujuan Instruksional Khusus Jumlah Pertemuan : Matriks : A. Transformasi Elementer. Transformasi Elementer pada baris
Minggu II Lanjutan Matriks Pokok Bahasan Sub Pokok Bahasan Tujuan Instruksional Umum Tujuan Instruksional Khusus Jumlah Pertemuan : Matriks : A. Transformasi Elementer. Transformasi Elementer pada baris
Komputasi untuk Sains dan Teknik -Menggunakan Matlab-
 Komputasi untuk Sains dan Teknik -Menggunakan Matlab- Supriyanto Suparno ( Website: http://supriyanto.fisika.ui.edu ) ( Email: [email protected] atau [email protected] ) Edisi III Revisi terakhir tgl:
Komputasi untuk Sains dan Teknik -Menggunakan Matlab- Supriyanto Suparno ( Website: http://supriyanto.fisika.ui.edu ) ( Email: [email protected] atau [email protected] ) Edisi III Revisi terakhir tgl:
METODE FINITE-DIFFERENCE UNTUK PROBLEM LINEAR
 METODE FINITE-DIFFERENCE UNTUK PROBLEM LINEAR Dr. Eng. Supriyanto, M.Sc Lab. Komputer, Departemen Fisika, Universitas Indonesia email: [email protected] atau [email protected] November 12, 2006 Suatu
METODE FINITE-DIFFERENCE UNTUK PROBLEM LINEAR Dr. Eng. Supriyanto, M.Sc Lab. Komputer, Departemen Fisika, Universitas Indonesia email: [email protected] atau [email protected] November 12, 2006 Suatu
Keunggulan Penyelesaian Persamaan Linear dengan Metode Dekomposisi LU dalam Komputerisasi
 Keunggulan Penyelesaian Persamaan Linear dengan Metode Dekomposisi LU dalam Komputerisasi Elvina Riama K. Situmorang 55) Program Studi Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi
Keunggulan Penyelesaian Persamaan Linear dengan Metode Dekomposisi LU dalam Komputerisasi Elvina Riama K. Situmorang 55) Program Studi Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi
Bentuk umum : SPL. Mempunyai penyelesaian disebut KONSISTEN. Tidak mempunyai penyelesaian disebut TIDAK KONSISTEN TUNGGAL BANYAK
 Bentuk umum : dimana x, x,..., x n variabel tak diketahui, a ij, b i, i =,,..., m; j =,,..., n bil. diketahui. Ini adalah SPL dengan m persamaan dan n variabel. SPL Mempunyai penyelesaian disebut KONSISTEN
Bentuk umum : dimana x, x,..., x n variabel tak diketahui, a ij, b i, i =,,..., m; j =,,..., n bil. diketahui. Ini adalah SPL dengan m persamaan dan n variabel. SPL Mempunyai penyelesaian disebut KONSISTEN
SOLUSI SISTEM PERSAMAAN LINEAR
 SOLUSI SISTEM PERSAMAAN LINEAR Bentuk umum persamaan linear dengan n peubah diberikan sebagai berikut : a1 x1 + a2 x2 +... + an xn = b ; a 1, a 2,..., a n R merupakan koefisien dari persamaaan dan x 1,
SOLUSI SISTEM PERSAMAAN LINEAR Bentuk umum persamaan linear dengan n peubah diberikan sebagai berikut : a1 x1 + a2 x2 +... + an xn = b ; a 1, a 2,..., a n R merupakan koefisien dari persamaaan dan x 1,
SISTEM PERSAMAAN LINEAR
 Pokok Bahasan : Sistem persamaan linier Sub Pokok Bahasan : Sistem persamaan linier Eliminasi Gauss Eliminasi Gauss Jordan Penyelesaian SPL dengan invers SISTEM PERSAMAAN LINEAR Tujuan : Menyelesaikan
Pokok Bahasan : Sistem persamaan linier Sub Pokok Bahasan : Sistem persamaan linier Eliminasi Gauss Eliminasi Gauss Jordan Penyelesaian SPL dengan invers SISTEM PERSAMAAN LINEAR Tujuan : Menyelesaikan
MATRIK dan RUANG VEKTOR
 MATRIK dan RUANG VEKTOR A. Matrik. Pendahuluan Sebuah matrik didefinisikan sebagai susunan persegi panjang dari bilangan bilangan yang diatur dalam baris dan kolom. Matrik ditulis sebagai berikut: a a
MATRIK dan RUANG VEKTOR A. Matrik. Pendahuluan Sebuah matrik didefinisikan sebagai susunan persegi panjang dari bilangan bilangan yang diatur dalam baris dan kolom. Matrik ditulis sebagai berikut: a a
MATRIKS Nuryanto, ST., MT.
 MateMatika ekonomi MATRIKS TUJUAN INSTRUKSIONAL KHUSUS Setelah mempelajari bab ini, anda diharapkan dapat : 1. Pengertian matriks 2. Operasi matriks 3. Jenis matriks 4. Determinan 5. Matriks invers 6.
MateMatika ekonomi MATRIKS TUJUAN INSTRUKSIONAL KHUSUS Setelah mempelajari bab ini, anda diharapkan dapat : 1. Pengertian matriks 2. Operasi matriks 3. Jenis matriks 4. Determinan 5. Matriks invers 6.
uiopasdfghjklzxcvbnmqwertyuiopasd fghjklzxcvbnmqwertyuiopasdfghjklzx wertyuiopasdfghjklzxcvbnmqwertyui opasdfghjklzxcvbnmqwertyuiopasdfg
 uiopasdfghjklzxcvbnmqwertyuiopasd Qwertyuiopasdfghjklzxcvbnmqwerty cvbnmqwertyuiopasdfghjklzxcvbnmq fghjklzxcvbnmqwertyuiopasdfghjklzx wertyuiopasdfghjklzxcvbnmqwertyui opasdfghjklzxcvbnmqwertyuiopasdfg
uiopasdfghjklzxcvbnmqwertyuiopasd Qwertyuiopasdfghjklzxcvbnmqwerty cvbnmqwertyuiopasdfghjklzxcvbnmq fghjklzxcvbnmqwertyuiopasdfghjklzx wertyuiopasdfghjklzxcvbnmqwertyui opasdfghjklzxcvbnmqwertyuiopasdfg
Pertemuan 2 Matriks, part 2
 Pertemuan 2 Matriks, part 2 Beberapa Jenis Matriks Khusus 1. Matriks Bujur Sangkar Suatu matriks dengan banyak baris = banyak kolom = n disebut matriks bujur sangkar berukuran n (berordo n). Barisan elemen
Pertemuan 2 Matriks, part 2 Beberapa Jenis Matriks Khusus 1. Matriks Bujur Sangkar Suatu matriks dengan banyak baris = banyak kolom = n disebut matriks bujur sangkar berukuran n (berordo n). Barisan elemen
OPERASI MATRIKS. a 11 a 12 a 13 a 14 A = a 21 a 22 a 23 a 24 a 31 a 32 a 33 a 34 a 41 a 42 a 43 a 44
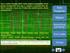 OPERASI MATRIKS Topik yang akan dibahas transpose perkalian TRANSPOSE Definisi: a 11 a 12 a 13 a 14 A = a 21 a 22 a 23 a 24 a 31 a 32 a 33 a 34 a 41 a 42 a 43 a 44 a 11 a 21 a 31 a 41 A T = a 12 a 22 a
OPERASI MATRIKS Topik yang akan dibahas transpose perkalian TRANSPOSE Definisi: a 11 a 12 a 13 a 14 A = a 21 a 22 a 23 a 24 a 31 a 32 a 33 a 34 a 41 a 42 a 43 a 44 a 11 a 21 a 31 a 41 A T = a 12 a 22 a
M AT E M AT I K A E K O N O M I MATRIKS DAN SPL I N S TITUT P ERTA N I A N BOGOR
 M AT E M AT I K A E K O N O M I MATRIKS DAN SPL TO N I BAKHTIAR I N S TITUT P ERTA N I A N BOGOR 2 0 1 2 Kesetimbangan Dua Pasar Permintaan kopi bergantung tidak hanya pada harganya tetapi juga pada harga
M AT E M AT I K A E K O N O M I MATRIKS DAN SPL TO N I BAKHTIAR I N S TITUT P ERTA N I A N BOGOR 2 0 1 2 Kesetimbangan Dua Pasar Permintaan kopi bergantung tidak hanya pada harganya tetapi juga pada harga
Penghitungan Polusi Udara Dalam Ruangan dengan Metode Eliminasi Gauss
 Penghitungan Polusi Udara Dalam Ruangan dengan Metode Eliminasi Gauss Tri Hastuti Yuniati (23515009) 1 Program Studi Magister Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung,
Penghitungan Polusi Udara Dalam Ruangan dengan Metode Eliminasi Gauss Tri Hastuti Yuniati (23515009) 1 Program Studi Magister Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung,
Pertemuan Ke 2 SISTEM PERSAMAAN LINEAR (SPL) By SUTOYO,ST.,MT
 Pertemuan Ke SISTEM PERSAMAAN LINEAR (SPL) By SUTOYO,ST,MT Pendahuluan Suatu sistem persamaan linier (atau himpunan persaman linier simultan) adalah satu set persamaan dari sejumlah unsur yang tak diketahui
Pertemuan Ke SISTEM PERSAMAAN LINEAR (SPL) By SUTOYO,ST,MT Pendahuluan Suatu sistem persamaan linier (atau himpunan persaman linier simultan) adalah satu set persamaan dari sejumlah unsur yang tak diketahui
MODUL ALJABAR LINEAR 1 Disusun oleh, ASTRI FITRIA NUR ANI
 214 MODUL ALJABAR LINEAR 1 Disusun oleh, ASTRI FITRIA NUR ANI Astri Fitria Nur ani Aljabar Linear 1 1/1/214 1 DAFTAR ISI DAFTAR ISI... i BAB I MATRIKS DAN SISTEM PERSAMAAN A. Pendahuluan... 1 B. Aljabar
214 MODUL ALJABAR LINEAR 1 Disusun oleh, ASTRI FITRIA NUR ANI Astri Fitria Nur ani Aljabar Linear 1 1/1/214 1 DAFTAR ISI DAFTAR ISI... i BAB I MATRIKS DAN SISTEM PERSAMAAN A. Pendahuluan... 1 B. Aljabar
ALJABAR LINIER MAYDA WARUNI K, ST, MT ALJABAR LINIER (I)
 ALJABAR LINIER MAYDA WARUNI K, ST, MT ALJABAR LINIER (I) 1 MATERI ALJABAR LINIER VEKTOR DALAM R1, R2 DAN R3 ALJABAR VEKTOR SISTEM PERSAMAAN LINIER MATRIKS, DETERMINAN DAN ALJABAR MATRIKS, INVERS MATRIKS
ALJABAR LINIER MAYDA WARUNI K, ST, MT ALJABAR LINIER (I) 1 MATERI ALJABAR LINIER VEKTOR DALAM R1, R2 DAN R3 ALJABAR VEKTOR SISTEM PERSAMAAN LINIER MATRIKS, DETERMINAN DAN ALJABAR MATRIKS, INVERS MATRIKS
BAB II KAJIAN PUSTAKA. operasi matriks, determinan dan invers matriks), aljabar max-plus, matriks atas
 BAB II KAJIAN PUSTAKA Pada bab ini akan diuraikan mengenai matriks (meliputi definisi matriks, operasi matriks, determinan dan invers matriks), aljabar max-plus, matriks atas aljabar max-plus, dan penyelesaian
BAB II KAJIAN PUSTAKA Pada bab ini akan diuraikan mengenai matriks (meliputi definisi matriks, operasi matriks, determinan dan invers matriks), aljabar max-plus, matriks atas aljabar max-plus, dan penyelesaian
BAB V DIAGONALISASI DAN DEKOMPOSISI MATRIKS. Sub bab ini membahas tentang faktorisasi matriks A berorde nxn ke dalam hasil
 BAB V DIAGONALISASI DAN DEKOMPOSISI MATRIKS. Diagonalisasi Sub bab ini membahas tentang faktorisasi matriks A berorde nn ke dalam hasil kali berbentuk PDP, di mana D adalah matriks diagonal. Jika diperoleh
BAB V DIAGONALISASI DAN DEKOMPOSISI MATRIKS. Diagonalisasi Sub bab ini membahas tentang faktorisasi matriks A berorde nn ke dalam hasil kali berbentuk PDP, di mana D adalah matriks diagonal. Jika diperoleh
PENYELESAIAN SISTEM PERSAMAAN LINEAR FUZZY KOMPLEKS MENGGUNAKAN METODE DEKOMPOSISI DOOLITTLE
 Jurnal Sains, Teknologi Industri, Vol. 11, No. 2, Juni 2014, pp. 166-174 ISSN 1693-2390 print/issn 2407-0939 online PENYELESAIAN SISTEM PERSAMAAN LINEAR FUZZY KOMPLEKS MENGGUNAKAN METODE DEKOMPOSISI DOOLITTLE
Jurnal Sains, Teknologi Industri, Vol. 11, No. 2, Juni 2014, pp. 166-174 ISSN 1693-2390 print/issn 2407-0939 online PENYELESAIAN SISTEM PERSAMAAN LINEAR FUZZY KOMPLEKS MENGGUNAKAN METODE DEKOMPOSISI DOOLITTLE
Matriks. Baris ke 2 Baris ke 3
 Matriks A. Matriks Matriks adalah susunan bilangan yang diatur menurut aturan baris dan kolom dalam suatu jajaran berbentuk persegi atau persegi panjang. Susunan bilangan itu diletakkan di dalam kurung
Matriks A. Matriks Matriks adalah susunan bilangan yang diatur menurut aturan baris dan kolom dalam suatu jajaran berbentuk persegi atau persegi panjang. Susunan bilangan itu diletakkan di dalam kurung
MUH1G3/ MATRIKS DAN RUANG VEKTOR
 MUHG3/ MATRIKS DAN RUANG VEKTOR TIM DOSEN Determinan Matriks Determinan Matriks Sub Pokok Bahasan Permutasi dan Determinan Matriks Determinan dengan OBE Determinan dengan Ekspansi Kofaktor Beberapa Aplikasi
MUHG3/ MATRIKS DAN RUANG VEKTOR TIM DOSEN Determinan Matriks Determinan Matriks Sub Pokok Bahasan Permutasi dan Determinan Matriks Determinan dengan OBE Determinan dengan Ekspansi Kofaktor Beberapa Aplikasi
a11 a12 x1 b1 Kumpulan Materi Kuliah #1 s/d #03 Tahun Ajaran 2016/2016: Oleh: Prof. Dr. Ir. Setijo Bismo, DEA.
 a11 a12 x1 b1 a a x b 21 22 2 2 Kumpulan Materi Kuliah #1 s/d #03 Tahun Ajaran 2016/2016: Oleh: Prof. Dr. Ir. Setijo Bismo, DEA. a11 a12 x1 b1 a a x b 21 22 2 2 a11 a12 x1 b1 a a x b 21 22 2 2 Setijo Bismo
a11 a12 x1 b1 a a x b 21 22 2 2 Kumpulan Materi Kuliah #1 s/d #03 Tahun Ajaran 2016/2016: Oleh: Prof. Dr. Ir. Setijo Bismo, DEA. a11 a12 x1 b1 a a x b 21 22 2 2 a11 a12 x1 b1 a a x b 21 22 2 2 Setijo Bismo
Operasi Eliminasi Gauss. Eliminasi Gauss adalah suatu cara mengoperasikan nilai-nilai di dalam
 Operasi Eliminasi Gauss Eliminasi Gauss adalah suatu cara mengoperasikan nilai-nilai di dalam matriks sehingga menjadi matriks yang lebih sederhana (ditemukan oleh Carl Friedrich Gauss). Caranya adalah
Operasi Eliminasi Gauss Eliminasi Gauss adalah suatu cara mengoperasikan nilai-nilai di dalam matriks sehingga menjadi matriks yang lebih sederhana (ditemukan oleh Carl Friedrich Gauss). Caranya adalah
BAB 2 ARRAY, OPERATOR DAN FORMAT DALAM FORTRAN
 BAB 2 ARRAY, OPERATOR DAN FORMAT DALAM FORTRAN TUJUAN Tujuan Instruksi Umum: Menerangkan Operator-Operator Yang Terdapat Dalam FORTRAN. Menerangkan Tentang Array. Menerangkan Tentang Format Specifier Tujuan
BAB 2 ARRAY, OPERATOR DAN FORMAT DALAM FORTRAN TUJUAN Tujuan Instruksi Umum: Menerangkan Operator-Operator Yang Terdapat Dalam FORTRAN. Menerangkan Tentang Array. Menerangkan Tentang Format Specifier Tujuan
II. SISTEM PERSAMAAN LANJAR I. PENDAHULUAN
 Solusi Sistem Persamaan Lanjar Homogen dengan Eliminasi Gauss-Jordan Sandy Socrates 135844 1 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha
Solusi Sistem Persamaan Lanjar Homogen dengan Eliminasi Gauss-Jordan Sandy Socrates 135844 1 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha
Penggunaan Metode Dekomposisi LU Untuk Penentuan Produksi Suatu Industri Dengan Model Ekonomi Leontief
 Penggunaan Metode Dekomposisi LU Untuk Penentuan Produksi Suatu Industri Dengan Model Ekonomi Leontief Achmad Dimas Noorcahyo - 13508076 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika
Penggunaan Metode Dekomposisi LU Untuk Penentuan Produksi Suatu Industri Dengan Model Ekonomi Leontief Achmad Dimas Noorcahyo - 13508076 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika
Pertemuan 14. persamaan linier NON HOMOGEN
 Pertemuan 14 persamaan linier NON HOMOGEN 10 Metode GAUSS Aljabar Linier Hastha 2016 10.2.2 METODE ELIMINASI GAUSS Apabila [A][X]=[B] maka dengan menyusun matriks baru yaitu matriks [A.B] akan didapat
Pertemuan 14 persamaan linier NON HOMOGEN 10 Metode GAUSS Aljabar Linier Hastha 2016 10.2.2 METODE ELIMINASI GAUSS Apabila [A][X]=[B] maka dengan menyusun matriks baru yaitu matriks [A.B] akan didapat
Part III DETERMINAN. Oleh: Yeni Susanti
 Part III DETERMINAN Oleh: Yeni Susanti Perhatikan determinan matriks ukuran 2x2 berikut: Pada masing-masing jumlahan dan Terdapat wakil dari setiap baris dan setiap kolom. Bagaimana dengan tanda + (PLUS)
Part III DETERMINAN Oleh: Yeni Susanti Perhatikan determinan matriks ukuran 2x2 berikut: Pada masing-masing jumlahan dan Terdapat wakil dari setiap baris dan setiap kolom. Bagaimana dengan tanda + (PLUS)
1.1 MATRIKS DAN JENISNYA Matriks merupakan kumpulan bilangan yang berbentuk segi empat yang tersusun dalam baris dan kolom.
 Bab MATRIKS DAN OPERASINYA Memahami matriks dan operasinya merupakan langkah awal dalam memahami buku ini. Beberapa masalah real dapat direpresentasikan dalam bentuk matriks. Masalah tersebut antara lain
Bab MATRIKS DAN OPERASINYA Memahami matriks dan operasinya merupakan langkah awal dalam memahami buku ini. Beberapa masalah real dapat direpresentasikan dalam bentuk matriks. Masalah tersebut antara lain
ISSN (Media Cetak) ISSN (Media Online) Implementasi Metode Eliminasi Gauss Pada Rangkaian Listrik Menggunakan Matlab
 JITEKH, Vol, No, Tahun 27, -5 ISSN 28-577(Media Cetak) ISSN 2549-4 (Media Online) Implementasi Metode Eliminasi Gauss Pada Rangkaian Listrik Menggunakan Matlab Silmi, Rina Anugrahwaty 2 Staff Pengajar
JITEKH, Vol, No, Tahun 27, -5 ISSN 28-577(Media Cetak) ISSN 2549-4 (Media Online) Implementasi Metode Eliminasi Gauss Pada Rangkaian Listrik Menggunakan Matlab Silmi, Rina Anugrahwaty 2 Staff Pengajar
Aljabar Linier Elementer. Kuliah 1 dan 2
 Aljabar Linier Elementer Kuliah 1 dan 2 1.3 Matriks dan Operasi-operasi pada Matriks Definisi: Matriks adalah susunan bilangan dalam empat persegi panjang. Bilangan-bilangan dalam susunan tersebut disebut
Aljabar Linier Elementer Kuliah 1 dan 2 1.3 Matriks dan Operasi-operasi pada Matriks Definisi: Matriks adalah susunan bilangan dalam empat persegi panjang. Bilangan-bilangan dalam susunan tersebut disebut
BAB 2 LANDASAN TEORI. yang dibicarakan yang akan digunakan pada bab selanjutnya. Bentuk umum dari matriks bujur sangkar adalah sebagai berikut:
 BAB 2 LANDASAN TEORI Pada bab ini dibicarakan mengenai matriks yang berbentuk bujur sangkar dengan beberapa definisi, teorema, sifat-sifat dan contoh sesuai dengan matriks tertentu yang dibicarakan yang
BAB 2 LANDASAN TEORI Pada bab ini dibicarakan mengenai matriks yang berbentuk bujur sangkar dengan beberapa definisi, teorema, sifat-sifat dan contoh sesuai dengan matriks tertentu yang dibicarakan yang
PERBANDINGAN KOMPLEKSITAS ALGORITMA PENCARIAN BINER DAN ALGORITMA PENCARIAN BERUNTUN
 PERBANDINGAN KOMPLEKSITAS ALGORITMA PENCARIAN BINER DAN ALGORITMA PENCARIAN BERUNTUN Yudhistira NIM 13508105 Mahasiswa Program Studi Teknik Informatika ITB Jalan Ganesha No.10 Bandung e-mail: [email protected]
PERBANDINGAN KOMPLEKSITAS ALGORITMA PENCARIAN BINER DAN ALGORITMA PENCARIAN BERUNTUN Yudhistira NIM 13508105 Mahasiswa Program Studi Teknik Informatika ITB Jalan Ganesha No.10 Bandung e-mail: [email protected]
MATRIKS A = ; B = ; C = ; D = ( 5 )
 MATRIKS A. DEFINISI MATRIKS Matriks adalah suatu susunan bilangan berbentuk segi empat dari suatu unsur-unsur pada beberapa sistem aljabar. Unsur-unsur tersebut bisa berupa bilangan dan juga suatu peubah.
MATRIKS A. DEFINISI MATRIKS Matriks adalah suatu susunan bilangan berbentuk segi empat dari suatu unsur-unsur pada beberapa sistem aljabar. Unsur-unsur tersebut bisa berupa bilangan dan juga suatu peubah.
2. MATRIKS. 1. Pengertian Matriks. 2. Operasi-operasi pada Matriks
 2. MATRIKS 1. Pengertian Matriks Matriks adalah himpunan skalar yang disusun secara empat persegi panjang menurut baris dan kolom. Matriks diberi nama huruf besar, sedangkan elemen-elemennya dengan huruf
2. MATRIKS 1. Pengertian Matriks Matriks adalah himpunan skalar yang disusun secara empat persegi panjang menurut baris dan kolom. Matriks diberi nama huruf besar, sedangkan elemen-elemennya dengan huruf
Modifikasi Metode Gauss atau Operasi Baris Elementer pada Solusi Sistim Persamaan Linier 3 Variabel dan 3 Persamaan
 Modifikasi Metode Gauss atau Operasi Baris Elementer pada Solusi Sistim Persamaan Linier 3 Variabel dan 3 Persamaan Edwin Julius Solaiman Fakultas Teknologi Informasi, Universitas Advent Indonesia Abstrak
Modifikasi Metode Gauss atau Operasi Baris Elementer pada Solusi Sistim Persamaan Linier 3 Variabel dan 3 Persamaan Edwin Julius Solaiman Fakultas Teknologi Informasi, Universitas Advent Indonesia Abstrak
BAB II KAJIAN TEORI. yang diapit oleh dua kurung siku sehingga berbentuk empat persegi panjang atau
 BAB II KAJIAN TEORI Pada bab ini akan diberikan kajian teori mengenai matriks dan operasi matriks, program linear, penyelesaian program linear dengan metode simpleks, masalah transportasi, hubungan masalah
BAB II KAJIAN TEORI Pada bab ini akan diberikan kajian teori mengenai matriks dan operasi matriks, program linear, penyelesaian program linear dengan metode simpleks, masalah transportasi, hubungan masalah
Pelatihan fortran JURUSAN TEKNIK SIPIL 2014 / 2015
 Pelatihan fortran JURUSAN TEKNIK SIPIL 2014 / 2015 STRUKTUR PROGRAM FORTRAN STRUKTUR DARI PROGRAM FORTRAN DIBAGI MENJADI 5 BAGIAN KOLOM DAN TIAP-TIAP BARIS DI DALAM PROGRAM DAPAT BERISI : 1) METACOMMAND
Pelatihan fortran JURUSAN TEKNIK SIPIL 2014 / 2015 STRUKTUR PROGRAM FORTRAN STRUKTUR DARI PROGRAM FORTRAN DIBAGI MENJADI 5 BAGIAN KOLOM DAN TIAP-TIAP BARIS DI DALAM PROGRAM DAPAT BERISI : 1) METACOMMAND
ALJABAR LINIER DAN MATRIKS
 ALJABAR LINIER DAN MATRIKS MATRIKS (DETERMINAN, INVERS, TRANSPOSE) Macam Matriks Matriks Nol (0) Matriks yang semua entrinya nol. Ex: Matriks Identitas (I) Matriks persegi dengan entri pada diagonal utamanya
ALJABAR LINIER DAN MATRIKS MATRIKS (DETERMINAN, INVERS, TRANSPOSE) Macam Matriks Matriks Nol (0) Matriks yang semua entrinya nol. Ex: Matriks Identitas (I) Matriks persegi dengan entri pada diagonal utamanya
STATEMEN GO TO DAN IF-THEN. Pertemuan IX
 STATEMEN GO TO DAN IF-THEN Pertemuan IX Statemen Alih Kontrol Pada bahasa pemrograman BASIC tidak hanya melakukan eksekusi baris demi baris atau secara berurutan yang tiap barisnya dieksekusi hanya satu
STATEMEN GO TO DAN IF-THEN Pertemuan IX Statemen Alih Kontrol Pada bahasa pemrograman BASIC tidak hanya melakukan eksekusi baris demi baris atau secara berurutan yang tiap barisnya dieksekusi hanya satu
BAB I PENDAHULUAN 1.1 Latar Belakang
 BAB I PENDAHULUAN 1.1 Latar Belakang Pembahasan mendasar mengenai matriks terutama yang berkaitan dengan matriks yang dapat didiagonalisasi telah jelas disajikan dalam referensi yang biasanya digunakan
BAB I PENDAHULUAN 1.1 Latar Belakang Pembahasan mendasar mengenai matriks terutama yang berkaitan dengan matriks yang dapat didiagonalisasi telah jelas disajikan dalam referensi yang biasanya digunakan
Contoh. C. Determinan dan Invers Matriks. C. 1. Determinan
 C. Determinan dan Invers Matriks C.. Determinan Suatu matriks persegi selalu dapat dikaitkan dengan suatu bilangan yang disebut determinan. Determinan dari matriks persegi dinotasikan dengan. Untuk matriks
C. Determinan dan Invers Matriks C.. Determinan Suatu matriks persegi selalu dapat dikaitkan dengan suatu bilangan yang disebut determinan. Determinan dari matriks persegi dinotasikan dengan. Untuk matriks
MODUL IV SISTEM PERSAMAAN LINEAR
 MODUL IV SISTEM PERSAMAAN LINEAR 4.. Pendahuluan. Sistem Persamaan Linear merupakan salah satu topik penting dalam Aljabar Linear. Sistem Persamaan Linear sering dijumpai dalam semua bidang penyelidikan
MODUL IV SISTEM PERSAMAAN LINEAR 4.. Pendahuluan. Sistem Persamaan Linear merupakan salah satu topik penting dalam Aljabar Linear. Sistem Persamaan Linear sering dijumpai dalam semua bidang penyelidikan
Tujuan. Mhs dapat mendemonstrasikan operasi matriks: penjumlahan, perkalian, dsb. serta menentukan matriks inverse
 Matriks Tujuan Mhs dapat mendemonstrasikan operasi matriks: penjumlahan, perkalian, dsb. serta menentukan matriks inverse Pengertian Matriks Adalah kumpulan bilangan yang disajikan secara teratur dalam
Matriks Tujuan Mhs dapat mendemonstrasikan operasi matriks: penjumlahan, perkalian, dsb. serta menentukan matriks inverse Pengertian Matriks Adalah kumpulan bilangan yang disajikan secara teratur dalam
5. PERSAMAAN LINIER. 1. Berikut adalah contoh SPL yang terdiri dari 4 persamaan linier dan 3 variabel.
 1. Persamaan Linier 5. PERSAMAAN LINIER Persamaan linier adalah suatu persamaan yang variabel-variabelnya berpangkat satu. Disamping persamaan linier ada juga persamaan non linier. Contoh : a) 2x + 3y
1. Persamaan Linier 5. PERSAMAAN LINIER Persamaan linier adalah suatu persamaan yang variabel-variabelnya berpangkat satu. Disamping persamaan linier ada juga persamaan non linier. Contoh : a) 2x + 3y
JURUSAN PENDIDIKAN MATEMATIKA FMIPA UNIVERSITAS NEGERI YOGYAKARTA
 CATATAN KULIAH ALJABAR LINEAR MUSTHOFA JURUSAN PENDIDIKAN MATEMATIKA FMIPA UNIVERSITAS NEGERI YOGYAKARTA 20 SISTEM PERSAMAAN LINEAR Tujuan : Menyelesaikan sistem persamaan linear. OPERASI BARIS ELEMENTER
CATATAN KULIAH ALJABAR LINEAR MUSTHOFA JURUSAN PENDIDIKAN MATEMATIKA FMIPA UNIVERSITAS NEGERI YOGYAKARTA 20 SISTEM PERSAMAAN LINEAR Tujuan : Menyelesaikan sistem persamaan linear. OPERASI BARIS ELEMENTER
ALGORITMA ELIMINASI GAUSS INTERVAL DALAM MENDAPATKAN NILAI DETERMINAN MATRIKS INTERVAL DAN MENCARI SOLUSI SISTEM PERSAMAAN INTERVAL LINEAR
 Buletin Ilmiah Math. Stat. dan Terapannya (Bimaster) Volume 04, No. 3 (2015), hal 313 322. ALGORITMA ELIMINASI GAUSS INTERVAL DALAM MENDAPATKAN NILAI DETERMINAN MATRIKS INTERVAL DAN MENCARI SOLUSI SISTEM
Buletin Ilmiah Math. Stat. dan Terapannya (Bimaster) Volume 04, No. 3 (2015), hal 313 322. ALGORITMA ELIMINASI GAUSS INTERVAL DALAM MENDAPATKAN NILAI DETERMINAN MATRIKS INTERVAL DAN MENCARI SOLUSI SISTEM
Reduksi Rank pada Matriks-Matriks Tertentu
 Reduksi Rank pada Matriks-Matriks Tertentu E. Apriliani, B. Ari Sanjaya September 6, 7 Abstract. Dekomposisi nilai singular (Singular Value Decomposition - SVD) adalah suatu metode untuk menuliskan suatu
Reduksi Rank pada Matriks-Matriks Tertentu E. Apriliani, B. Ari Sanjaya September 6, 7 Abstract. Dekomposisi nilai singular (Singular Value Decomposition - SVD) adalah suatu metode untuk menuliskan suatu
Algoritma Brute Force
 Algoritma Brute Force Definisi Brute Force Brute force adalah sebuah pendekatan yang lempang (straightforward( straightforward) ) untuk memecahkan suatu masalah, biasanya didasarkan pada pernyataan masalah
Algoritma Brute Force Definisi Brute Force Brute force adalah sebuah pendekatan yang lempang (straightforward( straightforward) ) untuk memecahkan suatu masalah, biasanya didasarkan pada pernyataan masalah
Teori Algoritma. Algoritma Perulangan
 Alam Santosa Teori Algoritma Perulangan Algoritma Perulangan Seperti pernah dibahas sebelumnya, kemampuan komputer adalah melakukan pekerjaan yang sama tanpa merasa lelah maupun bosan. Syarat utama memanfaatkan
Alam Santosa Teori Algoritma Perulangan Algoritma Perulangan Seperti pernah dibahas sebelumnya, kemampuan komputer adalah melakukan pekerjaan yang sama tanpa merasa lelah maupun bosan. Syarat utama memanfaatkan
6- Operasi Matriks. MEKANIKA REKAYASA III MK Unnar-Dody Brahmantyo 1
 6- Operasi Matriks Contoh 6-1 : Budi diminta tolong oleh ibunya untuk membeli 2 kg gula dan 1 kg kopi. Dengan uang Rp. 10.000,- Budi mendapatkan uang kembali Rp. 3.000,-. Dihari yang lain, Budi membeli
6- Operasi Matriks Contoh 6-1 : Budi diminta tolong oleh ibunya untuk membeli 2 kg gula dan 1 kg kopi. Dengan uang Rp. 10.000,- Budi mendapatkan uang kembali Rp. 3.000,-. Dihari yang lain, Budi membeli
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI 2.1 Noise Pada saat melakukan pengambilan gambar, setiap gangguan pada gambar dinamakan dengan noise. Noise dipakai untuk proses training corrupt image, gambarnya diberi noise dan
BAB 2 LANDASAN TEORI 2.1 Noise Pada saat melakukan pengambilan gambar, setiap gangguan pada gambar dinamakan dengan noise. Noise dipakai untuk proses training corrupt image, gambarnya diberi noise dan
BAB II LANDASAN TEORI. yang biasanya dinyatakan dalam bentuk sebagai berikut: =
 BAB II LANDASAN TEORI 2.1 Matriks Definisi 2.1 (Lipschutz, 2006): Matriks adalah susunan segiempat dari skalarskalar yang biasanya dinyatakan dalam bentuk sebagai berikut: Setiap skalar yang terdapat dalam
BAB II LANDASAN TEORI 2.1 Matriks Definisi 2.1 (Lipschutz, 2006): Matriks adalah susunan segiempat dari skalarskalar yang biasanya dinyatakan dalam bentuk sebagai berikut: Setiap skalar yang terdapat dalam
Menentukan Nilai Eigen Tak Dominan Suatu Matriks Definit Negatif Menggunakan Metode Kuasa Invers dengan Shift
 Jurnal Penelitian Sains Volume 14 Nomer 1(A) 14103 Menentukan Nilai Eigen Tak Dominan Suatu Matriks Definit Negatif Menggunakan Metode Kuasa Invers dengan Shift Yuli Andriani Jurusan Matematika FMIPA,
Jurnal Penelitian Sains Volume 14 Nomer 1(A) 14103 Menentukan Nilai Eigen Tak Dominan Suatu Matriks Definit Negatif Menggunakan Metode Kuasa Invers dengan Shift Yuli Andriani Jurusan Matematika FMIPA,
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI Pada bab ini akan dibahas beberapa definisi dan teorema dengan atau tanpa bukti yang akan digunakan untuk menentukan regularisasi sistem singular linier. Untuk itu akan diberikan terlebih
BAB 2 LANDASAN TEORI Pada bab ini akan dibahas beberapa definisi dan teorema dengan atau tanpa bukti yang akan digunakan untuk menentukan regularisasi sistem singular linier. Untuk itu akan diberikan terlebih
