MODEL MATEMATIKA STRUKTUR UMUR INFEKSI VIRUS HIV DENGAN KOMBINASI TERAPI OBAT MUHAMMAD BUWING

Transkripsi

1 MODEL MATEMATIKA STRUKTUR UMUR INFEKSI VIRUS HIV DENGAN KOMBINASI TERAPI OBAT MUHAMMAD BUWING SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR BOGOR 2008

2 PERNYATAAN MENGENAI TESIS DAN SUMBER INFORMASI Dengan ini saya menyatakan bahwa tesis dengan judul Model Matematika Struktur Umur Infeksi Virus HIV dengan Kombinasi Terapi Obat adalah karya saya sendiri dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi manapun. Sumber informasi dari karya yang diterbitkan maupun yang tidak diterbitkan dari penulis lain disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir thesis ini. Bogor, 14 Agustus 2008 Muhammad Buwing NIM. G

3 ABSTRACT MUHAMMAD BUWING. Mathematical Model of Age Structure of HIV Virus Infection with Drugs Therapy Combination. Under direction of PAIAN SIANTURI and ALI KUSNANTO. Human Immunodeficiency Virus (HIV) is a virus that attacks blood cell leucocyt. Various anti viral drugs are applied for therapy: Reverse Transcriptase Inhibitor (RTI), Protease Inhibitor (PI) and Entry Inhibitor (EI). Here, three mathematical models are studied i.e. no drugs therapy, therapy combination of RTI and PI, and therapy combination of EI and PI. The reproduction number R is obtained from each model and it is studied to know the influence of therapy combination to viral population. The result shows that in the no drugs therapy, each virus may infect more than one cell. With high PI efficacy for therapy combination of RTI and PI as well as therapy combination of EI and PI, the viral population can be decreased. From two combination therapies with the smaller control value of virus replication r, it is shown that the therapy combination of EI and PI are more effective than therapy combination of RTI and PI. At the bigger value r, it is shown that therapy combination of RTI and PI are more effective than therapy combination of EI and PI. Keywords: Human Immunodeficiency Virus, drugs therapy combination, reproduction number, viral population.

4 RINGKASAN MUHAMMAD BUWING. Model Matematika Struktur Umur Infeksi Virus HIV dengan Kombinasi Terapi Obat. Dibimbing oleh PAIAN SIANTURI dan ALI KUSNANTO. Human Immunodeficiency Virus (HIV) adalah virus yang menyerang sel darah putih sebagai sistem kekebalan tubuh manusia. Waktu yang dilewati virus sejak masuk ke dalam sel darah putih sehat disebut dengan umur infeksi. Dari struktur umur infeksi inilah dibentuk suatu model matematika. Walau belum ditemukannya obat secara total bagi penderita HIV, namun berbagai macam terapi obat terhadap virus HIV telah banyak digunakan, diantaranya kombinasi terapi obat Reverse Transcriptase Inhibitor (RTI) dan Protease Inhibitor (PI) serta Entry Inhibitor (EI) dan Protease Inhibitor (PI). Dalam penelitian ini, model struktur umur infeksi virus HIV tanpa dan dengan kombinasi terapi obat dikaji dan dibandingkan melalui Bilangan Reproduksi untuk melihat pengaruh terapi terhadap populasi virus. Dampak kombinasi terapi dan perbandingan keefektifan dua kombinasi terapi dapat diketahui dengan mengkaji Bilangan Reproduksi R dan populasi virus V pada model struktur umur infeksi virus HIV dengan kombinasi terapi obat. Penelitian ini mengkaji tiga model matematika yakni Model I (tanpa terapi Obat), Model II (kombinasi terapi obat RTI dan PI) dan Model III (kombinasi terapi obat EI dan PI). Hasil kajian menunjukkan bahwa dari Model I (tanpa terapi obat), virus akan menginfeksi lebih dari satu sel darah putih pada umur infeksi a > hari, artinya jika tanpa terapi obat, maka virus akan menginfeksi populasi sel pada umur infeksi lebih dari hari ( + 10 jam). Pada Model II, terdapat nilai konstanta pengontrol replikasi virus r yang sangat memengaruhi besar kecilnya nilai kemujaraban obat yang digunakan. Kajian dilakukan dengan menggunakan alat bantu sofware komputer Matematica. Pada kombinasi terapi obat RTI dan PI untuk r = 1 dan dengan kemujaraban obat PI 40%, berakibat populasi virus cenderung menurun dengan kemujaraban obat RTI lebih besar atau sama dengan 84%. Pada kemujaraban obat PI 50%, populasi virus cenderung menurun dengan kemujaraban obat RTI lebih besar atau sama dengan 65%. Pada kemujaraban obat PI 60%, populasi virus cenderung menurun dengan kemujaraban obat RTI lebih besar atau sama dengan 16%. Untuk r = 2 dengan kemujaraban obat PI 40% pada Model II, berakibat populasi virus cenderung menurun dengan kemujaraban obat RTI lebih besar atau sama dengan 58%. Pada kemujaraban obat PI 50%, populasi virus akan cenderung turun dengan kemujaraban obat RTI lebih besar atau sama dengan 41%. Pada kemujaraban obat PI 60%, populasi virus akan cenderung turun dengan kemujaraban obat RTI lebih besar atau sama dengan 7%. Untuk r = 5 dengan kemujaraban obat PI 40%, berakibat populasi virus cenderung menurun dengan kemujaraban obat RTI lebih besar atau sama dengan 30%. Pada kemujaraban obat PI 50%, populasi virus akan cenderung menurun dengan kemujaraban obat RTI lebih besar atau sama dengan 19%. Pada kemujaraban obat PI 60%, populasi virus akan cenderung menurun dengan kemujaraban obat RTI lebih besar atau sama dengan 3%.

5 Jadi secara umum, pada Model II dengan nilai sebarang r, semakin besar nilai kemujaraban obat PI diberikan, maka semakin cepat populasi virus berkurang. Pada Model III, pada kemujaraban obat PI 40%, berakibat populasi virus cenderung menurun dengan kemujaraban obat EI lebih besar atau sama dengan 37%. Pada kemujaraban obat PI 50%, virus cenderung menurun dengan kemujaraban obat EI lebih besar atau sama dengan 23%. Pada kemujaraban obat PI 60%, maka virus cenderung turun dengan kemujaraban obat EI lebih besar atau sama dengan 5%. Jadi secara umum, pada Model III semakin besar nilai kemujaraban obat obat PI diberikan maka semakin cepat populasi virus berkurang sesuai dengan berjalannya waktu. Hasil kajian perbandingan Model I, II dan III dengan penetapan r = 1, dan nilai kemujaraban obat PI 50% menunjukkan bahwa tanpa terapi obat, berakibat virus akan menginfeksi populasi sel darah putih pada umur infeksi lebih dari hari (lebih dari 10 jam), sedang dengan kombinasi terapi menunjukkan bahwa sesuai berjalannya waktu populasi virus cenderung menurun pada nilai kemujaraban RTI lebih besar atau sama dengan 65% dan EI lebih besar atau sama dengan 23%. Keefektifan dua kombinasi terapi obat sangat bergantung pada nilai r. Hasil kajian menunjukkan pada r = 1 dan 2, Model III (kombinasi terapi obat EI dan PI) lebih efektif dari Model II (kombinasi terapi obat RTI dan PI), sedangkan pada r = 5, kombinasi terapi obat Model II lebih efektif dari Model III. Jadi secara umum bahwa semakin kecil nilai r diberikan menunjukkan bahwa Model III lebih efektif dari Model II, sebaliknya semakin besar nilai r diberikan maka Model II lebih efektif dari Model III. Kata kunci : Human Immunodeficiency Virus, Kombinasi Terapi obat, Bilangan Reproduksi, Populasi virus.

6 Hak Cipta milik Institut Pertanian Bogor, tahun 2008 Hak Cipta dilindungi undang-undang 1. Dilarang mengutip sebagian atau seluruh hasil karya tulis ini tanpa mencantumkan atau menyebutkan sumber. a. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilimiah, penyusunan laporan, penulisan kritik, atau tinjauan suatu masalah b. Pengutipan tidak merugikan kepentingan yang wajar Institut Pertanian Bogor. 2. Dilarang mengumumkan dan memperbanyak sebagian atau seluruh karya tulis dalam bentuk apapun tanpa izin Institut Pertanian Bogor.

7 MODEL MATEMATIKA STRUKTUR UMUR INFEKSI VIRUS HIV DENGAN KOMBINASI TERAPI OBAT MUHAMMAD BUWING Tesis Sebagai salah satu syarat untuk memperoleh gelar Magister Sains pada Departemen Matematika SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR 2008

8 Penguji Luar Komisi pada Ujian Tesis : Ir. Ngakan Komang Kutha Ardana, M.Sc

9 Judul Tesis Nama NIM : Model Matematika Struktur Umur Infeksi Virus HIV dengan Kombinasi Terapi Obat : Muhammad Buwing : G Disetujui, Komisi Pembimbing Dr. Paian Sianturi. Ketua Drs. Ali Kusnanto M.Si. Anggota Diketahui Ketua Program Studi Matematika Terapan Dekan Sekolah Pasca Sarjana Dr. Ir. Endar H. Nugrahani, MS. Prof. Dr. Ir. Khairil A. Notodiputro, M.S. Tanggal Ujian : 14 Agustus 2008 Tanggal Lulus :

10 PRAKATA Puji dan syukur penulis panjatkan kepada Allah SWT atas segala karunia- Nya sehingga karya ilmiah ini berhasil diselesaikan. Judul yang dipilih dalam penelitian yang dilaksanakan sejak bulan Juni 2007 ini adalah Model Matematika Struktur Umur Infeksi Virus HIV dengan Kombinasi Terapi Obat. Terima kasih penulis ucapkan kepada Bapak Dr. Paian Sianturi dan Bapak Drs. Ali Kusnanto M.Si selaku pembimbing yang telah banyak membimbing dan mengarahkan serta Bapak Ir. Ngakan Komang Kutha Ardana, M.Sc selaku penguji yang telah banyak memberikan saran. Ungkapan terima kasih juga penulis sampaikan kepada Departemen Agama Republik Indonesia untuk beasiswa yang tersedia dan kepada rekan-rekan mahasiswa atas diskusinya. Semoga atas semua kebaikan dapat bernilai ibadah dan dibalas oleh Allah SWT dengan kebaikan yang berlipat. Terakhir kepada ibu, istri, mertua dan seluruh keluarga yang memberikan motivasi, semangat, do a dan kasih sayang penulis menyampaikan penghargaan dan terima kasih. Kepada Muhammad Raihan Alfaruq, Muhammad Farhan Ashiddiqi dan Muhammad Dzaky Ihsan Fachry penulis mohon maaf atas kurangnya waktu sebab kesibukan selama proses penulisan tesis ini. Semoga karya ilmiah ini bermanfaat. Bogor, 14 Agustus 2008 Muhammad Buwing

11 RIWAYAT HIDUP Penulis dilahirkan di Medan pada tanggal 15 Oktober 1969 dari Ayah Kromorejo dan Ibu Darni. Penulis merupakan putra ketujuh dari sepuluh bersaudara. Tahun 1989 penulis lulus dari SMA Negeri 3 Medan Sumatera Utara dan pada tahun yang sama lulus seleksi masuk IAIN Medan melalui Seleksi Masuk IAIN. Penulis memilih Jurusan Tadris Matematika, Fakultas Tarbiyah. Kesempatan untuk melanjutkan program magister pada program studi Matematika Terapan dan pada perguruan tinggi IPB diperoleh pada tahun Penulis adalah Guru Tsanawiyah di MTsN Kabanjahe Kabupaten Karo Sumatera Utara sejak Juli Mata pelajaran yang diajarkan adalah Matematika.

12 DAFTAR ISI Halaman DAFTAR TABEL... xiii DAFTAR GAMBAR...xiv DAFTAR LAMPIRAN...xv PENDAHULUAN Latar Belakang... 1 Tujuan Penelitian... 2 TINJAUAN PUSTAKA Sistem Persamaan Diferensial Linear... 3 Titik Tetap... 3 Titik Tetap Stabil... 3 Nilai Eigen dan Vektor Eigen... 3 Analisis Kestabilan Titik Tetap... 4 Bilangan Reproduksi ( R )... 4 MODEL MATEMATIKA Interaksi Virus Terhadap Sel Darah Putih Sehat... 5 Kombinasi Terapi... 7 Asumsi Model... 8 Model... 8 Model I : Tanpa Terapi Obat... 8 Terapi Obat... 9 Model II : Kombinasi Terapi Obat RTI dan PI 9 Model III : Kombinasi Terapi Obat EI dan PI 10 Nilai Parameter PEMBAHASAN Model I : Tanpa Terapi Obat Model II : Kombinasi Terapi Obat RTI dan PI Model III : Kombinasi Terapi Obat EI dan PI Perbandingan Model II dan III Terhadap Muatan Virus Pemberian Nilai Konstanta ρ pada Bilangan Reproduksi Model II dan Model III Perbandingan Model I, II dan III Terhadap Muatan Virus Pemberian Nilai Konstanta ρ pada Populasi Virus Populasi Virus Model II... 22

13 Populasi Virus Model III Perbandingan Populasi Virus Model II dan III KESIMPULAN DAFTAR PUSTAKA LAMPIRAN... 30

14 DAFTAR TABEL Halaman 1 Definisi Notasi Tanpa Terapi Obat Nilai Parameter Pemberian Nilai r Terapi RTI dan PI Pemberian Nilai ε PI Terapi EI dan PI Pemberian Nilai r pada Dua Bilangan Reproduksi Pemberian Nilai r pada Populasi Virus terapi RTI dan PI Pemberian Nilai ε PI pada Populasi Virus Terapi EI dan PI Pemberian Nilai r Untuk Populasi Virus Pada Model II dan III... 27

15 DAFTAR GAMBAR Halaman 1 Proses Infeksi Virus HIV Terhadap Sel Darah Putih Sehat Diagram penyebaran virus Peran Obat RTI dan PI terhadap virus HIV Skema Model Struktur Umur Infeksi Virus HIV Plot perubahan fungsi Laju Produksi Virus untuk nilai q = 10, 1, Plot Bilangan Reproduksi Virus Tanpa terapi Obat Plot perubahan fungsi η( εrti ) untuk r = 1, 2, Plot Bilangan Reproduksi Terapi kombinasi RTI dan PI dengan r = 1, 2 dan 5 serta ε PI =0.4, 0.5 dan Plot Bilangan Reproduksi Terapi kombinasi EI dan PI dengan ε PI =0.4, 0.5 dan Perbandingan terapi kombinasi Terhadap Bilangan Reproduksi II dan III Perbandingan Model I, II dan III Nilai kemujaraban obat RTI dengan penetapan kemujaraban obat PI, ε PI = 0.4, 0.5, 0.6 dan r = 1, 2, Nilai kemujaraban obat EI dengan penetapan kemujaraban obat PI, ε PI = 0.4, 0.5 dan Perbandingan terapi kombinasi dengan penetapan kemujaraban obat PI, ε PI =

16 DAFTAR LAMPIRAN Halaman 1 Penurunan Bilangan Reproduksi Virus (R 0 ) Tanpa Terapi Obat Penyederhanaan Bilangan Reproduksi Virus HIV dari terapi kombinasi RTI dan PI Plot gambar dengan menggunakan software Mathematica... 34

17 1 PENDAHULUAN Latar Belakang Human Immunodeficiency Virus (HIV) adalah virus penyebab Aquired Immuno Deficiency Syndrome (AIDS) yang melumpuhkan sistem kekebalan tubuh seseorang. Virus HIV ditemukan pada awal tahun 1980 dan dilaporkan bahwa penyakit AIDS sudah menyebar pada sebagian besar daerah di belahan bumi. Sudah lebih dari 60 juta orang terinfeksi, dan sepertiga dari mereka meninggal dunia (Fauci, 2003). Sampai saat ini, belum ditemukan obat penyembuhan secara total bagi penderita virus HIV. Walaupun begitu, telah ditemukan beberapa jenis terapi obat untuk menghambat laju pembentukan virus baru. Terapi tersebut berupa obat anti virus yakni Protease Inhibitor (PI), Entry Inhibitor (EI), dan Reverse Transcriptase Inhibitor (RTI) ( Madigan dan Martinko 2006). Jika obat anti virus dengan kombinasi digunakan dengan benar, maka diharapkan terjadi penekanan bertambahnya virus HIV di dalam sel darah putih, sehingga kekebalan tubuh akan kembali meningkat ke tahap normal. Keteraturan mengonsumsi obat anti virus ini dapat mencegah resistensi virus terhadap obat tersebut (Zein 2006). Infeksi Virus HIV dimulai dari penyerangan virus ke dalam sel darah putih. Waktu yang dilewati sejak virus menembus sel inilah yang disebut dengan umur infeksi. Berdasar umur infeksi lalu dibentuk model struktur umur infeksi virus HIV yang disusun oleh Nelson et al. (2004). Dalam tulisan ini akan dibahas model struktur umur infeksi virus HIV dengan terapi kombinasi obat serta pengaruhnya terhadap dinamika virus, dengan membedakan kombinasi terapi obat menjadi dua tipe yakni: 1 Kombinasi I : Kombinasi RTI dan PI 2 Kombinasi II: Kombinasi EI dan PI. Dua tipe diatas dimodelkan dalam sistem persamaan diferensial biasa dan parsial. Parameter yang digunakan dalam analisis akan diambil dari Rong et al. (2007).

18 2 Tujuan Penelitian Penulisan ini bertujuan : 1 Mengkaji model struktur umur dengan dan tanpa kombinasi terapi obat. 2 Mengkaji persamaan Bilangan Reproduksi pada masing-masing model dan populasi virus pada dua model kombinasi terapi obat dengan menggunakan parameter parameter yang telah diberikan. 3 Melakukan kajian pada model terhadap persamaan Bilangan Reproduksi dan populasi virus dengan menggunakan software komputer Matematica.

19 3 TINJAUAN PUSTAKA Sistem Persamaan Diferensial Linear Jika suatu Sistem Persamaan Diferensial (SPD) dinyatakan sebagai x& = Ax + b, x(0) = x, x R 0 n (1) n Dengan A adalah matriks koefisien berukuran n n dan vektor konstan b R, maka sistem tersebut dinamakan SPD linear orde 1 dengan kondisi awal x (0) = x. Sistem (1) disebut homogen, jika b=0 dan non homogen jika b 0. 0 [Tu 1994] Titik Tetap Diberikan SPD dx n = x& = f ( x); x R (2) dt Titik x* disebut titik tetap jika f(x*)=0. Titik tetap disebut juga titik kritis atau kesetimbangan. [Tu 1994] Titik Tetap Stabil Misalkan x* adalah titik tetap sebuah persamaan diferensial dan x(t) adalah solusi dengan kondisi awal x(0)=x 0, dimana x 0 x *. Titik x * dikatakan titik tetap stabil, jika untuk setiap ε > 0, terdapat r > 0, sedemikian sehingga * x 0 x r <, maka * x() t x ε < untuk t > 0. [Vershult 1990] Nilai Eigen dan Vektor Eigen Jika A adalah matriks nä n, maka sebuah vektor taknol x di dalam R n disebut vektor eigen dari A, jika Ax adalah sebuah kelipatan skalar dari x; jelasnya: Ax = λ x (3) untuk skalar sebarang λ. Skalar λ disebut nilai eigen dari A, dan x disebut sebagai vektor eigen dari A terkait dengan λ.

20 4 Untuk memperoleh nilai eigen dari sebuah matriks A, nä n, persamaan (3) dapat ditulis kembali sebagai (A - λ I) x = 0 (4) dengan I matriks Identitas. Persamaan (4) mempunyai solusi tak nol jika dan hanya jika det (A - λ I) = A - λ I = 0. (5) Persamaan (5) disebut persamaan karakteristik dari matriks A, skalar-skalar yang memenuhi persamaan ini adalah nilai-nilai eigen A. [Anton 2000] Analisis Kestabilan Titik Tetap Analisa kestabilan untuk setiap titik tetap yang berbeda untuk setiap nilai eigen yakni: 1 Sistem x& = Ax adalah stabil jika dan hanya jika setiap nilai eigen dari A bernilai negatif. 2 Sistem x& = Ax adalah tidak stabil jika dan hanya jika minimal satu nilai eigen dari A bernilai positif. [Borrelli dan Coleman 1998] Bilangan Reproduksi ( R ) Bilangan Reproduksi ( R ) adalah rata-rata banyaknya sel darah putih yang terinfeksi oleh sebuah virus selama virus tersebut hidup, dengan asumsi semua sel bersifat rentan. Ketika 1 R < 1, berarti masing-masing virus menginfeksi kurang dari satu sel darah putih. Hal ini akan berakibat bahwa penyakit akan hilang dari populasi. 2 R > 1, berarti masing-masing virus menginfeksi lebih dari satu sel. Hal ini berakibat bahwa penyakit akan menyerang populasi sel. [Heffernan et al. 2005]

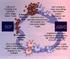
21 5 MODEL MATEMATIKA Interaksi Virus Terhadap Sel Darah Putih Sehat AIDS adalah penyakit yang disebabkan oleh virus HIV. Virus ini merusak sistem kekebalan tubuh manusia, sehingga tubuh mudah diserang berbagai penyakit lain yang dapat berakibat fatal. Berkurangnya kekebalan tubuh itu sendiri disebabkan berkurangnya sel darah putih sehat karena diserang oleh virus HIV. Setelah virus HIV memasuki sel darah putih sehat dalam tubuh seseorang, maka tubuh itu terinfeksi dan virus mulai bekerja memperbanyak diri (replikasi). Menurut pemeriksaan laboratorium, selama masa infeksi 2-12 minggu, seseorang sangat infeksius, dan mudah menularkan kepada orang lain. Hampir 30-50% penderita HIV mengalami masa infeksi akut yakni demam, pembesaran kelenjar getah bening, keringat malam, ruam kulit, sakit kepala dan batuk (Zein 2006). Proses infeksi virus HIV terhadap sel darah putih sehat dapat dilihat pada Gambar 1. 1 Virus masuk ke dalam sel darah putih sehat, 2 Enzim virus yakni RT (Reverse Transcriptase) pada genom RNA virus membuat salinan DNA, 3 DNA virus bergabung dengan DNA inang, membentuk RNA virus dalam jumlah banyak, 4 RNA virus membentuk protein virus, 5 Protein virus membentuk Protease virus, 6 Virus-virus matang keluar dari inang Gambar 1 Proses Infeksi Virus HIV terhadap sel Darah Putih Sehat (Feng dan Rong 2006)

22 6 Proses infeksi diawali masuknya virus ke dalam sel darah putih sehat. Di dalam sel, enzim virus yakni Reverse Transcriptase (RT) pada genom Ribonucleic Acid (RNA) virus, membuat suatu salinan Deoxyribonucleic Acid (DNA). DNA virus akan bergabung dengan DNA inang membentuk RNA virus dalam jumlah banyak, lalu RNA virus akan membentuk protein virus. Dari protein virus dihasilkan protease virus untuk menghasilkan virus baru yang siap menyerang sel darah putih sehat lainnya. Perelson (2002) menunjukkan diagram penyebaran virus tersebut pada Gambar 2. T * k Laju Infeksi p Laju produksi virus Sel darah putih terinfeksi Virus V Sel Darah Putih sehat s δ c m mati mati mati Gambar 2 Diagram penyebaran virus Pada Gambar 2, sel darah putih sehat (T) terinfeksi Virus (V) dengan laju k sehingga terbentuk sel darah putih terinfeksi (T * ). Sel darah putih diasumsikan diproduksi dengan laju s dan mati pada laju m. Sel terinfeksi akan mati secara alami dengan laju δ. Virus baru berkembang dengan laju p. Virus akan mati secara alami dengan laju c. Waktu yang dilewati sejak virus menembus sel darah putih disebut dengan umur infeksi. Berdasar umur infeksi inilah lalu dibentuk model struktur umur infeksi virus HIV ( Nelson et al ).

23 7 Kombinasi Terapi Kombinasi terapi obat diharapkan mampu menekan virus HIV dalam sel darah putih. Kombinasi obat meliputi RTI dan PI, serta EI dan PI. Peran dari RTI dan PI dapat dijelaskan pada Gambar 3. 1 Virus masuk ke dalam sel darah putih sehat 2 RTI menghalangi enzim virus yakni RT membuat salinan DNA 3 RNA virus tidak dihasilkan dalam jumlah banyak 4 RNA virus membentuk protein virus yang tidak sempurna 5 PI menghalangi protein virus membentuk Protease virus 6 Virus mati Gambar 3 Peran obat RTI dan PI terhadap virus HIV (Feng dan Rong 2006) Selama proses enzim virus yakni RT membuat suatu salinan DNA dari genom RNA virus, jika ada RTI, maka genom RNA virus tidak akan dicopy ke dalam DNA, dan virus baru tidak akan dihasilkan. Ketika virus mereplikat, DNA nya dibaca untuk menghasilkan protein-protein virus yang kemudian menghasilkan Protease virus. Protease virus diperlukan untuk menghasilkan virus. Jika protease virus dihambat dengan obat PI, maka virus baru tidak akan dihasilkan (Zein 2006). Kombinasi terapi obat EI dan PI bermanfaat menghalangi masuknya virus ke dalam sel darah putih sehat dan menghalangi infeksi yang berkelanjutan (Zein 2006). Untuk lebih memudahkan pemahaman tulisan ini, diberikan skema Model Struktur Umur Infeksi pada Gambar 4.

24 8 Model Struktur Umur Tanpa Terapi Obat Terapi Obat Kombinasi Obat Reverse Transcriptase Inhibitor dan Protease Inhibitor Entry Inhibitor dan Protease Inhibitor Gambar 4 Skema Model Struktur Umur Infeksi Virus HIV Dalam tulisan ini yang dianalisis secara rinci adalah model struktur umur dengan menggunakan terapi kombinasi obat yakni kombinasi RTI dan PI serta EI dan PI. Asumsi Model Beberapa asumsi mendasar yang digunakan untuk penyusunan model matematika adalah : 1 Virus yang baru dihasilkan adalah virus terinfeksi. 2 Tidak ada mikro organisme lain yang menyerang sel darah putih sehat selain virus HIV. 3 Semua sel darah putih bersifat rentan terinfeksi. Model Model yang akan disusun berdasar asumsi di atas menggunakan tiga variabel yakni populasi sel darah putih sehat T, sel terinfeksi T *, dan virus V. Model tersebut terdiri dari: Model I : Tanpa Terapi Obat Model struktur umur infeksi HIV tanpa terapi obat diberikan oleh Nelson et al. (2004) :

25 9 d T () t = s mt kvt, dt T*(,) at + T*(,) at = δ () at*(,), at t a d V () t = p () at *(,) a t da cv, dt T *(0, t) = kvt, 0 (6) dengan penjelasan notasi diberikan dalam Tabel 1. Tabel 1 Definisi Notasi Tanpa Terapi Obat Notasi T () t Keterangan Populasi sel darah putih sehat pada waktu t T *( a, t ) Populasi sel darah putih terinfeksi dengan umur infeksi a (waktu yang telah dilewati sejak virus menembus sel) pada waktu t V(t) Virus yang terinfeksi pada waktu t s m Laju produksi sel darah putih sehat Laju kematian sel darah putih sehat δ ( a) Laju kematian sel darah putih terinfeksi bergantung umur infeksi a c Laju kematian virus k p( a ) Laju infeksi sel darah putih Laju produksi virus dengan umur infeksi a Terapi Obat Terapi obat dilakukan dengan kombinasi obat yang dimodelkan dengan Model II : Terapi Kombinasi Obat RTI dan PI dan Model III : Terapi Kombinasi Obat EI dan PI. Model II : Kombinasi Terapi RTI dan PI Rong et al. (2007) memberikan model struktur umur dengan terapi kombinasi RTI dan PI yakni :

26 10 d T () t = s mt kvt + ηε ( RTI ) β() at *(,) a t da, dt 0 0 T *( at, ) + T *( at, ) = δ( at ) *( at, ) η( εrti ) β( at ) *( at, ), t a d V () t = (1 εpi )(1 β( a )) p () at *(,) a t da cv, dt T *(0, t) = kvt, (7) dengan β ( a) merupakan proporsi sel terinfeksi pada umur infeksi a, ε RTI adalah kemujaraban obat RTI, dan ε PI menunjukkan kemujaraban obat PI. ε RTI, ε PI œ [0,1]. Model III : Kombinasi Terapi Obat EI dan PI Rong et al. (2007) memberikan model struktur umur dengan terapi kombinasi EI dan PI yakni : d T () t = s mt (1 ε EI ) kvt dt T *( a, t) + T *( a, t) = δ ( at ) *( a, t) t a d V () t = (1 εpi )(1 β( a )) p () at *(,) a t da cv, dt 0 T *(0, t) = (1 ε ) kvt PI (8) dengan ε EI merupakan kemujaraban obat EI. ε EI œ [0,1]. Nilai Parameter Nilai parameter yang digunakan dalam simulasi diambil dari Rong et al. (2007) sebagai berikut :

27 11 Tabel 2 Nilai Parameter Notasi Definisi Nilai a 1 Waktu ketika enzim virus (RT) mulai membuat salinan DNA 0.25 hari δ Laju kematian sel terinfeksi 1 hari -1 c Laju kematian virus 23 hari -1 s Laju pengerahan sel darah putih 10 4 ml -1 hari -1 sehat m Laju kematian sel darah putih sehat 0.01 hari -1 k Laju perubahan sel darah putih 2.4ä10-8 ml hari -1 sehat menjadi terinfeksi p * Level maksimum produksi virus virus hari -1

28 12 PEMBAHASAN Untuk mengetahui perkembangan virus, dilakukan kajian terhadap Bilangan Reproduksi dan populasi virus. Bilangan Reproduksi tersebut meliputi Bilangan Reproduksi model tanpa terapi obat dan Bilangan Reproduksi model terapi kombinasi obat, sedangkan populasi virus hanya meliputi populasi virus model terapi kombinasi obat. Kombinasi obat dilakukan dengan dua macam cara. Cara pertama dengan kombinasi obat RTI dan PI (Kombinasi I) dan cara kedua dengan kombinasi obat EI dan PI (Kombinasi II). Pada dua jenis kombinasi terapi tersebut akan dikaji keefektifannya. Nelson et al. (2004) merumuskan laju produksi virus yakni : ( a a1 ) p*(1 e θ ) jika : a a1 p(a) = (9) 0 lainnya dengan q merupakan konstanta laju produksi virus. a 1 adalah waktu ketika enzim virus (RT) mulai membuat salinan DNA. Dengan mengambil a 1 =0.25 hari dan p * =6.4201ä10 3 virus hari -1, diperoleh plot perubahan fungsi p(a) pada Gambar p (a) 7000 q = q = q = Umur infeksi (hari) a Gambar 5 Plot perubahan fungsi p(a) untuk nilai q = 10, 1, 0.1.

29 13 Model I : Tanpa Terapi Obat Dari Model I diperoleh titik kesetimbangan yakni E (T, T *, V) = (s/m, 0, 0) (lihat lampiran1 halaman 31, 32). Pada titik kesetimbangan ini diperoleh Matriks Jacobi: J E = m 0 0 δ ( a) 0 p( a) ks m ks m. c Dengan penghitungan det (J E -λi) = 0 diperoleh nilai eigen yakni : λ 1 = m (10) λ 2,3 = 1 1 ks c a c a c a p a 2 2 m 2 ( + δ( )) ± ( + δ( )) 4[ δ( ) ( ) ]. (11) Kestabilan akan diperoleh jika semua nilai eigen bernilai negatif. Karena semua parameter bernilai positif, maka nilai eigen λ 1 dan λ2 akan bernilai negatif. Agar nilai eigen λ 3 bernilai negatif maka haruslah sehingga ks 4[ cδ ( a) p( a) ] > 0, m cδ ( a) > p( a) ks, m cδ ( a) ks pa ( ) m > 1. (12) Dari (12) diperoleh Bilangan Reproduksi virus untuk Model I yang didefinisikan dengan R 0 dan dirumuskan : R 0 kp( a) s =. (13) mcδ ( a) Dari (9) dan (13) diperoleh:

30 14 R 0 kp = * θ ( a a1 [1 e ) ] 0 untuk : a a lainnya. 1 (14) Dengan mengambil q=1, a 1 =0.25 hari, p * =6.4201ä10 3 virus hari -1, k=2.4ä10-8 ml hari -1, s =10 4 ml -1 hari -1, c = 23 hari -1, δ(a) =1 hari -1 dan m = 0.01 hari -1, dihasilkan plot Bilangan Reproduksi virus tanpa terapi obat (14) pada Gambar R a Umur Infeksi (a) dalam hari Gambar 6 Plot Bilangan Reproduksi Virus tanpa terapi obat Dari Gambar 6 diperoleh bahwa pada saat R 0 > 1, berarti masing-masing virus menginfeksi lebih dari satu sel darah putih yakni pada umur infeksi a > hari. Jadi pada kondisi tanpa terapi obat, virus dalam tubuh manusia dapat menginfeksi populasi sel darah putih pada umur infeksi a > 0.412, berarti penyakit dapat menyerang populasi sel darah putih dalam umur infeksi lebih besar dari hari ( lebih besar dari 10 jam). Model II : Kombinasi Terapi Obat RTI dan PI Bilangan Reproduksi virus HIV dari kombinasi terapi obat RTI dan PI didefinisikan dengan R 1 dan dirumuskan : a1 η ( εrti R ) 1 = e M 0, (15) (lihat Rong et al. 2007), dengan

31 15 dan sk θ δ M cm δθ ( + δ) * a1 0 = (1 ε PI ) p e, (16) η( εrti )=-ρln(1- ε RTI ), (17) dengan δ = δ(a) dan r konstanta pengontrol replikasi virus yang menentukan perubahan bentuk fungsi. Dengan pemberian nilai r = 1, 2, 5 pada (17) diperoleh plot perubahan fungsi η( ε RTI ) pada Gambar 7. η( RTI ) r=5 r=2 r= RTI Gambar 7 Plot perubahan fungsi η( εrti ) untuk r = 1, 2 dan 5 Dari (15), (16) dan (17) diperoleh : 1 (1 ) a 1 R = ε ρ M. (18) RTI 0 (Lihat lampiran 2 halaman 33). Untuk melihat dampak kombinasi terapi obat RTI dan PI terhadap virus HIV ditetapkan nilai kemujaraban obat ε PI = 0.4, 0.5 dan 0.6. Untuk mengetahui kondisi bebas penyakit maka dipilih R 1 lebih kecil dari satu. Untuk menyelidiki apakah populasi virus akan turun dapat dikaji dengan pemberian nilai konstanta pengontrol replikasi virus (ρ) dengan nilai sebesar 1, 2 dan 5, dan nilai kemujaraban obat PI yang berbeda. Perbandingan model II

32 16 dengan pemberian nilai ε PI = 0.4, 0.5 dan 0.6 penurunan populasi virus HIV dapat dijelaskan dalam Gambar 8. (i) Untuk ρ = 1 (ii) Untuk ρ = 2 R R RTI RTI (iii) Untuk ρ = 5 R Keterangan: : ε PI = 0.4 : ε PI = 0.5 : ε PI = RTI Gambar 8 Plot Bilangan Reproduksi terapi kombinasi RTI dan PI dengan ρ = 1, 2 dan 5, serta ε PI = 0.4, 0.5 dan 0.6 Lebih jelasnya dapat dilihat pada tabel berikut :

33 17 Tabel 3 Pemberian Nilai ρ Terapi RTI dan PI Gambar 8 ρ Nilai ε RTI pada Nilai ε RTI pada Nilai ε RTI pada ε PI = 0.4 ε PI = 0.5 ε PI = 0.6 (i) 1 ε RTI 0.84 ε RTI 0.65 ε RTI 0.16 (ii) 2 ε RTI 0.58 ε RTI 0.41 ε RTI 0.07 (iii) 5 ε RTI 0.30 ε RTI 0.19 ε RTI 0.03 Dari Gambar 8 dan Tabel 3 diperoleh bahwa pada kondisi bebas penyakit (R 1 < 1), untuk : 1 Nilai ε PI = 0.4 (40%), dengan ρ =1, R 1 turun secara nonlinear pada nilai ε RTI lebih besar atau sama dengan 84%, dengan nilai ρ =2 R 1 turun pada nilai ε RTI lebih besar atau sama dengan 58% dan dengan ρ =5 R 1 turun pada nilai ε RTI lebih atau sama dengan 30%. 2 Nilai ε PI = 0.5 (50%), dengan ρ =1, R 1 turun secara nonlinear pada nilai ε RTI lebih besar atau sama dengan 65%, dengan nilai ρ =2 R 1 turun pada nilai ε RTI lebih besar atau sama dengan 41% dan dengan ρ =5 R 1 turun pada nilai ε RTI lebih besar atau sama dengan 19%. 3 Nilai ε PI = 0.6 (60%), dengan ρ =1, R 1 turun secara nonlinear pada nilai ε RTI lebih dari atau sama dengan 16%, dengan nilai ρ =2 R 1 turun pada nilai ε RTI lebih besar atau sama dengan 7% dan dengan ρ =5 R 1 turun pada nilai ε RTI lebih besar atau sama dengan 3%. Pada kondisi tersebut di atas mengindikasikan bahwa populasi virus akan berkurang. Model III : Kombinasi Terapi Obat EI dan PI Bilangan Reproduksi virus HIV dari terapi kombinasi obat EI dan PI didefininisikan dengan R 2 dan dirumuskan dengan : R = (1 ε ) M. (19) 2 EI 0 (lihat Rong et al. 2007).

34 18 Untuk melihat dampak kombinasi terapi obat EI dan PI terhadap virus HIV, diberikan nilai kemujaraban obat PI, ε PI = 0.4, 0.5 dan 0.6. Bilangan Reproduksi R 2 dipilih lebih kecil satu untuk melihat kondisi bebas penyakit (Heffernan et al. 2005). Dengan pemberian nilai kemujaraban obat ε PI = 0.4, 0.5 dan 0.6, dari (16) dan (19) diperoleh plot Bilangan Reproduksi R 2 pada Gambar R Keterangan : : ε PI = 0.4 : ε PI = 0.5 : ε PI = EI Gambar 9 Plot Bilangan Reproduksi kombinasi terapi EI dan PI dengan ε PI = 0.4, 0.5 dan 0.6. Lebih jelasnya dapat dilihat pada tabel berikut : Tabel 4 Pemberian Nilai ε PI Terapi EI dan PI Gambar 9 Pemberian ε PI Nilai ε EI (i) 0.4 ε EI 0.37 (ii) 0.5 ε EI 0.23 (iii) 0.6 ε EI 0.05 Dari gambar 9 diperoleh bahwa dengan pemberian nilai kemujaraban obat: 1 ε PI = 0.4 (40%), pada kondisi bebas penyakit (R 2 < 1), R 2 turun secara linear pada nilai ε EI lebih besar atau sama dengan 37%. 2 ε PI = 0.5 (50%), pada kondisi bebas penyakit (R 2 < 1), R 2 turun secara linear pada nilai ε EI lebih besar atau sama dengan 23%. 3 ε PI = 0.6 (60%), pada kondisi bebas penyakit (R 2 < 1), R 2 turun secara linear pada nilai ε EI lebih besar atau sama dengan 5%. Pada kondisi tersebut di atas mengindikasikan bahwa populasi virus akan berkurang.

35 19 Perbandingan Model II dan III Terhadap Muatan Virus Dari kedua jenis kombinasi terapi akan dibandingkan keefektifannya dikaji dari pemberian nilai konstanta ρ pada Bilangan Reproduksi Model II dan Model III. Pemberian Nilai Konstanta ρ pada Bilangan Reproduksi Model II dan Model III Dalam bagian ini akan dibandingkan pengaruh dari dua terapi kombinasi terhadap muatan virus. Untuk mengaji dampak kombinasi terapi obat terhadap virus HIV ditetapkan nilai kemujaraban obat PI ε PI = 0.5. Bilangan Reproduksi dipilih lebih kecil dari satu pada kondisi bebas penyakit dengan R 1 lebih kecil dari satu dan R 2 juga lebih kecil satu. Untuk menyelidiki apakah virus akan mati dapat dikaji pada pemberian nilai konstanta ρ dengan nilai sebesar 1, 2 dan 5. Kematian Virus dapat dijelaskan dalam kajian pada Gambar 10. R 1, R Keterangan : : Model II (RTI dan PI) dengan r=1 : Model II (RTI dan PI) dengan r=2 : Model II (RTI dan PI) dengan r=5 : Model III (EI dan PI) RT, EI Gambar 10 Perbandingan terapi kombinasi terhadap Bilangan Reproduksi Model II dan III (Rong et al. 2007)

36 20 Lebih jelasnya dapat dilihat pada tabel berikut : Tabel 5 Pemberian Nilai ρ pada Dua Bilangan Reproduksi Gambar 10 ε RTI untuk nilai R 1 (ε RTI ) < 1 ε EI untuk nilai R 2 (ε EI ) < 1 ρ =1 ε RTI 0.65 ε EI 0.23 ρ =2 ε RTI 0.41 ε EI 0.23 ρ =5 ε RTI 0.19 ε EI 0.23 Dari ketiga kondisi di atas, dari Gambar 10 dan Tabel 5 diperoleh bahwa pada kondisi bebas penyakit (R 1 < 1 dan R 2 < 1) : 1 Pada ρ =1, R 1 turun secara nonlinear pada nilai ε RTI lebih besar atau sama dengan 65% sedang R 2 turun secara linear pada nilai ε EI lebih besar atau sama dengan 23%. Hal ini mengindikasikan bahwa populasi virus akan menurun. Jadi untuk menurunkan muatan virus, pada kondisi ini Model III lebih efektif dari Model II. 2 Pada ρ =2, R 1 turun secara nonlinear pada nilai ε RTI lebih besar atau sama dengan 41% sedang R 2 turun secara linear pada nilai ε EI lebih besar atau sama dengan 23%. Hal ini mengindikasikan bahwa populasi virus akan menurun. Jadi untuk menurunkan muatan virus, pada kondisi ini Model III lebih efektif dari Model II. 3 Pada ρ =5, R 1 turun secara nonlinear pada nilai ε RTI lebih besar atau sama dengan 19% sedang R 2 turun secara linear pada nilai ε EI lebih besar atau sama dengan 23%. Hal ini mengindikasikan bahwa populasi virus akan menurun. Jadi untuk menurunkan muatan virus, pada kondisi ini Model II lebih efektif dari Model III. Dari kondisi tersebut diperoleh bahwa nilai ρ memengaruhi besar kecilnya kemujaraban obat RTI tetapi tidak berpengaruh pada besar kecilnya kemujaraban obat EI.

37 21 Perbandingan Model I, II dan III Terhadap Muatan Virus Model I, II dan III, dibandingkan untuk melihat bagaimana muatan virus jika tanpa dan dengan terapi obat. Pada Model I, karena tidak ada terapi, Bilangan Reproduksi hanya dikaji dari umur infeksi virus, sedang pada Model II dan III karena kemujaraban obat ε PI ditetapkan dengan pemberian nilai sebesar 0.5 (50%), maka Model II dengan r =1, Bilangan Reproduksi dikaji dari nilai kemujaraban obat RTI dan Model III, Bilangan Reproduksi dikaji dari nilai kemujaraban obat EI. Masing-masing Bilangan Reproduksi dari ketiga model dikaji pada kondisi bebas penyakit, R 1 <1, R 2 <1 dan kondisi populasi sel terjangkit penyakit oleh populasi virus, R 0 >1. Untuk mengetahui perbandingan model tanpa dan dengan terapi obat, yakni model I, II dan III digambarkan pada Gambar 11. (i) Model I (ii) Model II (iii) Model III R R R a RTI EI Gambar 11 Perbandingan Model I, II dan III Dari Gambar 11 diperoleh bahwa : 1 Tanpa terapi obat, virus akan menginfeksi lebih dari satu sel darah putih pada umur infeksi a > hari, hal ini berakibat bahwa jika tanpa terapi obat, virus akan menginfeksi populasi sel darah putih pada umur infeksi lebih dari hari ( lebih dari 10 jam). 2 Dengan terapi kombinasi obat RTI dan PI pada kemujaraban obat PI 50%, populasi virus akan cenderung menurun pada kemujaraban obat RTI lebih besar atau sama dengan 65%.

38 22 3 Dengan terapi kombinasi obat EI dan PI pada kemujaraban obat PI 50%, populasi virus akan cenderung menurun pada kemujaraban obat EI lebih besar atau sama dengan 23%. Pemberian Nilai Konstanta ρ Pada Populasi Virus Keefektifan dua kombinasi terapi dapat juga dijelaskan dengan mengkaji Populasi virus dari kedua jenis model terapi kombinasi : 1 Populasi Virus Model II 2 Populasi Virus Model III. Populasi Virus Model II Populasi virus dari kombinasi terapi obat Model II (RTI dan PI) didefinisikan dengan V 2 dan dirumuskan : V 2 mr = k (1 K ) ( 1 1), (lihat Rong et al. 2007), dengan 1 (20) η( ε RTI ) [ ( RTI )] a1 1 [1 e δ + K = η ε ]. (21) δ + η( ε ) RTI Untuk menyelidiki seberapa besar nilai kemujaraban obat RTI berakibat virus akan mati, dilakukan pemberian nilai ρ. Dengan pemberian nilai kemujaraban obat PI 40%, 50% dan 60% serta nilai ρ = 1, 2 dan 5 pada (20) dan (21), nilai kemujaraban obat RTI pada kematian virus dapat dijelaskan dalam Gambar 12.

39 23 Untuk ρ = 1 (i) ε PI = 0.4 (ii) ε PI = 0.5 (iii) ε PI = 0.6 V (ä1000) V (ä V 2 (ä1000) RTI RTI RTI Untuk ρ = 2 (i) ε PI = 0.4 (ii) ε PI = 0.5 (iii) ε PI = 0.6 V ( 1000) RTI V 2 ( 1000) RTI V 2 ( 1000) RTI Untuk ρ = 5 (i) ε PI = 0.4 (ii) ε PI = 0.5 (iii) ε PI = 0.6 V 2 V ( 1000) RTI ( 1000) RTI V 20 2 ( 1000) RTI Gambar 12 Nilai kemujaraban obat RTI dengan penetapan kemujaraban obat PI, ε PI =0.4, 0.5, 0.6 dan r = 1, 2, 5 (Rong et al. 2007)

40 24 Lebih jelasnya dapat dilihat pada tabel berikut : Tabel 6 Pemberian nilai ρ pada populasi virus terapi RTI dan PI Gambar 12 ρ Nilai ε RTI pada Nilai ε RTI pada Nilai ε RTI pada ε PI = 0.4 ε PI = 0.5 ε PI = 0.6 (i) 1 ε RTI 0.84 ε RTI 0.65 ε RTI 0.16 (ii) 2 ε RTI 0.58 ε RTI 0.41 ε RTI 0.07 (iii) 5 ε RTI 0.30 ε RTI 0.19 ε RTI 0.03 Dari Gambar 12 dan Tabel 6 diperoleh bahwa untuk : 1 Nilai ε PI = 0.4 (40%), pada ρ =1 populasi virus akan menurun dengan kemujaraban obat RTI, ε RTI lebih besar atau sama dengan 84%, pada ρ =2 populasi virus akan menurun dengan kemujaraban obat RTI, ε RTI lebih besar atau sama dengan 58%, pada ρ =5 populasi virus akan menurun dengan kemujaraban obat RTI, ε RTI lebih besar atau sama dengan 30%. 2 Nilai ε PI = 0.5 (50%), pada ρ =1 populasi virus akan menurun dengan kemujaraban obat RTI, ε RTI lebih besar atau sama dengan 65%, pada ρ =2 populasi virus akan menurun dengan kemujaraban obat RTI, ε RTI lebih besar atau sama dengan 41%, pada ρ =5 populasi virus akan menurun dengan kemujaraban obat RTI, ε RTI lebih besar atau sama dengan 19%. 3 Nilai ε PI = 0.6 (60%), pada ρ =1 populasi virus akan menurun dengan kemujaraban obat RTI, ε RTI lebih besar atau sama dengan 16%, pada ρ =2 populasi virus akan menurun dengan kemujaraban obat RTI, ε RTI lebih besar atau sama dengan 7%, pada ρ =5 populasi virus akan menurun dengan kemujaraban obat RTI, ε RTI lebih besar atau sama dengan 3%. Jadi kemujaraban obat RTI bergantung dari besar kecilnya ρ. Populasi Virus Model III Populasi virus dari kombinasi terapi obat EI dan PI didefinisikan dengan V 3 dan dirumuskan dengan :

41 25 V 3 mr ) = k (1 ε ) ( 2 1. EI (lihat Rong et al. 2007). Untuk menyelidiki seberapa besar nilai keakuratan obat EI berakibat virus akan mati, dapat dikaji dengan pemberian nilai keakuratan obat ε PI = 0.4, 0.5 dan 0.6 pada (22). Pengkajian nilai keakuratan obat EI dapat dikaji pada Gambar 13. (22) (i) ε PI = 0.4 (ii) ε PI = 0.5 (iii) ε PI = 0.6 V 3 ( 1000) V 3 ( 1000) V ( 1000) EI EI EI Gambar 13 Nilai kemujaraban obat EI dengan penetapan kemujaraban obat PI, ε PI =0.4, 0.5 dan 0.6 (Rong et al. 2007) Lebih jelasnya dapat dilihat pada tabel berikut : Tabel 7 Pemberian Nilai ε PI Pada Populasi Virus Terapi EI dan PI Gambar 13 Pemberian ε PI Nilai ε EI (i) 0.4 ε EI 0.37 (ii) 0.5 ε EI 0.23 (iii) 0.6 ε EI 0.05 Dari gambar 13 dan Tabel 7 diperoleh bahwa dengan pemberian nilai kemujaraban obat:

42 26 1 ε PI = 0.4 (40%), populasi virus akan menurun pada nilai ε EI lebih besar atau sama dengan 37%. 2 ε PI = 0.5 (50%), populasi virus akan menurun pada nilai ε EI lebih besar atau sama dengan 23%. 3 ε PI = 0.6 (60%), populasi virus akan menurun pada nilai ε EI lebih besar atau sama dengan 5%. Perbandingan Populasi Virus Model II dan III Dari populasi virus kedua model kombinasi terapi dibandingkan melalui kajian pada Gambar 14. (i) r = 1 (ii) r = 2 V 2, V 3 ( 1000) 140 V 2, V 3 ( 1000) RTI, EI RTI, EI (iii) r = 5 V, V ( 1000) RTI, EI Keterangan : : Kombinasi terapi RTI dan PI : Kombinasi terapi EI dan PI Gambar 14 Perbandingan terapi kombinasi dengan penetapan kemujaraban obat PI, ε PI = 0.5 (Rong et al. 2007)

43 27 Lebih jelasnya dapat dilihat pada tabel berikut : Tabel 8 Pemberian Nilai ρ untuk Populasi Virus Pada Model II dan III Gambar 14 ρ Kemujaraban Obat EI Kemujaraban Obat RTI (i) 1 ε EI 0.23 ε RTI 0.65 (ii) 2 ε EI 0.23 ε RTI 0.41 (iii) 5 ε EI 0.23 ε RTI 0.19 Dari Gambar 14 dan Tabel 8 di atas, diperoleh bahwa keefektifan obat kombinasi RTI dan PI serta EI dan PI sangat bergatung pada nilai ρ. Dari Terapi Kombinasi obat RTI dan PI dan Terapi obat EI dan PI, dengan asumsi penetapan kemanjuran obat PI 50% (ε PI = 0.5) dan nilai ρ, hasil kajian menunjukkan : 1 Untuk nilai konstanta ρ =1 dan 2, Model III ( terapi kombinasi obat EI dan PI) lebih efektif dari Model II (terapi kombinasi obat RTI dan PI). 2 Untuk nilai konstanta ρ = 5, Model II (terapi kombinasi obat RTI dan PI) lebih efektif dari Model III (terapi kombinasi obat EI dan PI).

44 28 KESIMPULAN Dengan melakukan kajian pada Bilangan Reproduksi terhadap Model I (tanpa terapi obat), Model II (kombinasi terapi obat RTI dan PI) dan Model III (kombinasi terapi obat EI dan PI) serta kajian populasi virus pada Model II dan III, dengan pemberian nilai kemujaraban obat PI 40%, 50% dan 60% serta pemberian nilai konstanta pengontrol replikasi virus r sebesar 1, 2 dan 5, dari hasil kajian dapat ditarik beberapa kesimpulan : 1 Pada Model I (tanpa terapi obat), virus akan menginfeksi populasi sel darah putih pada umur infeksi a > hari (a > 10 jam), artinya jika tanpa terapi obat, maka penyakit HIV akan terjangkit pada tubuh seseorang pada umur infeksi lebih dari 10 jam. 2 Pada Model II (kombinasi terapi obat RTI dan PI), diperoleh bahwa semakin besar pemberian nilai kemujaraban obat PI dengan nilai konstanta pengontrol replikasi virus r sebarang, sesuai dengan berjalannya waktu mengakibatkan semakin cepat populasi virus menurun. 3 Pada Model III (kombinasi terapi obat EI dan PI), menunjukkan bahwa semakin besar pemberian nilai kemujaraban obat PI, sesuai dengan berjalannya waktu mengakibatkan semakin cepat populasi virus menurun. 4 Untuk Keefektifan dua kombinasi terapi obat, dari kajian Bilangan Reproduksi dan populasi virus diperoleh bahwa semakin kecil r maka Model III ( kombinasi terapi obat EI dan PI) lebih efektif dari Model II ( kombinasi terapi obat RTI dan PI) dan semakin besar r diperoleh Model II lebih efektif dari Model III.

45 29 DAFTAR PUSTAKA Anton H Elementary Linear Algebra. Eighth edition. Lehigh Press, Inc. USA Borrelli RL, Coleman CS Differential Equations A Modeling Perspective. John Wiley and Sons, Inc. USA. Fauci AS HIV and AIDS: 20 years of science, Nat. Med., 9, pp Feng Z, Rong L The influence of anti-viral drug therapy on the evolution of HIV-1 pathogens, in Disease Evolution: Models, Concepts, and Data Analyses, Feng Z., Dieckmann U., and Levin S. A., eds., AMS, Providence, RI, pp Heffernan JM, Smith RJ, and Wahl LM Perspectives on the basic reproductive ratio, Journal of The Royal Society Interface, pp Madigan MT, Martinko JM Brock Biology Of Microorganisms, eleventh edition, Pearson Education, USA. Nelson PW, Gilchrist MA, Coombs D, Hyman JM, Perelson AS An agestructured model of HIV infection that allows for variations in the production rate of viral particles and the death rate of productively infected cells, Math. Biosci., Eng., 1, pp Perelson AS Modelling viral and immune system dynamics, Nature Rev. Immunol., 2, pp Rong L, Feng Z, and Perelson AS Mathematical Analysis Of Age- Structured HIV-1 Dynamics With Combination Antiretroviral Therapy, SIAM J. APPL. MATH. Vol. 67, No. 3, pp Tu PNV Dynamical Systems. An Introduction with Applications in Economics and Biology. Springer-Verlag, New York. Verhulst F Nonlinear Differential Equations and Dynamical Systems. Springer-Verlag, Berlin. Zein U Pertanyaan Seputar HIV/AIDS yang Perlu Anda Ketahui. USU Press

46 LAMPIRAN 30

47 31 Lampiran1. Penurunan Bilangan Reproduksi Virus ( R 0 )Tanpa terapi Obat [Persamaan (13)] Dari persamaan (6), titik kesetimbangan diperoleh jika d T () t = 0, dt d T *( a, t) = 0, V () t = 0dengan T * (0, t) = kvt t dt maka: d d dari persamaan (6) dengan T () t = 0, T *( a, t) = 0, V () t = 0, menjadi: dt t dt 0 = s mt kvt, sehingga T s = m + kv, dan d T *(,) () *(,), ( ada ) = δ sehingga T *( a, t) = kvte δ, da dan p( at ) *( at, ) da 0 0 = p( at ) *( at, ) da cv, sehingga V =. c 0 Titik kesetimbangan diperoleh E (T, T *, V)=( s m, 0, 0). Persamaan (6) memiliki Matriks Jacobi: Sehingga m kv 0 kt J = 0 δ ( a) kt 0 p( a) c J s (,0,0) m m 0 = 0 δ ( a) 0 p( a) ks m ks m. c Nilai eigen diperoleh dari A λi = 0.

48 32 m λ 0 ks m 0 δ( a) λ ks m = 0, 0 pa ( ) c λ sehingga: ks ( m λ)[( δ( a) λ)( c λ) ( p( a) )] = 0 m ks m λ λ λ c δ a cδ a p a m 2 ( )[ + [ + ( )] + ( ) ( ) ] = 0 λ 1 = m λ 2,3 = 1 1 ks c + δ a ± c + δ a cδ a p a 2 2 m 2 [ ( )] [ ( )] 4[ ( ) ( ) ] Kestabilan diperoleh jika nilai eigen λ 1, λ 2 dan λ 3 seluruhnya negatif. Dari Nilai ks eigen λ 3 jika: 4[ cδ ( a) p( a) ] = 0 maka λ 3 = 0, jika 4[ cδ ( a) p( a) ks ] > 0 m m ks maka λ 3 < 0, dan jika 4[ cδ ( a) p( a) ] < 0 maka λ 3 > 0. m ks Jadi agar λ 3 bernilai negatif, maka haruslah 4[ cδ ( a) p( a) ] > 0. m Untuk memperoleh Bilangan Reproduksi dipilih: ks 4[ cδ ( a) p( a) ] > 0 m sehingga cδ ( a) > pa ( ) ks m ks pa ( ) m cδ ( a) > 1. Bilangan Reproduksi tanpa terapi obat diperoleh: kp( a) s R 0 =. mcδ ( a)

49 33 Lampiran 2. Penyederhanaan Bilangan Reproduksi virus HIV Pada Terapi Kombinasi RTI dan PI [Persamaan (18)]. a1 η ( εrti R ) 1 = e M 0,...lihat (15) Karena η(ε RTI )= -ρln(1-ε RTI ), maka : R = e M a1 [ ρln(1 εrti )] 1 0 = e = e a1 [ ρln(1 εrti )] ρ a1 [ln(1 εrti ) ] ρ ln(1 εrti ) a1 = [ e ] M M 0 0 M R = [ e ] M ln(1 ε ) 1 1 RTI ρa 0 ρ 1 = (1 ε ) a M RTI 0 0

50 34 Lampiran 3. Program Matematica 1. Untuk gambar 5 p@a_, a1_, θ_d := p I1 I θ H a a1l MM; p = ; a=plot[p[a,0.25,10],{a,0,10},plotrange {0,8000},Axes Origin {0,0},PlotStyle RGBColor[1,0,0]]; b=plot[p[a,0.25,1],{a,0,10},plotrange {0,8000},AxesO rigin {0,0},PlotStyle RGBColor[1,0,0]]; c=plot[p[a,0.25,0.1],{a,0,10},]; Show[{a,b,c},AxesLabel {"a","p(a)"}] 2. Untuk gambar 6 R0@a_, a1_, θ_d := ksh p H1 H θ Ha a1l LL L ; mcδ p = ;k= ;s= 10 4 ;m= 0.01; δ=1; c= 23; a=plot[r0[a,0.25,1],{a,0,10},plotrange {0,8},AxesOri gin {0,0},PlotStyle RGBColor[0,0,1], AxesLabel {"a","r0"}] G[a_]:=1; b=plot[g[a],{a,0, }] kons=table[ ,{i,0,1,0.01}]; bts=table[i,{i,0,1,0.01}]; m=length[kons]; table1=table[{kons[[i]],bts[[i]]},{i,1,m}]; c = ListPlot[table1] ; Show[{a,b,c}] 3. Untuk gambar 7 η[ RT_]:=-ρ Log[1- RT ]; ρ=1; a=plot[η[ RT],{ RT,0,1},PlotRange {0,20},AxesOrigin {0,0},PlotStyle RGBColor[0,0,1], AxesLabel {" RT","η RT"}] η[ RT_]:=-ρ Log[1- RT ]; ρ=2; b=plot[η[ RT],{ RT,0,1},PlotRange {0,20},AxesOrigin {0,0},PlotStyle RGBColor[0,0,1], AxesLabel {" RT","η RT"}] η[ RT_]:=-ρ Log[1- RT ]; ρ=5; c=plot[η[ RT],{ RT,0,1},PlotRange {0,20},AxesOrigin {0,0},PlotStyle RGBColor[0,0,1], AxesLabel {" RT","η RT"}] Show[{a,b,c}] 4. Gambar 8 (i)

51 35 RT_D := a1h ρ RTDL mo; skθ mo = cmδhθ+δl H1 PL p δ a1 ;a1= 0.25; s = 10 4 ; k= ; θ=1; c = 23; m = 0.01; δ=1; p = ; ρ=1; P= 0.4; a=plot[r1[ RT],{ RT,0,1},PlotStyle {RGBColor[1,0,0],Th ickness[.011]}] r11@ RT_D := a1 H ρ Log@1 RTDL mo; skθ mo = cmδhθ+δl H1 PI1L p δ a1 ;a1= 0.25; s= 10 4 ;k= ; θ=1; c = 23; m = 0.01; δ=1; p= ; ρ=1; PI1 = 0.5; b=plot[r11[ RT],{ RT,0,1},PlotStyle {RGBColor[0,0.5,0],Thickness[.011]}] r12@ RT_D := a1 H ρ Log@1 RTDL mo; skθ mo = cmδhθ+δl H1 PI2L p δ a1 ;a1= 0.25; s= 10 4 ;k= ; θ=1; c = 23; m = 0.01; δ=1; p= ; ρ=1; PI2 = 0.6; c=plot[r12[ RT],{ RT,0,1},PlotStyle {RGBColor[1.,0,1], Thickness[.011]}] G[σ_]:=1; d=plot[g[σ],{σ,0,1},plotstyle {RGBColor[0,0,1],Thickne ss[.011]}] bts=table[i,{i,0,1,0.01}]; konstan=table[0.23,{i,0,1,0.01}]; n=length[konstan]; table1=table[{konstan[[i]],bts[[i]]},{i,1,n}]; kons=table[0.65,{i,0,1,0.01}]; m=length[kons];table2=table[{kons[[i]],bts[[i]]},{i,1,m }]; e = ListPlot[table2] ;kons1=table[0.84,{i,0,1,0.01}]; m1=length[kons]; table3=table[{kons1[[i]],bts[[i]]},{i,1,m1}]; f = ListPlot[table3] ; kons2=table[0.16,{i,0,1,0.01}]; m2=length[kons]; table4=table[{kons2[[i]],bts[[i]]},{i,1,m2}]; g = ListPlot[table4] ; Show@8 a, b, c, d, e, f, g <, AxesLabel 8" RTI ", "R 1 "<D 5. Gambar 8(ii)

52 36 RT_D := a1h ρ RTDL mo; skθ mo = cmδhθ+δl H1 PL p δ a1 ;a1= 0.25; s = 10 4 ; k= ; θ=1; c = 23; m = 0.01; δ=1; p = ; ρ=2; P= 0.4; a=plot[r1[ RT],{ RT,0,1},PlotStyle {RGBColor[1,0,0],Th ickness[.011]}] r11@ RT_D := a1 H ρ Log@1 RTDL mo; skθ mo = cmδhθ+δl H1 PI1L p δ a1 ;a1= 0.25; s = 10 4 ; k= ; θ=1; c = 23; m = 0.01; δ=1; p = ; ρ=2; PI1 = 0.5; b=plot[r11[ RT],{ RT,0,1},PlotStyle {RGBColor[0,0.5,0],Thickness[.011]}] r12@ RT_D := a1 H ρ Log@1 RTDL mo; skθ mo = cmδhθ+δl H1 PI2L p δ a1 ;a1= 0.25; s = 10 4 ; k= ; θ=1; c = 23; m = 0.01; δ=1; p = ; ρ=2; PI2 = 0.6; c=plot[r12[ RT],{ RT,0,1},PlotStyle {RGBColor[1.,0,1], Thickness[.011]}] G[σ_]:=1; d=plot[g[σ],{σ,0,1},plotstyle {RGBColor[0,0,1],Thickne ss[.011]}] bts=table[i,{i,0,1,0.01}]; konstan=table[0.23,{i,0,1,0.01}]; n=length[konstan]; table1=table[{konstan[[i]],bts[[i]]},{i,1,n}]; kons=table[0.58,{i,0,1,0.01}]; m=length[kons]; table2=table[{kons[[i]],bts[[i]]},{i,1,m}]; e = ListPlot[table2] ; kons1=table[0.41,{i,0,1,0.01}]; m1=length[kons]; table3=table[{kons1[[i]],bts[[i]]},{i,1,m1}]; f = ListPlot[table3] ; kons2=table[0.07,{i,0,1,0.01}]; m2=length[kons]; table4=table[{kons2[[i]],bts[[i]]},{i,1,m2}]; g = ListPlot[table4] ; Show@8 a, b, c, d, e, f, g <, AxesLabel 8" RTI ", "R 1 "<D 6. Gambar 8 (iii)