BAB 2 MAKALAH. Makalah Pertama
|
|
|
- Suryadi Hartanto
- 5 tahun lalu
- Tontonan:
Transkripsi
1 Makalah Pertama Judul BAB MAKALAH : Penentuan Luas Lahan Datardengan Metode Pendekatan LingkaranBerbasisGoogle Earth/Google Maps Dipresentasikan pada : Seminar Nasional Matematika dan Pendidikan Matematika UNS 016 yang diselenggarakan oleh Fakultas Keguruan dan Ilmu Pendidikan Universitas Sebelas Maret pada tanggal 16 November 016 Publikasi : Seminar dan Prosiding Makalah Kedua Judul : Penentuan Luas Lahan dengan Menggunakan Metode Pendekatan Segitiga Sferik (Teorema Girard)dengan Bantuan Google Maps Dipresentasikan pada : Seminar Nasional Pendidikan Matematika UAD 016 yang diselenggarakan oleh Fakultas Keguruan dan Ilmu Pendidikan Universitas Ahmad Dahlan pada tanggal 31 Desember 016 Publikasi : Seminar dan Prosiding/Jurnal (dalam proses)
2 MAKALAH 1 Penentuan Luas Lahan Datar dengan Metode Pendekatan Lingkaran Berbasis Google Earth/Google Maps xiii
3 Penentuan Luas Lahan Datar dengan Metode Pendekatan Lingkaran BerbasisGoogle Earth/Google Maps Devi 1, Adi Setiawan 1, Eko Sediyono 1 Program Studi Matematika (Fakultas Sains dan Matematika, Universitas Kristen Satya Wacana) Program Studi Magister Sistem Informasi (Fakultas Teknologi Informasi, Universitas Kristen Satya Wacana) 1 devilialolok@gmail.com, 1 adi_setia_03@yahoo.com, eko@staff.uksw.edu Abstrak Kebutuhan akan lahan sangatlah penting bagi setiap makhluk hidup karena lahan merupakan bagian dari permukaan bumi yang mempunyai karakter dan fungsi yang luas dengan berbagai macam kekayaan yang terkandung di dalamnya. Salah satu pemanfaatan lahan adalah melakukan pengukuran luas lahan. Pada penelitian ini, metode yang digunakan untuk menghitung luas lahan yaitu metode pendekatan lingkaran dengan berbasis Google Earth/Google Maps. Ada tiga objek penelitian yang dilakukan diantaranya yaitu: Lapangan Sepak Bola UKSW, Rawa Pening dan Kota Salatiga. Dengan bantuan Google Earth diperoleh titik-titik koordinat berupa garis lintang dan garis bujur untuk menghitung jarak antar dua titik dengan asumsi bumi berbentuk bola dan elipsoida. Jarak antar dua titik diterapkan pada metode pendekatan luas lingkaran untuk memperoleh luas total dari ketiga lahan yang menjadi objek penelitian. Luas yang diperoleh dibandingkan dengan luas yang menjadi acuan.untuk Lapangan Sepak Bola UKSW yang menjadi acuan adalah luas berdasarkan hasil perhitungan manual ( m ), dan Rawa Pening luas acuan adalah Google Maps(19.79 km ), serta Kota Salatiga luas acuan adalah data dari BPS Kota Salatiga ( km ). Dengan metode pendekatan lingkaran yang mengasumsikan bumi berbetuk bola dan elipsoda maka luas Lapangan Sepak Bola UKSW, luas Rawa Pening, luas Kota Salatiga berturut-turut adalah m dan m, km dan km, km dan km.prosentasi luas dari ketiga objek penelitian dibandingkan luas acuan masing-masing lahan diperoleh 97% sampai dengan 108%. Kata kunci: LuasLahan, Google Earth, Google Maps, Metode Pendekatan Lingkaran PENDAHULUAN Kebutuhan akan lahan sangatlah penting bagi setiap makhluk hidup karena lahan merupakan bagian dari permukaan bumi yang mempunyai karakter dan fungsi yang luas dengan berbagai macam kekayaan yang terkandung di dalamnya (Maulana, 016). Setiap bidang lahan ini tentu memiliki fungsi sesuai peruntukannya seperti tertuang pada UURI Nomor 6 Tahun 007 Tentang Penataan Ruang. Oleh karena itu pemanfaatan lahan harus dilakukan secara terencana dan terkendali. Salah satu pemanfaatan lahan yaitu dengan cara pengukuran dan menentukan posisi titik-titik batas dari suatu lahan. SEMINAR MATEMATIKA DAN PENDIDIKAN MATEMATIKA UniversitasSebelasMaret, 16 November 016
4 Seiring berkembangnya ilmu pengetahuan dan teknologi penentuan posisi suatu titik di permukaan bumi dapat dilakukan dengan mudah. Penentuan titiktitik dapat dilakukan dengan memanfaatkan media informasi. Salah satunya dengan memanfaatkan bantuan Google Earth/ Google Maps. Program ini memetakan bumi dari superimposisi gambar yang dikumpulkan dari pemetaan satelit, fotografi udara dan globe GIS 3D (Mohammed, et al., 013). Pada penelitian ini penulis memanfaatkan Google Earth/ Google Maps untuk memperoleh titik-titik koordinat berupa koordinat garis lintang (latitude) dan garis bujur (longlitude) yang digunakan untuk menentukan luas suatu lahan. Titik-titik koordinat yang telah diperoleh dihubungkan sehingga membentuk suatu poligon yang menyerupai lahan yang akan ditentukan luasnya. Untuk menentukan luas lahan dibutuhkan suatu metode yang dapat membantu untuk melakukan perhitungan lahan tersebut.ada berbagai metode yang dapat diterapkan untuk menghitung luas suatu lahan.pada penelitian ini peneliti menggunakan metode pendekatan lingkaran untuk menentukan luas suatu lahan. Metode pendekatan lingkaran ini diterapkan untuk menentukan luas lahan datar diantaranya yaitu: lahan kecil adalah Lapangan Sepak Bola UKSW Salatiga, dan lahan yang berukuran sedang adalah Rawa Pening Kabupaten Semarang Jawa Tengah, terakhir lahan yang cukup luas adalah Kota Salatiga, Jawa Tengah. Hasil perhitungan luas lahan akan dibandingkan dengan luas yang sesungguhnya dari ketiga lahan tersebut. METODE PENELITIAN Pada penelitian ini, metode yang digunakan adalah metode pendekatan lingkaran dengan asumsi bumi berbentuk bola dan berbentuk elipsoida yang memanfaatkan Google Earth/Google Maps untuk memperoleh titik-titik koordinat, dan dilengkapi data yang dibutuhkan dalam penelitian. a. Google Earth/Google Maps Google Earth merupakan sebuah program globe virtual yang sebenarnya disebut Earth Viewer dan dibuat oleh Keyhole, Inc. Program ini memetakan bumi dari superimposisi gambar yang dikumpulkan dari pemetaan satelit, fotografi udara dan globe GIS 3D (Mohammed, et al., 013). Google Maps merupakan sebuah jasa peta global yang disediakan oleh Google secara gratis dan online (Mahdia & Noviyanto, 013). Google Earth/GoogleMaps memberi kemudahan bagi pengguna untuk memperoleh informasi lokasi.lebih dari sekedar memberikan informasi lokasi, Google Earth memungkinkan pengguna untuk menambahkan konten mereka sendiri seperti foto atau deskripsi dari daerah atau landmark (Becek& Khairunnisa, 011).Selain itu, Google Earth lebih menghemat biaya, waktu serta tenaga. SEMINAR MATEMATIKA DAN PENDIDIKAN MATEMATIKA 016 UniversitasSebelasMaret, 16 November 016
5 b. Bumi dianggap Berbentuk Bola Menurut Meeus (1998) jika geografis dua titik di permukaan bumi diketahui, dengan jarak terpendek s antara titik-titik ini, diukur sepanjang permukaan bumi, maka jarak antar dua titik dapat dihitung.jika tidak ada akurasi yang besar diperlukan, kita dapat mempertimbangkan bumi sebagai bola dengan rata-rata radius kilometer. GAMBAR 1. SUDUT JARAK d ANTAR DUA TITIK Menentukan sudut jarak d antar dua titik yaitu P(φ 1,L 1 ) dan Q(φ,L ) seperti pada GAMBAR 1 dapat dituliskan sebagai berikut : dengan,, i=1,,, i=1,. Jika sudut d dalam derajat, maka jarak kedua titik adalah s kilometer, yaitu c. Bumi dianggap Berbentuk Elipsoida Awalnya bumi diasumsikan berbentuk bola, kemudian lebih kompleks dari itu, bumi diasumsikan sebagai elipsoida (Meeus, 1998).Dengan menganggap bahwa kedua titik yang digunakan berada di bawah permukaan laut. Dalam hal iniaadalah jari-jari bumi pada garis katulistiwa dan f adalah flattening,maka dapat dihitung,, SEMINAR MATEMATIKA DAN PENDIDIKAN MATEMATIKA UniversitasSebelasMaret, 16 November 016
6 dengan dalam radian,,,, Jarak kedua titiktersebut adalah d. Perhitungan Luas dengan Metode Pendekatan Lingkaran Menurut Setiawan, et al., (016), metode pendekatan lingkaran sebenarnya adalah pengembangan dari metode pendekatan poligon. Pada GAMBAR titik O adalah titik pusat daerah perhatian.titik P dan Q adalah titik di perbatasan dan sudut simpul dari poligon. Daerah OPQ, yang merupakan bagian dari wilayah dapat didekati ke daerah OTS. Jari-jari lingkaran dengan panjang yang sama adalah OT atau OS dengan panjang OT adalah rata-rata dari OP dan OU serta. Luas sektor lingkaran batas bawah adalah OUQ dengan jari-jari OQ dan batas atas adalah OPR dengan jari-jari lingkaran OP atau OR. GAMBAR. SEKTOR LINGKARAN SEBAGAI DAERAH PERKIRAAN WILAYAH PERHATIAN SEMINAR MATEMATIKA DAN PENDIDIKAN MATEMATIKA UniversitasSebelasMaret, 16 November 016
7 Pada TABEL 1 menunjukan pengambilan koordinat titik-titik tepi Lapangan SepakBola UKSW yang dilakukan dengan menggunakan bantuan Google Earthyang kemudian dibandingkan dengan hasil perhitungan manual. TABEL1. KOORDINAT TITIK-TITIK TEPI LAPANGAN BOLA UKSW PADA GOOGLE EARTH No. Lintang Bujur No. Lintang Bujur (Latitude) (Longlitude) (Latitude) (Longlitude) Untuk data Rawa Pening terdiri dari 418 titik koordinat dan Salatiga terdiri dari 368 titik koordinat. HASIL DAN PEMBAHASAN Dalam penelitian ini, untuk menentukan luas daerah Lapangan Sepak Bola Universitas Kriten Satya Wacana (UKSW), Rawa Pening dan Kota Salatiga metode yang diusulkan adalah pendekatan lingkaran. Pada penelitian awal peneliti melakukan pengukuran manual di lapangan sepak bola dengan membentangkan pita ukur untuk menentukan panjang dan lebar lapangan. Dengan menggunakan rumus persegi panjang, maka luas lapangan diperoleh sebesar m. GAMBAR 3. POLIGON YANG DIGUNAKAN UNTUK MENDEKATI LAPANGAN UKSW (SUBER: IMAGE 016 DIGITALGLOBE) SEMINAR MATEMATIKA DAN PENDIDIKAN MATEMATIKA UniversitasSebelasMaret, 16 November 016
8 TABEL 1 dihitung dengan mengunakan metode pendekatan lingkaran yang merupakan pengembangan dari metode pendekatan poligon dengan menganggap bahwa jarak antar dua titik berupa bola bumi dan elipsoida. Dalam hal ini, yang merupakan titik pusat dari lahan yang menjadi perhatian adalah dan , titik-titik pada TABEL 1 merupakan titik tepi lahan seperti pada GAMBAR 3. TABEL. JARAK ANTARA TITIK KOORDINAT PUSAT DAN TITIK KOORDINAT TEPI No. Lintang (Latitude) Bujur (Longlitude) Bola (m) Elipsoida (m) Jari-jari (r) L r m m Dengan menggunakan persamaan (1) dan () diperoleh jarak seperti pada TABEL, kemudin dirata-rata sehingga diperoleh jarak total.dengan menggunkan rumus lingkaran,luas lapangan dengan asumsi bumi berbentuk bola diperoleh sebesar m.sedangkan dengan asumsi bumi berbentuk elipsoida diperoleh luas lapangan sebesar m. Hal ini dapat dilakukan untuk perhitungan luas Rawa Pening dan Luas kota Salatiga. Disisi lain, jika dilakukan pengambilan titik-titik koordinat selama 4 hari berturut-turut dengan mengambil 4 titik, 8 titik dan 16 titik koordinaat. Untuk 4 titik koordinat dengan asumsi bumi berbentuk bola dan elipsoida diperoleh luas rata-rata sebesar m dan m, dengan standar deviasi sebesar dan Dan untuk 8 titik koordinat dengan mengasumsikan bumi berbentuk bola dan elipsoida diperoleh luas rata-rata sebesar m dan m, yang mempunyai standar deviasi sebesar dan Sedangkan untuk 16 titik koordinat dengan mengasumsikan bumi berbentuk bola dan elipsoida diperoleh luas rata-rata sebesar m dan m. Dan SEMINAR MATEMATIKA DAN PENDIDIKAN MATEMATIKA UniversitasSebelasMaret, 16 November 016
9 mempunyai standar deviasi sebesar dan Dapat disimpulkan bahwa sedikit atau banyaknya titik koordinat yang digunakan akan sangat berpengaruh terhadap hasil perhitungan luas. Semakin banyak titik yang digunakan akan semakin baik. Hasil perhitungan luas lahan dengan menggunakan pendekatan lingkaran pada Google Earth dan hasil perhitungan manual mengunakan rumus persegi panjang diperoleh selisih. Selisih hasil perhitungan luas menggunakan meode pendekatan lingkaran dengan asumsi bumi berbentuk bola dan perhitungan manual adalah m. Selanjutnya selisih hasil perhitungan luas menggunakan metode pendekatan lingkaran dengan asumsi bumi berbentuk elipsoida dan perhitungan manual adalah m.pada perhitungan ini yang dijadikan acuan adalah luas perhitungan manual. Prosentase pengukuran luas menggunakan metode pendekatan lingkaran dengan asumsi bumi berbentuk bola dan elipsoida adalah % dan %. GAMBAR 4. PETA RAWA PENING (SUMBER: MAP DATA 016 GOOGLE) Penelitian selanjutnya adalah perhitungan luas Rawa Pening (GAMBAR 4) dengan menggunakan metode pendekatan lingkaran dengan asumsi bumi berbentuk bola dan elipsoida.hasil perhitungan yang diperoleh dibandingkan dengan luas perhitungan menggunakan Google Maps, berdasarkan penelitian yang dilakukan oleh Suwargana(01). Dengan menggunakan program R i untuk mengolah data yang terdiri dari 418 titik koordinat, baik garis lintang maupun garis bujur diperoleh luas dengan asumsi bumi berbentuk bola sebesar km dan luas dengan asumsi bumi berbentuk elipsoida sebesar km dan Menurut Suwargana(01) luas Rawa Pening terakhir pada tahun 006 mencapai km dan berdasarkan perhitungan Google Maps luas Rawa Pening yaitu km. Sehingga terdapat selisih antara luas ketiganya.pertama untuk metode SEMINAR MATEMATIKA DAN PENDIDIKAN MATEMATIKA UniversitasSebelasMaret, 16 November 016
10 pendekatan lingkaran dengan asumsi bumi berbentuk bola dan luas berdasarkan penelitian Suwargana (01) adalah km, sedangkan selisi dengan asumsi bumi berbentuk elipsoida adalah km.kedua untuk metode pendekatan lingkaran dengan asumsi bumi berbentuk bola dan luas berdasarkan perhitungan Google Maps adalah km, sedangkan selisih dengan asumsi bumi berbentuk elipsoida adalah km. Terdapat selisih yang sangat besar antara hasil perhitungan dengan metode pendekatan lingkaran dan luas berdasarkan penelitian Suwargana (01), namun untuk selisih luas perhitungan dengan metode pendekatan lingkaran dan luas hasil perhitungan menggunakan Google Mapstidak terlalu besar.persentasi pengukuran luas menggunakan metode pendekatan lingkaran dengan asumsi bumi berbentuk bola dan elipsoida adalah 97.47% dan 97%. GAMBAR 5. PETA KOTA SALATIGA (SUMBER: MAP DATA 016 GOOGLE) Terakhir penelitian dilakukan dengan menghitung luas Kota Salatiga (GAMBAR 5) menggunakan metode yang sama dengan penelitian sebelumnya. Hasil yang diperoleh dibandingkan dengan luas Kota Salatiga berdasarkan informasi yang diperoleh dari Badan Pusat Statistik (BPS) Salatiga dan hasil perhitungan dengan menggunakan Google Maps.Jika bumi di asumsikan bola dan elipsoida maka diperoleh luas Kota Salatiga sebesar km dan km. Berdasarkan (BPS, 016) luas wilayah Kota Salatiga tercatat sebesar km, sedangkan berdasarkan hasil perhitungan menggunakan Google Mapsluas Kota Salatiga sebesar53.31 km. Sehingga terdapat pula selisih luas yang cukup besar antara metode pendekatan lingkaran, informasi BPS Salatiga dan perhitungan luas menggunakan Google Maps.Selisih antara pendekatan lingkaran dengan bumi diasumsikan bola dan informasi dari BPS Salatiga adalah SEMINAR MATEMATIKA DAN PENDIDIKAN MATEMATIKA UniversitasSebelasMaret, 16 November 016
11 km, sedangkan dengan bumi yang diasumsikan elipsida adalah km.untuk metode pendekatan lingkaran dengan asumsi bumi adalah bola dan elipsida dengan perhitungan luas menggunakan Google Maps diperoleh selisih sebesar km dan km.pada penelitian ini, luas yang menjadi acuan adalah luas berdasarkan data iniformasi dari BPS kota Salatiga dengan prosentasi sebesar % untuk bumi diasumsikan bola dan % untuk bumi diasumsikan elipsoida. Hasil pengukuran yang dilakukan tidak selalu persis sama, karena hal ini dipengaruhi oleh permukaan tanah, semakin datar lahan yang diukur maka tingkat kesalahan hitung semakin kecil (Yunita, et al., 013). Hal lainyang mempengaruhi ketepatan pengambilan titik-titik koordinat pada Google Earth adalah saat mengklik korsor dan sedikit atau banyaknya titik koordinat yang dugunakan sangat mempengaruhi hasil perhitungan luas. Apabila menggunakan Google Earth atau Google Maps sangat bergantung pada kekuatan signal yang digunakan dan dalam pengambilan data tidak selalu sama setiap waktu. SIMPULANDAN SARAN Berdasarkan hasil dari analisis data maka dapat disimpulkan bahwa: 1. Perhitungan luas Lapangan Sepak Bola UKSW menggunakan metode pendekatan lingkaran dengan asumsi bumi berbentuk bola dan elipsoidadiperoleh luas berturut-turut m dan m.hasil tersebut dibandingkan dengan hasil perhitungan manual dengan luas sebesar m. Selisih perhitungan berdasarkan metode pendekatan lingkaran dan perhitungan manual dengan mengasumsikan bumi berbentuk bola dan elipsoida adalah m dan m.. Perhitungan luas Rawa Pening dengan menggunakan metode pendekatan lingkaran dengan asumsi bumi berbentuk bola dan elipsoida diperoleh luas berturut-turut yaitu km dan km. Luas yang diperoleh dibandingkan dengan luas berdasarkan informasi dari penelitian Suwargana (01) dan berdasarkan perhitungan Google Maps yang mempunyai luas berturut-turut sebesar km dan km. Selisih luas berdasarkan penelitian Suwargana (01) dan metode pendekatan lingkaran dengan asumsi bumi berbentuk bola dan berbentuk elipsoida yaitu km dan km. Sedangkan selisi antara metode lingkaran dengan hasil perhitungan google maps dengan asumsi bumi berbentuk bola dan elipsoida adalah km dan km. 3. Perhitungan luas Kota Salatiga dengan menggunakan metode pendekatan lingkaran dengan asumsi bumi berbentuk bola dan elipsoida diperoleh luas sebesar km dan km. Luas tersebut kemudian dibandingkan dengan data dari BPS Kota Salatiga dan hasil perhitungan menggunakan Google Mapsdengan luas berturut-turut sebesar km SEMINAR MATEMATIKA DAN PENDIDIKAN MATEMATIKA UniversitasSebelasMaret, 16 November 016
12 dan km. Untuk metode pendekatan lingkaran dan data dari BPS Kota Salatiga diperoleh selisi sebesar km dan km. Sedangkan untuk metode pendekatan lingkaran dengan asumsi bumi adalah bola dan elipsida dengan perhitungan luas menggunakan Google Maps diperoleh selisih sebesar km dan km. Perhitungan luas lahan dari ketiga lahan yang menjadi objek penelitian dengan acuan luas sesungguhnya dari masing-masing lahan 97% sampai dengan 108%.Penelitian ini dapat dikembangkan dengan menggunakan metode pendekatanheron pada permukaan bola atau padapermukaan elipsoidayang mungkin dapat memperkecil selisih perhitungan yang masih cukup besar. DAFTAR PUSTAKA Badan Pusat Statistik Salatiga, (016). Kota Salatiga dalam Angka 016.Salatiga: BPS Kota Salatiga. Becek,K., Khairunnisa, I., (011). On the Positional Accuracy Of The Google Earth Imaginary. Spatial Information Processing Ipaper no Brunei Darusalam. Mahdia, F., Noviyanto, F., (013). Pemanfaatan Google Maps Api untuk Pembangunan Sistem Informasi Manajemen Bantuan Logistik Pasca Bencana Alam Berbasis Mobile Web (Studi Kasus: Badan Penanggulangan Bencana Daerah Kota Yogyakarta). Jurnal Sarjana Teknik Informatika Universitas Ahmad Dahlan, 1(1), Maulana, Bani.( 016). Pengertian Lahan. Diunduh pada tanggal 0 Maret 016, pukul 14.0 WIB Meeus, J. (1998). Astronomical Algorithm nd ed.usa: Williman-Bell, Inc. Mohammed, Nagi Zomrawi., Ghazi, A., &Mustafa, Husam Eldin. (013). Positional Accuracy Testing Of Google Earth.International Jurnal Of Multidisciplinary Sciences And Enginering, 4 (6), 6-9. Setiawan, A., Sediyono, E.&Alivah, E. (Ed.). (016).The Use of Google Maps and Circle Approach Method in Land Area Measurement. Proceeding InternasionalConference On Theoritical and Applied Statistics. Surabaya: Institut Teknologi Sepuluh Nopember. Suwargana, N., (01). Pemantauan Luas Rawa Pening Periode 199, 001 dan 006 Berbasis Data LANDSAT-TM dan IKONOS.Prosiding Seminar Nasional Limnologi IVTahun 01. Bogor: IPB International Convention Center. Yunita, A., Suprayogi, A., &Hania ah. (011). Kajian Ketelitian Pemanfaatan Citra Quickbrid Pada Google Earth Untuk Pemetaan Bidang Tanah (Studi Kasus : Kabupaten Karanganyar). Jurnal Geodesi UNDIP, (), SEMINAR MATEMATIKA DAN PENDIDIKAN MATEMATIKA UniversitasSebelasMaret, 16 November 016
13 MAKALAH Penentuan Luas Lahan Menggunakan Metode Pendekatan Segitiga Sferik (Teorema Girard) dengan Bantuan Google Maps xiv
14 PENENTUAN LUAS LAHAN MENGGUNAKAN METODE PENDEKATAN SEGITIGA SFERIK (TEOREMA GIRARD) DENGAN BANTUAN GOOGLE MAPS Devi 1, Adi Setiawan, Eko Sediyono 3 1 Program Studi Matematika (Fakultas Sains dan Matematika, Universitas Kristen Satya Wacana), Program Studi Matematika (Fakultas Sains dan Matematika, Universitas Kristen Satya Wacana), 3 Program Studi Magister Sistem Informasi (Fakultas Teknologi Informasi, Universitas Kristen Satya Wacana), devilialolok@gmail.com 1, adi_setia_03@yahoo.com, ekosed1@yahoo.com 3 Abstrak Seiring dengan berkembangnya ilmu pengetahuan dan teknologi, ketersediaan peta sangat dibutuhkan. Peta dapat diakses melalui sebuah aplikasi, seperti Google Maps. Aplikasi ini merupakan sebuah jasa peta global yang disediakan oleh Google secara gratis dan online. Google Maps juga dapat dimanfaatkan untuk memperoleh titik-titik koordinat berupa garis lintang dan garis bujur, kemudian diolah untuk memperoleh luas lahan. Metode yang diterapkan untuk menghitung luas lahan adalah metode pendekatan segitiga sferik dengan asumsi bumi berbentuk bola dan elipsoida. Pada penelitian ini, lahan yang menjadi objek penelitian adalah Kabupaten Semarang. Berdasarkan perhitungan menggunakan pedekatan segitiga sferik diperoleh luas Kabupaten Semarang dengan asumsi bumi berbentuk bola dan elipsoida sebesar km dan km. Hasil perhitungan luas dibandingkan dengan data yang diperoleh dari Badan Pusat Statistik (BPS) Kabupaten Semarang sebesar km dan berdasarkan perhitungan Google Maps sebesar km. Luas yang menjadi acuan adalah berdasarkan data yang diperoleh dari BPS Kabupaten Semarang. Terdapat selisih antara hasil perhitungan luas lahan menggunakan metode pendekatan segitiga sferik dan luas yang menjadi acuan dengan asumsi bumi berbentuk bola dan elipsoida berturut-turut adalah km dan km. Berdasarkan luas acuan dengan asumsi bumi berbentuk bola dan elipsoida diperoleh prosentase sebesar 5.37% lebih banyak dari luas acuan dan 4.88% lebih banyak dari luas acuan. Metode pendekatan segitiga sferik tidak selalu bisa digunakan karena apabila jumlah sudut dalam koordinat segitiga sferik secara praktis lebih kecil dari π, maka hasil perhitungan tidak akurat, sehingga metode ini hanya bisa digunakan untuk lahan yang relatif lebih luas seperti pada Kabupaten Semarang. Kata kunci: Google Maps, luas lahan, metode pendekatan segitiga sferik.
15 A. Pendahuluan Seiring dengan berkembangnya ilmu pengetahuan dan teknologi, ketersediaan peta sangat dibutuhkan. Dewasa ini, teknik pemetaan sudah sangat berkembang. Peta dapat diakses melalui sebuah aplikasi, misal: Google Maps. Google Maps merupakan sebuah jasa peta global yang disediakan oleh Google secara gratis dan online (Mahdia & Noviyanto, 013, pp ). Selain untuk menentukan sebuah lokasi, Google Maps dapat dimanfaatkan untuk memperoleh titik-titik koordinat berupa garis lintang (latitude) dan garis bujur (longlitude). titik-titik koordinat yang diperoleh diolah untuk menentukan luas suatu lahan. Seperti yang kita ketahui bahwa keadaan lahan dipermukaan bumi tidak teratur seperti danau atau pulau (Setiawan, et al., 016), sehingga penentuan luas akan menjadi sulit untuk dilakukan. Penentuan luas lahan dapat dilakukan dengan menerapkan berbagai metode. Dalam makalah ini, penentuan luas lahan dilakukan dengan menggunakan metode pendekatan segitiga sferik dengan tidak diperhatikan konturnya. Metode ini digunakan untuk mengolah titik-titik koordinat yang diperoleh dari Google Maps untuk menentukan luas lahan yang menjadi perhatian. Namun sebelum menghitung luas, terlebih dahulu dilakukan perhitungan jarak antara dua titik dengan asumsi bumi berbentuk bola dan elipsoida. Sebelumnya penulis telah melakukan penelitian awal menggunakan metode pendekatan lingkaran. Lahan yang menjadi objek penelitian adalah Lapangan Sepak Bola UKSW, Rawa Pening dan Kota Salatiga (Devi, et al., 016). Pada makalah ini, lahan yang menjadi daerah perhatian adalah Kabupaten Semarang, Jawa Tengah. Dengan menggunakan metode pendekatan Segitiga Sferik akan diperoleh luas dari daerah yang menjadi perhatian. Hasil perhitungan luas lahan yang diperoleh akan dibandingkan dengan luas lahan yang menjadi acuan. B. Metode Penelitian Dalam penelitian ini, akan dibahas tentang cara mencari jarak antar dua titik dengan bumi diasumsikan berbentuk bola dan elipsoida, perhitungan luas Kabupaten Semarang menggunakan metode pendekatan segitiga sferik dengan memanfaatkan Google Maps, cara perhitungan luas lahan dan data yang digunakan dalam penelitian. a. Google Maps Google Maps merupakan sebuah jasa peta global yang disediakan oleh Google secara gratis dan online (Mahdia & Noviyanto, 013, p.1). Google Maps memberi kemudahan bagi pengguna untuk memperoleh informasi lokasi. Selain itu, Google Maps lebih menghemat biaya, waktu serta tenaga. Namun, Google Maps sangat bergantung pada kekuatan signal yang digunakan dan dalam pengambilan data tidak selalu sama setiap waktu. b. Bumi Diasumsikan Berbentuk Bola Gambar 1. Koordinat Bola Pada Gambar 1 sudut L 1 adalah sudut antara OE 1 dengan OE, sudut L adalah sudut antara OE 1 dengan OE 3. Sedangkan untuk sudut φ 1 adalah sudut
16 antara OE dengan OP, dan untuk sudut φ adalah sudut OE 3 dengan OQ. untuk sudut θ 1 adalah sudut OP dengan sumbu z dan sudut θ adalah sudut OQ dengan sumbu z. Jika tidak ada akurasi yang besar diperlukan, maka dapat dipertimbangkan bahwa bumi berbentuk bola dengan ratarata radius 6371 kilometer (Meeus, 1998, pp ). Menentukan sudut jarak d antar dua titik yaitu P (φ 1,L 1 ) dan Q (φ,l ) seperti pada Gambar 1 dapat dituliskan sebagai berikut : cos d sin1 sin cos 1 cos cos( L1 L ) Contoh 1: Misalkan diketahui titik P dengan koordinat φ 1 = , L 1 = dan titik Q dengan koordinat φ = , L = Menentukan sudut jarak d yaitu cos d sin sin cos cos cos dengan, =koordinat garis lintang, i=1,, i L =koordinat garis bujur, i=1,. i Bukti: misalkan dan sehingga dalam sistem koordinat bola dapat dinyatakan dengan v1 r sin1 cos 1, r sin1 sin1, r cos 1 v r sin cos, r sin sin, r cos dan hasil kali dot adalah v v r sin sin cos cos 0 0 sin90 cos cos90 sin cos sehingga v1 v r sin 1 sin cos1 cos cos( L1 L ) dan akibatnya cos d sin1 sin cos 1 cos cos( L1 L ) Jika sudut d dalam derajat, maka jarak kedua titik adalah s kilometer, yaitu 6371 d s 180 sedangkan jika d dalam radian maka s= 6371d., dengan d dalam radian maka d=0.0057, sehingga diperoleh jarak antar dua titik yaitu s=6371 d atau s= km. c. Bumi Diasumsikan Berbentuk Elipsoida Awalnya bumi diasumsikan berbentuk bola, kemudian lebih kompleks dari itu, bumi diasumsikan sebagai elipsoida (Meeus, 1998, pp ). r sin1 sin sin 1 sin r cos1 cos Dengan menganggap bahwa kedua titik r cos 1 cos sin1 sin (cos 1 cos sin1 sinyang ) digunakan berada pada permukaan r cos 1 cos sin1 sin cos( 1 ). laut. Dalam hal ini a adalah jari-jari bumi Dengan mengingat bahwa pada garis katulistiwa dan f adalah 0 90 flattening, maka dapat dihitung maka 1 0 F, 1 G, L1 L, sin sin90 S sin Gcos cos C cos Gcos sin S tan, C SC R, dengan ω dalam radian, a , D a, H 1 F sin, F sin, 1 f, R 1, H C 3R 1, S
17 sehingga jarak kedua titik tersebut adalah s D(1 fh sin F cos G fh cos F sin ). 1 G Contoh : dari Contoh 1 dapat dicari jarak antar titik dengan asumsi bumi berbentuk elipsoida sebagai berikut F , G , , S sin cos sin cos C cos sin , -6, cos sin , R e dengan ω dalam radian, , D, H, 1 H , sehingga diperoleh jarak antar dua titik s= km. d. Pendekatan Segitiga Sferik Metode ini digunakan untuk menghitung luas Kabupaten Semarang, Jawa Tengah, yang merupakan pengembangan dari metode pendekatan segitiga. Dalam makalah Alivah, et al. (016, p.451) tidak menggunakan metode pendekatan segitiga sferik karena lahan yang menjadi objek penelitian relatif sempit. Berikut adalah metode pendekatan segitiga sferik dengan memisalkan a, b, c sebagai panjang sisisisi dari segitiga sferik ABC pada luasan bola yang berjari-jari R yang terletak berturut-turut di hadapan titik-titik sudut A, B, C (Sangadji, 009, pp ). Luas segitiga sferik adalah ABC R dengan α= A, β= B, γ= C dalam radian maka cos c cos a cos b arccos sin sin a b, 180 cos b cos c cos a arccos sin sin a c, 180 cos c cos a cos b arccos sin sin a b. 180 Misalkan diketahui koordinat A( , ), B( , ), C( , ) seperti pada Gambar dengan jari-jari bumi R= Dengan mengasumsikan bumi berbentuk bola maka diperoleh jarak AB= km, BC= km, AC= km, sehingga diperoleh AB 180 a1 cos R, 360 BC 180 b1 cos R, 360
18 AC 180 c1 cos R, 360 AB 180 a sin R 360, segitiga sferik dengan mengasumsikan bumi berbentuk bola dan elipsoida seperti pada Contoh 1 dan Contoh. f. Data berupa Titik-titik Koordinat dari Kabupaten Semarang BC 180 b sin R 360 AC 180 c sin R 360 sehingga α,β,γ adalah arccos a b c, b c arccos b c a a c c1 b1 a1 arccos a b Akibatnya ABC, km. e. Perhitungan Luas Lahan Perhitungan luas dapat dilakukan dengan membagi lahan pada peta dalam beberapa persegi panjang seperti pada Gambar, yaitu dengan mengambil dua titik pada batas atas maupun batas bawah lahan. Berikutnya persegi panjang dibagi menjadi dua segitiga dan dihitung menggunakan metode pendekatan,, Gambar. Simulasi 4 titik koordinat pada bagian batas atas dan 4 titik koordinat pada bagian batas bawah Kabupaten Semarang Tabel 1 dan Tabel merupakan pengambilan titik-titik tepi Kabupaten Semarang sebanyak 4 titik koordinat pada bagian batas atas dan batas bawah yang berupa garis lintang dan garis bujur. Tabel 1. Titik-titik Koordinat Batas Atas Kabupaten Semarang No. Garis Lintang Garis Bujur Tabel. Titik-titik Koordinat Batas Bawah Kabupaten Semarang No. Garis Lintang Garis Bujur
19 Data pada Tabel 1, Tabel, Tabel 3 dan Tabel 4 diambil pada tanggal 3 November 016 dengan menggunakan bantuan Google Maps. Analog dengan perhitungan pada contoh segitiga sferik, maka diperoleh luas ABDFGEC dengan asumsi bumi berbentuk bola sebesar km. Perhitungan juga dapat dilakukan dengan mengasumsikan bumi berbentuk elipsoida. Langkah-langkah perhitungan ini deterapkan untuk menghitung luas lahan dengan 31 titik koordinat. Hasil luas yang diperoleh dibandingkan dengan luas acuan. Berikut adalah data lengkap dari lahan yang menjadi objek perhatian yang terdiri dari 31 titik koordinat batas atas dan batas bawah. Tabel 3. Titik-titik Koordinat Batas Atas Kabupaten Semarang No. Garis Lintang Garis Bujur Tabel 4. Titik-titik Koordinat Batas Bawah Kabupaten Semarang No. Garis Lintang Garis Bujur C. Hasil Penelitian dan Pembahasan Dalam penentuan luas lahan Kabupaten Semarang metode yang digunakan adalah metode pendekatan segitiga sferik. Titik-titik koordinat pada Tabel 3 dan Tabel 4 diolah dengan menggunakan bantuan R i untuk
20 memperoleh luas lahan yang menjadi perhatian. Pada perhitungan ini, dengan mengasumsikan bumi berbentuk bola luas Kabupaten Semarang diperoleh luas lahan sebesar km. Sedangkan luas lahan dengan asumsi bumi berbentuk elipsoida diperoleh luas lahan sebesar km. Gambar 3. Kabupaten Semarang, Jawa Tengah Luas lahan yang diperoleh dikurangi dengan luas Kota Salatiga dengan luas lahan sebesar km (BPS, 016, p.3) dan Rawa Pening luas lahan sebesar 6.7 km (Wikipedia, 016) yang bukan merupakan bagian dari Kabupaten Semarang seperti yang terlihat pada Gambar 3. Kedua lahan tersebut berada dalam batas wilayah Kabupaten Semarang namun bukan termasuk wilayah Kabupaten Semarang, sehingga diperoleh luas Kabupaten Semarang dengan mengasumsikan bumi berbentuk bola sebesar km dan untuk asumsi bumi berbentuk elipsoida sebesar km. Apabila dilakukan pengambilan titik-titik koordinat selama 5 hari berturut-turut (5-9 November 016) dengan mengasumsikan bumi berbentuk bola dan elipsoida diperoleh luas rata-rata dan standar deviasi seperti yang disajikan pada Tabel 5. Tabel 5. Hasil Perhitungan Luas Ratarata dan Standar Deviasi Kabupaten Semarang Hari Luas Bola (km ) Elipsoida (km ) Rata-rata S Deviasi Hasil perhitungan luas lahan yang diperoleh dibandingkan dengan luas yang diperoleh dari data Badan Pusat Statistik (BPS) kabupaten Semarang sebesar km (BPS, 016, p.3) dan berdasarkan perhitungan menggunakan Google Maps sebesar km. Terdapat selisi luas antara hasil perhitungan dengan luas yang menjadi pembanding. Selisih antara perhitungan menggunakan metode pendekatan segitiga sferik dan data dari BPS kabupaten Semarang dengan mengasumsikan bumi berbentuk bola adalah km dan berbentuk elipsoida adalah km. Sedangkan selisih antara perhitungan menggunakan metode pendekatan segitiga sferik dan perhitungan menggunakan Google Maps dengan asumsi bumi berbentuk bola sebesar km dan berbentuk elipsoida sebesar.870 km. Pada penelitian ini yang menjadi luas acuan adalah perhitungan berdasarkan data yang diperoleh dari Badan Pusat Statistik (BPS) Kabupaten Semarang. Berdasarkan luas acuan diperoleh prosentase luas Kabupaten Semarang yang dihitung menggunakan metode pendekatan segitiga sferik dengan asumsi bumi berbentuk bola adalah 5.37% lebih banyak dari luas acuan dan berbentuk elipsoida adalah 4.88% lebih banyak dari luas acuan. Dengan tingkat kepercayaan 95% maka diperoleh interval kepercayaan dengan
21 asumsi bumi berbentuk bola sebesar untuk batas bawah dan untuk batas atas. Sedangkan untuk asumsi bumi berbentuk elipsoida diperoleh interval kepercayaan dengan batas bawah sebesar dan batas atas sebesar Pada penelitian ini, metode pendekatan segitiga sferik tidak selalu bisa digunakan karena apabila jumlah sudut dalam koordinat segitiga sferik secara praktis lebih kecil dari π, maka hasil perhitungan tidak akurat, sehingga metode ini hanya bisa digunakan untuk lahan yang relatif lebih luas seperti pada lahan Kabupaten Semarang. Luas lahan yang digunakan BPS Kabupaten Semarang mungkin menggunakan jarak Euclid yang tidak mengasumsikan bumi berbentuk bola tetapi berupa bidang datar, sehingga luas lahan berdasarkan data dari BPS Kabupaten Semarang lebih kecil dari hasil perhitungan luas lahan menggunakan metode pendekatan segitiga sferik. Aplikasi Google Maps juga dapat dimanfaatkan untuk menghitung jarak antar dua titik (Ibrahim & Mohsen, 014, p.117), namun akurasi titik pada Google Maps tidak konstan melainkan selalu berubah-ubah dari waktu ke waktu (Mohammed, et al., 013, p.9). Hal lain yang mempengaruhi ketepatan pengambilan titik-titik koordinat pada Google Maps adalah saat mengklik korsor kuat atau tidaknya saat kita mengklik (Devi, et al., 016). Selain daripada itu, hasil pengukuran yang dilakukan tidak selalu persis sama, karena hal ini dipengaruhi oleh permukaan tanah, semakin datar lahan yang diukur maka tingkat kesalahan perhitungan akan semakin kecil (Yunita, et al., 013, p.). D. Simpulan dan Saran Simpulan Perhitungan luas Kabupaten Semarang menggunakan metode pendekatan segitiga sferik dengan asumsi bumi berbentuk bola dan elipsoida sebesar km dan km. Prosentase perhitungan luas lahan dengan asumsi bumi berbentuk bola dan elipsoida berturut-turut adalah 5.37% lebih banyak dari luas acuan dan 4.88% lebih banyak dari luas acuan. Saran Penelitian ini dapat dikembangkan dengan meggunakan metode lain yang mungkin lebih baik dari metode pendekatan segitiga sferik. E. Ucapan Terima Kasih Penulis mengucapkan terima kasih kepada Direktorat Jenderal Pendidikan Tinggi, Indonesia untuk pendanaan penelitian dengan skema Hibah Kompetensi No. 001/K6/KL/SP/PENELITIAN/016. F. Daftar Pustaka Alivah, E., Setiawan, A. & Sediyono, E. (016). Penentuan luas lahan dengan bantuan Google Earth. Prosiding, Seminar Nasional 3rd CGISE dan FIT ISI yang diselenggarakan oleh FTek UGM, tanggal 7 Oktober 016. Yogyakarta: Universitas Gadjah Mada. BPS Kabupaten Semarang, (016). Kabupaten Semarang dalam Angka 016. Kab. Semarang: BPS Kabupaten Semarang. BPS Kota Salatiga, (016). Kota Salatiga dalam Angka 016. Salatiga: BPS Kota Salatiga. Devi., Setiawan, A. & Sediyono, E. (016). Penentuan luas lahan datar dengan metode pendekatan lingkaran berbasis Google Earth/Google Maps. Telah
22 dipresentasikan di Seminar Nasional Matematika dan Pendidikan Matematika 016 yang diselenggarakan oleh FKIP UNS, tanggal 16 November 016. Surakarta: Universitas Sebelas Maret. Ibrahim, O., Mohsen, K., (014). Design and Implementation an Online Location Based Services Using Google Maps for Android Mobile. International Journal of Computer Networks and Communications Security, (3), Mahdia, F., Noviyanto, F., (013). Pemanfaatan Google Maps Api untuk Pembangunan Sistem Informasi Manajemen Bantuan Logistik Pasca Bencana Alam Berbasis Mobile Web (Studi Kasus: Badan Penanggulangan Bencana Daerah Kota Yogyakarta). Jurnal Sarjana Teknik Informatika Universitas Ahmad Dahlan, 1(1), Meeus, J. (1998). Astronomical Algorithm. ( th ed.). USA: Williman-Bell, Inc. Yogyakarta: Universitas Negeri Yogyakarta Setiawan, A., Sediyono, E. & Alivah, E. (016). The Use of Google Maps and Circle Approach Method in Land Area Measurement. Telah dipresentasikan di Internasional Conference On Theoritical and Applied Statistics yang diselenggarakan oleh ITS Surabaya, tanggal 19-0 Oktober 016. Surabaya: Institut Teknologi Sepuluh Nopember. Yunita, A., Suprayogi, A., & Hania ah. (011). Kajian Ketelitian Pemanfaatan Citra Quickbrid Pada Google Earth Untuk Pemetaan Bidang Tanah (Studi Kasus : Kabupaten Karanganyar). Jurnal Geodesi UNDIP, (), Wikipedia. (016). Rawa Pening. Diakses tanggal 6 November 016 dari wa_pening. Mohammed, N., Ghazi, A. & Mustafa, H. (013). Positional Accuracy Testing Of Google Earth. International Journal Of Multidisciplinary Sciences & Engineering, 4(6), 6-9. Sangadji. (009). Formula Heron: Tinjauan di Geometri Euclid dan Geometri Sferik. Prosiding Seminar Nasional Matematika dan Pendidikan Matematika Pembelajaran Matematika dan Aplikasinya yang diselenggarakan oleh Jurusan Pendidikan Matematika FMIPA UNY, tanggal 05 Mei 009.
Prosiding Seminar Matematika dan Pendidikan Matematika ISBN:
 PENERAPAN METODE KERUCUT TERPANCUNG DAN BUJUR SANGKAR DALAM PERHITUNGAN LUAS LAHAN BERKONTUR MENGGUNAKAN BANTUAN MEDIA INFORMASI GOOGLE EARTH/GOOGLE MAPS Evania Nur Alivah 1, Adi Setiawan 1, Eko Sediyono
PENERAPAN METODE KERUCUT TERPANCUNG DAN BUJUR SANGKAR DALAM PERHITUNGAN LUAS LAHAN BERKONTUR MENGGUNAKAN BANTUAN MEDIA INFORMASI GOOGLE EARTH/GOOGLE MAPS Evania Nur Alivah 1, Adi Setiawan 1, Eko Sediyono
GEOMETRI EUKLID VERSUS GEOMETRI SFERIK. Sangadji *
 GEOMETRI EUKLID VERSUS GEOMETRI SFERIK Sangadji * ABSTRAK GEOMETRI EUKLID VERSUS GEOMETRI SFERIK. Pada makalah ini akan dibahas hubungan antara formula Pythagoras dan formula sinus dari segitiga pada geometri
GEOMETRI EUKLID VERSUS GEOMETRI SFERIK Sangadji * ABSTRAK GEOMETRI EUKLID VERSUS GEOMETRI SFERIK. Pada makalah ini akan dibahas hubungan antara formula Pythagoras dan formula sinus dari segitiga pada geometri
PENCARIAN LOKASI JALUR NUGRAHA EKAKURIR (JNE) TERDEKAT MENGGUNAKAN HAVERSINE FORMULA (STUDI KASUS KOTA SAMARINDA)
 PENCARIAN LOKASI JALUR NUGRAHA EKAKURIR (JNE) TERDEKAT MENGGUNAKAN HAVERSINE FORMULA (STUDI KASUS KOTA SAMARINDA) Dyna Marisa Khairina 1), Febrian Wicaksana Ramadhinata 2),Heliza Rahmania Hatta 3) 1),2),3
PENCARIAN LOKASI JALUR NUGRAHA EKAKURIR (JNE) TERDEKAT MENGGUNAKAN HAVERSINE FORMULA (STUDI KASUS KOTA SAMARINDA) Dyna Marisa Khairina 1), Febrian Wicaksana Ramadhinata 2),Heliza Rahmania Hatta 3) 1),2),3
PEMETAAN LOKASI OBJEK PAJAK UNTUK PAJAK BUMI DAN BANGUNAN MENGGUNAKAN TEKNOLOGI SENSOR FUSION PADA PERANGKAT BERGERAK DENGAN SISTEM OPERASI ANDROID
 PEMETAAN LOKASI OBJEK PAJAK UNTUK PAJAK BUMI DAN BANGUNAN MENGGUNAKAN TEKNOLOGI SENSOR FUSION PADA PERANGKAT BERGERAK DENGAN SISTEM OPERASI ANDROID Cipta Andrian 5106100170 Jurusan Teknik Informatika Fakultas
PEMETAAN LOKASI OBJEK PAJAK UNTUK PAJAK BUMI DAN BANGUNAN MENGGUNAKAN TEKNOLOGI SENSOR FUSION PADA PERANGKAT BERGERAK DENGAN SISTEM OPERASI ANDROID Cipta Andrian 5106100170 Jurusan Teknik Informatika Fakultas
JURNAL SISTEM PENCARIAN JARAK TERDEKAT MENGGUNAKAN METODE HAVERSINE BERBASIS ANDROID
 JURNAL SISTEM PENCARIAN JARAK TERDEKAT MENGGUNAKAN METODE HAVERSINE BERBASIS ANDROID DISTANCE TO THE NEAREST SEARCH SYSTEM USING HAVERSINE METHOD ANDROID BASED Oleh: MUHAMMAD ARIZAL FAHRIBI C. F. NPM :
JURNAL SISTEM PENCARIAN JARAK TERDEKAT MENGGUNAKAN METODE HAVERSINE BERBASIS ANDROID DISTANCE TO THE NEAREST SEARCH SYSTEM USING HAVERSINE METHOD ANDROID BASED Oleh: MUHAMMAD ARIZAL FAHRIBI C. F. NPM :
Analisa Pantauan dan Klasifikasi Citra Digital Remote Sensing dengan Data Satelit Landsat TM Melalui Teknik Supervised Classification
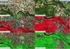 Analisa Pantauan dan Klasifikasi Citra Digital Remote Sensing dengan Data Satelit Landsat TM Melalui Teknik Supervised Classification (Studi Kasus Kabupaten Minahasa Tenggara, Provinsi Sulawesi Utara)
Analisa Pantauan dan Klasifikasi Citra Digital Remote Sensing dengan Data Satelit Landsat TM Melalui Teknik Supervised Classification (Studi Kasus Kabupaten Minahasa Tenggara, Provinsi Sulawesi Utara)
Penyajian Data Pelanggan pada Lima Area PT. Telekomunikasi Indonesia, Tbk. Kandatel Pekalongan Menggunakan Google Earth
 Scientific Journal of Informatics Vol. 1, No. 2, November 2014 p-issn 2407-7658 http://journal.unnes.ac.id/nju/index.php/sji e-issn 2460-0040 Penyajian Data Pelanggan pada Lima Area PT. Telekomunikasi
Scientific Journal of Informatics Vol. 1, No. 2, November 2014 p-issn 2407-7658 http://journal.unnes.ac.id/nju/index.php/sji e-issn 2460-0040 Penyajian Data Pelanggan pada Lima Area PT. Telekomunikasi
S 10 Studi Simulasi Tentang Penerapan Grafik Pengendali Berdasarkan Analisis Komponen Utama (Principal Component Analysis)
 PROSIDING ISBN : 978 979 6353 6 3 S 0 Studi Simulasi Tentang Penerapan Grafik Pengendali Berdasarkan Analisis Komponen Utama (Principal Component Analysis) Wirayanti ), Adi Setiawan ), Bambang Susanto
PROSIDING ISBN : 978 979 6353 6 3 S 0 Studi Simulasi Tentang Penerapan Grafik Pengendali Berdasarkan Analisis Komponen Utama (Principal Component Analysis) Wirayanti ), Adi Setiawan ), Bambang Susanto
Studi Simulasi Grafik Pengendali Non Parametrik Berdasarkan Fungsi Distribusi Empirik
 Studi Simulasi Grafik Pengendali Non Parametrik Berdasarkan Fungsi Empirik S 6 Jantini Trianasari Natangku 1), Adi Setiawan ), Lilik Linawati ) 1) Mahasiswa Program Studi Matematika FSM-UKSW Email : n4n4_00190@yahoo.co.id
Studi Simulasi Grafik Pengendali Non Parametrik Berdasarkan Fungsi Empirik S 6 Jantini Trianasari Natangku 1), Adi Setiawan ), Lilik Linawati ) 1) Mahasiswa Program Studi Matematika FSM-UKSW Email : n4n4_00190@yahoo.co.id
BAB II TINJAUAN PUSTAKA DAN DASAR TEORI
 BAB II TINJAUAN PUSTAKA DAN DASAR TEORI 2.1 Tinjauan Pustaka Tabel 2.1 Tinjauan Pustaka Penulis Objek Metode Febri Nugroho (2016) Anugerah Panembahan Attunggal (2016) Ismail (2013) Muhammad Aji Pratama
BAB II TINJAUAN PUSTAKA DAN DASAR TEORI 2.1 Tinjauan Pustaka Tabel 2.1 Tinjauan Pustaka Penulis Objek Metode Febri Nugroho (2016) Anugerah Panembahan Attunggal (2016) Ismail (2013) Muhammad Aji Pratama
BAB 2 TINJAUAN PUSTAKA
 BAB 2 TINJAUAN PUSTAKA Tinjauan pustaka merupakan pembahasan mengenai penelitian-penelitian yang sudah dilakukan sebelumnya dan berkaitan dengan topik yang dibahas, serta perbandingan antara penelitian-penelitian
BAB 2 TINJAUAN PUSTAKA Tinjauan pustaka merupakan pembahasan mengenai penelitian-penelitian yang sudah dilakukan sebelumnya dan berkaitan dengan topik yang dibahas, serta perbandingan antara penelitian-penelitian
2. Untuk interval 0 < x < 360, nilai x yang nantinya akan memenuhi persamaan trigonometri cos x 2 sin x = 2 3 cos adalah
 Soal Babak Semifinal OMITS 007. Hubungan antara a dan b agar fungsi f x = a sin x + b cos x mempunyai nilai stasioner di x = π adalah a. a = b b. a = b d. a = b e. a = b a = b. Untuk interval 0 < x < 60,
Soal Babak Semifinal OMITS 007. Hubungan antara a dan b agar fungsi f x = a sin x + b cos x mempunyai nilai stasioner di x = π adalah a. a = b b. a = b d. a = b e. a = b a = b. Untuk interval 0 < x < 60,
BAB II TINJAUAN PUSTAKA DAN DASAR TEORI. (Abdul Fatah dan Agung Budi Cahyono, 2013) dengan judul Sistem Informasi
 BAB II TINJAUAN PUSTAKA DAN DASAR TEORI 2.1 Tinjauan Pustaka Penelitian yang pernah dilakukan di Institut Teknologi Sepuluh November (Abdul Fatah dan Agung Budi Cahyono, 2013) dengan judul Sistem Informasi
BAB II TINJAUAN PUSTAKA DAN DASAR TEORI 2.1 Tinjauan Pustaka Penelitian yang pernah dilakukan di Institut Teknologi Sepuluh November (Abdul Fatah dan Agung Budi Cahyono, 2013) dengan judul Sistem Informasi
Matematika EBTANAS Tahun 1999
 Matematika EBTANAS Tahun 999 EBT-SMA-99-0 Akar-akar persamaan kuadrat + = 0 adalah α dan β. Persamaan kuadrat baru yang akar-akarnya (α + ) dan (β + ) + = 0 + 7 = 0 + = 0 + 7 = 0 + = 0 EBT-SMA-99-0 Akar-akar
Matematika EBTANAS Tahun 999 EBT-SMA-99-0 Akar-akar persamaan kuadrat + = 0 adalah α dan β. Persamaan kuadrat baru yang akar-akarnya (α + ) dan (β + ) + = 0 + 7 = 0 + = 0 + 7 = 0 + = 0 EBT-SMA-99-0 Akar-akar
STUDI SIMULASI UJI KOEFISIEN KORELASI SPEARMAN DAN KENDALL DARI SAMPEL YANG DIBANGKITKAN BERDASARKAN ESTIMASI DENSITAS KERNEL MULTIVARIAT
 STUDI SIMULASI UJI KOEFISIEN KORELASI SPEARMAN DAN KENDALL DARI SAMPEL YANG DIBANGKITKAN BERDASARKAN ESTIMASI DENSITAS KERNEL MULTIVARIAT Studi Kasus: Beberapa Kurs Mata Uang Asing Terhadap Rupiah Rangga
STUDI SIMULASI UJI KOEFISIEN KORELASI SPEARMAN DAN KENDALL DARI SAMPEL YANG DIBANGKITKAN BERDASARKAN ESTIMASI DENSITAS KERNEL MULTIVARIAT Studi Kasus: Beberapa Kurs Mata Uang Asing Terhadap Rupiah Rangga
Wilfried Suhr Gambar 1. Waktu-waktu kontak dalam peristiwa transit Venus.
 TUGAS I ASTROFISIKA (FI 567) BESARAN MENDASAR DALAM ASTRONOMI & ASTROFISIKA: Penentuan 1 AU SEMESTER GANJIL 2014 2015 DOSEN: JUDHISTIRA ARIA UTAMA, M.SI. (KODE: 2582) Dalam aktivitas laboratorium astronomi
TUGAS I ASTROFISIKA (FI 567) BESARAN MENDASAR DALAM ASTRONOMI & ASTROFISIKA: Penentuan 1 AU SEMESTER GANJIL 2014 2015 DOSEN: JUDHISTIRA ARIA UTAMA, M.SI. (KODE: 2582) Dalam aktivitas laboratorium astronomi
MATEMATIKA DASAR TAHUN 1987
 MATEMATIKA DASAR TAHUN 987 MD-87-0 Garis singgung pada kurva y di titik potong nya dengan sumbu yang absisnya positif mempunyai gradien 0 MD-87-0 Titik potong garis y + dengan parabola y + ialah P (5,
MATEMATIKA DASAR TAHUN 987 MD-87-0 Garis singgung pada kurva y di titik potong nya dengan sumbu yang absisnya positif mempunyai gradien 0 MD-87-0 Titik potong garis y + dengan parabola y + ialah P (5,
BAB II TINJAUAN PUSTAKA DAN DASAR TEORI. Dari penelitian yang telah dilakukan oleh peneliti- peneliti sebelumnya
 BAB II TINJAUAN PUSTAKA DAN DASAR TEORI 2.1 Tinjauan Pustaka yaitu : Dari penelitian yang telah dilakukan oleh peneliti- peneliti sebelumnya 1. Kuriunus Mala (2014) melakukan penelitian tentang aplikasi
BAB II TINJAUAN PUSTAKA DAN DASAR TEORI 2.1 Tinjauan Pustaka yaitu : Dari penelitian yang telah dilakukan oleh peneliti- peneliti sebelumnya 1. Kuriunus Mala (2014) melakukan penelitian tentang aplikasi
MAKALAH SEGITIGA BOLA. disusun guna memenuhi tugas mata kuliah Astronomi. Program Studi Pendidikan Fisika. oleh. 1. Dyah Larasati ( )
 MAKALAH SEGITIGA BOLA disusun guna memenuhi tugas mata kuliah Astronomi Program Studi Pendidikan Fisika oleh 1. Dyah Larasati (4201412042) 2. Lina Kurniawati (4201412091) 3. Qonia Kisbata Rodiya (4201412116)
MAKALAH SEGITIGA BOLA disusun guna memenuhi tugas mata kuliah Astronomi Program Studi Pendidikan Fisika oleh 1. Dyah Larasati (4201412042) 2. Lina Kurniawati (4201412091) 3. Qonia Kisbata Rodiya (4201412116)
Sistem Informasi Geografis (SIG) Geographic Information System (SIG)
 Sistem Informasi Geografis (SIG) Geographic Information System (SIG) 24/09/2012 10:58 Sistem (komputer) yang mampu mengelola informasi spasial (keruangan), memiliki kemampuan memasukan (entry), menyimpan
Sistem Informasi Geografis (SIG) Geographic Information System (SIG) 24/09/2012 10:58 Sistem (komputer) yang mampu mengelola informasi spasial (keruangan), memiliki kemampuan memasukan (entry), menyimpan
20. TRANSFORMASI. A. Translasi (Pergeseran) ; T = b. a y. a y. x atau. = b. = b
 . TRANSFORMASI A. Translasi (Pergeseran) ; T b a + b a atau b a B. Refleksi (Pencerminan). Bila M matriks refleksi berordo, maka: M atau M. Matriks M karena refleksi terhadap sumbu, sumbu, garis, dan garis
. TRANSFORMASI A. Translasi (Pergeseran) ; T b a + b a atau b a B. Refleksi (Pencerminan). Bila M matriks refleksi berordo, maka: M atau M. Matriks M karena refleksi terhadap sumbu, sumbu, garis, dan garis
 Pertemuan 1. Membuat Sudut Siku-Siku. Pengukuran Guna Pembuatan Peta dengan Alat-alatalat Sederhana Can be accessed on: http://haryono_putro.staff.gunadarma.ac.id/ Email: haryono_putro@gunadarma.ac.id
Pertemuan 1. Membuat Sudut Siku-Siku. Pengukuran Guna Pembuatan Peta dengan Alat-alatalat Sederhana Can be accessed on: http://haryono_putro.staff.gunadarma.ac.id/ Email: haryono_putro@gunadarma.ac.id
SISTEM INFORMASI GEOGRAFIS PENUNJANG OLAHRAGA DI SURABAYA Alwy Husein, ; Arif Basofi, S.Kom, M.T, OCA, ;
 SISTEM INFORMASI GEOGRAFIS PENUNJANG OLAHRAGA DI SURABAYA Alwy Husein, 7408030053; Arif Basofi, S.Kom, M.T, OCA, 197609212003121002 ; Reesa Akbar, S.T, ECNA, 197507292001121001 Abstrak - Olahraga adalah
SISTEM INFORMASI GEOGRAFIS PENUNJANG OLAHRAGA DI SURABAYA Alwy Husein, 7408030053; Arif Basofi, S.Kom, M.T, OCA, 197609212003121002 ; Reesa Akbar, S.T, ECNA, 197507292001121001 Abstrak - Olahraga adalah
Gregorius Anung Hanindito 1 Eko Sediyono 2 Adi Setiawan 3. Abstrak
 ANALISIS PANTAUAN DAN KLASIFIKASI CITRA DIGITAL PENGINDRAAN JAUH DENGAN DATA SATELIT LANDASAT TM MELALUI TEKNIK SUPERVISED CLASSIFICATION (STUDI KASUS KABUPATEN MINAHASA TENGGARA, PROVINSI SULAWESI UTARA)
ANALISIS PANTAUAN DAN KLASIFIKASI CITRA DIGITAL PENGINDRAAN JAUH DENGAN DATA SATELIT LANDASAT TM MELALUI TEKNIK SUPERVISED CLASSIFICATION (STUDI KASUS KABUPATEN MINAHASA TENGGARA, PROVINSI SULAWESI UTARA)
SIG FASILITAS UMUM UNTUKPENGGUNA JALAN BERBASIS MOBILE PHONE MENGGUNAKAN OS ANDROID
 SIG FASILITAS UMUM UNTUKPENGGUNA JALAN BERBASIS MOBILE PHONE MENGGUNAKAN OS ANDROID Fadhoelor Rohman (3508 100 031) Pembimbing : Agung Budi Cahyono, ST, M.Sc, DEA PENDAHULUAN Latar Belakang Rumusan Masalah
SIG FASILITAS UMUM UNTUKPENGGUNA JALAN BERBASIS MOBILE PHONE MENGGUNAKAN OS ANDROID Fadhoelor Rohman (3508 100 031) Pembimbing : Agung Budi Cahyono, ST, M.Sc, DEA PENDAHULUAN Latar Belakang Rumusan Masalah
SIDANG TUGAS AKHIR RG
 SIDANG TUGAS AKHIR RG 091536 KAJIAN KETELITIAN PLANIMETRIS CITRA RESOLUSI TINGGI PADA GOOGLE EARTH UNTUK PEMBUATAN PETA DASAR SKALA 1: 10000 KECAMATAN BANJAR TIMUR KOTA BANJARMASIN NOORLAILA HAYATI 3507100044
SIDANG TUGAS AKHIR RG 091536 KAJIAN KETELITIAN PLANIMETRIS CITRA RESOLUSI TINGGI PADA GOOGLE EARTH UNTUK PEMBUATAN PETA DASAR SKALA 1: 10000 KECAMATAN BANJAR TIMUR KOTA BANJARMASIN NOORLAILA HAYATI 3507100044
Gambar 1. prinsip proyeksi dari bidang lengkung muka bumi ke bidang datar kertas
 MODUL 3 REGISTER DAN DIGITASI PETA A. Tujuan Praktikum - Praktikan memahami dan mampu melakukan register peta raster pada MapInfo - Praktikan mampu melakukan digitasi peta dengan MapInfo B. Tools MapInfo
MODUL 3 REGISTER DAN DIGITASI PETA A. Tujuan Praktikum - Praktikan memahami dan mampu melakukan register peta raster pada MapInfo - Praktikan mampu melakukan digitasi peta dengan MapInfo B. Tools MapInfo
2.1 Soal Matematika Dasar UM UGM c. 1 d d. 3a + b. e. 3a + b. e. b + a b a
 Soal - Soal UM UGM. Soal Matematika Dasar UM UGM 00. Jika x = 3 maka + 3 log 4 x =... a. b. c. d. e.. Jika x+y log = a dan x y log 8 = b dengan 0 < y < x maka 4 log (x y ) =... a. a + 3b ab b. a + b ab
Soal - Soal UM UGM. Soal Matematika Dasar UM UGM 00. Jika x = 3 maka + 3 log 4 x =... a. b. c. d. e.. Jika x+y log = a dan x y log 8 = b dengan 0 < y < x maka 4 log (x y ) =... a. a + 3b ab b. a + b ab
Penentuan Batas Pengelolaan Wilayah Laut Antara Provinsi Jawa Timur dan Provinsi Bali Berdasarkan Undang-Undang Republik Indonesia Nomor 23 Tahun 2014
 G199 Penentuan Batas Pengelolaan Wilayah Laut Antara Provinsi Jawa Timur dan Provinsi Bali Berdasarkan Undang-Undang Republik Indonesia Nomor 23 Tahun 2014 Rainhard S Simatupang 1), Khomsin 2) Jurusan
G199 Penentuan Batas Pengelolaan Wilayah Laut Antara Provinsi Jawa Timur dan Provinsi Bali Berdasarkan Undang-Undang Republik Indonesia Nomor 23 Tahun 2014 Rainhard S Simatupang 1), Khomsin 2) Jurusan
MANIPULASIGAMBARUNTUK GAMBAR SEMUA ARAH (OMNIDIRECTIONAL IMAGE)
 MANIPULASIGAMBARUNTUK GAMBAR SEMUA ARAH (OMNIDIRECTIONAL IMAGE) Sukma Meganova Effendi 1, Dadet Pramadihanto 2, Imam Dui Agusalim 3 1 Program Studi Mekatronika, Politeknik Mekatronika Sanata Dharma Kampus
MANIPULASIGAMBARUNTUK GAMBAR SEMUA ARAH (OMNIDIRECTIONAL IMAGE) Sukma Meganova Effendi 1, Dadet Pramadihanto 2, Imam Dui Agusalim 3 1 Program Studi Mekatronika, Politeknik Mekatronika Sanata Dharma Kampus
F O R T O P O L I O KILOMETER 8.514
 F O R T O P O L I O Sabang 8.514 KM Merauke KILOMETER 8.514 I N D O N E S I A Orang Indonesia pertama yang masuk Peringkat 1 dari 4.161.999 users di seluruh dunia, untuk kategori Number Of Uploeded dan
F O R T O P O L I O Sabang 8.514 KM Merauke KILOMETER 8.514 I N D O N E S I A Orang Indonesia pertama yang masuk Peringkat 1 dari 4.161.999 users di seluruh dunia, untuk kategori Number Of Uploeded dan
S - 19 UJI NORMALITAS BERDASARKAN METODE ANDERSON- DARLING, CRAMER-VON MISES DAN LILLIEFORS MENGGUNAKAN METODE BOOTSTRAP
 S - 19 UJI NORMALITAS BERDASARKAN METODE ANDERSON- DARLING, CRAMER-VON MISES DAN LILLIEFORS MENGGUNAKAN METODE BOOTSTRAP Janse Oktaviana Fallo 1, Adi Setiawan 2, Bambang Susanto 3 1,2,3 Program Studi Matematika
S - 19 UJI NORMALITAS BERDASARKAN METODE ANDERSON- DARLING, CRAMER-VON MISES DAN LILLIEFORS MENGGUNAKAN METODE BOOTSTRAP Janse Oktaviana Fallo 1, Adi Setiawan 2, Bambang Susanto 3 1,2,3 Program Studi Matematika
Abstrak PENDAHULUAN.
 PENENTUAN BATAS PENGELOLAAN WILAYAH LAUT DAERAH ANTARA PROVINSI JAWA TIMUR DAN PROVINSI BALI BERDASARKAN UNDANG-UNDANG REPUBLIK INDONESIA NOMOR 23 TAHUN 2014 PENENTUAN BATAS PENGELOLAAN WILAYAH LAUT DAERAH
PENENTUAN BATAS PENGELOLAAN WILAYAH LAUT DAERAH ANTARA PROVINSI JAWA TIMUR DAN PROVINSI BALI BERDASARKAN UNDANG-UNDANG REPUBLIK INDONESIA NOMOR 23 TAHUN 2014 PENENTUAN BATAS PENGELOLAAN WILAYAH LAUT DAERAH
Pemetaan Situasi dengan Metode Koordinat Kutub di Desa Banyuripan, Kecamatan Bayat, Kabupaten Klaten
 Jurnal Integrasi Vol. 8, No. 1, April 2016, 50-55 p-issn: 2085-3858 Article History Received February, 2016 Accepted March, 2016 Pemetaan Situasi dengan Metode Koordinat Kutub di Desa Banyuripan, Kecamatan
Jurnal Integrasi Vol. 8, No. 1, April 2016, 50-55 p-issn: 2085-3858 Article History Received February, 2016 Accepted March, 2016 Pemetaan Situasi dengan Metode Koordinat Kutub di Desa Banyuripan, Kecamatan
Pendahuluan. Latar Belakang. Teknik Geomatika Institut Teknologi Sepuluh Nopember
 Pendahuluan Latar Belakang Peradaban manusia berkembang begitu cepat. Manusia tidak merasa kebingungann lagi untuk berpergian dari satu tempat ke tempat lainnyaa dengan bantuan alat GPS (Global Positioning
Pendahuluan Latar Belakang Peradaban manusia berkembang begitu cepat. Manusia tidak merasa kebingungann lagi untuk berpergian dari satu tempat ke tempat lainnyaa dengan bantuan alat GPS (Global Positioning
PERBANDINGAN DAN FUNGSI TRIGONOMETRI
 PERBANDINGAN DAN FUNGSI TRIGONOMETRI D. Rumus Perbandingan Trigonometri di Semua Kuadran Dalam pembahasan sebelumna, kita telah melihat nilai perbandingan trigonometri untuk sudut sudut istimewa ang besarna
PERBANDINGAN DAN FUNGSI TRIGONOMETRI D. Rumus Perbandingan Trigonometri di Semua Kuadran Dalam pembahasan sebelumna, kita telah melihat nilai perbandingan trigonometri untuk sudut sudut istimewa ang besarna
Rancang Bangun Aplikasi Pencarian Tempat Indekos Pada Perangkat Mobile Android
 JURNAL TEKNIK POMITS Vol. 2, No. 1, (2014) ISSN: 2337-3539 (2301-9271 Print) 1 Rancang Bangun Aplikasi Pencarian Tempat Indekos Pada Perangkat Mobile Android Adriyanra, Dwi Sunaryono, Adhatus Solichah
JURNAL TEKNIK POMITS Vol. 2, No. 1, (2014) ISSN: 2337-3539 (2301-9271 Print) 1 Rancang Bangun Aplikasi Pencarian Tempat Indekos Pada Perangkat Mobile Android Adriyanra, Dwi Sunaryono, Adhatus Solichah
Trigonometri. Trigonometri
 Penggunaan Rumus Sinus dan Cosinus Jumlah Dua Sudut, Selisih ; Dua Sudut, dan Sudut Ganda Rumus Jumlah dan Selisih Sinus dan Cosinus ; Menggunakan Rumus Jumlah dan Selisih Sinus dan Cosinus ; Pernahkah
Penggunaan Rumus Sinus dan Cosinus Jumlah Dua Sudut, Selisih ; Dua Sudut, dan Sudut Ganda Rumus Jumlah dan Selisih Sinus dan Cosinus ; Menggunakan Rumus Jumlah dan Selisih Sinus dan Cosinus ; Pernahkah
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI 2.1. Tinjauan Pustaka Penelitian mengenai sistem pelacakan pernah dilakukan sebelumnya oleh Taufiq Hasan yang berjudul Pembangunan Sistem Pencarian Lokasi Kuliner Di Yogyakarta Dengan
BAB II LANDASAN TEORI 2.1. Tinjauan Pustaka Penelitian mengenai sistem pelacakan pernah dilakukan sebelumnya oleh Taufiq Hasan yang berjudul Pembangunan Sistem Pencarian Lokasi Kuliner Di Yogyakarta Dengan
DISAIN AWAL PROTOTYPE G2A UNTUK ANALISA DATA PERTANIAN DAN PEDESAAN
 DISAIN AWAL PROTOTYPE G2A UNTUK ANALISA DATA PERTANIAN DAN PEDESAAN Hanna Arini Parhusip 1 dan Ramos Somnya 2 Pusat Studi Simitro, Fakultas Teknologi Informasi Universitas Kristen Satya Wacana ABSTRAK.
DISAIN AWAL PROTOTYPE G2A UNTUK ANALISA DATA PERTANIAN DAN PEDESAAN Hanna Arini Parhusip 1 dan Ramos Somnya 2 Pusat Studi Simitro, Fakultas Teknologi Informasi Universitas Kristen Satya Wacana ABSTRAK.
Konsep Geodesi untuk Data Spasial. by: Ahmad Syauqi Ahsan
 Konsep Geodesi untuk Data Spasial by: Ahmad Syauqi Ahsan Geodesi Menurut definisi klasik dari F.R. Helmert, Geodesi adalah sebuah sains dalam pengukuran dan pemetaan permukaan bumi. Pembahasan tentang
Konsep Geodesi untuk Data Spasial by: Ahmad Syauqi Ahsan Geodesi Menurut definisi klasik dari F.R. Helmert, Geodesi adalah sebuah sains dalam pengukuran dan pemetaan permukaan bumi. Pembahasan tentang
MENGENAL GERAK LANGIT DAN TATA KOORDINAT BENDA LANGIT BY AMBOINA ASTRONOMY CLUB
 MENGENAL GERAK LANGIT DAN TATA KOORDINAT BENDA LANGIT BY AMBOINA ASTRONOMY CLUB A. Gerak Semu Benda Langit Bumi kita berputar seperti gasing. Ketika Bumi berputar pada sumbu putarnya maka hal ini dinamakan
MENGENAL GERAK LANGIT DAN TATA KOORDINAT BENDA LANGIT BY AMBOINA ASTRONOMY CLUB A. Gerak Semu Benda Langit Bumi kita berputar seperti gasing. Ketika Bumi berputar pada sumbu putarnya maka hal ini dinamakan
INFERENSI PARAMETER SIMPANGAN BAKU POPULASI NORMAL DENGAN METODE BAYESIAN OBYEKTIF
 INFERENSI PARAMETER SIMPANGAN BAKU S - POPULASI NORMAL DENGAN METODE BAYESIAN OBYEKTIF Adi Setiawan Program Studi Matematika Fakultas Sains dan Matematika Universitas Kristen Satya Wacana, Jl Diponegoro
INFERENSI PARAMETER SIMPANGAN BAKU S - POPULASI NORMAL DENGAN METODE BAYESIAN OBYEKTIF Adi Setiawan Program Studi Matematika Fakultas Sains dan Matematika Universitas Kristen Satya Wacana, Jl Diponegoro
PEMETAAN MEREK DAN DESAIN INDUSTRI UMKM BERPOTENSI HKI DI KABUPATEN KUDUS BERBASIS SISTEM INFORMASI GEOGRAFIS MENGGUNAKAN GOOGLE MAP API
 PEMETAAN MEREK DAN DESAIN INDUSTRI UMKM BERPOTENSI HKI DI KABUPATEN KUDUS BERBASIS SISTEM INFORMASI GEOGRAFIS MENGGUNAKAN GOOGLE MAP API Andy Prasetyo Utomo, Suciningtyas Universitas Muria Kudus andyutomo@gmail.com
PEMETAAN MEREK DAN DESAIN INDUSTRI UMKM BERPOTENSI HKI DI KABUPATEN KUDUS BERBASIS SISTEM INFORMASI GEOGRAFIS MENGGUNAKAN GOOGLE MAP API Andy Prasetyo Utomo, Suciningtyas Universitas Muria Kudus andyutomo@gmail.com
BAB I PENDAHULUAN. Sistem informasi geografis (geographic information system/gis) yang
 BAB I PENDAHULUAN I.1. Latar Belakang Sistem informasi geografis (geographic information system/gis) yang selanjutnya akan disebut SIG merupakan sistem informasi berbasis komputer yang digunakan untuk
BAB I PENDAHULUAN I.1. Latar Belakang Sistem informasi geografis (geographic information system/gis) yang selanjutnya akan disebut SIG merupakan sistem informasi berbasis komputer yang digunakan untuk
SELEKSI OLIMPIADE TINGKAT KABUPATEN/KOTA TAHUN 2004 TIM OLIMPIADE MATEMATIKA INDONESIA TAHUN 2005
 SELEKSI OLIMPIADE TINGKAT KABUPATEN/KOTA TIM OLIMPIADE MATEMATIKA INDONESIA TAHUN 200 Bidang Matematika Waktu : 90 Menit DEPARTEMEN PENDIDIKAN NASIONAL DIREKTORAT JENDERAL PENDIDIKAN DASAR DAN MENENGAH
SELEKSI OLIMPIADE TINGKAT KABUPATEN/KOTA TIM OLIMPIADE MATEMATIKA INDONESIA TAHUN 200 Bidang Matematika Waktu : 90 Menit DEPARTEMEN PENDIDIKAN NASIONAL DIREKTORAT JENDERAL PENDIDIKAN DASAR DAN MENENGAH
POPULERISASI MATEMATIKA
 DISAIN ODEMA (Ornament Decorative Mathematics) UNTUK POPULERISASI MATEMATIKA Hanna Arini Parhusip Prodi Matematika,Fakultas Sains dan Matematika, Universitas Kristen Satya Wacana ABSTRAK. ODEMA (Ornament
DISAIN ODEMA (Ornament Decorative Mathematics) UNTUK POPULERISASI MATEMATIKA Hanna Arini Parhusip Prodi Matematika,Fakultas Sains dan Matematika, Universitas Kristen Satya Wacana ABSTRAK. ODEMA (Ornament
Evaluasi Belajar Tahap Akhir Nasional Tahun 1985 Matematika
 Evaluasi Belajar Tahap Akhir Nasional Tahun 98 Matematika EBTANAS-SMP-8- Jika A = {,, 8,, 4}, B = {,,,,, } dengan himpunan semesta C = (c c bilangan cacah }, maka himpunan {., 4, 6, 9,,, } =... A' B' (A
Evaluasi Belajar Tahap Akhir Nasional Tahun 98 Matematika EBTANAS-SMP-8- Jika A = {,, 8,, 4}, B = {,,,,, } dengan himpunan semesta C = (c c bilangan cacah }, maka himpunan {., 4, 6, 9,,, } =... A' B' (A
(A) 3 (B) 5 (B) 1 (C) 8
 . Turunan dari f ( ) = + + (E) 7 + +. Turunan dari y = ( ) ( + ) ( ) ( + ) ( ) ( + ) ( + ) ( + ) ( ) ( + ) (E) ( ) ( + ) 7 5 (E) 9 5 9 7 0. Jika f ( ) = maka f () = 8 (E) 8. Jika f () = 5 maka f (0) +
. Turunan dari f ( ) = + + (E) 7 + +. Turunan dari y = ( ) ( + ) ( ) ( + ) ( ) ( + ) ( + ) ( + ) ( ) ( + ) (E) ( ) ( + ) 7 5 (E) 9 5 9 7 0. Jika f ( ) = maka f () = 8 (E) 8. Jika f () = 5 maka f (0) +
SOAL UJIAN SELEKSI CALON PESERTA OLIMPIADE SAINS NASIONAL 2016 TINGKAT PROVINSI
 HAK CIPTA DILINDUNGI UNDANG-UNDANG SOAL UJIAN SELEKSI CALON PESERTA OLIMPIADE SAINS NASIONAL 2016 TINGKAT PROVINSI BIDANG MATEMATIKA Waktu : 210 menit KEMENTERIAN PENDIDIKAN DAN KEBUDAYAAN DIREKTORAT JENDERAL
HAK CIPTA DILINDUNGI UNDANG-UNDANG SOAL UJIAN SELEKSI CALON PESERTA OLIMPIADE SAINS NASIONAL 2016 TINGKAT PROVINSI BIDANG MATEMATIKA Waktu : 210 menit KEMENTERIAN PENDIDIKAN DAN KEBUDAYAAN DIREKTORAT JENDERAL
BAB IV ANALISIS PERHITUNGAN ARAH KIBLAT DENGAN MENGGUNAKAN AZIMUT PLANET. A. Algoritma Penentuan Arah Kiblat dengan Metode Azimut Planet
 BAB IV ANALISIS PERHITUNGAN ARAH KIBLAT DENGAN MENGGUNAKAN AZIMUT PLANET A. Algoritma Penentuan Arah Kiblat dengan Metode Azimut Planet Pada dasarnya azimut planet adalah busur yang diukur dari titik Utara
BAB IV ANALISIS PERHITUNGAN ARAH KIBLAT DENGAN MENGGUNAKAN AZIMUT PLANET A. Algoritma Penentuan Arah Kiblat dengan Metode Azimut Planet Pada dasarnya azimut planet adalah busur yang diukur dari titik Utara
SEGITIGA BOLA DAN ARAH KIBLAT
 SEGITIGA BOLA DAN ARAH KIBLAT Pengetahuan tentang arah kiblat yang benar sangat penting bagi ummat Islam. Ketika ummat Islam malaksanakan ibadah shalat, terdapat sebuah kewajiban untuk menghadap kiblat
SEGITIGA BOLA DAN ARAH KIBLAT Pengetahuan tentang arah kiblat yang benar sangat penting bagi ummat Islam. Ketika ummat Islam malaksanakan ibadah shalat, terdapat sebuah kewajiban untuk menghadap kiblat
BAB I PENDAHULUAN menjadikan kota Saumlaki semakin berkembang dengan pesat.
 16 BAB I PENDAHULUAN 2.1 Latar Belakang Kota Saumlaki, terletak di Propinsi Maluku, Indonesia. Saumlaki dahulu adalah kota kecamatan dalam wilayah Kabupeten Maluku Tenggara, yang kemudian melalui pemekaran
16 BAB I PENDAHULUAN 2.1 Latar Belakang Kota Saumlaki, terletak di Propinsi Maluku, Indonesia. Saumlaki dahulu adalah kota kecamatan dalam wilayah Kabupeten Maluku Tenggara, yang kemudian melalui pemekaran
Matematika Proyek Perintis I Tahun 1979
 Matematika Proyek Perintis I Tahun 979 MA-79-0 Irisan himpunan : A = { x x < } dan himpunan B = { x < x < 8 } ialah himpunan A. { x x < 8 } { x x < } { x < x < 8 } { x < x < } { x < x } MA-79-0 Apabila
Matematika Proyek Perintis I Tahun 979 MA-79-0 Irisan himpunan : A = { x x < } dan himpunan B = { x < x < 8 } ialah himpunan A. { x x < 8 } { x x < } { x < x < 8 } { x < x < } { x < x } MA-79-0 Apabila
Dr. Ramadoni Syahputra Jurusan Teknik Elektro FT UMY
 SISTEM-SISTEM KOORDINAT Dr. Ramadoni Syahputra Jurusan Teknik Elektro FT UMY Sistem Koordinat Kartesian Dalam sistem koordinat Kartesian, terdapat tiga sumbu koordinat yaitu sumbu x, y, dan z. Suatu titik
SISTEM-SISTEM KOORDINAT Dr. Ramadoni Syahputra Jurusan Teknik Elektro FT UMY Sistem Koordinat Kartesian Dalam sistem koordinat Kartesian, terdapat tiga sumbu koordinat yaitu sumbu x, y, dan z. Suatu titik
PERSIAPAN TES SKL KELAS X, MATEMATIKA IPS Page 1
 PERSIAPAN TES SKL X, MATEMATIKA 1. Pangkat, Akar dan Logaritma Menentukan hasil operasi bentuk pangkat (1 6) Menentukan hasil operasi bentuk akar (7 11) Menentukan hasil operasi bentuk logarithma (12 15)
PERSIAPAN TES SKL X, MATEMATIKA 1. Pangkat, Akar dan Logaritma Menentukan hasil operasi bentuk pangkat (1 6) Menentukan hasil operasi bentuk akar (7 11) Menentukan hasil operasi bentuk logarithma (12 15)
SUSUNAN KOORDINAT BAGIAN-1. Oleh: Fitria Khasanah, M. Pd
 SUSUNAN KOORDINAT BAGIAN-1 Oleh: Fitria Khasanah, M. Pd Program Studi Pendidikan Matematika Fakultas Keguruan dan Ilmu Pendidikan Universitas PGRI Yogyakarta 2010 Letak Suatu Titik pada Garis Lurus O g
SUSUNAN KOORDINAT BAGIAN-1 Oleh: Fitria Khasanah, M. Pd Program Studi Pendidikan Matematika Fakultas Keguruan dan Ilmu Pendidikan Universitas PGRI Yogyakarta 2010 Letak Suatu Titik pada Garis Lurus O g
ORIENTASI PADA PRA PLOTTING PETA BERSISTEM KOORDINAT LOKAL TERHADAP SISTEM KOORDINAT FIX (TETAP)
 Orientasi pada Pra Plotting... ORIENTASI PADA PRA PLOTTING PETA BERSISTEM KOORDINAT LOKAL TERHADAP SISTEM KOORDINAT FIX (TETAP) Yuwono 1), AdiKurniawan 2) 1) Jurusan Teknik Geomatika, ITS, 2) Jurusan Teknik
Orientasi pada Pra Plotting... ORIENTASI PADA PRA PLOTTING PETA BERSISTEM KOORDINAT LOKAL TERHADAP SISTEM KOORDINAT FIX (TETAP) Yuwono 1), AdiKurniawan 2) 1) Jurusan Teknik Geomatika, ITS, 2) Jurusan Teknik
P E N D A H U L U A N Latar Belakang
 KLASIFIKASI KEKERAPAN KUNJUNGAN LOKASI BERBASIS LOCATION BASED SERVICE (LBS) MENGGUNAKAN SELF-ORGANIZING MAP (SOM) Oleh : Dhanang Fitra Riaji (NRP : 2208205737) PROGRAM MAGISTER JURUSAN TEKNIK INDUSTRI
KLASIFIKASI KEKERAPAN KUNJUNGAN LOKASI BERBASIS LOCATION BASED SERVICE (LBS) MENGGUNAKAN SELF-ORGANIZING MAP (SOM) Oleh : Dhanang Fitra Riaji (NRP : 2208205737) PROGRAM MAGISTER JURUSAN TEKNIK INDUSTRI
PERANGKAT LUNAK UNTUK PERHITUNGAN SUDUT ELEVASI DAN AZIMUTH ANTENA STASIUN BUMI BERGERAK DALAM SISTEM KOMUNIKASI SATELIT GEOSTASIONER
 PERANGKAT LUNAK UNTUK PERHITUNGAN SUDUT ELEVASI DAN AZIMUTH ANTENA STASIUN BUMI BERGERAK DALAM SISTEM KOMUNIKASI SATELIT GEOSTASIONER Veni Prasetiati Jurusan Teknik Elektro Fakultas Teknik, Universitas
PERANGKAT LUNAK UNTUK PERHITUNGAN SUDUT ELEVASI DAN AZIMUTH ANTENA STASIUN BUMI BERGERAK DALAM SISTEM KOMUNIKASI SATELIT GEOSTASIONER Veni Prasetiati Jurusan Teknik Elektro Fakultas Teknik, Universitas
TAHUN PELAJARAN 2003/2004 SMK. Matematika Teknik Industri (E3-1) PAKET 1 (UTAMA) SELASA, 11 MEI 2004 Pukul
 0-04 E--P9-0-4 DOKUMEN NEGARA SANGAT RAHASIA UJIAN NASIONAL TAHUN PELAJARAN 00/004 SMK Matematika Teknik Industri (E-) PAKET (UTAMA) SELASA, MEI 004 Pukul 07.0 09.0 DEPARTEMEN PENDIDIKAN NASIONAL Hak Cipta
0-04 E--P9-0-4 DOKUMEN NEGARA SANGAT RAHASIA UJIAN NASIONAL TAHUN PELAJARAN 00/004 SMK Matematika Teknik Industri (E-) PAKET (UTAMA) SELASA, MEI 004 Pukul 07.0 09.0 DEPARTEMEN PENDIDIKAN NASIONAL Hak Cipta
BAB II TINJAUAN PUSTAKA DAN DASAR TEORI. Untuk membangun aplikasi ini, ada beberapa dasar penelitian seperti,
 BAB II TINJAUAN PUSTAKA DAN DASAR TEORI 2.1 Tinjauan Pustaka Untuk membangun aplikasi ini, ada beberapa dasar penelitian seperti, pencarian lokasi apotek menggunkan sistem operasi android berbasis google
BAB II TINJAUAN PUSTAKA DAN DASAR TEORI 2.1 Tinjauan Pustaka Untuk membangun aplikasi ini, ada beberapa dasar penelitian seperti, pencarian lokasi apotek menggunkan sistem operasi android berbasis google
BAB IV ANALISIS KOMPARASI ALGORITMA EQUATION OF TIME JEAN MEEUS DAN SISTEM NEWCOMB
 BAB IV ANALISIS KOMPARASI ALGORITMA EQUATION OF TIME JEAN MEEUS DAN SISTEM NEWCOMB A. Uji Komparasi dan Analisis Hasil Perhitungan Equation of Time Jean Meeus dan Newcomb Menggunakan Parameter Almanak
BAB IV ANALISIS KOMPARASI ALGORITMA EQUATION OF TIME JEAN MEEUS DAN SISTEM NEWCOMB A. Uji Komparasi dan Analisis Hasil Perhitungan Equation of Time Jean Meeus dan Newcomb Menggunakan Parameter Almanak
INFERENSI PARAMETER MEAN POPULASI NORMAL DENGAN METODE BAYESIAN OBYEKTIF
 INFERENSI PARAMETER MEAN POPULASI NORMAL DENGAN METODE BAYESIAN OBYEKTIF Adi Setiawan Program Studi Matematika Industri dan Statistika, Fakultas Sains dan Matematika Universitas Kristen Satya Wacana Jl
INFERENSI PARAMETER MEAN POPULASI NORMAL DENGAN METODE BAYESIAN OBYEKTIF Adi Setiawan Program Studi Matematika Industri dan Statistika, Fakultas Sains dan Matematika Universitas Kristen Satya Wacana Jl
ILMU UKUR TANAH 2 PENENTUAN POSISI
 ILMU UKUR TANAH 2 PENENTUAN POSISI Oleh: Andri Oktriansyah JURUSAN SURVEI DAN PEMETAAN UNIVERSITAS INDO GLOBAL MANDIRI PALEMBANG 2017 1. Penentuan Posisi Penentuan posisi titik dikelompokkan dalam dua
ILMU UKUR TANAH 2 PENENTUAN POSISI Oleh: Andri Oktriansyah JURUSAN SURVEI DAN PEMETAAN UNIVERSITAS INDO GLOBAL MANDIRI PALEMBANG 2017 1. Penentuan Posisi Penentuan posisi titik dikelompokkan dalam dua
PERANCANGAN SISTEM PENGELOLAAN PENANGGULANGAN BENCANA ALAM GARUT BERBASIS SISTEM INFORMASI GEOGRAFIS
 PERANCANGAN SISTEM PENGELOLAAN PENANGGULANGAN BENCANA ALAM GARUT BERBASIS SISTEM INFORMASI GEOGRAFIS Rubi Setiawan 1, Dede Kurniadi 2, H. Bunyamin 3 Jurnal Algoritma Sekolah Tinggi Teknologi Garut Jl.
PERANCANGAN SISTEM PENGELOLAAN PENANGGULANGAN BENCANA ALAM GARUT BERBASIS SISTEM INFORMASI GEOGRAFIS Rubi Setiawan 1, Dede Kurniadi 2, H. Bunyamin 3 Jurnal Algoritma Sekolah Tinggi Teknologi Garut Jl.
DAFTAR PUSTAKA. 1. Abidin, Hasanuddin Z.(2001). Geodesi satelit. Jakarta : Pradnya Paramita.
 DAFTAR PUSTAKA 1. Abidin, Hasanuddin Z.(2001). Geodesi satelit. Jakarta : Pradnya Paramita. 2. Abidin, Hasanuddin Z.(2002). Survey Dengan GPS. Cetakan Kedua. Jakarta : Pradnya Paramita. 3. Krakiwsky, E.J.
DAFTAR PUSTAKA 1. Abidin, Hasanuddin Z.(2001). Geodesi satelit. Jakarta : Pradnya Paramita. 2. Abidin, Hasanuddin Z.(2002). Survey Dengan GPS. Cetakan Kedua. Jakarta : Pradnya Paramita. 3. Krakiwsky, E.J.
Pemetaan Tingkat Kekeringan Berdasarkan Parameter Indeks TVDI Data Citra Satelit Landsat-8 (Studi Kasus: Provinsi Jawa Timur)
 Pemetaan Tingkat Kekeringan Berdasarkan Parameter Indeks TVDI Data Citra Satelit Landsat-8 (Studi Kasus: Provinsi Jawa Timur) Diah Witarsih dan Bangun Muljo Sukojo Jurusan Teknik Geomatika, Fakultas Teknik
Pemetaan Tingkat Kekeringan Berdasarkan Parameter Indeks TVDI Data Citra Satelit Landsat-8 (Studi Kasus: Provinsi Jawa Timur) Diah Witarsih dan Bangun Muljo Sukojo Jurusan Teknik Geomatika, Fakultas Teknik
Pembahasan Seleksi Nasional Masuk Perguruan Tinggi Negeri (SNMPTN) Bidang Matematika. Kode Paket 634. Oleh : Fendi Alfi Fauzi 1. x 0 x 2.
 Pembahasan Seleksi Nasional Masuk Perguruan Tinggi Negeri SNMPTN) Bidang Matematika Kode Paket 6 Oleh : Fendi Alfi Fauzi. lim x 0 cos x x tan x + π )... a) b) 0 c) d) e) Jawaban : C Pembahasan: lim x 0
Pembahasan Seleksi Nasional Masuk Perguruan Tinggi Negeri SNMPTN) Bidang Matematika Kode Paket 6 Oleh : Fendi Alfi Fauzi. lim x 0 cos x x tan x + π )... a) b) 0 c) d) e) Jawaban : C Pembahasan: lim x 0
FORMULA HERON: TINJAUAN DI GEOMETRI EUKLID DAN GEOMETRI SFERIK 1. Sangadji 2
 PROSIDING ISBN : 978 979 16353 3 FORMUL HERON: TINJUN DI GEOMETRI EUKLID DN GEOMETRI SFERIK 1 T 8 Sangadji strak Formula Heron mempunyai dua versi. Versi pertama adalah Formula Heron dalam geometri Euklid
PROSIDING ISBN : 978 979 16353 3 FORMUL HERON: TINJUN DI GEOMETRI EUKLID DN GEOMETRI SFERIK 1 T 8 Sangadji strak Formula Heron mempunyai dua versi. Versi pertama adalah Formula Heron dalam geometri Euklid
Buku Pendalaman Konsep. Trigonometri. Tingkat SMA Doddy Feryanto
 Buku Pendalaman Konsep Trigonometri Tingkat SMA Doddy Feryanto Kata Pengantar Trigonometri merupakan salah satu jenis fungsi yang sangat banyak berguna di berbagai bidang. Di bidang matematika sendiri,
Buku Pendalaman Konsep Trigonometri Tingkat SMA Doddy Feryanto Kata Pengantar Trigonometri merupakan salah satu jenis fungsi yang sangat banyak berguna di berbagai bidang. Di bidang matematika sendiri,
Dr. Amar, S.T., M.T. Curriculum Vitae. Daftar Riwayat Hidup. 1. Identitas Diri NIP
 Dr. Amar, S.T., M.T NIP. 19710303 199803 1 001 Curriculum Vitae Daftar Riwayat Hidup Identitas Diri 1 Nama Lengkap Dr. Amar, ST., MT. 2 Jabatan Fungsional Lektor Kepala 3 Jabatan Struktural 4 NIP 19680714
Dr. Amar, S.T., M.T NIP. 19710303 199803 1 001 Curriculum Vitae Daftar Riwayat Hidup Identitas Diri 1 Nama Lengkap Dr. Amar, ST., MT. 2 Jabatan Fungsional Lektor Kepala 3 Jabatan Struktural 4 NIP 19680714
OPTIMASI PENCAPAIAN TARGET PADA SIMULASI PERENCANAAN JALUR ROBOT BERGERAK DI LINGKUNGAN DINAMIS
 OPTIMASI PENCAPAIAN TARGET PADA SIMULASI PERENCANAAN JALUR ROBOT BERGERAK DI LINGKUNGAN DINAMIS Yisti Vita Via Jurusan Teknik Informatika, Fakultas Teknologi Informasi, Institut Teknologi Sepuluh Nopember
OPTIMASI PENCAPAIAN TARGET PADA SIMULASI PERENCANAAN JALUR ROBOT BERGERAK DI LINGKUNGAN DINAMIS Yisti Vita Via Jurusan Teknik Informatika, Fakultas Teknologi Informasi, Institut Teknologi Sepuluh Nopember
BAB IV ANALISIS PEMIKIRAN SAADOEDDIN DJAMBEK TENTANG ARAH KIBLAT. A. Penentuan Arah Kiblat Pemikiran Saadoeddin Djambek
 BAB IV ANALISIS PEMIKIRAN SAADOEDDIN DJAMBEK TENTANG ARAH KIBLAT A. Penentuan Arah Kiblat Pemikiran Saadoeddin Djambek Sebagian ahli Falak menyatakan bahwa arah kiblat adalah jarak terdekat, berupa garis
BAB IV ANALISIS PEMIKIRAN SAADOEDDIN DJAMBEK TENTANG ARAH KIBLAT A. Penentuan Arah Kiblat Pemikiran Saadoeddin Djambek Sebagian ahli Falak menyatakan bahwa arah kiblat adalah jarak terdekat, berupa garis
B. y = 1 x 2 1 UN-SMK-TEK Jika A = 2 0
 UN-SMK-TEK-04-0 Jarak kota A ke kota B pada peta 0 cm. Jika skala peta : 0.000, maka jarak kedua kota sebenarnya adalah..., km km 0 km.00 km.000 km UN-SMK-TEK-04-0 Hasil perkalian dari (4a) - (a) =...
UN-SMK-TEK-04-0 Jarak kota A ke kota B pada peta 0 cm. Jika skala peta : 0.000, maka jarak kedua kota sebenarnya adalah..., km km 0 km.00 km.000 km UN-SMK-TEK-04-0 Hasil perkalian dari (4a) - (a) =...
ANALISA PETA LINGKUNGAN PANTAI INDONESIA (LPI) DITINJAU DARI ASPEK KARTOGRAFIS BERDASARKAN PADA SNI
 ANALISA PETA LINGKUNGAN PANTAI INDONESIA (LPI) DITINJAU DARI ASPEK KARTOGRAFIS BERDASARKAN PADA SNI 19-6726-2002 Pristantrina Stephanindra, Ir.Yuwono MT Program Studi Teknik Geomatika, Fakultas Teknik
ANALISA PETA LINGKUNGAN PANTAI INDONESIA (LPI) DITINJAU DARI ASPEK KARTOGRAFIS BERDASARKAN PADA SNI 19-6726-2002 Pristantrina Stephanindra, Ir.Yuwono MT Program Studi Teknik Geomatika, Fakultas Teknik
MODUL 3 REGISTER DAN DIGITASI PETA
 MODUL 3 REGISTER DAN DIGITASI PETA A. Tujuan Praktikum - Praktikan memahami dan mampu melakukan register peta raster pada MapInfo - Praktikan mampu melakukan digitasi peta dengan MapInfo B. Tools MapInfo
MODUL 3 REGISTER DAN DIGITASI PETA A. Tujuan Praktikum - Praktikan memahami dan mampu melakukan register peta raster pada MapInfo - Praktikan mampu melakukan digitasi peta dengan MapInfo B. Tools MapInfo
PENGARUH FENOMENA LA-NINA TERHADAP SUHU PERMUKAAN LAUT DI PERAIRAN KABUPATEN MALANG
 Pengaruh Fenomena La-Nina terhadap SPL Feny Arafah PENGARUH FENOMENA LA-NINA TERHADAP SUHU PERMUKAAN LAUT DI PERAIRAN KABUPATEN MALANG 1) Feny Arafah 1) Dosen Prodi. Teknik Geodesi Fakultas Teknik Sipil
Pengaruh Fenomena La-Nina terhadap SPL Feny Arafah PENGARUH FENOMENA LA-NINA TERHADAP SUHU PERMUKAAN LAUT DI PERAIRAN KABUPATEN MALANG 1) Feny Arafah 1) Dosen Prodi. Teknik Geodesi Fakultas Teknik Sipil
DAFTAR PUSTAKA. 2. Google Earth, (2007), Explore, Search and Discover, google.com.
 41 DAFTAR PUSTAKA 1. Dewantara, T, (2007), Kajian Akurasi Geometrik Citra Quickbird Orthogonal untuk Penentuan Posisi dan Luas Obyek dalam Menjamin Kepastian Obyek Pajak Bumi dan Bangunan (studi kasus
41 DAFTAR PUSTAKA 1. Dewantara, T, (2007), Kajian Akurasi Geometrik Citra Quickbird Orthogonal untuk Penentuan Posisi dan Luas Obyek dalam Menjamin Kepastian Obyek Pajak Bumi dan Bangunan (studi kasus
PREDIKSI SOAL UAN MATEMATIKA 2009 KELOMPOK TEKNIK
 PREDIKSI SOAL UAN MATEMATIKA 2009 KELOMPOK TEKNIK 1. Jarak kota P dan kota R pada sebuah peta adalah 20 cm. Jika skala pada peta tersebut 1:2.500.000, maka jarak sebenarnya dua kota tersebut adalah. A.
PREDIKSI SOAL UAN MATEMATIKA 2009 KELOMPOK TEKNIK 1. Jarak kota P dan kota R pada sebuah peta adalah 20 cm. Jika skala pada peta tersebut 1:2.500.000, maka jarak sebenarnya dua kota tersebut adalah. A.
Lampiran Nomor Surat : S - 20/LPDP/2016 Tanggal : 4 Januari 2016
 Lampiran Nomor Surat : S - 0/LPDP/06 Tanggal : Januari 06 No. Rektor Perguruan Tinggi Rektor Institut Agama Islam Negeri (IAIN) Sunan Ampel, Surabaya Rektor Institut Agama Islam Negeri (IAIN) Walisongo,
Lampiran Nomor Surat : S - 0/LPDP/06 Tanggal : Januari 06 No. Rektor Perguruan Tinggi Rektor Institut Agama Islam Negeri (IAIN) Sunan Ampel, Surabaya Rektor Institut Agama Islam Negeri (IAIN) Walisongo,
RESAMPLING BERDASARKAN ESTIMASI DENSITAS KERNEL BIVARIAT
 RESAMPLING BERDASARKAN ESTIMASI DENSITAS KERNEL BIVARIAT Adi Setiawan Program Studi Matematika Fakultas Sains dan Matematika Universitas Kristen Satya Wacana Jl. Diponegoro 52-60 Salatiga 50711 e-mail
RESAMPLING BERDASARKAN ESTIMASI DENSITAS KERNEL BIVARIAT Adi Setiawan Program Studi Matematika Fakultas Sains dan Matematika Universitas Kristen Satya Wacana Jl. Diponegoro 52-60 Salatiga 50711 e-mail
BAB IV ANALISIS FORMULA PENENTUAN ARAH KIBLAT DENGAN THEODOLIT DALAM BUKU EPHEMERIS HISAB RUKYAT 2013
 BAB IV ANALISIS FORMULA PENENTUAN ARAH KIBLAT DENGAN THEODOLIT DALAM BUKU EPHEMERIS HISAB RUKYAT 2013 A. Konsep Penentuan Arah Kiblat Dengan Theodolit Dalam Buku Ephemeris Hisab Rukyat 2013 Konsep penentuan
BAB IV ANALISIS FORMULA PENENTUAN ARAH KIBLAT DENGAN THEODOLIT DALAM BUKU EPHEMERIS HISAB RUKYAT 2013 A. Konsep Penentuan Arah Kiblat Dengan Theodolit Dalam Buku Ephemeris Hisab Rukyat 2013 Konsep penentuan
BAB I PENDAHULUAN. yang akurat dan diperbaharui (update) yang dikenal dengan istilah Sistem
 BAB I PENDAHULUAN I.1. Latar Belakang Informasi geografis biasanya digambarkan dalam peta manual dengan ragam informasi yang tertulis dalam lembaran kertas (atlas). Tetapi kini, dengan adanya teknologi,
BAB I PENDAHULUAN I.1. Latar Belakang Informasi geografis biasanya digambarkan dalam peta manual dengan ragam informasi yang tertulis dalam lembaran kertas (atlas). Tetapi kini, dengan adanya teknologi,
Dosen : Haryono Putro, ST.,SE.,MT.
 ILMU UKUR TANAH (Geodetic Engineering) Dosen : Haryono Putro, ST.,SE.,MT. Can be accessed on: http://haryono_putro.staff.gunadarma.ac.id/ Email: haryono_putro@gunadarma.ac.id Materi I.U.T. 1. Pendahuluan
ILMU UKUR TANAH (Geodetic Engineering) Dosen : Haryono Putro, ST.,SE.,MT. Can be accessed on: http://haryono_putro.staff.gunadarma.ac.id/ Email: haryono_putro@gunadarma.ac.id Materi I.U.T. 1. Pendahuluan
BAB 6 KESIMPULAN DAN SARAN 6.1 Kesimpulan Berdasarkan analisis, desain, implementasi perangkat lunak, dan pembahasan pada bab-bab sebelumnya, maka
 BAB 6 KESIMPULAN DAN SARAN 6.1 Kesimpulan Berdasarkan analisis, desain, implementasi perangkat lunak, dan pembahasan pada bab-bab sebelumnya, maka dapat ditarik kesimpulan: 1. Aplikasi web Sistem Monitoring
BAB 6 KESIMPULAN DAN SARAN 6.1 Kesimpulan Berdasarkan analisis, desain, implementasi perangkat lunak, dan pembahasan pada bab-bab sebelumnya, maka dapat ditarik kesimpulan: 1. Aplikasi web Sistem Monitoring
BAB IV APLIKASI DAN UJI AKURASI DATA GLOBAL POSITIONING SYSTEM (GPS) DAN AZIMUTH MATAHARI PADA SMARTPHONE BERBASIS ANDROID UNTUK HISAB ARAH KIBLAT
 BAB IV APLIKASI DAN UJI AKURASI DATA GLOBAL POSITIONING SYSTEM (GPS) DAN AZIMUTH MATAHARI PADA SMARTPHONE BERBASIS ANDROID UNTUK HISAB ARAH KIBLAT Dalam tahap uji akurasi ini, analisis yang hendak penulis
BAB IV APLIKASI DAN UJI AKURASI DATA GLOBAL POSITIONING SYSTEM (GPS) DAN AZIMUTH MATAHARI PADA SMARTPHONE BERBASIS ANDROID UNTUK HISAB ARAH KIBLAT Dalam tahap uji akurasi ini, analisis yang hendak penulis
PENGGUNAAN METODE BAYESIAN OBYEKTIF DALAM INFERENSI PARAMETER POPULASI SERAGAM
 PENGGUNAAN METODE BAYESIAN OBYEKTIF DALAM INFERENSI PARAMETER POPULASI SERAGAM Adi Setiawan Program Studi Matematika, Fakultas Sains dan Matematika Universitas Kristen Satya Wacana Jl. Diponegoro 52-6
PENGGUNAAN METODE BAYESIAN OBYEKTIF DALAM INFERENSI PARAMETER POPULASI SERAGAM Adi Setiawan Program Studi Matematika, Fakultas Sains dan Matematika Universitas Kristen Satya Wacana Jl. Diponegoro 52-6
MAKALAH SISTEM TRANSFORMASI KOORDINAT 2 DIMENSI DISUSUN OLEH : HERA RATNAWATI 16/395027/TK/44319
 MAKALAH SISTEM TRANSFORMASI KOORDINAT DIMENSI DISUSUN OLEH : HERA RATNAWATI 16/9507/TK/19 DEPARTEMEN TEKNIK GEODESI FAKULTAS TEKNIK UNIVERSITAS GADJAH MADA 017 1 KATA PENGANTAR Puji dan syukur kehadirat
MAKALAH SISTEM TRANSFORMASI KOORDINAT DIMENSI DISUSUN OLEH : HERA RATNAWATI 16/9507/TK/19 DEPARTEMEN TEKNIK GEODESI FAKULTAS TEKNIK UNIVERSITAS GADJAH MADA 017 1 KATA PENGANTAR Puji dan syukur kehadirat
Analisis Perbedaan Perhitungan Arah Kiblat pada Bidang Spheroid dan Ellipsoid dengan Menggunakan Data Koordinat GPS
 JURNAL TEKNIK POMITS Vol. 2, No. 1, (Juni, 2013) ISSN: 2301-9271 1 Analisis Perbedaan Perhitungan pada Bidang Spheroid dan Ellipsoid dengan Menggunakan Data Koordinat GPS Andhika Prastyadi Nugroho dan
JURNAL TEKNIK POMITS Vol. 2, No. 1, (Juni, 2013) ISSN: 2301-9271 1 Analisis Perbedaan Perhitungan pada Bidang Spheroid dan Ellipsoid dengan Menggunakan Data Koordinat GPS Andhika Prastyadi Nugroho dan
SMARTPHONE SEBAGAI ALAT BANTU NAVIGASI UNTUK PENGENDARA SEPEDA BERBASISKAN ANDROID TUGAS AKHIR
 SMARTPHONE SEBAGAI ALAT BANTU NAVIGASI UNTUK PENGENDARA SEPEDA BERBASISKAN ANDROID TUGAS AKHIR Sebagai persyaratan guna meraih gelar Sarjana Strata 1 Teknik Informatika Universitas Muhammadiyah Malang
SMARTPHONE SEBAGAI ALAT BANTU NAVIGASI UNTUK PENGENDARA SEPEDA BERBASISKAN ANDROID TUGAS AKHIR Sebagai persyaratan guna meraih gelar Sarjana Strata 1 Teknik Informatika Universitas Muhammadiyah Malang
BAB I PENDAHULUAN. electronic map yang ditunjukkan oleh garis lintang dan bujur sehingga
 BAB I PENDAHULUAN 1.1 Latar Belakang Pada dasarnya mobile device dibuat dengan tujuan hanya untuk komunikasi suara dan pengiriman pesan. Namun berbeda dengan sekarang, ada beberapa aspek yang membuat komunikasi
BAB I PENDAHULUAN 1.1 Latar Belakang Pada dasarnya mobile device dibuat dengan tujuan hanya untuk komunikasi suara dan pengiriman pesan. Namun berbeda dengan sekarang, ada beberapa aspek yang membuat komunikasi
PENGKONSTRUKSIAN GRAFIK PENGENDALI BERDASAR BOXPLOT BIVARIAT
 S-3 PENGKONSTRUKSIAN GRAFIK PENGENDALI BERDASAR BOXPLOT BIVARIAT Frangky Masipupu 1), Adi Setiawan ), Bambang Susanto 3) 1) Mahasiswa Program Studi Matematika ) 3) Dosen Program Studi Matematika Program
S-3 PENGKONSTRUKSIAN GRAFIK PENGENDALI BERDASAR BOXPLOT BIVARIAT Frangky Masipupu 1), Adi Setiawan ), Bambang Susanto 3) 1) Mahasiswa Program Studi Matematika ) 3) Dosen Program Studi Matematika Program
SISTEM KOORDINAT GEOGRAFIK
 SISTEM KOORDINAT GEOGRAFIK Oleh: Ir. Djawahir, M.Sc Untuk mengidentifikasi posisi titik di bumi atau yang terkait dengan bumi, dikembangkanlah Sistem Koordinat Geografik dengan mendefinisikan bentuk bumi
SISTEM KOORDINAT GEOGRAFIK Oleh: Ir. Djawahir, M.Sc Untuk mengidentifikasi posisi titik di bumi atau yang terkait dengan bumi, dikembangkanlah Sistem Koordinat Geografik dengan mendefinisikan bentuk bumi
2009 ACADEMY QU IDMATHCIREBON
 NASKAH UJIAN NASIONAL TAHUN PELAJARAN 2008/2009 Jenjang Sekolah : SMA/MA Hari/Tanggal : Rabu/22 April 2009 Program Studi : IPA Waktu : 08.00 10.00 Petunjuk: Pilihlah satu jawababan yang tepat! 1. Perhatikan
NASKAH UJIAN NASIONAL TAHUN PELAJARAN 2008/2009 Jenjang Sekolah : SMA/MA Hari/Tanggal : Rabu/22 April 2009 Program Studi : IPA Waktu : 08.00 10.00 Petunjuk: Pilihlah satu jawababan yang tepat! 1. Perhatikan
TRIGONOMETRI BAB 7. A. Perbandingan Trigonometri pada Segitiga Siku-siku
 BAB 7 TRIGONOMETRI A. Perbandingan Trigonometri pada Segitiga Siku-siku Gambar disamping menunjukkan segitiga dengan besar sudut α o c a Sisi di hadapan sudut siku-siku yaitu sisi c disebut sisi miring
BAB 7 TRIGONOMETRI A. Perbandingan Trigonometri pada Segitiga Siku-siku Gambar disamping menunjukkan segitiga dengan besar sudut α o c a Sisi di hadapan sudut siku-siku yaitu sisi c disebut sisi miring
PEMANFAATAN GOOGLEMAPS UNTUK PEMETAAN DAN PENCARIAN DATA PERGURUAN TINGGI NEGERI DI INDONESIA
 SISFO-Jurnal Sistem Informasi PEMANFAATAN GOOGLEMAPS UNTUK PEMETAAN DAN PENCARIAN DATA PERGURUAN TINGGI NEGERI DI INDONESIA Umi Laili Yuhana 1, I G.L.A. Oka Cahyadi P. 2, Hadziq Fabroyir 1 1 Jurusan Teknik
SISFO-Jurnal Sistem Informasi PEMANFAATAN GOOGLEMAPS UNTUK PEMETAAN DAN PENCARIAN DATA PERGURUAN TINGGI NEGERI DI INDONESIA Umi Laili Yuhana 1, I G.L.A. Oka Cahyadi P. 2, Hadziq Fabroyir 1 1 Jurusan Teknik
MATEMATIKA TEKNIK II BILANGAN KOMPLEKS
 MATEMATIKA TEKNIK II BILANGAN KOMPLEKS 2 PENDAHULUAN SISTEM BILANGAN KOMPLEKS REAL IMAJINER RASIONAL IRASIONAL BULAT PECAHAN BULAT NEGATIF CACAH ASLI 0 3 ILUSTRASI Carilah akar-akar persamaan x 2 + 4x
MATEMATIKA TEKNIK II BILANGAN KOMPLEKS 2 PENDAHULUAN SISTEM BILANGAN KOMPLEKS REAL IMAJINER RASIONAL IRASIONAL BULAT PECAHAN BULAT NEGATIF CACAH ASLI 0 3 ILUSTRASI Carilah akar-akar persamaan x 2 + 4x
Matematika EBTANAS Tahun 1986
 Matematika EBTANAS Tahun 986 EBT-SMA-86- Bila diketahui A = { x x bilangan prima < }, B = { x x bilangan ganjil < }, maka eleman A B =.. 3 7 9 EBT-SMA-86- Bila matriks A berordo 3 dan matriks B berordo
Matematika EBTANAS Tahun 986 EBT-SMA-86- Bila diketahui A = { x x bilangan prima < }, B = { x x bilangan ganjil < }, maka eleman A B =.. 3 7 9 EBT-SMA-86- Bila matriks A berordo 3 dan matriks B berordo
MATEMATIKA. Sesi TRANSFORMASI 2 CONTOH SOAL A. ROTASI
 MATEMATIKA KELAS XII IPA - KURIKULUM GABUNGAN 14 Sesi NGAN TRANSFORMASI A. ROTASI Rotasi adalah memindahkan posisi suatu titik (, y) dengan cara dirotasikan pada titik tertentu sebesar sudut tertentu.
MATEMATIKA KELAS XII IPA - KURIKULUM GABUNGAN 14 Sesi NGAN TRANSFORMASI A. ROTASI Rotasi adalah memindahkan posisi suatu titik (, y) dengan cara dirotasikan pada titik tertentu sebesar sudut tertentu.
