Pertemuan 2 & 3 DEKOMPOSISI SPEKTRAL DAN DEKOMPOSISI NILAI SINGULAR
|
|
|
- Adi Gunardi
- 9 tahun lalu
- Tontonan:
Transkripsi
1 Pertemuan 2 & 3 DEKOMPOSISI SPEKTRAL DAN DEKOMPOSISI NILAI SINGULAR
2 Ingat : Vektor dan Matriks Ortogonal vektor dan a dan b saling ortogonal jika a dan b saling ortonormal jika a dan b di normalisasi (normalized) : u dan v saling ortonormal : dan
3 Ilustrasi 1 Saling ortogonal karena dan dan Saling ortonormal karena dimana Saling ortogonal dan saling ortonormal karena dan
4 Matriks ortogonal Matriks dikatakan ortogonal jika or Ini berarti setiap kolom (baris) dari Q saling ortonormal, yakni dan, untuk adalah matriks ortogonal (periksa)
5 Eigenvalues and Eigenvectors dan vector Pasangan disebut pasanganpasanagan nilai eigen dan vektor eigen yang bersesuaian jika setiap memenuhi persamaan Nilai-nilai igen dapat diperoleh dengan menyelesaikan prsamaan (determinan) Jika A simetri, maka semua nilai eigen bernilai riil Jika A definit positif maka semua nilai eigen bernilai positif Secara umum dapat bernilai kompleks Pada umumnya dalam statistik multivariat kita bekerja pada vektor-vektor eigen yang normnya 1 (normalized)
6 Jika vektor-vektor eigen ortonormal maka kita punya persamaan matriks (lihat teks) atau Hasil ini memegang peranan dalam dekomposisi spektral atau ortogonal diagonal
7 Dekomposisi spektral dari matrik simeri Definit positif simetri Dekomposisi spektral nilai-nilai eigen dari A Vektor-vektor eigen (normalized) yang bersesuaian dengan (ortonormal)
8 Sifat-sifat matriks simetri simetri Mempunyai k pasangan nilai eigen dan vektor eigen Vektor-vektor eigen yang bersesuaian dengan nilainilai eigen, semuanya ortonormal Semua nilai eigen bernilai riil Jika salah satu nilai eigen bernilai nol, berimplikasi A singular Jika A nonsingular, maka terdapat invers
9 Contoh
10 Lanjutan Mudah diperiksa bahwa P ortogonal
11 Matriks Definit positif & Form Kuadratik Misalkan matriks simetri dan vector A disebut definit positif jika x A x disebut bentuk kuadratik Matriks simetri definit positif jika dan hanya jika semua nilai eigennya positif Definit positif dari bentuk kuadratik dapat di interpretasikan sebagai kuadrat jarak
12 Rangkuman Misal matriks simetri berukuran. Maka mempunyai k pasang nilai eigen dan vektor eigen Vektor-vektor eigen dapat dipilih sehingga memenuhi dan saling mutually perpendicular Matrik simetri mempunyai dekomposisi spektral dimana adalah nilai-nilai eigen dari A dan adalah vektor-vektor eigen (yang dinormalisasi/uniter) yang bersesuaian dengan dan
13 Matrik defenit positif dengan dekomposisi spektral matriks yang kolom-kolomnya merupakan Misalkan vektor-vrktor eigen yang dinormalisir, maka dimana dan matriks diagonal CC: Dalam hal ini A harus definit positif, dimana semua nilai-nilai eigennnya juga positif
14 A matriks definit positif dengan dekomposisi spektral dan inversnya maka disebut matriks akar kuadrat atau matriks standar deviasi dimana dan
15 Ilustrasi 1 matriks simetri Nilai-nilai eigen diperoleh dengan menyelesaikan persamaan Untuk Untuk, vektor eigennya,, dinormalisasi menjadi vektor eigennya, dinormalisasi menjadi Dekomposisi spektral dari A adalah CC : disini ada nilai eigen bernilai negatif ( definit positif. Akibatnya, tidak berlaku?? ), jadi A bukan matriks
16 Ilustrasi 2 (A definit positif) Nilai-nilai eigen Vektor2 eigen dinormalisasi dinormalisasi dinormalisasi Dekomposisi spektral
17 Karena A definit positif (semua nilai eigen positif), maka
18 DEKOMPOSISI NILAI SINGULAR
19 Nilai Singulir dan Dekomposisi Singulir Maka dekomposisi singulir adalah dimana r buah vektor unit ortog berukuran mx1 r buah vektor unit ortog berukuran kx1 dengan entri (i,i) adalah pasanagn nilai eigen dan vektor eigen
20 Ilustrasi Tentukan dekomposisi nilai singulir dari matriks Solusi A nilai-nilai eigen nilai-nilai eigen Jadi
21 Matriks-matriks khusus
22 Perkalian Kronecker Definisi 2.1 Misalkan A dan B dua buah matriks masing-masing berukuran maka perkalian Kronecker (Kronecker product) dari A dan B dan dinotasikan sebagai yaitu suatu matriks berukuran didefinisikan sebagai, Misal dan = maka
23 Operator Operator yang mentransformasikan matriks kedalam bentuk vektor disebut operator vec disingkat. Jika A adalah matriks berukuran maka dengan kolom ke-i adalah adalah sebuah vektor berukuran dan dinyatakan sebagai Misal maka
24 Matriks Komutasi (Commutation matriks) Suatu matriks bujur sangkar P disebut matriks komutasi jika setiap baris dan setiap kolom dari matrik P hanya mengandung sebuah elemen 1, dan yang lainnya adalah nol. Matriks Identitas termasuk salah satu matrik komutasi. Definisi adalah matriks berukuran Misalkan yakni baris ke-i dan kolom-j. dengan elemen tidak nol, yaitu 1 pada posisi Maka matriks komutasi berukuran dinotasikan dengan dan didefenisikan sebagai
25 Contoh membentuk matriks Komutasi Misalakan diberikan dua matriks identitas dan kolom pertama dari dan kolom pertama dari maka sehingga adalah adalah
26 Selanjutnya, kolom pertama dari dan kolom kedua dari adalah adalah maka sehingga Selanjutnya, kolom pertama dari dan kolom ketiga dari maka sehingga adalah adalah
27 Selanjutnya, kolom kedua dari dan kolom pertama dari adalah adalah maka sehingga Selanjutnya, kolom kedua dari dan kolom kedua dari maka sehingga adalah adalah
28 Selanjutnya, kolom kedua dari dan kolom ketiga dari adalah adalah maka sehingga Diperoleh Matriks komutasinya adalah
29 Dapat ditunjukkan bahwa (sifat) Perhatikan bahwa untuk memperoleh matriks komutasi, setiap kolom pada matriks identitas pertama dikalikan dengan setiap kolom pada matriks identitas yang kedua. Matriks diperoleh dari perkalian kolom ke-i pada matriks identitas pertama dengan kolom ke-j pada matriks identitas yang kedua
30 Perkalian Hadamart (The Hadamard Product) Operator dari perkalian Hadamard dinotasikan dengan yakni suatu operator yang mengalikan dua matriks berukuran sama dengan elemen-elemen yang indeksnya bersesuaian Misalkan A dan B dua matriks berukuran sama yakni maka perkalian Hadamard dari matriks A dan B didefenisikan sebagai
Tujuan. Mhs dapat mendemonstrasikan operasi matriks: penjumlahan, perkalian, dsb. serta menentukan matriks inverse
 Matriks Tujuan Mhs dapat mendemonstrasikan operasi matriks: penjumlahan, perkalian, dsb. serta menentukan matriks inverse Pengertian Matriks Adalah kumpulan bilangan yang disajikan secara teratur dalam
Matriks Tujuan Mhs dapat mendemonstrasikan operasi matriks: penjumlahan, perkalian, dsb. serta menentukan matriks inverse Pengertian Matriks Adalah kumpulan bilangan yang disajikan secara teratur dalam
ALJABAR LINIER MAYDA WARUNI K, ST, MT ALJABAR LINIER (I)
 ALJABAR LINIER MAYDA WARUNI K, ST, MT ALJABAR LINIER (I) 1 MATERI ALJABAR LINIER VEKTOR DALAM R1, R2 DAN R3 ALJABAR VEKTOR SISTEM PERSAMAAN LINIER MATRIKS, DETERMINAN DAN ALJABAR MATRIKS, INVERS MATRIKS
ALJABAR LINIER MAYDA WARUNI K, ST, MT ALJABAR LINIER (I) 1 MATERI ALJABAR LINIER VEKTOR DALAM R1, R2 DAN R3 ALJABAR VEKTOR SISTEM PERSAMAAN LINIER MATRIKS, DETERMINAN DAN ALJABAR MATRIKS, INVERS MATRIKS
Pertemuan 2 Matriks, part 2
 Pertemuan 2 Matriks, part 2 Beberapa Jenis Matriks Khusus 1. Matriks Bujur Sangkar Suatu matriks dengan banyak baris = banyak kolom = n disebut matriks bujur sangkar berukuran n (berordo n). Barisan elemen
Pertemuan 2 Matriks, part 2 Beberapa Jenis Matriks Khusus 1. Matriks Bujur Sangkar Suatu matriks dengan banyak baris = banyak kolom = n disebut matriks bujur sangkar berukuran n (berordo n). Barisan elemen
MATRIKS. Notasi yang digunakan NOTASI MATRIKS
 MATRIKS Beberapa pengertian tentang matriks : 1. Matriks adalah himpunan skalar (bilangan riil atau kompleks) yang disusun atau dijajarkan secara empat persegi panjang menurut baris-baris dan kolom-kolom.
MATRIKS Beberapa pengertian tentang matriks : 1. Matriks adalah himpunan skalar (bilangan riil atau kompleks) yang disusun atau dijajarkan secara empat persegi panjang menurut baris-baris dan kolom-kolom.
Minggu II Lanjutan Matriks
 Minggu II Lanjutan Matriks Pokok Bahasan Sub Pokok Bahasan Tujuan Instruksional Umum Tujuan Instruksional Khusus Jumlah Pertemuan : Matriks : A. Transformasi Elementer. Transformasi Elementer pada baris
Minggu II Lanjutan Matriks Pokok Bahasan Sub Pokok Bahasan Tujuan Instruksional Umum Tujuan Instruksional Khusus Jumlah Pertemuan : Matriks : A. Transformasi Elementer. Transformasi Elementer pada baris
Eigen value & Eigen vektor
 Eigen value & Eigen vektor Hubungan antara vektor x (bukan nol) dengan vektor Ax yang berada di R n pada proses transformasi dapat terjadi dua kemungkinan : 1) 2) Tidak mudah untuk dibayangkan hubungan
Eigen value & Eigen vektor Hubungan antara vektor x (bukan nol) dengan vektor Ax yang berada di R n pada proses transformasi dapat terjadi dua kemungkinan : 1) 2) Tidak mudah untuk dibayangkan hubungan
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI Pada bab ini akan dipaparkan mengenai konsep dasar tentang matriks meliputi definisi matriks, jenis-jenis matriks, operasi matriks, determinan, kofaktor, invers suatu matriks, serta
BAB 2 LANDASAN TEORI Pada bab ini akan dipaparkan mengenai konsep dasar tentang matriks meliputi definisi matriks, jenis-jenis matriks, operasi matriks, determinan, kofaktor, invers suatu matriks, serta
Aljabar Linear Elementer
 BAB I RUANG VEKTOR Pada kuliah Aljabar Matriks kita telah mendiskusikan struktur ruang R 2 dan R 3 beserta semua konsep yang terkait. Pada bab ini kita akan membicarakan struktur yang merupakan bentuk
BAB I RUANG VEKTOR Pada kuliah Aljabar Matriks kita telah mendiskusikan struktur ruang R 2 dan R 3 beserta semua konsep yang terkait. Pada bab ini kita akan membicarakan struktur yang merupakan bentuk
BAB II KAJIAN PUSTAKA. operasi matriks, determinan dan invers matriks), aljabar max-plus, matriks atas
 BAB II KAJIAN PUSTAKA Pada bab ini akan diuraikan mengenai matriks (meliputi definisi matriks, operasi matriks, determinan dan invers matriks), aljabar max-plus, matriks atas aljabar max-plus, dan penyelesaian
BAB II KAJIAN PUSTAKA Pada bab ini akan diuraikan mengenai matriks (meliputi definisi matriks, operasi matriks, determinan dan invers matriks), aljabar max-plus, matriks atas aljabar max-plus, dan penyelesaian
Contoh. C. Determinan dan Invers Matriks. C. 1. Determinan
 C. Determinan dan Invers Matriks C.. Determinan Suatu matriks persegi selalu dapat dikaitkan dengan suatu bilangan yang disebut determinan. Determinan dari matriks persegi dinotasikan dengan. Untuk matriks
C. Determinan dan Invers Matriks C.. Determinan Suatu matriks persegi selalu dapat dikaitkan dengan suatu bilangan yang disebut determinan. Determinan dari matriks persegi dinotasikan dengan. Untuk matriks
TINJAUAN PUSTAKA Analisis Biplot Biasa
 TINJAUAN PUSTAKA Analisis Biplot Biasa Analisis biplot merupakan suatu upaya untuk memberikan peragaan grafik dari matriks data dalam suatu plot dengan menumpangtindihkan vektor-vektor dalam ruang berdimensi
TINJAUAN PUSTAKA Analisis Biplot Biasa Analisis biplot merupakan suatu upaya untuk memberikan peragaan grafik dari matriks data dalam suatu plot dengan menumpangtindihkan vektor-vektor dalam ruang berdimensi
Matriks biasanya dituliskan menggunakan kurung dan terdiri dari baris dan kolom: A =
 Bab 2 cakul fi080 by khbasar; sem1 2010-2011 Matriks Dalam BAB ini akan dibahas mengenai matriks, sifat-sifatnya serta penggunaannya dalam penyelesaian persamaan linier. Matriks merupakan representasi
Bab 2 cakul fi080 by khbasar; sem1 2010-2011 Matriks Dalam BAB ini akan dibahas mengenai matriks, sifat-sifatnya serta penggunaannya dalam penyelesaian persamaan linier. Matriks merupakan representasi
8 MATRIKS DAN DETERMINAN
 8 MATRIKS DAN DETERMINAN Matriks merupakan pengembangan lebih lanjut dari sistem persamaan linear. Oleh karenanya aljabar matriks sering juga disebut dengan aljabar linear. Matriks dapat digunakan untuk
8 MATRIKS DAN DETERMINAN Matriks merupakan pengembangan lebih lanjut dari sistem persamaan linear. Oleh karenanya aljabar matriks sering juga disebut dengan aljabar linear. Matriks dapat digunakan untuk
II. TINJAUAN PUSTAKA. nyata (fenomena-fenomena alam) ke dalam bagian-bagian matematika yang. disebut dunia matematika (mathematical world).
 5 II. TINJAUAN PUSTAKA 2.1. Pemodelan Matematika Definisi pemodelan matematika : Pemodelan matematika adalah suatu deskripsi dari beberapa perilaku dunia nyata (fenomena-fenomena alam) ke dalam bagian-bagian
5 II. TINJAUAN PUSTAKA 2.1. Pemodelan Matematika Definisi pemodelan matematika : Pemodelan matematika adalah suatu deskripsi dari beberapa perilaku dunia nyata (fenomena-fenomena alam) ke dalam bagian-bagian
SOLUSI PENDEKATAN TERBAIK SISTEM PERSAMAAN LINEAR TAK KONSISTEN MENGGUNAKAN DEKOMPOSISI NILAI SINGULAR
 Buletin Ilmiah Math. Stat. dan Terapannya (Bimaster) Volume 03, No. 1 (2014), hal 91 98. SOLUSI PENDEKATAN TERBAIK SISTEM PERSAMAAN LINEAR TAK KONSISTEN MENGGUNAKAN DEKOMPOSISI NILAI SINGULAR Febrianti,
Buletin Ilmiah Math. Stat. dan Terapannya (Bimaster) Volume 03, No. 1 (2014), hal 91 98. SOLUSI PENDEKATAN TERBAIK SISTEM PERSAMAAN LINEAR TAK KONSISTEN MENGGUNAKAN DEKOMPOSISI NILAI SINGULAR Febrianti,
Matriks. Modul 1 PENDAHULUAN
 Modul Matriks Dra. Sri Haryatmi Kartiko, M.Sc. I PENDAHULUAN lmu pengetahuan dewasa ini menjadi semakin kuantitatif. Data numerik dengan skala besar, hasil pengukuran berupa angka sering dijumpai oleh
Modul Matriks Dra. Sri Haryatmi Kartiko, M.Sc. I PENDAHULUAN lmu pengetahuan dewasa ini menjadi semakin kuantitatif. Data numerik dengan skala besar, hasil pengukuran berupa angka sering dijumpai oleh
Lampiran 1 Pembuktian Teorema 2.3
 LAMPIRAN 16 Lampiran 1 Pembuktian Teorema 2.3 Sebelum membuktikan Teorema 2.3, terlebih dahulu diberikan beberapa definisi yang berhubungan dengan pembuktian Teorema 2.3. Definisi 1 (Matriks Eselon Baris)
LAMPIRAN 16 Lampiran 1 Pembuktian Teorema 2.3 Sebelum membuktikan Teorema 2.3, terlebih dahulu diberikan beberapa definisi yang berhubungan dengan pembuktian Teorema 2.3. Definisi 1 (Matriks Eselon Baris)
MODUL V EIGENVALUE DAN EIGENVEKTOR
 MODUL V EIGENVALUE DAN EIGENVEKTOR 5.. Pendahuluan Biasanya jika suatu matriks A berukuran mm dan suatu vektor pada R m, tidak ada hubungan antara vektor dan vektor A. Tetapi seringkali kita menemukan
MODUL V EIGENVALUE DAN EIGENVEKTOR 5.. Pendahuluan Biasanya jika suatu matriks A berukuran mm dan suatu vektor pada R m, tidak ada hubungan antara vektor dan vektor A. Tetapi seringkali kita menemukan
BAB III PEREDUKSIAN RUANG INDIVIDU DENGAN ANALISIS KOMPONEN UTAMA. Analisis komponen utama adalah metode statistika multivariat yang
 BAB III PEREDUKSIAN RUANG INDIVIDU DENGAN ANALISIS KOMPONEN UTAMA Analisis komponen utama adalah metode statistika multivariat yang bertujuan untuk mereduksi dimensi data dengan membentuk kombinasi linear
BAB III PEREDUKSIAN RUANG INDIVIDU DENGAN ANALISIS KOMPONEN UTAMA Analisis komponen utama adalah metode statistika multivariat yang bertujuan untuk mereduksi dimensi data dengan membentuk kombinasi linear
BAB 2 TINJAUAN PUSTAKA
 5 BAB 2 TINJAUAN PUSTAKA 2.1 Matriks 2.1.1 Definisi Matriks Matriks adalah suatu kumpulan angka-angka yang juga sering disebut elemenelemen yang disusun secara teratur menurut baris dan kolom berbentuk
5 BAB 2 TINJAUAN PUSTAKA 2.1 Matriks 2.1.1 Definisi Matriks Matriks adalah suatu kumpulan angka-angka yang juga sering disebut elemenelemen yang disusun secara teratur menurut baris dan kolom berbentuk
DIAGONALISASI MATRIKS KOMPLEKS
 Buletin Ilmiah Mat Stat dan Terapannya (Bimaster) Volume 04, No 3 (2015), hal 337-346 DIAGONALISASI MATRIKS KOMPLEKS Heronimus Hengki, Helmi, Mariatul Kiftiah INTISARI Matriks kompleks merupakan matriks
Buletin Ilmiah Mat Stat dan Terapannya (Bimaster) Volume 04, No 3 (2015), hal 337-346 DIAGONALISASI MATRIKS KOMPLEKS Heronimus Hengki, Helmi, Mariatul Kiftiah INTISARI Matriks kompleks merupakan matriks
PENDAHULUAN LANDASAN ANALISIS
 10 PENDAHULUAN Latar Belakang Biplot merupakan metode eksplorasi analisis data peubah ganda yang dapat memberikan gambaran secara grafik tentang kedekatan antar objek, keragaman peubah, korelasi antar
10 PENDAHULUAN Latar Belakang Biplot merupakan metode eksplorasi analisis data peubah ganda yang dapat memberikan gambaran secara grafik tentang kedekatan antar objek, keragaman peubah, korelasi antar
MATRIKS A = ; B = ; C = ; D = ( 5 )
 MATRIKS A. DEFINISI MATRIKS Matriks adalah suatu susunan bilangan berbentuk segi empat dari suatu unsur-unsur pada beberapa sistem aljabar. Unsur-unsur tersebut bisa berupa bilangan dan juga suatu peubah.
MATRIKS A. DEFINISI MATRIKS Matriks adalah suatu susunan bilangan berbentuk segi empat dari suatu unsur-unsur pada beberapa sistem aljabar. Unsur-unsur tersebut bisa berupa bilangan dan juga suatu peubah.
I PENDAHULUAN II LANDASAN TEORI
 I PENDAHULUAN 1.1 Latar Belakang Matriks merupakan istilah yang digunakan untuk menunjukkan jajaran persegi panjang dari bilangan-bilangan dan setiap matriks akan mempunyai baris dan kolom. Salah satu
I PENDAHULUAN 1.1 Latar Belakang Matriks merupakan istilah yang digunakan untuk menunjukkan jajaran persegi panjang dari bilangan-bilangan dan setiap matriks akan mempunyai baris dan kolom. Salah satu
BAB V DIAGONALISASI DAN DEKOMPOSISI MATRIKS. Sub bab ini membahas tentang faktorisasi matriks A berorde nxn ke dalam hasil
 BAB V DIAGONALISASI DAN DEKOMPOSISI MATRIKS. Diagonalisasi Sub bab ini membahas tentang faktorisasi matriks A berorde nn ke dalam hasil kali berbentuk PDP, di mana D adalah matriks diagonal. Jika diperoleh
BAB V DIAGONALISASI DAN DEKOMPOSISI MATRIKS. Diagonalisasi Sub bab ini membahas tentang faktorisasi matriks A berorde nn ke dalam hasil kali berbentuk PDP, di mana D adalah matriks diagonal. Jika diperoleh
7. NILAI-NILAI VEKTOR EIGEN. Nilai Eigen dan Vektor Eigen Diagonalisasi Diagonalisasi Ortogonal
 7. NILAI-NILAI VEKTOR EIGEN Nilai Eigen dan Vektor Eigen Diagonalisasi Diagonalisasi Ortogonal Nilai Eigen, Vektor Eigen Diketahui A matriks nxn dan x adalah suatu vektor pada R n, maka biasanya tdk ada
7. NILAI-NILAI VEKTOR EIGEN Nilai Eigen dan Vektor Eigen Diagonalisasi Diagonalisasi Ortogonal Nilai Eigen, Vektor Eigen Diketahui A matriks nxn dan x adalah suatu vektor pada R n, maka biasanya tdk ada
Matriks Jawab:
 Matriks A. Operasi Matriks 1) Penjumlahan Matriks Jika A dan B adalah sembarang Matriks yang berordo sama, maka penjumlahan Matriks A dengan Matriks B adalah Matriks yang diperoleh dengan cara menjumlahkan
Matriks A. Operasi Matriks 1) Penjumlahan Matriks Jika A dan B adalah sembarang Matriks yang berordo sama, maka penjumlahan Matriks A dengan Matriks B adalah Matriks yang diperoleh dengan cara menjumlahkan
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI 2.1 Sistem Persamaan Linier Sistem Persamaan dengan m persamaan dan n bilangan tak diketahui ditulis dengan : Dimana x 1, x 2, x n : bilangan tak diketahui a,b : konstanta Jika SPL
BAB 2 LANDASAN TEORI 2.1 Sistem Persamaan Linier Sistem Persamaan dengan m persamaan dan n bilangan tak diketahui ditulis dengan : Dimana x 1, x 2, x n : bilangan tak diketahui a,b : konstanta Jika SPL
BAB I PENDAHULUAN 1.1 Latar Belakang
 BAB I PENDAHULUAN 1.1 Latar Belakang Pembahasan mendasar mengenai matriks terutama yang berkaitan dengan matriks yang dapat didiagonalisasi telah jelas disajikan dalam referensi yang biasanya digunakan
BAB I PENDAHULUAN 1.1 Latar Belakang Pembahasan mendasar mengenai matriks terutama yang berkaitan dengan matriks yang dapat didiagonalisasi telah jelas disajikan dalam referensi yang biasanya digunakan
LEMBAR AKTIVITAS SISWA MATRIKS (WAJIB)
 LEMBAR AKTIVITAS SISWA MATRIKS (WAJIB) Nama Siswa Kelas : : Kompetensi Dasar (Kurikulum 2013): 3.1 Menganalisis konsep, nilai determinan dan sifat operasi matriks serta menerapkannya dalam menentukan invers
LEMBAR AKTIVITAS SISWA MATRIKS (WAJIB) Nama Siswa Kelas : : Kompetensi Dasar (Kurikulum 2013): 3.1 Menganalisis konsep, nilai determinan dan sifat operasi matriks serta menerapkannya dalam menentukan invers
a11 a12 x1 b1 Kumpulan Materi Kuliah #1 s/d #03 Tahun Ajaran 2016/2016: Oleh: Prof. Dr. Ir. Setijo Bismo, DEA.
 a11 a12 x1 b1 a a x b 21 22 2 2 Kumpulan Materi Kuliah #1 s/d #03 Tahun Ajaran 2016/2016: Oleh: Prof. Dr. Ir. Setijo Bismo, DEA. a11 a12 x1 b1 a a x b 21 22 2 2 a11 a12 x1 b1 a a x b 21 22 2 2 Setijo Bismo
a11 a12 x1 b1 a a x b 21 22 2 2 Kumpulan Materi Kuliah #1 s/d #03 Tahun Ajaran 2016/2016: Oleh: Prof. Dr. Ir. Setijo Bismo, DEA. a11 a12 x1 b1 a a x b 21 22 2 2 a11 a12 x1 b1 a a x b 21 22 2 2 Setijo Bismo
03-Pemecahan Persamaan Linier (2)
 -Pemecahan Persamaan Linier () Dosen: Anny Yuniarti, M.Comp.Sc Gasal - Anny Agenda Bagian : Matriks Invers Bagian : Eliminasi = Faktorisasi: A = LU Bagian : Transpos dan Permutasi Anny Bagian MATRIKS INVERS
-Pemecahan Persamaan Linier () Dosen: Anny Yuniarti, M.Comp.Sc Gasal - Anny Agenda Bagian : Matriks Invers Bagian : Eliminasi = Faktorisasi: A = LU Bagian : Transpos dan Permutasi Anny Bagian MATRIKS INVERS
Bab 2 LANDASAN TEORI
 17 Bab 2 LANDASAN TEORI 2.1 Aljabar Matriks 2.1.1 Definisi Matriks Matriks adalah suatu kumpulan angka-angka yang juga sering disebut elemen-elemen yang disusun secara teratur menurut baris dan kolom sehingga
17 Bab 2 LANDASAN TEORI 2.1 Aljabar Matriks 2.1.1 Definisi Matriks Matriks adalah suatu kumpulan angka-angka yang juga sering disebut elemen-elemen yang disusun secara teratur menurut baris dan kolom sehingga
Matriks adalah susunan segi empat siku-siku dari objek yang diatur berdasarkan baris (row) dan kolom (column). Objek-objek dalam susunan tersebut
 Matriks adalah susunan segi empat siku-siku dari objek yang diatur berdasarkan baris (row) dan kolom (column). Objek-objek dalam susunan tersebut dinamakan entri dalam matriks atau disebut juga elemen
Matriks adalah susunan segi empat siku-siku dari objek yang diatur berdasarkan baris (row) dan kolom (column). Objek-objek dalam susunan tersebut dinamakan entri dalam matriks atau disebut juga elemen
Operasi Pada Matriks a. Penjumlahan pada Matriks ( berlaku untuk matriks matriks yang berukuran sama ). Jika A = a ij. maka matriks A = ( a ij)
 MATRIKS a a a... a n a a a... an A a a a... a n............... am am am... a mn Matriks A dengan m baris dan n kolom (A m n). Notasi Matriks : a, dimana a adalah elemen pada baris ke i kolom ke j Kesamaan
MATRIKS a a a... a n a a a... an A a a a... a n............... am am am... a mn Matriks A dengan m baris dan n kolom (A m n). Notasi Matriks : a, dimana a adalah elemen pada baris ke i kolom ke j Kesamaan
BAB 7 TRANSFORMASI LINEAR PADA RUANG VEKTOR
 BAB 7 TRANSFORMASI LINEAR PADA RUANG VEKTOR A. DEFINISI DASAR 1. Definisi-1 Suatu pemetaan f dari ruang vektor V ke ruang vektor W adalah aturan perkawanan sedemikian sehingga setiap vektor v V dikawankan
BAB 7 TRANSFORMASI LINEAR PADA RUANG VEKTOR A. DEFINISI DASAR 1. Definisi-1 Suatu pemetaan f dari ruang vektor V ke ruang vektor W adalah aturan perkawanan sedemikian sehingga setiap vektor v V dikawankan
PAM 252 Metode Numerik Bab 3 Sistem Persamaan Linier
 PAM 252 Metode Numerik Bab 3 Sistem Persamaan Linier Mahdhivan Syafwan Jurusan Matematika FMIPA Universitas Andalas Semester Genap 2013/2014 1 Mahdhivan Syafwan Metode Numerik: Sistem Persamaan Linier
PAM 252 Metode Numerik Bab 3 Sistem Persamaan Linier Mahdhivan Syafwan Jurusan Matematika FMIPA Universitas Andalas Semester Genap 2013/2014 1 Mahdhivan Syafwan Metode Numerik: Sistem Persamaan Linier
Reduksi Rank pada Matriks-Matriks Tertentu
 Reduksi Rank pada Matriks-Matriks Tertentu E. Apriliani, B. Ari Sanjaya September 6, 7 Abstract. Dekomposisi nilai singular (Singular Value Decomposition - SVD) adalah suatu metode untuk menuliskan suatu
Reduksi Rank pada Matriks-Matriks Tertentu E. Apriliani, B. Ari Sanjaya September 6, 7 Abstract. Dekomposisi nilai singular (Singular Value Decomposition - SVD) adalah suatu metode untuk menuliskan suatu
Pertemuan 3 & 4 INTERPRETASI GEOMETRI DAN GENERALISASI VARIANS. Interpretasi Geometri pada Sampel. Generalisasi varians
 Pertemuan 3 & 4 INTERPRETASI GEOMETRI DAN GENERALISASI VARIANS Interpretasi Geometri pada Sampel Generalisasi varians , Interpretasi Geometri pada Sampel Sample Geometry and Random Sampling Data sampel
Pertemuan 3 & 4 INTERPRETASI GEOMETRI DAN GENERALISASI VARIANS Interpretasi Geometri pada Sampel Generalisasi varians , Interpretasi Geometri pada Sampel Sample Geometry and Random Sampling Data sampel
Trihastuti Agustinah
 TE 9467 Teknik Numerik Sistem Linear Trihastuti Agustinah Bidang Studi Teknik Sistem Pengaturan Jurusan Teknik Elektro - FTI Institut Teknologi Sepuluh Nopember O U T L I N E OBJEKTIF TEORI CONTOH 4 SIMPULAN
TE 9467 Teknik Numerik Sistem Linear Trihastuti Agustinah Bidang Studi Teknik Sistem Pengaturan Jurusan Teknik Elektro - FTI Institut Teknologi Sepuluh Nopember O U T L I N E OBJEKTIF TEORI CONTOH 4 SIMPULAN
SATUAN ACARA PERKULIAHAN MATA KULIAH : ALJABAR LINIER KODE / SKS : IT / 2 SKS
 SATUAN ACARA PERKULIAHAN MATA KULIAH : ALJABAR LINIER KODE / SKS : IT0143231 / 2 SKS Deskripsi: - Mata kuliah ini mempelajari konsep aljabar linear sebagai dasar untuk membuat algoritma dalam permasalahan
SATUAN ACARA PERKULIAHAN MATA KULIAH : ALJABAR LINIER KODE / SKS : IT0143231 / 2 SKS Deskripsi: - Mata kuliah ini mempelajari konsep aljabar linear sebagai dasar untuk membuat algoritma dalam permasalahan
GARIS-GARIS BESAR PROGRAM PEMBELAJARAN
 GARIS-GARIS BESAR PROGRAM PEMBELAJARAN Mata Kuliah : Aljabar Linear Kode / SKS : TIF-5xxx / 3 SKS Dosen : - Deskripsi Singkat : Mata kuliah ini berisi Sistem persamaan Linier dan Matriks, Determinan, Vektor
GARIS-GARIS BESAR PROGRAM PEMBELAJARAN Mata Kuliah : Aljabar Linear Kode / SKS : TIF-5xxx / 3 SKS Dosen : - Deskripsi Singkat : Mata kuliah ini berisi Sistem persamaan Linier dan Matriks, Determinan, Vektor
Vektor. Vektor. 1. Pengertian Vektor
 Universitas Muhammadiyah Sukabumi Artikel Aljabar Vektor dan Matriks Oleh : Zie_Zie Vektor Vektor 1. Pengertian Vektor a. Definisi Vektor adalah suatu besaran yang mempunyai nilai (besar) dan arah. Contohnya
Universitas Muhammadiyah Sukabumi Artikel Aljabar Vektor dan Matriks Oleh : Zie_Zie Vektor Vektor 1. Pengertian Vektor a. Definisi Vektor adalah suatu besaran yang mempunyai nilai (besar) dan arah. Contohnya
MODUL ALJABAR LINEAR 1 Disusun oleh, ASTRI FITRIA NUR ANI
 214 MODUL ALJABAR LINEAR 1 Disusun oleh, ASTRI FITRIA NUR ANI Astri Fitria Nur ani Aljabar Linear 1 1/1/214 1 DAFTAR ISI DAFTAR ISI... i BAB I MATRIKS DAN SISTEM PERSAMAAN A. Pendahuluan... 1 B. Aljabar
214 MODUL ALJABAR LINEAR 1 Disusun oleh, ASTRI FITRIA NUR ANI Astri Fitria Nur ani Aljabar Linear 1 1/1/214 1 DAFTAR ISI DAFTAR ISI... i BAB I MATRIKS DAN SISTEM PERSAMAAN A. Pendahuluan... 1 B. Aljabar
BAB 2 LANDASAN TEORI. yang dibicarakan yang akan digunakan pada bab selanjutnya. Bentuk umum dari matriks bujur sangkar adalah sebagai berikut:
 BAB 2 LANDASAN TEORI Pada bab ini dibicarakan mengenai matriks yang berbentuk bujur sangkar dengan beberapa definisi, teorema, sifat-sifat dan contoh sesuai dengan matriks tertentu yang dibicarakan yang
BAB 2 LANDASAN TEORI Pada bab ini dibicarakan mengenai matriks yang berbentuk bujur sangkar dengan beberapa definisi, teorema, sifat-sifat dan contoh sesuai dengan matriks tertentu yang dibicarakan yang
BAB II TINJAUAN PUSTAKA
 BAB II TINJAUAN PUSTAKA 2.1 Matriks Matriks adalah himpunan bilangan real yang disusun secara empat persegi panjang, mempunyai baris dan kolom dengan bentuk umum : Tiap-tiap bilangan yang berada didalam
BAB II TINJAUAN PUSTAKA 2.1 Matriks Matriks adalah himpunan bilangan real yang disusun secara empat persegi panjang, mempunyai baris dan kolom dengan bentuk umum : Tiap-tiap bilangan yang berada didalam
Latihan 7 : Similaritas, Pendiagonalan Matriks, Polinom Matriks
 Latihan 7 : Similaritas, Pendiagonalan Matriks, Polinom Matriks 6. Tentukan polinomial karakteristik dari matriks transformasi A=. Andaikan A adalah matriks persegi berdimensi x. Polinom karakteristik
Latihan 7 : Similaritas, Pendiagonalan Matriks, Polinom Matriks 6. Tentukan polinomial karakteristik dari matriks transformasi A=. Andaikan A adalah matriks persegi berdimensi x. Polinom karakteristik
BAB II TINJAUAN PUSTAKA
 5 BAB II TINJAUAN PUSTAKA A Matriks 1 Pengertian Matriks Definisi 21 Matriks adalah kumpulan bilangan bilangan yang disusun secara khusus dalam bentuk baris kolom sehingga membentuk empat persegi panjang
5 BAB II TINJAUAN PUSTAKA A Matriks 1 Pengertian Matriks Definisi 21 Matriks adalah kumpulan bilangan bilangan yang disusun secara khusus dalam bentuk baris kolom sehingga membentuk empat persegi panjang
Aljabar Linier Elementer. Kuliah 1 dan 2
 Aljabar Linier Elementer Kuliah 1 dan 2 1.3 Matriks dan Operasi-operasi pada Matriks Definisi: Matriks adalah susunan bilangan dalam empat persegi panjang. Bilangan-bilangan dalam susunan tersebut disebut
Aljabar Linier Elementer Kuliah 1 dan 2 1.3 Matriks dan Operasi-operasi pada Matriks Definisi: Matriks adalah susunan bilangan dalam empat persegi panjang. Bilangan-bilangan dalam susunan tersebut disebut
Analisa Numerik. Matriks dan Komputasi
 Analisa Numerik Matriks dan Komputasi M AT R I K S Matriks adalah suatu susunan angka atau bilangan, variabel, atau parameter yang berbentuk empat persegi dan biasanya ditutup dengan tanda kurung K O N
Analisa Numerik Matriks dan Komputasi M AT R I K S Matriks adalah suatu susunan angka atau bilangan, variabel, atau parameter yang berbentuk empat persegi dan biasanya ditutup dengan tanda kurung K O N
BAB II MATRIKS POSITIF. Pada bab ini akan dibahas mengenai Teorema Perron, yaitu teori hasil kontribusi
 BAB II MATRIKS POSITIF Pada bab ini akan dibahas mengenai Teorema Perron, yaitu teori hasil kontribusi dari seorang matematikawan German, Oskar Perron. Perron menerbitkan tulisannya tentang sifat-sifat
BAB II MATRIKS POSITIF Pada bab ini akan dibahas mengenai Teorema Perron, yaitu teori hasil kontribusi dari seorang matematikawan German, Oskar Perron. Perron menerbitkan tulisannya tentang sifat-sifat
LEMBAR AKTIVITAS SISWA MATRIKS
 Nama Siswa Kelas : : LEMBAR AKTIVITAS SISWA MATRIKS Notasi dan Ordo Matriks Lengkapilah isian berikut! Suatu matriks biasanya dinotasikan dengan huruf kapital, misalnya: A. PENGERTIAN MATRIKS 1) Tabel
Nama Siswa Kelas : : LEMBAR AKTIVITAS SISWA MATRIKS Notasi dan Ordo Matriks Lengkapilah isian berikut! Suatu matriks biasanya dinotasikan dengan huruf kapital, misalnya: A. PENGERTIAN MATRIKS 1) Tabel
Matriks. Baris ke 2 Baris ke 3
 Matriks A. Matriks Matriks adalah susunan bilangan yang diatur menurut aturan baris dan kolom dalam suatu jajaran berbentuk persegi atau persegi panjang. Susunan bilangan itu diletakkan di dalam kurung
Matriks A. Matriks Matriks adalah susunan bilangan yang diatur menurut aturan baris dan kolom dalam suatu jajaran berbentuk persegi atau persegi panjang. Susunan bilangan itu diletakkan di dalam kurung
Matematika Teknik INVERS MATRIKS
 INVERS MATRIKS Dalam menentukan solusi suatu SPL selama ini kita dihadapkan kepada bentuk matriks diperbesar dari SPL. Cara lain yang akan dikenalkan disini adalah dengan melakukan OBE pada matriks koefisien
INVERS MATRIKS Dalam menentukan solusi suatu SPL selama ini kita dihadapkan kepada bentuk matriks diperbesar dari SPL. Cara lain yang akan dikenalkan disini adalah dengan melakukan OBE pada matriks koefisien
REDUKSI RANK PADA MATRIKS-MATRIKS TERTENTU
 J. Math. and Its Appl. ISSN: 89-65X Vol. 4, No., November 7, 8 REDUKSI RANK PADA MATRIKS-MATRIKS TERTENTU Erna Apriliani, Bandung Arry Sanjoyo Jurusan Matematika FMIPA Institut Teknologi Sepuluh Nopember,
J. Math. and Its Appl. ISSN: 89-65X Vol. 4, No., November 7, 8 REDUKSI RANK PADA MATRIKS-MATRIKS TERTENTU Erna Apriliani, Bandung Arry Sanjoyo Jurusan Matematika FMIPA Institut Teknologi Sepuluh Nopember,
DETERMINAN. Determinan matriks hanya didefinisikan pada matriks bujursangkar (matriks kuadrat). Notasi determinan matriks A: Jika diketahui matriks A:
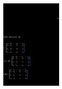 DETERMINAN Definisi Determinan Matriks Determinan matriks adalah bilangan tunggal yang diperoleh dari semua permutasi elemen matriks bujur sangkar.jika subskrip permutasi elemen matriks adalah genap (inversi
DETERMINAN Definisi Determinan Matriks Determinan matriks adalah bilangan tunggal yang diperoleh dari semua permutasi elemen matriks bujur sangkar.jika subskrip permutasi elemen matriks adalah genap (inversi
MUH1G3/ MATRIKS DAN RUANG VEKTOR
 MUHG3/ MATRIKS DAN RUANG VEKTOR TIM DOSEN Determinan Matriks Determinan Matriks Sub Pokok Bahasan Permutasi dan Determinan Matriks Determinan dengan OBE Determinan dengan Ekspansi Kofaktor Beberapa Aplikasi
MUHG3/ MATRIKS DAN RUANG VEKTOR TIM DOSEN Determinan Matriks Determinan Matriks Sub Pokok Bahasan Permutasi dan Determinan Matriks Determinan dengan OBE Determinan dengan Ekspansi Kofaktor Beberapa Aplikasi
Aljabar Linear. & Matriks. Evangs Mailoa. Pert. 5
 Aljabar Linear & Matriks Pert. 5 Evangs Mailoa Pengantar Determinan Menurut teorema 1.4.3, matriks 2 x 2 dapat dibalik jika ad bc 0. Pernyataan ad bc disebut sebagai determinan (determinant) dari matriks
Aljabar Linear & Matriks Pert. 5 Evangs Mailoa Pengantar Determinan Menurut teorema 1.4.3, matriks 2 x 2 dapat dibalik jika ad bc 0. Pernyataan ad bc disebut sebagai determinan (determinant) dari matriks
MATRIKS. Definisi: Matriks adalah susunan bilangan-bilangan yang berbentuk segiempat siku-siku yang terdiri dari baris dan kolom.
 Page- MATRIKS Definisi: Matriks adalah susunan bilangan-bilangan yang berbentuk segiempat siku-siku yang terdiri dari baris dan kolom. Notasi: Matriks dinyatakan dengan huruf besar, dan elemen elemennya
Page- MATRIKS Definisi: Matriks adalah susunan bilangan-bilangan yang berbentuk segiempat siku-siku yang terdiri dari baris dan kolom. Notasi: Matriks dinyatakan dengan huruf besar, dan elemen elemennya
BAB II LANDASAN TEORI. yang biasanya dinyatakan dalam bentuk sebagai berikut: =
 BAB II LANDASAN TEORI 2.1 Matriks Definisi 2.1 (Lipschutz, 2006): Matriks adalah susunan segiempat dari skalarskalar yang biasanya dinyatakan dalam bentuk sebagai berikut: Setiap skalar yang terdapat dalam
BAB II LANDASAN TEORI 2.1 Matriks Definisi 2.1 (Lipschutz, 2006): Matriks adalah susunan segiempat dari skalarskalar yang biasanya dinyatakan dalam bentuk sebagai berikut: Setiap skalar yang terdapat dalam
DIKTAT PERKULIAHAN. EDISI 1 Aljabar Linear dan Matriks
 DIKTAT PERKULIAHAN EDISI 1 Aljabar Linear dan Matriks Penulis : Ednawati Rainarli, M.Si. Kania Evita Dewi, M.Si. JURUSAN TEKNIK INFORMATIKA UNIVERSITAS KOMPUTER INDONESIA BANDUNG 011 IF/011 1 DAFTAR ISI
DIKTAT PERKULIAHAN EDISI 1 Aljabar Linear dan Matriks Penulis : Ednawati Rainarli, M.Si. Kania Evita Dewi, M.Si. JURUSAN TEKNIK INFORMATIKA UNIVERSITAS KOMPUTER INDONESIA BANDUNG 011 IF/011 1 DAFTAR ISI
II. TINJAUAN PUSTAKA. Suatu matriks didefinisikan dengan huruf kapital yang dicetak tebal, misalnya A,
 II. TINJAUAN PUSTAKA 2.1 Konsep-konsep Matriks Definisi Matriks Suatu matriks didefinisikan dengan huruf kapital yang dicetak tebal, misalnya A, B, X, Y. Elemen-elemen di dalamnya disebut skalar yang berasal
II. TINJAUAN PUSTAKA 2.1 Konsep-konsep Matriks Definisi Matriks Suatu matriks didefinisikan dengan huruf kapital yang dicetak tebal, misalnya A, B, X, Y. Elemen-elemen di dalamnya disebut skalar yang berasal
BAB II TEORI KODING DAN TEORI INVARIAN
 BAB II TEORI KODING DAN TEORI INVARIAN Pada bab 1 ini akan dibahas definisi kode, khususnya kode linier atas dan pencacah bobot Hammingnya. Di samping itu, akan dijelaskanan invarian, ring invarian dan
BAB II TEORI KODING DAN TEORI INVARIAN Pada bab 1 ini akan dibahas definisi kode, khususnya kode linier atas dan pencacah bobot Hammingnya. Di samping itu, akan dijelaskanan invarian, ring invarian dan
MENENTUKAN INVERS MOORE PENROSE DARI MATRIKS KOMPLEKS
 MENENTUKAN INVERS MOORE PENROSE DARI MATRIKS KOMPLEKS skripsi disajikan sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains Program Studi Matematika oleh Astin Wita Yunihapsari 4150407021 JURUSAN
MENENTUKAN INVERS MOORE PENROSE DARI MATRIKS KOMPLEKS skripsi disajikan sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains Program Studi Matematika oleh Astin Wita Yunihapsari 4150407021 JURUSAN
Aljabar Linear Elementer MUG1E3 3 SKS
 // ljabar Linear Elementer MUGE SKS // 9:7 Jadwal Kuliah Hari I Selasa, jam. Hari II Kamis, jam. Sistem Penilaian UTS % US % Quis % // 9:7 M- ljabar Linear // Silabus : Bab I Matriks dan Operasinya Bab
// ljabar Linear Elementer MUGE SKS // 9:7 Jadwal Kuliah Hari I Selasa, jam. Hari II Kamis, jam. Sistem Penilaian UTS % US % Quis % // 9:7 M- ljabar Linear // Silabus : Bab I Matriks dan Operasinya Bab
SATUAN ACARA PERKULIAHAN MATA KULIAH : ALJABAR LINIER JURUSAN : TEKNIK KOMPUTER JUMLAH SKS : Definisi, Notasi, dan Operasi Vektor 2.
 SATUAN ACARA PERKULIAHAN MATA KULIAH : ALJABAR LINIER JURUSAN : TEKNIK KOMPUTER JUMLAH SKS : 3 Minggu Ke Pokok Bahasan dan TIU Sub Pokok Bahasan Sasaran Belajar Cara Pengajaran Media Tugas Referens i 1
SATUAN ACARA PERKULIAHAN MATA KULIAH : ALJABAR LINIER JURUSAN : TEKNIK KOMPUTER JUMLAH SKS : 3 Minggu Ke Pokok Bahasan dan TIU Sub Pokok Bahasan Sasaran Belajar Cara Pengajaran Media Tugas Referens i 1
MATRIK dan RUANG VEKTOR
 MATRIK dan RUANG VEKTOR A. Matrik. Pendahuluan Sebuah matrik didefinisikan sebagai susunan persegi panjang dari bilangan bilangan yang diatur dalam baris dan kolom. Matrik ditulis sebagai berikut: a a
MATRIK dan RUANG VEKTOR A. Matrik. Pendahuluan Sebuah matrik didefinisikan sebagai susunan persegi panjang dari bilangan bilangan yang diatur dalam baris dan kolom. Matrik ditulis sebagai berikut: a a
MATRIKS Nuryanto, ST., MT.
 MateMatika ekonomi MATRIKS TUJUAN INSTRUKSIONAL KHUSUS Setelah mempelajari bab ini, anda diharapkan dapat : 1. Pengertian matriks 2. Operasi matriks 3. Jenis matriks 4. Determinan 5. Matriks invers 6.
MateMatika ekonomi MATRIKS TUJUAN INSTRUKSIONAL KHUSUS Setelah mempelajari bab ini, anda diharapkan dapat : 1. Pengertian matriks 2. Operasi matriks 3. Jenis matriks 4. Determinan 5. Matriks invers 6.
BAB 2 ALJABAR MATRIKS UNTUK STATISTIKA
 BAB 2 ALJABAR MATRIKS UNTUK STATISTIKA Analisis data, khususnya estimasi parameter dalam regresi multivariat, banyak melibatkan operasi matriks. Dalam bab ini akan dibahas teori matriks yang banyak terkait
BAB 2 ALJABAR MATRIKS UNTUK STATISTIKA Analisis data, khususnya estimasi parameter dalam regresi multivariat, banyak melibatkan operasi matriks. Dalam bab ini akan dibahas teori matriks yang banyak terkait
Yang dibahas : Ortogonal Basis ortogonal Ortonormal Matrik ortogonal Komplemen ortogonal Proyeksi ortogonal Faktorisasi QR
 Ortogonal Yang dibahas : Ortogonal Basis ortogonal Ortonormal Matrik ortogonal Komplemen ortogonal Proyeksi ortogonal Faktorisasi QR Ortogonal Himpunan vektor {v, v,.., v k } dalam R n disebut himpunan
Ortogonal Yang dibahas : Ortogonal Basis ortogonal Ortonormal Matrik ortogonal Komplemen ortogonal Proyeksi ortogonal Faktorisasi QR Ortogonal Himpunan vektor {v, v,.., v k } dalam R n disebut himpunan
BAB 4 RUANG VEKTOR EUCLID. Dr. Ir. Abdul Wahid Surhim, MT.
 BAB 4 RUANG VEKTOR EUCLID Dr. Ir. Abdul Wahid Surhim, MT. KERANGKA PEMBAHASAN 1. Ruang n Euclid 2. Transformasi Linier dari R n dan R m 3. Sifat-sifat Transformasi Linier 4.1 RUANG N EUCLID Jika di bab
BAB 4 RUANG VEKTOR EUCLID Dr. Ir. Abdul Wahid Surhim, MT. KERANGKA PEMBAHASAN 1. Ruang n Euclid 2. Transformasi Linier dari R n dan R m 3. Sifat-sifat Transformasi Linier 4.1 RUANG N EUCLID Jika di bab
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI 2.1 Aljabar Matriks 2.1.1 Definisi Matriks Matriks adalah suatu kumpulan angka-angka yang juga sering disebut elemen-elemen yang disusun secara teratur menurut baris dan kolom sehingga
BAB 2 LANDASAN TEORI 2.1 Aljabar Matriks 2.1.1 Definisi Matriks Matriks adalah suatu kumpulan angka-angka yang juga sering disebut elemen-elemen yang disusun secara teratur menurut baris dan kolom sehingga
BAB 6 RUANG HASIL KALI DALAM. Dr. Ir. Abdul Wahid Surhim, MT.
 BAB 6 RUANG HASIL KALI DALAM Dr. Ir. Abdul Wahid Surhim, MT. KERANGKA PEMBAHASAN 1. Hasil Kali Dalam 2. Sudut dan Keortogonalan pada Ruang Hasil Kali Dalam 3.Basis Ortogonal, Proses Gram-Schmidt 4.Perubahan
BAB 6 RUANG HASIL KALI DALAM Dr. Ir. Abdul Wahid Surhim, MT. KERANGKA PEMBAHASAN 1. Hasil Kali Dalam 2. Sudut dan Keortogonalan pada Ruang Hasil Kali Dalam 3.Basis Ortogonal, Proses Gram-Schmidt 4.Perubahan
MATRIKS. a A mxn = 21 a 22 a 2n a m1 a m2 a mn a ij disebut elemen dari A yang terletak pada baris i dan kolom j.
 MATRIKS A. Definisi Matriks 1. Definisi Matriks dan Ordo Matriks Matriks adalah susunan bilangan (elemen) yang disusun menurut baris dan kolom dan dibatasi dengan tanda kurung. Jika suatu matriks tersusun
MATRIKS A. Definisi Matriks 1. Definisi Matriks dan Ordo Matriks Matriks adalah susunan bilangan (elemen) yang disusun menurut baris dan kolom dan dibatasi dengan tanda kurung. Jika suatu matriks tersusun
5. PERSAMAAN LINIER. 1. Berikut adalah contoh SPL yang terdiri dari 4 persamaan linier dan 3 variabel.
 1. Persamaan Linier 5. PERSAMAAN LINIER Persamaan linier adalah suatu persamaan yang variabel-variabelnya berpangkat satu. Disamping persamaan linier ada juga persamaan non linier. Contoh : a) 2x + 3y
1. Persamaan Linier 5. PERSAMAAN LINIER Persamaan linier adalah suatu persamaan yang variabel-variabelnya berpangkat satu. Disamping persamaan linier ada juga persamaan non linier. Contoh : a) 2x + 3y
uiopasdfghjklzxcvbnmqwertyuiopasd fghjklzxcvbnmqwertyuiopasdfghjklzx wertyuiopasdfghjklzxcvbnmqwertyui opasdfghjklzxcvbnmqwertyuiopasdfg
 uiopasdfghjklzxcvbnmqwertyuiopasd Qwertyuiopasdfghjklzxcvbnmqwerty cvbnmqwertyuiopasdfghjklzxcvbnmq fghjklzxcvbnmqwertyuiopasdfghjklzx wertyuiopasdfghjklzxcvbnmqwertyui opasdfghjklzxcvbnmqwertyuiopasdfg
uiopasdfghjklzxcvbnmqwertyuiopasd Qwertyuiopasdfghjklzxcvbnmqwerty cvbnmqwertyuiopasdfghjklzxcvbnmq fghjklzxcvbnmqwertyuiopasdfghjklzx wertyuiopasdfghjklzxcvbnmqwertyui opasdfghjklzxcvbnmqwertyuiopasdfg
Konsep Dasar. Modul 1 PENDAHULUAN
 Modul 1 Konsep Dasar M PENDAHULUAN Drs. Suryo Guritno, M.Stats., Ph.D. ateri yang akan dibahas dalam modul ini adalah konsep-konsep dasar aljabar matriks yang meliputi pengertian matriks, vektor dan skalar;
Modul 1 Konsep Dasar M PENDAHULUAN Drs. Suryo Guritno, M.Stats., Ph.D. ateri yang akan dibahas dalam modul ini adalah konsep-konsep dasar aljabar matriks yang meliputi pengertian matriks, vektor dan skalar;
MATRIKS. Matriks adalah himpunan skalar (bilangan riil/kompleks) yang disusun secara empat persegi panjang (menurut baris dan kolom)
 MTRIKS DEFINISI Bentuk umum =(aij),i=,,...m J=,,...m a a a n baris a a..a n baris MTRIKS Matriks adalah himpunan skalar (bilangan riil/kompleks) yang disusun secara empat persegi panjang (menurut baris
MTRIKS DEFINISI Bentuk umum =(aij),i=,,...m J=,,...m a a a n baris a a..a n baris MTRIKS Matriks adalah himpunan skalar (bilangan riil/kompleks) yang disusun secara empat persegi panjang (menurut baris
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI Pada bab ini akan dibahas beberapa definisi dan teorema dengan atau tanpa bukti yang akan digunakan untuk menentukan regularisasi sistem singular linier. Untuk itu akan diberikan terlebih
BAB 2 LANDASAN TEORI Pada bab ini akan dibahas beberapa definisi dan teorema dengan atau tanpa bukti yang akan digunakan untuk menentukan regularisasi sistem singular linier. Untuk itu akan diberikan terlebih
KS KALKULUS DAN ALJABAR LINEAR Eigen Value Eigen Vector TIM KALIN
 KS091206 KALKULUS DAN ALJABAR LINEAR Eigen Value Eigen Vector TIM KALIN TUJUAN INSTRUKSIONAL KHUSUS Setelah menyelesaikan pertemuan ini mahasiswa diharapkan: Dapat menghitung eigen value dan eigen vector
KS091206 KALKULUS DAN ALJABAR LINEAR Eigen Value Eigen Vector TIM KALIN TUJUAN INSTRUKSIONAL KHUSUS Setelah menyelesaikan pertemuan ini mahasiswa diharapkan: Dapat menghitung eigen value dan eigen vector
BAB 3 FUNGSI MONOTON MATRIKS
 BAB 3 FUNGSI MONOTON MATRIKS Pada bab ini akan dibahas fungsi monoton matriks. Dalam mengkontruksi fungsi monoton matriks banyak istilah yang harus kita ketahui sebelumnya. Beberapa konsep yang akan dibahas
BAB 3 FUNGSI MONOTON MATRIKS Pada bab ini akan dibahas fungsi monoton matriks. Dalam mengkontruksi fungsi monoton matriks banyak istilah yang harus kita ketahui sebelumnya. Beberapa konsep yang akan dibahas
BAB VII MATRIKS DAN SISTEM LINEAR TINGKAT SATU
 BAB VII MATRIKS DAN SISTEM LINEAR TINGKAT SATU Sistem persamaan linear orde/ tingkat satu memiliki bentuk standard : = = = = = = = = = + + + + + + + + + + Diasumsikan koefisien = dan fungsi adalah menerus
BAB VII MATRIKS DAN SISTEM LINEAR TINGKAT SATU Sistem persamaan linear orde/ tingkat satu memiliki bentuk standard : = = = = = = = = = + + + + + + + + + + Diasumsikan koefisien = dan fungsi adalah menerus
Matriks. Matriks B A B. A. Pengertian Matriks. B. Operasi Hitung pada Matriks. C. Determinan dan Invers
 Matriks B B 3. Pengertian Matriks B. Operasi Hitung pada Matriks C. Determinan dan Invers Matriks D. Penerapan Matriks dalam Sistem Persamaan Linear Sumber: www.smanela-bali.net Pernahkah kalian mengamati
Matriks B B 3. Pengertian Matriks B. Operasi Hitung pada Matriks C. Determinan dan Invers Matriks D. Penerapan Matriks dalam Sistem Persamaan Linear Sumber: www.smanela-bali.net Pernahkah kalian mengamati
I. TINJAUAN PUSTAKA. distribusi normal multivariat, yaitu suatu kombinasi linier dari elemen-elemennya adalah
 I. TINJAUAN PUSTAKA 1.1 Distribusi Normal Multivariat Akan dibahas dua definisi dari multivariat normal. Definisi yang pertama didefinisikan melalui fungsi kepekatan peluangnya, dan definisi yang kedua
I. TINJAUAN PUSTAKA 1.1 Distribusi Normal Multivariat Akan dibahas dua definisi dari multivariat normal. Definisi yang pertama didefinisikan melalui fungsi kepekatan peluangnya, dan definisi yang kedua
BAB II KAJIAN TEORI. linier, varian dan simpangan baku, standarisasi data, koefisien korelasi, matriks
 BAB II KAJIAN TEORI Pada bab II akan dibahas tentang materi-materi dasar yang digunakan untuk mendukung pembahasan pada bab selanjutnya, yaitu matriks, kombinasi linier, varian dan simpangan baku, standarisasi
BAB II KAJIAN TEORI Pada bab II akan dibahas tentang materi-materi dasar yang digunakan untuk mendukung pembahasan pada bab selanjutnya, yaitu matriks, kombinasi linier, varian dan simpangan baku, standarisasi
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI 2.1 Noise Pada saat melakukan pengambilan gambar, setiap gangguan pada gambar dinamakan dengan noise. Noise dipakai untuk proses training corrupt image, gambarnya diberi noise dan
BAB 2 LANDASAN TEORI 2.1 Noise Pada saat melakukan pengambilan gambar, setiap gangguan pada gambar dinamakan dengan noise. Noise dipakai untuk proses training corrupt image, gambarnya diberi noise dan
MATRIKS. 3. Matriks Persegi Matriks persegi adalah matriks yang mempunyai baris dan kolom yang sama.
 MATRIKS Matriks adalah susunan berbeda dalam bentuk persegi panjang yang diatur pada baris dan kolom. NOTASI MATRIKS DAN ORDO MATRIKS Notasi matriks biasanya dituliskan dalam huruf kapital (huruf besar)
MATRIKS Matriks adalah susunan berbeda dalam bentuk persegi panjang yang diatur pada baris dan kolom. NOTASI MATRIKS DAN ORDO MATRIKS Notasi matriks biasanya dituliskan dalam huruf kapital (huruf besar)
1.1. Definisi, Notasi, dan Operasi Vektor 1.2. Susunan Koordinat Ruang R n 1.3. Vektor di dalam R n 1.4. Persamaan garis lurus dan bidang rata
 SATUAN ACARA PERKULIAHAN (SAP) MATA KULIAH : MATEMATIKA INFORMATIKA 2 JURUSAN : S1-TEKNIK INFORMATIKA KODE MATA KULIAH : IT-045214 Referensi : [1]. Yusuf Yahya, D. Suryadi. H.S., Agus S., Matematika untuk
SATUAN ACARA PERKULIAHAN (SAP) MATA KULIAH : MATEMATIKA INFORMATIKA 2 JURUSAN : S1-TEKNIK INFORMATIKA KODE MATA KULIAH : IT-045214 Referensi : [1]. Yusuf Yahya, D. Suryadi. H.S., Agus S., Matematika untuk
TINJAUAN PUSTAKA. dianalisis dan hasilnya ditransformasi menjadi matriks berukuran??
 TINJAUAN PUSTAKA Data Disagregat dan Agregat Berdasarkan cara pengumpulannya, data dapat dibedakan atas data internal dan data eksternal. Data internal berasal dari lingkungan sendiri sedangkan data eksternal
TINJAUAN PUSTAKA Data Disagregat dan Agregat Berdasarkan cara pengumpulannya, data dapat dibedakan atas data internal dan data eksternal. Data internal berasal dari lingkungan sendiri sedangkan data eksternal
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI 2.1. Repeated Measurement Dalam repeated measurement setiap perlakuan menunjukkan pengukuran terhadap satu sampel (unit eksperimen ) atau beberapa sampel yang memiliki karakter sama
BAB 2 LANDASAN TEORI 2.1. Repeated Measurement Dalam repeated measurement setiap perlakuan menunjukkan pengukuran terhadap satu sampel (unit eksperimen ) atau beberapa sampel yang memiliki karakter sama
MATEMATIKA INFORMATIKA 2 TEKNIK INFORMATIKA UNIVERSITAS GUNADARMA FENI ANDRIANI
 MATEMATIKA INFORMATIKA 2 TEKNIK INFORMATIKA UNIVERSITAS GUNADARMA FENI ANDRIANI SAP (1) Buku : Suryadi H.S. 1991, Pengantar Aljabar dan Geometri analitik Vektor Definisi, Notasi, dan Operasi Vektor Susunan
MATEMATIKA INFORMATIKA 2 TEKNIK INFORMATIKA UNIVERSITAS GUNADARMA FENI ANDRIANI SAP (1) Buku : Suryadi H.S. 1991, Pengantar Aljabar dan Geometri analitik Vektor Definisi, Notasi, dan Operasi Vektor Susunan
BAB 4 : SISTEM PERSAMAAN LINIER
 BAB 4 : SISTEM PERSAMAAN LINIER 4.1 PERSAMAAN LINIER Misalnya x 2 Matematika analitik membicarakan ilmu ukur secara aljabar. Garis lurus pada bidang x 1 dan x 2 dapat dinyatakan sebagai persamaan a 1 x
BAB 4 : SISTEM PERSAMAAN LINIER 4.1 PERSAMAAN LINIER Misalnya x 2 Matematika analitik membicarakan ilmu ukur secara aljabar. Garis lurus pada bidang x 1 dan x 2 dapat dinyatakan sebagai persamaan a 1 x
Aljabar Linear Elementer MA SKS. 07/03/ :21 MA-1223 Aljabar Linear 1
 Aljabar Linear Elementer MA SKS 7//7 : MA- Aljabar Linear Jadwal Kuliah Hari I Hari II jam jam Sistem Penilaian UTS 4% UAS 4% Quis % 7//7 : MA- Aljabar Linear Silabus : Bab I Matriks dan Operasinya Bab
Aljabar Linear Elementer MA SKS 7//7 : MA- Aljabar Linear Jadwal Kuliah Hari I Hari II jam jam Sistem Penilaian UTS 4% UAS 4% Quis % 7//7 : MA- Aljabar Linear Silabus : Bab I Matriks dan Operasinya Bab
SATUAN ACARA PERKULIAHAN UNIVERSITAS GUNADARMA
 Mata Kuliah : Matematika Diskrit 2 Kode / SKS : IT02 / 3 SKS Program Studi : Sistem Komputer Fakultas : Ilmu Komputer & Teknologi Informasi. Pendahuluan 2. Vektor.. Pengantar mata kuliah aljabar linier.
Mata Kuliah : Matematika Diskrit 2 Kode / SKS : IT02 / 3 SKS Program Studi : Sistem Komputer Fakultas : Ilmu Komputer & Teknologi Informasi. Pendahuluan 2. Vektor.. Pengantar mata kuliah aljabar linier.
DETERMINAN, INVERS, PENYELESAIAN SISTEM PERSAMAAN LINEAR
 DETERMINAN, INVERS, PENYELESAIAN SISTEM PERSAMAAN LINEAR DETERMINAN Definisi Setiap matriks kuadrat/persegi mempunyai suatu nilai khusus yang diseut determinan. determinan adalah jumlah hasil kali elementer
DETERMINAN, INVERS, PENYELESAIAN SISTEM PERSAMAAN LINEAR DETERMINAN Definisi Setiap matriks kuadrat/persegi mempunyai suatu nilai khusus yang diseut determinan. determinan adalah jumlah hasil kali elementer
BAB III MENENTUKAN PRIORITAS DALAM AHP. Wharton School of Business University of Pennsylvania pada sekitar tahun 1970-an
 BAB III MENENTUKAN PRIORITAS DALAM AHP Pada bab ini dibahas mengenai AHP yang dikembangkan oleh Thomas L Saaty di Wharton School of Business University of Pennsylvania pada sekitar tahun 970-an dan baru
BAB III MENENTUKAN PRIORITAS DALAM AHP Pada bab ini dibahas mengenai AHP yang dikembangkan oleh Thomas L Saaty di Wharton School of Business University of Pennsylvania pada sekitar tahun 970-an dan baru
6 Sistem Persamaan Linear
 6 Sistem Persamaan Linear Pada bab, kita diminta untuk mencari suatu nilai x yang memenuhi persamaan f(x) = 0. Pada bab ini, masalah tersebut diperumum dengan mencari x = (x, x,..., x n ) yang secara sekaligus
6 Sistem Persamaan Linear Pada bab, kita diminta untuk mencari suatu nilai x yang memenuhi persamaan f(x) = 0. Pada bab ini, masalah tersebut diperumum dengan mencari x = (x, x,..., x n ) yang secara sekaligus
MULTIMEDIA PEMBELAJARAN DIAGONALISASI MATRIKS
 MULTIMEDIA PEMBELAJARAN DIAGONALISASI MATRIKS 1 Kirana Permata Putri, 2 Ardi Pujiyanta(0529056601) 1,2 Program Studi Teknik Informatika Universitas Ahmad Dahlan Prof. Dr. Soepomo, S.H., Janturan, Umbulharjo,
MULTIMEDIA PEMBELAJARAN DIAGONALISASI MATRIKS 1 Kirana Permata Putri, 2 Ardi Pujiyanta(0529056601) 1,2 Program Studi Teknik Informatika Universitas Ahmad Dahlan Prof. Dr. Soepomo, S.H., Janturan, Umbulharjo,
SUMMARY ALJABAR LINEAR
 SUMMARY ALJABAR LINEAR SUMANANG MUHTAR GOZALI KBK ANALISIS UNIVERSITAS PENDIDIKAN INDONESIA BANDUNG 2010 2 KATA PENGANTAR Bismillahirrahmanirrahim Segala puji bagi Allah Rabb semesta alam. Shalawat serta
SUMMARY ALJABAR LINEAR SUMANANG MUHTAR GOZALI KBK ANALISIS UNIVERSITAS PENDIDIKAN INDONESIA BANDUNG 2010 2 KATA PENGANTAR Bismillahirrahmanirrahim Segala puji bagi Allah Rabb semesta alam. Shalawat serta
BAB I PENDAHULUAN. 3) Untuk mengetahui apa yang dimaksud dengan invers matriks. 4) Untuk mengetahui apa yang dimaksud dengan determinan matriks
 1.1 LATAR BELAKANG BAB I PENDAHULUAN Teori matriks merupakan salah satu cabang ilmu aljabar linier yang menjadi pembahasan penting dalam ilmu matematika. Sejalan dengan perkembangan ilmu pengetahuan, aplikasi
1.1 LATAR BELAKANG BAB I PENDAHULUAN Teori matriks merupakan salah satu cabang ilmu aljabar linier yang menjadi pembahasan penting dalam ilmu matematika. Sejalan dengan perkembangan ilmu pengetahuan, aplikasi
