KESEIMBANGAN BENDA TERAPUNG
|
|
|
- Ari Widjaja
- 9 tahun lalu
- Tontonan:
Transkripsi
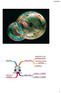
1 /8/ KEEIMBANGAN BENDA TERAPUNG Mepelajari asalah : Prinsip huku Archiees Prinsip keseibangan an kestabilan Menghitung besar gaya apung an letak pusat apung Mengevaluasi kestabilan bena terena atau terapung
2 /8/
3 /8/
4 /8/
5 /8/ 5
6 /8/ 6
7 /8/ Kesipulan Bena yang terrena i ala air engalai gaya berat seniri bena (G) yang bekerja vertikal ke bawah an gaya apung (B) yang bekerja vertikal ke atas. Besar gaya apung saa engan berat zat cair yang ipinahkan bena. Gaya berat bekerja paa pusat berat bena (G); an gaya apung bekerja paa pusat apung (B), yang saa engan pusat berat zat cair yang ipinahkan bena. G > B Bena tenggela G = B Bena elayang (terena) G < B Bena engapung Bena terena akan stabil jika pusat berat G beraa i bawah pusat apung B. Bena terapung ala kesetibangan stabil apabila pusat beratnya G beraa i bawah pusat apung (B). Bena terapung engan konisi tertentu apat pula ala kesetibangan stabil eskipun pusat beratnya beraa i atas pusat apung. Konisi stabilitas bena apat iketahui berasarkan tinggi etasentru. 7
8 /8/ M M M Menghitung tinggi etasentru GM BM BM I BG OG Apabila : Bena Bena Bena BG OB tabil Netral Tiak Diana engan : GM = tinggi etasentru Io = oen inersia tapang bena yang terpotong perukaan zat cair = volue zat cair yang ipinahkan bena BG = jarak antara pusat berat an pusat apung OG = jarak antara pusat berat an asar OB = jarak antara pusat apung an asar tabil TUGA oal :tabilitas Bena Terapung. Batu i uara epunyai berat 5 N, seang beratnya i ala air aalah N. Hitung volue an rapat relatif batu itu.. Balok segi epat engan ukuran 75 c x 5 c x 5 c engapung i air engan sisi panjangnya sejajar uka air. Apabila bagian ari balok yang beraa i atas perukaan air aalah c, hitung berat balok.. Kubus kayu engan panajang sisi-sisinya,5 epunyai rapat relatif,6 engapung i air. Hitung bagian kubus yang terena ala air.. Balok kayu engan panjang, lebar, an tingginya, engapung secara horizontal i air engan sisi tingginya vertikal. Rapat relatif kayu =,7. Hitung volue air yang ipinahkan an letak pusat apung. 5. Kubus kayu sisi,5 engapung i ala air. Berapakah berat beban yang harus iletakan i atas balok supaya balok terena seluruhnya. Rapat relatif kayu =,7. 8
9 /8/ 6. uatu balok ponton engan lebar B=6,, panjang L= an sarat =,5 engapung i air tawar ( = kg/). Hitung: a. Berat balok ponton b. arat apabila beraa i air laut ( = 5 kg/ ) c. Beban yang apat iukung oleh ponton i air tawar apabila sarat aksiu yang iijinkan aalah,. 7. Kubus engan sisi 5 c an rapat relatif,9 engapung i air engan salah satu sisinya sejajar uka air. Berapakah beban harus iletakkan i atas kubus supaya kubus tersebut tenggela i ala air. 8. Balok kayu engapung i air tawar engan bagian yang beraa i atas perukaan air aalah c. Apabila balok tersebut iapungkan i ala inyak engan rapat relatif,8; bagian balok yang beraa i atas perukaan inyak aalah 7,5 c. berapakah rapat reatif balok. 9. Tangki berbentuk kotak engan panjang an lebar,5 iisi air tawar an air raksa sapai ¾ kali tingginya. Berat tangki aalah 75 N. volue air aalah 9 kali volue air raksa. Tangki tersebut iletakan i air laut sehingga engapung engan bagian yang beraa i atas air aalah setinggi,. Apabila rapat relatif air raksa aalah,6 tentukan tinggi aksiu tangki. Rapat assa air laut an air tawar aalah kg/ an kg/. 9
10 /8/.Pelapung siliner engan iaeter an tinggi engapung engan subunya vertikal. Berat pelapung aalah ton. eliiki stabilitas pelapung..balok berpenapang bujur sangkar engan panjang sisinya,5 an tinggi H engapung i ala air. Rapat relatif balok,8. Berapakah tinggi H supaya balok apat terapung stabil engan sisi tingginya vertikal..iliner beriaeter eter an tingginya eter terbuat ari bahan engan rapat relatif,8. Bena tersebut engapung i ala air engan subunya vertikal. Hitunglah tinggi etasentru an seliiki stabilitas bena..balok terbuat ari bahan engan rapat relatif,8. epunyai panjang L=, an tapang lintang bujur sangkar engan sisi,8 iapungkan i ala air engan subu panjangnya vertikal. Hitung tinggi etasentru an seliiki stabilitas bena..iliner beriaeter 5 c an rapat relatif,9. Apabila siliner engapung i ala air engan subunya vertikal, tentukan panjang aksiu siliner.
11 /8/ 5.iliner engan iaeter,5 an panjang engapung secara vertikal i laut. Rapat assa air laut aalah kg/. Tentukan rapat assa bahan siliner apabila bena ala konisi tiak stabil. 6.iliner kayu engan rapat relatif,7 engapung i air tawar engan sisi panjangnya vertikal. Apabila panjang an iaeter siliner aalah L an D, berapakah perbaningan antara D an L seeikian sehingga siliner apat engapung stabil. 7.Balok engan panjang L=,, lebar B=,8 an tinggi H=,6 iapungkan i ala air engan sisi tingginya vertikal. Rapat relatif balok aalah =,8. eliiki stabilitas bena. Apabila i atas balok tersebut iletakan plat besi engan panjang an lebar yang saa engan balok an tebalnya T=,, seliiki stabilitas bena gabungan. Rapat relatif besi =7,85. 8.Ponton segiepat engan panjang, lebar an tinggi epunyai berat kn. Di bagian atas ponton iletakan siliner engan iaeter 7 an berat 6 kn. Pusat berat siliner an ponton ianggap terletak paa garis vertikal yang saa an elalui pusat berat ponton. Hitung tinggi etasentru. Rapat relatif air laut,.
12 /8/ 9.uatu balok engan panjang epunyai tapang lintang bujur sangkar engan sisi c epunyai rapat relatif,5. Bagian bawah balok tersebut setebal,5 c epunyai rapat relatif 8. Balok iapungkan engan posisi beriri (lihat gabar). eliiki stabilitas bena Apabila bena tiak stabil, berapakah panjang bagian balok yang epunyai rapat relatif,5 supaya bena bisa engapung stabil.. iliner terbuat ari ua bahan beriaeter,5 engapung i ala air. Bagian atas sepanjang, terbuat ari kayu engan rapat relatif,8; seangkan bagian bawah epunyai rapat relatif 5. Hitung panjang bagian bawah agar siliner apat engapung engan sisi panjang vertikal.. iliner engan panjang L, iaeter D an rapat relatif engapung ala zat cair engan rapat relatif. Tunjukan bahwa siliner akan engapung stabil gn, ubunya vertikal apabila L D/ ubunya horisontal apabila L D
13 /8/. Ponton ibuat engan enghubungkan ua buah balok sepanjang, lebar, an tinggi,5 yang engapung i ala air tawar. Rapat relatif balok kayu =,6. eliiki stabilitas balok tunggal an eliiki stabilitas ponton. Apabila i atas ponton terapat beban seberat 75 kg engan pusat berat paa jarak,5 ari sisi atas balok. Beban tersebut beraa paa tengah-tengah ponton.. Pelapung siliner beriaeter an panjang epunyai berat kn iapungkan iair laut (=,) engan subu eanjangnya vertikal. eliiki stabilitas bena. Apabila pelapung tiak stabil, berapakah gaya tarik yang harus iberikan paa rantai yang ipasang paa pusat asar siliner supaya siliner ala konisi stabil (engapung stabil)..kerucut paat engapung i ala air engan subunya vertikal seeikian sehingga puncaknya beraa i bawah. Apabila suut puncak kerucut aalah o, tentukan rapat relatif bena seeikian sehingga bena ala kesetibangan stabil.
14 /8/ 5.Kerucut terbuat ari bahan engan rapat relatif =,7 engapung i atas zat cair engan rapat relatif =,9. Hitung suut puncak kerucut iniu seeikian sehingga kerucut apat engapung engan puncaknya ibawah. 6.Pelapung siliner beriaeter D=, an tinggi H=,75 epunyai berat 5 N engapung i air laut (=,5) engan subu vertical. Di pusat sisi atas siliner iberi beban. Letak pusat berat beban aalah,5 ari sisi atas siliner. Berapakah berat beban aksiu supaya pelapung tetap ala konisi stabil. 7.Kapal engan panjang 6 lebar 8, an berat 5 MN. Muatan iatas kapal seberat 5 kn bergerak paa arah lebar sejauh sehingga enyebabkan kapal iring o. Moen Inersia tapang kapal paa elevasi uka air aalah 7% ari oen inersia segi epat yang engelilinginya. Pusat apung terletak paa,5 i bawah uka air. Tentukan tinggi etasentru an posisi pusat berat kapal. Rapat assa air laut =5 kg/. 8.Ponton bujur sangkar engan sisi 6 an tinggi, engapung i atas air. Apabila iatas ponton iberi beban seberat ton, bagian ari ponton yang terena air aalah,6. Beban beraa paa tengahtengah ponton. Pusat berat ponton aalah,6 iatas asar an pusat berat beban, iatas sisi ponton. eliiki stabilitas ponton. Berapa beban aksiu sehingga ponton tiak stabil.
15 /8/ Jawaban Tugas No. Gaya apung (B) aalah saa engan perbeaan antara berat batu i uara an i ala air: B Wiuara 5 B.. g. x9,8x , Wiair N Menurut huku Archiees, gaya apung (B) aalah saa engan berat air yang ipinahkan batu. Berat air yang ipinahkan batu (B) aalah saa engan perkalian antara volue air yang ipinahkan () an berat jenis air. Dari keua nilai B i atas, olue air aalah saa engan volue batu, sehingga volue batu aalah =,. Berat batu i uara aalah saa engan berat jenis batu ikalikan volue batu, Pusat apung(b) aalah titik p ana gaya apung bekerja. Pusat apung ini erupakan pusat berat ari volue zat cair yang ipinahkan W iuara 5. x9,8x, 5kg/. g. air 5,5 Jawaban Tugas No. Tinggi balok yang terena i ala air: 5 c, olue bagian balok yang terena i air:,x,5x,75,5 Berat balok = berat zat cair yang ipinahkan air. x,5 5 kgf 5
16 /8/ Jawaban Tugas No. Misal W : berat kubus, B : gaya apung : kealaan bagian kubus yang terena air Rapat relatif : bena air Berat bena : Gaya apung : bena Paa konisi engapung, berat bena aalah saa engan gaya apung:. air,6x 6, kgf W bena. 6 x,5 75, N B air. air _ yg_ ipinahkan x(,5x,5 x) 5, W B 75, 5,, Jai kealaan kubus yang terena air=,. Jawaban Tugas No. olue balok : =.x,x,=, Berat Balok : W Balok. g.. air. W,7xx9,8x, 8, N olue air yang ipinahkan : Berat _ balok berat _ jenis _ air 8, x9,8,8 Kealaan bagian balok yg terena air : olue_ air _ yg _ ipinahkan tapang _ balok _ p _ uka_ air Letak pusat apung :,8,, A, x, OB, 5 Jai letak pusat apung aalah,5 ari asar balok. 6
17 /8/ Jawaban Tugas No.5# olue balok : =,5 x,5 x,5 =,5 Berat Balok : olue air yang ipinahkan : W,7x x,5 87, 5kgf W Kealaan bagian balok yg terena air : W Balok.. air. 87,5 A, 875 air,875, A,5x,5 5 Jawaban Tugas No.5# Jika iatas Balok iberi beban engan berat W,aka berat total balok+beban aalah: W total W W, 5 87 W Apabila balok terena seluruhnya, berarti kealaan balok yg terena air aalah =,5. olue air yang ipinahkan bena : A A.,5x,5x,5, 5 Gaya apung : B air. A x,5 5, kgf Dengan enyaakan berat total an gaya apung : Wtotal B 87,5 W 5, W 7, 5kgf Jai berat beban i atas balok aalah W =7,5 kgf 7
18 /8/ Jawaban Tugas No.6 a. Dala keaaa terapung, berat bena aalah saa engan berat air yang ipinahkan bena (B) : G B. g. B. L. x9,8x6,x,x,5.59.8n Jai berat bena aalah (G):59,8 kn b. Mencari sarat (raft) i air laut : Rapat assa air laut : Paa konisi engapung, berat bena aalah saa engan gaya apung: c. Mencari sarat aksiu (raft ax) aks =,, gaya apung. ax G 5 kg/ B G. g. B. L. g. B. L x9,8x6, x,.59,8kn total Bak g. B. L. x9,8x6,x,x, 6 Jai beban yg pt iukung aalah:.,6-.59,8=5,6kn,6 N Jawaban Tugas No.7# isi kubus : B=5 c Rapat relatif : =,9 b Berat bena :,9x 9 kg/ G. b. g B. b. g Misalkan tinggi kubus yang terena air aalah Gaya apung : B A.. a. g B.. a. g Dala Keaaan engapung :G=B B. b. g B.. a. g b B B,9x,5, 5 a 8
19 /8/ Jawaban Tugas No.7# Jika iatas kubus iberi beban engan berat W,aka berat total kubus an beban aalah: W W W W total,5 x9x9,8 W 7,95 W Apabila kubus terena seluruhnya, berarti kealaan kubus yang terena air aalah =,5. Gaya apung paa keaaan tersebut : B. air. g,5 x x9,8 5, 8 N Dengan enyaakan berat total an gaya apung : W total W B 5,8N G 7,95 W 5,8 Jawaban Tugas No.8 Misal h aalah tinggi balok yang beraa i atas perukaan zat cair. Di ala air tawar a= h = c Di ala inyak : =,8 h = 7,5 c Misalkan tinggi balok H an luas asar balok A c. Gaya apung i air tawar: B A( H,) air. g A( H,75) Gaya apung i inyak: B nyak. Berat balok : G. b. g A. H. b. g g Paa konisi engapung, berat bena aalah saa engan gaya apung: G B A. H. an b. g G A( H B,) G a. g B 9
20 /8/ H. H G b b H B H a, AH b a g,75 H A( H,75) 8H 6 g Dengan enyaakan persaaan i atas: H 8H 6 H, ubstitusi nilai tersebut ke ala persaaan awal :,. x, 5 kg/ Balok b balok air 5kg/ kg/ b,5 Jawaban Tugas No.9 Luas tapang tangki : A=L x B = x,5 =,5 Misalkan tinggi tangki aalah H, seang an aalah volue air an air raksa. olue air an air raksa : Atau :,5x,75H,75 H _ elain itu, =9 sehingga 9 + =,75H,75H 5 Berat tangki, air an air raksa aalah : W 75 W t,75h 9x,75H,675H _ W W x9,8x,675h,6xx9,8x,75h 75 65,795H _ N
21 /8/ Gaya apung : B =A. air laut.g=,5xx9,8=5, N Dala keaaan engapung W= B, sehingga: H 5, 75 65,795 H 5, Bagian tangki yang beraa i atas perukaan air aalah,, berarti bagian yang terena aalah: H, Dengan enyaakan keua bentuk nilai i atas iapat 75 65,795H H, 5, 5, H, ,795H iapat: H,959 Jawaban Tugas No. Berat pelapung : G = ton Misalkan bagian ari pelapung yang terena air aalah. Gaya apung: B D.. air B.. 768, 58 Dala keaaan engapung : G = B =768,58, aka =, Jarak pusat apung terhaap asar OB, siliner :, Jarak pusat berat terhaap asar siliner OG, 5 : Jarak antara pusat berat an pusat apung: BG OG OB,5,, 878
22 /8/ Moent inersia tapang pelapung yang terpotong uka air: I xd x, olue air yang ipinahkan: D x x,, Jarak antara pusat apung an titik etasentru : I,9768 BM, 5, Tinggi etasentru: GM BM BG,5,878, 76 Karena GM >, berarti pelapung ala konisi stabil Jawaban Tugas No. Bena air Berat bena :,8,8x 8 kgf / bena G D. H. Dala keaaan engapung : G = B, sehingga : Bena Bena D. H. D.. Air xh,8x, Air, Jarak pusat apung terhaap asar OB, siliner :, Jarak pusat berat terhaap asar siliner OG, 5 : Jarak antara pusat berat an pusat apung: Bena BG OG OB,5,,
23 /8/ Moent inersia tapang pelapung yang terpotong uka air: I xd x, olue air yang ipinahkan: D x x, 6,969 Jarak antara pusat apung an titik etasentru : I,976 BM, 9,966 Tinggi etasentru: GM BM BG,,, 66 Karena GM <, berarti bena ala konisi tiak stabil Jawaban Tugas No. Bena air,8,8x 8 kgf / bena Berat bena : G,5. H. Bena, g,5.. g Gaya Apung : B air. Dala keaaan engapung : G = B, sehingga : Bena,5. H. Bena. g,5.. Air. g xh. H, 8H Jarak pusat apung terhaap asar : OB, H H Jarak pusat berat terhaap asar : OG, 5H Jarak antara pusat berat an pusat apung: Air BG OG OB, H
24 /8/ Moent inersia tapang pelapung yang terpotong uka air: I. B. B x,5 5,8x olue air yang ipinahkan: B,5 x,8h, H Jarak antara pusat apung an titik etasentru : I 5,8x,65 BM,H Bena akan stabil jika BM >BG :,65 H H, H H,5 Jai bena akan stabil apabila tinggi balok aksiu, Jawaban Tugas No. Bena air Luas Tapang lintang balok:,8,8x 8 kgf / bena B. H,8x,8,6 Berat bena : G A. L. Bena,6 x, x8 5 kgf Berat air yang ipinahkan: Dala keaaan engapung : G = B, sehingga : A B. A. x,6 x 6 _ kgf 5 6., 8,8 Jarak pusat apung terhaap asar Balok OB, : L, Jarak pusat berat terhaap asar Balok : OG, 5 Jai Jarak antara pusat berat an pusat apung: Air BG OG OB,5,,
25 /8/ I Moent inersia tapang bujursangkar yang terpotong uka air:. B. H x,8x,8, olue air yang ipinahkan: A.,6 x,8,5 Jarak antara pusat apung an titik etasentru : I, BM, 6667,5 Tinggi etasentru: GM BM BG,6667,, Karena GM <, berarti bena ala konisi tiak stabil Jawaban Tugas No.,9,9x 9 kg/ Bena bena air G D. H. Gaya Apung : Bena Berat bena : B D.. Air,5 xhx9,88 H _ kgf x,5 xx 59, _ kgf Dala keaaan engapung : G B,88 H 59,, 9H,9 Jarak pusat apung terhaap asar : OB, 5H, Jarak pusat berat terhaap asar OG :, 5H Jarak antara pusat berat an pusat apung: BG OG OB,5H,5H, 5H 5
26 /8/ Moent inersia tapang pelapung yang terpotong uka air: I xd x(,5),89x 6 6 olue air yang ipinahkan: D BM x(,5) Tinggi etasentru: I x,9h,89x,9h Bena akan stabil apabila BM>BG,9H _,65 H,65,5H H,5 H Jai tinggi siliner aksiu aalah,5. Jawaban Tugas No.5 Misal W aalah berat bena an an aalah rapat assa air laut an bahan siliner. W. g.. g. D h. g.,5. g Gaya apung : B D... g Paa konisi engapung, berat bena (W) aalah saa engan gaya apung (B), sehingga:,5. g D... g. h x., 5 olue air yang ipinahkan D. D x : Jarak pusat apung bena ari asar siliner OB x Jarak pusat berat bena ari asar siliner OG h x, 5 Jarak antara pusat berat bena an pusat apung BG OG OB,5 6
27 /8/ Moent inersia tapang lingkaran yang terpotong uka air: I xd 6 x() 6 6 Jarak antara pusat apung an Titik etasentru: I 6, 75 BM 6,5 iliner ala konisi stabil apabila tinggi etasentru BM>BG 6,75 6,75,5,5 5 ab.5 () xx.5 Diapat: a,6 kg/ b 9,75 kg/ 87 Apabila keua hasil tersebut isubstitusikan keala persaaan Diapat:,856 untuk a 87,6 kg/ an,6 untuk b 9,75 kg/ 7
28 /8/ Jawaban Tugas No.6 Rapat relatif siliner kayu : b =,7. Berat bena : balok,7 b, 7 air Paa konisi engapung, berat bena (G) aalah saa engan gaya apung (B), sehingga: D G D. L. b. g Gaya apung : L b b. g D.. a. g. L Jarak pusat apung bena ari asar siliner Jarak pusat berat bena ari asar siliner Jarak antara pusat berat bena an pusat apung B D.. a. g a L OB,5b L L OG, 5L BG OG OB,5L,5 L,5L b b b air Moent inersia tapang lingkaran yang terpotong uka air: I 6 xd olue air yang ipinahkan : D. D x b xl Jarak antara pusat apung an Titik etasentru: D 6 D L D L 8,96 I BM iliner akan stabil apabila BM>BG b,5l b b b D 6 D bl D L D 6 L 8x,7x,7 b 8 b b 8
29 /8/ Jawaban Tugas No.7 RAPAT MAA AIR: a RAPAT MAA BENDA : b Berat bena : G. g. Berat air yang ipinahkan: B Bena Bena air g. L. B. H 9,8x,8x,6 x, x8 Air. g. L. B.,8,8x 8 kg/ Bena.767, N,767 kn Dala keaaan engapung :,8 Jarak pusat apung terhaap asar Balok OB, : H,6 Jarak pusat berat terhaap asar Balok OG :, Jarak antara pusat berat an pusat apung: bena x9,8x, x,8x 7,88 _ kn,767 7,88, 8 BG OG OB,,, 6 Moent inersia tapang segi epat : I x I y. L. B. B. L x, x,8 x,8x, olue air yang ipinahkan:,667 L. B., x,8x,8,8 Jarak antara pusat apung an titik etasentru : Tinggi etasentru: I,667 BM,,8 GM BM BG,,6, 5 Karena GM >, berarti bena ala konisi stabil,6667 Dari keua hasil nilai tersebut abil yang terkecil, yaitu I x =,667 9
30 /8/ Apabila iatas balok itepatkan plat setebal T=, Berat plat : Gt L. B. T. g. Berat total bena : Berat air yang ipinahkan: Plat 7,85xx9,8x, x,8x, 66,68N,6668kN W G Gt,767,6668, 8 kn B Dala keaaan engapung : Air. g. L. B. x9,8x, x,8x 7,88 _ kn W B,8 7,88, 5585,5585 Jarak pusat apung terhaap asar Balok OB, 795 : Jarak pusat berat gabungan terhaap asar Balok ihitung berasarkan oen statis terhaap asar balok: WxOG x,5h x H,5T,8xOG OG G,87 Gt,767x,5 x,6,6668x,6,5x, BG OG OB,87,795, 66 olue air yang ipinahkan: L. B., x,8x,5585,68 I,667 BM, 955,68 Tinggi etasentru: GM BM BG,955,66, 9 Karena tinggi etasentru bertana positif, berarti bena ala konisi stabil
31 /8/ Jawaban Tugas No.8 Berat Ponton: W = kn Berat iliner : W =6 kn W W W 6 6 kn Berat total keua bena : Gaya apung: B Dala keaaan engapung W=B, sehingga : 6,8,, Jarak antara pusat apung an asar ponton OB, 65 : Jarak pusat berat gabungan an asar ponton ihitung engan oen statis terhaap asar Balok : W xog WxOG x,5 6 x,5 OG, 75 W W 6 x xxx x9,8 86 N,8 _ N Dala gabar, G an G aalah pusat berat ponton an siliner, seang G aalah pusat berat bena gabungan Moent inersia tapang ponton uka air : I olue air yang ipinahkan:. L. B xx 8, x x, 59,9 Jarak antara pusat apung an titik etasentru : Jarak antara pusat apung an pusat berat: Tinggi etasentru: I 8, BM 6, ,9 BG OG OB,75,65, 76 GM BM BG 6,775,76, 5 Karena GM >, berarti bena ala konisi stabil
32 /8/ Jawaban Tugas No.9 a. tabilitas Bena Terapung,5x 5 kg/ 8,x 8 kg =,5 = 8, / Panjang bena g : L=-,5=97,5 c Panjang bena g : L=,5 c Luas tapang lintang bena g A =,x,=, Berat bena Berat bena Berat total keua bena : Gaya apung: 69,775 9,, 6875 W g. A. L 5 x9,8x, x,975 9, 95 N. Jarak antara pusat apung terhaap asar : W g. A. L 8 x9,8x, x,5 78, 8N. W W W 9,95 78,8 69, 775 N A... g, xx x9,8 9, B air Dala keaaan engapung W=B, sehingga :,687 OB, 75 Jarak pusat berat ke asar O : OG W xog W 9,95x WxOG W,975,5,5 78,8x 9,95 78,8,675 I Jarak antara pusat apung an pusat berat: BG OG OB,675,75, Moent inersia tapang lintang bena :. bh x,x,, olue air yang ipinahkan: A., x,6875,75
33 /8/ Jarak antara pusat apung an titik etasentru : Tinggi etasentru: I BM, 888 GM BM BG,888,, 85 Karena GM <, berarti bena ala konisi tiak stabil b. Panjang L supaya Bena Terapung stabil Misalkan L Panjang bena g akan ihitung jarak antara pusat berat bena gabungan G an asar O. Berat bena W. g. A. L 5 x9,8x, xl 96, L _ Berat bena W g. A. L 8 x9,8x, x,5 78, 8N. Berat total keua bena : W W W 96,L 78, 8 L 96,L x,5 78,8x,5 W xog WxOG OG W W 96,L 78,8 L,5L, L,8 N Gaya apung: B 9, Dala keaaan engapung W=B, sehingga : 96,L 78,8 Jarak pusat apung ari asar :OB 9, 96,L 78,8,5L 9,,5x,5L,,5L,, Jarak antara pusat apung an pusat berat: BG OG OB L,5L,,5L L,8 Jarak antara pusat apung an titik etasentru : BM I,,5L,,,,,5L,
34 /8/ Bena akan stabil apabila BM>BG,,5L,,, L L L,5L,8,5L, L,8,,5L,5L,, Bentuk iatas apat iseerhanakan enjai L,7L L,8877,6666 Bena akan terapung stabil apabila panjang bena enga rapat assa lebih kecil atau saa engan,8877 Jawaban Tugas No. Bena bagian atas Bena bagian bawah Berat bena : Bena,8 bena,8x 8 kg/ air Bena, bena 5,x 5. kg/ air G,5 x, x8 9, 7kgf Misalkan h aalah panjang bena bagian bawah : Berat bena : G Berat bena total:,5 5 xhx5 5,7h _ kgf G G G 9,7 5, h
35 /8/ Pusat berat bena gabungan terhaap asar ihitung engan oen statis terhaap asar Balok : O O O G G G G xo G G G xo G xo G G G 9,7x h,5 9,7 G xo xo G G 5,7hx,5h 5,7h,79h 9,7h 9,65 5,7h 9,7 Gaya apung : B x,5 xx 9,87 _ kgf Dala keaaan engapung G = B sehingga: 9,7 5,7h 9,87 5,7h 9,7 5h,8 9,87 OB Jarak pusat apung terhaap asar Balok : Jarak antara pusat apung an pusat berat :,5h,,79h 9,7h 9,65 BG OG OB,5h, 5,7h 9,7,79h 9,7h 9,65,5h, 5,7h 9,7 5,7h 9,7,79h 9,7h 9,65 6,596h 96,5h 5,78 5,7h 9,7 9,875h 57,8h,97 5,7h 9,7 h,h,8 5,h,8 5
36 /8/ Moent inersia tapang iliner yang terpotong air : I 6.. D olue air yang ipinahkan: D. Jarak antara pusat apung an titik etasentru : BM I 6 6,965x 5h,8 D D 6 6,5,5,965x Bena akan stabil bila BM > GM :,965x h,h,8 5h,8 5,h,8 h h,h,h,8,965x,76975 Penyelesaian ari persaaan tersebut enghasilkan: h=,=,c. Jai supaya bena stabil aka panjang bena bagian bawah iniu aalah, c. 6
37 /8/ Jawaban Tugas No. a. iliner engapung engan subunya vertikal b = b _ kgf / a = a _ kgf / Berat bena G G D Lx Gaya Apung B Dala keaaan engapung G=B, sehingga : D Lx D x L, 5L Jarak antara pusat apung terhaap asar : Jarak antara pusat Berat terhaap asar : Jarak antara pusat apung an pusat berat : BG OG OB,5L B D x OB, 5L L OG, 5L,5L,5L L Moent inersia tapang siliner yang terpotong air : I 6 D olue air yang ipinahkan: D. 7
38 /8/ Jarak antara pusat apung an titik etasentru : D 8L L L D BM L I Bena akan stabil apabila: BM>BG, sehingga: D 6 6 D D b. iliner,engapung engan subunya horisontal D 6 terbukti Karena berat jenis siliner () aalah setengah berat jenis zat cair (), berarti siliner terena setengah bagiannya (uka air elalui pusat lingkaran)., 5D Pusat apung aalah saa engan pusat berat setengah lingkaran PB r D Jarak Pusat Berat ari asar: OB D Jarak Pusat apung ari asar: OG D D 8L D Jarak antara pusat apung an pusat berat: BG BM OG I OB Moent inersia tapang siliner yang terpotong air : olue air yang ipinahkan: Jarak antara pusat apung an titik etasentru : 8 DL D L D D D D I DL x D. L D. L 8 L D Bena akan stabil apabila : BM>BG L D L D D L D 8
39 /8/ Jawaban Tugas No. p= berat jenis ponton a= berat jenis air a. Balok tunggal: Berat bena G G LBH. p x,x,5 x6 5, Bagian balok yang terena air aalah. LB. Jarak antara pusat apung terhaap asar : Jarak antara pusat Berat terhaap asar : Jarak antara pusat apung an pusat berat : p a,6,6x 6kgf / p x,xx Berat air yang ipinahkan B a : Karena engapung, aka B=G, sehingga iapat kealaan: 5, 5 kgf _ kgf OB, 75 H OG, 5 BG OG OB,5,75, 5 Moent inersia tapang siliner yang terpotong air : I Jarak antara pusat apung an titik etasentru : Tinggi etasentru : I,5 BM, 5 x,x,5 LB xx,, 5 GM BM BG,5,5 Jai bena ala keseibangan netral (akan engguling) 9
40 /8/ b. PONTON Berat papan i atas balok iabaikan. Moen inersia total terhaap subu ponton, I t I AX,5 x,,5 I LxBx,5x,6,6,5x, Bagian balok ponton yang terena air aalah =,5, (karena berat papan iabaikan). olue air yang ipinahkan: Jarak antara pusat apung an titik etasentru :. A. x x,x,5,9 I,6 BM t,,9 Jarak pusat apung ponton an pusat berat ponton terhaap asar balok ponton aalah saa engan konisi a, sehingga: BG OG OB,5,75, 5 Tinggi etasentru : GM BM BG,,5, 5 stabil c. Apabila i atas PONTON terapat beban seberat Wb=75 kgf. Berat ponton :Wp=G=9 kgf Berat ponton :an beban : Wpb= =.65 kgf,65xog B 9x,5x,5 Berat air yang ipinahkan : Kealaan balok ponton yang terena air : Jarak antara pusat apung terhaap asar : etelah aa beban, bagian balok ponton yang terena air Aalah. x x,x x 6 _ kgf 65, 75 6,75 OB, 75 Jarak antara pusat Berat ihitung engan oen statis terhaap titik : WpbxOG WpxOG Wb xog 75,5,5 OG,9
41 /8/ Jarak pusat apung an pusat berat : BG OG OB,9,75, 76 Karena balok ponton tiak tenggela aka oen inersia sebelu an sesuah aa beban aalah saa: I t,6 olue air yang ipinahkan:. A. x x,x,76,696 Jarak antara pusat apung an titik etasentru : I,6 BM, 77,696 Tinggi etasentru: GM BM BG,77,76, 56 PONTON TETAP TABIL Jawaban Tugas No. a. Menyeliiki stabilitas bena : Gaya apung Berat iliner : G kn : Karena engapung, aka B=G, sehingga iapat kealaan: G B 7,7, 5655,5655 Jarak antara pusat apung terhaap asar OB :, 88 Jarak antara pusat Berat terhaap asar : Jarak antara pusat apung an pusat berat : D xx,x9,8 7.7N 7,7 _ kn L OG, BG OG OB,,88, 77 B g
42 /8/ Moent inersia tapang lintang bena yang terpotong air : I D x, olue air yang ipinahkan: 6 Jarak antara pusat apung an titik etasentru : I,9768 BM, 997,997 Tinggi etasentru : GM BM BG,997,77, 75 Tinggi etasentru aalah negatif, jai bena ala konisi tiak stabil. Berarti bena tiak bisa engapung engan subu panjangnya vertikal. A. x x,5655,997 b. Pusat asar bena iberi gaya tarik: Misalkan P aalah gaya tarik yang bekerja paa rantai i pusat asar pelapung. Berat bena an gaya tarik P aalah: G P. Gaya apung : B P N D g xx,x9,8 7.7N 7,7 _ kn Dala keaaan engapung, aka B=G+P :. P. P P Jarak antara pusat apung ari OB asar :.6 Dala keaaan gaya tarik i, letak pusat berat berubah. Letak pusat Berat ihitung berasarkan oen terhaap titik. G P xog P xog GxOG x Px OG 8 P
43 /8/ Jarak pusat berat bena an gaya tarik P terhaap asar aalah: BG OG OB olue air yang ipinahkan: 8 P P 6 P 5 A. x 9,998x 77 Moent inersia tapang lintang bena setelah aanya gaya tarik P aalah saa engan sebelu aanya gaya tarik, yaitu =,9768 BM I, ,998 x P P 9.785,7 P Bena akan stabil apabila BM>BG 9.785,7 8. P P P.6 P.6 P.,5 P.6 x.,5 P 75.,8 P 5.,8 N 5, 8kN Jai gaya tarik iniu yang harus iberikan aalah P = 5,8 kn
44 /8/ Jawaban Tugas No. Misalkan: h : tinggi kerucut D: iaeter asar kerucut : setengah suut puncak kerucut : bagian kerucut yang terena air : rapat assa kerucut : rapat assa air D / D tg D htg h h * * D / D * tg D htg h h Berat Kerucut : G D x x gh h. tg x xhx g h tg x g Berat air uyang ipinahkan ihitung engan cara yang saa seperti i atas Untuk kealaan air yang ipinahkan bena sebesar. B.. tg g upaya bena engapung B=G:.. tg g. h. tg g Jarak pusat apung ari puncak kerucut O : Jarak pusat berat ari puncak kerucut: Jarak antara pusat berat an pusat apung: h h. engan OB OG h BG OG OB Diaeter lingkaran paa perukaan air : D =.tg. h h
45 /8/ Moent inersia tapang lingkaran kerucut paa perukaan air : I * D x. tg. 6 olue air yang ipinahkan: 6 Jarak antara pusat apung an titik etasentru : tg BM tg Oleh karena tg =D/h an =h. /, aka I BM B g h. D h tg tg D 6h tg Untuk kesetibangan stabil, BM BG : D 6h h D h tg tg tg h tg D,697,6885,88 Jai supaya kerucut stabil aka rapat relatif kerucut aalah,6885 5
46 /8/ Jawaban Tugas No.5 air x air,7x 7kg/ air x air,9,9x 9kg/ Misalkan: h : tinggi kerucut D: iaeter asar kerucut D : iaeter tapang kerucut : kealaan kerucut yang terena air : suut puncak kerucut D / D tg D htg h h W Berat Kerucut : D x xh.. g htg h. Berat zat cair yang ipinahkan : B x. tg. g. g xh. tg. g Oleh karena bena engapung, aka B=G, sehingga:.. tg g. h. tg g h h 6
47 /8/ Jarak pusat apung ari puncak kerucut O : Jarak pusat berat ari puncak kerucut: OB OG h h Jarak antara pusat berat an pusat apung: BG OG OB h h h Moent inersia tapang lingkaran kerucut paa perukaan air : I * D x. tg. 6 6 olue air yang ipinahkan: tg g B g g tg tg Jarak antara pusat apung an titik etasentru : I tg BM. tg tg Agar bena ala kesetibangan stabil, titik etasentru M harus i atas atau beripit engan G : BM BG.. tg h h tg h 7
48 /8/ tg tg tg ,878 Jai suut puncak kerucut aalah =,9 = 56 6,7 Jawaban Tugas No.6 Berat Pelapung : G 5 N Gaya apung : B A... g Berat Beban = W. Berat Pelapung an Beban = (W+5). xx,5xx9,8 7897,75 Paa konisi engapung, aka B=G+W, sehingga: 7897,75 W 5 Jarak antara pusat apung terhaap asar : W ,75 OB W 5 579,75 8
49 /8/ Jarak antara pusat Berat an beban terhaap asar ihitung berasarkan oen statis terhaap titik,: W W OG BG G xog 5 xog GxOG 5x,5x,75,5,5W 5 W OG OB,5,5W 5 W W H,5 W,75 W ,75,5 Moent inersia tapang iliner yang terpotong uka air : I D x, olue air yang ipinahkan: Jarak antara pusat apung an titik etasentru : BM I A. x,987 W 5.55,5 Bena akan stabil apabila BM>BG W 5 x 7897,75 W 9,586 W 5 9,586,5,5W W 5 W 5 W ,75 88,9,5W W 5 W , ,5 9
50 /8/.9.5,9 9.7,W W 5 W.7,W 68.5,9 Penyelesaian ari persaaan tersebut enghasilkan : W. 796 N W 5, 5N Jai berat beban iniu seeikian sehingga bena ala konisi stabil aalah W =.796 N Jawaban Tugas No.7 Berat Kapal : W = 5 MN = 5 x 6 NBerat uatan : W=5kN=5x N Lebar Kapal : B = 8,. Jarak bergesernya uatan : l = Panjang Kapal : L= 6 Keiringan suut : = Moen yang enyebabkan goyangan: M 5 x 6 kn 5
51 /8/ Moen tersebut enyebabkan bergesernya titik tangkap W an G ke G. Karena berat uatan jauh lebih kecil ari berat kapal aka berat tersebut iabaikan terhaap kapal. Bergesernya titik tangkap enyebabkan Moent : WxGM sin 5x xgm sin kn Jai tinggi etasentru aalah,76 M M GM M 6 6 5x xgm sin 5x xgm sin,76 Karena tinggi etasentru GM positif berarti kapal ala konisi stabil Untuk encari posisi pusat berat ihitung jarak BM: Mencari oen inersia tapang kapal paa uka air: I 7% xisegiepat,7x LB I,7x 6x8,, 7 I BM olue air yang ipinahkan: W. g 6 5x 5x9,8 9,76 Jarak antara pusat apung an titik etasentru :,7 BM, 9,76 Oleh karena pusat apung terletak paa,5 (BP) i bawah uka air aka titik etasentru: PM BP BM,5,, 7 Jai titik etasentru M beraa paa,7 i bawah uka air : PG PM GM,7,76, 8 Jai Pusat berat beraa paa,8 i bawah uka air : 5
52 /8/ Jawaban Tugas No.8 a. MENYELIDIKI TABILITA BENDA : Gaya apung Berat Ponton : G : Berat beban : ton Berat Total : B G Jarak pusat apung ari asar : OB,5x,6, B 6x6x,6x.6 kgf, 6ton Dala keaaan engapung, aka B=G, sehingga : G,6 G,6 7,6ton Pusat berat bena an beban terhaap asar ihitung engan oen statis terhaap asar : O G G xo G G xo 7,6x,6 G G,x,,6 xo G, O G G,9 xo G G G xo G Jarak antara pusat apung an pusat berat : BG OG OB,9,, 6 Moent inersia tapang balok yang terpotong uka air : I olue air yang ipinahkan: 6x6x,6,6 BB x 6 8 Jarak antara pusat apung an titik etasentru : I 8 BM 5,,6 Tinggi etasentru : GM BM BG 5,,6, 667 Karena GM > berarti bena ala konisi stabil 5
53 /8/ b. MENGHITUNG BEBAN MAKIMUM: Beban aksiu aalah:w + W Gaya apung : B 6,x G B Jarak pusat berat ari asar : OB Jarak antara pusat apung ari asar : Jarak antara pusat apung an pusat berat : BG OG OB Berat Beban + ponton : G=7,6 6,xx 6. _ kgf W 7,6 6 W 7,6 6 OG 7,6x,6 7,6 Wx, W,W W,W W 6 _ ton,56 7,6 W 7,6 7,56 7,6 I 8 W Moent inersia tapang balok yang terpotong uka air : 7,6 7 olue air yang ipinahkan: 7,6 6 6x W x W 6 7,6 Jarak antara pusat apung an titik etasentru : BM Bena akan stabil apabila BM>BG 8,W,56 W W 7,6 W 7,6 8,W,56 W W 7,6 7,6 7 I 7,6 7 75,68 7,8W W 5,W W 7,6W 75, 8 W 7,6 Dari persaaan tersebut tiak eberikan nilai W yang berarti tiak Aa beban aksiu yang eenuhi persaaan tersebut. Beban aksiu lebih itentukan oleh tenggelanya ponton aripaa Tergulingnya. Beban aksiu yang apat iukung aalah beban Yang enyebabkan ponton tenggela, yang besarnya aalah : 9,76 5
54 /8/ 7,6 W 6x6x, x W 5,6 _ ton Untuk engetahui kebenaran ari pernyataan tersebut, aka beban W = 5,6 ton igunakan untuk enghitung konisi stabilitas ponton. Dengan beban tersebut konisi ponton aalah sebagai berikut ini. 5,6W x,,56 Jarak pusat berat ari asar OG, 667 : 5,6 7,6 Jarak antara pusat apung ari asar : Jarak antara pusat apung an pusat berat : W 7,6 5,6 7,6 OB, BG OG OB,667,6, 67 Jarak antara pusat apung an titik etasentru : I 8 BM, 5 Tinggi etasentru : W 7,6 GM BM BG,5,67, Jai ponton ala konisi stabil, tetapi hapir tenggela. 5
Soal :Stabilitas Benda Terapung
TUGAS 3 Soal :Stabilitas Benda Terapung 1. Batu di udara mempunyai berat 500 N, sedang beratnya di dalam air adalah 300 N. Hitung volume dan rapat relatif batu itu. 2. Balok segi empat dengan ukuran 75
KESEI MBANGAN BENDA TERAPUNG
Please purchase Pcap Printer on http//www.verypf.co/ to reove this waterark. KEE MBANAN BENA TERAPUN Mepelajari asalah Prinsip huku Archiees Prinsip keseianan an kestailan Menhitun esar aya apun an letak
VIII. ALIRAN MELALUI LUBANG DAN PELUAP
VIII. ALIRAN MELALUI LUBANG DAN PELUAP 8.. Penahuluan Lubang aalah bukaan paa ining atau asar tangki imana zat cair mengalir melaluinya. Lubang tersebut bisa berbentuk segi empat, segi tiga, ataupun lingkaran.
BAB III LANDASAN TEORI. Beton bertulang merupakan kombinasi antara beton dan baja. Kombinasi
16 BAB III LANDASAN TEORI 3.1. Umum Beton bertulang merupakan kombinasi antara beton an baja. Kombinasi keuanya membentuk suatu elemen struktur imana ua macam komponen saling bekerjasama alam menahan beban
Kombinasi Gaya Tekan dan Lentur
Mata Kuliah Koe SKS : Perancangan Struktur Beton : CIV-204 : 3 SKS Kombinasi Gaya Tekan an Lentur Pertemuan 9,10,11 Sub Pokok Bahasan : Analisis an Desain Kolom Penek Kolom aalah salah satu komponen struktur
BAB V FONDASI RAKIT. Fondasi rakit merupakan bagian bawah struktur yang berbentuk rakit melebar keseluruh bagian dasar bangunan.
BAB V FONASI RAKIT I. PENAHULUAN Fondasi rakit erupakan bagian bawah struktur yang berbentuk rakit elebar keseluruh bagian dasar bangunan. Fondasi rakit digunakan jika lapis tanah eiliki kapasitas dukung
ANALISAPERHITUNGANWAKTU PENGALIRAN AIR DAN SOLAR PADA TANGKI
ANALISAPERITUNGANWAKTU PENGALIRAN AIR DAN SOLAR PADA TANGKI Nurnilam Oemiati Staf Pengajar Jurusan Sipil Fakultas Teknik Universitas Muhammaiyah Palembang Email: [email protected] Abstrak paa
PERENCANAAN PENULANGAN LENTUR DAN GESER BALOK PERSEGI MENURUT SNI 03-847-00 Slamet Wioo Staf Pengajar Peniikan Teknik Sipil an Perenanaan FT UNY Balok merupakan elemen struktur yang menanggung beban layan
BESARNYA KOEFISIEN HAMBAT (CD) SILT SCREEN AKIBAT GAYA ARUS DENGAN MODEL PELAMPUNG PARALON DAN KAYU
BESARNYA KOEFISIEN HAMBAT (CD) SILT SCREEN AKIBAT GAYA ARUS DENGAN MODEL PELAMPUNG PARALON DAN KAYU Davi S. V. L Bangguna 1) 1) Staff Pengajar Program Stui Teknik Sipil, Fakultas Teknik, Universitas Sintuwu
BAB III BERAT VOLUME TANAH
BAB III BERAT VOLUME TANAH 3.1 Referensi Das, Braja M. Mekanika Tanah I. Bab Koposisi Tanah : Hubungan Antara Berat Volue, Angka Pori, Kaar Air an Berat Spesifik. 3.2 Dasar Teori Prinsip percobaan yang
BAB V KAPASITOR. (b) Beda potensial V= 6 volt. Muatan kapasitor, q, dihitung dengan persamaan q V = ( )(6) = 35, C = 35,4 nc
BAB KAPASITOR ontoh 5. Definisi kapasitas Sebuah kapasitor 0,4 imuati oleh baterai volt. Berapa muatan yang tersimpan alam kapasitor itu? Jawab : Kapasitas 0,4 4 0-7 ; bea potensial volt. Muatan alam kapasitor,,
VIII. TORSI Definisi Torsi. (couples) yang menghasilkan perputaran terhadap sumbu longitudinalnya. [Torsi]
![VIII. TORSI Definisi Torsi. (couples) yang menghasilkan perputaran terhadap sumbu longitudinalnya. [Torsi]](/thumbs/54/33346769.jpg "VIII. TORSI Definisi Torsi. (couples) yang menghasilkan perputaran terhadap sumbu longitudinalnya. [Torsi]")
[orsi] VIII. OSI 8.1. Definisi orsi orsi adah suatu peuntiran sebuah batang yang diakibatkan oleh kopelkopel (couples) yang enghasilkan perputaran terhadap subu longitudinnya. Kopel-kopel yang enghasilkan
PETUNJUK UMUM Pengerjaan Soal Tahap Final Diponegoro Physics Competititon Tingkat SMA
PETUNJUK UMUM Pengerjaan Soal Tahap Final Diponegoro Physics Copetititon Tingkat SMA 1. Ujian Eksperien berupa Naskah soal beserta lebar jawaban dan kertas grafik. 2. Waktu keseluruhan dala eksperien dan
F = M a Oleh karena diameter pipa adalah konstan, maka kecepatan aliran di sepanjang pipa adalah konstan, sehingga percepatan adalah nol, d dr.
Hukum Newton II : F = M a Oleh karena iameter pipa aalah konstan, maka kecepatan aliran i sepanjang pipa aalah konstan, sehingga percepatan aalah nol, rr rr( s) rs rs( r r) rrs sin o Bentuk tersebut apat
KALOR DAN KELEMBABAN SOAL DAN PENYELESAIAN FISIKA BANGUNAN FAKULTAS TEKNIK UNIVERSITAS NEGERI MEDAN Oleh: JURUSAN PENDIDIKAN TEKNIK BANGUNAN
SOAL DAN PENYELESAIAN FISIKA BANGUNAN KALOR DAN KELEMBABAN Oleh: MUHAMAD YUNUS NIM. 59 JURUSAN PENDIDIKAN TEKNIK BANGUNAN FAKULTAS TEKNIK UNIVERSITAS NEGERI MEDAN 3 . Bagaianakah berlangsungnya pengalihan
dan E 3 = 3 Tetapi integral garis dari keping A ke keping D harus nol, karena keduanya memiliki potensial yang sama akibat dihubungkan oleh kawat.
E 3 E 1 -σ 3 σ 3 σ 1 1 a Namakan keping paling atas aalah keping A, keping keua ari atas aalah keping B, keping ketiga ari atas aalah keping C an keping paling bawah aalah keping D E 2 muatan bawah keping
Soal Latihan Mekanika I. (3-11 November 2011)
Soal Latihan (3-11 Noveber 2011) Kerjakan soal-soal berikut selaa 1 inggu untuk elatih keapuan Anda. Kerjakan 2-3 soal per hari. Sebelu engerjakan soal-soal tersebut, sebaiknya Anda engerjakan soalsoal
3. Kegiatan Belajar Medan listrik
3. Kegiatan Belajar Mean listrik a. Tujuan Kegiatan Pembelajaran Setelah mempelajari kegiatan belajar 3, iharapkan Ana apat: Menjelaskan hubungan antara kuat mean listrik i suatu titik, gaya interaksi,
Soal Seleksi Provinsi 2009 Bidang studi Fisika Waktu: 3 jam
Soal Seleksi Provinsi 2009 Bidang studi Fisika Waktu: 3 ja 1 (Nilai 15) Sebuah bola pada ketinggian h dari perukaan lantai, ditebakkan secara horizontal dengan kecepatan v 0. Bola engenai lantai dan eantul
9. Dari gambar berikut, turunkan suatu rumus yang dikenal dengan rumus Darcy.
SOAL HIDRO 1. Saluran drainase berbentuk empat persegi panjang dengan kemiringan dasar saluran 0,015, mempunyai kedalaman air 0,45 meter dan lebar dasar saluran 0,50 meter, koefisien kekasaran Manning
Hidrostatika. Civil Engineering Department University of Brawijaya. Kesetimbangan Benda Terapung. TKS 4005 HIDROLIKA DASAR / 2 sks
TKS 4005 HIDROLIKA DASAR / 2 sks Hidrostatika Kesetimbangan Benda Terapung Ir. Suroso, M.Eng., Dipl.HE Dr. Eng. Alwafi Pujiraharjo Department University of Brawijaya Statika Fluida Membahas sistem yang
BAB III METODE ANALISIS
BAB III METODE ANALISIS 3.1 Penyajian Laporan Dala penyajian bab ini dibuat kerangka agar eudahkan dala pengerjaan laporan. Berikut ini adalah diagra alir tersebut : Studi Pustaka Model-odel Eleen Struktur
METODE PENELITIAN Data Langkah-Langkah Penelitian
METODE PENELITIAN Data Inonesia merupakan salah satu negara yang tiak mempunyai ata vital statistik yang lengkap. Dengan memperhatikan hal tersebut, sangat tepat menggunakan Moel CPA untuk mengukur tingkat
BAB 3 MODEL DASAR DINAMIKA VIRUS HIV DALAM TUBUH
BAB 3 MODEL DASA DINAMIKA VIUS HIV DALAM TUBUH 3.1 Moel Dasar Moel asar inamika virus HIV alam tubuh menggunakan beberapa asumsi sebagai berikut: Mula-mula tubuh alam keaaan tiak terinfeksi virus atau
Solusi Treefy Tryout OSK 2018
Solusi Treefy Tryout OSK 218 Bagian 1a Misalkan ketika kelereng encapai detektor bawah untuk pertaa kalinya, kecepatan subu vertikalnya adalah v 1y. Maka syarat agar kelereng encapai titik tertinggi (ketika
KESETIMBANGAN BENDA TEGAR
1 KESEIMNGN END EGR (Soal abahan Persiapan Ujian Perbaikan) 1. n enyusun 5 buah batang ebentuk huruf R seperti pada gabar. entukanlah Koordinat titik berat tersebut! 2. Ru enyusun 4 buah batang ebentuk
IV. ANALISA RANCANGAN
IV. ANALISA RANCANGAN A. Rancangan Fungsional Dalam penelitian ini, telah irancang suatu perontok pai yang mempunyai bentuk an konstruksi seerhana an igerakkan engan menggunakan tenaga manusia. Secara
SELEKSI OLIMPIADE TINGKAT KABUPATEN/KOTA 2014 TIM OLIMPIADE FISIKA INDONESIA 2015
SEEKSI OIMPIDE TINGKT KBUPTEN/KOT 14 TIM OIMPIDE FISIK INDONESI 15 Bidang Fisika Waktu : 18 enit KEMENTRIN PENDIDIKN DN KEBUDYN DIREKTORT JENDER PENDIDIKN DSR DN MENENGH DIREKTORT PEMBINN SEKOH MENENGH
UN SMA IPA 2009 Matematika
UN SMA IPA 009 Matematika Koe Soal P88 Doc. Name: UNSMAIPA009MATP88 Doc. Version : 0-0 halaman 0. Perhatikan premis-premis berikut ini : :Jika Ai muri rajin maka Ai muri panai :Jika Ai muri panai maka
Fluida. Pada temperatur normal, zat dapat berwujud: Fluida
LUID luia aa teperatur noral, zat apat erwuju: luia? aatan/soli Cair/Liqui Gas luia Zat an apat enalir an eiliki entuk seperti waah an enapunna to-ato an olekul-olekul eas ererak luia okok ahasan luia
UJIAN TENGAH SEMESTER KALKULUS/KALKULUS1
Jurusan Matematika FMIPA IPB UJIAN TENGAH SEMESTER KALKULUS/KALKULUS1 Sabtu, 4 Maret 003 Waktu : jam SETIAP NOMOR MEMPUNYAI BOBOT 10 1. Tentukan: (a) (b) x sin x x + 1 ; x (cos (x 1)) :. Diberikan fungsi
Modul 5 Saluran Transmisi
Saluran Transisi Organisasi Moul 5 Saluran Transisi A. Penahuluan page 3 B. Paraeter Prier Saluran Transisi page 9 C. Paraeter Sekuner Saluran Transisi page 5 D. Koefisien Pantul an SW page 7 E. Tegangan
ANTIREMED KELAS 11 FISIKA
ANTIREED KELAS 11 FISIKA UTS Fisika Latihan Doc. Nae: AR11FIS01UTS Version : 014-10 halaan 1 01. erak sebuah benda eiliki persaaan posisi r = (-6-3t)i + (8 + 4t) Seua besaran enggunakan satuan dasar SI.
Formulasi Lentur BAB ANALSS KASUS LENTUR DAN GESER PADA BALOK ELASTS Suatu elemen balok ikatakan alam konisi lentur murni, jika balok tersebut menerima beban ang berupa momen lentur secara konstan tanpa
BAB III UJICOBA KALIBRASI KAMERA
BAB III UJICOBA KALIBRASI KAMERA 3.1 Spesifikasi kamera Kamera yang igunakan alam percobaan paa tugas akhir ini aalah kamera NIKON Coolpix 7900, engan spesifikasi sebagai berikut : Resolusi maksimum :
SOAL UJIAN SELEKSI CALON PESERTA OLIMPIADE SAINS NASIONAL 2013 TINGKAT PROPINSI
SOAL UJIAN SELEKSI CALON PESERTA OLIMPIADE SAINS NASIONAL 013 TINGKAT PROPINSI FISIKA Waktu : 3,5 ja KEMENTERIAN PENDIDIKAN DAN KEBUDAYAAN DIREKTORAT JENDERAL PENDIDIKAN MENENGAH DIREKTORAT PEMBINAAN SEKOLAH
Lampiran 1. Rancangan Pintu Air dari Bahan Fiberglass
LAMPIRAN 60 Lapiran 1. Ranangan Pintu Air dari Bahan Fiberglass 61 Lapiran 1. (lanjutan) 62 Lapiran 2. Ranangan Pintu Air dari Bahan Beton Serat 63 Lapiran 2. (lanjutan) 64 Lapiran 3. Perhitungan Modulus
Lampiran 1 - Prosedur pemodelan struktur gedung (SRPMK) untuk kontrol simpangan antar tingkat menggunakan program ETABS V9.04
50 Lapiran 1 - Prosedur peodelan struktur gedung (SRPMK) untuk kontrol sipangan antar tingkat enggunakan progra ETABS V9.04 Pada sub bab ini, analisis struktur akan dihitung serta ditunjukan dengan prosedur
BAHAN KUIS PRA-UTS MEKANIKA, Oktober 2011
tosi-ipb.blogspot.co ekanika I BAHAN KUIS PRA-UTS EKANIKA, 3-4 Oktober 0 Untuk kalangan sendiri Tidak diperjualbelikan Silakan kerjakan soal-soal berikut, pahai dengan baik. Soal Kuis akan diabil dari
BAB III PROSES PERANCANGAN DAN PERHITUNGAN
BB III PROSES PERNCNGN DN PERHITUNGN 3.1 Diagram alir penelitian MULI material ie an material aluminium yang iekstrusi Perancangan ie Proses pembuatan ie : 1. Pemotongan bahan 2. Pembuatan lubang port
BAB IV BUOYANCY DAN STABILITAS BENDA MENGAPUNG
A IV UOYANCY DAN STAIITAS ENDA ENAPUN Tujuan Pembelajaran Umum :. ahasiswa memahami konsep kesetimbangan statis untuk menyelesaikan gaya-gaya yang bekerja pada kasus benda yang mengapung, 2. ahasiswa mampu
KAPASITOR. Pengertian Kapasitor
7/3/3 KAPASITOR Pengertian Kapasitor Dua penghantar berekatan yang imaksukan untuk iberi muatan sama tetapi berlawanan jenis isebut kapasitor. Sifat menyimpan energi listrik / muatan listrik. Kapasitas
B C D E... 2h g. =v 2h g T AB. B, y. = 2 v' =2e v 2h T BC
1. Gerak benda di antara tubukan erupakan erak parabola. Sebut posisi ula-ula benda adalah titik A, posisi terjadinya tubukan pertaa kali adalah titik B, posisi terjadi tubukan kedua kalinya adalah titik
BAB II DASAR TEORI. II.1 Saham
BAB II DASAR TEORI Paa bab ini akan ijelaskan asar teori yang igunakan selama pelaksanaan Tugas Akhir ini: saham, analisis funamental, analisis teknis, moving average, oscillator, an metoe Relative Strength
Perhitungan Tahanan Kapal dengan Metode Froude
9/0/0 Perhitungan Tahanan Kapal dengan etode Froude Froude enganggap bahwa tahanan suatu kapal atau odel dapat dipisahkan ke dala dua bagian: () tahanan gesek dan () tahanan sisa. Tahanan sisa ini disebabkan
BAB IV ESTIMASI DIMENSI ELEMEN STRUKTUR. 1 basement. Denah bangunan hotel seperti terlihat pada gambar 4.1 : Gambar 4.1.
BAB IV ESTIMASI DIMENSI ELEMEN STRUKTUR 4.1. Denah Bangunan Dalam tugas akhir ini penulis akan merancang geung hotel 7 lantai an 1 basement. Denah bangunan hotel seperti terlihat paa gambar 4.1 : Gambar
METODE MENGIKAT KEBELAKANG
METODE MENGIKAT KEBELAKANG Metoe mengikat ke belakang aalah menentukan suatu titik baru engan jalan mengaakan pengukuran suut paa titik yang tiak iketahui koorinatnya. Ketentuan yang harus ipenuhi aalah
BAB 6 P E G A S M E K A N I S
BAB 6 P E G A S M E K A N I S Pegas, aalah suatu elemen mesin yang memperoleh gaya bila iberi perubahan bentuk. Pegas mekanis ipakai paa Mesin untuk menesakan gaya, untuk menyeiakan lenturan an untuk menyimpan
MOMENTUM SUDUT DAN ROTASI BENDA TEGAR
BAB 7 Drs. Pristiadi Utoo, M.Pd. MOMENTUM SUDUT DAN ROTASI BENDA TEGAR STANDAR KOMPETENSI : Menerapkan konsep dan prinsip ekanika klasik siste kontinu dala enyelesaikan asalah. KOMPETENSI DASAR Setelah
RANCANG BANGUN ALAT UKUR UJI TEKANAN DAN LAJU ALIRAN FLUIDA MENGGUNAKAN POMPA CENTRIFUGAL
Jurnal J-Ensitec: Vol 0 No. 0, Mei 06 RANCANG BANGUN ALAT UKUR UJI TEKANAN DAN LAJU ALIRAN FLUIDA MENGGUNAKAN POMPA CENTRIFUGAL Gugun Gunai, Asep Rachmat, Teknik Mesin, Fakultas Teknik Universitas Majalengka
BAB III ANALISA TEORETIK
BAB III ANALISA TEORETIK Pada bab ini, akan dibahas apakah ide awal layak untuk direalisasikan dengan enggunakan perhitungan dan analisa teoretik. Analisa ini diperlukan agar percobaan yang dilakukan keudian
Keseimbangan benda terapung
Keseimbangan benda terapung Pendahuluan Benda yang terendam di dalam air akan mengalami gaya gaya sbb: a. Berat sendiri benda atau gaya gravity ( Fg )=m.g dengan arah vertikal ke bawah di titik berat benda
11/4/2011 KOHERENSI. koheren : memiliki θ yang tetap (tidak berubah terhadap waktu) y 1 y 2
11/4/011 1 11/4/011 KOHERENSI koheren : memiliki θ yang tetap (tiak berubah terhaap waktu) θ = π y 1 y θ = 0 y 1 y 11/4/011 INTERFERENSI CELAH GANDA G G T 4 T 3 T G T 1 T pusat T 1 G T T 3 T 4 Cahaya bersifat
2.3 Perbandingan Putaran dan Perbandingan Rodagigi. Jika putaran rodagigi yang berpasangan dinyatakan dengan n 1. dan z 2
.3 Perbaningan Putaran an Perbaningan Roagigi Jika putaran roagigi yang berpasangan inyatakan engan n (rpm) paa poros penggerak an n (rpm) paa poros yang igerakkan, iameter lingkaran jarak bagi (mm) an
BAB V PERENCANAAN STRUKTUR
BAB V PERENCANAAN STRUKTUR 5.1. TINJAUAN UMUM Dala perencanaan suatu bangunan pantai harus ditetapkan terlebih dahulu paraeter-paraeter yang berperan dalan perhitungan struktur. Paraeterparaeter tersebut
PERSAMAAN DIFFERENSIAL. Disusun untuk memenuhi tugas mata kuliah Matematika
PERSAMAAN DIFFERENSIAL Disusun untuk memenuhi tugas mata kuliah Matematika Disusun oleh: Aurey Devina B 1211041005 Irul Mauliia 1211041007 Anhy Ramahan 1211041021 Azhar Fuai P 1211041025 Murni Mariatus
SURVEYING (CIV-104) PERTEMUAN 11 : METODE PENGUKURAN LUAS
SURVEYING (CIV-04) PERTEMUAN : METODE PENGUKURAN LUAS UNIVERSITAS PEMBANGUNAN JAYA Jl. Boulevar Bintaro Sektor 7, Bintaro Jaa Tangerang Selatan 54 MANFAAT PERHITUNGAN LUAS Pengukuran luas ini ipergunakan
PROSPEK PENGEMBANGAN USAHA PAKAN IKAN DI PROVINSI BENGKULU
PROSPEK PENGEMBANGAN USAHA PAKAN IKAN DI PROVINSI BENGKULU A. Penahuluan Pakan erupakan salah satu koponen penting ala kegiatan buiaya ikan. Disatu sisi pakan erupakan suber ateri an energi untuk enopang
PERHITUNGAN BERAT KAPAL KOSONG
PERHITUNGAN BERAT KAPA KOSONG 1.1 Ukuran Utaa Kapal Berikut ini adalah ukuran utaa kapal yang akan dihitung dala proses peluncuran kapal : Ite Value Satuan Jenis kapal General Cargo pp 94.656 wl 98.442
ANALISIS STABILITAS LERENG DENGAN SIMPLIFIED BISHOP METHOD dan JANBU MENGGUNAKAN PROGRAM MATHCAD
ANALISIS STABILITAS LERENG DENGAN SIMPLIFIED BISHOP METHOD an JANBU MENGGUNAKAN PROGRAM MATHCAD YOSEPHINA NOVALIA NRP : 0521034 Pembimbing : Ir. Ibrahim Surya, M.Eng. FAKULTAS TEKNIK JURUSAN TEKNIK SIPIL
(x- x 1. Contoh soal: jawab: x 2 + y 2 = 2 2 x 2 + y 2 = 4. x 2 + y 2 = 4. jawab: (x 5) 2 + (y 2) 2 = 4 2
LINGKRN (x- x ) (x- x ) + (y- y ) (y- y ) = 0 Contoh soal: Pengertian : Lingkaran adalah tepat kedudukan titik-titik yang berjarak konstan/saa terhadap sebuah titik tertentu. Sebuah titik tertentu itu
PENGARUH KECEPATAN ANGIN TERHADAP EVAPOTRANSPIRASI BERDASARKAN METODE PENMAN DI KEBUN STROBERI PURBALINGGA
PENGARUH KECEPATAN ANGIN TERHADAP EVAPOTRANSPIRASI BERDASARKAN METODE PENMAN DI KEBUN STROBERI PURBALINGGA Nurhayati Fakultas Sains an Teknologi, UIN Ar-Raniry Bana Aceh [email protected] Jamru
BAB 7 P A S A K. Gambar 1. Jenis-Jenis Pasak
BAB 7 P A S A K Pasak atau keys merupakan elemen mesin yang igunakan untuk menetapkan atau mengunci bagian-bagian mesin seperti : roa gigi, puli, kopling an sprocket paa poros, sehingga bagian-bagian tersebut
= mv Momentum akhir setelah tumbukan pertama:
1.79. Sebuah bola baja berassa = 50 g jatuh dari ketinggian h = 1,0 pada perukaan horisontal sebuah papan tebal. Tentukan oentu total yang diberikan bola pada papan setelah terpental beberapa kali, bila
(x- x 1. Contoh soal: jawab: x 2 + y 2 = 2 2 x 2 + y 2 = 4. x 2 + y 2 = 4. jawab: (x 5) 2 + (y 2) 2 = 4 2
BB XI. LINGKRN (x- x ) (x- x ) + (y- y ) (y- y ) 0 Contoh soal: Pengertian : Lingkaran adalah tepat kedudukan titik-titik yang berjarak konstan/saa terhadap sebuah titik tertentu. Sebuah titik tertentu
Keseimbangan benda terapung
Keseimbangan benda terapung Pendahuluan Benda yang terendam di dalam air akan mengalami gaya berat sendiri benda atau gaya gravity ( Fg ) dengan arah vertikal ke bawah dan gaya tekanan air dengan arah
Hukum Coulomb. a. Uraian Materi
Hukum oulomb a. Tujuan Kegiatan Pembelajaran Setelah mempelajari kegiatan belajar, iharapkan ana apat: - menjelaskan hubungan antara gaya interaksi ua muatan listrik, besar muatan-muatan, an jarak pisah
Analisis Stabilitas Lereng
Analisis Stabilitas Lereng Lereng Slope Stability Dr.Eng.. Agus Setyo Muntohar, S.T.,M.Eng.Sc. Faktor Keamanan (Factor of Safety) Faktor aman (FS): nilai baning antara gaya yang menahan an gaya yang menggerakkan.
BAB III PERENCANAAN PEMILIHAN TALI BAJA PADA ELEVATOR BARANG. Q = Beban kapasitas muatan dalam perencanaan ( 1 Ton )
BAB III PERENCANAAN PEMILIHAN TALI BAJA PADA ELEVATOR BARANG 3.1 Perencanaan Beban Total Paa Elevator Barang Q total = Q + WM + WO ( Persamaan 2.1.10 ) Q = Beban kapasitas muatan alam perencanaan ( 1 Ton
BAB 4 ANALISIS DAN MINIMISASI RIAK TEGANGAN DAN ARUS SISI DC
BAB ANAL DAN MNMA RAK EGANGAN DAN ARU DC. Penahuluan ampai saat ini, penelitian mengenai riak sisi DC paa inverter PWM lima-fasa paa ggl beban sinusoial belum pernah ilakukan. Analisis yang ilakukan terutama
BAB 4. HASIL DAN PEMBAHASAN
BAB 4. HASIL DAN PEMBAHASAN Analisa pelat lantai gedung rawat inap RSUD Surodinawan Kota Mojokerto dengan enggunakan teori garis leleh ebutuhkan beberapa tahap perhitungan dan analsis aitu perhitungan
Metacentra dan Titik dalam Bangunan Kapal
Metacentra dan Titik dalam Bangunan Kapal 1. Titik Berat (Centre of Gravity) Setiap benda memiliki tittik berat. Titik berat inilah titik tangkap dari sebuah gaya berat. Dari sebuah segitiga, titik beratnya
GETARAN PEGAS SERI-PARALEL
1 GETARAN PEGAS SERI-PARALEL I. Tujuan Percobaan 1. Menentukan konstanta pegas seri, paralel dan seri-paralel (gabungan). 2. Mebuktikan Huku Hooke. 3. Mengetahui hubungan antara periode pegas dan assa
BAB VI PERENCANAAN TEKNIS
BAB I PERENCANAAN TEKNIS I.1. Umum Paa Bab telah ipilih satu alternatif jalur penyaluran an sistem pengolahan air buangan omestik Ujung Berung Regency. Paa bab ini akan itentukan imensi jaringan pipa,
1 Kapasitor Lempeng Sejajar
FI1201 Fisika Dasar IIA Kapasitor 1 Kapasitor Lempeng Sejajar Dosen: Agus Suroso Paa bab sebelumnya, telah ibahas mean listrik i sekitar lempeng-yang-sangat-luas yang bermuatan, E = σ 2ε 0 ˆn, (1) engan
1 Kapasitor Lempeng Sejajar
FI1201 Fisika Dasar IIA Kapasitor 1 Kapasitor Lempeng Sejajar Dosen: Agus Suroso Paa bab sebelumnya, telah ibahas mean listrik i sekitar lempeng-yang-sangat-luas yang bermuatan, E = σ 2ε 0 ˆn, (1) engan
BAB V PERENCANAAN TEKNIS RINCI
BAB V PERENCANAAN TEKNIS RINCI 5. PERHITUNGAN DIMENSI SALURAN 5.. Perhitungan Diensi Saluran Tersier Saluran tersier tidak direncanakan sebagai jalur navigasi sehingga perhitungan diensi untuk salutan
Contoh 1. = 3, 75 cm 3 Ditanya : m Jawab : m = ρv = 19,3 x 3,75 = 27,375 gra m
Contoh. Seotong eas yang bentuknya seerti seeda akan di tentukan assanya. Eas di asukkan dala gelas ukur yang sebelunya telah berisi air, seerti gabar. Ternyata, skala yang ditunjukan oleh eukaan air dala
Solusi Tutorial 6 Matematika 1A
Solusi Tutorial 6 Matematika A Arif Nurwahi ) Pernyataan benar atau salah. a) Salah, sebab ln tiak terefinisi untuk 0. b) Betul. Seerhananya, titik belok apat ikatakan sebagai lokasi perubahan kecekungan.
, serta notasi turunan total ρ
LANDASAN TEORI Lanasan teori ini berasarkan rujukan Jaharuin (4 an Groesen et al (99, berisi penurunan persamaan asar fluia ieal, sarat batas fluia ua lapisan an sistem Hamiltonian Penentuan karakteristik
Studi Perbandingan antara Gaya Menggantung dengan Gaya Jalan Di Udara terhadap Perestasi Lompat Jauh Pada Siswa putra Kelas VIII Putra SMPN 1 Sape
Stui Perbaningan antara Gaya Menggantung engan Gaya Jalan Di Uara terhaap Perestasi Lompat Jauh Paa Siswa putra Kelas VIII Putra SMPN 1 Sape Irfan., M.Or. Program Stui Penjaskesrek STKIP Taman Siswa Bima
(x- x 1. Contoh soal: jawab: x 2 + y 2 = 2 2 x 2 + y 2 = 4. x 2 + y 2 = 4. jawab: (x 5) 2 + (y 2) 2 = 4 2
BB XI. LINGKRN (x- x ) (x- x ) + (y- y ) (y- y ) = 0 Contoh soal: Pengertian : Lingkaran adalah tepat kedudukan titik-titik yang berjarak konstan/saa terhadap sebuah titik tertentu. Sebuah titik tertentu
Garis alir pada fluida mengalir terdapat dua jenis, yaitu:
DINAMIKA FLUIDA Garis alir pada fluida engalir terdapat dua jenis, yaitu:. Aliran lainar adalah aliran fluida yang engikuti suatu garis lurus atau elengkung yang jelas ujung dan pangkalnya serta tidak
Dinamika 3 TIM FISIKA FTP UB. Fisika-TEP FTP UB 10/16/2013. Contoh PUSAT MASSA. Titik pusat massa / centroid suatu benda ditentukan dengan rumus
Fisika-TEP FTP UB /6/3 Dinaika 3 TIM FISIKA FTP UB PUSAT MASSA Titik pusat assa / centroid suatu benda ditentukan dengan ruus ~ x x ~ y y ~ z z Diana: x, y, z adalah koordinat titik pusat assa benda koposit.
SOAL OLIMPIADE SAINS NASIONAL (OSN) 2007 Bidang studi : FISIKA Tingkat : SMA Waktu : 4 jam
Dapatkan soal-soal lainnya di http://foru.pelatihan-osn.co SOAL OLIPIADE SAINS NASIONAL (OSN) 007 Bidang studi : FISIKA Tingkat : SA Waktu : 4 ja 1. (nilai 0) A. Sebuah obil bergerak enuruni suatu jalan
Soal No. 2 Seorang anak hendak menaikkan batu bermassa 1 ton dengan alat seperti gambar berikut!
Fluida Statis Fisikastudycenter.com- Contoh Soal dan tentang Fluida Statis, Materi Fisika kelas 2 SMA. Cakupan : tekanan hidrostatis, tekanan total, penggunaan hukum Pascal, bejana berhubungan, viskositas,
PERSAMAAN SCHRODINGER YANG BERGANTUNG WAKTU
PERSAMAAN SCHRODINGER YANG BERGANTUNG WAKTU Perbeaan pokok antara mekanika newton an mekanika kuantum aalah cara menggambarkannya. Dalam mekanika newton, masa epan partikel telah itentukan oleh keuukan
TOPIC. 10. ShippingEducationEbooks www.ebokship.plusadvisor.com SumberEbookShippingTerlengkap DiIndonesia Youneedgoodadvisor www.plusadvisor.com PERCOBAAN STABILITAS INCLINING EXPERIMENT Tujuan percobaan
dimana p = massa jenis zat (kg/m 3 ) m= massa zat (kg) V= Volume zat (m 3 ) Satuan massa jenis berdasarkan Sistem Internasional(SI) adalah kg/m 3
Zat dan Wujudnya Massa Jenis Jika kau elihat kapas yang berassa 1 kg dan batu berassa 1 kg, apa ada di benaku? Massa Jenis adalah perbandingan antara assa benda dengan volue benda Massa jenis zat tidak
Pendahuluan Definisi Aturan Problems DERIVATIVE (TURUNAN) Kus Prihantoso Krisnawan. November 18 th, Yogyakarta. Krisnawan Pertemuan 1
DERIVATIVE (TURUNAN) Kus Prihantoso Krisnawan November 18 th, 2011 Yogyakarta Garis Singgung Garis Singgung Kecepatan Sesaat Garis Singgung Garis Singgung Kecepatan Sesaat Garis Singgung Garis Singgung
3 TEORI KONGRUENSI. Contoh 3.1. Misalkan hari ini adalah Sabtu, hari apa setelah 100 hari dari sekarang?
Paa bab ini ipelajari aritmatika moular yaitu aritmatika tentang kelas-kelas ekuivalensi, imana permasalahan alam teori bilangan iseerhanakan engan cara mengganti setiap bilangan bulat engan sisanya bila
DAFTAR NOTASI. : Tinggi blok tegangan persegi ekuivalen. : Koefisien momen lapangan arah x. : Koefisien momen tumpuan arah y
DAFTAR NOTASI 1. Perencanaan Pelat (Lantai) As a b clx cty fc fy h ly lx Mlx Mtx : Luas tulangan : Tinggi blok tegangan persegi ekuivalen : Panjang memanjang pelat : Koefisien momen lapangan arah x : Koefisien
matriks A. PENGERTIAN MATRIKS Persija Persib baris
Kolom 1. Pengertian Matriks matriks A. PENGERTIAN MATRIKS Dalam kehiupan sehari-hari an alam matematika, berbagai keterangan seringkali isajikan alam bentuk matriks. Contoh 1: Hasil pertaningan grup I
3 TEORI KONGRUENSI. Contoh 3.1. Misalkan hari ini adalah Sabtu, hari apa setelah 100 hari dari sekarang?
Paa bab ini ipelajari aritmatika moular yaitu aritmatika tentang kelas-kelas ekuivalensi, imana permasalahan alam teori bilangan iseerhanakan engan cara mengganti setiap bilangan bulat engan sisanya bila
BAB USAHA DAN ENERGI I. SOAL PILIHAN GANDA
1 BAB USAHA DAN ENERGI I. SOAL PILIHAN GANDA 01. Usaha yang dilakukan oleh suatu gaya terhadap benda sama dengan nol apabila arah gaya dengan perpindahan benda membentuk sudut sebesar. A. 0 B. 5 C. 60
PERILAKU KOMPONEN STRUKTUR LENTUR PROFIL I BERDASARKAN FORMULA AISC
PERILAKU KOMPONEN STRUKTUR LENTUR PROFIL I BERDASARKAN FORMULA AISC A. PENDAHULUAN. Aa ua kegagalan yang apat terjai paa komponen struktur lentur profil I yang mengelami lentur. Kegagalan pertama profil
METODE MATRIK APLIKASI METODE MATRIK UNTUK ANALISA STRUKTUR BALOK
METOE MATRIK APIKASI METOE MATRIK UNTUK ANAISA STRUKTUR BAOK PENGERTIAN UMUM Metoe matrik aalah suatu pemikiran baru paa analisa struktur, yang berkembang bersamaan engan populernya penggunaan computer
BAB IV KESEIMBANGAN BENDA TERAPUNG
BAB I KESEIMBANGAN BENDA TERAPUNG Tujuan Intruksinal Umum (TIU) Mahasiswa diharapkan dapat merencanakan suatu bangunan air berdasarkan knsep mekanika fluida, teri hidrstatika dan hidrdinamika. Tujuan Intruksinal
DEFERENSIAL PARSIAL BAGIAN I
DEFEENSAL PASAL BAGAN Diferenial parial olume uatu iliner berjari-jari r engan ketinggian h inatakan oleh r h Yakni bergantung kepaa ua bearan, aitu r an h. Jika r kita jaga tetap an ketinggian h kita
TEKNIK PEMBESIAN PELAT FONDASI
TEKNIK PEMBESIAN Hotma Prawoto Sulistyai Program Diploma Teknik Sipil Sekolah Vokasi Universitas Gajah Maa 1 UPPER STRUCTURE Bagian bangunan yang beraa i atas permukaan tanah SUB STRUCTURE Bagian bangunan