' x KAJIAN ALGORITMA KOMPUTASI PERSAMAAN DIFFERENSIAL PARSIAL (PDP) Agus Sujono *)
|
|
|
- Utami Sutedja
- 7 tahun lalu
- Tontonan:
Transkripsi
1 KAJIAN AGORITMA KOMPUTASI PERSAMAAN DIFFERENSIA PARSIA (PDP) Agus Sujono *) ABSTRACT The method of numerical analysis is very useful to solve many problems that very difficult to hold by conventional analytical analysis. But its need much power of computing if the method is not good. Some of the popular methods are Gauss-Seidel, elimination Gauss and Doolittle, that have different algorithms of computing, that to be compared. The result of the compare of the algorithms is the time execution or the flops is depend on the degree of the element of the matrix, but in many cases the Gauss-Seidel method is the better to use. 1. PENDAHUUAN Kemajuan komputer yang sangat cepat telah banyak memberi nuansa baru dalam bidang metoda komputasi, yang banyak mengarah pada metoda komputasi numeris. Sebab dengan metoda ini waktu komputasi dapat dipersingkat dan volume komputasi tidak terlalu dibatasi oleh karena kemampuan sumber daya yang ada. Selain itu juga banyak solusi bisa diperoleh dengan metoda ini dan bila dengan metode analitis terlalu sulit untuk memecahkannya. Oleh karena itu untuk mendukung komputasi diberbagai bidang, metoda komputasi numeris perlu terus dikembangkan, yaitu dengan membuat algoritma komputasinya. Hal ini termasuk mencari metoda yang paling menguntungkan, agar dapat lebih bnyak hal dapat ditangani dan lebih cepat pengerjaannya. Berikut ini kajian algoritma aplikasi dari permasalan perpindahan panas, mekanika fluida dan struktur / konstruksi baja, yang diselesaikan dengan metoda komputasi numeris Persoalan Perpindahan Panas. Diambil contoh masalah perpindahan panas konduksi, dalam suatu bahan yang cukup besar pada kondisi transien, untuk koordinat kartesian x, y, z : T T T q 1 T ' x y z k t dimana : T = suhu, t = waktu, q = panas yang terjadi *) Agus Sujono : staf pengajar Teknik Mesin, Fak.Teknik, UNS 1. Persoalan Mekanika Fluida Aliran fluida secara umum mempunyai kecepatan yang tidak sama disetiap tempat, dan bila fluida tersebut adalah kompresibel, maka kondisinya berubah, lebihlebih bila keadaan tidak ajeg (non steady state) maka akan selalu berubah terhadap waktu. Hal ini menimbulkan persamaan diferensial parsial multi-dimensional, sebagai berikut : Rumus vektor bentuk : 0
2 ( o ) =. u = 0 u ( u) ( u. ) u u p b 0 t R F T 1 ( T) ( u. ) T t R P e e r o T ij u x i j r 0 dimana : u = vektor kecepatan, T = suhu, R e = Renold number P r = Prandtl number, F r = Froudle number 1.. Persoalan Struktur Konstruksi Dalam struktur rangka ruang banyak digunakan metoda matrik, sebab komponen rangka batang berjumlah sangat banyak, sehingga bila diselesaikan secara manual akan sangat lama dan melelahkan. Perhitungan gaya akan didasarkan pada persamaan kekakuan dari batang yang bersangkutan didalam sistim konstruksi terpadu sebagai berikut : {P} = [K] {} dimana : P = gaya, K = kekakuan, = defleksi P1 P P P4 P 5 P6 P 7 P8 P 9 P10 P 11 P1 EA 1 EIz 0 1 EI y 0 0 GJ EI y 4 EI y EIz 4 EIz = EA Simetris EA 1 EIz 6EIz 1 EIz 1 EI y 6EI y 1 EI y GJ GJ 6EI y EI y 6EI y 4 EI y 6EIz EIz 6EIz 4 EIz Matrik ini adalah hanya satu elemen saja, padahal kenyataannya berjumlah banyak, sehingga untuk penyelesaiannya tidak efisien bila dengan perhitungan matrik biasa, maka telah ada metoda perhitungan dengan matrik jarang (sparse matrix).. Teori Analisis Algotitma 1
3 Masalah di dalam analisis algoritma dibagi menjadi atas : 1. Masalah Numeris, yaitu membuat model matematika.. Masalah Simbol dan Teks yaitu string atau format grammars. Keduanya akan menyusun suatu algoritma untuk membentuk sebuah program. Algoritma didefinisikan sebagai suatu barisan instruksi tersebut memiliki suatu arti yang jelas (clear meaning) dan dapat dijalankan dengan sejumlah usaha dalam jangka waktu tertentu. Algorima terkadang berupa : 1. Solusi optimal. Baik tetapi bukan merupakan solusi optimal yang penting (heuristik). Untuk penyelesaian masalah-masalah tersebut dapat diselesaikan dengan menggunakan beberapa algoritma, kemudian memilih algoritma yang tepat. Ada tujuan mengapa suatu algoritma dipilih yaitu : 1. Suatu algorima seharusnya mudah dimengerti, disandikan dan didebug. yang dipentingkan adalah penulisan suatu program yang akan digunakan sekali atau beberapa kali. Biaya untuk penulisan program lebih besar daripada biaya unuk running program.. Suatu algoritma seharusnya dapat menyebabkan penggunaan komputer menjadi lebih efisien, khususnya algoritma tersebut dapat berjalan secepat mungkin. Untuk suatu problem dengan solusi yang dipergunakan beberapa kali, biaya untuk running program lebih besar daripada biaya untuk menulis program. Mengukur running time dari suatu program tergantung dari beberapa faktor di bawah ini : 1. Masukan (input) program. Kualitas dari sandi (code) yang dihasilkan oleh kompiler yang dipergunakan untuk menulis (create) objek program.. Perlaku dan kecepatan instruksi-instruksi mesin yang dipergunakan untuk mengeksekusi program. 4. Kompleksitas waktu algoritma yang menjadi dasar suatu program. Comment [A1]: Running time dari suatu program seharusnya didefinisikan sebagai suatu fungsi dari masukan, biasanya pada ukuran masukan n, ditulis T(n). Running time pada beberapa program, benar-benar merupakan suatu fungsi dari masukan tertentu (bukan hanya ukuran dari masukan). Dalam hal ini, jika T(n) adalah Worst Case, yaitu running time maksimal dari semua running time pada masukan dengan ukuran n, maka T(n) adalah time complexity dari program. Pernyataan 1 dan, running time T(n) dapat dinyatakan dalam satuan standar waktu (misalnya detik). Notasi Big-Oh dipergunakan pada growth rate suatu fungsi. Running time T(n) dari beberapa program adalah O(n ), dapat dibaca big-oh dari n kwadrat. Pernyataan ini berarti bahwa ada konstanta positif c dan n 0 sedemikian hingga untuk setiap n sedemikian sehingga untuk setiap n n o, T(n) cn. Running time T(n) O(f(n)) jika terdapat konstanta positif c sedemikian sehingga T(n) cf(n) untuk setiap n n 0, program dikatakan memiliki growth rate f(n). Fungsi f(n) merupakan batas atas (upper bound) pada growth rate T(n). Untuk menspesifikasikan batas bawah (lower bound) pada growth rate T(n) dapat dipergunakan notasi W(g(n)), dibaca dengan big-omega dari g(n), artinya terdapat suatu konstanta c sedemikian sehingga T(n) cg(n). Suatu prinsip
4 asimetrikantara big-oh dan big Omega seringkali cepat pada beberapa masalah algoritma dan tidak cepat pada semua masukkan. Berpedoman pada fungsi-fungsi running time dari program, dengan mempertimbangkan program-program yang memiliki growth rate serendah mungkin sejak growth rate akhirnya menentukan berapa besarnya n, maslah dapat diselesaikan dengan komputer. Growth rate dari suatu worst case running time bukanlah suatu kejadian tunggal atau perlu, yang terpenting adalah kriteria untuk mengevaluasi algoritma atau program yaitu : 1. Jika suatu program hanya dipergunakan beberapa kali saja, maka biaya untuk menulis dan debugging akan mendominasi keseluruhan biaya running time saat itu, dan sudah tentu akan berpengaruh pula pada biaya keseluruhan, sehingga perlu dipilih algoritma yang aksesnya dapat diimplementaskan dengan benar.. Jika suatu program hanya membutuhkan sedikit masukan, maka growth rate dari running time akan lebih kecil, dan terlihat dari konstanta c pada rumusan di atas.. Algoritma yang sukar tetapi efisisen, biasanya tidak diinginkan, karena selain penulis program akan sukar untuk memahami algoritma tersebut. 4. Ada beberapa contoh algoritma efisien yang menggunakan begitu banyak ruang untuk diimplementasikan tanpa menggunakan pengingat sekunder yang berjalan lambat, hal ini lebih banyak dijumpai dibandingkan dengan harus membatalkan algoritma tersebut. 5. Pada algoritma numeris, ketepatan dan stabilitasnya sama pentingnya dengan efisiensi algoritma. Menghitung running time dari berbagai macam program merupakan masalah yang sangat kompleks terutama dalam hal matematikanya. Andaikan T 1 (n) dan T (n) adalah running time dari fragmen program yaitu P 1 dan P. T 1 (n) dinyatakan sebagai O(f(n)) dan T (n) sebagai O(g(n)), maka T 1 (n) + T (n) adalah running time dari P 1 diikuti oleh P. Dalam hal ini T 1 (n) + T (n) dapat ditulis sebagai O(max(f(n),g(n))). Untuk setiap konstanta c 1 dan c, n 1 dan n, jika n n1, maka T 1 (n) c 1 f(n) dan jika n n maka T (n) c g(n). Diambil n 0 = max(n 1,n ), jika n n0 maka T 1 (n) +T (n) c 1 f(n) + C g(n). Oleh karena itu T 1 (n) + T (n) adlah O(max(f(n),g(n))) yang kemudian dikenal sebagai rule of sum..1. Rule of Sum Rule of sum dapat dipergunakan untuk menentukan running time dari suatu barisan langkah-langkah program dimana masing-masing langkah mungkin merupakan suatu fragmen program sembarang dengan kalang (loop) dan cabang (branch). Andaikan ada langkah program dengan running time 0(n ), O(n ) dan (n log n), maka running time dari langkah pertama yang dieksekusi secara berurutan adalah O(max(n,n ) yaitu O(n ). Running time dari ketiga langkah bersamaan adalah O(max(n,n, nlogn)) yaitu O(n ). Secara umum, running time dari suatu barisan berhingga langkah-langkah dengan menggunakan faktor konstan adalah sama dengan running time dari langkah yang memiliki running time terbesar... Rule of Product Jika T 1 (n) dan T (n) memiliki running time O(f(n)) dan O(g(n)), maka T 1 (n).t (n) memiliki running time O(f(n),g(n)) yang kemudian disebut sebagai rule of product.
5 O(cf(n)) sama dengan O(f(n)) untuk sembarang bilangan positif c. Bila running time = O(n ). Program tersebut membutuhkan waktu yang sebanding dengan kwadrat anggota dari item yang diurutkan. Secara umum, aturan untuk menganalisa suatu program adalah sebagai berikut: 1. Running time dari tiap-tiap tugas, membaca dan menulis ungkapan sebesar O(1).. Running time dari suatu barisan ungkapan (statement) ditentukan oleh rule for sums. Running time dari beberapa barisan akan menjadi running time terbesar dari barisan-barisan yang ada di dalammnya.. Running time dari ungkapan IF adalah biaya dari ungkapan-ungkapan yang mengkondisikan apakah instruksi akan dieksekusi atau tidak, ditambah dengan waktu eksekusi dari kondisi tersebut. Waktu yang dibutuhkan untuk ungkapan IF-THEN-ESE adalah waktu untuk mengevaluasi kondisi ditambah waktu terbesar yang dibutuhkan untuk mengeksekusi ungkapan jika kondisi tersebut benar dan waktu untuk mengeksekusi ungkapan jika kondisi tersebut salah. 4. Waktu untuk mengeksekusi suatu kalang (loop) adalah jumlah semua waktu yang dibutuhkan untuk mengeksekusi badan kalang (body loop) dan waktu untuk mengeksekusi kondisi agar kalang berhenti.. PENERAPAN PADA PDP Persamaan diferensial parsial (PDP) linier orde dua (Partial Diferential Equation /PDE), seringkali mengacu kepada, seperti tertulis di atas, sebagai elliptik, hiperbolik atau parabolik. Klasifikasi seperti hal tersebut di atas, bisa jika persamaannya telah dikurangi dengan transformasi yang cocok dari variabel-variabel indenpenden, ke bentuk n n u u Ai Bi x cu D 0 (1-1) xi i1 i1 i dimana koefisien A i, dihitung pada titik (x 1, x,...x n ) bisa 1, -1 atau nol. Disini u adalah variabel mandiri, dan x i adalah variabel bebas. Catatlah ketiadaan turunan campuran dalam bentuk u/ x i x j (i j). Selama koefisien Ai, Bi, C, dan D adalah fungsi dari variabel mandiri x 1, x,...,x n, klasifikasi PDE dapat bermacam-macam sesuai dengan titik yang tertentu yang di diperhatikan pada ruang (x 1, x,...x n ). Sangat sering, salah satu variabel mandiri bisa jadi waktu t dan sisanya adalah sebuah jarak koordinat x, y, dan z. Dapat ditunjukan bahwa, untuk dua dimensi bidang xy dengan mandiri kita mempunyai bentuk persamaan : u sebagai sebuah variabel u x u u 0 y disebut persamaan aplace. Dapat ditunjukan dalam bidang xy, jika kita mempunyai fungsi f(x,y) kemudian mengikuti : u f ( x, y) disebut persamaan Poisson. Metode numerik untuk menyelesaikan persamaan diferensial elliptik dipergunakan sama pada kedua persamaan aplace dan Poisson. Persamaan menjelaskan bagaimana u bervariasi dibagian dalam sebuah wilayah tertutup. Fungsi ditetapkan pada batas wilayah oleh kondisi 4
6 batas. Kondisi batas bisa menspesifikasikan nilai u pada semua titik pada batas atau beberapa kombinasi. Metode memecahkan masalah persamaan diferensial parsial. Diantaranya, metode Gauss-Seidel, Eliminasi Gauss, dan Doolittle. Persamaan linear simultan dari bentuk : A* v b adalah Beberapa metode faktorisasi matrik A yang ada, diantaranya adalah Doolittle, Metode Gauss-Seidel, Eliminasi Gauss, yang akan dikaji.. KAJIAN AGORITMA Untuk menganalisa permasalahan program PDP, dipergunakan pendekatan dengan membetuk kisi-kisi diskrit dimana jarak h sejajar dengan sumbu x dan sejajar sumbu y, dan sejajar sumbu z adalah sama. Dengan : x i = ih 1, y j = jh, z k = kh h h q 1 nx 1 b ny 1 h c nz 1 nx = banyaknya titik pada tiap baris sumbu x ny = banyaknya titik pada tiap baris sumbu y nz = banyaknya titik pada tiap baris sumbu z Sehingga setiap titik u ijk u(x i,y j,z k ), PDE dapat diwakili oleh bentuk persamaan linear f ( x, y, z ) i j k u u u i, j, k i, j, k i, j, k 1 1 h1 u u u u u u i, j1, k i, j, k i, j1, k i, j, k 1 i, j, k i, j, k1 h h = -(h 1 + h + h )u i,j,k + h h u i - 1,j,k + h h u i + 1,j,k + h 1 h u i,j,k h 1 h u i,j + 1,k =(h 1 h h )f(x i,y j,z k ) Di sini terlihat bahwa setiap u i,j,k selalu didukung oleh 6 titik tetangganya yaitu u i-1,j,k, u i+1,j,k, u i,j- 1,k, u i,j+1,k, u i,j,k+1, and u i,j,k-1 Kemudian dibentuk Matrik A (matrik penthadiagonal) dengan elemen-elemen : v( 1) B( 1) v( ) B( ).... v( nn) B( nn) 5
7 A (label(j,i), label(j,i)) = -(h 1 + h + h ) A (label(j,i), label(j - 1,i)) = h 1 h A (label(j,i), label(j + 1,i)) = h 1 h A (label(j,i), label(j,i - 1)) = h h 1 A (label(j,i), label(j,i + 1)) = h h dimana label(j,i) = matrik yang elemen-elemennya berisi nomor label misal, label(j,i) = c, then v(c) is u(x i,y j,z k ) at c. Sehingga dapat tersusun bentuk matrik sebagai berikut : Terlihat bahwa akan terbentuk nn seperti persamaan linear simultan : A* v b.1. Kajian Algoritma Gauss Seidel function [v] = GSeidel(A,B); global nx ny nz u; nn = nx*ny*nz; x = zeros(nn,1); 1. for i=1:nn. v(i) = B(i);. for j=i:i-1 4. v(i) = v(i) - A(i,j)*v(j); 5. end; 6. for j=i+1:nn 7. v(i) = v(i) - A(i,j)*x(j); 8. end; 9. v(i) = v(i)/a(i,i); 10. end; Misal n = nn 1. Baris hingga 5 memiliki maksimum kalang sebesar (n-1) sehingga worst case running time. Baris 6 hingga 8 memiliki maksimum kalang sebesar (n-1) sehingga worst case running time 6
8 . Baris 1 hingga 10 memiliki kalang sebesar (n) sehingga waktu yang dibutuhkan sama dengan n 4. Worst case running time dari baris 1 sampai dengan baris 10 adalah : Total = n. n -1 n 1 = n. n - = n - n = O(n ).. Kajian Algoritma Gauss function [v] = Gauss(A,B); global nx ny nz; nn = nx*ny*nz; 1. for j=1:nn-1. for i=j+1:nn. m(i,j)= A(i,j)/A(j,j); 4. A(i,j)= 0; 5. B(i)= B(i) - m(i,j)*b(j); 6. for k=j+1:nn 7. A(i,k)= A(i,k) - m(i,j)*a(j,k); 8. end; 9. end; 10. end; 11. for i=nn:-1:1 1. v(i)= B(i); 1. for j=i+1:nn 14. v(i)= v(i) - A(i,j)*v(j); 15. end; 16. v(i)= v(i)/a(i,i); 17. end; Misal n = nn 1. Baris 6 hingga 8 memiliki maksimum kalang sebesar (n-1) sehingga worst case running time 7
9 . Baris hingga 9 memiliki maksimum kalang sebesar (n-1) sehingga worst case running time. Baris 1 hingga 10 memiliki maksimum kalang sebesar (n-1) sehingga worst case running time 4. Worst case running time dari baris 1 sampai dengan baris 10 adalah : Total = n -1 n 1 n 1 = n - n + n -1 = O(n ) 5. Baris 1 hingga 15 memiliki maksimum kalang sebesar (n-1) sehingga worst case running time 6. Baris 11 hingga 17 memiliki maksimum kalang sebesar (n) sehingga worst case running time 7. Worst case running time dari baris 1 sampai dengan baris 10 adalah : Total = nn -1 = n - n = O(n ) 8. Total Worst case running time dari baris 1 sampai dengan baris 17 adalah : Total = max(n,n ) = O(n ).. Kajian Algoritma Doolittle function [v] = dlitlle(a,b); global nx ny nz; nn = nx*ny*nz; % Triangularization for j=1:nn-1. for i=j+1:nn. A(i,j) = A(i,j)/A(j,j); 4. for k=j+1:nn 5. A(i,k) = A(i,k) - A(i,j)*A(j,k); 6. end; 7. end; 8. end; Misal n = nn 1. Baris 4 hingga 6 memiliki maksimum kalang sebesar (n-1) sehingga worst case running time 8
10 . Baris hingga 7 memiliki maksimum kalang sebesar (n-1) sehingga worst case running time. Baris hingga 8 memiliki maksimum kalang sebesar (n-1) sehingga worst case running time 4. Worst case running time dari baris 1 sampai dengan baris 10 adalah : Total = n -1 n 1 n 1 = n - n + n -1 = O(n ) % Forward Elimination for i=1:nn. z(i) = B(i);. for j=1:i-1 4. z(i) = z(i) - A(i,j)*z(j); 5. end; 6. end; Misal n = nn 1. Baris hingga 5 memiliki maksimum kalang sebesar (n-1) sehingga worst case running time. Baris 1 hingga 6 memiliki maksimum kalang sebesar (n) sehingga worst case running time. Worst case running time dari baris 1 sampai dengan baris 6 adalah : Total = n -1 n = n - n = O(n ) % Back Substitution for i=nn:-1:1. v(i) = z(i);. for j=i+1:nn 4. v(i) = v(i) - A(i,j)*v(j); 5. end; 6. v(i) = v(i)/a(i,i); 7. end; 9
11 Misal n = nn 1. Baris hingga 5 memiliki maksimum kalang sebesar (n-1) sehingga worst case running time. Baris 1 hingga 7 memiliki maksimum kalang sebesar (n-1) sehingga worst case running time. Worst case running time dari baris 1 sampai dengan baris 7 adalah : Total = n -1 n 1 = n - n +1 = O(n ) Jumlah seluruh worst case running time untuk program di atas adalah : T(n) = max(n,n,n ) = O(n ) 4. HASI DAN KESIMPUAN Metoda xx xx 4x4x4 5x5x5 Flops Time Flops Time Flops Time Flops Time Gauss-Seidel 115 0, , , , Gauss , , , ,9 Doolittle , , , Flops Time : adalah jumlah proses komputasi pada eksekusi pada program Matlab. : adalah jumlah waktu yang diperlukan untuk eksekusi. Dari hasil esekusi pada program MATAB dapat ditarik kesimpulan bahwa secara umum metoda Gauss-Seidel merupakan algoritma komputasi numeris yang memberikan waktu eksekusi terbaik. 5. DAFTAR PUSTAKA Chapra SC, Canale RR, 1990, Numerical Methode for Engineers, McGraw Hill, New York Etter DM, 199, Engineering Problem Solving with Matlab, Prentice Hall, New Jersey Kingston JH, 1991, Algorithms and Data Structures, Addison-Wesley Publishing Co, Sydney Penny J, indfield, 1995, Numerical Methods Using Matlab, Ellis Horwood, New York 10
12 11
Pengantar Analisa Algoritma
 Pengantar Analisa Algoritma Pendahuluan Suatu permasalahan memungkinkan untuk diselesaikan dengan lebih dari satu algoritma (pendekatan) Bagaimana kita memilih satu diantara beberapa algoritma tersebut.
Pengantar Analisa Algoritma Pendahuluan Suatu permasalahan memungkinkan untuk diselesaikan dengan lebih dari satu algoritma (pendekatan) Bagaimana kita memilih satu diantara beberapa algoritma tersebut.
Analisa Kompleksitas Algoritma. Sunu Wibirama
 Analisa Kompleksitas Algoritma Sunu Wibirama Referensi Cormen, T.H., Leiserson, C.E., Rivest, R.L., Stein, C., Introduction to Algorithms 2nd Edition, Massachusetts: MIT Press, 2002 Sedgewick, R., Algorithms
Analisa Kompleksitas Algoritma Sunu Wibirama Referensi Cormen, T.H., Leiserson, C.E., Rivest, R.L., Stein, C., Introduction to Algorithms 2nd Edition, Massachusetts: MIT Press, 2002 Sedgewick, R., Algorithms
Algoritma dan Struktur Data. Performansi Algoritma
 Algoritma dan Struktur Data Performansi Algoritma Teknik Informatika Universitas Muhammadiyah Malang 2016 Mana yang lebih baik? pilihan 1 : Algoritma biasa dengan komputer yang cepat. pilihan 2 : Menggunakan
Algoritma dan Struktur Data Performansi Algoritma Teknik Informatika Universitas Muhammadiyah Malang 2016 Mana yang lebih baik? pilihan 1 : Algoritma biasa dengan komputer yang cepat. pilihan 2 : Menggunakan
PENDAHULUAN A. Latar Belakang 1. Metode Langsung Metode Langsung Eliminasi Gauss (EGAUSS) Metode Eliminasi Gauss Dekomposisi LU (DECOLU),
 PENDAHULUAN A. Latar Belakang Persoalan yang melibatkan model matematika banyak muncul dalam berbagai disiplin ilmu pengetahuan, seperti dalam bidang fisika, kimia, ekonomi, atau pada persoalan rekayasa.
PENDAHULUAN A. Latar Belakang Persoalan yang melibatkan model matematika banyak muncul dalam berbagai disiplin ilmu pengetahuan, seperti dalam bidang fisika, kimia, ekonomi, atau pada persoalan rekayasa.
BAB 4 PENYELESAIAN SISTEM PERSAMAAN LINEAR
 BAB 4 PENYELESAIAN SISTEM PERSAMAAN LINEAR A. Latar Belakang Persoalan yang melibatkan model matematika banyak muncul dalam berbagai disiplin ilmu pengetahuan, seperti dalam bidang fisika, kimia, ekonomi,
BAB 4 PENYELESAIAN SISTEM PERSAMAAN LINEAR A. Latar Belakang Persoalan yang melibatkan model matematika banyak muncul dalam berbagai disiplin ilmu pengetahuan, seperti dalam bidang fisika, kimia, ekonomi,
Kompleksitas Algoritma
 Kompleksitas Algoritma Sebuah algoritma tidak saja harus benar, tetapi juga harus mangkus (efisien). Algoritma yang bagus adalah algoritma yang mangkus. Kemangkusan algoritma diukur dari berapa jumlah
Kompleksitas Algoritma Sebuah algoritma tidak saja harus benar, tetapi juga harus mangkus (efisien). Algoritma yang bagus adalah algoritma yang mangkus. Kemangkusan algoritma diukur dari berapa jumlah
Aplikasi OBE Untuk Mengurangi Kompleksitas Algoritma Program Penghitung Determinan Matriks Persegi
 Aplikasi OBE Untuk Mengurangi Kompleksitas Algoritma Program Penghitung Determinan Matriks Persegi Alif Bhaskoro / 13514016 Program Studi Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi
Aplikasi OBE Untuk Mengurangi Kompleksitas Algoritma Program Penghitung Determinan Matriks Persegi Alif Bhaskoro / 13514016 Program Studi Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi
Metode Beda Hingga untuk Penyelesaian Persamaan Diferensial Parsial
 Metode Beda Hingga untuk Penyelesaian Persamaan Diferensial Parsial Ikhsan Maulidi Jurusan Matematika,Universitas Syiah Kuala, ikhsanmaulidi@rocketmail.com Abstract Artikel ini membahas tentang salah satu
Metode Beda Hingga untuk Penyelesaian Persamaan Diferensial Parsial Ikhsan Maulidi Jurusan Matematika,Universitas Syiah Kuala, ikhsanmaulidi@rocketmail.com Abstract Artikel ini membahas tentang salah satu
Kompleksitas Algoritma
 Kompleksitas Algoritma Pendahuluan Sebuah algoritma tidak saja harus benar, tetapi juga harus mangkus (efisien). Algoritma yang bagus adalah algoritma yang mangkus. Kemangkusan algoritma diukur dari berapa
Kompleksitas Algoritma Pendahuluan Sebuah algoritma tidak saja harus benar, tetapi juga harus mangkus (efisien). Algoritma yang bagus adalah algoritma yang mangkus. Kemangkusan algoritma diukur dari berapa
Matematika Diskrit Kompleksitas Algoritma. Instruktur : Ferry Wahyu Wibowo, S.Si., M.Cs.
 Matematika Diskrit Kompleksitas Algoritma Instruktur : Ferry Wahyu Wibowo, S.Si., M.Cs. Pendahuluan Sebuah masalah dapat mempunyai banyak algoritma penyelesaian. Contoh: masalah pengurutan (sort), ada
Matematika Diskrit Kompleksitas Algoritma Instruktur : Ferry Wahyu Wibowo, S.Si., M.Cs. Pendahuluan Sebuah masalah dapat mempunyai banyak algoritma penyelesaian. Contoh: masalah pengurutan (sort), ada
Analisis Kecepatan Sorting Dengan Notasi Big O
 Analisis Kecepatan Sorting Dengan Notasi Big O Rama Aulia NIM : 13506023 Program Studi Teknik Informatika, Institut Teknologi Bandung Jl. Ganesha 10, Bandung E-mail : ramaaulia@yahoo.co.id Abstrak Sorting
Analisis Kecepatan Sorting Dengan Notasi Big O Rama Aulia NIM : 13506023 Program Studi Teknik Informatika, Institut Teknologi Bandung Jl. Ganesha 10, Bandung E-mail : ramaaulia@yahoo.co.id Abstrak Sorting
Analisa dan Perancangan Algoritma. Ahmad Sabri, Dr Sesi 1: 9 Mei 2016
 Analisa dan Perancangan Algoritma Ahmad Sabri, Dr Sesi 1: 9 Mei 2016 Apakah algoritma itu? Asal istilah: Al Khwarizmi (± 800 M), matematikawan dan astronomer Persia. Pengertian umum: "suatu urutan langkah-langkah
Analisa dan Perancangan Algoritma Ahmad Sabri, Dr Sesi 1: 9 Mei 2016 Apakah algoritma itu? Asal istilah: Al Khwarizmi (± 800 M), matematikawan dan astronomer Persia. Pengertian umum: "suatu urutan langkah-langkah
BAB III ANALISIS KOMPLEKSITAS ALGORITMA
 BAB III ANALISIS KOMPLEKSITAS ALGORITMA 3.1 Kompleksitas Algoritma Suatu masalah dapat mempunyai banyak algoritma penyelesaian. Algoritma yang digunakan tidak saja harus benar, namun juga harus efisien.
BAB III ANALISIS KOMPLEKSITAS ALGORITMA 3.1 Kompleksitas Algoritma Suatu masalah dapat mempunyai banyak algoritma penyelesaian. Algoritma yang digunakan tidak saja harus benar, namun juga harus efisien.
Kompleksitas Algoritma
 Kompleksitas Algoritma Bahan Kuliah IF2120 Matematika Disktit Rinaldi M/IF2120 Matdis 1 Rinaldi M/IF2120 Matdis 2 Pendahuluan Sebuah masalah dapat mempunyai banyak algoritma penyelesaian. Contoh: masalah
Kompleksitas Algoritma Bahan Kuliah IF2120 Matematika Disktit Rinaldi M/IF2120 Matdis 1 Rinaldi M/IF2120 Matdis 2 Pendahuluan Sebuah masalah dapat mempunyai banyak algoritma penyelesaian. Contoh: masalah
BAB II TINJAUAN PUSTAKA. Kriptografi (cryptography) berasal dari Bahasa Yunani: cryptós artinya
 BAB II TINJAUAN PUSTAKA 2.1 Kriptografi Kriptografi (cryptography) berasal dari Bahasa Yunani: cryptós artinya secret (rahasia), sedangkan gráphein artinya writing (tulisan), jadi kriptografi berarti secret
BAB II TINJAUAN PUSTAKA 2.1 Kriptografi Kriptografi (cryptography) berasal dari Bahasa Yunani: cryptós artinya secret (rahasia), sedangkan gráphein artinya writing (tulisan), jadi kriptografi berarti secret
Kompleksitas Algoritma
 Kompleksitas Algoritma Pendahuluan Mengapa kita memerlukan algoritma yang mangkus? Waktu komputasi (dalam detik) 10 5 10 4 10 3 10 2 1 0 1 10-1 1 hari 1 jam 1 detik 1 menit 5 1 0 1 5 2 0 10-4 x 2 n 10-6
Kompleksitas Algoritma Pendahuluan Mengapa kita memerlukan algoritma yang mangkus? Waktu komputasi (dalam detik) 10 5 10 4 10 3 10 2 1 0 1 10-1 1 hari 1 jam 1 detik 1 menit 5 1 0 1 5 2 0 10-4 x 2 n 10-6
STUDI PERPINDAHAN PANAS DENGAN MENGGUNAKAN SISTEM KOORDINAT SEGITIGA
 STUDI PERPINDAHAN PANAS DENGAN MENGGUNAKAN SISTEM KOORDINAT SEGITIGA Oleh : Farda Nur Pristiana 1208 100 059 JURUSAN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT TEKNOLOGI SEPULUH
STUDI PERPINDAHAN PANAS DENGAN MENGGUNAKAN SISTEM KOORDINAT SEGITIGA Oleh : Farda Nur Pristiana 1208 100 059 JURUSAN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT TEKNOLOGI SEPULUH
Logika dan Algoritma Yuni Dwi Astuti, ST 2
 ALGORITMA Istilah algoritma pertama kali diperkenalkan oleh seorang ahli matematika yaitu Abu Ja far Muhammad Ibnu Musa Al Khawarizmi. Yang dimaksud dengan algoritma adalah : Urutan dari barisan instruksi
ALGORITMA Istilah algoritma pertama kali diperkenalkan oleh seorang ahli matematika yaitu Abu Ja far Muhammad Ibnu Musa Al Khawarizmi. Yang dimaksud dengan algoritma adalah : Urutan dari barisan instruksi
Design and Analysis of Algorithm
 Design and Analysis of Algorithm Week 3: Notasi Asymptotic dan Kelas Dasar Efisiensi Dr. Putu Harry Gunawan 1 1 Department of Computational Science School of Computing Telkom University Dr. Putu Harry
Design and Analysis of Algorithm Week 3: Notasi Asymptotic dan Kelas Dasar Efisiensi Dr. Putu Harry Gunawan 1 1 Department of Computational Science School of Computing Telkom University Dr. Putu Harry
Simulasi Perpindahan Panas pada Lapisan Tengah Pelat Menggunakan Metode Elemen Hingga
 JURNAL SAINS DAN SENI ITS Vol. 4, No.2, (2015) 2337-3520 (2301-928X Print) A-13 Simulasi Perpindahan Panas pada Lapisan Tengah Pelat Menggunakan Metode Elemen Hingga Vimala Rachmawati dan Kamiran Jurusan
JURNAL SAINS DAN SENI ITS Vol. 4, No.2, (2015) 2337-3520 (2301-928X Print) A-13 Simulasi Perpindahan Panas pada Lapisan Tengah Pelat Menggunakan Metode Elemen Hingga Vimala Rachmawati dan Kamiran Jurusan
PEMANFAATAN SOFTWARE MATLAB DALAM PEMBELAJARAN METODE NUMERIK POKOK BAHASAN SISTEM PERSAMAAN LINEAR SIMULTAN
 PEMANFAATAN SOFTWARE MATLAB DALAM PEMBELAJARAN METODE NUMERIK POKOK BAHASAN SISTEM PERSAMAAN LINEAR SIMULTAN Any Muanalifah Dosen Jurusan Tadris Matematika FITK IAIN Walisongo Abstrak Persoalan yang melibatkan
PEMANFAATAN SOFTWARE MATLAB DALAM PEMBELAJARAN METODE NUMERIK POKOK BAHASAN SISTEM PERSAMAAN LINEAR SIMULTAN Any Muanalifah Dosen Jurusan Tadris Matematika FITK IAIN Walisongo Abstrak Persoalan yang melibatkan
Menentukan Distribusi Temperatur dengan Menggunakan Metode Crank Nicholson
 Jurnal Penelitian Sains Volume 13 Nomer 2(B) 13204 Menentukan Distribusi Temperatur dengan Menggunakan Metode Crank Nicholson Siti Sailah Jurusan Fisika FMIPA, Universitas Sriwijaya, Sumatera Selatan,
Jurnal Penelitian Sains Volume 13 Nomer 2(B) 13204 Menentukan Distribusi Temperatur dengan Menggunakan Metode Crank Nicholson Siti Sailah Jurusan Fisika FMIPA, Universitas Sriwijaya, Sumatera Selatan,
KAJIAN DISKRETISASI DENGAN METODE GALERKIN SEMI DISKRET TERHADAP EFISIENSI SOLUSI MODEL RAMBATAN PANAS TANPA SUKU KONVEKSI
 KAJIAN DISKRETISASI DENGAN METODE GALERKIN SEMI DISKRET TERHADAP EFISIENSI SOLUSI MODEL RAMBATAN PANAS TANPA SUKU KONVEKSI Suhartono dan Solikhin Zaki Jurusan Matematika FMIPA UNDIP Abstrak Penelitian
KAJIAN DISKRETISASI DENGAN METODE GALERKIN SEMI DISKRET TERHADAP EFISIENSI SOLUSI MODEL RAMBATAN PANAS TANPA SUKU KONVEKSI Suhartono dan Solikhin Zaki Jurusan Matematika FMIPA UNDIP Abstrak Penelitian
Persamaan Diferensial
 TKS 4003 Matematika II Persamaan Diferensial Konsep Dasar dan Pembentukan (Differential : Basic Concepts and Establishment ) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya Pendahuluan
TKS 4003 Matematika II Persamaan Diferensial Konsep Dasar dan Pembentukan (Differential : Basic Concepts and Establishment ) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya Pendahuluan
MODUL 3 FAKTORISASI LU, PARTISI MATRIK DAN FAKTORISASI QR
 MODUL 3 FAKTORISASI LU, PARTISI MATRIK DAN FAKTORISASI QR KOMPETENSI: 1. Memahami penggunaan faktorisasi LU dalam penyelesaian persamaan linear.. Memahami penggunaan partisi matrik dalam penyelesaian persamaan
MODUL 3 FAKTORISASI LU, PARTISI MATRIK DAN FAKTORISASI QR KOMPETENSI: 1. Memahami penggunaan faktorisasi LU dalam penyelesaian persamaan linear.. Memahami penggunaan partisi matrik dalam penyelesaian persamaan
Penghitungan Polusi Udara Dalam Ruangan dengan Metode Eliminasi Gauss
 Penghitungan Polusi Udara Dalam Ruangan dengan Metode Eliminasi Gauss Tri Hastuti Yuniati (23515009) 1 Program Studi Magister Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung,
Penghitungan Polusi Udara Dalam Ruangan dengan Metode Eliminasi Gauss Tri Hastuti Yuniati (23515009) 1 Program Studi Magister Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung,
KOMPUTASI DISTRIBUSI SUHU DALAM KEADAAN MANTAP (STEADY STATE) PADA LOGAM DALAM BERBAGAI DIMENSI
 Prosiding Seminar Nasional Penelitian, Pendidikan & Penerapan MIPA, Hotel Sahid Raya Yogyakarta, 8 Februari KOMPUTASI DISTRIBUSI SUHU DALAM KEADAAN MANTAP (STEADY STATE) PADA LOGAM DALAM BERBAGAI DIMENSI
Prosiding Seminar Nasional Penelitian, Pendidikan & Penerapan MIPA, Hotel Sahid Raya Yogyakarta, 8 Februari KOMPUTASI DISTRIBUSI SUHU DALAM KEADAAN MANTAP (STEADY STATE) PADA LOGAM DALAM BERBAGAI DIMENSI
ISSN (Media Cetak) ISSN (Media Online) Implementasi Metode Eliminasi Gauss Pada Rangkaian Listrik Menggunakan Matlab
 JITEKH, Vol, No, Tahun 27, -5 ISSN 28-577(Media Cetak) ISSN 2549-4 (Media Online) Implementasi Metode Eliminasi Gauss Pada Rangkaian Listrik Menggunakan Matlab Silmi, Rina Anugrahwaty 2 Staff Pengajar
JITEKH, Vol, No, Tahun 27, -5 ISSN 28-577(Media Cetak) ISSN 2549-4 (Media Online) Implementasi Metode Eliminasi Gauss Pada Rangkaian Listrik Menggunakan Matlab Silmi, Rina Anugrahwaty 2 Staff Pengajar
BAB X MATRIK DAN SISTEM PERSAMAAN LINIER SIMULTAN
 1 BAB X MATRIK DAN SISTEM PERSAMAAN LINIER SIMULTAN Pembahasan berikut ini akan meninjau salah satu implementasi operasi matrik untuk menyelesaikan sistem persamaan linier simultan. Selain menggunakan
1 BAB X MATRIK DAN SISTEM PERSAMAAN LINIER SIMULTAN Pembahasan berikut ini akan meninjau salah satu implementasi operasi matrik untuk menyelesaikan sistem persamaan linier simultan. Selain menggunakan
BAB I KONSEP DASAR PERSAMAAN DIFERENSIAL
 BAB I KONSEP DASAR PERSAMAAN DIFERENSIAL Tujuan Instruksional: Mampu memahami definisi Persamaan Diferensial Mampu memahami klasifikasi Persamaan Diferensial Mampu memahami bentuk bentuk solusi Persamaan
BAB I KONSEP DASAR PERSAMAAN DIFERENSIAL Tujuan Instruksional: Mampu memahami definisi Persamaan Diferensial Mampu memahami klasifikasi Persamaan Diferensial Mampu memahami bentuk bentuk solusi Persamaan
PERBANDINGAN KOMPLEKSITAS ALGORITMA METODE-METODE PENYELESAIAN SISTEM PERSAMAAN LANJAR
 PERBANDINGAN KOMPLEKSITAS ALGORITMA METODE-METODE PENYELESAIAN SISTEM PERSAMAAN LANJAR Achmad Dimas Noorcahyo NIM 3508076 Program Studi Teknik Informatika, Institut Teknologi Bandung Jalan Ganeca 0, Bandung
PERBANDINGAN KOMPLEKSITAS ALGORITMA METODE-METODE PENYELESAIAN SISTEM PERSAMAAN LANJAR Achmad Dimas Noorcahyo NIM 3508076 Program Studi Teknik Informatika, Institut Teknologi Bandung Jalan Ganeca 0, Bandung
Syarif Abdullah (G ) Matematika Terapan FMIPA Institut Pertanian Bogor.
 Syarif Abdullah (G551150381) Matematika Terapan FMIPA Institut Pertanian Bogor e-mail: syarif_abdullah@apps.ipb.ac.id 25 Maret 2016 Ringkasan Kuliah ke-6 Analisis Numerik (16 Maret 2016) Materi : System
Syarif Abdullah (G551150381) Matematika Terapan FMIPA Institut Pertanian Bogor e-mail: syarif_abdullah@apps.ipb.ac.id 25 Maret 2016 Ringkasan Kuliah ke-6 Analisis Numerik (16 Maret 2016) Materi : System
METODE ITERATIF YANG DIPERCEPAT UNTUK Z-MATRIKS ABSTRACT
 METODE ITERATIF YANG DIPERCEPAT UNTUK Z-MATRIKS Mildayani 1, Syamsudhuha 2, Aziskhan 2 1 Mahasiswa Program Studi S1 Matematika 2 Dosen Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Riau Kampus
METODE ITERATIF YANG DIPERCEPAT UNTUK Z-MATRIKS Mildayani 1, Syamsudhuha 2, Aziskhan 2 1 Mahasiswa Program Studi S1 Matematika 2 Dosen Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Riau Kampus
BAB I PENDAHULUAN Latar Belakang Masalah
 BAB I PENDAHULUAN 1.1. Latar Belakang Masalah Dalam kehidupan sehari-hari banyak permasalahan yang muncul di lingkungan sekitar. Hal tersebut dapat dikembangkan melalui pemodelan matematika. Sehingga dengan
BAB I PENDAHULUAN 1.1. Latar Belakang Masalah Dalam kehidupan sehari-hari banyak permasalahan yang muncul di lingkungan sekitar. Hal tersebut dapat dikembangkan melalui pemodelan matematika. Sehingga dengan
BAB 1 Konsep Dasar 1
 BAB 1 Konsep Dasar 1 BAB Solusi Persamaan Fungsi Polinomial BAB 3 Interpolasi dan Aproksimasi Polinomial 3 BAB 4 Metoda Numeris untuk Sistem Nonlinier 4 BAB 5 Metoda Numeris Untuk Masalah Nilai Awal 5
BAB 1 Konsep Dasar 1 BAB Solusi Persamaan Fungsi Polinomial BAB 3 Interpolasi dan Aproksimasi Polinomial 3 BAB 4 Metoda Numeris untuk Sistem Nonlinier 4 BAB 5 Metoda Numeris Untuk Masalah Nilai Awal 5
PDP linear orde 2 Agus Yodi Gunawan
 PDP linear orde 2 Agus Yodi Gunawan Pada bagian ini akan dipelajari tiga jenis persamaan diferensial parsial (PDP) linear orde dua yang biasa dijumpai pada masalah-masalah dunia nyata, yaitu persamaan
PDP linear orde 2 Agus Yodi Gunawan Pada bagian ini akan dipelajari tiga jenis persamaan diferensial parsial (PDP) linear orde dua yang biasa dijumpai pada masalah-masalah dunia nyata, yaitu persamaan
PROGRAM STUDI S1 SISTEM KOMPUTER UNIVERSITAS DIPONEGORO. Oky Dwi Nurhayati, ST, MT email: okydn@undip.ac.id
 PROGRAM STUDI S1 SISTEM KOMPUTER UNIVERSITAS DIPONEGORO Oky Dwi Nurhayati, ST, MT email: okydn@undip.ac.id Kinerja yang perlu ditelaah pada algoritma: beban komputasi efisiensi penggunaan memori Yang perlu
PROGRAM STUDI S1 SISTEM KOMPUTER UNIVERSITAS DIPONEGORO Oky Dwi Nurhayati, ST, MT email: okydn@undip.ac.id Kinerja yang perlu ditelaah pada algoritma: beban komputasi efisiensi penggunaan memori Yang perlu
Pertemuan 13 persamaan linier NON HOMOGEN
 Pertemuan 13 persamaan linier NON HOMOGEN 10 Metode CRAMER Aljabar Linier Hastha 2016 10. PERSAMAAN LINIER NONHOMOGEN 10.1 PERSAMAAN LINIER Misalnya x 2 Matematika analitik membicarakan ilmu ukur secara
Pertemuan 13 persamaan linier NON HOMOGEN 10 Metode CRAMER Aljabar Linier Hastha 2016 10. PERSAMAAN LINIER NONHOMOGEN 10.1 PERSAMAAN LINIER Misalnya x 2 Matematika analitik membicarakan ilmu ukur secara
Prasyarat : - Status Matakuliah. Deskripsi Singkat Matakuliah :
 Nama Matakuliah Kode / SKS : Fisika Komputasi : MAP4113 / 2 SKS Prasyarat : - Status Matakuliah : Wajib Deskripsi Singkat Matakuliah : Matakuliah Fisika Komputasi mempelajari bagaimana menggunakan komputer
Nama Matakuliah Kode / SKS : Fisika Komputasi : MAP4113 / 2 SKS Prasyarat : - Status Matakuliah : Wajib Deskripsi Singkat Matakuliah : Matakuliah Fisika Komputasi mempelajari bagaimana menggunakan komputer
METODE ITERASI KSOR UNTUK MENYELESAIKAN SISTEM PERSAMAAN LINEAR ABSTRACT
 METODE ITERASI KSOR UNTUK MENYELESAIKAN SISTEM PERSAMAAN LINEAR Adek Putri Syafriani, Syamsudhuha 2, Zulkarnain 2 Mahasiswa Program Studi S Matematika 2 Dosen Jurusan Matematika Fakultas Matematika dan
METODE ITERASI KSOR UNTUK MENYELESAIKAN SISTEM PERSAMAAN LINEAR Adek Putri Syafriani, Syamsudhuha 2, Zulkarnain 2 Mahasiswa Program Studi S Matematika 2 Dosen Jurusan Matematika Fakultas Matematika dan
Sistem Persamaan Aljabar Linier
 Sistem Persamaan Aljabar Linier Dimana: a ij = koefisien konstanta; x j = unknown ; b j = konstanta; n = banyaknya persamaan Metode-Metode untuk menyelesaikan Sistem Persamaan Aljabar Linier: 1. Metode
Sistem Persamaan Aljabar Linier Dimana: a ij = koefisien konstanta; x j = unknown ; b j = konstanta; n = banyaknya persamaan Metode-Metode untuk menyelesaikan Sistem Persamaan Aljabar Linier: 1. Metode
Solusi Persamaan Laplace Menggunakan Metode Crank-Nicholson. (The Solution of Laplace Equation Using Crank-Nicholson Method)
 Prosiding Seminar Nasional Matematika, Universitas Jember, 19 November 2014 320 Persamaan Laplace Menggunakan Metode Crank-Nicholson (The Solution of Laplace Equation Using Crank-Nicholson Method) Titis
Prosiding Seminar Nasional Matematika, Universitas Jember, 19 November 2014 320 Persamaan Laplace Menggunakan Metode Crank-Nicholson (The Solution of Laplace Equation Using Crank-Nicholson Method) Titis
RENCANA PEMBELAJARAN SEMESTER
 RENCANA PEMBELAJARAN SEMESTER F-0653 Issue/Revisi : A0 Tanggal Berlaku : 1 Juli 2015 Untuk Tahun Akademik : 2015/2016 Masa Berlaku : 4 (empat) tahun Jml Halaman : 17 halaman Mata Kuliah : Analisis Numerik
RENCANA PEMBELAJARAN SEMESTER F-0653 Issue/Revisi : A0 Tanggal Berlaku : 1 Juli 2015 Untuk Tahun Akademik : 2015/2016 Masa Berlaku : 4 (empat) tahun Jml Halaman : 17 halaman Mata Kuliah : Analisis Numerik
Kompleksitas Komputasi
 Kompleksitas Komputasi Big O Notation O(f(n)) Kompleksitas komputasi pada sebuah algoritma dibagi menjadi dua bagian, yaitu Kompleksitas Waktu T(n) Kompleksitas Ruang S(n) Kompleksitas Waktu diukur dari
Kompleksitas Komputasi Big O Notation O(f(n)) Kompleksitas komputasi pada sebuah algoritma dibagi menjadi dua bagian, yaitu Kompleksitas Waktu T(n) Kompleksitas Ruang S(n) Kompleksitas Waktu diukur dari
02-Pemecahan Persamaan Linier (1)
 -Pemecahan Persamaan Linier () Dosen: Anny Yuniarti, M.Comp.Sc Gasal - Anny Agenda Bagian : Vektor dan Persamaan Linier Bagian : Teori Dasar Eliminasi Bagian 3: Eliminasi Menggunakan Matriks Bagian 4:
-Pemecahan Persamaan Linier () Dosen: Anny Yuniarti, M.Comp.Sc Gasal - Anny Agenda Bagian : Vektor dan Persamaan Linier Bagian : Teori Dasar Eliminasi Bagian 3: Eliminasi Menggunakan Matriks Bagian 4:
LU DECOMPOSITION (FAKTORISASI MATRIK)
 LU DECOMPOSITION (FAKTORISASI MATRIK) Dr. Eng. Supriyanto, M.Sc Lab. Komputer, Departemen Fisika, Universitas Indonesia email: supri@fisika.ui.ac.id atau supri92@gmail.com 5 Februari 2005 Pada semua catatan
LU DECOMPOSITION (FAKTORISASI MATRIK) Dr. Eng. Supriyanto, M.Sc Lab. Komputer, Departemen Fisika, Universitas Indonesia email: supri@fisika.ui.ac.id atau supri92@gmail.com 5 Februari 2005 Pada semua catatan
Mata Kuliah :: Matematika Rekayasa Lanjut Kode MK : TKS 8105 Pengampu : Achfas Zacoeb
 Mata Kuliah :: Matematika Rekayasa Lanjut Kode MK : TKS 8105 Pengampu : Achfas Zacoeb Sesi XII Differensial e-mail : zacoeb@ub.ac.id www.zacoeb.lecture.ub.ac.id Hp. 081233978339 PENDAHULUAN Persamaan diferensial
Mata Kuliah :: Matematika Rekayasa Lanjut Kode MK : TKS 8105 Pengampu : Achfas Zacoeb Sesi XII Differensial e-mail : zacoeb@ub.ac.id www.zacoeb.lecture.ub.ac.id Hp. 081233978339 PENDAHULUAN Persamaan diferensial
Solusi Sistem Persamaan Linear Ax = b
 Solusi Sistem Persamaan Linear Ax = b Kie Van Ivanky Saputra April 27, 2009 K V I Saputra (Analisis Numerik) Kuliah Sistem Persamaan Linier c April 27, 2009 1 / 9 Review 1 Substitusi mundur pada sistem
Solusi Sistem Persamaan Linear Ax = b Kie Van Ivanky Saputra April 27, 2009 K V I Saputra (Analisis Numerik) Kuliah Sistem Persamaan Linier c April 27, 2009 1 / 9 Review 1 Substitusi mundur pada sistem
BAB 4 : SISTEM PERSAMAAN LINIER
 BAB 4 : SISTEM PERSAMAAN LINIER 4.1 PERSAMAAN LINIER Misalnya x 2 Matematika analitik membicarakan ilmu ukur secara aljabar. Garis lurus pada bidang x 1 dan x 2 dapat dinyatakan sebagai persamaan a 1 x
BAB 4 : SISTEM PERSAMAAN LINIER 4.1 PERSAMAAN LINIER Misalnya x 2 Matematika analitik membicarakan ilmu ukur secara aljabar. Garis lurus pada bidang x 1 dan x 2 dapat dinyatakan sebagai persamaan a 1 x
Solusi Persamaan Linier Simultan
 Solusi Persamaan Linier Simultan Obyektif : 1. Mengerti penggunaan solusi persamaan linier 2. Mengerti metode eliminasi gauss. 3. Mampu menggunakan metode eliminasi gauss untuk mencari solusi 1. Sistem
Solusi Persamaan Linier Simultan Obyektif : 1. Mengerti penggunaan solusi persamaan linier 2. Mengerti metode eliminasi gauss. 3. Mampu menggunakan metode eliminasi gauss untuk mencari solusi 1. Sistem
Setelah mempelajari topik Analisis Algoritma di kuliah SDA, ada beberapa kompetensi yang perlu Anda kuasai:
 Setelah mempelajari topik Analisis Algoritma di kuliah SDA, ada beberapa kompetensi yang perlu Anda kuasai: Menentukan kompleksitas waktu (Big-Oh) dari beberapa algoritma (logaritmik, linier, kuadratik,
Setelah mempelajari topik Analisis Algoritma di kuliah SDA, ada beberapa kompetensi yang perlu Anda kuasai: Menentukan kompleksitas waktu (Big-Oh) dari beberapa algoritma (logaritmik, linier, kuadratik,
6 Sistem Persamaan Linear
 6 Sistem Persamaan Linear Pada bab, kita diminta untuk mencari suatu nilai x yang memenuhi persamaan f(x) = 0. Pada bab ini, masalah tersebut diperumum dengan mencari x = (x, x,..., x n ) yang secara sekaligus
6 Sistem Persamaan Linear Pada bab, kita diminta untuk mencari suatu nilai x yang memenuhi persamaan f(x) = 0. Pada bab ini, masalah tersebut diperumum dengan mencari x = (x, x,..., x n ) yang secara sekaligus
Sidang Tugas Akhir - Juli 2013
 Sidang Tugas Akhir - Juli 2013 STUDI PERBANDINGAN PERPINDAHAN PANAS MENGGUNAKAN METODE BEDA HINGGA DAN CRANK-NICHOLSON COMPARATIVE STUDY OF HEAT TRANSFER USING FINITE DIFFERENCE AND CRANK-NICHOLSON METHOD
Sidang Tugas Akhir - Juli 2013 STUDI PERBANDINGAN PERPINDAHAN PANAS MENGGUNAKAN METODE BEDA HINGGA DAN CRANK-NICHOLSON COMPARATIVE STUDY OF HEAT TRANSFER USING FINITE DIFFERENCE AND CRANK-NICHOLSON METHOD
Desain dan Analisis Algoritma Pencarian Prediksi Hasil Penjumlahan Beberapa Urutan Berkala dengan Metode Eliminasi Gauss
 JURNAL TEKNIK ITS Vol. 6, No., (7) ISSN: 7-59 (-97 Print) A-75 Desain dan Analisis Algoritma Pencarian Prediksi Hasil Penjumlahan Beberapa dengan Metode Eliminasi Gauss Daniel Henry, Victor Hariadi, dan
JURNAL TEKNIK ITS Vol. 6, No., (7) ISSN: 7-59 (-97 Print) A-75 Desain dan Analisis Algoritma Pencarian Prediksi Hasil Penjumlahan Beberapa dengan Metode Eliminasi Gauss Daniel Henry, Victor Hariadi, dan
METODE GAUSS-SEIDEL PREKONDISI UNTUK MENCARI SOLUSI SISTEM PERSAMAAN LINEAR. Alhumaira Oryza Sativa 1 ABSTRACT ABSTRAK
 METODE GAUSS-SEIDEL PREKONDISI UNTUK MENCARI SOLUSI SISTEM PERSAMAAN LINEAR Alhumaira Oryza Sativa 1 1 Mahasiswa Program Studi S1 Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Riau
METODE GAUSS-SEIDEL PREKONDISI UNTUK MENCARI SOLUSI SISTEM PERSAMAAN LINEAR Alhumaira Oryza Sativa 1 1 Mahasiswa Program Studi S1 Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Riau
KARAKTERISTIK KINERJA ALGORITMA RECURSIVE DECOUPLING PADA SISTEM MULTIPROSESOR BERBASIS PVM
 KARAKTERISTIK KINERJA ALGORITMA RECURSIVE DECOUPLING PADA SISTEM MULTIPROSESOR BERBASIS PVM Tri Prabawa Program Studi Teknik Informatika, STMIK AKAKOM Yogyakarta Jl. Raya Janti 143, Yogyakarta 55198 E-mail
KARAKTERISTIK KINERJA ALGORITMA RECURSIVE DECOUPLING PADA SISTEM MULTIPROSESOR BERBASIS PVM Tri Prabawa Program Studi Teknik Informatika, STMIK AKAKOM Yogyakarta Jl. Raya Janti 143, Yogyakarta 55198 E-mail
ALGORITHM. 2 Analysis Algorithm. Dahlia Widhyaestoeti, S.Kom dahlia74march.wordpress.com
 ALGORITHM 2 Analysis Algorithm Dahlia Widhyaestoeti, S.Kom dahlia.widhyaestoeti@gmail.com dahlia74march.wordpress.com Analysis Suatu Algoritma Studi yang menyangkut analis algoritma ada 2 hal : 1. Perbandingan
ALGORITHM 2 Analysis Algorithm Dahlia Widhyaestoeti, S.Kom dahlia.widhyaestoeti@gmail.com dahlia74march.wordpress.com Analysis Suatu Algoritma Studi yang menyangkut analis algoritma ada 2 hal : 1. Perbandingan
BAB 4 Sistem Persamaan Linear. Sistem m persamaan linear dalam n variabel LG=C adalah himpunan persamaan linear
 BAB 4 Sistem Persamaan Linear berbentuk Sistem m persamaan linear dalam n variabel LG=C adalah himpunan persamaan linear Dengan koefisien dan adalah bilangan-bilangan yang diberikan. Sistem ini disebut
BAB 4 Sistem Persamaan Linear berbentuk Sistem m persamaan linear dalam n variabel LG=C adalah himpunan persamaan linear Dengan koefisien dan adalah bilangan-bilangan yang diberikan. Sistem ini disebut
BAB 2 TINJAUAN PUSTAKA
 BAB 2 TINJAUAN PUSTAKA 2.1 Konsep Dasar Algoritma Algoritma adalah kumpulan instruksi atau perintah yang dibuat secara jelas dan sistematis berdasarkan urutan yang logis (logika) untuk penyelsaian suatu
BAB 2 TINJAUAN PUSTAKA 2.1 Konsep Dasar Algoritma Algoritma adalah kumpulan instruksi atau perintah yang dibuat secara jelas dan sistematis berdasarkan urutan yang logis (logika) untuk penyelsaian suatu
CHAPTER 3 ALGORITHMS 3.1 ALGORITHMS
 CHAPTER 3 ALGORITHMS 3.1 ALGORITHMS Algoritma Definisi 1. Algoritma adalah himpunan hingga perintah yang terinci dalam melakukan perhitungan atau pemecahan masalah. Contoh 1. Program komputer adalah suatu
CHAPTER 3 ALGORITHMS 3.1 ALGORITHMS Algoritma Definisi 1. Algoritma adalah himpunan hingga perintah yang terinci dalam melakukan perhitungan atau pemecahan masalah. Contoh 1. Program komputer adalah suatu
Design and Analysis Algorithm
 Design and Analysis Algorithm Pertemuan 02 Drs. Achmad Ridok M.Kom Fitra A. Bachtiar, S.T., M. Eng Imam Cholissodin, S.Si., M.Kom Aryo Pinandito, MT Contents 31 2 Analisis Algoritma Analisis Efisiensi
Design and Analysis Algorithm Pertemuan 02 Drs. Achmad Ridok M.Kom Fitra A. Bachtiar, S.T., M. Eng Imam Cholissodin, S.Si., M.Kom Aryo Pinandito, MT Contents 31 2 Analisis Algoritma Analisis Efisiensi
Modifikasi Metode Gauss atau Operasi Baris Elementer pada Solusi Sistim Persamaan Linier 3 Variabel dan 3 Persamaan
 Modifikasi Metode Gauss atau Operasi Baris Elementer pada Solusi Sistim Persamaan Linier 3 Variabel dan 3 Persamaan Edwin Julius Solaiman Fakultas Teknologi Informasi, Universitas Advent Indonesia Abstrak
Modifikasi Metode Gauss atau Operasi Baris Elementer pada Solusi Sistim Persamaan Linier 3 Variabel dan 3 Persamaan Edwin Julius Solaiman Fakultas Teknologi Informasi, Universitas Advent Indonesia Abstrak
SISTEM PERSAMAAN LINEAR DAN ELIMINASI GAUSS
 SISTEM PERSAMAAN LINEAR DAN ELIMINASI GAUSS Dr. Eng. Supriyanto, M.Sc Lab. Komputer, Departemen Fisika, Universitas Indonesia email: supri@fisika.ui.ac.id atau supri92@gmail.com 5 Februari 2005 Abstract
SISTEM PERSAMAAN LINEAR DAN ELIMINASI GAUSS Dr. Eng. Supriyanto, M.Sc Lab. Komputer, Departemen Fisika, Universitas Indonesia email: supri@fisika.ui.ac.id atau supri92@gmail.com 5 Februari 2005 Abstract
BAB 2 LANDASAN TEORI. 2.1 Algoritma
 13 BAB 2 LANDASAN TEORI 2.1 Algoritma Dalam matematika dan komputasi, algoritma merupakan kumpulan perintah untuk menyelesaikan suatu masalah. Perintah-perintah ini dapat diterjemahkan secara bertahap
13 BAB 2 LANDASAN TEORI 2.1 Algoritma Dalam matematika dan komputasi, algoritma merupakan kumpulan perintah untuk menyelesaikan suatu masalah. Perintah-perintah ini dapat diterjemahkan secara bertahap
PAM 252 Metode Numerik Bab 3 Sistem Persamaan Linier
 PAM 252 Metode Numerik Bab 3 Sistem Persamaan Linier Mahdhivan Syafwan Jurusan Matematika FMIPA Universitas Andalas Semester Genap 2013/2014 1 Mahdhivan Syafwan Metode Numerik: Sistem Persamaan Linier
PAM 252 Metode Numerik Bab 3 Sistem Persamaan Linier Mahdhivan Syafwan Jurusan Matematika FMIPA Universitas Andalas Semester Genap 2013/2014 1 Mahdhivan Syafwan Metode Numerik: Sistem Persamaan Linier
Komputasi untuk Sains dan Teknik
 Komputasi untuk Sains dan Teknik Dr. Eng. Supriyanto, M.Sc Edisi I Laboratorium Jaringan Komputer Departemen Fisika-FMIPA Univeristas Indonesia 2006 Untuk Muflih Syamil dan Hasan Azmi... Mottoku : Tenang,
Komputasi untuk Sains dan Teknik Dr. Eng. Supriyanto, M.Sc Edisi I Laboratorium Jaringan Komputer Departemen Fisika-FMIPA Univeristas Indonesia 2006 Untuk Muflih Syamil dan Hasan Azmi... Mottoku : Tenang,
Persamaan Diferensial Parsial CNH3C3
 Persamaan Diferensial Parsial CNH3C3 Week 3: Pengantar, konsep dasar dan klasikasi PDP Tim Ilmu Komputasi Coordinator contact: Dr. Putu Harry Gunawan phgunawan@telkomuniversity.ac.id 1 Kontrak kuliah 2
Persamaan Diferensial Parsial CNH3C3 Week 3: Pengantar, konsep dasar dan klasikasi PDP Tim Ilmu Komputasi Coordinator contact: Dr. Putu Harry Gunawan phgunawan@telkomuniversity.ac.id 1 Kontrak kuliah 2
Algoritma dan Struktur Data
 Algoritma dan Struktur Data Click to edit Master subtitle style Pertemuan 3 Pengantar Analisis Efisiensi Algoritma Analisa efisiensi algoritma bertujuan mengestimasi waktu dan memori yang dibutuhkan untuk
Algoritma dan Struktur Data Click to edit Master subtitle style Pertemuan 3 Pengantar Analisis Efisiensi Algoritma Analisa efisiensi algoritma bertujuan mengestimasi waktu dan memori yang dibutuhkan untuk
BAB 2 LANDASAN TEORI. Algoritma Optimal Mismatch ini mencari data secara berurut pada tiap
 BAB 2 LANDASAN TEORI 2.1 Algoritma Optimal Mismatch Algoritma Optimal Mismatch ini mencari data secara berurut pada tiap karakter dalam teks sehingga pencarian seperti ini disebut pencarian sekuensial
BAB 2 LANDASAN TEORI 2.1 Algoritma Optimal Mismatch Algoritma Optimal Mismatch ini mencari data secara berurut pada tiap karakter dalam teks sehingga pencarian seperti ini disebut pencarian sekuensial
Metode Kekakuan Langsung (Direct Stiffness Method)
 Metode Kekakuan angsung (Direct Stiffness Method) matriks kekakuan U, P U, P { P } = [ K ] { U } U, P U 4, P 4 gaya perpindahan P K K K K 4 U P K K K K 4 U P = K K K K 4 U P 4 K 4 K 4 K 4 K 44 U 4 P =
Metode Kekakuan angsung (Direct Stiffness Method) matriks kekakuan U, P U, P { P } = [ K ] { U } U, P U 4, P 4 gaya perpindahan P K K K K 4 U P K K K K 4 U P = K K K K 4 U P 4 K 4 K 4 K 4 K 44 U 4 P =
PENYELESAIAN SISTEM PERSAMAAN LINEAR FUZZY KOMPLEKS MENGGUNAKAN METODE DEKOMPOSISI DOOLITTLE
 Jurnal Sains, Teknologi Industri, Vol. 11, No. 2, Juni 2014, pp. 166-174 ISSN 1693-2390 print/issn 2407-0939 online PENYELESAIAN SISTEM PERSAMAAN LINEAR FUZZY KOMPLEKS MENGGUNAKAN METODE DEKOMPOSISI DOOLITTLE
Jurnal Sains, Teknologi Industri, Vol. 11, No. 2, Juni 2014, pp. 166-174 ISSN 1693-2390 print/issn 2407-0939 online PENYELESAIAN SISTEM PERSAMAAN LINEAR FUZZY KOMPLEKS MENGGUNAKAN METODE DEKOMPOSISI DOOLITTLE
GARIS BESAR PROGRAM PENGAJARAN (GBPP)
 GARIS BESAR PROGRAM PENGAJARAN (GBPP) Mata Kuliah : Analisis Numerik & Pemrograman Kode/Bobot : TSP-303/3 SKS Deskripsi Singkat : Mata Kuliah ini mempelajari tentang analisis numerik dan bahasa pemrograman
GARIS BESAR PROGRAM PENGAJARAN (GBPP) Mata Kuliah : Analisis Numerik & Pemrograman Kode/Bobot : TSP-303/3 SKS Deskripsi Singkat : Mata Kuliah ini mempelajari tentang analisis numerik dan bahasa pemrograman
METODE ELEMEN BATAS UNTUK MASALAH TRANSPORT
 METODE ELEMEN BATAS UNTUK MASALAH TRANSPORT Agusman Sahari. 1 1 Jurusan Matematika FMIPA UNTAD Kampus Bumi Tadulako Tondo Palu Abstrak Dalam paper ini mendeskripsikan tentang solusi masalah transport polutan
METODE ELEMEN BATAS UNTUK MASALAH TRANSPORT Agusman Sahari. 1 1 Jurusan Matematika FMIPA UNTAD Kampus Bumi Tadulako Tondo Palu Abstrak Dalam paper ini mendeskripsikan tentang solusi masalah transport polutan
Hubungan Kompleksitas Algoritma dengan Cara Belajar
 Hubungan Kompleksitas Algoritma dengan Cara Belajar Ryan Ignatius Hadiwijaya / 13511070 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10
Hubungan Kompleksitas Algoritma dengan Cara Belajar Ryan Ignatius Hadiwijaya / 13511070 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10
OPERASI MATRIKS. a 11 a 12 a 13 a 14 A = a 21 a 22 a 23 a 24 a 31 a 32 a 33 a 34 a 41 a 42 a 43 a 44
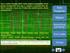 OPERASI MATRIKS Topik yang akan dibahas transpose perkalian TRANSPOSE Definisi: a 11 a 12 a 13 a 14 A = a 21 a 22 a 23 a 24 a 31 a 32 a 33 a 34 a 41 a 42 a 43 a 44 a 11 a 21 a 31 a 41 A T = a 12 a 22 a
OPERASI MATRIKS Topik yang akan dibahas transpose perkalian TRANSPOSE Definisi: a 11 a 12 a 13 a 14 A = a 21 a 22 a 23 a 24 a 31 a 32 a 33 a 34 a 41 a 42 a 43 a 44 a 11 a 21 a 31 a 41 A T = a 12 a 22 a
Seminar Nasional Aplikasi Teknologi Informasi 2004 Yogyakarta, 19 Juni 2004
 Seminar Nasional plikasi eknologi Informasi 4 Yogyakarta, 9 Juni 4 plikasi Metode homas untuk Mengefisiensikan Penyelesaian Sistem Persamaan Linier pada Persoalan Perambatan Panas dengan Skema Implisit
Seminar Nasional plikasi eknologi Informasi 4 Yogyakarta, 9 Juni 4 plikasi Metode homas untuk Mengefisiensikan Penyelesaian Sistem Persamaan Linier pada Persoalan Perambatan Panas dengan Skema Implisit
Penyelesaian Masalah Syarat Batas dalam Persamaan Diferensial Biasa Orde Dua dengan Menggunakan Algoritma Shooting Neural Networks
 Penyelesaian Masalah Syarat Batas dalam Persamaan Diferensial Biasa Orde Dua dengan Menggunakan Algoritma Shooting Neural Networks Dewi Erla Mahmudah 1, Ratna Dwi Christyanti 2, Moh. Khoridatul Huda 3,
Penyelesaian Masalah Syarat Batas dalam Persamaan Diferensial Biasa Orde Dua dengan Menggunakan Algoritma Shooting Neural Networks Dewi Erla Mahmudah 1, Ratna Dwi Christyanti 2, Moh. Khoridatul Huda 3,
PENYELESAIAN PERSAMAAN POISSON 2D DENGAN MENGGUNAKAN METODE GAUSS-SEIDEL DAN CONJUGATE GRADIENT
 Teknikom : Vol. No. (27) E-ISSN : 2598-2958 PENYELESAIAN PERSAMAAN POISSON 2D DENGAN MENGGUNAKAN METODE GAUSS-SEIDEL DAN CONJUGATE GRADIENT Dewi Erla Mahmudah, Muhammad Zidny Naf an 2 STMIK Widya Utama,
Teknikom : Vol. No. (27) E-ISSN : 2598-2958 PENYELESAIAN PERSAMAAN POISSON 2D DENGAN MENGGUNAKAN METODE GAUSS-SEIDEL DAN CONJUGATE GRADIENT Dewi Erla Mahmudah, Muhammad Zidny Naf an 2 STMIK Widya Utama,
FAKULTAS TEKNIK UNIVERSITAS NEGERI YOGYAKARTA
 No. LSKD/EKO/DEL221/01 Revisi : 02 Tgl : 27/11/2012 Hal 1 dari 14 1. Kompetensi Setelah melakukan praktik, mahasiswa diharapkan memiliki kompetensi: dapat memahami script files dan struktur pengaturan
No. LSKD/EKO/DEL221/01 Revisi : 02 Tgl : 27/11/2012 Hal 1 dari 14 1. Kompetensi Setelah melakukan praktik, mahasiswa diharapkan memiliki kompetensi: dapat memahami script files dan struktur pengaturan
BAB 1 PENDAHULUAN. hal, persamaan ini timbul langsung dari perumusan mula dari persoalannya, didalam hal
 BAB 1 PENDAHULUAN 1.1 Latar Belakang Persamaan Simultan timbul hampir disetiap cabang matematik, dalam beberapa hal, persamaan ini timbul langsung dari perumusan mula dari persoalannya, didalam hal lain
BAB 1 PENDAHULUAN 1.1 Latar Belakang Persamaan Simultan timbul hampir disetiap cabang matematik, dalam beberapa hal, persamaan ini timbul langsung dari perumusan mula dari persoalannya, didalam hal lain
APLIKASI METODE BEDA HINGGA SKEMA EKSPLISIT PADA PERSAMAAN KONDUKSI PANAS
 Sulistyono, Metode Beda Hingga Skema Eksplisit 4 APLIKASI METODE BEDA HINGGA SKEMA EKSPLISIT PADA PERSAMAAN KONDUKSI PANAS Bambang Agus Sulistyono Program Studi Pendidikan Matematika FKIP UNP Kediri bb7agus@gmail.com
Sulistyono, Metode Beda Hingga Skema Eksplisit 4 APLIKASI METODE BEDA HINGGA SKEMA EKSPLISIT PADA PERSAMAAN KONDUKSI PANAS Bambang Agus Sulistyono Program Studi Pendidikan Matematika FKIP UNP Kediri bb7agus@gmail.com
Desain dan Analisis Algoritma Pencarian Prediksi Hasil Penjumlahan Beberapa Urutan Berkala dengan Metode Eliminasi Gauss
 JURNAL TEKNIK ITS Vol. 6, No. (7), 7-5 (-98X Print) A665 Desain dan Analisis Algoritma Pencarian Prediksi Hasil Penjumlahan Beberapa dengan Metode Eliminasi Gauss Daniel Henry, Victor Hariadi, dan Rully
JURNAL TEKNIK ITS Vol. 6, No. (7), 7-5 (-98X Print) A665 Desain dan Analisis Algoritma Pencarian Prediksi Hasil Penjumlahan Beberapa dengan Metode Eliminasi Gauss Daniel Henry, Victor Hariadi, dan Rully
Penyelesaian Persamaan Poisson 2D dengan Menggunakan Metode Gauss-Seidel dan Conjugate Gradient
 Teknikom : Vol. No. (27) ISSN : 2598-2958 (online) Penyelesaian Persamaan Poisson 2D dengan Menggunakan Metode Gauss-Seidel dan Conjugate Gradient Dewi Erla Mahmudah, Muhammad Zidny Naf an 2 STMIK Widya
Teknikom : Vol. No. (27) ISSN : 2598-2958 (online) Penyelesaian Persamaan Poisson 2D dengan Menggunakan Metode Gauss-Seidel dan Conjugate Gradient Dewi Erla Mahmudah, Muhammad Zidny Naf an 2 STMIK Widya
BAB 2 LANDASAN TEORI. 2.1 Pengoptimalan, Optimisasi, Algoritma, dan Analisis Algoritma
 7 BAB 2 LANDASAN TEORI 2.1 Pengoptimalan, Optimisasi, Algoritma, dan Analisis Algoritma 2.1.1 Definisi Pengoptimalan Dalam Kamus Besar Bahasa Indonesia, pengoptimalan diartikan sebagai proses, cara, perbuatan
7 BAB 2 LANDASAN TEORI 2.1 Pengoptimalan, Optimisasi, Algoritma, dan Analisis Algoritma 2.1.1 Definisi Pengoptimalan Dalam Kamus Besar Bahasa Indonesia, pengoptimalan diartikan sebagai proses, cara, perbuatan
PENGGUNAAN BIG O NOTATION UNTUK MENGANALISA EFISIENSI ALGORITMA
 PENGGUNAAN BIG O NOTATION UNTUK MENGANALISA EFISIENSI ALGORITMA Ikhsan Fanani NIM : 13505123 Program Studi Teknik Informatika, Institut Teknologi Bandung Jl. Ganesha 10, Bandung E-mail : ikhsan_fanani@yahoo.com
PENGGUNAAN BIG O NOTATION UNTUK MENGANALISA EFISIENSI ALGORITMA Ikhsan Fanani NIM : 13505123 Program Studi Teknik Informatika, Institut Teknologi Bandung Jl. Ganesha 10, Bandung E-mail : ikhsan_fanani@yahoo.com
BAB II LANDASAN TEORI
 17 BAB II LANDASAN TEORI 2.1 Algoritma Dalam matematika dan komputasi, algoritma merupakan kumpulan perintah untuk menyelesaikan suatu masalah. Perintah-perintah ini dapat diterjemahkan secara bertahap
17 BAB II LANDASAN TEORI 2.1 Algoritma Dalam matematika dan komputasi, algoritma merupakan kumpulan perintah untuk menyelesaikan suatu masalah. Perintah-perintah ini dapat diterjemahkan secara bertahap
Aturan Untuk Menentukan Kompleksitas Waktu Asimptotik. Penjelasannya adalah sebagai berikut: T(n) = (n + 2) log(n 2 + 1) + 5n 2
 Aturan Untuk Menentukan Kompleksitas Waktu Asimptotik 1. Jika kompleksitas waktu T(n) dari algoritma diketahui, Contoh: (i) pada algoritma cari_maksimum T(n) = n 1 = O(n) (ii) pada algoritma pencarian_beruntun
Aturan Untuk Menentukan Kompleksitas Waktu Asimptotik 1. Jika kompleksitas waktu T(n) dari algoritma diketahui, Contoh: (i) pada algoritma cari_maksimum T(n) = n 1 = O(n) (ii) pada algoritma pencarian_beruntun
Analisis Kompleksitas Algoritma dalam Operasi BigMod
 Analisis Kompleksitas Algoritma dalam Operasi BigMod Calvin sadewa / 13512066 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung
Analisis Kompleksitas Algoritma dalam Operasi BigMod Calvin sadewa / 13512066 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung
PERBANDINGAN KOMPLEKSITAS ALGORITMA PENCARIAN BINER DAN ALGORITMA PENCARIAN BERUNTUN
 PERBANDINGAN KOMPLEKSITAS ALGORITMA PENCARIAN BINER DAN ALGORITMA PENCARIAN BERUNTUN Yudhistira NIM 13508105 Mahasiswa Program Studi Teknik Informatika ITB Jalan Ganesha No.10 Bandung e-mail: if18105@students.if.itb.ac.id
PERBANDINGAN KOMPLEKSITAS ALGORITMA PENCARIAN BINER DAN ALGORITMA PENCARIAN BERUNTUN Yudhistira NIM 13508105 Mahasiswa Program Studi Teknik Informatika ITB Jalan Ganesha No.10 Bandung e-mail: if18105@students.if.itb.ac.id
PERANGKAT LUNAK BANTU ANALISIS NUMERIK METODE DETERMINAN CRAMER, ELIMINASI GAUSS DAN LELARAN GAUSS-SEIDEL UNTUK MENYELESAIKAN SISTEM PERSAMAAN LINEAR
 PERANGKAT LUNAK BANTU ANALISIS NUMERIK METODE DETERMINAN CRAMER, ELIMINASI GAUSS DAN LELARAN GAUSS-SEIDEL UNTUK MENYELESAIKAN SISTEM PERSAMAAN LINEAR Tacbir Hendro Pudjiantoro A B S T R A K Salah satu
PERANGKAT LUNAK BANTU ANALISIS NUMERIK METODE DETERMINAN CRAMER, ELIMINASI GAUSS DAN LELARAN GAUSS-SEIDEL UNTUK MENYELESAIKAN SISTEM PERSAMAAN LINEAR Tacbir Hendro Pudjiantoro A B S T R A K Salah satu
PENERAPAN METODE ELEMEN HINGGA UNTUK SOLUSI PERSAMAAN STURM-LIOUVILLE
 PENERAPAN METODE ELEMEN HINGGA UNTUK SOLUSI PERSAMAAN STURM-LIOUVILLE Viska Noviantri Mathematics & Statistics Department, School of Computer Science, Binus University Jln. K.H. Syahdan No. 9, Palmerah,
PENERAPAN METODE ELEMEN HINGGA UNTUK SOLUSI PERSAMAAN STURM-LIOUVILLE Viska Noviantri Mathematics & Statistics Department, School of Computer Science, Binus University Jln. K.H. Syahdan No. 9, Palmerah,
I. PENDAHULUAN. dan kotoran manusia atau kotoran binatang. Semua polutan tersebut masuk. ke dalam sungai dan langsung tercampur dengan air sungai.
 I. PENDAHULUAN 1.1 Latar Belakang dan Masalah Dalam kehidupan, polusi yang ada di sungai disebabkan oleh limbah dari pabrikpabrik dan kotoran manusia atau kotoran binatang. Semua polutan tersebut masuk
I. PENDAHULUAN 1.1 Latar Belakang dan Masalah Dalam kehidupan, polusi yang ada di sungai disebabkan oleh limbah dari pabrikpabrik dan kotoran manusia atau kotoran binatang. Semua polutan tersebut masuk
BAB 2 LANDASAN TEORI
 5 BAB 2 LANDASAN TEORI 2.1. Pengertian Algoritma Algoritma adalah prosedur komputasi yang didefinisikan dengan baik yang mengambil beberapa nilai yaitu seperangkat nilai sebagai input dan output yang menghasilkan
5 BAB 2 LANDASAN TEORI 2.1. Pengertian Algoritma Algoritma adalah prosedur komputasi yang didefinisikan dengan baik yang mengambil beberapa nilai yaitu seperangkat nilai sebagai input dan output yang menghasilkan
Penyelesaian Barisan Rekursif dengan Kompleksitas Logaritmik Menggunakan Pemangkatan Matriks
 Penyelesaian Barisan Rekursif dengan Kompleksitas Logaritmik Menggunakan Pemangkatan Matriks Luqman Arifin Siswanto - 13513024 Program Sarjana Informatika Sekolah Teknik Elektro dan Informatika Institut
Penyelesaian Barisan Rekursif dengan Kompleksitas Logaritmik Menggunakan Pemangkatan Matriks Luqman Arifin Siswanto - 13513024 Program Sarjana Informatika Sekolah Teknik Elektro dan Informatika Institut
FAKULTAS TEKNIK UNIVERSITAS NEGERI YOGYAKARTA
 No. LSKD/EKO/DEL221/1 Revisi : 2 Tgl : 27/11/212 Hal 1 dari 13 1. Kompetensi Setelah melakukan praktik, mahasiswa diharapkan memiliki kompetensi: dapat memahami script files dan struktur pengaturan aliran.
No. LSKD/EKO/DEL221/1 Revisi : 2 Tgl : 27/11/212 Hal 1 dari 13 1. Kompetensi Setelah melakukan praktik, mahasiswa diharapkan memiliki kompetensi: dapat memahami script files dan struktur pengaturan aliran.
Pendahuluan. Ukuran input (input s size)
 Kompleksitas Algoritma Sesi 14 Pendahuluan Sebuah algoritma tidak saja harus benar, tetapi juga harus mangkus (efisien). Algoritma yang mangkus ialah algoritma yang meminimumkan kebutuhan waktu dan ruang.
Kompleksitas Algoritma Sesi 14 Pendahuluan Sebuah algoritma tidak saja harus benar, tetapi juga harus mangkus (efisien). Algoritma yang mangkus ialah algoritma yang meminimumkan kebutuhan waktu dan ruang.
STRUKTUR DATA KULIAH KE : 3 ALGORITMA
 STRUKTUR DATA KULIAH KE : 3 ALGORITMA Ciri-ciri algoritma 1. Input 2. Output 3. Definite 4. Efective 5. Terminate : masukan : keluaran : jelas : efektif : berakhir 1. Input 2. Output terdapat nol masukan
STRUKTUR DATA KULIAH KE : 3 ALGORITMA Ciri-ciri algoritma 1. Input 2. Output 3. Definite 4. Efective 5. Terminate : masukan : keluaran : jelas : efektif : berakhir 1. Input 2. Output terdapat nol masukan
BAB 4 MODEL RUANG KEADAAN (STATE SPACE)
 BAB 4 MODEL RUANG KEADAAN (STATE SPACE) KOMPETENSI Kemampuan untuk menjelaskan pengertian tentang state space, menentukan nisbah alih hubungannya dengan persamaan ruang keadaan dan Mengembangkan analisis
BAB 4 MODEL RUANG KEADAAN (STATE SPACE) KOMPETENSI Kemampuan untuk menjelaskan pengertian tentang state space, menentukan nisbah alih hubungannya dengan persamaan ruang keadaan dan Mengembangkan analisis
04-Ruang Vektor dan Subruang
 04-Ruang Vektor dan Subruang Vektor (1) Dosen: Anny Yuniarti, M.Comp.Sc Gasal 2011-2012 Anny2011 1 Agenda Bagian 1: Ruang Vektor Bagian 2: Nullspace of A: Solusi Ax = 0 Bagian 3: Rank dan Row-reduced-form
04-Ruang Vektor dan Subruang Vektor (1) Dosen: Anny Yuniarti, M.Comp.Sc Gasal 2011-2012 Anny2011 1 Agenda Bagian 1: Ruang Vektor Bagian 2: Nullspace of A: Solusi Ax = 0 Bagian 3: Rank dan Row-reduced-form
BAB I PENDAHULUAN. dengan ilmu rekayasa struktur dalam bidang teknik sipil. Perkembangan ini
 BAB I PENDAHULUAN I. Umum Saat ini perkembangan ilmu pengetahuan sudah sangat pesat, begitu juga dengan ilmu rekayasa struktur dalam bidang teknik sipil. Perkembangan ini didukung oleh kemajuan teknologi
BAB I PENDAHULUAN I. Umum Saat ini perkembangan ilmu pengetahuan sudah sangat pesat, begitu juga dengan ilmu rekayasa struktur dalam bidang teknik sipil. Perkembangan ini didukung oleh kemajuan teknologi
