Asep Juarna*, T. Basaruddin**
|
|
|
- Fanny Yulia Gunardi
- 7 tahun lalu
- Tontonan:
Transkripsi
1 PARALELISASI METODA RUNGE-KUTTA UNTUK MENYELESAIKAN MASALAH SISTEM PERSAMAAN DIFERENSIAL ORDINER YANG DIHASILKAN DARI REDUKSI MASALAH PERSAMAAN PARABOLIK LINIER : LAPORAN PENDAHULUAN ABSTRACT Asep Juarna*, T. Basaruddin** Illl ID995 PARALLELIZATION OF RUNGE-KUTTA METHOD TO SOLVE ORDINARY DIFFERENTIAL EQUATION PROBLEMS RESULTED FROM REDUCED PARABOLIC- LINEAR EQUATION PROBLEMS: PRELIMENARY REPORT. Using finite difference method, parabolic-linear equation can be reduced into ordinary differential equation problem. Since reduced problems are initial boundary problems and almost became stif, an implicit method diagonal implicit Runge-Kutta formulate in this case, can be used as an appropriate solution for the problems. To increase the computation performance, parallelization is implemented in two ways, i.e., method and system parallelization. ABSTRAK PARALELISASI METODA RUNGE-KUTTA UNTUK MENYELESAIKAN MASALAH SISTEM PERSAMAAN DIFERENSIAL ORDINER YANG DIHASILKAN DARI REDUKSI MASALAH PERSAMAAN PARABOLIK LINIER : LAPORAN PENDAHULUAN Dengan menggunakan nietoda beda hingga penulis telah mereduksi masalah persamaan parabolik linier menjadi masalah sistem persamaan diferensial ordiner. Masalah tereduksi adalah masalah syarat awal. Karena masalah terakhir ini hampir stif, adalah tepat jika nietoda implisit dipilih sebagai pemecah masalah; dalam kaitan ini sebuah formula Runge-Kutta implisit diagonal telah dipilih. Untuk meningkatkan kinerja komputasi, penulis telah melakukan paralelisasi terhadap semua kegiatan komputasinya dengan dua cara secara serempak. Kedua cara tersebut adalah paralelisasi metoda dan paralelisasi sistcm. PENDAHULUAN Dewasa ini komputasi paralel merupakan metoda komputasi yang pemakaiannya tidak dapat lagi dihindari. Tidak sedikit masalah yang memerlukan solusi segera. Bagi permasalahan pendek dan sederhana kebutuhan solusi segera tersebut dapat saja dipenuhi dengan metoda komputasi sekuensial, tetapi tidak demikian halnya jika yang dihadapi adalah permasalahan panjang dan rumit. Perkembangan komputasi paralel juga ditunjang oleh kemudahan dalam memperoleh perangkat keras penunjang. Staf Pengajar STMIK Giinadarma - Jakarta Staf Pusat limit Koniputer Universitas Indonesia - Jakarta 39
2 Secara umum komputasi paralel adalah suatu upaya untuk mereduksi waktu komputasi dengan cara memecah masalah menjadi beberapa bagian, menugaskan sebuah prosesor untuk setiap bagian masalah, dan kemudian menyelesaikan setiap bagian tersebut secara serempak Dalam tulisan ini komputasi paralel dibicarakan dalam kaitannya sebagai metoda komputasi untuk memecahkan permasalahan syarat awal, PSA (IVP, initial value problem) melalui suatu metoda Metoda yang digunakan dan lebih jauh dikembangkan ke arah paralel adalah metoda Runge-Kutta. Pembicaraan lebih jauh tentang komputasi paralel akan disajikan pada Pasa! 2, sedangkan pembicaraan tentang PSA dan metoda Runge-Kutta akan disajikan pada Pasal 4. Ditinjau dari cara paralelisasi itu diselenggarakan untuk memecahkan suatu PSA dengan suatu metoda, maka dapat dibedakan dua katagori paralelisasi; keduanya adalah: 1. paralelisasi metoda, atau sering diacu sebagai paralelisasi terhadap waktu, dan 2. paralelisasi sistem, atau sering diacu sebagai paralelisasi terhadap ruang Paralelisasi metoda adalah cara paralelisasi yang bergantung pada potensi metoda itu sendiri. Potensi paralel suatu metoda dapat dikembangkan dengan sendirinya atau dengan formulasi ulang metoda tersebut. Paralelisasi sistem memerlukan suatu metoda eksternal yang tidak berkaitan Iangsung dengan penyelesaian PSA itu sendiri. Pembicaraan kedua cara paralelisasi ini akan disajikan masing-masing pada Pasal 5 dan Pasal 6. Tulisan ini merupakan kombinasi penerapan kedua cara paralelisasi dalam menyelesaikan sebuah sistem persamaan diferensial ordiner (PDO) berderajat satu sebagai hasil reduksi sebuah persamaan diferensial parsial (PDP) dua dimensi dan berderajat dua. Persamaan tersebut adalah persamaan difusi dengan suku konveksi : d 2 U du (1) Persamaan difusi di atas mempunyai koefisien difusi 1 dan koefisien konveksi K. Setelah Pasal 2 membicarakan Komputasi Paralel, maka selanjutnya Pasal 3 akan menyajikan PDP dan reduksinya menjadi PDO. Tulisan ini diakhiri dengan beberapa kesimpulan sementara dan saran tentang alternatif penyelesaian masalah. Pada tulisan ini, notasi matematika menggunakan aturan sebagai-berikut : cetak tebal untuk menyatakan vektor atau matriks dan cetak tipis untuk menyatakan skalar. 4
3 SEPINTAS TENTANG KOMPUTASI PARALEL Terdapat 3 kelas komputer yang dapat dikatagorikan ke dalam komputer paralel; ketiganya adalah : 1. SIMD (Single Instruction stream, Multiple Data stream), dan 2. MISD (Multiple Instruction stream, Single Data stream), 3. MIMD (Multiple Instruction stream, Multiple Data stream). Secara singkat berikut ini adalah perbedaan ketiganya. SIMD mempunyai N prosesor identik yang bekerja secara sinkron, yaitu : pada setiap langkah komputasi setiap prosesor mengerjakan instruksi yang sama terhadap data (atau sekumpulan data) berbeda. Pada komputer MISD, pada setiap langkah komputasi setiap prosesornya secara serempak melakukan instruksi berbeda pada data (atau sekumpulan data) yang sama. Setiap prosesor kelas komputer MIMD melakukan instruksi berbeda pada data (atau sekumpulan data) yang berbeda pula. Jelas bahwa MIMD ini potensial untuk beroperasi secara tak-sinkron. Terdapat beberapa indikator komputasi paralel pada komputer paralel dengan p prosesor. Berikut ini 5 indikator yang berkaitan dengan tulisan ini 1. S(p) = percepatan {speed-up ratio), yaitu rasio antar vvaktu yang diperlukan untuk menyelesaikan suatu masalah secara sekuensial terbaik terhadap waktu yang diperlukan untuk menyelesaikan masalah yang sama secara paralel. 2. S(a) = penguatan {algorithmic speed-up ratio), yaitu ukuran penguatan yang diakibatkan oleh penggunaan p prosesor. Idealnya S(a) = p. Keadaan ideal ini bisa turun misalnya karena overhead yang diakibatkan sinkronisasi dan komunikasi antar prosesor. 3. Efisiensi, mengukur efektivitas penggunaan prosesor. Efisiensi ideal = 1%, dan akan turun karena : beberapa prosesor idle, sinkroniasi, dan komunikasi. 4. Granularitas {grain size) yaitu jumlah instruksi yang dapat dilaksanakan secara serempak sebelum sinkronisasi diperlukan. Terdapat tiga tipe granularitas, yaitu fine-grain jika jumlah instruksi'sebelum sinkronisasi tersebut adalah 9(1), mediumgrain jika jumlah instruksi adalah 6(1), dan coarse-grain jika jumlah instruksi adalah (1). 5.6 = Rasio antara waktu komunikasi terhadap komputasi. Nilai rasio ini menunjukkan kontribusi komunikasi terhadap overhead. 41
4 REDUKSI PDP MENJADI SISTEM PDO Dari uraian Taylor dapat diturunkan dua persamaan berikut: dan : 2Ar fix - Ax) - 2 f{x) + f(x + Ax) Ax 2 O(Ax 2 ) Persamaan (2) dan (3) dikenal sebagai pendekatan beda hingga (finite difference approximation), lebih spesifik lagi formula beda tengah (central difference formula). Dengan kedua persamaan di atas maka permasalahan (1) direduksi menjadi : dv(t) 1 dt 2 Ax- Ax)U(x- Av)-4U(x) + (2- K AX)U(X+AX)} (4) Pada persamaan-persamaan di atas Ax adalah suatu elemen besaran X yang membagi selang [,a] menjadi N bagian sama besar. Karena pada i = dan i = N diberikan syarat awal, maka pennasalahan yang ditinjau adalah titik-titik x i, i = 1,2,...,N-l. Selanjutnya jika V- X (t) adalah pendekatan untuk Uft), kemudian UQ = V () dan U a = V^ maka persamaan (4) dapat dilihat sebagai sistem N-\ persamaan diferensial ordiner berderajat satu sebagai bcrikut : d -V = AV + b (5, atau : -A 2-x-Av 2+ATAV -4 2-ATAV (2) (3) <* 2 + vav -4 2-Kbx. 2 + K Ar -4 (2 + KAX)V (6) (2 - K Ax)V n _ Terlihat bahwa matriks A adalah matriks tridiagonal konstan (N-l) x (N-l). 42
5 PSA DAN METODA RUNGE-KUTTA 1MPLISIT Sebuah PSA dapat dituliskan sebagai : y'=f(f,y), t=[f o,i t ], yoo)=yo (? ) Persamaan di atas merupakan sistem persamaan diferensial ordiner berderajat satu y dengan sebuah vektor nilai awal y. Solusi Runge-Kutta pada akhir selang integrasi t,t n+] ] dengan selang tahap h = t n+] - / untuk masalah PSA di atas adalah : dimana: yn +,=y n +^Z^k ni (8) ( * ^ l Z (9) Pada persamaan (8) y n adalah hasil komputasi numerik yang merupakan nilai pendekatan untuk y(/ n ). Selisih kedua besaran ini merupakan ukuran yang selanjutnya akan menentukan lebar-langkah (step-size) h secara adaptif. Teknik komputasi ini dikatakan bersifat adaptif terhadap h atau sering disebut juga sebagai teknik peubah lebar-langkah (variable step-size technique). Terdapat dua katagori utama metoda Runge-Kutta; keduanya adalah metoda Runge-Kutta Eksplisit, dan metoda Runge-Kutta Implisit. Selanjutnya dikenal pula katagori ketiga, yaitu metoda Runge-Kutta Semi Ekslpisit atau Semi Implisit atau Runge-Kutta Implisit Diagonal, RKID (DIRK, Diagonally Implicit Runge-Kufta). RKID sebenamya masih termasuk. katagori implisit. Berkaitan dengan katagorisasi di atas maka batas atas somasi pada persamaan (9) adalah i-1 untuk RK eksplisit, untuk RKID, dan s untuk RK implisit. Pilihan penggunaan kedua katagori metoda Runge-Kutta dilakukan berdasarkan ke-stif-an (stiffness) persoalan. Metoda Runge-Kutta Eksplisit dan metoda eksplisit lainnya sudah cukup stabil untuk permasalahan non-stiff, sedangkan masalah stif dan agak stif (mildy stiff) harus menggunakan metoda implisit. PSA (7) dikatakan stif pada selang I = [a,b] jika V/ el, berlaku : 1. Re(A,) < (i = l,2,...,s),dan Max, v / Min, N 43
6 dimana A i adalah nilai-nilai eigen dari matriks koefisien sistem, A, yaitu jika persamaan (7) dituliskan sebagai y' = f (/,y) = A(/) y + b(, baik melalui proses linierisasi dicirikan dengan kebergantungan matriks A dan vektor b terhadap variabel t ataupun tidak dicirikan dengan matriks A dan vektor b yang konstan. Tidak ada batasan baku tentang nilai rasio ke-stif-an {stiffness ratio) S(x). Di antara beberapa pendapat tersebut penulis mengutip pendapat Lambert yaitu (1) untuk permasalahan tidak stif, { O 2 ) untuk permasalahan hampir stif, dan { 6 ) untuk ^permasalahan stif. Masalah hampir stif akan lebih baik dikerjakan dengan metoda implisit dibandingkan dengan metoda eksplisit. Telah dilakukan perhitungan S(x) pada sistem (6) untuk K =.5 dan Ax =.25. Hasilnya terlihat pada Tabel 1. Tabel 1. Rasio ke-stif-an, S(x) sebagai fungsi derajat PDO, m m = N-l S(x) Karena S(x) berkisar antara 9(1) sampai 8(1), yaitu selang masalah agak stif, maka metoda Runge-Kutta yang dipakai adalah RK implisit. Selanjutnya dengan alasan-alasan seperti yang akan dijelaskan pada Pasal 4, maka RK implisit yang ak?.n dipakai adalah RKID. Tabel butcher RKID, yang memperlihatkan koefisien formula : a, b, dan c, seperti terlihat pada pada persamaan (8) dan (9), untuk formula RKID dengan derajat-tahap (stage-order) - s, ditunjukkan pada gambar di bawah ini. a «21 «22 «s Gambar 1. Tabel butcher untuk RKID Kombinasi persamaan-persamaan (7), (8), dan (9), serta Gambar 1. menghasilkan: 44
7 (1) dimana: J m = Jacobian(f) = A untuk PDO linier, I m = matriks satuan. PARALELISASI METODA : RKID PARALEL Sebuah formula RK implisit dengan derajat-tahap s membutuhkan pemecahan sm-buah persamaan simultan atau s-buah sistem PDO pada setiap langkah integrasi. Matriks a formula RK implisit ini, sepcrti ditunjukkan oleh tabel butcher, adalah matriks penuh. Metoda penyelesaian standar masalah ini adatah melalui faktorisasi LU dilanjutkan dengan penyelesaian sistem L dan U. Jumlah flops penyelesaian ini adalah : Berbeda dengan RK implisit, maka matriks a formula RKID adalah matriks segitiga atas. Tidak diperlukan faktorisasi LU pada penyelesaian masalah ini. Jadi jumlah flops yang diperlukan adalah ms 2. Sedikitnya jumlah flops yang diperlukan sebuah RKID mendorong orang untuk mencari atau menurunkan formula RKID, atau bahkan melakukan formulasi ulang bentuk RK implisit, jika mungkin, menjadi bentuk blok-rkid. Penulis memfokuskan tulisannya kepada upaya terakhir ini. Bentuk tabel butcher dari blok-rkid terlihat pada Gambar 2. A Cp B] Gambar 2. Tabel butcher untuk blok-rkid 45
8 Gambar 2 di atas adalah hasil formuiasi ulang RK implisit menjadi blok-rkid. A dan D adalah dua matriks berukuran maksimum q x q, dimana A adalah matriks bujur sangkar, penuh ataupun tidak, dan D adalah matriks diagonal yang tidak pertu sama untuk semua D. Sementara itu C dan B adalah dua matriks kolom dengan panjang kolom maksimum adalah q. Karena D adalah matriks diagonal maka semua k pada lajur blok pertama dapat dipecahkan secara serempak; Inilah potensi RKID dalam paralelisasi metoda sehingga blok-rkid di atas disebut sebagai RKID Paralcl (RKIDP). Selanjutnya, segera setelah semua k pada lajur ke-i selesai dipecahkan maka hal yang sama dapat dilakukan pada lajur ke-(i+l). Formula RKIDP di atas membutuhkan minimal q-buah prosesor, dan secara lengkap diacu sebagai RKIDP s-tahap p-paralel <?-prosesor (s-stage p-parallel q- processor RKIDP). Sebagai contoh berikut ini diberikan sebuah formula RK implisit 4- stage : 1 3/5 171/44 2/5-43/2 3/5-215/44 39/2 1 3/5 11/72 25/72 11/72 25/72 Gambar 3. Sebuah formula RK Implisit s-tahap Segera terlihat bahvva terhadap formula pada Gambar 3 di atas dapat dilakukan formuiasi ulang sehingga diperoleh formula 4-tahap 2-paralel 2-prosesor. Telah ditunjukkan pada akhir Pasal 3 bahwa matriks koefisien sistem PDO adalah matriks tridiagonal konstan berukuran (N-l) x (N-l). Jika formula Runge-Kutta Implisit yang dipakai adalah seperti pada Gambar 3 maka persamaan (9) akan menjadi: I n ~ ha u A ha^ A ha 4] A I ha 32 A ha 42 A A I» -ha,, A I k2 I k3f 3 JLkJ Ay o +b] Ay«+b Vektor kj dan k 2 dapat dipecahkan secara serempak. Hal yang sama dapat dilakukan pada k 3 dan k 4 setelah dua nilai k sebelumnya diperoleh. Perhatikan bahwa komponcn setiap vektor k adalah (N-l)-buah k. Dengan paralelisasi metoda inaka prosedur penyelesaian permasalahan syarat awal pada sebuah langkah komputasi dapat dituliskan dalam pseudocode berikut: (11) 46-
9 Pseudocode SEC PAR SEC proses 1.1 : for i = 1 to m : hitung &, ; proses 1.2 : for i =1 to m : hitung k 2 - t PAR SEC proses 2.1 : for i - ] to m : hitung k %; proses 2.2: PAR for i =1 to m for i = / to m : hitung k A - t proses 3.i.: hitung: y = ( Salah satu indikator komputasi paralel adalah speed-up ratio pada jumlah prosesor p, S p. S p didefinisikan sebagai rasio antara waktu algoritma sekuensial tercepat terhadap waktu algoritma paralel untuk suatu permasalahan yang diberikan Agak berbeda dengan defmisi di atas, maka pada tulisan ini algoritma sekuensial adalah prosedur komputasi dengan menggunakan formula RKID, sedangkan algoritma paralel adalah prosedur komputasi dengan menggunakan RKIDP dari formula RKID, yaitu dengan menggunakan pseudocode 11. Dari pengertian terakhir terlihat bahwa untuk formula pada Gambar 3 dan pseudocode 11 akan diperoleh speed-up ideal sebcsar 2. Paralelisasi metoda di atas telah dipergunakan oleh Suhartanto untuk menyelesaikan sistem PDO f(x,y) = Ly, dimana L adalah matriks tridiagonal sebagai berikut: \ Dari hasil percobaannya diperoleh nilai speed-up : (N = 1) dan meningkat sampai (N = 25). Hasil ini cukup dekat dengan speed-up ideal. (12) 47
10 PARALELISASI SISTEM : REDUKSI SIKLIK Pada pseudocode 11 di atas tampaknya terdapat satu peluang untuk menaikkan speed-up. Peluang itu adalah paralelisasi pada proses-proses : 1.1, 1.2, 2.1, dan 2.2, yaitu paralelisasi dalam menghitung semua komponen dalam setiap vektor k yang masing-masing berjumlah N-l. Dari persamaan (11) terlihat bahwa bentuk persamaan untuk memecahkan setiap vektor k adalah sama. Dengan mengingat bentuk A seperti pada persamaan (5), maka komponen persamaan (11) untuk k i pada akhir langkah komputasi pertama, sebagai contoh, adalah : 1 + 4a -(2-K dx)a -(2 + K dx)a 1 + 4«-{2-K dx)a -(2 + K dx)a dx)a -(2-K -(2 + K dx)a 1 + 4o " l.n-2 L*M.N-I J -4y lj + {2-K dx)y 2fi (2+K dx)y l - 4> 2> +{2-K dx)n xo (13) (2 + K N. 2 +(2-K dx)y N _ N_] Tujuan reduksi siklis adalah mempartisi sebuah sistem persamaan tridiagonal menjadi beberapa blok persamaan sedeniikian rupa sehingga setiap blok dapat dapat dipecahkan secara serempak bersama blok lainnya. Teknik reduksi ini dilakukan melalui serangkaian proses eliminasi. Setiap proses eliminasi akan menggandakan jumlah persamaan. Misalnya: ci y setelah eliminasi pertama berubah menjadi Gambar 4. 48
11 a? b a? b?\ Gambar 5. Gambar 4 adalah matriks koefisien A dari sistem persamaan linier Ax = y (14) Pada gambar tersebut terlihat bahwa eliminasi pertama telah mempartisi sebuah persamaan tridiagonal empat peubah menjadi dua blok persamaan yang dapat dipecahkan secara serempak : blok atas memecahkan dua peubah pertama scmentara blok bawah memecahkan dua peubah kedua. Indeks atas pada Gambar 5. menunjukkan bahwa eliminasi telah dilakukan sebanyak satu kali. Secara umum terhadap hasil eliminasi ke-n dapat dilakukan eliminasi Icbih lanjut sehingga diperoleh lebih banyak lagi blok persamaan yang dapat dipecahkan secara serempak. Teknik eliminasi akan dijelaskan bcrikut ini. Untuk kasus lebih umum Gambar 4 sekarangberukuran mxm sehingga bentuknya menjadi: A = (15) n,-!, b m J Perhatikan persamaan ke-(i-l), ke-i, dan ke-(i+l) untuk i = 3,4,...,m-2 sebagai berikut (16) Persamaan ke-(i-l) digunakan untuk mengeliminasi x- ra dari persamaan ke-i, sedangkan persamaan ke-(i+l) digunakan untuk mengeliminasi x i+] dari persamaan ke-i. Hasilnya adalah transformasi persamaan (14) menjadi : 49
12 dimana : a (X) x +b ) x +c ) x -,(') (17) i+i _ yj ) c (18) ). Persamaan (18) juga berlaku untuk a^'j,a ( n ]),b^]),b^,c, (1),dan c^ kecuali untuk : - b, + p, a^, dan Perhatikan bahwa dua indeks.\' berlirutan dalam persamaan (17) berselisih 2. dengan demikian transformasi matriks (15) akibat eliminasi pertama ini menghasilkan persamaan (19). Untuk memperjelas formulasi ulang persamaan (19) menjadi bentuk Gambar 5 maka disertakanlah variabel x-nva. c l (1) ci" x 2 x! (2) O.n.1 x ma x Persamaan (2) dapat diformulasi ulang menjadi: 5
13 !i o (21) Dapat disimpulkan bahwa prosedur reduksi-siklis terdiri atas : 1. assignment persamaan (18) 2. assignment persamaan (2) 3. formulasi persamaan (21) Persamaan (21) terdiri atas dua blok persamaan yang saling lepas schingga keduanya dapat diselesaikan secara sercmpak. Terhadap persamaan di atas juga dapat dilakukan prosedur yang sama sehingga diperoleh persamaan dengan empat, dclapan. sampai 2 n blok persamaan, dengan n adalah derajat reduksi-siklis, yaitu frekuensi pemanggilan prosedur reduksi-siklis. Segera setelah derajat reduksi-siklis tercapai, maka langkah selanjutnya adalah eliminasi gauss bagi persamaan : Ax = y, yang terdiri dari : 1. faktorisasi : A = LU 2. dapatkan z dari : Lz = y 3. dapatkan x dari : Ux = z. Untuk matriks A seperti pada persamaan (15) maka faktorisasi LU menghasilkan : U, /, i U 2 L = dan U = (22) dengan : 51
14 w, =, danuntuki = 2,3,...,m Akhimya, paralelisasi sistem reduksi siklis ini dirangkunikan dengan prosediir sistem berikut: Prosedur Sistem 1. for i = 1 to n do prosedur reduksi-siklis 2, for j = 1 to 2 n do in para lei eliminasi gauss (blok-j) Pseudocode lengkap yang menyertakan paralelisasi metoda dan paralelisasi sistem adalah: Pseudocode SEC 2. PAR 3. SEC 4. Prosedur Sistem (k ] J 5. Prosedur Sistem (k 2 J 6. PAR 7. SEC 8. Posedur Sistem (k 3 J 9. Prosedur Sistem (k 4 J 1. PAR for i =1 to m (A 11. proses 3.i.: hitung : y in+] = y in + h\ ^b- KESIMPULAN DAN SARAN Beberapa kesimpulan sementara yang dapat diturunkan dari pembicaraan di atas adalah : 1. Masalah Persamaan Difusi di atas dapat direduksi menjadi sistem PDO dengan matriks koefisien sistem thdiagonal-toeplitz serta mempunya jenis ke-stif-an: hampir stif. 52
15 2. Dengan menggunakan formula RKID Paralel berderajat-tahap 4 dan mempunyai jumlah blok 2, serta sistem PDO yang yang diuji mempunyai kemiripan (tridiagonal-toeplitz-simetri), pseudocode 7 menghasilkan speed-up cukup dekat dengan kondisi ideal. 3. Pseudocode 11 yang mengabungkan paralelisasi sitem, yaitu prosedur reduksi-siklis dan prosedur eliminasi-gauss, ke dalam pseudocode 7 diperkirakan akan menirigkatkan speed-up yang diperoleh dengan pseudocode 7 Hal ini terutama akan terjadi untuk ukuran sistem yang besar. Berikut ini beberapa saran untuk peningkatan speedup atau penelitian Icbili lanjut: 1. Speed-up yang dihasilkan oleh pseudocode 7 akan lebih tinggi (di atas 2) jika menggunakan formula RKIDP sebagai berikut: a. berderajat-tahap lebih dari 4 dengan jumlah blok lebih dari 2, b. berderajat-tahap 4 dengan jumlah blok 2 tetapi mempunyai struktur tabel butcher sebagai berikut: c. kombinasi (a) dan (b). Q c, Q A 4* A» 3 A 43 D 4 rjt nt I>T nt /3j /?T ZJ, X>4 2. Teknik lain dari reduksi siklis bisa dikembangkan misalnya dengan eliminasi tahap dua dan seterusnya terhadap matriks (2) sehingga akhirnya dihasilkan satu persamaan dengan satu peubah, satu sistem diagonal. 3. Teknik lain untuk merubah Gambar 4 menjadi Gambar 5 adalah metoda itcrasi, yaitu dengan membawa elemen a 3 dan c 2 ke ruas kanan, memberi nilai dugaan kepada peubah x yang bersangkutan (dalam hal ini x 3 dan x 2 ), lakukan itcrasi sehingga dua nilai terakhir kedua peubah tersebut berselisih sekecil mungkin. Teknik ini sangat bergantung kepada laju konvergensi; laju konvergensi yang lambat akan menjadikan overhead komputasi terlalu besar. 53
16 4. Implementasi program akan dilakukan dengan Transputer 8 prosesor, dengan bahasa pemrograman ccam2. Implementasi lain dapat saja dilakukan dengan menggunakan PVM. DAFTAR PUSTAKA 1. SELIM G. Akl., "The Design and Analysis of Parallel Algorithms", Prentice- Hall Inc., New Jersey, ROGER ALEXANDER, "Diagonally Implicit Runge-Kutta Methods for Stiff O.D.E. 's", SIAM J. Numer. Anal., Vol. 4, No. 6, hal , December BJORSTAD, P, dkk., "Efficient Matrix Multiplication on SIMD Computers". SIAM J. Matrix Anal. Appl. Vol. 13, No. 1, hal , January DOWERS, K, dkk., "Block Tridiagonal Systems on The Alliant FX>'8. Dalam Proceeding of The Fourth SIAM Conference on Parallel Processing for Scientific Computing", Jack Dongara, dkk (ed). Chicago-Illinois, 11-19, December FREEMAN, T.L. dan PHILLIPS, C, "Parallel Numerical Algorithms". Prentice-Hall, New York, GOLUB, GENE. H. dan VAN LOAN, CHARLES. F., "Matrix Computation", The John Hopkins University Press. Baltimore, HALL, G. dan WATT, J.M. (ed)., "Modern Numerical Methods for Ordinary Differential Equations", Clarendon Press, Oxford, JACKSON, K.R. dan NORSETT, S.P., "The Potential for Parallelism in Runge- Kutta Methods. Part I : RK Formulas in Standard Form", SIAM J. Numcr. Anal., Vol. 32, No. 1, hal , February SMITH, G.D., "Numerical Solutions of Partial Differential Equations : Finite Difference Methods", Clarendon Press, Oxford, SUHARTANTO, H., "Unjuk Kerja Metoda Runge-Kutta Paralel Untuk Mencari Solusi Sistem Persamaan Diferensial Biasa", Laporan Akhir Kegiatan Pcnelitian Pusat Antar Universitas Bidang Ilmu Komputer Universitas Indonesia,
17 DISKUSI SUPRIYONO 1. Bagaimana tingkat stabilitas RKID? 2. Berapa nilai dari beberapa parameter dalam RKID? ASEP JUARNA 1. Secara umum semua metode implisit lebih stabil dari pada metode eksplisit. Dua indikator stabilitas adalah komponen sistem yaitu stiffness ratio > (1) akan stabil jika menggunakan metode implisit, dan komponen metode yaitu dengan test function y' = ay akan diperoleh region of stability pada metode implisit lebih besar dari pada metode eksplisit. 2. RKID ini mempunyai derajat formula p = 8 dan derajat stage = 4 yang termasuk S- stable. RENO ALAMSYAH 1. Mengapa speed up ratio hasil eksperimen lebih kecil dari pada speed up ideal? 2. Mengapa speed up ratio hasil eksperimen untuk n = 1 (1,84) lebih kecil dari pada n= 1(1,85)? ASEP JUARNA 1. Speed up ideal djdasarkan pada asumsi bahwa communication cost antar prosesor sama dengan nol (pengiriman data tidak perlu waktu) dan setiap prosesor tidak pernah idle (menunggu), sedang pada kenyataannya kedua hal ini tidak mungkin terjadi terutama pada kasus komputasi assyncronous. 2. Komputasi yang baik mempunyai computation to communication ratio (ccratio) >1. Makin besar ukuran sistem (n), makin besar ukuran cc-ratio kumulatif sehingga overhead cost makin kecil dan mengakibatkan speed up makin mendekati ideal (walaupun tidak pernah tercapai). 55
18 TOTTITJIPTOSUMIRAT Apakah paralelisasi dalam metode RXID dapat digunakan untuk pemecahan masalah di bidang Biologi seperti penyerapan radioisotope tracer ( 32 P) oleh mikroba di dalam rumen (perut) hewan ternak ruminansia? Mohon penjelasan. ASEP JUARNA Setiap permasalahan yang dapat dimodelkan menjadi persamaan diferensial parsial orde2 dan 2 dimensi, dapat dideskritisasi menjadi sistem Persamaan Diferensial Ordiner (PDO). Setiap PDO pasti dapat diselesaikan dengan RKID secara paralel (paralelisasi metode), sedang paralelisasi sistem bergantung pada matriks koefisien sistem PDO. Sistem PDO dalam makalah ini mempunyai matriks koefisien konstan tridiagonal, sehingga mengalami paralelisasi ganda. 56
KARAKTERISTIK KINERJA ALGORITMA RECURSIVE DECOUPLING PADA SISTEM MULTIPROSESOR BERBASIS PVM
 KARAKTERISTIK KINERJA ALGORITMA RECURSIVE DECOUPLING PADA SISTEM MULTIPROSESOR BERBASIS PVM Tri Prabawa Program Studi Teknik Informatika, STMIK AKAKOM Yogyakarta Jl. Raya Janti 143, Yogyakarta 55198 E-mail
KARAKTERISTIK KINERJA ALGORITMA RECURSIVE DECOUPLING PADA SISTEM MULTIPROSESOR BERBASIS PVM Tri Prabawa Program Studi Teknik Informatika, STMIK AKAKOM Yogyakarta Jl. Raya Janti 143, Yogyakarta 55198 E-mail
KAJIAN DISKRETISASI DENGAN METODE GALERKIN SEMI DISKRET TERHADAP EFISIENSI SOLUSI MODEL RAMBATAN PANAS TANPA SUKU KONVEKSI
 KAJIAN DISKRETISASI DENGAN METODE GALERKIN SEMI DISKRET TERHADAP EFISIENSI SOLUSI MODEL RAMBATAN PANAS TANPA SUKU KONVEKSI Suhartono dan Solikhin Zaki Jurusan Matematika FMIPA UNDIP Abstrak Penelitian
KAJIAN DISKRETISASI DENGAN METODE GALERKIN SEMI DISKRET TERHADAP EFISIENSI SOLUSI MODEL RAMBATAN PANAS TANPA SUKU KONVEKSI Suhartono dan Solikhin Zaki Jurusan Matematika FMIPA UNDIP Abstrak Penelitian
EFEK DISKRITASI METODE GALERKIN SEMI DISKRET TERHADAP AKURASI DARI SOLUSI MODEL RAMBATAN PANAS TANPA SUKU KONVEKSI
 JURNAL MATEMATIKA DAN KOMPUTER EFEK DISKRITASI METODE GALERKIN SEMI DISKRET TERHADAP AKURASI DARI SOLUSI MODEL RAMBATAN PANAS TANPA SUKU KONVEKSI Kushartantya dan Awalina Kurniastuti Jurusan Matematika
JURNAL MATEMATIKA DAN KOMPUTER EFEK DISKRITASI METODE GALERKIN SEMI DISKRET TERHADAP AKURASI DARI SOLUSI MODEL RAMBATAN PANAS TANPA SUKU KONVEKSI Kushartantya dan Awalina Kurniastuti Jurusan Matematika
ASPEK STABILITAS DAN KONSISTENSI METODA DALAM PENYELESAIAN NUMERIK PERSAMAAN DIFERENSIAL BIASA DENGAN MENGGUNAKAN METODA PREDIKTOR- KOREKTOR ORDE 4
 ASPEK STABILITAS DAN KONSISTENSI METODA DALAM PENYELESAIAN NUMERIK PERSAMAAN DIFERENSIAL BIASA DENGAN MENGGUNAKAN METODA PREDIKTOR- KOREKTOR ORDE 4 Asep Juarna, SSi, MKom. Fakultas Ilmu Komputer, Universitas
ASPEK STABILITAS DAN KONSISTENSI METODA DALAM PENYELESAIAN NUMERIK PERSAMAAN DIFERENSIAL BIASA DENGAN MENGGUNAKAN METODA PREDIKTOR- KOREKTOR ORDE 4 Asep Juarna, SSi, MKom. Fakultas Ilmu Komputer, Universitas
SATUAN ACARA PERKULIAHAN UNIVERSITAS GUNADARMA
 Mata Kuliah Kode / SKS Program Studi Fakultas : Pengolahan Paralel : AK012215 / 2 SKS : Sistem Komputer : Ilmu Komputer & Teknologi Informasi 1 Pendahuluan Agar mahasiswa mengerti akan apa yang dimaksud
Mata Kuliah Kode / SKS Program Studi Fakultas : Pengolahan Paralel : AK012215 / 2 SKS : Sistem Komputer : Ilmu Komputer & Teknologi Informasi 1 Pendahuluan Agar mahasiswa mengerti akan apa yang dimaksud
SATUAN ACARA PERKULIAHAN MATA KULIAH ALGORITMA PENGOLAHAN PARALEL (S1/ TEKNIK INFORMATIKA)
 SATUAN ACARA PERKULIAHAN MATA KULIAH ALGORITMA PENGOLAHAN PARALEL (S1/ TEKNIK INFORMATIKA) Minggu Media Tugas Referensi 1 Pendahuluan butuhan akan komputer paralel Quinn, Agar mahasiswa mengerti akan apa
SATUAN ACARA PERKULIAHAN MATA KULIAH ALGORITMA PENGOLAHAN PARALEL (S1/ TEKNIK INFORMATIKA) Minggu Media Tugas Referensi 1 Pendahuluan butuhan akan komputer paralel Quinn, Agar mahasiswa mengerti akan apa
SATUAN ACARA PERKULIAHAN MATA KULIAH PENGOLAHAN PARALEL (S1/ TEKNIK KOMPUTER)
 SATUAN ACARA PERKULIAHAN MATA KULIAH PENGOLAHAN PARALEL (S1/ TEKNIK KOMPUTER) Minggu Media Tugas Referensi 1 Pendahuluan butuhan akan komputer paralel Quinn, Agar mahasiswa mengerti akan apa yang dimaksud
SATUAN ACARA PERKULIAHAN MATA KULIAH PENGOLAHAN PARALEL (S1/ TEKNIK KOMPUTER) Minggu Media Tugas Referensi 1 Pendahuluan butuhan akan komputer paralel Quinn, Agar mahasiswa mengerti akan apa yang dimaksud
STUDI KOMPARASI KINERJA ALGORITMA REDUKSI SIKLIS DENGAN ALGORITMA PEMISAHAN REKURSIF PADA SISTEM MULTIPROSESOR BERBASIS PVM
 STUDI KOMPARASI KINERJA ALGORITMA REDUKSI SIKLIS DENGAN ALGORITMA PEMISAHAN REKURSIF PADA SISTEM MULTIPROSESOR BERBASIS PVM Tri Prabawa Program Studi Teknik Informatika, STMIK AKAKOM Yogyakarta Jl. Raya
STUDI KOMPARASI KINERJA ALGORITMA REDUKSI SIKLIS DENGAN ALGORITMA PEMISAHAN REKURSIF PADA SISTEM MULTIPROSESOR BERBASIS PVM Tri Prabawa Program Studi Teknik Informatika, STMIK AKAKOM Yogyakarta Jl. Raya
Metode Beda Hingga untuk Penyelesaian Persamaan Diferensial Parsial
 Metode Beda Hingga untuk Penyelesaian Persamaan Diferensial Parsial Ikhsan Maulidi Jurusan Matematika,Universitas Syiah Kuala, [email protected] Abstract Artikel ini membahas tentang salah satu
Metode Beda Hingga untuk Penyelesaian Persamaan Diferensial Parsial Ikhsan Maulidi Jurusan Matematika,Universitas Syiah Kuala, [email protected] Abstract Artikel ini membahas tentang salah satu
PENYELESAIAN PERSAMAAN POISSON 2D DENGAN MENGGUNAKAN METODE GAUSS-SEIDEL DAN CONJUGATE GRADIENT
 Teknikom : Vol. No. (27) E-ISSN : 2598-2958 PENYELESAIAN PERSAMAAN POISSON 2D DENGAN MENGGUNAKAN METODE GAUSS-SEIDEL DAN CONJUGATE GRADIENT Dewi Erla Mahmudah, Muhammad Zidny Naf an 2 STMIK Widya Utama,
Teknikom : Vol. No. (27) E-ISSN : 2598-2958 PENYELESAIAN PERSAMAAN POISSON 2D DENGAN MENGGUNAKAN METODE GAUSS-SEIDEL DAN CONJUGATE GRADIENT Dewi Erla Mahmudah, Muhammad Zidny Naf an 2 STMIK Widya Utama,
Penyelesaian Persamaan Poisson 2D dengan Menggunakan Metode Gauss-Seidel dan Conjugate Gradient
 Teknikom : Vol. No. (27) ISSN : 2598-2958 (online) Penyelesaian Persamaan Poisson 2D dengan Menggunakan Metode Gauss-Seidel dan Conjugate Gradient Dewi Erla Mahmudah, Muhammad Zidny Naf an 2 STMIK Widya
Teknikom : Vol. No. (27) ISSN : 2598-2958 (online) Penyelesaian Persamaan Poisson 2D dengan Menggunakan Metode Gauss-Seidel dan Conjugate Gradient Dewi Erla Mahmudah, Muhammad Zidny Naf an 2 STMIK Widya
Persamaan Diferensial
 TKS 4003 Matematika II Persamaan Diferensial Konsep Dasar dan Pembentukan (Differential : Basic Concepts and Establishment ) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya Pendahuluan
TKS 4003 Matematika II Persamaan Diferensial Konsep Dasar dan Pembentukan (Differential : Basic Concepts and Establishment ) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya Pendahuluan
PENGANTAR MATEMATIKA TEKNIK 1. By : Suthami A
 PENGANTAR MATEMATIKA TEKNIK 1 By : Suthami A MATEMATIKA TEKNIK 1??? MATEMATIKA TEKNIK 1??? MATEMATIKA TEKNIK Matematika sebagai ilmu dasar yang digunakan sebagai alat pemecahan masalah di bidang keteknikan
PENGANTAR MATEMATIKA TEKNIK 1 By : Suthami A MATEMATIKA TEKNIK 1??? MATEMATIKA TEKNIK 1??? MATEMATIKA TEKNIK Matematika sebagai ilmu dasar yang digunakan sebagai alat pemecahan masalah di bidang keteknikan
Penyelesaian Masalah Syarat Batas dalam Persamaan Diferensial Biasa Orde Dua dengan Menggunakan Algoritma Shooting Neural Networks
 Penyelesaian Masalah Syarat Batas dalam Persamaan Diferensial Biasa Orde Dua dengan Menggunakan Algoritma Shooting Neural Networks Dewi Erla Mahmudah 1, Ratna Dwi Christyanti 2, Moh. Khoridatul Huda 3,
Penyelesaian Masalah Syarat Batas dalam Persamaan Diferensial Biasa Orde Dua dengan Menggunakan Algoritma Shooting Neural Networks Dewi Erla Mahmudah 1, Ratna Dwi Christyanti 2, Moh. Khoridatul Huda 3,
Solusi Sistem Persamaan Linear Ax = b
 Solusi Sistem Persamaan Linear Ax = b Kie Van Ivanky Saputra April 27, 2009 K V I Saputra (Analisis Numerik) Kuliah Sistem Persamaan Linier c April 27, 2009 1 / 9 Review 1 Substitusi mundur pada sistem
Solusi Sistem Persamaan Linear Ax = b Kie Van Ivanky Saputra April 27, 2009 K V I Saputra (Analisis Numerik) Kuliah Sistem Persamaan Linier c April 27, 2009 1 / 9 Review 1 Substitusi mundur pada sistem
PENGARUH PERUBAHAN NILAI PARAMETER TERHADAP NILAI ERROR PADA METODE RUNGE-KUTTA ORDE 3
 PENGARUH PERUBAHAN NILAI PARAMETER TERHADAP NILAI ERROR PADA METODE RUNGE-KUTTA ORDE 3 Tornados P. Silaban 1, Faiz Ahyaningsih 2 1) FMIPA, UNIMED, Medan, Indonesia email: [email protected] 2)
PENGARUH PERUBAHAN NILAI PARAMETER TERHADAP NILAI ERROR PADA METODE RUNGE-KUTTA ORDE 3 Tornados P. Silaban 1, Faiz Ahyaningsih 2 1) FMIPA, UNIMED, Medan, Indonesia email: [email protected] 2)
6 Sistem Persamaan Linear
 6 Sistem Persamaan Linear Pada bab, kita diminta untuk mencari suatu nilai x yang memenuhi persamaan f(x) = 0. Pada bab ini, masalah tersebut diperumum dengan mencari x = (x, x,..., x n ) yang secara sekaligus
6 Sistem Persamaan Linear Pada bab, kita diminta untuk mencari suatu nilai x yang memenuhi persamaan f(x) = 0. Pada bab ini, masalah tersebut diperumum dengan mencari x = (x, x,..., x n ) yang secara sekaligus
KEBUTUHAN KOMPUTER PARALEL
 PEMROSESAN KEBUTUHAN KOMPUTER Simulasi sirkulasi global laut di Oregon State University Lautan dibagi ke dalam 4096 daerah membentang dari timur ke barat, 1024 daerah membentang dari utara ke selatan dan
PEMROSESAN KEBUTUHAN KOMPUTER Simulasi sirkulasi global laut di Oregon State University Lautan dibagi ke dalam 4096 daerah membentang dari timur ke barat, 1024 daerah membentang dari utara ke selatan dan
Solusi Persamaan Laplace Menggunakan Metode Crank-Nicholson. (The Solution of Laplace Equation Using Crank-Nicholson Method)
 Prosiding Seminar Nasional Matematika, Universitas Jember, 19 November 2014 320 Persamaan Laplace Menggunakan Metode Crank-Nicholson (The Solution of Laplace Equation Using Crank-Nicholson Method) Titis
Prosiding Seminar Nasional Matematika, Universitas Jember, 19 November 2014 320 Persamaan Laplace Menggunakan Metode Crank-Nicholson (The Solution of Laplace Equation Using Crank-Nicholson Method) Titis
Simulasi Perpindahan Panas pada Lapisan Tengah Pelat Menggunakan Metode Elemen Hingga
 JURNAL SAINS DAN SENI ITS Vol. 4, No.2, (2015) 2337-3520 (2301-928X Print) A-13 Simulasi Perpindahan Panas pada Lapisan Tengah Pelat Menggunakan Metode Elemen Hingga Vimala Rachmawati dan Kamiran Jurusan
JURNAL SAINS DAN SENI ITS Vol. 4, No.2, (2015) 2337-3520 (2301-928X Print) A-13 Simulasi Perpindahan Panas pada Lapisan Tengah Pelat Menggunakan Metode Elemen Hingga Vimala Rachmawati dan Kamiran Jurusan
BAB I KONSEP DASAR PERSAMAAN DIFERENSIAL
 BAB I KONSEP DASAR PERSAMAAN DIFERENSIAL Tujuan Instruksional: Mampu memahami definisi Persamaan Diferensial Mampu memahami klasifikasi Persamaan Diferensial Mampu memahami bentuk bentuk solusi Persamaan
BAB I KONSEP DASAR PERSAMAAN DIFERENSIAL Tujuan Instruksional: Mampu memahami definisi Persamaan Diferensial Mampu memahami klasifikasi Persamaan Diferensial Mampu memahami bentuk bentuk solusi Persamaan
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI 2.1 Sistem Persamaan Linier Sistem Persamaan dengan m persamaan dan n bilangan tak diketahui ditulis dengan : Dimana x 1, x 2, x n : bilangan tak diketahui a,b : konstanta Jika SPL
BAB 2 LANDASAN TEORI 2.1 Sistem Persamaan Linier Sistem Persamaan dengan m persamaan dan n bilangan tak diketahui ditulis dengan : Dimana x 1, x 2, x n : bilangan tak diketahui a,b : konstanta Jika SPL
PEMODELAN ALGORITMA GAXPY PADA SISTEM MULTIPROSESOR
 PEMODELAN ALGORITMA GAXPY PADA SISTEM MULTIPROSESOR Tri Prabawa 1) Program Studi Teknik Informatika, STMIK AKAKOM Yogyakarta Jl Raya Janti 143, Yogyakarta 55198 e-mail : tprabawa@akakomacid ABSTRAK Dalam
PEMODELAN ALGORITMA GAXPY PADA SISTEM MULTIPROSESOR Tri Prabawa 1) Program Studi Teknik Informatika, STMIK AKAKOM Yogyakarta Jl Raya Janti 143, Yogyakarta 55198 e-mail : tprabawa@akakomacid ABSTRAK Dalam
Sagita Charolina Sihombing 1, Agus Dahlia Pendahuluan
 Jurnal Matematika Integratif. Vol. 14, No. 1 (2018), pp. 51 60. p-issn:1412-6184, e-issn:2549-903 doi:10.24198/jmi.v14.n1.15953.51-60 Penyelesaian Persamaan Diferensial Linier Orde Satu dan Dua disertai
Jurnal Matematika Integratif. Vol. 14, No. 1 (2018), pp. 51 60. p-issn:1412-6184, e-issn:2549-903 doi:10.24198/jmi.v14.n1.15953.51-60 Penyelesaian Persamaan Diferensial Linier Orde Satu dan Dua disertai
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI 2.1 Sistem Persamaan Diferensial Banyak sekali masalah terapan dalam ilmu teknik, ilmu fisika, biologi, dan lain-lain yang telah dirumuskan dengan model matematika dalam bentuk pesamaan
BAB II LANDASAN TEORI 2.1 Sistem Persamaan Diferensial Banyak sekali masalah terapan dalam ilmu teknik, ilmu fisika, biologi, dan lain-lain yang telah dirumuskan dengan model matematika dalam bentuk pesamaan
METODE DEKOMPOSISI ADOMIAN UNTUK MENYELESAIKAN PERMASALAHAN NILAI BATAS PADA PERSAMAAN DIFERENSIAL PARSIAL NONLINEAR ABSTRACT
 METODE DEKOMPOSISI ADOMIAN UNTUK MENYELESAIKAN PERMASALAHAN NILAI BATAS PADA PERSAMAAN DIFERENSIAL PARSIAL NONLINEAR Birmansyah 1, Khozin Mu tamar 2, M. Natsir 2 1 Mahasiswa Program Studi S1 Matematika
METODE DEKOMPOSISI ADOMIAN UNTUK MENYELESAIKAN PERMASALAHAN NILAI BATAS PADA PERSAMAAN DIFERENSIAL PARSIAL NONLINEAR Birmansyah 1, Khozin Mu tamar 2, M. Natsir 2 1 Mahasiswa Program Studi S1 Matematika
Mata Kuliah :: Matematika Rekayasa Lanjut Kode MK : TKS 8105 Pengampu : Achfas Zacoeb
 Mata Kuliah :: Matematika Rekayasa Lanjut Kode MK : TKS 8105 Pengampu : Achfas Zacoeb Sesi XII Differensial e-mail : [email protected] www.zacoeb.lecture.ub.ac.id Hp. 081233978339 PENDAHULUAN Persamaan diferensial
Mata Kuliah :: Matematika Rekayasa Lanjut Kode MK : TKS 8105 Pengampu : Achfas Zacoeb Sesi XII Differensial e-mail : [email protected] www.zacoeb.lecture.ub.ac.id Hp. 081233978339 PENDAHULUAN Persamaan diferensial
METODE ELEMEN BATAS UNTUK MASALAH TRANSPORT
 METODE ELEMEN BATAS UNTUK MASALAH TRANSPORT Agusman Sahari. 1 1 Jurusan Matematika FMIPA UNTAD Kampus Bumi Tadulako Tondo Palu Abstrak Dalam paper ini mendeskripsikan tentang solusi masalah transport polutan
METODE ELEMEN BATAS UNTUK MASALAH TRANSPORT Agusman Sahari. 1 1 Jurusan Matematika FMIPA UNTAD Kampus Bumi Tadulako Tondo Palu Abstrak Dalam paper ini mendeskripsikan tentang solusi masalah transport polutan
SOLUSI NON NEGATIF MASALAH NILAI AWAL DENGAN FUNGSI GAYA MEMUAT TURUNAN
 SOLUSI NON NEGATIF MASALAH NILAI AWAL DENGAN FUNGSI GAYA MEMUAT TURUNAN Muhafzan Jurusan Matematika Fakultas Matematika Ilmu Pengetahuan Alam Universitas Andalas Kampus Unand Limau Manis Pag 25163 email:
SOLUSI NON NEGATIF MASALAH NILAI AWAL DENGAN FUNGSI GAYA MEMUAT TURUNAN Muhafzan Jurusan Matematika Fakultas Matematika Ilmu Pengetahuan Alam Universitas Andalas Kampus Unand Limau Manis Pag 25163 email:
Menentukan Distribusi Temperatur dengan Menggunakan Metode Crank Nicholson
 Jurnal Penelitian Sains Volume 13 Nomer 2(B) 13204 Menentukan Distribusi Temperatur dengan Menggunakan Metode Crank Nicholson Siti Sailah Jurusan Fisika FMIPA, Universitas Sriwijaya, Sumatera Selatan,
Jurnal Penelitian Sains Volume 13 Nomer 2(B) 13204 Menentukan Distribusi Temperatur dengan Menggunakan Metode Crank Nicholson Siti Sailah Jurusan Fisika FMIPA, Universitas Sriwijaya, Sumatera Selatan,
PENGOLAHAN PARALEL. Kebutuhan akan Komputer Paralel PENDAHULUAN. Dahulu:
 PENGOLAHAN PARALEL PENDAHULUAN PENDAHULUAN 1 Kebutuhan akan Komputer Paralel Dahulu: Ilmu klasik didasarkan pada observasi, teori dan eksperimen Observasi dari fenomena menghasilkan hipotesa Teori dikembangkan
PENGOLAHAN PARALEL PENDAHULUAN PENDAHULUAN 1 Kebutuhan akan Komputer Paralel Dahulu: Ilmu klasik didasarkan pada observasi, teori dan eksperimen Observasi dari fenomena menghasilkan hipotesa Teori dikembangkan
MODIFIKASI METODE CAUCHY DENGAN ORDE KONVERGENSI EMPAT. Masnida Esra Elisabet ABSTRACT
 MODIFIKASI METODE CAUCHY DENGAN ORDE KONVERGENSI EMPAT Masnida Esra Elisabet Mahasiswa Program Studi S1 Matematika Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Riau Kampus
MODIFIKASI METODE CAUCHY DENGAN ORDE KONVERGENSI EMPAT Masnida Esra Elisabet Mahasiswa Program Studi S1 Matematika Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Riau Kampus
PEMBUKTIAN RUMUS BENTUK TUTUP BEDA MUNDUR BERDASARKAN DERET TAYLOR
 Jurnal Matematika UNAND Vol. VI No. Hal. 68 76 ISSN : 233 29 c Jurusan Matematika FMIPA UNAND PEMBUKTIAN RUMUS BENTUK TUTUP BEDA MUNDUR BERDASARKAN DERET TAYLOR WIDIA ASTUTI Program Studi Matematika, Fakultas
Jurnal Matematika UNAND Vol. VI No. Hal. 68 76 ISSN : 233 29 c Jurusan Matematika FMIPA UNAND PEMBUKTIAN RUMUS BENTUK TUTUP BEDA MUNDUR BERDASARKAN DERET TAYLOR WIDIA ASTUTI Program Studi Matematika, Fakultas
METODE ORDE-TINGGI UNTUK MENENTUKAN AKAR DARI PERSAMAAN NONLINEAR ABSTRACT
 METODE ORDE-TINGGI UNTUK MENENTUKAN AKAR DARI PERSAMAAN NONLINEAR I. P. Edwar, M. Imran, L. Deswita Mahasiswa Program Studi S Matematika Laboratorium Matematika Terapan, Jurusan Matematika Fakultas Matematika
METODE ORDE-TINGGI UNTUK MENENTUKAN AKAR DARI PERSAMAAN NONLINEAR I. P. Edwar, M. Imran, L. Deswita Mahasiswa Program Studi S Matematika Laboratorium Matematika Terapan, Jurusan Matematika Fakultas Matematika
SOLUSI NUMERIK PERSAMAAN INTEGRO-DIFERENSIAL VOLTERRA-FREDHOLM NONLINEAR MENGGUNAKAN FUNGSI TRIANGULAR ABSTRACT ABSTRAK
 SOLUSI NUMERIK PERSAMAAN INTEGRO-DIFERENSIAL VOLTERRA-FREDHOLM NONLINEAR MENGGUNAKAN FUNGSI TRIANGULAR Suci Dini Anggraini 1, Khozin Mu tamar 2 1 Mahasiswa Program Studi S1 Matematika 2 Dosen Jurusan Matematika
SOLUSI NUMERIK PERSAMAAN INTEGRO-DIFERENSIAL VOLTERRA-FREDHOLM NONLINEAR MENGGUNAKAN FUNGSI TRIANGULAR Suci Dini Anggraini 1, Khozin Mu tamar 2 1 Mahasiswa Program Studi S1 Matematika 2 Dosen Jurusan Matematika
PENDAHULUAN. -. Pengolahan data numerik dalam jumlah yang sangat besar. -. Kebutuhan akan ketersediaan data yang senantiasa up to date.
 PENDAHULUAN 1 Kebutuhan akan Pengolahan Paralel Motivasi : - Pengolahan data numerik dalam jumlah yang sangat besar - Kebutuhan akan ketersediaan data yang senantiasa up to date Contoh 11 : Simulasi sirkulasi
PENDAHULUAN 1 Kebutuhan akan Pengolahan Paralel Motivasi : - Pengolahan data numerik dalam jumlah yang sangat besar - Kebutuhan akan ketersediaan data yang senantiasa up to date Contoh 11 : Simulasi sirkulasi
PARALELISASI PERKALIAN MATRIKS SPARSE VEKTOR DENGAN CUBLAS
 PARALELISASI PERKALIAN MATRIKS SPARSE VEKTOR DENGAN CUBLAS Murni Pusat Studi Komputasi Matematika, Universitas Gunadarma Jl. Margonda Raya no. 100, Depok 16424, Jawa Barat [email protected]
PARALELISASI PERKALIAN MATRIKS SPARSE VEKTOR DENGAN CUBLAS Murni Pusat Studi Komputasi Matematika, Universitas Gunadarma Jl. Margonda Raya no. 100, Depok 16424, Jawa Barat [email protected]
KONSEP DASAR PERSAMAAN DIFERENSIAL
 KONSEP DASAR PERSAMAAN DIFERENSIAL A. PENGERTIAN PERSAMAAN DIFERENSIAL Dalam pelajaran kalkulus, kita telah berkenalan dan mengkaji berbagai macam metode untuk mendiferensialkan suatu fungsi (dasar). Sebagai
KONSEP DASAR PERSAMAAN DIFERENSIAL A. PENGERTIAN PERSAMAAN DIFERENSIAL Dalam pelajaran kalkulus, kita telah berkenalan dan mengkaji berbagai macam metode untuk mendiferensialkan suatu fungsi (dasar). Sebagai
SOLUSI POLINOMIAL TAYLOR PERSAMAAN DIFERENSIAL-BEDA LINEAR DENGAN KOEFISIEN VARIABEL ABSTRACT
 SOLUSI POLINOMIAL TAYLOR PERSAMAAN DIFERENSIAL-BEDA LINEAR DENGAN KOEFISIEN VARIABEL Siti Nurjanah 1, Musraini M 2 1 Mahasiswa Program Studi S1 Matematika 2 Dosen Jurusan Matematika Fakultas Matematika
SOLUSI POLINOMIAL TAYLOR PERSAMAAN DIFERENSIAL-BEDA LINEAR DENGAN KOEFISIEN VARIABEL Siti Nurjanah 1, Musraini M 2 1 Mahasiswa Program Studi S1 Matematika 2 Dosen Jurusan Matematika Fakultas Matematika
METODE GAUSS-SEIDEL PREKONDISI UNTUK MENCARI SOLUSI SISTEM PERSAMAAN LINEAR. Alhumaira Oryza Sativa 1 ABSTRACT ABSTRAK
 METODE GAUSS-SEIDEL PREKONDISI UNTUK MENCARI SOLUSI SISTEM PERSAMAAN LINEAR Alhumaira Oryza Sativa 1 1 Mahasiswa Program Studi S1 Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Riau
METODE GAUSS-SEIDEL PREKONDISI UNTUK MENCARI SOLUSI SISTEM PERSAMAAN LINEAR Alhumaira Oryza Sativa 1 1 Mahasiswa Program Studi S1 Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Riau
SOLUSI NUMERIK PERSAMAAN INTEGRAL VOLTERRA-FREDHOLM NONLINEAR MENGGUNAKAN FUNGSI BASIS BARU ABSTRACT
 SOLUSI NUMERIK PERSAMAAN INTEGRAL VOLTERRA-FREDHOLM NONLINEAR MENGGUNAKAN FUNGSI BASIS BARU Vanny Octary 1 Endang Lily 2 1 Mahasiswa Program Studi S1 Matematika 2 Dosen Jurusan Matematika Fakultas Matematika
SOLUSI NUMERIK PERSAMAAN INTEGRAL VOLTERRA-FREDHOLM NONLINEAR MENGGUNAKAN FUNGSI BASIS BARU Vanny Octary 1 Endang Lily 2 1 Mahasiswa Program Studi S1 Matematika 2 Dosen Jurusan Matematika Fakultas Matematika
BAB 1 Konsep Dasar 1
 BAB 1 Konsep Dasar 1 BAB Solusi Persamaan Fungsi Polinomial BAB 3 Interpolasi dan Aproksimasi Polinomial 3 BAB 4 Metoda Numeris untuk Sistem Nonlinier 4 BAB 5 Metoda Numeris Untuk Masalah Nilai Awal 5
BAB 1 Konsep Dasar 1 BAB Solusi Persamaan Fungsi Polinomial BAB 3 Interpolasi dan Aproksimasi Polinomial 3 BAB 4 Metoda Numeris untuk Sistem Nonlinier 4 BAB 5 Metoda Numeris Untuk Masalah Nilai Awal 5
UJIAN AKHIR SEMESTER METODE NUMERIS I
 PETUNJUK UJIAN AKHIR SEMESTER METODE NUMERIS I DR. IR. ISTIARTO, M.ENG. KAMIS, 8 JUNI 017 OPEN BOOK 150 MENIT 1. Saudara tidak boleh menggunakan komputer untuk mengerjakan soal ujian ini.. Tuliskan urutan/cara/formula
PETUNJUK UJIAN AKHIR SEMESTER METODE NUMERIS I DR. IR. ISTIARTO, M.ENG. KAMIS, 8 JUNI 017 OPEN BOOK 150 MENIT 1. Saudara tidak boleh menggunakan komputer untuk mengerjakan soal ujian ini.. Tuliskan urutan/cara/formula
PENERAPAN METODE ELEMEN HINGGA UNTUK SOLUSI PERSAMAAN STURM-LIOUVILLE
 PENERAPAN METODE ELEMEN HINGGA UNTUK SOLUSI PERSAMAAN STURM-LIOUVILLE Viska Noviantri Mathematics & Statistics Department, School of Computer Science, Binus University Jln. K.H. Syahdan No. 9, Palmerah,
PENERAPAN METODE ELEMEN HINGGA UNTUK SOLUSI PERSAMAAN STURM-LIOUVILLE Viska Noviantri Mathematics & Statistics Department, School of Computer Science, Binus University Jln. K.H. Syahdan No. 9, Palmerah,
PENDAHULUAN. Motivasi : -. Pengolahan data numerik dalam jumlah yang sangat besar. -. Kebutuhan akan ketersediaan data yang senantiasa up to date.
 PENDAHULUAN 1 Kebutuhan akan Pengolahan Paralel Motivasi : - Pengolahan data numerik dalam jumlah yang sangat besar - Kebutuhan akan ketersediaan data yang senantiasa up to date Contoh 11 : Simulasi sirkulasi
PENDAHULUAN 1 Kebutuhan akan Pengolahan Paralel Motivasi : - Pengolahan data numerik dalam jumlah yang sangat besar - Kebutuhan akan ketersediaan data yang senantiasa up to date Contoh 11 : Simulasi sirkulasi
METODE PSEUDO ARC-LENGTH DAN PENERAPANNYA PADA PENYELESAIAN SISTEM PERSAMAAN NONLINIER TERPARAMETERISASI
 Jurnal Matematika UNAND Vol. 5 No. 4 Hal. 9 17 ISSN : 233 291 c Jurusan Matematika FMIPA UNAND METODE PSEUDO ARC-LENGTH DAN PENERAPANNYA PADA PENYELESAIAN SISTEM PERSAMAAN NONLINIER TERPARAMETERISASI RAHIMA
Jurnal Matematika UNAND Vol. 5 No. 4 Hal. 9 17 ISSN : 233 291 c Jurusan Matematika FMIPA UNAND METODE PSEUDO ARC-LENGTH DAN PENERAPANNYA PADA PENYELESAIAN SISTEM PERSAMAAN NONLINIER TERPARAMETERISASI RAHIMA
IMPLEMENTASI METODE DEKOMPOSISI LU PADA REGRESI LINIER BERGANDA
 Seminar Nasional Teknologi Informasi & Komunikasi Terapan (Semantik ) ISBN 979-6 - 55 - Semarang, 3 Juni IMPLEMENTASI METODE DEKOMPOSISI LU PADA REGRESI LINIER BERGANDA Yuniarsi Rahayu Fakultas Ilmu Komputer
Seminar Nasional Teknologi Informasi & Komunikasi Terapan (Semantik ) ISBN 979-6 - 55 - Semarang, 3 Juni IMPLEMENTASI METODE DEKOMPOSISI LU PADA REGRESI LINIER BERGANDA Yuniarsi Rahayu Fakultas Ilmu Komputer
REDUKSI RANK PADA MATRIKS-MATRIKS TERTENTU
 J. Math. and Its Appl. ISSN: 89-65X Vol. 4, No., November 7, 8 REDUKSI RANK PADA MATRIKS-MATRIKS TERTENTU Erna Apriliani, Bandung Arry Sanjoyo Jurusan Matematika FMIPA Institut Teknologi Sepuluh Nopember,
J. Math. and Its Appl. ISSN: 89-65X Vol. 4, No., November 7, 8 REDUKSI RANK PADA MATRIKS-MATRIKS TERTENTU Erna Apriliani, Bandung Arry Sanjoyo Jurusan Matematika FMIPA Institut Teknologi Sepuluh Nopember,
OPERASI MATRIKS. a 11 a 12 a 13 a 14 A = a 21 a 22 a 23 a 24 a 31 a 32 a 33 a 34 a 41 a 42 a 43 a 44
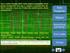 OPERASI MATRIKS Topik yang akan dibahas transpose perkalian TRANSPOSE Definisi: a 11 a 12 a 13 a 14 A = a 21 a 22 a 23 a 24 a 31 a 32 a 33 a 34 a 41 a 42 a 43 a 44 a 11 a 21 a 31 a 41 A T = a 12 a 22 a
OPERASI MATRIKS Topik yang akan dibahas transpose perkalian TRANSPOSE Definisi: a 11 a 12 a 13 a 14 A = a 21 a 22 a 23 a 24 a 31 a 32 a 33 a 34 a 41 a 42 a 43 a 44 a 11 a 21 a 31 a 41 A T = a 12 a 22 a
BAB 4 PENYELESAIAN SISTEM PERSAMAAN LINEAR
 BAB 4 PENYELESAIAN SISTEM PERSAMAAN LINEAR A. Latar Belakang Persoalan yang melibatkan model matematika banyak muncul dalam berbagai disiplin ilmu pengetahuan, seperti dalam bidang fisika, kimia, ekonomi,
BAB 4 PENYELESAIAN SISTEM PERSAMAAN LINEAR A. Latar Belakang Persoalan yang melibatkan model matematika banyak muncul dalam berbagai disiplin ilmu pengetahuan, seperti dalam bidang fisika, kimia, ekonomi,
PENDAHULUAN A. Latar Belakang 1. Metode Langsung Metode Langsung Eliminasi Gauss (EGAUSS) Metode Eliminasi Gauss Dekomposisi LU (DECOLU),
 PENDAHULUAN A. Latar Belakang Persoalan yang melibatkan model matematika banyak muncul dalam berbagai disiplin ilmu pengetahuan, seperti dalam bidang fisika, kimia, ekonomi, atau pada persoalan rekayasa.
PENDAHULUAN A. Latar Belakang Persoalan yang melibatkan model matematika banyak muncul dalam berbagai disiplin ilmu pengetahuan, seperti dalam bidang fisika, kimia, ekonomi, atau pada persoalan rekayasa.
Syarif Abdullah (G ) Matematika Terapan FMIPA Institut Pertanian Bogor.
 Syarif Abdullah (G551150381) Matematika Terapan FMIPA Institut Pertanian Bogor e-mail: [email protected] 25 Maret 2016 Ringkasan Kuliah ke-6 Analisis Numerik (16 Maret 2016) Materi : System
Syarif Abdullah (G551150381) Matematika Terapan FMIPA Institut Pertanian Bogor e-mail: [email protected] 25 Maret 2016 Ringkasan Kuliah ke-6 Analisis Numerik (16 Maret 2016) Materi : System
BAB III : SISTEM PERSAMAAN LINIER
 3.1 PENDAHULUAN BAB III : SISTEM PERSAMAAN LINIER Penyelesaian suatu sistem n persamaan dengan n bilangan tak diketahui banyak dijumpai dalam permasalahan teknik. Di dalam Bab ini akan dipelajari sistem
3.1 PENDAHULUAN BAB III : SISTEM PERSAMAAN LINIER Penyelesaian suatu sistem n persamaan dengan n bilangan tak diketahui banyak dijumpai dalam permasalahan teknik. Di dalam Bab ini akan dipelajari sistem
METODE ITERATIF YANG DIPERCEPAT UNTUK Z-MATRIKS ABSTRACT
 METODE ITERATIF YANG DIPERCEPAT UNTUK Z-MATRIKS Mildayani 1, Syamsudhuha 2, Aziskhan 2 1 Mahasiswa Program Studi S1 Matematika 2 Dosen Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Riau Kampus
METODE ITERATIF YANG DIPERCEPAT UNTUK Z-MATRIKS Mildayani 1, Syamsudhuha 2, Aziskhan 2 1 Mahasiswa Program Studi S1 Matematika 2 Dosen Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Riau Kampus
SOLUSI PENYEBARAN PANAS PADA BATANG KONDUKTOR MENGGUNAKAN METODE CRANK-NICHOLSON
 SOLUSI PENYEBARAN PANAS PADA BATANG KONDUKTOR MENGGUNAKAN METODE CRANK-NICHOLSON Viska Noviantri Mathematics & Statistics Department, School of Computer Science, Binus University Jl. K.H. Syahdan No. 9,
SOLUSI PENYEBARAN PANAS PADA BATANG KONDUKTOR MENGGUNAKAN METODE CRANK-NICHOLSON Viska Noviantri Mathematics & Statistics Department, School of Computer Science, Binus University Jl. K.H. Syahdan No. 9,
PENERAPAN METODE ADAMS-BASHFORTH-MOULTON ORDE EMPAT UNTUK MENENTUKAN SOLUSI PERSAMAAN DIFERENSIAL LINIER HOMOGEN ORDE TIGA KOEFISIEN KONSTAN
 Jurnal Matematika UNAND Vol. 5 No. 2 Hal. 21 25 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND PENERAPAN METODE ADAMS-BASHFORTH-MOULTON ORDE EMPAT UNTUK MENENTUKAN SOLUSI PERSAMAAN DIFERENSIAL LINIER
Jurnal Matematika UNAND Vol. 5 No. 2 Hal. 21 25 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND PENERAPAN METODE ADAMS-BASHFORTH-MOULTON ORDE EMPAT UNTUK MENENTUKAN SOLUSI PERSAMAAN DIFERENSIAL LINIER
PROGRAM FRAKSIONAL LINIER DENGAN KOEFISIEN INTERVAL. Annisa Ratna Sari 1, Sunarsih 2, Suryoto 3. Jl. Prof. H. Soedarto, S.H. Tembalang Semarang
 PROGRAM FRAKSIONAL LINIER DENGAN KOEFISIEN INTERVAL Annisa Ratna Sari 1, Sunarsih 2, Suryoto 3 1,2,3 Jurusan Matematika FSM Universitas Diponegoro Jl. Prof. H. Soedarto, S.H. Tembalang Semarang Abstract.
PROGRAM FRAKSIONAL LINIER DENGAN KOEFISIEN INTERVAL Annisa Ratna Sari 1, Sunarsih 2, Suryoto 3 1,2,3 Jurusan Matematika FSM Universitas Diponegoro Jl. Prof. H. Soedarto, S.H. Tembalang Semarang Abstract.
Analisis Reduksi Model pada Sistem Linier Waktu Diskrit
 JURNAL SAINS DAN SENI ITS Vol. 5 No. 2 (216) 2337-352 (231-928X Print) A-25 Analisis Reduksi Model pada Sistem Linier Waktu Diskrit Yunita Indriana Sari dan Didik Khusnul Arif Jurusan Matematika, Fakultas
JURNAL SAINS DAN SENI ITS Vol. 5 No. 2 (216) 2337-352 (231-928X Print) A-25 Analisis Reduksi Model pada Sistem Linier Waktu Diskrit Yunita Indriana Sari dan Didik Khusnul Arif Jurusan Matematika, Fakultas
Implementasi Hypergraph Partitioning pada Paralelisasi Perkalian Matriks-Vektor
 Implementasi Hypergraph Partitioning pada Paralelisasi Perkalian Matriks-Vektor Murni dan Tri Handhika Pusat Studi Komputasi Matematika Universitas Gunadarma, Depok {murnipskm, trihandika}@staff.gunadarma.ac.id
Implementasi Hypergraph Partitioning pada Paralelisasi Perkalian Matriks-Vektor Murni dan Tri Handhika Pusat Studi Komputasi Matematika Universitas Gunadarma, Depok {murnipskm, trihandika}@staff.gunadarma.ac.id
Reduksi Rank pada Matriks-Matriks Tertentu
 Reduksi Rank pada Matriks-Matriks Tertentu E. Apriliani, B. Ari Sanjaya September 6, 7 Abstract. Dekomposisi nilai singular (Singular Value Decomposition - SVD) adalah suatu metode untuk menuliskan suatu
Reduksi Rank pada Matriks-Matriks Tertentu E. Apriliani, B. Ari Sanjaya September 6, 7 Abstract. Dekomposisi nilai singular (Singular Value Decomposition - SVD) adalah suatu metode untuk menuliskan suatu
METODE ITERASI BARU BERTIPE SECANT DENGAN KEKONVERGENAN SUPER-LINEAR. Rino Martino 1 ABSTRACT
 METODE ITERASI BARU BERTIPE SECANT DENGAN KEKONVERGENAN SUPER-LINEAR Rino Martino 1 1 Mahasiswa Program Studi S1 Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Riau Kampus Binawidya
METODE ITERASI BARU BERTIPE SECANT DENGAN KEKONVERGENAN SUPER-LINEAR Rino Martino 1 1 Mahasiswa Program Studi S1 Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Riau Kampus Binawidya
Perbandingan Algoritma Golub Kahan dan QR Simetri untuk Dekomposisi Nilai Singular
 J. Math. and Its Appl. ISSN: 1829-605X Vol. 3, No. 1, May 2006, 19 25 Perbandingan Algoritma Golub Kahan dan QR Simetri untuk Dekomposisi Nilai Singular Dieky Adzkiya, E. Apriliani, Bandung A.S. Jurusan
J. Math. and Its Appl. ISSN: 1829-605X Vol. 3, No. 1, May 2006, 19 25 Perbandingan Algoritma Golub Kahan dan QR Simetri untuk Dekomposisi Nilai Singular Dieky Adzkiya, E. Apriliani, Bandung A.S. Jurusan
BAB VII MATRIKS DAN SISTEM LINEAR TINGKAT SATU
 BAB VII MATRIKS DAN SISTEM LINEAR TINGKAT SATU Sistem persamaan linear orde/ tingkat satu memiliki bentuk standard : = = = = = = = = = + + + + + + + + + + Diasumsikan koefisien = dan fungsi adalah menerus
BAB VII MATRIKS DAN SISTEM LINEAR TINGKAT SATU Sistem persamaan linear orde/ tingkat satu memiliki bentuk standard : = = = = = = = = = + + + + + + + + + + Diasumsikan koefisien = dan fungsi adalah menerus
STUDI PERPINDAHAN PANAS DENGAN MENGGUNAKAN SISTEM KOORDINAT SEGITIGA
 STUDI PERPINDAHAN PANAS DENGAN MENGGUNAKAN SISTEM KOORDINAT SEGITIGA Oleh : Farda Nur Pristiana 1208 100 059 JURUSAN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT TEKNOLOGI SEPULUH
STUDI PERPINDAHAN PANAS DENGAN MENGGUNAKAN SISTEM KOORDINAT SEGITIGA Oleh : Farda Nur Pristiana 1208 100 059 JURUSAN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT TEKNOLOGI SEPULUH
METODE ITERASI KSOR UNTUK MENYELESAIKAN SISTEM PERSAMAAN LINEAR ABSTRACT
 METODE ITERASI KSOR UNTUK MENYELESAIKAN SISTEM PERSAMAAN LINEAR Adek Putri Syafriani, Syamsudhuha 2, Zulkarnain 2 Mahasiswa Program Studi S Matematika 2 Dosen Jurusan Matematika Fakultas Matematika dan
METODE ITERASI KSOR UNTUK MENYELESAIKAN SISTEM PERSAMAAN LINEAR Adek Putri Syafriani, Syamsudhuha 2, Zulkarnain 2 Mahasiswa Program Studi S Matematika 2 Dosen Jurusan Matematika Fakultas Matematika dan
PENYELESAIAN SISTEM PERSAMAAN LINEAR DENGAN GENERALISASI METODE JACOBI
 PENYELESAIAN SISTEM PERSAMAAN LINEAR DENGAN GENERALISASI METODE JACOBI Sandra Roza 1*, M. Natsir 2, Asli Sirait 2 1 Mahasiswa Program Studi S1 Matematika 2 Dosen JurusanMatematika Fakultas Matematika dan
PENYELESAIAN SISTEM PERSAMAAN LINEAR DENGAN GENERALISASI METODE JACOBI Sandra Roza 1*, M. Natsir 2, Asli Sirait 2 1 Mahasiswa Program Studi S1 Matematika 2 Dosen JurusanMatematika Fakultas Matematika dan
PERBANDINGAN METODE GAUSS-SEIDEL PREKONDISI DAN METODE SOR UNTUK MENDAPATKAN SOLUSI SISTEM PERSAMAAN LINEAR. Merintan Afrina S ABSTRACT
 PERBANDINGAN METODE GAUSS-SEIDEL PREKONDISI DAN METODE SOR UNTUK MENDAPATKAN SOLUSI SISTEM PERSAMAAN LINEAR Merintan Afrina S Mahasiswa Program Studi S1 Matematika Fakultas Matematika dan Ilmu Pengetahuan
PERBANDINGAN METODE GAUSS-SEIDEL PREKONDISI DAN METODE SOR UNTUK MENDAPATKAN SOLUSI SISTEM PERSAMAAN LINEAR Merintan Afrina S Mahasiswa Program Studi S1 Matematika Fakultas Matematika dan Ilmu Pengetahuan
METODE GAUSS-SEIDEL PREKONDISI DENGAN MENGGUNAKAN EKSPANSI NEUMANN ABSTRACT
 METODE GAUSS-SEIDEL PREKONDISI DENGAN MENGGUNAKAN EKSPANSI NEUMANN Juanita Adrika, Syamsudhuha 2, Asmara Karma 2 Mahasiswa Program Studi S Matematika 2 Dosen Fakultas Matematika dan Ilmu Pengetahuan Alam
METODE GAUSS-SEIDEL PREKONDISI DENGAN MENGGUNAKAN EKSPANSI NEUMANN Juanita Adrika, Syamsudhuha 2, Asmara Karma 2 Mahasiswa Program Studi S Matematika 2 Dosen Fakultas Matematika dan Ilmu Pengetahuan Alam
Pertemuan 14. persamaan linier NON HOMOGEN
 Pertemuan 14 persamaan linier NON HOMOGEN 10 Metode GAUSS Aljabar Linier Hastha 2016 10.2.2 METODE ELIMINASI GAUSS Apabila [A][X]=[B] maka dengan menyusun matriks baru yaitu matriks [A.B] akan didapat
Pertemuan 14 persamaan linier NON HOMOGEN 10 Metode GAUSS Aljabar Linier Hastha 2016 10.2.2 METODE ELIMINASI GAUSS Apabila [A][X]=[B] maka dengan menyusun matriks baru yaitu matriks [A.B] akan didapat
Metode Simpleks (Simplex Method) Materi Bahasan
 Metode Simpleks (Simplex Method) Kuliah 03 TI2231 Penelitian Operasional I 1 Materi Bahasan 1 Rumusan Pemrograman linier dalam bentuk baku 2 Pemecahan sistem persamaan linier 3 Prinsip-prinsip metode simpleks
Metode Simpleks (Simplex Method) Kuliah 03 TI2231 Penelitian Operasional I 1 Materi Bahasan 1 Rumusan Pemrograman linier dalam bentuk baku 2 Pemecahan sistem persamaan linier 3 Prinsip-prinsip metode simpleks
JAWABAN ANALITIK SEBAGAI VALIDASI JAWABAN NUMERIK PADA MATA KULIAH FISIKA KOMPUTASI ABSTRAK
 JAWABAN ANALITIK SEBAGAI VALIDASI JAWABAN NUMERIK PADA MATA KULIAH FISIKA KOMPUTASI ABSTRAK Kasus-kasus fisika yang diangkat pada mata kuliah Fisika Komputasi akan dijawab secara numerik. Validasi jawaban
JAWABAN ANALITIK SEBAGAI VALIDASI JAWABAN NUMERIK PADA MATA KULIAH FISIKA KOMPUTASI ABSTRAK Kasus-kasus fisika yang diangkat pada mata kuliah Fisika Komputasi akan dijawab secara numerik. Validasi jawaban
BAB I PENDAHULUAN. 1.1 Latar Belakang
 BAB I PENDAHULUAN 1.1 Latar Belakang Persamaan diferensial biasa (ordinary differential equations (ODEs)) merupakan salah satu alat matematis untuk memodelkan dinamika sistem dalam berbagai bidang ilmu
BAB I PENDAHULUAN 1.1 Latar Belakang Persamaan diferensial biasa (ordinary differential equations (ODEs)) merupakan salah satu alat matematis untuk memodelkan dinamika sistem dalam berbagai bidang ilmu
METODE PSEUDOSPEKTRAL CHEBYSHEV PADA APROKSIMASI TURUNAN FUNGSI
 Jurnal Matematika UNAND Vol. VI No. 1 Hal. 50 57 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND METODE PSEUDOSPEKTRAL CHEBYSHEV PADA APROKSIMASI TURUNAN FUNGSI ILHAM FEBRI RAMADHAN Program Studi Matematika
Jurnal Matematika UNAND Vol. VI No. 1 Hal. 50 57 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND METODE PSEUDOSPEKTRAL CHEBYSHEV PADA APROKSIMASI TURUNAN FUNGSI ILHAM FEBRI RAMADHAN Program Studi Matematika
PENYELESAIAN MASALAH NILAI EIGEN UNTUK PERSAMAAN DIFERENSIAL STURM-LIOUVILLE DENGAN METODE NUMEROV
 Buletin Ilmiah Mat. Stat. dan Terapannya (Bimaster) Volume 04, No. 3 (2015), hal 415-422 PENYELESAIAN MASALAH NILAI EIGEN UNTUK PERSAMAAN DIFERENSIAL STURM-LIOUVILLE DENGAN METODE NUMEROV Iyut Riani, Nilamsari
Buletin Ilmiah Mat. Stat. dan Terapannya (Bimaster) Volume 04, No. 3 (2015), hal 415-422 PENYELESAIAN MASALAH NILAI EIGEN UNTUK PERSAMAAN DIFERENSIAL STURM-LIOUVILLE DENGAN METODE NUMEROV Iyut Riani, Nilamsari
PAM 573 Persamaan Diferensial Parsial Topik: Metode Beda Hingga pada Turunan Fungsi
 PAM 573 Persamaan Diferensial Parsial Topik: Metode Beda Hingga pada Turunan Fungsi Mahdhivan Syafwan Program Magister Jurusan Matematika FMIPA Universitas Andalas Semester Genap 2016/2017 1 Mahdhivan
PAM 573 Persamaan Diferensial Parsial Topik: Metode Beda Hingga pada Turunan Fungsi Mahdhivan Syafwan Program Magister Jurusan Matematika FMIPA Universitas Andalas Semester Genap 2016/2017 1 Mahdhivan
METODE ITERASI JACOBI DAN GAUSS-SEIDEL PREKONDISI UNTUK MENYELESAIKAN SISTEM PERSAMAN LINEAR DENGAN M-MATRIKS ABSTRACT
 METODE ITERASI JACOBI DAN GAUSS-SEIDEL PREKONDISI UNTUK MENYELESAIKAN SISTEM PERSAMAN LINEAR DENGAN M-MATRIKS Efriani Widya 1, Syamsudhuha 2, Bustami 2 1 Mahasiswa Program Studi S1 Matematika 2 Dosen Jurusan
METODE ITERASI JACOBI DAN GAUSS-SEIDEL PREKONDISI UNTUK MENYELESAIKAN SISTEM PERSAMAN LINEAR DENGAN M-MATRIKS Efriani Widya 1, Syamsudhuha 2, Bustami 2 1 Mahasiswa Program Studi S1 Matematika 2 Dosen Jurusan
03-Pemecahan Persamaan Linier (2)
 -Pemecahan Persamaan Linier () Dosen: Anny Yuniarti, M.Comp.Sc Gasal - Anny Agenda Bagian : Matriks Invers Bagian : Eliminasi = Faktorisasi: A = LU Bagian : Transpos dan Permutasi Anny Bagian MATRIKS INVERS
-Pemecahan Persamaan Linier () Dosen: Anny Yuniarti, M.Comp.Sc Gasal - Anny Agenda Bagian : Matriks Invers Bagian : Eliminasi = Faktorisasi: A = LU Bagian : Transpos dan Permutasi Anny Bagian MATRIKS INVERS
PAM 252 Metode Numerik Bab 5 Turunan Numerik
 Pendahuluan PAM 252 Metode Numerik Bab 5 Turunan Numerik Mahdhivan Syafwan Jurusan Matematika FMIPA Universitas Andalas Semester Genap 2013/2014 1 Mahdhivan Syafwan Metode Numerik: Turunan Numerik Permasalahan
Pendahuluan PAM 252 Metode Numerik Bab 5 Turunan Numerik Mahdhivan Syafwan Jurusan Matematika FMIPA Universitas Andalas Semester Genap 2013/2014 1 Mahdhivan Syafwan Metode Numerik: Turunan Numerik Permasalahan
PENYELESAIAN PERSAMAAN LINEAR-NON LINEAR DAN PERSAMAAN DIFFERENSIAL DENGAN METODE KESAMAAN
 309 Jurnal KIP Vol II No. 3, Nopember 2013 Februari 2014 PENYELESAIAN PERSAMAAN LINEAR-NON LINEAR DAN PERSAMAAN DIFFERENSIAL DENGAN METODE KESAMAAN Abraham Salusu [email protected] Program Studi
309 Jurnal KIP Vol II No. 3, Nopember 2013 Februari 2014 PENYELESAIAN PERSAMAAN LINEAR-NON LINEAR DAN PERSAMAAN DIFFERENSIAL DENGAN METODE KESAMAAN Abraham Salusu [email protected] Program Studi
PERBANDINGAN KOMPLEKSITAS ALGORITMA METODE-METODE PENYELESAIAN SISTEM PERSAMAAN LANJAR
 PERBANDINGAN KOMPLEKSITAS ALGORITMA METODE-METODE PENYELESAIAN SISTEM PERSAMAAN LANJAR Achmad Dimas Noorcahyo NIM 3508076 Program Studi Teknik Informatika, Institut Teknologi Bandung Jalan Ganeca 0, Bandung
PERBANDINGAN KOMPLEKSITAS ALGORITMA METODE-METODE PENYELESAIAN SISTEM PERSAMAAN LANJAR Achmad Dimas Noorcahyo NIM 3508076 Program Studi Teknik Informatika, Institut Teknologi Bandung Jalan Ganeca 0, Bandung
PENYELESAIAN PERSAMAAN PANAS BALIK (BACKWARD HEAT EQUATION) Oleh: RICHA AGUSTININGSIH
 TUGAS AKHIR PENYELESAIAN PERSAMAAN PANAS BALIK (BACKWARD HEAT EQUATION) Oleh: RICHA AGUSTININGSIH 1204100019 JURUSAN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT TEKNOLOGI SEPULUH
TUGAS AKHIR PENYELESAIAN PERSAMAAN PANAS BALIK (BACKWARD HEAT EQUATION) Oleh: RICHA AGUSTININGSIH 1204100019 JURUSAN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT TEKNOLOGI SEPULUH
Sidang Tugas Akhir - Juli 2013
 Sidang Tugas Akhir - Juli 2013 STUDI PERBANDINGAN PERPINDAHAN PANAS MENGGUNAKAN METODE BEDA HINGGA DAN CRANK-NICHOLSON COMPARATIVE STUDY OF HEAT TRANSFER USING FINITE DIFFERENCE AND CRANK-NICHOLSON METHOD
Sidang Tugas Akhir - Juli 2013 STUDI PERBANDINGAN PERPINDAHAN PANAS MENGGUNAKAN METODE BEDA HINGGA DAN CRANK-NICHOLSON COMPARATIVE STUDY OF HEAT TRANSFER USING FINITE DIFFERENCE AND CRANK-NICHOLSON METHOD
II LANDASAN TEORI. Contoh. Ditinjau dari sistem yang didefinisikan oleh:
 5 II LANDASAN TEORI 2.1 Keterkontrolan Untuk mengetahui persoalan sistem kontrol mungkin tidak ada, jika sistem yang ditinjau tidak terkontrol. Walaupun sebagian besar sistem terkontrol ada, akan tetapi
5 II LANDASAN TEORI 2.1 Keterkontrolan Untuk mengetahui persoalan sistem kontrol mungkin tidak ada, jika sistem yang ditinjau tidak terkontrol. Walaupun sebagian besar sistem terkontrol ada, akan tetapi
PEMBUKTIAN BENTUK TUTUP RUMUS BEDA MAJU BERDASARKAN DERET TAYLOR
 Jurnal Matematika UAD Vol. 5 o. 4 Hal. 8 ISS : 233 29 c Jurusan Matematika FMIPA UAD PEMBUKTIA BETUK TUTUP RUMUS BEDA MAJU BERDASARKA DERET TAYLOR ADE PUTRI, RADHIATUL HUSA Program Studi Matematika, Fakultas
Jurnal Matematika UAD Vol. 5 o. 4 Hal. 8 ISS : 233 29 c Jurusan Matematika FMIPA UAD PEMBUKTIA BETUK TUTUP RUMUS BEDA MAJU BERDASARKA DERET TAYLOR ADE PUTRI, RADHIATUL HUSA Program Studi Matematika, Fakultas
PENENTUAN HARGA OPSI SAHAM DENGAN MENGGUNAKAN METODE BEDA HINGGA CRANK-NICHOLSON (C-N)
 PENENTUAN HARGA OPSI SAHAM DENGAN MENGGUNAKAN METODE BEDA HINGGA CRANK-NICHOLSON (C-N) OKI TJANDRA SURYA KURNIAWAN 1 1 Jurusan Matematika, Fakultas MIPA, Universitas Udayana, email: [email protected]
PENENTUAN HARGA OPSI SAHAM DENGAN MENGGUNAKAN METODE BEDA HINGGA CRANK-NICHOLSON (C-N) OKI TJANDRA SURYA KURNIAWAN 1 1 Jurusan Matematika, Fakultas MIPA, Universitas Udayana, email: [email protected]
BAB II TINJAUAN PUSTAKA. apapun yang melalui beberapa pengolahan berarti (Tse, 2012). Mencerahkan citra,
 BAB II TINJAUAN PUSTAKA A. Tinjauan Pustaka Pengolahan citra adalah sebuah bentuk pengolahan sinyal dimana masukannya berupa sebuah citra, dan keluarannya dapat berupa citra kembali atau apapun yang melalui
BAB II TINJAUAN PUSTAKA A. Tinjauan Pustaka Pengolahan citra adalah sebuah bentuk pengolahan sinyal dimana masukannya berupa sebuah citra, dan keluarannya dapat berupa citra kembali atau apapun yang melalui
PEMODELAN ARUS LALU LINTAS ROUNDABOUT
 Jurnal Matematika UNAND Vol. 3 No. 1 Hal. 43 52 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND PEMODELAN ARUS LALU LINTAS ROUNDABOUT NANDA ARDIELNA, MAHDHIVAN SYAFWAN Program Studi Matematika, Fakultas
Jurnal Matematika UNAND Vol. 3 No. 1 Hal. 43 52 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND PEMODELAN ARUS LALU LINTAS ROUNDABOUT NANDA ARDIELNA, MAHDHIVAN SYAFWAN Program Studi Matematika, Fakultas
PERANCANGAN ARSITEKTUR PEMARALELAN UNTUK MENCARI SHORTEST PATH DENGAN ALGORITMA DIJKSTRA
 PERANCANGAN ARSITEKTUR PEMARALELAN UNTUK MENCARI SHORTEST PATH DENGAN ALGORITMA DIJKSTRA Eko Adi Sarwoko Jurusan Matematika FMIPA UNDIP Abstrak Perancangan arsitektur pemaralelan merupakan salah satu tahap
PERANCANGAN ARSITEKTUR PEMARALELAN UNTUK MENCARI SHORTEST PATH DENGAN ALGORITMA DIJKSTRA Eko Adi Sarwoko Jurusan Matematika FMIPA UNDIP Abstrak Perancangan arsitektur pemaralelan merupakan salah satu tahap
Model Linear Kuadratik untuk Sistem Deskriptor Berindeks Satu dengan Factor Discount dan Output Feedback
 Model Linear Kuadratik untuk Sistem Deskriptor Berindeks Satu dengan Factor Discount dan Output Feedback Nilwan Andiraja 1, Julia Sasmita Maiza 2 1, 2 Jurusan Matematika, Fakultas Sains dan Teknologi,
Model Linear Kuadratik untuk Sistem Deskriptor Berindeks Satu dengan Factor Discount dan Output Feedback Nilwan Andiraja 1, Julia Sasmita Maiza 2 1, 2 Jurusan Matematika, Fakultas Sains dan Teknologi,
BAB I PENDAHULUAN Latar Belakang Masalah
 BAB I PENDAHULUAN 1.1. Latar Belakang Masalah Dalam kehidupan sehari-hari banyak permasalahan yang muncul di lingkungan sekitar. Hal tersebut dapat dikembangkan melalui pemodelan matematika. Sehingga dengan
BAB I PENDAHULUAN 1.1. Latar Belakang Masalah Dalam kehidupan sehari-hari banyak permasalahan yang muncul di lingkungan sekitar. Hal tersebut dapat dikembangkan melalui pemodelan matematika. Sehingga dengan
PENYELESAIAN MASALAH STURM-LIOUVILLE DARI PERSAMAAN GELOMBANG SUARA DI BAWAH AIR DENGAN METODE BEDA HINGGA
 PENYELESAIAN MASALAH STURM-LIOUVILLE DARI PERSAMAAN GELOMBANG SUARA DI BAWAH AIR DENGAN METODE BEDA HINGGA oleh FIQIH SOFIANA M0109030 SKRIPSI ditulis dan diajukan untuk memenuhi sebagian persyaratan memperoleh
PENYELESAIAN MASALAH STURM-LIOUVILLE DARI PERSAMAAN GELOMBANG SUARA DI BAWAH AIR DENGAN METODE BEDA HINGGA oleh FIQIH SOFIANA M0109030 SKRIPSI ditulis dan diajukan untuk memenuhi sebagian persyaratan memperoleh
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI 21 Analisis Regresi Perubahan nilai suatu variabel tidak selalu terjadi dengan sendirinya, namun perubahan nilai variabel itu dapat disebabkan oleh berubahnya variabel lain yang berhubungan
BAB 2 LANDASAN TEORI 21 Analisis Regresi Perubahan nilai suatu variabel tidak selalu terjadi dengan sendirinya, namun perubahan nilai variabel itu dapat disebabkan oleh berubahnya variabel lain yang berhubungan
ASPEK STABILITAS DAN KONSISTENSI METODA DALAM PENYELESAIAN NT'MERIK PERSAMAAN DIFERENSIAL BIASA DENGAN MENGGUNAKAN METODA PREDIKTOR- KOREKTOR ORDE 4
 ASPEK STABILITAS DAN KONSISTENSI METODA DALAM PENYELESAIAN NT'MERIK PERSAMAAN DIFERENSIAL BIASA DENGAN MENGGUNAKAN METODA PREDIKTOR- KOREKTOR ORDE 4 Asep Juarna, SSi, MKom. Fakultas Ilmu Komputer, Universitas
ASPEK STABILITAS DAN KONSISTENSI METODA DALAM PENYELESAIAN NT'MERIK PERSAMAAN DIFERENSIAL BIASA DENGAN MENGGUNAKAN METODA PREDIKTOR- KOREKTOR ORDE 4 Asep Juarna, SSi, MKom. Fakultas Ilmu Komputer, Universitas
KOMPUTASI PARALEL PERSAMAAN DIFUSI NEUTRON PADA REAKTOR CEPAT DENGAN MENGGUNAKAN INTEL THREADING BUILDING BLOCKS
 KOMPUTASI PARALEL PERSAMAAN DIFUSI NEUTRON PADA REAKTOR CEPAT DENGAN MENGGUNAKAN INTEL THREADING BUILDING BLOCKS Imam Taufiq Jurusan Fisika FMIPA Universitas Andalas Kampus Limau Manis, Padang 25163 Email
KOMPUTASI PARALEL PERSAMAAN DIFUSI NEUTRON PADA REAKTOR CEPAT DENGAN MENGGUNAKAN INTEL THREADING BUILDING BLOCKS Imam Taufiq Jurusan Fisika FMIPA Universitas Andalas Kampus Limau Manis, Padang 25163 Email
Bab 2 LANDASAN TEORI
 17 Bab 2 LANDASAN TEORI 2.1 Aljabar Matriks 2.1.1 Definisi Matriks Matriks adalah suatu kumpulan angka-angka yang juga sering disebut elemen-elemen yang disusun secara teratur menurut baris dan kolom sehingga
17 Bab 2 LANDASAN TEORI 2.1 Aljabar Matriks 2.1.1 Definisi Matriks Matriks adalah suatu kumpulan angka-angka yang juga sering disebut elemen-elemen yang disusun secara teratur menurut baris dan kolom sehingga
METODE FINITEDIFFERENCE INTERVAL UNTUK MENYELESAIKAN PERSAMAAN PANAS
 METODE FINITEDIFFERENCE INTERVAL UNTUK MENYELESAIKAN PERSAMAAN PANAS Aziskhan, Mardhika W.A, Syamsudhuha Jurusan MatematikaFMIPA Universitas Riau Abstract. The aim of this paper is to solve a heat equation
METODE FINITEDIFFERENCE INTERVAL UNTUK MENYELESAIKAN PERSAMAAN PANAS Aziskhan, Mardhika W.A, Syamsudhuha Jurusan MatematikaFMIPA Universitas Riau Abstract. The aim of this paper is to solve a heat equation
Matriks - Definisi. Sebuah matriks yang memiliki m baris dan n kolom disebut matriks m n. Sebagai contoh: Adalah sebuah matriks 2 3.
 MATRIKS Pokok Bahasan Matriks definisi Notasi matriks Matriks yang sama Panambahan dan pengurangan matriks Perkalian matriks Transpos suatu matriks Matriks khusus Determinan suatu matriks bujursangkar
MATRIKS Pokok Bahasan Matriks definisi Notasi matriks Matriks yang sama Panambahan dan pengurangan matriks Perkalian matriks Transpos suatu matriks Matriks khusus Determinan suatu matriks bujursangkar
KOMPUTASI NUMERIK GERAK PROYEKTIL DUA DIMENSI MEMPERHITUNGKAN GAYA HAMBATAN UDARA DENGAN METODE RUNGE-KUTTA4 DAN DIVISUALISASIKAN DI GUI MATLAB
 KOMPUTASI NUMERIK GERAK PROYEKTIL DUA DIMENSI MEMPERHITUNGKAN GAYA HAMBATAN UDARA DENGAN METODE RUNGE-KUTTA4 DAN DIVISUALISASIKAN DI GUI MATLAB Tatik Juwariyah Fakultas Teknik Universitas Pembangunan Nasional
KOMPUTASI NUMERIK GERAK PROYEKTIL DUA DIMENSI MEMPERHITUNGKAN GAYA HAMBATAN UDARA DENGAN METODE RUNGE-KUTTA4 DAN DIVISUALISASIKAN DI GUI MATLAB Tatik Juwariyah Fakultas Teknik Universitas Pembangunan Nasional
PROSEDUR PARALELISASI PERKALIAN MATRIKS PADA GRAPHICS PROCESSING UNIT (GPU)
 PROSEDUR PARALELISASI PERKALIAN MATRIKS PADA GRAPHICS PROCESSING UNIT (GPU) Murni Pusat Studi Komputasi Matematika, Universitas Gunadarma Jl. Margonda Raya no. 100, Depok 16424, Jawa Barat [email protected]
PROSEDUR PARALELISASI PERKALIAN MATRIKS PADA GRAPHICS PROCESSING UNIT (GPU) Murni Pusat Studi Komputasi Matematika, Universitas Gunadarma Jl. Margonda Raya no. 100, Depok 16424, Jawa Barat [email protected]
FORMULA PENGGANTI METODE KOEFISIEN TAK TENTU ABSTRACT
 FORMULA PENGGANTI METODE KOEFISIEN TAK TENTU Syofia Deswita 1, Syamsudhuha 2, Agusni 2 1 Mahasiswa Program Studi S1 Matematika 2 Dosen Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas
FORMULA PENGGANTI METODE KOEFISIEN TAK TENTU Syofia Deswita 1, Syamsudhuha 2, Agusni 2 1 Mahasiswa Program Studi S1 Matematika 2 Dosen Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas
