10. Transformasi Fourier
|
|
|
- Susanto Agusalim
- 8 tahun lalu
- Tontonan:
Transkripsi
1 10. Transformasi Fourier Dalam beberapa bab ke depan, kita akan membahas transformasi Fourier, sifatsifatnya, dan aplikasinya. Seperti halnya pada pembahasan deret Fourier, pendekatan yang diambil dalam pembahasan transformasi Fourier di sini sama pendekatan dalam buku Fourier Analysis and Its Applications karangan G.B. Folland (Wadsworth, 1992) Pengantar yakni Pada Bab 4, kita telah membahas deret Fourier pada interval [ L, L] sembarang, f(x) = n= c n e inπx/l, x L, c n = 1 L f(x)e inπx/l dx, n N. 2L L Dengan sedikit modifikasi, kita dapat menuliskan ulang rumus di atas sebagai f(x) = 1 2L c n,l = L L n= c n,l e inπx/l, f(x)e inπx/l dx. Selanjutnya misalkan ξ := π L dan ξ n := n ξ = nπ L. Maka f(x) = 1 n= c n,l e iξ nx ξ, c n,l = L L f(x)e iξ nx dx. 43
2 Jika f(x) 0 cukup cepat untuk x, maka c n,l tidak akan berbeda banyak apabila daerah pengintegralannya diperluas dari [ L, L] ke (, ), yakni c n,l f(x)e iξ nx dx = f(ξ n ), n N. Dalam hal ini, f(x) 1 n= f(ξ n )e iξ nx ξ, x L. Ini mirip jumlah Riemann dari f pada (, ). Jika L, maka ξ 0 dan ξ n semakin memadati R, sehingga dapat digantikan = dan rumus di atas menjadi f(x) = 1 f(ξ) = f(ξ)e iξx dξ, x R, (1) f(x)e iξx dx, ξ R. (2) Kalkulasi ini tentu saja masih merupakan kalkulasi kasar, namun untuk f tertentu kalkulasi ini berlaku. Rumus (2) disebut transformasi Fourier dari f, dan rumus (1) merupakan rumus inversi Fourier, yang merupakan cara untuk memperoleh f kembali dari f yang akan kita buktikan kelak secara cermat Ruang L 1 (R) dan L 2 (R) Untuk merapikan definisi transformasi Fourier dan mempelajari sifat-sifatnya, kita perlu beberapa asumsi, istilah dan notasi. Pertama, fungsi yang akan kita bahas selnjutnya adalah fungsi yang terdefinisi pada R. Seperti ketika kita mendefinisikan deret Fourier, kita asumsikan bahwa f terintegralkan (mutlak) pada R. Untuk itu, kita definisikan ruang L 1 = L 1 (R) sebagai ruang semua fungsi f yang terintegralkan mutlak pada R, yakni L 1 := f : } f(x) dx <. Ruang L 1 dilengkapi norm 1 yang rumusnya adalah f 1 := 44 f(x) dx.
3 Sebagai perluasan dari L 2 (a, b), kita juga mendefinisikan ruang L 2 = L 2 (R) sebagai ruang semua fungsi f yang kuadratnya terintegralkan, yakni L 2 := f : } f(x) 2 dx <. Ruang L 2 dilengkapi norm 2 yang rumusnya adalah tinjau dan [ 1/2. f 2 := f(x) dx] 2 Catat bahwa tidak ada hubungan urutan di antara L 1 dan L 2. f(x) = g(x) = x 2/3, jika 0 < x < 1, 0, jika x lainnya x 2/3, jika x > 1, 0, jika x lainnya. Maka f L 1 tetapi f / L 2, sementara g L 2 tetapi g / L 1. Sebagai contoh, Walaupun demikian, ada dua fakta yang kelak berguna bagi kita mengenai kedua ruang ini, yaitu: (1) Jika f L 1 dan f terbatas pada R, maka f L 2. Persisnya f M f 2 M f f(x) 2 dx M f(x) dx <. (2) Jika f L 2 dan f bernilai 0 di luar suatu interval [a, b], maka f L 1. Persisnya f(x) dx = b a 1 f(x) dx (b a) 1/2[ b 1/2 f(x) dx] 2 <. a Catatan. Ruang L 1 dan L 2 merupakan kasus khusus dari ruang Lebesgue L p = L p (R), 1 p yang beranggotakan semua fungsi f sedemikian sehingga f(x) p dx < Transformasi Fourier Misalkan f L 1, yakni f 1 = f(x) dx <. Transformasi Fourier dari f, yang kita tuliskan sebagai f, didefinisikan oleh f(ξ) = R f(x)e iξx dx, ξ R. 45
4 Seperti halnya dalam pembahasan deret Fourier, pertanyaan kita adalah bagaimana kita dapat memperoleh f kembali dari f. Kesamaan (1) menyarankan kita untuk mendefinisikan invers transformasi Fourier dari g, yang dituliskan sebagai ǧ, sebagai ǧ(x) = 1 g(ξ)e ixξ dξ, x R. Teorema inversi Fourier, yang akan kita bahas nanti, menyatakan bahwa asalkan f dan f terintegralkan. R ( f)ˇ(x) = f(x), h.d.m. Sebelum sampai ke sana, kita pelajari dahulu sifat-sifat dasar transformasi Fourier. Teorema. Jika f L 1, maka f terbatas pada R. Bukti. Perhatikan bahwa untuk setiap ξ R berlaku f(ξ) e iξx f(x) dx = f(x) dx = f 1. Jadi f terbatas pada R, f := ess sup x R f(x) f 1. (QED) Teorema. Jika f L 1, maka f kontinu pada R. Bukti. Untuk setiap ξ dan h R, sehingga f(ξ + h) f(ξ) = f(ξ + h) f(ξ) e iξx (e ihx 1)f(x) dx, e ihx 1 f(x) dx. Integran di ruas kanan didominasi oleh 2 f(x) dan menuju 0 apabila h 0. Jadi, menurut Teorema Kekonvergenan Terdominasi Lebesgue, ruas kanan mestilah menuju 0 apabila h 0, dan akibatnya ruas kiri juga menuju 0 apabila h 0. (QED) Teorema (Riemann-Lebesgue) Jika f L 1, maka lim f(ξ) = 0. ξ Bukti. Perhatikan bahwa f(ξ) = f(x)e iξ(x+ π ξ ) dx = f(x π ξ )e iξx dx. Karena itu 2 f(ξ) = f(ξ) ( f(ξ)) = 46 ( f(x) f ( x π ξ ) ) e iξx dx,
5 sehingga 2 f(ξ) f(x) f ( x π ) dx. ξ Karena f L 1, maka (menggunakan kekontinuan dalam norma di L 1 ) ruas kanan akan menuju 0 apabila ξ. Dengan demikian ruas kiri pun mestilah menuju 0 apabila ξ. (QED) Akibat. Transformasi Fourier F memetakan fungsi f di L 1 ke fungsi Ff = f di C 0 (R). Catatan. C 0 (R) adalah ruang fungsi kontinu dan terbatas pada R limit nol di ±. Notasi Ff akan kita gunakan secara bergantian notasi f untuk menyatakan transformasi Fourier dari f. berikut. Berkenaan translasi dan dilasi, transformasi Fourier mempunyai sifat sebagai Teorema Misalkan f L 1 dan a R. (i) Jika g(x) := f(x a), maka ĝ(ξ) = e iaξ f(ξ); (ii) Jika g(x) := e iax f(x), maka ĝ(ξ) = f(ξ a). Selanjutnya, misalkan δ > 0. (iii) Jika g(x) := δ 1 f(x/δ), maka ĝ(ξ) = f(δξ); (iv) Jika g(x) = f(δx), maka ĝ(ξ) = δ 1 f(ξ/δ). Berkenaan operasi turunan dan perkalian peubah bebasnya, transformasi Fourier mempunyai sifat sebagai berikut. Teorema Misalkan f L 1. Jika f kontinu dan mulus bagian demi bagian pada R, dan f L 1, maka (f ) (ξ) = iξ f(ξ). Sebaliknya, jika g(x) := xf(x) terintegralkan mutlak pada R, maka ĝ(ξ) = i( f) (ξ). Berikut ini adalah beberapa contoh transformasi Fourier dari fungsi-fungsi tertentu. Contoh 1. Jika f = χ [ a,a] (a > 0), maka f(ξ) sin aξ = 2 ξ. Contoh 2. Jika f(x) = 1 x 2 +a 2 (a > 0), maka f(ξ) = π a e a ξ. 47
6 Contoh 3. Jika f(x) = e ax2 (a > 0), maka f(ξ) = a e ξ Contoh 1 dapat dihitung langsung, sementara Contoh 2 memerlukan teorema residu (untuk suatu integral fungsi kompleks yang berpadanan). Untuk Contoh 3, perhatikan 2 2a. bahwa f memenuhi persamaan diferensial f (x) + axf(x) = 0. Kenakan transformasi Fourier pada persamaan ini, kita peroleh persamaan diferensial yang dipenuhi oleh f, dan akhirnya kita peroleh rumus untuk f Soal Latihan 1. Buktikan dua teorema terakhir di atas. 2. Buktikan tiga contoh transformasi Fourier di atas. 48
12. Teorema Inversi Fourier dan Transformasi Fourier di L 2 (R)
 1. Teorema Inversi Fourier dan Transformasi Fourier di L (R) 1.1 Teorema Inversi Fourier Dari hasil hitung-hitungan kasar di awal bagian ke-10, kita ingin membuktikan bahwa, dalam kondisi tertentu, kita
1. Teorema Inversi Fourier dan Transformasi Fourier di L (R) 1.1 Teorema Inversi Fourier Dari hasil hitung-hitungan kasar di awal bagian ke-10, kita ingin membuktikan bahwa, dalam kondisi tertentu, kita
7. Transformasi Fourier
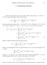 Pengantar Analisis Fourier dan eori Aproksimasi 33 7. ransformasi Fourier Pada bab sebelumnya kita telah melihat bahwa setiap fungsi f L 1 ([0, 1] L ([0, 1] dapat dinyatakan sebagai deret Fourier f(x =
Pengantar Analisis Fourier dan eori Aproksimasi 33 7. ransformasi Fourier Pada bab sebelumnya kita telah melihat bahwa setiap fungsi f L 1 ([0, 1] L ([0, 1] dapat dinyatakan sebagai deret Fourier f(x =
13. Aplikasi Transformasi Fourier
 13. plikasi ransformasi Fourier Misal adalah operator linear pada fungsi yang terdefinisi pada R dengan sifat: jika [f(x] = g(x, maka [f(x + s] = g(x + s untuk setiap s R. Maka, fungsi f(x = e ax (a C
13. plikasi ransformasi Fourier Misal adalah operator linear pada fungsi yang terdefinisi pada R dengan sifat: jika [f(x] = g(x, maka [f(x + s] = g(x + s untuk setiap s R. Maka, fungsi f(x = e ax (a C
11. Konvolusi. Misalkan f dan g fungsi yang terdefinisi pada R. Konvolusi dari f dan g adalah fungsi f g yang didefinisikan sebagai.
 11. Konvolusi Operasi konvolusi yang akan kita bahas di sini sebetulnya pernah kita jumpai pada pembahasan deret Fourier (ketika membuktikan kekonvergenan jumlah parsialnya). Operasi konvolusi merupakan
11. Konvolusi Operasi konvolusi yang akan kita bahas di sini sebetulnya pernah kita jumpai pada pembahasan deret Fourier (ketika membuktikan kekonvergenan jumlah parsialnya). Operasi konvolusi merupakan
Fourier Analysis & Its Applications in PDEs - Part I
 Fourier Analysis & Its Applications in PDEs Hendra Gunawan http://personal.fmipa.itb.ac.id/hgunawan/ Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA WIDE 2010 5-6 August
Fourier Analysis & Its Applications in PDEs Hendra Gunawan http://personal.fmipa.itb.ac.id/hgunawan/ Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA WIDE 2010 5-6 August
0. Pendahuluan. 0.1 Notasi dan istilah, bilangan kompleks
 0. Pendahuluan Analisis Fourier mempelajari berbagai teknik menganalisis sebuah fungsi dengan menguraikannya sebagai deret atau integral fungsi tertentu (yang sifat-sifatnya telah kita kenal dengan baik,
0. Pendahuluan Analisis Fourier mempelajari berbagai teknik menganalisis sebuah fungsi dengan menguraikannya sebagai deret atau integral fungsi tertentu (yang sifat-sifatnya telah kita kenal dengan baik,
Fourier Analysis & Its Applications in PDEs - Part II
 Fourier Analysis & Its Applications in PDEs Hendra Gunawan http://personal.fmipa.itb.ac.id/hgunawan/ Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA WIDE 2010 5-6 August
Fourier Analysis & Its Applications in PDEs Hendra Gunawan http://personal.fmipa.itb.ac.id/hgunawan/ Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA WIDE 2010 5-6 August
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
11. FUNGSI MONOTON (DAN FUNGSI KONVEKS)
 11. FUNGSI MONOTON (DAN FUNGSI KONVEKS) 11.1 Definisi dan Limit Fungsi Monoton Misalkan f terdefinisi pada suatu himpunan H. Kita katakan bahwa f naik pada H apabila untuk setiap x, y H dengan x < y berlaku
11. FUNGSI MONOTON (DAN FUNGSI KONVEKS) 11.1 Definisi dan Limit Fungsi Monoton Misalkan f terdefinisi pada suatu himpunan H. Kita katakan bahwa f naik pada H apabila untuk setiap x, y H dengan x < y berlaku
4. Deret Fourier pada Interval Sebarang dan Aplikasi
 4. Deret Fourier pada Interval Sebarang dan Aplikasi Kita telah mempelajari bagaimana menguraikan fungsi periodik dengan periode 2 yang terdefinisi pada R sebagai deret Fourier. Deret trigonometri tersebut
4. Deret Fourier pada Interval Sebarang dan Aplikasi Kita telah mempelajari bagaimana menguraikan fungsi periodik dengan periode 2 yang terdefinisi pada R sebagai deret Fourier. Deret trigonometri tersebut
17. Transformasi Wavelet Kontinu dan Frame
 17. Transformasi Wavelet Kontinu dan Frame Pada 16 kita mempelajari basis ortonormal {e 2πimx g(x n)} dengan g = χ [,1). Transformasi f f(x)g(x n)e 2πimx dx, m, n Z, dikenal sebagai transformasi Fourier
17. Transformasi Wavelet Kontinu dan Frame Pada 16 kita mempelajari basis ortonormal {e 2πimx g(x n)} dengan g = χ [,1). Transformasi f f(x)g(x n)e 2πimx dx, m, n Z, dikenal sebagai transformasi Fourier
BAB V KEKONVERGENAN BARISAN PADA DAN KETERKAITAN DENGAN. Pada subbab 4.1 telah dibahas beberapa sifat dasar yang berlaku pada koleksi
 BAB V KEKONVERGENAN BARISAN PADA DAN KETERKAITAN DENGAN Pada subbab 4.1 telah dibahas beberapa sifat dasar yang berlaku pada koleksi semua fungsi yang terintegralkan Lebesgue, 1. Sebagaimana telah dirumuskan
BAB V KEKONVERGENAN BARISAN PADA DAN KETERKAITAN DENGAN Pada subbab 4.1 telah dibahas beberapa sifat dasar yang berlaku pada koleksi semua fungsi yang terintegralkan Lebesgue, 1. Sebagaimana telah dirumuskan
UJI KONVERGENSI. Januari Tim Dosen Kalkulus 2 TPB ITK
 UJI KONVERGENSI Januari 208 Tim Dosen Kalkulus 2 TPB ITK Uji Integral Teorema 3 Jika + k= u k adalah deret dengan suku-suku tak negatif, dan jika ada suatu konstanta M sedemikian hingga s n = u + u 2 +
UJI KONVERGENSI Januari 208 Tim Dosen Kalkulus 2 TPB ITK Uji Integral Teorema 3 Jika + k= u k adalah deret dengan suku-suku tak negatif, dan jika ada suatu konstanta M sedemikian hingga s n = u + u 2 +
Hendra Gunawan. KK Analisis & Geometri FMIPA-ITB. Bandung, Maret 2001 [Edisi Revisi II: Mei 2014]
![Hendra Gunawan. KK Analisis & Geometri FMIPA-ITB. Bandung, Maret 2001 [Edisi Revisi II: Mei 2014] Hendra Gunawan. KK Analisis & Geometri FMIPA-ITB. Bandung, Maret 2001 [Edisi Revisi II: Mei 2014]](/thumbs/72/67819562.jpg) Analisis Fourier dan Wavelet 1 Catatan Kuliah Analisis Fourier dan Wavelet Oleh Hendra Gunawan KK Analisis & Geometri FMIPA-ITB Bandung, Maret 2001 [Edisi Revisi II: Mei 2014] 1 2 Hendra Gunawan Daftar
Analisis Fourier dan Wavelet 1 Catatan Kuliah Analisis Fourier dan Wavelet Oleh Hendra Gunawan KK Analisis & Geometri FMIPA-ITB Bandung, Maret 2001 [Edisi Revisi II: Mei 2014] 1 2 Hendra Gunawan Daftar
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
4. Deret Fourier pada Interval Sebarang dan Aplikasi
 8 Hendra Gunawan 4. Deret Fourier pada Interval Sebarang dan Aplikasi Kita telah mempelajari bagaimana menguraikan fungsi periodik dengan periode 2 yang terdefinisi pada R sebagai deret Fourier. Deret
8 Hendra Gunawan 4. Deret Fourier pada Interval Sebarang dan Aplikasi Kita telah mempelajari bagaimana menguraikan fungsi periodik dengan periode 2 yang terdefinisi pada R sebagai deret Fourier. Deret
DASAR-DASAR ANALISIS MATEMATIKA
 (Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: [email protected]. December 11, 2007 Misalkan f terdefinisi pada suatu himpunan H. Kita katakan bahwa f naik pada H apabila
(Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: [email protected]. December 11, 2007 Misalkan f terdefinisi pada suatu himpunan H. Kita katakan bahwa f naik pada H apabila
BAB III INTEGRAL LEBESGUE. Pada bab sebelumnya telah disebutkan bahwa ruang dibangun oleh
 BAB III INTEGRAL LEBESGUE Pada bab sebelumnya telah disebutkan bahwa ruang dibangun oleh fungsi-fungsi terukur dan memenuhi sifat yang berkaitan dengan integral Lebesgue. Kajian mengenai keterukuran suatu
BAB III INTEGRAL LEBESGUE Pada bab sebelumnya telah disebutkan bahwa ruang dibangun oleh fungsi-fungsi terukur dan memenuhi sifat yang berkaitan dengan integral Lebesgue. Kajian mengenai keterukuran suatu
5.1 Fungsi periodik, fungsi genap, fungsi ganjil
 Bab 5 DERET FOURIER Pada Bab sebelumnya kita telah membahas deret Taylor. Syarat fungsi agar dapat diekspansi ke dalam deret Taylor adalah fungsi tersebut harus terdiferensial pada setiap tingkat. Untuk
Bab 5 DERET FOURIER Pada Bab sebelumnya kita telah membahas deret Taylor. Syarat fungsi agar dapat diekspansi ke dalam deret Taylor adalah fungsi tersebut harus terdiferensial pada setiap tingkat. Untuk
Analisis Fourier dan Wavelet
 0 Hendra Gunawan Analisis Fourier dan Wavelet Hendra Gunawan KK Analisis & Geometri FMIPA-ITB Bandung, 2017 Analisis Fourier dan Wavelet 1 Daftar Isi Kata Pengantar 5 0 Pendahuluan 7 0.1 Notasi dan istilah,
0 Hendra Gunawan Analisis Fourier dan Wavelet Hendra Gunawan KK Analisis & Geometri FMIPA-ITB Bandung, 2017 Analisis Fourier dan Wavelet 1 Daftar Isi Kata Pengantar 5 0 Pendahuluan 7 0.1 Notasi dan istilah,
BAGIAN KEDUA. Fungsi, Limit dan Kekontinuan, Turunan
 BAGIAN KEDUA Fungsi, Limit dan Kekontinuan, Turunan 51 52 Hendra Gunawan Pengantar Analisis Real 53 6. FUNGSI 6.1 Fungsi dan Grafiknya Konsep fungsi telah dipelajari oleh Gottfried Wilhelm von Leibniz
BAGIAN KEDUA Fungsi, Limit dan Kekontinuan, Turunan 51 52 Hendra Gunawan Pengantar Analisis Real 53 6. FUNGSI 6.1 Fungsi dan Grafiknya Konsep fungsi telah dipelajari oleh Gottfried Wilhelm von Leibniz
16. Analisis Multi Resolusi
 16. Analisis Multi esolusi Esensi dari basis ortonormal yang dibangun oleh sebuah wavelet adalah sifat multi resolusi-nya, sehingga kita dapat menganalisis suatu signal pada berbagai frekuensi di suatu
16. Analisis Multi esolusi Esensi dari basis ortonormal yang dibangun oleh sebuah wavelet adalah sifat multi resolusi-nya, sehingga kita dapat menganalisis suatu signal pada berbagai frekuensi di suatu
asimtot.wordpress.com BAB I PENDAHULUAN
 BAB I PENDAHULUAN. Latar Belakang Kalkulus Differensial dan Integral sangat luas penggunaannya dalam berbagai bidang seperti penentuan maksimum dan minimum. Suatu fungsi yang sering digunakan mahasiswa
BAB I PENDAHULUAN. Latar Belakang Kalkulus Differensial dan Integral sangat luas penggunaannya dalam berbagai bidang seperti penentuan maksimum dan minimum. Suatu fungsi yang sering digunakan mahasiswa
Keterbatasan Operator Riesz di Ruang Morrey
 J. Math. and Its Appl. ISSN: 829-605X Vol. 3, No., May 2006, 27 40 Keterbatasan Operator Riesz di Ruang Morrey Gani Gunawan, Hendra Gunawan Departemen Matematika FMIPA ITB Abstrak Dengan menggunakan transformasi
J. Math. and Its Appl. ISSN: 829-605X Vol. 3, No., May 2006, 27 40 Keterbatasan Operator Riesz di Ruang Morrey Gani Gunawan, Hendra Gunawan Departemen Matematika FMIPA ITB Abstrak Dengan menggunakan transformasi
3 LIMIT DAN KEKONTINUAN
 Menurut Bartle dan Sherbet (1994), Analisis matematika secara umum dipahami sebagai tubuh matematika yang dibangun oleh berbagai konsep limit. Pada bab sebelumnya kita telah mempelajari limit barisan,
Menurut Bartle dan Sherbet (1994), Analisis matematika secara umum dipahami sebagai tubuh matematika yang dibangun oleh berbagai konsep limit. Pada bab sebelumnya kita telah mempelajari limit barisan,
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
Catatan Kuliah MA1123 Kalkulus Elementer I
 Catatan Kuliah MA1123 Kalkulus Elementer I Oleh Hendra Gunawan, Ph.D. Departemen Matematika ITB Sasaran Belajar Setelah mempelajari materi Kalkulus Elementer I, mahasiswa diharapkan memiliki (terutama):
Catatan Kuliah MA1123 Kalkulus Elementer I Oleh Hendra Gunawan, Ph.D. Departemen Matematika ITB Sasaran Belajar Setelah mempelajari materi Kalkulus Elementer I, mahasiswa diharapkan memiliki (terutama):
10. TEOREMA NILAI RATA-RATA
 10. TEOREMA NILAI RATA-RATA 10.1 Maksimum dan Minimum Lokal Misalkan f terdefinisi pada suatu interval terbuka (a, b) dan c (a, b). Kita katakan bahwa f mencapai nilai maksimum lokal di c apabila f(x)
10. TEOREMA NILAI RATA-RATA 10.1 Maksimum dan Minimum Lokal Misalkan f terdefinisi pada suatu interval terbuka (a, b) dan c (a, b). Kita katakan bahwa f mencapai nilai maksimum lokal di c apabila f(x)
ANALISIS REAL. (Semester I Tahun ) Hendra Gunawan. October 3, Dosen FMIPA - ITB
 (Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: [email protected]. October 3, 2011 6.3 Limit Sepihak, Limit di Tak Hingga, dan Limit Tak Hingga Bila sebelumnya kita mempelajari limit barisan,
(Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: [email protected]. October 3, 2011 6.3 Limit Sepihak, Limit di Tak Hingga, dan Limit Tak Hingga Bila sebelumnya kita mempelajari limit barisan,
16. BARISAN FUNGSI. 16.1 Barisan Fungsi dan Kekonvergenan Titik Demi Titik
 16. BARISAN FUNGSI 16.1 Barisan Fungsi dan Kekonvergenan Titik Demi Titik Bila pada bab-bab sebelumnya kita membahas fungsi sebagai sebuah objek individual, maka pada bab ini dan selanjutnya kita akan
16. BARISAN FUNGSI 16.1 Barisan Fungsi dan Kekonvergenan Titik Demi Titik Bila pada bab-bab sebelumnya kita membahas fungsi sebagai sebuah objek individual, maka pada bab ini dan selanjutnya kita akan
INTERGRAL INTEGRAL TAK TENTU INTEGRAL SUBSTITUSI MENU
 INTERGRAL OLEH : KELOMPOK 5 KETUA TEORI 1. I GEDE DIKA VIRGA SAPUTRA 2. I WAYAN HERMAWAN 3. EGI AZIKIN MAULANA KETUA SOAL 1. I MADE DUPI ANDIKA 2. I PUTU BAGUS MAHENDRA INTEGRAL TAK TENTU INTEGRAL SUBSTITUSI
INTERGRAL OLEH : KELOMPOK 5 KETUA TEORI 1. I GEDE DIKA VIRGA SAPUTRA 2. I WAYAN HERMAWAN 3. EGI AZIKIN MAULANA KETUA SOAL 1. I MADE DUPI ANDIKA 2. I PUTU BAGUS MAHENDRA INTEGRAL TAK TENTU INTEGRAL SUBSTITUSI
Daftar Isi 5. DERET ANALISIS REAL. (Semester I Tahun ) Hendra Gunawan. Dosen FMIPA - ITB September 26, 2011
 (Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: [email protected]. September 26, 2011 Diberikan sejumlah terhingga bilangan a 1,..., a N, kita dapat menghitung jumlah a 1 + + a N. Namun,
(Semester I Tahun 2011-2012) Dosen FMIPA - ITB E-mail: [email protected]. September 26, 2011 Diberikan sejumlah terhingga bilangan a 1,..., a N, kita dapat menghitung jumlah a 1 + + a N. Namun,
8. Deret Fourier yang Diperumum dan Hampiran Terbaik di L 2 (a, b)
 8. Deret Fourier yang Diperumum dan Hampiran Terbaik di L (a, b) 8.1 Deret Fourier yang Diperumum Jika {ϕ n } 1 adalah basis ortonormal untuk L (a, b) dan f L (a, b), maka f, ϕ n disebut koefisien Fourier
8. Deret Fourier yang Diperumum dan Hampiran Terbaik di L (a, b) 8.1 Deret Fourier yang Diperumum Jika {ϕ n } 1 adalah basis ortonormal untuk L (a, b) dan f L (a, b), maka f, ϕ n disebut koefisien Fourier
BAB 3 REVIEW SIFAT-SIFAT STATISTIK PENDUGA KOMPONEN PERIODIK
 BAB 3 REVIEW SIFAT-SIFAT STATISTIK PENDUGA KOMPONEN PERIODIK 3. Perumusan Penduga Misalkan N adalah proses Poisson non-homogen pada interval 0, dengan fungsi intensitas yang tidak diketahui. Fungsi intensitas
BAB 3 REVIEW SIFAT-SIFAT STATISTIK PENDUGA KOMPONEN PERIODIK 3. Perumusan Penduga Misalkan N adalah proses Poisson non-homogen pada interval 0, dengan fungsi intensitas yang tidak diketahui. Fungsi intensitas
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA1201 KALKULUS 2A (Kelas 10) Bab 8: Bentuk Tak Tentu d
 MA1201 KALKULUS 2A (Kelas 10) Bab 8: dan Do maths and you see the world ? Pengantar Bentuk tak tentu? Bentuk apa? Bentuk tak tentu yang dimaksud adalah bentuk limit dengan nilai seolah-olah : 0 0 ; ; 0
MA1201 KALKULUS 2A (Kelas 10) Bab 8: dan Do maths and you see the world ? Pengantar Bentuk tak tentu? Bentuk apa? Bentuk tak tentu yang dimaksud adalah bentuk limit dengan nilai seolah-olah : 0 0 ; ; 0
BAB II TINJAUAN PUSTAKA
 5 BAB II TINJAUAN PUSTAKA Dalam bab ini dijelaskan beberapa definisi dan teorema yang digunakan dalam pembahasan berikutnya. 2.1 Teori Peluang Definisi 2.1.1 (Percobaan Acak) (Ross 2000) Suatu percobaan
5 BAB II TINJAUAN PUSTAKA Dalam bab ini dijelaskan beberapa definisi dan teorema yang digunakan dalam pembahasan berikutnya. 2.1 Teori Peluang Definisi 2.1.1 (Percobaan Acak) (Ross 2000) Suatu percobaan
MA1201 KALKULUS 2A Do maths and you see the world
 Catatan Kuliah MA20 KALKULUS 2A Do maths and you see the world disusun oleh Khreshna I.A. Syuhada, MSc. PhD. Kelompok Keilmuan STATISTIKA - FMIPA Institut Teknologi Bandung 203 Catatan kuliah ini ditulis
Catatan Kuliah MA20 KALKULUS 2A Do maths and you see the world disusun oleh Khreshna I.A. Syuhada, MSc. PhD. Kelompok Keilmuan STATISTIKA - FMIPA Institut Teknologi Bandung 203 Catatan kuliah ini ditulis
KALKULUS BAB II FUNGSI, LIMIT, DAN KEKONTINUAN. DEPARTEMEN TEKNIK KIMIA Universitas Indonesia
 KALKULUS BAB II FUNGSI, LIMIT, DAN KEKONTINUAN DEPARTEMEN TEKNIK KIMIA Universitas Indonesia BAB II. FUNGSI, LIMIT, DAN KEKONTINUAN Fungsi dan Operasi pada Fungsi Beberapa Fungsi Khusus Limit dan Limit
KALKULUS BAB II FUNGSI, LIMIT, DAN KEKONTINUAN DEPARTEMEN TEKNIK KIMIA Universitas Indonesia BAB II. FUNGSI, LIMIT, DAN KEKONTINUAN Fungsi dan Operasi pada Fungsi Beberapa Fungsi Khusus Limit dan Limit
Catatan Kuliah KALKULUS II BAB V. INTEGRAL
 BAB V. INTEGRAL Anti-turunan dan Integral TakTentu Persamaan Diferensial Sederhana Notasi Sigma dan Luas Daerah di Bawah Kurva Integral Tentu Teorema Dasar Kalkulus Sifat-sifat Integral Tentu Lebih Lanjut
BAB V. INTEGRAL Anti-turunan dan Integral TakTentu Persamaan Diferensial Sederhana Notasi Sigma dan Luas Daerah di Bawah Kurva Integral Tentu Teorema Dasar Kalkulus Sifat-sifat Integral Tentu Lebih Lanjut
BAB I PENDAHULUAN 1.1 Latar Belakang
 1 BAB I PENDAHULUAN 1.1 Latar Belakang Pada awalnya deret Fourier diperkenalkan oleh Joseph Fourier pada tahun 1807 untuk memecahkan model masalah persamaan panas pada suatu lempeng logam (Fourier, 1878).
1 BAB I PENDAHULUAN 1.1 Latar Belakang Pada awalnya deret Fourier diperkenalkan oleh Joseph Fourier pada tahun 1807 untuk memecahkan model masalah persamaan panas pada suatu lempeng logam (Fourier, 1878).
3. Kekonvergenan Deret Fourier
 3. Kekonvergenan Deret Fourier Sekarang kita akan membahas kekonvergenan deret Fourier, khususnya kekonvergenan titik demi titik. Melalui Contoh 2 yang dibahas pada bab sebelumnya kita mengetahui bahwa
3. Kekonvergenan Deret Fourier Sekarang kita akan membahas kekonvergenan deret Fourier, khususnya kekonvergenan titik demi titik. Melalui Contoh 2 yang dibahas pada bab sebelumnya kita mengetahui bahwa
BAB I DERIVATIF (TURUNAN)
 BAB I DERIVATIF (TURUNAN) Pada bab ini akan dipaparkan pengertian derivatif suatu fungsi, beberapa sifat aljabar derivatif, aturan rantai, dan derifativ fungsi invers. A. Pengertian Derivatif Pengertian
BAB I DERIVATIF (TURUNAN) Pada bab ini akan dipaparkan pengertian derivatif suatu fungsi, beberapa sifat aljabar derivatif, aturan rantai, dan derifativ fungsi invers. A. Pengertian Derivatif Pengertian
BAB II TEOREMA NILAI RATA-RATA (TNR)
 BAB II TEOREMA NILAI RATA-RATA (TNR) Teorema nilai rata-rata menghubungkan nilai suatu fungsi dengan nilai derivatifnya (turunannya), dimana TNR merupakan salah satu bagian penting dalam kuliah analisis
BAB II TEOREMA NILAI RATA-RATA (TNR) Teorema nilai rata-rata menghubungkan nilai suatu fungsi dengan nilai derivatifnya (turunannya), dimana TNR merupakan salah satu bagian penting dalam kuliah analisis
LIMIT DAN KEKONTINUAN
 LIMIT DAN KEKONTINUAN Departemen Matematika FMIPA IPB Bogor, 2012 (Departemen Matematika FMIPA IPB) Kalkulus I Bogor, 2012 1 / 37 Topik Bahasan 1 Limit Fungsi 2 Hukum Limit 3 Kekontinuan Fungsi (Departemen
LIMIT DAN KEKONTINUAN Departemen Matematika FMIPA IPB Bogor, 2012 (Departemen Matematika FMIPA IPB) Kalkulus I Bogor, 2012 1 / 37 Topik Bahasan 1 Limit Fungsi 2 Hukum Limit 3 Kekontinuan Fungsi (Departemen
METODE GARIS SINGGUNG DALAM MENENTUKAN HAMPIRAN INTEGRAL TENTU SUATU FUNGSI PADA SELANG TERTUTUP [, ]
![METODE GARIS SINGGUNG DALAM MENENTUKAN HAMPIRAN INTEGRAL TENTU SUATU FUNGSI PADA SELANG TERTUTUP [, ] METODE GARIS SINGGUNG DALAM MENENTUKAN HAMPIRAN INTEGRAL TENTU SUATU FUNGSI PADA SELANG TERTUTUP [, ]](/thumbs/53/31205711.jpg) METODE GARIS SINGGUNG DALAM MENENTUKAN HAMPIRAN INTEGRAL TENTU SUATU FUNGSI PADA SELANG TERTUTUP [, ] Zulfaneti dan Rahimullaily* Program Studi Pendidikan Matematika STKIP PGRI Sumbar Abstract: There is
METODE GARIS SINGGUNG DALAM MENENTUKAN HAMPIRAN INTEGRAL TENTU SUATU FUNGSI PADA SELANG TERTUTUP [, ] Zulfaneti dan Rahimullaily* Program Studi Pendidikan Matematika STKIP PGRI Sumbar Abstract: There is
BAB IV DERET FOURIER
 BAB IV DERET FOURIER 4.1 Fungsi Periodik Fungsi f(x) dikatakan periodik dengan perioda P, jika untuk semua harga x berlaku: f (x + P) = f (x) ; P adalah konstanta positif. Harga terkecil dari P > 0 disebut
BAB IV DERET FOURIER 4.1 Fungsi Periodik Fungsi f(x) dikatakan periodik dengan perioda P, jika untuk semua harga x berlaku: f (x + P) = f (x) ; P adalah konstanta positif. Harga terkecil dari P > 0 disebut
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016. Hendra Gunawan
 MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 4.2 Sifat-Sifat Fungsi Kontinu Diberikan f dan g, keduanya terdefinisi pada himpunan A, kita definisikan f + g, f g, fg, f/g secara
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 4.2 Sifat-Sifat Fungsi Kontinu Diberikan f dan g, keduanya terdefinisi pada himpunan A, kita definisikan f + g, f g, fg, f/g secara
Analisis Riil II: Diferensiasi
 Definisi Turunan Definisi dan Teorema Aturan Rantai Fungsi Invers Definisi (Turunan) Misalkan I R sebuah interval, f : I R, dan c I. Bilangan riil L dikatakan turunan dari f di c jika diberikan sebarang
Definisi Turunan Definisi dan Teorema Aturan Rantai Fungsi Invers Definisi (Turunan) Misalkan I R sebuah interval, f : I R, dan c I. Bilangan riil L dikatakan turunan dari f di c jika diberikan sebarang
Barisan dan Deret Agus Yodi Gunawan
 Barisan dan Deret Agus Yodi Gunawan Barisan. Definisi. Barisan tak hingga adalah suatu fungsi dengan daerah asalnya himpunan bilangan bulat positif dan daerah kawannya himpunan bilangan real. Notasi untuk
Barisan dan Deret Agus Yodi Gunawan Barisan. Definisi. Barisan tak hingga adalah suatu fungsi dengan daerah asalnya himpunan bilangan bulat positif dan daerah kawannya himpunan bilangan real. Notasi untuk
BAB III FUNGSI TERUKUR LEBESGUE. Setelah dibahas mengenai ukuran Lebesgue dan beberapa sifatnya pada
 BAB III FUNGSI TERUKUR LEBESGUE Setelah dibahas mengenai ukuran Lebesgue dan beberapa sifatnya pada Bab II, selanjutnya pada bab ini akan dipelajari gagasan mengenai fungsi terukur Lebesgue. Gagasan mengenai
BAB III FUNGSI TERUKUR LEBESGUE Setelah dibahas mengenai ukuran Lebesgue dan beberapa sifatnya pada Bab II, selanjutnya pada bab ini akan dipelajari gagasan mengenai fungsi terukur Lebesgue. Gagasan mengenai
Bab 16. LIMIT dan TURUNAN. Motivasi. Limit Fungsi. Fungsi Turunan. Matematika SMK, Bab 16: Limit dan Turunan 1/35
 Bab 16 Grafik LIMIT dan TURUNAN Matematika SMK, Bab 16: Limit dan 1/35 Grafik Pada dasarnya, konsep limit dikembangkan untuk mengerjakan perhitungan matematis yang melibatkan: nilai sangat kecil; Matematika
Bab 16 Grafik LIMIT dan TURUNAN Matematika SMK, Bab 16: Limit dan 1/35 Grafik Pada dasarnya, konsep limit dikembangkan untuk mengerjakan perhitungan matematis yang melibatkan: nilai sangat kecil; Matematika
Karena deret tersebut konvergen pada garis luarnya, kita dapat menukar orde integrasi dan penjumlahan pada ruas kanan.
 Transformasi- 3. Invers Transformasi- Formasi inversi untuk memperoleh dari x(n) dari X() dapat diperoleh menggunakan teorema integral Cauchy yang merupakan teorema penting dalam variabel kompleks. Transformasi-
Transformasi- 3. Invers Transformasi- Formasi inversi untuk memperoleh dari x(n) dari X() dapat diperoleh menggunakan teorema integral Cauchy yang merupakan teorema penting dalam variabel kompleks. Transformasi-
3 LIMIT DAN KEKONTINUAN
 Menurut Bartle dan Sherbet (994), Analisis matematika secara umum dipahami sebagai tubuh matematika yang dibangun oleh berbagai konsep limit. Pada bab sebelumnya kita telah mempelajari limit barisan, kekonvergenan
Menurut Bartle dan Sherbet (994), Analisis matematika secara umum dipahami sebagai tubuh matematika yang dibangun oleh berbagai konsep limit. Pada bab sebelumnya kita telah mempelajari limit barisan, kekonvergenan
BAB I PENDAHULUAN Latar Belakang Masalah
 BAB I PENDAHULUAN 1.1. Latar Belakang Masalah Analisis merupakan salah satu cabang matematika yang mempelajari antara lain barisan, limit, deret, kekontinuan, kekonvergenan, integral, dan yang lainnya.
BAB I PENDAHULUAN 1.1. Latar Belakang Masalah Analisis merupakan salah satu cabang matematika yang mempelajari antara lain barisan, limit, deret, kekontinuan, kekonvergenan, integral, dan yang lainnya.
: D C adalah fungsi kompleks dengan domain riil
 BAB 4. INTEGRAL OMPLES 4. Integral Garis ompleks Misalkan ( : D adalah fungsi kompleks dengan domain riil b D [ a, b], maka integral (, dimana ( x( + iy( dapat dengan mudah a b dihitung, yaitu a i contoh
BAB 4. INTEGRAL OMPLES 4. Integral Garis ompleks Misalkan ( : D adalah fungsi kompleks dengan domain riil b D [ a, b], maka integral (, dimana ( x( + iy( dapat dengan mudah a b dihitung, yaitu a i contoh
DASAR-DASAR ANALISIS MATEMATIKA
 (Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: [email protected]. December 26, 2007 Misalkan f kontinu pada interval [a, b]. Apakah masuk akal untuk membahas luas daerah
(Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: [email protected]. December 26, 2007 Misalkan f kontinu pada interval [a, b]. Apakah masuk akal untuk membahas luas daerah
BAB III FUNGSI YOUNG DAN KOMPLEMEN YOUNG
 BAB III FUNGSI YOUNG DAN KOMPLEMEN YOUNG Pada bab ini, dibahas tentang definisi fungsi Young dengan domain real diperluas dan komplemennya. Sebelumnya, dalam studi deret Fourier, W. H. Young telah menganalisis
BAB III FUNGSI YOUNG DAN KOMPLEMEN YOUNG Pada bab ini, dibahas tentang definisi fungsi Young dengan domain real diperluas dan komplemennya. Sebelumnya, dalam studi deret Fourier, W. H. Young telah menganalisis
BAB I PENDAHULUAN. Integral Lebesgue merupakan suatu perluasan dari integral Riemann.
 BAB I PENDAHULUAN 1.1 Latar Belakang Masalah Integral Lebesgue merupakan suatu perluasan dari integral Riemann. Sebagaimana telah diketahui, pengkonstruksian integral Riemann dilakukan dengan cara pemartisian
BAB I PENDAHULUAN 1.1 Latar Belakang Masalah Integral Lebesgue merupakan suatu perluasan dari integral Riemann. Sebagaimana telah diketahui, pengkonstruksian integral Riemann dilakukan dengan cara pemartisian
II. LANDASAN TEORI ( ) =
 II. LANDASAN TEORI 2.1 Fungsi Definisi 2.1.1 Fungsi Bernilai Real Fungsi bernilai real adalah fungsi yang domain dan rangenya adalah himpunan bagian dari real. Definisi 2.1.2 Limit Fungsi Jika adalah suatu
II. LANDASAN TEORI 2.1 Fungsi Definisi 2.1.1 Fungsi Bernilai Real Fungsi bernilai real adalah fungsi yang domain dan rangenya adalah himpunan bagian dari real. Definisi 2.1.2 Limit Fungsi Jika adalah suatu
Dwi Lestari, M.Sc: Konvergensi Deret 1. KONVERGENSI DERET
 1. KONVERGENSI DERET Suatu barisan disebut konvergen jika terdapat bilangan Z yang setiap lingkungannya memuat semua. Jika bilangan Z itu ada maka dapat ditulis: lim sehingga dapat dikatakan bahwa barisan
1. KONVERGENSI DERET Suatu barisan disebut konvergen jika terdapat bilangan Z yang setiap lingkungannya memuat semua. Jika bilangan Z itu ada maka dapat ditulis: lim sehingga dapat dikatakan bahwa barisan
Ringkasan Kalkulus 2, Untuk dipakai di ITB 1
 Ringkasan Kalkulus 2, Untuk dipakai di ITB Deret Tak Hingga Pada bagian ini akan dibicarakan penjumlahan berbentuk a +a 2 + +a n + dengan a n R Sebelumnya akan dibahas terlebih dahulu pengertian barisan
Ringkasan Kalkulus 2, Untuk dipakai di ITB Deret Tak Hingga Pada bagian ini akan dibicarakan penjumlahan berbentuk a +a 2 + +a n + dengan a n R Sebelumnya akan dibahas terlebih dahulu pengertian barisan
BAGIAN PERTAMA. Bilangan Real, Barisan, Deret
 BAGIAN PERTAMA Bilangan Real, Barisan, Deret 2 Hendra Gunawan Pengantar Analisis Real 3 0. BILANGAN REAL 0. Bilangan Real sebagai Bentuk Desimal Dalam buku ini pembaca diasumsikan telah mengenal dengan
BAGIAN PERTAMA Bilangan Real, Barisan, Deret 2 Hendra Gunawan Pengantar Analisis Real 3 0. BILANGAN REAL 0. Bilangan Real sebagai Bentuk Desimal Dalam buku ini pembaca diasumsikan telah mengenal dengan
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016. Hendra Gunawan
 MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 3. Topologi Garis Bilangan Real 3.1 Teori Limit Limit, supremum, dan infimum Titik limit 3.2 Himpunan Buka dan Himpunan Tutup 3.3
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 3. Topologi Garis Bilangan Real 3.1 Teori Limit Limit, supremum, dan infimum Titik limit 3.2 Himpunan Buka dan Himpunan Tutup 3.3
DEFINISI TIPE RIEMANN UNTUK INTEGRAL LEBESGUE 1. Drajad Maknawi 2 dan Muslich 3 Jurusan Matematika FMIPA UNS. Abstrak
 DEFINISI TIPE RIEMANN UNTUK INTEGRAL LEBESGUE 1 An-2 1. PENDAHULUAN Drajad Maknawi 2 dan Muslich 3 Jurusan Matematika FMIPA UNS Abstrak Tujuan dari tulisan ini adalah membahas tentang integral Lebesgue
DEFINISI TIPE RIEMANN UNTUK INTEGRAL LEBESGUE 1 An-2 1. PENDAHULUAN Drajad Maknawi 2 dan Muslich 3 Jurusan Matematika FMIPA UNS Abstrak Tujuan dari tulisan ini adalah membahas tentang integral Lebesgue
DASAR-DASAR ANALISIS MATEMATIKA
 (Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: [email protected]. November 19, 2007 Secara geometris, f kontinu di suatu titik berarti bahwa grafiknya tidak terputus
(Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: [email protected]. November 19, 2007 Secara geometris, f kontinu di suatu titik berarti bahwa grafiknya tidak terputus
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016. Hendra Gunawan
 MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 5. Kalkulus Diferensial 5.1 Konsep Turunan Beberapa Definisi yang Setara Kekontinuan dan Keterdiferensialan secara Kontinu 5.2 Sifat-Sifat
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 5. Kalkulus Diferensial 5.1 Konsep Turunan Beberapa Definisi yang Setara Kekontinuan dan Keterdiferensialan secara Kontinu 5.2 Sifat-Sifat
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016. Hendra Gunawan
 MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 5.3 Kalkulus Turunan Pada bagian ini kita akan membahas sejumlah aturan untuk diferensial dan aturan untuk turunan, yg mempunyai kemiripan
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 5.3 Kalkulus Turunan Pada bagian ini kita akan membahas sejumlah aturan untuk diferensial dan aturan untuk turunan, yg mempunyai kemiripan
MA3231. Pengantar Analisis Real. Hendra Gunawan, Ph.D. Semester II, Tahun
 MA3231 Pengantar Analisis Real Semester II, Tahun 2016-2017 Hendra Gunawan, Ph.D. Tentang Mata Kuliah MA3231 Mata kuliah ini merupakan mata kuliah wajib bagi mahasiswa program studi S1 Matematika, dengan
MA3231 Pengantar Analisis Real Semester II, Tahun 2016-2017 Hendra Gunawan, Ph.D. Tentang Mata Kuliah MA3231 Mata kuliah ini merupakan mata kuliah wajib bagi mahasiswa program studi S1 Matematika, dengan
Bagian 2 Matriks dan Determinan
 Bagian Matriks dan Determinan Materi mengenai fungsi, limit, dan kontinuitas akan kita pelajari dalam Bagian Fungsi dan Limit. Pada bagian Fungsi akan mempelajari tentang jenis-jenis fungsi dalam matematika
Bagian Matriks dan Determinan Materi mengenai fungsi, limit, dan kontinuitas akan kita pelajari dalam Bagian Fungsi dan Limit. Pada bagian Fungsi akan mempelajari tentang jenis-jenis fungsi dalam matematika
Bab 2 Fungsi Analitik
 Bab 2 Fungsi Analitik Bab 2 ini direncanakan akan disampaikan dalam 4 kali pertemuan, dengan perincian sebagai berikut: () Pertemuan I: Fungsi Kompleks dan Pemetaan. (2) Pertemuan II: Limit Fungsi, Kekontiuan,
Bab 2 Fungsi Analitik Bab 2 ini direncanakan akan disampaikan dalam 4 kali pertemuan, dengan perincian sebagai berikut: () Pertemuan I: Fungsi Kompleks dan Pemetaan. (2) Pertemuan II: Limit Fungsi, Kekontiuan,
Suku Banyak Chebyshev
 Bab 3 Suku Banyak Chebyshev Suku banyak Chebyshev, yang diberi nama oleh Pafnuty Chebyshev, merupakan suatu deret dari suku banyak ortogonal yang dapat dituliskan secara rekursif. Suku banyak ini dibedakan
Bab 3 Suku Banyak Chebyshev Suku banyak Chebyshev, yang diberi nama oleh Pafnuty Chebyshev, merupakan suatu deret dari suku banyak ortogonal yang dapat dituliskan secara rekursif. Suku banyak ini dibedakan
VARIABEL KOMPLEKS SUMANANG MUHTAR GOZALI KBK ALJABAR & ANALISIS
 VARIABEL KOMPLEKS SUMANANG MUHTAR GOZALI KBK ALJABAR & ANALISIS UNIVERSITAS PENDIDIKAN INDONESIA BANDUNG 2009 2 DAFTAR ISI DAFTAR ISI 2 1 Sistem Bilangan Kompleks (C) 1 1 Pendahuluan...............................
VARIABEL KOMPLEKS SUMANANG MUHTAR GOZALI KBK ALJABAR & ANALISIS UNIVERSITAS PENDIDIKAN INDONESIA BANDUNG 2009 2 DAFTAR ISI DAFTAR ISI 2 1 Sistem Bilangan Kompleks (C) 1 1 Pendahuluan...............................
3 LIMIT DAN KEKONTINUAN
 Menurut Bartle dan Sherbet (1994), Analisis matematika secara umum dipahami sebagai tubuh matematika yang dibangun dari berbagai konsep limit. Pada bab sebelumnya kita telah mempelajari limit barisan,
Menurut Bartle dan Sherbet (1994), Analisis matematika secara umum dipahami sebagai tubuh matematika yang dibangun dari berbagai konsep limit. Pada bab sebelumnya kita telah mempelajari limit barisan,
Beberapa Pertidaksamaan Tipe Ostrowski
 Beberapa Pertidaksamaan Tipe Ostrowski Rani Fransiska Departemen Marematika, FMIPA UI, Kampus UI Depok 1644 ranifransiska@uiacid Abstrak Pertidaksamaan Ostrowski adalah suatu pertidaksamaan integral untuk
Beberapa Pertidaksamaan Tipe Ostrowski Rani Fransiska Departemen Marematika, FMIPA UI, Kampus UI Depok 1644 ranifransiska@uiacid Abstrak Pertidaksamaan Ostrowski adalah suatu pertidaksamaan integral untuk
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
KALKULUS MULTIVARIABEL II
 Pada Bidang Bentuk Vektor dari KALKULUS MULTIVARIABEL II (Minggu ke-9) Andradi Jurusan Matematika FMIPA UGM Yogyakarta, Indonesia Pada Bidang Bentuk Vektor dari 1 Definisi Daerah Sederhana x 2 Pada Bidang
Pada Bidang Bentuk Vektor dari KALKULUS MULTIVARIABEL II (Minggu ke-9) Andradi Jurusan Matematika FMIPA UGM Yogyakarta, Indonesia Pada Bidang Bentuk Vektor dari 1 Definisi Daerah Sederhana x 2 Pada Bidang
Bab III. Integral Fungsi Kompleks
 Bab III Integral Fungsi ompleks Integrasi suatu fungsi kompleks f() = u + iv dilakukan pada bidang Argand, sehingga integrasinya menyerupai integral garis pada integral vektor. Hal ini terjadi mengingat
Bab III Integral Fungsi ompleks Integrasi suatu fungsi kompleks f() = u + iv dilakukan pada bidang Argand, sehingga integrasinya menyerupai integral garis pada integral vektor. Hal ini terjadi mengingat
Disampaikan pada Diklat Instruktur/Pengembang Matematika SMA Jenjang Dasar Tanggal 6 s.d. 19 Agustus 2004 di PPPG Matematika
 PENGANTAR KALKULUS Disampaikan pada Diklat Instruktur/Pengembang Matematika SMA Jenjang Dasar Tanggal 6 s.d. 9 Agustus 004 di PPPG Matematika Oleh: Drs. SETIAWAN, M. Pd. Widyaiswara PPPG Matematika Yogyakarta
PENGANTAR KALKULUS Disampaikan pada Diklat Instruktur/Pengembang Matematika SMA Jenjang Dasar Tanggal 6 s.d. 9 Agustus 004 di PPPG Matematika Oleh: Drs. SETIAWAN, M. Pd. Widyaiswara PPPG Matematika Yogyakarta
KONSEP DASAR PERSAMAAN DIFERENSIAL
 KONSEP DASAR PERSAMAAN DIFERENSIAL A. PENGERTIAN PERSAMAAN DIFERENSIAL Dalam pelajaran kalkulus, kita telah berkenalan dan mengkaji berbagai macam metode untuk mendiferensialkan suatu fungsi (dasar). Sebagai
KONSEP DASAR PERSAMAAN DIFERENSIAL A. PENGERTIAN PERSAMAAN DIFERENSIAL Dalam pelajaran kalkulus, kita telah berkenalan dan mengkaji berbagai macam metode untuk mendiferensialkan suatu fungsi (dasar). Sebagai
SISTEM HUKUM KEKEKALAN LINEAR
 Bab 3 SISTEM HUKUM KEKEKALAN LINEAR 3.1 Sistem Linear Hiperbolik Sistem linear dalam pengertian Tugas Akhir ini adalah suatu sistem hukum kekekalan dengan bentuk umum, t u + d A α (t) xα u = 0 (3.1.1)
Bab 3 SISTEM HUKUM KEKEKALAN LINEAR 3.1 Sistem Linear Hiperbolik Sistem linear dalam pengertian Tugas Akhir ini adalah suatu sistem hukum kekekalan dengan bentuk umum, t u + d A α (t) xα u = 0 (3.1.1)
TURUNAN, EKSTRIM, BELOK, MINIMUM DAN MAKSIMUM
 TURUNAN, EKSTRIM, BELOK, MINIMUM DAN MAKSIMUM Fungsi f dikatakan mencapai maksimum mutlak di c jika f c f x untuk setiap x I. Di sini f c dinamakan nilai maksimum mutlak. Dan c, f c dinamakan titik maksimum
TURUNAN, EKSTRIM, BELOK, MINIMUM DAN MAKSIMUM Fungsi f dikatakan mencapai maksimum mutlak di c jika f c f x untuk setiap x I. Di sini f c dinamakan nilai maksimum mutlak. Dan c, f c dinamakan titik maksimum
KALKULUS MULTIVARIABEL II
 Definisi KALKULUS MULTIVARIABEL II (Minggu ke-7) Andradi Jurusan Matematika FMIPA UGM Yogyakarta, Indonesia Definisi 1 Definisi 2 ontoh Soal Definisi Integral Garis Fungsi f K R 2 R di Sepanjang Kurva
Definisi KALKULUS MULTIVARIABEL II (Minggu ke-7) Andradi Jurusan Matematika FMIPA UGM Yogyakarta, Indonesia Definisi 1 Definisi 2 ontoh Soal Definisi Integral Garis Fungsi f K R 2 R di Sepanjang Kurva
MAT 602 DASAR MATEMATIKA II
 MAT 60 DASAR MATEMATIKA II Disusun Oleh: Dr. St. Budi Waluya, M. Sc Jurusan Pendidikan Matematika Program Pascasarjana Unnes 1 HIMPUNAN 1. Notasi Himpunan. Relasi Himpunan 3. Operasi Himpunan A B : A B
MAT 60 DASAR MATEMATIKA II Disusun Oleh: Dr. St. Budi Waluya, M. Sc Jurusan Pendidikan Matematika Program Pascasarjana Unnes 1 HIMPUNAN 1. Notasi Himpunan. Relasi Himpunan 3. Operasi Himpunan A B : A B
SYARAT DIRICHLET. 1, 1 < t < 0
 SYARAT DIRICHET Misalkan f t adalah fungsi yang licin bagian demi bagian, berperioda, maka deret fourier konvergen. Ke nilai f t untuk setiap titik di mana fungsi f kontinu.. Ke nilai f t + + f t bagi
SYARAT DIRICHET Misalkan f t adalah fungsi yang licin bagian demi bagian, berperioda, maka deret fourier konvergen. Ke nilai f t untuk setiap titik di mana fungsi f kontinu.. Ke nilai f t + + f t bagi
MA2111 PENGANTAR MATEMATIKA Semester I, Tahun 2015/2016. Hendra Gunawan
 MA2111 PENGANTAR MATEMATIKA Semester I, Tahun 2015/2016 Hendra Gunawan 5 KUANTOR II: METODE MEMILIH (c) Hendra Gunawan (2015) 2 Masih Berurusan dengan Kuantor Sekarang kita akan membahas metode memilih,
MA2111 PENGANTAR MATEMATIKA Semester I, Tahun 2015/2016 Hendra Gunawan 5 KUANTOR II: METODE MEMILIH (c) Hendra Gunawan (2015) 2 Masih Berurusan dengan Kuantor Sekarang kita akan membahas metode memilih,
Matematika
 Fungsi dan Kekontinuan D3 Analis Kimia FMIPA Universitas Islam Indonesia Ilustrasi 1 Nol mutlak, yaitu temperatur T C di mana semua aktivitas molekular berhenti, dapat didekati namun tidak pernah dapat
Fungsi dan Kekontinuan D3 Analis Kimia FMIPA Universitas Islam Indonesia Ilustrasi 1 Nol mutlak, yaitu temperatur T C di mana semua aktivitas molekular berhenti, dapat didekati namun tidak pernah dapat
Kalkulus 2. Teknik Pengintegralan ke - 3. Tim Pengajar Kalkulus ITK. Institut Teknologi Kalimantan. Januari 2018
 Kalkulus 2 Teknik Pengintegralan ke - 3 Tim Pengajar Kalkulus ITK Institut Teknologi Kalimantan Januari 2018 Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari 2018 1 / 27 Daftar
Kalkulus 2 Teknik Pengintegralan ke - 3 Tim Pengajar Kalkulus ITK Institut Teknologi Kalimantan Januari 2018 Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari 2018 1 / 27 Daftar
DASAR-DASAR ANALISIS MATEMATIKA
 (Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: [email protected]. December 1, 2007 Diberikan sebuah fungsi yang terdefinisi pada interval (a, b) kecuali mungkin di
(Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: [email protected]. December 1, 2007 Diberikan sebuah fungsi yang terdefinisi pada interval (a, b) kecuali mungkin di
LEMBAR AKTIVITAS SISWA INDUKSI MATEMATIKA
 Nama Siswa Kelas : : LEMBAR AKTIVITAS SISWA INDUKSI MATEMATIKA Latihan 1 1. A. NOTASI SIGMA 1. Pengertian Notasi Sigma Misalkan jumlah n suku pertama deret aritmatika adalah S n = U 1 + U 2 + U 3 + + U
Nama Siswa Kelas : : LEMBAR AKTIVITAS SISWA INDUKSI MATEMATIKA Latihan 1 1. A. NOTASI SIGMA 1. Pengertian Notasi Sigma Misalkan jumlah n suku pertama deret aritmatika adalah S n = U 1 + U 2 + U 3 + + U
BAB IV PERTIDAKSAMAAN. 1. Pertidaksamaan Kuadrat 2. Pertidaksamaan Bentuk Pecahan 3. Pertidaksamaan Bentuk Akar 4. Pertidaksamaan Nilai Mutlak
 BAB IV PERTIDAKSAMAAN 1. Pertidaksamaan Kuadrat. Pertidaksamaan Bentuk Pecahan 3. Pertidaksamaan Bentuk Akar 4. Pertidaksamaan Nilai Mutlak 86 LEMBAR KERJA SISWA 1 Mata Pelajaran : Matematika Uraian Materi
BAB IV PERTIDAKSAMAAN 1. Pertidaksamaan Kuadrat. Pertidaksamaan Bentuk Pecahan 3. Pertidaksamaan Bentuk Akar 4. Pertidaksamaan Nilai Mutlak 86 LEMBAR KERJA SISWA 1 Mata Pelajaran : Matematika Uraian Materi
DASAR-DASAR TEORI RUANG HILBERT
 DASAR-DASAR TEORI RUANG HILBERT Herry P. Suryawan 1 Geometri Ruang Hilbert Definisi 1.1 Ruang vektor kompleks V disebut ruang hasilkali dalam jika ada fungsi (.,.) : V V C sehingga untuk setiap x, y, z
DASAR-DASAR TEORI RUANG HILBERT Herry P. Suryawan 1 Geometri Ruang Hilbert Definisi 1.1 Ruang vektor kompleks V disebut ruang hasilkali dalam jika ada fungsi (.,.) : V V C sehingga untuk setiap x, y, z
KALKULUS (IT 131) Fakultas Teknologi Informasi - Universitas Kristen Satya Wacana. Bagian 4. Derivatif ALZ DANNY WOWOR
 KALKULUS (IT 131) Fakultas Teknologi Informasi - Universitas Kristen Satya Wacana Bagian 4 Derivatif ALZ DANNY WOWOR Cakupan Materi A. Defenisi Derivatif B. Rumus-rumus Derivatif C. Aplikasi Derivatif
KALKULUS (IT 131) Fakultas Teknologi Informasi - Universitas Kristen Satya Wacana Bagian 4 Derivatif ALZ DANNY WOWOR Cakupan Materi A. Defenisi Derivatif B. Rumus-rumus Derivatif C. Aplikasi Derivatif
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016. Hendra Gunawan
 MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 3.2 Himpunan Buka dan Himpunan Tutup Titik limit dari suatu himpunan tidak harus merupakan anggota himpunan tersebut. Pada interval
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 3.2 Himpunan Buka dan Himpunan Tutup Titik limit dari suatu himpunan tidak harus merupakan anggota himpunan tersebut. Pada interval
Gambar 1. Gradien garis singgung grafik f
 D. URAIAN MATERI 1. Definisi dan Rumus-rumus Turunan Fungsi a. Definisi Turunan Sala satu masala yang mendasari munculnya kajian tentang turunan adala gradien garis singgung. Peratikan Gambar 1. f(c +
D. URAIAN MATERI 1. Definisi dan Rumus-rumus Turunan Fungsi a. Definisi Turunan Sala satu masala yang mendasari munculnya kajian tentang turunan adala gradien garis singgung. Peratikan Gambar 1. f(c +
FUNGSI KONTINU. sedemikian sehingga jika x adalah titik dari A (c), maka f (x) berada pada Vg (f (c)). (Lihat Gambar 5.1.1).
 FUNGSI KONTINU 51 FUNGSI KONTINU 511 Definisi A R, f: A R, dan c A Kita mengatakan bahwa f kontinu di c jika, diberi persekitaran Vg (f (c)) dari f (c) terdapat persekitaran (c) dari c sedemikian sehingga
FUNGSI KONTINU 51 FUNGSI KONTINU 511 Definisi A R, f: A R, dan c A Kita mengatakan bahwa f kontinu di c jika, diberi persekitaran Vg (f (c)) dari f (c) terdapat persekitaran (c) dari c sedemikian sehingga
DERET FOURIER DAN APLIKASINYA DALAM FISIKA
 Matakuliah: Fisika Matematika DERET FOURIER DAN APLIKASINYA DALAM FISIKA Di S U S U N Oleh : Kelompok VI DEWI RATNA PERTIWI SITEPU (8176175004) RIFKA ANNISA GIRSANG (8176175014) PENDIDIKAN FISIKA REGULER
Matakuliah: Fisika Matematika DERET FOURIER DAN APLIKASINYA DALAM FISIKA Di S U S U N Oleh : Kelompok VI DEWI RATNA PERTIWI SITEPU (8176175004) RIFKA ANNISA GIRSANG (8176175014) PENDIDIKAN FISIKA REGULER
Catatan Kuliah MA1123 KALKULUS ELEMENTER I BAB III. TURUNAN
 BAB III. TURUNAN Kecepatan Sesaat dan Gradien Garis Singgung Turunan dan Hubungannya dengan Kekontinuan Aturan Dasar Turunan Notasi Leibniz dan Turunan Tingkat Tinggi Penurunan Implisit Laju yang Berkaitan
BAB III. TURUNAN Kecepatan Sesaat dan Gradien Garis Singgung Turunan dan Hubungannya dengan Kekontinuan Aturan Dasar Turunan Notasi Leibniz dan Turunan Tingkat Tinggi Penurunan Implisit Laju yang Berkaitan
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
