BAB I PENDAHULUAN 1.1 Latar Belakang
|
|
|
- Adi Indradjaja
- 8 tahun lalu
- Tontonan:
Transkripsi
1 1 BAB I PENDAHULUAN 1.1 Latar Belakang Pada awalnya deret Fourier diperkenalkan oleh Joseph Fourier pada tahun 1807 untuk memecahkan model masalah persamaan panas pada suatu lempeng logam (Fourier, 1878). Meskipun motivasi awal adalah menyelesaikan model tersebut, namun kemudian deret Fourier dikembangkan untuk menyelesaikan banyak permasalahan dalam matematika dan fisika seperti penyelesaian persamaan diferensial biasa maupun parsial. Salah satu permasalahan yang menarik pada deret Fourier adalah tentang kemonotonan koefisien-koefisien deret Fourier, yaitu monoton turun dan konvergen ke nol karena merupakan salah satu syarat cukup agar deret tersebut konvergen seragam. Barisan koefisien dengan sifat monoton turun dan menuju ke nol dari c sin nx. (1.1.1) tersebut dimasukkan dalam klas yang disebut klas MS (monotone sequences). Dalam analisis Fourier, sifat-sifat koefisien deret sinus (1.1.1) pertama kali dibahas oleh Chaundy dan Jollife (1916). Setelah beberapa puluh tahun kemudian Shah (1962), memperluas klas MS dengan cara memperlemah syarat kemonotonan ke dalam suatu klas yang disebut CQMS (classical quasi-monotone sequences). Selanjutnya Garret dkk. (1980) menyatakan bahwa jika {c } bervariasi terbatas (bounded variation) dengan syarat tertentu maka deret (1.1.1) konvergen, kemudian Basar dan Altay (2003) menyatakan bahwa ruang barisan bervariasi terbatas merupakan ruang Banach. Lebih lanjut, beberapa peneliti seperti Stanojevic (1990), Leindler (2001, 2002, 2005, 2007, 2010, 2011), Zhou (1994, 2005, 2007, 2010, 2011), dan Tikhonov (2007, 2008, 2009, 2011) berturut-turut memperlemah syarat monoton klas MS ke dalam klas ORVQMS (O-regularly varying quasimonotone
2 2 sequences), RBVS (rest bounded variation sequences), GBVS (group bounded variation sequences) dan GMS (general monotone sequences). Zhou dkk. (2010) berhasil membuktikan bahwa klas monoton dapat digeneralisasi menjadi klas MVBVS (mean value bounded variation sequence). Lebih lanjut diperoleh MS CQMS RBVS GMS GBVS MVBVS. Jika syarat monoton di dalam klas MVBVS diperlemah lagi maka kekonvergenan seragam deret sius (1.1.1) tidak terjamin. Menurut Zhou dkk. (2010) klas MVBVS merupakan generalisasi terakhir (ultimate generalization) dari klas bervariasi terbatas sisa (rest bounded variation). Namun demikian ternyata Korus (2010) berhasil mematahkan pendapat tersebut dengan memperkenalkan klas baru yang merupakan generalisasi dari klas MVBVS yaitu klas SBVS (supremum bounded variation sequences) dan klas SBVS2 (supremum bounded variation sequences of 2nd type) yang telah berhasil dibuktikan bahwa MVBVS SBVS SBVS2. Pengembangan lebih lanjut Korus (2011) memperkenalkan klas MVBVDS (mean value bounded variation double sequences), SBVDS1 (supremum bounded variation double sequences od 1st type) dan SBVDS2 (supremum bounded variation double sequences of 2nd type), yang merupakan barisan ganda dan masing-masing klas lebih umum daripada klas MVBVS, SBVS dan SBVS2. Sebelum diperkenalkan klas MVBVS dan SBVS Liflyand dan Tikhonov (2009) mengembangkan klas GMS ke GMS (p-general monotone sequence) yang terdiri dari klas monoton barisan bilangan, serta dari klas GM (general monotone) ke klas GM (p-general monotone ) yang merupakan klas fungsi. Salah satu sifat dari klas GMS dan GM adalah bervariasi terbatas (bounded variation) yang merupakan hal penting dalam beberapa topik seperti kekonvergenan deret Fourier (Liflyand dan Tikhonov, 2011). Selanjutnya klas GMS dapat diterapkan untuk masalah aproksimasi deret trigometri terhadap polinomial trigonometri orde n, sedangkan klas GM dapat diterapkan pada keterintegralan tranformasi Fourier. Kemudian Korus (2011) memperkenalkan klas SBVF (supremum bounded variation functions) dan SBVF2 (supremum bounded variation functions of 2nd
3 3 type) yang memuat klas monoton tentang fungsi. Berdasarkan uraian di atas klas GMS dapat digeneralisasi menjadi klas MBVS dan SBVS dalam arah barisan bervariasi terbatas sisa (rest bounded variation). Kemudian dengan adanya klas SBVS2 perlu adanya asumsi yang harus dipenuhi agar klas tersebut terdefinisi dengan baik (well defined) yaitu lim c = 0 untuk klas barisan dan lim f(x) = 0 untuk klas fungsi, maka perlu dilakukan penelitian lebih lanjut dengan menghilangkan asumsi tersebut. Salah satu caranya yaitu dengan menggeneralisasi klas GMS dan GM dalam arah bervariasi-p terbatas sisa (rest bounded p-variation) untuk barisan bilangan tunggal dan ganda maupun fungsi, yang tidak menggunakan asumsi tersebut dan dapat diganti dengan asumsi lain, Dengan mengganti asumsi tersebut akan diperoleh klas yang lebih luas dan selanjutnya akan diteliti sifat-sifat klas tersebut yang berkaitan dengan kekonvergenan seragam deret sinus, sehingga syarat cukup kekonvergen dapat menggunakan asumsi baru tersebut. Selain syarat kekonvergenan menggunakan asumsi baru tersebut, mengingat klas-klas yang diteliti merupakan barisan selisih maka sangat berkaitan dengan klas barisan bervariasi terbatas. Kemudian menurut Moricz (1988), barisan koefisien-koefisien deret Fourier yang bervariasi terbatas dan monoton turun terjamin konvergen. Oleh karena itu diduga pada konstruksi klas baru jika dibatasi pada barisan bervariasi terbatas dengan syarat tertentu, kekonvergenan deret Fourier sinus tejamin. Ada suatu cara untuk membatasi klas barisan pada klas bervariasi terbatas yaitu dengan menggunakan norma tertentu. Kemudian dengan norma tertentu konstruksi klas barisan tersebut merupakan ruang bernorma sehingga klas baru tersebut bervariasi terbatas. Selanjutnya dengan klas baru bervariasi terbatas merupakan ruang Banach terhadap norma tertentu. Hal tersebut digunakan untuk menjamin kekonvergenan deret Fourier sinus. Kemudian karena alasan itu dapat diteliti pula kelengkapan dari ruang barisan tersebut. 1.2 Perumusan Masalah Penelitian Berdasarkan uraian dalam latar belakang, secara umum rumusan masalah penelitian ini adalah: Mengkonstruksi dan menyelidiki sifat-sifat generalisasi klas monoton dari klas GM termasuk kaitannya dengan ruang Banach dengan
4 4 norma tertentu dan konsep-konsep yang terkait di dalamnya serta konsistensinya pada kekonvergenan seragam deret maupun integral sinus. Secara terperinci perumusan masalah penelitian ini adalah mengkaji masalah-masalah sebagai berikut: 1. Generalisasi klas monoton deret tunggal dari klas GM ke klas yang lebih umum dalam arah bervariasi-p terbatas sisa dengan 1 p < beserta syarat cukup kekonvergenan. 2. Generalisasi klas monoton deret ganda dari klas SBVDS dan SBVS2 ke klas yang lebih umum dalam arah bervariasi-p terbatas sisa dengan 1 p < beserta syarat cukup kekonvergenan. 3. Generalisasi klas monoton fungsi dari klas GM ke klas yang lebih umum dalam arah bervariasi-p terbatas sisa dengan 1 p < beserta syarat cukup kekonvergenan. 4. Meneliti struktur dan sifat-sifat dari ruang-ruang generalisasi klas monoton. 1.3 Tujuan Penelitian Tujuan penelitian ini dibagi dalam dua bagian, yaitu tujuan umum dan tujuan khusus. 1) Tujuan umum: a) Ikut mengembangkan bidang matematika. b) Ikut mengembangkan apresiasi matematika di Indonesia. 2) Tujuan khusus. a) Pengembangan klas monoton barisan bilangan tunggal GM ke klas monoton barisan bilangan dalam arah bervariasi-p terbatas sisa dengan 1 p <, mempelajari karakteristik masing-masing klas beserta hubungan antar klas, menyelidiki syarat cukup agar deret sinus tunggal konvergen seragam serta struktur ruang klas baru terhadap norma tertentu dan penerapan dari klas tersebut. b) Pengembangan klas monoton barisan bilangan ganda SBVDS dan SBVS2 masing-masing ke klas monoton barisan bilangan dalam
5 5 arah bervariasi-p terbatas sisa dengan 1 p <, mempelajari karakteristik masing-masing klas beserta hubungan antar klas serta menyelidiki syarat cukup agar deret sinus ganda konvergen seragam dan strukur ruang baru terhadap norma tertentu. c) Pengembangan klas monoton fungsi GM ke klas monoton fungsi dalam arah bervariasi-p terbatas sisa dengan 1 p <, mempelajari karakteristik masing-masing klas beserta hubungan antar klas serta serta menyelidiki syarat cukup agar integral sinus tunggal konvergen seragam, struktur ruang klas baru dengan norma tertentu dan penerapan dari klas tersebut. 1.4 Manfaat Penelitian Berdasarkan tujuan penelitian di atas, manfaat penelitian yang diharapkan adalah sebagai berikut: 1) Memberikan sumbangan pemikiran bagi pengembangan ilmu matematika dalam bidang analisis khususnya klas monoton barisan. 2) Memperluas penerapan matematika analisis khususnya barisan. 1.5 Tinjauan Pustaka Deret Fourier dari suatu fungsi periodik f merupakan deret trigonometri untuk f. Jika f periodik dengan periode 2π dan terintegral pada interval [0,2π] maka koefisien-koefisien Fourier dari deret Fourier dapat dihitung. Selanjutnya timbul pertanyaan apakah deret Fourier yang terjadi sama dengan fungsi semula. Untuk menjawab pertanyaan tersebut beberapa peneliti melakukan beberapa kajian, diantaranya adalah Dirichlet (1829) yang memberikan hasil, jika f periodik dengan periode 2π dan mulus bagian demi bagian, maka deret Fourier tersebut konvergen ke f(x) jika x titik kontinu dan konvergen ke [f(x 0) + f(x + 0)] jika x titik diskontinu. Kemudian Jordan (1881) menyatakan bahwa, Diberikan f fungsi periodik dengan periode 2π, jika f bervariasi terbatas pada interval terbuka I maka deret Fourier tersebut
6 6 konvergen ke [f(x 0) + f(x + 0)] untuk setiap x I dan jika f kontinu maka deret Fourier tersebut konvergen ke f. Selanjutnya Chaundy dan Jollife (1916) mendapat hasil sebagai berikut: Jika c n c n+1 dan c n 0, maka syarat perlu dan cukup agar deret sinus (1.1.1) konvergen seragam ke f adalah nc n 0. Barisan koefisien (1.1.1) dengan sifat monoton turun dan konvergen ke nol tersebut dimasukkan dalam klas yang disebut klas MS (monotone sequences). Beberapa peneliti tertarik untuk menggeneralisasi klas MS dengan syarat deret (1.1.1) tetap konvergen seragam. Pada dasarnya ada dua cara untuk menggeneralisasi klas tersebut. Cara pertama dilakukan berdasarkan tipe barisan-barisan quasi-monoton (quasi-monotone) dan cara kedua berdasarkan barisan bervariasi terbatas sisa (rest bounded variation). Shah (1962) telah memperkenalkan klas barisan quasi monoton standar, dituliskan CQMS (classical quasi monotone sequences), yaitu CQMS = {a } R λ > 0 sehingga a n turun. Klas yang lebih umum dari CQMS adalah klas ORVQMS ( O-regularly varying quasi-monotone sequences) yang diberikan sebagai berikut: ORVQMS = a = {a }: a R, {λ } naik dan a λ turun. Sedangkan penelitian dengan cara kedua untuk memperumum kondisi klas monoton dilakukan dengan cara yang disebut klas bervariasi terbatas sisa (Leindler, 2001), yang dituliskan RBVS (rest bounded variation sequence) dengan RBVS = {a } R C > 0, a a Ca. Klas-klas CQMS dan RBVS tidak dapat dibandingkan dalam arti tidak saling memuat (Leindler, 2002). Kemudian Le dan Zhou ( 2005) mendefinisikan klas baru yang disebut GBVS (group bounded variation sequences) yaitu GBVS = {a } C: N N dan C > 0, a a C maks a.
7 7 Klas GBVS yang dibangun merupakan klas yang lebih luas dari RBVS dan CQMS, yaitu: MS CQMS RBVS GBVS. Setelah melakukan penelitian lebih lanjut, Zhou dan Le (2005) menyimpulkan bahwa klas monoton RBVS mempunyai karakteristik monoton satu sisi (one sided) yaitu: terdapat C > 0 dan k N dengan sifat untuk setiap n k, a Ca dan dikendalikan oleh a. Untuk barisan {a } GBVS dapat ditunjukkan bahwa untuk k n 2k, berlaku a = a + a a + a Ca + a dan hal ini dapat dinyatakan sebagai klas monoton dua sisi (two sided), karena a dikendalikan tidak hanya oleh a tetapi oleh a. Inti perluasan klas RBVS ke klas GBVS adalah perluasan klas monoton satu sisi ke dua sisi. Namun demikian dengan definisi dari GBVS, dapat disimpulkan bahwa a a + a Ca, sehingga a Ca untuk semua k n 2k, yang berarti bahwa syarat keanggotaan di dalam klas GBVS masih satu sisi, dengan a = a a. Selanjutnya pada tahun 2007, Tikhonov mendefinisikan klas GMS (general monotone sequences) sebagai berikut: GMS = {a } C: C > 0, a a C a. Klas GMS masih memuat RBVS tetapi tidak memuat GBVS (Tikhonov, 2008) yaitu MS CQMS RBVS GMS GBVS. Kemudian Yu dan Zhou (2007) memperkenalkan klas NBVS (non-onesided bounded variation sequences) yang merupakan generalisasi dari GBVS.
8 8 Intinya perluasan GBVS ke NBVS adalah perluasan dari klas satu sisi ke klas dua sisi dengan definisi berikut: NBVS = {a } C, a a C ( a + a ) untuk suatu konstanta positif C. Telah dibuktikan bahwa MS CQMS RBVS GMS GBVS NBVS. Generalisasi klas monoton yang termasuk dalam arah bervariasi terbatas sisa masih dapat dikembangkan menjadi klas MVBVS (mean value bounded variation sequences) (Zhou dkk, 2010), yang tetap memenuhi teorema kekonvergenan seragam dari deret (1.1.1), dengan definisi berikut: [] MVBVS = {a } C: C > 0 dan λ 2, a a C n a [ ], dengan [x] menyatakan bilangan bulat terbesar yang kurang dari atau sama dengan x. Klas ini merupakan generalisasi dari klas dua sisi ke klas n sisi (n sided). Klas MBVS tetap mempertahankan teorema klasik dari Chaundy dan Jollife dengan mengganti {c } barisan monoton turun menjadi {c } MVBVS yang dinyatakan sebagai berikut; Jika {c } MVBVS dan c 0, maka syarat perlu dan cukup agar deret (1.1.1) konvergen seragam adalah nb 0 untuk n. Generalisasi klas monoton yang mengacu pada kekonvergenan seragam deret (1.1.1) dalam arah bervariasi terbatas sisa menurut Zhou (2005) sudah berakhir, namun pendapat tersebut berhasil dipatahkan oleh Korus (2010) dengan memperkenalkan klas SBVS (supremum bounded variation sequences) dengan definisi berikut SBVS = C {a } C C > 0 dan γ 1, a n sup [/] a, n γ dan klas SBVS2 (supremum bounded variation sequences of second type) SBVS2 =
9 9 C {a } C C > 0, {b }, a n sup a, n 1, dengan konstanta C, λ dan γ hanya tergantung pada barisan {a } dengan b n. Kemudian Korus (2010) berhasil membuktikan bahwa MVBVS SBVS SBVS2. Lebih lanjut teorema klasik oleh Chaundy dan Jollife masih tetap berlaku jika {c } MVBVS digantikan dengan {c } SBVS2. Selanjutnya Korus (2011) mengembangkan deret sinus ganda untuk dua variabel sebagai berikut. Diberikan a = a C dan diperhatikan deret sinus a sin jx sin ky. (1.5.1) Seperti ide deret sinus (1.1.1) untuk satu variabel, untuk menyelidiki kekonvergenan seragam deret sinus ganda koeisien-koefisien deret (1.5.1) dianggap menjadi anggota klas kemonotonan barisan-barisan ganda. Korus (2010) telah memperkenalkan klas SBVDS1 (supremum bounded variation double sequences of first type) dan SBVDS2 (supremum bounded variation double sequences of second type). Barisan ganda a = a C disebut barisan ganda bervarisi terbatas supremum tipe pertama ditulis SBVSDS1, jika terdapat konstanta C > 0, bilangan bulat λ 2 dan barisan b,, b,, b, masing-masing divergen ke tak hingga dan hanya tergantung a sehingga Δ a C m maks a, m λ, n 1,,, Δ a C maks a n, m 1, n λ,,, Δ a C sup a mn, m, n λ,, dengan a = a a,,
10 10 a = a a,, a = a = a = a a, a, + a,. Selanjutnya barisan ganda a = a C disebut barisan ganda bervariasi terbatas supremum ditulis SBVSDS2, jika terdapat konstanta C > 0, bilangan bulat λ 1 dan barisan naik monoton {b }, yang menuju ke tak hingga dan hanya tergantung a sehingga Δ a C m sup a, m λ, n 1, Δ a C n sup a, m 1, n λ, Δ a C sup a mn, m, n λ. Dengan klas MBVDS dapat dinyatakan teorema baru yang dibuktikan oleh Korus dan Moricz (2009) sebagai berikut: Jika {c } MVBVDS dan kl c 0, untuk k + l maka deret (1.5.1) konvergen biasa (regular) seragam. Lebih lanjut Moricz (2009) mendefinisikan klas MBVF(R ), dan Korus (2011) mendefinisikan klas SBVF(R ) dan SBVF2(R ) sebagai berikut. Fungsi kompleks f yang didefinisikan pada R disebut fungsi (i) (ii) bervariasi terbatas nilai rata-rata (mean bounded variation functions) ditulis MBVF(R ) jika terdapat konstanta-konstanta C, A > 0 dan λ 2 yang hanya tergantung f dan memenuhi untuk a > A. f (x) dx C f(x) dx a bervariasi terbatas supremum (supremum bounded variation functions) ditulis SBVF(R ) jika terdapat konstanta-konstanta C, A > 0 dan λ 2 yang hanya tergantung f dan memenuhi
11 11 (iii) untuk a > A. f (x) dx C a sup / f(x) dx bervariasi terbatas supremum tipe kedua (supremum bounded variation functions of second type) ditulis SBVF2(R ) jika terdapat konstantakonstanta C, A > 0 dan fungsi positif B yang didefinisikan pada [0, ), naik monoton menuju tak hingga dengan B(x) x, hanya tergantung f dan memenuhi untuk a > A. f (x) dx C a sup () f(x) dx Kemudian klas MVBVF(R ) digunakan untuk menyelidiki syarat cukup untuk f: R C dan t R agar barisan integral sinus f(x) sin tx dx = {F (t)} (1.5.2) terbatas seragam pada R dan dikatakan terbatas seragam dari barisan fungsi (1.5.2) berarti terbatas seragam pada setiap interval terbuka I R. Berdasarkan (1.5.2), Moricz (2009) telah menggunakan anggota dari MVBV(R ) untuk membuktikan teorema berikut ; Diberikan f MVBV(R ), (i) Jika f: R C dan I. f terbatas, dengan I: R R (1.5.3) maka barisan integral (1.5.2) terbatas seragam. (ii) Jika f: R [0, ) dan barisan integral (1.5.2) terbatas seragam, maka kondisi (1.5.3) berlaku. Sebelum adanya konsep klas MBVS dan SBVS, Liflyand dan Tikhonov (2009) mengembangkan konsep kemonotonan lain untuk barisan, yaitu klas GMS (general p-monotone sequences) dengan definisi berikut : GMS =
12 12 / (a, β): a = {a } C; β = {β } [0, ), C > 0, a Cβ untuk 1 p <. Berikut ini Teorema untuk klas GMS, dengan p = 1, yang dibuktikan oleh Dyachenco dan Tikhonov (2008). Jika ({c }, β) GMS dan nβ 0 untuk n, maka deret (1.1.1) konvergen seragam pada [0,2π]. Kemudian Liflyand dan Tikhonov (2011), mengembangkan klas untuk fungsi, yaitu klas GM (general p-monotone ): GM = (h, β): β(x) 0; h (,) Cβ(x), untuk semua x R dengan h fungsi komplex yang didefinisikan pada R, β fungsi real non-negatif yang didefinisikan pada R, C suatu konstanta positif dan 1 p <. Selanjutnya mengingat fakta untuk klas barisan tunggal berlaku MS CQMS RBVS GMS MVBVS SBVS SBVS2, untuk barisan ganda berlaku MVBVDS SBVDS1 SBVDS2 dan untuk klas fungsi berlaku MVBF(R ) SBVF(R ) SBVF2(R ), serta perkembangan tentang klas kemonotonan, ditemukan peluang untuk melakukan penelitian lebih lanjut tentang pengembangan klas tersebut baik untuk barisan bilangan maupun fungsi beserta penerapannya. 1.6 Keaslian Penelitian Sejauh penelusuran yang dilakukan Peneliti, belum ditemukan penelitian lanjutan dalam arah sisa bervariasi-p terbatas selain klas GMS dan GM. Mengingat adanya perkembangan tentang klas monoton sehingga akan dilakukan penelitian lebih lanjut tentang klas tersebut baik untuk barisan bilangan maupun fungsi. Selanjutnya berdasarkan kajian yang telah peneliti lakukan, terdapat perbedaan mendasar pada generalisasi klas kemonotonan barisan tunggal dalam arah sisa bervariasi-p terbatas dengan klas-klas sebelumnya yang sudah ada.
13 13 Konstruksi pada klas-klas yang telah ada seperti MS, CQMS, RBVS, GMS, MVBVS, SBVS dan SBVS2 disyaratkan bahwa barisan {a } yang menjadi anggotanya harus memenuhi lim a = 0. Hal ini terjadi supaya pada konstruksi klas SBVS2 dengan barisan {b }, b n memenuhi lim a C lim n sup a < (1.6.1) Karena dengan C n sup a C n sup {([b ] + i) a } a = maks a,, a (), i = 0,1, 2, dan lim a = lim a = 0, sehingga C lim n sup a C lim n sup {(n + i) a } <. Oleh karena itu pada konstruksi generalisasinya seperti pada diagram Gambar yaitu klas NBVS p, MVBVS p, SBVS p, SBVS2 p dan SBVS2 ( ), barisan pengendali a = {a } pada ruas kanan dari (1.6.1) diganti dengan barisan real non-negatif β = {β } dengan asumsi lim β = 0 yang tidak tergantung barisan a = {a }. Dengan demikian asumsi lim a = 0 dihapuskan dan konstruksi baru menjadi klas yang lebih umum. Pada barisan ganda konstruksi baru yaitu klas MVBVDS, SBVDS2 dan SBVSD2 ( ), didefinisikan sejalan dengan konstruksi barisan tunggal yaitu barisan ganda pengendali a = a digantikan dengan barisan ganda real non-negatif β = β dengan asumsi lim β = 0. Akibatnya konstruksi baru bersifat lebih umum.
14 14 Kemudian pada konstruksi klas fungsi yang telah ada seperti klas MVBF(R ), SBVF(R ), SBVF2(R ), disyaratkan bahwa fungsi f yang menjadi anggotanya harus memenuhi lim f(x) = 0. Sejalan dengan klas barisan tunggal supaya pada konstruksi klas SBVF2(R ), yang memenuhi dengan f (x) dx C a sup f(x) dx, (1.6.2) () C lim a sup f(x) dx <. () Selanjutnya pada konstruksi baru yaitu klas NBVF (R ), MVBVF (R ), SBVF p (R + ) dan SBVF2, (R ) fungsi pengendali pada ruas kanan (1.6.2) diganti dengan fungsi real non-negatif β yang didefinisikan pada R dengan asumsi 1.7 Metodologi Penelitian lim β(x) = 0. Penelitian ini dilaksanakan dengan studi literatur, buku-buku pendukung dan jurnal-jurnal ilmiah untuk mendapatkan pemahaman yang baik, kemudian mengembangkan hasil-hasil penelitian terkait dengan penelitian yang sudah dimuat dalam jurnal. Hasil-hasil yang telah dicapai dikomunikasikan dalam seminar nasional maupun internasional. Sebagian hasil penelitian dipublikasikan dalam bentuk prosiding atau dalam jurnal nasional maupun internasional. Secara ringkas metode penelitian yang dilakukan adalah: 1. Menggeneralisasi klas barisan tunggal dari klas GM ke klas monoton barisan bilangan dalam arah sisa bervariasi-p terbatas dengan 1 p <, mempelajari sifat-sifat konstruksi yang baru beserta hubungan antar klas, mempelajari keterkaitan dengan ruang Banach dan penerapan klas tersebut. 2. Menggeneralisasi klas barisan ganda SBVDS dan SBVDS2 masingmasing ke klas monoton barisan bilangan dalam arah sisa bervariasi-p
15 15 terbatas dengan 1 p <, mempelajari sifat-sifat klas dari konstruksi yang baru beserta hubungan antar klas dan mempelajari keterkaitan dengan ruang Banach. 3. Menggeneralisasi konstruksi dari klas fungsi GM ke klas monoton fungsi dalam arah sisa bervariasi-p terbatas dengan 1 p < serta mempelajari sifat-sifat klas yang baru beserta hubungan antar klas, mempelajari keterkaitan dengan ruang Banach dan penerapan klas tersebut. Secara umum penelitian ini terdiri dari tiga tahap dengan uraian berikut. Tahap I Mula-mula dicermati kembali landasan teori yang menjadi dasar dan jembatan dalam menyelesaikan masalah-masalah pada Tahap I ini secara komprehensif, sehingga diperoleh hasil penelitian yang mendasari penelitian tahap berikutnya. Tahap-tahap dan rincian rencana kegiatan penelitian pada tahap ini adalah sebagai berikut. Klas monoton barisan tunggal: Diperhatikan dan diselidiki proses konstruksi tentang klas monoton barisan tunggal. Selanjutnya dengan memperhatikan struktur yang telah ada, dipelajari sifat klas-klas tersebut, keterkaitan dengan ruang Banach separabel dan terapannya dari klas-klas tersebut. Klas monoton barisan ganda: Dengan memperhatikan konstruksi sifat maupun terapan pada klas monoton barisan tunggal akan dipelajari klas monoton barisan ganda, selanjutnya dipelajari sifat barisan ganda dan keterkaitan dengan ruang Banach separabel. Kemonotonan fungsi: Diperhatikan kembali hasil-hasil pada barisan tunggal di atas akan dipelajari klas monoton fungsi yang telah ada beserta sifat klas-klas tersebut, keterkaitan dengan ruang Banach serabel dan terapan klas tersebut.
16 16 Tahap II Tahap ini merupakan bagian utama penelitian ini. Penelitian dilakukan dengan mencermati kembali hasil-hasil yang telah diperoleh dalam Tahap I dan membuat konstruksi baru yang merupakan generalisasi dari konsep klas monoton barisan bilangan yang telah ada. Tahap-tahap dan rincian rencana kegiatan penelitian pada tahap ini adalah sebagai berikut. Generalisasi klas monoton barisan tunggal: Diperhatikan dan diselidiki proses konstruksi dari klas monoton barisan tunggal. Selanjutnya dengan memperhatikan konsep yang sudah ada pada tahap sebelumnya, akan dikonstruksikan definisi baru tentang klas monoton barisan tunggal beserta sifat-sifatnya termasuk keterkaitan dengan ruang Banach dengan norma tertentu. Generalisasi klas monoton barisan ganda: Diperhatikan kembali hasil pembahasan pada barisan tunggal tahap sebelumnya dan konsep klas monoton yang telah ada. Selanjutnya akan dikonstruksikan definisi baru tentang kemonotonan barisan ganda baru beserta sifat-sifatnya termasuk keterkaitan dengan norma tertentu. Generalisasi klas monoton fungsi: Diperhatikan kembali hasil-hasil pada barisan tunggal di atas dan konsep klas monoton yang sudah ada pada tahap sebelumnya. Selanjutnya akan dikonstruksikan definisi baru tentang klas monoton fungsi baru beserta sifatsifatnya termasuk keterkaitan dengan ruang Banach dengan norma tertentu. Tahap III: Dalam tahap ini yang akan dibahas adalah uji kekonvergenan dan beberapa penerapan dari konstruksi baru yang telah diperoleh pada tahap sebelumnya. Tahap-tahap dan rincian rencana kegiatan penelitian pada tahap ini adalah sebagai berikut. Uji kekonvergenan konstruksi baru klas monoton barisan tunggal bilangan pada deret sinus tunggal dan penerapannya. Sesuai dengan tujuan khusus pada peneltian di atas yaitu menyelidiki tentang syarat cukup kekonvergenan seragam pada deret sinus. Dengan menggantikan koefisien deret sinus dengan anggota klas
17 17 monoton barisan tunggal bilangan yang baru dibuktikan kekonvergenan seragam deret tunggal sinus tetap berlaku dengan syarat tertentu. Selanjutnya diselidiki keterkaitan dengan ruang Banach separabel dan penerapan klas tersebut pada masalah aproksimasi, dengan demikian diharapkan dapat lebih memahami konstruksi dari klas monoton barisan tunggal bilangan. Uji kekonvergenan konstruksi baru klas monoton barisan ganda bilangan pada deret sinus ganda. Dengan cara yang sama seperti yang dilakukan pada klas monoton barisan tunggal di atas akan dibuktikan berlakunya kekonvergenan seragam pada deret sinus ganda dengan syarat tertentu. Dengan menggantikan koefisien deret ganda sinus dengan anggota klas monoton barisan ganda bilangan yang baru dengan syarat tertentu sehingga dapat dibuktikan kekonvergenan seragam deret ganda sinus tersebut dan diselidiki keterkaitan dengan ruang Banach separabel. Uji kekonvergenan seragam konstruksi baru klas monoton fungsi pada integral sinus dan penerapannya. Mula-mula diperhatikan cara yang sama seperti yang dilakukan pada konstruksi sebelumnya kemudian diteliti untuk uji kekonvergenan seragam dari konstruksi yang baru dengan syarat syarat tertentu pada integral sinus. Selanjutnya diselidiki keterkaitan dengan ruang Banach separabel dan dibahas penerapan anggota klas tersebut pada keterintegralan transformasi Fourier dan diharapkan dapat memberikan pemahaman yang lebih dalam dari klas monoton fungsi. Secara ringkas alur penelitian yang dilakukan disajikan dalam bentuk diagram pada Gambar Sistematika Penulisan Tulisan ini terdiri dari tujuh bab, yang telah diawali dengan Bab I yang mengemukakan latar belakang, perumusan masalah penelitian, tujuan penelitian, manfaat penelitian, tinjauan pustaka, keaslian penelitian, metodologi penelitian dan sistematika penulisan. Selanjutnya dalam Bab II akan ditinjau konsep-konsep dasar tentang barisan, deret, konsep klas monoton barisan, konsep klas monoton fungsi, yang merupakan landasan teori tulisan ini. Inti tulisan akan disampaikan dalam Bab III hingga Bab VI. Dalam Bab III akan dibahas konstruksi baru tentang klas monoton barisan tunggal bilangan.
18 18 Pembahasan Bab III meliputi konstruksi klas barisan bervariasi-p terbatas supremum (supremum bounded p-variation sequences) dan sifat-sifatnya, generalisasi barisan selisih dari klas barisan tersebut dan sifat-sifatnya, kekonvergenan seragam deret sinus tunggal dan keterkaitan dengan ruang Banach separabel. Bab IV membahas tentang klas barisan ganda, yang meliputi klas barisan ganda bervariasi-p terbatas supremum (supremum bounded p-variation double sequences) dan sifat-sifatnya, generalisasi barisan selisih dari klas barisan klas barisan tersebut dan sifat-sifatnya, dan kekonvergenan seragam deret sinus ganda beserta keterkaitan dengan ruang banach separabel. Bab V membahas tentang klas fungsi, yang meliputi klas fungsi bervariasi-p terbatas supremum (supremum bounded p-variation functions), relasi antar klas dan sifat-sifatnya, kekonvergenan seragam integral sinus beserta keterkaitan dengan ruang Banach. Bab VI membahas beberapa penerapan dari klas monoton, yang meliputi penerapan dari klas monoton barisan tunggal bilangan dan penerapan dari klas monoton fungsi. Akhirnya dalam Bab VII akan diberikan beberapa kesimpulan dan masalah terbuka.
19 19 KLAS MONOTON QUASI MONOTONE CQMS, ORVQMS REST BOUNDED VARIATION GMS REST BOUNDED VARIATION RBVS, GBVS, NBVS, MVBVS REST BOUNDED p-variation GMS& GMS P REST BOUNDED p-variation GM & GM P GENERALISASI GENERALISASI ke klas barisan ke klas fungsi NBVS, MVBVS, SBVS2, NBVF (R ), MVBVF (R ), SBVF, (R ), SBVF2, (R ) GENERALISASI ke klas double sequences MVBVDS, SBVDS2 GENERALISASI Barisan selisih barisan tunggal SBVS2 ( ) GENERALISASI Barisan selisih barisan ganda SBVSD2 ( ) Syarat cukup kekonvergenan seragam berkaitan dengan ruang Banach PENERAPAN Pada masalah aproksimasi PENERAPAN Pada transformasi Fourier Gambar Alur penelitian yang dilakukan (yang diarsir).
Relasi Inklusi Klas Barisan p-supremum Bounded Variation Sequences
 NATURAL-A Journal of Scientific Modeling & Computation, Volume 1 No.1 2013 1 Relasi Inklusi Klas Barisan p-supremum Bounded Variation Sequences Moch. Aruman Imron 1, Ch. Rini Indrati 2, Widodo 3 1 Jurusan
NATURAL-A Journal of Scientific Modeling & Computation, Volume 1 No.1 2013 1 Relasi Inklusi Klas Barisan p-supremum Bounded Variation Sequences Moch. Aruman Imron 1, Ch. Rini Indrati 2, Widodo 3 1 Jurusan
BAB IV DERET FOURIER
 BAB IV DERET FOURIER 4.1 Fungsi Periodik Fungsi f(x) dikatakan periodik dengan perioda P, jika untuk semua harga x berlaku: f (x + P) = f (x) ; P adalah konstanta positif. Harga terkecil dari P > 0 disebut
BAB IV DERET FOURIER 4.1 Fungsi Periodik Fungsi f(x) dikatakan periodik dengan perioda P, jika untuk semua harga x berlaku: f (x + P) = f (x) ; P adalah konstanta positif. Harga terkecil dari P > 0 disebut
DASAR-DASAR TEORI RUANG HILBERT
 DASAR-DASAR TEORI RUANG HILBERT Herry P. Suryawan 1 Geometri Ruang Hilbert Definisi 1.1 Ruang vektor kompleks V disebut ruang hasilkali dalam jika ada fungsi (.,.) : V V C sehingga untuk setiap x, y, z
DASAR-DASAR TEORI RUANG HILBERT Herry P. Suryawan 1 Geometri Ruang Hilbert Definisi 1.1 Ruang vektor kompleks V disebut ruang hasilkali dalam jika ada fungsi (.,.) : V V C sehingga untuk setiap x, y, z
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
DERET FOURIER DAN APLIKASINYA DALAM FISIKA
 Matakuliah: Fisika Matematika DERET FOURIER DAN APLIKASINYA DALAM FISIKA Di S U S U N Oleh : Kelompok VI DEWI RATNA PERTIWI SITEPU (8176175004) RIFKA ANNISA GIRSANG (8176175014) PENDIDIKAN FISIKA REGULER
Matakuliah: Fisika Matematika DERET FOURIER DAN APLIKASINYA DALAM FISIKA Di S U S U N Oleh : Kelompok VI DEWI RATNA PERTIWI SITEPU (8176175004) RIFKA ANNISA GIRSANG (8176175014) PENDIDIKAN FISIKA REGULER
BAB 1 PENDAHULUAN. 1 ; untuk k = n 0 ; untuk k n. e [n]
![BAB 1 PENDAHULUAN. 1 ; untuk k = n 0 ; untuk k n. e [n] BAB 1 PENDAHULUAN. 1 ; untuk k = n 0 ; untuk k n. e [n]](/thumbs/68/58947103.jpg) BAB 1 PENDAHULUAN 1.1. Latar Belakang Barisan bilangan real adalah suatu fungsi bernilai real yang didefinisikan pada himpunan N = 0, 1, 2,.... Dengan kata lain, barisan bilangan real adalah suatu fungsi
BAB 1 PENDAHULUAN 1.1. Latar Belakang Barisan bilangan real adalah suatu fungsi bernilai real yang didefinisikan pada himpunan N = 0, 1, 2,.... Dengan kata lain, barisan bilangan real adalah suatu fungsi
4. Deret Fourier pada Interval Sebarang dan Aplikasi
 4. Deret Fourier pada Interval Sebarang dan Aplikasi Kita telah mempelajari bagaimana menguraikan fungsi periodik dengan periode 2 yang terdefinisi pada R sebagai deret Fourier. Deret trigonometri tersebut
4. Deret Fourier pada Interval Sebarang dan Aplikasi Kita telah mempelajari bagaimana menguraikan fungsi periodik dengan periode 2 yang terdefinisi pada R sebagai deret Fourier. Deret trigonometri tersebut
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
BAB II KAJIAN TEORI. pada penulisan bab III. Materi yang diuraikan berisi tentang definisi, teorema, dan
 BAB II KAJIAN TEORI Pada bab ini akan dibahas beberapa hal yang digunakan sebagai landasan pada penulisan bab III. Materi yang diuraikan berisi tentang definisi, teorema, dan beberapa kajian matematika,
BAB II KAJIAN TEORI Pada bab ini akan dibahas beberapa hal yang digunakan sebagai landasan pada penulisan bab III. Materi yang diuraikan berisi tentang definisi, teorema, dan beberapa kajian matematika,
BAB I PENDAHULUAN Latar Belakang Masalah
 BAB I PENDAHULUAN 1.1. Latar Belakang Masalah Analisis merupakan salah satu cabang matematika yang mempelajari antara lain barisan, limit, deret, kekontinuan, kekonvergenan, integral, dan yang lainnya.
BAB I PENDAHULUAN 1.1. Latar Belakang Masalah Analisis merupakan salah satu cabang matematika yang mempelajari antara lain barisan, limit, deret, kekontinuan, kekonvergenan, integral, dan yang lainnya.
5.1 Fungsi periodik, fungsi genap, fungsi ganjil
 Bab 5 DERET FOURIER Pada Bab sebelumnya kita telah membahas deret Taylor. Syarat fungsi agar dapat diekspansi ke dalam deret Taylor adalah fungsi tersebut harus terdiferensial pada setiap tingkat. Untuk
Bab 5 DERET FOURIER Pada Bab sebelumnya kita telah membahas deret Taylor. Syarat fungsi agar dapat diekspansi ke dalam deret Taylor adalah fungsi tersebut harus terdiferensial pada setiap tingkat. Untuk
4. Deret Fourier pada Interval Sebarang dan Aplikasi
 8 Hendra Gunawan 4. Deret Fourier pada Interval Sebarang dan Aplikasi Kita telah mempelajari bagaimana menguraikan fungsi periodik dengan periode 2 yang terdefinisi pada R sebagai deret Fourier. Deret
8 Hendra Gunawan 4. Deret Fourier pada Interval Sebarang dan Aplikasi Kita telah mempelajari bagaimana menguraikan fungsi periodik dengan periode 2 yang terdefinisi pada R sebagai deret Fourier. Deret
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
0. Pendahuluan. 0.1 Notasi dan istilah, bilangan kompleks
 0. Pendahuluan Analisis Fourier mempelajari berbagai teknik menganalisis sebuah fungsi dengan menguraikannya sebagai deret atau integral fungsi tertentu (yang sifat-sifatnya telah kita kenal dengan baik,
0. Pendahuluan Analisis Fourier mempelajari berbagai teknik menganalisis sebuah fungsi dengan menguraikannya sebagai deret atau integral fungsi tertentu (yang sifat-sifatnya telah kita kenal dengan baik,
10. Transformasi Fourier
 10. Transformasi Fourier Dalam beberapa bab ke depan, kita akan membahas transformasi Fourier, sifatsifatnya, dan aplikasinya. Seperti halnya pada pembahasan deret Fourier, pendekatan yang diambil dalam
10. Transformasi Fourier Dalam beberapa bab ke depan, kita akan membahas transformasi Fourier, sifatsifatnya, dan aplikasinya. Seperti halnya pada pembahasan deret Fourier, pendekatan yang diambil dalam
3 LIMIT DAN KEKONTINUAN
 Menurut Bartle dan Sherbet (1994), Analisis matematika secara umum dipahami sebagai tubuh matematika yang dibangun oleh berbagai konsep limit. Pada bab sebelumnya kita telah mempelajari limit barisan,
Menurut Bartle dan Sherbet (1994), Analisis matematika secara umum dipahami sebagai tubuh matematika yang dibangun oleh berbagai konsep limit. Pada bab sebelumnya kita telah mempelajari limit barisan,
3 LIMIT DAN KEKONTINUAN
 Menurut Bartle dan Sherbet (994), Analisis matematika secara umum dipahami sebagai tubuh matematika yang dibangun oleh berbagai konsep limit. Pada bab sebelumnya kita telah mempelajari limit barisan, kekonvergenan
Menurut Bartle dan Sherbet (994), Analisis matematika secara umum dipahami sebagai tubuh matematika yang dibangun oleh berbagai konsep limit. Pada bab sebelumnya kita telah mempelajari limit barisan, kekonvergenan
UJI KONVERGENSI. Januari Tim Dosen Kalkulus 2 TPB ITK
 UJI KONVERGENSI Januari 208 Tim Dosen Kalkulus 2 TPB ITK Uji Integral Teorema 3 Jika + k= u k adalah deret dengan suku-suku tak negatif, dan jika ada suatu konstanta M sedemikian hingga s n = u + u 2 +
UJI KONVERGENSI Januari 208 Tim Dosen Kalkulus 2 TPB ITK Uji Integral Teorema 3 Jika + k= u k adalah deret dengan suku-suku tak negatif, dan jika ada suatu konstanta M sedemikian hingga s n = u + u 2 +
BAB III KEKONVERGENAN LEMAH
 BAB III KEKONVERGENAN LEMAH Bab ini membahas inti kajian tugas akhir. Di dalamnya akan dibahas mengenai kekonvergenan lemah beserta sifat-sifat yang terkait dengannya. Sifatsifat yang dikaji pada bab ini
BAB III KEKONVERGENAN LEMAH Bab ini membahas inti kajian tugas akhir. Di dalamnya akan dibahas mengenai kekonvergenan lemah beserta sifat-sifat yang terkait dengannya. Sifatsifat yang dikaji pada bab ini
Ayundyah Kesumawati. April 29, Prodi Statistika FMIPA-UII. Deret Tak Terhingga. Ayundyah. Barisan Tak Hingga. Deret Tak Terhingga
 Kesumawati Prodi Statistika FMIPA-UII April 29, 2015 Akar Barisan a 1, a 2, a 3, a 4,... adalah susunan bilangan-bilangan real yang teratur, satu untuk setiap bilangan bulat positif. adalah fungsi yang
Kesumawati Prodi Statistika FMIPA-UII April 29, 2015 Akar Barisan a 1, a 2, a 3, a 4,... adalah susunan bilangan-bilangan real yang teratur, satu untuk setiap bilangan bulat positif. adalah fungsi yang
KONSEP DASAR PERSAMAAN DIFERENSIAL
 KONSEP DASAR PERSAMAAN DIFERENSIAL A. PENGERTIAN PERSAMAAN DIFERENSIAL Dalam pelajaran kalkulus, kita telah berkenalan dan mengkaji berbagai macam metode untuk mendiferensialkan suatu fungsi (dasar). Sebagai
KONSEP DASAR PERSAMAAN DIFERENSIAL A. PENGERTIAN PERSAMAAN DIFERENSIAL Dalam pelajaran kalkulus, kita telah berkenalan dan mengkaji berbagai macam metode untuk mendiferensialkan suatu fungsi (dasar). Sebagai
BAB I PENDAHULUAN. umum ruang metrik dan memperluas pengertian klasik dari ruang Euclidean R n, sehingga
 BAB I PENDAHULUAN 1.1 Latar Belakang dan Permasalahan Permulaan munculnya analisis fungsional didasari oleh permasalahan pada kurang memadainya metode analitik klasik pada fisika dan astronomi matematika.
BAB I PENDAHULUAN 1.1 Latar Belakang dan Permasalahan Permulaan munculnya analisis fungsional didasari oleh permasalahan pada kurang memadainya metode analitik klasik pada fisika dan astronomi matematika.
Barisan dan Deret Agus Yodi Gunawan
 Barisan dan Deret Agus Yodi Gunawan Barisan. Definisi. Barisan tak hingga adalah suatu fungsi dengan daerah asalnya himpunan bilangan bulat positif dan daerah kawannya himpunan bilangan real. Notasi untuk
Barisan dan Deret Agus Yodi Gunawan Barisan. Definisi. Barisan tak hingga adalah suatu fungsi dengan daerah asalnya himpunan bilangan bulat positif dan daerah kawannya himpunan bilangan real. Notasi untuk
16. BARISAN FUNGSI. 16.1 Barisan Fungsi dan Kekonvergenan Titik Demi Titik
 16. BARISAN FUNGSI 16.1 Barisan Fungsi dan Kekonvergenan Titik Demi Titik Bila pada bab-bab sebelumnya kita membahas fungsi sebagai sebuah objek individual, maka pada bab ini dan selanjutnya kita akan
16. BARISAN FUNGSI 16.1 Barisan Fungsi dan Kekonvergenan Titik Demi Titik Bila pada bab-bab sebelumnya kita membahas fungsi sebagai sebuah objek individual, maka pada bab ini dan selanjutnya kita akan
III. HASIL DAN PEMBAHASAN
 III. HASIL DAN PEMBAHASAN 3.1 Perumusan Masalah Misalkan adalah proses Poisson nonhomogen pada interval dengan fungsi intensitas yang tidak diketahui. Fungsi intensitas diasumsikan terintegralkan lokal
III. HASIL DAN PEMBAHASAN 3.1 Perumusan Masalah Misalkan adalah proses Poisson nonhomogen pada interval dengan fungsi intensitas yang tidak diketahui. Fungsi intensitas diasumsikan terintegralkan lokal
BAB IV REDUKSI BIAS PADA PENDUGAAN
 BAB IV REDUKSI BIAS PADA PENDUGAAN 4.1. Asimtotik Orde-2 Berdasarkan hasil simulasi pada Helmers dan Mangku (2007) kasus kernel seragam, aproksimasi asimtotik orde pertama pada ragam dan bias, gagal memprediksikan
BAB IV REDUKSI BIAS PADA PENDUGAAN 4.1. Asimtotik Orde-2 Berdasarkan hasil simulasi pada Helmers dan Mangku (2007) kasus kernel seragam, aproksimasi asimtotik orde pertama pada ragam dan bias, gagal memprediksikan
3 LIMIT DAN KEKONTINUAN
 Menurut Bartle dan Sherbet (1994), Analisis matematika secara umum dipahami sebagai tubuh matematika yang dibangun dari berbagai konsep limit. Pada bab sebelumnya kita telah mempelajari limit barisan,
Menurut Bartle dan Sherbet (1994), Analisis matematika secara umum dipahami sebagai tubuh matematika yang dibangun dari berbagai konsep limit. Pada bab sebelumnya kita telah mempelajari limit barisan,
Deret Binomial. Ayundyah Kesumawati. June 25, Prodi Statistika FMIPA-UII. Ayundyah (UII) Deret Binomial June 25, / 14
 Deret Binomial Ayundyah Kesumawati Prodi Statistika FMIPA-UII June 25, 2015 Ayundyah (UII) Deret Binomial June 25, 2015 1 / 14 Pendahuluan Deret Binomial Kita telah mengenal Rumus Binomial. Untuk bilangan
Deret Binomial Ayundyah Kesumawati Prodi Statistika FMIPA-UII June 25, 2015 Ayundyah (UII) Deret Binomial June 25, 2015 1 / 14 Pendahuluan Deret Binomial Kita telah mengenal Rumus Binomial. Untuk bilangan
BAB I PENDAHULUAN Latar Belakang Masalah
 BAB I PENDAHULUAN Pada bab ini akan dibahas mengenai latar belakang masalah, perumusan masalah, batasan masalah, maksud dan tujuan penulisan, tinjauan pustaka serta sistematika penulisan skirpsi ini. 1.1.
BAB I PENDAHULUAN Pada bab ini akan dibahas mengenai latar belakang masalah, perumusan masalah, batasan masalah, maksud dan tujuan penulisan, tinjauan pustaka serta sistematika penulisan skirpsi ini. 1.1.
Definisi 1 Deret Tak Hingga adalah suatu ekspresi yang dapat dinyatakan dalam bentuk:
 DERET TAK HINGGA Definisi 1 Deret Tak Hingga adalah suatu ekspresi yang dapat dinyatakan dalam bentuk: u k = u 1 + u 2 + u 3 + + u k + Bilangan-bilangan u 1, u 2, u 3, disebut suku-suku dalam deret tersebut.
DERET TAK HINGGA Definisi 1 Deret Tak Hingga adalah suatu ekspresi yang dapat dinyatakan dalam bentuk: u k = u 1 + u 2 + u 3 + + u k + Bilangan-bilangan u 1, u 2, u 3, disebut suku-suku dalam deret tersebut.
BAB 4 KEKONSISTENAN PENDUGA DARI FUNGSI SEBARAN DAN FUNGSI KEPEKATAN WAKTU TUNGGU DARI PROSES POISSON PERIODIK DENGAN TREN FUNGSI PANGKAT
 29 BAB 4 KEKONSISTENAN PENDUGA DARI FUNGSI SEBARAN DAN FUNGSI KEPEKATAN WAKTU TUNGGU DARI PROSES POISSON PERIODIK DENGAN TREN FUNGSI PANGKAT 4.1 Perumusan Penduga Misalkan adalah proses Poisson nonhomogen
29 BAB 4 KEKONSISTENAN PENDUGA DARI FUNGSI SEBARAN DAN FUNGSI KEPEKATAN WAKTU TUNGGU DARI PROSES POISSON PERIODIK DENGAN TREN FUNGSI PANGKAT 4.1 Perumusan Penduga Misalkan adalah proses Poisson nonhomogen
BAB 3 REVIEW SIFAT-SIFAT STATISTIK PENDUGA KOMPONEN PERIODIK
 BAB 3 REVIEW SIFAT-SIFAT STATISTIK PENDUGA KOMPONEN PERIODIK 3. Perumusan Penduga Misalkan N adalah proses Poisson non-homogen pada interval 0, dengan fungsi intensitas yang tidak diketahui. Fungsi intensitas
BAB 3 REVIEW SIFAT-SIFAT STATISTIK PENDUGA KOMPONEN PERIODIK 3. Perumusan Penduga Misalkan N adalah proses Poisson non-homogen pada interval 0, dengan fungsi intensitas yang tidak diketahui. Fungsi intensitas
BAB I PENDAHULUAN. : k N} dan A(m) menyatakan banyaknya m suku pertama (x n ) yang menjadi suku (x nk ), maka A(m)
 BAB I PENDAHULUAN 1.1. Latar Belakang Masalah Konvergensi barisan bilangan real mempunyai banyak peranan dan aplikasi yang cukup penting pada beberapa bidang matematika, antara lain pada teori optimisasi,
BAB I PENDAHULUAN 1.1. Latar Belakang Masalah Konvergensi barisan bilangan real mempunyai banyak peranan dan aplikasi yang cukup penting pada beberapa bidang matematika, antara lain pada teori optimisasi,
BAB I PENDAHULUAN Latar Belakang Masalah
 BAB I PENDAHULUAN 1.1. Latar Belakang Masalah Pemetaan linear merupakan salah satu jenis pemetaan yang dikenal dalam bidang matematika, khususnya dalam bidang matematika analisis. Diberikan ruang vektor
BAB I PENDAHULUAN 1.1. Latar Belakang Masalah Pemetaan linear merupakan salah satu jenis pemetaan yang dikenal dalam bidang matematika, khususnya dalam bidang matematika analisis. Diberikan ruang vektor
BAB V KEKONVERGENAN BARISAN PADA DAN KETERKAITAN DENGAN. Pada subbab 4.1 telah dibahas beberapa sifat dasar yang berlaku pada koleksi
 BAB V KEKONVERGENAN BARISAN PADA DAN KETERKAITAN DENGAN Pada subbab 4.1 telah dibahas beberapa sifat dasar yang berlaku pada koleksi semua fungsi yang terintegralkan Lebesgue, 1. Sebagaimana telah dirumuskan
BAB V KEKONVERGENAN BARISAN PADA DAN KETERKAITAN DENGAN Pada subbab 4.1 telah dibahas beberapa sifat dasar yang berlaku pada koleksi semua fungsi yang terintegralkan Lebesgue, 1. Sebagaimana telah dirumuskan
-LIMIT- -KONTINUITAS- -BARISAN- Agustina Pradjaningsih, M.Si. Jurusan Matematika FMIPA UNEJ
 -LIMIT- -KONTINUITAS- -BARISAN- Agustina Pradjaningsih, M.Si. Jurusan Matematika FMIPA UNEJ [email protected] Konsep Limit Fungsi mendasari pembentukan kalkulus dierensial dan integral. Konsep ini
-LIMIT- -KONTINUITAS- -BARISAN- Agustina Pradjaningsih, M.Si. Jurusan Matematika FMIPA UNEJ [email protected] Konsep Limit Fungsi mendasari pembentukan kalkulus dierensial dan integral. Konsep ini
BAB I PENDAHULUAN. 1.1 Latar Belakang Masalah
 BAB I PENDAHULUAN 1.1 Latar Belakang Masalah Teori titik tetap merupakan teori matematika yang sering digunakan untuk menjamin eksistensi solusi masalah nilai awal dan syarat batas persamaan diferensial
BAB I PENDAHULUAN 1.1 Latar Belakang Masalah Teori titik tetap merupakan teori matematika yang sering digunakan untuk menjamin eksistensi solusi masalah nilai awal dan syarat batas persamaan diferensial
Pertemuan ke-10: UJI PERBANDINGAN, DERET BERGANTI TANDA, KEKONVERGENAN MUTLAK, UJI RASIO, DAN UJI AKAR
 Pertemuan ke-0: UJI PERBANDINGAN, DERET BERGANTI TANDA, KEKONVERGENAN MUTLAK, UJI RASIO, DAN UJI AKAR Departemen Matematika FMIPA IPB Bogor, 205 (Departemen Matematika FMIPA IPB) Kalkulus II Bogor, 205
Pertemuan ke-0: UJI PERBANDINGAN, DERET BERGANTI TANDA, KEKONVERGENAN MUTLAK, UJI RASIO, DAN UJI AKAR Departemen Matematika FMIPA IPB Bogor, 205 (Departemen Matematika FMIPA IPB) Kalkulus II Bogor, 205
BAGIAN KEDUA. Fungsi, Limit dan Kekontinuan, Turunan
 BAGIAN KEDUA Fungsi, Limit dan Kekontinuan, Turunan 51 52 Hendra Gunawan Pengantar Analisis Real 53 6. FUNGSI 6.1 Fungsi dan Grafiknya Konsep fungsi telah dipelajari oleh Gottfried Wilhelm von Leibniz
BAGIAN KEDUA Fungsi, Limit dan Kekontinuan, Turunan 51 52 Hendra Gunawan Pengantar Analisis Real 53 6. FUNGSI 6.1 Fungsi dan Grafiknya Konsep fungsi telah dipelajari oleh Gottfried Wilhelm von Leibniz
SYARAT DIRICHLET. 1, 1 < t < 0
 SYARAT DIRICHET Misalkan f t adalah fungsi yang licin bagian demi bagian, berperioda, maka deret fourier konvergen. Ke nilai f t untuk setiap titik di mana fungsi f kontinu.. Ke nilai f t + + f t bagi
SYARAT DIRICHET Misalkan f t adalah fungsi yang licin bagian demi bagian, berperioda, maka deret fourier konvergen. Ke nilai f t untuk setiap titik di mana fungsi f kontinu.. Ke nilai f t + + f t bagi
BAB III INTEGRAL LEBESGUE. Pada bab sebelumnya telah disebutkan bahwa ruang dibangun oleh
 BAB III INTEGRAL LEBESGUE Pada bab sebelumnya telah disebutkan bahwa ruang dibangun oleh fungsi-fungsi terukur dan memenuhi sifat yang berkaitan dengan integral Lebesgue. Kajian mengenai keterukuran suatu
BAB III INTEGRAL LEBESGUE Pada bab sebelumnya telah disebutkan bahwa ruang dibangun oleh fungsi-fungsi terukur dan memenuhi sifat yang berkaitan dengan integral Lebesgue. Kajian mengenai keterukuran suatu
BAB I PENDAHULUAN ( )
 BAB I PENDAHULUAN 1.1. Latar Belakang Persamaan diferensial merupakan persamaan yang melibatkan turunan dari satu atau lebih variabel tak bebas terhadap satu atau lebih variabel bebas dan dituliskan dengan
BAB I PENDAHULUAN 1.1. Latar Belakang Persamaan diferensial merupakan persamaan yang melibatkan turunan dari satu atau lebih variabel tak bebas terhadap satu atau lebih variabel bebas dan dituliskan dengan
Pertemuan 1 dan 2 KONSEP DASAR PERSAMAAN DIFERENSIAL
 Pertemuan 1 dan 2 KONSEP DASAR PERSAMAAN DIFERENSIAL A. PENGERTIAN PERSAMAAN DIFERENSIAL Dalam pelajaran kalkulus, kita telah berkenalan dan mengkaji berbagai macam metode untuk mendiferensialkan suatu
Pertemuan 1 dan 2 KONSEP DASAR PERSAMAAN DIFERENSIAL A. PENGERTIAN PERSAMAAN DIFERENSIAL Dalam pelajaran kalkulus, kita telah berkenalan dan mengkaji berbagai macam metode untuk mendiferensialkan suatu
URAIAN POKOK-POKOK PERKULIAHAN
 Pertemuan ke-: 10, 11, dan 12 Penyusun : Kosim Rukmana Materi: Barisan Bilangan Real 7. Barisan dan Limit Barisan 6. Teorema Limit Barisan 7. Barisan Monoton URAIAN POKOK-POKOK PERKULIAHAN 7. Barisan dan
Pertemuan ke-: 10, 11, dan 12 Penyusun : Kosim Rukmana Materi: Barisan Bilangan Real 7. Barisan dan Limit Barisan 6. Teorema Limit Barisan 7. Barisan Monoton URAIAN POKOK-POKOK PERKULIAHAN 7. Barisan dan
Dari contoh di atas fungsi yang tak diketahui dinyatakan dengan y dan dianggap
 BAB II TINJAUAN PUSTAKA A. Persamaan Diferensial Definisi 2.1 Persamaan diferensial Persamaan diferensial adalah suatu persamaan yang memuat variabel bebas, variabel tak bebas, dan derivatif-derivatif
BAB II TINJAUAN PUSTAKA A. Persamaan Diferensial Definisi 2.1 Persamaan diferensial Persamaan diferensial adalah suatu persamaan yang memuat variabel bebas, variabel tak bebas, dan derivatif-derivatif
8. Deret Fourier yang Diperumum dan Hampiran Terbaik di L 2 (a, b)
 8. Deret Fourier yang Diperumum dan Hampiran Terbaik di L (a, b) 8.1 Deret Fourier yang Diperumum Jika {ϕ n } 1 adalah basis ortonormal untuk L (a, b) dan f L (a, b), maka f, ϕ n disebut koefisien Fourier
8. Deret Fourier yang Diperumum dan Hampiran Terbaik di L (a, b) 8.1 Deret Fourier yang Diperumum Jika {ϕ n } 1 adalah basis ortonormal untuk L (a, b) dan f L (a, b), maka f, ϕ n disebut koefisien Fourier
DASAR-DASAR ANALISIS MATEMATIKA
 (Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: [email protected]. November 19, 2007 Secara geometris, f kontinu di suatu titik berarti bahwa grafiknya tidak terputus
(Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: [email protected]. November 19, 2007 Secara geometris, f kontinu di suatu titik berarti bahwa grafiknya tidak terputus
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016. Hendra Gunawan
 MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 3. Topologi Garis Bilangan Real 3.1 Teori Limit Limit, supremum, dan infimum Titik limit 3.2 Himpunan Buka dan Himpunan Tutup 3.3
MA5031 Analisis Real Lanjut Semester I, Tahun 2015/2016 Hendra Gunawan 3. Topologi Garis Bilangan Real 3.1 Teori Limit Limit, supremum, dan infimum Titik limit 3.2 Himpunan Buka dan Himpunan Tutup 3.3
BAB III TRANSFORMASI MATRIKS DERET DIRICHLET HOLOMORFIK. A. Transformasi Matriks Mengawetkan Kekonvergenan
 BAB III TRANSFORMASI MATRIKS DERET DIRICHLET HOLOMORFIK A. Transformasi Matriks Mengawetkan Kekonvergenan Pada bagian A ini pembahasan dibagi menjadi dua bagian, yang pertama membahas mengenai transformasi
BAB III TRANSFORMASI MATRIKS DERET DIRICHLET HOLOMORFIK A. Transformasi Matriks Mengawetkan Kekonvergenan Pada bagian A ini pembahasan dibagi menjadi dua bagian, yang pertama membahas mengenai transformasi
DERET TAK HINGGA. Contoh deret tak hingga :,,, atau. Barisan jumlah parsial, dengan. Definisi Deret tak hingga,
 DERET TAK HINGGA Contoh deret tak hingga :,,, atau. Barisan jumlah parsial, dengan Definisi Deret tak hingga,, konvergen dan mempunyai jumlah S, apabila barisan jumlah jumlah parsial konvergen menuju S.
DERET TAK HINGGA Contoh deret tak hingga :,,, atau. Barisan jumlah parsial, dengan Definisi Deret tak hingga,, konvergen dan mempunyai jumlah S, apabila barisan jumlah jumlah parsial konvergen menuju S.
MA3231 Analisis Real
 MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
MA3231 Analisis Real Hendra Gunawan* *http://hgunawan82.wordpress.com Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA Program Studi S1 Matematika ITB, Semester II 2016/2017
Modul KALKULUS MULTIVARIABEL II
 Modul KALKULUS MULTIVARIABEL II Oleh Ayundyah Kesumawati, S.Si., M.Si. (Program Studi Statistika) FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS ISLAM INDONESIA 26 Daftar Isi Daftar Isi iv Daftar
Modul KALKULUS MULTIVARIABEL II Oleh Ayundyah Kesumawati, S.Si., M.Si. (Program Studi Statistika) FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS ISLAM INDONESIA 26 Daftar Isi Daftar Isi iv Daftar
II. TINJAUAN PUSTAKA. Turunan fungsi f adalah fungsi lain f (dibaca f aksen ) yang nilainya pada ( ) ( ) ( )
 II. TINJAUAN PUSTAKA 2.1 Definisi Turunan Turunan fungsi f adalah fungsi lain f (dibaca f aksen ) yang nilainya pada sebarang bilangan c adalah asalkan limit ini ada. Jika limit ini memang ada, maka dikatakan
II. TINJAUAN PUSTAKA 2.1 Definisi Turunan Turunan fungsi f adalah fungsi lain f (dibaca f aksen ) yang nilainya pada sebarang bilangan c adalah asalkan limit ini ada. Jika limit ini memang ada, maka dikatakan
Fungsi Gamma. Pengantar Matematika Teknik Kimia. Muthia Elma
 Fungsi Gamma Pengantar Matematika Teknik Kimia Muthia Elma Fungsi Gamma Defenisi Merupakan salah satu fungsi khusus yang biasanya disajikan dalam pembahasan kalkulus tingkat lanjut Dalam aplikasinya fungsi
Fungsi Gamma Pengantar Matematika Teknik Kimia Muthia Elma Fungsi Gamma Defenisi Merupakan salah satu fungsi khusus yang biasanya disajikan dalam pembahasan kalkulus tingkat lanjut Dalam aplikasinya fungsi
BAB I PENDAHULUAN. 1.1 Latar Belakang
 BAB I PENDAHULUAN 1.1 Latar Belakang Dalam ilmu matematika, banyak pembahasan di bidang analisis dan topologi yang memerlukan pengertian ruang Hilbert. Ruang Hilbert merupakan konsep abstrak yang mendasari
BAB I PENDAHULUAN 1.1 Latar Belakang Dalam ilmu matematika, banyak pembahasan di bidang analisis dan topologi yang memerlukan pengertian ruang Hilbert. Ruang Hilbert merupakan konsep abstrak yang mendasari
BAB V KESIMPULAN. Berdasarkan uraian pada Bab III dan Bab IV maka dapat disimpulkan sebagai
 BAB V KESIMPULAN Berdasarkan uraian ada Bab III dan Bab IV maka daat disimulkan sebagai berikut 1. Keluarga emetaan K C,δ (R, R) dan L C,δ (R, R) adalah beberaa bentuk keluarga emetaan demi linear dari
BAB V KESIMPULAN Berdasarkan uraian ada Bab III dan Bab IV maka daat disimulkan sebagai berikut 1. Keluarga emetaan K C,δ (R, R) dan L C,δ (R, R) adalah beberaa bentuk keluarga emetaan demi linear dari
12. Teorema Inversi Fourier dan Transformasi Fourier di L 2 (R)
 1. Teorema Inversi Fourier dan Transformasi Fourier di L (R) 1.1 Teorema Inversi Fourier Dari hasil hitung-hitungan kasar di awal bagian ke-10, kita ingin membuktikan bahwa, dalam kondisi tertentu, kita
1. Teorema Inversi Fourier dan Transformasi Fourier di L (R) 1.1 Teorema Inversi Fourier Dari hasil hitung-hitungan kasar di awal bagian ke-10, kita ingin membuktikan bahwa, dalam kondisi tertentu, kita
SISTEM BILANGAN REAL
 DAFTAR ISI 1 SISTEM BILANGAN REAL 1 1.1 Sifat Aljabar Bilangan Real..................... 1 1.2 Sifat Urutan Bilangan Real..................... 6 1.3 Nilai Mutlak dan Jarak Pada Bilangan Real............
DAFTAR ISI 1 SISTEM BILANGAN REAL 1 1.1 Sifat Aljabar Bilangan Real..................... 1 1.2 Sifat Urutan Bilangan Real..................... 6 1.3 Nilai Mutlak dan Jarak Pada Bilangan Real............
11. Konvolusi. Misalkan f dan g fungsi yang terdefinisi pada R. Konvolusi dari f dan g adalah fungsi f g yang didefinisikan sebagai.
 11. Konvolusi Operasi konvolusi yang akan kita bahas di sini sebetulnya pernah kita jumpai pada pembahasan deret Fourier (ketika membuktikan kekonvergenan jumlah parsialnya). Operasi konvolusi merupakan
11. Konvolusi Operasi konvolusi yang akan kita bahas di sini sebetulnya pernah kita jumpai pada pembahasan deret Fourier (ketika membuktikan kekonvergenan jumlah parsialnya). Operasi konvolusi merupakan
Ringkasan Kalkulus 2, Untuk dipakai di ITB 1
 Ringkasan Kalkulus 2, Untuk dipakai di ITB Deret Tak Hingga Pada bagian ini akan dibicarakan penjumlahan berbentuk a +a 2 + +a n + dengan a n R Sebelumnya akan dibahas terlebih dahulu pengertian barisan
Ringkasan Kalkulus 2, Untuk dipakai di ITB Deret Tak Hingga Pada bagian ini akan dibicarakan penjumlahan berbentuk a +a 2 + +a n + dengan a n R Sebelumnya akan dibahas terlebih dahulu pengertian barisan
II. TINJAUAN PUSTAKA. variabel x, sehingga nilai y bergantung pada nilai x. Adanya relasi kebergantungan
 II. TINJAUAN PUSTAKA 2.1 Persamaan Diferensial Differential Equation Fungsi mendeskripsikan bahwa nilai variabel y ditentukan oleh nilai variabel x, sehingga nilai y bergantung pada nilai x. Adanya relasi
II. TINJAUAN PUSTAKA 2.1 Persamaan Diferensial Differential Equation Fungsi mendeskripsikan bahwa nilai variabel y ditentukan oleh nilai variabel x, sehingga nilai y bergantung pada nilai x. Adanya relasi
Memahami definisi barisan tak hingga dan deret tak hingga, dan juga dapat menentukan
 4 BARISAN TAK HINGGA DAN DERET TAK HINGGA JUMLAH PERTEMUAN : 5 PERTEMUAN TUJUAN INSTRUKSIONAL KHUSUS : Memahami definisi barisan tak hingga dan deret tak hingga, dan juga dapat menentukan kekonvergenan
4 BARISAN TAK HINGGA DAN DERET TAK HINGGA JUMLAH PERTEMUAN : 5 PERTEMUAN TUJUAN INSTRUKSIONAL KHUSUS : Memahami definisi barisan tak hingga dan deret tak hingga, dan juga dapat menentukan kekonvergenan
MA1201 KALKULUS 2A Do maths and you see the world
 Catatan Kuliah MA20 KALKULUS 2A Do maths and you see the world disusun oleh Khreshna I.A. Syuhada, MSc. PhD. Kelompok Keilmuan STATISTIKA - FMIPA Institut Teknologi Bandung 203 Catatan kuliah ini ditulis
Catatan Kuliah MA20 KALKULUS 2A Do maths and you see the world disusun oleh Khreshna I.A. Syuhada, MSc. PhD. Kelompok Keilmuan STATISTIKA - FMIPA Institut Teknologi Bandung 203 Catatan kuliah ini ditulis
BAB I PENDAHULUAN. 1.1 Latar Belakang Masalah
 BAB I PENDAHULUAN 1.1 Latar Belakang Masalah Integral merupakan salah satu konsep penting dalam matematika dan banyak aplikasinya. Dalam kehidupan sehari-hari integral dapat diaplikasikan dalam berbagai
BAB I PENDAHULUAN 1.1 Latar Belakang Masalah Integral merupakan salah satu konsep penting dalam matematika dan banyak aplikasinya. Dalam kehidupan sehari-hari integral dapat diaplikasikan dalam berbagai
PENGANTAR MATEMATIKA TEKNIK 1. By : Suthami A
 PENGANTAR MATEMATIKA TEKNIK 1 By : Suthami A MATEMATIKA TEKNIK 1??? MATEMATIKA TEKNIK 1??? MATEMATIKA TEKNIK Matematika sebagai ilmu dasar yang digunakan sebagai alat pemecahan masalah di bidang keteknikan
PENGANTAR MATEMATIKA TEKNIK 1 By : Suthami A MATEMATIKA TEKNIK 1??? MATEMATIKA TEKNIK 1??? MATEMATIKA TEKNIK Matematika sebagai ilmu dasar yang digunakan sebagai alat pemecahan masalah di bidang keteknikan
11. FUNGSI MONOTON (DAN FUNGSI KONVEKS)
 11. FUNGSI MONOTON (DAN FUNGSI KONVEKS) 11.1 Definisi dan Limit Fungsi Monoton Misalkan f terdefinisi pada suatu himpunan H. Kita katakan bahwa f naik pada H apabila untuk setiap x, y H dengan x < y berlaku
11. FUNGSI MONOTON (DAN FUNGSI KONVEKS) 11.1 Definisi dan Limit Fungsi Monoton Misalkan f terdefinisi pada suatu himpunan H. Kita katakan bahwa f naik pada H apabila untuk setiap x, y H dengan x < y berlaku
7. Transformasi Fourier
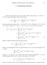 Pengantar Analisis Fourier dan eori Aproksimasi 33 7. ransformasi Fourier Pada bab sebelumnya kita telah melihat bahwa setiap fungsi f L 1 ([0, 1] L ([0, 1] dapat dinyatakan sebagai deret Fourier f(x =
Pengantar Analisis Fourier dan eori Aproksimasi 33 7. ransformasi Fourier Pada bab sebelumnya kita telah melihat bahwa setiap fungsi f L 1 ([0, 1] L ([0, 1] dapat dinyatakan sebagai deret Fourier f(x =
MODUL RESPONSI MAM 4222 KALKULUS IV
 MODUL RESPONSI MAM 4222 KALKULUS IV Mata Kuliah Wajib 2 sks untuk mahasiswa Program Studi Matematika Oleh Dr. WURYANSARI MUHARINI KUSUMAWINAHYU, M.Si. PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS
MODUL RESPONSI MAM 4222 KALKULUS IV Mata Kuliah Wajib 2 sks untuk mahasiswa Program Studi Matematika Oleh Dr. WURYANSARI MUHARINI KUSUMAWINAHYU, M.Si. PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS
BARISAN BILANGAN REAL
 BAB 2 BARISAN BILANGAN REAL Di sekolah menengah barisan diperkenalkan sebagai kumpulan bilangan yang disusun menurut pola tertentu, misalnya barisan aritmatika dan barisan geometri. Biasanya barisan dan
BAB 2 BARISAN BILANGAN REAL Di sekolah menengah barisan diperkenalkan sebagai kumpulan bilangan yang disusun menurut pola tertentu, misalnya barisan aritmatika dan barisan geometri. Biasanya barisan dan
2 BARISAN BILANGAN REAL
 2 BARISAN BILANGAN REAL Di sekolah menengah barisan diperkenalkan sebagai kumpulan bilangan yang disusun menurut "pola" tertentu, misalnya barisan aritmatika dan barisan geometri. Biasanya barisan dan
2 BARISAN BILANGAN REAL Di sekolah menengah barisan diperkenalkan sebagai kumpulan bilangan yang disusun menurut "pola" tertentu, misalnya barisan aritmatika dan barisan geometri. Biasanya barisan dan
Penerapan Aproksimasi Fejer dalam Membuktikan Teorema Weierstrass
 Jurnal Matematika, Statistika & Komputasi 1 Penerapan Aproksimasi Fejer dalam Membuktikan Teorema Weierstrass Islamiyah Abbas 1, Naimah Aris 2, Jusmawati M 3. Abstrak Dalam skripsi ini dibahas pembuktian
Jurnal Matematika, Statistika & Komputasi 1 Penerapan Aproksimasi Fejer dalam Membuktikan Teorema Weierstrass Islamiyah Abbas 1, Naimah Aris 2, Jusmawati M 3. Abstrak Dalam skripsi ini dibahas pembuktian
Prosiding Matematika ISSN:
 Prosiding Matematika ISSN: 2460-6464 Pengaruh Faktor Sigma Pada Ekspansi Fungsi Periodik Melalui Eksplorasi Deret Fourier Termodifikasi The Influence of Sigma Factor on The Expansion of The Periodic Function
Prosiding Matematika ISSN: 2460-6464 Pengaruh Faktor Sigma Pada Ekspansi Fungsi Periodik Melalui Eksplorasi Deret Fourier Termodifikasi The Influence of Sigma Factor on The Expansion of The Periodic Function
II. LANDASAN TEORI ( ) =
 II. LANDASAN TEORI 2.1 Fungsi Definisi 2.1.1 Fungsi Bernilai Real Fungsi bernilai real adalah fungsi yang domain dan rangenya adalah himpunan bagian dari real. Definisi 2.1.2 Limit Fungsi Jika adalah suatu
II. LANDASAN TEORI 2.1 Fungsi Definisi 2.1.1 Fungsi Bernilai Real Fungsi bernilai real adalah fungsi yang domain dan rangenya adalah himpunan bagian dari real. Definisi 2.1.2 Limit Fungsi Jika adalah suatu
3. Kekonvergenan Deret Fourier
 3. Kekonvergenan Deret Fourier Sekarang kita akan membahas kekonvergenan deret Fourier, khususnya kekonvergenan titik demi titik. Melalui Contoh 2 yang dibahas pada bab sebelumnya kita mengetahui bahwa
3. Kekonvergenan Deret Fourier Sekarang kita akan membahas kekonvergenan deret Fourier, khususnya kekonvergenan titik demi titik. Melalui Contoh 2 yang dibahas pada bab sebelumnya kita mengetahui bahwa
BAB I PENDAHULUAN Latar Belakang Masalah
 BAB I PENDAHULUAN 1.1. Latar Belakang Masalah Integral tipe Stieltjes merupakan salah satu topik yang banyak dipelajari dalam matematika analisis. Beberapa di antaranya adalah integral Riemann-Stieltjes,
BAB I PENDAHULUAN 1.1. Latar Belakang Masalah Integral tipe Stieltjes merupakan salah satu topik yang banyak dipelajari dalam matematika analisis. Beberapa di antaranya adalah integral Riemann-Stieltjes,
II. TINJAUAN PUSTAKA. dan Integral Bawah Darboux, Integral Darboux, Teorema Bolzano Weierstrass,
 II. TINJAUAN PUSTAKA Dalam bab ini akan dibahas beberapa konsep mendasar meliputi Integral Atas dan Integral Bawah Darboux, Integral Darboux, Teorema Bolzano Weierstrass, serta teorema-teorema yang mendukung
II. TINJAUAN PUSTAKA Dalam bab ini akan dibahas beberapa konsep mendasar meliputi Integral Atas dan Integral Bawah Darboux, Integral Darboux, Teorema Bolzano Weierstrass, serta teorema-teorema yang mendukung
LIMIT DAN KEKONTINUAN
 LIMIT DAN KEKONTINUAN Departemen Matematika FMIPA IPB Bogor, 2012 (Departemen Matematika FMIPA IPB) Kalkulus I Bogor, 2012 1 / 37 Topik Bahasan 1 Limit Fungsi 2 Hukum Limit 3 Kekontinuan Fungsi (Departemen
LIMIT DAN KEKONTINUAN Departemen Matematika FMIPA IPB Bogor, 2012 (Departemen Matematika FMIPA IPB) Kalkulus I Bogor, 2012 1 / 37 Topik Bahasan 1 Limit Fungsi 2 Hukum Limit 3 Kekontinuan Fungsi (Departemen
Deret Fourier. (Pertemuan XI) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya. Fungsi Genap dan Fungsi Ganjil
 TKS 4007 Matematika III Deret Fourier (Pertemuan XI) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya Fungsi Genap dan Fungsi Ganjil Perhitungan koefisien-koefisien Fourier sering kali
TKS 4007 Matematika III Deret Fourier (Pertemuan XI) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya Fungsi Genap dan Fungsi Ganjil Perhitungan koefisien-koefisien Fourier sering kali
BAGIAN PERTAMA. Bilangan Real, Barisan, Deret
 BAGIAN PERTAMA Bilangan Real, Barisan, Deret 2 Hendra Gunawan Pengantar Analisis Real 3 0. BILANGAN REAL 0. Bilangan Real sebagai Bentuk Desimal Dalam buku ini pembaca diasumsikan telah mengenal dengan
BAGIAN PERTAMA Bilangan Real, Barisan, Deret 2 Hendra Gunawan Pengantar Analisis Real 3 0. BILANGAN REAL 0. Bilangan Real sebagai Bentuk Desimal Dalam buku ini pembaca diasumsikan telah mengenal dengan
DASAR-DASAR ANALISIS MATEMATIKA
 (Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: [email protected]. December 26, 2007 Misalkan f kontinu pada interval [a, b]. Apakah masuk akal untuk membahas luas daerah
(Bekal untuk Para Sarjana dan Magister Matematika) Dosen FMIPA - ITB E-mail: [email protected]. December 26, 2007 Misalkan f kontinu pada interval [a, b]. Apakah masuk akal untuk membahas luas daerah
RUANG LIPSCHITZ. Departemen Pendidikan Matematika FPMIPA UPI. *Surel: : (, ) Ϝ
 RUANG LIPSCHITZ Muhammad Rifqi Agustian 1), Rizky Rosjanuardi 2), Endang Cahya 3) 1), 2), 3) Departemen Pendidikan Matematika FPMIPA UPI *Surel: [email protected] ABSTRAK. Diberikan ruang
RUANG LIPSCHITZ Muhammad Rifqi Agustian 1), Rizky Rosjanuardi 2), Endang Cahya 3) 1), 2), 3) Departemen Pendidikan Matematika FPMIPA UPI *Surel: [email protected] ABSTRAK. Diberikan ruang
BAB II PENGANTAR SOLUSI PERSOALAN FISIKA MENURUT PENDEKATAN ANALITIK DAN NUMERIK
 BAB II PENGANTAR SOLUSI PERSOALAN FISIKA MENURUT PENDEKATAN ANALITIK DAN NUMERIK Tujuan Instruksional Setelah mempelajari bab ini pembaca diharapkan dapat: 1. Menjelaskan cara penyelesaian soal dengan
BAB II PENGANTAR SOLUSI PERSOALAN FISIKA MENURUT PENDEKATAN ANALITIK DAN NUMERIK Tujuan Instruksional Setelah mempelajari bab ini pembaca diharapkan dapat: 1. Menjelaskan cara penyelesaian soal dengan
SIFAT KELENGKAPAN RUANG METRIK BERNILAI KOMPLEKS
 Prosiding Seminar Nasional Matematika dan Pembelajarannya. Jurusan Matematika, FMIPA UM. 13 Agustus 016 SIFAT KELENGKAPAN RUANG METRIK BERNILAI KOMPLEKS Dahliatul Hasanah FMIPA Universitas Negeri Malang
Prosiding Seminar Nasional Matematika dan Pembelajarannya. Jurusan Matematika, FMIPA UM. 13 Agustus 016 SIFAT KELENGKAPAN RUANG METRIK BERNILAI KOMPLEKS Dahliatul Hasanah FMIPA Universitas Negeri Malang
BAB I PENDAHULUAN. Integral Lebesgue merupakan suatu perluasan dari integral Riemann.
 BAB I PENDAHULUAN 1.1 Latar Belakang Masalah Integral Lebesgue merupakan suatu perluasan dari integral Riemann. Sebagaimana telah diketahui, pengkonstruksian integral Riemann dilakukan dengan cara pemartisian
BAB I PENDAHULUAN 1.1 Latar Belakang Masalah Integral Lebesgue merupakan suatu perluasan dari integral Riemann. Sebagaimana telah diketahui, pengkonstruksian integral Riemann dilakukan dengan cara pemartisian
BAB I DERIVATIF (TURUNAN)
 BAB I DERIVATIF (TURUNAN) Pada bab ini akan dipaparkan pengertian derivatif suatu fungsi, beberapa sifat aljabar derivatif, aturan rantai, dan derifativ fungsi invers. A. Pengertian Derivatif Pengertian
BAB I DERIVATIF (TURUNAN) Pada bab ini akan dipaparkan pengertian derivatif suatu fungsi, beberapa sifat aljabar derivatif, aturan rantai, dan derifativ fungsi invers. A. Pengertian Derivatif Pengertian
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI A. Matriks 1. Pengertian Matriks Definisi II. A. 1 Matriks didefinisikan sebagai susunan segi empat siku- siku dari bilangan- bilangan yang diatur dalam baris dan kolom (Anton, 1987:22).
BAB II LANDASAN TEORI A. Matriks 1. Pengertian Matriks Definisi II. A. 1 Matriks didefinisikan sebagai susunan segi empat siku- siku dari bilangan- bilangan yang diatur dalam baris dan kolom (Anton, 1987:22).
Ayundyah Kesumawati. April 29, Prodi Statistika FMIPA-UII. Uji Deret Positif. Ayundyah. Uji Integral. Uji Komparasi. Uji Rasio.
 Uji Uji Deret Kesumawati Prodi Statistika FMIPA-UII April 29, 2015 Uji Deret Uji Deret yang mempunyai suku-suku positif menjadi bahasan pada uji integral ini. Uji integral ini menggunakan ide dimana suatu
Uji Uji Deret Kesumawati Prodi Statistika FMIPA-UII April 29, 2015 Uji Deret Uji Deret yang mempunyai suku-suku positif menjadi bahasan pada uji integral ini. Uji integral ini menggunakan ide dimana suatu
Penerapan Aproksimasi Fejer dalam Membuktikan Teorema Weierstrass
 Vol. 11, No. 2, 139-148, Januari 2015 Penerapan Aproksimasi Fejer dalam Membuktikan Teorema Weierstrass NaimahAris 1, Jusmawati M 2,Islamiyah Abbas 3, Abstrak Dalam tulisan ini dibahas pembuktian teorema
Vol. 11, No. 2, 139-148, Januari 2015 Penerapan Aproksimasi Fejer dalam Membuktikan Teorema Weierstrass NaimahAris 1, Jusmawati M 2,Islamiyah Abbas 3, Abstrak Dalam tulisan ini dibahas pembuktian teorema
INTISARI KALKULUS 2. Penyusun: Drs. Warsoma Djohan M.Si. Open Source. Not For Commercial Use
 INTISARI KALKULUS 2 Penyusun: Drs. Warsoma Djohan M.Si. Program Studi Matematika - FMIPA Institut Teknologi Bandung Januari 200 Pengantar Kalkulus & 2 merupakan matakuliah wajib tingkat pertama bagi semua
INTISARI KALKULUS 2 Penyusun: Drs. Warsoma Djohan M.Si. Program Studi Matematika - FMIPA Institut Teknologi Bandung Januari 200 Pengantar Kalkulus & 2 merupakan matakuliah wajib tingkat pertama bagi semua
SISTEM BILANGAN REAL
 DAFTAR ISI SISTEM BILANGAN REAL. Sifat Aljabar Bilangan Real......................2 Sifat Urutan Bilangan Real..................... 6.3 Nilai Mutlak dan Jarak Pada Bilangan Real.............4 Supremum
DAFTAR ISI SISTEM BILANGAN REAL. Sifat Aljabar Bilangan Real......................2 Sifat Urutan Bilangan Real..................... 6.3 Nilai Mutlak dan Jarak Pada Bilangan Real.............4 Supremum
BAB III FUNGSI TERUKUR LEBESGUE. Setelah dibahas mengenai ukuran Lebesgue dan beberapa sifatnya pada
 BAB III FUNGSI TERUKUR LEBESGUE Setelah dibahas mengenai ukuran Lebesgue dan beberapa sifatnya pada Bab II, selanjutnya pada bab ini akan dipelajari gagasan mengenai fungsi terukur Lebesgue. Gagasan mengenai
BAB III FUNGSI TERUKUR LEBESGUE Setelah dibahas mengenai ukuran Lebesgue dan beberapa sifatnya pada Bab II, selanjutnya pada bab ini akan dipelajari gagasan mengenai fungsi terukur Lebesgue. Gagasan mengenai
EKSISTENSI TITIK TETAP DARI SUATU TRANSFORMASI LINIER PADA RUANG BANACH
 EKSISTENSI TITIK TETAP DARI SUATU TRANSFORMASI LINIER PADA RUANG BANACH Nur Aeni Prodi Matematika, Fakultas Sains dan Teknologi, UINAM nuraeniayatullah@gmailcom Info: Jurnal MSA Vol 3 No 1 Edisi: Januari
EKSISTENSI TITIK TETAP DARI SUATU TRANSFORMASI LINIER PADA RUANG BANACH Nur Aeni Prodi Matematika, Fakultas Sains dan Teknologi, UINAM nuraeniayatullah@gmailcom Info: Jurnal MSA Vol 3 No 1 Edisi: Januari
OPERATOR PADA RUANG BARISAN TERBATAS
 OPERATOR PADA RUANG BARISAN TERBATAS Muslim Ansori *,Tiryono 2, Suharsono S 2,Dorrah Azis 2 Jurusan Matematika FMIPA Universitas Lampung,2 Jln. Soemantri Brodjonegoro No Bandar Lampung email: [email protected]
OPERATOR PADA RUANG BARISAN TERBATAS Muslim Ansori *,Tiryono 2, Suharsono S 2,Dorrah Azis 2 Jurusan Matematika FMIPA Universitas Lampung,2 Jln. Soemantri Brodjonegoro No Bandar Lampung email: [email protected]
DEFINISI TIPE RIEMANN UNTUK INTEGRAL LEBESGUE 1. Drajad Maknawi 2 dan Muslich 3 Jurusan Matematika FMIPA UNS. Abstrak
 DEFINISI TIPE RIEMANN UNTUK INTEGRAL LEBESGUE 1 An-2 1. PENDAHULUAN Drajad Maknawi 2 dan Muslich 3 Jurusan Matematika FMIPA UNS Abstrak Tujuan dari tulisan ini adalah membahas tentang integral Lebesgue
DEFINISI TIPE RIEMANN UNTUK INTEGRAL LEBESGUE 1 An-2 1. PENDAHULUAN Drajad Maknawi 2 dan Muslich 3 Jurusan Matematika FMIPA UNS Abstrak Tujuan dari tulisan ini adalah membahas tentang integral Lebesgue
Bab 16. LIMIT dan TURUNAN. Motivasi. Limit Fungsi. Fungsi Turunan. Matematika SMK, Bab 16: Limit dan Turunan 1/35
 Bab 16 Grafik LIMIT dan TURUNAN Matematika SMK, Bab 16: Limit dan 1/35 Grafik Pada dasarnya, konsep limit dikembangkan untuk mengerjakan perhitungan matematis yang melibatkan: nilai sangat kecil; Matematika
Bab 16 Grafik LIMIT dan TURUNAN Matematika SMK, Bab 16: Limit dan 1/35 Grafik Pada dasarnya, konsep limit dikembangkan untuk mengerjakan perhitungan matematis yang melibatkan: nilai sangat kecil; Matematika
BAB I PENDAHULUAN 1.1. Latar Belakang Masalah
 BAB I PENDAHULUAN 1.1. Latar Belakang Masalah Ilmu matematika merupakan ilmu dasar yang digunakan di berbagai bidang. Teori titik tetap merupakan salah satu cabang dalam ilmu matematika, khususnya matematika
BAB I PENDAHULUAN 1.1. Latar Belakang Masalah Ilmu matematika merupakan ilmu dasar yang digunakan di berbagai bidang. Teori titik tetap merupakan salah satu cabang dalam ilmu matematika, khususnya matematika
CNH2B4 / KOMPUTASI NUMERIK
 CNH2B4 / KOMPUTASI NUMERIK TIM DOSEN KK MODELING AND COMPUTATIONAL EXPERIMENT 1 REVIEW KALKULUS & KONSEP ERROR Fungsi Misalkan A adalah himpunan bilangan. Fungsi f dengan domain A adalah sebuah aturan
CNH2B4 / KOMPUTASI NUMERIK TIM DOSEN KK MODELING AND COMPUTATIONAL EXPERIMENT 1 REVIEW KALKULUS & KONSEP ERROR Fungsi Misalkan A adalah himpunan bilangan. Fungsi f dengan domain A adalah sebuah aturan
