BAB 2 DISTRIBUSI INDUK DAN DISTRIBUSI SAMPEL
|
|
|
- Djaja Tan
- 8 tahun lalu
- Tontonan:
Transkripsi
1 BAB DISTRIBUSI IDUK DA DISTRIBUSI SAMEL.. EDAHULUA Jika suatu bsaran mmiliki nilai ssungguhnya sdangkan hasil ukurnya adalah maka kita mngharapkan hasil pngamatan mndkati, namun knyataannya tidak slalu dmikian. Jika dilakukan pngukuran brulang mungkin hasilnya brbda dari hasil ukur prtama. Jika pngukuran diulangi sampai banyak kali maka akan diprolh sbaran data. Ada data yang tlalu kcil, ada yang trlalu bsar. Walaupun dmikian kita brharap smua data hasil ukur masih brada di skitar nilai sbnarnya asalkan kita dapat mmprbaiki ralat sistmatis. Jika dilakukan pngukuran sampai tak hingga kali maka kita dapat mlukiskan distribusi data yang ssungguhnya. amun sayangnya hal ini tidak mungkin dilakukan dan bisanya hanya dalam hipotsis. Distribusi ini disbut distribusi induk. Untuk data yang diprolh dari pngukuran dalam umlah trbatas, maka distribusinya mrupakan distribusi sampl. Jika umlah pngukuran mndkati tak hingga maka distribusi sampl mndkati distribusi induk a kali b kali Gambar.. Distribusi data dngan kali pngukuran a, 3 kali pngukuran b
2 Gambar.. Histogram pngukuran panang balok. Kurva gaussian yaitu garis pnuh diprolh dari prhitungan dngan rata-rata =9,9 cm dan dviasi standar s =,5 cm. Kurva garis putus-putus mnyatakan distribusi induk dngan rata-rata =, cm dan dviasi standar =,5 cm. Contoh: Mahasiswa mngukur panang balok sbanyak kali. Hasil pngamatannya stlah dikorksi dngan ralat sistmatis brada diantara 8 cm dan bbrapa pngamatan hasilnya sama. Gambar mnyatakan histogram frkunsi pngukuran. Sumbu y mnyatakan umlah pngukuran. Jika hasil pngukuran brupa distribusi dngan ksalahan acak maka bntuknya mngikuti Gaussian atau distribusi ksalahan normal. Sumbu digambar mulai dari -d/ +d/. Jika kurva dinormalisasi shingga luas darah di bawah kurva samadngan maka disbut fungsi distribusi probabilitas. Untuk mnyatakan paramtr dari distribusi induk digunakan huruf Yunani sdangkan untuk mnyatakan paramtr distribusi sampl digunakan huruf latin. aramtr distribusi ksprimn sampl akan sama dngan paramtr distribusi induk ika umlah pngukuran mncapai batas tak hingga. Jika ksprimn dilakukan sbanyak kali maka paramtr induk = lim paramtr ksprimn Jika dilakukan pngukuran sbanyak dan masing-masing pngukuran dibri labl,...,,, 3 maka umlah dari sluruh pngukuran adalah: i i 3...
3 Untuk pnydrhanaan biasa ditulis dngan: i.. MEA, MEDIA DA MODUS Rata-rata untuk populasi sampl: i. Man untuk populasi induk: lim i. Man sama dngan nilai rata-rata dari. Gambar.3 Distribusi asimtrik yang mnggambarakan posisi man, mdian dan modus dari variabl. Mdian dari populasi induk / mrupakan nilai tngah dari populasi induk. Adanya / mmbuat sparoh dari data lbih kcil dari / dan sparoh data lbih bsar dari /. Jadi /.3 i / i / Modus adalah nilai yang paling sring muncul most probabl valu, ma..3. DEVIASI Dviasi.4 ma ma i dari smua pngukuran didfinisikan sbagai slisih antara i dan : i dngan nilai rata-rata distribusi induk 3
4 i i.5 Dalam prhitungan, dviasi biasanya dihitung trhadap man dan bukan trhadap mdian atau modus. Rata-rata dviasi i harus sama dngan nol. lim lim lim i i.6 Rata-rata mutlak dviasi didfinisikan sbagai rata-rata dari harga mutlak dviasi: lim i.7 Dviasi rata-rata mrupakan ukuran pnybaran pngamatan yang diharapkan di skitar man. aramtr lain yang lbih mudah digunakan scara analitik dan lbih mncrminkan pnybaran pngamatan adalah dviasi standar. Varian didfinisikan sbagai limit rata-rata dari kuadrat dviasi trhadap nilai : lim i lim i.8 Dviasi standar adalah akar varian. Ruas kanan prs..8 sring diungkapkan dngan rata-rata dari kuadrat, minus kuadrat rata-rata. Dalam mkanika kuantum dituliskan. Dviasi standar mrupakan rms akar kuadrat rata-rata dari dviasi. Untuk populasi sampl, dviasi standar kuadrat dinyatakan dngan: atau dviasi standar s i.9 s i dimana faktor - pada pnybut untuk mnyatakan bahwa paramtr ditntukan dari data dan bukan paramtr bbas di luar data..4 MEA DA DEVIASI STADAR DARI DISTRIBUSI ROBABILITAS Dfinisi dan standar dviasi trkait dngan distribusi induk dari populasi induk. Fungsi probabilitas didfinisikan sdmikian rupa shingga pada batas umlah 4
5 pngamatan yang sangat bsar, proporsi mnghasilkan nilai antara dan +d dibrikan olh d = d. d pngamatan trhadap variabl yang ilai man mrupakan nilai harap dari atau ditulis, dan varian mrupakan nilai harap dari kuadrat dviasi dari trhadap, atau ditulis. ilai harap smbarang fungsi, f didfinisikan sbagai rata-rata brbobot dari f mliputi sluruh nilai yang mungkin dari variabl, dimana stiap nilai f dibri bobot dngan distribusi rapat probabilitas. Distribusi diskrit Jika fungsi probabilitas mrupakan fungsi diskrit dari nilai obsrvabl, maka umlah sluruh pngamatan individual i pada prs.. diganti dngan umlah sluruh nilai ROBABILITAS pngamatan, dikalikan dngan banyaknya pngamatan trsbut yang diharapkan tradi. Jika trdapat n kmungkinan nilai obsrvabl yang brbda dan ditulis sbagai dngan indk bralan dari sampai n tanpa nilai yang sama, maka dari pngamatan total dapat diprolh umlah pngamatan bagi stiap obsrvabl sbanyak. Slanutnya man dapat dinyatakan: lim lim i n n lim. Bandingkan dngan distribusi frkunsi: fi f i i fi i f i i Dngan cara yang sama, varian pada prs..8 dapat dinyatakan dalam bntuk fungsi probabilitas mnadi: n n lim lim i i. Umumnya nilai harap dari smbarang fungsi f dinyatakan dngan: f f. n 5
6 Contoh: Di dalam klas trdiri dari 4 orang dngan sbaran umur sbagai brikut: o, Umur, Jumlah, Jumlah 6 4 Ungkapan tsbut dapat dinyatakan dngan = 4 = = 5 = 3 = 6 = 3 4 = = 5 = 4 = 6 = 5 = 5 4 rtanyaan: Brapakah pluang ssorang brumur 5 tahun? Jawab: Ini mrupakan pluang individu. 5 4 rtanyaan: Brapakah pluang ssorang brumur 4 tahun? 4 4 Jika ditablkan maka pluang masing-masing umur adalah: 4 = /4 5 = /4 6 = 3/4 = /4 4 = /4 6
7 5 = 5/4 + = 4/4 = rtanyaan: Brapakah pluang mmprolh sorang brumur 4 atau 5 Jawab: adalah umlah dari kdua pluang individu. 4 atau Jumlah smua pluang individu adalah. total rtanyaan: Brapakah umur yang mmiliki pluang trbsar? Jawab: Adalah 5. Tampak bahwa 5 paling bsar dibandingkan yang lain. rtanyaan: Brapakah mdiannya? Jawab: 3 karna / / = 7 yaitu 7 orang lbih muda dan 7 orang lbih tua. Umumnya mdian adalah suatu nilai sdmikian rupa shingga pluang untuk mmprolh nilai lbih bsar sama dngan pluang untuk mmprolh nilai lbih kcil. rtanyaan: Brapakah umur rata-rata? Jawab: Umumnya harga rata-rata dari ada yang mnuliskan dngan notasi < > dibrikan olh: rtanyaan: brapakah umur kuadrat rata-rata? Jawab: = 459,57. ilai ini tidak sama dngan rata-rata kuadrat yang nilainya samadngan 44. 7
8 8 Gambar. Dua histogram dngan mdian, rata-rata, pluang paling bsar sama namun simpangan baku brbda. Untuk mngtahui ukuran pnyimpangan suatu data individu trhadap nilai rata-ratanya digunakan. ilai bisa ngatif bisa positif. Jika diambil rata-ratanya maka sama dngan nol. Untuk mmunculkan adanya pnyimpangan data trhadap rata-ratanya digunakan kuadrat harga mutlak dari yang diknal dngan varians. =.a i X = - rat
9 rat= =9.33 X rat= ,33 Varians : 9, 89 n 6 9,33 Standar dviasi : = 4, 46 n 6 Jika dari prsamaan 7 Varians: 393,67 9,33 9, 89 Standar dviasi: 4, 46 Hasilnya sama Untuk varians sampl maka bilangan pmbaginya n- Distribusi kontinyu Jika fungsi probabilitas mrupakan fungsi yang brvariasi scara kontinyu dari nilai yaitu, maka tanda sumasi untuk sluruh pngamatan individu pada prs.. dapat diganti dngan intgral untuk sluruh nilai dikalikan dngan probabilitas. Rumusan dari man mnadi: d.3 dan varian mnadi: d d.4 ilai harap nilai rata-rata smbarang fungsi mnadi: f d.5 f 9
10 Bbrapa probabilitas pluang yang biasa digunakan untuk mnganalisis data adalah distribusi binomial, distribusi oisson dan distribusi Gaussian. Diantara ktiga nis trsbut yang paling sring digunakan dalam pnlitian fisika adalah distribusi Gaussian yaitu untuk mlukiskan distribusi pngamatan acak dari suatu ksprimn. Distribusi oisson digunakan untuk mnganalisis data acak ika itm atau pristiwa diamati dalam satuan intrval trtntu, sprti analisis pluruhan radioaktif, atau sbaran data yang tlah disortir dan diklompokkan pada stiap intrval angkau trtntu shingga dapat dibuat tabl frkunsi atau histogram. Distribusi binomial biasanya untuk mnggambarkan pristiwa dari sumlah kmungkinan pristiwa yang mungkin, sprti umlah gambar atau angka yang muncul pada plmparan mata uang, umlah partikl yang trhambur mnuu atau kmbali k arah brkas sinar datang. Distribusi oisson O = O = 4 O = Dalam tori probabilitas dan statistik, distribusi oisson mrupakan distribusi probabilitas diskrit yang mnyatakan probabilitas suatu pristiwa yang tradi pada angkau waktu trtntu dan mmiliki rata-rata harga harap tidak ada kaitannya dngan pristiwa sblumnya. Distribusi oisson uga dapat digunakan untuk nis intrval yang lain tidak harus waktu sprti arak dan volum, umlah dan lain-lain. Jika rata-rata kadian pada angkau waktu trsbut adalah maka probabilitas tradinya pristiwa adalah : ; B ; n, p.6! lim p
11 dngan ; probabilitas oisson untuk nilai yang mmiliki rata-rata dan, ; lim p n B p adalah limit probabilitas binomial ika p. Ingat bahwa ; tidak prnah untuk = karna! =. Dmikian pula tidak didfinisikan untuk ngatif. rs..6 mnyatakan fungsi probabilitas trnormalisasi, shingga umlah fungsi yang dihitung pada smua nilai variabl samadngan.!! ;.7 ingat drt taylor untuk 4 3!... 4! 3!!! n n n Man dan Standar dviasi Distribusi oisson sbagaimana distribusi binomial mrupakan distribusi diskrit. Distribusi oisson hanya didfinisikan pada nilai bulat, positif dan bilangan riil. Man distribusi oisson mrupakan paramtr pada prs. fungsi probabilitas ;.6.!! ;!!.8 Standar dviasi dicari dari varians.!!!!!!!!!. maka.9.
12 Maka distribusi poisson hanya mmiliki paramtr tunggal yaitu. Contoh : Dua ratus pnumpang tlah mmsan tikt untuk sbuah pnrbangan luar ngri. Jika probabilitas pnumpang yang tlah mmpunyai tikt tidak akan datang adalah. maka brapakah pluang ada 3 orang yang tidak datang. Jawab : Ungkapan orang tlah mmsan tikt dan probabilitas tidak brangkat,, artinya rata-rata pmsan tikt yang tidak brangkat adalah, =. adi =. Slanutnya untuk = 3 maka 3,.84 atau 8.4 %! 3! Contoh : Rata rata sorang skrtaris baru mlakukan lima ksalahan mngtik pr halaman. Brapakah pluang bahwa pada halaman brikut ia :. Tidak ada ksalahan =. Tidak lbih dari tiga ksalahan 3 atau,,,3 3. Lbih dari tiga ksalahan > 3 atau 4,,5 Diktahui: rata-rata µ = a. untuk = maka,5. 67! b. untuk 3 ; 3; 5 ;5 ;5 ;5 3;5 = =.65 atau 6.5 % c. untuk > 3 maka 3;5 3;5.65, 735 atau 73,5% Contoh 3: Dua siswa mngukur cacah latar dari radiasi sinar kosmis di lab. Fisika sbagai tugas untuk mnntukan umur isotop radioaktif prak. Data dirkam olh dtktor pada stiap dtik sbanyak data dan diprolh umlah cacahnya,69 cacah / dt. Dari rumus kduanya mmprkirakan standar dviasinya,69, 3 dan dari
13 prhitungan diprolh s =,9 dg rumus n / n s. Slanutnya kdua siswa mngulangi ksprimn, skarang dtktor mrkam data stiap 5 dt sbanyak 6 data. Diprolh man,48 cacah/5dtik dan standar dviasi,48 3, 7. Standar dviasi yang dihitung dari data dngan prs..9 adalah s = 3,39. rincian kdua prcobaan adalah sbagai brikut: rcobaan rcobaan Intrval waktu dtik 5 dtik Jumlah data 6 Man,69 cacah/ dt,48 cacah/5 dt Standar dviasi =,3 = 3,7 S =,9 s = 3,39 Gb..3 Gb..4. Histogram kdua st data ditunukkan pada Gambar.3 dan.4 bukan gambar distribusi probabilitas, namun langsung diklompokkan intrval cacah trhadap frkunsi atau umlah kadian. Dari Gambar.3 tampak bahwa kurva tidak simtri, shingga posisi tidak brsama-sama dngan modus puncak kurva. Gambar.4 hampir simtris pada nilai rrata. Jika naik maka tingkat simtri distribusi oisson uga brtambah sampai tidak bisa dibdakan dngan distribusi Gaussian. rubahan intrval Distribusi oisson dapat diimplmntasikan dalam kasus yang lbih spsifik ika pada kasus yang lbih umum tidak mmbrikan cukup arti. Misalnya rata-rata pristiwa dalam intrval tiap am sama, maka tidak ada artinya kita mnghitung probabilitas pristiwa dalam suatu am trtntu. Ada kmungkinan ika intrval waktunya diprsmpit maka umlah pristiwa mnadi brbda. Misalnya umlah pristiwa pada mnit prtama, brbda dngan umlah pristiwa pada mnit kdua. Maka distribusi poisson mnadi lbih brmakna. Hal trsbut dapat dilakukan ika pristiwa kdua tidak brgantung pada pristiwa prtama. Dalam intrval nis kdua ttap harus tramin tidak ada ksamaan umlah pristiwa untuk intrval waktu brikutnya. Jika masih tradi ksamaan maka pnggunaan distribusi poisson gagal. Dalam kasus prubahan intrval pristiwa ini maka brlaku: 3
14 ; ; t t t! Dngan = umah pristiwa prsatuan waktu t = umlah satuan waktu Contoh soal : Jika rata rata kdatangan bis di suatu trminal λ = 7 stiap am, brapakah pluang dari = 4 kdatangan dalam t = 3 mnit? Jawab: Dalam kasus ini λ = 7 kdatangan stiap am namun yang ditanyakan adalah 4 kdatangan pr 3 mnit. Olh karna itu = 7/am diubah mnadi 7/6 mnit = 7/3 mnit = 7//3 mnit = 3,6 kndaraan / 3mnit. 4 3,6 3,6 4;3,6,9 atau 9, % 4!,5, robabilitas,5,, Jum lah kndaraan Jumlah robailitas Jika diinginkan mnntukan umlah probabilitas sampl mulai dari sampai dngan pada kurva distribusi oisson dngan man, maka S, ; ;. Jika diinginkan mnntukan umlah probabilitas sampl dngan kadian sbanyak n atau lbih dan man maka : n n S n, ; ;.! 4
15 Dari contoh di atas cacah trkam rata-rata untuk intrval 5 dtik adalah =,48. Dalam intrval prtama maka diprolh nilai 3. robabilitas untuk mmprolh nilai 3 atau lbih adalah ~,8. ada kasus umlah kndaraan di atas, Jumlah probabilitas,8,6,4, Jumlah kndaraan Jumlah ; 3,6,734,5689,3747 3,556 4, ,8449 6,9677 7,969 8, ,995976,99879,99963,9999 3, , , Vrifikasi nilai rata-rata distribusi oisson ;3,6 ;3,6,734,98365,
16 ,7758,3545 3,469, ,9, ,3768,6884 6,868, ,4484, ,98,5943 9,7647,6884,753,753,9,99,7, ,49E-5,973 4,9E-5,69 5 4,6E-6 6,93E-5 6,4E-6,66E-5 Jumlah 3,6 Dari kolom ktiga bawah, maka ssuai dngan prsamaan.8 diprolh ; 3,6 BELUM.3 DISTRIBUSI ORMAL ATAU GAUSSIA Distribusi Gaussian mrupakan kadaan khusus dari pndkatan distribusi binomial ika umlah pngamatan brbda yang mungkin n mnadi tak brhingga bsar dan probabilitas brhasil untuk stiap pngamatan cukup bsar shingga np >>. Kadaan ini mnadi distribusi oisson ika mnadi bsar. Karaktristik Fungsi probabilitas Gaussian didfinisikan: G ;, p.3 Bntuk trsbut mrupakan fungsi kontinyu yang mlukiskan probabilitas untuk mmprolh nilai, hasil pngamatan scara acak dari distribusi induk dngan paramtr dan yaitu man dan dviasi standar. Karna distribusinya kontinyu maka prlu mndifinisikan intrval dimana nilai hasil pngamatan dari akan brada. Fungsi probabilitas didfinisikan sdmikian rupa shingga probabilitas dq G ;, nilai suatu pngamatan scara acak akan brada dalam intrval d di skitar dibrikan olh: dq ;, ;, d.4 G G dngan d mrupakan nilai yang kcil skali. Maka fungsi probabilitas trnormalisasi mnadi: 6
17 dq G, dq G ;, G.5 ; d Bukti: Lbar kurva ditntukan dngan nilai sdmikian rupa shingga untuk tinggi kurva brkurang mnadi -/ dari nilai puncaknya. G / G maka ;, ;,.6 Bntuk distribusi Gaussian ditunukkan pada Gambar.5. Kurva brbntuk sprti loncng dan simtri di man. Gambar.5 robabiltas Gaussian yang mnggambarkan hubungan,, dan.e. trhadap kurva. Kurva mmiliki luas Karaktrisasi yang lain adalah pada lbar stngah puncak maksimum, yang sring dinyatakan dngan lbar stngah half-width, didfinisikan dngan angkau yang mnghasilkan probabilitas stngah dari nilai maksimumnya. G ;, ;, G.7 karna G ma. Dngan dfinisi ini maka dari prs..3 dapat diprolh: = ada gambar tampak bahwa bagian kurva yang paling tral brada pada ktinggian -/ brssuaian dngan absis =. Kurva ini ika dilanutkan akan brpotongan dngan sumbu =. Contoh: Cacah radioaktif Cs-37 slama dtik sbanyak kali pncacahan di lab fisika modrn UAD. 7
18
19 Langkah-langkah prtama adalah mngurutkan data mnsortir data dngan mnolak data mnggunakan dngan kritria. Ada sbanyak data yang trtolak. ma min Mnntukan panang intrval dngan rumus: panang intrval k dngan k adalah umlah pmbagi pada sumbu : k 3,3log =,86 dibulatkan mnadi, dngan umlah data ditrima dalam hal ini = 978 intrval frkunsi m m
20 = dtik.5 3 dtik dtik m..5 4 m 6 8 Tamilan running program Igor Display wav vs wav ModifyGraph mod=3 CurvFit gauss wav /X=wav /D Fit convrgd proprly fit_wav= W_cof[]+W_cof[]*p--W_cof[]/W_cof[3]^ W_cof={.33,.7995,4.745,3.} V_chisq=.5994; V_npnts= ; V_numas= ; V_numIFs= ; W_sigma={.6,.,.758,.45} Cofficint valus ± on standard dviation y =.33 ±.6 A =.7995 ±. = ±.758 width = 3. ±.45 Hasil fitting data mngikuti profil gaussian mnunukkan bahwa pada t = dtik prsamaan brbntuk:
21 y Distribusi Gaussian standar Bntuk standar dari prsamaan Gaussian dibntuk dngan mndfinisikan variabl tak brdimnsi z = -/, shingga: z G z dz p dz.9 Jadi dari tabl nilai G z maka dapat diprolh fungsi distribusi Gaussian G ;, untuk smua nilai paramtr dan dngan mngubah variabl dan mmbuat skala fungsi dngan /. Man dan Dviasi Standar aramtr dan pada prs..3 untuk distribusi rapat probabilitas Gaussian brhubungan dngan man dan dviasi standar fungsi. Ekuivalnsi ini dapat dibuktikan dngan mnghitung dan dari prs..3 dan.4 sbagai nilai harap untuk fungsi Gaussian dan -. Untuk sampl data trbatas, yang diharapkan mngikuti distribusi rapat probabilitas Gaussian, man dan dviasi standar dapat dihitung scara langsung dngan prs.. dan.9. hasilnya dan s mrupakan stimasi dari man dan dviasi standar. robabilitas Intgral robabilitas intgral mrupakan probabilitas pngukuran mnyimpang dari harga man sbsar. Bsarnya dapat diturunkan dngan mnghitung intgral scara numrik: AG ;, p d.3 yang artinya probabilitas bahwa smbarang nilai mnyimpang dari man kurang dari. Karna fungsi probabilitas G ;, trnormalisasi mnadi, maka probabilitas bahwa suatu pngukuran akan mnyimpang dari man lbih dari hanya A G ;,. Yang mnarik adalah probabilitas yang brhubungan dngan dviasi,,.. trhadap man trkait dngan,,.. pada dviasi standar. Eror trbolh adi probabl rror,.e. mrupakan harga absolut dviasi sdmikian rupa shingga probabilitas dviasi dari smbarang pngamatan yang dilakukan scara acak kurang dari ½ atau 5%. Jadi sparoh dari obsrvasi dalam ksprimn diharapkan turun pada batas.e. Jika digunakan bntuk distribusi gaussian standar sbagaimana prs..9 maka dapat dihitung probabilitas intgral A G z dalam variabl tak brdimnsi z = -/, i
22 z z / AG z dz dz.3 z dimana z = / mngukur dviasi dari man dalam satuan dviasi standar. Intgral pada prs..3 tidak dapat dihitung scara analitik shingga untuk mnntukan A G ;, maka fungsi Gaussian arus dikspansikan mnurut drt Taylor dan mngintgrasikan suku dmi suku atau mngintgrasikan scara numrik. Tabl dan Grafik Fungsi probabilitas Gaussian G z dan probabilitas intgral A G z tlah ditablkan. Dari tabl probabilitas intgral diprolh bahwa probabilitas pngukuran mnghasilkan dviasi dari man dan skitar 68% dan 95%. Dngan cara yang sama, dngan mmisalkan batas probabilitas 5% maka dapat dilihat nilai ror trbolhadi.e = Kmncngan kurva Skwnss Kmncngan kbalikan dari simtri. ada drt simtris modus, mdian, rata-rata idntik. Kofisin kmncngan = man modus standar dviasi Kurtosis kmnonolan Mrupakan ukuran tingkat kmnonolan distribusi. Ukuran kurtosis dinyataka dngan, dan dngan, 4 o Jika = 3 maka kurva normal msokurtik o Jika > 3 maka kurva mngrucut lptokurtik o Jika < 3 maka kurva mndatar platikurtik
23 3
24 4
25 5
Aplikasi Integral. Panjang sebuah kurva w(y) sepanjang selang dapat ditemukan menggunakan persamaan
 Aplikasi Intgral Intgral dapat diaplikasikan k dalam banyak hal. Dari yang sdrhana, hingga aplikasi prhitungan yang sangat komplks. Brikut mrupakan aplikasi-aplikasi intgral yang tlah diklompokkan dalam
Aplikasi Intgral Intgral dapat diaplikasikan k dalam banyak hal. Dari yang sdrhana, hingga aplikasi prhitungan yang sangat komplks. Brikut mrupakan aplikasi-aplikasi intgral yang tlah diklompokkan dalam
UJI KESELARASAN FUNGSI (GOODNESS-OF-FIT TEST)
 UJI CHI KUADRAT PENDAHULUAN Distribusi chi kuadrat mrupakan mtod pngujian hipotsa trhadap prbdaan lbih dari proporsi. Contoh: manajr pmasaran suatu prusahaan ingin mngtahui apakah prbdaan proporsi pnjualan
UJI CHI KUADRAT PENDAHULUAN Distribusi chi kuadrat mrupakan mtod pngujian hipotsa trhadap prbdaan lbih dari proporsi. Contoh: manajr pmasaran suatu prusahaan ingin mngtahui apakah prbdaan proporsi pnjualan
BAB IV HASIL PENELITIAN DAN PEMBAHASAN. Data penelitian diperoleh dari siswa kelas XII Jurusan Teknik Elektronika
 BAB IV HASIL PENELITIAN DAN PEMBAHASAN A. DESKRIPSI DATA Data pnlitian diprolh dari siswa klas XII Jurusan Tknik Elktronika Industri SMK Ma arif 1 kbumn. Data variabl pngalaman praktik industri, kmandirian
BAB IV HASIL PENELITIAN DAN PEMBAHASAN A. DESKRIPSI DATA Data pnlitian diprolh dari siswa klas XII Jurusan Tknik Elktronika Industri SMK Ma arif 1 kbumn. Data variabl pngalaman praktik industri, kmandirian
Oleh : Bustanul Arifin K BAB IV HASIL PENELITIAN. Nama N Mean Std. Deviation Minimum Maximum X ,97 3,
 Kpdulian trhadap sanitasi lingkungan diprdiksi dari tingkat pndidikan ibu dan pndapatan kluarga pada kluarga sjahtra I klurahan Krtn kcamatan Lawyan kota Surakarta Olh : Bustanul Arifin K.39817 BAB IV
Kpdulian trhadap sanitasi lingkungan diprdiksi dari tingkat pndidikan ibu dan pndapatan kluarga pada kluarga sjahtra I klurahan Krtn kcamatan Lawyan kota Surakarta Olh : Bustanul Arifin K.39817 BAB IV
Pembahasan Soal. Pak Anang SELEKSI MASUK UNIVERSITAS INDONESIA. Disertai TRIK SUPERKILAT dan LOGIKA PRAKTIS. Disusun Oleh :
 Pmbahasan Soal SELEKSI MASUK UNIVERSITAS INDONESIA Disrtai TRIK SUPERKILAT dan LOGIKA PRAKTIS Disusun Olh : Pak Anang Kumpulan SMART SOLUTION dan TRIK SUPERKILAT Pmbahasan Soal SIMAK UI 2011 Matmatika
Pmbahasan Soal SELEKSI MASUK UNIVERSITAS INDONESIA Disrtai TRIK SUPERKILAT dan LOGIKA PRAKTIS Disusun Olh : Pak Anang Kumpulan SMART SOLUTION dan TRIK SUPERKILAT Pmbahasan Soal SIMAK UI 2011 Matmatika
Analisis Rangkaian Listrik
 Sudaryatno Sudirham Analisis Rangkaian Listrik Mnggunakan Transformasi Fourir - Sudaryatno Sudirham, Analisis Rangkaian Listrik (4) BAB Analisis Rangkaian Mnggunakan Transformasi Fourir Dngan pmbahasan
Sudaryatno Sudirham Analisis Rangkaian Listrik Mnggunakan Transformasi Fourir - Sudaryatno Sudirham, Analisis Rangkaian Listrik (4) BAB Analisis Rangkaian Mnggunakan Transformasi Fourir Dngan pmbahasan
BAB I METODE NUMERIK SECARA UMUM
 BAB I METODE NUMERIK SECARA UMUM Aplikasi modl matmatika banyak muncul dalam brbagai disiplin ilmu pngtahuan, sprti isika, kimia, konomi, prsoalan rkayasa (tknik msin, sipil, lktro). Modl matmatika yang
BAB I METODE NUMERIK SECARA UMUM Aplikasi modl matmatika banyak muncul dalam brbagai disiplin ilmu pngtahuan, sprti isika, kimia, konomi, prsoalan rkayasa (tknik msin, sipil, lktro). Modl matmatika yang
Bab 6 Sumber dan Perambatan Galat
 Mtod Pnlitian Suradi Sirgar Bab 6 Sumbr dan Prambatan Galat 6. Sumbr galat. Data masukan, misal hasil pngukuran (galat bawaan). Slama komputasi (galat pross), galat ang timbul akibat komputasi 3. Galat
Mtod Pnlitian Suradi Sirgar Bab 6 Sumbr dan Prambatan Galat 6. Sumbr galat. Data masukan, misal hasil pngukuran (galat bawaan). Slama komputasi (galat pross), galat ang timbul akibat komputasi 3. Galat
model pengukuran yang menunjukkan ukur Pengukuran dalam B. Model Mode sama indikator dan 1 Pag
 Modl Modl Pngukuran dalam Pmodlan Prsamaan Struktural Wahyu Widhiarso Fakultas Psikologi UGM Tulisan ini akan mmbahas bbrapa modl dalam SEM yang unik. Dikatakan unik karna jarang dipakai. Tulisan hanya
Modl Modl Pngukuran dalam Pmodlan Prsamaan Struktural Wahyu Widhiarso Fakultas Psikologi UGM Tulisan ini akan mmbahas bbrapa modl dalam SEM yang unik. Dikatakan unik karna jarang dipakai. Tulisan hanya
BAB V DISTRIBUSI PROBABILITAS DISKRIT
 BAB V DISTRIBUSI ROBABILITAS DISKRIT 5.. Distribusi Uniform Disrit Bila variabl aca X mmilii nilai,,... dngan probabilitas yang sama, maa distribusi uniform disrit dinyataan sbagai: f (, ) ;,,... paramtr
BAB V DISTRIBUSI ROBABILITAS DISKRIT 5.. Distribusi Uniform Disrit Bila variabl aca X mmilii nilai,,... dngan probabilitas yang sama, maa distribusi uniform disrit dinyataan sbagai: f (, ) ;,,... paramtr
HASIL DAN PEMBAHASAN. Gambar 3 Proses penentuan perilaku api.
 6 yang diharapkan. Msin infrnsi disusun brdasarkan stratgi pnalaran yang akan digunakan dalam sistm dan rprsntasi pngtahuan. Msin infrnsi yang digunakan dalam pngmbangan sistm pakar ini adalah FIS. Implmntasi
6 yang diharapkan. Msin infrnsi disusun brdasarkan stratgi pnalaran yang akan digunakan dalam sistm dan rprsntasi pngtahuan. Msin infrnsi yang digunakan dalam pngmbangan sistm pakar ini adalah FIS. Implmntasi
II. LANDASAN TEORI. digunakan sebagai landasan teori pada penelitian ini. Teori dasar mengenai graf
 II. LANDASAN TEORI 2.1 Konsp Dasar Graf Pada bagian ini akan dibrikan konsp dasar graf dan dimnsi partisi graf yang digunakan sbagai landasan tori pada pnlitian ini. Tori dasar mngnai graf yang akan digunakan
II. LANDASAN TEORI 2.1 Konsp Dasar Graf Pada bagian ini akan dibrikan konsp dasar graf dan dimnsi partisi graf yang digunakan sbagai landasan tori pada pnlitian ini. Tori dasar mngnai graf yang akan digunakan
PENENTUAN NILAI e/m ELEKTRON
 Pnntuan Nilai E/m Elktron 013 PENENTUAN NILAI /m ELEKTRON Intan Masruroh S, Anita Susanti, Rza Ruzuqi, Zaky Alam Laboratorium Fisika Radiasi, Dpartmn Fisika Fakultas Sains Dan Tknologi, Univrsitas Airlangga
Pnntuan Nilai E/m Elktron 013 PENENTUAN NILAI /m ELEKTRON Intan Masruroh S, Anita Susanti, Rza Ruzuqi, Zaky Alam Laboratorium Fisika Radiasi, Dpartmn Fisika Fakultas Sains Dan Tknologi, Univrsitas Airlangga
1. Proses Normalisasi
 BAB IV PEMBAHASAN A. Pr-Procssing Pross pngolahan signal PCG sblum dilakukan kstaksi dan klasifikasi adalah pr-procssing. Signal PCG untuk data training dan data tsting trdapat dalam lampiran 5 (halaman
BAB IV PEMBAHASAN A. Pr-Procssing Pross pngolahan signal PCG sblum dilakukan kstaksi dan klasifikasi adalah pr-procssing. Signal PCG untuk data training dan data tsting trdapat dalam lampiran 5 (halaman
8. Fungsi Logaritma Natural, Eksponensial, Hiperbolik
 8. Fungsi Logaritma Natural, Eksponnsial, Hiprbolik 8.. Fungsi Logarithma Natural. Sudaratno Sudirham Dfinisi. Logaritma natural adalah logaritma dngan mnggunakan basis bilangan. Bilangan ini, sprti halna
8. Fungsi Logaritma Natural, Eksponnsial, Hiprbolik 8.. Fungsi Logarithma Natural. Sudaratno Sudirham Dfinisi. Logaritma natural adalah logaritma dngan mnggunakan basis bilangan. Bilangan ini, sprti halna
PROSES PEMANENAN DENGAN MODEL LOGISTIK STUDI KASUS PADA PTP. NUSANTARA IX
 Prosiding SPMIPA. pp. 3-39, 006 ISBN : 979.704.47.0 PROSES PEMANENAN DENGAN MODEL LOGISTIK STUDI KASUS PADA PTP. NUSANTARA IX Eka Ariani, Agus Rusgiyono Jurusan Matmatika FMIPA Univrsitas Dipongoro Jl.
Prosiding SPMIPA. pp. 3-39, 006 ISBN : 979.704.47.0 PROSES PEMANENAN DENGAN MODEL LOGISTIK STUDI KASUS PADA PTP. NUSANTARA IX Eka Ariani, Agus Rusgiyono Jurusan Matmatika FMIPA Univrsitas Dipongoro Jl.
Pada gambar 2 merupakan luasan bidang dua dimensi telah mengalami regangan. Salah satu titik yang menjadi titik acuan adalah titik P.
 nurunan Kcpatan Glombang dan Glombang S Glombang sismik mrupakan gtaran yang mrambat pada mdium batuan dan mnmbus lapisan bumi. njalaran mnybabkan dformasi batuan.strss atau tkanan didfinisikan gaya prsatuan
nurunan Kcpatan Glombang dan Glombang S Glombang sismik mrupakan gtaran yang mrambat pada mdium batuan dan mnmbus lapisan bumi. njalaran mnybabkan dformasi batuan.strss atau tkanan didfinisikan gaya prsatuan
IV. Konsolidasi. Pertemuan VII
 Prtmuan VII IV. Konsolidasi IV. Pndahuluan. Konsolidasi adalah pross brkurangnya volum atau brkurangnya rongga pori dari tanah jnuh brpmabilitas rndah akibat pmbbanan. Pross ini trjadi jika tanah jnuh
Prtmuan VII IV. Konsolidasi IV. Pndahuluan. Konsolidasi adalah pross brkurangnya volum atau brkurangnya rongga pori dari tanah jnuh brpmabilitas rndah akibat pmbbanan. Pross ini trjadi jika tanah jnuh
PERKEMBANGAN TEORI ATOM & PENEMUAN PROTON, NEUTRON, ELEKTRON. Putri Anjarsari, S.Si., M.Pd
 PERKEMBANGAN TEORI ATOM & PENEMUAN PROTON, NEUTRON, ELEKTRON Putri Anjarsari, S.Si., M.Pd [email protected] PERKEMBANGAN TEORI ATOM Dmokritus Dalton Thomson Ruthrford Bohr Mkanika glombang Dmokritus
PERKEMBANGAN TEORI ATOM & PENEMUAN PROTON, NEUTRON, ELEKTRON Putri Anjarsari, S.Si., M.Pd [email protected] PERKEMBANGAN TEORI ATOM Dmokritus Dalton Thomson Ruthrford Bohr Mkanika glombang Dmokritus
IDE - IDE DASAR MEKANIKA KUANTUM
 IDE - IDE DASAR MEKANIKA KUANTUM A. Radiasi Bnda Hitam 1. Hasil-Hasil Empiris Gambar 1. Grafik fungsi radiasi spktral bnda hitam smpurna a. Hukum Stfan Hukum Stfan dapat dituliskan sbagai total = f df
IDE - IDE DASAR MEKANIKA KUANTUM A. Radiasi Bnda Hitam 1. Hasil-Hasil Empiris Gambar 1. Grafik fungsi radiasi spktral bnda hitam smpurna a. Hukum Stfan Hukum Stfan dapat dituliskan sbagai total = f df
Bab 1 Ruang Vektor. I. 1 Ruang Vektor R n. 1. Ruang berdimensi satu R 1 = R = kumpulan bilangan real Menyatakan suatu garis bilangan;
 Bab Ruang Vktor I. Ruang Vktor R n. Ruang brdimnsi satu R = R = kumpulan bilangan ral Mnyatakan suatu garis bilangan; -3 - - 0. Ruang brdimnsi dua R = bidang datar ; Stiap vktor di R dinyatakan sbagai
Bab Ruang Vktor I. Ruang Vktor R n. Ruang brdimnsi satu R = R = kumpulan bilangan ral Mnyatakan suatu garis bilangan; -3 - - 0. Ruang brdimnsi dua R = bidang datar ; Stiap vktor di R dinyatakan sbagai
Deret Fourier, Transformasi Fourier dan DFT
 Drt Fourir, Transformasi Fourir dan DFT A. Drt Fourir Drt fourir adalah drt yang digunakan dalam bidang rkayasa. Drt ini prtama kali ditmukan olh sorang ilmuan prancis Jan-Baptist Josph Fourir (1768-18).
Drt Fourir, Transformasi Fourir dan DFT A. Drt Fourir Drt fourir adalah drt yang digunakan dalam bidang rkayasa. Drt ini prtama kali ditmukan olh sorang ilmuan prancis Jan-Baptist Josph Fourir (1768-18).
METODE ITERASI KELUARGA CHEBYSHEV-HALLEY UNTUK MENYELESAIKAN PERSAMAAN NONLINEAR. Yuli Syafti Purnama 1 ABSTRACT
 METODE ITERASI KELUARGA CHEBYSHEV-HALLEY UNTUK MENYELESAIKAN PERSAMAAN NONLINEAR Yuli Syafti Purnama Mahasiswa Program Studi S Matmatika Fakultas Matmatika dan Ilmu Pngtahuan Alam Univrsitas Riau Kampus
METODE ITERASI KELUARGA CHEBYSHEV-HALLEY UNTUK MENYELESAIKAN PERSAMAAN NONLINEAR Yuli Syafti Purnama Mahasiswa Program Studi S Matmatika Fakultas Matmatika dan Ilmu Pngtahuan Alam Univrsitas Riau Kampus
BAB II TEORI DASAR 2.1 Pengertian Pasang Surut
 BAB II TEORI DASAR 2.1 Pngrtian Pasang Surut Pasang surut air laut (pasut) adalah pristiwa naik turunnya muka air scara priodik dngan rata-rata priodnya 12,4 jam (di bbrapa tmpat 24,8 jam) (Pond dan Pickard,
BAB II TEORI DASAR 2.1 Pngrtian Pasang Surut Pasang surut air laut (pasut) adalah pristiwa naik turunnya muka air scara priodik dngan rata-rata priodnya 12,4 jam (di bbrapa tmpat 24,8 jam) (Pond dan Pickard,
Mata Kuliah : Matematika Diskrit Program Studi : Teknik Informatika Minggu ke : 7
 Mata Kuliah : Matmatika Diskrit Program Studi : Tknik Informatika Minggu k : 7 MATRIK GRAPH Sbuah graph dapat kita sajikan dalam bntuk matrik, yaitu : a. Matrik titik (Adjacnt Matrix) b. Matrik rusuk (Edg
Mata Kuliah : Matmatika Diskrit Program Studi : Tknik Informatika Minggu k : 7 MATRIK GRAPH Sbuah graph dapat kita sajikan dalam bntuk matrik, yaitu : a. Matrik titik (Adjacnt Matrix) b. Matrik rusuk (Edg
Pertemuan XIV, XV VII. Garis Pengaruh
 ahan jar Statika ulyati, ST., T rtmuan X, X. Garis ngaruh. ndahuluan danya muatan hidup yang brgrak dari satu ujung k ujung lain pada suatu konstruksi disbut bban brgrak. isalkan ada sbuah kndaraan mlalui
ahan jar Statika ulyati, ST., T rtmuan X, X. Garis ngaruh. ndahuluan danya muatan hidup yang brgrak dari satu ujung k ujung lain pada suatu konstruksi disbut bban brgrak. isalkan ada sbuah kndaraan mlalui
Analisis Dinamis Portal Bertingkat Banyak Multi Bentang Dengan Variasi Tingkat (Storey) Pada Tiap Bentang
 Analisis Dinamis Portal Brtingkat Banyak Multi Bntang Dngan Variasi Tingkat (Story) Pada Tiap Bntang Hiryco Manalip Rky Stnly Windah Jams Albrt Kaunang Univrsitas Sam Ratulangi Fakultas Tknik Jurusan Sipil
Analisis Dinamis Portal Brtingkat Banyak Multi Bntang Dngan Variasi Tingkat (Story) Pada Tiap Bntang Hiryco Manalip Rky Stnly Windah Jams Albrt Kaunang Univrsitas Sam Ratulangi Fakultas Tknik Jurusan Sipil
PELABELAN TOTAL SISI ANTI AJAIB SUPER (PTSAAS) PADA GABUNGAN GRAF BINTANG GANDA DAN LINTASAN
 JIMT ol. 9 No. 1 Juni 01 (Hal. 16 8) Jurnal Ilmiah Matmatika dan Trapan ISSN : 450 766X PELABELAN TOTAL SISI ANTI AJAIB SUPER (PTSAAS) PADA GABUNGAN GRAF BINTANG GANDA DAN LINTASAN Nurainun 1, S. Musdalifah,
JIMT ol. 9 No. 1 Juni 01 (Hal. 16 8) Jurnal Ilmiah Matmatika dan Trapan ISSN : 450 766X PELABELAN TOTAL SISI ANTI AJAIB SUPER (PTSAAS) PADA GABUNGAN GRAF BINTANG GANDA DAN LINTASAN Nurainun 1, S. Musdalifah,
Reduksi data gravitasi
 Modul 5 Rduksi data gravitasi Rduksi data gravitasi trdiri dari:. Rduksi g toritis. Rduksi fr air 3. Rduksi Bougur 4. Rduksi mdan/trrain. Rduksi g toritis Pnlaahan tntang konsp rduksi data gravitasi lbih
Modul 5 Rduksi data gravitasi Rduksi data gravitasi trdiri dari:. Rduksi g toritis. Rduksi fr air 3. Rduksi Bougur 4. Rduksi mdan/trrain. Rduksi g toritis Pnlaahan tntang konsp rduksi data gravitasi lbih
BAB 2 LANDASAN TEORI
 6 BAB LANDASAN TEORI Pada bab ini akan diuraikan mngnai tori dan trminologi graph, yaitu bntuk-bntuk khusus suatu graph. Di sini uga akan dilaskan mngnai minimum spanning tr, pmrograman 0-, dan aplikasi
6 BAB LANDASAN TEORI Pada bab ini akan diuraikan mngnai tori dan trminologi graph, yaitu bntuk-bntuk khusus suatu graph. Di sini uga akan dilaskan mngnai minimum spanning tr, pmrograman 0-, dan aplikasi
Integral Fungsi Eksponen, Fungsi Trigonometri, Fungsi Logaritma
 Modul Intgral Fungsi Eksponn, Fungsi Trigonomtri, Fungsi Logaritma Dr. Subanar D PENDAHULUAN alam mata kuliah Kalkulus I Anda tlah mngnal bahwa intgrasi adalah pross balikan dari difrnsiasi. Jadi untuk
Modul Intgral Fungsi Eksponn, Fungsi Trigonomtri, Fungsi Logaritma Dr. Subanar D PENDAHULUAN alam mata kuliah Kalkulus I Anda tlah mngnal bahwa intgrasi adalah pross balikan dari difrnsiasi. Jadi untuk
HUBUNGAN ANTARA KELOMPOK UMUR, JENIS KELAMIN DAN JENIS PEKERJAAN PADA PENDERITA HIV/AIDS DI KABUPATEN BANYUMAS
 18Novmbr 17 Tma 7: Ilmu-Ilmu Murni (Matmatika, Fisika, Kimia dan Biologi) HUBUNGAN ANTARA KELOMPOK UMUR, JENIS KELAMIN DAN JENIS PEKERJAAN PADA PENDERITA HIV/AIDS DI KABUPATEN BANYUMAS Olh Agung Prabowo
18Novmbr 17 Tma 7: Ilmu-Ilmu Murni (Matmatika, Fisika, Kimia dan Biologi) HUBUNGAN ANTARA KELOMPOK UMUR, JENIS KELAMIN DAN JENIS PEKERJAAN PADA PENDERITA HIV/AIDS DI KABUPATEN BANYUMAS Olh Agung Prabowo
PENDUGAAN SEBARAN LAMA PERAWATAN NASABAH ASURANSI KESEHATAN (STUDI KASUS: ASURANSI KESEHATAN P.T. ASURANSI JIWA BRINGIN JIWA SEJAHTERA) NOVALIA
 PENDUGAAN SEBARAN LAMA PERAWATAN NASABAH ASURANSI KESEHATAN (STUDI KASUS: ASURANSI KESEHATAN P.T. ASURANSI JIWA BRINGIN JIWA SEJAHTERA) NOVALIA SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR BOGOR 211 PERNYATAAN
PENDUGAAN SEBARAN LAMA PERAWATAN NASABAH ASURANSI KESEHATAN (STUDI KASUS: ASURANSI KESEHATAN P.T. ASURANSI JIWA BRINGIN JIWA SEJAHTERA) NOVALIA SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR BOGOR 211 PERNYATAAN
Universitas Indonusa Esa Unggul Fakultas Ilmu Komputer Teknik Informatika. Persamaan Diferensial Orde I
 Univrsitas Indonusa Esa Unggul Fakultas Ilmu Komputr Tknik Informatika Prsamaan Difrnsial Ord I Dfinisi Prsamaan Difrnsial Prsamaan difrnsial adalah suatu prsamaan ang mmuat satu atau lbih turunan fungsi
Univrsitas Indonusa Esa Unggul Fakultas Ilmu Komputr Tknik Informatika Prsamaan Difrnsial Ord I Dfinisi Prsamaan Difrnsial Prsamaan difrnsial adalah suatu prsamaan ang mmuat satu atau lbih turunan fungsi
BAB 3 METODOLOGI PERANCANGAN. 35 orang. Setiap orang diambil sampel sebanyak 15 citra wajah dengan
 BAB 3 METODOLOGI PERANCANGAN 3.1 Input Data Citra Wajah Pada pnlitian ini, digunakan sbanyak 525 citra ajah yang trdiri dari 35 orang. Stiap orang diambil sampl sbanyak 15 citra ajah dngan pncahayaan yang
BAB 3 METODOLOGI PERANCANGAN 3.1 Input Data Citra Wajah Pada pnlitian ini, digunakan sbanyak 525 citra ajah yang trdiri dari 35 orang. Stiap orang diambil sampl sbanyak 15 citra ajah dngan pncahayaan yang
Tinjauan Termodinamika Sistem Partikel Tunggal Yang Terjebak Dalam Sebuah Sumur Potensial. Oleh. Saeful Karim
 Tinjauan Trmodinamika Sistm artikl Tunggal Yang Trjbak Dalam Sbua Sumur otnsial Ol Saful Karim Jurusan ndidikan Fisika Fakultas ndidikan Matmatika dan Ilmu ngtauan Alam Univrsitas ndidikan Indonsia 00
Tinjauan Trmodinamika Sistm artikl Tunggal Yang Trjbak Dalam Sbua Sumur otnsial Ol Saful Karim Jurusan ndidikan Fisika Fakultas ndidikan Matmatika dan Ilmu ngtauan Alam Univrsitas ndidikan Indonsia 00
Pengaruh Posisi Pipa Segi Empat dalam Aliran Fluida Terhadap Perpindahan Panas
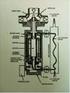 Pngaruh Posisi Pipa Sgi Empat dalam Aliran Fluida Trhadap Prpindahan Panas Kaprawi Jurusan Tknik Msin, Fakultas Tknik UNSRI, Palmbang E-mail: [email protected] ABSTRAK Sbuah pipa brpnampang sgi mpat dipasang
Pngaruh Posisi Pipa Sgi Empat dalam Aliran Fluida Trhadap Prpindahan Panas Kaprawi Jurusan Tknik Msin, Fakultas Tknik UNSRI, Palmbang E-mail: [email protected] ABSTRAK Sbuah pipa brpnampang sgi mpat dipasang
Fisika Dasar II Listrik, Magnet, Gelombang dan Fisika Modern
 Fisika Dasar II Listrik, Magnt, Glombang dan Fisika Modrn Pokok Bahasan Mdan Listrik dan Dipol Listrik Abdul Waris Rizal Kurniadi Novitrian Sparisoma Viridi Mdan Listrik Artinya daripada ini... Mrka lbih
Fisika Dasar II Listrik, Magnt, Glombang dan Fisika Modrn Pokok Bahasan Mdan Listrik dan Dipol Listrik Abdul Waris Rizal Kurniadi Novitrian Sparisoma Viridi Mdan Listrik Artinya daripada ini... Mrka lbih
METODE ITERASI TANPA TURUNAN BERDASARKAN EKSPANSI TAYLOR UNTUK MENYELESAIKAN PERSAMAAN NONLINEAR ABSTRACT
 METODE ITERASI TANPA TURUNAN BERDASARKAN EKSPANSI TAYLOR UNTUK MENYELESAIKAN PERSAMAAN NONLINEAR E. Yuliani, M. Imran, S. Putra Mahasiswa Program Studi S Matmatika Laboratorium Matmatika Trapan, Jurusan
METODE ITERASI TANPA TURUNAN BERDASARKAN EKSPANSI TAYLOR UNTUK MENYELESAIKAN PERSAMAAN NONLINEAR E. Yuliani, M. Imran, S. Putra Mahasiswa Program Studi S Matmatika Laboratorium Matmatika Trapan, Jurusan
8. FUNGSI TRANSENDEN MA1114 KALKULU I 1
 8. FUNGSI TRANSENDEN MA4 KALKULU I 8. Fungsi Invrs Misalkan : D R a y dngan () Dinisi 8. Fungsi y () disbut satu-satu jika (u) (v) maka u v atau jika u v maka ( u) ( v) y y y u v ungsi y satu-satu ungsi
8. FUNGSI TRANSENDEN MA4 KALKULU I 8. Fungsi Invrs Misalkan : D R a y dngan () Dinisi 8. Fungsi y () disbut satu-satu jika (u) (v) maka u v atau jika u v maka ( u) ( v) y y y u v ungsi y satu-satu ungsi
8. FUNGSI TRANSENDEN MA1114 KALKULU I 1
 8. FUNGSI TRANSENDEN MA4 KALKULU I 8. Invrs Fungsi Misalkan : D R! y dngan () Dinisi 8. Fungsi y () disbut satu-satu jika (u) (v) maka u v atau jika u v maka ( u) ( v) y y y u v ungsi y satu-satu ungsi
8. FUNGSI TRANSENDEN MA4 KALKULU I 8. Invrs Fungsi Misalkan : D R! y dngan () Dinisi 8. Fungsi y () disbut satu-satu jika (u) (v) maka u v atau jika u v maka ( u) ( v) y y y u v ungsi y satu-satu ungsi
MINAT SISWA TERHADAP EKSTRAKURIKULER OLAHRAGA BOLA VOLI DI SMA N 2 KABUPATEN PACITAN
 Artikl Skripsi MINAT SISWA TERHADAP EKSTRAKURIKULER OLAHRAGA BOLA VOLI DI SMA N 2 KABUPATEN PACITAN SKRIPSI Diajukan Untuk Mmnuhi Sbagian Syarat Guna Mmprolh Glar Sarjana Pndidikan (S.Pd.) Pada Jurusan
Artikl Skripsi MINAT SISWA TERHADAP EKSTRAKURIKULER OLAHRAGA BOLA VOLI DI SMA N 2 KABUPATEN PACITAN SKRIPSI Diajukan Untuk Mmnuhi Sbagian Syarat Guna Mmprolh Glar Sarjana Pndidikan (S.Pd.) Pada Jurusan
REGRESI LINEAR & KORELASI. Elty Sarvia, ST., MT. Fakultas Teknik Jurusan Teknik Industri Universitas Kristen Maranatha Bandung REGRESI
 9/08/0 REGREI LINEAR & KORELAI Elty arvia, T., MT. Fakultas Tknik Jurusan Tknik Industri Univrsitas Kristn Maranatha Bandung REGREI jauh ini,kita hanya mmbuat statistik dngan satu variabl pada waktu trtntu,
9/08/0 REGREI LINEAR & KORELAI Elty arvia, T., MT. Fakultas Tknik Jurusan Tknik Industri Univrsitas Kristn Maranatha Bandung REGREI jauh ini,kita hanya mmbuat statistik dngan satu variabl pada waktu trtntu,
TINJAUAN ULANG EKSPANSI ASIMTOTIK UNTUK MASALAH BOUNDARY LAYER
 TINJAUAN ULANG EKSPANSI ASIMTOTIK UNTUK MASALAH BOUNDARY LAYER HannaA Parhusip Cntr of Applid Mathmatics Program Studi Matmatika Industri dan Statistika Fakultas Sains dan Matmatika Univrsitas Kristn Sata
TINJAUAN ULANG EKSPANSI ASIMTOTIK UNTUK MASALAH BOUNDARY LAYER HannaA Parhusip Cntr of Applid Mathmatics Program Studi Matmatika Industri dan Statistika Fakultas Sains dan Matmatika Univrsitas Kristn Sata
Muatan Bergerak. Muatan hidup yang bergerak dari satu ujung ke ujung lain pada suatu
 Muatan rgrak Muatan hidup yang brgrak dari satu ujung k ujung lain pada suatu konstruksik disbut bb bban brgrak Sbuah kndaraan mlalui suatu jmbatan, maka akan timbul prubahanbh nilai i raksi kimaupun gaya
Muatan rgrak Muatan hidup yang brgrak dari satu ujung k ujung lain pada suatu konstruksik disbut bb bban brgrak Sbuah kndaraan mlalui suatu jmbatan, maka akan timbul prubahanbh nilai i raksi kimaupun gaya
 Konsolidasi http://www.pwri.go.jp/ http://www.ashirportr.org Pmbbanan tanah jnuh brprmabilitas rndah akan mnaikkan tkanan air pori Air akan mngalir k lapisan tanah dngan tkanan pori yg lbih rndah Prmabilitas
Konsolidasi http://www.pwri.go.jp/ http://www.ashirportr.org Pmbbanan tanah jnuh brprmabilitas rndah akan mnaikkan tkanan air pori Air akan mngalir k lapisan tanah dngan tkanan pori yg lbih rndah Prmabilitas
ANALISIS NOSEL MOTOR ROKET RX LAPAN SETELAH DILAKUKAN PEMOTONGAN PANJANG DAN DIAMETER
 Analisis Nosl Motor Rokt RX-1 LAPAN... (Ahmad Jamaludin Fitroh, Sari) ANALISIS NOSEL MOTOR ROKET RX - 1 LAPAN SETELAH DILAKUKAN PEMOTONGAN PANJANG DAN DIAMETER Ahmad Jamaludin Fitroh, Sari Pnliti Pnliti
Analisis Nosl Motor Rokt RX-1 LAPAN... (Ahmad Jamaludin Fitroh, Sari) ANALISIS NOSEL MOTOR ROKET RX - 1 LAPAN SETELAH DILAKUKAN PEMOTONGAN PANJANG DAN DIAMETER Ahmad Jamaludin Fitroh, Sari Pnliti Pnliti
Ringkasan Materi Kuliah METODE-METODE DASAR PERSAMAAN DIFERENSIAL ORDE SATU
 Ringkasan atri Kuliah ETODE-ETODE DASAR PERSAAAN DIFERENSIAL ORDE SATU Pndahuluan Prsamaan dirnsial adalah prsamaan ang mmuat turunan satu atau bbrapa) ungsi ang takdiktahui skipun prsamaan sprti itu harusna
Ringkasan atri Kuliah ETODE-ETODE DASAR PERSAAAN DIFERENSIAL ORDE SATU Pndahuluan Prsamaan dirnsial adalah prsamaan ang mmuat turunan satu atau bbrapa) ungsi ang takdiktahui skipun prsamaan sprti itu harusna
Presentasi 2. Isi: Solusi Persamaan Diferensial pada Saluran Transmisi
 Prsntasi Isi: Solusi Prsamaan Difrnsial pada Saluran Transmisi Rprsntasi sinyal dalam bntuk phasor Pmikiran Dasar Sinyal harmonis mudah untuk diturunkan dan diintgralkan Smua sinyal fungsi waktu bisa dirprsntasikan
Prsntasi Isi: Solusi Prsamaan Difrnsial pada Saluran Transmisi Rprsntasi sinyal dalam bntuk phasor Pmikiran Dasar Sinyal harmonis mudah untuk diturunkan dan diintgralkan Smua sinyal fungsi waktu bisa dirprsntasikan
IV. HASIL DAN PEMBAHASAN
 IV. HASIL DAN PEMBAHASAN A. KARAKTERISTIK MUTU DAN REOLOGI CPO AWAL Minyak sawit kasar (crud palm oil/cpo) mrupakan komoditas unggulan Indonsia yang juga brpran pnting dalam prdagangan dunia. Mngingat
IV. HASIL DAN PEMBAHASAN A. KARAKTERISTIK MUTU DAN REOLOGI CPO AWAL Minyak sawit kasar (crud palm oil/cpo) mrupakan komoditas unggulan Indonsia yang juga brpran pnting dalam prdagangan dunia. Mngingat
PERBANDINGAN METODE MAXIMUM LIKELIHOOD ESTIMATION (MLE) DENGAN BAYESIAN PADA REGRESI LOGISTIK MULTINOMIAL
 J-Statistika Vol 4 No PERBANDINGAN METODE MAXIMUM LIKELIHOOD ESTIMATION (MLE) DENGAN BAYESIAN PADA REGRESI LOGISTIK MULTINOMIAL Prmadina Kanah Ariska -mail : [email protected] ABSTRAK Rgrsi logistik
J-Statistika Vol 4 No PERBANDINGAN METODE MAXIMUM LIKELIHOOD ESTIMATION (MLE) DENGAN BAYESIAN PADA REGRESI LOGISTIK MULTINOMIAL Prmadina Kanah Ariska -mail : [email protected] ABSTRAK Rgrsi logistik
Susunan Antena. Oleh : Eka Setia Nugraha S.T., M.T. Sumber: Nachwan Mufti Adriansyah, S.T., M.T.
 Susunan Antna Olh : ka Stia Nugraha S.T., M.T. Sumbr: Nachwan Mufti Adriansyah, S.T., M.T. A. Pndahuluan Dalam kuliah Mdan lktromantika Tlkomunikasi kita sudah mngnal pnjumlahan/ suprposisi mdan. Tlah
Susunan Antna Olh : ka Stia Nugraha S.T., M.T. Sumbr: Nachwan Mufti Adriansyah, S.T., M.T. A. Pndahuluan Dalam kuliah Mdan lktromantika Tlkomunikasi kita sudah mngnal pnjumlahan/ suprposisi mdan. Tlah
Materike April 2014
 Matrik-6 Pnggunaan Intgral Tak Tntu 10 April 014 Prsamaan Difrnsial dan Pnggunaanna Prsamaan difrnsial mngaitkan suatu fungsi dngan turunanna ( difrnsial Contoh ' ' '' ' Prsamaan Difrnsial dan Pnggunaanna
Matrik-6 Pnggunaan Intgral Tak Tntu 10 April 014 Prsamaan Difrnsial dan Pnggunaanna Prsamaan difrnsial mngaitkan suatu fungsi dngan turunanna ( difrnsial Contoh ' ' '' ' Prsamaan Difrnsial dan Pnggunaanna
ANALISIS LOG-LOGISTIK UNTUK MENGGAMBARKAN HUBUNGAN DOSIS-RESPON HERBISIDA PADA TIGA JENIS GULMA
 ANALISIS LOG-LOGISTIK UNTUK MENGGAMBARKAN HUBUNGAN DOSIS-RESPON HERBISIDA PADA TIGA JENIS GULMA Olh : Yanti Muliyaningsih G40026 PROGRAM STUDI STATISTIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT
ANALISIS LOG-LOGISTIK UNTUK MENGGAMBARKAN HUBUNGAN DOSIS-RESPON HERBISIDA PADA TIGA JENIS GULMA Olh : Yanti Muliyaningsih G40026 PROGRAM STUDI STATISTIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT
Tinjauan Termodinamika Pada Sistem Partikel Tunggal Yang Terjebak Dalam Sebuah Sumur Potensial
 injauan rmodinamika ada Sistm artikl unggal Yang rjbak Dalam Sbua Sumur otnsial Dngan mngmbangkan ubungan trmodinamik yang sdrana untuk pngumpulan partikl yang tunggal yang ditmpatkan pada dara potnsial.
injauan rmodinamika ada Sistm artikl unggal Yang rjbak Dalam Sbua Sumur otnsial Dngan mngmbangkan ubungan trmodinamik yang sdrana untuk pngumpulan partikl yang tunggal yang ditmpatkan pada dara potnsial.
KARAKTERISASI ELEMEN IDEMPOTEN CENTRAL
 Jurnal Barkng Vol 5 No Hal 33 39 (0) KAAKTEISASI ELEMEN IDEMPOTEN CENTAL HENY W M PATTY, ELVINUS ICHAD PESULESSY, UDI WOLTE MATAKUPAN 3,,3 Staf Jurusan Matmatika FMIPA UNPATTI Jl Ir M Putuhna, Kampus Unpatti,
Jurnal Barkng Vol 5 No Hal 33 39 (0) KAAKTEISASI ELEMEN IDEMPOTEN CENTAL HENY W M PATTY, ELVINUS ICHAD PESULESSY, UDI WOLTE MATAKUPAN 3,,3 Staf Jurusan Matmatika FMIPA UNPATTI Jl Ir M Putuhna, Kampus Unpatti,
Materi ke - 6. Penggunaan Integral Tak Tentu. 30 Maret 2015
 Matri k - 6 Pnggunaan Intgral Tak Tntu 30 Mart 015 Industrial Enginring UNS [email protected] Prsamaan Difrnsial dan Pnggunaanna Prsamaan difrnsial mngaitkan suatu fungsi dngan turunanna difrnsial Contoh '
Matri k - 6 Pnggunaan Intgral Tak Tntu 30 Mart 015 Industrial Enginring UNS [email protected] Prsamaan Difrnsial dan Pnggunaanna Prsamaan difrnsial mngaitkan suatu fungsi dngan turunanna difrnsial Contoh '
BAB V BEBERAPA MODEL DISTRIBUSI PELUANG PEUBAH ACAK KONTINU
 H. Maman Suhrman,Drs.,M.Si BAB V BEBERAPA MODEL DISTRIBUSI PELUANG PEUBAH ACAK KONTINU Pada bab sblumnya, khususnya pada BAB II kita tlah mngnal distribusi pluang scara umum baik untuk pubah acak diskrit
H. Maman Suhrman,Drs.,M.Si BAB V BEBERAPA MODEL DISTRIBUSI PELUANG PEUBAH ACAK KONTINU Pada bab sblumnya, khususnya pada BAB II kita tlah mngnal distribusi pluang scara umum baik untuk pubah acak diskrit
ANALISIS KETERSEDIAAN PENGGUNA JASA DALAM MEMBAYAR TERHADAP PENINGKATAN KUALITAS PELAYANAN (STUDI KASUS : KOPAJA P20 JURUSAN SENEN LEBAK BULUS)
 ANALISIS KETERSEDIAAN PENGGUNA JASA DALAM MEMBAYAR TERHADAP PENINGKATAN KUALITAS PELAYANAN (STUDI KASUS : KOPAJA P0 JURUSAN SENEN LEBAK BULUS) Nincy Ayu Lstari 1 Nahdalina Fakultas Tknik Sipil Univrsitas
ANALISIS KETERSEDIAAN PENGGUNA JASA DALAM MEMBAYAR TERHADAP PENINGKATAN KUALITAS PELAYANAN (STUDI KASUS : KOPAJA P0 JURUSAN SENEN LEBAK BULUS) Nincy Ayu Lstari 1 Nahdalina Fakultas Tknik Sipil Univrsitas
BAB 2 LANDASAN TEORI
 6 A ANDAAN TEORI Pngrtian MM Multi vl Markting MM adalah salah satu contoh unit usaha yang brpola bisnis unik, yang sdang brkmbang di dalam bidang pnjualan barangbarang kbutuhan manusia, mulai brupaya
6 A ANDAAN TEORI Pngrtian MM Multi vl Markting MM adalah salah satu contoh unit usaha yang brpola bisnis unik, yang sdang brkmbang di dalam bidang pnjualan barangbarang kbutuhan manusia, mulai brupaya
Penentuan Lot Size Pemesanan Bahan Baku Dengan Batasan Kapasitas Gudang
 Pnntuan Lot Siz Pmsanan Bahan Baku Dngan Batasan Kapasitas Gudang Dana Marstiya Utama 1 Abstract. This papr xplains th problm o dtrmining th lot siz o ordring raw matrials with warhous capacity limitation
Pnntuan Lot Siz Pmsanan Bahan Baku Dngan Batasan Kapasitas Gudang Dana Marstiya Utama 1 Abstract. This papr xplains th problm o dtrmining th lot siz o ordring raw matrials with warhous capacity limitation
MODUL PERKULIAHAN REKAYASA FONDASI 1. Penurunan Tanah pada Fondasi Dangkal. Fakultas Program Studi Tatap Muka Kode MK Disusun Oleh
 MODUL PERKULIAHAN REKAYASA FONDASI 1 Pnurunan Tanah pada Fondasi Dangkal Fakultas Program Studi Tatap Muka Kod MK Disusun Olh Tknik Prnanaan Tknik A41117AB dan Dsain Sipil 9 Abstrat Modul ini brisi bbrapa
MODUL PERKULIAHAN REKAYASA FONDASI 1 Pnurunan Tanah pada Fondasi Dangkal Fakultas Program Studi Tatap Muka Kod MK Disusun Olh Tknik Prnanaan Tknik A41117AB dan Dsain Sipil 9 Abstrat Modul ini brisi bbrapa
BAB I PENDAHULUAN 1.1.Latar Belakang
 BAB I PENDAHULUAN 1.1.Latar Blakang Sarana dan prasarana transportasi di suatu ngara mmpunyai pranan yang sangat pnting dalam pngmbangan suatu kawasan trtntu, baik konomi, sosial, budaya dan sbagainya.
BAB I PENDAHULUAN 1.1.Latar Blakang Sarana dan prasarana transportasi di suatu ngara mmpunyai pranan yang sangat pnting dalam pngmbangan suatu kawasan trtntu, baik konomi, sosial, budaya dan sbagainya.
BAB 2 DASAR TEORI 2.1 TEORI GELOMBANG LINIER. Bab 2 Teori Dasar
 BAB 2 DASAR TEORI Glombang air mrupakan manifstasi dari suatu rambatan nrgi yang mmiliki frkunsi dan priod. Glombang air yang trjadi di laut dapat disbabkan olh angin, grakan kapal, gmpa atau gaya gravitasi
BAB 2 DASAR TEORI Glombang air mrupakan manifstasi dari suatu rambatan nrgi yang mmiliki frkunsi dan priod. Glombang air yang trjadi di laut dapat disbabkan olh angin, grakan kapal, gmpa atau gaya gravitasi
Online Jurnal of Natural Science, Vol.3(1): ISSN: March 2014
 Onlin Jurnal of Natural Scinc, ol.3(1): 65-74 ISSN: 338-0950 March 014 PELABELAN TOTAL SISI AJAIB SUPER (TSAS) PADA GABUNGAN GRAF ULAT BULU DAN BIPARTITE LENGKAP I W. Sudarsana 1, Fitria and S. Musdalifah
Onlin Jurnal of Natural Scinc, ol.3(1): 65-74 ISSN: 338-0950 March 014 PELABELAN TOTAL SISI AJAIB SUPER (TSAS) PADA GABUNGAN GRAF ULAT BULU DAN BIPARTITE LENGKAP I W. Sudarsana 1, Fitria and S. Musdalifah
SIMULASI DESAIN COOLING SYSTEM DAN RUNNER SYSTEM UNTUK OPTIMASI KUALITAS PRODUK TOP CASE
 SIMULASI DESAIN COOLING SYSTEM DAN RUNNER SYSTEM UNTUK OPTIMASI KUALITAS PRODUK TOP CASE Fabio Dwi Bagus Irawan 1,a, Cahyo Budiyantoro 1,b, Thoharudin 1,c 1 Program Studi Tknik Msin, Fakultas Tknik, Univrsitas
SIMULASI DESAIN COOLING SYSTEM DAN RUNNER SYSTEM UNTUK OPTIMASI KUALITAS PRODUK TOP CASE Fabio Dwi Bagus Irawan 1,a, Cahyo Budiyantoro 1,b, Thoharudin 1,c 1 Program Studi Tknik Msin, Fakultas Tknik, Univrsitas
Debuging Program dengan EasyCase
 Modul asyc 1 Dbuging Program dngan EasyCas Di susun Olh : Di dukung olh : Portal dukasi Indonsia Opn Knowlodg and Education http://ok.or.id Modul asyc 2 KATA PENGANTAR Puji syukur kpada guru sjatiku Gusti
Modul asyc 1 Dbuging Program dngan EasyCas Di susun Olh : Di dukung olh : Portal dukasi Indonsia Opn Knowlodg and Education http://ok.or.id Modul asyc 2 KATA PENGANTAR Puji syukur kpada guru sjatiku Gusti
ANALISIS STABILITAS DAN ADAPTABILITAS GALUR PADI DATARAN TINGGI DI LIMA LINGKUNGAN
 65 ANALISIS STABILITAS DAN ADAPTABILITAS GALUR PADI DATARAN TINGGI DI LIMA LINGKUNGAN (Stability and Adaptability Analysis of Highland Ric Gnotyps across Fiv Diffrnt Environmnts) Shrly Rahayu 1,2, Dsta
65 ANALISIS STABILITAS DAN ADAPTABILITAS GALUR PADI DATARAN TINGGI DI LIMA LINGKUNGAN (Stability and Adaptability Analysis of Highland Ric Gnotyps across Fiv Diffrnt Environmnts) Shrly Rahayu 1,2, Dsta
Gambar IV.6. Gambaran kontur bidang sesar yang menggambarkan bentuk ramp-flat-ramp pada border fault di Sub-cekungan Kiri.
 Pada pta struktur waktu (Gambar IV.4) trlihat bntuk ssar utama yang cukup unik dibagian tngah. Bntuk ini dipngaruhi olh konfigurasi Batuan Dasar yang dihasilkan olh struktur brumur Pra-Trsir. Pada pta
Pada pta struktur waktu (Gambar IV.4) trlihat bntuk ssar utama yang cukup unik dibagian tngah. Bntuk ini dipngaruhi olh konfigurasi Batuan Dasar yang dihasilkan olh struktur brumur Pra-Trsir. Pada pta
RANCANG BANGUN PATCH RECTANGULAR ANTENNA 2.4 GHz DENGAN METODE PENCATUAN EMC (ELECTROMAGNETICALLY COUPLED)
 RANCANG BANGUN PATCH RECTANGULAR ANTENNA 2.4 GHz DENGAN METODE PENCATUAN EMC (ELECTROMAGNETICALLY COUPLED) Winny Friska Uli,Ali Hanafiah Ramb Konsntrasi Tknik Tlkomunikasi, Dpartmn Tknik Elktro Fakultas
RANCANG BANGUN PATCH RECTANGULAR ANTENNA 2.4 GHz DENGAN METODE PENCATUAN EMC (ELECTROMAGNETICALLY COUPLED) Winny Friska Uli,Ali Hanafiah Ramb Konsntrasi Tknik Tlkomunikasi, Dpartmn Tknik Elktro Fakultas
KOMPUTASI DAN DINAMIKA FLUIDA
 KOMPUTASI DAN DINAMIKA FLUIDA TUGAS Olh RIRIN SISPIYATI NIM : 006003 Program Studi Matmatia INSTITUT TEKNOLOGI BANDUNG 009 Ercis 40 Ta as initial spctrum a bloc function nonzro for ½. Animat th initial
KOMPUTASI DAN DINAMIKA FLUIDA TUGAS Olh RIRIN SISPIYATI NIM : 006003 Program Studi Matmatia INSTITUT TEKNOLOGI BANDUNG 009 Ercis 40 Ta as initial spctrum a bloc function nonzro for ½. Animat th initial
PENENTUAN POLA - POLA GRAF TERHUBUNG BERLABEL BERORDE ENAM TANPA GARIS PARALEL DENGAN BANYAKNYA GARIS 5. (Skripsi) Oleh SITI FATIMAH
 PENENTUAN POLA - POLA GRAF TERHUBUNG BERLABEL BERORDE ENAM TANPA GARIS PARALEL DENGAN BANYAKNYA GARIS 5 (Skripsi) Olh SITI FATIMAH FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG BANDAR
PENENTUAN POLA - POLA GRAF TERHUBUNG BERLABEL BERORDE ENAM TANPA GARIS PARALEL DENGAN BANYAKNYA GARIS 5 (Skripsi) Olh SITI FATIMAH FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG BANDAR
BAB II TINJAUAN PUSTAKA. berbagai macam seperti gambar dibawah (Troitsky M.S, 1990).
 BAB II TINJAUAN USTAKA 2.1 Struktur Rangka Baja Extrnal rstrssing Scara toritis pningkatan kkuatan pada rangka baja untuk jmbatan dapat dilakukan dngan pmasangan prkuatan pratkan kstrnal pada rangka trsbut.
BAB II TINJAUAN USTAKA 2.1 Struktur Rangka Baja Extrnal rstrssing Scara toritis pningkatan kkuatan pada rangka baja untuk jmbatan dapat dilakukan dngan pmasangan prkuatan pratkan kstrnal pada rangka trsbut.
KAJIAN POTENSI PENGGUNA JALAN TOL MALANG KEPANJEN
 KAJIAN POTENSI PENGGUNA JALAN TOL MALANG KEPANJEN Ad Yudha Iswara, Fahry Husin, Ludfi Djakfar, Hndi Bowoputro Jurusan Tknik Sipil Fakultas Tknik Univrsitas Brawijaya Jalan MT. Haryono 167 Malang 65145,
KAJIAN POTENSI PENGGUNA JALAN TOL MALANG KEPANJEN Ad Yudha Iswara, Fahry Husin, Ludfi Djakfar, Hndi Bowoputro Jurusan Tknik Sipil Fakultas Tknik Univrsitas Brawijaya Jalan MT. Haryono 167 Malang 65145,
FUNGSI DOMINASI ROMAWI PADA LINE GRAPH
 Bultin Ilmiah Mat. Stat. dan Trapannya (Bimastr) Volum 04, No. 2 (2015), hal 119 126. FUNGSI DOMINASI ROMAWI PADA LINE GRAPH Ysi Januarti, Mariatul Kiftiah, Nilamsari Kusumastuti INTISARI Himpunan D disbut
Bultin Ilmiah Mat. Stat. dan Trapannya (Bimastr) Volum 04, No. 2 (2015), hal 119 126. FUNGSI DOMINASI ROMAWI PADA LINE GRAPH Ysi Januarti, Mariatul Kiftiah, Nilamsari Kusumastuti INTISARI Himpunan D disbut
PENGARUH MODEL ROLE PLAYING BERBASIS PERMAINAN TRADISIONAL BALI TERHADAP KETERAMPILAN BERBICARA PADA MATA PELAJARAN BAHASA INDONESIA SISWA KELAS III
 Jurusan PGSD Vol: 4 No: Tahun: 06 PENGARUH MODEL ROLE PLAYING BERBASIS PERMAINAN TRADISIONAL BALI TERHADAP KETERAMPILAN BERBICARA PADA MATA PELAJARAN BAHASA INDONESIA SISWA KELAS III Kadk Yuda wibawa,
Jurusan PGSD Vol: 4 No: Tahun: 06 PENGARUH MODEL ROLE PLAYING BERBASIS PERMAINAN TRADISIONAL BALI TERHADAP KETERAMPILAN BERBICARA PADA MATA PELAJARAN BAHASA INDONESIA SISWA KELAS III Kadk Yuda wibawa,
BAB II TINJAUAN KEPUSTAKAAN
 BAB II TINJAUAN KEPUTAKAAN II.1 PENDAHULUAN Yild lin adalah suatu pmcahan yang dapat digunakan dalam plat bton dimana trjadinya tgangan llh dan rotasi scara plastis muncul. Tori ini dapat digunakan dalam
BAB II TINJAUAN KEPUTAKAAN II.1 PENDAHULUAN Yild lin adalah suatu pmcahan yang dapat digunakan dalam plat bton dimana trjadinya tgangan llh dan rotasi scara plastis muncul. Tori ini dapat digunakan dalam
Hendra Gunawan. 29 November 2013
 MA1101 MATEMATIKA 1A Hndra Gunawan Smstr I, 013/014 9 Novmbr 013 Latihan (Kuliah yang Lalu) Ssorangygtingginya~1,60 m brdiri ditpiatastbing, mlihat lh k laut yang brada ~18,40 m di bawahnya. Pada saatitu
MA1101 MATEMATIKA 1A Hndra Gunawan Smstr I, 013/014 9 Novmbr 013 Latihan (Kuliah yang Lalu) Ssorangygtingginya~1,60 m brdiri ditpiatastbing, mlihat lh k laut yang brada ~18,40 m di bawahnya. Pada saatitu
SAMBUNGAN BALOK PENDUKUNG MOMEN
 BAB VI SABUNGAN BALOK ENDUKUNG OEN 1. TUJUAN ERKULIAHAN A. TUJUAN UU ERKULIAHAN (TU) Stlah mmplajari matri tntang sambungan balok pndukung momn, scara umum anda diharapkan : 1. ampu mnjlaskan pngrtian
BAB VI SABUNGAN BALOK ENDUKUNG OEN 1. TUJUAN ERKULIAHAN A. TUJUAN UU ERKULIAHAN (TU) Stlah mmplajari matri tntang sambungan balok pndukung momn, scara umum anda diharapkan : 1. ampu mnjlaskan pngrtian
MODEL PERSEDIAAN DETERMINISTIK DENGAN MEMPERTIMBANGKAN MASA KADALUARSA DAN PENURUNAN HARGA JUAL
 ISSN : 407 846 -ISSN : 460 846 MODEL PERSEDIAAN DETERMINISTIK DENGAN MEMPERTIMBANGKAN MASA KADALUARSA DAN PENURUNAN HARGA JUAL Chrish Rikardo *, Taufik Limansyah, Dharma Lsmono Magistr Tknik Industri,
ISSN : 407 846 -ISSN : 460 846 MODEL PERSEDIAAN DETERMINISTIK DENGAN MEMPERTIMBANGKAN MASA KADALUARSA DAN PENURUNAN HARGA JUAL Chrish Rikardo *, Taufik Limansyah, Dharma Lsmono Magistr Tknik Industri,
PENGGUNAAN ABU SEKAM PADI SEBAGAI ADSORBEN DALAM PENGOLAHAN AIR LIMBAH YANG MENGANDUNG LOGAM Cu. Mochtar Hadiwidodo *)
 PENGGUNAAN ABU SEKAM PADI SEBAGAI ADSORBEN DALAM PENGOLAHAN AIR LIMBAH YANG MENGANDUNG LOGAM u Mochtar Hadiwidodo *) Abstract Th industrial dvlopmnt hav bn incrasd togthr with th incrasmnt of th socity
PENGGUNAAN ABU SEKAM PADI SEBAGAI ADSORBEN DALAM PENGOLAHAN AIR LIMBAH YANG MENGANDUNG LOGAM u Mochtar Hadiwidodo *) Abstract Th industrial dvlopmnt hav bn incrasd togthr with th incrasmnt of th socity
VI. EFISIENSI PRODUKSI DAN PERILAKU RISIKO PRODUKTIVITAS PETANI PADA USAHATANI CABAI MERAH
 VI. EFISIENSI PRODUKSI DAN PERILAKU RISIKO PRODUKTIVITAS PETANI PADA USAHATANI CABAI MERAH.. Faktor-Faktor yang Mmpngaruhi Produktivitas Cabai Mrah dan Nilai Elastisitas Input trhadap Produktivitas...
VI. EFISIENSI PRODUKSI DAN PERILAKU RISIKO PRODUKTIVITAS PETANI PADA USAHATANI CABAI MERAH.. Faktor-Faktor yang Mmpngaruhi Produktivitas Cabai Mrah dan Nilai Elastisitas Input trhadap Produktivitas...
EVALUASI DAYA GABUNG PERSILANGAN JAGUNG DENGAN METODE DIALLEL
 EVALUASI DAYA GABUNG PERSILANGAN JAGUNG DENGAN ETODE DIALLEL Hruna Tanty athmatics & Statistics Dpartmnt, School of Computr Scinc, Binus Univrsity Jl. K. H. Syahdan No. 9 Palmrah Jakarta Barat 11480 [email protected]
EVALUASI DAYA GABUNG PERSILANGAN JAGUNG DENGAN ETODE DIALLEL Hruna Tanty athmatics & Statistics Dpartmnt, School of Computr Scinc, Binus Univrsity Jl. K. H. Syahdan No. 9 Palmrah Jakarta Barat 11480 [email protected]
APLIKASI METODE STATED PREFERENCE PADA PEMILIHAN MODA ANGKUTAN UMUM PENUMPANG (RUTE MAKASSAR MAJENE)
 APLIKASI METODE STATED PREFERENCE PADA PEMILIHAN MODA ANGKUTAN UMUM PENUMPANG (RUTE MAKASSAR MAJENE) Abdul Gaus Program Studi Tknik Siil Fakultas Tknik Univrsitas Khairun Trnat Tl/Fax (091) 38049 Irnawaty
APLIKASI METODE STATED PREFERENCE PADA PEMILIHAN MODA ANGKUTAN UMUM PENUMPANG (RUTE MAKASSAR MAJENE) Abdul Gaus Program Studi Tknik Siil Fakultas Tknik Univrsitas Khairun Trnat Tl/Fax (091) 38049 Irnawaty
Ensembel Kanonik Klasik
 nsmbl Kanonik Klasik Mnghitung Banyak Status Kaaan Sistm Misal aa ua sistm A an B yang bolh brtukar nrgi tai tiak bolh tukar artikl. Misal status kaaan an nrgi masing-masing sistm aalah sbb: Status A nrgi
nsmbl Kanonik Klasik Mnghitung Banyak Status Kaaan Sistm Misal aa ua sistm A an B yang bolh brtukar nrgi tai tiak bolh tukar artikl. Misal status kaaan an nrgi masing-masing sistm aalah sbb: Status A nrgi
ATMOSFER HIDROSTATIS DIATAS WATUKOSEK DARI DATA TEKANAN VERTIKAL TAHUN 2009
 Sminar Nasional Statistika IX Institut Tknologi Spuluh Nopmbr, 7 Novmbr 2009 ATMOSFER HIDROSTATIS DIATAS TUKOSEK DARI DATA TEKANAN VERTIKAL TAHUN 2009 Lalu Husnan Wijaya *, Dian Yudha Risdianto ** Pnliti
Sminar Nasional Statistika IX Institut Tknologi Spuluh Nopmbr, 7 Novmbr 2009 ATMOSFER HIDROSTATIS DIATAS TUKOSEK DARI DATA TEKANAN VERTIKAL TAHUN 2009 Lalu Husnan Wijaya *, Dian Yudha Risdianto ** Pnliti
ANALISIS PERPINDAHAN PANAS KONVEKSI PAKSA NANOFLUIDA AIR-Al2O3 DALAM SUB-BULUH VERTIKAL SEGIENAM
 ISSN : 2355-9365 -Procding of Enginring : Vol.4, No.1 April 2017 Pag 632 Abstrak ANALISIS PERPINDAHAN PANAS KONVEKSI PAKSA NANOFLUIDA AIR-Al2O3 DALAM SUB-BULUH VERTIKAL SEGIENAM FORCED CONVECTION HEAT
ISSN : 2355-9365 -Procding of Enginring : Vol.4, No.1 April 2017 Pag 632 Abstrak ANALISIS PERPINDAHAN PANAS KONVEKSI PAKSA NANOFLUIDA AIR-Al2O3 DALAM SUB-BULUH VERTIKAL SEGIENAM FORCED CONVECTION HEAT
JURUSAN FISISKA UNIVERSITAS NEGERI MALANG
 Solusi Prsamaan Schrödingr onlinir Untuk Mndiskripsikan Soliton Dari Prambatan Pulsa Optik Dalam Mdium Disprsif onlinir Munawar Kholil JURUSA FISISKA UIVERSITAS EGERI MALAG ITISARI sbuah pulsa optik dapat
Solusi Prsamaan Schrödingr onlinir Untuk Mndiskripsikan Soliton Dari Prambatan Pulsa Optik Dalam Mdium Disprsif onlinir Munawar Kholil JURUSA FISISKA UIVERSITAS EGERI MALAG ITISARI sbuah pulsa optik dapat
ISOMORFISMA PADA GRAF P 4
 ISOMORFISMA PADA GRAF P Eka Adhistiasari, I Ktut Budayasa 2 Jurusan Matmatika, Fakultas Martmatika dan Ilmu Pngtahuan Alam, UNESA Kampus Ktintang 6023,Surabaya Email : tias-adhis@yahoocoid, ktutbudayasa@yahoocom
ISOMORFISMA PADA GRAF P Eka Adhistiasari, I Ktut Budayasa 2 Jurusan Matmatika, Fakultas Martmatika dan Ilmu Pngtahuan Alam, UNESA Kampus Ktintang 6023,Surabaya Email : tias-adhis@yahoocoid, ktutbudayasa@yahoocom
PELABELAN PRIME CORDIAL UNTUK GRAF BUKU DAN GRAF MATAHARI YANG DIPERUMUM
 JIMT Vol. 4 No. Juni 07 (Hal 56-69) ISSN : 450 766X PELABELAN PRIME CORDIAL UNTUK GRAF BUKU DAN GRAF MATAHARI YANG DIPERUMUM S.Pranata, I. W. Sudarsana dan S.Musdalifah 3,,3 Program Studi Matmatika Jurusan
JIMT Vol. 4 No. Juni 07 (Hal 56-69) ISSN : 450 766X PELABELAN PRIME CORDIAL UNTUK GRAF BUKU DAN GRAF MATAHARI YANG DIPERUMUM S.Pranata, I. W. Sudarsana dan S.Musdalifah 3,,3 Program Studi Matmatika Jurusan
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI. MICRO BUBBLE GENERATOR Micro Bubbl Gnrator (MBG) mrupakan suatu alat yang difungsikan untuk mnghasilkan glmbung udara dalam ukuran mikro, yaitu glmbung dngan diamtr 00 μm []. Aplikasi
BAB II LANDASAN TEORI. MICRO BUBBLE GENERATOR Micro Bubbl Gnrator (MBG) mrupakan suatu alat yang difungsikan untuk mnghasilkan glmbung udara dalam ukuran mikro, yaitu glmbung dngan diamtr 00 μm []. Aplikasi
BAB III TEORI DASAR ANTENA SLOT DAN ANTENA ARRAY
 BAB III TEORI DASAR ATEA SLOT DA ATEA ARRAY 3. Antna Slot Slot antna biasanya digunakan pada frkunsi antara 300 MHz dan 4 GHz. Antna ini sangat populr karna dapat dipotong dan dipasang pada prmukaan apapun,
BAB III TEORI DASAR ATEA SLOT DA ATEA ARRAY 3. Antna Slot Slot antna biasanya digunakan pada frkunsi antara 300 MHz dan 4 GHz. Antna ini sangat populr karna dapat dipotong dan dipasang pada prmukaan apapun,
Pengaruh Rasio Tinggi Blok Tegangan Tekan Dan Tinggi Efektif Terhadap Lentur Balok Bertulangan Tunggal
 Rcivd: March 2017 Accptd: March 2017 Publishd: April 2017 Pngaruh Rasio Tinggi Blok Tgangan Tkan Dan Tinggi Efktif Trhadap Lntur Balok Brtulangan Tunggal Agus Sugianto 1*, Andi Marini Indriani 2 1,2 Dosn
Rcivd: March 2017 Accptd: March 2017 Publishd: April 2017 Pngaruh Rasio Tinggi Blok Tgangan Tkan Dan Tinggi Efktif Trhadap Lntur Balok Brtulangan Tunggal Agus Sugianto 1*, Andi Marini Indriani 2 1,2 Dosn
INFLUENCE OF LIMES COLUMN VARIATION DISTANCE IN SOFT CLAY STABILIZATION A REVIEW OF INDEX COMPRESSION (Cc) PARAMATER
 INFLUENCE OF LIMES COLUMN VARIATION DISTANCE IN SOFT CLAY STABILIZATION A REVIEW OF INDEX COMPRESSION (Cc) PARAMATER PENGARUH VARIASI JARAK KOLOM KAPUR DALAM STABILISASI LEMPUNG LUNAK PADA TINJAUAN NILAI
INFLUENCE OF LIMES COLUMN VARIATION DISTANCE IN SOFT CLAY STABILIZATION A REVIEW OF INDEX COMPRESSION (Cc) PARAMATER PENGARUH VARIASI JARAK KOLOM KAPUR DALAM STABILISASI LEMPUNG LUNAK PADA TINJAUAN NILAI
KAJIAN AWAL MEKANISME REAKSI ELEKTROLISIS NaCl MENJADI NaClO 4 UNTUK MENENTUKAN TAHAPAN REAKSI YANG EFEKTIF DARI PROSES ELEKTROLISIS NaCl
 KAJIAN AWAL MEKANISME REAKSI ELEKTROLISIS NaCl MENJADI NaClO 4 UNTUK MENENTUKAN TAHAPAN REAKSI YANG EFEKTIF DARI PROSES ELEKTROLISIS NaCl Bayu Prianto Pnliti Bidang Matrial Dirgantara Abstrak Amonium prklorat
KAJIAN AWAL MEKANISME REAKSI ELEKTROLISIS NaCl MENJADI NaClO 4 UNTUK MENENTUKAN TAHAPAN REAKSI YANG EFEKTIF DARI PROSES ELEKTROLISIS NaCl Bayu Prianto Pnliti Bidang Matrial Dirgantara Abstrak Amonium prklorat
PENGARUH MODEL PROBLEM BASED LEARNING (PBL) TERHADAP HASIL BELAJAR SISWA PADA MATERI POKOK OPTIKA GEOMETRIS
 PENGARUH MODEL PROBLEM BASED LEARNING (PBL) TERHADAP HASIL BELAJAR SISWA PADA MATERI POKOK OPTIKA GEOMETRIS Rani Dliana Panggaban 1 dan Pintor Simamora 1 Alumni Mahasiswa Program Studi Pndidikan Fisika
PENGARUH MODEL PROBLEM BASED LEARNING (PBL) TERHADAP HASIL BELAJAR SISWA PADA MATERI POKOK OPTIKA GEOMETRIS Rani Dliana Panggaban 1 dan Pintor Simamora 1 Alumni Mahasiswa Program Studi Pndidikan Fisika
Faculty of Economic Riau University, Pekanbaru, Indonesia
 Pngaruh Pngumuman Right Issu Trhadap Rturn Saham, Abnormal Rturn, Frkunsi Prdagangan, Volum Prdagangan, Risiko Saham dan Kapitalisasi Pasar Pada Prusahaan Proprty, Ral Estat and Building Construction yang
Pngaruh Pngumuman Right Issu Trhadap Rturn Saham, Abnormal Rturn, Frkunsi Prdagangan, Volum Prdagangan, Risiko Saham dan Kapitalisasi Pasar Pada Prusahaan Proprty, Ral Estat and Building Construction yang
PENENTUAN RUTE TERPENDEK DENGAN MENGGUNAKAN ALGORITMA CHEAPEST INSERTION HEURISTIC (STUDI KASUS: PT.
 Bultin Ilmiah Math. Stat. dan Trapannya (Bimastr) Volum 04, No. 3 (2015), hal 295 304. PENENTUAN RUTE TERPENDEK DENGAN MENGGUNAKAN ALGORITMA CHEAPEST INSERTION HEURISTIC (STUDI KASUS: PT. Wicaksana Ovrsas
Bultin Ilmiah Math. Stat. dan Trapannya (Bimastr) Volum 04, No. 3 (2015), hal 295 304. PENENTUAN RUTE TERPENDEK DENGAN MENGGUNAKAN ALGORITMA CHEAPEST INSERTION HEURISTIC (STUDI KASUS: PT. Wicaksana Ovrsas
